А 1 а 2 решение: Упростить выражение: 1) (а-2)(а-1)-а(а+1) 2) (b-5)(b+10)+(b+6)(b-8) 3) — Школьные Знания.com

alexxlab

Содержание

Как заговорить на уровне А1-А2

Обозначения А1-С2 используются для определения уровня владения английским языком. Иногда проводятся аналогии и с другими языками, однако они имеют свою специфику в представленных к уровню требованиях. Уровни А1-А2 считаются начальным этапом в изучении английского языка. Коротко охарактеризовать его можно так — хватает для выживания. То есть, это тот уровень, которого хватит для разговора на бытовую тему, а также туристической поездки. Несмотря на невысокие требования, чтобы достичь уровня А2 надо приложить значительные усилия.

Что такое уровень А1-А2

Человек, который освоил уровень А2, прошел через следующие этапы:

  • Beginner;
  • Elementary — А1;
  • Upper-Elementary;
  • Pre-Intermediate — А2.

Beginner — это уровень владения языком, при котором человек с английским никогда не сталкивался, не имеет о нем представления. На уровень Elementary ученик переходит, когда в его арсенале есть хоть немного простых слов, а также общее представление о языке. К этому уровню относятся те люди, которые начинают учить английский заново.

Чтобы перейти от начального уровня к А1, необходимо иметь базовые знания о простейших грамматических конструкциях. Должен быть набор из лексики до 100 единиц. На уровне Upper-Elementary требования возрастают. Словарный запас должен быть 300–500 слов, что позволяет поддерживать разговор на знакомую тему. Если в Elementary человек не воспринимает английскую речь на слух, то на следующем уровне уже надо уметь опознавать базовые конструкции. Круг тем, которые обсуждаются на этом этапе простой, но широкий:

  • биография, семья;
  • досуг и хобби;
  • работа и отдых;
  • праздники и выходные;
  • увлечения;
  • дата и числа;
  • транспорт и магазины.

То есть все то, что необходимо для поддержания знакомства, а также ориентирования в незнакомом месте. Срок обучения на уровне А1 длиться до 6 месяцев. В курс входит не только лексика, но и грамматика:

  • артикли;
  • три времени Simple;
  • построение предложения;
  • местоимения, прилагательные, наречия, предлоги;
  • исчисляемое, неисчисляемое;
  • конструкция There is/are.

Pre-Intermediate не отличается по тематике. Немного расширяется словарный запас, добавляются времена Present Continuous и Present Perfect, а также расширяется количество разговорных тем.

Обучение на этом этапе должно вселить интерес к дальнейшему изучению языка. Также одной из его главных целей является проработка основ функционирования английского. В языке есть правила, показывающие, как необходимо говорить в конкретных ситуациях, и именно их надо усвоить на этом этапе. Лексический запас должен оправдывать девиз уровня — выживание. То есть предполагается ситуация, в которой ученик находится в незнакомом городе и новый язык должен помочь найти место назначения, считывать дорожные знаки, ориентироваться по вывескам и объявлениям, завести простой диалог с прохожим.

Как выучиться на уровень А1-А2

Уже с самого начала необходимо решить, где и как ученик будет изучать язык. Лучше не перескакивать с одной формы обучения на другую, не менять преподавателей без веских причин.

Но для начала лучше разобраться с формами обучения:

  • самообразование;
  • курсы;
  • интернет-занятия;
  • репетиторство.

Самообразование не рекомендуется новичкам. В английском легко заучить неправильное произношение, заработав акцент. Также достаточно распространено непонимание разницы в использовании разных времен. Все это потом придется переучивать, однако уже с большим трудом.

Главный недостаток курсов в том, что они очень медлительны, а план урока подразумевает, что у всех учеников одинаковые способности. То есть, расписанные на 6 месяцев обычно растягиваются на год, при этом качество обучения не гарантируется.

Онлайн-занятия почти ничем не отличаются от самообразования. Разница лишь в том, что ученик сам обрабатывает кем-то подобранный материал. Проблема таких занятий такая же, как и советских учебников — они не актуальны. А еще они не предусматривают прохождение каких-либо практических заданий, развития речи и навыков чтения и аудирования.

Как выучить английский на А2 с репетитором

Индивидуальный формат обучения считается одним из самых быстрых в плане усвоения учеником информации. То есть, освоить уровень Pre-Intermediate можно быстрее чем за 4 месяца, при этом не потеряв в качестве.

Современные репетиторы ориентированы на то, чтобы собирать и воплощать в жизнь новейшие технологии и методики преподавания. Они стараются:

  • максимально упростить материал;
  • сделать информацию доступной, применимой в повседневной жизни;
  • организовать интерактивные занятия.

Ученик вовлекается в процесс раскрытия темы, то есть он не пассивно слушает, но участвует в формулировке правила, пытается объяснить его. Все эти действия активируют процесс запоминания.

Рекомендуется избегать репетиторов, которые слишком любят выдавать распечатки с упражнениями. С учеником надо в первую очередь общаться, а уже потом пытаться загрузить работой.

Найти настоящего специалиста можно на сайте Буки. Этот ресурс удобен в поиске репетиторов, потому что дает возможность узнать не только стандартную информацию, но и специфическую.

К стандартной информации можно отнести:

  • опыт преподавания;
  • место работы и обучения;
  • отзывы учеников;
  • предмет и специализацию.

Специфической можно назвать раздел о себе, где репетитор пытается коротко описать свои главные преимущества, рассказать о методах преподавания и их успешности.

Вся информация контролируется модераторами сайта, а значит — документально подтверждена. Например, при указании образования преподаватели прилагают копию соответствующих документов.

Выводы

Чтобы заложить надежные основы для обучения языку, нужно грамотно подойти к изучению уровня А1-А2. В этом поможет репетитор, который в понятной форме объяснит принципы использования основных грамматических структур, научит правильно строить предложения и говорить на понятные темы. Также важно правильно построить артикуляцию и произношение звуков, чтобы избежать акцента.

Чтобы найти хорошего репетитора, который поможет достичь всех целей, рекомендуется обращаться в компанию Буки.

Тракторная категория АЗ, А4, А2, А1 — основные сведения о правах

Какой спецтехникой можно управлять после получения прав с категорией А1-А4?

Получение прав для вождения транспортного средства любого вида является большим преимуществом, если вы находитесь в поиске соответствующей работы. Важно понимать, что стандартное водительское удостоверение для вождения легкового автомобиля не является подтверждением квалификации для управления трактором или любой другой специальной техникой. Если вы устраиваетесь на работу трактористом, следует изучать соответствующую теорию и сдавать другой экзамен. Далее нужно записаться на курсы для присвоения категории.

В данной статье мы поговорим о тракторных правах категории А1/2/3/4. Этот документ даёт право на управление транспортными средствами, скорость передвижения которых не превышает 50 км/ч. Это значит, что вы можете садиться за руль техники для уборки снега, осушителей водоёмов, вездеходов и других видов внедорожников. Документ данного вида также даёт возможность управлять самоходными машинами, предназначенными для выполнения ремонта дорожного полотна и строительных работ. Тракторы данного типа не используют рельсы, однако некоторые модели могут быть оснащены гусеницами вместо колёс.

ТС этого вида функционируют за счёт независимого привода. Объём двигателя не превышает 50 см3. Транспортные средства могут быть оснащены электрическим двигателем, мощность которого превышает 4 кВт. В эту категорию не входят тракторы, применяемые для движения по дорогам и способные развивать скорость более 50 км/ч. Присвоение категории А3 не даёт право управлять военной техникой. Как и автомобильные, тракторные права А3 имеют соответствующие категории. Предлагаем рассмотреть их характеристики.

Особенности категорий прав А1-4

После присвоения конкретной категории машинист получает возможность управлять транспортными средствами определённого вида. Есть возможность увеличения количества категорий, чтобы водитель смог садиться за руль любого трактора или специальной техники.

Основные характеристики категорий:

  1. Категория А1. Внедорожники, относящиеся к группе мотоциклов – это могут быть транспортные средства, подходящие для поездок по снегу или бездорожью.
  2. Категория А2. Внедорожники, которые обладают максимальной массой в 3.5 тонны. Количество свободных мест в таком транспорте не должно превышать 8. Такое внедорожное транспортное средство отдалённо напоминает обычную машину, однако оно используется для бездорожья.
  3. Категория А3. Внедорожник, общая масса которого превышает 3.5 тонны. Исключениями являются ТС, которые попадают в 4-ю категорию.
  4. Категория А4. В эту группу входит автомобильный транспорт различного вида, который способен перемещаться по бездорожью и имеет более 8 дополнительных мест в салоне или кузове.

Последние 3 группы являются аналогами категорий для обыкновенного автотранспорта (В, С и D), однако такая техника используется только для поездки вне дороги. Именно поэтому сдача экзаменов необходима для получения прав. Рассмотрим разновидности тракторных категорий:

  1. В – транспорт с гусеницами или колёсами с общей мощностью ДВС до 25 кВт.
  2. С – трактор с колёсами и ДВС мощностью до 110 кВт.
  3. D – ТС с колёсами и ДВС мощностью выше 110 кВт.
  4. Е – трактор с гусеницами и ДВС мощностью выше 25 кВт.

Как получить тракторные права категории А в Гостехнадзоре?

Все категории прав, включая права категории А3 сегодня выдаются только в Гостехнадзоре. Другим способом получить документ данного вида невозможно. Данная организация ответственна за прохождение потенциальными водителями обучающего курса и сдачи практики. На удостоверении ставится подпись сотрудника Гостехнадзора.

Чтобы оформить права на управление трактором или транспортным средством, подходящим под категорию А4, необходимо пройти специальный курс обучения. Основным требованием является предоставление медицинской справки, которая подтверждает способность управлять трактором. Чтобы получить доступ к выполнению работ на одном из агрегатов требуется обзавестись ВУ, оформленным по современным стандартам.

Важно! Раньше можно было иметь временное разрешение, однако с 2015 года его упразднили. Теперь необходимо обязательно обзавестись постоянным удостоверением.

Некоторые водители тракторов, которые практиковались вне проезжей части, принимают решение о приобретении поддельной копии ВУ тракториста. Они делают это с уверенностью, что обладают всеми необходимыми практическими навыками для выполнения поставленной задачи. Это заблуждение может привести к несоблюдению техники безопасности, ошибкам в процессе строительных или дорожных работ. Также в случае выявления факта наличия поддельных прав водитель будет отвечать на основании предписаний закона. Другими словами, наиболее простым и правильным решением будет сдача на права категории А1-4 в официально зарегистрированной организации. Это позволит устроиться на работу на законных основаниях.

Важно! Если возникают вопросы по поводу процедуры сдачи экзамена или прохождения теоретической части, всегда есть возможность проконсультироваться с сотрудником автошколы.

Как проходит сдача экзамена?

Если вы уже получили водительское удостоверение категории В или С, то можно получить удостоверение тракториста категории А1-4 без необходимости посещения занятий в автошколе. Достаточно сдать теорию и практику в Госавтоинспекции. Если вы сомневаетесь, что сможете успешно сдать теорию, то можно договориться о прохождении курса повторно в одной из аудиторий автошкол. Если вы хотите получить категорию А2 после 2-летнего стажа вождения, достаточно просто написать заявление и сделать медицинскую справку.

Для получения удостоверения тракториста необходимо сдать экзамен. Он проходит в два этапа: ответы на теоретические вопросы, связанные с ПДД, и практическая часть. Все подробности прохождения можно узнать у представителя учебного заведения. Для получения прав категории А3 кандидат должен соответствовать следующим требованиям:

  1. Клиент школы может получить удостоверение тракториста категории А1 в возрасте 16 лет.
  2. После достижения возраста в 17 лет есть возможность управлять спецтехникой практически всех категорий.
  3. В 18 лет можно начинать управлять транспортом категории D.
  4. В 19 лет открывается возможность получить категорию А2 и А3 в тракторных правах А3.
  5. В 22 года можно оформить категорию А4.

Также для допуска к управлению транспортным средством необходимо получить медицинскую справку определённого вида. Важно пройти профессиональную подготовку на основе требований потенциального работодателя.

Важно! Следует выбрать проверенное учебное заведение, которое обладает хорошей репутацией среди клиентов. В этом случае можно рассчитывать, что экзамен будет сдан на хорошую оценку.

Береговые станции морских районов А1 и А2 ГМССБ порта Ванино прошли освидетельствование

Радиус действия береговой станции морского района А1 составляет 48 морских миль, береговой станции морского района А2 – 130 морских миль

Комиссия Федерального агентства морского и речного транспорта выдала ФГУП «Росморпорт» свидетельство от 05. 11.2020 № GMDSS-3/1-3186-2020 о соответствии береговой станции Ванино морского района А1 Глобальной морской системы связи при бедствии (ГМССБ) и свидетельство от 05.11.2020 № GMDSS-3/1-3187-2020 о соответствии береговой станции Ванино морского района А2 ГМССБ Резолюции ИМО А.801(19) и требованиям приказа Минтранса России от 23.07.2015 № 226. Об этом сообщила пресс-служба Росморречфлота.

Ранее, в 2015 году, береговые станции Ванино также успешно проходили освидетельствование на их соответствие действующим требованиям, предъявляемым к работе данного оборудования в системе ГМССБ. Обе береговые станции введены в эксплуатацию в 2004 году.

Береговая станция Ванино морского района А1 ГМССБ состоит из центра управления связью, расположенного на территории морского порта Ванино, и базовой радиостанции в г. Советская Гавань на сопке Кекурная.

Береговая станция Ванино морского района А2 ГМССБ состоит из центра управления связью, расположенного на территории морского порта Ванино, приемной радиостанции, которая расположена в г. Советская Гавань на сопке Кекурная, и передающей радиостанции, расположенной в районе поселка Токи на мысе Мучукей-Дуа.

С помощью береговых станций Ванино морских районов А1, А2 ГМССБ осуществляется: несение радиовахты и радиообмен с судами на частотах ГМССБ в УКВ и ПВ-диапазонах; оперативная связь между судами и морским спасательно-координационным центром ФГБУ «АМП Сахалина, Курил и Камчатки» для организации спасательных операций; выполнение процедур обработки вызова бедствия, срочности и безопасности с использованием технологии цифрового избирательного вызова с судами в море, находящимися в пределах района, граница которого определена в соответствии с критериями, установленными Международной морской организацией для береговых радиостанций морского района А1, А2 ГМССБ и для обеспечения безопасности.

Немецкий на слух для начинающих: уровень А1‑А2

Экономика немецкоязычных стран по темпам развития занимает первое место в Европе и входит в пятерку лидеров среди стран мира. Немецким языком владеет значительно большее количество европейцев, чем, например, испанским или французским.

Немецкий язык может показаться сложным на первых порах, но в течение трех-четырех месяцев постоянного изучения вы с легкостью сможете разговаривать на несложные бытовые темы. Для этого составьте план и график обучения.

Ежедневные занятия от 30 минут до часа приблизят вас к поставленной цели

Используйте тот материал, который вам интересен: от пособия до подкастов, немецкоязычных журналов или сериалов. Когда начнете чувствовать, что теряете мотивацию – измените методику изучения или учебник. Вы должны получать удовольствие от процесса обучения, а не перенапрягаться. Также позаботьтесь о контроле ваших успехов  со стороны: семья, друзья или коллеги. Это способствует упорному труду и его результативности.

Изучение немецкого языка можно совмещать с изучением английского, поскольку эти языки генетически родственны. Используйте таблицы похожих слов для быстрого усвоения новых слов. K. Fund Media предлагает несколько видеороликов, которые помогут стартовать с начального уровня.

1. Диалог «Знакомство»

Deutsch lernen mit Videos / Learn German with videos!

2. «Мой путь в Германию. В автобусе»

Mein Weg nach Deutschland – 1. Im Bus

3. «Это моя новая квартира»

Learn German for Free / Lektion 15 Das ist meine neue Wohnung

4. Легкий немецкий. «Здравствуйте»

Hello! | Easy German 100

5. Сказка «Рождественская история»

Eine Weihnachtsgeschichte märchen | Gutenachtgeschichte für kinder

6. Сказка Братьев Гримм «Брат и сестра»

 Grimms Märchen – Brüderlein und Schwesterlein

7. «Сказка «Дюймовочка»

Däumelinchen märchen | Gutenachtgeschichte für kinder

Форматы бумаги А0, А1, А2, А3, А4, А5, А6 для полиграфии и не только

Содержание:

Классификация бумаги.

Все листы бумаги, производимые на фабриках, имеют фиксированные размеры, для удобства понимания их принято разделять на семь форматов. Размеры были выведены определенным способом, чтобы минимизировать количество отходов, остававшихся от производства того или иного типа листа. При появлении надобности произвести печать полиграфического изделия на нестандартном листе, клиенту придется оплатить полную стоимость, включая отходы, которые останутся после создания специализированного листа. Формат А является самым используемым и популярным стандартом для печати во всем мире. Формирование размеров осуществляется следующим образом: из одного листа А0 получается два листа А1, из А1 два листа А2, данное правило работает со всеми листами стандарта «А», отходы при производстве отсутствуют. Детально ознакомиться с размерами всех основных существующих листов формата «А» можно в нижеприведенной таблице.

Размер форматов бумаги:

ФОРМАТДЛИНАШИРИНА
А084,1118,9
А184,159,4
А24259,4
А34229,7
А42129,7
А52114,8
А610,514,8

Размеры форматов бумаги А0, А1, А2, А3, А4, А5, А6

А4 – это самый популярный формат, востребованными являются А3 и А5, данные виды бумаги используются в следующих целях:

  • Создание чертежей.
  • Рисование картин, создание макетов строений.
  • Печать.
  • Создание планов, конструкторской и проектировочной документации.
  • Запись информации и данных.

Форматы для полиграфии.

Полиграфисты и создатели оборудования для произведения печати пришли к единому стандарту листа SRA3, он имеет размеры 320 на 450 миллиметров. Такая ширина и высота является оптимальной, так как из данного листа можно получить изделия на следующих форматах:

  • А3 – 1 штука.
  • A4 – 2 изделия.
  • А5 – 4 штуки.
  • А6 – 8 изделий.
  • DL (европейский стандарт) – 6 изделий.
  • Карманный календари (100 на 70 миллиметров) – 16 штук.
  • Визитки (90 на 50) – 24 штуки.

Между изделиями будет присутствовать обрез 2 миллиметра, с каждой стороны.

Другие виды.

Кроме формата «А» существуют «B» и «C», второй используется для полиграфической продукции, последний исключительно для конвертов. Класс «B» имеет градацию размеров от 0 до 10, данное решение используется на территории Соединенных Штатов Америки и Канады.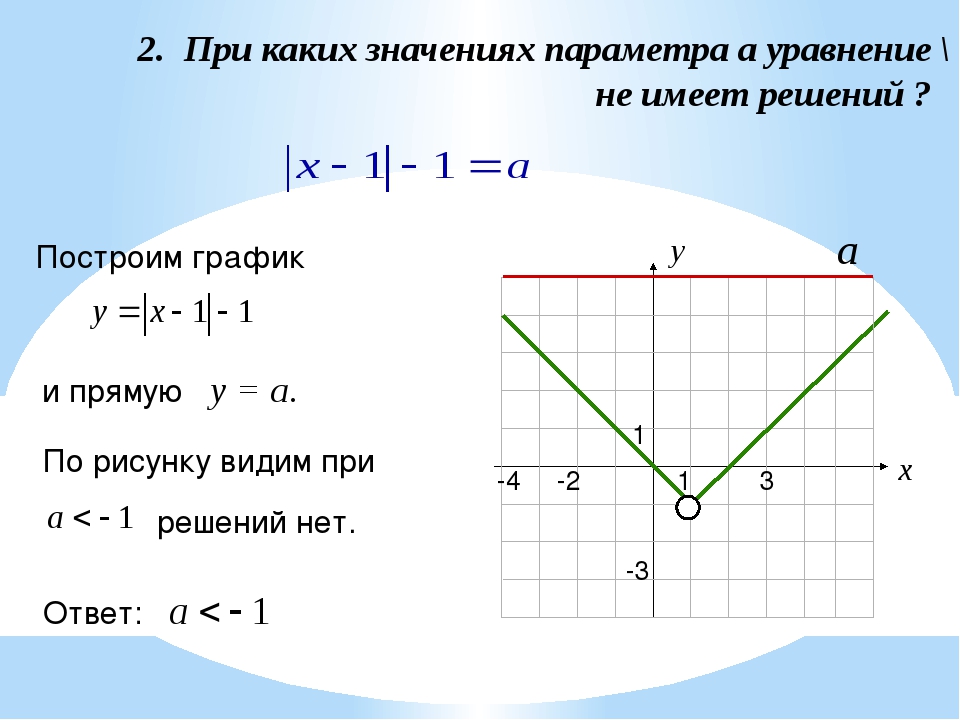 Длина листов варьируется от 141.4 сантиметров и до 4.4, ширина от 100 до 3.1 см. Класс «С» имеет градацию от С0 до С10, минимальная длина и ширина 4.4 и 3.1 сантиметр, максимальная 141.4 и 100.

Дополнительная классификация.

Кроме размеров бумагу делят на десять категорий по назначению:

  1. Для печати.
  2. Печать баннеров
  3. Декоративная.
  4. Техническая.
  5. Уф печать
  6. Впитывающая.
  7. Курительная.
  8. Электротехническая.
  9. Для письма, чертежей.
  10. Основа.
  11. Светочувствительная
  12. Упаковочная.
  13. Широкоформатная печать

Имеются следующие дополнительные характеристики:

  • Плотность.
  • Цвет.
  • Степень прозрачности.
  • Белизна.
  • Наличие дополнительного покрытия на поверхности листа.

Благодаря вышеописанным качествам удобно определять для чего можно использовать бумагу, можно дать общую оценку ее качества.

Видео

Выводы.

Понимания образования полиграфических и стандартных размеров листов, позволяет заказчику услуги сэкономить на печати продукции.

Разбираем задания ЦТ по русскому языку: А1-А2

Централизованное тестирование

Чтобы выполнить задания А1-А2 в ЦТ 2019 года по русскому языку, необходимо было знать правописание безударных гласных в корне слова. Предлагаем попрактиковаться на похожих заданиях, составленных преподавателями Адукар, и проверить, насколько хорошо ты знаешь это правило.

Обычно в заданиях А1-А2 просят указать слова, в корнях которых пишется буква А или Е. Для того, чтобы выполнить задание правильно, необходимо помнить следующие правила:

  1. В безударном положении употребляется та буква, которая пишется в том же слоге, когда она находится под ударением.

  2. Если под ударением пишется Ё, то без ударения в том же слоге пишется Е.

  3. В словах старославянского происхождения в безударном положении пишется неполногласное сочетание с одним гласным а-ра, ла; в параллельных исконно русских словах пишется полногласное сочетание с двумя гласными о-оро, оло.

  4. Если правописание гласного в безударном положении нельзя проверить ударным положением, то написание гласного надо запомнить (или проверить его написание по словарю).

  5. В корнях -гар-(-гор-), -клан-(-клон-),-твар-(-твор-) независимо от того, какая гласная пишется под ударением (А или О), в безударном положении пишется О.

  6. В корнях -зар-(-зор-) независимо от того, какая гласная пишется под ударением (А или О), в безударном положении пишется А.

  7. В корнях -плав-(-плов-) независимо от того, какая гласная пишется под ударением (А, О, или Ы), в безударном положении пишется А.

  8. В корнях -раст-(-ращ-,-рос-) перед СТ и Щ пишется А, перед с пишется О.

  9. В корнях -скак-, (-скоч-) независимо от того, какая гласная пишется под ударением (А или О), в безударном положении перед К пишется А, перед Ч пишется О.

  10. В корне -лаг- (-лож-) перед Г пишется А, перед Ж пишется О.

  11. В корне -кас-(-кос-). Если за корнем следует суффикс А, то в корне пишется А, если этого суффикса нет, то в корне пишется О.

  12. Корень -мак- (-мач-) пишется в словах, имеющих значение «погружать в жидкость». Корень -мок- (-моч-) пишется в словах, имеющих значение «пропускать жидкость, становиться мокрым».

  13. Корень -равн- пишется в словах, имеющих значение «одинаковый, наравне, равный».

  14. Корень -ровн- пишется в словах, имеющих значение «гладкий, прямой».

  15. Корни -бир-/бер-, -жиг-/жег-, -стил-/стел-, -блист-/блест-, -мир-/мер-, -тир-/тер-, -дир-/дер-, -пир-/пер-, -чит-/чет-. Если за корнем следует суффикс А, то в корне пишется И, если суффикса нет, то в корне пишется Е.

А теперь пройди небольшой тестик по этому правилу:

Как успехи? Больше тестов по теме ты найдёшь в ЦТ онлайн. Для закрепления правила посмотри видеоурок по этой теме от преподавателя Адукар:

Надеемся, мы помогли разобрать задания, аналогичные заданиям А1-А2 в ЦТ, и у тебя не возникнет с ними проблем. Если нет, заглядывай в группу ВКонтакте по русскому языку Адукар, смотри видеоуроки на нашем YouTube-канале или приходить заниматься на курсы подготовки к ЦТ. Удачи!

***

Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях ВКонтакте, Instagram, Facebook и поделись постом с друзьями. А мы сделаем ещё больше материалов, которые пригодятся тебе для учёбы.

Перепечатка материалов с сайта adukar.by возможна только с письменного разрешения редакции. [email protected]

ГДЗ по алгебре 7 класс Ершова самостоятельные и контрольные

Авторы: А.П. Ершова, В.В. Голобородько.

Нелегко представить нашу сегодняшнюю стремительную жизнь, жизнь полную высоких технологий, технического прогресса и всеобщей цифровизации без знаний математики. Не зря изучению математики в школе уделяется огромное внимание, однако эта наука сложна, поэтому каждому школьнику пригодится ГДЗ по алгебре и геометрии за 7 класс самостоятельные и контрольные Ершова.

Седьмой класс и его особенности

К седьмому классу учащиеся уже многое знают: изучены основные математические понятия и термины, приобретены навыки решения задач и уравнений, заложены первоначальные познания в предмете геометрия. И именно в седьмом классе вместо математики дети начинают изучать две совершенно разные науки: алгебра и геометрия. И вместе с новыми предметами в жизнь школьника входят дополнительные сложности, ведь практически это в два раза больше нагрузки, больше подготовки к урокам и больше решений домашних заданий. Предметы сложные, требуют постоянной концентрации внимания, запоминания новых законов, формул, математических приёмов. Алгебра и геометрия это не те науки, задачи по которым можно решить благодаря интуиции и логике. Обучение требует постоянной концентрированности и самодисциплины.

Решебник в помощь

Облегчить понимание изучения данных предметов и призван решебник по алгебре для 7 класса самостоятельные и контрольные работы, авторы: А.П. Ершова, В.В. Голобородько.

И ещё целый ряд сложных понятий. Алгебра один из тех предметов, где нельзя допустить недопонимание хотя бы одной темы. Именно поэтому достаточно часто на уроках проводятся самостоятельные и контрольные работы, чтобы учитель имел представление о том, насколько ученикам понятна та или иная тема. Сборник ГДЗ помогает школьникам без труда подготовиться к проверочной работе. А значит и написать на хорошую оценку.

Решебник по алгебре за 7 класса ср и кр от Ершовой — экономия бюджета

Учебник содержит в себе примеры решений всех заданий, используемых при проверке знаний:

  • приведены необходимые формулы;

  • подробно разобраны примеры решений линейных уравнений;

  • решение задач с помощью системы уравнений;

  • изображены примеры построения графика функций.

И ещё целый ряд не менее сложных заданий. К седьмому классу уже не каждый взрослый сможет объяснить ребёнку какие-либо непонятные моменты, приходиться прибегать к помощи репетиторов. А с помощью решебника ученик сможет повторить тему и подготовиться к контрольной работе самостоятельно.

Решите линейные уравнения с одним неизвестным a + (1 / a) = 2 Tiger Algebra Solver

Переставьте:

Переставьте уравнение, вычтя то, что находится справа от знака равенства с обеих сторон уравнения:

a + (1 / a) — (2) = 0

Пошаговое решение:

Шаг 1: 

 1
 Упростить -
            а
Уравнение в конце шага 1: 
 1
  (а + -) - 2 = 0
        а

Шаг 2:

Переписывание целого как эквивалентной дроби:

2. 1 Добавление дроби к целому

Перепишем целое как дробь, используя в качестве знаменателя:

 a a • a
     а = - = —————
          1 а

Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель

 
 Сложение дробей, имеющих общий знаменатель: 
 
 
 2.2 Сложение двух эквивалентных дробей 
 Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель 
 
 Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если возможно: 
 
 a • a + 1 а  2  + 1
 знак равно
     а а
 
 Уравнение в конце шага 2: 
 (a  2  + 1)
  ———————— - 2 = 0
     а
 
 Шаг 3: 
 
 Переписывание целого как эквивалентной дроби: 
 
 
 3.1 Вычитание целого из дроби 
 
 Перепишем целое как дробь, используя в качестве знаменателя: 
 
 2 2 • a
    2 = - = —————
         1 а
 
 Калькулятор полиномиальных корней: 
 
 3.2 Найдите корни (нули): F (a) = a  2  + 1 
 Калькулятор полиномиальных корней — это набор методов, направленных на поиск значений a, для которых F (a) = 0 
 
 Rational Roots Test — один из вышеупомянутых инструментов. Он мог бы найти только рациональные корни, которые представляют собой числа a, которые можно выразить как частное двух целых чисел 
 
 Теорема рационального корня утверждает, что если многочлен равен нулю для рационального числа P / Q, то P является множителем конечной константы и Q является множителем ведущего коэффициента 
 
 В этом случае ведущий коэффициент равен 1, а конечная константа — 1.
 
 Фактор (ы): 
 
 ведущего коэффициента: 1 
 конечной константы: 1 
 
 Давайте проверим …. 
  900 
  
    P     Q     P / Q     F (P / Q)     Делитель  
 
   -1     1     -1,00     2,00     1     1     1.00     2,00     
  
 
 
 Калькулятор полиномиальных корней не обнаружил рациональных корней 
 
 
 Сложение дробей с общим знаменателем: 
 
 
 3.3 Сложение двух эквивалентных дробей 
 
2 
 (a  +1) - (2 • a) a  2  - 2a + 1
 знак равно
        а а
 
 Попытка разложить на множители путем разделения среднего члена 
 
 3.4 Факторинг a  2  — 2a + 1 
 
 Первый член равен, a  2 , его коэффициент равен 1. 
 Средний член, -2a, его коэффициент -2. 
 Последний член, «константа», равен +1 
 
 Шаг-1: Умножьте коэффициент первого члена на константу 1 • 1 = 1 
 
 Шаг-2: Найдите два множителя 1, сумма которых равна коэффициенту среднего члена, который равен -2. 
 
 
  
   -1   +  -1   =  -2   Вот и все  
  
 
 
 Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два найденных множителя. на шаге 2, приведенном выше, -1 и -1 
 a  2  — 1a — 1a — 1 
 
 Шаг 4: сложите первые 2 члена, извлекая одинаковые множители: 
 a • (a-1) 
 Сложите последние 2 члена, извлекая общие множители: 
 1 • (a-1) 
 Шаг-5: сложите четыре члена шага 4: 
 (a-1) • (a-1) 
 Какая желаемая факторизация 
 
 
 Умножение экспоненциальных выражений: 
 
 
 3.5 Умножьте (a-1) на (a-1) 
 
 Правило гласит: Чтобы умножить экспоненциальные выражения с одинаковым основанием, сложите их показатели. 
 
 В нашем случае общая база равна (a-1), а показатели степени: 
 1, поскольку (a-1) — это то же число, что и (a-1)  1  
 и 1, поскольку (a- 1) — это то же число, что и (a-1)  1  
 Следовательно, произведение будет, (a-1)  (1 + 1)  = (a-1)  2  
 
 Уравнение в конце шага 3: 
 
 (а - 1)  2 
  ———————— = 0
     а
 
 Шаг 4: 
 
 Когда дробь равна нулю: 
 
 4.1 Когда дробь равна нулю ... 
 Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должен быть равен нулю.
 Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
 Вот как:
 (a-1)  2 
  —————— • а = 0 • а
    а
 
 Теперь, в левой части, a отменяет знаменатель, в то время как в правой части ноль, умноженный на что-либо, все еще равно нулю.
 Уравнение теперь принимает форму: 
 (a-1)  2  = 0
 
 Решение уравнения с одной переменной: 
 
 
 4.2 Решите: (a-1)  2  = 0 
 
 (a- 1)  2  представляет собой, по сути, произведение двух членов, которое равно нулю 
 
 Для того, чтобы произведение было равно нулю, по крайней мере один из этих членов должен быть равен нулю. Поскольку все эти члены равны друг другу, это фактически означает: a-1 = 0 
 
 Добавьте 1 к обеим сторонам уравнения: 
 a = 1 
 
 
 
 Приложение: решение квадратного уравнения напрямую 
 
 Решение  2  -2a + 1 = 0 непосредственно 
 Ранее мы разложили этот многочлен на множители, разделив средний член.давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
 
 Парабола, найдя вершину: 
 
 
 5.1. Найдите вершину y = a  2  -2a + 1 
 
 Параболы имеют наибольшее или самая низкая точка называется Вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). 
 
 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения. 
 
 Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
 
 Для любой параболы, Aa  2  + Ba + C, a -координата вершины задается как -B / (2A). В нашем случае координата a равна 1.0000 
 
 Подставив в формулу параболы 1.0000 для a, мы можем вычислить координату y: 
 y = 1.0 * 1.00 * 1.00 — 2.0 * 1.00 + 1.0 
 или y = 0.000 
 
 
 Parabola, Графическое изображение вершины и пересечения по оси X: 
 
 Корневой график для: y = a  2  -2a + 1 
 Vertex at {a, y} = {1.00, 0.00} 
 a-Intercept (Root): 
 One Root at { а, у} = {1.00, 0.00} 
 Обратите внимание, что корень совпадает с вершиной 
 и осью симметрии 
 совпадает с линией a = 0 
 
 Решите квадратное уравнение, заполнив квадрат 
 
 5.2 Решение  2  -2a + 1 = 0 завершив Квадрат. 
 
 Вычтем 1 из обеих частей уравнения: 
 a  2  -2a = -1 
 
 Теперь умный бит: возьмите коэффициент при a, равный 2, разделите его на два, получив 1, и возведите его в квадрат 1 
 
 Добавьте 1 к обеим частям уравнения: 
 В правой части получим: 
 -1 + 1 или, (-1/1) + (1/1) 
 Общий знаменатель двух дробей равен 1 Добавление (-1/1) + (1/1) дает 0/1 
 Таким образом, добавляя к обеим сторонам, мы наконец получаем: 
 a  2  -2a + 1 = 0 
 
 Добавление 1 завершило левую часть в полный квадрат: 
 a  2  -2a + 1 = 
 (a-1) • (a-1) = 
 (a-1)  2  
 Вещи, которые равны одному и тому же, также равны друг другу .Поскольку 
 a  2  -2a + 1 = 0 и 
 a  2  -2a + 1 = (a-1)  2  
, то согласно закону транзитивности 
 (a-1)  2  = 0 
 
 Мы будем называть это уравнение уравнением. # 5.2.1 
 
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. 
 
 Обратите внимание, что квадратный корень из 
 (a-1)  2  равен 
 (a-1)  2/2  = 
 (a-1)  1  = 
 a-1 
 
 Теперь, применяя Принцип квадратного корня для уравнения.# 5.2.1 получаем: 
 a-1 = √ 0 
 
 Добавьте 1 к обеим сторонам, чтобы получить: 
 a = 1 + √ 0 
 Квадратный корень из нуля равен нулю 
 
 Это квадратное уравнение имеет только одно решение. Это потому, что добавление нуля аналогично вычитанию нуля. 
 
 Решение: 
 a = 1 
 
 
 Решите квадратное уравнение с помощью квадратичной формулы 
 
 
 5.3 Решение  2  -2a + 1 = 0 по квадратичной формуле. 
 
 Согласно квадратичной формуле, a, решение для Aa  2  + Ba + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: 
   
 — B ± √ B  2  -4AC 
 a = ———————— 
 2A 
 
 В нашем случае A = 1 
 B = -2 
 C = 1 
 
 Соответственно, B  2  — 4AC = 
 4 — 4 = 
 0 
 
 Применение формулы корней квадратного уравнения: 
 
 2 ± √ 0 
 a = ———— 
 2 
 
 Корень квадратный из нуля равен нулю 
 
 Это квадратное уравнение имеет только одно решение.2 «. 
 
 Пошаговое решение: 
 
 Шаг 1: 
 
 Попытка разложить на множители путем разделения среднего члена 
 
 1.1 Факторинг a  2  + a + 1 
 
 Первый член равен, a  2  его коэффициент равно 1. 
 Средний член: + a, его коэффициент равен 1. 
 Последний член, «константа», равен +1 
 
 Шаг-1: Умножьте коэффициент первого члена на константу 1 • 1 = 1 
 
 Шаг 2: Найдите два множителя 1, сумма которых равна коэффициенту среднего члена, равному 1.
 
 
  
   -1   +  -1   =  -2   
 
    1   +   1   = 2 
 
 =   =   =   =   
 Наблюдение: Два таких фактора не могут быть найдены !! 
 Заключение: Трехчлен не может быть разложен на множители 
 
 Уравнение в конце шага 1: 
 
 a  2  + a + 1 = 0
 
 Шаг 2: 
 
 Парабола, поиск вершины: 
 
 2.1 Найдите вершину y = a  2  + a + 1 
 
 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). 
 
 Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения. 
 
 Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины. 
 
 Для любой параболы, Aa  2  + Ba + C, a -координата вершины задается как -B / (2A).В нашем случае координата a равна -0,5000 
 
 Подставив в формулу параболы -0,5000 для a, мы можем вычислить координату y: 
 y = 1,0 * -0,50 * -0,50 + 1,0 * -0,50 + 1,0 
 или y = 0,750 
 
 Парабола, графическая вершина и пересечение по оси X: 
 
 Корневой график для: y = a  2  + a + 1 
 Ось симметрии (пунктирная линия) {a} = {- 0,50} 
 Vertex at {a, y} = {-0,50, 0,75} 
 Функция не имеет действительных корней 
 
 Решите квадратное уравнение, заполнив квадрат 
 
 2.2 Решение  2  + a + 1 = 0, заполнив Квадрат. 
 
 Вычтем 1 из обеих частей уравнения: 
 a  2  + a = -1 
 
 Теперь умный бит: возьмите коэффициент при a, равный 1, разделите на два, получая 1/2 и, наконец, возведите в квадрат. это дает 1/4 
 
 Добавьте 1/4 к обеим частям уравнения: 
 В правой части мы имеем: 
 -1 + 1/4 или, (-1/1) + (1/4) 
. общий знаменатель двух дробей равен 4. Сложение (-4/4) + (1/4) дает -3/4 
 Таким образом, сложив обе части, мы, наконец, получаем: 
 a  2  + a + (1/4) = — 3/4 
 
 При сложении 1/4 левая часть завершилась в виде полного квадрата: 
 a  2  + a + (1/4) = 
 (a + (1/2)) • (a + (1/2) ) = 
 (a + (1/2))  2  
 Вещи, которые равны одному и тому же, также равны друг другу.Так как 
 a  2  + a + (1/4) = -3/4 и 
 a  2  + a + (1/4) = (a + (1/2))  2  
 то по закону транзитивности, 
 (a + (1/2))  2  = -3/4 
 
 Мы будем называть это уравнение уравнением. # 2.2.1 
 
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. 
 
 Обратите внимание, что квадратный корень из 
 (a + (1/2))  2  равен 
 (a + (1/2))  2/2  = 
 (a + (1/2))  1  = 
 a + (1/2) 
 
 Теперь, применяя принцип квадратного корня к уравнению.# 2.2.1 получаем: 
 a + (1/2) = √ -3/4 
 
 Вычтем 1/2 с обеих сторон, чтобы получить: 
 a = -1/2 + √ -3/4 
 В математике, i называется мнимой единицей. Это удовлетворяет i  2  = -1. Оба i и -i являются квадратными корнями из -1 
 
 Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
 a  2  + a + 1 = 0 
 имеет два решения: 
 a = -1 / 2 + √ 3/4 • i 
 или 
 a = -1/2 — √ 3/4 • i 
 
 Обратите внимание, что √ 3/4 можно записать как 
 √ 3 / √ 4, что равно √ 3/2 
 
 
 Решите квадратное уравнение через квадратную формулу 
 
 2.3 Решение  2  + a + 1 = 0 по квадратичной формуле. 
 
 Согласно квадратичной формуле, a, решение для Aa  2  + Ba + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: 
   
 — B ± √ B  2  -4AC 
 a = ———————— 
 2A 
 
 В нашем случае A = 1 
 B = 1 
 C = 1 
 
 Соответственно, B  2  — 4AC = 
 1 — 4 = 
 -3 
 
 Применение формулы корней квадратного уравнения: 
 
 -1 ± √ -3 
 a = ————— 
 2 
 
 В наборе действительных чисел отрицательные числа не имеют квадратных корней.Был изобретен новый набор чисел, названный комплексным, чтобы отрицательные числа имели квадратный корень. Эти числа записываются (a + b * i) 
 
 И i, и -i являются квадратными корнями из минус 1 
 
 Соответственно, √ -3 = 
 √ 3 • (-1) = 
 √ 3 • √ -1 = 
 ± √ 3 • i 
 
 √ 3, округленное до 4 десятичных цифр, составляет 1,7321 
 Итак, теперь мы смотрим на: 
 a = (-1 ± 1,732 i) / 2 
 
 Два мнимых решения: 
 
 
 a = (-1 + √-3) / 2 = (- 1 + i√ 3) / 2 = -0.5000 + 0,8660i
или: 
 a = (- 1-√-3) / 2 = (- 1-i√ 3) / 2 = -0.5000-0.8660i
 
 
 Было найдено два решения: 
  1.  a = (- 1-√-3) / 2 = (- 1-i√ 3) / 2 = -0.5000-0.8660i
  2.  a = (- 1 + √- 3) / 2 = (- 1 + i√ 3) / 2 = -0.5000 + 0.8660i
 Вирусная математическая задача с двумя ответами разделяет Интернет 
  •  Пользователь Twitter @pjmdoll поделился математической задачей: 8 ÷ 2 (2 + 2) =?
  •  Некоторые люди получили ответ 16, а некоторые — 1.
  •  Путаница связана с различием между современными и историческими интерпретациями порядка действий.
  •  Правильный ответ сегодня — 16. Ответ 1 был бы правильным 100 лет назад.
  •  Посетите домашнюю страницу INSIDER, чтобы узнать больше.
 Известно, что вирусные математические уравнения разделяют людей в Интернете. Некоторые задачи настолько сложны, что кажутся невозможными, даже если они предназначены для учеников начальной школы.
   Подробнее : 10 вирусных математических уравнений, которые поставили в тупик Интернет 
 Эта последняя вирусная проблема, о которой поделился пользователь Twitter @pjmdoll, является одним из таких уравнений.
 —em ♥ ︎ (@pjmdolI) 28 июля 2019 г.
 Уравнение: 8 ÷ 2 (2 + 2) =?
 Каждый получает разные ответы.
 —laur♏️ (@lauram_williams) 30 июля 2019 г.
 —becca 10✧ * .✰LILY + BARBS DAY (@spaceywhy) 30 июля 2019 г.
 —maggie (@BatmanOfficial_) 29 июля 2019 г.
 —George W.Куш (@supermaddd) 29 июля 2019 г.
 —Light💜 ᴮᵃⁿᵍᵗᵃⁿ ᶠᵒʳᵉᵛᵉʳ 💜 (@SakuraTsukimine) 29 июля 2019 г.
 Вот правильный способ решения 8 ÷ 2 (2 + 2) =?
 Сначала сложите числа в скобках.
 8 ÷ 2 (4) =?
 Теперь произведите умножение и деление слева направо.
 8 ÷ 2 (4) = 4 (4) = 16.
 Путаница вызвана различием между современной и исторической интерпретацией порядка операций, известной как PEMDAS:
  1.  Круглые скобки
  2.  Показатели
  3.  Умножение и деление (слева направо)
  4.  Сложение и вычитание (слева направо)
 Похожая математическая задача стала вирусной в 2011 году, когда люди не могли прийти к единому мнению относительно ответа на 48 ÷ 2 (9 + 3).Преш Талвалкер, автор книги «Радость теории игр: введение в стратегическое мышление», объяснил противоречие на своем канале YouTube MindYourDecisions и в сообщении в своем блоге.
 Люди, получившие число 1 в качестве ответа на эту проблему, использовали устаревшую версию порядка операций, сначала умножая 2 (4), а затем деля 8 на 8, согласно Талуокеру. Этот ответ был бы правильным 100 лет назад. Но вставив уравнение в современный калькулятор, мы получим 16.Вы должны добавить еще один набор круглых скобок, чтобы получить ответ 1.
 Люди получают разные ответы в зависимости от того, как они применяют порядок действий.
 Талия Лакриц / ИНСАЙДЕР
 Талуокер объясняет, что часть путаницы также вызвана тем, что в задаче двусмысленно установлен символ разделения.
 «В учебниках всегда есть правильные скобки, или они объясняют, что нужно разделять», — пишет он в своем блоге. «Поскольку математический набор текста сегодня намного проще, мы почти никогда не видим ÷ как символ, вместо этого дроби записываются с числителем вертикально над знаменателем».
 Вы можете посмотреть полное объяснение этого уравнения Талуокером ниже.
 
 Приготовление разведений — математические модули Ohlone Biotechnology | Колледж Олон, Мир культур, объединившихся в обучении 
 Прежде чем мы начнем, давайте вспомним, что такое разбавление из нашего последнего модуля, Модуль 4 — Терминология разбавления.Разведение   — это когда одно вещество (часто, но не всегда, вода) добавляется к другому веществу, чтобы уменьшить концентрацию исходного вещества. «Исходное вещество» — это основной раствор  . Растворенное вещество — это вещество, растворенное в растворе. Вещество, в котором растворено растворенное вещество, — это растворитель  .
 В этом модуле мы рассмотрим один конкретный вопрос: как мы можем сделать менее концентрированный раствор из более концентрированного раствора?
 Чтобы выполнить разбавление, вам необходимо иметь представление о двух математических концепциях: использование формулы и знакомство со свойством умножения равенства *.
  * См. «Модуль 9 — Решение уравнений» для более глубокого обзора свойства равенства умножения. 
 Формула — это математическое уравнение, содержащее две или более переменных. В любом случае, когда мы должны использовать формулу для решения проблемы, нам необходимо определить несколько ключевых компонентов:
  1.  Правильная формула,
  2.  Значение каждой из переменных,
  3.  значения переменных, специфичных для проблемы, и
  4.  Как решить уравнение для неизвестной величины.
 Каждый из этих компонентов имеет одинаковую ценность. К счастью, у нас есть формула для решения простых задач разбавления. Формула следующая — запоминайте ее и ее составные части!
 c1v1 = c2v2
 Разложение формулы для простого разбавления 
 У нас есть правильная формула. Но что означает каждая из переменных?
 Переменная «C» представляет концентрацию. «C» встречается в формуле дважды, как c1 и c2. Переменная «V» представляет объем.»V» также появляется дважды с нижними индексами. Позвольте переменным с нижним индексом «1» быть информацией для исходного раствора, а переменным с нижним индексом «2» представлять окончательное решение.
 При приближении к проблеме разбавления вам обычно задают концентрацию основного раствора C1. (Помните, что [] означает концентрацию). Возможно, вам дадут окончательную концентрацию, или вам придется разобраться в этом самостоятельно. Как показано на изображении выше, части формулы C  1  V  1  = C  2  V  2  следующие:
  •  C  1 : концентрация основного раствора
  •  C  2 : концентрация конечного раствора
  •  V  1 : объем основного раствора
  •  V  2 : Объем окончательного раствора
 При использовании формулы важно поддерживать согласованность этих переменных.
 Использование C 
 1  V  1  = C  2  V  2 : Пример 1
 Сколько галлонов исходного раствора апельсинового сока с «Концентрацией: 90% сока» вам нужно смешать с водой, чтобы приготовить 2 галлона апельсинового сока с концентрацией 20%?
  1.  Во-первых, спросите себя: «Создаю ли я менее концентрированный раствор из более концентрированного раствора?» Если да, отлично! Используйте C  1  V  1  = C  2  V  2 .
  2.  Определите значения, которые соответствуют правильным переменным:
    1.  Базовая концентрация = 90%, C  1 
    2.  Требуемый объем основного раствора = Неизвестно, В  1 
    3.  Требуемая конечная концентрация: 20%, C  2 
    4.  Требуемый конечный объем: 2 галлона, V  2 
  3.  Введите эти значения в C  1  V  1  = C  2  V  2  и решите для неизвестного, V  1 :
     C1V1 = C2V2 
     (90%) (V1) = (20%) (2 галлона) 
     V1 = (20%) (2 галлона) (90%)
     V1 = 0.44 галлона 90% концентрированного апельсинового сока
 Хотя вы, вероятно, не будете готовить два целых галлона апельсинового сока, этот пример показывает, как решить C  1  V  1  = C  2  V  2  уравнения.
 Использование C 
 1  V  1  = C  2  V  2 : Пример 2
 Рассмотрим следующее: сколько литров исходного раствора с концентрацией 3 мг / л необходимо для создания 4 литров конечного раствора с концентрацией 2,25 мг / л?
  1.  Вы действительно создаете менее концентрированный раствор из более концентрированного раствора — вот что такое разбавление.Вы можете использовать C  1  V  1  = C  2  V  2 .
  2.  Определите значения, соответствующие переменным: C1 = 3 мг / л, C2 = 2,25 мг / л, V1 = неизвестно, V2 = 4L
  3.  Запишите уравнение, подставьте значения и упростите: C1V1 = C2V2 (3 мг / л) (V1) = (2,25 мг / л) (4 л) V1 = (2,25 мг / л) (4 л) 3 мг / L = 3 л
  4.  Обобщите ответ:  Для приготовления 4 л окончательного раствора потребуется 3 л исходного раствора. 
 Проверьте понимание # 1: Использование C 
 1  V  1  = C  2  V  2 
  Используйте C  1  V  1  = C  2  V  2  для решения следующих проблем с разбавлением.Решения находятся в конце этого руководства. 
  1.  Как бы вы создали 2 мл 0,1 М раствора ТРИС-буфера из 1 М ТРИС-буфера?
  2.  Сколько из основного раствора глюкозы 2 г / л необходимо для приготовления 3 л раствора 1 г / л?
  3.  Какова концентрация конечного раствора, если 7 мл воды добавить к 4 мл раствора 3 г / мл?
 Проверка понимания: дополнительная практика 
  Ответьте на следующие вопросы, используя C  1  V  1  = C  2  V  2 .Решения находятся в конце этого руководства. 
  1.  Сколько из 4 мг / мл исходного раствора амилозы-лазури потребуется для приготовления 5 мл конечного раствора 0,5 мг / мл?
  2.  Какова концентрация конечного раствора, если 4 л исходного раствора 50 мг / л используются для создания 120 л конечного раствора?
  3.  Если вы начнете с 50 мл 0,20 М раствора NaCl и разбавите его до 1000 мл, какова будет концентрация конечного раствора?
  4.  Сколько 8,0 М раствора HCl нужно использовать для получения 500 мл 0.050 М окончательное решение?
  5.  Если вы начнете с 250 мл раствора NaCl с концентрацией 4 г / мл, какой будет концентрация в конечном растворе, если вы добавите 70 мл воды?
  6.  Сколько 0,2 М раствора глюкозы можно приготовить из 50 мл исходного раствора глюкозы 0,50 М?
  1.  Как бы вы создали 2 мл 0,1 М раствора ТРИС-буфера из 1 М ТРИС-буфера?
    1.  «Могу ли я создать менее концентрированный раствор из более концентрированного раствора?» Да! Используйте C  1  V  1  = C  2  V  2 .
    2.  Определите правильные значения для переменных: C  1  = 1M, V  1  = неизвестно, C  2  = 0,1 M, V  2  = 2 мл
    3.  Введите значения в C  1  V  1  = C  2  V  2  и решите: C1V1 = C2V2 (1 M) (V1) = (0,1 M) (2 мл) V1 = (0,1 M) ( 2 мл) (1 M) V1 = (0,1 M) (2 мл) (1 M) V1 = 0,2 мл исходного раствора 1 M ТРИС-буфер
  2.  Какова концентрация конечного раствора, если 7 мл воды добавить к 4 мл раствора 3 г / мл?
    1.  Вы создаете менее концентрированный раствор из более концентрированного раствора, добавляя воду (разбавитель).
    2.  Определите правильные значения переменных. Это немного сложно. Ваш окончательный объем, V  2 , составит 7 мл + 4 мл = 11 мл. C  1  — ваш исходный раствор — 3 г / мл. Вопрос просит вас найти конечную концентрацию раствора, C  2 . V  1  составляет 4 мл.
    3.  Подключите и решите неизвестное: C1V1 = C2V2 (3 г / мл) (4 мл) = C2 (11 мл) (3 г / мл) (4 мл) (11 мл) = C21,09 г / мл = С2, конечная концентрация раствора
 Проверка понимания: дополнительная практика 
  1.  Сколько из исходного раствора амилозы-лазурной с концентрацией 4 мг / мл потребуется для получения 5 мл 0.Конечный раствор 5 мг / мл?
     C  1  = 4 мг / мл 
     C  2  = 0,5 мг / мл 
     V  1  = неизвестно 
     V  2  = 5 мл 
     Окончательный ответ: вам потребуется 0,625 мл исходного раствора.
  2.  Какова концентрация конечного раствора, если 4 л исходного раствора 50 мг / л используются для создания 120 л конечного раствора?
     C  1  = 50 мг / л 
     C  2  = неизвестно 
     V  1  = 4 л 
     V  2  = 120 л 
     Окончательный ответ: 1.67 мг / л — конечная концентрация.
  3.  Если вы начнете с 50 мл 0,20 М раствора NaCl и разбавите его до 1000 мл, какова будет концентрация конечного раствора?
     C  1  = 0,20 M 
     C  2  = неизвестно 
     V  1  = 50 мл 
     V  2  = 1000 мл 
     Окончательный ответ: 0,01 M — конечная концентрация.
  4.  Сколько 8,0 М раствора HCl следует использовать для приготовления 500 мл 0,050 М конечного раствора?
     С  1  = 8.0 M 
     C  2  = 0,050 M 
     V  1  = неизвестно 
     V  2  = 500 мл 
     Окончательный ответ: следует использовать 3,1 мл 8,0 M раствора HCl
    .
  5.  Если вы начнете с 250 мл раствора NaCl с концентрацией 4 г / мл, какой будет концентрация в конечном растворе, если вы добавите 70 мл воды?
     C  1  = 4 г / мл 
     C  2  = неизвестно 
     V  1  = 250 мл 
     V  2  = 320 мл 
     Окончательный ответ: Концентрация конечного раствора будет ≈ 3.1 г / мл.
  6.  Сколько 0,2 М раствора глюкозы можно приготовить из 50 мл исходного раствора глюкозы 0,50 М?
     C  1  = 0,50 M 
     C  2  = 0,20 M 
     V  1  = 50 мл 
     V  2  = неизвестно 
     Окончательный ответ: 125 мл 0,2 M раствора глюкозы.
 Определение того, является ли целое число решением уравнения 
 Результаты обучения 
  •  Определите, является ли целое число решением уравнения
 Определить, является ли число решением уравнения 
 Решение уравнения похоже на поиск ответа на загадку.Алгебраическое уравнение утверждает, что два алгебраических выражения равны. Решение уравнения — это определение значений переменной, которые делают уравнение истинным. Любое число, которое делает уравнение истинным, называется решением уравнения. Это ответ на загадку!
 Решение уравнения 
 Решение уравнения — это значение переменной, которое делает истинное утверждение при подстановке в уравнение. 
 Процесс поиска решения уравнения называется решением уравнения.
 Найти решение уравнения — это значит найти значение переменной, которая делает уравнение истинным. Сможете ли вы распознать решение [латекс] x + 2 = 7? [/ Latex] Если вы сказали [latex] 5 [/ latex], вы правы! Мы говорим, что [latex] 5 [/ latex] является решением уравнения [latex] x + 2 = 7 [/ latex], потому что когда мы заменяем [latex] x [/ latex] [latex] 5 [/ latex], полученное утверждение верно.
 [латекс] \ begin {array} {} \\ \ hfill x + 2 = 7 \ hfill \\ \ hfill 5 + 2 \ stackrel {?} {=} 7 \ ​​hfill \\ \\ \ hfill 7 = 7 \ quad \ checkmark \ hfill \ end {array} [/ latex]
 Поскольку [latex] 5 + 2 = 7 [/ latex] — верное утверждение, мы знаем, что [latex] 5 [/ latex] действительно является решением уравнения.
 Символ [latex] \ stackrel {?} {=} [/ Latex] спрашивает, равна ли левая часть уравнения правой части. Как только мы узнаем, мы можем изменить знак равенства [latex] \ text {(=)} [/ latex] или знак неравенства [latex] \ text {(\ not =).} [/ Latex]
 Определите, является ли число решением уравнения. 
  1.  Подставьте число вместо переменной в уравнение.
  2.  Упростите выражения с обеих сторон уравнения.
  3.  Определите, истинно ли полученное уравнение.
    •  Если это правда, число является решением.
    •  Если это не так, число не является решением.
 пример 
 Определите, является ли [латекс] x = 5 [/ latex] раствором [латекса] 6x — 17 = 16 [/ latex].
 Решение
 [латекс] 6x-17 = 16 [/ латекс]
 Замените x [латекс] \ color {red} {5} [/ latex]. [латекс] 6 \ cdot \ color {красный} {5} -17 = 16 [/ латекс]
 Умножить. [латекс] 30-17 = 16 [/ латекс]
 Вычесть. [латекс] 13 = 16 [/ латекс]
 Итак, [латекс] x = 5 [/ latex] не является решением уравнения [латекс] 6x — 17 = 16 [/ latex].
 пример 
 Определите, является ли [латекс] y = 2 [/ latex] раствором [латекса] 6y — 4 = 5y — 2 [/ latex].
Показать решение
 Решение 
 Здесь переменная появляется с обеих сторон уравнения. Мы должны заменить [latex] 2 [/ latex] на каждый [latex] y [/ latex].
 [латекс] 6y-4 = 5y-2 [/ латекс]
 Замените y [латекс] \ color {red} {2} [/ latex]. [латекс] 6 (\ color {red} {2}) — 4 = 5 (\ color {red} {2}) — 2 [/ latex]
 Умножить. [латекс] 12-4 = 10-2 [/ латекс]
 Вычесть. [латекс] 8 = 8 [/ латекс]
 Поскольку [latex] y = 2 [/ latex] приводит к истинному уравнению, мы знаем, что [latex] 2 [/ latex] является решением уравнения [latex] 6y — 4 = 5y — 2 [/ латекс].
 В следующем видео мы покажем больше примеров того, как проверить, является ли целое число решением линейного уравнения.
 
 Мягкий вопрос — «Нет решения» — это то же самое, что «Не определено»? 
 Ради разнообразия ….
 Реальная практика  математики  имеет тенденцию неявно использовать более гибкую семантику, чем фактически явно описано. Одна интерпретация состоит в том, что семантика основана не на  функциях , а на  частичных функциях .2} $ имеет источник $ \ mathbb {R} $ (набор действительных чисел), цель $ \ mathbb {R} $ и домен $ [- 1,1] $.
 Пусть $ I $ обозначает набор с одним элементом. Напомним, понятие «элемент множества $ S $» эквивалентно понятию «функция $ I \ to S $». Помня о том, что нотация должна быть больше похожа на частичные функции, чем на функции, это означает, что должна существовать идея «частичного элемента».
 Набор всех частичных функций от $ I \ до S $ состоит из всех обычных функций и одной новой частичной функции: той, чья область определения пуста. 2} $, если мы будем следовать приведенному выше правилу, чтобы вставить значение $ 2 $, мы получим, что $ f (2) $ является неопределенным вещественным номер.
 Одной из неудобств этой нотации является неоднозначность того, что должно означать «$ = $». В частности, хотя $ f (2) $ является неопределенным действительным числом, было бы разумно настаивать на том, что $ f (2) = undefined $ не является истинным утверждением; вместо этого это неопределенное значение истинности. Я недостаточно продумал особенности этой нотации, чтобы решить, как обращаться с «$ = $».
 Еще одна особенность, которая встречается на практике, — это обобщенные элементы, например в виде неопределенных переменных и выражений, их включающих.x = 0 $, это определение имеет смысл в терминах обобщенных элементов; это более или менее эквивалентно «неопределенному действительному числу», описанному выше. И если интерпретировать в контексте обобщенных элементов,  действительно имеет смысл сказать $ x \ in \ emptyset $.
 4.5: Концентрация растворов — Химия LibreTexts 
 Многие люди имеют качественное представление о том, что подразумевается под концентрацией  . Любой, кто варил растворимый кофе или лимонад, знает, что слишком много порошка дает сильно ароматный и высококонцентрированный напиток, а слишком маленькое — разбавленный раствор, который трудно отличить от воды.В химии концентрация раствора — это количество  растворенного вещества , которое содержится в определенном количестве  растворителя  или раствора. Знание концентрации растворенных веществ важно для контроля стехиометрии реагентов для реакций в растворе. Химики используют множество различных методов для определения концентраций, некоторые из которых описаны в этом разделе.
 Молярность 
 Наиболее распространенной единицей концентрации является  молярность , что также является наиболее полезным для расчетов, включающих стехиометрию реакций в растворе.Молярность (M) определяется как количество молей растворенного вещества, присутствующего ровно в 1 л раствора. Это эквивалентно количеству миллимолей растворенного вещества, присутствующего ровно в 1 мл раствора:
 \ [молярность = \ dfrac {моль \: of \: solute} {литры \: of \: solution} = \ dfrac {ммоль \: of \: solute} {миллилитры \: of \: solution} \ label {4.5 .1} \]
 Таким образом, единицами молярности являются моль на литр раствора (моль / л), сокращенно \ (М \). Водный раствор, содержащий 1 моль (342 г) сахарозы в достаточном количестве воды, чтобы получить конечный объем 1.00 л имеет концентрацию сахарозы 1,00 моль / л или 1,00 М. В химической записи квадратные скобки вокруг названия или формулы растворенного вещества представляют молярную концентрацию растворенного вещества. Следовательно,
 \ [[\ rm {сахароза}] = 1,00 \: M \]
 читается как «концентрация сахарозы 1,00 молярная». Отношения между объемом, молярностью и молями могут быть выражены как
 \ [V_L M_ {mol / L} = \ cancel {L} \ left (\ dfrac {mol} {\ cancel {L}} \ right) = моль \ label {4.5.2} \]
 или
 \ [V_ {mL} M_ {ммоль / мл} = \ cancel {mL} \ left (\ dfrac {mmol} {\ cancel {mL}} \ right) = ммоль \ label {4.5.3} \]
 На рисунке \ (\ PageIndex {1} \) показано использование формул \ (\ ref {4.5.2} \) и \ (\ ref {4.5.3} \).
Рисунок \ (\ PageIndex {1} \): Приготовление раствора известной концентрации с использованием твердого вещества
 Пример \ (\ PageIndex {1} \): Расчет молей по концентрации NaOH
 Рассчитайте количество молей гидроксида натрия (NaOH) в 2,50 л 0,100 M NaOH.
  Дано:  идентичность растворенного вещества, а также объем и молярность раствора
  Запрошено:  количество растворенного вещества в молях
  Стратегия: 
 Используйте уравнение \ ref {4.5.2} или Equation \ ref {4.5.3}, в зависимости от единиц, указанных в задаче.
  Решение: 
 Поскольку нам задают объем раствора в литрах и спрашивают количество молей вещества, уравнение \ ref {4.5.2} более полезно:
 \ (моль \: NaOH = V_L M_ {моль / л} = (2,50 \: \ cancel {L}) \ left (\ dfrac {0.100 \: mol} {\ cancel {L}} \ right) = 0,250 \: моль \: NaOH \)
 Упражнение \ (\ PageIndex {1} \): вычисление молей по концентрации аланина
 Вычислите количество миллимолей аланина, биологически важной молекулы, в 27.2 мл 1,53 М аланина.
  Ответ 
 41,6 ммоль
 Концентрации также часто указываются в зависимости от массы к массе (м / м) или по отношению к массе к объему (м / об), особенно в клинических лабораториях и инженерных приложениях. Концентрация, выраженная на основе м / м, равна количеству граммов растворенного вещества на грамм раствора; Концентрация на основе м / об — это количество граммов растворенного вещества на миллилитр раствора.Каждое измерение можно выразить в процентах, умножив соотношение на 100; результат выражается в процентах по массе или в процентах по массе. Концентрации очень разбавленных растворов часто выражаются в  частей на миллион  ( частей на миллион ), что составляет граммы растворенного вещества на 10  6  г раствора, или в  частях на миллиард  ( частей на миллиард ), что составляет граммов растворенного вещества на 10  9  г раствора. Для водных растворов при 20 ° C 1 ppm соответствует 1 мкг на миллилитр, а 1 ppb соответствует 1 нг на миллилитр.Эти концентрации и их единицы приведены в Таблице \ (\ PageIndex {1} \).
 Таблица \ (\ PageIndex {1} \): Общие единицы концентрации
  Концентрация   Шт. 
 м / м г растворенного вещества / г раствора
 м / об г растворенного вещества / мл раствора
 частей на миллион г растворенного вещества / 10  6  г раствора
 мкг / мл
 частей на миллиард г растворенного вещества / 10  9  г раствора
 нг / мл
 Подготовка растворов 
 Чтобы приготовить раствор, который содержит определенную концентрацию вещества, необходимо растворить желаемое количество молей растворенного вещества в достаточном количестве растворителя, чтобы получить желаемый конечный объем раствора.Рисунок \ (\ PageIndex {1} \) иллюстрирует эту процедуру для раствора дигидрата хлорида кобальта (II) в этаноле. Обратите внимание, что объем  растворителя  не указан. Поскольку растворенное вещество занимает место в растворе, необходимый объем растворителя почти всегда на  меньше , чем желаемый объем раствора. Например, если желаемый объем был 1,00 л, было бы неправильно добавлять 1,00 л воды к 342 г сахарозы, потому что это привело бы к получению более 1,00 л раствора.Как показано на рисунке \ (\ PageIndex {2} \), для некоторых веществ этот эффект может быть значительным, особенно для концентрированных растворов.
Рисунок \ (\ PageIndex {2} \): Приготовление 250 мл раствора (NH  4 )  2  Cr  2  O  7  в воде. Растворенное вещество занимает пространство в растворе, поэтому для приготовления 250 мл раствора требуется менее 250 мл воды.
 Пример \ (\ PageIndex {2} \)
 Раствор содержит 10,0 г дигидрата хлорида кобальта (II), CoCl  2  • 2H  2  O, в этаноле, достаточном для приготовления ровно 500 мл раствора.Какова молярная концентрация \ (\ ce {CoCl2 • 2h3O} \)?
  Дано:  масса растворенного вещества и объем раствора
  Запрошено:  концентрация (M)
  Стратегия: 
 Чтобы найти количество молей \ (\ ce {CoCl2 • 2h3O} \), разделите массу соединения на его молярную массу. Рассчитайте молярность раствора, разделив количество молей растворенного вещества на объем раствора в литрах.
  Решение: 
 Молярная масса CoCl  2  • 2H  2  O составляет 165.87 г / моль. Следовательно,
 \ [молей \: CoCl_2 \ cdot 2H_2O = \ left (\ dfrac {10.0 \: \ cancel {g}} {165 .87 \: \ cancel {g} / mol} \ right) = 0 .0603 \: mol
 \ nonumber \]
 Объем раствора в литрах
 \ [volume = 500 \: \ cancel {mL} \ left (\ dfrac {1 \: L} {1000 \: \ cancel {mL}} \ right) = 0 .500 \: L
 \ nonumber \]
 Молярность — это количество молей растворенного вещества на литр раствора, поэтому молярность раствора составляет
.
 \ [молярность = \ dfrac {0.0603 \: mol} {0,500 \: L} = 0,121 \: M = CoCl_2 \ cdot H_2O
 \ nonumber \]
 Упражнение \ (\ PageIndex {2} \)
 Раствор, показанный на рисунке \ (\ PageIndex {2} \), содержит 90,0 г (NH  4 )  2  Cr  2  O  7  в достаточном количестве воды, чтобы получить конечный объем ровно 250 мл. Какова молярная концентрация дихромата аммония?
  Ответ 
 \ [(NH_4) _2Cr_2O_7 = 1,43 \: M
 \ nonumber \]
 Чтобы приготовить конкретный объем раствора, который содержит указанную концентрацию растворенного вещества, нам сначала нужно вычислить количество молей растворенного вещества в желаемом объеме раствора, используя соотношение, показанное в уравнении \ (\ ref {4.5.2} \). Затем мы переводим количество молей растворенного вещества в соответствующую массу необходимого растворенного вещества. Эта процедура проиллюстрирована в примере \ (\ PageIndex {3} \).
 Пример \ (\ PageIndex {3} \): D5W Решение
 Так называемый раствор D5W, используемый для внутривенного замещения биологических жидкостей, содержит 0,310 М глюкозы. (D5W представляет собой примерно 5% раствор декстрозы [медицинское название глюкозы] в воде.) Рассчитайте массу глюкозы, необходимую для приготовления пакета D5W объемом 500 мл. Глюкоза имеет молярную массу 180.16 г / моль.
  Дано:  молярность, объем и молярная масса растворенного вещества
  Запрошено:  Масса растворенного вещества
  Стратегия: 
  1.  Рассчитайте количество молей глюкозы в указанном объеме раствора, умножив объем раствора на его молярность.
  2.  Получите необходимую массу глюкозы, умножив количество молей соединения на его молярную массу.
  Решение: 
  A  Сначала мы должны вычислить количество молей глюкозы, содержащихся в 500 мл 0.310 M раствор:
 \ (V_L M_ {моль / л} = моль \)
 \ (500 \: \ cancel {mL} \ left (\ dfrac {1 \: \ cancel {L}} {1000 \: \ cancel {mL}} \ right) \ left (\ dfrac {0 .310 \: моль \: глюкоза} {1 \: \ cancel {L}} \ right) = 0 .155 \: моль \: глюкоза \)
  B  Затем мы переводим количество молей глюкозы в требуемую массу глюкозы:
 \ (масса \: of \: глюкоза = 0,155 \: \ cancel {моль \: глюкоза} \ left (\ dfrac {180.16 \: g \: глюкоза} {1 \: \ cancel {моль \: глюкоза}} \ справа) = 27.9 \: г \: глюкоза \)
 Упражнение \ (\ PageIndex {3} \)
 Другой раствор, обычно используемый для внутривенных инъекций, — это физиологический раствор, 0,16 М раствор хлорида натрия в воде. Рассчитайте массу хлорида натрия, необходимую для приготовления 250 мл физиологического раствора.
  Ответ 
 2,3 г NaCl
 Раствор желаемой концентрации можно также приготовить путем разбавления небольшого объема более концентрированного раствора дополнительным растворителем.Базовый раствор — это коммерчески приготовленный раствор известной концентрации, который часто используется для этой цели. Разбавление основного раствора является предпочтительным, поскольку альтернативный метод взвешивания крошечных количеств растворенного вещества трудно осуществить с высокой степенью точности. Разбавление также используется для приготовления растворов из веществ, которые продаются в виде концентрированных водных растворов, таких как сильные кислоты.
 Процедура приготовления раствора известной концентрации из основного раствора показана на рисунке \ (\ PageIndex {3} \).Это требует расчета желаемого количества молей растворенного вещества в конечном объеме более разбавленного раствора, а затем расчета объема исходного раствора, который содержит это количество растворенного вещества. Помните, что разбавление данного количества исходного раствора растворителем не влияет на количество молей присутствующего растворенного вещества , а не . Таким образом, соотношение между объемом и концентрацией основного раствора и объемом и концентрацией желаемого разбавленного раствора составляет
.
 \ [(V_s) (M_s) = моли \: of \: solute = (V_d) (M_d) \ label {4.5.4} \]
, где нижние индексы  s  и  d  обозначают исходный и разбавленный растворы, соответственно. Пример \ (\ PageIndex {4} \) демонстрирует вычисления, связанные с разбавлением концентрированного исходного раствора.
Рисунок \ (\ PageIndex {3} \): Приготовление раствора известной концентрации путем разбавления исходного раствора. (a) Объем ( V   s ), содержащий желаемые моли растворенного вещества (M  s ), измеряют из исходного раствора известной концентрации.(b) Отмеренный объем исходного раствора переносят во вторую мерную колбу. (c) Измеренный объем во второй колбе затем разбавляется растворителем до объемной отметки [( V   s ) (M  s ) = ( V   d ) (M  d ). ].
 Пример \ (\ PageIndex {4} \)
 Какой объем 3,00 М исходного раствора глюкозы необходим для приготовления 2500 мл раствора D5W в Примере \ (\ PageIndex {3} \)?
  Дано:  Объем и молярность разбавленного раствора
  Запрошено:  объем основного раствора
  Стратегия: 
  1.  Рассчитайте количество молей глюкозы, содержащихся в указанном объеме разбавленного раствора, умножив объем раствора на его молярность.
  2.  Чтобы определить необходимый объем исходного раствора, разделите количество молей глюкозы на молярность исходного раствора.
  Решение: 
  A  Раствор D5W в Примере 4.5.3 содержал 0,310 М глюкозы. Начнем с использования уравнения 4.5.4 для расчета количества молей глюкозы, содержащихся в 2500 мл раствора:
 \ [моль \: глюкоза = 2500 \: \ cancel {mL} \ left (\ dfrac {1 \: \ cancel {L}} {1000 \: \ cancel {mL}} \ right) \ left (\ dfrac { 0.310 \: моль \: глюкоза} {1 \: \ cancel {L}} \ right) = 0,775 \: моль \: глюкоза \]
  B  Теперь мы должны определить объем исходного раствора 3,00 M, который содержит это количество глюкозы:
 \ [объем \: of \: stock \: soln = 0,775 \: \ cancel {mol \: gluosis} \ left (\ dfrac {1 \: L} {3 .00 \: \ cancel {mol \: глюкоза}} \ right) = 0,258 \: L \: или \: 258 \: mL \]
 При определении необходимого объема исходного раствора мы должны были разделить желаемое количество молей глюкозы на концентрацию исходного раствора, чтобы получить соответствующие единицы.Кроме того, количество молей растворенного вещества в 258 мл исходного раствора такое же, как количество молей в 2500 мл более разбавленного раствора;  только количество растворителя изменилось . Полученный ответ имеет смысл: разбавление основного раствора примерно в 10 раз увеличивает его объем примерно в 10 раз (258 мл → 2500 мл). Следовательно, концентрация растворенного вещества должна уменьшиться примерно в 10 раз, как это происходит (3,00 M → 0,310 M).
 Мы также могли бы решить эту проблему за один шаг, решив уравнение 4.5.4 для  V   s  и подставив соответствующие значения:
 \ [V_s = \ dfrac {(V_d) (M_d)} {M_s} = \ dfrac {(2 .500 \: L) (0,310 \: \ cancel {M})} {3 .00 \: \ отменить {M}} = 0 .258 \: L \]
 Как мы уже отмечали, часто существует несколько правильных способов решения проблемы.
 Упражнение \ (\ PageIndex {4} \)
 Какой объем 5,0 М маточного раствора NaCl необходим для приготовления 500 мл физиологического раствора (0,16 М NaCl)?
  Ответ 
 16 мл
 Концентрации ионов в растворе 
 В примере \ (\ PageIndex {2} \) — концентрация раствора, содержащего 90. {2-} (водн.) \ Label {4.5.5} \]
 Таким образом, 1 моль единиц формулы дихромата аммония растворяется в воде с образованием 1 моль анионов Cr  2  O  7   2- и 2 моль катионов NH  4   +  (см. Рисунок \ (\ PageIndex { 4} \)).
Рисунок \ (\ PageIndex {4} \): Растворение 1 моля ионного соединения. В этом случае растворение 1 моля (NH  4 )  2  Cr  2  O  7  дает раствор, содержащий 1 моль Cr  2  O  7   2− ионов и 2 моль NH  4   +  иона.(Молекулы воды для ясности не показаны с точки зрения молекул.)
 При проведении химической реакции с использованием раствора соли, такого как дихромат аммония, важно знать концентрацию каждого иона, присутствующего в растворе. Если раствор содержит 1,43 M (NH  4 )  2  Cr  2  O  7 , то концентрация Cr  2  O  7   2− также должна быть 1,43 M, поскольку существует один Cr  2  O  7   2− ионов на формульную единицу.Однако на формульную единицу приходится два иона NH  4   + , поэтому концентрация ионов NH  4   +  составляет 2 × 1,43 M = 2,86 М. Поскольку каждая формульная единица (NH  4 )  2  Cr  2  O  7  при растворении в воде образует  трех ионов  (2NH  4   +  + 1Cr  2  O  7   2−), общая концентрация  ионов в решение 3 × 1,43 M = 4,29 M.
 Пример \ (\ PageIndex {5} \)
 Каковы концентрации всех веществ, полученных из растворенных веществ, в этих водных растворах?
  1.  0.21 М NaOH
  2.  3,7 M (CH  3 )  2  CHOH
  3.  0,032 M дюйм (NO  3 )  3 
  Дано:  Молярность
  Запрошено:  концентраций
  Стратегия: 
  A  Классифицируйте каждое соединение как сильный электролит или как неэлектролит.
  B  Если соединение неэлектролит, его концентрация такая же, как молярность раствора.- (водн.) \)
  B  Поскольку каждая формульная единица NaOH производит один ион Na  +  и один ион OH –, концентрация каждого иона такая же, как концентрация NaOH: [Na  + ] = 0,21 M и [ OH  — ] = 0,21 M.
  •   A  Формула (CH  3 )  2  CHOH представляет собой 2-пропанол (изопропиловый спирт) и содержит группу –OH, поэтому это спирт. Напомним из раздела 4.1, что спирты — это ковалентные соединения, которые растворяются в воде с образованием растворов нейтральных молекул.Таким образом, спирты не являются электролитами.
      B  Таким образом, единственными растворенными веществами в растворе являются (CH  3 )  2  молекулы CHOH, поэтому [(CH  3 )  2  CHOH] = 3,7 M.
  •   A  Нитрат индия — это ионное соединение, которое содержит ионы In  3   +  и ионы NO  3  —, поэтому мы ожидаем, что он будет вести себя как сильный электролит в водном растворе:
     \ (In (NO _3) _3 (s) \ xrightarrow {H_ 2 O (l)} In ^ {3+} (aq) + 3NO _3 ^ — (aq) \)
      B  Одна формульная единица In (NO  3 )  3  производит один ион In  3   +  и три NO  3  — иона, поэтому 0.032 M In (NO  3 )  3  раствор содержит 0,032 M In  3   +  и 3 × 0,032 M = 0,096 M NO  3   — , то есть [In  3   +  ] = 0,032 M и [NO  3  –] = 0,096 M
    •  Упражнение \ (\ PageIndex {5} \)
     Каковы концентрации всех веществ, полученных из растворенных веществ, в этих водных растворах?
    1.  0,0012 M Ba (OH)  2 
    2.  0.{2-}] = 0,17 \: M \)
        Ответ c 
       \ ([(CH_3) _2CO] = 0,50 \: M \)
       .
      Добавить комментарий 
      Ваш адрес email не будет опубликован. Обязательные поля помечены *
       
       
        
       2024 © Все права защищены.