Содержание
Умножение степеней, деление, таблица
Что такое степень числа
Алгебра дает нам такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
- an — степень, где
a — основание степени
n — показатель степени
Соответственно, an= a·a·a·a…·a
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и на калькуляторе — вот несколько подходящих:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3). Неважно в какой класс перешел ребенок — таблица пригодится всегда.
Неважно в какой класс перешел ребенок — таблица пригодится всегда.
Число | Вторая степень | Третья степень |
1 | 1 | 1 |
2 | 4 | 8 |
3 | 9 | 27 |
4 | 16 | 64 |
5 | 25 | 125 |
6 | 36 | 216 |
7 | 49 | 343 |
8 | 64 | 512 |
9 | 81 | 729 |
10 | 100 | 1000 |
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления.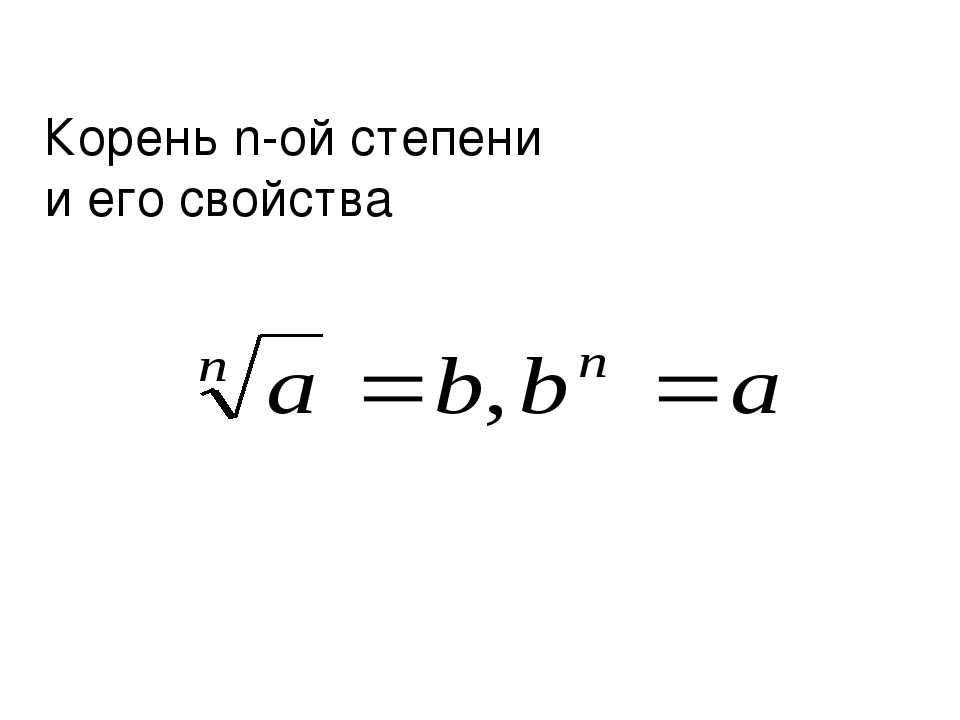 Всего их пять штук и ниже мы их рассмотрим.
Всего их пять штук и ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
an · am = am+n
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
(an)m = an· m
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.
(a · b)n = an · bn
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b)n = an : bn
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Умножение чисел с одинаковыми степенями
Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35+3 = 38 = 6561
- 28 · 81= 28 · 23 = 211 = 2048
Умножение чисел с разными степенями
Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:
А именно:
an · bn = (a · b)n
Если же разные и степени, и основания и одно из оснований не преобразуется в число с той же степенью, как у другого числа (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
Деление степеней с одинаковыми основаниями
Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми степенями
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
an : bn = (a : b)n, где
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Деление чисел со степенями
Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше.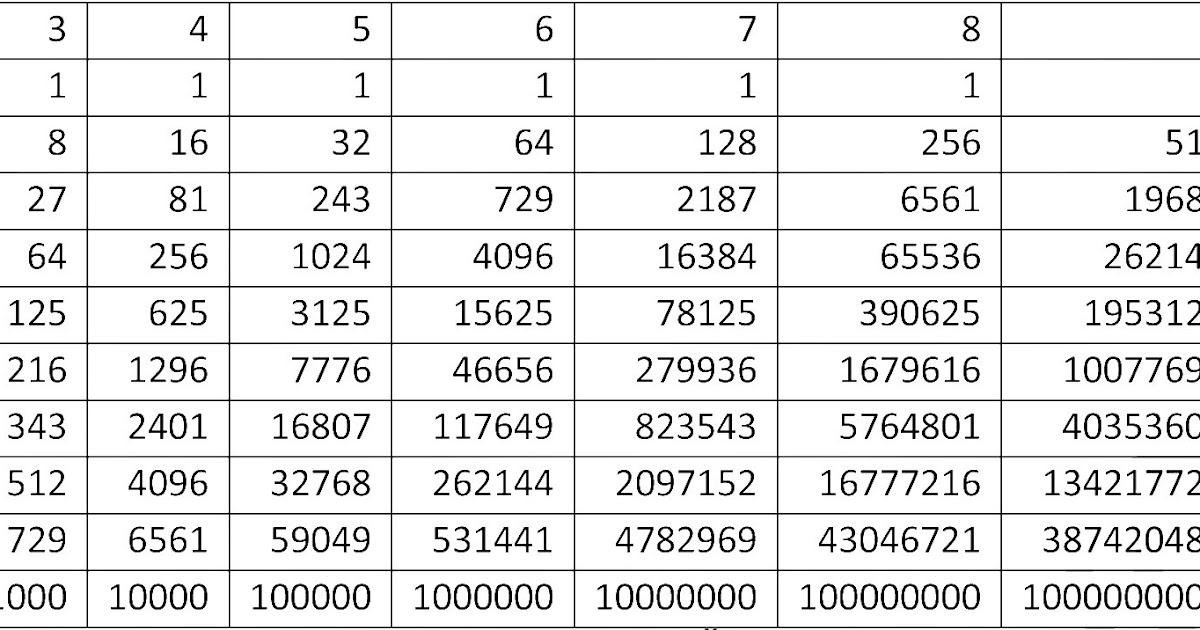 {n}=\underbrace{b*b*b*…*b}_{n \; раз}=a. $$
{n}=\underbrace{b*b*b*…*b}_{n \; раз}=a. $$
Число \(n\) при этом называют показателем корня.
Если \(n=2\), то перед вами корень 2-й степени или обычный квадратный корень.
Если \(n=3\), то корень 3-й степени и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.
Пример 1
$$ \sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2
$$ \sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3
$$ \sqrt[3]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4
$$ \sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим \(2,668…\) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть \(\sqrt[3]{19}\).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:
$$ \sqrt[3]{8} \le \sqrt[3]{19} \le \sqrt[3]{27} $$
$$ 2 \le \sqrt[3]{19} \le 3 $$
Получается, что наш корень лежит между числами 2 и 3.
Корень четной и нечетной степени
Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 5
$$ \sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.
Пример 6
$$ \sqrt[4]{-27} $$
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. k} $$
k} $$
Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №16 Название темы: Арифметический корень натуральной степени.
Перечень тем, рассматриваемых на уроке:
- преобразование и вычисление арифметических корней,
- свойства арифметического корня натуральной степени,
- корень нечетной степени из отрицательного числа,
- какими свойствами обладает арифметический корень натуральной степени.
Глоссарий
- Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
- Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
- Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.

- Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.
- Сканави М. И., Зайцев В. В., Рыжков В. В. «Элементарная математика». – Книга по требованию, 2012.
- Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
- Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.
Объяснение темы «Арифметический корень натуральной степени»
Решим задачу.
Площадь квадрата S=16 м².
Обозначим сторону квадрата а, м.
Тогда, а² = 16.
Решим данное уравнение:
a=4 и а= –4.
Проверим решение:
4² = 16;
(–4)² = 16.
Ответ: длина стороны квадрата равна 4 м.
Определение:
Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Определение:
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Обозначение: .
Определение:
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
Обозначение: .
Например:
.
.
.
На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.
Определение:
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Определение:
Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Обозначение: – корень n-й степени, где
n–степень арифметического корня;
а– подкоренное выражение.
Давайте рассмотрим такой пример: .
Мы знаем, что (–4)³ = –64, следовательно, .
Еще один пример: .
Мы знаем, что (–3)5 = –243, следовательно, .
На основании этих примеров, можно сделать вывод:
, при условии, что n –нечетное число.
Свойства арифметического корня натуральной степени:
Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:
- .
Примеры:
.
.
- .
Примеры:
.
.
- .
Пример:
.
- .
Пример:
.
- Для любогоа справедливо равенство:
Пример:
Найдите значение выражения , при 3 <x< 6.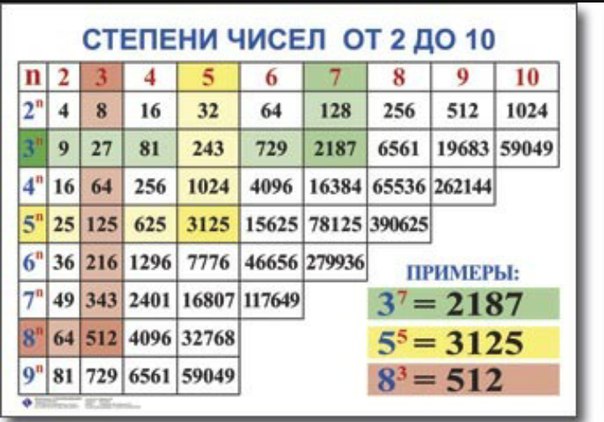
Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:
=|x – 3| = х – 3, т.к. х>3;
=|x – 6|=6 – x, т.к. х<6.
Получаем: х – 3 + 6 – х= 3.
Примеры заданий.
Первый пример.
Задача:
Выберите верные утверждения:
Разбор задания.
Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.
Ответ: ; ;
Второй пример.
Задача:
Выделите самое маленькое число:
Разбор задания:
Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число –
Ответ: 4.
Возведение в степень и извлечение корня из числа онлайн.
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби . Обратная операция также верна ,
Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Корни и степени. Квадратный корень, кубический корень.
youtube.com/embed/BvMYQ5eCBGg» frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями. ».
».
Мы возвели 8 в «квадрат» (т.е. ко второй степени) и получили в ячейке «А2» результат вычисления.
Вариант №2. С использованием функции
В Microsoft Office Excel есть удобная функция «СТЕПЕНЬ», которую вы можете активизировать для осуществления простых и сложных математических расчетов.
Функция выглядит следующим образом:
=СТЕПЕНЬ(число;степень)
ВНИМАНИЕ!
- Цифры для этой формулы указываются без пробелов и других знаков.
- Первая цифра – значение «число». Это основание (т.е. цифра, которую мы возводим). Microsoft Office Excel допускает введение любого вещественного числа.
- Вторая цифра – значение «степень». Это показатель, в который мы возводим первую цифру.
- Значения обоих параметров могут быть меньше нуля (т.е. со знаком «-»).
Формула возведения в степень в Excel
Примеры использования функции СТЕПЕНЬ().
С использованием мастера функций:
- Запускаем мастера функций с помощью комбинации горячих клавиш SHIFT+F3 или жмем на кнопку в начале строки формул «fx» (вставить функцию).
 Из выпадающего списка «Категория» выбираем «Математические», а в нижнем поле указываем на нужную нам функцию и жмем ОК.
Из выпадающего списка «Категория» выбираем «Математические», а в нижнем поле указываем на нужную нам функцию и жмем ОК. - В появившимся диалоговом окне заполняем поля аргументами. К примеру, нам нужно возвести число «2» в степень «3». Тогда в первое поле вводим «2», а во второе — «3».
- Нажимаем кнопку «ОК» и получаем в ячейке, в которую вводили формулу, необходимое нам значение. Для данной ситуации это «2» в «кубе», т.е. 2*2*2 = 8. Программа подсчитала все верно и выдала вам результат.
Если лишние клики вы считаете сомнительным удовольствием, предлагаем еще один простой вариант.
Ввод функции вручную:
- В строке формул ставим знак «=» и начинаем вводить название функции. Обычно достаточно написать «сте» — и система сама догадается предложить вам полезную опцию.
- Как только увидели такую подсказку, сразу жмите на клавишу «Tab». Или можете продолжить писать, вручную вводить каждую букву. Потом в скобках укажите необходимые параметры: два числа через точку с запятой.

- После этого нажимаете на «Enter» — и в ячейке появляется высчитанное значение 8.
Последовательность действий проста, а результат пользователь получает достаточно быстро. В аргументах вместо чисел могут быть указаны ссылки на ячейки.
Корень в степени в Excel
Чтобы извлечь корень с помощью формул Microsoft Excel, воспользуемся несколько иным, но весьма удобным способом вызова функций:
- Перейдите по закладке «Формулы». В разделе инструментов «Библиотека функций» щелкаем по инструменту «Математические». А из выпадающего списка указываем на опцию «КОРЕНЬ».
- Введите аргумент функции по запросу системы. В нашем случае необходимо было найти корень из цифры «25», поэтому вводим его в строку. После введения числа просто нажимаем на кнопку «ОК». В ячейке будет отражена цифра, полученная в результате математического вычисления корня.
ВНИМАНИЕ! Если нам нужно узнать корень в степени в Excel то мы не используем функцию =КОРЕНЬ(). Вспомним теорию из математики:
«Корнем n-ой степени от числа а называется число b, n-ая степень которого равна а», то есть:
n√a = b; bn = a. (1/n)- где a-число; n-степень:
(1/n)- где a-число; n-степень:
Или через такую функцию: =СТЕПЕНЬ(32;1/5)
В аргументах формулы и функции можно указывать ссылки на ячейки вместо числа.
Как в Excel написать число в степени?
Часто вам важно, чтобы число в степени корректно отображалось при распечатывании и красиво выглядело в таблице. Как в Excel написать число в степени? Здесь необходимо использовать вкладку «Формат ячеек». В нашем примере мы записали цифру «3» в ячейку «А1», которую нужно представить в -2 степени.
Последовательность действий следующая:
- Правой кнопкой мыши щелкаем по ячейке с числом и выбираем из выскакивающего меню вкладку «Формат ячеек». Если не получилось – находим вкладку «Формат ячеек» в верхней панели или жмем комбинацию клавиш CTRL+1.
- В появившемся меню выбираем вкладку «Число» и задаем формат для ячейки «Текстовый». Жмем ОК.
- В ячейке A1 вводим рядом с числом «3» число «-2» и выделяем его.
- Снова вызываем формат ячеек (например, комбинацией горячих клавиш CTRL+1) и теперь для нас только доступна вкладка «Шрифт», в которой отмечаем галочкой опцию «надстрочный».
 И жмем ОК.
И жмем ОК. - В результате должно отображаться следующее значение:
Пользоваться возможностями Excel просто и удобно. С ними вы экономите время на осуществлении математических подсчетов и поисках необходимых формул.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения
Формулы сокращенного умножения включают в себя следующие группы формул:
Степень суммы
Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:
| (x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y) |
и т. д.
д.
Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.
Таблица 1. – Степень суммы
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) суммы (x + y)2 = x2 + 2xy + y2 |
Куб (третья степень) суммы (x + y)3 = |
Четвертая степень суммы (x + y)4 = x4 + 4x3y + |
Пятая степень суммы (x + y)5 = x5 + 5x4y + |
Шестая степень суммы (x + y)6 = x6 + 6x5y + |
| … |
Общая формула для вычисления суммы
(x + y)n
с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.
Степень разности
Если в формулах из Таблицы 1 заменить y на – y , то мы получим группу формул «Степень разности» (Таблица 2.):
Таблица 2. – Степень разности
| Название формулы | Формула |
| Квадрат (вторая степень) разности | (x – y)2 = x2 – 2xy + y2 |
| Куб (третья степень) разности | (x – y)3 = x3 – 3x2y + 3xy2 – y3 |
| Четвертая степень разности | (x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4 |
| Пятая степень разности | (x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5 |
| Шестая степень разности | (x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6 |
| … | … |
Квадрат (вторая степень) разности (x – y)2 = x2 – 2xy + y2 |
Куб (третья степень) разности (x – y)3 = |
Четвертая степень разности (x – y)4 = x4 – 4x3y + |
Пятая степень разности (x – y)5 = x5 – 5x4y + |
Шестая степень разности (x – y)6 = x6 – 6x5y + |
| … |
Квадрат многочлена
Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:
Словами эту формулу можно выразить так: — «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».
Куб трехчлена
Следующая формула называется «Куб трехчлена»:
(x + y + z)3 =
= x3 + y3 + z3 + 3x2y +
+ 3x2z + 3xy2 +
+ 3xz2 +
+ 3y2z + 3yz2 + 6xyz .
Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.
Что такое «степень N»?
За последние несколько месяцев многие спрашивали меня, что означает «степень N». Фраза очень проста, но имеет много разных уровней смысла и понимания.
С математической точки зрения он представляет постоянно растущее число возможностей. Это метафора того, что мы, нанотехнологи, делаем.
Это метафора того, что мы, нанотехнологи, делаем.
Традиционная наука редуктивна: сужает известные возможности до тех пор, пока мы не придем к заключению. Мы идем в противоположном направлении к неизвестному.Мы стремимся открыть процессы в природе, которые человечество еще не постигло или не вообразило.
Это путешествие, открывающее в чистом виде. Конечно, мы идем дальше в рамках науки или, точнее, в рамках множества различных научных дисциплин (таких как инженерия, химия, биология, геология, информатика, сельское хозяйство, медицинские науки и т. Д.), Но они служат нашим пункт отправления, а не конечный пункт назначения.
Концепция объекта или сущности, находящихся «во власти N», представляет экспоненциальный потенциал для роста, обучения, лидерства и процветания, причем процветание является нашей конечной целью.
N также является начальной буквой трех наших областей концентрации:
Нанотехнология относится к нашей способности манипулировать материей на молекулярном уровне. Работа на этом наномасштабном уровне привела к множеству прорывов в нашем понимании того, как функционирует материя. Еще более захватывающим является то, что он открывает нам глаза на потенциал использования этого понимания для разработки технологий, которые позволяют находить новые решения проблем в областях, которые ранее были трудноразрешимыми.
Работа на этом наномасштабном уровне привела к множеству прорывов в нашем понимании того, как функционирует материя. Еще более захватывающим является то, что он открывает нам глаза на потенциал использования этого понимания для разработки технологий, которые позволяют находить новые решения проблем в областях, которые ранее были трудноразрешимыми.
Nature представляет собой дисциплину биомимикрии, которая включает наблюдение естественных атрибутов материи, объектов, систем и существ.Основываясь на этом фундаментальном понимании, мы затем стремимся воспроизвести эти процессы и манипулировать ими, чтобы обнаружить, что возможно при их использовании с другими процессами или материалами.
Сети — это настоящий рубеж научных открытий. Как только мы поймем основы материи и процессов, нам остается понять, как эти явления взаимодействуют друг с другом. Как обрабатывается информация, которая принимает форму молекулярных взаимодействий? Это ведет к более широкому потенциалу использования этого обмена молекулярной информацией для использования нанотехнологий для создания новых функциональных возможностей как неотъемлемого свойства при решении сложных проблем.
Благодаря этой структуре открытий мы собрали динамичную команду ученых, которые работают совместно (в нескольких дисциплинах), чтобы исследовать потенциал материалов следующего поколения, которые могут, например, определять окружающую среду вокруг них, расширять информацию, генерировать энергия и изменение физических характеристик.
Это новый рубеж науки, который функционирует на молекулярном уровне и имеет гораздо более широкое применение в отношении добычи ресурсов, управления окружающей средой, здравоохранения, обработки информации и производства ценных продуктов и услуг, которые будут определять будущее Альберты. , Канада и остальной мир.
Это сила N, которая подводит итог тому, что мы делаем в лаборатории Ingenuity Lab.
Что такое экспонента?
MATH
ОБЗОР: ПОЛЕЗНАЯ МАТЕМАТИКА ДЛЯ ВСЕХ
РАЗДЕЛ
3. 2. ЧТО ТАКОЕ ДОКАЗАТЕЛЬ?
2. ЧТО ТАКОЕ ДОКАЗАТЕЛЬ?
назад к экспонентам, стр. 1
Сначала давайте посмотрим, как
работать с переменными с заданной мощностью, например, 3 .
Там
пять правил работы с показателями:
1. a м * a n = a (m + n)
2. (a * b) n = a n * b n
3. ( м ) n = (m * n)
4. a м / a n = a (m-n)
5.(a / b) n = a n / b n
Давайте подробно рассмотрим каждый из них.
1. a m * a n = a (m + n) говорит, что когда вы берете
число a, умноженное на себя m раз, и умножьте это на
то же число a, умноженное само на себя n раз, это то же самое, что взять
это число a и возвести его в степень, равную сумме m + n.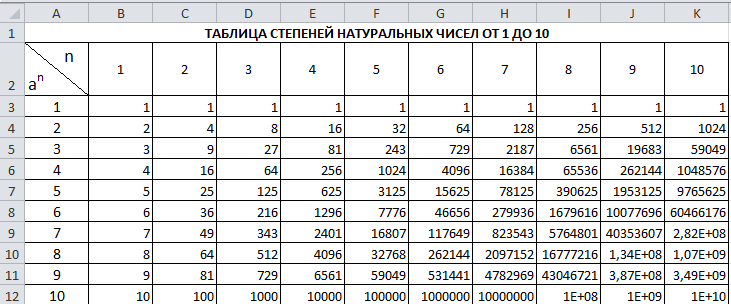
Вот пример, где
a = 3
m = 4
n = 5а м *
n = (m + n)3 4 *
3 5 = 3 (4 + 5) = 3 9 = 19 683
2. (а * б) н =
a n * b n говорит, что при умножении
два числа, а затем умножьте это произведение на себя n раз, это
то же самое, что умножить первое число на себя n раз и умножить
что на второе число, умноженное на себя n раз.
Давайте рассмотрим пример, где
a = 3
b = 6
n = 5(а
* b) n = a n * b n(3
* 6) 5 = 3 5 * 6 518 5 = 3 5 * 6 5 = 243
* 7,776 = 1,889,568
3. ( м ) n =
( м ) n =
а (м * н) говорит, что когда вы берете
число, a, и умножьте его на себя m раз, затем умножьте это
произведение на себя n раз, это то же самое, что умножение числа
a само по себе m * n раз.
Давайте разберемся на примере
гдеa = 3
m = 4
n = 5( м ) n =
а (м * п)(3 4 ) 5 = 3 (4 *
5) = 3 20 =
3 486 784 401
4. a м / a n =
a (m-n) говорит, что когда вы
возьмите число a и умножьте его на себя m раз, затем разделите
этот продукт умножается на себя n раз, это то же самое
как умноженное на себя m-n раз.
Вот пример, где
а = 3
м = 4
п = 5a м / a n = a (m-n)
3 4 /3 5 = 3 (4-5) = 3 -1 (Помните, как поднять
число до отрицательной степени.)3 4 /3 5 =
1/3 1 = 1/3
5. (а / б) n =
a n / b n говорит
что когда вы делите число, a на другое число, b, а затем
умножьте это частное
само по себе n раз, это то же самое, что умножение числа на само себя
n раз, а затем разделив этот продукт на число b, умноженное
сам по себе n раз.
Давайте рассмотрим пример, где
а = 3
б = 6
п = 5(a / b) n = a n / b n
(3/6) 5 =
3 5 /6 5Помните, что 3/6 можно уменьшить
до 1/2. Итак, имеем:(1/2) 5 =
243 / 7,776 = 0.03125
Понимание экспонентов подготовит вас к использованию логарифмов.
в логарифмах
Для
подробнее об этом сайте свяжитесь с Distance
Координатор по образованию.
Авторские права © 2004 г.
регентами Миннесотского университета, равные возможности
работодатель и педагог.
экспонентов
Показатель числа говорит , сколько раз использовать число при умножении.
В 8 2 «2» означает использование 8 дважды при умножении,
, поэтому 8 2 = 8 × 8 = 64
Словами: 8 2 можно было бы назвать «8 в степени 2» или «8 во второй степени», или
просто «8 в квадрате»
Показатели также называются степенями или индексами.
Еще несколько примеров:
Пример:
5 3 = 5 × 5 × 5 = 125
- Словами: 5 3 можно было бы назвать «5 в третьей степени», «5 в степени 3» или просто
«5 кубов»
Пример:
2 4 = 2 × 2 × 2 × 2 = 16
- Словами: 2 4 можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто
«2–4»
Показатели упрощают запись и использование множества умножений
Пример: 9 6 легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Вы можете умножить любое число на само столько раз , сколько хотите, используя экспоненты. 4 = 2 × 2 × 2 × 2 = 16
4 = 2 × 2 × 2 × 2 = 16
Отрицательные экспоненты
Отрицательный? Что может быть противоположностью умножения? Разделение!
Итак, мы каждый раз делим на число, что аналогично умножению на 1 число
Пример: 8 -1 = 1 8 = 0,125
Мы можем продолжить так:
Пример: 5 -3 = 1 5 × 1 5 × 1 5 = 0.008
Но зачастую проще сделать так:
5 -3 также можно рассчитать как:
1 5 × 5 × 5 = 1 5 3 = 1 125 = 0,008
Отрицательный? Переверните позитив!
Последний пример показал более простой способ работы с отрицательными показателями:
|
Другие примеры:
| Отрицательная экспонента | , обратный положительной экспоненте | Ответ | ||
|---|---|---|---|---|
| 4 -2 | = | 1/4 2 | = | 1/16 = 0,0625 |
| 10 -3 | = | 1/10 3 | = | 1/1000 = 0.001 |
| (-2) -3 | = | 1 / (-2) 3 | = | 1 / (- 8) = -0,125 |
Что, если показатель степени равен 1 или 0?
| 1 | Если показатель степени равен 1, то у вас есть только само число (например, 9 1 = 9 ) | |
| 0 | Если показатель степени равен 0, то вы получите 1 (например, 9 0 = 1 ) | |
А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенный» . |
Все имеет смысл
Если вы посмотрите на эту таблицу, вы увидите положительный результат, ноль или
отрицательные показатели на самом деле являются частью одного и того же (довольно простого) паттерна:
| Пример: Полномочия 5 | |||
|---|---|---|---|
| .. и т.д .. | |||
| 5 2 | 5 × 5 | 25 | |
| 5 1 | 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 5 | 0.2 | |
| 5 -2 | 1 5 × 1 5 | 0,04 | |
. . и т.д .. . и т.д .. | |||
Будьте осторожны при группировке
Чтобы избежать путаницы, используйте круглые скобки () в таких случаях:
| С (): | (-2) 2 = (-2) × (-2) = 4 |
| Без (): | -2 2 = — (2 2 ) = — (2 × 2) = -4 |
| С (): | (ab) 2 = ab × ab |
| Без (): | ab 2 = a × (b) 2 = a × b × b |
Правила экспоненты | Законы экспонентов
Правила экспоненты, законы экспоненты и примеры.
Что такое показатель степени
Основание a в степени n равно умножению числа a, n раз:
a n =
a × a × . .. × a
.. × a
п раз
a — основание, n — показатель степени.
Примеры
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Правила и свойства экспонентов
| Название правила | Правило | Пример |
|---|---|---|
| Правила продукта | a n ⋅ a m = a n + m | 2 3 ⋅ 2 4 = 2 3 + 4 = 128 |
| a n ⋅ b n = ( a ⋅ b ) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Правила частных | a n / a м = a n — м | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n = ( a / b ) n | 4 3 /2 3 = (4/2) 3 = 8 | |
| Силовые правила | ( b n ) м = b нм | (2 3 ) 2 = 2 3⋅2 = 64 |
| b n m = b ( n m ) | 2 3 2 = 2 (3 2 ) = 512 | |
| м √ ( b n ) = б n / м | 2 √ (2 6 ) = 2 6/2 = 8 | |
| b 1/ n = n √ b | 8 1/3 = 3 √8 = 2 | |
| Отрицательные показатели | b -n = 1/ b n | 2 -3 = 1/2 3 = 0. 125 125 |
| Нулевые правила | b 0 = 1 | 5 0 = 1 |
| 0 n = 0, для n > 0 | 0 5 = 0 | |
| Единые правила | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| Минус одно правило | (-1) 5 = -1 | |
| Производное правило | ( x n ) ‘ = n ⋅ x n -1 | ( x 3 ) ‘ = 3⋅ x 3-1 |
| Интегральная линейка | ∫ x n dx = x n +1 / ( n +1) + C | ∫ x 2 dx = x 2 + 1 / (2 + 1) + C |
Показатели продукта правила
Правило продукта с той же базой
a n ⋅ a m = a n + m
Пример:
2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Правило произведения с таким же показателем
a n ⋅ b n = ( a ⋅ b ) n
Пример:
3 2 ⋅ 4 2 = (3⋅4) 2 =
12 2 = 12⋅12 = 144
См . : Показатели умножения
: Показатели умножения
Правила частного экспонента
Правило частных с таким же основанием
a n / a м = a n — м
Пример:
2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4
Правило частных с тем же показателем
a n / b n = ( a / b ) n
Пример:
4 3 /2 3 = (4/2) 3 =
2 3 = 2⋅2⋅2 = 8
См .: Показатели деления
Правила степени экспоненты
Правило силы I
( a n ) m = a nm
Пример:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
Правило власти II
a n m = a ( n m )
Пример:
2 3 2 = 2 (3 2 )
= 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Силовое правило с радикалами
м √ ( a n ) = a n / м
Пример:
2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Правило отрицательных показателей
b -n = 1/ b n
Пример:
2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.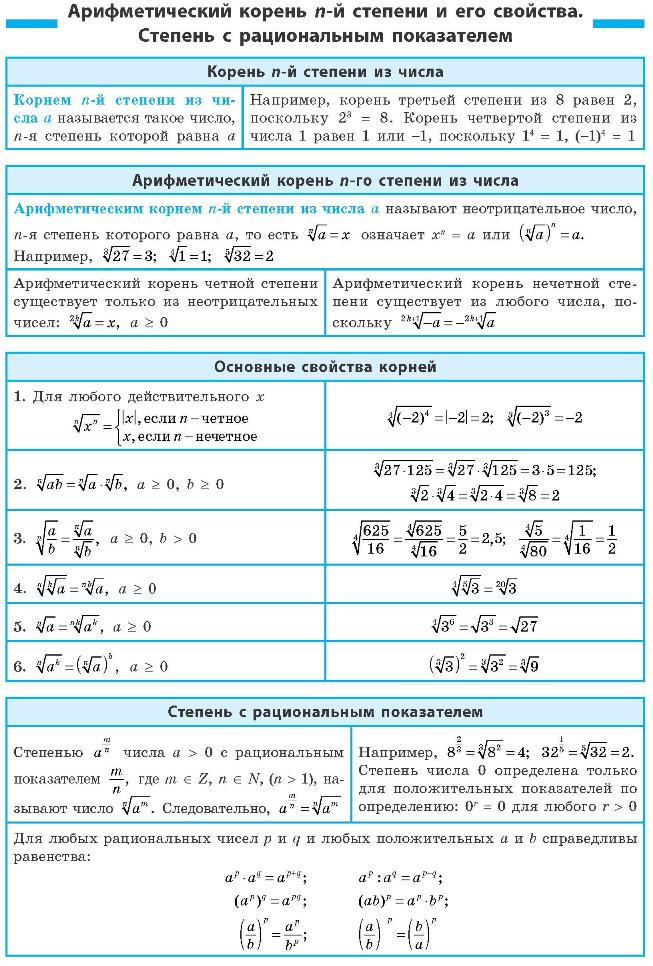 125
125
См .: Отрицательные показатели
Калькулятор экспонент ►
См. Также
экспонентов: основные правила | Purplemath
Purplemath
Экспоненты — это сокращение для многократного умножения одного и того же самого на себя. Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 3 .«Показатель», равный 3 в этом примере, означает, сколько раз умножается значение. То, что умножается, в этом примере равно 5, называется «базой».
Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 3 » произносится как «пять в третьей степени» или «пять в третьей степени».
MathHelp.com
Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе». Итак, «5 3 » обычно произносится как «пять кубов».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы лучше будем иметь дело с «27», чем с «3 3 ».Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « xxxxxx ».
У экспонентов есть несколько правил, которые мы можем использовать для упрощения выражений.
Чтобы упростить это, я могу думать в терминах того, что означают эти показатели. «До третьей» означает «умножение трех копий», а «до четвертой» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме.Сначала я расширяюсь:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
Теперь я могу убрать скобки и сложить все множители:
( xxx ) ( xxxx ) = xxxxxxx
Это семь копий переменной.«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
xxxxxxx = x 7
Собираем все вместе, шаги следующие:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
= xxxxxxx
= x 7
Тогда упрощенная форма ( x 3 ) ( x 4 ) будет:
Обратите внимание, что x 7 также равно x (3 + 4) .Это демонстрирует первое основное правило экспоненты:
Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты:
( x м ) ( x n ) = x (m + n)
Однако мы НЕ можем упростить ( x 4 ) ( y 3 ), потому что основания разные: ( x 4 ) ( y 3 ) = xxxxyyy = ( x 4 ) ( y 3 ).Ничего не сочетается.
Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом:
( a 5 b 3 ) ( a b 7 ) = ( a 5 ) ( a ) ( b 3 ) ( б 7 )
Теперь я хочу добавить мощности на a и b .Однако у второго или , похоже, нет мощности. Что мне добавить для этого срока?
Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:
( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( a 5 ) ( a 1 ) ( b 3 ) ( б 7 )
Теперь могу комбинировать:
( a 5 ) ( a 1 ) ( b 3 ) ( b 7 ) = a 5 + 1 b 3 + 7 = a 6 b 10
Если сложить все вместе, моя ручная работа будет выглядеть так:
( a 5 b 3 ) ( a b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) =
В следующем примере есть две силы, одна из которых в некотором смысле находится «внутри» другой.
Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, заключенного в круглые скобки. В этом случае база четвертой степени равна x 2 . Умножение четырех копий этой базы дает мне:
Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как:
( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( xx ) ( xx ) ( xx ) ( xx )
Убрав скобки, получим:
( xx ) ( xx ) ( xx ) ( xx ) = xxxxxxxx
Это строка из восьми копий переменной.«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
xxxxxxxx = x 8
Собираем все вместе:
( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 )
= ( xx ) ( xx ) ( xx ) ( xx )
= xxxxxxxx
= x 8
Обратите внимание, что ( x 2 ) 4 = x 8 , и что 2 × 4 = 8.Это демонстрирует правило второй степени:
Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:
Если у вас есть продукт в круглых скобках и сила в скобках, то сила идет на каждый элемент внутри. Например:
( xy 2 ) 3 = ( xy 2 ) ( xy 2 ) ( xy 2 )
= ( xxx ) ( y 2 y 2 y 2 )
= ( xxx ) ( yyyyyy )
= x 3 y 6
= ( x ) 3 ( y 2 ) 3
Другой пример:
Предупреждение: это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению.
Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильный. На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.
Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) 2 , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому:
( x — 2) 2 = ( x — 2) ( x — 2)
= x ( x -2) — 2 ( x -2)
= xx -2 x -2 x + 4
= x 2 — 4 x + 4.
Ошибка в виде ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается делать все в своей голове, вместо того, чтобы показать свою работу.Делайте все аккуратно, и вы вряд ли совершите эту ошибку.
Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что у c внутри скобок это «в степени 1».)
( a 2 ) 4 ( b 3 ) 4 ( c 1 ) 4
= ( a 2 × 4 ) ( b 3 × 4 ) ( c 1 × 4 )
= a 8 b 12 c 4
Партнер
Есть еще одно правило, которое может или не может быть рассмотрено в вашем классе на данном этапе:
Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе).
Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:
Упростить [(3
x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0
Кого волнует эта фигня в квадратных скобках? Я точно не знаю, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха!
[(3 x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0 = 1
Между прочим, как только ваш класс охватит «до нуля», вы должны ожидать упражнения, подобного приведенному выше, на следующем тесте.Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с показателями степени. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество отработанных примеров.)
Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.
URL: https://www.purplemath.com/modules/exponent.htm
Обзор правил для экспонентов
Обзор правил для экспонентов Ниже приведен список правил для экспонентов и один или два примера использования каждого правила:
| Правило нулевой экспоненты: a 0 = 1, это говорит, что все, что возведено в нулевую степень, равно 1. | |
| Правило мощности (от степеней к степеням): ( м ) n = мин , это говорит о том, что для возведения степени в степень вам необходимо умножить степень. Есть несколько других правил, которые соответствуют правилу мощности, например, правило произведения к степеням и правило отношения к степеням. | |
| Правило отрицательной экспоненты :, это говорит о том, что отрицательные показатели в числителе перемещаются в знаменатель и становятся положительными показателями.Отрицательные показатели в знаменателе перемещаются в числитель и становятся положительными показателями. Перемещайте только отрицательные показатели. | |
| Правило произведения : a m ∙ a n = a m + n , это говорит о том, что для умножения двух степеней с одинаковым основанием вы сохраняете основание и складываете степени. | |
| Правило частных :, это говорит о том, что для деления двух показателей с одинаковым основанием вы сохраняете основание и вычитаете степени.Это похоже на сокращение фракций; когда вы вычитаете степени, поместите ответ в числитель или знаменатель в зависимости от того, где находится высшая степень. Если в знаменателе указана более высокая степень, поместите разницу в знаменатель и наоборот, это поможет избежать отрицательных показателей. |
Теперь, когда мы рассмотрели правила для экспонент, вот шаги, необходимые для упрощения экспоненциальных выражений (обратите внимание, что мы применяем правила в том же порядке, что и правила были написаны выше):
| Шаг 1 : | Примените правило нулевой экспоненты.Измените все, что доведено до нулевой степени, на 1. |
| Шаг 2 : | Примените правило мощности. Умножьте (или распределите) показатель за пределами круглых скобок с каждым показателем внутри скобок, помните, что если показатель не показан, то показатель степени равен 1. |
| Шаг 3 : | Примените правило отрицательной экспоненты. Отрицательные показатели в числителе перемещаются в знаменатель и становятся положительными показателями.Отрицательные показатели в знаменателе перемещаются в числитель и становятся положительными показателями. Перемещайте только отрицательные показатели. Обратите внимание, что порядок, в котором перемещаются предметы, не имеет значения. |
| Шаг 4 : | Примените правило продукта. Чтобы умножить два показателя степени с одинаковым основанием, вы сохраняете основание и складываете степени. |
| Шаг 5 : | Примените правило частного. Это похоже на сокращение фракций; когда вы вычитаете степени, поместите ответ в числитель или знаменатель в зависимости от того, где находится высшая степень.Если в знаменателе указана более высокая степень, поместите разницу в знаменатель и наоборот, это поможет избежать отрицательных показателей степени и повторения шага 3. |
| Шаг 6 : | Возвести каждый коэффициент (или число) в соответствующую степень, а затем упростить или уменьшить оставшиеся дроби. |
Пример 1 — Упростить:
Пример 2 –Simplify:
Щелкните здесь для практических задач
Пример 3 –Simplify:
Щелкните здесь для практических задач
Пример 4 –Simplify:
Щелкните здесь для практических задач
Пример 5 –Simplify:
Щелкните здесь для практических задач
Калькулятор экспонент
Введите значения в любые два поля ввода, чтобы найти третье.
Связанный научный калькулятор | Калькулятор журнала | Калькулятор корня
Что такое показатель степени?
Возведение в степень — это математическая операция, записанная как a n , включающая основание a и показатель степени n . В случае, когда n является положительным целым числом, возведение в степень соответствует многократному умножению основания, n раз.
а н = а × а × … × а
n раз
Калькулятор выше принимает отрицательные основания, но не вычисляет мнимые числа.Он также не принимает дроби, но может использоваться для вычисления дробных показателей, если показатели вводятся в их десятичной форме.
Основные законы и правила экспоненты
При умножении экспонент с одной и той же базой экспоненты складываются.
a n × a м = a (n + m)
Пример: 2 2 × 2 4 = 4 × 16 = 64
2 2 × 2 4 = 2 (2 + 4) = 2 6 = 64
Когда показатель степени отрицательный, отрицательный знак удаляется возвратом основания и увеличением его до положительного показателя степени.
| Пример: 2 (-3) = 1 ÷ 2 ÷ 2 ÷ 2 | = |
При делении показателей степени с одинаковым основанием вычитаются показатели степени.
| Пример: | = | = |
| = 2 (2-4) = 2 -2 = | = |
Когда показатели увеличиваются до другого показателя, показатели умножаются.
(a м ) n = a (m × n)
Пример: (2 2 ) 4 = 4 4 = 256
(2 2 ) 4 = 2 (2 × 4) = 2 8 = 256
Когда умноженные основания возводятся в степень, экспонента распределяется по обеим основаниям.
(a × b) n = a n × b n
Пример: (2 × 4) 2 = 8 2 = 64
(2 × 4) 2 = 2 2 × 4 2 = 4 × 16 = 64
Аналогичным образом, когда разделенные основания возводятся в степень, показатель степени распределяется по обоим основаниям.
| Пример: ( | ) 2 | = | × | = |
Когда показатель степени равен 1, основание остается прежним.
а 1 = а
Когда показатель степени равен 0, результатом возведения в степень любого основания всегда будет 1, хотя некоторые
дебаты окружают 0 0 равным 1 или неопределенному. Для многих приложений удобно задать 0 0 как 1.
а 0 = 1
Ниже показан пример аргумента для 0 = 1 с использованием одного из ранее упомянутых законов экспоненты.
Если n × м = (n + m)
Тогда n × a 0 = a (n + 0) = a n
Таким образом, единственный способ, чтобы a n не изменились при умножении, и этот закон экспоненты остался верным, — это чтобы значение 0 было равно 1.
Когда показатель степени представляет собой дробь, где числитель равен 1, берется корень n th из основания. Ниже показан пример с дробной степенью, где числитель не равен 1. Он использует как отображаемое правило, так и правило для умножения экспоненты с аналогичными основаниями, рассмотренными выше. Обратите внимание, что калькулятор может вычислять дробные показатели, но они должны вводиться в калькулятор в десятичной форме.
Также возможно вычислить показатели с отрицательным основанием.Они следуют тем же правилам, что и показатели с положительным основанием. Показатели с отрицательными основаниями, возведенными в положительные целые числа, равны своим положительным аналогам по величине, но различаются в зависимости от знака. Если показатель степени является четным положительным целым числом, значения будут равны независимо от положительного или отрицательного основания. Если показатель степени является нечетным положительным целым числом, результат снова будет иметь ту же величину, но будет отрицательным. Хотя правила для дробных показателей с отрицательным основанием такие же, они предполагают использование мнимых чисел, поскольку невозможно извлечь корень из отрицательного числа.Пример приведен ниже для справки, но обратите внимание, что предоставленный калькулятор не может вычислять мнимые числа, и любые входные данные, которые дают мнимое число, вернут результат «NAN», что означает «не число». Численное решение по существу такое же, как и в случае с положительным основанием, за исключением того, что число должно быть обозначено как мнимое.
.


 Из выпадающего списка «Категория» выбираем «Математические», а в нижнем поле указываем на нужную нам функцию и жмем ОК.
Из выпадающего списка «Категория» выбираем «Математические», а в нижнем поле указываем на нужную нам функцию и жмем ОК.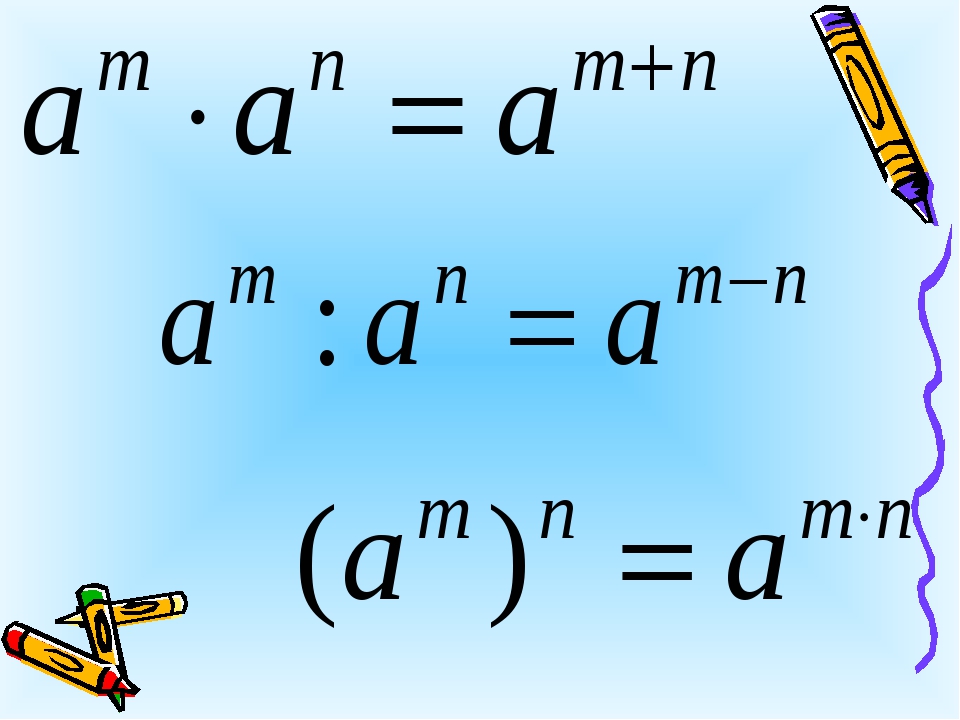
 И жмем ОК.
И жмем ОК. е. 1 / а н )
е. 1 / а н )