2
Содержание
Арксинус. Решение простейших уравнений с синусом. Часть 2
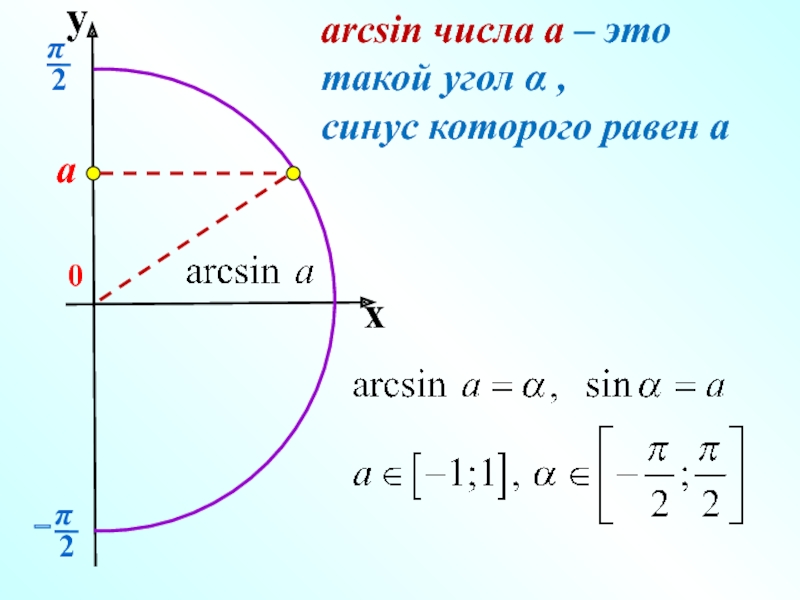
Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т.е.
\(\arcsin a=x\) \(<=>\) \(\sin x=a\)
Примеры:
\(\arcsin{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin \frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)
\(\arcsin 1=\frac{π}{2}\) потому что \(\sin\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)
\(\arcsin 0=0\) потому что \(\sin 0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)
\(\arcsin\sqrt{3}\) – не определен, потому что \(\sqrt{3}>1\)
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:
Как вычислить арксинус?
Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?
Например, вычислите значение арксинуса:
а) \(\arcsin(-\frac{1}{2})\)
б) \(\arcsin(\frac{\sqrt{3}}{2})\)
в) \(\arcsin(-1)\)
а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\).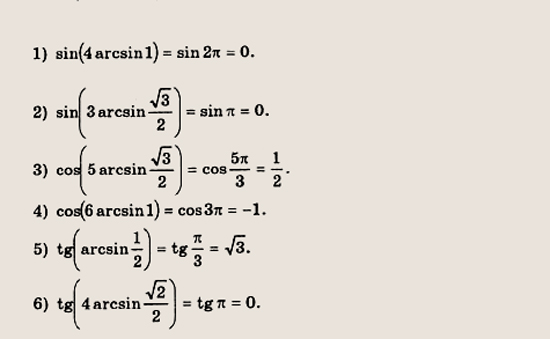 Ответ очевиден:
Ответ очевиден:
\(\arcsin(-\frac{1}{2})=-\frac{π}{6}\)
б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).
\(\arcsin(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)
в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin x=-1\), \(x=\) ?
\(\arcsin(-1)=-\frac{π}{2}\)
Тригонометрический круг со всеми стандартными арксинусами:
Зачем нужен арксинус? Решение уравнения \(\sin x=a\)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin x=\frac{1}{2}\).
Это не вызывает затруднений:
\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)
Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.
А теперь решите уравнение: \(\sin x=\frac{1}{3}\).
Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin\frac{1}{3}\).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right.\) Без арксинусов решить уравнение \(\sin x=\frac{1}{3}\) не получилось бы. Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
Как и уравнение \(\sin x=0,125\), \(\sin x=-\frac{1}{9}\), \(\sin x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:
С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{3}}\).
Решение:
Ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{1}{\sqrt{2}}\).
Решение:
Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:
Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:
\(\arcsin \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)
Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).
Ответ: \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac{7}{6}\).
Решение:
И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right.\) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.
Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.
Ответ: решений нет.
Думаю, вы уловили закономерность.
Если \(\sin x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
\(\arcsin({-a})=-\arcsin a\)
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:
Примеры:
\(\arcsin(-0,7)=-\arcsin 0,7\)
\(\arcsin(-\frac{\sqrt{3}}{2})=-\arcsin\frac{\sqrt{3}}{2}=-\frac{π}{6}\)
\(\arcsin(-\frac{\sqrt{7}}{2}) \neq -\arcsin\frac{\sqrt{7}}{2}\)
Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).
Пример. Решите тригонометрическое уравнение: \(\sin x=-\frac{1}{\sqrt{3}}\).
Решение:
Можно воспользоваться готовой формулой и написать:
\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)
Но я фанатка круга, поэтому:
Ответ: \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)
На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.
Смотрите также:
Синус
Тригонометрические уравнения
| arcsin(0) = 0° | arcsin(0.8660254038) = 120° | arcsin(-0.8660254038) = 240° |
| arcsin(0.01745240644) = 1° | arcsin(0.8571673007) = 121° | arcsin(-0.8746197071) = 241° |
| arcsin(0.0348994967) = 2° | arcsin(0.8480480962) = 122° | arcsin(-0.8829475929) = 242° |
| arcsin(0.05233595624) = 3° | arcsin(0.8386705679) = 123° | arcsin(-0.8910065242) = 243° |
| arcsin(0.06975647374) = 4° | arcsin(0.8290375726) = 124° | arcsin(-0.8987940463) = 244° |
| arcsin(0.08715574275) = 5° | arcsin(0.8191520443) = 125° | arcsin(-0.906307787) = 245° |
| arcsin(0.1045284633) = 6° | arcsin(0.8090169944) = 126° | arcsin(-0.9135454576) = 246° |
| arcsin(0.1218693434) = 7° | arcsin(0.79863551) = 127° | arcsin(-0.9205048535) = 247° |
| arcsin(0.139173101) = 8° | arcsin(0. 7880107536) = 128° 7880107536) = 128° | arcsin(-0.9271838546) = 248° |
| arcsin(0.156434465) = 9° | arcsin(0.7771459615) = 129° | arcsin(-0.9335804265) = 249° |
| arcsin(0.1736481777) = 10° | arcsin(0.7660444431) = 130° | arcsin(-0.9396926208) = 250° |
| arcsin(0.1908089954) = 11° | arcsin(0.7547095802) = 131° | arcsin(-0.9455185756) = 251° |
| arcsin(0.2079116908) = 12° | arcsin(0.7431448255) = 132° | arcsin(-0.9510565163) = 252° |
| arcsin(0.2249510543) = 13° | arcsin(0.7313537016) = 133° | arcsin(-0.956304756) = 253° |
| arcsin(0.2419218956) = 14° | arcsin(0.7193398003) = 134° | arcsin(-0.9612616959) = 254° |
| arcsin(0.2588190451) = 15° | arcsin(0.7071067812) = 135° | arcsin(-0.9659258263) = 255° |
| arcsin(0.2756373558) = 16° | arcsin(0.6946583705) = 136° | arcsin(-0.9702957263) = 256° |
arcsin(0. 2923717047) = 17° 2923717047) = 17° | arcsin(0.6819983601) = 137° | arcsin(-0.9743700648) = 257° |
| arcsin(0.3090169944) = 18° | arcsin(0.6691306064) = 138° | arcsin(-0.9781476007) = 258° |
| arcsin(0.3255681545) = 19° | arcsin(0.656059029) = 139° | arcsin(-0.9816271834) = 259° |
| arcsin(0.3420201433) = 20° | arcsin(0.6427876097) = 140° | arcsin(-0.984807753) = 260° |
| arcsin(0.3583679495) = 21° | arcsin(0.629320391) = 141° | arcsin(-0.9876883406) = 261° |
| arcsin(0.3746065934) = 22° | arcsin(0.6156614753) = 142° | arcsin(-0.9902680687) = 262° |
| arcsin(0.3907311285) = 23° | arcsin(0.6018150232) = 143° | arcsin(-0.9925461516) = 263° |
| arcsin(0.4067366431) = 24° | arcsin(0.5877852523) = 144° | arcsin(-0.9945218954) = 264° |
| arcsin(0.4226182617) = 25° | arcsin(0.5735764364) = 145° | arcsin(-0. 9961946981) = 265° 9961946981) = 265° |
| arcsin(0.4383711468) = 26° | arcsin(0.5591929035) = 146° | arcsin(-0.9975640503) = 266° |
| arcsin(0.4539904997) = 27° | arcsin(0.544639035) = 147° | arcsin(-0.9986295348) = 267° |
| arcsin(0.4694715628) = 28° | arcsin(0.5299192642) = 148° | arcsin(-0.999390827) = 268° |
| arcsin(0.4848096202) = 29° | arcsin(0.5150380749) = 149° | arcsin(-0.9998476952) = 269° |
| arcsin(0.5) = 30° | arcsin(0.5) = 150° | arcsin(-1) = 270° |
| arcsin(0.5150380749) = 31° | arcsin(0.4848096202) = 151° | arcsin(-0.9998476952) = 271° |
| arcsin(0.5299192642) = 32° | arcsin(0.4694715628) = 152° | arcsin(-0.999390827) = 272° |
| arcsin(0.544639035) = 33° | arcsin(0.4539904997) = 153° | arcsin(-0.9986295348) = 273° |
| arcsin(0.5591929035) = 34° | arcsin(0.4383711468) = 154° | arcsin(-0. 9975640503) = 274° 9975640503) = 274° |
| arcsin(0.5735764364) = 35° | arcsin(0.4226182617) = 155° | arcsin(-0.9961946981) = 275° |
| arcsin(0.5877852523) = 36° | arcsin(0.4067366431) = 156° | arcsin(-0.9945218954) = 276° |
| arcsin(0.6018150232) = 37° | arcsin(0.3907311285) = 157° | arcsin(-0.9925461516) = 277° |
| arcsin(0.6156614753) = 38° | arcsin(0.3746065934) = 158° | arcsin(-0.9902680687) = 278° |
| arcsin(0.629320391) = 39° | arcsin(0.3583679495) = 159° | arcsin(-0.9876883406) = 279° |
| arcsin(0.6427876097) = 40° | arcsin(0.3420201433) = 160° | arcsin(-0.984807753) = 280° |
| arcsin(0.656059029) = 41° | arcsin(0.3255681545) = 161° | arcsin(-0.9816271834) = 281° |
| arcsin(0.6691306064) = 42° | arcsin(0.3090169944) = 162° | arcsin(-0.9781476007) = 282° |
| arcsin(0.6819983601) = 43° | arcsin(0. 2923717047) = 163° 2923717047) = 163° | arcsin(-0.9743700648) = 283° |
| arcsin(0.6946583705) = 44° | arcsin(0.2756373558) = 164° | arcsin(-0.9702957263) = 284° |
| arcsin(0.7071067812) = 45° | arcsin(0.2588190451) = 165° | arcsin(-0.9659258263) = 285° |
| arcsin(0.7193398003) = 46° | arcsin(0.2419218956) = 166° | arcsin(-0.9612616959) = 286° |
| arcsin(0.7313537016) = 47° | arcsin(0.2249510543) = 167° | arcsin(-0.956304756) = 287° |
| arcsin(0.7431448255) = 48° | arcsin(0.2079116908) = 168° | arcsin(-0.9510565163) = 288° |
| arcsin(0.7547095802) = 49° | arcsin(0.1908089954) = 169° | arcsin(-0.9455185756) = 289° |
| arcsin(0.7660444431) = 50° | arcsin(0.1736481777) = 170° | arcsin(-0.9396926208) = 290° |
| arcsin(0.7771459615) = 51° | arcsin(0.156434465) = 171° | arcsin(-0.9335804265) = 291° |
arcsin(0. 7880107536) = 52° 7880107536) = 52° | arcsin(0.139173101) = 172° | arcsin(-0.9271838546) = 292° |
| arcsin(0.79863551) = 53° | arcsin(0.1218693434) = 173° | arcsin(-0.9205048535) = 293° |
| arcsin(0.8090169944) = 54° | arcsin(0.1045284633) = 174° | arcsin(-0.9135454576) = 294° |
| arcsin(0.8191520443) = 55° | arcsin(0.08715574275) = 175° | arcsin(-0.906307787) = 295° |
| arcsin(0.8290375726) = 56° | arcsin(0.06975647374) = 176° | arcsin(-0.8987940463) = 296° |
| arcsin(0.8386705679) = 57° | arcsin(0.05233595624) = 177° | arcsin(-0.8910065242) = 297° |
| arcsin(0.8480480962) = 58° | arcsin(0.0348994967) = 178° | arcsin(-0.8829475929) = 298° |
| arcsin(0.8571673007) = 59° | arcsin(0.01745240644) = 179° | arcsin(-0.8746197071) = 299° |
| arcsin(0.8660254038) = 60° | arcsin(0) = 180° | arcsin(-0.8660254038) = 300° |
arcsin(0. 8746197071) = 61° 8746197071) = 61° | arcsin(-0.01745240644) = 181° | arcsin(-0.8571673007) = 301° |
| arcsin(0.8829475929) = 62° | arcsin(-0.0348994967) = 182° | arcsin(-0.8480480962) = 302° |
| arcsin(0.8910065242) = 63° | arcsin(-0.05233595624) = 183° | arcsin(-0.8386705679) = 303° |
| arcsin(0.8987940463) = 64° | arcsin(-0.06975647374) = 184° | arcsin(-0.8290375726) = 304° |
| arcsin(0.906307787) = 65° | arcsin(-0.08715574275) = 185° | arcsin(-0.8191520443) = 305° |
| arcsin(0.9135454576) = 66° | arcsin(-0.1045284633) = 186° | arcsin(-0.8090169944) = 306° |
| arcsin(0.9205048535) = 67° | arcsin(-0.1218693434) = 187° | arcsin(-0.79863551) = 307° |
| arcsin(0.9271838546) = 68° | arcsin(-0.139173101) = 188° | arcsin(-0.7880107536) = 308° |
| arcsin(0.9335804265) = 69° | arcsin(-0.156434465) = 189° | arcsin(-0. 7771459615) = 309° 7771459615) = 309° |
| arcsin(0.9396926208) = 70° | arcsin(-0.1736481777) = 190° | arcsin(-0.7660444431) = 310° |
| arcsin(0.9455185756) = 71° | arcsin(-0.1908089954) = 191° | arcsin(-0.7547095802) = 311° |
| arcsin(0.9510565163) = 72° | arcsin(-0.2079116908) = 192° | arcsin(-0.7431448255) = 312° |
| arcsin(0.956304756) = 73° | arcsin(-0.2249510543) = 193° | arcsin(-0.7313537016) = 313° |
| arcsin(0.9612616959) = 74° | arcsin(-0.2419218956) = 194° | arcsin(-0.7193398003) = 314° |
| arcsin(0.9659258263) = 75° | arcsin(-0.2588190451) = 195° | arcsin(-0.7071067812) = 315° |
| arcsin(0.9702957263) = 76° | arcsin(-0.2756373558) = 196° | arcsin(-0.6946583705) = 316° |
| arcsin(0.9743700648) = 77° | arcsin(-0.2923717047) = 197° | arcsin(-0.6819983601) = 317° |
| arcsin(0.9781476007) = 78° | arcsin(-0. 3090169944) = 198° 3090169944) = 198° | arcsin(-0.6691306064) = 318° |
| arcsin(0.9816271834) = 79° | arcsin(-0.3255681545) = 199° | arcsin(-0.656059029) = 319° |
| arcsin(0.984807753) = 80° | arcsin(-0.3420201433) = 200° | arcsin(-0.6427876097) = 320° |
| arcsin(0.9876883406) = 81° | arcsin(-0.3583679495) = 201° | arcsin(-0.629320391) = 321° |
| arcsin(0.9902680687) = 82° | arcsin(-0.3746065934) = 202° | arcsin(-0.6156614753) = 322° |
| arcsin(0.9925461516) = 83° | arcsin(-0.3907311285) = 203° | arcsin(-0.6018150232) = 323° |
| arcsin(0.9945218954) = 84° | arcsin(-0.4067366431) = 204° | arcsin(-0.5877852523) = 324° |
| arcsin(0.9961946981) = 85° | arcsin(-0.4226182617) = 205° | arcsin(-0.5735764364) = 325° |
| arcsin(0.9975640503) = 86° | arcsin(-0.4383711468) = 206° | arcsin(-0.5591929035) = 326° |
arcsin(0. 9986295348) = 87° 9986295348) = 87° | arcsin(-0.4539904997) = 207° | arcsin(-0.544639035) = 327° |
| arcsin(0.999390827) = 88° | arcsin(-0.4694715628) = 208° | arcsin(-0.5299192642) = 328° |
| arcsin(0.9998476952) = 89° | arcsin(-0.4848096202) = 209° | arcsin(-0.5150380749) = 329° |
| arcsin(1) = 90° | arcsin(-0.5) = 210° | arcsin(-0.5) = 330° |
| arcsin(0.9998476952) = 91° | arcsin(-0.5150380749) = 211° | arcsin(-0.4848096202) = 331° |
| arcsin(0.999390827) = 92° | arcsin(-0.5299192642) = 212° | arcsin(-0.4694715628) = 332° |
| arcsin(0.9986295348) = 93° | arcsin(-0.544639035) = 213° | arcsin(-0.4539904997) = 333° |
| arcsin(0.9975640503) = 94° | arcsin(-0.5591929035) = 214° | arcsin(-0.4383711468) = 334° |
| arcsin(0.9961946981) = 95° | arcsin(-0.5735764364) = 215° | arcsin(-0.4226182617) = 335° |
arcsin(0. 9945218954) = 96° 9945218954) = 96° | arcsin(-0.5877852523) = 216° | arcsin(-0.4067366431) = 336° |
| arcsin(0.9925461516) = 97° | arcsin(-0.6018150232) = 217° | arcsin(-0.3907311285) = 337° |
| arcsin(0.9902680687) = 98° | arcsin(-0.6156614753) = 218° | arcsin(-0.3746065934) = 338° |
| arcsin(0.9876883406) = 99° | arcsin(-0.629320391) = 219° | arcsin(-0.3583679495) = 339° |
| arcsin(0.984807753) = 100° | arcsin(-0.6427876097) = 220° | arcsin(-0.3420201433) = 340° |
| arcsin(0.9816271834) = 101° | arcsin(-0.656059029) = 221° | arcsin(-0.3255681545) = 341° |
| arcsin(0.9781476007) = 102° | arcsin(-0.6691306064) = 222° | arcsin(-0.3090169944) = 342° |
| arcsin(0.9743700648) = 103° | arcsin(-0.6819983601) = 223° | arcsin(-0.2923717047) = 343° |
| arcsin(0.9702957263) = 104° | arcsin(-0.6946583705) = 224° | arcsin(-0. 2756373558) = 344° 2756373558) = 344° |
| arcsin(0.9659258263) = 105° | arcsin(-0.7071067812) = 225° | arcsin(-0.2588190451) = 345° |
| arcsin(0.9612616959) = 106° | arcsin(-0.7193398003) = 226° | arcsin(-0.2419218956) = 346° |
| arcsin(0.956304756) = 107° | arcsin(-0.7313537016) = 227° | arcsin(-0.2249510543) = 347° |
| arcsin(0.9510565163) = 108° | arcsin(-0.7431448255) = 228° | arcsin(-0.2079116908) = 348° |
| arcsin(0.9455185756) = 109° | arcsin(-0.7547095802) = 229° | arcsin(-0.1908089954) = 349° |
| arcsin(0.9396926208) = 110° | arcsin(-0.7660444431) = 230° | arcsin(-0.1736481777) = 350° |
| arcsin(0.9335804265) = 111° | arcsin(-0.7771459615) = 231° | arcsin(-0.156434465) = 351° |
| arcsin(0.9271838546) = 112° | arcsin(-0.7880107536) = 232° | arcsin(-0.139173101) = 352° |
| arcsin(0.9205048535) = 113° | arcsin(-0. 79863551) = 233° 79863551) = 233° | arcsin(-0.1218693434) = 353° |
| arcsin(0.9135454576) = 114° | arcsin(-0.8090169944) = 234° | arcsin(-0.1045284633) = 354° |
| arcsin(0.906307787) = 115° | arcsin(-0.8191520443) = 235° | arcsin(-0.08715574275) = 355° |
| arcsin(0.8987940463) = 116° | arcsin(-0.8290375726) = 236° | arcsin(-0.06975647374) = 356° |
| arcsin(0.8910065242) = 117° | arcsin(-0.8386705679) = 237° | arcsin(-0.05233595624) = 357° |
| arcsin(0.8829475929) = 118° | arcsin(-0.8480480962) = 238° | arcsin(-0.0348994967) = 358° |
| arcsin(0.8746197071) = 119° | arcsin(-0.8571673007) = 239° | arcsin(-0.01745240644) = 359° |
Внеклассный урок — Арксинус
Арксинус
Арксинус в переводе с латинского означает дуга и синус. Это обратная функция.
При этом | a | ≤ 1. Обозначается так: arcsin a. |
Говоря иначе:
arcsin a = t, следовательно sin t = a. Условия: модуль а не больше 1; t в отрезке [-π/2; π/2] (| a | ≤ 1; –π/2 ≤ t ≤ π/2) |
Пример-пояснение:
Найдем arcsin 1/2.
Решение.
Выражение arcsin 1/2 показывает, что синус угла t равен 1/2 (sin t = 1/2).
Далее просто находим точку этого синуса на числовой окружности, что и является ответом:
точка 1/2, находящася на оси у, соответствует точке π/6 на числовой окружности.
Значит, arcsin 1/2 = π/6.
Обратите внимание:
если sin π/6 = 1/2, то arcsin 1/2 = π/6.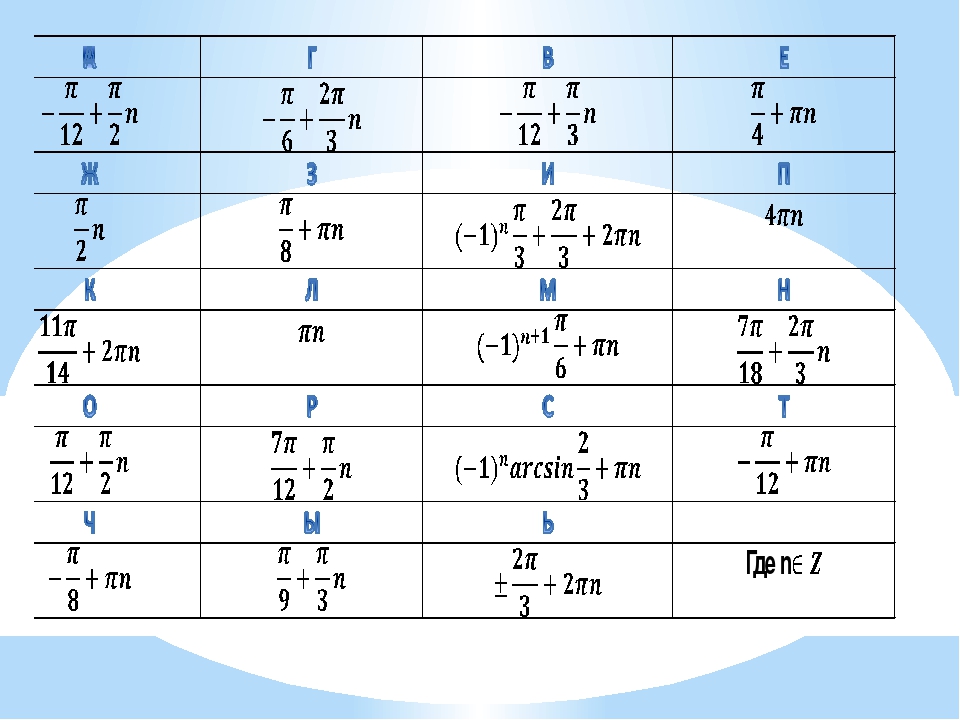
То есть в первом случае по точке на числовой окружности находим значение синуса, а во втором – наоборот, по значению синуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арксинус.
Формулы.
(1)
t = arcsin a + 2πk t = π – arcsin a + 2πk Эти две формулы можно объединить в одну: (k – любое целое число; n – любое целое число; | a | ≤ 1) Значение четного n: Значение нечетного n: Если n – четное число, то получается первая формула. Если n – нечетное число, то получается вторая формула. |
(2)
|
√2
Пример 1: Вычислить arcsin (– ——).
2
Решение.
Решая пример, следуем буквально по таблице над нашим примером.
Итак:
√2
а = – ——.
2
√2
Тогда sin t = – ——, при этом t входит в отрезок [–π/2; π/2]
2
π
Значит t = – —— (входит в отрезок [–π/2; π/2])
4
√2 π
Ответ: arcsin (– ——) = – —
2 4
Акцентируем ваше внимание: синусом числа –π/4 является -√2/2, а арксинусом -√2/2 является –π/4. Движение в обратном порядке. Cинусом числа является точка на оси координат, а арксинусом – точка на числовой окружности.
Движение в обратном порядке. Cинусом числа является точка на оси координат, а арксинусом – точка на числовой окружности.
√3
Пример 2: Вычислить arcsin ——
2
Решение.
√3
Пусть arcsin —— = t.
2
√3
Тогда sin t = ——.
2
Точка t находится в отрезке [–π/2; π/2]. Вычисляем значение t.
√3
Число —— соответствует значению sin π/3, при этом π/3 находится в отрезке [–π/2; π/2].
2
Значит:
t = π/3.
Итог:
√3
arcsin —— = π/3.
2
Пример решен.
Функция ASIN — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ASIN в Microsoft Excel.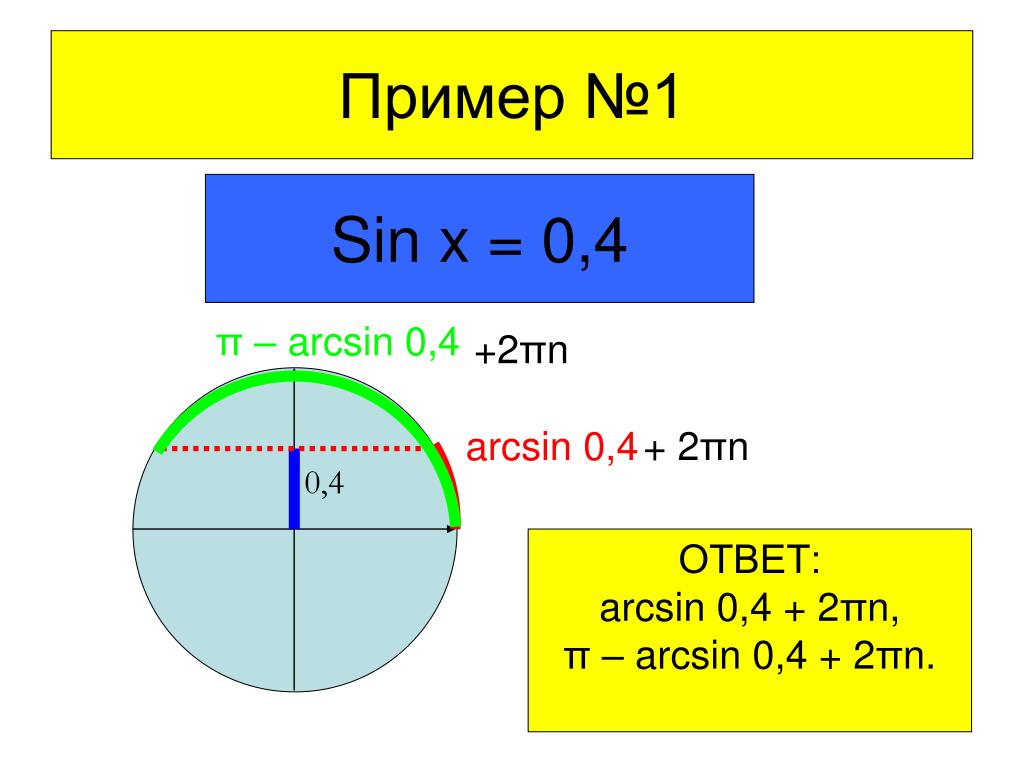
Описание
Возвращает арксинус числа. Арксинус числа — это угол, синус которого равен числу. Угол определяется в радианах в диапазоне от -пи/2 до пи/2.
Синтаксис
ASIN(число)
Аргументы функции ASIN описаны ниже.
Замечания
Чтобы выразить арксинус в градусах, умножьте результат на 180/ПИ( ) или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.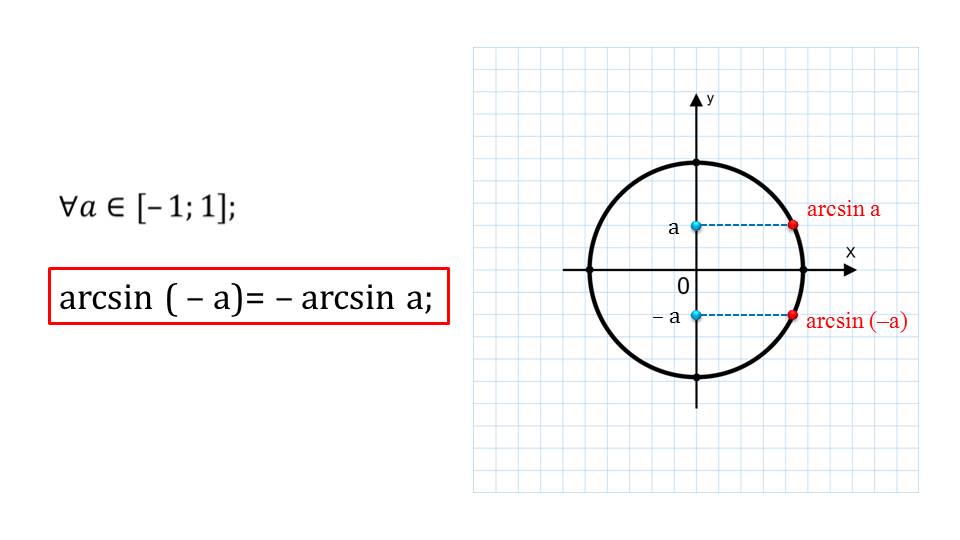 Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
|
|
|---|---|---|
|
=ASIN(-0,5)
|
Арксинус числа -0,5 в радианах, -пи/6 (-0,5236)
|
-0,523598776
|
|
=ASIN(-0,5)*180/ПИ()
|
Арккосинус числа -0,5 в градусах
|
-30
|
|
=ГРАДУСЫ(ASIN(-0,5))
|
Арккосинус числа -0,5 в градусах
|
-30
|
Арксинус, арккосинус — свойства, графики, формулы
Арксинус, arcsin
Определение и обозначения
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений –π/2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См. Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin t. Интегрируем по частям, учитывая что –π/2 ≤ t ≤ π/2, cos t ≥ 0:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| < 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
Арксинус. Решение уравнений вида arcsin t=a | План-конспект урока по алгебре (10 класс) по теме:
Описание методической разработки
Название Разработка урока
Краткая аннотация Урок составлен по технологии проблемно-диалогического обучения с учетом требований, предъявляемых ФГОС. Применяется парно-групповая форма работы, что дает возможности для формирования коммуникативных и личностных УУД. Для подведения итогов урока применен метод «Сезоны года». Этот этап очень важен, поскольку позволяет выяснить не только то, что ребята усвоили хорошо, а также на то, что необходимо обратить внимание на следующем уроке.
Учебный предмет Алгебра
Форма учебной работы Классно — урочная
Тема урока: Арксинус. Решение уравнений вида arcsin t=a (алгебра, 10 класс)
Тип урока: урок повторение
Цель урока: закрепить знание формул при решении уравнений, отрабатывать навыки решение уравнений вида sin t=a, cos t=a.
Методы обучения: словесные, наглядные.
Оборудование: 1. А.Г.Мордкович, Алгебра, 10-11классы, учебник
А.Г.Мордкович, Алгебра, 10-11классы, задачник
2. Проектор, компьютер
3. Компьютерная презентация (5 слайдов) (прилагается к разработке урока).
Ход урока
I. Организационный момент.
Ребята, давайте поздороваемся локтями. Цель: снятие напряжения
Учащиеся из первых парт складывают руки за головой, из второй- руки на талии, из третьей-руки на бедрах так, чтобы локти у всех были разведены в разные стороны. За 1 минуту поздороваться как можно с большим количеством одноклассников.
Цель нашего урока — закрепить знание формул при решении уравнений, отрабатывать навыки решение уравнений вида sin t=a, cos t=a.
II. Актуализация знаний учащихся (повторение теоретического материала):
- Устный опрос
-Дайте определение арккосинуса
-Запишите формулу корней уравнения cos t=a.
— Найдите решения уравнений cos t=0, cos t=1, cos t=-1
— Чему равен arccos (-a)?
-Дайте определение арксинуса
— Запишите формулу корней уравнения sin t=a.
— Найдите решения уравнений sin t=0, sin t=1, sin t=-1.
— Чему равен arcsin (-a)?
2. Устный счет Презентация: Слайд 4
А) Вычислить: arccos (), arccos (-), arccos (), arccos (),
arccos 1, arccos (-1), arcsin (), arcsin (), arcsin (-arcsin 0, arcsin 1.
Б) Решить уравнения: Презентация: Слайд 5
cos t= — t= +2πn,
cos t= — t= +2πn,
cos t=1 t=2πk
III. Решение примеров
№ 313 (а,б)
а) sin t= t= (-1)n arcsin + πn = (-1)n + πn, n-целое число.
б) sin t= t= (-1)n arcsin + πn = (-1)n + πn, n-целое число.
№ 314 (в,г)
в) sin t= t= (-1)n arcsin )+ πn = (-1)n )+ πn= (-1)n+1 + πn, n-целое число.
г) sin t=- t= (-1)n arcsin(- )+ πn = (-1)n+1 + πn, n-целое число.
IV. Физминутка Презентация: Слайд 3
V. Решение примеров
№315(а,б)
а) sin t= t= (-1)n arcsin )+ πn, n-целое число
б) sin t= 1,02 1,02>1 ответ: нет решения
№316 (работа в парах с взаимопроверкой) Презентация: Слайд 6
а) sin (arccos х+ arсcos (-х))= sin (arccos х +π- arccos х)= sin π=0
б) cos (arcsin х+ arcsin (-х))= cos (arcsin х – arcsin х)= cos 0=1
№319
Найдите область допустимых значений выражения:
а) arcsin х, arcsin х =t, тогда sin t=х, х- область значений функции, значит, х принадлежит
б) arcsin (5-2х)
-1 ≤5-2х≤1
-1-5≤ -2х≤1-5
-6 ≤-2х≤-4 :(-2)
2 ≤ х ≤3
Ответ: х принадлежит
г) arcsin (х2-3)
-1 ≤ х2-3≤1,
-1+3 ≤ х2≤1+3,
2 ≤ х2 ≤4,
√2 ≤ х ≤ 2,
-2 ≤ х ≤ -√2,
Ответ: х принадлежит [√2; 2] υ[-2 ; -√2]
№321 (а) Решите уравнение:
(2cos х+1)(2sin х -√3)=0
Решаем совокупность уравнений:
2cos х+1=0 , cos х =- х= +2πn,
2sin х -√3=0, sin х= х=(-1)n arcsin + πn = (-1)n + πn, n-целое число.
VI. Домашнее задание: № 313(в,г), 314(а,б), 317,321(б,в,г)
VII. Итог урока. Релаксация
Метод «Сезоны года»
Цель: получить обратную связь от учеников, выяснить их содержательное и эмоциональное впечатления от прошедшего урока.
Материал: листочки разных цветов, отражающие времена года: белый – зима, красный — лето, зеленый – весна и желтый – осень.
красный-урок понравился, было интересно, научился многому
зеленый — урок понравился, было любопытно
желтый- урок оставил равнодушным, было скучновато, еще не до конца разобрался
белый- урок не понравился, было скучно, ничего не понял
Проведение: учитель предлагает ученикам оценить свое состояние после урока с помощью ассоциаций, связанных с сезонами года. Каждый обучающийся выбирает один или несколько листочков, отражающий его эмоциональное отношение к уроку и комментируют свой выбор. Заполненные карточки обучающиеся приклеивают на доске. Из получившейся картинки можно узнать об уроке.
Калькулятор арксинуса — вычисляет арксинус (x)
Используйте этот калькулятор арксинуса, чтобы легко вычислить арксинус числа. Онлайн-инструмент для вычисления арксинуса с выводом в градусах или радианах. Поддерживает ввод десятичных чисел (0,5, 6, -1 и т. Д.) И дробей (1/4, 2/3, 4/3, 1/3 и т. Д.).
Функция арксинуса
Арксинус является одной из обратных тригонометрических функций (антитригонометрических функций) и является обратной функцией синуса. Иногда его записывают как sin -1 (x), но этого обозначения следует избегать, так как его можно спутать с обозначением экспоненты (степень, возведенная в степень).Арксинус используется для получения угла из тригонометрического отношения синуса, которое представляет собой отношение между стороной, противоположной углу, и самой длинной стороной треугольника.
Диапазон значений функции от -1 до 1, как и результаты нашего калькулятора arcsin. Диапазон значений угла обычно составляет от -90 ° до 90 °. Существует ряд правил arcsin, например sin (arcsin (x)) = x или arcsinα + arcsinβ = arcsin (α√ (1-β 2 ) + β√ (1-α 2 )) , а также косинус арксинуса: cos (arcsin (x)) = sin (arccos (x)) = √ (1-x 2 ), который может помочь вам в исчислении тригонометрии.
Как вычислить арксинус числа?
Самый простой способ вычислить это с помощью нашего калькулятора arcsin, описанного выше, который будет выводить результаты как в градусах, так и в радианах. Другие способы включают другую заданную информацию, такую как значения других тригонометрических функций для того же угла или других углов в том же треугольнике.
Вот таблица общих значений arcsin:
| x | arcsin (x) (°) | arcsin (x) (рад.) |
|---|---|---|
| -1 | -90 ° | -π / 2 |
| -√3 / 2 | -60 ° | -π / 3 |
| -√2 / 2 | -45 ° | -π / 4 |
| -1/2 | -30 ° | -π / 6 |
| 0 | 0 ° | 0 |
| 1/2 | 30 ° | π / 6 |
| √2 / 2 | 45 ° | π / 4 |
| √3 / 2 | 60 ° | π / 3 |
| 1 | 90 ° | π / 2 |
π — это, конечно, математическая константа, примерно равная 3.14159.
Использование арксинуса для нахождения угла
Для прямоугольного треугольника на рисунке ниже с известной длиной стороны a = 52 и гипотенузы c = 60 можно использовать функцию обратного косинуса arcsin, чтобы найти угол α в точке A.
Сначала вычислите синус α, разделив противоположную сторону на гипотенузу. Это приводит к sin (α) = a / c = 52/60 = 0,8666. Используйте обратную функцию с этим результатом, чтобы вычислить угол α = arcsin (0.8666) = 60 ° (1,05 радиана).
Калькулятор
Arcsin. Нахождение обратной функции синуса.
С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной.И так, чего же ты ждешь?
Что такое арксинус?
Арксинус — это функция, обратная синусоиде. Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале.
Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0.Следовательно, если кто-то хочет вычислить arcsin (0), ответ может быть 0, 2π (360 °) или -π (-180 °), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением .
| Сокращение | Определение | Домен arcsin x для реального результата | Диапазон обычных основных значений |
|---|---|---|---|
| arcsin (x) sin -1 x, asin | х = грех (у) | -1 ≤ х ≤ 1 | -π / 2 ≤ y ≤ π / 2 -90 ° ≤ y ≤ 90 ° |
Arcsin (x) — наиболее распространенное обозначение, так как sin -1 x может привести к путанице (потому что sin -1 x ≠ 1 / sin (x)).Аббревиатура asin обычно используется в языках программирования.
График arcsin x
Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса:
| x | арксин (х) | График | |
|---|---|---|---|
| ° | рад | ||
| -1 | -90 ° | -π / 2 | Компьютерщик 3, CC BY-SA 4.0 через Wikimedia Commons |
| -√3 / 2 | -60 ° | -π / 3 | |
| -√2 / 2 | -45 ° | -π / 4 | |
| -1/2 | -30 ° | -π / 6 | |
| 0 | 0 ° | 0 | |
| 1/2 | 30 ° | π / 6 | |
| √2 / 2 | 45 ° | π / 4 | |
| √3 / 2 | 60 ° | π / 3 | |
| 1 | 90 ° | π / 2 | |
Хотите знать, откуда взялся этот график arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x:
Jaro.p CC BY-SA 3.0, через Wikimedia Commons
Обратный синус, тригонометрические функции и другие отношения
Связь между тригонометрическими функциями и арксинусом может помочь вам еще лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка.
Напоминаем: для прямоугольного треугольника функция синуса берет угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, принимает отношение противоположности / гипотенузы (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что:
- Синус:
sin (arcsin (x)) = x - Косинус:
cos (arcsin (x)) = √ (1-x²) - Касательная:
tan (arcsin (x)) = x / √ (1-x²)
Другие полезные отношения с арксинусом:
-
arcsin (x) = π / 2 - arccos (x) -
arcsin (-x) = -arcsin (x)
Иногда также нужны интеграл и производная от arcsin:
интеграл от arcsin:
arcsin (x) dx = x arcsin (x) + √ (1 - x²) + Cпроизводная от arcsin:
d / dx arcsin (x) = 1 / √ (1 - x²)где x ≠ -1, 1
Пример использования калькулятора arcsin
Арксинус — полезная функция e.грамм. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус:
- для α:
sin (α) = a / c, поэтому α = arcsin (a / c) - для β:
sin (β) = b / c, поэтому β = arcsin (b / c)
Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:
- Введите значение, по которому вы хотите найти арксинус .В нашем случае это 6/10. Таким образом, вы можете ввести значение 0,6, но форма 6/10 также будет работать. Просто помните, что значение должно быть между -1 и 1.
- И … все! Калькулятор arcsin выполнил свою работу, и вы нашли арксинус своего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °
Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника.
Калькулятор — arcsin (0) — Solumaths
Описание:
Функция arcsin позволяет вычислять арксинус числа.
Функция арксинуса является обратной функцией функции синуса.
arcsin онлайн
Описание:
Функция arcsine является обратной функцией
синусоидальная функция,
это позволяет вычислить арксинус числа онлайн .
Число, к которому вы хотите применить функцию арксинуса, должно принадлежать диапазону [-1,1].
- Расчет арксинуса
Чтобы вычислить арксинус числа, просто введите число и примените
функция arcsin . Таким образом, для при вычислении
арксинус числа, следующего за 0,4, необходимо ввести
arcsin (`0,4`)
или напрямую 0.2) `.
Функция arcsin позволяет вычислять арксинус числа. 2)`
Первообразная арксинус:
Калькулятор первообразной функции арксинуса.2) `
Предел арксинуса:
Калькулятор пределов позволяет вычислять пределы функции арксинуса.
Предел для arcsin (x) — limit_calculator (`» arcsin «(x)`)
Арксинус обратной функции:
Функция , обратная арксинусу , является синусоидальной функцией, отмеченной как sin.
Графическая арксинус:
Графический калькулятор может строить функцию арксинуса в интервале ее определения.
Свойство функции arcsine:
Функция арксинуса — нечетная функция.
Расчет онлайн с помощью arcsin (арксинус)
Функция тригонометрии arcsin () — обратный синус — определение математического слова
Функция тригонометрии arcsin () — обратный синус — определение математического слова — Math Open Reference
Функция arcsin — это функция, обратная синусоиде.
Возвращает угол, синус которого является заданным числом.
Попробуй это
Перетащите любой
вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arcsin ().
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.
Эти обратные функции имеют то же имя, но с дугой впереди.
(На некоторых калькуляторах кнопка arcsin может быть помечена как asin, а иногда
sin -1 .)
Итак, обратное к греху — это arcsin и т. Д. Когда мы видим «arcsin A», мы понимаем его как «угол, грех которого равен A».
| sin30 = 0.5 | Означает: синус 30 градусов равен 0,5 |
| arcsin 0,5 = 30 | Означает: Угол, грех которого равен 0,5, равен 30 градусам. |
Используйте arcsin, если вы знаете синус угла и хотите узнать фактический угол.
См. Также Обратные функции — тригонометрия
Пример — использование arcsin для нахождения угла
На рисунке выше нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что
поэтому нам нужно знать угол, грех которого равен 0.5, или формально:
Используя калькулятор, чтобы найти arcsin 0,5, мы находим, что это 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить
триггерные функции на любой угол, включая большие и отрицательные углы. Но когда мы
Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, которые имеют один и тот же синус.
Например, 45 ° и 360 + 45 ° будут иметь одинаковый синус. Подробнее об этом см.
Обратные тригонометрические функции.
Чтобы решить эту проблему,
диапазон
обратных триггерных функций ограничены
таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и область значений arcsin
Напомним, что область определения функции — это набор допустимых входных данных для нее. Диапазон — это набор возможных выходов.
Для y = arcsin x:
По соглашению диапазон arcsin ограничен от -90 ° до + 90 °.
Итак, если вы используете калькулятор для решения, скажем, arcsin 0,55, из бесконечного числа возможностей он вернет 33,36 °,
тот, который находится в диапазоне функции.
Что попробовать
- На рисунке выше нажмите «сбросить» и «скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arcsin, вычислите значение угла C из длин сторон
- Нажмите «показать подробности», чтобы проверить ответ. 2
Arcsin
Arcsine, записанный как arcsin или sin -1 (не путать с), является функцией обратного синуса.Синус имеет инверсию только в ограниченной области ≤x≤. На рисунке ниже часть графика, выделенная красным, показывает часть графика sin (x), которая имеет инверсию.
Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза. Поскольку синус является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике ее обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через линию y = x.
График y = arcsin (x) показан ниже.
Как видно из рисунка, y = arcsin (x) является отражением sin (x) в ограниченной области ≤x≤ через линию y = x. Область arcsin (x), -1≤x≤1, является диапазоном sin (x), а ее диапазон, ≤y≤, является областью sin (x).
Калькулятор арксинуса
Ниже приведен калькулятор, позволяющий определить значение arccos числа от -1 до 1 или значение косинуса угла.
Использование специальных углов для поиска arcsin
Хотя мы можем найти значение арксинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения синуса и арксинуса которых, возможно, стоит запомнить.Ниже приведена таблица, показывающая эти углы (θ) как в радианах, так и в градусах, и их соответствующие значения синуса sin (θ).
Один из методов, который может помочь запомнить эти значения, — это выразить все значения sin (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° до 90 °, sin (0 °) = 0 =. Последующие значения sin (30 °), sin (45 °), sin (60 °) и sin (90 °) следуют шаблону, так что использование значения sin (0 °) в качестве эталона для нахождения значений синуса для последующих углов, мы просто увеличиваем число под знаком корня в числителе на 1, как показано ниже.
Значения синуса от 0 ° до -90 ° соответствуют той же схеме, за исключением того, что значения являются отрицательными, а не положительными, поскольку синус отрицателен в квадранте IV. Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем идентифицировать значения sin (θ) на основе положения θ в единичном круге, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный. в квадрантах III и IV.
После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения синуса или арксинуса для особых углов.
Обратные свойства
Как правило, функции и их обратные показывают взаимосвязь
f (f -1 (x)) = x и f -1 (f (x)) = x
при условии, что x находится в области определения функции. То же самое верно для sin (x) и arcsin (x) в их соответствующих ограниченных областях:
sin (arcsin (x)) = x, для всех x в [-1, 1]
и
arcsin (sin (x)) = x для всех x в [,]
Эти свойства позволяют нам оценивать состав тригонометрических функций.
Состав арксинуса и синуса
Если x находится в пределах домена, вычислить комбинацию арксинуса и синуса относительно просто.
Состав других тригонометрических функций
Мы также можем составлять композиции, используя все другие тригонометрические функции: косинус, тангенс, косеканс, секанс и котангенс.
Пример:
Найдите cos (arcsin ()).
Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции.Учитывая arcsin () = θ, мы можем найти, что sin (θ) =. Правый треугольник ниже показывает θ и отношение его противоположной стороны к гипотенузе треугольника.
Чтобы найти косинус, нам нужно найти смежную сторону, так как cos (θ) =. Пусть b — длина соседней стороны. Используя теорему Пифагора,
3 2 + b 2 = 5 2
9 + b 2 = 25
б 2 = 16
б = 4
Мы знаем, что arcsin () = θ, поэтому мы можем переписать задачу и найти cos (θ), используя построенный выше треугольник и тот факт, что cos (θ) =:
cos (arcsin ()) = cos (θ) =
Тот же процесс можно использовать с выражением переменной.
Пример:
Найдите загар (arcsin (2x)).
Учитывая arcsin (2x) = θ, мы можем найти, что sin (θ) =, и построить следующий треугольник:
Чтобы найти касательную, нам нужно найти смежную сторону, так как tan (θ) =. Пусть b — длина соседней стороны. Используя теорему Пифагора,
(2x) 2 + b 2 = 1 2
4x 2 + b 2 = 1
b 2 = 1 — 4x 2
б =
и
tan (arcsin (2x)) = tan (θ) =, где
Использование арксинуса для решения тригонометрических уравнений
Арксинус также может использоваться для решения тригонометрических уравнений, включающих синусоидальную функцию.
Примеры:
Решите следующие тригонометрические уравнения относительно x, где 0≤x <2π.
1. 2sin (x) =
2sin (x) =
грех (х) =
Синус положительный в двух квадрантах, квадранте I и квадранте II, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x.
2. 2sin 2 (x) + 5sin (x) — 3 = 0
2sin 2 (x) + 5sin (x) — 3 = 0
(2sin (x) — 1) (sin (x) + 3) = 0
2sin (x) — 1 = 0 или sin (x) + 3 = 0
sin (x) = или sin (x) = -3
x = arcsin () или x = arcsin (-3)
Решение для x = arcsin (),
x = или
Мы не можем найти x = arcsin (-3), потому что оно не определено, поэтому x = или являются единственными решениями.
Арксин из 1 | Justfreetools
Арксинус — это функция, обратная синусу.
Арксинус 1 равен функции обратного синуса 1, которая равна
равно π / 2 радиан или 90 градусов:В настоящее время у нас есть около 940 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
На этой странице вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитов и калькуляторы лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и инструментах (как писать смайлы в Интернете и т. Д.)
В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом.
Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Это наиболее часто используемые пользователями по всему миру.
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите даже малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
.

 Найти угол зная синус этого угла.
Найти угол зная синус этого угла.