Содержание
Урок 6. обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
- Рассмотреть свойства арксинуса и арккосинуса;
- Рассмотреть свойства арктангенса и арккотангенса;
- Объяснять расположение промежутков монотонности;
- Определять наибольшее и наименьшее значение функции;
- Применять знания при решении задач.
Глоссарий по теме
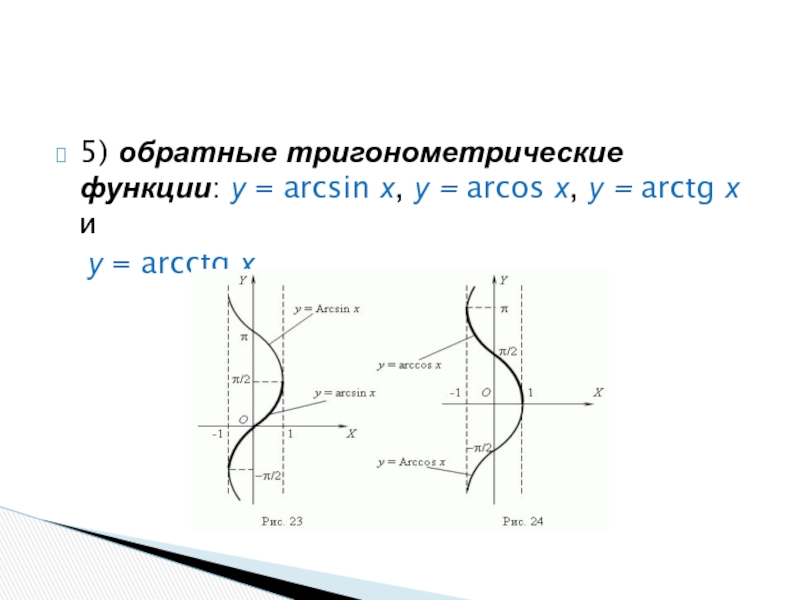
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
Он имеет область определения и множество значений .
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Объяснение нового материала
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Свойства | Функции y=arcsin х |
E(f) | |
D(f) | |
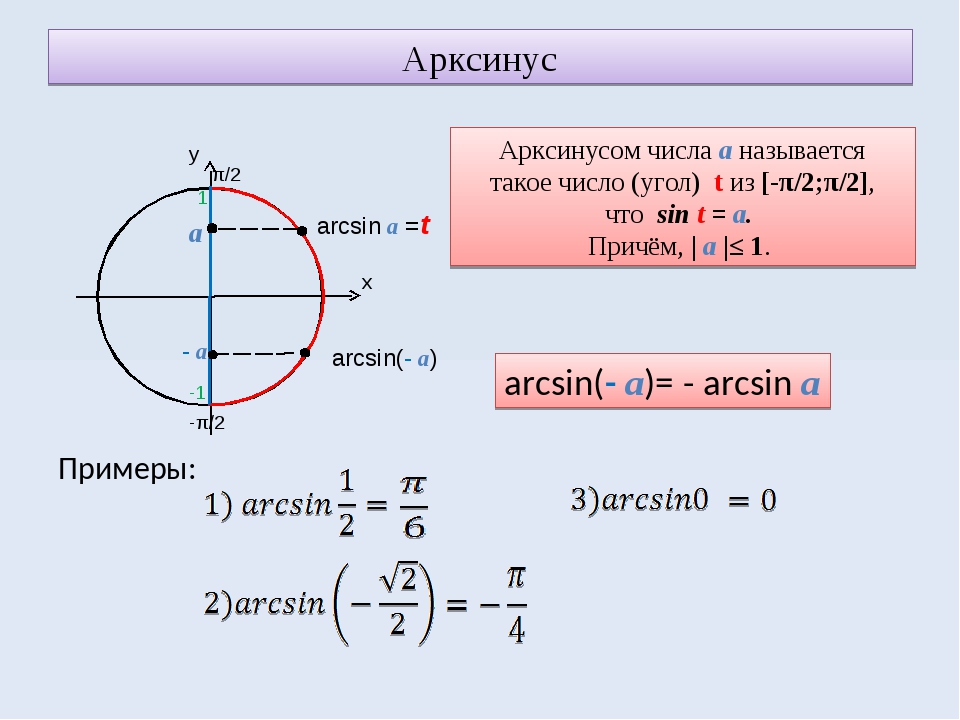
Чётность | Нечётная, т.к. arcsin(-x)= — arcsin x |
Промежутки монотонности | Возрастающая |
Рис. 1 График функции y=arcsin х
1 График функции y=arcsin х
Рассмотрим свойства функции y=arcos x и построим ее график.
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ).
Свойства | Функции y=arccos х |
E(f) | |
D(f) |
|
Чётность | Ни чётная, ни нечётная |
Промежутки монотонности | Убывающая |
Рис.2 График функции y=arccos х
Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ).
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ).
Свойства | y=arctg х | y=arcctg х |
E(f) | R | R |
D(f) | ||
Чётность | Нечётная | Нечётная |
Промежутки монотонности | Возрастающая | Убывающая |
Рис. 3 График функции y=arctgx
3 График функции y=arctgx
Рис.4 График функции y=arcсtgx
Примеры и разборы решения заданий тренировочного модуля:
Пример 1.
Найдите значение выражения
Обозначим , по определения арктангенса получаем х=60°, т.е. нам нужно найти
Ответ:
Пример 2.
Решите неравенство
;
;
;
;
Накладываем ограничения по свойствам арксинуса:
;
Ответ:
2.4.3. Обратные тригонометрические функции
Глава 2. Алгебраические выражения
2.4.
2.4.3.
Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам
и
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента
существует единственный элемент
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу соответствует единственный элемент
и наоборот, каждому элементу
соответствует единственный элемент Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается
и каждому элементу
ставит в соответствие такой элемент
что f (x) = y; этот факт записывают так:
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов.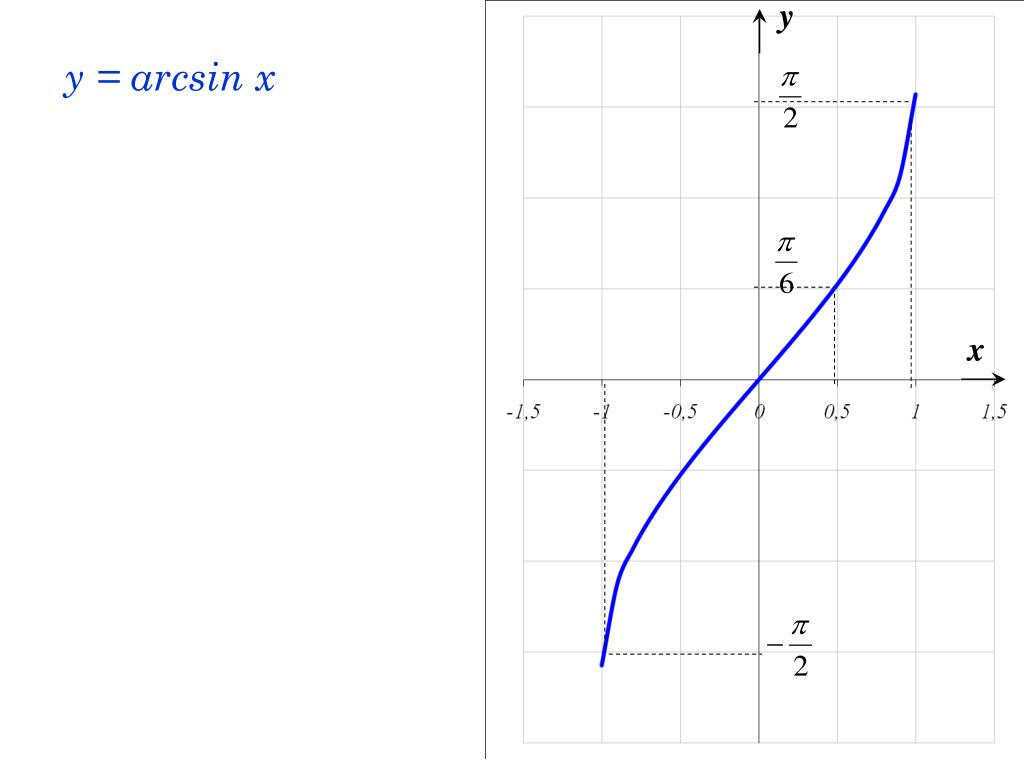 Область определения обратной функции совпадает с областью значений самой функции:
Область определения обратной функции совпадает с областью значений самой функции:
Область значений обратной функции совпадает с множеством определения самой функции:
Рассмотрим функцию f (x) = sin x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
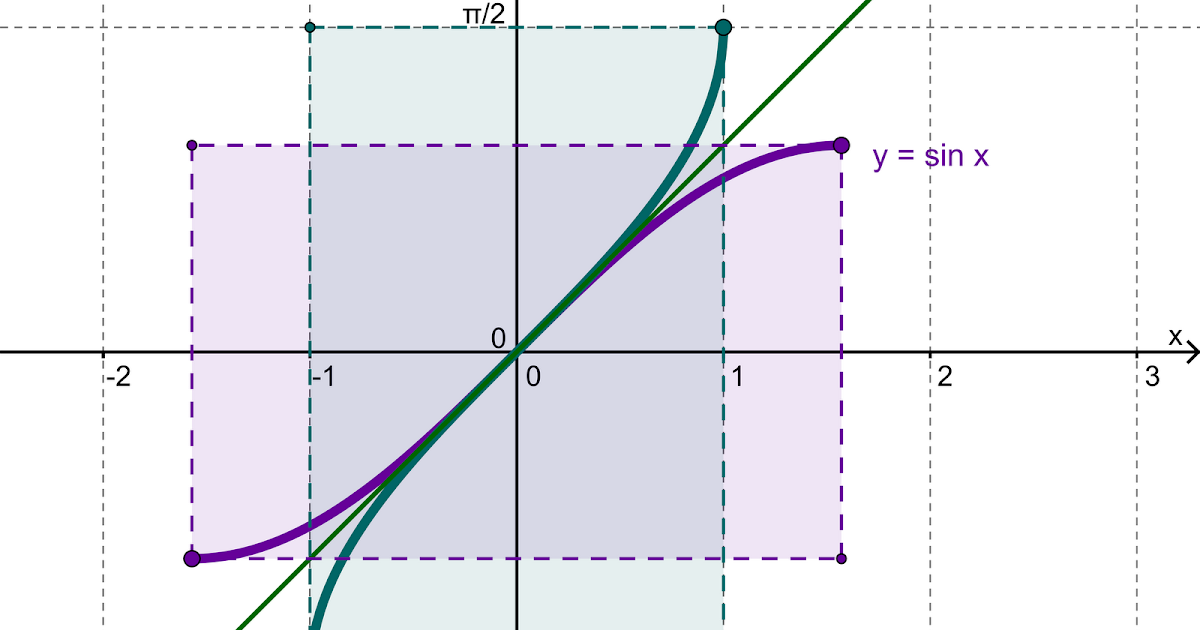
Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
|
1 |
| Рисунок 2.4.3.1. Арксинус |
|
Модель 2.11.
|
Аналогично, на промежутке D (f–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) = [0; π]
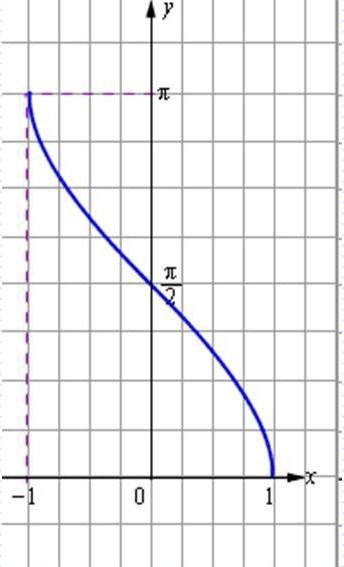
Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
|
2 |
| Рисунок 2.4.3.2. Арккосинус |
|
Модель 2.12.
|
Рассмотрим функцию f (x) = tg x для
Тогда
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
и областью значений
Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
|
3 |
| Рисунок 2.4.3.3. Арктангенс |
|
Модель 2.
|
Для построения арккотангенса выберем промежуток x (0; π). Тогда
Построим обратную функцию с областью определения
и областью значений
Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
|
4 |
| Рисунок 2.4.3.4. Арккотангенс |
|
Модель 2.14.
|
Итак, запись b = arcsin a обозначает, что
и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
Пример 1
Докажите тождество
Пример 2
Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).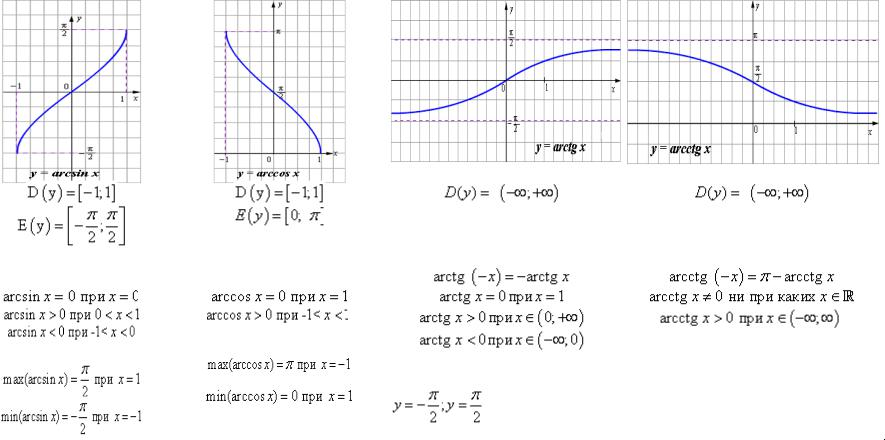
|
Обозначим через y переменную, для которой выполняется равенство:
Здесь поставлен знак «+», поскольку y − угол первой или четвёртой четверти, в которых косинус положителен. Равенство sin (arcsin x) = x справедливо по определению функции арксинус. Значит, Вычислим sin (arccos x) = sin z, где
Здесь поставлен знак плюс, поскольку z − угол первой или второй четверти, в которых синус положителен. Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда Итак,
Ответ.
|
Обратные тригонометрические функции
Определение обратных тригонометрических функций
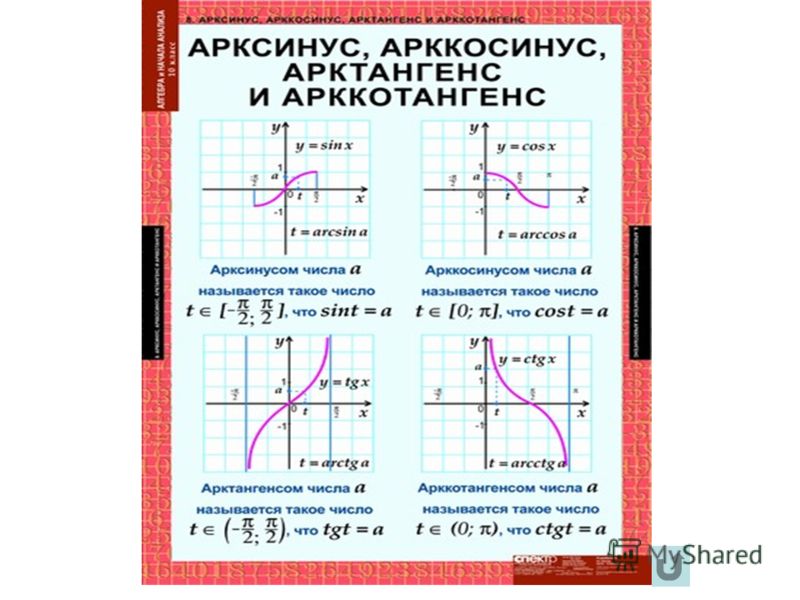
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x. Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.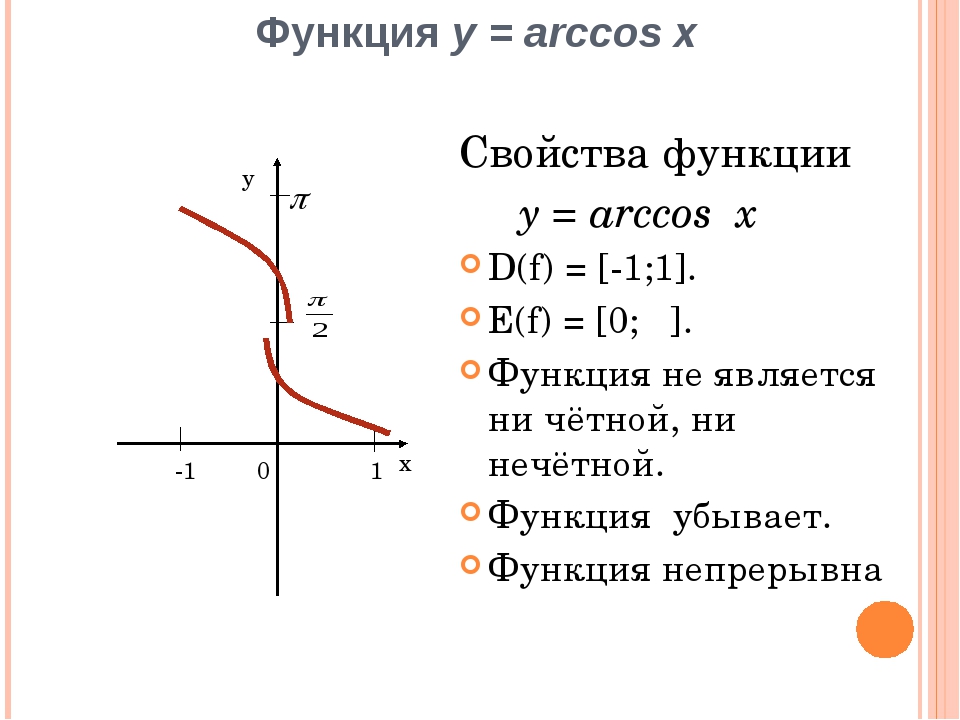
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
- Арксинус ( y = arcsin x )
- – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .
- Арккосинус ( y = arccos x )
- – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
- Арктангенс ( y = arctg x )
- – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
- Арккотангенс ( y = arcctg x )
- – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x. См. разделы Синус, косинус, Тангенс, котангенс.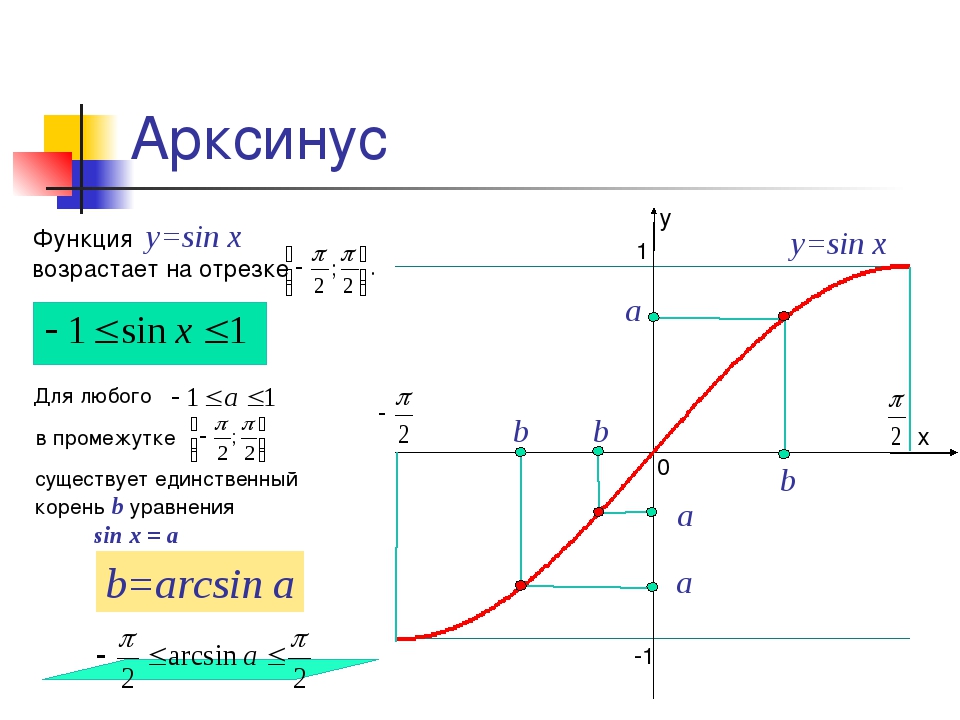
y = arcsin x
y = arccos x
y = arctg x
y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x
arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x
Формулы, связывающие обратные тригонометрические функции
См. Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.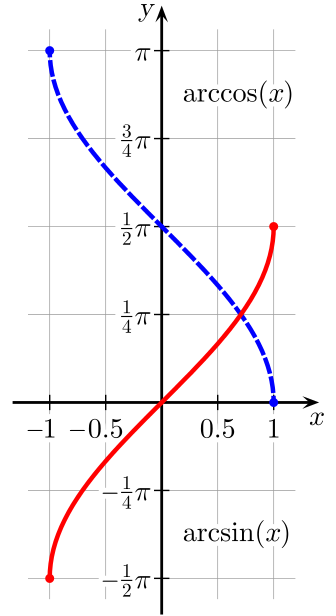 Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано:
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
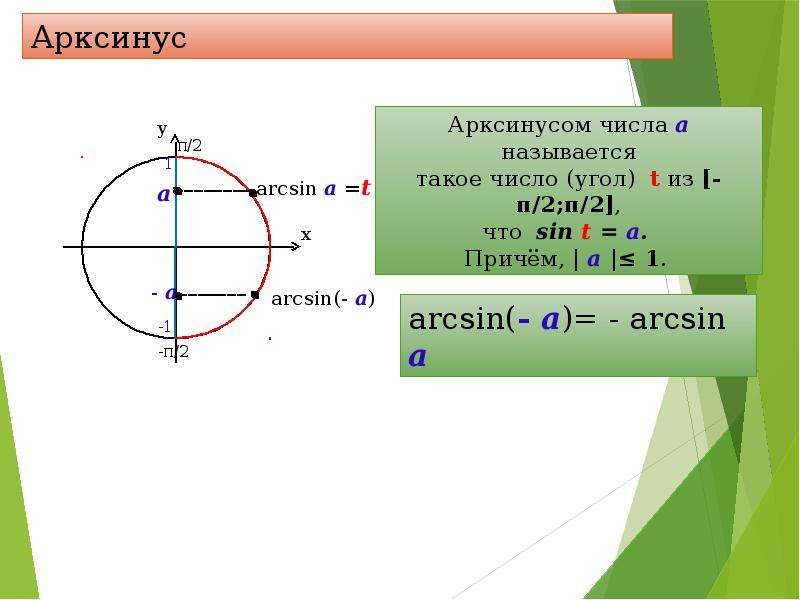
Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Помните, мы уже встречались с обратными функциями.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
При этом
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Это арксинус.
Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка , синус которого равен . Да, это
Да, это
Строим график функции
Свойства функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при
5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.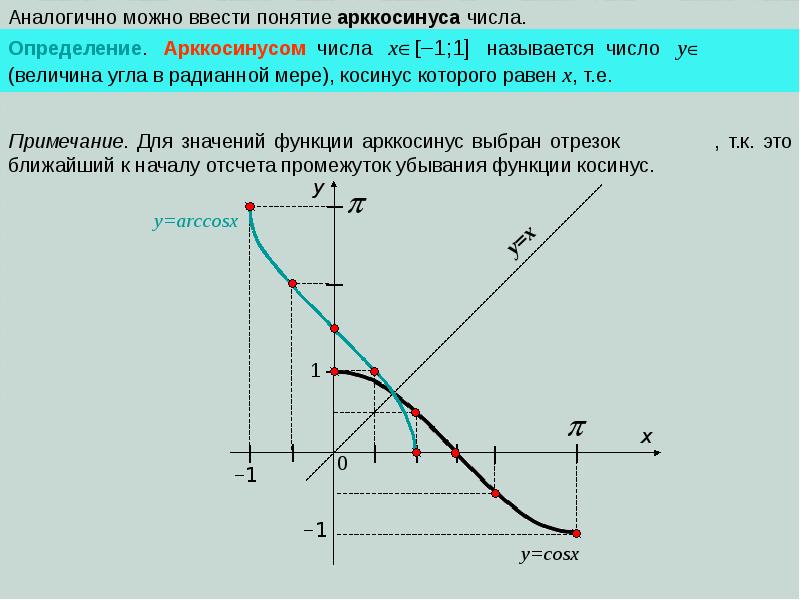
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что
Значит, , поскольку ;
, так как ;
, так как ,
, так как ,
Вот график арккосинуса:
Свойства функции
1. Область определения
2. Область значений
3.
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .
Область определения арктангенса — промежуток Область значений — интервал .
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
, значит,
, значит,
, значит,
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
Свойства функции
1. Область определения
Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
График функции :
Свойства функции
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Урок_Обратные тригонометрические функции арксинус и арккосинус
Министерство образования Московской области
Государственное бюджетное профессиональное образовательное учреждение
Московской области
«Павлово-Посадский техникум»
Тема урока:
Обратные тригонометрические функции арксинус и арккосинус.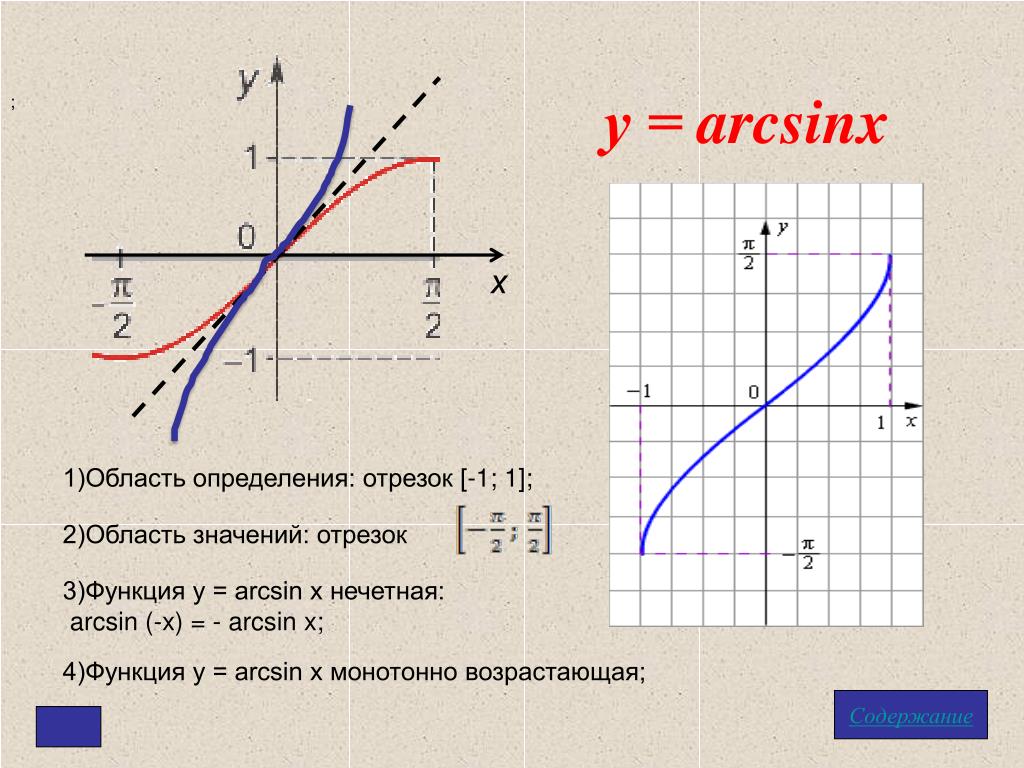
(Методическая разработка открытого урока
с использованием электронного обучения)
Разработал:
преподаватель математики
Стрелкин Д.А.
Дата проведения: 18.10.2017 г.
Наименование ЭОР
Система электронного обучения:
система опроса FLOW
Рассмотрено
на заседании цикловой методической комиссии
общих естественнонаучных и математических
дисциплин
Протокол №____ от «___»__________ 20____г.
Председатель ЦМК __________ Позднякова Г.Е
г. Павловский Посад,
2017-2018 учебный год
Пояснительная записка:
Тема “Обратные тригонометрические функции” является сложной для восприятия и осмысления студентов первого курса.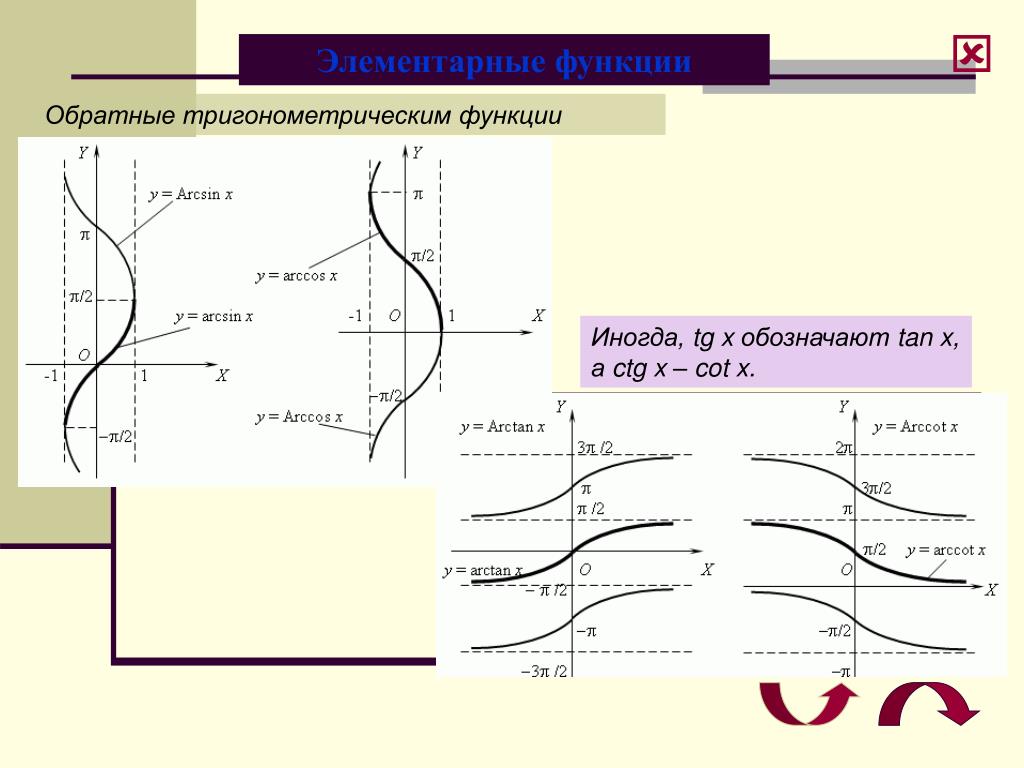 Поэтому очень важно последовательно и наглядно формировать понятие обратных тригонометрических функций и вырабатывать устойчивый навык их применения.
Поэтому очень важно последовательно и наглядно формировать понятие обратных тригонометрических функций и вырабатывать устойчивый навык их применения.
Успех освоения данной темы зависит от знания основных определений и свойств тригонометрических функций, умения находить значения тригонометрических функций на окружности и выполнять построения графиков.
Особое внимание нужно уделить связи обратных тригонометрических функций с исходными, их графику, умению пользоваться окружностью для поиска значений обратных тригонометрических функций, а так же восприятию новых формул.
Первичное представление об обратных тригонометрических функциях предпочтительно вводить, используя их связь с исходными тригонометрических функций, а так же использовать модель числовой окружности для нахождения значений обратных тригонометрических функций.
Остановлюсь на основных этапах рассуждения при знакомстве с обратными тригонометрическими функциями.
Понятие обратной функции для тригонометрических функций основывается на понятии обратных функций из школьного курса.
Для функции синуса обратные функции существуют на множестве числовых отрезков, но для удобства мы выбираем отрезок . Функция, обратная к синусу, называется арксинус и записывается y=arсsin(x).
У обратной функции есть свой график, необходимо его построить и записать свойства обратной функции.
Значения обратных тригонометрических функций удобно искать по числовой окружности.
Рассуждения при введении арккосинуса, арктангенса и арккотангенса аналогичны.
Конспект урока по теме: “Обратные тригонометрические функции арксинус и арккосинус”.
Задача урока – познакомиться с функциям арксинуса и арккосинуса, научиться находить их значения.
Цели урока:
закрепление знаний тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;
закрепление навыка построения графиков функций и описания свойств функцийй;
освоение приёмов нахождения значений обратных тригонометрических функций;
развитие логического мышления, смысловой памяти, навыков самостоятельной работы, самопроверки;
воспитание аккуратности и чёткости в оформлении решения, интереса к предмету, уважения к одногрупникам.

формирование учебно-познавательных, информационных, коммуникативных компетенций.
Оборудование: экран, проектор, система опроса Флоу, раздаточные карточки с готовыми чертежами тригонометрических кругов, карточки с домашним заданием.
Форма организации обучения – урок. Методы обучения, используемые на уроке – словесные, наглядные, репродуктивные, проблемно-поисковые, индивидуального и фронтального опроса, устного и письменного самоконтроля, самостоятельной работы.
Вспомним понятие обратной функции.
Функция f (с областью определения X и областью значений Y) называется обратимой на некотором промежутке, если каждому значению х на этом промежутке соответствует единственное значение у, и наоборот каждому у соответствует единственное значение х.
а) если g – функция, обратная к функции f, то и функция f – обратная к функции g; области определения и области значений взаимно обратных функций f и g взаимно обратны, т. е. область определения функции g совпадает с областью значений функции f и наоборот;
е. область определения функции g совпадает с областью значений функции f и наоборот;
б) графики функций y = f(x) и y = g(x) симметричны относительно прямой y = x;
в) функция, обратная нечетной функции, тоже нечетна;
г) любая монотонная функция обратима, причем функция, обратная к возрастающей (убывающей), – возрастающая (убывающая).
Новый материал.
Функция арксинус.
На доске презентация, слайд 1.
Функция монотонна на каждом из следующих отрезков: ,, и т.д. и принимает на них все значения от -1 до 1. Значит на каждом из указанных промежутков функция имеет обратную. Обычно обратную функцию рассматривают на промежутке , это связано с удобством построения её графика и поиска значений по числовой окружности.
Обозначают обратную функцию (читается «арксинус икс»).
Определение. Если синус которого равен .
Для чего же нужна обратная функция и как она работает?
Давайте вспомним, как работает сама функция . Мы подставляем вместо угол в радианах, функция синуса выдает нам число, которое соответствует этому углу. Например . Обратная функция работает наоборот. Мы ей даем число, а получаем – угол.
Пример.
Если
Если
Если
То есть, вычисляя , мы ищем такой угол из отрезка , синус которого равен .
Чтобы найти , задаем себе вопрос: синус какого угла из отрезка равен ?
Очень просто находить значения арксинуса по числовой окружности.
(Объяснение тех же примеров по презентации на экране )
Ученики срисовывают себе числовую окружность и слушают пояснения учителя.
Чтобы лучше усвоить материал, выполните задание: (пять минут на работу самостоятельно, далее разбор с учителем, желающих сдать решенные задания оценить и поставить отметку в журнал)
Задание 1. Вычислите:
Вычислите:
Дать возможность учащимся самим объяснить свое решение. Особое внимание уделить проговариванию правила «Чтобы найти , задаем себе вопрос: синус какого угла из отрезка равен ».
ОТВЕТЫ И ОБЪЯСНЕНИЯ
т.к.
т.к.
т.к.
, т.к.
, т.к.
не существует, т.к. не существует угла, синус которого равен 2.
Теперь перейдем к построению графика функции . Слева нарисуйте график в пределах , справа постарайтесь нарисовать график обратной функции. (можно оценить первых трех человек, кто самостоятельно и правильно нарисовал график)
По окончанию 5 минут, ученикам показывается правильный вариант графика на презентации, делаются необходимые пояснения, они срисовывают его в тетрадь.
Давайте опишем свойства этой функции:
()свойства.
Функция арккосинус.
А теперь давайте перейдем к графику косинуса (на экране).
Как вы думаете, какой промежуток удобнее всего выбрать для обратной функции косинуса? Промежуток .
Определение. Если косинус которого равен .
Пример.
На экране числовая окружность, студенты перерисовывают ее в тетрадь и слушают пояснения учителя.
Чтобы найти , задаем себе вопрос: косинус какого угла из отрезка равен ?
Попробуйте самостоятельно выполнить задание, использую числовую окружность и определение арккосинуса (по желанию можно взять несколько тетрадей на проверку).
Задание 2. Найдите значение выражения.
ОТВЕТЫ.
т.к.
т.к.
т.к.
не существует
т.
 к.
к.т.к.
т.к.
График функции арккосинус и его свойства.
Ученики срисовывают график с презентации и записывают его свойства.
Домашнее задание.
Выучить определение арксинуса и арккосинуса, выучить правила нахождения значений арксинуса и арккосинуса.
№1.
Подведение итогов, рефлексия.
–Что такое арксинус и арккосинус?
-По какому правилу их можно найти?
– Что вызвало наибольшее затруднение на уроке?
(Оцениваю работу студентов на уроке).
Онлайн вычисление обратных тригонометрических функций
Калькулятор онлайн расчитывает обратные тригонометрические функции дугу (число) по заданному значению ее тригонометрической функции: арксинус (arcsin) возвращает угол по значению его синуса; арккосинус (arccos) возвращает угол по значению его косинуса; арктангенс (arctg) возвращает угол по значению его тангенса.
В разделе I. Для справки приведены графики обратных тригонометрических функций.
Помощь на развитие проекта premierdevelopment.ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Для справки:
Арксинус числа a, обозначается arcsin(a) — значение угла x в интервале [−π/2, π/2], при котором sin(x) = a.
Обратная функция y = arcsin (x) определена при x ∈ [−1, 1], область значений арксинуса равна y ∈ [−π/2, π/2].
График функции арксинуса
Арккосинус числа a, обозначается arccos(a) — значение угла x в интервале [0, π], при котором cos(x) = a.
Обратная функция y = arccos (x) определена при x ∈ [−1, 1], область значений арккосинуса равна y ∈ [0, π].
График функции арккосинуса
Арктангенс числа a, обозначается arctan(a) — значение угла x в интервале [−π/2, π/2], при котором tan(x) = a.
Обратная функция y = arctan (x) определена при x ∈ R, область ее значений равна y ∈ [−π/2, π/2].
График функции арктангенса
II. Примечание:
- Если обратная тригонометрическая функция не определена в указанной точке, то ее значение не появится в результирующей таблице. Функции arcsin и arccos определены только на отрезке [-1,1].
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолачанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Обратная функция sin x. Арксинус, арккосинус
Обратные тригонометрические функции
(круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .
Арксинус
(обозначается как arcsin x
; arcsin x
— это угол, sin
его равняется x
).
Арксинус
(y = arcsin x
) — обратная тригонометрическая функция к sin
(x = sin y
), которая имеет область определения и множество значений . Другими словами возвращает угол по значению его sin
.
Функция y=sin x
непрерывна и ограничена на всей своей числовой прямой. Функция y=arcsin x
— строго возрастает.
Свойства функции arcsin .
График арксинуса.
Получение функции arcsin .
Есть функция y = sin x
. На всей своей области определения она кусочно-монотонная, таким образом, обратное соответствие y = arcsin x
не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает каждое значение области значений — . Т.к. для функции y = sin x
на интервале все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x
, у которой график является симметричным графику функции y = sin x
на отрезке относительно прямой y = x
.
Определение и обозначения
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1
и множество значений -π/2 ≤
y ≤ π/2
.
sin(arcsin
x)
= x
;
arcsin(sin
x)
= x
.
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin
x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1
и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
;
arccos(cos
x)
= x
.
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos
x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат.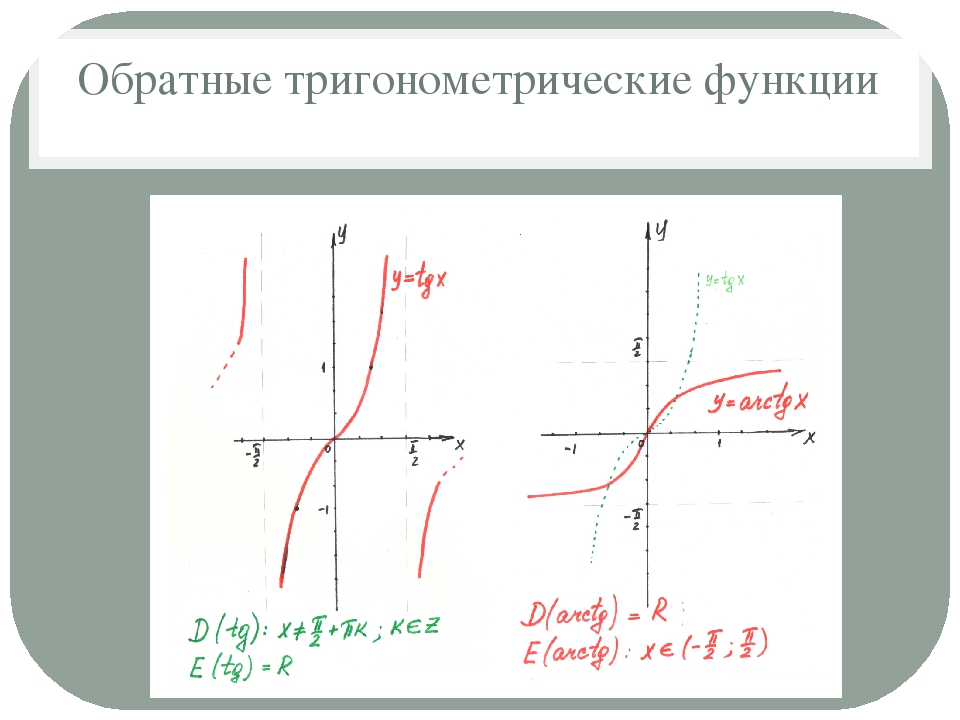 Чтобы устранить многозначность, область значений ограничивают интервалом ,
Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. также:
Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См.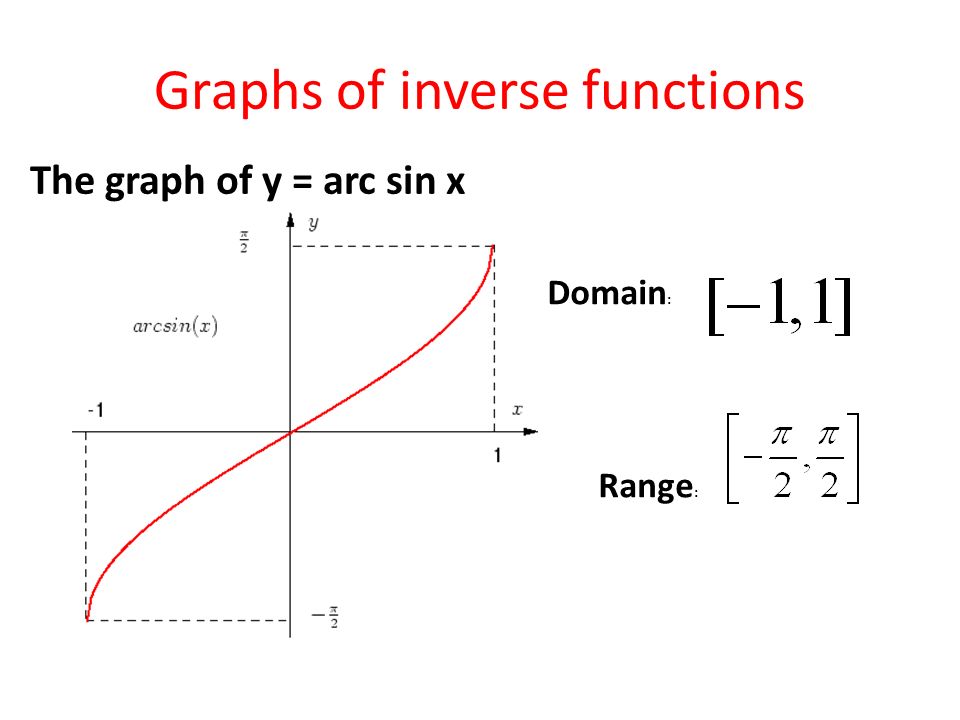 также:
также:
Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков
:
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2
,
cos
t ≥ 0
:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| 1
имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn
(где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны
. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
), имеющая область определения и множество значений .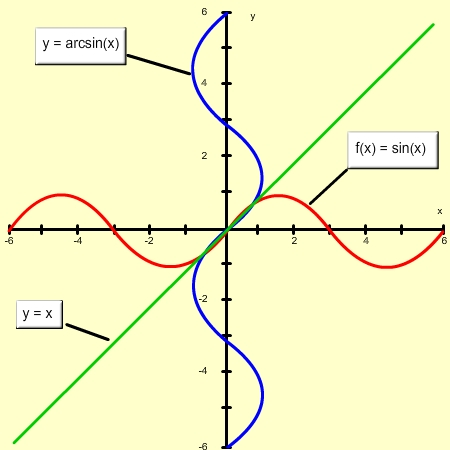
Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
), имеющая область определения и множество значений .
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x
.
См. разделы Синус, косинус , Тангенс, котангенс .
y = arcsin
x
y = arccos
x
y = arctg
x
y = arcctg
x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin
x)
= x
при
sin(arcsin
x)
= x
arccos(cos
x)
= x
при
cos(arccos
x)
= x
arctg(tg
x)
= x
при
tg(arctg
x)
= x
arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x
Формулы, связывающие обратные тригонометрические функции
См.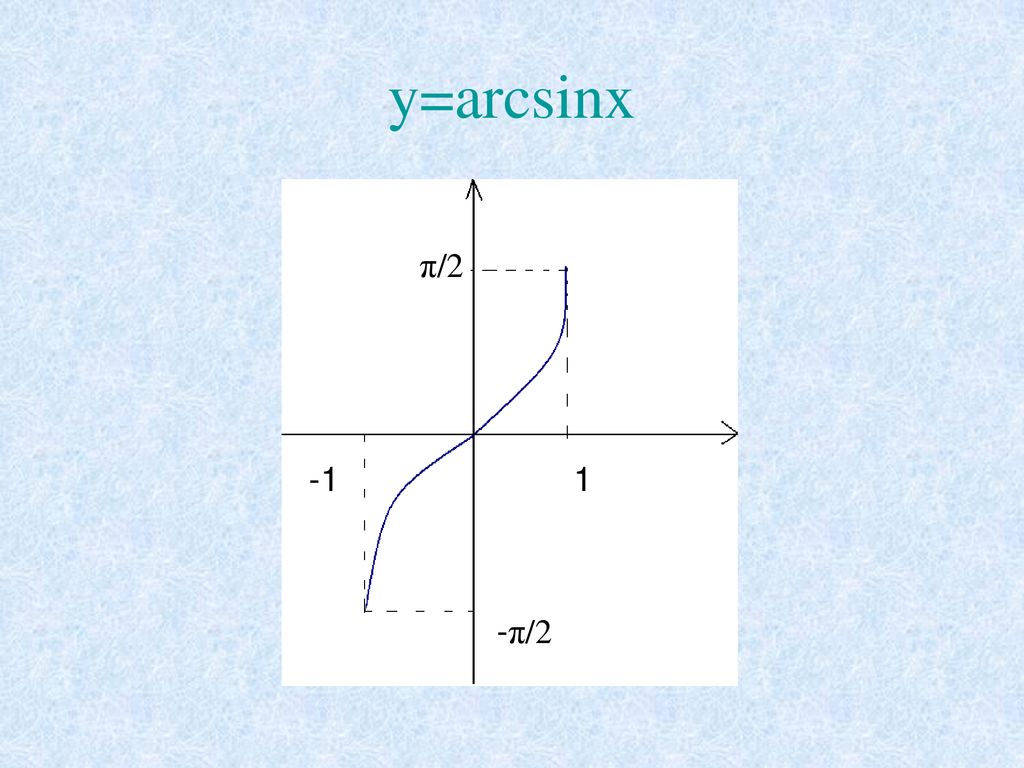 также:
также:
Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
(круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .
Арккосинус
, обратная функция к cos (x = cos y), y =
arccos x
определен при и имеет множество значений . Другими словами возвращает угол по значению его cos
.
Арккосинус
(обозначение: arccos x
; arccos x
— это угол , косинус которого равняется x
и так далее).
Функция y = cos x
непрерывна и ограничена на всей своей числовой прямой.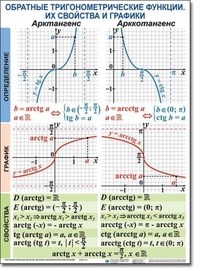 Функция y = arccos x
Функция y = arccos x
является строго убывающей.
Свойства функции arcsin .
Получение функции arccos .
Дана функция y = cos x
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — . На этом отрезке y = cos x
строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция y = arccos x
, график которой симметричен графику y = cos x
на отрезке относительно прямой y = x
.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin
и arcsin
, у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1.
Укажите функции изображенные на рисунке.
Ответ:
рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg
числа a – это такое значение угла α, что его тангенс равен а.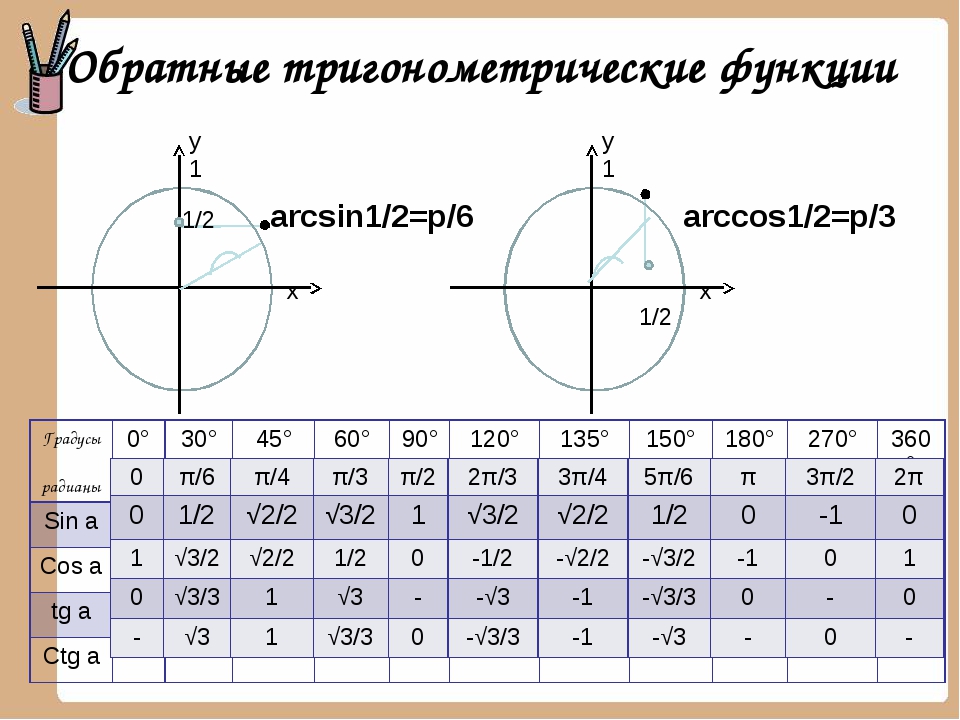
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2.
Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ:
рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α
, то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Calculus — Попытка получить обратную тригонометрическую функцию
Вам нужны формулы, производные от $ \ arcsin (u) $, $ \ arccos (u) $, $ \ arctan (u) $, $ \ mathrm {arcsec} (u) $ и, предположительно, $ \ mathrm { arccot} (u) $ и $ \ mathrm {arccsc} (u) $. {- 1}) ‘(b) = \ frac {1} {g’ (a)} $.2-1}}.
{- 1}) ‘(b) = \ frac {1} {g’ (a)} $.2-1}}.
\ end {align *}
Обратные тригонометрические функции
Аргумент обратной функции: \ (x \)
Угол (значение обратной функции): \ (y \)
Набор действительных чисел: \ (\ mathbb {R} \)
Действительное число: \ (a \)
- Обратные тригонометрические функции включают следующие функции \ (6 \): арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс.
- Поскольку исходные тригонометрические функции периодичны, обратные функции, вообще говоря, многозначны.Чтобы гарантировать взаимно однозначное соответствие между двумя переменными, области исходных тригонометрических функций могут быть ограничены их основными ветвями. Например, функция \ (y = \ sin x \) рассматривается только на интервале \ (x \ in \ left [{- \ large {\ frac {\ pi} {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right] \). На этом интервале однозначно определяется обратная синусоидальная функция.
- Арксинус, обратный синусу (арксинус)
Арксинус числа \ (a \) (обозначается \ (\ arcsin a \)) — это значение угла \ (x \) в интервале \ (x \ in \ left [{- \ large {\ frac {\ pi} {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right], \), при котором \ (\ sin x = а.\) Обратная функция \ (y = \ arcsin x \) определена для \ (x \ in \ left [{-1,1} \ right], \), ее диапазон равен \ (y \ in \ left [{- \ large {\ frac {\ pi} {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right] \). - Обратный косинус (арккосинус)
Арккосинус числа \ (a \) (обозначается arccos \ (\ arccos a \)) — это значение угла \ (x \) в интервале \ (\ left [ {0, \ pi} \ right] \), при котором \ (\ cos x = a \). Обратная функция \ (y = \ arccos x \) определена для \ (x \ in \ left [{-1,1} \ right] \), ее диапазон равен \ (y \ in \ left [{0, \ pi} \ right] \). - Арктангенс (арктангенс)
Арктангенс числа a (обозначается \ (\ arctan a \)) — это значение угла \ (x \) в открытом интервале \ (\ left ({- \ large {\ frac {\ pi} {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right), \) при котором \ (\ tan x = a \). Обратная функция \ (y = \ arctan x \) определена для всех \ (x \ in \ mathbb {R} \), диапазон арктангенса равен \ (\ left ({- \ large {\ frac {\ pi } {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right). \)
Обратная функция \ (y = \ arctan x \) определена для всех \ (x \ in \ mathbb {R} \), диапазон арктангенса равен \ (\ left ({- \ large {\ frac {\ pi } {2}} \ normalsize, \ large {\ frac {\ pi} {2}} \ normalsize} \ right). \) - Арккотангенс, обратный котангенсу (арккотангенс)
Арккотангенс числа \ (a \) (обозначается \ (\ text {arccot} a \)) — это значение угла \ (x \) в открытом интервале \ ( \ left [{0, \ pi} \ right], \), при котором \ (\ cot x = a \).Обратная функция \ (y = \ text {arccot} x \) определена для всех \ (x \ in \ mathbb {R} \), ее диапазон равен \ (y \ in \ left [{0, \ pi} \ верно]\). - Арксеканс числа \ (a \) (обозначается \ (\ text {arcsec} a \)) — это значение угла \ (x, \), при котором \ (\ сек х = а \). Обратная функция \ (y = \ text {arcsec} x \) определена для \ (x \ in \) \ (\ left ({- \ infty, — 1} \ right] \ cup \) \ (\ left [ {1, \ infty} \ right) \), его диапазон — это множество \ (y \ in \) \ (\ left [{0, \ large {\ frac {\ pi} {2}} \ normalsize} \ right ) \ cup \) \ (\ left ({\ large {\ frac {\ pi} {2}} \ normalsize, \ pi} \ right] \).

- Обратный косеканс (арккосеканс)
Арккосеканс числа \ (a \) (обозначается \ (\ text {arccsc} a \)) — это значение угла \ (x, \), при котором \ (\ csc х = а \). Обратная функция \ (y = \ text {arccsc} x \) определена для \ (x \ in \) \ (\ left ({- \ infty, — 1} \ right] \ cup \ left [{1, \ infty} \ right) \), его диапазон — это множество \ (y \ in \) \ (\ left [{- \ large {\ frac {\ pi} {2}} \ normalsize, 0} \ right) \ cup \ left ({0, \ large {\ frac {\ pi} {2}} \ normalsize} \ right] \). - Основные значения функций арксинуса и арккосинуса (в градусах)
- Основные значения функций арктангенса и арккотангенса (в градусах)
Функция обратной синусоиды — концепция
Поскольку синус не является однозначной функцией, домен должен быть ограничен от -pi / 2 до pi / 2, что называется ограниченной синусоидальной функцией.-1 (x) или arcsin (x). Обратные функции меняют местами значения x и y, поэтому диапазон обратного синуса составляет от -pi / 2 до / 2, а домен — от -1 до 1. При оценке проблем используйте идентификаторы или начинайте с внутренней функции.
При оценке проблем используйте идентификаторы или начинайте с внутренней функции.
Я хочу поговорить об обратной синусоидальной функции, но прежде мне нужно немного рассказать об обратных функциях и дать вам пример, когда f x равно x в квадрате не имеет обратного.Вот график, на котором f x равно x в квадрате, у него нет обратного, потому что он не 1 к 1, и помните, что тест для 1 к 1 — это тест горизонтальной линии. Если горизонтальная линия проходит более чем через 1 точку на графике функции, она не обратима, но мы можем сделать ее обратимой, ограничив область определения, и как мы это делаем, мы просто берем ее кусок, который равен 1 к 1, как правый наконечник. Итак, давайте сосредоточимся на этом фрагменте, я назову его g of x, и это x в квадрате для x, большего или равного 0.Таким образом, это ограничение домена делает эту функцию 1 к 1, и теперь мы можем ее инвертировать. И это обратный результат: g, обратный x, равен корню x, поэтому эта идея, идея ограничения домена, чтобы сделать функцию от 1 до 1, заключается в том, как мы делаем триггерные функции обратимыми и как мы получаем эти обратные триггерные функции.
Давайте посмотрим на синус. Синус очень сильно отличается от 1 к 1, в нем бесконечно много таких волн, поэтому вы не можете инвертировать синусоидальную функцию таким образом. Вы должны ограничить домен, поэтому мы ограничиваем его значением от отрицательного числа пи более 2 до числа пи более 2.Этот фрагмент равен 1 к 1, и давайте назовем эту функцию f от x равной синусу x для x между отрицательным числом пи более 2 и числом пи более 2. Это называется ограниченной функцией синуса, и важно помнить, что функция обратного синуса, которую я Я собираюсь записать это обратное, обратное, извините, ограниченная функция синуса, ограниченная функция синуса, так что снова это этот маленький красный кусочек здесь. Инверсия этой функции записывается как инверсный синус, этот отрицательный верхний индекс 1 не является показателем ни здесь, ни здесь, это фактически символ для инверсии функции синуса, поэтому убедитесь, что вы это помните.
Иногда это пишется так, а иногда и так — арксинус, так что это два имени для инверсии этой функции. Теперь нужно помнить одну вещь, если домен исходной функции находится между минусом пи более 2 и пи более 2, диапазон обратного синуса будет между отрицательным пи более 2 и пи более 2. Так что я запишу это. здесь отрицательное число пи больше 2 меньше или равно, я назову его y меньше или равно пи больше 2. Диапазон синусоидальной функции находится между отрицательными 1 и 1, область обратной синусоидальной функции будет между отрицательные 1 и 1 извините, что это домен.Поэтому всякий раз, когда вы инвертируете функцию, диапазон и домен снова переключаются, самое важное, что нужно помнить об обратных триггерных функциях, — это то, что мы сначала должны ограничить домен и сделать функцию от 1 до 1, чтобы сделать их обратимыми.
обратных функций, часть 3
обратных функций, часть 3
Обратные функции
Часть 3: Производные обратных триггерных функций
Функция обратного синуса также называется функцией арксинуса .Помимо обратного обозначения sin -1 x , используются обозначения arcsin x и asin x . Мы будем использовать обозначение arcsin x , которое вы можете представить как «угол, синус которого равен x » — с пониманием того, что значение arcsin x (угол) должно быть в радианах и должно быть между — pi / 2 и pi / 2 (включительно).
В Части 2 мы построили обратную (ограниченную) синусоидальную функцию как «функцию, определяемую интегралом»:
То есть arcsin x является специфической первообразной подынтегральной функции.В частности, мы уже знаем формулу производной для функции арксинуса:
В этой части мы увидим, как найти такую формулу производной напрямую. Если бы мы сначала знали производную, мы могли бы построить F (x) из этой информации — вместо того, чтобы она выпадала «из ниоткуда». Как только техника станет ясной, мы будем использовать ее, чтобы найти формулу для функции обратной тангенсации. В самом деле, это метод, который можно попробовать при поиске формулы, обратной любой дифференцируемой функции .
Нашей отправной точкой является уравнение y = sin x . Обратная синусоидальная функция по определению является обратной функцией, определяемой этим уравнением (с уже отмеченным ограничением области определения). Таким образом, если мы поменяем местами x и y , мы обнаружим, что обратный синус определяется уравнением x = sin y , с x в качестве независимой переменной и y в качестве зависимой переменной.
- Неявно дифференцируйте уравнение sin y = x и решите относительно dy / dx .[Это очень простой расчет — вы, вероятно, сможете сделать это быстрее с карандашом и бумагой, чем с помощью вашей системы компьютерной алгебры.]
- Результат шага 1 включает cos y , который нам нужно выразить в терминах x . Мы знаем, что sin y = x , и мы знаем соотношение между sin y и cos y . Что это за отношения? Решите его для cos y в терминах sin y , а затем замените sin y на x .
- Не торопитесь с формулой cos y . Решение для cos y включает в себя квадратный корень, и нам нужно знать, брать ли квадратный корень положительный или отрицательный. На следующих рисунках показан график cos y (с y в качестве независимой переменной) красным цветом и график положительного квадратного корня из 1 — sin 2 y синим цветом. Где их ценности одинаковые? Где они разные? Как это связано с функцией арксинуса? Правильно ли вы выбрали знак на предыдущем шаге?
- Подставьте результат шагов 2 и 3 в результат шага 1, чтобы найти явную формулу для dy / dx как функции x .Напомним, что в этом расчете y было сокращением для arcsin x . Таким образом, теперь у вас должна быть формула для производной функции арксинуса. Согласуется ли это с тем, что мы дали выше?
- Объясните своими словами, откуда взялась интегральная формула для arcsin x .
Теперь мы обратим наше внимание на касательную функцию и обратную к ней, а именно на задачу нахождения производной ее обратной.
- На следующем рисунке показаны три периода функции касательной.Как мы должны ограничить область, чтобы иметь обратимую функцию?
- Какая связь между tan x и sec x ? Это понадобится вам на следующем шаге. [Если вы не помните, вы можете получить его из отношения между sin x и cos x .]
- Обратная функция касательной (арктангенс, обозначается arctan x ) удовлетворяет уравнению tan y = X , где x — независимая переменная, а y — зависимая переменная.Используйте метод неявного дифференцирования, разработанный выше, чтобы найти формулу для производной arctan x как явной функции от x .
|
CCP Home |
Материалы | Интегральное исчисление | Содержание модуля | Назад | Вперед |
Функции арксинуса, арккосинуса и арктангенса
Функции арксинуса, арккосинуса и арктангенса
Функция арксинуса
Предпосылки: Функция арксинуса — это , обратная функции синуса
(пока функция синуса ограничена определенным доменом).Щелкните здесь, чтобы просмотреть обратные функции.
Напомним, что функция синуса принимает угол x
в качестве входных данных и возвращает синус этого угла в качестве выходных данных:
Например, если вход 30 °, то выход 0,5.
Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и
вернуть 30 ° на выходе.
Но существует проблема. Обратите внимание, что есть много углов с синусом 0,5:
Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное
отображение будет один-ко-многим и, следовательно, не будет удовлетворять
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как
отношение
называется Arcsine (с заглавной A и сокращением Arcsin), а функция называется arcsine
(со строчной буквой «а» и сокращением arcsin). Вот как они определены:
Определение: Арксинус x , обозначаемый Arcsin ( x ), определяется как « набор всех углов , синус которых равен x ».Это отношение «один ко многим» . Вот пример:
Определение: Арксинус x , обозначенный arcsin ( x ), определяется как определяется как
‘ один угол между −π / 2 и + π / 2 радиан
(или между -90 ° и + 90 °), синус которого равен x ’.
Это взаимно однозначная функция . Вот пример:
Определение: Из всех значений, возвращаемых отношением Арксинус,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения Арксинуса.(Примером является значение 30 °, показанное выше красным.)
График:
Красная кривая на графике справа — это функция арксинуса.
Обратите внимание, что для любых x от -1 до +1 он возвращает один
значение от −π / 2 до + π / 2 радиан.
Если мы добавим серую кривую к красной кривой, мы получим график
Отношение арксинуса. Вертикальная линия, проведенная где-то между x =
−1 и +1 коснутся этой кривой во многих местах, и это означает, что
отношение Арксинус вернет много значений.
На этом графике угол y измерен в радианах.
Если вы хотите измерить y в градусах , тогда
просто измените вертикальный масштаб, чтобы
что y изменяется от −360 ° до 360 ° вместо от
От −2π до 2π радиан;
в остальном форма графика не изменится.
Если сравнить график арксинуса с графиком синуса
тогда вы видите, что одно можно получить от другого, поменяв местами
горизонтальная и вертикальная оси.
Домен и диапазон:
Область определения функции арксинуса составляет от -1 до +1 включительно, а диапазон — от
От −π / 2 до π / 2 радиан включительно (или от −90 ° до 90 °).
Функция арксинуса может быть
распространяется на комплексные числа, в которых
если домен состоит из комплексных чисел.
Специальные значения функции арксинуса
(Щелкните здесь, чтобы получить более подробную информацию)
Решение уравнения sin ( θ ) = c для θ
с помощью арксинуса и Arcsin e
Предположим, что угол θ неизвестен, но известен его синус
быть c .Тогда для нахождения этого угла необходимо решить это уравнение
для θ :
sin ( θ ) = c
Если это, скажем, простая задача прямоугольного треугольника, и мы, , знаем , что
угол θ должен быть где-то между 0 и 90 °, тогда
решение — это единственное значение:
θ = arcsin ( c )
С другой стороны, если это более сложная проблема, и нам нужно найти
все возможные углы , синус которых равен c , тогда решение
это весь набор значений:
θ = Arcsin ( c )
Решения в этих двух случаях следуют непосредственно из
определения функции арксинуса и отношения арксинус.Обратите внимание, что если c больше 1 или меньше -1, то есть
нет реальных решений. Однако есть комплексные решения.
Оценка Arcsin ( c )
Если c — число, тогда весь набор значений Arcsin ( c )
можно найти, используя следующую процедуру. См. График справа
где точки — желаемые значения.
- Первое значение (главное значение), обозначенное θ PV , находится как
оценка arcsin ( c ) с помощью калькулятора или Algebra Coach. - Второе значение, называемое θ 2 , находится по
используя симметрию кривой Арксинус. Обратите внимание, что две синие стрелки на
граф имеют одинаковую длину. Это означает, что θ 2 настолько же меньше π, как
θ PV больше нуля. В форме формулы:θ 2 = π — θ PV
(Щелкните здесь, чтобы увидеть метод CAST для поиска
θ 2 .) - Все остальные значения выше и ниже этих двух значений
можно найти из этих двух значений, добавив или
вычитая кратные 2π. Если мы используем целое число n для подсчета
которое кратно другим значениям может быть получено из этой формулы:Например, если мы положим n = −1, то получим значения для
две самые низкие точки на графике. - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:
Как использовать функцию арксинуса в Algebra Coach
- Введите arcsin (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan .
(Параметр возвращает главное значение возвращает одно значение;
не оценивает параметр полезен, если вам нужны все значения
отношения Arc — но вам придется вычислить их самостоятельно.) - Установите опцию с точной / плавающей запятой .(Точный режим позволяет
используйте специальные значения.) - Установите режим градус / радиан. вариант.
- Установить p не представляет собой вариант π.
(Если вы хотите, чтобы арксинус возвращал специальные значения в радианном режиме
затем включите это.) - Включите комплексные числа , если вы хотите иметь возможность оценивать
арксинус комплексного числа или числа больше 1.
- Установите опцию arcsin, arccos и arctan .
- Нажмите кнопку «Упростить».
Алгоритм для функции арксинуса
Нажмите здесь
чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арксинуса.
Функция арккосинуса
Предпосылки: Функция арккосинуса — это , обратная функции косинуса
(пока функция косинуса ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.
Напомним, что функция косинуса принимает угол x
в качестве входных данных и возвращает косинус этого угла в качестве выходных данных:
Например, если вход 60 °, то выход 0,5.
Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и
вернуть 60 ° в качестве вывода.
Но существует проблема. Обратите внимание, что есть много углов, косинус которых равен 0,5:
Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное
отображение будет один-ко-многим и, следовательно, не будет удовлетворять
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как
отношение
называется Arccosine (с заглавной A и аббревиатурой Arccos) и функция называется arccosine
(со строчной буквой «а» и сокращением arccos). Вот как они определены:
Определение: Арккосинус x , обозначаемый Arccos ( x ), определяется как
« набор всех углов , косинус которых равен x ».Это отношение «один ко многим» . Вот пример:
Определение: Арккосинус x , обозначенный arccos ( x ), определяется как
‘ один угол между 0 и π радиан
(или от 0 ° до 180 °), косинус которого составляет x ’.
Это взаимно однозначная функция . Вот пример:
Определение: Из всех значений, возвращаемых отношением Арккосинус,
тот, который совпадает со значением, возвращаемым функцией arccosine
называется главным значением отношения Арккосинуса.(Пример — значение 60 °, показанное выше красным.)
График:
Красная кривая на графике справа — это функция арккосинуса.
Обратите внимание, что для любых x от -1 до +1 он возвращает один
значение от 0 до + π радиан.
Если мы добавим серую кривую к красной кривой, мы получим график
Отношение арккосинуса. Вертикальная линия, проведенная где-то между x =
−1 и +1 коснутся этой кривой во многих местах, и это означает, что
отношение Арккосинус вернет много значений.
На этом графике угол y измерен в радианах.
Если вы хотите измерить y в градусах , тогда
просто измените вертикальный масштаб, чтобы
что y изменяется от −360 ° до 360 ° вместо от
От −2π до 2π радиан;
в остальном форма графика не изменится.
Если сравнить график арккосинуса с графиком косинуса
тогда вы видите, что одно можно получить от другого, поменяв местами
горизонтальная и вертикальная оси.
Домен и диапазон:
Область функции арккосинуса составляет от -1 до +1 включительно, а диапазон — от
От 0 до π радиан включительно (или от 0 ° до 180 °).
Функция арккосинуса может быть
распространяется на комплексные числа, в которых
если домен состоит из комплексных чисел.
Специальные значения функции арккосинуса
(Щелкните здесь, чтобы получить более подробную информацию)
Решение уравнения cos ( θ ) = c для θ
с помощью арккосинуса и Arccos ine
Предположим, что угол θ неизвестен, но известен его косинус
быть c .Тогда для нахождения этого угла необходимо решить это уравнение
для θ :
cos ( θ ) = c
Если это, скажем, простая задача прямоугольного треугольника, и мы, , знаем , что
угол θ должен быть где-то между 0 и 90 °, тогда
решение — это единственное значение:
θ = arccos ( c )
С другой стороны, если это более сложная проблема, и нам нужно найти
все возможные углы , косинус которых равен c , тогда решение
это весь набор значений:
θ = Arccos ( c )
Решения в этих двух случаях следуют непосредственно из
определения функции арккосинуса и отношения арккосинуса.Обратите внимание, что если c больше 1 или меньше -1, то есть
нет реальных решений. Однако есть комплексные решения.
Оценка Arccos ( c )
Если c — число, то весь набор значений Arccos ( c )
можно найти, используя следующую процедуру. См. График справа
где точки — желаемые значения.
- Первое значение (главное значение), обозначенное θ PV , находится как
оценка arccos ( c ) с помощью калькулятора или Algebra Coach. - Второе значение, называемое θ 2 , находится по
используя симметрию кривой Арккосинуса. Обратите внимание, что две синие стрелки на
граф имеют одинаковую длину. Это означает, что θ 2 настолько же меньше 2π, сколько
θ PV больше нуля. В форме формулы:θ 2 = 2 π — θ PV
(Щелкните здесь, чтобы увидеть метод CAST для поиска
θ 2 .) - Все остальные значения выше и ниже этих двух значений
можно найти из этих двух значений, добавив или
вычитая кратные 2π. Если мы используем целое число n для подсчета
которое кратно другим значениям может быть получено из этой формулы:Например, если мы положим n = −1, то получим значения для
две самые низкие точки на графике. - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:
Как использовать функцию арккосинуса в Algebra Coach
- Введите arccos (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan .
(Параметр возвращает главное значение возвращает одно значение;
не оценивает параметр полезен, если вам нужны все значения
отношения Arc — но вам придется вычислить их самостоятельно.) - Установите опцию с точной / плавающей запятой .(Точный режим позволяет
используйте специальные значения.) - Установите режим градус / радиан. вариант.
- Установить p не представляет собой вариант π.
(Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.) - Включите комплексные числа , если вы хотите иметь возможность оценивать
арккосинус комплексного числа или числа больше 1.
- Установите опцию arcsin, arccos и arctan .
- Нажмите кнопку «Упростить».
Алгоритм для функции арккосинуса
Нажмите здесь
чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арккосинуса.
Функция арктангенса
Фон: Функция арктангенса — это , обратная функции тангенса
(пока касательная функция ограничена определенной областью).Щелкните здесь, чтобы просмотреть обратные функции.
Напомним, что функция тангенса принимает угол x
в качестве входных данных и возвращает тангенс этого угла в качестве выходных данных:
Например, если на входе 45 °, то на выходе 1,0.
Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и
вернуть 45 ° в качестве вывода.
Но существует проблема. Обратите внимание, что есть много углов, тангенс которых равен 1,0:
Мы говорим, что это сопоставление многие-к-одному .Это означает, что обратное
отображение будет один-ко-многим и, следовательно, не будет удовлетворять
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как
отношение
называется арктангенсом (с заглавной буквы A и сокращением арктангенс), а функция называется арктангенс
(со строчной буквой «а» и сокращением arctan). Вот как они определяются:
Определение: Арктангенс x , обозначаемый Arctan ( x ), определяется как
‘ набор всех углов , тангенс которых равен x ’.Это отношение «один ко многим» . Вот пример:
Определение: Арктангенс x , обозначенный arctan ( x ), определяется как
‘ один угол между −π / 2 и + π / 2 радиан
(или от -90 ° до + 90 °) с касательной x ’.
Это взаимно однозначная функция . Вот пример:
Определение: Из всех значений, возвращаемых отношением арктангенса,
тот, который совпадает со значением, возвращаемым функцией арктангенса
называется главным значением отношения арктангенса.(Пример — значение 45 °, показанное выше красным.)
График:
Красная кривая на графике справа — это функция арктангенса.
Обратите внимание, что для любых x он возвращает один
значение от −π / 2 до + π / 2 радиан.
Если мы добавим серые кривые к красной кривой, мы получим график
Отношение арктангенса. Вертикальная линия, проведенная в любом месте
коснется этого набора кривых во многих местах, и это означает, что
отношение арктангенса вернет много значений.
На этом графике угол y измерен в радианах.
Если вы хотите измерить y в градусах , тогда
просто измените вертикальный масштаб, чтобы
что y изменяется от -180 ° до 180 ° вместо от
От −π до π радиан;
в остальном форма графика не изменится.
Если сравнить график арктангенса с графиком касательного
тогда вы видите, что одно можно получить от другого, поменяв местами
горизонтальная и вертикальная оси.
Домен и диапазон:
Область функции арктангенса — все действительные числа, а диапазон — от
От −π / 2 до π / 2 без учета радиан (или от −90 ° до 90 °).
Функция арктангенса может быть
распространяется на комплексные числа, в которых
если домен состоит из комплексных чисел.
Специальные значения функции арктангенса
(Щелкните здесь, чтобы получить более подробную информацию)
Решение уравнения tan ( θ ) = c для θ
с использованием арктангенса и арктангенса
Предположим, что угол θ неизвестен, но известен его тангенс.
быть c .Тогда для нахождения этого угла необходимо решить это уравнение
для θ :
тангенс ( θ ) = c
Если это, скажем, простая задача прямоугольного треугольника, и мы, , знаем , что
угол θ должен быть где-то между 0 и 90 °, тогда
решение — это единственное значение:
θ = арктангенс ( c )
С другой стороны, если это более сложная проблема, и нам нужно найти
все возможные углы , тангенс которых равен c , тогда решение
это весь набор значений:
θ = Арктангенс ( c )
Решения в этих двух случаях непосредственно следуют из определений
функции арктангенса и отношения арктангенса.
Оценка Arctan ( c )
Если c — число, то весь набор значений Arctan ( c )
можно найти, используя следующую процедуру. См. График справа
где точки — желаемые значения.
- Первое значение (главное значение), обозначенное θ PV , находится как
оценка arctan ( c ) с помощью калькулятора или Algebra Coach. - Все остальные значения выше и ниже этого значения могут быть найдены
используя тот факт, что соседние значения удалены друг от друга на расстояние π.Если мы используем целое число n для подсчета числа, кратного π, то другой
значения могут быть получены из этой формулы:θ = θ PV + π n
(Щелкните здесь, чтобы увидеть метод CAST для поиска
θ 2 .) - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:θ = θ PV + 180 ° · n
Как использовать функцию арктангенса в Algebra Coach
- Введите arctan (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию arcsin, arccos и arctan .
(Параметр возвращает главное значение возвращает одно значение;
не оценивает параметр полезен, если вам нужны все значения
отношения Arc — но вам придется вычислить их самостоятельно.) - Установите опцию с точной / плавающей запятой .(Точный режим позволяет
используйте специальные значения.) - Установите режим градус / радиан. вариант.
- Установить p не представляет собой вариант π.
(Если вы хотите, чтобы арктангенс возвращал специальные значения в радианах
затем включите это.) - Включите комплексные числа , если вы хотите иметь возможность оценивать
арктангенс комплексного числа.
- Установите опцию arcsin, arccos и arctan .
- Нажмите кнопку «Упростить».
Алгоритм для функции арктангенса
Нажмите здесь
чтобы увидеть алгоритм, используемый компьютерами для вычисления функции арктангенса.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
математических слов: обратный синус
Обратный синус
sin -1
Sin -1
arcsin
Arcsin
Функция, обратная синусу.
Основная идея : Найти грех -1 (½),
мы спрашиваем «что
угол имеет синус, равный ½? »
ответ 30 °. В результате мы говорим sin -1 (½)
= 30 °.
В радианах это sin -1 (½)
= π / 6.
Подробнее : На самом деле существует много углов, которые
синус равен ½.
Мы действительно спрашиваем, «какой самый простой, самый основной угол, который
синус равен ½? »Как и прежде,
ответ — 30 °.Таким образом sin -1 (½)
= 30 ° или sin -1 (½) = π / 6.
Подробности : Что такое sin -1 (–½)?
Выбираем ли мы 210 °, –30 °, 330 °,
или под другим углом? Ответ –30 °.
Обратным синусом выбираем угол на правой половине блока
круг, имеющий размер как можно ближе к нулю. Таким образом sin -1 (–½)
= –30 ° или sin –1 (–½)
= –Π / 6.
В
другими словами, диапазон sin -1 равен
ограничено [–90 °, 90 °] или.
Примечание: arcsin означает «арксинус»,
или радианная мера дуги на окружности, соответствующая
к заданному значению синуса.
Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида,
косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны, их обратные значения не являются функциями. Каждая триггерная функция может иметь свой
домен ограничен, однако, чтобы сделать его инверсию функцией.Некоторые математики пишут эти ограниченные триггерные функции и их
переворачивается с заглавной буквы (например, Sin или Sin -1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не делает различий между заглавными и не заглавными буквами
триггерные функции.
См.
также
обратный
тригонометрия,
обратные триггерные функции, интервальное обозначение
Оценка обратной синусоидальной функции
Определения
Общие
Обратная синусоидальная функция, в современных обозначениях, записанная как arcsin (x), дает угол θ, так что:
\ sin \ theta = x
Поскольку значения синусоидальной функции находятся в диапазоне от -1 до 1, область аргумента x в функции arcsin ограничена тем же диапазоном: [-1,1].

 13.
13.