Содержание
Что такое Аксиома и Теорема? Определение, примеры, доказательства.
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
|
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Звучит она так:
Через любую точку, которая расположена вне данной прямой, можно провести только одну прямую параллельную данной.
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
- прямая, которая пересекает одну параллельную прямую, обязательно пересекает и другую;
- если две прямые параллельны третьей, то между собой они также параллельны.
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин.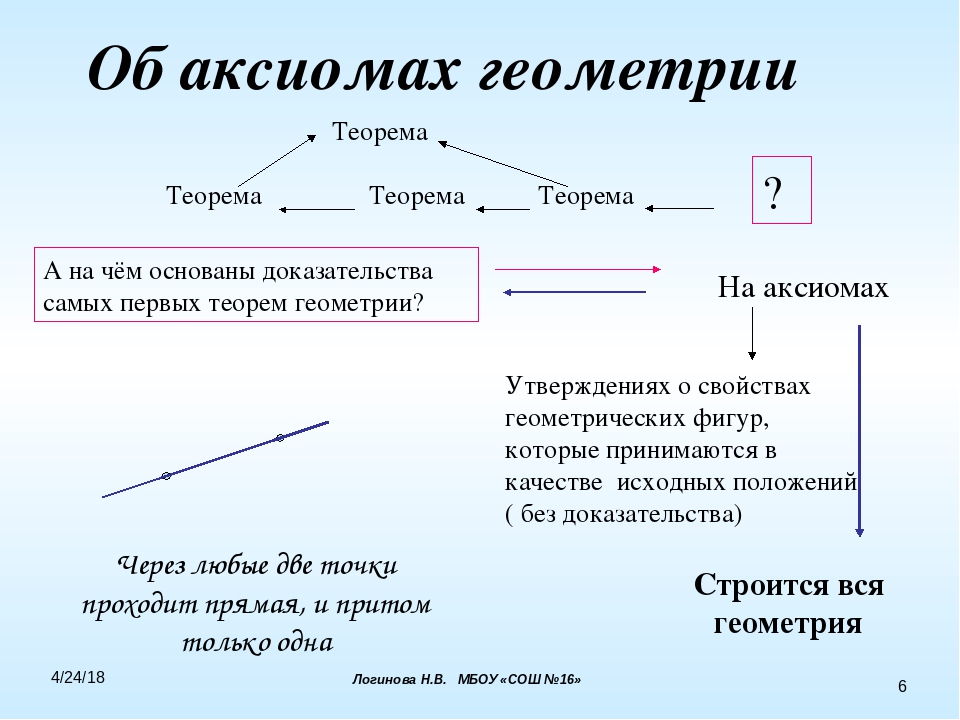 В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
|
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
- Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.
- Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
- Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
- прямая теорема: в треугольнике против равных сторон лежат равные углы.
- обратная теорема: в треугольнике против равных углов лежат равные стороны.

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
- Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
- Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
- Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
- Обратная противоположной: если прямые не параллельны, соответственные углы не равны.
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
- при b² + c² – a² > 0 угол α будет острым;
- при b² + c² – a² = 0 угол α будет прямым, что соответствуем теореме Пифагора;
- при b² + c² – a² < 0 угол α будет тупым.
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Формула:
где a, b, c — стороны треугольника,
α, β, γ — углы, которые находятся на противоположных сторонах.
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов.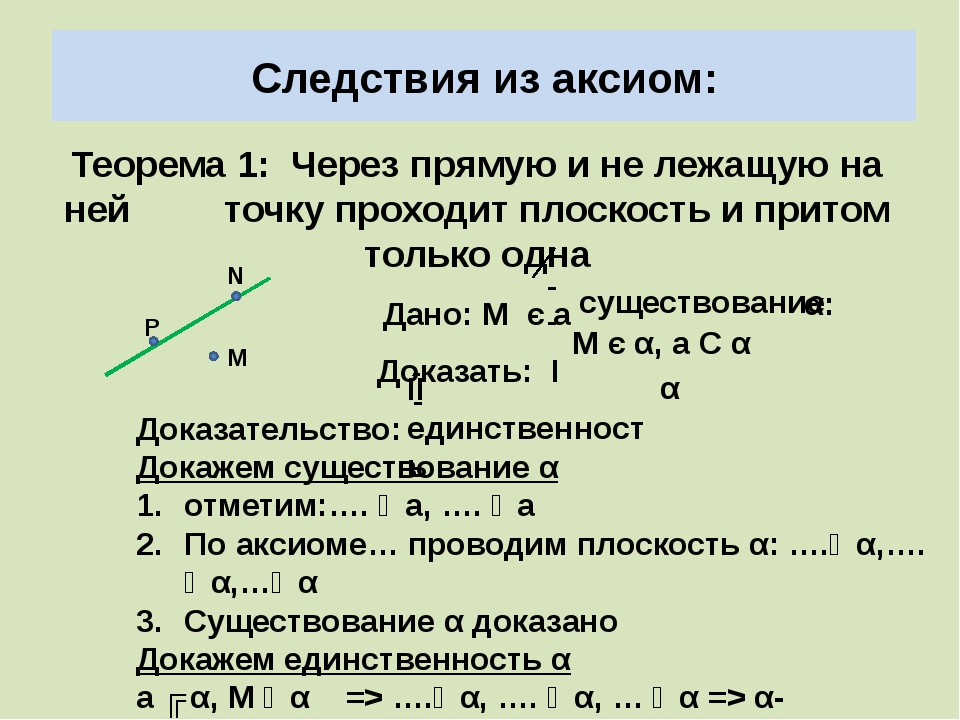 У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником.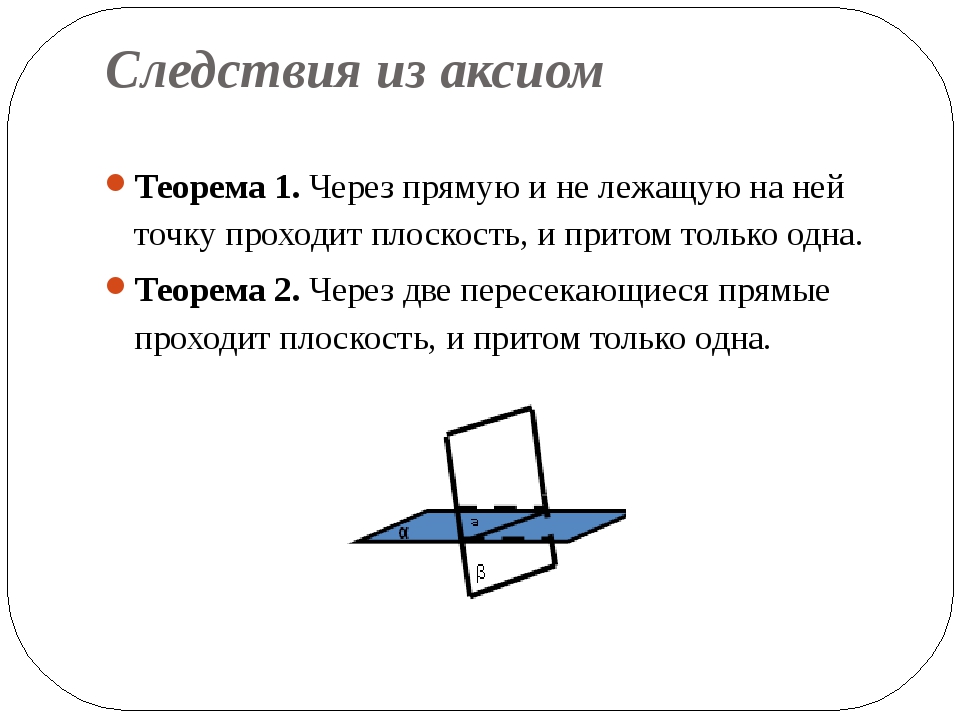 Это свойство, но не его признак.
Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный вводный урок математики в онлайн-школе Skysmart и попробуйте сами!
Понятие Теорема и Аксиома Лемма, Следствия введение в матема…
Сразу хочу сказать, что здесь никакой воды про теорема, и только нужная информация. Для того чтобы лучше понимать что такое
Для того чтобы лучше понимать что такое
теорема,аксиома,лемма,следствия,аксиоматизация теории , настоятельно рекомендую прочитать все из категории введение в математику. основы
теорема (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем,
аксиома ми называются утверждения, которые в рамках конкретной теории принимаются истинными без всяких доказательств или обоснований.
В математических текстах теоремами обычно называют только те доказанные утверждения, которые находят широкое применение в решении математических задач. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределенные утверждения).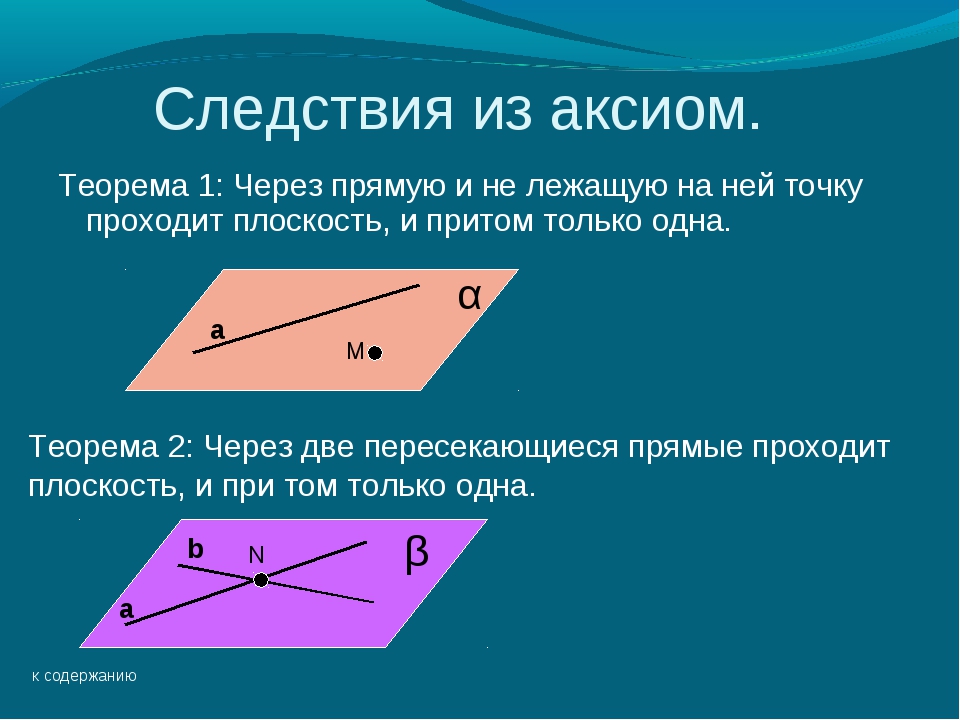 Менее важные утверждения-теоремы обычно называют
Менее важные утверждения-теоремы обычно называют
лемма ми,предложениями,
следствия ми, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называютгипотезами.
Наиболее знаменитыми являются теоремы Ферма, Пифагора и Птолемея.
Лемма (греч. λημμα — предположение) — доказанное утверждение, полезное не само по себе, а для доказательства других утверждений. Примеры известных лемм —лемма Евклида, лемма Жордана, лемма Гаусса, лемма Накаямы, лемма Гриндлингера, Лемма Лоренца, Лемма Лебедева.
Аксиома (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое в основе доказательства других ее положений.
Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной . Об этом говорит сайт https://intellect.icu . Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.
Об этом говорит сайт https://intellect.icu . Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.
В современной науке аксиомы — это те положения теории, которые принимаются за исходные, причем вопрос об истинности решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.
Аксиоматизация теории — явное указание конечного или счетного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, все дальнейшее изложение должно основываться исключительно лишь на этих аксиомах, не опираясь на обычное конкретное значение этих объектов и их отношений. Утверждения на основе аксиом называются теоремами.
Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и Евклидовой геометрии .
Набор аксиом называется непротиворечивым, если из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание. Аксиомы являются своего рода «точками отсчета» для построения теорий в любой науке, при этом сами они не доказываются, а выводятся непосредственно из эмпирического наблюдения (опыта) или обосновываются в более глубокой теории.
Австрийский математик Курт Гедель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система) начиная с определенного уровня сложности либо внутренне противоречива, либо неполна (то есть в достаточно сложных системах найдется хотя бы одно высказывание, истинность и ложность которого не может быть доказана средствами самой этой системы ).
Примеры аксиом
- Аксиома выбора
- Аксиома параллельности Евклида
- Аксиома Архимеда
- Аксиома объемности
- Аксиома регулярности
- Аксиома полной индукции
- Аксиома Колмогорова
- Аксиома булеана
- Аксиоматика
- Аксиоматика теории множеств
- Аксиоматика вещественных чисел
- Аксиоматика Евклида
- Аксиоматика Гильберта
Следствие — утверждение, которое выводится непосредственно из аксиомы или теоремы.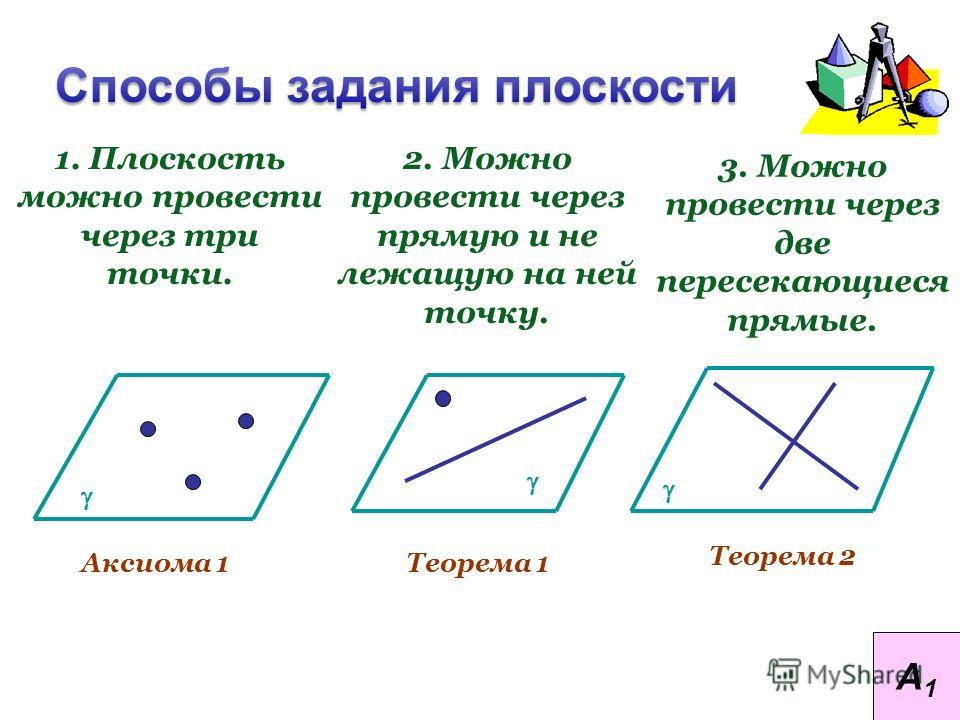 Следствие, как и теорему, необходимо доказывать.
Следствие, как и теорему, необходимо доказывать.
Приведем примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
История
Впервые термин «аксиома» встречается у Аристотеля (384—322 до н. э.) и перешел в математику от философов Древней Греции. Евклид различает понятия «постулат» и «аксиома», не объясняя их различия. Со времен Боэция постулаты переводят как требования (petitio), аксиомы — как общие понятия. Первоначально слово «аксиома» имело значение «истина, очевидная сама по себе». В разных манускриптах Начал Евклида разбиение утверждений на аксиомы и постулаты различно, не совпадает их порядок. Вероятно переписчики придерживались разных воззрений на различие этих понятий.
Отношение к аксиомам как к неким неизменным самоочевидным истинам сохранялось долгое время. Например, в словаре Даля аксиома — это «очевидность, ясная по себе и бесспорная истина, не требующая доказательств».
Сейчас аксиомы обосновываются не сами по себе, а в качестве необходимых базовых элементов теории. Критерии формирования набора аксиом в рамках конкретной теории часто являются прагматическими: краткость формулировки, удобство манипулирования, минимизация числа исходных понятий и т. п. Такой подход не гарантирует истинность принятых аксиом. Лишь подтверждение теории является одновременно и подтверждением набора ее аксиом.
См. также
Статью про теорема я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое теорема,аксиома,лемма,следствия,аксиоматизация теории
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.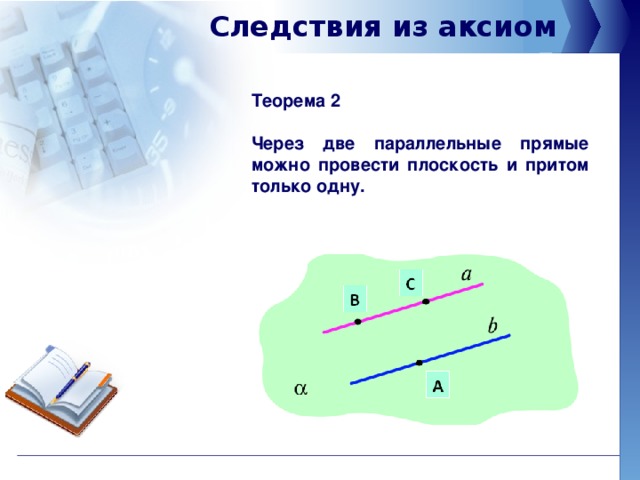 Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
введение в математику. основы
В чем разница между леммой, аксиомой, определением, следствием и т. Д.?
Некоторые из них сильно отличаются от других:
Axiom: This is what you are taking to be the ground truth. For instance, Peano axioms axiomatize natural numbers, and you can use Dedekind cuts to axiomatize reals (You can read Dedekind’s cut and axioms for more info)
Вы можете использовать это несколько взаимозаменяемо со словом «определение». (Вы можете сказать, что это то, как вы «определяете» натуральные или действительные числа), но в целом определение имеет следующий вид:
«Defintion: Мы говорим, что натуральное число BOO, если оно удовлетворяет следующим аксиомам:
1) Если вы добавите одно к любому номеру BOO, итоговое число не будет BOO.
2) Если вы добавите его к любому номеру, который не является BOO, итоговое число BOO.
3) 1 не BOO.
Теперь давайте сделаем предложение. (Как правило, это просто утверждение, которое может быть либо истинным, либо ложным. Это то, что они предлагают, это, я думаю, в основном используется, если они не собираются это доказывать какое-то время).
Предложение: «Каждый номер BOO — ровный».
Теорема. Это по существу математическая истина; любой, кто утверждает, что один из них лучше дает вам доказательство этого. Поскольку мы докажем вышеприведенное предложение, перепишем его так:
Теорема: «Каждое число BOO равномерное».
Теперь, чтобы помочь нам это доказать, мы докажем две мини-теоремы, более часто называемые леммами.
Лемма 1: «2 — BOO»
Доказательство: 1 не BOO по аксиоме 3, поэтому по аксиоме 2, 1 + 1 = 2 является BOO.
Лемма 2: «Если n — BOO, n + 2 — BOO»
Доказательство. Если n — BOO, то по аксиоме 1 n + 1 не находится в BOO, но тогда по аксиоме 2 (n + 1) +1 = n + 2 находится в BOO.
Теперь доказательство теоремы будет состоять в том, чтобы показать, что каждое число формы 2 + 2 + 2 + . .. + 2 делится на 2. Вы можете использовать тот факт, что умножение на 1/2 распределяется по суммированию, но это потребует, пожалуй, большего количества определений, чем то, что вы хотите использовать. Вы также можете использовать что-то, называемое индукцией, которое является методом доказательства. Это зависит от того, как вы хотите определить четность.
.. + 2 делится на 2. Вы можете использовать тот факт, что умножение на 1/2 распределяется по суммированию, но это потребует, пожалуй, большего количества определений, чем то, что вы хотите использовать. Вы также можете использовать что-то, называемое индукцией, которое является методом доказательства. Это зависит от того, как вы хотите определить четность.
Теперь давайте назовем следствием из нашей теоремы:
Следствие: 2 четное. (Мы знаем, что это следует из нашей теоремы, поскольку мы доказали ранее, что каждое число BOO четное, и мы знаем, что 2 — BOO.)
Закон: Это относится к большим наблюдениям, вы можете написать «закон BOOs как: каждый номер — BOO или BOO + 1». Законы не так распространены, но у нас есть несколько крупных: Закон больших чисел и законы Де Моргана. Вы можете представить, что они очень большие или полезные теоремы. (Существует множество больших и полезных теорем, таких как центральная предельная теорема, которые не называются законами).
Надеюсь, что он отвечает на игрушку!
Как работает доказательство Гёделя / Хабр
Его теоремы о неполноте разгромили поиск математической теории всего.
 Почти сто лет спустя мы всё ещё пытаемся осмыслить последствия этого.
Почти сто лет спустя мы всё ещё пытаемся осмыслить последствия этого.
В 1931 году австрийский логик Курт Гёдель провернул, вероятно, один из самых потрясающих интеллектуальных трюков в истории.
Математики той эпохи искали неколебимые основы математики: набор базовых фактов, аксиом, которые были бы непротиворечивыми и полными, играя роль строительных блоков всех математических истин.
Однако шокирующие теоремы Гёделя о неполноте, опубликованные им всего лишь в 25-летнем возрасте, разбили эту мечту. Он доказал, что любой набор аксиом, который вы можете предложить на роль основы математики, неизбежно будет неполным. Всегда найдутся истинные утверждения, касающиеся чисел, которые невозможно будет доказать при помощи этих аксиом. Он также показал, что ни один набор аксиом нельзя использовать для доказательства их собственной непротиворечивости.
Его теоремы о неполноте означают, что математической теории всего быть не может, и нельзя объединить множество доказуемых утверждений со множеством истинных. То, что математики могут доказать, зависит от начальных предположений, а не от какой-то фундаментальной истины, из которой происходят все ответы.
То, что математики могут доказать, зависит от начальных предположений, а не от какой-то фундаментальной истины, из которой происходят все ответы.
За 89 лет, прошедших с открытия Гёделя, математики уже натыкались на подобные вопросы без ответов, существование которых предсказывали его теоремы. К примеру, сам Гёдель помог установить, что континуум-гипотеза, касающаяся мощностей бесконечностей, неразрешима – как и проблема остановки, в которой требуется определить, завершится ли когда-нибудь выполнение компьютерной программы с определёнными входными данными, или она будет работать вечно. Неразрешимые вопросы возникали даже и в физике, что говорит о том, что гёделева неполнота влияет не только на математику, но и в каком-то (не совсем понятном) смысле, на реальность.
Далее идёт краткая, упрощённая и неформальная сводка того, как Гёдель доказал свои теоремы.
Нумерация Гёделя
Главным ходом Гёделя стало сопоставление утверждений, касающихся системы аксиом, с утверждениями, сделанными в рамках этой системы – с утверждениями, касающимися чисел. Такое сопоставление позволяет системе аксиом спокойно рассуждать о себе самой.
Такое сопоставление позволяет системе аксиом спокойно рассуждать о себе самой.
Первый шаг – сопоставить любое возможное математическое утверждение, или последовательность утверждений, с уникальным номером, который называется номером Гёделя.
Немного исправленная версия нумерации Гёделя, представленная в книге 1958 года «Доказательство Гёделя» за авторством Эрнеста Нагеля и Джеймса Ньюмена, начинается с 12 элементарных символов, служащих словарём для выражения набора базовых аксиом. К примеру, утверждение о существовании чего-либо можно выразить символом ∃, а сложение – символом +. Символ s, обозначающий «следующий элемент», даёт возможность обозначать числа: к примеру, ss0 обозначает двойку.
Затем этим двенадцати символам назначаются номера Гёделя с 1 по 12.
Затем буквы, обозначающие переменные, начиная с x, y и z, сопоставляются с простыми числами, большими 12 (13, 17, 19,..).
Затем каждая из комбинаций этих символов и переменных – то есть, любая арифметическая формула или последовательность формул, которые только можно составить – получает свой номер Гёделя.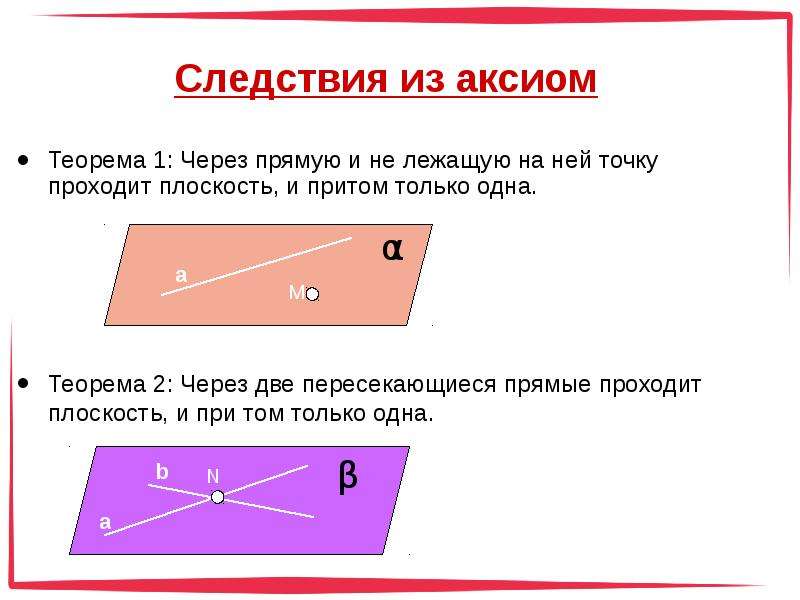
Рассмотрим, к примеру, утверждение 0 = 0. Три её символа соответствуют номерам Гёделя 6, 5 и 6. Гёделю нужно заменить эту последовательность из трёх номеров одним уникальным – номером, который не выдаст ни одна другая последовательность символов. Для этого он берёт три первых простых числа (2, 3 и 5), возводит каждое из них в степень, равную соответствующему номеру в последовательности, и перемножает их. Таким образом 0 = 0 превращается в 26 × 35 × 56, или 243 000 000.
Эта разметка работает потому, что никакие две формулы не дадут один и тот же номер Гёделя. Номера Гёделя – целые числа, а числа можно разложить на простые множители единственным способом. Поэтому единственный способ разложить 243 000 000 на множители — это 26 × 35 × 56, то есть, расшифровать этот номер Гёделя можно только одним способом: написав формулу 0 = 0.
Затем Гёдель пошёл ещё дальше. Математическое доказательство состоит из последовательности формул. Поэтому Гёдель назначил каждой последовательности формул свой номер Гёделя. В данном случае он также начинает с последовательности простых чисел – 2, 3, 5, и т.д. Затем он возводит каждое из них в степень, соответствующую номеру Гёделя для формулы, находящейся на том же порядковом месте в последовательности (допустим, 2243 000 000, если первой идёт формула 0 = 0), и перемножает всё вместе.
Поэтому Гёдель назначил каждой последовательности формул свой номер Гёделя. В данном случае он также начинает с последовательности простых чисел – 2, 3, 5, и т.д. Затем он возводит каждое из них в степень, соответствующую номеру Гёделя для формулы, находящейся на том же порядковом месте в последовательности (допустим, 2243 000 000, если первой идёт формула 0 = 0), и перемножает всё вместе.
Арифметизация математики
Замечательно, что даже утверждения, касающиеся арифметических формул, т.н. метаматематические утверждения, можно перевести в формулы, и назначить им собственные номера Гёделя.
Рассмотрим сначала формулу ~(0 = 0), означающую «ноль не равен нулю». Она явно ложная. Тем не менее, у неё есть номер Гёделя: 2 в степени 1 (номер Гёделя для символа ~), умноженное на 3 в степени 8 (номер Гёделя для символа «левая скобка»), и так далее, что в итоге даёт 21 × 38 × 56 × 75 × 116 × 139.
Поскольку мы можем генерировать номера Гёделя для всех формул, даже ложных, мы можем осмысленно рассуждать о них, используя их номера Гёделя.
Рассмотрим утверждение «Первый символ формулы ~(0 = 0) это тильда». Это истинное метаматематическое утверждение, касающееся ~(0 = 0), превращается в утверждение о номере Гёделя конкретной формулы – а именно, что его первая степень равняется 1, то есть, номеру Гёделя для тильды. Иначе говоря, наше утверждение говорит о том, что в 21 × 38 × 56 × 75 × 116 × 139 есть только один множитель «2». Если бы ~(0 = 0) начиналась с любого другого символа, кроме тильды, в её номере ГЁ было бы, по меньшей мере, два множителя 2. Так что, если сформулировать точнее, 2 является множителем 21 × 38 × 56 × 75 × 116 × 139, а 22 — не является.
Мы можем преобразовать последнее предложение в точную математическую формулу, и записать её при помощи элементарных символов. У этой формулы, естественно, будет свой номер Гёделя, который мы сможем подсчитать, сопоставив её символы степеням простых чисел.
Если вам интересно, то формулировка получается такая: существует такое целое х, что х, помноженное на 2, будет равно 21 × 38 × 56 × 75 × 116 × 139, но не существует такого целого х, чтобы оно, помноженное на 4, давало 21 × 38 × 56 × 75 × 116 × 139. Соответствующая формула выглядит так:
(∃x)(x × ss0 = sss … sss0) ⋅ ~(∃x)(x × ssss0 = sss … sss0)
Где sss … sss0 обозначает 21 × 38 × 56 × 75 × 116 × 139 копий символа следующего элемента s. Символ ⋅ означает «и», и представляет собой более краткую запись для фундаментального словаря: p ⋅ q означает ~(~p ∨ ~q).
Данный пример, как писали Нагель и Ньюмен, «иллюстрирует общую и глубокую идею, лежащую в основе открытия Гёделя: мы можем очень точно говорить о типографических свойствах длинных последовательностей символов, но не напрямую, а через свойства разложения на простые множители больших целых чисел.
Преобразовать в символы можно и метаматематические утверждения. „Существует некая последовательность формул с номером Гёделя х, доказывающая формулу с номером Гёделя k“ – или, короче говоря, „формула с номером Гёделя k доказуема“. Именно возможность „арифметизировать“ подобные заявления и заложила основы переворота.
G само по себе
Дополнительно Гёдель догадался о том, что можно подставить собственный номер Гёделя, обозначающий формулу, в саму формулу – а это уже ведёт к нескончаемым проблемам.
Чтобы понять, как работает эта подстановка, рассмотрим формулу (∃x)(x = sy). Она означает „существует переменная x, являющаяся следующим элементом для y“, или, проще говоря, „у »y» есть следующий элемент“. Как и у всех формул, у неё есть свой номер Гёделя – некое большое целое число, назовём его m.
Теперь введём число m в формулу вместо символа y. Получится новая формула (∃x)(x = sm), означающая „у m есть следующий элемент“. Как назвать номер Гёделя для этой формулы? Нам нужно передать три особенности: мы начали с формулы, имеющей номер Гёделя m.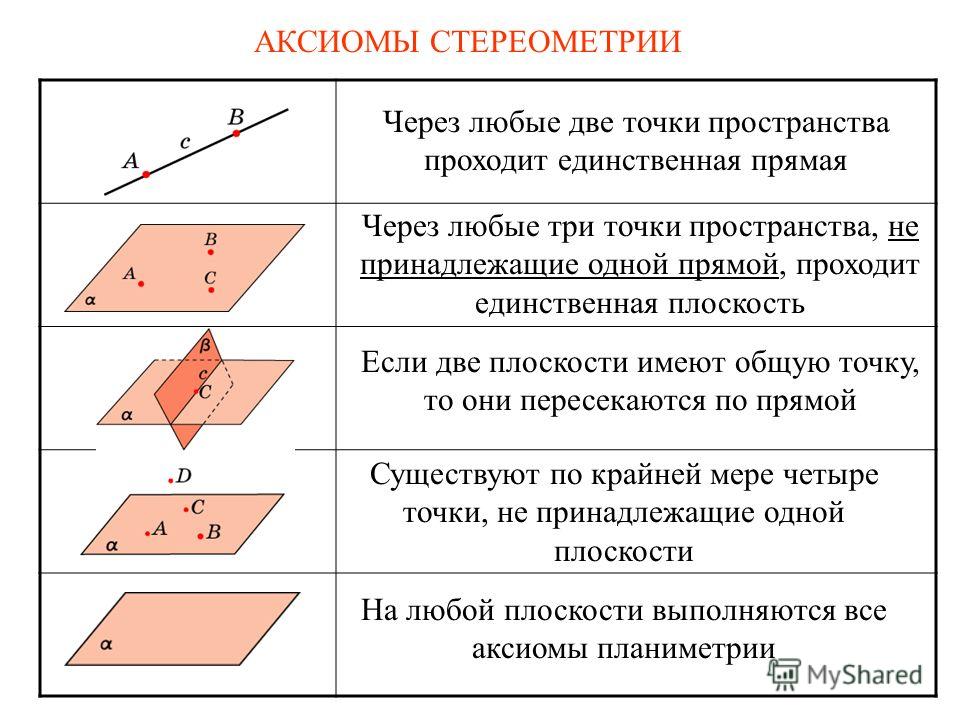 В ней мы заменили символ y на символ m. И, согласно ранее описанной схеме сопоставления, номер Гёделя у символа y равен 17. Давайте тогда обозначим номер Гёделя новой формулы sub(m, m, 17).
В ней мы заменили символ y на символ m. И, согласно ранее описанной схеме сопоставления, номер Гёделя у символа y равен 17. Давайте тогда обозначим номер Гёделя новой формулы sub(m, m, 17).
Подстановка формирует основу доказательства Гёделя.
Студент Курт Гёдель в Вене. Теоремы о неполноте он опубликовал в 1931 году, через год после получения диплома.
Он рассмотрел следующее математическое утверждение: „Формулу с номером Гёделя sub(y, y, 17) нельзя доказать“. Вспоминая только что принятые нами обозначения, мы знаем, что формулу с номером Гёделя sub(y, y, 17) мы получаем, взяв формулу с номером Гёделя y (некая неизвестная переменная) и подставив эту переменную y везде, где в формуле стоит символ с номером Гёделя, равным 17 (то есть, везде, где встречается y).
Голова уже начинает кружиться, но, тем не менее, мы определённо можем перевести наше метаматематическое утверждение, „формулу с номером Гёделя sub(y, y, 17) нельзя доказать“, в формулу с уникальным номером Гёделя. Назовём его n.
Назовём его n.
И последний этап подстановок: Гёдель создаёт новую формулу, подставляя число n везде, где в предыдущей формуле стоит y. Его новая формула получается следующей: „Формулу с номером Гёделя sub(n, n, 17) нельзя доказать“. Назовём эту формулу G.
У G, естественно, есть номер Гёделя. Каков этот номер? Вуаля – он должен равняться sub(n, n, 17). По определению, sub(n, n, 17) – это номер Гёделя для формулы, которая получается путём взятия формулы с номером Гёделя n и подстановки n везде, где в формуле встречается символ с номером Гёделя, равным 17. И G именно такая формула и есть! Поскольку целые числа раскладываются на простые множители уникальным способом, нам становится понятно, что формула G говорит нам только о самой формуле G, и более ни о какой другой.
G говорит о том, что её саму нельзя доказать.
Но можно ли доказать G? Если бы это было возможно, это означало бы, что существует некая последовательность формул, доказывающих формулу с номером Гёделя, равным sub(n, n, 17).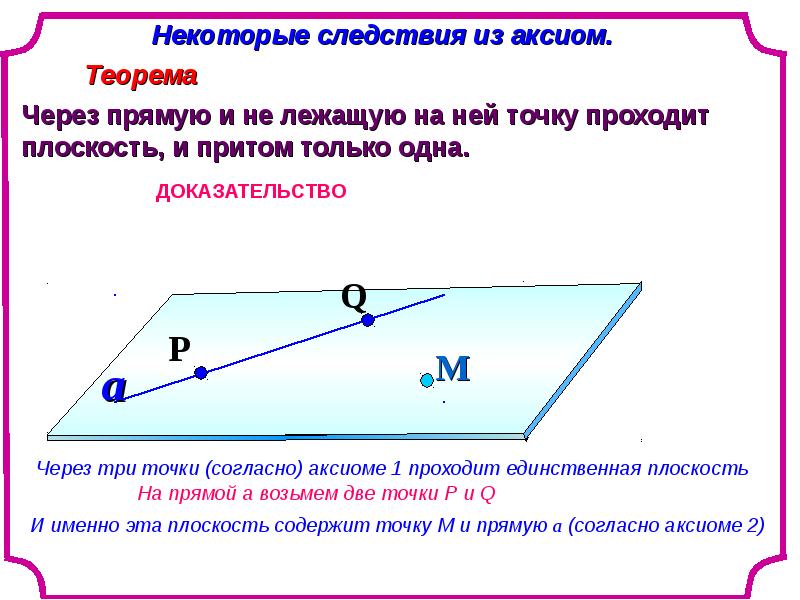 Но это противоположность формулы G, утверждающей, что такого доказательства не существует. Противоположные утверждения, G и ~G, в непротиворечивой системе аксиом не могут быть одновременно истинными. Поэтому G должна быть недоказуемой.
Но это противоположность формулы G, утверждающей, что такого доказательства не существует. Противоположные утверждения, G и ~G, в непротиворечивой системе аксиом не могут быть одновременно истинными. Поэтому G должна быть недоказуемой.
Однако, несмотря на то, что G доказать нельзя, она определённо правдива. G говорит, что „формулу с номером Гёделя sub(n, n, 17) нельзя доказать“, а именно это мы и установили! Поскольку G – истинное, но недоказуемое утверждение, существующее в рамках аксиоматической системы, которую мы использовали для его построения, эта система неполна.
Можно подумать, что мы можем просто добавить некую дополнительную аксиому, использовать её для доказательства G, и разрешить этот парадокс. Но это невозможно. Гёдель показал, что дополненная система аксиом позволит создать новую истинную формулу G’ по той же схеме, что и ранее, которую нельзя будет доказать в рамках новой, дополненной системы. Пытаясь построить полную математическую систему, вы будете лишь безуспешно гоняться за собственным хвостом.
Отсутствие доказательства непротиворечивости
Теперь мы знаем, что если набор аксиом непротиворечив, он неполон. Это первая теорема Гёделя о неполноте. Из неё легко следует вторая – ни один набор аксиом не может доказать свою непротиворечивость.
Что означало бы, если бы набор аксиом мог доказать, что он никогда не вызовет противоречий? Это означало бы, что существует последовательность формул, построенных на этих аксиомах, доказывающих формулу, которая метаматематически означает „этот набор аксиом непротиворечив“. Но тогда, согласно первой теореме, этот набор аксиом обязательно был бы неполным.
Однако сказать, что „набор аксиом неполон“, это то же самое, что сказать „существует истинная формула, которую нельзя доказать“. А это равнозначно нашей формуле G. А мы знаем, что аксиомы не могут доказать G.
Так Гёдель построил доказательство от противного: если бы набор аксиом мог доказать собственную непротиворечивость, тогда мы могли бы доказать G. Но мы этого сделать не можем. Следовательно, ни один набор аксиом не доказывает собственную непротиворечивость.
Следовательно, ни один набор аксиом не доказывает собственную непротиворечивость.
Доказательство Гёделя убило поиски непротиворечивой и полной математической системы. Математики „не смогли осознать всю глубину“ неполноты, писали Нагель и Ньюмен в 1958. И сегодня это утверждение остаётся истинным.
См. также:
Пределы доказуемости
Грегори Чейтин
«В мире науки» №6, 2006
Из идей сложности и случайности, впервые высказанных Готфридом Лейбницем в его «Рассуждении о метафизике» (1686), и их подтверждения в современной теории информации следует, что невозможно создать «самую общую теорию всего» в математике.
В 1956 году журнал Scientific American опубликовал статью Эрнста Нагеля (Ernest Nagel) и Джеймса Ньюмана (James R. Newman) «Доказательство Гёделя». Через два года ее авторы выпустили одноименную книгу, которая переиздается до сих пор. В те дни я был еще ребенком, но до сих пор помню трепет, который испытал, открыв ее в Нью-йоркской публичной библиотеке.
Меня поразило то, как Курт Гёдель (Kurt Gödel) использовал математику, чтобы показать, что ее собственные возможности ограничены. Он опроверг высказанное около столетия назад Давидом Гильбертом утверждение о существовании полной теории математики, т.е. конечной совокупности принципов, из которых с помощью последовательного использования правил математической логики можно вывести все положения математики. Гёдель показал, что существуют истинные математические утверждения, которые не могут быть доказаны таким образом. Его выводы основаны на двух самоотносимых парадоксах: «данное утверждение ложно» и «данное утверждение недоказуемо». (Более подробные сведения о теореме неполноты Гёделя можно найти на сайте Scientific American.)
Всю жизнь я разбирался с доказательством Гёделя и теперь, полвека спустя, издал собственную книжку. В какой-то степени это моя версия книги Нагеля и Ньюмана, однако доказательство Гёделя — не главная ее тема. Моя работа основана на измерении информации и доказательстве того, что некоторые математические факты не удается втиснуть в теорию, потому что они слишком сложны.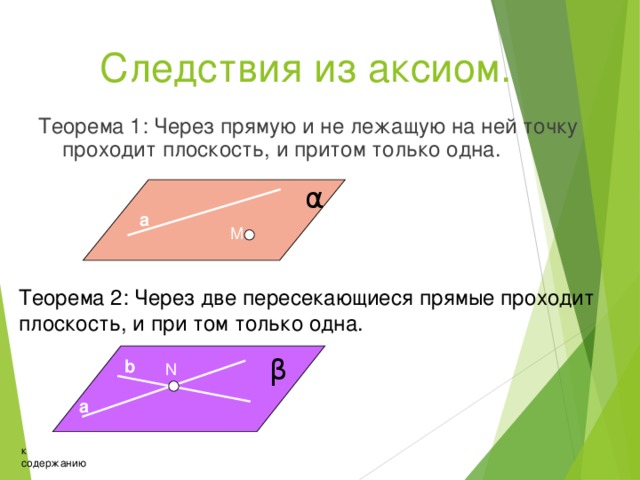 Согласно моему подходу, Гёдель открыл только верхушку айсберга: существует бесконечное множество верных математических теорем, которые невозможно доказать, исходя из конечной системы аксиом.
Согласно моему подходу, Гёдель открыл только верхушку айсберга: существует бесконечное множество верных математических теорем, которые невозможно доказать, исходя из конечной системы аксиом.
Сложность и законы науки
В 1686 году было издано философское эссе Готфрида Лейбница (Gottfried W. Leibniz) «Рассуждения о метафизике» (Discours de métaphysique), в котором поставлен вопрос: как отличить факты, которые можно описать неким законом, от фактов, никаким законам не подчиняющихся? В четвертом разделе своего эссе Лейбниц высказал очень простую и глубокую мысль: теория должна быть проще данных, которые она объясняет, иначе она не объясняет ничего. Концепция научного закона становится бессмысленной, если допускает неограниченный уровень математической сложности, потому что в таком случае всегда можно сформулировать закон независимо от того, насколько случайны и беспорядочны факты. И наоборот, если единственный закон, объясняющий какие-то данные, оказывается слишком сложным, то рассматриваемые данные на самом деле не подчиняются никакому закону.
Современная математическая теория алгоритмической информации позволила дать точные количественные определения понятиям сложности и простоты. Обычная теория информации определяет объем информации числом битов, необходимых для ее кодирования. Например, для кодирования простого ответа «да/нет» нужен один бит. В отличие от этого, объем алгоритмической информации определяется длиной компьютерной программы, необходимой для генерации данных. Минимальное число битов, необходимых для хранения программы, называется количеством алгоритмической информации данных. Например, бесконечный ряд натуральных чисел 1, 2, 3,… содержит очень мало алгоритмической информации: все числа ряда можно получить с помощью коротенькой компьютерной программы. Не имеет значения, сколько времени понадобится для выполнения вычислений и какой объем памяти придется использовать, важна лишь длина программы в битах. (Разумеется, точное значение количества алгоритмической информации зависит от выбранного языка программирования, однако для рассматриваемых в данной статье вопросов это несущественно.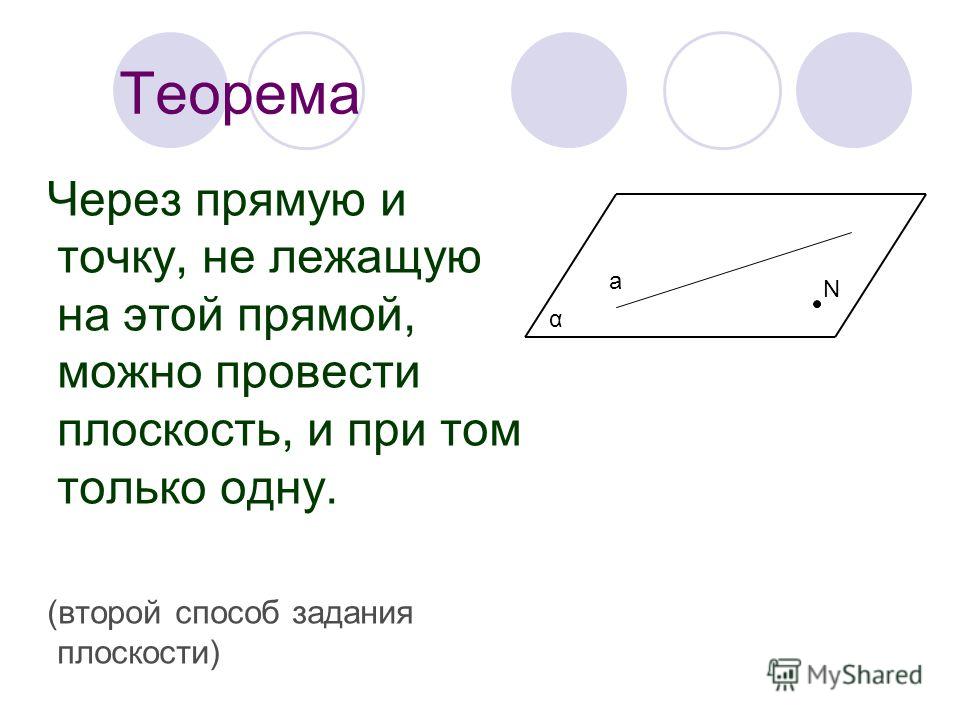 )
)
В качестве другого примера возьмем число π, равное 3,14159… Количество алгоритмической информации в нем тоже невелико: для последовательного вычисления всех его знаков нужен довольно короткий алгоритм. А вот случайное число, содержащее всего миллион знаков, скажем, 1,341285…64, характеризуется гораздо бóльшим количеством алгоритмической информации. Поскольку в таком числе нет определяющей структуры, длина самой короткой программы, необходимой для его написания, будет близка к длине самого числа:
Начать
Напечатать «1,341285…64»
Конец
(В программу должны быть включены все цифры, замененные многоточием.) Никакая более короткая программа не позволит рассчитать подобную последовательность цифр: ее невозможно сжать, в ней нет избыточности. Самое лучшее, что можно сделать, — просто передать ее, как она есть. Такие последовательности называются неприводимыми или алгоритмически случайными.
Как же соотносятся вышесказанное с научными законами и фактами? Идея заключается в том, чтобы взглянуть на науку глазами программиста: научная теория подобна компьютерной программе, предсказывающей результаты наблюдений, т. е. экспериментальные данные. Такая точка зрения опирается на два фундаментальных принципа. Согласно первому («бритва Оккама»), из двух теорий, объясняющих некоторые данные, следует предпочесть более простую. Иначе говоря, наилучшей теорией является самая короткая программа, позволяющая рассчитать результаты наблюдений. Второй принцип, изложенный Лейбницем, в современных понятиях звучит так: теория, объем которой в битах равен количеству объясняемых ею данных, бесполезна, поскольку теорией такого размера можно описать совершенно случайные данные. Полезная теория обеспечивает сокращение количества информации: осмысление данных — это их сжатие в краткие алгоритмические описания. Чем проще теория, тем лучше понимание сути явления.
е. экспериментальные данные. Такая точка зрения опирается на два фундаментальных принципа. Согласно первому («бритва Оккама»), из двух теорий, объясняющих некоторые данные, следует предпочесть более простую. Иначе говоря, наилучшей теорией является самая короткая программа, позволяющая рассчитать результаты наблюдений. Второй принцип, изложенный Лейбницем, в современных понятиях звучит так: теория, объем которой в битах равен количеству объясняемых ею данных, бесполезна, поскольку теорией такого размера можно описать совершенно случайные данные. Полезная теория обеспечивает сокращение количества информации: осмысление данных — это их сжатие в краткие алгоритмические описания. Чем проще теория, тем лучше понимание сути явления.
Достаточная причина
Лейбниц, живший за два с половиной века до появления компьютерных программ, очень близко подошел к современному понятию алгоритмической информации. Лейбниц знал, что все можно представить в виде двоичных кодов, и создал одно из первых вычислительных устройств; рассматривая понятия сложности и простоты, он осознавал огромный потенциал вычислений.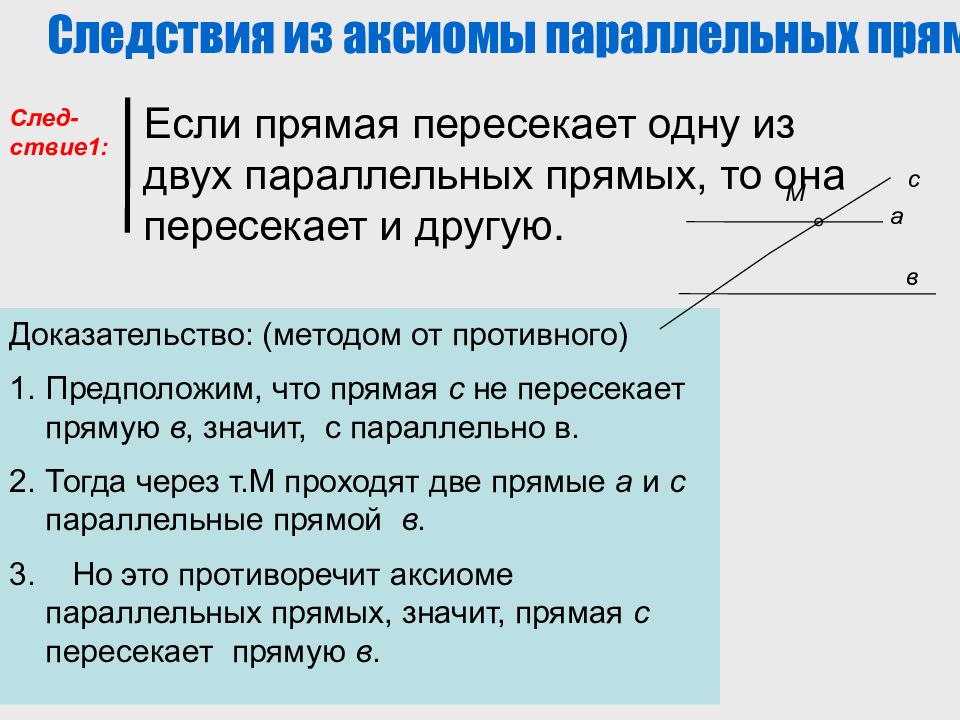 Если бы Лейбниц объединил все известные ему элементы, то, скорее всего, усомнился бы в одном из устоев своей философии — принципе достаточной причины, согласно которому все происходящее имеет причину. Более того, если какое-то положение истинно, то оно истинно по какой-то причине. Бывает, что в суете и хаосе повседневной жизни в это трудно поверить. Даже если мы не всегда можем увидеть причину (возможно потому, что цепочка рассуждений слишком длинна и запутанна), ее видит Бог. Вот и всё! Здесь Лейбниц соглашался с древнегреческими авторами этой идеи.
Если бы Лейбниц объединил все известные ему элементы, то, скорее всего, усомнился бы в одном из устоев своей философии — принципе достаточной причины, согласно которому все происходящее имеет причину. Более того, если какое-то положение истинно, то оно истинно по какой-то причине. Бывает, что в суете и хаосе повседневной жизни в это трудно поверить. Даже если мы не всегда можем увидеть причину (возможно потому, что цепочка рассуждений слишком длинна и запутанна), ее видит Бог. Вот и всё! Здесь Лейбниц соглашался с древнегреческими авторами этой идеи.
Математики, несомненно, безоговорочно принимают принцип достаточной причины Лейбница, потому что всегда стремятся всё доказать. Даже если истинность теоремы очевидна, и миллионы примеров подтверждают ее, математики все равно требуют обобщенного доказательства, на меньшее они не согласны. И здесь концепция алгоритмической информации может внести удивительный вклад в философские рассуждения об источниках и пределах познания. Она показывает, что некоторые математические факты истинны безо всяких причин, и бросает вызов принципу достаточной причины. Как будет показано ниже, существует бесконечное число неприводимых математических фактов, истинность которых нельзя объяснить никакой теорией. Они неприводимы не только вычислительно, но и логически. «Доказать» эти факты можно только одним способом: признать их аксиомами без всяких рассуждений.
Как будет показано ниже, существует бесконечное число неприводимых математических фактов, истинность которых нельзя объяснить никакой теорией. Они неприводимы не только вычислительно, но и логически. «Доказать» эти факты можно только одним способом: признать их аксиомами без всяких рассуждений.
Понятие «аксиома» тесно связано с логической неприводимостью. Аксиомы — это математические положения, которые мы считаем самоочевидными и не пытаемся доказать, исходя из более простых принципов. Все математические теории основаны на аксиомах, из которых выводятся следствия, называемые теоремами. Именно так поступал Евклид два тысячелетия назад: его труды по геометрии стали классическим примером математического изложения.
В древней Греции, чтобы убедить сограждан проголосовать именно так, а не иначе, вы должны были бы привести им свои доводы. Вероятно, именно поэтому греки пришли к мысли, что математические положения нужно доказывать, а не выводить опытным путем. (В отличие от греков, древнейшие цивилизации Месопотамии и Египта, похоже, полагались на эксперимент. ) Метод логических рассуждений оказался чрезвычайно плодотворным: с его помощью были созданы современная математика, математическая физика и все точные науки, включая технологию создания компьютеров — в высшей степени математичных и логичных машин. Утверждаю ли я, что подход, на котором математика и вся наука строились в течение двух тысячелетий, терпит крах? В каком-то смысле да. Моим контрпримером, иллюстрирующим ограниченность возможностей логики и рассуждений, моим источником бесконечного потока недоказуемых математических положений является число, которое я назвал «омега» (Ω).
) Метод логических рассуждений оказался чрезвычайно плодотворным: с его помощью были созданы современная математика, математическая физика и все точные науки, включая технологию создания компьютеров — в высшей степени математичных и логичных машин. Утверждаю ли я, что подход, на котором математика и вся наука строились в течение двух тысячелетий, терпит крах? В каком-то смысле да. Моим контрпримером, иллюстрирующим ограниченность возможностей логики и рассуждений, моим источником бесконечного потока недоказуемых математических положений является число, которое я назвал «омега» (Ω).
Число
Ω
Первый шаг к открытию числа Ω был сделан в знаменитой статье, опубликованной ровно через 250 лет после издания эссе Лейбница. В 1936 году на страницах «Трудов Лондонского математического общества» (Proceedings of the London Mathematical Society) Алан Тьюринг впервые представил математическую модель простой универсальной вычислительной машины. Кроме того, он задался вопросом: можно ли определить, остановится когда-нибудь компьютерная программа или нет? Так была сформулирована знаменитая проблема останова.
Разумеется, запустив программу, вы можете со временем обнаружить, что она остановилась. Фундаментальная проблема заключается в том, чтобы решить, когда вы сдадитесь и престанете ждать, если программа не останавливается. Для множества частных случаев она может быть решена, но Тьюринг показал, что общего решения не существует. Никакой алгоритм и никакая математическая теория не позволят определить, какая программа остановится, а какая нет. (Современное доказательство данного положения Тьюринга можно найти на сайте Scientific American.) Кстати, употребляя слово «программа» в современном смысле, я имею в виду совокупность самой компьютерной программы и данных, которые она обрабатывает.
Следующим шагом на пути к числу Ω становится рассмотрение множества всех возможных программ. Остановится ли когда-нибудь выбранная случайным образом программа? Вероятность останова и есть Ω. Определим сначала, как осуществить случайный выбор программы. Программа представляет собой последовательность битов, поэтому для выбора значения каждого последующего бита будем просто бросать монету. Сколько битов должна содержать программа? Будем бросать монету до тех пор, пока компьютер не перестанет запрашивать следующий бит. Число Ω есть вероятность того, что при введении такой случайной последовательности битов машина когда-нибудь остановится. (Численное значение Ω зависит от выбора языка программирования, но удивительные свойства этого числа с ним не связаны. Когда же язык выбран, Ω приобретает определенную величину, так же, как число π или число 5.)
Сколько битов должна содержать программа? Будем бросать монету до тех пор, пока компьютер не перестанет запрашивать следующий бит. Число Ω есть вероятность того, что при введении такой случайной последовательности битов машина когда-нибудь остановится. (Численное значение Ω зависит от выбора языка программирования, но удивительные свойства этого числа с ним не связаны. Когда же язык выбран, Ω приобретает определенную величину, так же, как число π или число 5.)
Поскольку число Ω выражает вероятность, оно должно быть больше нуля, но меньше единицы, т.к. некоторые программы останавливаются, а некоторые – нет. Число Ω, записанное в двоичном коде, будет иметь вид вроде 0,1110100… Последовательность битов после запятой неприводима, а сами они оказываются неприводимыми математическими фактами (каждый факт состоит в том, является ли данный бит нулем или единицей).
Число Ω можно определить как бесконечную сумму, и каждая программа длиной N битов вносит в нее свой вклад, равный ½N. Иными словами, каждая N-битовая программа, которая останавливается, добавляет единицу к N-ному биту двоичного представления числа Ω. Сложив все биты, соответствующие остановившимся программам, мы можем получить точное значение Ω. Создается впечатление, что Ω можно вычислить точно, как √2 или π. Однако это не так: число Ω строго определено и имеет вполне конкретное значение, но рассчитать его невозможно, поскольку это позволило бы решить проблему останова, у которой действительно нет решения. Если говорить конкретнее, знание первых N битов числа Ω позволяет определить, остановится ли когда-нибудь любая программа длиной до N битов, из чего следует, что для нахождения N битов числа Ω требуется программа длиной не менее N битов. Заметьте, я не утверждаю, что нельзя определить некоторое число битов числа Ω. Например, зная, что компьютерные программы 0, 10 и 110 останавливаются, мы можем говорить, что с точностью до первых трех битов Ω имеет вид 0,111.
Иными словами, каждая N-битовая программа, которая останавливается, добавляет единицу к N-ному биту двоичного представления числа Ω. Сложив все биты, соответствующие остановившимся программам, мы можем получить точное значение Ω. Создается впечатление, что Ω можно вычислить точно, как √2 или π. Однако это не так: число Ω строго определено и имеет вполне конкретное значение, но рассчитать его невозможно, поскольку это позволило бы решить проблему останова, у которой действительно нет решения. Если говорить конкретнее, знание первых N битов числа Ω позволяет определить, остановится ли когда-нибудь любая программа длиной до N битов, из чего следует, что для нахождения N битов числа Ω требуется программа длиной не менее N битов. Заметьте, я не утверждаю, что нельзя определить некоторое число битов числа Ω. Например, зная, что компьютерные программы 0, 10 и 110 останавливаются, мы можем говорить, что с точностью до первых трех битов Ω имеет вид 0,111. Дело в том, что первые N битов Ω нельзя вычислить с помощью программы, которая была бы существенно короче N битов.
Дело в том, что первые N битов Ω нельзя вычислить с помощью программы, которая была бы существенно короче N битов.
Самое главное, что Ω дает нам бесконечное число неприводимых битов. Любая программа конечной длины, сколько миллиардов битов она бы ни содержала, не поможет нам определить оставшиеся биты, которых бесконечно много. Иными словами, при любом конечном наборе аксиом мы имеем бесконечное число истин, которые не могут быть доказаны с помощью этого набора.
Из неприводимости числа Ω следует, что всеобъемлющей математической теории существовать не может. Бесконечное множество битов Ω составляет бесконечное множество математических фактов (является ли каждый выбранный бит единицей или нулем), которые не могут быть выведены из каких бы то ни было принципов, более простых, чем сама последовательность битов. Значит, сложность математики бесконечна, тогда как любая отдельная теория «всего на свете» характеризуется конечной сложностью и, следовательно, не может охватить все богатство мира математических истин. Из сказанного отнюдь не следует, что от доказательств нет никакого толка, и я ни в коем случае не против логических рассуждений. На самом деле, неприводимые принципы (аксиомы) всегда составляли часть математики. Просто число Ω показывает, что их гораздо больше, чем предполагалось ранее.
Из сказанного отнюдь не следует, что от доказательств нет никакого толка, и я ни в коем случае не против логических рассуждений. На самом деле, неприводимые принципы (аксиомы) всегда составляли часть математики. Просто число Ω показывает, что их гораздо больше, чем предполагалось ранее.
Возможно, математикам не нужно пытаться все доказать. Иногда им следует просто добавлять новые аксиомы, когда дело доходит до неприводимых фактов. Проблема в том, чтобы понять, что они неприводимы, и признать, что их невозможно доказать. Однако математики никогда не сдадутся, в отличие от физиков, которые всегда готовы обойтись правдоподобными рассуждениями вместо строгих доказательств, и охотно выводят новые законы, чтобы осмыслить свежие экспериментальные данные. Возникает интересный вопрос: похожа ли математика на физику?
Математика и физика
Принято считать, что математика и физика совершенно не похожи друг на друга. Физики описывают мир, исходя из результатов экспериментов и наблюдений. Законы, управляющие Вселенной, будь то законы Ньютона или Стандартная модель физики элементарных частиц, должны устанавливаться эмпирически и затем приниматься за аксиомы, которые невозможно доказать логическим путем, а можно лишь проверить экспериментально. Математики же в некотором смысле независимы от мира. Их выводы и теоремы, например, свойства целых или вещественных чисел, никак не зависят от окружающей нас реальности. Математические истины должны быть верны в любом мире. И все же определенное сходство есть. В физике, и вообще в естественных науках, ученые формулируют законы, сублимируя результаты наблюдений. Затем они показывают, как результаты наблюдений могут быть выведены из получившихся законов. В математике происходит нечто подобное: математики сжимают результаты вычислительных экспериментов в аксиомы, а затем выводят из них теоремы.
Законы, управляющие Вселенной, будь то законы Ньютона или Стандартная модель физики элементарных частиц, должны устанавливаться эмпирически и затем приниматься за аксиомы, которые невозможно доказать логическим путем, а можно лишь проверить экспериментально. Математики же в некотором смысле независимы от мира. Их выводы и теоремы, например, свойства целых или вещественных чисел, никак не зависят от окружающей нас реальности. Математические истины должны быть верны в любом мире. И все же определенное сходство есть. В физике, и вообще в естественных науках, ученые формулируют законы, сублимируя результаты наблюдений. Затем они показывают, как результаты наблюдений могут быть выведены из получившихся законов. В математике происходит нечто подобное: математики сжимают результаты вычислительных экспериментов в аксиомы, а затем выводят из них теоремы.
Если бы Гильберт оказался прав, то математика была бы замкнутой системой, в которой нет места новым идеям. Существовала бы статичная замкнутая теория, объясняющая в математике все, и это было бы похоже на диктатуру. Чтобы математика развивалась, нужны новые идеи и простор для творчества. Недостаточно усердно работать, выводя все возможные следствия из фиксированного числа базовых принципов. Лично мне больше нравятся открытые системы, я не люблю жестких, авторитарных способов мышления.
Чтобы математика развивалась, нужны новые идеи и простор для творчества. Недостаточно усердно работать, выводя все возможные следствия из фиксированного числа базовых принципов. Лично мне больше нравятся открытые системы, я не люблю жестких, авторитарных способов мышления.
Имре Лакатош (Imre Lakatos), бежавший в 1956 году из Венгрии и впоследствии занимавшийся философией науки в Англии, тоже считал, что математика похожа на физику. Он ввел понятие квазиэмпиричности, чтобы показать, что и математике не чужды эксперименты. Например, еще в 1742 году Кристиан Гольдбах опытным путем пришел к предположению, что любое четное число больше двух можно представить в виде суммы двух простых чисел. Предположение Гольдбаха успешно проверено для чисел до 1014, но строго не доказано. Мне кажется, что математика квазиэмпирична. Иными словами, она отличается от физики (которая истинно эмпирична), но, вероятно, не так сильно, как полагает большинство людей.
Новые аксиомы
Идея добавления новых аксиом не чужда математикам. Возьмем для примера пятый постулат Евклида: через выбранную точку, лежащую вне прямой, можно провести только одну прямую, параллельную данной. Столетиями геометры ломали голову, пытаясь доказать это, исходя из остальных постулатов Евклида. Не удалось. Наконец, математики поняли, что пятую аксиому можно заменить и получить неевклидову геометрию криволинейных пространств, в частности сферического и седлообразного. Другим примером может служить закон исключенного среднего в логике и аксиома выбора в теории множеств, которыми охотно пользуется в своих доказательствах большинство математиков. Но ведь есть ученые, которые их не признают и исследуют так называемую интуиционистскую логику и конструктивистскую математику. Оказывается, математика пока не стала монолитной системой абсолютных истин!
Возьмем для примера пятый постулат Евклида: через выбранную точку, лежащую вне прямой, можно провести только одну прямую, параллельную данной. Столетиями геометры ломали голову, пытаясь доказать это, исходя из остальных постулатов Евклида. Не удалось. Наконец, математики поняли, что пятую аксиому можно заменить и получить неевклидову геометрию криволинейных пространств, в частности сферического и седлообразного. Другим примером может служить закон исключенного среднего в логике и аксиома выбора в теории множеств, которыми охотно пользуется в своих доказательствах большинство математиков. Но ведь есть ученые, которые их не признают и исследуют так называемую интуиционистскую логику и конструктивистскую математику. Оказывается, математика пока не стала монолитной системой абсолютных истин!
Другой очень интересной аксиомой может стать утверждение «P не равно NP», где P и NP – названия классов задач. К классу NP относятся задачи, для которых предлагаемое решение можно проверить очень быстро. Например, для задачи «найти множители числа 8 633» предлагаемое решение «97 и 89» быстро проверяется простым перемножением. (Существует строгое определение понятия «быстро», но подробности здесь не имеют значения.) Класс P составляют задачи, которые можно быстро решить, не имея предварительного предположения. Вопрос, ответа на который не знает никто, состоит в том, можно ли быстро решить любую задачу класса NP. (Есть ли способ быстро найти множители числа 8 633?) Иначе говоря, тождественны ли классы P и NP? Это один из пунктов списка «Проблем тысячелетия» Математического института Клэя (Clay Millennium Prize Problem), за решение каждой из которых назначена награда в $1 млн.
Например, для задачи «найти множители числа 8 633» предлагаемое решение «97 и 89» быстро проверяется простым перемножением. (Существует строгое определение понятия «быстро», но подробности здесь не имеют значения.) Класс P составляют задачи, которые можно быстро решить, не имея предварительного предположения. Вопрос, ответа на который не знает никто, состоит в том, можно ли быстро решить любую задачу класса NP. (Есть ли способ быстро найти множители числа 8 633?) Иначе говоря, тождественны ли классы P и NP? Это один из пунктов списка «Проблем тысячелетия» Математического института Клэя (Clay Millennium Prize Problem), за решение каждой из которых назначена награда в $1 млн.
Большинство специалистов по вычислительной технике убеждено, что P не равно NP, но строгое доказательство пока не найдено. Истинность такого предположения подтверждается множеством эмпирических свидетельств, но можно ли на этом основании принять его в качестве аксиомы? Специалисты по вычислительной технике именно так и поступили. Правда, остается вопрос о надежности некоторых широко применяемых криптографических систем: считается, что взломать их невозможно, но никто не может этого доказать.
Правда, остается вопрос о надежности некоторых широко применяемых криптографических систем: считается, что взломать их невозможно, но никто не может этого доказать.
Экспериментальная математика
На стыке физики и математики возникла экспериментальная математика: открытие новых математических закономерностей путем компьютерной обработки большого числа примеров. Такой подход не столь убедителен, как короткое доказательство, но может быть убедительнее длинного, сложного доказательства и в некоторых случаях вполне приемлем. В прошлом данную концепцию отстаивали и Дьердь Пойа (George Pólya), и Лакатош, убежденные сторонники эвристических методов и квазиэмпирической природы математики. Он применяется и обосновывается в книге «Новый вид науки» (A New Kind of Science) Стивена Вольфрама (Stephen Wolfram), вышедшей в 2002 году.
Масштабные компьютерные вычисления могут быть очень убедительными, но избавляют ли они от необходимости доказательств? И да, и нет. Вычисления и доказательства дают свидетельства разного рода. В особо важных случаях я считаю необходимыми и те, и другие, поскольку доказательства могут содержать ошибки, а компьютерные вычисления могут, по несчастью, быть остановлены как раз перед обнаружением контрпримера, который опроверг бы предполагаемый вывод.
Вычисления и доказательства дают свидетельства разного рода. В особо важных случаях я считаю необходимыми и те, и другие, поскольку доказательства могут содержать ошибки, а компьютерные вычисления могут, по несчастью, быть остановлены как раз перед обнаружением контрпримера, который опроверг бы предполагаемый вывод.
Рассмотренные вопросы чрезвычайно интересны, но далеки от решения. Со времени публикации статьи о доказательстве Гёделя прошло 50 лет, а сейчас, в 2006 году, мы все еще не знаем, насколько серьезна неполнота, и не следует ли из-за нее пересмотреть математические методы. Возможно, через 50 лет ответ будет найден.
Дополнительная литература:
- Главу о Лейбнице см. в книге: Men of Mathematics. E.T. Bell. Reissue. Touchstone, 1986.
- Более полные сведения о квазиэмпирическом взгляде на математику см.: New Directions in the Philosophy of Mathematics. Edited by Thomas Tymoczko. Princeton University Press, 1998.
- Gödel’s Proof.
 Revised edition. E. Nagel, J.R. Newman and D.R. Hofstadter. New York University Press, 2002.
Revised edition. E. Nagel, J.R. Newman and D.R. Hofstadter. New York University Press, 2002. - Mathematics by Experiment: Plausible Reasoning in the 21st Century. J. Borwein and D. Bailey. A.K. Peters, 2004.
- О философии Гёделя и связи его работ с трудами Лейбница см.: Incompleteness: The Proof and Paradox of Kurt Gödel. Rebecca Goldstein. W.W. Norton 2005.
- Meta Math!: The Quest for Omega. Gregory Chaitin. Pantheon Books, 2005.
- Краткие биографии математиков доступны на сайте Школы математики и статистики Университета Св. Эндрю (Шотландия).
- Домашняя станица Грегори Чейтина.
Разница между аксиомой и теоремой
Ключевое отличие: Аксиома и теорема — это утверждения, которые чаще всего используются в математике или физике. Аксиома — это утверждение, которое принимается за истину. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, которое было доказано.
Аксиома и теорема — это утверждения, которые чаще всего используются в математике или физике. Аксиома — это утверждение, которое принимается за истину. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, которое было доказано.
Аксиома — это утверждение, которое принимается за истину. Это не нужно доказывать. Теорема, с другой стороны, является утверждением, которое было доказано.
Согласно Dictionary.com, аксиома определяется как:
- Самоочевидная истина, не требующая доказательств.
- Общепризнанный принцип или правило.
- Логика, Математика. Утверждение, которое предполагается без доказательства ради изучения последствий, вытекающих из него.
По сути, аксиомы — это предположения, которые не нужно доказывать. Они обычно принимаются как истинные, либо потому, что в них нет противоречий, либо потому, что мы, очевидно, знаем, что это правда. Аксиома слова происходит от греческого слова, которое означает «то, что считается достойным или подходящим» или «то, что оценивается как очевидное». Аксиома может иногда использоваться взаимозаменяемо с постулатом или предположением.
Теорема, с другой стороны, нуждается в доказательстве. Dictionary.com определяет теорему как:
- Математика.
 Теоретическое суждение, утверждение или формула, воплощающие что-то, что нужно доказать из других суждений или формул.
Теоретическое суждение, утверждение или формула, воплощающие что-то, что нужно доказать из других суждений или формул. - Правило или закон, особенно тот, который выражается уравнением или формулой.
- Логика. Предложение, которое может быть выведено из предпосылок или предположений системы.
- Идея, убеждение, метод или утверждение обычно принимаются как истинные или стоящие без доказательств.
Теорема — это утверждение, которое было доказано путем тестирования или расчета. Это может быть доказано на основе теорем, которые были ранее доказаны или на основе аксиом. Теоремы состоят из двух частей: гипотезы и выводы.
НОУ ИНТУИТ | Лекция | Теории и модели
Аннотация: Рассматриваются аксиомы равенства на произвольных сигнатурах, критерии существования для соответствующих теории, вопросы полноты теорий
Аксиомы равенства
Пусть сигнатура включает в себя двуместный предикат
равенства (записываемый традиционно ). Интерпретация этой
Интерпретация этой
сигнатуры называется нормальной,если предикат равенства
интерпретируется как тождественное совпадение элементов носителя.
Возникает естественный вопрос. Пусть имеется некоторая
теория (множество замкнутых формул) в языке, сигнатура
которого включает равенство. Мы знаем что теория имеет модель
(интерпретацию, в которой все формулы из истинны) тогда и
только тогда, когда она непротиворечива. В каком случае она
имеет нормальную модель (нормальную интерпретацию, в которой все
формулы из истинны)?
Чтобы ответить на этот вопрос, введем аксиомы равенства. Пусть произвольная сигнатура. Аксиомами равенства
в сигнатуре будут формулы
(называемые аксиомами рефлексивности, симметричности и
транзитивности). Это еще не все. Для каждого функционального
символа мы формулируем аксиому равенства, которая говорит, что
его значение не меняется, если аргументы заменить на равные.
Например, для двуместного функционального символа
соответствующая аксиома выглядит так:
Для предикатных символов аксиомы равенства говорят, что
истинный предикат остается истинным, если заменить аргументы на
равные.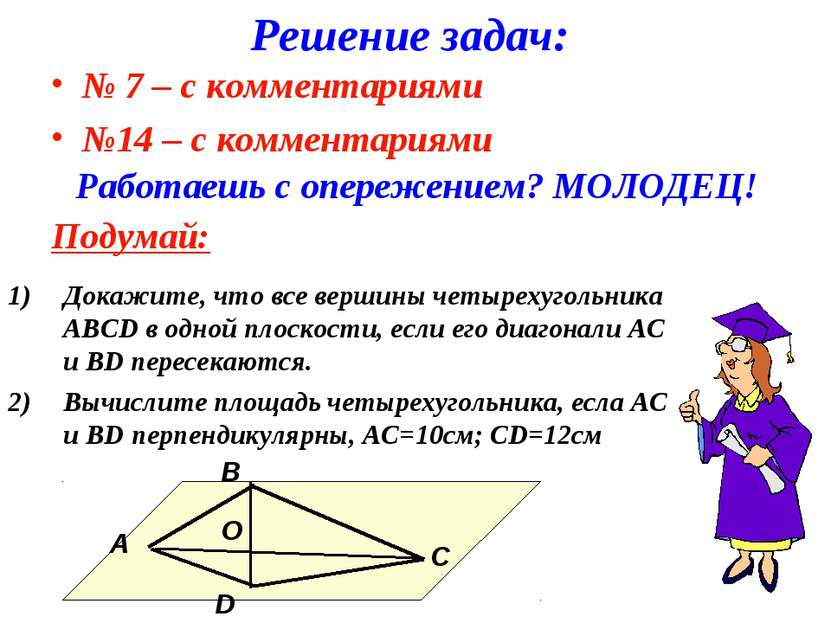 Например, для двуместного предикатного символа аксиома
Например, для двуместного предикатного символа аксиома
такова:
(Нет необходимости специально говорить, что предикат остается
ложным при замене аргументов на равные, так как равенство
симметрично.)
Теорема 59 (полноты для нормальных моделей).
Теория сигнатуры с равенством имеет
нормальную модель тогда и только тогда, когда она остается непротиворечивой
при добавлении аксиом равенства.
Прежде всего заметим, что теоремы о корректности и полноте
(раздел «Полнота исчисления предикатов») позволяют говорить о совместности вместо непротиворечивости.
В нормальной модели теории аксиомы равенства
истинны, так что в одну сторону утверждение теоремы очевидно.
Нам осталось показать, что если теория совместна с аксиомами
равенства, то она имеет нормальную модель.
Возьмем произвольную интерпретацию, в которой истинны формулы
из и аксиомы равенства. Пусть — ее носитель. В
Пусть — ее носитель. В
этой интерпретации предикат не обязан быть настоящим равенством;
он представляет собой некоторое бинарное отношение на .
Поскольку выполнены аксиомы равенства, это отношение
рефлексивно, симметрично и транзитивно (является отношением
эквивалентности). Следовательно, множество разбивается на
классы эквивалентности; множество этих классов обозначим
(его можно назвать фактор-множеством по данному отношению
эквивалентности). Класс элемента будем обозначать .
Аксиомы равенства позволяют корректно определить интерпретацию c
носителем . В самом деле, истинность аксиомы для
функционального символа (приведенной выше в качестве
примера) гарантирует, что класс зависит лишь от
классов и , но не от выбора
и внутри класса. Аналогичным образом аксиомы для предикатных символов позволяют
корректно определить предикаты на классах.
Полученная интерпретация с носителем по построению
нормальна. Осталось убедиться, что в ней истинны те же самые
Осталось убедиться, что в ней истинны те же самые
формулы, что и в (в том числе все формулы
теории ). Это почти очевидно с интуитивной точки зрения: отличается
от лишь тем, что каждый элемент представлен несколькими
равноправными копиями, которые со всех точек зрения ведут себя
одинаково.
Формально говоря, мы доказываем, что формула истинна в
интерпретации на оценке тогда и только тогда,
когда истинна в на оценке ,
при которой значение любой переменной есть класс, содержащий значение
переменной при оценке . Это легко сделать
индукцией по построению формулы .
111. Покажите, что из аксиом равенства для сигнатуры
выводится формула
если подстановка в правой части корректна. (Указание:
это очевидно следует из теоремы о полноте, но можно провести
и чисто синтаксическое рассуждение индукцией по построению
формулы .)
112. Покажите, что если теория (не обязательно с равенством)
имеет модель мощности , то она имеет и модель
любой большей мощности. (Указание: элементы модели можно
(Указание: элементы модели можно
«клонировать» в произвольном количестве.)
Из теоремы о полноте для нормальных моделей легко следует аналог
теоремы о компактности (теорема 50) для нормальных моделей.
Теорема 60 (компактности для нормальных моделей).
Если всякое конечное подмножество теории в сигнатуре
с равенством имеет нормальную модель, то и теория
имеет нормальную модель.
Любое конечное подмножество теории остается непротиворечивым
при добавлении аксиом равенства (поскольку имеет нормальную модель).
Значит, и вся теория остается непротиворечивой при
добавлении аксиом равенства (вывод противоречия использует
конечное число формул) и потому имеет нормальную модель.
113. Применив теорему о компактности, докажите, что всякий частичный
порядок может быть продолжен до линейного. (Указание. Рассмотрим
Рассмотрим
частично упорядоченное множество как модель теории, в сигнатуре
которой есть равенство, порядок и константы для всех элементов
множества, а формулами являются равенства и неравенства между
константами. Добавим к ней утверждение о сравнимости любых двух
элементов. Покажите, что любое конечное множество формул
полученной теории непротиворечиво, используя тот факт, что
частичный порядок на конечном множестве продолжается до линейного.)
114. Используя теорему о компактности, докажите, что для всякого поля сушествует его расширение , в котором всякий
многочлен с коэффициентами из имеет корень. (Указание. Утверждение о
существовании корня у многочлена с данными коэффициентами можно
записать в виде формулы. Любое конечное множество таких формул
совместно с аксиомами поля, так как можно по очереди
присоединить корни соответствующих многочленов.)
115. Пусть — множество замкнутых формул в сигнатуре с
равенством. Покажите, что замкнутая формула этой
Покажите, что замкнутая формула этой
сигнатуры истинна во всех нормальных моделях тогда и
только тогда, когда она выводима из и аксиом равенства.
Утверждение последней задачи является аналогом
теоремы 51 для теорий с равенством.
Иногда вообще рассматривают только такие теории. При этом
равенство является обязательным элементом сигнатуры, аксиомы
равенства (их число зависит от сигнатуры) считаются частью
исчисления предикатов, а интерпретации рассматриваются только
нормальные. При этом теория имеет [нормальную] модель тогда и
только тогда, когда она непротиворечива [вместе с аксиомами
равенства]; формула выводима из теории [и аксиом
равенства] тогда и только тогда, когда она верна во всех
[нормальных] моделях теории и т. п. (в квадратных скобках
указаны подразумеваемые слова).
Терминология
— Разница между аксиомами, теоремами, постулатами, следствиями и гипотезами
Исходя из логики, аксиома или постулат — это утверждение, которое считается самоочевидным. И аксиомы, и постулаты считаются истинными без каких-либо доказательств или демонстраций. По сути, то, что очевидно или заявлено как истина и принято, но не имеет доказательств, называется аксиомой или постулатом. Аксиомы и постулаты служат основой для вывода других истин.
И аксиомы, и постулаты считаются истинными без каких-либо доказательств или демонстраций. По сути, то, что очевидно или заявлено как истина и принято, но не имеет доказательств, называется аксиомой или постулатом. Аксиомы и постулаты служат основой для вывода других истин.
Древние греки осознавали разницу между этими двумя понятиями.Аксиомы — это самоочевидные предположения, общие для всех отраслей науки, а постулаты относятся к конкретной науке.
Аксиомы
Аристотель сам использовал термин «аксиома», который происходит от греческого «аксиома», что означает «считать стоящим», но также «требовать». У Аристотеля были и другие названия аксиом. Он называл их «обычными вещами» или «общими мнениями». В математике аксиомы можно разделить на «логические аксиомы» и «нелогические аксиомы».Логические аксиомы — это предложения или утверждения, которые считаются универсально истинными. Нелогические аксиомы, иногда называемые постулатами, определяют свойства для области конкретной математической теории или логические утверждения, которые используются в дедукции для построения математических теорий. «Вещи, которые равны одному и тому же, равны друг другу» — это пример известной аксиомы, установленной Евклидом.
«Вещи, которые равны одному и тому же, равны друг другу» — это пример известной аксиомы, установленной Евклидом.
Постулаты
Термин «постулат» происходит от латинского «postular», глагола, означающего «требовать».Учитель потребовал от учеников аргументировать определенные утверждения, на которых он мог основываться. В отличие от аксиом, постулаты стремятся уловить особенности конкретной структуры. «Можно провести прямую линию из любой точки в любую другую точку», «Можно построить конечную прямую непрерывно по прямой линии» и «Можно описать круг с любым центром и любым радиусом» несколько примеров постулатов, проиллюстрированных Евклидом.
В чем разница между аксиомами и постулатами?
• Аксиома обычно верна для любой области науки, в то время как постулат может быть конкретным для конкретной области.
• Невозможно доказать с помощью других аксиом, в то время как постулаты доказываются с помощью аксиом.
Терминология
— В чем именно разница между определением и аксиомой?
С точки зрения теории доказательств разницы нет.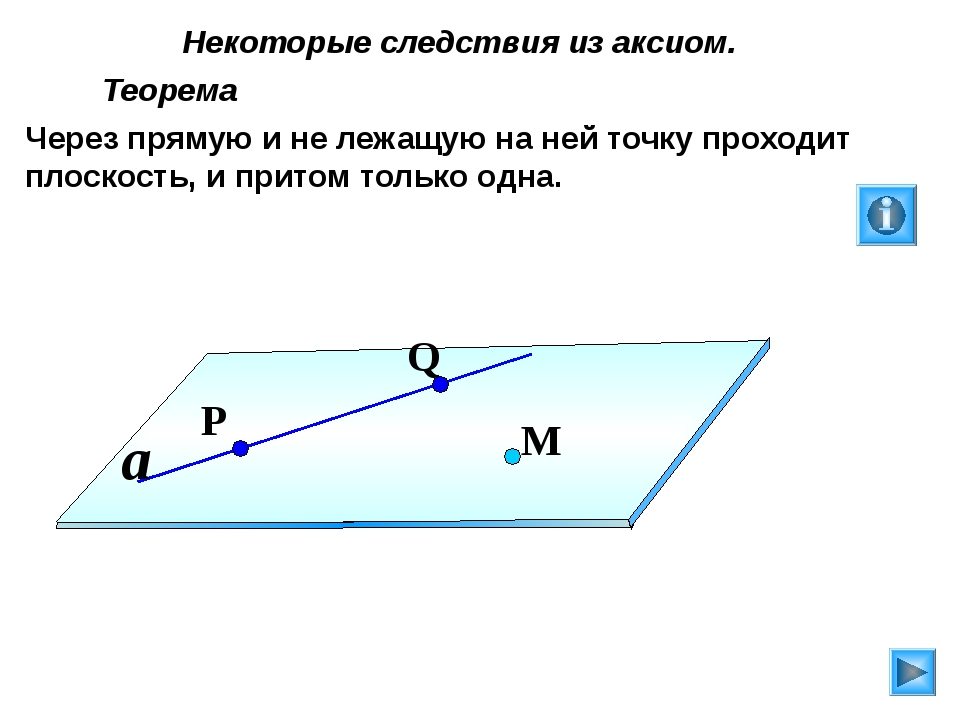 Они оба фактически заявляют об истинности чего-либо, не предоставляя доказательств этого.
Они оба фактически заявляют об истинности чего-либо, не предоставляя доказательств этого.
Разница возникает, когда применяется теория моделей, которая требуется для применения математических результатов (применяемых явно или неявно).Определение полностью содержится в математической системе. С этим нельзя не согласиться, потому что это просто артефакт того, как написана система. Иногда также можно переписать систему, чтобы исключить определение, которое является «оскорбительным».
Аксиома, с другой стороны, выходит за пределы моделируемой системы. Эти аксиомы определяют круг проблем, для которых применимы математические системы. Если кто-то не согласен с аксиомой, он просто заявляет, что математическая система не применима к определенному классу проблем, потому что вы не желаете принимать аксиомы.
С практической точки зрения, есть некоторая разница между написанием определения и написанием аксиомы. У вас есть немного больше свободы при назывании и определении определений, потому что вы полностью контролируете их значение. Когда дело доходит до аксиом, вам, как правило, приходится взаимодействовать с тем, что другие определяют, что они означают. Например, в математической системе я могу переопределить «+», чтобы иметь значение, обычно не связанное с сложением. Это может быть эффективным для визуального изображения концепции и обеспечения того, чтобы читатель ее запомнил (при условии, что она достаточно близка к сложению, чтобы не вызвать когнитивного диссонанса).Однако, если я предложу аксиому, которая требует, чтобы что-то было «непрерывным», и мое использование «непрерывного» на самом деле не то же самое, что и более согласованное определение, теперь я могу вызвать большую путаницу. К аксиомам обычно обращаются заранее, прежде чем ваш собственный стиль просочится в нотацию и многословие. Если в аксиомах использовать стандартную терминологию, то это с большей вероятностью запутает того, кто просматривает кучу документов в поисках решения своей проблемы.
Когда дело доходит до аксиом, вам, как правило, приходится взаимодействовать с тем, что другие определяют, что они означают. Например, в математической системе я могу переопределить «+», чтобы иметь значение, обычно не связанное с сложением. Это может быть эффективным для визуального изображения концепции и обеспечения того, чтобы читатель ее запомнил (при условии, что она достаточно близка к сложению, чтобы не вызвать когнитивного диссонанса).Однако, если я предложу аксиому, которая требует, чтобы что-то было «непрерывным», и мое использование «непрерывного» на самом деле не то же самое, что и более согласованное определение, теперь я могу вызвать большую путаницу. К аксиомам обычно обращаются заранее, прежде чем ваш собственный стиль просочится в нотацию и многословие. Если в аксиомах использовать стандартную терминологию, то это с большей вероятностью запутает того, кто просматривает кучу документов в поисках решения своей проблемы.
Отличный пример аксиомы проявляется в физике: «замкнутая система. «Замкнутая система — это система, в которой энергия не пересекает границу системы (производная потока энергии равна нулю). Это может быть определение в некоторых абстрактных сценариях, но почти во всех случаях это аксиома. Не все системы удовлетворяют требованиям». аксиома замкнутой системы (фактически, технически говоря, ни одна система не удовлетворяет ей на 100%, кроме, возможно, Вселенной в целом). Применимость любого математического моделирования в аксиоматическом предположении замкнутой системы ограничена тем, насколько хорошо «замкнутая система» описывает система, которую кто-то изучает.
«Замкнутая система — это система, в которой энергия не пересекает границу системы (производная потока энергии равна нулю). Это может быть определение в некоторых абстрактных сценариях, но почти во всех случаях это аксиома. Не все системы удовлетворяют требованиям». аксиома замкнутой системы (фактически, технически говоря, ни одна система не удовлетворяет ей на 100%, кроме, возможно, Вселенной в целом). Применимость любого математического моделирования в аксиоматическом предположении замкнутой системы ограничена тем, насколько хорошо «замкнутая система» описывает система, которую кто-то изучает.
С другой стороны, могут быть случаи, когда кто-то предпочтет использовать его в смысле определения. Например, если вы работали с абстрактной математической конструкцией и нашли подмножество этой конструкции, поведение которой аналогично закрытой системе в термодинамике, вы можете выбрать , чтобы определить как закрытую систему, соответствующую этому подмножеству вашей конструкции. Можно было бы исследовать класс кольцевых генераторов и заметить, что некоторые из них демонстрируют поведение, подобное энтропийному распаду.Можно выбрать определение такого поведения с помощью терминов термодинамики, таких как «закрытая система», потому что она хорошо фиксирует отношения, на которых вы сосредоточены. Однако, поскольку это чисто инкапсулировано в вашей математике, ничего страшного, если это не «официальное определение». Это определение не должно взаимодействовать с тысячами статей о термодинамически закрытых системах в такой степени, как если бы ваша конструкция была применима только к закрытым системам. В таком случае вам следует рассматривать это как аксиому.
Можно было бы исследовать класс кольцевых генераторов и заметить, что некоторые из них демонстрируют поведение, подобное энтропийному распаду.Можно выбрать определение такого поведения с помощью терминов термодинамики, таких как «закрытая система», потому что она хорошо фиксирует отношения, на которых вы сосредоточены. Однако, поскольку это чисто инкапсулировано в вашей математике, ничего страшного, если это не «официальное определение». Это определение не должно взаимодействовать с тысячами статей о термодинамически закрытых системах в такой степени, как если бы ваша конструкция была применима только к закрытым системам. В таком случае вам следует рассматривать это как аксиому.
В целом, эффективно думать об «определении» как о чем-то внутреннем по отношению к вашей работе, в то время как «аксиома» имеет тенденцию подключаться к большему объему работы, определяя, какие классы проблем позволяют применять вашу работу.
Разница между аксиомой и теоремой
Аксиома против теоремы
Аксиома — это утверждение, которое считается истинным на основании логики; однако это невозможно доказать или продемонстрировать, потому что это просто считается самоочевидным. По сути, все, что заявлено как истина и принято, но не имеет никаких доказательств или имеет какой-либо практический способ доказательства, является аксиомой. Это также иногда называют постулатом или предположением.
По сути, все, что заявлено как истина и принято, но не имеет никаких доказательств или имеет какой-либо практический способ доказательства, является аксиомой. Это также иногда называют постулатом или предположением.
Основа истины аксиомы часто игнорируется. Это просто так, и нет необходимости в дальнейших размышлениях. Однако многие аксиомы все еще оспариваются разными умами, и только время покажет, чокнутые они или гении.
Аксиомы можно разделить на логические и нелогические.Логические аксиомы — это общепринятые и действительные утверждения, в то время как нелогические аксиомы обычно представляют собой логические выражения, используемые при построении математических теорий.
В математике выделить аксиому намного проще. Аксиома — это часто утверждение, которое считается истинным ради выражения логической последовательности. Они являются основными строительными блоками доказывающих утверждений. Аксиомы служат отправной точкой для других математических утверждений. Эти утверждения, основанные на аксиомах, называются теоремами.
Эти утверждения, основанные на аксиомах, называются теоремами.
Теорема, по определению, — это утверждение, доказываемое на основе аксиом, других теорем и некоторого набора логических связок. Теоремы часто доказываются с помощью строгих математических и логических рассуждений, и процесс доказательства, конечно, будет включать в себя одну или несколько аксиом и других утверждений, которые уже считаются истинными.
Теоремы часто выражаются для вывода, и эти выводы считаются доказательством выражения. Два компонента доказательства теоремы называются гипотезой и заключением.Следует отметить, что теоремы чаще подвергаются сомнению, чем аксиомы, потому что они подлежат большему количеству интерпретаций и различных методов вывода.
Нетрудно рассматривать некоторые теоремы как аксиомы, поскольку есть и другие утверждения, которые интуитивно предполагаются истинными. Однако их более уместно рассматривать как теоремы, поскольку они могут быть выведены с помощью принципов дедукции.
Резюме:
1. Аксиома — это утверждение, которое считается истинным без каких-либо доказательств, в то время как теория требует доказательства, прежде чем она будет признана истинной или ложной.
2. Аксиома часто самоочевидна, в то время как теории часто требуются другие утверждения, такие как другие теории и аксиомы, чтобы стать действительной.
3. Естественно, теоремы ставят под сомнение больше, чем аксиомы.
4. В основном теоремы выводятся из аксиом и набора логических связок.
5. Аксиомы являются основными строительными блоками логических или математических утверждений, поскольку они служат отправными точками теорем.
6. Аксиомы можно разделить на логические и нелогические.
7. Две составляющие доказательства теоремы называются гипотезой и заключением.
: Если вам понравилась эта статья или наш сайт. Пожалуйста, расскажите об этом. Поделитесь им с друзьями / семьей.
Укажите
Ян. «Разница между аксиомой и теоремой». DifferenceBetween.net. 9 февраля 2010 г.
«Разница между аксиомой и теоремой». DifferenceBetween.net. 9 февраля 2010 г.
% PDF-1.5
%
1 0 obj
>
эндобдж
2 0 obj
>
эндобдж
3 0 obj
> поток
2013-10-03T17: 03: 27-04: 00TeX2013-10-09T07: 34: 56-07: 002013-10-09T07: 34: 56-07: 00Это MiKTeX-pdfTeX 2.9.4902 (1.40.14) MiKTeX pdfTeX-1.40.14; изменен с помощью iText 2.1.6 с помощью 1T3XTFalseapplication / pdfuuid: 681d3637-9c96-4a9e-a4c7-60c2d45f97a6uuid: 965cf784-1484-44d3-af1b-fd73ea2ae61b
конечный поток
эндобдж
4 0 obj
>
эндобдж
7 0 объект
>>>
эндобдж
6 0 obj
> поток
x ڵ XMo6W ؋, Zt. vd-; lkk9Pd + r = qyo8`K & H / ף ~
vd-; lkk9Pd + r = qyo8`K & H / ף ~
Каково точное значение этих похожих слов в математике: свойство, аксиома, постулат, теорема, правило, закон, принцип. В чем разница между ними.
Аксиома — это утверждение, которое без доказательства считается самоочевидным.
Постулат — истинное утверждение, которое не требует доказательств.
Подробнее о постулате
Постулат используется для вывода других логических утверждений для решения проблемы.
Постулаты также называются аксиомами.
Результат, который был подтвержден (с использованием уже известных фактов).
Пример: «Теорема Пифагора» доказала, что для прямоугольного треугольника a2 + b2 = c2
Функции обычно представлены правилом функции, в котором зависимая переменная y выражается через независимую переменную x.Пара входного значения и соответствующего ему выходного значения называется упорядоченной парой и может быть записана как (a, b).
-2 голос против
Теорема — это утверждение, доказываемое цепочкой рассуждений. Теорема не самоочевидна. Он выводится после рассмотрения результатов нескольких логических утверждений (часто включая другие теоремы). Знаменитый пример этого — теорема Пифагора, у которой есть почти 400 доказательств.
Законы — это утверждения, основанные на наблюдении.Законы не доказаны. Законы демонстрируются на основе многократных наблюдений. Он выражает причинную связь между сущностями при определенных условиях и часто выражается математически. Законы термодинамики (так часто цитируемые без математического контекста и искаженные именно по этой причине) являются хорошими примерами.
Теория — это устоявшееся и уважаемое объяснение природного явления, полученное путем подтверждения его принципов научным методом — проверкой, подтверждением, наблюдением и экспериментированием.
Факт — это истинное утверждение при определенных условиях. Вещь, которая, бесспорно, так и есть. Факты, как правило, можно воспроизвести для проверки. Единственный встречный пример немедленно понижает статус факта до ложного утверждения.
Факты, как правило, можно воспроизвести для проверки. Единственный встречный пример немедленно понижает статус факта до ложного утверждения.
Научное доказательство — успешная демонстрация изучаемой гипотезы с использованием доказательств и анализа. Во многих смыслах это заблуждение, поскольку наука фактически ничего не может доказать. В этом смысле «доказательство» — это упрощенный способ сказать «значительно увеличенная уверенность».
Правило — это неформальная аксиома, выражающая философскую точку зрения. Правило определяет, как субъект ведет себя при определенных обстоятельствах. Правило указывает на повышенную вероятность определенного исхода, когда субъект находится в определенном состоянии. «Правила» Ньютона или бритва Оккама являются примерами.
Гипотеза — это утверждение, которое (пока) не доказано, но которое интуитивно кажется верным, или для которого у автора есть более сложные причины, чтобы считать его вероятным. Некоторые обманчиво простые из них сопротивляются столетиям нападок выдающихся математиков.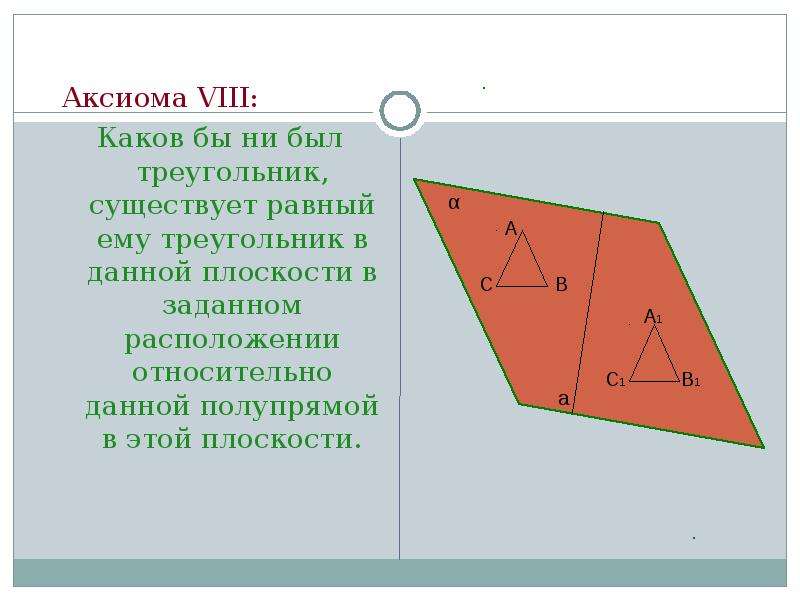
поделиться | цитировать | улучшить этот ответ
ответил 12 мая ’15 в 3:08
основная сумма
Основная сумма денег, взятых в долг или вложенных
В математике свойства демонстрируют общие правила, которые используются в вычислениях. Наиболее часто используемые свойства в повседневной математике — это свойства сложения и умножения. Коммутативное свойство сложения, например, гласит, что независимо от того, как вы упорядочиваете числа при сложении, результат один и тот же.
Ответы от Google в Интернете …
Надеюсь, это поможет!
Оскар
истории логики | Древняя, средневековая, современная и современная логика
Предшественники древней логики
Существовала средневековая традиция, согласно которой греческий философ Парменид (V век до нашей эры) изобрел логику, живя на скале в Египте. Эта история — чистая легенда, но она отражает тот факт, что Парменид был первым философом, который использовал расширенные аргументы в пользу своих взглядов, а не просто предлагал видение реальности. Но использование аргументов — это не то же самое, что их изучение, и Парменид никогда систематически не формулировал и не изучал принципы аргументации как таковые. В самом деле, нет никаких свидетельств того, что он хотя бы знал о неявных правилах вывода, использованных при изложении его доктрины.
Эта история — чистая легенда, но она отражает тот факт, что Парменид был первым философом, который использовал расширенные аргументы в пользу своих взглядов, а не просто предлагал видение реальности. Но использование аргументов — это не то же самое, что их изучение, и Парменид никогда систематически не формулировал и не изучал принципы аргументации как таковые. В самом деле, нет никаких свидетельств того, что он хотя бы знал о неявных правилах вывода, использованных при изложении его доктрины.
Возможно, аргументация Парменида была вдохновлена практикой ранней греческой математики среди пифагорейцев.Таким образом, примечательно, что у Парменида, как сообщается, был учитель-пифагорей. Но история пифагореизма в этот ранний период окутана тайной, и трудно отделить факты от легенды.
Если Парменид не знал общих правил, лежащих в основе его аргументов, то, возможно, это не так для его ученика Зенона Элейского (V век до н. Э.). Зенон был автором многих аргументов, известных под общим названием «Парадоксы Зенона», с целью вывести невозможные последствия из непарменидовского взгляда на вещи и, таким образом, опровергнуть такую точку зрения и косвенно установить монистическую позицию Парменида. Логическая стратегия обоснования претензии путем демонстрации того, что ее противоположность приводит к абсурдным последствиям, известна как reductio ad absurdum. Тот факт, что все аргументы Зенона были в этой форме, предполагает, что он осознавал и размышлял над общей закономерностью.
Логическая стратегия обоснования претензии путем демонстрации того, что ее противоположность приводит к абсурдным последствиям, известна как reductio ad absurdum. Тот факт, что все аргументы Зенона были в этой форме, предполагает, что он осознавал и размышлял над общей закономерностью.
Парадокс Зенона
Парадокс Зенона, проиллюстрированный Ахиллесом в гонке на черепахе.
Британская энциклопедия, Inc.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Другие авторы тоже способствовали растущему интересу греков к умозаключениям и доказательствам.Ранние риторы и софисты — например, Горгий, Гиппий, Продик и Протагор (все 5 век до н. Э.) — культивировали искусство защиты или критики тезиса с помощью аргументов. Эта забота о методах аргументации иногда просто приводила к вербальной демонстрации навыков ведения дебатов, которые Платон называл «эристикой». Но верно также и то, что софисты сыграли важную роль в доведении аргументации до центральной позиции, которую она заняла уникальным образом в греческой мысли.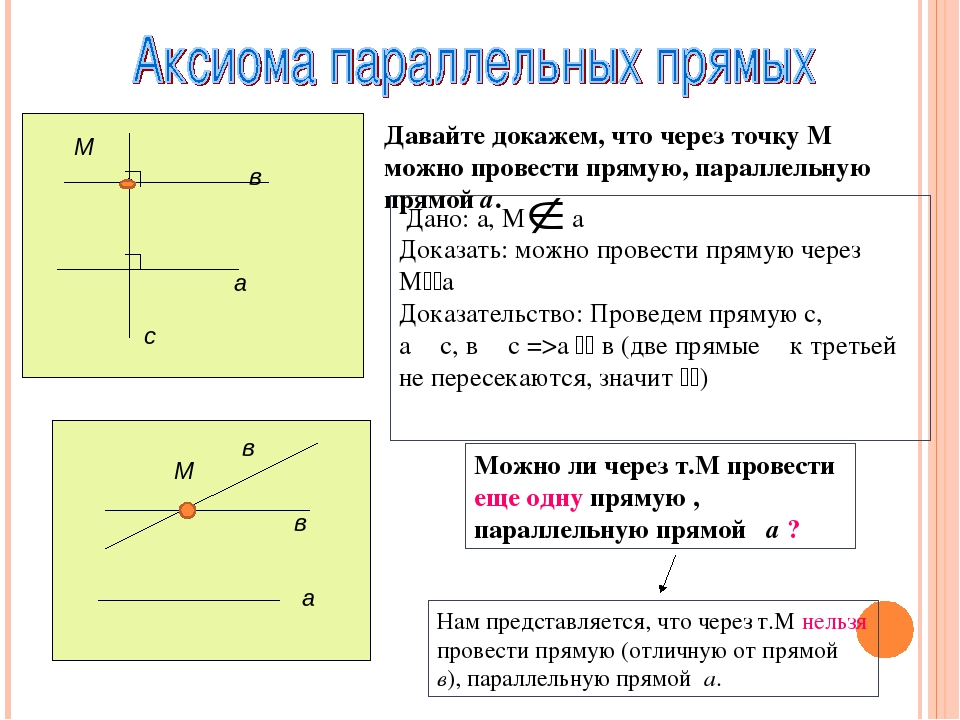 Например, софисты были одними из первых, кто потребовал, чтобы моральные претензии были оправданы причинами.
Например, софисты были одними из первых, кто потребовал, чтобы моральные претензии были оправданы причинами.
Определенные учения софистов и риторов имеют важное значение для ранней истории логики. Например, Сообщается, что Протагор был первым, кто различал разные типы предложений: вопросы, ответы, молитвы и предписания. Продик, похоже, утверждал, что никакие два слова не могут означать одно и то же. Соответственно, он уделял много внимания тщательному различению и определению значений очевидных синонимов, включая многие этические термины.
Сократ ( ок. 470–399 до н. Э.), Как говорят, посещал лекции Продика. Как и Продик, он следовал определениям вещей, особенно в области этики и ценностей. Эти исследования, проведенные посредством дебатов и аргументов, как это описано в трудах Платона (428 / 427–348 / 347 гг. До н. Э.), Усилили интерес греков к аргументации и подчеркнули важность осторожности и строгости в использовании языка.
Платон продолжил дело, начатое софистами и Сократом. В книге Sophist он отличал утверждение от отрицания и провел важное различие между глаголами и именами (включая как существительные, так и прилагательные). Он заметил, что полное утверждение ( логотипов ) не может состоять из одного только имени или глагола, но требует хотя бы одного из каждого. Это наблюдение указывает на то, что анализ языка развился до точки исследования внутренних структур высказываний в дополнение к отношениям высказываний в целом друг к другу.Это новое развитие было возведено в высокое искусство учеником Платона Аристотелем (384–322 гг. До н. Э.).
В книге Sophist он отличал утверждение от отрицания и провел важное различие между глаголами и именами (включая как существительные, так и прилагательные). Он заметил, что полное утверждение ( логотипов ) не может состоять из одного только имени или глагола, но требует хотя бы одного из каждого. Это наблюдение указывает на то, что анализ языка развился до точки исследования внутренних структур высказываний в дополнение к отношениям высказываний в целом друг к другу.Это новое развитие было возведено в высокое искусство учеником Платона Аристотелем (384–322 гг. До н. Э.).
Платон беседует со своими учениками
Платон беседует со своими учениками, мозаика из Помпеи, I век до н. в Национальном археологическом музее Неаполя.
К. М. Диксон / Heritage-Images
В трудах Платона есть отрывки, в которых он предполагает, что практика аргументации в форме диалога (платоническая «диалектика») имеет большее значение, чем ее случайное использование для исследования конкретной проблемы. Предполагается, что диалектика — это самостоятельная наука или, возможно, общий метод достижения научных выводов в других областях. Эти основополагающие, но неубедительные замечания указывают на новый уровень общности греческих рассуждений о рассуждениях.
Предполагается, что диалектика — это самостоятельная наука или, возможно, общий метод достижения научных выводов в других областях. Эти основополагающие, но неубедительные замечания указывают на новый уровень общности греческих рассуждений о рассуждениях.
Основные определения и аксиомы
Основные определения и аксиомы
Конечная математика
Роберт С. Уилсон
1. Определения и аксиомы
Примитивное понятие: набор — это совокупность объектов.Объекты в
коллекции называются элементами набора. построенный с использованием
следующие определения и аксиомы.
Это не определение, потому что мы не определяем «коллекцию» или
«объект». Не все коллекции являются наборами. Наборы будут коллекциями
который можно построить из следующих определений и аксиом.
Определение 1.1 : Пусть A и B два множества.
Если каждый элемент A также является элементом B, то мы говорим, что A является
подмножество B, обозначаемое.
Аксиома 1 : Если A — это множество, а B — подмножество
из A, то B также является множеством.
Определение 1.2 : Пусть A и B два множества.
A = B тогда и только тогда, когда
Теорема 1.1 : Если
A — это набор тогда
Определение 1.3 : Пусть A и B — два множества.
Объединение A и B, обозначенное
— это набор вещей, которые являются либо элементами A, либо элементами
Б.
Аксиома 2 : Если A и B установлены, то также
их союз.
Теорема 1.2: Пусть
A и B — два набора, тогда
Определение 1.4 : Пусть A и B — два множества.
Пересечение A и B обозначено
— это набор вещей, которые являются элементами как A, так и B.
Теорема 1.3 : Пусть
A и B — два набора.
Теорема 1.4 : Если
A и B — два множества, так же как и их пересечение.
Определение 1.5 : Пусть A и B — два множества.
Разница между A и B — это набор вещей, которые находятся в A, но не
в B. Разность A и B обозначается буквами A — B.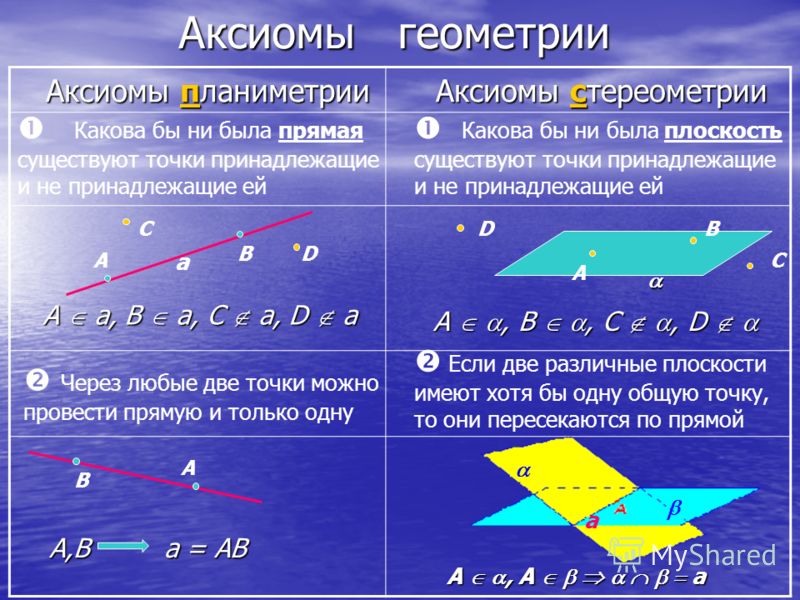
Определение 1.6 : Пусть U — универсальное множество
и пусть A — подмножество U. Тогда дополнение к A относительно
U — это U — A.Обозначение для дополнения к A будет A ‘
.
Теорема 1.5 : Если
A и B являются множествами, тогда A — B.
Теорема 1.6 :
Дополнением набора является набор.
Определение 1.7 : Пусть S — некоторое множество. Множество всех подмножеств S
называется множеством степеней S и обозначается P (S).
Аксиома 3 : Если S — множество, то и его
набор мощности.
Определение 1.8 : Пусть a и b два
элементы. Упорядоченная пара a и b, обозначенная (a, b), определяется
быть
(а, б) = {{а}, {а, б}}
Теорема 1.7 :
(a, b) = (c, d) тогда и только тогда, когда a = c и b = d.
Определение 1.9 : Пусть A и B — два множества.
Декартово произведение A и B, обозначенное A x B, — это множество всех
упорядоченные пары, первая координата которых исходит из A, а вторая
координата исходит от Б.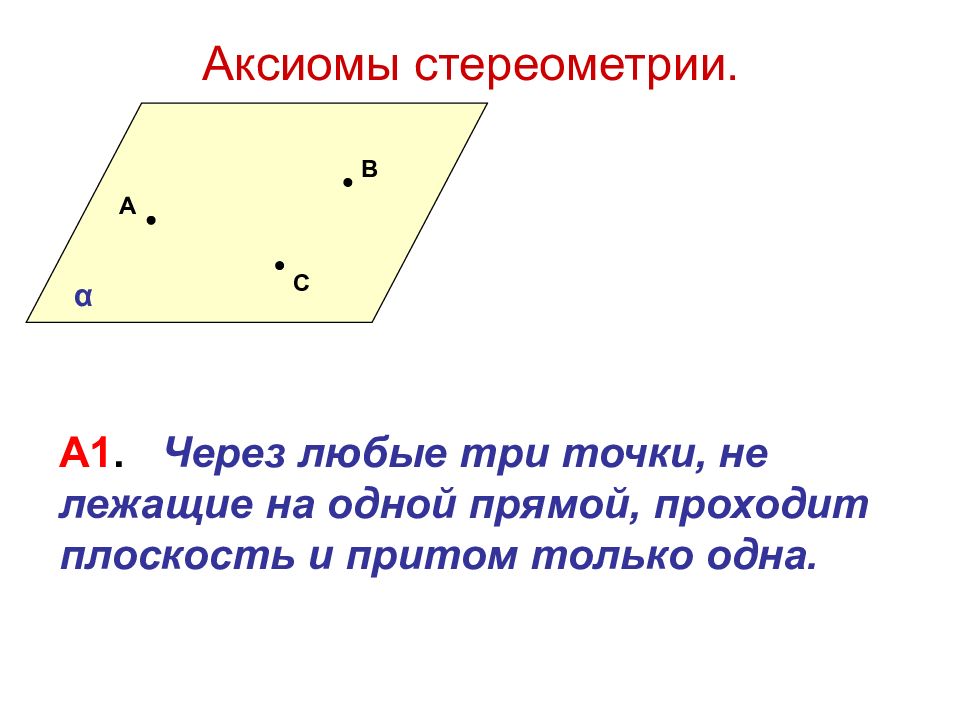
Теорема 1.8 :
Декартово произведение двух множеств — это множество.
Условные обозначения: Порядок операций : Если у вас есть процедура
где новые наборы производятся из существующих наборов, принимая
объединений, пересечений, различий и декартовых произведений, тогда мы
Согласитесь, что без скобок возьмем
- декартовы произведения сначала,
- пересечений и различий рядом и
- союзов в последнюю очередь.
Если есть круглые скобки, они говорят нам выполнять операции в
скобки в указанном выше порядке, прежде чем делать что-либо еще.
Теорема 1.9 : Пусть
А быть набором. Тогда
Теорема 1.10 :
Пусть A — множество. Тогда
2. Установить операции
.



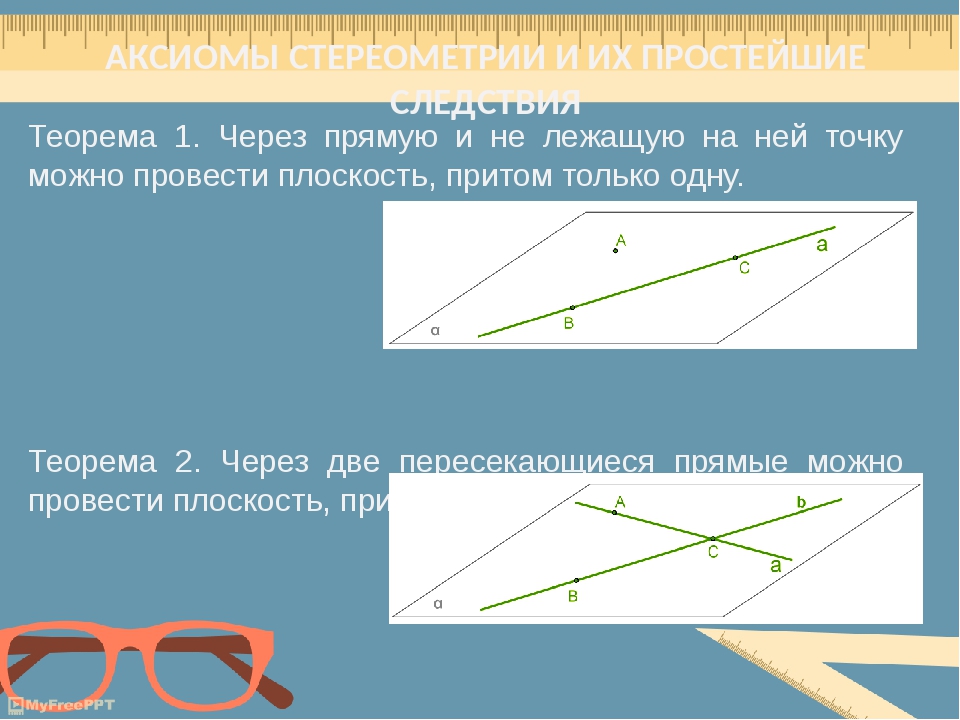 Revised edition. E. Nagel, J.R. Newman and D.R. Hofstadter. New York University Press, 2002.
Revised edition. E. Nagel, J.R. Newman and D.R. Hofstadter. New York University Press, 2002.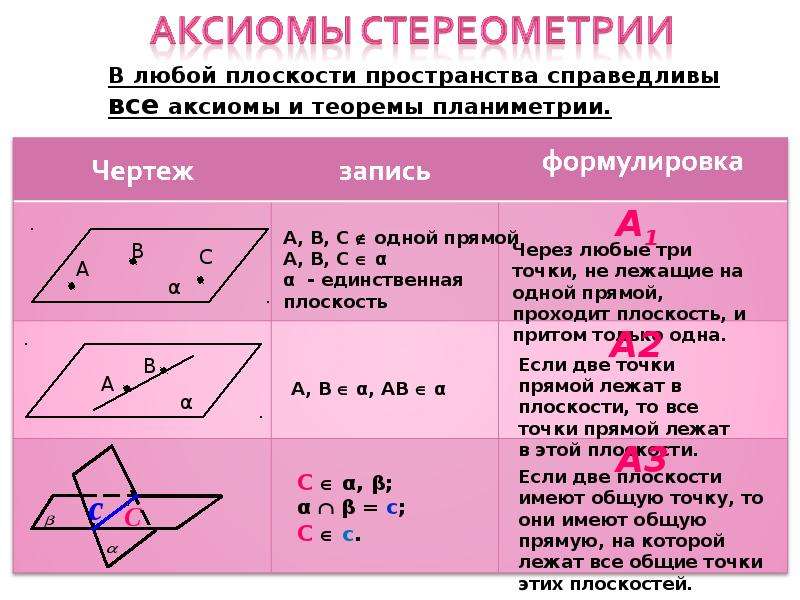 Теоретическое суждение, утверждение или формула, воплощающие что-то, что нужно доказать из других суждений или формул.
Теоретическое суждение, утверждение или формула, воплощающие что-то, что нужно доказать из других суждений или формул.