Содержание
Логарифмические выражения
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
При возведении в степень произведения в эту же степень возводится каждый множитель.
Так же необходимо знать следующее свойство:
Рассмотрим примеры:
*Данный контент (более 20 подробно решённых примеров) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задания В11. Логарифмические выражения | Подготовка к ЕГЭ по математике
Часть 4.
Здесь смотрим части 1, 2, 3, 5
При решении задач, что мы сегодня рассматриваем, нам понадобятся свойства логарифмов. Кстати, – видео по теме
Числовые логарифмические выражения
Задание 1.
Найдите значение выражения .
Решение: + показать
Задание 2.
Найдите значение выражения .
Решение: + показать
Представим как и далее воспользуемся следующим свойством логарифмов:
при :
А теперь применяем основное логарифмическое тождество:
Ответ: 49.
Задание 3.
Найдите значение выражения .
Решение: + показать
Задание 4.
Найдите значение выражения .
Решение: + показать
Задание 5.
Найдите значение выражения .
Решение: + показать
Ответ: 12.
Задание 6.
Найдите значение выражения .
Решение: + показать
Складывать логарифмы не имеем право, у них разные основания.
Работаем с каждым слагаемым по отдельности:
Тогда
Ответ: 1,5.
Задание 7.
Найдите значение выражения .
Решение: + показать
Задание 8.
Найдите значение выражения .
Решение: + показать
Ответ: 2.
Задание 9.
Найдите значение выражения .
Решение: + показать
Задание 10.
Найдите значение выражения .
Решение: + показать
Ответ: 9.
Задание 11.
Найдите значение выражения .
Решение: + показать
Ответ: 1.
Задание 12.
Найдите значение выражения .
Решение: + показать
Ответ: 9.
Задание 13.
Найдите значение выражения .
Решение: + показать
Ответ: 0.
Задание 14.
Вычислите значение выражения: .
Решение: + показать
В самом конце мы применили основное логарифмическое тождество, а до этого – следствие из свойства 7 логарифмов.
Ответ: 2.
Задание 15.
Найдите значение выражения .
Решение: + показать
Обратите внимание, это не произведение логарифмов. У логарифма по основанию подлогарифмным выражением является .
У логарифма по основанию подлогарифмным выражением является .
Ответ: 0,25.
Буквенные логарифмические выражения
Задание 1.
Найдите , если .
Решение: + показать
При имеем:
Ответ: -32.
Задание 2.
Найдите значение выражения , если .
Решение: + показать
🙂 После плодотворной работы не помешало бы и отдохнуть немного… –>+ показать
Жизнь полна неожиданностей, неправда ли?
Вы можете пройти обучающий тест по теме «Преобразование логарифмических выражений».
Вычисление значения логарифмического выражения
В этой статье вы познакомитесь со всеми типами логарифмических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.
16 видео помогут вам понять как использовать свойства логарифмов при упрощении логарифмических выражений.
Вы можете попытаться решить каждый пример самостоятельно, и затем свериться с ответом. А можете сначала посмотреть видео с решением аналогичного задания.
Пример 1. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 6
Видеорешение аналогичного задания:
Пример 2. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 30
Видеорешение аналогичного задания:
Пример 3. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 0,125
Видеорешение аналогичного задания:
Пример 4. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 1,5
Видеорешение аналогичного задания:
Пример 5. Найти значение выражения: Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 6. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 7. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,75
Видеорешение аналогичного задания:
Пример 8. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 216
Видеорешение аналогичного задания:
Пример 9. Найти значение выражения:
Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 1
Видеорешение аналогичного задания:
Пример 10. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,75
Видеорешение аналогичного задания:
Пример 11. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 1
Видеорешение аналогичного задания:
Пример 12. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 3
Видеорешение аналогичного задания:
Пример 13. Найти значение выражения:Посмотреть ответ:
показать
Ответ: -2
Видеорешение аналогичного задания:
Пример 14. Найти значение выражения:Посмотреть ответ:
показать
Ответ: 0,5625
Видеорешение аналогичного задания:
Пример 15. Найти значение выражения:Посмотреть ответ:
показать
Ответ: -0,2
Видеорешение аналогичного задания:
Пример 16. Найти значение выражения:
Посмотреть ответ:
показать
Ответ: 25
Видеорешение аналогичного задания:
И.В. Фельдман, репетитор по математике.
Свойства логарифмов и примеры их решений (ЕГЭ — 2021)
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться \( 1\). {\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
{\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).
Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).
И по условию, эта степень равна \( 2\): \( \displaystyle {{x}^{2}}=x+2\). {2}}-x-2=0\).
{2}}-x-2=0\).
Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.
\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)
Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\). Если корней несколько, в ответе укажите меньший из них.
Решение:
\( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\).
В первую очередь напишем ОДЗ:
\( \displaystyle \left\{ \begin{array}{l}x+1>0\\x+1\ne 1\\2x+5>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0\\x>-\frac{5}{2}\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0.\end{array} \right.\)
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание \( \displaystyle x+1\), чтобы получить аргумент \( \displaystyle 2x+5\)?
Хотите читать учебник без ограничений? Зарегистрируйтесь:
Во вторую. То есть:
\( \displaystyle {{\left( x+1 \right)}^{2}}=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}+2x+1=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2. \end{array} \right.\)
\end{array} \right.\)
Казалось бы, меньший корень равен \( \displaystyle -2\). Но это не так: согласно ОДЗ корень \( \displaystyle x=-2\) – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: \( \displaystyle x=2\).
Ответ: \( \displaystyle x=2\).
Логарифмы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции.
Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание,
а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и
все свойства логарифмов.
Логарифм произведения, сумма логарифмов
Теоретический материал по теме — логарифм произведения.
Пример
Задание. Представить $\log _{5} 6$ в виде суммы логарифмов.
Решение. $\log _{5} 6=\log _{5}(2 \cdot 3)=\log _{5} 2+\log _{5} 3$
Слишком сложно?
Примеры решения задач с логарифмами не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Упростить $\log _{5} 4+\log _{5} 3$
Решение. $\log _{5} 4+\log _{5} 3=\log _{5}(4 \cdot 3)=\log _{5} 12$
Логарифм частного, разность логарифмов
Теоретический материал по теме — логарифм частного.
Пример
Задание. Известно, что $\log _{5} 2=a$,
а $\log _{5} 3=b$. Выразить $\log _{5} \frac{2}{3}$ через $a$ и $b$.
Решение. $\log _{5} \frac{2}{3}=\log _{5} 2-\log _{5} 3=a-b$
Пример
Задание. {2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$
{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$
Второй корень не принадлежит ОДЗ, а значит решение $x=2$
Ответ. $x=2$
Пример
Задание. Решить уравнение $\ln (x+1)=\ln (2 x-3)$
Решение. Находим ОДЗ:
$$\left\{\begin{array}{l}
x+1>0 \\
2 x-3>0
\end{array} \Rightarrow\left\{\begin{array}{l}
x>-1 \\
2 x>3
\end{array} \Rightarrow\left\{\begin{array}{l}
x>-1 \\
x>\frac{3}{2}
\end{array} \Rightarrow\left(\frac{3}{2} ;+\infty\right)\right.\right.\right.$$
Решаем уравнение $x+1=2 x-3: x=4 \in$ ОДЗ.
Итак, решением исходного логарифмического уравнения
также является это значение.
Ответ. $x=4$
Решение логарифмических неравенств
Теоретический материал по теме — логарифмические неравенства.
Пример
Задание. Решить неравенство $\log _{0,5}(x-1)>-1$
Решение. {-1}$ или $x-1<2 \Rightarrow x<3$
{-1}$ или $x-1<2 \Rightarrow x<3$
В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$
Ответ. $x \in(1 ; 3)$
Пример
Задание. Решить неравенство $\log _{5} 5>\log _{5} x$
Решение. Данное неравенство равносильно системе:
$$\left\{\begin{array}{l}
5>x, \\
x>0
\end{array} \Rightarrow\left\{\begin{array}{l}
x0
\end{array} \Rightarrow x \in(0 ; 5)\right.\right.$$
Ответ. $x \in(0 ; 5)$
Читать первую тему — формулы и свойства логарифмов,
раздела логарифмы.
Как решать логарифмы егэ профиль. Решение логарифмичеких уравнений
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы?
Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм
.
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.

- Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители.
 Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9. - log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения
, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
log 2 x
= 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений
. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c
одержали, обязательно нужно привести к уравнению вида:log a
f
(x
) = log a
g
(x
)
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел
, одно из которых вообще не является логарифмом. - Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.

Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения
, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a
f
(x
) + log a
g
(x
) = log a
f
(x
) · g
(x
)
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
a
= log b
b
a
Здесь нужно понимать: когда мы говорим «Любое основание b
», то подразумеваем, что b
все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения
Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения
, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0
Давайте посмотрим, что происходит в нашем случае:
1 = log 2 2 1 = log 2 2
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания
. Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
Давайте запишем одно из этих правил:
log a
b
n
= n
· log a
b
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n
«мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k
.
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n
), окажется в числителе. А то, что было степенью у основания, a
k
, отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log 2 2(9x
2 + 5) = log 2 (8x
4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x
2 + 5) = 8x
4 + 14
Давайте раскроем скобки слева. Получим:
Получим:
18x
2 + 10 = 8x
4 + 14
Перенесем все из левой части в правую:
8x
4 + 14 − 18x
2 − 10 = 0
Приведем подобные и получим:
8x
4 − 18x
2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x
4 − 9x
2 + 2 = 0
Перед нами обычное биквадратное уравнение
, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D
= 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x
, а x
2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная
. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x
2 + 5 (эта функция всегда положительна), либо 8x
4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x
= 1/2 и x
= −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x
= −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x
= 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V
— знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак
. Вот такая галочка V изменилась бы на такую — Λ. - Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо.
 Что действительно нужно, так это возвести обе части в квадрат
Что действительно нужно, так это возвести обе части в квадрат
, чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому
А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому
логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a
или b
, именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.

В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Логарифмические уравнения. 10-11 класс
Стоит напомнить всем, что логарифмическими называют уравнения, в которых переменная или функция от «икс» находится под знаком логарифма.
При равносильных преобразованиях справедливая формула перехода от логарифмического до простого уравнения
logaf(x)=c⇔f(x)=ac.
ОДЗ: основание логарифма должно быть больше нуля и не равняться единице,
функция – положительной
{x>0, x≠1, f(x)>0}.
Важно знать частные случаи простейших логарифмических уравнений:
правая сторjна равна нулю (с=0) или единицы (с=1):
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Эти формулы Вы должны знать на память, поскольку их чаще всего применяют при сведении логарифмов до простейшего типа.
С целью научить Вас раскрывать логарифмические уравнения, а также подготовить к ВНО тестированию нами решены 40 примеров, которые в полной мере охватывают все известные методы решения логарифмических уравнений, которые Вас учат в 10-11 классе школьной программы, и дальше на первых курсах в ВУЗ-ах.
Схема вычисления логарифмических уравнений
- если возможно, выписать область допустимых значений логарифмов и функций, которые в него входят.
- свести уравнение к простейшему типу путем элементарных преобразований, которые заключаются в вынесении степени из основания логарифма (или наоборот), логарифмированию и потенцированию (возведение в степень по основанию (экспонента, основы =10, 2, π)
- в случаях сложных уравнений вводят замену переменных и сводят к квадратным или другим известным уравнениям.

Вычисление уравнений с логарифмом
Пример 16.1 Решить уравнение logax=c.
Решение: Имеем простейшее логарифмическое уравнение, которое решается методом сведения к одному основанию логарифмов:
logax=c
(здесь a>0, a≠1),
logax=c•1,
logax=c•logaa,
logax= logaac
Здесь использовали свойства логарифма, единицу расписали как логарифм основания, после чего множитель c внесли под логарифм.
Далее опустили основы и приравняли выражения в логарифмах:
x=ac.
ОДЗ: x>0.
Ответ: ac – Г.
Пример 16.2 Решить уравнение log1/2(x)=-4.
А | Б | В | Г | Д |
ø | -16 | 1/16 | 1/16; 16 | 16 |
Решение: ОДЗ функции под логарифмом: x>0.
Сводим уравнение к одному основанию логарифмов
При равных основах приравниваем выражения под логарифмами:
x=(1/2)-4,
x=24,
x=16.
Ответ: 16 – Д.
Пример 16.3 Решить уравнение log2(-x)=5.
А | Б | В | Г | Д |
ø | 32 | -32 | 1/32 | -1/32 |
Решение: Выполняем раскрытия логарифмов по данной в начале инструкции:
ОДЗ – -x>0,x<0.
Упростим уравнения
log2(-x)=5
log2(-x)=5•1
log2(-x)=5• log22
log2(-x)= log225
опустим основы и приравняем логарифмические выражения:
-x=25,
-x=32,
x=-32.
Ответ: -32 – У.
Пример 16.4 Решить уравнение lg(x2-x)=1-lg(5).
А | Б | В | Г | Д |
ø | -3; 2 | -2; 1 | -2; 3 | -1; 2 |
Решение: ОДЗ: x2-x>0,
x(x-1)>0
Решим неравенство методом интервалов
x(x-1)=0,
x1=0,
x2=1.
x∈(-∞;1)∪(1;+∞).
На этом множестве значений и ищем решение уравнения, сперва сведя к одной основе логарифмы
по теореме Виета:
x1+x2=1,
x1•x2=-2.
x1=-1,
x2=2.
Оба корня принадлежат ОДЗ.
Ответ: -1; 2 – Д.
ОДЗ неравенства могут быть сложнее, чем сами уравнения, тогда достаточно сами корни уравнения подставить в неравенство (или систему неравенств) и определить, принадлежат ли корни области допустимых значений логарифмческого уравнения.
Пример 16.5 Сколько корней имеет уравнение lg(x4-10x2)=lg3x3?
А | Б | В | Г | Д |
Ни одного | один | два | три | четыре |
Решение: В логарифме имеем биквадратное выражение, которое при условиях на ОДЗ требует вычислений. 2)=lg3x3 имеет один корень.
2)=lg3x3 имеет один корень.
Ответ: один – Б.
Пример 16.6 Решить уравнение log6(x-2)+log6(x-1)=1 и указать промежуток, которому принадлежит его корень.
Решение: Выпишем систему неровностей для ОДЗ:
По правилу, что сумма логарифмов чисел равна логарифму их произведения ln(a)+ln(b)=ln(a•b) и свойству log66=1, сведем логарифмы к общему основанию:
При преобразованиях получили квадратное уравнение, корни которого находим по теореме Виета:
x1+x2=3
x1•x2=-4.
x1=-1<2 (не принадлежит ОДЗ)
x2=4.
x=4 – единственный корень заданного уравнения, он принадлежит промежутку (3,9;4,1).
Ответ: (3,9;4,1) – Б.
Пример 16.9 Решить уравнение (log2x)2-2log2x-3=0 и указать сумму его корней.
Решение: ОДЗ: x>0.
логарифмическое уравнение
(log2x)2-2log2x-3=0
сведем к квадратному заменой log2x=t.
t2-2•t-3=0
По формулам Виета имеем:
t1+t2=2 – сумма корней уравнения;
t1•t2=3 – их произведение, тогда
t1=-1 и t2=3 – корни квадратного уравнения.
Возвращаемся к замене, и вычисляем простые логарифмические уравнения
Оба корня принадлежат ОДЗ, по условию найдем их сумму:
x1+x2=0,5+8=8,5.
Ответ: 8,5 – Д.
С простых примеров на раскрытие логарифмических уравнений Вы увидели, что достаточно знать несколько формул и базовые свойства логарифма и уже можно самостоятельно решать уравнения. Для простых условий это работает, но напоминаем, что курс ВНО подготовки содержит 40 примеров, причем ряд задач сочетают в себе не только логарифмы, но и корни, модули, показательные выражения. Вы научитесь сводить уравнения к квадратным, логарифмировать и еще много чего нового.
Решение логарифмических уравнений — объяснения и примеры
Как вы хорошо знаете, логарифм — это математическая операция, обратная возведению в степень. Логарифм числа сокращается как « log ».
Логарифм числа сокращается как « log ».
Прежде чем мы сможем решить логарифмические уравнения, давайте сначала познакомимся со следующими правилами логарифмов:
Правило произведения гласит, что сумма двух логарифмов равна произведению логарифмов.Первый закон представлен как;
⟹ log b (x) + log b (y) = log b (xy)
Разность двух логарифмов x и y равна отношению логарифмов.
⟹ журнал b (x) — журнал b (y) = журнал (x / y)
⟹ журнал b (x) n = n журнал b (x)
⟹ log b x = (log a x) / (log a b)
Логарифм любого положительного числа по основанию этого числа всегда равен 1.
b 1 = b ⟹ log b (b) = 1.
Пример:
- Логарифм от числа 1 до любого ненулевого основания всегда равен нулю.
b 0 = 1 ⟹ журнал b 1 = 0.
Как решать логарифмические уравнения?
Уравнение, содержащее переменные в показателях степени, известно как экспоненциальное уравнение. Напротив, уравнение, которое включает логарифм выражения, содержащего переменную, называется логарифмическим уравнением.
Цель решения логарифмического уравнения — найти значение неизвестной переменной.
В этой статье мы узнаем, как решить два общих типа логарифмических уравнений, а именно:
- Уравнения, содержащие логарифмы на одной стороне уравнения.
- Уравнения с логарифмами на противоположных сторонах от знака равенства.
Как решить уравнения с односторонним логарифмом?
Уравнения с логарифмами на одной стороне принимают логарифм b M = n ⇒ M = b n .
Чтобы решить этот тип уравнений, выполните следующие действия:
- Упростите логарифмические уравнения, применив соответствующие законы логарифмов.
- Перепишите логарифмическое уравнение в экспоненциальной форме.

- Теперь упростим показатель степени и решим переменную.
- Проверьте свой ответ, подставив его обратно в логарифмическое уравнение. Обратите внимание, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
Пример 1
Логарифм решения 2 (5x + 7) = 5
Решение
Перепишем уравнение в экспоненциальной форме
log 2 (5x + 7) = 5 ⇒ 2 5 = 5x + 7
⇒ 32 = 5x + 7
⇒ 5x = 32-7
5x = 25
Разделите обе стороны на 5, чтобы получить
x = 5
Пример 2
Решите относительно x в логарифме (5x -11) = 2
Решение
Поскольку основание этого уравнения не дано, мы предполагаем основание 10.
Теперь измените логарифм в экспоненциальной форме.
⇒ 10 2 = 5x — 11
⇒ 100 = 5x -11
111 = 5x
111/5 = x
Следовательно, x = 111/5 — это ответ.
Пример 3
Логарифм решения 10 (2x + 1) = 3
Решение
Перепишите уравнение в экспоненциальной форме
log 10 (2x + 1) = 3n⇒ 2x + 1 = 10 3
⇒ 2x + 1 = 1000
2x = 999
. Разделив обе стороны на 2, получим;
х = 499.5
Проверьте свой ответ, подставив его в исходное логарифмическое уравнение;
⇒ log 10 (2 x 499,5 + 1) = log 10 (1000) = 3, поскольку 10 3 = 1000
Пример 4
Оценить ln (4x -1) = 3
Решение
Перепишем уравнение в экспоненциальной форме как;
ln (4x -1) = 3 ⇒ 4x — 3 = e 3
Но, как известно, e = 2,718281828
4x — 3 = (2.718281828) 3 = 20.085537
x = 5.271384
Пример 5
Решите логарифмическое уравнение log 2 (x +1) — log 2 (x — 4) = 3
Решение
Сначала упростите логарифмы, применив правило частного, как показано ниже.
журнал 2 (x +1) — журнал 2 (x — 4) = 3 ⇒ log 2 [(x + 1) / (x — 4)] = 3
Теперь перепишите уравнение в экспоненциальной форме
⇒2 3 = [(x + 1) / (x — 4)]
⇒ 8 = [(x + 1) / (x — 4)]
Перемножьте уравнение крест-накрест
⇒ [(x + 1) = 8 (x — 4)]
⇒ x + 1 = 8x -32
7x = 33 …… (Сбор одинаковых терминов)
x = 33/7
Пример 6
Решите относительно x, если log 4 (x) + log 4 (x -12) = 3
Решение
Упростите логарифм, используя следующее правило произведения;
журнал 4 (x) + журнал 4 (x -12) = 3 ⇒ журнал 4 [(x) (x — 12)] = 3
⇒ журнал 4 (x 2 — 12x) = 3
Преобразуйте уравнение в экспоненциальную форму.
⇒ 4 3 = x 2 — 12x
⇒ 64 = x 2 — 12x
Поскольку это квадратное уравнение, мы решаем его факторизацией.
x 2 -12x — 64 ⇒ (x + 4) (x — 16) = 0
x = -4 или 16
Когда x = -4 подставляется в исходное уравнение, мы получаем отрицательный ответ что мнимое. Поэтому 16 — единственное приемлемое решение.
Как решить уравнения с логарифмами с обеих сторон уравнения?
Уравнения с логарифмами по обе стороны от знака равенства принимают log M = log N, что совпадает с M = N.
Процедура решения уравнений с логарифмами по обе стороны от знака равенства.
- Если логарифмы имеют общую основу, упростите задачу, а затем перепишите ее без логарифмов.
- Упростите, собирая одинаковые члены и решая переменную в уравнении.
- Проверьте свой ответ, вернув его в исходное уравнение. Помните, что приемлемый ответ приведет к положительному аргументу.
Пример 7
Логарифм решения 6 (2x — 4) + log 6 ( 4) = log 6 (40)
Решение
Во-первых, упростите логарифмы.
журнал 6 (2x — 4) + журнал 6 (4) = журнал 6 (40) ⇒ журнал 6 [4 (2x — 4)] = журнал 6 (40)
Теперь опустите логарифмы
⇒ [4 (2x — 4)] = (40)
⇒ 8x — 16 = 40
⇒ 8x = 40 + 16
8x = 56
x = 7
Пример. 8
Решите логарифмическое уравнение: log 7 (x — 2) + log 7 (x + 3) = log 7 14
Решение
Упростите уравнение, применив правило произведения .
Логарифм 7 [(x — 2) (x + 3)] = log 7 14
Отбросьте логарифмы.
⇒ [(x — 2) (x + 3)] = 14
Распределите ФОЛЬГУ, чтобы получить;
⇒ x 2 — x — 6 = 14
⇒ x 2 — x — 20 = 0
⇒ (x + 4) (x — 5) = 0
x = -4 или x = 5
когда x = -5 и x = 5 подставляются в исходное уравнение, они дают отрицательный и положительный аргумент соответственно. Поэтому x = 5 — единственное приемлемое решение.
Поэтому x = 5 — единственное приемлемое решение.
Пример 9
Логарифм решения 3 x + log 3 (x + 3) = log 3 (2x + 6)
Решение
Учитывая уравнение; log 3 (x 2 + 3x) = log 3 (2x + 6), отбросьте логарифмы, чтобы получить;
⇒ x 2 + 3x = 2x + 6
⇒ x 2 + 3x — 2x — 6 = 0
x 2 + x — 6 = 0 ……………… (Квадратное уравнение)
Фактор множителя квадратное уравнение получить;
(x — 2) (x + 3) = 0
x = 2 и x = -3
Проверяя оба значения x, мы получаем x = 2, что является правильным ответом.
Пример 10
Журнал решения 5 (30x — 10) — 2 = log 5 (x + 6)
Решение
log 5 (30x — 10) — 2 = log 5 (x + 6)
Это уравнение можно переписать как;
⇒ log 5 (30x — 10) — log 5 (x + 6) = 2
Упростим логарифмы
log 5 [(30x — 10) / (x + 6)] = 2
Записать логарифм в экспоненциальной форме.
⇒ 5 2 = [(30x — 10) / (x + 6)]
⇒ 25 = [(30x — 10) / (x + 6)]
При перекрестном умножении получаем;
⇒ 30x — 10 = 25 (x + 6)
⇒ 30x — 10 = 25x + 150
⇒ 30x — 25x = 150 + 10
⇒ 5x = 160
x = 32
Предыдущий урок | Главная страница | Следующий урок
Решение логарифмических уравнений — ChiliMath
Обычно существует два типа логарифмических уравнений. Внимательно изучите каждый случай, прежде чем приступить к рассмотрению приведенных ниже примеров.
Типы логарифмических уравнений
- Первый тип выглядит так.
Если у вас есть один логарифм на каждой стороне уравнения с одинаковым основанием, вы можете установить аргументы, равные друг другу, и решить. Аргументами здесь являются алгебраические выражения, представленные \ color {blue} M и \ color {red} N.
- Второй тип выглядит так.

Если у вас есть один логарифм на на одной стороне уравнения, вы можете выразить его в виде экспоненциального уравнения и решить.
Давайте научимся решать логарифмические уравнения на нескольких примерах.
Примеры решения логарифмических уравнений
Пример 1: Решите логарифмическое уравнение.
Поскольку мы хотим преобразовать левую часть в одно логарифмическое уравнение, мы должны использовать правило произведения в обратном порядке, чтобы сжать его. Вот правило на всякий случай, если вы забыли.
- Распределить: \ left ({x + 2} \ right) \ left (3 \ right) = 3x + 6
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу.
- Затем решите линейное уравнение. Я знаю, что у тебя есть эта часть!
Просто большое предостережение. ВСЕГДА проверяйте решенные значения с помощью исходного логарифмического уравнения.
Запомнить :
- Хорошо, может иметь значения x, такие как положительные, 0 и отрицательные числа.
- Однако НЕ ДОПУСКАЕТСЯ иметь логарифм отрицательного числа или логарифм нуля, 0, при замене или вычислении в исходное уравнение логарифма.
⚠︎ ВНИМАНИЕ! Логарифм отрицательного числа и логарифм нуля не определены.
{\ log _b} \ left ({{\ rm {negative \, \, number}}} \ right) = {\ rm {undefined}}
{\ log _b} \ left (0 \ right) = {\ rm {undefined}}
Теперь давайте проверим наш ответ, является ли x = 7 допустимым решением. Подставьте его обратно в исходное логарифмическое уравнение и проверьте, верно ли оно.
Да! Поскольку x = 7 проверяет, у нас есть решение в \ color {blue} x = 7.2} — 2x
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу
- Решите квадратное уравнение, используя метод факторизации.
 Но вам нужно сдвинуть все на одну сторону, заставив противоположную сторону равной 0.
Но вам нужно сдвинуть все на одну сторону, заставив противоположную сторону равной 0.
- Установите каждый коэффициент равным нулю, затем решите относительно x.
x — 5 = 0 означает, что x = 5
x + 2 = 0 означает, что x = — 2
Итак, возможные решения: x = 5 и x = — 2.Не забывайте всегда подставлять возможные решения обратно в исходное логарифмическое уравнение.
Давайте проверим наши возможные ответы x = 5 и x = — 2, если они будут действительными решениями. Подставьте его обратно в исходное логарифмическое уравнение и проверьте, верно ли оно.
После проверки наших значений x мы обнаружили, что x = 5 определенно является решением. Однако x = -2 генерирует некоторые отрицательные числа внутри скобок (логарифм нуля и отрицательные числа не определены), что заставляет нас исключить x = -2 как часть нашего решения.
Следовательно, окончательное решение будет просто \ color {blue} x = 5. Мы не принимаем во внимание x = -2, потому что это постороннее решение.
Пример 3: Решите логарифмическое уравнение.
Это интересная проблема. Здесь мы имеем различие логарифмических выражений по обе стороны уравнения. Упростите или сожмите журналы с обеих сторон, используя правило Quotient Rule, которое выглядит следующим образом.
- Разница в журналах говорит нам использовать правило частного.Преобразуйте операцию вычитания снаружи в операцию деления внутри скобок. Сделайте это с обеими сторонами уравнений.
- Я думаю, что мы готовы установить каждый аргумент равным друг другу, так как мы можем уменьшить проблему до одного логарифмического выражения для каждой стороны уравнения.
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу. Обратите внимание, что это рациональное уравнение. Один из способов решить эту проблему — получить Cross Product .
- Это выглядит так после получения перекрестного продукта.

- Упростите обе стороны распределительным свойством. На этом этапе мы понимаем, что это всего лишь квадратное уравнение. Тогда ничего страшного. Сдвиньте все в одну сторону, и это заставит одну сторону уравнения равняться нулю.
- Это легко фактурируемо. Теперь установите каждый коэффициент равным нулю и решите относительно x.
- Итак, это наши возможные ответы.
Я предоставлю вам проверить наши возможные ответы обратно в исходное логарифмическое уравнение.Вы должны убедиться, что \ color {blue} x = 8 — единственное решение, а x = -3 — нет, поскольку он генерирует сценарий, в котором мы пытаемся получить логарифм отрицательного числа. Нехорошо!
Пример 4: Решите логарифмическое уравнение.
Если вы видите «журнал» без явного или письменного основания, предполагается, что он имеет основание 10. Фактически, логарифм с основанием 10 известен как десятичный логарифм .
Нам нужно сжать обе части уравнения в одно логарифмическое выражение.С левой стороны мы видим различие журналов, что означает, что мы применяем правило Quotient Rule, в то время как с правой стороны требуется правило продукта, потому что они представляют собой сумму журналов.
Есть только одна вещь, на которую вы должны обратить внимание на левую сторону. Вы видите этот коэффициент \ Large {1 \ over 2} \ ,?
Что ж, мы должны представить это как экспоненту, используя правило мощности в обратном порядке.
- Поднимите этот коэффициент \ large {1 \ over 2} как показатель степени (см. Крайний левый член)
- Упростите показатель степени (все еще относится к крайнему левому члену)
- Затем сожмите бревна с обеих сторон уравнения.Используйте правило частного слева и правило продукта справа.
- Здесь я использовал разные цвета, чтобы показать, что, поскольку у нас одна и та же база (если не указано явно, предполагается, что это база 10), можно установить их равными друг другу.

- Удаление журналов и просто приравнивание аргументов внутри круглых скобок.
- На этом этапе вы можете решить рациональное уравнение, выполнив перекрестное произведение. Переместите все члены в одну сторону уравнения, затем вычтите их.
- Установите каждый коэффициент равным нулю и решите относительно x.
Пора проверить свои потенциальные ответы. Когда вы проверите x = 0 обратно в исходное логарифмическое уравнение, вы получите выражение, которое включает в себя получение логарифма нуля, который не определен, что означает — нехорошо! Итак, мы должны игнорировать или отбросить \ color {red} x = 0 как решение.
Проверка \ Large {x = {3 \ over 4}} подтверждает, что действительно \ Large {\ color {blue} {x = {3 \ over 4}}} является единственным решением.
Пример 5: Решите логарифмическое уравнение.
Эта проблема связана с использованием символа \ ln вместо \ log для обозначения логарифма.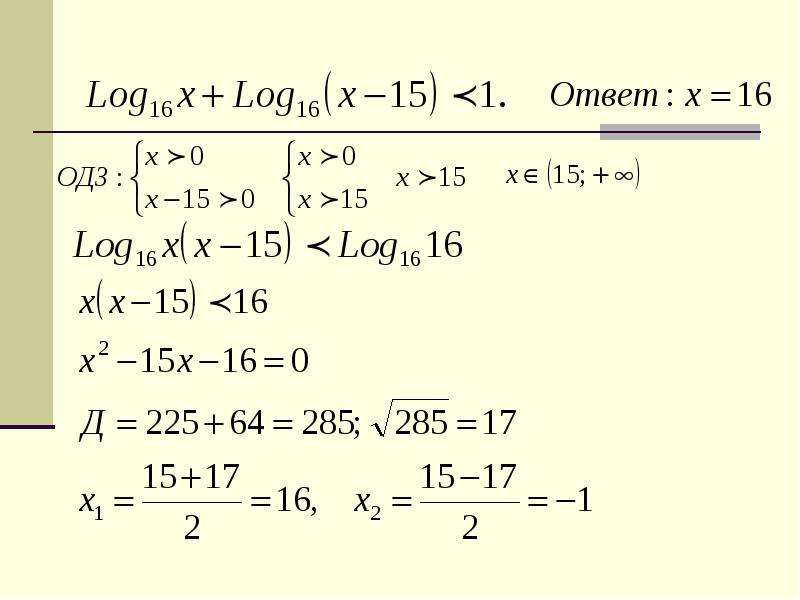
Думайте о \ ln как о особом логарифме с основанием e, где e \ приблизительно 2,71828.
- Используйте правило продукта с правой стороны
- Сначала запишите переменную, а затем константу, чтобы быть готовым к использованию метода FOIL.
- Упростите два бинома, умножив их вместе.
- На этом этапе я просто закодировал выражение в круглых скобках цветом, чтобы показать, что мы готовы установить их равными друг другу.
- Ага! Здесь мы говорим, что содержимое в левой скобке равно содержимому в правой скобке.
Не забудьте символ \ pm.
- Далее, упрощая, мы должны получить следующие возможные ответы.
Проверьте, являются ли найденные выше потенциальные ответы возможными, подставив их обратно в исходные логарифмические уравнения.
Вы должны убедиться, что ЕДИНСТВЕННЫМ допустимым решением является \ large {\ color {blue} x = {1 \ over 2}}, что делает \ large {\ color {red} x = — {1 \ over 2}} лишним. отвечать.
отвечать.
Пример 6: Решите логарифмическое уравнение.
В этом уравнении есть только одно логарифмическое выражение. Мы рассматриваем это как второй случай, когда у нас
Мы преобразуем уравнение из логарифмической формы в экспоненциальную, а затем решим его.
- Я закодировал части логарифмического уравнения цветом, чтобы показать, куда они идут при преобразовании в экспоненциальную форму.4} = 81.
Вы должны убедиться, что значение \ color {blue} x = 12 действительно является решением логарифмического уравнения.
Пример 7: Решите логарифмическое уравнение.
Соберите все логарифмические выражения на одной стороне уравнения (оставьте его слева) и переместите константу в правую часть. Используйте правило частного, чтобы выразить разницу журналов в виде дробей в скобках логарифма.
- Переместите все логарифмические выражения в левую часть уравнения, а константу — вправо.
 {\ color {красный} 1} = 5.
{\ color {красный} 1} = 5.
- Это рациональное уравнение из-за наличия переменных в числителе и знаменателе.
Я бы решил это уравнение, используя правило перекрестного произведения. Но сначала я должен выразить правую часть уравнения с явным знаменателем, равным 1. То есть 5 = {\ large {{5 \ over 1}}}
- Выполните перекрестное умножение, а затем решите полученное линейное уравнение.
Когда вы проверяете x = 1 обратно в исходное уравнение, вы должны согласиться с тем, что \ large {\ color {blue} x = 1} является решением логарифмического уравнения.
Пример 8: Решите логарифмическое уравнение.
Эта проблема очень похожа на №7. Давайте соберем все логарифмические выражения слева, оставив константу справа. Поскольку у нас есть разница журналов, мы будем использовать правило Quotient Rule.
- Переместите выражения журнала влево, а константу оставьте вправо.
- Примените правило частного, поскольку они представляют собой разность журналов.

- Я использовал здесь разные цвета, чтобы показать, куда они уходят после перезаписи в экспоненциальной форме.
- Обратите внимание, что выражение внутри круглых скобок остается на своем текущем месте, а \ color {red} 5 становится показателем степени основания.
- Чтобы решить это рациональное уравнение, примените правило перекрестного произведения.
- Упростите правую часть с помощью свойства распределения. Похоже, мы имеем дело с квадратным уравнением.
- Переместите все в левую сторону и сделайте правую сторону равной нулю.
Выносим трехчлен за скобки.Установите каждый коэффициент равным нулю, затем решите относительно x.
- Когда вы решаете для x, вы должны получить эти значения x как потенциальные решения.
Убедитесь, что вы проверили возможные ответы из исходного логарифмического уравнения.
Согласитесь, что \ color {blue} x = -32 — единственное решение. Это делает \ color {red} x = 4 посторонним решением, так что не обращайте на него внимания.
Это делает \ color {red} x = 4 посторонним решением, так что не обращайте на него внимания.
Пример 9: Решите логарифмическое уравнение
Я надеюсь, что теперь вы получили основное представление о том, как подходить к этому типу проблемы.Здесь мы видим три логических выражения и константу. Давайте разделим логарифмические выражения и константу на противоположных сторонах уравнения.
- Давайте оставим лог-выражения слева, а константу — справа.
- Начните с сжатия выражений журнала с помощью правила продукта для обработки суммы журналов.
- Затем дополнительно уплотните выражения журнала, используя правило частного, чтобы учесть разницу в журналах.
- На этом этапе я использовал разные цвета, чтобы показать, что готов выразить логарифмическое уравнение в его экспоненциальной форме.
- Сохраните выражение внутри символа группировки ( синий ) в том же месте, сделав константу \ color {red} 1 с правой стороны как показатель степени основания 7.

- Решите это рациональное уравнение, используя перекрестное произведение. Выразите 7 как \ large {7 \ over 1}.
- Переместите все члены в левую часть уравнения. Выносим за скобки трехчлен. Затем установите каждый коэффициент равным нулю и решите относительно x.
- Это ваши потенциальные ответы.Всегда проверяйте свои ценности.
Очевидно, что когда мы подставляем x = -8 обратно в исходное уравнение, получается логарифм с отрицательным числом. Следовательно, вы исключаете \ color {red} x = -8 как часть вашего решения.
Таким образом, единственное решение — \ color {blue} x = 11.
Пример 10: Решите логарифмическое уравнение.
- Сохраните логарифмическое выражение слева и переместите все константы в правую сторону.
- Думаю, мы готовы преобразовать это логарифмическое уравнение в экспоненциальное уравнение.3} = 27. Перед нами простое радикальное уравнение.

Отметьте этот отдельный урок, если вам нужно напомнить, как решать различные типы радикальных уравнений.
- Чтобы избавиться от радикального символа в левой части, возведите обе части уравнения в квадрат.
- После возведения в квадрат обеих сторон, похоже, у нас есть линейное уравнение. Просто решите это как обычно.
Верните свой потенциальный ответ в исходное уравнение.
После этого вы должны убедиться, что действительно \ color {blue} x = -104 — верное решение.
Практика с рабочими листами
Возможно, вас заинтересует:
Уплотняющие логарифмы
Расширяющиеся логарифмы
Объяснение логарифма
Правила логарифмирования
Базовые правила журнала и расширяющиеся выражения журнала
Purplemath
Вы изучили различные правила для управления и упрощения выражений с показателями степени, например, правило, согласно которому x 3 × x 5 равно x 8 , потому что вы можете складывать экспоненты. Аналогичные правила для логарифмов.
Аналогичные правила для логарифмов.
Правила журнала:
1) журнал b ( mn ) = журнал b ( m ) + журнал b ( n )
2) бревно b ( м / n ) = бревно b ( м ) — бревно b ( n )
3) журнал b ( м n ) = n · журнал b ( м )
MathHelp.com
В менее формальных терминах правила журнала могли бы быть выражены как:
1) Умножение внутри журнала можно превратить в сложение вне журнала, и наоборот.
2) Деление внутри журнала можно превратить в вычитание вне журнала, и наоборот.
3) Показатель степени для всего, что находится внутри бревна, можно вынести вперед как множитель, и наоборот.
Предупреждение: как и в случае с экспонентами, приведенные выше правила работают только , если основания совпадают. Например, выражение «log d ( m ) + log b ( n )» нельзя упростить, потому что основания («d» и «b») не совпадают, просто как x 2 × y 3 нельзя упростить, потому что основания ( x и y ) не совпадают.
Расширяющиеся логарифмы
Правила журнала могут использоваться для упрощения (или, точнее, для «уплотнения») выражений, для «расширения» выражений или для поиска значений. Начнем с расширения.
Когда в инструкциях говорится «расширить», они означают, что они дали мне одно выражение журнала с большим количеством вещей внутри него, и они хотят, чтобы я использовал правила журнала, чтобы разбить журнал на множество отдельных терминов журнала, каждый из которых имеет только одна вещь внутри своего конкретного журнала.То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
В этом случае у меня внутри журнала есть «2 x ». Поскольку «2 x » — это умножение, я могу разделить это выражение в соответствии с первым из приведенных выше правил журнала и превратить его в сложение вне журнала:
журнал 3 (2 x ) = журнал 3 (2) + журнал 3 ( x )
Тогда ответ, который они ищут:
Примечание: не пытайтесь вычислить «журнал 3 (2)» в вашем калькуляторе.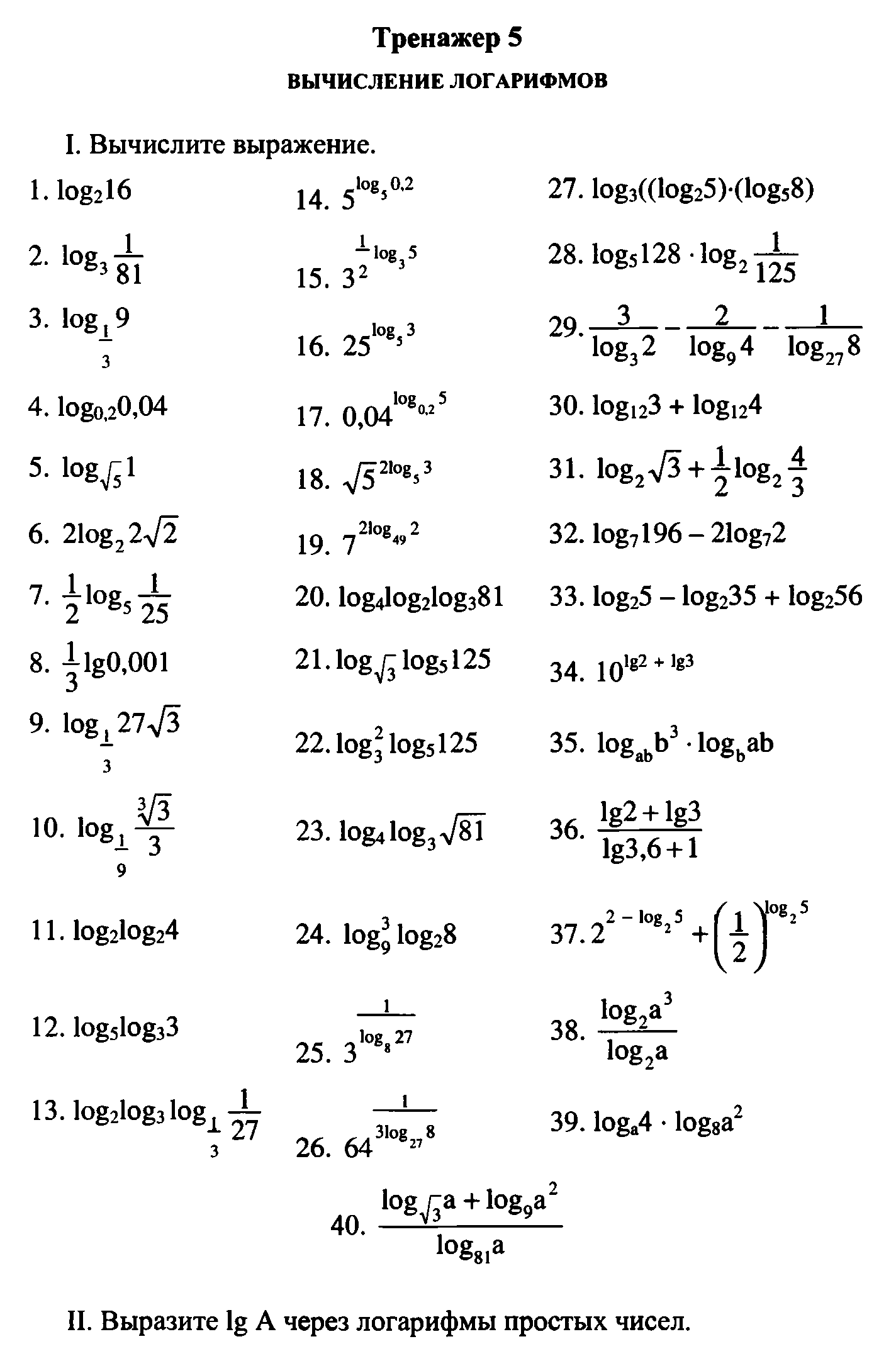 Хотя вы были бы правы, если бы сказали, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить в своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Хотя вы были бы правы, если бы сказали, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить в своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Если вы дадите «ответ» в виде десятичного приближения, вы должны ожидать потерю баллов.
У меня внутри журнала деление.Согласно второму правилу журнала, приведенному выше, его можно разделить на части как вычитание вне журнала, так:
журнал 4 ( 16 / x ) = журнал 4 (16) — журнал 4 ( x )
Первый член в правой части приведенного выше уравнения можно упростить до точного значения, применив основное определение логарифма. В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
Затем исходное выражение полностью раскрывается как:
журнал 4 ( 16 / x ) = 2 — журнал 4 ( x )
Всегда не забывайте находить время, чтобы проверить, можно ли упростить какие-либо термины в вашем расширении (например, журнал 4 (16) выше).
Показатель внутри бревна можно вынести вперед как множитель:
log 5 ( x 3 ) = 3 · log 5 ( x ) = 3log 5 ( x )
Приведенные выше примеры представляют собой очень простое использование правил журнала применительно к раскрытию выражений журнала. На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
URL: https://www.purplemath.com/modules/logrules.htm
Решение логарифмических уравнений с экспонентами
Purplemath
Второй тип логарифмического уравнения требует использования отношения:
—Взаимосвязь—
y = b x
……….. эквивалентно …………
(означает то же самое, что и)
журнал b ( y ) = x
В анимированной форме два уравнения связаны, как показано ниже:
MathHelp.com
Обратите внимание, что основание как в экспоненциальной форме уравнения, так и в логарифмической форме уравнения — «b», но x и y меняют сторону при переключении между двумя уравнениями.Если вы помните это — то, что было как аргумент журнала, становится «равным», и все, что было как «равно», становится экспонентой в экспоненте, и наоборот — тогда у вас не должно быть слишком много проблема с решением уравнений журнала.
Поскольку это уравнение имеет форму «журнал (чего-то) равен числу», а не «журнал (чего-то) равен журналу (чего-то еще)»), я могу решить уравнение, используя Соотношение:
журнал 2 ( x ) = 4
2 4 = x
16 = х
Я могу решить эту проблему, преобразовав логарифмический оператор в его эквивалентную экспоненциальную форму, используя The Relationship:
Но 8 = 2 3 , поэтому я могу приравнять степени двойки:
Обратите внимание, что это также можно было решить, работая непосредственно с определением логарифма.
Какая мощность при установке на «2» даст вам 8? Конечно же, сила 3!
Если вы хотите много работать, вы также можете сделать это в своем калькуляторе, используя формулу замены базы:
Подключите это к своему калькулятору, и вы получите «3» в качестве своего ответа. Хотя этот метод смены базы не особенно полезен в данном случае, вы можете видеть, что он действительно работает. (Попробуйте это на своем калькуляторе, если вы еще этого не сделали, чтобы быть уверенным, что вы знаете, какие клавиши нажимать и в каком порядке.Эта техника понадобится вам в последующих задачах.
Я не говорю, что вы обязательно захотите, чтобы решал уравнения, используя формулу замены базы, или всегда используя определение журналов, или какой-либо другой конкретный метод. Но я предлагаю вам убедиться, что вы знакомы с различными методами, и что вы не должны паниковать, если вы и ваш друг использовали , всего разных методов для решения одного и того же уравнения.
Журнал решения
2 ( x ) + лог 2 ( x — 2) = 3
Я пока ничего не могу сделать с этим уравнением, потому что у меня его еще нет в форме «журнал (чего-то) равно числу». Поэтому мне нужно использовать правила журнала, чтобы объединить два члена в левой части уравнения:
журнал 2 ( x ) + журнал 2 ( x — 2) = 3
журнал 2 [( x ) ( x — 2)] = 3
журнал 2 ( x 2 -2 x ) = 3
Теперь уравнение устроено удобным образом.На этом этапе я могу использовать Отношение, чтобы преобразовать логарифмическую форму уравнения в соответствующую экспоненциальную форму, а затем я могу решить результат:
журнал 2 ( x 2 -2 x ) = 3
2 3 = x 2 -2 x
8 = x 2 -2 x
0 = x 2 — 2 x — 8
0 = ( x -4) ( x + 2)
x = 4, –2
Но если x = –2, то «log 2 ( x )» из исходного логарифмического уравнения будет иметь отрицательное число в качестве аргумента (как и термин «log 2 ( x — 2) «).Поскольку журналы не могут иметь нулевых или отрицательных аргументов, решение исходного уравнения не может быть x = –2.
Тогда мое решение:
Имейте в виду, что вы всегда можете проверить свои ответы на любое упражнение «решение», вставив эти ответы обратно в исходное уравнение и проверив, что решение «работает». В этом случае я вставлю свое значение решения в любую сторону исходного уравнения и проверю, что каждая сторона оценивает одно и то же число:
левая сторона:
журнал 2 ( x ) + журнал 2 ( x — 2)
= журнал 2 (4) + журнал 2 (4-2) 3
= журнал 2 (4) + журнал 2 (2)
= журнал 2 (2 2 ) + журнал 2 (2 1 )
= 2 + 1 = 3
Правая часть исходного уравнения уже была упрощена до «3», поэтому это решение проверяется.
Это уравнение может показаться слишком сложным, но это всего лишь еще одно логарифмическое уравнение. Чтобы решить эту проблему, мне нужно дважды применить The Relationship. Я начинаю с исходного уравнения и работаю с «внешним» журналом:
Отношение преобразует вышеуказанное в:
Теперь я применяю Отношение во второй раз:
Тогда решение:
Журнал решения
2 ( x 2 ) = (журнал 2 ( x )) 2
Во-первых, я расширю квадрат справа, чтобы он был явным произведением двух журналов:
журнал 2 ( x 2 ) = [журнал 2 ( x )] 2
журнал 2 ( x 2 ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я применяю правило журнала, чтобы переместить «квадрат» изнутри журнала в левой части уравнения, вынимая его перед этим журналом в качестве множителя:
2 · журнал 2 ( x ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я перенесу этот член из левой части уравнения в правую:
0 = [журнал 2 ( x )] [журнал 2 ( x )] — 2 · журнал 2 ( x )
Это уравнение может показаться плохим, но внимательно присмотритесь.На данный момент это не более чем упражнение по факторингу. Итак, я фактор, а затем я решу факторы, используя The Relationship:
.
0 = [журнал 2 ( x )] [журнал 2 ( x ) — 2]
журнал 2 ( x ) = 0 или журнал 2 ( x ) — 2 = 0
2 0 = x или лог 2 ( x ) = 2
1 = x или 2 2 = x
1 = x или 4 = x
Тогда мое решение:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении логарифмических уравнений (или пропустите виджет и продолжите урок).Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvelog2.htm
OpenAlgebra.com: Решение логарифмических уравнений
Используйте однозначное свойство логарифмов для решения логарифмических уравнений.
Плейлист по решению лог-уравнений
Если нам дано уравнение с логарифмом одного и того же основания с обеих сторон, мы можем просто приравнять аргументы.
Шаг 1 : Используйте правила экспонент, чтобы изолировать логарифмическое выражение (с одинаковым основанием) с обеих сторон уравнения.
Шаг 2 : Установите одинаковые аргументы.
Шаг 3 : Решите полученное уравнение.
Шаг 4 : Проверьте свои ответы.
Обязательно проверьте, решают ли полученные решения исходное логарифмическое уравнение. В этом учебном пособии мы поставим галочку рядом с решением после того, как определим, что оно действительно решает уравнение. Этот процесс иногда приводит к посторонним решениям, поэтому мы должны проверить свои ответы.
Решить .
Конечно, подобные уравнения очень особенные. Большинство проблем, с которыми мы столкнемся, не имеют логарифма с обеих сторон.Шаги по их решению приведены ниже.
Шаг 1 : Используйте свойства логарифма, чтобы изолировать журнал с одной стороны.
Шаг 2 : Примените определение логарифма и перепишите его как экспоненциальное уравнение.
Шаг 3 : Решите полученное уравнение.
Шаг 4 : Проверьте свои ответы.
Если ответ на логарифмическое уравнение делает аргумент отрицательным, то он не имеет значения. Это не исключает отрицательных ответов.Мы должны обязательно проверить все наши решения.
Обучающее видео : Решение логарифмических уравнений
Решить .
Совет : Не все отрицательные решения являются посторонними! Посмотрите на предыдущий набор проблем и убедитесь, что на некоторые из них есть отрицательные ответы. Галочка означает, что мы действительно вставили ответы, чтобы убедиться, что они действительно решают исходный текст. Пожалуйста, не пропускайте этот шаг, часто встречаются посторонние решения.
Видео на YouTube :
Алгебра — решение логарифмических уравнений
Решите каждое из следующих уравнений.
a \ ({\ log _5} \ left ({2x + 4} \ right) = 2 \) Показать решение
Чтобы решить их, нам нужно привести уравнение в точную форму, в которой находится это. Нам нужен единственный лог в уравнении с коэффициентом, равным единице, и константой по другую сторону от знака равенства.2} = 25 \]
Обратите внимание, что это уравнение, которое мы можем легко решить.
\ [2x = 21 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = \ frac {{21}} {2} \]
Теперь, как и в первом наборе примеров, нам нужно снова вставить это в исходное уравнение и посмотреть, будет ли оно давать отрицательные числа или нули в логарифмах. Если да, то это не может быть решением, а если нет, то это решение.
\ [\ begin {align *} {\ log _5} \ left ({2 \ left ({\ frac {{21}} {2}} \ right) + 4} \ right) & = 2 \\ {\ log _5} \ left ({25} \ right) & = 2 \ end {align *} \]
Только положительные числа в логарифме, поэтому \ (x = \ frac {{21}} {2} \) на самом деле является решением.
b \ (\ log x = 1 — \ log \ left ({x — 3} \ right) \) Показать решение
В этом случае у нас есть два логарифма в задаче, поэтому нам придется объединить их в один логарифм, как мы это сделали в первом наборе примеров. Выполнение этого для этого уравнения дает
\ [\ begin {align *} \ log x + \ log \ left ({x — 3} \ right) & = 1 \\ \ log \ left ({x \ left ({x — 3} \ right)} \ вправо) & = 1 \ end {выровнять *} \]
Теперь, когда мы получили уравнение в правильной форме, мы преобразуем его в экспоненциальную форму.2} — 3x — 10 & = 0 \\ \ left ({x — 5} \ right) \ left ({x + 2} \ right) & = 0 \ hspace {0,25in} \ Rightarrow \ hspace {0,25in} x = — 2, \, \, x = 5 \ end {align *} \]
Итак, у нас есть два возможных решения. Давайте проверим их обоих.
\ (* х = — 2: \)
\ [\ log \ left ({- 2} \ right) = 1 — \ log \ left ({- 2 — 3} \ right) \]
У нас есть отрицательные числа в логарифмах, поэтому это не может быть решением. 2} — 6 \ left (2 \ right)} \ right) & = 3 + {\ log _2} \ left ({1 — 2} \ right) \\ {\ log _2} \ left ({4 — 12} \ right) & = 3 + {\ log _2} \ left ({- 1} \ right) \ end {align *} \]
В этом случае, несмотря на то, что потенциальное решение положительно, мы получаем отрицательные числа в логарифмах, и поэтому оно не может быть решением.
Следовательно, мы получаем единственное решение этого уравнения, \ (x = — 4 \).
Чтений: Использование определения логарифма для решения логарифмических уравнений
Мы уже видели, что каждое логарифмическое уравнение
log b ( x ) = y эквивалентно экспоненциальному уравнению b y = x . Мы можем использовать этот факт вместе с правилами логарифмов для решения логарифмических уравнений, в которых аргумент является алгебраическим выражением. {{3}} = {6} {x} — {10} [/ latex]
3
Использование определения логарифма для решения логарифмических уравнений
Для любого алгебраического выражения
S и вещественных чисел b и c , где b > 0, b ≠ 1,
log
b ( S ) = c тогда и только тогда, когда b c = S
Пример 1
Использование алгебры для решения логарифмического уравнения
- Решить [латекс] \ displaystyle {2} {ln {{x}}} + {3} = {7} [/ latex]
- Вычесть 3:
[латекс] \ displaystyle {2} {ln {{x}}} = {4} [/ latex] - Разделить на 2:
[латекс] \ displaystyle {ln {{x}}} = {2} [/ latex] - Записываем в экспоненциальной форме:
[latex] \ displaystyle {x} = {e} ^ {{2}} [/ latex]
- Вычесть 3:
- Решить [латекс] \ displaystyle {6} + {ln {{x}}} = {10} [/ latex]
Использование алгебры до и после использования определения натурального логарифма
- Решить [латекс] \ displaystyle {2} {ln {{({6} {x})}}} = {7} [/ latex]
- Разделить на 2:
[латекс] \ displaystyle {ln {{({6} {x})}}} = \ frac {{7}} {{2}} [/ latex] - Используйте определение ln:
[latex] \ displaystyle {6} {x} = {e} ^ {{{(\ frac {{7}} {{2}})}}} [/ latex] - Разделить на 6:
[латекс] \ displaystyle {x} = \ frac {{1}} {{6}} {e} ^ {{{(\ frac {{7}} {{2}})}} } [/ латекс]
- Разделить на 2:
- Решить [латекс] \ displaystyle {2} {ln {{({x} + {1})}}} = {10} [/ latex]
- Используя график, чтобы понять решение логарифмического уравнения, решите [latex] \ displaystyle {ln {{x}}} = {3} [/ latex] Графики y = ln x и y = 3 крестик в точке ( e 3 , 3), что приблизительно равно (20.0855, 3).
- Используйте графический калькулятор, чтобы оценить приблизительное решение логарифмического уравнения 2 x = 1000, решите с точностью до 2 десятичных знаков.
x ≈ 9,97
Как и в случае с экспоненциальными уравнениями, мы можем использовать свойство однозначности для решения логарифмических уравнений. Однозначное свойство логарифмических функций говорит нам, что для любых действительных чисел
x > 0, S > 0, T > 0 и любого положительного действительного числа b , где b ≠ 1,
журнал b S = журнал b T тогда и только тогда, когда S = T
Например,
Если журнал 2 ( x — 1) = log 2 (8), то x — 1 = 8.
Итак, если
x — 1 = 8,
, то мы можем решить для
x , и мы получим x = 9. Чтобы проверить, мы можем заменить x = 9 в исходное уравнение: log 2 (9 — 1) = log 2 (8) = 3. Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны. Это также применимо, когда аргументы являются алгебраическими выражениями. Следовательно, когда дано уравнение с журналами с одинаковым основанием на каждой стороне, мы можем использовать правила логарифмов, чтобы переписать каждую сторону как единый логарифм.Затем мы используем тот факт, что логарифмические функции взаимно однозначны, чтобы установить аргументы, равные друг другу, и найти неизвестное.
Например, рассмотрим уравнение
[латекс] \ displaystyle {log {{({3} {x} — {2})}}} — {log {{({2})}}} = {log {{ ({x} + {4})}}} [/ латекс]. Чтобы решить это уравнение, мы можем использовать правила логарифмов, чтобы переписать левую часть как единый логарифм, а затем применить свойство «один к одному», чтобы найти
[латекс] \ displaystyle {log {{({3} { x} — {2})}}} — {log {{({2})}}} = {log {{({x} + {4})}}} [/ latex]
| Примените правило частного логарифмов | [латекс] \ displaystyle {журнал {{(\ frac {{{3} {x} — {2}}} {{2}})}}} = {журнал {{({x} + {4}) }}} [/ latex] |
| Примените свойство логарифма один к одному. | [латекс] \ displaystyle \ frac {{{3} {x} — {2}}} {{2}} = {x} + {4} [/ latex] |
| Умножьте обе части уравнения на 2 | [латекс] \ displaystyle {3} {x} — {2} = {3} {x} + {8} [/ latex] |
| Вычтем 2 x и прибавим 2 | [латекс] \ displaystyle {x} = {10} [/ latex] |
Чтобы проверить результат, замените
на
[латекс] \ displaystyle {журнал {{({3} {({10})} — {2})}}} — {журнал {{({2})}}} = {журнал {{({( {10})} + {4})}}} [/ латекс]
[латекс] \ displaystyle {log {{({28})}}} — {log {{({2})}}} = {log {{({14})}}} [/ latex]
[латекс] \ Displaystyle {журнал {{(\ frac {{28}} {{2}})}}} = {журнал {{({14})}}} [/ латекс]
Решение проверяет.
Использование однозначного свойства логарифмов для решения логарифмических уравнений
Для любых алгебраических выражений
S и T и любого положительного действительного числа b , где b ≠ 1, log b S = log b T тогда и только тогда, когда S = т
Обратите внимание: при решении уравнения, включающего логарифмы, всегда проверяйте, правильный ли ответ или является ли это посторонним решением. {{2}} — {2} {x} — {3} = {0} [/ latex] Фактор с использованием FOIL: [latex] \ displaystyle {({x} — {3})} {({x} + {1})} = {0} [/ латекс]
Если продукт равен нулю, один из факторов должен быть равен нулю: [latex] \ displaystyle {x} — {3} = {0} {\ text {или}} {x} + {1} = {0} [ / латекс]
Решите относительно x : [latex] \ displaystyle {x} = {3} {\ text {or}} {x} = — {1} [/ latex]
Анализ
Есть два решения:
x = 3 или x = –1.{{2}})}}} = {ln {{1}}} [/ latex]
OpenStax, Precalculus, «Экспоненциальные и логарифмические уравнения», под лицензией CC BY 3.0.
.
