Чему равен arcsin sinx: Чему равен arcsin(sinx) и arccos(cosx)? — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )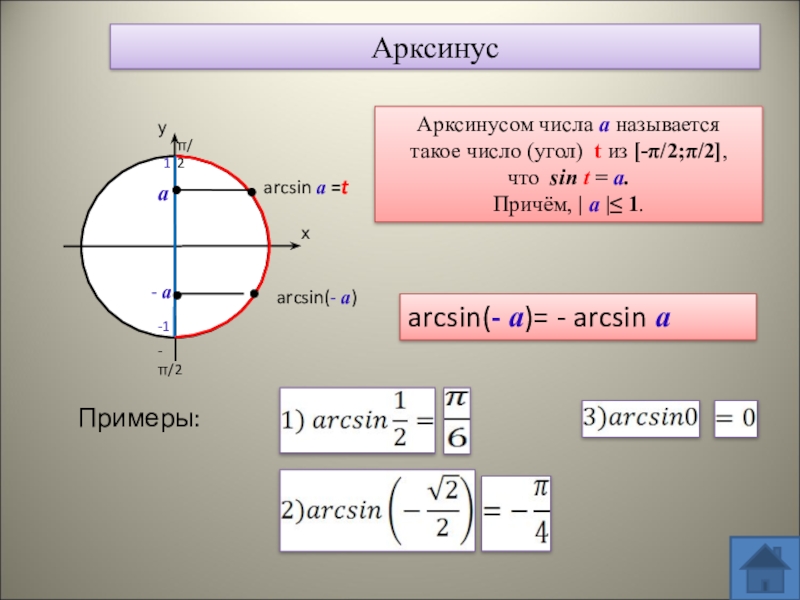
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )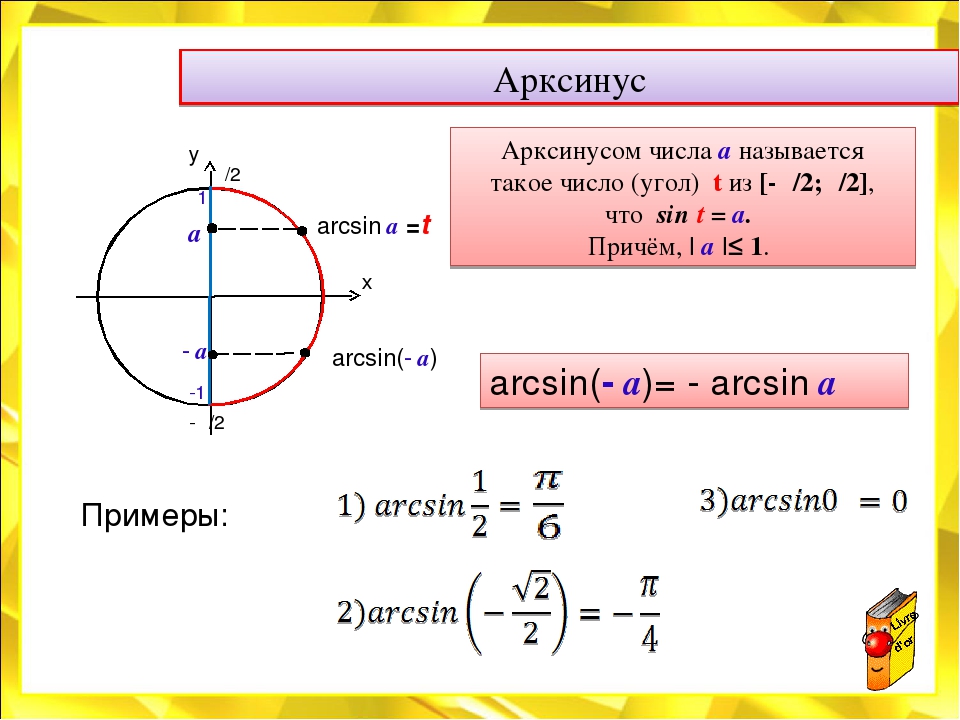
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень 2)/2)
100	Преобразовать из градусов в радианы	88 град.

График arcsin cos x. Вывод формул обратных тригонометрических функций

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

К понятиям арксинус, арккосинус, арктангенс, арккотангенс

учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы.
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4.

Или arctg(-1,3).

Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…

Что означает выражение

arcsin 0,4 ?

Это угол, синус которого равен 0,4
! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.

И всё.

Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:

arc
sin
0,4

угол,
синус которого
равен 0,4

Как пишется, так и слышится.) Почти. Приставка arc
означает дуга
(слово арка
знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.

Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.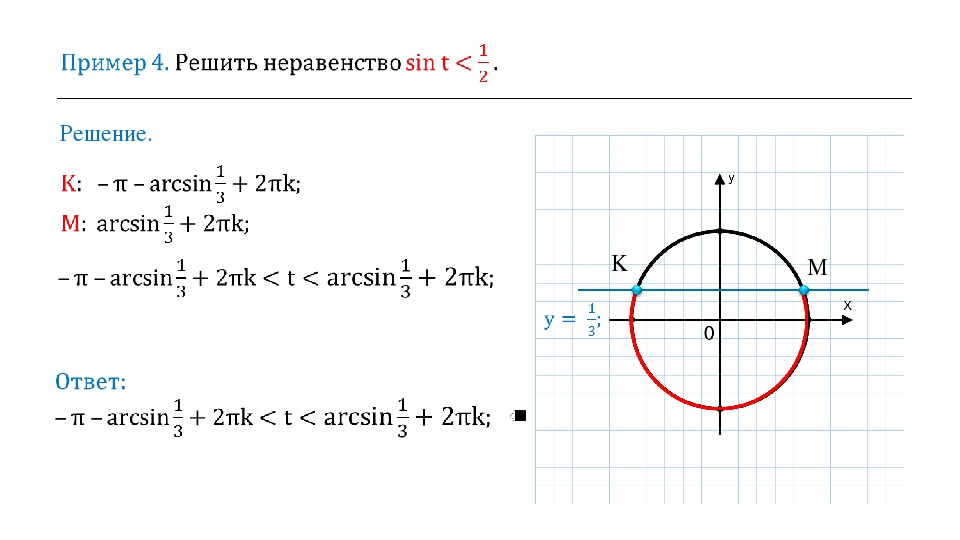

Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.

Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.

Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!

Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)

Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки.
Чтобы печатать меньше.)

Внимание! Элементарная словесная и осознанная
расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных
заданиях только она и спасает.

А можно переходить от арков к обычным градусам или радианам?
— слышу осторожный вопрос.)

Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)

Например: что такое arcsin 0,5?

Вспоминаем расшифровку:
arcsin 0,5 — это угол, синус которого равен 0,5.
Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов
. Вот и все дела: arcsin 0,5 — это угол 30°.
Можно смело записать:

arcsin 0,5 = 30°

Или, более солидно, через радианы:

Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.

Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс…
То легко разберётесь, например, с таким монстром.)

Несведущий человек отшатнётся в ужасе, да. ..) А сведущий вспомнит расшифровку:
арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!

Достаточно сообразить, что:

Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1)
— это угол 45°. Или, что едино, Пи/4. Аналогично:

и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.

Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!

Частенько, в подобных примерах, внутри арков стоят отрицательные
значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:

Нужно вам, скажем, определить значение выражения:

Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного
значения внутри арккосинуса к положительному
по второй формуле:

Внутри арккосинуса справа уже положительное
значение. То, что

вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:

Вот и всё.

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)

Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень.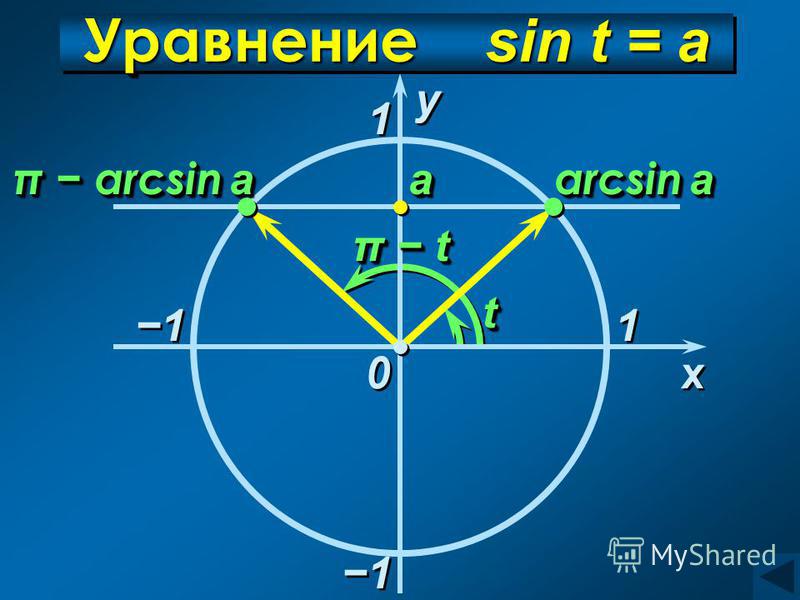 Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С

Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве

Что будем изучать:

1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.

6. Примеры.

Что такое арксинус?

Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность.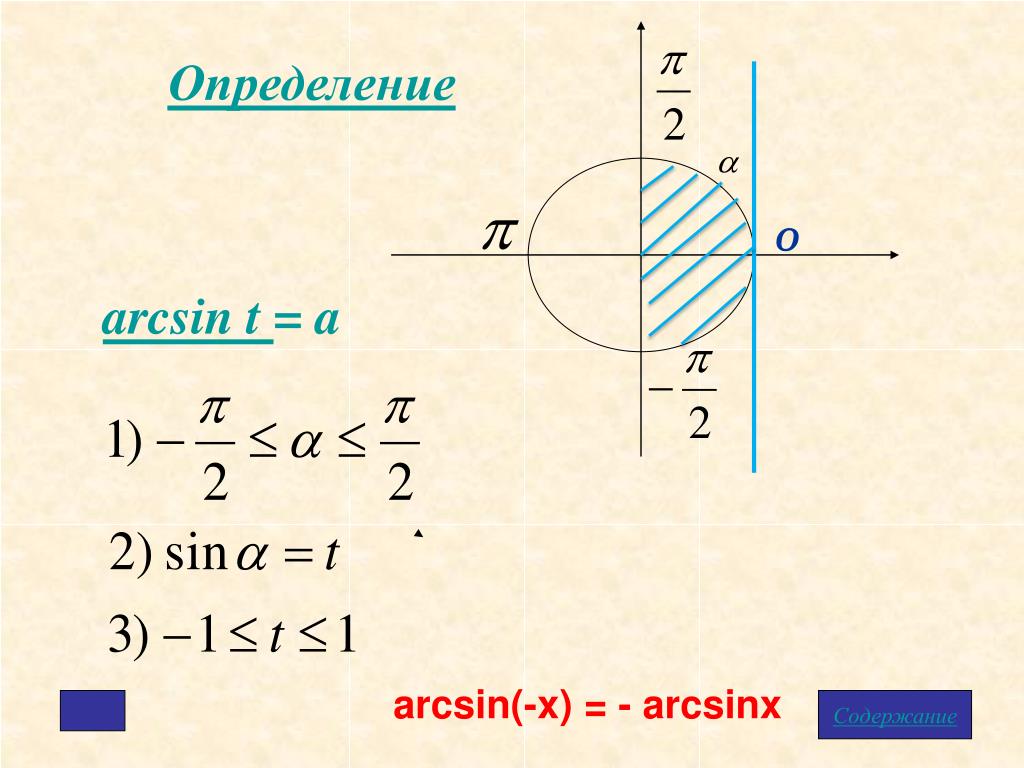 Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.

Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?

Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.

Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).

И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.

Немного истории арксинуса

История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.

Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.

Определение арксинуса

Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.

Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk

Перепишем:

x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).

Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:

Есть три случая, в которых предпочитают записывать решения более простым способом:

sin(x)=0, то x= πk,

sin(x)=1, то x= π/2 + 2πk,

sin(x)=-1, то x= -π/2 + 2πk.

Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).

Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.

Примеры

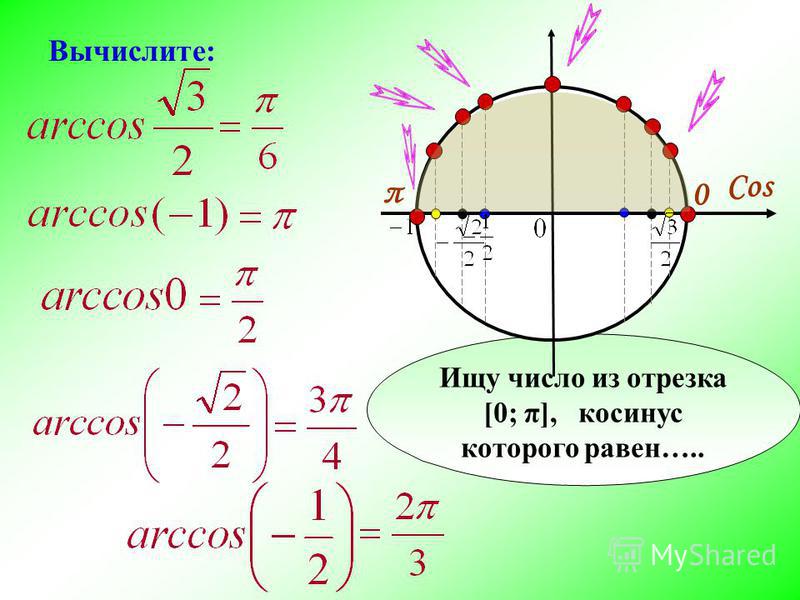
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.

2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.

3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.

4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.

5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk

6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.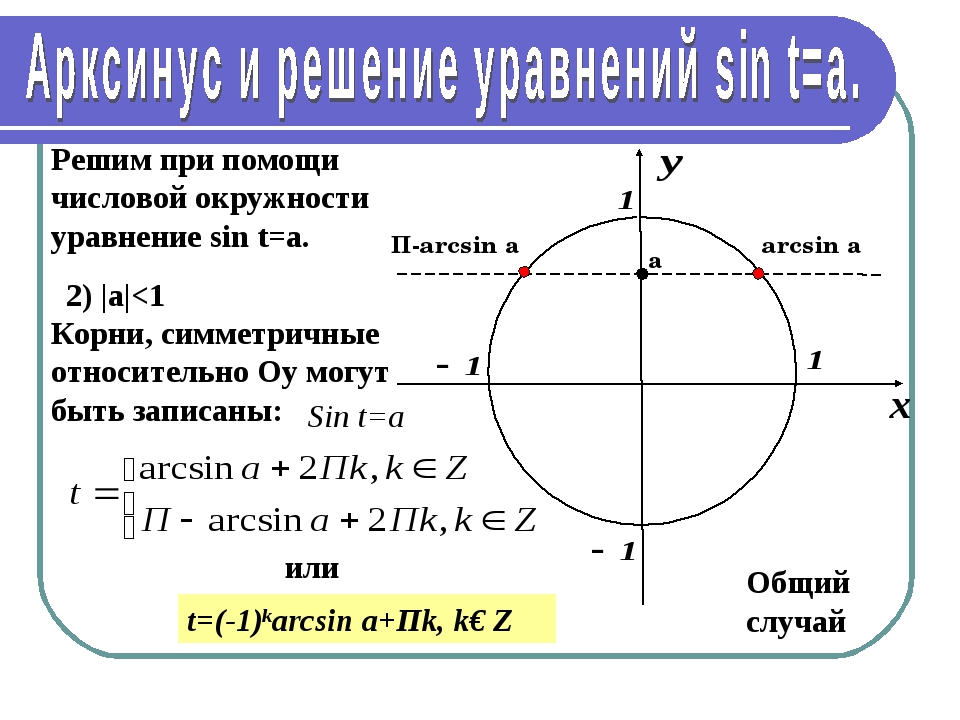

7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk

Задачи на арксинус для самостоятельного решения

1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.

Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.

Определение обратных тригонометрических функций

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней.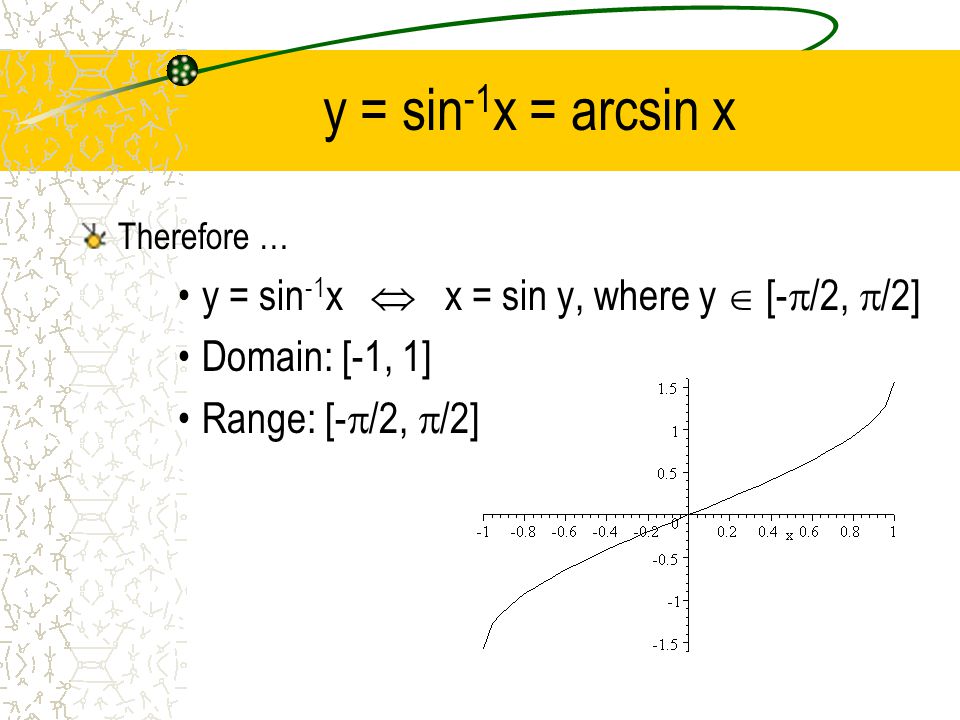 Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn

(где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны
. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус (y = arcsin
x
)

— это функция, обратная к синусу (x = sin
y

Арккосинус (y = arccos
x
)

— это функция, обратная к косинусу (x = cos
y
), имеющая область определения и множество значений .

Арктангенс (y = arctg
x
)

— это функция, обратная к тангенсу (x = tg
y
), имеющая область определения и множество значений .

Арккотангенс (y = arcctg
x
)

— это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x
.
См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin
x

y = arccos
x

y = arctg
x

y = arcctg
x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin
x)
= x
при
sin(arcsin
x)
= x

arccos(cos
x)
= x
при
cos(arccos
x)
= x

arctg(tg
x)
= x
при
tg(arctg
x)
= x

arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x

Формулы, связывающие обратные тригонометрические функции

Формулы суммы и разности

при или

при и

при или

при и

при

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.

Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.

Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сопоставить графики sin
и arcsin
, у двух тригонометрических функций можно найти общие закономерности.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

Функция определена на отрезке [-1; 1].
ОДЗ для arccos — .
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.

Задание 1.
Укажите функции изображенные на рисунке.

Ответ:
рис. 1 – 4, рис.2 — 1.

В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.

Арктангенс

Arctg
числа a – это такое значение угла α, что его тангенс равен а.

Если рассмотреть график арктангенса, можно выделить следующие свойства:

График бесконечен и определен на промежутке (- ∞; + ∞).
Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
Y = 0 при x = 0.
Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арккотангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

Интервал определения функции – бесконечность.
Область допустимых значений – промежуток (0; π).
F(x) не является ни четной, ни нечетной.
На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2.
Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ:
рис. 1 – 1, рис. 2 – 4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.

Также существуют соотношения для arctg и arcctg:

Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.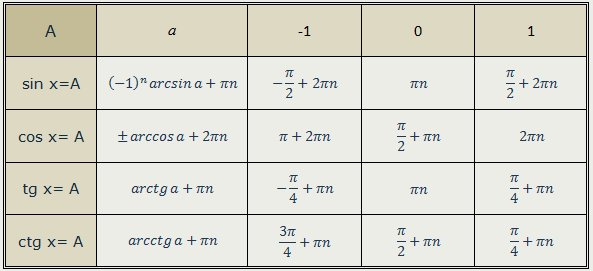

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

Если вспомнить формулу arcsin (sin α) = α
, то можно свести поиск ответов к решению системы из двух уравнений:

Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов.

Основные формулы

Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.

В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin
x)
= x

cos(arccos
x)
= x

tg(arctg
x)
= x
(-∞ ctg(arcctg
x)
= x
(-∞

Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при

Если переменная x
не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n
— целое):
sin
x = sin(-
x-π)

;
sin
x = sin(π-x)

;
sin
x = sin(x+2
πn)

;

cos
x = cos(-x)

;
cos
x = cos(2
π-x)

;
cos
x = cos(x+2
πn)

;

tg
x = tg(x+πn)

;
ctg
x = ctg(x+πn)

Например, если известно, что то
arcsin(sin
x)
=
arcsin(sin( π — x ))
= π — x .

Легко убедиться, что при π — x
попадает в нужный интервал. Для этого умножим на -1
: и прибавим π
:
или Все правильно.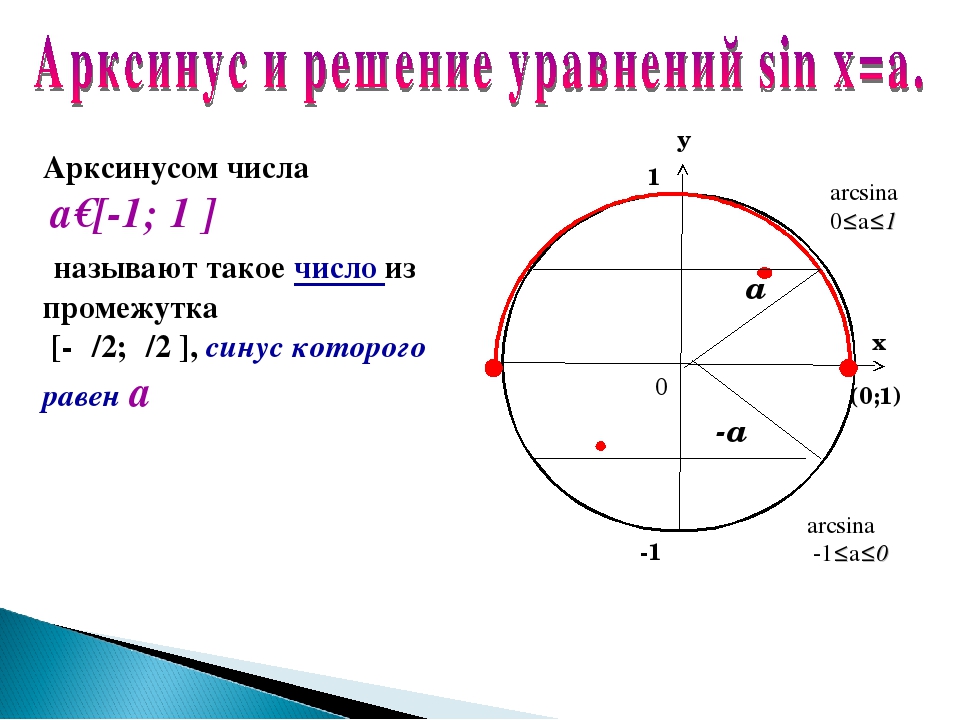

Обратные функции отрицательного аргумента

Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.

arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x

Поскольку то умножив на -1
, имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.

Аналогично для остальных функций.
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x

arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x

arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x

Выражение арксинуса через арккосинус и арктангенса через арккотангенс

Выразим арксинус через арккосинус.

Формула справедлива при Эти неравенства выполняются, поскольку

Чтобы убедиться в этом, умножим неравенства на -1
: и прибавим π/2
:
или Все правильно.

Аналогично выражаем арктангенс через арккотангенс.

Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот

Поступаем аналогичным способом.

Формулы суммы и разности

Аналогичным способом, получим формулу суммы арксинусов.

Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin
x
,
Y = arcsin
y
.
Формула применима при
.
Далее замечаем, что, поскольку arcsin(-
x) = — arcsin
x,
arcsin(-
y) = — arcsin
y,
то при разных знаках у x
и y
,
X
и Y
также разного знака и поэтому неравенства выполняются. Условие различных знаков у x
и y
можно написать одним неравенством: .
То есть при формула справедлива.

Теперь рассмотрим случай x > 0

и y > 0

,
или X > 0

и Y > 0

.
Тогда условие применимости формулы заключается в выполнении неравенства: .
Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0

,
до π
,
то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;

;

;

.

Поскольку и ;
то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;

.

Подставляем sin
X = sin arcsin
x = x
:

;

;

;

.

Итак, полученная формула справедлива при или .

Теперь рассмотрим случай x > 0, y > 0
и x 2 + y 2 > 1

.
Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :

Итак,

при и.

Заменив x
и y
на — x
и — y
,
имеем

при и.

Выполняем преобразования:

при и.

Или

при и.

Итак, мы получили следующие выражения для суммы арксинусов:

при или ;

при и ;

при и .

Тест. Уравнение sinx = a

Будьте внимательны! У Вас есть 20 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса.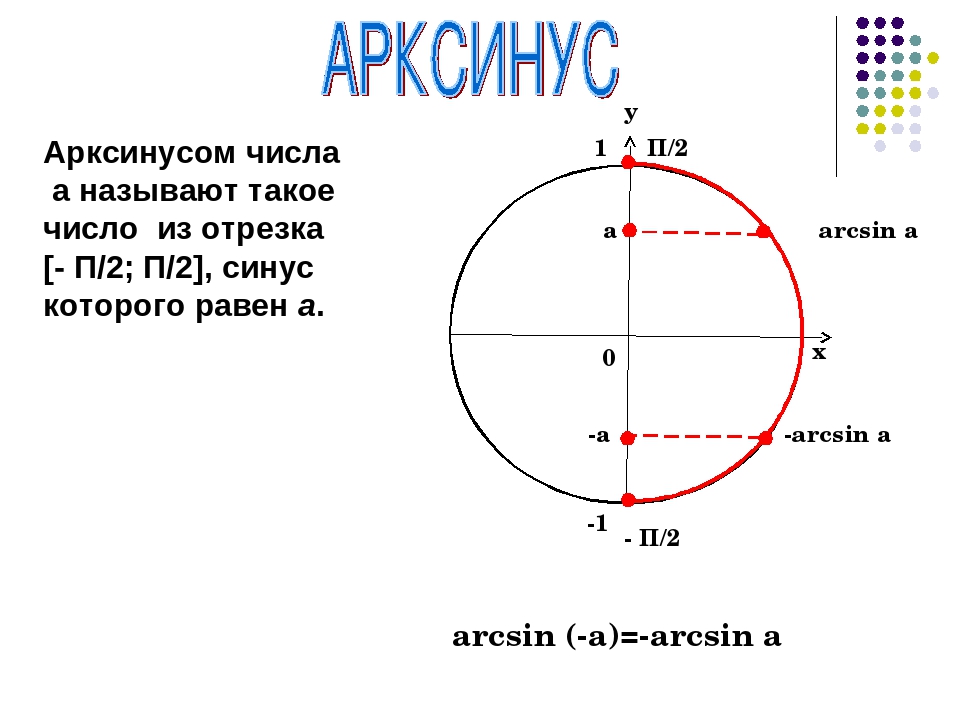 Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!

Список вопросов теста

Вопрос 1

Как называется уравнение, которое содержит переменную под знаком тригонометрических функций?

Вопрос 2

Дополните:
Синусом угла α называется . .. точки Рα, полученной поворотом точки Р (1;0) вокруг начала координат на угол α.

Варианты ответов

абсцисса

ордината

Вопрос 3

Дополните:
Арксинусом числа а, модуль которого не больше единицы, называется. ..

Варианты ответов

Вопрос 4

Согласны ли вы, что:

Варианты ответов

Уравнение sin x = a, где а≤1, на отрезке -π2;π2 имеет только один корень.

Для любого а из промежутка [-1;1] справедлива формула:
arсsin (-а) = -arcsin а.

Уравнение sin x = a имеет корни только при -1 ≤ а ≤ 1.

Уравнение sin x = a, где а≤1, на отрезке -π2;π2 имеет бесконечное множество корней.

Для любого а из промежутка [-1;1] справедлива формула:
arсsin (-а) = π — arcsin а.

Уравнение sin x = a имеет корни только при a < -1 и а > 1.

Вопрос 5

Найдите решения уравнения sin x=22 на промежутке [0;2π].

Варианты ответов

Вопрос 6

Найдите решения уравнения sin x=-22 на промежутке [0;2π].

Варианты ответов

Вопрос 7

Сопоставьте уравнения с их решениями:

Варианты ответов

x=πk,k∈Z

x=π2+2πk,k∈Z

x=-π2+2πk,k∈Z

Вопрос 8

Выберите общую формулу нахождения корней уравнения sin x = a, │a│≤ 1.

Варианты ответов

x=±arcsin a+2πk,k∈Z

x=(-1)narcsin a+πn,n∈Z

x=arcsin a+πk,k∈Z

x=π-arcsin a-2πk,k∈Z

Вопрос 9

Решите уравнение sin 2x-1=-22.

Варианты ответов

x=(-1)k+1π8+12+πk2,k∈Z

x=±π8+2πk,k∈Z

x=(-1)karcsin 12+2πk,k∈Z

x=-1arcsin 22+π3+πk,k∈Z

Вопрос 10

Чему равен arcsin(0,3)? Значение округлите до тысячных.

Арксинус и арккосинус. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале [−∞;+∞] и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.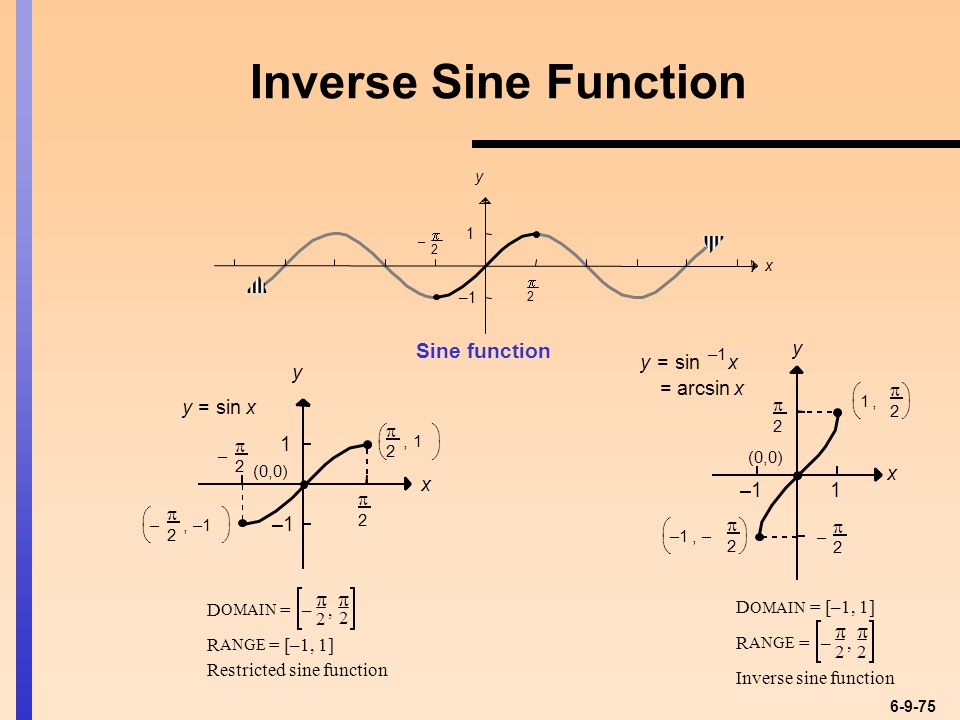 1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

Область определения функции: .

Область значений функции: .

Функция является нечетной: .

Функция возрастает.

Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т. к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т. к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале [−∞;+∞] и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию.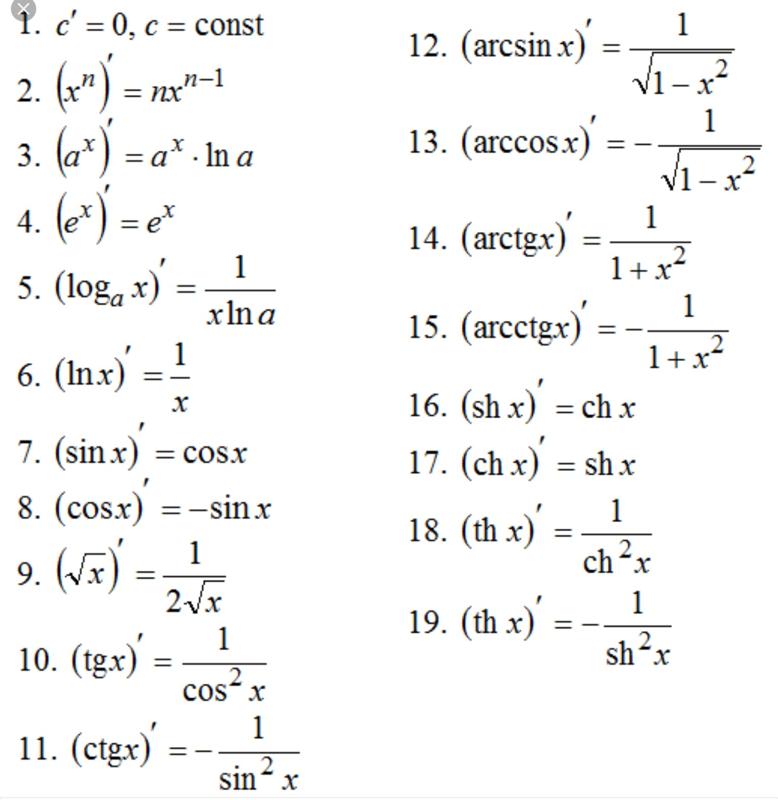 Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

Область определения функции: .

Область значений функции: .

Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).

Функция убывает.

Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3.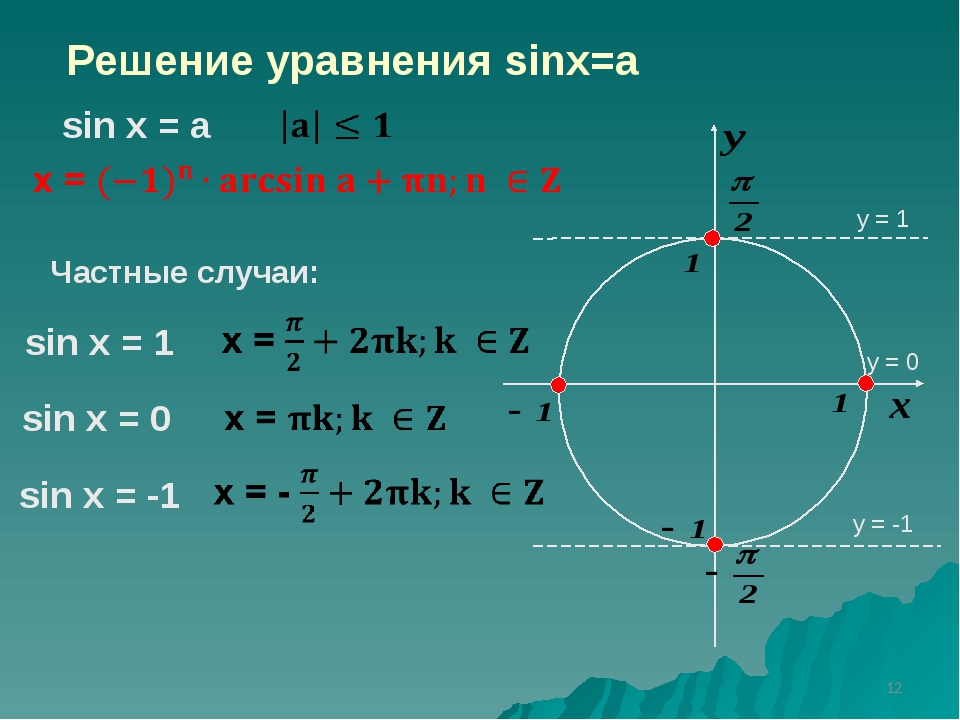 Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

Урок по теме: «Обратные тригонометрические функции»

Тип урока: «Обобщения, систематизации
знаний»

Цели
урока:

повторение основных свойств обратных
тригонометрических функций,

вычисление значений обратных
тригонометрических функций,

решение уравнений, содержащих обратные
тригонометрические функции,

решение экзаменационных заданий ЕГЭ группы B и
группы C.

Оборудование:

доска (в начале урока),

доска (в конце урока),

10 карточек для опроса,

10 компьютеров для тестирования,

3 таблицы.

Ход урока

Организационный момент: вступительное слово
учителя о целях урока.

            I:
Фронтальный опрос

1)       Что называется арксинусом
числа а? (Арксинусом числа a?[-1;1]
называется такое число a?[-?/2; ?/2], синус
которого равен а)

2)       Что называется
арккосинусом числа а? (Арккосинусом числа a?[-1;1]
называется такое число a?[0; ?], косинус
которого равен а)

3)       Что называется
арктангенсом числа а? (Арктангенсом числа a?R
называется такое число a?(-?/2; ?/2), тангенс
которого равен а)

4)       Что называется
арккотангенсом числа а? (Арккотангенсом
числа a?R называется такое число a?(0; ?), котангенс
которого равен а
5)       Чему равен sin(arcsin a), cos(arccos
a), tg(arctg a). ctg(arcctg a)? Какие значения принимает a?

sin(arcsin a)=a, cos(arccos a)=a, a?[-1;1]

tg(arctg a)=a, ctg(arcctg a)=a.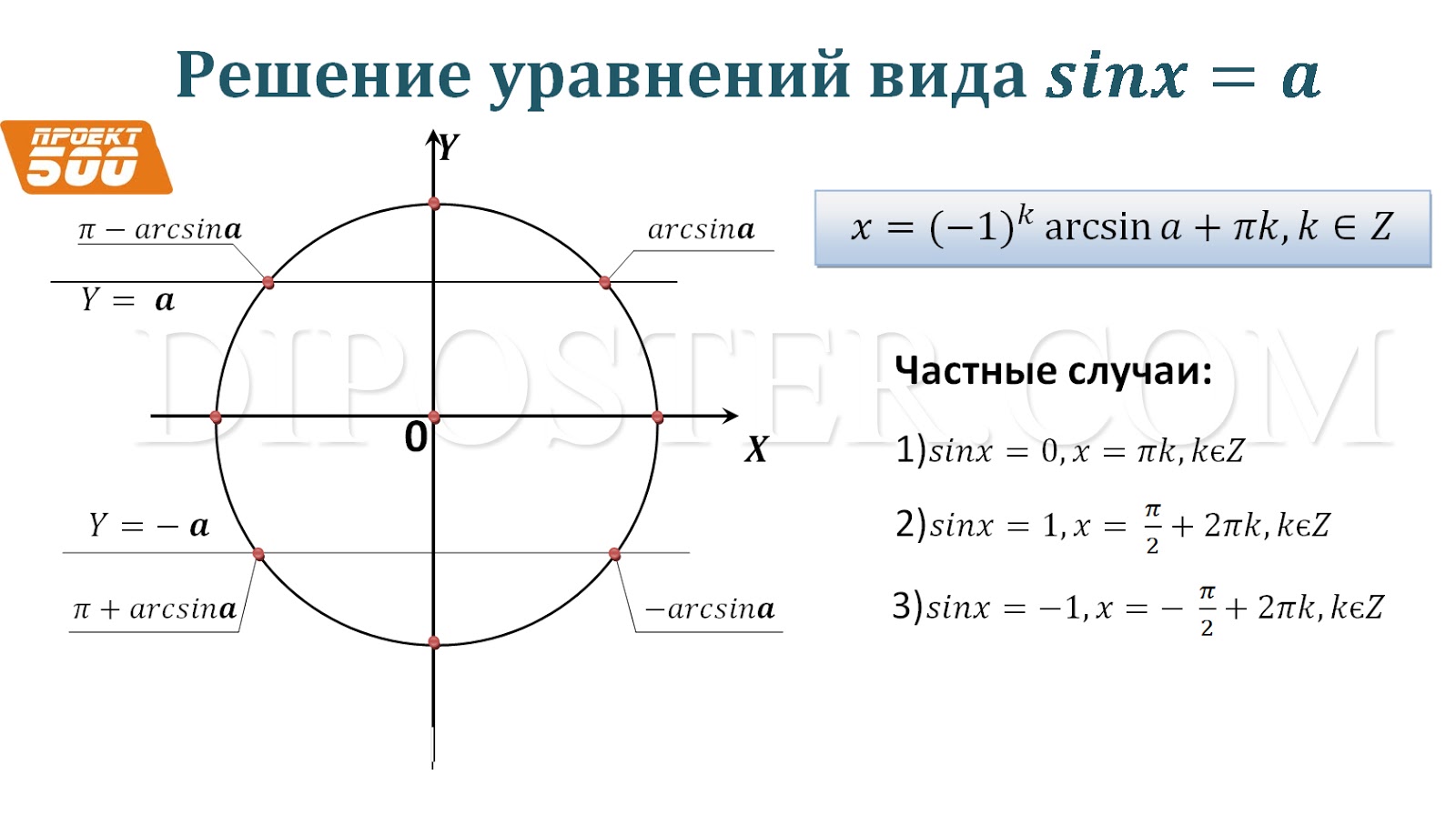 a?R

6)       Чему равен arcsin(sin x), arccos(cos x),
arctg(tg x), arcctg(ctg x)? Какие значения принимает x?

arcsin(sin x)=x, x?[-?/2; ?/2]

arcos(cos x)=x, x?[0; ?]

arcctg(tg x)=x, x?(-?/2; ?/2)

arcctg(ctg x)=x, x?(0; ?)

II: Устные
упражнения

Вычислить:

3) не сущ

5) не сущ

III. Решение
заданий на нахождение обратных
тригонометрических функций. (Трое учащихся у
доски)

IV. Решение заданий из ЕГЭ.

I группа: B. 6 (часть B). Тест (со взаимопроверкой;
ответы на откидной доске.)

1) вариант 56:

2) вариант 57:

3) вариант 58:

4) вариант 59:

5) вариант 60:

V. Фронтальный опрос.

1) Как решить уравнение

Таблица №1

           или

2) Как решить уравнение:

Таблица №2

какое используется тождество?

3) Как решить уравнение:

Таблица №3

или

Какое используется тождество?

VI. Решение уравнений. (Трое учащихся у доски)

Решение

Уравнение равносильно системе

Ответ: x=-1/3

Решение

Ответ: x=1

Решение

n?Z
n?Z

               , n?Z




k?Z пост.
корень

Ответ: , n?Z

VII. Решение заданий.
II группа на компьютерах.

Тест со взаимопроверкой; ответы показываются
на компьютере, и оцениваются компьютером

1) Вычислить:

1)

Решить уравнение:

Решение

Ответ: x=2

2)

Найти область определения функции

Ответ: [2;4]

II. Решение задания С-2 из ЕГЭ

Найти множество значений функции , если x?[arсcos
0,8;5 /12]

Решение:

, n?Z

Ответ: [0,5;1]

VIII. Итог урока.

Учитель оценивает учащихся за работу на уроке.

Арксинус, арккосинус, арктангенс числа. Корни тригонометрических уравнений.

←Тригонометрический круг

Тригонометрические уравнения→

Решим уравнение sin x = a. Здесь a — число. Решаем его графически, то есть решаем систему уравнений

Для этого рисуем графики у = sin x и у = a

Как видно из графика, решений у этого уравнения — бесконечное множество. Функция у = sin x — периодическая, в одном периоде — два решения, а потом они оба повторяются через 2π, то есть необходимо просто прибавить или отнять от предыдущего значения корня ±2π.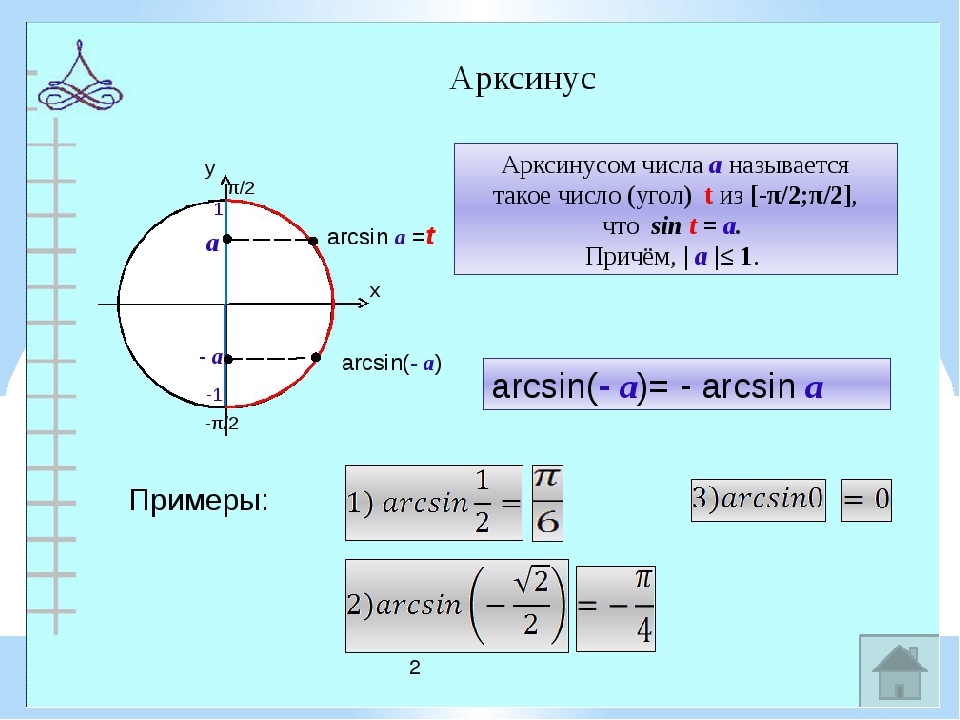

Строим те же графики на тригонометрическом круге. В этом случае мы график функции у = sin x заменяем на круг, а правая часть уравнения становится прямой, параллельной Ох. Смотрим на круге: Точки пересечения круга с прямой дают нам два решения: α₁ и α₂ . Причем, (смотрите на круге): α₂ = π — α₁ ! И тогда решениями уравнения будут точки

Еще из курса геометрии мы знаем некоторые значения синусов, косинусов, тангенсов и котангенсов для конкретных углов, а именно: для углов в 0°, 30°, 45°, 60°, 90°. А что же делать с остальными? И тут нам поможет арк(функция). Арк(функция) является обратной функцией для тригонометрических функций.

Рассмотрим конкретную функцию знакомого угла: sin 30° = 0,5. Тогда arcsin 0,5 = 30°. Собственно, эта формула и читается, как пишется. Угол (arc — это угол), синус которого равен 0,5, равен 30°. Все верно! То есть, если мы не знаем значения угла для какого-то синуса, мы его, этот угол, можем записать через арксинус.

Решим простое уравнение для

x ∈ [0; 2π].

sin x = 0,35

Первый угол определить через геометрию мы не сможем, ну, и не надо! Решениями этого уравнения будут значения:

Теперь рассмотрим уравнение для

x ∈ [0; 2π]

с отрицательным значением:

sin x = — 0,35

Опить два корня, и первый по модулю (величине) будет таким же, как и в первом примере, но со знаком «минус». запишем результат:

Получается, что нам нет нужды рассматривать весь круг, все возможные значения для арксинуса укладываются в интервал [-π/2; π/2 ], все остальные значения находим уже по кругу. другими словами:

-π/2 ≤ arcsin a ≤ π/2

А модуль арксинусов вообще определяется первой четвертью круга, в четвертой просто появляется знак «минус».

Запишем теперь, как будет выглядеть полное решение уравнения sin x = a

⇒

Смотрите: Получется, что, если четное количество π (2πn), арксинус с плюсом, а если нечетное (π(2n+1)) — арксинус со знаком «плюс». Можно объединить запись коней!

x_1,2 = arcsin a · (-1)ⁿ + πn, n ∈ Z

Здесь, если n — четное число, «минус» пропадает, и арксинус с «плюсом», если n — нечетное, то арксинус с «минусом».

Теперь по аналогии с арксинусом и помощью картинок определим остальные значения тригонометрических функций.

cos x = b

Так как косинус определяется координатой х, то и пересекать круг будем прямыми, проходящими через соответствующие точки на оси Ох.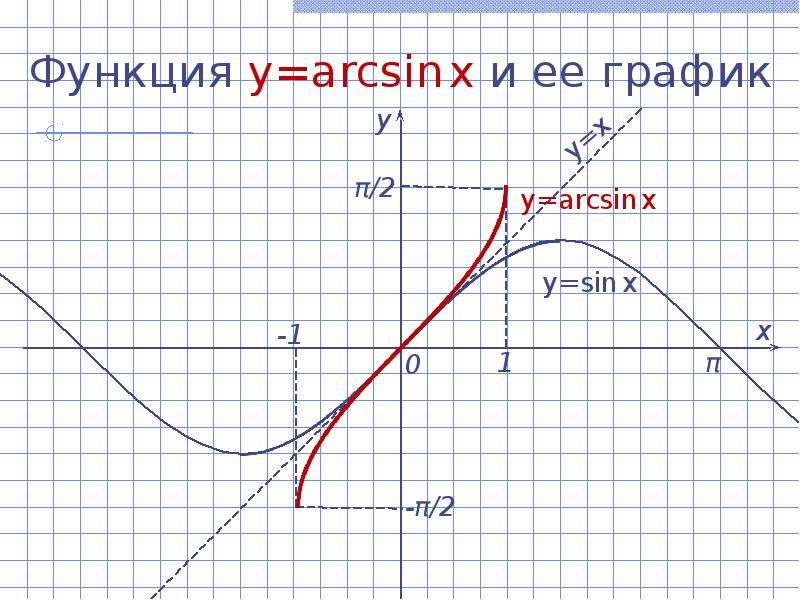 На этом круге решаем уравнение положительного значения арккосинуса. И в том случае можем смело утверждать, что = Получается:

cos x = 0,4

Решение уравнения:

⇒

x = ± arccos 0,4 + 2πn, n ∈ Z

Теперь рассмотрим урвнение

cos x = — 0,6

Здесь тоже очевидно, что = .

Решение уравнения

⇒

x = ± arccos (-0,6) + 2πn, n ∈ Z

Общая формула для cos x = b будет:

x_1,2 = ± arccos b + 2πn, n ∈ Z

Обратите внимание, что все значения арккосинуса находятся в первой и второй четвертях круга. То есть

0 ≤ arccos b ≤ π

Ну, и дополнительное напоминание — у тупых углов косинус отрицательный.

Тангес угла определяется, как

. Соответственно, ось со значениями у тангенса проходит там, где знаменатель дроби cos x =1. Там-то и появляется ось, все значения на которой будут соответствовать тангенсу угла φ, а прямая, проведенная через центр круга, покажет углы, тангенс которых равен числу на оси. Угол всегда определяется от нуля до проведенной линии. Соответственно, у отрицательных значений углы будут тупые.

В отличие от синуса и косинуса, у тангенса углы повторяются не через 2π,а через π. Итак,

tg x = 1,5

Решение данного уравнения будет следующим:

x = arctg 1,5 + πn, n ∈ Z

Все значения для арктангенса, как видно из рисунка, укладываются в интервал

-π/2 < arctg d < π/2

Формула для определения корней уравнения

tg x = d

будет: x = arctg d + πn, n ∈ Z

Теперь про арккотангенс числа. Конечно же он существует, и им можно пользоваться. Но зачем? Ведь любое уравнение с котангенсом легко превращается в уравнение тангенсом, поскольку .

Подведем итоги:

*уравнение*	корни уравнения
sin x = a	x_1,2 = arcsin a · (-1)ⁿ + πn, n ∈ Z	-π/2 ≤ arcsin a ≤ π/2
cos x = b	x_1,2 = ± arccos b + 2πn, n ∈ Z	0 ≤ arccos b ≤ π
tg x = d	x = arctg d + πn, n ∈ Z	-π/2 < arctg d < π/2

Арксинус, формула, график функции арксинус, урок и презентация

Дата публикации: 09 апреля 2017.

Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Скачать:
Тригонометрические уравнения. Арксинус (PPTX)

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С

Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арксинуса.
6. Примеры.

Что такое арксинус?

Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.

Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).

Немного истории арксинуса

Определение арксинуса

Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.

Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk

Перепишем:

x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).

Есть три случая, в которых предпочитают записывать решения более простым способом:

sin(x)=0, то x= πk,

sin(x)=1, то x= π/2 + 2πk,

sin(x)=-1, то x= -π/2 + 2πk.

Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).

Таблица значений арксинуса

Таблица значений синуса

Таблица значений арксинуса

Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.

Примеры

4. Решить уравнение: sin(x) = -√2/2.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2 ) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2 )= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.

6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1)ⁿ — arcsin(3/5) + πk.

Задачи на арксинус для самостоятельного решения

Arcsin

Arcsine, записанный как arcsin или sin ^-1 (не путать с), является функцией обратного синуса. Синус имеет инверсию только в ограниченной области, ≤x≤. На рисунке ниже часть графика, выделенная красным, показывает часть графика sin (x), которая имеет инверсию.

Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза. Поскольку синус является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз.

Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике ее обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через линию y = x.

График y = arcsin (x) показан ниже.

Как видно из рисунка, y = arcsin (x) является отражением sin (x) в ограниченной области ≤x≤ через линию y = x.Область arcsin (x), -1≤x≤1, является диапазоном sin (x), а ее диапазон, ≤y≤, является областью sin (x).

Калькулятор арксинуса

Ниже приведен калькулятор, позволяющий определить значение arccos числа от -1 до 1 или значение косинуса угла.

Используя специальные углы, найти arcsin

Хотя мы можем найти значение арксинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения синуса и арксинуса которых, возможно, стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) как в радианах, так и в градусах, и их соответствующие значения синуса sin (θ).

Один из методов, который может помочь запомнить эти значения, — это выразить все значения sin (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° до 90 °, sin (0 °) = 0 =. Последующие значения sin (30 °), sin (45 °), sin (60 °) и sin (90 °) следуют шаблону, так что использование значения sin (0 °) в качестве эталона для нахождения значений синуса для последующих углов, мы просто увеличиваем число под знаком корня в числителе на 1, как показано ниже.

Значения синуса от 0 ° до -90 ° соответствуют той же схеме, за исключением того, что значения являются отрицательными, а не положительными, поскольку синус отрицателен в квадранте IV. Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin (θ) на основе положения θ в единичном круге, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный. в квадрантах III и IV.

После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения синуса или арксинуса для особых углов.

Обратные свойства

Как правило, функции и их обратные показывают взаимосвязь

f (f ^-1 (x)) = x и f ^-1 (f (x)) = x

при условии, что x находится в области определения функции. То же самое верно для sin (x) и arcsin (x) в их соответствующих ограниченных областях:

sin (arcsin (x)) = x, для всех x в [-1, 1]

arcsin (sin (x)) = x для всех x в [,]

Эти свойства позволяют нам оценивать состав тригонометрических функций.

Состав арксинуса и синуса

Если x находится в пределах домена, вычислить комбинацию арксинуса и синуса относительно просто.

Состав других тригонометрических функций

Мы также можем составлять композиции, используя все другие тригонометрические функции: косинус, тангенс, косеканс, секанс и котангенс.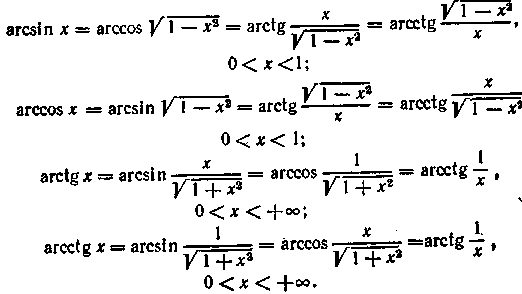

Пример:

Найдите cos (arcsin ()).

Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции.Учитывая arcsin () = θ, мы можем найти, что sin (θ) =. Правый треугольник ниже показывает θ и отношение его противоположной стороны к гипотенузе треугольника.

Чтобы найти косинус, нам нужно найти смежную сторону, так как cos (θ) =. Пусть b — длина соседней стороны. Используя теорему Пифагора,

3 ² + b ² = 5 ²

9 + b ² = 25

б ² = 16

б = 4

Мы знаем, что arcsin () = θ, поэтому мы можем переписать задачу и найти cos (θ), используя построенный выше треугольник и тот факт, что cos (θ) =:

cos (arcsin ()) = cos (θ) =

Тот же процесс можно использовать с выражением переменной.

Пример:

Найдите загар (arcsin (2x)).

Учитывая arcsin (2x) = θ, мы можем найти, что sin (θ) =, и построить следующий треугольник:

Чтобы найти касательную, нам нужно найти смежную сторону, так как tan (θ) =. Пусть b — длина соседней стороны. Используя теорему Пифагора,

(2x) ² + b ² = 1 ²

4x ² + b ² = 1

b ² = 1 — 4x ²

б =

tan (arcsin (2x)) = tan (θ) =, где

Использование арксинуса для решения тригонометрических уравнений

Арксинус также можно использовать для решения тригонометрических уравнений, включающих синусоидальную функцию.

Примеры:

Решите следующие тригонометрические уравнения относительно x, где 0≤x <2π.

1. 2sin (x) =

2sin (x) =

грех (х) =

Синус положительный в двух квадрантах, квадранте I и квадранте II, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x.

2. 2sin ² (x) + 5sin (x) — 3 = 0

2sin ² (x) + 5sin (x) — 3 = 0

(2sin (x) — 1) (sin (x) + 3) = 0

2sin (x) — 1 = 0 или sin (x) + 3 = 0

sin (x) = или sin (x) = -3

x = arcsin () или x = arcsin (-3)

Решение для x = arcsin (),

x = или

Мы не можем найти x = arcsin (-3), потому что оно не определено, поэтому x = или являются единственными решениями.

Функция обратной синусоиды

Функция обратной синусоиды

Функция y = sin ^-1 x = arcsin x и ее график:

Поскольку y = sin ^-1 x является обратной функцией y = sin x, функция y = sin ^-1 x тогда и только тогда, когда sin y = x . Но, поскольку y = sin x не является взаимно однозначным, его область должна быть ограничена, чтобы y = sin ^-1 x была функцией. Чтобы получить график y = sin ^-1 x, начните с графика y = sin x.
Ограничить область определения функции однозначным region — обычно используется (выделено красным справа) для sin ^-1 x. Это оставляет диапазон ограниченной функции неизменным как [-1, 1].
Отразите этот график поперек линии y = x, чтобы получить график y = sin ^-1 x (y = arcsin x), черная кривая справа. Обратите внимание, что y = sin ^-1 x имеет домен [-1, 1] и диапазон. Он строго увеличивается на всей своей территории.
Итак, когда вы просите калькулятор построить график y = sin ^-1 x, вы получите график, показанный справа. (Окно просмотра составляет [-2, 2] x [-2, 2].)

Вычисление y = sin

^-1 x:

Пример 1: Вычислить sin

^-1 (1/2)

Большинство людей более знакомо (и более комфортно) с тригонометрическими функциями, чем с их обратными.Следовательно, первый шаг в оценке этого выражения — сказать, что если y = sin ^-1 (1/2), то sin y = 1/2. Эта простая тригонометрическая функция имеет бесконечное количество решений:

Пять из этих решений обозначены вертикальными линиями на графике y = sin x ниже.

Итак, значение sin ^-1 (1/2) определяется приведенными выше выражениями? Нет! Жизненно важно помнить, что функция обратной синусоиды является однозначной и однозначной функцией. Только одно из бесконечного числа решений, приведенных выше, является желаемым результатом. Который из? Помните, что диапазон sin ^-1 x равен, который обозначен синим цветом на рисунке выше. действительно важно знать область и диапазон обратных тригонометрических функций! (Почему этот синий интервал отмечен на оси x, если он представляет диапазон sin ^-1 x? Потому что диапазон обратной функции равен области главной функции.) Единственное решение y = sin x, которое попадает в требуемый диапазон, — это (сплошная красная линия на рисунке выше). Следовательно,

Пример 2: Что такое

Справа показана диаграмма единичный круг. Обратите внимание, что кандидаты на решение включают:

Однако только одно из этих значений находится в диапазоне sin ^-1 x (), поэтому:

Производная y = sin ^-1 x:

Производная y = sin ^-1 x: (Щелкните здесь, чтобы получить вывод. )

Графики y = sin ^-1 x и его производной показаны справа. Область y ‘равна (-1,1). Поскольку y = sin ^-1 x всегда увеличивается, y ‘> 0 для всех x в своей области.

Интегралы, включающие функцию обратной синусоиды

Так как,. Это означает, что функция арксинуса возникает при обсуждении интегралов (и площадей) «относительно нормально выглядящих» алгебраических функций.Например:

Это заштрихованная область, показанная на снимке экрана TI-89 справа. (Окно [-0,5, 1,1] x [0, 3].)

последнее обновление 16 января 2009 г., Джерри Л. Стэнбро

$ \ arcsin (\ sin x) $ объяснение? | Newbedev
Поскольку $ \ sin (x) $ всегда находится в интервале $ [- 1,1] $, где определено $ \ arcsin $,
$ \ arcsin (\ sin (x)) $ определен для всех действительных $ x $.
$ \ arcsin (y) $ определяется как число $ x $ в интервале $ [- \ pi / 2, \ pi / 2] $, где $ \ sin (x) = y $. Итак, для $ x $ в интервале $ [- \ pi / 2, \ pi / 2] $,
$ \ arcsin (\ sin (x)) = x $ удовлетворяет этому определению. Для $ x $ в интервале $ [\ pi / 2, 3 \ pi / 2] $, $ \ arcsin (\ sin (x)) $ не может быть $ x $, но может быть $ \ pi — x $, который находится в интервале $ [- \ pi / 2, \ pi / 2] $ (обратите внимание, что $ \ sin (\ pi — x) = \ sin (x) $). Итак, это касается этой части графика:
Теперь обратите внимание, что $ \ sin (x) $ периодичен с периодом $ 2 \ pi $, поэтому график
выглядит так же, если вы сдвинете его влево или вправо на $ 2 \ pi $.Это позаботится обо всем остальном.
Для $ \ pi \ ge x \ ge \ frac {1} {2} \ pi $ имеем $ \ sin [x] = \ sin [\ pi-x] $. Поэтому у нас есть
$$
\ arcsin (\ sin [x]) = \ arcsin (\ sin [\ pi-x]) = \ pi-x
$$
Аналогично для $ — \ pi \ le x \ le — \ frac {\ pi} {2} $ имеем $ \ sin [x] = \ sin [- \ pi-x] $. Поэтому у нас есть
$$
\ arcsin (\ sin [x]) = \ arcsin (\ sin [- \ pi-x]) = \ arcsin (- \ sin [\ pi + x]) = — \ arcsin (\ sin (\ pi + x) ) = — \ pi-x
$
Я думаю, что остальная часть графика следует тому же аргументу. Прикрепил график, не знаю, поможет ли.
Итак, пусть $ f (x) = \ sin (x) $ и пусть $ g (x) = \ arcsin (x) $.Пусть $ \ operatorname {Dom} (f) $ — это область определения $ f $, а $ \ operatorname {Rng} (f) $ — диапазон $ f $. Таким образом, мы имеем
$$
\ begin {align}
\ operatorname {Dom} (f) & = \ mathbb {R} \\
\ operatorname {Rng} (f) & = [- 1,1] \\
\ operatorname {Dom} (g) & = [- 1,1] \\
\ operatorname {Rng} (g) & = \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right]
\ end {align}
$
Если мы ограничим $ \ operatorname {Dom} (f) $ до $ \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] $, то $ f $ и $ g $ противоположны друг другу и
$$
(е \ сирк г) (х) = (г \ сирк е) (х) = х
$
на $ \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] $.
Пусть теперь $ \ operatorname {Dom} (f) = \ mathbb {R} $ и рассмотрим $ (f \ circ g) (x) $. Этот график должен оставаться неизменным, поскольку для любого $ x \ not \ in [-1,1] $, $ (f \ circ g) (x) $ не определено, и поэтому на $ \ mathbb {R} нельзя нарисовать картинку. \ setminus [-1,1] $.
С другой стороны, когда мы полагаем $ \ operatorname {Dom} (f) = \ mathbb {R} $ и рассматриваем $ (g \ circ f) (x) $, эта композиция определена над всем $ \ mathbb { R} $, но ведет себя двумя разными способами:
1.) На интервалах $ \ left [\ frac {\ pi (2k-1)} {2}, \ frac {\ pi \ cdot (2k + 1)} {2} \ right] $, когда $ k $ нечетно: когда $ x $ переходит от $ \ frac {\ pi (2k-1)} {2} $ к $ \ frac {\ pi (2k + 1)} {2} $, $ f (x) $ переходит от $ -1 $ до $ 1 $.Таким образом, $ (g \ circ f) $ переходит от $ \ frac {\ pi (2k-1)} {2} $ к $ \ frac {\ pi (2k + 1)} {2} $, образуя прямую с положительным наклоном .
2.) На интервалах $ \ left [\ frac {\ pi (2k-1)} {2}, \ frac {\ pi \ cdot (2k + 1)} {2} \ right] $, когда $ k $ четно: когда $ x $ переходит от $ \ frac {\ pi (2k-1)} {2} $ к $ \ frac {\ pi (2k + 1)} {2} $, $ f (x) $ идет от $ 1 $ до $ -1 $. Таким образом, $ (g \ circ f) $ переходит от $ \ frac {\ pi (2k + 1)} {2} $ к $ \ frac {\ pi (2k-1)} {2} $, образуя линию с отрицательным наклоном .
Вот почему вы видите образец мозаики при построении графика $ (g \ circ f) $ и не видите никаких изменений в $ (f \ circ g) $.
Как найти домен и диапазон arcsin sin class 12 maths CBSE
Подсказка: В этом вопросе нам нужно найти область определения и диапазон тригонометрической функции arcsin (sinx). Для этого мы сначала оценим эту функцию, а затем вычислим область и диапазон в соответствии с областью и диапазоном решения функции. Домен — это интервал, который сообщает нам значение x, которое мы можем поместить в функцию, чтобы функция оставалась хорошо определенной.Диапазон — это интервал, в котором находится решение, когда мы помещаем значение x в функцию.
Полное пошаговое решение:
Нам дана функция как arcsin (sinx). Нам нужно найти домен и диапазон функции.
Для этого давайте сначала разберемся, что такое домен и диапазон. Для функции f (x) все значения x, которые делают функцию корректной, лежат в интервале, называемом доменом. Диапазон — это интервал, в котором находится решение f (x), когда значения x взяты из области.
Для нахождения домена и диапазона arcsin (sinx) давайте упростим его. Мы знаем, что arcsin означает, что мы имеем дело с обратной стороной греха. Итак, возьмем sinx = u.
Обратное sinx = u даст нам arcsin = x.
Теперь, подставив значение u, мы получим $ \ arcsin \ left (\ sin x \ right) = x $.
Таким образом, функция arcsin (sinx) будет иметь тот же домен и диапазон, что и x.
Таким образом, функцию f (x) можно определить как f (x) = x.
Мы знаем, что для любого значения x функция определена правильно.Следовательно, областью определения функции будут все действительные числа, то есть область $ \ left (- \ infty, \ infty \ right) $.
Поскольку функция дает нам одинаковые значения, все значения x и x могут находиться в диапазоне $ \ left (- \ infty, \ infty \ right) $. {- 1}} $.2}}}}} = {\ frac {{\ frac {\ pi} {2}}} {1} — \ frac {0} {1}} = {\ frac {\ pi} {2}.} \ ]
Пример 9.
Используя цепное правило, выведите формулу производной обратной синусоидальной функции.
Решение.
Функция \ (y \ left (x \ right) = \ arcsin x \) определена на открытом интервале \ (\ left ({- 1,1} \ right). \) Синус обратного синуса равен
\ [\ sin \ left ({\ arcsin x} \ right) = x. \]
Возьмем производную от обеих частей (левая часть рассматривается как составная функция).2}}}} = {\ frac {2} {5} \ text {sign} \ left ({- 3} \ right)} = {\ frac {2} {5} \ cdot \ left ({- 1} \ right)} = {- \ frac {2} {5}.} \]
Калькулятор обратного синуса
— Расчет arcsin (x)
Найдите угол в градусах или радианах, используя обратный синус с помощью калькулятора arcsin ниже.
Как найти Arcsin
Arcsin — это тригонометрическая функция для вычисления обратного синуса. Arcsin также можно выразить как sin ^-1 (x).
Arcsin используется для отмены или отмены синусоидальной функции.Если вы знаете синус угла, вы можете использовать arcsin для вычисления угла.
Поскольку arcsin — это функция, обратная синусоиде, а многие углы имеют одно и то же значение синуса, arcsin является периодической функцией. Каждое значение arcsin может привести к нескольким значениям угла. Первичный результат для arcsin известен как главное значение и представляет собой угол в диапазоне от -90 ° до 90 °.
Чтобы вычислить arcsin, используйте научный калькулятор и функцию asin или просто воспользуйтесь калькулятором выше.Большинство научных калькуляторов требуют, чтобы значение угла было в радианах, чтобы вычислить грех.
Формула обратной синусоиды
Формула обратного синуса:
у = грех (х) | x = arcsin (y)
Таким образом, если y равно синусу x , то x равно arcsin y .
График обратной синусоиды
Если вы построите график функции arcsin для каждого возможного значения синуса, он образует кривую от (-1, –π2) до (1, π2).
Поскольку значение синусоиды всегда находится в диапазоне от -1 до 1, обратная синусоидальная кривая начинается при x = -1 и заканчивается при x = 1. Поскольку пик синусоиды находится в π2 радиан, а угол падения волны составляет –π2 радиан, значение y заканчивается в этих точках.
Таблица обратных синусов
В таблице ниже показаны общие значения синуса и arcsin или угол для каждого из них.
Таблица, показывающая общие значения синуса и значения обратного синуса для каждого в градусах и радианах.
Синус Угол (градусы) Угол (радианы)
-1 -90 ° –π2
–√6 + √24 -75 ° –5π12
–√32 -60 ° –π3
–√22 -45 ° –π4
–12 -30 ° –π6
–√6 — √24 -15 ° –π12
0 0 ° 0
√6 — √24 15 ° π12
12 30 ° π6
√22 45 ° π4
√32 60 ° π3
√6 + √24 75 ° 5π12
1 90 ° π2
Возможно, вас заинтересуют наши калькуляторы обратного косинуса и арктангенса.

Синус	Угол (градусы)	Угол (радианы)
-1	-90 °	–π2
–√6 + √24	-75 °	–5π12
–√32	-60 °	–π3
–√22	-45 °	–π4
–12	-30 °	–π6
–√6 — √24	-15 °	–π12
0	0 °	0
√6 — √24	15 °	π12
12	30 °	π6
√22	45 °	π4
√32	60 °	π3
√6 + √24	75 °	5π12
1	90 °	π2