Содержание
Урок геометрии в 10 классе «Построение сечений многогранников»
Тема: «Построение сечений многогранников».
Учитель математики МКОУ «Урахинская СОШ» Аликадиева М. Л.
Предмет: геометрия
Класс: 10
Используемые педагогические технологии:
технология проектного обучения, информационные технологии.
Тема урока: Построение сечений многогранников.
Тип урока: урок закрепления и развития знаний.
Формы работы на уроке: фронтальная, индивидуальная
Цели:
Образовательные:
Проверить знание теоретического материала о многогранниках .
Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, строить сечения, намечать ход решения задачи, предвидеть конечный результат.
Отработать навыки решения задач на построение сечений многогранников в программе GeoGebra. Развивать графическую культуру и математическую речь.
Развивать графическую культуру и математическую речь.
Формировать навыки использования компьютерных технологий на уроках геометрии.
Развивающие:
Развивать познавательный интерес учащихся.
Формировать и развивать у учащихся пространственное воображение.
Воспитательные:
Воспитывать самостоятельность, аккуратность, трудолюбие.
Воспитывать умения работать индивидуально над задачей.
Воспитывать волю и настойчивость для достижения конечных результатов.
Техническое обеспечение:
Компьютерный класс, программное обеспечение динамической математики GeoGebra, проектор.
Раздаточный материал:
Инструкция по построению многогранников и их сечений.
Бланки-карточки с заданиями для практической работы, бланки-карточки с ответами.
Структура урока.
1. | Приветствие. | 1 мин |
2. | Постановка цели и задачи урока. | 2 мин |
3. | Исторические сведения | 6 мин |
4. | Повторение изученного материала. | 6мин |
5. | Построение сечений многогранников в GeoGebra | 18мин |
6. | Практическая работа на построение сечений в GeoGebra | 8 мин |
7. | Домашнее задание | 2 мин |
8. | Заключение | 2 мин |
ХОД УРОКА
1-2. Организационный момент. Постановка цели и задач.
Организационный момент. Постановка цели и задач.
Учитель: Здравствуйте, ребята! Тема нашего урока «Построение сечений многогранников». На уроке мы обобщим и систематизируем пройденный теоретический материал, и применим его к практическим задачам на построение сечений в программе GeoGebra.
— Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью.
На предыдущих уроках мы с вами рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами продолжим строить сечения пирамиды плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани. Построим сечение куба и наклонной призмы. Для этого мы будем использовать программу GeoGebra.
3. Исторические сведения.
В качестве домашнего задания вам было предложено написание рефератов или небольших выступлений об истории развития геометрии, о жизни великих математиков, об их знаменитых открытиях и теоремах. Доклады и рефераты получились очень интересные, но на уроке мы заслушаем только три мини-выступления, отвечающие на вопрос, что изучает стереометрия, как возникла и развивалась и где находит своё применение?
1 ученик. Понятие стереометрии, что изучает.
2 ученик. Евклид – основоположник геометрии, греческая архитектура.
3 ученик. Математическая теория живописи. «Золотое сечение» — формула совершенного человеческого тела по Леонардо да Винчи.
В стереометрии изучаются красивые математические объекты. Их формы находят своё применение в искусстве, архитектуре, строительстве. « Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии, а греческая архитектура – внешнее выражение геометрии Евклида», — писал архитектор Корбюзье.
Прошли века, но роль геометрии не изменилась. Она по прежнему остается «грамматикой архитектора». Геометрические формы находят своё применение в искусстве, архитектуре, строительстве.
Математическая теория живописи – это теория перспективы, представляющая, по словам Леонардо да Винчи, «тончайшее исследование и изобретение, основанное на изучении математики, которое силой линий заставляло казаться отдаленным то, что близко, и большим то, что невелико». Развернувшееся в эпоху Возрождения строительство инженерных сооружений возродило и расширило применявшиеся в античном мире приёмы проекционных изображений. Архитекторы и скульпторы встали перед необходимостью создания учения о живописной перспективе на геометрической основе. Многочисленные примеры построения перспективных изображений имеются в работах гениального итальянского художника и выдающегося ученого Леонардо да Винчи. Он впервые говорит о сокращении масштаба разных отрезков удаляющихся в глубь картины, кладет начало панорамной перспективе, указывает правила распределения теней, высказывает уверенность в существовании некой математической формулы красоты отношения размеров человеческого тела – формулы «золотого сечения».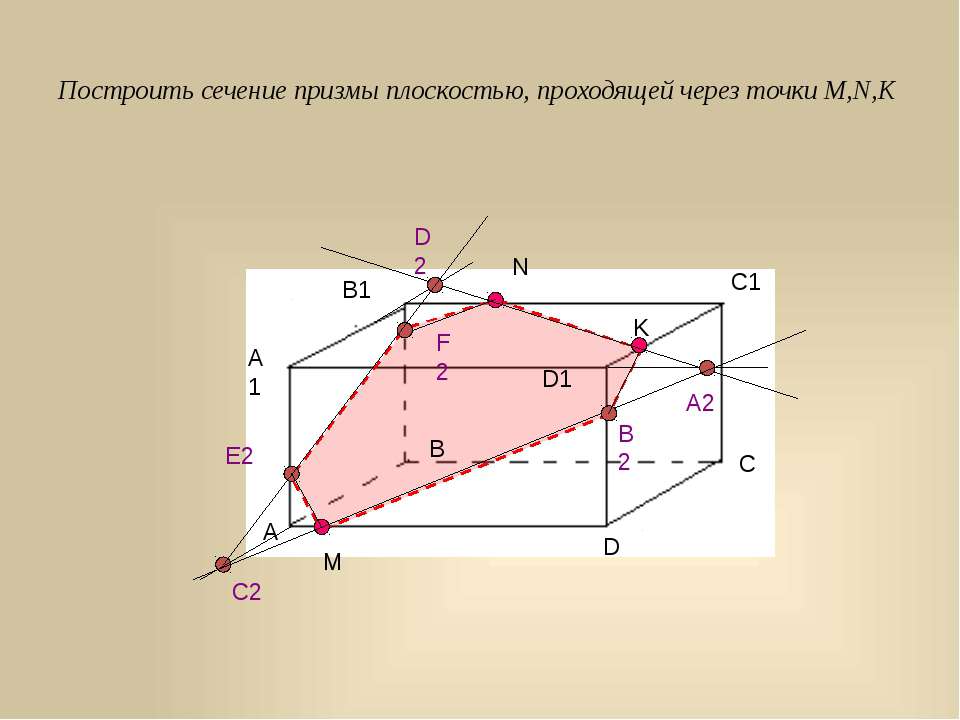
Таким образом мы плавно подошли к теме нашего урока, в его следующий этап будут слова Леонардо да Винчи :
«Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет».
Это высказывание определяет следующий этап нашего урока: повторение теоретического материала.
4. Повторение изученного материала.
— Давайте повторим некоторые вопросы теории.
Что такое секущая плоскость?
Как можно задать секущую плоскость?
Что такое сечение тетраэдра, куба, (параллелепипеда)?
Какие многоугольники могут получиться при построении сечений тетраэдра?
А какие многоугольники мы можем получить при построении сечений параллелепипеда, многогранника ?
Изучение темы «Решение задач на построение сечений» облегчается с помощью различных компьютерных программ. Одной из таких программ является программное обеспечение динамической математики GeoGebra. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
Одной из таких программ является программное обеспечение динамической математики GeoGebra. Она подходит для изучения и обучения на любом из этапов образования, облегчает создание математических построений и моделей обучающимися, которые позволяют проводить интерактивные исследования при перемещении объектов и изменение параметров.
— Сечение призмы и пирамиды плоскостью: как построить сечение многогранника в GeoGebra
( Ответы учащихся)
Для построения сечения любого многогранника плоскостью — необходима плоскость:
-через 3 точки не лежащие на одной прямой,
-через 2 пересекающие прямые,
-через 2 параллельные прямые,
—
через прямую и не лежащую на ней точку.
Выбрать из опций нужный.
5. Построение сечений многогранников в GeoGebra
Открываем Программу GeoGebra. Кликнем «Вид», «Полотно3Д»
(Раздаю учащимся инструкцию для построения сечений призмы и пирамиды)
. Выбрать инструмент «Призма» или «Пирамида».
Выбрать инструмент «Призма» или «Пирамида».
Для построения плоскости сечения воспользуемся различными функциями в инструменте «Плоскость через 3 точки» и т д. Чтобы понять, как провести плоскость с помощью той или иной функции выберем ее и наведем на ее обозначение.
3. После добавления плоскости выберем инструмент «Кривая пересечения».
4. Выберем плоскость, которая образует сечение, затем в «Панели объектов» нажмем на призму или же пирамиду.
5. Для того, чтобы лучше увидеть сечение щелкнем правой кнопкой мыши по плоскости, которую мы провели, и выберем режим 2D на эту плоскость.
6. В 2D режиме мы увидим сечение. Щелкнув правой кнопкой мыши по сечению выберем «Свойства», «Цвет» (сверху) затем выберем яркий цвет и ползунок заливки передвинем на большее число процентов. При таком цвете лучше видна плоскость сечения.
7. Переходим на «Панель объектов» и скроем плоскость, щелкнув по его значку.
— Ребята, мы же построим сначала еще один вид построения сечения куба плоскостью, инструментом «Перпендикулярная плоскость»
Построение сечения куба плоскостью
Построить сечение куба плоскостью перпендикулярной его диагонали.
В настройках выберем шрифт, «Обозначение», выбрать «Только для точек».
Кликнуть «Вид», «Пирамида»,
Кликнем «Куб». На плоскости ставим две точки. Куб построен.
На панели инструментов кликнем «Прямая»
Щелкнем две диагональные вершины куба. Прямая, содержащая диагональ построена.
Кликнем инструмент «Точка». Построим точку на прямой.
Кликнем инструмент «Перпендикулярная плоскость»
Кликнем по точке, потом по прямой, получим плоскость. Левой кнопкой мыши, передвинем до середины. Плоскость является секущей.
Выделим сечение.
Кликнем инструмент «Кривая пересечения». Переходим на «Панель объектов», щелкнем по объекту куб, и по плоскости (на их именах). Сечение
построено. Можно выбрать другой цвет. Саму плоскость можно отключить и оставить сечение.
Полезна возможность «GeoGebra» строить выносной чертеж сечения.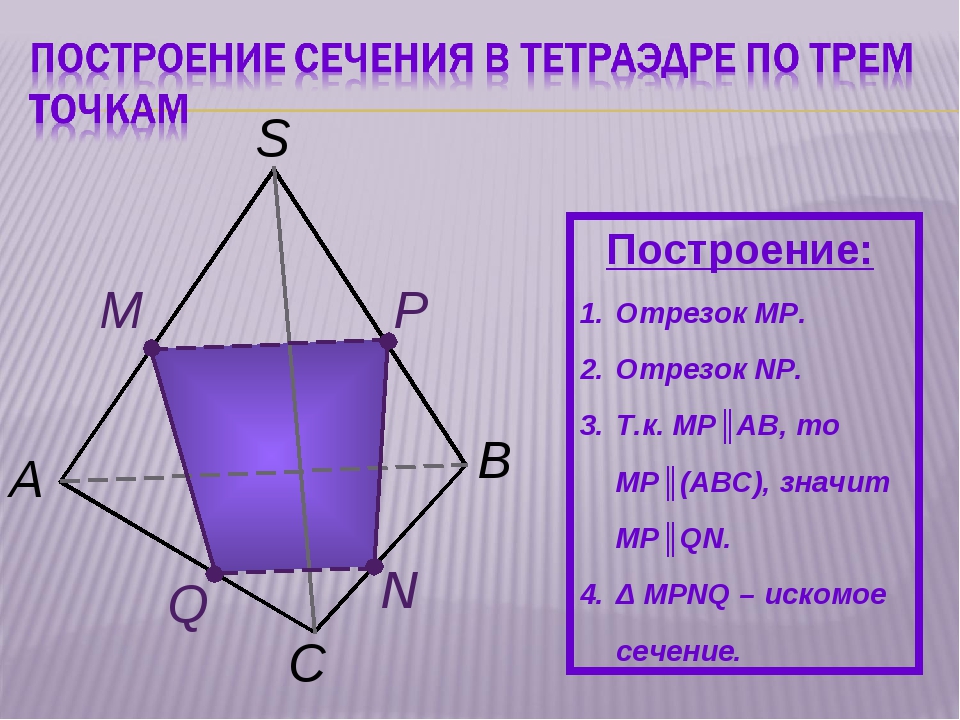
Для этого достаточно щелкнуть по нему на «Панели объектов» правой кнопкой мыши на многоугольник. Из контекстного меню выбрать
«Создать 2Д вид на многоугольник». Выносной чертеж будет меняться по мере того, как будет меняться сечение.
Точно также можно построить сечение параллелепипеда, например,
его сечение плоскостью, проходящее через три точки на ребрах:, выбрав инструмент «Плоскость через 3 точки». Это вы сможете сделать дома.
Рассмотрим применение программы GeoGebra на примере задач.
Задача 1
На ребрах AB, BC, CD тетраэдра DABC отмечены точки M, N, P. Построить сечение тетраэдра плоскостью MNP.
Программу GeoGebra открыта.
В меню Вид выберем «Полотно 3D» (Полотно 2D можно закрыть)
Кликнем инструмента «Призма», Выбрать «Тетраэдр», создадим тетраэдр DABC.
С помощью инструмента «Точка» на ребрах AB, BC, CD тетраэдра DABC отметим точки M, N, P (переименовать точку можно выделив ее и вызывая контекстное меню правой кнопкой мыши, выбрать соответствующий пункт).
Построим прямую инструментом «Прямая», по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке E, которая и будет второй общей точкой плоскостей MNP и ABC Для этого выбрав инструмент «Прямая», нужно щелкнуть поочерёдно по точкам N, P и B, C и с помощью инструмента «Пересечение», отметить точку E – точку пересечения прямых NP и BC.Ребята, посмотрите, эти плоскости пересекаются по прямой ME.
Прямая ME пересекает ребро AC в некоторой точке Q.
Выбрать прямую ME , выбрав инструмент «Прямая» и щелкнув поочерёдно по точкам M, E. С помощью инструмента «Пересечение» отметим точку Q – точку пересечения прямой ME и ребра AC.
Четырёхугольник МNPQ – искомое сечение.
Выделим его используя инструмент «Многоугольник», поочерёдно щелкая по точками M, N, P, Q, M.
Дважды щелкнув по объектам «Tetrahedron» и «Четырёхугольник», можно вызвать контекстное меню с настройками, в которых можно выбрать цвет заливки и прозрачность соответствующего объекта.
Также при построении сечений необходим инструмент «Параллельная прямая», позволяющий строить прямую параллельную данной через заданную точку. Для построения достаточно выбрать соответствующий инструмент и щелкнуть по прямой и точке, через которую требуется провести прямую.
Задача 2.
Построить сечение наклонной призмы плоскостью (ABC), проходящее через точку на боковом ребре параллельно основанию.
Строим наклонную произвольную пятиугольную призму.
Кликнем «Вид». «Полотно». «Многоугольник».
Инструмент «Точка». Ставим точку на боковом ребре призмы.
Кликнем инструмент «Параллельная плоскость». Щелкнем по точке на ребре и по плоскости основания. Плоскость сечения построена.
«Кривая пересечения». Выделяем сечение.
При построении можно использовать ползунки.
6. Практическая работа в программной среде GeoGebra на построение сечений.
Ученики получают бланки-карточки для практической работы и садятся за компьютеры для выполнения практической работы. На бланках также расположено несколько различных примеров построения сечений. Практическая работа состоит из 2 заданий на построение сечений тетраэдра и параллелепипеда. Учитель контролирует выполнение работы и помогает учащимся в случае затруднений.
Проверка выполнения работы.
Ученики получают бланки с ответами. Проверяют работы друг друга, отмечая правильно построенные сечения. Учитель оценивает работы учащихся.
7. Домашнее задание.
— В качестве домашнего задания я попрошу вас решить задачи, аналогичные задачам в практической работе. Построить сечение параллелепипеда плоскостью, проходящее через три точки.
8. Рефлексия. Заключение.
В данной работе:
Мы ознакомились с возможностями применения среды GeoGebra в геометрических построениях.
Рассмотрели примеры использования инструментов.
Подробно описали команды для геометрических построений, рассмотрели примеры использования таких команд.
Приведены примеры решения заданий с подробным пошаговым описанием действий на примерах задач из школьного курса.
На этапе рефлексии деятельности учащиеся анализируют, где и почему были допущены ошибки, каким способом они были исправлены, повторяют алгоритмы, вызвавшие затруднения, оценивают свою деятельность на уроке.
Список используемых источников и программно-педагогических средств:
https://ru.wikipedia.org/wiki/GeoGebra
http://3d-geometry.ru/pages/geogebra.html
Л.С. Атанасян. Геометрия. 10-11 классы,- М: Просвещение, 2015г.
Программное обеспечение динамической математики GeoGebra
Урок по теме «Задачи на построение сечений параллелепипеда».
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ. Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Подробнее
Сечения многогранников
Сечения многогранников Цель работы Показать как решать задачи на построение сечений Задачи работы Объяснить понятие плоского сечения Что значит построить сечение Методы построения сечений многогранников
Подробнее
C 1 сентября по 30 декабря
Тематическое планирование по геометрии (заочное отделение) в 10 классе Учебник: Л.С. Атанасян, Геометрия 10-11 классы, Просвещение, 2011г. Дидактические материалы по геометрии 10 класс Б.Г. Зив, Просвещение,
Подробнее
Построение сечений многогранников
Построение сечений многогранников Для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно уметь строить на рисунке их сечения различными плоскостями. Рассмотрим взаимное
Рассмотрим взаимное
Подробнее
Задачи: Обучающие: Развивающие:
Технологическая карта урока (7 класс ). Ф.И.О. учителя: Стихина Ольга Николаевна 2. Класс: 7 Предмет:Геометрия 3. Тема урока: Призгаки параллельности прямых Тип урока: Урок изучения нового материала Геометрия
Подробнее
Урок по теме «Сфера и шар»
Акчурина Е.В. Урок по теме «Сфера и шар» Тема: Сфера и шар Цели и задачи урока: Обучающие: — ввести понятие сферы, шара и полушара; — рассмотреть сечения шара плоскостью; — ввести понятие касательной прямой
Подробнее
Календарно-тематическое планирование
Данная программа курса по геометрии в 10 классе разработана на основе Федерального государственного образовательного стандарта основного общего образования, утв. Приказом Минобрнауки России от 17. 12.2010
12.2010
Подробнее
Многогранники. Призма
Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,
Подробнее
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Предмет: геометрия 9 Б 9 Д 9 Е Номер урока в КТП: 56 Преподаватель: УМК, учебник: Геометрия: Учебник для 7-9 классов общеобразовательных учреждений /А. В. Погорелов. М.: Просвещение,
Подробнее
по геометрии 10 «А» класс
Государственное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа 312 с углубленным изучением французского языка Фрунзенского района Санкт-Петербурга «Согласовано» «Рассмотрено»
Подробнее
Урок по теме «Прямой круговой цилиндр»
Акчурина Е.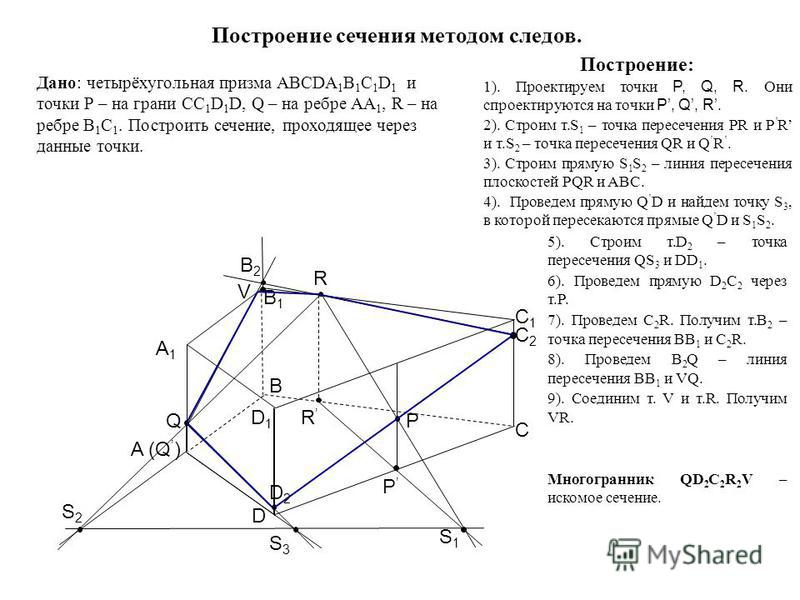 В. Урок по теме «Прямой круговой цилиндр» Тема: Прямой круговой цилиндр Цели и задачи урока: Обучающие: — ввести понятие цилиндра; — ввести понятие прямого кругового цилиндра и его элементов
В. Урок по теме «Прямой круговой цилиндр» Тема: Прямой круговой цилиндр Цели и задачи урока: Обучающие: — ввести понятие цилиндра; — ввести понятие прямого кругового цилиндра и его элементов
Подробнее
Конспект открытого урока
Конспект открытого урока «11» мая 2013 г. Класс 10 «А» Предмет математика Учитель Новгородова Н.И. Цель посещения в рамках обобщения опыта работы Тема урока «Построение сечений многогранников» Тип урока:
Подробнее
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
1 1. Сведения о программе (примерной/типовой/ или авторской), на основании которой разработана рабочая программа, с указанием наименования, если есть авторов и места, года издания 1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа учебного курса по геометрии для 10 класса разработана на основе Примерной программы среднего (полного) общего образования (базовый уровень) с учетом требований федерального
Подробнее
Стереометрия: пирамиды.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной
Подробнее
12+ УДК 373:51 ББК 22.1я72 Г68
УДК 373:51 ББК 22.1я72 Г68 Г68 Гордин Р. К. ЕГЭ 2018. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / Под ред. И. В. Ященко. М.: МЦНМО, 2018. 128 с. ISBN 978-5-4439-1214-1 Пособия
Подробнее
Учебно- методический комплекс
Учебно- методический комплекс курсов класса учителя (Ф.И.О.) «ГЕОМЕТРИЯ» 12 «А» Лебедевой Светланы Николаевны государственного бюджетного общеобразовательного учреждение Самарской области «Школа-интернат
Подробнее
D
Открытый урок по геометрии в 0 классе Тема: «Расстояния между прямыми и плоскостями в прямоугольном параллелепипеде» Цели урока: ) Образовательные: вспомнить и систематизировать те знания, которые ученики
Подробнее
СУММА УГЛОВ ТРЕУГОЛЬНИКА
ТЕМА УРОКА: СУММА УГЛОВ ТРЕУГОЛЬНИКА ТИП УРОКА: УРОК ФОРМИРОВАНИЯ НОВЫХ ЗНАНИЙ Данилова Светлана Леонидовна учитель математики МБОУ Лицея 1 г. Сургут ЦЕЛЕВАЯ НАПРАВЛЕННОСТЬ УРОКА Данный урок является первым
Сургут ЦЕЛЕВАЯ НАПРАВЛЕННОСТЬ УРОКА Данный урок является первым
Подробнее
Краткое содержание курса
Аннотация Тематическое планирование учебного курса по геометрии для 10 класса составлено на основе Примерной программы среднего (полного) общего образования по математике в соответствии с федеральным компонентом
Подробнее
Учитель: Стрельцова Марина Витальевна.
План конспект урока геометрии в 11 «а» классе Тема: «Сечение цилиндра. Призма, вписанная в цилиндр и описанная около цилиндра. Формула вычисления объема, боковой, полной поверхности цилиндра» Учитель:
Подробнее
параллелепипеда АD=а, АВ=b, АА 1 =с. (Ответ: V a b
c Государственное автономное образовательное учреждение общеобразовательная школа-интернат Республики Коми «Коми республиканский лицей-интернат для одаренных детей из сельской местности» Елизарова Н. Г.,
Г.,
Подробнее
Задание 8, 14. Стереометрия
Задание 8, 4. Стереометрия Основные определения Аксиомы стереометрии Теорема. Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой
Подробнее
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 17 г.белгорода «Согласовано» Руководитель ШМО Н.А.Ильминская Протокол от 20 г. «Согласовано» Заместитель директора
Подробнее
Урок по теме «Треугольник». 7-й класс
Урок по теме «Треугольник». 7-й класс Николаева Наталия Геннадьевна Цели урока: Образовательные: o ввести определение треугольника и его элементов, периметра треугольника, понятие равных треугольников.
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа по геометрии 10 класса составлена на основе примерной программы министерства образования Российской Федерации с учетом федерального компонента государственного стандарта
Подробнее
Среда «Живая геометрия»
15/2010 МАТЕМАТИКА 17 И. САВЕЛЬЕВА, Москва В наш век ИКТ педагогика не отстает от других областей и активно внедряет применение компьютерных технологий в образование. Появление новых компьютерных программ
Подробнее
ПРЯМОЙ И НАКЛОННЫЙ КОНУС
ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг
Подробнее
«УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС
УРОК ГЕОМЕТРИИ ПО ТЕМЕ: «УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС — 1 ЦЕЛИ: Образовательная введение нового понятия; отработка знаний, умений и навыков по нахождению угла между прямой и плоскостью; умение
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа по геометрии составлена на основе авторской программы по геометрии Л. С, Атанасяна, В.Ф. Бутузова и др. 10 класс (базовый уровень). /Сост. Т.А. Бурмистрова М., Просвещение,
С, Атанасяна, В.Ф. Бутузова и др. 10 класс (базовый уровень). /Сост. Т.А. Бурмистрова М., Просвещение,
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена на основании нормативных документов:.федеральный Закон от 29.2.202 273-ФЗ «Об образовании в Российской Федерации». 2.Приказ Министерства образования и
Подробнее
Урок Построение сечения параллелепипеда 11 класс
МБОУ КАРСУНСКАЯ СРЕДНЯ ШКОЛА
ИМЕНИ Д.Н. ГУСЕВА
Построение сечения параллелепипеда
Учитель математики
Втюрина Н.В.
Карсун, 2019 г.
Построение сечения параллелепипеда
Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.
Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.
Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки .
Задача 1. Дано
Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .
Задача 1. Шаг 1.
Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .
Задача 1. Шаг 2.
Шаг 2.
Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром – .
Задача 1. Шаг 3.
Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.
Задача 1. Шаг 4.
Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки
Задача 2. Дано.
Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .
Задача 2. Шаг 1.
Шаг 1.
Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра – .
Задача 2. Шаг 2
Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.
Задача 2. Шаг 3.
Шаг 4. Находим точку пересечения отрезком ребра – точку .
Задача 2. Шаг 4
Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.
Задача 2. Шаг 5
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки
Построить сечение параллелепипеда плоскостью, проходящей через точки
Задача 3. Дано.
Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.
Задача 3. Шаг 1
Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .
Задача 3. Шаг 2.
Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром – точка .
Задача 3. Шаг 3.
Шаг 4. Теперь надо найти точку в плоскости передней грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую и найдем пересечение этой прямой с прямой – точка .
Задача 3. Шаг 4
Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер – точку , и ребра – точку .
Задача 3. Шаг 5.
Шаг 6. Соединяем точки и получаем многоугольник сечения.
Задача 3. Шаг 6
Окончательный вид сечения с другого ракурса:
Окончательный вид
Задача 4. Построить сечение параллелепипеда плоскостью, проходящей через точки . Точка в задней грани.
Задача 4. Дано
Шаг 1. Проводим прямую через две точки одной плоскости – и . Определяем точку пересечения данной прямой ребра – .
Задача 4. Шаг 1.
Шаг 2. Продолжение прямой пересечется с продолжением прямой – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .
Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .
Задача 4. Шаг 2.
Шаг 3. Точка – точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.
Задача 4. Шаг 3
Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.
Задача 4. Шаг 4.
Окончательный вид сечения с другого ракурса:
Сечения куба, призмы, пирамиды
Для
решения большинства задач из раздела стереометрии необходимы знания и навыки в
построении сечения объёмных тел. Именно об этом мы сейчас с вами и поговорим.
Именно об этом мы сейчас с вами и поговорим.
Итак,
секущей плоскостью называют любую плоскость, по обе стороны от которой
имеются точки данной фигуры.
Секущая
плоскость пересекает грани многогранника по отрезкам.
Многоугольник,
сторонами которого являются эти отрезки, называется сечением
многогранника.
Построить
сечение многогранника плоскостью – это значит указать
точки пересечения секущей плоскости с рёбрами многогранника и соединить эти
точки отрезками, принадлежащими граням многогранника.
Теперь
давайте вспомним, что нам необходимо знать для построения плоскости.
Итак,
построить плоскость можно: с помощью трёх точек, не лежащих на одной прямой;
с
помощью двух пересекающихся прямых;
с
помощью прямой и точки, которая не лежит на прямой;
а
также с помощью двух параллельных прямых.
Метод
следов включает три важных пункта: сначала нужно построить
линию пересечения (след) секущей плоскости с плоскостью основания многогранника;
затем найти точки пересечения секущей плоскости с рёбрами многогранника, а
после этого построить и заштриховать сечение.
В
основе построения сечения методом следов лежат две теоремы:
1)
если две точки прямой принадлежат плоскости, то и вся прямая принадлежит
плоскости;
2)
если плоскость проходит через прямую, параллельную другой плоскости, и эти
плоскости пересекаются, то линия их пересечения параллельна первой прямой.
Метод
вспомогательных сечений применяется при построении сечений в
тех случаях, когда неудобно находить след секущей плоскости. Например, след
получается очень далеко от заданной фигуры.
Суть
комбинированного метода построения сечений многогранников состоит в
применении теорем о параллельности прямых и плоскостей в пространстве в
сочетании с методом следов или методом вспомогательных сечений.
Обратите
внимание: тетраэдр имеет четыре грани, поэтому его сечениями могут быть только
треугольники и четырёхугольники. А вот параллелепипед имеет шесть граней,
поэтому его сечениями могут быть треугольники, четырёхугольники, пятиугольники
и шестиугольники.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. В основании прямой призмы лежит равнобедренная
трапеция с основаниями, равными см
и см,
и боковой стороной, равной см.
Боковое ребро призмы равно см.
Найдите площадь сечения призмы плоскостью, проходящей через большую сторону
основания и середину противоположного бокового ребра призмы.
Решение.
Задача
вторая. На ребре правильного
тетраэдра с
длиной ребра взята
точка такая,
что .
Найдите площадь сечения тетраэдра плоскостью, содержащей точку и
перпендикулярной ребру .
Решение.
Задача
третья. В основании четырёхугольной пирамиды лежит
квадрат ,
а две боковые грани и
представляют
собой прямоугольные треугольники с прямым .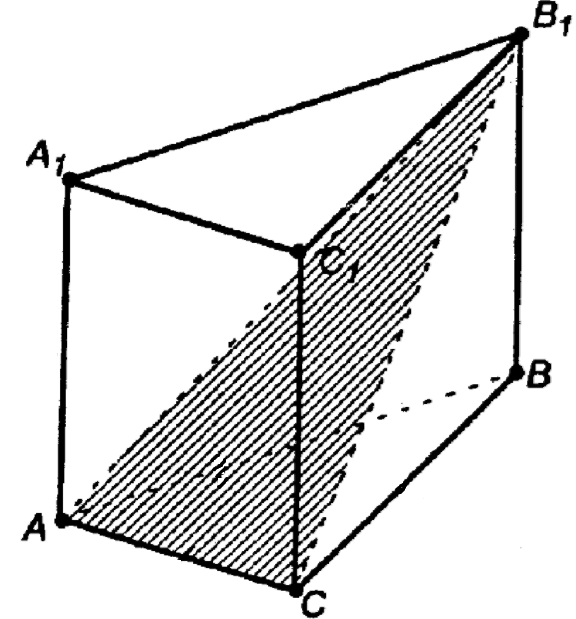
Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения
диагоналей основания и параллельной грани ,
если .
Решение.
Урок по теме «Сечение многогранников» / Открытый урок
Цель: углубление, обобщение, систематизация, закрепление полученных знаний и навыков построения сечений
Задачи:
1. Сформировать у школьников мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для получения новых знаний.
3. Развивать у учащихся мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки
исследовательской работы над задачей.Оборудование: Атанасян Л. С. и др. Геометрия 10-11 класс (М.Просвещение.2010), компьютер,
проектор, экран, презентация для сопровождения урока, раздаточный материал учащихся,
СD: Виртуальнаяшкола Кирилла и Мефодия (Уроки геометрии 10класс)
План урока: 1. Организационныймомент (1мин)
Организационныймомент (1мин)
2. Проверка домашнегозадания (4-5мин)
3. Актуализация (3-4мин)
4. Применение знаний встандартной ситуации (закрепление) (21-23мин)
5. Самостоятельнаяработа (10мин)
6. Домашнеезадание (2мин)
7. Подведение итогаурока (2мин)
1. Организационный момент (приветствие,сообщение темы, целей и плана урока)
2. Проверка домашнего задания (задачи №1, 2, презентация слайд № 3, 4) разборрешения задач домашней работы по этапам, с объяснением теоретической составляющей)
3. Актуализация (блиц-опрос)
Что называется многогранником
Что называется сечением многогранника (слайд № 5)
Что является базовым при построениисечений (слайд № 6)
Какие методы построения сеченийиспользуются при решении задач
4. Закрепление: Просмотр решения задачи (анимация №3 «сечение параллелепипеда»,урок №13 по теме «Многогранники», СD Виртуальная школа Кирилла и Мефодия, Уроки геометрии 10 класс), обсуждение
Решение задач (обсуждение плана построения, построение каждым в тетради и проверка с помощью подготовленной презентации, слайды 7-10)
1.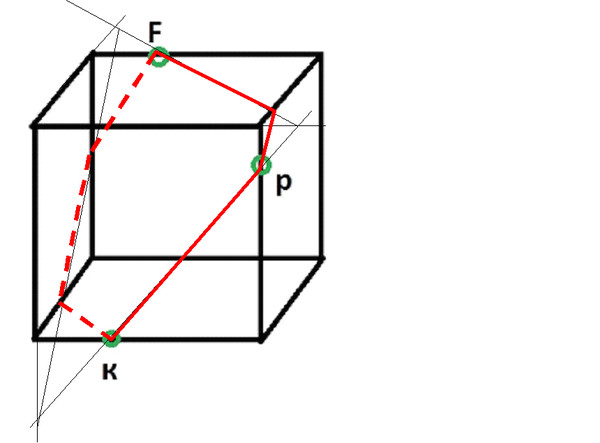 Построить сечение,определяемое параллельными прямыми АА1 и СС1
Построить сечение,определяемое параллельными прямыми АА1 и СС1
2. Построитьсечение куба плоскостью, проходящей через М и прямую АС3.
Построть сечение куба, проходящее через точки Р,М,К
4.Определить вид сечениякуба АВСДА1В1С1Д1 плоскостью,проходящей через ребро А1Д1 и середину ребраВВ1
5. Самостоятельнаяработа на построение сечений, проходящих через данные точки, по готовым чертежам с взаимопроверкой (слайд №11-условие, №12-решение)
6. Домашнеезадание: № 84,85 [1,с.32] дополнительно: Составить две задачи на построение сечений многогранников с использованием полученных знаний. (творческое задание)
7. Итог урока:
Что нового вы узнали на уроке?
Каким образом строится сечение параллелепипеда?
Какие многоугольники могутполучиться в сечении параллелепипеда?
Литература:
1. Атанасян Л.С. и др. Геометрия. /Учебник для 10-11классов общеобразовательных учрежденийМ. Просвещение.20102.
2. Смирнов В.А.,Смирнова И.М. Геометрия / Учебник для 10-11 классов. М.Мнемозина.20083.
3. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»
4. Электронное издание«Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы»
5. Электронное издание«Виртуальная школа Кирилла и Мефодия: Уроки геометрии 10 класс»
| 25 мая 2020 г. | |||
| Алгебра и начала математического анализа. Задачи с экономическим содержанием на выплаты неравными платежами | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 21 мая 2020 г. | |||
| Алгебра. Построение графика функции, содержащей модуль | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Геометрия. Использование подобия треугольников при решении задач Использование подобия треугольников при решении задач | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 13 мая 2020 г. | |||
| Алгебра и начала математического анализа. Задачи с экономическим содержанием | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| Геометрия. Объемы шара, конуса и цилиндра | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 7 мая 2020 г. | |||
| Геометрия. Многоугольники | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Алгебра. Построение графика кусочно-заданной функции Построение графика кусочно-заданной функции | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 5 мая 2020 г. | |||
| Алгебра и начала математического анализа. Теория вероятностей | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| Геометрия. Площадь поверхности цилиндра и конуса | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 4 мая 2020 г. | |||
| Алгебра. Решение уравнений, неравенств и их систем. Практикум | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Геометрия. Окружность Окружность | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 24 апреля 2020 г. | |||
| Алгебра и начала математического анализа. Решение задач с параметром | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| Геометрия. Многогранники. Площади боковых поверхностей призмы и пирамиды | Математика 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 22 апреля 2020 г. | |||
| Алгебра. Теория вероятностей. Комбинаторика при решении задач теории вероятностей | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Геометрия. Решение задач о равновеликих фигурах Решение задач о равновеликих фигурах | Математика 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 10 апреля 2020 г. | |||
| Правильные многогранники | Стереометрия 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| Функционально-графический метод решения задач с параметром | Алгебра и начала математического анализа 11 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
| 8 апреля 2020 г. | |||
| Площади треугольников и четырехугольников | Геометрия 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Теория вероятностей. Теоремы сложения и умножения вероятностей Теоремы сложения и умножения вероятностей | Алгебра 9 класс | 30 минут | Шайкина Виктория Николаевна, старший преподаватель кафедры естественно-математических дисциплин, ГБУ ДПО ЧИППКРО |
Построение сечений многогранников — презентация онлайн
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 1 им. Гриши Акулова
г.Донецка, Ростовской области
Урок геометрии, 10 класс
Автор: Кущий Надежда Васильевна,
учитель математики
• Развитие пространственного воображения обучаемых, их
логического мышления и индуктивного анализа.
• Формирования навыков решения задач на построение
сечений многогранников.
• Обучение умению анализировать свои действия для
достижения поставленной цели, развитие самоконтроля.
2
1. Сообщение темы и цели урока.
2. Проверка опорных знаний и умений обучаемых.
(Сл. 4-7)
3. Решение задач с объяснением хода решения учителем.
(Сл. 8, 10, 11)
4. Применение пространственного моделирования для
решения задач. (Сл. 9, 12, 13, 14)
5. Подведение итогов.
6. Домашнее задание. (Сл. 15)
3
Построить сечение многогранника,
проходящее через выделенные элементы
4
Построить сечение, проходящее через точку О,
параллельно грани ABCD
О
B
A
C
D
5
Построить сечение многогранника,
проходящее через выделенные элементы
6
Построить сечение многогранника ,
проходящее через выделенные элементы
Провести дополнительное построению параллельно выполненному
сечению
7
Построить сечение четырехугольной
пирамиды, проходящее через заданные точки
S
M
Q
N
B
C
X
P
Y
A
K
D
8
Построить сечение призмы, проходящее через точки
K – принадлежит ребру АА1
L – принадлежит грани АА1В1В
M – принадлежит грани АВС
A1
B1
C1
K
L
X
A
Y
B
M
C
9
Построить сечение параллелепипеда, проходящее через
заданные точки
Способ 1
B1
C1
Н
A1
D1
I
B
C
F
K
A
D
L
10
Построить сечение параллелепипеда, проходящее через
заданные точки
Способ 2
B1
C1
Н
A1
D1
I
B
C
Y
F
K
A
D
L
X
11
Построить сечение призмы, проходящее через
заданные точки
Н
B1
A1
K
C1
D1
Q
C
B
X
R
P
A
D
12
Построить сечение параллелепипеда, проходящее
через заданные точки
Способ 1
X
N
M
C1
B1
D1
A1
K
R
B
C
P
A
D
Q
13
Построить сечение параллелепипеда, проходящее
через заданные точки
X
N
M
C1
B1
Z
D1
A1
K
R
B
C
P
A
Q
D
Способ 2
Y
14
Построить сечение тетраэдра, проходящее через точки
Q – принадлежит грани ABC;
R – принадлежит ребру AB;
S – принадлежит ребру DB.
D
S
A
R
Q
T
U
X
B
C
15
1. Атанасян Л.С., и др. Геометрия 10-11. – М.: Просвещение, 2008.
2. Литвиненко В.Н., Многогранники. Задачи и решения. – М.: Вита-Пресс,
1995.
3. Смирнов В.А., Смирнова И. М., ЕГЭ 100 баллов. Геометрия. Сечение
многогранников. – М.: Экзамен, 2011.
4. Учебно-методическое приложение к газете «Первое сентября»
«Математика». Федотова О., Кабакова Т. Интегрированный урок
«Построение сечений призмы», 9/2010.
5. http://www.cartoonclipartfree.com/Cliparts_Free/Schule_Free/Cartoon_Clipa
rt_Free_Page_1.html мальчик за партой
16
Оценка и решение для объема призм
В последнем разделе вы разработали формулу объема для призмы, V = Bh , где B представляет собой площадь основания призмы, а h представляет высоту призмы. Вы также использовали формулу объема для решения задач, связанных с прямоугольными призмами.
Однако не все призмы являются прямоугольными. Рассмотрим небоскребы из разных городов, которые показаны ниже.
Рассмотрим небоскребы из разных городов, которые показаны ниже.
Флэтайрон-билдинг в Нью-Йорке представляет собой треугольную призму , поскольку крыша и контур улицы представляют собой совпадающие прямоугольные треугольники. | Башня JPMorgan Chase Tower в Хьюстоне представляет собой пятиугольную призму , поскольку крыша и очертания улицы представляют собой конгруэнтные пятиугольники. | Башня в Форт-Уэрте представляет собой восьмиугольную призму , поскольку крыша и очертания улицы представляют собой совпадающие восьмиугольники. |
Источник: Edificio Fuller (Flatiron) Edit, lmelenchon, Wikimedia Commons | Источник: Тауэр, 500 Трокмортон, Форт-Уэрт, Техас, Магнус Манске, Wikimedia Commons |
В этом разделе вы сосредоточитесь на треугольных призмах, которые представляют собой призмы с треугольным основанием.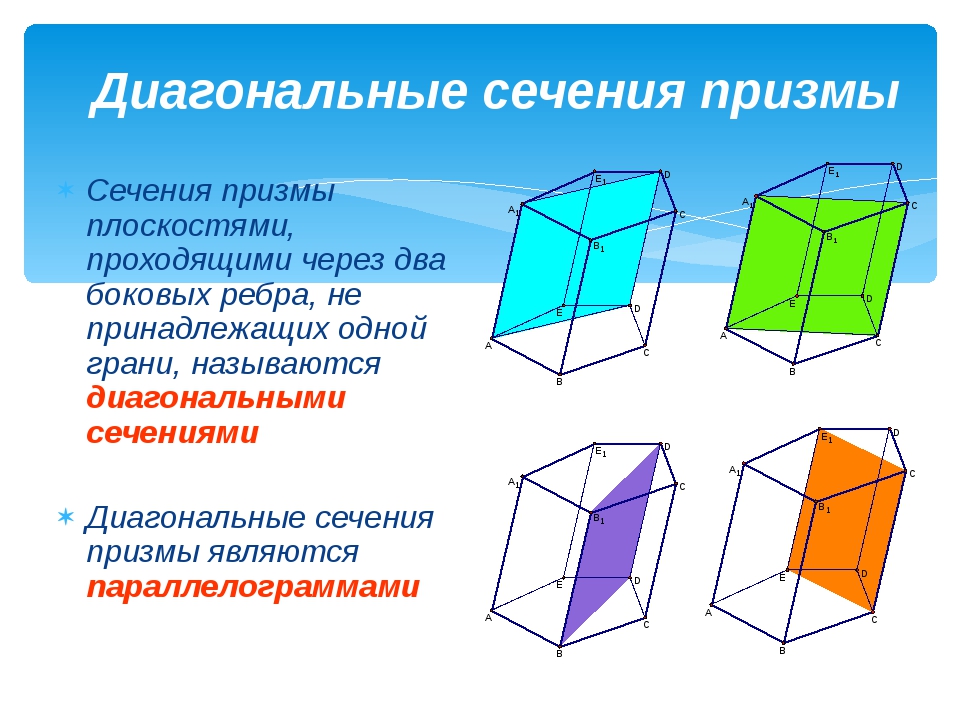
Воспользуйтесь интерактивом, чтобы создать несколько треугольных призм.Используйте размеры в интерактивном режиме, чтобы произвести расчеты, чтобы заполнить таблицу ниже. Запишите объем призмы с интерактивного экрана. Используйте таблицу, чтобы ответить на следующие вопросы.
Нужны дополнительные направления?
Скопируйте приведенную ниже таблицу в свои заметки или текстовый редактор, чтобы ввести данные в таблицу.
| Номер призмы | Площадь базы | Высота призмы | Объем призмы |
1 | 6.18 | 5 | 30,9 |
2 | |||
3 | |||
4 |
Посмотреть примеры ответов.
Что такое прямоугольная призма? — Определение и примеры — Урок математики [видео 2021 года]
Правила для призм
Есть пять правил для идентификации призмы:
Правило 1: заключается в том, что грани призмы должны быть многоугольниками. Таким образом, даже если может показаться, что цилиндры — это призмы, они не подходят под определение. Это потому, что их грани представляют собой круги или овалы, которые не имеют сторон и, следовательно, не являются многоугольниками. Так что банка — это не призма.Ни сторон, ни многоугольников, ни призмы.
У призмы могут быть треугольники в качестве граней.
Правило 2: гласит, что стороны призмы должны быть параллелограммами.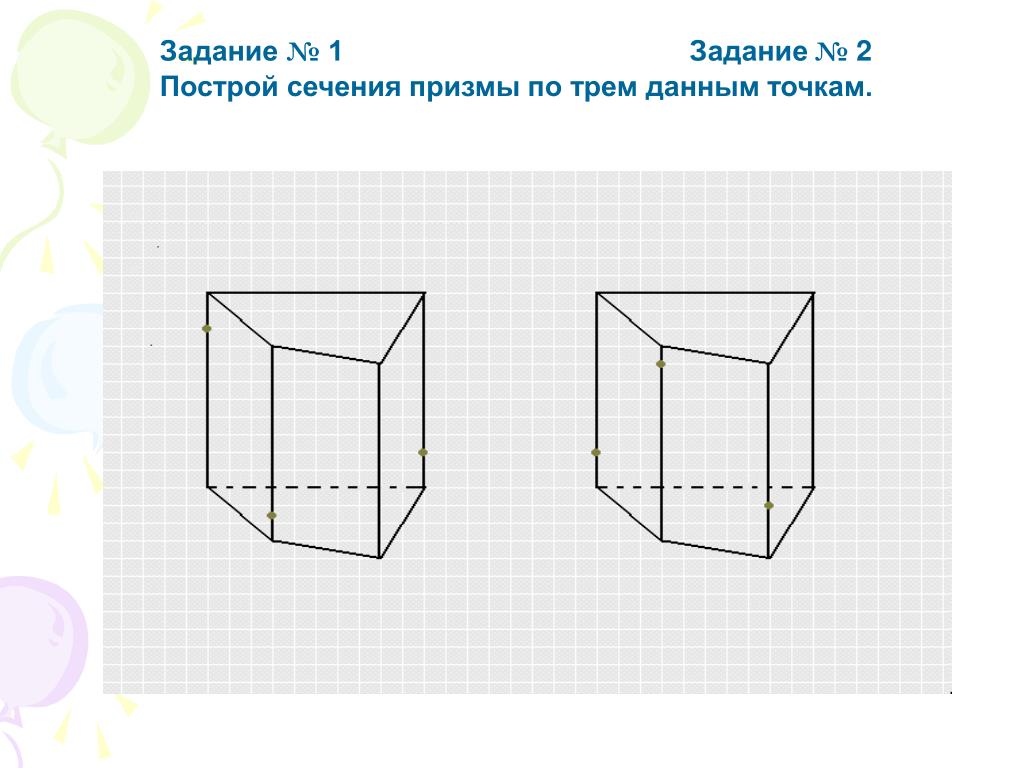 Параллелограммы — это четырехугольники, противоположные стороны которых параллельны. Рассмотрим короб и треугольную призму, все стороны которых параллелограммы.
Параллелограммы — это четырехугольники, противоположные стороны которых параллельны. Рассмотрим короб и треугольную призму, все стороны которых параллелограммы.
Правило 3: Третье правило гласит, что грани призмы должны быть параллельны. Если одна грань лежит под углом к другой, они в какой-то момент пересекутся, и фигура не является призмой. Кроме того, если грани не параллельны, стороны не будут параллелограммами.
Например, на этом рисунке задняя поверхность расположена под углом по сравнению с передней поверхностью. В результате две стороны не являются параллелограммами. Непараллельные грани создают стороны, не являющиеся параллелограммами.
Правило 4: гласит, что основания должны совпадать. Конгруэнтный означает точно такую же форму и размер.
Фигура с гранями разной формы создает стороны, не являющиеся параллелограммами.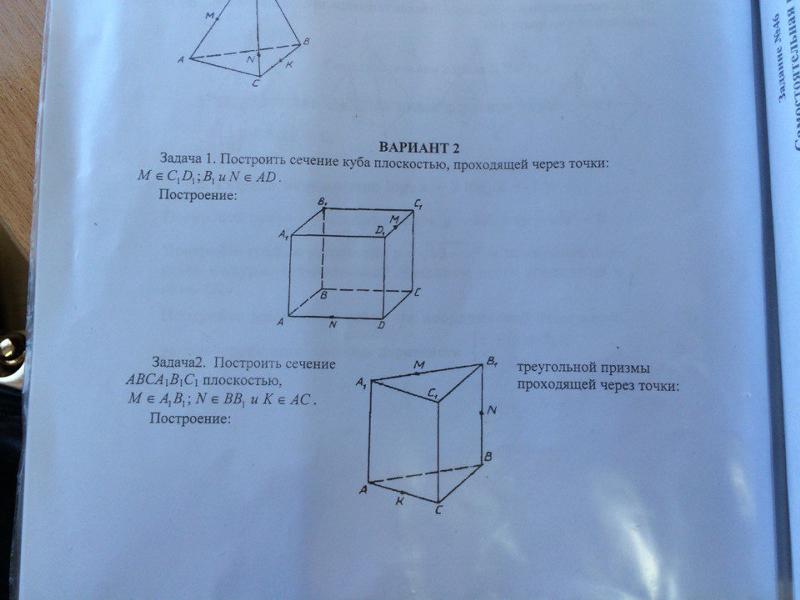 Поскольку лица не совпадают, эта фигура не является призмой.
Поскольку лица не совпадают, эта фигура не является призмой.
Правило 5: Наконец, правило пять гласит, что если взять поперечное сечение призмы, параллельное ее граням, то поперечное сечение будет конгруэнтно граням призмы.Это происходит потому, что грани совпадают и параллельны. Это верно независимо от того, где вы его разрежете.
Думайте об этом как о буханке хлеба. Если его нарезать параллельно концам, независимо от того, где вы нарезаете, ломтики будут иметь одинаковую форму.
Косые призмы
При соблюдении всех этих правил важно понимать, что есть кое-что, что не является правилом.Углы между сторонами и гранями не обязательно должны быть прямыми. Наклонная призма имеет наклонные стороны, но грани все еще конгруэнтны и параллельны.
Наклонная призма имеет наклонные стороны, но грани все еще конгруэнтны и параллельны.
Хотя стороны призмы этого типа наклонены, ее пятиугольные грани конгруэнтны и параллельны, а стороны по-прежнему параллелограммы.
Прямоугольные призмы
Итак, что же все это дает нам в отношении прямоугольных призм? Поскольку существует много разных форм, которые могут служить гранями, существует много разных типов призм.На самом деле призмы названы по форме их граней. Итак, прямоугольная призма — это просто призма с прямоугольниками на гранях. Это замкнутая трехмерная форма, но она основана на двух прямоугольниках. Есть много обычных предметов, которые на самом деле являются прямоугольными призмами.
Эта шкатулка представляет собой трехмерный объект с прямоугольными верхом и низом.Это делает его прямоугольной призмой!
Точно так же матрас — это прямоугольная призма.
Матрас имеет прямоугольные верх и низ. Конгруэнтные и параллельные прямоугольные грани образуют прямоугольную призму.
И еще пример:
Эта книга стоит на узких прямоугольниках.Но это все же трехмерная фигура, основанная на двух прямоугольниках, так что это прямоугольная призма.
Резюме урока
Призма — это два многоугольника, соединенных вместе, чтобы образовать замкнутую трехмерную форму.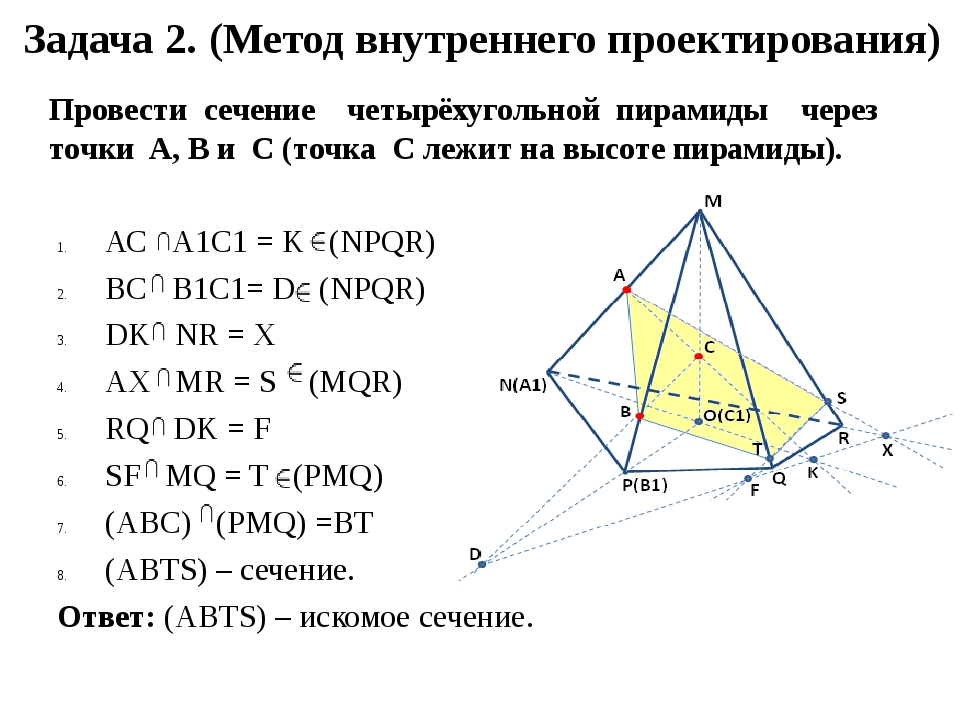 Правила, определяющие призму, гласят, что грани должны быть многоугольниками, стороны должны быть параллелограммами, а грани должны быть параллельны. Трехмерная форма, которая является призмой, также должна иметь конгруэнтные грани, а поперечные сечения, параллельные граням, должны совпадать с гранями.Цилиндры не являются призмами из-за круглой верхней и нижней части.
Правила, определяющие призму, гласят, что грани должны быть многоугольниками, стороны должны быть параллелограммами, а грани должны быть параллельны. Трехмерная форма, которая является призмой, также должна иметь конгруэнтные грани, а поперечные сечения, параллельные граням, должны совпадать с гранями.Цилиндры не являются призмами из-за круглой верхней и нижней части.
Косые призмы имеют наклонные стороны, но являются призмами, поскольку имеют параллельные и совпадающие грани. Прямоугольная призма — это просто призма с прямоугольными гранями. Поскольку грани прямоугольной призмы должны быть прямоугольниками, по крайней мере две ее стороны всегда будут прямоугольниками, даже если остальные стороны являются квадратами.
Объем призм и пирамид — Видео и стенограмма урока
Типы призм
Начнем с призм.Вы, наверное, видели всевозможные призмы. Есть стеклянные, которые используются для фокусов со светом, например, для превращения солнечного света в радугу.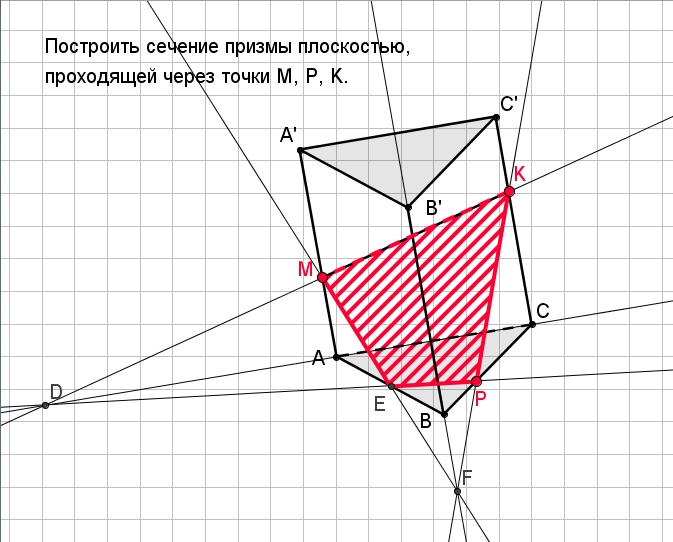 Палатки тоже могут быть призмами. Если вы любитель шоколада, то знаете, что Toblerone упаковывает шоколад в коробки в форме призмы.
Палатки тоже могут быть призмами. Если вы любитель шоколада, то знаете, что Toblerone упаковывает шоколад в коробки в форме призмы.
Призма представляет собой трехмерную форму с плоскими сторонами и двумя параллельными гранями. Что это обозначает? Все приведенные выше примеры — треугольные призмы. Обратите внимание, что каждая грань представляет собой треугольник. Это параллельные грани.А по бокам? Ага, они плоские. Они тоже параллелограммы. Один из способов думать о призмах состоит в том, что если вы сделаете срез в любом месте, параллельном лицу, форма всегда будет одинаковой.
Не все призмы треугольные. Также есть квадратные призмы. К ним относятся кубы, у которых все шесть сторон одинаковы, но пока грани квадраты, это квадратная призма. Видите ли, призмы определяются этими гранями. Если у лица пять сторон? Это пятиугольная призма. Также сарай. Это может быть сарай.
Объем призм
Допустим, вам нужно найти объем призмы. Например, вы в походе и хотите наполнить палатку вашего приятеля зефиром. Вам нужно спланировать такие вещи.
Хорошо, объем призмы довольно прост. Начните с области лица. Если это треугольник, это 1/2 * b * h. Если квадрат, то s2 и так далее. Затем вы просто умножаете его на высоту призмы. Таким образом, объем призмы — это площадь основания (B), умноженная на высоту между основаниями (h), которую мы можем просто записать как B * h.
Теперь вернемся к той палатке. Лицевая сторона представляет собой треугольник. Если основание 4 фута в длину и 4 фута в высоту, то площадь будет 1/2 * 4 * 4, или 8 квадратных футов. Длина этой палатки 7 футов, так что это высота. Объем всего B * h или 8 * 7, что составляет 56 кубических футов. Итак, вам понадобится 56 кубических футов зефира. Это много зефира.
Рассмотрим другой пример. Допустим, вы отказались от шуток в кемпинге и устраиваете вечеринку с вином и сыром.У вас может быть кусок сыра, который вы пытаетесь нарезать кубиками. Каждый куб равен одному кубическому сантиметру. Сколько кубиков можно получить из этого сыра?
Это прямоугольная призма, поэтому вам нужно знать площадь прямоугольника и высоту. Лицо сыра 3 см в длину и 7 см в ширину. Площадь прямоугольника равна длине, умноженной на ширину. 3 * 7 = 21 квадратный сантиметр. Высота этого блока 14 см. Итак, объем B * h, или 21 * 14, что составляет 294 кубических сантиметра. Итак, у вас будет 294 крошечных кубика сыра.О, и если вы похожи на меня, не забудьте вычесть несколько, которые вы съедите, пока будете нарезать.
Типы пирамид
Теперь давайте посмотрим на пирамиды. Люди часто путают призмы и пирамиды. Но вы никогда не увидите радуги, если повесите в окне пирамиду. Когда люди думают о пирамидах, они думают о пирамидах в Египте. Почему? Потому что они потрясающие!
Пирамида — это форма, основание которой соединено с вершиной. Стороны пирамиды всегда образуют треугольники.Основания могут иметь любую форму с трех и более сторон. Те, что в Египте, представляют собой квадратные пирамиды, что означает, что их основания — квадраты. У вас также могут быть треугольные пирамиды и пирамиды с большим количеством сторон у основания.
Объем пирамид
Хорошо, держу пари, вы всегда задавались вопросом, сколько камня в одной из этих египетских пирамид? Чтобы найти объем пирамиды , вам нужно умножить площадь основания (B) на высоту (h), затем разделить на три, или 1/3 * B * h.Почему 1/3? Потому что базовое умножение на высоту даст вам объем призмы. Поскольку вершина пирамиды — это точка, вы знаете, что она имеет меньший объем. Это 1/3 объема.
Хорошо, самая большая пирамида в Египте — Великая пирамида Гизы. Это квадратная пирамида, у которой каждая сторона основания составляет около 750 футов в длину. Таким образом, площадь базы составляет 7502 или 562 500 квадратных футов. Первоначально пирамида была около 480 футов в высоту. Таким образом, объем равен 1/3 * B * h или 1/3 * 562 500 * 480. Это 90 000 000 кубических футов.
Звучит огромно, правда? Кстати, самая большая пирамида в мире находится не в Египте. Это в Мексике. Это Великая пирамида Чолула, и ее объем превышает 100 миллионов кубических футов. Однако сегодня он покрыт растениями и увенчан церковью.
Давайте посмотрим на меньший пример. Вот треугольная пирамида. Его высота всего 6 дюймов. Но послушайте, так проще построить. Основание — треугольник. Помните, что площадь треугольника равна 1/2 * b * h.
Важно не запутаться с терминами.Мы работаем с двумя вещами, называемыми базой, и двумя вещами, называемыми высотой. Но давайте сделаем шаг за шагом и начнем с треугольника.
База 3 дюйма. И его высота составляет 4 дюйма. Подключите это к 1/2 * b * h, и у вас будет 1/2 * 3 * 4, или 6 квадратных дюймов. Это наша большая Б. Запомните формулу объема: 1/3 * B * h. Это будет 1/3 * 6 * 6, что составляет 12 кубических дюймов. Туристы могут не приехать посмотреть на нашу скромную пирамиду, но это пирамида.
Резюме урока
Таким образом, призмы могут быть треугольной, квадратной или другой формы.Объем призмы равен B * h, где B — площадь основания, а h — высота призмы.
Пирамиды могут иметь основания в виде треугольников, квадратов или других форм. Объем пирамиды составляет 1/3 * B * h, где B — площадь основания, а h — высота пирамиды.
Результаты обучения
По завершении этого урока вы сможете:
- Создавать призмы и пирамиды
- Определите объем призм
- Определите объем пирамид
Этот анимационный эпизод показывает антипризму сверху вниз. | Трехмерные фигуры, треугольные призмы | ||
Этот анимационный эпизод показывает антипризму, разворачивающуюся в две пирамиды. | Трехмерные фигуры | ||
В этой анимированной последовательности показан конус сверху вниз. | Трехмерные фигуры, конусы | ||
Эта анимированная последовательность показывает куб сверху вниз. | Трехмерные фигуры, кубики | ||
В этой анимированной последовательности показан цилиндр сверху вниз. | Трехмерные фигуры, цилиндры | ||
Эта анимированная последовательность показывает октаэдр сверху вниз. | Трехмерные фигуры | ||
Этот анимационный эпизод показывает пирамиду сверху вниз. | Трехмерные фигуры, пирамиды | ||
Этот анимационный эпизод показывает прямоугольную призму сверху вниз. | Трехмерные фигуры, прямоугольные призмы | ||
Эта анимированная последовательность показывает тетраэдр сверху вниз. | Трехмерные фигуры | ||
На этом анимационном кадре сверху вниз изображена треугольная призма. | Трехмерные фигуры | ||
В этом видео студенты изучают основы антипризм в контексте нью-йоркской башни Свободы, имеющей антипризменный дизайн.Они изучают свойства антипризм, уделяя особое внимание тем, у кого квадратное основание. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Прямоугольные призмы | ||
В этом видео студенты изучают основы прямоугольных призм в контексте жилой башни в Нью-Йорке: 432 Park Avenue.Они изучают свойства прямоугольных призм с квадратным основанием и без него, а также архитектурные требования, влияющие на использование обоих типов прямоугольных призм. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Прямоугольные призмы | ||
В этом видео студенты изучают реальное применение треугольных призм: здание Flat Iron в Нью-Йорке.Это здание является идеальным примером реальной призмы, а также обеспечивает привязку к геометрии прямоугольного треугольника. В этом видео описывается геометрия здания Flat Iron Building, а также его архитектура. Он включает в себя анимацию, демонстрирующую ключевые особенности треугольных призм. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Треугольные призмы | ||
В этом видео студенты изучают основы призм и антипризм.Они изучают свойства треугольных призм, прямоугольных призм, треугольных антипризм и прямоугольных антипризм. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Прямоугольные призмы, треугольные призмы | ||
В этой программе мы исследуем свойства трехмерных фигур.Мы делаем это в контексте двух реальных приложений. В первой мы рассмотрим трехмерную структуру пирамид майя. Эти лестнично-ступенчатые конструкции предоставляют уникальную возможность также исследовать последовательности и серии. Во втором приложении мы рассматриваем Шанхайскую башню как пример конструкций цилиндрической формы. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Трехмерные фигуры | ||
Мы посетим Древнюю Грецию, чтобы узнать о Платоновых Телах.Это введение в более общую тему трехмерных фигур. Это видео включает расшифровку видео: https://media4math.com/library/video-transcript-geometry-applications-3d-geometry-segment-1-introduction Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Трехмерные фигуры | ||
Прямоугольные призмы.Пирамиды майя по сути представляют собой стопки прямоугольных призм. Громкость каждого последующего уровня — это процентное уменьшение его нижнего соседа. Это вводит понятие геометрической последовательности и ряда, включая бесконечный ряд. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Трехмерные фигуры, пирамиды | ||
Шанхайская башня в Китае представляет собой стопку цилиндрических форм, где каждый последующий слой представляет собой процентное уменьшение своего нижнего соседа.Как и в предыдущем разделе, здесь вводится понятие геометрической последовательности и ряда. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Трехмерные фигуры, цилиндры | ||
В этой программе мы исследуем свойства четырехугольника.Мы делаем это в контексте двух реальных приложений. В первом мы исследуем архитектуру Фрэнка Ллойда Райта как приложение квадратов и прямоугольников; в частности, мы смотрим на его дом Fallingwater. Во втором приложении мы смотрим на уникальное здание в форме параллелограмма в Испании, известное как Пуэрта-де-Европа. Это дает возможность изучить свойства параллелограммов и трапеций. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Приложения четырехугольника, определение четырехугольника | ||
Стоунхендж наиболее известен как круглая структура.Но примечательна конструкция стойки и перемычки, и этот тип конструкции включает в себя четырехугольные формы. От привычных дверных проемов домов до величественных входов в древние храмы — конструкция столбов и перемычек дает четкое представление о природе четырехугольников. В этом сегменте также описаны ключевые концепции, разработанные на протяжении всей программы. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Приложения четырехугольника, определение четырехугольника | ||
Архитектурный шедевр Фрэнка Ллойда Райта «Падающая вода» также представляет собой потрясающее собрание четырехугольников.Некоторые из прямоугольных форм в этом здании, кажется, бросают вызов гравитации, поскольку мы исследуем свойства квадратов и прямоугольников, которые позволили Фрэнку Ллойду Райту выйти за рамки дизайна и структуры. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Приложения четырехугольника, определение четырехугольника | ||
Башни Пуэрта-де-Европа в Мадриде соединяют параллелограммы спереди и по центру.Эти наклонные башни, похожие на современные башни Пизы, кажется, бросают вызов гравитации, но полагаются на стабильность, обеспечиваемую их четырехугольной структурой. Исследуются и анализируются лежащие в основе параллелограмм и трапеции. Стенограмма видео для этого руководства доступна по ссылке Ссылка Примечание. Загружается руководство Media4Math по видео с субтитрами. Другие видео с субтитрамиЧтобы увидеть полную коллекцию видео с субтитрами, нажмите на ссылкуСсылка | Приложения четырехугольника, определение четырехугольника | ||
Определение термина «антипризма.»Примечание. Загружается файл PNG. Примечание. Загружаемый файл представляет собой файл JPG. Связанные ресурсыЧтобы увидеть полное собрание терминов глоссария в Visual Glossary, щелкните по этой ссылке:https://media4math.com/Visual-Glossary | Трехмерные фигуры | ||
Определение термина «призма.»Примечание. Загружается файл PNG. Примечание. Загружаемый файл представляет собой файл JPG. Связанные ресурсыЧтобы увидеть полное собрание терминов глоссария в Visual Glossary, щелкните по этой ссылке:https://media4math.com/Visual-Glossary | Трехмерные фигуры | ||
Формула площади поверхности сферы. Примечание. Загружаемый файл представляет собой файл JPG. Связанные ресурсыЧтобы увидеть полную коллекцию формул, щелкните по этой ссылке:https://media4math.com/math-formulas | Площадь |
13 Потрясающий объем пирамид и призм Активность
Объем и площадь поверхности — одни из самых сложных понятий для моих учеников в 7-м классе.Я чувствую, что они путают их, и им нужно действительно понимать, что каждый влечет за собой. Я хотел бы убедиться, что ученики достаточно хорошо понимают объем, прежде чем мы перейдем к поверхностной области. Хотя каждый год я, наверное, пробовал что-то немного другое. Один из лучших способов заложить фундамент — заниматься открытием. Многие студенты приходят в наш класс не с достаточными базовыми знаниями, и ведение их через процесс открытий отлично помогает создать этот фон.В этом посте я расскажу больше об открытии, которое я использую для этой темы, и еще о двенадцати увлекательных занятиях, которые помогут студентам действительно получить прочную основу для определения объема пирамид и призм.
В этом сообщении блога вы увидите много занятий, но всегда важно, чтобы на протяжении всего обучения учащиеся продолжали обсуждать «почему». Например, почему объем треугольной призмы составляет половину прямоугольной призмы? Дайте им возможность ответить на этот и подобные вопросы несколько раз.Покажите им примеры призм, подобных этой, и попросите их обсудить это с партнером.
Кроме того, мы не можем просто полагаться на учеников, которые перенесут целую кучу формул из своих заметок в свою долговременную память. Им необходимо глубокое понимание, чтобы понимать эти формулы и держаться за них. Таким образом, упражнения должны формировать концептуальное понимание, а не просто запоминать формулы для теста. Ладно, хватит лекции — это просто уроки, которые я продолжаю изучать снова и снова со своими учениками, поэтому я хотел бы избавить кого-нибудь от душевной боли, которая возникает, когда ученики хорошо справляются с последним тестом, но не Представьте, о чем вы говорите, всего несколько недель спустя.Давайте рассмотрим несколько забавных заданий, которые увлекут учащихся, изучая объем призм и пирамид.
Вот список:
Лаборатория открытий
Лабиринты объема
Игра с QR-кодом
Карты задач
Загадка
Вырезание, складывание
Якорная диаграмма и другие якорные диаграммы
PBS Видео и урок
Строительство крыши Деятельность
Что вы заметили?
Создайте свой собственный рабочий лист
Целевая игра с рабочим листом
Объем песни на YouTube
Погрузимся в
Этот список мероприятий включает в себя различные виды деятельности.Некоторые из них лучше всего подходят для небольших групп, а другие — для всего класса. Вы найдете одни отличные ресурсы для начального обучения, а другие можно просмотреть позже в этом году. Давайте посмотрим на эти упражнения и заставим наших студентов раскачивать объем пирамид и призм!
Лаборатория открытий дает учащимся возможность действительно увидеть того, что они пытаются решить. Это побуждает их придавать смысл и лучше всего работает до формальных инструкций или заметок. Чтобы сделать этот объем лаборатории по обнаружению прямоугольных призм, все, что вам нужно, это какие-то маленькие кубики, с которыми студенты могут работать.Студентам дается прямоугольная призма, составленная из кубиков, и они должны вычислить, сколько в ней кубических единиц, не разбирая ее и не считая кубики. Я люблю эту лабораторию открытий. Моим студентам тоже понравилось. Сначала они не знали, что делать, а потом было так здорово наблюдать, как они придумывают стратегии. Каждая группа придумала свою уникальную стратегию ответа на этот вопрос.
Сначала студенты пытались сосчитать каждый кубик. Затем они попытались найти более эффективные способы.Я не могу объяснить, как здорово было видеть, как в их мозгу крутятся колеса. И имейте в виду, что группа студентов, которой я изначально занималась, боролась с математикой. Это открытие действительно заставляет студентов задуматься. Кроме того, это дает им некоторую предысторию, которая им необходима, чтобы помнить об этом надолго.
Математические лабиринты — отличный вариант традиционного рабочего листа. Студенты приступают к практике, в которой они нуждаются в решении задач, и получают удовлетворение от работы над финишной чертой лабиринта.Я каждый день использую лабиринты для работы с колокольчиками, и не дай бог, я когда-либо попытаюсь оставить ученикам что-нибудь еще, чтобы начать занятия.
Этот том лабиринта призм на самом деле состоит из трех лабиринтов. Для выполнения каждого из них ученики решают 12-15 задач на призму, чтобы добраться до финиша. В первых двух лабиринтах ученики находят объем призмы. В третьем лабиринте ученикам дается объем, и им нужно найти высоту или ширину отсутствующей стороны.
В лабиринтах мне нравится то, что они позволяют легко визуально проверить, как идут дела у учеников.Я могу смотреть на путь и мгновенно сообщать студентам об их успехах. Или студенты могут быстро проверить свою работу, увидев пройденный путь. Эта способность быстро видеть, что ученики, а что нет, позволяет мне быстро дать им обратную связь, прежде чем они решат все задачи неправильно и получат все эти плохие практики.
Хотите еще больше забавных математических лабиринтов, подобных приведенному выше, присылать вам каждый месяц бесплатно? Просто присоединитесь к эксклюзивному клубу «Лабиринт месяца» и получите свой собственный бесплатный математический лабиринт, который будет автоматически отправляться вам каждый месяц.
Да! Зарегистрируйтесь в бесплатном клубе «Лабиринт месяца»!
Не могу дождаться встречи с вами там.
Если вам требуется совместная деятельность для учащихся, чтобы они могли больше практиковаться, не ищите ничего, кроме этой игры с QR-кодом «Том с треугольными и прямоугольными призмами». В нем 16 вопросов, половина из них — задачи с текстом. У остальных или задач есть изображение формы, а учащиеся вычисляют объем. Самое интересное, что студенты могут проверять свои ответы с помощью QR-кодов. Им это нравится.Кроме того, они не знают, сколько очков они получат от карты, которую выбрали сначала. После того, как они все сделали правильно, они сверяют очки. Игры с QR-кодом просто добавляют немного новизны и удерживают учащихся. (Подробнее читайте в статье «5 способов использования QR-кодов в математическом классе».)
Мне нравится универсальность карточек задач. Вы можете использовать их практически для чего угодно. Иногда я даже использую их в качестве подстаканника или передаю в офис (после того, как мы посчитаем их, и они, конечно же, отправятся на переработку!).Их нельзя недооценивать. А если серьезно, то карточки с задачами — отличное занятие для партнера или обзор для всего класса. Мы используем их примерно каждую неделю в моем классе. На прошлой неделе мы использовали карточки с заданиями, чтобы играть в футбол всем классом, а на прошлой неделе мы использовали их в качестве задания для партнеров.
В этом наборе карточек задач «Объем прямоугольных и треугольных призм» есть вопросы различных типов. Они побуждают студентов не просто рассчитать объем прямоугольных и треугольных призм.Некоторые вопросы заставляют учащихся складывать вещи. Также они должны найти объем неправильных призм.
Одно из моих предложений — напечатать ответы на обратной стороне карточек. Позвольте учащимся проверить свои ответы и сразу же получить обратную связь. Это дает им возможность исправить свои ошибки до того, как они полностью закрепятся на каких-либо вредных привычках.
Если вы ищете какую-нибудь старую добрую практику, этот сборник «Загадка призм» отлично подойдет. Он добавляет несколько глупых загадок.Я обязательно подчеркиваю ученикам, что загадки — глупые. Это одна из тех ситуаций, когда вы просто принимаете глупость. Некоторые дети действительно решают загадку, и тогда вы слышите стоны глупости.
Примите пошлое!
В этом упражнении 16 задач. Восемь из них включают изображение прямоугольной или треугольной призмы. Остальные восемь — сюжетные задачи. Есть 2 рабочих листа, так что вы можете использовать один время от времени, а затем другой, когда будете просматривать. Кроме того, они отлично подходят для выполнения домашних заданий или занятий в центре.
С помощью этого упражнения «Раскладывание-вверх» вы можете показать учащимся, почему объем пирамиды составляет одну треть от прямоугольной призмы. Используя предоставленный шаблон, учащиеся создают бумажные пирамиды и соединяют их вместе. Затем они смогут сделать выводы о том, что происходит. Какое прекрасное открытие для этой концепции! Как и в случае с другими открытиями, вы увидите, как учащиеся устанавливают собственные связи. Они с большей вероятностью запомнят эти связи после такого рода деятельности, чем просто заучивание формул.
Якорные диаграммы бывают разными именами. В последнее время я видел их под названием «шпаргалки», особенно для средних классов. Когда я использую якорные диаграммы, я распечатываю их по две на страницу, а затем мы помещаем их в свои блокноты. Они становятся ориентиром для студентов. Кроме того, мы можем вернуться к ним, когда будем рассматривать тест на конец года.
Что касается объема призм, вот две отличные диаграммы привязок, которые стоит проверить. Первая справочная страница (показанная ниже) принадлежит миссис А.Математика Ньюэлла. Как видите, это отличное дополнение к записным книжкам учащихся в качестве справочника для решения объемных задач. Следующая диаграмма привязок взята из Cazoom Maths и является отличным визуальным напоминанием о различных формулах (для этой бесплатной услуги требуется подписка по электронной почте).
Эти якорные диаграммы не являются действиями сами по себе, но с ними можно выполнять действия. Например, в качестве предварительного набора вы можете попросить всех учеников ответить на вопросы, основанные на шпаргалке.Когда я это делаю, я обычно даю каждому ребенку, ответившему на вопрос, по «Веселому ранчо». Это просто заставляет их взглянуть на диаграмму и увидеть, как она может быть им полезна.
Это видео с PBS представляет собой базовое видео, которое показывает, как определить объем прямоугольной призмы. Кроме того, к нему прилагаются некоторые дополнительные материалы. Если вы ищете урок без подготовки, чтобы усилить или восстановить объем прямоугольных призм, это сработает для вас. Он включает в себя план урока с дополнительными и дополнительными упражнениями.
Это упражнение «Строительство крыши» от PBS Learning начинается с видео, в котором показано, как рассчитать объем треугольной призмы. Если вы нажмете на вкладку вспомогательных материалов, вы увидите подробный план урока. Я бы порекомендовал следовать их плану уроков. Они дают студентам много возможностей поговорить о математике. Студенты могут определить объем некоторых повседневных предметов и оценить, какой из предметов имеет больший объем. Затем им дается вызов на крышу. В целом это даст вашим ученикам практический опыт определения объема треугольных и прямоугольных призм.
Мне нравится использовать: «Что вы заметили?» мероприятия из Family Math Night в качестве предварительного набора. В этом сообщении блога представлены некоторые идеи о том, как использовать эту стратегию. В примере, показанном в сообщении, они дали студентам несколько призм и диаграмму с их размерами и объемом, но ничего не помечено. Это прекрасно работает, потому что ученики должны распознавать закономерности. Мне нравится, когда ученики пишут свои ответы на SmartPal или на доске. Есть так много разных способов сделать это.
Можно сделать что-то подобное с треугольными призмами. Еще вы могли бы сделать прямоугольную призму и треугольную призму с одинаковыми размерами. Затем попросите учащихся сделать выводы о том, почему треугольная форма составляет половину объема прямоугольной. Варианты использования этой стратегии безграничны.
Может быть, ваши ученики не справляются с одной частью тома, и вам для этого нужны некоторые задачи. Этот веб-сайт позволяет вам настроить свой рабочий лист, выбрав конкретные формы и единицы измерения, которые вы хотите.Вы просто устанавливаете флажки и бум, у вас есть проблемы, которые вам нужны. Затем эти задачи можно легко геймифицировать, превратив их из традиционного рабочего листа в забавную игру. Читайте дальше, чтобы узнать, как я играю в Target Game с рабочими листами, или ознакомьтесь с этой стратегией футбольной игры.
Иногда я чувствую себя побитым рекордом, когда говорю о рабочих листах апсайклинга. (Кстати, вы когда-нибудь использовали фразу «побитый рекорд» со своими учениками? Они не понимают, о чем вы говорите, и тогда вы просто чувствуете себя очень старым!) В любом случае, мне нравится находить способы использовать рабочий лист в забавные и увлекательные способы.На этом веб-сайте вы найдете множество бесплатных рабочих листов. Кроме того, у них есть некоторые, за которые нужно платить.
Я использую вопросы и играю в игру, называемую целевой игрой, потому что она придает больше опыта. Если вы хотите узнать больше о специфике целевой игры, ознакомьтесь с этим постом. Обычно дети могут бросить мяч в цель после того, как ответят на несколько вопросов о проблеме, которую они решают. Это приносит немного удовольствия в то, что может показаться скучным занятием. В результате этой игры у учащихся даже появляется мозговой перерыв.
Когда я показываю подобные видео в своем классе, некоторые ученики, кажется, оживают. В зависимости от группы детей и того, как вы ее представляете, подобные видео могут иметь большое влияние. В этом видео показана песня об объеме треугольных и прямоугольных призм на мелодию «Хэппи» Фарелла. После того, как вы будете смотреть его весь день на всех уроках, вы будете думать об этом в течение следующих трех недель (извините за это, но вас предупредили!). Это весело, и если вы попросите учащихся посмотреть его пару раз, они обязательно его запомнят.Я до сих пор помню песню 10-летней давности, которую я использовал на уроках ELL. Всякий раз, когда я вижу кого-нибудь из учеников этого класса, они все еще могут спеть мне это.
Попробуй одно
Видеть такое количество занятий может стать ошеломляющим, поэтому я всегда призываю людей просто попробовать что-то новое. Лично я считаю свой класс лабораторией. Мы пробуем разные вещи и смотрим, работают ли они. Если они работают, мы продолжаем их выполнять, а если они не работают, мы можем либо внести некоторые коррективы, либо оставить их позади.Моя задача — попробовать что-то новое, что привлечет внимание ваших учеников.
Большое спасибо за чтение. До скорого!
Связанные
Призма идентичности бренда: что это такое и как ее использовать
Призма идентичности бренда — это хорошо известная маркетинговая модель, также известная как призма идентичности бренда Капферера. Это шестиугольная призма, которая представляет шесть ключевых элементов, составляющих идентичность бренда.
Призма идентичности бренда внесла важный вклад в наше понимание роли рассказывания историй в брендинге.Он остается незаменимым помощником для предприятий, стремящихся укрепить свой бренд способами, которые последовательно отражают их происхождение и основные ценности.
6 элементов призмы идентичности бренда
В этой статье мы разберем 6 элементов призмы идентичности бренда и поможем вам внедрить их в ваш бренд в целом.
Ваш путеводитель по призме фирменного стиля
—
Что такое призма идентичности бренда Капферера?
–
Призма идентичности бренда — это концепция, разработанная в 1986 году профессором маркетинговой стратегии Жаном-Ноэлем Капферером для визуализации того, как бренд выражается через определенные аспекты.Капферер отточил шесть жизненно важных характеристик идентичности бренда и решил, что лучший способ представить, как они взаимодействуют как части целого, — это поместить их в форму призмы.
Бренд имеет очень специфические характеристики, которые определяют его помимо логотипа и других материалов визуального дизайна. По словам Капферера, бренды, которым удается идеально гармонизировать и выражать эти характеристики, — это те, которым удается создать сильную и отличительную идентичность бренда. Цель призмы — помочь брендам распознать части своей идентичности и заставить их работать вместе, чтобы рассказать историю бренда.
Объяснение 6 частей призмы идентичности бренда
—
Чтобы призма идентичности бренда работала как единое целое, вы должны начать с ее отдельных частей. Мы проведем вас через каждую грань призмы, а затем покажем, как применить эти строительные блоки к вашему собственному бренду.
Кампания Airbnb «Живи там» говорит о том, чем известен Airbnb — о домах вдали от дома. через Airbnb
1. Телосложение
Physique описывает физические характеристики вашего бренда, то есть все, что ваши клиенты могут визуально воспринимать о вас.В эту категорию входят логотип, руководство по стилю, иконография, цветовая палитра и представление самого продукта.
Например,
Airbnb предлагает услугу вместо физического продукта. Это означает, что их телосложение важно подчеркнуть, потому что их аудитории гораздо легче понять осязаемое изображение, чем концепцию. Таким образом, вместо продукта их реклама показывает конечный результат использования их услуг: люди, комфортно проживающие в местах, которые не являются их домами, но могут быть ими.
Вместе все визуальные элементы создают единый привлекательный внешний вид, который составляет основу их бренда.
2. Личность
Если телосложение — это лицо вашего бренда, то индивидуальность — это голос. Индивидуальность вашего бренда связана не только с тем, что вы говорите, но и с тем, как вы это говорите, и не ограничивается вербальным общением.
Personality воплощает в себе все, от выбора шрифта до тона любого общения. Иногда это называют «человеческими характеристиками» бренда. Он должен ответить на вопрос «кто вы?» Если бы человек сидел в комнате с вашим брендом, что бы он увидел, услышал и обсудил с вами?
Личность бренда Nike легко узнать как уверенную, вдохновляющую и бесстрашную.через Nike
Фирменный стиль Nike, например, проявляется как в знаменитой «галочке», так и в расположении спортсменов в рамке рядом с напористым текстом. Он уверенный, конкурентоспособный, рискованный и спортивный. История, которую он рассказывает, — это история триумфа, независимо от счета. Nike добивается согласованности в индивидуальности своего бренда с помощью спортсменов, которых они выбирают изображать, позиций, которые они занимают, их выбора шрифта и их разреженного, командного языка.
3. Культура
Мы только что отправили вам ваш первый урок.
Культура — это история происхождения вашего бренда. Где родился ваш бренд? Где оно живет? Какую систему убеждений и ценности она приписывает и почему?
«Культура» — это очень обсуждаемый аспект новых инновационных компаний. В нем есть способ выразить, как компания изо дня в день воплощает свою миссию, и он затрагивает людей, которые там работают, а также клиентов, которые взаимодействуют с продуктом.
Главный вопрос, который следует задать, чтобы определить культуру вашей компании: для чего живет мой бренд? Культура привносит в ваш бренд цель, выходящую за рамки продукта.
4. Отношения
Отношения — это взаимодействие между брендом и потребителями.
Это больше, чем денежная транзакция: подумайте о том, как ваш бренд поддерживает здоровые отношения со своими клиентами от первоначального взаимодействия до периода после покупки.
Кого вы хотите привлечь своим брендом? Иллюстрация Musique !.
В зависимости от характера вашего бренда хорошие отношения могут варьироваться от взаимодействия с социальными сетями до внимательной помощи в магазине.В конце концов, прочные отношения — это то, что отвечает ожиданиям клиентов и приносит вам лояльность к бренду.
Apple — отличный пример бренда, который признает и поддерживает свои отношения с клиентами. Не только интерфейс ориентирован на удобство использования, но и магазины Apple спроектированы так, чтобы быть местами, где легко найти помощь, а также продукты.
Отношения подчеркивают безупречное знакомство, удовлетворение потребностей клиентов и развитие без изоляции клиентов.
5. Отражение
Reflection описывает, кем вы хотите видеть своего покупателя. Кого бы вы в идеале хотели достичь? Здесь важна конкретность. Для компании, которая продает биоразлагаемые косметические продукты, это могут быть работающие женщины в возрасте от 20 лет, которые живут в космополитических районах и придерживаются веганской диеты.
Как только вы определитесь со своим идеальным клиентом, вы можете уверенно направить свой бренд на этого человека, учитывая все остальные характеристики призмы.
6. Собственное изображение
Клиенты Ralph Lauren могут почувствовать себя частью сюжетной линии. via Ralph Lauren
Образ себя — это то, как клиенты визуализируют свое идеальное «я». Понимание этого позволяет брендам более эффективно обслуживать своих клиентов. Подумайте, как их покупки и взаимодействие с вами улучшают их жизнь.
Собственный имидж является вдохновляющим как для бренда, так и для аудитории. Потребитель хочет видеть себя в идеале, а ваш бренд может стремиться помочь им достичь их идеалов.
Бренд
Ralph Lauren, как известно, фокусируется на построении сюжетной линии, в которой покупатели могут почувствовать себя персонажами: высококлассные, здоровые американцы, наслаждающиеся природой, как показано в их рекламных кампаниях.
Собираем призму
—
Всего существует шесть аспектов призмы идентичности бренда: телосложение, личность, культура, отношения, отражение и самооценка. Они разделены на призме, но сгруппированы в следующие более крупные категории.
Изображение отправителя указывает на то, как бренд представляет себя.Телосложение и личность подпадают под эту группу.
Изображение получателя показывает, как покупатели видят бренд. Отражение и самооценка относятся к этой категории.
Две другие категории — это интернализация и экстернализация. Внешний вид касается всей продукции бренда, видимой для клиентов, такой как логотип, реклама, продукты и услуги, и поэтому представлен отношением.
Интернализация включает ценности, кадровую политику, менеджмент и т. Д. И напрямую касается культуры.
Хотя эти плакаты разные, прочная основа бренда привела к неизменной идентичности: яркий красный цвет в сочетании с ликующими образами. Дизайн goopanic.
В совокупности эти категории завершают призму идентичности бренда и обеспечивают дорожную карту для вашего бренда, чтобы эффективно общаться с вашей аудиторией.
Как использовать призму идентификации бренда
—
Призма идентичности бренда творит чудеса, когда вы анализируете свой бренд по каждому из его аспектов. Продвигаясь через призму, задавайте себе такие вопросы: какова моя миссия? Кого я бы выбрал для представления своего бренда? С какими впечатлениями я хочу, чтобы люди покидали мой магазин? Помните, что ваша главная цель — создать последовательность в своей персоне, и ваши ответы должны подкреплять друг друга.
После того, как вы создали персонализированную призму идентичности бренда, подумайте о том, чтобы обобщить свой бренд в единую концепцию бренда, описав, кем вы являетесь как бизнес. Обязательно держите призму под рукой в качестве справочника, которым можно руководствоваться во всем, от повседневного общения до важных решений. Пересматривайте и регулярно обновляйте его, чтобы он оставался актуальным для изменений в ваших бизнес-целях.
Посмотрите на свой бренд в новом свете
—
Призма идентичности бренда — это способ развития вашего бренда, чтобы клиенты могли мгновенно узнать его индивидуальность и ценность для своей жизни.Призма — полезный и ясный способ выработать стратегию брендинга, соответствующую вашей миссии.
Используя призму в качестве ориентира, вы можете развиваться в соответствии с этой стратегией и следить за тем, как ваши собственные грани призмы меняются с течением времени, чтобы убедиться, что каждый из них постоянно поддерживает ваш бренд на долгие годы.
Нужна помощь специалиста по брендингу?
Наши дизайнеры позаботятся о вас.
Призмы с примерами
Перейти к площади или объему поверхности.
Призма — это твердый объект с:
- одинаковые концы
- плоские грани
- и тот же сечение по всей длине!
Поперечное сечение — это форма, полученная прямым разрезом объекта.
Поперечное сечение данного объекта — треугольник …
.. имеет одинаковое поперечное сечение по всей длине…
… значит, это треугольная призма .
изображения / prism-grow.js
Попробуйте нарисовать фигуру на листе бумаги А теперь представьте, что он выходит из листа бумаги … |
Без кривых!
Призма — это многогранник, а это значит, что все грани плоские!
Например, цилиндр не является призмой , потому что у него изогнутые стороны.
Базы
Концы призмы параллельны
, и каждый из них называется основанием.
Стороны
Боковые грани призмы — параллелограммы
(четырехсторонние формы с параллельными противоположными сторонами)
Это все призмы:
и более!
Пример: гексагональный кристалл льда.
Похоже на шестиугольник, но из-за некоторой толщины это на самом деле шестиугольная призма!
Фотография НАСА / Алексей Клятов.
Обычная и неправильная призмы
Все предыдущие примеры — это призмы Regular , поскольку поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).
Вот пример неправильной призмы :
| Неправильная пятиугольная призма: | ||
| Поперечное сечение | ||
| Он «неправильный», потому что поперечное сечение не имеет «правильной» формы. | ||
Правая и наклонная призма
Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:
Площадь призмы
Площадь поверхности = 2 × площадь основания
+ периметр основания × длина
Пример: какова площадь поверхности призмы, у которой площадь основания 25 м
2 , периметр основания 24 м, а длина 12 м:
Площадь поверхности = 2 × площадь основания + периметр основания × длина
= 2 × 25 м 2 + 24 м × 12 м
= 50 м 2 + 288 м 2
= 338 м 2
(Примечание: у нас есть инструмент для расчета площади)
Объем призмы
Объем призмы — это площадь одного конца, умноженная на длину призмы.
Объем = Площадь основания × Длина
Пример: каков объем призмы с площадью основания 25 м
2 и длиной 12 м:
Объем = Площадь × Длина
= 25 м 2 × 12 м
= 300 м 3
Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( наклонный ), но помните, что высота находится под прямым углом к основанию:
И вот почему:
Стек может наклоняться, но имеет тот же объем
Подробнее о боковых гранях
Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)
Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!
Но если два конца не параллельны , это не призма .
639 640 863, 1826, 1827 864, 3379, 3377, 3378, 7649
.

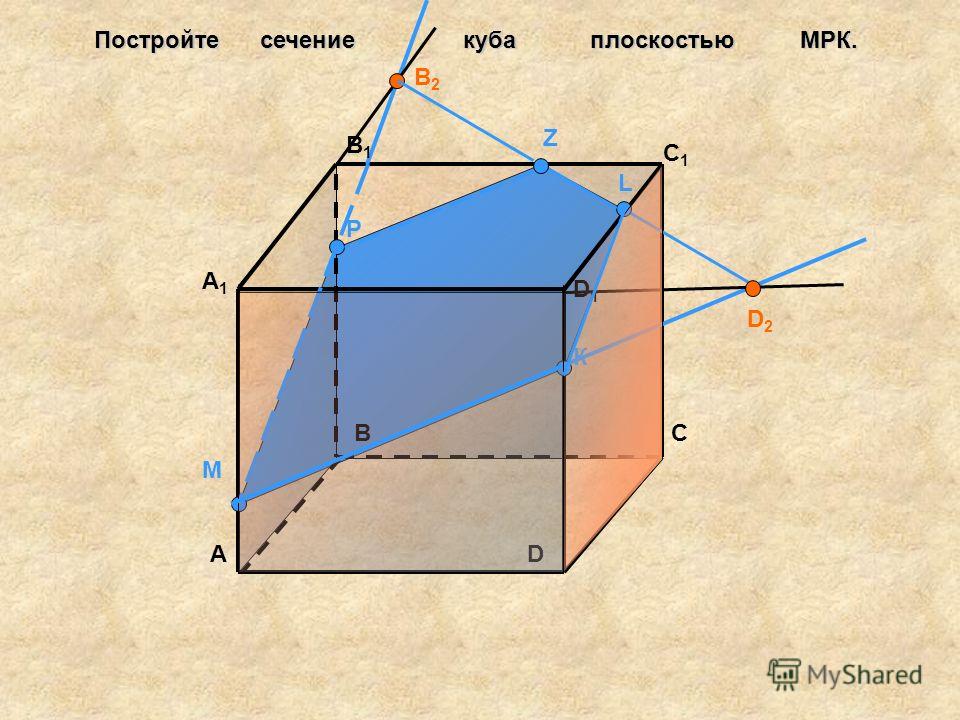 Организационный момент.
Организационный момент.