Содержание
УРАВНЕНИЯ — это… Что такое УРАВНЕНИЯ?
где lg — логарифм по основанию 10.
Дифференциальные уравнения. Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы.
Интегральные уравнения. Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения. Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x — 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения. Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом. 1. Если равные величины увеличить на одно и то же число, то результаты будут равны. 2. Если из равных величин вычесть одно и то же число, то результаты будут равны. 3. Если равные величины умножить на одно и то же число, то результаты будут равны. 4. Если равные величины разделить на одно и то же число, то результаты будут равны. Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения. Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения. Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители. Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 — x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:
Решения мы находим, полагая каждый из множителей равным нулю:
Таким образом, корни равны x = -1,
, т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений. Два линейных уравнения с двумя неизвестными можно записать в виде
Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей
и
отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации — система
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений. Общая теория рассматривает m линейных уравнений с n переменными:
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
где Aji — алгебраическое дополнение элемента aij в матрице (aij). В более общем плане существуют следующие теоремы. Пусть r — ранг матрицы (aij), s — ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца из чисел bi. Тогда: (1) если r = s, то существует n — r линейно независимых решений; (2) если r
В более общем плане существуют следующие теоремы. Пусть r — ранг матрицы (aij), s — ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца из чисел bi. Тогда: (1) если r = s, то существует n — r линейно независимых решений; (2) если r
См. также АЛГЕБРА.
Энциклопедия Кольера. — Открытое общество.
2000.
- ЧИСЛО e
- КОНЕЧНЫЕ РАЗНОСТИ
Смотреть что такое «УРАВНЕНИЯ» в других словарях:
Уравнения — Уравнение равенство вида или , где f и g функции (в общем случае векторные) одного или нескольких аргументов, а также задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут… … Википедия
уравнения — решать дифференциальные уравнения • решение … Глагольной сочетаемости непредметных имён
Уравнения Эйлера — Лагранжа — Уравнения Эйлера Лагранжа (в физике также уравнения Лагранжа Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов.
 В частности, эти… … Википедия
В частности, эти… … ВикипедияУравнения Навье — Стокса — Механика сплошных сред Сплошная среда Классическая меха … Википедия
Уравнения Рейнольдса — (англ. RANS (Reynolds averaged Navier Stokes)) уравнения Навье Стокса (уравнения движения вязкой жидкости) осредненные по Рейнольдсу. Используются для описания турбулентных течений. Метод осреднения Рейнольдса заключается в замене случайно… … Википедия
Уравнения Эйлера-Лагранжа — Уравнения Эйлера Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом действия,… … Википедия
Уравнения Прока — Уравнения Прока обобщение уравнений Максвелла, призванное описывать массивные частицы со спином 1. Уравнения Прока обычно записываются в виде , где антисимметричный тензор электромагнитного поля … Википедия
Уравнения Петерсона ― Кодацци — Уравнения Петерсона ― Майнарди ― Кодацци ― уравнения, составляющие вместе с уравнением Гаусса необходимые и достаточные условия интегрируемости системы, к которой сводится задача восстановления поверхности по её первой и второй квадратичным… … Википедия
Уравнения Рауса — Уравнения Рауса дифференциальные уравнения движения механической системы в переменных Рауса.
 Предложены Э. Раусом (англ.)русск. в 1867 г. Для системы с s степенями свободы, находящейся под действием потенциальных сил, уравнения… … Википедия
Предложены Э. Раусом (англ.)русск. в 1867 г. Для системы с s степенями свободы, находящейся под действием потенциальных сил, уравнения… … ВикипедияУравнения Фаддеева — Уравнения Фаддеева это уравнения, которые описывают все возможные взаимодействия в системе трёх частиц в полной квантовомеханической формулировке. Установлены Л. Д. Фаддеевым. Уравнения могут быть решены итерационным способом. В… … Википедия
Вообще любое уравнение — это математическая модель чашечных весов (рычажных, равноплечих, коромысловых — названий много), изобретенных в древнем Вавилоне 7000 лет назад или еще раньше. Более того, я даже думаю, что именно чашечные весы, использовавшиеся на древнейших базарах, и стали прообразом уравнений. И если смотреть на любое уравнение не как на непонятный набор цифр и букв, связанный двумя параллельными палочками, а как на чаши весов, то и со всем остальным проблем не будет:
Любое уравнение подобно уравновешенным чашам весов
Так уж получилось, что уравнений в нашей жизни с каждым днем все больше, а понимания, что такое уравнение и в чем его смысл — все меньше.
х + 2 = 8 (500.1)
Т.е. в школе конечно же объясняют, что в таких случаях чтобы найти х, нужно из правой части вычесть 2:
х = 8 — 2 (500.3)
Это, конечно же, абсолютно правильное действие, но почему нужно именно вычесть, а не, например, прибавить или разделить, в школьных учебниках объяснения нет. Просто есть правило, которое нужно тупо выучить:
При переносе члена уравнения из одной части в другую его знак меняется на противоположный.
А как сие правило понимать школьнику 10 лет от роду и в чем его смысл, это вы уж сами думайте-решайте. Более того, выяснилось, что и мои близкие родственники тоже никогда не понимали смысла уравнений, а просто заучивали на память то, что требовалось (и вышеуказанное правило в частности), а уж потом применяли это, как бог на душу положит.
Сразу хочу сказать, что хоть я 10 лет учился в школе, но при этом никаких правил и определений, относящихся к техническим дисциплинам, никогда не учил. Т.е. если что-то понятно, то оно и так запомнится, а если что-то не понятно, то какой смысл его зубрить, не понимая смысла, если оно все равно забудется? А кроме того, если мне что-то не понятно, значит, оно мне и не надо (это я только недавно осознал, что если я чего-то не понимал в школе, то это была не моя вина, а вина преподавателей, учебников и вообще системы образования).
Такой подход обеспечивал мне массу свободного времени, которого в детстве так не хватает на всякие игры и развлечения. При этом я участвовал в различных олимпиадах по физике, химии, а одну районную по математике даже выиграл.
А теперь продолжим
Простейшие уравнения, аналогия с весами
Вообще-то детей приучают сравнивать различные предметы еще в дошкольном возрасте, когда они еще и говорить-то толком не умеют. Начинают как правило с геометрических сравнений. Например, показывают ребенку два кубика и ребенок должен определить, какой кубик больше, а какой меньше. А если они одинаковые, то это и есть равенство по размеру.
Когда чаши весов находятся на одном горизонтальном уровне (стрелки чашечных весов, показанные на рисунке 500.1 оранжевым и голубым цветом, совпадают, горизонтальный уровень показан черной жирной чертой), то это значит, что на правой чаше весов находится столько же груза, сколько на левой чаше. В простейшем случае это могут быть гири весом в 1 кг:
Рисунок 500.1.
И тогда мы получаем простейшее уравнение 1 = 1. Впрочем уравнение это только для меня, в математике подобные выражения называют равенством, но суть от этого не меняется. Если мы с левой чаши весов уберем гирю и положим на нее что угодно, хоть яблоки, хоть гвозди, хоть красную икру и при этом чаши весов будут на одном горизонтальном уровне, то это будет по-прежнему означать, что 1 кг любого из указанных продуктов равен 1 кг гирьки, оставшейся на правой части весов.
Конечно же, в те далекие времена, когда появились чашечные весы, все было значительно проще. Во-первых, не было такой меры веса, как килограмм, а были денежные единицы, соответствующие мерам весов, например, таланты, шекели, фунты, гривны и пр. (кстати, меня давно удивляло, что есть фунт — денежная единица и фунт — мера веса, есть гривна — денежная единица, а когда-то гривна была мерой веса, и только недавно, когда я узнал, что талант — это не только денежная единица древних иудеев, упоминаемая в Ветхом завете, но и мера веса, принятая в древнем Вавилоне, все встало на свои места).
Точнее сначала были меры весов, как правило зерна злаковых культур, а уже потом появились деньги, этим мерам весов соответствующие.
В те далекие времена продавцу не нужно было долго и подробно объяснять, сколько будет стоить тот или иной товар. Достаточно было положить на одну чашу весов продаваемый товар, а на вторую покупатель клал деньги — очень просто и наглядно и даже знание местного наречия не требуется, можно торговать в любой точке мира. Но вернемся к уравнениям.
Если рассматривать уравнение (500.1) с позиции весов, то оно означает, что на левой чаше весов находится неизвестное количество килограммов и еще 2 килограмма, а на правой чаше — 8 килограммов:
х + 2кг, = 8кг, (500.1.2)
Примечание: В данном случае нижнее подчеркивание символизирует дно чаш весов, при расчетах на бумаге эта линия может больше напоминать дно чаши весов.
Итак, что нам нужно сделать, что узнать неизвестное количество килограммов? Правильно! Снять с левой и с правой части весов по 2 килограмма, тогда чаши весов останутся на одном горизонтальном уровне, т.е.у нас будет по прежнему равенство:
х + 2кг, — 2кг = 8кг, — 2кг (500.2.2)
Соответственно
х, = 8кг — 2кг, (500.3.2)
х, = 6 кг, (500.4.2)
Рисунок 500.2.
Часто математика оперирует не килограммами, а некими абстрактными безразмерными единицами и тогда запись решения уравнения (500.1) например в черновике будет выглядеть так:
х + 2, = 8, (500.1)
х + 2, — 2 = 8, — 2 (500.
х, = 8 — 2, (500.3)
х = 6 (500.4)
Что и отражено на рисунке 500.2.
Примечание: Формально для еще более лучшего понимания после уравнения (500.2) должно следовать еще одно уравнение вида: х + 2 — 2, = 8 — 2, означающее, что действие завершилось и мы опять имеем дело с равновесными чашами весом. Однако на мой взгляд в такой совсем уж полной записи решения необходимости нет.
В чистовиках обычно используется сокращенная запись решения уравнения, причем сокращаются не только столь необходимые на мой взгляд на начальном этапе изучения уравнений символы чаш весов, но даже и целые уравнения. Так сокращенная запись решения уравнения (500.1) в чистовике согласно приводимым в учебниках примерам будет выглядеть так:
х + 2 = 8 (500.1.1)
х = 8 — 2 (500.3.1)
х = 6 (500.
В итоге, при использовании аналогии с весами мы составили дополнительное уравнение (500.2) по сравнению с предлагаемым учебниками то ли методом решения, то ли формой записи этого решения. На мой взгляд это уравнение, к тому же записанное приблизительно в такой форме, т.е. с символичным обозначением чаш весов — это и есть то недостающее звено, важное для понимания смысла уравнений.
Т.е. при решении уравнений мы ничего и никуда с обратным знаком не переносим, а выполняем одинаковые математические действия с левой и с правой частью уравнения.
Просто сейчас принято записывать решение уравнений в сокращенной форме, приведенной выше. За уравнением (500.1.1) сразу следует уравнение (500.3.1), отсюда и следует правило обратных знаков, которое впрочем многим проще запомнить, чем вникать в смысл уравнений.
Примечание: Против сокращенной формы записи я ничего не имею, более того. продвинутые пользователи могут эту форму еще более сокращать, однако делать это следует лишь после того, когда общий смысл уравнений уже четко усвоен.
А еще расширенная запись позволяет понять главные правила решения уравнений:
1. Если мы производим одинаковые математические действия с левой и правой частью уравнений, то равенство сохраняется.
2. Не важно, какая часть в рассматриваемом уравнении левая, а какая правая, мы можем свободно менять их местами.
Эти математические действия могут быть любыми. Мы можем вычитать одно и то же число из левой и из правой части, как показано выше. Мы можем прибавлять одно и то же число к левой и правой части уравнения, например:
х — 2, = 8, (500.5.1)
х — 2, + 2 = 8, + 2 (500.5.2)
х, = 8 + 2, (500.5.3)
х = 10 (500.5.4)
Мы можем делить или умножать обе части на одно и то же число, например:
3х, = 12, (500.6.1)
3х, : 3 = 12, : 3 (500.
х, = 12 : 3, (500.6.3)
х = 4 (500.6.4)
или
3х — 6, = 12, (500.7.1)
3х — 6, + 6 = 12, + 6 (500.7.2)
3х, = 18, (500.7.3)
3х, : 3 = 18, : 3 (500.7.4)
х = 6 (500.7.5)
Мы можем интегрировать или дифференцировать обе части. Мы можем делать все, что угодно с левой и правой частью, но если эти действия будут одинаковыми для левой и правой части, то равенство сохранится (чаши весов останутся на одном горизонтальном уровне).
Конечно же действия нужно выбирать такие, которые позволят максимально быстро и просто определить неизвестную величину.
С этой точки зрения классический метод обратного действия как бы более прост, но как быть, если ребенок еще не изучал отрицательные числа? А между тем составленное уравнение имеет следующий вид:
5 — х = 3 (500.
Т.е. при решении этого уравнения классическим методом один из возможных вариантов решения, дающий самую короткую запись, следующий:
— х = 3 — 5 (500.8.2)
— х = — 2 (500.8.3)
х = 2 (500.8.4)
И самое главное — как тут объяснить ребенку почему уравнение (500.8.3) тождественно уравнению (500.8.4)?
Это значит, что в данном случае даже при использовании классического метода экономить на записи нет никакого смысла и сначала нужно избавиться от неизвестной величины в левой части, имеющей отрицательный знак.
5 — х = 3 (500.8)
5 = 3 + х (500.8.5)
3 + х = 5 (500.8.6)
х = 5 — 3 (500.8.7)
х = 2 (500.8.4)
При этом полная запись будет выглядеть так:
5 — х, = 3, (500.8)
5 — х, + х = 3, + х (500.
5, = 3 + х, (500.9.3)
3 + х, = 5, (500.8.6)
3 + х, — 3 = 5, — 3 (500.9.3)
х, = 5 — 3, (500.8.7)
х = 2 (500.8.4)
Добавлю еще раз. Полная запись решения нужна не для учителей, а для лучшего понимания метода решения уравнений. А когда мы меняем местами левую и правую части уравнения, то это все равно что мы меняем взгляд на весы с точки зрения покупателя на точку зрения продавца, тем не менее равенство при этом сохраняется.
К сожалению, я так и не смог добиться от своей дочери полной записи решения даже в черновиках. У нее железный довод: «нас так не учили». А между тем сложность составляемых уравнений увеличивается, процент угадываний, какое действие нужно выполнить для определения неизвестной величины, уменьшается, оценки падают. Что с этим делать, не знаю…
Примечание: в современной математике принято различать равенства и уравнения, т.
Простейшие уравнения, аналогия со временем
Конечно же, аналогия с весами при решении уравнений является далеко не единственной. Например, решение уравнений можно рассматривать и во временном аспекте. Тогда условие, описываемое уравнением (500.1), будет звучать так:
После того, как мы добавили к неизвестному количеству х еще 2 единицы, у нас стало 8 единиц (настоящее время). Однако нас по тем или иным причинам не интересует, сколько их стало, а интересует сколько их было в прошедшем времени. Соответственно, чтобы узнать, сколько у нас было этих самых единиц, нам нужно произвести обратное действие, т.
Пример решения уравнения со скобками
Эту статью я написал летом, когда дочь окончила 4 класс, но не прошло и полгода, как им в школе начали задавать решение уравнений следующего вида:
(97 + 75 : (50 — 5х)) · 3 = 300 (500.10)
Никто в классе решить это уравнение не смог, а между тем в его решении при применении предложенного мной способа нет ничего сложного, вот только полная форма записи будет занимать слишком много места:
(97 + 75 : (50 — 5х)) · 3, : 3 = 300, : 3 (500.10.2)
97 + 75 : (50 — 5х), = 300 : 3, (500.10.3)
97 + 75 : (50 — 5х), = 100, (500.10.4)
97 + 75 : (50 — 5х), — 97 = 100, — 97 (500.
75 : (50 — 5х), = 100 — 97, (500.10.6)
75 : (50 — 5х), = 3, (500.10.7)
75 : (50 — 5х), · (50 — 5х) = 3, · (50 — 5х) (500.10.8)
75, = 3 · (50 — 5х), (500.10.9)
75, : 3 = 3 · (50 — 5х), : 3 (500.10.10)
75 : 3, = 50 — 5х, (500.10.11)
25, = 50 — 5х, (500.10.12)
25, + 5х = 50 — 5х, + 5х (500.10.13)
25 + 5х, = 50, (500.10.14)
25 + 5х, — 25 = 50, — 25 (500.10.15)
5х, = 50 — 25, (500.10.16)
5х, = 25, (500.10.17)
5х, : 5 = 25, : 5 (500.10.18)
х, = 25 : 5, (500.10.19)
х = 5 (500.10.20)
Однако на данном этапе в такой полной форме записи нет никакой необходимости.
97 + 75 : (50 — 5х), : 3 = 300, : 3, (500.10.2)
97 + 75 : (50 — 5х), = 100, (500.10.4)
97 + 75 : (50 — 5х), — 97 = 100 — 97, (500.10.5)
75 : (50 — 5х), = 3, (500.10.7)
75 : (50 — 5х), · (50 — 5х) = 3, · (50 — 5х) (500.10.8)
75, = 3 · (50 — 5х), (500.10.9)
75, : 3 = 3 · (50 — 5х), : 3 (500.10.10)
25, = 50 — 5х, (500.10.12)
25, + 5х = 50 — 5х, + 5х (500.10.13)
25 + 5х, = 50, (500.10.14)
25 + 5х, — 25 = 50, — 25 (500.10.15)
5х, = 25, (500.10.17)
5х, : 5 = 25, : 5 (500.
х = 5 (500.10.20)
Итого на данном этапе потребовалось записать 14 уравнений для решения исходного.
При этом запись решения уравнения в чистовике может выглядеть так:
97 + 75 : (50 — 5х) = 300 : 3 (500.10.3)
97 + 75 : (50 — 5х) = 100 (500.10.4)
75 : (50 — 5х) = 100 — 97 (500.10.6)
75 : (50 — 5х) = 3 (500.10.7)
75 = 3 · (50 — 5х) (500.10.9)
75 : 3 = 50 — 5х (500.10.11)
25 = 50 — 5х (500.10.12)
25 + 5х = 50 (500.10.14)
5х = 50 — 25 (500.10.16)
5х = 25 500.10.17)
х = 25 : 5 (500.10.19)
х = 5 (500.10.20)
Т.е. при сокращенной форме записи нам все равно придется составить 12 уравнений.
P.S. Только когда дело дошло до двойных скобок, дочь заинтересовалась предложенным мной методом решения уравнений, но при этом в ее форме записи даже в черновике все равно уравнений в 2 раза меньше, потому что она пропускает итоговые уравнения типа (500.10.4), (500.10.7) и им подобные, а при записи сразу оставляет место для следующего математического действия. В итоге запись в ее черновике выглядела примерно так:
(97 + 75 : (50 — 5х)) · 3, : 3 = 300, : 3 (500.10.2)
97 + 75 : (50 — 5х), — 97 = 100, — 97 (500.10.5)
75 : (50 — 5х), · (50 — 5х) = 3, · (50 — 5х) (500.10.8)
75, : 3 = 3 · (50 — 5х), : 3 (500.10.10)
25, + 5х = 50 — 5х, + 5х (500.10.13)
25 + 5х, — 25 = 50, — 25 (500.10.15)
5х, : 5 = 25, : 5 (500.10.18)
х = 5 (500.10.20)
В итоге получилось всего 8 уравнений, что даже меньше, чем требуется при сокращенной записи решения. В принципе я не возражаю, вот только была бы от этого польза.
Вот собственно и все, что мне хотелось сказать по поводу решения простейших уравнений, содержащих одну неизвестную величину. Для решения уравнений, содержащих две неизвестных величины, потребуется больше знаний. |
2 класс. Математика. Понятие «уравнение». Корень уравнения. Решение уравнений — Понятие «уравнение». Корень уравнения. Решение уравнений
Комментарии преподавателя
§1. Что такое уравнение?
Вам уже знакомы такие математические понятия, как «выражение», «равенство», «неравенство».
«Уравнение» — это еще одно математическое понятие, с ним мы и познакомимся в этом уроке.
Давайте попробуем решить следующую задачу:
|
|
Фрекен Бок испекла 5 пирожков и положила их на тарелку.
Когда она отошла от стола, Карлсон подлетел и взял несколько пирожков.
На тарелке осталось только 2 пирожка.
Сколько пирожков взял Карлсон?
|
|
На основании условий задачи мы можем сделать такую запись: Всего Фрекен Бок испекла 5 пирожков. Запишем число 5.
Карлсон взял пирожки, следовательно, количество пирожков уменьшилось, поэтому поставим знак « – ».
Сколько Карлсон взял пирожков, неизвестно, поэтому вместо числа оставим пустую клетку.
Всего на тарелке осталось 2 пирожка.
Запишем = 2.
|
|
Теперь давайте вместо пустой клетки – неизвестного числа, вставим букву, например, а. Получится следующая запись: 5 – а = 2
Такие равенства, в которых есть неизвестные числа, обозначенные буквой, называютуравнениями.
§2. Корень уравнение и метод подбора при решении уравнения
В уравнениях могут присутствовать любые математические знаки, как «–», так «+», например: 5 – а = 2, 5 + а = 9
В уравнениях неизвестное число принято обозначать малыми буквами латинского алфавита: a, b, c и т.д. Часто используют буквы x, y, z.
Например:
6 + у = 13
z – 8 = 3
х + 5 = 9
Вернемся к задаче про пирожки.
Полученное нами уравнение выглядит таким образом: 5 – а = 2.
Давайте попытаемся определить, какое число спряталось за буквой а?
Для этого будем подставлять вместо а разные числа до тех пор, пока не найдем число, подстановка которого сделает это равенство верным.
Подставим вместо а число 1.
Получим 5 – 1 = 2.
Но это неверное равенство, так как 5 – 1 = 4, а не 2.
Значит, а не может быть равным 1.
Подставим вместо а число 2.
Получим 5 – 2 = 2.
Это тоже неверное равенство, т.к. 5 – 2 = 3, а не 2.
Следовательно, а не может быть равным 2.
Подставим вместо а число 3.
Получим 5 – 3 = 2.
Мы получили верное равенство.
Значит, в уравнении 5 – а = 2 за буквой а спряталось число 3.
Число, которое превращает уравнение в верное равенство, называется корнем уравнения.
Следовательно, в нашем случае число 3 является корнем уравнения 5 – а = 2.
Способ, с помощью которого мы нашли корень уравнения, называется методом подбора.
Итак, подведем итоги урока:
Уравнение – это равенство, в котором есть неизвестное число, обозначенное латинской буквой.
Число, которое превращает уравнение в верное равенство, называется корнем уравнения.
ИСТОЧНИКИ
https://vimeo.com/112468248
http://znaika.ru/catalog/2-klass/matematika/Ponyatie-%C2%ABuravnenie%C2%BB.-Koren-uravneniya.-Reshenie-uravneniy
http://www.youtube.com/watch?v=Hbm7kWk5J34
http://www.youtube.com/watch?v=uzAgNOT5D0E
Файлы
Нет дополнительных материалов для этого занятия.
Что такое корень уравнения
Корнем уравнения называют число, подстановка которого в уравнение вместо переменной (обычно \(x\)), дает одинаковые значения выражений справа и слева от знака равно.
Решая, например, уравнение \(2x+1=x+4\) находим ответ: \(x=3\). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:
\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)
И никакое другое число, кроме тройки такого равенства нам не даст.{2}+15\cdot(-2)+22=0\)
\(2\cdot4-30+22=0\)
\(0=0\) — сошлось, значит \(-2\) — корень уравнения
Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для линейных уравнений достаточно одних только равносильных преобразований, для квадратных – уже используются формулы дискриминанта и т.д. Каждому типу уравнений – свой метод.
Ответы на часто задаваемые вопросы
Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень — ноль. Можете проверить подстановкой.
Вопрос: Когда в уравнении нет корней?
Ответ: В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством.2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).
Скачать статью
Что такое корень уравнения. Уравнение Объяснение темы уравнение и его корни
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Yandex.RTB R-A-339285-1
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Определение 1
Уравнением
называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6: x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · (x − 1) = 19 , x + 6 · (x + 6 · (x − 8)) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · (8 + 1) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · (x + 17) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Определение 2
Уравнение
– это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Определение 3
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + (y − 6) 2 + (z + 0 , 6) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Пример 1
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Определение 4
Корнем уравнения
называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Пример 2
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Пример 3
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · (x − 1) · (x − 2) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или { — 2 , 1 , 5 } .
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Определение 5
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Пример 4
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3 , 4) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В предложенном видео речь идет о понятии уравнения и его корнях. Для начала рассмотрена задача о гусях. В задаче стая гусей отвечает гусю, что если бы их было столько, сколько сейчас, да еще столько, да еще полстолька, да еще четверть столько, да еще он, то их было бы сто гусей. Вопрос: Сколько гусей в стае?
Неизвестное число гусей в стае обозначили через Х.
В результате получили: Х + Х +1/2Х+ 1/4Х + 1 = 100.
В этом равенстве присутствует неизвестная нам величина Х, значение которой мы ищем. Это значение мы можем найти из составленного нами равенства. Подобные равенства называют уравнениями с одной переменной, или уравнениями с одним неизвестным.
Искомую неизвестную величину принято обозначать буквой Х, хотя можно обозначать любой буквой. Впервые неизвестную величину обозначил буквой и составил уравнение в явном виде с неизвестным древнегреческий математик Диофант в своем труде «Арифметика».
В составленном уравнении необходимо найти такое значение переменной, которое превращает уравнение в правильное числовое равенство. Такое значение неизвестной называют корнем уравнения.
Делаем вывод, что корнем уравнения называется значение переменной, превращающее уравнение в верное числовое равенство. Решить уравнение означает найти множество его корней, число которых может быть различным. Корень может быть один, их может быть несколько, а может и не быть ни одного. В конечном итоге, чтобы решить уравнение, необходимо определить все его корни или убедиться, что у уравнения нет корней.
Количество корней уравнения может быть разным в зависимости от вида уравнения. В некоторых случаях и число может быть бесконечным, а может быть равно нулю. Для убедительности автор предлагает рассмотреть примеры уравнений, которые имеют разное количество корней. Это уравнения Х + 1 = 6, (Х — 1)(Х — 5)(Х — 8) = 0, Х = Х + 4, 3(Х + 5) = 3Х + 15. В первом случае корень один, так как только в случае, когда Х = 5, уравнение становится верным числовым равенством 6 = 6. Второе уравнение имеет три корня. Это числа 1, 5, 8. Именно при этих значениях переменной выражения в скобках по очереди принимают значение 0. При умножении на 0 все выражение становиться равным 0. Получаем равенство 0 = 0. Третье уравнение не имеет корней, потому что при любом значении Х правая часть принимает значение больше, чем левая. Четвертое уравнение в свою очередь имеет бесконечное число корней в силу применения сочетательного свойства умножения. После раскрытия скобок и левая, и правая части уравнения имеют одинаковый вид: 3Х + 15 = 3Х = 15.
Далее автор вводит понятие допустимых значений неизвестного. Для этого рассматриваются уравнения 17 — 3Х = 2Х — 2 и (25 — Х)/(Х — 2) = Х + 9. Если в первом случае неизвестное Х может принимать любые значения, то во втором при Х = 2 получаем деление на 0. Следовательно, значения переменной, которые можно подставлять в уравнение в первом случае все числа, а во втором — все числа, кроме 2.
Область определения уравнения — это множество значений переменно, при которых обе части уравнения имеют смысл.
После этого вводится понятие равносильности уравнений. Рассматриваются уравнения Х 2 = 36 и (Х — 6)(Х + 6) = 0. У этих уравнений одинаковые корни; такие уравнения принято называть равносильными.
При решении уравнений их заменяют равносильными уравнениями, но более простыми по форме. Необходимо помнить некоторые правила замены уравнения на равносильное уравнение. Во время переноса слагаемого через знак равенства знак слагаемого меняем на противоположный. При умножении или делении обеих частей уравнения на одно и то же число, неравное 0, уравнение останется равносильным. Можно выполнять тождественные преобразования, если они не влияют на область определения уравнения.
Получив общее представление о равенствах , и познакомившись с одним из их видов — числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств — об уравнениях. В этой статье мы разберем, что такое уравнение
, и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения
:
Определение.
Уравнение
– это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p
, t
, u
и т.п., но наиболее часто используются буквы x
, y
и z
.
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
, y=3
и т.п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
, z−2=5
, 3·t=9
, 8:x=2
.
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18
и x+3·(x+2·(x−2))=3
. Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9
, также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8
, 7−3=z+1
или 3·x−4=2·(x+12)
.
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений
, изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
Уравнением
называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7
– уравнение с переменной x
, а 3·z−1+z=0
– уравнение с переменной z
.
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
Уравнения с одной, двумя, тремя и т.д. переменными
– это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1
– это уравнение с одной переменной x
, в свою очередь уравнение вида x−y=3
– это уравнение с двумя переменными x
и y
. И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
. Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
, y
и z
.
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a
в уравнение a+1=5
подставить число 2
, то получится неверное числовое равенство 2+1=5
. Если же мы в это уравнение подставим вместо a
число 4
, то получится верное равенство 4+1=5
.
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
Корень уравнения
– это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5
. Согласно озвученному определению корня уравнения, число 4
есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5
, а число 2
не является его корнем, так как ему отвечает неверное равенство вида 2+1=5
.
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
имеет корень 4
, а уравнение 0·x=5
не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
, мы получим неверное равенство 0=5
.
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4
имеет единственный корень 6
, корнями уравнения x 2 =9
являются два числа −3
и 3
, уравнение x·(x−1)·(x−2)=0
имеет три корня 0
, 1
и 2
, а решением уравнения x=x
является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества
в фигурных скобках. Например, если корнями уравнения являются числа −1
, 2
и 4
, то пишут −1
, 2
, 4
или {−1, 2, 4}
. Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
, и корнями этого уравнения являются числа 3
и 5
, то можно записать x=3
, x=5
, также переменной часто добавляют нижние индексы x 1 =3
, x 2 =5
, как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
, целых чисел Z
, действительных чисел R
. Например, если корнем уравнения с переменной x
является любое целое число, то пишут , а если корнями уравнения с переменной y
является любое действительное число от 1
до 9
включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
Решением уравнения с двумя, тремя и т.д. переменными
называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
. Подставим в него вместо x
число 1
, а вместо y
число 2
, при этом имеем равенство 1+2=7
. Очевидно, оно неверное, поэтому, пара значений x=1
, y=2
не является решением записанного уравнения. Если же взять пару значений x=4
, y=3
, то после подстановки в уравнение мы придем к верному равенству 4+3=7
, следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
.
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7
. Решение этого уравнения x=4
, y=3
кратко можно записать как (4, 3)
.
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений
.
Список литературы.
- Математика
. 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0. - Алгебра:
учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3. - Алгебра:
9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- обобщить и систематизировать знания по теме
“Уравнения”; - способствовать развитию логического мышления и
речи учащихся.
Технические средства обучения:
мультимедийный
проектор.
Ход урока
1. Домашнее задание:
п. 6, № 113, 117, 120.
2. Математический диктант
(под
копирку).
Дети сдают диктанты, обмениваются тетрадями,
проверяют друг у друга работы. Ответы
проецируются на доску.
3. Сообщение темы урока.
Каким было последнее задание в диктанте?
(Решить уравнение).
Учиться решать уравнения вы начали ещё в
начальных классах. С этой темой мы встречались в 5
и 6 классах, узнавая каждый раз что – то новое об
уравнениях. Задачей нашего сегодняшнего урока
является обобщение и систематизация знаний об
уравнениях.
4. Изучение нового материала
(с
применением компьютерной презентации).
1) – Запишите тему нашего урока “Уравнение и
его корни”. (Слайд 1)
2) – Давайте постараемся дать определение
уравнению. Что же это такое? (Слайд 2)
Равенство, содержащее переменную,
называется уравнением с одной переменной или
уравнением с одним неизвестным.
3) Помня определение уравнения, определите,
является ли данная запись уравнением:
а) х + 2 = 1,3;
г) 16 * 5 – 8 = 72;
д) 1.5 х + 2.8 = 5,8. (Слайд 3)
Дети объясняют свои ответы, подчёркивая,
является ли данная запись равенством и содержит
ли она переменную.
4) — Вспомните, пожалуйста, что называют корнем
уравнения.
Корнем уравнения
называется значение
переменной, при котором уравнение обращается в
верное равенство.
Проверим ваши ответы. (Слайд 4)
5) – Как узнать, является ли данное число корнем
уравнения или нет? (Надо подставить число в
уравнение вместо переменной, посмотреть,
обратится ли при этом уравнение в верное
равенство или нет.)
Выясните, является ли число 2 корнем уравнения:
а) 4 + 3х = 10;
б) (х – 5)(х + 1) = 11;
в) 6(3х – 1) = 12х + 6. (Слайд 5)
Учащиеся подставляют число 2 в каждое
уравнение, проверяя, обращает ли оно данное
уравнение в верное равенство. Делают
соответствующий вывод.
6) – Следующее задание выполним письменно.
Определите, какие из чисел – 2, — 1, 0, 2, 3 являются
корнем уравнения х 2 + 3х = 10. (Слайд 6)
Задание выполняется учащимися в тетради.
Некоторые ученики по очереди делают
соответствующие записи на доске.
Образец выполнения задания:
Корнем уравнения х 2 + 3х = 10 число
а) -2 не является, так как (-2) 2 + 3 * (-2) = 4 – 6 = —
2, а -2 10;
б) – 1 не является, так как (- 1) 2 + 3 * (- 1) = 1 – 3
= -2, а – 2 10;
в) 0 не является, так как 0 2 + 3 * 0 = 0, а 0 10;
г) 2 является, так как 2 2 + 3 * 2 = 4 + 6 = 10, а 10 = 10;
д) 3 не является, так как 3 2 + 3 * 3 = 9 + 9 = 18, а 18 10.
7) Физ. пауза.
А теперь немного отдохнём. Сядьте удобно.
1. Делаем вертикальные движения глазами вверх –
вниз.
2. Горизонтальные движения глазами вправо –
влево.
3. “Нарисуем глазами линию” (на плакате
изображено несколько линий, дети “ведут” по ним
глазами от точки до точки).
Следующие упражнения выполняем стоя.
4. – Поднимаем сначала правое плечо вверх, потом
левое, опускаем сначала правое плечо, потом
левое. Так продолжаем поочерёдно.
5. “Роняем руки”.
6. “Стряхиваем воду с кистей рук”.
Постарайтесь сами составить уравнение, корнем
которого было бы число 3. (Слайд 7)
После самостоятельного выполнения задания
некоторые учащиеся зачитывают получившиеся у
них уравнения, класс определяет, правильно ли
выполнено задание.
9) – Как вы думаете, что значит решить уравнение?
Решить уравнение – значит найти его корни или
доказать, что корней нет. (Слайд 8)
10) – Какие из данных уравнений не имеют корней:
б) 4(х + 1) = 4х +7;
в) 3х + 12 = 3(х + 4). (Слайд 9)
Дети дают ответы, обосновывая их.
11) – Что называется модулем числа?
Чему равен модуль положительного числа?
Модуль нуля? Отрицательного числа?
Может ли модуль числа равняться
отрицательному числу?
Как вы думаете, имеют ли данные уравнения корни
и, если имеют, то сколько:
в) l х l = — 1;
г) l х l = 2,5. (Слайд 10)
12) – Сегодня мы знакомимся с новым для вас
понятием – это равносильные уравнение.
Попробуйте догадаться, какие же уравнения
называются равносильными.
Уравнения, имеющие одни и те же корни,
называются равносильными уравнениями. (Слайд
11)
13) – Какое уравнение равносильно уравнению 3х –
10 = 50? (Слайд 12)
Учащиеся составляют уравнения, равносильные
данному, записывают их в тетрадь, некоторые из
составленных уравнений зачитываются и
обсуждаются классом.
14) – При решении уравнений используются
свойства, которые мы с вами учили в 6 классе.
Давайте их вспомним. (Слайд 13)
1) Если в уравнении перенести слагаемое из одной
части в другую, изменив его знак на
противоположный, то получится уравнение,
равносильное данному.
2) Если обе части уравнения умножить или
разделить на одно и то же отличное от нуля число,
то получится уравнение, равносильное данному.
15) – Замените уравнения равносильными
уравнениями с целыми коэффициентами:
а) 0,1х = — 5;
б) – 0,19 у = 3;
в) — 0,7х = — 4,9. (Слайд 14)
Замените уравнения равносильными уравнениями
вида ах = b:
а) 8х + 15 = 39;
б) 16 – 2х = 10. (Слайд 15)
5. Подведение итогов урока
. (Слайд 16)
Дайте определение уравнения с одной
переменной.
Что называют корнем уравнения?
Все ли уравнения имеют корни?
Что значит решить уравнение?
Какие уравнения называются равносильными?
Назовите свойства, которые используются при
решении уравнений.
Использованная литература.
Учебник “Алгебра. 7 класс” под редакцией С. А.
Теляковского, Москва “Просвещение”, 2009 год.
Что такое уравнение? Как решать уравнения?
Уравнение — одно из краеугольных понятий всей математики. Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
То, что это слово однокоренное со словами «равный», «равенство», возражений, думаю, ни у кого не вызывает.
Уравнение — это два математических выражения, соединённых между собой знаком «=» (равно).
Но… не каких попало. А таких, в которых (хотя бы в одном) содержится неизвестная величина. Или, по-другому, переменная величина. Или, сокращённо, просто «переменная». Которая обычно обозначается буквой «х».
Переменных может быть одна, может быть несколько. В школьной математике чаще всего рассматриваются уравнения с одной переменной. И мы тоже пока что будем рассматривать уравнения с одной переменной. С двумя переменными или более — в специальных уроках.
Что значит решить уравнение?
Идём дальше.
Переменная, входящая в уравнение, может принимать любые допустимые математикой значения. На то она и переменная. 🙂 При каких-то значениях переменной получается верное числовое равенство, а при каких-то — нет.
Так вот:
Решить уравнение означает найти ВСЕ такие значения переменной, при подстановке которых в исходное уравнение получается верное равенство. Или, более научно, верное тождество. Или доказать, что таких значений переменной не существует.
Что такое верное равенство? Это равенство, не вызывающее сомнений даже у человека, абсолютно не отягощённого глубокими математическими познаниями. Например, 5=5, 0=0, -10=-10. И так далее. 🙂
Значения переменной, при подстановке которых достигается это самое верное равенство, называются очень красиво и научно — корни уравнения.
Корень может быть один, может быть несколько. А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А бывает и такое, что нельзя найти такие иксы, которые давали бы нам верное равенство. Принципиально нельзя. По определённым причинам. Нету таких иксов…
В таких случаях обычно говорят, что уравнение не имеет корней.
Для чего нужны уравнения?
Вопрос смешной. Для жизни! В школе, как правило, уравнения нужны для решения текстовых задач. Это, напоминаю, задачи на движение, на работу, на проценты и многие другие.
А во взрослой жизни без уравнений невозможны было бы ответить даже на самые обычные, но жизненно важные вопросы повседневности: какая будет погода завтра, выдержит ли заданную нагрузку здание. Или лифт. Или самолёт. Куда попадёт ракета… И не было бы сейчас среди нас ни синоптиков, ни инженеров, ни бухгалтеров, ни экономистов, ни программистов… За ненадобностью. Внушает?)
Почему это так? А потому, что уравнениями описываются почти все известные человеку природные явления и процессы. Изменение давления и температуры воздуха с высотой, закон всемирного тяготения, размножение бактерий, радиоактивный распад, химические реакции, электричество, спрос и предложение — в основе всего этого лежат математические уравнения! Простые, сложные — всякие. Какое явление или ситуация, такое и уравнение.)
Итак, запоминаем:
Уравнения — очень мощный и универсальный инструмент для решения самых разных прикладных задач.
А какие бывают уравнения?
Уравнений в математике несметное количество. Самых разных видов. Но всё многообразие уравнений можно условно разделить всего на 4 категории:
1. Линейные,
2. Квадратные,
3. Дробные (или дробно-рациональные),
4. Прочие.
Разные категории уравнений требуют и разного подхода к их решению: линейные уравнения решаются одним способом, квадратные — другим, дробные — третьим, тригонометрические, логарифмические, показательные и прочие — тоже решаются своими методами.
Прочих уравнений, разумеется, больше всего, да…) Это и иррациональные, и тригонометрические, и показательные, и логарифмические, и многие другие уравнения. И даже дифференциальные уравнения (для студентов), где роль неизвестного играет не число, а функция. Или даже семейство функций. 🙂
В соответствующих уроках мы подробно разберём все эти типы уравнений. А здесь у нас — базовые приёмы и правила.
Называются эти правила — тождественные (или — равносильные) преобразования уравнений. Их всего два. И нигде их не обойти. Так что знакомимся!
Как решать уравнения? Тождественные (равносильные) преобразования уравнений.
Решение любого уравнения заключается в поэтапном преобразовании входящих в него выражений. Но преобразований не абы каких, а таких, чтобы от шага к шагу суть всего уравнения не менялась. Несмотря на то, что после каждого преобразования уравнение будет видоизменяться и, в конечном счёте, станет совсем не похоже на исходное.
Такие преобразования в математике называются равносильными или тождественными. Их довольно много, но среди всего многообразия тождественных преобразований уравнений выделяется два базовых. О них и пойдёт речь в этом уроке. Да-да, всего два! Но — крайне важных! И каждое из них заслуживает отдельного внимания.
Применение этих двух тождественных преобразований в том или ином порядке гарантирует успех в решении 99% уравнений математики. Заманчиво, правда?
Итак, вперёд!
Первое тождественное преобразование:
К обеим частям уравнения можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Суть уравнения от этого не изменится.
Это преобразование вы применяете всюду, наивно думая, что переносите какие-то члены из одной части уравнения в другую, меняя знаки. 🙂
Например, такое крутое уравнение:
Тут и думать нечего, перебрасываем тройку вправо, меняя минус на плюс:
А что же происходит в действительности? А на самом деле вы… прибавляете к обеим частям уравнения тройку!
Вот что у вас происходит:
И результат получается тем же самым:
Вот и всё. Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Дело в том, что привычный нам перенос слагаемых из одной части в другую со сменой знака — это просто сокращённый вариант первого тождественного преобразования.
И зачем нам так глубоко копать? В уравнениях — незачем. Переносите себе спокойно и не парьтесь. Только знаки менять не забывайте.) А вот в неравенствах привычка к переносу может и слегка обескуражить, да…
Это было первое тождественное преобразование. Переходим ко второму.
Второе тождественное преобразование:
Обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение.
Это тождественное преобразование мы вы постоянно применяете, когда решаете что-нибудь совсем уж жуткое типа:
Тут каждому ясно, что х=3. А вот как вы получили этот ответ? Подобрали? Угадали?
Чтобы не подбирать и не гадать (мы с вами математики, а не гадалки), нужно понять, что вы просто поделили обе части уравнения на четвёрку. Которая нам и мешает.
Вот так:
Эта палка с делением означает, что на четвёрку делятся обе части нашего уравнения. Через дроби эта процедура выглядит так:
Слева четвёрки благополучно сокращаются, остаётся икс в гордом одиночестве. А справа при делении 12 на 4 получается, понятное дело, тройка. 🙂
И все дела.)
Звучит невероятно, но эти два (всего два!) простых преобразования лежат в основе решения всех уравнений математики! Да-да, именно всех, я нисколько не преувеличиваю! От линейных и квадратных в школе до дифференциальных в ВУЗе.)
Ну что, посмотрим на тождественные преобразования уравнений в действии?
Применение тождественных преобразований к решению уравнений.
Начнём с первого тождественного преобразования. Переноса вправо-влево.
Пример для новичков:
1 — х = 3 — 2х
Дело нехитрое. Это линейное уравнение. Работаем прямо по заклинанию: «С иксами влево, без иксов — вправо».
Эта мантра — универсальная инструкция по применению первого тождественного преобразования. Вот и смотрим на уравнение. Какое слагаемое с иксом у нас справа? Что? 2х? Не-а!) Справа у нас -2х (минус два икс)! Поэтому при переносе в левую часть минус поменяется на плюс:
1 — х +2х = 3
Полдела сделано, иксы собрали слева. Осталось все числа собрать справа. Слева в уравнении стоит единичка. Опять вопрос — с каким знаком? Ответ «с никаким» не катит.) Слева перед единицей и вправду ничего не написано. А это значит, что перед ней стоит знак «плюс». Так уж в математике повелось: ничего не написано — значит, плюс.)
И поэтому вправо единичка перенесётся уже с минусом:
-х + 2х = 3 — 1
Вот почти и всё. Слева приводим подобные, а справа — считаем. И получаем:
х = 2
Это было совсем примитивное уравнение.
Теперь пример покруче, для старшеклассников:
Решить уравнение:
Уравнение логарифмическое. Ну и что? Какая разница? Всё равно первым шагом делаем базовое тождественное преобразование («С иксами влево ….»). Для этого слагаемое с иксом (то есть, —log3x) переносим влево. Со сменой знака:
А числовое выражение (log34) переносим вправо. Также со сменой знака, разумеется:
Вот и всё. Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
х=3
Что? Хотите синусы? Пожалуйста, вот вам синусы:
И снова всё то же самое! Выполняем первое тождественное преобразование — переносим sin x влево (с минусом), а -0,25 переносим вправо (с плюсом):
Получили простейшее тригонометрическое уравнение с синусом, решить которое (для знающих) также не составляет никакого труда.
Видите, насколько универсально первое равносильное преобразование! Встречается везде и всюду и не обойти его никак… Именно поэтому так важно уметь его делать на автомате и без ошибок.
Собственно, ошибиться здесь можно лишь в одном — забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательность никто не отменял, да…)
Ну что, продолжаем наши игры? Развлекаемся теперь со вторым преобразованием!)
Решить уравнение:
7х=28
Крутяк, прямо скажем.) Ладно, это эмоции…
Смотрим и соображаем: что нам мешает в этом уравнении? Что-что… Да семёрка мешает! Хорошо бы от неё избавиться. Да так, чтобы исходное уравнение не испортить.)
Но как? Перенести вправо? Ээээ… Стоп! Нельзя.) Семёрка с иксом умножением связана. Коэффициент, видите ли.) Нельзя её оторвать от икса и вправо перенести. Вот всё выражение 7х целиком — пожалуйста (вопрос — зачем?). А семёрку отдельно — никак нет.
Самое время про умножение/деление вспомнить! Нам ведь в ответе чистый икс нужен, не так ли? А семёрка — мешает. Вот и делим левую часть на семь. «Очищаем» икс от коэффициента. Так нам надо. Но тогда и правую часть тоже надо поделить на семь: этого уже математика требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 28 на 7 замечательно делится. Получится 4.
Ответ: х=4
Или такое уравнение:
Что здесь нам мешает? Дробь 1/6, не так ли? Вот давайте и избавимся от неё. Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Но мы же не только делить, мы ещё и умножать умеем!) Вспоминаем из младших классов, после какого действия у нас пропадает дробь? Правильно! Дробь у нас пропадает при умножении на число, равное (или кратное) её знаменателю. Вот и умножим обе части нашего уравнения на 6. Слева всё равно чистый икс получится, а умножение правой части на 6 — не самая трудная работа.)
Вот и всё.) Умножение обеих частей уравнения на нужное число позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, запросто можно и ошибок наляпать. Короче дорога — меньше ошибок!
Теперь снова на машину времени и — в старшие классы:
Решить уравнение:
Чтобы добраться до икса и тем самым решить это крутое тригонометрическое уравнение, нам надо сначала получить слева чистый косинус, безо всяких коэффициентов. А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
Но тогда и правую часть тоже придётся разделить на двойку: это уже МАТЕМАТИКЕ надо. Делим:
Получили справа табличное значение косинуса. И теперь уравнение решается за милую душу.)
Вот и вся премудрость. Как видите, тождественные преобразования уравнений — штука полезная. И при этом не самая сложная. Перенос да умножение/деление. Однако далеко не у всех они получаются с первого раза и без ошибок, ох не у всех… Основные проблемы здесь две.
Проблема первая (для малоопытных):
Иногда ученик думает, что упрощение уравнений делается по одному, раз и навсегда установленному правилу. И никак не может уловить и понять это правило: в каких-то примерах начинают с домножения (или деления), в каких-то — с переноса. Где-то три раза переносят и ни разу не домножают…
Например, такое линейное уравнение:
10х + 5 = 5х — 20
С чего начинать? Можно начать с переноса:
10х — 5х = -20 — 5
А можно сначала поделить обе части на пятёрку, а затем уж переносить. Тогда сразу числа попроще станут:
Как видим, и так и сяк решать можно. И это — в примитивном примере! Вот и возникает у неопытных учеников вопрос: «Как правильно?»
По-всякому правильно! Кому как удобнее. 🙂 Универсального рецепта здесь нет и быть не может. Математика предлагает вам на выбор два вида преобразований уравнений. А порядок этих самых преобразований зависит исключительно от исходного уравнения, а также от личных предпочтений и привычек решающего.
Проблема вторая (для всех…ну… почти):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать скобки. Умножать и делить дроби. Работать со степенями… Короче, в наличии весь набор элементарных действий математики. Со всеми вытекающими…
Обе эти проблемы устраняются только одним способом — практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
УРАВНЕНИЯ | Энциклопедия Кругосвет
Содержание статьи
УРАВНЕНИЯ. Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида (x – 1)2 = (x – 1)(x – 1) выполняется при всех значениях переменной x. Для обозначения тождества часто вместо обычного знака равенства = пишут знак є, который читается «тождественно равно». Тождества используются в алгебре при записи разложения многочленов на множители (как в приведенном выше примере). Встречаются они и в тригонометрии в таких соотношениях, как sin2x + cos2x = 1, а в общем случае выражают формальное отношение между двумя на первый взгляд различными математическими выражениями.
Если уравнение, содержащее переменную x, выполняется только при определенных, а не при всех значениях x, как в случае тождества, то может оказаться полезным определить те значения x, при которых это уравнение справедливо. Такие значения x называются корнями или решениями уравнения. Например, число 5 является корнем уравнения 2x + 7= 17.
Уравнения служат мощным средством решения практических задач. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется теорией уравнений.
ТИПЫ УРАВНЕНИЙ
Алгебраические уравнения.
Уравнения вида fn = 0, где fn – многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида
fn = a0 xiyj … vk + a1 xlym … vn + ј + asxpyq … vr,
где x, y,…, v – переменные, а i, j,…, r – показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так:
f(x) = a0xn + a1xn – 1 +… + an – 1x + an
или, в частном случае, 3x4 – x3 + 2x2 + 4x – 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида f(x) = 0. Если a0 № 0, то n называется степенью уравнения. Например, 2x + 3 = 0 – уравнение первой степени; уравнения первой степени называются линейными, так как график функции y = ax + b имеет вид прямой. Уравнения второй степени называются квадратными, а уравнения третьей степени – кубическими. Аналогичные названия имеют и уравнения более высоких степеней.
Трансцендентные уравнения.
Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:
где lg – логарифм по основанию 10.
Дифференциальные уравнения.
Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы. См. также ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Интегральные уравнения.
Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения.
Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x – 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения.
Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом.
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения.
Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения.
Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители.
Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 – x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:
Таким образом, корни равны x = –1, , т.е. всего 3 корня.
Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений.
Два линейных уравнения с двумя неизвестными можно записать в виде
Решение такой системы находится с помощью определителей
Оно имеет смысл, если Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей и отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации – система
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений.
Общая теория рассматривает m линейных уравнений с n переменными:
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
где Aji – алгебраическое дополнение элемента aijв матрице (aij). В более общем плане существуют следующие теоремы. Пусть r – ранг матрицы (aij), s – ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца из чисел bi. Тогда: (1) если r = s, то существует n – r линейно независимых решений; (2) если r , то уравнения несовместны и решений не существует.
Что такое уравнения? | Помощь с математикой
С помощью основных арифметических операций мы решили задачи, подобные приведенным ниже:
| Проблема | Решение |
| 2 + 3 = __ | 2 + 3 = 5 |
| 4 x 6 = __ | 4 х 6 = 24 |
| 28 ÷ 4 = __ | 28 ÷ 4 = 7 |
В этих задачах у нас есть пробелы рядом со знаком равенства вместо ответа e.грамм. = __
В уравнениях мы используем буквы вместо пробелов. Мы можем написать и решить вышеуказанные проблемы, используя такие буквы:
| Проблема | Решение |
| 2 + 3 = n | п = 5 |
| 4 x 6 = | а = 24 |
| 28 ÷ 4 = b | б = 7 |
В приведенных выше задачах используются n, a и b, но можно использовать любые буквы.
Буквы просто заполнители — как пробел. Мы почти всегда используем буквы, но вы можете использовать что угодно!
5 + 6 = n
n = 11
OR
5 + 6 =
= 11
Что действительно важно, так это то, что он представляет — ответ — в данном случае 11
Убедитесь, что вашего ребенка не смущает использование букв. Вероятно, это первый раз, когда он или она использовали буквы вне письменной или устной речи.
Зачем нужны письма
Использование букв в качестве заполнителей действительно может помочь с некоторыми числовыми проблемами, потому что они позволяют нам записать проблему в виде уравнения.Решая уравнение, мы находим ответ на проблему.
Решение уравнений означает поиск того, что представляет собой буква или чему она равна.
Примеры
| Проблема | Уравнение | Решение |
| Хочу купить рубашку стоимостью 25 долларов. У меня 8 долларов. Сколько еще мне нужно? | п + 8 = 25 | п = 17 |
| Мой папа похудел на 35 фунтов и теперь весит 175 фунтов.Сколько он весил до того, как похудел? | п — 35 = 175 | п = 210 |
| Через 8 недель я собираюсь в отпуск, и я хотел бы получить 160 долларов, когда поеду. Сколько мне нужно откладывать каждую неделю? | п х 8 = 160 | п = 20 |
На следующей странице в этом разделе будет показано, как решать уравнения, подобные приведенным выше.
Уравнения и формулы
Что такое уравнение?
Уравнение говорит, что две вещи равны.У него будет знак равенства «=», например:
.
Это уравнение говорит: то, что слева (x + 2) равно тому, что справа (6)
Таким образом, уравнение похоже на оператор «, это равно , что »
(Примечание: это уравнение имеет решение x = 4 , прочтите, как решать уравнения.
Что такое формула?
Формула — это факт или правило, в котором используются математические символы.
Обычно в нем:
- знак равенства (=)
- две или более переменных (x, y и т. Д.), Которые заменяют значения, которые мы еще не знаем
Он показывает нам, как вещи связаны друг с другом.
Пример:
Формула для определения объема ящика:
V = lwh
V обозначает объем, l — длину, w — ширину и h — высоту.
Если l = 10, w = 4 и h = 5, то:
V = 10 × 4 × 5 = 200
Это все уравнения, но лишь некоторые из них являются формулами:
| x = 2 y -7 | Формула (относящаяся к x и y ) |
| a 2 + b 2 = c 2 | Формула (относящаяся к a , b и c ) |
| x /2 + 7 = 0 | Не формула (просто уравнение) |
Без равных
Иногда формула пишется без знака «=»:
Пример: Формула объема ящика:
л / ч
Но в некотором смысле знак «=» все еще присутствует, потому что мы можем написать V = lwh , если захотим.
Субъект формулы
«Субъект» формулы — это единственная переменная (обычно слева от «=»), которой равны все остальные.
Пример: в формуле
s = ut + ½ при 2
«s» является предметом формулы
Изменение темы
Очень мощная вещь, которую может сделать алгебра, — это «перестроить» формулу так, чтобы в качестве объекта использовалась другая переменная.
Пример: измените объем формулы прямоугольника (
V = lwh ) так, чтобы ширина была предметом
Начать с: V = lwh
разделите обе стороны на h: В / ч = lw
разделите обе стороны на l: В / (hl) = w
сменные стороны: w = V / (hl)
Итак, если нам нужен ящик объемом 12, длиной 2 и высотой 2, мы можем вычислить его ширину:
Вт = В / (гл)
= 12 / (2 × 2)
= 12/4
= 3
Алгебра — Определения
Это может помочь вам сначала прочитать Введение в алгебру
Что такое уравнение
Уравнение говорит, что две вещи равны.У него будет знак равенства «=», например:
.
Это уравнение говорит: то, что слева (x + 2), равно тому, что справа (6)
Таким образом, уравнение похоже на оператор «, это равно , что »
Части уравнения
Так
люди могут говорить об уравнениях, существует имен для разных частей (лучше, чем говорить «вот эта штука»!)
Здесь мы
есть уравнение, в котором 4x — 7 равно 5, и все его части:
A Переменная — это символ числа, которое мы еще не знаем.Обычно это буква типа x или y.
Число называется константой .
Коэффициент — это число, используемое для умножения переменной ( 4x означает 4 умножить на x , поэтому 4 — это коэффициент)
Переменные сами по себе (без номера рядом с ними) фактически имеют коэффициент 1 ( x на самом деле 1x )
Иногда коэффициент представляет собой букву типа a или b вместо числа:
Пример: ax
2 + bx + c
- x — переменная
- a и b — коэффициенты
- c постоянная
Оператор — это символ (например, +, × и т. Д.), Который показывает операцию (т. Е. Мы хотим что-то сделать со значениями).
A Член — это либо одно число, либо переменная, либо числа и переменные, умноженные вместе.
Выражение — это группа терминов (термины разделены знаками + или -)
Итак, теперь мы можем сказать такие вещи, как «это выражение имеет только два члена», или «второй член является константой», или даже «вы уверены, что коэффициент действительно равен 4?»
Показатели
Показатель степени (например, 2 в x 2 ) говорит , сколько раз использовать при умножении.
Примеры:
8 2 = 8 × 8 = 64
y 3 = y × y × y
y 2 z = y × y × z
Показатели упрощают запись и использование множества умножений
Пример: y 4 z 2 проще, чем y × y × y × y × z × z
Полином
Пример полинома: 3x 2 + x — 2
Многочлен может иметь константу , переменную и степень 0,1,2,3 ,…
Но в нем никогда не бывает деления на переменную.
Моном, бином, трехчлен
Существуют специальные названия многочленов с 1, 2 или 3 членами:
Понятия «Нравится»
подобных терминов — это термин , переменные которых (и их показатели, такие как 2 в x 2 ) совпадают.
Другими словами, термины, которые «похожи» друг на друга. (Примечание: коэффициенты могут быть разными)
Пример:
Все ли похожи на термины , потому что все переменные xy 2
Что такое уравнения? | TheSchoolRun
Часто контрольные работы SAT , начиная с 4-го класса, включают вопросы, которые знакомят детей с основами алгебры , например:
- В этом случае ребенку нужно будет решить левую часть уравнения, которая 40.
- Затем им нужно будет вычислить, что для определения значения треугольников им нужно будет вычислить 40 минус звезда, то есть 20, так что значение двух треугольников вместе составит 20.
- Поскольку половина 20 равна 10, значение треугольника равно 10.
По новой учебной программе детей 6-го класса изучают алгебру . Им потребуется разработать следующие уравнения:
Очень похоже на приведенные выше уравнения с пробелами, им нужно будет вычислить 6 x 3 = 18, а затем отнять 8 от 18, чтобы найти y, что равно 10.
Эти уравнения могут стать сложнее:
В алгебре, когда число помещается рядом с буквой, это означает, что букву и число нужно умножить. Следовательно, чтобы вычислить 8y, ребенку нужно будет вычислить 8 x 10 = 80. Затем им нужно будет отнять 5 от 80, чтобы получить 75, поэтому b равно 75.
Более способные дети 6-го класса могут начать выполнять более сложные задачи. алгебраические уравнения, такие как следующие:
- В этом случае им нужно сначала вычислить значение левой части уравнения: 9 x 5 + 6, что равно 51.
- Тогда им нужно будет помнить, что правая часть уравнения также должна быть равна 51, чтобы они знали, что 4b равно 51 + 5, что равно 56.
- Затем им нужно будет разделить 56 на 4, чтобы найдите b, что равно 14.
Всегда полезно записать ответы в уравнение и снова обработать его, чтобы убедиться, что вы правы :
Важным правилом алгебры является то, что когда вы видите умножение в уравнение вместе со сложением или вычитанием, умножение должно быть выполнено сначала , поэтому это числовое предложение:
будет равно 17, а не 26, потому что сначала выполняется 4 x 2, а затем добавляется 9.
Если вам сначала требуется выполнить сложение или вычитание, это будет заключено в скобки , поэтому для приведенного выше числового предложения, если нам необходимо сначала вычислить 9 + 4, они будут помещены в скобки, а затем число 2 будет помещено рядом с ними в начале, чтобы показать, что нам нужно найти два лота из 9 + 4:
Правила о порядке завершения вычислений преподаются как BODMAS (Brackers, Other / Indices , Деление, умножение, сложение и вычитание).
Введение в уравнения | Безграничная алгебра
Что такое уравнение?
В уравнении с одной переменной переменная имеет решение или значение, которое делает уравнение истинным.
Цели обучения
Объясните, что представляет собой уравнение для одной переменной, и причины использования этого уравнения.
Основные выводы
Введите здесь ключевые моменты.
Ключевые моменты
- Уравнение — это математическое утверждение, которое утверждает эквивалентность двух выражений.
- Когда уравнение содержит переменную, такую как [latex] x [/ latex], переменная считается неизвестным значением .
- Значения переменных, которые делают уравнение истинным, являются решениями уравнения и могут быть найдены путем решения уравнения.
- Решение уравнения можно проверить или проверить, подставив его значение вместо переменной в уравнении.
Ключевые термины
- решение : значение, которое может быть заменено переменной, чтобы уравнение стало истинным.
- неизвестно : переменная в уравнении, для которого необходимо решить.
- уравнение : математическое утверждение, которое утверждает эквивалентность двух выражений.
Уравнение — это математическое утверждение, которое утверждает эквивалентность двух выражений. Например, утверждение, что «два плюс пять равняется семи», представлено уравнением [латекс] 2 + 5 = 7 [/ латекс].
Во многих случаях уравнение содержит одну или несколько переменных.Они по-прежнему записываются, помещая каждое выражение по обе стороны от знака равенства ([latex] = [/ latex]). Например, уравнение [латекс] x + 3 = 5 [/ латекс], читаемое как «[латекс] x [/ латекс] плюс три равно пяти», утверждает, что выражение [латекс] x + 3 [/ латекс] равно к значению 5.
В уравнениях может быть более одной переменной. Например, [латекс] x + y + 7 = 13 [/ latex] — это уравнение с двумя переменными. Однако этот урок посвящен исключительно уравнениям с одной переменной.
Решение уравнений
Если уравнение содержит такую переменную, как [latex] x [/ latex], эта переменная считается неизвестным значением .Во многих случаях мы можем найти возможные значения для [latex] x [/ latex], которые сделают уравнение истинным. [латекс] [/ латекс]
Например, рассмотрим уравнение, о котором мы говорили выше: [латекс] x + 3 = 5 [/ латекс]. Вы, наверное, уже догадались, что единственное возможное значение [latex] x [/ latex] — 2, потому что вы знаете, что [latex] 2 + 3 = 5 [/ latex] — истинное уравнение. Мы используем знак равенства, чтобы показать, что мы знаем значение данной переменной. В этом случае мы пишем [латекс] x = 2 [/ latex] (читается как «[latex] x [/ latex] равно двум»).
Значения переменных, которые делают уравнение истинным, называются решениями уравнения. В свою очередь, решение уравнения означает определение того, какие значения переменных делают уравнение истинным.
Уравнение выше было довольно простым; Нам было легко идентифицировать решение как [латекс] x = 2 [/ latex]. Однако становится полезным иметь процесс поиска решений для неизвестных, когда проблемы становятся более сложными.
Решения для проверки
Если число найдено как решение уравнения, то замена этого числа на место переменной должна сделать уравнение истинным.Таким образом, мы можем легко проверить, является ли число истинным решением данного уравнения.
Например, давайте проверим, является ли [latex] x = 3 [/ latex] решением уравнения [latex] 2x + 31 = 37 [/ latex].
Заменяя 3 на [латекс] x [/ латекс], получаем:
[латекс] 2 (3) + 31 = 37 \ 6 + 31 = 37 [/ латекс]
Это равенство является верным. Следовательно, мы можем сделать вывод, что [латекс] x = 3 [/ latex], по сути, является решением уравнения [латекс] 2x + 31 = 37 [/ latex].
Решение уравнений: сложение и умножение свойств равенства
Свойства равенств на сложение и умножение — полезные инструменты для решения уравнений.
Цели обучения
Решите уравнения, используя свойства равенства и умножения
Основные выводы
Ключевые моменты
- Уравнения часто выражают отношения между заданными величинами (называемыми «известными») и количествами, которые еще предстоит определить (называемыми «неизвестными»).
- Свойство сложения равенства гласит, что любое действительное число может быть добавлено к обеим сторонам уравнения.
- Свойство вычитания равенства гласит, что любое действительное число может быть вычтено из обеих частей уравнения. Свойство умножения равенства утверждает, что любое действительное число может быть умножено на обе стороны уравнения.
- Свойство деления равенства гласит, что любое вещественное число, отличное от нуля, может делить обе части уравнения.
Ключевые термины
- равенство : состояние двух или более объектов, имеющих одинаковое значение.
Уравнение — это математическое утверждение, которое утверждает эквивалентность двух выражений. В современных обозначениях это обозначается размещением выражений по обе стороны от знака равенства (=). Например, [latex] x + 3 = 5 [/ latex] утверждает, что [latex] x + 3 [/ latex] равно 5.
Уравнения часто выражают отношения между заданными величинами («известные») и количествами, которые еще предстоит определить («неизвестные»). По математическому соглашению неизвестные обозначаются буквами в конце алфавита [латекс] (x, y, z…) [/ latex], а известные — буквами в начале алфавита [латекс] (a, b , c…) [/ латекс].
Процесс выражения неизвестных в уравнении через известные им называется решением уравнения . В уравнении с одной неизвестной значение той неизвестной, для которой уравнение является истинным, называется решением или корнем уравнения.
Если известно, что какое-либо уравнение в алгебре истинно, следующие свойства могут быть использованы для создания другого истинного уравнения. Для каждого свойства предоставляется как формальное определение, так и определение на простом английском языке.
Дополнительное свойство равенства
Если [латекс] a = b [/ латекс], то [латекс] a + c = b + c [/ латекс].
Другими словами, к обеим сторонам уравнения можно прибавить любое действительное число.
Свойство равенства вычитания
Если [латекс] a = b [/ латекс], то [латекс] a-c = b-c [/ латекс].
Другими словами, из обеих частей уравнения можно вычесть любое действительное число.
Свойство равенства при умножении
Если [латекс] a = b [/ латекс], то [латекс] ca = cb [/ латекс].
Другими словами, любое действительное число можно умножить на обе части уравнения.
Раздел имущества равенства
Если [latex] a = b [/ latex] и [latex] c \ neq 0 [/ latex], то [latex] \ dfrac {a} {c} = \ dfrac {b} {c} [/ latex ].
Другими словами, любое действительное число, отличное от нуля, может делить обе части уравнения.
Решение уравнений с использованием свойств равенства
Пример 1
Счет за ремонт автомобиля составил 458 долларов, а стоимость запчастей — 339 долларов.Стоимость рабочей силы составляла 34 доллара в час. Напишите и решите уравнение, чтобы найти количество рабочих часов, затраченных на ремонт.
Пусть [latex] x [/ latex] равно неизвестному значению: количеству рабочих часов. Таким образом, уравнение:
[латекс] 34x + 339 = 458 [/ латекс].
На английском языке стоимость рабочей силы (34 доллара США), умноженная на количество рабочих часов [latex] (x) [/ latex], плюс стоимость деталей (339 долларов США), равняется общему счету за ремонт. (458 долларов).
Чтобы найти неизвестное, сначала отмените операцию сложения (используя свойство вычитания), вычтя 339 долларов из обеих частей уравнения:
[латекс] \ begin {align} 34x + 339-339 & = 458-339 \\ 34x & = 458-339 \\ 34x & = 119 \ end {align} [/ latex]
Затем отмените операцию умножения (используя свойство деления), разделив обе части уравнения на 34:
.
[латекс] \ begin {align} \ dfrac {34x} {34} & = \ dfrac {119} {34} \\ x & = \ dfrac {119} {34} \\ x & = 3.5 \ end {align} [/ latex]
Это означает, что ремонт автомобиля занял 3,5 часа.
Пример 2
Решите следующее уравнение, используя свойства равенства:
[латекс] \ dfrac {1} {8} x-5 = 3 [/ латекс]
Сначала используйте свойство сложения, чтобы добавить 5 к обеим сторонам уравнения:
[латекс] \ begin {align} \ dfrac {1} {8} x-5 + 5 & = 3 + 5 \\ \ dfrac {1} {8} x & = 3 + 5 \\ \ dfrac {1} {8 } x & = 8 \ end {align} [/ latex]
Во-вторых, используйте свойство умножения, чтобы умножить обе части уравнения на 8:
.
[латекс] \ begin {align} 8 \ cdot \ dfrac {1} {8} x & = 8 \ cdot 8 \\ x & = 64 \ end {align} [/ latex]
Это решение уравнения.
Рациональные уравнения
Рациональное уравнение устанавливает два рациональных выражения, равных друг другу, и включает неизвестные значения, которые делают уравнение истинным.
Цели обучения
Решите рациональные уравнения, найдя общий знаменатель
Основные выводы
Ключевые моменты
- При решении рационального уравнения найдите общий знаменатель или воспользуйтесь методом перекрестного умножения.
- Если знаменатели в рациональном уравнении совпадают, числители также должны быть одинаковыми.Поэтому используйте следующую стратегию: найдите общий знаменатель, установите числители, равные друг другу, а затем найдите переменную, если необходимо.
Ключевые термины
- перекрестное умножение : умножение числителя каждой стороны уравнения на знаменатель другой стороны.
- рациональное выражение : набор математических терминов, которые можно выразить как частное двух многочленов.
- знаменатель : Число или выражение, записанное под чертой в виде дроби (например,г., 2 дюйма [латекс] 1/2 [/ латекс]).
- числитель : Число или выражение, записанное над линией в виде дроби (например, 1 в [латексе] 1/2 [/ латексе]).
Решение рационального уравнения (те же знаменатели)
Для уравнения, которое включает две дроби или рациональные выражения, перекрестное умножение является полезной стратегией для упрощения уравнения или определения значения переменной.
Например, начните со следующего уравнения:
[латекс] \ dfrac {x} {8} = \ dfrac {3} {8} [/ latex]
Выход перекрестного умножения:
[латекс] \ begin {align} 8x & = 8 \ cdot 3 \\ 8x & = 24 \ end {align} [/ latex]
Теперь решите для [latex] x [/ latex], разделив обе части уравнения на [latex] 8 [/ latex]:
[латекс] \ begin {align} \ dfrac {8x} {8} & = \ dfrac {24} {8} \\ x & = 3 \ end {align} [/ latex]
Мы могли бы также использовать простую алгебру.Начните с того же уравнения:
[латекс] \ dfrac {x} {8} = \ dfrac {3} {8} [/ latex]
Изолируйте переменную слева, умножив обе стороны на [латекс] 8 [/ латекс]:
[латекс] \ left (\ dfrac {8} {1} \ right) \ cdot \ dfrac {x} {8} = \ left (\ dfrac {8} {1} \ right) \ cdot \ dfrac {3} {8} [/ латекс]
Знаменатели с обеих сторон сокращаются, давая:
[латекс] x = 3 [/ латекс]
Вы также можете прийти к такому выводу с помощью дедуктивного мышления. Обратите внимание, что рациональные выражения по обе стороны от знака равенства имеют одинаковый знаменатель.Если у вас есть рациональное уравнение, в котором знаменатели с обеих сторон уравнения одинаковы, , то их соответствующие числители также должны иметь одинаковое значение , даже если они могут быть выражены в разных терминах. Это предлагает стратегию: найти общий знаменатель, приравнять числители друг к другу и найти неизвестные.
Решение рационального уравнения (разные знаменатели)
Несколько реальных ситуаций можно смоделировать с помощью уравнений, которые устанавливают, что две дроби или отношения равны друг другу — например, нахождение неизвестных размеров определенных форм.
Два треугольника называются «подобными», если у них равны соответствующие углы. Это то же самое, что и у треугольников с равным соотношением сторон.
Подобные геометрические формы: Два геометрических объекта похожи, если они оба имеют одинаковую форму или если один имеет ту же форму, что и зеркальное отображение другого. На этом изображении фигуры, показанные одним цветом, похожи.
Два треугольника ниже похожи. Если длина [латекс] \ overline {AC} [/ latex] составляет 10 дюймов, [latex] \ overline {EF} [/ latex] составляет 14 дюймов, а [latex] \ overline {AB} [/ latex] — 17 дюймов. , какова длина [латекса] \ overline {EG} [/ latex]?
Подобные треугольники : Соответствующие углы аналогичной формы отмечены одним и тем же символом.Например, [латекс] \ угол A [/ латекс] (т.е. угол [латекс] A [/ латекс]) соответствует [латексу] \ углу E [/ латексу], и они равны.
Начнем с написания рационального уравнения:
[латекс] \ dfrac {\ overline {AC}} {\ overline {EF}} = \ dfrac {\ overline {AB}} {\ overline {EG}} [/ latex]
Теперь давайте подставим реальные числа:
[латекс] \ dfrac {10} {14} = \ dfrac {17} {x} [/ латекс]
Теперь перемножим:
[латекс] \ begin {align} \ dfrac {10} {14} \ cdot (x) \ cdot (14) & = \ dfrac {17} {x} \ cdot (x) \ cdot (14) \\ 10 \ cdot x & = 14 \ cdot 17 \\ 10x & = 238 \ end {align} [/ latex]
Наконец, разделите обе части уравнения на 10:
.
[латекс] x = 23.8 [/ латекс] дюймов.
Следовательно, [латекс] \ overline {EG} [/ latex] имеет длину 23,8 дюйма.
Радикальные уравнения
Уравнения с радикалами часто решаются возведением в квадрат обеих сторон.
Цели обучения
Решите радикальное уравнение, возведя в квадрат обе части уравнения и проверив ложные решения
Основные выводы
Ключевые моменты
- Решая уравнения, в которых используются радикалы, начните с вопроса: есть ли [латекс] x [/ латекс] под квадратным корнем? Ответ на этот вопрос определит ваш подход к проблеме.
- Если под квадратным корнем нет [латекс] x [/ латекс] — если под радикалами указаны только числа — уравнение может быть решено почти так же, как если бы оно не содержало радикалов.
- Однако, если есть [латекс] x [/ латекс] под квадратным корнем, переместите все, кроме этого радикала, в одну сторону, а затем возведите обе части уравнения в квадрат.
- Квадрат обеих сторон потенциально может привести к посторонним решениям (например, ложным ответам), поэтому важно проверять свои ответы после решения!
Ключевые термины
- корень : корень (числа или количества).
- квадрат : вторая степень числа, значения, члена или выражения.
- постороннее решение : ответ на уравнение, возникающее в процессе решения проблемы, но не верный ответ на исходную проблему.
- корень : число, которое при добавлении в уравнение дает ноль.
Решая уравнения, содержащие радикалы, начните с вопроса: есть ли [латекс] x [/ латекс] под квадратным корнем? Ответ на этот вопрос определит подход к проблеме.Если нет [латекс] x [/ латекс] под квадратным корнем — если только числа под радикалами — проблема может быть решена почти так же, как если бы в ней не было радикалов.
Решение радикальных уравнений без переменных под радикальным символом
Пример
Решите это уравнение:
[латекс] \ sqrt 2 x + 5 = 7- \ sqrt 3 x [/ латекс]
Сначала выделите переменную на одной стороне уравнения:
[латекс] \ begin {align} \ sqrt 2 x + \ sqrt 3 x + 5-5 & = 7-5- \ sqrt 3 x + \ sqrt 3 x \\ \ sqrt 2x + \ sqrt 3x & = 7-5 \ end { align} [/ латекс]
Затем, поскольку оба члена в левой части уравнения содержат [latex] x [/ latex], вычтите [латекс] x [/ latex].(Помните, что [латекс] \ sqrt 2 [/ latex] и [latex] \ sqrt 3 [/ latex] — разные термины и не могут быть объединены.)
[латекс] x (\ sqrt 2+ \ sqrt 3) = 2 [/ латекс]
Теперь разделите обе части уравнения на [latex] (\ sqrt 2+ \ sqrt 3) [/ latex], чтобы найти [latex] x [/ latex]:
[латекс] x = \ dfrac 2 {\ sqrt 2 + \ sqrt 3} [/ латекс]
Ключевым моментом, на который следует обратить внимание при решении подобных задач, является то, что обе части уравнения не нужно возводить в квадрат. [latex] 2 \ sqrt {2} [/ latex] может показаться сложным, но это просто число — оно действует в уравнении точно так же, как число [latex] 10 [/ latex] или [latex] \ frac {1} {3} [/ latex] или [латекс] \ pi [/ latex].
Шаги к решению радикального уравнения с переменной под радикалом
Если под квадратным корнем стоит [латекс] x [/ latex] или переменная, то к проблеме нужно подходить по-другому. В этом случае необходимо возвести обе стороны в квадрат, чтобы избавиться от корня. 2 \\ 10x-2 & = 100 \\ 10x-2 + 2 & = 100 + 2 \ \ 10x & = 102 \\ \ dfrac {10x} {10} & = \ dfrac {102} {10} \\ x & = 10.2 \ end {align} [/ latex]
Однако, проверив этот результат, мы обнаруживаем, что [latex] \ sqrt {100} = — 10 [/ latex]. Это неверно, потому что квадратный корень определяется как только положительный корень, [латекс] 10 [/ латекс]. Это значит, что [latex] 10.2 [/ latex] — это посторонний раствор . Поскольку это единственный ответ, который мы нашли, ответ на эту проблему — «нет решения».
Эта задача демонстрирует, насколько важно проверять свои решения всякий раз, когда вы возводите обе части уравнения в квадрат.
Уравнения с абсолютным значением
Чтобы решить уравнение с абсолютным значением, сначала выделите абсолютное значение, а затем решите положительный и отрицательный случаи.
Цели обучения
Разбейте уравнение абсолютного значения на два уравнения, чтобы найти переменную
Основные выводы
Ключевые моменты
- Абсолютные значения всегда положительны, поскольку они представляют собой расстояние.
- Уравнение абсолютного значения может иметь одно, два или ни одного решения.
Ключевые термины
- абсолютное значение : Величина (т.е. неотрицательное значение) числа безотносительно его знака; расстояние числа от нуля.
Абсолютное значение — одна из простейших функций и, как ни парадоксально, одна из самых проблемных. На первый взгляд, нет ничего проще: абсолютное значение просто означает , расстояние, на которое число находится от нуля . Абсолютное значение [latex] -5 [/ latex] равно [latex] 5 [/ latex], а абсолютное значение [latex] 5 [/ latex] также равно [latex] 5 [/ latex], поскольку оба [ latex] -5 [/ latex] и [latex] 5 [/ latex] находятся на расстоянии [latex] 5 [/ latex] единиц от [latex] 0 [/ latex].Математически это представлено следующим образом:
[латекс] \ левый | -5 \ справа | = 5 [/ латекс] и [латекс] \ влево | 5 \ право | = 5 [/ латекс]
Следующая числовая строка также иллюстрирует это определение:
Абсолютное значение: Абсолютное значение действительного числа можно рассматривать как его расстояние от нуля. На этом изображении, например, [латекс] \ left | -3 \ right | = 3 [/ латекс].
Типы решений уравнений абсолютных значений
Рассмотрим следующие три уравнения.Они выглядят очень похожими — меняется только количество — но решения совершенно разные. Эти три уравнения демонстрируют, как уравнения абсолютных значений могут иметь одно, два или ни одного решения.
Уравнение 1
[латекс] \ левый | х \ право | = 10 [/ латекс]
Какие значения делают это уравнение верным?
[латекс] x = 10 [/ latex] работает, как и [latex] x = -10 [/ latex]. Поэтому наше решение:
[латекс] x = \ pm 10 [/ латекс]
Уравнение 2
[латекс] \ левый | х \ право | = -10 [/ латекс]
Здесь ни [latex] x = 10 [/ latex], ни [latex] x = -10 [/ latex] не работают.Напомним, что абсолютное значение — это мера расстояния, поэтому оно никогда не может быть отрицательным. Таким образом, это уравнение не имеет решения .
Уравнение 3
[латекс] \ левый | х \ право | = 0 [/ латекс]
Какие значения делают это уравнение верным? [latex] x = 0 [/ latex] — единственное решение.
Решение уравнений абсолютных значений
Следующие шаги описывают, как решить уравнение абсолютного значения:
- Выделите член абсолютного значения алгебраически.
- Создайте два отдельных уравнения: для первого оставьте новое уравнение, найденное на шаге 1, но удалите знаки абсолютного значения; во-вторых, сохраните уравнение, найденное на шаге 1, удалите знаки абсолютного значения, и умножьте одну сторону на -1.
- Решите пару уравнений.
Например, давайте решим следующее уравнение относительно [латекс] x [/ латекс]:
[латекс] 3 \ левый | 2x + 1 \ вправо | -7 = 5 [/ латекс]
Шаг 1
Сначала выделите алгебраически абсолютное значение, прибавив 7 к обеим частям уравнения, а затем разделив обе части на 3:
[латекс] \ begin {align} 3 \ left | 2x + 1 \ вправо | -7 +7 & = 5 +7 \\ 3 \ left | 2x + 1 \ вправо | & = 12 \\ \ dfrac {3 \ left | 2x + 1 \ right |} {3} & = \ dfrac {12} {3} \\ \ left | 2x + 1 \ вправо | & = 4 \ end {align} [/ latex]
Шаг 2
Теперь составьте два отдельных уравнения.Первое — это уравнение, которое мы нашли на шаге 1, но без знаков абсолютного значения:
[латекс] 2x + 1 = 4 [/ латекс]
Второе уравнение — это уравнение, которое мы нашли на шаге 1, без знаков абсолютного значения, и с другой стороной, умноженной на -1:
.
[латекс] 2x + 1 = -4 [/ латекс]
Шаг 3
Теперь решите оба уравнения. Для первого:
[латекс] \ begin {align} 2x + 1 & = 4 \\ 2x + 1-1 & = 4-1 \\ 2x & = 3 \\ \ dfrac {2x} {2} & = \ dfrac {3} {2} \\ x & = \ dfrac {3} {2} \ end {align} [/ latex]
Для второго уравнения:
[латекс] \ begin {align} 2x + 1 & = — 4 \\ 2x + 1-1 & = — 4-1 \\ 2x & = — 5 \\ \ dfrac {2x} {2} & = \ dfrac {-5 } {2} \\ x & = \ dfrac {-5} {2} \ end {align} [/ latex]
Следовательно, у этой задачи есть два ответа:
[латекс] x = \ dfrac {3} {2} [/ latex] и [латекс] x = \ dfrac {-5} {2} [/ latex]
Что такое уравнение и его виды? — Математика для детей
Определение уравнения
Уравнение — это утверждение, в котором говорится, что значения двух математических выражений равны.Проще говоря, уравнение говорит о том, что две вещи равны. Обозначается знаком равенства «=».
Пример уравнения: 8 + 2 = 12-2
В приведенном выше уравнении говорится, что левая часть уравнения равна правой части. Таким образом, уравнение — это утверждение, в котором говорится, что «это равно тому».
Различные типы уравнений в математике
Студенты могут столкнуться с этими различными типами уравнений в математике, а точнее алгебре:
1.Линейные уравнения
Линейный означает наличие одной линии. Это уравнения типа Y = ax + b, где «a» и «b» — числа, а «x» не может быть нулем. В этих уравнениях «x» не имеет показателей. Y = 4x + 3 — линейное уравнение.
2. Квадратные уравнения
Это уравнение второй степени, в котором одна переменная из всех содержит показатель степени 2. ax2 + bx + c = 0 — квадратное уравнение, в котором x не равно нулю.
3. Радикальные уравнения
Это уравнения, у которых максимальный показатель переменной равен ½ и содержит более одного члена.Здесь переменная находится внутри радикального символа, обычно в квадратном корне. √x + 10 = 26 — радикальное уравнение.
4. Тригонометрические уравнения
Это уравнения, в которых на переменные влияют тригонометрические функции. Cos 2x = 1 + Sin 4x — это тригонометрическое уравнение.
5. Полиномиальные уравнения
Полиномиальное уравнение — это уравнение, исключающее самый высокий предел экспоненты. Здесь все «x» — числа, а уравнение состоит из нескольких членов.(x7 + 2 × 4-5) * 3x = 0
6. Экспоненциальные уравнения
Это уравнения, в которых вместо показателей степени используются переменные. ab = 0 — экспоненциальное уравнение.
Решение уравнения
(x + 1) 2 = x2 — 2
Нам нужно сначала расширить переменные в левой части уравнения формулой (a + b) 2 = a2 + 2ab + b2
X2 + 2x + 1 = x2-2
Теперь x2 с обеих сторон отменяется, поэтому остается
2x + 1 = -2
2x = -3
X = -3/2
X = -1.5
Решите следующие уравнения
1. 4 + n = 6
а. 4 б. 2 в. 10 дн. 0
2. 4 * 7 = v + 9
а. 28 б. 9 в. 19 дн. -19
3. м / 10 = 9 * 6
а. 5.4 б. 540 ок. 64 г. -5,4
4. 10 * 11 = x-3
а. 110 б. -113 с. 113 дн. 107
5. (-5-v) / 3 = 1
a. -8 б. 8 с. 1,67 г. 15
6. 7 = w — (- 7) / 5
а. 56 б. 5.6 с. 35 дн. 3,5
7. 2п-6 = 8 + 5 (п + 9)
а. 19.6 б. -19,6 с. 59 дн.-59
8. 8 (x + 4) -4 = 4x-1
а. -7.25 б. 29 с. 7.25 г. 32
9. 8 (t + 5) + 2 = 4.8t + 4
a. 1187 г.р. 11.87 г. 11.78 г. -11,87
10. (3в / 3) — 3в = -5
а. -2,5 б. 2.5 в. -6 с. 15
Язык алгебры — Написание уравнений
Уравнение
математическое предложение, содержащее знак равенства. Это говорит нам, что два
выражения означают одно и то же или представляют одно и то же число.Уравнение
может содержать переменные и константы. Используя уравнения, мы можем выразить математику
краткие факты в легко запоминающихся формах и быстрое решение проблем.
Вот несколько
примеры уравнений. Вы можете думать о письмах как о контейнерах или коробках,
которые могут содержать разные числа.
Пример
1
3z
+ 2 = 14 х — 9 = 20 п
+ 2п = 3
Самое главное
навык, развиваемый в алгебре, — это способность перевести словесную задачу на
правильное уравнение, чтобы вы могли легко решить проблему.Давай попробуем
несколько примеров:
Пример
2
Число n умноженное на 3 равно 120.
Это очень просто. Слово «раз» говорит вам, что вы должны умножать
переменная n на 3, и что результат равен 120. Вот как написать
это уравнение:
3н
= 120
Вот
тот, который немного сложнее.
Пример
3.
Десять
долларов составляли две трети всех потраченных денег.
Что мы
пытаетесь найти в этом заявлении? Неизвестная сумма — это общая сумма потраченных денег.
Назовем это m. Мы знаем, что десять долларов равны двум третям m, поэтому
мы можем записать уравнение так:
Пример
4.
Тим отработал 7 часов в субботу и косил 3 газона.Сколько времени, на
в среднем, потратил ли он на каждую лужайку?
Пусть буква
«t» представляет собой среднее время на газон, неизвестное значение. Потом,
3т будет означать, что время косить все три газона, и мы знаем, что
это равно 7 часам. Мы можем записать уравнение так:
3 т
= 7 часов
.

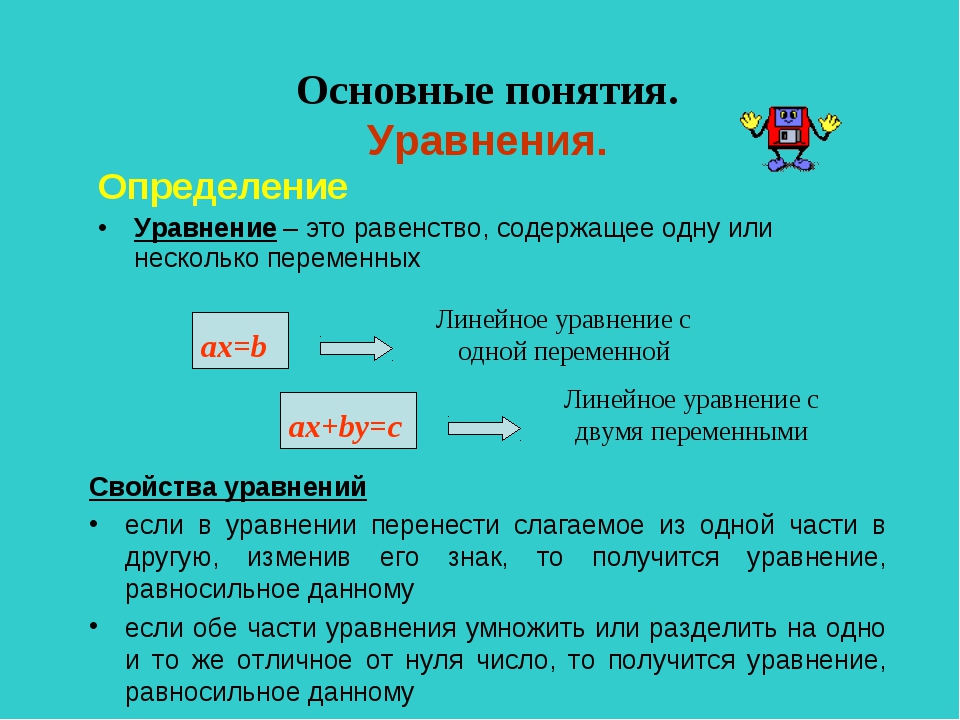 Во всяком случае у меня сложилось такое впечатление при попытке объяснить старшей дочери смысл простейшего математического уравнения типа:
Во всяком случае у меня сложилось такое впечатление при попытке объяснить старшей дочери смысл простейшего математического уравнения типа: Мне такое положение дел не понравилось, поэтому я и решил написать данную статью (растет младший, ему через несколько лет опять придется это объяснять, да и немногочисленным читателям моего сайта это тоже может пригодиться).
Мне такое положение дел не понравилось, поэтому я и решил написать данную статью (растет младший, ему через несколько лет опять придется это объяснять, да и немногочисленным читателям моего сайта это тоже может пригодиться).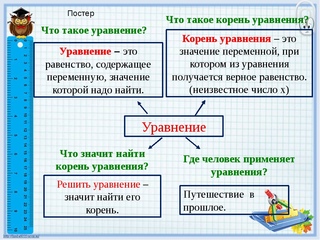 Но время шло, количество дисциплин, оперирующих абстрактными понятиями, только увеличивалось и соответственно мои оценки снижались. На первом курсе института количество дисциплин, оперирующих абстрактными понятиями, составляло абсолютное большинство и я конечно же был полным троечником. Но потом, когда мне по ряду причин пришлось самому без помощи лекций и конспектов разбираться с сопроматом и я его как бы понял, дело пошло на лад и закончилось красным дипломом. Впрочем сейчас не об этом, а о том, что в связи с указанной спецификой мои понятия и определения могут значительно отличаться от преподаваемых в школе.
Но время шло, количество дисциплин, оперирующих абстрактными понятиями, только увеличивалось и соответственно мои оценки снижались. На первом курсе института количество дисциплин, оперирующих абстрактными понятиями, составляло абсолютное большинство и я конечно же был полным троечником. Но потом, когда мне по ряду причин пришлось самому без помощи лекций и конспектов разбираться с сопроматом и я его как бы понял, дело пошло на лад и закончилось красным дипломом. Впрочем сейчас не об этом, а о том, что в связи с указанной спецификой мои понятия и определения могут значительно отличаться от преподаваемых в школе. Затем задача усложняется, ребенку показывают предметы различных форм, различных цветов и выбрать одинаковые предметы ребенку становится все сложнее. Однако мы не будем так сильно усложнять задачу, а остановимся лишь на одном виде равенства — денежно-весовом.
Затем задача усложняется, ребенку показывают предметы различных форм, различных цветов и выбрать одинаковые предметы ребенку становится все сложнее. Однако мы не будем так сильно усложнять задачу, а остановимся лишь на одном виде равенства — денежно-весовом. Остается лишь заплатить за этот килограмм согласно установленной продавцом цене. Другое дело, что вам может не нравиться цена, или возникли сомнения в точности весов — но это уже вопросы экономико-правовых отношений, к математике прямого отношения не имеющие.
Остается лишь заплатить за этот килограмм согласно установленной продавцом цене. Другое дело, что вам может не нравиться цена, или возникли сомнения в точности весов — но это уже вопросы экономико-правовых отношений, к математике прямого отношения не имеющие. Например 60 зерен соответствовали одному шекелю (сиклю), 60 шекелей — одной мине, а 60 мин — одному таланту. Поэтому изначально весы использовались для того, чтобы проверить, не являются ли предлагаемые деньги фальшивыми, а уже потом появились гирьки, как эквивалент денег, обвесы и обсчеты, электронные весы и пластиковые карты, но сути дела это никак не меняет.
Например 60 зерен соответствовали одному шекелю (сиклю), 60 шекелей — одной мине, а 60 мин — одному таланту. Поэтому изначально весы использовались для того, чтобы проверить, не являются ли предлагаемые деньги фальшивыми, а уже потом появились гирьки, как эквивалент денег, обвесы и обсчеты, электронные весы и пластиковые карты, но сути дела это никак не меняет. Более того, математики уже давно придумали специальные символы — скобки, так вот любые скобки можно рассматривать как борта чаш весов, во всяком случае на первом этапе постижения смысла уравнений. Тем не менее нижнее подчеркивание я для большей наглядности оставлю.
Более того, математики уже давно придумали специальные символы — скобки, так вот любые скобки можно рассматривать как борта чаш весов, во всяком случае на первом этапе постижения смысла уравнений. Тем не менее нижнее подчеркивание я для большей наглядности оставлю. 2)
2) 4)
4)
 6.2)
6.2) 8)
8) 9.2)
9.2) е. 1 = 1 — это просто численное равенство, а если в одной из частей равенства есть неизвестная, которую необходимо найти, то это уже уравнение. Как по мне, то такое дифференцирование значений не имеет большого смысла, а лишь усложняет восприятие материала. Я считаю, что любое равенство можно называть уравнением, а любое уравнение основано на равенстве. А кроме того, возникает вопрос х = 6, это уже равенство или это еще уравнение?
е. 1 = 1 — это просто численное равенство, а если в одной из частей равенства есть неизвестная, которую необходимо найти, то это уже уравнение. Как по мне, то такое дифференцирование значений не имеет большого смысла, а лишь усложняет восприятие материала. Я считаю, что любое равенство можно называть уравнением, а любое уравнение основано на равенстве. А кроме того, возникает вопрос х = 6, это уже равенство или это еще уравнение?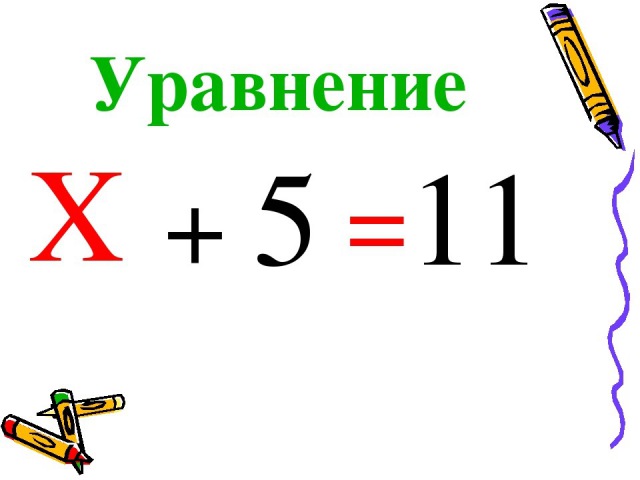 е. от 8 отнять 2 (уравнение 500.3). Такой подход точно соответствует излагаемому в учебниках, но на мой взгляд, является не таким наглядным, как аналогия с весами. Впрочем мнения по этому поводу могут быть разные.
е. от 8 отнять 2 (уравнение 500.3). Такой подход точно соответствует излагаемому в учебниках, но на мой взгляд, является не таким наглядным, как аналогия с весами. Впрочем мнения по этому поводу могут быть разные. 10.5)
10.5) Раз уж мы добрались до двойных скобок, то не обязательно для математических операций в левой и правой части составлять отдельное уравнение, поэтому запись решения в черновике вполне может выглядеть так:
Раз уж мы добрались до двойных скобок, то не обязательно для математических операций в левой и правой части составлять отдельное уравнение, поэтому запись решения в черновике вполне может выглядеть так: 10.18)
10.18) Экономия в записи при этом минимальная, а вот с пониманием требуемых действий у пятиклассника действительно могут возникнуть проблемы.
Экономия в записи при этом минимальная, а вот с пониманием требуемых действий у пятиклассника действительно могут возникнуть проблемы.