Содержание
Методические указания. Механика
Методические указания. Механика
Методические указания. Механика
19 февраля 2007 г.
Оглавление
Глава 1
Механика
1.1 Кинематика
1.1.1 Время и расстояние
Основная единица времени – секунда. В эталонных часах, использующих
излучение атомов цезия, секунда определяется как 9192631770 периодов
колебаний излучения. Предыдущее астрономическое определение секунды
(1/86400 доля суток) очень близко к современному, но неудобно для
использования, так как длительность суток изменяется из-за неравномерности
вращения Земли. Сейчас дважды в год астрономическое время корректируется
по атомным часам: добавляется недостающая или вычитается лишняя
секунда.
На Генеральной конференции мер и весов в 1983 году метр определен как
расстояние, которое свет проходит за 1/299792458 долю секунды. В
пределах точности это определение совпадает с более ранним (эталонная
«линейка»).
1.
 1.2 Системы отсчета. Координаты
1.2 Системы отсчета. Координаты
Чтобы описать движение, нужно указывать положение тел. Проще всего
это сделать для тел малых размеров. Тела, размерами которых при
описании движения можно пренебречь, называют материальными
точками.
Для указания положения и описания движения тел и частиц специально
выбирают одно из тел. Его называют телом отсчета. Все измерения
проводятся от выбранного тела отсчета.
Декартовы координаты. На плоскости из выбранного начала
отсчета O проводятся под прямым углом две координатные оси X и Y
(рис. 1.1). Из интересующей нас точки опускаются перпендикуляры
на оси и прочитываются на них координаты и . Координаты
точки принято записывать в круглых скобках числами через запятую:
.
Расстояние от начала отсчета до частицы определяется из теоремы
Пифагора:
При координатах двух точек () и () расстояние между
ними
Отношение координат дает тангенс угла, под которым видна точка из
начала отсчета O по отношению к оси X (рис.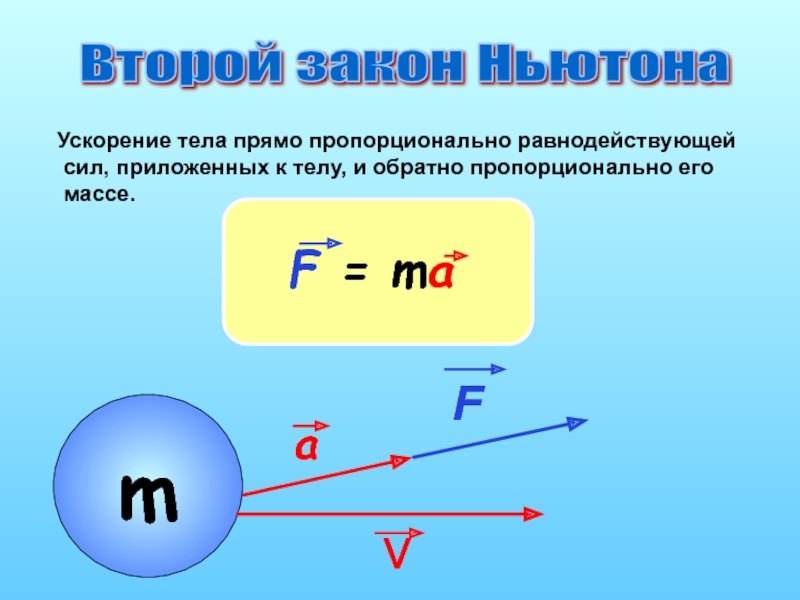 1.1):
1.1):
Числа – это полярные координаты точки. В физике удобнее
работать с углами не в градусной, а в радианной мере. Из вершины угла
описывают окружность и задают величину угла отношением длины отсекаемой
дуги к радиусу (рис. 1.2):
Другими словами, угол в радианной мере – это число, показывающее, во
сколько раз дуга длиннее радиуса: .
В пространстве из начала отсчета выходят три взаимно перпендикулярных
координатных оси X, Y и Z. Через точку проводятся три плоскости,
перпендикулярные осям. Их пересечения с осями и задают координаты частицы
().
Расстояние от начала координат до выбранной точки дается выражением
Расстояние между двумя точками в пространстве определяется формулой:
1.1.3 Векторы
Положение точки можно задать и направленным отрезком (вектором).
Радиус-вектор частицы проводится из начала координат в точку M, где
находится частица. Радиус-вектор указывает, в каком направлении и на
каком расстоянии от начала отсчета находится точка. Векторы при записи
выделяются стрелкой сверху или черточкой (в книгах – жирным шрифтом:
).
Если частица перешла из точки A в точку B, то изменение ее положения
называется перемещением и описывается направленным отрезком (рис. 1.3). Частица не обязательно двигалась от A к B по прямой. При любых
промежуточных этапах перемещение от начальной точки A до конечной точки
B однозначно задается вектором .
Результат последовательных перемещений, переводящих частицу из точки A
в точку B, а затем в точку C, таков же, как и одного перемещения из точки A
сразу в C. Значит, векторы перемещения можно складывать:
Чтобы сложить два вектора, в конец первого слагаемого переносим
начало второго слагаемого . Замыкающая стрелка от начала первого к
Замыкающая стрелка от начала первого к
концу второго вектора дает сумму . Такое правило сложения векторов
называется правилом треугольника. Складывать можно не только
перемещения, но и любые другие векторы (скорости, силы…) Правило сложения
обобщается на случай любого числа слагаемых: они выстраиваются в ломаную
линию, каждое последующее слагаемое откладывается от конца предыдущего.
Вектор, проведенный из начала в конец этой ломаной линии, дает сумму (рис.
1.4).
Вектор противоположен по направлению вектору . Разность
векторов определяется как сумма и :
то есть, чтобы вычесть вектор, прибавляем его с противоположным
знаком.
1.1.4 Прямолинейное движение. Скорость. Ускорение
Простейшее движение – вдоль прямой. При этом изменяется координата тела
в зависимости от времени , что записывается кратко в виде:
Средней скоростью на промежутке времени от до называется
отношение перемещения к интервалу времени:
(1. 1) 1) |
При стремлении интервала времени и перемещения к нулю в пределе
получается мгновенная скорость:
| (1.2) |
Здесь обозначает предел (сокращенное limit) выражения в скобках при
, стремящемся к нулю.
Более компактно мгновенную скорость принято записывать так:
| (1.3) |
Обозначения и можно понимать как бесконечно малые
изменения координаты и времени. Операция (1.3), или, что то же, (1.2),
называется вычислением производной для функции , или
дифференцированием координаты по времени. Малые приращения
и называют дифференциалами (от иностранного слова
difference).
Ускорение – это скорость изменения скорости:
| (1.4) |
От координаты получается вторая производная (производная от производной).
1.1.5 Пример – квадратичная зависимость
Пусть , где – постоянный коэффициент. Тогда, опуская знак
предела везде, кроме последнего равенства, получим
Теперь устремляем к нулю:
Выражение уже не содержит никакого интервала и зависит только от одного
времени .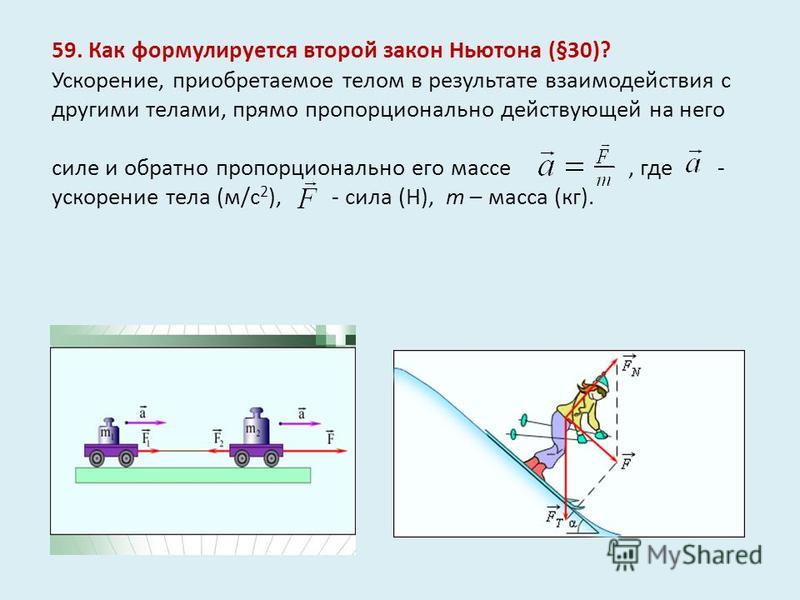 Это и есть мгновенная скорость для данной зависимости .
Это и есть мгновенная скорость для данной зависимости .
Заметим, что сначала надо вычислить и по возможности упростить выражение,
а уж потом переходить к пределу. Если, наоборот, сразу положить ,
получится неопределенность 0/0.
Ускорение в этом примере
то есть постоянно.
1.1.6 Правила дифференцирования
Производная от постоянной величины равна нулю: .
Производная суммы функций равна сумме производных: .
Производная произведения:
В частности, для произведения функции на постоянную величину
Производная частного:
Производная сложной функции:
Производные от наиболее важных функций (величины постоянны):
Пользуясь таблицей и правилами дифференцирования, можно найти
производные от любой комбинации указанных функций.
1.1.7 Графическое представление движения
На рисунке 1.5 приведен график зависимости положения частицы от
времени, то есть график функции . Он гораздо нагляднее, чем таблица
Он гораздо нагляднее, чем таблица
или формула.
Видно, например, что на интервале времени от 1 до 3,5 с координата растет.
Значит, в течение этого промежутка частица удаляется от начала координат.
Затем виден участок (3,5 6 с), на котором координата постоянна. Значит, на
некоторое время частица остановилась. Уменьшение координаты (участок 6 7 с) означает, что частица двинулась назад.
Геометрически мгновенная скорость – это тангенс угла между касательной
к непрерывной кривой и осью . Короче можно говорить просто
наклон вместо тангенс угла наклона касательной.
1.1.8 Пример
В момент времени с к графику проведена касательная. Измерив катеты
треугольника, изображенного на рисунке, получаем м/с.
Совершенно так же по графику скорости находится ускорение.
Наклон касательной к графику скорости – это и есть ускорение в данный
момент времени.
1.1.9 Движение в пространстве
Основные формулы
Траектория есть линия, описываемая частицей при движении в пространстве.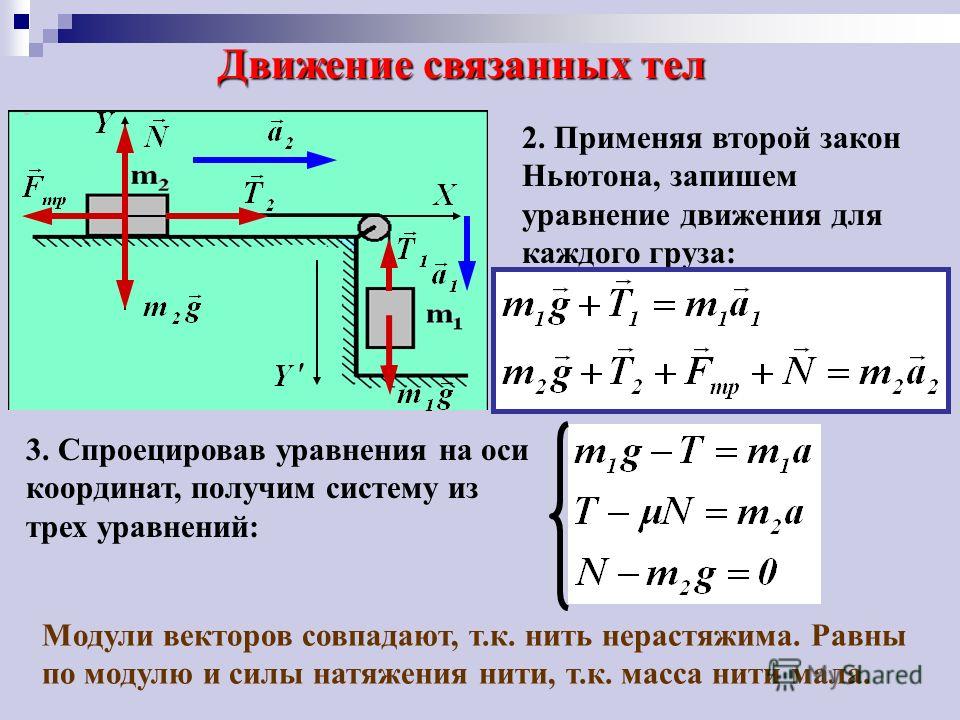
Ускорение частицы при движении по кривой траектории можно разложить на
две взаимно перпендикулярные компоненты: центростремительное
(перпендикулярное вектору скорости ) и тангенциальное (параллельное скорости, и, значит, траектории в данной точке). Выполняются
равенства
где – радиус кривизны траектории в данной точке.
1.1.10 Пример
Определим радиус кривизны траектории тела, брошенного под углом к
горизонту, в верхней и начальной точках. В верхней точке траектории
скорость равна и направлена горизонтально (вертикальная
составляющая скорости обращается в нуль). Ускорение перпендикулярно
скорости, то есть в этой точке все ускорение – чисто центростремительное.
Тогда можно записать: , откуда радиус кривизны
траектории:
В
начальной точке центростремительная, перпендикулярная скорости
составляющая ускорения , а скорость равна . Имеем:
, и радиус кривизны
Этот радиус больше , то есть траектория в начальной точке менее
кривая. Тангенциальное ускорение в начальной точке . Оно
Оно
отрицательно, то есть величина скорости в этот момент уменьшается.
1.2 Динамика
1.2.1 Сила. Законы Ньютона
Основные понятия и формулы
Между физическими телами существуют взаимодействия, количественно
характеризуемые силами.
Первый закон Ньютона: в инерциальной системе отсчета тело, на которое
нет внешних воздействий, движется равномерно и прямолинейно (в частности,
может и покоиться).
Второй закон Ньютона:
Здесь – масса тела, – его ускорение, – векторная сумма сил,
действующих на тело.
Третий закон Ньютона: при взаимодействии двух тел (допустим, 1 и 2)
силы их взаимодействия противоположны,
Второй и третий законы Ньютона позволяют определять действующие силы
по известному движению. Так были найдены силы тяготения, упругости,
трения и пр. Полученные закономерности применяют для определения
движения тел в новых условиях.
1.2.2 Пример – силы взаимодействия
Пусть бруски масс и соприкасаются, и первый брусок толкают с
заданной силой (рис. 1.6).
1.6).
Тела, как известно из опыта, могут двигаться вместе, сохраняя
соприкосновение. Для такого движения найдем ускорение , одинаковое для
обоих тел. Из второго закона Ньютона
На тело действует пока неизвестная сила со стороны первого.
Записываем второй закон Ньютона:
На
тело действует известная сила и сила со стороны второго тела .
Значит, равнодействующая сил, приложенных к , равна .
Тогда
По
третьему закону Ньютона . Видим, что это равенство
выполняется: силы и одинаковы по величине и направлены в
противоположные стороны (см. рис. 1.6). При этом совершенно не существенно,
как взаимодействуют тела (сколько точек соприкосновения, каковы упругие
свойства материалов и т.д.). Все, что нам понадобилось – второй и третий
законы Ньютона и тот опытный факт, что тела могут ускоряться вместе,
сохраняя соприкосновение. Тела могли бы быть склеены или вообще быть
частями единого тела.
1.2.3 Пример – силы при криволинейном движении
Рассмотрим движение по окружности, когда известно центростремительное
ускорение тела. Пусть автомобиль с массой кг проезжает по
Пусть автомобиль с массой кг проезжает по
выпуклому мосту, имеющему радиус кривизны м, со скоростью
км/час (10 м/с). С какой силой автомобиль давит на мост в его
середине?
Центростремительное ускорение м/с. Вектор
ускорения направлен вниз. На автомобиль действует сила тяжести и
сила со стороны моста (сила реакции) . Из уравнения движения
, откуда Н. По третьему
закону Ньютона, автомобиль давит на мост с силой, противоположной
, то есть равной по величине и направленной вниз. Заметим, что
неподвижный автомобиль давил бы с силой Н, то есть заметно
сильнее. Если еще увеличить скорость, давление может уменьшиться до
нуля. Отрицательным оно не станет, так как автомобиль оторвется от
моста.
1.2.4 Пример – задача о блоке
Разберем задачу, которая позволяет понять, как следует применять
законы Ньютона. Пусть две массы и соединены невесомой
нерастяжимой нитью, перекинутой через неподвижный блок (рис. 1.7).
Неподвижный значит только, что ось блока закреплена, но вращается на оси
он свободно. Масса блока пренебрежимо мала. Надо найти движение этой
Масса блока пренебрежимо мала. Надо найти движение этой
системы, то есть ускорения тел. Удобен стандартный порядок решения
задач:
1. Сначала изображаются силы, действующие на каждое тело. В данном
случае на действует сила тяжести и сила натяжения нити . На
действует и . Мы считаем, что натяжение одинаково вдоль
всей нити. Это следует из ее нулевой массы и из того, что блок не оказывает
сопротивления вращению.
2. Затем необходимо записать уравнения движения, то есть второй закон
Ньютона для каждого тела. Если выбрать за положительное направление вниз,
то уравнения движения имеют вид
Здесь не нужно заранее указывать, какое тело двигается вниз, а какое – вверх.
При правильном решении нужное направление получится автоматически, оно
определится знаком ускорения.
В двух уравнениях три неизвестных: и . Нужно еще одно
уравнение. Оно находится из взаимосвязи ускорений тел.
3. Поскольку уравнений движения недостаточно, необходимо выписать
уравнения связей. Используем нерастяжимость нити. Если масса опустилась на 1 м, то на столько же должна подняться масса . Модули
смещений одинаковы. Но тогда одинаковы модули скоростей и ускорений. По
направлению же ускорения тел противоположны. Следовательно, недостающее
уравнение имеет вид
4. Когда полная система уравнений получена, ее нужно решить. Для этого
можно исключать по очереди неизвестные или использовать другие приемы. В
данном случае вместо подставляем :
Теперь вычтем из верхнего уравнения нижнее:
откуда
Найдем еще натяжение:
5. Очень важно проанализировать результаты. Прежде всего полезно
проверять размерность. В приведенном решении размерность правильная –
ускорения записаны как , умноженное на безразмерный коэффициент; сила
имеет размерность массы, умноженной на ускорение. Если размерность ответа
неверна, наверняка в решении есть ошибка.
Далее важно проверить, не противоречит ли полученное решение здравому
смыслу. В данной задаче, если получается, например, отрицательное
В данной задаче, если получается, например, отрицательное
натяжение или ускорение какого-то тела оказалось (при некоторых
значениях масс) больше , надо пересмотреть решение и найти ошибку.
Полученный ответ выдерживает такую проверку: всегда (при любых
положительных массах) , а ускорения не превышают по абсолютной
величине . Это легко понять – нить всегда тянет вверх и замедляет
падение.
Важным элементом анализа ответа является рассмотрение предельных
случаев. В нашем решении можно положить, например, . Тогда
массы должны находиться в равновесии. Это выполняется (получается
). Если одна из масс нулевая, вторая должна падать
свободно, с ускорением . Это выполняется (положим ), что тоже
убеждает в правильности результата. Примерно тот же результат будет,
если масса не нулевая, но просто очень мала. При ускорения , то есть тяжелое тело опускается, легкое –
поднимается.
Анализ не только служит проверкой, но и помогает лучше понять результат,
а иногда и заметить какие-то его особенности. В данной задаче, например,
В данной задаче, например,
сила, действующая на подвес блока и равная , меньше суммарной
силы тяжести, действующей на тела (если массы не равны). Покажите
это самостоятельно. Попробуйте объяснить физический смысл этого
условия.
1.2.5 Пример – наклонная плоскость
Рассмотрим тело, которое положили на наклонную плоскость (рис. 1.8).
Пусть задан коэффициент трения тела о плоскость и угол наклона плоскости. Требуется найти, будет ли тело соскальзывать, и если будет, то с
каким ускорением.
На тело действует сила тяжести , направленная вниз, сила
нормального давления , перпендикулярная плоскости, и сила трения ,
направленная вдоль плоскости вверх. Удобно ввести систему координат с осью
X вдоль плоскости и осью Y перпендикулярно ей. Запишем второй закон
Ньютона в проекциях на эти направления:
Здесь учтено, что ускорение тела в направлении Y равно нулю. Скатывающая
сила – это проекция силы тяжести на ось X, а величина –
это проекция силы тяжести на ось Y.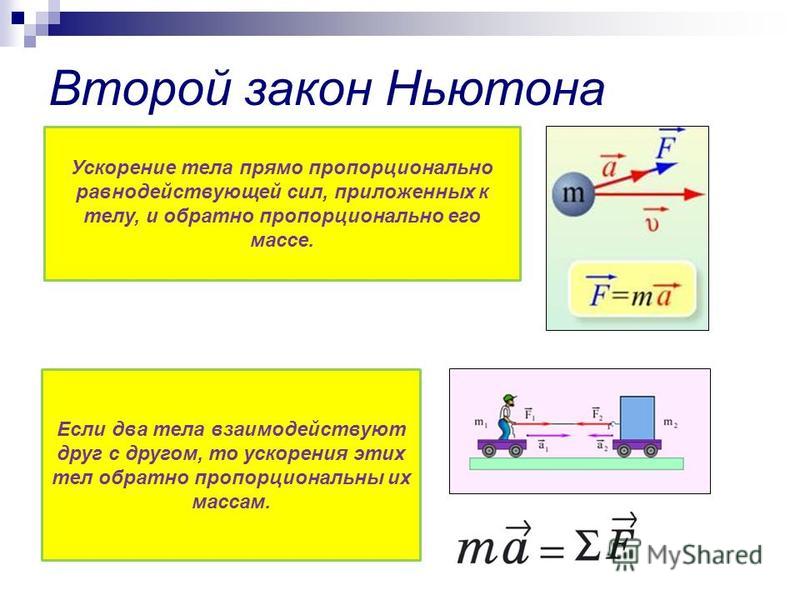
Из второго уравнения находится сила нормального давления:
Остается найти движение вдоль плоскости. Возможны два варианта: тело либо
скользит вниз, либо лежит неподвижно. В этом легко убедиться, положив
монету на книгу и изменяя наклон. Рассмотрим оба случая.
- Пусть тело скользит вниз. Тогда известна сила трения
и из уравнения движения по оси X находим ускорение :
- Предположим, что тело покоится. Тогда известно ускорение:
и из уравнения движения находим силу трения:
Сила трения в этом случае уравновешивает скатывающую силу.
Какой же из вариантов выбрать? Это должно следовать из условий задачи.
Необходимо определить, при каких условиях реализуется первый вариант, а при
каких – второй.
Рассмотрим случай покоя. Найденная сила трения не
должна превышать максимального значения , при котором
наступает проскальзывание. Неравенство
выполняется для углов, не превышающих так называемого предельного угла,
или угла трения :
Если угол наклона плоскости меньше угла трения, тело покоится. Если же угол
Если же угол
больше, оно скользит вниз.
Таким образом, результат задачи следует записать так:
Можно было проанализировать и вариант скольжения. Для него ускорение должно быть положительным. Это дает то же самое условие выполнения
варианта: .
При угле, равном углу трения, оба решения, конечно, совпадают:
. На практике трение скольжения
может быть несколько меньше трения покоя, так что тело может лежать на
плоскости, но если его толкнуть, будет двигаться вниз с небольшим ускорением.
Подберите такой режим на опыте. Убедитесь, что он получается в узком
интервале углов наклона.
1.3 Работа и энергия
1.3.1 Пример – подпрыгивающий мячик
С какой скоростью, направленной вниз, надо бросить мячик с высоты ,
чтобы после удара о пол мячик поднялся на высоту ?
Начальная потенциальная энергия мячика , кинетическая – ,
где – искомая скорость. После отскока в верхней точке энергия равна
. Закон сохранения энергии:
Откуда .
1.3.
 2 Пример – связанные грузы
2 Пример – связанные грузы
Два груза массы и связаны нитью, переброшенной через
неподвижный блок. В начальный момент первый груз удерживают на высоте
над полом. Затем его без толчка отпускают. Какое количество теплоты
выделится при ударе первого груза о пол?
Решение
Закон сохранения механической энергии дает
Кинетическая энергия первого тела при абсолютно неупругом ударе перейдет
целиком в тепло . Тогда
Выражая из первого уравнения и подставляя во второе, получим
ответ:
1.3.3 Пример – скорость снаряда
Сила, действующая на снаряд массы в стволе орудия, нарастает
равномерно от нуля до на участке ствола длины , не меняется на
участке ствола длины и, наконец, равномерно уменьшается до нуля на
участке ствола длины . Какова скорость снаряда при вылете из ствола?
(Рис. 1.9)
Из закона сохранения энергии следует, что работа силы действующей на
заряд перейдет в его кинетическую энергию.
Работу найдем как площадь под графиком функции силы от смещения.
Окончательно получаем
1.3.4 Пример – соскальзывание с полусферы
С вершины гладкой полусферы радиуса небольшое тело. Найдите его
скорость на высоте (отсчитываемой от подножья). На какой высоте тело
оторвется от полусферы?
Будем отсчитывать потенциальную энергию от подножья полусферы.
Рассмотрим момент, когда угол между радиусом, проведенным в точку, где
находится тело, и вертикалью равен . Тогда высота . Из закона
сохранения энергии
имеем .
Рассмотрим динамику движения. По второму закону Ньютона сумма
проекций сил и реакции опоры (см. рис. 1.10) должна равняться
произведению массы на центростремительное ускорение:
При движении скорость растет, а уменьшается. Следовательно,
уменьшается сила реакции. Отрыв тела от поверхности сферы произойдет при
. Подставляя выражение для скорости, получим:
И,
учитывая, что , получаем ответ:
1.
 3.5 Пример – прыжок со второго этаха
3.5 Пример – прыжок со второго этаха
Оцените среднюю силу, приходящуюся на ноги человека при ударе о землю при
прыжке со второго этажа.
Выберем высоту второго этажа . Тогда скорость при приземлении
тела определится из уравнения
При ударе о землю торможение происходит на некотором пути . Эту
величину оценим как (высота приседания человека). Тогда
Откуда . И, при массе человека 70 кг, .
1.3.6 Пример – груз на пружине
Груз массы , подвешенный на пружине жесткости , находится на
подставке. Пружина при этом не деформирована. Подставку быстро убирают.
Определите максимальное удлинение пружины и максимальную скорость
груза.
В нижнем положении, когда растяжение максимально, и скорость равна
нулю, суммарная работа силы тяжести и силы упругости также равна
нулю:
Откуда .
Скорость тела будет максимальна, когда сумма сил, действующих на тело,
равна нулю:
Тогда
Подставляя в последнее уравнение , получим ответ:
1.
 4 Столкновения
4 Столкновения
1.4.1 Пример – распад ядра
В результате распада движущегося ядра появились два осколка массы и
с импульсами и , разлетающиеся под углом . Определите
выделившуюся при распаде ядра энергию .
Пусть – начальный импульс частицы. Запишем закон сохранения
импульса и энергии:
Откуда получаем
1.4.2 Пример – полет Мюнхгаузена на ядре
Артиллерист стреляет из пушки ядром массы так, чтобы оно упало в
неприятельском лагере. На вылетевшее ядро садится барон Мюнхгаузен, масса
которого . Какую часть пути до неприятельского лагеря ему придется идти
пешком?
Пусть ядро вылетает со скоростью под углом к горизонту. Тогда
дальность полета (расстояние до неприятельского лагеря)
При посадке на ядро барона направление скорости, то есть угол, не
меняется. Величина скорости полета определяется из закона сохранения
импульса:
Тогда . И ядро пролетит лишь
Ответ: барону придется пройти 35/36 пути.
1.5 Движение в гравитационном поле
1.
 5.1 Пример – притяжение к Земле и Луне
5.1 Пример – притяжение к Земле и Луне
На каком расстоянии (выраженном в радиусах Земли) от Земли на прямой
Земля-Луна силы притяжения тела к Земле и Луне равны по величине?
Расстояние до Луны в 60 раз больше радиуса Земли. Масса Луны в 81 раз
меньше земной.
Пусть масса рассматриваемого тела, а , и , массы и
расстояния от тела до центров Земли и Луны соответственно. Запишем условие
равенства сил притяжения:
Используя сотношения между параметрами получаем:
откуда получаем ответ
1.6 Механические колебания
1.6.1 Пример – груз на пружине
Груз массы г совершает гармонические колебания с частотой
Гц под действием упругой пружины. Найти жесткость пружины.
Воспользуемся формулой для круговой частоты колебаний тела на
пружинне
Откуда получаем ответ
1.6.2 Пример – маятник и падение
Шарик, подвешенный на длинной нити, отклонили на малый угол и отпустили.
В этот же момент времени другой такой же шарик начал свободно падать из
точки подвеса нити. Какой из шариков быстрее достигнет точки равновесия
Какой из шариков быстрее достигнет точки равновесия
первого шарика?
Пусть длина нити равна . Тогда первый шарик достигнет положения
равновесия за четверть периода
а
свободно падающий за время
Первый долетит быстрее.
1.7 Статика
Раздел механики статика рассматривает условия равновесия тел. Легко
придумать два необходимых условия равновесия, которые будут всегда
выполняться в случае равновесия.
- Сумма сил действующих на тело находящееся в равновесии
равна нулю. Тело не двигается как целое. - Сумма моментов сил действующих на тело равна нулю. Тело
не должно вращаться.
1.7.1 Пример – груз на тросе
Найти силу натяжения троса в системе изображенной на рисунке 1.11.
В данном случае, для решения задачи достаточно воспользоваться только
первым условием равновесия – балансом сил. В качестве рассматриваемого тела
В качестве рассматриваемого тела
удобно выбрать небольшой кусок троса в области подвеса груза, точка .
Сумма векторов сил прикладываемых к этой точке должна давать ноль.
Запишем уравнение для проекций сил на вертикальную ось, явно указав знаки
компонент.
откуда получаем ответ
1.7.2 Пример – цепочка
Цепочка массы подвешена за концы так, что вблизи точек подвеса она
образует с горизонталью угол . Определите силу натяжения цепочки в ее
нижней точке и в точках подвеса (рис. 1.12, а).
Для определения натяжения цепочки в точках подвеса приравняем нулю
сумму вертикальных проекций сил (рис. 1.12, б)
откуда получаем ответ
Для определения натяжения в нижней точке рассмотрим половину цепочки и
приравняем сумму горизонтальных проекций сил нулю (рис. 1.12, в).
откуда получаем ответ
1.7.3 Пример – стержень в углу 1
Попробуем приставить однородный стержень длины наклонно к стене
комнаты.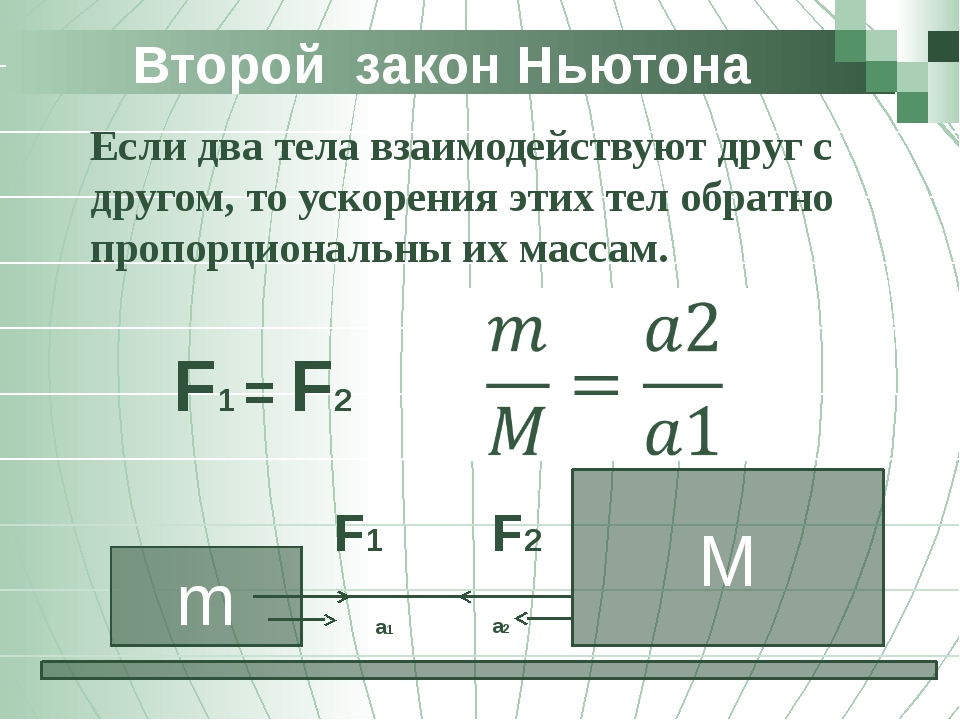
аб |
Пусть стержень составляет угол с горизонтом и пол гладкий, то
есть трения между стержнем и полом нет (рис. 1.13, а). Возможно ли
равновесие?
На рисунке изображены силы, которые должны действовать на стержень со
стороны Земли (), стенки (и ) и пола (). Очевидно,
что на ось X имеет отличную от нуля проекцию единственная сила –
. Тогда уравнение равновесия сил может быть выполнено лишь
при . Следовательно, сила трения также равна нулю, а
.
Но тогда условие равенства нулю суммы моментов сил не выполняется.
Выбрав ось вращения, например, проходящей через центр стержня, получим
для момента силы :
Равновесие невозможно. Стержень непременно упадет на пол.
1.7.4 Пример – стержень в углу 2
Пусть между стержнем и полом есть трение, а стена гладкая. Возможно ли
равновесие теперь?
Силы, действующие в этом случае, изображены на рисунке 1. 13, б). Здесь
13, б). Здесь
через обозначена сила трения. Условие равновесия сил в проекциях на оси
X и Y дает:
Выберем ось вращения проходящей через нижнюю точку стержня (точка
O на рисунке) и запишем условие равенства нулю суммы моментов
сил:
Из
этих уравнений сразу получаются выражения для всех трех неизвестных
сил:
При малых углах tgмал, и сила трения из этого решения получится
очень большой. Однако она не может превышать значения – силы
трения скольжения:
Значит, полученные формулы для могут выполняться лишь при углах
не меньше некоторого критического . Значение критического угла
соответствует случаю, когда сила трения покоя максимальна:
Отсюда для критического угла получается соотношение:
Равновесие возможно лишь при углах больше критического.
Если попытаться установить стержень с меньшим углом, то есть ближе к
горизонтальному положению, то формально равновесие возможно только при
. Этого можно добиться, только удерживая стержень в нижней
точке дополнительной внешней силой. Одно же трение будет неспособно
Одно же трение будет неспособно
обеспечить устойчивость, и стержень упадет.
1.7.5 Как выбрать ось вращения?
Для записи условия равновесия моментов сил в рассмотренной задаче можно
было выбрать и любую другую ось. Так, для оси, проходящей через верхнюю
точку стержня, для рис. 1.13, б) получим:
(Убедитесь, что ответ при этом не изменится).
Если тело не вращается (как должно быть в статике), то оно не вращается
относительно любой неподвижной оси. Разумно выбирать ось так, чтобы
уравнение моментов было максимально простым. Выбрав ось проходящей через
точку O, мы автоматически обратили моменты двух из четырех сил в нуль, так
как плечи сил и равны нулю.
формула и определение + маленький опыт
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
Элементарный опыт по второму закону Ньютона
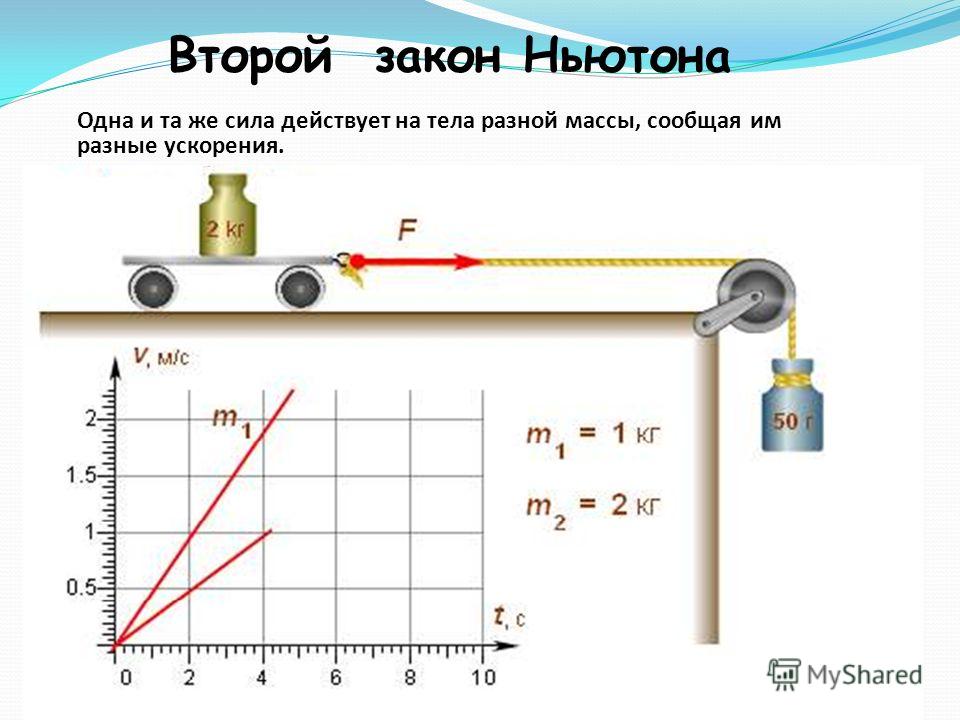
Начнем с практической части. Нагрузите чем-нибудь две сумки или два пакета. Один чуть-чуть, а второй очень сильно. Только пакеты берите покрепче. А теперь примерно с одинаковой силой по очереди резко поднимите оба пакета вверх. Вы увидите, что легкий пакет практически взлетит, а вот тяжелый перемещаться будет намного медленнее.
А теперь другой опыт положите на землю футбольный мячик и пните его пару раз. Один раз легонько, а второй раз со всей силы. Понаблюдайте, как изменится скорость мяча после пинка. В первом случае он потихоньку откатится на небольшое расстояние, во втором улетит далеко и на весьма приличной скорости. Ну вот и все, с практической частью закончили. Теперь немного порассуждаем.
Действие равнодействующей силы
Мы знаем, что скорость тела изменяется под действием приложенной к нему силы. Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением.
То есть, фактически, все случаи приложения различных сил в конкретный момент времени можно свести к действию одной равнодействующей силы. Таким образом, чтобы найти, как изменилась скорость тела, нам надо знать, какая сила действует на тело.
Какое ускорение получает тело?
В зависимости от величины и направления силы тело получит то или иное ускорение. Это четко видно в опыте с мячом. Когда мы подействовали на тело небольшой силой, мяч ускорился не очень сильно. Когда же сила воздействия увеличилась, то мяч приобрел гораздо большее ускорение. То есть, ускорение связано с приложенной силой прямо пропорционально. Чем больше сила воздействия, тем большее ускорение приобретает тело.
От чего еще зависит ускорение, полученное телом в результате воздействия на него? Вспомним первую часть нашего опыта. Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим.
То есть, второй вывод это то, что масса тела напрямую связана с ускорением, приобретаемым телом в результате воздействия силы. При этом, масса тела обратно пропорциональна полученному ускорению. Чем больше масса, тем меньше будет величина ускорения.
Второй Закон Ньютона: формула и определение
Исходя из всего вышесказанного, приходим к тому, что можно записать второй закон Ньютона в виде следующей формулы:
a =F / m ,
где a ускорение, F сила воздействия, m масса тела.
Соответственно, второму закону Ньютона можно дать такое определение: ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела. Это и есть второй закон Ньютона.
Не правда ли, все оказалось довольно просто и понятно?
Нужна помощь в учебе?
Предыдущая тема: Инерциальные системы отсчета: первый закон Ньютона
Следующая тема:   Третий закон Ньютона: определение, формула + рассуждения по теме
применение законов Ньютона в работе / Блог компании MBA Consult / Хабр
В этой статье Джеймс Клир (James Clear), расскажет, как использовать законы Ньютона для повышения продуктивности в повседневной жизни.
В 1687 году Исаак Ньютон опубликовал свою революционную книгу «Математические принципы естественной философии», в которой изложил три закона динамики. Таким образом, Ньютон заложил основы классической механики и изменил взгляды человечества на физику и науку в целом.
Но большинство людей не догадывается, что три закона динамики Ньютона можно по аналогии использовать и для повышения продуктивности, упрощения рабочего процесса и улучшения своей жизни.
Позвольте мне такую аналогию назвать законами продуктивности Ньютона.
Первый закон продуктивности Ньютона
Первый закон динамики: Тело остается в состоянии покоя или продолжает движение с постоянной скоростью, если на него не действует внешняя сила (т.е. движущееся тело стремится продолжать движение, а покоящееся — оставаться в состоянии покоя).
Инертность — фундаментальный закон вселенной. Первый закон Ньютона применим и к продуктивности. Тело в состоянии покоя стремится оставаться в покое.
Хорошая новость? Закон работает и по-другому. Движущееся тело стремится продолжать движение. В отношении продуктивности это означает только одно: Самое важное — найти способ начать. Начав, продолжать движение гораздо легче.
Движущееся тело стремится продолжать движение. В отношении продуктивности это означает только одно: Самое важное — найти способ начать. Начав, продолжать движение гораздо легче.
Итак, какой же наилучший способ начать, когда находишься во власти инертности?
По своему опыту могу сказать, что проверенным методом начать работу является правило двух минут.
Вот как звучит правило двух минут в применении к продуктивности: Чтобы преодолеть инертность, найдите способ приступить к выполнению задачи в течение менее двух минут.
Обратите внимание, что речь не идет о завершении работы. Фактически, не нужно даже непосредственно работать. Но благодаря первому закону Ньютона, вы часто будете замечать, что, начав эту небольшую часть задания в течение двух минут, продолжать работать будет гораздо легче.
Приведу несколько примеров…
- Возможно, прямо сейчас вам не хочется отправляться на пробежку. Но если вы обуете кроссовки и наполните водой бутылку, этого небольшого стартового действия будет достаточно, чтобы заставить вас выйти из дома.

- Возможно, прямо сейчас вы смотрите на пустой экран и не можете заставить себя начать писать отчет. Но если в течение двух минут вы напишете какие-то случайные предложения, то может оказаться, что необходимые фразы начнут сами рождаться под вашими пальцами.
- Возможно, прямо сейчас вам нужно выполнить творческое задание, а вы не можете заставить себя хоть что-то нарисовать. Но если вы начертите на листе бумаги случайную линию, а затем превратите ее в собаку, то сможете ощутить, как начинается прилив творческих сил.
Мотивация часто приходит после старта. Найдите способ начать с малого. Движущееся тело стремится продолжать движение.
Второй закон продуктивности Ньютона
Второй закон динамики: F=ma. Векторная сумма сил, действующих на тело, равна произведению массы этого тела и вектора ускорения этого тела (т.е. сила равна произведению массы и ускорения).
Давайте рассмотрим составляющие этого уравнения и то, как оно может быть применено к продуктивности.
В данном уравнении надо обратить внимание на один важный момент. Сила F — векторная величина. Вектор характеризуется величиной (сколько работы вы выполняете) и направлением (куда направлена эта работа). Другими словами, если вы хотите придать телу ускорение в определенном направлении, то имеет значение, как величина прилагаемого усилия, так и направление этого усилия.
Знаете что? В жизни все происходит точно так же.
Если вы хотите быть продуктивны, это зависит не только от того, насколько напряженно вы трудитесь (величина), но также от того, куда вы прилагаете усилия (направление). Это справедливо как для крупных, значимых дел нашей жизни, так и для небольших повседневных задач.
Например, одни и те же способности можно приложить в различных направлениях и получить абсолютно разные результаты.
Проще говоря, у вас есть только определенное количество сил, которое вы можете вложить в вашу работу, и направление приложения сил так же важно, как и то, насколько напряженно вы трудитесь.
Третий закон продуктивности Ньютона
Третий закон динамики: Если одно тело воздействует на второе, то второе тело тоже воздействует на первое с силой, равной по величине, но противоположной по направлению (т.е. силы равны и противоположны по направлению).
У каждого из нас есть средняя скорость, с которой мы работаем в повседневной жизни. Наш обычный уровень продуктивности и эффективности обычно является балансом производительных и непроизводительных сил, согласно формуле Ньютона — равных по величине и противоположных по направлению.
В нашей жизни есть производительные усилия — концентрация, позитив и мотивация. Есть также усилия непроизводительные — стресс, недосыпание и попытки заниматься одновременно слишком многими делами.
Если мы хотим стать более эффективными и продуктивным, у нас есть два варианта.
Первый: добавить производительных усилий. Это вариант «продавливания». Мы пересиливаем себя, выпиваем дополнительную чашку кофе и работаем еще напряженней. Именно для этого люди принимают препараты, помогающие им сконцентрироваться, или смотрят мотивирующие видео, чтобы «накачать» себя. Все это — попытки повысить свои производительные силы и превозмочь непроизводительные.
Именно для этого люди принимают препараты, помогающие им сконцентрироваться, или смотрят мотивирующие видео, чтобы «накачать» себя. Все это — попытки повысить свои производительные силы и превозмочь непроизводительные.
Очевидно, что делать это можно лишь пока ты не выгоришь до конца, но на коротком отрезке времени стратегия «продавливания» может дать хороший результат.
Второй вариант: устранить силы противодействия. Упростите себе жизнь, научитесь говорить «нет», смените обстановку, сократите количество взятых на себя обязанностей или каким-либо другим способом устраните силы, которые вас сдерживают.
Если вы уменьшаете непроизводительные силы в своей жизни, ваша продуктивность возрастает естественным образом. Это как если бы вы чудесным образом избавились от руки, которая вас тянет назад. (Как я люблю говорить: если бы вы устранили все факторы, мешающие вам стать продуктивным, вам не потребовались бы советы по повышению продуктивности.)
Большинство людей старается «продавить» и силой проложить себе путь через препятствия. Недостаток этой стратегии заключается в том, что по-прежнему приходится иметь дело с другими силами. Я считаю, что гораздо меньше стресса предполагает вариант, при котором мы устраняем противодействующие силы и даем возможность нашей продуктивности расти естественным образом.
Недостаток этой стратегии заключается в том, что по-прежнему приходится иметь дело с другими силами. Я считаю, что гораздо меньше стресса предполагает вариант, при котором мы устраняем противодействующие силы и даем возможность нашей продуктивности расти естественным образом.
Законы продуктивности Ньютона
Законы динамики Ньютона, в значительной степени, проливают свет на то, как быть продуктивным.
- Движущееся тело стремится продолжать движение. Найдите способ приступить к делу в течение не более двух минут.
- Вопрос не только в том, чтобы напряженно работать, но также в том, чтобы работать над правильными вещами. Ваши силы ограниченны, направление их приложения также важно.
- Продуктивность является балансом противоположных сил. Если вы хотите быть более продуктивным, вы можете либо «продавить» препятствия, либо устранить силы противодействия. Второй вариант менее стрессовый.
P.S. Рекомендуем ещё одну статью по теме – 14 советов, как сделать 2015 год самым продуктивным.
Автор перевода — Давиденко Вячеслав, основатель компании MBA Consult
Измерение ускорения свободного падения на различных высотах при помощи математического маятника
- Участник: Мингалеев Артур Эдуардович
- Руководитель: Баскова Мария Аркадьевна
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря.
1. Введение
Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается. Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:
- Ознакомиться с историей открытия свободного падения тел;
- Изучить методы измерения ускорения свободного падения на поверхности Земли;
- Провести самостоятельные измерения ускорения свободного падения при помощи математического маятника;
- Провести измерения на различных высотах.
Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.
Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела. Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
Погрешность составила не более 10%.
В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.
2. Основная часть
2.1. Исторические сведения об открытии свободного падения и методах его измерения
Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление. Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли.
Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с «постоянным ускорением»; темп увеличения скорости тела не меняется, т. е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня. Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью. Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
S1 : S2 : S3 : … = 1 : 2 : 3 : … (при V0 = 0)
Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
S1 : S2 : S3 = t12 : t22 : t32 (2)
Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
2.2. Практическая значимость нахождения значения ускорения свободного падения
Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
2.3. Методы измерения ускорения свободного падения
На самом деле методов по измерению ускорения свободного падения достаточно много. Приведу только те, которые сам испробовал.
1) Измерение ускорения свободного падения с помощью наклонной плоскости
Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Записывая второй закон Ньютона в проекциях на оси координат:
Ох: – Fтр+ mgsinα = ma
Oy: N – mgcosα = 0
и учитывая, что N = mgcosα; Fтр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:
|
g = |
a |
|
sinα – μcosα |
При этом ускорение a можно вычислить из формулы
так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:
Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.
Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.
При равномерном движении бруска эти силы будут попарно равны: Fтр = Fупр, Fтяж = N, т. е. Fупр = μFтяж, тогда коэффициент трения равен
Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.
2) Определение
g благодаря давлению жидкости
Как известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.
Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м3.
При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.
3) Измерение ускорения свободного падения с помощью математического маятника
Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Подготовка к проведению работы
В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника
Тогда период
и ускорения свободного падения может быть вычислено по формуле
Результаты измерений и вычислений представлены в разделе 2.5
2.4. Теоретические расчеты по определению ускорения свободного падения различных высотах
Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
где G — гравитационная постоянная (G = 6,6743 · 10–11 (H ·м2)/кг2).
При вычислениях я применял такие значения:
R = 6370 · 103 м – радиус Земли на широте Казани;
M = 5,9722 · 1024 кг – масса Земли.
Таким образом теоретическое значение gт = 9,823386 м/с2.
Согласно формуле
естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.
Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.
Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:
|
|
|
|
|
|
|
|
|
|
|
|
2.5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
Как уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Ход работы
Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.
- Я установил на краю стола штатив. У его верхнего конца укрепил с помощью муфты кольцо и подвесил к нему шарик на нити. Шарик должен висеть и свободно совершать колебания.
- Нить я взял метровой длины для удобства вычислений.
- Отклонив шарик на небольшое расстояние (5-8 см), я возбудил колебания маятника.
- Измерил в пяти экспериментах время t 20 колебаний маятника и вычислил tср:
|
tср = |
t1 + t2 + t3 + t4 + t5 |
|
5 |
- Затем вычислил среднюю абсолютную погрешность измерения времени:
|
∆tср = |
│t1 – tср│ + │t2 – tср│+ │t3– tср│ + │t4– tср│ + │t5– tср│ |
|
5 |
- Вычислил ускорение свободного падения по формуле:
Таблица результатов измерений в классе
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
| |||
|
|
|
| |||
|
|
|
|
- Я определил относительную погрешность измерения времени εt.
|
ε = |
∆t |
= |
∆tи + ∆tотсчета |
= |
1 с + 1 с |
= |
2 c |
= |
2 с |
= 0,05 = 5% |
|
t |
t |
t |
tсредн |
39,94 с |
- Определил относительную погрешность измерения длины маятника:
|
εl = |
∆l |
= |
∆lи + ∆lотсчета |
= |
половина цены деления + цена деления |
= |
|
l |
l |
длина маятника |
|
= |
0,0005 м + 0,001 м |
= |
0,0015 м |
= |
0,0015 м |
= 0,0015 = 0,15% |
|
l |
l |
1 м |
- Вычислил относительную погрешность измерения g:
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3% - Определил абсолютную погрешность вычисления ускорения свободного падения:
∆g = εggсредняя = 0,053 · 9,73971 м/с2 = 0,5162 м/с2 ≈ 0,520
Итог моих измерений и вычислений:
9,37 ≤ g ≤ 10,41
Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».
Таблица результатов измерений на станции метро Кремлевская
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
| |||
|
|
|
| |||
|
|
|
|
При измерениях в метро пришлось использовать длину нити 63,5 см.
Относительная погрешность измерения времени εt = 0,063 = 6,3%.
Относительная погрешность измерения длины маятника: εl = 0,24%
Относительная погрешность измерения g: εg = 6,78%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с2.
Итог моих измерений и вычислений:
9,33 ≤ g ≤ 10,59
Таблица результатов измерений на 36-м этаже небоскреба «Лазурные небеса»
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
| |||
|
|
|
| |||
|
|
|
|
Здесь при измерениях пришлось длину нити еще сократить до 51 см.
Относительная погрешность измерения времени εt = 7%.
Относительная погрешность измерения длины маятника: εl = 0,29%
Относительная погрешность измерения g: εg = 7,58%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с2.
Итог моих измерений и вычислений:
9,11 ≤ g ≤ 10,61
Таблица сравнения теоретически полученных значений g (м/с2) и полученных экспериментально
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
3. Заключение
При подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.
Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.
Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается. Экспериментально полученные значения хорошо это показывают.
Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.
В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.
Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.
Конспект урока «Третий закон Ньютона» | План-конспект занятия по физике (10 класс):
10 «Б» класс
Тема урока: «Третий закон Ньютона».
Тип урока: урок изучения нового учебного материала.
Цели урока.
Стратегические:
— Формирование научной картины мира.
— Развитие критического мышления.
— Формирование научного миропонимания.
Тактические:
— Ликвидировать пробелы в знаниях.
— Сформировать умение пользоваться учебной литературой.
— Развить умение обобщать и систематизировать знания.
— Сформировать умение использовать теоретические знания на практике.
— Сформировать интерес к физике как науке.
— Сформировать умение раскрывать взаимосвязь между изученным теоретическим материалом и явлениями в жизни.
— Развить умение анализировать данные и делать вывод.
— Развить общие учебные (в т.ч. познавательные) умения.
Оперативные:
Когнитивная область.
Уровень знания: ученик должен знать определение силы, массы, формулировку третьего закона Ньютона, его математическую интерпретацию, записать формулу третьего закона Ньютона на доске, знать единицы измерения массы и силы, условие равенства сил, понятие инерции, свойство аддитивности массы.
Уровень понимания: ученик должен приводить примеры проявления третьего законов Ньютона из окружающего мира, понимать формулировку третьего закона Ньютона, словесно интерпретировать его математическую интерпретацию, понятие массы и силы, инерции, процесс сравнения и измерения сил.
Уровень применения: ученик должен уметь применять третий закон Ньютона при объяснении физических явлений и решении задач, свойство аддитивности массы, переводить единицы массы и силы в единицы измерения СИ, изображать на рисунке третий законы Ньютона.
Аффективная область.
Уровень восприятия: ученик осознает важность учения, внимательно слушает высказывания учителя и учащихся, активно участвует в дискуссии.
Уровень реагирования: ученик выполняет домашнее задание, поручения учителя, проявляет интерес к физике, самостоятельность при обучении.
Уровень усвоения ценностной ориентации: ученик целенаправленно изучает различные точки зрения, выносит собственное суждение, проявляет убежденность в защите своего убеждения.
Этапы урока | Формы, методы обучения | Средства обучения | Время |
Организационный момент. | Фронтальная, словесный (беседа). | Слово учителя и учащихся, журнал, ручка. | 2 мин |
Проверка ранее изученного учебного материала, домашнего задания. | Фронтальная, словесный, репродуктивный, практический. | Слово учителя и учащихся, мел, доска, учебник, тетрадь. | 5 мин |
Формирование новых знаний умений, навыков. | Фронтальная, словесный (объяснение), репродуктивный, объяснительно-иллюстративный, наглядный. | Слово учителя и учащихся, мел, доска, печатное слово (учебник), поясняющие рисунки на доске. | 21 мин |
Закрепление изученного материала. | Фронтальная, репродуктивный, практический. | Слово учителя и учащихся, учебник, задачник, физический словарь. | 10 мин |
Инструктаж по выполнению домашнего задания. | Фронтальная, словесный (беседа, комментарии). | Слово учителя, мел, доска, журнал. | 2 мин |
Ход урока.
1. Приветствие учащихся учителем, выявление отсутствующих учащихся.
2. В начале урока учитель проводит с учащимися фронтальный устный опрос. Учитель задает вопросы нескольким учащимся, остальные ученики дополняют ответ своих одноклассников. В это время два ученика показывают на доске решение домашних задач.
Вопросы.
- Дайте определение силы.
- Какие две силы считаются в механике равными?
- Как связано ускорение тела с силой?
- Что такое инерция? Приведите примеры ее проявления.
- Какое утверждение содержит второй закон Ньютона?
- Каким образом, используя второй закон Ньютона, можно определить массу тела?
- Какие условия необходимы для того, чтобы тело двигалось с постоянным ускорением?
3.
Третий закон Ньютона.
Примеров взаимодействия тел и сообщения ими друг другу ускорений можно привести сколь угодно много. Когда вы, находясь в одной лодке, начнете за веревку подтягивать другую лодку, то и ваша лодка обязательно будет двигаться вперед. Действуя на другую лодку, вы заставляете ее действовать на свою лодку.
Если вы ударите ногой по футбольному мячу или толкнете плечом товарища, то ощутите обратное действие на ногу или плечо. Все это проявления закона взаимодействия тел.
Действия тел друг на друга носят характер взаимодействия не только при непосредственном контакте тел. Положите на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что они начнут двигаться навстречу друг другу.
Заметные изменения скоростей обоих взаимодействующих тел наблюдаются лишь в тех случаях, когда массы этих тел не сильно отличаются друг от друга. Если же взаимодействующие тела значительно различаются по массе, заметное ускорение получает только то из них, которое имеет меньшую массу. Так, при падении камня Земля заметно ускоряет движение камня, но ускорение Земли (а ведь камень тоже притягивает Землю) практически обнаружить нельзя, так как оно очень мало.
Выясним с помощью опыта, как связаны между собой силы взаимодействия двух тел.
Возьмем достаточно сильный магнит и железный брусок и установим их на катки для уменьшения трения о стол. К концам магнита и бруска прикрепим одинаковые пружины, закрепленные другими концами на столе. Магнит и брусок притянутся друг к другу и растянут пружины. Опыт показывает, что к моменту прекращения движения пружины растянуты совершенно одинаково. Это означает, что на оба тела со стороны пружин действуют одинаковые по модулям и противоположные по направлениям силы:
Так как магнит покоится, то сила равна по модулю и противоположна по направлению силе , с которой на него действует брусок:
Точно так же равны по модулям и противоположны по направлению силы, действующие на брусок со стороны магнита и пружины:
Отсюда следует, что силы, с которыми взаимодействуют магнит и брусок, равны по модулям и противоположны по направлению:
На основе подобных опытов можно сформулировать третий закон Ньютона:
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
Это означает, что если на тело А со стороны тела В действует сила , то одновременно на тело В со стороны тела А будет действовать сила , причем
.
Используя второй закон Ньютона, можно определить:
Отсюда следует, что
т. е. отношение модулей ускорении а1 и а2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое — большее.
Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.
В настоящее время наиболее широко в физике и технике применяется система единиц, в которой в качестве основной величины взята не сила, а масса. Единица же силы устанавливается на основе второго закона Ньютона.
В Международной системе единиц (СИ) за единицу массы — один килограмм (1 кг) — принята масса эталонной гири из сплава платины и иридия, которая хранится в Международном бюро мер и весов в Севре, близ Парижа. Точные копии этой гири имеются во всех странах. Приближенно массу 1 кг имеет литр воды при комнатной температуре.
За единицу силы в Международной системе единиц принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2.
Эта единица называется ньютоном (сокращенное обозначение — Н). Наименование ньютона:
1 Н = 1 кг·1 м/с2.
4.
Далее учитель вызывает к доске учащихся, которые решают задачи по изученной теме.
№ 1. Может ли автомобиль двигаться равномерно по горизонтальному шоссе с выключенным двигателем?
Ответ: нет, так как в этом случае движущийся автомобиль не является свободным телом (телом, на которое не оказывают воздействие другие тела), потому что при движении тела по какой-либо поверхности всегда имеется сила трения, препятствующая данному движению.
№ 2. О ветровое стекло движущегося автомобиля ударился комар. Сравнить силы, действующие на комара и автомобиль во время удара.
Ответ: согласно третьему закону Ньютона, эти силы равны по модулю и противоположны по направлению.
№ 3. Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 м/с2. Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН?
5. На дом учитель задает учащимся прочитать § 25, 26, 27, 28, ответить на вопросы после §, решить две задачи.
№ 1. Тело массой 3 кг падает в воздухе с ускорением 8 м/с2. Найдите силу сопротивления воздуха.
№ 2. Тепловоз на горизонтальном участке пути длиной 600 м развивает постоянную силу тяги 147 кН. Скорость поезда возрастает при этом от 36 до 54 км/ч. Определите силу сопротивления движению, считая ее постоянной. Масса поезда 1000 т.
Урок 21. релятивистские эффекты — Физика — 11 класс
Физика, 11 класс
Урок №21. Релятивистские эффекты
На уроке рассматриваются понятия: энергия покоя, полная энергия частиц; связь массы и энергии в специальной теории относительности; релятивистский импульс частицы, релятивистская кинетическая энергия; принцип соответствия.
Глоссарий урока:
Релятивистская механика — раздел физики, где описывается движение частиц со скоростями близкими к скорости света.
Закон взаимосвязи энергии и массы — тело обладает энергией и при нулевой скорости, такую энергию называют энергией покоя.
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии.
Безмассовыми называют частицы массы, которых в состоянии покоя равны нулю, они существуют только в движении, при этом во всех инерциальных системах отсчёта их импульс и энергия не равны нулю.
Массовыми называют частицы, для которых масса является важной характеристикой, мерой инертности тела.
Принцип соответствия – это подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматриваются как частный случай релятивистских законов при скоростях намного меньших скорость света.
Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай.
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 239 – 241.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 147 – 149
Дополнительная литература:
- Анциферов Л.И., Физика: электродинамика и квантовая физика. 11кл. Учебник для общеобразовательных учреждений – М.: Мнемозина, 2001. – С. 253-260.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 311-315.
- Айзексон У., Эйнштейн. Жизнь гения; пер. с анг. А.Ю. Каннуниковой. – М: АСТ, 2016 – С.144-157
Основное содержание темы
«Основы физики претерпели неожиданные и радикальные изменения благодаря смелости молодого и революционно мыслящего гения.»
Вернер Гейзенберг
Эти слова и множество других восхищённых эпитетов будут высказаны в адрес гениального учёного Альберта Эйнштейна. Эйнштейн не боялся опровергать общепринятые утверждения. Он разрушил представление об абсолютном времени и незыблемости пространства. Его теория утверждала, что есть движущиеся системы координат со своим относительным временем. А пространство существует, пока в нём существует всё материальное. Время идёт тем медленнее, если быстрее движется тело. Такие удобные и понятные принципы классической физики: о постоянстве массы, длины, времени, скорости — опровергаются следствиями из постулатов специальной теории относительности Эйнштейна.
Альберт (Einstein) Эйнштейн
14 марта 1879 г. – 18 апреля 1955 г.
Физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 года, общественный деятель-гуманист.
По законам классической физики: масса – это мера инертности тела. Но Эйнштейн утверждает другое: масса – это мера энергии, содержащейся в теле.
Любое тело обладает энергией уже в силу своего существования. Альбертом Эйнштейном была установлена пропорциональность между энергией и массой:
На первый взгляд, простая формула, является фундаментальным законом природы, законом взаимосвязи энергии и массы.
Согласно этой формуле тело обладает энергией даже при нулевой скорости, в таком случае энергию называют E энергией покоя. А массу, которая входит в формулу Эйнштейна назовём m0 массой покоя.
Как же будет выглядеть закон взаимосвязи массы и энергии для движущегося тела? К нему добавляем радикал (релятивистский множитель) из преобразований Лоренца:
Такую формулу называют релятивистской энергией или полной энергией движущегося тела.
Релятивистская механика — раздел физики, где описываются движения тел и частиц со скоростями близкими к скорости света, где используются преобразования Лоренца, перехода из одной инерциальной системы в другую, когда одна система движется относительно другой со скоростью вдоль оси ОХ.
Любые изменения физических величин, связанные с сокращением размеров:
эффект замедления времени:
изменение массы тела при изменении энергии:
закон сложения скоростей:
в специальной теории относительности называют релятивистскими изменениями.
По законам классической физики полная энергия равна сумме кинетической и потенциальной энергий тела или частицы
Отсюда выразим кинетическую энергию тела
Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии
В классической физике кинетическая энергия вычисляется по формуле
Получим ещё одно выражение
Выразим кинетическую энергию из формулы релятивистской энергии:
Поставим релятивистский радикал, который можно преобразовать при малых скоростях и получим релятивистскую кинетическую энергию частицы:
Или другой способ выражения кинетической энергии, если использовать классическую кинетическую энергию, то получим
— выражение для определения релятивистской кинетической энергии.
Путём не сложных математических вычислений можно доказать, что формула определения кинетической энергии в классической физикеи формула кинетической энергии в релятивистской физике равны между собой.
Давайте проверим работают ли главные законы механики — законы Ньютона в релятивистской физике.
Первый закон Ньютона: существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первый постулат СТО Эйнштейна: все физические явления протекают одинаково во всех инерциальных системах отсчёта, или никакими опытами, проводимыми в инерциальной системе отсчёта, невозможно установить её движение относительно других инерциальных систем.
Внимание! Они не противоречат друг другу!
Третий закон Ньютона: силы с которыми тела действуют друг на друга равны по модулю и направлены вдоль одной прямой в противоположные стороны. Этот закон тоже работает в релятивистской физике (смотрите первый постулат СТО).
А что же со вторым законом классической механики? Второй закон Ньютона: ускорение тела прямо пропорционально силе и обратно пропорционально его массе.
Рассмотрим предельный случай: если на тело долгое время t (время стремится к бесконечности) действовать с постоянной силой F = const, то ускорение будет постоянным a = const. Ускорение в свою очередь, зависит от скорости, с которой движется тело:
Отсюда скорость тоже будет стремиться к бесконечности, а это невозможно (смотрите второй постулат СТО), так как скорость тела или частицы не может быть больше предельного значения скорости света ()!
Но давайте рассмотрим другую формулировку второго закона Ньютона, когда сила прямо пропорциональна изменению импульсов тела ко времени этого изменения:
В классической механике импульс равен произведению массы тела или частицы на его скорость: , где m – постоянная величина, мера инертности тела.
В релятивистской механике выражение импульса можно записать, используя преобразования Лоренца:
При скоростях намного меньших, чем скорость света 𝟅с, формула принимает вид классической механики Ньютона
Эти проявления — подтверждение законов Ньютона и классических представлений о пространстве и времени, рассматривают как частный случай релятивистских законов при скоростях намного меньших скорости света и называют принципом соответствия. Согласно принципу соответствия любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, должна включать предыдущую теорию, как предельный случай. То есть законы классической механики подтверждаются релятивистской, но только для частиц или тел, движущихся с малыми скоростями.
В природе существуют такие частицы (фотоны, мюоны, нейтрино), скорость которых равна или близка к скорости света. Массы таких частиц в состоянии покоя равны нулю, эти частицы называют безмассовыми. Они существуют только в движении, но во всех инерциальных системах отсчёта их импульс и энергия не равны нулю. Тогда подтверждается утверждение Эйнштейна, что масса – это мера энергии тела. Частицы, для которых масса является важной характеристикой — мерой инертности, называют массовыми.
Найдём соотношение между энергией и импульсом:
Взаимно уничтожаются подкоренные выражения, сокращается произведение массы на скорость света, и мы получим простое соотношение энергии и импульса, где нет зависимости от массы.
Энергия и импульс связаны соотношением
Поэтому во всех инерциальных системах отсчёта импульс и энергия не равны нулю. При превращениях элементарных частиц, обладающих массой покоя , в частицы у которых , их энергия покоя целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя.
Во всех инерциальных системах отсчёта импульс частицы и её энергия связаны соотношением:
или
— эта формула является фундаментальным соотношением энергии и импульса для массовых частиц релятивистской механики. Эти соотношения экспериментально подтверждены.
Следовательно, для безмассовых частиц, где или , выражение примет вид
Основное выражение энергии через её импульс записывают так:
Отсюда, масса, движущейся частицы, будет равна
Если частица покоится, то её значение можно определить из основной формулы Эйнштейна взаимосвязи массы и энергии:
В обычных условиях, при нагревании тела или его охлаждении, при химической реакции, эти приращения массы происходят, их можно вычислить, но изменения массы не так заметны. Энергию, полученную из расщепления ядер на атомных электростанциях, используют на благо человека, где незначительные массы радиоактивного топлива вырабатывают энергию, питающую электроэнергией огромные города. Но, к сожалению, такую энергию, высвобождающуюся при цепной реакции, люди использовали и военных целях, для уничтожения городов, людей. Поэтому, только в последствии, понимая ответственность за свои открытия, учёные искренне становятся общественными деятелями: правозащитниками и борцами за мир.
Рассмотрим задачи тренировочного блока урока:
1. Чтобы выработать количество энергии, которой обладает тело массой 1 кг, Красноярской ГЭС потребуется времени _________ суток (1,5·107; 173,6; 182,3). Мощность Красноярской ГЭС 6000МВт.
Дано:
m = 1 кг
P = 6000 МВт = 6·109 Вт
t — ? (сутки)
Воспользуемся выражением, описывающим зависимость энергии тела от массы:
И зависимостью мощности от работы и времени:
Выразим секунды в часах, а затем в сутках:
Ответ: 173,6 суток.
2. Чему равен импульс протона, летящего со скоростью 8,3·107 м/с? На сколько будет допущена ошибка, если пользоваться формулами классической физики? Данные поученных вычислений занесите в таблицу:
Физические величины | Показатели |
Масса покоя протона, m | 1,67·10-27 кг |
Скорость света, с | 3·108 м/с |
Скорость движения протона, 𝟅 | 8,3·107 м/с |
Импульс протона по классическим законам, рк | ? |
Импульс протона по релятивистским законам, рр | ? |
Разница в вычислениях импульса протона, | ? |
Воспользуемся формулами для определения импульса релятивистским и классическим способами:
Вычислим разницу показаний:
Физические величины | Показатели |
Масса покоя протона, m | 1,67·10-27кг |
Скорость света, с | 3·108 м/с |
Скорость движения протона, 𝟅 | 8,3·107 м/с |
Импульс протона по классическим законам, рк | 1,38·10-19кг·м/с |
Импульс протона по релятивистским законам, рр | 5,2·10-19 кг·м/с |
Разница в вычислениях импульса протона, | в 3,8 раза |
Каков физический смысл 2-го закона Ньютона? : Дискуссионные темы (Ф)
Zloj писал(а):
Это набор слов, а не трактовка.
Любая трактовка — это набор слов.
Zloj писал(а):
Трактовка вышеприведенной записи только одна — под действием силы F тело массы m приобретает ускорение w.
Что «Трактовка вышеприведенной записи только одна» очень легко поверить.
Хочется, однако, узнать, почему именно этот закон не может рассматриваться как утверждение о равенстве сил?
Добавлено спустя 25 минут 22 секунды:
chiba писал(а):
Это только частное следствие 2 закона Ньютона и не работает в случае, например, реактивного движения.
А, если время измерять по неисправным часам, у которых секунды разной продолжительности, то формула поменяется ещё круче.
Если слева пишется , то понятно, что ограничиваемся случаем постоянной массы.
chiba писал(а):
Математическая формулировка 2 закона Ньютона выглядит как
.
Это более общая форма, но ана мало что изменит.
Если писать производную вместо дифференциалов, то снова справа стоит очень понятная штука — сила (например сила Гука).
А что стоит слева? (равное производной от импульса).
chiba писал(а):
Озвучить математическую формулировку 2го закона Ньютона можно так:
Результирующая сила , действующая на тело в течение времени , приводит к изменению импульса тела на величину .
Неточность: справа стоит импульс силы, а не сила.
Физически бесконечно малый импульс силы равен произведению , но прямым физическим смыслом обладает только одна операция — измерение (сравнение с эталоном).
Произведение — это математическая операция, она физического смысла не имеет.
Если писать производную или , то основной вопрос будет звучать как что стоит слева, а, если писать дифференциалы, то — что стоит справа.
Утверждение такое: если слева стоит сила, то и справа должна стоять сила — не площадь, не температура и не стоимость — только сила.
Это потому, что имеется только одна физически осмысленная операция — измерение.
Физический смысл математическим операциям приписывать нельзя — физика не нуждается в математике (математика для неё лишь один из множества инструментов).
Выяснить же пытаемся только физический смысл закона.
Всё это к тому, чтобы задаться вопросом, а не являются ли три закона Ньютона тремя частными случаями одного более общего закона?: типа, всякое действие влечёт адекватное противодействие (даже первый закон тоже).
Добавлено спустя 3 минуты 44 секунды:
Munin писал(а):
Когда мы не знаем силы — его можно использовать как определение силы (с известной массой).
Можно, но тут интересен только случай, когда это соотношение не может быть определением ни для одной входящей в него величины.
Munin писал(а):
Когда мы знаем и то и другое — его можно использовать для расчёта движения.
Ключевое слово «расчёта».
Интересует же только физический смысл.
Представим, что математики нет совсем; что именно тогда утверждает этот закон?
Второй закон движения Ньютона
Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены. Первый закон — иногда называемый законом инерции — гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет 0 м / с / с. Объекты в равновесии (состояние, в котором все силы уравновешены) не будут ускоряться. Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или несбалансированная сила.Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Второй закон движения Ньютона относится к поведению объектов, для которых все существующие силы не уравновешены. Второй закон гласит, что ускорение объекта зависит от двух переменных — чистой силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно — от массы объекта.По мере увеличения силы, действующей на объект, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.
Большое уравнение
Второй закон движения Ньютона можно формально сформулировать следующим образом:
Ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и чистая сила, и обратно пропорционально массе объекта.
Это словесное утверждение можно выразить в виде уравнения следующим образом:
a = F нетто / м
Приведенное выше уравнение часто преобразовывается в более знакомую форму, как показано ниже. Чистая сила равна произведению массы на ускорение.
F net = m • a
Во всем этом обсуждении упор был сделан на чистую силу .Ускорение прямо пропорционально чистой силе ; чистая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение создается чистой силой . СЕТЕВАЯ СИЛА. Важно помнить об этом различии. Не используйте значение просто «какой-либо одной силы» в приведенном выше уравнении. Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила — это векторная сумма всех сил.Если известны все индивидуальные силы, действующие на объект, то можно определить результирующую силу. При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы для силы, массы и ускорения в приведенное выше уравнение, можно записать следующую эквивалентность единиц.
1 Ньютон = 1 кг • м / с 2
Определение стандартной метрической единицы силы определяется приведенным выше уравнением.Один ньютон определяется как количество силы, необходимое для придания 1 кг массы ускорения в 1 м / с / с.
Ваша очередь практиковаться
Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и решив неизвестную величину. Попробуйте сами, а затем используйте кнопки, чтобы просмотреть ответы.
| Чистая сила (н.) | Масса (кг) | Разгон (м / с / с) | |
| 1. | 10 | 2 | |
| 2. | 20 | 2 | |
| 3. | 20 | 4 | |
| 4. | 2 | 5 | |
| 5. | 10 | 10 |
Второй закон Ньютона как руководство к мышлению
Числовая информация в таблице выше демонстрирует некоторые важные качественные отношения между силой, массой и ускорением.Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса остается постоянной). Точно так же сравнение значений в строках 2 и 4 демонстрирует, что уменьшение вдвое чистой силы приводит к уменьшению вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.
Кроме того, качественную взаимосвязь между массой и ускорением можно увидеть, сравнив числовые значения в приведенной выше таблице.Обратите внимание на строки 2 и 3, что удвоение массы приводит к уменьшению вдвое ускорения (если сила остается постоянной). Точно так же строки 4 и 5 показывают, что уменьшение массы на вдвое приводит к удвоению ускорения (если сила остается постоянной). Ускорение обратно пропорционально массе.
Анализ табличных данных показывает, что такое уравнение, как F net = m * a, может быть руководством к размышлениям о том, как изменение одной величины может повлиять на другую величину.Какое бы изменение ни производилось в чистой силе, такое же изменение произойдет и с ускорением. Удвойте, утроите или учетверите чистую силу, и ускорение будет делать то же самое. С другой стороны, какое бы изменение массы ни произошло, с ускорением произойдет противоположное или обратное изменение. Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Направление чистой силы и ускорения
Как указано выше, направление результирующей силы совпадает с направлением ускорения.Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости проверьте ускорение по сравнению с предыдущим блоком.)
В заключение, второй закон Ньютона дает объяснение поведения объектов, на которых силы не уравновешиваются.Закон гласит, что несбалансированные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально чистой силе и обратно пропорционально массе.
Мы хотели бы предложить …
Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive.Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащемуся исследовать влияние изменений приложенной силы, чистой силы, массы и трения на ускорение объекта.
Ракетостроение!
Ракеты НАСА (и другие) ускоряются от стартовой площадки, сжигая огромное количество топлива. Когда топливо сгорает и расходуется для приведения в движение ракеты, масса ракеты изменяется.Таким образом, одна и та же движущая сила может со временем привести к увеличению значений ускорения. Используйте виджет Rocket Science ниже, чтобы изучить этот эффект.
Проверьте свое понимание
1. Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.
2. К энциклопедии прилагается чистая сила 15 Н, которая заставляет ее ускоряться со скоростью 5 м / с 2 .Определите массу энциклопедии.
3. Предположим, что салазки ускоряются со скоростью 2 м / с 2 . Если чистая сила утроится, а масса — вдвое, то каково новое ускорение салазок?
4. Предположим, что салазки ускоряются со скоростью 2 м / с 2 . Если чистая сила утроится, а масса уменьшится вдвое, то каково новое ускорение салазок?
Второй закон движения Ньютона: концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения . Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным — внешняя сила действует извне из интересующей системы .Например, на рис. 1 (а) интересующая нас система — это вагон плюс ребенок в нем. Две силы, действующие со стороны других детей, — это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок 1 (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на ней, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, а иногда определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет многократно пересмотрена в нашем путешествии по физике.
Рис. 1. Различные силы, действующие на одну и ту же массу, вызывают разное ускорение.а) двое детей толкают телегу с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система — это повозка и ее водитель. Вес системы w и опора земли N также показаны для полноты и, как предполагается, отменяют. Вектор f представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, в сумме образуют чистую силу, F net .На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение ( a ‘> a ), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему.Это предположение было проверено экспериментально и показано на рисунке 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы — это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.А пока мы определим трение как силу, которая противодействует движению мимо друг друга соприкасающихся объектов. На рисунке 1 (b) показано, как векторы, представляющие внешние силы, складываются вместе, чтобы получить результирующую силу,
.
F net .
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
[латекс] \ text {a} \ propto {\ text {F} _ {net}} \\ [/ latex]
, где символ ∝ означает «пропорционально», а F net — это чистая внешняя сила .(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение — не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой благодаря нашему упрощению.
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.И действительно, как показано на рисунке 2, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
.
[латекс] \ text {a} \ propto {\ frac {1} {m}} \\ [/ latex]
, где м — масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, так же как оно прямо линейно пропорционально чистой внешней силе.
Рис. 2. Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(а) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.
Было обнаружено, что ускорение объекта только зависит от чистой внешней силы и массы объекта.Объединение двух только что приведенных пропорций дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.
[латекс] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex].
Это часто записывается в более знакомой форме
F нетто = м a .
Если рассматривать только величину силы и ускорения, это уравнение просто
F net = ma.
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон представляет собой причинно-следственную связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
F net = м используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 . То есть, поскольку F net = m a ,
1 Н = 1 кг ⋅ м / с 2 .
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 N = 0.225 фунтов
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, — это сила тяжести, обычно называемая его массой масс Вт. Вес можно обозначить как вектор w, потому что он имеет направление; вниз — это, по определению, направление силы тяжести, и, следовательно, вес — это сила, направленная вниз.Величина веса обозначается как w . Галилей показал, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий вниз к Земле. Он испытывает только направленную вниз силу тяжести, величина которой составляет w . Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, составляет F net = ма .Поскольку объект испытывает только направленную вниз силу тяжести, F net = w . Мы знаем, что ускорение объекта под действием силы тяжести составляет g , или a = g . Подставляя их во второй закон Ньютона, получаем
Масса
Это уравнение для веса — силы тяжести, действующей на массу m:
w = мг
Так как g = 9,80 м / с 2 на Земле, вес 1.0 кг объекта на Земле составляет 9,8 Н, как мы видим:
w = мг = (1,0 кг) (9,80 м / с 2 ) = 9,8 Н.
Напомним, что g может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что оно находится в состоянии свободного падения . То есть единственная сила, действующая на объект, — это сила тяжести.В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.
Ускорение свободного падения g незначительно меняется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является внутренним свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения всего 1.67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое в физике мы называем «свободным падением». Мы воспользуемся приведенным выше определением веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса — очень разные физические величины, хотя они тесно связаны. Масса — это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес — это сила тяжести, которая зависит от силы тяжести.Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах — ньютонах.
Распространенные заблуждения: масса против веса
В обиходе масса и вес часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса — это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «пуля» в английских единицах измерения). С другой стороны, вес — это мера силы тяжести, действующей на объект. Вес равен массе объекта (м), умноженной на ускорение свободного падения (g). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах). Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения.Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с большей или меньшей силой тяжести. Например, ускорение свободного падения на Луне составляет 1,67 м / с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м / с 2 ). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» намного меньше, хотя и не выглядите худее.Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Эксперимент на вынос: масса и вес
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении.Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример 1.Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Какое у него ускорение?
Рис. 3. Сила полезного действия на газонокосилку справа составляет 51 Н. С какой скоростью газонокосилка ускоряется вправо?
Стратегия
Поскольку даны F net и m, ускорение можно вычислить непосредственно из второго закона Ньютона, как указано в F net = m a .{2} \\ [/ латекс].
Обсуждение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что скоро человек достигнет максимальной скорости.
Пример 2. Какая ракетная тяга разгоняет салазки?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой T, для четырехракетной двигательной установки, показанной на рисунке 4. Начальное ускорение салазок составляет 49 м / с2, масса системы — 2100 кг, а сила трения. противодействие движению, как известно, составляет 650 Н.
Рис. 4. Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются.Земля оказывает на систему направленную вверх силу N, равную по величине и противоположную по направлению ее весу w. Система здесь — сани, его ракеты и всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение (f), нарисована крупнее шкалы.
Стратегия
Несмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу.Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин.Следовательно, мы начинаем с
F net = ma,
, где F net — чистая сила в горизонтальном направлении. Из рисунка 4 видно, что тяга двигателя увеличивается, а трение противодействует тяги. В форме уравнения чистая внешняя сила равна
.
Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
[латекс] 4T = \ text {ma} + f = \ left (\ text {2100 кг} \ right) \ left ({\ text {49 м / с}} ^ {2} \ right) + \ text { 650 Н} \ [/ латекс]
[латекс] 4Т = 1.{4} \ text {N} \\ [/ латекс].
Обсуждение
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g. (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с 2 . Когда мы говорим, что ускорение составляет 45 g, это 45 × 9.80 м / с 2 , что составляет примерно 440 м / с 2 .) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона — это больше, чем определение; это соотношение между ускорением, силой и массой.Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Сводка раздела
- Ускорение, a , определяется как изменение скорости, означающее изменение ее величины или направления, или и того, и другого.
- Внешняя сила — это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона выглядит так: [latex] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ латекс].
- Это часто записывается в более привычной форме: F net = m a .
- Вес объекта w определяется как сила тяжести, действующая на объект массой м .Объект испытывает ускорение свободного падения g :
w = м г .
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение — это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Концептуальные вопросы
1. Какое утверждение верно? (а) Чистая сила вызывает движение. (б) Чистая сила вызывает изменение движения. Объясните свой ответ и приведите пример.
2. Почему мы можем пренебрегать такими силами, как силы, удерживающие тело вместе, когда мы применяем второй закон движения Ньютона?
3. Объясните, как выбор «интересующей системы» влияет на то, какие силы необходимо учитывать при применении второго закона движения Ньютона.
4. Опишите ситуацию, в которой чистая внешняя сила, действующая на систему, не равна нулю, но ее скорость остается постоянной.
5. Система может иметь ненулевую скорость, в то время как чистая внешняя сила, действующая на нее , равна нулю.Опишите такую ситуацию.
6. Камень брошен вверх. Какая чистая внешняя сила действует на скалу, когда она находится на вершине своей траектории?
7. (a) Приведите пример различных чистых внешних сил, действующих на одну и ту же систему, вызывая разные ускорения. (б) Приведите пример одной и той же чистой внешней силы, действующей на системы разной массы, вызывая разные ускорения. (c) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
8. Если ускорение системы равно нулю, не действуют ли на нее внешние силы? А как насчет внутренних сил? Объясни свои ответы.
9. Если к объекту приложена постоянная ненулевая сила, что вы можете сказать о скорости и ускорении объекта?
10. Сила тяжести, действующая на баскетбольный мяч на рисунке 2, игнорируется. Если принять во внимание гравитацию и , каково направление чистой внешней силы на баскетбольный мяч — выше горизонтали, ниже горизонтали или все еще горизонтально?
Задачи и упражнения
Вы можете предположить, что данные, взятые с иллюстраций, имеют точность до трех цифр.
1. Спринтер весом 63,0 кг начинает забег с ускорением 4,20 м / с. 2 . Какая чистая внешняя сила действует на него?
2. Если спринтер из предыдущей задачи разгоняется с такой скоростью на 20 м, а затем сохраняет эту скорость до конца 100-метрового рывка, сколько у него времени для забега?
3. Пылесос толкает тележку для белья весом 4,50 кг таким образом, чтобы чистая внешняя сила, действующая на нее, составляла 60,0 Н. Вычислите величину ее ускорения.
4. Поскольку астронавты на орбите явно невесомые, необходим умный метод измерения их массы, чтобы отслеживать прирост или потерю массы и корректировать рацион. Один из способов сделать это — приложить известную силу к космонавту и измерить возникающее ускорение. Предположим, что действует чистая внешняя сила 50,0 Н и измеренное ускорение астронавта составляет 0,893 м / с 2 . (а) Рассчитайте ее массу. (b) При приложении силы к космонавту, аппарат, в котором он движется по орбите, испытывает равную и противоположную силу.Обсудите, как это повлияет на измерение ускорения космонавта. Предложите метод, позволяющий избежать отдачи автомобиля.
5. На рис. 3 чистая внешняя сила на газонокосилке 24 кг заявлена равной 51 Н. Если сила трения, препятствующая движению, равна 24 Н, то какую силу F (в ньютонах) прикладывает человек косилка? Предположим, косилка движется со скоростью 1,5 м / с при снятии усилия F . Как далеко уйдет косилка до остановки?
6.Те же ракетные салазки, изображенные на рисунке 5, замедляются со скоростью 196 м / с 2 . Какая сила необходима, чтобы вызвать это замедление? Предположим, что ракеты выключены. Масса системы 2100 кг.
Рисунок 5.
7. (a) Если салазки ракеты, показанные на рисунке 6, запускаются с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы составляет 2100 кг, тяга T составляет 2,4 × 10 4 Н, а сила трения, препятствующая движению, известна как 650 Н.б) Почему ускорение не в четыре раза меньше, чем у всех горящих ракет?
Рисунок 6.
8. Какое замедление у ракетных санок, если они останавливаются за 1,1 с со скорости 1000 км / ч? (Из-за такого замедления один испытуемый потерял сознание и временно потерял сознание.)
9. Предположим, двое детей толкают третьего ребенка в повозке горизонтально, но в противоположных направлениях. Первый ребенок прикладывает силу 75,0 Н, второй — 90.{2} \\ [/ latex] при скорости 90,0 км / ч. На этой скорости силы, противодействующие движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта.) Какова величина силы, которую мотоцикл оказывает на мотоцикл в обратном направлении. земля, чтобы произвести его ускорение, если масса мотоцикла с водителем составляет 245 кг?
11. Ракетные салазки, показанные на рисунке 8, ускоряются со скоростью 49,0 м / с. 2 . Его пассажирская масса 75.0 кг. (а) Рассчитайте горизонтальную составляющую силы, которую сиденье оказывает на его тело. Сравните это с его весом, используя соотношение. (b) Рассчитайте направление и величину общей силы, которую сиденье оказывает на его тело.
Рисунок 8.
12. Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью 201 м / с 2 . В этой задаче силы прилагаются к сиденью и удерживающим ремням.
13. Вес космонавта вместе с его скафандром на Луне составляет всего 250 Н.Сколько они весят на Земле? Какая масса на Луне? На земле?
14. Предположим, масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей составляет 30 000 Н. (а) Рассчитайте величину ускорения при вертикальном взлете с Луны. б) Может ли он взлететь с Земли? Если нет, то почему? Если бы это было возможно, вычислите величину его ускорения.
Глоссарий
- ускорение:
- скорость, с которой скорость объекта изменяется за период времени
- свободное падение:
- ситуация, в которой единственной силой, действующей на объект, является сила тяжести
- трение:
- — сила соприкасающихся объектов друг с другом; Примеры включают шероховатую поверхность и сопротивление воздуха
- чистая внешняя сила:
- векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу ускоряться
- Второй закон движения Ньютона:
- чистая внешняя сила F чистая на объекте с массой m пропорциональна и в том же направлении, что и ускорение объекта, a , и обратно пропорциональна массе; математически определяется как [latex] \ mathbf {\ text {a}} = \ frac {{\ mathbf {\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex]
- система
- определяется границами наблюдаемого объекта или набора объектов; все силы, возникающие извне системы, считаются внешними силами
- вес
- сила w из-за силы тяжести, действующей на объект массой [латекс] м [/ латекс]; математически определяется как: w = mg , где g — величина и направление ускорения свободного падения
Избранные решения проблем и упражнения
1.265 N
3. 13,3 м / с 2
7. (a) 12 м / с 2 (b) Ускорение не в четверть от того, что было при горящих ракетах, потому что сила трения все еще такая же большая, как и при всех горящих ракетах.
9. (a) Система — это ребенок в вагоне плюс вагон.
Рисунок 9
(б)
(c) a = 0,130 м / с 2 в направлении толчка второго ребенка.
(г) a = 0,00 м / с 2
11.(а) 3,68 × 10 3 Н. Эта сила в 5,00 раз превышает его вес. (b) 3750 Н; 11,3º над горизонтом
13. 1,5 × 10 3 Н, 150 кг, 150 кг
Сила, масса и ускорение — второй закон Ньютона
Фотография
Multiflash создает последовательные изображения через равные промежутки времени на одном кадре.
Метод 1. Использование цифровой камеры в режиме множественной вспышки
Созданное изображение можно передавать прямо на компьютер.
Метод 2: Использование видеокамеры
Воспроизведите видео кадр за кадром и поместите прозрачный ацетатный лист на экран телевизора, чтобы записать положение объектов.
Метод 3. Использование камеры и дискового стробоскопа с приводом от двигателя
Вам нужна камера, которая будет фокусироваться на изображениях объектов на расстоянии до 1 метра. Фотокамере потребуется настройка B, при которой затвор остается открытым для непрерывной экспозиции. Используйте большую диафрагму, например f3,5. Цифровые камеры немедленно предоставляют изображение для анализа.В некоторых камерах может потребоваться закрыть фотоэлемент, чтобы затвор оставался открытым.
Установите стробоскоп перед камерой так, чтобы прорези в диске позволяли свету от объекта попадать в объектив камеры через равные промежутки времени по мере вращения диска.
Расстояние между линзой и диском может составлять всего 1 см. Диск с прорезями должен приводиться в движение мотором с использованием синхронного двигателя, чтобы интервалы времени между экспозициями были постоянными.
Вы можете изменять частоту «экспонирования», заклеивая нежелательные щели черной лентой.Делайте это симметрично. Например, диск с 2 открытыми прорезями при 300 об / мин дает 10 экспозиций в секунду.
Чем уже щель, тем резче, но темнее изображение. Сильное освещение объектов или использование источника света в качестве движущегося объекта позволяет использовать более узкую щель.
Осветите объект как можно ярче, но как можно меньше на черном матовом фоне. Слайд-проектор — хороший источник света для этой цели.
Метод 4: Использование ксенонового стробоскопа
Это обеспечивает более четкое изображение, чем при использовании дискового стробоскопа, при условии хорошего затемнения.Общие указания такие же, как для метода 3. Направьте свет от стробоскопа вдоль пути объекта.
При съемке с несколькими вспышками избегайте частоты вспышки в диапазоне 15–20 Гц и избегайте мерцания красного света. Некоторые люди могут плохо себя чувствовать из-за мерцания. Редко у некоторых людей бывает светочувствительная эпилепсия.
Общие советы по успеху
Необходимо устроить частичное затемнение. См. Инструкцию
.
Управление классом в полумраке
Используйте белый или серебристый предмет, например, большой полированный стальной мяч или мяч для гольфа, на темном фоне.В качестве альтернативы можно использовать движущийся источник света, например лампу, прикрепленную к ячейке, с подходящими электрическими соединениями. В этом случае положите подушку на пол, чтобы предотвратить поломку.
Используйте видоискатель, чтобы убедиться, что объект находится в фокусе на протяжении всего своего движения и что достаточный диапазон его движения находится в пределах поля зрения камеры.
Поместите сетку измерений на заднем плане, чтобы можно было проводить измерения. Черная карточка с полосами белой изоленты, скажем, на расстоянии 10 см, обеспечивает сильный контраст и позволяет выделяться освещенному движущемуся объекту.
В качестве альтернативы сетке можно использовать линейку счетчика. Его масштаб обычно не виден на окончательном изображении, но вы можете спроецировать фотографию на экран. Перемещайте проектор до тех пор, пока линейка шкалы на изображении не станет такого же размера, как линейка шкалы, расположенная рядом с экраном. После этого вы можете проводить измерения прямо с экрана.
Используйте штатив и / или систему зажимов и подставок для крепления оборудования. Убедитесь, что любая система максимально жесткая и устойчивая.
Работа в команде имеет значение, особенно в методе 3.Один человек мог управлять камерой, другой — системой стробоскопа, если необходимо, а третий — объектом, который нужно сфотографировать.
- Включить лампу и затемнить комнату.
- Проверьте фокусировку камеры, f 3,5, настройку B.
- Проверьте поле зрения, чтобы убедиться, что весь эксперимент будет записан.
- Стробоскоп Line Up.
- Обратный отсчет 3-2-1-0. Откройте заслонку непосредственно перед началом эксперимента и закройте ее по окончании эксперимента.
5.3 Второй закон Ньютона — University Physics Volume 1
Второй закон Ньютона тесно связан с его первым законом.Он математически показывает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях, связанных с применением силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение силы, массы и ускорения, нам нужно отточить некоторые идеи, о которых мы упоминали ранее.
Сила и ускорение
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости.Изменение скорости по определению означает ускорение. Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ненулевое ускорение .
В разделе «Силы» мы определили внешнюю силу как силу, действующую на объект или систему, которая возникает вне объекта или системы. Давайте рассмотрим эту концепцию дальше. Интуитивно понятное представление о внешнем верно — это вне интересующей системы. Например, на (Рисунок) (а) интересующая система — это автомобиль плюс человек в нем.Две силы, проявленные двумя учениками, — это внешние силы. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в автомобиле держится за рулевое колесо, представляет собой внутреннюю силу между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы нейтрализуют друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними.Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция многократно пересматривается при изучении физики.
Рисунок 5.10 Различные силы, действующие на одну и ту же массу, вызывают разное ускорение. (а) Два студента толкают заглохшую машину. Показаны все внешние силы, действующие на автомобиль. (b) Силы, действующие на автомобиль, переносятся на координатную плоскость (диаграмма свободного тела) для упрощения анализа.(c) Эвакуатор может создавать большую внешнюю силу при той же массе и, следовательно, большее ускорение.
Из этого примера вы можете видеть, что разные силы, действующие на одну и ту же массу, вызывают разное ускорение. На (Рис.) (А) двое учеников толкают машину с водителем. Показаны стрелки, представляющие все внешние силы. Интересующая система — это автомобиль и его водитель. Вес
системы и опоры земли
также показаны для полноты и, как предполагается, отменяются (поскольку не было вертикального движения и дисбаланса сил в вертикальном направлении, чтобы создать изменение в движении).Вектор
представляет трение, действующее на автомобиль, и действует влево, противодействуя движению автомобиля. (Мы обсудим трение более подробно в следующей главе.) На (Рисунок) (b) все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу
.
Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки.Поскольку справа действуют две силы, векторы показаны коллинеарно. Наконец, на (Рисунок) (c), большая чистая внешняя сила вызывает большее ускорение
когда эвакуатор тянет машину.
Кажется разумным, что ускорение будет прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении. Это предположение было проверено экспериментально и проиллюстрировано на (Рисунок). Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения
и чистая внешняя сила
как пропорциональность
где символ
означает «пропорционально.(Напомним из книги «Силы», что чистая внешняя сила представляет собой векторную сумму всех внешних сил и иногда обозначается как
) Эта пропорциональность показывает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе. После выбора интересующей системы определите внешние силы и игнорируйте внутренние. Было бы огромным упрощением игнорировать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в телах учеников, не говоря уже о бесчисленных силах между атомами в объектах.Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.
Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. Как показано на (Рисунок), та же самая чистая внешняя сила, приложенная к баскетбольному мячу, вызывает гораздо меньшее ускорение, когда она применяется к кроссоверу. Пропорциональность записывается как
.
, где м, — масса системы, а и — величина ускорения.Эксперименты показали, что ускорение прямо обратно пропорционально массе, так же как оно прямо пропорционально чистой внешней силе.
Рисунок 5.11 Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (а) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Игнорируйте влияние силы тяжести на мяч.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение. (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации.По мере того, как вы решите больше задач и научитесь рисовать их в Рисование диаграмм свободного тела, появится серия шаблонов для диаграмм свободного тела.
Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Комбинируя две только что приведенные пропорциональности, получаем второй закон Ньютона .
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе.В форме уравнения второй закон Ньютона равен
.
где
— ускорение,
— это чистая сила, а м — масса. Это часто записывается в более привычной форме
.
, но первое уравнение дает более полное представление о том, что означает второй закон Ньютона. Если рассматривать только величину силы и ускорения, это уравнение можно записать в более простой скалярной форме:
Закон — это причинно-следственная связь между тремя величинами, которая не просто основана на их определениях.Справедливость второго закона основана на экспериментальной проверке. Диаграмма свободного тела, которую вы научитесь рисовать в «Рисование диаграмм свободного тела», является основой для написания второго закона Ньютона.
Пример
Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле ((Рисунок)). Масса косилки 24 кг. Какое у него ускорение?
Рисунок 5.12 (a) Чистое усилие на газонокосилке составляет 51 Н. вправо. С какой скоростью газонокосилка ускоряется вправо? (б) Показана диаграмма свободного тела для этой задачи.
Стратегия
Эта проблема связана только с движением в горизонтальном направлении; нам также дана чистая сила, обозначенная одним вектором, но мы можем подавить векторную природу и сосредоточиться на применении второго закона Ньютона. С
и м. , ускорение можно рассчитать непосредственно из второго закона Ньютона как
Решение
Величина ускорения а составляет
.Ввод известных значений дает
Если заменить ньютон на килограммы, умноженные на метры в секунду в квадрате, получим
.
Значение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. Это результат векторной связи, выраженной во втором законе Ньютона, то есть вектор, представляющий чистую силу, является скалярным кратным вектору ускорения.В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, поскольку в вертикальном направлении не происходит ускорения (косилка движется только по горизонтали). Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку.Такое усилие не продлится слишком долго, потому что человек скоро наберет максимальную скорость.
Проверьте свое понимание
На момент запуска HMS Titanic был самым массивным мобильным объектом из когда-либо построенных, с массой
единиц.
. При силе 6 МН
был применен к кораблю, какое ускорение он испытает?
[показывать-ответ q = ”fs-id116503
66 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id116503
66 ″]
[/ hidden-answer]
В предыдущем примере мы имели дело с чистой силой только для простоты.Однако на газонокосилку действует несколько сил. Вес
(подробно обсуждается в разделе «Масса и вес») тянет косилку вниз к центру Земли; это создает контактное усилие на земле. Земля должна оказывать на газонокосилку восходящую силу, известную как нормальная сила
.
, который мы определяем в Common Forces. Эти силы уравновешены и поэтому не вызывают вертикального ускорения. В следующем примере мы показываем обе эти силы.Продолжая решать проблемы, используя второй закон Ньютона, не забудьте показать множественные силы.
Пример
Какая сила больше?
(a) Автомобиль, показанный на (Рисунок), движется с постоянной скоростью. Какая сила больше,
или
? Объяснять.
(b) Эта же машина сейчас ускоряется вправо. Какая сила больше,
или
Объясните.
Рис. 5.13 Автомобиль показан (а) движущимся с постоянной скоростью и (б) ускоряющимся. Как соотносятся силы, действующие на автомобиль, в каждом конкретном случае? а) Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль, по сравнению с силой трения? б) Что знание того, что автомобиль ускоряется, говорит нам о горизонтальной силе, действующей на автомобиль, по сравнению с силой трения?
Стратегия
Мы должны рассмотреть первый и второй законы Ньютона, чтобы проанализировать ситуацию.Нам нужно решить, какой закон применяется; это, в свою очередь, расскажет нам о соотношении сил.
Решение
- Силы равны. Согласно первому закону Ньютона, если результирующая сила равна нулю, скорость постоянна.
- В этом случае
должно быть больше
Согласно второму закону Ньютона, для ускорения требуется чистая сила.
Значение
Эти вопросы могут показаться тривиальными, но обычно на них отвечают неверно.Чтобы автомобиль или любой другой объект двинулся, его нужно разогнать до желаемой скорости; для этого требуется, чтобы сила двигателя была больше силы трения. Когда автомобиль движется с постоянной скоростью, результирующая сила должна быть равна нулю; в противном случае автомобиль будет ускоряться (набирать скорость). Чтобы решить проблемы, связанные с законами Ньютона, мы должны понять, применять ли первый закон Ньютона (где
) или второй закон Ньютона (где
не равно нулю).Это станет очевидным, когда вы увидите больше примеров и попытаетесь решить проблемы самостоятельно.
Пример
Какая ракетная тяга ускоряет этот снегоход?
До пилотируемых космических полетов ракетные сани использовались для проверки самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.
Рассчитайте величину силы, прилагаемой каждой ракетой, которая называется ее тягой T , для четырехракетной двигательной установки, показанной на (Рисунок).Начальное ускорение салазок
, масса системы 2100 кг, сила трения, противодействующая движению, 650 Н.
Рис. 5.14 Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Система здесь представляет собой салазки, их ракеты и их всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение
нарисован в крупном масштабе.
Стратегия
Хотя силы действуют как вертикально, так и горизонтально, мы предполагаем, что вертикальные силы компенсируются, потому что нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на (Рисунок).
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей.Мы определили направление силы и ускорения как действующее «вправо», поэтому нам нужно учитывать только величины этих величин в расчетах. Следовательно, мы начинаем с
где
— чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует тяги. В форме уравнения чистая внешняя сила равна
.
Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
Следовательно, общая тяга
и индивидуальные тяги
Значение
Цифры довольно большие, поэтому результат может вас удивить.Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости, и установка была разработана для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g ’s. (Напомним, что g , ускорение свободного падения, равно
. Когда мы говорим, что ускорение составляет 45 g с, это
.
, что составляет примерно
.) Хотя живые предметы больше не используются, наземная скорость 10 000 км / ч была получена с помощью ракетных саней.
В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон Ньютона — это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.
Проверьте свое понимание
Спортивный автомобиль массой 550 кг сталкивается с грузовиком массой 2200 кг, и во время столкновения результирующая сила, действующая на каждое транспортное средство, равна силе, прилагаемой другим. Если величина ускорения грузовика
какова величина ускорения спортивного автомобиля?
[показывать-ответ q = ”fs-id1165039454293 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039454293 ″]
[/ hidden-answer]
Составная форма второго закона Ньютона
Мы разработали второй закон Ньютона и представили его в виде векторного уравнения (рисунок).Это векторное уравнение можно записать в виде трехкомпонентных уравнений:
Второй закон — это описание того, как тело механически реагирует на окружающую среду. Влияние окружающей среды — чистая сила
реакция тела — ускорение
, а сила отклика обратно пропорциональна массе м . Чем больше масса объекта, тем меньше его реакция (его ускорение) на влияние окружающей среды (заданная результирующая сила).Следовательно, масса тела является мерой его инерции, как мы объясняли в Первом законе Ньютона.
Пример
Сила на футбольном мяче
Игрок перебрасывает футбольный мяч весом 0,400 кг через поле; он подвергается ускорению, заданному
Найдите (а) результирующую силу, действующую на мяч, и (б) величину и направление результирующей силы.
Стратегия
Векторов в
и
, которые указывают направление силы вдоль оси x и оси y соответственно, поэтому мы применяем второй закон Ньютона в векторной форме.
Решение
- Применяем второй закон Ньютона:
- Величина и направление находятся с использованием компонентов
:
Значение
Мы должны помнить, что второй закон Ньютона является векторным уравнением. В (а) мы умножаем вектор на скаляр, чтобы определить результирующую силу в векторной форме. Хотя векторная форма дает компактное представление вектора силы, она не говорит нам, насколько он «большой» или куда он идет, в интуитивно понятных терминах.В (b) мы определяем действительный размер (величину) этой силы и направление, в котором она движется.
Пример
Масса автомобиля
Найдите массу автомобиля, если чистая сила равна
.
дает ускорение
.
Стратегия
Векторное деление не определено, поэтому
не может быть выполнено. Однако масса m является скаляром, поэтому мы можем использовать скалярную форму второго закона Ньютона,
.
.
Решение
Мы используем
и подставляем величины двух векторов:
и
Следовательно,
Значение
Сила и ускорение были даны в
и
, но ответ, масса м , является скаляром и поэтому не дается в
и
форма.
Пример
Несколько сил на частицу
Частица массой
На
действуют четыре силы величин.
, с направлениями, показанными на схеме свободного тела на (Рисунок). Что такое ускорение частицы?
Рис. 5.15 Четыре силы в плоскости xy действуют на частицу массой 4,0 кг.
Стратегия
Поскольку это двумерная задача, мы должны использовать диаграмму свободного тела.Первая,
необходимо разделить на компоненты x и y . Затем мы можем применить второй закон в каждом направлении.
Решение
Рисуем диаграмму свободного тела, как показано на (Рисунок). Теперь применим второй закон Ньютона. Мы рассматриваем все векторы, разделенные на компоненты x и y :
Таким образом, чистое ускорение равно
.
, который является вектором величины
.
направлено на
к положительной оси x .
Значение
В повседневной жизни можно найти множество примеров, когда на один объект действуют три или более сил, например, кабели, идущие от моста Золотые Ворота, или футболиста, которого атакуют три защитника. Мы видим, что решение этого примера является просто продолжением того, что мы уже сделали.
Проверьте свое понимание
На автомобиль действуют силы, как показано ниже. Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трение можно не учитывать.а) Какова чистая сила, действующая на машину? б) Какое ускорение у автомобиля?
[показать-ответ q = ”153079 ″] Показать ответ [/ раскрыть-ответ] [скрытый-ответ a =” 153079 ″] а.
; б.
[/ hidden-answer]
Второй закон и импульс Ньютона
Ньютон фактически сформулировал свой второй закон в терминах количества движения: «Мгновенная скорость изменения количества движения тела равна чистой силе, действующей на тело.»(« Мгновенная скорость »подразумевает, что задействована производная.) Это может быть задано векторным уравнением
Это означает, что второй закон Ньютона обращается к центральному вопросу движения: что вызывает изменение движения объекта? Импульс был описан Ньютоном как «количество движения», способ объединения скорости объекта и его массы. Мы посвящаем линейный импульс и столкновения изучению импульса .
Пока достаточно определить импульс
как произведение массы объекта м и его скорости
:
Поскольку скорость — вектор, импульс тоже.
Импульс легко визуализировать. Поезд, движущийся со скоростью 10 м / с, имеет больше импульса, чем поезд, движущийся со скоростью 2 м / с. В повседневной жизни мы говорим об одной спортивной команде как о «имеющей импульс», когда она набирает очки против команды соперника.
Если подставить (рисунок) в (рисунок), то получим
Когда м постоянно, мы имеем
Таким образом, мы видим, что импульсная форма второго закона Ньютона сводится к форме, приведенной ранее в этом разделе.
Лаборатория 3 — Второй закон Ньютона
Введение
Сэр Исаак Ньютон выдвинул много важных идей в своей знаменитой книге The Principia . Его три закона движения — самые известные из них.
Кажется, что первый закон противоречит нашему повседневному опыту. Первый закон Ньютона гласит, что любой объект в состоянии покоя, на который не действуют внешние силы, будет оставаться в состоянии покоя, и что любой объект в движении, на который не действуют внешние силы, будет продолжать движение по прямой линии с постоянной скоростью.Если мы катим мяч по полу, мы знаем, что он в конечном итоге остановится, что, по-видимому, противоречит Первому закону. Наш опыт, кажется, согласуется с идеей Аристотеля о том, что «импульс», данный мячу, исчерпывается по мере его катания. Но Аристотель ошибался, как и наше первое впечатление о движении мяча.
Суть в том, что мяч действительно испытывает внешнюю силу, то есть трение, когда он катится по полу. Эта сила заставляет мяч замедляться (то есть имеет «отрицательное» ускорение).Согласно второму закону Ньютона объект будет ускоряться в направлении чистой силы . Поскольку сила трения противоположна направлению движения, это ускорение заставляет объект замедлять свое поступательное движение и в конечном итоге останавливаться.
Цель этого лабораторного упражнения — проверить второй закон Ньютона.
Обсуждение принципов
Второй закон Ньютона в векторной форме имеет вид
Эта сила заставляет шарик, катящийся по полу, замедляться (то есть иметь «отрицательное» ускорение).Согласно второму закону Ньютона, объект будет ускоряться в направлении действующей силы. Если
F
— это величина чистой силы, и если
м
— масса объекта, то ускорение определяется по формуле
(2)
а =
| F |
| м |
Поскольку сила трения имеет направление, противоположное направлению движения, это ускорение заставляет объект замедлять свое поступательное движение и в конечном итоге останавливаться.Обратите внимание, что уравнение. (1) и уравнение. (2) a =
| F |
| m |
записываются в векторной форме. Это означает, что второй закон Ньютона верен во всех направлениях. Вы всегда можете разделить силы и результирующее ускорение на соответствующие составляющие в направлениях
x
,
y
и
z
.
Рассмотрим тележку на гусенице с низким коэффициентом трения, как показано на рис. 1. К тележке прикреплена легкая струна, которая проходит через шкив в конце гусеницы, а к концу этой струны прикреплена вторая масса.Вес подвешенной массы обеспечивает натяжение тетивы, что способствует ускорению тележки по рельсам. Этому движению будет сопротивляться небольшая сила трения.
Мы предполагаем, что струна не имеет массы (или ее можно пренебречь) и между струной и шкивом нет трения. Следовательно, натяжение струны будет одинаковым во всех точках струны. Это приводит к тому, что обе массы имеют одинаковую величину ускорения, но направление ускорения будет разным. Тележка будет ускоряться вправо, в то время как подвешенная масса будет ускоряться в направлении вниз, как показано на рис.1.
Рисунок 1 : Двухмассовая система
Мы возьмем положительное направление в направлении ускорения двух масс, как показано системой координатных осей на рис. 1. Диаграммы свободного тела для двух масс показаны на рис. 2. Давайте посмотрим на силы. действуя на каждую массу.
Рисунок 2 : Диаграммы свободного тела для двух масс
Для падающей массы
м 1
отсутствуют силы, действующие в горизонтальном направлении.В вертикальном направлении он тянется вниз под действием силы тяжести, придавая объекту вес
W = m 1 g
и вверх за счет натяжения
T
в струне. См. Рис. 2b. Таким образом, второй закон Ньютона, примененный к падающей массе в направлении
y
, будет следующим:
(6)
F net, 1 = m 1 g — T = m 1 a
где направление , направленное вниз, было выбрано положительным.На рис. 2а показаны силы, действующие на
м 2
. Тележка в вертикальном направлении не движется. Следовательно, результирующая сила в вертикальном направлении будет равна нулю, как и ускорение. В горизонтальном направлении натяжение струны действует на тележку в направлении
+ x
, в то время как сила трения между шинами тележки и поверхностью гусеницы действует в направлении
— x
. Второй закон Ньютона в направлениях
x
и
y
соответственно равен
(7)
F net, 2x = T — f = m 2 a
(8)
F net, 2y = F N — m 2 g = 0
Поскольку тележка и подвешенная масса связаны веревкой, которая не растягивается, оба ускорения, появляющиеся в уравнении.(6)
F net, 1 = m 1 g — T = m 1 a
и уравнение. (7)
F net, 2x = T — f = m 2 a
представляют те же физические свойства. Напряженность такая же из-за третьего закона Ньютона. Объедините уравнение. (6)
F net, 1 = m 1 g — T = m 1 a
и уравнение. (7)
F net, 2x = T — f = m 2 a
для исключения
T
.
(9)
m 1 g = (m 1 + m 2 ) a + f
Обратите внимание, что уравнение.(9)
m 1 g = (m 1 + m 2 ) a + f
имеет форму линейного уравнения
y = mx + b
, где m — наклон, а
b
— это перехват
и
.
Объектив
Цель этого эксперимента — проверить справедливость второго закона Ньютона, который гласит, что результирующая сила, действующая на объект, прямо пропорциональна его ускорению. Уравнение (9)
m 1 g = (m 1 + m 2 ) a + f
было получено на основании этого закона.Поэтому мы можем рассмотреть уравнение. (9) быть предсказанием второго закона. В этом эксперименте мы постараемся проверить это конкретное предсказание и тем самым предоставить доказательства справедливости второго закона.
Оборудование
Гусеница с низким коэффициентом трения со шкивом
Корзина
Нить
Остаток средств
Программное обеспечение DataStudio
Два фотоката
Ассорти масс
Весовая вешалка
Компьютер
Сигнальный интерфейс
Процедура
Вы проведете несколько испытаний, сохраняя общую массу
M = m 1 + m 2
постоянной при изменении
m 1
и, следовательно,
m 2
, чтобы получить другое значение
a
. для каждого значения
м 1
.Построив график
и
против
м 1 г
, вы сможете найти
M
, общую массу системы из уравнения. (9)
m 1 g = (m 1 + m 2 ) a + f
.
К тележке прикреплен металлический флажок, который заставит два фотозатвора, размещенных на фиксированном расстоянии друг от друга, реагировать, когда тележка проходит через них. Компьютер, подключенный к фотозатвору, будет измерять и отображать временные интервалы, прошедшие, пока флаг проходит через два фотозабора.По этим временным интервалам и длине флага компьютер вычислит скорости
v 1
и
v 2
тележки на каждом из фотозатворов. Кроме того, из компьютерных данных вы можете определить интервал времени
Δt
, который требуется тележке для перемещения между фотозатвором. Тогда ускорение
a
между двумя воротами можно рассчитать по формуле
где
v 1
— скорость на первом фотозатворе, а
v 2
— скорость на втором фотозатворе.
Наладка оборудования
1
Используя регулировочные винты под ними, выровняйте гусеницу, чтобы тележка не двигалась, когда она размещается в центре гусеницы.
Поскольку тележка имеет некоторое трение, проверьте, выровнена ли гусеница, слегка подтолкнув тележку вправо и сравнив движение с аналогичным толчком влево.
2
Разместите фотошаблоны достаточно далеко друг от друга.
Убедитесь, что флажок тележки находится перед первыми воротами, когда подвеска полностью поднята рядом со шкивом, как показано на рис.3а.
Кроме того, убедитесь, что флаг тележки проходит через второй фотозатвор до того, как вешалка упадет на землю. См. Рис. 3b.
Это обеспечит ускорение тележки в области между двумя фотозатвором.
3
Отрегулируйте высоту каждой заслонки так, чтобы небольшой металлический флажок на тележке блокировал световой луч фотозатвора, когда он проходит.
Рисунок 3 : Настройка фотозатвора
Рисунок 4 : Экспериментальная установка
4
Подключите фотозатвор 1 к цифровому каналу 1, а фотозатвор 2 — к цифровому каналу 2.Если фотозатворы подключены правильно, красный светодиод на фотозатворе загорится, когда инфракрасный луч заблокирован.
5
Откройте соответствующий файл Capstone, связанный с этой лабораторной работой. На рис. 5 показан начальный экран в Capstone.
Рисунок 5 : Отображение второго закона Ньютона
6
Длина небольшого металлического флажка на тележке разная для каждой тележки. Измерьте свою тележку и запишите это на листе.
7
Вы должны ввести значение длины флажка и расстояния между фотозатвором, как показано на рис. 6. Не забудьте нажать кнопку «Сохранить».
Рисунок 6 : Ввод длины флажка
Сбор данных
8
Поместите тележку в конце гусеницы подальше от шкива. Добавьте в тележку три гири по 50 грамм.
9
Взвесьте весовую подвеску и запишите на листе массу
M h
.
10
Подсоедините один конец веревки к подвеске груза, а другой конец — к тележке, поместив веревку на шкив. См. Рис.3.
11
Удерживайте тележку в таком положении, чтобы при отпускании тележка ускорялась.
Когда будете готовы к записи данных, нажмите кнопку Start .
Освободите тележку и поймайте ее, когда она достигнет конца пути.
Нажмите кнопку Stop , чтобы завершить запись данных.
Данные о времени и скорости для каждого фотозатвора будут автоматически представлены в таблице.См. Рис.7.
Рисунок 7 : Пример таблицы данных
12
Скорость тележки плавно увеличивается в течение промежутка времени, пока флаг проходит через луч фотозатвора. В какой-то момент в течение этого интервала времени мгновенная скорость тележки равна средней скорости за интервал. Этот момент времени отображается в столбце «Время (с)» рядом с соответствующей скоростью.
13
Время, затраченное тележкой на прохождение между фотозаборами 1 и 2, составляет
Δt
.Это вычисляется путем вычитания значения времени в столбце Velocity in Gate, Ch2 из значения времени в столбце Velocity in Gate, Ch 2.
Вычислите
Δt
и запишите это в Таблицу данных 1 на рабочем листе.
14
Используйте этот временной интервал вместе с двумя скоростями
v 1
и
v 2
в уравнении. (10), чтобы вычислить ускорение тележки между двумя фотозатвором и записать этот результат в Таблицу данных 1.
15
Переместите одну 50-граммовую гирю из тележки на вешалку.
Примечание : Вы должны поддерживать постоянную общую массу, поэтому любую массу, снятую с тележки, необходимо добавить на подвеску для грузов.
16
Повторите шаги с 11 по 15 еще три раза, пока у вас не будет в общей сложности четырех прогонов с разными значениями подвешенной массы для каждого прогона. Рассчитайте и запишите ускорение для каждого случая.
Контрольная точка 1:
Попросите своего технического специалиста проверить значения в вашей таблице, прежде чем продолжить.
Анализ результатов
17
Используя график Excel
m 1 g
по сравнению с
a
. См. Приложение G.
18
Используйте опцию линии тренда в Excel, чтобы нарисовать линию наилучшего соответствия для данных и определить наклон и интервал
y
. См. Приложение H.
Запишите эти значения на листе.
19
По величине уклона определяют общую массу системы.
20
Используйте весы, чтобы измерить массу тележки.Добавьте это к массе подвески груза и добавленным массам, чтобы получить общую массу
M
системы.
21
Сравните эту измеренную массу с массой, определенной по наклону графика, вычислив разницу в процентах. Запишите это на листе. См. Приложение Б.
Контрольная точка 2:
Попросите своего технического специалиста проверить ваш рабочий лист и график Excel.
Авторские права © 2012 Advanced Instructional Systems Inc.и государственный университет Северной Каролины | Кредиты
Сила, масса и ускорение: второй закон движения Ньютона
Первый закон движения Исаака Ньютона гласит: «Покоящееся тело будет оставаться в покое, а тело в движении будет оставаться в движении, если на него не действует внешняя сила». Что же тогда происходит с телом при приложении к нему внешней силы? Эта ситуация описывается вторым законом движения Ньютона.
Согласно НАСА, этот закон гласит: «Сила равна изменению количества движения за изменение во времени.Для постоянной массы сила равна массе, умноженной на ускорение ». В математической форме это записывается как F = м a
F — сила, м — масса и a — ускорение. математика, лежащая в основе этого, довольно проста. Если вы удвоите силу, вы удвоите ускорение, но если вы удвоите массу, вы уменьшите ускорение вдвое.
Ньютон опубликовал свои законы движения в 1687 году в своей основополагающей работе «Philosophiæ Naturalis» Principia Mathematica »(« Математические принципы естественной философии »), в которой он формализовал описание того, как массивные тела движутся под действием внешних сил.
Ньютон расширил более раннюю работу Галилео Галилея, который разработал первые точные законы движения масс, по словам Грега Ботуна, профессора физики в Университете Орегона. Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью, независимо от размера и массы. Ньютон также раскритиковал и расширил работу Рене Декарта, который также опубликовал свод законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.
Ускорение и скорость
Второй закон Ньютона гласит, что когда на массивное тело действует постоянная сила, она заставляет его ускоряться, то есть изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация рассматривается из движущейся инерциальной системы отсчета, это тело может казаться ускоряющимся, замедляющимся или меняющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета движутся относительно друг друга.
Полужирные буквы F и a в уравнении указывают, что сила и ускорение являются векторными величинами , что означает, что они имеют как величину, так и направление. Сила может быть одной силой или сочетанием более чем одной силы. В этом случае мы бы записали уравнение как ∑ F = м a
Большой Σ (греческая буква сигма) представляет векторную сумму всех сил, или результирующую силу, действующую на тело.
Довольно сложно представить приложение постоянной силы к телу в течение неопределенного промежутка времени. В большинстве случаев силы могут применяться только в течение ограниченного времени, создавая так называемый импульс . Для массивного тела, движущегося в инерциальной системе отсчета без каких-либо других сил, таких как трение, действующих на него, определенный импульс вызовет определенное изменение его скорости. Тело может ускориться, замедлиться или изменить направление, после чего оно продолжит движение с новой постоянной скоростью (если, конечно, импульс не заставит тело остановиться).
Однако есть одна ситуация, в которой мы действительно сталкиваемся с постоянной силой — силой, вызванной гравитационным ускорением, которая заставляет массивные тела оказывать на Землю нисходящую силу. В этом случае постоянное ускорение свободного падения записывается как g , а Второй закон Ньютона становится F = mg . Обратите внимание, что в этом случае F и g обычно не записываются как векторы, потому что они всегда указывают в одном направлении, вниз.
Произведение массы на гравитационное ускорение, мг , известно как вес , что представляет собой просто еще один вид силы.Без гравитации массивное тело не имеет веса, а без массивного тела гравитация не может создавать силу. Чтобы преодолеть гравитацию и поднять массивное тело, вы должны создать направленную вверх силу m a , которая больше, чем сила тяжести, направленная вниз mg .
Второй закон Ньютона в действии
Ракеты, путешествующие в космосе, охватывают все три закона движения Ньютона.
Если ракете необходимо замедлить, ускориться или изменить направление, для ее толчка используется сила, обычно исходящая от двигателя.Величина силы и место, в котором она обеспечивает толчок, могут изменять либо скорость (часть величины ускорения), либо направление, либо и то, и другое.
Теперь, когда мы знаем, как массивное тело в инерциальной системе отсчета ведет себя, когда на него действует внешняя сила, например, как двигатели, создающие толкающий маневр, маневрируют ракетой, что происходит с телом, которое проявляет эту силу? Эта ситуация описывается третьим законом движения Ньютона.
Дополнительный отчет от Рэйчел Росс, автора Live Science.
См. Также:
Дополнительные ресурсы
4.3 Второй закон движения Ньютона — Физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Устно и математически описать второй закон Ньютона
- Используйте второй закон Ньютона для решения проблем
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут учащимся освоить следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (D) вычисляет влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Перед тем, как начать этот раздел, просмотрите силы, ускорение, ускорение свободного падения (g), трение, инерцию и первый закон Ньютона.
Раздел Основные термины
| в свободном падении | Второй закон движения Ньютона | вес |
Описание второго закона движения Ньютона
Поддержка учителей
Поддержка учителей
[BL] [OL] Просмотрите концепции инерции и первый закон Ньютона.Объясните: согласно первому закону Ньютона изменение движения вызывается внешней силой. Например, подброшенный мяч меняет свою скорость и направление, когда по нему попадает летучая мышь.
[BL] [OL] [AL] Напишите уравнение для второго закона Ньютона и покажите, как его можно решить для всех трех переменных: F , m и a . Объясните практическое значение для каждого случая. Спросите студентов, как бы вели себя две другие переменные, если бы одна величина оставалась постоянной.
Предупреждение о заблуждении
Студенты могут перепутать термины , равные , и , пропорциональные .
Первый закон Ньютона рассматривал тела в покое или тела, движущиеся с постоянной скоростью. Другое состояние движения, которое следует учитывать, — это когда объект движется с изменяющейся скоростью, что означает изменение скорости и / или направления движения. Этот тип движения рассматривается во втором законе движения Ньютона, который гласит, как сила вызывает изменения в движении.Второй закон движения Ньютона используется для расчета того, что происходит в ситуациях, связанных с силами и движением, и показывает математическую взаимосвязь между силой, массой и ускорением . Математически второй закон чаще всего записывается как
Fnet = maorΣF = ma, Fnet = maorΣF = ma,
4,2
, где F net (или ∑ F ) — чистая внешняя сила, м — масса системы, а — — ускорение. Обратите внимание, что F net и ∑ F одинаковы, поскольку чистая внешняя сила является суммой всех внешних сил, действующих на систему.
Во-первых, что мы подразумеваем под изменением движения ? Изменение движения — это просто изменение скорости: скорость объекта может стать медленнее или быстрее, направление, в котором движется объект, может измениться, или обе эти переменные могут измениться. Изменение скорости по определению означает, что произошло ускорение. Первый закон Ньютона гласит, что только ненулевая чистая внешняя сила может вызвать изменение движения, поэтому чистая внешняя сила должна вызывать ускорение. Обратите внимание, что ускорение может относиться к замедлению или ускорению.Ускорение также может относиться к изменению направления движения без изменения скорости, потому что ускорение — это изменение скорости, деленное на время, необходимое для того, чтобы это изменение произошло, скорость и определяется скоростью и направлением .
Из уравнения Fnet = ma, Fnet = ma мы видим, что сила прямо пропорциональна массе и ускорению, что имеет смысл. Чтобы ускорить два объекта из состояния покоя до одной и той же скорости, можно ожидать, что для ускорения более массивного объекта потребуется больше силы.Точно так же для двух объектов одинаковой массы приложение большей силы к одному ускорит его до большей скорости.
Теперь давайте изменим второй закон Ньютона, чтобы найти ускорение. Получаем
a = Fnetmora = ΣFm.a = Fnetmora = ΣFm.
4.3
В этой форме мы видим, что ускорение прямо пропорционально силе, которую мы записываем как
, где символ ∝∝ означает , пропорциональный .
Эта пропорциональность математически выражает то, что мы только что сказали словами: ускорение прямо пропорционально чистой внешней силе.Когда две переменные прямо пропорциональны друг другу, тогда, если одна переменная удваивается, другая переменная должна удваиваться. Аналогичным образом, если одна переменная уменьшается вдвое, другая переменная также должна быть уменьшена вдвое. Обычно, когда одна переменная умножается на число, другая переменная также умножается на то же число. Кажется разумным, что ускорение системы должно быть прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему. Объект испытывает большее ускорение, когда на него действует большая сила.
Из уравнения a = Fnet / ma = Fnet / m также ясно, что ускорение обратно пропорционально массе, которую мы записываем как
a 1m.a ∝ 1m.
4,5
Обратно пропорциональный означает, что если одна переменная умножается на число, другая переменная должна быть разделена на на то же число. Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.Эта взаимосвязь проиллюстрирована на рис. 4.5, который показывает, что заданная чистая внешняя сила, приложенная к баскетбольному мячу, вызывает гораздо большее ускорение, чем при приложении к автомобилю.
Рис. 4.5 Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (а) Мальчик толкает баскетбольный мяч, чтобы сделать передачу. Влияние силы тяжести на мяч игнорируется. (б) Тот же мальчик, толкающий с одинаковой силой заглохшую машину, дает гораздо меньшее ускорение (трение незначительно).Обратите внимание, что диаграммы свободного тела для мяча и для автомобиля идентичны, что позволяет нам сравнивать эти две ситуации.
Применение второго закона Ньютона
Поддержка учителей
Поддержка учителей
[BL] Узнайте, как преобразовывать единицы измерения.
[OL] [AL] Попросите студентов привести примеры второго закона Ньютона.
Предупреждение о заблуждении
Учащиеся могут спутать вес, который представляет собой силу, и г, , что означает ускорение свободного падения.
[BL] [OL] [AL] Спросите студентов, думают ли они, что космонавт весит на Луне столько же, сколько они на Земле. Поговорим о разнице между массой и весом.
Прежде чем применять второй закон Ньютона, важно рассмотреть единицы измерения.
Уравнение Fnet = maFnet = ma используется для определения единиц силы в терминах трех основных единиц массы, длины и времени (напомним, что ускорение состоит из единиц длины, разделенных на квадрат времени). Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 .То есть, поскольку Fnet = ma, Fnet = ma, мы имеем
1N = 1 кг × 1 м / с2 = 1 кг⋅мс2,1N = 1 кг × 1 м / с2 = 1 кг⋅мс2.
4,6
Одним из наиболее важных применений второго закона Ньютона является вычисление веса (также известного как сила тяжести), который математически обычно представляется как W . Когда люди говорят о гравитации, они не всегда понимают, что это ускорение. Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что чистая внешняя сила, действующая на объект, ответственна за его ускорение.Если сопротивление воздуха незначительно, чистая внешняя сила, действующая на падающий объект, представляет собой только силу тяжести (т. Е. Вес объекта).
Вес может быть представлен вектором, потому что он имеет направление. Вниз определяется как направление, в котором тянет сила тяжести, поэтому вес обычно считается направленной вниз силой. Используя второй закон Ньютона, мы можем вычислить уравнение веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только силу тяжести (т.е., гравитационная сила или вес), который представлен вторым законом У. Ньютона, согласно которому Fnet = ma.Fnet = ma. Поскольку единственная сила, действующая на объект, — это сила тяжести, мы имеем Fnet = W.Fnet = W. Мы знаем, что ускорение объекта под действием силы тяжести составляет g , поэтому мы имеем a = g.a = g. Подставляя эти два выражения во второй закон Ньютона, получаем
Это уравнение для веса — силы тяжести на массу м . На Земле g = 9,80 м / с2, g = 9.80 м / с2, поэтому вес (без учета направления веса) объекта массой 1,0 кг на Земле составляет
Вт = mg = (1,0 кг) (9,80 м / с2) = 9,8 NW = mg = (1,0 кг) (9,80 м / с2) = 9,8 Н.
4,8
Хотя в большинстве стран мира в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Напомним, что хотя сила тяжести действует вниз, ей можно присвоить положительное или отрицательное значение, в зависимости от того, какое положительное направление находится в выбранной вами системе координат.Обязательно учтите это при решении задач с весом. Когда направление вниз считается отрицательным, как это часто бывает, ускорение свободного падения становится равным
g = -9,8 м / с 2 .
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении. В этом случае единственной силой, действующей на объект, является сила тяжести. На поверхности Земли, когда объекты падают вниз к Земле, они никогда не находятся в истинном свободном падении, потому что всегда существует некоторая восходящая сила из-за сопротивления воздуха, которое действует на объект (и есть также сила плавучести воздуха, которая аналогична сила плавучести в воде, которая удерживает лодки на плаву).
Гравитация незначительно меняется на поверхности Земли, поэтому вес объекта очень слабо зависит от его местоположения на Земле. Вес резко меняется от поверхности Земли. На Луне, например, ускорение свободного падения составляет всего 1,67 м / с 2 . Поскольку вес зависит от силы тяжести, масса в 1,0 кг весит 9,8 Н на Земле и всего около 1,7 Н на Луне.
Важно помнить, что вес и масса очень разные, хотя они тесно связаны.Масса — это количество материи (сколько материала ) в объекте и не меняется, но вес — это сила тяжести на объекте, пропорциональная силе тяжести. Их легко спутать, потому что наш опыт ограничен Землей, а вес объекта по существу одинаков, независимо от того, где вы находитесь на Земле. Путаницу усугубляет то, что в повседневном языке термины масса и вес часто используются как синонимы; например, в наших медицинских записях наш вес часто указывается в килограммах, но никогда не в ньютонах.
Snap Lab
Масса и вес
Поддержка учителя
Поддержка учителя
Объясните: хотя весы показывают массу, они фактически измеряют вес. Весы откалиброваны, чтобы показывать правильную массу на Земле. На Луне они дадут разные результаты, потому что на Луне сила тяжести слабее.
В этом упражнении вы будете использовать весы для определения массы и веса.
- Что измеряют весы для ванной?
- Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении.
- Пружины позволяют измерить ваш вес (при условии, что вы не ускоряетесь). Это сила в ньютонах (или фунтах). В большинстве стран измерение теперь делится на 9,80, чтобы получить значение в килограммах, что соответствует массе. Весы определяют вес, но откалиброваны для отображения массы.
- Если бы вы отправились на Луну и встали на свои весы, обнаружила бы она ту же массу , что и на Земле?
Проверка захвата
Стоя на весах в ванной, нажмите на соседний стол.Что происходит с чтением? Почему?
- Показание увеличивается, потому что часть вашего веса прикладывается к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание увеличивается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, которая действует в направлении, противоположном вашему весу.
- Показание уменьшается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание уменьшается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении, противоположном вашему весу.
Советы для успеха
Только чистая внешняя сила влияет на ускорение объекта. Если на объект действует более одной силы, и вы вычисляете ускорение, используя только одну из этих сил, вы не получите правильное ускорение для этого объекта.
Watch Physics
Второй закон движения Ньютона
В этом видео рассматривается второй закон движения Ньютона и то, как чистая внешняя сила и ускорение связаны друг с другом и с массой.Он также охватывает единицы силы, массы и ускорения и рассматривает отработанный пример.
Проверка захвата
Верно или неверно — если вы хотите уменьшить ускорение объекта до половины от его первоначального значения, вам нужно будет уменьшить чистую внешнюю силу вдвое.
- Истинно
- Ложь
Рабочий пример
Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н, параллельную земле.Масса косилки 240 кг. Какое у него ускорение?
Рисунок 4.6
Стратегия
Поскольку даны F net и м , ускорение можно рассчитать непосредственно по второму закону Ньютона: F net = м a .
Решение
Решая второй закон Ньютона для ускорения, мы находим, что величина ускорения, a , равна a = Fnetm.а = Fnetm. Ввод данных значений чистой внешней силы и массы дает
a = 51 N240 kga = 51 N240 кг
4,9
Вставка единиц кг⋅м / с2кг⋅м / с2 для N дает
a = 51 кг⋅м / с2240 кг = 0,21 м / с2. A = 51 кгм / с2240 кг = 0,21 м / с2.
4,10
Обсуждение
Ускорение происходит в том же направлении, что и чистая внешняя сила, которая параллельна земле и направо. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах.Например, сила, прилагаемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению, потому что нам дано, что чистая внешняя сила направлена в направлении, в котором толкает человек. Кроме того, вертикальные силы должны нейтрализоваться, если нет ускорения в вертикальном направлении (косилка движется только горизонтально). Найденное ускорение приемлемо для человека, толкающего косилку; скорость косилки должна увеличиваться на 0,21 м / с каждую секунду, что возможно. Время, в течение которого газонокосилка разгоняется, не будет очень долгим, потому что скоро человек достигнет максимальной скорости.На этом этапе человек может толкать немного меньше, потому что ему нужно только преодолеть трение.
Рабочий пример
Какая ракетная тяга ускоряет эти салазки?
До пилотируемых космических полетов ракетные сани использовались для проверки самолетов, ракетного оборудования и физиологических воздействий на людей при высоких ускорениях. Ракетные сани представляли собой платформу, установленную на одном или двух рельсах и приводимую в движение несколькими ракетами. Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой, T , для четырехракетной двигательной установки, показанной ниже.Начальное ускорение салазок составляет 49 м / с2,49 м / с2, масса системы — 2100 кг, сила трения, препятствующая движению, — 650 Н.
Рисунок 4.7
Стратегия
Интересующая система — ракетные сани. Хотя силы действуют на систему вертикально, они должны нейтрализоваться, поскольку система не ускоряется вертикально. Остается рассмотреть только горизонтальные силы. Мы назначим направление вправо как положительное. См. Диаграмму свободного тела на рисунке 4.8.
Решение
Начнем со второго закона Ньютона и ищем способы определить тягу T двигателей. Поскольку все силы и ускорения линейны, нам нужно учитывать только величины этих величин в расчетах. Начнем с
, где FnetFnet — чистая внешняя сила в горизонтальном направлении. Из рисунка 4.8 видно, что тяга двигателя в одном направлении (которое мы называем положительным направлением), тогда как трение противодействует тяге.В форме уравнения чистая внешняя сила равна
.
Fnet = 4T − f. Fnet = 4T − f.
4,12
Второй закон Ньютона говорит нам, что F net = м a , поэтому мы получаем
После небольшой алгебры решаем общую тягу 4 T :
, что означает, что индивидуальная тяга составляет
Вставка известных значений дает
T = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 N.T = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 N.
4,16
Обсуждение
Цифры довольно большие, поэтому результат может вас удивить.Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости и проверить устройство, предназначенное для защиты летчиков-истребителей от аварийных катапультирований. Были получены скорости 1000 км / ч, с ускорением 45 g . (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с2,9,80 м / с2. Ускорение 45 g составляет 45 × 9,80 м / с2,45 × 9,80 м / с2, что составляет примерно 440 м / с. s2,440 м / с2. Живые предметы больше не используются, и теперь с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч.В этом примере, как и в предыдущем примере, интересующая система ясна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение и что этот выбор не всегда очевиден.
Практические задачи
9.
Если 1 Н равен 0,225 фунта, сколько фунтов составляют 5 Н силы?
- 0,045 фунта
- 1,125 фунта
- 2,025 фунта
- 5.000 фунтов
10.
Какое усилие необходимо приложить к объекту массой 5 кг, чтобы он разогнался со скоростью 20 м / с 2 ?
- 1 н.
- 10 N
- 100 N
- 1,000 N
Проверьте свое понимание
Поддержка учителя
Поддержка учителя
Используйте вопросы в Проверьте свое понимание , чтобы оценить, достигли ли учащиеся целей обучения по разделу.Если учащиеся не справляются с какой-либо конкретной целью, экзамен Check Your Understanding поможет определить, что вызывает проблему, и направит учащихся к соответствующему содержанию.
11.
Каково математическое утверждение второго закона движения Ньютона?
- F = м a
- F = 2 м a
- F = maF = ma
- F = м a 2
12.
Второй закон Ньютона описывает взаимосвязь между какими величинами?
- Сила, масса и время
- Сила, масса и перемещение
- Сила, масса и скорость
- Сила, масса и ускорение
13.
Что такое ускорение?
- Ускорение — это скорость изменения рабочего объема.
- Ускорение — это скорость изменения силы.
- Ускорение — это скорость изменения скорости.
- Ускорение — это скорость изменения массы.
.
