Чтобы найти наибольший общий делитель нескольких натуральных чисел надо: чтобы найти наибольший общий делитель нескольких натуральных чисел надо — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Внеклассный урок — Наибольший общий делитель (НОД). Наименьшее общее кратное (НОК).

Наибольший общий делитель (НОД).

Наименьшее общее кратное (НОК)

Наибольший общий делитель.

Наибольший общий делитель – это наибольшее натуральное число, на которое делятся без остатка числа a и b.

Чтобы найти НОД нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

3) найти произведение оставшихся множителей.

Пример: найдем НОД чисел 48 и 36. Для этого находим делители обоих чисел (рис.1):

Итак, 48 = 2 · 2 · 2· 2 · 3, а 36 = 2 · 2 · 3 · 3.

Из множителей, входящих в разложение первого числа, вычеркнем те, которые не входят в разложение второго числа -т. е. две двойки (рис.2)

В столбце с вычеркнутыми числами остаются множители 2 · 2 · 3. Их произведение равно 12. Это число и является НОД чисел 48 и 36. То есть 12 — наибольшее общее число, на которое делятся 48 и 36.

Если НОД натуральных чисел равен 1, то эти числа называют взаимно простыми (например, числа 24 и 35).

Наименьшее общее кратное.

Наименьшее общее кратное чисел a и b – это наименьшее натуральное число, которое делится на оба эти числа.

Чтобы найти НОК нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример: найдем НОК тех же чисел 48 и 36.

Как и в случае с НОД, сначала находим делители обоих чисел. Впрочем, мы уже нашли их в предыдущем примере (рис. 3):

Из разложения второго числа вычеркиваем множители, которые входят в разложение первого числа (рис.4).

Теперь выпишем множители, входящие в разложение первого числа, добавим к ним оставшийся множитель из разложения второго числа (3), перемножим их и получим результат:

2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 = 144.

Число 144 – это и есть НОК чисел 48 и 36. То есть 144 – это минимальное число, которое делится без остатка и на 48, и на 36.

Персональный сайт — НОД и НОК

Наибольший общий делитель (НОД). Наименьшее общее кратное (НОК)

Наибольший общий делитель – это наибольшее натуральное число, на которое делятся без остатка числа a и b.

Чтобы найти НОД нескольких натуральных чисел, надо:

1) разложить их на простые множители;

3) найти произведение оставшихся множителей.

Пример: найдем НОД чисел 48 и 36. Для этого находим делители обоих чисел (рис.1):

Итак, 48 = 2 · 2 · 2· 2 · 3, а 36 = 2 · 2 · 3 · 3.

Если НОД натуральных чисел равен 1, то эти числа называют взаимно простыми (например, числа 24 и 35).

Чтобы найти НОК нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример: найдем НОК тех же чисел 48 и 36.

Из разложения второго числа вычеркиваем множители, которые входят в разложение первого числа (рис.4).

2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 = 144.

Наибольший общий делитель нескольких натуральных чисел. Взаимно простые числа.

Григорьева Алиса Алексеевна

Тема: наибольший общий делитель нескольких натуральных чисел. Взаимно простые числа.

Тип урока: Урок применения знаний.

Цель урока: В результате изучения материала ученики должны усвоить смысл понятий «наибольший общий делитель нескольких натуральных чисел», знать определение этих понятий; приобрести навыки отыскания Н. О.Д.

Уметь аккуратно и математически верно оформлять задачи.

Ход урока

I. Актуализация опорных знаний:

1. Определи, делится ли число а на число в, и если делится, найди частное:

1),

2) ,

3) ,

4) ,

Вопросы:

1) На какие множители разложили число а?

2) Какие числа называются простыми?

3) Какие числа называются составными?

4) Что вы можете сказать о единице?

5) Признаки делимости на 2, 3, 5

II. Мотивация противоречия между имеющимися знаниями о Н.О.Д. и новыми фактами

Задача 1

Какое наибольшее количество одинаковых подарков можно составить из 12 шоколадок и 18 конфет? Сколько шоколадок и сколько конфет будет в каждом подарке?

Т. к. во всех подарках должно быть поровну шоколадок и поровну конфет, то каждое из чисел 12 и 18 должно делится на число подарков.

Что надо для этого сделать?

Найдем делители для 12 и 18

Следовательно, одинаковых подарков можно сделать 6, в них будет по 2 шоколадки и 3 конфеты.

Определение: Наибольшее натуральное число на которое делится каждое из данных натуральных чисел, называют наибольшим общим делителем этих чисел.

Однако на практике эти способы применимы лишь в случае, когда числа невелики. Универсальным способом поиска Н.О.Д. является разложение данных чисел на простые множители.

Мы решим нашу задачу для двух двухзначных чисел, усложним задачу о новогодних подарках.

Задача 2

Какое наибольшее число одинаковых подарков можно сделать из 320 орехов, 240 конфет и 200 пряников. Сколько конфет, орехов и пряников будет в каждом подарке?

Ответ: 40 подарков, в каждом из которых будет 8 орехов, 6 конфет и 5 пряников.

Алгоритм нахождения Н.О.Д.

Прочитать в учебнике алгоритм и записать в свою тетрадь. На доске таблица.

Задача 3

На ферме приготовили к продаже партию птиц: 18 гусей, 24 утки и 25 куриц. Поставщику было поручено доставить товар на продажу в мясные точки с которыми был заключен договор, но с одним лишь условием – весь товар следовало разделить на одинаковые партии.

В разложении нет одинаковых множителей

Числа 18 и 25 называются взаимно простыми, т.е у них только один наибольший общий делитель – единица.

Можем ли мы без разложения найти эти числа?

Какая пара четных чисел не может оказаться взаимно простой?

Закрепление:

Задача 4 Решение на доске

1) Найти

2) Найти

В разложении чисел 56 и 81 нет одинаковых множителей. Их Н.О.Д. равен 1.

3) Найти

Видим, что все простые множители числа 45 входят в разложение 450. Действительно, 450 делится на 45, поэтому 45 и будет наибольшим общим делителем этих чисел.

III. Закрепление

1) устная работа: № 660, 662 (1). По таблицам

2) Известно, что

а) Н.О.Д (а,в) = 14, . Найдите несколько возможных значений а и в

б) Н.О.Д (а,56) = 14,

Найдите значение а. Сколько решений имеет задача? Какие простые множители обязательно входят в разложение числа а?

в) Н.О.Д (х, у)=1

Найдите х и у. Сколько решений имеет задача?

3) Работа с учебником: № 656, № 663

IV. Знакомство с сочинениями о простых числах.

V. Домашнее задание – п.2 № 676, № 677 (1,4)

Задача 1

Найдите наибольший общий делитель чисел наиболее удобным способом:

1) 14 и 140

2) 4914 и 4915

3) 6, 81 и 9054

4) 3150 и 1848

Задача 2

Имеется по 48 синих, желтых и зеленых карандашей, 72 красных карандаша и 120 картинок для раскрашивания. Какое наибольшее число одинаковых наборов можно составить из картинок и карандашей. По сколько предметов в каждом наборе?

№ 664

НОД и взаимно простые числа

Слайд №2
	Цели: 10.05.2012 ввести понятия наибольшего общего делителя; формировать навык нахождения наибольшего общего делителя; отрабатывать умение решать задачи на использование НОД чисел; обобщить имеющиеся у учащихся знания о наибольшем общем делителе натуральных чисел, о взаимно простых числах. 2 www.konspekturoka.ru
Слайд №3
	10.05.2012 www.konspekturoka.ru 3 Изучение нового материала Решите уравнения, записывая только ответы. 84 : л = 14; л = 6 84 : т = 7; т = 12 84 : е = 21; е = 4 84 : л = 4; л = 21 84 : ь = 3; ь = 28 84 : д = 28; д = 3 84 : е = 6; е = 14 84 : и = 12; и = 7 Расположите ответы в порядке возрастания. Назовите, какое слово получилось. Дайте определение делителя натурального числа.
Слайд №4
	10.05.2012 www.konspekturoka.ru 4 Делитель – это натуральное число, на которое делится данное натуральное число без остатка.
Слайд №5
	10.05.2012 www.konspekturoka.ru 5 Разложите на простые множители число 875 Назовите наибольший делитель, отличный от самого числа. Как его найти? 875 = 53 ? 7 875 : 5 = 175 Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы.
Слайд №6
	10.05.2012 www.konspekturoka.ru 6 Разложите на простые множители число 2376 2376 = 23 ? 3? · 11 Назовите наибольший делитель, отличный от самого числа. Как его найти? Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы. 2376 : 2 = 1188
Слайд №7
	10.05.2012 www.konspekturoka.ru 7 Разложите на простые множители число 5625 5625 = З2 ? 54 Назовите наибольший делитель, отличный от самого числа. Как его найти? Чтобы найти наибольший делитель, надо число разделить на наименьший делитель, отличный от единицы. 5625 : 3 = 1875
Слайд №8
	10.05.2012 www.konspekturoka.ru 8 Для каждой пары чисел: 18 и 9; 10 и 7; 15 и 20; 14 и 35; 48 и 36; Найдите все делители каждого числа. Подчеркните их общие делители. 18: 1, 2, 3, 6, 9,18. 9: 1, 3, 9. 10: 1, 10. 7: 1, 7. 15: 1, 3, 5, 15. 20: 1, 2, 4, 5, 10, 20. 14: 1, 2, 7, 14. 35: 1, 5, 7, 35. 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. 36: 1, 2, 3, 4, 6, 9,12, 18, 36. Выделите их наибольший общий делитель.
Слайд №9
	Этот способ удобен, когда количество делителей, хотя бы у одного из чисел, невелико (способ 1). 10.05.2012 9 www.konspekturoka.ru Обозначают: НОД (48; 36) = 12 Запишем НОД для чисел НОД (18; 9) = 9, НОД (10; 7) = 1, НОД (15; 20) = 5, НОД (14; 35) = 7, НОД (48; 36) = 12.
Слайд №10
	10.05.2012 www.konspekturoka.ru 10 Способ 2. 1. Разложите числа на простые множители. 2. Выпишите общие простые множители. 3. Найдите произведение полученных простых множителей. НОД(24;60) = 2 ? 2 ? 3 = 12. 24 = 2 ? 2 ? 2 ? 3; 60 = 2 ? 2 ? 3 ? 5
Слайд №11
	10.05.2012 www.konspekturoka.ru 11 НОД(50; 175) = ? 50 = 2 ? 5 ? 5; 175 = 5 ? 5 ? 7 НОД(50;175) = 5 ? 5= 25
Слайд №12
	10.05.2012 www.konspekturoka.ru 12 НОД (675; 875) = ? 675 = 3 ? 3 ? 3 · 5 · 5; 875 = 5 · 5 ? 5 ? 7 НОД(675;875) = 5 ? 5= 25
Слайд №13
	10. 05.2012 www.konspekturoka.ru 13 НОД (7920; 594) = ? НОД(7920;594) = 2 ? 3 ? 3 · 11 = 198 7920 = 2 ? 2 ? 2 · 2 · 3 · 3 · 5 · 11 594 = 2 · 3 ? 3 ? 3 · 11
Слайд №14
	10.05.2012 14 www.konspekturoka.ru Алгоритм нахождения наибольшего общего делителя нескольких чисел. Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) из множителей, входящих в каждое разложение подчеркнуть общие множители; 3) найти произведение подчеркнутых множителей. Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Слайд №15
	Что нужно сделать, чтобы ответить на вопрос задачи? Задача. 32 яблока 40 груш НОД (32; 40) = 8. Ответ: 8 наборов. 10.05.2012 15 www.konspekturoka.ru В одной корзине 32 яблока, в другой корзине 40 груш. Какое наибольшее количество одинаковых наборов можно составить, используя эти фрукты. Найти наибольшее число, на которое делятся числа 32 и 40, то есть найти их наибольший общий делитель.
Слайд №16
	10.05.2012 www.konspekturoka.ru 16 35: 1, 5, 7, 35 88: 1, 2, 4, 8, 11, 22, 44, 88 Для каждой пары чисел: 35 и 88; 25 и 9; 5 и 3; 7 и 8; Найдите все делители каждого числа. Подчеркните их общие делители. НОД (35; 88) = 1. НОД (25; 9) = 1; НОД( 5; 3) = 1; НОД (7; 8) = 1. Выделите их наибольший общий делитель. 25: 1, 5, 259: 1, 3, 9 5: 1, 5 3: 1, 3 7: 1, 7 8: 1, 8
Слайд №17
	10.05.2012 www.konspekturoka.ru 17 НОД (35; 88) = 1 НОД (25; 9) = 1 НОД( 5; 3) = 1 НОД (7; 8) = 1 Такие числа называются взаимно простыми. Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Слайд №18
	Древние греки придумали замечательный способ, позволяющий искать наибольший общий делитель двух натуральных чисел без разложения на множители. Он носил название «Алгоритма Евклида». Он заключается в том, что наибольшим общим делителем двух натуральных чисел является последний, отличный от нуля, остаток при последовательном делении чисел. 10.05.2012 18 www.konspekturoka.ru Историческая минутка. Положим, требуется найти НОД (455; 312), Тогда 455 : 312 = 1 (ост. 143), получаем 455 = 312 ? 1 + 143 312 : 143 = 2 (ост. 26), 312 = 143 ? 2 + 26 143 : 26 = 5 (ост. 13), 143 =26 ? 5 + 13 26: 13 = 2 (ост. 0), 26 = 13 ? 2 Последний делитель или последний, отличный от нуля остаток 13 будет искомым НОД (455; 312) = 13.
Слайд №19
	Как узнать, сколько ребят было на елке? 10. 05.2012 19 www.konspekturoka.ru Ребята получили на новогодней елке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок было в каждом подарке? Найти НОД чисел 123 и 82. Количество апельсинов и яблок должно делиться на одно и то же наибольшее число. НОД (123; 82) = 41, значит, 41 человек. 123 : 41 = 3 (ап.) 82 : 41 = 2 (ябл.) Ответ: ребят 41, апельсинов 3, яблок 2. Сколько ребят -? Сколько яблок — ? Сколько апельсинов -?
Слайд №20
	10.05.2012 www.konspekturoka.ru 20 Найдите наибольший общий делитель числителя и знаменателя дробей. НОД (20; 30) = 10 НОД (8; 24) = 8 НОД (15; 35) = 5 НОД(13; 26) = 13 НОД (8; 9) = 1 НОД (24; 60) = 12
Слайд №21
	Задача Найти НОД чисел 424 и 477. НОД (424; 477) = 53, значит, 53 пассажира в одном автобусе. 424 : 53 = 8 (авт.) — в лес. 477 : 53 = 9 (авт.) — на озеро. 8 + 9 = 17 (авт.) Ответ: 17 автобусов, 53 пассажира в каждом. 10.05.2012 21 www.konspekturoka.ru Для поездки за город работникам завода было выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?
Слайд №22
	Ответить на вопросы: Какое число называют общим делителем данных натуральных чисел? Какое число называют наибольшим общим делителем двух натуральных чисел? Какие числа называют взаимно простыми? Как найти наибольший общий делитель нескольких натуральных чисел? Если числа взаимно простые, то какому числу равен их наибольший общий делитель? Верно ли: «Если числа простые, то они взаимно простые»? Ответ обоснуйте. 10.05.2012 22 www.konspekturoka.ru

Алгоритм нахождения НОД и НОК натуральных чисел

Правило нахождения наибольшего общего делителя (НОД).

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1) разложить их на простые множители;

3) найти произведение оставшихся множителей.

Пример. Найдем НОД (48;36). Воспользуемся правилом.

1. Разложим числа 48 и 36 на простые множители.

48 = 2 · 2 · 2 · 2 · 3

36 = 2 · 2 · 3 · 3

2. Из множителей, входящих в разложение числа 48 вычеркнем те, которые не входят в разложение числа 36.

48 = 2 · 2 · 2 · 2 · 3

Остаются множители 2, 2 и 3.

3. Перемножим оставшиеся множители и получим 12. Это число и является наибольшим общим делителем чисел 48 и 36.

НОД (48;36) = 2 · 2 · 3 = 12.

Правило нахождения наименьшего общего кратного (НОК).

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример. Найдем НОК (75;60). Воспользуемся правилом.

1. Разложим числа 75 и 60 на простые множители.

75 = 3 · 5 · 5

60 = 2 · 2 · 3 · 3

2. Выпишем множители, входящие в разложение числа 75: 3, 5, 5.

НОК (75;60) = 3 · 5 · 5 · …

3. Добавим к ним недостающие множители из разложения числа 60, т.е. 2, 2.

НОК (75;60) = 3 · 5 · 5 · 2 · 2

4. Найдем произведение получившихся множителей

НОК (75;60) = 3 · 5 · 5 · 2 · 2 = 300.

Правило нахождения наибольшего общего делителя (НОД).

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1) разложить их на простые множители;

3) найти произведение оставшихся множителей.

Пример. Найдем НОД (48;36). Воспользуемся правилом.

1. Разложим числа 48 и 36 на простые множители.

48 = 2 · 2 · 2 · 2 · 3

36 = 2 · 2 · 3 · 3

2. Из множителей, входящих в разложение числа 48 вычеркнем те, которые не входят в разложение числа 36.

48 = 2 · 2 · 2 · 2 · 3

Остаются множители 2, 2 и 3.

3. Перемножим оставшиеся множители и получим 12. Это число и является наибольшим общим делителем чисел 48 и 36.

НОД (48;36) = 2 · 2 · 3 = 12.

Правило нахождения наименьшего общего кратного (НОК).

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1) разложить их на простые множители;

2) выписать множители, входящие в разложение одного из чисел;

3) добавить к ним недостающие множители из разложений остальных чисел;

4) найти произведение получившихся множителей.

Пример. Найдем НОК (75;60). Воспользуемся правилом.

1. Разложим числа 75 и 60 на простые множители.

75 = 3 · 5 · 5

60 = 2 · 2 · 3 · 3

2. Выпишем множители, входящие в разложение числа 75: 3, 5, 5.

НОК (75;60) = 3 · 5 · 5 · …

3. Добавим к ним недостающие множители из разложения числа 60, т.е. 2, 2.

НОК (75;60) = 3 · 5 · 5 · 2 · 2

4. Найдем произведение получившихся множителей

НОК (75;60) = 3 · 5 · 5 · 2 · 2 = 300.

Письменный опрос по теме НОД и НОК. Математика, 6 класс

ФИ
_______________________________

Закончите предложения.

1.
Наибольшее
натуральное число, на которое делятся без остатка числа a
и b, называют
______________________________________________________________________________
этих чисел.

2.
Натуральные
числа называют ___________________________________________________ , если их
наибольший общий делитель равен 1.

3.
Чтобы
найти наибольший общий делитель нескольких натуральных чисел, надо:

1. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. Из
множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые
________________________________________________________________________________________________________________________________________________________

3. Найти
_______________________________________________ оставшихся множителей.

4.
Наименьшим
общим кратным натуральных чисел a
и b называют наименьшее натуральное
число, которое
____________________________________________________________________________________________________________________________________________________________

5.
Чтобы
найти наименьшее общее кратное нескольких натуральных чисел, надо:

1.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ФИ
_______________________________

Закончите предложения.

1.
Наибольшее
натуральное число, на которое делятся без остатка числа a
и b, называют ______________________________________________________________________________
этих чисел.

2.
Натуральные
числа называют ___________________________________________________ , если их
наибольший общий делитель равен 1.

3.
Чтобы
найти наибольший общий делитель нескольких натуральных чисел, надо:

3. Найти
_______________________________________________ оставшихся множителей.

5.
Чтобы
найти наименьшее общее кратное нескольких натуральных чисел, надо:

2. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3. ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4. __________________________________________________________________________________________________________________________________________________________________________________________________________________________________

keepslide.com — НОД И НОК ЧИСЕЛ
учитель математики МОУ… | Facebook

НОД И НОК ЧИСЕЛ
учитель математики МОУ лицея №1 Бугаева Вера Михайловна г.Комсомольска–на–Амуре

Наибольший обЩий делитель
Наибольшее натуральное число на которое де-лятся без остатка числа a и b, называют наи-большим общим делителем чисел a и b. Например: НОД чисел 48 и 36 равен 12, т.е. наи- большему из натуральных чисел, ко- торое делит нацело и 48, и 36. НОД(48;36)=12.

ПОМНИ!
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо: разложить их на простые множители; из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел; найти произведение оставшихся множителей. Например: НОД (96, 72)=24 96=2 • 2 • 2 • 2 • 2 • 3, 72=2 • 2 • 2 • 3 • 3 Остались множители: 2 • 2 • 2 • 3=24.

ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№1. Найдите НОД чисел: а)108 и 72; б) 150 и 225 . Решение. Разложим числа на простые множители: 108 2 72 2 150 2 225 5 54 2 36 2 75 5 45 5 27 3 18 2 15 5 9 3 9 3 9 3 3 3 3 3 3 3 3 3 1 1 1 1 1 1 Найдем одинаковые множители ( выделены одним цветом) НОД(108; 72) = 36, т.к. НОД(150; 225) = 75, т.к. 2 • 2 • 3 • 3 = 36. 5 • 5 • 3 = 75.

Числа правят миром.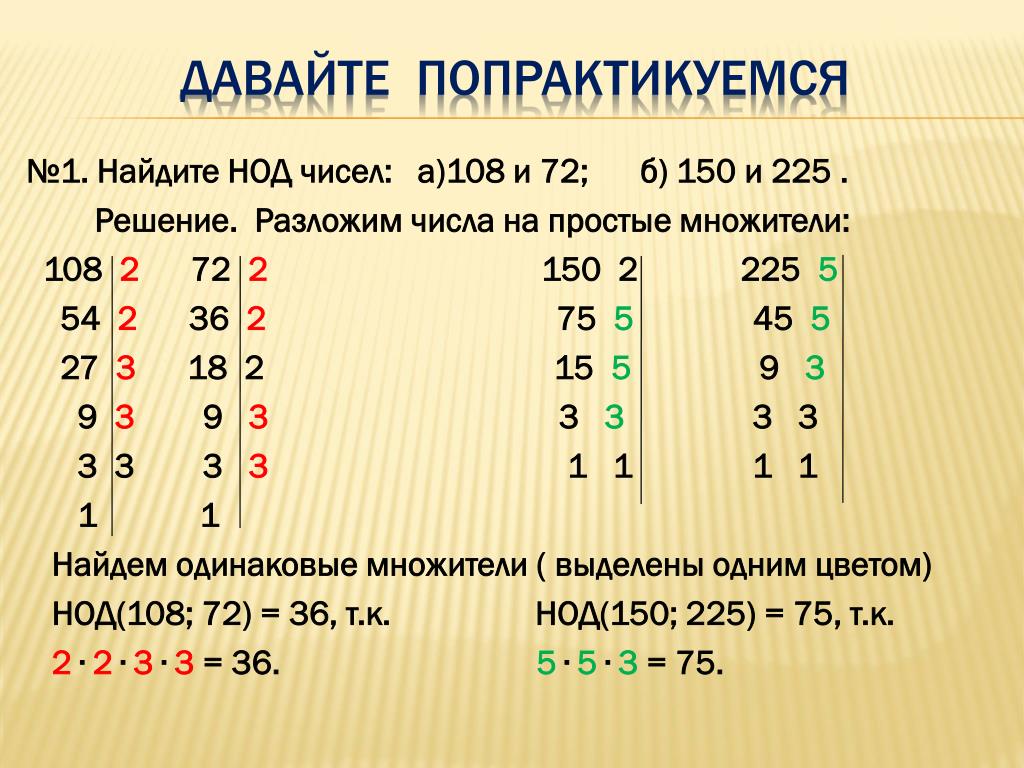 Пифагор
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Взаимно простые числа
Найти наибольший общий делитель чисел: а) 22 и 39; б) 56 и 31; в) 73 и 45; г) 44 и 63. Если вы решали все примеры верно, то в ответе всегда получалась 1.

Наименьшее общее кратное
Наименьшим общим кратным натуральных чи-сел a и b называют наименьшее натуральное число, которое кратно и a, и b. Например: НОК чисел 75 и 60 равен300, т.е. наименьшему из натуральных чисел, которые делятся без остатка на числа 75 и 60. НОК(75 и 60) =300

ПОМНИ!
Чтобы найти наименьшее общее кратное несколь- ких натуральных чисел , надо: разложить их на простые множители; выписать множители, входящие в разложение одного из чисел; добавить к ним недостающие множители из разложений остальных чисел; найти произведение получившихся множите- лей.

•
Давайте попрактикуемся
№2. Найдите НОК чисел: а) 108 и 72; б) 150 и 225. Решение. Разложим числа на простые множители: 108 2 72 2 150 2 225 5 54 2 36 2 75 5 45 5 27 3 18 2 15 5 9 3 9 3 9 3 3 3 3 3 3 3 3 3 1 1 1 1 НОК(150; 225) = 5 • 5 • 3 • 3 • 2 = 450 НОК(108; 72) = 2 • 2 • 3 • 3 • 3 • 2 = 216

Реши самостоятельно
№1.Найдите: а) НОД (81 и 243) б) НОК(15 и 18) в) НОД(72 и 108) г) НОК(36 и 48) д) НОД(168 и 180) е) НОК(252 и 360) ж) НОД(360 и 1050) з) НОК(396 и 180) и)НОД(270;450 и 555) к) НОК(72;120 и 264)

Позволяет решать различные задачи
Сокращение дробей
Отыскание общего знаменателя дробей
Применение НОД и нок чисел
№2. Сократите дроби: а) ; б) ; в) ; г) . №3. Приведите дроби к общему знаменателю: а) и ; б) и .

ПРОВЕРЬ СЕБЯ
№1. а) 81; б) 90; в) 36 ; г) 144; д) 12; е)2520 ; ж) 30; з) 1980; и) 15; к) 3960. №2. а) ; б) ; в) ; г) . №3. и ; и . Попытайся сократить такую дробь: . Трудно? А как выполнить это задание быстро и легко, не раскладывая числа на простые множители? Оказывается это возможно осуществить с помощью алгоритма Евклида.

Алгоритм евклида
Во многих случаях, когда числитель и знаменатель делятся на число (например на 19, на 37 и т.д.), а признака делимости мы не знаем, НОК числителя и знаменателя находят с помо-щью, так называемого, алгоритма Евклида. Суть его проста: делится большее число на меньшее. Затем меньшее делится на первый остаток. При этом получается второй остаток. Дальше первый остаток делится на второй и процесс продолжается. Он конечен и последний неравный нулю остаток и будет наибольший общим делителем. Прием этот занимателен, он называется –алгоритм Евклида – реко-мендуем его испробовать. Продемонстрируем его на примере.

Сократить дробь: .
Для того, чтобы сократить данную дробь найдем с помощью алгоритма Евкли- да НОД чисел 5959 и 13433. Делим 13433 на 5959. 13433 5959 11918 2 5959 1515 4545 3 1515 1414 1414 1 1414 101 101 14 404 = 404 0 Последний неравный нулю остаток, т. е. 101 и будет наибольшим общим дели- телем. Разделим на 101 числитель и знаменатель. Получим дробь: .

РЕШИ самостоятельно
№1. С помощью алгоритма Евклида сократить дроби: а) б) в) г) д) ; ; ; ; . №2. Найдите НОД чисел: а) 2304 и 5220; б) 8136 и 12250; в) 1348 и 1126; г) 42628 и 33124; д) 71004 и 154452. №3. Какой наименьшей длины должна быть доска, чтобы ее можно было раз- резать поперек на части, равные 20см и 27см, не получив обрезков? №4. Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если имеется 12 зайцев, 24 лисицы, 16 морковок и 48 яблок? №5. Найдите НОК и НОД чисел, затем сравните произведение этих чисел с произведением НОК и НОД: а) 14 и21; б) 24 и 36; в) 32 и 48; г) 18 и24; д) 25 и 35.

РЕШАЕМ И ПРОВЕРЯЕМ
№1.
№2.
№3.
№4.
№5.
а) НОД (14; 21) = 7; б) НОД (24; 36) = 12; НОК (14; 21) = 42. НОК (24; 36) = 72. в) НОД (32; 48) = 16; г) НОД (18; 24) = 6; НОК (32; 48) = 96. НОК (18; 24) = 72. д) НОД (25; 35) = 5; НОК (25; 35) =175.

Замечательное свойство НОК и НОД
Заметили ли вы, что для любых натуральных чисел a и b выпол- няется равенство: НОД(a;b) НОК(a;b) = a b Это свойство позволяет по заданным числам и известному НОД находить НОК этих чисел. a b НОК(a;b) =
НОД(a;b)

Предлагаю решить задачи
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в коробке. Какое наименьшее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну? Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Белочка», если надо использовать все конфеты? Сколько конфет «Ласточка» и «Белочка» будет в каждом подар-ке? Для поездки за город работникам завода было выделено несколько ав-тобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе? Конфеты «Сладкая математика» продаются по 12 штук в коробке, а кон-феты «Геометрия с орехами» – по 15 штук в коробке. Какое наимень-шее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну? Коля, Серёжа и Ваня регулярно ходили в кинотеатр. Коля бывал в нём каждый 3-й день, Серёжа — каждый 7-й, Ваня — каждый 5-й. Сегодня все ребята были в кино. Когда все трое встретятся в кинотеатре в сле-дующий раз?

ответы
№1. НОД (36; 48) = 12; 36 : 12 = 3 (шт) конфет «Белочка» 48 : 12 = 4 (шт) конфет « Ласточка»
№2. НОД (424; 477) = 53; (424 + 477) : 53 = 17 (чел)
№3. 5 коробок «Сладкая математика», 4 коробки «Геометрия с ореха- ми» . НОК(15; 12) = 60, 60 : 12 = 5, 60 : 15 = 4. 2 $ математически правильным образом?

Спасибо, andvance!

Обновление

Я задумался над проблемой еще раз и хочу более подробно объяснить, что скрипт Python должен уметь делать.2 \\
\ hline
1 и 15,845 и 0,24232239557963048 \\
2 и 22.480 и 0.4846105998701098 \\
3 и 27.623 и 0.72692651083 \\ 4 и 32,003 и 0,9692579815933621 \\ 5 и 35.901 и 1.2115343992719871 \\ 6 и 39.463 и 1.4538572457953847 \\ \ hline \ end {array}

`R Программа для поиска H.C.F. или G.C.D.`

В этой статье вы научитесь находить НОД (Наибольший общий делитель), создав пользовательскую функцию двумя разными способами.

Чтобы понять этот пример, вы должны знать следующие темы программирования R:

Наивысший общий множитель (H.C.F) или наибольший общий делитель (G.C.D) двух чисел - это наибольшее положительное целое число, которое идеально делит два заданных числа.

Например, H.C.F для 12 и 14 равняется 2.

`Пример: программа для поиска GCD`

  # Программа для поиска H. C.F двух входных чисел
# определить функцию
hcf <- function (x, y) {
# выберите меньшее число
if (x> y) {
меньше = у
} еще {
меньше = х
}
for (я в 1: меньше) {
if ((x %% i == 0) && (y %% i == 0)) {
hcf = я
}
}
возврат (hcf)
}
# принять ввод от пользователя
num1 = as.целое число (readline (prompt = "Введите первое число:"))
num2 = as.integer (readline (prompt = "Введите второе число:"))
print (paste ("H.C.F. of", num1, "and", num2, "is", hcf (num1, num2)))

Выход

  Введите первое число: 72
Введите второе число: 120
[1] «H.C.F. 72 и 120 составляет 24»

Эта программа запрашивает два целых числа и передает их функции, которая возвращает H.C.F.

В функции мы сначала определяем меньшее из двух чисел, поскольку кодировка H.C.F может быть меньше или равняться наименьшему числу.

Затем мы используем цикл для , чтобы перейти от 1 к этому числу.

На каждой итерации мы проверяем, идеально ли наше число делит оба входных числа.

Если да, то мы сохраняем номер как H.C.F. По завершении цикла мы получаем наибольшее число, которое идеально делит оба числа.

Вышеупомянутый метод прост для понимания и реализации, но неэффективен. Гораздо более эффективный метод поиска H.К.Ф. - алгоритм Евклида.

`Алгоритм Евклида для поиска GCD`

Этот алгоритм основан на том, что H.C.F. двух чисел делит и их разницу.

В этом алгоритме мы делим большее на меньшее и берем остаток. Теперь разделите меньшее на этот остаток. Повторяйте, пока остаток не станет 0.

Например, если мы хотим найти H.C.F. 54 и 24, мы делим 54 на 24. Остаток равен 6.

Теперь мы делим 24 на 6, а остаток равен 0.Следовательно, 6 - это требуемый H.C.F. Мы можем сделать это в Python следующим образом.

`Пример 2: НОД с использованием алгоритма Евклида`

  hcf <- function (x, y) {
while (y) {
temp = y
у = х %% у
x = температура
}
возврат (х)
}

Здесь мы зацикливаемся, пока y не станет равным нулю.

На каждой итерации мы помещаем значение y в x , а остаток (x% y) в y , используя временную переменную.

Когда y становится равным нулю, мы имеем H.К.Ф. размером x .

Код

`для наибольшего общего делителя в Python`

код для наибольшего общего делителя в Python - qaru

Присоединяйтесь к Stack Overflow , чтобы учиться, делиться знаниями и строить свою карьеру.

Спросил 8 лет, 11 месяцев назад

Просмотрено 323к раз

Закрыт . Этот вопрос должен быть более конкретным. В настоящее время он не принимает ответы.

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он фокусировался только на одной проблеме, отредактировав это сообщение.

Закрыт 1 год назад.

Наибольший общий делитель (НОД) чисел a и b - это наибольшее число, которое делит их оба без остатка.

Одним из способов найти НОД двух чисел является алгоритм Евклида, который основан на наблюдении, что если r - это остаток от деления a на b , то gcd (a, b) = gcd ( б, г) . В качестве базового случая мы можем использовать gcd (a, 0) = a .

Напишите функцию с именем gcd, которая принимает параметры a и b и возвращает их наибольший общий делитель.

Сампатсрис

11k1010 золотых знаков5959 серебряных знаков9090 бронзовых знаков

Создан 24 июн.

Люк DLuke D

1,65933 золотых знака1414 серебряных знаков1515 бронзовых знаков

2

Это в стандартной библиотеке.

  >>> из фракций import gcd
>>> gcd (20,8)
4

Исходный код модуля inspect в Python 2.7:

  >>> печать inspect.getsource (gcd)
def gcd (a, b):
    "" "Вычислите наибольший общий делитель a и b.

    Если b == 0, результат будет иметь тот же знак, что и b (так что когда
    b делится на него, результат получается положительным). 
    "" "
    в то время как b:
        а, б = б, а% б
    вернуть

Начиная с Python 3.5, gcd находится в модуле math ; один из дробей устарел. Более того, inspect.getsource больше не возвращает поясняющий исходный код ни для одного из методов.

Создан 24 июн.

пользователь545424

14.4k1010 золотых знаков4949 серебряных знаков6666 бронзовых знаков

16

Алгоритмы с m-n могут работать очень долго.

Этот работает намного лучше:

  def gcd (x, y):
    а y! = 0:
        (х, у) = (у, х% у)
    вернуть х

Создан 22 сен.

нетомнетом

3,11222 золотых знака1818 серебряных знаков2121 бронзовый знак

9

Эта версия кода использует алгоритм Евклида для поиска GCD.

  def gcd_recursive (a, b):
    если b == 0:
        вернуть
    еще:
        вернуть gcd_recursive (b, a% b)

Создан 20 фев.

Анкуш

38333 серебряных знака88 бронзовых знаков

3

  gcd = лямбда m, n: m, если не n, иначе gcd (n, m% n)

Создан 02 ноя.

Йонас Быстрём

22.2k121 золотой знак9292 серебряных знака137137 бронзовых знаков

0

с использованием рекурсии ,

  def gcd (a, b):
    вернуть a если не b иначе gcd (b, a% b)

с использованием , а ,

  def gcd (a, b):
  в то время как b:
    а, б = б, а% б
  вернуть

с использованием лямбда,

  gcd = лямбда a, b: a если не b иначе gcd (b, a% b)

>>> gcd (10,20)
>>> 10

Создан 31 янв.

1

  def gcd (m, n):
    return gcd (abs (m-n), min (m, n)) if (m-n) else n

Создан 29 июн.

дансальмодансалмо

10.3k55 золотых знаков5050 серебряных знаков4949 бронзовых знаков

2

Очень краткое решение с использованием рекурсии:

  def gcd (a, b):
    если b == 0:
        вернуть
    вернуть gcd (b, a% b)

Создан 16 мая '18 в 15: 022018-05-16 15:02

  a = int (raw_input ('1-е число \ n'))
b = int (raw_input ('2-е число \ n'))

def gcd (m, n):
    г = абс (м-п)
    если (m-n) == 0:
        вернуть n
    еще:
        вернуть НОД (z, min (m, n))


распечатать gcd (a, b)

Другой подход, основанный на алгоритме Евклида.

Создан 29 июн.

  def gcdRecur (a, b):
    '' '
    a, b: положительные целые числа

    возвращает: положительное целое число, наибольший общий делитель a и b.
    '' '
    # Базовый случай - когда b = 0
    если b == 0:
        вернуть

    # Рекурсивный случай
    return gcdRecur (b, a% b)

Марко Гресак

7,38255 золотых знаков3434 серебряных знака4646 бронзовых знаков

Создан 15 ноя.

ШАМШАМЫ

1911 бронзовый знак

Я думаю, что другой способ - использовать рекурсию. Вот мой код:

  def gcd (a, b):
    если a> b:
        с = а - б
        gcd (b, c)
    элиф а <б:
        с = Ь - а
        gcd (a, c)
    еще:
        вернуть

Создан 27 окт.

dexhunter

54777 серебряных знаков2121 бронзовый знак

1

на питоне с рекурсией:

  def gcd (a, b):
    если a% b == 0:
        вернуть б
    вернуть gcd (b, a% b)

Создан 27 июл.

Keajerkeajer

1922 бронзовых знака

  def gcd (a, b):
    если b> a:
        вернуть gcd (b, a)
    г = а% б
    если r == 0:
        вернуть б
    вернуть gcd (r, b)

lennon310

11. 8k1111 золотых знаков4040 серебряных знаков5555 бронзовых знаков

Создан 03 дек.

  def gcd (a, b):

    если (a

  def gcd (a, b):

    т = мин (а, б)

    # Продолжайте цикл, пока t не разделит оба a и b равномерно
    пока a% t! = 0 или b% t! = 0:
        t - = 1

    вернуть т

Создан 25 янв.

2

Мне пришлось сделать что-то подобное для домашнего задания с использованием циклов while. Не самый эффективный способ, но если вы не хотите использовать функцию, это работает:

  число1 = 20
num1_list = []
число2 = 40
num2_list = []
х = 1
у = 1
в то время как x <= num1:
    если num1% x == 0:
        num1_list.append (x)
    х + = 1
а y <= num2:
    если num2% y == 0:
        num2_list.append (y)
    у + = 1
xy = список (набор (num1_list) .intersection (num2_list))
печать (xy [-1])

Создан 16 апр.

  def _grateest_common_devisor_euclid (p, q):
    если q == 0:
        вернуть p
    еще:
        напоминание = p% q
        return _grateest_common_devisor_euclid (q, напоминание)

печать (_grateest_common_devisor_euclid (8,3))

Создан 07 июн.

Сай пратик

10.1,955 золотых знаков3939 серебряных знаков5959 бронзовых знаков

  числа = [];
count = input ("СКОЛЬКО ЧИСЕЛ ВЫ ХОТИТЕ ВЫЧИСЛИТЬ НОД? \ n")
для я в диапазоне (0, количество):
  число = ввод ("ВВЕДИТЕ НОМЕР: \ n")
  numbers.append (число)
numbers_sorted = отсортировано (числа)
print 'ЧИСЛА, СОРТИРОВАННЫЕ В УВЕЛИЧЕНИИ ПОРЯДКА \ n', числа_сортировано
gcd = числа_сортировано [0]

для i в диапазоне (1, count):
  делитель = НОД
  делимое = отсортированное по числам [i]
  остаток = делитель% дивиденда
  если остаток == 0:
  gcd = делитель
  еще :
    пока не остаток == 0:
      divisor_one = делитель
      divisor_one = остаток
      остаток = divisor_one% divisor_one
      gcd = divisor_one

напечатайте 'GCD OF', count, 'NUMBERS IS \ n', gcd

Создан 08 июн.

1

Обмен значениями у меня не сработал.Поэтому я просто создал зеркальную ситуацию для чисел, которые вводятся либо в b:

  def gcd (a, b):
    если a> b:
        г = а% б
        если r == 0:
            вернуть б
        еще:
            вернуть gcd (b, r)
    если a

Делимитрий

2,81344 золотых знака2525 серебряных знаков3636 бронзовых знаков

Создан 18 июн.

тройхроитройхрой

4911 серебряный знак99 бронзовых знаков

2

  # Эта программа найдет hcf заданного списка чисел. A = [65, 20, 100, 85, 125] # создает и инициализирует список чисел

def наибольший_общий_дивизор (_A):
  итератор = 1
  коэффициент = 1
  a_length = len (_A)
  наименьшее = 99999

# получить наименьшее число
для числа в _A: #iterate through array
  if number <наименьшее: # если текущее не наименьшее число
    наименьшее = число # установить на наибольшее

в то время как итератор <= наименьшее: # итерация от 1 ... наименьшее число
для индекса в диапазоне (0, a_length): #loop through array
  if _A [index]% iterator! = 0: # если элемент не делится поровну на 0
    break #stop и перейти к следующему элементу
  if index == (a_length - 1): # если мы дойдем до последнего элемента массива
    factor = iterator # это означает, что все они делятся на 0
iterator + = 1 # давайте увеличим, чтобы проверить, делится ли массив на следующий итератор
# распечатайте коэффициент
фактор печати

print "Наивысший общий множитель:",
для элемента в A:
  элемент печати,
print "is:",

great_common_devisor (A)

Создан 25 марта 2015 г. в 19: 232015-03-25 19:23

  def gcdIter (a, b):
gcd = min (a, b)
для i в диапазоне (0, min (a, b)):
    если (a% gcd == 0 и b% gcd == 0):
        вернуть gcd
        перерыв
    gcd- = 1

Создан 25 мая 2018 в 15: 472018-05-25 15:47

Par basPar bas

14311 серебряный знак22 бронзовых знака

3

Вот решение, реализующее концепцию Итерация :

  def gcdIter (a, b):
    '' '
    a, b: положительные целые числа

    возвращает: положительное целое число, наибольший общий делитель a и b. '' '
    если a> b:
        результат = b
    результат = а

    если результат == 1:
        возврат 1

    пока результат> 0:
        если% result == 0 и b% result == 0:
            вернуть результат
        результат - = 1

Создан 15 фев.

Бикрамджит Сингх

65911 золотой знак77 серебряных знаков2121 бронзовый знак

Очень активный вопрос .Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.

`Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками python или задайте свой вопрос.`

lang-py

Stack Overflow лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie

Настроить параметры

`Наибольший общий множитель`

Наибольший общий множитель (GCF) двух или более чисел является наибольшим общим делителем. Наибольший общий множитель может быть найден с использованием ряда методов, таких как перечисление факторов, использование факторизации простых чисел или алгоритм Евклида, среди других. GCF двух чисел, таких как 12 и 16, можно обозначить как GCF (12, 16).

Для меньших чисел составить список факторов обычно не так сложно, и это помогает найти наибольший общий фактор.

`Список факторов для поиска GCF`

Чтобы найти наибольший общий делитель 8 и 12:

Первое: перечислите факторы

Факторы 8:	1, 2, 4, 8
Факторы 12:	1, 2, 3, 4, 6, 12

Далее: сравните эти факторы и определите наибольший фактор, общий для двух чисел

Наибольший общий делитель 8 и 12 равен 4.

Это также можно записать как GCF (8, 12) = 4.

`Использование разложения на простые множители для нахождения GCF`

Чтобы найти наибольший общий делитель 36 и 48,

Первое: найдите разложение на простые множители

У чисел 36 и 48 простые делители 2, 2 и 3 общие.

Далее: умножьте эти простые множители: 2 × 2 × 3 = 12

GCF (36, 48) = 12

Знание того, как найти наибольший общий множитель, помогает выразить обыкновенные дроби в их простейшей форме.

`Использование алгоритма Евклида для поиска GCF`

Факторизация простых чисел и перечисление факторов для нахождения GCF могут быстро стать утомительными, поскольку числа становятся больше. Алгоритм Евклида для поиска GCF является одним из ряда более эффективных алгоритмов поиска GCF.

Алгоритм

Евклида - это алгоритм с делением в столбик, основанный на том принципе, что GCF двух чисел не меняется, если большее число заменяется его разницей на меньшее число.Итак, GCF (18, 34) совпадает с GCF (34-18, 18) или GCF (16, 18). Мы не будем вдаваться в подробности, чтобы доказать, почему алгоритм Евклида работает, но чтобы использовать алгоритм для поиска GCF, выполните следующие действия:

Разделите большее число на меньшее. Если остаток равен 0, делителем является ОКФ. Если нет, переходите к следующему шагу.
Разделите меньшее число (предыдущий делитель) на остаток. Если новый остаток равен 0, делителем является GCF.
Продолжить процесс деления предыдущего делителя на остаток до тех пор, пока не останется остаток.Делитель, который дает остаток от 0, является GCF исходных двух чисел.

Пример

Найдите GCF (114, 288):

Обратите внимание, что частное не имеет значения для этого алгоритма, и мы не решаем фактическую исходную задачу деления в столбик.

После четырехкратного деления остаток равен 0, а последний делитель равен 6. Следовательно, согласно алгоритму, GCF (114, 288) = 6. Это можно проверить, разделив 114 и 288 на 6:

.

114 ÷ 6 = 19

288 ÷ 6 = 48

19 и 48 не имеют общих факторов, подтверждая, что 6 - это GCF 114 и 288.

Этот алгоритм также можно использовать для нахождения GCF для более чем двух чисел путем нахождения GCF между первыми двумя числами, а затем вычисления GCF результата и следующего числа. Это можно записать как:

GCF (a, b, c) = GCF (GCF (a, b), c)

`Наибольший общий делитель - задача интервью`

`Наибольший общий делитель`

Сложность: Средняя

Вопрос: Google

Понимание проблемы:

Даны два целых числа, например A и B, вы должны найти наибольший общий делитель или наибольший общий делитель числа заданы целые числа .

  Например: ВХОД: 10 15
             ВЫХОД: 5
             
             ВХОД: 36 48
             ВЫХОД: 12

  Объяснение: 5 - это наибольшее целое число, которое множится как 10, так и 15. Точно так же 12 - это наибольшее целое число, которое полностью делит 36 и 48.

Возможные дополнительные вопросы: →

Есть ли на входе отрицательные числа? ( Ответ: Нет, только положительные целые числа! )

Решения

Мы увидим два решения, чтобы найти GCD или HCF двух чисел →

Решение Brute Force → Это простое решение, основанное на нахождении всех простых множителей обоих чисел и выборе общих множителей.
Евклидов алгоритм → Евклидов алгоритм помогает нам выполнять итерацию в направлении НОД гораздо более оптимизированным образом.
Оптимизированный алгоритм Евклида → Оптимизация стандартной евклидовой операции для сокращения времени при больших числах!

1. Решение методом перебора

Идея решения

Простая идея состоит в том, чтобы найти множители обоих заданных чисел, а затем умножить общие множители, чтобы получить GCD.

Пример: →

  Факторы числа 30: 2x3x5
Множители числа 20: 2x2x5
Поскольку общие множители равны 2x5, НОД будет 2x5 = 10

Шаги решения

Мы начнем цикл с 1 и будем продолжать до тех пор, пока переменная цикла не станет меньше обоих чисел.
Если переменная цикла полностью разделяет оба числа, мы сохраним это в переменной result .
Когда цикл окончательно завершен, значение, сохраненное в переменной результата, является выходом.

Псевдокод

  int getGCD (int number1, int number2)
{
   int результат = 1
   for (от int i = 2 до min (число1, число2))
   {
      если (я% число1 == 0 и я% число2 == 0)
          результат = я
   }
   вернуть результат
}

Анализ сложности

Сложность времени: O (min (number1, number2)) , это минимум из двух целых чисел ( Почему?)

Сложность пространства: О (1)

2.Евклидов алгоритм

Мы увидим более эффективное решение, использующее евклидов алгоритм для GCD.

Идея решения

Евклидов алгоритм основан на том принципе, что НОД двух чисел остается неизменным, если большее из двух чисел заменяется его разностью на меньшее число. Этот процесс продолжает уменьшать большее число, пока оно не станет равным меньшему числу. Когда это происходит, мы получаем НОД.

Шаги решения

Мы будем продолжать уменьшать большее число среди двух чисел на разницу между ними, пока оба не станут равными и мы не получим GCD.

Псевдокод

  int getGCD (int number1, int number2)
{
   в то время как (число1! = число2)
   {
     если (число1> число2)
       число1 = число1 - число2
     еще
       число2 = число2 - число1
   }
   номер возврата1
}

Анализ сложности

Сложность времени: O (max (number1, number2))

(Почему? Подсказка: Рассмотрим случай, когда существует большая разница между числами )

Пространственная сложность: O (1)

★ Можете ли вы подумать об оптимизации алгоритма Евклида? Можем ли мы заменить вычитание более эффективными операторами?

3.Оптимизированный алгоритм Евклида

Идея решения

Проблема с указанным выше алгоритмом заключается в повторяющихся вычислениях (вычитании) в случае, когда одно из чисел очень велико. Чтобы этого избежать, мы можем изменить операцию вычитания на деление. Алгоритм завершится, как только будет найден нулевой остаток.

Шаги решения

Мы заменим большее число остатком от деления большего числа на меньшее.
Если остаток равен нулю, у нас есть НОД.

Псевдокод

  int getGCD (int number1, number2)
{
   если (число2 == 0)
       номер возврата1
   return getGCD (число2, число1% число2)
}

Анализ сложности

Сложность времени: O (log (number1 + number2)) (Почему?)

Сложность пространства: Подумайте! ( Подсказка: Какое пространство рекурсивного стека используется?)

Критические идеи для размышления!

Можете ли вы представить себе различные свойства GCD и его связь с LCM?
Узнайте больше о сложности оптимизированного алгоритма Евклида.
Как найти НОД для отрицательных целых чисел? А как насчет чисел с плавающей запятой ??
А как насчет сложности итеративной реализации оптимизированного евклидова кода?

`Сравнение решений`

Предлагаемые задачи для решения

Программа для поиска НОК двух чисел с помощью НОД.
Программа для поиска НОД чисел с плавающей запятой.
Программа для поиска общего рациона трех чисел.
Программа для поиска НОД массива целых чисел.
Программа для нахождения суммы квадратов N натуральных чисел.

Удачного кодирования! Наслаждайтесь алгоритмами !!

`простых чисел и GCD`

простых чисел и GCD

Простое число - это целое число \ (p \) больше единицы, где его делят только 1 и \ (p \). например 2, 3, 5, 7, 11, 13, 17, 19,… простые числа.
Непростое целое число больше единицы составляет составное . То есть \ (n \) является составным числом, если существует некоторое целое число \ (a \) с \ (1
Теорема: Составное целое число \ (n \) имеет простой множитель, меньший или равный \ (\ sqrt {n} \).
Проба: По определению мы знаем, что существует \ (a \) с \ (1
По основной теореме \ (a \) можно записать как произведение простых чисел.Пусть \ (p \) будет одним из простых чисел факторизации \ (a \). Теперь \ (p \) - простое число, а \ (p \ le a \ le \ sqrt {n} \). ∎
Это дает нам по крайней мере один алгоритм проверки того, является ли число простым. Попробуйте простое число 2 до \ (\ lfloor \ sqrt {n} \ rfloor \), чтобы увидеть, есть ли деление (\ (n \ mathop {\ mathrm {mod}} a = 0 \)). Если нет, то просто. Или вместо того, чтобы проверять все простые числа, просто проверьте все целые числа: возможно, быстрее, чем вычисление простых чисел.
Теорема: Существует бесконечное количество простых чисел.
Проба: Предположим, нет, что мы можем перечислить все простые числа: \ (p_1, p_2, \ ldots, p_n \). Тогда пусть \ (q = p_1 p_2 \ cdots p_n + 1 \).
Значение \ (q \) не делится ни на одно из простых чисел в нашем списке: его остаток равен единице при делении на каждое из них. Таким образом, оно должно быть либо другим простым числом, либо делиться на другое простое число, не указанное в списке. ∎

Для двух целых чисел \ (a \) и \ (b \) наибольший общий делитель для then является наибольшим целым числом \ (d \) такое, что \ (d \ mid a \) и \ (d \ mid б \).3 \ раз 5 \ раз 7 = 7560 \).

Теорема: Для положительных целых чисел \ (a \) и \ (b \) имеем \ (ab = \ mathrm {gcd} (a, b) \ cdot \ mathrm {lcm} (a, b) \ ).

Пробная идея: Имея в виду нахождение их с помощью разложения на простые множители, мы можем умножить два результата вместе и получить все одинаковые степени простых чисел.

 Эта теорема дает гораздо лучший алгоритм, чем метод простой факторизации: используйте метод Евклида и верните \ (a \ times b / \ mathrm {gcd} (a, b) \).