Cos x 1 2 решение: решить уравнение: cosx=1/2 — Школьные Знания.com — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

cos 1 2 на окружности

Вы искали cos 1 2 на окружности? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos x 1 2, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «cos 1 2 на окружности».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как cos 1 2 на окружности,cos x 1 2,cos x 1 2 решение,cos x чему равен x,cos х 1 2,cosx 1 2 x,y cos x 1 2,y cosx 1 2,кос равен 1,кос х 1,косинус 2 икс равен 1,косинус 2 икс равен 1 2,косинус 2 минус 1,косинус x 1 2,косинус икс равен 1,косинус икс равен 1 2,косинус равен 1 2,косинус х равен,косинус х равен 1,косинус х равен 1 2,косинус х равен минус 1 2,решение cosx 1 2,решите уравнение cosx 1 2,решить уравнение cosx 1,соs2х,чему равен cos 1 2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и cos 1 2 на окружности. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos x 1 2 решение).

Где можно решить любую задачу по математике, а так же cos 1 2 на окружности Онлайн?

Решить задачу cos 1 2 на окружности вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Уравнение cos x = а

Мы знаем, что значения косинуса заключены в промежутке [-1; 1], т.е. -1 ≤ cos α ≤ 1. Поэтому если |а| > 1, то уравнение cos x = а не имеет корней. Например, уравнение cos x = -1,5 корней не имеет.

Рассмотрим несколько задач.

Задача 1.

Решить уравнение cos x = 1/2.

Решение.

Вспомним, что cos x – это абсцисса точки окружности с радиусом, равным 1, полученной в результате поворота точки Р (1; 0) на угол х вокруг начала координат.

Абсцисса 1/2 есть у двух точек окружности М₁ и М₂. Так как 1/2 = cos π/3, то точку М₁ мы можем получить из точки Р (1; 0) путем поворота на угол х₁ = π/3, а также на углы х = π/3 + 2πk, где k = +/-1, +/-2, …

Точка М₂ получается из точки Р (1; 0) поворотом на угол х₂ = -π/3, а также на углы -π/3 + 2πk, где k = +/-1, +/-2, …

Итак, все корни уравнения cos x = 1/2 можно найти по формулам
х = π/3 + 2πk
х = -π/3 + 2πk,

где k € Z.

Две представленные формулы можно объединить в одну:

х = +/-π/3 + 2πk, k € Z.

Задача 2.

Решить уравнение cos x = -1/2 .

Решение.

Абсциссу, равную – 1/2 , имеют две точки окружности М₁ и М₂. Так как -1/2 = cos 2π/3, то угол х₁ = 2π/3, а потому угол х₂ = -2π/3.

Следовательно, все корни уравнения cos x = -1/2 можно найти по формуле: х = +/-2π/3 + 2πk, k € Z.

Таким образом, каждое из уравнений cos x = 1/2 и cos x = -1/2 имеет бесконечное множество корней. На отрезке 0 ≤ х ≤ π каждое из этих уравнений имеет только один корень: х₁ = π/3 – корень уравнения cos x = 1/2 и х₁ = 2π/3 – корень уравнения cos x = -1/2.

Число π/3 называют арккосинусом числа 1/2 и записывают: arccos 1/2 = π/3, а число 2π/3 – арккосинусом числа (-1/2) и записывают: arccos (-1/2) = 2π/3.

Вообще уравнение cos x = а, где -1 ≤ а ≤ 1, имеет на отрезке 0 ≤ х ≤ π только один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке (π/2; π].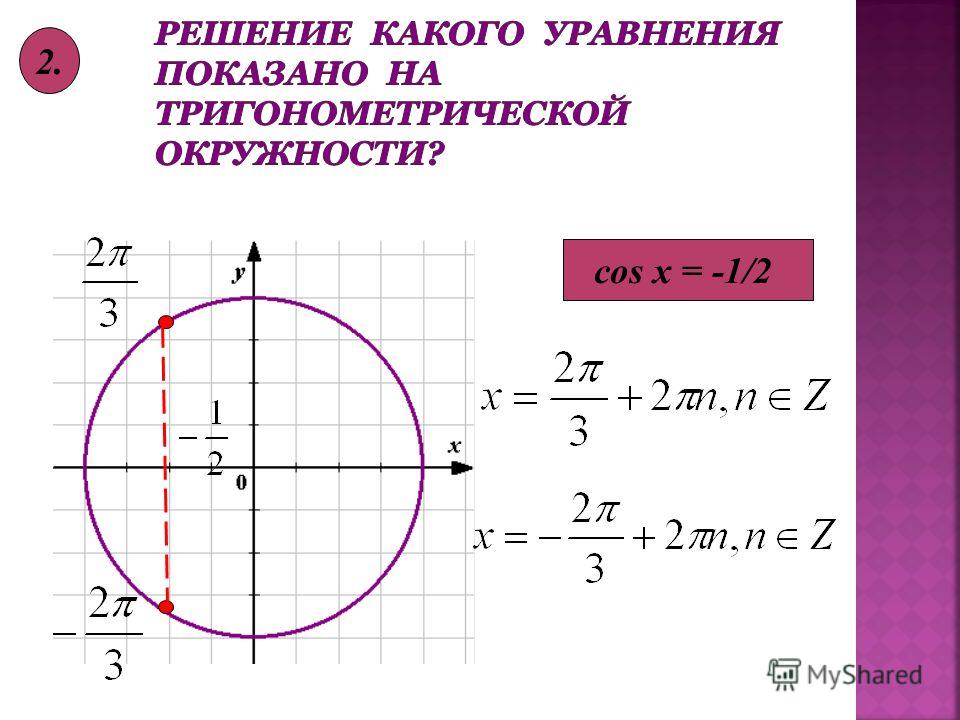 Этот корень называют арккосинусом числа а и обозначают: arccos а.

Таким образом, арккосинусом числа а € [-1; 1 ] называется такое число а € [0; π], косинус которого равен а:

arccos а = α, если cos α = а и 0 ≤ а ≤ π (1).

Например, arccos √3/2 = π/6, так как cos π/6 = √3/2 и 0 ≤ π/6 ≤ π;
arccos (-√3/2) = 5π/6, так как cos 5π/6 = -√3/2 и 0 ≤ 5π/6 ≤ π.

Аналогично тому, как это сделано в процессе решения задач 1 и 2, можно показать, что все корни уравнения cos x = а, где |а| ≤ 1, выражаются формулой

х = +/-arccos а + 2 πn, n € Z (2).

Задача 3.

Решить уравнение cos x = -0,75.

Решение.

По формуле (2) находим, х = +/-arccos (-0,75) + 2 πn, n € Z.

Значение arcos (-0,75) можно приближенно найти на рисунке, измерив угол при помощи транспортира. Приближенные значения арккосинуса также можно находить с помощью специальных таблиц (таблицы Брадиса) или микрокалькулятора. Например, значение arccos (-0,75) можно вычислить на микрокалькуляторе, получив приблизительное значение 2,4188583. Итак, arccos (-0,75) ≈ 2,42. Следовательно, arccos (-0,75) ≈ 139°.

Ответ: arccos (-0,75) ≈ 139°.

Задача 4.

Решить уравнение (4cos x – 1)(2cos 2x + 1) = 0.

Решение.

1) 4cos x – 1 = 0, cos x = 1/4, х = +/-arcos 1/4 + 2 πn, n € Z.

2) 2cos 2x + 1 = 0, cos 2x = -1/2, 2х = +/-2π/3 + 2 πn, х = +/-π/3 + πn, n € Z.

Ответ. х = +/-arcos 1/4 + 2 πn, х = +/-π/3 + πn.

Можно доказать, что для любого а € [-1; 1] справедлива формула arccos (-а) = π – arccos а (3).

Эта формула позволяет выражать значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел. Например:

arccos (-1/2) = π – arccos 1/2 = π – π/3 = 2π/3;

arccos (-√2/2) = π – arсcos √2/2 = π – π/4 = 3π/4

из формулы (2) следует, что корни уравнения, cos x = а при а = 0, а = 1 и а = -1 можно находить по более простым формулам:

cos х = 0 х = π/2 + πn, n € Z (4)

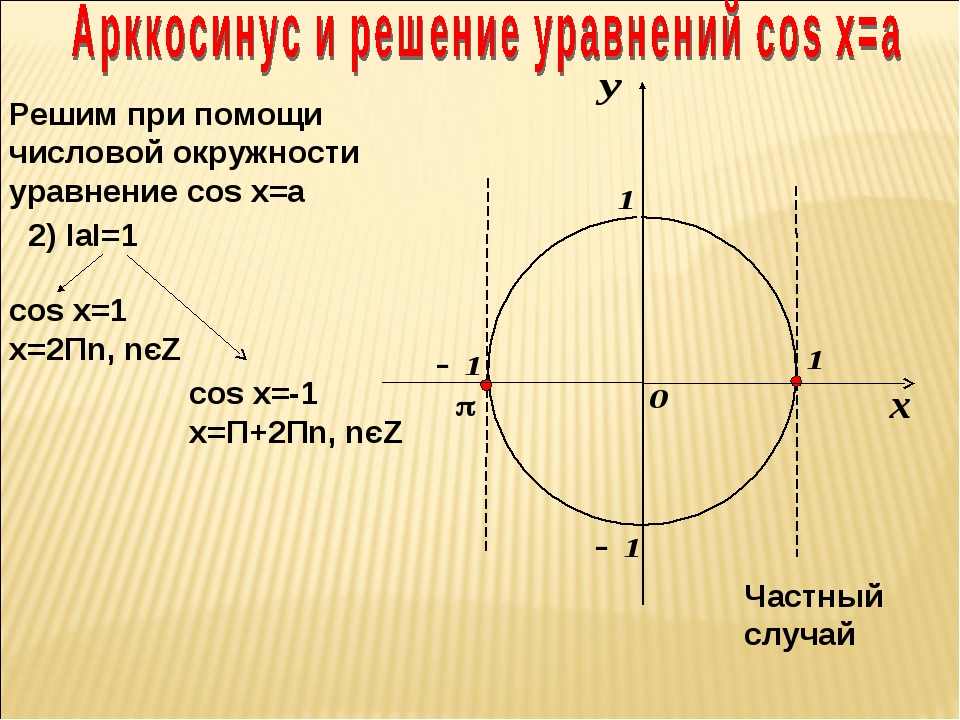
cos х = 1 х = 2πn, n € Z (5)

cos х = -1 х = π + 2πn, n € Z (6).

Урок решить уравнение синус 2х 1 2. Тригонометрические уравнения — формулы, решения, примеры. можно познакомиться с функциями и производными

Когда-то я стал свидетелем разговора двух абитуриентов:

– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!

– И у меня такая же проблема.

Так и хотелось им сказать: «Не запоминать надо, а понимать!»

Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:

Числовая окружность

Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной.
Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.

Свойства числовой окружности

Каждое действительное число находится на одной точке числовой окружности.
На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …

Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A
.

Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z.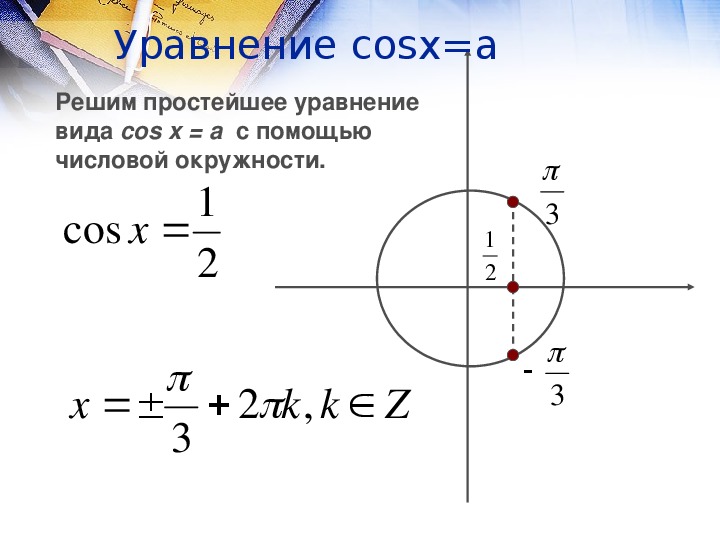 Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).

Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.

Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.

Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z.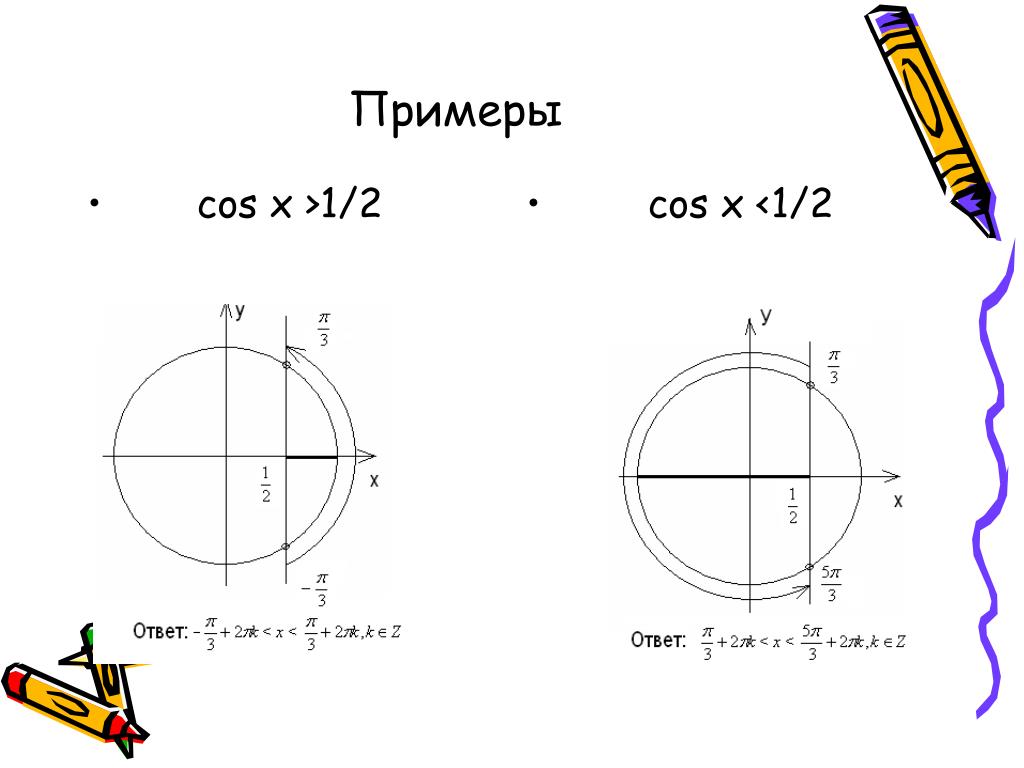 k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).

Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.

Шестнадцать основных точек числовой окружности

На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.

Теперь можем указать по одному числу на точках:

π/3 на С1 и

Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).

Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a)
простейших уравнений.

Решить уравнения

1) sinx=1⁄(2)
.

– Что от нас требуется?

– Найти все те числа x, синус которых равен 1/2
.

Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x
. На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».

2) sinx=-√3⁄2
.

Нам надо найти все числа на точках C4 и C3.

3) sinx=1
. На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.

Ответ: x=π/2+2πk , k∈Z .

4) sinx=-1
.

Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.

Ответ: x=-π/2+2πk , k∈Z .

5) sinx=0
.

На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .

Ответ: x=πk ,k∈Z
.

6) cosx=√2⁄2
.

Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x.
На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.

Ответ: x=±π/4+2πk , k∈Z .

7) cosx=-1⁄2
.

Надо найти числа на точках C_2 и C_3 .

Ответ: x=±2π/3+2πk , k∈Z
.

10) cosx=0
.

Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.

Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .

Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе

Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.

Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).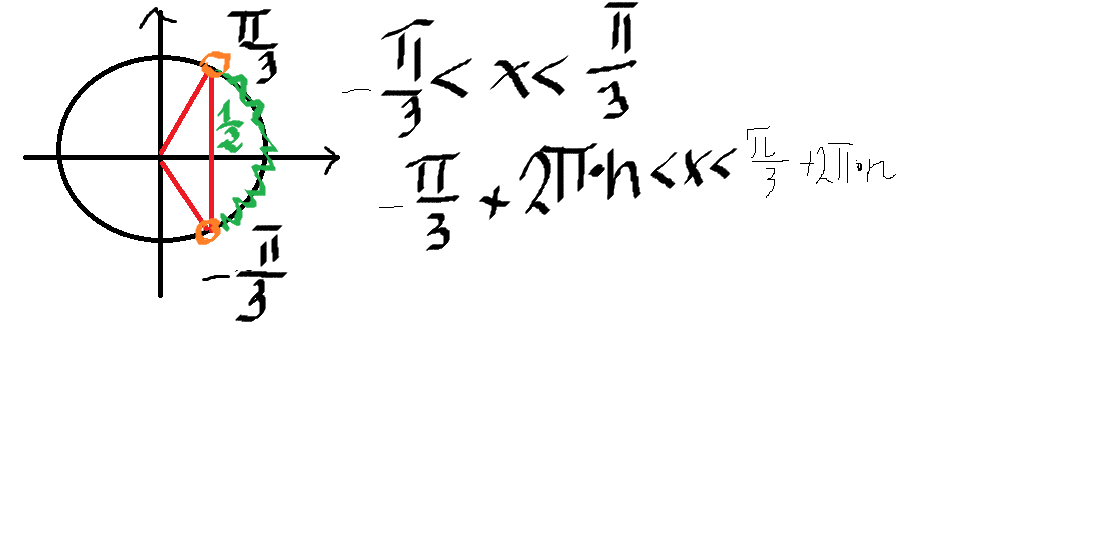

Примеры.

1. Уравнения, сводящиеся к простейшим.

1) Решить уравнение

Решение:

Ответ:

2) Найти корни уравнения

(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .

Решение:

Ответ:

2. Уравнения, сводящиеся к квадратным.

1) Решить уравнение 2 sin 2 x – cosx –1 = 0.

Решение:
Используя формулу sin 2 x = 1 – cos 2 x, получаем

Ответ:

2) Решить уравнение cos 2x = 1 + 4 cosx.

Решение:
Используя формулу cos 2x = 2 cos 2 x – 1, получаем

Ответ:

3) Решить уравнение tgx – 2ctgx + 1 = 0

Решение:

Ответ:

3. Однородные уравнения

1) Решить уравнение 2sinx – 3cosx = 0

Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим

Ответ:

2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x

Решение:

Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим

sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0

Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x.
Получим

tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k
, k

б) tgx = 2, x= arctg2 + 2 k
, k
.

Ответ:
arctg4 + 2 k
, arctg2 + 2 k, k

4. Уравнения вида a
sinx + b
cosx = с, с
≠ 0.

1) Решить уравнение .

Решение:

Ответ:

5. Уравнения, решаемые разложением на множители.

1) Решить уравнение sin2x – sinx = 0.

Корнем уравнения f
( х
) = φ ( х
) может служить только число 0. Проверим это:

cos 0 = 0 + 1 – равенство верно.

Число 0 единственный корень данного уравнения.

Ответ:
0.

Вы можете заказать подробное решение вашей задачи !!!

Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.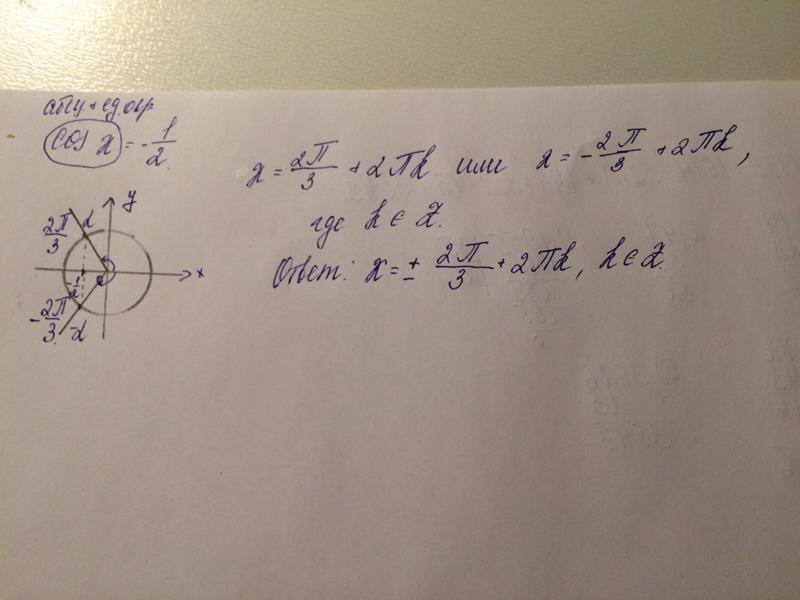 n arcsin a + \pi n, n \in Z`

2. Уравнение `cos x=a`

При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.

При `|a| \leq 1` имеет бесконечное множество решений.

Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Частные случаи для синуса и косинуса в графиках.

3. Уравнение `tg x=a`

Имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arctg a + \pi n, n \in Z`

4. Уравнение `ctg x=a`

Также имеет бесконечное множество решений при любых значениях `a`.

Формула корней: `x=arcctg a + \pi n, n \in Z`

Формулы корней тригонометрических уравнений в таблице

Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений

Решение любого тригонометрического уравнения состоит из двух этапов:

с помощью преобразовать его до простейшего;
решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Задачи с параметром на единственность, количество решений и нахождение множества решений.
Иррациональные уравнения и неравенства.

Московский физико-технический институт Иррациональные уравнения и неравенства Методическое пособие по подготовке к олимпиадам Составитель: Паркевич Егор Вадимович Москва 04 Введение В этой работе мы рассмотрим
Подробнее
( 3) log 3 ( 125) = ( 5 3 ) = x=53. = log 5 = 3

Решение некоторых заданий одного из вариантов досрочного экзамена ЭГЭ по математике в 2012 году, полученное с помощью программы UMS B5 x+28 =9 Отметим ОДЗ. x+28 0 x+28 =9 Воспользуемся свойством радикалов.
Подробнее
ЕГЭ 2018 Профильный уровень

ЕГЭ 2018 Профильный уровень Задания с параметрами Ильина Зоя Владимировна, старший преподаватель Кафедры естественно-математических Дисциплин ТОГИРРО 2 марта, 2018 г Решение уравнений с параметром Найдите
Подробнее
Иррациональные неравенства

Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного
Подробнее
МЕТОДИЧЕСКОЕ ПОСОБИЕ

ВОЕННО-ТЕХНИЧЕСКИЙ КАДЕТСКИЙ КОРПУС Дисциплина: «Математика, основы информатики и вычислительной техники» МЕТОДИЧЕСКОЕ ПОСОБИЕ для кадет Тема: Уравнения и неравенства с параметрами. Преподаватель: Молоткова
Подробнее
ОТВЕТЫ ,4 25 0,8 НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК

МАТЕМАТИКА, класс Ответы и критерии, Апрель Вариант/ задания ОТВЕТЫ В В В В4 В В В7 С 4 7 4 arccos 7 44,7 9 8 + n, n, 4 8 7 4,4,8 4 4, 4, 9,,4 ( ; ) ( log 😉 + n,, 8 49 8,7 ( 4; ) ( ; + ), 8 9, 4 8 + 7
Подробнее
ОЛИМПИАДА «ФИЗТЕХ» ПО МАТЕМАТИКЕ. 11 класс

МОСКОВСКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ ОЛИМПИАДА «ФИЗТЕХ» ПО МАТЕМАТИКЕ 11 класс БИЛЕТ 1 ШИФР Заполняется ответственным секретарём 1 Дана линейная функция f(x) Известно, что расстояние между точками пересечения
Подробнее
РАЗДЕЛ 14. ЗАДАЧИ С ПАРАМЕТРАМИ

РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных
Подробнее
Параметры и квадратный трёхчлен.
3
И. В. Яковлев Материалы по математике MathUs.ru Параметры и квадратный трёхчлен. В данной статье мы рассматриваем задачи с параметрами, так или иначе сводящиеся к исследованию квадратных уравнений и неравенств.
Подробнее
Исследование тригонометрических функций

И. В. Яковлев Материалы по математике MthUs.ru Исследование тригонометрических функций Напомним, что функция fx называется периодической, если существует такое число T 0, что для любого x из области определения
Подробнее
Тема 39. «Производные функций»

Тема 39. «Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная
Подробнее
Исследование тригонометрических функций

И. В. Яковлев Материалы по математике MthUs.ru Исследование тригонометрических функций Напомним, что функция fx) называется периодической, если существует такое число T 0, что для любого x из области определения
Подробнее
Минимаксные задачи в тригонометрии

И. В. Яковлев Материалы по математике MathUs.ru Минимаксные задачи в тригонометрии В настоящем листке рассматриваются уравнения, для решения которых используются оценки правой и левой частей. Чтобы стало
Подробнее
Тригонометрические неравенства

И В Яковлев Материалы по математике MathUsru Тригонометрические неравенства Предполагается, что читатель умеет решать простейшие тригонометрические неравенства Мы же переходим к более сложным задачам Задача
Подробнее
Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Симметрия в задачах с параметрами 1. (МГУ, ф-т почвоведения, 001 ) При каких значениях b уравнение имеет ровно один корень? tg b = log
Подробнее
Тренировочные задачи

И В Яковлев Материалы по математике MathUsru Тренировочные задачи Квадратные уравнения и неравенства с параметрами 3 МГУ, ВМК, 003 При всех значениях параметра d решите уравнение 4 x + d 49 x = 4 4 x Олимпиада
Подробнее
ОТВЕТЫ НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК

МАТЕМАТИКА, класс Ответы и критерии, Февраль 0 Вариант/ задания ОТВЕТЫ В В В В4 В5 В6 В7 С 0 6 0 9 4,5 6 n, n Z 7 5 0 6,5-0,5 64 5 7 90,6 9,5 0, 4,75 9 6 0 n, n Z 7 4 6 5 0,5 7 0,45 5 0640 4 7,7 0 -,75
Подробнее
ОТВЕТЫ НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК

МАТЕМАТИКА, класс Ответы и критерии, Апрель 0 Вариант/ задания ОТВЕТЫ В В В В В В В7 С — 0,, 000, 0-8 000 70 ( 0 0, 7, 7 0 ± + n, n — 9 9 9 8 0 ( 0 9 77-9,8 0, 9 + k, k 8 00 0, 7 0 000 8, 7 0 000 0 ( 8
Подробнее
Задачи с параметром в ЕГЭ

Л. А. Штраус, И.В. Баринова Задачи с параметром в ЕГЭ Методические рекомендации y=-x 0 -a- -a х -5 Ульяновск 05 Штраус Л.А. Задачи с параметром в ЕГЭ [Текст]: методические рекомендации / Л.А. Штраус, И.В.
Подробнее
ID_4970 1/7 neznaika.pro

Уравнения, неравенства, системы с параметром Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
Подробнее
г. Классная работа.

5.0. 014 г. Классная работа. Уравнения и системы уравнений с параметрами. Опыт вступительных экзаменов в вузы показывает, что решение уравнений и неравенств, содержащих параметры, вызывает большие затруднения
Подробнее
Тема 41 «Задания с параметром»

Тема 41 «Задания с параметром» Основные формулировки заданий с параметром: 1) Найти все значения параметра, при каждом из которых выполняется определенное условие. ) Решить уравнение или неравенство с
Подробнее
Решение уравнений. Полезные сведения

Решение уравнений Полезные сведения Решение уравнений сводится к тождественным преобразованиям выражений, стоящих слева и справа от знака равенства. Преобразования считаются тождественными и между последовательно
Подробнее
УДК 51(075.8) ББК 22.1 ISBN

Министерство образования Республики Беларусь УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯНКИ КУПАЛЫ» Ю.Ю. Гнездовский, В. Н. Горбузов, П.Ф. Проневич ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
Подробнее
Методы решения задач с параметром

Научно-исследовательская работа «Старт в науке» Тема работы: Методы решения задач с параметром Выполнил: Власов Никита Денисович учащийся 11 класса МБОУ «СОШ 5 с углубленным изучением отдельных предметов»
Подробнее
Неравенство Коши-Буняковского.

Московский физико-технический институт Неравенство Коши-Буняковского. Методическое пособие по подготовке к олимпиадам. Составитель: Паркевич Егор Вадимович Москва 014 Теоретический материал. В этой работе
Подробнее
Тренировочные задачи

И В Яковлев Материалы по математике MathUsru Тренировочные задачи Квадратные уравнения и неравенства с параметрами 2 Докажите, что уравнение имеет решение при любом a: а) a 2 + )x 2 + a + a 2 + a)x a 2
Подробнее
; ctg α = 1 sin 2 α = 1 + ctg2 α

Министерство науки и образования Российской Федерации Московский Государственный Университет Геодезии и Картографии Т. М. Королёва, Е. Г. Маркарян, Ю. М. Нейман ПОСОБИЕ ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ В
Подробнее
Симметрия в задачах с параметрами

И. В. Яковлев Материалы по математике MathUs.ru Симметрия в задачах с параметрами Симметрия одно из ключевых понятий математики и физики. Вы знакомы с геометрической симметрией фигур и вообще различных
Подробнее
Учебный центр «Резольвента»

ООО «Резольвента», www.resolventa.ru, [email protected], (495) 509-8-10 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К. Л. САМАРОВ УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЯМИ Учебное
Подробнее
Обратные тригонометрические функции

И. В. Яковлев Материалы по математике MathUs.ru Обратные тригонометрические функции Перед этим листком следует повторить статью «Введение в аркфункции», в которой приводятся определения арксинуса, арккосинуса,
Подробнее
Учебный центр «Резольвента»

ООО «Резольвента», www. resolventa.ru, [email protected], (495) 509-8-0 Учебный центр «Резольвента» К. Л. САМАРОВ, С.С. САМАРОВА ТРИГОНОМЕТРИЯ В ЕГЭ ПО МАТЕМАТИКЕ Учебно-методическое пособие для подготовки
Подробнее
Методы решения заданий с параметрами.

МБОУ Покровская улусная многопрофильная гимназия МР Хангаласский улус РС (Я) Методы решения заданий с параметрами. доклад учителя математики ПУМГ Владимирова Михаила Даниловича г. Покровск 2016 г. 1 Содержание
Подробнее
Тригонометрические уравнения с модулем

И. В. Яковлев Материалы по математике MathUs.ru Тригонометрические уравнения с модулем Этот листок посвящён тригонометрическим уравнениям, в которых тригонометрические функции от неизвестной величины содержатся
Подробнее
РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ

РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Оглавление РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ I Рациональные алгебраические уравнения Равносильность уравнений Равносильность уравнений на множестве Равносильность
Подробнее
Параметры и квадратный трёхчлен.
2
И. В. Яковлев Материалы по математике MathUs.ru Параметры и квадратный трёхчлен. 2 Данная статья посвящена вопросам расположения корней квадратного трёхчлена в зависимости от параметра. Вычисление корней
Подробнее
Обратные тригонометрические функции. 2

И. В. Яковлев Материалы по математике MathUs.ru Обратные тригонометрические функции. Перед этим листком следует повторить статью «Обратные тригонометрические функции.», в которой приводятся определения
Подробнее
1 Корни и их количество

1 Функции, их графики и связанные с ними доказательства Оглавление 1 Корни и их количество…1 1.1 Корни уравнения…1 1.1.a Корни уравнения…1 1. Число корней… 1. Число корней… 1.4 Функциональное
Подробнее
Билет Билеты Решения

1 Билеты 1 16. Решения Билет 1 1. Дана линейная функция f(x). Известно, что расстояние между точками пересечения графиков y = x + 1 и y = f(x) равно, а расстояние между точками пересечения графиков y =
Подробнее
Задание 18. Задачи с параметром

Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
Подробнее
4.6. Иррациональные уравнения

4.6. Иррациональные уравнения Иррациональным уравнением называют уравнение, содержащее под знаком радикала переменную, относительно которой оно решается. Областью допустимых значений уравнения являются
Подробнее
Учебный центр «Резольвента»

ООО «Резольвента», www. resolventa.ru, [email protected], (495) 509-8-0 Учебный центр «Резольвента» Кандидат физико-математических наук, доцент С. С. САМАРОВА РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ Учебно-методическое
Подробнее
Тригонометрические уравнения
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах.
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°…
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
Пример №1. cos(x) = ½
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
Или запомнить такой прием:
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2): π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на …=-225°=135°=495°=…
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: …,60°-360°, 60°, 60°+360°,…
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= −π/3 + 2πk, (n, k)∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y, вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
Пример №4: −10ctg(x) = 10
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π…) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = −√3/2):
1. Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
2. Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
3. Точки пересечения с окружностью и будут являться корнями уравнения.
4. Значение одной точки (без разницы, как в нее попадете) +2πk.
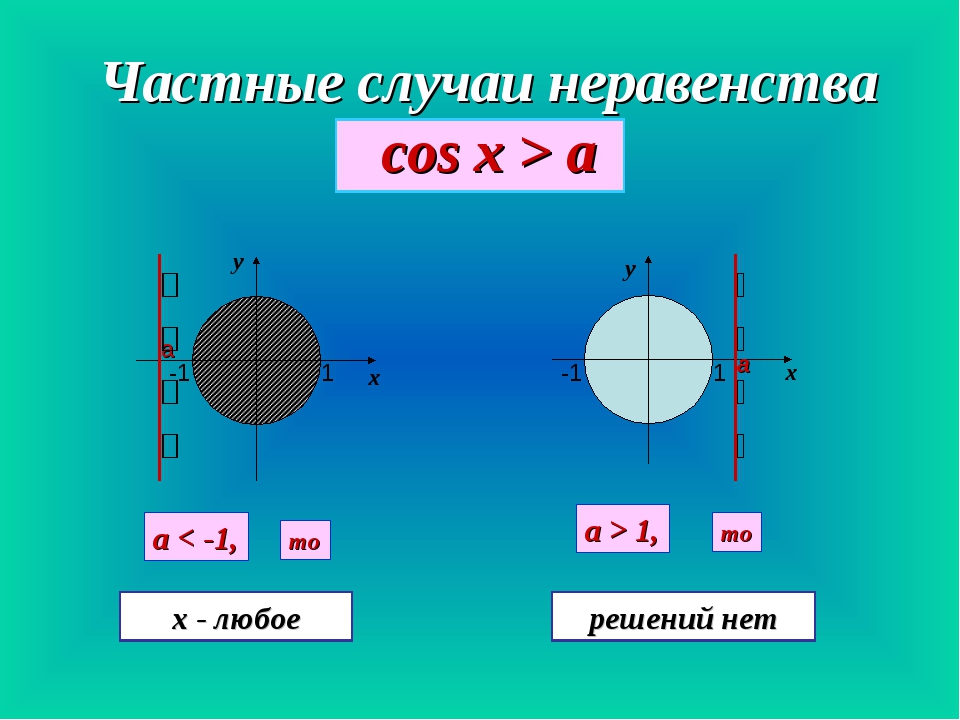
Азов достаточно, прежде чем идти дальше закрепите полученные знания.
Будь в курсе новых статеек, видео и легкого математического юмора.
Cos x = -1/2
Отправитель: Pierre Boivin
тригонометрическое уравнение, расширяющее решение. 2cos -5cos-3 = 0 для диапазона от -360 до 720 градусов
Когда я множу [2cos (квадрат) — 5cos -3], я получаю (2cos + 1) (cos — 3).
2cos + 1 = 0, 2cos = -1, cos = -0,5,. Используя inv cos на калькуляторе, я получаю угол в 120 градусов.
Когда я строю график, я получаю два значения: от 90 до 180 градусов и от 180 до 270 градусов. Как мне найти эти два значения. Как использовать 120 градусов по отношению к оси x.Может быть, мой фактоттинг ошибочен.
заранее спасибо
Меня зовут Пьер Иам, я учусь на курсах корреспонденции.
Привет Пьер,
Ваш факторинг в порядке. Сложность возникает при попытке решить cos x = -1/2. Я бы быстро набросал график одного цикла y = cos x для x от 0 ^o до 360 ^o.
Обратите внимание, что график пересекает ось x под углом 90 ^o и 270 ^o. Если вы нарисуете горизонтальные линии ay y = 1/2 и y = -1/2, вы увидите, что есть два значения x, в Q и R, где cos x = -1/2 и два значения x, в P и S, где cos x = 1/2.
Ключ к нахождению Q и R — это сначала найти P. Либо используя обратный косинус на вашем калькуляторе, либо используя треугольник «30-60-90», вы можете найти, что P = 60 ^o. Теперь из симметрии диаграммы P находится на 30 ^o слева от точки пересечения на 90 ^o, поэтому Q составляет 30 ^o справа от 90 ^o. Таким образом, Q равно 90 ^o + 30 ^o = 120 ^o. Для другой пары точек R находится на 30 ^o слева от 270 ^o, а S на 30 ^o справа.Таким образом, R равно 270 ^o — 30 ^o = 240 ^o, а S равно 270 ^o + 30 ^o = 300 ^o. 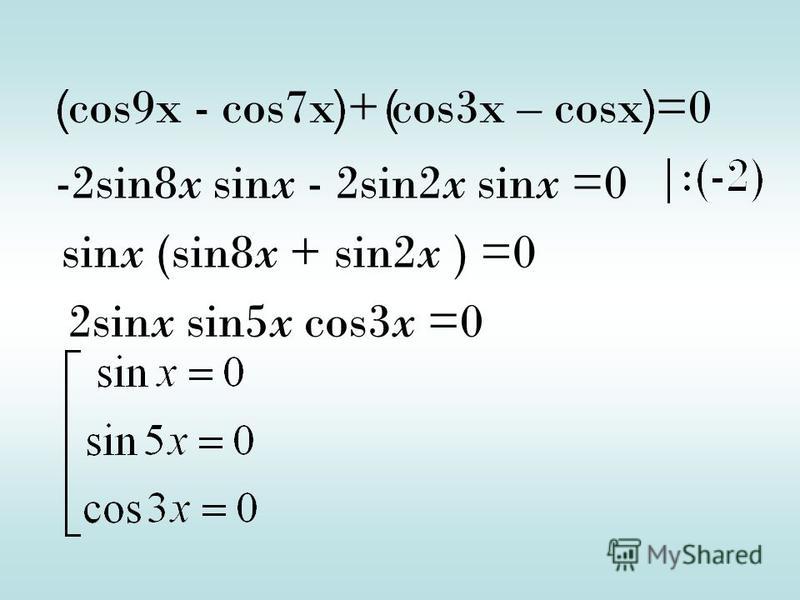Следовательно, cos x = -1/2 при 120 ^o и 240 ^o.
Это только значения x между 0 ^o и 360 ^o. Вы можете сложить или вычесть целые числа, кратные 360 ^o, и получить множество других решений.
Ура,
Пенни
Перейти в Центр математики
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Примечание: Если вы хотите получить обзор тригонометрии, нажмите
тригонометрия.
Пример 1: Решите относительно x в следующем уравнении.

Есть бесконечное множество решений этой проблемы.
Сначала выделите косинусный член.
Чтобы найти x, мы должны изолировать x. Как нам изолировать x? Мы могли бы взять
инверсия (арккосинус) обеих сторон. Однако обратные функции могут только
применяться к взаимно однозначным функциям, а функция косинуса не
один к одному.
Давайте ограничим область, чтобы функция была однозначной на ограниченном
домен при сохранении исходного диапазона. Функция косинуса
один к одному на интервале
Если мы ограничим
области функции косинуса к этому интервалу, мы можем взять арккосинус
обеих частей каждого уравнения.

Угол x — это опорный угол. Мы знаем это

Следовательно, если
,
тогда
Период
равно
и период
равно
,
это означает, что существуют другие решения
каждый
единицы измерения. Точные решения
где n — целое число.
Приблизительные значения этих решений:
где n — целое число.
Вы можете проверить каждое решение алгебраически, подставив каждое решение в
исходное уравнение. Если после подстановки левая часть
исходное уравнение равно правой части исходного уравнения,
решение действительно.
Вы также можете проверить решения графически, построив график функции, сформированной
путем вычитания правой части исходного уравнения из левой части
исходное уравнение.Решениями исходного уравнения являются
x-пересечения этого графа.
Алгебраическая проверка:
Проверить решение
х = 0,8569321
Левая сторона:
Правая сторона:
Поскольку левая часть исходного уравнения равна правой части
исходное уравнение, когда вы подставляете 0,8569321 вместо x, тогда 0,8569321 будет
решение.

Проверить решение
х = -0,19026544
Левая сторона:
Правая сторона:
Поскольку левая часть исходного уравнения равна правой части
исходное уравнение при замене
-0.19026544 для x, тогда
-0.19026544 — это решение.

Мы только что алгебраически проверили, что точные решения
и эти решения повторяются каждый
единицы измерения. Приблизительные значения этих решений:
и 0,8569321, и эти решения повторяются каждые
единицы измерения.
Графическая проверка:

Изобразите уравнение
(образуется вычитанием
правая часть исходного уравнения от левой части исходного
уравнение).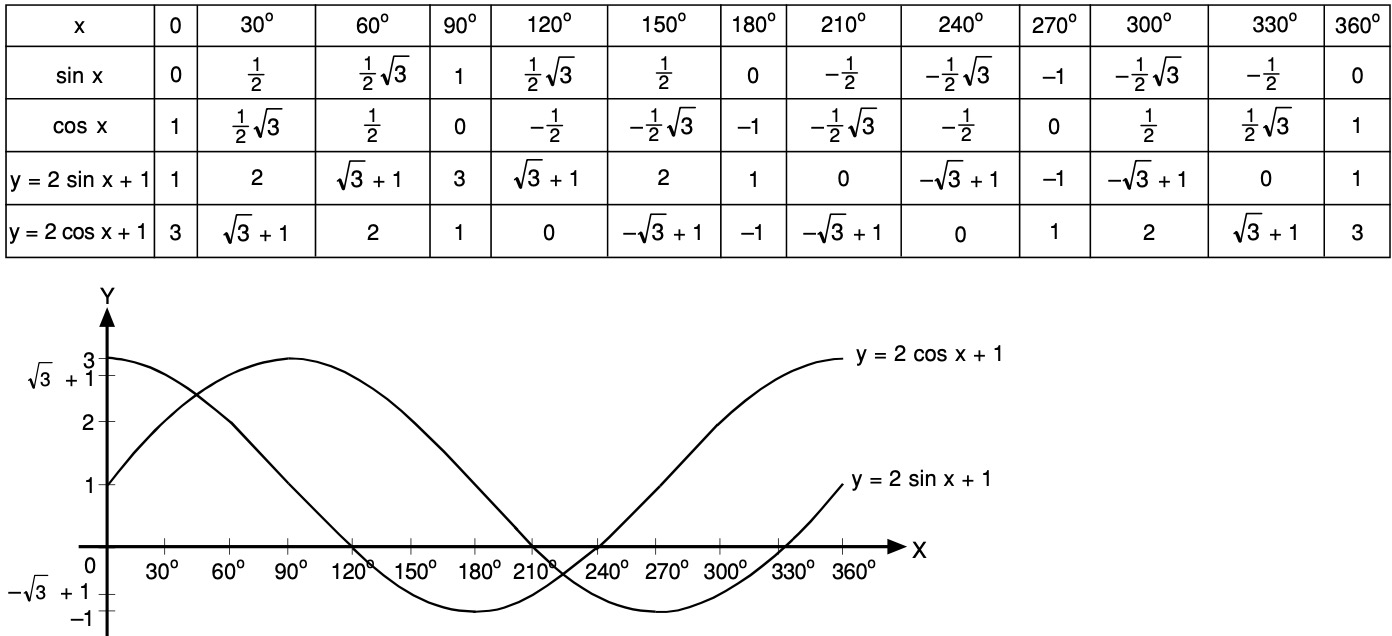 Обратите внимание, что график пересекает ось x много раз, указывая на множество
решения.Давайте проверим несколько из этих x-перехватов с решениями, которые мы
полученный.
Убедитесь, что график пересекает ось x в точке
-0,19026544. Поскольку период
,
вы можете убедиться, что график также
снова пересекает ось абсцисс в точке
и в
,
7.997049, 10.091444 и др.
Убедитесь, что график пересекает ось x в точке
0,8569321. Поскольку период
,
вы можете убедиться, что график также
снова пересекает ось абсцисс в точке
и в
,
7.1401171 и др.
Примечание: если проблема заключалась в том, чтобы найти решения в интервале
,
затем вы выбираете эти решения из множества бесконечных
решения, принадлежащие множеству
1.90412966, г.
2.9513271,
5.0457221 и

Если вы хотите проработать другой пример, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой
Например, щелкните «Проблема».
Если вы хотите перейти к следующему разделу, нажмите «Далее».
Если вы хотите вернуться к оглавлению уравнения, щелкните
Содержание.
[Алгебра]
[Тригонометрия]
[Геометрия]
[Дифференциальные уравнения]
[Исчисление]
[Комплексные переменные]
[Матричная алгебра]
С.Домашняя страница O.S MATHematics

Автор:
Нэнси Маркус

Авторские права 1999-2021 MathMedics, LLC. Все права защищены.

Свяжитесь с нами

Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США

пользователей онлайн за последний час
Решение тригонометрических уравнений с использованием тригонометрических тождеств
Уравнение, содержащее
тригонометрические функции
называется

тригонометрическое уравнение

.

Пример:

грех
2
Икс
+
потому что
2
Икс
знак равно
1
2
грех
Икс
—
1
знак равно
0
загар
2
2
Икс
—
1
знак равно
0
Решение тригонометрических уравнений с использованием тригонометрических тождеств

Тригонометрические тождества
являются уравнениями, включающими тригонометрические функции, которые верны для любого значения задействованных переменных. Вы можете использовать тригонометрические тождества вместе с алгебраическими методами для решения тригонометрических уравнений.
Посторонние решения

An
посторонний раствор
является корнем преобразованного уравнения, который не является корнем исходного уравнения, поскольку он был исключен из области определения исходного уравнения.
Когда вы решаете тригонометрические уравнения, иногда вы можете получить уравнение для одной тригонометрической функции, возведя в квадрат каждую сторону, но этот метод может дать посторонние решения.

Пример :

Найти все решения уравнения в интервале
[
0
,
2
π
)
.
2
грех
2
Икс
знак равно
2
+
потому что
Икс
Уравнение содержит функции синуса и косинуса.
Мы перепишем уравнение так, чтобы оно содержало только косинусные функции, используя тождество Пифагора.
грех
2
Икс
знак равно
1
—
потому что
2
Икс
.
2
(
1
—
потому что
2
Икс
)
знак равно
2
+
потому что
Икс
2
—
2
потому что
2
Икс
знак равно
2
+
потому что
Икс
—
2
потому что
2
Икс
—
потому что
Икс
знак равно
0
2
потому что
2
Икс
+
потому что
Икс
знак равно
0
Факторинг
потому что
Икс
мы получаем,
потому что
Икс
(
2
потому что
Икс
+
1
)
знак равно
0
.
Используя
свойство нулевого продукта
, мы получим
потому что
Икс
знак равно
0
, а также
2
потому что
Икс
+
1
знак равно
0
который дает
потому что
Икс
знак равно
—
1
2
.
В интервале
[
0
,
2
π
)
, мы знаем это
потому что
Икс
знак равно
0
когда
Икс
знак равно
π
2
а также
Икс
знак равно
3
π
2
.С другой стороны, мы также знаем, что
потому что
Икс
знак равно
—
1
2
когда
Икс
знак равно
2
π
3
а также
Икс
знак равно
4
π
3
.
Следовательно, решения данного уравнения в интервале
[
0
,
2
π
)
находятся
{
π
2
,
3
π
2
,
2
π
3
,
4
π
3
}
.
Решатель тригонометрических уравнений
Решение тригонометрических уравнений. Тригонометрические уравнения и неравенства. Общий метод решения уравнения — преобразовать его в форму только одного отношения. Мы читаем уравнение слева направо по горизонтали, как предложение. Таким образом, вы ищете значения θ в третьем и четвертом квадрантах, которые имеют опорный угол π / 3. Чтобы найти решения этих уравнений, нам нужно использовать обратные триггерные функции. Расчеты для получения результата детализированы, поэтому можно будет решить уравнения типа `cos (x) = 1 / 2` или` 2 * sin (x) = sqrt (2) `с этапами расчета. Почти все тригонометрические тождества, включая взаимные тождества, пифагоровы тождества, тождества факторов, тождества со-функций, тождества четно-нечетных, формулы суммы-разности, формулы двойного и половинного угла, а также суммы-к-произведению и произведения-к -Суммы формулы. Следующая таблица представляет собой частичный список типичных уравнений. Квадратичная формула говорит, что если у вас есть квадратное уравнение в форме ax2 + bx + c = 0, где a равно […] Решите тригонометрическое уравнение $ 3 \ cos x + 2 \ sin x = 1 $ Задать вопрос Задано 5 лет, 3 месяца назад.Если вы находитесь за веб-фильтром, убедитесь, что домены *. Иногда невозможно решить тригонометрическое уравнение с помощью тождеств, имеющих кратный угол, например \ (\ sin (2x) \) или \ (\ cos (3x) \). Решение тригонометрических уравнений может быть немного сложным, потому что не существует стандартной процедуры для решения тригонометрических уравнений. 1 2 Решения таких тригонометрических уравнений, которые лежат в интервале [0, 2π], называются главными решениями. Затем, используя эти результаты, мы можем получить решения. Решение тригонометрических уравнений.Запатентованная обучающая система Virtual Nerd предоставляет контекстную информацию, подсказки и ссылки на вспомогательные обучающие материалы, синхронизированные с видео, продолжительностью от 3 до 7 минут. Khan Academy — некоммерческая организация 501 (c) (3). Возможно, вы захотите вернуться и взглянуть на тригонометрические функции любого угла, где мы видим предысторию следующих решений. Спланируйте свой 60-минутный урок по математике или предварительному вычислению и исчислению с помощью полезных советов от Тиффани Доуди. Для этой системы уравнений MATLAB может найти решение в замкнутой форме для th2 и th3 в терминах обратной тригонометрической функции, если заданы th4 и th5. .00: 00: 00: hr min sec Объясните, почему многие тригонометрические уравнения имеют бесконечно много решений. Мы можем использовать знания о преобразовании триггерных функций с помощью этих тождеств для решения более сложных уравнений. Решение тригонометрических уравнений — это просто поиск решений уравнений, как мы делали с линейными, квадратными и радикальными уравнениями, но с использованием вместо них триггерных функций. Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте. Однако логарифмы в уравнении на данный момент являются просто числами, поэтому мы относимся к ним так же, как и ко всем числам с помощью такого рода уравнений.Домашнее задание 376-379 35-47 нечетное, 49-53 нечетное, 61-71 нечетное Домашнее задание Страница 376-379 35-47 нечетное, 49-53 нечетное, 61-71 нечетное В этом разделе вы научитесь: Использовать стандартные алгебраические методы решения тригонометрических уравнений Решение тригонометрических уравнений квадратичного типа Решение тригонометрических уравнений с множественными углами Используйте обратные тригонометрические функции для решения тригонометрических уравнений Два основных раздела 7. Решите относительно x в следующем уравнении. Выделяем sin (x), прибавляя 4 и извлекая квадратный корень из обеих частей.(a) Покажите, что уравнение 5 cos2 x = 3 (1 + sin x) может быть записано как 5 sin2 x + 3 sin x — 2 = 0. Решение для Решите уравнение для решений в интервале [0,2x) с помощью первое решение для тригонометрической функции. Решения этих уравнений для тригонометрической функции от переменной x, где x лежит между 0≤x≤2π, называются основными примечаниями к обзору — раздел 5. Напомним, что уравнения на этом этапе имеют тенденцию выглядеть более запутанными, чем мы привыкли иметь дело. с участием. Я практиковался, чтобы улучшить и уточнить свое понимание, но я все еще немного неуверен в некоторых областях.co. Пример 5: Решите тригонометрическое уравнение с помощью тождества. rebekah_renteria. Последняя активность 5 лет 3 месяца назад. 362 — 373 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ • При решении двух тригонометрических уравнений два неизвестных. Например, cos (1) то же самое, что cos 1 Rad.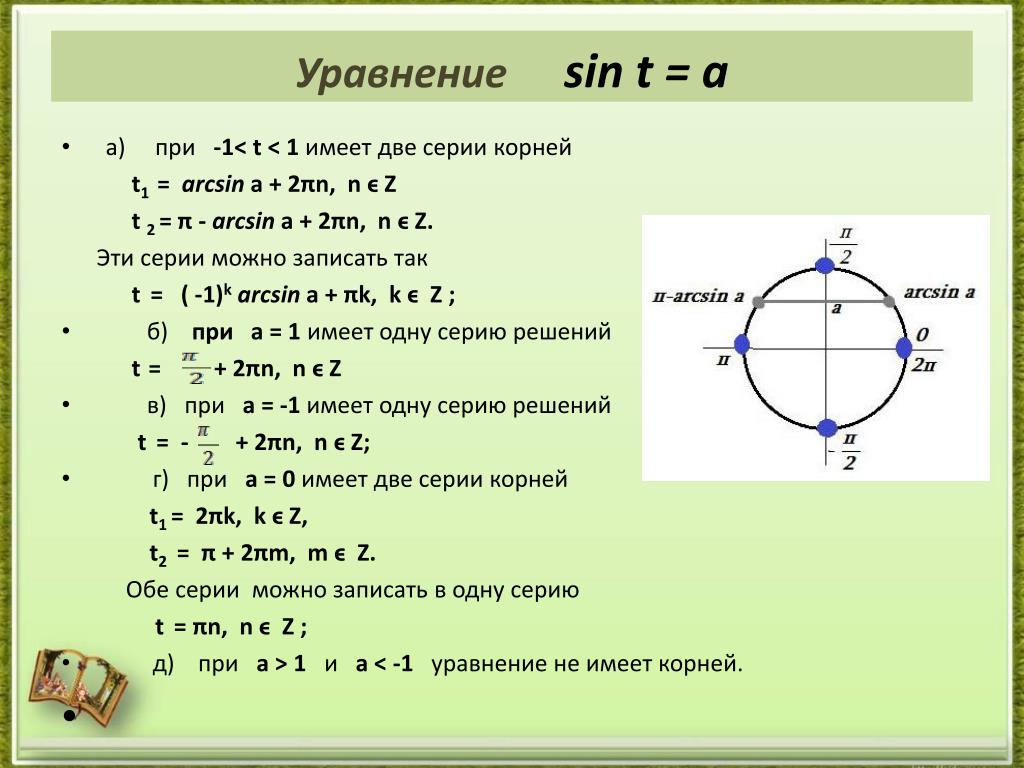 До сих пор мы вводили тригонометрические функции, но не исследовали их полностью. Чтобы узнать, какой метод использовать, вам нужно узнать о каждом методе, а затем решить, какой из них вы будете использовать для конкретного уравнения. Узнайте больше о тригонометрических уравнениях.Раздел 1-6: Решение триггерных уравнений с помощью калькуляторов, Часть II. Обычно существует два способа решить тригонометрическое уравнение, алгебраический метод и графический метод. Он берет строку с одним или несколькими уравнениями и анализирует строку для решения уравнений. Когда два тригонометрических графика, такие как синус и косинус, пересекаются, мы называем эту точку пересечения решением системы уравнений. Последняя активность 2 года 9 месяцев назад. Найдите решение (я) следующих уравнений. Онлайн-калькулятор и решатель для тригонометрических уравнений с функцией косинуса вида cos x = a.Решением основных уравнений можно заняться с помощью тригонометрического метода R. 1 — это один конец очень известного тригонометрического тождества, и замена его на 3. Бесплатная программа для решения уравнений абсолютного значения, ответы на шестое издание по алгебре и тригонометрии, применение (алгебра, бесплатная математика для четырехклассников от наименьшего до наибольшего десятичных знаков для печати рабочий лист, квадратное уравнение 3 точки решить онлайн, разложение трехчленов на двойные переменные. Простейшие тригонометрические уравнения. naikermaths. Мохамед Ахмед, 14 апреля 2018 г.Всякий раз, когда вы ищете руководства по решению неравенств или даже радикальных уравнений, используйте факторинг-полиномы. Этот решатель тригонометрических уравнений найдет точные или приближенные решения в заданном диапазоне. Этот класс может решать линейные, полиномиальные, тригонометрические уравнения. Этот калькулятор попытается решить систему из 2, 3, 4, 5 одновременных уравнений любого типа, включая полиномиальные, рациональные, иррациональные, экспоненциальные. Иллюстрация: Решите уравнение: cos θ = 0 Решение Решение тригонометрических уравнений Направления: Используя цифры от 1 до 9, не более одного раза каждую, найдите уравнение, решение которого является наибольшим значением x (от 0 до 360 или от 0 до 2π ).Онлайн-калькулятор доказательства тригонометрических идентичностей с решением и шагами. В этой теме рассматриваются: — Определение тригонометрических функций единичного круга — Тригонометрические тождества — Графики синусоидальных и тригонометрических функций — Обратные тригонометрические функции и решение тригонометрических уравнений — Моделирование с помощью тригонометрических функций — Параметрические функции Решение тригонометрических уравнений с использованием формул суммы и разности. решение уравнений Этот раздел иллюстрирует процесс решения уравнений различных форм. Два способа визуализировать решения: (1) график в координатной плоскости и (2) единичный круг.Используйте единичный круг, поскольку он помогает находить решения, когда у вас есть опорный угол. 5_practice_solutions. Триггерные уравнения с полууглами и множественными углами Ниже приведены иллюстрации работы с тригонометрическими уравнениями с множественными углами. 0 Прошедшее время Время. Если вам нужна помощь с рабочим листом или алгебраическими выражениями, алгебра-уравнение. Если задан интервал, найдите только те решения, которые находятся в интервале. Шаги, предпринятые для решения уравнения, будут зависеть от формы, в которой 8.Наконец, мы рассмотрим, как решать более общие тригонометрические уравнения. pdf: Размер файла: 503 kb: Скачать файл. Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Решите тригонометрические уравнения» и тысяч других математических навыков. Пример: Решите следующее; 3cos x — 1 = 0. sin x = -4/8. com — это бесплатный математический веб-сайт, который объясняет математику простым способом и включает множество примеров, от подсчета до исчисления. Если вы забыли точную формулу, вот она. Определение недопустимых значений для триггерных выражений.⋮. Этот пост является частью серии: Trig Help. 6 sin x + 9 = 6 Выберите правильный вариант… Решите простое тригонометрическое уравнение. Борн. 3sin x — 11sin x = 4-8sin x = 4. Выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов. Microsoft Math Solver. 1. Ниже приведен калькулятор фазового сдвига амплитудного периода для тригонометрических функций, который поможет вам с легкостью вычислить вертикальный сдвиг, амплитуду, период и фазовый сдвиг синусоидальных и косинусных функций.Уравнение, включающее тригонометрические функции неизвестного угла, называется тригонометрическим уравнением. Как избежать распространенных математических ошибок. 2 грех х — 1 = 0 2 грех х = 1 грех х = 1/2. Уравнения могут быть такими простыми, как это, или более сложными, например sin2 x — 2 cos x — 2 = 0. Решите тригонометрические уравнения, проблемы с ответами. Выберите правильный ответ. Единственная проблема с уравнениями, которые мы там решили, заключается в том, что почти все они имели решения, которые исходили из горстки «стандартных» углов, и, конечно же, есть много уравнений, которых просто нет.Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Существует бесконечное количество способов выбрать набор параметрических уравнений для кривой, определенной как прямоугольное уравнение. pdf из MATH PRE CAL в школе Cosumnes Oaks High. Некоторые простые тригонометрические уравнения Пример Предположим, мы хотим решить уравнение sinx = 0. Это показано в разделе Решение тригонометрического уравнения 2 sin (θ) = -1 Решение: Перепишите приведенное выше уравнение в простой форме, как показано ниже.Без использования калькулятора найдите решение (я) к \ (16 = — 9 \ sin \ left ({7x} \ right) — 4 \), которые находятся в \ (\ displaystyle \ left [{- 2 \ pi, \ frac {{9 \ pi}} {4}} \ right] \). В комплекте с масштабируемыми уравнениями, а также примером задачи с подсказкой и решением. 5 (и 360 — 70. В предыдущем разделе мы начали решать тригонометрические уравнения. Метод решения тригонометрических уравнений с помощью подстановки Как решить систему тригонометрических уравнений — это аналогичный вопрос, но мне трудно следовать ответу и применять его к этому конкретная проблема.Любые советы будут оценены. Другой способ записать x = sin (y) — y = arcsin (x). В интервале [0, 2π] два угла, соответствующие этим критериям, можно бесплатно загрузить с помощью Advanced Trigonometry Calculator. Используемая техника включает алгебру, справочные треугольники и специальные углы. rebekah_renteria. То же значение имеют решения систем линейных уравнений. СЧЕТЧИК ПАМЯТИ. Последняя активность 2 года 9 месяцев назад. 1. Подробные пошаговые решения ваших задач «Доказательство тригонометрических идентичностей» онлайн с помощью нашего математического решателя и калькулятора.Например, значения тригонометрических функций при загрузке шаблона решения триггерного уравнения. Узнайте о тригонометрии с помощью нашего бесплатного математического решателя с пошаговыми решениями. В этом разделе мы рассмотрим решение тригонометрических уравнений. . Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Бесплатная программа для решения математических задач отвечает на ваши домашние вопросы по тригонометрии с пошаговыми пояснениями. Рассмотрим следующий пример: Решите следующее уравнение: Раздел 1-4: Решение триггерных уравнений. com — это всегда идеальное место для посещения! Решить тригонометрические уравнения численным методом и методом секущих для получения решения.Решение тригонометрических уравнений с несколькими углами. В элементарной алгебре квадратная формула — это формула, которая дает решение (я) квадратного уравнения. Решение может быть выражено в радианах или градусах. (Если вам не сказали решать «в общих чертах», не забудьте включить интервал, как показано ниже. 2-й грех (½) = 30 решение тригонометрических уравнений Примечание. Если вы хотите получить обзор тригонометрии, нажмите на тригонометрию. Бесплатная тригонометрическая калькулятор уравнений — пошаговое решение тригонометрических уравнений. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство.Ver en YouTube Используйте обратные тригонометрические функции, чтобы найти два наименьших положительных решения cos (5. При алгебраическом решении мы сначала изолируем тригонометрическую функцию, а затем используем обратную к этой функции функцию для определения переменной. Пример 1: Пример 2: Пример 3: Nool; Математика. 6 $ \ begingroup $ Я хотел бы решить это Узнайте, как решать тригонометрические уравнения и как использовать тригонометрические тождества для решения различных задач. \ circ = 0.Эта странная истина является следствием того факта, что тригонометрические функции являются периодическими и повторяются каждые 360 градусов или 2Π радиана. Введите ваше сложное математическое выражение на его целостность и в последний раз нажмите кнопку «Enter», через несколько мгновений будет отображено решение для вашего выражения. Глава 7: Решение триггерных уравнений. Калькулятор степени. Если существует более одной триггерной функции, перепишите уравнение в терминах только одной триггерной функции. Некоторые из нас со школьных времен помнят, что тригонометрические функции могут быть выражены как рациональные функции тангенса полурагумента, поэтому давайте сделаем это: перепишем уравнение в терминах tan.\ circ \)). Тригонометрические уравнения возникают в различных ситуациях, например, в Законе преломления, и в различных дисциплинах, включая физику, химию и технику. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. 9 терминов. com — это просто идеальный сайт для выезда! Получите бесплатный виджет «Решатель тригонометрических уравнений» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Рассмотрим функцию. Доступны ежемесячные, полугодовые и годовые планы. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется Решением тригонометрических уравнений.решить относительно x, y или любой другой переменной любого уравнения (линейного, квадратичного. Тригонометрическое уравнение также будет иметь общее решение, выражающее все значения, которые удовлетворяли бы данному уравнению, и оно выражается в обобщенной форме через ‘ n ‘. Обратные тригонометрические отношения для синуса, косинуса, тангенса, косеканса, секанса и котангенса соответственно следующие: арксинус, арккосинус, арктангенс, арккосеканс, арккосеканс и арккотангенс. Укажите, что sin (x) = 2 или sin (x) = -2 5. Добро пожаловать в MathPortal.com. 4. Столкнувшись с этими уравнениями, вспомните, что \ (y = \ sin (2x) \) — это горизонтальное сжатие с коэффициентом 2 от функции \ (y = \ sin x \). Тригонометрическое уравнение — это любое уравнение, содержащее тригонометрическую функцию. 5 (3sin x — 4 = 11sin x. Например, тождество sin2 x + cos2 x = 1 верно, независимо от того, когда учитываются квадратные уравнения тригонометрии, жизнь хороша. Бесплатная программа для решения математических задач отвечает на ваши вопросы по алгебре, геометрии, тригонометрии, исчислению и статистические домашние задания с пошаговыми пояснениями, как у репетитора по математике.матрица89. Бесплатная программа для решения математических задач отвечает на ваши домашние задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как репетитор по математике. Мы можем составить наше уравнение следующим образом: Синус равен, поэтому мы можем заменить его в: перекрестное умножение дает нам. 1 Решение тригонометрических уравнений и тождеств 413 Попробуйте сейчас 2. Решение тригонометрических уравнений Глава Инструкции к экзамену. 3 — Решение тригонометрических уравнений. Решая тригонометрические уравнения, мы находим все углы, которые делают уравнение истинным.Когда вы нажимаете кнопку, эта страница пытается применить 25 различных триггеров. Онлайн-программа для решения математических задач с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач. Решения являются главными решениями, если переменная уравнения лежит в интервале 0 и 2π. Калькулятор тригонометрических уравнений Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора тригонометрических уравнений. cos x = 1/3. В этом разделе мы исследуем методы, необходимые для решения более сложных тригонометрических уравнений.Получите помощь в Интернете или с помощью нашего математического приложения. 3 — Решение тригонометрических уравнений. Владелец этого веб-сайта — математик Милош Петрович. Используйте предоставленные подсказки. Например, sin x + 2 = 1 — это пример тригонометрического уравнения. 3. Я написал следующий код: Vets = {Cos [2a1] (I + Cos [2a2]) + Sin [2a1] Sin Рабочий лист решения тригонометрических уравнений: Это упражнение позволяет студенту попрактиковаться в решении 8 тригонометрических уравнений. ) Затем нажмите кнопку и, для получения наилучших результатов, выберите «Решить за интервал», чтобы сравнить свой ответ. Чтобы решить тригонометрические уравнения, вам необходимо использовать тождества и исходные углы для запоминания наряду с алгеброй.Бесконечная алгебра 2 — Рабочий лист 102 — Решение тригонометрических уравнений Дата создания: 20150401145714Z Вопрос: Решите тригонометрические уравнения на интервале 0 QX 07:11 Контрольная точка решения тригонометрических уравнений Для таких задач мы используем обратные тригонометрические отношения. Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. 5х + 0. Примечание. Если вы хотите получить обзор тригонометрии, щелкните по тригонометрии.как решать тригонометрические уравнения на питоне. Тригонометрическое уравнение — это уравнение, которое содержит тригонометрические функции, такие как синус и косинус. Получите доступ ко всем курсам и более 150 HD-видео по подписке.