Содержание
Внесение множителя под знак корня: правила, примеры, решения
В этой статье мы продолжим говорить о том, как преобразовывать иррациональные выражения, а конкретно о том, как внести множитель под знак корня. Сначала поясним, в чем состоит смысл такого преобразования, приведем теоретические обоснования и сформулируем основные правила, после чего проиллюстрируем их на примерах решений задач.
Понятие внесения множителя под знак корня
Начнем с определения этого преобразования.
Определение 1
Внесение множителя под знак корня представляет собой преобразование произведения B·Cn, где B и C являются числами или выражениями, а n – натуральным числом, в тождественно равное выражение Bn·Cn или -Bn·Cn.
Первое знакомство с этим видом преобразования, как правило, происходит сразу после изучения понятия квадратного корня и его свойств в рамках школьного курса алгебры. При этом определение берется только для n, равного 2, то есть для выражений с квадратным корнем.
Позже, когда начинают изучаться корни n-ной степени, разбираются и случаи с более сложными выражениями.
Учитывая все сказанное выше, легко понять, почему данное преобразование называется именно так: в его результате множитель B перемещается под знак корня. Также очевидно, что изменить таким образом можно не любые выражения, а только конкретные произведения некоторых чисел (выражений) и корней, под знаками которых также расположено некоторое число или выражение. В качестве примера можно привести 5·3, -0,7·x+2·y3, x-2·1-x4 и т.д.
В результате мы должны прийти к выражению вполне определенного вида. Так, указанные выше примеры после преобразования будут выглядеть так: 52·3, -0,73·x+2·y3, -x-24·1-x4. Возможно и дальнейшее упрощение этих выражений, если такая необходимость есть.
После того, как мы определились, что из себя представляет внесение множителя под знак корня, можно перейти к теоретическим обоснованиям преобразования. В следующем пункте мы объясним, когда -Bn·Cn следует заменять на Bn·Cn, а когда Bn·Cn на -Bn·Cn.
Теоретические основы внесения множителя под корень
Ранее, когда мы объясняли, как можно изменить иррациональные выражения, применяя основные свойства корня, у нас получился ряд важных результатов. Здесь нам потребуются два из них:
Определение 2
- Выражение A можно заменить на Ann в случае нечетного n. Если же n является четным числом, то возможна замена на Ann для всех значений переменных, которые принадлежат области допустимых значений для данного выражения и при которых A не будет отрицательным (это условие можно записать как A≥0). То есть если n – нечетное число, то A=Ann, A≥0,-Ann, A<0.
- Выражение An·Bn заменяется на A·Bn при условии, что n – натуральное число.
Воспользовавшись этими правилами, мы можем внести множитель под знак радикала (корня) после следующих преобразований:
- при нечетном n – B·Cn=Bnn·Cn=Bn·Cn
- при четном n– B·Cn=Bnn·Cn=Bn·Cn, B≥0,-Bnn·Cn=-Bn·Cn, B<0
Допустим, B представляет из себя число, большее 0, либо выражение, которое будет неотрицательным при любых значениях переменных из области допустимых значений.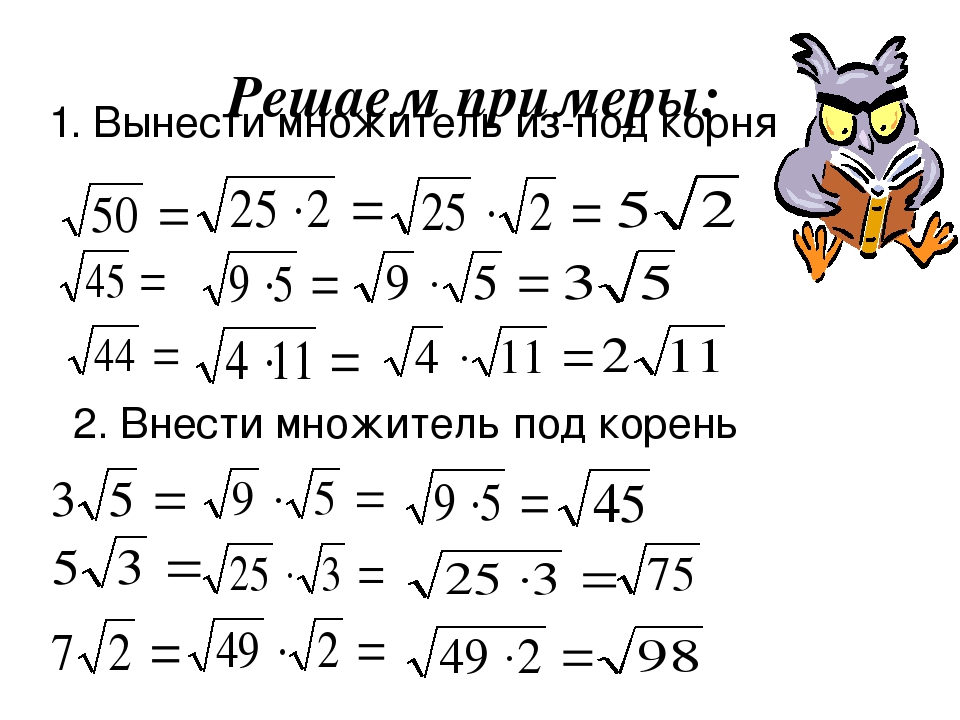
Тогда B·Cn=Bnn·Cn=Bn·Cn. А если B будет отрицательным числом или его значения не будут положительны при любых переменных, то B·Cn=-Bnn·Cn=-Bn·Cn.
В следующем пункте мы сформулируем эти положения в виде правил, которые будем в дальнейшем применять для решения задач.
Основные правила внесения множителя под знак радикала
Выше мы уже рассказывали, что действия, которые нужно предпринять для внесения множителя под корень, будут зависеть от значения показателя n, точнее от того, четный он или нечетный, а также от вида самого выражения. Запишем несколько правил для всех возможных случаев.
Определение 3
Если показателем корня является нечетное число, то необходимые преобразования будут выглядеть следующим образом: B·Cn=Bnn·Cn=Bn·Cn.
Определение 4
Если показателем корня является четное число, а B является некоторым выражением с неотрицательным значением (x2, 5·x4+3·y2·z2+7 и др.) или же просто положительным числом, то нам нужно действовать так: B·Cn=Bnn·Cn=Bn·Cn.
Определение 5
Если показателем корня будет четное число, но B при этом будет числом, меньшим 0, или выражением с неположительными значениями (к примеру, −2·x2, −(x2+y2+1) и т.п.), то вносить множитель под корень нужно так: B·Cn=-Bnn·Cn=-Bn·Cn.
Определение 6
Если показатель корня четный, однако по выражению B невозможно сразу сказать, какие значения оно примет на области допустимых значений, нам нужно:
- решить неравенства B≥0 и B<0 на области допустимых значений исходного выражения;
- получив некоторые множества решений, выполнить на первом из них преобразование B·Cn=Bnn·Cn=Bn·Cn, а на втором B·Cn=-Bnn·Cn=-Bn·Cn.
Теперь посмотрим, как правильно применять эти положения на практике.
Решения задач на внесение множителя под корень
Для начала рассмотрим наиболее простой случай с нечетным показателем корня.
Пример 1
Условие: преобразуйте выражения 2·35, -0,25·-384·x·y-13·y23 и x-1·x+1x-167, внеся множитель под знак корня.
Решение
Во всех трех выражениях корни имеют нечетные показатели. Тогда мы можем представить вносимые множители в виде корней и перейти от произведения корней к корню произведения. Подсчитаем каждый пример отдельно.
- 2·35=255·35=25·35. Результат можно еще упростить, выполнив нужные действия под корнем: 25·35=32·35=965.
- Здесь сначала нужно преобразовать десятичную дробь в обыкновенную, чтобы упростить дальнейшие вычисления. После этого вносим множитель под знак корня и получаем:-0,25·-384·x·y-13·y23==-14·-384·x·y-13·y23==-1433·-384·x·y-13·y23==-14·-384·x·y-13·y23==6·x·y-13·y23=6·x·y-2·y23
- Здесь выполняем преобразования сразу:
x-1·x+1x-167=(x-1)77·x+1(x-1)67==(x-1)7·x+1x-167
Полученному выражению можно придать еще более простой вид, преобразовав рациональное выражение под корнем, которое получилось после внесения множителя. Сделаем это:
x-17·x+1x-167=x-17·x+1(x-1)67==(x-1)·x+17=x2-17
Ответ: 2·35=965, -0,25·-384·x·y-13·y23=6·x·y-2·y23, x-1·x+1x-167=x2-17
Далее переходим к задачам, в которых нужно преобразовать корень с четным показателем.
Пример 2
Условие: внесите множитель под знак радикала в выражениях 5·3, 12·16·q4-q4 и x2+1·1x·(x2+1), а потом по возможности упростите выражения.
Решение
Первое выражение мы уже приводили в качестве примера в первом пункте. Проверим получившийся результат 52·3. Поскольку здесь у нас квадратный корень, а множитель перед ним является положительным числом, то нам нужно выполнить следующие действия: 5·3=52·3=52·3. Все, что нам осталось, – это упростить полученный результат: 52·3=75.
Во втором случае показатель корня является четным числом, а вносимое число больше 0, значит, сразу переходим к преобразованиям:
12·16·q4-q4=1244·16·q4-q4==124·16·q4-q4=q4-q4=0
В третьем случае очевидно, что x2+1будет принимать значения больше 0 при любых значениях переменной x (поскольку при сложении неотрицательной при любом значении переменной выражения x2и единицы мы получим положительное число), значит:
x2+1·1x·x2+1=x2+12·1x·x2+1==x2+12·1x·x2+1=(x2+1)2x·x2+1=x2+1x
Ответ: 5·3=75, 12·16·q4-q4=0, x2+1·1x·x2+1=x2+1x.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 3
Условие: преобразуйте выражения -102·(0,1)7·a4 и 2·-3-y2·x, внеся множитель под знак корня.
Решение
Первое выражение имеет четный показатель корня и отрицательный множитель, который надо внести. Значит, для решения нам надо использовать третье правило, сформулированное в предыдущем пункте:
-102·0,17·a4=-10244·0,17·a4==-1024·0,17·a4=-108·0,17·a4=-10·a4
Во втором выражении показатель корня тоже является четным числом. Выражение 2·(−3−y2) будет отрицательно при любом y, поскольку произведение положительного и отрицательного числа есть число также отрицательное. Значит, можно записать следующее:
2·-3-y2·x=-2·-3-y22·x==-2·-3-y22·x=-22·-3-y22·x==-4·y4+6·y2+9·x=-4·x·y4+24·x·y2+36·x
Ответ: -102·0,17·a4=-10·a4, 2·-3-y2·x=-4·x·y4+24·x·y2+36·x.
Еще один случай, который нам надо разобрать, – работа с четным показателем корня и переменными, способными принимать произвольные значения. Вообще такие преобразования лежат за пределами школьного курса алгебры, поскольку они относятся к задачам повышенной сложности, однако мы все же решим одну такую задачу.
Пример 4
Условие: даны выражения x-2·1-x4 и x+6x-4·x2+x-2. Выполните внесение множителя под знак корня.
Решение
Первое выражение мы уже приводили в качестве примера в первом пункте. Проверим получившийся результат и поясним ход преобразования. Поскольку в x-2·1-x4 есть четный показатель корня (4), а выражение x−2 может принять разные значения (больше 0, меньше 0, равные 0), то нам придется использовать последнее правило из предыдущего пункта. Область допустимых значений x будет определена условием 1−x≥0. Как мы узнаем, когда переменная примет положительное, а когда отрицательное значение? Для этого нам надо составить и решить две системы неравенств: x-2≥01-x≥0⇔x≥2x≤1⇔∅ и x-2<01-x≥0⇔x<2x≥1⇔x≤1.
Решений у первой системы нет. Значит, наше выражение x−2 не может быть положительным ни при каких значениях переменной. А вот вторая система имеет решение в виде множества x≤1, совпадающее с областью допустимых значений. Поэтому можно записать следующее:
x-2·1-x4=-x-244·1-x4==-(x-2)4·1-x4
Во втором выражении x+6x-4·x2+x-2 имеется четный показатель корня, а выражение x+6x-4 на первый взгляд может принимать любые значения. Выясним, когда они будут положительными, а когда отрицательными. Как и в примере выше, составим и решим две системы неравенств: x+6x-4≥0x2+x-2≥0 и x+6x-4<0x2+x-2≥0.
Первую систему можно решить, используя метод интервалов, а вторую – любым способом решения квадратных неравенств.
x+6x-4≥0x2+x-2≥0⇔(-∞, -6]∪[4, +∞)(-∞, -2]∪[1, +∞)⇔⇔(-∞, -6]∪[4, +∞)x+6x-4<0x2+x-2≥0⇔(-6, 4)(-∞, -2]∪[1, +∞)⇔⇔(-6, -2]∪[1, 4)
Следовательно, значение выражения x+6x-4 будет неотрицательным при x∈(−∞, −6]∪[4, +∞), и x+6x-4·x2+x-2=x+6x-42·x2+x-2==x+6x-42·x2+x-2
А отрицательным значение будет при x∈(−6, −2]∪[1, 4), и x+6x-4·x2+x-2=-x+6x-42·x2+x-2==-x+6x-42·x2+x-2
Выражение, которое получилось в итоге, может быть приведено к виду рациональной дроби.
Ответ: x-2·1-x4=-(x-2)4·1-x4 и
x+6x-4·x2+x-2==x+6x-42·x2+x-2, x∈(-∞, -6]∪[4, +∞)-x+6x-42·x2+x-2, x∈(-6, -2]∪[1, 4)
В заключении отметим, что вносить число под знак корня часто требуется в случаях, когда нужно сравнить значения выражений с корнями. Также советуем вам прочесть материал, посвященный противоположному преобразованию – вынесению множителя из-под корня.
Как внести число под корень
Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную перед знаком корня степень должно дать число, указанное под этим самым знаком. Часто для решения задач, в которых присутствуют корни, недостаточно только рассчитать значение. Приходится осуществлять и дополнительные операции, одной из которых является внесение числа, переменной или выражения под знак корня.
Определите показатель степени корня. Показателем называют целое число, указывающее степень, в которую надо возвести результат вычисления корня, чтобы получить подкоренное выражение (то число, из которого извлекается этот корень).
Показатель степени корня пишется в виде верхнего индекса перед значком корня. Если этот индекс не указан, значит это квадратный корень, степень которого равна двойке. Например, показатель корня √3 равен двум, показатель ³√3 равен трем, показатель корня ⁴√3 равен четырем и т.д.
Возведите число, которое требуется внести под знак корня, в степень, равную показателю этого корня, определенную вами на предыдущем шаге. Например, если нужно внести число 5 под знак корня ⁴√3, то показателем степени корня является четверка и вам надо посчитать результат возведения 5 в четвертую степень 5⁴=625. Сделать это можно любым удобным вам способом — в уме, с помощью калькулятора или соответствующих онлайн-сервисов, размещенных в интернете.
Внесите полученное на предыдущем шаге значение под знак корня в качестве множителя подкоренного выражения. Для использованного в предыдущем шаге примера с внесением под корень ⁴√3 числа 5 (5*⁴√3), это действие можно записать так: 5*⁴√3=⁴√(625*3).
Упростите полученное подкоренное выражение, если это возможно.
Для примера из предыдущих шагов это означает, что нужно просто перемножить числа, стоящие под знаком корня: 5*⁴√3=⁴√(625*3)=⁴√1875. На этом операция внесения числа под корень будет завершена.
Если в задаче присутствуют неизвестные переменные, то описанные выше шаги можно проделать в общем виде. Например, если требуется внести под корень четвертой степени неизвестную переменную x, а подкоренное выражение равно 5/x³, то вся последовательность действий может быть записана так: x*⁴√(5/x³)=⁴√(x⁴*5/x³)=⁴√(x*5).
Арифметический квадратный корень. Вынесение, внесение множителя под знак корня
Математика->Модуль числа. Корень числа->квадратный корень->
Тестирование онлайн
Квадратный корень. Вычисления
Квадратный корень. Вычисления (часть 2)
Квадратный корень. Алгебраические выражения и преобразования
Квадратный корень. Алгебраические выражения и преобразования (часть 2)
Квадратный корень.
Алгебраические выражения и преобразования (часть 3)Тождество
Вынесение множителя из-под знака квадратного корня
Внесение множителя под знак квадратного корня
Значение переменной в выражении с квадратным корнем
Вынесение и внесение множителя (средний уровень)
Алгебраические преобразования с квадратным корнем (выше среднего)
Алгебраические преобразования, вычисление. Повторение (выше среднего)
Алгебраические выражения и преобразования (часть 3)Арифметический квадратный корень
Обозначение знака квадратного арифметического корня , подразумеваем , но «2» не пишется.
Неотрицательный квадратный корень из числа a называется арифметическим квадратным корнем из числа a. Например,
Выражения не имеют смысла!
Тождество
При любом значении a имеет место равенство
Согласно определению модуля
получим
Вынесение и внесения множителя под знак корня
При любом значении a и при любом положительном значении b верно равенство
Обратное равенство имеет вид
Среднее арифметическое и среднее геометрическое чисел
Средним арифметическим двух чисел a и b называется выражение
Средним геометрическим двух неотрицательных чисел a и b называется выражение
Среднее арифметическое неотрицательных чисел a и b не меньше их среднего геометрического.
Если среднее арифметическое двух неотрицательных чисел равно их среднему геометрическому, то эти числа равны.
Внесение (вынесение) множителя из-под знака корня
Сегодня рассмотрим следующую тему: как вносить или выносить множитель из-под знака корня. Именно множитель (!!!) в предыдущей публикации были слагаемые — их никуда выносить нельзя. Я рассмотрю данную тему на примере квадратного корня, однако аналогичные преобразования могут быть выполнены с корнями любой четной степени.
x≤0 означает, что переменная x неположительна.
Никакой знак минус перед переменной не укажет вам на знак переменной! Запись —x>0 является всего лишь линейным неравенством с одной переменной, решая которое (умножаем обе части неравенства на -1, меняем знак неравенства на противоположный), получаем x<0, что говорит о том, что переменная отрицательна.
Вынесение из-под знака корня.
Здесь нам пригодится уже знакомое тождество
Пример: Вынести множитель из-под знака корня:
Выполняем следующую цепочку преобразований, главная цель которой заключается в том, чтобы у максимального числа множителей под знаком корня выделить вторую степень (т.
3≥0, значит b≥0, а значит -2b≤0. Получили, что множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
Внести под знак корня
Естественная область определения: —a≥0, значит a≤0, а значит 3a≤0. Множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
Внести под знак корня
Естественная область определения: a-5≥0, значит 5-a≤0. Множитель перед знаком корня отрицательный, поэтому знак минус оставляем перед корнем, внося под корень положительный множитель:
Как написать корень на клавиатуре и в Word: второй и третьей степени
Работать с формулами не всегда приходится в удобных для этого редакторах. Иногда написать знак корня квадратного или третьей степени может потребоваться просто в браузере или в любом текстовом редакторе при внесении правок в документ.
В таком случае можно воспользоваться различными способами написания корня на клавиатуре, которые рассмотрены в данной статье.
Оглавление: 1. Как написать квадратный корень - На клавиатуре, используя NUM-блок - Используя таблицу символов - В Word через список символов - В Word вставить формулу от числа 2. Как написать корень 3 степени - На клавиатуре, используя NUM-блок - Используя таблицу символов - В Word через список символов - В Word вставить формулу от числа
Как написать квадратный корень
Рассмотрим несколько способов написания знака квадратного корня на клавиатуре — в любом приложении или только в Word.
На клавиатуре, используя NUM-блок
Самый простой способ написать квадратный корень — это использовать NUM-блок на клавиатуре, который позволяет путем ввода определенных комбинаций получать различные знаки.
Напомним: NUM-блок — это блок в правой части полномасштабной клавиатуры (на ноутбучных клавиатурах он бывает расположен в другом месте или активироваться на других клавишах при нажатии NUM LOCK).
Убедитесь, что NUM-блок активирован, для этого нажмите клавишу NUM LOCK. Обычно на клавиатуре есть светодиоды, которые горят, когда NUM-блок активирован.
После этого переключите раскладку клавиатуры на английскую, зажмите клавишу Alt и введите комбинацию 251 (на NUM-блоке).
Когда вы отпустите кнопку Alt, появится знак корня: √
Таким образом квадратный корень можно ввести практически в любой программе.
Используя таблицу символов
В операционной системе Windows для случаев, когда необходимо написать особый символ, есть специальная таблица с этими символами. Чтобы ее вызвать, введите в поиске слова “Таблица символов” и запустите найденное приложение.
Найдите в списке доступных символов знак квадратного корня — он находится во второй половине таблицы.
Обратите внимание
Единожды отыскав знак корня, потом повторно его искать будет легче.
Когда найдете нужный символ, нажмите на него, далее нажмите “Выбрать” и “Копировать”.
После этого у вас в буфере обмена будет квадратный корень. Теперь его можно вставить в любую программу обычным способом — нажать правой кнопкой на место для ввода символов и выбрав “Вставить”.
В Word через список символов
Похожая таблица символов есть и в Word, и ею тоже можно воспользоваться чтобы вставить значок квадратного корня в текст. Для этого переключитесь в программе в верхнем меню на пункт “Вставка”, выберите вариант “Символ” и нажмите “Другие символы”.
Откроется почти такая же таблица, как была рассмотрена выше, за одним лишь исключением — здесь более удобный поиск. Выберите сверху набор “Математические операторы”, и вы быстро найдете в списке символов квадратный корень. Нажмите на него и выберите пункт “Вставить”.
После этого в тексте появится знак корня.
Обратите внимание
Этот знак корня можно использовать для копирования в другие программы. Просто выделите его, нажмите правой кнопкой и выберите “Копировать”, а потом вставьте в нужном приложении.
В Word вставить формулу от числа
Еще один способ добавить знак квадратного корня в Word — это использовать вставку формулы. Подойдет такой вариант, если не нужно, чтобы корень квадратный был встроен внутрь текста.
Вставка квадратного корня через формулу выполняется следующим образом. Нажмите в Word раздел “Вставка” и выберите “Формула”.
Далее нажмите “Радикал”.
Выберите вариант вставки квадратного корня от числа.
Остается только ввести число от которого будет отображаться квадратный корень.
Обратите внимание
Через вставку формулы можно вставить и обычный квадратный корень, не указывая от какого числа он берется. Для этого нужно после выбора пункта “Формула” в разделе “Вставка” сверху выбрать в списке доступных вариантов значок обычного квадратного корня.
Как написать корень 3 степени
А теперь рассмотрим способ написать корень третьей степени различными вариантами. Все варианты, описанные выше, подходят и в этом случае, но придется внести некоторые корректировки, чтобы написать корень 3 степени.
На клавиатуре, используя NUM-блок
Переключите язык на английский, зажмите Alt и напишите комбинацию 0179.
После этого отобразится цифра 3 в степени: ³
Далее снова зажмите Alt и напишите рассмотренную выше комбинацию квадратного корня — 251.
Итого получится корень в 3 степени: ³√
Обратите внимание
После каждого написанного символа нужно отпускать Alt, чтобы он отобразился.
Используя таблицу символов
В таблице символов можно найти цифру 3 в степени. И если написать ее, то после можно поставить знак квадратного корня, и получится в итоге корень 3 степени, что нам и нужно.
Запустите утилиту “Таблица символов” через поиск или любым другим удобным способом.
После этого найдите в ней цифру 3 в степени, нажмите на нее и выберите пункт “Выбрать”.
Цифра 3 отобразится в области для копирования.
Теперь нужно найти квадратный корень и вновь выбрать пункт “Выбрать”.
Потом остается скопировать полученный результат и его можно будет использовать в любой программе.
Обратите внимание
В таблице символов несколько вариантов цифры “3”, некоторые из которых больше остальных, другие меньше. Можно выбрать оптимальный вариант.
В Word через список символов
Похожий способ на тот, что был описан выше. Заходим в Word на вкладку “Вставка” и выбираем “Другие символы”.
Здесь надо найти цифру 3 в степени. Для этого переключитесь в раздел “доп. фонетические знаки”, нажмите на цифру 3 в степени и нажмите “Вставить”.
Далее остается найти в разделе “Математические операторы” значок корня, выбрать его и нажать “Вставить”.
В Word вставить формулу от числа
Заключительный способ — вставить корень третьей степени в Word через формулу. Для этого нажмите “Вставка” и выберите пункт “Формула”.
Далее необходимо выбрать “Радикал”.
Здесь среди доступных вариантов выберите последний из доступных шаблонов — это корень третьей степени. Нажмите на него.
Теперь остается только написать число, от которого необходимо взять корень 3 степени.
Загрузка…
Арифметический квадратный корень. Мини-курс. Уроки 6 — 10. — Math
Арифметический квадратный корень. Мини-курс. Уроки 6 — 10.
Как вынести множитель из-под знака корня? Вынесение множителя из-под корня. Алгебра 8 класс. Примеры с решением. Математика. Образование. Пример 1: Вынести множитель из-под знака корня.
Урок 7. Вынесение общего множителя из-под знака корня в выражениях с переменными.
Алгебра 8 класс. Вынесение общего множителя из под знака корня в выражениях с переменными. Вынесение общего множителя из под знака корня в буквенных выражениях.
Математика. Образование. Примеры с решением. Арифметический квадратный корень.
Урок 8. Внесение множителя под знак корня.
Внесение множителя под знак корня. Арифметический квадратный корень. Как правильно вносить множитель под знак корня. Внесение множителя под знак корня в числовых выражениях. Внесение множителя под знак корня в выражениях с переменными. Что необходимо учитывать при внесении множителя под знак корня в выражениях с переменными. Когда надо ставить знак минус перед корнем при внесении множителя под корень, примеры с решением, алгебра 8 класс, математика, образование.
- Пример 1: Внесите множитель под знак корня.
- Пример 2: Внесите множитель под знак корня в выражениях с переменными.
Урок 9.
Сравнение чисел с корнем. Сравнение иррациональных чисел.
Сравнение чисел с корнем. Сравнение иррациональных чисел. Как сравнить числа с корнем. Арифметический квадратный корень. Свойства корня. Алгебра 8 класс. Внесение множителя под знак корня для сравнения чисел. Иррациональные числа. Числа с корнем. Примеры с решением.
- Пример 1: Сравнить числа.
- Пример 2: Сравнить числа, внеся множитель под знак корня.
- Пример 3: Расположить числа в порядке возрастания.
Урок 10. Оценка значений арифметического квадратного корня.
Как оценить значение квадратного корня? Алгебра 8 класс. Примеры с решением.
- Пример 1: Укажите два последовательных целых числа, между которыми находится значение корня.
- Пример 2: Укажите все целые числа, расположенные на координатной прямой между 7 и корень из 102.
youtube.com/embed/00Md7alXjk0″ frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Арифметический квадратный корень. Ответы к заданиям из видео уроков.
Арифметический квадратный корень. Мини-курс. Уроки 11 — 16.
Арифметический квадратный корень. Мини-курс. Уроки 17 — 24.
Как найти квадратные корни и кубические корни в Microsoft Excel —
При работе с Microsoft Excel квадратный корень чисел можно найти двумя способами. Вы можете использовать функцию, уже запрограммированную в формате Excel, которая называется функцией «SQRT». И второй метод — вручную добавить формулу для квадратного корня числа, для которого вы хотите получить значение квадратного корня. Давайте посмотрим, как вы можете использовать оба метода.
Но прежде чем мы перейдем к тому, как можно использовать оба метода нахождения квадратного корня числа, вам необходимо знать основы использования таблиц Excel. Иногда мы допускаем незначительные ошибки в наших записях на листе Excel, которые могут дать нам ответы, которые не являются точными или ожидаемыми.
Чтобы избежать таких ошибок, необходимо всегда помнить следующие важные основы использования листов Excel. И даже если вы забыли использовать их и обнаружили ошибку, вы можете перепроверить список ниже, чтобы убедиться, что ошибка произошла из-за пропуска этих шагов.
- ‘знак равно‘ знак. Знак равенства является наиболее важной частью формулы. Вы упускаете это, и формула или функция, которую вы ввели, просто будет выглядеть как простой текст. Добавление ‘=’ в ячейку перед вводом формулы или функции является одной из частей реализации формулы в этой ячейке.
- Скобки (). Скобки играют очень важную роль в формулах и функциях в Excel. Поэтому убедитесь, что вы добавили скобки в вашу функцию так, как они должны быть добавлены. Для большинства функций скобки обычно содержат значение или номера ячеек, по которым будет реализована формула.
- Наконец, ключ ввода. Нажмите клавишу ввода после закрытия скобок или заполнения формулы, чтобы наконец сделать функцию, функцию.
Важно отметить, что пропущение любого из них не даст вам ответов на этот вопрос или даже может привести к ошибке. Так что запомни это.
Способ 1
Функция SQRT в Microsoft Excel
- Откройте свой лист Excel на пустую страницу. Или, если вы уже создали файл данных, откройте его. Основная идея состоит в том, чтобы иметь числа, для которых вам нужен квадратный корень.
Работа с Microsoft Excel может быть хорошим опытом. Это помогает своим пользователям во многих отношениях. - Например, скажем, я хочу знать квадратный корень из числа 7. Я напишу функцию, как показано на рисунке ниже.
= SQRT (число)Я начну со знака равенства и добавив его в ячейку, в которой я хочу отобразить квадратный корень из значений, я начну печатать «sqrt». После того, как вы наберете s, список формул начнет появляться в раскрывающемся списке для этой ячейки. Теперь, когда я увижу формулу «sqrt», я дважды щелкните по ней и сделаю так, чтобы она появилась в выбранной ячейке.
Начните вводить функцию
Открывающая скобка автоматически появляется, когда вы дважды щелкаете по формуле, вы добавляете здесь номер / значение ячейки, закрываете скобку и нажимаете ввод.
Двойной щелчок по формуле, которая появляется в раскрывающемся списке ячейки, приводит к открытию скобки.
После открытой скобки вы либо введете номер ячейки, либо само число / значение
Добавляя число, для которого вы хотите найти квадратный корень в скобках в функции.Ответ в обоих случаях будет одинаковым независимо от того, добавите ли вы само значение или номер ячейки.
Квадратный корень для числа 7.
Это ваш квадратный корень для ответа 7. Если вы не уверены, нужно ли вам добавлять номер ячейки или значение напрямую, я бы посоветовал вам добавить номер ячейки. Потому что существует высокая вероятность того, что вам, возможно, придется внести некоторые изменения в свой лист Excel. Если число в ячейке A2 изменилось, и если вы написали A2 в формуле своих функций, значение для квадратного корня изменится автоматически.
(1/3). Единственное отличие здесь — это номер 3. Вы также можете использовать функцию Power, как показано на рисунке ниже, чтобы найти корень куба числа.Использование функции Power в Excel, чтобы найти Cub Root
Мощность (номер ячейки, мощность)
Ответ для кубического корня.Как вручную найти квадратный корень
Как вручную найти квадратный корень
Как найти квадратный корень вручную
Вот почти забытое искусство: с появлением электронных
калькуляторы, скорее всего, доживут до XXI века только на бумаге и
в воспоминаниях стариков.Из какого числа вы хотите найти квадратный корень?
Вот один из них, который мы будем использовать:46656
Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр,
начиная с десятичной точки.То есть никакая пара цифр не должна пересекаться
десятичная точка. (Например, разделите 1225 на «12 25», а не на
«1 22 5»; 6.5536 на «6,55 36», а не на «6,5 53 6». )Затем вы можете поместить несколько линий на каждую пару цифр и полосу на
слева, что-то вроде длинного деления.+ --- ---- ---- | 4 66 56Найдите наибольшее число, квадрат которого меньше или равен ведущему
пара цифр. В этом случае первая пара цифр — 4; самое большое число
квадрат которого меньше или равен 4 равен 2.Поместите это число слева, и над первой парой цифр.
2 + --- ---- ---- 2 | 4 66 56Теперь возведите это число в квадрат и вычтите из пары первых цифр.
2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 0Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой
число на 2, поместите его слева от разницы, которую вы только что вычислили, и
оставьте рядом с ним пустой десятичный знак.2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0Затем опустите следующую пару цифр и поместите ее вправо
разницы.2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0 66Найдите наибольшее число для этого пустого десятичного разряда, чтобы
число, умноженное на уже существующее число плюс десятичный разряд, будет меньше
чем текущая разница.Например, если 1 * 41 равно ≤ 66, то 2 * 42
≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле,
и в следующем десятичном разряде в строке результатов вверху.2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66Теперь вычтите продукт, который вы только что нашли.
2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 25Теперь повторите, как прежде: возьмите число в левом столбце (здесь 41) и
удвойте его последнюю цифру (что даст вам 42).Скопируйте это ниже в левый столбец и
оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для
Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18
что равно 58. ) Также опустите следующую пару цифр справа.2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 42_ 25 56Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556.Здесь,
получается, что 426 * 6 = 2556 точно.2 1 6 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 426 | 25 56 | - 25 56 + ------------- 0Когда разница равна нулю, у вас есть точный квадратный корень, и вы
Выполнено. В противном случае вы можете продолжать находить больше десятичных знаков до тех пор, пока
как ты хочешь.Вот еще один пример с меньшим количеством аннотаций.
7. 2 8 0 1 ... + ---------------------- 7 | 53. 00 00 00 00 00 | 49 + ---------------------- 142 | 4 00 | 2 84 + ---------------------- 1448 | 1 16 00 | 1 15 84 + ---------------------- 14560 | 16 00 | 0 + ---------------------- 145601 | 16 00 00 | 14 56 01 + ---------------------- | 1 43 99 00 . ». В этом руководстве мы рассмотрим каждый метод.
Найдите корень n-й степени числа в Excel
Рис. 1. Пример таблицы, показывающей корень n-й степени числа
Настройка данныхСоздайте ниже таблицу с числом, корнем N и N в качестве заголовков и столбцом примечаний для пояснения.
Рисунок 2. Пример данных для нахождения корня n-й степени числа
N-й корень с использованием функции POWERФункция СТЕПЕНЬ возвращает результат данного числа, которое возведено в указанную степень.
Синтаксис= МОЩНОСТЬ ( номер , мощность )Где
- Число : базовое число, которое мы хотим возвести в определенную степень
- Степень - показатель степени, до которого возводится основание числа;
- При нахождении корня n-й степени числа степень представляется как « 1 / n »
В ячейке E3 введите формулу:
= МОЩНОСТЬ ( B3 , 1 / C3 )Эта формула вычисляет квадратный корень из 25, который равен 5.
»Возвращает те же результаты В большинстве случаев задача, которую вам нужно решить, будет более сложной, чем простое применение формулы или функции. Если вы хотите сэкономить часы на исследованиях и разочарованиях, попробуйте нашу живую службу Excelchat! Наши эксперты по Excel доступны круглосуточно и без выходных, чтобы ответить на любые ваши вопросы по Excel. Мы гарантируем подключение в течение 30 секунд и индивидуальное решение в течение 20 минут.
Как вычислить квадратный корень в Excel (с помощью простых формул)
Удивительно, как вы можете найти несколько способов сделать то же самое в Excel.В конце концов, существует так много потрясающих функций и возможностей.
Очень простая и часто используемая задача - вычислить квадратный корень в Excel.
И, как я уже сказал, есть несколько способов сделать это в Excel (формулы, VBA, Power Query).
В этом уроке я покажу вам различные способы вычисления квадратного корня в Excel (и вы можете выбрать любой метод, который вам больше нравится).
Но прежде чем я перейду к тому, как это вычислить, позвольте мне быстро рассказать о том, что такое квадратный корень (не стесняйтесь переходить к следующему разделу, если я буду слишком наставлять).
Что такое квадратный корень?
Когда вы умножаете число (скажем, X) на само себя, вы получаете значение (скажем, Y).
Здесь X - квадратный корень из Y.
Например, 10, умноженное на 10, равно 100.
Здесь 10 - квадратный корень из 100.
Вот и все! Это просто. Но посчитать это не так-то просто.
Например, если я прошу вас вычислить квадратный корень из 50, я уверен, что вы не сможете вычислить его в уме (если вы не математический гений).
Вот подробная статья в Википедии на случай, если вам интересно узнать о ней больше.
В этом уроке я покажу вам несколько способов (обещаю простые) для вычисления квадратного корня в Excel .
Итак, приступим!
Вычислить квадратный корень с помощью функции SQRT
Да, в Excel есть специальная функция, цель существования которой - дать вам квадратный корень
Функция SQRT принимает один единственный аргумент (может быть числом или ссылкой на число) и возвращает квадратный корень из этого числа.
Чтобы вычислить квадратный корень из 100 в Excel, вы можете использовать следующую формулу:
= SQRT (100)
Вышеупомянутая формула даст вам 10, что является квадратным корнем из 100.
Вы можете также используйте ссылку на ячейку в функции SQRT, как показано ниже:
Примечание. Другой результат здесь может быть -10, но формула возвращает только положительное значение.
Хотя эта функция отлично работает с положительными числами, если вы дадите ей отрицательное число, она вернет ошибку # ЧИСЛО.
Это понятно, поскольку в математике отрицательное число не имеет квадратного корня. Даже если число отрицательное, если вы умножите его само на себя, результат будет положительным.
Но если вам все еще нужен квадратный корень из отрицательного числа (при условии, что он был положительным), вам может потребоваться сначала преобразовать отрицательное число в положительное, а затем найти квадратный корень из него.
Например, если вы хотите получить квадратный корень из -100, вы можете использовать функцию SQRT с функцией ABS:= SQRT (ABS (-100))
Функция ABS дает вам абсолютное значение и игнорирует отрицательный знак.
Примечание. В Excel есть еще две функции, связанные с квадратным корнем:
- SQRTPI - Эта функция возвращает квадратный корень из числа, умноженного на константу Pi (π)
- IMSQRT - Эта функция возвращает квадратный корень из комплексного числа
Вычислить квадратный корень с помощью экспоненциального оператора
Другой способ вычисления квадратного корня (или кубического корня или N-го корня) в Excel - использование экспоненциального оператора.1/2 даст два разных результата. Это связано с тем, что экспоненциальный оператор получает предпочтение перед делением и вычисляется первым. Использование скобок решает эту проблему.
Вычислить квадратный корень с помощью функции POWER
Еще один простой способ вычислить квадратный корень в Excel (или кубический корень, или корень N-й степени) - использовать функцию POWER.
Ниже приведен синтаксис функции СТЕПЕНЬ:
= СТЕПЕНЬ (число, мощность)
Требуется два аргумента:
- базовое число (может быть любым действительным числом)
- степень / экспонента, к которой это основание число увеличивается
В отличие от функции КОРЕНЬ, вы можете использовать функцию СТЕПЕНЬ для вычисления корней (например, квадратного корня или кубического корня) или степени (например, квадрат или куб) числа.
Ниже приведена формула, которая даст вам квадратный корень из 100 в Excel:
= МОЩНОСТЬ (100,1 / 2)
или
= МОЩНОСТЬ (100, 0,5)
На случай, если вы хотите кубический корень, вы можете использовать следующую формулу:
= МОЩНОСТЬ (100,1 / 3)
И аналогично, если вам нужен квадрат числа, вы можете использовать ту же формулу с соответствующим вторым аргументом.
= POWER (100,2)
Если вы используете отрицательное число в функции POWER, оно вернет ошибку #NUM.
Получение квадратного корня с помощью Power Query
Хотя приведенные выше формулы очень быстрые, и если вы работаете с большим объемом данных, и это то, что вам нужно делать довольно часто, вы также можете рассмотреть возможность использования Power Query.
Этот метод больше подходит, когда у вас есть большой набор данных, в котором вы хотите вычислить квадратный корень значений в столбце, и вы получаете новый набор данных каждый день / неделю / месяц / квартал. Использование Power Query минимизирует усилия, поскольку вы можете просто подключить новые данные и обновить запрос, и он даст вам результат.
Для этого примера я буду использовать простой набор данных, как показано ниже, где мне нужно вычислить квадратный корень для значений в столбце B.
Ниже приведены шаги для вычисления квадратного корня с помощью Power Query в Excel:
- Выберите любую ячейку в наборе данных
- Щелкните вкладку «Вставка»
- Щелкните значок «Таблица» (он находится в группе «Таблицы»). Это откроет диалоговое окно Create Table.
- Проверьте диапазон и отметьте опцию «Моя таблица имеет заголовки».Щелкните ОК. Это преобразует табличные данные в таблицу Excel.
- Щелкните вкладку «Данные»
- В группе «Получить и преобразовать» щелкните параметр «Из таблицы / диапазона». Откроется редактор Power Query.
- В редакторе запросов щелкните заголовок столбца
- Щелкните вкладку «Преобразование»
- В группе «Число» щелкните научную опцию
- Щелкните квадратный корень. Это мгновенно изменит значения в выбранном столбце и даст вам квадратные корни из исходных чисел.
- Щелкните вкладку «Файл».
- Щелкните «Закрыть и загрузить».
Приведенные выше шаги позволят создать новый рабочий лист в книге Excel и вставить таблицу из Power Query. Эта новая таблица будет иметь квадратные корни исходных табличных данных.
Если у вас есть отрицательные значения в ячейках, вы получите ошибку #NUM в результирующей таблице.
Несмотря на то, что для того, чтобы заставить это работать с Power Query, требуется несколько шагов, огромное преимущество Power Query заключается в том, что теперь вы можете просто обновлять и получать новые результаты, когда вы получаете новые данные.
Например, если вы теперь получаете новые данные в следующем месяце, вам нужно просто скопировать и вставить эти данные в таблицу, которую мы создали (на шаге 4), перейти в любую ячейку в таблице, полученной из Power Query, справа - нажмите и нажмите "Обновить".
Итак, хотя для выполнения этой операции в первый раз требуется несколько щелчков мышью, после установки вы легко преобразуете новые данные с помощью простого обновления.
Помимо квадратного корня, вы также можете использовать функцию Power в Power Query, чтобы получить кубический корень или корень N-й степени (или получить квадрат или куб чисел).
Вставка символа квадратного корня (√) в Excel
Хотя немного не по теме, я подумал, что я также дам вам знать, как вставить квадратный корень в Excel.
Это может быть полезно, если вы хотите отобразить значение рядом с символом квадратного корня и квадратным корнем из него. Что-то вроде того, что показано ниже.
И точно так же, как у нас есть разные формулы для вычисления значения квадратного корня в Excel, у нас также есть несколько методов для вставки символа квадратного корня.
Вставить символ квадратного корня с помощью сочетания клавиш
Если вы используете цифровую клавиатуру, вот сочетание клавиш для вставки символа квадратного корня:
ALT + 251
Удерживая клавишу ALT, нажмите цифровые клавиши 2,5 и 1 на цифровой клавиатуре. Теперь, когда вы оставите ключи, будет вставлен символ квадратного корня.
Вставка символа квадратного корня с формулой
Вы также можете использовать формулу для получения символа квадратного корня в Excel.
Это может быть полезно, когда имеется столбец значений, и вы хотите быстро добавить ко всем ним символ квадратного корня.
Чтобы получить символ квадратного корня, вы можете использовать следующую формулу:
= UNICHAR (8730)
Поскольку это формула, вы также можете комбинировать ее с другими формулами или ссылками на ячейки.
Например, если у вас есть столбец значений и вы хотите добавить символ квадратного корня ко всем этим значениям, вы можете использовать формулу, как показано ниже:= UNICHAR (8730) & A1
Примечание. хотите получить квадратный корень пару раз, вы можете получить его один раз, используя сочетание клавиш или формулу, а затем просто скопируйте и вставьте его.
Вставить символ квадратного корня путем изменения пользовательского числового формата
И, наконец, третий способ добавить символ квадратного корня - изменить форматирование ячейки таким образом, чтобы оно отображалось всякий раз, когда вы вводите что-либо в ячейку
Ниже Ниже приведены шаги по изменению форматирования ячеек для автоматического добавления символа квадратного корня:
- Выберите ячейки, в которых должен автоматически отображаться символ квадратного корня
- Удерживая клавишу Ctrl, нажмите клавишу 1.Откроется диалоговое окно «Форматирование ячеек».
- В панели «Категория» слева щелкните параметр «Пользовательский».
- В поле «Тип» введите √General
- Нажмите кнопку «ОК»
. ячейки автоматически получают символ квадратного корня.
Одним из преимуществ этого метода является то, что он не меняет значения в ячейке. Он только меняет то, как он отображается.
Это означает, что вы можете использовать эти значения в формулах и вычислениях, не беспокоясь о влиянии символа квадратного корня.Вы можете подтвердить это, выбрав ячейку и посмотрев на строку формул (которая показывает фактическое значение в ячейке).
Надеюсь, вы нашли этот урок полезным!
Вам также могут понравиться следующие руководства по Excel:
Квадратный корень из 125 - Как найти квадратный корень из 125?
125 - идеальное кубическое число. 125 можно выразить как сумму двух квадратов двумя разными способами: 125 = 10 2 + 5 2 или 11 2 + 2 2 .
Квадратный корень из 125 выражается как 5 √5. В этом уроке мы вычислим квадратный корень из 125 методом деления в столбик.- Квадратный корень из 125 : 5√5
- Квадрат 125: 15,625
Что такое квадратный корень из 125?
- Квадратный корень - это математическая операция, обратная квадрату.
- Квадратный корень из 125 - это значение, полученное после извлечения квадратного корня из 125.
- √125 = 11.1803398875
- Упрощенная радикальная форма квадратного корня из 125 составляет 5 √5.
Является ли квадратный корень из 125 рациональным или иррациональным?
- Невозможно найти такое целое число, которое в квадрате дает 125
- Его можно приблизительно записать в виде квадрата 11,180, которое является неповторяющимся десятичным числом без завершения.
- Это показывает, что это не идеальный квадрат, что также доказывает, что квадратный корень из 125 является иррациональным числом.
Как найти квадратный корень из 125?
Существует множество методов вычисления квадратного корня из 125. Давайте попробуем здесь разложение на простые множители и метод деления в столбик.
Квадратный корень из 125 путем простого факторизации
Чтобы упростить извлечение квадратного корня из 125, сначала представим 125 как произведение его простых множителей.
Разложение 125 на простые множители составляет 5 × 5 × 5. Квадратный корень из 125 равен 5 √5.Квадратный корень из 125 методом длинного деления
- Шаг 1: Начиная справа, мы объединим цифры в пары, поставив над ними полосу.У нас будет две пары, т.е.1 и 25
- Шаг 2 : Мы делим крайнее левое число на наибольшее число, квадрат которого меньше или равен числу в крайней левой паре.
- Шаг 3 : Удвойте делитель и введите его с пробелом справа. Угадайте наибольшую возможную цифру, чтобы заполнить пробел, который также станет новой цифрой в частном, так что, когда новый делитель умножается на новое частное, произведение меньше или равно деленному. Разделите и запишите остаток.
- Шаг 4: Повторите этот процесс, чтобы получить нужные десятичные разряды.
Таким образом, √125 = 11,1803398875
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
- Метод разложения на простые множители используется для записи квадратного корня из неполного квадратного числа в простейшей радикальной форме. Например: 45 = 3 × 3 × 5 = 3 2 × 5.
- 125 - не идеальный квадрат; следовательно, его квадратный корень - иррациональное число.Отсюда следует, что квадратный корень из любого числа «n», которое не является полным квадратом, всегда будет иррациональным числом.
- Квадратный корень из 125 в радикальной форме выражается как 5√5.
- Как Сэм найдет квадратный корень из 75 и квадратный корень из 25, используя метод деления в длину до трех знаков после запятой?
- Является ли √-125 действительным числом?
Часто задаваемые вопросы о квадратном корне из 125
Что такое квадратный корень из 125?
Квадратный корень из 125 равен 11.
180.Является ли 125 числом куба?
Да, 125 - число в кубе целого числа 5. (125 = 5 × 5 × 5)
Что такое упрощенный квадратный корень из 125?
Квадратный корень из 125 в простейшей форме равен 5 √5.
Является ли квадратный корень из 125 действительным числом?
Да, квадратный корень 125 является действительным числом.
Что такое квадрат 125?
125 × 125 = 15 625
Элементы квадратного корня и пошаговое вычисление
Элементы квадратного корня
Когда мы решаем квадратный корень этим методом, мы должны знать, на какие части делится квадратный корень.Составные части:
- Радикал - это символ, обозначающий квадратный корень.
- Подкоренное выражение - это число, квадратный корень которого мы вычисляем.
- Корень, это квадратный корень из подкоренного выражения.
- Вспомогательные линии, они помогут нам вычислить квадратный корень.
- Остаток - это последний номер процесса вычисления квадратного корня.
Вычисление квадратного корня по шагам
Когда вычисляется квадратный корень из числа, необходимо понимать, что результатом может быть не натуральное число, а десятичное число.Мы изучим вычисление квадратных корней, в которых решениями являются натуральные числа.
Чтобы вычислить квадратный корень из числа с несколькими десятичными цифрами, действуем следующим образом:
Номер делится на группы по две цифры, начиная справа.
Вычислите число, которое при умножении на себя наиболее близко к первой группе чисел слева, но не превышает ее. Таким образом получается первое число корня, и мы помещаем его справа от подкоренного выражения на первой вспомогательной строке.Затем квадрат этого числа уменьшается из первой группы.
Справа от остатка написана вторая группа и число справа отделяется.
Число слева от разделенного числа делится на удвоение полученного корня. Частное записывается справа от делителя, и вся часть числа, полученная в результате деления, умножается на такое же частное.
Если этот продукт может быть уменьшен из делимого, за которым следует разделенное число, частное - это номер корня; в противном случае попробуйте меньшее число.- Шаги $$ 3 $$ и $$ 4 $$ повторяются до тех пор, пока не исчезнут группы подкоренного выражения.
Например, давайте сначала попробуем с числом, которое представляет собой полный квадрат:
Давайте вычислим корень из $$ 582,169 $$, то есть $$ 763 $$, потому что $$ 763 \ cdot763 = 582,169 $$.
Пошагово будет:
1) Мы группируем в $$ 2 $$ за один раз цифры числа $$ 582169 $$, то есть $$ 58 \ \ 21 \ \ 69 $$. Запишем так:
2) Мы ищем число, которое выросло до $$ 2 $$, близкое к $$ 58 $$, в данном случае это число $$ 7 $$, так как $$ 7 \ cdot7 = 49 $$.Запишем:
3) Этот результат уменьшен с $$ 58 $$ и, следовательно, он: $$ 58-49 = 9 $$, и мы перемещаемся вниз на две следующие цифры, $$ 21 $$. И отделяем последнее число - $$ 1 $$. Пишем это так:
58. 21.697 -49 7,7 = 49 92.1 4) В третьей вспомогательной строке мы записываем двойную сумму $$ 7 $$ (то есть $$ 14 $$), а затем число, которое находится слева от разделенной цифры (то есть $$ 1 $ $) делится на $$ 14 $$.
В данном случае $$ 92: 14 $$, и мы получаем ближайшее целое число, равное $$ 6 $$. (Мы пишем $$ 6 $$ рядом с $$ 7 $$ в первой строке).
Мы производим вычитание, перемещаемся вниз на следующие две цифры и отделяем последнюю (теперь $$ 9 $$).Запишется так:
58.21.69 76 -49 7,7 = 49 92,1 7,2 = 14 -876 146 · 6 = 876 456. 95) Делаем то же, что и на предыдущем шаге. А именно, мы умножаем $$ 76 $$ на два (удваиваем), и $$ 456 $$ делим на это удвоение (то есть $$ 152 $$), что дает $$ 3 $$.
Когда мы выполняем вычитание, оно приходит к нулю и, следовательно, нет необходимости продолжать.
Мы пишем $$ 3 $$ в первой строке, и искали корень: $$ 763 $$.
58.21,69 763 -49 7,7 = 49 92,1 7,2 = 14 -876 146 · 6 = 876 456. 976 · 2 = 152 -4569 1523 · 3 = 4569 0 Квадратный корень из 582,169 $$ равен 763 $$.
Давайте теперь посмотрим на пример числа, которое не является полным квадратом, а является десятичным числом:
Корень $$ 5836,369 $$
1) номер подкоренного выражения делится на группы по две цифры.Разделение осуществляется по десятичному знаку (если он есть) справа налево.
Если на стороне десятичных знаков нет четного числа цифр, ясно, что цифра будет одна: в таком случае мы добавляем ноль.
Если бы в части целого числа мы оставили одно число, оно бы осталось таким. В нашем случае мы должны добавить ноль рядом с $$ 9 $$.
Написано, это будет:2) Мы ищем число, которое, умноженное само на себя, составляет $$ 58 $$ или ближайшее меньшее число, имея в виду, что результат не может быть больше, чем $$ 58 $$.
В этом случае число будет $$ 7 $$, потому что $$ 7 \ cdot7 = 49 $$. Напишем:
3) Мы вычитаем $$ 49 $$ из первой группы двух чисел корня, которая равна $$ 9 $$. Мы перемещаемся вниз на следующие цифры $$ 2 $$, то есть $$ 36 $$. Теперь отделяем последнее число, $$ 6 $$. Напишем:
58.36,36.90 7 -49 7,7 = 49 93.6 4) Мы записываем двойную сумму $$ 7 $$ (то есть $$ 14 $$) в третьей вспомогательной строке и число, которое находится слева от разделенного числа (то есть $$ 6 $ $) делится на $$ 14 $$. В этом случае ближайшее целое число - $$ 6 $$. (Мы пишем $$ 6 $$ рядом с $$ 7 $$ в первой строке).
Вычитаем, опускаем следующие две цифры и отделяем последнюю. В этом случае мы движемся вниз по $ 36 $.
Поскольку они находятся справа от десятичной точки, в первой строке (где мы пишем) мы также помещаем десятичную точку. Напишем:
58.36,36.90 76, -49 7,7 = 49 93.6 7,2 = 14 -876 146 · 6 = 876 603,6 5) Теперь повторяем предыдущий шаг. Мы умножаем $$ 76 $$ на два (мы удваиваем), и $$ 603 $$ делим на это удвоение (то есть $$ 152 $$), что дает $$ 3,9 $$; следовательно, взяв всю часть, мы имеем $$ 3 $$.
Выполняемая операция: $$ 1523 \ cdot3 $$. Записываем результат под последним оставшимся отдыхом и делаем вычитание.
Перемещаемся на следующие две цифры вниз. В первой строке пишем 3. Это записывается как:
58.36,36.90 76,3 -49 7,7 = 49 93.6 7,2 = 14 -876 146 · 6 = 876 603,6 76 · 2 = 152 -4569 1523 · 3 = 4569 1467.90 6) Повторяется тот же предыдущий шаг. Мы умножаем корень, который мы написали к настоящему моменту $$ (76,3) $$, на $$ 2 $$, но игнорируя десятичную точку, то есть $$ 763 \ cdot2 = 1526 $$.
Результат записывается в следующей вспомогательной строке, и первые четыре числа остатка $$ (1467) $$ делятся на результат умножения, давая число $$ 9 $$ как первое число, которое не является числом. ноль деления.
Мы пишем $$ 9 $$ в строке корня, а $$ 9 $$ умножаем на $$ 15269 $$, то есть $$ 137421 $$. Это число, которое мы должны вычесть из последнего остатка, который составлял 146790 долларов США, что составляет 9369 долларов США.
58.36,36.90 76,3 -49 7,7 = 49 93.6 7,2 = 14 -876 146 · 6 = 876 603,6 76 · 2 = 152 -4569 1523 · 3 = 4569 1467.90 763 · 2 = 1526 -137421 15269 · 9 = 137421 9369 На этом этапе мы можем сказать, что приблизительно квадратный корень из $$ 5836 369 $$ равен 76,39 $$ с напоминанием о $$ 9369 $$.
Эта операция, используемая в качестве примера, не завершена. Если мы продолжим, то получится 76,3
$$. Процесс повторяется до тех пор, пока напоминание не станет нулевым. Но мы замечаем, что квадратный корень не является целым числом, поскольку $ 5836,369 $$ не является полным квадратом.
Квадратный корень из 8 - Как найти квадратный корень из 8 на примерах
Значение корня 8
Значение корня 8 равно \ [\ sqrt {8} \] = 2.82842712475
Если вы рассмотрите первые три десятичных знака \ [\ sqrt {8} \] = 2,828
Теперь, когда вы знаете значение корня 8, давайте узнаем, как вычислить его значение здесь. Хотя значение корня 8 легко найти с помощью калькулятора, вы должны знать, как найти его значение вручную.
Квадратный корень числа представлен символом √. Этот символ известен как радикальный символ или основание. Число под этим основанием системы счисления называется подкоренным.
Оценим теперь значение квадратных корней.
Как вычислить квадратные корни?
Существует два метода вычисления квадратных корней: один использует простые множители числа, а другой - метод деления. Чтобы оценить квадратный корень из полного квадрата, мы всегда применяем первый метод. Однако для вычисления квадратного корня из числа, которое не является точным квадратом, в десятичной системе счисления используется метод деления.
Чтобы найти значение √8, вы должны сначала выразить число 8 как произведение его простых множителей.{3}} \] или \ [\ sqrt {2} \] x \ [\ sqrt {2} \] x \ [\ sqrt {2} \]
=> \ [\ sqrt {8} \] = 2x \ [\ sqrt {2} \]
=> \ [\ sqrt {8} \] = 2 \ [\ sqrt {2} \]
Теперь мы знаем, что \ [\ sqrt {2} \] = 1,41421 ...
Следовательно, \ [\ sqrt {8} \] = 2 x 1,41421 ..
=> \ [\ sqrt {8} \] = 2,82842 ..
Более быстрый способ оценки квадратный корень из большего числа используется для определения его диапазона. Например, вы вычисляете квадратный корень из x. Рассмотрим любые два других числа, скажем, n и m таким образом, что n2
Квадратный корень из большего числа также можно вычислить, сначала выразив его как произведение его множителей. Затем вы можете разбить множители (меньшие числа) на их последующие простые множители. Таким образом, расчет становится проще и требует меньше времени.
Метод нахождения квадратного корня из 8
Напоминаем, что 22 = 4, а 32 = 9.Следовательно, ответ на корень 8 находится между числами 2 и 3. Однако, поскольку квадрат 3 равен 9, который больше 8, значение корня 8 находится между числами 2,8 и 2,9.
Точный ответ квадратного корня из 8: 2,82842712475. это намного ближе к тому ответу, который мы оценили.
Ну, а вы знали ответ на квадратный корень из 8 в степени 3? Чтобы решить эту проблему, вам нужно сначала узнать значение корня 8. Затем умножьте это значение на себя 3 раза, чтобы получить ответ.
Следовательно, ответ на квадратный корень из 8 в степени 3 будет (2,828) x 3 = 22,627.
Знаете ли вы, что такое квадратный корень из 8 в степени 3? Чтобы решить эту проблему, нам нужно извлечь квадратный корень из 8. Затем мы берем это значение и умножаем на себя 3 раза.
Таким образом, квадратный корень из 8 в степени 3 = (2,828 x 2,828 x 2,828) = 22,627. Вам было бы легче найти значение корня 8 с помощью этого простого метода.
Вот таблица квадратных корней чисел от 1 до 100 для справки. Вы можете использовать эти значения для своих расчетов.
Квадратный корень чисел от 1 до 100
\ [\ sqrt {1} \]
84 1.000 sqrt {26} \]
5,099
\ [\ sqrt {51} \]
7.141
\ [\ sqrt {76} \]
8.718
\ [\ sqrt {2} \]
1,414
\ [\ sq \]
5,196
\ [\ sqrt {52} \]
7,211
\ [\ sqrt {77} \]
8,775
007
[\ sqrt {3} \]
1,732
\ [\ sqrt {28} \]
5.292
\ [\ sqrt {53} \]
7,280
\ [\ sqrt {78} \]
8,832
\ [sq \]
2,000
\ [\ sqrt {29} \]
5,385
\ [\ sqrt {54} \]
7,348
84 \ 9068 sqrt {79} \]
8,888
\ [\ sqrt {5} \]
2.236
\ [\ sqrt {30} \]
5,477
\ [\ sqrt {55} \]
7,416
\ [\ sqrt {80} \]
8.944
\ [\ sqrt {6} \]
2.449
\ [\ sqrt {31} \]
687 \
sqrt {56} \]
7,483
\ [\ sqrt {81} \]
9.000
\ [\ sqrt {7} \]
2,646
\ [\ sqrt {32} \]
5,657
\ [\ sqrt { \]
7,550
\ [\ sqrt {82} \]
9,055
\ [\ sqrt {8} \]
84 2,87
84 2,87 9 [\ sqrt {33} \]
5,745
\ [\ sqrt {58} \]
7.616
\ [\ sqrt {83} \]
9,110
\ [\ sqrt {9} \]
3.000
\ [sq \]
5,831
\ [\ sqrt {59} \]
7,681
\ [\ sqrt {84} \]
9,165
907
[\ sqrt {10} \]
3,162
\ [\ sqrt {35} \]
5.916
\ [\ sqrt {60} \]
7.746
\ [\ sqrt {85} \]
9.220
rt \ [11} \]
3,317
\ [\ sqrt {36} \]
6.000
\ [\ sqrt {61} \]
7,810
84
sqrt {86} \]
9,274
\ [\ sqrt {12} \]
3.464
\ [\ sqrt {37} \]
6,083
\ [\ sqrt {62} \]
7,874
\ [] \ sqrt {87} \
9,327
\ [\ sqrt {13} \]
3,606
\ [\ sqrt {38} \]
84 6,164 \
84 6,164 \
sqrt {63} \]
7,937
\ [\ sqrt {88} \]
9.381
\ [\ sqrt {14} \]
3,742
\ [\ sqrt {39} \]
6,245
\ [\ sqrt { \]
8.000
\ [\ sqrt {89} \]
9,434
\ [\ sqrt {15} \]
903,873 [\ sqrt {40} \]
6,325
\ [\ sqrt {65} \]
8.062
\ [\ sqrt {90} \]
9,487
\ [\ sqrt {16} \]
4.000
\ [sqrt { \]
6,403
\ [\ sqrt {66} \]
8,124
\ [\ sqrt {91} \]
9,539
007
[\ sqrt {17} \]
4,123
\ [\ sqrt {42} \]
6.481
\ [\ sqrt {67} \]
8,185
\ [\ sqrt {92} \]
9,592
\ [\ sq \]
4,243
\ [\ sqrt {43} \]
6,557
\ [\ sqrt {68} \]
8,246
84 \
sqrt {93} \] 9,644
\ [\ sqrt {19} \]
4.359
\ [\ sqrt {44} \]
6.633
\ [\ sqrt {69} \]
8.307
\ [\ sqrt {94} \ [\ sqrt {94}]
9,695
\ [\ sqrt {20} \]
4,472
\ [\ sqrt {45} \]
004 6,708 \
004 6,708 9000 9000 sqrt {70} \]
8,367
\ [\ sqrt {95} \]
9.747
\ [\ sqrt {21} \]
4,583
\ [\ sqrt {46} \]
6,782
\ [\ sqrt { \]
8,426
\ [\ sqrt {96} \]
9,798
\ [\ sqrt {22} \]
84 4,690
84 4,690 [\ sqrt {47} \]
6,856
\ [\ sqrt {72} \]
8.485
\ [\ sqrt {97} \]
9,849
\ [\ sqrt {23} \]
4,796
\ [sq \]
6,928
\ [\ sqrt {73} \]
8,544
\ [\ sqrt {98} \]
9,899
907
9,899
907
[\ sqrt {24} \]
4,899
\ [\ sqrt {49} \]
7.000
\ [\ sqrt {74} \]
8.602
\ [\ sqrt {99} \]
9.950
\ [\ sq \]
5.000
\ [\ sqrt {50} \]
7.071
\ [\ sqrt {75} \]
8.660 \
[ sqrt {100} \]
10.000
Квадратный корень и Квадратный корень [Видео и практика]
Квадратный корень и Совершенный квадрат
Квадратный корень и Полный квадрат. Квадратный корень из числа - это результат, обратный возведению числа в квадрат или возведению числа во вторую степень. Квадратный корень - это число, которое при умножении само на себя равно этому значению. Например, квадратный корень из 4 равен 2, потому что 2 умноженное на само число равно 4.
4 - это полный квадрат. Полный квадрат - это значение, состоящее из квадратного корня из целого числа. Квадратный корень из 4 равен 2, поэтому квадратный корень представляет собой целое число, что означает, что четверка является полным квадратом. Другой пример идеального квадрата - 9.
Квадратный корень из 9 равен 3. Квадратный корень - это целое число, что означает, что 9 - это полный квадрат. Квадратный корень равен 3. 3 - это не полный квадрат, потому что квадратный корень из 3 не является целым числом. Квадратный корень 3 на самом деле является иррациональным числом.
Вы можете найти значение на своем калькуляторе, но оно продолжается вечно. Корни могут быть выражены в экспоненциальной форме в виде дробей. Квадратный корень из 3, который мы могли бы записать, равен 3 в степени 1/2. Они эквивалентны.
Вы можете записать кубический корень из 8 также как дробь, как показатель степени с дробью, так что это будет от 8 до 1/3 степени.Кубический корень из восьми.
(1/3). Единственное отличие здесь — это номер 3. Вы также можете использовать функцию Power, как показано на рисунке ниже, чтобы найти корень куба числа.
)
) Также опустите следующую пару цифр справа.
». В этом руководстве мы рассмотрим каждый метод.
»Возвращает те же результаты 
Например, если вы хотите получить квадратный корень из -100, вы можете использовать функцию SQRT с функцией ABS:
Это откроет диалоговое окно Create Table.
Например, если у вас есть столбец значений и вы хотите добавить символ квадратного корня ко всем этим значениям, вы можете использовать формулу, как показано ниже:
Квадратный корень из 125 выражается как 5 √5. В этом уроке мы вычислим квадратный корень из 125 методом деления в столбик.
Разделите и запишите остаток.
180.
Если этот продукт может быть уменьшен из делимого, за которым следует разделенное число, частное - это номер корня; в противном случае попробуйте меньшее число.
21.69
9
9
Написано, это будет: