заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Таблица Брадиса тригонометрические функции sin x, cos x, tg x от аргумента в радианах. Значения тригонометрических функций.

Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)

Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)

Квадрат синуса, косинуса, тангенса, котангенса (альфа)

Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

Синус, косинус в кубе

Синус, косинус, тангенс, котангенс половинного угла

Формулы тригонометрических функций двойного угла

Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:

cos(2α)- через sin и cos:

cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

Формулы тригонометрических функций тройного угла

Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

Формулы суммы тригонометрических функций

Формулы разницы тригонометрических функций

Формулы тригонометрических функций суммы углов

Формулы тригонометрических функций разницы углов

Тригонометрические формулы преобразования разности аргументов

Формулы произведения тригонометрических функций, (sin cos tg ctg)

Значения синуса, косинуса, тангенса, котангенса

sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

Значения функций для некоторых углов, α

Тригонометрические формулы приведения

В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).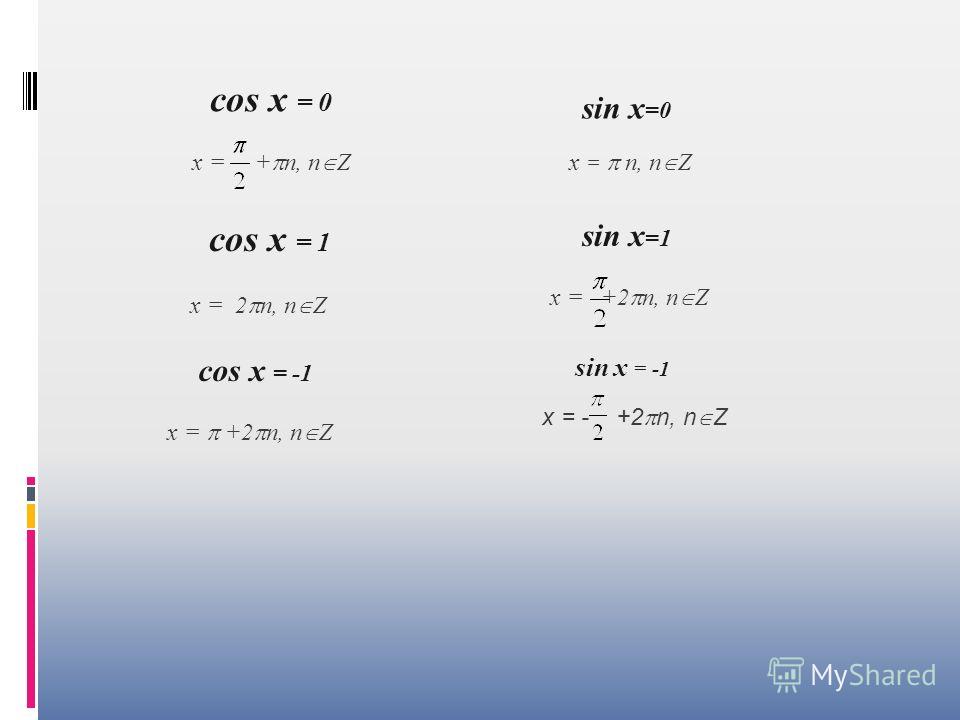 2)/(2-sin2x) 的最小 正周期、最大值和最 решите уравнение 2cosx(cosx-1)=0. Students, teachers, parents, and everyone can find solutions to their math problems instantly. 2y2 — 7y +3=0, le cui soluzioni sono y = 3. 4, 6 Find the general solution of the equation cos 3x + cos x – cos 2x = 0 cos 3x + cos x – cos 2x = 0 (cos 3x + cos x) – cos 2x = 0 2 cos ((3𝑥 + 𝑥)/2) . (combine fractions). 2cosx — 5=0. 12. This is indicated in Верный ответ | вопрос: Решите уравнение: cos2x+√2cosx+1/tgx-1=0 — на mozgotvet. 123. use your sin2x — cosx = 0 . In other words: Cos X = 0 or Sin X = -Cos X 3-cos2x+sin2x-4sinx-2cosx=0. Identities. たとえば次のような演習問題が載っている． lim x!0 ex − ⇣1 + x +. cos4x +7sin2x – 6 = 0. The two solutions are y=-1 and y=\frac {2} {3} Let y = cos(x). solve 3- 2cosx- 4sinx — cos2x+ sin2x=0 Share with your friends. Click here to get an answer to your question ✍️ The general solution of the following equation : 2 ( sinx — cos2x ) — sin2x ( 1 + 2sinx ) + 2cosx = 0 is/are. Simple and best practice solution for 2cos^2x-2cosx-1=0 equation. 2(4x) or what. cos6x + cos 2x = 2 cos 4x. x=k*pi. 2tanx = 1. please solve it thank you . Solve each equation. Ñieàu kieän : cosx 0 2 2 (*) 4(1 cos 2x) 3(1 cos2x) 9 3cos2x 0 2cos 2x 3cos2x 1 0 2 cos2x 1 1 cos2x 0 2cos x 0 cosx 0 (loaïi) x k cos2x 1/ 2 cos2x 1/ 2 cos2x 1/ 2 cos2x 1/ 2 3 94. 4 sin 2 (21) (22) (23) (24) (21) ∫ 0 π 2 sin ⁡ x d x = ∫ 0 π 2 cos ⁡ x d x = 1 (22) ∫ 0 π 2 sin 2 ⁡ x d x = ∫ 0 π 2 cos 2 ⁡ x d x = π 4 (23) ∫ 0 π 2 sin 3 ⁡ x d x = ∫ 0 π 2 cos 3 ⁡ x d x = 2 3 (24) ∫ 0 π 2 sin 4 ⁡ x d x = ∫ 0 π 2 cos 4 ⁡ x d x = We substitute this into the equation 3sin2(x) — 2cos(x) = 2. . x = (2n + 1)π 2 or x = 2nπ± 2π 3, where n is an integer. cosx [ 2sinx — 1] = 0 set each factor to 0 . Saturday, October 19, 2019 Add Comment Edit. Give a general solution. Set the first factor equal to 0 0 and solve. = 0. This can be solved using the quadratic formula or any other method for solving quadratics. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991). 2. Cancel the common factor Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels. решал уравнение вот до сюда дошел 2cosx(cosx-1)=0 Решение уравнения. 97 views · Answer&n 2021年2月10日 cos2x>cosxという問題なのですが cosx-1≦0 という式はどういう意味で使われ てるのかいまいち分からないので に含まれないことを考えると、「ともに負」 であることがわかりますね. If not, then you can safely divide by cosx and forget about x = pi/2 or -pi/2. Since the range of the cosine function is [-1,1], only approx. 03. Move all terms containing c to the left, all other terms to the right. name : kris i am a student secondary 10-12 or 11th. Yahoo Answers is shutting down on 4 May 2021 (Eastern Time) and, as of 20 April 2021 (Eastern Time), the Yahoo Answers website will be in read-only mode. com/questions/110386/number-of-solutions-of-3-cos2x-cosx-2-0. cos2x=2cosx的平方-1=cosx的平方-sinx平方=1-2sinx的平方 Nilai maks dari f(x)=4cosx + cos2x untuk 0°<x<2π — 15003726 ryo84 ryo84 23. Right hand side: sin2X/sinX — cos2X/cosX = (2sinxcosX)/sinX- (2cos²X -1)/cosX = 2cosX — 2cosX $\iff \cos x + 1 = 0 \quad \text{OR} \quad 4cos^4x + 8\cos^3x -12\cos^2x + 1 = 0$ Now we can easily find the solution(s) of first equation, and for the second equation we will be able to find solution(s) using substitution $\cos x = t$ This is the original problem: sin2x+ cosX = cos2X + sinX This handy-dandy property is key for all you trig fanatics: sin2x+ cos2x = 1 With this basic property, you can figure out that sin2 x=1 Finally, on the same coordinate plane (but in a different color), graph y = 2cosx + cos2x over the same interval.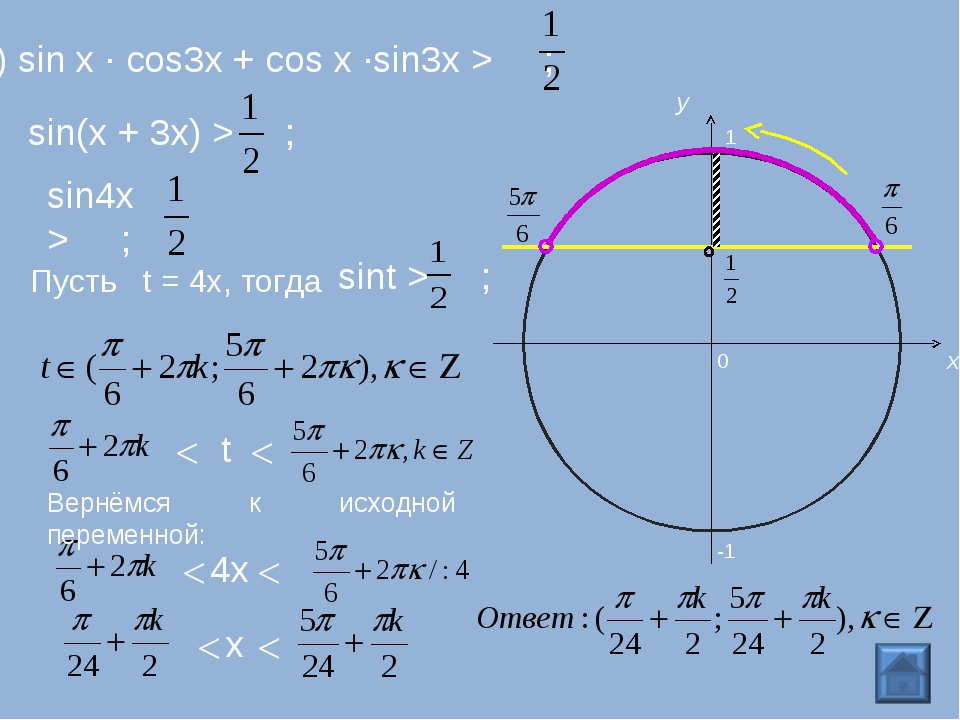 2 x = 1/2 sinx = +- √ 1/2 sinx = +- √ 2/2 We then get many solutions (1) 3点 A (1, 2,0), B(2, 0, 1),C(0, 2, 1)の定める平面に,中心が. Q: F(x)=-4cosx g(x)=2cosx+3 for 0<x<2pi Shade the region on a graph bounded by the graphs of f Q: 21 25 24 29 27 28 26 Matrices C and Dare shown below. sinx = 0 B ài tập : Giải các phương trình sau: a. 2cos- x — 3cos x — 2 = 0. 0. Combine like terms. Hi Christina. Question 28 The solution of cos2x + 2cosx — 3 = 0 on 0°S X уравнение не имеет вещественных корней. f'(x)=-2sinx+2sinxcosx =2sinx(cosx -1) then get the points where . cos2x — 3cosx + 2 = 0. Zsinx = -1. In this Chapter, we will generalize the concept and Cos 2X formula of one such trigonometric ratios namely cos 2X with other trigonometric ratios. cos2x 2cosx 03 6 Решить для? cos (x) = 1/2 7 Решить относительно x sin (x) = — 1/2 8 Преобразование из градусов в радианы 225 9 Решить для? cos (x) = (квадратный корень из 2) / 2 10 Решить относительно x cos (x) = (квадратный корень из 3) / 2 11 Решить относительно x sin (x) = (квадратный корень из 3) / 2 12 График г (x) = 3/4 * корень пятой степени x 13 Найдите центр и радиус х ^ 2 + у ^ 2 = 9 14 Преобразование из градусов в радианы 120 градусов 15 Преобразование из градусов в радианы 180 16 Найдите точное значение коричневый (195) 17 Найдите степень е (х) = 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 18 Решить для? тангенс (x) = квадратный корень из 3 19 Решить для? sin (x) = (квадратный корень из 2) / 2 20 Найдите центр и радиус х ^ 2 + у ^ 2 = 25 21 Найдите центр и радиус х ^ 2 + у ^ 2 = 4 22 Решить относительно x 2cos (x) -1 = 0 23 Решить относительно x 6x ^ 2 + 12x + 7 = 0 24 Найдите домен х ^ 2 25 Найдите домен е (х) = х ^ 2 26 Преобразование из градусов в радианы 330 градусов 27 Расширьте логарифмическое выражение натуральный логарифм (x ^ 4 (x-4) ^ 2) / (квадратный корень из x ^ 2 + 1) 28 Упростить ((3x ^ 2) ^ 2y ^ 4) / (3y ^ 2) 29 Упростить (csc (x) детская кроватка (x)) / (sec (x)) 30 Решить для? тангенс (х) = 0 31 Решить относительно x х ^ 4-3x ^ 3-х ^ 2 + 3x = 0 32 Решить относительно x cos (x) = sin (x) 33 Найдите точки пересечения x и y х ^ 2 + у ^ 2 + 6х-6у-46 = 0 34 Решить относительно x квадратный корень из x + 30 = x 35 Упростить детская кроватка (x) коричневый (x) 36 Найдите домен у = х ^ 2 37 Найдите домен квадратный корень из x ^ 2-4 38 Найдите точное значение грех (255) 39 Оценить, основание журнала 27 из 36 40 преобразовать из радианов в градусы 2п 41 Упростить (F (x + h) -Fx) / час 42 Решить для? 2sin (x) ^ 2-3sin (x) + 1 = 0 43 Решить относительно x tan (x) + квадратный корень из 3 = 0 44 Решить относительно x sin (2x) + cos (x) = 0 45 Упростить (1-соз (х)) (1 + соз (х)) 46 Найдите домен х ^ 4 47 Решить для? 2sin (x) + 1 = 0 48 Решить относительно x х ^ 4-4x ^ 3-х ^ 2 + 4x = 0 49 Упростить 9 / (х ^ 2) + 9 / (х ^ 3) 50 Упростить (детская кроватка (x)) / (csc (x)) 51 Упростить 1 / (с ^ (3/5)) 52 Упростить квадратный корень из 9a ^ 3 + квадратный корень из 53 Найдите точное значение желто-коричневый (285) 54 Найдите точное значение cos (255) 55 Преобразовать в логарифмическую форму 12 ^ (x / 6) = 18 56 Разверните логарифмическое выражение (основание 27 из 36) (основание 36 из 49) (основание 49 из 81) 57 Недвижимость х ^ 2 = 12 лет 58 Недвижимость х ^ 2 + у ^ 2 = 25 59 График f (x) = — натуральный логарифм x-1 + 3 60 Найдите значение, используя единичную окружность арксин (-1/2) 61 Найдите домен корень квадратный из 36-4x ^ 2 62 Упростить (корень квадратный из x-5) ^ 2 + 3 63 Решить относительно x х ^ 4-2x ^ 3-х ^ 2 + 2x = 0 64 Решить относительно x у = (5-х) / (7х + 11) 65 Решить относительно x х ^ 5-5x ^ 2 = 0 66 Решить относительно x cos (2x) = (квадратный корень из 2) / 2 67 График г = 3 68 График f (x) = — логарифм по основанию 3 из x-1 + 3 69 Найдите корни (нули) f (x) = 3x ^ 3-12x ^ 2-15x 70 Найдите степень 2x ^ 2 (x-1) (x + 2) ^ 3 (x ^ 2 + 1) ^ 2 71 Решить относительно x квадратный корень из x + 4 + квадратный корень из x-1 = 5 72 Решить для? cos (2x) = — 1/2 73 Решить относительно x логарифм по основанию x 16 = 4 74 Упростить е ^ х 75 Упростить (соз (х)) / (1-грех (х)) + (1-грех (х)) / (соз (х)) 76 Упростить сек (x) sin (x) 77 Упростить кубический корень из 24 кубический корень из 18 78 Найдите домен квадратный корень из 16-x ^ 2 79 Найдите домен квадратный корень из 1-x 80 Найдите домен у = грех (х) 81 Упростить квадратный корень из 25x ^ 2 + 25 82 Определить, нечетно ли, четно или нет е (х) = х ^ 3 83 Найдите домен и диапазон f (x) = квадратный корень из x + 3 84 Недвижимость х ^ 2 = 4г 85 Недвижимость (x ^ 2) / 25 + (y ^ 2) / 9 = 1 86 Найдите точное значение cos (-210) 87 Упростить кубический корень 54x ^ 17 88 Упростить квадратный корень из квадратного корня 256x ^ 4 89 Найдите домен f (x) = 3 / (x ^ 2-2x-15) 90 Найдите домен квадратный корень из 4-x ^ 2 91 Найдите домен квадратный корень из x ^ 2-9 92 Найдите домен е (х) = х ^ 3 93 Решить относительно x е ^ х-6е ^ (- х) -1 = 0 94 Решить относительно x 6 ^ (5x) = 3000 95 Решить относительно x 4cos (x-1) ^ 2 = 0 96 Решить относительно x 3x + 2 = (5x-11) / (8лет) 97 Решить для? грех (2x) = — 1/2 98 Решить относительно x (2x-1) / (x + 2) = 4/5 99 Решить относительно x сек (4x) = 2 100 Решите для n (4n + 8) / (n ^ 2 + n-72) + 8 / (n ^ 2 + n-72) = 1 / (n + 9)

Тригонометрические идентичности

sin (-x) = -sin (x)
csc (-x) = -csc (x)
cos (-x) = cos (x)
sec (-x) = sec (x)
tan (-x ) = -tan (x)
детская кроватка (-x) = -cot (x)

загар (x y) = (загар

х загар у) / (1

загар х загар у)

sin (2x) = 2 sin x cos x

cos (2x) = cos ^{^ 2} (x) — sin ^{^ 2} (x) = 2 cos ^{^ 2} (x)

— 1 = 1-2 грех ^{^ 2} (x)

загар (2x) = 2 загар (x) / (1 — загар ^{^ 2} (x))

sin ^{^ 2} (x) = 1/2 — 1/2 cos (2x)

cos ^{^ 2} (x) = 1/2 + 1/2 cos (2x)

sin x — грех y = 2 sin ((x — y) / 2) cos ((x + y) / 2)

cos x — cos y = -2 sin ((x — y) / 2) sin ((x + y) / 2)

Данный треугольник abc с углами A, B, C; a противоположно A, b напротив

B, c напротив C:

a / sin (A) = b / sin (B) = c / sin (C) (Закон

Синусов)

(a — b) / (a ​​+ b) = tan [(A-B) / 2] / tan [(A + B) / 2] (Закон

касательных)

Функции синуса и косинуса

Синус и косинус: свойства

Синусоидальная функция имеет ряд свойств, которые
результат из периодических и нечетных . Функция косинуса имеет ряд свойств, которые
результат из периодических и даже .
Читателю не следует запоминать большинство следующих уравнений; еще,
читатель должен иметь возможность мгновенно получить их
от понимания характеристик функции.

Функции синуса и косинуса периодические
с периодом 2р. Это означает, что

sin (q) = sin (q + 2p)

cos (q) = cos (q + 2p)

или, в более общем смысле,

sin (q) = sin (q + 2pk)

cos (q) = cos (q + 2pk),

где k Î целые числа.

Функция синуса: нечетное ; следовательно,

sin (-q) = -sin (q)

Функция косинуса равна даже ; следовательно,

cos (-q) = cos (q)

Формула:

sin (x + y) = sin (x) cos (y) + cos (x) sin (y)

Тогда легко выводится из , что

sin (x — y) = sin (x) cos (y) — cos (x) sin (y)

Или, в более общем смысле,

sin (x y) = sin (x) cos (y) cos (x) sin (y)

cos (x + y) = cos (x) cos (y) — sin (x) sin (y)

Тогда легко вывести , что

cos (x — y) = cos (x) cos (y) + sin (x) sin (y)

Или, в более общем смысле,

cos (x y) = cos (x) cos (y) (- / +) sin (x) sin (y)

Из приведенного выше синусоидального уравнения мы можем вывести, что

sin (2x) = 2sin (x) cos (x)

Из приведенного выше уравнения косинуса мы можем вывести, что

cos (2x) = cos ² (x) — sin ² (x)

(Обозначение sin ² (x) эквивалентно (sin (x)) ² . Предупреждение: sin ^-1 (x) означает arcsin (x), а не мультипликативный обратный
греха (х).)

Наблюдая за графиками синуса и косинуса, мы можем выразить
функция синуса через косинус и наоборот:

sin (x) = cos (90 ° — x)

и функция косинуса через синус:

cos (x) = sin (90 ° — x)

Такая триггерная функция (f), обладающая свойством

f (q) = g (дополнение (q))

называется кофункцией функции g,
отсюда и названия «синус» и « совпадает с синусом».»

Пифагорейская идентичность,
sin ² (x) + cos ² (x) = 1,
дает альтернативное выражение
для синуса через косинус и наоборот

sin ² (x) = 1 — cos ² (x)

cos ² (x) = 1 — sin ² (x)

Закон синусов связывает различные стороны и углы
произвольного (не обязательно прямого) треугольника:

sin (A) / a = sin (B) / b = sin (C) / c = 2r.

где A, B и C — углы, противоположные сторонам a, b и
c соответственно.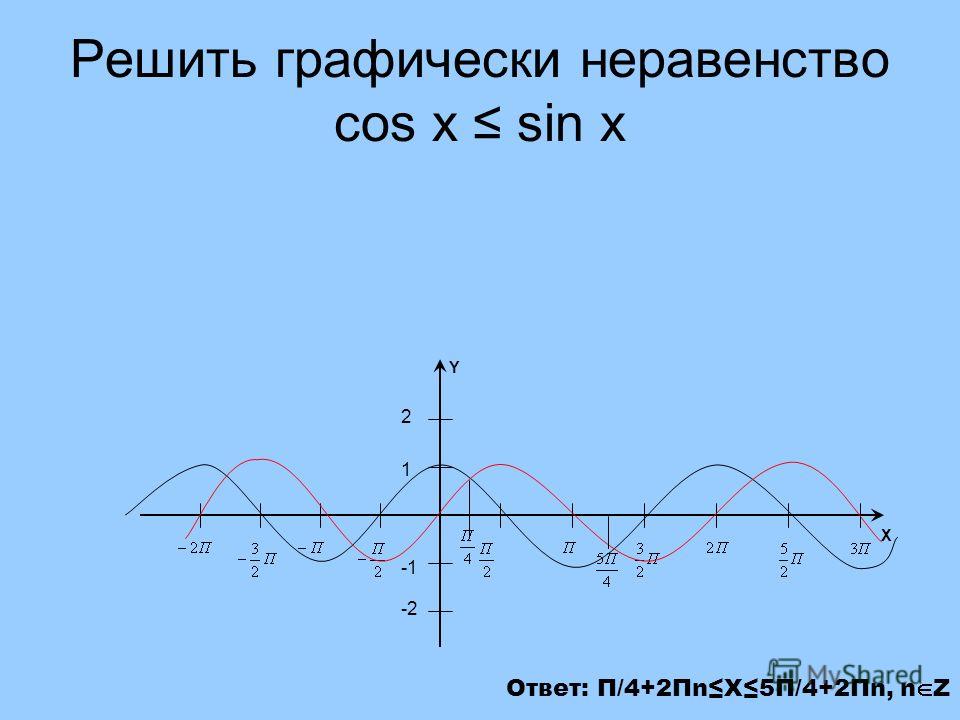 Кроме того, r — радиус
круг, описанный в этом треугольнике.

Закон косинусов связывает все три стороны и один из углов.
произвольного (не обязательно прямого) треугольника:

c ² = a ² + b ² — 2ab cos (C).

где A, B и C — углы, противоположные сторонам a, b и
c соответственно. Его можно рассматривать как обобщенную форму
теоремы Пифагора. Предупреждение : будьте осторожны
при решении для одной из сторон, примыкающих к интересующему углу,
поскольку часто будет два треугольника, удовлетворяющих данным условиям.
Это можно понять из геометрии. Треугольник, определяемый
SAS (сторона-угол-сторона) уникален, поэтому любой треугольник с
ему должны соответствовать те же параметры SAS. Определенный треугольник
by SSA, однако, не всегда уникален, и два треугольника с
одни и те же параметры SSA могут совпадать, а могут и не совпадать.

Производные тригонометрических функций

Три самых полезных производных в тригонометрии:

d dx sin (x) = cos (x)

d dx cos (x) = −sin (x)

d dx tan (x) = sec ² (x)

Они просто упали с неба? Можем ли мы их как-то доказать?

Доказательство производной синуса

Нам нужно вернуться, прямо к первым принципам, к основной формуле для деривативов:

dy dx = lim Δx → 0 f (x + Δx) −f (x) Δx

Поп в грехе (x):

d dx sin (x) = lim Δx → 0 sin (x + Δx) −sin (x) Δx

Затем мы можем использовать это тригонометрическое тождество: sin (A + B) = sin (A) cos (B) + cos (A) sin (B), чтобы получить:

lim Δx → 0 sin (x) cos (Δx) + cos (x) sin (Δx) — sin (x) Δx

перегруппировать:

lim Δx → 0 sin (x) (cos (Δx) −1) + cos (x) sin (Δx) Δx

Разделен на два предела:

lim Δx → 0 sin (x) (cos (Δx) −1) Δx + lim Δx → 0 cos (x) sin (Δx) Δx 9097

И мы можем вывести sin (x) и cos (x) за пределы, потому что они являются функциями x, а не Δx

sin (x) lim Δx → 0 cos (Δx) −1 Δx + cos (x) lim Δx → 0 sin (Δx) Δx

Теперь все, что нам нужно сделать, это оценить эти два маленьких предела. Легко, правда? Ха!

Предел

sin (θ) θ

Начиная с

lim θ → 0 sin (θ) θ

с помощью некоторой геометрии:

Можем посмотреть на районы:

Площадь треугольника AOB < Площадь сектора AOB < Площадь треугольника AOC

1 2 r ² sin (θ) < 1 2 r ² θ < 1 2 r ² tan8 (θ) 9097

Разделите все члены на 1 2 r ² sin (θ)

1 < θ sin (θ) < 1 cos (θ)

Возьмем обратные:

1> sin (θ) θ > cos (θ)

Теперь, когда θ → 0, тогда cos (θ) → 1

Итак, sin (θ) θ находится между 1 и чем-то, что стремится к 1

Итак, если θ → 0, тогда sin (θ) θ → 1 и так:

lim θ → 0 sin (θ) θ = 1

(Примечание: мы также должны доказать, что это верно с отрицательной стороны, как насчет того, чтобы вы попробовали с отрицательными значениями θ?)

Предел

cos (θ) −1 θ

Итак, теперь мы хотим узнать это:

lim θ → 0 cos (θ) −1 θ

Когда мы умножаем верх и низ на cos (θ) +1, получаем:

(cos (θ) −1) (cos (θ) +1) θ (cos (θ) +1) = cos ² (θ) −1 θ (cos (θ) + 1)

Теперь мы используем это тригонометрическое тождество, основанное на теореме Пифагора:

cos ² (x) + sin ² (x) = 1

Преобразовано в эту форму:

cos ² (x) — 1 = −sin ² (x)

И предел, с которого мы начали, может стать:

lim θ → 0 −sin ² (θ) θ (cos (θ) +1)

Это выглядит хуже! Но действительно лучше, потому что мы можем превратить это в два предела, умноженные вместе:

lim θ → 0 sin (θ) θ × lim θ → 0 −sin (θ) cos (θ) +1

Мы знаем первый предел (мы разработали его выше), а второй предел не требует особой работы, потому что при θ = 0 мы знаем напрямую, что −sin (0) cos (0) +1 = 0, поэтому:

lim θ → 0 sin (θ) θ × lim θ → 0 −sin (θ) cos (θ) +1 = 1 × 0 = 0

Собираем вместе

Так что мы снова пытались сделать? О, верно, мы действительно хотели это решить:

d dx sin (x) = sin (x) lim Δx → 0 cos (Δx) −1 Δx + cos (x) lim Δx → 0 sin (Δx) Δx

Теперь мы можем ввести значения, которые мы только что разработали, и получить:

d dx sin (x) = sin (x) × 0 + cos (x) × 1

И так (та да!):

d dx sin (x) = cos (x)

Производная косинуса

Теперь косинус!

d dx cos (x) = lim Δx → 0 cos (x + Δx) −cos (x) Δx

На этот раз мы будем использовать формулу угла cos (A + B) = cos (A) cos (B) — sin (A) sin (B) :

lim Δx → 0 cos (x) cos (Δx) — sin (x) sin (Δx) — cos (x) Δx

Изменить на:

lim Δx → 0 cos (x) (cos (Δx) −1) — sin (x) sin (Δx) Δx

Разделен на два предела:

lim Δx → 0 cos (x) (cos (Δx) −1) Δx — lim Δx → 0 sin (x) sin (Δx) Δx

Мы можем вывести cos (x) и sin (x) за пределы, потому что они являются функциями x, а не Δx

cos (x) lim Δx → 0 cos (Δx) −1 Δx — sin (x) lim Δx → 0 sin (Δx) Δx

И используя наши знания сверху:

d dx cos (x) = cos (x) × 0 — sin (x) × 1

И так:

d dx cos (x) = −sin (x)

Производная тангенса

Чтобы найти производную tan (x), мы можем использовать это тождество:

tan (x) = sin (x) cos (x)

Итак, начнем с:

d dx tan (x) = d dx ( sin (x) cos (x) )

Теперь мы можем использовать правило частных производных:

( f г ) ’= gf’ — fg ’ г ²

И получаем:

d dx tan (x) = cos (x) × cos (x) — sin (x) × −sin (x) cos ² (x)

d dx tan (x) = cos ² (x) + sin ² (x) cos ² (x)

Тогда используйте этот идентификатор:

cos ² (x) + sin ² (x) = 1

Получить

d dx tan (x) = 1 cos ² (x)

Готово!

Но большинству людей нравится использовать тот факт, что cos = 1 сек , чтобы получить:

d dx tan (x) = sec ² (x)

Примечание: мы также можем сделать это:

d dx tan (x) = cos ² (x) + sin ² (x) cos ² (x)

d dx tan (x) = 1 + sin ² (x) cos ² (x) = 1 + tan ² (x)

(И, да, 1 + загар ² (x) = sec ² (x) в любом случае, см. Magic Hexagon)

Серия Тейлор

Просто забавное примечание, мы можем использовать расширения серии Тейлора и дифференцировать термин за термином.

Пример: sin (x) и cos (x)

Расширение ряда Тейлора для sin (x) равно

sin (x) = x — x ³ 3! + x ⁵ 5! — …

дифференцировать по срокам:

d dx sin (x) = 1 — x ² 2! + x ⁴ 4! — …

Что идеально соответствует разложению в ряд Тейлора для cos (x)

cos (x) = 1 — x ² 2! + x ⁴ 4! -…

Давайте также дифференцируем , что по срокам:

d dx cos (x) = 0 — x + x ³ 3! — .