Содержание
Умножение степеней, деление, таблица
Что такое степень числа
Алгебра дает нам такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
- an — степень, где
a — основание степени
n — показатель степени
Соответственно, an= a·a·a·a…·a
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и на калькуляторе — вот несколько подходящих:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3). Неважно в какой класс перешел ребенок — таблица пригодится всегда.
Неважно в какой класс перешел ребенок — таблица пригодится всегда.
Число | Вторая степень | Третья степень |
1 | 1 | 1 |
2 | 4 | 8 |
3 | 9 | 27 |
4 | 16 | 64 |
5 | 25 | 125 |
6 | 36 | 216 |
7 | 49 | 343 |
8 | 64 | 512 |
9 | 81 | 729 |
10 | 100 | 1000 |
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук и ниже мы их рассмотрим.
Всего их пять штук и ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
an · am = am+n
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
(an)m = an· m
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.
(a · b)n = an · bn
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b)n = an : bn
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Умножение чисел с одинаковыми степенями
Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35+3 = 38 = 6561
- 28 · 81= 28 · 23 = 211 = 2048
Умножение чисел с разными степенями
Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:
А именно:
an · bn = (a · b)n
Если же разные и степени, и основания и одно из оснований не преобразуется в число с той же степенью, как у другого числа (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
Деление степеней с одинаковыми основаниями
Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми степенями
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
an : bn = (a : b)n, где
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Деление чисел со степенями
Если степени разные, но основания одинаковые, то действия производим согласно правилу, описанному выше. А именно:
А именно:
Если же разные и степени, и основания, то возводим в степень каждое число и только потом умножаем:
Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.
Умножение и деление степеней с одинаковыми основаниями
Умножение степеней с одинаковыми основаниями
При умножении степеней с одинаковыми основаниями их показатели складываются.
Рассмотрим, почему показатели складываются. Во-первых, возведение в степень — это сокращённая запись умножения:
23 = 2 · 2 · 2.
Во-вторых, умножение числа самого на себя, имеющего при этом разные степени, означает, что это число берётся сомножителем столько раз, сколько указывают показатели степеней:
| 23 · 22 = | (2 · 2 · 2) | · | (2 · 2) | = |
3 множ. | 2 множ. |
| = | 2 · 2 · 2 · 2 · 2 | = 25. |
| 5 множ. |
Из примера становится понятно, что при сложении показателей степеней мы получаем общую сумму сомножителей, поэтому для любого выражения будет верна формула:
ax · ay = ax+y.
Примеры умножения степеней
Пример 1. Запишите в виде степени:
n3n5.
Решение:
n3n5 = n3 + 5 = n8.
Пример 2. Упростите:
xy2z3x4y5z6.
Решение: Чтобы легче было провести умножение степеней с одинаковыми основаниями, можно сначала сгруппировать степени по основаниям:
(xx4)(y2y5)(z3z6).
Теперь выполним умножение степеней:
(xx4)(y2y5)(z3z6) = (x1 + 4)(y2 + 5)(z3 + 6) = x5y7z9.
Следовательно:
xy2z3x4y5z6 = x5y7z9.
Пример 3. Выполните умножение:
а) nxn5;
б) xxn;
в) amam.
Решение:
а) nxn5 = nx + 5;
б) xxn = xn + 1;
в) amam = am + m = a2m.
Пример 4. Упростите выражение:
а) —a2 · (-a)2 · a;
б) -(-a)2 · (-a) · a.
Решение:
а) —a2 · (-a)2 · a = —a2 · a2 · a = -(a2a2a) = -(a2 + 2 + 1) = —a5;
б) -(-a)2 · (-a) · a = —a2 · (-a) · a = a3 · a = a4.
Деление степеней с одинаковыми основаниями
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Рассмотрим частное двух степеней с одинаковыми основаниями:
n12 : n5,
где n — это число, не равное нулю, так как на 0 делить нельзя. Запишем частное в виде дроби:
Представим n12 в виде произведения n7 · n5. Тогда числитель и знаменатель дроби можно будет сократить на общий множитель n5:
| n12 | = | n7 · n5 | = n7. |
| n5 | n5 |
Верность совершённого действия легко проверить с помощью умножения:
n7 · n5 = n7+5 = n12.
Следовательно, общая формула для деления степеней с одинаковым основанием будет выглядеть так:
ax : ay = ax-y.
Примеры деления степеней
Пример 1. Частное степеней замените степенью с тем же основанием:
| а) | a5 | ; б) | m18 | . |
| a | m10 |
Решение:
| а) | a5 | = | a4 · a | = a4; |
| a | a |
| б) | m18 | = | m8 · m10 | = m8. |
| m10 | m10 |
Пример 2. Выполните деление:
а) x7 : x2;
б) n10 : n5;
в) a30 : a10.
Решение:
а) x7 : x2 = x7 — 2 = x5;
б) n10 : n5 = n10 — 5 = n5;
в) a30 : a10 = a30 — 10 = a20.
Пример 3. Чему равно значение выражения:
| а) | an | ; б) | mx | ; в) | b5 · b8 | . |
| a2 | m | b3 |
Решение:
| в) | b5 · b8 | = | b2 · b3 · b8 | = b2 · b8 = b10. |
| b3 | b3 |
Урок математики в 7 классе по теме «Умножение и деление степеней с одинаковыми показателями»
Предмет: Алгебра
Класс: 7
Учитель: Егерь Ирина Викторовна , учитель математики
МБОУ города Иркутска СОШ №11 с углублённым изучением отдельных предметов
Тема программы: Степень с натуральным показателем и ее свойства (10 ч)
Тема урока: Умножение и деление степеней с одинаковыми показателями
Цель урока:
— обучающая: изучить правила действий над степенями с одинаковыми показателями,
научиться применять правила при вычислении значений выражений и преобразовании выражений;
— развивающая: развивать математическую речь, формировать умение анализировать, рассуждать, доказывать;
— воспитательная: воспитание познавательной активности, ответственности и аккуратности;
формирование навыков культуры диалога.
Технологии: обучение в сотрудничестве, проблемное обучение.
Тип урока: урок изучения нового материала.
Методы обучения: словесный, практический, наглядный.
Формы обучения: индивидуальная, фронтальная, групповая.
Оборудование: доска, мел, карточки для самостоятельной работы
Литература: Мордкович А.Г., Александрова Л.А. Алгебра 7 класс. М.: Мнемозина, 2013.
Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ,2014.
http://school—assistant.ru/
Ход урока:
I. Орг. момент
Орг. момент
II. Актуализация знаний
Вспомним тему предыдущего урока, для этого устно выполните следующие задания (по ходу выполнения, учащиеся формулируют свойства степеней, определение степени на которые ссылаются при выполнении задания):
Вычислите:
|
|
|
|
|
|
|
|
|
|
|
|
Проверяем ответы к заданиям. Возникает затруднение при выполнении заданий №7,8,9.
Возникает затруднение при выполнении заданий №7,8,9.
III. Создание проблемной ситуации и диалогический выход из неё
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV. Самостоятельная работа с самопроверкой по эталону
Два ученика выполняют задания самостоятельно на скрытых досках, остальные-в тетрадях. Затем они проверяют работу по алгоритму и сопоставляют с решением на доске. Ошибки исправляются, выясняются их причины. Если задание выполнено верно, то рядом ученики ставят «+».
Карточки
-
вариант.
1.Представьте произведение степеней в виде степени:
а) 35 • 25 б) х7у7; в) 23у3.
2. Представьте дробь в виде степени:
а) ; б) ; в) .
-
вариант.
1.Представьте произведение степеней в виде степени:
а) 43 • 33 б) х6у6; в) 52х2.
2. Представьте дробь в виде степени:
а) ; б) ; в) .
V. Домашнее задание: §18 №18.18, №18.19, опорный конспект — правила умножения и деления степеней с одинаковыми показателями.
VI. Рефлексия деятельности.
Рефлексия деятельности.
— Что нового узнали на уроке? Что повторили?
— Как перемножить степени с одинаковыми показателями?
— Как разделить друг на друга степени с одинаковыми показателями?
— Верно ли равенство: а) 34 • 54 = 158; б) (-6)5 • ( -3)5 = 20 ?
— Чью работу вы можете сегодня отметить?
— Как оцениваете свою работу?
Деление степеней с одинаковыми основаниями
Пусть надо a9 ÷ a3; здесь, согласно смыслу деления, дано произведение = a9 и дан один множитель = a3. Надо найти другой множитель. Напишем данное произведение (a9) подробнее
a · a · a · a · a · a · a · a · a
и отделим, например, подчеркивая, данный множитель, т. е. a3 или a · a · a. Тогда мы увидим, каков другой множитель, а именно осталось неподчеркнутым
е. a3 или a · a · a. Тогда мы увидим, каков другой множитель, а именно осталось неподчеркнутым
a · a · a · a · a · a,
что = a6. Итак,
a9 ÷ a3 = a6.
Пусть надо b47 ÷ b18. Данное произведение есть b47 или такое произведение, где b повторяется множителем 47 раз; отделим один данный множитель, b18, или произведение, где b повторяется 18 раз множителем. Тогда мы сообразим, что искомым множителем является произведение, где b повторяется 29 раз множителем, т. е. b29. Итак, b47 ÷ b18 = b29.
Также
x15 ÷ x5 = x10
(a + b)7 ÷ (a + b) = (a + b)6
323 ÷ 320 = 33 = 27 и т. д.
Вообще
am ÷ an = am-n (если m > n)
или словами: при делении степеней с одинаковыми основаниями основание степени остается без изменения, а показатель делителя вычитается из показателя делимого (если показатель делимого больше показателя делителя).
Пусть теперь надо
20a5b4c2d ÷ 5a3b3c2.
Здесь дано произведение (20a5b4c2d) и один множитель 5a3b3c2; надо найти другой множитель. У произведения коэффициент (+20), он получился от умножения коэффициента данного множителя (+5) на коэффициент искомого множителя. Чтобы найти этот коэффициент, надо (+20) ÷ (+5), получим +4. В данном произведении a взято множителем 5 раз, в данном множителе a входит множителем 3 раза. Поэтому в искомом множителе a должно входить множителем 2 раза, т. е. в искомом множителе должно быть a2. В данном произведении b берется множителем 4 раза, а в данном множителе – 3 раза; следовательно, в искомом множителе b должно входить множителем лишь 1 раз. В данном произведении имеем c2 (c берется множителем 2 раза) и в данном множителе имеем c2. Поэтому в искомом множителе c не должно вовсе входить. В данном произведении имеется множитель d, а в данном множителе d вовсе нет; поэтому d должно иметься в искомом множителе. Итак,
В данном произведении имеется множитель d, а в данном множителе d вовсе нет; поэтому d должно иметься в искомом множителе. Итак,
20a5b4c2d ÷ 5a3b3c2 = 4a2bd.
Еще примеры:
В предыдущем встречались деления, вроде c2 ÷ c2; a ÷ a; b3 ÷ b3; и т. д. Здесь уместно заметить, что частное от деления какого-либо числа на самое себя всегда равно 1.
Умножение и деление степеней 7 класс
Тема урока: Умножение и деление степеней
Учитель: Демчук В. В.
Место работы, должность: учитель математики МБОУ «СОШ№14» г.Евпатории
Класс: 7 класс
Предмет: Алгебра
Учебник: Ю.Н. Макарычев «Алгебра. 7 класс».
Цель урока: вывести правила умножения и деления степеней с одинаковыми основаниями; дать определение нулевой степени числа, не равного нулю; формировать умение выполнять указанные действия со степенями.
Задачи урока:
Образовательные задачи урока (формирование познавательных УУД):
познакомить учащихся со степенью с натуральным показателем;
тренировать способность к использованию выведенного алгоритма;
организовать деятельность учащихся по приобретению необходимых умений и навыков;
повторить и закрепить;
2. Воспитательные задачи урока ( формирование коммуникативных и личностных УУД):
содействовать развитию познавательного интереса учащихся к предмету;
прививать учащимся навыки организации самостоятельной работы;
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
3. Развивающие задачи урока: (формирование регулятивных УУД)
развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;
Предметными результатами являются использование при решении математических задач, их обосновании и проверке найденного решения знание остепени с натуральными показателями и их свойствах
4. Метапредметные
Метапредметные
— способствовать формированию умений применять приемы обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию;
— развитие математического кругозора, мышления, речи, внимания и памяти;
— формирование отдельных составляющих исследовательской деятельности: делать выводы и умозаключения;
— развитие вычислительной культуры.
Тип урока:
Урок изучения и первичного закрепления новых знаний
Используемые учебники и учебные пособия:
Учебник для общеобразовательных учреждений /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковскогоей С.А. Теляковского
Оборудование: ПК, И/доска, проектор, USB носитель, презентация раздаточный материал
I Организационный момент. Мотивационный момент.
1)ПРИВЕТСТВИЕ:
Добрый день всем, ребята, настроимся на работу. На предыдущих уроках вы уже открыли для себя удивительный мир степеней. Многие ученые во все времена занимались вопросами их изучения. Это знаменитый Пифагор, Рене Декарт(который первым ввел обозначение- степени)Но я хочу обратить ваше внимание на слова М Ломоносова, которые будут эпиграфом урока «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»
Многие ученые во все времена занимались вопросами их изучения. Это знаменитый Пифагор, Рене Декарт(который первым ввел обозначение- степени)Но я хочу обратить ваше внимание на слова М Ломоносова, которые будут эпиграфом урока «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»
2)Кто отсутствует? ПРОВЕРКА готовности к уроку
II. Актуализация знаний
Устная работа
Для дальнейшей работы по этой теме, нам нужно будет вспомнить элементарные правила степеней.
1. Что называется степенью?
2. Что называют основанием степени?
3. Что такое показатель степени? где в этом выражении основание и показатель?
4. Какое число получается при возведении положительного числа в степень?
5. Какое число получается при возведении отрицательного числа в степень?
6. Закончить фразу: любое число в 1 степени это…(это же число).
Теперь вычислим (слайд 1)
1.
2. Вычислить:
а) ∙; б) +; в) .
3. Какие числа нужно возвести в квадрат, чтобы получить:
а) 16; б) 121; в) .
4. Какие числа надо возвести в куб, чтобы получить:
а) -8; б) 125; в)- .
Давайте подумаем где используется степень (слайды 2-7)
III.Постановка темы и определение цели урока.
Теперь чтобы определить тему нашего урока, я предлагаю вам решить ребусы (слайды 8,9)
Какое еще действие можно выполнять с степенью? (умножение)
Открываем тетради, записываем число, классная работа.
Запишите тему урока: Умножение и деление степеней. (слайд 10)
Изучение нового материала (Создание проблемной ситуации:)
А представьте в виде степени такие выражения…
а) 23∙ 22 = ??? б) 35 : 32 = ???
в) 4237∙ 4225 ???
Как посчитать?
(Ученики могут сказать ответ в б) 45 или 46или 8∙4 = 32; но в задании д) у них ответа не будет)
Кто может расписать этот пример? (ученик выходит к доске)
23 ∙ 22 = (2∙2∙2)∙(2∙2) =2∙2∙2∙2∙2= 23+2 = 25
Что вы заметили?
Чему равно основание? : везде 2 и было 2 и осталось 2
А что стало с показателем?
Как мы его получили? З + 2 = 5 — Мы их сложили.
Откройте учебник на стр. 100 и посмотрите, такое ли там правило?
Прочитайте его. (Все читают правило в учебнике)
ПРИ УМНОЖЕНИИ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ОСНОВАНИЯМИ ОСНОВАНИЕ ОСТАВЛЯЮТ ПРЕЖНИМ, А ПОКАЗАТЕЛИ СКЛАДЫВАЮТ
В тетрадях запишем это правило в буквенном выражении:
аn ∙ аm = аn + m для любого а и натуральных m и n
(записываю на доске)
Приведите по одному примеру на это правило и запишите их в тетради.
(Ребята записывают примеры, затем несколько учеников зачитывают свои примеры.)
Это правило можно применять при умножении двух и более степеней
Например: 54 ∙53 ∙ 5 = 54+3+1 = 58
Физкультминутка.
Посчитайте, сколько ламп освещения в кабинете.
— Ребята, как умножаются степени, мы с вами теперь знаем?
Чему еще сегодня будем учиться?
-ДЕЛИТЬ СТЕПЕНИ.
Вернёмся к нашему примеру на деление степеней.
35 : 32 = (запишем в виде дроби: в числителе делимое, а в знаменателе делитель) = = и сократим = 3∙3∙3 = 33
Посмотрите внимательно, основание степени у нас изменилось?
Ученики: — НЕТ, оно осталось прежним
А чему равен показатель степени?
Ученики: 5-2 = 3
Какое у нас получается правило?
Вы начните его, а я помогу закончить:
ПРИ ДЕЛЕНИИ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ОСНОВАНИЯМИ ОСНОВАНИЯ ОСТАВЛЯЮТ ПРЕЖНИМ, А….. ИЗ ПОКАЗАТЕЛЯ ДЕЛИМОГО ВЫЧИТАЮТ ПОКАЗАТЕЛЬ ДЕЛИТЕЛЯ
Откройте учебник на стр. 100 и посмотрите, такое ли там правило?
Прочитайте его.
В тетрадях запишем это правило в буквенном выражении:
аn : аm = аn — m при условии, что а ≠ 0 m > n
(на доске фиксирую таблицу с правилом)
Приведите по одному примеру на это правило и запишите их в тетради.
(Одного ученика попросить прочитать свой пример)
Если m=n, то можно записать: аm : аm = аm – m = а0 = 1 при а ≠ 0 (т.к. 00 не имеет смысла)
Например: 60 = 1 2,70 = 1 х0 = 1 (х≠0)
Какое ещё действие мы учились выполнять? – ДЕЛИТЬ степени
(жду ответ и показываю на цель урока на слово ДЕЛИТЬ)
V.Усвоение новых знаний и способов действий.
Для закрепления знаний заполним магический квадрат
А теперь подумаем где можно использовать умножение и деление степеней, рассмотри задачи: (слайд 11,12)
Первичное закрепление
Учебник «Алгебра 7 класс» автор Макарычев Ю.Н.
№ 403, 414 (устно отвечают по цепочке, 1 ряд эксперты), № 407, 409 (а,в,д,е), 410 (а,в,д), 416(а,в,е),417(а,г)
№ 403.
Решение:
а) x5x8 = x5 + 8 = x13; е) yy12 = y1 + 12 = y13;
ж) 2624 = 26 + 4 + 210; з) 757 = 75 + 1 = 76.
№ 414.
Решение:
а) x5 : x3 = x5 – 3 = x2;
в) a21 : a = a21 – 1 = a20;
з) 0,79 : 0,74 = 0,79 – 4 = 0,75.
№ 407.
Решение:
Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:
6 = 1 + 5; 6 = 2 + 4; 6 = 3 + 3.
Значит, a6 = a ∙ a5; a6 = a2 ∙ a4; a6 = a3 ∙ a3.
№ 409.
Решение:
а) m3m2m8 = m3 + 2 + 8 = m13; в) xx4x4x = x1 + 4 + 4 + 1 = x10;
д) 78 ∙ 7 ∙ 74 = 78 + 1 + 4 = 713; е) 5 ∙ 52 ∙ 53 ∙ 55 = 51 + 2 + 3 + 4 = 511.
№ 410.
При выполнении этого упражнения ученики сами определяют основание степени, которое будет являться общим для двух степеней.
Решение:
а) 58 ∙ 25 = 58 ∙ 52 = 58 + 2 = 510;
в) 615 ∙ 36 = 615 ∙ 62 = 615 + 2 = 617;
д) 0,45 ∙ 0,16 = 0,45 ∙ 0,42 = 0,45 + 2 = 0,47;
№ 416.
Решение:
а) 56 : 54 = 56 – 4 = 52 = 25;
в) 0,510 : 0,57 = 0,510 – 7 = 0,53 = 0,125;
е) .
№ 417.
Решение:
а) = 86 : 84 = 86 – 4 = 82 = 64;
б) = 0,87 : 0,84 = 0,87 – 4 = 0,83 = 0,512;
в) = (–0,3)5 : (–0,3)3 = (–0,3)5 – 3 = (–0,3)2 = 0,09;
VI.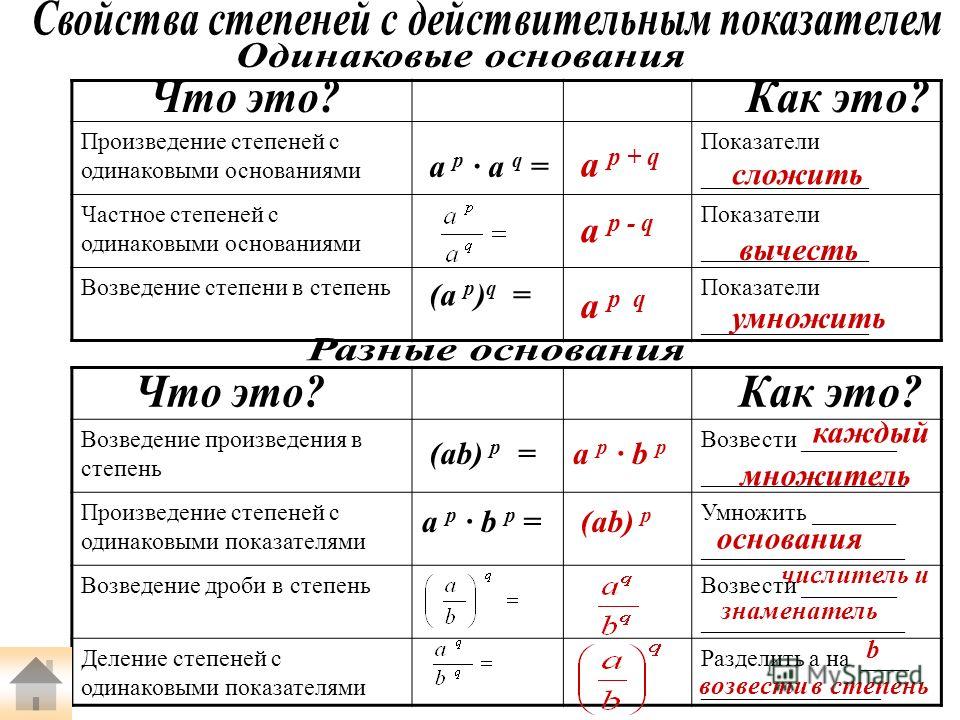 Рефлексия учебной деятельности на уроке, подведение итогов.
Рефлексия учебной деятельности на уроке, подведение итогов.
– Какой знак имеет результат возведения любого числа в квадрат?
– Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.
– Чему равно значение выражения 20; (–1)1?
Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова…
Сегодня я узнал…
Было трудно…
Я понял, что…
Теперь я умею…
Я научился…
У меня получилось …
У меня получилось…
Мне понравилось…
Кто какие ключевые слова урока может нам записать на доске?
Резерв.. № 411.
Решение:
а) 24 ∙ 2 = 24 + 1 = 25 = 32;
б) 26 ∙ 4 = 26 ∙ 22 = 26 + 2 = 28 = 256;
в) 8 ∙ 27 = 23 ∙ 27 = 23 + 7 = 210 = 1024;
г) 16 ∙ 32 = 24 ∙ 25 = 24 + 5 = 29 = 512.
2. Используя правила умножения и деления степеней, упростите выражение.
а) x8 ∙ x3 : x5; б) x20 : x10 ∙ x;
в) x7 : x3 : x3; г) x14 : x9 ∙ x5.
Решение:
а) x8 ∙ x3 : x5 = x8 + 3 : x5 = x11 : x5 = x11 – 5 = x6;
б) x20 : x10 ∙ x = x20 – 10 ∙ x = x10 ∙ x = x10 + 1 = x11;
в) x7 : x3 : x3 = x7 – 3 : x3 = x4 : x3 = x4 – 3 = x;
г) x14 : x9 ∙ x5 = x14 – 9 ∙ x5 = x5 ∙ x5 = x5 + 5 = x10.
№ 405
VII. Информация о домашнем задании.
Решить задания: п. 19 выучить определения, №408, 412, 419 (б,г,е).
7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Умножение и деление степеней с одинаковыми основаниями.
Комментарии преподавателя
На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула )
Основные определения:
Здесь a — основание степени,
n — показатель степени,
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
По-иному: если а – любое число; n и k натуральные числа, то:
Отсюда правило 1:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Разъясняющие примеры:
1)
2)
Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
Дано число а – любое; числа n и k – натуральные. Доказать:
Доказательство основано на определении степени.
То есть
Пример 1: Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
а)
б)
в)
г)
д)
е)
ж)
Здесь использовано обобщение:
з)
и)
к)
л)
м)
Пример 2: Вычислите (можно использовать таблицу основных степеней).
а) (по таблице)
б)
Пример 3: Запишите в виде степени с основанием 2.
а)
б)
в)
г)
Пример 4: Определите знак числа:
, а – отрицательное, так как показатель степени при -13 нечетный.
По-иному:
Пример 5: Замените (·) степенью числа с основанием r:
Имеем , то есть .
На этом уроке мы изучим деление степеней с одинаковыми основаниями. Вначале вспомним определение степени и теорему об умножении степеней с одинаковыми основаниями. Далее мы сформулируем теорему о делении степеней с одинаковыми основаниями, решим разъясняющие задачи и докажем теорему в общем случае. Затем мы применим теорему для решения различных задач, а также решим типичные задачи с использованием обеих теорем.
Затем мы применим теорему для решения различных задач, а также решим типичные задачи с использованием обеих теорем.
Тема: Степень с натуральным показателем и ее свойства
Урок: Деление степеней с одинаковыми основаниями (формула )
Основные определения:
Здесь a — основание степени,
n — показатель степени,
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Разъясняющие задачи
1)
2)
Вывод: частные случаи подтвердили правильность теоремы №2. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k таких, что n > k.
Доказательство теоремы 2.
Первый способ.
Воспользуемся теоремой 1. Применим ее для степеней и .
. Разделим обе части на .
Второй способ.
Доказательство основано на определении степени
Сократим k сомножителей.
То есть для любого а и любых натуральных n и k таких, что n > k.
Пример 1: Вычислить.
Для решения следующих примеров воспользуемся теоремой 2.
а)
б)
Пример 2: Упростить.
а)
б)
в)
Пример 3: Решить уравнение.
а)
б)
Пример 4: Вычислить:
Для решения следующих примеров будем пользоваться обеими теоремами.
а) =6 или быстрее =6
б) ==81 или быстрее =81
в) == или быстрее
Пример 5: Упростить:
а) = или быстрее
б)
в) или быстрее
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/umnozhenie-stepeney-s-odinakovymi-osnovaniyami-formula-a-sup-n-sup-8727a-sup-k-sup-a-sup-n-k-sup?konspekt&chapter_id=2
http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/delenie-stepeney-s-odinakovymi-osnovaniyami?konspekt&chapter_id=2
Источник видео: http://www.youtube.com/watch?v=IQPWIC6GXuI
Произведение степеней с разными основаниями.
 Умножение и деление чисел со степенями. Степень с иррациональным показателем
Умножение и деление чисел со степенями. Степень с иррациональным показателем
Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.
a m · a n = a m + n
, где
«a
» — любое
число, а «m
», «n
» — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 =
b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 =
6 17 - Представить в виде степени.

(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями
. Оно не относится к их сложению.
Нельзя
заменять сумму
(3 3 + 3 2)
на 3 5
. Это понятно, если
посчитать
(3 3 + 3 2) = (27 + 9) = 36
, а
3 5 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений,
а из показателя степени делимого вычитают показатель степени делителя.
=
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 =
4 5m + 6 + m + 2: 4 4m + 3 =
4 6m + 8 − 4m − 3 = 4 2m + 5 - Пример.
 Найти значение выражения, используя свойства степени.
Найти значение выражения, используя свойства степени.
=
=
=
=
=
2 11 − 5 = 2 6 = 64Важно!
Обратите внимание, что в свойстве 2 речь шла только
о делении степеней с одинаковыми основаниями.
Нельзя
заменять разность
(4 3 −4 2)
на 4 1
. Это понятно, если посчитать
(4 3 −4 2) = (64 − 16) = 48
, а
4 1 = 4Будьте внимательны!
Свойство № 3
Возведение степени в степень
Запомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней
перемножаются.(a n) m = a n · m
, где
«a
» — любое
число, а «m
», «n
» — любые натуральные числа.Свойства 4
Степень произведения
Запомните!
При возведении в степень произведения каждый из множителей
возводится в степень. Затем полученные результаты перемножаются.(a · b) n = a n · b n
, где
«a
», «b
» — любые рациональные
числа; «n
» — любое натуральное число.- Пример 1.
(6 · a 2 · b 3 · c) 2 =
6 2 · a 2 · 2 · b 3 · 2
· с 1 · 2 = 36 a 4 · b 6
· с 2 - Пример 2.

(−x 2 · y) 6 =
((−1) 6 · x 2 · 6 · y 1 · 6) =
x 12 · y 6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней,
применяют и в обратном порядке.(a n · b n)=
(a · b) nТо есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 =
10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 =
1
В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.Например,
4 5 · 3 2 = 4 3 ·
4 2 · 3 2 = 4 3 · (4 · 3) 2 =
64 · 12 2 = 64 · 144 = 9216Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 ·
(−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 =
4 · 1 = 4Свойства 5
Степень частного (дроби)
Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель,
и первый результат разделить на второй.
(a: b) n = a n: b n
, где
«a
», «b
» — любые рациональные
числа, b ≠ 0, n
— любое натуральное число.- Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице. - Пример 1.
Каждая арифметическая операция порою становится слишком громоздкой для записи и её стараются упростить. Когда-то так было и с операцией сложения. Людям было необходимо проводить многократное однотипное сложение, например, посчитать стоимость ста персидских ковров, стоимость которого составляет 3 золотые монеты за каждый. 3+3+3+…+3 = 300. Из-за громоздкости было придумано сократить запись до 3 * 100 = 300. Фактически, запись «три умножить на сто» означает, что нужно взять сто троек и сложить между собой. Умножение прижилось, обрело общую популярность. Но мир не стоит на месте, и в средних веках возникла необходимость проводить многократное однотипное умножение.3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.
Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.
Свойства степени
Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.
1-е свойство.
Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.
2-е свойство.
3-е свойство.
Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.
4-е свойство.
Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.
Свойство работает только при делении, при вычитании не применяется!
5-е свойство.
6-е свойство.
Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.
7-е свойство.
Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.
8-е свойство.
9-е свойство.
Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.
Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.
10-е свойство.
Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.
11-е свойство.
Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.
12-е свойство.
Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.
Применение степеней и их свойств
Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.
Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.
Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.
Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.
Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.
Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.
С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.
Показательные уравнения и неравенства
Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками
.
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных
могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных
и различные степени
одинаковых переменных
, должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание
степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме
степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные
.
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат
, результат будет равен сумме или разнице этих чисел в четвёртой
степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице
показателей делимых чисел.
При делении степеней с одинаковым основанием их показатели вычитаются.
.
Так, y 3:y 2 = y 3-2 = y 1 . То есть, $\frac = y$.
И a n+1:a = a n+1-1 = a n . То есть $\frac = a^n$.3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Вычислить.
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями
. Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Как умножать степени
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
Умножение степеней с одинаковыми основаниями
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства
. Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение степеней с одинаковыми основаниями (формула )
1. Основные определения
Основные определения:
n
— показатель степени,
— n
-ая степень числа.
2. Формулировка теоремы 1
Теорема 1.
Для любого числа а
и любых натуральных n
и k
справедливо равенство:
По-иному: если а
– любое число; n
и k
натуральные числа, то:
Отсюда правило 1:
3. Разъясняющие задачи
Вывод:
частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а
и любых натуральных n
и k.
4. Доказательство теоремы 1
Дано число а
– любое; числа n
и k –
натуральные. Доказать:
Доказательство основано на определении степени.
5. Решение примеров с помощью теоремы 1
Пример 1:
Представьте в виде степени.
Для решения следующих примеров воспользуемся теоремой 1.
ж)
6. Обобщение теоремы 1
Здесь использовано обобщение:
7. Решение примеров с помощью обобщения теоремы 1
8. Решение различных задач с помощью теоремы 1
Пример 2:
Вычислите (можно использовать таблицу основных степеней).
а) (по таблице)
б)
Пример 3:
Запишите в виде степени с основанием 2.
а)
Пример 4:
Определите знак числа:
, а –
отрицательное, так как показатель степени при -13 нечетный.
Пример 5:
Замените (·) степенью числа с основанием r:
Имеем , то есть .
9. Подведение итогов
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
1. Школьный помощник (Источник).
1. Представьте в виде степени:
а) б) в) г) д)
3. Запишите в виде степени с основанием 2:
4. Определите знак числа:
а)
5. Замените (·) степенью числа с основанием r:
а) r 4 · (·) = r 15 ; б) (·) · r 5 = r 6
Умножение и деление степеней с одинаковыми показателями
На этом уроке мы изучим умножение степеней с одинаковыми показателями. Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Напоминание основных определений и теорем
Здесь a
— основание степени,
— n
-ая степень числа.
Теорема 1.
Для любого числа а
и любых натуральных n
иk
справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2.
Для любого числа а
и любых натуральных n
и k,
таких, что n
> k
справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Теорема 3.
Для любого числа а
и любых натуральных n
иk
справедливо равенство:
Все перечисленные теоремы были о степенях с одинаковыми основаниями
, на этом уроке будут рассмотрены степени с одинаковыми показателями
.
Примеры на умножение степеней с одинаковыми показателями
Рассмотрим следующие примеры:
Распишем выражения по определению степени.
Вывод:
из примеров можно заметить, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, то есть для любых а
и b
и любого натурального n.
Формулировка и доказательство теоремы 4
Для любых чисел а
и b
и любого натурального n
справедливо равенство:
Доказательство
теоремы 4.
По определению степени:
Итак, мы доказали, что .
Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.
Формулировка и доказательство теоремы 5
Сформулируем теорему для деления степеней с одинаковыми показателями.
Для любого числа а
и b ()
и любого натурального n
справедливо равенство:
Доказательство
теоремы 5.
Распишем и по определению степени:
Формулировка теорем словами
Итак, мы доказали, что .
Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Решение типичных задач с помощью теоремы 4
Пример 1:
Представить в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
Для решения следующего примера вспомним формулы:
Обобщение теоремы 4
Обобщение теоремы 4:
Решение примеров с помощью обобщенной теоремы 4
Продолжение решения типичных задач
Пример 2:
Запишите в виде степени произведения.
Пример 3:
Запишите в виде степени с показателем 2.
Примеры на вычисление
Пример 4:
Вычислить самым рациональным способом.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
2. Школьный помощник (Источник).
1. Представить в виде произведения степеней:
а) ; б) ; в) ; г) ;
2. Запишите в виде степени произведения:
3. Запишите в виде степени с показателем 2:
4. Вычислить самым рациональным способом.
Урок математики по теме «Умножение и деление степеней»
Разделы:
Математика
Педагогическая цель
:
различать свойства умножения и деления степеней с натуральным показателем; применять эти свойства в случае с одинаковыми основаниями;
уметь выполнять преобразования степеней с разными основаниями и уметь выполнять преобразования в комбинированных заданиях.
Задачи
:
Деятельностные единицы учения:
определение степени с натуральным показателем; компоненты степени; определение частного; сочетательный закон умножения.
I. Организация демонстрации овладение учащимися имеющимися знаниями. (шаг 1)
а) Актуализация знаний:
2) Сформулировать определение степени с натуральным показателем.
a n =a a a a … а (n раз)
b k =b b b b a… b (k раз) Обосновать ответ.
II. Организация самооценивания обучаемого степенью владения актуальным опытом.
(шаг 2)
Тест для самопроверки: (индивидуальная работа в двух вариантах.)
А1) Представьте произведение 7 7 7 7 x x x в виде степени:
А2) Представить в виде произведения степень (-3) 3 х 2
A3) Вычислите: -2 3 2 + 4 5 3
Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.
К тесту даю ключ для самопроверки. Критерии: зачёт – не зачёт.
III. Учебно-практическая задача (шаг 3) + шаг 4. (сформулируют свойства сами ученики)
В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.
На кластере появляется запись:
Формулируется тема урока. Умножение степеней.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждения: каким действием проверяется деление? а 5: а 3 = ? что а 2 а 3 = а 5
Возвращаюсь к схеме – кластер и дополняем запись – ..при делении вычитаем и дописываем тему урока. …и деление степеней.
IV. Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: а m а n = а m+n ; а m: а n = а m-n
V. Организация изучения нового материала. (шаг 5)
а) По учебнику: №403 (а, в, д) задания с разными формулировками
№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи.
б) При каком значении m справедливо равенство? а 16 а m = а 32 ; х h х 14 = х 28 ; х 8 (*) = х 14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а) Ловушки для учеников
: х 3 х n = х 3n ; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2 .
VI. Обобщение изученного, проведение диагностической работы (что побуждает учеников, а не учителя изучать данную тему)(шаг 6)
Диагностическая работа.
Тест
(ключи поместить на обратной стороне теста).
Варианты заданий: представьте в виде степени частное х 15: х 3 ; представьте в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; при каком m справедливо равенство а 16 а m = а 32 ; найдите значение выражения h 0: h 2 при h =0,2; вычислите значение выражения (5 2 5 0) : 5 2 .
Итог урока. Рефлексия.
Делю класс на две группы.
Найдите аргументы I группа: в пользу знания свойств степени, а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств. Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
VII. Домашнее задание.
Историческая справка. Какие числа называют числами Ферма.
П.19. №403, №408, №417
Используемая литература:
Свойства степеней, формулировки, доказательства, примеры.
После того как определена степень числа, логично поговорить про свойства степени
. В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.
Навигация по странице.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел
, можно получить и обосновать следующие свойства степени с натуральным показателем
:
- если a>0 , то a n >0 для любого натурального n ;
- если a=0 , то a n =0 ;
- если a 2·m >0 , если a 2·m−1 n ;
- если m и n такие натуральные числа, что m>n , то при 0m n , а при a>0 справедливо неравенство a m >a n .
- a m ·a n =a m+n ;
- a m:a n =a m−n ;
- (a·b) n =a n ·b n ;
- (a:b) n =a n:b n ;
- (a m) n =a m·n ;
- если n – целое положительное число, a и b – положительные числа, причем an n и a −n >b −n ;
- если m и n – целые числа, причем m>n , то при 0m n , а при a>1 выполняется неравенство a m >a n .
Сразу заметим, что все записанные равенства являются тождественными
при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений
часто применяется в виде a m+n =a m ·a n .
Теперь рассмотрим каждое из них подробно.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени
: для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.
Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .
Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .
Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями
: для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .
Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из связи умножения с делением следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.
Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .
Теперь рассмотрим свойство степени произведения
: натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .
Приведем пример: .
Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующее свойство представляет собой свойство частного в натуральной степени
: частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .
Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .
Запишем это свойство на примере конкретных чисел: .
Теперь озвучим свойство возведения степени в степень
: для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .
Например, (5 2) 3 =5 2·3 =5 6 .
Доказательством свойства степени в степени является следующая цепочка равенств: .
Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Для начала обоснуем, что a n >0 при любом a>0 .
Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .
Переходим к отрицательным основаниям степени.
Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По правилу умножения отрицательных чисел каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.
Докажем, что при m>n и 0m n . Для этого запишем разность a m −a n и сравним ее с нулем. Записанная разность после вынесения a n за скобки примет вид a n ·(a m−n −1) . Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .
Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .
Свойства степеней с целыми показателями
Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.
Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.
Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями
:
При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.
Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .
Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .
Аналогично .
И .
По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Запишем и преобразуем разность левой и правой частей этого неравенства: . Так как по условию an n , следовательно, b n −a n >0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
- свойство произведения степеней с одинаковыми основаниями при a>0 , а если и , то при a≥0 ;
- свойство частного степеней с одинаковыми основаниями при a>0 ;
- свойство произведения в дробной степени при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
- свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
- свойство степени в степени при a>0 , а если и , то при a≥0 ;
- свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .
- a p ·a q =a p+q ;
- a p:a q =a p−q ;
- (a·b) p =a p ·b p ;
- (a:b) p =a p:b p ;
- (a p) q =a p·q ;
- для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
- для иррациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .
Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a0 справедливо неравенство a p p , а при p p >b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .
Аналогично, при m m >b m , откуда , то есть, и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 , а при a>1 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .
Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями
:
Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.
- Алгебра – 10 класс. Тригонометрические уравнения
Урок и презентация на тему: «Решение простейших тригонометрических уравнений»
Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы […] - Открыт конкурс на позицию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»:
Обязанности: продажа мобильных телефонов и аксессуаров для мобильной связи сервисное обслуживание абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС консультирование […] - Параллелепипед формулы
Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.
Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.
Любой параллелепипед характеризуется 3 […] - Принять закон о Родовых поместьях
Принять федеральный закон о безвозмездном выделении каждому желающему гражданину Российской Федерации или семье граждан участка земли для обустройства на нем Родового Поместья на следующих условиях: 1. Участок выделяется для […] - Общество защиты прав потребителя астана
Для того, что бы получить pin-код для доступа к данному документу на нашем сайте, отправьте sms-сообщение с текстом zan на номер
Абоненты GSM-операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […] - ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА БРЯНСКОЙ ОБЛАСТИ
Квитанция об оплате госпошлины(Скачать-12,2 kb)
Заявления на регистрацию для физ.лиц(Скачать-12 kb)
Заявления на регистрацию для юр.лиц(Скачать-11,4 kb)
1. При регистрации новой машины:
1.заявление 2.паспорт […] - ПРАВОПИСАНИЕ Н И НН В РАЗНЫХ ЧАСТЯХ РЕЧИ
С.Г.ЗЕЛИНСКАЯ
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Теоретическая зарядка
1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […] - Пивоев В.М. Философия и методология науки: учебное пособие для магистров и аспирантов
Петрозаводск: Изд-во ПетрГУ, 2013. ― 320 с.ISBN 978-5-821-1647-0
PDF 3 mb
Учебное пособие предназначено для студентов старших курсов, магистров и аспирантов социального и […]
Правило деления степеней. При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:
Слайд 11 из презентации «Деление и умножение степеней»
к урокам алгебры на тему «Степень»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке алгебры, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Деление и умножение степеней.ppt» можно в zip-архиве размером 1313 КБ.
«Деление и умножение степеней» — a2 a3 = a2+3 = a5. a3 = a · a · a. Найдем произведение a2 и a3. 100. 2+3. 5 раз. 64 = 144 = 1 0000 =. Умножение и деление степеней. 3 раза. a2 a3 =.
«Степени двойки» — 1024+. Правила перевода из одной системы счисления в другую. Гусельникова Е.В. Школа №130. Содержание. Таблица степеней двойки. Переведём число 1998 из десятичной в двоичную систему. Кислых В.Н. 11Э Зинько К.О. 11Э. Преподаватель: Выполнили: Рассмотрим схему преобразования на примере.
«Степень с отрицательным показателем» — Степень с отрицательным показателем. 5 12?3 (27?3). -2. -1. Вычислите: -3.
«Степень с рациональным показателем» — по теме: «Степень с рациональным показателем». Цели урока: I. Организационная часть. Проверка домашнего задания 1.Математический диктант 2. Взаимопроверка III.Самостоятельная работа IV. Обобщающий урок. Ход урока. Подготовка к контрольной работе V. Подведение итогов урока VI. II.
«Степень с целым показателем» — Представьте выражение в виде степени. X-12. Расположите в порядке убывания. Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен. Вычислите. Упростите.
«Свойства степени» — Обобщение знаний и умений по применению свойств степени с натуральным показателем. Вычислительная пауза. Свойства степени с натуральным показателем. Проверь себя! Применение знаний для решения различных по сложности задач. Тест. Физминутка. Развитие настойчивости, мыслительной активности и творческой деятельности.
Правило деление степеней
1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):
(abc…) n = a n b n c n …
Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3
Практически более важно обратное преобразование:
a n b n c n … = (abc…) n
т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.
Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 =[(a +b)(a 2 – ab +b 2)] 2 =(a 3 +b 3) 2
2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:
Пример 5. Пример 6.
Обратное преобразование:. Пример 7.. Пример 8..
3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
Пример 9.2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого
Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.
5. При возведении степени в степень показатели степеней перемножаются:
Пример 13. (2 3) 2 =2 6 =64. Пример 14.
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками
.
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных
могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных
и различные степени
одинаковых переменных
, должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание
степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме
степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные
.
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат
, результат будет равен сумме или разнице этих чисел в четвёртой
степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Алгебра – 7 класс.n$.
mathematics-tests.com
Степени и корни
Операции со степенями и корнями. Степень с отрицательным
,
нулевым и дробным
показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m
· a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели
вычитаются
.
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b
) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² =
2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями.
Во всех нижеприведенных формулах символ означает арифметический корень
(подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень
подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени.
До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным
, нулевым
и дробным
показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем.
Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m
: a n
= a m — n
может быть использована не только при m
, большем, чем n
, но и при m
, меньшем, чем n
.
П р и м е р. a
4: a
7 = a
4 — 7 = a
— 3 .
Если мы хотим, чтобы формула a m
: a n
= a m
— n
была справедлива при m = n
, нам необходимо определение нулевой степени.
Степень с нулевым показателем.
Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (–
5) 0 = 1, (–
3 / 5) 0 = 1.
Степень с дробным показателем.
Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла.
Есть несколько таких выражений.
где a
≠ 0 , не существует.
В самом деле, если предположить, что x
– некоторое число, то в соответствии с определением операции деления имеем: a
= 0· x
, т.e. a
= 0, что противоречит условию: a
≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x
, то согласно определению операции деления имеем: 0 = 0 · x
. Но это равенство имеет место при любом числе x
, что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x
= 0 –
это значение не удовлетворяет данному уравнению
2) при x
> 0 получаем: x / x
= 1, т.e. 1 = 1, откуда следует,
что x
– любое число; но принимая во внимание, что в
нашем случае x
> 0 , ответом является x
> 0 ;
- Правила техники безопасности при работе утюгом
Правила техники безопасности при работе утюгом. 1.Перед включением утюга в электросеть нужно проверить изоляцию шнура и положение утюга на подставке. 2.Включение и […] - Проблемы водного налога
Состояние, анализ и проблемы совершенствования водного налога
При заборе воды сверх установленных квартальных (годовых) лимитов водопользования налоговые ставки в части такого превышения […] - как составить приказ о переходе с 223фз на 44 фз
Сергей Антонов 30 Ответ написан год назад
Профессор 455 Ответ написан год назад
Например: приказ об отмене применения положения о закупках.
Оценка ответа: 0
Добавить […] - Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если « a » и « b » положительные числа, то разделить число « a » на число « […] - Разрешения D1, 960Н, 720Р, 960Р, 1080Р
Системы видеонаблюдения получают все большее распространение по всему миру. Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […] - Конституционное право Российской Федерации. Баглай М.В.
6-е изд., изм. и доп. — М.: Норма, 200 7 . — 7 84 с.
Настоящий учебник, представляющий собой шестое, измененное и дополненное, издание, написан известным […]
Экспоненты умножения и деления | Правила | Примеры
Показатели используются для выражения многих чисел в одном выражении. Когда два экспоненциальных члена с одинаковым основанием умножаются, их степени складываются, а основание остается прежним. Однако, когда два экспоненциальных члена с одинаковым основанием делятся, их степени вычитаются.
Умножение экспоненциальных членов
Умножение показателей с одной и той же базой и с разными базами включает в себя применение идентичностей.Мы обобщаем свойства показателей и приходим к тождествам.
Умножение экспонент с одинаковым основанием
Рассмотрим m × a n , где «a» — это общее основание, а «m» и «n» — степени. Когда мы умножаем два экспоненциальных члена на одно и то же основание, получаем: 2 2 × 2 3 = (2 × 2) × (2 × 2 × 2) = 2 5 . Мы получим тот же результат, если сложим экспоненты. 2 2 × 2 3 = 2 (2 + 3) = 2 5 .{\ left \ {{{p_1} + {p_2} + {p_3} + …} \ right \}}} \)
Умножение экспонент с разным основанием и одинаковой степенью
Рассмотрим умножение показателей с разными основаниями и одинаковыми показателями, как в случае с m × b m . Например, возьмем: 11 4 × 3 4
11 4 = 11 × 11 × 11 × 11 и 3 4 = 3 × 3 × 3 × 3
11 4 × 3 4 = (11 × 11 × 11 × 11) × (3 × 3 × 3 × 3)
= 11 × 3 × 11 × 3 × 11 × 3 × 11 × 3
= 33 × 33 × 33 × 33 = 33 4 .Это также можно записать и решить как: 11 4 × 3 4 = (11 × 3) 4 = 33 4 . Следовательно, когда мы умножаем показатели с разным основанием и одним и тем же показателем, мы применяем тождество:
Экспоненциальные члены с делением
Показатели с одной и той же базой
Рассмотрим m ÷ a n , где «a» — общее основание, а «m» и «n» — степени. Теперь разделим два экспоненциальных члена с одинаковым основанием: 3 7 ÷ 3 4 .
3 7 = 3 × 3 × 3 × 3 × 3 × 3 × 3 и 3 4 = 3 × 3 × 3 × 3
3 7 ÷ 3 4 = \ (\ dfrac {3 × 3 × 3 × 3 × 3 × 3 × 3} {3 × 3 × 3 × 3} \) = 3 3
Это также можно записать и решить как: 3 7 ÷ 3 4 = 3 (7-4) = 3 3 . Обратите внимание, что при делении экспоненциальных членов, если основания совпадают, мы находим разницу показателей. Следовательно, здесь используется идентификатор:
Деление экспонент с разным основанием и одинаковым показателем
Рассмотрим m ÷ b m , где показатели степени имеют разные основания и одинаковые показатели.Например, решим: 12 3 ÷ 3 3 .
12 3 = 12 × 12 × 12 и 3 3 = 3 × 3 × 3
12 3 ÷ 3 3 = (12 ÷ 3) 3 = 4 3
Это можно сделать как 12 3 ÷ 3 3 = (12 ÷ 3) 3 = 4 3 . Следовательно, при делении показателей с разным основанием и одинаковым показателем мы применяем тождество:
Как умножить и разделить дробные показатели?
Прежде чем понять, как умножать или делить дробные показатели с одинаковым основанием, давайте рассмотрим несколько примеров дробных показателей с одинаковым основанием.{(\ frac {3} {2} — \ frac {1} {2})} \) = 3 1 = 3. Здесь мы применили тождество a m ÷ a n = a млн
Как умножить и разделить экспоненты с переменными?
Идентификаторы, которые используются в числах, также используются в показателях степени с переменными. Давайте вспомним их, а затем воспользуемся ими в следующих примерах:
- a м × a n = a m + n
- a м × b м = (a × b) м
- a m ÷ a n = a m-n
- a м ÷ b м = (a ÷ b) м
Переменная как база
Давайте посмотрим, как использовать тождества, когда база является переменной.Например, решите: y 2 × (2y) 3
Применим тождество: a m × b m = (a × b) m , y 2 × (2y) 3 = y 2 × 2 3 × y 3 = 2 3 × y (2 + 3) = 8y 5
Переменная как экспонента
Давайте посмотрим, как использовать тождества, когда показатель степени является переменной.Например, решите: 5 (2x -1) ÷ 5 (x + 1)
Применим тождество: a m ÷ a n = a mn , получаем 5 (2x -1 — x — 1) = 5 (x -2)
Связанные темы
переменных с показателями — как их умножить и разделить
Как их умножить и разделить
Что такое переменная с экспонентой?
A Переменная — это символ числа, которое мы еще не знаем.Обычно это буква типа x или y.
Показатель степени (например, 2 в x 2 ) указывает, сколько раз
использовать переменную при умножении.
Пример:
y 2 = yy
( yy означает y , умноженное на y , потому что в алгебре поставить две буквы рядом друг с другом означает их умножить)
Аналогично z 3 = zzz и x 5 = xxxxx
Показатели 1 и 0
Показатель 1
Когда показатель степени равен 1, у нас есть только сама переменная (например, x 1 = x )
Обычно мы не пишем «1», но иногда полезно помнить, что x — это также x 1
Показатель 0
Когда показатель степени равен 0, мы не умножаем ни на что, и ответ будет просто «1»
(например, y 0 = 1 )
Умножение переменных на экспоненты
Итак, как нам умножить это:
(г 2 ) (г 3 )
Мы знаем, что y 2 = yy и y 3 = yyy , поэтому давайте выпишем все умножения:
y 2 y 3 = yy yyy
Это 5 y, умноженные вместе, поэтому новый показатель степени должен быть 5:
y 2 y 3 = y 5
Но почему считают «у», когда показатели уже говорят нам, сколько?
Показатели говорят нам, что есть два «y», умноженные на 3 «y», в сумме получается 5 «y»:
y 2 y 3 = y 2 + 3 = y 5
Итак, самый простой способ — это всего лишь сложить экспоненты !
(Примечание: это один из законов экспонент)
Смешанные переменные
Когда у нас есть набор переменных, просто сложите показатели для каждой, как это (нажмите кнопку воспроизведения):
(Помните: переменная без показателя степени действительно имеет показатель степени 1, например: y равно y 1 )
с константами
Часто встречаются константы (числа вроде 3, 2.9, ½ и т. Д.).
Не бойтесь! Просто умножьте константы по отдельности и поместите результат в ответ:
(Примечание: «·» означает умножение, которое мы используем, когда «×» можно спутать с буквой «x»)
Вот более сложный пример с константами и показателями:
Отрицательные экспоненты
Отрицательные показатели среднего деления!
| x -1 = 1 x | x -2 = 1 x 2 | x -3 = 1 x 3 | и др… |
Ознакомьтесь с этой идеей, она очень важна и полезна!
Разделение
Итак, как нам это сделать? y 3 y 2
Выпишем все умножения: ггг гг
Теперь удалите все совпадающие «y», которые имеют значение
как сверху, так и снизу (потому что y y = 1)
И у нас остается: y
Таким образом, 3 «y» над линией уменьшаются на 2 «y» ниже линии, оставляя только 1 «y»:
y 3 y 2 = yyy yy = y 3-2 = y 1 = y
ИЛИ, мы могли бы сделать это так:
y 3 y 2 = y 3 y -2 = y 3-2 = y 1 = y
Итак… просто вычтите показателей переменных, на которые мы делим!
Вот более крупная демонстрация, включающая несколько переменных:
Буквы «z» полностью исключены! (Что имеет смысл, потому что z 2 / z 2 = 1)
Чтобы увидеть, что происходит, запишите все умножения, затем «вычеркните» верхние и нижние переменные:
x 3 y z 2 x y 2 z 2
знак равно
ххх у zz х уу zz
знак равно
x xx y zz x y y zz
знак равно
х х у
знак равно
x 2 y
Но еще раз, почему подсчитывают переменных, когда показатель степени говорит вам, сколько ?
Как только вы почувствуете себя уверенно, вы сможете сделать все довольно быстро «на месте», например:
Свойства умножения и деления экспонент — концепция
Существуют разные правила, которым нужно следовать при умножении показателей степени и при делении показателей степени.Если мы умножаем одинаковые основания, мы просто складываем экспоненты. Если мы делим, мы просто вычитаем экспоненты. Если показатель степени находится за пределами круглых скобок, он распространяется на внутренние члены. Важно понимать правила умножения показателей на , чтобы мы могли упростить выражения с показателями.
Когда вы перейдете к главе об экспонентах, ваш учитель будет задавать много-много домашних заданий.В основном потому, что они, вероятно, будут короткими. Что ж, вы должны быть очень осторожны, потому что часто, когда я назначаю много задач экспонента, студенты делают большинство из них неправильно, потому что они пытаются ускориться. Пожалуйста, будьте осторожны, когда решаете эти задачи с показателями, есть много мест, где можно сделать ошибки. Одно из мест, где студенты делают ошибки, — это запоминать все эти свойства показателей, которые мы рассмотрим через секунду, а затем они запутались в своем мозгу. Я собираюсь пройтись по ним, но попрошу вас не запоминать их, если вы не думаете, что вы как студент уровня A.Ничего страшного, если вы хорошо запоминаете и похожи на ученика с отличием, вы также можете попробовать запомнить их. Но будьте очень осторожны: многие ошибки случаются, когда учащиеся просто действуют неосторожно и делают глупые ошибки, потому что им казалось, что они запомнили свойства.
И еще одна вещь, прежде чем мы перейдем к этому, это просто свойства умножения и деления с показателями, есть другие свойства, связанные с показателями, которые равны нулю, и отрицательными показателями, мы вернемся к ним в другом видео.Но пока давайте просто проверим это, я собираюсь сделать это как с помощью переменных, так и с помощью чисел, вы, ребята, можете понять, что я имею в виду. x к n, к степени m равно x к n, умноженному на m. Вот что это значит, если вы используете числа, 3 в квадрате в четвертой степени будет равно 3 в восьмой степени. Вот как это будет выглядеть с точки зрения чисел, и мы поймем, почему именно так, когда начнем выполнять все больше и больше практических задач.
Вот еще одно свойство: если у меня 3 умножить на 2 в четвертой степени, как xy для m, это будет равно x, умноженному на m, умноженному на y, на m.Таким образом, это будет от 3 до четвертого умножить на 2 до четвертого, это почти как эта маленькая экспонента распределяется по каждой из этих частей в основе, пока они находятся в скобках. Вот еще одно свойство: вы устали пытаться их запоминать, не беспокойтесь с запоминанием. Вы можете поработать над этим, и я покажу вам это, когда мы будем решать проблемы. x к n умножить на x к m равно x к n плюс m. Что это обозначает? Это означает, что если у вас одна и та же база, например, 3 к 1 умножить на 3 во второй степени, посмотрите, как все они являются одной и той же базой, но с разными показателями, которые можно упростить, добавив этих парней 1 плюс 2.
Опять же, если вы не умеете запоминать, не запоминайте их, мы пройдемся по ним и сделаем их более понятными всего за секунду. Затем один x к n, деленный на x к m, равен разности показателей. Итак, если бы у меня было 3 в четвертой степени поверх 3 в квадрате, это было бы то же самое, что и 3 в 4, убрав 2 или 3 в квадрате.
И последнее, но не менее важное: если у вас есть дробь, возведенная в экспоненту, это похоже на то, как эта экспонента распределяется по обеим частям этой базы.Как 3 половинки до четвертого — это то же самое, что 3 до четвертого, как 2 до четвертого. Так что я просто скажу это в последний раз, когда я знаю, что я уже говорил это много раз, если вы не тот, чей хороший запоминатель даже не пытается запоминать их, потому что вы получите они перемешались в твоей голове. Всегда лучше записать каждое число и получить его правильно, чем использовать простой метод для запоминания, но вы ошибаетесь.
Умножение и деление на 10 — Полный курс арифметики
Примеры.
| 265 ÷ 10 | = 26 . 5 | Начиная с 265 справа, отделите одной десятичной цифрой . |
| 265 ÷ 100 | = 2 . 65 | Разделите на две десятичные цифры . |
| 265 ÷ 1000 | = . 265 | Разделите тремя десятичными цифрами . |
Когда мы делим целое число на степень 10,
В ответе будет столько десятичных цифр, сколько нулей.
8 ÷ 100 = . 08
Два нуля. Две десятичные цифры.
Снова, как и в Уроке 2, рассмотрим этот массив:
По мере продвижения вверх по списку — сдвигая цифры на одну позицию вправо — число было , разделенное на на 10, потому что каждое место справа стоит в 10 раз меньше.(При перемещении от 26 , 58 к 2 , 658, мы переходим от 2 десятков к 2 единиц .) Однако это выглядит так, как если бы десятичная точка сдвинулась на одну позицию влево, или, с целое число 26580, что 0 было снято.
По мере продвижения по списку — по мере продвижения цифр влево через
десятичная точка — каждое число умножено на 10.
Итак, мы можем легко умножить или разделить на степень 10 благодаря нашей системе
позиционной нумерации.
Каждое место принадлежит следующей степени 10.
На этом этапе, пожалуйста, «переверните» страницу и сделайте
Проблемы.
или
Перейдите к разделу 2: Значение процентов
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Умножение и деление экспонентов — математика для старших классов
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Умножение и деление десятичных знаков на степень 10
При умножении или делении чисел на степень 10 (например, 10, 100, 1000 и т. Д.) Цифры остаются неизменными, только их положение относительно десятичной точки (или значение их места) и количество нулей меняется.
Распространенным ярлыком при умножении и делении на степень 10 является «перемещение десятичной точки». Однако по мере того, как ваши дети узнают больше о важной фундаментальной концепции ценности места, убедитесь, что они понимают, что это значение мест, в которых расположены числа, увеличивается или уменьшается.
Полномочия 10
Степень 10 используется для отображения многократного умножения или деления на 10. Они часто используются для отображения очень больших или очень маленьких чисел.Их можно записать в экспонентах. Здесь вы найдете больше информации об экспонентах. В таблице ниже показано их использование.
Степень 10 Диаграмма
| Номер | 10 000 | 1 000 | 100 | 10 |
|---|---|---|---|---|
| Разговорный | Десять тысяч | Одна тысяча | Сто | Тен |
| Повторное умножение | 10 х (10 х 10 х 10) | (10 х 10 х 10) | 10 х 10 | 10 х 1 |
| Мощность | 4 | 3 | 2 | 1 |
| Экспоненциальная форма | 10 4 | 10 3 | 10 2 | 10 1 |
| Разговорный | 10 в 4-й степени * | 10 в 3-й степени | 10 во 2-й степени | 10 в 1-й степени |
* Также обозначается от 10 до 4 или степени 4.
Показатели и степени 10 можно использовать для аккуратного и аккуратного представления большого числа с большим количеством нулей. Это показано в таблице ниже, которая является продолжением предыдущей.
| Номер | 100 000 000 000 | 10 000 000 | 1 000 000 | 100 000 |
|---|---|---|---|---|
| Разговорный | Сто миллионов | Десять миллионов | Один миллион | Сто тысяч |
| Повторное умножение | 10 х 10 х (10 х 10 х 10) х (10 х 10 х 10) | 10 х (10 х 10 х 10) х (10 х 10 х 10) | (10 х 10 х 10) х (10 х 10 х 10) | (10 х 10) х (10 х 10 х 10) |
| Мощность | 8 | 7 | 6 | 5 |
| Экспоненциальная форма | 10 8 | 10 7 | 10 6 | 10 5 |
| Разговорный | 10 в восьмой степени | 10 в 7-й степени | 10 в шестой степени | 10 в пятой степени |
Умножение целых чисел на степени 10
Мы уже видели, что при умножении на 10 значение каждой цифры увеличивается в 10 раз и, следовательно, перемещается на одну позицию влево.Умножение на 100 увеличивает значения цифр в 100 раз, перемещая их на две позиции влево, а умножение на 1000 увеличивает их значение в 1000 раз и перемещает их на три позиции влево. Глядя на приведенную выше таблицу «Степени 10», вы можете помочь вашим детям увидеть, как появляется шаблон, в котором цифры перемещают количество разрядов влево, соответствующее степени.
Избегайте или, по крайней мере, будьте осторожны при использовании метода «сложения одинакового количества нулей», так как это может привести к проблемам при умножении десятичных чисел. E.грамм. 6,29 x 100 не равно 6,2900
Умножение десятичных знаков на степень 10
Существуют аналогичные шаблоны при умножении целых и десятичных чисел на степень 10. Умножение десятичной дроби на 10 увеличивает значение каждой цифры на 10. Умножение десятичной дроби на степень 10 увеличивает значение каждой цифры на количество единиц. раз, что эквивалентно этой степени 10. Когда значение цифры изменяется, эта цифра перемещается в соответствующее место. Тот же самый эффект может быть реализован путем «перемещения десятичной точки», но, как упоминалось ранее, лучше видеть, как изменение значения разряда в цифре помещается как представление умножения.
Примеры выше включены в качестве первых трех примеров в таблицу ниже и записаны в экспоненциальной форме
| 2,43 x 10 1 = 24,3 | 1,76 x 10 3 = 1,760 |
| 2,43 x 10 2 = 243 | 0,134 x 10 5 = 13 400 |
| 2,43 x 10 3 = 2,430 | 0,246 x 10 6 = 246 000 |
| 0,12 x 10 2 = 12 | 0.246 x 10 5 = 24 600 |
| 0,134 x 10 4 = 1,340 | 0,246 x 10 4 = 2,430 |
| 15,67 x 10 6 = 15,670,000 | 0,07 x 10 3 = 70 |
| 1,567 x 10 8 = 156,700,000 | 0,07 x 10 6 = 70 000 |
Просмотрите приведенные выше примеры, демонстрирующие умножение на степень 10, и обсудите взаимосвязь между показателем степени и изменением значения цифр и относительным положением десятичной точки.Постарайтесь выявить какие-либо закономерности.
Деление по 10 степеням
Деление целых и десятичных чисел на степень 10 имеет противоположный эффект умножению. Значение цифр уменьшается, а не увеличивается, и цифры перемещаются вправо, а не влево на диаграмме разряда.
Примеры выше включены в качестве первых трех примеров в таблицу ниже и записаны в экспоненциальной форме
| 745 ÷ 10 1 = 74.5 | 2,430 ÷ 10 2 = 2,43 |
| 745 ÷ 10 2 = 7,45 | 2,430 ÷ 10 4 = 0,243 |
| 745 ÷ 10 3 = 0,745 | 13,400 ÷ 10 5 = 0,134 |
| 133 ÷ 10 3 = 0,133 | 134,000 ÷ 10 6 = 0,134 |
| 1,2300 ÷ 10 5 = 0,123 | 1,340 ÷ 10 4 = 0,134 |
Просмотрите приведенные выше примеры, показывающие деление на степень 10, и обсудите взаимосвязь между показателем степени и изменением значения цифр и относительным положением десятичной точки.







