Урок 3. квадратные уравнения, неравенства и их системы — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №3. Квадратные уравнения, неравенства и их системы.

Перечень вопросов, рассматриваемых в теме:

• систематизация знаний учащихся о решении квадратных уравнений и неравенств;
• установление зависимости количества и расположения корней квадратного уравнения от его коэффициентов и значения дискриминанта;
• способы решения квадратных уравнений и неравенств с параметрами.

Глоссарий по теме:

Параметр — (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода.

Основная литература:

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М.: Просвещение, 2017.

Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.

Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.

Теоретический материал для самостоятельного изучения

В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.

Квадратные уравнения.

На уроке будем рассматривать различные способы решения квадратных уравнений.

Как определить, сколько корней имеет уравнение, подскажет дискриминант.

Дискриминант – это число, которое находим по формуле

Если D <0 корней нет, если D = 0 один корень, если D> 0 два корня.

Если дискриминант D> 0 , корни можно найти по формуле:

Если D = 0 , то

Рассмотрите пример. Решить уравнение

Шаг 1. Выпишем коэффициенты a, b, c. 

Шаг 2. Найдем дискриминант. D=16.

Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:

Заметим:

1.Перед решением квадратного уравнения привести его к стандартному виду.

2. Избавьтесь от минуса перед . Для этого надо умножить всё уравнение на -1.

3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.

4. Проверяйте корни по теореме Виета. Это просто, когда a=1.

Рассмотрите другие формулы:

, где второй коэффициент b=2k – четное число.

Приведенное квадратное уравнение , старший коэффициент равен a= 1, проще решать по теореме Виета.

Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.

Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.

Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.

Рассмотрим несколько примеров:

Пример 1.

Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.

Пример 2.

Применяем метод сложения. Выполнив сложение, получаем уравнение , далее x= ±5. Находим у= ±2. Составляем возможные пары чисел.

Записываем ответ: (5; 2), (5; -2), (-5; 2), (- 5; -2).

Пример 3. Иногда проще ввести новые переменные.

Пусть xy=u, x+y=v. Тогда систему можно записать в более простом виде:

Решение смотри в примере 1.

Часть 2. Квадратные неравенства.

Теперь, когда мы разобрали решение квадратных уравнений, переходим к решению квадратных неравенств
ax^2+ bx + c больше или меньше нуля.  

Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».

Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.

Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.

Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.

Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:

если а>0 + — +, если а <0 — + -. Или путём подстановки произвольного значения квадратный трехчлен.

Рассмотрим несколько примеров:

D=0 все точки параболы выше оси и только одна х=2 на оси ОХ -нет решений.

D<0 коэффициент а=2>0 ветви вверх. Парабола выше оси, все значения положительны, значит х- любое число. Неравенство не имеет решений.

Далее рассмотрим схему решения системы неравенств.

Алгоритм решения системы неравенств.

1.Решить первое неравенство системы, изобразить его графически на оси x.

2.Решить второе неравенство системы, изобразить его графически на оси x.

3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Часть 3

Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Первый шаг в решении — найти особое значение параметра.

Второй шаг – определить допустимые значения.

Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.

Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.

Рассмотрите примеры решения неравенства с параметром.

Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.

Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.

Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.

Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.

Задания тренировочного модуля с разбором.

Пример 1.

При каких значениях параметра, а квадратное уравнение

имеет только один корень?

Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.

Пример 2.

Определите, на каком интервале значения квадратного трехчлена отрицательны?

Решаем неравенство: . Находим дискриминант квадратного трехчлена D= 1-4∙2∙ (-1) =1+8=9. Находим корни . Расставляем точки на числовой прямой.

Старший коэффициент а=2 ветви параболы вверх. Знаки чередуются + — +. Записываем ответ: — 0,5< х <1.

от чего зависит вид графика функции

Функция вида y = a*x² + b*x + c, где a, b, c – некоторые вещественные числа, причем а отлично от нуля, а x и y – переменные, называется квадратичной функцией. Графиком квадратичной функции y = a*x² + b*x + c является линия, называемая в математике параболой. Общий вид параболы представлен на рисунке ниже.

График квадратичной функции

Исследуем расположение графика квадратичной функции, в зависимости от формы и вида квадратного трехчлена. Первым критерием, влияющим на общий вид графика квадратичной функции, является знак при старшем коэффициенте.

Если при старшем коэффициенте в квадратном трехчлене стоит знак «плюс», то парабола будет иметь ветви направленные вверх. Если при старшем коэффициенте в квадратном трехчлене стоит знак «минус», то парабола будет иметь ветви направленные вниз.

Следующим критерием является значение дискриминанта квадратного уравнения.

Формула корней квадратного уравнения a*x² + b*x+ c = 0.

x = (-b ± √D)/(2*a), где D = b² — 4 *a*c.

В формуле корней квадратного уравнения выражение D (b² — 4*a*c) называется дискриминантом квадратного уравнения a*x² + b*x + c = 0. Такое название пришло из латинского языка, в переводе означает «различитель». В зависимости от того, какое значение имеет дискриминант, квадратное уравнение будет иметь два или один корень либо не иметь корней.

Если дискриминант больше нуля, то квадратное уравнение имеет два корня: (x = (-b ± √D)/(2*a)). Если дискриминант равен нулю, то квадратное уравнение имеет один корень: (x = (-b/(2*a)). Если дискриминант отрицателен, то квадратное уравнение не имеет корней.

Корнем квадратного уравнения a*x² + b*x + c = 0 называют любое значение переменной х, такое, что квадратный трехчлен a*x² + b*x + c обращается в нуль. Обращение в нуль значение функции равносильно тому, что график функции будет в этой точке пересекать ось Ох.

Следовательно, в зависимости от, того какое будет значение дискриминанта, вершина параболы будет расположена относительно оси координат одним из следующих трех способов: ниже оси Ох, на оси Ох, выше оси Ох. На следующем рисунке показаны основные расположения графика квадратичной функции, в зависимости от перечисленных выше двух критериев.

Нужна помощь в учебе?

Предыдущая тема: Квадратичная функция: ее график и свойства
Следующая тема:&nbsp&nbsp&nbspПостроение графика квадратичной функций: алгоритм и примеры

Квадратное уравнение. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.

Квадратным уравнением называется уравнение вида:

                 ,

где
x — переменная,
a,b,c — постоянные (числовые) коэффициенты.

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта

Формула дискриминанта:

.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

• D>0 — уравнение имеет 2 различных вещественных корня
• D=0 — уравнение имеет 2 совпадающих вещественных корня
• D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)

В общем случае корни уравнения равны:

                 .

Очевидно, в случае с нулевым дискриминантом, оба корня равны

                 .

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

В таком случае корни уравнения вычисляются по формуле:

Теорема Виета.

Приведенным квадратным уравнением называется уравнение вида

                ,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

                 .

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х²

KotlinAsFirst2016/chapter02.adoc at master · Kotlin-Polytech/KotlinAsFirst2016 · GitHub

KotlinAsFirst2016/chapter02.adoc at master · Kotlin-Polytech/KotlinAsFirst2016 · GitHub

This repository has been archived by the owner. It is now read-only.

Permalink

Cannot retrieve contributors at this time

До этого мы рассматривали ситуации, когда вычисление результата функций происходило без рассмотрения вариантов.
Это возможный, но сравнительно редкий случай в программировании.
Существует очень много задач, где приходится рассматривать различные варианты,
и для этой цели программисты придумали ветвления.

Максимум из двух

В качестве простого примера рассмотрим функцию, результат которой равен наибольшему из её параметров.

fun max(m: Int, n: Int) = if (m > n) m else n

Здесь if..else — оператор или конструкция ветвления, переводится с английского как если..иначе.
После ключевого слова if в скобках следует условие ветвления m > n.
Если условие истинно, в качестве результата используется выражение сразу за условием ветвления, в данном случае m.
Если же условие ложно, используется выражение за ключевым словом else, в данном случае n.
Конструкцию можно прочитать по-русски как «Если m > n, (то) m, иначе n».

Число корней квадратного уравнения

Рассмотрим более сложный пример.
Следующая функция рассчитывает число корней квадратного уравнения ax² + bx + c = 0.
Напомним, что квадратное уравнение имеет два корня, если его дискриминант больше 0,
один корень, если дискриминант равен 0, и ноль корней в противном случае.
Для реализации этого алгоритма следует вначале рассчитать дискриминант,
а затем применить конструкцию if..else.
Функция на Котлине может быть записана так:

fun quadraticRootNumber(a: Double, b: Double, c: Double): Int {
    // Применяем готовую функцию из первой части
    val d = discriminant(a, b, c)
    // Для сравнения на равенство применяем ==
    return if (d > 0.0) 2 else if (d == 0.0) 1 else 0
}

Здесь мы применили запись функции в виде блока и использовали промежуточную переменную d.
Последняя строчка функции читается как «вернуть: если d > 0.0, (то) 2, иначе, если d = 0.0, (то) 1, иначе 0».
Обратите внимание на возможность так называемой «каскадной» записи конструкции if. .else
в виде if..else if..else if..else if..else (с неограниченным количеством промежуточных элементов).

Операции сравнения

В обоих примерах в условиях мы использовали операции сравнения. Таких операций имеется восемь:

• > строго больше;

• >= больше или равно, аналог математического ≥

• < строго меньше;

• <= меньше или равно, аналог математического ≤

• x in a..b — x принадлежит интервалу от a до b, аналог математического a ≤ x ≤ b;

• x !in a..b — x НЕ принадлежит интервалу от a до b;

• != не равно, аналог математического ≠

• == равно (используется два знака равенства, чтобы не путать данную операцию с инициализацией / вычислением результата =).

Операции == и != в Котлине применимы для сравнения аргументов произвольных типов.
В частности, разрешается сравнивать на равенство строки — они равны, если имеют равную длину, и соответствующие их символы совпадают: «abc» != «cba».

Остальные операции применимы только в том случае,
если для аргументов определена специальная функция сравнения compareTo — об этом мы будем говорить позже.
Первое время, нам придётся применять их только для числовых типов.

Математически, результат всех операций сравнения имеет тип Boolean с ровно двумя возможными значениями: true, false.

Табличная форма ветвлений (when)

Каскадную запись if..else if..else часто можно представить более изящно в табличной форме, используя конструкцию when (когда).
Для примера quadraticRootNumber это делается так:

fun quadraticRootNumber(a: Double, b: Double, c: Double): Int {
    // Применяем готовую функцию из первой части
    val d = discriminant(a, b, c)
    // Для сравнения на равенство применяем ==
    return when {
        d > 0. 0  -> 2
        d == 0.0 -> 1
        else     -> 0
    }
}

Конструкция when состоит из последовательности записей вида условие -> результат.
В последней записи условие заменяется на ключевое слово else (иначе).

Частый случай применения when — ситуация, когда одно и то же выражение необходимо
последовательно сравнить на равенство с несколькими другими.
Для примера, рассмотрим задачу формирования словесной нотации для оценки.
Согласно принятым сейчас стандартам, оценка «5» записывается как «отлично», «4» как «хорошо»,
«3» как «удовлетворительно» и «2» как «неудовлетворительно».
Представим подобное преобразование в виде функции на Котлине, используя when:

fun gradeNotation(grade: Int): String = when (grade) {
    5 -> "отлично"
    4 -> "хорошо"
    3 -> "удовлетворительно"
    2 -> "неудовлетворительно"
    else -> "несуществующая оценка $grade"
}

Эта функция принимает на вход целочисленную оценку (grade) и формирует на выходе соответствующую ей строку.
Напомним, что строкам в Котлине соответствует тип String и записываются они в двойных кавычках.

Для проверки возможного значения grade мы используем конструкцию when (grade),
в которой оно последовательно сравнивается с 5, 4, 3 и 2.
Обратите внимание, что в нашей записи when имеется и пятый случай (else).
Его присутствие необходимо, так как функция должна знать, какой результат ей следует вернуть на выход,
для любого допустимого значения входа (в данном случае это тип Int с его диапазоном допустимых значений).
Строго говоря, ветка else здесь соответствует ошибочной ситуации,
которая может предусматривать специальную обработку — но об этом позже.
В функции gradeNotation в этой ситуации мы формируем строку «несуществующая оценка»,
дописывая к ней значение переданной оценки, например: «несуществующая оценка 0».

Логические функции и операции

Условие в операторе if часто в свою очередь вычисляется с помощью функции с результатом типа Boolean.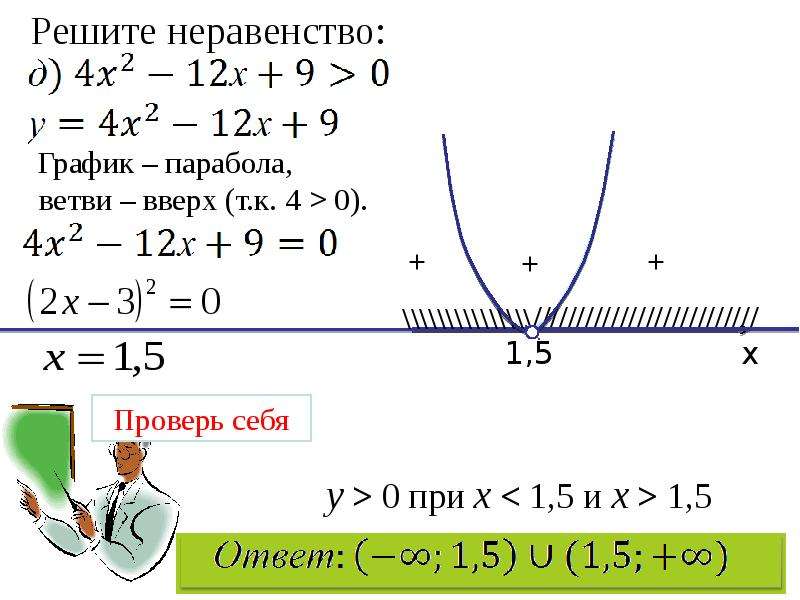
Пусть, например, имеется круг на плоскости с центром в точке (x₀, y₀) и радиусом r,
а также точка на плоскости с координатами (x, y). Необходимо определить, лежит ли точка внутри круга.
Особенность данной задачи в том, что у неё есть только два ответа: ДА или НЕТ,
либо, более формально, ИСТИННО (true) или ЛОЖНО (false).

Для решения данной задачи необходимо воспользоваться неравенством круга: (x-x0)2 + (y-y0)2 ≤ r2.
Если точка (x, y) удовлетворяет этому неравенству, то она лежит внутри круга,
если же нет, то она находится снаружи. Функция очень проста и записывается так:

fun pointInsideCircle(x: Double, y: Double, x0: Double, y0: Double, r: Double) =
        sqr(x - x0) + sqr(y - y0) <= sqr(r)

Здесь вновь используется функция sqr из урока 1 для вычисления квадратов чисел.
Тип результата функции pointInsideCircle — Boolean.
При написании тестовых функций для неё удобно использовать готовые функции assertTrue и assertFalse, например:

@Test
fun pointInsideCircle() {
    // (1, 1) inside circle: center = (0, 0), r = 2
    assertTrue(pointInsideCircle(1. 0, 1.0, 0.0, 0.0, 2.0))
    // (2, 2) NOT inside circle: center = (0, 0), r = 2
    assertFalse(pointInsideCircle(2.0, 2.0, 0.0, 0.0, 2.0))
}

Обе функции имеют один параметр типа Boolean.
assertTrue (проверить на истину) приводит к неудачному исходу теста, если её аргумент равен false,
и продолжает выполнение теста, если он равен true.
assertFalse (проверить на ложь) работает с точностью до наоборот.

Функцию pointInsideCircle в свою очередь можно использовать для решения более сложных задач.
Например, условие принадлежности точки пересечению или объединению двух кругов может выглядеть так:

// Фрагмент программы...
val x = 0.5
val y = 0.5
// Пересечение: логическое И
if (pointInsideCircle(x, y, 0.0, 0.0, 1.0) && pointInsideCircle(x, y, 1.0, 1.0, 1.0)) { ... }
// Объединение: логическое ИЛИ
if (pointInsideCircle(x, y, 0.0, 0.0, 1. 0) || pointInsideCircle(x, y, 1.0, 1.0, 1.0)) { ... }
// Не принадлежит
if (!pointInsideCircle(x, y, 0.0, 0.0, 1.0)) { ... }

В этом примере используются логические операции:

• && — логическое И, результат равен true, если ОБА аргумента true

• || — логическое ИЛИ, результат равен true, если ХОТЯ БЫ ОДИН из аргументов равен true

• ! — логическое НЕ, результат равен true, если аргумент false

Сложный пример: биквадратное уравнение

Рассмотрим теперь более сложный случай. Пусть нам необходимо написать функцию,
рассчитывающую минимальный из имеющихся корней биквадратного уравнения: ax⁴ + bx² + c = 0.
Данное уравнение решается путём замены y = x², решения квадратного уравнения ay² + by + c = 0
и последующего решения уравнения x² = y с подставленными корнями квадратного уравнения y₁ и y₂.
Попробуем сначала записать алгоритм решения задачи в виде последовательности действий:

1. Если a равно 0, уравнение вырождается в bx² + c = 0. Вырожденное уравнение:

   • при b равном 0 не имеет решений (или имеет бесконечно много)

   • при c / b > 0 также не имеет решений

   • в противном случае минимальный корень — это x = -sqrt(-c / b)

2. Рассчитаем дискриминант d = b2 - 4ac.

3. Если d меньше 0, у квадратного уравнения нет решений, как и у биквадратного.

4. В противном случае найдём корни квадратного уравнения y1 = (-b + sqrt(d))/(2a) и y2 = (-b - sqrt(d))/(2a).

5. Вычислим y3 = Max(y1, y2).

6. Если y₃ < 0, у уравнения x2 = y3 нет решений.

7. В противном случае, минимальный корень биквадратного уравнения — это x = -sqrt(y3).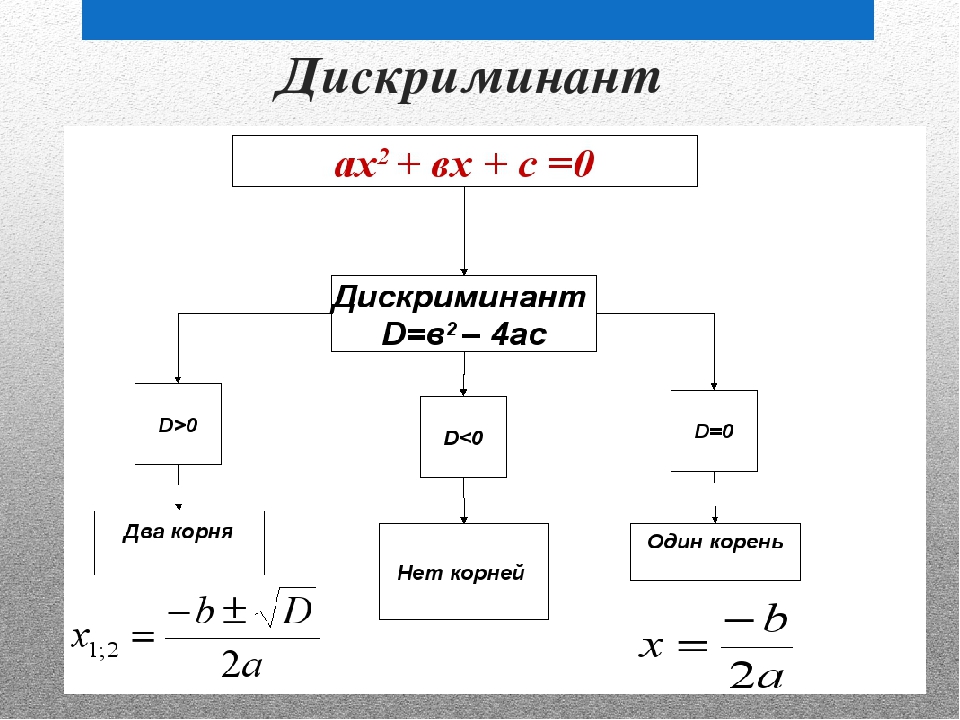

Запишем теперь то же самое на Котлине. Для обозначения ситуации, когда решений нет, будем использовать
специальную константу Double.NaN, так называемое не-число.
На практике она может получиться как результат некоторых некорректных действий с вещественными числами,
например, после вычисления квадратного корня из -1.

fun minBiRoot(a: Double, b: Double, c: Double): Double {
    // 1: в главной ветке if выполняется НЕСКОЛЬКО операторов
    if (a == 0.0) {
        if (b == 0.0) return Double.NaN // ... и ничего больше не делать
        val bc = -c / b
        if (bc < 0.0) return Double.NaN // ... и ничего больше не делать
        return -Math.sqrt(bc)
        // Дальше функция при a == 0.0 не идёт
    }
    val d = discriminant(a, b, c)   // 2
    if (d < 0.0) return Double.NaN  // 3
    // 4
    val y1 = (-b + Math.sqrt(d)) / (2 * a)
    val y2 = (-b - Math.sqrt(d)) / (2 * a)
    val y3 = Math.max(y1, y2)       // 5
    if (y3 < 0.0) return Double. NaN // 6
    return -Math.sqrt(y3)           // 7
}

Данная реализация активно использует оператор return.
Если в предыдущих примерах он использовался исключительно в конце функций,
то в этом примере он встречается в теле функции многократно в конструкции вида if (something) return result.
Такая конструкция читается как «если что-то, результат функции равен тому-то (и дальше ничего делать не надо)».
Заметьте, что в данном случае вторая часть оператора if — ветка else — отсутствует.
Это эквивалентно записи if (something) return result else {}, то есть в ветке «иначе» не делается ничего.
В случае, если условие в if не выполнено, функция пропускает оператор return
и выполняет оператор, следующий за оператором if.

Всегда ли может отсутствовать ветка else? Нет, не всегда.
Это зависит от контекста, то есть конкретного варианта использования if. .else.
В примере вроде val x = if (condition) 1 else 2 исчезнование ветки else не позволит функции «понять»,
чему же должно быть равно значение x, что приведёт к ошибке:

'if' must have both main and 'else' branches if used as an expression.

В переводе с английского — оператор if должен иметь как главную ветку, так и ветку else, если он используется как выражение.
Два наиболее распространённых случая такого рода — val x = if …​ или return if …​.
В обоих случаях у if есть результат, который затем используется для записи в x
или для формирования результата функции.

Обратите также внимание на самый первый оператор if в minBiRoot.
Он выглядит как if (a == 0.0) { …​ } с несколькими операторами в фигурных скобках.
По умолчанию, if может иметь только один оператор как в главной ветке, так и в ветке else.
Если в случае истинности или ложности условия необходимо выполнить несколько операторов,
их следует заключить в фигурные скобки, образуя блок операторов.
Блок операторов выполняется последовательно, так же, как и тело функции.
Блок может содержать любые операторы, в том числе и другие операторы if.

Проверим нашу реализацию minBiRoot с помощью тестовой функции.
Для этого нам необходимо проверить различные случаи:

1. a = b = 0, например 0x⁴ + 0x² + 1 = 0 — корней нет.

2. a = 0, c / b > 0, например 0x⁴ + 1x² + 2 = 0 — корней нет.

3. a = 0, c / b < 0, например 0x⁴ + 1x² — 4 = 0 — корни есть, в данном случае минимальный из них -2.

4. d < 0, например 1x⁴ -2x² + 4 = 0 — корней нет.

5. d > 0, но оба корня y отрицательны, например 1x⁴ + 3x² + 2 = 0, y₁ = -2, y₂ = -1, корней нет.

6. d > 0, хотя бы один корень y положителен, например 1x⁴ — 3x² + 2 = 0, y₁ = 1, y₂ = 2, минимальный корень -1.41.

Тестовая функция может выглядеть так:

@Test
fun minBiRoot() {
    assertEquals(Double.NaN, minBiRoot(0.0, 0.0, 1.0), 1e-2)
    assertEquals(Double.NaN, minBiRoot(0.0, 1.0, 2.0), 1e-2)
    assertEquals(-2.0, minBiRoot(0.0, 1.0, -4.0), 1e-10)
    assertEquals(Double.NaN, minBiRoot(1.0, -2.0, 4.0), 1e-2)
    assertEquals(Double.NaN, minBiRoot(1.0, 3.0, 2.0), 1e-2)
    assertEquals(-1.41, minBiRoot(1.0, -3.0, 2.0), 1e-2)
}

Обратите внимание, что функция assertEquals при работе с типом Double имеет третий аргумент — максимально допустимую погрешность. Учитывая, что расчёты с вещественными числами выполняются приближённо,
это важная часть теста. Например, заменив в последнем вызове 1e-2 на 1e-3 (0.01 на 0.001),
мы обнаружим, что тест перестал проходить — точное значение корня будет -1.41421356…​,
а заданное нами -1.41 с погрешностью 0.00421356…​, что больше по модулю, чем 0.001.

Упражнения

Упражнения для урока 2 разбиты на две задачи — одну про if..else и другую про логические функции.
Откройте вначале файл srс/lesson2/task1/IfElse.kt в проекте KotlinAsFirst.
Выберите любую из задач в нём. Придумайте её решение и запишите его в теле соответствующей функции.

Откройте файл test/lesson2/task1/Tests.kt,
найдите в нём тестовую функцию — её название должно совпадать с названием написанной вами функции.
Запустите тестирование, в случае обнаружения ошибок исправьте их и добейтесь прохождения теста.

Внимательно прочитайте текст тестовой функции. Какие случаи ей проверяются и как?
Существуют ли другие важные случаи, которые следовало бы проверить?
Проверьте ещё один или два случая, добавив в текст тестовой функции новые вызовы assertEquals.

Откройте теперь файл srс/lesson2/task2/Logical.kt, содержащий задачи на написание логических функций.
Решите одну из них, обратите внимание на имеющиеся тестовые функции — они находятся в файле test/lesson2/task2/Tests.kt.

Решите ещё хотя бы одну задачу из урока 2 на ваш выбор.
Убедитесь в том, что можете решать такие задачи уверенно и без посторонней помощи.
После этого вы можете перейти к следующему разделу.

You can’t perform that action at this time.

You signed in with another tab or window. Reload to refresh your session.
You signed out in another tab or window. Reload to refresh your session.

Как решать квадратные уравнения через дискриминант

Умение решать квадратные уравнения, очень важный пункт в изучении математики. В решении многих задач алгебры, геометрии, а также физики, химии и других предметов, присутствует часть, где необходимо найти корни квадратного уравнения. Если вы готовитесь к экзаменам ОГЭ или ЕГЭ или другим каким-либо аттестациям по математике, то вам нужно обязательно изучить эту тему подробнее, потому что даже знание основных формул, не дает полного понимания этой темы. Прочитав статью полностью, вы разберетесь во всех нюансах решения полных и неполных квадратных уравнений.

Итак, как же решать квадратные уравнения?

В этой статье мы рассмотрим:

1. что такое квадратное уравнение;
2. основные формулы нахождения корней квадратного уравнения;
3. как определить количество решений квадратного уравнения;
4. как можно графически решить квадратное уравнение;
5. что значит неполное квадратное уравнение и способы их решения;
6. какое квадратное уравнение называется приведенным, теорема Виета;
7. использование квадратных уравнений в решении текстовых задач.

Что такое квадратное уравнение

Уравнение вида

называется квадратным уравнением, где — некоторые числа, причем . Как квадратное уравнение отличить от кубического или линейного? Ответ прост: наивысшая степень переменной — 2 (вторая).

Давайте чуть подробнее остановимся на коэффициентах. В уравнении — называется первым коэффициентом (или старшим), (если  , то квадратное уравнение «вырождается» в линейное уравнение ), — называется вторым коэффициентом или коэффициентом при , и — свободным членом.

Основные формулы нахождения корней квадратного уравнения

Чтобы решить квадратное уравнение, нужно подставить значения в формулу дискриминанта

и затем значение дискриминанта в формулы корней

Это базовые формулы нахождения корней квадратного уравнения

Как определить количество решений квадратного уравнения

В зависимости от того какой дискриминант, можно определить сколько решений у квадратного уравнения.

Если , то квадратное уравнение (1) имеет 2 различных корня и , .

Если , то квадратное уравнение (1) имеет одно решение или два равных корня .

Если , то квадратное уравнение (1) не имеет действительных корней или говорят решений нет.

Давайте теперь рассмотрим примеры квадратных уравнений и найдем их корни.

1)

Для начала нужно определить чему равны  :

старший коэффициент при ,  ,

второй коэффициент при , ,

свободный член .

Найдем дискриминант, подставив в формулу значения   

Так как , то корней два. Найдем их по формулам:

Итак, уравнение имеет два корня .

2)

Выпишем коэффициенты: .

Найдем дискриминант: .

Так как , то корней два. Найдем их:

Обратите внимание, я каждый раз прописываю все формулы не смотря на то, что отлично их знаю. Совет: никогда не ленитесь также их прописывать. Во-первых, прописывая их каждый раз вы лучше запоминаете их. Во-вторых, проверяющий будет знать, что вы знаете формулы, и если где-то не правильно посчитано, то скорее всего из-за невнимательности. В-третьих, у вас вообще меньше шансов ошибиться — это проверено статистически.

Как можно графически решить квадратное уравнение

Давайте теперь рассмотрим наши уравнения на координатной плоскости, как же они будут выглядеть визуально? И можно ли по рисунку определить корни?

1)

Рассмотрим квадратичную функцию .

Графиком квадратичной функции является парабола, на координатной плоскости она будет выглядеть вот так:

рисунок 1

Обратите внимание, парабола пересекает ось Ох в точках и , которые являются корнями уравнения . Мы рассматриваем точки пересечения с осью Ох, так как она совпадает с прямой .

Итак, становится понятно, какой визуальный смысл заложен в квадратном уравнении: квадратный трехчлен , имеющий форму параболы, в зависимости от того сколько корней имеет, столько раз  пересекает ось абсцисс (ось Ох).

Если 2 корня, то парабола пересекает ось Ох в двух точках, как парабола q пересекает ось абсцисс в точках D и E, а парабола r — в точках H и I. (рисунок 2)

рисунок 2

Если корень один, то парабола пересекает ось Ох в одной точке, так параболы p и h, касаются оси Ох в точках M и N соответственно (рисунок 3).

рисунок 3

Если корней нет, то парабола не пересекает ось Ох (рисунок 4).

рисунок 4

Итак, точки пересечения парабол с осью Ох и есть корни квадратных уравнений. Если по рисунку можно определить их значение, то корни найдены. Но часто эти значения приблизительны и поэтому такой способ решения практически не используют.

Что значит неполное квадратное уравнение и способы их решения

Иногда в квадратном уравнении отсутствует какое-либо слагаемое, и тогда ребята часто впадают в ступор, «а как же решать тогда уравнение?» Ответ прост: также как и полное квадратное уравнение, лишь только учитывая, что какой-то из коэффициентов равен нулю. Но давайте разбираться поэтапно.

Квадратное уравнение называется полным, если все коэффициенты ,

а если или , то квадратное уравнение называется неполным (случай когда не рассматриваем, поскольку в этом случае пропадает слагаемое с  и квадратное уравнение вырождается в линейное).

Итак.

1) Если , , то уравнение будет выглядеть так:

то есть отсутствует слагаемое с . Можно как и в полном квадратном уравнении найти дискриминант , но так как , то , и если один из коэффициентов отрицательный, то , а корней будет 2.

Но путь этот громоздкий в смысле числовых вычислений, поэтому есть более простой способ, без использования формул дискриминанта .

Давайте внимательно посмотрим на данное уравнение

мы как и в линейном уравнении можем разделить переменную с   и свободное слагаемое, то есть перенесем коэффициент в другую сторону от знака равно, при этом не забывая поменять знак на противоположный:

разделим обе стороны на :

если правая сторона от , то получим следующие корни уравнения:

если же — то корней нет.

2) Если , , то уравнение будет выглядеть так:

В этом случае тоже можно использовать формулы дискриминанта и корней уравнения. Но мы рассмотрим сразу другой способ.

Во-первых, можно вынести за скобку из обоих слагаемых

получили произведение двух множителей и , их произведение равно 0, тогда когда хотя бы один из множителей равен 0. Значит, мы приравниваем к 0 каждый из них и решаем новые, уже линейные уравнения.

в первом уравнении все понятно, во втором как при решении линейного уравнения, переносим свободное слагаемое в право от равно и делим обе стороны на коэффициент перед :

В этом случае получили два корня .

3) Если , то получаем уравнение

В этом случае корни совпадают и равны 0, то есть .

Какое квадратное уравнение называется приведенным, теорема Виета

Рассмотрим случай, когда в полном квадратном уравнении , тогда уравнение будет иметь вид:

и называется приведенным.

Такое квадратное уравнение также решают через формулы дискриминанта.

Но иногда решая приведенное квадратное уравнение, очень удобно находить корни по теореме Виета.

Согласно этой теореме должно выполнятся два условия:

причем оба условия должны выполнятся одновременно, поэтому его правильнее записать так

Часто в книгах эти условия записываются в другом порядке:

— по своему опыту, советую использовать первый вариант — так легче подобрать корни.

Чтобы было понятно как действует теорема Виета, нужно рассмотреть эти условия на конкретных примерах.

1) Дано квадратное уравнение .

Здесь . Нам нужно найти какие два числа при умножении друг на друга будут давать , а в сумме . Явно существует только два числа, произведение которых равно 3 — это 1 и 3, их сумма как раз будет равна 4:

Значит, корни уравнения .

Еще несколько примеров, чтобы все было понятно:

2) . Здесь сумма равна -4. То есть значения чисел те же, но знаки другие. Поэтому попробуем . Значит, корни .

3)  Корни .

4)  Корни .

5) , казалось бы, такие большие числа! Как найти подходящие корни? И кстати, решая через формулы дискриминанта, нас бы ждали громоздкие вычисления!

Но не будем впадать в панику, и просто посмотрим какие подходящие варианты чисел могут подойти в данном случае:    Значит, корни .

6) .

Еще раз акцентирую ваше внимание, что сумма корней равна , поэтому во втором условии всегда будет противоположный знак, чем у коэффициента b.

рисунок 5

Когда значение свободного коэффициента , то оба корня имеют одинаковые знаки, то есть оба либо положительные, либо отрицательные.

Соответственно, если , то корни находятся по разные стороны от 0, то есть один отрицательный, а другой положительный.

7) 

Обратите внимание, в первом варианте системы подобраны корни не верно, об этом говорит то, что во втором условии не выполнилось равенство. А во второй системе выполняются оба условия. Значит, корни уравнения .

В этот раз первый вариант корней сразу выполнил оба условия и  получаем .

Конечно, не во всех приведенных квадратных уравнениях легко по теореме Виета подобрать корни, и после нескольких тщетных попыток условия не выполняются. В таких случаях приходится находить корни через формулы дискриминанта, и чаще всего выясняется, что дискриминант либо отрицательный, либо = 0.

Использование квадратных уравнений в решении текстовых задач

Ну и конечно же, нужно рассмотреть, где же используются квадратные уравнения.

Итак, задача о нахождении периметра участка для постройки вокруг него забора.

Существует дачный участок прямоугольной формы. Известно, что длина этого участка на 10 м длиннее его ширины, а площадь участка равна 6 соткам (то есть 600 кв.м.). Найти длину забора вокруг этого участка.

В тех случаях, когда изначально не известны исходные параметры (в нашем случае не известно ни длины, ни ширины участка), а известна только зависимость их между собой, то вводим неизвестную переменную . Я обычно через обозначаю меньший из параметров, но это не важно — главное соблюсти все условия.

Пусть м. — ширина участка, тогда длина — ( +10) м. Так как площадь участка находится путем умножения длины на ширину, и у нас площадь равна 600 кв.м., то получим квадратное уравнение:

раскроем скобки и перенесем свободное слагаемое в левую сторону от равно, приведем его к стандартному общему виду:

Я по теореме Виета найду корни. Получаем . По условиям теоремы

Оба условия выполняются верно. Значит, корни уравнения .

Второй корень нам не подходит по смыслу задачи, так как ширина участка не может быть отрицательной. Значит, ширина участка равна 20 м., а длина соответственно 20+10=30 м.  Проверим, площадь участка:

Корень найден правильно. Найдем теперь периметр участка, чтобы узнать длину забора:

Получили длину забора вокруг участка: 100 м.

Тема квадратных уравнений обычно не вызывает сложностей у ребят. Особенно решение уравнений явно общего вида с использованием формул дискриминанта. Но когда квадратное уравнение задано не явно и необходимо его преобразовать и привести к общему виду, вот тогда возникают трудности. Такие виды уравнений я рассмотрю в следующей статье.

Дискриминант

★ Дискриминант

В дискриминантом многочлена p = a 0 a 1 x (1) ⋯ a n x n (а н х) {\свойства стиль отображения значение Р=ох{0} ох{1}х \cdots ох{н}х^{н}}, a n (а) ≠ 0 {\свойства стиль отображения значение ох{Н}\neq 0}, является продуктом

D p = a n 2 n (Д р = н 2) − 2 ∏ i &lt, j α i − α j 2 (Дж 2) {\displaystyle Dp=a_{n}^{2n-2}\prod _{i D &gt, 0 {\displaystyle D&gt, 0} вещественных корней — два, и они вычисляются по формуле x 1, 2 = − b ± b 2 (Б 2) − 4 a c 2 a (4 с 2) {\displaystyle x_{1.{2}}{4}}}, тогда все корни являются комплексными.

Памятка по теме «Квадратное уравнение»

Квадратное уравнение

Квадратное уравнение – это уравнение вида ax2 + bx + c = 0, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.

Пример квадратного уравнения:

3×2 + 2x – 5 = 0.

Здесь а = 3, b = 2, c = –5.

Числа a, b и c – коэффициенты квадратного уравнения.

Число a называют первым коэффициентом, число b – вторым коэффициентом, а число c – свободным членом.

Приведенное квадратное уравнение.

Квадратное уравнение, в котором первый коэффициент равен 1, называют приведенным квадратным уравнением.

Примеры приведенного квадратного уравнения:

x2 + 10x – 11 = 0

x2 – x – 12 = 0

x2 – 6х + 5 = 0

здесь коэффициент при x2 равен 1 (просто единица во всех трех уравнениях опущена).

Неполное квадратное уравнение.

Если в квадратном уравнении ax2 + bx + c = 0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют неполным квадратным уравнением.

Примеры неполного квадратного уравнения:

-2×2 + 18 = 0

здесь есть коэффициент а, который равен -2, есть коэффициент c, равный 18, а коэффициента b нет – он равен нулю.

x2 – 5x = 0

здесь а = 1,  b = -5,  c = 0 (поэтому коэффициент c  в уравнении отсутствует).

Как решать квадратные уравнения.

Чтобы решить квадратное уравнение, надо совершить всего два действия:

1) Найти дискриминант D по формуле:

D = b2 – 4ac.

Если дискриминант – отрицательное число, то квадратное уравнение не имеет решения, вычисления прекращаются. Если D ≥ 0, то

2) Найти корни квадратного уравнения по формуле:

             –b ± √D
х1,2 = —————.
                  2а

Пример: Решить квадратное уравнение 3х2 – 5х – 2 = 0.

Решение:

Сначала определимся с коэффициентами нашего уравнения:

а = 3, b = –5, c = –2.

Вычисляем дискриминант:

D = b2 – 4ac = (–5)2 – 4 · 3 · (–2) = 25 + 24 = 49.

D > 0, значит, уравнение имеет смысл, а значит, можем продолжить.

Находим корни квадратного уравнения:

           –b + √D            5 + 7          12
х1 = ————— = ———— = —— = 2
               2а                    6              6

          –b – √D             5 – 7              2             1
х2 = ————— = ———— = – —— = – ——.
             2а                     6                  6             3

                                       1
Ответ: х1 = 2,  х2 = – ——.
                                       3

Формулы корней квадратного уравнения. Дискриминант.

Формула №1:

         —b ± √D
x =  ————,  где D = b2 – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12×2 + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b2 – 4ac = 72 – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         -b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x1 = ——— = —— = — = – —
           24           24       4          4

         -7 – 1       -8       -1         1
x2 = ——— = —— = — = – — .
           24           24       3          3

                        1                   1
Ответ: x1 = – —,    x2 = – —
                        4                   3

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D1
x = ————,   где D1 = k2 – ac
             a

Пример. Решим уравнение 5×2 – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8, a = 5,  c = 3. Мы уже можем найти дискриминант D1:

D1 = k2 – ac = (-8)2 – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      -k ± √D1       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x1 = ——— =  — = 3
            5            5

         8 – 7         1
x2 = ——— =  — = 0,2
             5           5 

Ответ: x1 = 3; x2 = 0,2.

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

Здесь будет файл: /data/edu/files/n1461134193.docx (Квадратное уравнение)

2 + bx + c #:

• Если #Delta> 0 # — полный квадрат, то #f (x) # имеет два различных рациональных вещественных нуля.

• Если #Delta> 0 # не является полным квадратом, то #f (x) # имеет два различных иррациональных действительных нуля.

• Если #Delta = 0 #, то #f (x) # имеет повторяющийся рациональный действительный ноль (кратности # 2 #).

• Если #Delta <0 #, то #f (x) # не имеет вещественных нулей. Он имеет комплексно сопряженную пару ненастоящих нулей.

Если коэффициенты действительны, но не рациональны, рациональность нулей не может быть определена с помощью дискриминанта, но мы все равно имеем:

Дискриминант входит в формулу корней квадратного уравнения для нулей # ax ^ 2 + bx + c #, а именно:

#x = (-b + -sqrt (b ^ 2-4ac)) / (2a) = (-b + -sqrt (Дельта)) / (2a) #

, из которого вы можете понять, почему нули имеют тот характер, который они имеют для разных значений # Delta #.2 + 18abcd #

• Если #Delta> 0 #, то #f (x) # имеет три различных действительных нуля.

• Если #Delta = 0 #, то #f (x) # имеет либо один действительный ноль кратности # 3 #, либо два различных действительных нуля, один из которых имеет кратность # 2 #, а другой — кратность # 1 #.

• Если #Delta <0 #, то #f (x) # имеет один действительный ноль и комплексно-сопряженную пару нереальных нулей.

Дискриминант кубического уравнения

Дискриминант квадратного уравнения

a x ² + bx + c = 0

это

Δ = b ² — 4 ac .

Если дискриминант Δ равен нулю, уравнение имеет двойной корень, то есть существует уникальный x , который делает уравнение нулевым, и он дважды считается корнем. Если дискриминант не равен нулю, есть два различных корня.

Кубические уравнения также имеют дискриминант. Для кубического уравнения

a x ³ + bx ² + cx + d = 0

дискриминант равен

Δ = 18 abcd — 4 b ³ d + b ²c² — 4 ac³ — 27 a ² d ².

Если Δ = 0, уравнение имеет кратный корень, но в противном случае оно имеет три различных корня.

Замена переменной может свести общее кубическое уравнение к так называемому «вдавленному» кубическому уравнению вида

x ³ + пикселей + q = 0

, в этом случае дискриминант упрощается до

Δ = — 4 p³ — 27 q ².

Вот пара интересных связей. Идея сведения кубического уравнения к кубическому с углублением восходит к Кардано (1501–1576).То, что в этом контексте называется углубленной кубикой, известно как форма Вейерштрасса (1815–1897) в контексте эллиптических кривых. То есть эллиптическая кривая вида

y ² = x ³ + ax + b

Считается, что

находится в форме Вейерштрасса. Другими словами, эллиптическая кривая имеет форму Вейерштрасса, если правая часть представляет собой углубленную кубику.

Кроме того, эллиптическая кривая должна быть невырожденной, что означает, что она должна удовлетворять требованиям

4 a³ + 27 b ² ≠ 0.

Другими словами, дискриминант правой части отличен от нуля. В контексте эллиптических кривых дискриминант определяется как

Δ = -16 (4 a³ + 27 b ²)

, который совпадает с дискриминантом выше, за исключением коэффициента 16, который упрощает некоторые вычисления с эллиптическими кривыми.

Примечание о полях

В контексте решения квадратных и кубических уравнений мы обычно неявно работаем с действительными или комплексными числами.Предположим, что все коэффициенты квадратного уравнения действительны. Если дискриминант положительный, есть два различных действительных корня. Если дискриминант отрицательный, есть два различных комплексных корня, и эти корни являются комплексно сопряженными друг другу.

Аналогичные замечания справедливы для кубических уравнений, когда все коэффициенты действительны. Если дискриминант положительный, существует три различных действительных корня. Если дискриминант отрицательный, существует один действительный корень и комплексно сопряженная пара комплексных корней.

В первом разделе я рассмотрел только, был ли дискриминант нулевым, и поэтому утверждения не зависят от поля, из которого берутся коэффициенты.

Для эллиптических кривых можно работать с множеством полей. Может быть, действительные или комплексные числа, но также и конечные поля. В большинстве сообщений блога, которые я писал об эллиптических кривых, поле представляет собой целые числа по модулю большого простого числа.

Больше сообщений, связанных с кубическими уравнениями

Посмотреть вопрос — каково значение дискриминанта?

какое значение дискриминанта?

Степень 2
Квадратичный многочлен \ ({\ displaystyle ax ^ {2} + bx + c \,} \, \) имеет дискриминант \ ({\ displaystyle b ^ {2} -4ac \, .{2} \,. \ End {align}}} \)
Дискриминант равен нулю тогда и только тогда, когда по крайней мере два корня равны.
Если коэффициенты являются действительными числами и дискриминант не равен нулю,
дискриминант отрицательный, если есть два действительных корня и два комплексно-сопряженных корня,
и положительный, если все корни либо действительные, либо все не действительные.

Равные или двойные корни

РАВНЫЕ ИЛИ ДВОЙНЫЕ КОРНИ

Если дискриминант b ² — 4ac равен нулю,

радикал в формуле корней квадратного уравнения обращается в ноль.

В этом случае корни равны; таких корней

иногда называют двойным корнем.

Рассмотрим уравнение

9x ² + 12x + 4 = 0

Сравнивая с общей квадратичной, замечаем, что

a = 9, b = 12 и c = 4

Дискриминант

Следовательно, корни равны.

ПРОВЕРКА: по формуле

Равенство корней проверено.

Корни могут быть равны, только если трехчлен
это. идеальный квадрат. Его коэффициенты равны.
Факторизация трехчлена в

9x ² + 12x + 4 = 0

видим, что

(3x + 2) ² = 0

Поскольку множитель 3x + 2 возведен в квадрат, фактически имеем

3x + 2 = 0

дважды, а у нас

дважды.

Дело в том, что надо считать один и тот же корень
дважды объясняет использование термина «двойной»
корень «. Двойной корень квадратного уравнения — это
всегда рационально, потому что двойной корень может возникнуть только тогда, когда радикал равен нулю.

РЕАЛЬНЫЕ И НЕРАВНЫЕ КОРНИ Когда дискриминант положительный, корни

должно быть настоящим. Также они должны быть неравными, поскольку
равные корни возникают только тогда, когда дискриминант
равно нулю.

Рациональные корни.

Если дискриминант — полный квадрат,
корни рациональны. Например, рассмотрим
уравнение

3x ² — x — 2 = 0

, в котором

a = 3, b = -1 и c = -2

Дискриминант

Мы видим, что дискриминант 25 представляет собой полный квадрат. Идеальный квадрат означает, что

радикал в квадратной формуле может быть удален, что корни уравнения рациональны, и что трехчлен можно факторизовать.Другими словами, когда мы оцениваем дискриминант и обнаруживаем, что он представляет собой идеальный квадрат, мы знаем, что

что трехчлен можно разложить на множители.

Таким образом,

, из которых

Мы видим, что информация, полученная из
дискриминант правильный. Корни настоящие,
неравный и рациональный.

Дискриминант квадратного уравнения | от Никсона Джорама

Квадратичное произошло от Quadratus , латинского слова, которое описывает вторую степень или операцию возведения в квадрат.

Мы определяем квадратное уравнение в следующем обобщенном формате.

f (x) = ax² + bx + c , где ‘a’ не равно нулю. Здесь ax² — квадратичный член, bx — линейный член ( bx¹ ) и c — постоянный член ( cx⁰ ).

Здесь ‘a’ равно , не равному нулю.Потому что предположим, что если ‘a’ равно нулю, то есть; коэффициент наивысшей степени равен нулю, тогда f (x) не будет квадратным уравнением.

Когда ‘a’ не равно 0, тогда у нас есть две возможности для значения ‘a’ .

1. a > 0
2. a <0

Когда a > 0, функция будет иметь минимальное значение, то есть для определенного значения x , функция выдаст минимальное значение.

Коэффициент члена наивысшей степени / квадратичный член больше нуля

Когда a <0, функция будет иметь максимальное значение, то есть для конкретного значения x функция будет дать максимальное значение.

Коэффициент члена наивысшей степени / квадратичный член меньше нуля

Для данного квадратного уравнения ( f (x) = ax² + bx + c) Дискриминант должен быть задан как,

Это производное от корня x (независимая переменная) в квадратном уравнении, когда он равен нулю.

f (x) = ax² + bx + c = 0

Здесь мы все знаем, что если отрицательное значение поместить внутри квадратного корня, это даст мнимое значение. Это; невозможно возвести значение в квадрат (умножить его на само себя) и получить отрицательное значение. Чтобы решить эту проблему, мы создали новый номер, i , который относится к «мнимому числу» , и его нет в наборе «Действительных чисел» .К этому новому числу отнеслись с большим скепсисом. Также i² = (- 1) .

Давайте изменим решение для x следующим образом:

Итак, теперь у нас есть 3 возможности для значения Δ для каждого диапазона ‘a’.

1. Δ> 0
2. Δ = 0
3. Δ <0

Когда a > 0 и Δ> 0,

x может иметь

или

Оба являются реальные значения, и это показывает, что функция будет иметь , два действительных корня , и функция будет разрезать ось x в двух разных точках.

Когда a > 0 и Δ = 0,

x может иметь

как единственное реальное решение. Это показывает, что функция будет иметь только один действительный корень (совпадающие с двумя действительными корнями) и будет касаться оси x в определенном месте.

Когда a > 0 и Δ <0,

x может иметь

или

Оба значения не являются действительными (то есть мнимыми значениями), и это показывает, что функция никогда не будет иметь реальных значений. корни , и функция никогда не будет обрезать ось x .Проще говоря, функция будет иметь два мнимых корня.

Проверьте следующие графики для понимания графики.

Надеюсь, теперь вы сможете понять, как это работает, когда a <0.

РЕШЕНИЕ: При использовании квадратной формулы для решения квадратного уравнения ax2 + bx + c = 0 дискриминант равен b2

РЕШЕНИЕ: При использовании квадратной формулы для решения квадратного уравнения ax2 + bx + c = 0 дискриминант равен b2 — 4ac. Дискриминант может быть положительным, нулевым или отрицательным.(Когда диск

Алгебра ->
Квадратичные уравнения и параболы
-> РЕШЕНИЕ: При использовании квадратной формулы для решения квадратного уравнения ax2 + bx + c = 0 дискриминант равен b2 — 4ac. Дискриминант может быть положительным, нулевым или отрицательным. (Когда диск

Войти в систему

Понимание дискриминанта

Давайте рассмотрим, что мы знаем о стандартной форме квадратного уравнения.