Содержание
Длина отрезка если известны координаты точек
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка.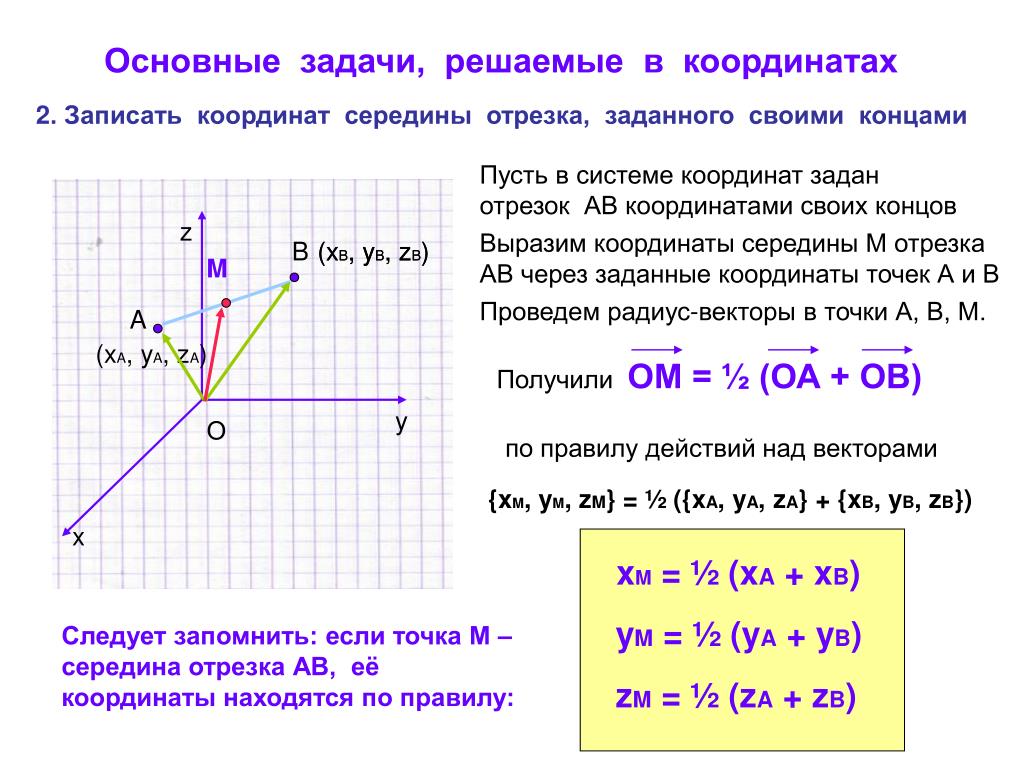 В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C – x A = x B – x C
Тогда возможно два равенства: x C – x A = x B – x C и x C – x A = – ( x B – x C )
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных – несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y – проекции точек A , B и C на оси координат (прямые О х и О y ).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:
( x A + x B 2 , y A + y B 2 )
Середина отрезка в пространстве
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z – проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А ( – 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = – 7 + 2 2 = – 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ: координаты середины отрезка А В – 5 2 , 7 2 .
Исходные данные: известны координаты треугольника А В С : А ( – 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , – 8 ) . Необходимо найти длину медианы А М .
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( – 8 ) 2 = – 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :
A M = ( 6 – ( – 1 ) ) 2 + ( – 3 – 0 ) 2 = 58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , – 4 ) . Необходимо рассчитать координаты точки А .
Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , – 4 ) . Необходимо рассчитать координаты точки А .
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M – x C 1 = 2 · 4 – 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M – y C 1 = 2 · 2 – 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M – z C 1 = 2 · ( – 4 ) – 0 = – 8
Ответ: координаты точки А ( 7 , 3 , – 8 ) .
примеры, решения, как найти середину отрезка по координатам
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.
Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.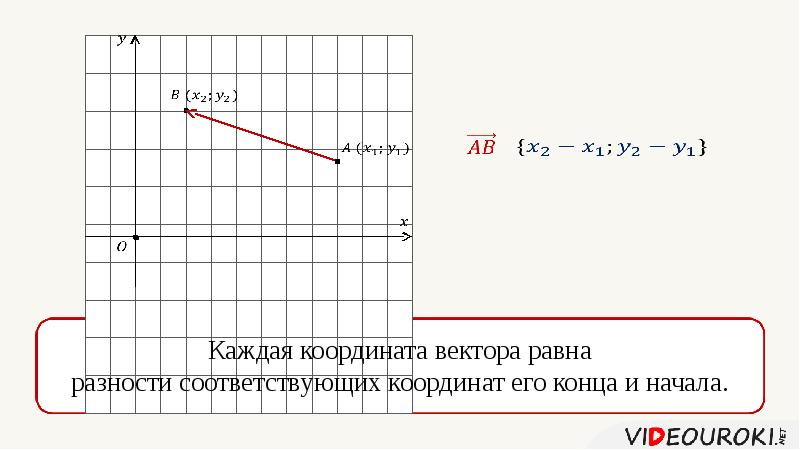
Середина отрезка на координатной прямой
Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.
Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.
|АС| = |СВ|⇔xC-xA=xB-xC
Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)
Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).
Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):
xA+xB2
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.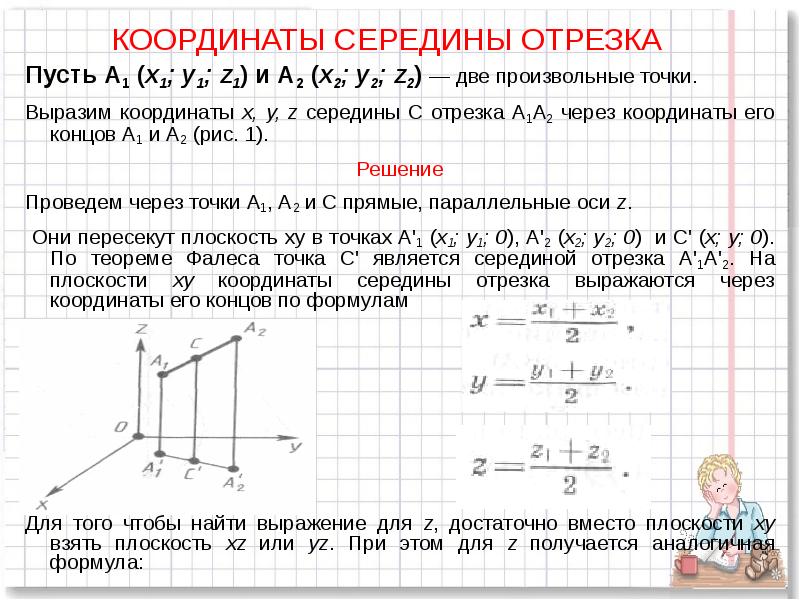 Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Середина отрезка в пространстве
Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.
Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы.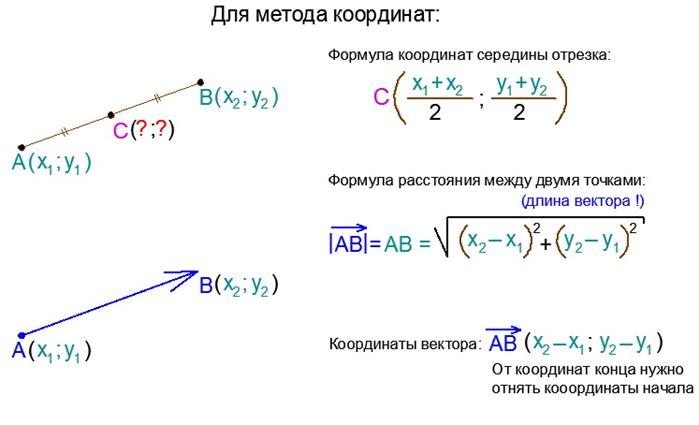 Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.
Решение
Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.
xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72
Ответ: координаты середины отрезка АВ-52, 72.
Пример 2
Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.
Решение
- По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:
xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:
AM=(6-(-1))2+(-3-0)2=58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 .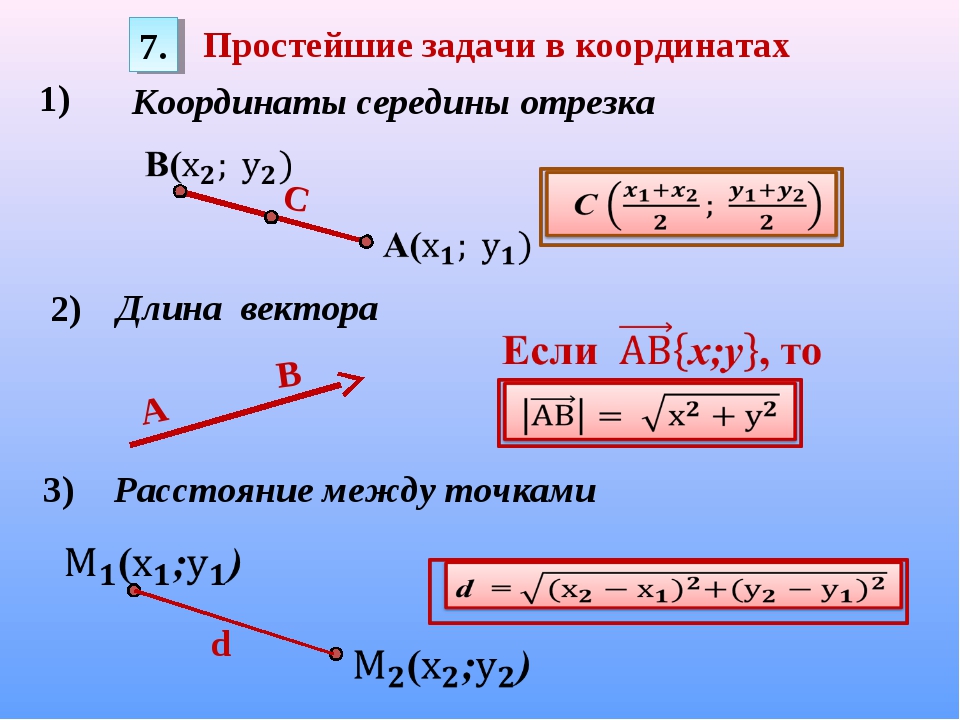 Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8
Ответ: координаты точки А (7,3,-8).
Формула вычисления длины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения
Отрезком
называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов
(x1; y1)
и
(x2; y2)
. На оси
X
и
Y
из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y
длина проекции равна y2-y1
, а на ось Х
длина проекции равна x2-x1
. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)²
. В данном случае |AB|
является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3)
и (2;5)
. Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5
. А это значит, что длина нашего отрезка равна 5:1/2
.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y)
исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1
.
Рассчитаем длину отрезка А
, для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²)
.
Если наш отрезок расположен между точками, координаты которых 2;4
и 4;1
, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61
.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.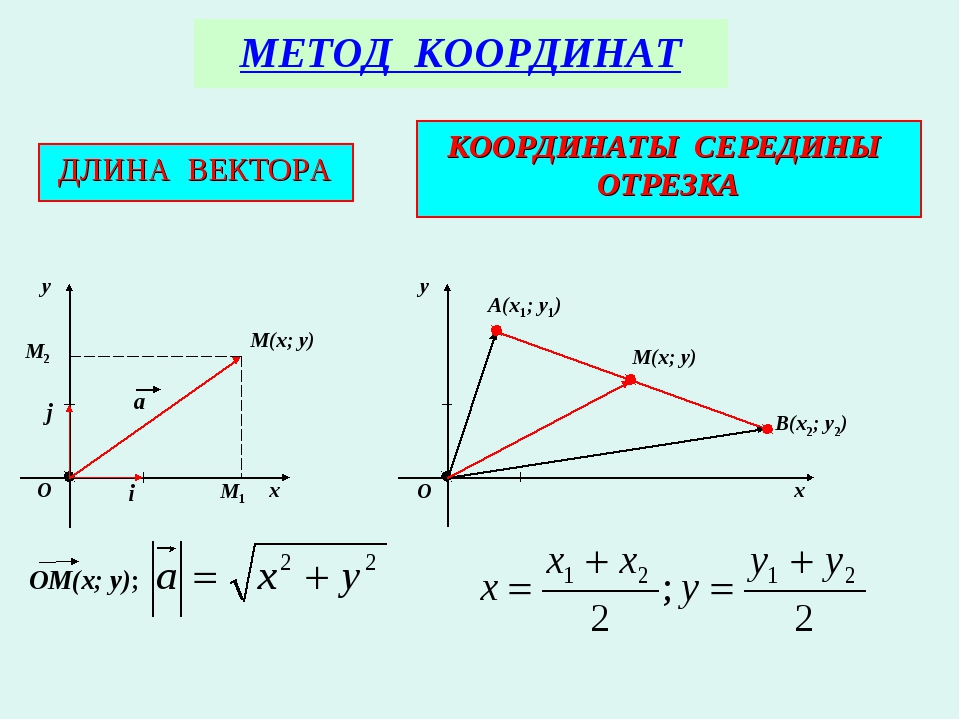
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1
;у 1
) и (х 2
;у 2
) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b
, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A
с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A
(6;8) относительно оси Ox
.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A
(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки
O
(0;0) и
A
(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A
(6;8) и B
(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O
(0;0) и A
(6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол
ВОА
в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу
ОА.
По теореме Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ
.
Найдите расстояние от точки A
с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A
с координатами (6;8) до начала координат.
Нахождение длины отрезка по координатам его концов. Нахождение координат середины отрезка: примеры, решения
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1.
Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами
x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами
этой точки.Пускай у вас сейчас есть две точки с координатами
x1,y1,z1 и x2,y2 и z2 соответственно.2))
Видео по теме
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти длину отрезка если известны координаты. Нахождение координат середины отрезка, примеры, решения
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Измерить отрезок — значит найти его длину. Длина отрезка
— это расстояние между его концами.
Измерение отрезков производится путём сравнения данного отрезка с другим отрезком, принятым за единицу измерения. Отрезок, принятый за единицу измерения, называется единичным отрезком
.
Если за единичный отрезок принят сантиметр, то для определения длины данного отрезка надо узнать, сколько раз в данном отрезке помещается сантиметр. В этом случае измерение удобно производить с помощью сантиметровой линейки.
Начертим отрезок AB
и измерим его длину. Приложим шкалу сантиметровой линейки к отрезку AB
так, чтобы её нулевая точка (0) совпала с точкой A
:
Если при этом окажется, что точка B
совпадает с некоторым делением шкалы — например, 5, то говорят: длина отрезка AB
равна 5 см, и пишут: AB
= 5 см.
Свойства измерения отрезков
Когда точка делит отрезок на две части (на два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.
Рассмотрим отрезок AB
:
Точка C
делит его на два отрезка: AC
и CB
. Мы видим, что AC
= 3 см, CB
= 4 см и AB
= 7 см. Таким образом, AC
+ CB
= AB
.
Любой отрезок имеет определённую длину, большую нуля.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Приведу подробный пример, как можно определить длину отрезка по заданным координатам, воспользовавшись сервисом онлайн на сайте Контрольная работа Ру.
Допустим, вам надо найти длину отрезка на плоскости
(в пространстве вы можете по-аналогии расчитывать, только надо изменить точку на размерность трёх)
Отрезок AB имеет концы с координатами A (1, 2) и B (3, 4).
Для того, чтобы вычислить длину отрезка AB воспользуйтесь следующими шагами:
1. Перейдите на страницу сервиса по нахождению расстояния между двумя точками онлайн:
Мы можем этим пользоваться, т.к. длина отрезка по коорд. как раз и равна расстоянию между точками A и B.
Чтобы задать правильную размерность точки A, то потяните за нижний правый край влево, как показано на рис.
После того, как ввели координаты первой точки A(1, 2), то нажмите на кнопку
3. На втором шаге вы увидите форму для ввода второй точки B, введите её координаты, как рис. ниже:
Точки a и b введены!
Решение:
| Даны точки a = | и b = |
Найдем расстояние между точками (s)
Отрезком
называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов
(x1; y1)
и
(x2; y2)
. На оси
X
и
Y
из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y
длина проекции равна y2-y1
, а на ось Х
длина проекции равна x2-x1
. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)²
. В данном случае |AB|
является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3)
и (2;5)
. Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5
. А это значит, что длина нашего отрезка равна 5:1/2
.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y)
исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1
.
Рассчитаем длину отрезка А
, для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²)
.
Если наш отрезок расположен между точками, координаты которых 2;4
и 4;1
, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61
.
Как найти координаты точки зная длину отрезка
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек – концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка – среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Как найти длину отрезка на координатной плоскости. Нахождение координат середины отрезка: примеры, решения
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком
.
Точка и отрезок − примеры геометрических фигур
.
Точки A
и B
называют концами отрезка
.
Существует единственный отрезок, концами которого являются точки A
и B.
Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5
обозначают одним из двух способов: AB
или BA.
Читают: «отрезок AB»
или «отрезок BA».
На рисунке 6
изображены три отрезка. Длина отрезка AB
равна 1
см. Он помещается в отрезке MN
ровно три раза, а в отрезке EF −
ровно 4
раза. Будем говорить, что длина отрезка
MN
равна 3
см, а длина отрезка EF −
4
см.
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN
и EF
мы измерили единичным отрезком
, длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины
, например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
.
Длина отрезка обладает следующим свойством.
Если на отрезке AB
отметить точку C,
то длина отрезка AB
равна сумме длин отрезков AC
и CB
(рис. 8
).
Пишут: AB = AC + CB.
На рисунке 9
изображены два отрезка AB
и CD.
Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB
и CD
равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB
называют расстоянием
между точками A
и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная
. Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E −
вершины ломаной
ABCDE,
точки A
и E −
концы ломаной
, а отрезки AB, BC, CD, DE −
ее звенья
(см. рис. 10
).
Длиной ломаной
называют сумму длин всех ее звеньев.
На рисунке 12
изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми
.
Пример 1
. Отрезок BC
на 3
см меньше отрезка AB,
длина которого равна 8
см (рис. 13
). Найдите длину отрезка AC.
Решение. Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13
см.
Пример 2
. Известно, что MK =
24
см, NP =
32
см, MP =
50
см (рис. 14
). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN =
50
− 32
= 18
(см).
Имеем: NK = MK − MN.
Отсюда NK =
24
− 18
= 6
(см).
Ответ: 6
см.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1
Определение 1
Отрезок
– прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка
– расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка
– точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа
x A и
x B . Точка C – середина отрезка A B: необходимо определить координату
x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и
B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов
A (x A , y A) и
B (x B , y B) определяются как
:
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Пример 1
Исходные данные:
на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ
: координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные:
известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ:
58
Пример 3
Исходные данные:
в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ:
координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1
;у 1
) и (х 2
;у 2
) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b
, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A
с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A
(6;8) относительно оси Ox
.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A
(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки
O
(0;0) и
A
(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A
(6;8) и B
(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O
(0;0) и A
(6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол
ВОА
в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу
ОА.
По теореме Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ
.
Найдите расстояние от точки A
с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A
с координатами (6;8) до начала координат.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1.
Разглядите для начала прямоугольную декартову систему координат.2))
Видео по теме
Калькулятор конечных точек
Добро пожаловать в калькулятор конечных точек Omni , где мы узнаем , как найти конечную точку сегмента линии , если мы знаем его другой конец и его среднюю точку. Как вы могли догадаться, эта тема связана с вычислением средней точки, и формула конечной точки очень похожа на вычисления, которые мы сделали там . Но прежде чем мы углубимся в детали, мы медленно рассмотрим определение конечной точки в геометрии, чтобы лучше понять, с чем мы здесь имеем дело.
Итак, сядьте поудобнее, заварите себе чашку чая в дорогу, и , давайте приступим. !
Определение конечной точки в геометрии
Говоря простым языком, конечная точка — это точка, которая находится на конце . Мы уверены, что это заявление было для вас таким же шоком, как и для нас, когда мы впервые его услышали. Но, с другой стороны, баклажан совсем не похож на яйца, так что вы никогда не будете слишком уверены, угадывая значение слова , не так ли?
Однако бывают случаи, например, когда вы делите пиццу на нескольких человек, когда вам нужно , немного точнее , и к кому еще мы можем обратиться для этого, если не к математикам ?
В своей простейшей форме определение конечной точки в геометрии фокусируется на линейных сегментах , т.е.е., прямые, соединяющие две точки. Ага, как вы уже догадались — эти точки называются конечными точками . Обратите внимание, что в соответствии с этим определением каждый сегмент имеет две конечные точки (если это не вырожденный случай, когда они являются одной и той же точкой, т.е. интервал является одной точкой).
Для простоты и расчетов мы назовем одну из них начальной точкой (как это сделано в калькуляторе конечных точек). Однако имейте в виду, что начало может быть и концом, если вы посмотрите на него с другой стороны .
Так вот, звучало жутко философски , вам не кажется? Но давайте оставим вопрос « Кто мы и куда мы идем?» вопросов, когда мы не можем заснуть. Нам следует сосредоточиться на упомянутых сегментах и на том, как найти конечные точки.
Как найти конечную точку ?
Чтобы получить конечную точку , нам для начала нужна некоторая точка отсчета . Другими словами, поскольку мы имеем дело с линейным сегментом и одним из его компонентов, , нам нужно знать, как выглядит остальная часть .
Самая простая и наиболее распространенная ситуация — когда нам не хватает конечной точки, хотя мы знаем начальную и среднюю точки . Последний — это просто, как следует из названия, точка, обозначающая середину сегмента. Это все, что нам нужно, чтобы найти конечную точку; в конце концов, он должен лежать на другом конце средней точки от начальной точки и находиться на таком же расстоянии.
Следовательно, интуитивно мы уже можем описать геометрически геометрически, как найти конечную точку .
- Учитывая начальную точку
Aи среднюю точкуB, , нарисуйте отрезок линии , который соединяет их. - Проведите линию , идущую дальше от
BотAк бог знает куда. - Измерьте расстояние от
AдоBи отметьте такое же расстояние отBв обратном направлении. Точка, которую вы отметили, — это конечная точка, которую вы ищете. - Выполните победный танец .
Однако есть люди (и мы не предполагаем, что мы именно такие), которым не очень нравится рисовать линии . В конце концов, для этого вам понадобится линейка, а Лорда трудно найти … (Да, это была ужасная шутка, и мы склоняем головы от стыда. Но все же с легким хихиканьем.)
В любом случае, для людей, которые предпочитают числа и вычисления (и мы могли бы предположить, что мы именно те люди), мы сосредоточимся на , как найти конечную точку алгебраически в следующем разделе.Пожалуйста, не бойтесь слова «алгебраически» — через секунду вы увидите, как оно переводится в « легко и без усилий » — , который является девизом нашего отсутствующего калькулятора конечных точек .
Формула конечной точки
В координатной геометрии мы обрабатываем объекты, встроенные в то, что мы называем евклидовым пространством . Сейчас не так важно понимать его математическое определение, но для наших целей достаточно знать, что это означает, что в таких пространствах, точки , скажем, A или B , имеют две координаты : A = (x₁, y₁) и B = (x₂, y₂) .
Цифры x₁ и x₂ обозначают положение точек относительно горизонтальной оси (обычно обозначается цифрами x ), а y70 и y₂ используются для вертикальной оси (чаще всего обозначается y ‘s). Вместе такая пара чисел (x₁, y₁) определяет точку в пространстве . Более того, координаты помогают нам анализировать более сложные объекты в нашем евклидовом пространстве .Например, они появляются в формуле конечной точки .
Допустим, у вас есть отрезок от A = (x₁, y₁) до … ну, мы еще не знаем. Теперь мы объясним , как найти конечную точку B = (x₂, y₂) , если мы знаем среднюю точку M = (x, y) .
Из определения средней точки мы знаем, что расстояние от A до M должно быть таким же, как и расстояние от M до B .Просто B с другой стороны. Это означает, что для нахождения B достаточно « переместить » M вдоль линии, проходящей через A и M на ту же длину, что и отрезок AM . Или, если хотите, можете использовать вектор AM .
Другими словами, у нас есть
x₂ = x + (x - x₁) = 2x - x₁ и
y₂ = y + (y - y₁) = 2y - y₁ .
Подводя итог, если вам нравится иметь всей необходимой информации в одном абзаце , то вот она.
💡 Конечная точка отрезка линии, идущего от A = (x₁, y₁) до средней точки M = (x, y) , является точкой B = (2x - x₁, 2y - y₁) . |
Обратите внимание, что выше мы упоминали линию, проходящую через A и M . Такие строки очень полезны, когда вы учитесь находить конечную точку или среднюю точку . В конце концов, сегмент AB содержится на этой строке. Если ваше упражнение или проблема требует дополнительной информации о них, обязательно ознакомьтесь с калькуляторами координатной геометрии Omni и найдите тот, который соответствует вашим потребностям. !
Уф, сколько времени было потрачено на теорию и формулы, тебе не кажется? Как насчет того, чтобы оставить эту техническую неразбериху и увидеть числовой пример ?
Пример: использование калькулятора конечных точек
Скажем, четыре месяца назад вы начали размещать видео на YouTube.Ничего особенного, просто несколько рецептов приготовления блюд, традиционных для вашего региона. Это началось как хобби, но, похоже, человека наслаждаются шоу , и вы видите, что количество зрителей линейно увеличивается со временем . Почему бы нам не попытаться найти недостающую конечную точку с помощью нашего калькулятора, чтобы проверить , сколько должно быть через четыре месяца?
Прежде всего, обратите внимание, что хотя проблема вовсе не кажется геометрической, мы действительно можем найти ответ, используя определение конечной точки из геометрии .В конце концов, отправной точкой, то есть нулевым месяцем, было время, когда вы начали публиковать видео, так что на тот момент у нас было 0 зрителей. Сейчас у нас четвертый месяц, и это будет наша середина (поскольку мы хотим узнать количество зрителей за следующие четыре месяца). Другими словами, конечная точка будет нашим ответом .
Допустим, что на данный момент, у вас 54000 подписчиков , и давайте попробуем перевести все эти данные таким образом, чтобы калькулятор конечных точек понимал, чего мы от него хотим.
Согласно приведенному выше разделу, чтобы найти ответ, нам нужна начальная точка и средняя точка . Обозначим их как A = (x₁, y₁) и M = (x, y) соответственно. Для нас x будет обозначать , количество месяцев в котором у нас , а y будет , количество зрителей . Поскольку нашей отправной точкой был нулевой месяц, а сейчас прошло 4 месяца, у нас есть (и мы можем ввести в калькулятор конечных точек)
x₁ = 0 ,
х = 4 .
Пришло время для абонентов . Опять же, отправной точкой было то время, когда у нас никого не было, а сейчас, по прошествии четырех месяцев, мы находимся на 54000 . Следовательно, имеем
y₁ = 0 ,
y = 54000 .
Как только мы введем все эти данные в калькулятор конечной точки, , он выдаст ответ . Но не будем пока это раскрывать! Как насчет того, чтобы увидеть , как найти конечную точку самостоятельно, используя формулу конечной точки ?
Давайте возьмем листок бумаги и вспомним информацию, о которой мы уже говорили выше.Наша отправная точка была в нулевом месяце с нулевым числом подписчиков , что означает, что наша отправная точка — A = (0, 0) . Сейчас , у нас четвертый месяц с 54000 подписчиками , что наполовину отличается от того, что мы хотели бы подсчитать. Это означает, что наша средняя точка — (4, 54,000) .
Все, что нам нужно сделать сейчас, это использовать формулу конечной точки из приведенного выше раздела. Если обозначить координаты конечной точки как B = (x₂, y₂) , то
x₂ = 2 * 4 - 0 = 8 ,
y₂ = 2 * 54 000 - 0 = 108 000 .3
Что такое отрезок линии в геометрии? — Определение, формула и пример — Видео и стенограмма урока
Формула для определения длины линейного сегмента
Если вы хотите найти длину линейного сегмента, вам нужно будет создать уравнение на основе информации, предоставленной вам в задаче.Можно использовать измерения для двух сегментов линии, чтобы найти длину третьего сегмента. Какова длина отрезка AC?
Уравнение будет следующим:
отрезок AB + отрезок BC = отрезок AC
5 + 3 = 8
Длина отрезка AC равна 8.
Отрезок прямой на декартовой плоскости
Линия сегменты также видны на графиках или декартовой плоскости .Вы можете определить длину линейного сегмента, посчитав единицы, которые покрывает линейный сегмент. Подсчет единиц на графике похож на подсчет количества блоков, пройденных между вашим домом и домом вашего друга.
Подсчитайте количество единиц между двумя конечными точками. На этом конкретном графике отрезок линии имеет длину 5 единиц.
Формула теоремы Пифагора
Вы можете найти длину диагональной линии, используя теорему Пифагора .
При нахождении длины отрезка в прямоугольном треугольнике вы можете использовать теорему Пифагора: квадрат плюс B в квадрате равен C в квадрате.
В этом примере при поиске длины линейного сегмента ST вы можете использовать длину линейных сегментов TU и SU.
Используя теорему Пифагора, мы можем увидеть, что 5 в квадрате плюс 7 в квадрате равняется 74. 5 в квадрате равно 25, а 7 в квадрате составляет 49. 25 плюс 49 равняется 74.Квадратный корень из 74 составляет примерно 8,6. Следовательно, длина сегмента ST составляет примерно 8,6 единицы.
Формула расстояния
Вы также можете использовать формулу расстояния , чтобы найти длину отрезка. Формулу расстояния можно использовать для определения длины отрезка ST. Найдите длину горизонтальной и вертикальной сторон, вычтя значения x и y. Затем выполните действия по теореме Пифагора, чтобы найти длину неизвестной стороны.
Не забудьте использовать точки на каждом конце отрезка, чтобы найти длину горизонтальной и вертикальной сторон.
Резюме урока
Таким образом, отрезок линии является частью линии с двумя отдельными конечными точками. Вы можете найти длину отрезка линии, решив уравнение, когда известна длина отрезка из двух отрезков. Длину линейных сегментов на декартовой плоскости можно найти, посчитав единицы, которые покрывает линейный сегмент.При работе с прямоугольным треугольником можно использовать теорему Пифагора и формулу расстояния , чтобы найти длину отрезка. Сегмент линии отличается от линии тем, что он не продолжается вечно.
Ключевые термины
отрезок линии: часть линии с двумя отдельными конечными точками
декартова плоскость: две перпендикулярные числовые линии, используемые для создания упорядоченных пар чисел
теорема Пифагора: уравнение, используемое с прямоугольным треугольником который утверждает, что квадрат гипотенузы равен сумме квадратов двух других сторон.
формула расстояния: выведено из теоремы Пифагора, уравнения, которое помогает найти расстояние между двумя точками.
Результаты обучения
После просмотра этого урока вы должны уметь делать следующее:
- Определить отрезок линии
- Определите расстояние между двумя точками
Что такое геометрия такси?
Если таксист остается на одной линии сетки, Есть еще названия City-Block- , Пример данной веб-страницы это глава в книге Мартина Гарднера (1). T-Line сегмент
Т-образный
Т-полигон
Если вы дадите третью точку C, это вопрос определения, В этом смысле существует также t-четырехугольник ADBC на этом рисунке со стороной 4. Следовательно, фигура также представляет собой t-16-угольник боковой длина 1, как ни странно. Т-образные квадраты?
Четырехугольник — это квадрат, когда все стороны равны и все углы 90 ° в евклидовой геометрии.
Другой выход на площадь дает уравнение | x | + | y | = 2 с D = | R.Вы можете передать его в такси геометрия легко. Вы испытаете на этом стр. что этот t-квадрат также является t-кругом. Это странно. T-Line верх
На т-образных линиях работать не стоит, т. Т-образный круг
Выписка передана к геометрии такси.
Это напоминает квадрат круг , где вы должны искать квадрат такой же площади, как есть круг. Если круг по центру в начале координат (0, 0), тогда уравнение будет x² + y² = r² в декартовой системе координат. В геометрии такси есть | x | + | y | = r.
Два круги
Есть еще корпуса с т-круги.
Т-эллипс
Расстояние b фокусов а постоянная сумма s определяет форму t-эллипса как обычный эллипс. Простая компьютерная программа обнаруживает, что числа двух
Пояснение: слева угловая точка есть уравнение s = 2x + b или s-b = 2x, или «s-b является четное число». Таким образом, s и b должны быть четными или нечетными одновременно. Диагональ должность Вы получите другие цифры, если очаги лежат по диагонали. Простая компьютерная программа обнаруживает, что цифры возникают, Как получить t-эллипс с помощью b = 6 и s = 10 1 Правая верхняя точка лежит на отрезке t-линии, проходящей через
Дополнение
Прогноз > Вы также можете использовать треугольник вместо квадрата. > Вы также можете дать трехмерное или многомерное Такси Немецкий Википедия Английский Бариль, Маргарита (MathWorld) Джим Уилсон Паскаль Тессон Роберт М.Дикау Демонстрационный проект Вольфрама Википедия Список литературы Отзыв: Адрес электронной почты на моей главной странице Это URL из © верх |
| A | B |
|---|---|
| Неопределенный термин | Базовая фигура, которая не определяется в терминах других фигур. |
| Коллинеарно | Точки, лежащие на одной линии. |
| Плоскость | Плоская поверхность, не имеющая толщины и бесконечно расширяющаяся. |
| Линия | Прямая траектория без толщины, продолжающаяся бесконечно. |
| Точка | Местоположение без размера. |
| Копланарный | Точки, лежащие в одной плоскости. |
| Конечная точка | Точка в конце сегмента или начальная точка луча. |
| Луч | Часть линии, которая начинается в конечной точке и продолжается бесконечно в одном направлении. |
| Постулат | Утверждение, которое без доказательства принимается как истинное, также называется аксиомой. |
| Вершина | Общая конечная точка сторон угла. |
| Противоположные лучи | Два луча, которые имеют общую конечную точку и образуют линию. |
| Сегмент | Часть линии, состоящая из двух конечных точек и всех точек между ними. |
| Расстояние | Абсолютное значение разности координат двух точек. |
| Конструкция | Метод создания фигуры, который считается математически точным. |
| Между | Для трех точек A, B и C, B находится между A и C тогда и только тогда, когда все три точки лежат на одной прямой и AB + BC = AC. |
| Координатная плоскость | Плоскость, которая разделена на четыре области горизонтальной линией, называемой осью x, и вертикальной линией, называемой осью y. |
| Координата | Число, используемое для определения местоположения точки. |
| Конгруэнтные сегменты | Два сегмента одинаковой длины. |
| Градус | Единица измерения угла. |
| Средняя точка | Точка, разделяющая сегмент на два конгруэнтных сегмента. |
| Bisect | Для разделения на две равные части. |
| Угол | Фигура, образованная двумя лучами с общей конечной точкой. |
| Измерение | Использование единиц измерения для определения размера или количества. |
| Биссектриса сегмента | Линия, луч или сегмент, которые делят сегмент на два конгруэнтных сегмента. |
| Вертикальные углы | Несмежные углы, образованные двумя пересекающимися линиями. |
| Прямой угол | Угол, образованный двумя противоположными лучами и составляющий 180 °. |
| Острый угол | Угол, который измеряется от 0 ° до 90 °. |
| Прямой угол | Угол размером 90 °. |
| Внутренняя часть угла | Совокупность всех точек между сторонами угла. |
| Тупой угол | Угол, который измеряется больше 90 ° и меньше 180 °. |
| Внешний вид угла | Набор всех точек вне угла. |
| Смежные углы | Два угла в одной плоскости с общей вершиной и общей стороной, но без общих внутренних точек. |
| Дополнительные углы | Два угла, сумма которых составляет 90 °. |
| Дополнительные углы | Два угла, сумма которых составляет 180 °. |
| Биссектриса угла | Луч, разделяющий угол на два равных угла. |
| Линейная пара | Пара смежных углов, чьи необычные стороны являются противоположными лучами. |
| Конгруэнтные углы | Углы одинаковой меры. |
| Изображение | Фигура, полученная в результате преобразования фигуры. |
| Прообраз | Исходная фигура в преобразовании. |
| Отражение | Преобразование по линии. |
| Преобразование | Изменение положения, размера или формы фигуры. |
| Вращение | Преобразование вокруг точки P, такое, что каждая точка и ее изображение находятся на одинаковом расстоянии от P. |
| Перемещение | Преобразование, при котором все точки фигуры перемещаются на одинаковое расстояние в в том же направлении. |
| ножка | Одна из двух сторон прямоугольного треугольника, образующих прямой угол. |
| Площадь | Количество неперекрывающихся единичных квадратов заданного размера, которые точно покрывают внутреннюю часть плоской фигуры. |
| Гипотенуза | Сторона, противоположная прямому углу в прямоугольном треугольнике. |
| Длина | Расстояние между двумя конечными точками сегмента. |
| основание | Любая сторона треугольника. |
| Высота | Фрагмент вершины, образующей прямой угол с линией, содержащей основание. |
| Радиус | Отрезок, конечными точками которого являются центр окружности и точка на окружности или расстояние от центра окружности до любой точки окружности. |
| Периметр | Сумма длин сторон замкнутой плоской фигуры. |
| pi | Отношение длины окружности к ее диаметру, обозначается греческой буквой π. |
| Окружность | Расстояние по окружности. |
| Диаметр | Сегмент, который проходит через центр окружности и концы которого находятся на окружности, или длина такого сегмента. |
Определения
Определения
Определения
1. точка — это упорядоченная пара реальных
числа.
2.Самолет — это комплект всего заказанного
пары действительных чисел.
3. Средняя точка между
(x 1 , y 1 ) и (x 2 , y 2 ) равно
4. Расстояние между
(x 1 , y 1 ) и (x 2 , y 2 ) равно
5. Уклон между (x 1 ,
y 1 ) и (x 2 , y 2 ) равно
6.Линия — это набор всех точек,
координаты — это решения линейного уравнения с двумя неизвестными.
7. Две прямые параллельны , если их
склоны такие же.
8. Две прямые перпендикулярны
если их наклоны противоположны друг другу.
9. Даны линия и точка, точка, в которой
линия, проходящая через данную точку, перпендикулярная данной прямой
пересекает данную линию, называется футов точки в
линия.
10. Окружность имеет центр и все
точки круга находятся на одинаковом расстоянии от центра. Этот
расстояние называется радиусом круга.
11. Хорда круга — это линия
отрезок, концы которого находятся на окружности.
12. Диаметр круга — это хорда, проходящая через центр круга.
13. Радиус круга — это отрезок прямой, идущий от центра круга к точке на окружности.
14. Линия, пересекающая круг точно в
одна точка называется касательной к окружности.
15. Если A, B и C — точки на
окружности, то угол ВАС называется вписанным углом .
16. Если O — центр круга и
B и C — точки на окружности, тогда угол BOC называется
центральный угол .
17. Параллелограмм — четверка.
двусторонняя фигура, где противоположные стороны параллельны.
18. Прямоугольник четырехсторонний
рисунок, где все четыре угла являются прямыми углами.
19. Ромб — четырехсторонняя фигура.
где все четыре стороны имеют одинаковую длину.
20. Тирангл — это равнобедренный
треугольник, если две его стороны имеют одинаковую длину.
21. Треугольник — это равносторонний
треугольник, если все три стороны имеют одинаковую длину.
22. медиана треугольника — это линия
отрезок от одного повернутого до середины противоположной стороны.
23. Высота треугольника равна
отрезок от одной вершины перпендикулярно противоположной стороне
24. Точка, где перпендикуляр
биссектрисы трех сторон треугольника пересекаются.
Центр окружности треугольника.
25. Круг, проходящий через все
три точки окружности называются описанной окружностью или
описанная окружность .
26. Точка, где три угла
биссектрисы треугольника называются центром внутреннего угла
треугольник.
27. Круг, к которому все три стороны
касательный треугольник называется вписанной окружностью или
вписанная окружность .
28. Точка, в которой три медианы
пересечение треугольника называется его центром тяжести или центром
Гравитация .
29.Точка, где три высоты
пересечения треугольника называется ортоцентром треугольника.
30. Линия Эйлера треугольника
проходит через центр окружности,
центроид, а
ортоцентр.
31. Круг из 9 точек с центром в
середина линии Эйлера и проходит через
середины трех сторон, ступни
высоты и середины отрезков прямых между
ортоцентр и вершины
треугольник.
32. правильный многоугольник — это один
где все стороны имеют одинаковую длину, а все углы равны
такого же размера.
33. Точка, где все
биссектрисы сходятся в правильный многоугольник, называется центр
многоугольника.
34. Отрезок от центра
Правильный многоугольник, перпендикулярный стороне, называется апофемой .
Использование Geogebra
В этой статье предлагаются советы и подсказки, которые помогут максимально эффективно использовать GeoGebra для решения геометрических задач.
GeoGebra — это программное обеспечение для динамической геометрии с множеством различных функций, и, поскольку оно имеет открытый исходный код, вы можете использовать его бесплатно. Возможно, вы захотите посетить этот веб-сайт и загрузить его, прежде чем читать остальную часть этой статьи. GeoGebra также встроен в различные проблемы на сайте NRICH, так что вы, возможно, уже использовали его, даже не осознавая!
Я часто использую GeoGebra, когда пытаюсь понять новую геометрическую проблему, и в этой статье я хотел бы поделиться некоторыми инструментами, которые я считаю полезными.Начнем очень просто, думая о точках и линиях. Ниже приведен апплет GeoGebra, который вы можете использовать для изучения, если вы еще не загрузили программное обеспечение для себя.
Точки и линии
Чтобы нарисовать точку, щелкните второй значок вместе (с синей буквой A), а затем щелкните страницу, где должна быть точка. Координаты вашей точки отображаются на панели алгебры сбоку. Если вы затем нажмете на инструмент перемещения (первый значок со стрелкой), вы можете перемещать точку.
GeoGebra пометит вашу первую точку A, вторую точку B и так далее. Если вы передумали относительно точки, вы можете удалить ее несколькими способами — выберите ее с помощью инструмента перемещения и нажмите «Удалить» или щелкните ее правой кнопкой мыши в графическом окне или на боковой панели алгебры и выберите «Удалить» в меню.
Вы также можете добавить новую точку с помощью панели ввода. Попробуйте ввести P = (0,2) на панели ввода. Новая точка, помеченная буквой P, должна появиться в точке с координатами (0,2).
После того, как вы нарисовали несколько точек, вы можете попробовать нарисовать несколько линий, используя третий значок на панели инструментов.Линия соединяет две точки. Попробуйте щелкнуть по двум точкам с помощью выбранного инструмента «Линия» и увидеть, как между ними появится прямая линия. После того, как вы нарисовали линию, ее уравнение появится на боковой панели алгебры.
Иногда бывает полезно нарисовать луч или отрезок линии, а не всю линию. Сегмент линии просто рисует отрезок между двумя выбранными вами точками, а луч начинается с одной точки, проходит через другую точку и продолжается дальше. Попробуй нарисовать все три. Обратите внимание, что когда вы рисуете линейный сегмент, его длина отображается на боковой панели алгебры.Это полезно, если вы хотите узнать
длины разных частей вашей диаграммы!
Параллель, перпендикуляр и многоугольники
Теперь мы можем рисовать точки и линии, давайте сделаем это немного интереснее! Апплет ниже имеет два новых элемента на панели инструментов. Первый имеет значок перпендикулярной линии. В меню есть много других специальных строк, которые вы можете построить; пока мы сосредоточимся только на первых двух, перпендикулярной и параллельной линиях.
Нарисуйте линию, а затем нарисуйте любую точку на линии или за ее пределами.Выберите инструмент «Перпендикулярная линия», затем щелкните свою линию и свою точку (в любом порядке). GeoGebra строит линию под прямым углом к вашей первой, проходя через выбранную вами точку! Кстати, если ваша диаграмма начинает немного загромождаться, но вы не хотите ничего удалять, вы всегда можете скрыть объект,
щелкнув правой кнопкой мыши и отменив выбор «показать объект», или переключив его на боковой панели алгебры.
После того, как вы попробовали нарисовать перпендикулярные линии, используйте инструмент параллельных линий, чтобы таким же образом нарисовать несколько параллельных линий.
Вы заметили другой новый инструмент? Это инструмент многоугольника, который полезен для рисования наборов отрезков прямых линий, из которых вы хотите образовать многоугольник. Просто выберите точки, которые вы хотите присоединить (или щелкните, чтобы создать новые точки), и когда вы закончите, снова щелкните первую точку, чтобы закрыть многоугольник. Обратите внимание, как площадь многоугольника отображается на боковой панели алгебры вместе с длиной каждого
сегмент. Перемещайте точки и наблюдайте, как изменяется площадь …
Если вы хотите нарисовать правильный многоугольник, выберите второй инструмент в меню многоугольника.На этот раз вам понадобится только одна длина стороны, чтобы указать многоугольник вместе с количеством сторон. Итак, выберите первые две точки, чтобы сформировать сторону, а затем введите желаемое количество сторон. Попробуйте нарисовать равносторонний треугольник, квадрат, правильный пятиугольник …
Вы могли заметить, что когда вы рисуете правильный многоугольник, некоторые вершины синие, а некоторые черные! Это потому, что в GeoGebra одни точки и линии зависят от других. Когда вы рисуете точку, она отображается синим цветом, и вы можете перемещать ее с помощью инструмента «Перемещение».Но точку, которая зависит от другого, нельзя поднять и переместить, она движется только вместе с объектом, от которого зависит. Эти точки выглядят как
чернить.
Вы также можете нарисовать точку, которая должна находиться на линии или в объекте, используя инструмент «Точка на объекте» на панели инструментов «Точки». Попробуйте построить точку внутри одного из ваших многоугольников. Когда вы пытаетесь переместить его за пределы формы, он останавливается на границе! Эти точки отображаются бледно-голубым цветом, чтобы показать, что они частично ограничены, но все еще могут быть перемещены.
Круги, измерения и преобразования
Когда мы создаем геометрию с помощью бумаги и карандаша, мы не просто используем прямые линии, у нас также есть циркуль, чтобы мы могли рисовать круги и дуги. В приведенном ниже апплете есть несколько дополнительных панелей инструментов. Попробуй нарисовать круг. Есть несколько вариантов: вы можете выбрать центр и точку на окружности, или вы можете выбрать центр, а затем указать радиус, или вы можете выбрать три точки на
длина окружности. Вы также можете просто нарисовать дугу или сектор.Почему бы не изучить нижеприведенный апплет?
После создания диаграммы вы можете узнать о некоторых измерениях. Следующий новый набор инструментов на панели инструментов включает несколько полезных инструментов измерения. Выберите инструмент измерения угла и щелкните две линии или три точки, чтобы измерить угол между ними. Вы можете использовать второй инструмент, чтобы нарисовать угол определенного размера. Также есть инструменты для измерения расстояний и площадей.
Третий новый набор инструментов позволяет выполнять некоторые отражения или вращения.Попробуйте нарисовать многоугольник и линию, а затем отразите ваш многоугольник в этой линии. Просто выберите инструмент «Отражение», щелкните объект, который вы хотите отразить, и линию, в которой вы хотите отразить. Изображение автоматически помечается точками, которые соответствуют объекту, поэтому, если ваш объект имеет точку, помеченную буквой A,
отраженному изображению соответствует точка A ‘.
Другие инструменты
Это лишь некоторые из инструментов, которые может предложить GeoGebra. Есть много других полезных функций, которые вы можете изучить и узнать о них.
Вот еще несколько функций, которые могут оказаться полезными:
Пересечение — отмечает точки пересечения двух объектов.
Середина / Центр — отмечает середину отрезка линии или центр круга.
Серединный перпендикуляр — рисует серединный перпендикуляр к отрезку прямой.
Биссектриса угла — рисует биссектрису угла.
Касательные — рисует касательную (и) к окружности, проходящей через заданную точку.
Ползунки — это объекты, которые определяют значение в диапазоне, чтобы вы могли создать диаграмму, которая изменяется в соответствии со значением, выбранным на ползунке.
