Урок 4. трапеция — Геометрия — 8 класс

Четырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.

CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.

∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK).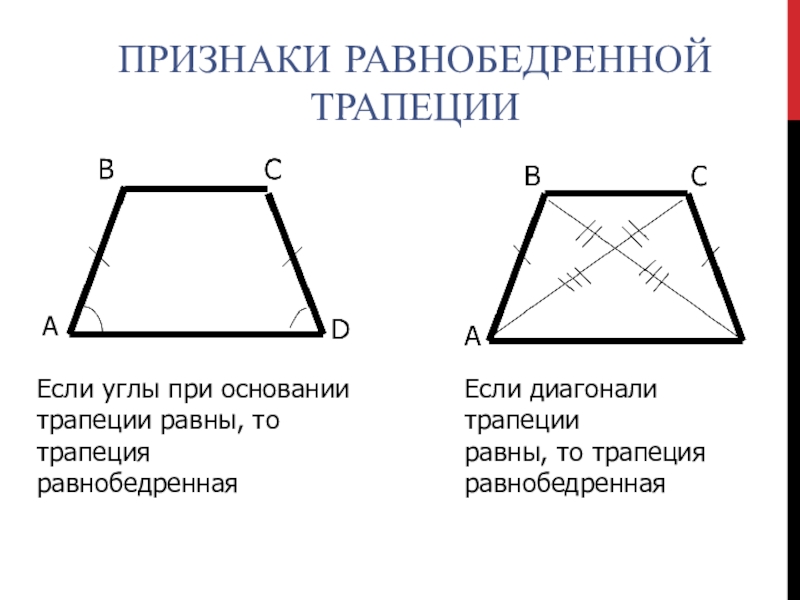 Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Второе свойство равнобедренной трапеции: диагонали равнобедренной трапеции равны.
Дано: ABCD – равнобедренная трапеция, BC || AD
Доказать: AC = BD.

Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция

Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK || AB, следовательно ABCK – параллелограмм, тогда AB = CK, ∠A = ∠CKD.
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция

Составим план доказательства второго признака, опираясь на который можно провести доказательство самостоятельно.
Проведем отрезок CK, параллельный BD.
План доказательства

1. CK || BD
2. Доказать, что BCKD – параллелограмм.
3. Доказать, что треугольник ACK – равнобедренный.
4. Найти равные углы.
5. Доказать равенство треугольников ABD и DCA.
6. Доказать равенство сторон AB и CD.
7. Сделать вывод.

Трапеция.

Определение, виды, свойства

Определения

Определение 1. Трапецией называется четырехугольник, у которого две стороны параллельны а две другие − нет.

На Рис.1 четырехугольники ABCD и EFGH являются трапециями.

Параллельные стороны трапеции называются основаниями трапеции, а непараллельные стороны − боковыми сторонами (Рис.2).

В трапеции ABCD (Рис.1) углы A и B называют углами при основании AB, а углы C и D называют углами при основании CD.

Определение 2. Высотой трапеции называется перпендикуляр, отпущенный из любой точки прямой, проходящей через один из оснований трапеции, на прямую, проходящую через другое основание.

На Рис.3 отрезки DM, ON, QP являются вершинами трапеции ABCD. Поскольку величина каждой из этих отрезков является расстоянием между параллельными прямыми, проходящими через основания трапеции, то они равны друг другу.

Определение 3. Средней линией трапеции называется отрезок, соединяющий средние точки боковых сторон.

На рисунке Рис.4 \( \small MN \) является средней линией трапеции \( \small ABCD, \) причем \( \small AM=MD,\;\; BN=NC. \)

Виды трапеций

Если боковые стороны трапеции равны, то трапеция называется равнобокой или равнобедренной (Рис.5).

Трапеция называется прямоугольной, если одна из боковых сторон перпендикуляна основаниям трапеции (Рис.6).

Трапеция называется разносторонней, если длина всех сторон разные (т.е. если трапеция не прямоульная и не равнобедренная)(Рис.7).

Свойства трапеции

Свойство 1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.

Доказательство. Пусть MN средняя линия трапеции ABCD (Рис.8). Докажем, что \( \small MN || AB, \)   \( \small MN=\frac12 (AB+CD). \)

Проведем прямую DN и обозначим точку ее пересечения с прямой AB точкой P. Так как MN является средней линией трапеции ABCD, то

Углы 1 и 2 вертикальные , следовательно

Углы 3 и 4 являются накрест лежащими, при рассмотрении параллельных прямых BP и CD пересеченные секущей CB, тогда (теорема 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей).

Исходя из равенств (1),(2) и (3) получим, что треугольники CND и NPC равны, по второму признаку равенства треугольников. Тогда BP = DC, DN = NP. Из равенств AM = MD и DN = NP следует, что MN является средней линией треугольника ADP. Тогда \( \small MN \ || \ AP \) ( или \( \small MN \ || \ AB \)) и \( \small MN =\frac 12 AP \). Но \( \small AP=AB +BP=AB+CD \). Тогда \( \small MN =\frac 12 (AB+CD).\)

Свойство 2. Сумма углов трапеции, прилежащих к одной боковой стороне равна 180°.

Доказательство. Рассмотрим трапецию ABCD (Рис.9).

Углы A и D являутся односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда \( \small \angle A+ \angle D=180°.\)

Свойство 3. Отрезок, слединяющий середины диагоналей трапеции лежит на средней линии трапеции и равен половине разности оснований.

Доказательство. Рассмотрим трапецию ABCD (Рис.10).

Поскольку точки P и Q являются средними точками диагоналей AC и BD, соответственно, то:

MP − является средней линией треугольника ADC, так как , . Тогда

QN − является средней линией треугольника BCD, так как , Тогда

Из и следует, что P находится на прямой, проходящей через среднюю линию MN, поскольку из точки M можно провести только одну прямую, параллельно CD (Аксиома 1 статьи Аксиома параллельных прямых).

Аналогично, из и следует, что Q находится на прямой, проходящей через среднюю линию MN, поскольку из точки N можно провести только одну прямую, параллельно CD.

Далее, учитывая (4) и (5), получим:

Откуда

Далее, учитывая свойство 1, получим:

Свойства равнобокой (равнобедренной) трапеции

Свойсво 1′. В равнобокой трапеции углы при каждом основании равны.

Доказательство. Рассмотрим равнобедренную (равнобокую) трапецию ABCD, где AD = BC (Рис.11).

Проведем высоты DM и CN. Поскольку DM = CN и AD = BC, то прямоугольники ADM и NCB равны гипотенузе и катету (см. статью Прямоугольный треугольник. Свойства, признаки равенства). Тогда \( \small \angle A=\angle B. \) Докажем, далее, что \( \small \angle ADC=\angle DCB. \) \( \small \angle A +\angle ADC=180° \) поскольку углы A и ADC являются односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle B +\angle DCB=180°. \) Учитывая, что \( \small \angle A=\angle B \), получим \( \small \angle ADC=\angle DCB. \)

Свойсво 2′. В равнобокой трапеции диагонали равны.

Доказательство.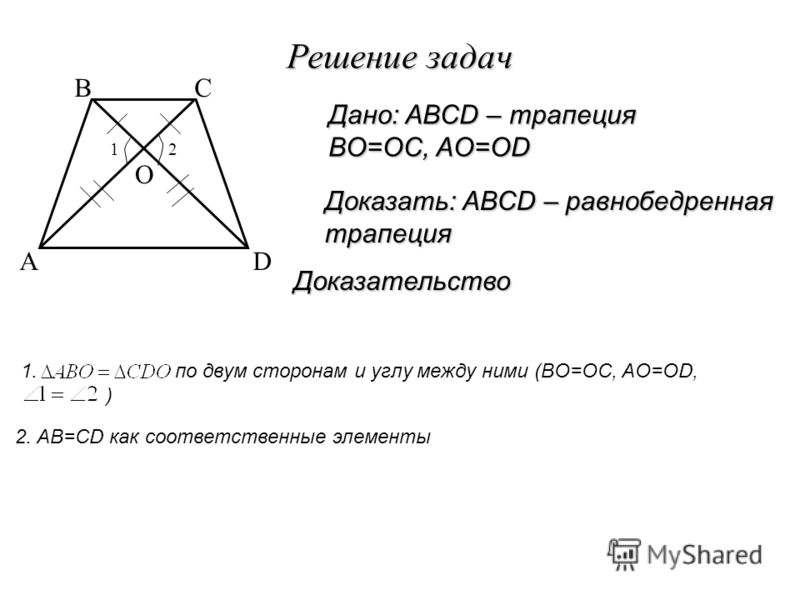 Рассмотрим треугольники ADC и DCB (Рис.12). Имеем CD общая сторона для обеих треугольников, AD = CB, \( \small \angle ADC=\angle DCB. \) Тогда треугольники равны по двум сторонам и углу между ними. Следовательно диагонали AC и DB трапеции ABCD равны.

Свойсво 3′. В равнобокой трапеции высота, приведенная из вершины тупого угла на основание, делит основание трапеции на отрезки, больший из которых равен половине суммы оснований, а меньший равен половине разности оснований.

Доказательство. Рассмотрим четырехугольник DMNC (Рис.11). Имеем:

Тогда четырехугольник DMNC является прямоугольником. Следовательно DC = MN. Поскольку треугольники ADM и NCB равны (см. доказательство следствия 1), то AM = NB. Следовательно:

Отсюда:

Далее

или

Равновеликие треугольники в трапеции доказательство.  Трапеция. Свойства и элементы трапеции. Теоремы: признаки равнобедренной трапеции

Описанная окружность и трапеция.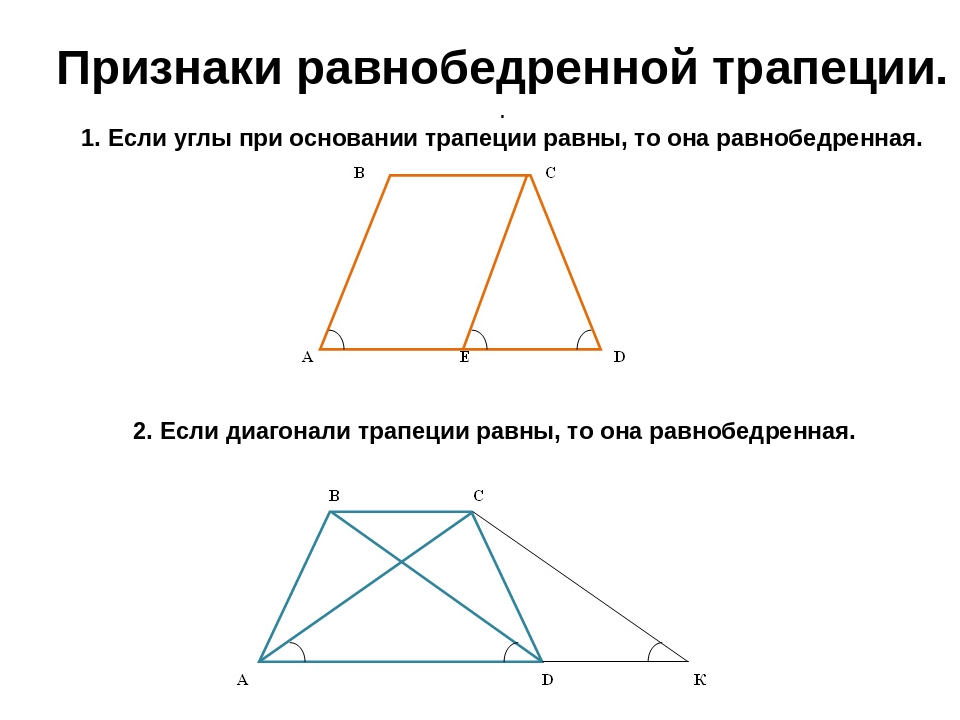 Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Вписанные и описанные трапеции

Другими словами, учебники — это более быстрый момент для исправления: в стране насчитывается менее десятка крупных титулов, в отличие от тысяч учителей в стране. Мы должны убедиться, что эти глубокие концептуальные ошибки в учебниках сведены к минимуму, если не устранить.

Трапеция представляет собой четырехугольник, который имеет две параллельные стороны, а два других — нет, а сумма его углов равна 360º. На рисунке выше вы заметите, что две стороны параллельны, а две другие стороны могут рассматриваться как параллельные или расходящиеся.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь

.

27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Параллельные стороны называются основаниями трапеции, а расстояние между ними — это высота. Ответ: параллелограмм представляет собой многоугольник из четырех параллельных сторон два на два. Трапеция также представляет собой многоугольник из четырех сторон, но с 4 сторон, два — только параллельные.

Ответ: Да, потому что они имеют все 4 стороны и, кроме того, две-две параллели. Мы говорили, что трапеция имеет большую базу и небольшую, чтобы решить проблему, из которой они взяты? Базовое значение представляет собой среднее значение двух значений. В качестве основной базы ценность базы этой трапеции — полусумма обоих, то есть. Трапеция, которая имеет непараллельные стороны, равна равнобедренной трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Теоремы: свойства трапеции

Стороны и равны, следовательно, равнобедренная трапеция. Диагонали равнобедренной трапеции одинаковы. и те же. Это тот, который имеет два угла 90º. Как вы можете видеть, непараллельная сторона перпендикулярна и, следовательно, имеет два прямых угла. Диагонали разные и не перпендикулярны.

Ответ: Каждая трапеция представляет собой четырехугольник, но это не параллелограмм, потому что у него нет параллельных сторон от двух до двух. Он имеет только две параллели с четырех сторон. Прежде чем вы начнете их изучать, вы должны четко понимать концепцию симметрии.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6.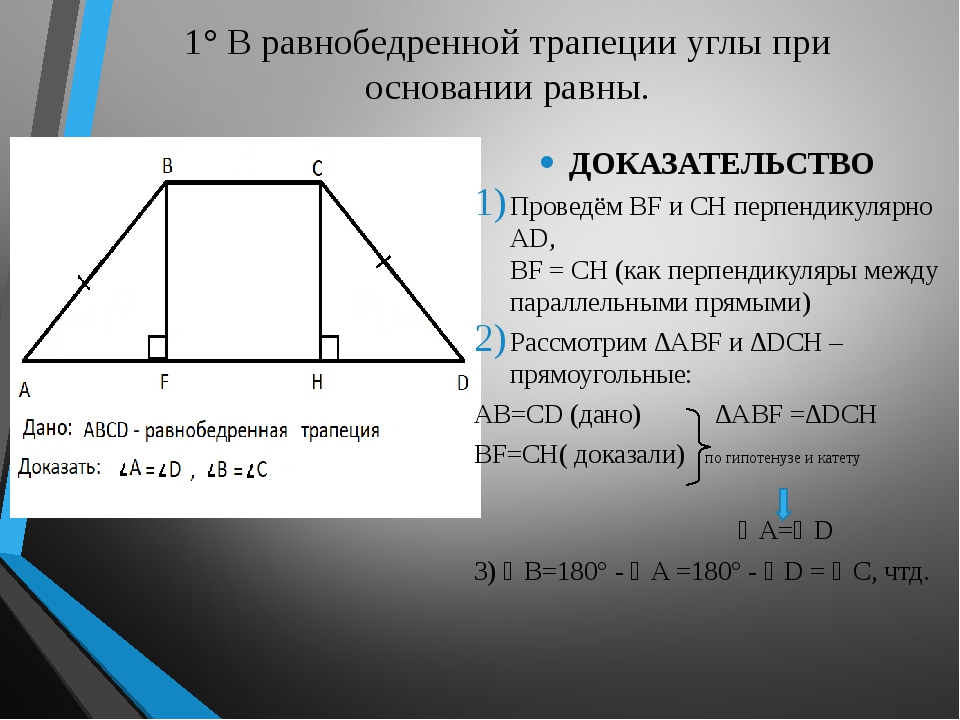 Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

Свойство диагоналей равнобедренной трапеции

Симметрия слова исходит из греческого син, означающего в то же время, и от слова метрона, означающего измерение. Мы нарисуем красную половину бабочки, которая у вас внизу. Две половины бабочки симметричны, то есть две половины имеют те же самые меры. Если эта бабочка с красной линией, которую мы называем осью симметрии, у вас она была в бумаге, а в двойнике — осью или красной линией, вы бы точно это увидели.

Если мы прорубим ось симметрии и удалим обе половины, мы увидим. Есть некоторые, которые говорят, что две половины одинаковы, другие идентичны. Истина заключается в том, что одинаковые и идентичные становятся одинаковыми, но эти две половины должны сказать, что они симметричны относительно оси, то есть оси симметрии.

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

Мы не говорим, что эти две половины бабочки одинаковы, хотя, хотя размеры и формы равны, однако их положение на плоскости не одно и то же, это наоборот. Чтобы узнать, совпадают ли два куска картона, вы ставите один поверх другого, и если они совпадают во всех своих точках, мы скажем, что они одинаковы. Если каждая из двух половинок бабочки помещает один поверх другого, правда в том, что они совсем не совпадают.

Диагональ равнобедренной трапеции

Давайте посмотрим на следующий рисунок, который очень легко рисовать, просто линейка и ручка. Это примерно половина простого обелиска. Чтобы закончить, нам нужна другая половина, нам не хватает ее симметричности, а именно. Если обе стороны расположены друг напротив друга.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Мы приближаемся к ним, и по точкам объединения двух половин мы рисуем красную линию, которую мы оставили. Если этот рисунок был на листе бумаги, вы увидите, что при складывании листа по красной линии или оси симметрии линии с одной стороны соответствуют тем, что расположены на другой стороне.

Геометрический элемент имеет только положение, не имеет размеров, длины, ширины или толщины. Точка может быть графически представлена ​​падением. Помните, что представления представляют точку, но дело не в этом, так как точка на карте может представлять город, но это не город. Точки обычно обозначаются или идентифицируются столичной латинской буквой на стороне.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам.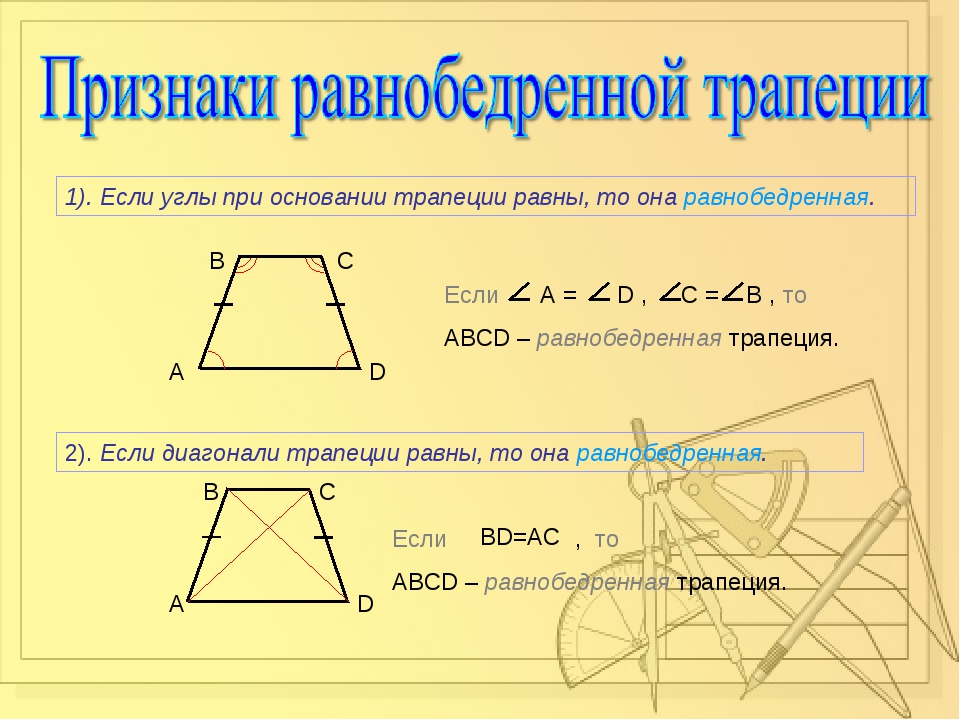 Покажем это на эскизе, также соединим центр с вершинами:

Положение линий в пространстве определяет их ориентацию: горизонтальную, вертикальную или наклонную. Параллельные линии — это прямые линии, которые, как бы долго они ни были, никогда не встречались, сохраняли одинаковое расстояние и никогда не пересекались. представляют собой две или более эквидистантные линии по всей длине.

Угол — это встреча двух прямых сегментов, ориентированных от общей точки. Пересечение между двумя сегментами называется вершиной угла, а стороны угла — двумя отрезками. Два угла являются последовательными, если одна сторона одного из них совпадает с одной стороной другого угла.

Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Два соседних угла смежны, если у них нет общих внутренних точек. Эти линии определяют четыре угла. Углы, которые не смежны, противоположны вершине. Мы говорим, что два угла конгруэнтны, если они накладываются друг на друга, все их элементы совпадают. Два противоположных угла вершины всегда конгруэнтны.

Конгруэнтные углы имеют равные измерения и наоборот углы, которые имеют равные измерения, являются конгруэнтными. Из двух указанных углов мы можем получить третий угол, измерение которого соответствует сумме измерений заданных углов. Единицей измерения угла в Международной системе является радиан.

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями.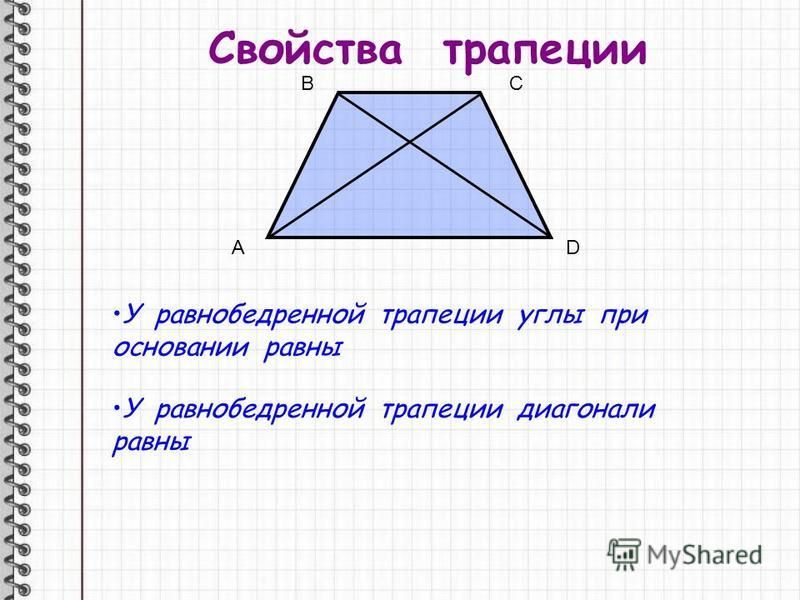

Диагонали и стороны трапеции

Угол в 360 градусов — это угол, который завершает круг. После этого полного оборота этот угол совпадает с углом нуля градусов, но имеет величину 360 градусов. Чтобы получить приблизительную меру угла, нанесенного на бумагу, мы используем инструмент, называемый транспортиром, который содержит отрезок прямой в его основании, представляет собой полукруг сверху, обозначенный единицами от 0 до.

Заметные элементы и стороны многоугольника, углы, вершины и диагонали. Регулярный многоугольник имеет равные стороны и углы. Четырехугольник многоугольник имеет четыре стороны, четыре вершины, четыре угла и две диагонали. Они четырехугольники: параллелограммы, трапеции и трапеция — четырехугольник, который имеет две параллельные стороны, которые являются основой трапеции.

Раздел 2. Четырехугольники

I
.
Справочные материалы.

1.
Трапеция, ее виды и свойства

Свойства
трапеции, которые часто используются
при решении задач:

1)
Диагонали трапеции разбивают её на
четыре треугольника с общей вершиной.
Площади треугольников, прилежащие к
боковым сторонам, равны.

2) В
любой трапеции середины оснований,
точка пересечения диагоналей и точка
пересечения прямых, на которой лежат
боковые стороны, лежат на одной прямой
(точки М, N, О и К).

Параллелограмм представляет собой четырехугольник, противоположные стороны которого параллельны и конгруэнтны, а противоположные углы также конгруэнтны. Это параллелограммы: квадрат, прямоугольник, ромб и собственно параллелограмм. Трапеция: четырехугольник, который имеет две параллельные стороны, которые являются основой трапеции.

Теорема: свойство произвольной трапеции

Пентагон: многоугольник с пятью вершинами, пятью сторонами и пятью углами. Треугольник и многоугольник трех сторон, три угла и три вершины. Геометрический треугольник рисования равносторонний. Равносторонний треугольник — имеет три конгруэнтные стороны.

3) В
равнобокой трапеции углы при основании
равны.

4) В
равнобокой трапеции прямая, проходящая
через середины оснований, перпендикулярна
основаниям и является осью симметрии
этой трапеции,

Мы называем треугольник объединением отрезков, образованных ими.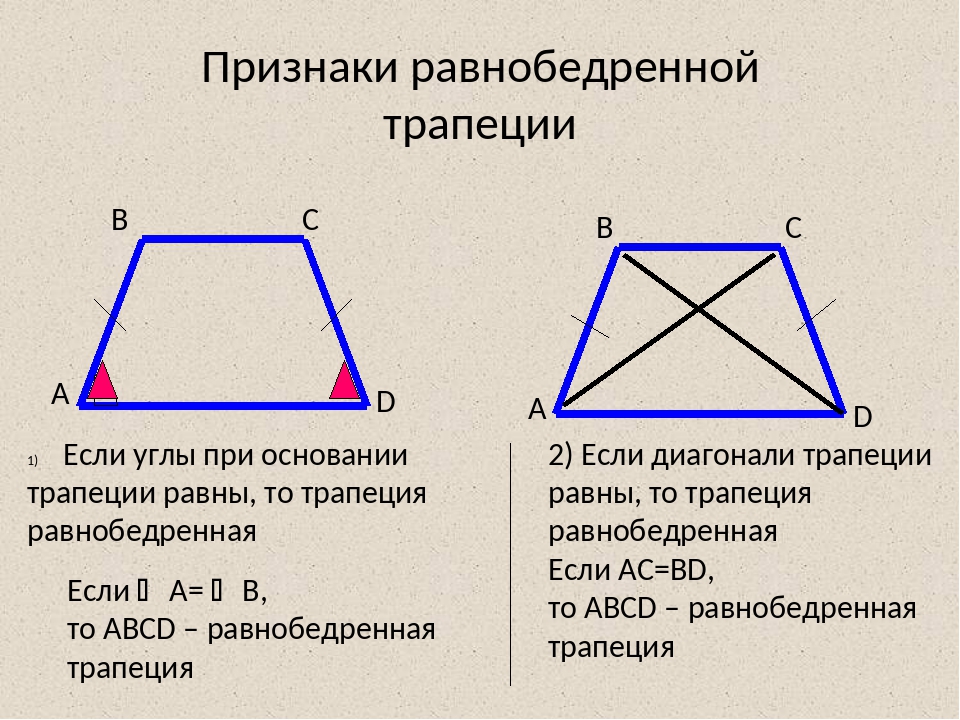 точек. Внешний угол — это сумма несмежных интерьеров. Равнобедренные: две стороны с равными мерами. Скалайн: не имеет сторон с равными мерами. В каждом треугольнике большая сторона выступает против большего угла.

Если угол вершины А равен 80 °, мера θ обозначенного угла равна. Большой угол треугольника. у нас есть: Периметр:! Архитектор. 4√2 км 3 км. Полученный сегмент параллелен третьей стороне и измеряется его половиной. то. Теорема Объединяя середины двух сторон любого треугольника.

5) В
равнобокой трапеции диагонали равны.

6) В
равнобокой трапеции высота, опущенная
на большее основание из конца меньшего
основания, делит его на два отрезка,
один из которых равен полуразности
оснований, а другой их полусумме.

Каждый выпуклый четырехугольник, имеющий противоположные конгруэнтные углы, является параллелограммом. Диагонали конгруэнтны и разрезаны пополам и конгруэнтны. Диагональ алмаза не является конгруэнтным. Диагонали находятся под углами внутренних углов.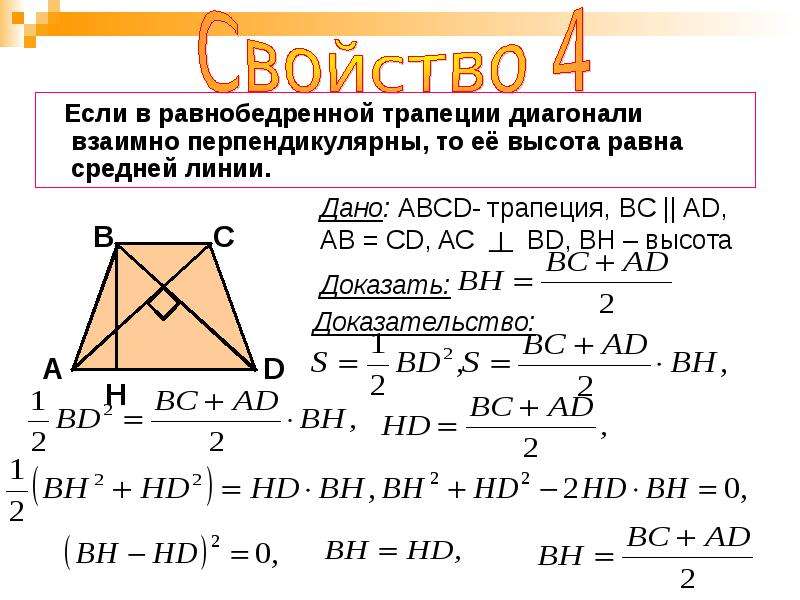 находятся в биссектрисах внутренних углов.

Средняя Линия Треугольника

Рассматривая множества параллелограммов. Каждый квадрат — как ромб, так и прямоугольник. Можно сказать, что: три прямоугольника имеют одинаковую площадь. Соотношение между количеством мужчин и женщин в промышленном подразделении составляет 7 для показанного рисунка. Будем изучать выпуклые многоугольники.

7) Во
всякой трапеции серединам боковых
сторон и середины диагоналей лежат на
одной прямой.

8) Во
всякой трапеции отрезок, соединяющий
середины диагоналей, параллелен
основаниям и равен полуразности
оснований.

Многоугольники получают различные наименования. Круг — это объединение окружности с ее внутренностью. Вычислите радиус этого круга. от высоты относительно наименьшей стороны € √. Фернандо. В 650 метрах от точки, где находится Фернандо. по прямой. в 350 метрах от отеля. Есть только один момент, когда вы можете одновременно слышать как Фернандо, так и Бруно. Жоао Гильерме и Бруно проиграли.

Фернандо достаточно кричит, что его можно услышать где угодно до 250 метров от того места, где он находится. также по прямой. Расстояние. Площадь треугольника равна 8 см². Таким образом. Ниже мы приводим краткое резюме и несколько упражнений с использованием теоремы Пифагора.

9) во
всякой трапеции сумма квадратов
диагоналей равна сумме квадратов боковых
сторон и удвоенного произведения
оснований.

10)
Трапецию можно вписать в окружность
тогда и только тогда, когда она равнобокая.

11)
Трапецию можно описать около окружности
тогда и только тогда, когда сумма
оснований равна сумме боковых сторон.

Наша цель в этой статье — показать применимость теоремы, ее важность в конструкциях посредством нескольких упражнений, которые решаются шаг за шагом. Отметим также, что из-за его важности теорема сильно заряжена в различных конкурсах. Итак, наслаждайтесь этой статьей, чтобы попрактиковаться и принять ваши сомнения.

Свойства средней линии трапеции

Теорема Пифагора; — Приложения; — Упражнения решены и многое другое. Утверждение теоремы Пифагора. В каждом прямоугольнике треугольника квадрат меры гипотенузы равен сумме квадратов мер ног. Бедра — это стороны правого угла, так как гипотенуза — это сегмент «спереди» под прямым углом.

2.Вписанные
и
o
писанные
четырёхугольники.

1)Если
четырёхугольник вписан в окружность,
то сумма противолежащих углов равна
180°.

Верно
и обратное: если сумма противолежащих
углов четырёхугольника равна 180°, то
около этого четырёхугольника можно
описать окружность.

2)Около
параллелограмма можно описать окружность
тогда и только тогда, когда этот
параллелограмм есть прямоугольник.

Это было краткое резюме по теореме Пифагора, существует гораздо больше теории на эту тему. Но теперь давайте применим то, что было представлено выше в вопросах конкуренции, этого достаточно для нашей цели. Заявления ниже, а затем резолюции. Мильор Фернандес, в прекрасном уважении к математике, написал стихотворение, из которого мы извлекаем фрагмент ниже.

На многие листы книги математики. Инкогнитой. Он посмотрел на нее своим бесчисленным взглядом и увидел ее от вершины до основания: странная фигура. ромбовидные глаза, трапециевидный рот, прямоугольное тело, синусы сфероида. Он сделал свою жизнь параллельной ей, пока они не встретились в Бесконечном. «Кто ты?» — спросил он с сильным рвением. Я — сумма квадратов хиксов. Инкогнита ошибалась, чтобы сказать, кто она. Чтобы соответствовать теореме Пифагора, она должна дать следующее. ответ.

3)Около
трапеции можно описать окружность, если
она равнобокая.

четырёхугольник
называется описанным около окружности,
если окружность касается всех его
сторон.

4)Если
четырёхугольник описан около окружности,
то суммы противолежащих сторон равны.

5)Если
в выпуклом четырёхугольнике суммы
противоположных сторон равны, то в этот
четырёхугольник можно вписать окружность.

3. Площади
четырёхугольников.

Площадь
выпуклого четырёхугольника равна
половине произведения диагоналей на
синус угла между ними.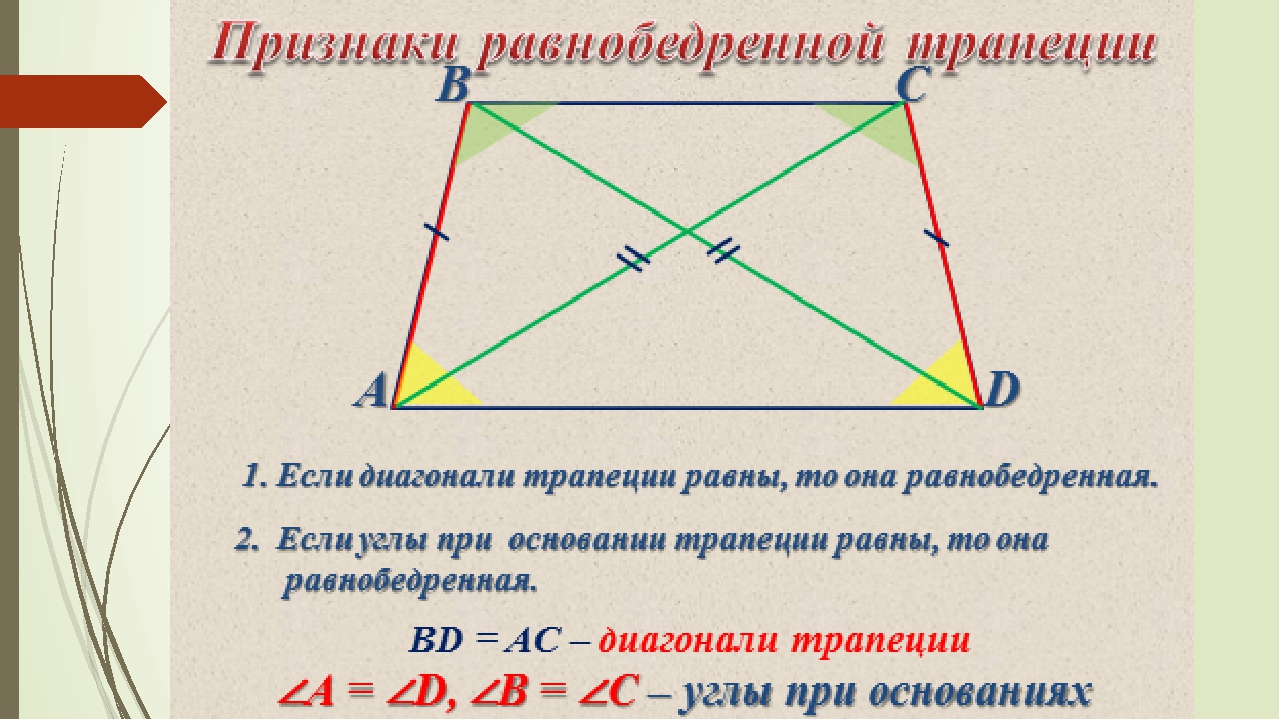

Ромб

1.
Диагонали ромба взаимно перпендикулярны
и делят углы пополам.

2.
Площадь определяется формулами:

Параллелограмм

1.
Сумма квадратов диагоналей равна сумме
квадратов всех его сторон.

2. Площадь
определяется формулой

II
.
Дополнительные материалы

1)Свойства
вписанного выпуклого четырехугольника
.

а)В
выпуклом вписанном четырехугольнике
сумма противоположных углов равна двум
прямым

б)Обратно:
если в выпуклом четырехугольнике сумма
противоположных углов равна двум прямым,
то около него можно описать окружность

Доказательство.

а)
Пусть АВСD есть вписанный выпуклый
четырехугольник; требуется доказать„
что

Так как
сумма всех четырех углов сякого выпуклого
четырехугольника равна 4d,
то достаточно доказать только одно из
требуемых равенств.

докажем,
например, что

Углы В
и D как вписанные, измеряются:
первый-половиной дуги ADC,
второй- половиной дуги АВС;

Следовательно,
сумма

б) Пусть
АВСD есть такой выпуклый
четырехугольник, у которого

Через
какие-нибудь три его вершины, например,
через A,В и С, проведем
окружность (что всегда можно сделать).

Четвертая
вершина D должна находиться
на этой окружности, пoтoму
что в противном случае вершина угла В
лежала бы или внутри круга, или вне его,
и тогда этот угол не измерялся бы
половиной дуги АВС; поэтому cyммa
измерялась
бы полусуммой дуг ADC и АВС
и, значит, сумма Следствия

1) из
всех параллелограммов только вокруг
прямоугольника можно описать окружность.

2) около
трапеции можно описать окружность
только тогда, когда она равнобокая.

2)
Свойство описанного четырехугольника.

В описанном четырехугольнике суммы
противоположных сторон равны.

Пусть
АВСD будет описанный
четырехугольник, Т.е, стороны его касаются
окружности; требуется доказать, что
АВ+СВ=ВС+АD

Обозначим
точки касания буквами M,
N, Р и Q. Так
как две касательные, проведенные из
одной точки окружности, равны, то АМ.=АQ,
ВМ=ВN, CN=СР, DP=DQ.

Следовательно,
АМ+МВ+СР+РD=AQ+QD+BN+NC.
Т.е. АВ+СD=АD+ВС.

III
. Вводные задачи.

Задача 1.

Средняя линия трапеции ABCD
равна 15.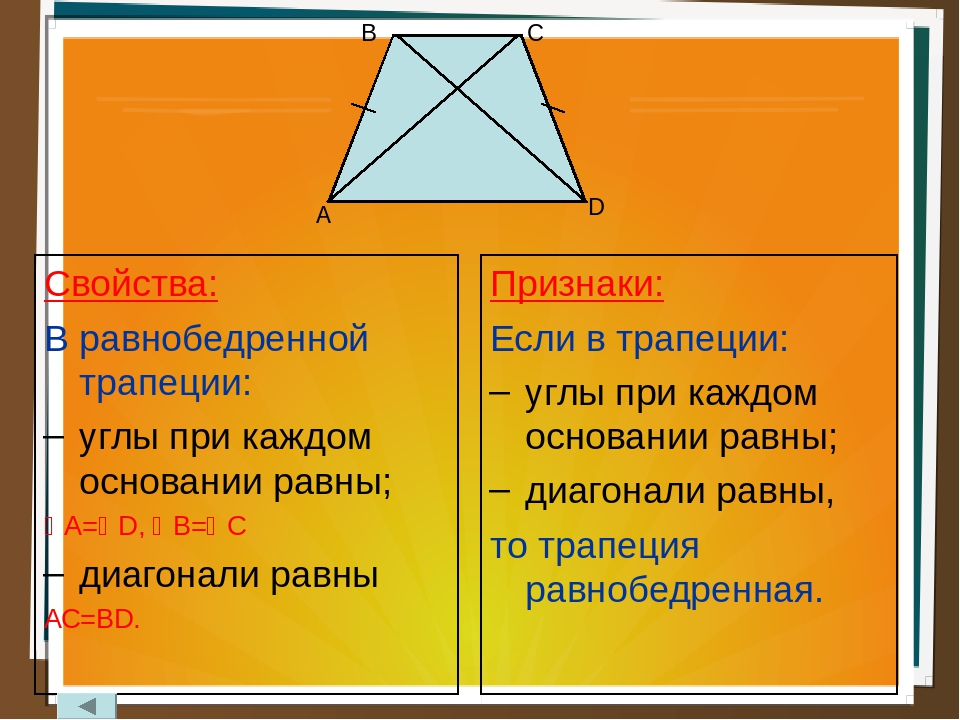
AD
– большее основание трапеции,
A

= 90°,
D

= 60°,
BAC

= 30°. Найдите длину стороны CD
.

В
∆ABC
(он прямоугольный) BC
=
– по свойству катета, лежащего против
угла в 30°.

BAC

= 30°, значит,
CAD
= 90° – 30° =
= 60°, следовательно, ∆ACD

равносторонний,
т. е. AC
= CD
= AD

= 2BC
.

Средняя линия MN
=
3BC
= 30,

BC
= 10, значит,
CD
= 2 · 10 = 20.

Ответ:
20.

Задача
2
.

Сторона AB
параллелограмма ABCD

равна а его диагонали равны 20 и
24. Найдите сторону BC
.

Для
любого выпуклого четырехугольника
справедливо

где
a
, b
, c
и d
– стороны
четырехугольника, а d
1 , d
2
– его диагонали.

В
параллелограмме

20 2 + 24 2 = 2(() 2
+ b
2), b
> 0; b
2 + 88 =
488,b
2 = 400, b
= 20.

Задача
3
.

Основания трапеции равны 4 и 10, а ее
боковые стороны – и 15. Найдите
косинус наименьшего угла этой трапеции.

1)
Проведем BM
∥
CD
, значит,
BMA

=D
,
ВСDМ
– параллелограмм, так как ВМ

|| MD
, ВМ
|| СD
. Следовательно,
ВС
= MD
= 4,
BM
= CD
= 15, AM

= AD
– MD
= 10 – 4 = 6.

2) В ∆AMB
против большей стороны
(выбирая из AB
и BM
) лежит больший
угол: AB
BM, значит,
BMA

A
.

Ответ: 0,8.

Задача 4.

Определите периметр равнобокой трапеции,
у которой длина меньшего основания
равна 7, диагонали перпендикулярны
боковым сторонам и равны
.

1)
Проведем в трапеции ABCD
высоту
CF
,
тогда

∆ACD
∼ ∆AFC
,

2) Пусть FD
= x
, тогда AF
= 7 + x

() 2 = (x
+ 7) (7 + 2x
),

36 · 2 = 49 + 21x
+ 2x
2 ,

2x
2 + 21x
– 23 = 0,

D
= 21 2 + 4 · 2 · 23 = 625,

х
1,2 =

3) Итак, AD
= 7 +2 = 9;

P
= 9 + 7 + 2 · 3 = 22.

Ответ:
22.

Задача 5.

В ромбе высота, проведенная из вершины
тупого угла, делит сторону ромба пополам.
Найдите периметр и высоту ромба, если
меньшая диагональ его равна 7

1)
В треугольнике ABD
BK
– высота и
медиана, значит, ∆ABD
-равнобедренный
с основанием AD
, т. е. AB
= BD
= 7
см. Тогда ∆ABD
-равносторонний, значит,
A

=
ABD

=
BDA

= 60°.

2) P
= 4AB
= 4 · 7 = 28 (см).

3)
BKD

– прямоугольный, BK
= AD
sin
BDK
.

BK
= 7 · sin 60° = (см). Ответ:

28 см; 3,5 см.

Задача 6.

Основание AB
трапеции ABCD
вдвое
длиннее основания CD
и вдвое длиннее
боковой стороны AD
. Длина диагонали
AC
равна 12, длина боковой стороны BC

равна 5. Найдите площадь трапеции.

1)
По условию AB
= 2AD
= 2DC
.

Пусть
M
– середина AB
, тогда AM
= MB

= CM
,
т.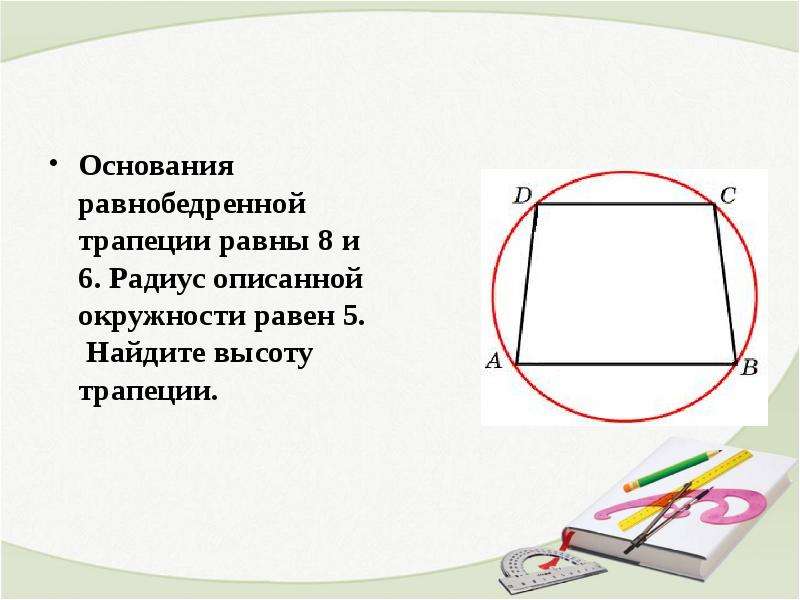 е. CM
– медиана треугольника
ABC
и CM
= AB
, значит, ∆ABC

прямоугольный с гипотенузой AB
.Вершина C параллелограмма
ABCD соединена с точкой N
на стороне AB. Отрезок CN
пересекает диагональ BD
в точке P. Площадь
треугольника BNP равна 8,
а площадь треугольника BCP
равна 12. Найдите площадь параллелограмма
ABCD.

1)
Треугольники BNP и BPC
имеют общую высоту BH=>

SBNP/SBPC=PN/PC=>PN/NC=2/3;

2)
Треугольники BPN и DPC
подобны по

двум
углам => SBPN/SDPC=(PN/PC) 2

SDPC=9/4;
SBPN
= (9/4)·8=18;

3)
SBCD=SBPC+SDPC=12+18=30;

4)
SABCD=2·SBCD=60;
Ответ: 60

На стороне AB параллелограмма
ABCD, как на диаметре,
построена окружность, проходящая через
точку пересечения диагоналей и середину
стороны AD. Найдите углы
параллелограмма.

Р

ешение:

1) По
условию, AB – диагональ=>
ABCD – ромб

P – середина АВ: по условию
Q – середина AD=>PQ
– средняя линия ∆ABD=BD=2PQ;PQ=R=>BD=2R;

PO=R – средняя
линия ∆АBD=>AD=2·PO=R

∆ABD – правильный =>

Ответ:
60 o и 120 o .

Угол между сторонами АВ и СD четырехугольника
ABCD=φ. Докажите, что AD 2 =AB 2 +BC 2 +CD 2 -2(AB·BCcosB
+ BC·CDcosC+CD·ABcosφ)

По
теореме косинусов AD 2 =AC 2 +CD 2 -2AC·CD·cosACD
и AC 2 =AB 2 +BC 2 -2AB·BCcosB. A
так как длина проекции отрезка АС на
прямую l
, перпендикулярную CD, равна
сумме длин проекций отрезков АВ и ВС на
прямую l, то ACcosACD=ABcosφ+BCcosC

V

.Задачи для
самостоятельного решения

№1. Докажите, что если ABCD прямоугольник,
а Р- произвольная точка, то

АР 2 +СР 2 =DP 2 +BP 2

№2. Перпендикуляр, опущенный из вершины
параллелограмма на диагональ, делит
ее на отрезки длиной 6 и 15. Найдите
большую сторону параллелограмма, если
известно, что разность сторон равна 7.

№3. Одно из оснований трапеции равно
24, а расстояние между серединами
диагоналей 4. найдите другое основание.

№4. Длины оснований равнобедренной
трапеции относятся как 5:12, а длина ее
высоты равна 17. Найдите радиус окружности,
описанной около трапеции, если средняя
линия равна высоте.

№5. В трапеции ABCD диагональ АС
перпендикулярна боковой стороне СD.
Окружность, описанная возле треугольника
АВС, касается прямой CD, пересекает
основание AD в точке М. Найдите площадь
трапеции АBCD, если АМ=8, СМ=4.

№6. Окружность, центр которой лежит
внутри квадрата PQRS, касается стороны
PQ в точке К, пересекает сторону PS в точках
А и В, а диагональ PR в точках С и D. Найдите
радиус окружности, если АВ=16, СD=2√92

№7. В параллелограмме ABCD угол АВС=3п/4.
окружность, описанная возле треугольника
АВD, касается прямой CD. Найдите площадь
параллелограмма, если диагональ BD=2

№8. Вершина С параллелограмма ABCD соединена
с точкой N на стороне АВ. Отрезок CN
пересекает диагональ BD в точке Р. Площадь
треугольника BNP равна 8, а S ВСР =12.
Найдите площадь параллелограмма АВСD.

№9.
Найдите площадь трапеции, основания
которой 6 и 26, а боковые стороны – 12 и
16.

Ответ:
153,6

№10. На
стороне АВ параллелограмма АВСD как на
диаметре построена окружность, проходящая
через точку пересечения диагоналей и
середину стороны АD. Найдите углы
параллелограмма.

Ответ:
60,120,60,120.

VI
.
Контрольные задачи.

Вариант № 1.

1) В равнобедренную трапецию, площадь
которой равна 80, вписана окружность
радиуса 4. Найдите периметр трапеции.

2) Найдите диаметр окружности, вписанной
в равнобедренную трапецию, если сумма
оснований трапеции 26, а разность оснований
равна 10.

3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К. Найдите периметр
параллелограмма, если АК = 12, СМ = 24, МК =
18.

Вариант
№ 2.

1) В круг с площадью 169π вписана
равнобедренная трапеция, меньшее
основание которой равно 10. найдите
площадь трапеции, если центр описанного
круга лежит на её большем основании.

2) Найдите диаметр окружности, вписанной
в равнобедренную трапецию, если сумма
оснований трапеции 15, а разность оснований
равна 9.

3)В параллелограмме АВСД биссектриса
угла Д пересекает сторону АВ в точке К
и прямую ВС в точке Р. Найдите периметр
∆ СДР, если ДК = 18, РК = 24, АД=15.

Вариант
№ 3.

1) В равнобедренную трапецию, площадь
которой 20, а синус одного из углов равен
0,8, вписана окружность. Найдите радиус
этой окружности.

2) Основание СМ и ОР трапеции СМОР равны
3 и 6 соответственно, диагонали трапеции
пересекаются в точке Н, а площадь
треугольника СРН равна 4. Найдите площадь
трапеции.

3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К. Найдите периметр
∆ АМК, если СД = 12, СМ = 14, СВ = 30.

Вариант
№ 4.

1) Найдите площадь равнобедренной
трапеции, если её высота равна 4, а тангенс
угла между диагональю и основанием
равен
.

2) В равнобедренную трапецию, площадь
которой равна 80, вписана окружность
радиуса 4. Найдите периметр трапеции.

решении
задач
…

Предыдущая статья: Жизнь после Picasa: бесплатные программы для организации фотоархива

Следующая статья: Темы для веб страниц информатика

Докажите что из одинаковых плиток имеющих форму равнобедренной трапеции

Главная » Разное » Докажите что из одинаковых плиток имеющих форму равнобедренной трапеции

391 Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости.

Источник:

Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №391
к главе «Глава V. Четырехугольники. §2. Параллелограмм и трапеция».

Все задачи >

Решение #1.

Условие задачи сформулировано некорректно. Доказательство невозможно.

Пример! Пусть S — площадь паркетной плитки в виде равнобедренной трапеции, S
₁ — некая площадь, ограниченная стенами. Тогда при S>S₁ паркет уложить нельзя.

Решение #2.

Следовательно, можно построить 3 параллелограмма, удовлетворяющие данному условию.

← 390 Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции.392 Основания прямоугольной трапеции равны а и b, один из углов равен а. Найдите: а) большую боковую сторону трапеции, если a=4 см, b = 7см, α=60°; б) меньшую боковую сторону трапеции, если a=10 см, b=15см, α=45°. →

• Вконтакте
• Facebook

Свойства трапеций и равнобедренных трапеций

2. Образование
3. Математика
4. Геометрия
5. Свойства трапеций и равнобедренных трапеций

Марк Райан

Трапеция с одной парой параллельных сторон параллельные стороны называются основаниями ). На следующем рисунке изображена трапеция слева и равнобедренная трапеция справа.

Пожалуй, самое сложное свойство обеих диаграмм — наличие дополнительных углов. Поскольку стороны параллельны, последовательные углы являются внутренними углами одной стороны и, следовательно, являются дополнительными. (Между прочим, все специальные четырехугольники, кроме воздушного змея, содержат следующие друг за другом дополнительные углы.)

Вот вам доказательство равнобедренной трапеции:

Заявление 1 :

Причина выписки 1 : Дано.

Заявление 2 :

Причина утверждения 2 : Ноги равнобедренной трапеции совпадают.

Заявление 3 :

Причина утверждения 3 : Верхние углы основания равнобедренной трапеции совпадают.

Заявление 4 :

Причина выписки 4 : Рефлексивное свойство.

Заявление 5 :

Причина утверждения 5 : SAS или Side-Angle-Side (2, 3, 4)

Заявление 6 :

Причина утверждения 6 : CPCTC (Соответствующие части конгруэнтных треугольников конгруэнтны).

Заявление 7 :

Причина утверждения 7 : Если углы, то стороны.

,

Докажите, что диагонали равнобедренной трапеции конгруэнтны

Чтобы доказать, что диагонали равнобедренной трапеции совпадают, рассмотрим равнобедренную трапецию, показанную ниже. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя одну и ту же трапецию.

Первый способ — показать, что треугольник ABC конгруэнтен треугольнику DCB

.
Дано : Равнобедренная трапеция ABCD с отрезком AB ≅ сегмент DC

Prove : сегмент AC ≅ сегмент BD

Поскольку трапеция равнобедренная, углы основания совпадают.

Следовательно, ∠CBA ≅ ∠BCD

Кроме того, отрезок BC должен отрезать BC по рефлексивному свойству конгруэнтности.

Согласно постулату SAS, треугольник ABC ≅ треугольник DCB.

Следовательно, сегмент AC ≅ сегмент BD

О чем нужно помнить, когда вы доказываете, что диагонали равнобедренной трапеции совпадают.

Вот некоторые вещи, которые вы должны знать о приведенном выше доказательстве.

• Утверждение , если трапеция равнобедренная, то базовые углы равны , также требует доказательства.Однако мы не будем здесь доказывать.

• Равные стороны равнобедренной трапеции всегда непараллельны. На трапеции выше мы показываем эти стороны красными отметками.

• Рефлексивное свойство относится к числу, которое всегда равно самому себе. Например, 9 = 9 или y = y являются примерами рефлексивного свойства.

• SAS означает «сторона, угол, сторона». Возможно, вам стоит повторить урок о конгруэнтных треугольниках.

• Чтобы доказать, что диагонали равнобедренной трапеции совпадают, вы также могли бы использовать треугольник ABD и треугольник DCA.

Другой способ доказать, что диагонали равнобедренной трапеции совпадают. На этот раз мы покажем, что треугольник BAD конгруэнтен треугольнику CDA

.
Дано : Равнобедренная трапеция ABCD с отрезком AB ≅ сегмент DC

Prove : сегмент AC ≅ сегмент BD

Поскольку трапеция равнобедренная, базовые углы совпадают

Следовательно, ∠BAD ≅ CDA

Обратите внимание, что на этот раз мы не используем те же базовые углы, что и перед. Базовые углы, которые мы сейчас используем, связаны с основанием сверху или сегментом AD.

Кроме того, отрезок AD ≅ переходит в отрезок AD по рефлексивному свойству конгруэнтности.

Согласно постулату SAS, треугольник BAD ≅ треугольник CDA

Следовательно, сегмент AC ≅ сегмент BD

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

,

Свойства трапеций и воздушных змеев

Теперь, когда мы видели несколько типов четырехугольники, которые параллелограммы, давайте узнаем о фигурах, не обладающих свойствами параллелограммов. Напомним, что параллелограммы были четырехугольниками, противоположные стороны были параллельны. В этом разделе мы рассмотрим четырехугольники, противоположные стороны могут пересекаться в какой-то момент.Мы изучим два типа четырехугольников. называются
трапеции и воздушных змеев . Начнем изучение с изучения некоторые свойства трапеций.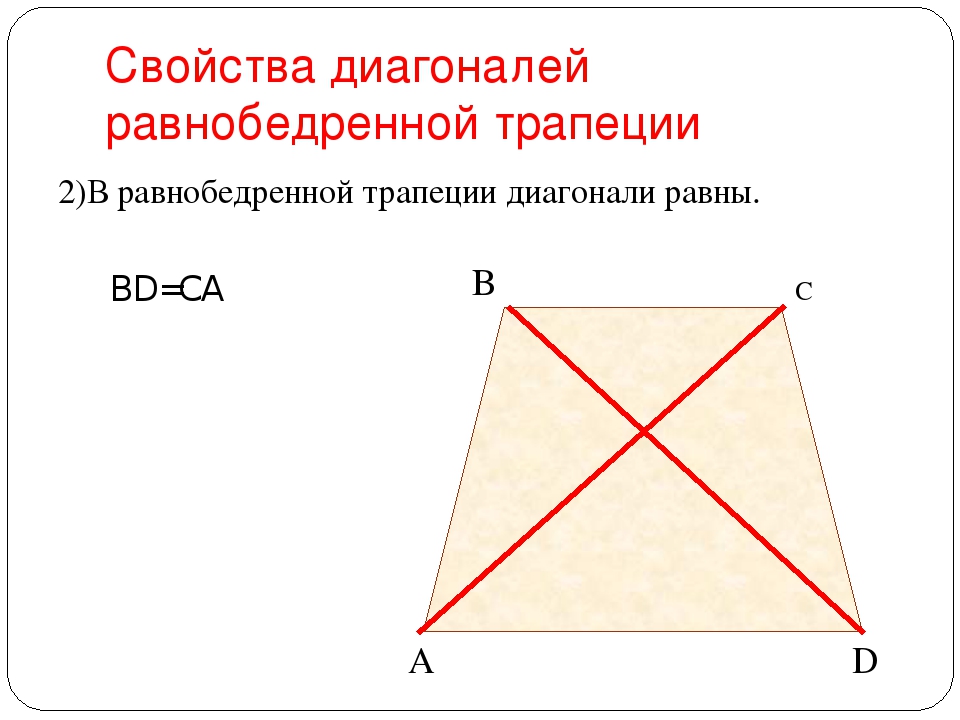

Трапеции

Определение: Трапеция — это четырехугольник с одной парой параллельных Стороны.

Поскольку у трапеции должна быть ровно одна пара параллельных сторон, нам потребуется докажите, что одна пара противоположных сторон параллельна, а другая не находится в нашем двухколоночные геометрические доказательства.Если мы забудем доказать, что одна пара противоположных стороны не параллельны, мы не исключаем возможность того, что четырехугольник — параллелограмм. Поэтому этот шаг будет абсолютно необходим, когда мы будем работать. на разные упражнения с трапециями.

Прежде чем мы углубимся в изучение трапеций, необходимо изучить названия различных частей этих четырехугольников, чтобы уточнить его стороны и углы.Все трапеции состоят из двух основных частей: оснований и опор . Противоположные стороны трапеции, параллельные друг другу, называются основаниями. Остальные стороны трапеции, которые пересекаются в некоторой точке при удлинении, называются ножками трапеции.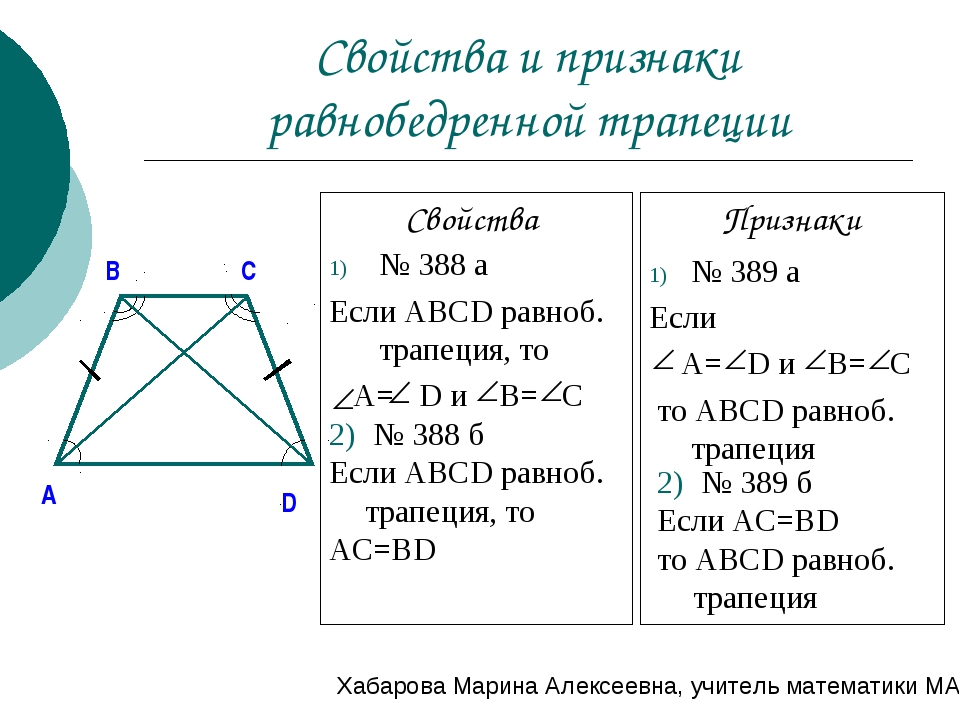

Верхняя и нижняя стороны трапеции проходят параллельно друг другу, поэтому они основания трапеции.Другие стороны трапеции будут пересекаться, если их удлинить, так что они ноги трапеции.

Отрезок, соединяющий середины ног трапеции, называется отрезком. мидсегмент . Длина этого сегмента всегда равна половине суммы основания трапеции, или

Рассмотрим трапецию ABCD, показанную ниже.

Средний сегмент, EF , показанный красным, имеет длину

.

Размер среднего сегмента зависит только от длины трапеции. основы. Однако есть одна важная особенность некоторых трапеций: полагается исключительно на свои ноги. Давайте теперь посмотрим на эти трапеции.

Равнобедренные трапеции

Определение: Равнобедренная трапеция — это трапеция, ноги которой совпадают.

По определению, если в четырехугольнике есть ровно одна пара параллельных прямых, тогда четырехугольник — трапеция. Определение равнобедренной трапеции добавляет еще одно уточнение: ноги трапеции должны быть конгруэнтными.

ABCD не является равнобедренной трапецией, потому что AD и BC не совпадают. Потому что EH и FG конгруэнтны, трапеция EFGH — равнобедренная трапеция.

Есть несколько теорем, которые помогут нам доказать, что трапеция равнобедренная. Эти свойства перечислены ниже.

(1) Трапеция является равнобедренной тогда и только тогда, когда углы основания совпадают.

(2) Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают.

(3) Если трапеция равнобедренная, то ее противоположные углы являются дополнительными.

Воздушные змеи

Определение: Воздушный змей — это четырехугольник с двумя разными парами смежных стороны, которые совпадают.

Напомним, что у параллелограммов тоже были пары равных сторон.Однако их конгруэнтные стороны всегда были противоположными сторонами. Воздушные змеи имеют две пары совпадающих сторон, которые встречаются в двух разных точках. Давайте посмотрим на иллюстрацию ниже, чтобы понять, что как выглядит воздушный змей.

Отрезок AB прилегает к отрезку BC и конгруэнтен ему. Сегменты AD и CD также смежные и конгруэнтные.

У воздушных змеев есть несколько свойств, которые помогут нам отличить их от других четырехугольников.

(1) Диагонали воздушного змея пересекаются под прямым углом.

(2) Воздушные змеи имеют ровно одну пару противоположных углов, которые совпадают.

Эти два свойства показаны на диаграмме ниже.

Обратите внимание, что на пересечении диагоналей образуется прямой угол, который в точке N.Также мы видим, что? K ?? M. Это наша единственная пара совпадающих углов, потому что ? J и? L имеют разные меры.

Попрактикуемся в выполнении некоторых задач, требующих использования свойств трапеций. и воздушных змеев, о которых мы только что узнали.

Упражнение 1

Найдите значение x на трапеции ниже.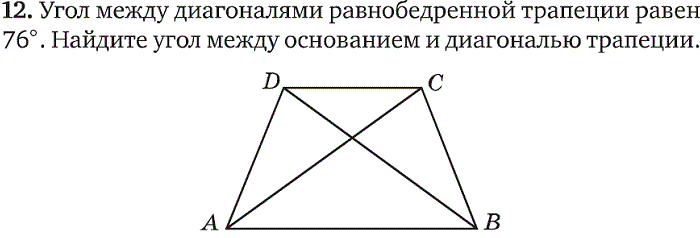

Ответ:

Поскольку нам даны длины оснований трапеции, мы можем вычислить какой длины должен быть средний сегмент.Давайте использовать формулу, которую мы использовали дано для среднего сегмента, чтобы понять это. (Помните, что это половина суммы основания.)

Итак, теперь, когда мы знаем, что длина среднего сегмента составляет 24 , мы можем перейти вперед и установите 24 равным 5x-1 .Переменная разрешима сейчас:

Упражнение 2

Найдите значение y на равнобедренной трапеции ниже.

Ответ:

На рисунке нам дана величина только одного угла, поэтому мы должны иметь возможность чтобы вывести больше информации на основе этого элемента.Поскольку четырехугольник равнобедренной трапеции, мы знаем, что углы основания равны. Это означает, что ? A также имеет размер 64 ° .

Теперь давайте разберемся, что такое сумма ? A и ? P :

.

Вместе они имеют в общей сложности 128 ° .Напомним по Polygon Interior Теорема суммы углов гласит, что внутренние углы четырехугольника должны быть 360 ° . Итак, давайте попробуем использовать это таким образом, который поможет нам определить меру . ? R . Сначала просуммируем все углы и установим его равным 360 ° .

Теперь мы видим, что сумма ? T и ? R составляет 232 ° .Поскольку сегмент TR является другой базой трапеции TRAP , мы знаем, что углы в точках T и R должны совпадать друг другу. Таким образом, если мы определим меры ? T и ? R по переменной x , имеем

Это значение означает, что размер ? T и ? R равен . 116 ° .Наконец, мы можем установить 116 равным выражению, показанному в ? R для определения стоимости y . У нас

Итак, получаем x = 9 .

Хотя приведенный выше метод был подробным способом решения упражнения, мы могли бы Также как раз использовано то свойство, что противоположные углы равнобедренных трапеций являются дополнительными.Решение таким образом происходит намного быстрее, поскольку нам нужно только найти, что за добавка угла 64 ° составляет. Получаем

Как только мы дойдем до этой точки в нашей проблеме, мы просто установим 116 равным 4 (3y + 2) и решите, как мы делали раньше.

Упражнение 3

Ответ:

Прочитав задачу, мы видим, что нам предоставили ограниченный объем информации. и хочу сделать вывод, что четырехугольник DEFG — это воздушный змей. Заметь EF и GF совпадают, поэтому, если мы сможем найти способ доказать, что DE и DG совпадают, это даст нам две различные пары смежных сторон, которые конгруэнтны, что является определением воздушного змея.

Нам также известно, что ? EFD и ? GFD совпадают. В прошлом мы узнали несколько теорем сравнения треугольников, которые могут быть применимы в этой ситуации, если мы сможем найти другую сторону или угол, которые совпадают.

Поскольку сегмент DF составляет сторону ? DEF и ? DGF , мы можем использовать рефлексивное свойство , чтобы сказать, что оно конгруэнтно самому себе.Таким образом, согласно постулату SAS у нас есть два совпадающих треугольника.

Далее, мы можем сказать, что сегменты DE и DG совпадают. потому что соответствующие части конгруэнтных треугольников конгруэнтны. Наша новая иллюстрация показано ниже.

Мы заключаем, что DEFG является воздушным змеем, потому что он имеет две отдельные пары смежных сторон, которые совпадают.Геометрическое доказательство этого упражнения из двух столбцов показано ниже.

,

Трапеция Трапецией основаниями боковыми равнобокой равнобедренной средней линией Теорема Пример Решение Ответ Пример Доказательство

Прототипы задания В6-2 (2013)

Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний

Подробнее

7 sin A. Найдите AB. 25

Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,

Подробнее

AC 6, cos A. Найдите BH.

Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите

Подробнее

Задание 3, 6, 16. Планиметрия

Задание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные

Подробнее

Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь.. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника. . Средняя линия

Подробнее

Геометрия

Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна

Подробнее

Тема 21 «Трапеция. Многоугольники».

Тема 1 «Трапеция. Многоугольники». Трапеция четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Параллельные стороны называются основаниями трапеции. Две другие стороны называются

Подробнее

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ

ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший

Подробнее

Задание 16.

Планиметрия

Задание 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы

Подробнее

В 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.

В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,

Подробнее

Основные теоремы и формулы

Основные теоремы и формулы Определение 1. Угловой величиной дуги называется отношение длины этой дуги к длине окружности, умноженное на 2π. Теорема 1. Величина центрального угла равна угловой величине

Подробнее

Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой. Найдите стороны параллелограмма. и 4. Найдите

Подробнее

tgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.

В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,

Подробнее

7 класс 1. Виды углов.

7 класс 1. Виды углов. Угол называется прямым, если он равен 90 0. Угол называется острым, если он меньше 90 0. Угол называется тупым, если он больше 90 0, но меньше 180 0. Прямой угол Острый угол Тупой

Подробнее

Тест 140. Правильный многоугольник. Признак

Тест 132. Многоугольник. Существование Существуют два треугольника, объединением которых являются: 1. треугольники двух видов: равносторонний и равнобедренный, но не равносторонний; 2. квадрат; 3. шестиугольник;

Подробнее

Основные определения, теоремы и формулы планиметрии.

Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне

Подробнее

Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен

Подробнее

Расстояние от точки до прямой

Расстояние от точки до прямой Пример 1. Стороны треугольника равны 15, 37 и 44 см. Из вершины большего угла треугольника проведен к его плоскости перпендикуляр, равный 16 см. Найти расстояние от его концов

Подробнее

Математика 8 класс Трапеция

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Трапеция Новосибирск Трапеция. Очень часто в задачах

Подробнее

Вписанные и описанные окружности

Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.

Подробнее

Тренировочные задачи

И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.

Подробнее

Вписанные и описанные окружности

Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.

Подробнее

ЗАДАНИЕ 15 Планиметрия Треугольник

ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками

Подробнее

«ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО ГЕОМЕТРИИ ДЛЯ 8 КЛАССА ТЕМАТИЧЕСКОЕ ТЕСТИРОВАНИЕ «ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ» Амосова Галина Владимировна, учитель математики и информатики ГБОУ СОШ 2 Василеостровского района г.

Подробнее

Многоугольники и их свойства

Задание 19 Планиметрические задачи Многоугольники и их свойства 1. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,

Подробнее

3. В прямоугольном треугольнике ABC С = 90, AB = 5, BC = 3, АC = 4. Найдите tg B. 4. В параллелограмме ABCD диагонали пересекаются в точке О,

ГЕОМЕТРИЯ, 8 класс Вариант 1, Апрель 2011 ГЕОМЕТРИЯ, 8 класс Вариант 1, Апрель 2011 2. В треугольнике MNK сторона MK равна 19 см. Найдите длину средней линии треугольника, параллельной MK. 8 см 8, см )

Подробнее

Анализ геометрических высказываний

Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы

Подробнее

Средняя линия треугольника

И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону

Подробнее

Билет 10. Билет 12. Билет 13. Билет 14

Билет 1 1. Первый признак равенства треугольников. 2. Параллелограмм. Определение, свойства. 3. Задача по теме «Координаты и векторы». Билет 2 1. Второй признак равенства треугольников. 2. Прямоугольник.

Подробнее

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.

ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB.\circ\)
.

2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.

Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*

1) Докажем параллельность.

Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.

2) Докажем формулу.

Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.

Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \

Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.

Таким образом:

\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*

С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.

Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.

Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.

2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.

Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.

\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию \(ABCD\)
.

Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.

Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.

2)

Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.

3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.

Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.

В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.

2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.

Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.

Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.

— [ Страница 2 ] —

3. Обсудить устно решения задач 1, 2, 3, приведённые в учебнике.

В связи с необходимостью проводить постоянную работу по развитию устной речи учащихся следует требовать от них не только построения сечений в рассматриваемых задачах, но и устного рассказа о ходе построения с соответствующими обоснованиями.

Для краткости записи решений можно использовать известную символику.

Более сложные задачи на построение сечений тетраэдра и параллелепипеда, когда данные точки, через которые проводится сечение, лежат внутри граней, могут быть рассмотрены на факультативных занятиях и спец курсах.

Для классной и домашней работы можно использо вать задачи 74, 75, 79-87, дополнительные задачи к главе I.

Задача 105. Изобразите тетраэдр DABC и отметьте точки M и N на р брах BD и CD и внутреннюю точку K грани ABC. Постройте сечение тетраэдра плоскостью MNK.

Р е ш е н и е. Обозначим секущую плоскость буквой.

Тогда M, N, M CDB, N CDB, CDB = MN.

Возможны два случая: 10) MN BC = P; 20) MN BC.

Рассмотрим их раздельно.

10) Проводим прямую MN. P, K, P ABC, K ABC, ABC = PK. Проводим прямую PK. Пусть она пересе кает стороны AC и AB в точках E и F. Проводим отрез ки NE и MF. Искомое сечение — четыр хугольник MNEF (рис. 1.31).

20) Через точку K проводим EF BC. Проводим отрез ки NE и MF. Искомое сечение — четыр хугольник MNEF.

Задача 85. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где K — середина ребра AA1, а L — середина CC1.

Докажите, что построенное сечение — параллелограмм.

Р е ш е н и е. Проведем отрезок KL. Согласно аксиоме А2 он лежит в плоскости сечения.

Так как точки K и L — середины боковых р бер, то отрезок KL проходит через середину диагонали AC1, а по этому согласно свойству 20 параллелепипеда (п. 13) он проходит через середину диагонали BD1 (точка O на ри сунке 1.32).

B, O, следовательно, BD1. Искомое сечение — четырехугольник BLD1K. Так как его диагонали KL и BD1 точкой пересечения делятся пополам, то четыр х угольник BLD1K — параллелограмм.

– &nbsp– &nbsp–

1. Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, K.

2. В задачах 1-3 найдите периметр сечения, если M, N, K — середины р бер и каждое ребро тетраэдра равно a.

– &nbsp– &nbsp–

1. Объясните, как построить сечение куба плоско стью, проходящей через три данные точки, являющие ся либо вершинами куба, либо серединами его р бер (три данные точки на рисунках выделены).

2. В задачах 1-4 и 6 найдите периметр сечения, если ребро куба равно a. В задаче 5 докажите, что AE = 1 a.

– &nbsp– &nbsp–

1. Объясните, как построить сечение параллелепи педа плоскостью, проходящей через точки B, D и M, если M — середина ребра B1C1.

2. Докажите, что построенное сечение есть равно бедренная трапеция.

3. Найдите стороны трапеции.

Р е ш е н и е.

1) Пусть — секущая плоскость, ABCD = BD, BCC1B1 = BM, MN BD, сечение — трапеция BDNM.

2) BB1M = DD1N, BM = DN, трапеция BDNM рав нобедренная.

– &nbsp– &nbsp–

При решении задач, связанных с сечением тетраэдра некоторой плоскостью, часто оказывается полезной теорема Менелая, в некоторых других задачах — теорема Чевы. Поэтому в классах с углубл нным изучением математики изучение пункта 14 «Задачи на построение сечений» целесообразно совместить с изучением теорем Менелая и Чевы (пункты 95 и 96). Привед м пример такой задачи.

Задача 1. В тетраэдре ABCD на р брах AB, AD и BC взяты соответственно точки K, L и M так, что AK: KB = = 2: 3, AL = LD, BM: MC = 4: 5.

Постройте сечение тетраэдра плоскостью KLM и найдите, в каком отношении эта плоскость делит ребро CD.

Р е ш е н и е.

1) Провед м отрезки KL и KM, а затем продолжим отрезки KL и BD, лежащие в плоскости ABD, до пересечения в точке E (рис. 1.33). Точки E и M лежат в секущей плоскости KLM и также в плоскости BCD.

Проведя отрезок ME, получим точку N, в которой секущая плоскость KLM пересекается с ребром CD.

Четыр хугольник KLNM — искомое сечение.

2) Найд м отношение CN: ND. С этой целью применим теорему Менелая к треугольникам ABD и BCD. На сторонах AB и AD треугольника ABD лежат точки K и L, а на продолжении стороны BD — точка E, прич м точки K, L и E лежат на одной прямой. Поэтому согласно теореме Менелая имеет место равенство

AK BE DL

= 1.

KB ED LA

– &nbsp– &nbsp–

MC BE находим искомое отношение CN: ND = 15: 8.

С целью использования теоремы Менелая в задаче 105 учебника можно дать дополнительное задание:

Найдите отношение, в котором плоскость MNK делит ребро AB, если CN: ND = 2: 1, BM = MD и точка K — середина медианы AL треугольника ABC. (Ответ: 3: 2.) Аналогичное дополнительное задание можно дать в задаче 106:

Найдите отношение, в котором плоскость MNK делит ребро BC, если она делит ребро AB в отношении 1: 4 (считая от точки A), точка K — середина ребра CD, а точка N лежит на медиане DL треугольника ACD, при ч м DN: NL = 3: 2. (Ответ: 4: 3.) На применение теоремы Чевы можно рассмотреть сле дующую задачу:

Задача 2. На р брах AB, BC и CA тетраэдра ABCD от мечены точки C1, A1, B1 так, что AC1: C1B = 1: 2, BA1: A1C = 2: 3, CB1: B1A = 3: 1.

Докажите, что плоскости ADA1, BDB1 и CAC1 пересекаются по прямой.

– &nbsp– &nbsp–

1. Повторить основные вопросы темы «Параллельность прямых и плоскостей», заслушав ответы учащихся. Эти вопросы сформулированы в карточках к зач ту № 1.

2. Провести математический диктант № 1.1. Диктант привед н в дидактических материалах .

3. Рассмотреть решения некоторых задач из карточек к зач ту и из учебника.

Изучение темы «Параллельность прямых и плоскос тей» завершается проведением контрольной работы № 1.2 и зач та № 1 по данной теме.

– &nbsp– &nbsp–

Контрольная работа № 1.2 Вариант 1

10. Прямые a и b лежат в параллельных плоскостях и. Могут ли эти прямые быть: а) параллельными;

20. Через точку O, лежащую между параллельными плоскостями и, проведены прямые l и m. Прямая l пересекает плоскости и в точках A1 и A2 соответст венно, прямая m — в точках B1 и B2. Найдите длину от резка A2B2, если A1B1 = 12 см, B1O: OB2 = 3: 4.

3. Изобразите параллелепипед ABCDA1B1C1D1 и по стройте его сечение плоскостью, проходящей через точ ки M, N и K, являющиеся серединами р бер AB, BC и DD1.

Вариант 2

10. Прямые a и b лежат в пересекающихся плоскостях и. Могут ли эти прямые быть: а) параллельными;

б) скрещивающимися? Сделайте рисунок для каждого возможного случая.

20. Через точку O, не лежащую между параллельны ми плоскостями и, проведены прямые l и m. Прямая l пересекает плоскости и в точках A1 и A2 соответст венно, прямая m — в точках B1 и B2. Найдите длину от резка A1B1, если A2B2 = 15 см, OB1: OB2 = 3: 5.

3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющие ся серединами р бер DC и BC, и точку K, такую, что K DA, AK: KD = 1: 3.

О т в е т ы:

Вариант 2 Вариант 1

10. Рис. 1.35, a b, a b.

10. Рис. 1.34, a b, a b.

3. Сечение — трапеция.

3. Сечение — пятиугольник.

Рис. 1.34 Рис. 1.35

Урок № 24 Зач т № 1. Параллельность прямых и плоскостей Карточка 1

1. Сформулируйте аксиомы А1, А2 и А3 стереометрии.

Сформулируйте и докажите следствия из аксиом.

2. Докажите, что через любую точку пространства, не лежащую на данной прямой, проходит прямая, парал лельная данной, и притом только одна.

3. Плоскость пересекает стороны AB и AC треуголь ника ABC соответственно в точках B1 и C1. Известно, что BC, AB: B1B = 5: 3, AC = 15 см. Найдите AC1.

Карточка 2

1. Сформулируйте определение параллельных прямой и плоскости. Сформулируйте и докажите теорему, выра жающую признак параллельности прямой и плоскости.

2. Докажите, что если одна из двух параллельных прямых пересекает данную плоскость, то и другая пря мая пересекает эту плоскость.

3. Каждое ребро тетраэдра DABC равно 2 см. По стройте сечение тетраэдра плоскостью, проходящей через точки B, C и середину ребра AD. Вычислите периметр сечения.

Карточка 3

1. Сформулируйте определение скрещивающихся пря мых. Сформулируйте и докажите теорему, выражающую признак скрещивающихся прямых.

2. Докажите, что если две прямые параллельны третьей прямой, то они параллельны.

3. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки A, C и M, где M — середина ребра A1D1.

Карточка 4

1. Сформулируйте определение параллельных плоскос тей. Сформулируйте и докажите теорему, выражающую признак параллельности двух плоскостей.

2. Докажите, что через каждую из двух скрещиваю щихся прямых проходит плоскость, параллельная дру гой прямой, и притом только одна.

3. ABCDA1B1C1D1 — куб, ребро которого 4 см. Построй те сечение куба плоскостью, проходящей через точки A, D1 и M, где M — середина ребра BC. Вычислите пери метр сечения.

Карточка 5

1. Докажите, что противоположные грани паралле лепипеда параллельны и равны.

2. Докажите, что если стороны двух углов соответ ственно сонаправлены, то такие углы равны.

3. Параллельные плоскости и пересекают сторону AB угла BAC соответственно в точках A1 и A2, а сторону AC этого угла соответственно в точках B1 и B2. Найдите AA1, если A1A2 = 6 см, AB2: AB1 = 3: 2.

Карточка 6

1. Докажите, что диагонали параллелепипеда пересе каются в одной точке и делятся этой точкой пополам.

2. Докажите, что если две параллельные плоскос ти пересечены третьей, то линии их пересечения парал лельны.

3. Точка C лежит на отрезке AB. Через точку A про ведена плоскость, а через точки B и C — параллельные прямые, пересекающие эту плоскость соответственно в точках B1 и C1. Найдите длину отрезка BB1, если AC: CB = 4: 3, CC1 = 8 см.

1. Карточки к зач ту, содержащие основные вопросы теории и некоторые типичные задачи, даются учащимся заблаговременно (примерно за две недели до проведения зач та).

2. Готовясь к зач ту, учащиеся делают какие то запи си. Эти записи (возможно, в виде черновиков), свиде тельствующие о повторении учебного материала и подго товке к зач ту, учащиеся показывают учителю в день проведения зач та. Они могут быть использованы на зач те. При этом на основе беседы и дополнительных вопросов учитель выясняет глубину усвоения темы учащимися.

3. Зач т проводит учитель с помощью наиболее под готовленных учащихся — консультантов. Для этого класс нужно разделить на несколько групп, в каждой из которых 4-5 учеников. Один из них является помощни ком учителя в проведении зач та. По предыдущим уро кам и в начале зач та учитель должен убедиться в том, что консультанты сами на хорошем уровне владеют учеб ным материалом.

4. В течение урока учитель вед т опрос многих уча щихся. В конце урока он утверждает оценки, выставлен ные консультантами. В отдельных случаях после урока учитель может проверить записи учащихся, выполнен ные на уроке, и после этого выставить окончательную оценку по зач ту.

5. Итоговую оценку за полугодие учитель выставляет на основе текущих оценок за самостоятельные и конт рольные работы, а также устного ответа учащихся.

Решающая роль при этом принадлежит оценке по зач ту.

П Е Р П Е Н Д И К УЛ Я Р Н О С Т Ь П Р Я М Ы Х

И ПЛОСКОСТЕЙ

§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ

И ПЛОСКОСТИ

– &nbsp– &nbsp–

Основные задачи урока Ввести понятие перпендикулярных прямых в простран стве, доказать лемму о перпендикулярности двух парал лельных прямых к третьей прямой, дать определение перпендикулярности прямой и плоскости, доказать теоре мы, в которых устанавливается связь между параллель ностью прямых и их перпендикулярностью к плоскости.

1. Напомнить понятие угла между двумя скрещиваю щимися прямыми, ввести понятие перпендикулярности двух прямых в пространстве. Отметить, что перпенди кулярные прямые могут пересекаться и могут быть скре щивающимися (см. рис. 43 учебника).

2. Доказать л е м м у: если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Доказательство основано на использовании понятия угла между прямыми и может быть проведено самими учащимися с опорой на текст и рисунок 44 учебника.

3. Сформулировать определение перпендикулярности прямой и плоскости. Ввести обозначение a. Проил люстрировать понятие перпендикулярности прямой и плоскости с помощью рисунка 45 и примеров из жизни.

4. Доказать т е о р е м у: если одна из двух параллель ных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Доказательство теоремы несложное. Оно основано на определении перпендикулярности прямой и плоскости и рассмотренной выше лемме и состоит из двух этапов:

1) x, x — произвольная прямая. Из условия a следует (по определению перпендикулярности прямой и плоскости), что a x;

2) так как a1 a (по условию) и a x, то (согласно лемме о перпендикулярности двух параллельных пря мых к третьей прямой) a1 x.

Итак, прямая a1 перпендикулярна к произвольной прямой x, лежащей в плоскости. А это означает, что a1.

5. Доказать о б р а т н у ю т е о р е м у: если две прямые перпендикулярны к плоскости, то они параллельны.

Доказательство проводится по учебнику (см. рис. 47, а, б). Повторить это доказательство можно на следующих уроках.

На первый взгляд может показаться странным, поче му эта теорема названа обратной предыдущей теореме.

Ведь в предыдущей теореме условие состояло в том, что a a1 и a, а заключением теоремы было: a1. В дан ной теореме условие состоит в том, что a и a1, а заключение — в том, что a a1.

Таким образом, с формальной точки зрения данная теорема не является обратной предыдущей, поскольку условие и заключение данной теоремы не совпадают со ответственно с заключением и условием предыдущей тео ремы. Тем не менее можно так сформулировать эти тео ремы, что каждая из них будет обратной другой.

Привед м эту формулировку.

Пусть прямая a перпендикулярна к плоскости. Тогда:

если a a1, то a1, и обратно:

если a1, то a a1.

6. Для классной и домашней работы можно исполь зовать задачи 116-118, 120.

Задача 116 а). Дан параллелепипед ABCDA1B1C1D1.

Докажите, что DC B1C1 и AB A1D1, если BAD = 90°.

Р е ш е н и е.

1) В параллелепипеде все грани — параллелограммы. Так как BAD = 90° (по условию), то грань ABCD — прямоуголь ник, поэтому AB AD и DC BC (рис. 2.1).

2) B1C1 BC (так как грань BB1C1C — параллелограмм) и BC DC. Отсюда по лемме о перпендикулярности двух па раллельных прямых к треть ей B1C1 DC. Рис. 2.1

3) Аналогично доказывает ся, что AB A1D1. Действитель но, A1D1 AD (так как AA1D1D — параллелограмм) и AB AD, по этому AB A1D1.

Задача 120. Через точку O пересечения диагоналей квад рата со стороной a проведена прямая OK, перпендикуляр ная к плоскости квадрата.

Найдите расстояние от точки K до вершин квадрата, если Рис. 2.2 OK = b.

Р е ш е н и е.

2) Треугольники KAO, KBO, KCO и KDO равны по двум катетам, откуда KA = KB = KC = KD (рис. 2.2).

KAO получаем AO = a 2. Так как KA =

– &nbsp– &nbsp–

Урок № 26 Тема урока: Признак перпендикулярности прямой и плоскости Основные задачи урока Изучить теорему, выражающую признак перпендику лярности прямой и плоскости; рассмотреть задачи на применение этой теоремы.

Примерный план проведения урока

1. Повторить теоретический материал предыдущего урока пут м опроса учащихся.

2. В качестве подготовительной работы к изучению нового материала решить задачу 119.

Задача 119. Прямая OA перпендикулярна к плоскос ти OBC, и точка O является серединой отрезка AD.

Докажите, что: а) AB = DB; б) AB = AC, если OB = OC;

в) OB = OC, если AB = AC.

Р е ш е н и е.

а) OA OBC по условию, следовательно, OA OB по определению перпендикулярности прямой к плоскости.

OA = OD по условию задачи, поэтому прямая OB являет ся серединным перпендикуля ром к отрезку AD, и, следова тельно, AB = DB (рис. 2.3).

б) Так как по условию OA OBC, то OA OC. Если OB = OC, то прямоугольные треугольники AOC и AOB равны по двум катетам, и, следовательно, равны их ги потенузы, т. е. AB = AC.

в) Если AB = AC, то прямо угольные треугольники AOC и Рис. 2.3 AOB равны по катету и гипотену зе, откуда следует, что OB = OC.

3. Доказать теорему, выражающую п р и з н а к п е р п е н д и к у л я р н о с т и п р я м о й и п л о с к о с т и: если прямая перпендикулярна к двум пересекающимся пря мым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

В процессе доказательства теоремы выделяются сле дующие этапы:

1) Вначале рассматриваем случай, когда прямая a про ходит через точку O пересечения прямых p и q, лежа щих на плоскости. Доказываем, что прямая a перпен дикулярна к любой прямой, лежащей в плоскости и про ходящей через точку O.

2) Используя лемму о перпендикулярности двух па раллельных прямых к третьей, делаем вывод о перпен дикулярности прямой a к любой прямой, лежащей в плоскости. Это означает, что a.

3) Рассматриваем теперь случай, когда прямая a не проходит через точку O пересечения p и q. В этом слу чае проводим через точку O прямую a1, параллельную пря мой a. В силу упомянутой леммы a1 p и a1 q, и поэто му согласно доказанному в первом случае a1. Отсю да по первой теореме п. 16 следует, что a. Это завершает доказательство теоремы.

4. В связи с тем что доказательство теоремы состоит из нескольких этапов, можно предложить учащимся за писать план доказательства в соответствии с содержани ем слайда 2.1.

Слайд может быть использован при подведении ито гов данного урока и на следующем уроке.

5. Для классной и домашней работы можно использо вать задачи 121, 124, 126, 128.

Задача 128. Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая OM так, что MA = MC, MB = MD. Докажите, что прямая OM перпен дикулярна к плоскости параллелограмма.

– &nbsp– &nbsp–

1. Сформулируйте определение перпендикулярно сти прямой и плоскости.

2. Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

– &nbsp– &nbsp–

Р е ш е н и е.

1) Так как MA = MC (по усло вию) и AO = OC (диагонали па раллелограмма точкой пересе чения делятся пополам), то отрезок MO — медиана равно бедренного треугольника AMC (рис. 2.4).

Следовательно, MO также высота этого треугольника, т. е.

2) Аналогично доказывается, Рис. 2.4 что MO BD.

3) Так как MO AC и MO BD, то по признаку пер пендикулярности прямой и плоскости MO ABCD.

Урок № 27 Тема урока: Теорема о прямой, перпендикулярной к плоскости Основные задачи урока Повторить доказательство теоремы, выражающей при знак перпендикулярности прямой и плоскости; рассмот реть теорему из п. 18: через любую точку пространства проходит прямая, перпендикулярная к данной плоско сти, и притом только одна.

Примерный план проведения урока

1. Повторить доказательство теоремы, выражающей признак перпендикулярности прямой и плоскости.

2. Проверить выборочно решения задач из домашней работы.

3. Сформулировать т е о р е м у: через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Наглядно утверждение теоремы представляется впол не очевидным, однако строгое ее доказательство не явля ется простым.

Учащимся, проявляющим повышенный интерес к ма тематике, можно предложить разобрать доказательство дома самим по учебнику. При этом следует обратить их внимание на то, что в первой части доказательства вво дится в рассмотрение плоскость, проходящая через данную точку M и перпендикулярная к данной прямой a.

Существование такой плоскости доказано в задаче с ре шением, привед нной в п. 17, а единственность такой плоскости доказана в задаче 133, которая также дана с решением. Таким образом, полное доказательство данной теоремы весьма громоздко, и поэтому учитель по своему усмотрению может изложить его с той или иной степе нью полноты в зависимости от уровня класса. Отдельные фрагменты доказательства (задача из п. 17, задача 133) можно рассмотреть на уроках № 28-30, посвящ нных повторению теории и решению задач по теме.

4. Провести фронтальный опрос учащихся, используя слайд 2.2.

– &nbsp– &nbsp–

5. Для классной и домашней работы можно исполь зовать задачи 122, 123, 125, 127.

Задача 122. Прямая CD перпендикулярна к плоско сти правильного треугольника ABC. Через центр O это го треугольника проведена прямая OK, параллельная прямой CD. Известно, что AB = 16 3 см, OK = 12 см, CD = 16 см. Найдите расстояния от точек D и K до вер шин A и B треугольника.

Р е ш е н и е.

1) По условию задачи OK CD, следовательно, OK ABC (рис. 2.5).

2) Точка O — центр правильного треугольника ABC, следовательно, OA = OB = OC = AB = 16 см.

– &nbsp– &nbsp–

Уроки № 28-30 Тема уроков: Решение задач на перпендикулярность прямой и плоскости. Повторение вопросов теории Основные задачи уроков Выработать навыки решения основных типов задач на перпендикулярность прямой и плоскости, повторить во просы теории.

1. Повторить вопросы теории в ходе опроса учащихся (пп. 15-18).

2. Решить выборочно задачи 129-137, использовать вопросы 1-9 к главе II.

3. Рассмотреть частично или полностью доказатель ство теоремы из п. 18.

4. Можно использовать задачи из дидактических ма териалов .

5. Можно провести математический диктант (№ 2 в дидактических материалах ).

6. Полезна работа на уроке со слайдом 2.3.

На уроке № 30 проводится самостоятельная работа.

Самостоятельная работа № 2.1 Вариант 1

10. Д а н о: AB, M и K — произвольные точки плос кости. Докажите, что AB MK.

2. Треугольник ABC правильный, точка O — его центр. Прямая OM перпендикулярна к плоскости ABC.

а)0 Докажите, что MA = MB = MC.

б) Найдите MA, если AB = 6 см, MO = 2 см.

– &nbsp– &nbsp–

Вариант 2

10. Д а н о: прямая MA перпендикулярна к плоскости треугольника ABC. Докажите, что MA BC.

2. Четыр хугольник ABCD — квадрат, точка O — его центр. Прямая OM перпендикулярна к плоскости квад рата.

а)0 Докажите, что MA = MB = MC = MD.

б) Найдите MA, если AB = 4 см, OM = 1 см.

Ответы:

В а р и а н т 1.

В а р и а н т 2.

Задача 129. Прямая AM перпендикулярна к плоскос ти квадрата ABCD, диагонали которого пересекаются в точке O. Докажите, что:

а) прямая BD перпендикулярна к плоскости AMO;

Р е ш е н и е.

а) MA ABCD, следовательно, MA BD по определе нию перпендикулярности прямой и плоскости, BD AC по свойству диагоналей квадрата (рис. 2.7).

Итак, BD AO и BD AM, следовательно, BD AMO по признаку перпендикулярности прямой и плоскости.

б) Так как BD MOA, то прямая BD перпендикуляр на к любой прямой, лежащей в плоскости MOA, в част ности BD MO.

Задача 134. Докажите, что все прямые, проходящие через данную точку M прямой a и перпендикулярные к этой прямой, лежат в плоскости, проходящей через точку M и перпендикулярной к прямой a.

Р е ш е н и е. Обозначим буквой плоскость, проходя щую через точку M прямой a и перпендикулярную к этой прямой, и рассмотрим произвольную прямую b, также про ходящую через точку M и перпендикулярную к прямой a.

Требуется доказать, что b (рис. 2.8). Допустим, что это не так. Тогда плоскость, проходящая через прямые a и b, пересекается с плоскостью по некоторой прямой b1, проходящей через точку M и отличной от прямой b. Так как a и b1, то a b1. Мы получили, что в плоскости через точку M проходят две прямые (b и b1), пер пендикулярные к прямой a, чего не может быть. Значит, предположение неверно и прямая b лежит в плоскости.

Рис. 2.7 Рис. 2.8

Задача 136. Докажите, что если точка X равноудалена от концов данного отрезка AB, то она лежит в плоскости, прохо дящей через середину отрезка AB и перпендикулярной к пря мой AB.

Р е ш е н и е. Обозначим бук вой плоскость, проходящую через середину O отрезка AB и Рис. 2.9 перпендикулярную к прямой AB (рис. 2.9). Пусть точка X равноудалена от концов отрезка AB, т. е. XA = XB. Требуется доказать, что X.

Если точка X лежит на прямой AB, то она совпадает с точкой O, и поэтому X.

Если точка X не лежит на прямой AB, то отрезок XO является медианой равнобедренного треугольника AXB и, следовательно, высотой этого треугольника, т. е.

Таким образом, прямая XO проходит через точку O прямой AB и перпендикулярна к прямой AB. Отсюда сле дует (см. задачу 134), что прямая XO лежит в плоскос ти, и поэтому X.

Задача 137. Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой пря мой.

Р е ш е н и е. Пусть a и b — взаимно перпендикулярные скрещивающиеся прямые. Докажем, что через прямую a проходит плоскость, перпенди кулярная к прямой b.

1) Через произвольную точ ку O прямой a провед м пря мую b1, параллельную прямой b. Тогда a b1, так как по усло вию a b (рис. 2.10).

2) Обозначим буквой плос кость, проходящую через пере секающиеся прямые a и b1, и провед м через точку O прямую c, перпендикулярную к плоско сти. Тогда c b1, а так как b b1, то c b.

3) Обозначим буквой плос кость, проходящую через пере секающиеся прямые a и c. Так как b a (по условию) и b c, Рис. 2.10 то b (по признаку перпендикулярности прямой и плоскости). Итак, через прямую a проходит плоскость, перпендикулярная к прямой b.

Аналогично доказывается, что через прямую b про ходит плоскость, перпендикулярная к прямой a.

§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ.

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

– &nbsp– &nbsp–

Основные задачи урока Ввести понятие расстояния от точки до плоскости, до казать теорему о тр х перпендикулярах, показать при менение этой теоремы при решении задач.

Примерный план проведения урока

1. Используя рисунок 51 учебника, ввести понятия перпендикуляра к плоскости, наклонной, проекции на клонной на плоскость. Рассматривая прямоугольный треугольник AMH (см. рис. 51), доказать, что перпен дикуляр, провед нный из данной точки к плоскости, меньше любой наклонной, провед нной из той же точки к этой плоскости. Длина перпендикуляра, провед нного из точки к плоскости, называется расстоянием от этой точки до плоскости.

2. Обратить внимание на замечания 1, 2, 3 в п. 19 учебника, в которых введены понятия расстояния между параллельными плоскостями, параллельными прямой и плос костью, скрещивающимися пря мыми. Полезно выполнить ри сунки и обосновать справедли вость утверждений, привед н ных в замечаниях.

З а м е ч а н и е 1. Если две плоскости параллельны, то все точки одной плоскости равно удалены от другой плоскости.

Пусть, A, M. Про ведем AA0 и MM0, тогда Рис. 2.11 AA0 MM0 (рис. 2.11), поэтому AA0 = MM0 (как отрезки параллельных прямых, заключ нные между параллель ными плоскостями).

Итак, расстояния от двух произвольных точек A и M плоскости до плоскости равны друг другу. То же са мое относится к расстояниям от точек плоскости до плоскости.

Расстояние от произвольной точки одной из парал лельных плоскостей до другой плоскости называется рас стоянием между параллельными плоскостями.

З а м е ч а н и е 2. Если прямая и плоскость параллель ны, то все точки прямой равноудалены от этой плоскости.

Доказательство утверждения приведено в решении за дачи 144, учащиеся могут прочитать его самостоятельно.

Можно предложить другой вариант доказательства.

Пусть a, A a, B a. Проведем AA1 и BB1 (рис. 2.12). Тогда AA1 BB1. Докажем, что AA1 = BB1.

Плоскость, проходящая через параллельные прямые AA1 и BB1, пересекается с плоскостью по прямой A1B1 и содержит прямую AB. Ясно, что AB A1B1 (если бы эти прямые пересекались, то прямая AB (т. е. прямая a) пересекалась бы с плоскостью, что противоречит усло вию a).

Итак, AA1 BB1 и AB A1B1. Следовательно, четыр х угольник ABB1A1 — параллелограмм, и поэтому AA1 = BB1.

Таким образом, расстояния от двух произвольных то чек A и B прямой a до параллельной ей плоскости рав ны между собой.

Если прямая и плоскость параллельны, то расстояни ем между прямой и плоскостью называется расстояние от произвольной точки прямой до этой плоскости.

З а м е ч а н и е 3. Если две прямые скрещивающиеся, то расстоянием между ними называется расстояние меж ду одной из них и плоскостью, проходящей через дру гую прямую параллельно первой прямой.

Целесообразно напомнить, как выполняется построе ние плоскости, содержащей одну из скрещивающихся прямых и параллельной другой прямой (рис. 2.13).

Рис. 2.12 Рис. 2.13

Пусть a b. Через произвольную точку M прямой b провед м прямую a1, параллельную a. Пересекающиеся прямые a1 и b определяют некоторую плоскость, па раллельную прямой a.

Из произвольной точки A прямой a проводим перпен дикуляр AA1 к плоскости. Длина этого перпендикуля ра и есть расстояние между скрещивающимися прямы ми a и b.

В дальнейшем в процессе решения задач можно пока зать, как построить общий перпендикуляр к двум дан ным скрещивающимся прямым a и b, т. е. отрезок, пер пендикулярный к прямым a и b, концы которого лежат на этих прямых.

3. Доказать теорему о тр х перпендикулярах и обрат ную ей теорему. При этом можно использовать рисунок 53 учебника или слайд 2.4.

– &nbsp– &nbsp–

4. Для классной и домашней работы можно использо вать задачи 138-145, 153.

Задача 143. Расстояние от точки M до каждой из вершин правильного треугольника ABC равно 4 см. Най дите расстояние от точки M до плоскости ABC, если AB = 6 см.

Р е ш е н и е.

1) По условию MA = MB = MC = 4. Пусть MO ABC (рис. 2.14), тогда OA = OB = OC (как проекции равных наклонных, см. задачу 139). Это означает, что точка O — центр окружности, описанной около треугольника ABC,

– &nbsp– &nbsp–

а OA — радиус этой окружности. Известно, что a3 = R 3, где a3 = AB, R = AO, поэтому AO = 6 = 2 3.

2) Из MAO получаем MO = MA2 – AO2, MO = 16 – 12 = 4 = 2.

О т в е т: 2 см.

Задача 145. Через вершину A прямоугольного тре угольника ABC с прямым углом C проведена прямая AD, перпендикулярная к плоскости треугольника.

а) Докажите, что треугольник CBD прямоугольный.

б) Найдите BD, если BC = a, DC = b.

Р е ш е н и е.

а) Отрезок AC — проекция наклонной DC на плос кость треугольника ABC (рис. 2.15). BC AC по условию, следовательно, BC DC по теореме о тр х перпендикуля рах и поэтому треугольник CBD прямоугольный.

б) BC = a, DC = b. Из BCD получаем BD = BC2 + CD2, BD = a2 + b2.

О т в е т: a2 + b2.

В дальнейшем в процессе решения задач важно обра тить внимание учащихся на обобщ нную теорему о тр х перпендикулярах, когда прямая a1 перпендикулярна к проекции наклонной, но не проходит через основание наклонной.

Урок № Тема урока: Угол между прямой и плоскостью Основные задачи урока Ввести понятие угла между прямой и плоскостью;

рассмотреть задачи, в которых используется это понятие.

Примерный план проведения урока

1. Проверить выборочно решение задач из домашней работы. Решения задач типа 138-142 и доказательство теоремы о тр х перпендикулярах можно обсудить устно, используя готовые рисунки и слайды.

2. Ввести понятие проекции точки на плоскость, про екции фигуры на плоскость. Доказать, что проекцией прямой на плоскость, не перпендикулярной к этой плос кости, является прямая. При этом используются рисун ки 54, 55 учебника.

3. Ввести определение угла между прямой и плоско стью.

4. Разобрать решение задачи 162, привед нное в учеб нике. Доказать, что угол между данной прямой и плос костью является наименьшим из всех углов, кото рые данная прямая образует с прямыми, провед нными в плоскости через точку пересечения прямой с плос костью.

Учащимся полезно сделать краткую запись доказа тельства, привед нного в слайде 2.5.

– &nbsp– &nbsp–

5. Для классной и домашней работы можно использо вать задачи 163-165, 146-148.

Задача 165. Из точки A, удал нной от плоскости на расстояние d, проведены к этой плоскости наклонные AB и AC под углом 30° к плоскости. Их проекции на пло скость образуют угол 120°. Найдите BC.

– &nbsp– &nbsp–

Уроки № 33-36 Тема уроков: Повторение теории. Решение задач на применение теоремы о тр х перпендикулярах, на угол между прямой и плоскостью Основные задачи уроков Повторить доказательство теоремы о тр х перпенди кулярах, понятие угла между прямой и плоскостью, за крепить навыки решения задач.

Примерный план проведения уроков

1. На каждом из уроков № 33-35 повторить вопро сы теории пут м опроса учащихся.

2. В процессе решения задач повторить соотношения между элементами прямоугольного треугольника, теоре мы синусов и косинусов.

3. Обратить особое внимание на решение некоторых типовых задач, которые будут использоваться в дальней шем при вычислении площадей поверхностей и объ мов многогранников. К таким задачам относятся, например, задачи 147, 151, 158, 161. Полезно использовать на уро ках привед нный ниже слайд 2.6, который предназначен для фронтальной работы с учащимися, обсуждения под ходов к решению задач из учебника.

4. На уроке № 36 целесообразно провести самостоя тельную работу контролирующего характера.

Самостоятельная работа № 2.2

Вариант 1 Из точки M провед н перпендикуляр MB, равный 4 см, к плоскости прямоугольника ABCD. Наклонные MA и MC образуют с плоскостью прямоугольника углы 45° и 30° соответственно.

а)0 Докажите, что треугольники MAD и MCD прямо угольные.

б)0 Найдите стороны прямоугольника.

в) Докажите, что треугольник BDC является проек цией треугольника MDC на плоскость прямоугольника, и найдите его площадь.

Вариант 2 Из точки M провед н перпендикуляр MD, равный 6 см, к плоскости квадрата ABCD. Наклонная MB образует с плоскостью квадрата угол 60°.

а)0 Докажите, что треугольники MAB и MCB прямо угольные.

б)0 Найдите сторону квадрата.

в) Докажите, что треугольник ABD является проек цией треугольника MAB на плоскость квадрата, и най дите его площадь.

Ответы:

б) AB = 4 см, BC = 4 3 см; в) 8 3 см2.

В а р и а н т 1.

б) 6 см; в) 3 см2.

В а р и а н т 2.

– &nbsp– &nbsp–

Задача 147. Из точки M провед н перпендикуляр MB к плоскости прямоугольника ABCD. Докажите, что тре угольники AMD и MCD прямоугольные.

Р е ш е н и е.

1) По условию задачи отрезок MB — перпендикуляр к плоскости прямоугольника, следовательно, отрезок AB есть проекция наклонной MA на плоскость прямоуголь ника (рис. 2.17). AD AB (так как ABCD — прямоуголь ник), следовательно, AD MA по теореме о тр х перпен дикулярах. Таким образом, угол MAD прямой и, значит, треугольник AMD прямоугольный.

2) Аналогично, так как DC BC, то DC MC и тре угольник MCD прямоугольный.

Задача 151. Прямая CD перпендикулярна к плоскости треугольника ABC. Докажите, что: а) треугольник ABC является проекцией треугольника ABD на плоскость ABC;

б) если CH — высота треугольника ABC, то DH — высо та треугольника ABD.

Р е ш е н и е.

а) По условию задачи отрезок DC — перпендикуляр к плоскости ABC, следовательно, точка C есть проекция точки D на плоскость ABC, отрезок CB — проекция на клонной DB, а отрезок CA — проекция наклонной DA на плоскость ABC (рис. 2.18).

Все точки отрезка AB лежат в плоскости ABC, поэто му проекцией отрезка AB на плоскость ABC является сам этот отрезок.

Итак, проекциями сторон треугольника ABD на плос кость ABC являются соответствующие стороны треуголь ника ABC.

Очевидно также, что проекция M1 любой внутренней точки M треугольника ABD лежит внутри треугольника ABC и обратно: любая внутренняя точка M1 треугольни ка ABC является проекцией на плоскость ABC некоторой внутренней точки M треугольника ABD. Это и означает, что треугольник ABC является проекцией треугольника ABD на плоскость ABC.

б) AB CH по условию, следовательно, AB DH по теореме о тр х перпендикулярах, т. е. DH — высота тре угольника ABD.

– &nbsp– &nbsp–

Задача 158. Через вершину B ромба ABCD проведена прямая BM, перпендикулярная к его плоскости. Найди те расстояние от точки M до прямых, содержащих сто роны ромба, если AB = 25 см, BAD = 60°, BM = 12,5 см.

Р е ш е н и е.

1) Проведем BK AD (рис. 2.19). Отрезок BK — про екция наклонной MK на плоскость ромба, AD BK, сле довательно, AD MK по теореме о тр х перпендикуля рах. Длина отрезка MK равна расстоянию от точки M до прямой AD.

Аналогично ME — расстояние от точки M до пря мой DC.

ABK получаем BK = AB sin 60°, BK = 25 3.

3) Треугольник MBK прямоугольный, так как MB ABC. Имеем

– &nbsp– &nbsp–

4) BK = BE (как высоты ромба). Прямоугольные тре угольники MBK и MBE равны по двум катетам, следо вательно, ME = MK = 25 см.

5) Расстояния от точки M до прямых AB и BC рав ны длине перпендикуляра MB, т. е. равны 12,5 см.

О т в е т: 25 см, 25 см, 12,5 см, 12,5 см.

Задача 161. Луч BA не лежит в плоскости неразв р нутого угла CBD. Докажите, что если ABC = ABD, причем ABC 90°, то проекцией луча BA на плоскость CBD является биссектриса угла CBD.

Р е ш е н и е.

1) Пусть AE CBD. В плоскости ABC провед м пер пендикуляр AM к прямой BC, а в плоскости ABD — пер пендикуляр AK к прямой BD. Так как ABC 90°, то точка M лежит на луче BC (а не на продолжении этого луча). Аналогично так как ABD 90°, то точка K ле жит на луче BD (рис. 2.20).

Так как BC AM, то BC EM (по теореме, обратной теореме о тр х перпендикулярах). Аналогично доказыва ется, что BD EK.

2) Прямоугольные треугольники ABK и ABM равны по гипотенузе (AB — общая гипотенуза) и острому углу (ABC = ABD), следовательно, BM = BK.

3) Прямоугольные треугольники BME и BKE равны по гипотенузе (BE — общая гипотенуза) и катету (BM = BK), следовательно, EM = EK.

4) Точка E равноудалена от сторон угла CBD, следо вательно, она лежит на биссектрисе этого угла, т. е. луч BE — биссектриса угла CBD.

§ 3. ДВУГРАННЫЙ УГОЛ.

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

Урок № 37 Тема урока: Двугранный угол Основные задачи урока Ввести понятия двугранного угла и его линейного угла, рассмотреть задачи на применение этих понятий.

Примерный план проведения урока

1. Ввести понятие двугранного угла, используя рису нок 58 учебника.

2. Ввести понятие линейного угла двугранного угла.

Доказать, что все линейные углы двугранного угла рав ны друг другу (см. рис. 59, а, б).

3. Дать определение градусной меры двугранного угла.

Рассмотреть примеры острого, прямого и тупого двугран ных углов, используя рисунок 60 учебника. Прямой дву гранный угол можно показать на пересечении двух стен классной комнаты, а также стены и потолка или пола.

4. Для классной и домашней работы можно использо вать выборочно задачи 166-170.

Следует обратить внимание учащихся на обозначение двугранных углов. Двугранный угол с ребром AB, на раз ных гранях которого отмечены точки C и D, называется двугранным углом CABD.

Задача 167. В тетраэдре DABC все ребра равны, точка M — середина ребра AC. Докажите, что DMB — линейный угол двугранного угла BACD.

Рис. 2.21 Рис. 2.22

Р е ш е н и е. Медианы BM и DM являются одновремен но высотами правильных треугольников ABC и ADC (рис. 2.21). Поэтому BM AC и DM AC, и, следователь но, DMB является линейным углом двугранного угла при ребре AC основания пирамиды.

Задача 170. Из вершины B треугольника ABC, сторо на AC которого лежит в плоскости, провед н к этой плоскости перпендикуляр BB1. Найдите расстояние от точки B до прямой AC и до плоскости, если AB = 2 cм, BAC = 150° и двугранный угол BACB1 равен 45°.

Р е ш е н и е.

1) Треугольник BAC тупоугольный с тупым углом A, поэтому основание высоты BK, провед нной из вершины B, лежит на продолжении стороны AC. Расстояния от точ ки B до прямой AC и до плоскости равны соответствен но BK и BB1 (рис. 2.22).

2) Так как AC BK, то AC KB1 по теореме, обратной теореме о трех перпендикулярах. Следовательно, BKB1 — линейный угол двугранного угла BACB1. По условию задачи BKB1 = 45°.

3) Из BAK имеем A = 30°, BK = BA sin 30°, BK = 1.

– &nbsp– &nbsp–

Урок № 38 Тема урока: Признак перпендикулярности двух плоскостей Основные задачи урока Ввести понятие угла между плоскостями; дать опре деление перпендикулярных плоскостей; доказать теоре му, выражающую признак перпендикулярности двух плоскостей; показать применение этой теоремы при ре шении задач.

Примерный план проведения урока

1. Проверить выборочно решение задач из домашней работы. Желательно использовать слайды с готовыми чертежами.

2. Обратить внимание учащихся на то, что при пере сечении двух плоскостей образуются четыре двугранных угла. Если — величина того из четыр х углов, который не превосходит каждый из остальных, то говорят, что угол между пересекающимися плоскостями равен. Яс но, что 0° 90°. Если = 90°, то плоскости называются перпендикулярными. В этом случае каждый из четыр х двугранных углов, образованных пересекающимися плос костями, прямой.

3. Доказать теорему, выражающую признак перпен дикулярности двух плоскостей. Доказательство теоремы можно провести устно по тексту учебника, используя ри сунок 62. Привед нное в учебнике традиционное доказа тельство, как правило, успешно усваивается учащимися.

4. Важно обратить внимание учащихся на следующие два факта, часто используемые при решении задач:

а) Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. (Это утверждение в несколько иной формулировке приведено в п. 23 учеб ника в виде следствия из теоремы.)

б) Перпендикуляр, провед нный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.

(Это утверждение доказано в привед нном в учебнике решении задачи 178.)

5. Для классной и домашней работы можно использо вать задачи 171-180.

Задача 171. Гипотенуза прямоугольного равнобедрен ного треугольника лежит в плоскости, а катет накло нен к этой плоскости под углом 30°. Найдите угол между плоскостью и плоскостью треугольника.

Р е ш е н и е.

1) Пусть ABC — данный треугольник, AB, CO. Тогда отрезок OB — проекция катета CB на плос кость. По условию задачи CBO = 30° (рис. 2.23).

2) Пусть в треугольнике COB CO = a, тогда CB = 2a.

3) Проведем CD AB, тогда AB DO по теореме, об ратной теореме о трех перпендикулярах, и CDO — ли нейный угол двугранного угла, образованного при пере сечении плоскости с плоскостью треугольника. Пусть

– &nbsp– &nbsp–

CDO = x. Это и есть искомый угол между плоскостью и плоскостью треугольника.

4) Из CDB получаем CBD = 45°, так как по усло вию треугольник ACB равнобедренный и прямоуголь

– &nbsp– &nbsp–

откуда = 45°, т. е. двугранный угол DABC равен 45°.

5) Так как BC DC и AC DC, то ACB — линейный угол двугранного угла BDCA.

Поскольку ACB = 60°, то двугранный угол BDCA ра вен 60°.

О т в е т: 90°, 45°, 60°.

Задача 174. Найдите двугранный угол ABCD тетраэд ра ABCD, если углы DAB, DAC и ACB прямые, AC = CB = 5, DB = 5 5.

Р е ш е н и е.

1) По условию задачи углы DAB и DAC прямые, следо вательно, DA AB и DA AC (рис. 2.25). Отсюда следует, что отрезок DA — перпендикуляр к плоскости ABC, и, следователь но, отрезок AC — проекция наклонной DC на плоскость ABC. Рис. 2.25

2) По условию задачи угол ACB прямой, т. е. BC AC, и, следовательно, BC DC по теореме о тр х перпенди кулярах. Таким образом, ACD — линейный угол дву гранного угла ABCD.

3) Из DCB: DC = DB2 – BC2, DC = 25 5 – 25 = 10.

4) Из DAC получаем ACD = x, cos x = AC, cos x = 5,

– &nbsp– &nbsp–

Основные задачи урока Ввести понятие прямоугольного параллелепипеда, рассмотреть свойства его граней, двугранных углов, диа гоналей.

Примерный план проведения урока

1. Сформулировать определение прямоугольного па раллелепипеда. Доказать, что все шесть граней прямо угольного параллелепипеда — прямоугольники.

2. Доказать, что все двугранные углы прямоугольно го параллелепипеда прямые.

3. Доказать т е о р е м у: квадрат диагонали прямо угольного параллелепипеда равен сумме квадратов тр х его измерений.

Обратить внимание на аналогию со свойством диаго нали прямоугольника. Можно отметить также, что эта теорема является одним из вариантов пространственной теоремы Пифагора.

Рассмотреть следствие из теоремы: диагонали прямо угольного параллелепипеда равны.

4. Для классной и домашней работы можно использо вать выборочно задачи 187-192.

Рис. 2.26 Рис. 2.27

Задача 191. Дан куб ABCDA1B1C1D1. Докажите, что плоскости ABC1 и A1B1D перпендикулярны.

Р е ш е н и е.

1) BC1 B1C по свойству диагоналей квадрата (рис. 2.26). DC BCC1, поэтому DC BC1, так как BC1 BCC1.

Таким образом, прямая BC1 перпендикулярна к двум пересекающимся прямым DC и CB1, лежащим в плоско сти A1B1D. Следовательно, прямая BC1 перпендикулярна к плоскости A1B1D по признаку перпендикулярности прямой и плоскости.

2) Плоскость ABC1 проходит через прямую BC1, пер пендикулярную к плоскости A1B1D, следовательно, ABC1 A1B1D по признаку перпендикулярности двух плос костей.

Задача 192. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.

Р е ш е н и е.

1) Пусть ребро куба ABCDA1B1C1D1 равно a. Тогда BD = a 2 (рис. 2.27). Так как D1D ABC, то прямая BD является проекцией прямой BD1 на плоскость грани ABCD, и поэтому угол между этими прямыми есть угол между диагональю BD1 и гранью ABCD. Таким образом, требу ется найти тангенс угла D1BD, величину которого обо значим.

2) Из D1DB получаем tg = 1, tg = a, tg = 2.

– &nbsp– &nbsp–

Урок № 40 Тема урока: Решение задач на прямоугольный параллелепипед Основные задачи урока Повторить свойства прямоугольного параллелепипеда, решить ряд задач на прямоугольный параллелепипед.

Примерный план проведения урока

1. Повторить вопросы теории пут м опроса учащихся.

2. Проверить выборочно решение задач из домашней работы, используя готовые чертежи, слайды.

3. Для классной и домашней работы можно использо вать задачи 193-196.

Задача 195. Найдите измерения прямоугольного па раллелепипеда ABCDA1B1C1D1, если AC1 = 12 см и диаго наль BD1 составляет с плоскостью грани AA1D1D угол 30°, а с ребром DD1 — угол 45°.

Р е ш е н и е.

Похожие работы:

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Институт наук о Земле Кафедра физической географии и экология Тюлькова Л.А ГЕОМОРФОЛОГИЯ учебно-методический комплекс. Рабочая программа для студентов направления 05.03.04 « Гидрометеорология», очной формы обучения Тюменский государственный университет Тюлькова Л.А. Геоморфология. Учебно-методический…»

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ «ГУСЕВСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ» УТВЕРЖДАЮ Директор ГБУ КО ПОО ГАПК Л.В. Грубинов 15 августа 2014 года ОСНОВНАЯ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ КАЛИНИНГРАДСКОЙ ОБЛАСТИ ПРОФЕССИОНАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ«ГУСЕВСКИЙ АГРОПРОМЫШЛЕННЫЙ…»

«Тема: ОБРАЗОВАНИЕ в РФ. Общие положения. ВУЗ. ПТО. СШО.ДОУ Дата обновления: 24.02.2015 Аналитический обзор Утверждены рекомендации по актуализации федеральных стандартов высшего образования с целью учета в них положений соответствующих профессиональных стандартов рекомендации по актуализации действующих федеральных государственных Методические образовательных стандартов высшего образования с учетом принимаемых профессиональных стандартов (утв. Минобрнауки России 22.01.2015 N ДЛ-2/05вн)…»

« ОБУЧЕНИЯ) Фамилия Имя Отчество Курс_ факультет коммуникаций и права Группа № _ Результаты рецензирования (графа заполняется преподавателем) _ _ _ _ _ _Преподаватель _ Минск 2014 СОДЕРЖАНИЕ КРАТКИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ РАЗДЕЛ 1. ОБЩЕЕ УЧЕНИЕ О КРИМИНАЛИСТИКЕ ТЕМА 1.1 ПРЕДМЕТ, ИСТОРИЯ, СИСТЕМА, ОБЪЕКТЫ И ЗАДАЧИ. ИСТОРИЯ И МЕТОДОЛОГИЯ…»

«Содержание Аннотация…1. Цели самостоятельной работы студентов. 2. Задачи самостоятельной работы студентов..5 3.Рекомендации по самостоятельному изучению дисциплины..5 4. Виды самостоятельной работы студентов..5 5. Требования к минимуму содержания дисциплины согласно Федеральному государственному образовательному стандарту… 6.Содержание самостоятельной работы по темам дисциплины. 7.Задания для самостоятельной работы студентов 7.1.Тематика рефератов и творческих работ по дисциплине..8…»

«План информационнообразовательных семинаров и вебинаров Первое полугодие 2015-2016 учебный год Октябрь Участие бесплатное. Всем участникам (регистрация обязательна) выдаются 16 октября 2015 16.00–17.00 (время московское) сертификаты об участии в Вебинар «Методические принципы разработки заданий семинарах и вебинарах. Международного конкурса «ПОНИ® в гостях у Пифагора» для учеников 2-4 классов и критерии их оценивания». На вебинаре анализируются цели проведения интеллектуальных состязаний,…»

«РОССИЙСКАЯ ФЕДЕРАЦИЯ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ Государственное образовательное учреждение высшего профессионального образования ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ «УТВЕРЖДАЮ»: Проректор по учебной работе Л.М. Волосникова 08.07. 2011г. Организация логопедической работы в дошкольных образовательных учреждениях Учебно-методический комплекс. Рабочая программа для студентов направления подготовки 050700.62 Специальное (дефектологическое) образование, профиль подготовки Логопедия, форма…»

«Государственное бюджетное профессиональное образовательное учреждение города Москвы «Первый Московский Образовательный Комплекс» Методические рекомендации по выполнению практических работ По профессиональному модулю ПМ 02. Конструирование швейных изделий МДК 02.02. Методы конструктивного моделирования швейных изделий, 3-й курс обучения 262019 Конструирование, моделирование и технология швейных изделий углубленная подготовка (наименование профиля подготовки) Москва ББК Г1 ОДОБРЕНЫ Разработаны на…»

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ УНИВЕРСИТЕТ ИТМО Е.П. Сучкова, М.С. Белозерова МЕТОДЫ ИССЛЕДОВАНИЯ МОЛОКА И МОЛОЧНЫХ ПРОДУКТОВ Учебно-методическое пособие Санкт-Петербург УДК 637.1/3 Сучкова Е.П., Белозерова М.С. Методы исследования молока и молочных продуктов: Учеб.-метод. пособие. – СПб.: Университет ИТМО; ИХиБТ, 2015. – 47 с. Приведены лабораторные работы по дисциплине «Методы исследования молока и молочных продуктов». Работы посвящены изучению современных методов…»

«Содержание 1. Общие положения..2. Характеристика направления подготовки..3. Характеристика профессиональной деятельности выпускников.3.1. Область профессиональной деятельности выпускника ОП ВО.3.2 Объекты профессиональной деятельности выпускника ОП ВО.3.3 Виды профессиональной деятельности выпускника ОП ВО.3.4 Обобщенные трудовые функции выпускников в соответствии с профессиональными стандартами..8 4. Результаты освоения образовательной программы.. 5. Структура образовательной программы…»

«ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ЗАЩИТЫ ПРАВ ПОТРЕБИТЕЛЕЙ И БЛАГОПОЛУЧИЯ ЧЕЛОВЕКА ФБУН «Федеральный научный центр медико-профилактических технологий управления рисками здоровью населения» ФГБОУ ВПО «Пермский государственный национальный исследовательский университет» АКТУАЛЬНЫЕ НАПРАВЛЕНИЯ РАЗВИТИЯ СОЦИАЛЬНО-ГИГИЕНИЧЕСКОГО МОНИТОРИНГА И АНАЛИЗА РИСКА ЗДОРОВЬЮ Материалы Всероссийской научно-практической конференции с международным участием (15–17 мая 2013 г.) Под редакцией академика РАМН…»

«РАБОЧАЯ ПРОГРАММА ПО ПРЕДМЕТУ «ТЕХНОЛОГИЯ» ДЛЯ 1 КЛАССА «Ж» Составитель: учитель начальных классов Тамбовцева Наталья Сергеевна Москва, 2014-2015 учебный год Пояснительная записка. Рабочая программа по технологии построена на основе требований Федерального государственного стандарта начального общего образования по образовательной области «Технология» и разработана в соответствии с Примерной программой начального общего образования, рабочей программой Н.И. Роговцевой, С.В. Анащенкова…»

«М. С. Соловейчик Н. С. Кузьменко РУССКИЙ ЯЗЫК МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к учебнику для 2 класса общеобразовательных организаций Пособие для учителя Издание 7-е, переработанное Смоленск Ассоциация XXI век УДК 372.881.116.11.046. ББК 74.268.1Рус С ОБРАТИТЕ ВНИМАНИЕ! Будьте осмотрительны при использовании методических пособий к учебнику, выпускаемых другими издательствами! Если кто-либо из авторов данного учебника не указан в качестве редактора, консультанта или рецензента, пособие может не…»

«СПЕЦИАЛИЗИРОВАННОЕ СТРУКТУРНОЕ ОБРАЗОВАТЕЛЬНОЕ ПОДРАЗДЕЛЕНИЕ ПОСОЛЬСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ В РЕСПУБЛИКЕ МАДАГАСКАР – ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ПРИ ПОСОЛЬСТВЕ РОССИИ НА МАДАГАСКАРЕ РАБОЧАЯ ПРОГРАММА учебного курса (литература) 5 КЛАСС 2014-2015 учебный год учитель: Егорова И.В. Пояснительная записка Рабочая программа составлена в соответствии с нормативными документами и методическими материалами: Федеральным компонентом государственного образовательного стандарта основного общего…»

«Рассмотрено на заседании МО протокол № от 24.08.2015г. «Проверено» «Утверждаю» _ заместитель директора по УВР директор МБОУ «Лицей «МОК №2» Самофалова Ю.В._ Свердлов В.Я. Рабочая программа по внеурочной деятельности Курс «Школа развития речи» 2015-2016 учебный год Учитель Асоян О.И., Бавыкина И.Е., Леденёва Г.А., Ивашкина Н.В., Саввина О.Ю., Свердлова Л.В. Класс 4 «А», «Б», «В», «Г», «Д», «Е» Предмет «Курс «РЕЧЬ». Юным умникам и умницам. Школа развития речи» (34 часа; 1 час в неделю)…»

«Министерство образования и науки Российской Федерации Амурский государственный университет Е.В. Пшеничникова ОСНОВЫ ПРОЕКТИРОВАНИЯ ОДЕЖДЫ ДЛЯ ИНДИВИДУАЛЬНОГО ПОТРЕБИТЕЛЯ Учебное пособие Рекомендовано Дальневосточным региональным учебнометодическим центром (ДВ РУМЦ) в качестве учебного пособия для студентов, обучающихся по направлению подготовки бакалавров 262000.62 «Технология изделий легкой промышленности», 100100.62 «Сервис» вузов региона Благовещенск Издательство АмГУ ББК 37. 24-2 я 73 П 93…»

«ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ Междисциплинарное учебное пособие CREAN ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ ЗАЩИТА ДЕТЕЙ ОТ ДИСКРИМИНАЦИИ Междисциплинарное учебное пособие Под редакцией Дагмар Кутсар и Ханны Уорминг Редактор перевода на русский язык Заботкина Вера Ивановна д-р филол. наук, проф., Проректор по инновационным международным проектам Российский государственный гуманитарный университет Европейский консорциум университетов, предлагающих магистерские программы по правам ребенка в рамках…»

«Содержание Раздел 1. Перечень планируемых результатов обучения по дисциплине, соотнесенных с планируемыми результатами освоения образовательной программы.. 4 1.1 Перечень планируемых результатов обучения по дисциплине. 4 1.2 Планируемые результаты освоения образовательной программы. 4 Раздел 2. Место дисциплины в структуре образовательной программы. 6 Раздел 3. Объем дисциплины.. 6 Раздел 4. Структура и содержание дисциплины. 7 Раздел 5. Перечень учебно-методического обеспечения для…»

«СОДЕРЖАНИЕ Требования к результатам освоения дисциплины 1. 4 Место дисциплины в структуре ОПОП 2. 5 Структура и содержание дисциплины 3. 6 Структура дисциплины 3.1. 6 Содержание дисциплины 3.2. 7 Перечень учебно-методического обеспечения для самостоятельной работы 4. 9 обучающихся по дисциплине Образовательные технологии 5. 9 Формы контроля освоения дисциплины 6. 9 Перечень оценочных средств для текущего контроля освоения дисциплины 6.1. 9 Состав фонда оценочных средств для проведения…»
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам , мы в течении 1-2 рабочих дней удалим его.

Исследовательская работа «Трапеция» | Образовательная социальная сеть

Слайд 16

2.Свойства равнобедренной трапеции A B K C M D N 1. Прямая, проходящая через середины оснований равнобедренной трапеции, перпендикулярна основаниям и является осью симметрии трапеции. Доказательство Пример

Слайд 17

Доказательство: Пусть в трапеции АВС D ВС// А D , АВ = С D , К – точка пересечения продолжений боковых сторон, М и N — середины оснований, тогда М , N и К лежат на одной прямой.

Слайд 18

Пример: (№24 ГИА 2014) В равнобедренной трапеции АВС D длина боковой стороны равна длина основания угол А при сновании равен 60 0 , О – точка пересечения диагоналей, К – точка пересечения продолжений боковых сторон трапеции. Найти длину отрезка КО. A B K C M D N О Решение: АВС D – равнобедренная трапеция. Прямая КО проходит через середину оснований и перпендикулярно к ним (КО┴ ВС, КО ┴А D ). Пусть М и N — середины оснований.

Слайд 19

KM – высота Δ BKC, KN – высота Δ AKD, ΔBOC ∞ ΔDOA, Обозначим МО = х, тогда N О = х — 21 KO= KM + MO =63 + 9 =72 Ответ: 72.

Слайд 20

a A B C D M b 2. Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. Доказательство Пример

Слайд 21

Доказательство : A B C D M b K a Проведем высоту CK . ΔABC = Δ DCK по гипотенузе и катету) следовательно AM = KD . BC = MK = a , т.к BCMK — прямоугольник AM = KD = (AD-BC):2 = (b- а ):2 Что и требовалось доказать.

Слайд 22

C B F D A 29 21 Пример ( № 24 Гиа 2014 )Средняя линия трапеции равна 21, а диагональ – 29. Найти высоту, проведенную к основанию. Дано: MN =21, AC = 29 Найти: CF =? Решение: AF = MN =21, FC =29 ( CF ┴ AD ), По теореме Пифагора для треугольника ACF : AC 2 = AF 2 + CF 2 CF 2 = AC 2 — AF 2 CF 2 =29 2 – 21 2 = 400, CF =20 Ответ: 20.

Слайд 23

3. В равнобедренной трапеции длины диагоналей равны. BD = AC Доказательство: Треугольники ABD и ACD равны по двум сторонам и углу между ними ( AB = CD , угол А равен углу D , так как трапеция равнобедренная, сторона AD – общая), следовательно BD = AC . Что и требовалось доказать.

Слайд 24

A B M N C P D K 4. Середины сторон равнобедренной трапеции являются вершинами ромба .( №21 ГИА 2012) Доказательство: Точки M , N , P и K — середины сторон АВ, CD и DA равнобедренной трапеции ABCD . Отрезки MN и KP параллельны AC и равны ее половине как средние линии треугольников ABC и ADC ; аналогично MK и NP параллельны BD и равны ее половине. Поэтому четырехугольник MNPK — параллелограмм. Треугольник Δ ABC =Δ DCA , MK и РК — средние линии этих треугольников, значит, MK = PK . Аналогично MN = NP по 2 сторонам и углу между ними. Таким образом, в параллелограмме MNPK все стороны равны, а значит, он является ромбом. Что и требовалось доказать.

Слайд 25

A a D B C b 5. Боковая сторона равнобедренной трапеции, в которую вписана окружность равна полусумме оснований Доказательство: Окружность вписана в трапецию значит AB + CD = BC + AD , AB = CD , поэтому 2*АВ= BC + AD Что и требовалось доказать.

Слайд 26

A a D B C b M N 6. Боковая сторона равнобедренной трапеции, в которую вписана окружность, равна средней линии трапеции. AB = MN 7. Периметр равнобедренной трапеции, в которую можно вписать окружность, равен 4*АВ

Слайд 27

A a D B C b H 8. Высота равнобедренной трапеции, в которую можно вписать окружность, равна Доказательство Из прямоугольного треугольника ABH найдем BH : AB 2 =AH 2 + BH 2 , BH 2 = AB 2 – AH 2 ) Что и требовалось доказать.

Слайд 28

A a D B C b O 9.

Слайд 29

10. Около равнобедренной трапеции можно описать окружность.

Слайд 30

11. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. AC┴BD

Слайд 31

3.Формулы площади трапеции 1. Площадь трапеции равна произведению полусуммы оснований на высоту: Пример

Слайд 32

Пример (№17 ГИА 2012): 6 16 10 10 Найти площадь трапеции изображенной на рисунке: Решение: По теореме Пифагора: a = 10, b = 6+16 = 22 Ответ: 128

Слайд 33

Формула площади трапеции, где a,b – основания трапеции, c.d – боковые стороны трапеции: Пример

Слайд 34

Доказательство: Рассмотрим трапецию АВС D с основанием А D и BC . Обозначим через К и М середины боковых сторон AB и CD . Рассмотрим еще одну точку — середину P диагонали BD . Тогда KP — средняя линия треугольника ABD , а PM — средняя линия треугольника BDC . KP и PM параллельны соответственно AD и BC , а поскольку AD и BC параллельны между собой, точки K , P и M лежат на одной прямой, параллельной основаниям трапеции. Кроме того, КМ=КР+РМ= ½ (А D + BC ) Что и требовалось доказать . A D B C K M a b P

Слайд 35

— середина AC , — середина BD Доказательство: Проведем в трапеции ABCD среднюю линию ML . По свойству средней линии трапеции ML || AD и ML || BC , ML = Так как в Δ BCD через середину стороны CD проведена прямая, параллельная основанию BC , то она является средней линией ΔВ CD , проходит через середину стороны BD — точку . = 1/2BC Значит, средняя линия трапеции проходит через точку . Аналогично доказывается, что = 1/2BC Что и требовалось доказать.

Слайд 36

Доказательство формулы Буракова: Пусть в трапеции ABCD основания AD и BC соответственно равны а и в Что и требовалось доказать.

Слайд 37

Доказательство свойства № 5: Обозначаем через L и Р середины оснований AD и ВС трапеции ABCD ; М-точка пересечения её диагоналей, К — точка пересечения продолжений боковых сторон. Докажем, что точки K , L . P лежат на одной прямой. Это следует из подобия треугольников BKC и AKD . В каждом из них отрезки KP и KL соответственно являются медианами, а значит, они делят угол при вершине K на одинаковые части. Точно также на одной прямой расположены точки M , P , L . (Здесь это следует из подобия треугольников BMC и DMC .) Значит, все четыре точки K , P , M и L лежат на одной прямой, т.е прямая KM проходит через P и L . Что и требовалось доказать.

Слайд 38

A B C D Доказательство свойства № 7: Прямые BC и AD — параллельны, AB – секущая, α + β = 180 0 — как сумма односторонних углов. Что и требовалось доказать .

Слайд 39

В трапеции ABCD известны длины оснований BC =16, AD = 19 и боковых сторон AB = 5, CD = 4. Найти площадь этой трапеции. Решение: a=16 , b=19, c=5, d=4 Ответ: 70.

Слайд 40

Площадь трапеции равна половине произведения диагоналей на синус угла между ними. A B C D Пример

Слайд 41

Пример (№17 ГИА 2011): Найти площадь трапеции, диагонали которой взаимно перпендикулярны и соответственно равны 19 и 26. Решение S= 0.5*19*26*sin 90 0 =19*13*1=247 Ответ: 247. A B C D

Как найти длину диагонали трапеции

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

доказательств для равнобедренных трапеций — видео и стенограмма урока

Базовые углы

Углы, образованные между непараллельными сторонами и параллельными сторонами, называемые базовыми углами , равны в равнобедренной трапеции.В трапеции ABCD Ирен на газоне углы C и D равны.

Чтобы доказать эту теорему, давайте проведем линию CE , параллельную AD , так что ADCE станет параллелограммом.

В этом параллелограмме мы знаем, что линия AD = линия CE .Мы также знаем, что строка AD = строка BC , поэтому мы также знаем, что строка BC = строка CE .

Теперь, поскольку линия BC и линия CE равны, треугольник BCE становится равнобедренным. Следовательно, углы CBE и CEB равны.

Мы понимаем, что линия AD и линия CE параллельны, а линия AE является поперечной.Таким образом, сумма внутренних углов на одной стороне, угла DAE и угла CEA составляет 180 градусов.

Итак,

Следовательно, углы DAB и CBA равны.

Далее мы знаем, что ADCE — параллелограмм, поэтому противоположные углы будут равны.

Теперь углы CBE и BCD будут равны, потому что они являются альтернативными внутренними углами для параллельных линий AE и CD .

Мы уже знаем, что углы CEB и CEB равны. Следовательно,

Таким образом, доказано, что углы основания равнобедренной трапеции равны.

Диагонали

Диагонали равнобедренной трапеции равны по длине. Итак, в равнобедренной трапеции ABCD Ирен диагонали AC и BD равны.

Чтобы доказать эту теорему, давайте сосредоточимся на двух образованных треугольниках: DAC и CBD . Здесь мы знаем, что линия AD = BC , углы ADC и BCD равны, а сторона CD является общей.Ирен вспоминает свойство стороны-угла-стороны треугольников: если в двух треугольниках две стороны и их угол первого треугольника конгруэнтны двум сторонам и их углу второго, то два треугольника конгруэнтны. .

Следовательно, треугольники DAC и CBD совпадают.

Следовательно, остальные соответствующие стороны равны, AC = BD .Таким образом, диагонали равны.

Противоположные углы

Сумма противоположных углов равнобедренной трапеции Ирен составляет 180 градусов. Она может доказать это, зная, что угол A равен углу B , а угол C равен углу D .

Она также знает, что AB параллельна CD , что делает пары углов A и D и B и C внутренними углами на одной стороне поперечной.Это означает, что эти пары составляют дополнительных или их сумма равна 180 градусам.

Теперь, заменяя равные углы,

Таким образом, она доказывает, что противоположные углы являются дополнительными в равнобедренной трапеции.

Основываясь на углах основания, диагонали и сумме противоположных углов, она может посадить свой сад и быть уверенной, что его форма действительно представляет собой равнобедренную трапецию.

Резюме урока

На этом уроке вы узнали, что трапеция с равными, непараллельными сторонами — это равнобедренная трапеция . Затем мы рассмотрели важные теоремы, связанные с ними, и подробно доказали их.

• Базовые углы (углы, образованные между непараллельными сторонами и параллельными сторонами) равны равнобедренной трапеции.
• Диагонали равнобедренной трапеции равны по длине.
• Сумма противоположных углов равнобедренной трапеции равна 180 градусам.

Видеоурок: Доказательство циклических четырехугольников

Стенограмма видео

В этом видео мы узнаем, как
Докажите, что четырехугольник вписанный, используя углы, полученные из его
диагонали. Начнем с определения циклического
четырехугольник. Вогнутый четырехугольник — это
четырехсторонний многоугольник, вершины которого вписаны в окружность.Например, это циклический
четырехугольник. Вписанный угол — это угол
получается, когда две хорды пересекаются по окружности круга. Вершина угла лежит на
окружность круга.

Прежде чем мы рассмотрим свойства
вписанного четырехугольника напомним две очень важные теоремы о вписанном
углы. Угол 𝜃 вписанный в круг
равна половине центрального угла два 𝜃, который образует ту же дугу на окружности.Другими словами, угол при
окружность равна половине угла в центре. Затем это приводит ко второму
теорема о вписанных углах, которая говорит нам, что вписанные углы, образуемые одним и тем же
дуги равны. Итак, давайте посмотрим, как это будет
полезно, когда мы смотрим на доказательство циклических четырехугольников.

Мы можем взять пример этого
вписанный четырехугольник 𝐴𝐵𝐶𝐷. И нарисуем его диагональную линию
сегменты.Используя дугу и учитывая, что
если углы, образуемые одной и той же дугой, равны, то можно сказать, что мера
угол 𝐷𝐴𝐶 равен мере угла 𝐷𝐵𝐶. Затем мы можем использовать то же свойство
с этой дугой 𝐴𝐵, чтобы показать, что мера угла должна быть равна
мера угла 𝐴𝐶𝐵.

Тогда мы можем наблюдать, что в любом
циклический четырехугольник, угол, образованный диагональю и стороной, равен углу
создается другой диагональю и противоположной стороной.В этом примере мы нашли две пары
равных углов. Но мы также можем использовать дугу 𝐵𝐶, чтобы
покажите, что мера угла 𝐵𝐴𝐶 равна мере угла. Использование дуги показало бы, что
мера угла 𝐴𝐵𝐷 равна мере угла.

Когда дело доходит до доказательства того, что
четырехугольник вписанный, нам нужно проверить, верно ли обратное утверждение этой теоремы.
правда. Посмотрим, сможем ли мы доказать это, если
если углы, образованные диагоналями, равны, то это означает, что
четырехугольник вписанный.Давайте возьмем другой
четырехугольник, along, вместе с его диагоналями. Если мы сможем доказать, что мера
угол 𝐷𝐴𝐶 равен мере угла, то четырехугольник равен
циклический. Это потому, что 𝐷𝐶 должна быть дугой
круга. Следовательно, 𝐴 и 𝐵 также должны быть
точки на том же круге. Следовательно, каждая вершина должна быть на
круг. И это по определению циклический
четырехугольник.

Конечно, не всегда
здесь должны быть два верхних угла, которые, как мы доказали, совпадают. Например, если бы мы могли доказать, что
мера угла 𝐴𝐷𝐵 равна мере угла 𝐴𝐶𝐵, тогда это будет
также покажите, что четырехугольник вписанный. Однако нам просто нужен один из этих
пары конгруэнтных углов, чтобы продемонстрировать, что четырехугольник вписанный. Вы также можете задаться вопросом, возможно,
каждый четырехугольник вписанный.Но давайте посмотрим на
другой пример.

Вот четырехугольник 𝐸𝐹𝐺𝐻. Мы можем наблюдать на глаз, что
мера угла 𝐺𝐸𝐻 не равна мере угла. Мы не могли нарисовать круг, который
проходит через все четыре вершины. Итак, 𝐸𝐹𝐺𝐻 не циклический
четырехугольник.

Теперь рассмотрим несколько примеров.
где мы доказываем, является ли четырехугольник вписанным или нет.

Есть ли круг, проходящий через
вершины четырехугольника 𝐴𝐵𝐶𝐷?

Если круг проезжает
через вершины этого четырехугольника, то это будет вписанный
четырехугольник.Есть несколько разных
угловые свойства, которые мы можем использовать, чтобы определить, является ли этот четырехугольник циклическим. Однако, учитывая, что у нас есть
диагонали обозначены, давайте проверим углы, образованные диагоналями. Затем мы можем задать вопрос, является ли
угол между диагональю и стороной равен
угол, созданный другой диагональю и противоположной стороной?

На данный момент у нас нет
конгруэнтные пары углов на диаграмме.Однако мы можем заметить, что это
угол 𝐶𝐴𝐵 — это угол, образованный стороной и диагональю. Угол 𝐶𝐷𝐵 — это созданный угол
по другой диагонали и с противоположной стороны. Итак, давайте посмотрим, соответствует ли это
угол 𝐶𝐴𝐵. Рассмотрим треугольник 𝐶𝐵𝐷
и напомним, что сумма внутренних углов треугольника равна 180 градусам. Таким образом, можно сказать, что
три угла в этом треугольнике, 54 градуса плюс 79 градусов плюс мера угла
𝐶𝐷𝐵, должен быть равен 180 градусам.Мы можем упростить левую часть
а затем вычтите 133 градуса с обеих сторон, что дает нам меру
угол 𝐶𝐷𝐵 составляет 47 градусов.

Это означает, что теперь у нас есть пара
равных углов. Мера угла равна
равна мере угла 𝐶𝐴𝐵. Следовательно, можно сказать, что угол
сделана с диагональю, и сторона равна по мере углу, созданному другой
диагональ и противоположная сторона.Следовательно, мы можем дать ответ
да. Поскольку мы показали, что это
циклический четырехугольник, мы могли бы нарисовать круг, который проходит через все четыре вершины
из 𝐴𝐵𝐶𝐷.

Давайте посмотрим на другой пример.

Является ли циклическим
четырехугольник?

На этом рисунке видно, что
у нас отмечены две диагонали 𝐴𝐶 и. Если мы сможем доказать, что угол
образованный диагональю, и сторона равна по мере углу, создаваемому другой
диагональ и противоположная сторона, то четырехугольник вписанный.Если они не равны, то это
не вписанный четырехугольник. Угол 𝐵𝐷𝐴 — это угол
создается по диагонали и по бокам. Угол, созданный другим
диагональ, а противоположная сторона — угол 𝐵𝐶𝐴. Если эти два угла совпадают,
тогда четырехугольник вписанный.

Еще пара углов, которые мы могли бы
проверка будет угол 𝐷𝐴𝐶 и угол 𝐷𝐵𝐶. Если бы мы знали, что всего одна пара
эти угловые меры совпадали, тогда этого было бы достаточно, чтобы показать, что
четырехугольник вписанный.Итак, давайте посмотрим, сможем ли мы поработать
это угловая мера.

Нам дано, что этот угол
мера 𝐵𝐸𝐴 составляет 90 градусов. И мы можем помнить, что углы
по прямой сумме до 180 градусов. Значит, угол 𝐵𝐸𝐶
также должен иметь размер 90 градусов. Теперь мы можем рассмотреть треугольник
𝐵𝐸𝐶 и помните, что сумма углов в треугольнике составляет 180 градусов. Итак, мы можем написать, что 63 градуса
плюс 90 градусов плюс мера угла 𝐵𝐶𝐸 составляет 180 градусов.Следовательно, мера угла
𝐵𝐶𝐸 равно 180 градусам, вычесть 153 градуса, что составляет 27 градусов. Следовательно, эти два угла измерения
созданные по диагоналям не равны. А это значит, что 𝐴𝐵𝐶𝐷 не
вписанный четырехугольник. Следовательно, мы можем дать ответ
нет.

В начале этого вопроса мы
также сказал, что мы можем проверить угловые размеры 𝐶𝐵𝐷 и. Вычисление этого угла равно
также 90 градусов, тогда мы могли бы установить, что угол 𝐶𝐴𝐷 равен 52 градусам.Но конечно 63 градуса — это не так.
равный 52 градусам, что еще раз показывает, что 𝐴𝐵𝐶𝐷 не является циклическим
четырехугольник.

В следующем вопросе мы проверим
если данная трапеция — вписанный четырехугольник.

Трапеция 𝐴𝐵𝐶𝐷 циклическая
четырехугольник?

Учитывая, что у нас есть трапеция, мы
должна иметь одну пару параллельных сторон. И они здесь отмечены. 𝐵𝐶 и 𝐴𝐷 параллельны. Поскольку у нас есть трансверсаль, мы
можно вычислить, что угол ate чередуется с углом 𝐴𝐷𝐵.Тоже 84 градуса. Мы можем обозначить пересечение
диагонали как точка 𝐸. И тогда мы можем присмотреться
в треугольнике 𝐵𝐸𝐶.

Мы можем определить меру этого
неизвестный угол 𝐵𝐶𝐸, помня, что внутренние углы в треугольнике в сумме составляют
180 градусов. Следовательно, 84 градуса плюс 52
градусов плюс мера угла 𝐵𝐶𝐸 равна 180 градусам. 84 градуса плюс 52 градуса дает
136 градусов.Вычитая 136 градусов из обоих
сторон дает нам, что угол 𝐵𝐶𝐸 составляет 44 градуса. Итак, как это помогает нам работать
если 𝐴𝐵𝐶𝐷 циклический или нет?

Что ж, давайте считать, что мы были
учитывая угол, образованный диагональю и стороной, угол 𝐴𝐷𝐵. Мы только что рассчитали угол
создается другой диагональю и противоположной стороной. Если эти две угловые меры равны
равные, то четырехугольник вписанный.Но, конечно, 84 градуса — это не так.
равняется 44 градусам. Итак, две угловые меры
не совпадают. Следовательно, 𝐴𝐵𝐶𝐷 не
циклический. Поэтому мы можем ответить на
вопрос с нет.

Пока мы видели конкретные
примеры различных четырехугольников. Однако в следующих двух примерах
мы рассмотрим общие утверждения о множествах четырехугольников, начиная с
определение того, являются ли все прямоугольники вписанными четырехугольниками или нет.

Все прямоугольники циклические
четырехугольники. (A) верно или (B) неверно.

Для начала напомним, что
вписанный четырехугольник — это четырехугольник, все четыре вершины которого вписаны в
круг. Один из способов доказать, что
четырехугольник является циклическим, демонстрируя, что угол, образованный диагональю и
сторона равна по мере углу, создаваемому другой диагональю и противоположной
боковая сторона.Итак, давайте рассмотрим свойства
прямоугольник, который определяется как четырехугольник с четырьмя углами по 90 градусов. В прямоугольнике также есть два
пары противоположных конгруэнтных сторон.

Мы знаем, что диагонали
прямоугольник делит прямоугольник на два равных треугольника. Вместе обе диагонали создают
четыре равных треугольника. То есть любой треугольник,
образованный двумя сторонами, и диагональ конгруэнтна любому другому треугольнику, который также
создается двумя сторонами и диагональю.Итак, для этого прямоугольника, который мы
можно назвать 𝐽𝐾𝐿𝑀, мы можем сказать, что треугольник 𝐽𝐾𝐿 конгруэнтен треугольнику
𝐿𝑀𝐽. Можно также сказать, что это то же самое
треугольник 𝐿𝑀𝐽 конгруэнтен треугольнику.

В этой последней паре конгруэнтных
треугольников, мы также можем утверждать, что две соответствующие угловые меры конгруэнтны
так как мера угла 𝑀𝐽𝐿 равна мере угла. Это означает, что угол, созданный
диагональ и сторона равны углу, образованному другой диагональю
и противоположная сторона.Так вот этот прямоугольник и вправду
любой прямоугольник должен быть вписанным четырехугольником.

В качестве альтернативного метода мы могли бы
Также учтите, что диагонали прямоугольника равны по длине и делят каждую пополам.
Другие. Это означает, что будет четыре
отрезки равной длины, идущие от точки пересечения. Их можно рассматривать как радиусы
идущий из центра круга. Любой метод позволит нам дать
ответ верный, так как все прямоугольники вписанные четырехугольники.

В этом примере мы установили
что все прямоугольники циклические. Однако важно отметить
эти квадраты, которые определяются как четырехугольники со всеми равными сторонами и
внутренние углы, равные 90 градусам, представляют собой подмножество прямоугольников. Следовательно, все квадраты тоже
вписанные четырехугольники.

Теперь посмотрим на другой тип
четырехугольника.

Все равнобедренные трапеции циклические.
четырехугольники.(A) верно или (B) неверно.

Начнем с того, что напомним, что
трапеция — это четырехугольник с одной парой параллельных сторон. Равнобедренная трапеция — особая
тип трапеции, который имеет дополнительное свойство, заключающееся в том, что две непараллельные стороны,
которые иногда называют ногами, имеют одинаковую длину. Итак, нарисуем равнобедренный
трапеция. У него одна пара параллельных сторон,
а две другие непараллельные стороны равны по длине.Затем мы можем использовать один из
свойства диагоналей равнобедренной трапеции. Диагонали равнобедренной кости
трапеция создает два равных треугольника на ногах. Они также создают два одинаковых
треугольники у оснований.

Будьте осторожны, но только это правило
относится к равнобедренным трапециям. Например, возьмем это
трапеция, которая не является равнобедренной. Диагонали не образуют двух
конгруэнтные треугольники на ногах.Но вернемся к равнобедренному телу
трапеции и посмотрите на углы. Мы можем определить пересечение
диагонали как точка 𝐸. А потом, потому что у нас есть два
конгруэнтных треугольников, мы можем идентифицировать соответствующие углы. Угол 𝐷𝐴𝐸 должен быть
равна мере угла 𝐶𝐵𝐸. Кроме того, мера угла
𝐴𝐷𝐸 равно мере угла 𝐵𝐶𝐸. Любая из этих пар конгруэнтных
углов продемонстрировали бы, что мера угла, образованного диагональю и стороной
равен углу, создаваемому другой диагональю и противоположной стороной.Это означает, что равнобедренная трапеция
𝐴𝐵𝐶𝐷 и любая равнобедренная трапеция — вписанный четырехугольник.

Хотя не все трапеции
вписанные четырехугольники, все равнобедренные трапеции. Так что мы можем дать верный ответ.

Можно резюмировать предыдущие два
примеры, говоря, что, хотя есть некоторые четырехугольники, которые могут быть показаны
быть циклическим, есть три типа, которые всегда будут циклическими. Это квадраты, прямоугольники и
равнобедренные трапеции.

Теперь подведем итоги ключевых моментов.
этого видео. Мы начали с того, что отметили, что циклический
четырехугольник — это четырехгранный многоугольник, вершины которого вписаны в окружность. В круговом четырехугольнике
угол, образованный диагональю и стороной, равен по мере углу, создаваемому
другая диагональ и противоположная сторона. Обратное также
правда. Таким образом, мы можем использовать один метод, чтобы
доказать, что четырехугольник вписан, — это продемонстрировать, что угол, образованный
диагональ и сторона равны по мере углу, образованному другой диагональю и
противоположная сторона.Наконец, мы также увидели, что все
квадраты, прямоугольники и равнобедренные трапеции — это циклические четырехугольники.

.