Содержание
Как найти площадь трапеции если известны. Как найти площадь трапеции
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность.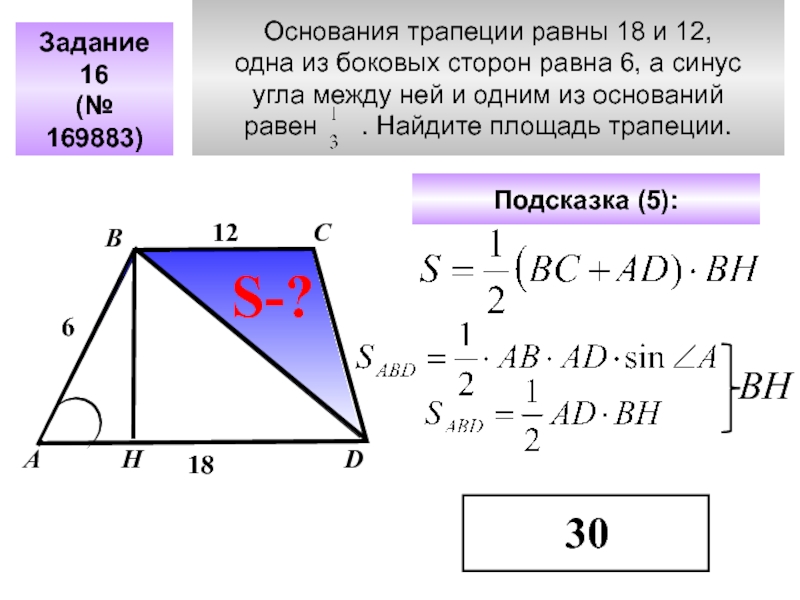 И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие.
Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение.
Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Задача решена.
Ответ:
площадь трапеции равна 4,5 дм 2 .
№ 2. Условие.
В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение.
Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ:
S = 20 см 2 .
№ 3. Условие.
Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение.
Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ:
Искомая площадь равна 45 см 2 .
№ 4. Условие.
Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение.
Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ
: х = √ {(а 1 2 + 5 а 2 2) / 6}.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а
– нижнее основание, b
– верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD.
 sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh
.
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S
Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S
) такова:
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние
;
— равнобокие
;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции
параллельна основаниям и равна их полусумме - Отрезок, соединяющий середины диагоналей
, равен половине разности оснований и лежит на средней линии. Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции
, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника) - Треугольники, лежащие на основаниях
трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции - Треугольники, лежащие на боковых сторонах
трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади) - В трапецию можно вписать окружность
, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) - Отрезок, параллельный основаниям
и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые
.
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые
, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.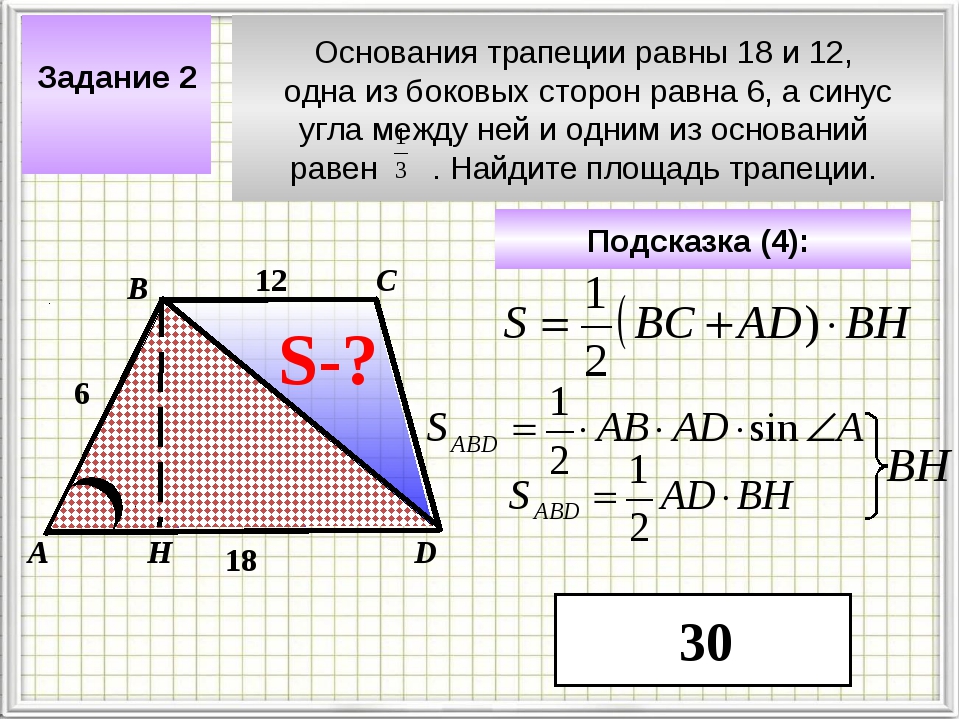
Тупые углы трапеции принадлежат меньшему
по длине основанию, а острые – большему
основанию.
Любую трапецию можно рассматривать как усеченный треугольник
, у которого линия сечения параллельна основанию треугольника.
Важно
. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.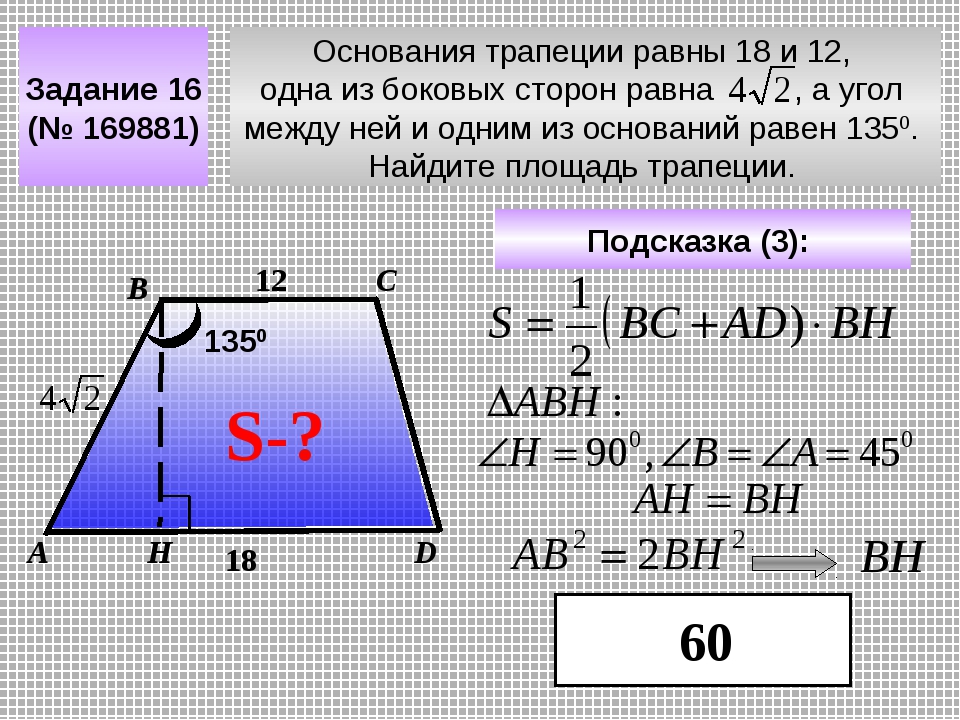
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия
– это линия, соединяющая середины боковых сторон. Высота
трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.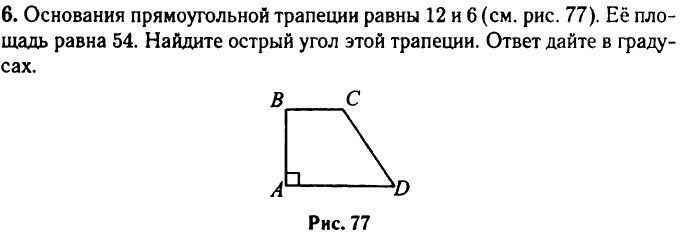 найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон.
Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b
и со средней линией l
, и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.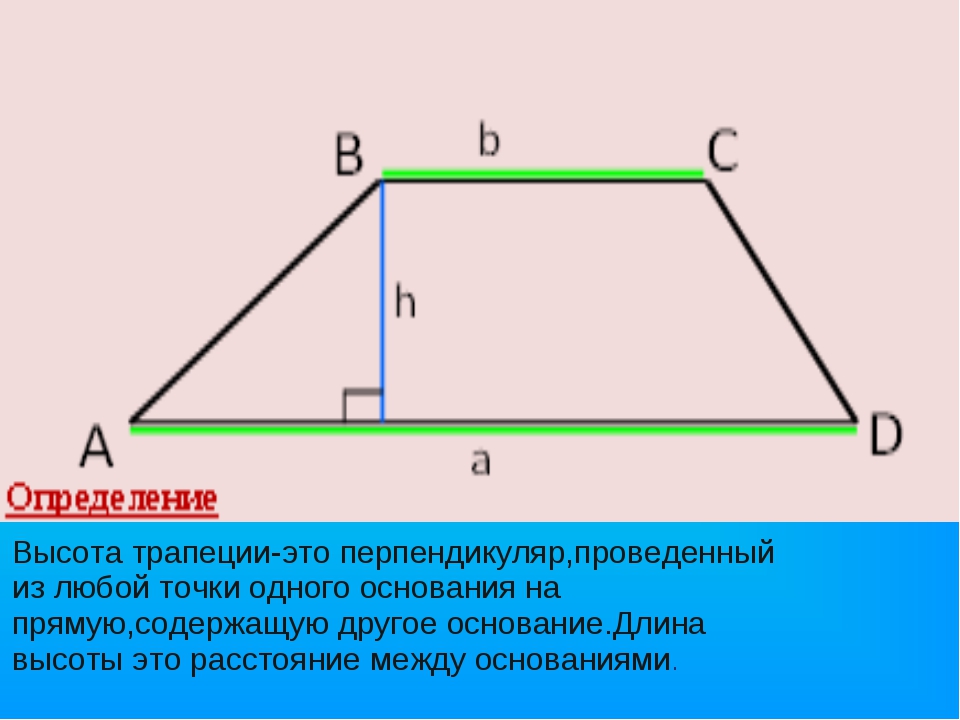
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно.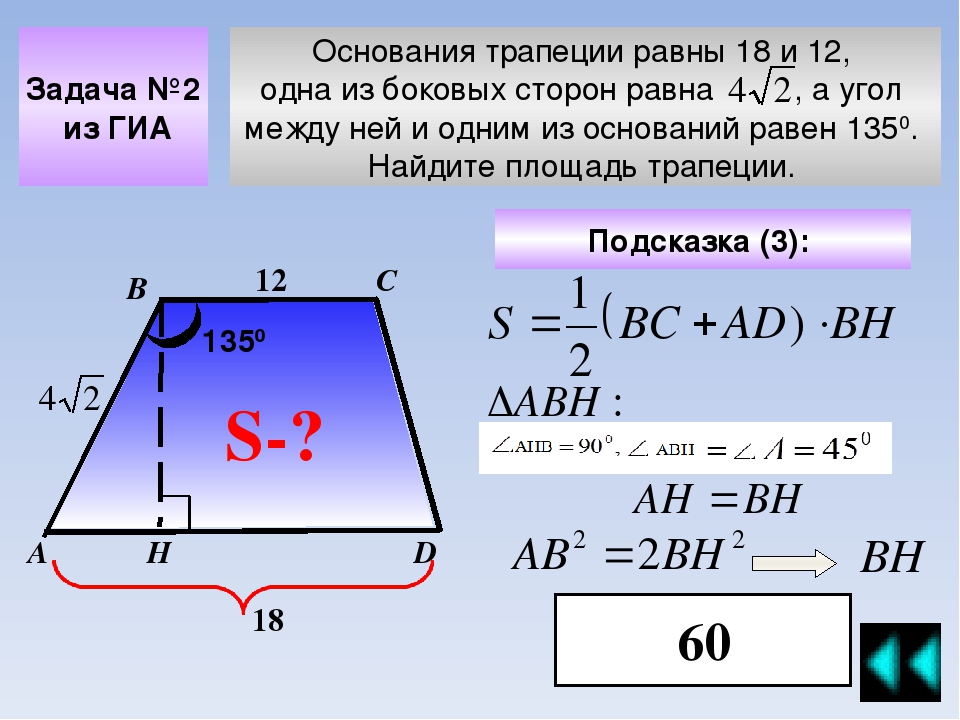 Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Меню
Многогранники: Тела вращения: Вспомогательные материалы: |
Задания » Трапеция В прямоугольной трапеции острый угол равен 45 градусов а высота проведенная из вершины тупого угла делит большее основание на отрезки 2 и 6 считая от точки. .. Найти площадь трапеции1. Острый угол прямоугольной трапеции в 3раза меньше тупого угла! Найдите эти углы!! 2. |
Задачи по школьной математике.
 Трапеция
Трапеция
Наибольший угол прямоугольной трапеции равен 120◦, а большая боковая сторона равна c. Найдите разность оснований.
Диагонали трапеции взаимно перпендикулярны, а средняя линия равна 5. Найдите отрезок, соединяющий середины оснований.
Высота равнобокой трапеции, проведенная из конца меньшего основания, делит ее большее основание на отрезки, равные 4 и 8. Найдите основания трапеции.
Найдите меньшее основание равнобокой трапеции, если высота, проведенная из конца меньшего основания, делит большее основание на отрезки, один из которых на 5 больше другого.
Боковая сторона равнобокой трапеции видна из точки пересечения диагоналей под углом, равным 60◦. Найдите диагонали трапеции, если ее высота равна h.
В равнобокой трапеции острый угол равен 60◦. Докажите, что меньшее основание равно разности большего основания и боковой стороны.
Меньшая боковая сторона прямоугольной трапеции равна 3, а большая образует угол, равный 30◦, с одним из оснований.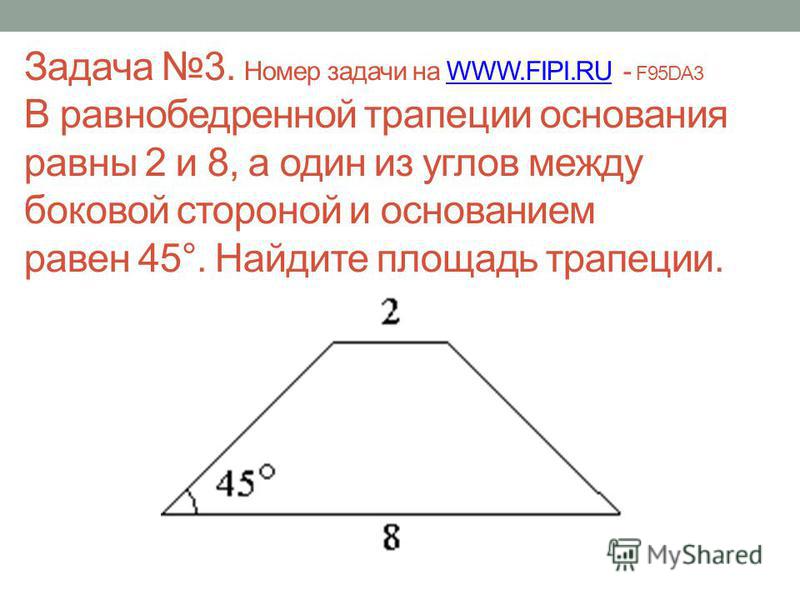 Найдите это основание, если на нем лежит точка пересечения биссектрис углов при другом основании.
Найдите это основание, если на нем лежит точка пересечения биссектрис углов при другом основании.
Докажите, что биссектрисы углов при боковой стороне трапеции пересекаются на ее средней линии.
Дана трапеция ABCD с основанием AD. Биссектрисы внешних углов при вершинах A и B пересекаются в точке P, а при вершинах C и D — в точке Q. Докажите, что отрезок PQ равен полупериметру трапеции.
 Докажите, что вторая боковая сторона перпендикулярна одной из диагоналей трапеции.
Докажите, что вторая боковая сторона перпендикулярна одной из диагоналей трапеции.

 Диагональ равна 10. Найдите площадь трапеции.
Диагональ равна 10. Найдите площадь трапеции.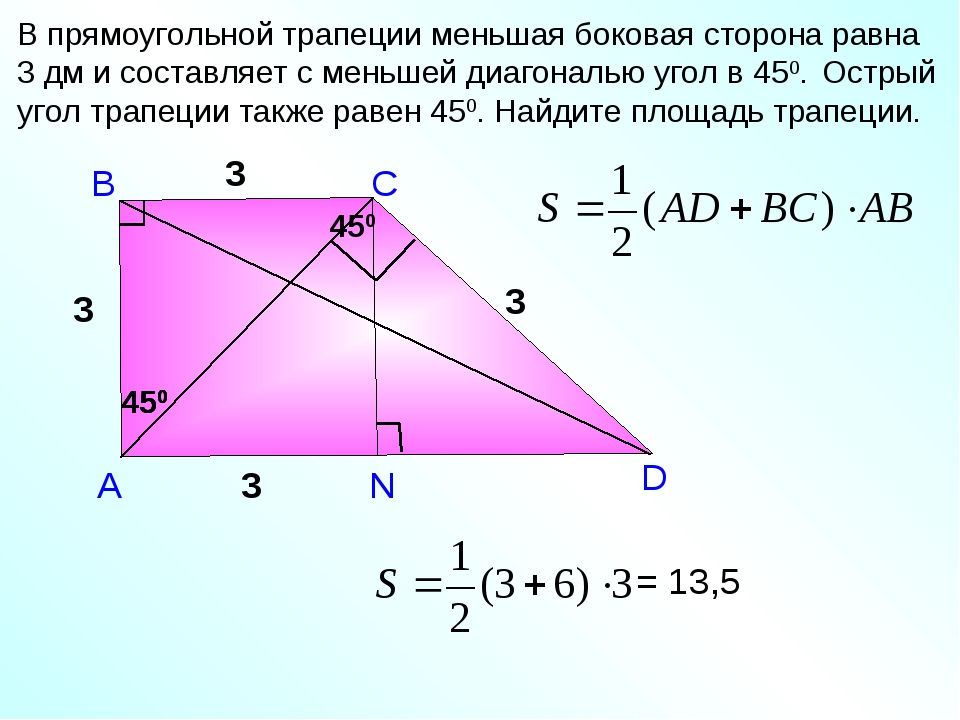 Найдите EC, если AB = 1, CD = 3 и BE = 2.
Найдите EC, если AB = 1, CD = 3 и BE = 2.Площадь произвольной трапеции формула. Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
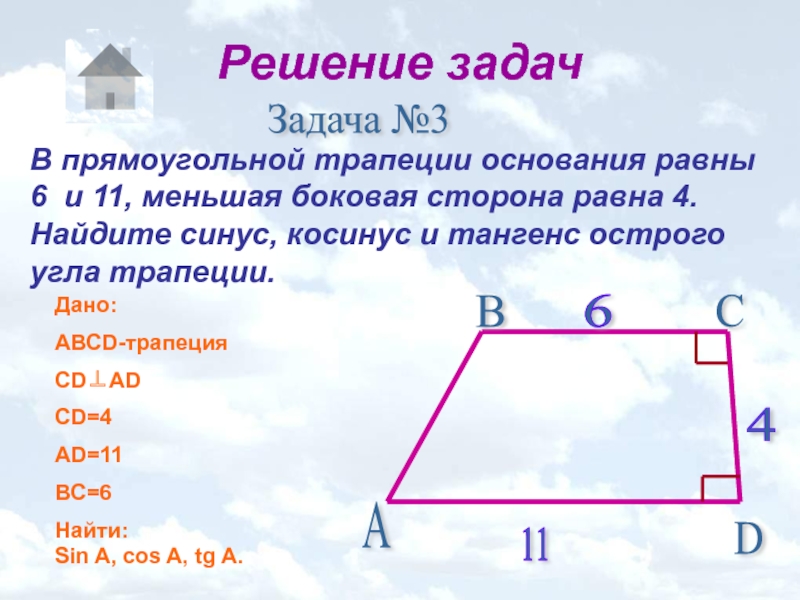 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.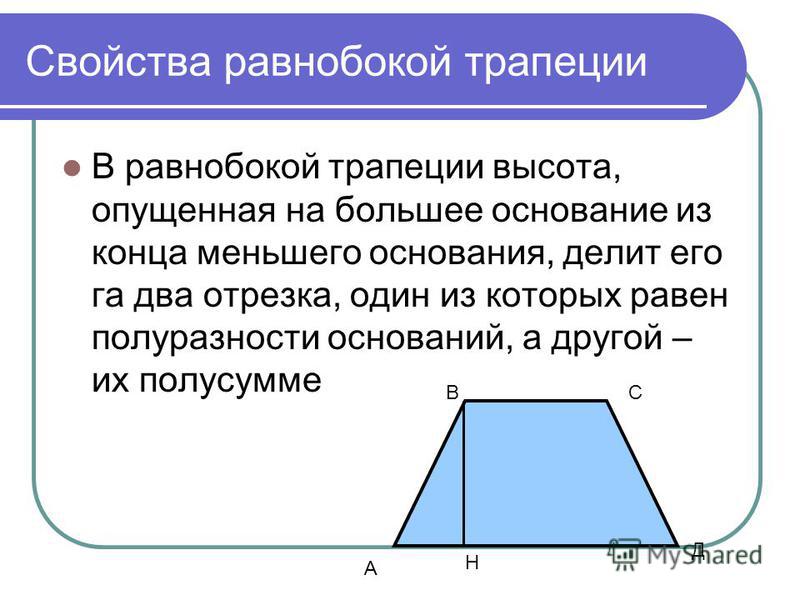
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки.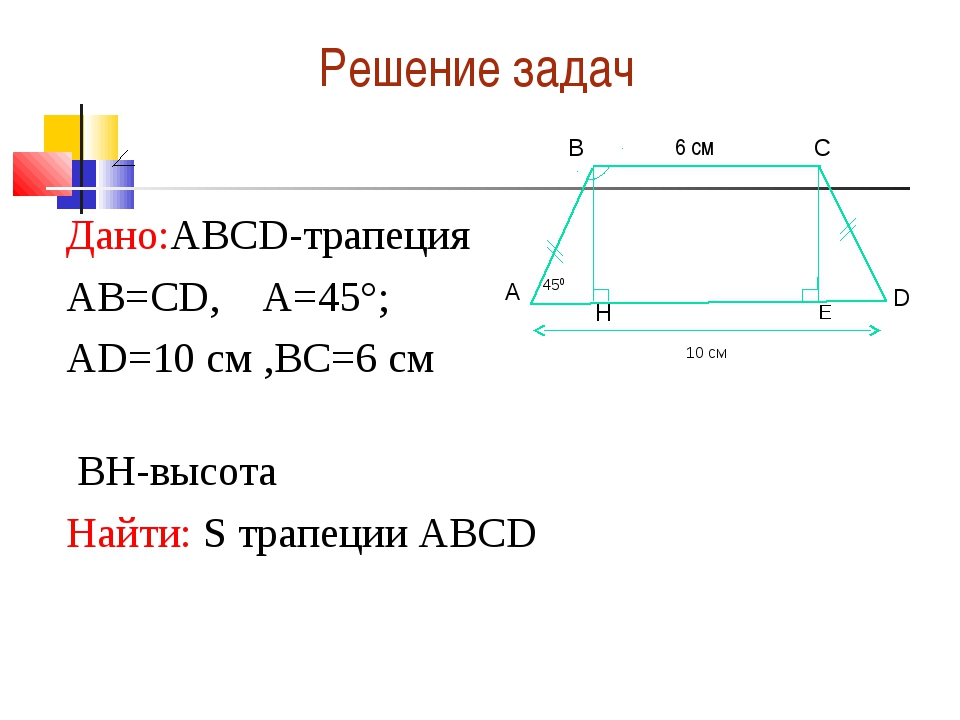 Он может быть как миллиметр, так и метр.
Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие.
Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение.
Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ:
площадь трапеции равна 4,5 дм 2 .
№ 2. Условие.
В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение.
Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх.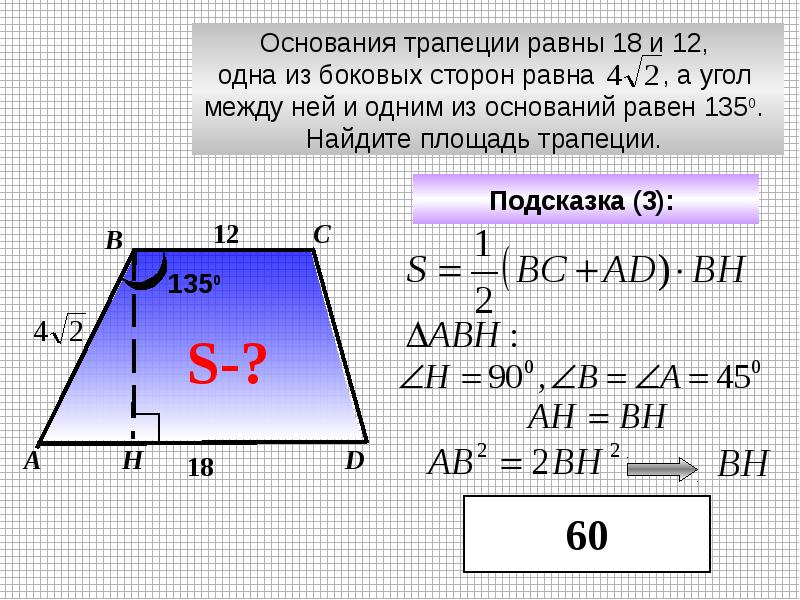 Так ЕН окажется внутри фигуры.
Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ:
S = 20 см 2 .
№ 3. Условие.
Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение.
Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ:
Искомая площадь равна 45 см 2 .
№ 4. Условие.
Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение.
Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ
: х = √ {(а 1 2 + 5 а 2 2) / 6}.
Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия
– это линия, соединяющая середины боковых сторон. Высота
трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а
– нижнее основание, b
– верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh
.
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S
) такова:
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c
*sin a
*(a
— c
*cos a
),
где с
— боковое бедро, a
— угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Площадь трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно и (для того, чтобы нарисовать высоту во втором треугольнике, необходимо будет продлить основание b). Площадь трапеции будет равна сумме полученных выражений, где мы вынесем высоту за скобку, и получим искомую формулу:
Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.
Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y.
Таким образом x+y=d-b, y=d-b-x.
Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту и . Приравнивая, получаем a2-x2=c2-y2 или x2-y2=a2-c2.
x2-(d-b-x)2=a2-c2 — Подставляем вместо х полученное выше выражение d-b-y.
x2-d2+bd+dx-b2+bd-bx-x2+dx-bx=a2-c2 — Раскрываем скобки.
x2-d2+2bd+2dx-b2-2bx-x2=a2-c2 — Приводим подобные слагаемые.
2dx-2bx=a2-c2+d2+b2-2bd — Переносим все вправо, оставляя слева только y.
2x(d-b)=a2-c2+(d-b)2 — Выносим общие множители.
Подставляем обратно y в формулу высоты .
Формула площади трапеции через стороны будет выглядеть так:
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону и среднюю линию
Тогда площадь трапеции равна
Как найти площадь трапеции если неизвестна высота. Все варианты того, как найти площадь трапеции
Трапецией называется такой четырехугольник, две стороны у которого параллельны (это основания трапеции, обозначенные на рисунке a и b), а другие две — нет (на рисунке АД и CB). Высота трапеции — это отрезок h, проведенный перпендикулярно к основаниям.
Как найти высоту трапеции при известных величинах площади трапеции и длин оснований?
Для вычисления площади S трапеции ABCD, воспользуемся формулой:
S = ((a+b) × h)/2.
Здесь отрезки a и b — это основания трапеции, h — это высота трапеции.
Преобразуя эту формулу, можем записать:
Используя эту формулу, получим значение h, если известны величина площади S и величины длин оснований a и b.
Пример
Если известно, что площадь трапеции S равна 50 см², длина основания a составляет 4 см, длина основания b составляет 6 см, то, чтобы найти высоту h, используем формулу:
Подставляем в формулу известные величины.
h = (2 × 50)/(4+6) = 100/10 = 10 см
Ответ: высота трапеции составляет 10 см.
Как находить высоту трапеции, если даны величины площади трапеции и длина средней линии?
Воспользуемся формулой вычисления площади трапеции:
Здесь m — средняя линия, h — высота трапеции.
Если возникает вопрос, как найти высоту трапеции, формула:
h = S/m, будет ответом.
Таким образом, можем найти величину высоты трапеции h, имея известные величины площади S и отрезка средней линии m.
Пример
Известна длина средней линии трапеции m, которая составляет 20 см, и площадь S, которая равна 200 см². Найдем значение величины высоты трапеции h.
Подставив значения S и m, получим:
h = 200/20 = 10 см
Ответ: высота трапеции составляет 10 см
Как найти высоту прямоугольной трапеции?
Если трапеция — это четырехугольник, с двумя параллельными сторонами (основаниями) трапеции. То диагональ — это отрезок, который соединяющий две противоположные вершины углов трапеции (отрезок АС на рисунке). Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.
Прямоугольной трапецией называется такая трапеция, где одна из боковых сторон перпендикулярна основаниям. В этом случае ее длина (АД) совпадает с высотой h.
Итак, рассмотрим прямоугольную трапецию ABCD, где AD — это высота, DC — это основание, AC — это диагональ. Воспользуемся теоремой Пифагора. Квадрат гипотенузы AC прямоугольного треугольника ADC равен сумме квадратов его катетов AB и BC.
Тогда можно записать:
AC² = AD² + DC².
AD — это катет треугольника, боковая сторона трапеции и, в то же время, ее высота. Ведь отрезок АД перпендикулярен основаниям. Его длина составит:
AD = √(AC² — DC²)
Итак, имеем формулу для вычисления высоты трапеции h = AD
Пример
Если длина основания прямоугольной трапеции(DC) равна 14 см, а диагональ (AC) составляет 15 см, для получения значения высоты(AD -боковой стороны) воспользуемся теоремой Пифагора.
Пусть х — это неизвестный катет прямоугольного треугольника(AD), тогда
AC² = AD² + DC² можно записать
15² = 14² + х²,
х = √(15²-14²) = √(225-196) = √29 см
Ответ: высота прямоугольной трапеции (АВ) составит √29 см, что приблизительно составит, 5.385 см
Как найти высоту равнобедренной трапеции?
Равнобедренной трапецией, называют трапецию, у которой длины боковых сторон равны между собой. Прямая, проведенная через середины оснований такой трапеции будет осью симметрии. Частным случаем является трапеция, диагонали которой перпендикулярны друг другу, тогда высота h, будет равна полусумме оснований.
Рассмотрим случай, если диагонали не перпендикулярны друг другу. В равнобочной (равнобедренной) трапеции равны углы при основаниях и длины диагоналей равны. Также известно, что все вершины равнобокой трапеции касаются линии окружности, проведенной вокруг этой трапеции.
Рассмотрим рисунок. ABCD- равнобедренная трапеция. Известно, что основания трапеции параллельны, значит, BC = b параллельно AD = a, сторона AB = CD = c, значит, углы при основаниях соответственно равны, можно записать угол BAQ = CDS = α, и угол ABC = BCD = β. Таким образом, делаем вывод о равенстве треугольника ABQ треугольнику SCD, значит, отрезок
AQ = SD = (AD — BC)/2 = (a — b)/2.
Имея по условию задачи величины оснований a и b, и длину боковой стороны с, найдем высоту трапеции h, равную отрезку BQ.
Рассмотрим прямоугольный треугольник ABQ. ВО — высота трапеции, перпендикулярна основанию AD, значит и отрезку AQ. Сторону AQ треугольника ABQ, найдем, воспользовавшись выведенной нами ранее формулой:
Имея значения двух катетов прямоугольного треугольника, найдем гипотенузу BQ= h. Используем теорему Пифагора.
AB²= AQ² + BQ²
Подставим данные задачи:
c² = AQ² + h².
Получим формулу для нахождения высоты равнобедренной трапеции:
h = √(c²-AQ²).
Пример
Дана равнобедренная трапеция ABCD, где основание AD = a = 10см, основание BC = b = 4см, а боковая сторона AB = c = 12см. При таких условиях, рассмотрим на примере, как найти трапеции высоту, равнобедренной трапеции АВСД.
Найдем сторону AQ треугольника ABQ, подставив известные данные:
AQ = (a — b)/2 = (10-4)/2=3см.
Теперь подставим значения сторон треугольника в формулу теоремы Пифагора.
h = √(c²- AQ²) = √(12²- 3²) = √135 = 11.6см.
Ответ. Высота h равнобедренной трапеции ABCD составляет 11.6 см.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника
.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике
: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве
, подготовка к ЕГЭ в Строгино
.
(S) трапеции, начните вычисление высоты (h) с нахождения полусуммы длин параллельных сторон: (a+b)/2. Затем на полученное значение разделите площадь — результат и будет искомой величиной: h = S/((a+b)/2) = 2*S/(a+b).
Зная длину средней линии (m) и площадь (S) можно упростить формулу из предыдущего шага. По определению средняя линия трапеции равна полусумме ее оснований, поэтому для вычисления высоты (h) фигуры просто разделите площадь на длину средней линии: h = S/m.
Можно определить высоту (h) такого и в том случае, если даны только длина одной из боковых сторон (с) и угол (α), образуемый ей и длинным основанием. В этом случае следует рассмотреть , образуемый этой стороной, высотой и коротким отрезком основания, который отсекает опущенная на него высота. Этот треугольник будет прямоугольным, известная сторона будет в нем гипотенузой, а высота — катетом. Отношение длин и гипотенузы равно противолежащего катету угла, поэтому для вычисления высоты трапеции умножьте известную длину стороны на синус известного угла: h = с*sin(α).
Такой же треугольник стоит рассмотреть и если даны длина боковой стороны (с) и величина угла (β) между ней и другим (коротким) основанием. В этом случае величина угла между боковой стороной (гипотенузой) и высотой (катетом) будет на 90° меньше известного из условий угла: β-90°. Так как отношение длин катета и гипотенузы равно косинусу угла между ними, то высоту трапеции вычислите умножением косинуса уменьшенного на 90° угла на длину боковой стороны: h = с*cos(β-90°).
Если вписана окружность известного радиуса (r), вычисления высоты (h) будет очень проста и не потребует никаких других параметров. Такая окружность по определению должна каждого из оснований только одной точкой и эти точки будут лежать на одной линии с центром . Это значит, что расстояние между ними будет равно диаметру (удвоенному радиусу), проведенному перпендикулярно основаниям, то есть совпадающим с высотой трапеции: h=2*r.
Трапецией считается такой четырехугольник, у которого две стороны параллельны, а две другие нет. Высотой трапеции называется отрезок, проведенный перпендикулярно между двумя параллельными прямыми. В зависимости от исходных данных ее можно вычислить по-разному.
Вам понадобится
- Знание сторон, оснований, средней линии трапеции, а так же, опционально, ее площадь и/или периметр.
Инструкция
Допустим, имеется трапеция с теми же данными, что и на рисунке 1. Проведем 2 высоты, получим , у которого 2 меньшие стороны катетами прямоугольных треугольников. Обозначим меньший катит за x. Он находится
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон. Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c
*sin a
*(a
— c
*cos a
),
где с
— боковое бедро, a
— угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
6 способов найти площадь трапеции
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
Иллюстрация: Лайфхакер
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
Иллюстрация: Лайфхакер
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
Иллюстрация: Лайфхакер
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
Иллюстрация: Лайфхакер
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
Иллюстрация: Лайфхакер
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
Иллюстрация: Лайфхакер
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
Площадь трапеции — веб-формулы
Трапеция — это четырехугольник, у которого есть только одна пара параллельных сторон. Чтобы вычислить площадь трапеций, возьмите среднее значение оснований и умножьте на его высоту.
Площадь трапеции определяется как:
A = (a + b) ∙ h / 2
a: длина вершины
б: длина основания
h: высота
Когда a = 0, форма становится треугольником.
Пример 1:
Какова площадь трапеции с основаниями 5 см и 8 см и высотой 6 см?
Решение :
Используя формулу площади трапеции, получим:
Площадь трапеции = 0.5 × в × (а + б)
Площадь трапеции = 0,5 × 6 × (5 + 8)
Площадь трапеции = 0,5 × 6 × 13
Площадь трапеции = 39 см 2
Пример 2:
Площадь трапеции составляет 52 см, 2 , а основания — 11 дюймов и 15 дюймов соответственно. Найдите его высоту.
Решение : Мы знаем, что площадь трапеции определяется выражением:
Площадь трапеции = 0,5 × h × (a + b), где h — высота, выделив h из формулы, мы сможем определить ее высоту
.
Площадь = 0.5 × в × (а + б)
или
52 = 0,5 × (11 + 15) × в
52 = 0,5 × 26 × в
52 = 13 ч
Таким образом:
h = 52/13 = 4 дюйма
Пример 3: Площадь трапеции составляет 15 см 2 , а расстояние между параллельными основаниями составляет 6 см. Если одно из параллельных оснований составляет 3 см, то какова длина другого параллельного основания?
Решение : Пусть a — длина неизвестной параллельной стороны, а b — известное основание.
Площадь трапеции = 0,5 × высота × (a + b) = 15 см 2
Подставляя значения, получим:
(0,5) × 6 × (3 + a) = 15
Умножить каждую сторону на 2
6 х (3 + а) = 30
Разделив каждую сторону на 6, получим
3 + а = 5
а = 2 см
Следовательно, длина другой параллельной стороны составляет 2 см.
Пример 4: Какова длина параллельных сторон трапеции, если ее площадь составляет 18 см. 2 , высота составляет 4 см, а длина ее более короткой стороны на 5 см короче ее длинной стороны?
Решение : Пусть y будет длиной большей стороны.
Длина более короткой стороны составляет (y — 5) см, так как более короткая сторона на 5 см короче длинной стороны.
Площадь трапеции = 18 см 2
По формуле для площади трапеции имеем:
(0,5) × 4 × [y + (y — 5)] = 18
Умножаем каждую сторону на 2,
4 × (2y — 5) = 36
Разделите каждую сторону на 4,
2лет — 5 = 9
Упростив уравнение, мы получим:
2y = 14 и y = 7 см
Таким образом, длина более длинной стороны равна y = 7 см, тогда как длина более короткой стороны равна y — 5 = 7 — 5 = 2 см
Пример 5: Площадь трапеция 160 см2.Параллельные стороны 18 см и 14 см. Найдите расстояние между параллельными сторонами.
Решение :
Дано A = 160 см 2 , a = 18 см и b = 14 см.
Площадь трапеции, A = (0,5) × (a + b) × h
Подставляя известные значения, получаем:
160 = (0,5) × (18 + 14) × h
т.е. (0,5) × (18 + 14) × h = 160
0,5 × 32 × в = 160
16 × h = 160
Разделить на 16 с каждой стороны,
в = 10 см
Таким образом, расстояние между параллельными сторонами составляет 10 сантиметров.
Онлайн-калькулятор площади
Калькулятор площади трапеции
- Цель использования
- потребности способность
- Комментарий / запрос
- требуется способность изменять левую и правую стороны
[1] 31.03.2021 02:55 Мужчина / До 20 лет / Другое / Немного /
- Цель использования
- найти область трапеции с неизвестной высотой
[2] 2021/02/26 00:48 Женский / До 20 лет / Начальная школа / Младший школьник / Совсем нет /
- Цель использования
- Поздняя работа по математике
[3] 2021/02/23 22:14 Женский / — / Высшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Помощь со школой
[4] 2021.01.21 00:14 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Полезно /
- Цель использования
- Расчеты для инженерного проекта в работе
[5] 2020 / 09/22 04:12 Женский / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Требуется площадь крыши в саду
[6] 2020.07.24 19:57 Мужской / 20 лет / средняя школа / университет / аспирант / очень /
- Цель использования
- помощь с домашним заданием
[7] 2020/01/30 10:10 Женщина / Моложе 20 лет старый / Начальная школа / Младший школьник / — /
- Цель использования
- Проектирование плана дома
- Комментарий / запрос
- Было бы неплохо, если бы была включена формула для определения длин диагональных сторон трапеции
[8] 2019/28/11/28 02:47 Женский / Уровень 20 лет / Домохозяйка / Очень /
- Цель использования
- Путать по формуле
[9] 2018/12/03 10: 50 Женский / До 20 лет / Начальная школа / Ученица неполной средней школы / Очень /
- Отчет об ошибке
- Shettale размером 110 × 110 × 110 × 87 футов и высотой 18 футов.Сколько бумаги требуется для крышки бака.
[10] 2018/06/24 01:51 Мужчина / 50-летний уровень / Пенсионеры A / Очень /
Как найти периметр и площадь трапеции [видео]
Площадь и периметр трапеции
Привет, и добро пожаловать в это видео о поиске площади и периметра трапеции!
Трапеция — это четырехсторонний многоугольник или «четырехугольник», у которого есть по крайней мере один набор параллельных сторон. У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу.Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах. Зная длину ног и оснований, мы можем найти периметра трапеции.
Периметр — это расстояние вокруг объекта. Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько ограждений купить.
Для трапеции формула периметра следующая: «Периметр трапеции, P равен размеру основания один плюс размер основания два плюс размер ноги один плюс размер ноги два.
Нам не нужно запоминать эту формулу, потому что, как и с любым другим типом многоугольника, это просто причудливый способ сказать, что складывает все стороны вместе !
Давайте найдем периметр этой трапеции:
Вот и все! Перейдем к области . Вот трапеция на миллиметровой бумаге:
Помните, что площадь — это мера того, сколько квадратных единиц уместится внутри фигуры. Сколько квадратов внутри нашей трапеции?
24 полных квадрата плюс восемь полуквадратных, что означает, что площадь трапеции составляет 28 квадратных единиц.Но что, если у нас нет миллиметровой бумаги или трапеции удобного размера? Вот почему нам нужна формула!
Формула для определения площади трапеции: «Площадь трапеции A равна h, высоте трапеции, умноженной на длину основания один плюс длину основания два, деленную на два».
Обратите внимание, что деление суммы оснований на два — это среднее значение этих длин. Поскольку в нашем примере задача находится на графике, мы можем видеть, что верхняя база, которую мы назовем базой 1, имеет длину три единицы.Наша нижняя база, база 2, имеет длину 11 единиц. Высота трапеции, которая представляет собой расстояние между основаниями, составляет четыре единицы:
Для площади нам не нужны измерения двух ножек, только два основания и высота, которую также можно назвать . высота . Поскольку у нас есть все три, мы можем вставить их в нашу формулу:
Это тот же ответ, который мы получили при подсчете!
Давайте попробуем еще одну:
Хорошо, она выглядит немного иначе, чем трапеция, которую мы только что сделали.Но мы можем сказать, что это трапеция, потому что у нее один набор из параллельных сторон . Мы можем использовать формулу, поэтому теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны являются основаниями, поэтому мы можем установить основание 1 равным 6 сантиметрам, а основание 2 — 3 сантиметра. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которые явно соответствовали бы высоте, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем судить по символу прямого угла.Так что 4 сантиметра — это высота, хоть и боком! Давайте подключим все это:
Эта формула также работает для определения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Вот и все, что нужно для определения периметра и площади трапеций.
Спасибо за просмотр и удачной учебы!
Площадь трапеции с медианой
В дополнение к стандартной формуле для площади трапеции с использованием ее оснований, мы также можем вычислить площадь трапеции с ее серединой и ее высотой.Медиана — это линия, соединяющая две средние точки ног трапеции — непараллельные стороны трапеции. Медиана также называется срединным сегментом или средней линией.
Задача
BCD — трапеция, AB || CD . EF — это линия, соединяющая середины ветвей AD и BC , AE = ED и BF = FC . h — высота трапеции. Найдите формулу для его площади, используя h и | EF |
Стратегия
Давайте посмотрим, как мы можем связать то, что мы знаем о медиане трапеции, с формулой, которая у нас уже есть для площади трапеции.Площадь трапеции составляет (короткое основание + длинное основание) · высота / 2, или A = ½ ( AB + DC ) · h.
В этой задаче у нас есть высота и середина или средний сегмент. Из теоремы о срединном сегменте трапеции мы получаем связь между средним сегментом и основаниями: | EF | = ½ ( AB + DC ). Глядя на две формулы, мы видим, что можем просто заменить EF на ½ ( AB + DC ) в формуле для площади и получить A = | EF | · h
Раствор
(1) A = ½ ( AB + DC ) · h // Площадь трапеции
(2) AE = ED , BF = FC // задано
(3) EF — средний сегмент // (2), Определение среднего сегмента
(4) | EF | = ½ ( AB + DC ) // (3), теорема о срединном сегменте трапеции
(5) A = | EF | · H // (1), (4), подстановка
Другой способ решения этой проблемы
В предыдущем разделе мы полагались на признание того, что формула для площади трапеции — A = ½ ( AB + DC ) · h выглядит очень похоже на формулу для длины среднего сегмента — | EF | = ½ ( AB + DC ), и произвела замену, которая привела к очень компактному и элегантному решению.
Но что, если мы не сразу узнаем, что формулы похожи, или не вспомним, что средний сегмент равен половине суммы оснований? Давайте посмотрим на другой способ решить эту проблему, не полагаясь на это.
Поскольку EF — это линия, соединяющая середины сторон, мы могли бы использовать теорему о треугольнике середины отрезка, но для этого нам понадобится треугольник. Итак, давайте нарисуем один, используя диагональ AC:
Решение, используя теорему о среднем сегменте треугольника
В треугольнике ΔACD, | EG | — это линия, параллельная основанию CD, которая начинается от середины стороны AD, поэтому согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания.Положим | EG | = x. Если x равен половине базы, то CD базы должен быть равен 2x.
Теперь посмотрим на другой треугольник ΔACB. Используя те же рассуждения, что и выше, | GF | начинается от середины стороны BC и параллельна AB — так что, согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания. Длина | GF | равно | EF | -x, поэтому основание AB равно 2 · (| EF | -x) или 2 · | EF | -2x.
Теперь давайте подставим эти значения в формулу для площади трапеции:
(1) A = ½ ( AB + CD ) · h
(2) AB = 2 · | EF | — 2x
(3) CD = 2x
(4) A = ½ (2 · | EF | -2x + 2x) · h = ½ (2 · | EF |) · h = | EF | · h
Площадь : Area of Trapezoids Study Guide
Area of Trapezoids
До сих пор мы в значительной степени имели дело с вариациями одной и той же площади A = bh формулы.Мы изменили его на A = lw для прямоугольников и даже на A = s 2 для квадратов, но по сути это то же самое. Сколько раз вы можете перемножить два числа?
Пора развлечься. Нет, не супер причудливый, а изрядно причудливый. Как иметь две базы — а не две головы — вместо одной.
Мы говорим ни о чем другом, как о трапециях , которые действительно легко найти. Пока только две из четырех его сторон параллельны друг другу, мы получаем трапецию.Они даже не обязательно должны быть одинаковой длины, что означает, что другие стороны могут делать все, что захотят, в значительной степени. Совсем ничего похожего на параллелограммы или прямоугольники.
Мы вам сказали. Странно. Настолько причудливые, что мы должны называть их Freakazoids.
Во всяком случае, все они выглядят по-разному. Даже если бы мы могли использовать одно уравнение для вычисления площади для всех из них, с чего бы мы начали? Это похоже на попытку попасть из Небраски в страну Оз. (Может быть, это не лучший пример. Объезд через Канзас, и мы золотые.)
Возьмем общую характеристику всех трапеций: параллельные стороны. Мы знаем, что две параллельные линии всегда будут на одинаковом расстоянии друг от друга, поэтому назовем это расстояние высотой . Для единообразия мы будем использовать х для высоты… снова.
Мы знаем, что две параллельные стороны не будут иметь одинаковую длину, потому что тогда у нас будет параллелограмм. Поэтому мы назовем эти две стороны основаниями , b 1 и b 2 .(Иногда вы увидите B и b вместо b 1 и b 2 . Это просто разные способы различения двух оснований.) Наша формула площади для любой трапеции с высотой h и базы b 1 и b 2 is:
A = ½ ( b 1 + b 2 ) h
3
9 может игнорировать шаткие стороны, которые не параллельны друг другу.
Пример задачи
Если основания трапеции имеют длину 4 и 5 при высоте 2, какова площадь трапеции?
Используя уравнение для площади трапеции, все, что нам нужно сделать, это указать длину оснований и высоту.
A = ½ ( b 1 + b 2 ) h
A = ½ (4 + 5) × 2
A = ½ × 9 × 2
A = 9 единиц 2
Пример задачи
Найдите высоту трапеции, которая имеет площадь 7 единиц 2 и основания 7 единиц и 21 единицу в длину.
Мы можем использовать ту же формулу площади для трапеции. На этот раз вместо A мы можем найти высоту h . Замените 21 единицу на b 1 , 7 единиц на b 2 и 7 единиц 2 на A . Вы знаете, что делать.
A = ½ ( b 1 + b 2 ) h
7 = ½ (21 + 7) h
7 = ½ × 28 × h
0.5 = h
Высота трапеции 0,5 единицы.
Какими бы причудливыми ни были трапеции, вы, наверное, уже знаете, что они бывают разных типов. Равнобедренные трапеции пытаются сделать их нормальными, делая две непараллельные стороны одинаковой длины. Правые трапеции имеют сторону, которая образует прямые углы с обоими основаниями.
Знание этих конкретных типов трапеций не меняет формулы для расчета площади.Это по-прежнему A = ½ ( b 1 + b 2 ) h . С другой стороны, это может быть полезно, если вам не даны сразу b 1 , b 2 и h .
Пример задачи
Какова площадь и периметр этой трапеции?
Это правая трапеция, поэтому мы можем рассматривать ее как прямоугольник и прямоугольный треугольник, соединенные вместе. Гипотенуза треугольника равна 5, и мы можем найти один из катетов, вычитая маленькое основание из большого, что дает нам длину 3.
Мы знаем гипотенузу и один из катетов прямоугольного треугольника. Вы можете сказать: «Теорема Пифагора»? Конечно, можем. Просто замените a на 3, b на h и c на 5.
a 2 + b 2 = c 2
3 2 + h 2 = 5 2
h 2 = 16
h = 4 единицы
Высота этой трапеции равна 4, и мы знаем, что ее основания 8 и 11.Поиск области должен быть легким.
A = ½ ( b 1 + b 2 ) h
A = ½ (8 + 11) × 4
A = ½ × 19 × 4
А = 38 шт. 2
Ну, все хорошо, а с периметром? Мы знаем, что периметр складывается из всех сторон. Мы уже знаем три стороны (два основания и неперпендикулярная сторона). К счастью для нас, высота равна одной из сторон для правой трапеции.
P = b 1 + b 2 + h + s
P = 8 + 11 + 4 + 5
P = 28 единиц
9,7: Использование свойств прямоугольников, треугольников и трапеций (часть 2)
Использование свойств треугольников
Теперь мы знаем, как найти площадь прямоугольника. Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике на рисунке \ (\ PageIndex {9} \) мы обозначили длину b и ширину h, так что это площадь bh.
Рисунок \ (\ PageIndex {9} \) — Площадь прямоугольника равна основанию b, умноженному на высоту h.
Мы можем разделить этот прямоугольник на два конгруэнтных треугольников (рисунок \ (\ PageIndex {10} \)). Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны. Площадь каждого треугольника равна половине площади прямоугольника или \ (\ dfrac {1} {2} \) bh. Этот пример помогает нам понять, почему формула для вычисления площади треугольника имеет вид A = \ (\ dfrac {1} {2} \) bh.
Рисунок \ (\ PageIndex {10} \) — прямоугольник можно разделить на два треугольника равной площади. Площадь каждого треугольника составляет половину площади прямоугольника.
Формула площади треугольника: A = \ (\ dfrac {1} {2} \) bh, где b — основание, а h — высота. Чтобы найти площадь треугольника, нужно знать его основание и высоту. Основание — это длина одной стороны треугольника, обычно стороны внизу. Высота — это длина линии, которая соединяет основание с противоположной вершиной и составляет с основанием угол 90 °.На рисунке \ (\ PageIndex {11} \) показаны три треугольника с отмеченными основанием и высотой каждого.
Рисунок \ (\ PageIndex {11} \) — Высота h треугольника — это длина отрезка линии, соединяющего основание с противоположной вершиной и образующего угол 90 ° с основанием.
Определение: Свойства треугольника
Для любого треугольника ΔABC сумма углов составляет 180 °. $$ m \ angle A + m \ angle B + m \ angle C = 180 ° $$ Периметр треугольника равен сумме длин сторон.$$ P = a + b + c $$ Площадь треугольника равна половине основания b, умноженной на высоту h. $$ A = \ dfrac {1} {2} bh \]
Пример \ (\ PageIndex {9} \):
Найдите площадь треугольника с основанием 11 дюймов и высотой 8 дюймов.
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | площадь треугольника |
| Шаг 3. Имя . Выберите переменную для ее представления. | пусть A = площадь треугольника |
| Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. | |
| Шаг 5. Решите уравнение. | A = 44 квадратных дюйма |
| Шаг 6. Чек . | $$ \ begin {split} A & = \ dfrac {1} {2} bh \\ 44 & \ stackrel {?} {=} \ Dfrac {1} {2} (11) 8 \\ 44 & = 44 \; \ checkmark \ end {split} $$ |
| Шаг 7. Ответьте на вопрос. | Площадь составляет 44 квадратных дюйма. |
Упражнение \ (\ PageIndex {17} \):
Найдите площадь треугольника с основанием 13 дюймов и высотой 2 дюйма.
- Ответ
13 кв.дюймы
Упражнение \ (\ PageIndex {18} \):
Найдите площадь треугольника с основанием 14 дюймов и высотой 7 дюймов.
- Ответ
49 кв. Дюймов
Пример \ (\ PageIndex {10} \):
Периметр треугольного сада составляет 24 фута. Длина двух сторон составляет 4 фута и 9 футов. Какова длина третьей стороны?
Решение
| Шаг 1. Прочтите задачу. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | длина третьей стороны треугольника |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть c = третья сторона |
| Шаг 4. Перевести . Напишите соответствующую формулу.Подставьте в данную информацию. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} 24 & = 13 + c \\ 11 & = c \ end {split} $$ |
| Шаг 6. Проверьте . | $$ \ begin {split} P & = a + b + c \\ 24 & \ stackrel {?} {=} 4 + 9 + 11 \\ 24 & = 24 \; \ checkmark \ end {split} $$ |
| Шаг 7. Ответьте на вопрос. | Третья сторона имеет длину 11 футов. |
Упражнение \ (\ PageIndex {19} \):
Периметр треугольного сада составляет 48 футов. Длина двух сторон 18 футов и 22 фута. Какова длина третьей стороны?
- Ответ
8 футов
Упражнение \ (\ PageIndex {20} \):
Длина двух сторон треугольного окна составляет 7 футов 5 футов. Периметр 18 футов.Какова длина третьей стороны?
- Ответ
6 футов
Пример \ (\ PageIndex {11} \):
Площадь треугольного церковного окна — 90 квадратных метров. База окна 15 метров. Какая высота окна?
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | высота треугольника |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть h = высота |
| Шаг 4. Перевести . Напишите соответствующую формулу. Подставьте в данную информацию. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} 90 & = \ dfrac {15} {2} h \\ 12 & = h \ end {split} $$ |
| Шаг 6. Чек . | $$ \ begin {split} A & = \ dfrac {1} {2} bh \\ 90 & \ stackrel {?} {=} \ Dfrac {1} {2} \ cdot 15 \ cdot 12 \\ 90 & = 90 \; \ checkmark \ end {split} $$ |
| Шаг 7. Ответьте на вопрос. | Высота треугольника 12 метров. |
Упражнение \ (\ PageIndex {21} \):
Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов.Какая высота?
- Ответ
14 дюймов
Упражнение \ (\ PageIndex {22} \):
Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота 5 футов. Что такое база?
- Ответ
6 футов
Равнобедренные и равносторонние треугольники
Помимо прямоугольного треугольника, некоторые другие треугольники имеют особые имена. Треугольник с двумя сторонами равной длины называется равнобедренным треугольником .Треугольник, у которого три стороны равной длины, называется равносторонним треугольником . На рисунке \ (\ PageIndex {12} \) показаны оба типа треугольников.
Рисунок \ (\ PageIndex {12} \) — В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.
Определение: равнобедренные и равносторонние треугольники
У равнобедренного треугольника две стороны одинаковой длины.
Равносторонний треугольник имеет три стороны одинаковой длины.
Пример \ (\ PageIndex {12} \):
Периметр равностороннего треугольника составляет 93 дюйма. Найдите длину каждой стороны.
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | Периметр = 93 дюйма |
| Шаг 2. Определите то, что вы ищете. | длина сторон равностороннего треугольника |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть s = длина каждой стороны |
| Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} 93 & = 3s \\ 31 & = s \ end {split} $$ |
| Шаг 6. Чек . | $$ \ begin {split} 93 & = 31 + 31 + 31 \\ 93 & = 93 \; \ checkmark \ end {split} $$ |
| Шаг 7. Ответьте на вопрос. | Каждая сторона 31 дюйм. |
Упражнение \ (\ PageIndex {23} \):
Найдите длину каждой стороны равностороннего треугольника с периметром 39 дюймов.
- Ответ
13 дюймов
Упражнение \ (\ PageIndex {24} \):
Найдите длину каждой стороны равностороннего треугольника с периметром 51 сантиметр.
- Ответ
17 см
Пример \ (\ PageIndex {13} \):
У Арианны есть 156 дюймов бисера, которые можно использовать для обрезки шарфа. Платок будет представлять собой равнобедренный треугольник с основанием 60 дюймов. Как долго она сможет сделать две равные стороны?
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | P = 156 дюймов |
| Шаг 2. Определите то, что вы ищете. | длины двух равных сторон |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть s = длина каждой стороны |
| Шаг 4. Перевести . Напишите соответствующую формулу. Подставьте в данную информацию. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} 156 & = 2s + 60 \\ 96 & = 2s \\ 48 & = s \ end {split} $$ |
| Шаг 6. Проверьте . | $$ \ begin {split} p & = a + b + c \\ 156 & \ stackrel {?} {=} 48 + 60 + 48 \\ 156 & = 156 \; \ checkmark \ end {split} $$ |
| Шаг 7. Ответьте на вопрос. | Арианна может сделать каждую из двух равных сторон по 48 дюймов в длину. |
Упражнение \ (\ PageIndex {25} \):
Палуба заднего двора имеет форму равнобедренного треугольника с основанием 20 футов. Периметр палубы 48 футов. Какова длина каждой из равных сторон колоды?
- Ответ
14 футов
Упражнение \ (\ PageIndex {26} \):
Парус лодки представляет собой равнобедренный треугольник с основанием 8 метров. Периметр — 22 метра. Какова длина каждой из равных сторон паруса?
- Ответ
7 мес.
Используйте свойства трапеций
Трапеция — это четырехсторонняя фигура, четырехугольник , две стороны которого параллельны, а две — нет.Параллельные стороны называются основаниями. Мы называем длину меньшего основания b и длину большего основания B. Высота h трапеции — это расстояние между двумя основаниями, как показано на рисунке \ (\ PageIndex {13} \).
Рисунок \ (\ PageIndex {13} \) — Трапеция имеет большее основание, B, и меньшее основание, b. Высота h — это расстояние между основаниями.
Формула площади трапеции:
\ [Area_ {trapezoid} = \ dfrac {1} {2} h (b + B) \]
Разделение трапеции на два треугольника может помочь нам понять формулу.Площадь трапеции — это сумма площадей двух треугольников. См. Рисунок \ (\ PageIndex {14} \).
Рисунок \ (\ PageIndex {14} \) — Разделение трапеции на два треугольника может помочь вам понять формулу для ее площади.
Высота трапеции — это также высота каждого из двух треугольников. См. Рисунок \ (\ PageIndex {15} \).
Рисунок \ (\ PageIndex {15} \)
Формула площади трапеции
\ [Area_ {trapezoid} = \ dfrac {1} {2} h (\ textcolor {blue} {b} + \ textcolor {red} {B}) \]
Если раздадим, то получим
Определение: Свойства трапеций
- Трапеция имеет четыре стороны.См. Рисунок 9.25.
- Две его стороны параллельны, а две — нет.
- Площадь A трапеции равна A = \ (\ dfrac {1} {2} \) h (b + B).
Пример \ (\ PageIndex {14} \):
Найдите площадь трапеции, высота которой 6 дюймов, а основания 14 и 11 дюймов.
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | площадь трапеции |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть A = площадь |
| Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot 6 (25) \\ A & = 3 (25) \\ A & = 75 \; квадратный\; дюймы \ end {split} $$ |
| Шаг 6. Проверка : разумен ли этот ответ? |
Если мы нарисуем прямоугольник вокруг трапеции с таким же большим основанием B и высотой h, его площадь должна быть больше, чем у трапеции.
Если мы нарисуем внутри трапеции прямоугольник с таким же основанием b и высотой h, его площадь должна быть меньше, чем у трапеции.
Площадь большего прямоугольника составляет 84 квадратных дюйма, а площадь меньшего прямоугольника — 66 квадратных дюймов.Таким образом, имеет смысл, что площадь трапеции составляет от 84 до 66 квадратных дюймов
| Шаг 7. Ответьте на вопрос. | Площадь трапеции составляет 75 квадратных дюймов. |
Упражнение \ (\ PageIndex {27} \):
Высота трапеции — 14 ярдов, а основание — 7 и 16 ярдов. Какой район?
- Ответ
161 кв. Ярд
Упражнение \ (\ PageIndex {28} \):
Высота трапеции 18 сантиметров, основания 17 и 8 сантиметров.Какой район?
- Ответ
255 кв. См
Пример \ (\ PageIndex {15} \):
Найдите площадь трапеции высотой 5 футов и основаниями 10,3 и 13,7 футов.
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | площадь трапеции |
| Шаг 3. Имя . Выберите переменную для ее представления. | Пусть A = площадь |
| Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot 5 (24) \\ A & = 12 \ cdot 5 \\ A & = 60 \; квадратный\; футов \ end {split} $$ |
| Шаг 6. Проверка : разумен ли этот ответ? Площадь трапеции должна быть меньше площади прямоугольника с основанием 13,7 и высотой 5, но больше площади прямоугольника с основанием 10,3 и высотой 5. | |
| Шаг 7. Ответьте на вопрос. | Площадь трапеции составляет 60 квадратных футов. |
Упражнение \ (\ PageIndex {29} \):
Высота трапеции 7 сантиметров, оснований 4.6 и 7,4 сантиметра. Какой район?
- Ответ
42 кв. См
Упражнение \ (\ PageIndex {30} \):
Высота трапеции 9 метров, оснований 6,2 и 7,8 метра. Какой район?
- Ответ
63 кв.м
Пример \ (\ PageIndex {16} \):
У Винни есть сад в форме трапеции. Трапеция имеет высоту 3.4 ярда, а основания — 8,2 и 5,6 ярда. Сколько квадратных ярдов будет доступно для посадки?
Решение
| Шаг 1. Прочтите о проблеме. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите то, что вы ищете. | площадь трапеции |
| Шаг 3. Имя .Выберите переменную для ее представления. | Пусть A = площадь |
| Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. | |
| Шаг 5. Решите уравнение. | $$ \ begin {split} A & = \ dfrac {1} {2} \ cdot (3.4) (13.8) \\ A & = 23.46 \; квадратный\; ярдов \ end {split} $$ |
Шаг 6. Проверить : Разумен ли этот ответ? Да.Площадь трапеции меньше площади прямоугольника с основанием 8,2 ярда и высотой 3,4 ярда, но больше площади прямоугольника с основанием 5,6 ярда и высотой 3,4 ярда. | |
| Шаг 7. Ответьте на вопрос. | У Винни 23,46 квадратных ярда, на которых он может сажать растения. |
Упражнение \ (\ PageIndex {31} \):
Линь хочет подстричь лужайку, имеющую форму трапеции.Основания составляют 10,8 ярда и 6,7 ярда, а высота — 4,6 ярда. Сколько квадратных ярдов дерна ему нужно?
- Ответ
40,25 кв. Ярд
Упражнение \ (\ PageIndex {32} \):
Кира хочет покрыть свой внутренний двор бетонной брусчаткой. Если внутренний дворик имеет форму трапеции с основанием 18 футов 14 футов и высотой 15 футов, сколько квадратных футов брусчатки ему понадобится?
- Ответ
240 кв.футов
Практика ведет к совершенству
Используйте свойства прямоугольников
В следующих упражнениях найдите (а) периметр и (б) площадь каждого прямоугольника.
- Длина прямоугольника составляет 85 футов, а ширина — 45 футов.
- Длина прямоугольника составляет 26 дюймов, а ширина — 58 дюймов.
- Прямоугольная комната 15 футов шириной и 14 футов длиной.
- Подъездная дорога имеет форму прямоугольника 20 футов шириной и 35 футов длиной.
В следующих упражнениях решите.
- Найдите длину прямоугольника с периметром 124 дюйма и шириной 38 дюймов.
- Найдите длину прямоугольника с периметром 20,2 ярда и шириной 7,8 ярда.
- Найдите ширину прямоугольника с периметром 92 метра и длиной 19 метров.
- Найдите ширину прямоугольника с периметром 16,2 метра и длиной 3,2 метра.
- Площадь прямоугольника 414 квадратных метров.Длина 18 метров. Какая ширина?
- Площадь прямоугольника 782 квадратных сантиметра. Ширина 17 сантиметров. Какая длина?
- Длина прямоугольника на 9 дюймов больше ширины. По периметру 46 дюймов. Найдите длину и ширину.
- Ширина прямоугольника на 8 дюймов больше его длины. По периметру 52 дюйма. Найдите длину и ширину.
- Периметр прямоугольника 58 метров. Ширина прямоугольника на 5 метров меньше длины.Найдите длину и ширину прямоугольника.
- Периметр прямоугольника 62 фута. Ширина на 7 футов меньше длины. Найдите длину и ширину.
- Ширина прямоугольника на 0,7 метра меньше длины. Периметр прямоугольника 52,6 метра. Найдите размеры прямоугольника.
- Длина прямоугольника на 1,1 метра меньше ширины. Периметр прямоугольника 49,4 метра. Найдите размеры прямоугольника.
- Периметр прямоугольника 150 футов. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.
- Длина прямоугольника в три раза больше ширины. Периметр 72 фута. Найдите длину и ширину прямоугольника.
- Длина прямоугольника на 3 метра меньше двойной ширины. Периметр — 36 метров. Найдите длину и ширину.
- Длина прямоугольника на 5 дюймов больше, чем в два раза ширины.По периметру 34 дюйма. Найдите длину и ширину.
- Ширина прямоугольного окна 24 дюйма. Площадь — 624 квадратных дюйма. Какая длина?
- Длина прямоугольного плаката составляет 28 дюймов. Площадь составляет 1316 квадратных дюймов. Какая ширина?
- Площадь прямоугольной крыши — 2310 квадратных метров. Длина 42 метра. Какая ширина?
- Площадь прямоугольного брезента составляет 132 квадратных фута. Ширина 12 футов. Какая длина?
- Периметр прямоугольного двора составляет 160 футов.Длина на 10 футов больше ширины. Найдите длину и ширину.
- Периметр прямоугольной картины 306 сантиметров. Длина на 17 сантиметров больше ширины. Найдите длину и ширину.
- Ширина прямоугольного окна на 40 дюймов меньше высоты. Периметр дверного проема — 224 дюйма. Найдите длину и ширину.
- Ширина прямоугольной площадки на 7 метров меньше длины. Периметр детской площадки 46 метров.Найдите длину и ширину.
Используйте свойства треугольников
В следующих упражнениях решайте задачи, используя свойства треугольников.
- Найдите площадь треугольника с основанием 12 дюймов и высотой 5 дюймов.
- Найдите площадь треугольника с основанием 45 см и высотой 30 см.
- Найдите площадь треугольника с основанием 8,3 метра и высотой 6,1 метра.
- Найдите площадь треугольника с основанием 24.2 фута и высотой 20,5 футов.
- Треугольный флаг имеет основание 1 фут и высоту 1,5 фута. Какая у него площадь?
- Треугольное окно имеет основание 8 футов и высоту 6 футов. Какая у него площадь?
- Если треугольник имеет стороны 6 футов и 9 футов, а периметр равен 23 футам, какова длина третьей стороны?
- Если треугольник имеет стороны 14 и 18 см, а периметр равен 49 см, какова длина третьей стороны?
- Что такое основание треугольника площадью 207 квадратных дюймов и высотой 18 дюймов?
- Какова высота треугольника площадью 893 квадратных дюйма и основанием 38 дюймов?
- Периметр треугольного отражающего бассейна составляет 36 ярдов.Длина двух сторон составляет 10 ярдов и 15 ярдов. Какова длина третьей стороны?
- Треугольный двор имеет периметр 120 метров. Длина двух сторон 30 метров и 50 метров. Какова длина третьей стороны?
- Равнобедренный треугольник имеет основание 20 сантиметров. Если периметр равен 76 сантиметрам, найдите длину каждой из других сторон.
- Равнобедренный треугольник имеет основание 25 дюймов. Если периметр составляет 95 дюймов, найдите длину каждой из других сторон.
- Найдите длину каждой стороны равностороннего треугольника с периметром 51 ярд.
- Найдите длину каждой стороны равностороннего треугольника с периметром 54 метра.
- Периметр равностороннего треугольника 18 метров. Найдите длину каждой стороны.
- Периметр равностороннего треугольника составляет 42 мили. Найдите длину каждой стороны.
- Периметр равнобедренного треугольника составляет 42 фута. Длина самой короткой стороны — 12 футов.Найдите длину двух других сторон.
- Периметр равнобедренного треугольника составляет 83 дюйма. Длина самой короткой стороны — 24 дюйма. Найдите длину двух других сторон.
- Блюдо имеет форму равностороннего треугольника. Каждая сторона 8 дюймов в длину. Найдите периметр.
- Плитка для пола имеет форму равностороннего треугольника. Каждая сторона 1,5 фута в длину. Найдите периметр.
- Дорожный знак в форме равнобедренного треугольника имеет основание 36 дюймов.Если периметр составляет 91 дюйм, найдите длину каждой из других сторон.
- Платок в форме равнобедренного треугольника имеет основу 0,75 метра. Если периметр составляет 2 метра, найдите длину каждой из других сторон.
- Периметр треугольника составляет 39 футов. Одна сторона треугольника на 1 фут длиннее второй. Третья сторона на 2 фута длиннее второй. Найдите длину каждой стороны.
- Периметр треугольника составляет 35 футов.Одна сторона треугольника на 5 футов длиннее второй. Третья сторона на 3 фута длиннее второй. Найдите длину каждой стороны.
- Одна сторона треугольника — это дважды наименьшая сторона. Третья сторона на 5 футов больше самой короткой. Периметр — 17 футов. Найдите длины всех трех сторон.
- Одна сторона треугольника в три раза больше наименьшей стороны. Третья сторона на 3 фута больше самой короткой. Периметр — 13 футов. Найдите длины всех трех сторон.
Используйте свойства трапеций
В следующих упражнениях решайте, используя свойства трапеций.
- Высота трапеции составляет 12 футов, а основания — 9 и 15 футов. Какой район?
- Высота трапеции 24 ярда, а основания 18 и 30 ярдов. Какой район?
- Найдите площадь трапеции высотой 51 метр и основаниями 43 и 67 метров.
- Найдите площадь трапеции высотой 62 дюйма и основаниями 58 и 75 дюймов.
- Высота трапеции составляет 15 сантиметров, а основания — 12,5 и 18,3 сантиметра. Какой район?
- Высота трапеции составляет 48 футов, а основание — 38,6 и 60,2 фута. Какой район?
- Найдите площадь трапеции высотой 4,2 метра и основанием 8,1 и 5,5 метра.
- Найдите площадь трапеции высотой 32,5 см и основаниями 54,6 и 41,4 см.
- Лорел делает знамя в форме трапеции.Высота баннера составляет 3 фута, а основания — 4 и 5 футов. Какая площадь у баннера?
- Нико хочет выложить плиткой пол в ванной. Пол имеет форму трапеции шириной 5 футов и длиной 5 и 8 футов. Какая площадь этажа?
- Терезе нужна новая столешница для кухонной стойки. Счетчик имеет форму трапеции шириной 18,5 дюйма и длиной 62 и 50 дюймов. Какая площадь прилавка?
- Елена вяжет шарф.Шарф будет иметь форму трапеции шириной 8 дюймов и длиной 48,2 дюйма и 56,2 дюйма. Какая площадь у шарфа?
Трапеция
Трапеция — это четырехугольник с одной парой параллельных сторон. На рисунке ниже показано несколько различных типов трапеций.
Примечание. Некоторые определяют трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, подразумевая, что он может содержать две пары параллельных сторон, что делает его параллелограммом.В рамках данной статьи мы определим трапецию как четырехугольник с одной парой параллельных сторон.
Грани трапеции
Параллельные стороны трапеции называются ее основаниями. Непараллельные стороны называются ножками. Высота (или высота) — это отрезок линии, используемый для измерения кратчайшего расстояния между двумя основаниями.
Углы трапеции
В трапеции пара углов, имеющих общее основание, называется базовыми углами.Для трапеций, показанных на диаграмме ниже, A и ∠D — это базовые углы, а ∠B и ∠C — базовые углы. Пара углов рядом с опорой дополнительные: ∠A + ∠B = 180 ° и ∠C + ∠D = 180 °.
Срединный отрезок трапеции
Середина трапеции — это отрезок прямой, соединяющий середину ее ног. Средний сегмент параллелен основаниям и имеет длину, равную половине суммы двух оснований.
На рисунке выше средний сегмент EF делит ветви AB и CD пополам и
Площадь трапеции
Площадь А трапеции равна половине произведения суммы ее оснований и ее высоты.
, где h — высота, а b 1 и b 2 — базовые длины.
Классификация трапеций
Трапеции можно классифицировать как разносторонние или равнобедренные в зависимости от длины ног. Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. В остальном это разносторонняя трапеция.
| Чешуйчатая трапеция | Равнобедренная трапеция |
|---|---|
| Ножки или углы основания не совпадают | Конгруэнтные ножки и углы основания |
Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов.Если одна из ножек перпендикулярна основанию, трапеция представляет собой прямую трапецию. В противном случае трапеция должна содержать два тупых угла и называется тупой трапецией.
| Правая трапеция | Тупая трапеция |
|---|---|
| Одна нога перпендикулярна основаниям. | Два угла тупые. |
Равнобедренные трапеции
Равнобедренная трапеция — это особая трапеция с совпадающими сторонами и углами основания.Он обладает следующими свойствами.
- Две диагонали равнобедренной трапеции совпадают. Они также образуют равные треугольники. На изображенной ниже равнобедренной трапеции диагонали AC и BD совпадают. Поскольку ноги равнобедренной трапеции конгруэнтны, а следующие пары треугольников имеют общее основание, ABD ≅ △ DCA и △ ABC ≅ △ DCB согласно постулату Сторона-Сторона-Сторона.
- Соотношение сегментов, составляющих диагонали трапеции, пропорционально. На диаграмме выше AE = DE, BE = CE и
- Равнобедренная трапеция имеет одну линию симметрии: высоту, разделяющую ее основания пополам.


 В прямоугольном треугольнике один из катетов равен 4дм, а гипотенуза 5дм. Найти площадь треугольникаОснование равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.Боковые стороны прямоугольной трапеции равны 5 и 13 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.Найдите площадь равнобокой трапеции, меньшее основание которой равно 2 см, тупой угол при нем равен 120, если известно, что в трапецию можно вписать окружностьБоковые стороны трапеции равны 12 м и 8 м, большее основание 26 м, а диагональ делит трапецию на два подобных треугольника. Определите длину этой диагонали. Трапеция: По свойству трапеции(углы при основании равнобедренной трапеции равны) сделать докозательство. Заранее спасибо!Большее основание трапеции относится к средней линии как 4:3, а меньшее основание равно 12см. Найдите среднюю линию трапеции. (напишите подробно)Можно развёрнутое решение? В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, площадь АОД = 32 см в квадрате, площадь ВОС = 8 см в квадрате.
В прямоугольном треугольнике один из катетов равен 4дм, а гипотенуза 5дм. Найти площадь треугольникаОснование равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.Боковые стороны прямоугольной трапеции равны 5 и 13 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.Найдите площадь равнобокой трапеции, меньшее основание которой равно 2 см, тупой угол при нем равен 120, если известно, что в трапецию можно вписать окружностьБоковые стороны трапеции равны 12 м и 8 м, большее основание 26 м, а диагональ делит трапецию на два подобных треугольника. Определите длину этой диагонали. Трапеция: По свойству трапеции(углы при основании равнобедренной трапеции равны) сделать докозательство. Заранее спасибо!Большее основание трапеции относится к средней линии как 4:3, а меньшее основание равно 12см. Найдите среднюю линию трапеции. (напишите подробно)Можно развёрнутое решение? В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, площадь АОД = 32 см в квадрате, площадь ВОС = 8 см в квадрате. Найдите меньшее основание трапеции, если большее из них равно 10Можно развёрнутое решение? В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, площадь АОД = 32 см в квадрате, площадь ВОС = 8 см в квадрате. Найдите меньшее основание трапеции, если большее из них равно 10 см.Найти растояние между двумя опорами высотой 7м и 5м, на которых лежит перекладина длиной 5м.Дана равнобокая трапеция с меньшим основанием 10 см, диагональю 20 см и высотой 12 см. Найдите среднюю линию трапеции.В прямоугольный трапеции большая боковая сторона равна сумме оснований, высота 12см. Найти площадь прямо-ка, стороны которого равны основаниям трапецииТрапеция АВСД вписана в окружность, угол А=60 градусов, угол АВД=90градусов, СД=4 см. А) найдите радиус окружности Б) какие значения может принимать угол ВМС, если М — произвольная точка окружности?Боковые стороны трапеции равны 17 см и 23 см, а основания 12 см и 28 см. Определите высоту трапеции.Основание прямой призмы является равнобедреной трапецией с основанием 4 см и 10 см и острым углом 45 градусов.
Найдите меньшее основание трапеции, если большее из них равно 10Можно развёрнутое решение? В трапеции АВСД (АД и ВС основания) диагонали пересекаются в точке О, площадь АОД = 32 см в квадрате, площадь ВОС = 8 см в квадрате. Найдите меньшее основание трапеции, если большее из них равно 10 см.Найти растояние между двумя опорами высотой 7м и 5м, на которых лежит перекладина длиной 5м.Дана равнобокая трапеция с меньшим основанием 10 см, диагональю 20 см и высотой 12 см. Найдите среднюю линию трапеции.В прямоугольный трапеции большая боковая сторона равна сумме оснований, высота 12см. Найти площадь прямо-ка, стороны которого равны основаниям трапецииТрапеция АВСД вписана в окружность, угол А=60 градусов, угол АВД=90градусов, СД=4 см. А) найдите радиус окружности Б) какие значения может принимать угол ВМС, если М — произвольная точка окружности?Боковые стороны трапеции равны 17 см и 23 см, а основания 12 см и 28 см. Определите высоту трапеции.Основание прямой призмы является равнобедреной трапецией с основанием 4 см и 10 см и острым углом 45 градусов. Найти площадь боковой и полной поверхности призмы если высота призмы 5 см3. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.В прямоугольный треугольник вписан ромб так, что его вершины лежат на сторонах треугольника. А угол, равный 60, является общим углом треугольника и ромба. Найдите стороны треугольника, если сторона ромба равна 6см. 10. Вписанная в трапецию окружность делит одну из боковых сторон на отрезки 4см и 9см. Найдите площадь трапеции, если одно из оснований равно 7см.Трапеция CDEK вписана в окружность (DE//CK), EK=5 см, KD=12 см, причем KD перпендикулярно CD. Найдите длину окружности.Площадь равнобедренной трапеции, описанной около круга, равна S. Определить площадь круга, если угол при основании трапеции равен 30 градусов.Основи прямокутної трапеції 21 і 28. Обчислити радіус вписаного в неї кола.Боковые стороны трапеции равны 13 см и 15 см, ее периметр равен 48 см.
Найти площадь боковой и полной поверхности призмы если высота призмы 5 см3. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.В прямоугольный треугольник вписан ромб так, что его вершины лежат на сторонах треугольника. А угол, равный 60, является общим углом треугольника и ромба. Найдите стороны треугольника, если сторона ромба равна 6см. 10. Вписанная в трапецию окружность делит одну из боковых сторон на отрезки 4см и 9см. Найдите площадь трапеции, если одно из оснований равно 7см.Трапеция CDEK вписана в окружность (DE//CK), EK=5 см, KD=12 см, причем KD перпендикулярно CD. Найдите длину окружности.Площадь равнобедренной трапеции, описанной около круга, равна S. Определить площадь круга, если угол при основании трапеции равен 30 градусов.Основи прямокутної трапеції 21 і 28. Обчислити радіус вписаного в неї кола.Боковые стороны трапеции равны 13 см и 15 см, ее периметр равен 48 см. Найдите среднюю линию трапеции.В равнобедренной трапеции основания равны 4 см и 12 см, а боковая сторона — 5 см. Найдите диагонали трапеции.У прмокутній трапеції основи = 16 см,і 26 см, а менша діагональ є бісектрисою тупого кута! Знайдіть периметр трапеції!Найти длину средней линии трапеции, длина основания которой численно равна корням уравнения √7x²-7x+2=0Знайдіть площу рівнобічної трапеції, у якої основи дорівнюють 6 см і 12 см, а бічна сторона 5 см.Знайдіть середню лінію рівнобічної трапеції, якщо її бічна сторона дорівнює 6 см, а периметр 48см.Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и ЕК.В трапецию ABCD можно вписать окружность. Известно, что AD=8, угол A=90*, угол D=60*. Найдите S(ABCD)
Найдите среднюю линию трапеции.В равнобедренной трапеции основания равны 4 см и 12 см, а боковая сторона — 5 см. Найдите диагонали трапеции.У прмокутній трапеції основи = 16 см,і 26 см, а менша діагональ є бісектрисою тупого кута! Знайдіть периметр трапеції!Найти длину средней линии трапеции, длина основания которой численно равна корням уравнения √7x²-7x+2=0Знайдіть площу рівнобічної трапеції, у якої основи дорівнюють 6 см і 12 см, а бічна сторона 5 см.Знайдіть середню лінію рівнобічної трапеції, якщо її бічна сторона дорівнює 6 см, а периметр 48см.Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости. Выясните взаимное расположение прямых CD и ЕК.В трапецию ABCD можно вписать окружность. Известно, что AD=8, угол A=90*, угол D=60*. Найдите S(ABCD)