Содержание
Закон Фарадея для самоиндукции
При постоянной индуктивности можно
записать
ЭДС самоиндукции прямо пропорциональна
индуктивности катушки и скорости
изменения силы тока в ней.
В
случае, когда скорость изменения силы
тока не постоянна, ЭДС самоиндукции
следует вычислять как производную
собственного магнитного потока, взятую
с обратным знаком.
Из закона Фарадея для самоиндукции
следует связь между единицами измерения
магнитных и электрических величин
Энергия магнитного поля
Магнитное поле обладает энергией.
Подобно тому, как в заряженном конденсаторе
имеется запас электрической энергии,
в катушке, по виткам которой протекает
ток, имеется запас магнитной энергии.
Энергия магнитного поля вычисляется
как половина произведения индуктивности
контура на квадрат силы тока в нем:
W=LI2/2
Отсюда для единиц измерения
Дж = Гн *А2
;
Дж=В* Кл
Домашнее задание (повышенная
сложность): Доказать, что индуктивность
соленоида пропорциональна квадрату
числа витков.
Переменный ток Лекция 5 Введение. Немного математики
радианная мера угла
Производные
Тригонометрической функции: (cosx)/
= — sinx (sin
x)/
= + cosx
Показательной
функции (xn)/
= nxn-1
Независимая переменная не координата
х, а время t
x ==>t
f(x)==>
f(t)
Производная сложной функции равна
произведению производной функции на
производную аргумента
(cosωx)/
= — ωsinωx
(Acosωx)/
= — Aωsinωx
(sinωx)/
= ωcosωx
(Asinωx)/
= ωAcosωx
Гармоническая функция
Гармонической называется функция,
которая изменяется по закону синуса
или косинуса:
x = Acos(ωt+α0)
x = Asin(ωt+α0)
A – амплитуда –
максимальное отклонение изменяющейся
величины от положения равновесия
(ωt+α0)
– фаза α
α0 – начальная фаза –
значение фазы в момент времени =0
ω – циклическая
частота или угловая скорость
ν=ω/2π — частота- число колебаний в
единицу времени
Т – период Т=1/ν = 2π/ ω – время одного
полного колебания
Фаза α и период Т связаны
соотношением: α =(ωt+α0)
= (2πt/Т+ α0)
Вращение рамки в однородном магнитном поле
Поместим рамку в однородное магнитное
поле
перпендикулярно силовым линиям и начнем
вращать ее с постоянной угловой
скоростью ω.
В начальный момент времени
нормаль к плоскости рамки параллельна
силовым линиям. Начальная фаза α = α0
=0.
Через время t рамка
повернется на угол α.
На рисунке α — угол между вектором
магнитной
индукции и силовыми линиями,
изменяется
со временем по закону α=ω t.
Магнитный поток через рамку
Ф=BS cosα
α=ω t
Ф=BS cos
ω t или Ф= Ф0
cos ω t,
где Ф0 = BS
– амплитуда магнитного потока.
Поскольку магнитный поток через рамку
изменяется со временем, в ней появляется
ЭДС индукции. Ее значение определяем
Ее значение определяем
по закону электромагнитной индукции
как производную от магнитного потока,
взятую с обратным знаком:
ei
= — Ф/
ei
=BS ω sin
ω t
ei
=e0 sin
ω t , где e0
= BSω –
амплитуда ЭДС индукции
Магнитный поток и ЭДС индукции изменяются
по гармоническому закону.
В начальный момент времени (t=0)
магнитный поток максимален, ЭДС
индукции равна нулю. В рассмотренном
примере начальная фаза α0
=0. Получен результат:
Ф=BS cos
ω t Ф0
= BS
ei
=e0
sin ω t
e0 =
BS ω
в начальный момент времени ( t=0):
Ф = Ф0 ei
=0
Возможно любое другое начальное
положение рамки. Например, такое:
Например, такое:
t=0
начальная фаза α0 =π/2
Положение
рамки через время t
угол между нормалью к плоскости рамки
и
силовыми линиями (фаза) равен α=ω t
+ π/2
Магнитный поток
Ф=BS cos
(ω t + π/2 ) = -Ф0
sin(ω t),
Ф0 = BS
ЭДС индукции ei
=-(-BS ω cos
ω t) =e0
cos ω t
, e0 =
BS ω
В начальный момент времени (t=0)
магнитный поток равен нулю, ЭДС
индукции максимальна: Ф=0, ei
= e0.
Электричество и магнетизм
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре
Введем коэффициент пропорциональности L
|
|
(8.16) |
Коэффициент пропорциональности L называется индуктивностью контура.
|
Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока. |
Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.
|
В системе СИ единицей измерения индуктивности является генри (Гн)
|
Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.
|
Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции. |
Видео 8.13. Закон Фарадея. Явление самоиндукции.
Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.
Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
|
|
(8.17) |
Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков
,
что необходимо учитывать при дифференцировании
Подставляя это выражение в (8. 17), получаем для неподвижного контура всреде
17), получаем для неподвижного контура всреде
|
|
(8.18) |
Если же индуктивность контура не зависит от силы тока в нём, то имеем
|
|
(8.19) |
Мы приходим к закону самоиндукции. В этом простейшем случае:
|
В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи. |
Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна
Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна
где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
|
|
(8.20) |
где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
|
|
(8. |
Рис. 8.31. Индуктивность соленоида
При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Самоиндукция. Индуктивность. Энергия магнитного поля.
Самоиндукция — является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
Явление самоиндукции подобно явлению инерции. Так же, как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет явления самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых ламп, последовательно со второй лампой включить катушку, то при замыкании цепи первая лампа загорается практически сразу, а вторая с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки очень часто перегорают при выключении света.
Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называетсягенри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
Единица индуктивности в СИ называетсягенри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
| 1 Гн = 1 Вб / 1 А. |
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.
Магнитный поток, пронизывающий все N витков соленоида, равен
| Φ = B S N = μ0 n2 S l I. |
Следовательно, индуктивность соленоида равна
|
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз, поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз, поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
|
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает |
Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2 R Δt.
Ток в цепи равен
Выражение для ΔQ можно записать в виде
ΔQ = –L I ΔI = –Φ (I) ΔI. |
В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I0 до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I0 до 0. Это дает
Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ (I) от тока I Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного треугольника.
Вычисление энергии магнитного поля |
Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
???Вопросы
- В чем заключается явление самоиндукции?
- В каких опытах можно наблюдать это явление?
- Дайте определение индуктивности? В каких единицах СИ она измеряется?
- Как вычислить энергию магнитного поля катушки с током?
Домашнее задание упр.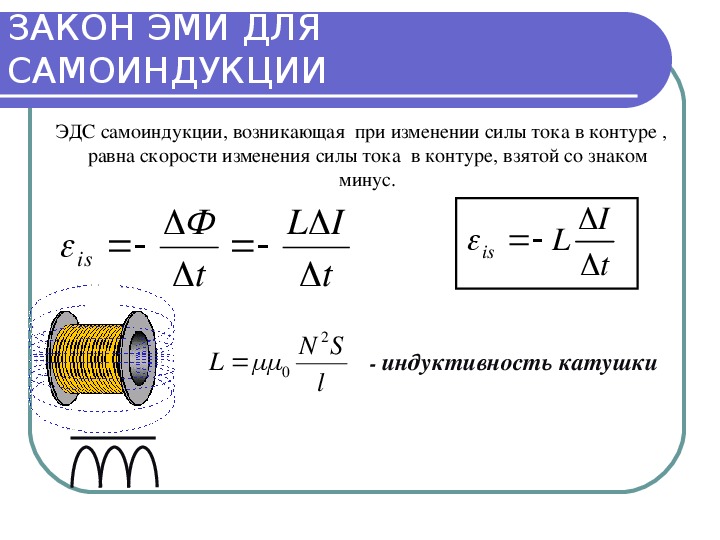 №25
№25
Закон самоиндукции определение. Явление самоиндукции
Магнитное поле
контура, в котором сила тока изменяется,
индуцирует ток не только в других
контурах, но и в себе самом. Это
явление получило название самоиндукции.
Опытным путём
установлено, что магнитный поток вектора
магнитной индукции поля, создаваемого
текущим в контуре током, пропорционален
силе этого тока:
где L– индуктивность
контура. Постоянная характеристика
контура, которая зависит от его формы
и размеров, а так же от магнитной
проницаемости среды, в которой находится
контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время
dtток в контуре изменится
наdI, то магнитный поток,
связанный с этим током, изменится наdФ
=LdIв результате чего в
этом контуре появится ЭДС самоиндукции:
Знак минус показывает, что ЭДС
самоиндукции (а, следовательно, и ток
самоиндукции) всегда препятствует
изменению силы тока, который вызвал
самоиндукцию.
Наглядным
примером явления самоиндукции служат
экстратоки замыкания и размыкания,
возникающие при включении и выключении
электрических цепей, обладающей
значительной индуктивностью.
Энергия магнитного поля
Магнитное поле
обладает потенциальной энергией, которая
в момент его образования (или изменения)
пополняется за счёт энергии тока в цепи,
совершающего при этом работу против
ЭДС самоиндукции, возникающей вследствие
изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС
самоиндукциии токIможно считать
постоянными, равняется:
.
(5)
Знак минус указывает, что
элементарная работа совершается током
против ЭДС самоиндукции. Чтобы определить
работу при изменении тока от 0 до I,
проинтегрируем правую часть, получим:
.
(6)
Эта работа численно равна
приросту потенциальной энергии ΔW п магнитного поля, связанного с этой
цепью, т.е.A= -ΔW п.
Выразим энергию магнитного
поля через его характеристики на примере
соленоида. Будем считать, что магнитное
Будем считать, что магнитное
поле соленоида однородно и в основном
расположено внутри его. Подставим в (5)
значение индуктивности соленоида,
выраженное через его параметры и значение
силы тока I, выраженное
из формулы индукции магнитного поля
соленоида:
, (7)
где N – общее число витков
соленоида; ℓ – его длина; S – площадь
сечения внутреннего канала соленоида.
, (8)
После подстановки имеем:
Разделив обе части на V,
получим объёмную плотность энергии
поля:
(10)
или, с учётом, что
получим,
.
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным
называется ток, изменяющийся с течением
времени и по величине и по направлению.
Примером переменного тока может служить
потребляемый промышленный ток. Этот
ток является синусоидальным, т.е.
мгновенное значение его параметров
меняются со временем по закону синуса
(или косинуса):
i
= I 0 sinωt,
u =
U 0 sin(ωt
+ φ 0). (12)
(12)
Переменный
синусоидальный ток можно получить, если
вращать рамку (контур) с постоянной
скоростью
в однородном
магнитном поле с индукцией B
(рис.5). При этом магнитный поток,
пронизывающий контур, изменяется по
закону
где S– площадь
контура, α = ωt– угол
поворота рамки за время t. Изменение
потока приводит к возникновению ЭДС
индукции
, (17)
направление которой определяется
по правилу Ленца.
Если
контур замкнут (рис.5), то по нему идёт
ток:
.
(18)
График изменения электродвижущей
силыи индукционного токаi
представлен на рис.6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой
и фазой φ = (ωt
+ φ 0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для
характеристики переменного тока вводятся
понятия действующего (эффективного)
значения тока и напряжения. Эффективным
Эффективным
значением силы переменного тока
называется сила такого постоянного
тока, который выделяет в данном проводнике
столько же тепла за время одного периода,
сколько выделяет тепла и данный переменный
ток.
,
. (13)
Приборы, включенные в цепь
переменного тока (амперметр, вольтметр),
показывают эффективные значения тока
и напряжения.
При изменении тока в проводнике, витке или индуктивной катушке изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока индуцирует в проводнике (витке, индуктивной катушке) ЭДС, действие которой направлено на поддержание предшествующего состояния поля. Такое явление называется самоиндукцией.
Направление ЭДС самоиндукции определяется по правилуЛенца.
Электродвижущая сила самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока
.
Следовательно, при возрастании тока в проводнике (индуктивной катушке) индуцированная в ней ЭДС самоиндукции будет направлена против тока, т. е. будет препятствовать его возрастанию (рис. 10, а),и, наоборот, при уменьшении тока в проводнике (индуктивной катушке) возникает ЭДС самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 10,6).
е. будет препятствовать его возрастанию (рис. 10, а),и, наоборот, при уменьшении тока в проводнике (индуктивной катушке) возникает ЭДС самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 10,6).
Способность различных проводников (индуктивных катушек)
индуцировать ЭДС самоиндукции оценивается индуктивностью L.
Единица индуктивности — генри (Гн). Такой индуктивностью обладает проводник, в котором возникает ЭДС самоиндукции, равная 1 В, при изменении тока на 1 А за 1 с:
Знак « — » в формуле отражает правило Ленца.
а — при увеличении тока; б — при уменьшении тока
На практике индуктивность часто измеряют в тысячных долях генри — миллигенри (мГн) и в миллионных долях генри — микрогенри (мкГн).
Значение индуктивности L
зависит от конструкции элементов цепи.
Так, для индуктивной катушки с числом витков w
, магнитопроводом длины, сечения S
и магнитной проницаемостью индуктивность
Если катушки своими полями не влияют друга на друга, то при последовательном соединении
индуктивных катушек с индуктивностями . .. общая индуктивность
.. общая индуктивность
При параллельном соединение
Запомните
Если ток в индуктивной катушке не изменяется, то ЭДС самоиндукции не возникает.
Явление самоиндукции в тех или иных проводниках характеризуется индуктивностью L. Индуктивность
— это размерный коэффициент пропорциональности между скоростью изменения тока во времени и индуцируемой при этом ЭДС.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При каких условиях возникает ЭДС самоиндукции?
2. В каких единицах измеряется индуктивность?
3. Как изменится ЭДС самоиндукции, если скорость изменения тока, проходящего через индуктивную катушку, возросла?
ВЗАИМОИНДУКЦИЯ
Если две индуктивные катушки находятся на некотором расстоянии друг от друга (рис..11) и по одной из них (1) проходит изменяющийся ток, то часть магнитного потока, возбуждаемая этим током, пронизывает витки второй индуктивной катушки (2) и в ней
возникает ЭДС, называемая ЭДС взаимоиндукции.
Если два замкнутых контура или две индуктивные катушки 1 и 2 (см. рис. 11) сцеплены с общим магнитным потоком , то такие контуры и индуктивные катушки называют индуктивно-
или магнитно-связанными
.
Под действием ЭДС взаимоиндукции в замкнутой цепи второй индуктивной катушки
взаимоиндукции. Он вызывает появление магнитного поля, которое пронизывает витки первой индуктивной катушки, в результате чего в ней также возникает ЭДС взаимоиндукции. Такое явление называется взаимоиндукцией
Величина ЭДС взаимоиндукции, возникающей во второй индуктивной катушке, зависит от размеров, расположения индуктивных катушек, магнитной проницаемости их сердечников, а также скорости изменения силы тока — в первой индуктивноикатушке.Эту зависимость можно выразить формулой.
Рис..11. Взаимоиндукция: Э — индуктивно-связанные катушки.
гдеМ
— величина, зависящая от размеров индуктивных катушек, их расположения и магнитной проницаемости среды между индуктивными катушками. Она называется взаимной индуктивностью и измеряется в генри (Гн). Знак « — » в этой формуле показывает, что ЭДС взаимоиндукции противодействует причине, вызывающей ее.
Она называется взаимной индуктивностью и измеряется в генри (Гн). Знак « — » в этой формуле показывает, что ЭДС взаимоиндукции противодействует причине, вызывающей ее.
Взаимоиндукция дает возможность связывать посредством магнитного поля различные электрические цепи. Явление взаимоиндукции широко используют в трансформаторах, радиотехнических устройствах и устройствах автоматики.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое явление называется взаимоиндукцией?
2. При каких условиях возникает ЭДС взаимоиндукции?
3. Какие катушки называют магнитносвязанными?
4. В каких единицах измеряется взаимная индуктивность?
ВИХРЕВЫЕ ТОКИ
Изменяющийся магнитный поток способен индуцировать ЭДС не только в проводах или витках индуктивных катушек, но и в массивных стальных сердечниках, кожухах и других металлических деталях электротехнических установок. Эти ЭДС являются причиной
появления индуцированных токов, которые действуют в массивных металлических деталях электротехнических устройств, замыкаясь накоротко в их толще. Такие токи получили название вихревых токов. Природа вихревых токов такая же, как и токов, индуцированных в обычных проводах или индуктивных катушках. Благодаря
Такие токи получили название вихревых токов. Природа вихревых токов такая же, как и токов, индуцированных в обычных проводах или индуктивных катушках. Благодаря
очень малому сопротивлению массивных проводников вихревые токи даже при небольшой индуцированной ЭДС достигают очень больших значений, вызывая чрезмерное нагревание этих проводников.
Способы уменьшения вредного действия вихревых токов.В электрических машинах и аппаратах вихревые токи обычно нежелательны, так как они вызывают нагрев металлических сердечников, создают потери энергии (так называемые потери от вихревых токов), снижают КПД электрических машин и аппаратов и ока;!Ь1вают согласно правилу Ленца размагничивающее действие. Для уменьшения вредного действия вихревых токовприменяют два основных способа.
1. Сердечники электрических машин и аппаратов выполняют из отдельных стальных листов толщиной 0,35- 1,0 мм, изолированных один от другого слоем изоляции (лаковой пленкой, окалиной, образующейся при отжиге листов, и пр. ). Благодаря этому преграждается путь распространению вихревых токов.
). Благодаря этому преграждается путь распространению вихревых токов.
2. В состав электротехнической стали, из которой изготовляют сердечники электрических машин и аппаратов, вводят 1- 5% кремния, что обеспечивает повышение ее электрического сопртивления. Благодаря этому достигается снижение силы вихревых токов, протекающих по сердечникам электрических машин и аппаратов.
Использование вихревых токов. Вихревые токи используют для плавки металлов, с их помощью нагревают металлические детали при сварке, наплавке и пайке, а также осуществляют поверхностный нагрев, необходимый для закалки металлических изделий.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что является причиной появления вихревых токов?
2. Какие способы уменьшения вредного действия вихревых токов вам
известны?
3. Где можно найти полезное применение вихревым токам?
Изменяющийся по величине ток всегда создаёт изменяющееся магнитное поле, которое, в свою очередь, всегда индуктирует ЭДС. При всяком изменении тока в катушке (или вообще в проводнике) в ней самой индуктируется ЭДС самоиндукции, она зависит от скорости изменения тока. Чем больше скорость изменения тока, тем больше ЭДС самоиндукции.
Чем больше скорость изменения тока, тем больше ЭДС самоиндукции.
Величина ЭДС самоиндукции зависит также от числа витков катушки и её размеров. Чем больше диаметр катушки и число её витков, тем больше ЭДС самоиндукции. Эта зависимость имеет большое значение в электротехнике. Направление ЭДС самоиндукции определяет Закон Ленца
:
ЭДС самоиндукции имеет всегда
такое направление, при котором она препятствует изменению вызвавшего её тока.
Иначе говоря, убывание тока в катушке влечёт за собой появление ЭДС самоиндукции, направленной по направлению тока, т. е. препятствующей его убыванию. И, наоборот, — при возрастании тока в катушке возникает ЭДС самоиндукции, направленная против тока, т. е. препятствующая его возрастанию. Если ток в катушке не изменяется, то никакой ЭДС самоиндукции не возникает. Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку со стальным сердечником, так как сталь значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции.
Продемонстрировать явление самоиндукции можно, проведя следующий эксперимент. Соберём электрическую цепь, состоящую из аккумулятора, разъединителя и двух параллельных цепей: в первой — лампочка и резистор, а во второй — лампочка и катушка, причём сопротивление обеих лампочек одинаковое, и сопротивление резистора и катушки также одинаково.
1. При включении разъединителя лампа Л1 загорится с задержкой, так как ЭДС самоиндукции катушки препятствует быстрому нарастанию тока в цепи лампы Л1 (рис. 1а и 1б).
2. При отключении разъединителя обе лампы кратковременно вспыхнут, так как ЭДС самоиндукции катушки выше ЭДС батареи. Когда ЭДС самоиндукции иссякает, то обе лампы одновременно гаснут (рис. 2а и 2б).
Явление самоиндукции имеет как положительные, так и отрицательные свойства, причём и те и другие проявляются при работе аппаратов и электрических цепей подвижного состава метрополитена:
- Индуктивный шунт
, подключённый параллельно обмоткам возбуждения тяговых электродвигателей, сглаживает колебания высокого напряжения на контактном рельсе (либо при кратковременном отрыве токоприёмников). Индуктивность этого шунта сравнима с индуктивностью обмоток возбуждения, а его ЭДС направлена всегда против ЭДС ОВ ТЭД. Таким образом, при снижении или снятии высокого напряжения с контактного рельса ЭДС индуктивного шунта препятствует снижению тока, а при повышении напряжения – препятствует нарастанию тока, что препятствует возникновению аварийного режима в силовой цепи и образованию кругового огня по коллектору электродвигателей.
Индуктивность этого шунта сравнима с индуктивностью обмоток возбуждения, а его ЭДС направлена всегда против ЭДС ОВ ТЭД. Таким образом, при снижении или снятии высокого напряжения с контактного рельса ЭДС индуктивного шунта препятствует снижению тока, а при повышении напряжения – препятствует нарастанию тока, что препятствует возникновению аварийного режима в силовой цепи и образованию кругового огня по коллектору электродвигателей.
- Если разомкнуть цепь, содержащую катушку с большой индуктивностью, то при размыкании контактов будет образовываться электрическая дуга, способная привести к разрушению коммутационного аппарата, поэтому в подобных случаях необходимо применять устройство дугогашения или (для низковольтных цепей) подключать параллельно контактам конденсатор.
Самоиндукция. Энергия магнитного поля.
Определение 1
Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.
В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).
Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.
Определение 2
Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.
Расчет индуктивности
Пример 1
Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:
Магнитное поле соленоида задается формулой:
B=μ0nI,
где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.
Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:
Φ=B·S·N=μ0n2Sl
Таким образом, индуктивность соленоида будет выражена формулой:
L=μ0n2S·l=μ0n2V,
где V=Sl – объем соленоида, содержащий магнитное поле.
Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:
Lμ=μ·L=μ0·μ·n2·V.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 3
ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:
δинд=δL=-∆Φ∆t=-L∆I∆t.
ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.
Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.
Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как Rполное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.
Ток в цепи составляет:
I=δLR=-LR∆I∆t
Выражение для ΔQ можем записать так:
∆Q=-L·I·∆I=-Φ(I)∆I
В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:
Q=LI022
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Самоиндукция — Основы электроники
Общеизвестно, что поезд, отходящий от станции, не может сразу развить нужную скорость.
Требуемая скорость достигается лишь по истечении некоторого промежутка времени. За этот промежуток значительная часть энергии локомотива затрачивается на преодоление инерции поезда т. е. на образование запаса кинетической энергии, и очень незначительная часть — на преодоление трения.
За этот промежуток значительная часть энергии локомотива затрачивается на преодоление инерции поезда т. е. на образование запаса кинетической энергии, и очень незначительная часть — на преодоление трения.
В силу того что движущийся поезд обладает запасом кинетической энергии, он не может остановиться мгновенно и будет по инерции двигаться еще некоторое время, т. е. до тех пор, пока не израсходуется на трение весь запас кинетической энергии, сообщенной ему локомотивом в начале движения.
Аналогичные явления имеют место и в замкнутой электрической цепи при включении и выключении тока.
В момент включения постоянного тока (рисунок 1) вокруг проводника образуется магнитное силовое поле.
Рисунок 1. Инерция электрического тока. При включении тока вокруг проводника появляется магнитное поле.
В первые мгновения после включения тока значительная часть энергии источника тока затрачивается на создание этого магнитного поля и лишь незначительная часть — на преодоление сопротивления проводника, вернее на нагревание током проводника.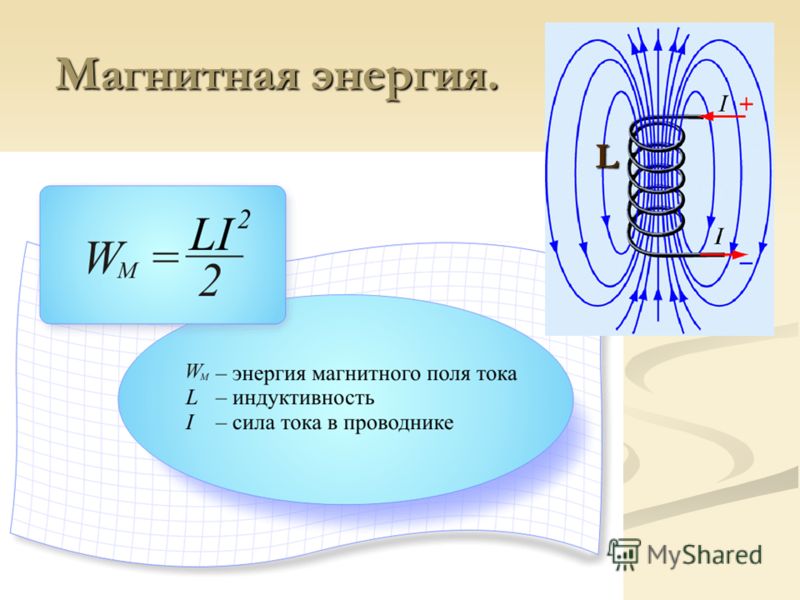 Поэтому в момент замыкания цепи ток не сразу достигает предельной своей величины. Предельная сила тока устанавливается в цепи лишь после окончания процесса образования вокруг проводника магнитного поля (рисунок 2).
Поэтому в момент замыкания цепи ток не сразу достигает предельной своей величины. Предельная сила тока устанавливается в цепи лишь после окончания процесса образования вокруг проводника магнитного поля (рисунок 2).
Рисунок 2. Влияние ЭДС самоиндукции на ток в цепи. При включении источника тока, ток в цепи устанавливается не сразу.
Если, не разрывая замкнутой цепи, выключить из нее источник тока, то ток в цепи прекратится не сразу, а будет протекать в ней, еще некоторое время уменьшаясь постепенно (рисунок 3) до тех пор, пока не исчезнет магнитное поле вокруг проводника, т. е. пока не израсходуется весь запас энергии, заключенной в магнитном поле.
Рисунок 2. Влияние ЭДС самоиндукции на ток в цепи. При выключении источника тока, ток в цепи прекращается не сразу.
Итак, магнитное поле является носителем энергии. Оно накопляет в себе энергию при включении источника постоянного тока и отдает ее обратно в цепь после выключения источника тока. Энергия магнитного поля, таким образом, имеет много общего с кинетической энергией движущегося предмета. Магнитное поле служит причиной «инерции» электрического тока.
Энергия магнитного поля, таким образом, имеет много общего с кинетической энергией движущегося предмета. Магнитное поле служит причиной «инерции» электрического тока.
Мы знаем, что всякий раз, когда изменяется магнитный поток, пронизывающий площадь, ограниченную замкнутой электрической цепью, в этой цепи появляется ЭДС индукции.
Кроме того, нам известно, что всякое изменение силы тока в цепи влечет за собой изменение числа магнитных силовых линий, охватываемых этой цепью. Если замкнутая цепь неподвижна, то число магнитных силовых линий, пронизывающих данную площадь, может измениться только тогда, когда новые линии войдут снаружи в пределы этой площади или когда существующие уже линии выйдут за пределы этой площади. И в том и в другом случае магнитные силовые линии при своем движении должны пересечь проводник. Пересекая проводник, магнитные силовые линии наводят в нем ЭДС индукции. Но так как в этом случае проводник индуктирует ЭДС в самом себе, то эта ЭДС называется ЭДС самоиндукции.
При включении источника постоянного тока в какую-либо замкнутую цепь площадь, ограниченную этой цепью, начинают пронизывать извне магнитные силовые линии. Каждая магнитная силовая линия, приходящая извне, пересекая проводник, наводит в нем ЭДС самоиндукции.
Электродвижущая сила самоиндукции, действуя против ЭДС источника тока, задерживает нарастание тока в цепи. Через несколько мгновений, когда возрастание магнитного потока вокруг цепи прекратится, ЭДС самоиндукции исчезнет и в цепи устанавливается сила тока, определяемая по закону Ома:
I=U/R
При выключении источника тока из замкнутой цепи магнитные силовые линии должны исчезнуть из пространства, ограниченного проводником. Каждая уходящая магнитная силовая линия при пересечении проводника наводит в нем ЭДС самоиндукции, имеющую одинаковое направление с ЭДС источника тока; поэтому ток в цепи прекратится не сразу, а будет протекать в том же направлении, постепенно уменьшаясь до того момента, пока полностью не исчезнет магнитный поток внутри цепи. Ток, протекающий по цепи после выключения из нее источника тока, называется током самоиндукции.
Ток, протекающий по цепи после выключения из нее источника тока, называется током самоиндукции.
Если при выключении источника цепь разрывается, то ток самоиндукции проявляется в виде искры в месте размыкания цепи.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Закон электромагнитной индукции самоиндукция энергия магнитного поля
«Физика — 11 класс»
Самоиндукция.
Если по катушке идет переменный ток, то:
магнитный поток, пронизывающий катушку, меняется во времени,
а в катушке возникает ЭДС индукции .
Это явление называют самоиндукцией.
По правилу Ленца при увеличении тока напряженность вихревого электрического поля направлена против тока, т.е. вихревое поле препятствует нарастанию тока.
При уменьшения тока напряженность вихревого электрического поля и ток направлены одинаково, т. е.вихревое поле поддерживает ток.
е.вихревое поле поддерживает ток.
На вышеприведенном рисунке:
при замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием, т.к. ЭДС самоиндукции в цепи второй лампы велика, и сила тока не сразу достигает своего максимального значения.
При размыкании ключа в катушке L возникает ЭДС самоиндукции, которая поддерживает уменьшающийся ток.
В момент размыкания через гальванометр идет ток размыкания, направленный против начального тока до размыкания.
Сила тока при размыкании может быть больше начального тока, т.е. ЭДС самоиндукции больше ЭДС источника тока.
Индуктивность
Величина индукции магнитного поля, создаваемого током, пропорционален силе тока, а магнитный поток пропорционален магнитной индукции.
Ф = LI
где L — индуктивность контура (иначе коэффициентом самоиндукции), т.е. это коэффициент пропорциональности между током в проводящем контуре и магнитным потоком.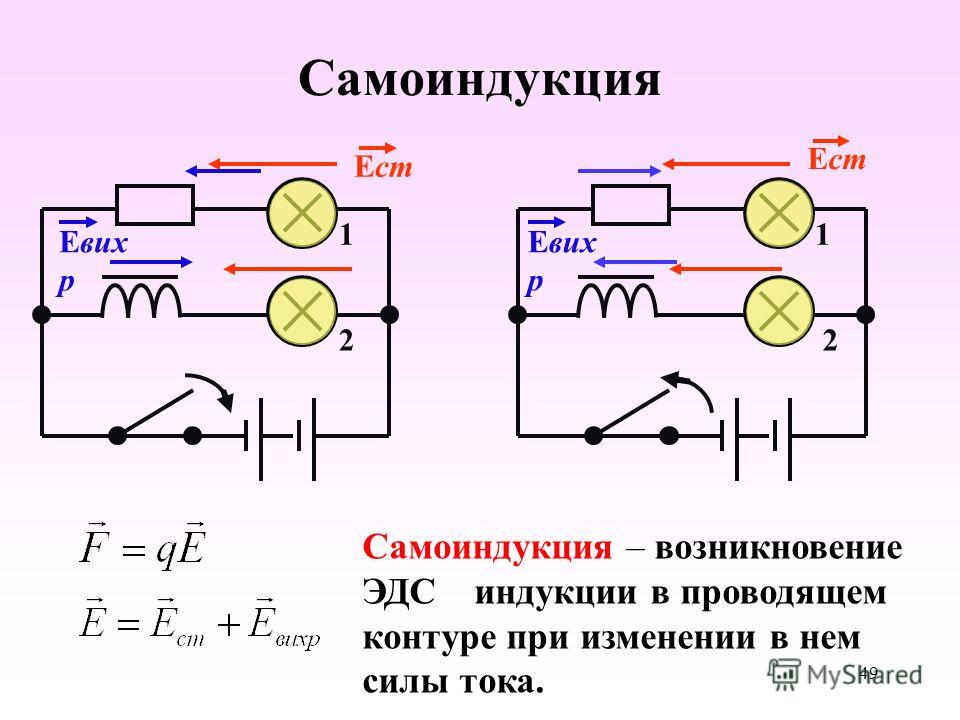
Используя закон электромагнитной индукции, получаем равенство
Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на 1 А за 1 с.
Индуктивность зависит от размеров проводника, его формы и магнитных свойств среды, в которой находится проводник, но не зависит от силы тока в проводнике.
Индуктивность катушки (соленоида) зависит от количества витков в ней.
Единицу индуктивности в СИ называется генри (1Гн).
Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.
Аналогия между самоиндукцией и инерцией.
Явление самоиндукции подобно явлению инерции в механике.
В механике:
Инерция приводит к тому, что под действием силы тело приобретает определенную скорость постепенно.
Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила.
В электродинамике:
При замыкании цепи за счет самоиндукции сила тока нарастает постепенно.
При размыкании цепи самоиндукция поддерживает ток некоторое время, несмотря на сопротивление цепи.
Явление самоиндукции выполняет очень важную роль в электротехнике и радиотехнике.
Энергия магнитного поля тока
По закону сохранения энергии энергия магнитного поля, созданного током, равна той энергии, которую должен затратить источник тока (например, гальванический элемент) на создание тока.
При размыкании цепи эта энергия переходит в другие виды энергии.
При замыкании цепи ток нарастает.
В проводнике появляется вихревое электрическое поле, действующее против электрического поля, созданного источником тока.
Чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля.
Эта работа идет на увеличение энергии магнитного поля тока.
При размыкании цепи ток исчезает.
Вихревое поле совершает положительную работу.
Запасенная током энергия выделяется.
Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.
Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L, определяется по формуле
Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.
Плотность энергии магнитного поля (т. е. энергия единицы объема) пропорциональна квадрату магнитной индукции: wм
В 2 ,
аналогично тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля wэ
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.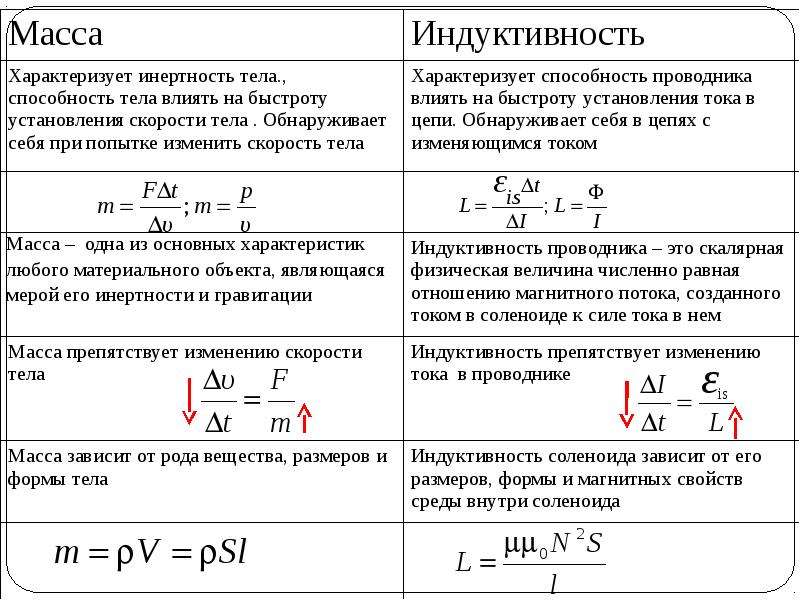
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°).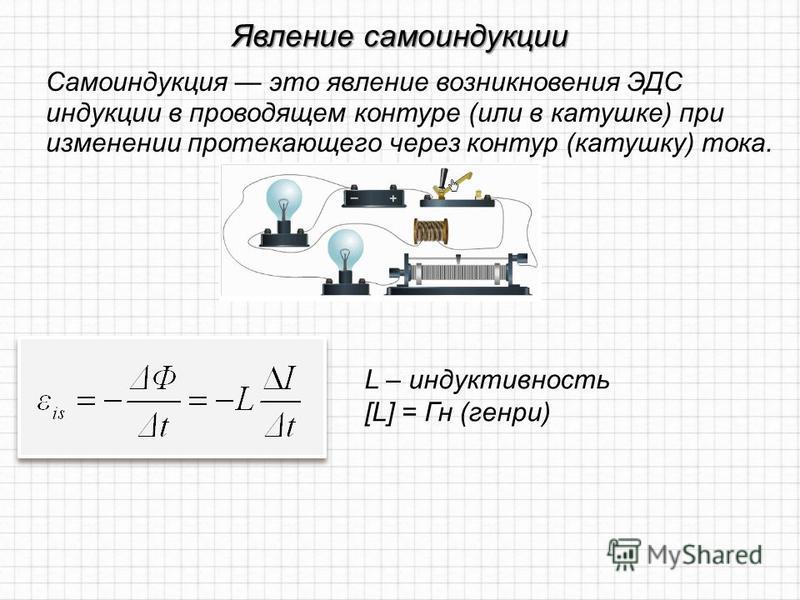 Если ( alpha ) = 90°, то магнитный поток равен 0.
Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec ) .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
 В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током.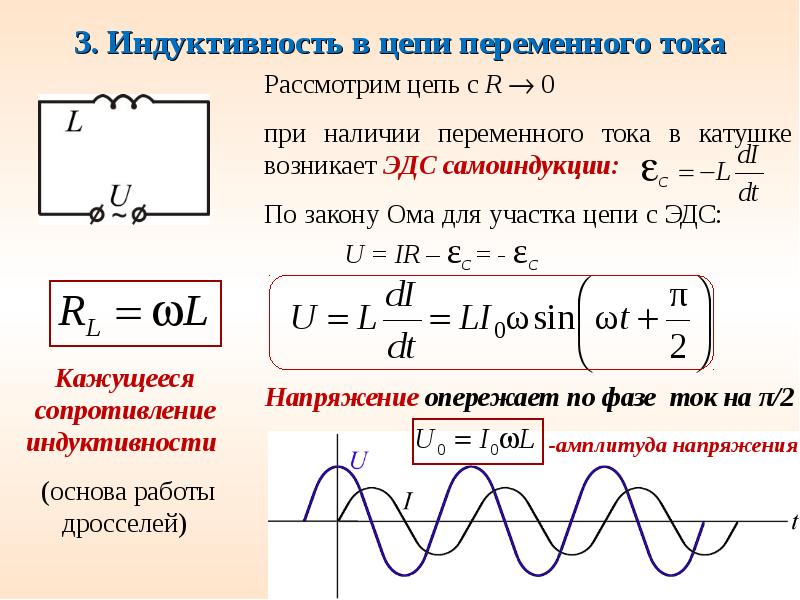 Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл. поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике
(B
I), следовательно магнитный поток пропорционален силе тока (Ф
I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме «Электромагнитная индукция»
1. Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).
Собственная индуктивность | Примечания по электронике
— основная информация о самоиндукции, о том, как она возникает, основная формула самоиндукции и соответствующие расчеты.
Учебное пособие по индуктивности и трансформатору Включает:
Индуктивность
Символы
Закон Ленца
Собственная индуктивность
Расчет индуктивного реактивного сопротивления
Теория индуктивного реактивного сопротивления
Индуктивность проволоки и катушек
Трансформеры
Самоиндукция — это эффект, который замечается, когда одна катушка испытывает влияние индуктивности.
Под действием собственной индуктивности и изменений тока индуцирует ЭДС или электродвижущую силу в том же проводе или катушке, создавая то, что часто называют обратной ЭДС.
Поскольку эффект наблюдается в том же проводе или катушке, которые генерируют магнитное поле, эффект известен как самоиндукция.
Определения самоиндукции
Полезно упомянуть различные определения, связанные с самоиндукцией.
- Самоиндукция: Самоиндукция определяется как явление, при котором изменение электрического тока в цепи вызывает индуцированную электродвижущую силу в той же цепи.
- Единица самоиндукции: Самоиндукция катушки считается равной одному генри, если изменение тока в цепи на один ампер в секунду создает в цепи электродвижущую силу в один вольт.
Основы самоиндукции
Когда ток проходит по проводу, особенно когда он проходит через катушку или индуктор, индуцируется магнитное поле. Он выходит наружу от провода или индуктора и может соединяться с другими цепями.Однако он также связан с цепью, из которой он настроен.
Магнитное поле можно представить в виде концентрических контуров магнитного потока, которые окружают провод, и более крупных, которые соединяются с другими из других контуров катушки, обеспечивая самосвязь внутри катушки.
Когда ток в катушке изменяется, это вызывает индуцирование напряжения в различных контурах катушки — результат самоиндукции.
Самоиндукция
С точки зрения количественной оценки влияния индуктивности, основная формула, приведенная ниже, дает количественную оценку этого эффекта.
Где:
VL = индуцированное напряжение в вольтах
N = количество витков в катушке
dφ / dt = скорость изменения магнитного потока в интервалах в секунду
Наведенное напряжение в катушке индуктивности также может быть выражено через индуктивность (в генри) и скорость изменения тока.
Самоиндукция — это способ работы одиночных катушек и дросселей. Дроссель используется в радиочастотных цепях, потому что он противодействует любому изменению, то есть радиочастотному сигналу, но допускает любое устойчивое, т.е.е. Постоянный ток течет.
Другие основные концепции электроники:
Напряжение
Текущий
Мощность
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
Радиочастотный шум
Вернуться в меню «Основные понятия электроники». . .
. .
Собственная индуктивность
Собственная индуктивность
Далее: Энергия, накопленная в
Up: индуктивность
Предыдущее: Взаимная индуктивность
Самостоятельная индуктивность
Нам не обязательно нужны две цепи для индуктивного эффекта.Рассмотреть возможность
одиночная проводящая цепь, вокруг которой течет ток
течет. Этот ток создает магнитное поле, которое
вызывает магнитный поток, связывающий
схема. Мы ожидаем, что поток будет прямо пропорционален
току, учитывая линейный характер законов магнитостатики,
и определение магнитного потока. Таким образом, мы можем написать
| (241) |
где константа пропорциональности называется самоиндукцией
схема.Как и взаимная индуктивность, самоиндукция
цепи измеряется в единицах генри, и является
чисто геометрическая величина, зависящая только от
форма цепи и количество витков в цепи.
Если ток, протекающий по цепи, изменяется на
количество во временном интервале, то
магнитный поток, соединяющий цепь, изменяется на величину
в том же временном интервале. В соответствии с
Закон Фарадея, ЭДС
| (242) |
генерируется по контуру.С
,
эту ЭДС также можно записать
| (243) |
Таким образом, ЭДС, генерируемая вокруг цепи за счет собственного тока, напрямую
пропорционально скорости изменения тока. Закон Ленца и
здравый смысл, требуйте, чтобы, если ток увеличивается, то ЭДС должна
всегда
действовать для уменьшения тока, а наоборот . Это легко оценить,
так как если
ЭДС действовала на увеличение
ток, когда ток возрастал, мы явно получили бы нефизический
положительный отзыв
эффект, в котором ток продолжал неограниченно расти.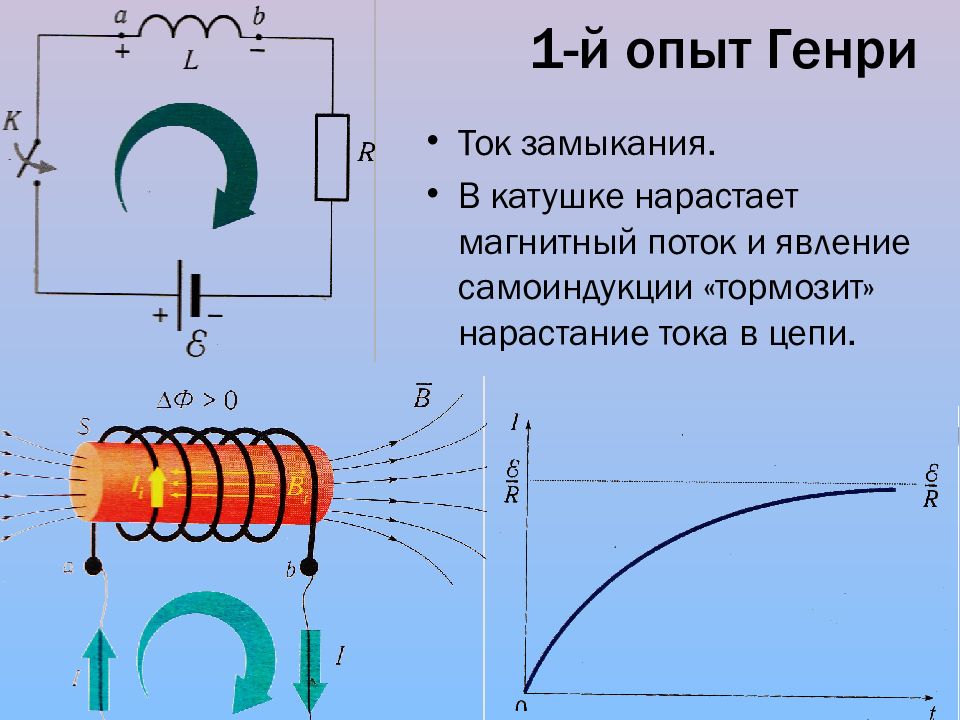 Следовательно, из
Следовательно, из
Уравнение (243), что
собственная индуктивность цепи обязательно должна быть положительным числом . Этот
это не относится к взаимной индуктивности, которая может быть как положительной, так и отрицательной.
Рассмотрим соленоид длины и сечения
область . Предположим, что у соленоида есть витки.
Когда в соленоиде течет ток, возникает однородное осевое поле величиной
| (244) |
генерируется в сердечнике соленоида.Напряженность поля вне ядра
является
незначительный. Магнитный поток, связывающий один виток соленоида, равен
. Таким образом, магнитный поток, связывающий все витки
соленоид
| (245) |
Согласно формуле. (241) собственная индуктивность соленоида определяется выражением
(241) собственная индуктивность соленоида определяется выражением
, что сводится к
| (246) |
Обратите внимание, что это положительно. Кроме того, это геометрическая величина, зависящая от
только от размеров соленоида, и количества витков в соленоиде.
Инженеры
хотели бы уменьшить все части электрического оборудования, независимо от того, насколько они сложны, до
эквивалентная схема , состоящая из сети
всего четыре разных типов
компонента. Этими четырьмя основными компонентами являются ЭДС , резисторы , конденсаторы ,
и индукторы . Катушка индуктивности — это просто чистая самоиндукция, и обычно она
На принципиальных схемах представлен небольшой соленоид. На практике индукторы
обычно состоят из коротких соленоидов с воздушным сердечником, намотанных из эмалированной медной проволоки.
Далее: Энергия, накопленная в
Up: индуктивность
Предыдущее: Взаимная индуктивность
2007-07-14
Самоиндуктивность и индукторы — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Сопоставьте скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
- Вывести самоиндукцию цилиндрического соленоида
- Вывести самоиндукцию прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндукцией .
Катушки индуктивности
(рисунок) показывает некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если ток I должен изменяться со временем — скажем, сразу после замыкания переключателя S, — тогда соответственно изменится магнитный поток.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС, где
Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть
Магнитное поле создается током I в контуре. Если бы – менялись со временем, магнитный поток через петлю также изменился бы, и в петле была бы индуцирована ЭДС.
Это также можно записать как
, где коэффициент пропорциональности L известен как самоиндукция проволочной петли.Если петля имеет N витков, это уравнение принимает вид
По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на (Рисунок) нормаль направлена вниз. При таком соглашении положительное значение на (Рисунок), поэтому L всегда имеет положительное значение .
Для контура с Н витков, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как
При использовании этого уравнения для определения L проще всего игнорировать знаки и рассчитать L как
Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.
Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор.Он представлен символом, показанным на (Рисунок), который напоминает катушку с проводом, основную форму индуктора. (Рисунок) показывает несколько типов индукторов, обычно используемых в схемах.
Символ, обозначающий катушку индуктивности в цепи.
Катушки индуктивности разнообразные. Независимо от того, заключены ли они в капсулу, как показано в трех верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой. (Источник: Windell Oskay)
В соответствии с законом Ленца отрицательный знак на (рис.) Указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока.Например, если бы ток, протекающий от A к B на (Рисунок) (a), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от A до B уменьшался, то индуцированная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока ((Рисунок) (b)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не возникала бы ЭДС.
Индуцированная ЭДС на катушке индуктивности всегда препятствует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).
Одно из распространенных применений индуктивности — это возможность светофора определять, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля.Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути ((Рисунок)). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.
Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (кредит: «Alexbuirds» / Wikimedia Commons)
Во вспышках фотокамер обнаруживаются большие наведенные напряжения. Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. Вспомните из статьи «Колебания при колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения.Также вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный свист трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки.
Самоиндуктивность катушки Индуцированная ЭДС 2.0 В измеряется на катушке из 50 плотно намотанных витков, в то время как ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Какова собственная индуктивность катушки? (б) Каков поток через каждый виток катушки при токе 5,0 А?
Стратегия
Обе части этой проблемы предоставляют всю информацию, необходимую для решения самоиндукции в части (a) или потока через каждый виток катушки в части (b). Необходимые уравнения (рисунок) для части (a) и (рисунок) для части (b).
Решение
- Игнорируя отрицательный знак и используя величины, мы имеем, из (Рисунок),
- Из (Рисунок), магнитный поток выражается в единицах тока так:
Значение Самоиндукция и магнитный поток, вычисленные в частях (a) и (b), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не изменяется во времени, поэтому ЭДС не индуцируется.
Проверьте свое понимание Ток протекает через катушку индуктивности на (Рисунок) от B до A вместо A до B , как показано.Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?
а. уменьшение; б. увеличение; Поскольку ток течет в противоположном направлении диаграммы, чтобы получить положительную ЭДС в левой части диаграммы (а), нам нужно уменьшить ток влево, что создает усиленную ЭДС там, где положительный конец находится слева. Чтобы получить положительную ЭДС в правой части диаграммы (b), нам нужно увеличить ток слева, что создает усиленную ЭДС там, где положительный конец находится справа.
Проверьте свое понимание Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?
Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем: самоиндуктивность
- Предположим, через катушку индуктивности протекает ток I .
- Определите магнитное поле, создаваемое током.Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получить магнитный поток,
- При известном магнитном потоке самоиндуктивность может быть определена по формуле (Рисунок),.
Чтобы продемонстрировать эту процедуру, мы теперь вычислим самоиндуктивности двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A и N витков провода.Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем считать, что магнитное поле распространяется по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде. При токе I , протекающем через катушки, магнитное поле, создаваемое внутри соленоида, составляет
.
, поэтому магнитный поток на один виток равен
Используя (рисунок), находим для самоиндукции соленоида
Если — количество витков на единицу длины соленоида, мы можем записать (рисунок) как
где — объем соленоида.Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока. Это верно для индукторов в целом.
Inductance — The Physics Hypertextbook
Обсуждение
введение
Готовы? Вот так.
Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит.Поле внутри задается формулой…
| B = μ 0 nI = μ 0 | № | I |
| ℓ |
В то же время соленоид — это еще и устройство для улавливания потока.
Φ B = NBA
Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, — это скорость изменения во времени.Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.
Давайте снова рассмотрим эти уравнения, но с изменяющимся во времени поворотом. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.
| дБ | = мк 0 | № | ди | |
| дт | ℓ | дт |
Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал.Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС — в данном случае самоиндуцированную или обратную ЭДС.
| ℰ = — | d Φ B | = — Н | ⎛ | мкм 0 | № | ди | ⎞ | А | |
| дт | ℓ | дт |
Немного изменив порядок вещей, мы получим это уравнение…
| ℰ = — | мкм 0 AN 2 | ди | |
| ℓ | дт |
, который может показаться не таким уж большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта константа называется индуктивностью (или, точнее, самоиндуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…
Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чья новаторская работа в области электромагнитной индукции сыграла важную роль в развитии окончательной теории. Если вы помните, закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы его чествуем символом L .
Индуктивность лучше всего определяется по ее роли в уравнении, полученном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.
На английском языке мы бы прочитали это как «самоиндукция ( L ) — это отношение обратной ЭДС () к временной скорости изменения тока, производящего ее ( dI / dt ).»Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы.
| Н = | В | = | Дж / К | = | (кг · м 2 / с 2 ) / (A · с) | = | кг м 2 | ⎤ | |
| А / с | пк / с | пк / с | A 2 с 2 |
Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо от и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт, когда ток изменяется со скоростью один ампер в секунду.
Индуктивность это что-то. Индуктивность — это сопротивление элемента схемы изменениям тока.Индуктивность в цепи — это аналог массы в механической системе.
| ℰ = — л | ди | ⇔ | причина изменения | = | сопротивление изменить | × | курс сдача | ⇔ | F = м | d v | |
| дт | дт |
индуктивный датчик петли
Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD — это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проезжает через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.
примеров
индуктивность зависит от геометрии
Соленоид ( A площадь поперечного сечения, N количество витков, ℓ длина, n количество витков на длину)
| Φ B | = N | В | А | ||
| Φ B | = N | мкм 0 NI | А | ||
| ℓ | |||||
| Φ B | = | мкм 0 AN 2 | I | ||
| ℓ | |||||
| d Φ B | = | мкм 0 AN 2 | ди | ||
| дт | ℓ | дт | |||
| л | = | мкм 0 AN 2 | = | мкм 0 Aℓn 2 | |
| ℓ |
коаксиальных проводников ( a внутренний радиус, b внешний радиус, длина ℓ)
| Φ B | = | ⌠ | Б | · | d A | ||||
| б | б | ||||||||
| Φ B | = | мкм 0 I | ℓ др | = | мкм 0 Iℓ | др | |||
| 2π r | 2π | r | |||||||
| а | а | ||||||||
| Φ B | = | мкм 0 ℓ | пер. | ⎛ | а | ⎞ | I | ||
| 2π | б | ||||||||
| d Φ B | = | мкм 0 ℓ | пер. | ⎛ | а | ⎞ | ди | ||
| дт | 2π | б | дт | ||||||
| л | = | мкм 0 ℓ | пер. | ⎛ | а | ⎞ | |||
| 2π | б | ||||||||
тороид ( A площадь поперечного сечения , радиус вращения R , число витков N )
| Φ B | = | № | В | А | |
| Φ B | ≈ | № | мкм 0 NI | А | |
| 2π R | |||||
| Φ B | ≈ | № | мкм 0 NA | I | |
| 2π R | |||||
| d Φ B | ≈ | мкм 0 AN 2 | ди | ||
| дт | 2π R | дт | |||
| л | ≈ | мкм 0 AN 2 | |||
| 2π R | |||||
прямоугольная петля ( w ширина, h высота, a радиус провода )
| Φ B | = | № | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | № |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | 2 | мкм 0 N 2 | ⎡ | y ln | ⎛ | х | ⎞ | + | x лин | ⎛ | y | ⎞ | ⎤ | I | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2π | а | а | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d Φ B | = | мкм 0 N 2 | ⎡ | y ln | ⎛ | х | ⎞ | + | x лин | ⎛ | y | ⎞ | ⎤ | ди | ||||||||||||||||||||||||||||||||||||||||||||||||||
| дт | π | а | а | дт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| л | = | мкм 0 N 2 | ⎡ | y ln | ⎛ | х | ⎞ | + | x лин | ⎛ | y | ⎞ | ⎤ | |||||||||||||||||||||||||||||||||||||||||||||||||||
| π | а | а | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта формула не совсем работает, поскольку она игнорирует краевые эффекты.Вы можете найти точную формулу (а также скрипты, которые будут рассчитывать индуктивность для вас) в Интернете на нескольких веб-сайтах по электротехнике.
Индуктивность | Физика
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы.Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность . Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.
Рис. 1. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор.Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что « E 2 индуцированный» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом.Мы выражаем это в форме уравнения как
[латекс] {\ text {emf}} _ {2} = — M \ frac {\ Delta {I} _ {1}} {\ Delta t} \\ [/ latex],
, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от Transformers. Единицами измерения для M являются (В с) / A = Ω ⋅ s, который назван генри (H) в честь Джозефа Генри.То есть 1 H = 1 Ω⋅s. Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] {\ text {emf}} _ {1} = — M \ frac {\ Delta {I} _ {2}} {\ Delta t} \\ [/ latex],
, где M то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть, а может и не быть желательной.Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля. (См. Рисунок 2.)
Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока Δ I через устройство.Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = — L \ frac {\ Delta I} {\ Delta t} [/ latex],
, где L — собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на рисунке 3.
Рисунок 3.
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока.Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера L , например, за счет встречной намотки катушек, как показано на рисунке 2. Катушка индуктивности 1 H — это большая индуктивность. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1.0 H, через который протекает ток 10 A. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как ЭДС = — L (Δ I / Δ t ), будет препятствовать изменению. Таким образом, ЭДС будет индуцирована ЭДС = — L (Δ I / Δ t ) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. Положительный знак означает это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный свист трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. Рисунок 4.)
Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля.Таким образом, в этом тексте индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = — Н (Δ Φ / Δ t ) и, по определению самоиндукции, как ЭДС = — L . (Δ I / Δ т ).Приравнивая эти доходности к
[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} = — L \ frac {\ Delta I} {\ Delta t} \\ [/ latex]
Решение для L дает
[латекс] L = N \ frac {\ Delta \ Phi} {\ Delta I} \\ [/ latex]
Это уравнение для самоиндукции L устройства всегда верно. Это означает, что самоиндукция L зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше Δ Φ / Δ I .Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь A соленоида является фиксированной, изменение магнитного потока составляет Δ Φ = Δ ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется выражением [латекс] B = {\ mu} _ {0} {nI} = {\ mu} _ {0} \ frac {NI} { \ ell} \\ [/ латекс]. {2} \ влево (1.{2} \ right)} {0.100 \ text {m}} \\ & = & 0.632 \ text {mH} \ end {array} \\ [/ latex].
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.
Рис. 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)
Физика для науки и техники II
из отдела академических технологий на Vimeo.
9,7 Самоиндукция
Рассмотрим две простые схемы. Катушка, которая подключена к клеммам источника питания, батареи, переключателя, и, скажем так, это наша схема номер один.Мы размещаем аналогичную катушку напротив этой, и в этой схеме у нас нет источника питания. Мы можем разместить здесь гальванометр, чтобы определять ток, и назовем его схемой номер два.
Допустим, источник питания, батарея, генерирует ε вольт электродвижущей силы. Конечно, когда переключатель выключен, через эту цепь не будет протекать ток. Когда мы включаем переключатель, мы собираемся закончить тем, что определенный ток будет течь по этой цепи от положительного конца к отрицательному, так что, как только переключатель будет замкнут.
Ну, во время этого процесса, как только мы включим этот переключатель, ток будет начинаться с 0 и начнет увеличиваться до своего максимального значения. Затем он достигнет своего максимального значения и, следовательно, будет проходить через этот контур с этим постоянным значением. Но во время нарастания тока, другими словами, когда он идет от 0 до максимального значения, соответствующее магнитное поле, которое он генерирует, также будет начинаться с 0 и увеличиваться в сторону максимального значения, потому что, как вы помните, величина тока прямо пропорциональна силе создаваемого магнитного поля.
Итак, во время этого процесса, когда магнитное поле растет с увеличением тока, и оно будет генерировать силовые линии магнитного поля через этот первый контур, допустим, первая катушка, и эти линии будут проходить через область, окружающую вторую катушку. По мере увеличения тока это магнитное поле будет увеличиваться. Следовательно, поток через область, окруженную второй катушкой, будет увеличиваться, и в результате этого увеличения потока, согласно закону Фарадея, мы получим наведенную ЭДС и, следовательно, индуцированный ток.Этот ток появится из закона Ленца, так что он будет противодействовать своей причине, поэтому он будет генерировать магнитное поле в направлении, противоположном этому. Это магнитное поле индуцированного тока. Чтобы иметь возможность генерировать магнитное поле в этом направлении, используя правое правило, индуцированный ток должен течь против часовой стрелки по всей этой цепи.
Конечно, этот ток будет обнаружен здесь гальванометром, и стрелка гальванометра будет двигаться в одном направлении.Он отклонится от своего первоначального 0 в любой точке или в любом месте. Что ж, если мы последуем этому случаю, то магнитное поле этого индуцированного тока вдоль этой второй петли будет проходить через область, окруженную первой петлей, как это. Поскольку ток нарастает в первом, поэтому индуцированный и будет генерировать второй. Магнитное поле второй катушки пройдет через область, окруженную первой катушкой. Следовательно, он будет генерировать изменение потока через первую катушку, и этот поток будет индуцировать электродвижущую силу вдоль первой катушки и, следовательно, также ток, и этот ток будет проявляться так, что он будет противодействовать своей причине.
Если мы проследим катушки, исходные катушки, и это вернется к тому факту, что i индуцировано во второй катушке, чтобы появиться, и это происходит, что исходный ток i отображается как увеличивающийся от своего максимума. значение. Следовательно, ток, наведенный на первую катушку, будет противодействовать этой причине. Другими словами, он будет пытаться противодействовать увеличению первоначального тока. Для этого он должен генерировать магнитное поле, противоположное направлению потока исходного тока.Следовательно, он должен работать в направлении, противоположном исходному току. И по этой причине мы не сможем закончить тем, что ток сразу перейдет от 0 до максимального значения. Для достижения этого значения потребуется некоторое время.
Что ж, мы можем заявить здесь, что, говоря, индуцированная электродвижущая сила также появляется в катушке, если мы изменяем ток в той же катушке. Это называется самоиндукцией, а создаваемая ЭДС, электродвижущая сила, называется «самоиндуцированной ЭДС».Теперь, следовательно, как только мы изменим ток в первой катушке, мы собираемся индуцировать ток через вторую катушку, и магнитное поле этого тока вызовет изменение потока через первую катушку. Таким образом, мы собираемся получить и , индуцированные вдоль первой катушки. И если ток увеличивается в первой катушке, этот индуцированный ток будет течь в направлении, противоположном направлению первоначального тока.
Следовательно, это приведет к тому, что исходный ток сразу достигнет своего максимального значения.Или, если i уменьшается, если исходный ток уменьшается, от его максимального значения до 0, тогда уменьшение магнитного поля будет генерировать или индуцировать электрический ток вдоль второй катушки. Этот ток будет течь в таком направлении, что будет противодействовать своей причине, и поэтому он будет течь в таком направлении, что создаваемое им магнитное поле будет в том же направлении, что и исходное магнитное поле. Это магнитное поле, опять же, будет генерировать изменение магнитного потока через область, окруженную первой катушкой.Это вызовет наведенный ток по первому, и в этом случае, опять же, он будет появляться в противовес своей первоначальной причине, а именно уменьшению исходного тока.
Следовательно, в этом случае этот ток будет проявляться в том же направлении, что и исходный ток. Поэтому позвольте мне выключить переключатель, ток не упадет до 0 сразу, и это займет некоторое время, и мы называем эту электродвижущую силу, которая появляется в результате изменения тока так же, как самоиндуцированная электродвижущая сила и связанный с ней ток как самоиндуцированный ток.
Хорошо. Если мы вспомним определение индуктивности для любого индуктора, мы имеем L, — это равное количество потоковых звеньев, деленное на ток. Отсюда, если мы произведем перекрестное умножение, Li будет равно N , умноженному на Φ B . Что ж, по закону Фарадея индуцированная электродвижущая сила равна — Н, раз количество витков, умноженное на изменение магнитного потока. Мы можем поместить это N в оператор производной, поскольку это константа, и записать это соотношение d из NΦ B над dt .Но NΦ B , исходя из определения индуктивности, равно L времени i . Следовательно, ε становится равным — d Li по сравнению с dt .
Поскольку индуктивность постоянна, мы можем вынести ее за пределы оператора производной. Тогда наведенная ЭДС становится равной — L di по сравнению с dt , и это выражение для самоиндуцированной электродвижущей силы. Он просто говорит нам, что если ток меняется, то мы получим самоиндуцированную ЭДС через ту же катушку.Если через какой-либо индуктор протекает постоянный ток, то самоиндуцированная ЭДС будет равна 0.
Итак, мы можем резюмировать, сказав, что, таким образом, в любом индукторе — это может быть простой катушечный соленоид или тороид — самоиндуцированная ЭДС возникает всякий раз, когда ток изменяется со временем. Величина электродвижущей силы не влияет на индуцированную электродвижущую силу. Учитывается только скорость изменения тока. Другими словами, поскольку мы генерируем самоиндуцированную электродвижущую силу в самой первой катушке, самоиндуцированная ЭДС и связанный с ней индуцированный ток не имеют ничего общего с величиной исходного тока.Это напрямую зависит от того, насколько быстро или медленно изменяется исходный ток.
Что ж, направление самоиндуцированной электродвижущей силы, опять же, определяется из закона Ленца, другими словами, самоиндуцированные действия противодействуют изменению, которое его вызывает. Таким образом, если мы добавим, мы можем сказать, что направление самоиндуцированной электродвижущей силы определяется законом Ленца. То есть противостоит своей причине.
В этом смысле, если вы посмотрите на пару интересных случаев, предполагая, что у нас есть индуктор, может быть соленоидом, тороидом или простой катушкой, и давайте предположим, что ток течет слева направо, и предположим, что i повышается.Следовательно, мы собираемся получить самоиндуцированную электродвижущую силу, и она проявится так, что будет противодействовать своей причине. Очевидно, что для протекания тока в этом направлении у нас должна быть наша оригинальная стрелка ЭДС. Он указывает вправо, чтобы ток шел слева направо. Таким образом, если и увеличиваются, мы собираемся закончить с самоиндуцированной ЭДС вдоль этого индуктора, так что она будет противодействовать своей причине. Другими словами, он будет вести себя так, как будто у нас есть другой источник питания, противостоящий этому току.Другими словами, создание индуцированного тока в направлении, противоположном этому исходному току.
С другой стороны, если мы рассматриваем ту же катушку индуктивности, в этом случае ток снова уменьшается в том же направлении. Итак, снова стрелка ЭДС указывает в направлении потока тока, но теперь ток становится все меньше и меньше, поэтому мы собираемся закончить с самоиндуцированной ЭДС через этот индуктор, но эта ЭДС будет проявляться в некотором роде. что он попытается противостоять своему делу. Для этого он будет генерировать индуцированный ток, который будет течь в том же направлении, что и исходный ток.Следовательно, он будет вести себя так, как если бы у нас наведена электродвижущая сила ε ‘, и он генерирует ток в том же направлении, что и исходный. Тогда как в предыдущем случае этот индуцированный ток будет иметь направление, противоположное направлению потока исходного тока.
Хотя это не очень хорошее представление, но оно поможет вам понять, потому что, помните, мы не можем действительно использовать стрелки ЭДС из-за электродвижущей силы, генерируемой в результате индукции.Что ж, именно из-за этих причин для первого случая мы можем рассматривать этот случай как момент, когда мы включаем переключатель, чтобы ток нарастал от его, от 0 до максимального значения. В то время как во втором случае мы можем визуализировать это как момент, когда мы выключаем выключатель, так что ток уменьшается от максимального значения до 0. В обоих случаях ни максимальное значение, ни значение 0 тока не будут достигнуты сразу. Это займет некоторое время из-за самоиндуцированной электродвижущей силы.
Страница не найдена | MIT
Перейти к содержанию ↓
- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
.

 21)
21)