Движение тел под действием нескольких сил: Движение под действием нескольких сил: движение на плоскости | LAMPA — ошкольное образовательное учреждение № 4 «Алёнушка»

3\cdot 0,7=Fтяги=0,03⋅15⋅103⋅10+15⋅103⋅0,7=

=300⋅15+15⋅700=15⋅(300+700)=15000=300\cdot 15+15\cdot 700=15\cdot(300+700)=15000=300⋅15+15⋅700=15⋅(300+700)=15000 (Н).

Ответ. Fтяги=15F_{тяги}=15Fтяги=15 кН.

Разберем еще одну задачу.

Условие

Брусок массой 400400400 г под действием груза массой 100100100 г проходит из состояния покоя путь 808080 см за 222 с. Найти коэффициент трения.

(Источник: Рымкевич А.П. Сборник задач по физике)

Решение

Это задача на движение связанных тел. В таких задачах надо знать, что сила, с которой нитка тянет два связанных тела, — одинакова. Давайте разберемся, почему это так. Пусть у нас есть два бруска, связанных невесомой нитью (то есть нитью с массой, равной нулю). Пусть нить тянет первое тело с силой T⃗1\vec{T}_1T⃗1, а второе тело — с силой T⃗2\vec{T}_2T⃗2.

Тогда по 3-му закону Ньютона тело 1 и тело 2 также действуют на саму нить с силами T⃗1′\vec{T}_1’T⃗1′ и T⃗2′\vec{T}_2’T⃗2′. Причем по тому же 3-му закону Ньютона:

T⃗1=−T⃗1′\vec{T}_1=-\vec{T}_1’T⃗1=−T⃗1′

T⃗2=−T⃗2′\vec{T}_2=-\vec{T}_2’T⃗2=−T⃗2′.

Теперь посмотрим только на нить:

Получается, что на нить действуют две силы: T⃗1′\vec{T}_1’T⃗1′ и T⃗2′\vec{T}_2’T⃗2′. Значит, мы можем найти равнодействующую. Пусть суммарная (равнодействующая) сила равна TTT.

Тогда по 2-му закону Ньютона T=m⋅aT=m\cdot aT=m⋅a, где mmm — это масса нити, aaa — ускорение, с которым движется нить. Но масса нашей нити m=0m=0m=0. А это значит, что и равнодействующая сил, приложенных к нити, должна быть равна 000:

T=0T=0T=0.

А это, в свою очередь, значит, что T⃗1′+T⃗2′=0\vec{T}_1’+\vec{T}_2’=0T⃗1′+T⃗2′=0. Или: T1′=T2′T_1’=T_2’T1′=T2′.

То есть нить «передает» силу через себя от одного груза к другому без потери этой силы.

Блок, который присутствует в нашей задаче, лишь «поворачивает» силу, не изменяя ее по величине.

Вернемся к решению нашей задачи.

Шаг 1. Первое, что нужно сделать, — это рисунок.

Шаг 2. Записываем 2-й закон Ньютона.

В этой задаче у нас участвуют два тела. Поэтому 2-й закон Ньютона нужно записать для двух тел:

для первого тела: T⃗1+F⃗тр+N⃗1+m1g⃗=m1a⃗1\vec{T}_1+\vec{F}_{тр}+\vec{N}_1+m_1\vec{g}=m_1\vec{a}_1T⃗1+F⃗тр+N⃗1+m1g⃗=m1a⃗1
для второго тела: T⃗2+m2g⃗=m2a⃗2\vec{T}_2+m_2\vec{g}=m_2\vec{a}_2T⃗2+m2g⃗=m2a⃗2.

Шаг 3. Выберем оси и запишем 2-й закон Ньютона в проекции на каждую из осей.

а) Сначала для тела 1:

На ось OXOXOX: T1−Fтр+0+0=m1a1\,\,T_1-F_{тр}+0+0=m_1a_1T1−Fтр+0+0=m1a1.

На ось OYOYOY: 0+0+N1−m1g=m1⋅0\,\,0+0+N_1-m_1g=m_1\cdot 00+0+N1−m1g=m1⋅0.

Итак: {T1−Fтр=m1a1N1−m1g=0.\begin{cases}T_1-F_{тр}=m_1a_1\\N_1-m_1g=0{.}\end{cases}{T1−Fтр=m1a1N1−m1g=0.

б) Для тела 2:

Обратите внимание на то, что движение второго тела одномерное. Оно происходит вдоль одной оси. Поэтому достаточно ввести лишь одну ось.

Уравнение, полученное из 2-го закона Ньютона для второго тела, в проекции на ось OYOYOY:

−T2+m2g=m2a2-T_2+m_2g=m_2a_2−T2+m2g=m2a2.

Шаг 4. Собираем все, что было получено ранее:

{T1−Fтр=m1a1N1−m1g=0−T2+m2g=m2a2T1=T2.\begin{cases}T_1-F_{тр}=m_1a_1\\N_1-m_1g=0\\-T_2+m_2g=m_2a_2\\T_1=T_2{.}\end{cases}⎩⎪⎪⎪⎨⎪⎪⎪⎧T1−Fтр=m1a1N1−m1g=0−T2+m2g=m2a2T1=T2.

Дополнительно надо учесть, что нить (обычно) является не только невесомой, но еще и нерастяжимой.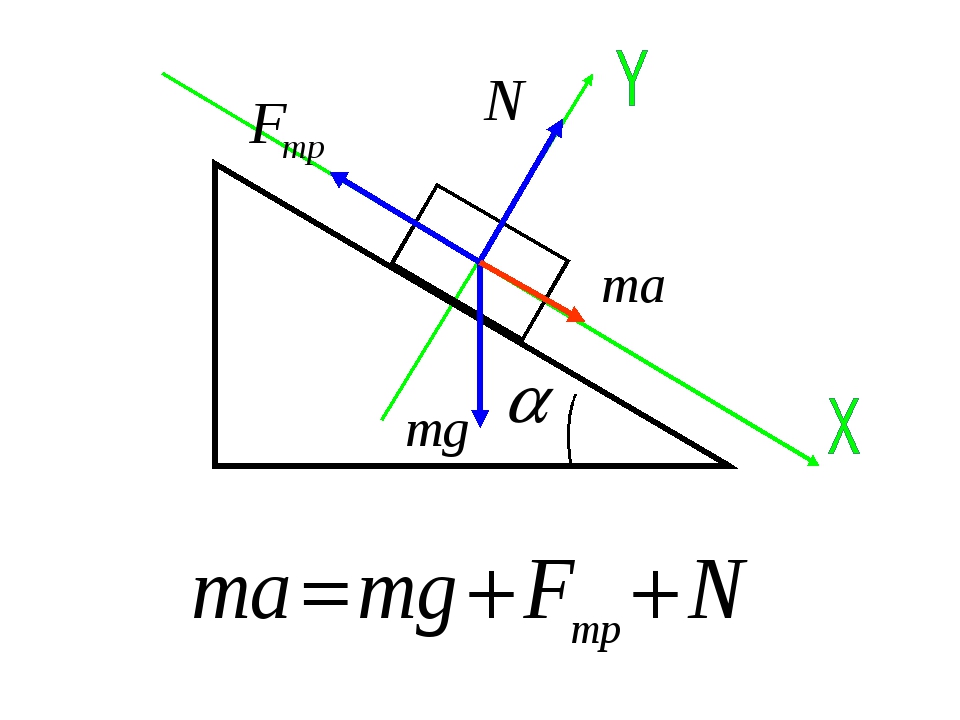

Содержание

Движение тела под действием нескольких сил

Теоретически тела могут двигаться при воздействии на них одной силы: силы упругости, силы тяготения или силы трения. Но в реальности такие движения в земных условиях можно наблюдать очень редко. В большинстве случаев наряду с силами упругости и тяготения на тело всегда действует сила трения.

При прямолинейном падении тела в жидкости или в газе на тело действует две силы – сила тяжести и сила сопротивления газа или жидкости.

Если пренебречь всеми другими силами, то можно считать, что в момент, когда падение тела только начинается (v = 0), на него действует только одна сила тяжести F_т. Сила сопротивления отсутствует. Но как только движение тела началось, сразу же появляется сила сопротивления – сила жидкого трения, которая растёт с увеличением скорости и направлена против неё.

Если сила тяжести остаётся постоянной, направленная в противоположную сторону сила сопротивления растёт вместе со скоростью тела, обязательно настанет тот момент, когда они по модулю станут равными друг другу.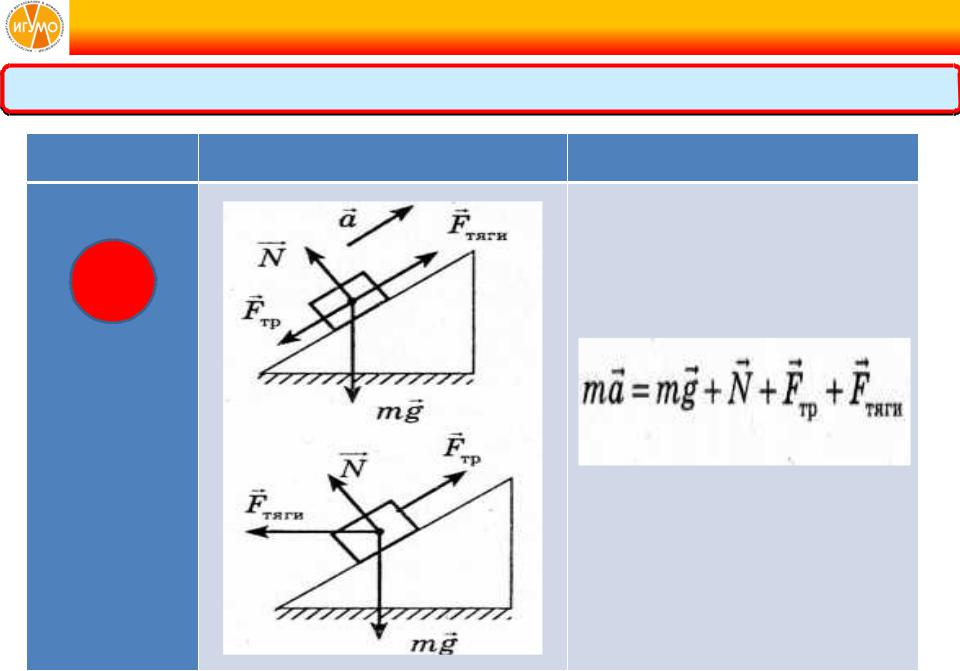 Как только это произойдёт, равнодействующая обеих сил станет равной нулю. Ускорение тела также станет равным нулю, и тело начнёт двигаться с постоянной скоростью.

Если тело падает в жидкости, кроме силы тяжести, необходимо учитывать и выталкивающую силу, направленную противоположно силе тяжести. Но так как эта сила постоянна и не зависит от скорости, то она не препятствует установлению постоянной скорости движения падающего тела.

Как решают задачи механики, если на тело действует несколько сил?

Вспомним второй закон Ньютона:

где F – это векторная сумма всех сил, приложенных к телу. Векторное сложение сил можно заменить их алгебраическим сложением их проекций на координатные оси. При решении задач по механике, необходимо сначала изобразить на чертеже векторы всех сил, действующих не тело, и ускорения тела (если известно его направление). После выбора направления координатных осей, необходимо найти проекции всех векторов на эти оси. Далее нужно составить уравнение второго закона Ньютона для проекций на каждую ось и решить полученные скалярные уравнения.

Если в условиях задачи рассматривается движение нескольких тел, то уравнение второго закона Ньютона применяют к каждому телу отдельно и затем совместно решают полученные уравнения.

Решим задачу.

Брусок массой m движется по наклонной плоскости с углом α. Коэффициент трения бруска о плоскость µ. Найдите ускорение а бруска.

Для решения задачи необходимо построить чертёж и изобразить на нём векторы всех сил, действующих на брусок.

На брусок действуют три силы: сила тяжести Fт = mg, сила трения Fтр и сила реакции опоры N (сила упругости). Совместно эти силы сообщают бруску ускорение ā, которое направлено вниз вдоль плоскости.

Направим оси координат X параллельно наклонной плоскости, а ось координат Y перпендикулярно наклонной плоскости.

Вспомним второй закон Ньютона в векторной форме:

Для решения задачи нам необходимо записать это уравнение в скалярной форме. Для этого необходимо найти проекции векторов на оси X и Y .

Проекции на ось X. Проекция aх положительна и равна модулю вектора ā: aх = a. Проекция (Fт)х положительна и равна, как видно из треугольника АВD, mg sin α. Проекция (Fтр)х отрицательна и равна – Fтр. Проекция N вектора N равна нулю: Nх = 0. Уравнение второго закона Ньютона в скалярной форме записывается поэтому так:

ma = mg sin α – Fтр.

Проекциии на ось Y.Проекция aу равна нулю (вектор a перпендикулярен оси Y!): a = 0. Проекция (Fт)у отрицательна. Из треугольника ADC видно, что (Fт)у = -mg cos α. Проекция N положительна и равна модулю вектора Nу = N. Проекция (F) равна нулю: (Fтр)у = 0. Тогда уравнение второго закона Ньютона запишем так:

0 = N – mg cos α.

Откуда

N = mg cos α.

Сила трения по модулю равна µN, отсюда Fтр = µ mg cos α.

Подставим это выражение вместо силы трения в первое полученное скалярное уравнение:

ma = mg sin α – µ mg cos α;

a = g(sin α – µ cos α).

Ускорение a, меньше, чем g. Если трение отсутствует (µ = 0), то ускорение скользящего по наклонной плоскости тела равно по модулю g sin α, и в таком случае оно также меньше g.

На практике наклонные плоскости и используются как устройства, позволяющее уменьшить ускорение (g) при движении тела вниз или вверх.

Урок по физике 10 класс Движение под действием нескольких сил.

Урок физики в 10 классе

Тема: Движение под действием нескольких сил. Алгоритм решения задач.

Тип урока: Закрепление изученного материала.

Цель урока: создать условия для восприятия и осмысления учащимися блока информации о движении тел под действием нескольких сил.

Задачи:

Образовательная:

— научить учащихся разбираться в условии задачи и пользоваться математическим аппаратом;

-продолжить развитие умений анализировать условия задач и ответов;

-продолжить формирование умений решать задачи.

Развивающая: Продолжить формирование у учащихся навыков умений мыслить, анализировать и делать выводы. Формирование таких приёмов умственной деятельности, как: выделение главного, обобщение, систематизация, постановка и решение проблемы и т.д. Развитие активности мышления, его самостоятельности, систематичности, гибкости.

Развитие внимания, памяти, воображения

Воспитательная: Формирование таких качеств личности, как творческий подход к решению познавательных и практических задач, чёткость и организованность в труде, умение контролировать свою деятельность, оценивать её.

Оборудование к уроку: мультипроектор, экран, презентация, раздаточный материал.

План урока:

1.Организационный момент.

2. Проверка знаний.

3.Актуализация знаний.

4.Объяснение нового материала.

5.Закрепление.

6.Подведение итогов и Д/З

Ход урока:

1.Организационный момент.

Проверка готовности обучающихся к уроку.

2. Проверка знаний.

1. СЛАЙД 1-3

Повторение материала (устно объяснить увиденное на рисунках на основе законов Ньютона)

2. СЛАЙД 4- 14

Быстро ответить на вопросы

3. СЛАЙД 15

Проверить и сдать задания.

СЛАЙД 16

Записать в тетрадь тему урока.

СЛАЙД 17

Что будем рассматривать на уроке.

3.Актуализация знаний.

СЛАЙД 18

Дайте характеристики силе по схеме:

1)Определение

2)Формула

3)Направление

Сила тяжести.

Сила упругости и её разновидности.

Сила трения.

Вес тела.

Сила Архимеда.

4.Объяснение нового материала.

Сегодня на уроке применим знания при решении задач, когда на тело действуют не одна, а несколько сил, в зависимости от условий задачи.

Вот одна из них:

Ящик массой 10 кг перемещают по полу, прикладывая к нему некоторую силу. В течение 5 с скорость ящика возросла с 2 м/с до 14,4 км/ч. Коэффициент трения скольжения между ящиком и полом равен 0,15. Определите эту силу.

Давайте вместе с вами решим эту задачу.

Ваша задача внимательно следить за каждым шагом решения и помогать мне.

А помогать мне можете, если будем вместе дискутировать, обсуждать, отвечать на вопросы, а помогать ещё нам будет презентация.

СЛАЙД 19 АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ

Первый вопрос: С чего обычно начинается решение задач.

Правильно, с анализа условия и записи дано. (си)

Далее, на ваш взгляд, что мы должны сделать?

Сделать пояснительный чертёж.

Начертили опору и ящик.

Далее расставляем силы, действующие на тело и покажем направление ускорения. Заметьте, что расставляем силы, действующие на ТЕЛО!!!

Какие силы действуют на тело? Перечислите их.

Сила тяжести, сила реакции опоры, сила трения и сила с которой тянут ящик. Вес тела не рассматривается, так как действует не на тело, а на опору.

Давайте выясним из условия задачи как движется тело?

Правильно, равноускоренно.

Следовательно, какой закон Ньютона приемлем для решения задачи?

Второй закон Ньютона в векторной форме.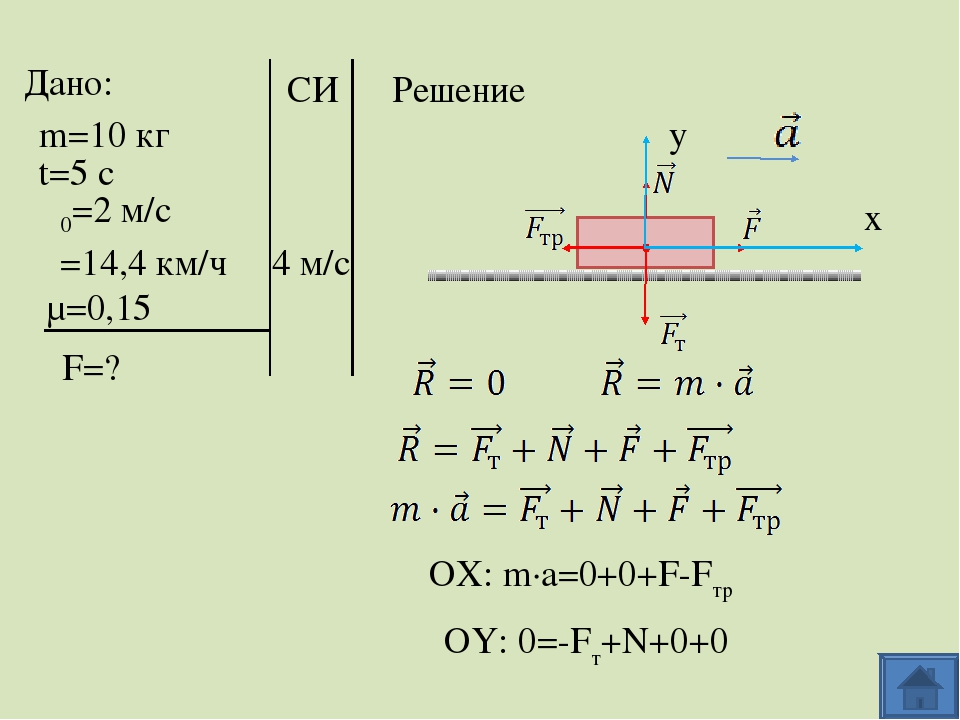 Равнодействующая сил состоит из четырёх сил.

Чтобы перейти из векторной формы к скалярной нужно найти проекции векторных величин на оси.

Следующий шаг, надо выбрать направление осей и спроецировать на них векторные величины.

Чтобы найти неизвестную величину, нужно ввести дополнительные данные.

Давайте запишем формулы силы тяжести, силы трения, ускорения.

Подставьте эти данные и выразите неизвестную величину решив систему двух уравнений.

Обучающие самостоятельно выражают неизвестную величину и проверяют свой ответ с помощью презентации.

Чтобы проверить правильность решения задачи, давайте проверим размерность найденной величины.

Если получится единица измерения Ньютон, значит мы правильно выразили её.

Теперь найдем численное значение и проанализируем ответ.

5.Закрепление. СЛАЙД 21-29

1. Давайте мысленно пройдем этапы решения задачи. (алгоритм решения задач)

2. Решим задачи на доске, следуя алгоритму.

Задача № 1. Автобус, масса которого с полной нагрузкой равна 15 т, трогается с места с ускорением 0,7 м/с². Найти силу тяги, если коэффициент сопротивления движению равен 0,03. (15кН)

Задача № 2. Подъемный кран поднимает груз массой 1 т. Какова сила натяжения троса в начале подъема, если груз двигается (очень кратковременно) с ускорением 25 м/с². (35кН)

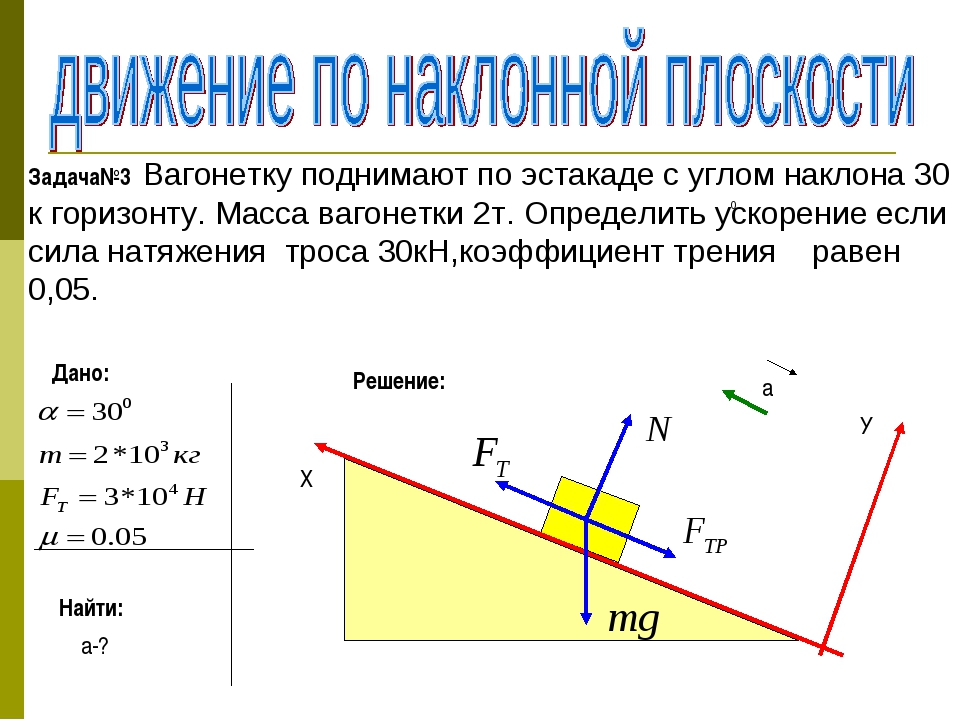
Задача №3. Вагонетку поднимают по эстакаде с углом наклона 30º к горизонту. Масса вагонетки 2 т. Определить ускорение если сила натяжения троса 30кН, коэффициент трения равен 0,05. (9,6 м/с2)

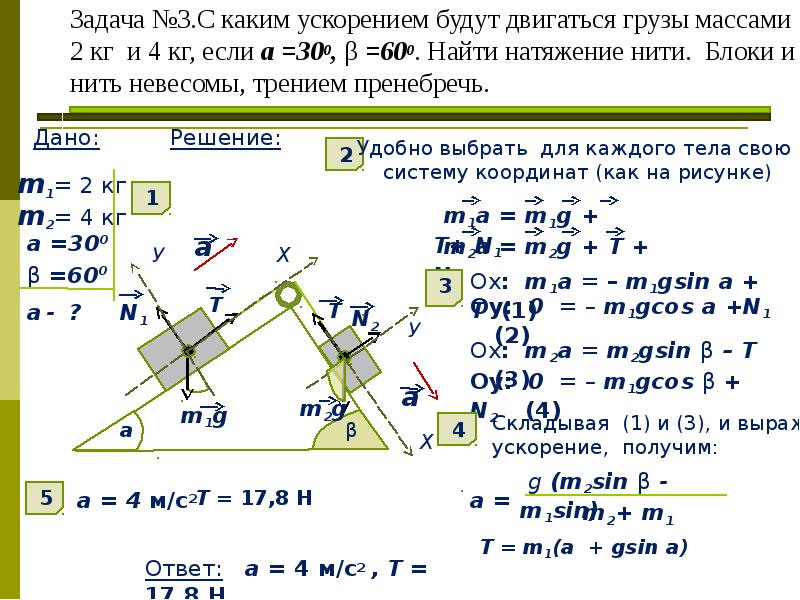
Задача№4. На шнуре, перекинутом через неподвижный блок, помещены грузы массами 0,3 и 0,2кг. С каким ускорением движется система? Какова сила натяжения шнура во время движения? (2м/с2, 2,4 Н)

Задача№5 . Конькобежец движется со скоростью 10м/с по окружности радиусом 30 м. Под каким углом к горизонту он должен наклониться, чтобы сохранить равновесие? (720)

6. Подведение итогов.

Сегодня мы закрепили алгоритм решения задач по динамике, который лежит в основе решения многих задач по физике.

7. Домашнее задание . СЛАЙД 30

1. Подготовка к контрольной работе

2. Решить задачу

Груз, подвешенный на нити длиной 60см, двигаясь равномерно, описывает в горизонтальной плоскости окружность. С какой скоростью движется груз, если во время его движения нить образует с вертикалью постоянный угол φ=30º? (0,42м/с)

Движение тел под действием нескольких сил

Задачи урока:

Образовательные:

повторение основных законов динамики;

закрепление умений определять действующие силы и их результирующую силу, решать задачи на законы динамики;

владение монологической речью, умение сравнивать, выбирать рациональные способы решения задач в новых ситуациях; владение способами само- и взаимооценки; умение коллективно работать.

Воспитательные:

развитие представления о движении тел под действием нескольких сил;

формирование знаний о динамических закономерностях, о влиянии условий на характер движения под действием нескольких сил.

Развивающие:

развитие речи, мышления, сенсорной сферы личности, эмоциональной, волевой и потребностно – мотивационной областей;

совершенствование умственной деятельности: выполнение операции анализа, синтеза, классификации, способности наблюдать, делать выводы, выделять существенные признаки движения.

Вопросы для повторения:

Сформулировать первый закон Ньютона.

Сформулировать второй закон Ньютона.

Сформулировать третий закон Ньютона.

Что такое сила трения, формула, направление?

Какой природы сила реакции опоры?

Что такое сила тяжести, направление?

Дайте определение веса тела?

Характерная особенность решения задач механики о движении материальной точки, требующих применения законов Ньютона, состоит в следующем:

Сделать схематический чертёж и указать все силы, действующие на данное тело в текущий момент времени.

Составить основное уравнение динамики в векторной форме F=F₁+F₂+…+F_n=mа

Найти проекции F_x и F_y составляющих сил по этим осям и затем составить основное уравнение динамики точки в проекции. Положительное направление осей удобно выбирать так, чтобы оно совпадало с направлением ускорения тела.

Само собой разумеется, что, если все силы действуют по одной прямой или по двум взаимно перпендикулярным направлениям, раскладывать их не надо и можно сразу записывать уравнение динамики в проекциях.

Составив основное уравнение динамики и, если можно, упростив его (проведя возможные сокращения), необходимо еще раз прочитать задачу и определить число неизвестных в уравнении. Если число неизвестных оказывается больше числа уравнений динамики, то недостающие соотношения между величинами, фигурирующими в задаче, составляют на основании формул кинематики, законов сохранения импульса и энергии.

После того как получена полная система уравнений, можно приступать к ее решению относительно искомого неизвестного.

Выписав числовые значения заданных величин в единицах одной системы, принятой для расчета, и подставив их в окончательную формулу, прежде чем делать арифметический подсчет, нужно проверить правильность решения методом сокращения наименований. В задачах динамики, особенно там, где ответ получается в виде сложной формулы, этого правила в начальной стадии обучения желательно придерживаться всегда, поскольку в этих задачах делают много ошибок.

Чтобы научиться решать задачи по динамике, нужно научиться задавать вопросы и искать на них ответы на всех этапах решения задач.

С каких вопросов начать?

1. Где должны располагаться точки, явлюющиеся началом вектора каждой из сил?	Если тело движется поступательно, то все точки совершают одинаковые перемещения. Размеры тела в этом случае не имеют значения. Поэтому для удобства все силы прикладываем к одной точке, находящейся в центре тяжести.
2. Как учесть все, действительно приложенные, силы и не изобразить лишнюю?	Сила – характеристика действия реального тела. Если не можешь ответить на следующий вопрос: со стороны какого тела приложена сила? – Следовательно силы нет.

Рассмотрим несколько примерв, в которых необходимо изобразить все приложенные силы.

1. Санки тянут по рыхлому снегу с силой F под углом ά к горизонту. Изобразите все силы, действующие на санки.

1. С чего начнём?	В центре прямоугольника ставим точку – это начало всех векторов сил.
2. Как правильно изобразить все силы?	Для каждой силы выясним: со стороны какого объекта приложена сила.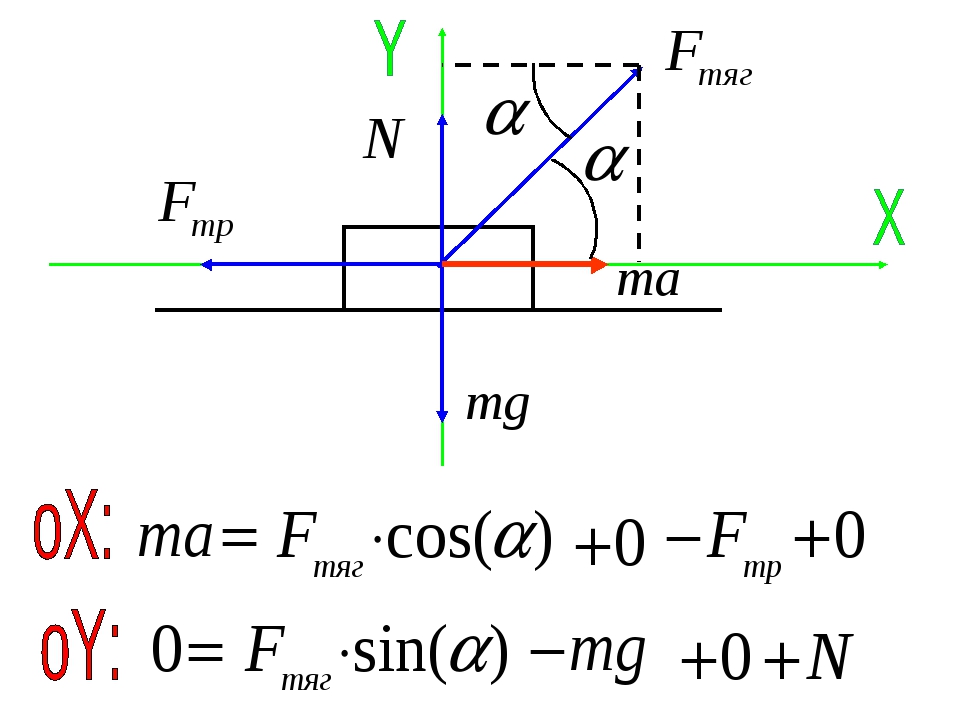

Сила	Что(кто) действует?
F_т Сила тяжести mg Сила трения F_тр Реакция опоры N	Тот кто тянет санки Земля Рыхлый снег Земля

А теперь самостоятельно изобразите, какие силы действуют:

3. Эти же санки катятся с горы.

4. На нити поднимают тело вертикально вверх.

5. Тело крепится к нити и опускается в жидкость.

Проекция сил в двухмерной системе координат.

Как спроектировать вектор силы на оси координат?	Из начала и конца вектора опускаем перпендикуляры до пересечения с осью координат
Как удобнее расположить систему координат?	Поместить начало координат в начало вектора
Как выразить проекцию через модуль вектора силы?	Вектор, его проекция на одну из осей и перпендикуляр образуют прямоугольный треугольник. Для угла ά: F_x=Fcosά F_y=Fsinά

Найдём проекцию на оси Х и У всех сил, приложенных к телу.

F_1x=Fcosά F_1y=Fsinά; F_2x=-F₂ F_2у=0; F_3х=0 F_3у=-F₃; F_4х=0 F_4у=F₄

Найдите самостоятельно проекции на оси Х и У всех сил, приложенных к телу.

1. Тело соскальзывает с наклонной плоскости.		2. Тело на верёвке.

Решение задач по динамике основано на применении 2-го закона Ньютона.

Задача. Найдите величину ускорения тела, соскальзывающего по наклонной плоскости с нулевой начальной скоростью. Угол наклона плоскости с горизонту 300. Коэффициент трения скольжения тела по плоскости 0,3.

Дано:

ά =30°

μ=0,3

а-?

Задача. Тележка массой 5 кг движется по горизонтальной поверхности под действием гири массой 2 кг, прикрепленной к концу нерастяжимой нити, перекинутой через неподвижный блок. Определить натяжение нити и ускорение движения тележки, если коэффициент трения тележки о плоскость 0,1. Массами блока и нити, а также трением в блоке пренебречь.

Дано: m₁=5 кг m₂=2 кг μ=0,1 Т-?; а-?	Решение: В данном случае рассматривается движение каждого тела отдельно.
	1. На тележку действуют силы: сила тяжести mg, сила реакции плоскости Т, сила трения F_тр, выберем прямоугольную систему координат хОу, направим ось х по направлению движения тележки, а ось у – вертикально вверх. Запишем второй закон Ньютона в векторной форме.
	2. На гирю m₂ действуют две силы: сила тяжести m₂g и сила натяжения нити Т₂. Запишем второй закон Ньютона для второго тела.
	3. Сила натяжения и ускорения системы тел равны, следовательно находим силу натяжения и ускорение.

Урок «Движение тела под действием нескольких сил» | План-конспект урока по физике (10 класс) на тему:

Модуль 10. 9 класс

Урок 19-20 Движение тела под действием нескольких сил.

Движение по вертикали и горизонтали. Решение задач

Цели урока.

обучающие: закрепить знания по теме «Законы Ньютона» при решении задач; отработать навыки применения законов Ньютона: объединить изученные законы в систему представлений о причине механического движения.

развивающие: развивать монологическую речь учащихся, умение ставить вопросы и отвечать

на них; ориентировать учащихся на использование теоретических знаний в жизни и практической деятельности.

воспитательные: воспитать любознательность, внимательность, усидчивость, трудолюбие, точность и четкость при ответе, умение видеть физику вокруг себя;

ПЕРВЫЙ МИНИ-МОДУЛЬ

Входное тестирование (используя раздаточный материал. См. приложение 1)

Мотивация. Сообщение темы, цели и задач урока

Сегодня к уроку вы должны были скачать материал, помещенный в разделе „Файлы“ на странице вашего класса на сайте «Дневник. ru». Скачанный материал надо было распечатать и вклеить в свою рабочую тетрадь по физике. Он содержит нужный нам алгоритм решения задач по динамике. И сегодня мы будем знакомиться с данным алгоритмом, и применять его для решения конкретных физических задач. Надо заметить, что данный вид задач и соответствующий алгоритм встречается не только в разделе физики механика. С ним вы будете работать, изучая законы электромагнетизма, оптики, ядерной физики, механических и электромагнитных колебаний, законы гидростатики и аэродинамики, то есть практически, везде всегда. Более 50% заданий ЕГЭ по физике невозможно решить, не приобретя те навыки и умения, которыми мы сегодня будем овладевать.

Учимся решать задачи на применение законов Ньютона.

Первый этап. Алгоритм решения.

Удобно задачи к данному разделу механики разбить на следующие группы:

— движение тела по горизонтали и вертикали

— тело на наклонной плоскости

— движение системы тел

— движение тела по окружности

При этом алгоритм решения задач из любой указанной выше группы стандартный:

На рисунке изображаем все тела и их связи, все силы, приложенные к каждому телу, вектор ускорения.
Выбираем систему отсчета (если надо, то для каждого тела выбрать свою систему отсчета) Для удобства начало СО надо поместить в центре тела, ось Х направить по ускорению. Если движение тела равномерное, направить по скорости. А если тело покоиться, то ось Х следует направить в сторону возможного или совершенного движения. Ось Y проводим перпендикулярно оси Х
Для каждого тела записывает второй закон Ньютона в векторном виде, то есть записать уравнение, в одной части которого произведение массы на ускорение, а в другой — векторная сумма всех сил, действующих на тело.
Проектируем данное уравнение на координатные оси и вместо активных сил подставляем соответствующие выражения:

Fтp=μN

Fapx=ρVg

Fтяж = mg и т. д.

Решаем полученную систему уравнений относительно неизвестного. Если уравнений недостаточно, и по условию задачи даны кинематические величины, то добавляем формулы кинематики

P.S.

Если тела соединены нерастяжимой нитью, то у них одинаковое ускорение
Если нить невесома, то по всей ее длине одинаковая сила упругости
Если в задаче речь идет о весе тела, то его заменяем силой реакции опоры N или силой реакции подвеса Т.
Если не надо учитывать силу трения скольжения, то проектировать на ось Y нет необходимости
Если в задаче есть система из блока подвижного и неподвижного, то у тел, с этими блоками связанными, ускорения различаются в 2 раза

Если возможно, то при записи уравнения движения (второго закона Ньютона) пренебречь действием внутренних сил в системе.

Второй этап. Применение алгоритма для тела, движущегося по горизонтали

Задача 1. (Работа учителя у доски)

Поезд массы m=500 т после прекращения тяги паровоза останавливается через t = 1 мин. С какой скоростью υ шел поезд до момента прекращения тяги паровоза, если коэффициент трения 0,2

На рисунке показываем состав и все силы, действующие на него, вектор ускорения (он направлен против вектора скорости, так как поезд тормозит)

Систему отсчета поместим в центре тела, ось х направим по ускорению, ось у перпендикулярно оси х.
Записываем второй закон Ньютона в векторном виде:

Проектируем полученные выражения на ось х и у:

Подставим для силы трения соответствующее выражение в (1):

Из (2) найдем силу реакции со стороны опоры

N = mg

Тогда:
Добавим уравнение кинематики:

Спроектируем это уравнение на ось х

Задача 2. (Работа ученика у доски с подачи учителя)

Какая горизонтальная сила F требуется, чтобы тело массой m = 2 кг, лежащее на горизонтальной поверхности, начало скользить по ней с ускорением а = 0,2 м/с2? Коэффициент трения между телом и поверхностью μ = 0,02.

На рисунке показываем тело и все силы, к нему приложенные, вектор ускорения;
Систему отсчета поместим в центре тела, ось х направим по ускорению, ось у перпендикулярно оси х.
Записываем второй закон Ньютона в векторном виде:

Проектируем полученные выражения на ось х и у:

Подставим для силы трения соответствующее выражение в (1):

Из (2) найдем силу реакции со стороны опоры

N = mg

Тогда:
Отсюда:

ВТОРОЙ МИНИ-МОДУЛЬ

(Работа у доски, и самостоятельная работа учащихся на местах с консультацией учителя)

Используя раздаточный материал или проектируя текст задач на мультимедийную доску

Задача 3

Паровоз на горизонтальном участке пути, имеющем длину 600 м, развивает силу тяги F=147кН. Масса поезда1000 т. При этом скорость возрастает от υ0 = 36 км/ч до υ=54 км/ч. Найдите силу сопротивления движению поезда, считая ее постоянной.

Задача 4

Тело массы m движется по горизонтальной поверхности под действием силы F, направленной под углом α к горизонту (см. рис.) Найти ускорение тела. Коэффициент трения между телом и плоскостью равен μ.

Третий этап. Применение алгоритма для тела, движущегося по вертикали.

Задача 1. (Работа учителя у доски)

Тело массы m движется вверх по вертикальной стене под действием силы F, направленной под углом α к вертикали (см. рис.). Найти ускорение тела. Коэффициент трения между телом и стеной равен μ.

На рисунке показываем тело и все силы, к нему приложенные, вектор ускорения;

Систему отсчета поместим в центре тела, ось х направим по ускорению, ось у перпендикулярно оси х.
Записываем второй закон Ньютона в векторном виде:

Проектируем полученные выражения на ось х и у:

Подставим для силы трения соответствующее выражение в (1):

Из (2) найдем силу реакции со стороны опоры

Тогда:

Задача 2. (Работа ученика у доски с помощью учителя)

Тело массы 40 г, брошенное вертикально вверх с начальной скоростью υ0 = 30 м/с, достигло высшей точки подъема спустя время t = 2,5 с. Найти среднюю силу сопротивления воздуха, действовавшую на тело во время полета.

Делаем рисунок, выбираем систему координат. В этом случае достаточно одной координатной оси, так как силы, действующие на тело, направлены вдоль одной прямой

Записываем второй чакон Ньютона в векторном виде, проектируем полученное выражение на ось х (или сразу проектируем, кто это уже может делать):

Отсюда определяем силу трения со стороны воздуха на тело действующую:

Так как этого уравнения оказалось недостаточным для решения данной задачи, добавим формулу кинематики:

И спроектируем на ось х:

Задача 3. (Работа ученика у доски с помощью учителя)

Шарик всплывает в жидкости с постоянной скоростью, причем плотность жидкости в 4 раза превышает плотность материала шарика. Найдите массу шарика, если во время подъема на шарик действует сила трения 0,ЗН.

Покажем силы, действующие на шарик во время равномерного подъема. Так как ускорения нет, ось х направим в ту сторону, куда движется тело, то есть по вектору скорости, а значит вертикально вверх

Записываем второй закон Ньютона в векторном виде, проектируем полученное выражение

на ось х:

Так как сила Архимеда

Согласно условию

Мотивация.

Результат решения следующей задачи можно будет в дальнейшем использовать как основную формулу при решении сложных комбинированных задач и не выводить каждый раз.

Задача 4. (Работа ученика у доски с помощью учителя).

Масса чемодана, стоящего на полу лифта 40кг. Определить вес чемодана, при движении лифта вверх и вниз с ускорением 0,6м/с2

Вес тела при движении с ускорением вверх: (перегрузка)
Вес тела при движении с ускорением вниз: (потеря веса вплоть до невесомости при условии, что ускорение тела равно ускорению свободного падения)

ТРЕТИЙ МИНИ-МОДУЛЬ

Решаем экспериментальную задачу:

Определите начальную скорость и время торможения тела, движущегося под действием силы трения.

Оборудование: деревянный брусок от лабораторного трибометра,

динамометр,

измерительная линейка.

Анализируем задачу (метод беседы):

Если брусок толкнуть рукой, сообщив ему начальную скорость υ, то, пройдя некоторый путь S, он остановится, так как на него действует сила трения Fтр., сообщая ему ускорение

Определив вес бруска с помощью динамометра, вычисляют его массу.

Для определения силы трения Fтр., брусок равномерно протягивают вдоль стола.

Так как , то

Измеряя тормозной путь S, можно подсчитать начальную скорость движения бруска. Для определения времени торможения бруска, следует воспользоваться формулой:

Выполнение практической части задачи

Самостоятельное решение задач

С какой наименьшей силой нужно толкать перед собой тележку, масса которой m = 12 кг, для того чтобы сдвинуть ее с места? Сила направлена вдоль ручки тележки и составляет с горизонтом угол α = 30°, а коэффициент трения между полом и тележкой μ = 0,4?

К одному концу веревки, перекинутой через блок, подвешен груз массы m= 10 кг (см. рис.) С какой силой F нужно тянуть вниз за другой конец веревки, чтобы груз поднимался с ускорением а = 1 м/с2?

ПОДВЕДЕНИЕ ИТОГОВ УРОКА, СООБЩЕНИЕ ДОМАШНЕГО ЗАДАНИЯ

Кирик

стр.71 № 3,4,5,6,7 (вариант А)

стр.72 № 7 (вариант В)

Приложение 1

ОСНОВЫ ДИНАМИКИ

I вариант

Любое тел при взаимодействии не может изменить свою скорость мгновенно, для этого нужно определенное время. Какая физическая величина является мерой этого свойства тела?

А. сила. Б. давление. В. масса Г. скорость.

Как выражается единица силы 1 Н через основные единицы СИ?

А. Б. В. Г.

Если векторная сумма всех сил, которые действуют на тело, равна нулю, то …

А…. направление движения тела изменяется.

Б…. скорости тела остается неизменной.

В…. скорости тела со временем возрастает.

Г…. скорость тела со временем уменьшается.

Какой физический закон утверждает, что действие одного тела на другое всегда сопровождается «противодействием»?

А. I закон Ньютона. Б. II закон Ньютона. В. III закон Ньютона. Г. Закон Гука.

Какая формула является математической записью закона Гука?

А. F = kx Б. F = μN В. Г. F = ρVg.

Как движется тело массой 2 т под действием силы, модуль которой равен 4 кН?

А. равномерно со скоростью 2 м/с. Б. равномерно со скоростью 0,5 м/с.

В. равноускоренно с ускорением 2 м/с2. Г. равноускоренно с ускорением 0,5 м/с2.

Вес — это …

А…. мера инертности тела.

Б…. мера гравитационного взаимодействия тела с Землей.

В…. сила, с которой Земля действует на тело вблизи ее поверхности.

Г…. сила, с которой тело действует на опору или подвес вследствие притяжения к Земле.

Сила взаимодействия между двумя телами

А…. прямо пропорциональна произведению масс эти тел и расстоянию между ними.

Б…. прямо пропорциональна произведению масс этих тел и обратно пропорциональна

расстоянию между ними.

В…. прямо пропорциональна произведению масс этих тел и обратно пропорциональна

квадрату расстояния между ними.

Г…. прямо пропорциональна квадрату расстояния между телами и обратно пропорциональна

произведению их масс.

Как изменится сила гравитационного взаимодействия между двумя материальными точками, если расстояние между ними увеличить в 3 раза?

А. увеличится в 3 раза. Б. уменьшится в 9 раз.

В. уменьшится в 6 раз. Г. уменьшится в 3 раза.

На каком рисунке показан вес тела?

А. Рис.1 . Б. Рис.2 В. Рис.3 Г. Рис.4 Д. Рис.5

Брусок неподвижно лежит на горизонтальной платформе, которая движется прямолинейно и равномерно. Какое направление имеет вектор силы трения, действующей на брусок?

А. Fтр=0. Б. 1. В. 2. Г. 3. Д. 4.

ОСНОВЫ ДИНАМИКИ

II вариант

Количественную меру действия одного тела на другое, вследствие которого тела приобретают ускорение, называют …

А…. массой Б. …силой. В. …скоростью. Г. …давлением.

Мы можем утверждать, что сила – это

давление Б. действие на другое тело В. напряжение, возникающее в теле

Г. энергия тела Д. определенный динамический эффект

Если на тело действует не скомпенсированная внешняя сила, то

тело должно иметь ускорение Б. тело должно двигаться В. скорость тела увеличивается

Г. тело движется то быстрей, то медленнее Д. ускорение тела все время увеличивается

Какая из следующих формул является записью II закона Ньютона?

А. F = kx. Б. . В. Г.

При измерении силы мышц руки при помощи силомера используют зависимость силы упругости пружины от ее деформации. Как зависит эта сила от модуля удлинения пружины?

А. сила прямо пропорциональна удлинению пружины х.

Б. сила прямо пропорциональна х2

В. сила обратно пропорциональна х.

Г. сила обратно пропорциональна х2.

Под действием силы 4 Н пружина растянулась на 0,2 дм. Какова жесткость пружины?

А. 0,8 Н/м. Б. 8 Н/м. В. 20 Н/м. Г. 200 Н/м.

Какое из следующих утверждений правильное?

масса и вес – это одно и то же, только у них разные единицы измерения
когда тело свободно падает, то масса тела равна 0
если масса тела удваивается, то вес не обязательно удваивается
масса тела не зависит от силы тяготения
тело, имеющее массу, не обязательно инертно.

Модуль силы взаимодействия между Землей и Луной …

А…. прямо пропорционален произведению масс Земли и Луны и расстоянию между ними.

Б…. прямо пропорционален произведению масс Земли и Луны и обратно пропорционален

расстоянию между ними.

В…. прямо пропорционален произведению масс Земли и Луны и обратно пропорционален

квадрату расстояния между ними.

Г…. прямо пропорционален квадрату расстояния между Землей и Луной и обратно

пропорционален произведению их масс.

Если расстояние между телами различной массы m1 и m2 уменьшится вдвое, то сила всемирного тяготения, с которой эти тела взаимодействуют друг с другом

увеличится в 2 раза Б. уменьшится в 2 раза В. уменьшится в 4 раза

Г. увеличится в 4 раза Д. останется неизменной

На каком рисунке показана сила тяжести, действующая на тело?

А. Рис.1 . Б. Рис.2 В. Рис.3 Г. Рис.4 Д. Рис.5

Как изменится сила трения скольжения при движении бруска по горизонтальной поверхности, если при неизменном значении силы нормального давления площадь соприкасающихся поверхностей увеличить в 2 раза?

А. не изменится. Б. увеличится в 2 раза. В. уменьшится в 2 раза.

Г. увеличится в 4 раза. Д. уменьшится в 4 раза

Движение тела под действием силы тяжести определение. Движение тела под действием нескольких сил. Движение тела под действием силы тяжести: формулы для решения задач

Действием сил всемирного тяготения в природе объясняются многие явления: движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.

Закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.

Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. Одним из проявлений силы всемирного тяготения является сила тяжести — так принято называть силу притяжения тел к Земле вблизи ее поверхности.

Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна

где g – ускорение свободного падения у поверхности Земли

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения.

Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли

Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, мы стоим у края отвесной скалы, рядом пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

Теперь представим, что мы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты.

Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне.

Так поэтапно мы перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет

С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения

где T = 27,3 сут – период обращения Луны вокруг Земли.

Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.

Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли.

Поэтому ускорение gЛ определится выражением

В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.

Рассмотрим вопрос об искусственных спутниках Земли. Искусственные спутники Земли движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли.

В зависимости от начальной скорости траектория космического тела может быть различной. Рассмотрим случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1 – такая скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим

Двигаясь с такой скоростью, спутник облетал бы Землю за время

Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.

Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной.

Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.

Рисунок 5 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·103 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·103 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.

Рисунок 5 — Космические скорости

Указаны скорости вблизи поверхности Земли: 1) υ = υ1 – круговая траектория;

2) υ1

4) υ = υ2 – параболическая траектория; 5) υ > υ2 – гиперболическая траектория;

6) траектория Луны

Таким образом, мы выяснили, что все движения в Солнечной системе подчиняются закону всемирного тяготения Ньютона.

Исходя из малой массы планет и тем более прочих тел Солнечной системы, можно приближенно считать, что движения в околосолнечном пространстве подчиняются законам Кеплера.

Все тела движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. Чем ближе к Солнцу небесное тело, тем быстрее его скорость движения по орбите (планета Плутон, самая далекая из известных, движется в 6 раз медленнее Земли).

Тела могут двигаться и по разомкнутым орбитам: параболе или гиперболе. Это случается в том случае, если скорость тела равна или превышает значение второй космической скорости для Солнца на данном удалении от центрального светила. Если речь идет о спутнике планеты, то и космическую скорость надо рассчитывать относительно массы планеты и расстояния до ее центра.

Цели:

Продолжение знакомства с разнообразием
равноускоренных движений.
Обучение сравнению разных видов движений,
нахождению общих черт и отличий, умению делать
выводы из наблюдаемых явлений.
Познакомить с методикой решения задач по данной
теме, показать универсальность законов
применяемых при решении задач.
Расширение кругозора.

Этапы уроков:

Этап определения цели урока
Этап актуализации знаний
Этап получения новых знаний по теме “Движение
тел под действием силы тяжести”
Этап подготовки к решению задач
Этап закрепления материала в процессе решения
кроссворда, задач, теста
Задание на дом

Сопровождение уроков:

Презентация “Движение тел под действием силы
тяжести”.
Кинофрагменты.
Опыты.

Оборудование уроков:

Компьютерный класс
Видеопроектор
Электронный дидактический материал для
учащихся
Приборы: трубка Ньютона, диски металлический и
бумажный

ХОД УРОКА

I.
С сегодняшнего дня мы будем
рассматривать характер и законы движения тел, на
которые действует только сила тяжести. Видов
движений под действием силы тяжести может быть
несколько: движение тел брошенных вертикально
вверх, вертикально вниз, горизонтально, под углом
к горизонту. Значение знаний этих законов трудно
недооценить. Они объясняют движение
парашютистов, снарядов, спортсменов на
трамплинах и т.д.

Свободное движение тел обладает следующей
особенностью: тело, брошенное горизонтально и
просто отпущенное с того же уровня падают
одновременно. Проследим движение таких тел на
модели.

На последних слайдах презентации № 18,19, 20, 21
представлены кинофрагменты (см. Приложение
6

):

Основная задача механики и движение тел
брошенных под углом к горизонту,
Падение снарядов, брошенных с самолета,
Полет баллистических ракет,
Полет космических ракет.

Кинофрагменты можно использовать перед
началом изучения темы для создания элемента
заинтересованности, в середине – для
обоснования рассмотрения данных видов движений
или в конце – при подведении итогов.

Выберем инерциальную систему отсчета. Свяжем ее с Землей.

Изобразим на чертеже направление ускорения каждого тела.

Т. к. мы не знаем точно, по часовой стрелке или против нее, будет двигаться система, направление движения выберем произвольно.

Судя по всему, ускорения тел
и
одинаковы, поскольку эти тела можно рассматривать как одно тело, движущееся с ускорением Но, так как нам надо найти силу давления перегрузка на груз, будем рассматривать их раздельно.

Изобразим силы, действующие на каждое тело
, исходя из того, что силы – результат действия одних тел на другие. Все силы будем прикладывать к центру масс тел.

На первое тело со стороны Земли действует сила тяжести

Со стороны нити на это тело действует сила упругости

Так как первое тело движется с ускорением вертикально вверх, то по величие сила упругости больше, чем сила тяжести.

На второе тело со стороны Земли действует сила тяжести В этом же направлении на второе тело действует сила давления со стороны перегрузка .

В противоположную сторону на второе тело со стороны нити действует сила

Так как вектор ускорения, с которым движется второе тело, направлен вниз, на чертеже эти силы изобразим так, чтобы их векторная сумма также была направлена вниз.

Для выполнения чертежа предположим, что нить по всей длине натянута одинаково и силы
и равны друг другу.

На перегрузок действует сила тяжести , направленная вертикально вниз, и сила реакции со стороны опоры

Сила давления, с которой перегрузок действует на опору, по третьему закону Ньютона равна силе, с которой опора действует на перегрузок.

Так как ускорение, с которым движется перегрузок, направлено вертикально вниз, сила тяжести, действующая на него, больше силы реакции опоры.

После того, как на чертеже изображены силы, действующие на каждое из движущихся тел, выберем направления для проецирования сил и ускорений.
Удобно направления для проецирования сил и ускорений выбирать так, чтобы они совпадали с направлениями ускорений движения соответствующих тел.

Выберем для каждого тела свое направление (хотя можно было бы ограничиться одним направлением).

Для проецирования сил, действующих на первое тело, и ускорения его движения, выберем направление вверх. Для проецирования сил, действующих на второе тело и перегрузок, и ускорения их движения, выберем направление вниз.

Запишем второй закон Ньютона в векторной форме для каждого из рассматриваемых тел:
сумма сил действующих на тело, равна произведению массы этого тела на ускорение, с которым тело движется.

Запишем уравнения в скалярной форме, в проекциях на выбранные направления.

Y
:

Y»
:

Процедура проецирования векторов сил и ускорений на выбранные направления позволила получить систему уравнений, в которую входят не векторные, а скалярные величины:

В этой системе, если сопоставить число неизвестных с числом уравнений, оказывается, что неизвестных больше, чем самих уравнений. Это означает, что необходимо записать дополнительные уравнения, включающие в себя уже имеющиеся неизвестные величины.

При написании этих уравнений будем исходить из следующих обстоятельств.

Во-первых, по третьему закону Ньютона, модуль силы давления перегрузка на второе тело и силы реакции опоры, действующей со стороны второго тела на перегрузок, равны друг другу:

Во-вторых, по условию задачи, нить нерастяжима. Ускорение при равноускоренном движении, если начальная скорость равна нулю, связано с перемещением и временем движения следующим образом: Это означает, что за равные промежутки времени тела будут совершать равные перемещения.

Таким образом, ускорения тел численно равны друг другу:

a
1 = a
2 = a
.

Для этого рассмотрим упрощенный чертеж. Исключим из рассмотрения перегрузок и ограничимся фрагментом, на котором отсутствует блок.

На первое тело со стороны нити действует сила но, по третьему закону Ньютона, со стороны тела на нить также действует сила, равная по величине и противоположная по направлению. Обозначим ее

Эта сила приложена к нити со стороны тела. Именно эта сила нас и интересует.

Таким образом: .

Точно также, на второе тело со стороны нити действует сил а на нить со стороны тела действует сила По третьему закону Ньютона

Оказывается, что на нить с двух сторон действуют силы
и

Нить так же, как и тела, движется с ускорением под действием этих сил. Запишем уравнение движения нити в скалярном виде:

Где M
– масса нити.

Если масса нити равна нулю M
= 0 , то В противном случае это равенство несправедливо.

Так как то можно сделать вывод о том, что .

Такое доказательство, строго говоря, необходимо при решении любой задачи на движение связанных тел, но поскольку оно всегда производится одинаковым образом, в дальнейшем его повторять не будем. При желании всегда можно обратиться к данной задаче и повторить доказательство для любого аналогичного случая.

С учетом всего вышеизложенного, перепишем систему уравнений:

Решать эту систему можно разными способами, например, наиболее распространенным и универсальным способом подстановки. Но в данном случае гораздо удобнее сложить правые и левые части уравнений.

В результате проведения этой операции получаем: (m
2 + m
3 – m
1) g
= (m
1 + m
2 + m
3)a
.

Отсюда искомое ускорение:

Как видно, в данном уравнении коэффициент, стоящий перед ускорением свободного падения, меньше единицы, следовательно, ускорение, с которым движется тело, меньше ускорения свободного падения.

Если сумма масс второго и третьего тела равна массе первого тела, грузы, висящие справа и слева, уравновешивают друг друга. Ускорение их движения равно нулю. Система либо покоится, либо, если ей сообщили какую-то скорость, движется с этой скоростью, сохраняя ее постоянной.

Зная ускорение движения системы, можно найти ответы на другие интересующие нас вопросы. В частности, можно, например, из первого уравнения выразить силу натяжения нити: T
= m
1 a
+ m
1 g
.

Найдя численное значение ускорения, его можно будет подставить в данное уравнение и определить численное значение силы натяжения T
.

Аналогичным образом можно выразить из второго или из третьего уравнения (лучше из третьего, как более простого) значение силы давления F
д: F
д = m
3 g
– m
3 a
.

Зная величину ускорения, можно найти величину силы давления перегрузка на груз. Эта сила является весом перегрузка.

Как видно, в случае, если система движется с ускорением, вес перегрузка меньше силы тяжести, действующей на него.

Введение

1. Движение тела под действием силы тяжести

1.1 Движение тела по круговой или эллиптической орбите вокруг планеты

1.2 Движение тела под действием силы тяжести в вертикальной плоскости

1.3 Движение тела, если начальная скорость направлена под углом к силе тяжести

2. Движение тела в среде с сопротивлением

3. Применение законов движения тела под действием силы тяжести с учётом сопротивления среды в баллистике

Заключение

Список литературы

Введение

По второму закону Ньютона причиной изменения движения, то есть причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения. Закон всемирного тяготения был открыт И.Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс. У тела в виде однородного шара центр масс совпадает с центром шара.

Рис.1. Гравитационные силы.

В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом И.Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная, как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной

G = 6,67·10 -11
Н·м 2
/кг 2

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики. Одним из проявлений силы всемирного тяготения является сила тяжести.

Сила тяжести — это сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения:

Любое тело, находящееся на Земле (или вблизи нее), вместе с Землей вращается вокруг ее оси, т.е. тело движется по окружности радиусом r с постоянной по модулю скоростью.

Рис.2. Движение тела, находящегося на поверхности Земли.

На тело на поверхности Земли действуют сила тяготения и сила со стороны земной поверхности

Их равнодействующая

сообщает телу центростремительное ускорение

Разложим силу тяготения на две составляющие, одна из которых будет, т.е.

Из уравнений (1) и (2) видим, что

Таким образом, сила тяжести — одна из составляющих силы тяготения, вторая составляющая сообщает телу центростремительное ускорение. В точке Μ на географической широте φ сила тяжести направлена не по радиусу Земли, а под некоторым углом α к нему. Сила тяжести направлена по, так называемой, отвесной прямой (по вертикали вниз).

Сила тяжести равна по модулю и направлению силе тяготения только на полюсах. На экваторе они совпадают по направлению, а по модулю отличие наибольшее.

где ω — угловая скорость вращения Земли, R — радиус Земли.

рад/с,ω = 0,727·10 -4
рад/с.

Так как ω очень мала, то F T
≈ F. Следовательно, сила тяжести мало отличается по модулю от силы тяготения, поэтому данным различием часто можно пренебречь.

Тогда F T
≈ F,

Из этой формулы видно, что ускорение свободного падения g не зависит от массы падающего тела, но зависит от высоты.

Если M – масса Земли, R З
– ее радиус, m – масса данного тела, то сила тяжести равна

где g – ускорение свободного падения у поверхности Земли:

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81м/с 2
. Зная ускорение свободного падения и радиус Земли

(R З
= 6,38·10 6
м), можно вычислить массу Земли M:

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рисунок иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.

Рис.3.Изменение силы тяготения, действующей на космонавта при удалении от Земли.

Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии r Л
= 3,84·10 6
м. Это расстояние приблизительно в 60 раз превышает радиус Земли R З. Следовательно, ускорение свободного а л, обусловленное земным притяжением, на орбите Луны составляет

где T = 27,3 сут. – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести. Собственное гравитационное поле Луны определяет ускорение свободного падения g л
на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение g л
определится выражением:

1. Движение тела под действием силы тяжести

Если на тело действует только сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости. При этом возможны следующие случаи движения тела:

1. Тело может двигаться по круговой или эллиптической орбите вокруг планеты.

2. Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное свободное падение.

3. Если начальная скорость тела направлена под углом к силе тяжести, то тело будет двигаться по параболе, либо по ветви параболы.

1.1 Движение тела по круговой или эллиптической орбите вокруг планеты

Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу R З. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ 1
. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим:

Двигаясь с такой скоростью, спутник облетал бы Землю за время

На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли. Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли. Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия

Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите. Период T обращения такого спутника равен

Здесь T 1
– период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6R З, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R о
называется геостационарной.

1.2 Движение тела под действием силы тяжести в вертикальной плоскости

Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное свободное падение.

Основной задачей механики, является определение положения тела в любой момент времени. Решением задачи для частиц, движущихся в поле тяжести Земли, являются уравнения, в проекциях на оси OX и OY:

Этих формул достаточно, чтобы решить любую задачу о движении тела под действием силы тяжести.

Тело брошено вертикально вверх

В этом случае v 0x
= 0, g x
= 0, v 0y
= v 0
, g y
= -g.

Движение тела в этом случае будет происходить по прямой линии, причем сначала вертикально вверх до точки, в которой скорость обратится в нуль, а затем вертикально вниз.

Рис.4.Движение тела, брошенного вверх.

При движении тела с ускорением в поле тяготения изменяется вес тела.

Весом тела называется сила, с которой тело действует на неподвижную относительно него опору или подвес.

Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы реакции) или подвеса (силы натяжения) Вес существенно отличается от силы тяжести:

Это силы разной природы: сила тяжести — гравитационная сила, вес — упругая сила (электромагнитной природы).

Они приложены к разным телам: сила тяжести — к телу, вес — к опоре.

Рис.5. Точки приложения силы тяжести и веса тела.

Направление веса тела не обязательно совпадает с отвесным направлением.

Сила тяжести тела в данном месте Земли постоянная и не зависит от характера движения тела; вес зависит от ускорения, с которым движется тело.

Рассмотрим, как изменяется вес тела, движущегося в вертикальном направлении вместе с опорой. На тело действуют сила тяжести и сила реакции опоры.

Рис.5. Изменение веса тела при движении с ускорением.

Основное уравнение динамики: . В проекции на ось Оу:

По третьему закону Ньютона модули сил N p1
= P 1
. Следовательно, вес тела P 1
= mg

, (тело испытывает перегрузки).

Следовательно, вес тела

Если a = g, то P = 0

Таким образом, вес тела при вертикальном движении может быть в общем случае выражен формулой

Мысленно разобьем неподвижное тело на горизонтальные слои. На каждый из этих слоев действует сила тяжести и вес вышележащей части тела. Этот вес будет становиться тем больше, чем ниже лежит слой. Поэтому под влиянием веса вышележащих частей тела каждый слой деформируется и в нем возникают упругие напряжения, которые возрастают по мере перехода от верхней части тела к нижней.

Рис.6.Тело, разбитое на горизонтальные слои.

Если тело свободно падает (a = g), то его вес равен нулю, в теле исчезают всякие деформации и, несмотря на сохраняющееся действие силы тяжести, верхние слои не будут давить на нижние.

Состояние, при котором в свободно движущемся теле исчезают деформации и взаимные давления, называется невесомостью. Причина невесомости заключается в том, что сила всемирного тяготения сообщает телу и его опоре одинаковое ускорение.

1.3 Движение тела, если начальная скорость направлена под углом к силе тяжести

Тело брошено горизонтально, т.е. под прямым углом к направлению силы тяжести.

При этом v 0x
= v 0
, g x
= 0, v 0y
= 0, g y
= — g , х 0
= 0, и, следовательно,

Чтобы определить вид траектории, по которой тело будет двигаться в этом случае, выразим время t из первого уравнения и подставим его во второе уравнение. В результате мы получим квадратичную зависимость у от х:

Это означает, что тело при этом будет двигаться по ветви параболы.

Рис.7. Движение тела, брошенного под углом к горизонту.

Движение тела, брошенного с некоторой начальной скоростью υ о
под углом α к горизонту, тоже представляет собой сложное движение: равномерное по горизонтальному направлению и одновременно происходящее под действием силы тяжести равноускоренное движение в вертикальном направлении. Так движется лыжник при прыжке с трамплина, струя воды из брандспойта и т.д.

Рис.8. Струя воды из брандспойта.

Изучение особенностей такого движения началось довольно давно, еще в XVI веке и было связано с появлением и совершенствованием артиллерийских орудий.

Представления о траектории движения артиллерийских снарядов в те времена были довольно забавными. Считалось, что траектория эта состоит из трех участков: А — насильственного движения, В — смешанного движения и С — естественного движения, при котором ядро падает на солдат противника сверху.

Рис.9. Траектория движения артиллерийского снаряда.

Законы полета метательных снарядов не привлекали особого внимания ученых до тех пор, пока не были изобретены дальнобойные орудия, которые посылали снаряд через холмы или деревья — так, что стреляющий не видел их полета.

Сверхдальняя стрельба из таких орудий на первых порах использовалась в основном для деморализации и устрашения противника, а точность стрельбы не играла вначале особенно важной роли.

Близко к правильному решению о полете пушечных ядер подошел итальянский математик Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге «Новая наука» были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века.

Однако, полное решение проблем, связанных с движением тел брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей. В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия. Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы. Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая.

Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха. Появилась и новая наука – баллистика. Прошло много-много лет, и теперь снаряды движутся столь быстро, что даже простое сравнение вида траекторий их движения подтверждает возросшее влияние сопротивления воздуха.

Рис.10. Идеальная и действительная траектории движения снаряда.

На нашем рисунке идеальная траектория движения тяжелого снаряда, вылетевшего из ствола пушки с большой начальной скоростью, показана пунктиром, а сплошной линией — действительная траектория полета снаряда при тех же условиях выстрела.

В современной баллистике для решения подобных задач используется электронно-вычислительная техника — компьютеры, а мы пока ограничимся простым случаем — изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений.

Полет пуль и снарядов представляет собой пример движения тел, брошенных под углом к горизонту. Точное описание характера такого движения возможно только при рассмотрении некоторой идеальной ситуации.

Посмотрим, как меняется скорость тела, брошенного под углом α к горизонту, в отсутствие сопротивления воздуха. В течение всего времени полета на тело действует сила тяжести. На первом участке траектории по направлению.

Рис 11. Изменение скорости вдоль траектории.

В наивысшей точке траектории – в точке С — скорость движения тела будет наименьшей, она направлена горизонтально, под углом 90° к линии действия силы тяжести. На второй части траектории полет тела происходит аналогично движению тела, брошенному горизонтально. Время движения от точки А до точки С будет равно времени движения по второй части траектории в отсутствие сил сопротивления воздуха.

Если точки «бросания» и «приземления» лежат на одной горизонтали, что то же самое можно сказать и о скоростях «бросания» и «приземления». Углы между поверхностью Земли и направлением скорости движения в точках «бросания» и «приземления» будут в этом случае тоже равны.

Дальность полета АВ тела, брошенного под углом к горизонту, зависит от величины начальной скорости и угла бросания. При неизменной скорости бросания V 0
с увеличением угла, между направлением скорости бросания и горизонтальной поверхностью от 0 до 45°, дальность полета возрастает, а при дальнейшем росте угла бросания – уменьшается. В этом легко убедиться, направляя струю воды под разными углами к горизонту или следя за движением шарика, выпущенного из пружинного «пистолета» (такие опыты легко проделать самому).

Траектория такого движения симметрична относительно наивысшей точки полета и при небольших начальных скоростях, как уже говорилось раньше, представляет собой параболу.

Максимальная дальность полета при данной скорости вылета достигается при угле бросания 45°. Когда угол бросания составляет 30° или 60°, то дальность полета тел для обоих углов оказывается одинаковой. Для углов бросания 75° и 15° дальность полета будет опять одна и та же, но меньше, чем при углах бросания 30° и 60°. Значит, наиболее «выгодным» для дальнего броска углом является угол в 45°, при любых других значениях угла бросания дальность полета будет меньше.

Если бросить тело с некоторой начальной скоростью v о
под углом 45° к горизонту, то его дальность полета будет в два раза больше максимальной высоты подъема тела, брошенного вертикально вверх с такой же начальной скоростью.

Максимальную дальность полета S тела, брошенного под углом α к горизонту, можно найти по формуле:

максимальную высоту подъема H по формуле:

При отсутствии сопротивления воздуха наибольшей дальности полета соответствовал бы угол наклона ствола винтовки равный 45°, но сопротивление воздуха значительно изменяет траекторию движения и максимальной дальности полета соответствует другой угол наклона ствола винтовки – больше 45°. Величина этого угла зависит также от скорости пули при выстреле. Если скорость пули при выстреле 870 м/с, то реальная дальность полета составит примерно 3,5 км, а не 77 км, как показывают «идеальные» расчеты.

Эти соотношения показывают, что расстояние, пройденное телом в вертикальном направлении, не зависит от величины начальной скорости – ведь ее значение не входит в формулу для расчета высоты Н. А дальность полета пули в горизонтальном направлении будет тем больше, чем больше ее начальная скорость.

Изучим движение тела, брошенного с начальной скоростью v 0
под углом α к горизонту, рассматривая его как материальную точку массы m При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.

Поместим начало координат О в начальном положении точки. Направим ось O y
вертикально вверх; горизонтальную ось O x
расположим в плоскости, проходящей через О y
и вектор v 0
, а ось O z
проведём перпендикулярно первым двум осям. Тогда угол между вектором v 0
и осью O x
будет равен α

Рис.12.Движение тела, брошенного под углом к горизонту.

Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести , проекции которой на оси координат равны: P x
=0 , P y
=-P =mg , P Z
=0

Подставляя эти величины в дифференциальные уравнения и замечая, что и т.д. мы после сокращения на m получим:

Умножая обе части этих уравнений на dt и интегрируя, находим:

Начальные условия в нашей задаче имеют вид:

x=0,

y=0 ,

Удовлетворяя начальным условиям, будем иметь:

Подставляя эти значения С 1
, С 2
и С 3
в найденное выше решение и заменяя V x
, V Y
, V z
на придём к уравнениям:

Интегрируя эти уравнения, получим:

Подстановка начальных данных даёт С 4
= С 5
= С 6
= 0, и мы окончательно находим уравнения движения точки М в виде:

Из последнего уравнения следует, что движение происходит в плоскости О xy

Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.

1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:

(2)

Это – уравнение параболы с осью, параллельной оси О y
. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).

2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси О x
расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью О х. Из уравнения:

получаем

Первое решение дает точку О, второе точку С. Следовательно, Х=Х 2
и окончательно

(3)

Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле β, для которого 2β=180° — 2α , т.е. если угол β=90°-α . Следовательно, при данной начальной скорости v 0
в одну и ту же точку С можно попасть двумя траекториями: настильной (α45°)

При заданной начальной скорости v 0
наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда sin 2 α = 1, т.е. при угле α=45°.

то найдется высота траектории Н:

(4)

Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством Заменяя здесь Х его значением, получим

При угле наибольшей дальности α=45° все найденные величины равны:

Полученные результаты практически вполне приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при ) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивление воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.

Движение тела, брошенного с высоты h.

Из пушки, установленной на высоте h, произвели выстрел под углом α к горизонту. Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.

Рис.13.Движение тела, брошенного с высоты.

Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.

а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.

б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными.

в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).

В этом примере – это только сила , вес ядра. Сопротивление воздуха учитывать не будем.

г) Составить дифференциальные уравнения по формулам:

Отсюда получим два уравнения: и .

д) Решить дифференциальные уравнения.

Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.

Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0, x = 0, y = h,,) в эти четыре уравнения: ,,

0 = С 2
, h = D 2
.

Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде

Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.

Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.

Здесь сила — сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:

Решив это уравнение, получим закон движения точки, а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции и .

2. Движение тела в среде с сопротивлением

движение сопротивление баллистика эллиптический орбита

Одной из важнейших задач аэро- и гидродинамики является исследование движения твёрдых тел в газе и жидкости. В частности изучение тех сил, с которыми среда действует на движущееся тело. Эта проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движения морских судов. На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (R х) направлена в сторону, противоположную движению тела (в сторону потока), — лобовое сопротивление, а вторая (R y) перпендикулярна этому направлению – подъёмная сила.

Где ρ – плотность среды; υ – скорость движения тела; S – наибольшее поперечное сечение тела.

Подъёмная сила может быть определена формулой:

Где С y
– безразмерный коэффициент подъёмной силы.

Если тело симметрично и его ось симметрии совпадает с направлением скорости, то на него действует только лобовое сопротивление, подъёмная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если рассмотреть движение цилиндра в такой жидкости, то картина линий тока симметрична и результирующая силы давления на поверхность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличении скорости обтекания). Вследствие вязкости среды в области, прилегающей к поверхности тела, образуется пограничный слой частиц, движущихся с меньшими скоростями. В результате тормозящего действия этого слоя и возникает вращение частиц, и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончающиеся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидкости или газа, направленное противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны. Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается коэффициентом сопротивления. Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения F , направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила. Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь S поверхности слоя, и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. Величина оказывает, как быстро меняется скорость при переходе от слоя к слою в направлении x , перпендикулярном направлению движения слоев, и называется градиентом скорости. Таким образом, модуль силы внутреннего трения

где коэффициент пропорциональности η , зависящий от природы жидкости. называется динамической вязкостью.

Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причём характер этой зависимости для жидкостей и газов различен (для жидкостей η с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения.

3. Применение законов движения тела под действием силы тяжести с учётом сопротивления среды в баллистике

Основной задачей баллистики является определение, под каким углом к горизонту, и с какой начальной скоростью должна лететь пуля определенной массы и формы, чтобы она достигла цели.

Образование траектории.

Во время выстрела пуля, получив под действием пороховых газов при вылете из канала ствола некоторую начальную скорость, стремится по инерции сохранить величину и направление этой скорости, а граната, имеющая реактивный двигатель, движется по инерции после истечения газов из реактивного двигателя. Если бы полет пули (гранаты) совершался в безвоздушном пространстве, и на нее не действовала бы сила тяжести, пуля (граната) двигалась бы прямолинейно, равномерно и бесконечно. Однако на пулю (гранату), летящую в воздушной среде, действуют силы, которые изменяют скорость ее полета и направление движения. Этими силами являются сила тяжести и сила сопротивления воздушной среды.

Вследствие совместного действия этих сил пуля теряет скорость и изменяет направление своего движения, перемещаясь в воздушной среде по кривой линии, проходящей ниже направления оси канала ствола.

Кривая линия, которую описывает в пространстве центр тяжести двигающейся пули (снаряда) в полете, называется траекторией. Обычно баллистика рассматривает траекторию над (или под) горизонтом оружия — воображаемой бесконечной горизонтальной плоскостью, проходящей через точку вылета. Движение пули, а следовательно, и фигура траектории зависят от многих условий. Пуля при полете в воздухе подвергается действию двух сил: силы тяжести и силы сопротивления воздуха. Сила тяжести заставляет пулю постепенно понижаться, а сила сопротивления воздуха непрерывно замедляет движение пули и стремится опрокинуть ее. В результате действия этих сил скорость полета постепенно уменьшается, а ее траектория представляет собой по форме неравномерно изогнутую кривую линию.

Действие силы тяжести.

Представим себе, что на пулю после вылета ее из канала ствола действует только одна сила тяжести. Тогда она начнет падать вертикально вниз, как и всякое свободно падающее тело. Если предположить, что на пулю при ее полете по инерции в безвоздушном пространстве действует сила тяжести, то под действием этой силы пуля опустится ниже от продолжения оси канала ствола: в первую секунду — на 4,9 м, во вторую секунду — на 19,6 м и т. д. В этом случае, если навести ствол оружия в цель, пуля никогда в нее не попадет, так как, подвергаясь действию силы тяжести, она пролетит под целью. Вполне очевидно, что, для того чтобы пуля пролетела определенное расстояние и попала в цель, необходимо направить ствол оружия куда-то выше цели, с тем чтобы траектория пули, изгибаясь под влиянием силы тяжести, пересекла центр цели. Для этого нужно, чтобы ось канала ствола и плоскость горизонта оружия составляли некоторый угол, который называется углом возвышения. Траектория пули в безвоздушном пространстве, на которую действует сила тяжести, представляет собой правильную кривую, которая называется параболой. Самая высокая точка траектории над горизонтом оружия называется ее вершиной. Часть кривой от точки вылета до вершины называется восходящей ветвью траектории, а от вершины до точки падения — нисходящей ветвью. Такая траектория пули характерна тем, что восходящая и нисходящая ветви совершенно одинаковы, а угол бросания и падения равны между собой.

Действие силы сопротивления воздушной среды.

На первый взгляд кажется маловероятным, чтобы воздух, обладающий такой малой плотностью, мог оказывать существенное сопротивление движению пули и этим значительно уменьшать ее скорость. Однако сопротивление воздуха оказывает сильное тормозящее действие на пулю, в связи с чем она теряет свою скорость. Сопротивление воздуха полету пули вызывается тем, что воздух представляет собой упругую среду и поэтому на движение в этой среде затрачивается часть энергии пули. Сила сопротивления воздуха вызывается тремя основными причинами: трением воздуха, образованием завихрений и образованием баллистической волны.

Как показывают фотоснимки пули, летящей со сверхзвуковой скоростью (свыше 340 м/сек), перед ее головной частью образуется уплотнение воздуха. От этого уплотнения расходится во все стороны головная волна. Частицы воздуха, скользя по поверхности пули и срываясь с ее боковых стенок, образуют за донной частью пули зону разреженного пространства, вследствие чего появляется разность давлений на головную и донную части. Эта разность создает силу, направленную в сторону, обратную движению пули и уменьшающую скорость ее полета. Частицы воздуха, стремясь заполнить пустоту, образовавшуюся за пулей, создают завихрение, в результате чего за дном пули тянется хвостовая волна.

Уплотнение воздуха впереди головной части пули тормозит ее полет; разреженная зона позади пули засасывает ее и этим еще больше усиливает торможение; ко всему этому стенки пули испытывают трение о частицы воздуха, что также замедляет ее полет. Равнодействующая этих трех сил и составляет силу сопротивления воздуха. Пуля (граната) при полете сталкивается с частицами воздуха и заставляет их колебаться. Вследствие этого перед пулей (гранатой) повышается плотность воздуха, и образуются звуковые волны. Поэтому полет пули (гранаты) сопровождается характерным звуком. При скорости полета пули (гранаты), меньшей скорости звука, образование этих волн оказывает незначительное влияние на ее полет, так как волны распространяются быстрее скорости полета пули (гранаты). При скорости полета пули, большей скорости звука, от набегания звуковых волн друг на друга создается волна сильно уплотненного воздуха — баллистическая волна, замедляющая скорость полета пули, так как пуля тратит часть своей энергии на создание этой волны.

Равнодействующая (суммарная) всех сил, образующихся вследствие влияния воздуха на полет пули (гранаты), составляет силу сопротивления воздуха. Точка приложения силы сопротивления называется центром сопротивления.

Влияние, оказываемое сопротивлением воздуха на полет пули очень велико — оно вызывает уменьшение скорости и дальности полета пули.

Действие на пулю сопротивления воздуха.

Величина силы сопротивления воздуха зависит от скорости полета, формы и калибра пули, а также от ее поверхности и плотности воздуха.

Сила сопротивления воздуха возрастает с увеличением калибра пули, скорости ее полета и плотности воздуха. Для того чтобы сопротивление воздуха меньше тормозило пулю во время полета, вполне очевидно, что нужно уменьшить ее калибр и увеличить ее массу. Эти соображения и привели к необходимости использования в стрелковом оружии пуль продолговатой формы, а с учетом сверхзвуковых скоростей полета пули, когда основной причиной сопротивления воздуха является образование уплотнения воздуха перед головной частью (баллистической волны), выгодны пули с удлиненной остроконечной головной частью. При дозвуковых скоростях полета гранаты, когда основной причиной сопротивления воздуха является образование разреженного пространства и завихрений, выгодны гранаты с удлиненной и суженной хвостовой частью.

Чем глаже поверхность пули, тем меньше сила трения и сила сопротивления воздуха.

Разнообразие форм современных пуль во многом определяется необходимостью уменьшить силу сопротивления воздуха.

Если бы полет пули совершался в безвоздушном пространстве, то направление ее продольной оси было бы неизменным и пуля падала бы на землю не головной частью, а дном.

Однако при действии на пулю силы сопротивления воздуха полет ее будет совсем иным. Под действием начальных возмущений (толчков) в момент вылета пули из канала ствола между осью пули и касательной к траектории образуется угол, и сила сопротивления воздуха действует не вдоль оси пули, а под углом к ней, стремясь не только замедлить движение пули, но и опрокинуть ее. В первый момент, когда пуля вылетает из канала ствола, сопротивление воздуха только тормозит ее движение. Но как только пуля начинает под действием силы тяжести опускаться вниз, частицы воздуха начнут давить не только на головную часть, но и на боковую поверхность ее.

Чем больше пуля будет опускаться, тем больше она будет и подставлять сопротивлению воздуха свою боковую поверхность. А так как частицы воздуха оказывают на головную часть пули значительно большее давление, чем на хвостовую, они стремятся опрокинуть пулю головной частью назад.

Следовательно, сила сопротивления воздуха не только тормозит пулю при ее полете, но и стремится опрокинуть ее головную часть назад. Чем больше скорость пули и чем она длиннее, тем сильнее на нее оказывает воздух опрокидывающее действие. Вполне понятно, что при таком действии сопротивления воздуха пуля во время своего полета начнет кувыркаться. При этом, подставляя воздуху то одну сторону, то другую, пуля быстро будет терять скорость, в связи, с чем дальность полета будет небольшой, а кучность боя — неудовлетворительной.

Заключение

Во всех рассмотренных примерах на тело действовала одна и та же сила тяжести. Однако движения при этом выглядели по-разному. Объясняется это тем, что характер движения любого тела в заданных условиях определяется его начальным состоянием. Недаром все полученные нами уравнения содержат начальные координаты и начальные скорости. Меняя их, мы можем заставить тело подниматься вверх или опускаться вниз по прямой линии, двигаться по параболе, достигая ее вершины, или опускаться по ней вниз; дугу параболы мы можем изогнуть сильнее или слабее и т.д. И в то же время все это многообразие движений можно выразить одной простой формулой:

Список литературы

1. Гершензон Е.М., Малов Н.Н. Курс общей физики. М.Просвещение, 1995.

2. Рымкевич П.А. Курс физики. М. Просвещение, 1975

3. Савельев И.В. Курс общей физики. М. Просвещение, 1983.

4. Трофимова Т.И. Курс физики. М. Просвещение, 1997

5. Чертов А.Г., Воробьёв А.А. Задачник по физике. М. Просвещение, 1988.

Урок-исследование ключевой ситуации «Движение тел под действием нескольких сил. Движение по окружности»

Автор: Андреева Валентина Михайловна

«Урок-исследование ключевой ситуации»


Движение под действием нескольких сил. Движение по окружности.

Из опыта преподавания физики должна сказать, что учащиеся с интересом решают задачи на движение тел под действием нескольких сил по наклонной плоскости, по горизонтали и вертикали, на движение связанных тел, но испытывают определенные трудности при решении задач на движение под действием нескольких сил по окружности. Если они могут определить силы, действующие на тело, то не всегда правильно могут изобразить силы на чертеже ( точку приложения силы), построить систему отсчета, в которой удобнее рассматривать движение тела. Да и в сборниках задач по физике данному вопросу уделяется недостаточно внимания ( мало задач). Поэтому при подготовке учащихся к ЕГЭ я уделяю этой теме большое внимание.

Постановка учебной проблемы: В окружающей нас жизни существенное значение имеют движущиеся тела: санки, велосипеды, автомобили и др. Практически всегда движение обусловлено действием нескольких тел: например, в условиях Земли это действие Земли, действие опоры или подвеса.
Наша задача — научиться определять характеристики (ускорение, скорость, угол наклона и др.) тела, к которому приложены 2-3 силы.

На уроке можно рассмотреть решение следующих задач.


Задача 1. Груз, подвешенный на нити длиной 60 см, двигаясь равномерно, описывает в горизонтальной плоскости окружность. С какой скоростью движется груз, если во время его движения нить образует с вертикалью постоянный угол 30?

Задача 2. Конькобежец движется со скоростью 10 м\с по окружности радиусом 30 м. Под каким углом к горизонту он должен наклониться, чтобы сохранить равновесие?

Задача 3. Шарик массой 500г, подвешенный на нерастяжимой нити длиной 1м, совершает колебания в вертикальной плоскости. Найти силу натяжения нити в момент, когда она образует с вертикалью угол 60. Скорость шарика в этот момент 1,5 м\с.
Сразу хочу сказать, что на уроке можно решить вместе с учащимися все три задачи или любые две, в зависимости от времени урока, от уровня подготовки учащихся к решению задач такого типа. Можно в качестве подготовки предыдущий урок посвятить движению тел под действием нескольких сил по окружности в вертикальной плоскости типа задач№1, №5 второго уровня.
Перед решением этих задач необходимо провести разминку, которая позволит уч-ся вспомнить и применить основные формулы и приемы решения задач по этой теме.

Разминка:

Тело движется по окружности с центром О в горизонтальной плоскости, Какая из стрелок правильно указывает направление ускорения?

а)1 б) 2 В 3
1

2

Шарик, подвешенный на нити длиной 2 м, раскачивается. В момент прохождения положения равновесия скорость шарика 3 м\с. Каково центростремительное ускорение шарика в этот момент?

а) 4,5 м\с б) 0,75 м\с в) 6 м\с

Тело движется по окружности радиусом 5м с постоянной угловой скоростью 4 об.\с. Определите центростремительное ускорение.

а) 3,2 рад.\с б) 80рад.\с в)20 рад.\с

Изобразите силы, действующие на тела:





а)тело на опоре б)тело на подвесе в) тело в положении 1

Определите проекцию силы F на координатные оси.


Y


F
O X
На ось ОХ:
a)F б) F в) F


На ось ОY:
а) F б) F в) F

Какая сила сообщит телу массой 4т ускорение 0,2 м\с.

а)20000 Н б) 800 Н в) 8000 Н

Автомобиль массой 2т проходит по выпуклому мосту, имеющему радиус кривизны 40м, со скоростью 36 км\ч. С какой силой автомобиль давит на мост в его середине?

а) 15000 Н б) 25000 Н в) 20000 Н

Ответы: 1. б 2.а 3. Б 5. На ось ОХ: а, на ось OY: б 6. в 7. а

После окончания разминки снова предъявляем классу условия задач.

Решаем задачу №1.

Идея решения: по условию задача динамическая, но найти надо кинематическую характеристику — скорость. Для этого надо знать ускорение, которое определяется на основе второго закона Ньютона.

Решение задачи.

A Y

L T1

X
O B
R T2 a


mg

1.Решение задачи полезно начать с построения чертежа. В процессе построения чертежа учащиеся выясняют, что на груз действуют 2 силы: сила тяжести и сила натяжения нити.
Определяем направление и точку приложения сил.
Для того, чтобы груз двигался по окружности с постоянной скоростью, необходима сила, направленная к центру этой окружности.

В данном случае, как мы выяснили, на груз действуют две силы: сила натяжения нити и сила тяжести. Ни одна из них не направлена к центру траектории движения камня. Но силу натяжения нити можно разложить на две составляющие: вертикальную и горизонтальную. Вертикальная составляющая равна силе тяжести. Именно поэтому камень ни падает вниз, ни поднимается вверх. Сила тяжести и сила вертикальная составляющая силы натяжения нити уравновешивают друг друга.
По второму закону Ньютона ускорение определяется равнодействующей силой. Направление равнодействующей и ускорения совпадают. Сила натяжения и сила тяжести являются сторонами параллелограмма, а равнодействующая сила его диагональю. Проведя на рисунке векторное сложение сил, делаем вывод, что соотношения между силами представлено верно.

2.Построим систему отсчета. Ось OY направим по линии действия силы тяжести вертикально вверх. Ось ОХ в данном случае ,удобнее направить по вектору ускорения (влево), чтобы при нахождении проекций векторных величин было меньше отрицательных.

3.Запишем 2-ой закон Ньютона для груза ( уравнение движения тела в векторной форме):
ma=T+mg

4.Определим проекции сил и ускорения на координатные оси:
ОХ: Тх= Т2, (mg)x=0 , ax=a, ma=T2
ma=m\R, T2=m\R…(1)

OY: Ty=T1, (mg)y= — mg, ay=0 , 0=T1 – mg , T1=mg …(2)

5.Из уравнений (1) и (2) составим систему T2=m\R
T1=mg
Разделим уравнение (1) на (2):T2/T1= (m/R)/mg, получим
=, =Rg…(3)
Из треугольника AOB получим, что ОВ=R=L …(4)

Подставим (4) в (3) , получим =Lg

V=

Вычисление: v= =1,3(м\с)

Ответ: 1,3 м\с.

Решаем задачу №2.
Идея решения: Данная задача по условию кинематическая, но , чтобы найти угол наклона конькобежца, необходимо использовать законы динамики, а именно 2-ой закон Ньютона.

Как и в задаче№1 на конькобежца действуют 2 силы: сила тяжести и сила реакции опоры. Очень важно, чтобы учащиеся приложили эти силы к центру массы конькобежца и правильно изобразили направление силы реакции опоры. Далее векторно складываем силы, тем самым определяем направление равнодействующей силы и ускорения.

Решение задачи.

1.Построим чертеж и выберем систему отсчета, удобную для решения задачи.
Y

A
N2 N


α
C B a X O

α N1
mg

2.Запишем 2-ой закон Ньютона для движения конькобежца в векторной форме:
ma=N+mg
3.Запишем 2-ой закон Ньютона в проекциях на координатные оси.
На ось OX: ax=a, Nx=N1, (mg)x=0, ma=N1, т.к.а=\R,то m/R=N1 …(1)
На осьOY: ay=0, Ny=N2, (mg)y= — mg , 0=N2-mg, mg=N2 …(2)
4.Поделим (2) на (1) N2/N1=mg/m/R
Из треугольника АВС N2/N1= , gR\
α==71
Ответ; 71


Решаем задачу №3




α T


a



mg




Решение:
При решении данной задачи удобнее ось ОY и ускорение а направить по линии действия силы натяжения. T+mg=ma, OY: T-mg=ma, T=m(g+a)
Т.к. R=L,то a=/L, T=m(g+/L)=3,6H.

Задачи для самостоятельного решения

Первый уровень.

Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800м со скоростью 20 м\с?

a=\R, a=0,5 м\

С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40м, чтобы центростремительное ускорение равнялось ускорению свободного падения?

a=g= /R , v = 20м\с

Подвешенный на нити шарик равномерно движется по окружности в горизонтальной плоскости. Какой вектор указывает направление вектора равнодействующей всех сил, приложенных к шарику?


2 1

3

4


Второй уровень.

1. Велосипедист массой 80 кг движется со скоростью 10м\с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.

Решение.

N=m(g+a)=m(g+\R)=1200H

2.С какой силой, направленной горизонтально, давит вагон трамвая массой 24 кг на рельсы, если он движется по закруглению радиусом 100м со скоростью 18 км\ч? Во сколько раз изменится эта сила, если скорость движения увеличится в 2 раза?

Решение.

N1=ma=m/R=6000H. Если скорость движения увеличится в 2 раза, то центростремительное ускорение увеличится в 4 раза, значит и сила увеличится в 4 раза.

3. С какой наибольшей скоростью автомобиль может проходить по горизонтальной дороге поворот радиусом 25м, если коэффициент шин о дорогу равен 0,4?

Решение.

Fтр.=ma=m\R, но с другой стороны Fтр.=N=mg
m\R=mg, v==10м\с

4. На рисунке грузик, привязанный к нити, обращается по окружности с центростремительным ускорением 3 м\с. С каким ускорением будет двигаться грузик, если нить порвется?

Решение.

Если нить порвется, то на грузик будет действовать только сила тяжести.
mg=ma, значит грузик будет двигаться с ускорением 10м\.

5. Реактивный самолет описывает петлю Нестерова. Скорость самолета в нижней точке петли равна 360 км\ч. Радиус петли 200м. Найти во сколько раз «тяжелее становится летчик, т. е. Какова перегрузка в нижней точке петли?

Решение.

Составим уравнение движения тела ( 2-ой закон Ньютона): mg+N=ma.
Найдем проекции сил: ОY: N-mg=-ma — для верхней точки
N=m(g-a)
OY: N-mg=ma – для нижней точки
N=m(g+a), N=P
Для нижней точки составим отношение:
m(g+a)/mg=1+a/g, a=/R, получим ,что 1+/gR=6 т.е. в нижней точке петли летчик «тяжелее» в 6 раз.

Третий уровень.

Тело массой 1кг, подвешенное на нити длиной 1м, описывает в горизонтальной плоскости окружность с постоянной угловой скоростью, совершая 1 об\с. Определите модуль силы упругости нити и угол, который образует нить с вертикалью.

Y
α

T
X
a

mg

Решение:

А).Найду Т. mg+T=ma, OX: T=ma, T=ma/ , т.к. R=L, a=/R=/L, то
T= m/L…(1). Скорость найду по формуле: v=R=2πnL…(2)
Подставлю (2) в (1),получу, что T=4mL.=40Н.
Б). Найду угол α . OY: T-mg=0, =mg/T=75,5

Велосипедист движется по горизонтальной дороге со скоростью υ = 18 км/ч. При повороте угол наклона велосипедиста с вертикалью равен 60⁰. Чему равен радиус дуги окружности, по которой движется велосипедист?

Решение.

Используем коллективное решение задачи №2. В итоге =gR/,
R=/g=4,25м.

Человек на мотоцикле едет по горизонтальной дороге со скоростью υ = 72 км/ч и делает поворот радиусом R = 100 м. На какой угол от вертикали должен отклониться мотоциклист, чтобы не упасть на повороте? (Принять g = 10м/).

Решение.

Используем коллективное решение задачи №1. В итоге =/Rg,
==22

Груз, подвешенный к невесомой нити, описывает горизонтальную окружность с постоянной скоростью ( конический маятник). Расстояние от точки подвеса до центра окружности Н=1м. Найти число оборотов за 1с.

Y
α

T
H X
a

Решение.

mg+T=ma, OX T=ma,
OY T=mg
Т.к. v=R, R=h, то T=mh…(1)
T=mg…(2)
Поделю (1) на (2), получу =h/g, h/g=1, =
Число оборотов n=/2π= =0,5 , т.е. пол-оборота.

5.Акробат на подвешенной к куполу цирка веревке длиной l движется равномерно в горизонтальной плоскости по окружности. При этом угол отклонения веревки от вертикали α. Найти натяжение веревки и число оборотов за минуту.

Решение.

T+mg=ma, OX: T=m/R…(1)
OY: mg-T=0, T=mg/
Скорость v=2πRn …(2) , а R=L…(3)
(2)и(3) подставлю в (1), получу n=mL/

Использованная литература:

Л.Э.Генденштейн, Л.А.Кирик, И.М.Гельфгат, И.Ю.Ненашев «Физика 10, задачник», «Мнемозина» 2009г.
Материалы ЕГЭ «ФИПИ» с 2005 — 2016 г.г.
А.П.Рымкевич, П.А.Рымкевич «Сборник задач по физике», Издательство «Просвещение»,1983 г.




«Урок-исследование ключевой ситуации»

comments powered by HyperComments

механиков | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

Исторически механика была одной из первых возникших точных наук.Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Механику можно разделить на три части: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.

Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) правильно описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение вещества и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Классическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Этот предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его книге Philosophiae Naturalis Principia Mathematica (1687), широко известной как Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.

В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.

Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не очень четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса — это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов — основная тема классической механики.

Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины — энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.

Примечательно то, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, вытекающие из законов Ньютона — сохранение энергии, импульса и углового момента — остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса — лишь одним из множества атрибутов материи.Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющаяся важность этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в современной науке.

механика | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга.Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Исторически механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

механика | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга.Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Исторически механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

механика | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга.Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Исторически механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Законы Ньютона | Безграничная физика

Первый закон: инерция

Первый закон движения Ньютона описывает инерцию. Согласно этому закону, покоящееся тело стремится оставаться в покое, а движущееся тело стремится оставаться в движении, если только на него не действует чистая внешняя сила.

Цели обучения

Определите первый закон движения

Основные выводы

Ключевые моменты

Три закона физики Ньютона являются основой механики.
Первый закон гласит, что покоящееся тело будет оставаться в покое до тех пор, пока на него не подействует чистая внешняя сила, и что движущееся тело будет оставаться в движении с постоянной скоростью до тех пор, пока на него не будет действовать чистая внешняя сила.
Чистая внешняя сила — это сумма всех сил, действующих на объект.
Тот факт, что на объект действуют силы, не обязательно означает наличие чистой внешней силы; силы, равные по величине, но действующие в противоположных направлениях, могут нейтрализовать друг друга.
Трение — это сила между движущимся объектом и поверхностью, по которой он движется. Трение — это внешняя сила, которая действует на объекты и заставляет их замедляться, когда на них не действует никакая другая внешняя сила.
Инерция — это тенденция движущегося тела оставаться в движении.Инерция зависит от массы, поэтому сложнее изменить направление движущегося тяжелого тела, чем направление более легкого движущегося объекта.

Ключевые термины

инерция : Свойство тела, которое сопротивляется любому изменению его равномерного движения; эквивалент его массе.
трение : Сила, которая сопротивляется относительному движению или тенденции к такому движению двух соприкасающихся тел.
равномерное движение : Движение с постоянной скоростью (с нулевым ускорением).Обратите внимание, что движущийся объект не изменит свою скорость, если на него не действует неуравновешенная сила.

История

Сэр Исаак Ньютон был английским ученым, интересовавшимся движением объектов в различных условиях. В 1687 году он опубликовал работу под названием Philosophiae Naturalis Principla Mathematica , в которой описал свои три закона движения. Ньютон использовал эти законы для объяснения и исследования движения физических объектов и систем. Эти законы составляют основу механики.Законы описывают взаимосвязь между силами, действующими на тело, и движениями, вызываемыми этими силами. Эти три закона заключаются в следующем:

Если объект не испытывает чистой силы, его скорость останется постоянной. Объект либо находится в состоянии покоя и его скорость равна нулю, либо он движется по прямой с постоянной скоростью.
Ускорение объекта параллельно и прямо пропорционально чистой силе, действующей на объект, происходит в направлении чистой силы и обратно пропорционально массе объекта.
Когда первый объект оказывает силу на второй объект, второй объект одновременно оказывает силу на первый объект, что означает, что сила первого объекта и сила второго объекта равны по величине и противоположны по направлению.

Первый закон движения

Скорее всего, вы уже слышали о первом законе движения Ньютона. Если вы не слышали это в приведенной выше форме, вы, вероятно, слышали, что «движущееся тело остается в движении, а тело в состоянии покоя остается в покое.Это означает, что движущийся объект не изменит своей скорости, если на него не действует неуравновешенная сила. Это называется равномерным движением. Эту концепцию легче объяснить на примерах.

Примеры

Если вы катаетесь на коньках и отталкиваетесь от края катка, согласно первому закону Ньютона вы продолжите путь до другой стороны катка. Но на самом деле этого не произойдет. Ньютон говорит, что движущееся тело будет оставаться в движении до тех пор, пока на него не подействует внешняя сила.В этом и большинстве других случаев реального мира эта внешняя сила — трение. Трение между коньками и льдом — это то, что заставляет вас замедляться и в конечном итоге останавливаться.

Давайте посмотрим на другую ситуацию. Обратитесь к этому примеру. Почему мы пристегиваемся ремнями безопасности? Очевидно, они там, чтобы защитить нас от травм в случае автомобильной аварии. Если автомобиль движется со скоростью 60 миль в час, водитель также движется со скоростью 60 миль в час. Когда автомобиль внезапно останавливается, к автомобилю прилагается внешняя сила, которая заставляет его замедляться.Но на водителя не действует сила, поэтому водитель продолжает двигаться со скоростью 60 миль в час. Ремень безопасности должен противодействовать этому и действовать как та внешняя сила, которая замедляет водителя вместе с автомобилем, предотвращая его повреждение.

Первый закон Ньютона : Первый закон Ньютона действует на водителя автомобиля

Инерция

Иногда этот первый закон движения называют законом инерции. Инерция — это свойство тела оставаться в покое или оставаться в движении с постоянной скоростью.Некоторые объекты обладают большей инерцией, чем другие, потому что инерция объекта эквивалентна его массе. Вот почему изменить направление валуна сложнее, чем бейсбольного мяча.

Doc Physics — Newton : Первый закон Ньютона очень противоречит здравому смыслу. Хотя, возможно, вы выучили это в начальной школе. Давайте посмотрим, какой умопомрачительный вывод есть на самом деле.

Второй закон: сила и ускорение

Второй закон гласит, что результирующая сила, действующая на объект, равна скорости изменения или производной его линейного количества движения.

Цели обучения

Определите второй закон движения

Основные выводы

Ключевые моменты

Три закона движения Ньютона объясняют взаимосвязь между силами, действующими на объект, и движением, которое они испытывают из-за этих сил. Эти законы лежат в основе механики.
Второй закон объясняет взаимосвязь между силой и движением, в отличие от скорости и движения. Для этого он использует концепцию линейного импульса.
Линейный импульс [латекс] \ text {p} [/ latex], является произведением массы [latex] \ text {m} [/ latex] и скорости [latex] \ text {v} [/ latex]: [ латекс] \ текст {p} = \ text {mv} [/ latex].
Второй закон гласит, что результирующая сила равна производной или скорости изменения ее количества движения.
Упростив это соотношение и вспомнив, что ускорение — это скорость изменения скорости, мы можем увидеть, что второй закон движения — это то, откуда происходит взаимосвязь между силой и ускорением.

Ключевые термины

чистая сила : комбинация всех сил, действующих на объект.
импульс : (тела в движении) произведение его массы и скорости.
ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).

Английский ученый сэр Исаак Ньютон исследовал движение физических объектов и систем в различных условиях.В 1687 году он опубликовал свои три закона движения в книге Philosophiae Naturalis Principla Mathematica . Законы составляют основу механики — они описывают взаимосвязь между силами, действующими на тело, и движением, вызываемым этими силами. Эти три закона гласят:

Если объект не испытывает чистой силы, его скорость останется постоянной. Объект либо находится в состоянии покоя и его скорость равна нулю, либо он движется по прямой с постоянной скоростью.
Ускорение объекта параллельно и прямо пропорционально чистой силе, действующей на объект, происходит в направлении чистой силы и обратно пропорционально массе объекта.
Когда первый объект оказывает силу на второй объект, второй объект одновременно оказывает силу на первый объект, что означает, что сила первого объекта и сила второго объекта равны по величине и противоположны по направлению.

Первый закон движения определяет только естественное состояние движения тела (то есть, когда результирующая сила равна нулю). Это не позволяет нам количественно оценить силу и ускорение тела. Ускорение — это скорость изменения скорости; это вызвано только действующей на него внешней силой.Второй закон движения гласит, что результирующая сила, действующая на объект, равна скорости изменения его количества движения.

Линейный импульс

Линейный импульс объекта — это векторная величина, которая имеет как величину, так и направление. Это произведение массы и скорости частицы в данный момент времени:

[латекс] \ text {p} = \ text {mv} [/ latex]

, где [латекс] \ text {p} = \ text {momentum} [/ latex], [latex] \ text {m} = \ text {mass} [/ latex] и [latex] \ text {v} = \ text {скорость} [/ латекс].Из этого уравнения мы видим, что объекты с большей массой будут иметь больший импульс.

Второй закон движения

Представьте два шара разной массы, движущиеся в одном направлении с одинаковой скоростью. Если они оба столкнутся со стеной одновременно, более тяжелый шар будет оказывать на стену большее усилие. Эта концепция, проиллюстрированная ниже, объясняет второй закон Ньютона, который подчеркивает важность силы и движения, а не только скорости. Он гласит: результирующая сила, действующая на объект, равна скорости изменения его количества движения.Из расчетов мы знаем, что скорость изменения такая же, как и у производной. Когда мы измеряем количество движения объекта, получаем:

Сила и масса : Эта анимация демонстрирует связь между силой и массой.

[латекс] \ displaystyle \ text {F} = \ frac {\ text {dp}} {\ text {dt}} \\\ text {F} = \ frac {\ text {d} (\ text {m} \ cdot \ text {v})} {\ text {dt}} [/ latex]

, где F = сила и t = время. Отсюда мы можем еще больше упростить уравнение:

[латекс] \ displaystyle \ text {F} = \ text {m} \ frac {\ text {d} (\ text {v})} {\ text {dt}} \\\ text {F} = \ text {m} \ cdot \ text {a} [/ latex]

где, [латекс] \ text {a} = \ text {ускорение} [/ latex].Как мы заявляли ранее, ускорение — это скорость изменения скорости или скорости, деленная на время.

Три закона механики Ньютона — Второй закон — Часть 1 : Здесь мы увидим, сколько людей могут запутать ваше понимание 2-го закона движения Ньютона из-за недосмотра, небрежности или жестоких намерений.

Три закона механики Ньютона — Второй закон — Часть вторая : Равновесие исследуется, и 1-й закон Ньютона рассматривается как частный случай 2-го закона Ньютона!

Третий закон: симметрия сил

Третий закон движения гласит, что для каждого действия существует равное и противоположное противодействие.

Цели обучения

Определите третий закон движения

Основные выводы

Ключевые моменты

Если объект A оказывает силу на объект B, объект B оказывает равную и противоположную силу на объект A.
Третий закон Ньютона можно увидеть во многих повседневных обстоятельствах. Когда вы идете, сила, которую вы используете для отталкивания от земли назад, заставляет вас двигаться вперед.
Тяга — это применение третьего закона движения. Вертолет с помощью тяги толкает воздух под винтом вниз и, следовательно, отрывается от земли.

Ключевые термины

симметрия : точное соответствие по обе стороны от разделительной линии, плоскости, центра или оси.
тяга : Сила, создаваемая движущей силой, как в реактивном двигателе.

Сэр Исаак Ньютон был ученым из Англии, интересовавшимся движением объектов в различных условиях. В 1687 году он опубликовал работу под названием Philosophiae Naturalis Principla Mathematica , в которой содержались его три закона движения.Ньютон использовал эти законы для объяснения и исследования движения физических объектов и систем. Эти законы составляют основу механики. Законы описывают взаимосвязь между силами, действующими на тело, и движение — это опыт, обусловленный этими силами. Три закона Ньютона:

Если объект не испытывает чистой силы, его скорость останется постоянной. Объект либо находится в состоянии покоя и его скорость равна нулю, либо он движется по прямой с постоянной скоростью.
Ускорение объекта параллельно и прямо пропорционально чистой силе, действующей на объект, происходит в направлении чистой силы и обратно пропорционально массе объекта.
Когда первый объект оказывает силу на второй объект, второй объект одновременно оказывает силу на первый объект, что означает, что сила первого объекта и сила второго объекта равны по величине и противоположны по направлению.

Третий закон движения Ньютона

Третий закон Ньютона в основном гласит, что на каждое действие существует равное и противоположное противодействие. Если объект A воздействует на объект B, из-за закона симметрии объект B будет оказывать на объект A силу, равную силе, действующей на него:

[латекс] \ small {\ rm {\ text {F} _ \ text {A} = — \ text {F} _ \ text {B}}} [/ latex]

В этом примере F _A — это действие, а F _B — это реакция.Вы, несомненно, были свидетелями этого закона движения. Например, возьмем пловца, который ногами отталкивается от стены, чтобы набрать скорость. Чем больше силы она прикладывает к стене, тем сильнее она отталкивается. Это потому, что стена оказывает на нее ту же силу, что и она. Она толкает стену в направлении позади себя, поэтому стена будет оказывать на нее силу в направлении впереди нее и толкать вперед.

Третий закон движения Ньютона : Когда пловец отталкивается от стены, он использует третий закон движения.

Возьмем в качестве другого примера концепцию тяги. Когда ракета запускается в космическое пространство, она выбрасывает газ назад с высокой скоростью. Ракета оказывает на газ большую обратную силу, а газ оказывает равную и противоположную силу реакции вперед на ракету, заставляя ее запускаться. Эта сила называется тягой. Тяга также используется в автомобилях и самолетах.

Третий закон Ньютона : Самое фундаментальное утверждение базовой физической реальности также чаще всего понимается неправильно.Как твоя мама, если она понимает Третий Ньютон. Затем спросите ее, почему все может двигаться, если у каждой силы есть пара противоположных сил все время, навсегда.

Равновесие трех сил

Очень простая концепция при работе с
силы
это идея равновесия или баланса .
В общем, на объект могут действовать несколько сил.
в то же время.
Сила — это
векторная величина
что значит
что у него есть как величина, так и направление, связанные с
Это.Две силы одинаковой величины, но разные направления
не равны силы.
Векторная сумма
всех сил, действующих на тело, составляет
единая сила называется чистой силой .
Если чистая сила равна нулю,
считается, что объект находится в состоянии равновесия .
Поскольку на объект, находящийся в равновесии, не действует результирующая сила,
затем из Ньютона
первый закон
движения, объект продолжает
двигаться
с постоянной скоростью.

На другой странице мы показываем простейший пример равновесия с
две силы, действующие на объект.
На этой странице мы рассмотрим случай
планер, на который в полете действуют три силы.
А на другой странице мы рассматриваем случай
приводимый в действие самолет в
крейсерский, где на самолет действуют четыре силы.

В примере 1 мы показываем компьютерный чертеж
планер, когда он спускается. На планер действуют три силы;
лифт (L),
перетащить (D),
а также
вес (Вт).Вес всегда направлен к центру земли, подъемная сила
направлено перпендикулярно траектории полета, а сопротивление — по траектории полета
дорожка. Траектория полета наклонена к горизонтали на
угол a .
Когда самолет находится в равновесии, векторная сумма этих трех сил
равно нулю. Поскольку это векторная сумма, есть два
составная часть
уравнения, одно вертикальное и одно горизонтальное, которые
показано под графиком.

W — L * cos (a) — D * sin (a) = V = 0

D * cos (a) — L * sin (a) = H = 0

где sin и cos —
тригонометрические функции синуса и косинуса,
V — чистая вертикальная сила, а H — чистая горизонтальная сила.
Поскольку мы смотрим на состояние равновесия, H и V равны нулю.

Самолет имеет постоянную скорость вперед и вниз по
траектория полета.Обратите внимание, что подъемная сила, сопротивление и вес продолжают увеличиваться.
действовать на самолет. В состоянии равновесия действие некоторых сил точно
уравновешивается или нейтрализуется другими силами.

В примере 2
спойлер
размещается на верхней части крыла планера, уменьшая подъемную силу и увеличивая сопротивление.
Вес остался прежним.
Планера больше нет
равновесие. Уравнения для сил остались прежними, но теперь есть
чистые горизонтальные и вертикальные силы; V и H не равны нулю.По мнению Ньютона
второй закон
движения, самолет начал бы ускоряться вниз и вправо. В примере 2
силы не уравновешены, и самолет не находится в равновесии.

Навигация ..

Руководство для начинающих Домашняя страница

Значение силы

Сила — это толкание или притяжение объекта, возникающее в результате взаимодействия объекта с другим объектом.Когда происходит взаимодействие между двумя объектами, на каждый из объектов действует сила. Когда взаимодействие , прекращается, два объекта больше не испытывают силы. Силы только существуют в результате взаимодействия.

Контакт против сил действия на расстоянии

Для простоты все силы (взаимодействия) между объектами можно разделить на две большие категории:

,
контактных сил и
силы, возникающие в результате действия на расстоянии

Контактные силы — это те типы сил, которые возникают, когда два взаимодействующих объекта воспринимаются как физически контактирующие друг с другом.Примеры контактных сил включают силы трения, силы натяжения, нормальные силы, силы сопротивления воздуха и приложенные силы. Эти особые силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.

Силы, действующие на расстоянии — это те типы сил, которые возникают, даже когда два взаимодействующих объекта не находятся в физическом контакте друг с другом, но все же способны толкать или тянуть, несмотря на их физическое разделение. Примеры сил, действующих на расстоянии, включают гравитационные силы.Например, Солнце и планеты оказывают друг на друга гравитационное притяжение, несмотря на их большое пространственное разделение. Даже когда ваши ноги отрываются от земли и вы больше не находитесь в физическом контакте с Землей, между вами и Землей существует гравитационное притяжение. Электрические силы — это силы, действующие на расстоянии. Например, протоны в ядре атома и электроны вне ядра испытывают электрическое притяжение друг к другу, несмотря на их небольшое пространственное разделение. А магнитные силы — это силы, действующие на расстоянии.Например, два магнита могут оказывать магнитное притяжение друг на друга, даже если они находятся на расстоянии нескольких сантиметров. Эти особые силы будут обсуждаться более подробно позже в Уроке 2, а также в других уроках.

Примеры сил контакта и воздействия на расстоянии приведены в таблице ниже.

Контактные силы	Силы дистанционных действий
Сила трения	Сила гравитации
Сила натяжения	Электрическая сила
Нормальная сила	Магнитная сила
Силы сопротивления воздуха
Приложенная сила
Spring Force

Ньютон

Сила — это величина, которая измеряется в стандартной метрической единице, известной как Ньютон .Ньютон сокращенно обозначается буквой «N». Сказать «10,0 Н» означает 10,0 Ньютона силы. Один ньютон — это сила, необходимая для того, чтобы придать массе массой 1 кг ускорение 1 м / с / с. Таким образом, можно констатировать следующую эквивалентность единицы:

1 Ньютон = 1 кг • м / с ²

Сила — векторная величина

Сила — это векторная величина. Как было сказано ранее, векторная величина — это величина, которая имеет как величину, так и направление.Чтобы полностью описать силу, действующую на объект, вы должны описать как величину (размер или числовое значение), так и направление. Таким образом, 10 Ньютонов не являются полным описанием силы, действующей на объект. Напротив, 10 Ньютонов вниз — это полное описание силы, действующей на объект; даны как величина (10 Ньютон), так и направление (вниз).

Поскольку сила — это вектор, имеющий направление, принято представлять силы с помощью диаграмм, на которых сила представлена стрелкой.Такие векторные диаграммы были введены в более раннем модуле и используются на протяжении всего изучения физики. Размер стрелки отражает величину силы, а направление стрелки показывает направление, в котором действует сила. (Такие диаграммы известны как диаграммы свободного тела и обсуждаются позже в этом уроке.) Кроме того, поскольку силы являются векторами, действие отдельной силы на объект часто нейтрализуется действием другой силы. Например, эффект направленной вверх силы 20 Ньютон, действующей на книгу, равен , аннулируется эффектом направленной вниз силы 20 Ньютон, действующей на книгу.В таких случаях говорят, что две отдельные силы уравновешивают друг друга ; на книгу не будет действовать неуравновешенная сила.

Можно представить другие ситуации, в которых две отдельные векторные силы уравновешивают друг друга («баланс»), но существует третья индивидуальная сила, которая не уравновешивается другой силой. Например, представьте книгу, скользящую по шероховатой поверхности стола слева направо. Нисходящая сила тяжести и восходящая сила стола, поддерживающего книгу, действуют в противоположных направлениях и, таким образом, уравновешивают друг друга.Однако сила трения действует влево, и нет силы, направленной вправо, чтобы уравновесить ее. В этом случае на книгу действует неуравновешенная сила, изменяющая ее состояние движения.

Точные детали построения диаграмм свободного тела обсуждаются позже. Пока что акцент делается на том факте, что сила — это векторная величина, имеющая направление. Важность этого факта станет очевидной, когда мы проанализируем отдельные силы, действующие на объект, позже в этом уроке.

Движение тела под действием нескольких сил

Урок по физике 10 класс Движение под действием нескольких сил.

Движение тел под действием нескольких сил

Урок «Движение тела под действием нескольких сил» | План-конспект урока по физике (10 класс) на тему:

Урок-исследование ключевой ситуации «Движение тел под действием нескольких сил. Движение по окружности»

механиков | Определение, примеры, законы и факты

механика | Определение, примеры, законы и факты

механика | Определение, примеры, законы и факты

механика | Определение, примеры, законы и факты

Законы Ньютона | Безграничная физика

Первый закон: инерция

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

История

Первый закон движения

Примеры

Инерция

Второй закон: сила и ускорение

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Линейный импульс

Второй закон движения

Третий закон: симметрия сил

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Третий закон движения Ньютона

Равновесие трех сил

Значение силы

Добавить комментарий Отменить ответ