Формула геометрии прогрессии: Геометрическая прогрессия — урок. Алгебра, 9 класс. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Геометрическая прогрессия и сумма ее членов 🐲 СПАДИЛО.РУ

Определение

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

Другими словами, последовательность (b_n) – геометрическая последовательность, если для натурального n выполняются условия:

b_n+1= b_n×q,

где q некоторое число, которое называется знаменатель прогрессии, и b_n≠0

Примером такой последовательности может быть ряд чисел 2; 10; 50; 250;…., откуда видно, что каждое последующее больше предыдущего в пять раз, значит, каждый член равен предыдущему, умноженному на одно и то же число 5. Или, например, ряд чисел 20; -2; 0,2; -0,02……, где видно, что каждое последующее умножали на одно и то же число (-0,1).

Так как по определению геометрической прогрессии мы имеем одно и то же число, то это и есть число q. Оно называется «знаменатель» геометрической прогрессии. Он находится путем деления соседних членов – последующего на предыдущий, то есть q=bn+1bn… Знаменатель не может быть равным нулю!

Для того чтобы задать геометрическую прогрессию, надо знать ее первый член и знаменатель. Например, если b₁=4, q=3, то получим прогрессию: 4; 12; 36; ….и так далее. Ну, а зная первый член и знаменатель, можно найти любой член геометрической прогрессии: b₂=b₁q; b₃=(b₁q)q=b₁q²; b₄==((b₁q)q)q=b₁q³. Так можно продолжать и дальше, но из этих записей видно, что можно найти n-ый член геометрической последовательности, если умножить первый член на знаменатель, степень которого на 1 меньше порядкового номера искомого члена, то есть bn=b1 qn−1 . Мы получили формулу n-ого члена геометрической прогрессии.

Формула n-ого члена геометрической прогрессии

bn=b1 ×qn−1

Рассмотри на примерах применение формулы bn=b1 qn−1 для указанного члена геометрической прогрессии.

Пример №1. Найти четвертый член геометрической прогрессии, если известно, что b₁=6, q=3. Составляем формулу для b₄:

b4=b1 q4−1=b1 q3

Подставляем в формулу значения, указанные в задании и вычисляем результат: b4=6×33=162.

Найти шестой член геометрической прогрессии 2; -6;……. Здесь для нахождения b₆ надо знать знаменатель q. Для его нахождения надо -6 разделить на 2, получим -3, то есть q=-3. Теперь составляем формулу для b₆, подставляем значения и вычисляем ответ:

b6=b1 q6−1=b1 q5=2×(−3)5=−486

Свойство геометрической прогрессии

Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов. Формула:

b2n=bn−1×bn+1

Верным является и утверждение, обратное данному: если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность чисел является геометрической прогрессией.

Другими словами, с помощью данной формулы можно найти неизвестный член геометрической прогрессии, соседние члены которого известны. Рассмотрим применение данного свойства на примерах.

Пример №2. Найти b₅, если задана геометрическая прогрессия, в которой b₄=32, b₆=128. Составляем формулу, подставляем в нее значения и вычисляем:

b25=b5−1×b5+1=b4 ×b6 =32×128=4096

Этим действием мы нашли квадрат пятого члена геометрической прогрессии, поэтому извлекаем квадратный корень из числа 4096 для нахождения значения b₅: b₅=√4096=64

Найти у, если дана геометрическая прогрессия …..24; у; 96. Видим, что у находится между соседними известными числами 24 и 96. Поэтому, следуя свойству, умножаем данные числа и извлекаем квадратный корень из полученного числа: у=√24×96=√2304=48.

Формула суммы n первых членов геометрической прогрессии

Формула суммы членов геометрической прогрессии с известными членами

Sn=bnq−b1q−1. . , где q≠1

Для нахождения суммы по данной формуле нужно знать первый и последний член геометрической прогрессии, а также ее знаменатель.

Также есть вторая формула, по которой можно находить сумму нескольких первых членов прогрессии, зная только первый ее член и знаменатель:Формула суммы членов геометрической прогрессии с известным первым членом и знаменателем

Sn=b1(qn−1)q−1.., где q≠1

Рассмотрим применение данных формул на примере, решив его двумя способами. Пример №3. Найти сумму пяти первых членов геометрической прогрессии, если известно, что b₁=2; b₅=162; q=-3. Способ №1 (первая формула). Составим формулу для нахождения S₅:

S5=b5q−b1q−1..

Подставим значения b₁=2; b₅=162 и найдем результат:

S5=162(−3)−2−3−1..=−486−2−4..=−488−4..=122

Способ №2 (вторая формула).

Sn=b1(qn−1)q−1.

Для решения нам нужен первый член и знаменатель: b₁=2; q=-3. Составим формулу:

S5=b1(q5−1)q−1.

Подставим в формулу данные значения и вычислим сумму:

S5=2((−3)5−1)−3−1. .=2(−243−1)−4..=−488−4..=122

Таким образом, мы увидели, что у нас получился один и тот же результат 122 в обоих способах решения. Выбор формулы зависит от данных в условии задачи.

Определение геометрической прогрессии: формула n-го члена прогрессии

Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число. Геометрическая прогрессия обозначается b1,b2,b3, …, bn, …

Свойства геометрической прогрессии

Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.

Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. 7 = 13122.

Нужна помощь в учебе?

Предыдущая тема: Электронный учебник по геометрии: все темы школьной программы
Следующая тема:&nbsp&nbsp&nbspФормула суммы n первых членов геометрической прогрессии + примеры

Формула n-го члена геометрической прогрессии

Формула n-го члена геометрической прогрессии — штука очень простая. Как по смыслу, так и по общему виду. Но задачки на формулу n-го члена встречаются всякие — от совсем примитивных до вполне себе серьёзных. И в процессе нашего знакомства мы обязательно рассмотрим и те и другие. Ну что, знакомимся?)

Итак, для начала собственно сама формула n-го члена геометрической прогрессии.

Вот она:

b_n = b₁·qⁿ^-1

Формула как формула, ничего сверхъестественного. Выглядит даже проще и компактнее, чем аналогичная формула для арифметической прогрессии. Смысл формулы тоже прост, как валенок.

Эта формула позволяет находить ЛЮБОЙ член геометрической прогрессии ПО ЕГО НОМЕРУ «n«.

Как вы видите, по смыслу полная аналогия с арифметической прогрессией. Знаем номер n — можем посчитать и член, стоящий под этим номером. Какой хотим. Не умножая последовательно на «q» много-много раз. Вот и весь смысл.)

Я понимаю, что на данном уровне работы с прогрессиями все входящие в формулу величины вам уже должны быть понятны, но считаю своим долгом всё-таки расшифровать каждую. На всякий случай.

Итак, поехали:

b₁ — первый член геометрической прогрессии;

q — знаменатель геометрической прогрессии;

n — номер члена;

b_n — энный (n-й) член геометрической прогрессии.

Эта формулка связывает четыре главных параметра любой геометрической прогрессии — b_n, b₁, q и n. И вокруг этих четырёх ключевых фигур и вертятся все-все задачки по прогрессии.

«А как она выводится?» — слышу любопытный вопрос… Элементарно! Смотрите!

Чему равен второй член прогрессии? Не вопрос! Прямо по смыслу геометрической прогрессии пишем:

b₂ = b₁·q

А третий член? Тоже не проблема! Второй член помножаем ещё раз на q.

Вот так:

b₃ = b₂·q

Вспомним теперь, что второй член, в свою очередь, у нас равен b₁·q и подставим это выражение в наше равенство:

b₃ = b₂·q = (b₁·q)·q = b₁·q·q = b₁·q²

Получаем:

b₃ = b₁·q²

А теперь прочитаем нашу запись по-русски: третий член равен первому члену, умноженному на q во второй степени. Улавливаете? Пока нет? Хорошо, ещё один шаг.

Чему равен четвёртый член? Всё то же самое! Умножаем предыдущий (т.е. третий член) на q:

b₄ = b₃·q = (b₁·q²)·q = b₁·q²·q = b₁·q³

Итого:

b₄ = b₁·q³

И снова переводим на русский язык: четвёртый член равен первому члену, умноженному на q в третьей степени.

И так далее. Ну и как? Уловили закономерность? Да! Для любого члена с любым номером количество одинаковых множителей q (т.е. степень знаменателя) всегда будет на единичку меньше, чем номер искомого члена n.

Стало быть, наша формула будет, без вариантов:

b_n = b₁·qⁿ^-1

Вот и все дела. )

Ну что, порешаем задачки, наверное?)

Решение задач на формулу n-го члена геометрической прогрессии.

Начнём, как обычно, с прямого применения формулы. Вот типичная задачка:

В геометрической прогрессии известно, что b₁ = 512 и q = -1/2. Найдите десятый член прогрессии.

Конечно, эту задачку можно вообще безо всяких формул решить. Прямо по смыслу геометрической прогрессии. Но нам ведь с формулой n-го члена размяться нужно, правда? Вот и разминаемся.

Наши данные для применения формулы следующие.

Известен первый член. Это 512.

b₁ = 512.

Известен также знаменатель прогрессии: q = -1/2.

Остаётся только сообразить, чему равен номер члена n. Не вопрос! Нас интересует десятый член? Вот и подставляем в общую формулу десятку вместо n.

И аккуратно считаем арифметику:

Ответ: -1

Как видим, десятый член прогрессии оказался с минусом. Ничего удивительного: знаменатель прогрессии у нас -1/2, т.е. отрицательное число. А это говорит нам о том, что знаки у нашей прогрессии чередуются, да.)

Здесь всё просто. А вот похожая задачка, но немного посложнее в плане вычислений.

В геометрической прогрессии известно, что:

b₁ = 3

Найдите тринадцатый член прогрессии.

Всё то же самое, только в этот раз знаменатель прогрессии — иррациональный. Корень из двух. Ну и ничего страшного. Формула — штука универсальная, с любыми числами справляется.

Работаем прямо по формуле:

Формула, конечно, сработала как надо, но… вот тут некоторые и зависнут. Что дальше делать с корнем? Как возвести корень в двенадцатую степень?

Как-как… Надо понимать, что любая формула, конечно, дело хорошее, но знание всей предыдущей математики при этом не отменяется! Как возвести? Да свойства степеней вспомнить! Превратим корень в степень с дробным показателем и — по формуле возведения степени в степень.

Вот так:

Ответ: 192

И все дела.)

В чём состоит основная трудность при прямом применении формулы n-го члена? Да! Основная трудность — это работа со степенями! А именно — возведение в степень отрицательных чисел, дробей, корней и тому подобных конструкций. Так что те, у кого с этим проблемы, настоятельная просьба повторить степени и их свойства! Иначе и в этой теме будете тормозить, да…)

А теперь порешаем типовые задачки на поиск одного из элементов формулы, если даны все остальные. Для успешного решения таких задач рецепт един и прост до ужаса — пишем формулу n-го члена в общем виде! Прямо в тетрадке рядышком с условием. А затем из условия соображаем, что нам дано, а чего не хватает. И выражаем из формулы искомую величину. Всё!

Например, такая безобидная задачка.

Пятый член геометрической прогрессии со знаменателем 3 равен 567. Найдите первый член этой прогрессии.

Ничего сложного. Работаем прямо по заклинанию.

Пишем формулу n-го члена!

b_n = b₁·qⁿ^-1

Что нам дано? Во-первых, дан знаменатель прогрессии: q = 3.

Кроме того, нам дан пятый член: b₅ = 567.

Всё? Нет! Ещё нам дан номер n! Это — пятёрка: n = 5.

Надеюсь, вы уже понимаете, что в записи b₅ = 567 скрыты сразу два параметра — это сам пятый член (567) и его номер (5). В аналогичном уроке по арифметической прогрессии я об этом уже говорил, но и здесь считаю не лишним напомнить.)

Вот теперь подставляем наши данные в формулу:

567 = b₁·3^5-1

Считаем арифметику, упрощаем и получаем простенькое линейное уравнение:

81b₁ = 567

Решаем и получаем:

b₁ = 7

Как вы видите, с поиском первого члена проблем никаких. А вот при поиске знаменателя q и номера n могут встречаться и сюрпризы. И к ним (к сюрпризам) тоже надо быть готовым, да.)

Например, такая задачка:

Пятый член геометрической прогрессии с положительным знаменателем равен 162, а первый член этой прогрессии равен 2.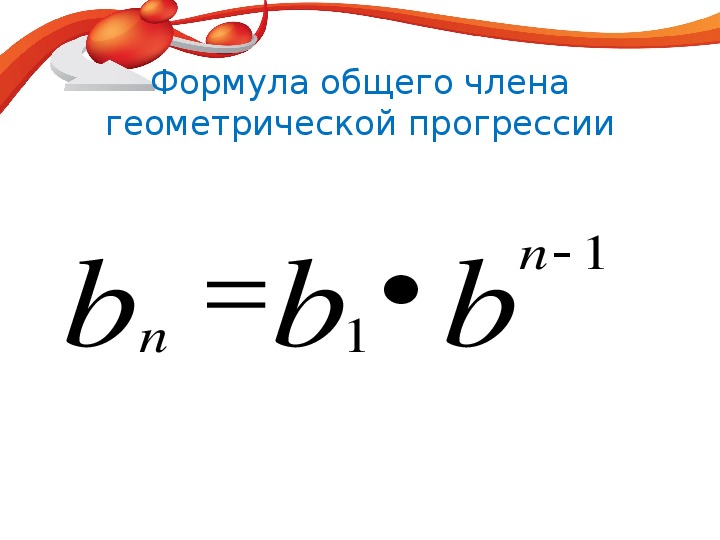 Найдите знаменатель прогрессии.

В этот раз нам даны первый и пятый члены, а найти просят знаменатель прогрессии. Вот и приступаем.

Пишем формулу n-го члена!

b_n = b₁·qⁿ^-1

Наши исходные данные будут следующими:

b₅ = 162

b₁ = 2

n = 5

Не хватает значения q. Не вопрос! Сейчас найдём.) Подставляем в формулу всё что нам известно.

Получаем:

162 = 2·q^5-1

2q⁴ = 162

q⁴ = 81

Простенькое уравнение четвёртой степени. А вот сейчас — аккуратно! На данном этапе решения многие ученики сразу же радостно извлекают корень (четвёртой степени) и получают ответ q=3.

Вот так:

q⁴ = 81

q = 3

Но вообще-то, это недоделанный ответ. Точнее, неполный. Почему? Дело в том, что ответ q = -3 тоже подходит: (-3)⁴ тоже будет 81!

Всё из-за того, что степенное уравнение xⁿ = a всегда имеет два противоположных корня при чётном n. С плюсом и с минусом:

Оба подходят.

Например, решая неполное квадратное уравнение (т.е. второй степени)

x² = 9

вы же почему-то не удивляетесь появлению двух корней x=±3? Вот и тут то же самое. И с любой другой чётной степенью (четвёртой, шестой, десятой и т.д.) будет так же. Подробности — в теме про арифметический корень n-й степени.

Поэтому правильное решение будет таким:

q⁴ = 81

q = ±3

Хорошо, со знаками разобрались. Какой же из них правильный — плюс или минус? Что ж, читаем ещё раз условие задачи в поисках дополнительной информации. Её, конечно, может и не быть, но в данной задаче такая информация имеется. У нас в условии прямым текстом сказано, что дана прогрессия с положительным знаменателем.

Поэтому ответ очевиден:

q = 3

Здесь-то всё просто. А как вы думаете, что было бы, если бы формулировка задачи была бы вот такой:

Пятый член геометрической прогрессии равен 162, а первый член этой прогрессии равен 2. Найдите знаменатель прогрессии.

В чём отличие? Да! В условии ничего не сказано про знак знаменателя. Ни прямо, ни косвенно. И вот тут задачка уже имела бы два решения!

q = 3 и q = -3

Да-да! И с плюсом и с минусом.) Математически сей факт означал бы, что существуют две прогрессии, которые подходят под условие задачи. И для каждой — свой знаменатель. Ради интереса, потренируйтесь и выпишите первые пять членов каждой из них.)

А теперь потренируемся номер члена находить. Эта задачка самая сложная, да. Но зато и более творческая.)

Дана геометрическая прогрессия:

3; 6; 12; 24; …

Под каким номером в этой прогрессии стоит число 768?

Первый шаг всё тот же: пишем формулу n-го члена!

b_n = b₁·qⁿ^-1

А теперь, как обычно, подставляем в неё известные нам данные. Гм… не подставляется! Где первый член, где знаменатель, где всё остальное?!

Где-где… А глазки нам зачем? Ресницами хлопать? В этот раз прогрессия задана нам напрямую в виде последовательности. Первый член видим? Видим! Это — тройка (b₁ = 3). А знаменатель? Пока не видим, но он очень легко считается. Если, конечно, понимать, что такое знаменатель геометрической прогрессии.

Вот и считаем. Прямо по смыслу геометрической прогрессии: берём любой её член (кроме первого) и делим на предыдущий.

Хотя бы вот так:

q = 24/12 = 2

Что ещё нам известно? Нам ещё известен некоторый член этой прогрессии, равный 768. Под каким-то номером n:

b_n = 768

Номер его нам неизвестен, но наша задача как раз и состоит в том, чтобы его отыскать.) Вот и ищем. Все необходимые данные для подстановки в формулу мы уже скачали. Незаметно для себя.)

Вот и подставляем:

768 = 3·2ⁿ^-1

Делаем элементарные тождественные преобразования — делим обе части на тройку и переписываем уравнение в привычном виде: неизвестное слева, известное — справа.

Получаем:

2ⁿ^-1 = 256

Вот такое интересное уравнение. Надо найти «n». Что, непривычно? Да, я не спорю. Вообще-то, это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное (в данном случае это — номер n) стоит в показателе степени.

На этапе знакомства с геометрической прогрессией (это девятый класс) показательные уравнения решать не учат, да… Это тема старших классов. Но страшного ничего нет. Даже если вы не в курсе, как решаются такие уравнения, попробуем найти наше n, руководствуясь простой логикой и здравым смыслом.

Начинаем рассуждать. Слева у нас стоит двойка в какой-то степени. Мы пока не знаем, что это конкретно за степень, но это и не страшно. Но зато мы твёрдо знаем, что эта степень равна 256! Вот и вспоминаем, в какой же степени двойка даёт нам 256. Вспомнили? Да! В восьмой степени!

256 = 2⁸

Если не вспомнили или с распознаванием степеней проблемы, то тоже ничего страшного: просто последовательно возводим двойку в квадрат, в куб, в четвёртую степень, пятую и так далее. Подбор, фактически, но на данном уровне — вполне прокатит.

Так или иначе, мы получим:

2ⁿ^-1 = 2⁸

А дальше что напрашивается? Правильно, просто убрать одинаковые основания (двойки) и приравнять показатели! Это можно, математика позволяет. Убираем двойки и получаем:

n-1 = 8

n = 9

Итак, 768 — это девятый член нашей прогрессии. Всё, задача решена.)

Ответ: 9

Что? Скучно? Надоела элементарщина? Согласен. И мне тоже. Шагаем на следующий уровень.)

Более сложные задачи.

А теперь решаем задачки покруче. Не то чтобы совсем уж сверхкрутые, но над которыми предстоит немного поработать, чтобы добраться до ответа.

Например, такая.

Найдите второй член геометрической прогрессии, если четвёртый её член равен -24, а седьмой член равен 192.

Это классика жанра. Известны какие-то два разных члена прогрессии, а найти надо ещё какой-то член. Причём все члены НЕ соседние. Что и смущает поначалу, да…

Как и в уроке по арифметической прогрессии, для решения таких задач рассмотрим два способа. Первый способ — универсальный. Алгебраический. Работает безотказно и с любыми исходными данными. Поэтому именно с него и начнём.)

Расписываем каждый член по формуле n-го члена!

Всё точь-в-точь как с арифметической прогрессией. Только в этот раз работаем с другой общей формулой. Вот и всё.) Но суть та же самая: берём и поочерёдно подставляем в формулу n-го члена наши исходные данные. Для каждого члена — свои.

Для четвёртого члена записываем:

b₄ = b₁·q³

-24 = b₁·q³

Есть. Одно уравнение готово.

Для седьмого члена пишем:

b₇ = b₁·q⁶

192 = b₁·q⁶

Итого получили два уравнения для одной и той же прогрессии.

Собираем из них систему:

Несмотря на её грозный вид, системка совсем простая. Самый очевидный способ решения — обычная подстановка. Выражаем b₁ из верхнего уравнения и подставляем в нижнее:

Немного повозившись с нижним уравнением (сократив степени и поделив на -24), получим:

q³ = -8

К этому же уравнению, между прочим, можно прийти и более простым путём! Каким? Сейчас я вам продемонстрирую ещё один секретный, но оч-чень красивый, мощный и полезный способ решения подобных систем. Таких систем, в уравнениях которых сидят только произведения. Хотя бы в одном. Называется метод почленного деления одного уравнения на другое.

Итак, перед нами система:

В обоих уравнениях слева — произведение, а справа — просто число. Это очень хороший знак.) Давайте возьмём и… поделим, скажем, нижнее уравнение на верхнее! Что значит, поделим одно уравнение на другое? Очень просто. Берём левую часть одного уравнения (нижнего) и делим её на левую часть другого уравнения (верхнего). С правой частью аналогично: правую часть одного уравнения делим на правую часть другого.

Весь процесс деления выглядит так:

Теперь, сократив всё, что сокращается, получим:

q³ = -8

Чем хорош этот способ? Да тем, что в процессе такого деления всё нехорошее и неудобное может благополучно сократиться и остаться вполне безобидное уравнение! Именно поэтому так важно наличие только умножения хотя бы в одном из уравнений системы. Нету умножения — нечего и сокращать, да…

А вообще, этот способ (как и многие другие нетривиальные способы решения систем) даже заслуживает отдельного урока. Обязательно его разберу поподробнее. Когда-нибудь…

Впрочем, неважно, как именно вы решаете систему, в любом случае теперь нам надо решить получившееся уравнение:

q³ = -8

Никаких проблем: извлекаем корень (кубический) и — готово!

Прошу заметить, что здесь при извлечении ставить плюс/минус не нужно. Нечётной (третьей) степени у нас корень. И ответ — тоже один, да.)

Итак, знаменатель прогрессии найден. Минус два. Отлично! Процесс идёт.)

Для первого члена (скажем, из верхнего уравнения) мы получим:

Отлично! Знаем первый член, знаем знаменатель. И теперь у нас появилась возможность найти любой член прогрессии. В том числе и второй.)

Для второго члена всё совсем просто:

b₂ = b₁·q = 3·(-2) = -6

Ответ: -6

Итак, алгебраический способ решения задачи мы с вами разложили по полочкам. Сложно? Не очень, согласен. Долго и нудно? Да, безусловно. Но иногда можно существенно сократить объём работы. Для этого есть графический способ. Старый добрый и знакомый нам по задачкам на арифметическую прогрессию.)

Рисуем задачу!

Да! Именно так. Снова изображаем нашу прогрессию на числовой оси. Не обязательно по линеечке, не обязательно выдерживать равные интервалы между членами (которые, кстати, и не будут одинаковыми, т.к. прогрессия — геометрическая!), а просто схематично рисуем нашу последовательность.

У меня получилось вот так:

А теперь смотрим на картинку и соображаем. Сколько одинаковых множителей «q» разделяют четвёртый и седьмой члены? Верно, три!

Стало быть, имеем полное право записать:

-24·q³ = 192

Отсюда теперь легко ищется q:

q³ = -8

q = -2

Вот и отлично, знаменатель у нас уже в кармане. А теперь снова смотрим на картинку: сколько таких знаменателей сидит между вторым и четвёртым членами? Два! Стало быть, для записи связи между этими членами знаменатель будем возводить в квадрат.

Вот и пишем:

b₂·q² = -24, откуда b₂ = -24/q²

Подставляем наш найденный знаменатель в выражение для b₂, считаем и получаем:

Ответ: -6

Как видим, всё гораздо проще и быстрее, чем через систему. Более того, здесь нам вообще даже не понадобилось считать первый член! Совсем.)

Вот такой простой и наглядный способ-лайт. Но есть у него и серьёзный недостаток. Догадались? Да! Он годится только для очень коротких кусочков прогрессии. Таких, где расстояния между интересующими нас членами не очень большие. А вот во всех остальных случаях картинку рисовать уже затруднительно, да… Тогда решаем задачу аналитически, через систему. ) А системы — штука универсальная. С любыми числами справляются.

Ещё одна эпичная задачка:

Второй член геометрической прогрессии на 10 больше первого, а третий член на 30 больше второго. Найдите знаменатель прогрессии.

Что, круто? Вовсе нет! Всё то же самое. Снова переводим условие задачи в чистую алгебру.

1) Расписываем каждый член по формуле n-го члена!

Второй член: b₂ = b₁·q

Третий член: b₃ = b₁·q²

2) Записываем связь между членами из условия задачи.

Читаем условие: «Второй член геометрической прогрессии на 10 больше первого». Стоп, это ценно!

Так и пишем:

b₂ = b₁+10

Читаем дальше: «…третий член на 30 больше второго».

И эту фразу переводим в чистую математику:

b₃ = b₂+30

Получили два уравнения. Объединяем их в систему:

Система на вид простенькая. Но что-то уж много различных индексов у буковок. Подставим-ка вместо второго и третьего членов их выражения через первый член и знаменатель! Зря, что ли, мы их расписывали?

Получим:

А вот такая система — уже не подарок, да… Как такое решать? К сожалению, универсального секретного заклинания на решение сложных нелинейных систем в математике нет и быть не может. Это фантастика! Но первое что должно приходить вам в голову при попытке разгрызть подобный крепкий орешек — это прикинуть, а не сводится ли одно из уравнений системы к красивому виду, позволяющему, например, легко выразить одну из переменных через другую?

Вот и прикинем. Первое уравнение системы явно проще второго. Его и подвергнем пыткам.) А не попробовать ли из первого уравнения что-то выразить через что-то? Раз уж мы хотим найти знаменатель q, то выгоднее всего нам было бы выразить b₁ через q.

Вот и попробуем проделать эту процедуру с первым уравнением, применяя старые добрые тождественные преобразования:

b₁q = b₁+10

b₁q — b₁ = 10

b₁(q-1) = 10

Всё! Вот мы и выразили ненужную нам переменную (b₁) через нужную (q). Да, не самое простое выражение получили. Дробь какую-то… Но и система у нас приличного уровня, да.)

А дальше дело техники. Обычный метод подстановки. Подставляем наше полученное выражение для b₁ в нижнее уравнение:

Типичное дробно-рациональное уравнение. Что делать — знаем.

Пишем ОДЗ (обязательно!):

q ≠ 1

Умножаем всё на знаменатель (q-1) и сокращаем все дроби:

10q² = 10q + 30(q-1)

Делим всё на десятку, раскрываем скобки, собираем всё слева:

q² — 4q + 3 = 0

Решаем получившееся квадратное уравнение и получаем два корня:

q₁ = 1

q₂ = 3

И что дальше? И какой из корней нам выбрать? Так, стоп! Чего же я туплю-то? А ОДЗ зачем мы выписывали? Для красоты?) Единица никак не катит! В отвал единицу!

Окончательный ответ один: q = 3.

Ответ: 3

Как вы видите, путь решения большинства задач на формулу n-го члена геометрической прогрессии всегда един: читаем внимательно условие задачи и с помощью формулы n-го члена переводим всю полезную информацию в чистую алгебру.

А именно:

1) Расписываем отдельно каждый данный в задаче член по формуле n-го члена.

2) Из условия задачи переводим связь между членами в математическую форму. Составляем уравнение или систему уравнений.

3) Решаем полученное уравнение или систему уравнений, находим неизвестные параметры прогрессии.

4) В случае неоднозначного ответа читаем внимательно условие задачи в поисках дополнительной информации (если таковая присутствует). Также сверяем полученный ответ с условиями ОДЗ (если таковые имеются).

А теперь перечислим основные проблемы, наиболее часто приводящие к ошибкам в процессе решения задач на геометрическую прогрессию.

1. Элементарная арифметика. Действия с дробями и отрицательными числами.

2. Действия со степенями и действия с корнями. Возведение в степень дробей, корней, отрицательных чисел. Извлечение корней n-й степени при решении уравнений.

3. Решение уравнений и (особенно!) систем уравнений. Тождественные преобразования уравнений.

Если хотя бы с одним из этих трёх пунктов проблемы, то неизбежно будете ошибаться и в этой теме. К сожалению… Так что не ленитесь и повторите то о чём упомянуто выше. И по ссылочкам — сходите. Иногда помогает.)

Видоизменённые и рекуррентные формулы.

А теперь рассмотрим парочку типичных экзаменационных задачек с менее привычной подачей условия. Да-да, вы угадали! Это видоизменённые и рекуррентные формулы n-го члена. С такими формулами мы уже с вами сталкивались и работали в соответствующем уроке по арифметической прогрессии. Здесь всё аналогично. Суть та же.

Например, такая задачка из ОГЭ:

Геометрическая прогрессия задана формулой b_n = 3·2ⁿ. Найдите сумму первого и четвёртого её членов.

В этот раз прогрессия нам задана не совсем привычно. В виде какой-то формулы. Ну и что? Эта формула — тоже формула n-го члена! Мы же с вами знаем, что формулу n-го члена можно записать как в общем виде, через буквы, так и для конкретной прогрессии. С конкретными первым членом и знаменателем.

В нашем случае нам, на самом деле, задана формула общего члена для геометрической прогрессии вот с такими параметрами:

b₁ = 6

q = 2

Проверим?) Запишем формулу n-го члена в общем виде и подставим в неё b₁ и q. Получим:

b_n = b₁·qⁿ^-1

b_n = 6·2ⁿ^-1

Упрощаем, используя разложение на множители и свойства степеней, и получаем:

b_n = 6·2ⁿ^-1 = 3·2·2ⁿ^-1 = 3·2ⁿ^-1+1 = 3·2ⁿ

Как видите, всё честно. Но наша с вами цель — не продемонстрировать вывод конкретной формулы. Это так, лирическое отступление. Чисто для понимания.) Наша цель — решить задачу по той формуле, что дана нам в условии. Улавливаете?) Вот и работаем с видоизменённой формулой напрямую.

Считаем первый член. Подставляем n=1 в общую формулу:

b₁ = 3·2¹ = 3·2 = 6

Вот так. Кстати, не поленюсь и ещё раз обращу ваше внимание на типовой ляп с подсчётом первого члена. НЕ НАДО, глядя на формулу b_n = 3·2ⁿ, сразу бросаться писать, что первый член — тройка! Это — грубейшая ошибка, да…)

Продолжаем. Подставляем n=4 и считаем четвёртый член:

b₄ = 3·2⁴ = 3·16 = 48

Ну и наконец, считаем требуемую сумму:

b₁ + b₄ = 6+48 = 54

Ответ: 54

Ещё задачка.

Геометрическая прогрессия задана условиями:

b₁ = -7;

b_n₊₁ = 3b_n

Найдите четвёртый член прогрессии.

Здесь прогрессия задана рекуррентной формулой. Ну и ладно.) Как работать с такой формулой — тоже знаем.

Вот и действуем. По шагам.

1) Считаем два последовательных члена прогрессии.

Первый член нам уже задан. Минус семь. А вот следующий, второй член, легко можно посчитать по рекуррентной формуле. Если понимать принцип её работы, конечно.)

Вот и считаем второй член по известному первому:

b₂ = 3b₁ = 3·(-7) = -21

2) Считаем знаменатель прогрессии

Тоже никаких проблем. Прямо по смыслу геометрической прогрессии, делим второй член на первый.

Получаем:

q = -21/(-7) = 3

3) Пишем формулу n-го члена в привычном виде и считаем нужный член.

Итак, первый член знаем, знаменатель — тоже. Вот и пишем:

b_n = -7·3ⁿ^-1

Осталось лишь посчитать четвёртый член:

b₄ = -7·3³ = -7·27 = -189

Ответ: -189

Как вы видите, работа с такими формулами для геометрической прогрессии ничем по своей сути не отличается от таковой для прогрессии арифметической. Важно лишь понимать общую суть и смысл этих формул. Ну и смысл геометрической прогрессии тоже надо понимать, да.) И тогда глупых ошибок не будет.

Ну что, порешаем самостоятельно?)

Совсем элементарные задачки, для разминки:

1. Дана геометрическая прогрессия, в которой b₁ = 243, а q = -2/3. Найдите шестой член прогрессии.

2. Общий член геометрической прогрессии задан формулой b_n = 5∙2ⁿ⁺¹. Найдите номер последнего трёхзначного члена этой прогрессии.

3. Геометрическая прогрессия задана условиями:

b₁ = -3;

b_n₊₁ = 6b_n

Найдите пятый член прогрессии.

Чуть посложнее:

4. Дана геометрическая прогрессия:

b₁=2048; q=-0,5

Чему равен шестой отрицательный её член?

Что, кажется суперсложно? Вовсе нет. Спасёт логика и понимание смысла геометрической прогрессии. Ну и формула n-го члена, само собой.

5. Третий член геометрической прогрессии равен -14, а восьмой член равен 112. Найдите знаменатель прогрессии.

6. Сумма первого и второго членов геометрической прогрессии равна 75, а сумма второго и третьего членов равна 150. Найдите шестой член прогрессии.

Ответы (в беспорядке): 6; -3888; -1; 800; -32; 448.

Вот почти и всё. Осталось лишь научиться нам считать сумму n первых членов геометрической прогрессии да открыть для себя бесконечно убывающую геометрическую прогрессию и её сумму. Очень интересную и необычную штуку, между прочим! Об этом — в следующих уроках.)

Прогрессия геометрическая — Энциклопедия по экономике

Читатель найдет здесь доступное описание основных экономико-математических методов, построенных как на традиционном аппарате математики и логики, известном из школьных программ (дроби, проценты, уравнения, прогрессии, геометрические и логические задачи), так и на основе методов исследования операций — современном математическом аппарате, специально созданном для решения тех задач, с которыми элементарная математика не справляется. Это методы оптимизации (линейное, нелинейное и динамическое программирование), теория вероятностей и математическая статистика, теория массового обслуживания (теория очередей), метод статистических испытаний (Монте-Карло), теория игр и статистических решений, сетевое планирование. [c.6]

Геометрическая прогрессия. Геометрической прогрессией называется последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число q. Число q называется знаменателем геометрической прогрессии. [c.52]

Сумма членов геометрической прогрессии [c.113]

К. к. представляет собой сумму членов геометрической прогрессии, где членом прогрессии является коэффициент изменения добычи, и определяется по формуле [c.16]

Сумма этой геометрической прогрессии составляет [c.182]

В данном случае мы имеем дело с геометрической прогрессией, поэтому применив известную из курса математики формулу суммы членов геометрической прогрессии, мы получаем выражение для будущей стоимости обычного n-периодного аннуитета [c.314]

Применив формулу суммы геометрической прогрессии, получаем [c.314]

Применив к этому выражению формулу суммы членов геометрической прогрессии, получаем искомое выражение для текущей стоимости аннуитета [c. 321]

Если члены аннуитета изменяются в соответствии с некоторыми законами (в частности, образуют арифметическую или геометрическую прогрессию), то общие формулы для определения будущей или приведенной стоимости аннуитета можно упростить. [c.293]

Оценка переменного аннуитета постнумерандо, платежи которого образуют геометрическую прогрессию а) будущая стоимость аннуитета [c.339]

Наращение по сложным процентам описывается геометрической прогрессией. Множитель наращения будет выглядеть как (1 + /). Наращенная сумма исчисляется по алгоритму [c.58]

Следует заметить, что этот коэффициент представляет собой сумму членов геометрической прогрессии, где первый член равен [c.91]

Практика уплаты процентов основывается на теории наращивания денежных средств по арифметической или геометрической прогрессии. Арифметическая прогрессия соответствует простым процентам, геометрическая — сложным, т.е. в зависимости от того, что является базой для начисления — переменная или постоянная величина — проценты также делятся на [c. 72]

Наращенные отдельные платежи РМТ, PMT( +i)1, PMT(l+i)2 представляют собой геометрическую прогрессию с первым членом R и множителем прогрессии (1 +/). Поэтому искомая сумма как сумма геометрической прогрессии для случая т=1, Р- равна [c.95]

Дисконтированные отдельные платежи РМТ( + г)»1, РМТ (1+1) 1У РМТ(( + г)»1)3 представляют собой геометрическую прогрессию с первым членом РМТ( + i) l и знаменателем (1 +/)» Ее сумма имеет вид [c.99]

В этом случае формула (11.16) трансформируется в формулу суммы членов бесконечно убывающей геометрической прогрессии, поэтому [c.460]

Неравные интервалы применяются в статистике, когда значения признака варьируют неравномерно и в значительных размерах, что характерно для большинства социально-экономических явлений, особенно при анализе макроэкономических показателей. Неравные интервалы могут быть прогрессивно возрастающими или убывающими в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом [c. 29]

В геометрической прогрессии величина интервалов исчисляется по формуле [c.29]

Если количество подчиненных увеличивается в арифметической прогрессии, то число потенциально возможных межличностных отношений между руководителем и подчиненными возрастает в геометрической прогрессии. Это происходит по той причине, что руководитель имеет дело с тремя типами межличностных контактов прямые двусторонние прямые множественные комбинация тех и других. Первые — это отношения между руководителем и конкретным подчиненным. Вторые — это отношения руководителя с двумя или более подчиненными. Третьи — это отношения между подчиненными. [c.315]

Можно автоматически заполнять большие блоки ячеек числами, значение которых подчиняется арифметической или геометрической прогрессии. Для значений типа дат можно создавать прогрессии с определенной периодичностью и шагом по месяцам, годам, рабочим дням и т. п. Команда меню Правка > Заполнить > Прогрессия выводит диалоговое окно Прогрессия для ввода параметров (рис. 5.22). [c.370]

Параметры диалогового окна заполняются с учетом типа прогрессии. Для числовых величин выбирается арифметическая или геометрическая прогрессия, задается шаг приращения либо указывается автоматическое определение шага. Для дат выбирается единица периодичности (день, рабочий день, месяц, год), шаг. Можно указать предельное значение ряда. [c.370]

Для числового ряда указывается Тип прогрессии (арифметическая, геометрическая), Шаг, Предельное значение. [c.371]

Модель (8.32) называется моделью с распределением Койка лаговых объясняющих переменных. Ее еще иногда называют моделью с геометрическим распределением, имея в виду, что коэффициенты при лаговых переменных образуют геометрическую прогрессию со знаменателем yi (напомним, что yjПреобразование модели (8.15) к виду (8.32) называется обратным преобразованием Койка. [c.203]

Отметим также следующее обстоятельство. Если остатки ряда модели подчинены процессу скользящей средней, уравнение с нормально распределенными ошибками будет содержать бесконечное число лагов переменной Y. Коэффициенты при них убывают в геометрической прогрессии, и можно ограничиться несколькими первыми членами. В этом случае метод максимального правдоподобия практически равносилен нелинейному методу наименьших квадратов. [c.205]

Мы снова можем вывести это, используя те же принципы. Нам необходимо вычислить сумму бесконечной геометрической прогрессии [c.35]

Обеспечьте максимально возможный доступ к вашей BBS. Ваша аудитория расширится в геометрической прогрессии, если вы обеспечите шлюз в Интернет из вашей BBS. Стоимость этой акции невелика, если учесть размер аудитории, которую вы получите. [c.284]

Такие доводы достаточно очевидно демонстрируют недостатки линейной функциональной структуры (при увеличении п выпуск падает в геометрической прогрессии, т.к. [c.182]

Когда-то, еще на заре восходящего капитализма, в таком снижении рождаемости его идеологи, наверно, не усмотрели бы никакой опасности. Как известно, эти идеологи, наоборот, в качестве подлинного социального пугала выдвинули иную опасность, кроющуюся якобы в чрезмерной плодовитости населения. Ведь именно тогда, в 1798 г., был впервые провозглашен Мальтусом пресловутый закон народонаселения, состоящий в постоянном стремлении, свойственном всем живым существам, размножаться быстрее, чем это допускается находящимся в их распоряжении количеством пищи . Этот закон утверждается Мальтусом как вечный и непреложный закон естества, действующий во все время и прж всевозможных условиях, в которых жил или продолжает жить человек . Мы можем,— формулировал свой закон Мальтус,— считать несомненным, что если размножение населения не встречает никакого препятствия, то оно удваивается каждые 25 лет ж возрастает в геометрической прогрессии , в то время как средства существования при самых благоприятных условиях для труда ни в каком случае не могут возрастать быстрее, чем в арифметической прогрессии 2. [c.126]

Тенденция геометрического роста населения предполагает постоянный коэффициент рождаемости, что при ограничении этого роста населения арифметической прогрессией средств существования означает соответствующее снижение естественного прироста за счет возрастания коэффициента смертности. Говоря иначе, весь избыток рождений сверх нормы, укладывающейся в рамки арифметической прогрессии, обрекается законом Мальтуса на вымирание. Всякому, кому не посчастливилось уже родиться [c.126]

Однако теория Мальтуса, как известно, самым блестящим образом — и притом по всем пунктам — окончательно провалилась. При Мальтусе, в 1800 г., население Англии составляло 16,2 млн. человек геометрическая прогрессия удвоения через каждые 25 лет дала бы к 1950 г. при нормальной смертности свыше 1 млрд. душ, арифметическая за счет повышения смертности дала бы 113,4 млн., а фактически, несмотря на резкое снижение смертности, население Соединенного королевства к 1950 г. едва достигло 50 млн. душ, А между тем Англия 1950 г. не беднее, а богаче Англии 1800 г. из расчета на душу населения. Оказалось, что именно средства существования в наше время способны возрастать много быстрее, чем население. Их относительное перепроизводство в капиталистическом мире то и дело достигает таких масштабов, что в порядке борьбы с кризисами перепроизводства буржуазия очень ревностно добивается резкого сокращения посевных площадей и продуктивного животноводства, а уже готовые продукты литания во избежание снижения на них рыночных цен целыми горами сжигаются или выбрасываются в море. И тем не менее, несмотря на столь явное, казалось бы, перепроизводство средств существования, в динамике населения капиталистических стран не только не выявляется никаких тенденций к геометрическим темпам роста, но, более того, здесь не приходится уже говорить даже об арифметической прогрессии. Следует же здесь говорить только разве о прямой регрессии ряда ежегодных приростов населения и о столь существенном их сокращении, при котором далеко не всегда обеспечивается даже простое его воспроизводство. И это несмотря на повсеместное — вопреки предпосылкам теории Мальтуса — сокращение смертности. Ежегодные приросты населения падают при этом, несмотря на сокращение смертности потому, что еще быстрее падают тоже наперекор основной предпосылке Мальтуса коэффициенты рождаемости во всех странах, И в этом теперь основной гвоздь проблемы. [c.127]

Одним из важнейших направлений конструкторской унификации является сокращение номенклатуры изделий, имеющих одинаковое или сходное эксплуатационное назначение. Оно реализуется в первую очередь путем создания параметрических рядов (гамм) изделий. Каждый ряд представляет собой совокупность изделий, аналогичных по кинематике, рабочему процессу, но различных по габаритным, мощностным или другим основным эксплуатационным параметрам (грузоподъемность грузового автомобиля или крана, рабочий объем двигателя, производительность компрессора и т. д.). Параметрический ряд, как правило, создается в соответствии с ГОСТ 8032—84 Предпочтительные числа и ряды предпочтительных чисел . Обычно пользуются четырьмя десятичными рядами R5 RIO , R20 R40 с соответствующими знаменателями геометрической прогрессии 1,6 1,25 1,12 1,06. Расчет параметрических рядов для выбора экономически рационального разрежения ряда производится по Типовым методикам оптимизации параметрического (типоразмерного) ряда и соответствующей типовой методике для многомерных рядов. Имеются экономико-математические модели их оптимизации, основанные как на классических методах в условиях непрерывности и дифференцируемости функции затрат и функции спроса и наличии экстремума общих затрат, так и неклассических методах оптимизации, разработанных, в частности, Институтом математики Сибирского отделения АН СССР. Параметрические ряды формируют в каждой отрасли перспективный типаж изделий, что весьма ограничивает их возможную номенклатуру. [c.107]

Чем выше значение коэффициента использования материала (Лим 1), тем при прочих равных условиях технологичнее данная конструкция, тем ниже ее себестоимость. Средние коэффициенты использования черных металлов в различных отраслях в среднем составляют в автомобилестроении — 0,68, тракторном и сельскохозяйственном машиностроении — 0,75, тяжелом, энергетическом и транспортном машиностроении — 0,79, электротехнической промышленности — 0,65, станкоинструмен-тальной промышленности — 0,69. Как видно из приведенных данных, коэффициенты использования материалов в настоящее время намного ниже единицы. Правильный выбор процесса формообразования деталей, сближение геометрических форм и размеров заготовки с размерами готовой детали является одним из главных тенденций технического прогресса в машиностроении. [c.124]

Группировка называется простой (монотетической), если для ее построения используется один группировочный признак. Если группировка проводится по нескольким признакам, она называется сложной (политетической). Обычно такая группировка проводится как комбинационная, т.е. группы, выделенные по одному признаку, подразделяются на подгруппы по другому признаку. Казалось бы, этот метод выделения групп должен быть лучше простой группировки -ведь трудно ожидать, что различия между группами можно уловить лишь на основе одного признака. Однако комбинация признаков приводит к дроблению совокупности в геометрической прогрессии число групп будет равно произведению числа группировочных признаков (/) на число выделенных категорий по каждому из них (т) k = / т. Данные становятся труднообозримыми, группы включают малое число единиц, групповые показатели становятся ненадежными. [c.119]

Хотя число финансовых коэффициентов, которые могли бы быть рассчитаны, растет в геометрической прогрессии по мере прибавления исходной информации, в этой главе будут рассмотрены только основные из них, поскольку на практике оказывается достаточным использование относительно небольшого числа показателей для того, чтобы верно оценить финансовое положение компании. Расчет же дополнительных показателей не только излишне усложняет, но и вносит порядочную путаницу в анализ. Рассматриваемые в этой главе показатели будут для иллюстрации рассчитываться на основании данных баланса и отчета о прибылях и убытках Aldine Manufa turing ompany, приведенных в табл. 6.1 и 6.2. [c.142]

Заметим, что переменные X не коррелируют с ошибками Е, так что, применив обратное преобразование Койка, мы решили проблему коррелированности регрессоров со случайными членами. Однако применение обычного метода наименьших квадратов к модели (8.32) оказывается на практике невозможным из-за бесконечно большого количества регрессоров. Разумеется, в силу того, что коэффициенты входящего в модель ряда убывают в геометрической прогрессии, и, стало быть, сам ряд быстро сходится, можно было бы ограничиться сравнительно небольшим числом лагов. Однако и в этом случае мы столкнулись бы по крайней мере с двумя трудно решаемыми проблемами. Во-первых, возникла бы сильная мультиколлинеарность, так как естественно ожидать, что лаговые переменные сильно коррели-рованы. Во-вторых, уравнение оказалось бы неидентифицируемым. В модели на самом деле присутствует всего четыре параметра. Между тем как, взяв всего лишь три лага, мы бы получили оценки пяти параметров. [c.203]

Нам необходимо вычислить сумму бесконечной геометрической прогрессии PV=a( +x+x3+. ..), гдеа = С/(1 + г), a x = ( +g)/( + r). Всноске4мы показали,что сумма такой профессии равна а/( — х). Подставим а и х в формулу и найдем, что [c.34]

Разделив все анкеты по среднему уровню одаренности на группы, отличающиеся друг от друга всего на долбалла, ж приняв численность наиболее многолюдной группы за 100, мы видим, что такие группы занимают центральное положение по среднему баллу одаренности. Численность же всех остальных групп, стоящих выше или ниже этого уровня одаренности, быстро падает. При этом повышение или понижение этого уровня в арифметической прогрессии всего на десятки процентов сопровождается сокращением численности соответствующей группы в геометрической прогрессии в десятки раз. [c.96]

Имея в виду теснейшую взаимную связь всех технических и экономических моментов общественно-производственного процесса, можно бы избрать для наблюдения в качестве показателя общей дипамики какой-нибудь один наиболее простой из этих моментов. Так, например, известны очень любопытные попытки принять за меру технического прогресса в целом темпы роста числа изобретений, патентуемых ежегодно в данной стране (Л. К. Мартене). При этом допущении нетрудно статистически установить для всех стран, имеющих патентное бюро, что число изобретений возрастает в них за последние два века в геометрической прогрессии. Можно установить и сравнительные темны этого роста. Они как будто представляют собой за последнее время довольно постоянную величину для каждой страны в отдельности, но довольно различную для разных стран. По имеющимся расчетам этого рода, уровень мировой техники возрастает за каждое десятилетие процентов на 20, достигая для СШЛ прироста в 33%, для Германии и довоенной России — 29, для Японии — 27, для Англии — 19, для Франции — 12%. [c.410]

Правда, Л. Н. Крицман имеет в виду не начальную эпоху капитализма, в последние полвека, т. е. период его полного расцвета ж даже отчасти начало его дряхлости и загнивания. Говоря о капитализме, что его историческое призвание — безудержное, измеряемое в геометрической прогрессии развитие производительности человеческого труда , Маркс предвидел также и такие условия, в которых капитализм изменяет этому призванию , тем самым доказывая, что он дряхлеет и все более и более изживает себя 8. И все же такой низкий прирост — за цельте полвека всего на 50%,—о котором говорит Л. Н, Крицмаи, является совершенно неправдоподобным. [c.412]

Показательная кривая первого порядка (y = aqx) характеризует процесс непрерывного возрастания с постоянным коэффициентом роста, т. е. по формуле геометрической прогрессии. Некоторые экономические показатели могут расти по такому закону, в особенности связанные прямо или косвенно с ростом населения, а поэтому в целях сравнительного анализа мы обобщили ряд народного дохода и по кривой такого типа, а также попытались выравнять этот ряд и по показательной кривой 2-го порядка. [c.127]

Конспект урока по геометрии «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии» 9 класс

Цели урока:

Образовательная: формирование понятия геометрической прогрессии, умений работать с формулой nго члена геометрической прогрессии, сформировать навыки применения формулы при выполнении упражнений;

Развивающая: продолжить развитие математического мышления, умений применять ранее изученный материал о последовательностях, развивать интеллектуальные умения: сравнивать, делать выводы, выявлять закономерности, анализировать;

Воспитательная: воспитание правильного отношения к своему здоровью, внимания, чувства ответственности и общематематической культуры.

Тип урока: объяснение нового материала.

Формы работы: фронтальная, индивидуальная, самостоятельная

Методы контроля: устный

План урока

I Организационный момент

II Повторение пройденного материала. Подготовка к изучению нового материала

III Изучение нового материала

IV Физ.минутка

V Закрепление учебного материала

VI Задание на дом

VII Рефлексия. Подведение итогов урока

Оборудование: компьютер, интерактивная доска, презентация «Геометрическая прогрессия», учебник «Алгебра 9» , Мордкович А.Г.

I Организационный момент.(2 мин)

Цель: проверить готовность учащихся и кабинета к работе, выявить отсутствующих; создать положительный настрой учащихся к работе.

Метод : беседа

Здравствуйте, ребята! Садитесь. Проверьте, пожалуйста, наличие у вас учебника, тетради, ручки, дневника. Дежурный , сообщите об отсутствующих.

Ребята! Французский писатель Анатоль Франс однажды заметил «Учиться можно только весело…чтобы переваривать знания, надо поглощать их с аппетитом» Так давайте, сегодня, на уроке будем следовать совету писателя. Будем внимательны, активны , будем поглощать знания с желанием, ведь они пригодятся вам в дальнейшей жизни.

— Какую тему мы изучали с вами на прошлых уроках? ( арифметическая прогрессия)

-Повторим определение (называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом , которое называется разностью d).

— Что ещё знаем и умеем находить для арифметической прогрессии? (d, n-й член, сумму n-первых членов)

Из сказанного сформулируем девиз сегодняшнего урока

« Прогрессио – движение вперёд!»

Ход урока

II.Повторение пройденного материала. Подготовка к изучению нового материала.

Цель: актуализировать знания учащихся, которые необходимы для сознательного восприятия нового материала; организовать фронтальную деятельность класса; развивать быстроту реакций, математическое мышление, умение правильно понимать вопрос.

Задачи учителя: предложить и решить примеры, с помощью которых учащимся будет легче воспринимать новый материал.

Форма работы: устная, фронтальная, индивидуальная.

Найдите значение выражения: 2ⁿ , при n= 1, 2, 3, 4,…, составьте последовательность

Ответы : 2,4,8, 16 ….

а) Найдите три первых члена последовательности, заданной условиями:

с₁ = 10, с_n₊₁= 5 с_n_.

б) Чему равно значение выражения: ;

в) Назовите член последовательности, который следует за C₅ ; С_n_;С_n₊₁?

г) Назовите член последовательности, который предшествует С₅ ;С_n₊₁;С_n_-2?

3. а) Вставьте в числовую последовательность число вместо вопросительного знака: 1. 7;?; 13; 16;

2. 5; 15; 25;?;

3. 4; 8;?; 32;

б) Выявите закономерность, которой подчиняются числа в каждой последовательности?

III Изучение нового материала.

Цель: познакомить учащихся с определением геометрической прогрессии и формулой n–го члена геометрической прогрессии; формировать умения и навыки распознавать геометрическую прогрессию и применять формулу n – го члена при выполнении упражнений.

Задачи учителя: создать условия для восприятия учащимися новых понятий изучаемого материала; добиваться усвоения методов воспроизведения изучаемого материала; отрабатывать умения; делать выводы.

Метод: проблемно-исследовательский.

Форма работы: письменная, устная работа, работа с учебником.

На доске записана последовательность 4; 8; 16; 32;

— Посмотрите, ребята, на данную последовательность, что вы про неё можете сказать?

— В дальнейшем все последовательности чисел, для которых, устанавливается нами открытая закономерность, будем называть геометрической прогрессией.

Итак, тема сегодняшнего урока «Геометрическая прогрессия. Формула n-го члена геометрической прогрессии».

Давайте вместе аналогично определению арифметической прогрессии попробуем дать определение геометрической прогрессии :

называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго равен предыдущему члену, умноженному на одно и то же число.

b_n_{+1 =}b_nq

где b_n_≠ 0, q – некоторое число.

— Ребята, запишите данную формулу в тетрадь и выразите q из формулы. q – будем называть знаменателем геометрической прогрессии.

Запомните! q0.

Вывод формулы n-го члена геометрической прогрессии.

(у доски будет работать ученик)

Цель: показать непосредственное следствие формулы n- го члена геометрической прогрессии из её определения.

b_n= b₁qⁿ^-1

Пример 2.

а) В геометрической прогрессии b₁ = 12, q = . Найти b_4.

б) В геометрической прогрессии b₁ = -2, q=3. Найти b₅.

— Что нам известно?

— Что надо найти?

— Какую формулу будем использовать?

Решение:

а) b₄= b₁q³ = 12 )³ =)³ = =

б) b₅ = b₁q⁴ = -2 3⁴ = -2 81= — 162(самостоятельно)

3. Сообщение о показательной функции.

Если b_n= b₁qⁿ^-1 = b₁qⁿ: q; b_n = qⁿпри m = , получим ; b_n = m qⁿ

Т.к. n – находится в показателе , то функцию вида ; у = m q^хназывают показательной, т.е. геометрическую прогрессию можно рассматривать как показательную на множестве N.

Применение показательной функции в природе.

В жизни нередко приходится встречаться с такими фактами, когда скорость

изменения какой-либо величины пропорциональна самой величине (размножение

бактерий, ход химической реакции и т. д.). В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид: y= у₀а^х

По закону показательной функции размножалось бы все живое на Земле, если

бы для этого имелись благоприятные условия, то есть не было естественных врагов

и было вдоволь пищи.

В природе, технике и экономике встречаются многочисленные процессы, в

ходе которых значение величины меняется в одно и то же число раз, то есть по

закону показательной функции. Эти процессы называются процессами

органического роста или органического затухания. Например, рост бактерий в

идеальных условиях соответствует процессу органического роста; радиоактивный

распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в Сберегательном банке, восстановление гемоглобина в крови, донора или раненого, потерявшего много крови, рост дрожжей, ферментов, микроорганизмов.

В природе и технике часто можно наблюдать процессы, которые подчиняются

законам выравнивания, описываемым показательной функцией. Например,

температура чайника изменяется со временем .Процессы выравнивания также можно наблюдать при включении и выключении электрического тока в цепи при падении тел в воздухе с парашютом. В биологии процесс выравнивания встречается при разрушении адреналина в крови; о работе

почек судят по их способности выводить радиоактивные вещества, количество

которых уменьшается по показательному закону.

Вы все слышали о цепных реакциях, теорию которых в 20-ых годах описал

молодой химик Н.Н.Семенов, а потом развили ученые-атомщики. Как управлять

этим процессом в мирных целях? На этот вопрос можно ответить только при

помощи знаний о показательной функции.

При прохождении света через мутную среду каждый слой этой среды

поглощает строго определенную часть падающего на него света.

Подобный же закон будет характеризовать процесс поглощения газа соответствующей средой, изменение скорости ветра и т.п.

Как видите во всех приведенных выше исследованиях использовалась

показательная функция.

IV. Физ.минутка

Цель: восстановление работоспособности учащихся, воспитание правильного отношения к своему здоровью.

— А сейчас немного отдохнём.

В весенний период идёт распространение вируса ГРИППА, ОРВИ . Недаром в народе говорят, что инфекция распространяется с геометрической прогрессией. Есть много различных способов профилактики и лечения ОРЗ.

— Какие профилактические мероприятия вы проводите?

Раз — подняться, подтянуться

Два — согнуться, разогнуться

Три — в ладоши три хлопка, головою три кивка.

На четыре — ноги шире.

Пять — руками помахать

Шесть — за стол тихонько сесть.

V. Закрепление учебного материала

Цель: закрепить и проверить практическое применение геометрической прогрессии при решении примеров и теста.

Задачи учителя: выработать умения применять новые знания, создать условия для понимания нового материала и правильного воспроизведения.

Метод: комбинированный.

Форма работы: письменная, практическая.

1.Повторение курса 9 класса.

Методы решения систем № 514 ( стр 107) Ответ:0,5 и 72

Решение упражнений из открытого банка ФИПИ.

В этом году вам предстоит пройти ГИА . Предлагаю выполнить несколько упражнений, которые позволят подготовиться к экзамену.

Взаимопроверка. Критерии оценивания:

3упр. – оценка «5»

2упр.– оценка «4»

1 упр. – оценка «3»

0 упр. – оценка «2».

Ф.И._________________________

I вариант

№ 1.Из последовательностей выбрать геометрическую прогрессию:

1. 3;6;9;…

2. 3; 9; 27;

3. 7; 12; 33;…

4. -8; -11; -34;…

№ 2. Найти b₄ геометрической прогрессии b_n=

Ответ:

№ 3. Сколько отрицательных членов данной последовательности

с_n= n²– 16 ?

Ответ:

Ф.И.____________________

II вариант

№ 1.Из последовательностей выбрать геометрическую прогрессию:

1. 10; 14; 18;…

2. 4; 13; 24;…

3. —3; -6; -9; …

4. 4; 16;64;…

№ 2. Найти b₃ геометрической прогрессии b_n=

Ответ:

№ 3. Сколько положительных членов данной последовательности

с_n= 25 — n² ?

Ответ:

Существует древняя история, а вместе с ней и задача, про шахматную доску. Однажды создатель шахмат показал правителю страны свое изобретение. А правителю настолько понравилось, что он разрешил мудрецу попросить для себя любую награду. Тот попросил заплатить за первую клетку доски 1 зерно пшеницы (или риса), за вторую — 2, и так далее: за каждую клетку вдвое больше предыдущей. Правитель быстро согласился, но через некоторое время узнал, что не может расплатиться с изобретателем…

И не удивительно, ведь уже подсчитано, что сумма данной геометрической прогрессии составляет 18 446 744 073 709 551 615 зерен.( 20-значное число). Это примерно в 1800 раз больше, чем в мире собирают за год, это даже больше, чем весь урожай, собранный за всю историю человечества!

Что нужно знать для определения количества зёрен? Сумма n-первых членов геометрической прогрессии.

Изучим её на следующем уроке.

VI Задание на дом

Цель: проверить усвоение материала урока.

Задачи учителя: сообщить домашнее задание, разъяснить методику его выполнения.

Форма работы: индивидуальная, дифференцированная.

Задание на дом. П. 16, п.5-повторение

«3» №476 (б), 484(б)

«4» №495(б)

«5» №512

VII Рефлексия. Подведение итогов урока

Цель: подведение итогов урока, развитие у учащихся навыков самоконтроля.

Задача учителя: дать оценку успешности достижения цели и наметить перспективу на будущее.

— Что нового мы узнали на уроке?

Мне хочется вернуться к нашему девизу «Прогрессио – движение вперёд!

Учащимся предлагается поставить на значок + на линии в том месте, которое отражает их отношение к занятию и степень участия в уроке:

1. Я считаю, что занятие было интересным___________________скучным.

2.Я научился многому ______________________малому.

3. Я думаю, что слушал других внимательно__________________невнимательно.

4. Я принимал участие в дискуссии часто________________________редко.

5. Результатами своей работы на уроке я доволен_________________не доволен.

Как вы думаете, а мы сегодня добились прогресса?

В чём заключается наш прогресс?

(Оценки за урок)

Всего вам хорошего! Спасибо за урок!

Сумма геометрической прогрессии | Онлайн калькулятор

Сумма геометрической прогрессии имеет несколько различных представлений, которые зависят от знаменателя прогрессии. Для возрастающей положительной, отрицательной или знакочередующейся прогрессии имеет место исключительно сумма нескольких первых членов геометрической прогрессии, количество которых должно быть ограничено, так как сама последовательность будет бесконечной.

Для прогрессии, знаменатель которой заключен между нулем и единицей, то есть является правильной дробью (0, сумма всей последовательности будет вполне однозначным конкретным числом, так как весь числовой ряд будет убывающим. Сумма бесконечно убывающей геометрической прогрессии имеет свою отдельную формулу, которую можно найти в соответствующем разделе, вместе с калькулятором.

Чтобы найти сумму первых членов геометрической прогрессии, необходимо знать первый член и знаменатель прогрессии. Если по условиям задачи дан какой-либо другой член прогрессии, кроме первого, тогда нужно будет сначала воспользоваться формулой первого члена геометрической прогрессии, чтобы вычислить его, и подставить полученное значение в онлайн калькулятор суммы.

Формула суммы первых трех, четырех или n членов геометрической прогрессии выводится с использованием среднего геометрического, как основного свойства данной прогрессии. Любое из чисел, стоящих в ряду, будет равно среднему геометрическому его соседей:

Если объединить это свойство с отношением двух последовательных членов прогрессии, которые неизменно равно одному и тому же числу — знаменателю, то путем нехитрых сокращений, сумма первых нескольких членов геометрической прогрессии приводится к такому виду:

В некоторых источниках встречается похожий вариант, но с другими знаками в скобках — по сути окончательного значения это не меняет, и для ручного расчета, когда даны первые несколько членов, уместно использовать более удобную на момент формулу.

Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

1. УРОК – ПРЕЗЕНТАЦИЯ. ТЕМА : Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

900igr.net

2. ЦЕЛЬ УРОКА :

Формирование понятия геометрической
прогрессии, используя сопоставление и
противопоставления понятию
арифметической прогрессии.
Познакомить со свойствами
геометрической прогрессии и формулой nго члена.
Закрепить на примерах решения задач.

3. Изучение понятия геометрической прогрессии и вывод формулы n-го члена геометрической прогрессии.

4. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущ

Геометрической прогрессией
называется
последовательность отличных от
нуля чисел, каждый член которой,
начиная со второго, равен
предыдущему члену, умноженному
на одно и тоже число.

5. Определение

Числовая
последовательность, в
которой каждый
следующий член
получается из
предыдущего
прибавлением одного и
того же числом
d,называется
арифметической
прогрессией.
Числовая
последовательность
отличных от нуля
чисел, в которой
каждый следующий
член получается из
предыдущего
умножением на одно
и тоже число q,
называется
геометрической
прогрессией.
Число d –
называется
разностью
Число q –
называется
знаменателем
арифметической геометрической
прогрессии.
прогрессии.

7. Обозначение

Арифметическая
прогрессия
a
n
Геометрическая
прогрессия
b
n

8. Допустимые значения

Арифметическая
прогрессия
a1 , d
любые числа
Геометрическая
прогрессия
,
b1 q
числа неравные
нулю

9. Рекуррентная формула

Арифметическая
прогрессия
Геометрическая
прогрессия
an 1 an d
bn 1 bn q
n N
n N

10. Нахождение

разность
арифметической
прогрессии
d a n 1 a
n
знаменатель
геометрической
прогрессии
q
b
b
n 1
n
n N
n N

11. Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.

b b q
b b q b q q b q
b b q b q q b q
b b q b q q b q
2
3
1
2
1
1
2
4
3
1
4
1
3
1
3
5
2
1
4

12. Итак,

b
n
n 1
b1 b

13. Формула n-го члена

арифметическая
прогрессия
геометрическая
прогрессия
an a1 d n 1 bn b1 b
n 1
n N
n N

14. Характеристическое свойство

арифметическая
прогрессия
a
n
a
n 1
a n 1
геометрическая
прогрессия
b
b
n
n 1 bn 1
2
или
2
n N
b
n
b b
n 1
n N
n 1

15. Геометрическая прогрессия в геометрии:

16. Решение задач

17. Задача 1

Найдите первые 5 членов
геометрической прогрессии , если
первый член -2, а знаменатель -0.5.
Ответ: -2; 1; -0,5; 0,25; — 0,125

18. Задача 2.

В правильный треугольник, сторона
которого равна 16 см, вписан второй
треугольник так, что его вершинами
являются середины сторон первого. Во
второй треугольник таким же способом
вписан третий и т.д. Найдите периметр
пятого треугольника.
Ответ: 3 см.

20. Задача 3 (решить двумя способами)

Найдите знаменатель геометрической
прогрессии, если ее четвертый член
25, а шестой член 16.
4
4
Ответ:
;
5
5

21. Задача 4.

1
Между числами
и 27 вставьте
9
четыре числа, чтобы получилась
геометрическая прогрессия.
Найдите эти числа.
1
Ответ:
; 1; 3; 9
3

22. Задача 5.

Дана геометрическая прогрессия (bn),
1
b
4
b5 216
в которой
и
b
2
b6 4
Найти первый член геометрической
прогрессии.
Ответ: 12 или
15
3
7

Калькулятор геометрической прогрессии — Расчет высокой точности

Цель использования: Использование для нахождения дисконтированных денежных потоков для моей жизни страховой полис

Цель использования: Здравствуйте, может кто подскажет геометрическую погрешность между -4 и -9 с пояснениями пожалуйста.Большое спасибо!

Цель использования: Расчет внутриигровых ресурсов
Комментарий / запрос: Очень точный, может отображать большие числа цифра за цифрой

Цель использования: Расчет моей пенсионной суммы : P
Комментарий / запрос: Точно и кратко

Цель использования: За результат

Цель использования: Learning The Math.
Комментарий / запрос: Изучение математики

Цель использования: Чтобы рассчитать возможные возвраты для ставки на сборщик.

Цель использования: математическая задача
Комментарий / Запрос: круто

Цель использования: Я искал калькулятор, чтобы найти общее отношение последовательности, когда даны первые 3 числа этой последовательности.Кажется, я не могу найти один из этих …

Цель использования: Фон Нейман оценка зондирования. 400 миллиардов звезд в галактике, сколько итераций перед воспроизводящим зондом дает число, эквивалентное одному зонду на звезду. Предположим, что исходный зонд производит 1 раз в месяц, пока не будет достигнуто T. Каждый зонд после этого делает то же самое по прибытии. Среднее время путешествия между звездами предполагает 50 лет.

Явные формулы для геометрических последовательностей

Результаты обучения

Напишите рекурсивную формулу для последовательности чисел.
Дайте два члена геометрической последовательности, найдите третий.
Решите прикладную задачу, используя геометрическую последовательность.

Использование рекурсивных формул для геометрических последовательностей

Рекурсивная формула позволяет нам найти любой член геометрической последовательности, используя предыдущий член.Каждый член является продуктом обычного отношения и предыдущего члена. Например, предположим, что обычное отношение равно 9. Тогда каждый член в девять раз больше предыдущего. Как и в любой рекурсивной формуле, необходимо указать начальный член.

Общее примечание: рекурсивная формула для геометрической последовательности

Рекурсивная формула для геометрической последовательности с общим соотношением [латекс] r [/ латекс] и первым членом [латекс] {a} _ {1} [/ latex]:
[латекс] {a} _ {n} = r \ cdot {a} _ {n — 1}, n \ ge 2 [/ латекс]

Как сделать: учитывая первые несколько членов геометрической последовательности, напишите ее рекурсивную формулу.

Укажите начальный срок.
Найдите обычное отношение, разделив любой термин на предыдущий.
Подставляет обычное отношение в рекурсивную формулу геометрической последовательности.

Пример: использование рекурсивных формул для геометрических последовательностей

Напишите рекурсивную формулу для следующей геометрической последовательности.

[латекс] \ left \ {6,9,13.5,20.25, \ dots \ right \} [/ latex]

Показать решение

Первый член равен 6.Обычное отношение можно найти, разделив второй член на первый член.

[латекс] r = \ dfrac {9} {6} = 1,5 [/ латекс]

Подставьте обычное соотношение в рекурсивную формулу для геометрических последовательностей и определите [латекс] {a} _ {1} [/ latex].

[латекс] \ begin {align} & {a} _ {n} = r \ cdot {a} _ {n — 1} \\ & {a} _ {n} = 1.5 \ cdot {a} _ {n — 1} \ text {for} n \ ge 2 \\ & {a} _ {1} = 6 \ end {align} [/ latex]

Анализ решения

Последовательность точек данных следует экспоненциальному шаблону.Обычное отношение также является основой экспоненциальной функции.

— вопросы и ответы

Нужно ли нам разделить второй член на первый член, чтобы найти обычное отношение?

Нет. Мы можем разделить любой член в последовательности на предыдущий член. Однако чаще всего делят второй член на первый член, потому что это часто самый простой метод определения общего отношения.

Попробуй

Напишите рекурсивную формулу для следующей геометрической последовательности.

[латекс] \ left \ {2, \ dfrac {4} {3}, \ dfrac {8} {9}, \ dfrac {16} {27}, \ dots \ right \} [/ latex]

Показать решение

[латекс] \ begin {align} & {a} _ {1} = 2 \\ & {a} _ {n} = \ frac {2} {3} \ cdot {a} _ {n — 1} \ текст {for} n \ ge 2 \ end {align} [/ latex]

Использование явных формул для геометрических последовательностей

Поскольку геометрическая последовательность представляет собой экспоненциальную функцию, область определения которой является набором положительных целых чисел, а обычное отношение является основой функции, мы можем написать явные формулы, которые позволят нам находить определенные термины.{3} && \ text {Divide} \\ & r = 2 && \ text {Решите для общего отношения} \ end {align} [/ latex]

Найдите второй член, умножив первый член на обычное отношение.

[латекс] \ begin {align} {a} _ {2} & = 2 {a} _ {1} \\ & = 2 \ left (3 \ right) \\ & = 6 \ end {align} [/ латекс]

Анализ решения

Обычное отношение умножается на первый член один раз, чтобы найти второй член, дважды, чтобы найти третий член, трижды, чтобы найти четвертый член, и так далее.Десятый член можно найти, умножив первый член на обыкновенное отношение девять раз или умножив на обыкновенное отношение в девятой степени.

Попробуй

Учитывая геометрическую последовательность с [латексом] {a} _ {2} = 4 [/ latex] и [latex] {a} _ {3} = 32 [/ latex], найдите [latex] {a} _ {6 }[/латекс].

Показать решение

[латекс] {a} _ {6} = 16 \ text {,} 384 [/ латекс]

Пример: написание явной формулы для

n -го члена геометрической последовательности

Напишите явную формулу для члена [latex] n \ text {th} [/ latex] следующей геометрической последовательности.{n} [/ латекс]

Пример: решение прикладных задач с помощью геометрических последовательностей

В 2013 году количество учеников в малой школе составляет 284 человека. По оценкам, количество учеников будет увеличиваться на 4% каждый год.

Напишите формулу для численности учащихся.
Оцените численность студентов в 2020 г.

Показать решение

Ситуацию можно смоделировать геометрической последовательностью с начальным семестром 284. Контингент студентов составит 104% по сравнению с предыдущим годом, поэтому обычное отношение равно 1.{n} [/ латекс]
Количество просмотров будет около 333.

Следующее видео представляет собой короткий урок по некоторым темам, затронутым в этом уроке.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

геометрических последовательностей и серии

Геометрические последовательности

Геометрическая последовательность: последовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r ., или геометрическая прогрессия. Используется при обращении к геометрической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r .

an = ran − 1 Геометрическая последовательность

И поскольку anan − 1 = r, постоянный множитель r называется общим отношением Константа r , которая получается делением любых двух последовательных членов геометрической последовательности; anan − 1 = r .. Например, следующая геометрическая последовательность,

9,27,81,243,729…

Здесь a1 = 9, а соотношение между любыми двумя последовательными членами равно 3.Можно построить общий член an = 3an − 1, где,

a1 = 9a2 = 3a1 = 3 (9) = 27a3 = 3a2 = 3 (27) = 81a4 = 3a3 = 3 (81) = 243a5 = 3a4 = 3 (243) = 729 ⋮

В общем, с учетом первого члена a1 и общего отношения r геометрической последовательности мы можем записать следующее:

a2 = ra1a3 = ra2 = r (a1r) = a1r2a4 = ra3 = r (a1r2) = a1r3a5 = ra3 = r (a1r3) = a1r4 ⋮

Из этого мы видим, что любую геометрическую последовательность можно записать в терминах ее первого элемента, ее общего отношения и индекса следующим образом:

an = a1rn − 1 Геометрическая последовательность

Фактически, любой общий член, являющийся экспонентой в числах n , является геометрической последовательностью.

Пример 1

Найдите уравнение для общего члена данной геометрической последовательности и используйте его для вычисления 10 ^th члена: 3,6,12,24,48…

Решение:

Начните с определения общего отношения,

г = 63 = 2

Обратите внимание, что соотношение между любыми двумя последовательными членами равно 2. Последовательность действительно представляет собой геометрическую прогрессию, где a1 = 3 и r = 2.

an = a1rn − 1 = 3 (2) n − 1

Следовательно, мы можем записать общий член an = 3 (2) n − 1, а член 10 ^th можно вычислить следующим образом:

a10 = 3 (2) 10−1 = 3 (2) 9 = 1,536

Ответ: an = 3 (2) n − 1; а10 = 1,536

Термины между данными элементами геометрической последовательности называются средними геометрическими. Термины между данными элементами геометрической последовательности..

Пример 2

Найдите все члены геометрической последовательности между a1 = −5 и a4 = −135. Другими словами, найдите все геометрические средние между 1 ^-м и 4 ^-м членами.

Решение:

Начнем с нахождения общего отношения r . В данном случае нам даны первый и четвертый слагаемые:

an = a1rn − 1 Используйте n = 4.a4 = a1r4−1a4 = a1r3

Подставляем a1 = −5 и a4 = −135 в приведенное выше уравнение, а затем решаем относительно r .

−135 = −5r327 = r33 = r

Затем используйте первый член a1 = −5 и общее отношение r = 3, чтобы найти уравнение для n -го члена последовательности.

an = a1rn − 1an = −5 (3) n − 1

Теперь мы можем использовать an = −5 (3) n − 1, где n — положительное целое число, чтобы определить пропущенные члены.

a1 = −5 (3) 1−1 = −5⋅30 = −5a2 = −5 (3) 2−1 = −5⋅31 = −15a3 = −5 (3) 3−1 = −5⋅32 = −45} средние геометрические a4 = −5 (3) 4−1 = −5⋅33 = −135

Ответ: −15, −45,

Первый член геометрической последовательности не может быть указан.

Пример 3

Найдите общий член геометрической последовательности, где a2 = −2 и a5 = 2125.

Решение:

Чтобы определить формулу для общего члена, нам нужны a1 и r. Нелинейная система с этими переменными может быть сформирована с использованием данной информации и an = a1rn − 1:

{a2 = a1r2−1a5 = a1r5−1 ⇒ {−2 = a1r2125 = a1r4 Используйте a2 = −2. Используйте a5 = 2125.

Решите относительно a1 в первом уравнении,

{−2 = a1r ⇒ −2r = a12125 = a1r4

Подставляем a1 = −2r во второе уравнение и решаем: r .

2125 = a1r42125 = (- 2r) r42125 = −2r3−1125 = r3−15 = r

Обратный заменитель, чтобы найти a1:

a1 = −2r = −2 (−15) = 10

Следовательно, a1 = 10 и r = −15.

Ответ: an = 10 (−15) n − 1

Попробуй! Найдите уравнение для общего члена данной геометрической последовательности и используйте его для вычисления его 6 ^{-го члена}: 2,43,89,…

Ответ: an = 2 (23) n − 1; а6 = 64243

Геометрическая серия

Геометрический ряд Сумма членов геометрической последовательности.представляет собой сумму членов геометрической последовательности. Например, сумма первых 5 членов геометрической последовательности, определенной как an = 3n + 1, выглядит следующим образом:

S5 = Σn = 153n + 1 = 31 + 1 + 32 + 1 + 33 + 1 + 34 + 1 + 35 + 1 = 32 + 33 + 34 + 35 + 36 = 9 + 27 + 81 + 243 + 729 = 1089

Можно добавить 5 натуральных чисел. Однако задача добавления большого количества терминов не стоит. Поэтому далее мы разработаем формулу, которую можно использовать для вычисления суммы первых n членов любой геометрической последовательности.В целом

Sn = a1 + a1r + a1r2 +… + a1rn − 1

Умножая обе стороны на r , мы можем написать,

rSn = a1r + a1r2 + a1r3 +… + a1rn

Вычитая эти два уравнения, получаем

Sn-rSn = a1-a1rnSn (1-r) = a1 (1-rn)

Предполагая, что r ≠ 1 деление обеих сторон на (1 − r) приводит нас к формуле для n -й частичной суммы геометрической последовательности Сумма первых n членов геометрической последовательности, заданной формулой: Sn = a1 (1 − rn) 1 − r, r ≠ 1.:

Sn = a1 (1 − rn) 1 − r (r ≠ 1)

Другими словами, n -я частичная сумма любой геометрической последовательности может быть вычислена с использованием первого члена и общего отношения. Например, чтобы вычислить сумму первых 15 членов геометрической последовательности, определенной как an = 3n + 1, используйте формулу с a1 = 9 и r = 3.

S15 = a1 (1 − r15) 1 − r = 9⋅ (1−315) 1-3 = 9 (−14,348,906) −2 = 64,570,077

Пример 4

Найдите сумму первых 10 членов заданной последовательности: 4, −8, 16, −32, 64,…

Решение:

Определите, существует ли общее соотношение между данными терминами.

г = −84 = −2

Обратите внимание, что отношение между любыми двумя последовательными членами равно -2; следовательно, данная последовательность является геометрической последовательностью. Используйте r = −2 и тот факт, что a1 = 4, чтобы вычислить сумму первых 10 членов,

Sn = a1 (1 − rn) 1 − rS10 = 4 [1 — (- 2) 10] 1 — (- 2) = 4 (1−1,024) 1 + 2 = 4 (−1,023) 3 = −1,364

Ответ: S10 = −1,364

Пример 5

Вычислить: Σn = 162 (−5) n.

Решение:

В этом случае нас просят найти сумму первых 6 членов геометрической последовательности с общим членом an = 2 (−5) n.Используйте это, чтобы определить член 1 ^st и обыкновенное отношение r :

а1 = 2 (−5) 1 = −10

Чтобы показать, что существует общее отношение, мы можем использовать следующие друг за другом следующие термины:

r = anan − 1 = 2 (−5) n2 (−5) n − 1 = (- 5) n− (n − 1) = (- 5) 1 = −5

Используйте a1 = −10 и r = −5, чтобы вычислить частичную сумму 6 ^th.

Sn = a1 (1 − rn) 1 − rS6 = −10 [1 — (- 5) 6] 1 — (- 5) = — 10 (1−15,625) 1 + 5 = −10 (−15,624) 6 = 26 040

Ответ: 26 040

Попробуй! Найдите сумму первых 9 членов заданной последовательности: −2, 1, −1 / 2,…

Ответ: S9 = −171128

Если общее отношение r бесконечной геометрической последовательности является дробью, где | r | <1 (то есть -1 n -я частичная сумма стремится к 1 по мере увеличения n .Например, если r = 110 и n = 2,4,6, мы имеем

1− (110) 2 = 1−0,01 = 0,991− (110) 4 = 1−0,0001 = 0,99991− (110) 6 = 1−0,000001 = 0,999999

Здесь мы видим, что этот коэффициент становится все ближе и ближе к 1 для все больших значений n . Это иллюстрирует идею предела, важную концепцию, широко используемую в математике более высокого уровня, которая выражается с помощью следующих обозначений:

limn → ∞ (1 − rn) = 1, где | r | <1

Читается, что «предел (1-rn), поскольку n приближается к бесконечности, равен 1.«Хотя это дает предварительный обзор того, что должно произойти в вашем продолжающемся изучении математики, на данный момент мы заинтересованы в разработке формулы для специальных бесконечных геометрических рядов. Рассмотрим n -ю частичную сумму любой геометрической последовательности,

Sn = a1 (1 − rn) 1 − r = a11 − r (1 − rn)

Если | r | <1, то существует предел частичных сумм, когда n приближается к бесконечности, и мы можем записать,

Sn = a11 − r (1 − rn) ⇒n → ∞ S∞ = a11 − r⋅1

Следовательно, сходящийся геометрический ряд — это бесконечный геометрический ряд, где | r | <1, сумма которого определяется формулой: S∞ = a11 − r.бесконечный геометрический ряд, где | r | <1; его сумму можно рассчитать по формуле:

S∞ = a11 − r

Пример 6

Найдите сумму бесконечного геометрического ряда: 32 + 12 + 16 + 118 + 154 + ⋯

Решение:

Определить обыкновенное отношение,

г = 1232 = 12⋅23 = 13

Поскольку знаменатель r = 13 является дробью от -1 до 1, это сходящийся геометрический ряд.Используйте первый член a1 = 32 и обыкновенное отношение, чтобы вычислить его сумму.

S∞ = a11 − r = 321− (13) = 32 23 = 32⋅32 = 94

Ответ: S∞ = 94

Примечание : В случае бесконечного геометрического ряда, где | r | ≥1, ряд расходится, и мы говорим, что нет суммы. Например, если an = (5) n − 1, то r = 5, и мы имеем

S∞ = Σn = 1∞ (5) n − 1 = 1 + 5 + 25 +

Мы видим, что эта сумма неограниченно растет и не имеет суммы.

Попробуй! Найдите сумму бесконечного геометрического ряда: Σn = 1∞ − 2 (59) n − 1.

Ответ: −9/2

Повторяющаяся десятичная дробь может быть записана как бесконечный геометрический ряд, значащий коэффициент которого равен степени 1/10. Таким образом, формулу сходящегося геометрического ряда можно использовать для преобразования повторяющегося десятичного числа в дробь.

Пример 7

Запишите в виде дроби: 1.181818…

Решение:

Начните с определения повторяющихся цифр справа от десятичной дроби и перепишите их в геометрической прогрессии.

0,181818… = 0,18 + 0,0018 + 0,000018 +… = 18100 + 1810 000 + 181 000 000 +…

В этой форме мы можем определить общее отношение,

г = 1810,000 18100 = 1810,000 × 10018 = 1100

Обратите внимание, что отношение между любыми двумя последовательными членами равно 1100. Используйте это, а также тот факт, что a1 = 18100, чтобы вычислить бесконечную сумму:

S∞ = a11 − r = 181001− (1100) = 1810099100 = 18100⋅10099 = 211

Следовательно, 0.181818… = 211 и имеем

1,181818… = 1 + 211 = 1211

Ответ: 1211

Пример 8

Определенный мяч отскакивает назад на две трети высоты, с которой он упал. Если этот мяч изначально падает с высоты 27 футов, приблизьте общее расстояние, которое он пролетит.

Решение:

Мы можем вычислить высоту каждого последующего отскока:

27⋅23 = 18 футов Высота первого отскока 18⋅23 = 12 футов Высота второго отскока 12⋅23 = 8 футов Высота третьего отскока

Общее расстояние, которое проходит мяч, складывается из расстояний, на которые мяч падает, и расстояний, на которые мяч поднимается.Расстояния, на которые падает мяч, образуют геометрическую серию

27 + 18 + 12 + ⋯ Дистанция падения мяча

, где a1 = 27 и r = 23. Поскольку r представляет собой дробную часть от -1 до 1, эту сумму можно рассчитать следующим образом:

S∞ = a11 − r = 271−23 = 2713 = 81

Следовательно, мяч падает на общую дистанцию 81 фут. Расстояния, на которые мяч поднимается, образуют геометрическую серию

18 + 12 + 8 + ⋯ Расстояние подъема мяча

, где a1 = 18 и r = 23.Вычислите эту сумму аналогично:

S∞ = a11 − r = 181−23 = 1813 = 54

Следовательно, мяч поднимается на общую дистанцию 54 фута. Приблизительно общее пройденное расстояние, сложив общее расстояние подъема и падения:

81 + 54 = 135 футов

Ответ: 135 футов

Основные выводы

Геометрическая последовательность — это последовательность, в которой отношение r между последовательными членами является постоянным.
Общий член геометрической последовательности может быть записан в терминах его первого члена a1, общего отношения r и индекса n следующим образом: an = a1rn − 1.
Геометрический ряд — это сумма членов геометрической последовательности.
Частичная сумма n геометрической последовательности может быть вычислена с использованием первого члена a1 и общего отношения r следующим образом: Sn = a1 (1-rn) 1-r.
Бесконечная сумма геометрической последовательности может быть вычислена, если общее отношение представляет собой дробь от -1 до 1 (то есть | r | <1) следующим образом: S∞ = a11-r.Если | r | ≥1, то суммы не существует.

Тематические упражнения

Часть A: Геометрические последовательности

Запишите первые 5 членов геометрической последовательности с учетом ее первого члена и общего отношения. Найдите формулу для его общего члена.

Учитывая геометрическую последовательность, найдите формулу для общего члена и используйте ее, чтобы определить 5 ^{-й член} в последовательности.

−3.6, −4,32, −5,184,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 1, x2, x24,…
Найдите общий член и используйте его для определения 20-го члена в последовательности: 2, −6x, 18×2,…
Количество клеток в культуре определенных бактерий удваивается каждые 4 часа.Если изначально присутствует 200 ячеек, напишите последовательность, которая показывает популяцию ячеек после каждых n -го 4-часового периода в течение одного дня. Напишите формулу, которая дает количество ячеек после любого 4-часового периода.
Определенный мяч отскакивает назад на половине высоты, с которой он упал. Если этот мяч изначально падает с 12 футов, найдите формулу, которая дает высоту мяча при отскоке n и используйте его, чтобы найти высоту мяча при отскоке 6 ^-го.
Для заданной геометрической последовательности, определяемой рекуррентным соотношением an = 4an − 1, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общего отношения r .
Учитывая геометрическую последовательность, определяемую рекуррентным соотношением an = 6an − 1, где a1 = 12 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общего отношения r .

Учитывая члены геометрической последовательности, найдите формулу для общего члена.

a4 = −2.4 × 10−3 и a9 = −7,68 × 10−7

Найдите все средние геометрические между заданными членами.

a2 = −20 и a5 = −20 000

Часть B: геометрическая серия

Рассчитайте указанную сумму.

∑n = 155n
∑n = 16 (−4) п
∑k = 1102k + 1
∑k = 1142k − 1
∑k = 110−2 (3) к
∑k = 185 (−2) к
∑n = 152 (12) n + 2
∑n = 14−3 (23) п
∑n = 1∞2 (13) n − 1
∑n = 1∞ (15) п
∑n = 1∞3 (2) n − 2
∑n = 1∞ − 14 (3) n − 2
∑n = 1∞12 (−16) п
∑n = 1∞13 (−25) п

Запишите как смешанное число.

Предположим, вы согласились работать за гроши в день в течение 30 дней.Вы заработаете 1 пенни в первый день, 2 пенни во второй день, 4 пенни в третий день и так далее. Сколько всего пенни вы заработаете в конце 30-дневного периода? Какая сумма в долларах?
Первоначальная ставка в рулетке 100 долларов делается (красное поле) и проигрывает. Чтобы компенсировать разницу, игрок удваивает ставку, делает ставку 200 долларов и проигрывает.Опять же, чтобы компенсировать разницу, игрок удваивает ставку до 400 долларов и проигрывает. Если игрок продолжает удваивать свою ставку таким образом и проигрывает 7 раз подряд, сколько всего он проиграет?
Определенный мяч отскакивает назад на половину высоты, с которой он упал. Если этот мяч изначально падает с 12 футов, приблизьте общее расстояние, которое он пролетит.
Мяч для гольфа отскакивает от цементного тротуара на три четверти высоты, с которой он упал. Если мяч изначально падает с 8 метров, приблизьте общее расстояние, которое он пролетит.
Структурированное поселение ежегодно приносит сумму в долларах, представленную как n , в соответствии с формулой pn = 6000 (0.80) п — 1. Какова общая сумма дохода от урегулирования через 10 лет?
Начните с квадрата, каждая сторона которого составляет 1 единицу, начертите еще один квадрат, соединив середины каждой стороны. Продолжайте писать квадраты таким образом до бесконечности, как показано на рисунке:
Найдите сумму площадей всех квадратов на рисунке.(Подсказка: начните с поиска последовательности, сформированной с использованием площадей каждого квадрата.)

Часть C: Последовательности и серии

Определите последовательность как арифметическую, геометрическую или ни то ни другое. Укажите общее различие или соотношение, если оно существует.

Определите последовательность как арифметическую или геометрическую, а затем вычислите указанную сумму.

Рассчитайте указанную сумму.

∑n = 150 (3n − 5)
∑n = 125 (4−8n)
∑n = 112 (−2) n − 1
∑n = 1∞5 (−12) n − 1
∑n = 1405
∑n = 1∞0.6n

Часть D: Обсуждение

Используйте методы, описанные в этом разделе, чтобы объяснить, почему 0,999… = 1.
Постройте геометрическую последовательность, где r = 1. Исследуйте n -ю частичную сумму такой последовательности.Какие выводы мы можем сделать?

ответы

1, 5, 25, 125, 625; ан = 5n − 1
2, 6, 18, 54, 162; ан = 2 (3) п − 1
2, -6, 18, -54, 162; ан = 2 (−3) п − 1
3, 2, 43, 89, 1627; ан = 3 (23) п − 1
1.2, 0,72, 0,432, 0,2592, 0,15552; ан = 1,2 (0,6) п − 1
an = — (- 23) n − 1, a5 = −1681
ан = −3.6 (1,2) п − 1, а5 = −7,46496
400 ячеек; 800 ячеек; 1600 ячеек; 3200 ячеек; 6400 ячеек; 12800 ячеек; pn = 400 (2) n − 1 ячеек

1,073,741,823 пенни; 10 737 418 долларов.23

Выведение суммы конечной и бесконечной геометрической прогрессии

Геометрическая прогрессия, GP
Геометрическая прогрессия (также известная как геометрическая последовательность) — это последовательность чисел, в которой соотношение любых двух соседних членов является постоянным.Постоянное отношение называется обычным отношением, r геометрической прогрессии. Таким образом, каждый член в геометрической прогрессии находится путем умножения предыдущего на r .

Примеры GP:

3, 6, 12, 24,… — геометрическая прогрессия с r = 2
10, -5, 2,5, -1,25,… — геометрическая прогрессия с r = -1/2

n ^th член геометрической прогрессии
Для каждого члена GP как a ₁, a ₂, a ₃, a _{4 ₄, a _{4 _{, a _m ,…, a _n , выразив все эти термины согласно первому члену a ₁, мы получим.{\, n — 1}}}}

долл. США

Где
a ₁ = первый член, a ₂ = второй член и так далее
a _n = последний член (или n ^th term) и
a _m = любой член перед последним термином

Сумма конечной геометрической прогрессии
Сумма в геометрической прогрессии (также называемая геометрическим рядом) равна
$ S = a_1 + a_2 + a_3 + a_4 + \, \ dots \, + a_n $

$ S = a_1 + a_1 r + a_1 r ^ 2 + a_1 r ^ 3 + \, \ dots \, + a_1 r ^ {\, n — 1} $ ← Уравнение (1)

Умножьте обе части уравнения (1) на r. {\, n})} {1 — r}

Приведенная выше формула подходит для GP с r <1.{\, n}} {1 - r} $

Для n → ∞ величина ( a ₁ r ⁿ) / (1- r ) → 0 для -1,0 <( r ≠ 0) <+1,0, таким образом ,

$ S = \ dfrac {a_1} {1 — r}

Решатель геометрической прогрессии, N-е значение и калькулятор суммы

Что такое геометрическая прогрессия?

Геометрическая прогрессия $ (g_n) _ {n \ in N} $ или геометрическая последовательность — это последовательность действительных чисел или переменных, каждый член которой получается из
предшествующий единице путем умножения на ненулевое действительное число.4, \ ldots $$

где ненулевая константа $ r $ — обычное отношение. Первый член $ g_1 $ называется начальным членом. Обратите внимание, что обычное отношение $ r $ не может быть нулевым.
С другой стороны, прогрессия $ (g_n) _ {n \ in N} $ является геометрической прогрессией с общим соотношением $ r $, если отношения между последовательными членами равны, то есть

$$ \ frac {g_2} {g_1} = \ frac {g_3} {g_2} = \ ldots = \ frac {g_n} {g_ {n-1}} = r $$

Если $ r> 1 $, то геометрическая прогрессия представляет собой возрастающую прогрессию и в нем содержится
$$ g_1 \ lt g_2 \ lt \ ldots \ lt g_ {n-1} \ lt g_n $$
Если $ 0 \ lt r \ lt 1 $, то геометрическая прогрессия является убывающей и содержит
$$ g_1> g_2> \ ldots> g_ {n-1}> g_n $$
Если $ r = 1 $, то геометрическая прогрессия — это постоянная прогрессия и выполняется
$$ g_1 = g_2 = \ ldots = g_ {n-1} = g_n $$
Постоянная прогрессия — это только прогрессия, одновременно геометрическая и геометрическая.

Члены между двумя непоследовательными членами геометрической прогрессии $ (g_n) _ {n \ in N} $ называются средними геометрическими терминами.
Например, геометрические средние между $ g_1 $ и $ g_5 $ равны $ g_2 $, $ g_3 $ и $ g_5. $
Если заданы два непоследовательных члена геометрической прогрессии $ (g_n) _ {n \ in N} $ и число средних геометрических между ними, то геометрическая прогрессия полностью определена.

Геометрический ряд — это сумма членов геометрической прогрессии. Геометрический ряд может быть бесконечным или конечным.{n-1}, $$
где $ g_1 $ — начальный член, а $ r \ ne0 $ — обыкновенное отношение.

Арифметических и геометрических последовательностей

Расследовать!

Для рисунков из точек ниже нарисуйте следующий рисунок в последовательности. Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \ (n \) -м шаблоне.

Теперь перейдем к вопросу о нахождении замкнутых формул для конкретных типов последовательностей.

Арифметические последовательности.

Если члены последовательности отличаются на константу, мы говорим, что последовательность равна арифметическим .Если начальный член (\ (a_0 \)) последовательности равен \ (a \), а общая разность равна \ (d \ text {,} \), то мы имеем,

Рекурсивное определение: \ (a_n = a_ {n-1} + d \) с \ (a_0 = a \ text {.} \)

Замкнутая формула: \ (a_n = a + dn \ text {.} \)

Откуда мы это знаем? Для рекурсивного определения нам нужно указать \ (a_0 \ text {.} \) Затем нам нужно выразить \ (a_n \) через \ (a_ {n-1} \ text {.} \) Если мы вызовем первый член \ (a \ text {,} \), затем \ (a_0 = a \ text {.} \) Для рекуррентного отношения, по определению арифметической последовательности, разница между последовательными членами является некоторой константой, скажем \ (д \ текст {.} \) Итак \ (a_n — a_ {n-1} = d \ text {,} \) или, другими словами,

\ begin {уравнение *}
a_0 = a \ qquad a_n = a_ {n-1} + d \ text {.}
\ end {уравнение *}

Чтобы найти замкнутую формулу, сначала напишите общую последовательность:

\ begin {align *}
а_0 \ amp = а \\
a_1 \ amp = a_0 + d = a + d \\
a_2 \ amp = a_1 + d = a + d + d = a + 2d \\
a_3 \ amp = a_2 + d = a + 2d + d = a + 3d \\
\ amp \ vdots
\ end {выровнять *}

Мы видим, что для нахождения \ (n \) -го члена нам нужно начать с \ (a \), а затем добавить \ (d \) несколько раз.Фактически, добавьте это \ (n \) раз. Таким образом, \ (a_n = a + dn \ text {.} \)

Пример 2.2.1.

Найдите рекурсивные определения и замкнутые формулы для арифметических последовательностей ниже. Предположим, что первым перечисленным термином является \ (a_0 \ text {.} \)

\ (2, 5, 8, 11, 14, \ ldots \ text {.} \)
\ (50, 43, 36, 29, \ ldots \ text {.} \)

Решение

Сначала мы должны проверить, действительно ли эти последовательности являются арифметическими, взяв разности последовательных членов. Это покажет общую разницу \ (d \ text {.} \)

\ (5-2 = 3 \ text {,} \) \ (8-5 = 3 \ text {,} \) и т. Д. Чтобы перейти от каждого термина к следующему, мы добавляем три, поэтому \ (d = 3 \ text {.} \) Следовательно, рекурсивное определение — \ (a_n = a_ {n-1} + 3 \) с \ (a_0 = 2 \ text {.} \) Замкнутая формула \ (a_n = 2 + 3n \ text {.} \)
Здесь общая разница \ (- 7 \ text {,} \), поскольку мы прибавляем \ (- 7 \) к 50, чтобы получить 43, и так далее. Таким образом, у нас есть рекурсивное определение \ (a_n = a_ {n-1} — 7 \) с \ (a_0 = 50 \ text {.} \) Замкнутая формула \ (a_n = 50 — 7n \ text {.} \)

А как насчет последовательностей типа \ (2, 6, 18, 54, \ ldots \ text {?} \) Это не арифметика, потому что разница между терминами непостоянна. Однако соотношение между последовательными членами постоянно. Мы называем такие последовательности геометрическими .

Рекурсивное определение геометрической последовательности с начальным членом \ (a \) и общим отношением \ (r \): \ (a_n = a_ {n-1} \ cdot r; a_0 = a \ text {.} \) To чтобы получить следующий член, мы умножаем предыдущий член на \ (r \ text {.{n} \ text {.} \)

Пример 2.2.2.

Найдите рекурсивную и замкнутую формулу для геометрических последовательностей ниже. Опять же, первым перечисленным термином является \ (a_0 \ text {.} \)

\ (\ Displaystyle 3, 6, 12, 24, 48, \ ldots \) 
\ (\ Displaystyle 27, 9, 3, 1, 1/3, \ ldots \)

Решение

Начните с проверки того, что эти последовательности действительно геометрически, разделив каждый член на его предыдущий член. Если это соотношение действительно постоянное, мы найдем \ (r \ text {.} \)

\ (6/3 = 2 \ text {,} \) \ (12/6 = 2 \ text {,} \) \ (24/12 = 2 \ text {,} \) и т. Д.{n} \ text {.} \)

В приведенных выше примерах и формулах мы предположили, что начальный член был \ (a_0 \ text {.} \). Если ваша последовательность начинается с \ (a_1 \ text {,} \), вы можете легко найти термин, который были \ (a_0 \) и используйте это в формуле. Например, если мы хотим получить формулу для последовательности \ (2, 5, 8, \ ldots \) и настаиваем на том, чтобы \ (2 = a_1 \ text {,} \), то мы можем найти \ (a_0 = -1 \) (поскольку последовательность арифметическая с общей разницей 3, имеем \ (a_0 + 3 = a_1 \)). Тогда закрытая формула будет \ (a_n = -1 + 3n \ text {.} \)

Подраздел Суммы арифметических и геометрических последовательностей

Расследовать!

В вашем соседнем продуктовом магазине есть автомат с кеглями.

Предположим, что автомат для конфет в настоящее время вмещает ровно 650 кеглей, и каждый раз, когда кто-то вставляет четверть, из автомата выходит ровно 7 кеглей.
1. Сколько кеглей останется в машине после того, как будут вставлены 20 четвертей?
2. Останется ли когда-нибудь в машине ровно ноль кеглей? Объяснять.
Что, если автомат выдаст 7 Skittles первому покупателю, вложившему четверть, 10 — второму, 13 — третьему, 16 — четвертому и т.д. в машину?
Теперь, что, если автомат выдаст 4 Skittles первому покупателю, 7 — второму, 12 — третьему, 19 — четвертому и т.д.

Посмотрите на последовательность \ ((T_n) _ {n \ ge 1} \), которая начинается \ (1, 3, 6, 10, 15, \ ldots \ text {.} \) Эти числа называются треугольными числами , поскольку они представляют количество точек в равностороннем треугольнике (подумайте о том, как вы расставляете 10 кеглей: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).

Это арифметическая последовательность? Нет, поскольку \ (3-1 = 2 \) и \ (6-3 = 3 \ ne 2 \ text {,} \), поэтому нет общей разницы. Последовательность геометрическая? Нет. \ (3/1 = 3 \), но \ (6/3 = 2 \ text {,} \), поэтому нет общего отношения. Что делать?

Обратите внимание, что различия между терминами и образуют арифметическую последовательность: \ (2, 3, 4, 5, 6, \ ldots \ text {.} \) Это означает, что \ (n \) -й член последовательности \ ((T_n) \) является суммой первых \ (n \) членов последовательности \ (1,2,3,4 , 5, \ ldots \ text {.} \) Мы говорим, что \ ((T_n) \) — это последовательность частичных сумм последовательности \ (1,2,3, \ ldots \) ( частичных сумм потому что мы не берем сумму всех бесконечно многих членов).

Это станет яснее, если мы запишем треугольные числа так:

\ begin {align *}
1 \ amp = 1 \\
3 \ amp = 1 + 2 \\
6 \ amp = 1 + 2 + 3 \\
10 \ amp = 1 + 2 + 3+ 4 \\
\ vdots \ amp \ qquad \ vdots \\
T_n \ amp = 1 + 2 + 3 + \ cdots + n \ text {.}
\ end {выровнять *}

Если мы знаем, как складывать члены арифметической последовательности, мы могли бы найти замкнутую формулу для последовательности, отличия которой являются членами этой арифметической последовательности. Подумайте, как мы могли бы найти сумму первых 100 натуральных чисел (то есть \ (T_ {100} \)). Вместо того, чтобы складывать их по порядку, мы перегруппируем и добавим \ (1 + 100 = 101 \ text {.} \) Следующая пара, которую нужно объединить, это \ (2 + 99 = 101 \ text {.} \) Затем \ (3+ 98 = 101 \ text {.} \) Продолжайте. Это дает 50 пар, каждая из которых в сумме дает \ (101 \ text {,} \), поэтому \ (T_ {100} = 101 \ cdot 50 = 5050 \ text {.} \) ¹

Это прозрение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его в детстве, когда его неприятный учитель начальных классов думал, что он будет держать класс занятым, требуя от них вычисления большой суммы.

В общем, используя такую же перегруппировку, мы обнаруживаем, что \ (T_n = \ frac {n (n + 1)} {2} \ text {.} \) Между прочим, это в точности то же самое, что \ ({n +1 \ choose 2} \ text {,} \), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий, которые происходят на вечеринке с \ (n + 1 \) людьми: первый человек трясет \ (n \) рук, следующий пожимает еще \ (n-1 \) рук и так далее.

Смысл всего этого в том, что некоторые последовательности, хотя и не арифметические или геометрические, могут быть интерпретированы как последовательность частичных сумм арифметических и геометрических последовательностей. К счастью, есть методы, которые можно использовать для быстрого вычисления этих сумм.

Подраздел Суммирование арифметических последовательностей: обратное и сложение

Вот метод, который позволяет нам быстро найти сумму арифметической последовательности.

Пример 2.2.4.

Найдите сумму: \ (2 + 5 + 8 + 11 + 14 + \ cdots + 470 \ text {.} \)

Решение

Идея состоит в том, чтобы имитировать, как мы нашли формулу для треугольных чисел. Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме составляют 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Назовем сумму \ (S \ text {.} \) Тогда

\ (S = \)	\ (2 \)	\ (+ \)	\ (5 \)	\ (+ \)	\ (8 \)	\ (+ \ cdots + \)	\ (467 \)	\ (+ \)	470
\ (+ \ quad S = \)	\ (470 \)	\ (+ \)	\ (467 \)	\ (+ \)	\ (464 \)	\ (+ \ cdots + \)	\ (5 \)	\ (+ \)	2
\ (2S = \)	\ (472 \)	\ (+ \)	\ (472 \)	\ (+ \)	\ (472 \)	\ (+ \ cdots + \)	\ (472 \)	\ (+ \)	\ (472 \)

Чтобы найти \ (2S \), мы прибавляем 472 к себе несколько раз.Какой номер? Нам нужно решить, сколько членов ( слагаемых ) в сумме. Поскольку члены образуют арифметическую последовательность, \ (n \) -й член в сумме (считая \ (2 \) как 0-й член) можно выразить как \ (2 + 3n \ text {.} \) Если \ ( 2 + 3n = 470 \), тогда \ (n = 156 \ text {.} \) Итак, \ (n \) находится в диапазоне от 0 до 156, что дает 157 членов в сумме. Это число 472 в сумме для \ (2S \ text {.} \) Таким образом,

\ begin {уравнение *}
2S = 157 \ cdot 472 = 74104 \ text {.}
\ end {уравнение *}

Теперь легко найти \ (S \ text {:} \)

\ begin {уравнение *}
S = 74104/2 = 37052 \ текст {.}
\ end {уравнение *}

Это будет работать для суммы любой арифметической последовательности . Назовите сумму \ (S \ text {.} \) Обратный и сложите. Это дает одно число, добавленное к самому себе много раз. Найдите количество раз. Умножить. Разделить на 2. Готово.

Пример 2.2.5.

Найдите замкнутую формулу для \ (6 + 10 + 14 + \ cdots + (4n — 2) \ text {.} \)

Решение

Опять же, у нас есть сумма арифметической последовательности. Сколько терминов в последовательности? Ясно, что каждый член в последовательности имеет вид \ (4k -2 \) (о чем свидетельствует последний член).Но для каких значений \ (k \)? Чтобы получить 6, \ (k = 2 \ text {.} \) Чтобы получить \ (4n-2 \), возьмите \ (k = n \ text {.} \) Итак, чтобы найти количество терминов, мы должны подсчитать количество целых чисел в диапазоне \ (2,3, \ ldots, n \ text {.} \) Это \ (n-1 \ text {.} \) (Есть \ (n \) числа от 1 до \ (n \ text {,} \) так что на один меньше, если мы начнем с 2.)

Теперь переверните и добавьте:

\ (S = \)	\ (6 \)	\ (+ \)	\ (10 \)	\ (+ \ cdots + \)	\ (4н-6 \)	\ (+ \)	\ (4н-2 \)
\ (+ \ quad S = \)	\ (4н-2 \)	\ (+ \)	\ (4н-6 \)	\ (+ \ cdots + \)	\ (10 \)	\ (+ \)	6
\ (2S = \)	\ (4n + 4 \)	\ (+ \)	\ (4n + 4 \)	\ (+ \ cdots + \)	\ (4n + 4 \)	\ (+ \)	\ (4n + 4 \)

Поскольку есть \ (n-1 \) членов, получаем

\ begin {уравнение *}
2S = (n-1) (4n + 4) \ qquad \ mbox {so} \ qquad S = \ frac {(n-1) (4n + 4)} {2} \ text {.}
\ end {уравнение *}

Помимо нахождения сумм, мы можем использовать эту технику для нахождения замкнутых формул для последовательностей, которые мы распознаем как последовательности частичных сумм.

Пример 2.2.6.

Используйте частичные суммы, чтобы найти замкнутую формулу для \ ((a_n) _ {n \ ge 0} \), которая начинается с \ (2, 3, 7, 14, 24, 37, \ ldots \ ldots \)

Решение

Во-первых, если вы посмотрите на различия между терминами, вы получите последовательность различий: \ (1,4,7,10,13, \ ldots \ text {,} \), которая является арифметической последовательностью. Написано по-другому:

\ begin {align *}
а_0 \ amp = 2 \\
а_1 \ amp = 2 + 1 \\
а_2 \ amp = 2 + 1 + 4 \\
а_3 \ amp = 2 + 1 + 4 + 7
\ end {выровнять *}

и так далее.Мы можем записать общий член \ ((a_n) \) в терминах арифметической последовательности следующим образом:

\ begin {уравнение *}
a_n = 2 + 1 + 4 + 7 + 10 + \ cdots + (1 + 3 (n-1))
\ end {уравнение *}

(мы используем \ (1 + 3 (n-1) \) вместо \ (1 + 3n \), чтобы индексы выровнялись правильно; для \ (a_3 \) мы складываем до 7, что составляет \ ( 1 + 3 (3-1) \)).

Мы можем перевернуть и сложить, но начальные 2 не соответствуют нашему шаблону. Это просто означает, что нам нужно убрать 2 из обратной части:

\ (a_n = \)	\ (2 \)	\ (+ \)	\ (1 \)	\ (+ \)	\ (4 \)	\ (+ \ cdots + \)	\ (1 + 3 (n-1) \)
\ (+ \ quad a_n = \)	\ (2 \)	\ (+ \)	\ (1 + 3 (n-1) \)	\ (+ \)	\ (1 + 3 (n-2) \)	\ (+ \ cdots + \)	\ (1 \)
\ (2a_n = \)	\ (4 \)	\ (+ \)	\ (2 + 3 (п-1) \)	\ (+ \)	\ (2 + 3 (п-1) \)	\ (+ \ cdots + \)	\ (2 + 3 (п-1) \)

Не считая первого члена (4), есть \ (n \) слагаемых в \ (2 + 3 (n-1) = 3n-1 \), поэтому правая часть становится \ (4+ (3n-1 ) п \ текст {.} \)

Наконец, решая \ (a_n \), получаем

\ begin {уравнение *}
a_n = \ d \ frac {4+ (3n-1) n} {2} \ text {.}
\ end {уравнение *}

На всякий случай проверяем \ (a_0 = \ frac {4} {2} = 2 \ text {,} \) \ (a_1 = \ frac {4 + 2} {2} = 3 \ text {,} \) и т.д. У нас есть правильная замкнутая формула.

Подраздел Суммирование геометрических последовательностей: умножение, сдвиг и вычитание

Чтобы найти сумму геометрической последовательности, мы не можем просто перевернуть и сложить. Вы понимаете почему? Причина, по которой мы добавляли один и тот же термин много раз к самому себе, заключается в том, что разница была постоянной.Таким образом, когда мы добавляли разницу в одном направлении, мы вычитали разницу в другом направлении, оставляя постоянную сумму. Для геометрических сумм у нас есть другая техника.

Пример 2.2.7.

Что такое \ (3 + 6 + 12 + 24 + \ cdots + 12288 \ text {?} \)

Решение

Умножьте каждый член на 2, обычное отношение. Вы получите \ (2S = 6 + 12 + 24 + \ cdots + 24576 \ text {.} \) Теперь вычтите: \ (2S — S = -3 + 24576 = 24573 \ text {.} \) Поскольку \ (2S — S = S \ text {,} \) у нас есть ответ.

Чтобы лучше понять, что произошло в приведенном выше примере, попробуйте написать это так:

\ (S = \)	\ (3 \, + \)	\ (6 + 12 + 24 + \ cdots + 12288 \)
\ (- \ qquad 2S = \)		\ (6 + 12 + 24 + \ cdots + 12288 \)	\ (+ 24576 \)
\ (- S = \)	\ (3 \, + \)	\ (0 + 0 + 0 + \ cdots + 0 \)	\ (- 24576 \)

Затем разделите обе части на \ (- 1 \), и мы получим тот же результат для \ (S \ text {.{n + 1}} {- 4} \)

Даже если это может показаться новой техникой, вы, вероятно, использовали ее раньше.

Пример 2.2.9.

Экспресс \ (0,464646 \ ldots \) в виде дроби.

Решение

Пусть \ (N = 0.46464646 \ ldots \ text {.} \) Рассмотрим \ (0.01N \ text {.} \) Получаем:

\ (N = \)	\ (0,4646464 \ ldots \)
\ (- \ qquad 0,01N = \)	\ (0,00464646 \ ldots \)
\ (0,99N = \)	\ (0.46 \)

Итак, \ (N = \ frac {46} {99} \ text {.} \) Что мы сделали? Мы рассматривали повторяющуюся десятичную дробь \ (0,464646 \ ldots \) как сумму геометрической последовательности \ (0,46, 0,0046, 0,000046, \ ldots \). Общее отношение равно \ (0,01 \ text {.} \) Единственная реальная разница в том, что что теперь мы вычисляем бесконечную геометрическую сумму , у нас нет лишнего «последнего» члена для рассмотрения. На самом деле, это результат взятия предела, как в исчислении, когда вы вычисляете бесконечных геометрических сумм.

Упражнения Упражнения

1.

Рассмотрим последовательность \ (5, 9, 13, 17, 21, \ ldots \) с \ (a_1 = 5 \)

Дайте рекурсивное определение последовательности.
Приведите замкнутую формулу для \ (n \) -го члена последовательности.
Является ли \ (2013 \) членом последовательности? Объяснять.
Сколько членов в последовательности \ (5, 9, 13, 17, 21, \ ldots, 533 \)?
Найдите сумму: \ (5 + 9 + 13 + 17 + 21 + \ cdots + 533 \ text {.{th} \) член \ (1, 6, 15, 28, 45, \ ldots \ text {,} \), где \ (b_0 = 1 \)

Решение

\ (a_n = a_ {n-1} + 4 \) с \ (a_1 = 5 \ text {.} \)
\ (a_n = 5 + 4 (n-1) \ text {.} \)
Да, поскольку \ (2013 = 5 + 4 (503-1) \) (поэтому \ (a_ {503} = 2013 \)).
133
\ (\ frac {538 \ cdot 133} {2} = 35777 \ text {.} \)
\ (b_n = 1 + \ frac {(4n + 6) n} {2} \ text {.} \)

2.

3.

4.

5.

6.

7.

8.

Найдите \ (x \) и \ (y \) такие, что \ (27,
x, y, 1 \) является частью арифметической последовательности.

Затем найдите \ (x \) и \ (y \), чтобы последовательность была частью геометрической последовательности.

(Предупреждение: \ (x \) и \ (y \) могут быть не целыми числами.)

Решение

Для арифметики: \ (x = 55/3 \ text {,} \) \ (y = 29/3 \ text {.} \) Для геометрических: \ (x = 9 \) и \ (y = 3 \ текст {.} \)

9.

Найдите \ (x \) и \ (y \) такие, что \ (5,
x, y, 32 \) является частью арифметической последовательности.(2/3) \ text {.} \)

10.

Существует ли пара целых чисел \ ((a, b) \) такая, что \ (a,
x_1, y_1, b \) является частью арифметической последовательности, а \ (a,
x_2, y_2, b \) является частью геометрической последовательности с \ (x_1, x_2, y_1, y_2 \) всеми целыми числами?

11.

Рассмотрим последовательность \ (2, 7, 15, 26, 40, 57, \ ldots \) (с \ (a_0 = 2 \)). Рассматривая различия между терминами, выразите последовательность как последовательность частичных сумм. Затем найдите замкнутую формулу для последовательности, вычислив \ (n \) -ю частичную сумму.n (2 + 3k) \ text {.} \) Чтобы найти замкнутую формулу, мы переворачиваем и складываем. Получаем \ (a_n = \ frac {(4 + 3n) (n + 1)} {2} \) (у нас там \ (n + 1 \), потому что в сумме есть \ (n + 1 \) слагаемые для\)).

12.

Начиная с любого прямоугольника, мы можем создать новый прямоугольник большего размера, прикрепив квадрат к длинной стороне. Например, если мы начнем с прямоугольника \ (2 \ times 5 \), мы приклеим квадрат \ (5 \ times 5 \), образуя прямоугольник \ (5 \ times 7 \):

Следующий прямоугольник будет сформирован путем присоединения квадрата \ (7 \ times 7 \) к верхней или нижней части прямоугольника \ (5 \ times 7 \).

Создайте последовательность прямоугольников, используя это правило, начиная с прямоугольника \ (1 \ times 2 \). Затем запишите последовательность из периметра для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \ (1 \ times 2 \) равен 6 — следующий член будет 10).
Повторите вышеупомянутую часть на этот раз, начиная с прямоугольника \ (1 \ times 3 \).
Найдите рекурсивные формулы для каждой из последовательностей периметров, которые вы нашли в частях (a) и (b).Не забудьте также указать начальные условия.
Являются ли последовательности арифметическими? Геометрический? Если нет, то близки ли они к к одному из них (т.е. являются ли различия или отношения почти постоянными)? Объяснять.

13.

Если у вас достаточно зубочисток, вы можете сделать большую треугольную сетку. Ниже представлены треугольные решетки размера 1 и размера 2. Для сетки размера 1 требуется 3 зубочистки, для сетки размера 2 требуется 9 зубочисток.

Пусть \ (t_n \) будет количеством зубочисток, необходимых для создания треугольной сетки размером \ (n \). Запишите первые 5 членов последовательности \ (t_1, t_2, \ ldots \ text {.} \)
Найдите рекурсивное определение последовательности. Объясните, почему вы правы.
Последовательность арифметическая или геометрическая? Если нет, то это последовательность частичных сумм арифметической или геометрической последовательности? Объясните, почему ваш ответ правильный.
Используйте результаты из части (c), чтобы найти замкнутую формулу для последовательности.Показать свою работу.

14.

Если бы вы заштриховали квадрат в \ (n \ times n \) на миллиметровой бумаге, вы могли бы сделать это скучным способом (со сторонами, параллельными краю листа) или интересным способом, как показано ниже:

Здесь интересно то, что квадрат \ (3 \ times 3 \) теперь имеет площадь 13. Наша цель — найти формулу для площади квадрата \ (n \ times n \) (диагонального).

Запишите несколько первых членов последовательности областей (предположим, \ (a_1 = 1 \ text {,} \) \ (a_2 = 5 \ text {,} \) и т. Д.).Последовательность арифметическая или геометрическая? Если нет, то это последовательность частичных сумм арифметической или геометрической последовательности? Объясните, почему ваш ответ правильный, ссылаясь на диагональные квадраты.
Используйте результаты из части (а), чтобы найти замкнутую формулу для последовательности. Показать свою работу. Обратите внимание: хотя здесь есть много способов найти замкнутую формулу, вам следует использовать именно частичные суммы.
Найдите замкнутую формулу как можно большим количеством других интересных способов.

15.

Вот удивительное использование последовательностей для ответа на вопрос о подсчете: сколько номерных знаков состоит из 6 символов с использованием только трех цифр 1, 2 и 3 и четырех букв a, b, c и d, так что нет цифра стоит после любой буквы? Например, «31ddac», «123321» и «ababab» являются допустимыми номерными знаками, а «13ba2c» — нет.

Сначала ответьте на этот вопрос, рассмотрев разные случаи: на скольких номерных знаках нет цифр? Сколько содержат одну цифру и т. Д.7 \ text {.} \)

Математические изображения | Геометрическая последовательность

Последовательность — это упорядоченный список чисел. Некоторые последовательности следуют шаблону.

Каждое число в последовательности называется термином .

Если мы рассматриваем последовательность как функцию, ее доменом являются натуральные числа.

Геометрическая последовательность (или геометрическая прогрессия) — это последовательность чисел, в которой каждый член после первого задается умножением
предыдущий фиксированным ненулевым числом, константой, называемой общим коэффициентом .

Любой член геометрической последовательности можно выразить формулой для общего члена:

Когда отношение r больше 1, мы имеем возрастающую последовательность (экспоненциальный рост).

Даже если соотношение очень мало, последовательность начинает медленно увеличиваться, но после достаточного количества шагов рост становится все больше и больше. Например, это
— результат после 300 шагов, если соотношение равно 1,01:

Если отношение r положительно и меньше 1, последовательность уменьшается, а общий член стремится к 0.

При отрицательном соотношении и последовательность чередуется.

Если отношение r находится между -1 и 0, переменная последовательность имеет общий член, стремящийся к 0.

Если отношение r меньше -1, чередующаяся последовательность по абсолютной величине стремится к бесконечности.
(без знака, если мы рассматриваем значение из-за переменного знака).

Мы можем рассматривать сумму n членов геометрической последовательности.

Мы можем вывести формулу:

В следующем приложении мы можем поиграть с разными случаями с положительным общим отношением:

Вы можете увидеть поведение, если общее отношение больше 1 (сумма растет и растет):

Если общее отношение меньше 1, кажется, что сумма приближается к числу:

Серия — это сумма бесконечных членов последовательности.

Если положительное значение r меньше 1, вы можете суммировать эти бесконечные числа, и результатом будет число.Можно сказать, что ряд сходится
(приближается к некоторому пределу).

Если положительное значение r больше или равно 1, то ряд не приближается к некоторому числу, потому что он становится все больше и больше.
Тогда можно сказать, что ряд расходится.

В следующем приложении мы можем поиграть с общим случаем. Теперь общий рацион может быть положительным или отрицательным:

Расходящиеся альтернативные серии:

Сходящийся альтернативный ряд:

Условием сходимости геометрического ряда с ненулевым знаменателем r является:

А формула такая:

СЛЕДУЮЩИЙ

Один наглядный пример суммирования геометрического ряда.Геометрический ряд с отношением меньше 1 сходится.

БОЛЬШЕ ССЫЛКИ

Геометрический ряд отношения 1/2 сходится. Мы можем изобразить эту серию в виде прямоугольника и последовательно разрезать его пополам. Здесь мы используем прямоугольник, поэтому все прямоугольники похожи.

Мы можем изучить несколько свойств экспоненциальных функций, их производных и введение в число e.

Используя убывающую положительную функцию, вы можете определить ряды.Интегральный тест — это инструмент, позволяющий определить, сходится ли ряд или расходится. Если ряд сходится, интегральный тест дает нам нижнюю и верхнюю границы.

Интеграл степенных функций был известен Кавальери от n = 1 до n = 9. Ферма смог решить эту задачу, используя геометрические прогрессии.

Существует стандартизация размера бумаги, которая называется DIN A. Последующие размеры бумаги в сериях A1, A2, A3, A4 и т. Д. Определяются путем уменьшения вдвое предыдущего размера бумаги по большему размеру.

Расширяющее вращение — это комбинация вращения и растяжения от одной и той же точки.

В равноугольной спирали угол между вектором положения и касательной постоянен.

Мы можем рассматривать это как дилатативное вращение.

Умножение на комплексное число — это преобразование комплексной плоскости: растягивающее вращение.

Из комплексного числа мы можем получить геометрическую прогрессию, получая степени натуральной экспоненты (последовательно умножая)