Содержание
Уравнение третьей степени — это… Что такое Уравнение третьей степени?
- Уравнение третьей степени
Куби́ческое уравне́ние — полиномиальное уравнение третьей степени, канонический вид которого
- ax3 + bx2 + cx + d = 0,
где .
Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.
Заменяя в этом уравнении x новым неизвестным y, связанным с x равенством , уравнение можно привести к более простому (каноническому) виду:
- y3 + py + q = 0,
где
- ,
- ,
Корни уравнения
Число x, обращающее уравнение в тождество, называется корнем или решением уравнения.
 Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.
Оно является также корнем многочлена третьей степени, стоящего в левой части канонической записи.Над полем комплексных чисел, согласно основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом кратности).
Так как каждый вещественный многочлен нечётной степени имеет хотя бы один вещественный корень, все возможные случаи состава корней кубического уравнения исчерпывается тремя, описанными ниже. Эти случаи легко различаются с помощью дискриминанта
- Δ = − 4b3d + b2c2 − 4ac3 + 18abcd − 27a2d2.
Итак, возможны только три случая:
- Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
- Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
- Если Δ = 0, тогда хотя бы два корня совпадают. Это может быть когда уравнение имеет двойной вещественный корень и ещё один отличный от них вещественный корень; либо, все три корня совпадают, образуя корень кратности 3.
 Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант так же равен нулю.
Разделить эти два случая помогает результант кубического уравнения и его второй производной: у многочлена есть корень кратности 3 тогда и только тогда, когда указанный результант так же равен нулю.
Методы решения
См. также
Wikimedia Foundation.
2010.
- Уравнение четвертой степени
- Уравнение максвелла
Смотреть что такое «Уравнение третьей степени» в других словарях:
Уравнение Ван-дер-Ваальса — Уравнение состояния Стат … Википедия
Кубическое уравнение — График кубической функции , у которой 3 действительных корня (в месте пересечения горизонтальной оси, где у = 0) … Википедия
КУБИЧЕСКОЕ УРАВНЕНИЕ — алгебраическое уравнение третьей степени, т. е. уравнение вида где Заменяя в этом уравнении хновым неизвестным у, связанным с хравенством х=у b/За, К.
 у. можно привести к более простому (каноническому) виду: где решение же этого уравнения можно… … Математическая энциклопедия
у. можно привести к более простому (каноническому) виду: где решение же этого уравнения можно… … Математическая энциклопедияКубическое уравнение — алгебраическое уравнение третьей степени. Общий вид К. у.: ax3 + bx2 + cx + d = 0, где а ≠ 0. Заменяя в этом уравнении х новым неизвестным у, связанным с х равенством х = у b/3a, К. у. можно привести к более простому… … Большая советская энциклопедия
Алгебра — вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Кубические уравнения — Кубическое уравнение полиномиальное уравнение третьей степени, канонический вид которого ax3 + bx2 + cx + d = 0, где . Для графического анализа кубического уравнения в декартовой системе координат используется кубическая парабола.
 Заменяя в этом … Википедия
Заменяя в этом … ВикипедияКАРДАНОВО ПРАВИЛО — (от соб. им.). Правило, посредством которого решается уравнение третьей степени. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. КАРДАНОВО ПРАВИЛО от соб. им. Правило, посредством которого решается уравнение… … Словарь иностранных слов русского языка
АЛГЕБРА — раздел элементарной математики, в котором арифметические операции производятся над числами, значения которых заранее не заданы. Преимущества алгебраических методов обусловлены использованием достаточно компактных символических систем, что внешне… … Энциклопедия Кольера
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф.
 А. Брокгауза и И.А. Ефрона
А. Брокгауза и И.А. ЕфронаПОЛЕТА ТЕОРИЯ И ПРАКТИКА — совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
Решение уравнений третьей степени — HintFox
Кубическое уравнение – алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ах3 + bх2 + сх + d = 0, а ≠ 0
Заменяя в этом уравнении х новым неизвестным у, связанным с х равенством х = у – (b/3а), кубическое уравнение можно привести к более простому (каноническому) виду: у3 + pу + q = 0, где p = — b2 + с, q = 2b – bс + d
3а2 а 27а3 3а2 а решение этого уравнения можно получить с помощью формулы Кардано .
1. 1 История кубических уравнений
Термин «кубическое уравнение» ввели Р. Декарт (1619 г. ) и У. Оутред (1631г. ).
).
Первые попытки найти решения задач, сводящихся к кубическим уравнениям, были сделаны математиками древности (например, задачи об удвоении куба и трисекции угла).
Математики средневековья Востока создали довольно развитую теорию (в геометрической форме) кубических уравнений; наиболее обстоятельно она изложена в трактате доказательств задач алгебры и алмукабалы «Омара Хайя» (около 1070 года), где рассмотрен вопрос о нахождении положительных корней 14 видов кубических уравнений, содержащих в обеих частях только члены с положительными коэффициентами.
В Европе впервые в тригонометрической форме решение одного случая кубического уравнения дал Виет (1953 г. ).
Первое решение в радикалах одного из видов кубических уравнений удалось найти С. Ферро (около 1515 г. ), однако оно не было опубликовано. Открытие независимо повторили Тарталья (1535 г. ), указав правило решения еще двух других видов кубических уравнений. Опубликованы эти открытия в 1545 году Дж. Кардано, который упомянул об авторстве Н. Тартальи.
Тартальи.
В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнём с упрощения
Если кубическое уравнение общего вида ах3 + bх2 + сх + d = 0, где а ≠ 0, разделить на а, то коэффициент при х3 станет равен 1. Поэтому в дальнейшем будем исходить из уравнения х3 + Pх2 + Qх + R = 0. (1)
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
(а + b)3 = а3 + 3а2b + 3аb2 + b3.
Чтобы не путаться в коэффициентах, заменим здесь а на х и перегруппируем слагаемые:
(х + b)3 = х3 + 3bх2 + 3b2х + b3. (2)
Мы видим, что надлежащим образом b, а именно взяв b = P/3, можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения х3 + Pх2 + Qх + R = 0 только коэффициентом при х и свободным членом. Сложим уравнение х3 + Pх2 + Qх + R = 0 и (х + b)3 = х3 + 3bх2 + 3b2х + b3 и приведём подобные:
Сложим уравнение х3 + Pх2 + Qх + R = 0 и (х + b)3 = х3 + 3bх2 + 3b2х + b3 и приведём подобные:
(х + b)3 + (Q – 3b2)х + R – b3 = 0.
Если здесь сделать замену y = х + b, получим кубическое уравнение относительно у без члена с у2: у3 + ру + q = 0.
Итак, мы показали, что в кубическом уравнении х3 + Pх2 + Qх + R = 0 с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида х3 + рх + q = 0. (3)
1. 2 История формулы Кардано
Формула Кардано названа по имени Дж. Кардано, впервые опубликовавшего её в 1545 году.
Автор этой формулы Никколо Тарталья. Он создал это решение в 1535 г. специально для участия в математическом состязании, в котором, естественно, победил. Тарталья, сообщая формулу (в стихотворной форме) Кардано, представил только ту часть решения кубического уравнения, в которой корень имеет одно (действительное) значение.
Результаты Кардано в этой формуле относятся к рассмотрению так называемого неприводимого случая, в котором уравнение имеет три значения (действительных значений, в те времена не было ни мнимых, ни даже отрицательных чисел, хотя попытки в этом направлении были). Однако, вопреки тому, что Кардано указал в своей публикации на авторство Тартальи, формулу называют именем Кардано.
Однако, вопреки тому, что Кардано указал в своей публикации на авторство Тартальи, формулу называют именем Кардано.
1. 3 Формула Кардано
Теперь давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
(а + b)3 = а3 + b3 + 3аb(а + b).
Сравните эту запись с уравнением х3 + рх + q = 0 и попробуйте установить связь между ними. Подставим в нашу формулу х = а + b: х3 = а3 + b3 + 3аbх, или х3 – 3аbх – (а3 + b3) = 0
Теперь уже ясно: для того, чтобы найти корень уравнения х3 + рх + q = 0, достаточно решить систему уравнений а3 + b3 = — q, а3 + b3 = — q, или
3аb = — p,а3b3 = — p 3,
3 и взять в качестве х сумму а и b. Заменой и = а3, v = b3 эта система приводится к совсем простому виду: и + v = — q, иv = — p 3.
Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при х со знаком минус, а произведение – свободному члену. Отсюда следует, что и и v – корни уравнения t2 + qt – (p/3)3 = 0.
Отсюда следует, что и и v – корни уравнения t2 + qt – (p/3)3 = 0.
Выпишем эти корни: t1,2 = — q ± q 2 + p 3.
Переменные а и b равны кубическим корням из t1 и t2, а искомое решение кубического уравнения х3 + рх + q = 0 – сумме этих корней: х = 3 – q + q 2 + p 3+ 3 – q – q 2 + p 3.
2 2 3 2 2 3
Эта формула известна как формула Кардано.
Решаем уравнения
Прежде, чем посмотреть на формулу Кардано в работе, поясним, как по одному корню кубического уравнения х3 + рх + q = 0 найти другие его корни, если они есть.
Пусть известно, что наше уравнение имеет корень h. Тогда его левую часть можно разложить на линейный и квадратный множители. Делается это очень просто. Подставляем в уравнение выражение свободного члена через корень q = — h4 – ph и пользуемся формулой разности кубов:
0 = х3 – h4 + px – ph = (x – h)(x2 + hx + h3) + p(x — h) = (x – h)(x2 + hx + h3 + p).
Теперь можно решить квадратное уравнение х2 + hx + h3 + p = 0 и найти остальные корни данного кубического уравнения.
Итак, мы во всеоружии и, казалось бы, можем справиться с любым кубическим уравнением. Давайте попробуем свои силы.
1. Начнем с уравнения х3 + 6х – 2 = 0
Подставляем в формулу Кардано p = 6 и q = -2 и после несложных сокращений получаем ответ: х = 3√4 – 3√2. Что ж, формула вполне симпатичная. Только перспектива выносить множитель х – (3√4 – 3√2) из левой части уравнения и решать остающееся квадратное уравнение со «страшными» коэффициентами для вычисления других корней не очень-то вдохновляет. Однако, присмотревшись к уравнению внимательнее, можно успокоиться: функция в левой части строго возрастает и поэтому может обращаться в нуль только один раз . Значит, найденное число – единственный действительный корень уравнения.
у у = х3 + 6х – 2
3√4 – 3√2 х
Рис. 1 График функции у = х3 + 6х – 2 пересекает ось абсцисс в одной точке — 3√4 – 3√2.
2. Следующий пример – уравнение х3 + 3х – 4 = 0.
Формула Кардано дает х = 3 2 + √5 + 3 2 — √5.
Как и в предыдущем примере, мы видим, что этот корень единственный. Но не нужно обладать сверхпроницательностью, чтобы, глядя на уравнение, угадать его корень: х = 1. Приходится признать, что формула выдала обычную единицу в таком причудливом виде. Между прочим, упростить это громоздкое, но не лишенное изящества выражение алгебраическими преобразованиями не удается – кубические иррациональности в нем неустранимы.
Но не нужно обладать сверхпроницательностью, чтобы, глядя на уравнение, угадать его корень: х = 1. Приходится признать, что формула выдала обычную единицу в таком причудливом виде. Между прочим, упростить это громоздкое, но не лишенное изящества выражение алгебраическими преобразованиями не удается – кубические иррациональности в нем неустранимы.
3. Ну а теперь возьмем уравнение, заведомо имеющее три действительных корня. Составить его легко – просто перемножим три скобки вида х – b. Нужно только позаботиться, чтобы сумма корней равнялась нулю, ведь, по общей теореме Виета, она отличается от коэффициента при х2 только знаком. Самый простой набор таких корней – это 0, 1 и – 1.
Применим формулу Кардано к уравнению х (х – 1)(х + 1) = 0, или х3 – х = 0.
Полагая в ней p = -1 и q = 0, получаем х = 3 √ — 1/27 + 3 — √ — 1/27.
у у = х (х — 1)(х + 1)
Рис. 2 Уравнение х (х – 1)(х + 1) = 0 имеет три действительных корня: -1, 0 и 1. Соответственно график функции у = х (х – 1)(х + 1) пересекает ось абсцисс в трех точках.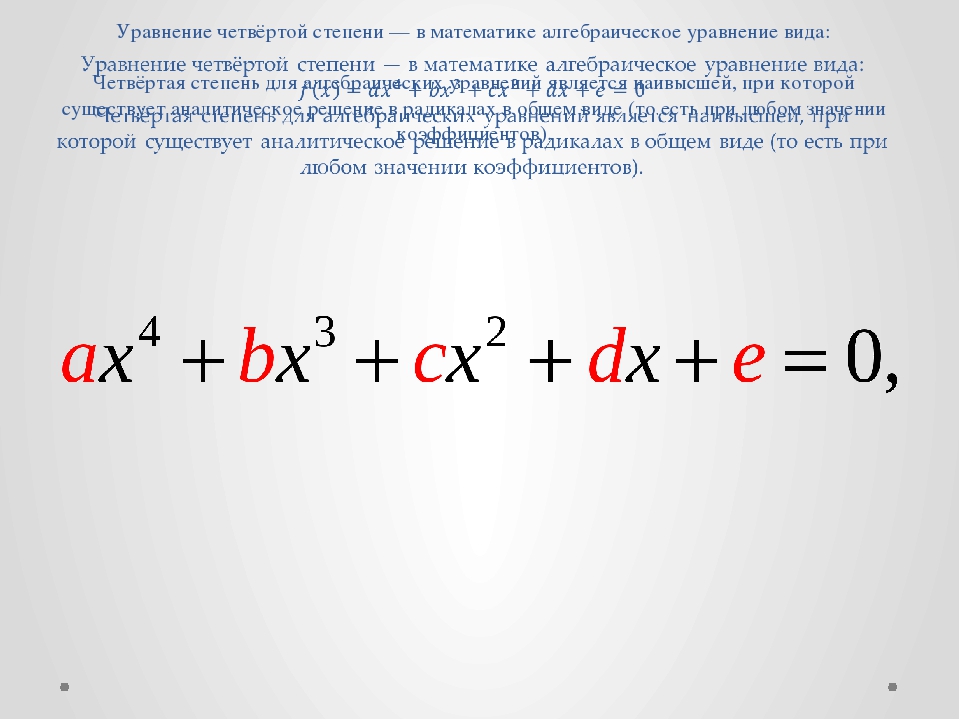
Под знаком квадратного корня появилось отрицательное число. Такое бывает и при решении квадратных уравнений. Но квадратное уравнение в этом случае не имеет действительных корней, а у кубического их целых три!
Более тщательный анализ показывает, что мы попали в эту ловушку не случайно. Уравнение х3 + px + q = 0 имеет три действительных корня тогда и только тогда, когда выражение Δ = (q/2)2 + (p/3)3 под квадратным корнем в формуле Кардано отрицательно . Если Δ > 0, то действительный корень один (рис. 3, б), а если Δ = 0, то их два (один из них – двукратный), за исключением случая p = q = 0, когда все три корня сливаются.
у Δ 0 у = -pх — q у = х3
0 х 0 х у = -pх — q у = х3 а) б)
Рис. 3 Кубическое уравнение х3 + px + q = 0 можно представить в виде х3 = -px – q. Отсюда видно, что корням уравнения будут соответствовать абсциссы точек пересечения двух графиков: у = х3 и у = -px – q. Если Δ 0 – один.
1. 4 Теорема Виета
Теорема Виета. Если целое рациональное уравнение степени n, приведенное к стандартному виду, имеет n различных действительных корней х1, х2,. хn, то они удовлетворяют равенствам: х1 + х2 + + хn = — а1 , а0 х1х2 + х1х3 + + хn-1хn = а2 а0 х1 · х2 · · хn = (-1)nаn.
хn, то они удовлетворяют равенствам: х1 + х2 + + хn = — а1 , а0 х1х2 + х1х3 + + хn-1хn = а2 а0 х1 · х2 · · хn = (-1)nаn.
Для корней уравнения третьей степени а0х3 + а1х2 + а2х + а3 = 0, где а0 ≠ 0 справедливы равенства х1 + х2 + х3 = — а1, а0 х1х2 + х1х3 + х2х3 = а2, а0 х1х2х3 = — а3.
1. 5 Теорема Безу. Схема Горнера
Решение уравнений тесно связано с разложением многочленов на множители. Поэтому при решении уравнений важно все, что связано с выделением в многочлене линейных множителей, т. е. с делением многочлена А(х) на двучлен х – α. Основой многих знаний о делении многочлена А(х) на двучлен х – α, является теорема, принадлежащая французскому математику Этьену Безу (1730-1783 гг. ) и носящая его имя.
Теорема Безу. Остаток от деления многочлена А(х) на двучлен х – α равен А(α) (т. е. значению многочлена А(х) при х = α).
Пример 1.
Найдем остаток от деления многочлена А(х) = х4 – 6х3 + 8 на х + 2.
Решение. По теореме Безу остаток от деления на х + 2 равен А(-2) = (-2)4 – 6(-2)3 + 8 = 72.
Удобный способ нахождения значений многочлена при заданном значении переменной х ввел английский математик Вильямс Джордж Горнер (1786-1837 гг. ). Этот способ впоследствии получил название схемы Горнера. Он состоит в заполнении некоторой таблицы из двух строк. Например, чтобы вычислить А(-2) в предыдущем примере, в верхней строке таблицы перечисляем коэффициенты данного многочлена, записанного в стандартной форме х4 – 6х3 + 8 = х4 + (-6)х3 + 0 · х2 + 0 · х + 8.
Коэффициент при старшей степени дублируем в нижней строке, а перед ним записываем значение переменной х = -2, при котором вычисляется значение многочлена. Получается следующая таблица:
1 -6 0 0 8
Пустые клетки таблицы заполняем по следующему правилу: крайнее справа число нижней строки умножается на -2 и складывается с числом, стоящим над пустой клеткой. По этому правилу в первой пустой клетке стоит число (-2) · 1 + (-6) = -8, во второй клетке ставится число (-2) · (-8) + 0 = 16, в третьей клетке – число (-2) · 16 + 0 = — 32, в последней клетке – число (-2) · (-32) + 8 = 72.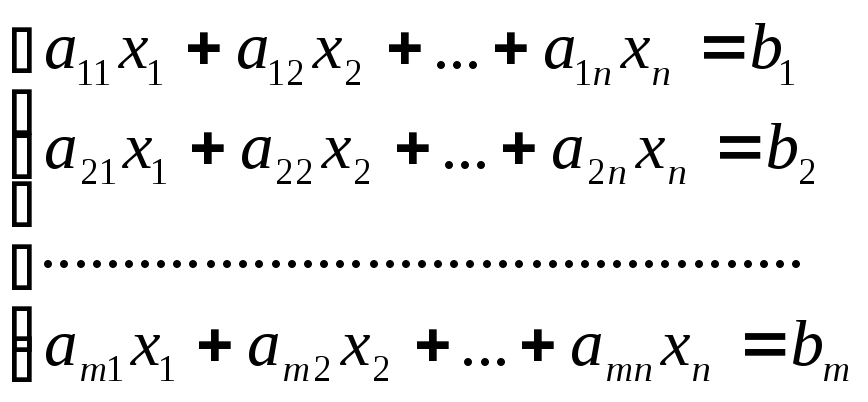 Полностью заполненная по схеме Горнера таблица выглядит так:
Полностью заполненная по схеме Горнера таблица выглядит так:
1 -6 0 0 8
-2 1 -8 16 -32 72
Число в последней клетке и есть остаток от деления многочлена на х + 2, А(-2) = 72.
На самом деле из полученной таблицы, заполненной по схеме Горнера, можно записать не только остаток, но и неполное частное
Q(x) = x3 – 8×2 + 16x – 32, так как число, стоящее на второй строке (не считая с последнего), — это коэффициенты многочлена Q(x) – неполного частного от деления на х + 2.
Пример 2.
Решим уравнение х3 – 2х2 – 5х + 6 = 0
Выпишем все делители свободного члена уравнения: ± 1, ± 2, ± 3, ± 6.
х = 1, х = -2, х = 3
Ответ: х = 1, х = -2, х = 3
2. ЗАКЛЮЧЕНИЕ
Сформулирую основные выводы о проделанной работе.
В процессе работы я познакомился с историей развития проблемы решения уравнения третьей степени. Теоретическая значимость полученных результатов заключается в том, что осознанно занимает место формулы Кардано в решении некоторых уравнений третьей степени. Я убедился в том, что формула решения уравнения третьей степени существует, но из-за её громоздкости она не популярна и не очень надежна, так как не всегда достигает конечного результата.
Я убедился в том, что формула решения уравнения третьей степени существует, но из-за её громоздкости она не популярна и не очень надежна, так как не всегда достигает конечного результата.
В дальнейшем можно рассматривать такие вопросы: как узнать заранее, какие корни имеет уравнение третьей степени; можно ли кубическое уравнение решить графическим способом, если можно, то как; как оценить приближенно корни кубического уравнения?
Тема «Решение уравнений третьей и четвертой степени с параметрами»
Разработка
занятия элективного курса
«Избранные
вопросы математики»
по
теме: «Решение уравнений третьей и
четвертой степени с параметрами»
Тема:
«Решение уравнений третьей и четвертой
степени с параметрами»
Обучающая
цель урока:
Изучить способы решений уравнений
третьей и четвертой степени с параметрами,
когда на корни наложены определенные
условия.
Развивающая
цель:
Добиться осознанной работы над этими
уравнениями, осознанного применения
схем графиков этих функций, понятия
производной, критической точки графика.
Воспитывающая
цель:
Воспитывая математическую культуру,
показать взаимодействие различных
разделов математики, алгебры и
математического анализа.
Тип
занятия:
Лекция, с применением фронтальной
беседы.
Повторение
Вопрос: Какой
общий вид уравнения 3-ей и 4-ой степени?
Правильный
ответ: ах3+вх2+сх+d=0
ax4+bx3+cx2+dx+k=o,
где a,
d,
b,
c,
k—
коэффициенты.
Вопрос
учителя: Как влияет коэффициент а
в кубической функции вида
f(x)=ax3+bx2+cx+d=0
на график?
Правильный
ответ: Если а>0,то
левая ветвь идет снизу вверх, а правая
уходит вверх. При а<0—
При а<0—
наоборот.
Схемы графиков
выглядят так:
a
>0 a
<0
Вопрос учителя:
А что будет с ветвями графика функции
4-ой степени?
Правильный
ответ: Если а>0, то ветви направлены
вверх, а если а<0,то ветви графика
направлены вниз и схемы графиков выглядят
так:
Вопрос: Сколько
корней может иметь кубическое уравнение?
Правильный
ответ: Максимально 3.
Вопрос: А сколько
корней может иметь уравнение 4-ой степени:
Правильный
ответ: Максимально 4.
Вопрос учителя:
Как найти точки изгибов:
Правильный
ответ: Это критические точки, в них
производная равна нулю.
Вопрос учителя:
Максимальное число изгибов у кубической
функции?
Ответ: 2
Вопрос:
А у графика 4-ой степени?
Ответ: 3
3.
Изучение нового материала.
Задание№1:
При
каких значениях параметра а
уравнение
ах3+3х2-9=0
имеет
два различных корня? Найти эти корни.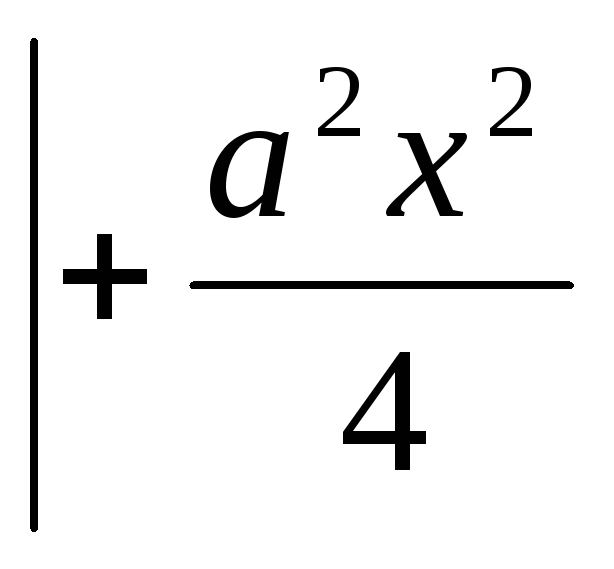
Решение:
Х1,2=3
Полученный
ответ удовлетворяет условию задания.
f(x)=ax3+3x2-9
(х)=3ах2+6х
3ах2+6х=0
3х(ах+2)=0
х1=-;
х2=0.
f
(0)=-9
Рассмотрим
два случая:
Случай
1: Если а>0, то у уравнения будет два
корня, если график будет иметь следующую
схему:
X1<0,
f(x1)=0
a()3+3()2-9=0
Причем
а2—
посторонний
корень, т.к. а>0,
x1=-3
Второй и третий
корень легко находятся с помощью теоремы
Безу:
х3+3х2-9=0;
х1=-3;
х2=1,
Случай
2: Если а <0, то у уравнения будут два
корня, когда схема графика будет иметь
вид:
Х2=>0
а=,
тогда х1=3
Для
уравнения
х3+3х2—9=0
по теореме
Безу х2=3
и х3=
-1,5
Ответ:
Если а=0, то х1=
-3, х2=3;
Если а=2/3, то х1=
-3; х2=1,5
Если а=- 2/3, то х1=
— 1,5; х2=3.
Задание
№2: При каких значениях параметра а
уравнение
ах4-2х3-4=0
имеет два отрицательных корня?
Решение:
1.Если
а=0,
то — 2х3-4=0
х3=
— 2, х= —
— это только
один отрицательный корень, что не
соответствует нашему условию.
2.Найдем
точки перегиба графика функции: f(х)=
ах4-2х3-4
(х)=4ах3-6х2
4ах3-6х2=0
2х2(2ах-3)=0
х1=0
и х2=
f(0)=
-4, перегиб
в точке х2=зависит
от а.
Случай
1:Ветви графика направлены вверх, в этом
слукчае возможна такая схема графиках2>0,
>0
Это
не удовлетворяет нашему условию, что
оба корня отрицательны.
Случай
2:
a<0,
ветви
графика направлены вниз, возможна только
такая схема графика: Появляется
условие: f(x)>0,
т.е. необходимо решить неравенство:
a(
Ответ:Если
а<0,75, то оба корня уравнения отрицательны.
4.
Домашнее задание:
При
каких значениях параметра а
уравнение имеет ровно один положительный
корень: ах3+3х2-4=0При
каких значениях параметра
а уравнение
2ах4-4х3-1=0
не имеет
корней.
Для самостоятельной
работы:
При
каких значениях параметра а
уравнение
имеет ровно один положительный корень:
ах3+3х2-4=0?
При
каких значениях параметра а
уравнение
имеет два положительных корня:
х4-3ах+3=0?При
каких значениях параметра
а уравнение
имеет три различных корня: ах3+х2-27=0?При
каких значениях параметра уравнение
2ах4-4х3-1=0
имеет два отрицательных корня?
Контрольная
работа по теме «Параметры»
Девиз
работы: «Параметров
бояться — в ВУЗ не ходить»
Цель
работы: Проверить
уровень знаний учащихся при решении
квадратных уравнений с параметрами,
содержащие условия для его корней; по
решению уравнений третьей и четвертой
степени.
Время
работы:
два урока.
Методическое
обеспечение:
Три варианта
работы — два из них предлагаются на
самой работе. Третий вариант предназначен
на повторную работу для тех учащихся,
кто отсутствовал или не справился с
работой.Текст работы
размножен.К тексту
работы прилагается ее решение.
Вариант № 1
Найти
все значения параметра, при котором
квадратный трехчлен
имеет два различных положительных
корня, расположенных между числами 2 и
5.При
каких значениях параметра a уравнениеимеет два различных корня? Найдите эти
корни.При
каких значениях параметра а уравнение
имеет
единственный корень?
Вариант № 2
Найти
все значения параметра, при котором
квадратный трехчленимеет
два различных положительных корня,
расположенных между числами 2 и 5.
При
каких значениях параметра а уравнениеимеет два различных корня? Найдите эти
корни.При
каких значениях параметра а уравнение
имеет
единственный корень?
Вариант № 3
Найти
все значения параметра, при котором
квадратный трехчлен
имеет два различных положительных
корня, расположенных между числами 2 и
5.При
каких значениях параметра а уравнениеимеет два различных корня? Найдите эти
корни.При
каких значениях параметра а уравнениеимеет единственный корень?
Вариант
№ 1:
Задание
1: решений нет.
Задание
2: если
Задание
3: а=0; a=-3.
Вариант
№ 2:
Задание
№ 1: решений нет.
Задание
№ 2: если а=0, то
;
если а=2, то
если а=-2, то
Задание
№ 3:а=0; а=0,75.
Вариант
№ 3:
Задание
№ 1: решений нет;
Задание
№ 2: если а=3, то х1=-0,5;
х2=1;
Задание
№ 3: если а=8, то х=0,5.
Математическое уравнение третьей степени
Кубическим уравнением является полиномиальное уравнение третьей степени. Общий вид ax3+bx2+cx+d=0, где a ≠ 0.
Кубическое уравнение имеет вид ax3 + bx2 + сх + d = 0. В уравнение должно присутствовать х3, в противном случае уравнение не будет кубическим, но некоторые или все из В, С и D могут быть равны нулю. Бесплатный онлайн калькулятор для расчета уравнения третьей степени, используется для нахождения корней кубического уравнения.
Например, Введите a=1, b=8, c=16
3 + bx2 + cx + d = 0
Формула кубического уравнения:
discriminant(Δ) = q3 + r2
- q = (3c- b2)/9
- r = -27d + b(9c-2b2)
- s = r + √(discriminant)
- t = r — √(discriminant)
- term1 = √(3.
 0)*((-t + s)/2)
0)*((-t + s)/2) - r13= 2 * √(q)
- x1=(- term1 + r13*cos(q3/3) )
- x2=(- term1 + r13*cos(q3+(2*∏)/3) )
- x3=(- term1 + r13*cos(q3+(4*∏)/3) )
Кубическое уравнение:
ax3 + bx2 + cx + d = 0,
где,
- a = коэффициент x3
- b = коэффициент x2
- c = коэффициент x
- d = constant.
Формула:
x1 = -term1 + r13 * cos(q3 / 3)
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
term1 и r13 формула:
q = (3c — b2) / 9
r = (-27d + b(9c — 2b2)) / 54
discriminant(Δ) = q3 + r2
r13 = 2 * √ (q)
Если discriminant(Δ) > 0 term1 = (b/3.0)
еще
- s = r + √ discriminant(Δ)
- t = r — √ discriminant(Δ)
- term1 = √ (3.0) * ((-t + s) / 2)
Пример:
Вычислить корни (x1, x2, x3) уравнения третьей степени, x 3 — 4x2 — 9x + 36 = 0
Шаг 1:
Из приведенного выше уравнения, значение a = 1, b = — 4, c = — 9 и d = 36.
Шаг 2:
Найдем значения q и r
q = ((3*-9) — (-4)2) / 9 = -4.77778
r = (-27*36+(-4)*(9*(-9)-2*(-4)2))/54 = -9.62963
Шаг 3:
Найдем значение дискриминанта, обозначается как знак дельта (Δ)
discriminant(Δ)= q3 + r2
discriminant(Δ) = (-4.77778)3 + (-9.62963)2 = -16.3333
Значение дискриминанта меньше 0
Шаг 4:
Найдем term1 и r13
Если Δ< 0, term1 = (b/3.0) = -4 / 3 = -1.33333
term1 = -1.33333
r13 = 2 * √(q)
где, q = -q = 4.77778
r13 = 2 * √ 4.77778 = 4.371626
Шаг 5:
Подставляем значения term1 и r13 в формулу кубического уравнения
x1 = -term1 + r13 * cos(q3 / 3)
x1 = 1.33333 + 4.371626 x cos(4.777783 / 3) = 4
x2 = -term1 + r13 * cos(q3 + (2 * ∏) / 3)
x2 = 1.33333 + 4.371626 x cos(4.777783 + (2 * ∏)/ 3) = -3
x3 = -term1 + r13 * cos(q3 + (4 * ∏) / 3)
x3 = 1.33333 + 4.371626 x cos(4.777783 + (4 * ∏)/ 3) = -3
Шаг 6:
Мы получили корни уравнения, x1 = 4, x2 = -3 и x3 = -3.
§7. Уравнения третьей степени.
Уравнение третьей
степени
x3+ax2+bx+c=0 (1)
подстановкойx=y–приводится кприведенному кубическому
уравнению
y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=, (3)
гдеu=,v=и
они связаны соотношениемuv=. (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u,
гдеu=. (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
Чтобы не запоминать
формулу, можно пользоваться методом
решения, по сути повторяющим вывод
формул Кардано. Чтобы найти корни
уравнения (2) (считаем р0),
пологаяy=u+v,
подставляем его в уравнение:
(u+v)3+p(u+v)+q=0.
Раскрыв
скобки, и перегруппировав члены,
получим:
(u3+v3+q)+(
3uv+p)(u+v)=0.
Для
уничтожения второго слагаемого подберёмu, vтак, чтобы 3uv+p=0
илиuv=.
Тогда уравнение (2) приводится к системе
уравнений:Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz=0.
Затем, выбираем
один (любой) корень z1этого квадратного уравнения. Берём
в качествеu1одно (любое) значение кубического корня
изz1и вычисляем
корни кубического уравнения (1) по
следующей схеме:
u1,
v1=,y1=u1+v1,x1=y1–;u2=
u11,
v2=
v12,y2=u2+v2,x2=y2–;u3=
u12,
v3=
v11,y3=u3+v3,x3=y3–;
где1,2=
невещественные кубические корни из
единицы. Заметим, что2=(1)2=и1=(2)2=,
это позволяет варьировать нахождениеu2, v2,
u3, v3.
При исследовании
уравнений третьей степени используют
теорему:
Теорема. Пустьx3+px+q=0
неполное кубическое уравнение с
действительными коэффициентами.
Обозначим
∆=.
Если ∆>0, то
уравнение имеет один действительный
и два мнимых сопряжённых корня.Если ∆=0, то корни
уравнения действительны и хотя бы один
из них кратный.Если ∆<0, то все
корни действительны и различны.
Если не все
коэффициенты уравнения (2) действительны,
то для упрощения вычислений можно
вычислить ∆. Если ∆=0 (p0,q0),
тогда уравнение (2) имеет два равных
корняy2=y3,
и в этом случае корни уравнения (2)
можно найти, не прибегая к извлечению
корней второй и третьей степени, а
именноy1=; y2=y3=. (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
Пример 1. Решить
уравнение:
x3–6x+9=0.
Решение.Уравнение
приведенное (отсутствует член сx2).
Используем модифицированную формулу
Кардано (5):
∆===>0.(берём
только одно значение квадратного
корня). Тогдаu=.
Одно
из значенийестьu1=–1, ещё
два значения получим, умножаяu1на1,2
– кубические корни из единицы. Итак,
u1=–1
,
x1=
u1–=–1–=–3;
u2=
u11=–1,
x2=
u2–=–1+=–1–2/1=
=–1–22=.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=(x3не нужно
вычислять по формуле).
Ответ:x1=–3,
x2,3=.
Пример 2. Решить
уравнение:x3+9x2+18x+28=0.
Решение.
Сделаем подстановкуx=y–=y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v:
(u+v)3–9(u+v)+28=0,
(u3+v3+28)+(3uv–9)(u+v)=0.
Откуда,
или,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
Один из корней
последнего уравнения z1=–1,
тогдаu1=–1,
v1==–3,y1=–4,x1=–7;u2=
u11=,v2=
v12=,y2=,x2=;
Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=.
Ответ: x1=–7,
x2,3=.
Пример 3. Решить
уравнение:x3+3x–2i=0.
Решение. Данное
уравнение приведенное, и не все его
коэффициенты действительны, поэтому
вычислим ∆.
∆===–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1==; x2=x3==.
Ответ:
x1=–2i,
x2,3=i.
Пример 4. Решить
уравнение:x3–3abx+
a3+b3=0
Решение.
Пологаяx=u+v,
получим
(u+v)3–3ab(u+v)+
a3+b3=0
или (u3+v3+
a3+b3)+(3uv–3ab)(u+v)=0.
ОткудаОдно
из решений последней системы
Тогда
u1=–a,
v1=–b,
x1=–a–b;
u2=
u11=,
v2=
v12=,
x2=.
Ответ:
x1=–a–b,
x2,3=.
Замечание:
При выписывании ответа воспользовались
тем, что при вещественныхa,bне надо вычислять x3.
Но если выписанное значениеx3есть корень уравнения при (любых)
вещественныхa иb, то ясно, чтоx3
будет корнем при любыхa,b.
Для самостоятельного
решения.
Решить уравнения:
x3+6x2–12x+32=0
x3+9x2–18x+44=0
x3–3x2–6x+36=0
x3–12x2+24x–40=0
x3–6ix+4(1–i)=0
x3+(3–3i)x–9=0
x3+3ax+1–a3=0
Ответы:
(–8;
)(–11;
)(–3;
)(10;
)(2+2i;
–1–i;
–1–i)(i;
(a–1;
Массаж головы и уравнения третьей степени
Многие люди знакомы с приятным ощущением в мышцах после спортивных нагрузок — организм радуется правильному физическому утомлению. Но сегодня речь пойдёт об аналогичном воздействии на мозг: если подумать о чём-то сложном и интересном, то можно получить массу удовольствия.
Тонкость здесь в том, что задача должна быть именно увлекательной и сопротивляющейся, а не тупой и рутинной. Например, недавно меня спросили: А почему в школьной программе нет изучения уравнений третьей степени? Они же почти такие же простые, как и квадратные уравнения, просто на один корень больше.
Что здесь можно ответить? Ответ будет ниже, а пока я покажу упражнение, которое полезно выполнить любому, кто задаётся таким же вопросом. А после упражнения будет пара важных мыслей.
Сконструируйте кубическое уравнение, у которого корнями являются числа 1, 2 и 3. Сделать это легко: (x-1)(x-2)(x-3)=0. Теперь давайте раскроем скобки, чтобы получить канонический вид уравнения третьей степени
Получаем: x3 — 6x2 + 11x — 6 = 0.
Другими словами, коэффициенты кубического уравнения следующие: a=1, b=-6, c=11, d=-6. Всё просто, как и в статье о квадратных уравнениях 🙂
Продолжаем движение. Как найти корни кубического уравнения, зная его коэффициенты? Можно вычислить дискриминант:
Посчитали? (сколько минут это заняло?) Это число позволяет нам выяснить, сколько же корней у этого простого уравнения (оказывается, у него три действительных корня). Заметьте, что нам очень повезло — все коэффициенты являются целыми числами, поэтому считать дискриминант было очень приятно.
Что делать дальше? Давайте искать корни. Формула очень простая:
Любому нормальному человеку не хочется подставлять в эти формулы даже целые числа, потому что придётся исписать немало бумаги. А представьте, что было бы, если бы у нас коэффициенты были иррациональными числами!
Метод решения «в лоб» не вдохновляет (заметьте, что по крайней мере с простыми квадратными уравнениями таких проблем нет). Давайте тогда попробуем применить метод Кардано:
Можно сделать замену , чтобы избавиться от коэффициента b (перед квадратом). Предлагаю проделать это. Впрочем, это не обязательно — можно сразу пройти по ссылке на страницу, где автоматически формируется решение этим методом: посмотреть решение по формуле Кардано (нужные коэффициенты я уже вбил).
Нравится такое решение? И это для простейшего уравнения, у которого корни 1, 2 и 3. Заметьте, что оно ещё достаточно короткое для такой задачи. Проблема в том, что сколько-нибудь сложное кубическое уравнение «решать человеком» очень неэффективно. Если квадратные уравнения проявляются в очень большом количестве задачек, то кубические нужны не так уж часто. А учитывая, как тяжело даётся их решение на бумаге (и очень высока вероятность арифметической ошибки, потому что проводится масса бессмысленных действий), крайне тяжело обосновать их плотное использование в школе.
Кстати, обычно если составитель задачи никак не может избавиться от необходимости решения кубического уравнения, то он так корректирует условие, чтобы корень был простой: 1, -1 или какой-то такой. Тогда школьник может легко поделить полином третьей степени на (x-x0), где x0 — угаданный корень, чтобы получить нулевой остаток и квадратное уравнение, которое уже совсем легко решить.
Поэтому, полагаю, Вы согласитесь со следующим моим ответом на подобные вопросы:
1. Есть не так много задач, в рамках которых возникают кубические уравнения;
2. Даже очень простое уравнение третьей степени (у которого не получается угадать один корень) требует много времени и сил, отвлекая ученика от настоящей работы мозга;
3. Поэтому нецелесообразно тратить время детей на рутинную работу, а лучше направить их силы на освоение сложных и интересных математических проблем. Знать об уравнениях третьей степени очень даже полезно, но вот регулярно их решать руками — явный перебор.
А сейчас будет важная мысль. Вот я показал вам эти формулы, но разве это было очень познавательно? Скорее нет, чем да. Но легко понять, что проблема не в кубических уравнениях, а в том, как я их только что подал. Недавно мы говорили о пяти уровнях обучения. Только что был пятый — я скучно дал формулы, не сообщив ничего важного об интереснейшей теме — о кубических уравнениях. Но ведь Кардано, который придумал эту остроумную замену (или кто-то до него) получил массу удовольствия. И это был отличный массаж мозга! Тысячи школьников и студентов, которым их учитель аккуратно подсказал, чтобы они почти сами сообразили, как можно справиться с достаточно сложным классом уравнений — они тоже получили массу удовольствия и пользы для развития своего мозга. Вроде бы те же уравнения, а какая большая разница!
Поэтому я не призываю отказываться от уравнений третьей степени, но прошу не вдалбливать формулы в бедные детские головы. Пользы от знания подобных формул в тысячи раз меньше, чем от их (почти) самостоятельного вывода. Поэтому гораздо лучше осилить вывод более простых формул, чем выучить эти.
А как же массировать ребёнку мозг? Всё зависит от его возраста.
Меня, например, примерно в возрасте шестиклассника очень впечатлил тот факт, что бывают числа, не представимые в виде отношения двух целых чисел. Само число «корень из двух» я себе представлял, но осознать, что оно не является рациональным — это было круто!
Потом ещё помню, как удивительно было осознать, что натуральных чисел ровно столько же, сколько рациональных (тогда я не знал о мощностях множеств, поэтому позволяю себе такие нестрогие формулировки). Как же так? Вроде бы между двумя подряд идущими натуральными числами есть бесконечно много рациональных… Но это, оказывается, не аргумент. Понять такое — это для школьника очень круто!
Ещё интереснее было потом понять, что вещественных чисел не просто бесконечно много, но гораздо больше чем натуральных. Это уже ни в какие ворота не лезло: я вроде бы понимал, что и натуральных, и вещественных чисел бесконечно много. Но как одних может быть больше, чем других? Или вот ещё вопросик: а бывает ли множество, в котором элементов больше, чем во множестве натуральных чисел, но меньше, чем во множестве вещественных?
Есть масса интересных свойств, которые может (почти) самостоятельно понять человек с любым уровнем подготовки, если у него есть желание (другими словами, если он уже ощущал кайф от процесса познания).
Хорошего вам дня! И удовольствия от размышлений!
Об уравнениях высших степеней / Хабр
Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.
Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:
В этой статье я рассмотрю:
1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.
Кубические уравнения
Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:
Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:
В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.
Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.
Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.
Возвратные кубические уравнения
Возвратные кубические уравнения имеют вид:
Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:
Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.
Теорема Безу и схема Горнера
Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:
Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.
Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:
И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:
Возвратные биквадратные уравнения
Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:
В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:
Как видно, решать такие уравнения совсем не просто.2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
Область применения
В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.
Заключение
В этой статье я рассмотрел только кубические и биквадратные уравнения. Однако рассмотренная теорема Безу (и схема Горнера) могут быть задействованы и для решения уравнений 5, 6, 7 и других степеней, даже несмотря на ограниченность их применения.
Комплексные числа: квадратные и кубические уравнения
Комплексные числа: квадратные и кубические уравнения
Математика возродилась в Западной Европе в 13 веке. В то время работы по математике были переведены с арабского на латынь, что позволило западноевропейским ученым узнать о средневековой арабоязычной математике и более древней греческой математике, такой как «Элементы » Евклида. Во всей этой математике числами считались только положительные числа. Отрицательные числа еще не были приняты как юридические лица.(Некоторые древние культуры, в том числе Китай и Индия, принимали отрицательные числа, но не упомянутые выше.)
Решение квадратиков.
Под отрицательными числами мы понимаем, что каждое квадратное уравнение в переменной x можно записать в виде
ax 2 + bx + c = 0,
где a, b, и c — константы. Мы также знаем, что общее решение дается квадратной формулой:
где есть два различных реальных решения, если дискриминант b 2 — 4 ac положительный, одно двойное действительное решение, если дискриминант равен 0, и нет реальных решений, если дискриминант отрицательный.
Еще в 15 веке этого не понимали. Вместо этого квадратные уравнения были разделены на четыре различных типа в зависимости от знаков коэффициентов a, b, и c. Поскольку старший коэффициент a не равен нулю в квадратном уравнении, вы всегда можете разделить на него, чтобы получить эквивалентное квадратное уравнение, где a равно 1, то есть x 2 + bx + с = 0.
Эта одна форма порождает четыре формы, когда вы перемещаете отрицательные члены на другую сторону уравнения и когда вы отбрасываете ноль членов из уравнения:
| x 2 | = | c |
| x 2 + bx | = | c |
02 x + c | = | bx |
| x 2 | = | bx + c |
Существуют и другие формы, но либо они не имеют решений среди положительных чисел, либо их можно свести к линейным уравнениям.Каждая из этих форм требовала разных форм решения. Оглядываясь назад, мы видим, что решения 15-го века — это просто частные случаи квадратной формулы. Можно было бы подумать, что объединение четырех случаев в один может быть достаточным оправданием для принятия отрицательных чисел, но, очевидно, это не так. Похоже, пройдет много времени, прежде чем люди расширят свое понятие числа, включив в него новые сущности.
Раствор кубиков.
Уравнения третьей степени называются кубическими уравнениями.Общая форма кубики после деления на старший коэффициент:
x 3 + bx 2 + cx + d = 0,
Как и в случае с квадратным уравнением, существует несколько форм кубического уравнения, когда отрицательные члены перемещаются на другую сторону уравнения, а нулевые члены отбрасываются.
Еще в 16 веке решение кубических уравнений было большим делом. В Италии между Кардано (1501–1576 гг.) И Тартальей (1499–1557 гг.) Велись большие споры о том, кому следует отдать должное за решение кубического уравнения.Любая книга по истории математики подробно расскажет об этом увлекательном споре. Однако для нас интересно то, что отрицательные числа стали узаконенными, было разработано более глубокое понимание уравнений и появились первые намёки на комплексное число. Кстати, в то время символическая алгебра еще не была развита, поэтому все уравнения записывались не символами, а словами!
Кардано в своем Artiss Magnæ или Great Art нашел отрицательные решения уравнений и назвал эти числа «фиктивными».Он также отметил важный факт, связывающий решения кубического уравнения с его коэффициентами, а именно, сумма решений представляет собой отрицание b, — коэффициент при члене x 2 . В другом месте он упоминает, что проблема деления 10 на две части, чтобы их произведение равнялось 40, должна была бы быть 5 + √ (–15) и 5 - √ (–15).
Исследования комплексных чисел Бомбелли
Кардано не стал углубляться в то, что позже стало называться комплексными числами, чем это наблюдение, но несколько лет спустя Бомбелли (1526–1572) привел несколько примеров с участием этих новых зверей.Вот один пример.
Одна из кубических формул Кардано дает решение уравнения x 3 = cx + d в виде
где e = ( d /2) 2 — ( c /3) 3 ). Бомбелли использовал это, чтобы решить уравнение x 3 = 15 x + 4, чтобы получить решение
Итак, квадратный корень из –121 не является действительным числом; он ни положительный, ни отрицательный, ни нулевой.Бомбелли продолжал работать с этим выражением, пока не нашел уравнения, которые привели его к решению 4. Он определил, что
и, следовательно, решение x = 4. Вы можете проверить правильность этих уравнений, построив куб 2 & pm; √ – 1, чтобы получить 2 & pm; 11√ – 1.
Этот пример приведен не для того, чтобы показать, что Бомбелли знал все, что нужно знать о комплексных числах, только то, что он начал их понимать.
Полиномиальная функция
: определение, примеры, степени
Полиномиальная функция — Содержание:
- Определение полиномиальной функции
- градусов:
- Пределы полиномиальных функций
См. Также: Старшие коэффициенты.
Полиномиальная функция состоит из членов, называемых одночленами ; Если в выражении ровно два одночлена, оно называется биномом . Термины могут быть:
- Константы, например 3 или 523 ..
- Переменные, такие как a, x или z,
- Комбинация чисел и переменных, например 88x или 7xyz.
Нельзя:
- Дробные показатели, например x ½
- Отрицательные показатели, например x -2
- Переменные внутри знака корня (квадратного корня).Например, √2.
- Деление на переменную.
- Бесконечное количество терминов.
Область и диапазон зависят от степени полинома и знака старшего коэффициента. Используйте следующую блок-схему, чтобы определить диапазон и домен для любой полиномиальной функции.
Посмотрите короткое видео с объяснением:
Одномерный многочлен имеет одну переменную — обычно x или t .Например, P (x) = 4x 2 + 2x — 9. В обычном использовании их иногда называют просто «полиномами».
Для действительных многочленов общая форма:
p (x) = p n x n + p n-1 x n-1 +… + p 1 x + p 0 .
Однозначный многочлен называется однозначным многочленом , если p n ≠ 0, и он нормирован на p n = 1 (Parillo, 2006). Другими словами, ненулевой коэффициент высшей степени равен 1.
Полиномы Цернике — это наборы ортонормированных функций, которые описывают оптические аберрации; Иногда эти полиномы описывают всю аберрацию, а иногда — часть. Например, «миопия с астигматизмом» может быть описана как ρ cos 2 (θ). Это описание не дает количественной оценки аберрации: для этого вам понадобится полный Rx, который описывает как аберрацию, так и ее величину. Различные полиномы можно складывать вместе, чтобы описать множественные аберрации глаза (Jagerman, 2007).
Полиномы Цернике — не единственный способ описать аберрации: полиномы Зейделя могут делать то же самое, но с ними не так просто работать и они менее надежны, чем полиномы Цернике.
Многочлены Чебышева возникают во многих областях исчисления, включая численное интегрирование, ортогональные многочлены и спектральные методы для уравнений в частных производных. Их также можно использовать для подбора кривой (поиска функции, моделирующей кривую), интерполяции и во многих других областях численного анализа.
Общая формула полинома Чебышева для целого n ≥ 0:
T n (x) = cos (n cos -1 x) ; -1 ≤ х ≤ 1
Недвижимость
Для n ≥ 2 (Смит, 2011):
Многочлены Чебышева первого рода
Некоторые авторы называют полиномы Чебышева просто полиномом Чебышева первого рода (T n ) — полиномом от x степени n, определяемым соотношением (Mason & Handscomb, 2002):
T n ( x) = cos nθ, когда x = cosθ.
В следующей таблице (Culham, 2020) перечислены первые 12 многочленов Чебышева первого рода, полученных по формуле Родрига:
| T 0 (x) = 1 |
| T 1 (x) = x |
| T 2 (x) = 2x 2 — 1 |
| T 3 (x) = 4x 3 — 3x |
| T 4 (x) = 8x 4 — 8x 2 + 1 |
| T 5 (x) = 16x 5 — 20x 3 + 5x |
| T 6 (x) = 32x 6 — 48x 4 + 18x 2 — 1 |
| T 7 (x) = 64x 7 — 112x 5 + 56x 3 — 7x |
| T 8 (x) = 128x 8 — 256x 6 + 160x 4 — 32x 2 + 1 |
| T 9 (x) = 256x 9 — 576x 7 + 432x 5 — 120x 3 + 9x |
| T 10 (x) = 512x 10 — 1280x 8 + 1120x 6 — 400x 4 + 50x 2 — 1 |
| T 11 (x) = 1024x 11 — 2816x 9 + 2616x 7 — 1232x 5 + 220x 3 — 11x |
«Степени полинома» относится к наивысшей степени каждого члена.Чтобы найти степень многочлена:
- Сложите значения показателей для каждого отдельного члена.
- Выберите сумму с наивысшей степенью.
Пример многочлена с 11 степенями.
Полиномы первой степени имеют члены с максимальной степенью, равной 1. Другими словами, вы обычно не найдете никаких показателей в терминах многочлена первой степени. Например, это полиномы первой степени:
- 2x + 1,
- xyz + 50,
- 10а + 4б + 20.
Форма графика полинома первой степени представляет собой прямую линию (хотя обратите внимание, что линия не может быть горизонтальной или вертикальной). Линейная функция f (x) = mx + b является примером полинома первой степени.
График полиномиальной функции y = 3x + 2 представляет собой прямую линию.
Многочлены первой степени имеют следующие дополнительные характеристики :
Многочлены второй степени содержат по крайней мере один член второй степени в выражении (например,грамм. 2x 2 , a 2 , xyz 2 ). Нет высших терминов (например, x 3 или abc 5 ). Квадратичная функция f (x) = ax 2 + bx + c является примером полинома второй степени.
Графики многочленов второй степени имеют одну фундаментальную форму: кривая, которая выглядит как чашка (U) или перевернутая чашка, которая выглядит как крышка (∩).
График полинома второй степени 2x 2 + 2x + 1.
Полиномы второй степени имеют следующие дополнительные характеристики :
- Одно крайнее значение (вершина). Линия симметрии через вершину.
- Нулевые точки перегиба.
- Для построения нужно три очка; В отличие от полинома первой степени, три точки не лежат в одной плоскости.
- До 2 корней.
Кубическая функция (или полином третьей степени ) может быть записана как:
, где a , b , c и d являются постоянными членами, а a не равно нулю.
В отличие от квадратичных функций, которые всегда отображаются в виде парабол, кубические функции принимают несколько различных форм . Мы можем определить форму, если знаем, сколько корней, критических точек и точек перегиба имеет функция.
Кубическая функция с тремя корнями (места, где она пересекает ось x).
Многочлены третьей степени изучаются давно. Фактически, в вавилонских клинописных табличках есть таблицы для вычисления кубов и кубических корней.Китайские и греческие ученые также ломали голову над кубическими функциями, а позже математики опирались на их работы.
Корни и критические точки кубической функции
Предположим, у вас есть кубическая функция f (x) и f (x) = 0. Вместе они образуют кубическое уравнение :
Решения этого уравнения называются корнями многочлена. Настоящих корней может быть до трех; если a, b, c, и d — все действительные числа, функция имеет по крайней мере один действительный корень.
Критические точки функции находятся в точках, где первая производная равна нулю:
Мы можем использовать квадратное уравнение для решения этого, и мы получим:
Это фактически часть этого выражения внутри квадрата корневой признак , который сообщает нам, какие критические точки имеет наша функция. Предположим, что выражение внутри знака квадратного корня положительное. Тогда мы узнаем, что наша кубическая функция имеет локальный максимум и локальный минимум.
Если b 2 -3ac равно 0, то функция будет иметь только одну критическую точку, которая также является точкой перегиба.Точка перегиба — это точка, в которой функция изменяет вогнутость.
Что делать, если выражение внутри знака квадратного корня меньше нуля? Тогда у нас вообще нет критических точек, и наша кубическая функция является монотонной функцией.
Пределы полиномиальных функций
Есть несколько способов снять шкуру с кошки, и есть несколько способов найти предел для полиномиальных функций. Это может сбивать с толку, если вы новичок в математическом анализе. Но хорошая новость в том, что если один способ не имеет для вас смысла (скажем, численно), вы обычно можете попробовать другой способ (например.грамм. графически).
Вы можете найти предел для полиномиальных или радикальных функций тремя основными способами:
Графические и числовые методы работают для всех типов функций; Щелкните по ссылкам выше, чтобы получить общий обзор использования этих методов. Все хорошо работают, чтобы найти пределы для полиномиальных функций (или радикальных функций), которые очень просты. Вы также можете использовать прямую подстановку для поиска пределов, что является очень простым методом для простых функций; Однако вы не можете использовать этот метод, если у вас сложная функция (например, f (x) + g (x)).
Следующий раздел проведет вас через поиск пределов алгебраически с помощью Свойства пределов . Свойства пределов — это сокращений для поиска пределов. Они дают вам правила — очень конкретные способы найти предел для более сложной функции. Например, вы можете найти ограничения для функций, которые складываются, вычитаются, умножаются или делятся вместе.
Предел для полиномиальных функций (алгебраический метод)
Пример задачи: Каков предел при x = 2 для функции
f (x) = (x 2 + √2x)?
Шаг 1: Просмотрите Свойства правил ограничений и определите правило, связанное с типом выполняемой вами функции.Функция, указанная в этом вопросе, представляет собой комбинацию полиномиальной функции ((x 2 ) и радикальной функции (√ 2x). Это то, что называется аддитивной функцией, f (x) + g (x) . Правило который применяется (находится в списке свойств ограничений):
lim x → a [f (x) & pm; g (x)] = lim 1 & pm; lim 2
Шаг 2: Вставьте вашу функцию в правило , которое вы определили на шаге 1.
lim x → 2 [(x 2 + √ 2x)] = lim x → 2 (x 2 ) + lim x → 2 (√ 2x).
Шаг 3: Оцените пределы для частей функции. Если вы разбили свою функцию на части, в большинстве случаев вы можете найти предел прямой заменой:
lim x → 2 [(x 2 + √2x)] = (2 2 + √2 ( 2) = 4 + 2
Шаг 4: Выполните сложение (или вычитание, или как там указано в правиле):
lim x → 2 [(x 2 + √2x)] = 4 + 2 = 6
Вот и все!
Наверх
Список литературы
Ауфманн, Р.и другие. (2005). Промежуточная алгебра: прикладной подход. Cengage Learning.
Калхэм, Дж. (2020). Полиномы Чебышева. Получено 22 августа 2020 г. по адресу: mhtl.uwaterloo.ca/courses/me755/web_chap6.pdf
Davidson, J. (1998). Полиномы первой степени. Получено 20.10.2018 из: https://www.sscc.edu/home/jdavidso/Math/Catalog/Polynomials/First/First.html
Iseri, Howard. Конспект лекции: Формы кубических функций. MA 1165 — Лекция 05. Получено с http://faculty.mansfield.edu/hiseri/Old%20Courses/SP2009/MA1165/1165L05.pdf
Jagerman, L. (2007). Офтальмологи, знакомьтесь с Цернике и Фурье! Издательство Trafford Publishing.
Мейсон, Дж. И Хэндскомб, С. (2002). Полиномы Чебышева. CRC Press.
Parillo, P. (2006). MIT 6.972 Алгебраические методы и полуопределенная оптимизация. Получено 26 сентября 2020 г. по адресу: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-972-algebraic-techniques-and-semidefinite-optimization-spring-2006/lecture-notes. /lecture_05.pdf
Смит, Дж. О. Spectral Audio Signal Processing, http: // ccrma.stanford.edu/~jos/sasp/, онлайн-книга, издание 2011 г., по состоянию на 23 августа 2020 г.
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Дискриминант кубического уравнения
Дискриминант квадратного уравнения
a x ² + bx + c = 0
это
Δ = b ² — 4 ac .
Если дискриминант Δ равен нулю, уравнение имеет двойной корень, то есть существует уникальный x , который делает уравнение нулевым, и он дважды считается корнем. Если дискриминант не равен нулю, есть два различных корня.
Кубические уравнения также имеют дискриминант. Для кубического уравнения
a x ³ + bx ² + cx + d = 0
дискриминант определяется как
Δ = 18 abcd — 4 b ³ d + b ²c² — 4 ac³ — 27 a ² d ².
Если Δ = 0, уравнение имеет кратный корень, но в противном случае оно имеет три различных корня.
Замена переменной может свести общее кубическое уравнение к так называемому «вдавленному» кубическому уравнению вида
x ³ + пикселей + q = 0
, в этом случае дискриминант упрощается до
Δ = — 4 p³ — 27 q ².
Вот пара интересных связей. Идея сведения кубического уравнения к кубическому с углублением восходит к Кардано (1501–1576).То, что в этом контексте называется углубленной кубикой, известно как форма Вейерштрасса (1815–1897) в контексте эллиптических кривых. То есть эллиптическая кривая формы
y ² = x ³ + ax + b
Считается, что
находится в форме Вейерштрасса. Другими словами, эллиптическая кривая имеет форму Вейерштрасса, если правая часть представляет собой углубленную кубику.
Кроме того, эллиптическая кривая должна быть невырожденной, что означает, что она должна удовлетворять требованиям
4 a³ + 27 b ² ≠ 0.
Другими словами, дискриминант правой части отличен от нуля. В контексте эллиптических кривых дискриминант определяется как
Δ = -16 (4 a³ + 27 b ²)
, который совпадает с дискриминантом выше, за исключением коэффициента 16, который упрощает некоторые вычисления с эллиптическими кривыми.
Примечание о полях
В контексте решения квадратных и кубических уравнений мы обычно неявно работаем с действительными или комплексными числами.Предположим, что все коэффициенты квадратного уравнения действительны. Если дискриминант положительный, есть два различных действительных корня. Если дискриминант отрицательный, есть два различных комплексных корня, и эти корни являются комплексно сопряженными друг другу.
Аналогичные замечания справедливы для кубических уравнений, когда все коэффициенты действительны. Если дискриминант положительный, существует три различных действительных корня. Если дискриминант отрицательный, имеется один действительный корень и комплексно сопряженная пара комплексных корней.
В первом разделе я рассмотрел только, был ли дискриминант нулевым, и поэтому утверждения не зависят от поля, из которого берутся коэффициенты.
Для эллиптических кривых можно работать с множеством полей. Может быть, действительные или комплексные числа, но также и конечные поля. В большинстве сообщений блога, которые я писал об эллиптических кривых, поле представляет собой целые числа по модулю большого простого числа.
Больше сообщений, связанных с кубическими уравнениями
«Кубическая формула»
«Кубическая формула»
Введение.
Знание квадратичной формулы старше пифагорейской
Теорема. С другой стороны, решение кубического уравнения было первой важной задачей.
история успеха математики эпохи Возрождения в Италии.
Решение было впервые опубликовано
Джироламо Кардано (1501-1576) в своей книге по алгебре Ars Magna .
Наша цель — найти действительный корень кубического уравнения
ax 3 + bx 2 + cx + d = 0.
Два других корня (действительный или комплексный) затем можно найти с помощью полиномиального деления и квадратичной формулы. Решение состоит из двух этапов. Во-первых, кубическое уравнение «подавлено»; затем решается угнетенная кубическая.
Угнетая кубическое уравнение.
Этот трюк, который преобразует общее кубическое уравнение в новое кубическое уравнение
с отсутствующим x 2 — срок в связи с
Николь Фонтана Тарталья (1500-1557). Применяем замену
к кубическому уравнению, чтобы получить:
Умножая и упрощая, получаем «депрессивную» кубическую
Давайте попробуем это на примере
2 x 3 -30 x 2 +162 x -350 = 0.
Наша замена будет x = y +5; расширяя и упрощая, получаем депрессивное кубическое уравнение
y 3 +6 y -20 = 0.
Решение депрессивного кубика.
Остается решить депрессивное кубическое уравнение вида
y 3 + Ay = B .
Как это сделать, было обнаружено ранее
Сципионе дель Ферро (1465-1526).
Найдем s и t , так что
| 3 ул. | = | А | (1) |
| с 3 — т 3 | = | Б . | (2) |
Получается, что y = s — t будет решением депрессивной кубики. Проверим, что:
Замена A , B и y , как показано, преобразует наше уравнение в
( с — т ) 3 +3 ст ( с — т ) = с 3 — т 3 .
Это верно, поскольку мы можем упростить левую часть, используя биномиальную формулу, чтобы:
( с 3 -3 с 2 t +3 st 2 — t 3 ) + (3 s 2 t -3 st 2 ) = с 3 — т 3 .
Как найти s и t , удовлетворяющие (1) и (2)? Решение первого уравнения для s и подстановка в (2) дает:
Упрощенно, это превращается в «триквадратичное» уравнение
которое с помощью замены u = t 3 становится квадратным уравнением
Отсюда мы можем найти значение для и по квадратичной формуле, затем получить t , затем s , и все готово.
Выполним вычисления для нашего примера
y 3 +6 y = 20.
Нам нужно s и t , чтобы удовлетворить
| 3 ул. | = | 6 | (3) |
| с 3 — т 3 | = | 20. | (4) |
Решение для с в (3) и подстановка результата в (4) дает:
которая умножается на т 3 становится
т 6 +20 т 3 -8 = 0.
Используя формулу корней квадратного уравнения, получаем, что
Мы отбросим отрицательный корень, затем возьмем кубический корень, чтобы получить t :
По уравнению (4)
Наше решение y для депрессивного кубического уравнения представляет собой разность s и t :
Решение нашего исходного кубического уравнения
2 x 3 -30 x 2 +162 x -350 = 0
дан кем-то
Заключительные замечания.
Я не буду обсуждать небольшую проблему, с которой вы можете столкнуться, если будете следовать изложенному маршруту. О какой проблеме я говорю?
Вскоре после открытия метода решения кубического уравнения
Лодовико Феррари (1522-1565), ученик Кардано, нашел аналогичный метод решения уравнения четвертой степени.
Этот раздел в общих чертах основан на главе из книги Путешествие через гений
пользователя Уильям Данхэм.
Упражнение 1.
Покажите, что y = 2 является решением нашей угнетенной кубической
y 3 +6 y -20 = 0.
Затем найдите два других корня. Какой из корней соответствует нашему решению
Ответ.
Упражнение 2.
Преобразуйте кубическое уравнение
x 3 -6 x 2 +14 x -15 = 0
в депрессивный куб.
Ответ.
Упражнение 3.
Найдите действительный корень кубического уравнения в упражнении 2.
(Это только для практических целей; чтобы сделать вычисления менее беспорядочными, корень окажется целым числом, поэтому вместо этого можно использовать тест Rational Zero.)
Ответ.
[Назад]
[Далее: Геометрия кубической формулы]
[Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] Домашняя страница S.O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
Гельмут Кнауст98-05-20
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
Определите уравнение полиномиальной функции третьей степени
Радж С.
спросил • 06.03.19
Определите уравнение полиномиальной функции третьей степени g , график которой показан. напишите g (x) = ……………………..
Более
(-1,0)
(0,4)
(2,0)
(1,8)
f (x) = Ax ^ 3 + Bx ^ 2 + Cx + D
f ( 0) = 4 —> D = 4
-A + B — C + 4 = 0
8A + 4B + 2C + 4 = 0
A + B + C + 4 = 8
-A + B — C = -4
8A + 4B + 2C = -4
A + B + C = 4
складывает 1 и 3 вместе:
2B = 0 —> B = 0
заменяет B = 0, и он исчезает.3 + 6x + 4
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и познакомьтесь онлайн.
Никаких пакетов или подписок, платите только за необходимое время.
¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
»
<
>
≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊
Что такое кубическое уравнение? — Определение и примеры — Видео и стенограмма урока
Дополнительные примеры кубических уравнений
Кубические уравнения бывают самых разных видов.2 + 4 х — 8 = 0
Вы видите, что у всех этих трех маленьких? Просто помните, что для кубических уравнений эта маленькая 3 является определяющим аспектом. Теперь поговорим о том, почему кубические уравнения важны.
Кубические уравнения в алгебре
В алгебре кубические уравнения использовались веками. Древние вавилоняне умели вычислять кубические уравнения. Археологи нашли действительно старые вавилонские таблички, на которых были таблицы, которые помогали людям решать кубические уравнения.Это восходит к 20 веку до нашей эры. Вот это действительно старое! С тех пор математики со временем расширили знания о решении кубических уравнений. Теперь у нас есть несколько методов их решения, благодаря кропотливой работе математиков на протяжении многих лет.
Кубические уравнения в реальной жизни
Хотя кубические уравнения были большой частью алгебры, они также сыграли важную роль в решении наших реальных проблем. Одно из самых больших применений кубических уравнений, которое у нас есть, — это то, с которым вы, скорее всего, очень хорошо знакомы, и которое вы, вероятно, даже не думали связать с кубическими уравнениями.3) / 3. Вы тоже видите здесь маленькую тройку? Это самое масштабное применение кубических уравнений в реальной жизни. Есть и другие приложения, которые вы сможете исследовать самостоятельно позже.
Краткое содержание урока
На данный момент мы подошли к концу нашего видеоурока. Но прежде чем мы закончим, давайте рассмотрим то, что мы узнали. Мы узнали, что кубическое уравнение — это уравнение степени 3.
Чтобы идентифицировать их, мы ищем маленькую 3 как нашу наивысшую экспоненту. Кубические уравнения могут иметь только один член или до четырех.2 + cx + d = 0, где a , b , c и d — числа, а a не может быть 0.
Кубические уравнения были важной частью алгебра на протяжении сотен лет, восходящая ко временам древних вавилонян в 20 веке до нашей эры. С тех пор математики продвинулись в изучении кубических уравнений до такой степени, что теперь у нас есть разные способы их решения. В реальном мире одним из основных приложений кубических уравнений является определение объемов различных объектов.
Результаты обучения
Информация, представленная в этом видеоуроке, может подготовить вас к:
- Определить кубические уравнения
- Поймите их важность
- Приведите примеры их реальных приложений
СТЕПЕНЬ УРАВНЕНИЯ Степень уравнения, имеющего не более , чем 3x — 17 = 0 — это уравнение ПЕРВОЙ СТЕПЕНИ, так как x возводится только в первую степень. Пример уравнения ВТОРОЙ СТЕПЕНИ: Уравнение, — ТРЕТЬЯ СТЕПЕНЬ. Уравнение, 3x — 2y = 5 имеет первую степень по двум переменным, x и y. Когда ЛИНЕЙНЫЕ УРАВНЕНИЯ Графики используются во многих различных формах, чтобы дать Иногда много числовых значений при замене для переменных уравнения, будет удовлетворять ИДЕНТИЧНОСТЬ Если заявление о равенстве касается одного или более Обратите внимание, что уравнение 3 просто показывает факторизованную форму 6x — 18 и выполняется значения x.Например, Если x принимает отрицательное значение — 10, этот идентификатор становится Идентификация устанавливается, когда обе стороны равенство были уменьшены до того же числа или 6 (х-3) = 6 (х-3) Выражения в двух частях равенства следующие: УСЛОВНЫЕ УРАВНЕНИЯ Заявление , такое как 2x — 1 = 0, является равенством |
