Формула отрицательного дискриминанта: Если в дискриминанте отрицательное число — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Если в дискриминанте отрицательное число

Читайте также:

B. Сделайте предложения отрицательными и вопросительными.
I. Решение задач с помощью массивов в среде VBA.
V. Сделайте следующие предложения отрицательными и вопросительными, ответьте на вопросы.
Worksheets(“Решение уравнения”).Range(“C5:D7”).Clear
XI. Системы обыкновенных дифференциальных уравнений.
Анализ и разрешение внутрифирменных конфликтов на основе теории соглашений
Без записи их уравнений
В. Управленческое решение
Важнейшее решение
Взаимодействие ВУЗа с работодателями как решение проблемы трудоустройства молодых специалистов в РФ
Виды дифференциальных уравнений
Виды квадратных матриц.

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример 42.4. Решить уравнение: .

Решение. Найдем дискриминант: = 36 – 52 = -16.

Тогда .

Ответ:

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Дата добавления: 2014-12-27 ; Просмотров: 11818 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Как решать квадратные уравнения?

1. Дискриминант положительный. Это значит, из него можно извлечь корень. 2-4cdot1cdot11=25-44=-19).

Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:

– если (D) положителен – уравнение будет иметь два корня;
– если (D) равен нулю – только один корень;
– если (D) отрицателен – корней нет.

Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt) входит в формулу для вычисления корней квадратного уравнения: (x_<1>=) (frac<-b+sqrt><2a>) и (x_<2>=) (frac<-b-sqrt><2a>) . Давайте рассмотрим каждый случай подробнее.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит (x_<1>) и (x_<2>) будут различны по значению, ведь в первой формуле (sqrt) прибавляется, а во второй – вычитается. 2+x+3) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Квадратное уравнение

Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:

Квадратное уравнение.

Квадратичная функция.

Дискриминант отрицательный. Решение есть!

Неполные квадратные уравнения.

Полезные свойства и закономерности коэффициентов.

Теорема Виета.

Квадратное уравнение и ЕГЭ.

Квадратное уравнение – это уравнение вида:

где коэффициенты a,b и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Пусть пока будет так. *Далее поясню, некорректность второго пункта.

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

Далее не трудно заметить, что число корней зависит от этого самого дискриминанта:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D < 0, то уравнение не имеет действительных корней.

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х₁= 3 х₂= 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1: Решить 2x²+8x–192=0

а=2 b=8 c= –192

D = b²–4ac = 8²–4∙2∙(–192) = 64+1536 = 1600

Ответ: х₁= 8 х₂= –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2: Решить x²–22x+121 = 0

а=1 b=–22 c=121

D = b²–4ac =(–22)²–4∙1∙121 = 484–484 = 0

Получили, что х₁= 11 и х₂= 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3: Решить x²–8x+72 = 0

а=1 b= –8 c=72

D = b²–4ac =(–8)²–4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Рекомендация: не пытайтесь представить комплексное число в реальной жизни, это всё равно, что представить бесконечность, четвёртое измерение или что-то сверх нашего сознания.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x²–16 = 0 => 4x² =16 => x² = 4 => x₁ = 2 x₂ = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x²–45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x₁ = 0 x₂ = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

— если для коэффициентов уравнения аx²+bx+c=0 выполняется равенство

a + b + с = 0, то

— если для коэффициентов уравнения аx²+bx+c=0 выполняется равенство

a + с = b, то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001x²–4995x – 6=0

Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит

Пример 2: 2501x²+2507x+6=0

Выполняется равенство a + с = b, значит

Закономерности коэффициентов.

1. Если в уравнении ax² + bx + c = 0 коэффициент «b» равен (а² +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx² + (а² +1)∙х+ а= 0 = > х₁= –а х₂= –1/a.

Пример. Рассмотрим уравнение 6х² +37х+6 = 0.

х₁= –6 х₂= –1/6.

2. Если в уравнении ax² – bx + c = 0 коэффициент «b» равен (а² +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx² – (а² +1)∙х+ а= 0 = > х₁= а х₂= 1/a.

Пример. Рассмотрим уравнение 15х² –226х +15 = 0.

х₁= 15 х₂= 1/15.

3. Если в уравнении ax² + bx – c = 0 коэффициент «b» равен (a² – 1), а коэффициент «c» численно равен коэффициенту «a», то его корни равны

аx² + (а² –1)∙х – а= 0 = > х₁= – а х₂= 1/a.

Пример. Рассмотрим уравнение 17х² +288х – 17 = 0.

х₁= – 17 х₂= 1/17.

4. Если в уравнении ax² – bx – c = 0 коэффициент «b» равен (а² – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx² – (а² –1)∙х – а= 0 = > х₁= а х₂= – 1/a.

Пример. Рассмотрим уравнение 10х²– 99х –10 = 0.

х₁= 10 х₂= – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

Теорема: Пусть квадратное уравнение aх² + bx + c = 0 имеет корни х₁и х₂, тогда справедливы формулы Виета

Доказательство:

Пример. Рассмотрим уравнение х²– 14х + 45 = 0. Запишем a=1 b= –14 c=45.

Ответ определить несложно, возможны следующие варианты произведений

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а ± b+c ≠ 0, то используется прием переброски, например:

2х² – 11х+5 = 0 (1) => х² – 11х+10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х₁ = 10 х₂= 1

Полученные корни уравнения необходимо разделить на 2 (так как от х² «перебрасывали» двойку), получим

х₁ = 5 х₂= 0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х²:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х₁ = 5 х₂= 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x²— 45x = 0 или 15х+42+9x²— 45x=0 или 15 -5x+10x² = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

3. Если получите большой дискриминант, то посмотрите как можно извлечь такой корень без калькулятора.

На этом всё. Надеюсь, статья была для вас полезной.

Получить материал статьи в формате PDF

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Решение квадратных уравнений с помощью дискриминанта.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах² + b x + c = 0, где коэффициенты a, b и с не равны нулю.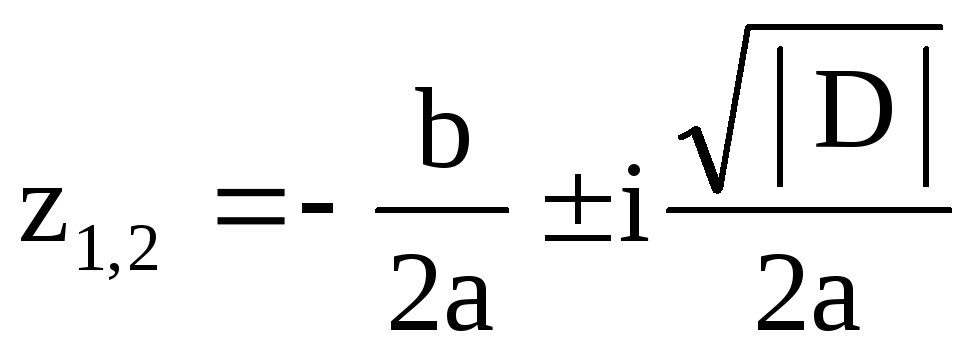 Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b² – 4ас .

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D < 0),то корней нет.

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х₁ = (-b — √D)/2a , и х₂ = (-b + √D)/2a .

Например. Решить уравнение х² – 4х + 4= 0.

D = 4² – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х² + х + 3 = 0.

D = 1² – 4 · 2 · 3 = – 23

Ответ: корней нет.

Решить уравнение 2х² + 5х – 7 = 0.

D = 5² – 4 · 2 · (–7) = 81

х₁ = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х₂ = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1.

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах² + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х² = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3² – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах², затем с меньшим – bx, а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х² равен единице и уравнение примет вид х² + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х².

На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х² + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6² – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х₁ = (-6 — 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3

х₂ = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D₁= 3² – 3 · (– 6) = 9 + 18 = 27

√(D₁) = √27 = √(9 · 3) = 3√3

х₁= (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х₂ = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x² + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного уравнения рисунок 3.

D₂ = 2² – 4 · (– 2) = 4 + 8 = 12

√(D₂) = √12 = √(4 · 3) = 2√3

х₁= (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х₂= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

Онлайн калькулятор: Дискриминант

В алгебре дискриминантом многочлена называется функция от многочлена, описывающая некоторые свойства корней, без их вычисления.

Из школьного курса хорошо известна формула дискриминанта квадратного многочлена . Дискриминант равен . Формула используется для вычисления корней квадратного уравнения.

Однако зная дискриминант можно предсказать некоторые свойства корней, не вычисляя их. В случае квадратичного полинома дискриминант равен нулю тольк в том случае, если имеется один двойной корень. Если дискриминант положителен — то имеются два различных вещественных корня, а если отрицательный — то два комплексно сопряженных.

Следующий калькулятор вычисляет дискриминант квадратичного полинома, а ниже него можно почитать немного теории.

Дискриминант квадратного многочлена

Квадратный многочлен

Дискриминант

Корни многочлена

content_copy Ссылка save Сохранить extension Виджет

Дискриминант

Дискриминант многочлена степени n: может быть определен через результант или через корни.

Через корни полинома, дискриминант выражается следующим образом:

Через результант дискриминант можно выразить так:

где Res — результант многочлена A и его первой производной A’. Если коротко, то результант это определитель Матрицы Сильвестра составленной из A и A’.

В случае квадратного многочлена A производная A’ будет равна . Еси записать матрицу Сильвестра для этих двух многочленов и посчитать детерминант, то мы придем к уже известному:.

Дискриминант полиномов более высоких степеней

Используя второе определение, можно вывести формулы для дискриминанта полиномов более высоких степеней (если перейти по ссылке ниже можно получить формулы для полиномов степеней 3 и 4 и других).
Последовательность OEIS A007878 содержит 5 членов суммы для вычисления дискриминанта полинома 3-й степени, 16 членов для 4-й, 59 членов для 5-й, и наконец 3815311 членов для полиномов 12-й степени.
Следующий калькулятор вычисляет дискриминант многочлена любой степени:

Дискриминант

Введите коэффициенты многочлена, через пробел начиная от более высокой степени к меньшей

Точность вычисления

Знаков после запятой: 2

Дискриминант

Входной многочлен

content_copy Ссылка save Сохранить extension Виджет

Квадратное уравнение

Предварительные навыки

Что такое квадратное уравнение и как его решать?

Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти.

Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением.

Например, следующие уравнения являются квадратными:

Решим первое из этих уравнений, а именно x²− 4 = 0.

Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных.

Итак, в уравнении x²− 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак:

Получили уравнение x²= 4. Ранее мы говорили, что уравнение считается решённым, если в одной части переменная записана в первой степени и её коэффициент равен единице, а другая часть равна какому-нибудь числу. То есть чтобы решить уравнение, его следует привести к виду x = a, где a — корень уравнения.

У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить.

Чтобы решить уравнение x²= 4, нужно ответить на вопрос при каком значении x левая часть станет равна 4. Очевидно, что при значениях 2 и −2. Чтобы вывести эти значения воспользуемся определением квадратного корня.

Число b называется квадратным корнем из числа a, если b²= a и обозначается как

У нас сейчас похожая ситуация. Ведь, что такое x²= 4? Переменная x в данном случае это квадратный корень из числа 4, поскольку вторая степень x прирáвнена к 4.

Тогда можно записать, что . Вычисление правой части позвóлит узнать чему равно x. Квадратный корень имеет два значения: положительное и отрицательное. Тогда получаем x = 2 и x = −2.

Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение , перед следует поставить знак ±

Затем найти арифметическое значение квадратного корня

Выражение x = ± 2 означает, что x = 2 и x = −2. То есть корнями уравнения x²− 4 = 0 являются числа 2 и −2. Запишем полностью решение данного уравнения:

Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно:

В обоих случаях левая часть равна нулю. Значит уравнение решено верно.

Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2)²= 25

Для начала проанализируем данное уравнение. Левая часть возведенá в квадрат и она равна 25. Какое число в квадрате равно 25? Очевидно, что числа 5 и −5

То есть наша задача найти x, при которых выражение x + 2 будет равно числам 5 и −5. Запишем эти два уравнения:

Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко:

Значит корнями уравнения (x + 2)²= 25 являются числа 3 и −7.

В данном примере как и в прошлом можно использовать определение квадратного корня. Так, в уравнения (x + 2)²= 25 выражение (x + 2) представляет собой квадратный корень из числа 25. Поэтому можно cначала записать, что .

Тогда правая часть станет равна ±5. Полýчится два уравнения: x + 2 = 5 и x + 2 = −5. Решив по отдельности каждое из этих уравнений мы придём к корням 3 и −7.

Запишем полностью решение уравнения (x + 2)²= 25

Из рассмотренных примеров видно, что квадратное уравнение имеет два корня. Чтобы не забыть о найденных корнях, переменную x можно подписывать нижними индексами. Так, корень 3 можно обозначить через x₁, а корень −7 через x₂

В предыдущем примере тоже можно было сделать так. Уравнение x²− 4 = 0 имело корни 2 и −2. Эти корни можно было обозначить как x₁= 2 и x₂= −2.

Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже.

Сделаем проверку для уравнения (x + 2)²= 25. Подставим в него корни 3 и −7. Если при значениях 3 и −7 левая часть равна 25, то это будет означать, что уравнение решено верно:

В обоих случаях левая часть равна 25. Значит уравнение решено верно.

Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так:

ax² + bx + c = 0,
где a, b, c — некоторые числа, x — неизвестное.

Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения.

Пусть дано уравнение 3x²+ 2x = 16. В нём переменная x возведенá во вторую степень, значит уравнение является квадратным. Приведём данное уравнение к общему виду.

Итак, нам нужно получить уравнение, которое будет похоже на уравнение ax²+ bx + c = 0. Для этого в уравнении 3x²+ 2x = 16 перенесем 16 из правой части в левую часть, изменив знак:

3x² + 2x − 16 = 0

Получили уравнение 3x²+ 2x − 16 = 0. В этом уравнении a = 3, b = 2, c = −16.

В квадратном уравнении вида ax²+ bx + c = 0 числа a, b и c имеют собственные названия. Так, число a называют первым или старшим коэффициентом; число b называют вторым коэффициентом; число c называют свободным членом.

В нашем случае для уравнения 3x²+ 2x − 16 = 0 первым или старшим коэффициентом является 3; вторым коэффициентом является число 2; свободным членом является число −16. Есть ещё другое общее название для чисел a, b и c — параметры.

Так, в уравнении 3x²+ 2x − 16 = 0 параметрами являются числа 3, 2 и −16.

В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения.

Например, если дано уравнение −5 + 4x²+ x = 0, то его желательно записать в нормальном виде, то есть в виде ax²+ bx + c = 0.

В уравнении −5 + 4x²+ x = 0 видно, что свободным членом является −5, он должен располагаться в конце левой части. Член 4x² содержит старший коэффициент, он должен располагаться первым. Член x соответственно будет располагаться вторым:

Квадратное уравнение в зависимости от случая может принимать различный вид. Всё зависит от того, чему равны значения a, b и с.

Если коэффициенты a, b и c не равны нулю, то квадратное уравнение называют полным. Например, полным является квадратное уравнение 2x²+ 6x − 8 = 0.

Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x²+ 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6), но отсутствует свободный член c.

Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения.

Пусть дано квадратное уравнение 2x²+ 6x − 8 = 0. В этом уравнении a = 2, b = 6, c = −8. Если b сделать равным нулю, то уравнение примет вид:

Получилось уравнение 2x²− 8 = 0. Чтобы его решить перенесем −8 в правую часть, изменив знак:

2x²= 8

Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2

У нас получилось уравнение, которое мы решали в начале данного урока. Чтобы решить уравнение x²= 4, следует воспользоваться определением квадратного корня. Если x²= 4, то . Отсюда x = 2 и x = −2.

Значит корнями уравнения 2x²− 8 = 0 являются числа 2 и −2. Запишем полностью решение данного уравнения:

В обоих случаях левая часть равна нулю, значит уравнение решено верно.

Уравнение, которое мы сейчас решили, является неполным квадратным уравнением. Название говорит само за себя. Если полное квадратное уравнение выглядит как ax²+ bx + c = 0, то сделав коэффициент b нулём получится неполное квадратное уравнение ax²+ c = 0.

У нас тоже сначала было полное квадратное уравнение 2x²+ 6x − 4 = 0. Но мы сделали коэффициент b нулем, то есть вместо числа 6 поставили 0. В результате уравнение обратилось в неполное квадратное уравнение 2x²− 4 = 0.

В начале данного урока мы решили квадратное уравнение x²− 4 = 0. Оно тоже является уравнением вида ax²+ c = 0, то есть неполным. В нем a = 1, b = 0, с = −4.

Также, неполным будет квадратное уравнение, если коэффициент c равен нулю.

Рассмотрим полное квадратное уравнение 2x²+ 6x − 4 = 0. Сделаем коэффициент c нулём. То есть вместо числа 4 поставим 0

Получили квадратное уравнение 2x²+ 6x=0, которое является неполным. Чтобы решить такое уравнение, переменную x выносят за скобки:

Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).

В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала:

Получилось два уравнения: x = 0 и 2x + 6 = 0. Первое уравнение решать не нужно — оно уже решено. То есть первый корень равен нулю.

Чтобы найти второй корень, решим уравнение 2x + 6 = 0. Это обычное линейное уравнение, которое решается легко:

Видим, что второй корень равен −3.

Значит корнями уравнения 2x²+ 6x = 0 являются числа 0 и −3. Запишем полностью решение данного уравнения:

Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно:

Следующий случай это когда числа b и с равны нулю. Рассмотрим полное квадратное уравнение 2x²+ 6x − 4 = 0. Сделаем коэффициенты b и c нулями. Тогда уравнение примет вид:

Получили уравнение 2x²= 0. Левая часть является произведением, а правая часть равна нулю. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Очевидно, что x = 0. Действительно, 2 × 0²= 0. Отсюда, 0 = 0. При других значениях x равенства достигаться не будет.

Проще говоря, если в квадратном уравнении вида ax²+ bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю.

Отметим, что когда употребляются словосочетания «b равно нулю» или «с равно нулю«, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении.

Например, если дано уравнение 2x²− 32 = 0, то мы говорим, что b = 0. Потому что если сравнить с полным уравнением ax²+ bx + c = 0, то можно заметить, что в уравнении 2x²− 32 = 0 присутствует старший коэффициент a, равный 2; присутствует свободный член −32; но отсутствует коэффициент b.

Наконец, рассмотрим полное квадратное уравнение ax²+ bx + c = 0. В качестве примера решим квадратное уравнение x²− 2x + 1 = 0.

Итак, требуется найти x, при котором левая часть станет равна нулю. Воспользуемся изученными ранее тождественными преобразованиями.

Прежде всего заметим, что левая часть уравнения представляет собой квадрат разности двух выражений. Если мы вспомним как раскладывать многочлен на множители, то получим в левой части (x − 1)².

Рассуждаем дальше. Левая часть возведенá в квадрат и она равна нулю. Какое число в квадрате равно нулю? Очевидно, что только 0. Поэтому наша задача найти x, при котором выражение x − 1 равно нулю. Решив простейшее уравнение x − 1 = 0, можно узнать чему равно x

Этот же результат можно получить, если воспользоваться квадратным корнем. В уравнении (x − 1)²= 0 выражение (x − 1) представляет собой квадратный корень из нуля. Тогда можно записать, что . В этом примере записывать перед корнем знак ± не нужно, поскольку корень из нуля имеет только одно значение — ноль. Тогда получается x − 1 = 0. Отсюда x = 1.

Значит корнем уравнения x²− 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает.

Не всегда бывают даны простые уравнения. Рассмотрим например уравнение x²+ 2x − 3 = 0.

В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения.

Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст.

Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения:

В получившемся уравнении перенесем −4 в правую часть, изменив знак:

Теперь воспользуемся квадратным корнем. В уравнении (x + 1)²= 4 выражение (x + 1) представляет собой квадратный корень из числа 4. Тогда можно записать, что . Вычисление правой части даст выражение x + 1 = ±2. Отсюда полýчится два уравнения: x + 1 = 2 и x + 1 = −2, корнями которых являются числа 1 и −3

Значит корнями уравнения x²+ 2x − 3 = 0 являются числа 1 и −3.

Выполним проверку:

Пример 3. Решить уравнение x²− 6x + 9 = 0, выделив полный квадрат.

Выделим полный квадрат из левой части:

Далее воспользуемся квадратным корнем и узнáем чему равно x

Значит корнем уравнения x²− 6x + 9 = 0 является 3. Выполним проверку:

Пример 4. Решить квадратное уравнение 4x²+ 28x − 72 = 0, выделив полный квадрат:

Выделим полный квадрат из левой части:

Перенесём −121 из левой части в правую часть, изменив знак:

Воспользуемся квадратным корнем:

Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их:

Пример 5. Решить уравнение 2x²+ 3x − 27 = 0

Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения.

Так, в прошлом примере первым членом уравнения был 4x². Его можно было представить в виде квадрата выражения 2x, то есть (2x)²= 2²x²= 4x². Чтобы убедиться что это правильно, можно извлечь квадратный корень из выражения 4x². Это квадратный корень из произведения — он равен произведению корней:

В уравнении 2x²+ 3x − 27 = 0 первый член это 2x². Его нельзя представить в виде квадрата какого-нибудь выражения. Потому что нет числá, квадрат которого равен 2. Если бы такое число было, то этим числом был бы квадратный корень из числа 2. Но квадратный корень из числа 2 извлекается только приближённо. А приближённое значение не годится для представления числá 2 в виде квадрата.

Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения.

Тогда можно разделить обе части нашего уравнения на 2. Это позвóлит избавиться от двойки перед x² что впоследствии даст нам возможность выделить полный квадрат:

Перепишем левую часть в виде трёх дробей со знаменателем 2

Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю:

Выделим полный квадрат.

При представлении члена в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на . При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.

Свернём полученный полный квадрат:

Приведём подобные члены:

Перенесём дробь в правую часть, изменив знак:

Воспользуемся квадратным корнем. Выражение представляет собой квадратный корень из числа

Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби:

Тогда наше уравнение примет вид:

Полýчим два уравнения:

Решим их:

Значит корнями уравнения 2x²+ 3x − 27 = 0 являются числа 3 и .

Корень удобнее оставить в таком виде, не выполняя деления числителя на знаменатель. Так проще будет выполнять проверку.

Выполним проверку. Подставим найденные корни в исходное уравнение:

В обоих случаях левая часть равна нулю, значит уравнение 2x²+ 3x − 27 = 0 решено верно.

Решая уравнение 2x²+ 3x − 27 = 0, в самом начале мы разделили обе его части на 2. В результате получили квадратное уравнение, в котором коэффициент перед x² равен единице:

Такой вид квадратного уравнения называют приведённым квадратным уравнением.

Любое квадратное уравнение вида ax²+ bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax²+ bx + c = 0 нужно разделить на a

Пример 6. Решить квадратное уравнение 2x²+ x + 2 = 0

Сделаем данное уравнение приведённым:

Выделим полный квадрат:

Получили уравнение , в котором квадрат выражения равен отрицательному числу . Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.

Следовательно, нет такого значения x, при котором левая часть стала бы равна . Значит уравнение не имеет корней.

А поскольку уравнение равносильно исходному уравнению 2x²+ x + 2 = 0, то и оно (исходное уравнение) не имеет корней.

Формулы корней квадратного уравнения

Выделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно.

Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся.

Взяв за основу буквенное уравнение ax²+ bx + c = 0, и выполнив некоторые тождественные преобразования, мы сможем получить формулы для вывода корней квадратного уравнения ax²+ bx + c = 0. В эти формулы можно будет подставлять коэффициенты a, b, с и получать готовые решения.

Итак, выделим полный квадрат из левой части уравнения ax²+ bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a

Теперь в получившемся уравнении выделим полный квадрат:

Перенесем члены и в правую часть, изменив знак:

Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби:

В числителе правой части вынесем за скобки a

Сократим правую часть на a

Поскольку все преобразования были тождественными, то получившееся уравнение имеет те же корни, что и исходное уравнение ax²+ bx + c = 0.

Уравнение будет иметь корни только тогда, если правая часть больше нуля или равна нулю. Это потому что в левой части выполнено возведéние в квадрат, а квадрат любого числа положителен или равен нулю (если в этот квадрат возвóдится ноль). А чему будет равна правая часть зависит от того, что будет подставлено вместо переменных a, b и c.

Поскольку при любом a не рáвным нулю, знаменатель правой части уравнения всегда будет положительным, то знак дроби будет зависеть от знака её числителя, то есть от выражения b²− 4ac.

Выражение b²− 4ac называют дискриминантом квадратного уравнения. Дискриминант это латинское слово, означающее различитель. Дискриминант квадратного уравнения обозначается через букву D

D = b²− 4ac

Дискриминант позволяет заранее узнать имеет ли уравнение корни или нет. Так, в предыдущем задании мы долго решали уравнение 2x²+ x + 2 = 0 и оказалось, что оно не имеет корней. Дискриминант же позволил бы нам заранее узнать, что корней нет. В уравнении 2x²+ x + 2 = 0 коэффициенты a, b и c равны 2, 1 и 2 соответственно. Подставим их в формулу D = b²−4ac

D = b² − 4ac = 1² − 4 × 2 × 2 = 1 − 16 = −15.

Видим, что D (оно же b²− 4ac) является отрицательным числом. Тогда нет смысла решать уравнение 2x²+ x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида , окажется что правая часть станет меньше нуля (из-за отрицательного дискриминанта). А квадрат числа не может быть отрицательным. Следовательно, корней у данного уравнения не будет.

Станóвится понятно почему древние люди считали выражение b²− 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней.

Итак, D равно b²− 4ac. Подставим в уравнении вместо выражения b²− 4ac букву D

Если дискриминант исходного уравнения окажется меньше нуля (D < 0), то уравнение примет вид:

В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным.

Если дискриминант исходного уравнения окажется больше нуля (D > 0), то уравнение примет вид:

В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем:

Получили уравнение . Из него полýчится два уравнения: и . Выразим x в каждом из уравнений:

Получившиеся два равенства это и есть универсальные формулы для решения квадратного уравнения ax²+ bx + c = 0. Их называют формулами корней квадратного уравнения.

Чаще всего эти формулы обозначаются как x₁ и x₂. То есть для вычисления первого корня используется формула c индексом 1; для вывода второго корня — формула с индексом 2. Обозначим свои формулы так же:

Очерёдность применения формул не важнá.

Решим например квадратное уравнение x²+ 2x − 8 = 0 с помощью формул корней квадратного уравнения. Коэффициенты данного квадратного уравнения это числа 1, 2 и −8. То есть, a = 1, b = 2, c = −8.

Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения.

Найдём дискриминант квадратного уравнения. Для этого воспользуемся формулой D = b²− 4ac. Вместо переменных a, b и c у нас будут коэффициенты уравнения x²+ 2x − 8 = 0

D = b²− 4ac = 2²− 4 × 1 × (−8) = 4 + 32 = 36

Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения:

Значит корнями уравнения x²+ 2x − 8 = 0 являются числа 2 и −4. Проверкой убеждаемся, что корни найдены верно:

Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению . Если дискриминант равен нулю, то правая часть уравнения примет вид:

И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем:

Далее выражаем x

Это ещё одна формула для вывода корня квадратного корня. Рассмотрим её применение. Ранее мы решили уравнение x²− 6x + 9 = 0, имеющее один корень 3. Решили мы его методом выделения полного квадрата. Теперь попробуем решить с помощью формул.

Найдём дискриминант квадратного уравнения. В этом уравнении a = 1, b = −6, c = 9. Тогда по формуле дискриминанта имеем:

D = b²− 4ac = (−6)²− 4 × 1 × 9 = 36 − 36 = 0

Дискриминант равен нулю (D = 0). Это означает, что уравнение имеет только один корень, и вычисляется он по формуле

Значит корнем уравнения x²− 6x + 9 = 0 является число 3.

Для квадратного уравнения, имеющего один корень также применимы формулы и . Но применение каждой из них будет давать один и тот же результат.

Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3

Если квадратное уравнение имеет только один корень, то желательно применять формулу , а не формулы и . Это позволяет сэкономить время и место.

Пример 3. Решить уравнение 5x²− 6x + 1 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения:

Значит корнями уравнения 5x²− 6x + 1 = 0 являются числа 1 и .

Ответ: 1; .

Пример 4. Решить уравнение x²+ 4x + 4 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле

Значит корнем уравнения x²+ 4x + 4 = 0 является число −2.

Ответ: −2.

Пример 5. Решить уравнение 3x²+ 2x + 4 = 0

Найдём дискриминант квадратного уравнения:

Дискриминант меньше нуля. Значит корней у данного уравнения нет.

Ответ: корней нет.

Пример 6. Решить уравнение (x + 4)²= 3x + 40

Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его:

Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль:

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения (x + 4)²= 3x + 40 являются числа 3 и −8.

Ответ: 3; −8.

Пример 7. Решить уравнение

Умнóжим обе части данного уравнения на 2. Это позвóлит нам избавиться от дроби в левой части:

В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения являются числа 23 и −1.

Ответ: 23; −1.

Пример 8. Решить уравнение

Умнóжим обе части на наименьшее общее кратное знаменателей обеих дробей. Это позвóлит избавиться от дробей в обеих частях. Наименьшее общее кратное чисел 2 и 3 это число 6. Тогда получим:

В получившемся уравнении раскроем скобки в обеих частях:

Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0

Приведём подобные члены в левой части:

В получившемся уравнении найдём дискриминант:

Значит корнями уравнения являются числа и 2.

Примеры решения квадратных уравнений

Пример 1. Решить уравнение x²= 81

Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода:

Ответ: 9, −9.

Пример 2. Решить уравнение x²− 9 = 0

Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим:

Ответ: 3, −3.

Пример 3. Решить уравнение x²− 9x = 0

Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки:

Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю.

Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено:

Ответ: 0, 9.

Пример 4. Решить уравнение x²+ 4x − 5 = 0

Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения.

Решим данное уравнение с помощью формул. Сначала найдём дискриминант:

D = b²− 4ac = 4²− 4 × 1 × (−5) = 16 + 20 = 36

Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их:

Ответ: 1, −5.

Пример 5. Решить уравнение

Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях:

В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль:

Приведём подобные члены:

Решим получившееся уравнение с помощью формул:

Ответ: 5, .

Пример 6. Решить уравнение x²= 6

В данном примере как и в первом нужно воспользоваться квадратным корнем:

Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых:

Но чаще всего корень оставляют в виде радикала:

Ответ:

Пример 7. Решить уравнение (2x + 3)²+ (x − 2)²= 13

Раскроем скобки в левой части уравнения:

В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены:

Получили неполное квадратное уравнение. Решим его:

Ответ: 0, −1,6.

Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0

Данное уравнение можно решить двумя способами. Рассмотрим каждый из них.

Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения.

Раскроем скобки:

Приведём подобные члены:

Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим:

Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные:

Решим получившееся уравнение с помощью формул корней квадратного уравнения:

Второй способ. Найти значения x, при которых сомножители левой части уравнения равны нулю. Этот способ удобнее и намного короче.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит:

Примеры решения задач

Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м². При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?

Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:

Обозначим ширину комнаты через x. А длину комнаты через 2x, потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:

Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:

2x × x

По условию задачи площадь должна быть 8 м². Значит выражение 2x × x следует приравнять к 8

2x × x = 8

Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.

Первое что можно сделать это выполнить умножение в левой части уравнения:

2x² = 8

В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.

Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2

Теперь воспользуемся квадратным корнем. Если x²= 4, то . Отсюда x = 2 и x = −2.

Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2. Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.

А длина была обозначена через 2x. Значение x теперь известно, подставим его в выражение 2x и вычислим длину:

2x = 2 × 2 = 4

Значит длина равна 4 м, а ширина 2 м. Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м²

4 × 2 = 8 м²

Ответ: длина комнаты составляет 4 м, а ширина 2 м.

Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м²

Решение

Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м². Умножим длину участка на его ширину и приравняем к 1200, получим уравнение:

x(x + 10) = 1200

Решим данное уравнение. Для начала раскроем скобки в левой части:

Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0

Решим получившееся уравнение с помощью формул:

Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30. Потому что ширина не может выражаться отрицательным числом.

Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10. Подставим в него найденное значение x и вычислим длину:

x + 10 = 30 + 10 = 40 м

Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30) получится 1200 м²

40 × 30 = 1200 м²

Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка.

Периметр прямоугольника это сумма всех его сторон. Тогда:

P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.

Ответ: длина изгороди огородного участка составляет 140 м.

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 2; −2.

Задание 2. Решить уравнение:

Решение:

Ответ: корней нет.

Задание 3. Решить уравнение:

Решение:

Ответ: 3; −3.

Задание 4. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 3; −13.

Задание 5. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 12; 4.

Задание 6. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 7; 5.

Задание 7. Решить уравнение:

Решение:

Ответ: 0; 1.

Задание 8. Решить уравнение:

Решение:

Ответ: 0; −3.

Задание 9. Решить уравнение:

Решение:

Ответ: 7; −7.

Задание 10. Решить уравнение:

Решение:

Ответ:

Задание 11. Решить уравнение:

Решение:

Ответ: 5; −5.

Задание 12. Решить уравнение:

Решение:

Ответ: 7; 2

Задание 13. Решить уравнение:

Решение:

Ответ: корней нет.

Задание 14. Решить уравнение:

Решение:

Ответ:

Задание 15. Решить уравнение:

Решение:

Ответ: 1; −5.

Задание 16. Решить уравнение:

Решение:

Ответ: 5; −9.

Задание 17. Решить уравнение:

Решение:

Ответ: −3; −4.

Задание 18. Решить уравнение:

Решение:

Ответ: .

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Дискриминант. Решение, примеры

Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.

Предлагаю вам подробный алгоритм решения неравенств методом интервалов
, следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств
.

Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i
2 = — 1.

Вместе с тем

(- i

) 2 = (- 1 i

) 2 = (- 1) 2 i

2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i

и — i

. Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi

равен — 1. Тогда

(а + bi

) 2 = — 1,

а
2 + 2аbi

— b

2 = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а

и b

должно равняться нулю. Если b

= 0, то из первого уравнения получается а

2 = — 1. Число а

действительное, и поэтому а

2 >
0. Неотрицательное число а

2 не может равняться отрицательному числу — 1. Поэтому равенство b

= 0 в данном случае невозможно. Остается признать, что а

= 0, но тогда из первого уравнения системы получаем: —b

2 = — 1, b

= ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i

и —i

, Условно это записывается в виде:

√-1 = ± i

.

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а

. Такими числами являются √ai

и -√ai

. Условно это записывается так:

√— а

= ± √ai

.

Под √a

здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i

, √-9= ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x

2 + 2х

+ 5 = 0; тогда

х
1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i

.

Итак, данное уравнение имеет два корня: х

1 = — 1 +2i

, х

2 = — 1 — 2i

. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Понятие комплексного числа

Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = b и c = d .
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i (b + d).
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
ac – bd + i (ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,

№ 4 .1.
В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множествавещественных чисел или множества комплексных чисел .

График функции

Фрагмент графика функции

Способы задания функции

[править]Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

[править]Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

[править]Графический способ

Осциллограмма задаёт значение некоторой функции графически.

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

[править]Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

факториал;
числа Фибоначчи;
функция Аккермана.

[править]Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

функция, возвращающая цифру в записи числа пи по её номеру;
функция, возвращающая число атомов во вселенной в определённый момент времени;
функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 253. Извлечение корней квадратных из отрицательных чисел.
Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i

2 = — 1.

Вместе с тем

(- i

) 2 = (- 1 i

) 2 = (- 1) 2 i

2 = -1.

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi

равен — 1. Тогда

(а + bi

) 2 = — 1,

а

2 + 2аbi

— b

2 = — 1

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а

и b

должно равняться нулю. Если b

= 0, то из первого уравнения получается а

2 = — 1. Число а

действительное, и поэтому а

2 >
0. Неотрицательное число а

2 не может равняться отрицательному числу — 1. Поэтому равенство b

= 0 в данном
случае невозможно. Остается признать, что а

= 0, но тогда из первого уравнения системы получаем: — b

2 = — 1, b

= ± 1.

√-1
= ± i

.

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а

. Такими числами являются √a

i

и -√a

i

. Условно это записывается так:

√— а

= ± √a

i

.

Под √a

здесь подразумевается арифметический, то есть положительный, корень. Например, √4
= 2, √9
=.3; поэтому

√-4
= + 2i

, √-9
= ± 3i

х

1,2 = — 1 ± √1 -5
= — 1 ± √-4
= — 1 ± 2i

.

Упражнения

2022. (У с т н о.) Решить уравнения:

а) x

2 = — 16; б) x

2 = — 2; в) 3x

2 = — 5.

2023. Найти все комплексные числа, квадраты которых равны:

а) i

; б) 1 / 2 — √ 3
/ 2 i

;

2024. Решить квадратные уравнения:

а) x

2 — 2x

+ 2 = 0; б) 4x

2 + 4x

+ 5 = 0; в) x

2 — 14x

+ 74 = 0.

Решить системы уравнений (№ 2025, 2026):

2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными.

2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются:

a) х

1 = 5 — i

, х

2 = 5 + i

; б) х

1 = 3i

, х

2 = — 3i

.

2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i

) (2i

— 4).

2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 —
i

1- 3i

.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0
, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2
– 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2

+ х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет
.

Решить уравнение 2х 2

+ 5х – 7 = 0
.

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1
.

Итак представим решение полных квадратных уравнений схемой на рисунке1.

ах 2

+ bx + c,
иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2

, затем с меньшим –
bx
, а затем свободный член с.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2

равен единице и уравнение примет вид х 2 + px + q = 0
. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а
, стоящий при х 2

.

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2

+ 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3
. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. Решить квадратное уравнение можно через дискриминант и с помощью теоремы Виета. Методика изучения квадратных уравнений, как и формулы дискриминанта достаточно неудачно прививается школьникам, как и многое в настоящем образовании.2–4*a*c.

Корни (решения) квадратного уравнения зависят от знака дискриминанта (D)
:
D>0
– уравнение имеет 2
различных действительных корня;
D=0
— уравнение имеет 1
корень (2
совпадающих корня):
D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
.

Общая формула для нахождения корней квадратного уравнения
:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4
уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6,
следовательно корнями могут быть значения (1, 6)
и (2, 3)
или пары с противоположным знаком. Сумма корней равна 7
(коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.

Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0)
,

или парабола ветвями вниз (a

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0)
парабола имеет две точки пересечения с осью Ox
.
Если дискриминант равен нулю (D=0)
то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D

Неполные квадратные уравнения

Что делать если дискриминант меньше нуля

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

x_1;2 =

−b ± √ b 2 − 4ac

Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

x_1;2 =

, где « D = b 2 − 4ac »

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай

D > 0
(дискриминант больше нуля)

D –> , где « D = b 2 − 4ac »
–> –> D = b 2 − 4ac
D = 5 2 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0

x_1;2 =

x₂ =−5 − 94x₁ =44x₂ =−144x₁ = 1x₂ = −324x₁ = 1x₂ = −312

Ответ: x₁ = 1; x₂ = −3

Вывод: когда « D > 0 » в квадратном уравнении два корня .

II случай

D = 0
(дискриминант равен нулю)

16x 2 − 8x + 1 = 0

D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0

x_1;2 =

x =

Ответ: x =

Вывод: когда « D = 0 » в квадратном уравнении один корень .

III случай

D
(дискриминант меньше нуля)

D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D

x_1;2 =

Ответ: нет действительных корней

Вывод: когда « D » в квадратном уравнении нет корней .

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример 42.4. Решить уравнение: .

Решение. Найдем дискриминант: = 36 – 52 = -16.

Тогда .

Ответ:

Дата добавления: 2014-12-27 ; Просмотров: 12919 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Если дискриминант больше нуля, то уравнение имеет два корня.
Если дискриминант равен нулю, то уравнение имеет один корень.
Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 3 · 2 = 16 – 24 = -8, D 2 – 6x + 9 = 0

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-6) 2 – 4 · 1 · 9 = 36 – 36 = 0, D = 0

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 – 4ac = (-4) 2 – 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Дискриминант — Концепция — Алгебра Видео от Brightstorm

Дискриминант — это член под квадратным корнем в квадратной формуле, который сообщает нам количество решений квадратного уравнения. Если , дискриминант положительный, мы знаем, что у нас есть 2 решения. Если он отрицательный, решений нет, а если дискриминант равен нулю, у нас есть одно решение. Дискриминант вычисляется путем возведения в квадрат члена «b» и четырехкратного вычитания члена «a», умноженного на член «c».

Дискриминант — действительно удобный инструмент, когда вам кажется, что вы получаете странный ответ. Вот почему. Дискриминант говорит вам, сколько существует решений квадратного уравнения или сколько пересечений по оси x существует для параболы. Он не говорит вам, каковы эти числа, каковы значения пересечения x, он просто говорит вам, сколько их должно быть. Звучит так, будто это бесполезно, но на самом деле это особенно важно, когда вы проверяете свою работу.
Вот как это выглядит. Дискриминант — это формула b в квадрате минус 4ac, помня, что a, b и c — это коэффициенты вашей квадратичной функции в стандартной форме. Он сообщает вам количество решений квадратного уравнения. Если дискриминант больше нуля, есть два решения. Если дискриминант меньше нуля, решений нет, а если дискриминант равен нулю, есть одно решение.
Это то, что вам просто необходимо запомнить. Это идет рука об руку с формулой корней квадратного уравнения.Так что, если вы, ребята, это усвоили, в этом будет большой смысл. Если вы еще не выучили квадратную формулу, вы, вероятно, узнаете ее завтра на уроке математики. Просто знайте, что вы смотрите на то, действительно ли b в квадрате минус 4ac больше нуля, меньше нуля или равно нулю. И это говорит мне, сколько ответов я должен получить. Он не говорит мне, каковы ответы, просто сколько из них мне нужно, чтобы решить проблему.

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения
Часть 3

Сегодня я хотел бы продолжить обсуждение дискриминанта квадратного уравнения.Вы можете просмотреть части 1 и 2 этого обсуждения здесь:

Дискриминант квадратного уравнения — Часть 1
Дискриминант квадратного уравнения — Часть 2

Напомним, что дискриминант квадратного уравнения ax ² + bx + c = 0 является величиной Δ , определяемой

Δ = b ² — 4 ac

То есть дискриминант — это просто выражение, которое появляется под квадратным корнем в формуле корней квадратного уравнения.

На прошлой неделе я попросил вас решить следующую задачу:

Пример: Найдите дискриминант x ² + 8 x + 7 = 0 . Затем опишите характер корней уравнения и опишите график функции y = x ² + 8 x + 7 .

Обязательно попробуйте решить эту проблему самостоятельно, прежде чем читать следующее решение.

Решение: В этом вопросе мы имеем a = 1, b = 8 и c = 7. Таким образом, дискриминант равен

Δ = b ² — 4 ac = 8 ² — 4 (1) (7) = 64 — 28 = 36 .

Поскольку дискриминант положительный, два корня квадратного уравнения являются различными действительными числами. Кроме того, поскольку 36 — это полный квадрат (6 ² = 36), корни на самом деле рациональны.

График функции y = x ² + 8 x + 7 — это направленная вверх парабола, которая пересекает ось x в двух точках.

Примечания: (1) В этом примере мы можем легко найти два корня уравнения путем факторизации:

x ² + 8 x + 7 = 0
( x + 1) ( x + 7) = 0
x + 1 = 0 или x + 7 = 0
x = –1 или x = –7

Итак, два корня — –1 и –7.

(2) Мы знаем, что парабола открывается вверх, потому что a = 1> 0.

(3) Также очень легко найти точку пересечения и параболы. Мы просто подставляем 0 вместо x в уравнение. Таким образом, мы получаем y = 7. Отсюда следует, что пересечение параболы y — это точка (0,7).

Отрицательные дискриминанты

До сих пор мы рассматривали случаи, когда дискриминант равен 0 и положителен.Сегодня поговорим о том, что происходит, если дискриминант отрицательный.

Если дискриминант квадратного уравнения ax ² + bx + c = 0 отрицательный, то мы получаем отрицательное число под квадратным корнем в квадратной формуле. Квадратный корень отрицательного числа — это мнимое число. Таким образом, мы пришли к двум сложным решениям.

Графически, если дискриминант отрицательный, график функции y = ax ² + bx + c является параболой, которая не пересекает x — ось.

Пример дается желтой параболой на изображении выше.

Пример: Найдите дискриминант x ² + 4 x + 8 = 0 . Затем опишите характер корней уравнения и опишите график функции y = x ² + 4 x + 8 .

Я опубликую решение этой проблемы завтра, а затем обсудю, что произойдет, если определитель будет отрицательным.Не стесняйтесь размещать свои собственные решения в комментариях.

Если вам понравилась эта статья, поделитесь ею со своими друзьями на Facebook:

Дискриминант

Дискриминант описывает характеристику корней многочленов. Он отличает разные многочлены одного типа друг от друга.

Существуют разные дискриминанты, используемые для разных степеней многочленов, но наиболее вероятно, что вы увидите, особенно в алгебре, b ² — 4ac, который используется для описания числа решений квадратичной.Хотя это только один дискриминант, термин «дискриминант» часто используется для обозначения этого конкретного дискриминанта. Этот дискриминант также используется как часть формулы корней квадратного уравнения в числителе.

Если дискриминант меньше 0, то квадратичная функция не имеет реального решения. Вы можете вспомнить это, вспомнив, что вы не можете извлечь квадратный корень из отрицательного числа (без использования мнимых чисел). В квадратной формуле дискриминант заключен в радикал, поэтому, если дискриминант отрицательный, вы не сможете вычислить реальное решение.

Пример

f (x) = 3x ² — 2x + 2

а = 3; b = -2; с = 2

b ² — 4ac = (-2) ² — 4 (3) (2)

= 4 — 24 = -20

Если дискриминант отрицательный, настоящего решения нет. Как видно на рисунке ниже, на графике нет нулей:

Если дискриминант равен 0, то квадратичный имеет одно решение. Вы можете вспомнить это, вспомнив, что квадратный корень из 0 равен 0.Ниже приведен пример этого дела:

Пример

f (x) = 4x ² — 4x + 1

a = 4; b = -4; с = 1

b ² — 4ac = (-4) ² — 4 (4) (1)

= 16-16 = 0

f (x) = 4x ² — 4x + 1

Дискриминант равен 0, и есть одно решение при x = & frac12

Если дискриминант больше 0, то квадратичный имеет два решения.Вы можете вспомнить это, вспомнив, что квадратный корень из положительного числа имеет два решения, одно положительное и одно отрицательное, как показано ниже:

Пример

f (x) = x ² — 2x — 3

a = 1; b = -2; с = -3

b ² — 4ac = (-2) ² — 4 (1) (- 3)

= 4 + 12 = 16

Поскольку дискриминант больше 0, существует два решения: x = -1 или x = 3.

См. Также формулу корней квадратного уравнения.

Онлайн калькулятор: Дискриминант

В алгебре дискриминант полинома — это полиномиальная функция его коэффициентов, что позволяет вывести некоторые свойства корней, не вычисляя их.

Вы, вероятно, знаете хорошо известную формулу дискриминанта квадратного многочлена, которая есть, и используете эту формулу для вычисления корней.

Однако дискриминант фактически позволяет нам вывести некоторые свойства корней, не вычисляя их.В случае квадратичного многочлена он равен нулю, если — и только если — многочлен имеет двойной корень. Он положительный, если у многочлена два действительных корня, и отрицательный, если корни комплексные.

Калькулятор ниже вычисляет дискриминант, и вы можете найти немного больше теории дискриминантов непосредственно под ним.

Дискриминант квадратичного полинома

content_copy Link save Save extension Widget

Дискриминант

Дискриминант полинома степени n : может быть определен либо в терминах частного результата, либо в терминах корней.

Дискриминант по корням равен

Технически можно вывести формулу квадратного уравнения, ничего не зная о дискриминанте. Затем, если вы вставите производные выражения для корней в приведенное выше определение, вы получите расширение.

В терминах частного от полученного результата дискриминант равен

, где Res является результатом A и первой производной A ‘. Результирующая, короче говоря, является определителем матрицы Сильвестра A и A ‘.

В случае квадратичного многочлена A есть, а A ‘равно. Если вы запишете матрицу Сильвестра для этих двух многочленов и получите определитель, вы снова получите.

Вычисление дискриминанта более высокой степени

Используя второе определение, вы можете вывести формулы для полинома более высоких степеней (в приведенной ниже ссылке есть формулы для степени 3 и степени 4), но они довольно сложные.
Последовательность OEIS A007878 перечисляет 5 членов для многочленов степени 3; 16 семестров для получения степени 4; 59 семестров по 5-й степени; и, наконец, 3 815 311 членов для многочленов степени 12.
Калькулятор ниже вычисляет дискриминант полинома более высокой степени из результата полинома и его производной

Дискриминант

Коэффициенты дивидендного полинома, разделенные пробелами, в порядке от старшей степени к младшей

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

Дискриминантные и сложные корни

Выражение $$ {b ^ 2} — 4ac $$, которое появляется под знаком радикала в формуле корней квадратного уравнения
\ [x = \ frac {{- b \ pm \ sqrt {{b ^ 2} — 4ac}} } {{2a}} \]

называется дискриминантом квадратного уравнения $$ a {x ^ 2} + bx + c = 0 $$.2} — 4 \ left (1 \ right) \ left (1 \ right)}}} {{2 \ left (1 \ right)}} $$
$$ = \ frac {{1 \ pm \ sqrt {- 3}}} {2} $$
$$ = \ frac {{1 \ pm \ sqrt 3 i}} {2} = \ frac {1} {2} \ pm \ frac {{\ sqrt 3}} { 2} i $$

Таким образом, корнями являются комплексные сопряжения $$ \ frac {1} {2} + \ frac {{\ sqrt 3}} {2} i $$ и $$ \ frac {1} {2} — \ frac { {\ sqrt 3}} {2} i $$

Квадратичная формула: обзор, объяснение и примеры

Прелесть квадратной формулы в том, что всегда работает для решения квадратных уравнений.

Точно так же, как мы знаем, что солнце взойдет завтра утром, мы знаем, что квадратная формула предоставит решения (действительные и мнимые) наших квадратных уравнений. Если вы ищете немного больше красоты (и намного меньше стирания) при решении квадратичных, продолжайте читать, чтобы просмотреть квадратную формулу, понять вывод квадратной формулы и увидеть примеры того, как использовать квадратную формулу!

Квадратичная формула : надежна, как восход солнца !

Вернуться к началу

Что такое квадратичная формула?

Давайте начнем с рассмотрения полной формулы корней квадратного уравнения, представленной ниже:

Квадратичная формула:

x = \ dfrac {-b \ pm \ sqrt {b ^ 2 — 4ac}} {2a}

Буквы a, b и c взяты из стандартная форма квадратного уравнения:

Стандартная форма квадратного уравнения:

y = ax ^ 2 + bx + c

Коэффициент перед x ^ 2 равен a, коэффициент перед x равен b, а коэффициент без переменной равен c.

Вы можете узнать больше о стандартной форме и других формах квадратных уравнений в нашей обзорной статье о формах квадратичных уравнений.

Истории квадратичной формулы

Ранняя история

Решение квадратных уравнений — не современное достижение. Фактически, древние вавилоняне завершали квадрат для решения квадратных уравнений задолго до того, как вообще появилось слово «алгебра», согласно Хакворту и Хоуленду в тексте «Вводный курс математики колледжа: история действительных чисел».

Представьте, что вы решаете квадратные уравнения на счетах, а не вытаскиваете калькулятор. Согласно Mathnasium, не только вавилоняне, но и китайцы решали квадратные уравнения, завершая квадрат с помощью этих инструментов.

В 700 году нашей эры математик из Индии Брахмагупта разработал общее решение квадратного уравнения, но только в 1100 году нашей эры решение, которое мы знаем сегодня, было разработано другим математиком из Индии по имени Бхаскара. пользователя Mathnasium.

Хакворт и Хауленд сообщили нам, что до тех пор, пока не существовала индуистская математика, математика, развитая в Индии, числа не появлялись в том виде, в каком мы их знаем, с системой с основанием 10. Другими словами, поскольку эти разработки происходили для решения квадратных уравнений, многие другие разработки произошли в математике. Знаменитые древние математики, такие как Пифагор, не понимали существования чисел, таких как \ sqrt {2} или \ pi. Фактически, как сказал нам Матнасиум, признание Бхаскара двух решений квадратного корня из числа помогло ему решить квадратные уравнения.Британника сообщает нам, что Бхаскара также смог приблизить значение \ pi как 3,141666.

Более новая история

Мухаммад Аль-Хорезми, «Отец алгебры»

Согласно Mathnasium, в период между Брахмагуптой и Бхаскарой арабский математик Аль-Хорезми также решал квадратные уравнения. По словам Хакворта и Хауленда, он написал текст под названием «Аль-джабр ва’ль мукабала», из которого мы получили слово «алгебра». Хакворт и Хауленд также сообщают нам, что в своем тексте Аль-Хорезми объясняет конкретными шагами, как решать уравнения, включая квадратные уравнения.В эпоху Возрождения, примерно в 1545 году нашей эры, Джироламо Кардано построил произведения Аль-Хорезми, как утверждает Матнасиум, включая воображаемые решения. В то время как работы Кардано включают воображаемые числа, Аль-Хорезми даже не включает отрицательные решения, согласно Hackwork и Howland.

Наконец, в 1637 году Рене Декарт включил квадратную формулу в том виде, в каком мы ее знаем сегодня, в свою работу «Геометрия», изложенную в Mathnasium.

Вывод квадратичной формулы

Мы можем вывести квадратную формулу, заполнив квадрат Стандартной формы квадратного уравнения.2 — 4ac}} {2a}

Потребовалось немного поработать, но теперь у нас есть доказано, что квадратичная формула будет работать во всех случаях!

Если вы хотите увидеть этот процесс в наглядной форме, ниже приведено короткое видео от YouTuber patrickJMT, показывающее, как вывести формулу корней квадратного уравнения:

Вернуться к началу

Когда использовать квадратичную формулу

Иногда, пытаясь решить квадратное уравнение с помощью факторизации, мы наталкиваемся на препятствие на дороге.Не каждое квадратное уравнение факторизуемо.

Хорошая новость о квадратной формуле заключается в том, что вы всегда можете ее использовать! Не существует квадратных уравнений, для которых квадратная формула не дает решения. Даже в тех случаях, когда нет реальных решений, квадратичная формула все равно даст решения! Ознакомьтесь с нашим разделом ниже о дискриминанте, чтобы узнать больше о том, как квадратная формула всегда дает подходящие решения.

Однако, когда квадратное уравнение факторизуемо, факторизация часто оказывается более эффективным методом решения уравнений. 2-x + 9 — это \ frac {1} {14} + \ frac {i \ sqrt {251}} {14} и \ frac {1} { 14} — \ frac {i \ sqrt {251}} {14}.

Вернуться к началу

Рабочий лист с бесплатными квадратичными формулами

Учителя математики: вам нужна простая в использовании таблица с квадратными формулами, содержащая краткие заметки и некоторые базовые практические задачи?

Предварительный просмотр листа с квадратными формулами:

Что такое дискриминант квадратного уравнения?

Теперь, когда мы решили уравнения с помощью формулы корней квадратного уравнения, определение дискриминанта покажется простым! Дискриминант — это часть формулы корней квадратного уравнения.2 — 4ac}} {2a}

Если дискриминант положительный , это означает, что мы извлекаем квадратный корень из положительного числа. У нас будет положительное и отрицательное реальное решение. Это уравнение будет иметь два реальных решения или пересечения по оси x.

Если дискриминант ноль , мы извлекаем квадратный корень из нуля, который равен нулю. Добавление нуля и вычитание нуля дают одно и то же значение, поэтому уравнение будет иметь только одну точку пересечения по оси x.

Наконец, если дискриминант отрицательный , мы извлекаем квадратный корень из отрицательного числа. У этого уравнения не будет реальных решений, но будет два мнимых решения, потому что i = \ sqrt {-1}.

В этой таблице показано, как использовать дискриминант для определения количества и типа решений квадратного уравнения:

Дискриминант Число решений уравнения

Положительное Два реальных решения

Отрицательное Два реальных решения

Дискриминант	Число решений уравнения
Положительное	Два реальных решения
Отрицательное	Два реальных решения
0 в Топ СОВЕТ: Дискриминанты и факторинг Дискриминант также можно использовать для определения факторизуемости уравнений.2} -4 \ color {красный} {(1)} \ color {зеленый} {(9)} 36-36 0 Мы знаем, что 0 = 0. Дискриминант со значением , равным 0 , говорит нам, что уравнение имеет только и одну точку пересечения по оси x . Мы можем увидеть, как функция попадает в точку x, построив график этого квадратного уравнения. Больше наглядного ученика? Посмотрите отличное видео-объяснение ниже о том, как найти дискриминант квадратичной: Вернуться к началу 5 лучших композиций с квадратичной формулой Что может быть лучше для запоминания формулы, чем слушать надоедливую песню? Да, есть несколько приятных песен, но песня, которая будет звучать в вашей голове, даже если вы захотите, чтобы она прекратилась, — это песня, которая лучше всего поможет вам запомнить формулу.Вот несколько отличных вариантов для вас! Набрав более трех миллионов просмотров, нам пришлось начать с полностью оригинальной композиции с квадратичной формулой. Вот еще одна оригинальная версия песни о квадратичной формуле — предупреждение: это может застрять у вас в голове. Вот отличная кавер-версия песни One Direction, использующая квадратную формулу. Хотя этот рэп может и не заставить вас застрять в этой формуле, в нем рассматриваются три метода решения квадратных уравнений! Чтобы завершить наш список, еще одна обложка.Хор в этой версии — действительно приятный способ петь формулу корней квадратного уравнения (начало в 1:00). Свободная практика с квадратичной формулой Чтобы получить ответы на бесплатные практические вопросы о квадратичной формуле, изучите практический курс Альберта по алгебре 1! Все вопросы Альберта включают объяснения решений и способы избежать типичных ошибок. Учителя математики: прочтите наше подробное руководство о том, как преподавать квадратные уравнения, включая стратегии, примеры из реальной жизни и необходимые навыки учащихся. Кроме того, лицензированные преподаватели Альберта могут назначить учащимся этот короткий тест по алгебре 1, в котором основное внимание уделяется решению квадратных уравнений. Наконец, ознакомьтесь с другими нашими подробными руководствами по алгебре 1, чтобы узнать больше о квадратиках. Калькулятор квадратичных формул \| Комплексный Если вам нужно решить уравнение вида `Ax² + Bx + C = 0` , этот калькулятор квадратной формулы здесь, чтобы помочь вам. Всего за несколько кликов вы сможете решить даже самые сложные задачи.В этой статье подробно описывается, что такое квадратная формула и что обозначают символы A, B и C. Также объясняется, как решать квадратные уравнения, которые имеют отрицательный определитель и не имеют действительных корней. Что такое квадратная формула? Квадратичная формула является решением полиномиального уравнения второй степени следующего вида: `Ax² + Bx + C = 0` Если вы можете переписать свое уравнение в этой форме, это означает, что оно может быть решено с помощью формулы корней квадратного уравнения.Решение этого уравнения также называется корнем уравнения. Квадратичная формула имеет следующий вид: `x = (-B ± √Δ) / 2A` где: Используя эту формулу, вы можете найти решения любого квадратного уравнения. Учтите, что есть три возможных варианта получения результата: Квадратное уравнение имеет два уникальных корня, когда Δ> 0. Тогда первое решение квадратной формулы: `x₁ = (-B + √Δ) / 2A` , а второе — `x₂ = (-B - √ Δ) / 2А` . Квадратное уравнение имеет только один корень, когда Δ = 0. Решение равно `x = -B / 2A` . Иногда его называют повторным или двойным корнем. Квадратное уравнение не имеет реальных решений при Δ <0. Вы также можете построить график функции `y = Ax² + Bx + C` . Его форма представляет собой параболу, а корни квадратного уравнения являются точками пересечения по оси x этой функции. Коэффициенты квадратного уравнения A, B и C — коэффициенты квадратного уравнения.Все они действительные числа, не зависящие от x. Если A = 0, то уравнение не квадратичное, а линейное. Если `B² <4AC` , то определитель Δ будет отрицательным. Это означает, что у такого уравнения нет реальных корней. Как использовать решатель квадратичных формул Запишите уравнение. Предположим, это `4x² + 3x - 7 = -4 - x` . Приведите уравнение к виду `Ax² + Bx + C = 0` . В этом примере мы сделаем это в следующие шаги: `4x² + 3x - 7 = -4 - x` `4x² + (3 + 1) x + (-7 + 4) = 0` `4x² + 4x - 3 = 0` Вычислить определитель. `Δ = B² - 4AC = 4² - 4 * 4 * (- 3) = 16 + 48 = 64` . Решите, будет ли определитель больше, равен или меньше нуля. В нашем случае определитель больше 0, что означает, что это уравнение имеет два уникальных корня. Вычислите два корня по формуле корней квадратного уравнения. `x₁ = (-B + √Δ) / 2A = (-4 + √64) / (2 * 4) = (-4 + 8) / 8 = 4/8 = 0,5` `x₂ = (-B - √Δ) / 2A = (-4 -√64) / (2 * 4) = (-4-8) / 8 = -12/8 = -1.5` Корни вашего уравнения: `x₁ = 0,5` и `x₂ = -1,5` . Вы также можете просто ввести значения A, B и C в наш калькулятор квадратного уравнения и позволить ему выполнять все вычисления за вас. Убедитесь, что вы записали правильное количество цифр с помощью нашего калькулятора значащих цифр. Решение квадратных уравнений с отрицательным определителем Даже если калькулятор квадратной формулы указывает, что уравнение не имеет действительных корней, можно найти решение квадратного уравнения с отрицательным определителем.Эти корни будут комплексными числами. Комплексные числа имеют действительную и мнимую части. Мнимая часть всегда равна числу i = √ (-1) , умноженному на действительное число. Posted in Разное Навигация по записям Шукшина чудики: Чудик — ToBeWell Разобрать по составу слово полезный: Страница не найдена Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Без рубрики Дет Полезн Разное Родител Семья Успокоит Уход 2024 © Все права защищены.

0 в Топ

СОВЕТ: Дискриминанты и факторинг

Дискриминант также можно использовать для определения факторизуемости уравнений.2} -4 \ color {красный} {(1)} \ color {зеленый} {(9)}

36-36

Мы знаем, что 0 = 0. Дискриминант со значением , равным 0 , говорит нам, что уравнение имеет только и одну точку пересечения по оси x . Мы можем увидеть, как функция попадает в точку x, построив график этого квадратного уравнения.

Больше наглядного ученика? Посмотрите отличное видео-объяснение ниже о том, как найти дискриминант квадратичной:

Вернуться к началу

5 лучших композиций с квадратичной формулой

Что может быть лучше для запоминания формулы, чем слушать надоедливую песню? Да, есть несколько приятных песен, но песня, которая будет звучать в вашей голове, даже если вы захотите, чтобы она прекратилась, — это песня, которая лучше всего поможет вам запомнить формулу.Вот несколько отличных вариантов для вас!

Набрав более трех миллионов просмотров, нам пришлось начать с полностью оригинальной композиции с квадратичной формулой.
Вот еще одна оригинальная версия песни о квадратичной формуле — предупреждение: это может застрять у вас в голове.
Вот отличная кавер-версия песни One Direction, использующая квадратную формулу.
Хотя этот рэп может и не заставить вас застрять в этой формуле, в нем рассматриваются три метода решения квадратных уравнений!
Чтобы завершить наш список, еще одна обложка.Хор в этой версии — действительно приятный способ петь формулу корней квадратного уравнения (начало в 1:00).

Свободная практика с квадратичной формулой

Чтобы получить ответы на бесплатные практические вопросы о квадратичной формуле, изучите практический курс Альберта по алгебре 1! Все вопросы Альберта включают объяснения решений и способы избежать типичных ошибок. Учителя математики: прочтите наше подробное руководство о том, как преподавать квадратные уравнения, включая стратегии, примеры из реальной жизни и необходимые навыки учащихся.

Кроме того, лицензированные преподаватели Альберта могут назначить учащимся этот короткий тест по алгебре 1, в котором основное внимание уделяется решению квадратных уравнений.

Наконец, ознакомьтесь с другими нашими подробными руководствами по алгебре 1, чтобы узнать больше о квадратиках.

Калькулятор квадратичных формул | Комплексный

Если вам нужно решить уравнение вида Ax² + Bx + C = 0 , этот калькулятор квадратной формулы здесь, чтобы помочь вам. Всего за несколько кликов вы сможете решить даже самые сложные задачи.В этой статье подробно описывается, что такое квадратная формула и что обозначают символы A, B и C. Также объясняется, как решать квадратные уравнения, которые имеют отрицательный определитель и не имеют действительных корней.

Что такое квадратная формула?

Квадратичная формула является решением полиномиального уравнения второй степени следующего вида:

Ax² + Bx + C = 0

Если вы можете переписать свое уравнение в этой форме, это означает, что оно может быть решено с помощью формулы корней квадратного уравнения.Решение этого уравнения также называется корнем уравнения.

Квадратичная формула имеет следующий вид:

x = (-B ± √Δ) / 2A

где:

Используя эту формулу, вы можете найти решения любого квадратного уравнения. Учтите, что есть три возможных варианта получения результата:

Квадратное уравнение имеет два уникальных корня, когда Δ> 0. Тогда первое решение квадратной формулы: x₁ = (-B + √Δ) / 2A , а второе — x₂ = (-B - √ Δ) / 2А .
Квадратное уравнение имеет только один корень, когда Δ = 0. Решение равно x = -B / 2A . Иногда его называют повторным или двойным корнем.
Квадратное уравнение не имеет реальных решений при Δ <0.

Вы также можете построить график функции y = Ax² + Bx + C . Его форма представляет собой параболу, а корни квадратного уравнения являются точками пересечения по оси x этой функции.

Коэффициенты квадратного уравнения

A, B и C — коэффициенты квадратного уравнения.Все они действительные числа, не зависящие от x. Если A = 0, то уравнение не квадратичное, а линейное.

Если B² <4AC , то определитель Δ будет отрицательным. Это означает, что у такого уравнения нет реальных корней.

Как использовать решатель квадратичных формул

Запишите уравнение. Предположим, это 4x² + 3x - 7 = -4 - x .
Приведите уравнение к виду Ax² + Bx + C = 0 . В этом примере мы сделаем это в следующие шаги:
4x² + 3x - 7 = -4 - x
4x² + (3 + 1) x + (-7 + 4) = 0
4x² + 4x - 3 = 0
Вычислить определитель.
Δ = B² - 4AC = 4² - 4 * 4 * (- 3) = 16 + 48 = 64 .
Решите, будет ли определитель больше, равен или меньше нуля. В нашем случае определитель больше 0, что означает, что это уравнение имеет два уникальных корня.
Вычислите два корня по формуле корней квадратного уравнения.
x₁ = (-B + √Δ) / 2A = (-4 + √64) / (2 * 4) = (-4 + 8) / 8 = 4/8 = 0,5
x₂ = (-B - √Δ) / 2A = (-4 -√64) / (2 * 4) = (-4-8) / 8 = -12/8 = -1.5
Корни вашего уравнения: x₁ = 0,5 и x₂ = -1,5 .

Вы также можете просто ввести значения A, B и C в наш калькулятор квадратного уравнения и позволить ему выполнять все вычисления за вас.

Убедитесь, что вы записали правильное количество цифр с помощью нашего калькулятора значащих цифр.

Решение квадратных уравнений с отрицательным определителем

Даже если калькулятор квадратной формулы указывает, что уравнение не имеет действительных корней, можно найти решение квадратного уравнения с отрицательным определителем.Эти корни будут комплексными числами.

Комплексные числа имеют действительную и мнимую части. Мнимая часть всегда равна числу i = √ (-1) , умноженному на действительное число.

Если в дискриминанте отрицательное число

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:

Если дискриминант положителен

Квадратное уравнение

Решение квадратных уравнений с помощью дискриминанта.

Онлайн калькулятор: Дискриминант

Дискриминант квадратного многочлена

Дискриминант

Дискриминант полиномов более высоких степеней

Дискриминант

Квадратное уравнение

Что такое квадратное уравнение и как его решать?

Формулы корней квадратного уравнения

Примеры решения квадратных уравнений

Примеры решения задач

Задания для самостоятельного решения

Навигация по записям

Дискриминант. Решение, примеры

Формула (уравнение) дискриминанта квадратного уравнения

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Решение квадратного уравнения через дискриминант

Может ли дискриминант быть меньше нуля

Давайте попробуем разобраться,

Физический смысл дискриминанта:

Что делать если дискриминант меньше нуля

I случай

II случай

III случай

Решение квадратных уравнений через дискриминант

Дискриминант — Концепция — Алгебра Видео от Brightstorm

Дискриминант квадратного уравнения

Комментарии

Дискриминант

Онлайн калькулятор: Дискриминант

Дискриминант квадратичного полинома

Дискриминант

Вычисление дискриминанта более высокой степени

Дискриминант

Дискриминантные и сложные корни

Квадратичная формула: обзор, объяснение и примеры

Что такое квадратичная формула?

Ранняя история

Более новая история

Вывод квадратичной формулы

Рабочий лист с бесплатными квадратичными формулами

Что такое дискриминант квадратного уравнения?

СОВЕТ: Дискриминанты и факторинг

5 лучших композиций с квадратичной формулой

Свободная практика с квадратичной формулой

Калькулятор квадратичных формул | Комплексный

Что такое квадратная формула?

Коэффициенты квадратного уравнения

Как использовать решатель квадратичных формул

Решение квадратных уравнений с отрицательным определителем

Добавить комментарий Отменить ответ