Интегрирование по частям: объяснение, решение примеров

Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:

Для
применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя.
Один из них обозначается через u, а остальная часть относится ко второму множителю и
обозначается через dv. Затем дифференцированием находится du и интегрированием —
функция v. При этом за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется.

Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция
содержит:

1) — логарифмические
функции, а также обратные тригонометрические функции (с приставкой «arc»), тогда на основании продолжительного опыта
интегрирования по частям эти функции обозначаются через u;

2) ,
,
— синус, косинус и экспоненту, умноженные
на P(x) — произвольный многочлен от икса, тогда эти функции обозначают
через dv, а многочлен — через u;

3) ,
,
,
, в этом случае интегрирование по частям
применяется дважды.

Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение
под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям
такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть
не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную
в самом начале урока формулу интегрирования по частям

,

получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом
(под знаком интеграла) — функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла,
под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная
тригонометрическая функция.

Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу:
нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям
состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал
проще первоначального.

Метод интегрирования по частям основан на использовании формулы дифференцирования
произведения двух функций:

Так как

то её можно записать в виде

,

который и был приведён в самом начале урока.

При нахождении интегрированием функции v для неё
получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям,
можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С,
равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить
не следует.

Есть у метода интегрирования по частям совершенно особенное применение: с его помощью
можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций
под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например,
функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула — это формула для
нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается
последовательным понижением степени. Так, если подынтегральная функция — синус в
четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей
степени и так далее. Описанной задаче посвящен последний параграф этого урока.

Пример 1. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. В подынтегральном выражении — логарифм, который, как мы уже знаем, разумно
обозначить через u. Полагаем, что ,
.

Тогда , .

Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом
(без интеграла) логарифмическую функцию, а во втором слагаемом
(под знаком интеграла) — функцию, не содержащую логарифма):

И снова логарифм. ..

Пример 2.  Найти неопределённый интеграл:

.

Решение. Пусть ,
.

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
,
.

Применяя формулу интегрирования по частям, получаем:

Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом
слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом
(под знаком интеграла) — функцию, не содержащую логарифма).

Находим изначальный интеграл:

Пример 3.  Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть ,
.

Тогда
,
.

Применяя формулу интегрирования по частям, получаем:

Второй интеграл находим методом замены переменной.

Возвращаясь к переменной x, получаем

.

Находим изначальный интеграл:

.

Пример 4. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что

находим

Проверить решение задач на неопределённый интеграл можно на
калькуляторе неопределённых интегралов онлайн.

Пример 6. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть ,
.

Тогда , .

По формуле интегрирования по частям находим:

Пример 10. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем
,
.

Тогда ,
.

По формуле интегрирования по частям получаем:

Ко второму слагаемому также применяем интегрирование по частям. Обозначаем
,
.

Тогда ,
.

Применив эти обозначения, интегрируем упомянутое слагаемое:

Теперь находим требуемый интеграл:

Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие,
которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из
практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях
нужно пользоваться соображением удобства, также приведённым в параграфе «Суть метода интегрирования по частям»:
за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется. Последний пример этого урока — решение именно такого интеграла.

Пример 11. Найти неопределённый интеграл методом интегрирования по частям:

.

Решение. Примем как руководство к действию общее соображение относительно обозначений.
Обозначаем
,
.

Тогда ,
.

По формуле интегрирования по частям получаем:

Случаев, когда требуется понижения степени подынтегральной функции, мы уже коснулись во
вводной части урока. Теперь — практика использования для этой цели метода интегрирования по частям.

Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу
для

,

найти I4.

Решение. Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали
бы и синус, и косинус. Используя тригонометрические тождества, получаем

Ко второму слагаемому — интегралу — применяем метод интегрирования по частям. Для этого обозначим

Тогда

Находим это второе слагаемое — интеграл:

Теперь находим рекуррентную формулу для исходного интеграла:

С помощью полученной формулы найдём I4:

Начало темы «Интеграл»

Продолжение темы «Интеграл»

Поделиться с друзьями

Интегрирование по частям, формулы и примеры решений

Содержание:

Рассмотрим функции $u=u(x)$ и
$v=v(x)$, которые имеют непрерывные
производные. {2}-1\right) \sin x+2 x \cos x+C$

2)$\int P_{n}(x) \arcsin x d x$  ;  
$\int P_{n}(x) \arccos x d x$  ;  
$\int P_{n}(x) \ln x d x$

Здесь принимают, что $d v=P_{n}(x) d x$, а в
качестве $u$ оставшиеся сомножители.

Пример

Задание. Найти интеграл
$\int \ln x d x$

Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.

$$\int \ln x d x\left\|\begin{array}{l}
u=\ln x \quad d v=d x \\
d u=\frac{d x}{x} \quad v=x
\end{array} \quad\right\|=x \ln x-\int x \cdot \frac{d x}{x}=$$

$=x \ln x-\int d x=x \ln x-x+C=x(\ln x-1)+C$

Ответ. $\int \ln x d x=x(\ln x-1)+C$

Больше примеров решений
Решение интегралов онлайн

Пример

Задание. Найти интеграл
$\int \arcsin x d x$

Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям. {2 x+1} \sin x}{5}+C$

Больше примеров решений
Решение интегралов онлайн

Читать дальше: простейшие дроби.

Метод интегрирования по частям

Формула интегрирования по частям

Формула интегрирования по частям имеет вид:
.

Метод интегрирования по частям состоит в применении этой формулы. При практическом применении стоит отметить, что u и v являются функциями от переменной интегрирования. Пусть переменная интегрирования обозначена как x (символ после знака дифференциала d в конце записи интеграла) . Тогда u и v являются функциями от x: u(x) и v(x).
Тогда
,     .
И формула интегрирования по частям принимает вид:
.

То есть подынтегральная функция должна состоять из произведения двух функций:
,
одну из которых обозначаем как u:   g(x) = u, а у другой должен вычисляться интеграл (точнее находиться первообразная):
, тогда dv = f(x) dx.

В некоторых случаях f(x) = 1. То есть в интеграле
,
можно положить g(x) = u, x = v.

Резюме

Итак, в данном методе, формулу интегрирования по частям стоит запомнить и применять в двух видах:
;
.

Интегралы, вычисляющиеся интегрированием по частям

Интегралы, содержащие логарифм и обратные тригонометрические (гиперболические) функции

По частям часто интегрируются интегралы, содержащие логарифм и обратные тригонометрические или гиперболические функции. При этом ту часть, которая содержит логарифм или обратные тригонометрические (гиперболические) функции обозначают через u, оставшуюся часть – через dv.

Вот примеры таких интегралов, которые вычисляются методом интегрирования по частям:
,   ,   ,   ,   ,   ,   .
Подробное решение этих интегралов >>>

Интегралы, содержащие произведение многочлена и sin x, cos x или e

^x

По формуле интегрирования частям находятся интегралы вида:
,   ,   ,
где P(x) – многочлен от x. При интегрировании, многочлен P(x) обозначают через u, а e^ax dx, cos ax dx или sin ax dx – через dv.

Вот примеры таких интегралов:
,   ,   .
Подробное решение этих интегралов >>>

Примеры вычисления интегралов методом интегрирования по частям

Примеры интегралов, содержащих логарифм и обратные тригонометрические функции

Пример

Вычислить интеграл:

Подробное решение

Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x,
dv = x² dx.
Тогда
,
.

.

Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений нужно обязательно добавить постоянную C, поскольку неопределенный интеграл – это множество всех первообразных. Также ее можно было добавлять и в промежуточных вычислениях, но это лишь загромождало бы выкладки.

Более короткое решение

Можно представить решение и в более коротком варианте. Для этого не нужно делать подстановки с u и v, а можно сгруппировать сомножители и применить формулу интегрирования по частям во втором виде.

.

Ответ

Другие примеры

Примеры решений подобных интегралов >>>

Примеры интегралов, содержащих произведение многочлена и sin x, cos x или ex

Пример

Вычислить интеграл:
.

Решение

Введем экспоненту под знак дифференциала:
e ^{– x} dx = – e ^{– x} d(–x) = – d(e ^{– x}).

Интегрируем по частям.
.
Также применяем метод интегрирования по частям.
.
.
.
Окончательно имеем:
.

Ответ

.

Другие примеры

Примеры решений подобных интегралов >>>

Автор: Олег Одинцов.     Опубликовано: 19-10-2014

Интегрирование по частям. Первая часть.

В этой теме мы подробно поговорим вычислении неопределённых интегралов с помощью так называемой «формулы интегрирования по частям». Нам понадобится таблица неопределенных интегралов и таблица производных. В первой части будут разобраны стандартные примеры, которые большей частью встречаются в типовых расчётах и контрольных работах. Более сложные примеры разобраны во второй части.

Постановка задачи в стандартном случае следующая. Допустим, под интегралом у нас расположены две функции разной природы: многочлен и тригонометрическая функция, многочлен и логарифм, многочлен и обратная тригонометрическая функция и так далее. В этой ситуации выгодно отделить одну функцию от другой. Грубо говоря, имеет смысл разбить подынтегральное выражение на части, – и разобраться с каждой частью по отдельности. Отсюда и название: «интегрирование по частям». Применение этого метода основано на следующей теореме:

Пусть функции $u(x)$ и $v(x)$ дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл $\int v \; du$. Тогда на этом же промежутке существует и интеграл $\int u \; dv$, при этом верно следущее равенство:

$$
\begin{equation}
\int u \; dv=u\cdot v-\int v\; du
\end{equation}
$$

Формулу (1) и называют «формулой интегрирования по частям». 2+14x-5)$. Т.е. запись $\ln x$ нужно воспринимать как своего рода обобщение.

Ещё один момент. Бывает, что формулу интегрирования по частям приходится применять несколько раз. Об этом поговорим подробнее в примерах №4 и №5. Теперь перейдём непосредственно к решению типичных задач. Решение задач, уровень которых чуть выше стандартных, разбирается во второй части.

Пример №1

Найти $\int (3x+4) \cos (2x-1) \; dx$.

Решение

Под интегралом расположен многочлен $3x+4$ и тригонометрическая функция $\cos (2x-1)$. Это классический случай для применения формулы (1), поэтому возьмём заданный интеграл по частям. Формула (1) требует, чтобы интеграл $\int (3x+4) \cos (2x-1) \; dx$ был представлен в форме $\int u \; dv$. Нам нужно выбрать выражения для $u$ и для $dv$. Можно в качестве $u$ принять $3x+4$, тогда $dv=\cos (2x-1)dx$. Можно взять $u=\cos (2x-1)$, тогда $dv=(3x+4)dx$. Чтобы сделать правильный выбор обратимся к правилу №2. Заданный интеграл $\int (3x+4) \cos (2x-1) \; dx$ подпадает под вид $\int P_n(x) \cos x \;dx$ (многочлен $P_n(x)$ в нашем интеграле имеет вид $3x+4$). Согласно правилу №2 нужно выбрать $u=P_n(x)$, т.е. в нашем случае $u=3x+4$. Так как $u=3x+4$, то $dv=\cos(2x-1)dx$.

Однако недостаточно просто выбрать $u$ и $dv$. Нам еще понадобятся значения $du$ и $v$. Так как $u=3x+4$, то:

$$ du=d(3x+4)=(3x+4)’dx=3dx.$$

Теперь разберёмся с функцией $v$. Так как $dv=\cos(2x-1)dx$, то согласно определению неопределённого интеграла имеем: $ v=\int \cos(2x-1)\; dx$. Чтобы найти нужный интеграл применим внесение под знак дифференциала:

$$ v=\int \cos(2x-1)\; dx=\frac{1}{2}\cdot \int \cos(2x-1)d(2x-1)=\frac{1}{2}\cdot \sin(2x-1)+C=\frac{\sin(2x-1)}{2}+C. $$

Однако нам нужно не всё бесконечное множество функций $v$, которое описывает формула $\frac{\sin(2x-1)}{2}+C$. Нам нужна какая-то одна функция из этого множества. Чтобы получить искомую функцию нужно вместо $C$ подставить какое-либо число. Проще всего, разумеется, подставить $C=0$, получив при этом $v=\frac{\sin(2x-1)}{2}$.

Итак, соберём всё вышеизложенное воедино. Мы имеем: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac{\sin(2x-1)}{2}$. Подставляя всё это в правую часть формулы (1) будем иметь:

$$
\int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx.
$$

Осталось, по сути, только найти $\int\frac{\sin(2x-1)}{2}\cdot 3dx$. Вынося константу (т.е. $\frac{3}{2}$) за знак интеграла и применяя метод внесения под знак дифференциала, получим:

$$
(3x+4)\cdot \frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx=

\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx= \\
=\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\int \sin(2x-1) \;d(2x-1)=
\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C=\\
=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C.

$$

Итак,

$$\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C.$$

В сокращенном виде процесс решения записывают так:

$$
\int (3x+4) \cos (2x-1) \; dx=\left | \begin{aligned} & u=3x+4; \; du=3xdx. \\ & dv=\cos(2x-1)dx; \; v=\frac{\sin(2x-1)}{2}. \end{aligned} \right |=\\
=(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx=
\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx=\\
=\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C=
\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C.
$$

Неопределённый интеграл по частям найден, осталось лишь записать ответ.

Ответ: $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$.

Полагаю, здесь не обойдётся без вопроса, поэтому попробую сформулировать его и дать ответ.

Вопрос

Почему мы приняли именно $u=3x+4$ и $dv=\cos(2x-1)dx$? Да, интеграл был решён. Но, может быть, если бы мы взяли $u=\cos (2x-1)$ и $dv=(3x+4)dx$ интеграл тоже был бы найден!

Ответ

Нет, если принять $u=\cos (2x-1)$ и $dv=(3x+4)dx$, то ничего хорошего с этого не выйдет, – интеграл не упростится. 2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C$.

Применение метода интегрирования по частям в несколько нестандартных случаях, не подпадающих под действие правил №1 и №2, будет дано во второй части.

Примеры интегрирования по частям

Примеры интегрирования по частям подобного состава задают студентам 1, 2 курсов. Данные задания задавали на контрольной работе в ЛНУ им. И. Франка. Чтобы формулы в задачах и ответах не повторялись же задачи описывать не будем. По условию заданий нужно или «Найти интеграл», или «Вычислить интеграл».
Пример 8. Интеграл находим по правилу интегрирования частями int(u*dv)=u*v-int(v*du). Здесь главное правильно выбрать функции под правило. (Для себя запомните что за dv если возможно выбирают периодические функции или такие, которые при дифференцировании с точностью до множителя дают сами себя — экспонента). В этом интеграле нужно синус внести под дифференциал

Дальнейшее интегрирование достаточно простое и на деталях останавливаться не будем.

Пример 9.Снова нужно применять правило интегрирования по частям u*dv. Здесь имеем произведение периодической функции на экспоненту, поэтому что лучше вносить под дифференциал выбирать Вам. Можно как экспоненту, так и косинус (в каждом варианте получим рекуррентную формулу).

Применяем интегрирование по частям повторно

Пришли к рекуррентной формуле. Если записать интеграл который искали и результат вычислений то получим два подобные слагаемые

Группируем их и находим искомый интеграл

Пример 10. Имеем готовую запись интеграла под правило u*dv. Находим du и выполняем интегрирование

Сводим второй интеграл под табличную формулу и вычисляем его

Пример 11. Обозначим за новую переменную cos(ln(x))=u і найдем du, затем внесением под дифференциал

К интегралу повторно применяем правило интегрирования по частям

Пришли к рекуррентной формуле

с которой и вычисляем неизвестный интеграл

Пример 12. Для нахождения интеграла выделим в знаменателе полный квадрат. Далее сведя знаменатель к известной формуле интегрирования получим арктангенс

Хорошо запомните порядок чередования множителей. Единица разделена на корень из свободного члена фигурирует перед арктангенсом, также этот множитель присутствует в арктангенс перед переменной.
Пример 13. Дело имеем с подобным интегралом, только в знаменателе квадратичная зависимость находится под корнем. Выделяем полный квадрат и сводим под формулу интегрирования, которая дает логарифм

Вот такие бывают примеры на контрольной или тестах. Хорошо запомните основные схемы интегрирования.
Если не можете решить интеграл сами, тогда обращайтесь за помощью.

Готовые решения контрольной по интегрированию

Интегрирование по частям. Интегралы квадратных трехчленов

Примеры на интегрирование функций по частям, а также интегралы от квадратных трехчленов взято из материалов контрольной работы, которую задают студентам 1, 2 курсов с математических дисциплин. Для экономии Вашего времени сами условия заданий пропущенные, везде нужно или «Найти неопределенный интеграл» или «Вычислить интеграл». Текста в комментариях к каждому заданию немного, но этого достаточно для усвоения материала и изучение методики и схем интегрирования.

Интегрирование по частям

Пример 8. Здесь необходимо интегрировать частями. Кто не знает как интегрировать по частях то сначала ознакомьтесь с этой статьей. За dv удобно выбрать экспоненту умноженную на dx. Вычисляем v, du и применяем интегрирование по частям

Ко второму интегралу повторно применяем правило интегрирования по частям

Если бы имели переменную в 3-й степени то интегрировали бы частями трижды и так далее. Другого метода вычислить такого сорта интегралы математики еще не придумали.
Пример 9. В этом интеграле за dv можем обозначать как экспоненту так и синус, поскольку его вторая производная тоже даст синус (со знаком минус). В каждом из случаев придем к рекуррентной формуле с которой и найдем интеграл

Пришли к рекуррентной формуле, когда справа и слева от знака равенства имеем искомый интеграл

Группируем слагаемые и делим правую сторону на коэффициент при интеграле

Пример 10.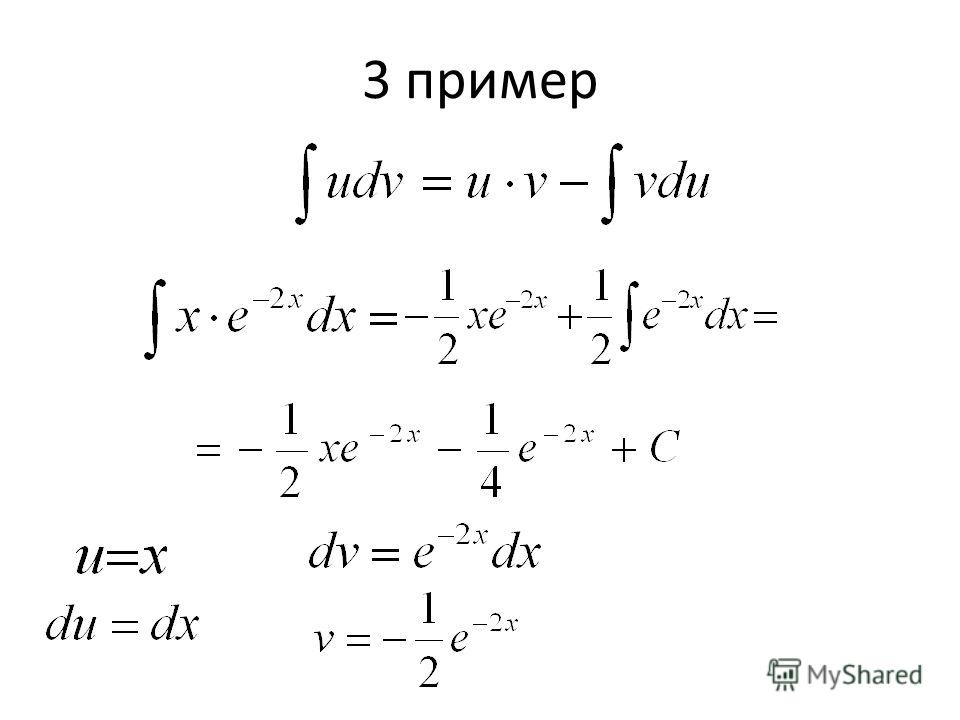 Несмотря на короткую запись, интеграл от арксинуса двойного «икс» нужно находить интегрированием по частям. Функции u, dv выбираем согласно представленным формулам

Последние две строки можно расписать переходом к новой переменной, а затем ее подстановки в интеграл, однако и такая запись будет правильным ответом для Вас.
Пример 11. Находим интеграл частями, для этого прямо применяем метод. Здесь в скобках выполняем упрощение в вычислениях дифференциала du

Для применения формулы интегрирования вносим переменную под дифференциал чтобы получить такой же выражение как под корнем

Постепенно Вы запомните что внесение под дифференциал позволяет опускать замены переменных и сразу переходить к готовым формул на интегралы. Теперь Вы знаете как интегрировать частями, другие примеры приведены в конце статьи.

Пример 12. Имеем квадратный трехчлен в знаменателе дроби. Для сведения к табличному интегралу следует его свести к разнице или сумме квадратов. В этом задании получим арктангенс

Для легкости чтения формул важные моменты выделены цветом.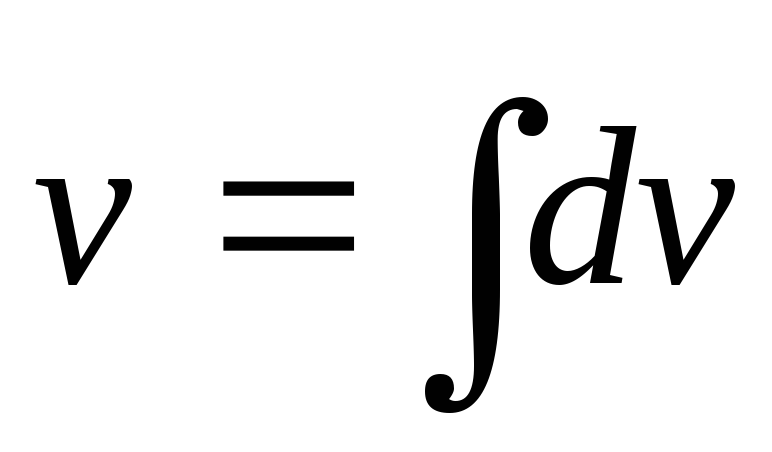 Поверьте что это помогает быстрее запомнить то, что на первый взгляд выглядит для одних понятным, а другим и после второго и третьего пересмотра тяжелым.
Пример 13. Несмотря на то, что квадратный трехчлен в знаменателе находится под корнем схема возведения к табличному интегралу подобная предыдущему примеру. Разница лишь в том что здесь получим логарифм, а не арктангенс. Важные моменты преобразований записано формулами

Задания вида 12, 13 на контрольных и тестах встречаются часто, поэтому хорошо их изучите.
Пример 14. В этом интеграле замена переменных несколько специфическая и вряд ли Вы ее запомните, однако без нее интеграл не найти. Поэтому внимательно рассмотрите, как преображается функция под интегралом при такой замене переменных

Под корнем в знаменателе выделяем разность квадратов. Поскольку перед скобками, которые содержат переменную стоит отрицательный знак то при интегрировании получим арксинус

Остальные ответы в следующих материалах. Помните что такого рода примеры задают на контрольных или тестах и внимательно разбирайте ответы к интегралам. 2}+C.$

6.143.$\int\cos(\ln x)\,dx.$

Решение.

$$\int \cos(\ln x)\, dx=\left[\begin{array}{lcl}u=\cos(\ln x) \Rightarrow du=-\frac{1}{x}\sin(\ln x)\, dx\\dv=dx\Rightarrow v=x\end{array}\right]=$$ $$=\cos(\ln x)x-\int x\cdot\left(-\frac{1}{x}\sin(\ln x)\right)\,dx=x\cos(\ln x)+\int\sin(\ln x)\,dx.$$

$$\int \sin(\ln x)\, dx=\left[\begin{array}{lcl}u=\sin(\ln x) \Rightarrow du=\frac{1}{x}\cos(\ln x)\, dx\\dv=dx\Rightarrow v=x\end{array}\right]=$$ $$=\sin(\ln x)x-\int x\cdot\left(\frac{1}{x}\cos(\ln x)\right)\,dx=x\sin(\ln x)-\int\cos(\ln x)\,dx.$$

Таким образом, $$\int\cos(\ln x)\,dx=x\cos(\ln x)+x\sin(\ln x)-\int\cos(\ln x)\, dx.$$

Пусть $\int\cos(\ln x)\, dx=I.$ Тогда запишем и решим уравнение 

$$I=x\cos(\ln x)+x\sin(\ln x)-I\Rightarrow$$ $$\Rightarrow 2I=x\cos(\ln x)+x\sin(\ln x)\Rightarrow$$ $$\Rightarrow I=\frac{1}{2}(x\cos(\ln x)+x\sin(\ln x).$$

Ответ: $\frac{1}{2}(x\cos(\ln x)+x\sin(\ln x))+C. 2-2x+3)\cos x\, dx.$

Интеграция по частям

Интеграция по частям — это особый метод интеграции, который часто бывает полезен, когда две функции перемножаются, но также полезен и другими способами.

Скоро вы увидите множество примеров, но сначала давайте рассмотрим правило:

∫u v dx = u∫v dx −∫u ‘(∫v dx) dx

• u — функция u (x)
• v — функция v (x)
• u ‘ — производная функции u (x)

Правило в виде диаграммы:

Давайте сразу рассмотрим пример:

Пример: Что такое ∫x cos (x) dx?

Хорошо, у нас есть x , умноженное на cos (x) , поэтому интегрирование по частям — хороший выбор.

Сначала выберите, какие функции для u и v :

Итак, теперь он в формате ∫ u v dx , мы можем продолжить:

Дифференциация u : u ‘= x’ = 1

Интегрировать v : ∫v dx = ∫cos (x) dx = sin (x) (см. Правила интеграции)

Теперь мы можем собрать это вместе:

Упростить и решить:

x sin (x) — ∫sin (x) dx

х грех (х) + соз (х) + С

Итак, мы выполнили следующие шаги:

• Выберите u и v
• Дифференцировать u: u ‘
• Интеграция v: ∫v dx
• Поместите u, u ‘и ∫v dx в: u∫v dx −∫u’ (∫v dx) dx
• Упростить и решить

На английском языке мы можем сказать, что ∫u v dx становится:

(интеграл u) минус интеграл (производная u, интеграл v)

Давайте попробуем еще несколько примеров:

Пример: что такое ∫ln (x) / x

² dx?

Сначала выберите u и v:

Дифференцировать u: ln (x) ‘= 1 x

Интегрировать v: ∫1 / x ² dx = ∫x ^-2 dx = −x ^-1 = −1 x (по правилу мощности)

Теперь сложим:

Упростить:

−ln (x) / x — ∫ − 1 / x ² dx = −ln (x) / x — 1 / x + C

— лин (x) + 1 x + C

Пример: Что такое ∫ln (x) dx?

Но есть только одна функция! Как выбрать u и v?

Эй! Мы можем просто выбрать v как «1»:

Дифференцировать u: ln (x) ‘= 1 / x

Интегрировать v: ∫1 dx = x

Теперь сложим:

Упростить:

x ln (x) — ∫1 dx = x ln (x) — x + C

Пример: что такое ∫e

^x x dx?

Выберите u и v:

Дифференцировать u: (e ^x ) ‘= e ^x

Интегрировать v: ∫x dx = x ² /2

Теперь сложим:

Что ж, это была грандиозная катастрофа! Все стало еще сложнее.

Может быть, мы могли бы выбрать другие u и v?

Пример: ∫e

^x x dx (продолжение)

Выберите по-разному u и v:

Дифференцировать u: (x) ‘= 1

Интегрировать v: ∫e ^x dx = e ^x

Теперь сложим:

Упростить:

x e ^x — e ^x + C

е ^х (х − 1) + С

Мораль истории: выбирайте u и v внимательно!

Выберите и , который станет проще, если вы его дифференцируете, и v , который не станет более сложным после интеграции.

Полезное эмпирическое правило — Я ПОЗДНУЮ. Выберите и в зависимости от того, что из них будет первым:

И последний (и хитрый) пример:

Пример: ∫e

^x sin (x) dx

Выберите u и v:

Дифференцировать u: sin (x) ‘= cos (x)

Интегрировать v: ∫e ^x dx = e ^x

Теперь сложим:

∫e ^x sin (x) dx = sin (x) e ^x −∫cos (x) e ^x dx

Выглядит хуже, но будем настаивать! Чтобы найти ∫cos (x) e ^x dx, мы можем снова использовать интеграцию по частям :

Выберите u и v:

Дифференцировать u: cos (x) ‘= -sin (x)

Интегрировать v: ∫e ^x dx = e ^x

Теперь сложим:

∫e ^x sin (x) dx = sin (x) e ^x — (cos (x) e ^x −∫ − sin (x) e ^x dx)

Упростить:

∫e ^x sin (x) dx = e ^x sin (x) — e ^x cos (x) −∫ e ^x sin (x) dx

Теперь у нас одинаковый интеграл с обеих сторон (за исключением вычитания одного). ..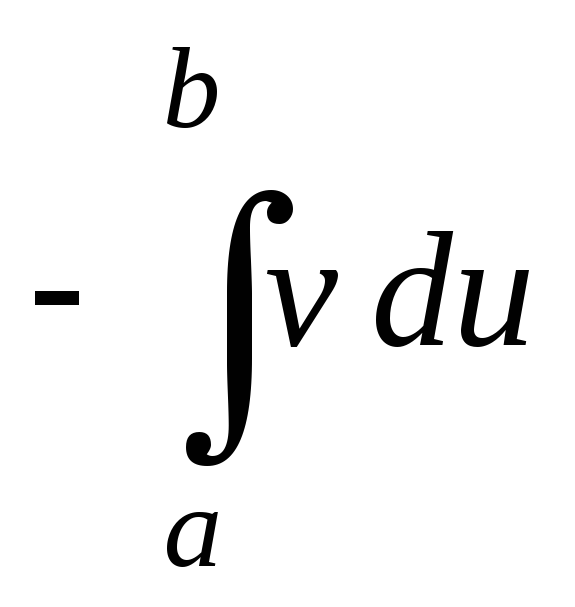

… так что переместим правую руку влево и получим:

2∫e ^x sin (x) dx = e ^x sin (x) — e ^x cos (x)

Упростить:

∫e ^x sin (x) dx = ½ e ^x (sin (x) — cos (x)) + C

Сноска. Откуда взялась «интеграция по частям»?

Он основан на Правиле продукта для деривативов:

(УФ) ‘= УФ’ + УФ

Объединить обе стороны и переставить:

∫ (uv) ‘dx = ∫uv’ dx + ∫u’v dx

uv = uv ‘dx + ∫u’v dx

uv ‘dx = uv — u’v dx

Некоторые люди предпочитают эту последнюю форму, но мне нравится заменять v ‘на w и v на w dx , что упрощает левую часть:

∫uw dx = u∫w dx — ∫u ‘(∫w dx) dx

Calculus II — Интеграция по частям

Показать общее уведомление

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST. Будем надеяться, что единственное неудобство будет заключаться в периодической потере / разрыве соединения, которую следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 1-1: Интеграция по частям

Давайте начнем с этого раздела с пары интегралов, которые мы уже должны уметь делать для начала. {6x}} \) отдельно, мы могли бы сделать интеграл достаточно легко.\ prime} \, dx}} = \ int {{f ‘\, g + f \, g’ \, dx}} \]

Левую часть достаточно легко интегрировать (мы знаем, что интегрирование производной просто «отменяет» производную), и мы разделим правую часть интеграла.

\ [fg = \ int {{f ‘\, g \, dx}} + \ int {{f \, g’ \, dx}} \]

Обратите внимание, что технически у нас должна была отображаться константа интегрирования слева после выполнения интегрирования. Мы можем отбросить его на этом этапе, поскольку другие константы интеграции будут отображаться в будущем, и они просто поглотят эту.

Наконец, перепишите формулу следующим образом, и мы придем к формуле интегрирования по частям.

\ [\ int {{f \, g ‘\, dx}} = fg — \ int {{f’ \, g \, dx}} \]

Однако это не самая простая формула. Итак, сделаем пару замен.

\ [\ begin {align *} u = f \ left (x \ right) \ hspace {0. 5in} v = g \ left (x \ right) \\ & du = f ‘\ left (x \ right) \, dx \ hspace {0,5 дюйма} dv = g ‘\ left (x \ right) \, dx \ end {align *} \]

Обе из них — стандартные замены Calculus I, к которым, надеюсь, вы уже привыкли.Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же.

Использование этих замен дает нам формулу, которую большинство людей считают формулой интегрирования по частям.

Интеграция по частям

\ [\ int {{u \, dv}} = uv — \ int {{v \, du}} \]

Чтобы использовать эту формулу, нам нужно будет идентифицировать \ (u \) и \ (dv \), вычислить \ (du \) и \ (v \), а затем использовать формулу. Также обратите внимание, что вычислить \ (v \) очень просто.Все, что нам нужно сделать, это интегрировать \ (dv \).

\ [v = \ int {{dv}} \]

Одна из самых сложных вещей при использовании этой формулы — это то, что вам необходимо правильно идентифицировать как \ (u \), так и \ (dv \). Не всегда будет ясно, каков правильный выбор, и иногда мы делаем неправильный выбор. Это не повод для беспокойства. Если мы сделаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.

Это приводит к очевидному вопросу: как узнать, правильно ли мы сделали выбор для \ (u \) и \ (dv \)? Ответ на самом деле довольно прост.{6x}} \, dx}} \]

Показать решение

Итак, на некотором уровне проблема здесь в \ (x \), стоящем перед экспонентой. Если бы этого не было, мы могли бы выполнить интеграл. Также обратите внимание, что при выполнении интеграции по частям все, что мы выбираем для \ (u \), будет дифференцироваться. Таким образом, кажется, что выбор \ (u = x \) будет хорошим выбором, поскольку при дифференцировании \ (x \) выпадет.

Теперь, когда мы выбрали \ (u \), мы знаем, что \ (dv \) будет всем остальным, что останется.{6x}} + c \ end {align *} \]

После того, как мы выполнили последний интеграл в задаче, мы добавим константу интегрирования, чтобы получить окончательный ответ.

Также обратите внимание, что, как отмечалось выше, мы знаем, что сделали правильный выбор для \ (u \) и \ (dv \), когда получили новый интеграл, который мы фактически вычисляем после применения формулы интегрирования по частям.

Теперь давайте посмотрим на интегрирование по частям для определенных интегралов.b \) в первом члене — это просто стандартное обозначение интегральной оценки, с которым вы должны быть знакомы на этом этапе. Все, что мы делаем, это оцениваем член, в данном случае uv , в \ (b \), затем вычитаем оценку члена в \ (a \).

На каком-то уровне нам здесь действительно не нужна формула, потому что мы знаем, что при вычислении определенных интегралов все, что нам нужно сделать, это вычислить неопределенный интеграл, а затем выполнить вычисление. На самом деле, это, вероятно, будет немного проще, поскольку нам не нужно отслеживать таким образом оценку каждого термина.{- 6}} \ end {align *} \]

Любой из методов вычисления определенных интегралов с интегрированием по частям довольно прост, так что выбор, который вы выберете, в значительной степени зависит от вас.

Поскольку нам нужно уметь вычислять неопределенный интеграл, чтобы вычислить определенный интеграл, а выполнение определенного интеграла сводится к не более чем вычислению неопределенного интеграла в паре точек, мы сконцентрируемся на вычислении неопределенных интегралов в остальной части этого раздел.Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.

Давайте взглянем еще на несколько примеров.

Пример 3 Вычислите следующий интеграл.

\ [\ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} \]

Показать решение

Есть два способа продолжить этот пример. Для многих первое, что они пробуют, — это умножить косинус на скобки, разделить интеграл и затем выполнить интегрирование по частям для первого интеграла.

Хотя это вполне приемлемый способ решения проблемы, это больше работы, чем нам действительно нужно. Вместо того, чтобы разделять интеграл, давайте вместо этого воспользуемся следующими вариантами для \ (u \) и \ (dv \).

\ [\ begin {align *} u & = 3t + 5 & \ hspace {0,5 дюйма} dv & = \ cos \ left ({\ frac {t} {4}} \ right) \, dt \\ du & = 3 \, dt & \ hspace {0,5 дюйма} v & = 4 \ sin \ left ({\ frac {t} {4}} \ right) \ end {align *} \]

Тогда интеграл равен

.

\ [\ begin {align *} \ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) — 12 \ int {{\ sin \ left ({\ frac {t} {4}} \ right) \, dt}} \\ & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) + 48 \ cos \ left ({\ frac {t} {4}} \ right) + c \ end {align *} \]

Обратите внимание, что мы вытащили все константы из интеграла, когда использовали формулу интегрирования по частям.2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {1} {5} \ int {{w \ cos \ left ({10w} \ right) \, dw}} \]

В этом примере, в отличие от предыдущих примеров, новый интеграл также потребует интегрирования по частям. 2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {w} {{50}} \ sin \ left ({10w} \ right) + \ frac {1} {{500}} \ cos \ left ({10w} \ вправо) + c \ end {align *} \]

Будьте осторожны с коэффициентом интеграла для второго применения интегрирования по частям.Поскольку интеграл умножается на \ (\ frac {1} {5} \), нам нужно убедиться, что результаты фактического выполнения интеграла также умножаются на \ (\ frac {1} {5} \). Забывание сделать это — одна из наиболее распространенных ошибок при интеграции по частям.

Как показал этот последний пример, иногда нам потребуется несколько приложений интегрирования по частям, чтобы полностью оценить интеграл. Это то, что произойдет, поэтому не волнуйтесь, когда это произойдет.

В следующем примере нам нужно признать важный момент, касающийся методов интеграции. Некоторые интегралы могут быть получены с использованием нескольких различных методов. Так обстоит дело с интегралом в следующем примере.

Пример 5 Вычислите следующий интеграл

\ [\ int {{x \ sqrt {x + 1} \, dx}} \]

1. Использование интеграции по частям.
2. Используя стандартную замену Calculus I.

Показать все решения Скрыть все решения

a Использование интеграции по частям.Показать решение

Сначала обратите внимание, что в этом интеграле нет триггерных функций или экспонент. Хотя довольно много интегралов по частям будет включать триггерные функции и / или экспоненты, не все из них будут слишком зациклены на идее ожидания их появления.

В этом случае мы будем использовать следующие варианты для \ (u \) и \ (dv \).

\ [\ begin {align *} u & = x & \ hspace {0,5 дюйма} dv & = \ sqrt {x + 1} \, dx \\ du & = dx & \ hspace {0.{\ frac {5} {2}}} + c \ end {align *} \]

b Используя стандартную замену Calculus I. Показать решение

Теперь сделаем интеграл с заменой. {\ frac {3} {2}}} + c \ end {align *} \]

Итак, в этом примере мы использовали два разных метода интеграции и получили два разных ответа.Тогда возникает очевидный вопрос: мы сделали что-то не так?

На самом деле, мы не сделали ничего плохого. Нам необходимо помнить следующий факт из исчисления I.

\ [{\ rm {If}} \, \, f ‘\ left (x \ right) = g’ \ left (x \ right) \, \, \, {\ rm {then}} \, \, \ , е \ влево (х \ вправо) = г \ влево (х \ вправо) + с \]

Другими словами, если две функции имеют одинаковую производную, то они будут отличаться не более чем на константу. Итак, как это применимо к указанной выше проблеме? Сначала определите следующее:

\ [f ‘\ left (x \ right) = g’ \ left (x \ right) = x \ sqrt {x + 1} \]

Затем мы можем вычислить \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) путем интегрирования следующим образом:

\ [е \ left (x \ right) = \ int {{f ‘\ left (x \ right) \, dx}} \ hspace {0. 5in} g \ left (x \ right) = \ int {{g ‘\ left (x \ right) \, dx}} \]

Мы будем использовать интегрирование по частям для первого интеграла и замену для второго интеграла. Тогда согласно тому, что \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) должны отличаться не более чем на константу. Давайте проверим это и посмотрим, так ли это. Мы можем убедиться, что они различаются не более чем на константу, если мы посмотрим на разницу между ними и сделаем небольшие алгебраические манипуляции и упрощения.{\ frac {3} {2}}} \ left (0 \ right) \\ \ hspace {2.0in} = 0 \ end {array} \]

Итак, в этом случае оказывается, что две функции — это одна и та же функция, поскольку разница равна нулю. Учтите, что это происходит не всегда. Иногда разница дает ненулевую константу. Пример этого можно найти в разделе «Константа интеграции» в примечаниях к исчислению I.

Итак, что мы узнали? Во-первых, иногда будет несколько методов вычисления интеграла.Во-вторых, мы увидели, что разные методы часто приводят к разным ответам. Наконец, хотя ответы разные, иногда с большим трудом можно показать, что они отличаются не более чем на константу.

Когда мы сталкиваемся с интегралом, первое, что нам нужно решить, — это то, есть ли более одного способа сделать интеграл. Если существует несколько способов, нам нужно будет определить, какой из них следует использовать. Общее практическое правило, которое я использую в своих классах, заключается в том, что вы должны использовать метод, который вы считаете наиболее простым.Возможно, это не самый простой способ, но это не значит, что это неправильный метод.

Одна из наиболее распространенных ошибок интеграции по частям — это слишком сильная привязанность людей к воспринимаемым шаблонам. Например, во всех предыдущих примерах использовался базовый шаблон, согласно которому \ (u \) принимался за многочлен, стоящий перед другой функцией, а затем позволял \ (dv \) быть другой функцией. Это не всегда будет происходить, поэтому нам нужно быть осторожными и не связываться с какими-либо шаблонами, которые, как нам кажется, мы видим.

Давайте взглянем на некоторые интегралы, которые не вписываются в приведенный выше шаблон.

Пример 6 Вычислите следующий интеграл.

\ [\ int {{\ ln x \, dx}} \]

Показать решение

Итак, в отличие от любого другого интеграла, который мы сделали до этого момента, в интеграле есть только одна функция и нет полинома перед логарифмом.

Первый выбор многих здесь — попытаться вписать это в шаблон сверху и сделать следующие выборы для \ (u \) и \ (dv \).

\ [u = 1 \ hspace {0,5 дюйма} dv = \ ln x \, dx \]

Однако это приводит к реальной проблеме, поскольку это означает, что \ (v \) должно быть,

\ [v = \ int {{\ ln x \, dx}} \]

Другими словами, нам нужно знать ответ заранее, чтобы решить проблему. Так что этот выбор просто не сработает.

Следовательно, если логарифм не принадлежит \ (dv \), он должен принадлежать вместо \ (u \).Итак, давайте использовать следующие варианты вместо

\ [\ begin {align *} u & = \ ln x & \ hspace {0,5 дюйма} dv & = \, dx \\ du & = \ frac {1} {x} dx & \ hspace {0,5 дюйма} v & = х \ конец {выравнивание *} \]

Тогда интеграл равен

.

\ [\ begin {align *} \ int {{\ ln x \, dx}} & = x \ ln x — \ int {{\ frac {1} {x} \, x \, dx}} \\ & = x \ ln x — \ int {{dx}} \\ & = x \ ln x — x + c \ end {align *} \]

Пример 7 Вычислите следующий интеграл.{\ frac {5} {2}}} + c \ end {align *} \]

Итак, в двух предыдущих примерах мы видели случаи, которые не совсем вписывались в какой-либо воспринимаемый шаблон, который мы могли бы получить из первых двух примеров. Это всегда то, к чему мы должны обращать внимание при интеграции по частям.

Давайте взглянем на другой пример, который также иллюстрирует другой метод интеграции, который иногда возникает из-за проблем интеграции по частям.

Пример 8 Вычислите следующий интеграл.\ theta} \ cos \ theta \, d \ theta}} \]

Показать решение

Хорошо, до сих пор мы всегда выбирали \ (u \) таким образом, чтобы при дифференцировании эта часть исчезла или, по крайней мере, превратила ее в интеграл в форму, которая упростила бы работу с . В этом случае, какую бы часть мы ни делали \ (u \), она никогда не уйдет в процессе дифференцирования.

Не имеет большого значения, какой мы выбираем \ (u \), поэтому мы выберем следующий путь.\ theta} \ sin \ theta} \ right) + c \]

Обратите внимание, что после деления на два мы добавляем постоянную интегрирования в этой точке.

Эту идею интегрирования до тех пор, пока вы не получите одинаковый интеграл по обе стороны от знака равенства, а затем простое решение для интеграла, неплохо запомнить. Это не так уж и часто, но когда это происходит, это может быть единственный способ на самом деле выполнить интеграл.

Также обратите внимание, что это на самом деле просто алгебра, по общему признанию, сделанная таким образом, что вы, возможно, не привыкли к этому, но на самом деле это просто алгебра.

На этом этапе вашей математической карьеры каждый может решить,

\ [x = 3 — x \ hspace {0,5 дюйма} \ to \ hspace {0,5 дюйма} x = \ frac {3} {2} \]

Мы все еще решаем «уравнение». Единственное отличие состоит в том, что вместо решения для \ (x \) в мы решаем для интеграла, и вместо хорошей константы «3» в приведенной выше задаче алгебры мы получили функцию «беспорядка».

У нас есть еще один пример. Как мы увидим, некоторые проблемы могут потребовать от нас выполнять интеграцию по частям много раз, и существует короткий метод, который позволит нам быстро и легко выполнять несколько приложений интеграции по частям.{\ frac {x} {2}}} \, dx}} \]

Показать решение

Мы начинаем с выбора \ (u \) и \ (dv \), как всегда. Однако вместо того, чтобы вычислять \ (du \) и \ (v \), мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \ (u \), пока не дойдем до нуля. В столбце, соответствующем \ (dv \), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается со знака «+», а затем чередуются знаки, как показано.{\ frac {x} {2}}} + c \ end {align *} \]

У нас есть интеграл. Это намного проще, чем записывать все различные \ (u \) и \ (dv \), которые нам пришлось бы делать в противном случае.

Итак, в этом разделе мы увидели, как выполнять интеграцию по частям. На более поздних уроках математики это, вероятно, будет одним из наиболее частых методов интеграции, с которыми вы столкнетесь.

Важно не зацикливаться на шаблонах, которые, как вы думаете, вы видели.В большинстве случаев любой шаблон, который, как вы думаете, вы видели, может (и будет) нарушен в какой-то момент времени. Будь осторожен!

7. Интеграция по частям

М. Борна

Иногда мы встречаем интеграцию, которая является продуктом двух функций. Мы можем интегрировать такие продукты с помощью Integration by Parts .

Если u и v являются функциями x , то
правило продукта для дифференциации, которое мы встретили ранее, дает нам:

`d / (dx) (uv) = u (dv) / (dx) + v (du) / (dx)`

Переставив, имеем:

`u (dv) / (dx) = d / (dx) (uv) -v (du) / (dx)`

Интегрируя всюду относительно x , получаем
формула для интегрирования по частям:

Эта формула позволяет превратить сложный интеграл в
более простые.Мы должны убедиться, что выбрали u и
дв осторожно.

ПРИМЕЧАНИЕ: Функция u выбрана так
что `(du) / (dx)` на проще , чем
u .

Приоритеты выбора
u

Если у вас есть сочетание функций в выражении, которое нужно интегрировать, используйте следующее для выбора `u` по порядку.

1. Пусть `u = ln x`

2.(nx) `

Пример 1

`intx \ sin 2x \ dx`

Решение

Нам нужно выбрать «u». В этом вопросе у нас нет ни одной из функций, предложенных в списке «приоритетов» выше.

Можно использовать u = x или u = sin 2x, но обычно работает только один из них. В общем, мы выбираем тот, который позволяет `(du) / (dx)`
иметь более простую форму, чем и .

Итак, для этого примера мы выбираем u = x , и поэтому `dv` будет» остатком «интеграла,
дв = sin 2 x dx .

У нас есть u = x, поэтому du = dx.

Также `dv = sin 2x \ dx` и интегрирование дает:

`v = intsin 2x \ dx`

`= (- cos 2x) / 2`

Подставляя эти 4 выражения в формулу интегрирования по частям, мы получаем (используя цветовую кодировку, чтобы было легче увидеть, откуда берутся данные):

`int \ color {green} {\ underbrace {u}} \ \ \ \ color {red} {\ underbrace {dv}} \ \` `= \ \ \ color {green} {\ underbrace {u}} \ \ \ \ color {blue} {\ underbrace {v}} \ \ — \ int \ color {blue} {\ underbrace {v}} \ \ \ color {magenta} {\ underbrace {du}} `

`int \ color {green} {\ fbox {: x:}} \ \ color {red} {\ fbox {: sin 2x dx:}} = \ color {green} {\ fbox {: x:}} \ \ color {blue} {\ fbox {: {- cos2x} / 2:}} — int \ color {blue} {\ fbox {: {- cos2x} / 2:} \ \ color {magenta} {\ fbox {: dx:}} `

`= (-xcos2x) / 2 + 1/2 int cos2x dx`

`= (-xcos2x) / 2 + 1/2 (sin2x) / 2 + K`

`= (-xcos2x) / 2 + (sin2x) / 4 + K`

Если вышеизложенное немного сложно понять (из-за разрывов строк), вот оно снова в другом формате:

Пример 2

`int x sqrt (x + 1) dx`

Ответ

`intxsqrt (x + 1) \ dx`

Мы могли бы использовать `u = x` или` u = sqrt (x + 1) `. 2) dx`.2) + К`

На этот раз мы интегрировали обратную тригонометрическую функцию (в отличие от более раннего типа, где мы получили обратные тригонометрические функции в нашем ответе). См. Интеграция: обратные тригонометрические формы.

Альтернативный метод интеграции по частям

Вот альтернативный метод решения проблем, который можно решить с помощью интеграции по частям. Возможно, вам будет легче следовать.

Танзалин Метод

Интеграция по частям

Интеграция по частям (IBP) — это особый метод интеграции продуктов функций.x} dx}, \; \;} \ kern0pt {\ int {x \ ln xdx},} \]

, в котором подынтегральное выражение является произведением двух функций, может быть решено с помощью интегрирования по частям.

Этот метод основан на правиле продукта для дифференциации.

Предположим, что \ (u \ left (x \ right) \) и \ (v \ left (x \ right) \) — дифференцируемые функции. Тогда правило продукта с точки зрения дифференциалов дает нам:

\ [{d \ left ({uv} \ right) = udv + vdu. {- x}}, \ ldots \) ​​

Чем ближе функция к вершине, тем больше вероятность, что ее следует использовать как \ (u.n} xdx}, \) \ (n \ ge 2. \)

Пример 1.

Вычислить \ (\ int {x \ sin \ left ({3x — 2} \ right) dx}. \)

Решение.

Используем интегрирование по частям: \ (\ int {udv} = uv — \ int {vdu}. \) Пусть \ (u = x, \) \ (dv = \ sin \ left ({3x — 2} \ right ) dx. \) Тогда

\ [
{v = \ int {\ sin \ left ({3x — 2} \ right) dx}}
= {- \ frac {1} {3} \ cos \ left ({3x — 2} \ right) ), \; \;} \ kern-0.3pt
{du = dx.}
\]

Следовательно, интеграл равен

\ [
{\ int {x \ sin \ left ({3x — 2} \ right) dx}}
= {{- \ frac {x} {3} \ cos \ left ({3x — 2} \ right) )}} — {{\ int {\ left ({- \ frac {1} {3} \ cos \ left ({3x — 2} \ right)} \ right) dx}}}
= {{- \ frac {x} {3} \ cos \ left ({3x — 2} \ right)} + {\ frac {1} {3} \ int {\ cos \ left ({3x — 2} \ right) dx}}}
= {{- \ frac {x} {3} \ cos \ left ({3x — 2} \ right)}} + {{\ frac {1} {3} \ cdot \ frac {1} {3} \ sin \ left ({3x — 2} \ right) + C}}
= {{\ frac {1} {9} \ sin \ left ({3x — 2} \ right)} — ​​{\ frac {x} { 3} \ cos \ left ({3x — 2} \ right)} + {C.2} xdx}} = {- x \ cot x} + {\ ln \ left | {\ sin x} \ right | } + {C.} \]

Пример 3.

Вычислить интеграл \ (\ int {x \ cos 2xdx}. \)

Решение.

Выбираем

\ [{u = x, \; \;} \ kern0pt {dv = \ cos 2xdx.} \]

Отсюда

\ [{du = dv, \; \;} \ kern0pt {v = \ int {\ cos 2xdx}} = {\ frac {1} {2} \ sin 2x.} \]

Подставляя эти выражения в формулу интегрирования по частям

\ [\ int {udv} = uv — \ int {vdu}, \]

у нас

\ [{\ int {x \ cos 2xdx}} = {x \ cdot \ frac {1} {2} \ sin 2x — \ int {\ frac {1} {2} \ sin 2xdx}} = {\ frac {x} {2} \ sin 2x — \ frac {1} {2} \ int {\ sin 2xdx}} = {\ frac {x} {2} \ sin 2x — \ frac {1} {2} \ cdot \ left ({- \ frac {1} {2} \ cos 2x} \ right) + C} = {\ frac {x} {2} \ sin 2x + \ frac {1} {4} \ cos 2x + C .} \]

Пример 4.

Интегрируйте \ (\ int {\ ln xdx}. \)

Решение.

Мы должны интегрировать по частям: \ (u = \ ln x, \) \ (dv = dx. 2}}}} \ normalsize dx}.2}}}}} = {- \ frac {{\ ln x}} {x} — \ frac {1} {x} + C.} \]

Пример 6.

Вычислить интеграл \ (\ int {{{\ log} _2} xdx}. \)

Решение.

Чтобы использовать интегрирование по частям, перепишем интеграл следующим образом:

\ [\ int {{{\ log} _2} xdx} = \ int {1 \ cdot {{\ log} _2} xdx} \]

Теперь мы можем применить правило ILATE, то есть

\ [{u = {\ log _2} x, \; \;} {dv = 1dx.} \]

Это дает

\ [{du = \ frac {{dx}} {{x \ ln 2}}, \; \;} {v = \ int {1dx} = x.} \]

Интегрируя по частям, получаем

\ [{\ int {{{\ log} _2} xdx}} = {x {\ log _2} x — \ int {x \ cdot \ frac {{dx}} {{x \ ln 2}}}} = {x {\ log _2} x — \ frac {1} {{\ ln 2}} \ int {dx}} = {x {\ log _2} x — \ frac {x} {{\ ln 2}} + C.} \]

Как интегрировать по частям: формулы и примеры

Первообразные могут быть достаточно сложными для решения сами по себе, но когда у вас есть две умноженные вместе функции, от которых нужно взять первообразную, может быть трудно понять, с чего начать. Вот тут и пригодится формула интегрирования по частям!

Эта удобная формула может значительно облегчить домашнюю работу по расчету, помогая найти первообразные, разработка которых в противном случае была бы сложной и трудоемкой. В этом руководстве мы объясним формулу, проведем вас через каждый шаг, который необходимо предпринять для интеграции по частям, и решим примеры задач, чтобы вы сами могли стать экспертом по интеграции по частям.

Что такое формула интеграции по частям?

Интегрирование по частям — это метод, используемый в исчислении для нахождения интеграла произведения функций через интеграл от их производной и первообразной. В принципе, если у вас есть уравнение с первообразной двумя функциями, умноженными вместе, и вы не знаете, как найти первообразную, формула интегрирования по частям преобразует первообразную функций в другую форму, чтобы было легче найти упростить / решить. Вот формула:

∫ f (x) g ’(x) dx = f (x) g (x) — ∫ f’ (x) g (x) dx

Вы начинаете с левой части уравнения (первообразной произведения двух функций) и преобразуете ее в правую часть уравнения.

Формулу интегрирования по частям можно также записать более компактно: с u вместо f (x), v вместо g (x), dv вместо g ‘(x) и du вместо f’ (x):

∫ u dv = uv — ∫ v du

Вы можете использовать интегрирование по частям, когда вам нужно найти первообразную сложной функции, которую трудно решить, не разбивая ее на две функции, умноженные вместе. Поначалу это может показаться не очень полезной формулой, поскольку ни одна из сторон уравнения не является значительно более упрощенной, чем другая, но, работая с примерами, вы увидите, насколько полезной может быть формула интегрирования по частям для решения первообразных.

Как решать проблемы с помощью интеграции по частям

Существует пять шагов к решению проблемы с использованием формулы интегрирования по частям:

# 1: Выберите свои u и v

# 2: Дифференцируйте вас, чтобы найти du

# 3: Интегрируйте v, чтобы найти ∫v dx

# 4: подставьте эти значения в уравнение интегрирования по частям

# 5: Упростите и решите

Может показаться сложным интегрировать по частям, но использовать формулу на самом деле довольно просто.Все первые три шага связаны с выбором / поиском различных переменных, чтобы их можно было включить в уравнение на четвертом шаге. Вы должны хорошо понимать, как дифференцировать и интегрировать, но если вы это сделаете, эти шаги просты.

В общем, ваша цель состоит в том, чтобы du было проще, чем u , а первообразное dv не было сложнее, чем v . По сути, вы хотите, чтобы правая часть уравнения оставалась как можно более простой, чтобы вам было легче ее упростить и решить.Тем не менее, не слишком переживайте, выбирая u и v. Если ваш первый выбор не работает, просто поменяйте их местами и интегрируйте по частям с новыми u и v, чтобы посмотреть, работает ли это лучше.

После того, как у вас есть переменные, все, что вам нужно сделать, это упростить, пока у вас не останется никаких первообразных, , и вы не получите ответ! Продолжайте читать, чтобы увидеть, как мы используем эти шаги для решения реальных проблем с образцами.

Интеграция по примерам деталей

Вот три примера задач разной сложности.Попробуйте решить каждую из них самостоятельно, а затем посмотрите, как мы использовали интеграцию по частям, чтобы получить правильный ответ.

Пример №1: Найти ∫ xsin (x) dx

Если бы вы просто взглянули на эту проблему, вы, возможно, не знали бы, как взять первообразную xsin (x). Вот тут и приходит на помощь интеграция по частям! Первый шаг — выбрать u и dv . Используя «x» как u , легко получить du , так что давайте начнем с этого.

u = x

dv = sin (x)

Для шагов 2 и 3 мы выделим и и интегрируем dv , чтобы получить du и v . Производная x равна dx (легко!), А первообразная sin (x) равна -cos (x).

du = dx

v = -cos (x)

Теперь пора подставить эти переменные в формулу интегрирования по частям: ∫ u dv = uv — ∫ v du.Это дает нам:

∫ xsin (x) dx = x (-cos (x)) — ∫ -cos (x) dx

Затем обработайте правую часть уравнения, чтобы упростить его. Сначала раздайте негативы:

= -xcos (x) + ∫ cos (x) dx

Первообразной cos (x) является sin (x), и не забудьте добавить произвольную константу C в конце:

= -xcos (x) + sin (x) + C

Вот и все, первообразную вы нашли!

Пример № 2: Найти ∫ x

² ln (x) dx

Опять же, сначала мы выберем u и dv .

u = ln (x)

dv = x ²

Затем мы используем эту информацию для определения du и v . Производная ln (x) равна (1 / x) dx, а первообразная x ² равна (⅓) x ³ .

du = (1 / x) dx

v = (⅓) x ³

Теперь, когда у нас есть все переменные, давайте включим их в уравнение интегрирования по частям:

∫x ² ln (x) dx = ln (x) ⋅ (⅓) x ³ −∫ (⅓) x ³ ⋅ (1 / x) dx

Теперь осталось упростить! Сначала перемножьте все:

= (x ³ ln (x)) / 3 — ∫x ² /3 dx

Затем возьмем первообразную ∫x ² /3.Добавьте константу, и все готово; в уравнении больше не осталось первообразных:

= (x ³ ln (x)) / 3 — (1/9) x ³ + C

Пример № 3: Найти ∫ ex sin (x) dx

Снова выберите u и dv :

u = sin (x)

dv = ex

Найдите du и v (производная sin (x) равна cox (x), а первообразная ex по-прежнему равна ex.

du = cos (x)

v = ex

Введите эти переменные в уравнение:

∫ex sin (x) dx = sin (x) ex -cos (x) ex dx

Все еще довольно запутано, и часть уравнения «∫cos (x) ex dx» по-прежнему имеет две функции, перемноженные вместе. Иногда, когда вы используете формулу интегрирования по частям, и все выглядит так же сложно, как и раньше, когда две функции умножаются вместе, может помочь снова использовать интеграцию по частям. Давай попробуем.

Ориентируясь только на часть уравнения «∫cos (x) ex dx», выберите другие u и dv . Производная cos (x) равна -sin (x), а первообразная ex по-прежнему ex (по крайней мере, это легко!).

u = cos (x)

dv = ex

du = -sin (x)

v = ex

Снова подставьте эти новые переменные в формулу:

∫ex sin (x) dx = sin (x) ex — (cos (x) ex −∫ − sin (x) ex dx)

Теперь упростим:

∫ex sin (x) dx = ex sin (x) — ex cos (x) −∫ ex sin (x) dx

Мы можем переместить «−∫ ex sin (x) dx» из правой части уравнения в левую:

2∫ex sin (x) dx = ex sin (x) — ex cos (x)

Упростите это снова и добавьте константу:

∫ex sin (x) dx = ex (sin (x) — cos (x)) / 2 + C

В правой части уравнения больше нет первообразных, так что вот вам ответ! Мы смогли найти первообразную этого запутанного уравнения, дважды проработав формулу интегрирования по частям.

Резюме: как интегрировать по частям

Формула интегрирования по частям может быть отличным способом найти первообразную произведения двух функций, которую вы иначе не знали бы, как взять первообразную. Вам необходимо хорошо знать производные и первообразные, чтобы использовать ее, но это простая формула, которая может помочь вам решать различные математические задачи. Шаги:

# 1: Выберите свои u и v

# 2: Дифференцируйте вас, чтобы найти du

# 3: Интегрируйте v, чтобы найти ∫v dx

# 4: подставьте эти значения в уравнение интегрирования по частям

# 5: Упростите и решите

Что дальше?

Хотите знать, какие уроки математики вам следует посещать? Узнайте, какие математические классы должны посещать старшие школьники, прочитав наше руководство.

Заинтересованы в математических соревнованиях, таких как Международная математическая олимпиада ? Прочтите наше руководство, чтобы узнать, как пройти квалификационные тесты.

Проблемы с математическим разделом SAT или ACT? У нас есть полные руководства по SAT Math и ACT Math, которые научат вас всему, что вам нужно для успешной работы в этих разделах.

7.1: Интегрирование по частям — математика LibreTexts

К настоящему моменту у нас есть довольно подробная процедура вычисления многих основных интегралов.2 \), что-то столь же простое, как \ (∫x \ sin x \, \, dx \), бросает нам вызов. Многие студенты хотят знать, существует ли правило продукта для интеграции. Нет, но есть метод, основанный на правиле произведения для дифференциации, который позволяет нам заменять один интеграл на другой. Мы называем эту технику интегрированием по частям.

Формула интеграции по частям

Если \ (h (x) = f (x) g (x) \), то, используя правило произведения, мы получаем

\ [h ′ (x) = f ′ (x) g (x) + g ′ (x) f (x).\ label {eq1} \]

Хотя сначала это может показаться контрпродуктивным, давайте теперь объединим обе стороны уравнения \ ref {eq1}:

\ [∫h ′ (x) \, \, dx = ∫ (g (x) f ′ (x) + f (x) g ′ (x)) \, \, dx. \ nonumber \]

Это дает нам

\ [h (x) = f (x) g (x) = ∫g (x) f ′ (x) \, dx + ∫f (x) g ′ (x) \, \, dx. \ nonumber \]

Теперь решаем относительно \ (∫f (x) g ′ (x) \, \, dx: \)

\ [∫f (x) g ′ (x) \, dx = f (x) g (x) −∫g (x) f ′ (x) \, \, dx. \ nonumber \]

Сделав замены \ (u = f (x) \) и \ (v = g (x) \), которые, в свою очередь, сделают \ (du = f ′ (x) \, dx \) и \ (dv = g ′ (x) \, dx \) имеем более компактную форму

\ [∫u \, dv = uv − ∫v \, du.\ nonumber \]

Интеграция по частям

Пусть \ (u = f (x) \) и \ (v = g (x) \) — функции с непрерывными производными. Тогда формула интегрирования по частям для интеграла, включающего эти две функции, будет:

\ [∫u \, dv = uv − ∫v \, du. \ label {IBP} \]

Преимущество использования формулы интегрирования по частям заключается в том, что мы можем использовать ее для замены одного интеграла на другой, возможно, более простой интеграл. Следующий пример иллюстрирует его использование.

Пример \ (\ PageIndex {1} \): использование интеграции по частям

Используйте интегрирование по частям с \ (u = x \) и \ (dv = \ sin x \, \, dx \) для оценки

\ [∫x \ sin x \, \, dx.\ nonumber \]

Решение

Выбирая \ (u = x \), мы получаем \ (du = 1 \, \, dx \). Поскольку \ (dv = \ sin x \, \, dx \), получаем

\ [v = ∫ \ sin x \, \, dx = — \ cos x. \ nonumber \]

Эти значения удобно отслеживать следующим образом:

• \ (и = х \)
• \ (dv = \ sin x \, \, dx \)
• \ (du = 1 \, dx \)
• \ (v = ∫ \ sin x \, \, dx = — \ cos x. \)

Применяя формулу интегрирования по частям (Equation \ ref {IBP}), получаем

\ [\ begin {align} ∫x \ sin x \, \, dx & = (x) (- \ cos x) −∫ (- \ cos x) (1 \, \, dx) \ tag {Substitute} \\ [4pt] & = — x \ cos x + ∫ \ cos x \, \, dx \ tag {Simplify} \ end {align} \]

Тогда используйте

\ [∫ \ cos x \, \, dx = \ sin x + C.2 \ соз х \, \, dx. \ nonumber \]

К сожалению, с новым интегралом мы не в лучшем положении, чем раньше. Важно помнить, что когда мы применяем интегрирование по частям, нам может потребоваться попробовать несколько вариантов для \ (u \) и \ (dv \), прежде чем найти подходящий вариант.

Во-вторых, вы можете задаться вопросом, почему, когда мы находим \ (v = ∫ \ sin x \, \, dx = — \ cos x \), мы не используем \ (v = — \ cos x + K. \) Чтобы увидеть, что это не имеет значения, мы можем переработать задачу, используя \ (v = — \ cos x + K \):

\ [\ begin {align *} ∫x \ sin x \, \, dx & = (x) (- \ cos x + K) −∫ (- \ cos x + K) (1 \, \, dx) \\ [4pt] & = — x \ cos x + Kx + ∫ \ cos x \, \, dx − ∫K \, \, dx \\ [4pt] & = — x \ cos x + Kx + \ sin x − Kx + C \\ [4pt] & = — x \ cos x + \ sin x + C.\ end {align *} \]

Как видите, в конечном решении это не имеет значения.

Наконец, мы можем проверить правильность нашей первообразной путем дифференцирования \ (- x \ cos x + \ sin x + C: \)

\ [\ begin {align *} \ dfrac {d} {\, dx} (- x \ cos x + \ sin x + C) = \ cancel {(- 1) \ cos x} + (−x) (- \ sin x) + \ cancel {\ cos x} \\ [4pt] = x \ sin x \ end {align *} \]

Следовательно, первообразная проверяется.

Упражнение \ (\ PageIndex {1} \)

Вычислить \ (∫ xe ^ {2x} \, dx \), используя формулу интегрирования по частям (Equation \ ref {IBP}) с \ (u = x \) и \ (dv = e ^ {2x} \, \, dx \).{2x} + C \ nonumber \]

Здесь возникает естественный вопрос: как мы узнаем, как выбирать \ (u \) и \ (dv \)? Иногда это результат проб и ошибок; однако аббревиатура LIATE часто помогает избавиться от некоторых догадок в нашем выборе. Этот акроним означает L огарифмических функций, I nverse тригонометрических функций, A алгебраических функций, T ригонометрических функций и E xponential функций.Эта мнемоника помогает определить подходящий выбор для \ (u \). Тип функции в интеграле, который появляется первым в списке, должен быть нашим первым выбором \ (u \).

Например, если интеграл содержит логарифмическую функцию , и алгебраическую функцию , мы должны выбрать \ (u \) в качестве логарифмической функции, потому что L стоит перед A в LIATE. Интеграл в примере \ (\ PageIndex {1} \) имеет тригонометрическую функцию (\ (\ sin x \)) и алгебраическую функцию (\ (x \)).Поскольку A стоит перед T в LIATE, мы выбрали \ (u \) в качестве алгебраической функции. Когда мы выбрали \ (u \), \ (dv \) выбирается как оставшаяся часть интегрируемой функции вместе с \ (\, dx \).

Почему работает эта мнемоника? Помните, что все, что мы выбираем как \ (dv \), должно быть чем-то, что мы можем интегрировать. Поскольку у нас нет формул интегрирования, позволяющих интегрировать простые логарифмические функции и обратные тригонометрические функции, имеет смысл не выбирать их в качестве значений для \ (dv \).Следовательно, они должны быть во главе списка как варианты выбора для \ (u \). Таким образом, мы помещаем LI в начало мнемоники. (Мы могли бы так же легко начать с IL, поскольку эти два типа функций не будут появляться вместе в задаче интегрирования по частям.) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно просто интегрировать и сделать хороший выбор для \ (dv \). Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы так же легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет значения, какая из них \ (u \), а какая \ (dv \).2} + С. \ end {align *} \]

Пример \ (\ PageIndex {3C} \): применение интеграции по частям более одного раза

Вычислить \ [∫ \ sin (\ ln x) \, dx. \ nonumber \]

Решение

Этот интеграл, похоже, имеет только одну функцию, а именно \ (\ sin (\ ln x) \), однако мы всегда можем использовать постоянную функцию 1 в качестве другой функции. В этом примере давайте выберем \ (u = \ sin (\ ln x) \) и \ (dv = 1 \, dx \). (Решение использовать \ (u = \ sin (\ ln x) \) легко. Мы не можем выбрать \ (dv = \ sin (\ ln x) \, dx \), потому что, если бы мы могли его интегрировать, мы не будет использовать интегрирование по частям в первую очередь!) Следовательно, \ (du = (1 / x) \ cos (\ ln x) \, dx \) и \ (v = ∫ 1 \, dx = x .\) После применения интегрирования по частям к интегралу и упрощения имеем

\ [∫ \ sin \ left (\ ln x \ right) \, dx = x \ sin (\ ln x) — \ int \ cos (\ ln x) \, dx. \ nonumber \]

К сожалению, этот процесс оставляет нам новый интеграл, очень похожий на исходный. Однако давайте посмотрим, что произойдет, когда мы снова применим интеграцию по частям. На этот раз выберем \ (u = \ cos (\ ln x) \) и \ (dv = 1 \, dx, \), образуя \ (du = — (1 / x) \ sin (\ ln x) \, dx \) и \ (v = ∫ 1 \, dx = x. \)

Подставляя, получаем

\ [∫ \ sin (\ ln x) \, dx = x \ sin (\ ln x) — (x \ cos (\ ln x) -∫ — \ sin (\ ln x) \, dx).\ nonumber \]

После упрощения получаем

\ [∫ \ sin (\ ln x) \, dx = x \ sin (\ ln x) −x \ cos (\ ln x) −∫ \ sin (\ ln x) \, dx. \ nonumber \]

Последний интеграл теперь такой же, как и исходный. Может показаться, что мы просто пошли по кругу, но теперь мы действительно можем вычислить интеграл. Чтобы увидеть, как это сделать более наглядно, подставьте \ (I = ∫ \ sin (\ ln x) \, dx. \). Таким образом, уравнение принимает вид

\ [I = х \ sin (\ ln x) −x \ cos (\ ln x) −I. \ nonumber \]

Сначала добавьте \ (I \) к обеим частям уравнения, чтобы получить

\ [2I = х \ sin (\ ln x) −x \ cos (\ ln x).\ nonumber \]

Далее разделите на 2:

\ [I = \ dfrac {1} {2} x \ sin (\ ln x) — \ dfrac {1} {2} x \ cos (\ ln x). \ nonumber \]

Подставляя снова \ (I = ∫ \ sin (\ ln x) \, dx \), получаем

\ [\ int \ sin (\ ln x) \, dx = \ dfrac {1} {2} x \ sin (\ ln x) — \ dfrac {1} {2} x \ cos (\ ln x). \ nonumber \]

Отсюда мы видим, что \ ((1/2) x \ sin (\ ln x) — (1/2) x \ cos (\ ln x) \) является первообразной от \ (\ sin (\ ln x) \, dx \). Для наиболее общего первообразного прибавьте \ (+ C \):

\ [∫ \ sin (\ ln x) \, dx = \ dfrac {1} {2} x \ sin (\ ln x) — \ dfrac {1} {2} x \ cos (\ ln x) + C .\ nonumber \]

Анализ

Если этот метод сначала покажется немного странным, мы можем проверить ответ дифференцированием:

\ [\ begin {align *} \ dfrac {d} {\, dx} \ left (\ dfrac {1} {2} x \ sin (\ ln x) — \ dfrac {1} {2} x \ cos (\ ln x) \ right) \\ [4pt] & = \ dfrac {1} {2} (\ sin (\ ln x)) + \ cos (\ ln x) ⋅ \ dfrac {1} {x} ⋅ \ dfrac {1} {2} x− \ left (\ dfrac {1} {2} \ cos (\ ln x) — \ sin (\ ln x) ⋅ \ dfrac {1} {x} ⋅ \ dfrac {1 } {2} x \ right) \\ [4pt] & = \ sin (\ ln x). 2 \ sin x \, dx.2 \ cos x + 2x \ sin x + 2 \ cos x + C \ nonumber \]

Интегрирование по частям для определенных интегралов

Теперь, когда мы успешно использовали интегрирование по частям для вычисления неопределенных интегралов, мы обратим наше внимание на определенные интегралы. Методика интегрирования на самом деле такая же, только мы добавляем шаг для вычисления интеграла на верхнем и нижнем пределе интегрирования.

Интеграция по частям для определенных интегралов

Пусть \ (u = f (x) \) и \ (v = g (x) \) — функции с непрерывными производными на [\ (a, b \)].{π / 2} _0x \ cos x \, dx = \ dfrac {π} {2} −1 \ nonumber \]

Интеграция по частям — Исчисление Том 2

Цели обучения

• Определите, когда следует использовать интеграцию по частям.
• Используйте формулу интегрирования по частям для решения задач интегрирования.
• Используйте формулу интегрирования по частям для определенных интегралов.

К настоящему времени у нас есть довольно подробная процедура вычисления многих основных интегралов. Однако, хотя мы можем интегрироваться, используя подстановку, что-то столь же простое, как кажется, бросает нам вызов.Многие студенты хотят знать, существует ли правило продукта для интеграции. Нет, но есть метод, основанный на правиле произведения для дифференциации, который позволяет нам заменять один интеграл на другой. Мы называем эту технику интеграцией по частям.

Формула интеграции по частям

Если, то, используя правило произведения, мы получаем Хотя сначала это может показаться контрпродуктивным, давайте теперь проинтегрируем обе части этого уравнения:

Это дает нам

Теперь решаем

Делая замены и которые, в свою очередь, делают, и мы получаем более компактную форму

Интеграция по частям

Позвольте и быть функции с непрерывными производными.Тогда формула интегрирования по частям для интеграла, включающего эти две функции, будет:

Преимущество использования формулы интегрирования по частям заключается в том, что мы можем использовать ее для замены одного интеграла на другой, возможно, более простой интеграл. Следующий пример иллюстрирует его использование.

Использование интеграции по частям

Используйте интеграцию по частям с

и для оценки

Анализ

На данный момент, вероятно, есть несколько вопросов, которые нуждаются в пояснении.Прежде всего, вам может быть любопытно, что бы произошло, если бы мы выбрали, и если бы мы сделали это, то у нас было бы и Таким образом, после применения интегрирования по частям у нас есть К сожалению, с новым интегралом мы не в лучше, чем раньше. Важно помнить, что когда мы применяем интеграцию по частям, нам может потребоваться попробовать несколько вариантов, прежде чем найти тот, который работает.

Во-вторых, вы можете задаться вопросом, почему, когда мы обнаруживаем, что мы не используем, Чтобы увидеть, что это не имеет значения, мы можем переделать проблему, используя

Как видите, в конечном решении это не имеет значения.

Наконец, мы можем проверить правильность нашего первообразного путем дифференцирования

Следовательно, первообразная проверяется.

Здесь возникает естественный вопрос: как мы узнаем, как выбирать? Иногда это вопрос проб и ошибок; однако аббревиатура LIATE часто помогает избавиться от некоторых догадок в нашем выборе. Это сокращение означает L огарифмических функций, I обратных тригонометрических функций, A алгебраических функций, T ригонометрических функций и E экспоненциальных функций.Эта мнемоника помогает сделать правильный выбор для

.

Тип функции в интеграле, который появляется первым в списке, должен быть нашим первым выбором.Например, если интеграл содержит логарифмическую функцию и алгебраическую функцию, мы должны выбрать логарифмическую функцию, потому что L стоит перед A в ЛАЙТ. Интеграл на (рисунок) имеет тригонометрическую функцию и алгебраическую функцию. Поскольку A стоит перед T в LIATE, мы выбрали в качестве алгебраической функции.Когда мы выбрали, будет выбрана оставшаяся часть функции, которая будет интегрирована вместе с

Почему работает эта мнемоника? Помните, что все, что мы выбираем, должно быть чем-то, что мы можем интегрировать. Поскольку у нас нет формул интегрирования, которые позволяют нам интегрировать простые логарифмические функции и обратные тригонометрические функции, имеет смысл не выбирать их в качестве значений для Следовательно, они должны быть во главе списка в качестве вариантов для выбора. LI в начале мнемоники.(Мы могли бы так же легко начать с IL, поскольку эти два типа функций не будут появляться вместе в задаче интегрирования по частям.) Экспоненциальные и тригонометрические функции находятся в конце нашего списка, потому что их довольно просто интегрировать и сделать правильный выбор Таким образом, у нас есть TE в конце нашей мнемоники. (Мы могли бы так же легко использовать ET в конце, поскольку, когда эти типы функций появляются вместе, обычно не имеет значения, какая из них, а какая — Алгебраические функции, как правило, легко как интегрировать, так и дифференцировать, и они приходят в середине мнемоники.

Использование интеграции по частям

Оценить

В некоторых случаях, как в следующих двух примерах, может потребоваться применить интеграцию по частям более одного раза.

Применение интеграции по частям более одного раза

Оценить

Применение интеграции по частям, когда LIATE не работает

Оценить

Применение интеграции по частям более одного раза

Оценить

Этот интеграл, похоже, имеет только одну функцию, а именно, однако, мы всегда можем использовать постоянную функцию 1 в качестве другой функции.В этом примере давайте выберем и (Решение использовать легко. Мы не можем выбрать, потому что, если бы мы могли его интегрировать, мы бы не использовали интеграцию по частям в первую очередь!) Следовательно, и после применения интеграции по частям к интегралу и упрощению имеем

К сожалению, этот процесс оставляет нам новый интеграл, очень похожий на исходный. Однако давайте посмотрим, что произойдет, когда мы снова применим интеграцию по частям. На этот раз выберем и сделаем и заменим, у нас

После упрощения получаем

Последний интеграл теперь такой же, как и исходный.Может показаться, что мы просто пошли по кругу, но теперь мы действительно можем вычислить интеграл. Чтобы увидеть, как это сделать более наглядно, подставьте подставку Таким образом, уравнение станет

Сначала прибавьте к обеим частям уравнения, чтобы получить

Далее разделите на 2:

Подставляя снова, получаем

Из этого мы видим, что это первообразная от. Для наиболее общего первообразного прибавляем

.

Анализ

Если этот метод сначала покажется немного странным, мы можем проверить ответ дифференцированием:

Оценить

Ключевые понятия

• Формула интегрирования по частям позволяет заменять один интеграл другим, возможно, более простым интегралом.
• Интегрирование по частям применимо как к определенным, так и к неопределенным интегралам.

Ключевые уравнения

• Интеграция по формуле частей
• Интегрирование по частям для определенных интегралов

Глоссарий

интеграция по частям

метод интегрирования, который позволяет заменять один интеграл на другой по формуле

.