Содержание
Физика 9 класс. Законы, правила, формулы
Кинематика
Динамика
- Силы трения
- Трение покоя
Максимальная сила трения покоя (Fтр)max пропорциональна силе нормального давления (N) и зависит от характера взаимодействия соприкасающихся поверхностей тел, определяемого коэффициентом трения (μ)
(Fтр)max=μ×N
СИ: Н - Трение скольжения
Сила трения скольжения (Fтр) пропорциональна силе давления (N), коэффициенту трения (μ) и направлена противоположно направлению движения тела.
Fтр=μ×N
СИ: Н - Коэффициент трения
Коэффициент трения (μ) вычисляют как отношение модулей силы трения (Fтр) и силы давления (N).
μ=Fтр/N - Движение тела под действием силы трения
1) Путь (l), пройденный движущимся телом под действием силы трения до полной остановки (тормозной путь), прямо пропорционален квадрату начальной скорости (v0) и обратно пропорционален коэффициенту трения (μ): , (g — ускорение свободного падения).
2) Время (t) движения тела под действием силы трения до момента полной остановки (время торможения) прямо пропорционально начальной скорости (v0) и обратно пропорционально коэффициенту трения (μ):
СИ: м, с
- Движение тела под действием нескольких сил
- Условие равновесия тела (как материальной точки).
Тело находится в равновесии (в покое или движется равномерно и прямолинейно), если сумма проекций всех сил (), действующих на тело, на любую ось (ОХ, ОY, O, …) равна нулю.
;
;СИ: Н
- Движение тела по наклонной плоскости
Ускорение тела, скользящего вниз по наклонной плоскости с углом наклона (α) и коэффициентом трения тела о плоскость (μ), не зависит от массы тела и равно: , (g — ускорение свободного падения)
СИ: м/с2 - Движение связанных тел через неподвижный блок
Ускорение двух тел, массами m1 и m2, связанных нитью, перекинутой через неподвижный блок, равно:
, (g — ускорение свободного падения)
СИ: м/с2
- Законы сохранения в механике
- Импульс тела
Импульс тела () — векторная величина, равная произведению массы (m) тела на его скорость ().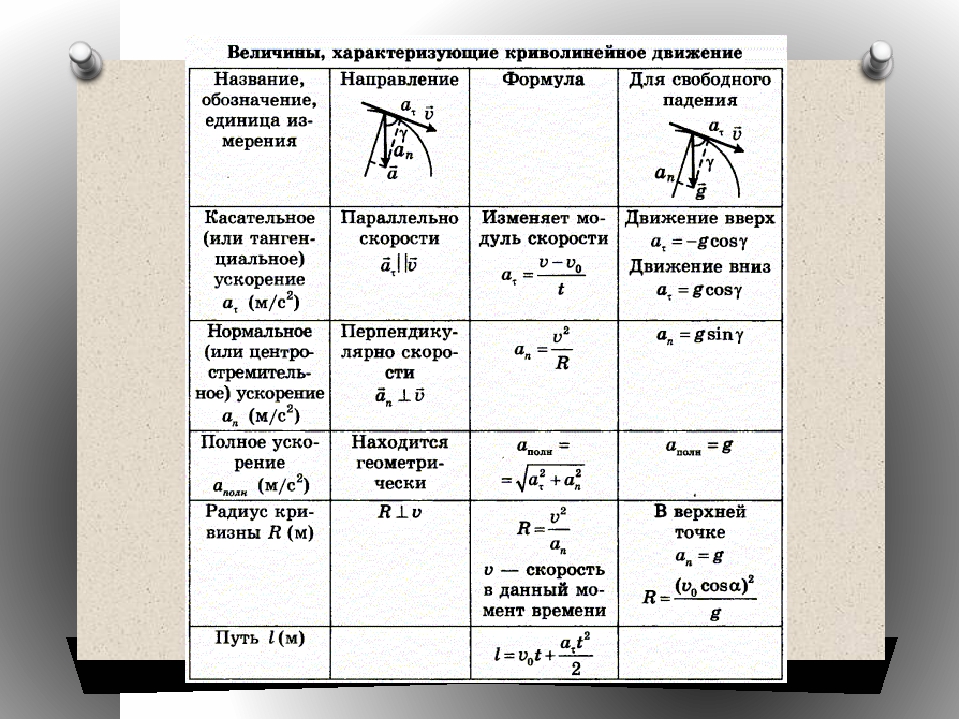
СИ: (кг×м)/с
- Импульс силы
Импульс силы ( — произведение силы на время t её действия) равен изменению импульса тела.СИ: Н×с
- Закон сохранения импульса
Геометрическая сумма импульсов тел (), составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.СИ: Н×с
- Механическая работа силы
Работа (А) постоянной силы равна произведению модулей векторов силы () и перемещения () на косинус угла между этими векторами.СИ: Дж
- Теорема о кинетической энергии
Работа (А) силы (или равнодействующей сил) равна изменению кинетической энергии (Ek1 и Ek2) движущегося тела.
,
где m — масса тела, v1, v2 — начальная и конечная скорости тела
СИ: Дж - Потенциальная энергия поднятого тела
Потенциальная энергия (ЕП) тела, поднятого на некоторую высоту (h) над нулевым уровнем, равна работе (А) силы тяжести (m×g) при падении тела с этой высоты до нулевого уровня.
A=ЕП=m×g×h
СИ: Дж - Работа силы тяжести
Работа (А) силы тяжести (mg) не зависит от пути, пройденного телом, а определяется разностью высот (Δh=h2-h1) положения тела в конце и в начале пути и равна разности его потенциальных энергий (EП2 и EП1).
A=-(EП2-EП1)=-m×g×Δh
СИ: Дж - Потенциальная энергия деформированного тела
Потенциальная энергия (ЕП) деформированного тела (пружины) равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна нулю.
ЕП = ,
где k — жесткость; х — деформация пружины.
СИ: Дж - Закон сохранения полной механической энергии
Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
ЕК2+ЕП2=ЕК1+ЕП1=const
СИ: Дж
- Движение жидкостей и газов по трубам
- Закон Бернулли
Давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость её движения меньше, и наоборот, в тех частях, где скорость больше, давление меньше.
,
где p1, v1, h1 — давление, скорость и вертикальная координата жидкости в одном сечении трубы; p2, v2, h2 — давление, скорость и вертикальная координата жидкости в другом сечении трубы;
ρ — плотность жидкости; g — ускорение свободного падения.
СИ: Па
Поделитесь с друзьями:
Дополнительные главы физики: кинематика. 9 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой по физике 9 класса. В процессе обучения учащиеся познакомятся с основными принципами и методами кинематики, увидят, как довольно сложные движения можно свести к комбинации более простых, и научатся решать разнообразные задачи.
Курс состоит из 11 обязательных и 1 лекционного модуля, 51 видеолекций с конспектами, 181 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
— Геометрия и физика
— Описание движения
— Ускорение
— Движение по окружности
— Малые приращения физических величин
— Движение тела, брошенного под углом к горизонту
— Криволинейное движение
— Кинематика плоского движения твердого тела
— Комбинация прямолинейных движений
— Кинематические связи
— Выбор системы отсчета
— Комбинация вращения и прямолинейного движения
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
Каждый ученик самостоятельно определяет для себя темп и удобное время учебы. Часть модулей открыта сразу, следующие модули открываются после того, как получен зачет по предыдущим. В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
12-а. Что такое кинематика
§ 12-а.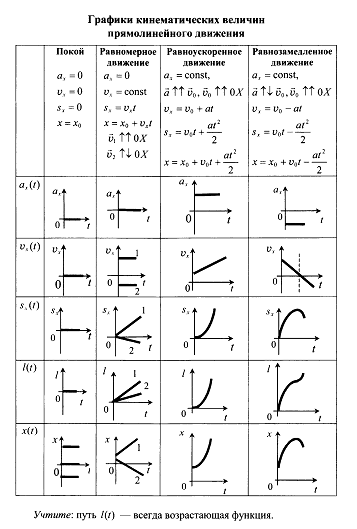 Что такое кинематика
Что такое кинематика
Вокруг нас множество движущихся тел. Их движение можно описать по-разному. Рассмотрим, например, словесное описание движения поезда. Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем 1 час стоял, и в пункт Б прибыл через 3 часа после возобновления движения, всё это время поддерживая скорость 50 км/ч.
Движение этого же поезда можно описать при помощи таблицы:
Пример табличного описания движения тела, например, поезда.
| Время t, ч | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Путь l, км | 0 | 100 | 200 | 200 | 250 | 300 | 350 |
По данным таблицы построим график, и мы получим описание движения при помощи графика. На нём три этапа: от 0 до 2 часов (движение со скоростью 100 км/ч), от 2 до 3 часов (стоянка) и от 3 до 6 часов (движение со скоростью 50 км/ч).
На нём три этапа: от 0 до 2 часов (движение со скоростью 100 км/ч), от 2 до 3 часов (стоянка) и от 3 до 6 часов (движение со скоростью 50 км/ч).
Каждый этап движения поезда на графике отражён прямой линией, которой в алгебре соответствует линейная функция y = kx + b, где k и b – числа. Применительно к нашей задаче про поезд, вместо y будем писать l, а вместо x будем писать t. Тогда мы получим описание движения формулами:
Табл. 12.3. Пример описания движения поезда с помощью формул, являющихся линейными функциями .
| Этап движения на графике | Интервал времени | Формула линии графика |
| I. (красный) | если 0 t , то | l = 100 · t + 0 |
| II. (чёрный) | если 2 t , то | l = 0 · t + 200 |
III. (синий) (синий) | если 3 t , то | l = 50 · t + 50 |
Как получаются эти формулы, мы изучим при решении задач, а пока убедимся, что они верные, например последняя. Значение t должно лежать в интервале от 3 до 6 часов. Возьмём значение 4 и подставим в формулу: l = 50 · 4 + 50. Вычисляем: 250 километров. В верхней таблице мы тоже видим, что за 4 часа поезд проехал 250 км. Взгляните и на график: для момента времени t = 4 ч получается путь l = 250 км.
Обобщим сказанное: рассмотренные способы описания движения – словесный, табличный, графический и формулами – равноправны. В зависимости от ситуации мы будем выбирать более удобный способ.
Кинематика (от греч. «кинематос» – движение) – раздел физики, изучающий способы математического описания движения тел без выяснения причин, вызвавших движение. Кинематика не интересуется тем, почему тело движется так, а не иначе. Она лишь отвечает на вопросы: как движение описать математически и что нового из такого описания можно почерпнуть?
Она лишь отвечает на вопросы: как движение описать математически и что нового из такого описания можно почерпнуть?
Тело, собственными размерами которого в данных условиях можно пренебречь, называют материальной точкой. Например, если самолёт совершает перелёт по маршруту Москва–Сочи, диспетчер вполне может считать самолёт точкой (именно так он и отображается на экране радара). Однако тот же самолёт, выруливающий на взлётную полосу, точкой считать нельзя – надо учитывать, например, размах крыльев, чтобы не повредить другие самолёты или мачты освещения на месте стоянки.
В физике линию, которую «описывает» материальная точка при движении в пространстве, называют траекторией. Траектория может быть видимой или невидимой. Например, линия движения самолёта в небе часто видна (см. рисунок), а линия движения автомобиля по шоссе не видна. Заметим, что с точки зрения геометрии линия не имеет ширины. Поэтому, говоря о траектории движения любого тела, мы всегда считаем его материальной точкой.
По виду траекторий все движения тел делят на прямолинейные и криволинейные. Например, траектория падения мяча, выпущенного из рук, – отрезок прямой, полёта пушечного снаряда – часть параболы, а кончика маятника настенных часов – дуга, то есть часть окружности.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsbox
Вопросы на зачёт за первое полугодие
Вопросы на зачёт по физике за первое полугодие 9 класс.
Что изучает раздел физики Кинематика. Что называется механическим движением? Характеристики механического движения?
Что называется телом отсчёта? Системой отсчёта? Какую систему отсчёта выбирают, когда тело движется по прямой, по плоскости, и в пространстве. Материальная точка?
Написать уравнения движения для тел, графики движения которых показаны на рисунке.
Какие виды движения вы знаете?
Написать формулы скорости для всех видов движения?
Написать формулы времени для всех видов движения?
Написать формулы ускорения для всех видов движения?
Написать формулы перемещения для всех видов движения?
Написать формулы координаты для всех видов движения?
Что называется относительностью движения. Формулы относительной скорости?
Формулы относительной скорости?
Что изучает раздел физики «Динамика» Что называется силой? От чего зависит результат действия силы?
Три закона Ньютона их определения и формулы.
Что называется инерцией, инерциальными системами отсчёта, инертность? Примеры?
Определение силы тяжести и силы всемирного тяготения? Формулы и рисунки к ним?
Определение силы упругости. Формула закона Гука? Рисунок. Виды деформации?
Определение веса тела. Рисунок веса тела. Перегрузки и невесомость. Формулы веса в этих случаях?
Сила трения? Виды сил трения? Формула силы трения. Причины силы трения. От чего зависит величина силы трения?
Равнодействующая сила. Как найти равнодействующую силу в различных случаях?
Что называется ускорением свободного падения, как определить, написать формулы? От чего зависит значение ускорения свободного падения?
Как представляют криволинейное движение. Нарисовать направление скорости и ускорения при криволинейном движении.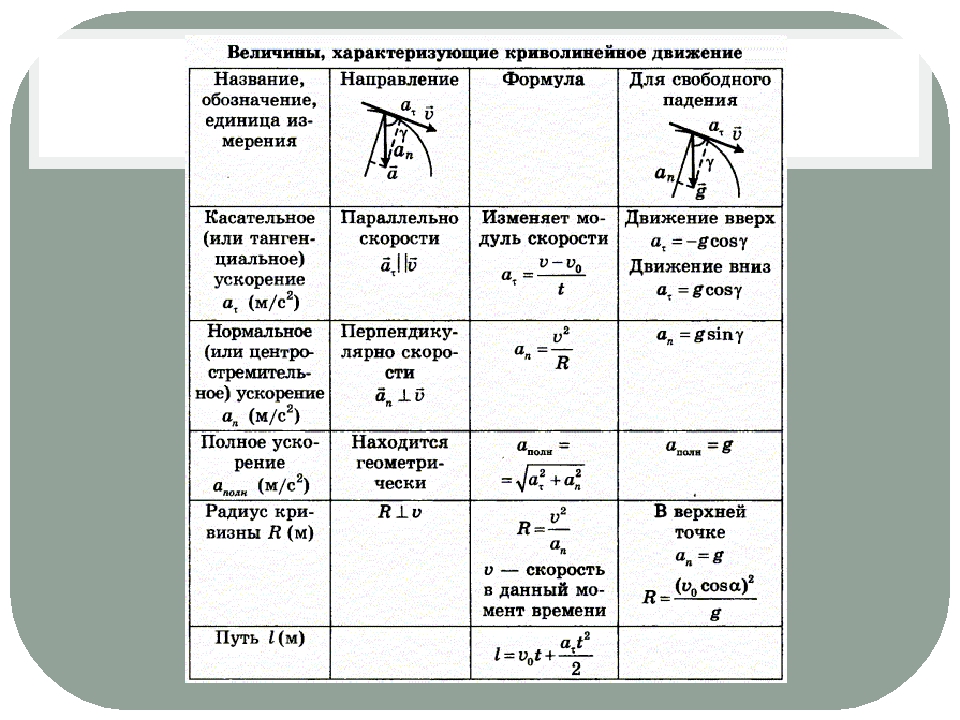 Формулы характеристик при криволинейном движении?
Формулы характеристик при криволинейном движении?
Импульс силы и импульс тела? Формулы и определения?
Закон сохранения импульса при упругом и неупругом ударе?
Энергия. Виды энергии? Дать определения и написать формулы?
Закон сохранения энергии?
Работа в механике. Когда работа положительна, отрицательна и равна нулю?
Мощность? Формулы мощности? Единицы мощности?
Уметь находить путь графическим способом.
Уметь решать все задачи из упражнений.
Брейн-ринг по физике — физика, мероприятия
Физическая викторина
по кинематике и динамике в 8-классах
Цели и задачи: В неформальной обстановке провести соревнование и повторить основные вопросы кинематики и динамики.
Развить навыки логического мышления.
Развить навыки командной работы.
Помочь выработать сплоченность коллектива.
Правила игры: В игре принимают участие команды по 6 человек из каждого класса.
Каждая команда имеет одинаковое время для обсуждения, по истечении которого, капитан сдает письменный ответ ведущему, а один из игроков «озвучивает его».
I ТУР (РАЗМИНКА)
БЛИЦ (ВОПРОС – ОТВЕТ)
ПЕРЕВЕДИТЕ В СИСТЕМУ СИ 54 КМ/Ч?
В КАКИХ ЕДИНИЦАХ ИЗМЕРЯЕТСЯ УСКОРЕНИЕ?
КАКОЙ БУКВОЙ ОБОЗНАЧАЕТСЯ ПРОЙДЕННЫЙ ПУТЬ?
ЯВЛЕНИЕ СОХРАНЕНИЯ СКОРОСТИ БЕЗ ДЕЙСТВИЯ СИЛ, НАЗЫВАЕТСЯ …
ЧЕМУ РАВНО УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ g?
КАКОЙ БУКВОЙ ОБОЗНАЧАЮТ СИЛУ РЕАКЦИИ ОПОРЫ?
КАК НАЗЫВАЕТСЯ УСКОРЕНИЕ ТЕЛА ДВИЖУЩЕГОСЯ ПО ОКРУЖНОСТИ?
ПРО КАКОГО УЧЕНОГО СКАЗАНО «ПУСТЬ СМЕРТНЫЕ РАДУЮТСЯ, ЧТО СУЩЕСТВОВАЛО ТАКОЕ УКРАШЕНИЕ РОДА ЧЕЛОВЕЧЕСКОГО»?
МОЖЕТ ЛИ ТЕЛО ОДНОВРЕМЕННО ПОКОИТЬСЯ И ДВИГАТЬСЯ?
ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОЙДЕННОГО ПУТИ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
ФОРМУЛА ОПРЕДЕЛЕНИЯ ПЕРИОДА
ФОРМУЛА ВТОРОГО ЗАКОНА НЬЮТОНА
В КАКИХ ЕДИНИЦАХ ИЗМЕРЯЮТ СИЛУ
ЧЕМУ РАВНО ЧИСЛО ПИ
КАК НАПРАВЛЕНА СКОРОСТЬ ТЕЛА ПРИ ДВИЖЕНИИ ПО ОКРУЖНОСТИ?
КАЖДЫЙ ВЕРНЫЙ ОТВЕТ 1балл.
II – ТУР (Ох, уж эти формулы)
Составить как можно больше формул из имеющихся латинских букв, обозначающих физические величины (карточки)
s, υ, t, a, T, ν, ρ, F, r, m, V
Каждая формула 1 балл
III тур (физика в загадках)
1 Синие крылья
Весь мир накрыли.
2 Своих глаз нет,
А видит далеко.
3. Я всегда со светом дружен,
Если солнышко в окне,
Я от зеркала, от лужи
Пробегаю по стене.
4. Летит птица орел,
Несет в зубах огонь,
Огненные стрелы пускает,
Никто ее не поймает.
5. По тропинкам я бегу,
Без тропинок не могу,
Где меня, ребята, нет,
Не зажжется в доме свет.
6 Книзу летит капельками,
А кверху – невидимкою.
7 Свет пропускает,
А тепло не выпускает.
8. Искры небо прожигают,
А до нас не долетают.
9. Под окошками гармонь
Горяча как огонь.
10. И в тайге, и в океане
Он отыщет путь любой.
Умещается в кармане
И ведет нас за собой.
IV – ТУР (ВЕСЕЛЫЕ ЗАДАЧКИ ГРИГОРИЯ ОСТЕРА)
Каждая задача по 2 балла.
Ученый с мировым именем Иннокентий сконструировал
средство передвижения, которое, рванув с места и отмахав
за минуту 121 километр, вдруг замирает, пыхтит, топчется
на одном месте и только через два часа снова бросается в
путь. За какое время ученый с мировым именем, катаясь на
своем средстве, проедет 605 километров?
Ответ: восемь часов и пять минут понадобятся ученому,
чтобы, трясясь и подпрыгивая, на своем средстве преодолеть
605 километров пути.
Лютый враг нежно прижался щекой к прикладу и нажал
курок. Пуля массой 10 г выскочила из винтовки и понеслась
искать невинную жертву со скоростью 800 м/с. А винтовка
А винтовка
в результате отдачи со скоростью 2 м/с послала врага в
нокаут. Вычисли массу, сбившую с ног врага.
Ответ: врага нокаутировало его собственное оружие массой
в 4 кг. Кто к нам с чем придет — от того и упадет.
Какую силу должен прилагать дежурный восьмиклассник Егор Букин,
чтобы одной рукой держать за шивороты в воздухе трех
первоклассников, общая масса которых 53 кг?
Ответ: 530 н. Для трех первоклассников этого вполне достаточно.
Дед, взявшись за репку, развивает силу тяги до 600 н,
бабка до 100 н, внучка до 50 н, жучка до 30 н, кошка до 10 н
и мышка до 2 н.
Справилась бы с репкой эта компания без мышки, если силы,
удерживающие репку в земле, равны 791 н? Почему?
Ответ: модуль равнодействующей силы, равный сумме модулей
сил, с которыми дедка тянет за репку, бабка за дедку,
внучка за бабку, жучка за внучку, кошка за жучку, а
мышка за кошку, будет равен 792 н. Вклад мускулистой мышки
Вклад мускулистой мышки
в этот могучий порыв равен 2н. Без мышкиных ньютонов
дело не пойдет.
V – ТУР (СМЕКАЙ)
НА РАЗМЫШЛЕНИЕ ПО 1 МИН
ПИСЬМЕННЫЕ КРАТКИЕ ОТВЕТЫ (БАЛЛЫ ПО СКОРОСТИ ОТВЕТА(3-2-1))
1. У ТРЕХ ТРАКТОРИСТОВ ЕСТЬ РОДНОЙ БРАТ ИВАН.
А У ИВАНА НЕТ БРАТЬЕВ. КАК ЭТО МОЖЕТ БЫТЬ?
2. ИМЕЕТСЯ 16м ТКАНИ. ПОРТНОЙ КАЖДЫЙ ДЕНЬ ОТРЕЗАЕТ ПО 2 МЕТРА.
ЧЕРЕЗ СКОЛЬКО ДНЕЙ ОН ОТРЕЖЕТ ПОСЛЕДНИЙ КУСОК?
3. ДЕРЕВО ДАЕШЬ – СЪЕДАЕТ, ОТ ВОДЫ – УМИРАЕТ.
4. ОДИН КИРПИЧ ВЕСИТ ОДИН КИЛОГРАММ И ЕЩЕ ПОЛКИРПИЧА. СКОЛЬКО ВЕСИТ ОДИН КИРПИЧ?
5. КАК НАЗЫВАЕТСЯ МАЛЕНЬКОЕ КОЛИЧЕСТВО ЖИДКОСТИ?
6. НА КАКОЕ ЧИСЛО НУЖНО РАЗДЕЛИТЬ 2, ЧТОБЫ ПОЛУЧИТЬ 4?
7. КАК НАЗЫВАЕТСЯ САМОЕ РАСПРОСТРАНЕННОЕ ВЕЩЕСТВО НА ЗЕМЛЕ?
8. МОЖЕТ ЛИ СТРАУС НАЗВАТЬ СЕБЯ ПТИЦЕЙ?
9. НА РУКАХ 10 ПАЛЬЦЕВ. СКОЛЬКО ПАЛЬЦЕВ НА 10 РУКАХ?
10. КАК ЗВАЛИ ЛОМОНОСОВА?
V – ТУР (ЭКСПЕРИМЕНТАЛЬНЫЙ)
ОТВЕТЫ ПРОДЕМОНСТРИРОВАТЬ
1. НА СТАКАН ПОЛОЖИТЬ ОТКРЫТКУ, А НА НЕЕ МОНЕТУ. УРОНИТЬ В СТАКАН МОНЕТУ, ЛЕЖАШУЮ НА ОТКРЫТКЕ, НЕ ХВАТАЯ ОТКРЫТКИ РУКОЙ.
НА СТАКАН ПОЛОЖИТЬ ОТКРЫТКУ, А НА НЕЕ МОНЕТУ. УРОНИТЬ В СТАКАН МОНЕТУ, ЛЕЖАШУЮ НА ОТКРЫТКЕ, НЕ ХВАТАЯ ОТКРЫТКИ РУКОЙ.
2.НУЖНО НАПОЛНИТЬ СТАКАН ВОДОЙ РОВНО НА ПОЛОВИНУ, НЕ ИСПОЛЬЗУЯ ЛИНЕЙКУ ИЛИ ЗАМЕНЯЮЩИЕ ЕЕ ПРИБОРЫ.
ДОКАЗАТЬ ЧТО НАБРАЛОСЬ ИМЕННО ПОЛ — СТАКАНА.
3.НУЖНО РАСПОЛОЖИТЬ СТАКАН НАД ДВУМЯ СТАКАНАМИ РАСПОЛОЖЕННЫМИ НА РАССТОЯНИИ 10 СМ ДРУГ ОТ ДРУГА ИСПОЛЬЗУЯ ЛИШЬ ЛИСТ БУМАГИ.
Протокол Жюри
Команда | Команда | Команда | ||||||
I тур | ||||||||
II тур | ||||||||
III тур | ||||||||
IV тур | ||||||||
V тур | ||||||||
VI тур | ||||||||
Итог | ||||||||
Председатель жюри:
Члены жюри:
Ответы:
I тур:
15 м/с
м/с2
s
Инерция
9.
 8 м/с2 (или 10)
8 м/с2 (или 10)N
центростремительное
И. Ньютон
может относительно разных тел отсчета.
s= υ0t+at2/2 или s=at2/2
T=n/t, T=2пr/ υ, T=1/ ν
F=ma
Н
3.14
по касательной к окружности
III тур
1. 360 м. (12 м/с)
2. на 2 м/с (1м)
3. 3,14 с (4 м/с2)
4. 16 Н
5. 15 м/с
6. 98 м/с или 100 м/с (490 м или 100 м)
IV тур
1 трактористы девушки
2. через 7 дней
3. огонь
4. 2 кг.
5. капля
6. на 0,5
7. Вода
8. страусы не говорят
9. 50
10. Михайло
V тур
1. щелчком по открытке выбить ее из под монеты.
2. поверхность воды должна соединить дно и верхнее отверстие.
3. сложить лист гармошкой.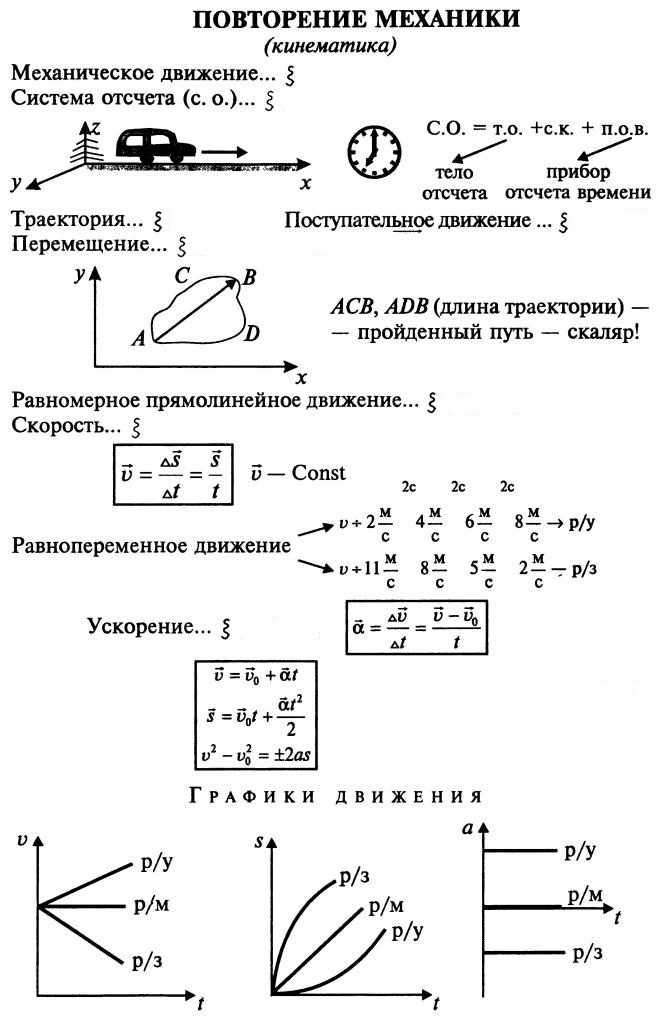
I ТУР | _________КЛАСС II ТУР ФОРМУЛЫ (___ КЛАСС) s, υ, t, a, T, ν, ρ, F, r, m, V | |
№ | ОТВЕТ | |
IV ТУР | _________КЛАСС | |
№ | ОТВЕТ | |
8
| Класс | Месяц | Тема | |
| 7 | Сентябрь | Измерение физических величин. Единицы физических величин. Цена деления. Погрешность измерения. Единицы физических величин. Цена деления. Погрешность измерения. | |
| 7 | Октябрь | Механическое движение. Путь. Перемещение. Равномерное движение. Скорость. Средняя скорость. Работа с графиками. Сложение скоростей для тел, движущихся параллельно. | |
| 7 | Ноябрь | Инерция. Взаимодействие тел. Масса. Плотность | |
| 7 | Январь | Силы в природе (тяжести, упругости, трения). Сложение сил. Равнодействующая. | |
| 7 | Май | Механическая работа, мощность, энергия. Простые механизмы, блок, рычаг. Момент силы. Правило моментов (для сил направленных вдоль параллельных прямых). Золотое правило механики. КПД. | |
| 7 | Май | Давление. Основы гидростатики. Закон Паскаля. Атмосферное давление. Гидравлический пресс. Сообщающиеся сосуды. Закон Архимеда. Плавание тел. Воздухоплавание. Закон Архимеда. Плавание тел. Воздухоплавание. | |
| 8 | Сентябрь | Тепловое движение. Температура. Внутренняя энергия. Теплопроводность. Конвекция. Излучение. | Только понятия без формул |
| 8 | Октябрь | Количество теплоты. Удельная теплоемкость вещества. Удельная теплота сгорания. Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел. Удельная теплота плавления. Испарение. Кипение. Удельная теплота парообразования. | |
| 8 | Ноябрь | Общее уравнение теплового баланса. КПД нагревателей. | |
| 8 | Декабрь | Влажность воздуха. | Только понятия без формул |
| 8 | Декабрь | Работа газа и пара при расширении. Двигатель внутреннего сгорания. Паровая турбина. КПД теплового двигателя. | Только понятия без формул |
| 8 | Январь | Работа с графиками: построение, расчёт площади под графиком, проведение касательных для учёта скорости изменения величины. | |
| 8 | Февраль | Электризация. Два рода зарядов. Взаимодействие заряженных тел. Проводники и диэлектрики. Электрическое поле. Делимость электрического заряда. Электрон. Строение атомов. | Только понятия без формул |
| 8 | Февраль | Электрический ток. Источники электрического тока. Электрическая цепь и ее составные части. Действие электрического тока. Сила тока. Электрическое напряжение. Электрическое сопротивление проводников. Закон Ома для участка цепи. Удельное сопротивление. | |
| 8 | Март | Последовательное и параллельное соединение проводников. Расчет простых цепей постоянного тока. Работа и мощность электрического тока. Закон Джоуля – Ленца. | |
| 8 | Апрель | Магнитное поле. Магнитное поле прямого тока. Магнитные линии магнитного поля. Магнитное поле катушки с током. Электромагниты. Постоянные магниты. Магнитное поле постоянных магнитов. Магнитное поле Земли. Действие магнитного поля на проводник с током. | Только понятия без формул |
| 8 | Май | Источники света. Распространение света. Тень и полутень. Камера – обскура. Отражение света. Законы отражения света. Плоское зеркало. Преломление света. Линзы. Построения в линзах. Оптическая сила линзы. Изображение, даваемое линзой. Фотоаппарат. Глаз и зрение. Близорукость и дальнозоркость. Очки. | Только понятия без формул |
| 9 | Октябрь | Кинематика. Материальная точка. Системы отсчёта. Равномерное прямолинейное движение. Мгновенная скорость. Средняя скорость. Равнопеременное движение. Ускорение. Свободное падение. Графики движения (пути, перемещения, координат от времени; скорости, ускорения и их проекций от времени и координат). Движение по окружности. Угловое перемещение и угловая скорость. Центростремительное (нормальное) и тангенциальное (касательное) ускорение. | |
| 9 | Ноябрь | Относительность движения. Закон сложения скоростей. Кинематические связи. Плоское движение твердого тела. | |
| 9 | Декабрь | Динамика. Силы. Векторное сложение сил. Масса. Центр масс. Законы Ньютона. | |
| 9 | Январь | Динамика систем с кинематическими связями. Блоки, скольжение наклонных плоскостей. | |
| 9 | Январь | Закон всемирного тяготения. Гравитация. Искусственные спутники. Первая космическая скорость. Перегрузки и невесомость. | |
| 9 | Февраль | Силы трения. Силы сопротивления при движении в жидкости и газе. Силы упругости. Закон Гука. | |
| 9 | Март | Импульс. Закон сохранения импульса. Движение центра масс. Реактивное движение. | |
| 9 | Апрель | Работа. Мощность. Энергия (гравитационная, деформированной пружины). Закон сохранения энергии. Упругие и неупругие взаимодействия. Диссипация энергии. Выделившееся количество теплоты. | |
| 9 | Апрель | Статика | |
| 9 | Май | Механические колебания. Маятник. Гармонические колебания. Волны. | |
| 9 | Май | Основы атомной и ядерной физики. | |
| 10 | Сентябрь | Газовые законы. Изопроцессы. Законы Дальтона и Авогадро. | |
| 10 | Октябрь | Молекулярно-кинетическая теория. Температура. | |
| 10 | Октябрь | Потенциальная энергия взаимодействия молекул. | Только понятия без формул |
| 10 | Ноябрь | Термодинамика. Внутренняя энергия газов. Количество теплоты. 1-й закон термодинамики. Теплоемкость. Адиабатные процессы. Цикл Карно. | |
| 10 | Ноябрь | Насыщенные пары, влажность. | |
| 10 | Декабрь | Поверхностное натяжение. Капилляры. | |
| 10 | Январь | Электростатика. Закон Кулона. Электрическое поле. Напряженность. Потенциал. Проводники и диэлектрики в электростатических полях. Конденсаторы. | |
| 10 | Февраль | ЭДС. Цепи постоянного тока. Законы Кирхгофа. Нелинейные элементы. | |
| 10 | Март | Работа и мощность электрического тока. | |
| 10 | Апрель | Электрический ток в средах. | |
| 10 | Май | Магнитное поле постоянного тока. Силы Лоренца и Ампера. |
Задание 1 ЕГЭ по физике 2019: разбор теории и практики
Задание 1
Это задание проверяет знания учащихся в области кинематики, к основным понятиям которой относятся понятия ускорение, скорости и перемещения. Так как это векторные величины, то в подавляющем большинстве учебников приведены формулы в векторном виде и подавляющее большинство моих коллег, с которыми мне доводилось общаться, также заставляют своих учеников учить формулы в векторном виде, что совершенно избыточно, на мой взгляд, и чаще мешает решать задания ЕГЭ, чем помогает. Конечно, важно знать, что скорость, ускорение и перемещение — это векторные величины, как и импульс, и сила. Но гораздо важнее, чтобы они понимали, что вычисляем мы, в конечном итоге, не вектора, а их проекции и модули. И вот с этим-то учащиеся часто путаются. К примеру, необходимо по графику скорости определить модуль или проекцию ускорения. Сколько формул для этого нужно учить — три, две или одну? Конечно же одну, для проекции ускорения. А модуль ускорения а = |ах|.
С перемещением ситуация ещё интереснее. Часто мне приходится сталкиваться с ситуацией, когда ученики из других школ, с которыми я занимаюсь подготовкой к экзамену по физике в центре подготовки к ЕГЭ в городе Ногинске, не понимают почему проекцию перемещения нужно находить по той или иной формуле. Они просто не могут понять откуда взялись те или иные формулы перемещения. Но зато они легко могут написать эти формулы в векторном виде, от которого, как правило, мало толку. Да, есть проблема — когда изучается кинематика, в 10 классе, дети ещё не знакомы с элементами математического анализа и не знают ни понятия производной, ни понятия интеграла. Но это и не обязательно. Достаточно показать на простом примере равномерного движения, что проекция перемещения может быть определена как площадь фигуры под графиком скорости и затем применить эту идею к равноускоренному движению. Это, в принципе, показано и в учебнике Пёрышкина для 9 класс, в разделе Кинематика, и в учебнике для 10 класса углублённого уровня Мякишева. Но тем не менее, почему-то многие ученики затрудняются с вычислением пройденного пути по графику скорости, который есть ни что иное как модуль перемещения при прямолинейном движении. Особенно, если график представляет собой ломаную линию.
- Найти ax в промежутке времени от 0 до 2 с.
- Найти модуль ускорения в промежутке от 6 до 7 с.
- Найти пройденный путь за первые 5 с движения
Вот несколько примеров.
1)
2) На промежутке от 6 до 7 с ускорение такое же как и на промежутке от 6 до 8 с, а он удобнее, поэтому
a = │ax│ = 7,5 м/с2
3) На графике площадь заштрихованной области и есть Sx, то есть:
ЕГЭ-2020. Физика. Решение задач
В книге содержатся материалы для успешной сдачи ЕГЭ: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену.
Купить
Девятый класс движения CBSE Science
Уравнение движения:
Связь между скоростью, расстоянием, временем и ускорением называется уравнениями движения. Есть три уравнения движения:
Первое уравнение движения:
Конечная скорость (v) движущегося объекта с равномерным ускорением (a) через время, t.
Пусть, начальная скорость = u.
Конечная скорость = v.
Время = t
Ускорение =
Мы знаем, что ускорение (a) `= (text {Изменение скорости}) / (text {Время занято})`
`=> a = (text {Конечная скорость-Начальная скорость}) / text {Время занято}`
`=> a = (v-u) / t`
`=> at = v-u`
`=> at-v = -u`
`=> — v = -u-at`
`=> v = u + at` — (i)
Это уравнение известно как первое уравнение движения.
Второе уравнение движения:
Расстояние, пройденное движущимся телом за время (t).
Пусть, Начальная скорость объекта = u
Конечная скорость объекта = v
Разгон =
Время = t
Пройденное расстояние за заданное время =
с.
Мы знаем,
Средняя скорость `= (текст {Начальная скорость + Конечная скорость}) / 2`
∴ Средняя скорость `= (u + v) / 2` —- (ii)
Мы знаем, что пройденное расстояние (я) за данный момент времени = Средняя скорость x Время
Или, с = Средняя скорость x Время —————— (iii)
После подстановки значения средней скорости из уравнения (ii) получаем
`=> s = (u + v) / 2xxt`
После подстановки значения «v» из первого уравнения движения мы получаем
`=> s = (u + (u + at)) / 2xxt`
`=> s = (u + u + at) / 2 xxt`
`=> s = (2u + at) / 2 xxt`
`=> s = (2ut + at ^ 2) / 2`
`=> s = (2ut) / 2 + (at ^ 2) / 2`
`=> s = ut + (at ^ 2) / 2`
`=> s = ut + 1/2 at ^ 2` —- (iv)
Приведенное выше уравнение известно как Второе уравнение движения.2 + 2 как` — (vi)
Это называется третьим уравнением движения.
Подход к динамике обучения, основанный на запросах
Подход к динамике обучения, основанный на запросах
СКОРОСТЬ
ОГРАНИЧЕНИЯ: подход к динамике обучения, основанный на запросах
Раздел
I — Общая информация
Раздел
II — Поддерживаемые учебные стандарты
Раздел
III — Обоснование учебного дизайна
Раздел
IV — Обзор ежедневных уроков
Раздел
V — Подробные планы уроков
Раздел
VI — Ресурсы поддержки
Секция
I — Общая информация
Уровень оценки: 11-12
Дисциплина: Физика
Учебная программа: кинематика
Обзор устройства
Студенческие группы выбирают конкретный участок проезжей части (1-3 квартала)
в районе и оцените практичность и целесообразность
опубликовано ограничение скорости на основе разумных физических, числовых и статистических аргументов.Эти аргументы развиваются с помощью различных высокотехнологичных, классных
лабораторные работы (эксперименты и симуляции) и онлайн-исследования.
Каждая группа представит результаты своего исследования в официальной презентации.
Ориентировочный вопрос для запроса:
А
Разумны ли местные ограничения скорости?
Срок поставки: 15 дней
ВЕРХ
Секция
II — Поддерживаемые научные стандарты
Иллинойс (ISBE) Стандарты:
| Стандартный | Описание |
| 13.B.5d | Анализировать затраты, выгоды и последствия научно-технической политики на местном , государственном, национальном и глобальном уровнях. |
| 11.A.5a | Сформулировать гипотезы, относящиеся к предшествующим исследованиям и знаниям. |
| 11.A.5b | Дизайн процедуры проверки выбранной гипотезы. |
| 11.A.5c | Поведение систематические контролируемые эксперименты для проверки выбранной гипотезы. |
| 11.A.5d | Применить статистические методы, позволяющие делать прогнозы и проверять точность результатов. |
| 11.A.5e | Отчет, демонстрировать и защищать результаты расследований для аудитории, которая может включают профессионалов и технических экспертов. |
| 12.D.4a | Объяснить и предсказывать движения в инерциальной и ускоренной системе отсчета. |
Поддерживаемая национальная наука (NSTA)
Стандарты
Преподавательский стандарт A: Учителя
науки планируют исследовательскую программу для своих студентов.:
Преподавательский стандарт B: Учителя естественных наук
направлять и способствовать обучению .
Преподавательский стандарт C: Учителя естественных наук
участвовать в постоянной оценке своего преподавания и обучения студентов.
Педагогический стандарт D: Учителя естественных наук
проектировать и управлять учебной средой, которая предоставляет студентам
время, место и ресурсы, необходимые для изучения науки e.
Педагогический стандарт E: Учителя естественных наук
развивать сообщества учащихся, отражающие интеллектуальную строгость
научное исследование и отношение социальных ценностей, способствующих науке
обучение.
Стандарт оценки A: A оценок
должны соответствовать решениям, которые они призваны информировать.
Стандарт оценки B: Достижение
и возможность изучать науку должна быть оценена.
Стандарт содержания A: В результате деятельности в 9-12 классах,
все студенты должны развить:
- способностей, необходимых для проведения научных исследований.
- понятий о научном исследовании.
Содержание Стандарт B: В результате
занятий в 9–12 классах, все учащиеся должны развивать и понимать
из . движения и силы.
Содержание Стандарт F: Как
В результате занятий в 9-12 классах все ученики должны развиваться и
понимание:
- личное и общественное здоровье.
- опасностей природного и техногенного характера.
TOP
Секция
III — Обоснование разработки инструкции
Зачем учить кинематике?
В то время как физика изучает взаимодействие между
материи и энергии, большинство этих взаимодействий происходит в движущемся или
ускорение системы отсчета.Кинематика — это система описания
то, как движутся вещи, имеет фундаментальное значение для наблюдения за любым сложным взаимодействием.
Кроме того, кинематика вводит идею использования скоростей для измерения некоторых
количество, которое меняется со временем.
Зачем нужен подход структурированного расследования?
Традиционные методы обучения кинематике интенсивны по математике и имеют тенденцию
быть сухим, состоящим из математических «сюжетных» задач, повторяющихся вычислений,
и механические операции (т.е. построение графиков вручную). Текущее состояние и национальная
стандарты, наряду со здравым смыслом, предполагают, что обучение более эффективно
когда это имеет смысл. Процесс исследования — это способ способствовать значимому
опыт обучения. В этом случае учащиеся сами выбирают проблему.
выбор (в рамках параметров исследования по ограничению скорости) и использование учебного класса
опыт и открытия, которые помогут им в решении проблем.
Кроме того, этот процесс запроса дает продукт (проблему, решение и
презентация), демонстрирующая концептуальное понимание и прикладные научные
рассуждения.Этот способ оценивания охватывает весь процесс обучения.
и, таким образом, является более «достоверным», чем комплексный экзамен по окончании курса.
ВЕРХ
Секция
IV — Обзор ежедневных уроков
День 1: Представьте проект,
Обсудите проблемы и подвопросы.
День 2: Графики движения
лаборатория
День 3: График движения
лаборатория
День 4: Обсудить результаты
лаборатории движения, группы разрабатывают исследовательские вопросы, планируют и распространяют
задачи
День 5: Интернет-исследования
День
День 6: Моделирование движения
(Интерактивная физика)
День 7: Формулы и
Вычисление I: Автомобильная видеолаборатория
День 8: Формулы и
Вычисления II: время реакции и время зависания.
День 9: Время реакции
& тормозной путь.
День 10: Завершить остановку
дистанционное упражнение. * Дополнительно: компьютерное моделирование трафика.
День 11: Работа над презентациями
День 12: Работа над презентациями
День 13: Групповые презентации
(Может понадобиться еще один день)
ВЕРХ
Секция
V — Подробные планы уроков
День первый:
Ограничения скорости
Задачи: Студент
- Вспомните термины, связанные с движением: расстояние, перемещение, скорость,
скорость, ускорение, сила, трение, миль / ч, м / с, быстро, медленно, скорости и т. д. - Обсудить причины установки ограничения скорости
- Определить дорожные / автомобильные условия, влияющие на безопасную скорость движения
- Определить физиологические условия, влияющие на безопасную скорость движения
Материалы:
Площадки для работы в малых группах
Классное обучение:
1.Обсудите автомобильные путешествия.
- Что делает одни автомобили лучше других?
(используйте «быстро», чтобы перейти к следующему вопросу) - Почему одни машины быстрее других? —
Что быстро? (основывается на следующем вопросе) - Есть ли словарь, который мы могли бы использовать, чтобы описать
как движется машина? (акцент на физических терминах)
2. Обсуждение безопасности автомобилей,
С партнером студенты должны идентифицировать
одна функция / проблема безопасности, связанная с поездкой на автомобиле, и почему это может
были разработаны.Затем он передается всему классу.
3. Ограничения скорости
На этом этапе дайте учащимся скорость
раздаточный материал для обсуждения и разделите класс на группы по 4 человека, чтобы обсудить
следующие:
- Что может быть физическим (дорога / машина)
причины ограничения скорости? - Что может быть физиологическим (связанным с людьми)
причины ограничения скорости? - Зачем городу устанавливать или изменять скорость
ограничение на конкретной дороге? - Из вышеперечисленных вопросов каждой группе следует
выберите три наиболее важных фактора, которые следует учитывать при
определение ограничения скорости.Каждая группа сообщит о своих выводах.
Оценка:
Листы обсуждения можно просмотреть
дать инструктору обратную связь об имеющихся знаниях студентов.
Преподаватель также должен уметь использовать эти ответы для определения групп.
которым может потребоваться дополнительное руководство при разработке хороших вопросов, чтобы направлять их
проект запроса.
День 2 и
3: Лаборатория построения графиков движения
Задачи: Студент
- Различают термины: смещение, скорость / скорость и ускорение
- Сравните и сопоставьте графики, изображающие одно и то же движение разными способами
(d v.т, в в. т, а в. т) - Объясните движение объекта на основе его графика
Материалы:
8 — 12 компьютерных станций (компьютер, лабораторный интерфейс, ультразвуковое движение
детектор)
Сетевой принтер
Раздаточный материал лаборатории: Описание движения
Обучение:
1. Продемонстрируйте правильную работу
компьютерное оборудование.
2. Распределите группы по 4 человека.Дайте
каждому студенту раздаточный материал и роль: диктофон, оператор компьютера, руководитель
(читает инструкцию) и ходунок.
- Разрешить учащимся работать над заданием
пакет. После двух дней работы обсудите формы графиков и вопросы пакета.
с классом.
Оценка:
Завершенные пакеты должны предоставлять
основа для оценки студентами предварительного понимания движения
построение графиков.
День 4: Итоги
Лаборатория графического моделирования движения и формализация запроса
Задачи: Студент
- Оцените личное понимание работы предыдущих дней.
- Работайте в группе, чтобы составить справочные вопросы об ограничениях скорости.
- Составьте план группового исследования с распределенными задачами.
Материалы:
Раздаточный материал лаборатории: Описание
Движение
Запрос описания проекта / рубрики
Одиночный компьютер с ультразвуковым движением
детектор и проекционный блок.
Обучение:
1.Обсудите результаты каждого построения графиков
Мероприятия. Убедитесь, что учащиеся не имеют конкретных свойств графиков, таких как
кривые вверх, кривые вниз, прямые и горизонтальные линии. Иметь индивидуальный
учащиеся демонстрируют в классе ускоренное движение и сопоставление графиков.
2. Вспомните действия с первого
день — возврат листов обсуждения с того дня, если они были собраны.
Представьте задачу, подключив обсуждение ограничения скорости к графику
лаборатории (задайте вопрос, как график движения может помочь определить
безопасная скорость движения?).Лаборатория построения графиков — один из нескольких инструментов, которые
применяться для понимания ограничений скорости
3. Разбейте ученика на группы (аналогично
в первый день) от четырех до пяти. Этим группам следует дать конкретную
задачи на остаток дня:
- выбрать дорогу для учебы
- предложить гипотезу об ограничении скорости
на дороге (т.е. выше, ниже, оставаться прежним) - определить ключевые физические, экологические, биологические,
и гуманистические подвопросы - определить существующие источники информации
который мог бы ответить на некоторые из этих вопросов - определить хотя бы один способ экспериментально
генерировать информацию, которая могла бы ответить на эти вопросы - назначить группе задачи по сбору информации
участники
Оценка:
Обучение во время графической деятельности
можно оценить из пакета, в то время как первоначальный запрос требует неофициальных
методы оценки, так как учитель должен переходить от группового опроса к групповому
этапы планирования.Инструктор должен проявлять осторожность, направляя студентов
в разработке вопросов, на которые можно ответить, не диктуя вопросы для ответа.
День 5: Он-лайн
Исследования
Задачи: Студент
- Оцените и измените подвопросы, разработанные накануне.
- Используйте существующую электронную информацию, чтобы составить основу для запроса.
- Найдите контактную информацию и ресурсы, которые можно использовать в качестве запроса
развивается.
Материалы:
Компьютерные станции с доступом в Интернет
(по одному на группу)
Запрос описания проекта / рубрики
Избранное
сайтов безопасности дорожного движения и ограничения скорости
Раздаточный материал: Web
Анализ сайта
Обучение:
1. Используя горячий список в качестве отправной точки,
студенты должны просматривать предоставленные сайты. Лист анализа должен быть
заполняется на каждом сайте.
2.После просмотра некоторых сайтов.
Следует поощрять поиск в Интернете.
Оценка:
Опять же, используются неформальные методы оценки, поскольку учитель должен двигаться
от группы к группе, исследующей исследование. Аналитические листы могут быть собраны
чтобы узнать, как студенты оценивают выбранные для них сайты.
День 6: Моделирование
Движение
Задачи: Студент
- Построение графиков постоянного и ускоренного движения на основе моделирования
данные. - Обобщить поведение ускоряющихся и неускоряющихся объектов
при представлении в виде графика.
Комментарии: Процесс
наблюдение за числами для постоянного и ускоренного движения — это умственная подготовка
для формул, которые будут изучены в следующие дни.
Материалы:
Компьютерные станции с интерактивным интерфейсом
Physics и Графический анализ и скорость файлов
Racer 1, Speed Racer 2, воскресенье
Привод 3
Сетевой принтер
Раздаточный материал : Движение
Графический запрос
Обучение:
1.Раздайте учащимся раздаточный материал и разрешите
им работать через действия.
Оценка:
Листы ответов можно собрать и просмотреть, чтобы проверить понимание учащимся
ускоренного и постоянного движения. При необходимости инструктор может обсудить
результаты в классе.
День 7: Кинематика
формулы I: Car Video Lab
Задачи: Студент
- Используйте основные кинематические уравнения для изучения реального замедления и
движения с постоянной скоростью. - Узнайте, как методы сбора данных ограничивают точность результатов.
- Разработайте экспериментальные стратегии для личного расследования ограничений скорости.
Материалы:
Компьютерные станции с доступом в Интернет
& QuickTime 4.0
Сетевой или локальный доступ к файлам
blackcar.mov,
cars.mov,
Brake.mov
Раздаточный материал: Реальный мир
движение
Обучение:
1.Начните с обсуждения того, как
может измерить скорость (скорость), чтобы представить идею скорости = расстояние / время.
2. Различайте ситуации, в которых
представляют средней скорости , как движение за длительную поездку с мгновенными
скорость с помощью спидометра.
3. Напомним, что ускорение меняется.
скорость. Обсудите, как измерить ускорение. Настоящая формула:
ускорение = (конечная скорость
— начальная скорость) / время.
4. Раздайте раздаточный материал и раздайте учащимся
возможность использовать эти формулы, изучая видео с движущимися автомобилями.
Оценка:
Можно собрать листы анализа движения, чтобы узнать, насколько хорошо учащиеся используют
формулы и применять их в контексте видео и движущихся автомобилей.
День 8: Формулы
II: Зависание и время реакции
Задачи: Студент
- Применяйте усовершенствованные формулы кинематики в реальных ситуациях.
- Получить представление о продолжительности времени реакции человека на подготовку
для последующей деятельности.
Материалы:
линейки 12 или 6 дюймов
малярная лента
метровых палочек
Раздаточный материал: Повесить
& Время реакции
Обучение:
1. Ввести новые формулы: и,
объясняя, что они основаны на двух предыдущих и учитывают
такие вещи, как пройденное расстояние при ускорении или трогании с места
начальная скорость.При желании могут быть показаны фактические производные.
2. Ввести понятие, что земля
сила тяжести вызывает постоянное ускорение, равное 9,8 м / с / с.
Также используйте мяч, подброшенный в воздух, чтобы визуально продемонстрировать, что время
свободно движущийся / падающий объект поднимается так же, как и время, которое он
берет, чтобы упасть.
3. Кратко объясните деятельность, раздайте
раздаточные материалы и позвольте студентам работать над заданиями.
Оценка:
Неформальное оценивание позволит учителю
чтобы проверить правильность выполнения процедур и расчетов, таким образом
обеспечение разумных сравнительных значений для завтрашней деятельности.
День 9 и
10: Время реакции и расстояние остановки
Задачи: Студент
- Сравните методы определения времени реакции человека.
- Изучите влияние времени реакции человека на вождение.
- Изучите влияние различных дорожных покрытий на вождение.
- Сравните смоделированные данные с реальным опытом.
Материалы:
Компьютеры с выходом в Интернет (один
на группу) и Графический анализ
Сетевой принтер
Ссылки на:
Реакция
Апплет Time Shockwave
Остановка
Аплет расстояния
Трафик
Апплет управления
Раздаточный материал: Реакция
Время и остановочное расстояние
Таблица
для записи времени реакции класса
Комментариев:
Netscape (или IE) 4.0 или лучше будет
уметь запускать эти апплеты. Сбой Netscape — это нормально
иногда при запуске Java-апплетов.
Обучение:
1. Раздайте учащимся раздаточный материал. Есть
электронная таблица, отображаемая в классе, чтобы учащиеся могли обмениваться данными из части
Я деятельности.
2. Разрешить учащимся проработать
виды деятельности. Это образец остановки
данные о расстоянии и график.
3. Перед тем, как студенты приступят к работе в течение дня
во-вторых, инструктор должен обсудить результаты предыдущего дня.
4. Учащиеся, закончившие досрочно, должны
разрешить «поиграть» с симулятором дорожного движения. Дайте им задачу
максимизация транспортного потока и описание их решения.
Оценка:
Неформальное оценивание позволит учителю увидеть, как выполняются процедуры
выполнено правильно. Сбор выполненных заданий продемонстрирует студенту
понимание того, как данные тормозного пути будут связаны с окончательным проектом.
День 11 и
! 2: Подготовка презентации
Задачи: Студенческие группы
будет
- Завершите и выполните задачи для представления запроса.
Материалы:
Некоторые компьютерные станции с Интернетом
и мультимедийное программное обеспечение
Артефактов, собранных студентами
Видеомагнитофон для кассет, созданных студентами (видео
плата захвата необязательна)
Обучение:
1. Студенты должны использовать время для подготовки
Справочный документ и презентация для соответствия требованиям рубрики.
Оценка:
Вместо того, чтобы оценивать
в наши дни инструктор должен указать студентам дополнительные ресурсы
и консультировать студентов по поводу сбора и анализа соответствующих данных.
День 13 и
14: Студенческие презентации
Цели:
Студенческие группы продемонстрируют свое
способность применять знания о кинематике для научных исследований.
Материалы:
Компьютер с доступом в Интернет и
проекционный блок
Обучение:
1. В студенческих группах 10-15 минут
представить свою проблему, методы, выводы и рекомендации, а также
отвечать на вопросы.
Оценка:
Преподаватель должен использовать рубрику
для оценки исследовательского проекта каждой группы.
ВЕРХ
Раздел VI Ресурсы
Для файлов Pdf требуется программа для чтения Acrobat, которую можно получить
с www.adobe.com. Следовать
ссылка для Acrobat Reader.
Плагины Quicktime 4 и программы просмотра можно получить на сайте www.apple.com.
Перейдите по ссылке для quicktime. Если у вас установлен Netscape 3.0 или лучше,
браузер может самообновляться при переходе на сайт.
ВЕРХ
Примечания к редакции кинематики | askIITians
- Инерциальная система отсчета: — Система отсчета, в которой действует ньютоновская механика, называется инерциальной системой отсчета или инерциальной системой отсчета. Система отсчета, в которой не работает ньютоновская механика, называется неинерциальной системой отсчета или неинерциальной системой отсчета.
- Средняя скорость v av и средняя скорость тела за промежуток времени? т определяется как,
v av = средняя скорость
=? с /? т
Примечание:
(a) Изменение скорости или направления движения приводит к изменению скорости
(b) Частица, которая совершает один оборот по круговой траектории с постоянной скоростью, считается обладающей нулевой скоростью и ненулевой скоростью.
(c) Частица не может иметь нулевую скорость с ненулевой скоростью.
- Среднее ускорение определяется как изменение скорости за интервал времени? т .
Мгновенное ускорение частицы — это скорость, с которой ее скорость изменяется в данный момент.
- Три уравнения движения для объекта с постоянным ускорением приведены ниже.
(а) v = u + при
(б) s = ut + 1/2 при 2
(c) v 2 = u 2 + 2as
Здесь u — начальная скорость, v — конечная скорость, a — ускорение, s — перемещение тела и t — время.
Примечание: примите знак «+ ve», когда тело ускоряется, и знак «–ve», когда тело замедляется.
- Смещение корпуса в n -й секунде определяется как,
с n = u + a /2 (2 n -1)
- Время позиционирования ( x против t ), скорость-время ( v vs t ) и время ускорения ( a vs t ) график для движения в одном измерении:
(i) Изменение смещения (x), скорости (v) и ускорения (a) во времени для различных типов движения.
| Рабочий объем (x) | Скорость (v) | Разгон (а) |
(а) В состоянии покоя |
| | |
(б) Движение с постоянной скоростью |
|
|
|
(c) Движение с постоянным ускорением |
|
|
|
(d) Движение с постоянным замедлением |
|
|
Скалярные величины: — Скалярные величины — это те величины, которые требуют только величины для их полной спецификации.(например, масса, длина, объем, плотность)
Векторные величины: — Векторные величины — это те величины, которые требуют как величины, так и направления для их полной спецификации. (например, перемещение, скорость, ускорение, сила)
Нулевой вектор (нулевые векторы): — Это вектор с нулевой величиной и произвольным направлением.
Когда нулевой вектор добавляется или вычитается из заданного вектора, результирующий вектор совпадает с заданным вектором.
Точечное произведение нулевого вектора с любым произвольным всегда равно нулю. Перекрестное произведение нулевого вектора с любым другим вектором также является нулевым вектором.
- Коллинеарный вектор: — Векторы, имеющие общую линию действия, называются коллинеарными векторами. Есть два типа.
Параллельный вектор ( θ = 0 °): — Два вектора, действующих в одном направлении, называются параллельными векторами.
Антипараллельный вектор ( θ = 180 °): — Два вектора, направленные в противоположных направлениях, называются антипараллельными векторами.
Копланарные векторы — Векторы, расположенные в одной плоскости, независимо от их направления, называются копланарными векторами.
Сложение вектора: —
Сложение вектора коммутативное —
Сложение векторов ассоциативно —
Векторное сложение распределительное —
- Треугольники Закон сложения векторов: — Если два вектора представлены двумя сторонами треугольника, взятыми в одном порядке, то их результат представлен третьей стороной треугольника, взятой в противоположном порядке.
Величина результирующего вектора: —
R = √ ( A 2 + B 2 +2 AB cos θ )
Здесь θ — угол между и.
Если β — угол между и,
тогда,
- Если три вектора, действующих одновременно на частицу, могут быть представлены тремя сторонами треугольника, взятыми в одном порядке, то частица останется в равновесии.
Итак,
- Параллелограммный закон сложения векторов: —
R = √ ( A 2 + B 2 +2 AB cos θ ),
Случаи 1: — Когда, θ = 0 °, тогда
R = A + B (максимум), β = 0 °
Случаи 2: — Когда, θ = 180 °, тогда
R = A — B (минимум), β = 0 °
Варианты 3: — Когда, θ = 90 °, тогда
R = √ ( A 2 + B 2 ), β = tan -1 (B / A)
- Процесс вычитания одного вектора из другого эквивалентен векторному сложению отрицательного значения вычитаемого вектора.
Итак,
(a) Точечное произведение или скалярное произведение: —
,
Здесь A — величина, B, — величина, а θ — угол между и.
(i) Перпендикулярный вектор: —
(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °),
Когда, Антипараллельный вектор (θ = 180 °),
(b) Перекрестное произведение или векторное произведение: —
Или,
Здесь A — величина, B — величина, θ — угол между и и — единичный вектор в направлении, перпендикулярном плоскости, содержащей и.
(i) Перпендикулярный вектор (θ = 90 °): —
(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °), (нулевой вектор)
Когда, θ = 180 °, (нулевой вектор)
В трех измерениях,
Площадь треугольника: —
Площадь параллелограмма: —
Объем параллелепипеда: —
(i) Перпендикулярный вектор: — В верхней части наклонной плоскости ( t = 0, u = 0 и a = g sin q ) уравнение движения будет иметь вид
(а) v = (g sinθ) t
(б) s = ½ (g sinθ) t 2
(в) v 2 = 2 (g sinθ) с
(ii) Если время, необходимое телу для достижения дна, составляет т , тогда с = ½ ( г sin θ ) т 2
t = √ (2s / g sin θ )
Но sin θ = ч / с или с = ч / sin θ
Итак, t = (1 / sin θ ) √ (2 h / g )
(iii) Скорость тела на дне
v = g (sin θ ) t
= √2 гх
- Относительная скорость объекта A относительно объекта B определяется как
V AB = V A — V B
Здесь V B называется скоростью опорного объекта.
- Изменение массы: — В соответствии с формулой изменения массы Эйнштейна релятивистская масса тела определяется как,
м = м 0 / √ (1- v 2 / c 2 )
Здесь m 0 — масса покоя тела, v — скорость тела и c — скорость света.
- Движение снаряда в плоскости: — Если частица с начальной скоростью u проецируется под углом θ (угол проекции) с осью x , то
Время полета, T = (2 u sin α ) / g
Горизонтальный диапазон, R = u 2 sin2 α / g
Максимальная высота, H = u 2 sin 2 α /2 g
Уравнение траектории, y = x tan α — ( gx 2 /2 u 2 cos 2 α )
(a) При падении: — Период времени, t = √ (2h / g) и скорость, v = √ (2gh
(b) При рвоте: — Период времени, t = u / g и высота, h = u 2 / 2g
- Состояние равновесия: —
(а)
(b) | F 1 + F 2 | ≥ | F 3 | ≥ | F 1 -F 2 |
Возможно, вам понравится:
CBSE класс 7 по математике | CBSE, класс 7, естественные науки | CBSE класс 11 по химии
3.5.Свободное падение — Университетская физика, том 1,
Цели обучения
К концу этого раздела вы сможете:
- Используйте кинематические уравнения с переменными y и g для анализа движения свободного падения.
- Опишите, как меняются значения положения, скорости и ускорения во время свободного падения.
- Найдите положение, скорость и ускорение как функции времени, когда объект находится в свободном падении.
Интересное применение от (Рис.) До (Рис.) Называется свободное падение , которое описывает движение объекта, падающего в гравитационном поле, например, вблизи поверхности Земли или других небесных объектов планетарного размера.Предположим, что тело падает по прямой линии, перпендикулярной поверхности, поэтому его движение одномерно. Например, мы можем оценить глубину вертикальной шахты, бросив в нее камень и прислушиваясь к удару камня о дно. Но «падение» в контексте свободного падения не обязательно означает, что тело перемещается с большей высоты на меньшую. Если мяч брошен вверх, уравнения свободного падения в равной степени применимы как к его подъему, так и к его спуску.
Гравитация
Самый замечательный и неожиданный факт о падающих объектах заключается в том, что если сопротивление воздуха и трение незначительны, то в данном месте все объекты падают к центру Земли с одинаковым постоянным ускорением , независимо от их массы .Этот экспериментально установленный факт является неожиданным, потому что мы настолько привыкли к эффектам сопротивления воздуха и трения, что ожидаем, что легкие объекты будут падать медленнее, чем тяжелые. Пока Галилео Галилей (1564–1642) не доказал обратное, люди считали, что более тяжелый объект имеет большее ускорение при свободном падении. Теперь мы знаем, что это не так. При отсутствии сопротивления воздуха тяжелые предметы падают на землю одновременно с более легкими при падении с той же высоты (рисунок).
Рис. 3.26 Молоток и перо падают с одинаковым постоянным ускорением, если сопротивление воздуха незначительно. Это общая характеристика гравитации, не уникальная для Земли, как продемонстрировал астронавт Дэвид Р. Скотт в 1971 году на Луне, где ускорение свободного падения составляет всего 1,67 м / с2, а атмосферы нет.
В реальном мире сопротивление воздуха может привести к тому, что более легкий объект будет падать медленнее, чем более тяжелый объект того же размера. Теннисный мяч падает на землю после того, как одновременно упал бейсбольный мяч.(Может быть трудно заметить разницу, если высота невелика.) Сопротивление воздуха препятствует движению объекта по воздуху и трению между объектами, например, между одеждой и лотком для белья или между камнем и бассейном. которую уронили — тоже противодействуют движению между ними.
Для идеальных ситуаций, описанных в этих первых нескольких главах, объект , падающий без сопротивления воздуха или трения , определяется как в свободном падении . Сила тяжести заставляет объекты падать к центру Земли.Таким образом, ускорение свободно падающих объектов называется ускорением силы тяжести . Ускорение силы тяжести постоянно, что означает, что мы можем применить кинематические уравнения к любому падающему объекту, где сопротивление воздуха и трение незначительны. Это открывает нам широкий класс интересных ситуаций.
Ускорение свободного падения настолько важно, что его величине присвоен собственный символ: g . Он постоянен в любом месте на Земле и имеет среднее значение
.
Хотя г варьируется от 9.От 78 м / с 2 до 9,83 м / с 2 , в зависимости от широты, высоты, нижележащих геологических образований и местной топографии, давайте воспользуемся средним значением 9,8 м / с 2 , округленным до двух значащих цифр. текст, если не указано иное. Пренебрегая этими эффектами на величину г в результате положения на поверхности Земли, а также эффектами, возникающими в результате вращения Земли, мы принимаем направление ускорения силы тяжести вниз (к центру Земли).Фактически, его направление определяет то, что мы называем вертикальным. Обратите внимание, имеет ли ускорение a в кинематических уравнениях значение + g или — g , зависит от того, как мы определяем нашу систему координат. Если определить направление вверх как положительное, то
, а если определить положительное направление вниз, то
.
Одномерное движение с участием силы тяжести
Лучший способ увидеть основные особенности движения, связанного с гравитацией, — это начать с простейших ситуаций, а затем переходить к более сложным.Итак, мы начнем с рассмотрения прямого движения вверх и вниз без сопротивления воздуха или трения. Эти предположения означают, что скорость (если есть) вертикальная. Если объект уронили, мы знаем, что начальная скорость в свободном падении равна нулю. Когда объект оставил контакт с тем, что держало или бросало, объект находится в свободном падении. Когда объект брошен, он имеет ту же начальную скорость в свободном падении, что и до того, как его выпустили. Когда объект соприкасается с землей или любым другим объектом, он больше не находится в свободном падении, и его ускорение g больше не действует.В этих условиях движение является одномерным и имеет постоянное ускорение величиной g . Мы обозначаем вертикальное смещение символом y .
Кинематические уравнения для объектов в свободном падении
Здесь мы предполагаем, что ускорение равно — g (при положительном направлении вверх).
Стратегия решения проблем: свободное падение
- Определитесь со знаком ускорения свободного падения.На (Рисунок) — (Рисунок) ускорение g отрицательное, что означает положительное направление вверх, а отрицательное направление — вниз. В некоторых задачах может быть полезно иметь положительное ускорение g , что указывает на положительное направление вниз.
- Нарисуйте схему проблемы. Это помогает визуализировать вовлеченную физику.
- Запишите известные и неизвестные из описания проблемы. Это помогает разработать стратегию выбора соответствующих уравнений для решения проблемы.
- Решите, какое из (Рисунок) — (Рисунок) использовать для решения неизвестных.
Пример
Свободное падение мяча (рисунок) показывает положение мяча с интервалом в 1 с и начальной скоростью 4,9 м / с вниз, который брошен с вершины здания высотой 98 м. (а) Сколько времени проходит до того, как мяч коснется земли? б) С какой скоростью он достигает земли?
Рис. 3.27 Позиции и скорости с интервалом в 1 секунду мяча, брошенного вниз из высокого здания, на 4.9 м / с.
Стратегия
Выберите начало координат наверху здания с положительным направлением вверх и отрицательным направлением вниз. Чтобы найти время, когда позиция составляет -98 м, мы используем (Рисунок) с
.
Решение
- [раскрыть-ответ q = ”801478 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 801478 ″] Подставьте указанные значения в уравнение:Это упрощается до
Это квадратное уравнение с корнями
.Положительный корень — это тот, который нас интересует, так как время
— это время, когда мяч выпущен наверху здания. (Время
представляет собой тот факт, что мяч, брошенный вверх от земли, находился бы в воздухе в течение 5,0 с, когда он пролетел мимо вершины здания, двигаясь вниз со скоростью 4,9 м / с.) [/ Hidden-answer]
- [показать-ответ q = ”736816 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 736816 ″] Используя (рисунок), мы имеем[/ hidden-answer]
Значение
Для ситуаций, когда два корня получаются из квадратного уравнения для переменной времени, мы должны посмотреть на физическое значение обоих корней, чтобы определить, какой из них правильный.С
соответствует времени, когда мяч был выпущен, отрицательный корень будет соответствовать времени до того, как мяч был выпущен, что не имеет физического смысла. Когда мяч ударяется о землю, его скорость не сразу равна нулю, но как только мяч взаимодействует с землей, его ускорение не равно g , и он ускоряется с другим значением за короткое время до нулевой скорости. Эта задача показывает, насколько важно установить правильную систему координат и сохранить согласованность знаков g в кинематических уравнениях.
Пример
Вертикальное движение бейсбольного мяча
Бэттер ударяет по бейсбольному мячу прямо вверх по своей тарелке, и мяч ловится через 5,0 с после удара (рисунок). а) Какова начальная скорость мяча? (б) Какой максимальной высоты достигает мяч? (c) Сколько времени нужно, чтобы достичь максимальной высоты? (г) Какое ускорение в верхней части его пути? (e) Какова скорость мяча, когда он пойман? Предположим, что мяч попадает в одно и то же место.
Рис. 3.28 Бейсбольный мяч, попавший прямо вверх, ловится ловушкой через 5,0 с.
Стратегия
Выберите систему координат с положительной осью y , которая направлена прямо вверх и с началом в точке, где мяч попадает и ловится.
Решение
- (рисунок) дает
, что дает
.
- На максимальной высоте,
.С
, (рисунок) дает
или
- Чтобы узнать время, когда
, используем (рисунок):
Это дает
. Поскольку мяч поднимается за 2,5 с, время падения составляет 2,5 с.
- [раскрыть-ответ q = ”430807 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 430807 ″] Ускорение равно 9.8 м / с2 везде, даже когда скорость равна нулю в верхней части траектории. Хотя скорость наверху равна нулю, вниз она изменяется со скоростью 9,8 м / с2. [/ Hidden-answer] - [раскрыть-ответ q = ”984068 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 984068 ″] Скорость приможно определить с помощью (Рисунок):
[/ hidden-answer]
Значение
Мяч возвращается с той скоростью, с которой он уходил.Это общее свойство свободного падения при любой начальной скорости. Мы использовали одно уравнение для перехода от броска к ловле, и нам не приходилось разбивать движение на два сегмента, восходящий и нисходящий. Мы привыкли думать, что гравитация вызывает свободное падение вниз к Земле. Важно понимать, как показано в этом примере, что объекты, движущиеся вверх от Земли, также находятся в состоянии свободного падения.
Проверьте свое понимание
Глыба льда отламывается от ледника и падает 30.0 м до попадания в воду. Если предположить, что он падает свободно (нет сопротивления воздуха), сколько времени нужно, чтобы удариться о воду? Какая величина увеличивается быстрее, скорость куска льда или пройденное расстояние?
[показывать-ответ q = ”fs-id11683274 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11683274 ″]
Время попадания в воду — 2,47 с. Пройденное расстояние увеличивается быстрее.
[/ hidden-answer]
Пример
Ракетный ускоритель
Маленькая ракета с ускорителем взлетает и устремляется вверх.Когда на высоте
и скоростью 200,0 м / с выпускает ускоритель. (а) Какую максимальную высоту достигает ракета-носитель? (б) Какова скорость ракеты-носителя на высоте 6,0 км? Пренебрегайте сопротивлением воздуха.
Рис. 3.29 Ракета выпускает ускоритель с заданной высотой и скоростью. Насколько высоко и с какой скоростью летит бустер?
Стратегия
Нам нужно выбрать систему координат для ускорения свободного падения, которое мы принимаем как отрицательное при движении вниз.Нам дана начальная скорость ускорителя и его высота. Мы рассматриваем точку выпуска как источник. Мы знаем, что скорость равна нулю в максимальном положении в пределах интервала ускорения; таким образом, скорость ускорителя равна нулю на его максимальной высоте, поэтому мы также можем использовать эту информацию. Из этих наблюдений мы используем (рисунок), который дает нам максимальную высоту бустера. Мы также используем (рисунок), чтобы указать скорость на уровне 6,0 км. Начальная скорость ускорителя 200,0 м / с.
Решение
- Из (Рисунок),
[Показать-ответ q = ”761449 ″] Показать ответ [/ Показать-ответ]
[Скрытый-ответ a =” 761449 ″].С
, мы можем решить для y:
Это решение дает максимальную высоту бустера в нашей системе координат, которая берет свое начало в точке выпуска, поэтому максимальная высота бустера составляет примерно 7,0 км. [/ Hidden-answer]
- [show-answer q = ”897934 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 897934 ″] Высота 6,0 км соответствуетв используемой нами системе координат.Остальные начальные условия:
.
. [/ Hidden-answer] У нас, из (Рисунок),
[раскрыть-ответ q = ”228115 ″] Показать ответ [/ раскрыть-ответ]
[hidden-answer a = ”228115 ″][/ hidden-answer]
Значение
У нас есть как положительное, так и отрицательное решение в (b). Поскольку наша система координат имеет положительное направление вверх, +142,8 м / с соответствует положительной восходящей скорости на высоте 6000 м во время восходящего участка траектории ракеты-носителя.Значение v = −142,8 м / с соответствует скорости на 6000 м на нисходящем участке. Этот пример также важен тем, что объекту задается начальная скорость в начале нашей системы координат, но начало координат находится на высоте над поверхностью Земли, что необходимо учитывать при формировании решения.
Сводка
- Объект в свободном падении испытывает постоянное ускорение, если сопротивление воздуха незначительно.
- На Земле все свободно падающие объекты имеют ускорение g за счет силы тяжести, что в среднем составляет
.
- Для объектов, находящихся в свободном падении, направление вверх обычно считается положительным для смещения, скорости и ускорения.
Концептуальные вопросы
Какое ускорение у камня, брошенного вверх по пути вверх? На пике своего полета? По пути вниз? Предположим, что сопротивление воздуха отсутствует.
Подброшенный вверх объект падает обратно на Землю. Это одномерное движение. (а) Когда его скорость равна нулю? (б) Меняет ли его скорость направление? (c) Имеет ли ускорение тот же знак при движении вверх и вниз?
[показывать-ответ q = ”fs-id1168327
4 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327
4 ″]
а.на вершине своей траектории; б. да, на вершине своей траектории; c. да
[/ hidden-answer]
Предположим, вы бросаете камень почти прямо в кокос на пальме, и камень просто не попадает в кокос на пути вверх, но ударяет по кокосу на пути вниз. Если пренебречь сопротивлением воздуха и небольшим горизонтальным изменением движения, чтобы учесть попадание и промах кокоса, как скорость камня, когда он ударяется о кокос на пути вниз, сравнивается с той, которая была бы, если бы он ударился о кокос? по пути наверх? Кокосовый орех с большей вероятностью сместится по пути вверх или вниз? Объяснять.
Серьезность падения зависит от вашей скорости при ударе о землю. Все факторы, кроме ускорения свободного падения, одинаковы, во сколько раз безопасное падение на Луну может быть выше, чем на Земле (гравитационное ускорение на Луне примерно в одну шестую от земного)?
[show-answer q = ”fs-id1168325788809 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1168325788809 ″]
Земля
; Луна
; Земля
Луна
[/ hidden-answer]
Во сколько раз космонавт мог бы прыгнуть на Луне выше, чем на Земле, если бы ее скорость взлета была одинаковой в обоих местах (гравитационное ускорение на Луне примерно в шесть раз меньше, чем на Земле)?
Проблемы
Рассчитайте смещение и скорость в моменты времени (а) 0.500 с, (б) 1,00 с, (в) 1,50 с и (г) 2,00 с для шара, брошенного прямо вверх с начальной скоростью 15,0 м / с. Возьмем точку выпуска
.
.
Рассчитайте смещение и скорость в моменты времени: (а) 0,500 с, (б) 1,00 с, (в) 1,50 с, (г) 2,00 с и (д) 2,50 с для камня, брошенного прямо вниз с начальной скоростью 14,0 м / с от моста Verrazano Narrows Bridge в Нью-Йорке. Высота проезжей части этого моста над водой составляет 70,0 м.
[показывать-ответ q = ”fs-id1168327
8 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327
8 ″]
а.
;
г.
;
г.
;
г.
;
e.
[/ hidden-answer]
Баскетбольный судья подбрасывает мяч прямо вверх для стартовой наводки. С какой скоростью баскетболист должен оторваться от земли, чтобы подняться на 1,25 м над полом в попытке поймать мяч?
Спасательный вертолет парит над человеком, чья лодка затонула.Один из спасателей бросает спасательный круг прямо в пострадавшего с начальной скоростью 1,40 м / с и отмечает, что для достижения воды требуется 1,8 с. (а) Перечислите известных в этой проблеме. б) На какой высоте над водой был выпущен предохранитель? Обратите внимание, что нисходящий поток вертолета снижает влияние сопротивления воздуха на падающий спасательный круг, так что ускорение, равное ускорению силы тяжести, является разумным.
[показывать-ответ q = ”fs-id1168327876420 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327876420 ″]
а.Знает:
;
г.
и начало у спасателей, находящихся на высоте 18,4 м над водой.
[/ hidden-answer]
Необоснованные результаты Дельфин на водном шоу выпрыгивает прямо из воды со скоростью 15,0 м / с. (а) Перечислите известных в этой проблеме. б) Насколько высоко его тело возвышается над водой? Чтобы решить эту часть, сначала обратите внимание, что окончательная скорость теперь известна, и определите ее значение.Затем определите неизвестное и обсудите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в поиске неизвестных, проверяющих единицы и обсудите, является ли ответ разумным. в) Как долго дельфин находится в воздухе? Не обращайте внимания на любые эффекты, связанные с его размером или ориентацией.
Дайвер подпрыгивает прямо от трамплина, избегая трамплина при спуске, и падает ногами в бассейн. Она стартует со скоростью 4.00 м / с, а ее точка взлета — 1,80 м над бассейном. а) Какая у нее самая высокая точка над доской? б) Сколько времени ее ноги в воздухе? в) Какова ее скорость, когда ее ноги касаются воды?
[показывать-ответ q = ”fs-id1168328246433 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168328246433 ″]
а.
; б. к вершине
умножить на 2 до доски = 0,82 с от доски до воды
, решение квадратного уравнения дает 1.13 с; c.
[/ hidden-answer]
(a) Вычислите высоту обрыва, если камень ударится о землю за 2,35 с, когда он брошен прямо со скалы с начальной скоростью 8,00 м / с. б) Сколько времени потребуется, чтобы достичь земли, если ее бросят прямо вниз с той же скоростью?
Очень сильный, но неумелый толкатель ядра стреляет прямо вертикально с начальной скоростью 11,0 м / с. Сколько времени ему нужно, чтобы уклоняться, если выстрел был произведен на высоте 2.20 м а он рост 1,80 м?
[show-answer q = ”fs-id1168328325887 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1168328325887 ″]
Время до апекса:
умножить на 2 равно 2,24 с, чтобы получить высоту 2,20 м. К высоте 1,80 м добавляются дополнительные 0,40 м.
.
Возьмите положительный корень, поэтому время на дополнительные 0,4 м составит 0,04 с. Общее время
.
[/ hidden-answer]
Вы бросаете мяч прямо вверх с начальной скоростью 15.0 м / с. Поднимаясь вверх, он проходит ветку дерева на высоте 7,0 м. Сколько дополнительного времени проходит, прежде чем мяч пересечет ветку дерева на обратном пути вниз?
Кенгуру может перепрыгнуть через объект высотой 2,50 м. (а) Учитывая только его вертикальное движение, вычислите его вертикальную скорость, когда он отрывается от земли. б) Как долго он в воздухе?
[show-answer q = ”fs-id1168328168679 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1168328168679 ″]
а.
; б.
умножить на 2 дает 1,44 с в воздухе
[/ hidden-answer]
Стоит у подножия одной из скал горы. Путешественник в Арапилесе, Виктория, Австралия, слышит, как с высоты 105,0 м вырывается скала. Он не может сразу увидеть камень, но видит, спустя 1,50 секунды. а) Как далеко путешественник находится над скалой, когда он ее видит? б) Сколько времени ему нужно двигаться, прежде чем камень ударится о его голову?
На Хаф-Доум в национальном парке Йосемити в Калифорнии находится утес высотой 250 м.Предположим, с вершины этого утеса вырывается валун. а) С какой скоростью он будет двигаться, когда ударится о землю? (b) Предполагая, что время реакции составляет 0,300 с, сколько времени потребуется туристу внизу, чтобы уклониться от дороги после того, как услышал звук отрывающейся скалы (без учета роста туриста, который в любом случае стал бы незначительным. если ударил)? Скорость звука в этот день составляет 335,0 м / с.
[показывать-ответ q = ”fs-id1168327989886 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327989886 ″]
а.
; б. время слышно после начала падения камня: 0,75 с, время достижения земли: 6,09 с
[/ hidden-answer]
Глоссарий
- ускорение свободного падения
- Ускорение объекта под действием силы тяжести
- свободное падение
- состояние движения, которое является результатом только силы тяжести
Видео | Номер | Марка |
|---|---|---|
Графики | ||
| Положение-время (d-t) Графики | ||
Гр-1 | 11 | |
Гр-2 | 11 | |
Гр-3 | 11 | |
| Скорость-время (v-t) Графики | ||
Гр-4 | 11 | |
Гр-5 | 11 | |
Гр-6 | 11 | |
Гр-7 | 11 | |
| Время разгона (a-t) Графики | ||
Гр-8 | 11 | |
| Сводка графиков | ||
Гр-9 | 11 | |
| Использование Один график для рисования других | ||
Гр-10 | 11 | |
Гр-11 | 11 | |
Математический | ||
Conv-1 | 11 и 12 | |
Движение | ||
| Кинематика постоянная скорость и постоянная скорость | ||
| Определения положения, расстояния, перемещения | Кин-1 | 11 и 12 |
| Как для расчета скорости и скорости | Кин-2 | 11 и 12 |
| Кинематика формулы ускорения с объектами, движущимися вперед и назад | ||
Кин-3 | 11 и 12 | |
Кин-4 | 11 и 12 | |
| Образец проблема, которая очень часто встречается на тестах.Объект ускоряется и позже притормаживает. | Кин-5 | 11 и 12 |
Кин-6 | 11 и 12 | |
Кин-7 | 11 и 12 | |
| Образец проблема, когда Супермен мчится, чтобы догнать пулю | Кин-8 | 11 и 12 |
| Объекты брошенный вверх или вниз | ||
Кин-9 | 11 и 12 | |
| Образец проблема с падением одного мяча и брошенным вторым 1 с позже. | Кин-10 | 11 и 12 |
| Образец проблема, когда Супермен должен поймать падающего студента | Кин-11 | 11 и 12 |
| Это это очень сложная задача с двумя поднятыми стрелами. | Кин-12 | 11 и 12 |
| Объекты движение по кривой или окружности | ||
Кин-13 | 11 и 12 | |
| Это пример задачи использует кинематические уравнения для решения ускорения и перемещение на колесе обозрения. | Кин-14 | 11 и 12 |
Кин-15 | 11 и 12 | |
Векторы | ||
Введение | ||
Вект-1 | 11 и 12 | |
Вект-2 | 11 | |
Вект-3 | 11 и 12 | |
Вектор | ||
| Как разбить вектор на составляющие и как вычислить составляющие | Вект-4 | 11 и 12 |
| Образцы разбиения векторов на составляющие | Вект-5 | 11 и 12 |
Вект-6 | 11 и 12 | |
Вект-7 | 11 и 12 | |
Вект-8 | 11 и 12 | |
Вект-9 | 11 и 12 | |
Сложение / Вычитание | ||
Вект-10 | 12 | |
Вект-11 | 11 и 12 | |
Вект-12 | 11 и 12 | |
Родственник | ||
Простой | ||
РелВ-1 | 11 и 12 | |
РелВ-2 | 11 и 12 | |
Подробнее | ||
РелВ-3 | 12 | |
РелВ-4 | 12 | |
РелВ-5 | 12 | |
РелВ-6 | 12 | |
РелВ-7 | 12 | |
Ньютона | ||
| Введение первого и второго закона Ньютона | ||
Тритон-1 | 11 и 12 | |
Тритон-2 | 11 и 12 | |
Тритон-3 | 11 и 12 | |
Тритон-4 | 11 и 12 | |
Ньют-5 | 11 и 12 | |
Ньют-6 | 11 и 12 | |
| Простой Проблемы второго закона Ньютона (без диаграмм свободного тела) | ||
| А пример проблемы с тянущим автомобилем.Используется трение, и проблема видоизменена во второй половине ролика. | Тритон-7 | 11 и 12 |
| А в этом примере задачи пуля проходит через блок. | Тритон-8 | 11 и 12 |
| Иногда вы не можете использовать уравнения x и y для решения проблемы.Это показывает как добавить силы к объекту под разными углами при взгляде сверху. | Ньют-9 | 12 |
| Бесплатно Основы схемы тела | ||
| Бесплатно Диаграммы кузова с указанием сил | FBD-1 | |
FBD-2 | 11 и 12 | |
FBD-3 | 11 и 12 | |
FBD-4 | 11 и 12 | |
FBD-5 | 11 и 12 | |
FBD-6 | 11 и 12 | |
FBD-7 | 11 и 12 | |
FBD-8 | 11 и 12 | |
FBD-9 | 11 и 12 | |
| Лифт Проблемы | ||
Элев-1 | 11 и 12 | |
Элев-2 | 11 и 12 | |
| Это Пример задачи охватывает все, что вам нужно знать о лифте. | Элев-3 | 11 и 12 |
| Это В примере задачи лифт движется вверх и вниз вместе с человеком стоя на весах | Элев-4 | 11 и 12 |
| Трение И законы Ньютона Проблемы с трением | ||
| Введение к коэффициент трения и принцип трения | Fric-1 | 11 и 12 |
| Как работы статического и кинетического трения | Fric-2 | 11 и 12 |
| Статический и проблема кинетического трения, показывающая разницу между два | Fric-3 | 11 и 12 |
| А проблема трения с коробкой и сила, давящая на нее | Fric-4 | 11 и 12 |
| Fn не% $ #! равно Fg (простая версия) | Fric-5 | 11 и 12 |
| Это Пример задачи включает в себя 2 коробки, тянущиеся с трением и сила под углом. | Fric-6 | 12 |
| Это это 1 из 2 сложных примеров задач, использующих штабелированные блоки, трение и схемы свободного тела | Fric-7 | 12 |
| Это это 2 из 2 сложных примеров задач с использованием штабелированных блоков, трения и схемы свободного тела | Fric-8 | 12 |
| Силы под углом на коробках | ||
Ф / Анг-1 | 11 и 12 | |
F / Ang-2 | 11 и 12 | |
F / Ang-3 | 11 и 12 | |
F / Ang-4 | 11 и 12 | |
Наклоны | ||
| Как для рисования FBD объекта на склоне или холме | Inc-1 | 12 |
| Проблема скольжения по склону, холму или пандусу с трением | Inc-2 | 12 |
Inc-3 | 12 | |
Inc-4 | 12 | |
Inc-5 | 11 и 12 | |
| Ньютона Третий закон | ||
Тритон (3) -1 | 11 и 12 | |
Тритон (3) -2 | 11 и 12 | |
Тритон (3) -3 | 11 и 12 | |
| Типичный Задача 2-го и 3-го закона Ньютона с вертолетом, поднимающим машину. | Тритон (3) -4 | 12 |
Тритон (3) -5 | 12 | |
Тритон (3) -6 | 12 | |
| Это проблема с образцом — это более сложная версия вытягиваемых ящиков и включает милых пингвинов | Тритон (3) -7 | 12 |
Шкив | ||
Простой | ||
Потяните-1 | 12 | |
Потяните-2 | 12 | |
Потяните-3 | 12 | |
Потяните-4 | 12 | |
Потяните-5 | 12 | |
Тяга-6 | 12 | |
| Подробнее расширенный взгляд на эту проблему | Потяните-7 | 12 |
Комплекс | ||
Потяните-8 | 12 | |
Прицеп-9 | 12 | |
Центростремительный | ||
Центростремительный | ||
| Ан. объяснение того, что такое центростремительное ускорение | ac-1 | 12 |
| центростремительный пример ускорения при повороте автомобиля | ac-2 | 12 |
Центростремительный | ||
Fc-1 | 12 | |
Fc-2 | 12 | |
Fc-3 | 12 | |
Fc-4 | 12 | |
Fc-5 | 12 | |
Fc-6 | 12 | |
Fc-7 | 12 | |
Fc-8 | 12 | |
Fc-9 | 12 | |
Fc-10 | 12 | |
Снаряд | ||
Уроки | ||
Проект-1 | 12 | |
Проект-2 | 12 | |
Проект-3 | 12 | |
Проект-4 | 12 | |
| Простой способ решить проблему с снарядом, но он работает, только если объект приземляется на том же уровне, на котором был произведен выстрел. | Проект-5 | 12 |
| Как для расчета максимальной высоты снаряда | Проект-6 | 12 |
Образец | ||
| Это проблема связана с тем, что самолет роняет объект. | Проект-7 | 12 |
| Барт Симпсон пытается перепрыгнуть ущелье, и самая сложная часть — найти скорость | Проект-8 | 12 |
| Как для расчета угла выстрела снаряда. | Проект-9 | 12 |
Столкновения | ||
| Импульс | ||
Объекты | ||
Столб-1 | 12 | |
Кол-2 | 12 | |
Объекты | ||
Кол-3 | 12 | |
Col-4 | 12 | |
Энергетика | ||
Col-5 | 12 | |
Col-6 | 12 | |
Col-7 | 12 | |
Col-8 | 12 | |
Col-9 | 12 | |
Энергия, | ||
Работа, | ||
NRG-1 | 11 и 12 | |
NRG-2 | 11 и 12 | |
NRG-3 | 11 и 12 | |
NRG-4 | 11 и 12 | |
NRG-5 | 11 и 12 | |
| Комплекс проблема американских горок.Найдите высоту, необходимую для петли | NRG-6 | |
эластичный | ||
NRG-7 | 12 | |
NRG-8 | 12 | |
NRG-9 | 12 | |
Мощность | ||
военнопленный-1 | 11 | |
КПД | ||
EFF-1 | 11 | |
ЭФФ-2 | 11 | |
EFF-3 | 11 | |
Планетарный | ||
Ньютона | ||
Грав-1 | 11 и 12 | |
Грав-2 | 11 и 12 | |
Кеплер | ||
ПМеч-1 | 12 | |
ПМеч-2 | 12 | |
ПМеч-3 | 12 | |
Использование | ||
ПМеч-4 | 12 | |
ПМеч-5 | 12 | |
ПМеч-6 | 12 | |
| кинетическая энергии, когда спутник находится на орбите, и его скорость в орбита | ПМеч-7 | 12 |
Электроэнергия | ||
Фомулас | ||
| Ан. введение в самые распространенные формулы | Элек-1 | 11 |
| Как использовать формулу Q = Ne | Элек-2 | 11 |
| Как использовать формулу V = E / Q | Элек-3 | 11 |
| Как использовать формулу I = Q / t | Элек-4 | 11 |
| Как использовать формулу R = V / I | Элек-5 | 11 |
| Как длина, площадь и сопротивление материала воздействию | Элек-6 | 11 |
| Как использовать формулу R = удельное сопротивление * L / A | Элек-7 | 11 |
| Как использовать 3 формулы мощности | Элек-8 | 11 |
| Использование тариф энергии для расчета стоимости электроэнергии | Элек-9 | 11 |
Электрический | ||
| Чертеж схемы и 4 части | Элек-10 | 11 |
| Пуск в вольтах и амперметрах в цепи | Элек-11 | 11 |
| Как для расчета тока в электрической цепи | Элек-12 | 11 |
Как | Элек-13 | 11 |
| Как для расчета сопротивления в электрической цепи | Элек-14 | 11 |
| Простой пример решения схемы | Элек-15 | 11 |
| Подробнее сложный пример решения схемы | Элек-16 | 11 |
Электромагнетизм | ||
Левый | ||
| Как найти магнитное поле вокруг провода | EM-1 | 11 |
| Как найти северный конец электромагнита | EM-2 | 11 |
| Как найти направление силы двигателя | EM-3 | 11 |
| Как для расчета моторной силы | EM-4 | 11 |
Генераторы | ||
| Как найти направление, в котором будет течь электричество | EM-5 | 11 |
| Как найти направление, в котором будет течь электричество | EM-6 | 11 |
| Как сделать простые расчеты трансформатора | EM-7 | 11 |
| Как для расчета нескольких трансформаторов | EM-8 | 11 |
| Как для расчета трансформатора, если КПД не 100% | EM-9 | 11 |
Волны | ||
Недвижимость | ||
Волна-1 | 11 и 12 | |
Волна-2 | 11 и 12 | |
Волна-3 | 11 и 12 | |
Волна-4 | 11 и 12 | |
Волна-5 | 11 и 12 | |
Волна-6 | 11 и 12 | |
Волна-7 | 11 и 12 | |
Волна-8 | 11 и 12 | |
Волна-9 | 11 и 12 | |
Волна-10 | 11 и 12 | |
Звук | ||
Волна-11 | 11 и 12 | |
Волна-12 | 11 и 12 | |
Волна-13 | 11 и 12 | |
Волна-14 | 11 и 12 | |
Волна-15 | 11 и 12 | |
Волна-16 | 12 | |
Волны | ||
Волна-17 | 12 | |
Волна-18 | 12 | |
Волна-19 | 12 | |
Волна-20 | 12 | |
Волна-21 | 12 | |
Оптика | ||
Рефракция | ||
Опт-1 | 10 | |
Опт-2 | 10 | |
Опт-3 | 10 | |
изогнутый | ||
Опт-4 | 10 | |
Опт-5 | 10 | |
Опт-6 | 10 | |
Опт-7 | 10 | |
Линзы | ||
Опт-8 | 10 | |
Опт-9 | 10 | |
Опт-10 | 10 | |
Опт-11 | 10 | |
Опт-12 | 10 | |
Опт-13 | 10 | |
Опт-14 | 10 | |
Графики | ||
GrEx-1 | 11 | |
GrEx-2 | 11 | |
Действительно | ||
| Физика Обещание: Некоторые вещи, которые сводят нас с ума, учителя физики. | ||
| 1 Миллион просмотров Видео с благодарностью: кажется, так давно мы достигли 1 миллион просмотров. Спасибо за поддержку | ||
Видео | ||
Наука | ||
г. | ||
| г. Каруана-Дингли получает премию Toronto Urban Hero Eductional Award !! Щелкните, чтобы увидеть статью newpapaer. | ||
| г. Каруана-Дингли получает статью в газету для своей коллекции | ||
| г. Каруана-Дингли разговаривает с Алексом Лифсоном из Rush !! | ||
| г. Каруана-Дингли во время завтрака по телевидению демонстрирует граммофоны | ||
| г. Каруана-Дингли о старинном охотнике, демонстрирующем граммофоны | ||
| г. Каруана-Дингли играет на гитаре в своем акустическом дуэте | ||
| г. Каруана-Дингли играет песню, которую он написал со своей рок-группой | ||
г. | ||
| Почему Г-н Морен — лучший учитель физики в истории | ||
| г. Костюмы Каруаны-Дингли и г-на Морина на Хэллоуин через Годы | ||
| г. Морин пытается подбодрить г-на Каруана-Дингли, напевая | ||
Как решать кинематические задачи: Часть II
Эта статья является второй главой в серии о том, как понимать и решать кинематические задачи.Первая глава посвящена положению, скорости и ускорению. Теперь, когда мы понимаем эти величины, мы собираемся использовать их для решения задач в одном измерении.
Четыре всадника кинематического апокалипсиса:
x f — x i = (v f — v i ) * t / 2
v f — v i = a * t
v f 2 = v i 2 + 2 * a * (x f — x i )
x f = x i + v i * t + ½a * t 2
Примечание: маленький f обозначает конечную (как конечную скорость или положение), а маленький i обозначает начальную.
Примечание. Эти уравнения работают только при постоянном ускорении, но почти все задачи имеют постоянное ускорение.
Для каждой одномерной кинематической задачи этапы практически одинаковы.
- Запишите каждую величину, которую дает вам задача (начальное и конечное положение, начальная и конечная скорость, ускорение, время и т. Д.)
- Запишите, какое количество вы пытаетесь найти
- Найдите кинематическое уравнение (или иногда два уравнения), чтобы связать эти величины.
- Решите алгебру.
Да, это действительно так просто. (На самом деле, большинство физических задач работают одинаково. Подробнее об алгоритме решения физических задач читайте в этой статье.)
Как избежать распространенных ошибок: скрытые величины
Иногда проблема может сообщить вам количество тайно; вы можете даже не осознавать, что получили это. Например, если они сообщают вам смещение (как далеко что-то переместилось), но не позиции, вы можете рассматривать смещение как x f и установить для x i значение 0.Точно так же, если проблема не говорит ничего особенного об ускорении, то ускорение, вероятно, является просто силой тяжести, a = g = 9,8 м / с 2 . Эти скрытые количества так же действительны, как и обычные количества, только их немного труднее обнаружить.
Как избежать распространенных ошибок: лучший результат
Особый пример скрытой величины — это когда вам говорят, что объект находится «на вершине своего полета / движения / траектории и т. Д.». Это означает, что они тайно говорят вам, что v f равно 0, потому что объект, движущийся в одном измерении, всегда имеет скорость 0 в верхней части своего пути.Интересно, почему? Что ж, если бы скорость росла, то через миллисекунду объект был бы выше (и, следовательно, он не мог бы оказаться на вершине своего пути). Точно так же, если бы объект имел скорость, направленную вниз, то она была бы выше за миллисекунду (так что он также не может быть наверху).
Как избежать распространенных ошибок: положительные и отрицательные числа
Отследить негативы бывает непросто. Ключ — это направление; вниз всегда отрицательно. Поэтому, если объект падает, он будет иметь отрицательную скорость.Если ускорение снижается (а это почти всегда), то ускорение отрицательное. И не забывайте из нашей первой главы, что можно иметь положительную скорость и отрицательное ускорение одновременно!
Пример: женщина и ее мяч
Женщина держит мяч на расстоянии 1 метра и бросает его вверх со скоростью 5 м / с. а) Как высоко достигает мяч? б) Сколько времени нужно мячу, чтобы коснуться земли? в) Насколько быстро мяч летит, когда ударяется о землю?
Давай узнаем!
Часть A: Как высоко достигает мяч?
Что мы знаем?
Начальное положение x i = 1 м
Начальная скорость v i = 5 м / с
Секретное количество: a = -9.8 м / с 2 (гравитация)
Секретное количество: В верхней части дуги мяча (то есть, когда она самая высокая) v f = 0 м / с
Что мы пытаемся найти?
Положение в верхней части броска, x f
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x f , x i , v f , v i и a
v f 2 = v i 2 + 2 * a * (x f — x i ) кажется подходящим!
Подключи и реши
v f 2 = v i 2 + 2 * a * (x f — x i )
(0 м / с) 2 = (5 м / с) 2 + 2 * (- 9.8 м / с 2 ) * (x f — 1 м)
0 = 25 (м 2 / с 2 ) — (19,6 м / с 2 ) * (x f — 1 м )
(19,6 м / с 2 ) * (x f — 1 м) = 25 м 2 / с 2
x f -1 м = (25 м 2 / с 2 ) / (19,6 м / с 2 )
x f –1 м = 1,28 м
x f = 2,28 м
Тада! Конечная высота = 2,28 метра
Часть B: Сколько времени нужно мячу, чтобы коснуться земли?
Что мы знаем?
Мы все еще знаем x i = 1 м, v i = 5 м / с и a = -9.8 м / с 2 , но теперь мы также знаем, что x f = 0 м (потому что высота земли 0 м)
Примечание. Поскольку мяч теперь находится на земле, а не наверху полета, v f ≠ 0, так что мяч находится вне стола.
Что мы пытаемся найти?
Время, т
Какое уравнение связывает эти величины?
Мы ищем уравнение, которое включает x f , x i , v i , a и t
Похоже, нам понадобится x f = x i + v i * т + ½a * т 2
Подключи и реши
x f = x i + v i * t + ½a * t 2
0 m = 1 m + (5 м / с) * t + ½ (-9.8 м / с 2 ) * t 2
— (4,9 м / с 2 ) * t 2 + (5 м / с) * t + 1 м = 0
Это квадратное уравнение (ax 2 + bx + c = 0), которое можно решить с помощью формулы корней квадратного уравнения.
t =
t =
t = или t =
t = или t =
t = -17 с или 1,2 с
Мы можем игнорировать t = -. 17, потому что нам не разрешено иметь отрицательное время (мы называем это нефизическим ответом), что оставляет нам время = 1,2 секунды!
Часть C)
Что мы знаем?
Мы все еще знаем x i = 1 м, v i = 5 м / с, a = -9.8 м / с 2 и x f = 0 м, но теперь мы также знаем, что t = 1,2 секунды, потому что мы только что решили это.
Что мы пытаемся найти?
Скорость, v f
Какое уравнение связывает эти величины?
У нас так много величин, что мы можем использовать любое из уравнений, но давайте возьмем v f — v i = a * t, потому что это просто, и мы еще не использовали его.
Подключи и реши
v f — v i = a * t
v f — 5 м / с = (-9.8 м / с 2 ) * 1,2 с
v f = 5 м / с — 11,8 м / с
v f = -6,8 м / с
Стрела, скорость при падении мяча на землю составляет 6,8 м / с (отсюда отрицательный знак)
Теперь мы знаем, как использовать наши кинематические уравнения для решения задач в одном измерении. В нашем следующем блоге мы обсудим, как «вырезать» векторы при подготовке к кинематике в двух измерениях.
Оставайтесь с нами! То же время летучей мыши, тот же канал летучей мыши.
Вы заинтересованы в работе с Джейкобом — в Нью-Йорке или в Интернете — над своими физическими работами?
Для более актуального чтения ознакомьтесь с другими сообщениями в блогах, написанными нашими преподавателями физики в Нью-Йорке и Бостоне:
уравнений движения | Блестящая вики по математике и науке
Графики очень интерактивны и помогают суммировать различные вещи в одном месте.Следовательно, они полезны для идентификации, отслеживания и моделирования движения объекта. Следующие типы графиков могут быть полезны в кинематике: графики положения-времени и графики скорости-времени.
График положения-времени:
Графики положения-времени — это самые простые графики в кинематике. Они позволяют описывать движение объекта как по положению, так и по времени. Ось yyy этих графиков представляет смещение объекта, а ось xxx представляет время.Таким образом, наклон графика «положение-время» дает скорость объекта.
Найдите скорость частицы в интервале (1,2) (1,2) (1,2).
Можно видеть, что наклон графика положение-время дает нам скорость за период времени. Таким образом,
v = s2 − s1t2 − t1 = 10−7,52−1 = 2,5 м / с. \ Begin {align}
v & = \ dfrac {s_2-s_1} {t_2-t_1} \\
& = \ dfrac {10-7.5} {2-1} \\
& = 2,5 \ текст {м / с}.
\ end {align} v = t2 −t1 s2 −s1 = 2−110−7,5 = 2,5 м / с.Также можно видеть, что смещение этого объекта задается функцией s (t) = 2,5t + 5s (t) = 2,5t + 5s (t) = 2,5t + 5. Таким образом, можно найти скорость этой функции, которая есть не что иное, как ее производная:
v (t) = ddt (2,5t + 5) = 2,5 м / зв (t) = \ dfrac {d} {dt} (2,5t + 5) = 2,5 \ text {m / s} .v (t) = dtd (2,5t + 5) = 2,5 м / с.
Отправьте свой ответ
Позиционно-временной график объекта
Найдите скорость объекта в интервале (2,4) (2,4) (2,4).
График скорости-времени:
Эти графики позволяют вычислить скорость объекта в данный момент времени. Ось yyy представляет скорость, а ось xxx — время. В основном они могут помочь в вычислении двух вещей:
перемещение объекта по интервалу,
ускорение объекта на интервале.
Из приведенного выше графика видно, что наклон графика скорость-время дает ускорение:
(Наклон графика скорости и времени) = a = v2 − v1t2 − t1.2.
\ end {align} a = t2 −t1 v2 −v1 = 4−210−6 = 2 м / с2.
Площадь под графиком показывает смещение, которое является площадью трапеции:
s = h (a + b) 2 = 2 (6 + 10) 2 = 16 м. \ Begin {align}
s & = \ dfrac {h (a + b)} 2 \\
& = \ dfrac {2 (6 + 10)} {2} \\
& = 16 \ текст {м}.
\ end {align} s = 2h (a + b) = 22 (6 + 10) = 16 м.
Также можно сделать вывод, что график задается функцией: v (t) = 2t + 2v (t) = 2t + 2v (t) = 2t + 2. Таким образом, ускорение будет производной
.
a = ddt (2t + 2) = 2 м / с2.2 + 4 \ вправо) \\
& = 16 \ текст {м}.
\ end {align} s = ∫24 2t + 2dt = [t2 + 2t] 24 = 42 + 8− (22 + 4) = 16 м.
Выше показан график скорости бега от времени. Как далеко проходит этот бегун за 1616 16 секунд?
Вертикальный масштаб фигуры установлен на vs = 8,0 м / с.v_ {s} = 8.0 \ text {м / с.} vs = 8.0 м / с.
Отправьте свой ответ
Скорость ракеты определяется следующей функцией:
v (t) = 3t2−2t − 1.2-2t-1.v (t) = 3t2−2t − 1.
Найти смещение ракеты за интервал времени (1,3) (1,3) (1,3).
Изображение предоставлено Wikimedia Commons.
Хотя использование графиков может показаться более запутанным, чем использование простых уравнений для решения вопросов, оно может дать важную интуицию при решении физических проблем и дать подсказки относительно того, как выводить уравнения движения в сложных случаях. В следующих разделах графики скорости-времени используются для получения фундаментальных уравнений, управляющих движением объектов.
.
