Формулы площади трапеции все: Все формулы площади трапеции. Найти онлайн — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Площадь прямоугольной трапеции | Треугольники

Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.

I. Площадь трапеции равна произведению полусуммы оснований на высоту.

Площадь прямоугольной трапеции ABCD,

AD∥BC,

равна

Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть

Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):

II. Площадь трапеции равна произведению средней линии на высоту.

Если MN — средняя линия прямоугольной трапеции ABCD,

то площадь

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:

III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

Для прямоугольной

трапеции

ABCD,

AD∥BC,

Так как sin(180º-α)=sin α, то также

Если AC=d1, BD=d2, ∠COD=φ, то

В частности, если диагонали трапеции перпендикулярны, то

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

Так как в трапецию можно вписать окружность, то

AD+BC=AB+CD=p. Следовательно,

или

Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:

Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула

Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.

или

Формула площади трапеции через угол. Все варианты того, как найти площадь трапеции

Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.

Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия
– это линия, соединяющая середины боковых сторон. Высота
трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:

Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :

Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:

Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.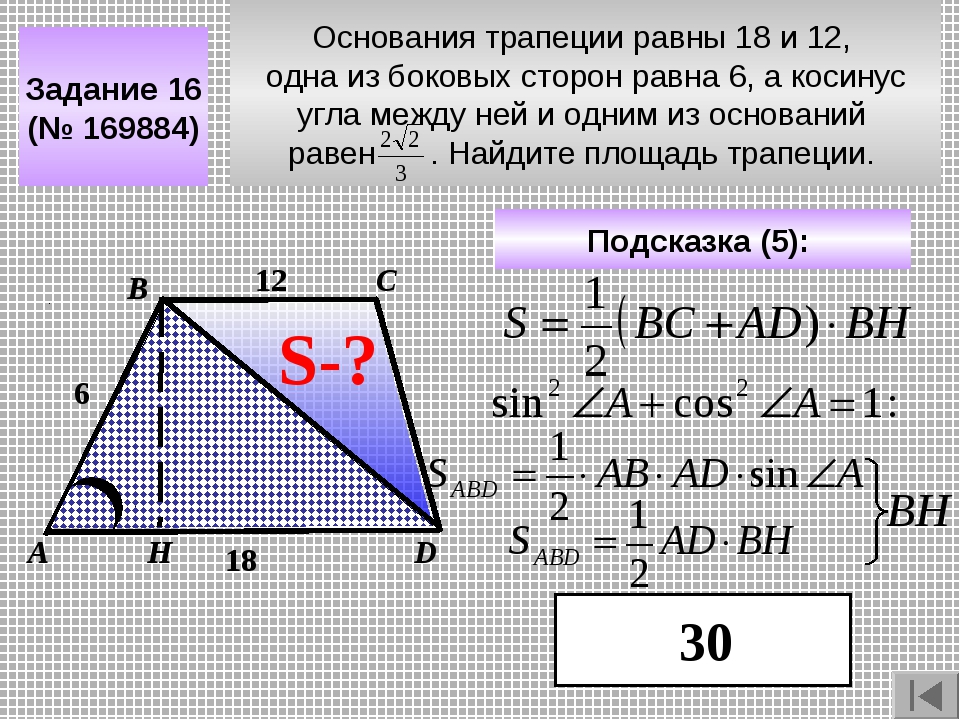 найдем площадь фигуры:

Площадь равнобокой трапеции

Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:

Помните, что диагонали равнобокой трапеции равны между собой!

То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.

Площадь криволинейной трапеции

Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.

Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:

Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:

Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.

Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:

Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:

Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.

Определяем трапецию

Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.

Свойства трапеции

Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:

Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!

У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.

Самые простые формулы площади трапеции

Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:

S = h*(a + b)/2.

В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.

Рассмотрим пример.

Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?

Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв.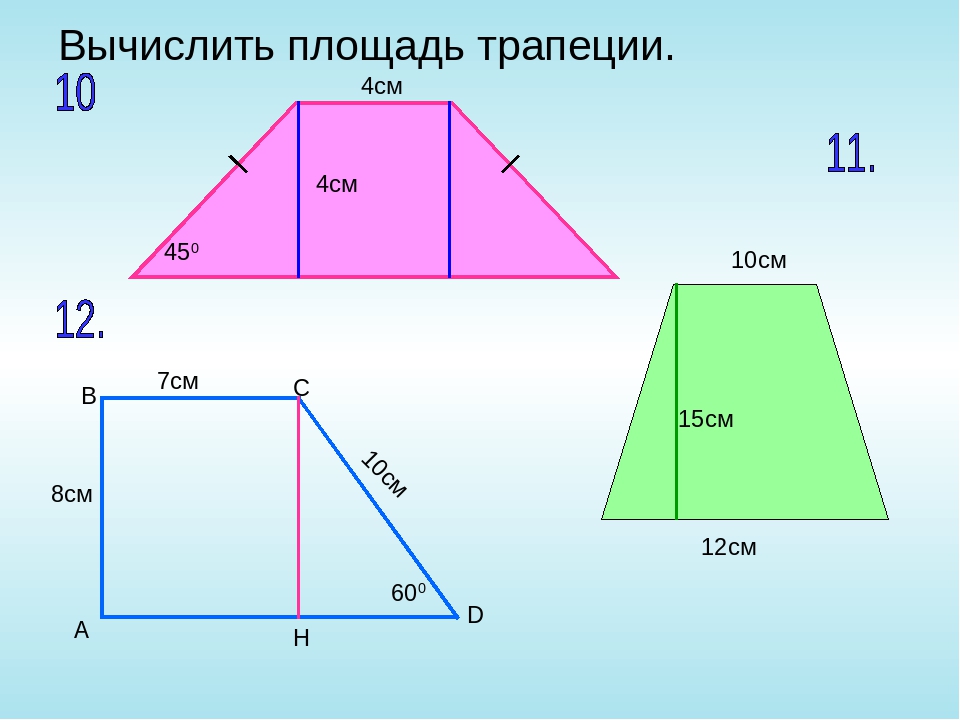 см.

Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.

Использование диагоналей для вычислений

Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:

S = ½ d 1 d 2 sina.

Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.

Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.

Ищем площадь равнобокой трапеции

Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок.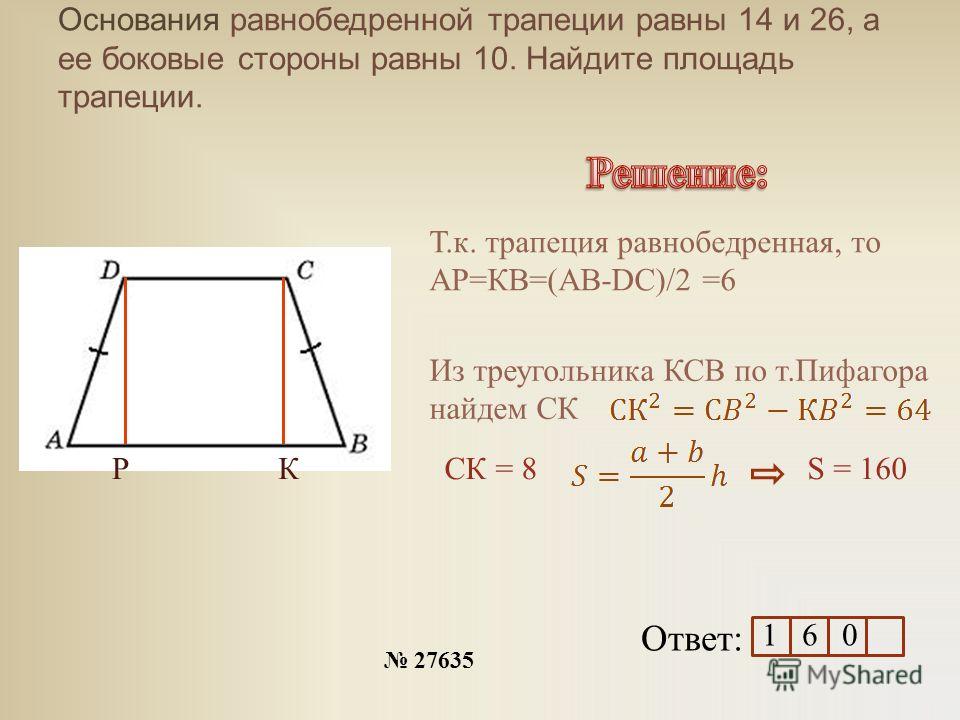 Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.

Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:

S = c
*sin a
*(a
— c
*cos a
),

где с
— боковое бедро, a
— угол при нижнем основании.

Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.

Находим площадь прямоугольной трапеции

Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.

Применяем смекалку

Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.

Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.

Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.

Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320.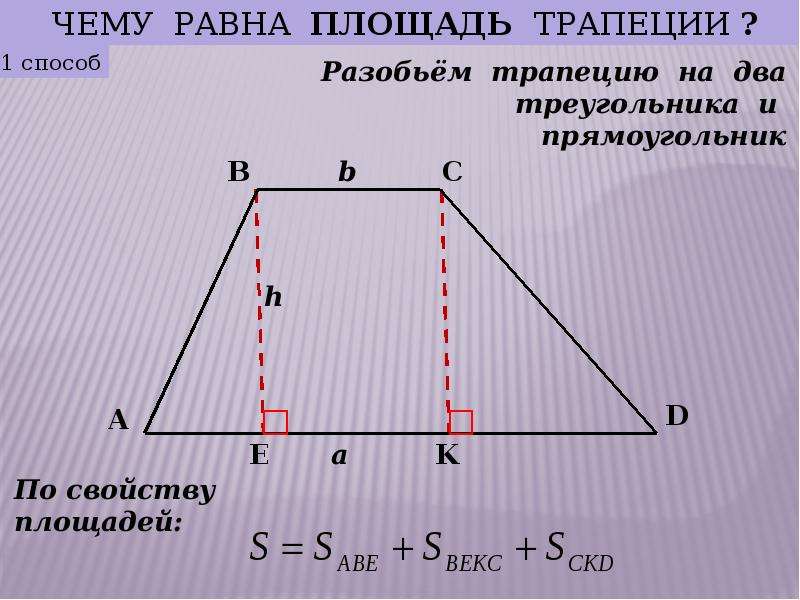 Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.

Используем формулу Пика

Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:

S = M/2 + N — 1,

в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.

Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.

Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.

Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:

Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?

Рассмотрим трапецию с основаниями a и b
и со средней линией l

, и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:

*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое.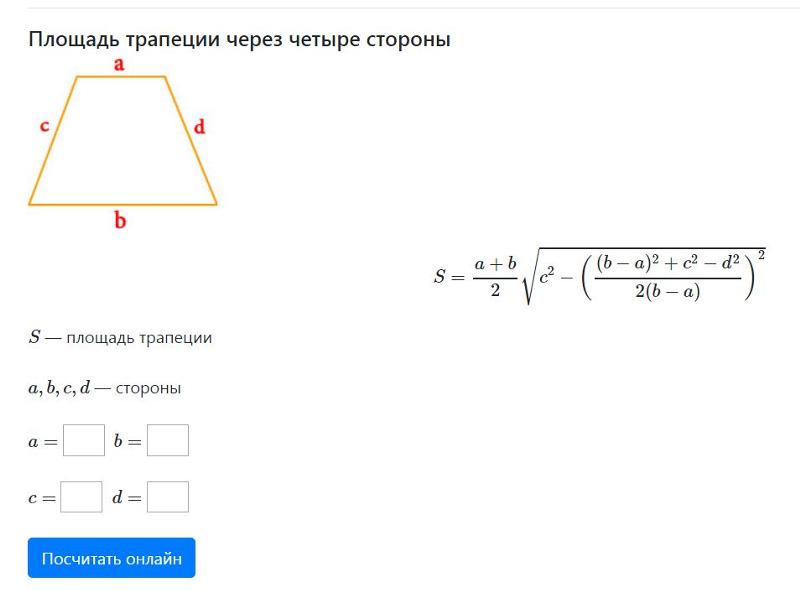 Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

Посмотреть ещё одно объяснение

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:

Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.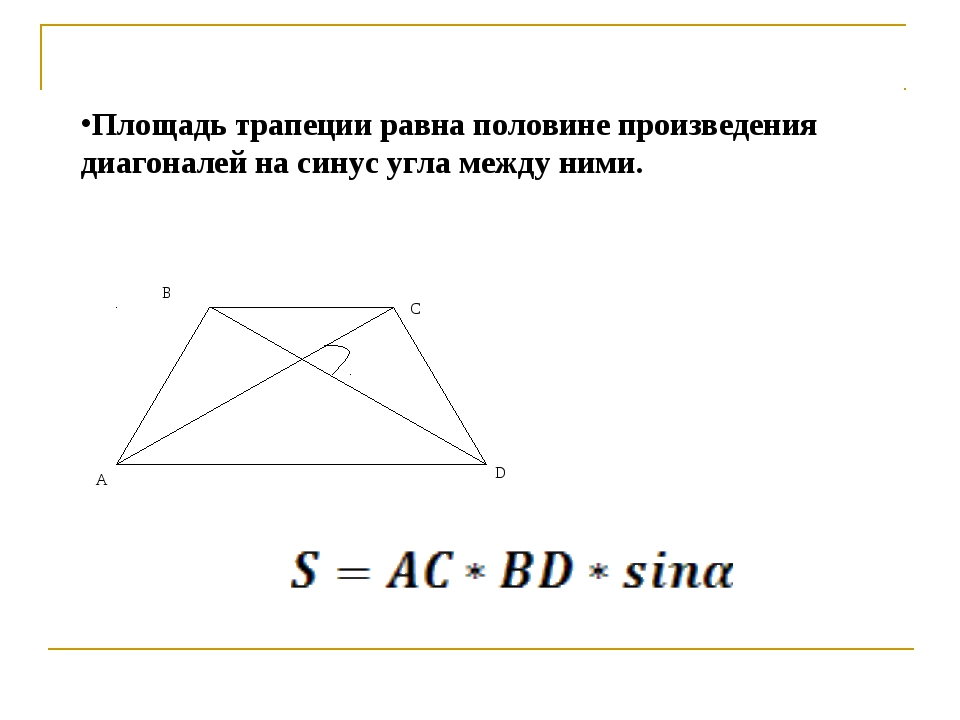

Теперь рассмотрим треугольник:

*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Площадь трапеции формула:

Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.

То есть, получается, что она равна произведению средней линии и высоты:

Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:

То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:

Но дело тут не в записи, конечно, а в понимании.

Скачать (посмотреть) материал статьи в формате *pdf

На этом всё.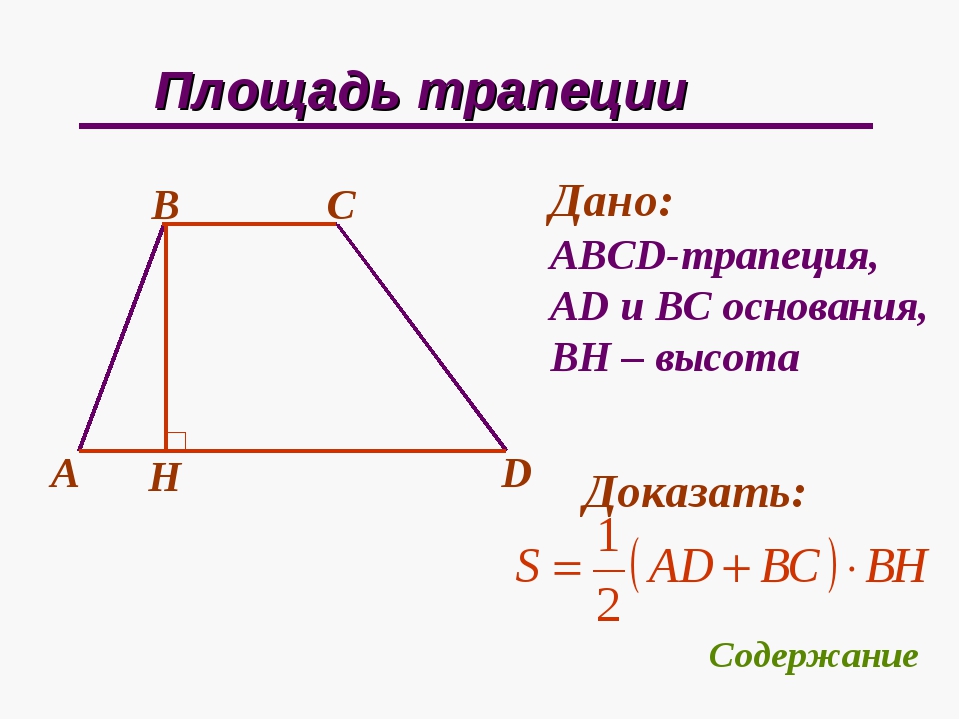 Успеха вам!

С уважением, Александр.

Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:

, где DP – внешняя высота в

Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:

Вынесем за скобку

Что и требовалось доказать.

Следствие из формулы площади трапеции:

Так как полусумма оснований равна MN — средней линии трапеции, то

2) Применение общей формулы площади четырехугольника
.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда

3) Метод сдвига диагонали

Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:

Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции.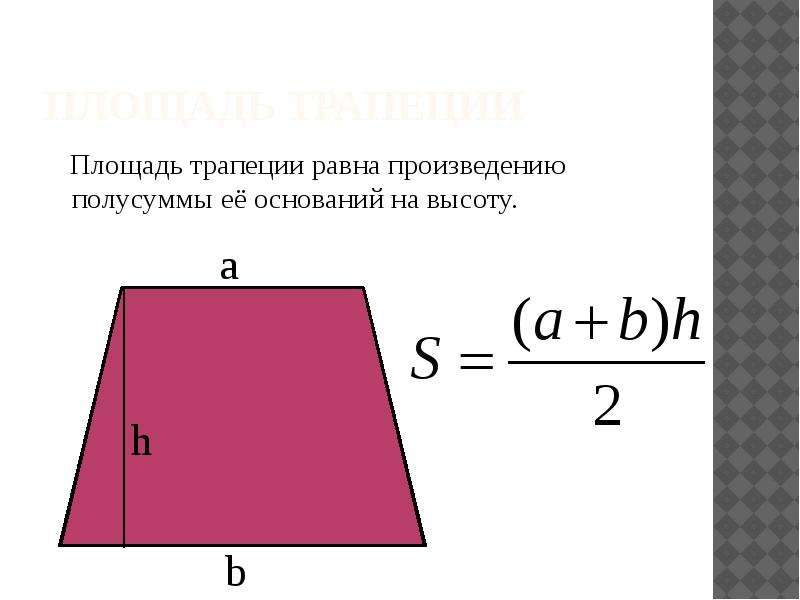 С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).

Спецприемы репетитора по математике.

Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:

Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:

Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.

В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции.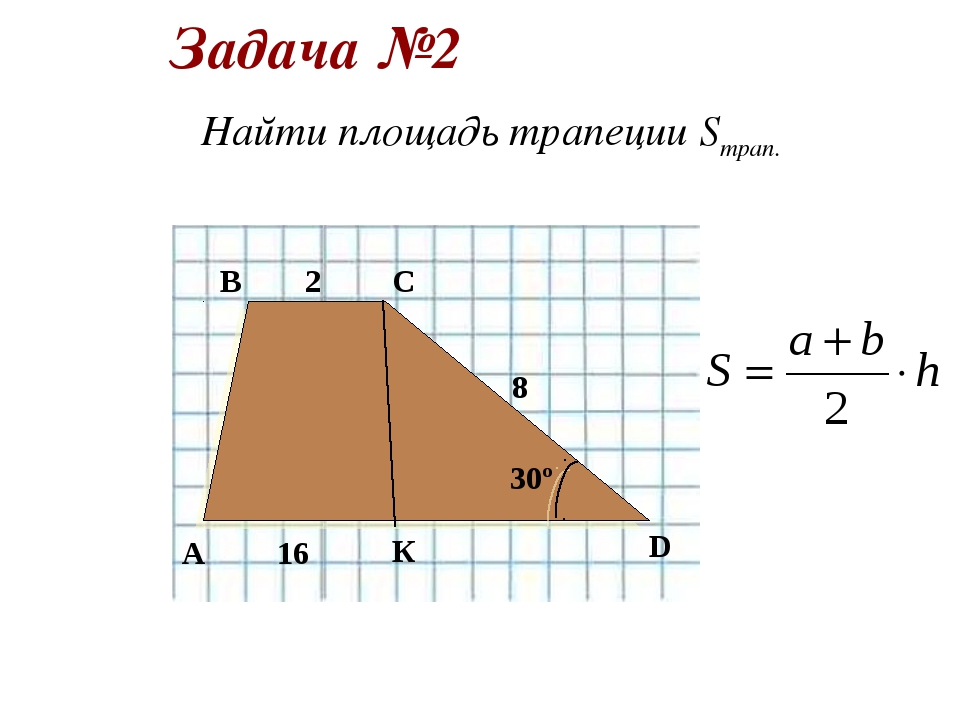 Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!

Задачи на площадь трапеции:

Замечание репетитора по математике
: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.

1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол .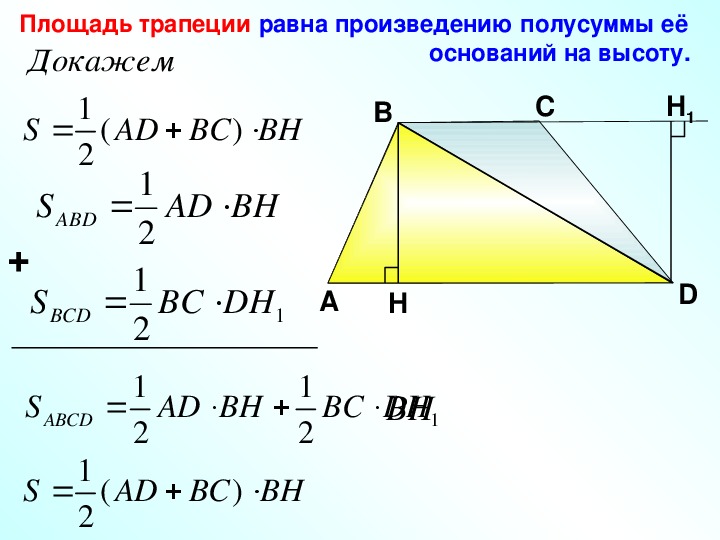 Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).

Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.

Колпаков А.Н.
Репетитор по математике в Москве
, подготовка к ЕГЭ в Строгино
.

В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.

Площадь трапеции

Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:

S = ½ * (a+b) * h

т.е. взять полусумму оснований, умноженную на высоту.

Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m.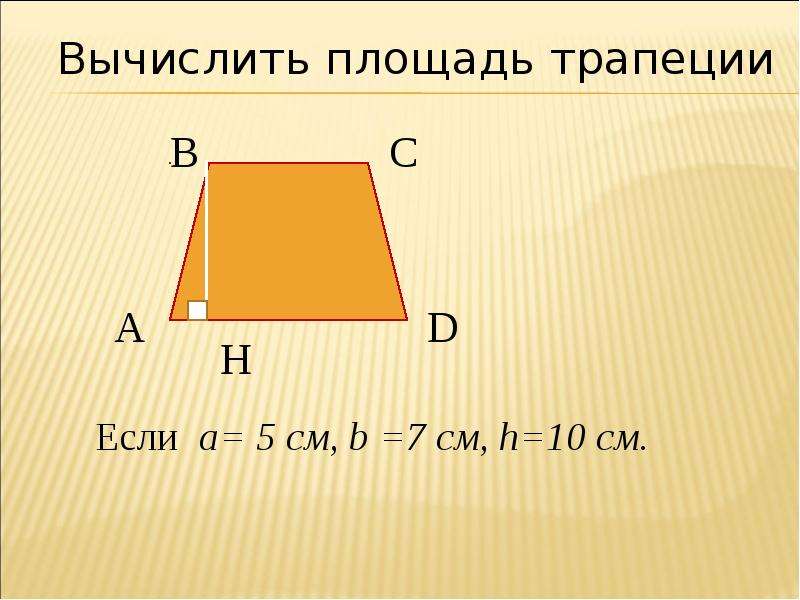 Тогда

Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:

Если известны длины диагоналей и угол между ними, то площадь ищется так:

S = ½ * d1 * d2 * sin α

где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.

При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:

S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))

Площадь равнобедренной трапеции

Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.

Найти площадь равнобедренной трапеции можно несколькими способами.

Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:

Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:

S = c * sin α * (a + c * cos α)

где а — верхнее основание, с — боковая сторона.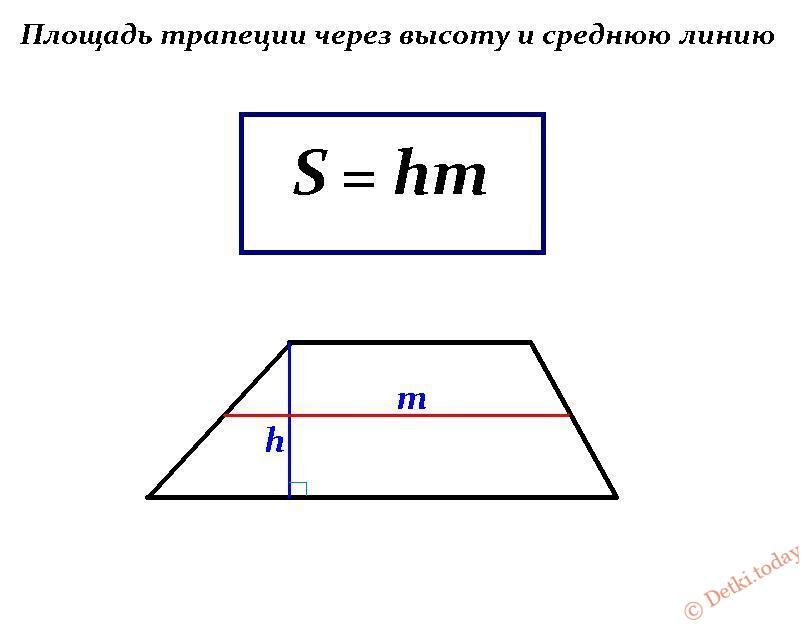

Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:

S = c * sin α * (b – c * cos α)

Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:

S = ½ * (b2 – a2) * tg α

Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:

S = ½ * d2 * sin α

Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.

Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:

S = m * c * sin α

Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.

Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:

S = 4r2 / sin α

Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):

Зная основания и угол, площадь равнобедренной трапеции вычисляется так:

S = a * b / sin α

(эта и последующие формулы верны только для трапеций с вписанной окружностью).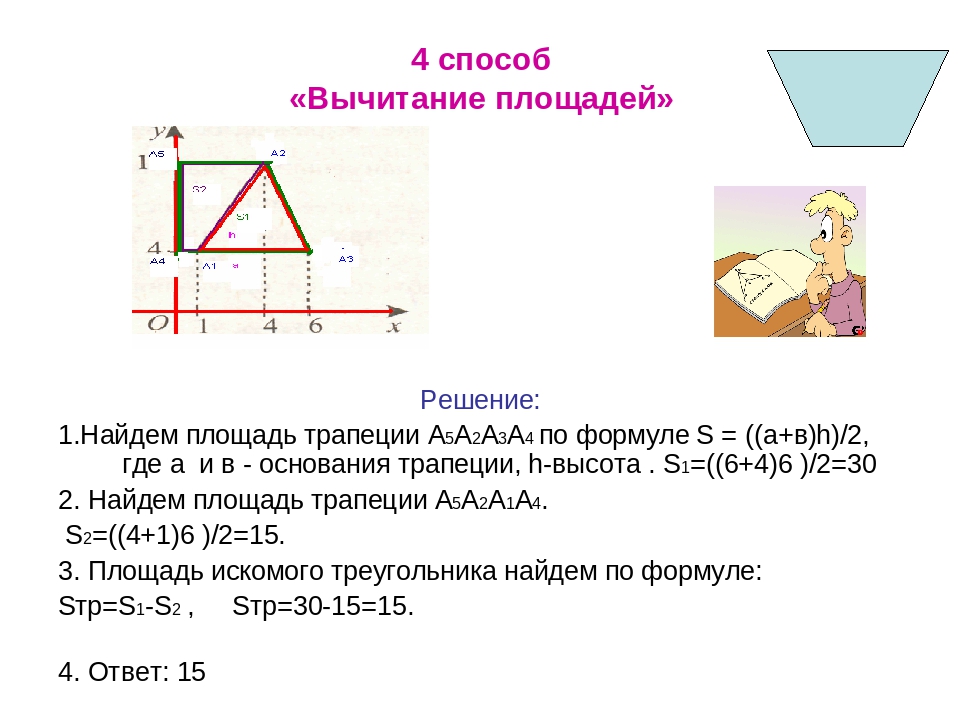

Через основания и радиус окружности площадь ищется так:

Если известны только основания, то площадь считается по формуле:

Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:

Площадь прямоугольной трапеции

Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.

Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.

Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.

Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:

S = (a + b) * h / 2

В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:

S = (a + b) * c / 2

Другой способ рассчитать площадь — перемножить длину средней линии на высоту:

или на длину боковой перпендикулярной стороны:

Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:

S = ½ * d1 * d2 * sin α

Если диагонали перпендикулярны, то формула упрощается до:

S = ½ * d1 * d2

Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:

S = (2r + c) * r

Если в трапецию вписана окружность, то площадь вычисляется так же:

где m — длина средней линии.

Площадь криволинейной трапеции

Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.

Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:

Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов.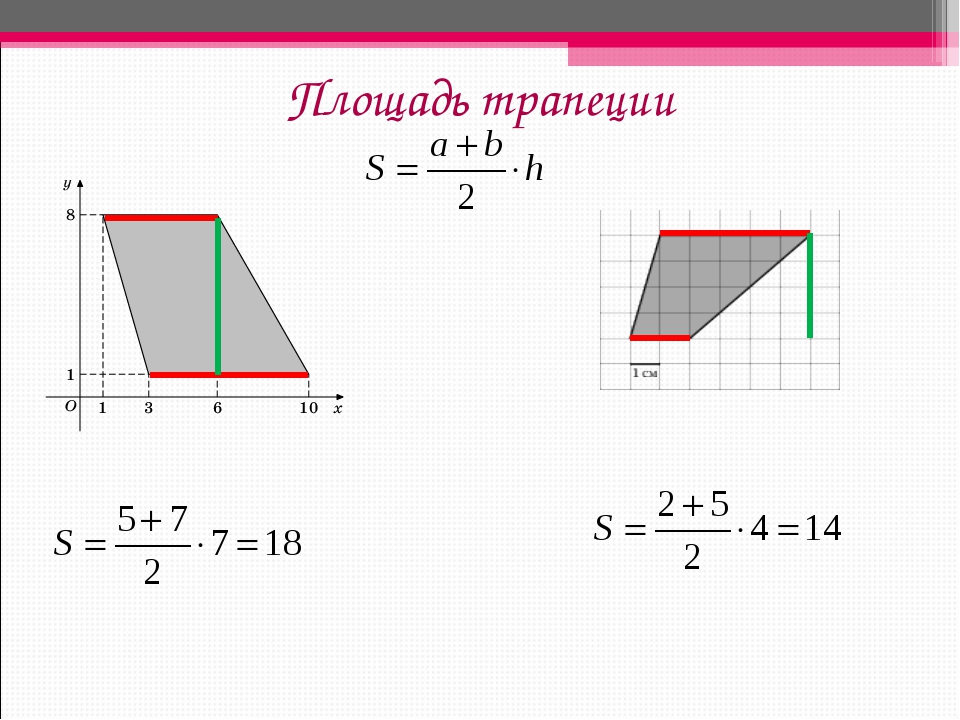 А сумма углов, прилежащих к боковой стороне, — 180 градусам.

формулы через стороны, диагонали, площадь

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.

Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.

Нахождение высоты трапеции

Через длины сторон

Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:

Через боковую сторону и прилежащий угол

Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.

Через диагонали и угол между ними

Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:

Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:

Средняя линия трапеции (m) равняется полусумме ее оснований, т. е m = ^(a+b)/₂.

Через площадь

Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).

Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.

Примеры задач

Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.

Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:

Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.

Задание 2
Площадь трапеции равна 26 см². Найдите ее высоту, если основания равны 10 и 3 см.

Решение
В данном случае можно применить последнюю из рассмотренных формул:

формулы и примеры Как решать трапецию

Чтобы понять, как решать задачи с трапецией, полезно запомнить три основных пути решения.

I. Провести две высоты.

Ia
. Четырехугольник BCKF — прямоугольник (так как у него все углы прямые). Следовательно, FK=BC.

AD=AF+FK+KD, отсюда AD=AF+BC+KD.

Треугольники ABF и DCK — прямоугольные.

(Следует учесть и другой вариант:

Ib.

В этом случае AD=AF+FD=AF+FK-DK=AF+BC-DK.)

Ic.
Если трапеция равнобедренная, решение задачи упрощается:

В этом случае прямоугольные треугольники ABF и DCK равны, например, по катету и гипотенузе (AB=CD по условию, BF=CK как высоты трапеции). Из равенства треугольников следует равенство соответствующих сторон:

AF=KD=(AD-FK):2=(AD-BC):2.

II. Провести прямую, параллельную боковой стороне.

IIa.
BM∥
CD. Так как BC∥
AD (как основания трапеции), то BCDM — параллелограмм. Следовательно, MD=BC, BM=CD, AM=AD-BC.

IIb.
В частности, для равнобедренной трапеции

BM∥
CD. Так как CD=AB, то и BM=AB. То есть получаем равнобедренный треугольник ABM и параллелограмм BCDM.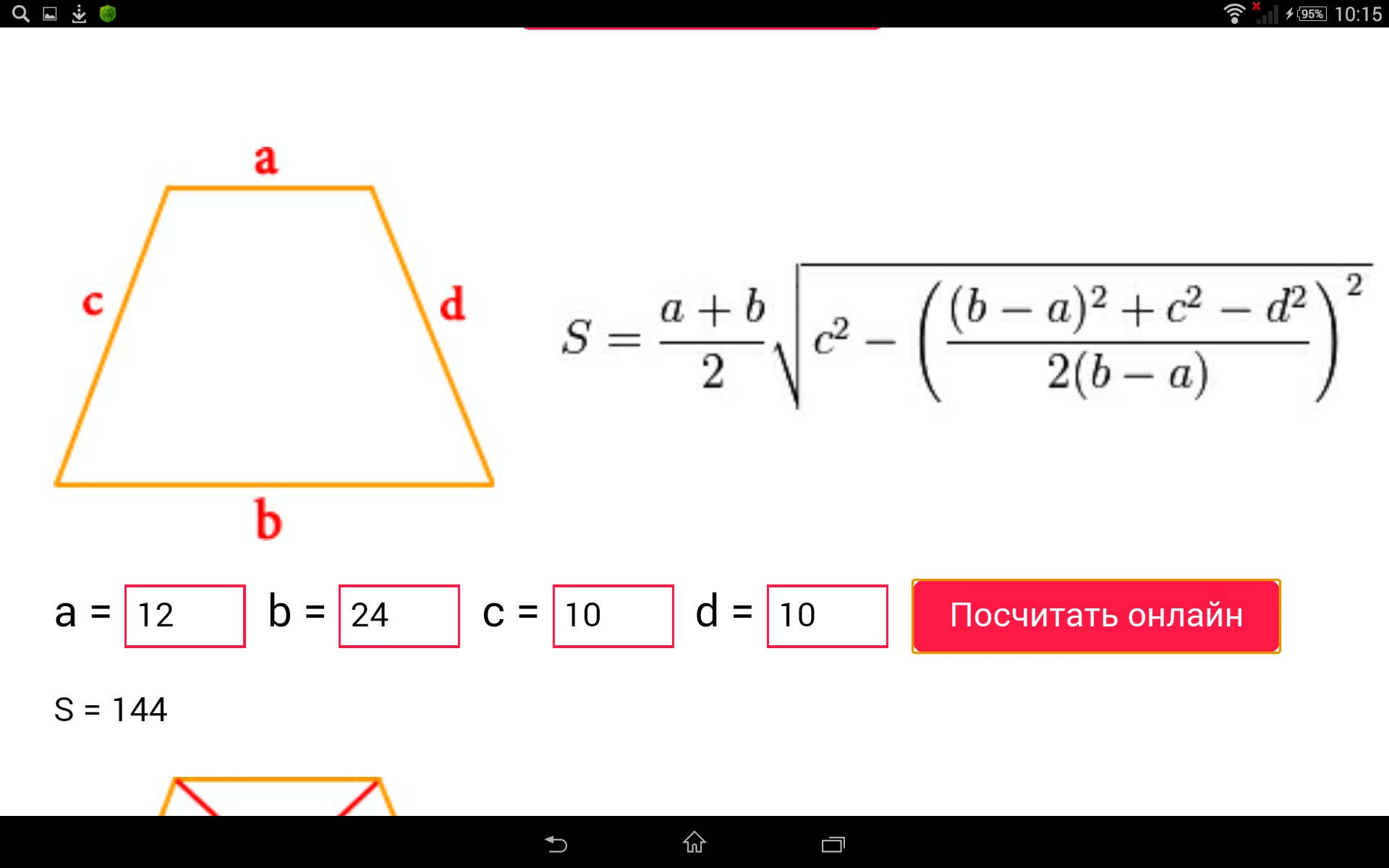

III. Продолжить боковые стороны и получить треугольник.

Прямые AB и CD пересекаются в точке P.

Треугольники APD и BPC подобны по двум углам (угол P — общий, ∠
PAD= ∠
PBC как соответственные при BC∥
AD и секущей AP).

Следовательно, их стороны пропорциональны:

Эти три подхода к решению задач на трапецию — основные. Помимо них, существует много других способов. Некоторые рассмотрены на этом сайте. Например, — как решать задачи с трапецией, у которой диагонали перпендикулярны.

Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.

Что нужно знать про трапецию?

Для начала вспомним, что трапецией
называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.

В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.

Формулы площади трапеции

Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.

Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h
.

Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b).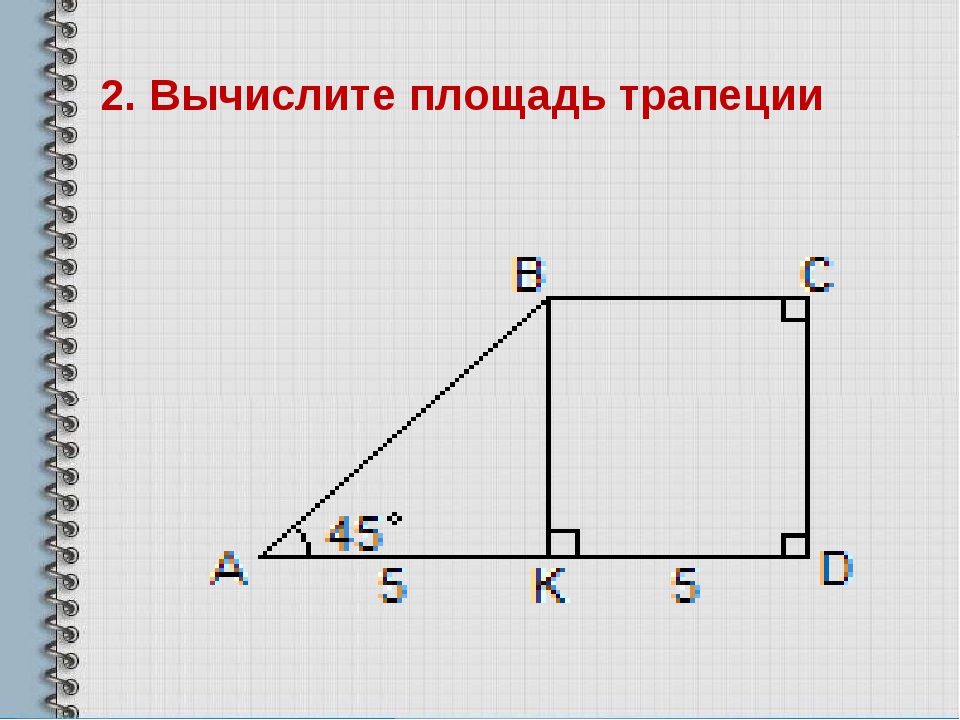 Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h
. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.

Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα
.

Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2
.

Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.

Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.

Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα
. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2
.

Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2
.

Формула площади криволинейной трапеции

Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.

Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a)
. В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.

Примеры задач

Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.

Задача №1:
Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.

Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.

Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.

Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .

Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.

Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .

Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.

Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.

Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).

Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).

Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.

Таким образом, ОЕ = х = √(5а 2 + b 2)/6.

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.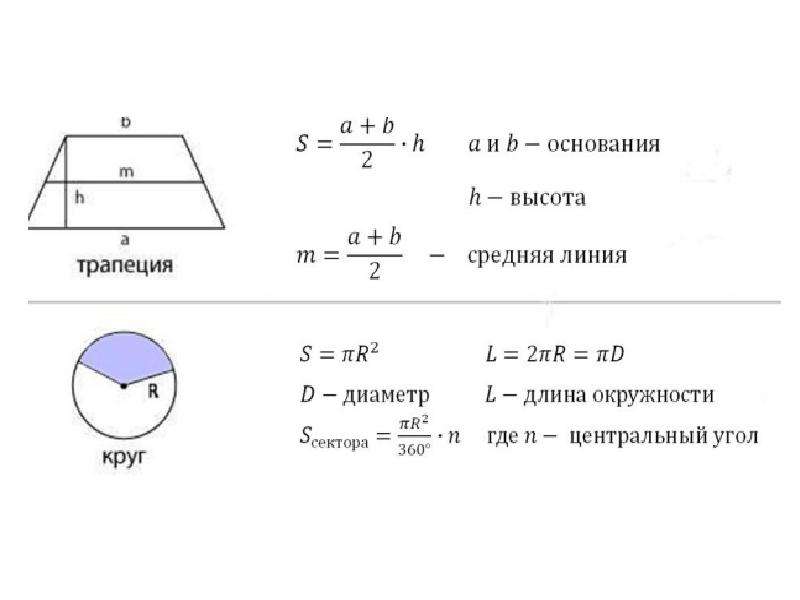

Трапеция
– четырехугольник у которого две стороны параллельны. Параллельные стороны – это основание, непараллельные стороны – боковые.

Существует несколько основных видов: криволинейная, равнобедренная, произвольная, прямоугольная. Вычисления площади трапеции по формуле разнятся в зависимости от конкретного типа геометрической фигуры.

Что такое трапеция: типы и отличия

Всего существует четыре типа, отличающихся между собой не только вариативностью углов, но и возможным наличием криволинейных отрезков.

Площадь произвольной трапеции

Вариативность расчета площади произвольной трапеции невелика. Ее можно вычислить относительно заданных размеров основания и высоты; посчитать через обозначенные четыре стороны фигуры; решить пример, зная длину средней линии и высоты; по указанным диагоналям и углом между ними; высчитать через основания и два угла.

Основная формула расчета данного способа:

Где а и b – параллельные стороны, а h – высота четырехугольника.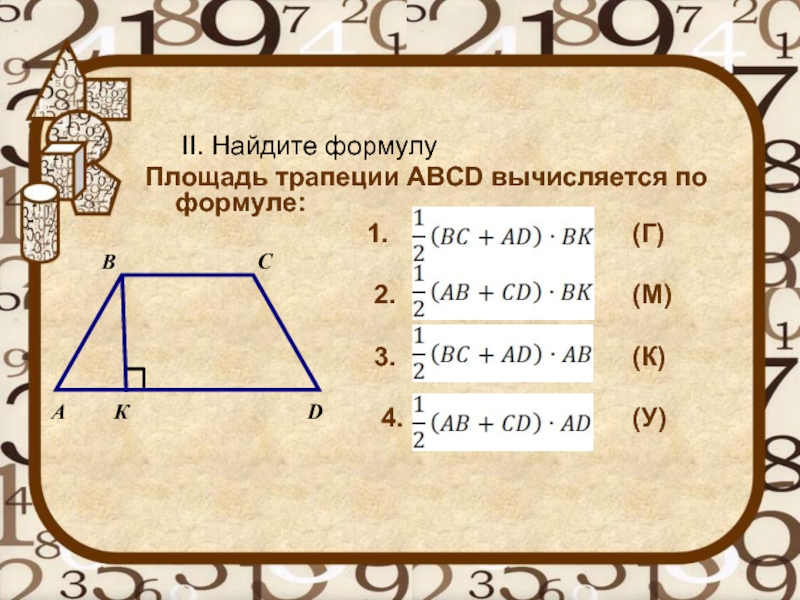

Пример задачи:
Дана плоская геометрическая фигура, параллельные стороны которой соответствуют длине 12 и 20 см, а высота равна – 10 см. Как найти площадь?

Решение:
Допустимое решение согласно вышеприведенной формуле S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 см².

Зная длину средней линии и высоту плоской фигуры, всегда можно найти площадь трапеции, выполнив буквально одно действие:

Где h – высота четырехугольника, а m – средняя линия (прямая, соединяющая середины боковых сторон).

Пример решения задачи:
Дана трапеция, в которой длина средней линии – 28 см, а высота фигуры – 19 см. Какова площадь плоского четырехугольника?

Решение:
Используя формулу S = hm, подставляем вместо букв цифровые значения из условия задачки. Получаем S = 28 х 19 = 532 см².

Этот метод не так прост, как предыдущие. Здесь взяты за основу основные теоремы геометрии, а потому принцип расчета площади трапеции выглядит следующим образом:

Где a, b, c, d – четыре стороны фигуры, причем сторона b в обязательном порядке должна быть длинней а.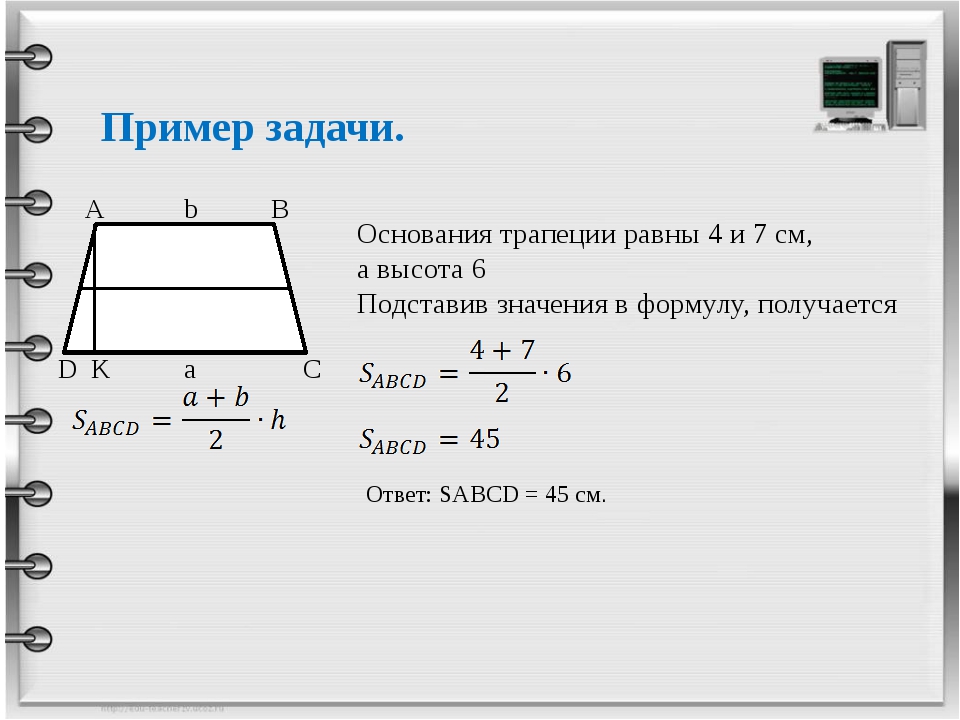

Пример вычисления:
Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?

Расчет:

Вычислить площадь трапеции также можно, зная размеры обеих диагоналей и значения угла между ними.

Обозначения: d₁ и d₂ — первая и вторая диагонали, α – угол между диагоналями.

Пример:
Вычислить площадь фигуры при следующих известных значениях — d₁ = 17 см, d₂ = 25 см, α = 35⁰.

Верное решение:
S = ½ х 17 х 25 х sin35 = 212,5 х 0,57 = 121,125 см².

Еще один вариант вычисления, основанный на расчете площади трапеции посредством длин двух оснований и двух углов.

Значения букв: b, a – длины оснований, α и β – углы.

Решение:

Обучающее видео

Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.

Видео «Трапеция: решение задач»

Видео для новичков – доходчиво изложенная информация, содержащая основные формулы вычисления площади трапеции.

Видео «Площадь трапеции»

Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.

Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.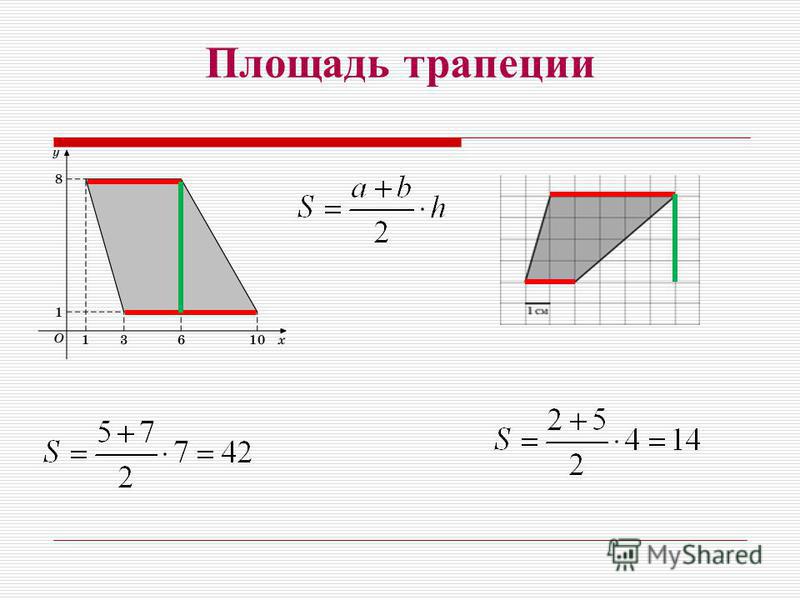

Как подготовиться к экзамену?

Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.

Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».

«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Добрый день, дорогие друзья! Сегодня у нас тема — трапеция решение задач по геометрии.
Прежде чем начинать разбирать задачи, давайте вспомним, что такое трапеция, и какие у неё есть элементы.

Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами.
Трапеции бывают прямоугольные, равнобедренные и простые.

В прямоугольных трапециях есть 2 прямых угла.
В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны.
В трапеции имеется средняя линия, которая соединяет середины боковых сторон.

А теперь задачи.

Острый угол равнобедренной трапеции равен 60°. Доказать, что основание ВС = AD — AB.

Доказательство.
Опустим из вершин трапеции высоты BM и CN на нижнее основание AD.
Получим два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника,
равен 30°.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы.
Т.е. АМ= с/2.
То же самое и в правом треугольнике — ND = с/2.
Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC, или верхнему основанию.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.

Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.
Основания трапеции равны AD и BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.

Решение:
На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции.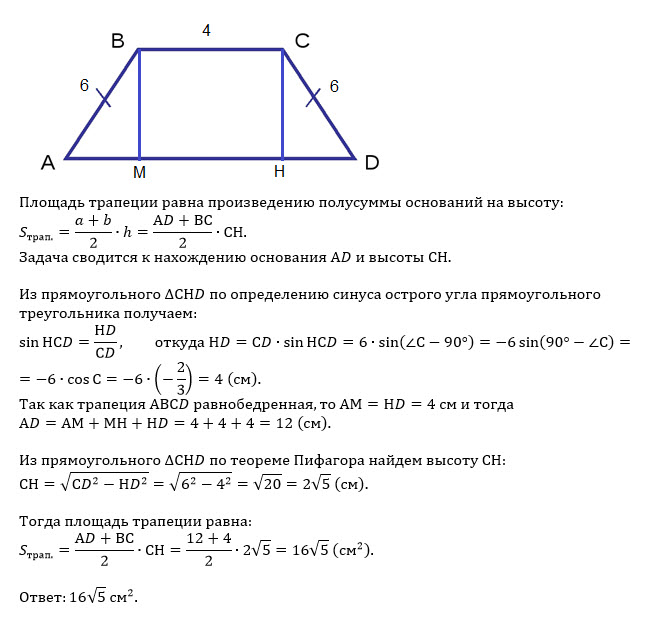
Средняя линия трапеции
, как мы знаем, равна полу-сумме оснований трапеции
, или (AD+BC)/2.
В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Отсюда, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.

Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции
.
Задача 3.
Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.

Решение:
Сделаем дополнительное построение. Проведём высоту ВМ.

Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету
— AB=CD, как боковые стороны равнобедренной трапеции.
Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми
.
Следовательно, AM=KD.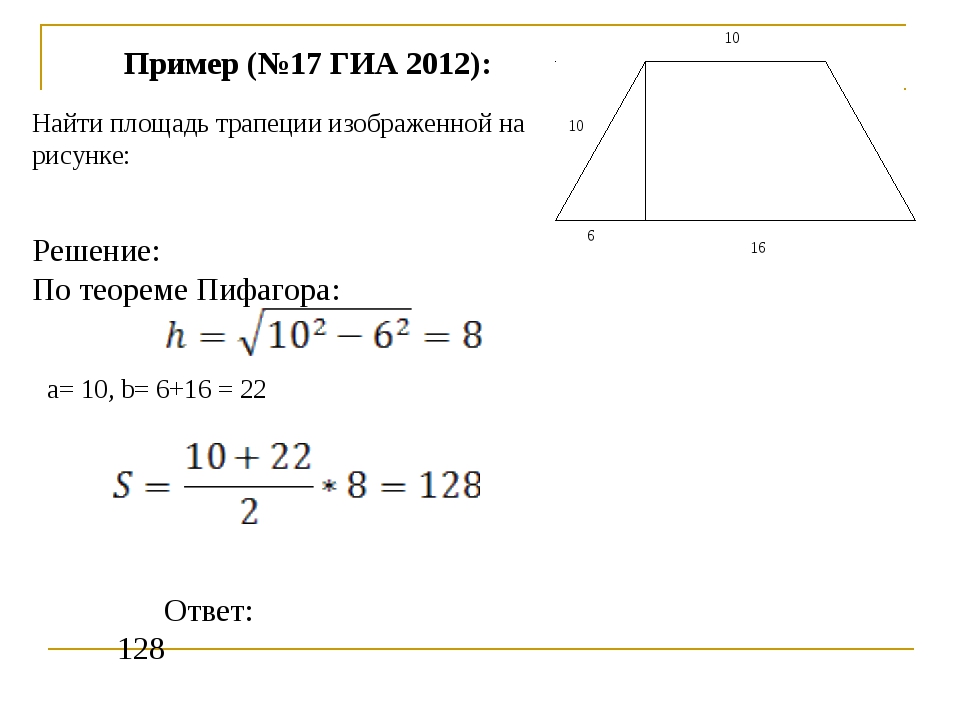 Получается, что разность между AK и KD равна разности между AK и AM.
А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник.
Отсюда меньшее основание трапеции равно 8 см.
Задача 4.
Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.

Решение:
Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам
.
По теореме Фалеса MN делит также и стороны AC и BD пополам.

Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна основанию и равна его половине
. Т.е. если MO=Х, то ВС=2Х.

Из треугольника ACD имеем ON — средняя линия.
Она тоже параллельна основанию и равна его половине.
Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х.

Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х.

Ответ: отношение оснований трапеции равно 1:2.
Поделитесь статьей с друзьями:
Похожие статьи

Площадь трапеции через синус угла и основания.

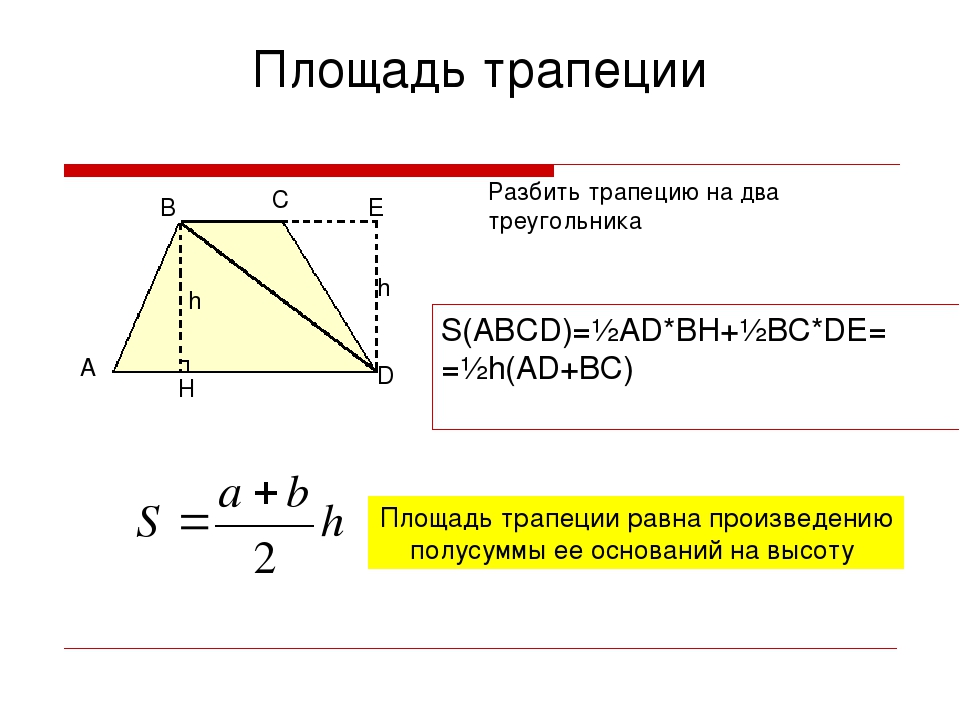Площадь трапеции

Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.

Трапеция. Определение, формулы и свойства

Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.

Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.

Примечание. В этом случае параллелограмм является частным случаем трапеции.

Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.

Трапеции бывают:

— разносторонние
;

— равнобокие
;

— прямоугольные

.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.

A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция

У разносторонней трапеции все стороны разной длины, а основания параллельны.

У боковые стороны равны, а основания параллельны.

У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.

Свойства трапеции

Средняя линия трапеции
параллельна основаниям и равна их полусумме
Отрезок, соединяющий середины диагоналей
, равен половине разности оснований и лежит на средней линии. Его длина
Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
Точка пересечения диагоналей трапеции
, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
Треугольники, лежащие на основаниях
трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Треугольники, лежащие на боковых сторонах
трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
В трапецию можно вписать окружность
, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Отрезок, параллельный основаниям
и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)

Углы трапеции

Углы трапеции бывают острые, прямые и тупые
.
Прямыми бывают только два угла.

У прямоугольной трапеции два угла прямые
, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.

Тупые углы трапеции принадлежат меньшему
по длине основанию, а острые – большему
основанию.

Любую трапецию можно рассматривать как усеченный треугольник
, у которого линия сечения параллельна основанию треугольника.
Важно
. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.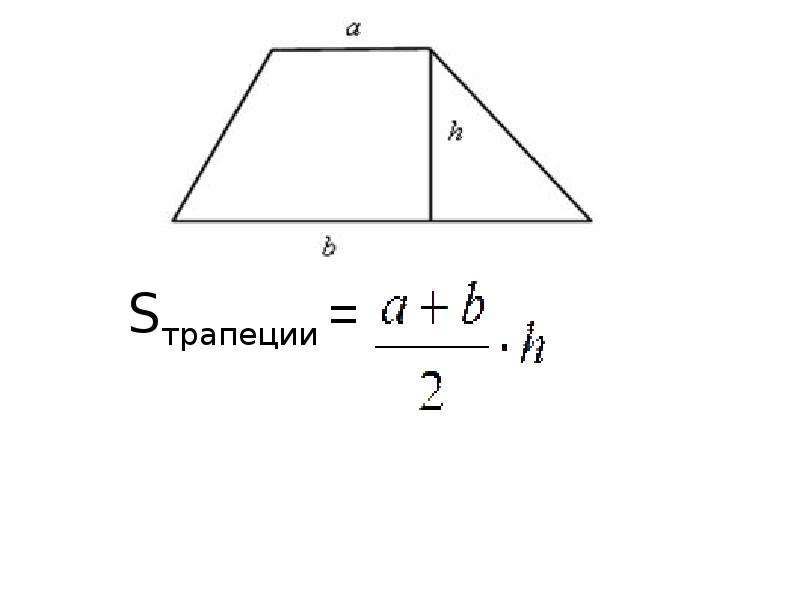

Как найти стороны и диагонали трапеции

Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:

В указанных формулах применяются обозначения, как на рисунке.

a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали

Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)

Прежде чем найти площадь трапеции, необходимо определится с известными элементами трапеции. Трапеция – это геометрический объект, а именно: четырёхугольник, который имеет две параллельные стороны (два основания). Другие две стороны – боковые. Если же параллельны будут и эти две стороны четырёхугольника, то это уже будет не трапеция, а параллелограмм. Если хотя бы один угол трапеции равен 90 градусов, то такая трапеция называется прямоугольной. Как найти площадь прямоугольной трапеции, рассмотрим позже.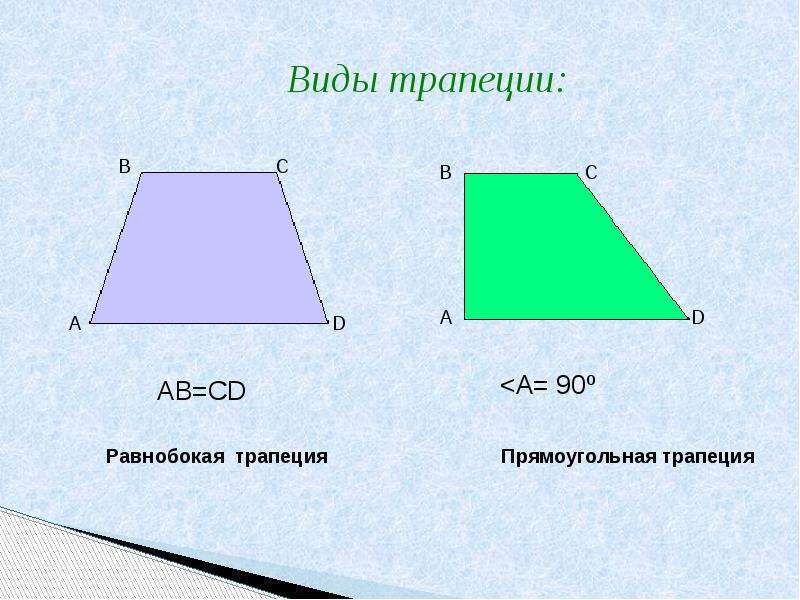 d2) – это синус угла, между диагоналями трапеции.

Существуют также различные формулы, выведенные из основных, а также формула для расчёта площади трапеции, когда известны все её стороны. Однако эта формула достаточно громоздкая и используется редко, ведь, зная все стороны трапеции можно просто определить высоту или её среднюю линию. Также в равнобедренную трапецию можно вписать окружность. В этом случае площадь трапеции будет высчитываться по формуле: 8*радиус окружности в квадрате.

Как найти площадь прямоугольной трапеции

Как и говорилось ранее, прямоугольной называется та трапеция, у которой хотя бы один угол прямой. Найти площадь такой трапеции очень просто. В основном, для поиска площади прямоугольной трапеции используются те же формулы, что и для обычной трапеции. Однако стоит помнить, что одна из боковых сторон такой трапеции и будет являться высотой. Также часто решение задач поиска площади прямоугольной трапеции сводится к поиску площади прямоугольника и треугольника, образованных опущенной высотой. Такие задачи достаточно просты.

, где DP – внешняя высота в

Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:

Вынесем за скобку

Что и требовалось доказать.

Следствие из формулы площади трапеции:

Так как полусумма оснований равна MN — средней линии трапеции, то

Спецприемы репетитора по математике.

Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:

Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.

Задачи на площадь трапеции:

Колпаков А.Н.
Репетитор по математике в Москве
, подготовка к ЕГЭ в Строгино
.

Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.

Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:

Площадь равнобокой трапеции

Помните, что диагонали равнобокой трапеции равны между собой!

То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.

Площадь криволинейной трапеции

Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.

Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:

Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.

Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

Средняя линия трапеции равна полусумме оснований и параллельна им.
У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.

Как найти площадь трапеции
.

Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:

где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.

Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.

Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.

Формула площади трапеции

В статье понятно и доступно разберем формулу площади трапеции, но для начала отработаем основные понятия!
Трапеция это геометрическая четырехугольная фигура, состоящая из двух параллельных линий называющихся основанием и двух боковых линии не являющиеся параллельными, называющиеся боковые стороны. Линия которая соединяет стороны как основные так и боковые посередине, называется — средней линией, высота выводится под углом 90⁰.
Площадью трапеции называется участок на плоскости, который ограничен данной фигурой, обозначается в единицах квадратных.

В случае если мы знаем величину средней линии k, формула меняется на более легкую, она приравнивается к половине суммы длины основных линий

В случае когда мы знаем длину всех сторон, можно рассчитать площадь используя данную формулу

Если разобрать данную формулу на примере, то мы получим следующее:
Рассмотрим для ясности: трапеция с длиной боковых линий х = 5 см, g = 4 см, основные линии y = 3 см, z = 7 см. Требуется найти S = ?.

Трапеция бывает однобокой, ещё ее называют равнобедренной — так как диагонали равны между собой. Для нее формула может складываться через радиус вписанной в нее окружности, диагонали и углы прилегающие к основанию.
В случае когда мы знаем длину диагоналей и угол находящийся между ними:

В том случае когда выводим формулу с помощью боковых сторон и углов прилегающих к основанию. Формула будет выглядеть так:

S = x * sin ?(y — x * cos ?)
S = x * sin ?(z + x * cos ?)

Вывод: Если нам известно одно основание из двух и величины углов принадлежащие этому основанию, мы без труда сможем узнать площадь трапеции.

Трапеция бывает криволинейной — это тогда, когда трапеция находится на оси координат, ограничена графиком продолжительной функции.

В случае когда основание трапеции находится на оси х и ограничено точками x1 = z, x2 = y. Вычислить площадь трапеции помогут интегралы

где F (z) — значение в точке z
F (y) — значение в точке y

Разберем для наглядности: Криволинейная трапеция, ограниченная функцией y = f(x). Функция F(x) = — x3 — 27×2 — 240x — 8. Нужно найти S = ?. Фигура ограничивается: графиком сверху y = f(x)., снизу ОХ осью, слева х = (-10), справа х = (-8).
Пользуемся данной формулой, получаем:

В условиях задачи дана функция. С помощью нее найдем значения точек.
1) F(-8) = -(-8)3 — 27 х (-8)2 — 240 х (-8) — 8 = 24-1728+1920 — 8 = 696
2) F(-10) = -(-10)3 — 27 х (-10)2 — 240 х (-10) — 8 = 1000-2700+240 — 8 = 692
3) F(-8) — F (-10) = 696 — 692 = 4
Ответ: S = 4

Вот собственно и всё по формулам площади для разных видов трапеций. Если у вас появились какие то вопросы, обязательно пишите их в комментариях. Успехов в учебе.
vamsochinenie.ru — база сочинений на самые разные темы.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Формула площади трапеции через четыре стороны. Все варианты того, как найти площадь трапеции

Трапеции обладают некоторыми интересными свойствами:

Средняя линия трапеции равна полусумме оснований и параллельна им.
У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.

Как найти площадь трапеции
.

где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

В этом случае площадь трапеции может быть найдена по формуле:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.

Геометрия трапеции

Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:

высота — расстояние между параллельными основаниями фигуры;
средняя линия — отрезок, соединяющий середины боковых сторон.

Данная геометрическая фигура широко распространена в реальной жизни.

Трапеция в реальности

В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:

дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
мода — форма одежды, обуви и аксессуаров;
архитектура — окна, стены, основания зданий;
производство — различные изделия и детали.

При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.

Периметр трапеции

Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:

P = a + b + c + d,

где a и c – основания фигуры, b и d – ее боковые стороны.

Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.

Примеры из реальной жизни

Платок

Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:

Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.

Откосы

К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде

Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.

Заключение

Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.

Этот калькулятор рассчитал 2192
задачи на тему «Площадь трапеции»

ПЛОЩАДЬ ТРАПЕЦИИ

Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:

Общая теория для вычисления площади трапеции.

Трапеция —

это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.

Точки называются вершинами трапеции

и обозначаются заглавными латинскими буквами.

Отрезки называются сторонами трапеции

и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.

Две параллельные стороны трапеции называются основаниями трапеции

.

Две не параллельные стороны трапеции называются боковыми сторонами трапеции

.

Рисунок №1: Трапеция ABCD

На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.

AB ǁ DC — основания трапеции ABCD.

AD, BC — боковые стороны трапеции ABCD.

Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.

Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.

Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.

Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.

Рисунок №2: Трапеция ABCD

На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.

Средняя линия трапеции
параллельна основаниям и равна их полусумме. То есть,.

Рисунок №3: Равнобедренная трапеция ABCD

На Рисунке №3, AD=BC.

Трапеция называется равнобедренной (равнобокой)
, если ее боковые стороны равны.

Рисунок №4: Прямоугольная трапеция ABCD

На Рисунке №4 угол D — прямой (равен 90 о).

Трапеция называется прямоугольной,
если угол при боковой стороне прямой.

Площадью S плоской
фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.

Площадь обладает несколькими свойствами:

1. Она не может быть отрицательной.

2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.

3. Если две фигуры равны, то и площади их равны.

4. Площадь квадрата, который построен на единичном отрезке, равна единице.

За единицу
измерения
площади
принимают площадь квадрата, сторона которого равна единице
измерения
отрезков.

При решении задач часто используются следующие формулы вычисления площади трапеции:

1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:

2. Площадь трапеции равна произведению ее средней линии на высоту:

3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:

4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:

Пример 1:
Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.

Решение:

Ответ:

Пример 2:
Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.

Решение:

Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:

Выразим из данной формулы сторону основания трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 3:
Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.

Решение:

Для нахождения высоты трапеции воспользуемся формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Пример 4:
Вычислить площадь трапеции с высотой h=24 и средней линией m=5.

Решение:

Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Пример 5:
Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.

Решение:

Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:

Выразим из данной формулы высоту трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 6:
Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.

Решение:

Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:

Выразим из данной формулы среднюю линию трапеции:

Таким образом, имеем следующее.

Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.

Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:

Площадь равнобокой трапеции

Помните, что диагонали равнобокой трапеции равны между собой!

То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.

Площадь криволинейной трапеции

Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.

Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:

Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.

Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.

Определяем трапецию

Свойства трапеции

Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!

Самые простые формулы площади трапеции

S = h*(a + b)/2.

Рассмотрим пример.

Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?

Использование диагоналей для вычислений

S = ½ d 1 d 2 sina.

Ищем площадь равнобокой трапеции

S = c
*sin a
*(a
— c
*cos a
),

где с
— боковое бедро, a
— угол при нижнем основании.

Находим площадь прямоугольной трапеции

Применяем смекалку

Используем формулу Пика

S = M/2 + N — 1,

Геометрия

— есть ли формула для расчета площади трапеции, зная длину всех ее сторон?

Эта проблема более тонкая, чем показывают некоторые другие ответы здесь. Многое зависит от того, определяется ли «трапеция» включительно (т.е. четырехугольник с как минимум одной парой параллельных сторон ) или исключительно (т.е. четырехугольник с ровно с одной парой параллельных сторон ). Первое определение широко считается более сложным с математической точки зрения, но второе определение более традиционное, до сих пор широко используется в системе образования до 12 лет в Соединенных Штатах и имеет некоторые преимущества.

Как указывалось в других ответах, если определить «трапецию» включительно, то любой параллелограмм автоматически станет трапецией, и, поскольку длины сторон параллелограмма не определяют его площадь, это невозможно (даже теоретически), чтобы там может быть формулой для площади трапеции через длину ее сторон.

Однако, если «трапеция» определяется как исключительно как , тогда все обстоит совсем иначе. Рассмотрим трапецию с параллельными основаниями длины $ a $ и $ b $ с $ b> a $.2} $$
Однако я не уверен, есть ли более простое выражение.

Математическое выражение: Площадь трапеции

00: 00: 03.150
В этом уроке мы узнаем о площади трапеции.

00: 00: 08.030
Сначала давайте рассмотрим эту трапецию с высотой «h» и двумя параллельными сторонами «a» и «b» соответственно.

00: 00: 17.140
Теперь, чтобы найти площадь трапеции A, сначала складываем «a» и «b» и делим добавленные числа на 2.

00: 00: 27.010
Это дает (a + b) / 2. Затем мы умножаем (a + b) / 2 на высоту трапеции «h».

00: 00: 38.070
Таким образом, теперь у нас есть формула для площади трапеции: A = ((a + b) / 2) h.

00: 00: 47.240
Обратите внимание, что очень важно указать единицу измерения. Поскольку это формула для площади, ее единицей будет квадрат.

00: 00: 57.020
Мы увидим больше объяснений этого в следующем примере.

00:01:02.040
Теперь давайте посмотрим на несколько примеров использования этой формулы.

00: 01: 07.030
Найдите площадь этой трапеции, когда ее высота равна 4 см, а параллельные стороны равны 5 см и 9 см соответственно.

00: 01: 17.080
Сначала мы начнем с формулы для площади трапеции, A = ((a + b) / 2) h.

00: 01: 26.080
Поскольку более короткая параллельная сторона задана как 5 см, мы можем заменить ‘a’ на 5.

00: 01: 33.150
Аналогичным образом, поскольку более длинная параллельная сторона задана как 9 см, мы можем заменить ‘b’ с 9.

00: 01: 41.230
Затем мы можем упростить, добавив 5 к 9. Это дает 14.

00: 01: 48.110
14 делится на 2, дает 7.

00: 01: 52.200
Теперь, поскольку высота задана как 4 см, мы можем заменить h на 4.

00: 01: 59.120
Умножение 7 на 4 дает 28.

00: 02: 03.180
Обратите внимание, что это число не имеет значения, если мы включите для него блок.

00: 02: 08.160
Поскольку стороны трапеции указаны в сантиметрах, единицей измерения площади будет квадрат

сантиметр.00: 02: 15.160
Следовательно, площадь трапеции составляет 28 квадратных сантиметров.

00: 02: 23.050
Следующий пример, учитывая, что площадь этой трапеции составляет 9 квадратных футов, а ее параллельные стороны составляют 2 фута и 4 фута соответственно. Найдите его высоту.

00: 02: 34.200
И снова мы начнем с формулы для площади трапеции: A = ((a + b) / 2) h.

00: 02: 44.040
Теперь, поскольку заданы площадь и 2 параллельные стороны, мы можем найти высоту, решив это уравнение для h.Вот как.

00: 02: 53.240
Поскольку площадь задана как 9 квадратных футов, мы можем заменить букву A на 9,

00: 03: 00.100
Точно так же, поскольку более короткая параллельная сторона задана как 2 см, мы можем заменить ‘a’ на 2.

00: 03: 08.100
Опять же, поскольку длинная параллельная сторона задана как 4 см, мы можем заменить ‘b’ на 4.

00: 03: 16.150
Мы можем упростить это уравнение, сложив 2 с 4. Это дает 6. 6, разделенное на 2, дает 3.

00: 03: 27.130
(3) h то же самое, что и 3h.

00: 03: 32.010
Теперь у нас 3h равно 9.

00: 03: 36.140
Давайте перепишем это уравнение, чтобы оно выглядело аккуратнее.

00: 03: 40.190
Чтобы найти ‘h’, нам нужно удалить 3. Мы можем сделать это, разделив обе части уравнения на 3.

00: 03: 49.040
Таким образом, мы получим ‘h ‘равно 9 над 3.

00: 03: 54.170
9 делится на 3, дает 3.

00: 03: 58.190
Теперь это число не имеет смысла, если мы не включим его единицу.

00: 04: 03.110
Поскольку параллельные стороны даны в футах, высота трапеции будет в футах.

00: 04: 09.120
Следовательно, высота этой трапеции составляет 3 фута.

00: 04: 15.010
Это все для этого урока. Попробуйте ответить на практический вопрос, чтобы углубить свое понимание.

Площадь трапеций — Концепция

Формула площади трапеции находится путем построения параллелограмма, состоящего из двух совпадающих трапеций.Для этого скопируйте трапецию, поверните копию на 180 градусов и переместите, чтобы создать параллелограмм. Площадь параллелограмма равна основанию, умноженному на соответствующую высоту; поскольку есть две трапеции, формула трапеций должна быть разделена пополам. Поскольку основания не совпадают, их необходимо суммировать отдельно.

Чтобы найти площадь любой трапеции, мы должны начать с того, что мы знаем.Мы знаем, что площадь любого параллелограмма равна основанию, умноженному на соответствующую высоту или высоту. Что ж, с трапецией у нас есть только одна пара параллельных оснований. Итак, я собираюсь обозначить эти основания 1 и 2 разными числами ниже, потому что они определенно не будут совпадать. Допустим, я знал высоту между этими двумя базами. Какой будет район? Или как бы мы вычислили площадь, исходя из того, что мы знаем?
Хитрость здесь в том, чтобы взять эту трапецию, продублировать ее в своей голове и повернуть на 180 градусов.Итак, что я собираюсь сделать, я собираюсь перерисовать эту трапецию, хотя я дублирую ее, поворачивая на 180 градусов и перемещая, и я собираюсь нарисовать ее с той стороны. Итак, я сказал, что у нас есть база 1 внизу, потому что мы повернулись на 180 градусов. Здесь основание 2, и у нас такая же высота. Если посмотреть на это, становится ясно, что у нас будет параллелограмм. То, что нам известно.
Итак, я собираюсь подойти сюда и напишу, что площадь нашего параллелограмма, которую я собираюсь обозначить как «пара», равна двукратной площади трапеции.
Теперь, почему я должен сказать, что площадь этого параллелограмма равна двукратной площади трапеции? Ну сколько у нас трапеций? У нас есть 2 трапеции. Итак, если я хочу узнать, какова площадь трапеции, потому что я знаю, как вычислить площадь параллелограмма, мне придется разделить это уравнение на 2. Итак, я скажу, что 2 делятся. на 2 равно 1, а площадь трапеции равна площади этого параллелограмма, разделенной пополам. Итак, как мы можем найти площадь этого параллелограмма?
Что ж, давайте начнем с того, что скажем, что является нашей базой, и я собираюсь взять здесь маркер другого цвета, и если у нас есть наша высота, у нас есть соответствующая база, которая тянется от конца до конца.И если этот кусок равен b1, и если этот кусок равен b2, то все расстояние здесь равно b1 плюс b2. Поэтому вместо того, чтобы писать область параллелограмма, я собираюсь написать базу, которая равна b1 плюс b2, я собираюсь записать это в скобках, умножая на любую нашу высоту. И мы знаем, какой у нас рост, это будет h. Нам это дано. И мы должны разделить это пополам и сказать, что это равно площади нашей трапеции.
Так что это было неплохо. Все, что нам нужно было сделать, это сказать: возьмите вашу трапецию, продублируйте ее, поверните, переместите.Вы создали параллелограмм и знаете формулу площади параллелограмма.
Уловка здесь заключалась в осознании того, что эта база прямо здесь или ваша, любая из ваших баз равна b1 плюс b2. Итак, формула площади для трапеции — это количество b1 плюс b2, вы собираетесь суммировать эти основания, умноженные на ваш рост, разделенные на 2.

Площадь трапеции

Этот урок покажет вам, как найти площадь трапеции двумя разными способами.

Разрезание трапеции и перестановка частей так, чтобы получились прямоугольник и треугольник.
Использование формулы для определения площади трапеций.

Первый метод поможет вам понять, почему работает формула для определения площади трапеций. Приступим! Разрежьте трапецию на три части и сделайте из
прямоугольник и треугольник.

Затем нам нужно сделать следующие четыре важных наблюдения.

Прямоугольник

Основание = 4
Высота = 8

Трапеция

Длина нижнего основания = 13
Длина верхнего основания = 4
Высота = 8

3.

Новый треугольник (с синими и оранжевыми линиями)

Длина основания = 9 = 13 — 4 = длина нижнего основания трапеции — 4
Высота = 8

Площадь трапеции = площадь прямоугольника + площадь вновь образованного треугольника.

Теперь наша стратегия будет заключаться в том, чтобы вычислить площадь прямоугольника и площадь вновь образованного треугольника и посмотреть, сможем ли мы волшебным образом создать формулу для нахождения площади трапеции.

Площадь прямоугольника = основание × высота = 4 × 8

Площадь треугольника = (основание × высота) / 2

Площадь треугольника = [(13 — 4) × 8] / 2 = [13 × 8 + — 4 × 8] / 2

Площадь треугольника = (13 × 8) / 2 + (- 4 × 8) / 2

Площадь трапеции = 4 × 8 + (13 × 8) / 2 + (- 4 × 8) ) / 2

Площадь трапеции = 8 × (4 + 13/2 + — 4/2)

Площадь трапеции = 8 × (4 — 4/2 + 13/2)

Площадь трапеции = 8 × (8/2 — 4/2 + 13/2)

Площадь трапеции = 8 × (4/2 + 13/2)

Площадь трапеции = (4/2 + 13/2) × 8

Площадь трапеции = 1/2 × (4 + 13) × 8

Пусть b ₁ = 4, пусть b ₂ = 13, и пусть h = 8

Тогда формула для получения площади трапеции равна до 1/2 × (b ₁ + b ₂) × h

Формула для определения площади трапеции

В общем случае, если b ₁ и b ₂ являются основаниями трапеции, а h — высотой трапеции, то мы можем использовать формулу ниже.

Примеры, показывающие, как найти площадь трапеции по формуле

Пример № 1:

Если b ₁ = 7 см, b ₂ = 21 см и h = 2 см, найдите A

Площадь = 1/2 × (b ₁ + b ₂) × h = 1/2 × (7 + 21) × 2 = 1/2 × (28) × 2

Площадь = 1/2 × 56 = 28 см ²

Пример № 2:

Если b ₁ = 15 см, b ₂ = 25 см и h = 10 см, найдите A

Площадь = 1/2 × (b ₁ + b ₂) × h = 1/2 × (15 + 25) × 10 = 1/2 × (40) × 10

Площадь = 1/2 × 400 = 200 см ²

Пример № 3:

Если b ₁ = 9 см, b ₂ = 15 см и h = 2 см, найдите A

Площадь = 1/2 × (b ₁ + b ₂) × h = 1/2 × (9 + 15) × 2 = 1/2 × (24) × 2

Площадь = 1/2 × 48 = 24 см ²

Область викторины, посвященной трапеции, чтобы узнать, действительно ли вы понимаете этот урок.

Купить полную электронную книгу геометрических формул. Все геометрические формулы объясняются хорошо подобранными текстовыми задачами, так что вы можете освоить геометрию.

Площадь трапеции — формула, примеры, определение

Трапеция — это четырехугольник с одной парой параллельных сторон (которые называются основаниями). Это означает, что другая пара сторон может быть непараллельной (так называемые ножки).Площадь трапеции — это количество единичных квадратов, которые могут быть помещены в нее, и измеряется в квадратных единицах (например, см ², м ², в ² и т. Д.). Например, если внутри трапеции можно уместить 15 квадратов длиной 1 см каждый, то ее площадь составит 15 см ².

Не всегда можно нарисовать единичные квадраты и измерить площадь трапеции. Существует формула для определения площади трапеции, которую мы собираемся изучить на этой странице.

Площадь Формулы трапеции

Чтобы найти площадь трапеции, достаточно знать длины двух ее параллельных сторон и расстояние (высоту) между ними.Площадь (A) трапеции с основаниями a и b и высотой h (перпендикулярное расстояние между a и b) составляет

A = ½ (a + b) h

Пример

Найдите площадь трапеции, основания которой 32 см и 12 см, а высота 5 см.

Решение

Основания a = 32 см; б = 12 см.

Высота h = 5 см.

Площадь трапеции,

A = ½ (a + b) h

A = ½ (32 + 12) (5) = ½ (44) (5) = 110 см ².

Как получить формулу площади трапеции?

Мы можем доказать формулу для определения площади трапеции двумя способами:

Доказательство параллелограммом
Доказательство с помощью треугольника

Мы увидим доказательство площади формулы трапеции с помощью треугольника. Рассмотрим указанную выше трапецию оснований a и b и высоту h. Чтобы доказать формулу,

Разделите одну из ножек на две равные части
Вырежьте треугольную часть трапеции (как показано ниже на верхнем рисунке схемы ниже)
Прикрепите его снизу (как показано на нижнем рисунке схемы ниже)

Таким образом, трапеция преобразуется в треугольник.Из приведенной выше диаграммы легко видно, что площади трапеции и треугольника одинаковы. Кроме того, мы можем видеть, что основание треугольника равно (a + b), а высота треугольника равна h.

Площадь трапеции = Площадь треугольника

Площадь трапеции = ½ × основание × высота = ½ (a + b) h

Таким образом, мы доказали формулу нахождения площади трапеции. Перейдем к решению нескольких примеров на основе площади трапеции.

Часто задаваемые вопросы о площади трапеции

Как найти площадь трапеции?

Площадь трапеции определяется по формуле A = ½ (a + b) h, где ‘a’ и ‘b’ — основания (параллельные стороны), а ‘h’ — высота (перпендикулярное расстояние между основания) трапеции.

Почему площадь трапеции ½ (a + b) h?

Рассмотрим трапецию с основаниями «a» и «b» и высотой «h». Мы можем вырезать часть треугольной формы из трапеции и прикрепить ее внизу так, чтобы вся трапеция превратилась в треугольник. Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации вы можете обратиться к разделу Как получить формулу трапеции? раздел этой страницы.

Как найти недостающую основу трапеции, если вы знаете местность?

Площадь трапеции с основаниями «a» и «b» и высотой «h» равна A = ½ (a + b) h. Если даны одно из оснований (скажем, ‘a’), высота и площадь, то мы просто подставим эти значения в приведенную выше формулу и решим это для недостающего основания (a) следующим образом:

A = ½ (a + b) h

Умножение обеих сторон на 2,

2А = (а + б) ч

Делим обе стороны на h,

2А / ч = а + б

Вычитая b с обеих сторон,

а = (2А / ч) — б

Как определить высоту трапеции с учетом площади и основания?

Площадь трапеции с основаниями «a» и «b» и высотой «h» равна A = ½ (a + b) h.Мы можем найти высоту трапеции с площадью и основаниями, решив приведенную выше формулу для h следующим образом:

A = ½ (a + b) h

Умножение обеих сторон на 2,

2А = (а + б) ч

Делим обе стороны на (a + b),

h = (2A) / (a + b).

Какова площадь равнобедренной трапеции со сторонами?

Если даны длины сторон равнобедренной трапеции, то мы разделим ее на два равнобедренных прямоугольных треугольника и прямоугольник.Мы находим площади каждой из этих фигур и складываем их, что дает площадь данной трапеции. Вы можете увидеть это подробно в Примере 2 в разделе «Решенные примеры» на этой странице.

Какова площадь трапеции с координатами?

Если даны координаты вершин трапеции, то мы можем найти длины ее оснований ‘a’ и ‘b’, используя формулу расстояния. Чтобы найти высоту h (расстояние по перпендикуляру между основаниями), мы можем использовать перпендикулярное расстояние от точки до формулы линии (для этого нам нужно найти уравнение линии для одного из оснований).2}} \).

Затем мы можем применить формулу A = ½ (a + b) h, чтобы найти площадь трапеции.

Как найти площадь равнобедренной трапеции без высоты?

Если высота трапеции не указана, а вместо нее указаны все ее стороны, то мы разделим ее на два равных прямоугольных треугольника и прямоугольник. Мы находим площади каждой из этих фигур и складываем их, что дает площадь данной трапеции. Вы можете увидеть это подробно в Примере 2 в разделе «Решенные примеры» на этой странице.

Формулы площади и формулы периметра

Формулы площади и формулы периметра — это формулы, которые часто появляются при выполнении различных домашних заданий. Примеры включают проблемы, связанные с давлением, механическим крутящим моментом и электрическим сопротивлением. Вы можете просто запомнить эти формулы, но зачем это делать, когда доступна эта удобная справочная информация?

Формула площади треугольника и формула периметра треугольника

Треугольник — это фигура, образованная тремя соединенными сторонами. Периметр — это сумма длин сторон.«Высота» (h) треугольника — это самая высокая точка, противоположная стороне, выбранной вами в качестве основания.

Периметр треугольника = a + b + c

Площадь треугольника = ½b · h

Формула площади параллелограмма и формула периметра параллелограмма

Параллелограмм представляет собой замкнутую фигуру, образованную четырьмя сторонами а противоположные стороны параллельны друг другу. «Высота» (h) параллелограмма — это расстояние от измеряемой стороны до его противоположной параллельной стороны.

Периметр параллелограмма = 2a + 2b

Площадь параллелограмма = b ⋅ h

Формула площади прямоугольника и формула периметра прямоугольника

Внутренний параллелограмм — это внутренний прямоугольник. все прямые углы.

Периметр прямоугольника = 2H + 2W

Площадь прямоугольника = H · W

Формула площади квадрата и формула периметра квадрата

Квадрат — это прямоугольник особого типа, состоящий из четырех стороны равной длины.

Периметр квадрата = 4s

Площадь квадрата = s ²

Формула площади трапеции и формула периметра трапеции

Трапеция — еще один особый четырехугольник (четырехугольник) где две стороны параллельны. «Высота» (h) трапеции — это расстояние между двумя параллельными сторонами.

Периметр трапеции = a + b ₁ + b ₂ + c

Площадь трапеции = ½ (b ₁ + b ₂) · h

904 Формула площади эллипса и формула периметра эллипса

Эллипс — это замкнутая фигура, на которой трассируется путь, когда сумма расстояний между двумя фиксированными точками является постоянной.Малая полуось овала — это кратчайшее расстояние от центра эллипса (r ₁), а большая полуось (r ₂) — самое длинное расстояние от центра.

Периметр эллипса

На самом деле вычислить периметр эллипса непросто. Если большая и малая полуоси примерно одинакового размера (в пределах 3x длины друг друга), периметр можно приблизительно определить по формуле:

Более точное приближение можно определить с помощью этого выражения:

точное решение может быть вычислено с помощью бесконечного ряда.Сначала вам нужно рассчитать эксцентриситет эллипса по формуле

Затем используйте это значение в выражении

Хотя формула периметра сложна, формула площади проста.

Площадь эллипса = πr ₁ r ₂

Формула площади круга и формула периметра круга

Окружность — это особый эллипс, в котором большая и малая полуоси имеют одинаковый размер.Все точки находятся на одинаковом расстоянии от центра. Это расстояние называется радиусом. Расстояние через самую широкую точку круга называется диаметром.

Периметр круга также известен как окружность.

Периметр круга = 2πr = πd

Площадь круга = πr ²

Формула площади шестиугольника и формула периметра шестиугольника

Правильный шестиугольник, где шестигранник каждая из сторон имеет одинаковую длину.Длина этих сторон равна расстоянию от центра до самой широкой точки шестиугольника.

Периметр шестиугольника = 6r

Площадь шестиугольника = (3√3) / 2 ⋅ r ²

Формула площади восьмиугольника и формула периметра восьмиугольника

восьмиугольная фигура с равной длиной сторон.

Периметр восьмиугольника = 8a

Площадь восьмиугольника = (2 + 2√2) a ²

Определение площади трапеции

Площадь трапеции равна половине ее высоты, умноженной на сумму длин двух ее оснований.

A = (1/2) h (b ₁ + b ₂)

Просматривая историю античного периода, а также средневековья, мы действительно находим упоминания статистики во многих странах .

Связь между параллелограммом и трапецией

Обратите внимание, что две копии одной и той же трапеции соединяются вместе, образуя параллелограмм. Высота параллелограмма равна высоте трапеции.

Длина основания параллелограмма равна сумме длин двух оснований (b₁ и b₂ ) трапеции.

Итак, площадь трапеции равна половине площади параллелограмма.

Примеры

Пример 1:

Часть настила имеет форму трапеции. Какова площадь этой секции

Решение:

Площадь трапеции:

= (1/2) h (b ₁ + b ₂)

Заменить b ₁ = 17, b ₂ = 39 и h = 16.

= (1/2) x 16 (17 + 39)

= 8 (56)

= 448 футов ²

Пример 2:

Длина одного основания трапеции составляет 27 футов , а длина другой базы — 34 фута. Высота 12 футов. Какая у него площадь?

Решение:

Площадь трапеции:

= (1/2) h (b ₁ + b ₂)

Заменить b ₁ = 27, b ₂ = 34 и h = 12.

= (1/2) x 12 (34 + 27)

= 6 (61)

= 366 футов ²

Пример 3:

Саймон говорит, что для определения площади трапеции , вы можете умножить высоту на верхнее основание и высоту на нижнее основание. Затем сложите два продукта и разделите сумму на 2. Прав ли Саймон? Поясните свой ответ.

Решение:

Да

Саймон использует свойство распределения, чтобы умножить каждое основание на высоту.Затем он находит, что умножение суммы BY на 1/2 аналогично делению на 2.

Пример 4:

Высота трапеции составляет 8 дюймов, а ее площадь — 96 квадратных дюймов. Одно основание трапеции на 6 дюймов длиннее другого. Какова длина оснований?

Решение:

Пусть «a» и «b» будут основаниями трапеции.

Одно основание трапеции на 6 дюймов длиннее другого основания.

Тогда

b ₁ = b ₂ + 6

Площадь трапеции = 96 дюймов ²

(1/2) h (b ₁ + b ₂) = 96

Заменить h = 8 и b ₁ = b ₂ + 6.

(1/2) x 8 (b ₂ + 6 + b ₂) = 96

4 (2b ₂ + 6) = 96

Разделите каждую сторону на 4.

2b ₂ + 6 = 24

Вычтем по 2 с каждой стороны.

2b ₂ = 18

Разделим каждую сторону на 2.

b ₂ = 9

Тогда

b ₁ = b ₂ + 6

b ₁ = 9 + 6

b ₁ = 15

Итак, длина оснований составляет 15 дюймов, а также см и 9 дюймов.

Помимо того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебра

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word по сложным процентам

ngles

Проблемы со словами с дополнительными и дополнительными углами

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейными неравенствами

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращения в процентах

Сокращения в таблице времен

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Домен и диапазон рациональных функций

Домен и диапазон рациональных функций функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Нахождение квадратного корня с использованием длинного di видение

Л.Метод CM для решения задач времени и работы

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении степени 17 на 16 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6