Содержание
Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.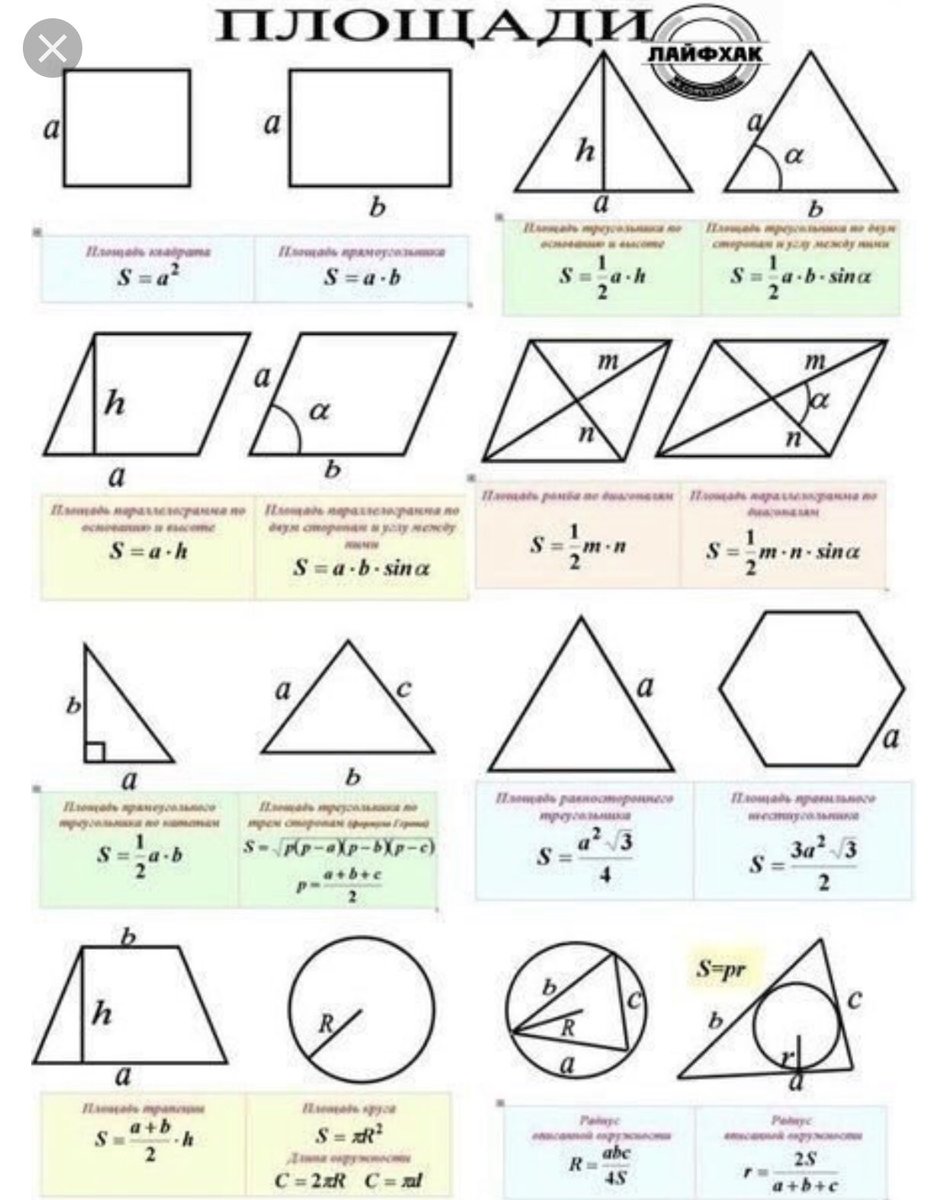
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .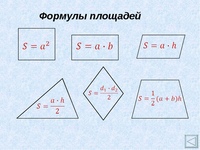
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4.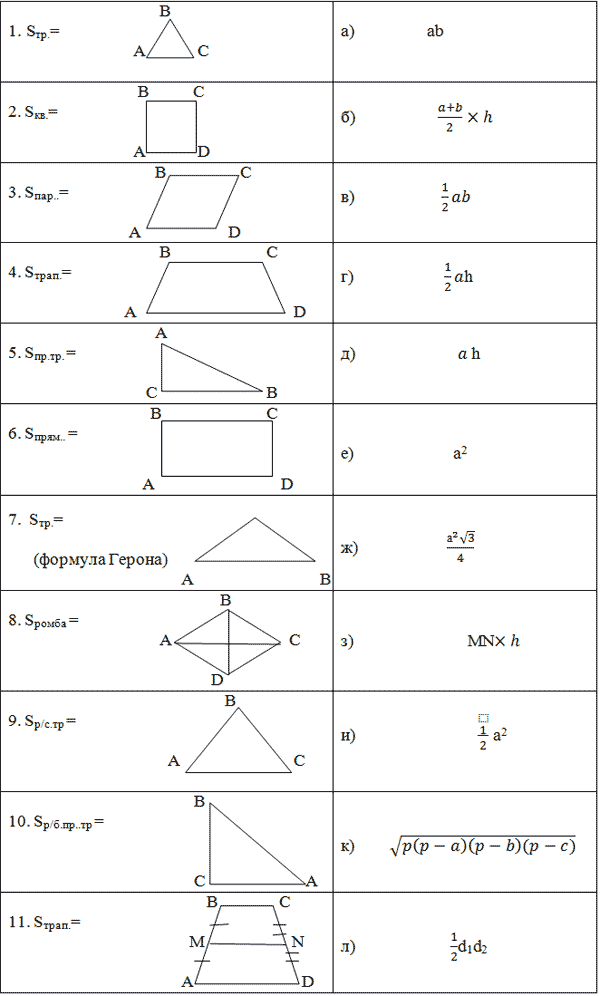 Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Формула вычисления площади для всех геометрических фигур
Стандартное обозначение площади — S
Площадь
Пусть длина стороны квадрата равна a, тогда формул квадрата:
S = a ⋅ a = a2
Прямоугльник
Пусть длины сторон прямоугольника равны a и b
S = a ⋅ b
Параллелограмм
Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
S = a ⋅ ha = b ⋅ hb
Трапеция
Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). 2\cdot \text{ctg}(\frac{\pi}{n})$
2\cdot \text{ctg}(\frac{\pi}{n})$
n — число ребер(вершин).
$\pi=3,14159265359$
Как найти площадь фигуры? Ответ на webmath.ru
Содержание:
Определения
Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.
Определение
Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.
Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее
площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение
площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.
Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и
вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю. {2}$$
{2}$$
Читать дальше: формула площади круга и примеры решений →
Площадь квадрата
Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть
Читать дальше: формула площади квадрата и примеры решений →
Площадь прямоугольника
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть
Читать дальше: формула площади прямоугольника и примеры решений →
Площадь параллелограмма
Чтобы найти площадь параллелограмма, нужно найти произведение стороны
$a$ параллелограмма на высоту
, проведенную к этой стороне, то есть
Читать дальше: формулы площади параллелограмма и примеры решений →
Площадь трапеции
Чтобы найти площадь трапеции, нужно длину средней линии
умножить на длину высоты
, опущенной к основанию:
Читать дальше: формулы площади трапеции и примеры решений →
Площадь ромба
Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:
Читать дальше: формулы площади ромба и примеры решений →
Площадь эллипса
Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число
$\pi$, то есть
Читать дальше: формула площади эллипса и примеры решений →
Все формулы по геометрии.
 Задача в3: площади фигур
Задача в3: площади фигур
Больше
половины всех задач В3 из вариантов ЕГЭ
— это задачи, в которых надо посчитать
площадь фигуры. Чтобы решить их, надо
знать формулы по геометрии — такие, как
площадь треугольника или площадь
параллелограмма — а также простые
приёмы, о которых мы расскажем.
Для
начала стоит выучить формулы площадей
фигур. Мы специально собрали их в удобную
таблицу. Распечатайте, выучите и
применяйте!
Конечно
же, не все формулы по геометрии есть в
нашей таблице. Например, для решения
задачи С4 применяются и другие формулы
площади треугольника. О них мы обязательно
расскажем.
А
что делать, если надо найти не площадь
трапеции или треугольника, а площадь
какой-либо сложной фигуры? Есть
универсальные способы! Покажем их на
примерах из банка заданий ФИПИ.
Как
найти площадь нестандартной фигуры?
Например, произвольного четырёхугольника?
Простой приём — разобьём эту фигуру
на такие, о которых мы всё знаем, и найдем
её площадь — как сумму площадей этих
фигур.
Разделим
этот четырёхугольник горизонтальной
линией на два треугольника с общим
основанием, равным 5. Высоты этих
треугольников равны 2 и 3. Тогда площадь
четырёхугольника равна сумме площадей
двух треугольников:
S
= 5 + 7,5 = 12,5.
Ответ:
12,5.
В
некоторых случаях площадь фигуры можно
представить как разность каких-либо
площадей.
Не
так-то просто посчитать, чему равны
основание и высота в этом треугольнике!
Зато мы можем сказать, что его площадь
равна разности площадей квадрата со
стороной 5 и трёх прямоугольных
треугольников. Видите их на рисунке?
Получаем:
S
= 25 – 5 – 5 – 4,5 = 10,5.
Ответ:
10,5.
Иногда
в задании В3 надо найти площадь не всей
фигуры, а её части. Обычно речь здесь
идет о площади сектора — части круга.
Найдите
площадь сектора круга радиуса 1, длина
дуги которого равна 2.
На
этом рисунке мы видим часть круга.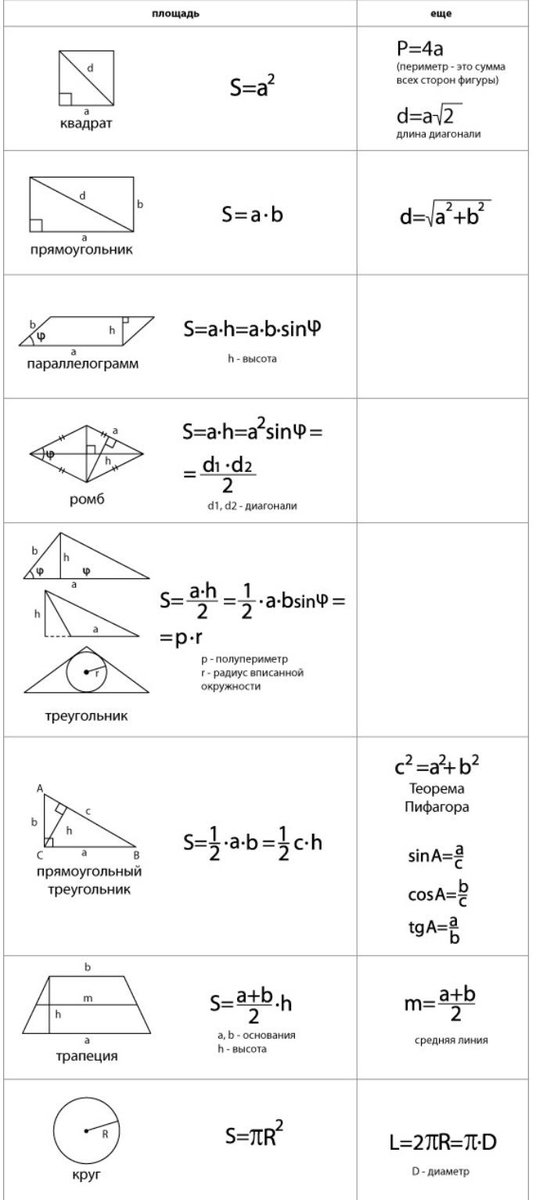
Площадь всего круга равна πR² = π, так
как R=1. Остается узнать, какая часть
круга изображена. Поскольку длина всей
окружности равна 2πR = 2π (так как R=1), а
длина дуги данного сектора равна 2,
следовательно, длина дуги в π раз меньше,
чем длина всей окружности. Угол, на
который опирается эта дуга, также в π
раз меньше, чем полный круг (то есть 360
градусов). Значит, и площадь сектора
будет в π раз меньше, чем площадь всего
круга.
Ответ:
1.
И
ещё примерно половина прототипов задачи
В3 — это простые задачи на тему «Координаты
и векторы». Для их решения вспомните,
что такое абсцисса точки (это ее координата
по Х) и что такое ордината (координата
по Y). Пригодятся также такие понятия,
как координаты вектора и длина вектора
(она находится по теореме Пифагора),
синус и косинус угла, угловой коэффициент
прямой, уравнение прямой, а также сумма,
разность и скалярное произведение
векторов, угол между векторами. Все
прототипы задачи В3 можно найти на сайте
mathege.ru.
Геометрия на егэ по математике
Геометрия
на ЕГЭ по математике — одна
из сложных тем для абитуриентов. Дело
Дело
в том, что когда-то экзамен по геометрии
в школе был обязательным, а сейчас —
нет. В результате у большинства
абитуриентов знания по геометрии
близки к нулю.
Геометрия
на ЕГЭ — это четыре задачи в части
и В (две по планиметрии и две
по стереометрии), а также задача
С2 и для многих недосягаемая С4.
Как же научиться их решать?
Начнем
с планиметрии. Прежде всего, вам нужно
выучить основные формулы
геометрии.
На нашем
сайте вы найдете курс геометрии
с нуля — основные определения,
формулы и теоремы, а также разбор
множества экзаменационных задач
по геометрии из части В.
Для
решения задачи С4 нужна более серьезная
подготовка.
Первый этап — теория.
Необходимый материал есть в учебнике
по геометрии за 7-9 класс (автор —
А. В. Погорелов или Л. С. Атанасян).
Выпишите в тетрадь определения
и формулировки теорем. Сделайте
чертежи. Доказывать теоремы старайтесь
самостоятельно.
Программа
по геометрии.
1.
Треугольники. Элементы треугольника.
Вершины и стороны. Высоты, медианы,
биссектрисы (определения).
2.
Построение треугольника: практические
задания.
а) Три стороны треугольника
АВС равны 4, 6 и 8 сантиметров
соответственно. Постройте треугольник
АВС с помощью циркуля и линейки.
б)
В треугольнике АВС угол В равен
48 градусов, сторона АВ равна двум,
ВС равна 9. Постройте треугольник
АВС.
в) В треугольнике АВС сторона ВС
равна 5, угол В равен 26°, угол С
равен 58°. Постройте треугольник АВС.
3.
Три признака равенства треугольников.
Неравенство треугольника.
4.
Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр
к отрезку;
б) биссектрису угла.
5.
Углы при параллельных прямых и секущей.
Вертикальные, смежные, соответственные,
односторонние и накрест лежащие
углы. Их определение и свойства.
6.
Теорема о сумме углов треугольника.
7.
Внешний угол треугольника.
8.
Постройте в одном и том же
треугольнике
а) три высоты. Рассмотрите
также случаи тупоугольного
и прямоугольного треугольника.
б) три биссектрисы.
в) три медианы.
9.
Равнобедренный треугольник. Определение
и свойства. Высота в равнобедренном
треугольнике.
10.
Средняя линия треугольника и ее свойства.
11.
Прямоугольный треугольник. Теорема
Пифагора.
12.
Определения синуса, косинуса и тангенса
— для острого угла прямоугольного
треугольника
— для произвольного
угла.
13.
Четырехугольники. Сумма углов
четырехугольника.
14.
Параллелограмм. Определение и свойства.
Площадь параллелограмма.
15.
Виды параллелограммов и их свойства.
(ромб, прямоугольник, квадрат).
16.
Трапеция. Средняя линия трапеции. Площадь
трапеции.
17.
Подобные треугольники. Три признака
подобия треугольников.
18.
Площадь треугольника. Формулы
и
.
19.
Теоремы синусов и косинусов.
20.
Чему равно отношение площадей подобных
фигур.
21.
Свойство медианы (в каком отношении
делятся медианы в точке пересечения?)
22.
Свойство биссектрисы (в каком отношении
биссектриса делит противоположную
сторону?)
23.
Окружность и круг. Длина окружности.
Площадь круга. Длина дуги и площадь
сектора.
24.
Теорема о радиусе, проведенном в точку
касания.
25.
Центральный и вписанный углы. Связь
между ними.
26.
Теоремы о вписанных углах.
27.
Теорема о пересекающихся хордах.
28.
Теорема об отрезках длин касательных,
проведенных из одной точки.
29.
Теорема о секущей и касательной.
30.
Дан треугольник АВС. Постройте
а)
окружность, вписанную в данный
треугольник
б) окружность, описанную
вокруг данного треугольника.
Где
находятся центры этих окружностей?
31.
Еще три формулы площади треугольника
(через радиус вписанной окружности,
через радиус описанной окружности
и формула Герона).
32.
Когда можно вписать окружность
в четырехугольник? Когда — описать
вокруг четырехугольника?
(Программа
по стереометрии будет размещена в
ближайшее время.)
Отдельно —
тема «Векторы». Напомним, что на ЕГЭ
по математике векторы встречаются
в задаче В3.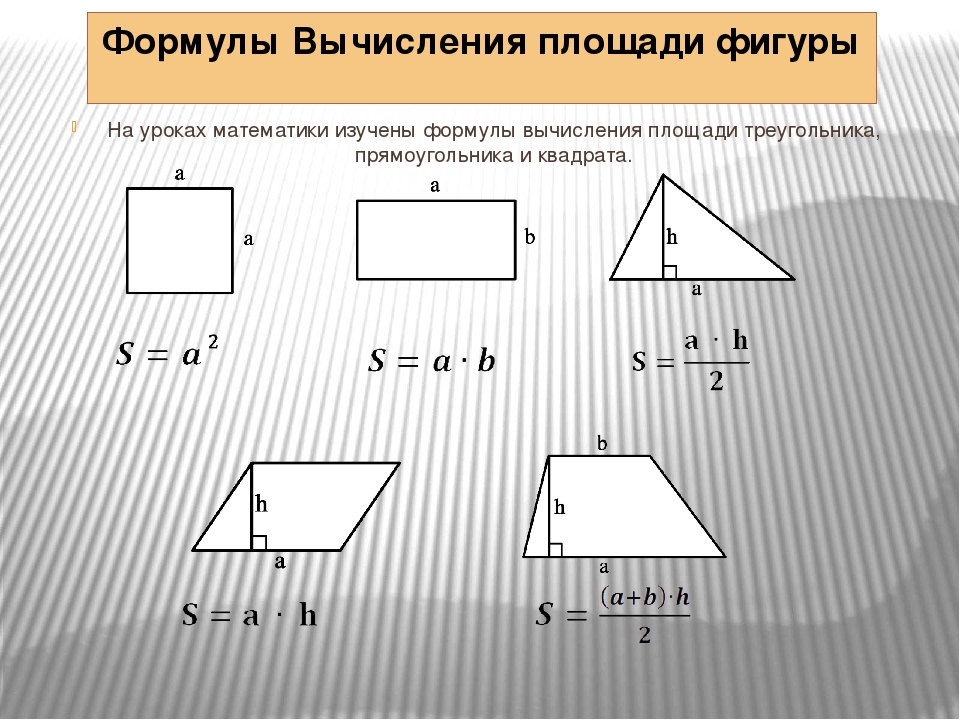 Они также пригодятся вам
Они также пригодятся вам
в решении задачи С2.
Освоив
теорию, можно приступать к решению
сложных задач по геометрии, входящих
в часть С ЕГЭ. Мы рекомендуем
вам сборники:
Р. К. Гордин «ЕГЭ
2012. Математика. Задача С4. Геометрия.
Планиметрия» и
А. Г. Корянов
и А. А. Прокофьев «Пособие
по решению заданий типа С4». Можно
найти на сайте alexlarin.net.
Разбирая
и решая задания ЕГЭ по геометрии,
вы заметите очень интересную вещь.
Простые задачи из части В, разобранные
на нашем сайте, часто оказываются
базовыми схемами, на которых строятся
сложные С4.
Решая
на ЕГЭ задачи С4 по геометрии,
обращайте особое внимание на оформление.
Помните совет, который дал абитуриентам
автор бестселлера «Математика —
абитуриенту» В. В. Ткачук. Вот он,
этот ценнейший совет:
«Подробность
решения должна быть такова, чтобы его
мог понять человек в 10 (десять)
раз глупее вас
Синус,
косинус и тангенс острого угла
прямоугольного треугольника
Изучение
тригонометрии мы начнем с прямоугольного
треугольника. Определим, что такое синус
Определим, что такое синус
и косинус, а также тангенс и котангенс
острого угла. Это основы тригонометрии.
Напомним,
что прямой
угол —
это угол, равный 90º. Другими словами,
половина развернутого угла.
Острый
угол —
меньший 90º.
Тупой
угол —
больший 90º. Применительно к такому
углу «тупой» — не оскорбление,
а математический термин 🙂
Нарисуем
прямоугольный треугольник. Прямой угол
обычно обозначается С. Обратим
внимание, что сторона, лежащая напротив
угла, обозначается той же буквой,
только маленькой. Так, сторона, лежащая
напротив угла А, обозначается а.
Угол
А обозначается соответствующей греческой
буквой α.
Гипотенуза
прямоугольного треугольника — это
сторона, лежащая напротив прямого угла.
Катеты —
стороны, лежащие напротив острых углов.
Катет а,
лежащий напротив угла α, называется
противолежащим
(по отношению к углу α). Другой
катет b, который лежит на одной
из сторон угла α, называется прилежащим.
Синус
острого угла в прямоугольном
треугольнике — это отношение
противолежащего катета к гипотенузе:
Косинус
острого угла в прямоугольном
треугольнике — отношение прилежащего
катета к гипотенузе:
Тангенс
острого угла в прямоугольном
треугольнике — отношение противолежащего
катета к прилежащему:
Другое
(равносильное) определение: тангенсом
острого угла называется отношение
синуса угла к его косинусу:
Котангенс
острого угла в прямоугольном
треугольнике — отношение прилежащего
катета к противолежащему (или, что
то же самое, отношение косинуса к синусу):
Обратите
внимание на основные соотношения
для синуса, косинуса, тангенса и
котангенса, которые приведены ниже. Они
пригодятся нам при решении задач.
Давайте
докажем некоторые из них.
Сумма
углов любого треугольника равна 180º.
Значит, сумма
двух острых углов прямоугольного
треугольника равнa 90º.С
одной стороны,как
отношение противолежащего катета
к гипотенузе. С другой стороны,,
поскольку для угла β катет а будет
прилежащим.
Получаем,
что cos β = sin A. Иными словами, cos (90º —
А) = sin A.
Возьмем
теорему Пифагора: a2
+ b2
= c2.
Поделим
обе части на cos2 A:
Мы
получили основное
тригонометрическое тождество:
Поделив
обе части основного тригонометрического
тождества на cos2 A,
получим:
Это
значит, что если нам дан тангенс острого
угла α, то мы сразу можем найти его
косинус.
Аналогично,
Хорошо,
мы дали определения и записали
формулы. А для чего все-таки нужны
синус, косинус, тангенс и котангенс?
Мы знаем,
что сумма
углов любого треугольника равна 180°.
Знаем
соотношение между сторонами
прямоугольного треугольника. Это теорема
Пифагора: a2
+ b2
= с2.
Получается,
что зная два угла в треугольнике,
можно найти третий. Зная две стороны
в прямоугольном треугольнике, можно
найти третью. Значит, для углов —
свое соотношение, для сторон — свое.
А что делать, если в прямоугольном
треугольнике известен один угол (кроме
прямого) и одна сторона, а найти
надо другие стороны?
С этим
и столкнулись люди в прошлом,
составляя карты местности и звездного
неба. Ведь не всегда можно непосредственно
измерить все стороны треугольника.
Синус,
косинус и тангенс — их еще
называют тригонометрическими
функциями угла —
дают соотношения между сторонами
и углами
треугольника. Зная угол, можно найти
все его тригонометрические функции
по специальным таблицам. А зная
синусы, косинусы и тангенсы углов
треугольника и одну из его сторон,
можно найти остальные.
Мы тоже
нарисуем таблицу значений синуса,
косинуса, тангенса и котангенса для
«хороших» углов от 0 до 90°.
Обратите
внимание на два красных прочерка в
таблице. При соответствующих значениях
углов тангенс и котангенс не существуют.
Разберем
несколько задач по тригонометрии
из Банка заданий ФИПИ.
1.
В треугольнике ABC угол C равен 90°,
sin A = 0,1. Найдите cos B.
Задача
решается за четыре секунды.
Поскольку
А+В = 90°, sin A = cos B = 0,1.
2.
В треугольнике ABC угол C равен 90°, АВ
= 5,
.
Найдите AC.
Имеем:
Отсюда
Найдем
АС по теореме Пифагора.
Задача
решена.
Часто
в задачах встречаются треугольники
с углами 90°, 30° и 60° или
с углами 90°, 45° и 45°. Основные
соотношения для них запоминайте наизусть!
Для
треугольника с углами 90°, 30° и 60°
катет, лежащий напротив угла в 30°,
равен половине
гипотенузы.
Треугольник
с углами 90°, 45° и 45° —
равнобедренный. В нем гипотенуза в
раз
больше катета.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. Формулы площади треугольника
Формулы площади квадрата
Формула площади прямоугольникаПлощадь прямоугольника равна произведению длин двух его смежных сторон S = a · b где S — Площадь прямоугольника, Формулы площади параллелограмма
Формулы площади ромба
Формулы площади трапеции
Формулы площади выпуклого четырехугольника
Формулы площади круга
Формулы площади эллипсаПлощадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. S = π · a · b где S — Площадь эллипса, Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
Площади фигур. Геометрия, 8 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Новости
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Переменка
Поиск по сайту
Отправить отзыв
-
Предметы -
Геометрия -
8 класс
-
Площадь многоугольника. Свойства площадей
-
Формулы площадей параллелограмма, треугольника и трапеции
-
Теорема Пифагора. Доказательство
Отправить отзыв
Нашёл ошибку?
Сообщи нам!
Copyright © 2021 ООО ЯКласс
Контакты
Пользовательское соглашение
Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора
Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = w × h
w = ширина
h = высота
Мы знаем, что w = 5 и h = 3 , поэтому:
Площадь = 5 × 3 = 15
Пример: Какова площадь этого круга?
Радиус = r = 3
| Площадь | = π × r 2 | |
| = π × 3 2 | ||
| = π × (3 × 3) | ||
| = 3.14159 … × 9 | ||
| = 28,27 (до 2 знаков после запятой) |
Пример: Какова площадь этого треугольника?
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Более сложный пример:
Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр
Сколько зарабатывает Сэм, обрабатывая эту область:
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B = 400 м 2 + 140 м 2 = 540 м 2
Сэм зарабатывает 0,10 доллара за квадратный метр
Сэм зарабатывает = 0,10 доллара × 540 млн 2 = 54 доллара
Что такое площадь?
Площадь — это размер поверхности!
Пример:
У всех этих фигур одинаковая площадь 9:
Это помогает представить , сколько краски покроет форму.
Площадь простых форм
Для определенных форм существуют специальные формулы:
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = w × h
w = ширина
h = высота
Ширина равна 5, а высота 3, поэтому мы знаем, что w = 5 и h = 3 :
.
Площадь = 5 × 3 = 15
Узнайте больше в Area of Plane Shapes.
Площадь по счету квадратов
Мы также можем нанести фигуру на сетку и подсчитать количество квадратов:
Прямоугольник имеет площадь 15
Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь составляет 15 м 2 (15 квадратных метров)
Квадратный метр vs Квадратный метр
Базовая единица площади в метрической системе — квадратных метров. — квадрат, каждая сторона которого имеет 1 метр:
1 квадратный метр
Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:
Есть также «квадратный мм», «квадратный см» и т. Д., Подробнее см. Метрическая площадь.
Приблизительная площадь при подсчете квадратов
Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.
В одну сторону:
- больше чем половина квадрата считается как 1
- меньше чем половина квадрата считается как 0
Как это:
Этот пятиугольник имеет площадь примерно 17
Или мы можем сосчитать один квадрат, когда кажется, что площади
в сумме дают .
Пример: Здесь площадь, обозначенная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):
Этот круг имеет площадь примерно 14
Но лучше всего использовать формулу (когда это возможно):
Пример: круг имеет радиус 2,1 метра:
Формула:
Площадь = π × r 2
Где:
Радиус 2.1м , итого:
Площадь = 3,1416 … × (2,1 м) 2
= 3,1416 … × (2,1 м × 2,1 м)
= 13,854 … м 2
Таким образом, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)
Область сложных форм
Иногда мы можем разбить фигуру на две или более простые формы:
Пример: Какова площадь этой формы?
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = a 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B
Площадь = 400 м 2 + 140 м 2
Площадь = 540м 2
Площадь путем сложения треугольников
Мы также можем разбить фигуру на треугольники:
Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:
Затем рассчитайте каждую площадь
(используя Area = ½b × h) и сложите их все.
Площадь по координатам
Когда мы знаем координаты каждой угловой точки, мы можем использовать метод «Площадь неправильных многоугольников».
Есть область многоугольника с помощью инструмента рисования, который тоже может помочь.
Квадрат (Геометрия)
(Перейти на площадь квадрата или периметра квадрата)
Квадрат — это плоская форма с 4 равными сторонами, каждый угол — прямой (90 °).
| означает «прямой угол» | ||
| показать равные стороны | ||
| Все стороны равны по длине | |
| Каждый внутренний угол составляет 90 ° | |
| Противоположные стороны параллельны (значит, это параллелограмм). |
Играть с квадратом:
Квадрат также соответствует определению прямоугольника (все углы равны 90 °), ромба (все стороны равны), параллелограмма (противоположные стороны параллельны и равны по длине) и правильного многоугольника (все углы равны и все стороны равный). Какой герой!
Площадь
Квадрата
Площадь — это длина стороны в квадрате : Площадь = a 2 = a × a |
Пример. У квадрата длина стороны 6 м. Какова его площадь?
Площадь = 6 м × 6 м = 36 м 2
| Площадь также составляет , половина диагонали в квадрате: Площадь = d 2 2 |
Периметр квадрата
Периметр — это расстояние по краю.
Периметр составляет , в 4 раза больше длины стороны: Периметр = 4a |
Пример. У квадрата длина стороны 12 см. Каков его периметр?
Периметр = 4 × 12 см = 48 см
Диагонали квадрата
У квадрата две диагонали, они равны по длине и пересекаются посередине.
Диагональ — это длина стороны , умноженная на квадратный корень из 2 : Диагональ «d» = a × √2 |
Пример. У квадрата длина стороны 5 м. Какова длина диагонали?
Длина по диагонали = a × √2
= 5 × 1.41421 …
= 7,071 м (до 3 знаков после запятой)
Калькулятор
Введите длину стороны , площадь, диагональ или периметр , а остальные значения рассчитываются в реальном времени.
Формула площади и объема для геометрических фигур
пи (π) = 3,1415926535 …
Формула периметра | |
| Квадрат | 4 × сторона |
| Прямоугольник | 2 × (длина + ширина) |
| Параллелограмм | 2 × (сторона1 + сторона2) |
| Треугольник | сторона1 + сторона2 + сторона3 |
| Правильный n-многоугольник | n × сторона |
| Трапеция | высота × (base1 + base2) / 2 |
| Trapezoid | base1 + base2 + height × [ csc (theta1) + csc (theta2)] |
| Окружность | 2 × pi × радиус |
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) |
Формула площади | |
| Квадрат | сторона 2 |
| Прямоугольник | длина × ширина |
| Параллелограмм | основание × высота |
| Треугольник | основание × высота / 2 |
| Правильный n-многоугольник | (1/4) × n × сторона 2 × кроватка (pi / n) |
| Трапеция | высота × (base1 + base2) / 2 |
| Окружность | pi × радиус 2 |
| Эллипс | пи × радиус1 × радиус2 |
| Куб (поверхность) | 6 × сторона 2 |
| Сфера (поверхность) | 4 × пи × радиус 2 |
| Цилиндр ( вс сторона стороны) | периметр круга × высота |
| 2 × pi × радиус × высота | |
| Цилиндр (вся поверхность) | Области верхнего и нижнего кругов + Площадь стороны |
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |
| Конус (поверхность) | пи × радиус × сторона |
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) |
Формула объема | |
| Куб | сторона 3 |
| Прямоугольная призма | сторона1 × сторона2 × сторона3 |
| Сфера | (4 / 3) × пи × радиус 3 |
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 |
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × пи × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота |
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 |
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Периметр, площадь и объем
1. В
периметр
из
многоугольник (или любая другая замкнутая кривая, например окружность) — это расстояние вокруг внешней стороны.
2. В
область
из
простая замкнутая плоская кривая — это количество внутреннего пространства.
3. В
объем
из
твердый
3
D
shape — это количество перемещаемого им пространства.
Некоторые формулы для общих
2
-мерные плоские фигуры и
3
-мерные тела приведены ниже. Ответов один, два,
или три измерения;
периметр
измеряется в
линейные единицы
,
область
измеряется в
квадратные единицы
, а также
объем
измеряется в
кубические единицы
.
1 .Формулы периметра | ||
| | |
Квадратный | п знак равно 4 s | s длина стороны квадрата. |
Прямоугольник | п знак равно 2 L + 2 W | L а также W — длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + c | а , б , а также c — длины сторон. |
п знак равно а + б + а 2 + б 2 | а а также б длины двух катетов треугольника | |
Круг | р это радиус и d это диаметр. | |
| ||
| | |
Квадратный | s длина стороны квадрата. | |
Прямоугольник | L а также W — длины сторон прямоугольника (длина и ширина). | |
Треугольник | А знак равно 1 2 б час | б а также час основание и высота |
Треугольник | А знак равно s ( s — а ) ( s — б ) ( s — c ) где s знак равно а + б + c 2 | а , б , а также c длины сторон и s полупериметр |
Параллелограмм | б длина основания и час это высота. | |
Трапеция | А знак равно б 1 + б 2 2 час | б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
| ||
| | |
Куб | s длина стороны. | |
Правая прямоугольная призма | L это длина, W ширина и ЧАС это высота. | |
Призма или цилиндр | А площадь основания, час это высота. | |
Пирамида или конус | А площадь основания, час это высота. | |
Сфера | р это радиус. | |
математических формул для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм. Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур. Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь и объем сферы
Д.Рассел
Трехмерный круг известен как сфера. Чтобы вычислить площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ).Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. Рассел
Конус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь и объем цилиндра
Д. Рассел
Вы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. Рассел
Прямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для них вам нужно знать длину ( л ), высоту ( х ) и ширину ( х ).С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (левый) + 2 (левый) + 2 (белый)
- Объем = л. С.
Площадь и объем пирамиды
Д. Рассел
С пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 b 2 h
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д.Рассел
При переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину ( l ) формы. Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих вычислений.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (бч) л
Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле используется высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = Ad
Площадь сектора круга
Д. Рассел
Площадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. Рассел
Эллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Semiminor Axis ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете видеть эту формулу, записанную с r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам необходимо знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, который имеет одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ), и это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были объединены в пары как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник — это тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( x ).
- Периметр = 2h + 2w
- Площадь = в x ш
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать только длину одной стороны ( s ), чтобы найти ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
Формулы площади
( пи
= = 3.141592 …)
Площадь
Формулы
Примечание: «ab» означает «а»
умножить на «б». «a
2 » означает «квадрат»,
что то же самое, что «а» умножить на «а».
Будьте осторожны !! Количество единиц. Используйте то же самое
единиц для всех измерений. Примеры
квадрат = a 2
прямоугольник = ab
параллелограмм = bh
трапеция = h / 2 (b 1 + b 2 )
3 круг =
3 круг =
pi r 2
эллипс = pi r 1 r 2
| треугольник = | — половина длины основания, умноженная на высоту треугольник |
| равносторонний треугольник = |
треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C
треугольник, заданный a, b, c = [s (s-a) (s-b) (s-c)]
когда s = (a + b + c) / 2 (формула Герона)
правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = длина от центра до угла
Квартир
Площадь измеряется в «квадратных» единицах.Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это
то же самое, это может быть просто длина одной стороны в квадрате.
Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам.
4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в формате 2 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается.
измерение.
Площадь прямоугольника — это длина сбоку.
раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что
это площадь?
НЕ ПРАВИЛЬНО …. 4 раза 6 = 24
ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута. Площадь 1/3 фута
умножить на 6 футов = 2 квадратных фута.
