Содержание
Модуль числа | Презентация к уроку по алгебре (7 класс) по теме:
Модуль числа
Цель:
изучение понятия модуля,
применение определения модуля при выполнении задач.
Задачи:
развивать умение применять теоретический материал при решении практических задач;
развивать интерес к математике через поиск примеров по данной теме;
расширить математический кругозор;
приобрести навыки исследовательской работы.
Считаю, что выбранная тема является актуальной:
Задачи, связанные с абсолютной величиной, часто встречаются на математических олимпиадах и вступительных экзаменах.
Понятие модуля широко применяется в различных разделах школьного курса математики.
Это понятие является одним из основных понятий элементарной математики. Осмысленное владение модулем позволяет воспринимать алгебру и геометрию, как единое целое. “Расстояние между точками” позволяет оценивать правильность найденных решений ряда уравнений, содержащих модуль, строить графики функций.
В ходе работы я использовала следующие методы:
Исследование литературы по теме.
Проведение поиска задач по теме.
Основная часть
Существенной характеристикой числа является понятие его абсолютной величины (модуля).
Модулем числа называют расстояние от точки, изображающей число на координатной прямой до начала отсчета.
В различных учебниках первоначальное понятие модуля вводится по-разному: как расстояние от точки, изображающей число, до начала отсчёта (Математика. Н.Я. Виленкин), как длина вектора (Математика. П.М. Эрдниев), как число “без знака” (Математика. Г.В. Дорофеев) и др.
В архитектуре – это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике – это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например, модуль зацепления, модуль упругости и т. п.
п.
Понятие модуля
Модуль (modulus) в переводе с латинского языка означает “мера, размер”.
Модуль числа а обозначают | а |. Этот термин “модуль” ввёл в 1806 г. французский математик Жорж Аргон.
Геометрический смысл модуля
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5.
Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6.
Пишут: |-6| = 6.
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули.
|-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета О, т.е. удалена от нее на 0 единичных отрезков.
|0| = 0
Так как модуль числа – это расстояние, он никогда не будет отрицательным.
Изучая понятие модуля, я рассмотрела доказательство следующей теоремы:
Абсолютная величина действительного числа a ≠ 0 равна большему из двух чисел a или -a.
Доказательство:
Если число a положительно, то -a отрицательно, т.е. –a a. Отсюда следует, что –a a.
Например, число 5 положительно, тогда -5 – отрицательно и -5
В этом случае |a| = a, т.е. |a| совпадает с большим из двух чисел a и -a.
Если a отрицательно, тогда -a положительно и a a, т.е. большим числом является -a. По определению, в этом случае, |a| = -a — равно большему из двух чисел -a и a.
Для нахождения модуля числа можно использовать следующую блок-схему.
Отработка алгоритма. Допустим, необходимо найти модуль чисел -3 и 7.
В учебниках приводятся различные упражнения с использованием модуля числа. Вот некоторые из них:
Запишите число, противоположное данному: 4; -4; +3; -3; -6,3; 6,3.
2. Найдите модуль каждого из чисел: |- 6 |, | 9 |, | — 5 |, | 0 |, |0,8 |.
3. Найти расстояние от М(-7) и N(6) до начала отчета на координатной прямой.
При решении задач, содержащих модуль числа, основным приемом является раскрытие знака модуля в соответствии с его свойствами.
В некоторых случаях модуль раскрывается однозначно.
Например: |x2 + y2| = x2 + y2, так как выражение под знаком модуля неотрицательно при любых х и у. Или |–z2 – 1| = z2 + 1, так как выражение под модулем отрицательно при любых z.
Уравнения, содержащие знак модуля, решаются следующими способами:
алгебраический,
графический,
последовательное раскрытие модулей,
метод интервалов.
Рассмотрим некоторые примеры решения уравнений и неравенств, содержащих знак модуля.
Решить уравнение: |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения:
x = 3 и x = -3.
Решить уравнение: |x — 3| = 4.
Это уравнение можно прочитать так: расстояние от точки до точки равно 4. С помощью графического метода можно определить, что уравнение имеет два решения: — 1 и 7.
С помощью графического метода можно определить, что уравнение имеет два решения: — 1 и 7.
Решить неравенство: |x + 7| .
Можно прочитать как: расстояние от точки до точки меньше четырёх. Ответ: (-11; -3).
Решить неравенство: |10 — x| ≥ 7.
Расстояние от точки 10 до точки х больше или равно семи.
Ответ: (-∞; 3]U [17, +∞)
Рассматривая модуль числа, я познакомилась с функцией y = |x|, графиком которой является ломаная линия, состоящая из двух лучей, являющихся биссектрисами I и II координатных четвертей.
Действительно,
Для x ≥ 0 имеем y = x.
Для x y = -x.
ЗАКЛЮЧЕНИЕ
В результате работы я:
повторила школьный материал по данной теме,
изучила решение уравнений и неравенств, содержащих знак модуля,
научилась строить график функции вида y = |x|,
Так как изучение модуля числа продолжается в старших классах, где рассматриваются свойства модуля, а также задачи различного уровня сложности, исследование данной темы будет продолжено. В следующем году я проведу исследование задач различного уровня сложности, а также олимпиадные и экзаменационные задачи.
В следующем году я проведу исследование задач различного уровня сложности, а также олимпиадные и экзаменационные задачи.
Модуль числа | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная 🙂 Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.
Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.
Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет. никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
(без знака!). Например,
Обратите внимание: модуль числа всегда неотрицателен:
Определение модуля
Вот оно:
От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.
Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 🙂
Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,
В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.
Или: так так как выражение под модулем неположительно при любых z.
Геометрическая интерпретация модуля
Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.
Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.
Вообще, если имеются два числа a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A до точки B.)
Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).
Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Отметим на числовой прямой точки, удовлетворяющие этому условию.
Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.
Перейдём к неравенствам. Решим неравенство .
Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.
Ответ: (-11; -3).
Другой пример. Решим неравенство |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ:
График функции
Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.
Корень из квадрата
Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что
Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .
Оно равно при и при , т. е. как раз .
Примеры заданий ЕГЭ
1. Найдите значение выражения при .
Заметим, что при . Следовательно, значение нашего выражения равно: .
2. Найдите значение выражения при .
Действуем аналогично:
В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.
Читайте также: Уравнения с модулем
Урок 17. противоположные числа. модуль числа — Математика — 6 класс
Математика
6 класс
Урок № 17
Противоположные числа. Модуль числа
Перечень рассматриваемых вопросов:
- Понятие противоположного числа.
- Понятие модуля числа.
- Решение различных заданий по теме «Противоположные числа. Модуль числа».
Тезаурус
Числа, которые отличаются только знаком, называются противоположными.
Модулем положительного числа называют само это число.
Модулем отрицательного числа называют противоположное ему (положительное) число.
Модулем числа 0 является число 0.
Основная литература
- Никольский С. М. Математика. 6 класс: Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е.Ф. Шершнёв, О.Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И.Ф. Задачи на смекалку: 5-6 кл. // И.Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Считается, что если перед целым числом поставить знак «+», то это не изменяет самого числа.
Например,
число 7 можно записать как + 7
число – 7 можно записать как + (– 7)
7 = + 7
– 7 = + (– 7)
Поэтому ряд целых чисел можно записывать в виде:
…, – 6, – 5, – 4, – 3, – 2, – 1, 0, + 1, + 2, + 3, + 4, + 5, + 6, …
Числа, которые отличаются только знаком, называются противоположными.
Например, противоположные числа:
– 7 и + 7
– 53 и 53
Модуль или абсолютная величина числа.
Разбор заданий тренировочного модуля
№ 1. Единичный выбор.
Ответ: + 107.
№2. Ввод с клавиатуры пропущенных элементов в текст.
Модуль числа
Мóдуль числá a — это расстояние от начала координат до точки А(a).
Чтобы понять это определение, подставим вместо переменной a любое число, например 3, и снова прочитаем его:
Мóдуль числá 3 — это расстояние от начала координат до точки А(3).
То есть модуль это ни что иное как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)
Расстояние от начала координат до точки А(3) составляет 3 (три единицы или три шага).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Мы искали модуль числа 3 и выяснили, что он равен 3. Так и записываем:
Так и записываем:
|3| = 3
Читается как «Модуль числа три равен три»
Теперь попробуем найти модуль числа −3. Опять же возвращаемся к определению и подставляем в него число −3. Только вместо точки A используем новую точку B. Точку A мы уже использовали в первом примере.
Модулем числа −3 называют расстояние от начала координат до точки B(−3).
Расстояние от одного пункта до другого не может быть отрицательным. Модуль это тоже расстояние, поэтому тоже не может быть отрицательным.
Модуль числа −3 равен 3. Расстояние от начала координат до точки B(−3) равно трём единицам:
|−3| = 3
Читается как «Модуль числа минус три равен три»
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом координат. То есть расстояние от начала координат до точки O(0) равно нулю:
|0| = 0
«Модуль нуля равен нулю»
Сделаем выводы:
- Модуль числа не может быть отрицательным;
- Для положительного числа и нуля модуль равен самомý числу, а для отрицательного – противоположному числу;
- Противоположные числа имеют равные модули.

Противоположные числа
Числа, отличающиеся только знаками называют противоположными.
Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числá −2 знак минуса, а у числá 2 знак плюса, но мы его не видим, поскольку плюс как говорилось ранее, не записывают.
Еще примеры противоположных чисел:
−1 и 1
−3 и 3
−5 и 5
−9 и 9
Противоположные числа имеют равные модули. Например, найдём модули чисел −3 и 3
|−3| и |3|
3 = 3
На рисунке видно, что расстояние от начала координат до точек A(−3) и B(3) одинаково равно трём шагам.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
конспект урока по математике «Модуль числа»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Модуль числа. Урок математики в 6 классе. Учитель математики Шаронова Л. М.
Урок математики в 6 классе. Учитель математики Шаронова Л. М.
Номер слайда 2
Расскажи мне, и я забуду,Покажи мне, и я запомню,Дай мне попробовать, и я научусь.(Древняя китайская пословица)
Номер слайда 3
01 FNRLAКакие из данных точек имеют противоположные координаты?Назовите координаты точек, отмеченных на координатной прямой. Какие числа называются противоположными?Среди данных чисел укажите пары противоположных чисел:
Какие числа называются противоположными?Среди данных чисел укажите пары противоположных чисел:
Номер слайда 4
Найдите значения выражения:-(-(-(-1)))-(-(-(-(-1))))-(-(-1))Найдите значения выражения:-(-с), если с=2,3 ; -4¼-(-(-а)), если а = -12,3 ; 7½
Номер слайда 5
Назовите число противоположное данному:7– 7– 44–(–5) 5–(+3)-3-6+2-9-8+(–6)–(–2)–(+9)–(–(–8))
Номер слайда 6
00,1 МОДУЛЬ01,50,8 Для того, чтобы узнать тему нашего урока, укажите число, противоположное данному , а во второй таблице найдите букву, соответствующую этому числу. 0,801,5 ОЬМДЛУ
0,801,5 ОЬМДЛУ
Номер слайда 7
Модуль числа. Урок математики в 6 классе. Учитель математики Шаронова Л. М.
Номер слайда 8
ON06 Расстояние от точки M(-6) до начала отсчёта О равно 6. -6 MРасстояние от точки N(6) до начала отсчёта О равно 6. Число 6 называют модулем числа. Модуль числа записывают так:-6 = 6, 6 = 6
-6 MРасстояние от точки N(6) до начала отсчёта О равно 6. Число 6 называют модулем числа. Модуль числа записывают так:-6 = 6, 6 = 6
Номер слайда 9
ON06 Расстояние от точки M(-6) до начала отсчёта О равно 6.-6 MРасстояние от точки N(6) до начала отсчёта О равно 6. Число 6 называют модулем числа. Модуль числа записывают так:-6 = 6, 6 = 6
Номер слайда 10
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а). т. к. точка с координатой 5 удалена от начала отсчета на 5 единичных отрезковт. к. точка с координатой 0 совпадает с началом отсчётат. к. точка с координатой -5 удалена от начала отсчёта на 5 единичных отрезков
т. к. точка с координатой 5 удалена от начала отсчета на 5 единичных отрезковт. к. точка с координатой 0 совпадает с началом отсчётат. к. точка с координатой -5 удалена от начала отсчёта на 5 единичных отрезков
Номер слайда 11
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а)А(а)а единиц0
Номер слайда 12
Модуль числа не может быть отрицательным (ведь это расстояние!)Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: -a = a
Противоположные числа имеют равные модули: -a = a
Номер слайда 13
Прикольно!Представь, что модуль – это баня, а знак «минус» — грязь. Оказываясь под знаком модуля, отрицательное число «моется» и выходит без знака «минус» — чистым. В бане могут «мыться» (т.е. стоять под знаком модуля) как положительные, так и отрицательные числа.
Номер слайда 14
Из истории математики. Модуль числа а обозначают |а|. Этот термин «модуль» ввел в 1806году французскийматематик Жорж Аргон.
Модуль числа а обозначают |а|. Этот термин «модуль» ввел в 1806году французскийматематик Жорж Аргон.
Номер слайда 15
Обозначение: Например: Чему равен модуль числа 0? Почему?
Номер слайда 16
Найдите модуль каждого из чисел:127,086,32072│12│=│7,08│=│- 6,32│=│0│=│ -72│=
Номер слайда 17
Найдите значение выражения│- 8│+│- 2│=│- 5│-│ 2│=│- 8│∙│ — 3│=│- 27│:│-9│=103243
Номер слайда 18
Найди модули чисел и запиши значение модулей. Расположи данные числа в порядке убывания модулей, сопоставь им соответствующие буквы, и ты узнаешь название самой северной точки одного из материков. На каком материке находится эта точка?ЮНЕСКЛИЧЧЕЛЮСКИН
Расположи данные числа в порядке убывания модулей, сопоставь им соответствующие буквы, и ты узнаешь название самой северной точки одного из материков. На каком материке находится эта точка?ЮНЕСКЛИЧЧЕЛЮСКИН
Номер слайда 19
Достигнут впервые участником 2-й Камчатской (Великой Северной) экспедиции штурманом С. И. Челюскиным вместе с казаками Фофановым и Гороховым в 1742 году. Челю́скин (мыс Восточно-Северный, мыс Челюскина) — северная оконечность (мыс) полуострова Таймыр и самая северная материковая точка Евразии.
Номер слайда 20
Поняли?А теперь…
Номер слайда 21
Номер слайда 22
Номер слайда 23
ВОПРОСЫ: Что называют модулем числа? Как обозначают модуль числа? Как найти модуль положительного числа или нуля? Как найти модуль отрицательного числа? Может ли модуль какого–нибудь числа быть отрицательным числом?
Номер слайда 24
Домашнее заданиезаписи учить; «особенное число 0»№ 896; № 898; № 913 доп.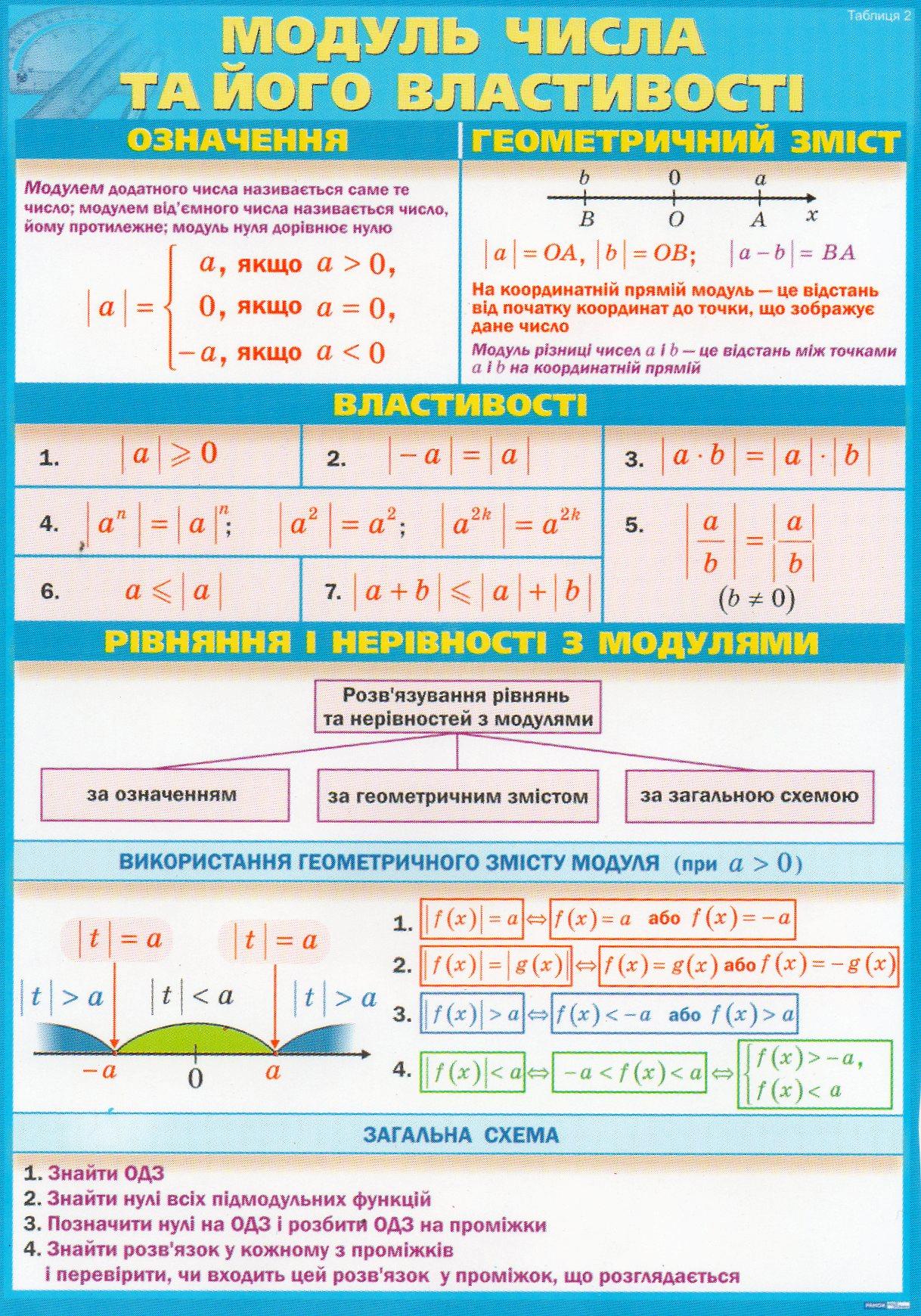
Номер слайда 25
Номер слайда 26
СПАСИБО ЗА РАБОТУ НА УРОКЕ!!!
Модуль числа
Давайте внимательно рассмотрим чертёж.
На координатной прямой отмечены начало отсчёта и две
точки А и В с
координатами 7 и – 7.
Что можно сказать о расстояниях ОА и ОВ. Правильно!
Они равны. Но как так получилось? Ведь точка А имеет
отрицательную координату, а точка В положительную,
а расстояния от них до начала отсчёта одинаковое.
Для такого расстояния придумано специальное название
– модуль числа.
Для нашего чертежа пишут так:
Определение
Модулем числа а
называют
расстояние (в единичных отрезках) от начала координат до точки А (а).
Модуль числа а обозначают так: .
Читают: «модуль а».
Например
Модулем положительного числа
называется
само это число.
Например
Модулем отрицательного числа
называется
противоположное ему число. Например
Например
Модуль числа 0 равен 0.
Так как точка с координатой 0 совпадает с
началом отсчёта О, т.е. удалена от неё на 0 единичных отрезков.
Пишут:
Модули противоположных чисел равны.
Например
Задание
Отметьте числа на координатной прямой, модуль
которых равен 3.
Решение:
Задание
Найдите значение выражения: , если a = 17, b = – 5,2.
Решение:
Задание
Найдите значение выражений:
Итоги
Модулем числа а называют расстояние (в единичных
отрезках) от начала координат до точки А (а).
Модулем положительного числа называется само это
число.
Модулем отрицательного числа называется
противоположное ему число.
Модуль числа 0 равен 0.
Модули противоположных чисел равны.
Дополнительные главы алгебры. 7 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой по математике 7 класса. Курс посвящен базовым темам алгебры и теории чисел. В рамках курса слушатели узнают, когда и зачем нужно вводить в задачах буквы, как грамотно работать с неравенствами, какие свойства есть у целых чисел и что формулы сокращенного умножения — это не только нудное раскрытие скобок. Знания, полученные на курсе, помогут не только на уроках математики в школе, но и позволят успешнее выступать на олимпиадах.
Курс состоит из 13 обязательных учебных модулей, 54 видеолекций с конспектами, 288 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
– Зачем нужны буквы
– Доли и проценты
– Четность
– Простые и составные числа
– Десятичная запись числа
– Признаки делимости
– Основная теорема арифметики
– НОД и НОК
– Делимость и деление с остатком
– Диофантовы уравнения
– Сравнения по модулю
– Формулы сокращенного умножения
– Основные свойства неравенств
Внутри каждого модуля есть:
– видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
– упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
– задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
Каждый ученик самостоятельно определяет для себя темп и удобное время учебы. Часть модулей открыта сразу, следующие модули открываются после того, как получен зачет по предыдущим. В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
| Вы готовы? | стр.58 | ||
| Понимание словаря | стр.59 | ||
| 3,1 | Рациональные числа и десятичные дроби | Твоя очередь | с.61 |
| Практическое руководство | п.64 | ||
| Независимая практика | п.65 | ||
| 3,2 | Добавление рациональных чисел | Твоя очередь | п.68 |
| Практическое руководство | с.72 | ||
| Независимая практика | стр.73 | ||
| 3,3 | Вычитание рациональных чисел | Твоя очередь | п.75 |
| Практическое руководство | с.79 | ||
| Независимая практика | с.80 | ||
| 3,4 | Умножение рациональных чисел | Твоя очередь | п.83 |
| Практическое руководство | п.86 | ||
| Независимая практика | п.87 | ||
| 3.5 | Деление рациональных чисел | Твоя очередь | п.89 |
| Практическое руководство | п.92 | ||
| Независимая практика | п.93 | ||
| 3,6 | Применение рациональных операций с числами | Твоя очередь | с.95 |
| Практическое руководство | п.98 | ||
| Независимая практика | п.99 | ||
| Готовы к работе? | с.101 | ||
| Смешанный обзор | с.102 | ||
| Обзор учебного пособия: модуль 1 | с.103 | ||
| Обзор руководства: модуль 2 | с.104 | ||
| Обзор руководства: модуль 3 | с.106 | ||
| Задача производительности | с.107 | ||
| Смешанный обзор | с.109 |
Алгебра 1 — Sevenstar
Описание курса:
Мы окружены числами. Помощь по Алгебре 1 поможет учащимся замечать и понимать эти числа, когда они исследуют порядки и закономерности, обнаруженные в Творении Бога. Этот курс является основой, содержащей базовые знания, необходимые для всех будущих курсов математики в средней школе.Материал, изучаемый в этом курсе, важен, но это может сделать каждый. Каждый может хорошо провести время, решая сотни реальных проблем, которые алгебра может помочь найти, и научиться применять этот инструмент для управления чудесными дарами нашего щедрого Создателя. Каждый модуль в этом курсе представлен пошагово прямо на экране компьютера. Практические занятия делают числа, графики и уравнения более реальными. Содержание этого курса связано с реальными приложениями, такими как спорт, путешествия, бизнес и здоровье.Этот курс разработан, чтобы дать студентам навыки и стратегии для решения всех видов математических задач. Учащиеся также приобретут уверенность, необходимую для того, чтобы справиться со всем, что им припасла математика в старшей школе.
Рекомендуемые требования:
Успешное завершение математики в 7-м классе с оценкой C или выше.
Обязательно ознакомьтесь с полной программой курса, чтобы убедиться, что ваш ученик усвоил все необходимые материалы для успешной учебы.Если у вас есть какие-либо вопросы о готовности вашего ученика пройти этот курс, запишите его на предварительный тест по алгебре 1. Это предоставит вам точную информацию о размещении, чтобы вы могли запросить соответствующий уровень курса для успеваемости вашего ученика.
Уровень:
Рекомендуется 9 класс
Утвердил:
Доступные типы курсов:
- 1 кредит — Полный курс (минимум 12 недель / максимум 12 месяцев)
- ½ кредита — 1 st только семестр (минимум 6 недель / максимум 6 месяцев)
- ½ кредита — 2 только за семестр (минимум 6 недель / максимум 6 месяцев)
- Имеется награда с отличием
Библейская интеграция Информация:
Бог решил открыть истину о Своей природе и путях в Сотворенном мире.Сложные модели, схемы и взаимосвязи, обнаруженные при изучении математики, указывают на природу и пути Бога. По мере того, как мы исследуем, открываем, проверяем и каталогизируем известные истины Его вселенной, погружаемся в неизвестное, принимаем решения, выявляем, оцениваем и решаем проблемы вокруг нас и стремимся больше узнать о вселенной, которую создал Бог, и о роли Бога. люди в нем прославляют Бога. Изучение математики приводит нас к более глубокому пониманию нашего Создателя и признательности за Его обеспечение и мудрость, поскольку мы используем это знание как инструмент, чтобы владеть миром природы и заботиться о нем.Чтобы увидеть, как именно эти истины исследуются в этом курсе, посетите страницу с информацией о курсе в курсе и нажмите «Руководящие принципы».
Необходимые материалы курса:
Калькулятор
Определение выражений и уравнений | Предалгебра
Результаты обучения
- Определять и записывать математические выражения, используя слова и символы
- Определять и записывать математические уравнения, используя слова и символы
- Определите разницу между выражением и уравнением
- Используйте экспоненциальную запись для выражения многократного умножения
- Записать экспоненциальное выражение в развернутом виде
Определить выражения и уравнения
В чем разница между фразой и предложением в английском языке? Фраза выражает отдельную мысль, которая сама по себе является неполной, а предложение — законченное утверждение.«Очень быстро бежал» — это фраза, а «Футболист бежал очень быстро» — это предложение. В предложении есть подлежащее и глагол.
В алгебре у нас есть выражений и уравнений . Выражение похоже на фразу. Вот несколько примеров выражений и их соотношения со словесными фразами:
| Выражение | слов | Фраза |
|---|---|---|
| [латекс] 3 + 5 [/ латекс] | [латекс] 3 \ text {plus} 5 [/ латекс] | сумма трех и пяти |
| [латекс] n — 1 [/ латекс] | [латекс] н [/ латекс] минус один | разница [латекс] н [/ латекс] и одна |
| [латекс] 6 \ cdot 7 [/ латекс] | [латекс] 6 \ text {times} 7 [/ латекс] | произведение шести и семи |
| [латекс] \ frac {x} {y} [/ латекс] | [латекс] x [/ латекс] разделить на [латекс] y [/ латекс] | частное [латекс] x [/ латекс] и [латекс] y [/ латекс] |
Обратите внимание, что фразы не образуют законченное предложение, потому что во фразе нет глагола.Уравнение — это два выражения, соединенных знаком равенства. Когда вы читаете слова, которые символы представляют в уравнении, вы получаете полное предложение на английском языке. Знак равенства дает глагол. Вот несколько примеров уравнений:
| Уравнение | Предложение |
|---|---|
| [латекс] 3 + 5 = 8 [/ латекс] | Сумма трех и пяти равна восьми. |
| [латекс] n — 1 = 14 [/ латекс] | [латекс] н [/ латекс] минус один равняется четырнадцати. |
| [латекс] 6 \ cdot 7 = 42 [/ латекс] | Произведение шести и семи равно сорока двум. |
| [латекс] x = 53 [/ латекс] | [латекс] х [/ латекс] равен пятидесяти трем. |
| [латекс] y + 9 = 2y — 3 [/ латекс] | [латекс] y [/ latex] плюс девять равно двум [латексу] y [/ latex] минус три. |
Выражения и уравнения
Выражение — это число, переменная или комбинация чисел, переменных и символов операций.
Уравнение состоит из двух выражений, соединенных знаком равенства.
пример
Определите, является ли каждое из них выражением или уравнением:
- [латекс] 16 — 6 = 10 [/ латекс]
- [латекс] 4 \ cdot 2 + 1 [/ латекс]
- [латекс] x \ div 25 [/ латекс]
- [латекс] y + 8 = 40 [/ латекс]
Решение
| 1. [латекс] 16 — 6 = 10 [/ латекс] | Это уравнение — два выражения связаны знаком равенства. |
| 2. [латекс] 4 \ cdot 2 + 1 [/ латекс] | Это выражение — без знака равенства. |
| 3. [латекс] x \ div 25 [/ латекс] | Это выражение — без знака равенства. |
| 4. [латекс] y + 8 = 40 [/ латекс] | Это уравнение — два выражения связаны знаком равенства. |
Упростите выражения с помощью экспонентов
Упростить числовое выражение — значит сделать все возможное.Например, чтобы упростить [latex] 4 \ cdot 2 + 1 [/ latex], мы сначала умножим [latex] 4 \ cdot 2 [/ latex], чтобы получить [latex] 8 [/ latex], а затем добавить [latex ] 1 [/ latex], чтобы получить [latex] 9 [/ latex]. Хорошая привычка — работать со страницей вниз, записывая каждый шаг процесса под предыдущим. Только что описанный пример будет выглядеть так:
[латекс] 4 \ cdot 2 + 1 [/ латекс]
[латекс] 8 + 1 [/ латекс]
[латекс] 9 [/ латекс]
Предположим, у нас есть выражение [латекс] 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 \ cdot 2 [/ latex].{5} [/ латекс]
пример
Запишите каждое выражение в экспоненциальной форме:
- [латекс] 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 \ cdot 16 [/ латекс]
- [латекс] \ text {9} \ cdot \ text {9} \ cdot \ text {9} \ cdot \ text {9} \ cdot \ text {9} [/ latex]
- [латекс] x \ cdot x \ cdot x \ cdot x [/ латекс]
- [латекс] a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a \ cdot a [/ latex]
Показать решение
Решение
| 1.{4} [/ латекс] | |
| Разверните выражение. | [латекс] 3 \ cdot 3 \ cdot 3 \ cdot 3 [/ латекс] |
| Умножение слева направо. | [латекс] 9 \ cdot 3 \ cdot 3 [/ латекс] |
| [латекс] 27 \ cdot 3 [/ латекс] | |
| Умножить. | [латекс] 81 [/ латекс] |
Обучение абсолютному значению числа в математике
Урок 2: Разработка концепции
Материалы: Каталожные карточки или цифровые «карточки», которые могут быть распределены среди класса
Стандарты:
- Под абсолютным значением рационального числа понимается его расстояние от 0 на числовой прямой.(6.NS.C.7.C)
Подготовка: Сделайте карточки для У меня есть… У кого есть?
Заключительная и оценочная игра
- Попросите учащихся написать и поделиться своими определениями и примерами из реальной жизни ситуаций абсолютной ценности.
- Играть У меня … у кого есть? Составьте набор из 15 учетных карточек с уравнениями абсолютных значений и 15 учетных карточек, содержащих значения переменной. Если учетные карточки недоступны или вы адаптируете это для дистанционного обучения, создайте способ, чтобы 30 приведенных ниже уравнений были распределены среди ваших учеников как можно более равномерно.
| Карты абсолютного значения | Карты переменного значения |
| | x + 5 | = 20 | x = 15 |
| | 5 — x | = 30 | x = –25 |
| | x + 6 | = 41 | x = 35 |
| | –27 — x | = 20 | x = –47 |
| –7 + | x | = 0 | x = –7 |
| | 25 — x | = 18 | x = 7 |
| | x + –5 | = 38 | x = 43 |
| | 37 — x | = 70 | x = –33 |
| 114 — | x | = 7 | x = 107 |
| | — x + 100 | = 21 | x = 121 |
| — | 1 + x | = -80 | x = 79 |
| | x | = 81 | x = –81 |
| | x + 3 | = 84 | x = 81 |
| | 25 + x | = 62 | x = –87 |
| | x — 26 | = 11 | x = 37 |
Каждая указанная карта абсолютного значения имеет два значения: x .Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум из заданных уравнений абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и т. Д., Пока последнее и первое значения не удовлетворяют требованиям последнее уравнение).
Распределите карточки или уравнения поровну. Убедитесь, что все они были розданы. Выберите ученика, который скажет «У меня есть», а затем прочтите значение или уравнение на его карточке. Затем попросите учащегося сказать: «У кого есть совпадение для моей карты?» Любой ученик, у которого есть совпадение, должен сказать: «У меня есть… у кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки.Вы можете попросить учащихся встать, когда игра начинается, и сесть, когда они предлагают ответ. Чтобы заинтересовать всех, предложите награду за успешное прохождение игры, поощряя вызовы к подозрительным ответам.
***
Ищете дополнительные бесплатные уроки математики и мероприятия для учеников средней школы? Обязательно ознакомьтесь с нашим центром бесплатных учебных ресурсов.
Четыре основных математических понятия, которые ваши дети изучают в 7–8 классах | Scholastic
Учащиеся 6 -го класса закладывают фундамент для математики, над которой они будут работать в 7-м -м классе и 8 -м классе .Многие из концепций являются продолжением работы 6 -го классов и позволяют глубже погрузиться в понимание и развитие, ведущее к алгебре. Учащиеся 7 -х и 8 -х классов готовятся к работе, которую они будут выполнять в средней школе по алгебре и геометрии. Эти строительные блоки будут иметь решающее значение для их общего понимания и успеха на уровне старшей школы.
1. Система счисления. В 7 -м классе учащиеся полностью поймут, как интерпретировать и вычислять все рациональные числа.Они могут складывать, вычитать, умножать и делить все десятичные дроби и дроби, а также представлять проценты. Они вычисляют как положительные, так и отрицательные числа, используя все четыре основные операции, и интерпретируют значение абсолютного значения. В 8 -м классе ученики переходят от рациональных чисел к иррациональным числам. Они понимают концепцию десятичного разложения и могут интерпретировать и находить как рациональные, так и иррациональные числа на числовой прямой.
Поощряйте своего ребенка:
- Используйте числовые линии при расчетах как с положительными, так и с отрицательными числами.Наличие вертикальной и / или горизонтальной числовой линии при выполнении домашнего задания может быть очень полезным.
- Мысленно оцените и рассчитайте чаевые, налог с продаж и проценты продаж при покупках и еде вне дома.
- Интерпретируйте положительные и отрицательные числа в реальной жизни, такие как температура, задолженность / задолженность, отрицательные и положительные начисления, выигрыш / проигрыш и т. Д.
- Узнавайте рациональные и иррациональные числа.
2. Выражения и уравнения. Ожидания учащихся сильно возрастают в 7 -м и 8 -м классах при изучении выражений и уравнений. Они начинают использовать переменные и решать многоступенчатые задачи реального мира. Учащиеся интерпретируют неравенства и рисуют их соответствующим образом. Они готовятся к алгебре, рассматривая и понимая линейные уравнения и находя наклон таблицы, графика и уравнения.
Поощряйте своего ребенка:
- Различайте равенство и неравенство (>, <, > , <) с помощью переменных:
- равенство: 4s + 20 = 46
- неравенство: 4s + 20 <46
- Рассматривайте и решайте многоступенчатые реальные задачи, используя переменные.Например, Как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов. Напишите неравенство для количества продаж, которые вам нужно совершить, и опишите решения .
- Изучите и изучите различные типы графиков и таблиц в Интернете или в газете.
- Разберитесь в значении наклона и как его найти с помощью графика, таблицы или уравнения:
3. Геометрия. Студенты уделяют большое внимание лексике по геометрии и точно используют свой словарный запас при письме.Они расширяют свое понимание объема и площади для расчета площади поверхности двух- и трехмерных объектов. Они также изучают формулы площади и окружности круга. В 8 -м классе они изучают теорему Пифагора и применяют ее к реальным и математическим задачам. Студенты также должны знать формулы для определения объема конусов, сфер и цилиндров.
Поощряйте своего ребенка:
- Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств.Например: дополнительных углов: два угла, которые в сумме дают 180 °.
- Создавайте словарные карточки для всего их математического словаря и еженедельно практикуйте их.
- Найдите разные двухмерные и трехмерные объекты в реальном мире и обсудите разницу между нахождением площади поверхности и объема каждого объекта.
- Понять теорему Пифагора и как использовать ее в реальном мире:
Источник изображения: FreeLearningChannel.com
4. Функции. В 8 -м ученики классов начнут узнавать о функциях. Студенты будут определять, сравнивать и оценивать функции. Они будут использовать функции для моделирования отношений между различными величинами. Они будут сравнивать функции алгебраически, графически, численно в таблицах или с помощью словесных описаний.
Поощряйте своего ребенка:
Источник изображения: Slideshare.net
У вас есть вопросы об этих концепциях или другие вопросы по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге.Или поделитесь ими с нами на странице Scholastic Parents в Facebook.
Изображение предоставлено: © DragonImages / Thinkstock
МАТЕМАТИКА G7: 7 класс по математике
Описание
Математика седьмого класса — это примерно
— Развитие понимания и применение пропорциональных отношений
— Развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями
— Решение задач, связанных с масштабными чертежами и неформальными геометрическими конструкциями, и работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом
— Делать выводы о популяциях на основе выборок.
О загружаемых ресурсах
История соотношений, карта учебной программы и обзор для 6-8 классов : Карта учебной программы и обзор истории соотношений предоставляют учителям четкое представление о модулях на каждом уровне с 6 по 8 класс.
Контрольный список CCLS для истории соотношений : Контрольный список CCLS для истории соотношений включает в себя диаграммы уровней классов, позволяющие быстро определить, когда выполняется каждый стандарт.
Поддержка беглости речи по математике для 6–8 классов : Общие базовые стандарты по математике призывают учащихся приобретать и демонстрировать не только концептуальное понимание и решение задач, но также процедурные навыки и беглость.
Scaffolding Instruction for ELLs: Resource Guide for Mathematics : предоставить преподавателям инструкции по использованию учебных материалов на EngageNY и предоставить дополнительные строительные леса для студентов ELL в соответствии с их уровнем владения английским языком.
Загрузки
Могут быть случаи, когда наши загружаемые ресурсы содержат гиперссылки на другие веб-сайты. Эти гиперссылки ведут на веб-сайты, опубликованные или управляемые третьими сторонами. UnboundEd и EngageNY не несут ответственности за содержание, доступность или политику конфиденциальности этих веб-сайтов.
Теги
- Нет тегов для этого ресурса
Кредиты
от EngageNY.org Департамента образования штата Нью-Йорк. Математика 7 класса.
Доступно на сайте engageny.org/resource/grade-7-mat Mathematics; по состоянию на 29 мая 2015 г.
Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
Открытые учебные программы CEMC — математика для 7 и 8 классов
Представление и сравнение чисел (N)
Часть A (Уроки 1–7)
Темы включают представление и сравнение положительных рациональных чисел (целых, дробных и десятичных), поиск кратных и множителей положительных целых чисел, а также определение наименьшего общего кратного (НОК) и наибольшего общего множителя ( GCF) пары натуральных чисел.
Часть B (Уроки 8–12)
Темы включают представление отрицательных дробей и отрицательных десятичных дробей, сравнение значений любых двух рациональных чисел, экспоненциальную запись, а также использование факторных деревьев и простых факторизаций, чтобы найти НОК или НОК пары положительные целые числа.
В этом уроке рассматриваются три разные системы счисления: целые числа, целые числа и рациональные числа.Выделены связи между различными системами счисления, чтобы заложить основу для сравнений и операций.
Математики часто используют числовую прямую для решения задач. В этом уроке мы рассмотрим числовую линию, уделяя особое внимание построению дробей.
В математике символы важны для общения.В этом уроке мы рассмотрим символы «больше» и «меньше». Кроме того, мы представляем два метода, используемых для сравнения дробей.
Рациональные числа можно записывать в виде дробей или десятичных знаков. В этом уроке мы обсудим связи между дробными и десятичными представлениями, в частности, когда дело доходит до нанесения чисел на числовой прямой.
В этом уроке мы рассмотрим, как создать список, кратный целому числу. Используя наши списки, мы определяем общие кратные двух целых чисел, уделяя особое внимание наименьшему общему кратному (НОК).
Факторы, как и кратные, имеют отношение к умножению.В этом уроке мы решаем проблемы, определяя множители положительных целых чисел.
Продолжая урок по факторам, мы сравниваем множители двух положительных целых чисел, чтобы найти общие множители; в частности, нас часто интересует определение наибольшего общего фактора (GCF). В заключение мы решаем задачи со словами, которые требуют от нас применения факторов к разным контекстам.
Дробные количества могут быть положительными или отрицательными. Как и отрицательные целые числа, отрицательные дроби лежат слева от нуля на числовой строке. В этом уроке мы наносим отрицательные дроби на числовую линию, чтобы помочь нам понять и сравнить значения этих чисел.
Рациональные числа можно записывать в виде дробей или десятичных знаков.В этом уроке мы сравниваем отрицательные десятичные числа, нанося их на числовую линию. Затем мы сравниваем отрицательные дроби с отрицательными десятичными знаками. Определены десятичные эквиваленты обыкновенных дробей и показаны стратегии преобразования дроби в десятичные. Наконец, мы узнаем, как сравнивать любые два рациональных числа.
На этом уроке мы учимся представлять многократное умножение с использованием экспоненциальной записи.Затем используется экспоненциальная запись для представления целых чисел в развернутой форме с использованием степеней десяти. Исследуются квадратные числа и кубические числа.
В этом уроке мы рассмотрим простые и составные числа. Мы узнаем, как представить составное число как произведение его простых множителей с помощью факторного дерева.
Факторизации на простые числа можно использовать для определения наибольшего общего множителя (GCF) и наименьшего общего кратного (LCM) пары положительных целых чисел. Мы исследуем, как это можно сделать, и используем эти стратегии для решения текстовых задач.
Операции (N)
Часть A (Уроки 1–11)
Темы включают в себя сложение и вычитание рациональных чисел, умножение и деление целого числа на положительное рациональное число, а также вычисление выражений с использованием порядка операций.
Часть B (Уроки 12–19)
Темы включают в себя умножение и деление целых, дробных и десятичных чисел, приближение квадратных корней из положительных целых чисел и вычисление выражений, включающих показатели степени, с использованием порядка операций.
Мы начинаем обсуждение сложения с изучения того, как числовые линии могут использоваться для отображения сложения. В этом уроке мы сосредоточимся на сложении целых чисел, а именно на том, как можно складывать положительные и отрицательные числа с помощью числовой строки.
Мы можем складывать целые числа без использования калькулятора или числовой строки. В этом уроке мы расширяем наше предыдущее обсуждение сложения целых чисел и исследуем стратегии выполнения сложения целых чисел в уме.
Этот урок исследует эквивалентные дроби в процессе подготовки к тому, когда мы должны складывать и вычитать дроби.В процессе поиска эквивалентных дробей вам будет предоставлена возможность попрактиковаться в нахождении общих кратных, использовании неправильных дробей и смешанных чисел, построении графика на числовой прямой и сравнении рациональных чисел.
В этом уроке мы основываемся на нашем понимании сложения и включаем рациональные числа.Для этого мы снова обращаемся к числовой прямой и применяем наши стратегии построения рациональных чисел, чтобы мы могли найти их сумму.
В этом уроке представлены стратегии сложения дробей без использования числовой прямой. Мы используем числовые линии как мотивацию для поиска общего знаменателя, затем переходим к сложению дробей без использования наглядных пособий.
Мы начнем обсуждение вычитания с целых чисел. В этом уроке мы рассмотрим операцию вычитания, покажем вычитание на числовой строке и узнаем, как вычитать целые числа как с числовой строкой, так и без нее.
Продолжая обсуждение вычитания, в этом уроке мы исследуем стратегии вычитания дробей.Наша цель — использовать эквивалентные дроби для решения задач на вычитание без использования калькулятора или числовой прямой.
В этом уроке исследуются стратегии умножения целых чисел на дроби и десятичные дроби. Решаем примеры и выделяем правила выполнения расчетов без использования калькулятора.
Умножение — это операция, которая используется для масштабирования или изменения размера количества. В этом уроке мы исследуем масштабные коэффициенты и обсудим, почему мы должны думать об умножении с точки зрения масштабирования.
В этом уроке мы узнаем, как выполнять вычисления, включающие деление целых чисел на дроби и десятичные дроби.На примерах мы выделяем правила выполнения этих вычислений без калькулятора.
Порядок операций проверяется и используется для выполнения вычислений с использованием целых, дробных и десятичных знаков. Кроме того, мы исследуем важность скобок; когда они нужны и когда их можно удалить из выражения.В заключение мы воспользуемся свойством распределенности для упрощения вычислений.
В этом уроке мы узнаем, как мысленно умножать целые числа. В частности, мы смотрим, как знак каждого целого числа в продукте влияет на знак продукта.
Деление — это операция, противоположная умножению, поэтому стратегии, которые мы изучаем для деления целых чисел, будут аналогичны тем, которые мы использовали при умножении целых чисел.В этом уроке мы исследуем, как знаки делимого и делителя влияют на знак частного.
Мы начнем этот урок с того, что рассмотрим умножение дроби на целое число. Затем мы расширяем наше понимание, включив в него умножение любых двух дробей. Кроме того, определенное внимание уделяется оценке стоимости продуктов.
В этом уроке мы рассмотрим, как разделить целое число на дробь. Затем мы исследуем, как адаптировать эту стратегию, чтобы разделить дробь на другую дробь без использования калькулятора.
Мы начинаем этот урок с изучения умножения десятичных чисел на степени десяти, включая обсуждение научных обозначений.Затем мы узнаем, как умножать два десятичных числа, во-первых, преобразовывая числа в дроби, а во-вторых, работая с самими десятичными числами.
В этом уроке мы разрабатываем стратегии для оценки выражений деления, содержащих целые и десятичные числа. Мы также расширяем эти стратегии, чтобы обсудить деление с двумя десятичными числами.
Этот урок посвящен взаимосвязи между возведением числа в квадрат и извлечением квадратного корня из числа. Мы обсуждаем точные квадраты и исследуем, как приблизительно вычислить квадратный корень из положительного целого числа, которое не является полным квадратом.
В этом уроке мы вернемся к порядку выполнения арифметических операций.Мы решаем задачи с целыми числами, дробями и десятичными знаками, уделяя особое внимание показателям степени.
Соотношения, нормы и пропорции (N)
Часть A (Уроки 1–5)
Темы включают соотношения письма и интерпретации; нахождение эквивалентных соотношений; преобразование между дробями, десятичными знаками и процентами; преобразование единиц измерения; и решение проблем, связанных с удельными ставками.
Часть B (Уроки 6–10)
Темы включают распознавание пропорциональных ситуаций в задачах со словами, таблицах и графиках; соединительный блок относится к пропорциональным отношениям и их представлению в таблицах, графиках и уравнениях; и дробные проценты и проценты больше 100 процентов.
В этом уроке обсуждается значение соотношения и рассказывается, как записывать и интерпретировать соотношения.В заключение мы решаем проблемы, которые требуют применения соотношения к большим количествам.
Мы начинаем обсуждение эквивалентных соотношений с диаграмм и исследуем, как два соотношения могут представлять одно и то же отношение между двумя величинами. Затем мы разрабатываем стратегии для численного нахождения эквивалентных соотношений.Этот урок завершается решением задач соотношения.
В этом уроке мы определяем процент и исследуем отношения между дробями, десятичными знаками и процентами. В заключение мы решим несколько словесных задач, связанных с процентами.
В этом уроке рассматриваются стратегии преобразования между различными метрическими единицами измерения длины, массы и вместимости.Затем мы применяем эти стратегии для преобразования единиц времени в единицы площади.
В этом уроке мы узнаем о показателях, которые представляют собой сравнение двух измерений с разными единицами измерения. Мы сосредотачиваемся на том, как записывать удельные расценки и как можно использовать удельные расценки для решения текстовых задач. Также включены несколько примеров того, как преобразовать курс в разные единицы.
В этом уроке мы исследуем понятие пропорциональности на таких примерах, как увеличение изображения и смешивание красок. Мы исследуем пропорциональные отношения между двумя величинами и учимся распознавать, когда ситуация пропорциональна, а когда нет.
В этом уроке мы исследуем, как распознать пропорциональную связь между двумя величинами, когда данные отображаются в таблице или на графике.
Соотношение между пропорциональными количествами часто задается в форме удельной нормы. В этом уроке мы исследуем, как эта единичная ставка проявляется в уравнении, таблице или графике, представляющем взаимосвязь между двумя величинами.
В этом уроке мы обсуждаем дробные проценты и проценты, превышающие 100 процентов.Некоторое внимание уделяется тому, где проценты появляются в повседневной жизни и как оценка может быть полезна при работе с процентами.
Пропорциональные ситуации могут быть представлены разными способами, включая: удельные расценки, таблицы, графики или уравнения. В этом уроке мы практикуем сравнение пропорциональных отношений, которые представлены по-разному.
Биссектрисы и свойства фигур (G)
Часть A (Уроки 1–6)
Темы включают построение биссектрис угла и серединного перпендикуляра, а также различные свойства треугольников, четырехугольников и многоугольников более общего вида. В частности, разные многоугольники классифицируются на основе длины их сторон и угловых размеров.
Часть B (Уроки 7–10)
Темы включают диагонали четырехугольника, терминологию и построение круга, а также применение кругов в реальном мире.
Этот урок знакомит с терминологией и обозначениями основных геометрических объектов с упором на письменное и устное общение.
Мы рассмотрим, как классифицировать треугольники по длинам сторон и угловым измерениям.Затем мы исследуем соотношение сторон и угла в треугольниках. Этот урок завершается применением свойств треугольника для построения угла в 60 градусов с помощью циркуля.
Циркуль и линейку можно использовать для точного деления угла пополам без выполнения измерения. В этом уроке мы обсудим свойства биссектрис угла и то, как использовать эти свойства для построения биссектрисы угла заданного угла, используя только циркуль и линейку.Мы расширяем наше обсуждение до треугольников и исследуем взаимосвязь трех биссектрис угла в любом треугольнике.
Продолжая обсуждение построений, мы рассмотрим свойства серединных перпендикуляров и то, как использовать эти свойства для построения серединного перпендикуляра заданного отрезка прямой, используя только циркуль и линейку.Мы расширяем наше обсуждение до треугольников и исследуем отношения трех серединных перпендикуляров в любом треугольнике.
В этом уроке мы рассмотрим свойства шести специальных четырехугольников. Мы исследуем сходства и различия между ними и используем диаграмму, чтобы представить все обсуждаемые нами отношения.
В этом уроке мы обсуждаем свойства многоугольников, расширяясь по четырехугольникам. В частности, мы исследуем сумму внутренних углов в многоугольнике и то, как многоугольники связаны с призмами. Этот урок завершается расширением, в котором исследуется, как можно разрезать призмы для получения различных многоугольных граней.
В этом уроке мы исследуем различные свойства диагоналей в четырехугольниках. В частности, мы рассматриваем, когда диагонали делят друг друга пополам, перпендикулярны друг другу или равны по длине. Затем мы используем эти свойства, чтобы помочь нам классифицировать четырехугольники.
Этот урок начинается с обсуждения того, как описать круг.Поскольку круги сильно отличаются от многоугольников, мы вводим новую терминологию для использования при изучении кругов. В частности, мы определяем центр, радиус, диаметр и длину окружности. Мы также исследуем, как использовать многоугольники, чтобы оценить длину окружности и площадь, заключенную в круг.
В этом уроке мы обсудим стратегии рисования точных кругов.В частности, мы смотрим на рисование окружностей, когда заданы центр и радиус, центр и точка, которые должны лежать на окружности, а также две или более точек, которые должны все лежать на окружности. Мы обсуждаем, где в реальном мире появляются большие круги и какие инструменты и стратегии можно использовать для их создания.
В этом уроке мы рассмотрим применение кругов за пределами колеса и обсудим роль кругов в проектировании круговых движений, использование кругов в дизайне конструкций и взаимодействие кругов разного диаметра в машинах, в которых используются шестерни.
Площадь, объем и углы (G)
Часть A (Уроки 1–5)
Темы включают вычисление площади параллелограммов, треугольников, трапеций и составных фигур; расчет площади поверхности, объема и емкости призм; и представление трехмерных объектов по-разному.
Часть B (Уроки 6–10)
Темы включают вычисление длины окружности и площади кругов; расчет объема и площади цилиндров; и свойства углов, образованных пересекающимися линиями, включая параллельные линии и трансверсали.
В этом уроке рассматривается определение площади и способ вычисления площади прямоугольника. Затем мы разрабатываем и применяем формулы для нахождения площадей параллелограммов, треугольников и трапеций.
Продолжая обсуждение площади, мы исследуем, как разложить и вычислить площадь составных фигур.
В этом уроке мы узнаем, как визуализировать поверхность трехмерного твердого тела с помощью сети. Затем мы вычисляем площадь поверхности призм и решаем задачи, связанные с площадью поверхности.
В этом уроке мы разработаем и применим формулу для определения объема призмы.Мы связываем объем и вместимость и исследуем, как конвертировать единицы объема.
Мы завершаем обсуждение призм и составных тел, научившись рисовать их на бумаге с треугольными точками. Мы также узнаем, как распознавать и рисовать различные 2D-виды 3D-объекта.
В этом уроке мы рассмотрим окружность и площадь кругов.Затем мы разрабатываем и применяем формулы для вычисления длины окружности и площади круга с учетом радиуса (или диаметра) круга.
Мы начинаем обсуждение цилиндров со сравнения цилиндров с призмами. Мы разрабатываем и применяем формулу для определения объема цилиндра и решаем задачи, связанные с объемом или вместимостью цилиндра.
Продолжая обсуждение цилиндров, в этом уроке мы исследуем сеть цилиндра и используем эту сеть, чтобы разработать формулу для площади поверхности цилиндра. Затем мы вычисляем площадь поверхности цилиндров и решаем задачи, связанные с площадью поверхности.
В этом уроке мы начнем обсуждение пересекающихся линий с изучения свойств углов, образованных двумя пересекающимися линиями.Мы определяем дополнительные, дополнительные и противоположные углы и используем угловые отношения, чтобы найти неизвестные углы на диаграмме.
Продолжая обсуждение пересекающихся линий, в этом уроке мы исследуем углы, образованные параллельными линиями и трансверсалиями. Мы определяем соответствующие, альтернативные и совпадающие внутренние углы и используем угловые отношения для определения неизвестных углов на диаграмме.
Преобразования фигур (G)
Часть A (Уроки 1–7)
Темы включают сопоставление многоугольников, правила сопоставления треугольников, нанесение точек на декартову плоскость, изображение многоугольника на декартовой плоскости при перемещениях, отражениях и / или поворотах на декартовой плоскости, а также мозаики.
Часть B (Уроки 8–11)
Темы включают подобие многоугольников, правила подобия треугольников, расширение многоугольников и косвенные измерения.
В этом уроке мы рассмотрим определение конгруэнтности и сопоставим стороны и углы двух конгруэнтных многоугольников. Мы также смотрим на периметр и площадь конгруэнтных многоугольников.
Продолжая обсуждение конгруэнтности, в этом уроке мы исследуем правила конгруэнтности для треугольников.Наша цель — показать конгруэнтность двух треугольников, сопоставив только три соответствующие части.
Этот урок знакомит с декартовой плоскостью. Мы исследуем, как построить декартову систему координат, как построить точки на декартовой плоскости, а также исследуем вертикальные / горизонтальные расстояния между двумя точками на декартовой плоскости.
В этом уроке мы начнем обсуждение преобразований с изучения переводов многоугольников. Мы учимся рисовать изображение многоугольника под переводом и соотносим определение конгруэнтности с переводами.
Продолжая обсуждение преобразований, мы исследуем отражения многоугольников.В этом уроке мы узнаем, как построить график изображения многоугольника под отражением на декартовой плоскости, и объясним, как изображение конгруэнтно исходному многоугольнику.
В этом уроке мы узнаем, как построить график изображения многоугольника при повороте. Мы также комбинируем все три преобразования и строим график изображения многоугольника при перемещении, отражении и вращении на декартовой плоскости.
Этот урок исследует искусство мозаики. Мы определяем тесселяцию и исследуем, какие полигоны могут тесселять плоскость. Затем, используя многоугольники, которые, как мы знаем, составляют мозаику плоскости, мы исследуем, как создавать интересные мозаичные конструкции.
В геометрии слово «аналогичный» используется для обозначения того, когда два объекта имеют одинаковую форму, но не обязательно одинакового размера.В этом уроке мы узнаем точное определение похожих многоугольников, исследуем масштабный коэффициент между двумя похожими многоугольниками и узнаем, как использовать масштабный коэффициент для решения проблем.
Каждый треугольник имеет три угла и три стороны, но оказывается, что нам не нужно знать размеры каждого из них, чтобы определить форму треугольника.В этом уроке мы исследуем минимальные условия, необходимые для проверки схожести двух треугольников. Мы изучаем правила подобия «Угол-угол», «Сторона-сторона-сторона» и «Сторона-угол-сторона» и практикуемся в построении подобных треугольников.
В этом уроке мы узнаем, как рисовать похожие многоугольники без измерения углов.Это можно сделать, выполнив преобразование определенного типа: расширение.
Косвенные измерения позволяют нам находить неизвестные длины без фактического измерения отрезков линий. В этом уроке мы исследуем, как использовать правила подобия треугольников для косвенных измерений в различных сценариях.
Представление узоров (A)
Часть A (Уроки 1–6)
Темы включают представление последовательностей с помощью таблиц, общих терминов и графиков, описание паттернов с помощью переменных и выражений, расширение последовательностей и решение проблем, связанных с неизвестными величинами.
Часть B (Уроки 7–11)
Темы включают эквивалентные выражения для общего члена последовательности, описание отношений и закономерностей с помощью уравнений, а также убывающие и встречающиеся естественным образом последовательности.
Мы начинаем обсуждение паттернов с изучения последовательностей чисел и изображений. В этом уроке мы сосредоточимся на формулировке шаблонного правила, которое описывает, как генерировать следующий член в последовательности.
В этом уроке исследуется взаимосвязь между номером термина и значением термина, то есть взаимосвязь между термином в последовательности и его положением в этой последовательности. Затем мы используем общий термин, чтобы найти значение термина в последовательности по его номеру термина.
Мы продолжаем находить общий термин последовательностей, уделяя особое внимание тому, как использовать переменную для представления неизвестной величины.Этот урок завершается обсуждением подстановки, где мы оцениваем выражения, подставляя число вместо переменной в общем термине.
На этом уроке мы встречаемся с последовательностями, которые имеют другой тип отношений, чем то, что мы видели ранее. Вы продолжите практиковаться в нахождении общего члена последовательности, завершив урок некоторыми прикладными задачами.
В этом уроке мы исследуем, как графически представить последовательность. С последовательностью, представленной на графике, мы затем используем график для определения номера термина, который соответствует данному термину в последовательности. Наконец, вы научитесь находить общий член последовательности по ее графику.
В этом уроке мы соединяем различные последовательности, которые мы изучили до сих пор.Мы продолжаем использовать таблицы, графики и общие термины для изучения закономерностей, которые представляют последовательности.
В этом уроке мы рассмотрим, как представить последовательность с помощью таблицы, общего термина или графика. Акцент делается на определении того, какое из этих трех представлений является наиболее подходящим в конкретной ситуации решения проблемы.
В этом уроке мы анализируем разные шаблоны, которые генерируют одну и ту же последовательность чисел. Мы генерируем различные выражения для представления различных интерпретаций шаблона и узнаем, как определить, эквивалентны ли два выражения.
В этом уроке мы узнаем разницу между выражением и уравнением и исследуем, как каждое из них можно использовать при описании шаблонов.В частности, мы используем выражения для общего члена последовательности, чтобы формировать уравнения для представления взаимосвязей в последовательностях.
В этом уроке мы определяем и исследуем убывающие последовательности. Вам предлагается подумать, как можно использовать стратегии нахождения общих членов возрастающих последовательностей, чтобы написать уравнение, представляющее убывающую последовательность.Мы также исследуем, как некоторые последовательности чисел, возникающие из физических ситуаций, не могут продолжаться вечно из-за границ реального мира.
В этом уроке мы выходим за рамки типичных последовательностей, обсуждаемых в этом разделе, и исследуем более естественные последовательности. Примеры сосредоточены на популярных головоломках и реальных сценариях роста и снижения стоимости.В заключение мы обсудим на примере, насколько очевидные закономерности могут иногда вводить в заблуждение.
Уравнения и теорема Пифагора (A)
Часть A (Уроки 1–5)
Темы включают использование переменных в выражениях и уравнениях, определение и исследование линейных отношений, а также решение уравнений путем проверки, проб и ошибок, а также с использованием визуальных моделей.
Часть B (Уроки 6–10)
Темы включают решение уравнений с использованием алгебраических методов, сравнение различий между вычислением выражения и решением уравнения, изучение уравнений с несколькими переменными и теорему Пифагора.
В этом уроке мы рассмотрим переменные и выражения. Мы обсуждаем общие обозначения для операций в алгебре и попрактикуемся в переводе английских фраз в математические выражения.
В этом уроке мы исследуем линейные отношения между двумя величинами. Мы узнаем, как определить линейную зависимость, представленную на графике, в таблице значений или в уравнении.
В этом уроке мы используем выражения и уравнения для моделирования и решения реальных проблем.
В этом уроке мы используем графики и визуальную модель весов на шкале, чтобы помочь решить уравнения. Мы также практикуем решение простых уравнений путем осмотра.
В этом уроке мы попрактикуемся в решении уравнений методом проб и ошибок.Эти методы применяются для решения задач со словами и для решения уравнений с дробными решениями.
В этом уроке мы визуализируем уравнения с помощью весов и сбалансированной шкалы. Мы решаем уравнения за одну операцию, используя алгебраические методы, и узнаем, как проверить решение уравнения.
Мы продолжаем решать уравнения с помощью алгебры, расширяя наши стратегии для решения уравнений с помощью более чем одной операции.
В этом уроке исследуется движение вперед и назад с помощью математической машины и выясняются различия между вычислением выражения и решением уравнения.
В этом уроке мы находим решения уравнений с двумя или более неизвестными величинами, используя метод проб и ошибок и алгебру.
В этом уроке мы исследуем взаимосвязь между длинами сторон прямоугольного треугольника. Мы разработаем теорему Пифагора и воспользуемся ею, чтобы найти недостающую длину стороны прямоугольного треугольника.
Сбор данных и графики (D)
Часть A (Уроки 1–5)
Темы включают различные типы данных; население, выборка и перепись; предвзятость при сборе данных, связанная с формулировкой вопросов, принятыми ответами и выбором группы выборки; таблицы и графики частоты и относительной частоты; чтение и построение круговых графиков; выбор подходящего типа графика для набора данных; смещение в представлении данных, возникающее из-за выбранного типа графика, структуры и формы графика, а также меток и масштабов осей.
Часть B (Уроки 6–9)
Темы включают в себя организацию непрерывных данных в виде графиков «стебель-лист» и частотных таблиц с интервалами; а также создание и чтение гистограмм и диаграмм рассеяния.
В этом уроке мы обсуждаем различные типы данных, включая первичные, вторичные, категориальные и числовые данные. Мы обсуждаем термины «население», «выборка» и «перепись» и узнаем разницу между дискретными и непрерывными числовыми данными.
В этом уроке мы исследуем, как на данные могут влиять формулировка вопросов обследования, типы ответов, принимаемых в обследовании, и группа выборки, которая используется в обследовании для представления совокупности.
В этом уроке мы узнаем, как систематизировать данные в таблицы частот, вычислять относительные частоты, а также создавать и сравнивать графики частоты и относительной частоты.
В этом уроке мы сосредоточимся на чтении и создании круговых диаграмм (или круговых диаграмм). Мы также обсуждаем соответствующие типы графиков (круг, столбец или линия), которые можно использовать для отображения различных наборов данных.
В этом уроке мы исследуем, как выбор, сделанный при создании графика, может привести к искажению основных данных.В частности, мы обсуждаем, как тип графика, структура и форма графика или метки осей и масштабы графика могут потенциально ввести в заблуждение зрителя.
В этом уроке мы сосредоточимся на работе с непрерывными наборами данных. Мы исследуем различные способы организации и построения графиков непрерывных данных, а также обсуждаем, как отображать парные наборы данных.
В этом уроке мы изучаем различные способы организации наборов числовых данных в интервалы. Мы начнем с организации данных с помощью диаграмм «ствол и лист», а затем исследуем, как можно использовать частотные таблицы, если мы разделим данные на интервалы. Мы обсуждаем преимущества и недостатки этих инструментов организации и практикуем выбор подходящих интервалов для заданных наборов данных.
Стандартные гистограммы не всегда являются подходящим способом отображения заданного набора числовых данных. Гистограмма — это аналогичный тип графика, на котором числовые данные сначала группируются в диапазоны, а затем частота каждого диапазона отображается с помощью столбца. В этом уроке мы обсудим особенности гистограммы и попрактикуемся в создании гистограмм из наборов числовых данных.Мы обсуждаем, какую информацию можно получить или потерять, представляя данные в виде гистограммы, и исследуем влияние выбора интервала на форму графика.
Диаграмма рассеяния — это график, состоящий из точек, сформированных с использованием значений двух переменных величин. Диаграммы разброса используются для отображения взаимосвязи между двумя рассматриваемыми переменными.В этом уроке мы обсудим особенности диаграммы рассеяния и попрактикуемся в создании диаграмм рассеяния из парных наборов данных. Мы обсуждаем роли, которые две переменные играют на диаграмме рассеяния, и исследуем, какая информация может быть раскрыта, когда мы рассматриваем форму, сформированную точками данных в целом.
Анализ данных (D)
Часть A (Уроки 1–4)
Темы включают определение среднего, медианного и режима наборов данных; изучение эффектов добавления данных в набор данных или удаления данных из набора данных; изучение влияния выбросов на среднее, медиану и моду; и практика делать выводы и делать прогнозы на основе данных в виде графиков.
Часть B (Уроки 5–8)
Темы включают интерпретацию данных, гистограмм и диаграмм рассеяния, а также выводы из этих диаграмм; описание отношений между двумя переменными на диаграмме рассеяния; оценка темпов изменений, связанных с диаграммами рассеяния; делать прогнозы, подкрепленные данными в гистограммах и диаграммах рассеяния; и используя соответствующие меры центральной тенденции для сравнения двух наборов данных.
Может быть полезно использовать одно значение для обобщения информации в большом наборе данных.Меры центральной тенденции, такие как среднее значение, медиана и мода, пытаются суммировать данные, измеряя середину (или центр) набора данных. В этом уроке мы узнаем, как определять среднее значение, медианное значение и режим для различных наборов данных, и обсудим, как их можно использовать для анализа данных.
В этом уроке мы обсуждаем эффекты добавления данных в набор данных (или удаления данных из него).Мы фокусируемся на том, как это может по-разному повлиять на среднее значение, медианное значение и моду.
Некоторые наборы данных содержат выбросы, то есть данные, отделенные от остальных значений в наборе данных. В этом уроке мы обсуждаем влияние выбросов на среднее, медианное значение и режим наборов данных, а также исследуем различные контексты, в которых одна конкретная мера может быть наиболее подходящей для обобщения данных.
В этом уроке мы попрактикуемся в интерпретации базовых данных, отображаемых на разных графиках. Мы обсуждаем разницу между утверждениями, которые можно проверить с помощью информации в графике, и прогнозами, которые поддерживаются тенденциями на графике, но не могут быть проверены с помощью одного только графика.
В этом уроке мы практикуемся в определении и интерпретации информации, представленной в гистограмме, и делаем выводы, подтверждаемые гистограммой.Мы также исследуем, как размер интервала гистограммы может повлиять на выводы, сделанные кем-то, кто анализирует данные в гистограмме.
На этом уроке мы практикуемся в определении и интерпретации информации, представленной на диаграмме рассеяния, и делаем выводы, подтверждаемые диаграммой рассеяния. Мы исследуем, как определить и описать общие отношения, которые могут существовать между двумя переменными на диаграмме рассеяния.
Точечные диаграммы часто используются для выявления и изучения взаимосвязи между двумя переменными. Когда кажется, что точки данных на диаграмме рассеяния примерно повторяют траекторию линии, мы можем использовать наши знания о линейных паттернах, чтобы изучить данные и сделать прогнозы. В этом уроке мы исследуем рисование линий, которые приблизительно соответствуют тенденции, наблюдаемой на точечной диаграмме, и оцениваем скорость изменения, связанную с точечной диаграммой.Мы сравниваем скорость изменения различных графиков рассеяния и используем их для прогнозов.
На этом уроке мы попрактикуемся в использовании показателей центральной тенденции для сравнения двух наборов данных, сделаем выводы и обсудим факторы, которые могут повлиять на то, какая мера центральной тенденции является наиболее подходящей для конкретного сравнения.Мы также исследуем, как сравнивать данные, представленные в гистограммах.
Вероятность (D)
Часть A (Уроки 1–4)
Темы включают случайные эксперименты, результаты и события; расчет теоретических вероятностей единичных событий; сравнение вероятностей разных событий; независимые мероприятия; экспериментальная вероятность; и использование вероятностей для предсказаний.
Часть B (Уроки 5–8)
Темы включают сравнение теоретических вероятностей и экспериментальных вероятностей; изучение того, как количество испытаний влияет на оценки вероятности; дополнительные мероприятия; настройка и запуск моделирования с использованием вероятностных моделей; и повторное посещение независимых событий.
Случайный эксперимент — это эксперимент, в котором известен набор возможных результатов, но фактический результат нельзя предсказать с какой-либо уверенностью.Теория вероятностей — это исследование случайных экспериментов, включая различные способы измерения вероятности того, что конкретный результат или событие произойдет. В этом уроке мы рассмотрим понятие вероятности и попрактикуемся в вычислении теоретических вероятностей различных событий в различных экспериментах.
Часто случайные эксперименты включают более одного объекта, например, эксперимент может включать подбрасывание честной монеты и бросание стандартного кубика.В этом уроке мы исследуем, как вычислить вероятность двух независимых событий, например, вероятность того, что голова подброшена и выпадет четное число. Мы определяем и идентифицируем независимые события, а также используем таблицы и древовидные диаграммы для систематического перечисления всех результатов эксперимента с целью расчета вероятностей различных событий.
Теоретическая вероятность — это соотношение, которое описывает то, что мы ожидаем от эксперимента, а экспериментальная вероятность — это соотношение, которое описывает то, что на самом деле произошло во время испытаний эксперимента.В этом уроке мы вычисляем экспериментальные вероятности различных событий и исследуем, как они соотносятся с известными теоретическими вероятностями. Мы также исследуем ситуации, когда экспериментирование является нашим единственным вариантом изучения вероятностей.
Если вы можете определить вероятность того, что определенное событие произойдет в эксперименте, то вы можете использовать эту информацию, чтобы делать прогнозы, связанные с этим экспериментом.В этом уроке мы используем теоретические и экспериментальные вероятности, чтобы делать прогнозы. Мы обсуждаем, насколько надежными или ненадежными могут быть наши прогнозы, и изучаем, как мы можем спланировать эксперименты таким образом, чтобы наши прогнозы были максимально надежными.
В этом уроке мы сравниваем теоретические вероятности с оценками вероятностей, полученными в результате экспериментов, и исследуем, как количество испытаний, выполненных в эксперименте, может повлиять на оценки вероятностей.
В этом уроке мы определяем и исследуем понятие дополнительных событий. Мы узнаем, как определение дополнительных событий может быть полезно при вычислении вероятностей.
Для многих реальных ситуаций, связанных с вероятностями, может быть сложно собрать данные напрямую путем проведения реальных экспериментов.В таких ситуациях математики часто проводят симуляции, которые с точки зрения вероятностей напоминают реальную ситуацию. В этом уроке мы узнаем, как выбрать подходящие модели для моделирования, и попрактикуемся в запуске моделирования для получения оценок вероятности.
В этом уроке мы рассмотрим, как определять вероятности независимых событий, используя списки, таблицы и древовидные диаграммы для отображения всех возможных результатов.
