Функции кусочные примеры: Кусочные функции. Как построить график кусочной функции

alexxlab

Содержание

Как построить график кусочной функции

☰

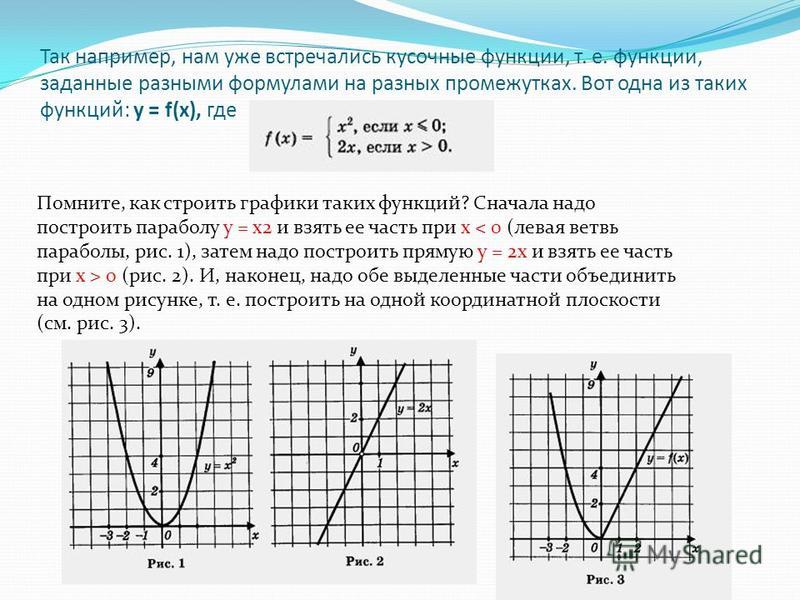
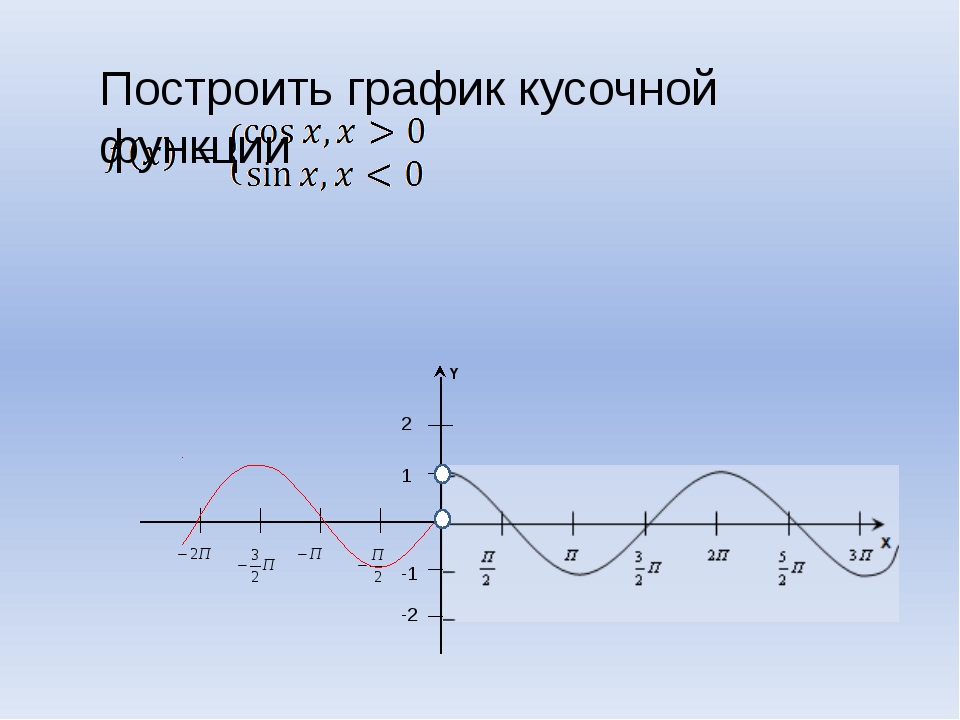
Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,

Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x2. Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x2 (сначала возводим в квадрат, потом учитываем минус).

Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.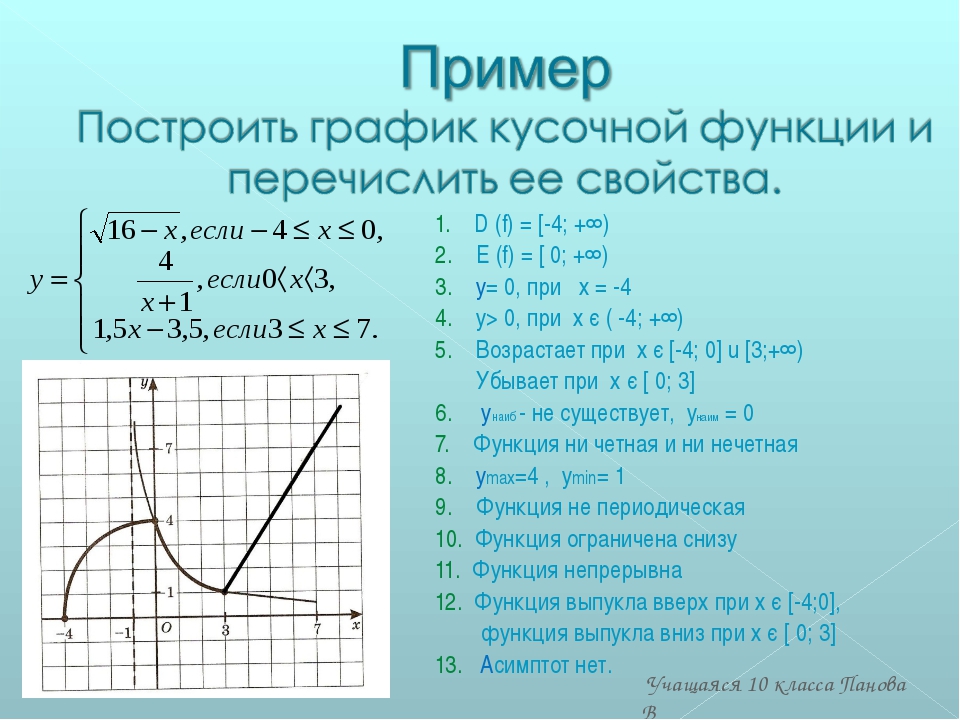

Для приведенного выше примера для формулы y = √x получим такой график:

Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.

Построим график функции f(x) = –x2. Получим перевернутую параболу:

В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:

Рассмотрим другой пример:

Графиком функции f(x) = (0.6x – 0.5)2 – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:

В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой:

построение графика, формула, знак модуля и примеры

Графики и формулы кусочно-линейных функций

Ситуация, когда движение или другое явление можно описать одной линейной функцией, определенной на интервале $-\infty \lt t \lt +\infty$, в действительности невозможна. Хотя бы потому, что возраст Вселенной велик, но не бесконечен.

На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т.п. Как задать подобную зависимость?

Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода.

Изобразим зависимость s(t) графически:

Первый отрезок AB легко записать: $ s_1 (t) = 5t,0 \le t \lt 2$

С отрезком BC тоже всё ясно: $s_2 (t) = 10,2 \le t \lt 3$

Осталось найти формулу для отрезка CD. Для него известен угловой коэффициент, равный скорости k = -4; знак «минус» оттого, что турист возвращается обратно. Формула имеет вид $s_3 (t) = -4t+b$. Также, нам известны координаты C(3;10).

Подставляем: $10 = -4 \cdot 3+b \Rightarrow b =22$.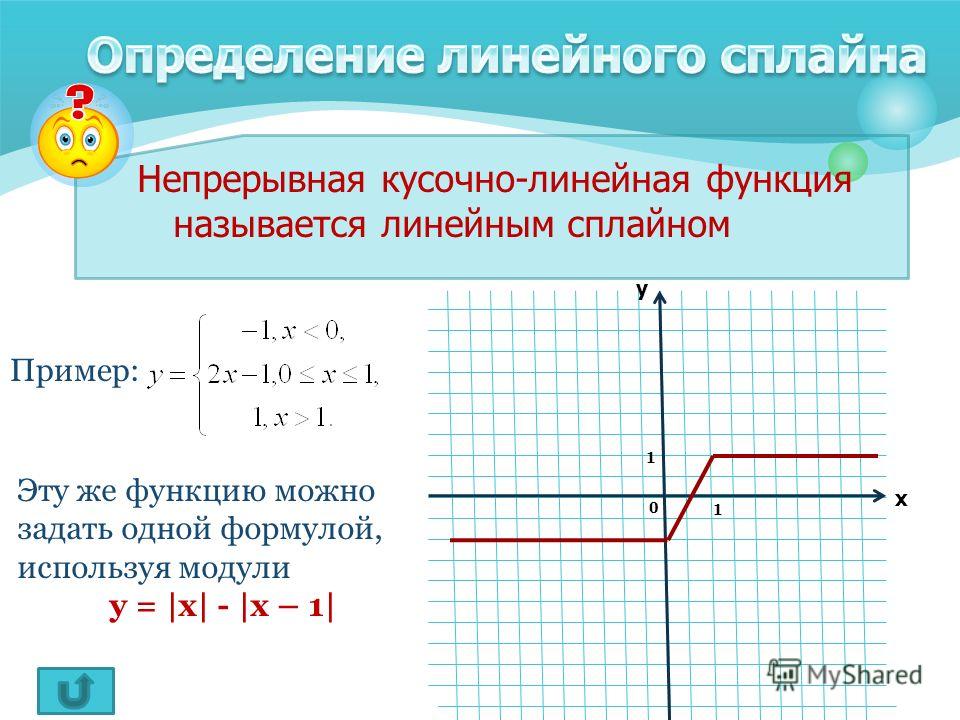 Осталось рассчитать момент возвращения:

$$0 = -4t_{back}+22 \Rightarrow t_{back} = 22:4 = 5,5$$ (ч)

Значит, формула движения на отрезке $CD:s_3 (t) = -4t+22,3 \le t \le 5,5.$

Получаем:

$$s(t) = {\left\{ \begin{array}{c} 5t,0 \le t \lt 2 \\ 10,2 \le t \lt 3 \\ -4t+22,3 \le t \le 5,5 \end{array} \right.} $$

Важным свойством заданной функции является выполнение условий согласования:

$$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$

Наша функция «сшита» на концах промежуточных интервалов.

В общем случае:

Функция вида

$$x f(x) = {\left\{ \begin{array}{c} k_1 x+b_1, x_1 \le x \lt x_2 \\ k_2 x+b_2,x_2 \le x \lt x_3 \\…\\ k_n x+b_n,x_n \le x \lt x_{n+1} \end{array} \right.}$$

называется кусочно-линейной.

При этом для функции на краях интервалов выполняются условия согласования:

$$f_i (x_{i+1} ) = f_{i+1} (x_{i+1} ),i = \overline {1,n-1} $$

Графиком кусочно-линейной функции является ломаная линия

Знак модуля в линейных функциях

По правилу раскрытия скобок модуля (см.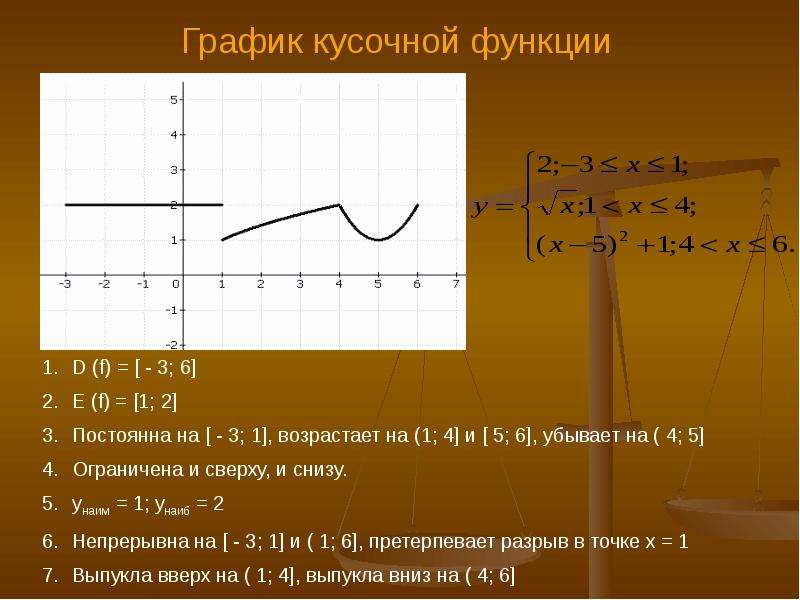 §4 данного справочника)

$$ |x| = \left[ \begin{array}{cc} x, x\ge0 \\ -x, x \lt 0\end{array} \right.$$

Внимание!

Если в формуле для линейной функции содержится знак модуля, то после его раскрытия получается кусочно-линейная функция.

Например:

$$ y = 2|x|+5 = {\left\{ \begin{array}{c} -2x+5, x\ge0 \\ 2x+5, x \lt 0\end{array} \right.} $$

Мы заменили квадратную скобку со значением «или» на фигурную скобку со значением «и», поскольку именно смысл объединения — «и того, и другого» — вкладывается в определение кусочно-линейной функции .

Примеры

Пример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:

а) $ y = |x| = {\left\{ \begin{array}{c} -x, x \lt0 \\ x, x \ge 0 \end{array} \right.}$

б) $ y = 2|x|-1 = {\left\{ \begin{array}{c} -2x-1, x \lt0 \\ 2x-1, x \ge 0 \end{array} \right.}$

в) $ y = |x+1| = {\left\{ \begin{array}{c} -x-1, x \lt0 \\ x+1, x \ge 0 \end{array} \right. }$

г) $ y = |x-2| = {\left\{ \begin{array}{c} -x+2, x \lt0 \\ x-2, x \ge 0 \end{array} \right.}$

Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:

$$ y = |2|x|-1| = {\left\{ \begin{array}{c} |-2x-1|, x\lt0 \\ |2x-1|,x \ge 0 \end{array} \right.} = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x-1 \lt 0 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x-1 \ge 0 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x-1 \lt 0 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x-1 \ge 0 \\ x \ge 0\end{array} \right.} \end{array} \right.}= $$

$$ = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x \lt 1 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x \ge 1 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x \lt 1 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x \ge 1 \\ x \ge 0\end{array} \right.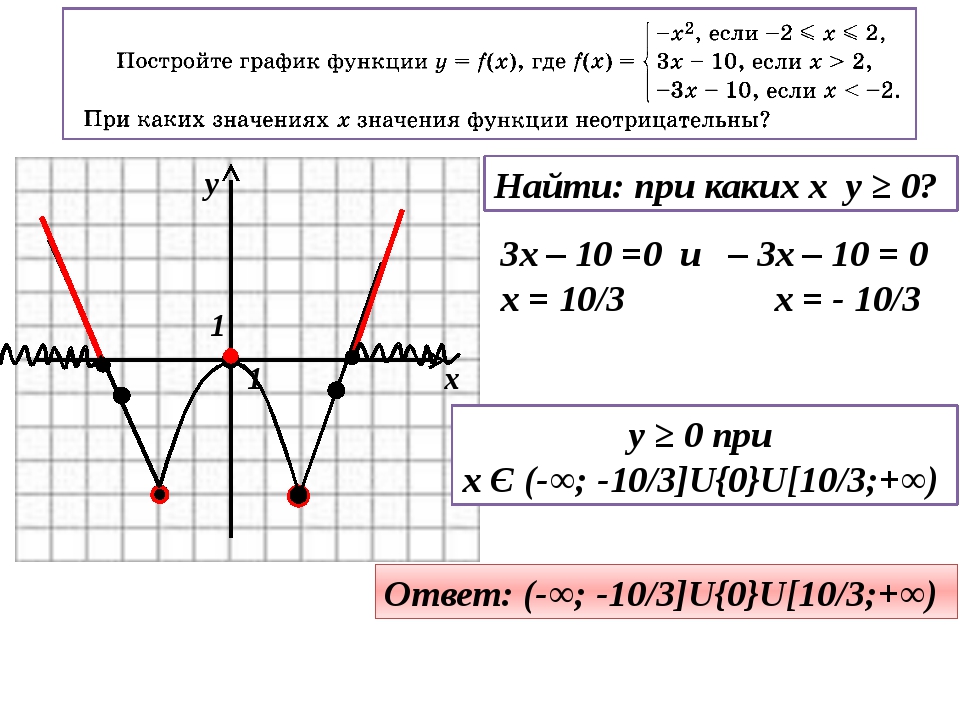 } \end{array} \right.}= {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} x \gt — \frac{1}{2} \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} x \le — \frac{1}{2} \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}x \lt \frac{1}{2} \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}x \ge \frac{1}{2} \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} -2x-1, x \le — \frac{1}{2} \\ 2x+1, — \frac{1}{2} \lt x \lt 0 \\ -2x+1, 0 \le x \lt \frac{1}{2} \\ 2x-1, x \ge \frac{1}{2} \end{array} \right.} $$

Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко.

Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования.

Шаг 1. Строим y = 2x-1

Шаг 2. Строим y = 2|x|-1 по правилу: |x| отражает часть графика для положительных $x \ge 0$ влево, зеркально относительно оси Y

Шаг 3. Строим y = |(2|x|-1)| по правилу: общий модуль отражает участок графика с отрицательными $y \lt 0$ вверх, зеркально относительно оси X

Или на одном графике:

Кусочно-заданная функция

Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва.

Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например:

y = {x – 3, при x > -3;
     {-(x – 3), при x < -3.

Такие функции называются кусочными или кусочно-заданными. Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Упражнения.

Построить графики кусочных функций:

1)       {-3, при -4 ≤ x < 0,
f(x) = {0, при x = 0,
          {1, при 0 < x ≤ 5.

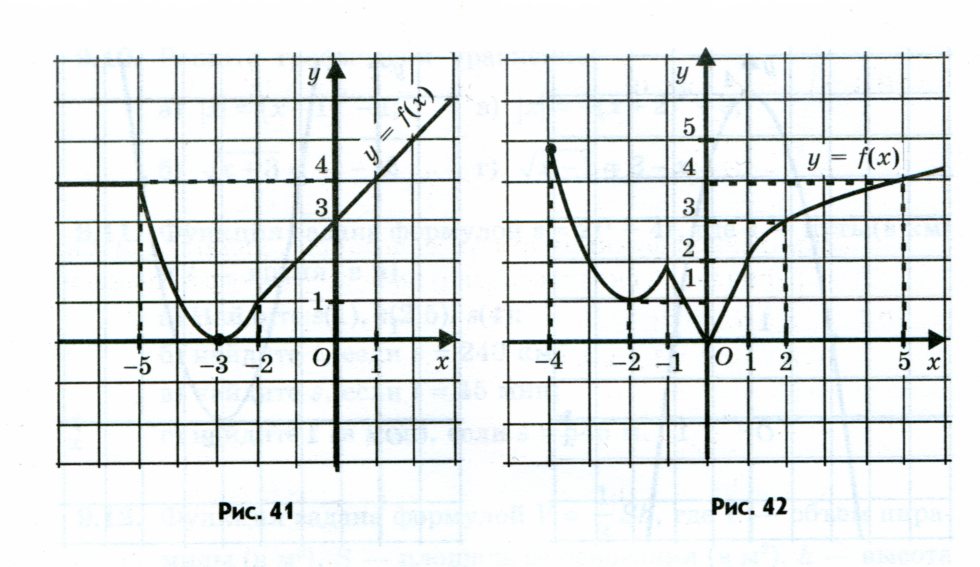
График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох.

Ответ: рисунок 1.

2)       {3, если x ≤ -4,
f(x) = {|x2 – 4|x| + 3|, если  -4 < x ≤ 4,
          {3 – (x – 4)2, если x > 4.

Рассмотрим отдельно каждую функцию и построим ее график.

Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.

График функции f(x) = |x2 – 4|x| + 3| может быть получен из параболы y = x2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.

График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4.

Ответ: рисунок 2.

3)       {8 – (x + 6)2, если x ≤ -6,
f(x) = {|x2 – 6|x| + 8|, если -6 ≤ x < 5,
          {3, если x ≥ 5.

Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох.  

Ответ: рисунок 3.

4) Построить график функции y = x – |x| + (x – 1 – |x|/x)2 .

Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая:

1) При x > 0 получим y = x – x + (x – 1 – 1)2 = (x – 2)2.

2) При x < 0 получим y = x + x + (x – 1 + 1)2 = 2x + x2.

Таким образом, перед нами кусочно-заданная функция:

y = {(x – 2)2, при x > 0;
     { x2 + 2x, при x < 0.

Графики обоих функций – параболы, ветви которых направлены вверх.

Ответ: рисунок 4.

5) Построить график функции y = (x + |x|/x – 1)2 .

Решение.

Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию:

1) При x > 0 получим y = (x + 1 – 1)2 = x2.

2) При x < 0 получим y = (x – 1 – 1)2 = (x – 2)2.

Перепишем.

y = {x2, при x > 0;
      {(x – 2)2, при x < 0.

Графики этих функций – параболы.

Ответ: рисунок 5.

6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой?

Решение.

Да, существует.

Примером может быть функция f(x) = x3. Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x3 – kx – b = 0 имеет действительный корень х0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х0; х03).

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Кусочно-заданная функция · Калькулятор Онлайн

Что умеет калькулятор?

На данной странице вы можете выполнить различные действия с кусочно-заданной функцией,
а также для большинства сервисов — получить подробное решение.

  • Производная кусочно-заданной функции
  • Построить график
  • Исследовать график
  • Определённый интеграл
  • Неопределённый интеграл от таких функций
  • Предел кусочно-заданной
  • Ряд Фурье (в примерах для нахождения ряда в основном используются кусочно-заданные функции)
  • Ряд Тейлора

Сначала задайте соответствующую функцию.

Как задавать условия?

Приведём примеры, как задавать условия:

x≠0
x не равен нулю
x > pi
x больше, чем число Пи
-pi/2
x меньше или равно, чем Пи пополам, но нестрого больше, чем Пи пополам
true
означает «в любых других случаях»
Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)
Абсолютное значение x
(модуль x или |x|)
arccos(x)
Функция — арккосинус от x
arccosh(x)
Арккосинус гиперболический от x
arcsin(x)
Арксинус от x
arcsinh(x)
Арксинус гиперболический от x
arctg(x)
Функция — арктангенс от x
arctgh(x)
Арктангенс гиперболический от x
exp(x)
Функция — экспонента от x (что и e^x)
log(x) or ln(x)
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
sin(x)
Функция — Синус от x
cos(x)
Функция — Косинус от x
sinh(x)
Функция — Синус гиперболический от x
cosh(x)
Функция — Косинус гиперболический от x
sqrt(x)
Функция — квадратный корень из x
sqr(x) или x^2
Функция — Квадрат x
ctg(x)
Функция — Котангенс от x
arcctg(x)
Функция — Арккотангенс от x
arcctgh(x)
Функция — Гиперболический арккотангенс от x
tg(x)
Функция — Тангенс от x
tgh(x)
Функция — Тангенс гиперболический от x
cbrt(x)
Функция — кубический корень из x
gamma(x)
Гамма-функция
LambertW(x)
Функция Ламберта
x! или factorial(x)
Факториал от x

В выражениях можно применять следующие операции:

Действительные числа
вводить в виде 7. 3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание
15/7
— дробь

Другие функции:

asec(x)
Функция — арксеканс от x
acsc(x)
Функция — арккосеканс от x
sec(x)
Функция — секанс от x
csc(x)
Функция — косеканс от x
floor(x)
Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x)
Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x)
Функция — Знак x
erf(x)
Функция ошибок (или интеграл вероятности)
laplace(x)
Функция Лапласа
asech(x)
Функция — гиперболический арксеканс от x
csch(x)
Функция — гиперболический косеканс от x
sech(x)
Функция — гиперболический секанс от x
acsch(x)
Функция — гиперболический арккосеканс от x

Постоянные:

pi
Число «Пи», которое примерно равно ~3. 14159..
e
Число e — основание натурального логарифма, примерно равно ~2,7183..
i
Комплексная единица
oo
Символ бесконечности — знак для бесконечности

Кусочно-постоянная функция

Пользователи также искали:



кусочно,

функция,

непрерывная,

Кусочно — постоянная,

кусочно дифференцируемая функция,

кусково неперервна функція,

кусочно монотонная,

кусочная функция,

заданная,

кусочная,

пример,

кусково,

неперервна,

функція,

производная,

заданной,

функции,

монотонная,

дифференцируемая,

Кусочно — постоянная функция,

кусочно — заданная функция,

кусочно — непрерывная функция,

производная кусочно заданной функции,

кусочно — непрерывная функция пример,

кусочно-постоянная функция,

функции. кусочно-постоянная функция,

Образец чтения свойств кусочно заданной функции. Кусочные функции

Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное
 или непрерывное
 и скачкообразное
 (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва.

Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например:

y = {x – 3, при x > -3;
{-(x – 3), при x

Такие функции называются кусочными
или кусочно-заданными
. Участки числовой прямой с различными формулами задания, назовем составляющими
область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками
. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями
. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Упражнения.

Построить графики кусочных функций:

1)
 {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0

График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох.

Ответ: рисунок 1.

2)
 {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4.

Рассмотрим отдельно каждую функцию и построим ее график.

Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.

График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.

График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4.

Ответ: рисунок 2.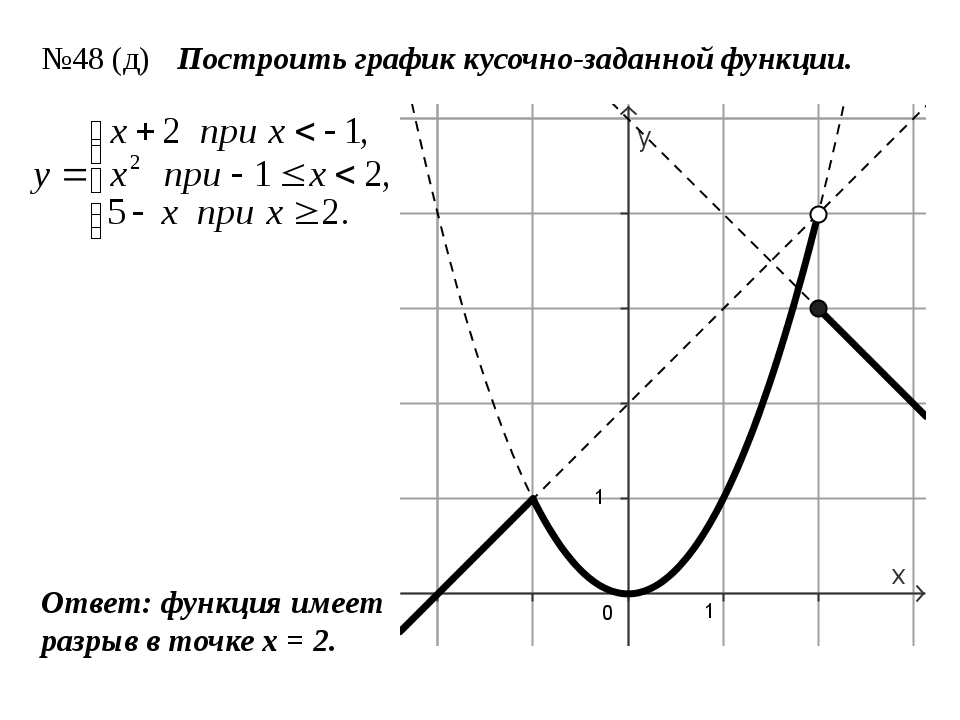

3)
 {8 – (x + 6) 2 , если x ≤ -6,
f(x) = {|x 2 – 6|x| + 8|, если -6 ≤ x {3, если x ≥ 5.

Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох.

Ответ: рисунок 3.

4)
 Построить график функции y = x – |x| + (x – 1 – |x|/x) 2 .

Решение.
 Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая:

1) При x > 0 получим y = x – x + (x – 1 – 1) 2 = (x – 2) 2 .

2) При x

Таким образом, перед нами кусочно-заданная функция:

y = {(x – 2) 2 , при x > 0;
{ x 2 + 2x, при x

Графики обоих функций – параболы, ветви которых направлены вверх.

Ответ: рисунок 4.

5)
 Построить график функции y = (x + |x|/x – 1) 2 .

Решение.

Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию:

1) При x > 0 получим y = (x + 1 – 1) 2 = x 2 .

2) При x

Перепишем.

y = {x 2 , при x > 0;
{(x – 2) 2 , при x

Графики этих функций – параболы.

Ответ: рисунок 5.

6)
Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой?

Решение.

Да, существует.

Примером может быть функция f(x) = x 3 . Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а 3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x 3 – kx – b = 0 имеет действительный корень х 0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х 0 ; х 0 3).

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.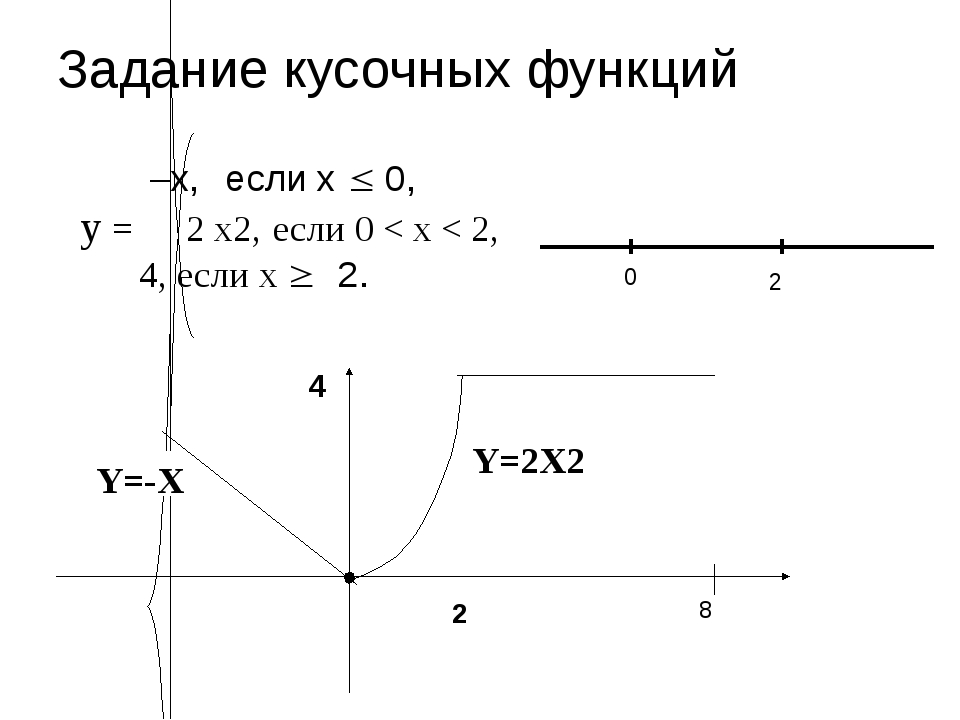

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №13

«Кусочные функции»

Сапогова Валентина и

Донская Александра

Руководитель-консультант:

г. Бердск

1. Определение основных целей и задач.

2. Анкетирование.

2.1. Определение актуальности работы

2.2. Практическая значимость.

3. История функций.

4. Общая характеристика.

5. Способы задания функций.

6. Алгоритм построения.

8. Используемая литература.

1. Определение основных целей и задач.

Цель:

Выяснить способ решения кусочных функций и, исходя из этого, составить алгоритм их построения.

Задачи:

— Познакомиться с общим понятием о кусочных функциях;

— Узнать историю термина «функция»;

— Провести анкетирование;

— Выявить способы задания кусочных функций;

— Составить алгоритм их построения;

2. Анкетирование.

Среди старшеклассников было проведено анкетирование на умение строить кусочные функции. Общее количество опрошенных составило 54 человека. Среди них 6% — работу выполнили полностью. 28% работу смогли выполнить, но с определёнными ошибками. 62% — работу не смогли выполнить, хоть и предпринимали какие-либо попытки, а оставшиеся 4% вообще не приступали к работе.

Из этого анкетирования можно сделать вывод, что ученики нашей школы, которые проходят программу имеют не достаточную базу знаний, ведь этот автор не уделяет особого внимания на задания подобного рода. Именно из этого вытекает актуальность и практическая значимость нашей работы.

2.1. Определение актуальности работы.

Актуальность:

Кусочные функции встречаются, как в ГИА, так и в ЕГЭ, задания, которые содержат функции подобного рода, оцениваются в 2 и более баллов. И, следовательно, от их решения может зависеть ваша оценка.

2.2. Практическая значимость.

Результатом нашей работы будет являться алгоритм решения кусочных функций, который поможет разобраться в их построении. И добавит шансы на получения желаемой вами оценки на экзамене.

3. История функций.

— «Алгебра 9 класс» и др.;

7

Урок по алгебре в 9А классе учителя Микитчук Ж.Н. МОУ «СОШ №23»
19.03.07г
Тема урока:
 «Кусочно-заданные функции»


Цели:

    обобщить и совершенствовать знания, умения и навыки учащихся по указанной теме; воспитывать у учащихся внимательность, сосредоточенность, настойчивость, уверенность в своих знаниях; развивать мыслительные способности, логическое мышление; речевую культуру, умение применять теоретические знания.

В результате обобщения темы учащиеся должны знать:

    понятие кусочно-заданной функции; формулы различных функций, соответствующие названия и изображения графиков;

уметь:

    строить график кусочно-заданной функции; читать график; задавать функцию аналитически по графику.

Ход урока

I. Организационно-психологический момент.

Начнем наш урок словами Д. К.Фадеева «Какую бы задачу вы не решали, в концевас ждёт счастливая минута – радостноечувство успеха, укрепление веры в свои силы.Пусть эти слова на нашем уроке обретут реальное подтверждение.II. Проверка домашнего задания.

Начнем урок как обычно с проверки д/з.-Повторите определение кусочной функции и план исследования функций.1). На доске

изобразить придуманные вами графики кусочных функций (рис.1,2,3)2).Карточки

.№1. Расставьте порядок исследования свойств функций:

    выпуклость; четность, нечётность; область значений; ограниченность; монотонность; непрерывность; наибольшее и наименьшее значение функции; область определения.

№2.Изобразите схематически графики функций:

А) у = kx + b, k0; Б) y = kx, k0;

В) у = , k0.

3).Устная работа

.
– 2мин

    Какая функция называется кусочной?

Кусочной называется функция, заданная разными формулами на разных промежутках.

    Из каких функций состоят кусочные функции, изображенные на рис. 1,2,3? Какие ещё названия функций вы знаете? Как называются графики соответствующих функций? Является ли графиком какой-либо функции, фигура, изображенная на рис.4? Почему?

Ответ:
 нет, т.к. по определению функции, каждому значению независимой переменной х ставится в соответствие единственное значение зависимой переменной у.
4) Самоконтроль —

3 минИз предложенных графиков и соответствующих формул, задающих функции, выберите верные. Из полученных букв ответов составьте знакомое слово.

Ответ: ГРАФИК
Где в жизни, в науке, в быту мы ещё встречаемся со словом ГРАФИК?-График зависимости массы от объёма,-объёма от давления;- график дежурства;- график движения поездов;-графики используются для представления различной информации, например, объём промышленного производства в Саратовской области в период с 1980 по 2002год.. По этому графику можно проследить за снижением и ростом производства в отдельные года.-Скажите, графиком какой функции представлена данная информация. Ответ: кусочная функция
.III. Сообщение темы, цели урока.

Тема урока:
 «Кусочно-заданные функции»Цель:
— на примере кусочно-заданной функции вспомнить план исследования функций;

    повторить шаги построения кусочно-заданной функции; применять обобщенные знания при решении нестандартных задач.

IV. Актуализация ранее усвоенных знаний.

Понятие функции впервые встретилось нам в 7 классе при изучении линейной зависимости. С точки зрения моделирования реальных процессов, эта зависимость соответствует равномерным процессам.Пример: Движение пешехода с постоянной скоростью за время t. Формула: s =vt, график – отрезки прямой, расположен в I четверти.
Основная тема 8-го класса – квадратичная функция, моделирующая равноускоренные процессы.Пример: изученная вами в 9-ом классе формула определения сопротивления нагретой лампы (R) при постоянной мощности (Р) и изменяющемся напряжении (U). ФормулаR = , график – ветвь параболы, расположен-ная в I четверти.
На протяжении трёх лет наши знания о функциях обогащались, количество изученных функций росло, пополнялся и набор заданий для решения которых приходится прибегать к графикам.Назовите эти типы заданий…- решение уравнений;
— решение систем уравнений;
— решение неравенств;
— исследование свойств функций.
V.Подготовка уч-ся к обобщающей деятельности.

Вспомним один из типов заданий, а именно – исследование свойств функций или чтение графика.Обратимся к учебнику. Страница 65 рис.20а из №250.Задание:
прочитать график функции. Порядок исследования функции перед нами.1. область определения – (-∞; +∞)
2. четность, нечётность – ни четная, ни нечётная
3. монотонность- возрастает [-3; +∞), убывает
[-5;-3], постоянна (-∞; -5];
4. ограниченность – ограничена снизу
5.
наибольшее и наименьшее значение функции – у наим = 0, у наиб – не существует;
6. непрерывность- непрерывна на всей области определения;
7. область значений – , выпукла и вниз и вверх (-∞; -5] и [-2; +∞).
VI. Воспроизведение знаний на новом уровне.

Вы знаете, что построение и исследование графиков кусочно-заданных функций, рассматриваются во второй части экзамена по алгебре в разделе функции и оцениваются 4-мя и 6-ю баллами. Обратимся к сборнику заданий.Страница 119 — №4.19-1).Решение:
1).у = —
x, — квадратичная функция, график – парабола, ветви вниз (а = -1, а
0). х -2 -1 0 1 2
у -4 -1 0 1 4
2) у= 3х – 10, — линейная функция, график – прямая
Составим таблицу некоторых значений
х 3 3
у 0 -1
3) у= -3х -10, — линейная функция, график – прямая
Составим таблицу некоторых значений
х -3 -3
у 0 -1
4)Построим графики функций в одной системе координат и выделим части графиков на заданных промежутках.

Найдем по графику, при каких значениях х значения функции неотрицательны.
Ответ:
f(x) 
0 при х = 0 и при 
3VII.Работа над нестандартными заданиями.

№4.29-1), стр. 121.
Решение:
1)Прямая (слева) у =
kx + b проходит через точки (-4;0) и (-2;2). Значит,-4
k + b = 0,-2
k + b = 2;
k = 1, b = 4, у = х+4. Ответ: х +4, если х
-2
у = , если -2
х £
3
3, если х
3

VIII.Контроль знаний.

Итак, подведём небольшой итог. Что мы повторили на уроке?План исследования функций, шаги построения графика кусочной функции, задание функции аналитически. Проверим как вы усвоили данный материал.Тестирование на «4»- «5», «3»



I вариант№ У

2
1
-1 -1 1 Х

    D(f) = , выпуклая и вверх и вниз на , выпуклая вверх и вниз на , убывает на ________ Ограничена ____________ у наим не существует, у наиб =_____ Непрерывна на всей области определения Е(f) = ____________ Выпукла и вниз и вверх на всей области определения

Графики
 кусочно – заданных
 функций

Мурзалиева Т.А. учитель математики МБОУ «Борская средняя общеобразовательная школа» Бокситогорский район Ленинградская область

Цель:

  • освоить метод линейного сплайна для построения графиков, содержащих модуль;
  • научиться применять его в простых ситуациях.

Под сплайном
 (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию.

Такие функции были известны математикам давно, начиная еще с Эйлера (1707-1783г.,швейцарский, немецкий и российский математик),
 но их интенсивное изучение началось, фактически, только в середине XX века.

В 1946 году Исаак Шёнберг (1903- 1990г., румынский и американский математик)
 впервые употребил этот термин. С 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании.

1 . Введение

2. Определение линейного сплайна

3. Определение модуля

4. Построение графиков

5. Практическая работа

Одно из основных назначений функций – описание реальных процессов, происходящих в природе.

Но издавна ученые – философы и естествоиспытатели выделяли два типа протекания процессов:
 постепенное

 ( непрерывное

 ) и
 скачкообразное.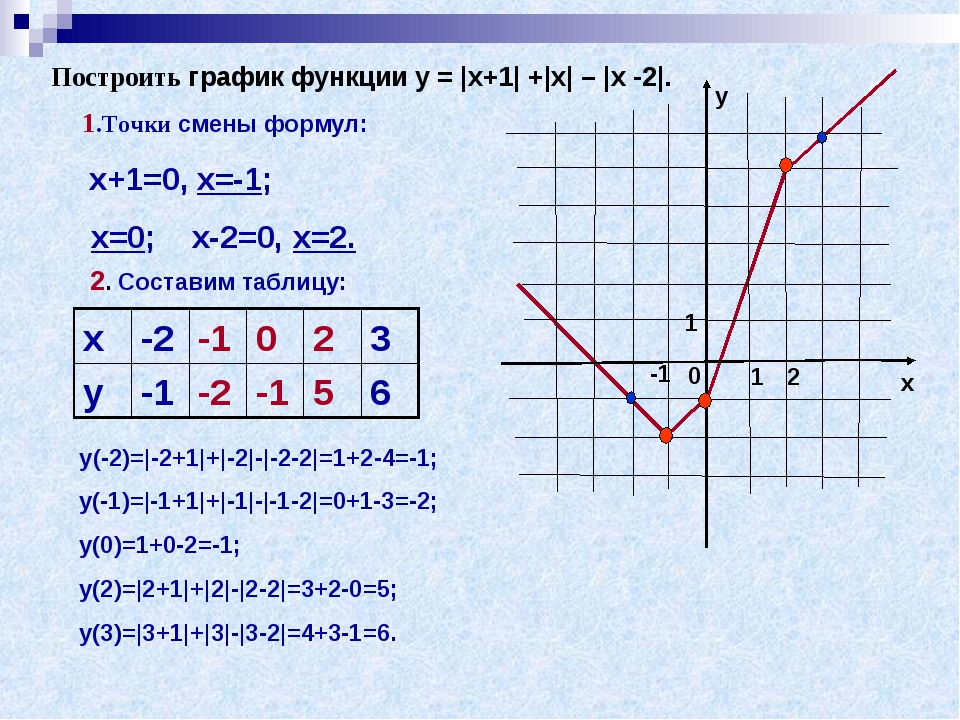

При падении тела на землю сначала происходит
 непрерывное нарастание

 скорости движения

 , а в момент столкновения с поверхностью земли
 скорость изменяется скачкообразно

 ,
 становясь равной нулю

 или меняя направление (знак) при «отскоке» тела от земли (например, если тело – мяч).

Но раз есть разрывные процессы, то необходимы средства их описаний. С этой целью вводятся в действие функции, имеющие

 разрывы

 .

a — формулой y = h(x), причем будем считать, что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда, если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. »

  • Один из способов введения таких разрывов
     следующий:

Пусть
 функция

 y = f(x)

при

 x


 определена формулой


 y = g(x),


а при

 xa


 — формулой


 y = h(x),


 причем будем считать
 , что каждая из функций

 g(x)

 и

 h(x)

 определена для всех значений х и разрывов не имеет.

Тогда
 ,
 если

 g(a) = h(a),

 то функция

 f(x)

 имеет при

 х=а

 скачок;

если же

 g(a) = h(a) =

 f(a),

 то «комбинированная» функция
 f
 разрывов не имеет. Если обе функции
 g
 и
 h
 элементарные,
 то
 f называется

 кусочно–элементарной.

Графики непрерывных функций

Построить график функции:

У = |X-1| + 1

Х=1 –точка смены формул

Слово «модуль»
 произошло от латинского слова «modulus», что в переводе означает «мера».

Модулем числа
 а

 называется расстояние

 (в единичных отрезках
) от начала координат до точки А (а)
 .

Это определение раскрывает геометрический смысл модуля.

Модулем
 (абсолютной величиной
) действительного числа а
 называется то самое число а
 ≥ 0, и противоположное число –а
 , если а

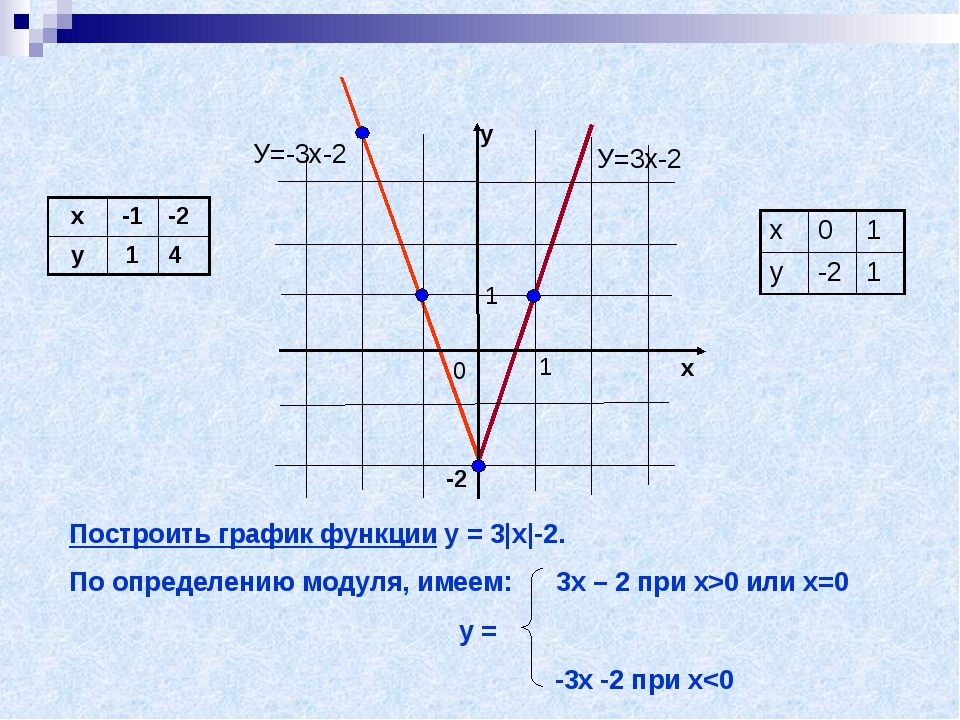
0 или х=0 у = -3х -2 при х »

Построить график функции

 у = 3|х|-2.

По определению модуля, имеем: 3х – 2 при х0 или х=0

-3х -2 при х

x n) »

.
 Пусть заданы х
 1
 х
 2
 х
 n
 – точки смены формул в кусочно-элементарных функциях.


Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале

и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв.

Непрерывная кусочно-линейная функция
 называется
 линейным сплайном

 .
 Её
 график

 есть
 ломаная с двумя бесконечными крайними звеньями

 – левым (отвечающим значениям x n
 ) и правым
 ( отвечающим значениям x x
 n
 )

Кусочно-элементарная функция может быть определена более чем двумя формулами

График –
 ломаная

 с двумя бесконечными крайними звеньями – левым (х1).

У=|x| — |x – 1|

Точки смены формул: х=0 и х=1.

У(0)=-1, у(1)=1.

График кусочно-линейной функции удобно строить,
 указывая

 на координатной плоскости
 вершины ломаной.

Кроме построения
 n

 вершин следует
 построить

 также
 две точки

 : одну левее вершины
 A

 1 ( x

 1;
 y

 ( x

 1)), другую – правее вершины
 An

 ( xn

 ;
 y

 ( xn

 )).

Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов

 .

Построить график функции
 у = х+ |x -2| — |X|.

Непрерывная кусочно-линейная функция называется линейным сплайном

1. Точки смены формул: Х-2=0,
 Х=2

 ;

 Х=0

2.Составим таблицу:

У(0
)= 0+|0-2|-|0|=0+2-0= 2
 ;

у(2
)=2+|2-2|-|2|=2+0-2= 0
 ;

у (-1
)= -1+|-1-2| — |-1|= -1+3-1= 1
 ;

у(3
)=3+|3-2| — |3|=3+1-3= 1
 .

Построить график функции у = |х+1| +|х| – |х -2|.

1
 .Точки смены формул:

х+1=0,
 х=-1

 ;

х=0

 ;
 х-2=0,
 х=2.

2
 .
 Составим таблицу:

y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1;

y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2;

y(0)=1+0-2=-1;

y(2)=|2+1|+|2|-|2-2|=3+2-0=5;

y(3)=|3+1|+|3|-|3-2|=4+3-1=6.

|x – 1| = |x + 3|

Решите уравнение:

Решение.

 Рассмотрим функцию y = |x -1| — |x +3|

Построим график функции /методом линейного сплайна/

  • Точки смены формул:

х -1 = 0, х = 1; х + 3 =0, х = — 3.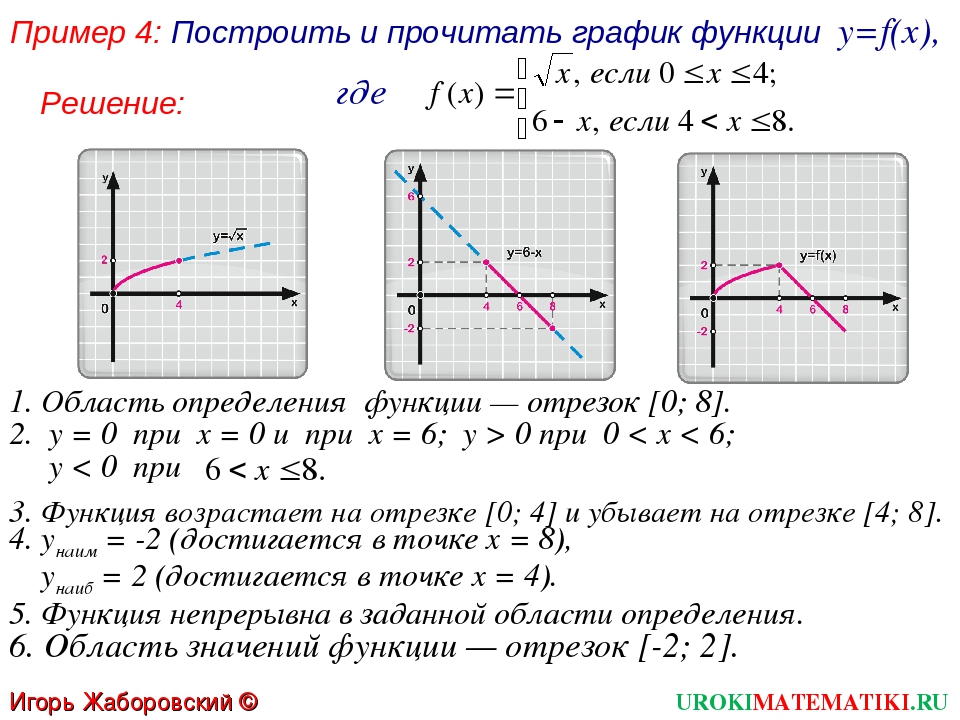

2. Составим таблицу:

y(- 4) =|- 4–1| — |- 4+3| =|- 5| — | -1| = 5-1=4;

y( -3
 )=|- 3-1| — |-3+3|=|-4| =
 4;

y( 1
 )=|1-1| — |1+3| =
 — 4
 ;

y(-1) = 0.

y(2)=|2-1| — |2+3|=1 – 5 = — 4.

Ответ: -1.

1. Построить графики кусочно-линейных функций методом линейного сплайна:

у = |x – 3| + |x|;

1).
 Точки смены формул:

2).
 Составим таблицу:

2. Построить графики функций, используя УМК «Живая математика
 »

А)
 у = |2x – 4| + |x +1|

1) Точки смены формул:

2) y() =

Б)
 Постройте графики функций, установите закономерность
 :

a) у = |х – 4| б) y = |x| +1

y = |x + 3| y = |x| — 3

y = |x – 3| y = |x| — 5

y = |x + 4| y = |x| + 4

Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов.

1. Меню «Графики».

2. Вкладка «Построить график».

.3. В окне «Калькулятор» задать формулу.

Постройте график функции:

1)
 У = 2х + 4

1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.

2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011

3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011

4. ВикипедиЯ свободная энциклопедия

http://ru.wikipedia.org/wiki/Spline

Кусочно — Piecewise — other.wiki

График кусочно-линейной функции ж ( Икс ) знак равно { — 3 — Икс если Икс ≤ — 3 Икс + 3 если — 3 ≤ Икс ≤ 0 3 — 2 Икс если 0 ≤ Икс ≤ 3 0,5 Икс — 4. 5 если 3 ≤ Икс {\ displaystyle f (x) = \ left \ {{\ begin {array} {lll} -3-x & {\ text {if}} & x \ leq -3 \\ x + 3 & {\ text {if}} & -3 \ leq x \ leq 0 \\ 3-2x & {\ text {if}} & 0 \ leq x \ leq 3 \\ 0.5x-4.5 & {\ text {if}} & 3 \ leq x \\\ end { массив}} \ right.}

В математике , А кусочно-определенная функция (также называемая функцию кусочно , а гибридную функцию , или определение, случаев ) является функцией определяется несколькими суб-функций, где каждая подфункция относится к другому интервалу в домене. Кусочное определение на самом деле является способом выражения функции, а не характеристикой самой функции.

Отдельным, но связанным понятием является понятие свойства, сохраняющееся кусочно для функции, используемое, когда область может быть разделена на интервалы, на которых это свойство сохраняется. В отличие от приведенного выше понятия, на самом деле это свойство самой функции. Кусочно-линейная функция (которая также бывает непрерывной) изображена в качестве примера.

Обозначения и интерпретация

График функции абсолютного значения, . y знак равно | Икс | {\ Displaystyle у = | х |}

Кусочные функции могут быть определены с использованием общей функциональной записи , где тело функции представляет собой массив функций и связанных поддоменов. Эти поддомены вместе должны охватывать весь домен ; часто также требуется, чтобы они попарно не пересекались, т.е. образовывали разбиение области. Для того чтобы общую функцию можно было назвать «кусочной», подобласти обычно должны быть интервалами (некоторые могут быть вырожденными интервалами, то есть одиночными точками или неограниченными интервалами). Для ограниченных интервалов количество подобластей должно быть конечным, для неограниченных интервалов часто требуется только локальное конечное число. Например, рассмотрим кусочное определение функции абсолютного значения :

| Икс | знак равно { — Икс , если  Икс < 0 + Икс , если  Икс ≥ 0. {\ displaystyle | x | = {\ begin {cases} -x, & {\ text {if}} x <0 \\ + x, & {\ text {if}} x \ geq 0. \ end {cases} }}

Для всех значений меньше нуля используется первая функция ( ), которая отменяет знак входного значения, делая отрицательные числа положительными. Для всех значений больше или равных нулю используется вторая функция ( ), которая тривиально оценивает само входное значение.
Икс {\ displaystyle x} — Икс {\ displaystyle -x} Икс {\ displaystyle x} Икс {\ displaystyle x}

Следующая таблица документирует функцию абсолютного значения при определенных значениях :
Икс {\ displaystyle x}

Здесь обратите внимание, что для оценки кусочной функции при заданном входном значении необходимо выбрать соответствующий субдомен, чтобы выбрать правильную функцию и получить правильное выходное значение.

Непрерывность и дифференцируемость кусочных функций.

Кусочная функция непрерывна на заданном интервале в своей области определения, если выполняются следующие условия:

  • составляющие его функции непрерывны на соответствующих интервалах (подобластях),
  • в каждой конечной точке субдоменов в этом интервале нет разрывов.

Изображенная функция, например, кусочно-непрерывна во всех своих подобластях, но не является непрерывной во всей области, так как она содержит скачок в точке . Закрашенный кружок указывает на то, что значение правой функциональной части используется в этой позиции.
Икс 0 {\ displaystyle x_ {0}}

Чтобы кусочная функция была дифференцируемой на заданном интервале в ее области определения, в дополнение к условиям непрерывности, указанным выше, должны выполняться следующие условия:

  • составляющие его функции дифференцируемы на соответствующих открытых интервалах,
  • односторонние производные существуют на всех концах интервалов,
  • в точках соприкосновения двух подынтервалов совпадают соответствующие односторонние производные двух соседних подынтервалов.

Приложения

В прикладном математическом анализе было обнаружено, что кусочные функции согласуются со многими моделями зрительной системы человека , где изображения воспринимаются на первом этапе как состоящие из гладких областей, разделенных краями. {2}}} \ right), & x \ in (-1,1) \ \ 0, & {\ text {иначе}} \ end {case}}} и некоторые другие общие функции Bump . Они бесконечно дифференцируемы, но аналитичность сохраняется только кусочно.

  • Непрерывные функции в вещественных числах не обязательно должны быть ограниченными или равномерно непрерывными, они всегда кусочно ограничены и кусочно равномерно непрерывны.

    • Смотрите также

    Рекомендации

    <img src=»//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

    кусочных функций

    Функция может быть в частях

    Мы можем создавать функции, которые ведут себя по-разному в зависимости от значения input (x).

    Функция из 3 частей

    Пример:

    • , когда x меньше 2, дает x 2 ,
    • , когда x равно 2, дает 6
    • , когда x больше 2, но меньше или равно 6, получается строка 10-x

    Это выглядит так:

    (сплошная точка означает «включая»,

    открытая точка означает «не включая»)

    А вот как мы это пишем:

    Домен (все значения, которые могут входить в функцию) — это все действительные числа до 6 включительно, которые мы можем записать так:

    Dom (f) = (-∞, 6] (с использованием обозначения интервалов)

    Dom (f) = {x | x ≤ 6} (с использованием нотации Set Builder)

    А вот несколько примеров значений:

    х Я
    −4 16
    -2 4
    0 0
    1 1
    2 6
    3 7

    Пример: вот еще одна кусочная функция:

    который выглядит так:

    Что такое ч (-1)?

    x ≤ 1, поэтому мы используем h (x) = 2, поэтому h (−1) = 2

    Что такое h (1)?

    x ≤ 1, поэтому мы используем h (x) = 2, поэтому h (1) = 2

    Что такое h (4)?

    x> 1, поэтому мы используем h (x) = x, поэтому h (4) = 4

    Кусочные функции позволяют создавать функции, которые делают все, что мы хотим!

    Пример: Гонорар врача зависит от продолжительности работы.

    • До 6 минут стоит 50 долларов
    • От 6 до 15 минут стоит 80 долларов
    • Более 15 минут стоит 80 долларов плюс 5 долларов за минуту свыше 15 минут

    Что мы можем написать так:

    Вы приходите на 12 минут, какова плата? $ 80

    Вы приходите на 20 минут, сколько стоит? 80 $ + 5 $ (20-15) = 105 9000 $ 5

    Функция абсолютного значения

    Функция абсолютного значения — известная кусочная функция.

    состоит из двух частей:

    • ниже нуля: -x
    • , начиная с 0: x

    f (x) = | x |

    Функция этажа

    Функция Floor — это особая кусочная функция. В нем бесконечное количество штук:

    Функция этажа

    кусочных функций — определение, график и примеры

    Есть случаи, когда выражение для функций зависит от заданного интервала входных значений. Когда это происходит, мы называем эти типы функций кусочно-определенными функциями .

    Кусочные функции определяются разными функциями в разных интервалах домена.

    На самом деле мы применяем кусочные функции в нашей жизни чаще, чем думаем. В налоговых скобках, при оценке тарифных планов для мобильных телефонов и даже в заработной плате (с учетом сверхурочных) используются кусочные функции.

    Вот почему мы выделили для этой функции специальный артикул.Из этой статьи вы узнаете следующее:

    • Определение кусочной функции.
    • Учимся оценивать кусочно-определенные функции через заданные интервалы.
    • Построение и интерпретация кусочных функций.

    Что такое кусочная функция?

    Чтобы полностью понять, что такое кусочные функции и как мы можем построить наши собственные кусочно-определенные функции, давайте сначала погрузимся в более глубокое понимание того, как это работает.

    Определение кусочной функции

    Кусочная функция — это функция, которая определяется различными формулами или функциями для каждого заданного интервала.Это также есть в названии: кусок. Функция определяется частями функций для каждой части домена .

    2x, для x> 0

    1, для x = 0

    -2x, для x <0

    Как видно из приведенного выше примера, f (x) является кусочной функцией, потому что она определяется однозначно для трех интервалов: x> 0, x = 0 и x <0.

    Как читать кусочные функции?

    Когда у нас есть заданная кусочно-определенная функция, мы можем интерпретировать ее, глядя на заданные интервалы.Если мы посмотрим на наш пример, мы можем прочитать его как:

    • Когда x> 0, f (x) равно 2x.
    • Когда x = 0, f (x) равно 1.
    • Когда x <0, f (x) равно -2x.

    При получении графика кусочной функции обязательно соблюдайте указанные интервалы, в которых f (x) имеет различные графики. Но прежде чем мы попробуем примеры, которые включают анализ графиков кусочных функций, давайте продолжим и узнаем, как мы можем сначала вычислить и построить график кусочных функций.

    Как решать кусочные функции?

    Теперь, когда мы узнали об этой уникальной функции, как нам убедиться, что мы возвращаем правильное значение для функции, заданной x ? Вот советы, которые следует помнить при решении и оценке кусочных функций:

    • Дважды проверьте, где x находится в заданном интервале.
    • Оцените значение, используя соответствующую функцию.

    Допустим, мы хотим найти f (8) , используя показанную нами кусочную функцию.

    2x, для x> 0

    1, для x = 0

    -2x, для x <0

    Так как 8 больше 0, функция, которую мы будем использовать для оценки f (8) , будет f (x) = 2x . Следовательно, имеем f (8) = 2 (8) = 16 . Это также означает, что f (-6) = -2 (-6) = 12 и f (0) = 1 .

    Как построить кусочный график функций?

    Как мы упоминали ранее, кусочные функции содержат разные функции для каждого из заданных интервалов.Это означает, что при построении графиков кусочных функций также ожидает построения графиков различных функций для каждого интервала .

    Вот несколько быстрых напоминаний при построении графиков кусочных функций:

    • Это помогает определить, как будет выглядеть каждая функция.
    • Для инклюзивных интервалов (т. Е. X ≥ 0), включая конечные точки.
    • Для исключительных интервалов (т. Е. X <0) исключите конечные точки, используя незаполненные точки.

    С какими общими функциями вы можете столкнуться при построении графиков кусочных функций? Вот некоторые ресурсы, и не стесняйтесь проверять ссылки, чтобы освежить свои знания о некоторых из часто используемых графиков:

    Это не единственные функции, которые могут использовать кусочные функции, поэтому обязательно проверьте библиотеку функций в вашем учебнике всякий раз, когда вам нужно.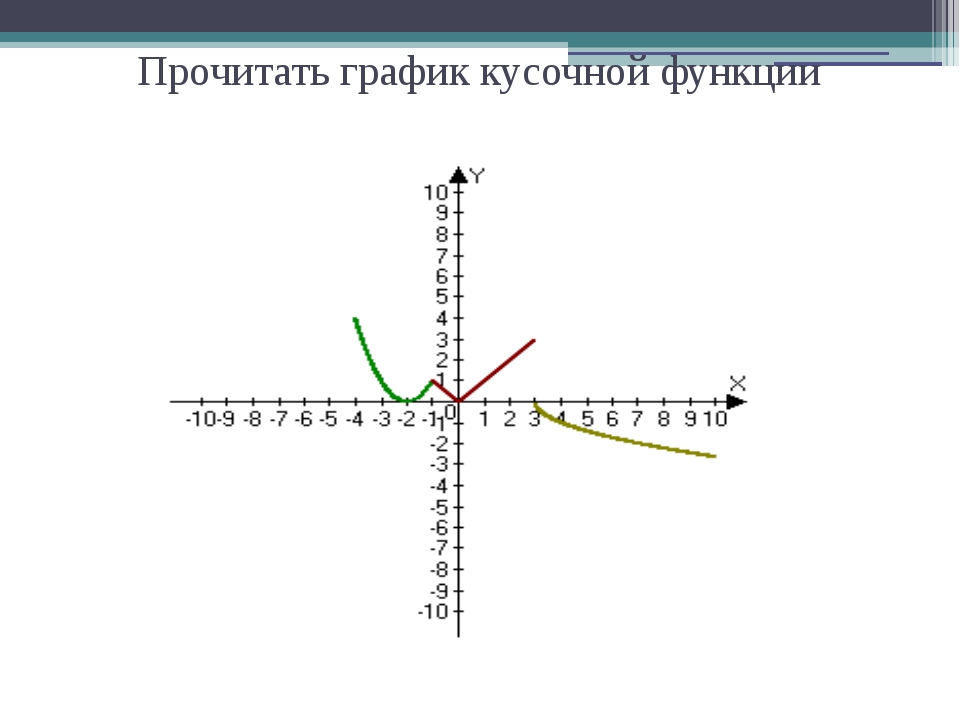 Давайте попробуем построить график кусочной функции, приведенной в первом разделе.

    2x, для x> 0

    1, для x = 0

    -2x, для x <0

    Когда x> 0 и x <0, f (x) возвращает линейную функцию . Найдите как минимум две пары точек, удовлетворяющих каждой функции, и используйте их для построения двух линейных графиков.

    Поскольку оба неравенства являются исключительными, мы оставляем точку в начале координат незаполненной. Теперь у нас осталось условие, когда x = 0.Поскольку значение является постоянным при f (x) = 1, нарисуем точку в точке (0,1).

    Этот график возвращает окончательный график для данной кусочной функции. Из графика видно, что f (x) имеет область значений и диапазон (-∞, ∞) и [0, -∞) соответственно.

    Мы рассмотрели все основные свойства и методы, которые мы можем использовать с кусочными функциями, поэтому пришло время проверить наши знания на этих примерах!

    Пример 1

    Оцените данную кусочную функцию при заданных значениях x , как показано ниже.

    √x, для x> 0

    5, для x = 0

    x / 6, для x <0

    a. ж (-36)

    б. f (0)

    c. f (49)

    Решение

    • Когда x = -36 (или меньше 0), выражение для f (x) будет x / 6 . Давайте вычислим f (-36) , используя выражение. Следовательно, мы имеем f (-36) = -36/6 = -6 .
    • Когда x = 0, f (x) является константой . Это означает, что у нас f (0) = 5 .
    • Когда x = 49 (и, следовательно, больше 0), выражение для f (x) будет √ x . Давайте вычислим f (49) , используя выражение. Следовательно, мы имеем f (49) = √ 49 = 7 .

    Пример 2

    Изобразите кусочную функцию, показанную ниже. Используя график, определите его домен и диапазон.

    2x, для x ≠ 0

    1, для x = 0

    Решение

    Для всех интервалов x, кроме тех, когда он равен 0, f (x) = 2x (что является линейным функция).Чтобы построить график линейной функции, мы можем использовать две точки, чтобы соединить линию. Просто убедитесь, что две точки удовлетворяют y = 2x . Не забудьте оставить точку отправления незаполненной.

    Поскольку f (x) = 1 , когда x = 0 , мы наносим закрашенную точку в (0,1). График выше показывает окончательный график кусочной функции.

    Поскольку график охватывает все значения x, доменом будет все действительные числа или (-∞, ∞). То же самое относится и к набору функций.Поскольку он распространяется в обоих направлениях, диапазон функции составляет (- ∞ , ∞ ) в обозначении интервала .

    Пример 3

    Изобразите кусочную функцию, показанную ниже.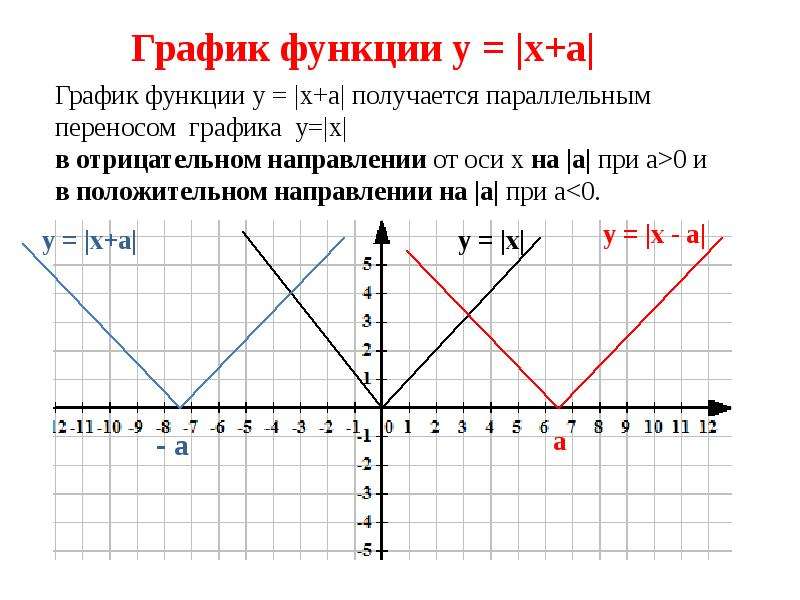 Используя график, определите его домен и диапазон.

    x 2 , для x ≤ 0

    5, для 0

    x / 2, для x ≥ 2

    Решение

    Давайте сначала разберем три интервала и определим, как график функции будет выглядеть так:

    • Когда x ≤ 0, f (x) становится квадратичной функцией с параболой, проходящей через начало координат и (-2, 4).Поскольку это применимо только к 0 и отрицательным числам, мы будем использовать только половину параболы.
    • Когда 0 f (x) будет представлять константу, которая представляет собой горизонтальную линию, проходящую через y = 5 . Обязательно оставьте (0,5) и (2,5) незаполненными, так как они не являются частью раствора.
    • Когда x ≥ 2, f (x) является функцией и проходит через (2, 1) и (6,3).

    Используя эту информацию, мы можем построить график f (x) .

    Изображение выше разбивает три компонента кусочной функции. Давайте продолжим и упростим этот график, чтобы мы могли проанализировать его по предметной области и диапазону.

    Поскольку все значения x распространяются в обоих направлениях, доменом будет , все действительные числа или (-∞, ∞). Поскольку график охватывает только значения y над осью x, диапазон функции составляет [0, ∞ ) в обозначении интервала .

    Пример 4

    Разговорная поэзия проводится в соседнем кафе.Они берут 6 долларов с человека за стол на от 1 до 5 человек. Они также предлагают фиксированную плату в размере 50 долларов за столик на 6 и более человек. Напишите функцию, которая связывает количество людей, x , и стоимость посещения мероприятия, f (x) .

    Решение

    Давайте продолжим и разберем задачу и найдем выражение f (x) для каждого интервала:

    • Для стола от 1 до 5 гостей, мы можем выразить это как 1 ≤ x ≤ 5 по x.Поскольку это будет стоить каждому гостю 6 долларов, общая сумма для x гостей составит 6x .
    • Теперь для стола с 6 или более людьми мы можем выразить интервал как x ≥ 6. Для этого интервала f (x) будет всегда равным 60 .

    Теперь мы можем суммировать это в виде кусочной функции:

    6x, для 1 ≤ x ≤ 5

    50, для x ≥ 6

    Эта кусочная функция представляет собой стоимость f (x) для x число гостей.

    Практические вопросы

    1. Оцените данную кусочную функцию при заданных значениях x , как показано ниже.

    √ (x-1), для x> 0

    5, для x = 0

    x + 1, для x <0

    a. ф (-8)

    б. ф (0)

    с. f (63)

    2. Оцените данную кусочную функцию при заданных значениях x, , как показано ниже.

    3x 2 , для x ≤ 0

    4x — 6, для 0

    2x, для x ≥ 2

    a. ф (-2)

    б. f (0,75)

    c. f (7)

    3. Постройте график кусочной функции, показанной ниже. Используя график, определите его домен и диапазон.

    2x 2 , для x ≠ 0

    8, для x = 0

    4. Изобразите кусочную функцию, показанную ниже. Используя график, определите его домен и диапазон.

    √ (-4x), для x ≤ 0

    2x, для 0

    -x 2 , для x ≥ 9

    5.Предположим, у вас есть летняя работа, за которую платят 12 долларов в час. Вы должны работать не менее 30 часов в неделю. Компания оплачивает сверхурочную работу в 1,5 раза больше почасовой ставки.

    а. Настройте кусочную функцию, которая представляет вашу еженедельную оплату.
    г. Изобразите построенную вами кусочную функцию.
    г. Сколько бы вы заработали, если бы в ту неделю проработали 48 часов?

    Предыдущий урок | Главная страница | Следующий урок

    кусочно-определенные функции | Колледж алгебры

    Результаты обучения

    • Написать кусочно определенные функции.
    • График кусочно-определенных функций.

    Иногда мы сталкиваемся с функцией, которая требует более одной формулы для получения заданного результата. Например, в функциях инструментария мы ввели функцию абсолютного значения [latex] f \ left (x \ right) = | x | [/ latex]. С областью всех действительных чисел и диапазоном значений больше или равным 0, абсолютное значение может быть определено как величина или модуль значения действительного числа независимо от знака.Это расстояние от 0 на числовой прямой. Все эти определения требуют, чтобы результат был больше или равен 0.

    Если мы вводим 0 или положительное значение, выход будет таким же, как и вход.

    [латекс] f \ left (x \ right) = x \ text {if} x \ ge 0 [/ латекс]

    Если мы вводим отрицательное значение, выход будет противоположным входному.

    [латекс] f \ left (x \ right) = — x \ text {if} x <0 [/ latex]

    Поскольку для этого требуются два разных процесса или части, функция абсолютного значения является примером кусочной функции.Кусочная функция — это функция, в которой используется более одной формулы для определения вывода для разных частей домена.

    Мы используем кусочные функции для описания ситуаций, в которых правило или отношение изменяется, когда входное значение пересекает определенные «границы». Например, в бизнесе мы часто сталкиваемся с ситуациями, когда стоимость единицы определенного предмета снижается, если заказанное количество превышает определенное значение. Налоговые скобки — еще один реальный пример кусочных функций.Например, рассмотрим простую налоговую систему, в которой доход до [латекс] 10 000 долларов [/ латекс] облагается налогом [латекс] 10% [/ латекс], а любой дополнительный доход облагается налогом [латекс] 20 \% [/ латекс] ]. Налог на общий доход, [латекс] S [/ латекс], будет [латекс] 0,1S [/ латекс], если [латекс] {S} \ le $ 10 000 [/ латекс] и [латекс] 1000 + 0,2 (S — 10 000 долларов) [/ латекс], если [латекс] S> 10 000 долларов [/ латекс].

    Общее примечание: кусочные функции

    Кусочная функция — это функция, в которой для определения вывода используется более одной формулы.Каждая формула имеет свою собственную область определения, а область определения функции представляет собой объединение всех этих меньших областей. Мы записываем эту идею так:

    [латекс] f \ left (x \ right) = \ begin {cases} \ text {формула 1, если x находится в домене 1} \\ \ text {формула 2, если x находится в домене 2} \\ \ text {формула 3, если x находится в домене 3} \ end {ases} [/ latex]

    В кусочной записи функция абсолютного значения равна

    .

    [латекс] | x | = \ begin {case} \ begin {align} x & \ text {if} x \ ge 0 \\ -x & \ text {if} x <0 \ end {align} \ end {cases} [/ латекс]

    Практическое руководство. Для данной кусочной функции напишите формулу и определите область для каждого интервала.


    1. Укажите интервалы, для которых применяются разные правила.
    2. Определите формулы, описывающие, как вычислить выход из входа в каждом интервале.
    3. Используйте фигурные скобки и операторы if для написания функции.

    Пример: написание кусочной функции

    Музей взимает 5 долларов с человека за экскурсию с группой от 1 до 9 человек или фиксированную плату в размере 50 долларов за группу из 10 и более человек. Напишите функцию , связывающую количество людей [латекс] n [/ латекс] со стоимостью [латекс] C [/ латекс].

    Показать решение

    Потребуются две разные формулы. Для [latex] n [/ latex] значений меньше 10, [latex] C = 5n [/ latex]. Для значений [latex] n [/ latex], равных 10 или больше, [latex] C = 50 [/ latex].

    [латекс] C (n) = \ begin {cases} \ begin {align} {5n} & \ hspace {2mm} \ text {if} \ hspace {2mm} {0} <{n} <{10} \ \ 50 & \ hspace {2mm} \ text {if} \ hspace {2mm} {n} \ ge 10 \ end {align} \ end {case} [/ latex]

    Анализ решения

    График представляет собой диагональную линию от [latex] n = 0 [/ latex] до [latex] n = 10 [/ latex] и константу после нее.В этом примере две формулы совпадают в точке встречи, где [latex] n = 10 [/ latex], но не все кусочные функции обладают этим свойством.

    Пример: работа с кусочной функцией

    Компания сотовой связи использует приведенную ниже функцию для определения стоимости [latex] C [/ latex] в долларах за [latex] g [/ latex] гигабайт передачи данных.

    [латекс] C \ left (g \ right) = \ begin {cases} \ begin {align} {25} \ hspace {2mm} & \ text {if} \ hspace {2mm} {0} <{g} < {2} \\ {25 + 10} \ left (g - 2 \ right) \ hspace {2mm} & \ text {if} \ hspace {2mm} {g} \ ge {2} \ end {align} \ end {case} [/ latex]

    Найдите стоимость использования 1.5 гигабайт данных и стоимость использования 4 гигабайт данных.

    Показать решение

    Чтобы определить стоимость использования 1,5 гигабайт данных, [latex] C (1.5) [/ latex], мы сначала смотрим, в какую часть домена попадает наш ввод. Поскольку 1.5 меньше 2, мы используем первую формула.

    [латекс] C (1,5) = 25 $ [/ латекс]

    Чтобы найти стоимость использования 4 гигабайт данных, [latex] C (4) [/ latex], мы видим, что введенное нами значение 4 больше 2, поэтому мы используем вторую формулу.

    [латекс] C (4) = 25 + 10 (4-2) = 45 долларов США [/ латекс]

    Анализ решения

    Мы можем видеть, где функция изменяется от постоянной к смещенной и растянутой идентичности при [latex] g = 2 [/ latex].Мы наносим графики для различных формул на общий набор осей, следя за тем, чтобы каждая формула применялась в соответствующей области.

    Как сделать: для данной кусочной функции нарисуйте график.

    1. Укажите на оси [latex] x [/ latex] границы, определяемые интервалами на каждой части домена.
    2. Постройте график на этом интервале для каждой части домена, используя соответствующее уравнение, относящееся к этой части. Не отображайте две функции на одном интервале, потому что это нарушит критерии функции.{2} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} \ le {1} \\ {3} \ hspace {2mm} & \ text {if} \ hspace {2mm} {1 } & lt {x} \ le 2 \\ {x} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} & gt {2} \ end {align} \ end {case} [/ latex]

      Показать решение

      Каждая из функций компонента взята из нашей библиотеки функций набора инструментов, поэтому мы знаем их форму. Мы можем представить себе построение графика каждой функции, а затем ограничение графика указанной областью. На конечных точках домена мы рисуем пустые кружки, чтобы указать, где конечная точка не включена из-за неравенства «меньше или больше»; мы рисуем замкнутый круг, в котором конечная точка включена из-за неравенства «меньше или равно» или «больше или равно».{2} \ text {if} x \ le 1 [/ латекс]; (b) [латекс] f \ left (x \ right) = 3 \ text {if 1 <} x \ le 2 [/ latex]; (c) [латекс] f \ left (x \ right) = x \ text {if} x> 2 [/ latex]

      Теперь, когда мы нарисовали каждую деталь по отдельности, мы объединяем их в одной координатной плоскости.

      Анализ решения

      Обратите внимание, что график действительно проходит тест вертикальной линии даже при [latex] x = 1 [/ latex] и [latex] x = 2 [/ latex], потому что точки [latex] \ left (1,3 \ right) [ / latex] и [latex] \ left (2,2 \ right) [/ latex] не являются частью графика функции, хотя [latex] \ left (1,1 \ right) [/ latex] и [latex ] \ left (2,3 \ right) [/ латекс] ар.{3} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} & lt {-1} \\ {-2} \ hspace {2mm} & \ text {if} \ hspace {2mm} { -1} & lt {x} & lt {4} \\ \ sqrt {x} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} & gt {4} \ end {align} \ end {case } [/ латекс]

      Показать решение

      Попробуй

      Вы можете использовать онлайн-инструмент построения графиков для построения графиков кусочно определенных функций. Посмотрите это обучающее видео, чтобы узнать, как это сделать.

      Постройте следующую кусочную функцию с помощью онлайн-инструмента построения графиков.{3} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} & lt {-1} \\ {-2} \ hspace {2mm} & \ text {if} \ hspace {2mm} { -1} & lt {x} & lt {4} \\ \ sqrt {x} \ hspace {2mm} & \ text {if} \ hspace {2mm} {x} & gt {4} \ end {align} \ end {case } [/ латекс]

      Вопросы и ответы

      Можно ли применить более одной формулы из кусочной функции к значению в домене?

      № Каждое значение соответствует одному уравнению в кусочной формуле.

      Внесите свой вклад!

      У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

      Улучшить эту страницуПодробнее

      Определение и запись кусочных функций

      Результаты обучения

      • Определить кусочную функцию
      • Вычислить кусочную функцию
      • Напишите кусочную функцию по приложению

      Кусочная функция — это функция, в которой используется более одной формулы для определения вывода по разным частям домена.

      Мы используем кусочные функции для описания ситуаций, когда правило или отношение изменяется, когда входное значение пересекает определенные «границы».«Например, мы часто сталкиваемся с ситуациями в бизнесе, когда стоимость единицы определенного товара снижается, если заказанное количество превышает определенное значение. Налоговые скобки — еще один реальный пример кусочных функций. Например, рассмотрим простую налоговую систему, в которой доходы до [латекс] 10 000 долларов [/ латекс] облагаются налогом [латекс] 10 \% [/ латекс], а любой дополнительный доход облагается налогом [латекс] 20 \% [/ латекс] . Налог на общий доход S составит [латекс] 0,1 [/ латекс] S, если [латекс] S \ le [/ латекс] [латекс] 10 000 долларов [/ латекс] и [латекс] 1000 + 0.2 (S — 10 000 долларов) [/ латекс], если S> [латекс] 10 000 долларов [/ латекс].

      Кусочная функция

      Кусочная функция — это функция, в которой для определения вывода используется более одной формулы. Каждая формула имеет свою собственную область определения, а область определения функции представляет собой объединение всех этих меньших областей. Мы записываем эту идею так:

      [латекс] f \ left (x \ right) = \ begin {cases} \ text {формула 1, если x находится в домене 1} \\ \ text {формула 2, если x находится в домене 2} \\ \ text {формула 3, если x находится в домене 3} \ end {ases} [/ latex]

      В кусочной записи функция абсолютного значения равна

      .

      [латекс] | x | = \ begin {case} x \ text {if} x \ ge 0 \\ -x \ text {if} x <0 \ end {cases} [/ latex]

      Вычислить кусочно-определенную функцию

      В первом примере мы покажем, как вычислить кусочно определенную функцию.Обратите внимание, как важно обращать внимание на домен, чтобы определить, какое выражение использовать для оценки ввода.

      Пример

      Дана функция [латекс] f (x) = \ begin {cases} 7x + 3 \ text {if} x <0 \\ 7x + 6 \ text {if} x \ ge {0} \ end {cases} [ / latex], оценка:

      1. [латекс] f (-1) [/ латекс]
      2. [латекс] f (0) [/ латекс]
      3. [латекс] f (2) [/ латекс]

      Показать решение

      1. [латекс] f (x) [/ latex] определяется как [latex] 7x + 3 [/ latex] для [latex] x = -1 \ text {потому что} -1 <0 [/ latex].

      Вычислить: [латекс] f (-1) = 7 (-1) + 3 = -7 + 3 = -4 [/ латекс]

      2. [латекс] f (x) [/ latex] определяется как [latex] 7x + 6 [/ latex] для [latex] x = 0 \ text {потому что} 0 \ ge {0} [/ latex].

      Вычислить: [латекс] f (0) = 7 (0) + 6 = 0 + 6 = 6 [/ латекс]

      3. [латекс] f (x) [/ latex] определяется как [latex] 7x + 6 [/ latex] для [latex] x = 2 \ text {потому что} 2 \ ge {0} [/ latex].

      Вычислить: [латекс] f (2) = 7 (2) + 6 = 14 + 6 = 20 [/ латекс]

      В следующем видео мы покажем, как оценить несколько значений с помощью кусочно определенной функции.

      В следующем примере мы покажем, как оценить функцию, которая моделирует стоимость передачи данных для телефонной компании.

      Пример

      Компания сотовой связи использует приведенную ниже функцию для определения стоимости [latex] C [/ latex] в долларах за [latex] g [/ latex] гигабайт передачи данных.

      [латекс] C \ left (g \ right) = \ begin {cases} {25} \ text {if} {0} <{g} <{2} \\ 10g + 5 \ text {if} {g} \ ge {2} \ end {case} [/ latex]

      Найдите стоимость использования [латекса] 1.5 [/ latex] гигабайт данных и стоимость использования [latex] 4 [/ latex] гигабайт данных.

      Показать решение

      Чтобы определить стоимость использования [latex] 1,5 [/ latex] гигабайт данных, C [latex] (1.5) [/ latex], мы сначала смотрим, на какую часть домена попадает наш ввод. Поскольку [latex] 1.5 [/ latex] меньше, чем [latex] 2 [/ latex], мы используем первую формулу.

      [латекс] C (1,5) = 25 $ [/ латекс]

      Чтобы определить стоимость использования [latex] 4 [/ latex] гигабайт данных, C [latex] (4) [/ latex], мы видим, что наш ввод [latex] 4 [/ latex] больше, чем [latex] ] 2 [/ latex], поэтому мы используем вторую формулу.

      [латекс] C (4) = 10 (4) + 5 = 45 долларов США [/ латекс]

      Функция из предыдущего примера представлена ​​на графике ниже. Мы можем видеть, где функция изменяется с постоянной на линию с положительным наклоном при [latex] g = 2 [/ latex]. Мы наносим графики для различных формул на общий набор осей, следя за тем, чтобы каждая формула применялась в соответствующей области.

      Написать кусочно-определенную функцию

      В последнем примере мы покажем, как написать кусочно-определенную функцию, которая моделирует стоимость экскурсии по музею.

      Пример

      Музей взимает [латекс] 5 [/ латекс] с человека за экскурсию для группы из [латекса] 1 [/ латекса] до [латекса] 9 [/ латекс] человек или фиксированный сбор в размере 50 долларов для группы из [ латекс] 10 [/ латекс] и более человек. Напишите функцию , связывающую количество людей [латекс] n [/ латекс] со стоимостью [латекс] C [/ латекс].

      Показать решение

      Потребуются две разные формулы. Для n — значения под [латекс] 10 [/ латекс], [латекс] C = 5n [/ латекс]. Для значений n, которые составляют [латекс] 10 [/ латекс] или больше, [латекс] C = 50 [/ латекс].

      [латекс] C (n) = \ begin {cases} {5n} \ text {if} {0} <{n} <{10} \\ 50 \ text {if} {n} \ ge 10 \ end { футляры} [/ латекс]

      График функции для предыдущего примера показан ниже. График представляет собой диагональную линию от [latex] n = 0 [/ latex] до [latex] n = 10 [/ latex] и константу после нее. В этом примере две формулы совпадают в точке встречи, где [latex] n = 10 [/ latex], но не все кусочные функции обладают этим свойством.

      В следующем видео мы показываем пример того, как написать кусочно-определенную функцию с учетом сценария.

      Как: для данной кусочной функции напишите формулу и определите область для каждого интервала


      1. Определите интервалы, в которых применяются разные правила.
      2. Определите формулы, описывающие, как вычислить выход из входа в каждом интервале.
      3. Используйте квадратные скобки и операторы «если» для написания функции.

      Сводка

      • Кусочная функция — это функция, в которой используется более одной формулы для определения вывода для разных частей домена.
      • Оценка кусочной функции означает, что вам нужно уделять пристальное внимание правильному выражению, используемому для данного ввода.

      кусочно-определенная функция

      А

      кусочно-определенный

      Функция — это функция, которая определяется не одним уравнением, а двумя или более. Каждое уравнение справедливо для некоторых

      интервал

      .


      Пример 1:

      Рассмотрим функцию, определенную следующим образом.

      y

      знак равно

      {

      Икс

      +

      2

      для

      Икс

      < 0 2 для 0 ≤ Икс ≤ 1 - Икс + 3 для Икс >

      1

      Функция в этом примере является кусочно-линейной, потому что каждая из трех частей графика представляет собой линию.

      Кусочно определенные функции также могут иметь разрывы («скачки»). Функция в приведенном ниже примере имеет разрывы на

      Икс

      знак равно

      —

      2

      а также

      Икс

      знак равно

      2

      .


      Пример 2:

      Изобразите функцию, определенную, как показано.

      y

      знак равно

      {

      1

      2

      Икс

      2

      для

      Икс

      < - 2 0для - 2 ≤ Икс < 2 1 2 Икс 2 для Икс ≥ 2

      Обратите внимание, что мы используем маленькие белые кружки на графике, чтобы указать, что конечная точка кривой не включена в график, и сплошные точки, чтобы указать конечные точки, которые включены.


      Пример 3:

      Изобразите график функции, определенной ниже.

      y

      знак равно

      {

      бревно

      Икс

      для

      0

      < Икс < 1 1 Икс - 2 для Икс ≥ 1

      Отрицательные значения

      Икс

      а также

      0

      не входят в

      домен

      потому что первая функция,

      бревно

      Икс

      , не определено для этих значений.Значение

      Икс

      знак равно

      2

      не включен в домен, потому что вторая функция не определена для этого значения (у нее есть вертикальная асимптота). Следовательно, область определения этой функции

      {

      Икс

      |

      0

      < Икс < 2 } ∪ { Икс | Икс >

      2

      }

      .Это может быть представлено с использованием обозначения интервалов как

      (

      0

      ,

      2

      )

      ∪

      (

      2

      ,

      ∞

      )

      .

      Кусочная функция: определение, как рисовать

      Состав:

      1. Что такое кусочная функция?
      2. Оценка
      3. Рисование вручную
      4. График на TI-89

      Кусочная функция — это функция, состоящая из разных частей.В частности, это функция, определенная для двух или более интервалов, а не с помощью одного простого уравнения для области. Это может быть или не быть непрерывной функцией.

      Кусочно-непрерывная функция является непрерывной, за исключением определенного количества точек. Другими словами, функция состоит из конечного числа непрерывных частей.


      Более математическое определение

      Кусочно-непрерывная функция f (x), определенная на интервале (a i (i = 1 , 2, 3…) такие, что a i


      Примеры функции, которая не является кусочно-непрерывной

      При попытке выяснить, является ли функция кусочно-непрерывной или нет, иногда легче определить, когда функция не соответствует строгому определению (вместо того, чтобы пытаться доказать, что это так!).

      Важной частью этого определения является то, что должны существовать односторонние ограничения . В качестве примера функция sin (1 / x) является , а не кусочно-непрерывной, потому что одностороннего предела f (0+) не существует.Если функция имеет такую ​​вертикальную асимптоту даже в конце интервала, то она не является кусочно-непрерывной.

      Пример неполной непрерывной функции: 1 / x. Предел не существует с одной стороны при x = 0 из-за вертикальной асимптоты. График: Desmos.com

      Возможно, удивительно, но в определении ничего не говорится, что каждая точка должна быть определена. В функции может отсутствовать, скажем, точка при x = 0. Но пока она удовлетворяет всем остальным требованиям (например, пока график непрерывен между неопределенными точками), она по-прежнему считается кусочно-непрерывной.

      Кусочно-гладкая

      Кусочно-непрерывная функция называется кусочно-гладкой, если производная кусочно-непрерывна.

      Предупреждение об использовании графиков для принятия решения

      Тот факт, что график выглядит как кусочно-непрерывная функция, не означает, что это так. Например, прямоугольная волновая функция является кусочной, и она определенно выглядит как кусочно-непрерывная функция. Однако функция не является непрерывной для целых чисел, поэтому она не является примером функции этого типа.

      Сначала определите, к какой части вашей функции она принадлежит. Например, предположим, что вы хотите оценить следующую функцию при x = 0.

      Первое, что следует отметить, это то, что эта конкретная функция состоит из двух частей, разделенных на x = -3.

      Если вы попытаетесь оценить это, вычислив 2x + 14 = 14 (первая часть), вы ошибетесь. При x = 0, x> — 3, так что это вторая часть кусочной функции, которая применяется к вашей ситуации. Фактическое значение будет равно 16 — 2x, поэтому:
      16 — 2 (0) = 16.

      Обычно это легче увидеть, если построить график функции. Ниже приводится простая процедура.

      Чтобы построить график кусочной функции, сначала посмотрите на неравенства. Для функции выше это будет

      1. На миллиметровой бумаге нарисуйте вертикальные пунктирные линии на каждом из перечисленных значений x. В нашем случае мы будем рисовать только одну линию с x = -3.
      2. Нарисуйте все указанные функции. Нарисуйте их очень легко карандашом. У вас будет две или более функций, которые могут пересекаться; не беспокойся об этом.

        Первые два шага для построения кусочной функции.


      3. Посмотрите еще раз на ваши интервалы и затемните / раскрасьте график ваших функций только в соответствующих интервалах: между вертикальными линиями, которые отмечают изменения.
      4. Наконец, сотрите рисунок светлым карандашом. Теперь у вас есть аккуратный график кусочной функции.

        5. Если вы построили график

        , он должен выглядеть идентично приведенному выше.

        Кусочные функции TI 89 «when (» Команда

        Кусочные функции — это функции, которые находятся в отдельных частях.Другими словами, вместо одного уравнения для ввода у вас может быть несколько, составляющих одну большую функцию. Хотя построение (и дифференцирование) кусочных функций вручную может стать проблематичным — особенно если вам нужно иметь дело с тремя или более уравнениями — TI89 упрощает построение кусочных функций с помощью команды «when (».

        Кусочные функции TI 89 «когда»: пример

        Пример задачи: изобразите следующие кусочные функции:

      • f (x) = 3x, x больше 0,
      • f (x) = x + 5, x меньше или равно 0.

      Шаг 1: Нажмите кнопку HOME .

      Шаг 2: Нажмите ромбовидную клавишу , а затем нажмите F1 , чтобы войти в редактор y =. Удалите все уравнения в редакторе y =, используя клавиши со стрелками и нажав клавишу CLEAR.

      Шаг 3: Находясь в слоте «y1 =», нажмите КАТАЛОГ , а затем нажмите точку «.» (для буквы «W» над клавишей точки). Вы сразу перейдете к команде «когда (».

      Шаг 4: Нажмите ENTER , чтобы перенести команду «when (» в слот «y1 =».

      Шаг 5: Находясь в команде «when (», нажмите: x 2nd. 0, 3 x, x + 5) ENTER.
      Это говорит TI-89, что всякий раз, когда x больше 0, возвращать 3x; всякий раз, когда x не больше 0 (это то же самое, что и всякий раз, когда x меньше или равно 0), вернуть x + 5

      Шаг 6: Нажмите ромбовидную кнопку , а затем нажмите F3 , чтобы просмотреть график.

      Примечание . Если вы не видите график, проверьте настройки окна. Нажмите ромбовидную клавишу, а затем нажмите F2, чтобы открыть окно.

      Ссылки

      Barron & Kastberg. Кусочно-линейные функции. EMT668 Урок 4. Департамент математического образования Университета Джорджии
      Получено с http://jwilson.coe.uga.edu/emt668/EMAT6680.Folders/Barron/unit/Lesson%204/4.html 11 ноября 2018 г.
      Эгберт, Ник. Кусочные функции. Получено с https://www.math.purdue.edu/~egbertn/fa2016/notes/lesson9.pdf, 11 ноября 2018 г. Графический калькулятор Desmos
      , Доши, Дж. (1998). Аналитические методы в технике.Alpha Science Int’l Ltd.
      Myint, T. & Debnath, L. (2007). Линейные дифференциальные уравнения с частными производными для ученых и инженеров. Springer Science and Business Media.

      ————————————————— —————————-

      Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

      Как рассчитать, примеры, практические задачи, рисунки

      Ошибка: Нажмите «Не робот», затем повторите попытку.

      Краткий обзор

      Если $$ x $$ приближается к одной из точек перехода функции, вам необходимо проверить оба односторонних предела.

      Примеры

      Пример 1

      Определите $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) $$, если $$ f $$ определен, как показано ниже.

      $$
      е (х) = \ влево \ {%
      \ begin {array} {ll}
      2x + 3, & x

      Шаг 1

      Оцените односторонние пределы. +} (5x-9) = 5 (4) -9 = 11
      \ end {выровнять *}
      $$

      Шаг 2

      Если односторонние ограничения совпадают, ограничение существует.

      Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) = 11 $$, если $$ f $$ определен, как указано выше.

      Пример 2

      Вычислить $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$, когда $$ f $$ определен следующим образом.+} \ sqrt x = \ sqrt 0 = 0
      \ end {выровнять *}
      $$

      Шаг 2

      Если односторонние ограничения различны, ограничение не существует.

      Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

      Пример 3

      Предположим, что $$ f $$ определен, как показано ниже. +} \ left (\ frac 2 3 x + b \ right) = \ frac {2 (5)} 3 + b = \ frac {10} 3 + b
      \ end {выровнять *}
      $$

      Шаг 2

      Установите два предела равными друг другу и решите.

      $$
      \\
      \ begin {align *}
      \ frac {10} 3 + b & = 7 \\ [6pt]
      b & = 7 — \ frac {10} 3 \\ [6pt]
      b & = \ frac {11} 3
      \ end {выровнять *}
      \\
      $$

      Ответ: $$ b = \ frac {11} 3 $$

      Практические задачи

      Задача 1

      Вычислить $$ \ displaystyle \ lim_ {x \ to 2} f (x) $$, если $$ f $$ определен следующим образом. +} \ left (3x + 4 \ right) = 3 (2) +4 = 10
      \ end {выровнять *}
      $$

      Шаг 2

      Отвечать

      Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to2} f (x) = 10 $$, если $$ f $$ определен, как указано выше.

      Проблема 2

      Вычислить $$ \ displaystyle \ lim_ {x \ to 4} f (x) $$, если $$ f $$ определен следующим образом. +} \ frac 1 4 x = \ frac 4 4 = 1
      \ end {выровнять *}
      $$

      Шаг 2

      Отвечать

      Ответ: $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 1 $$, если $$ f $$ определен, как указано выше.

      Проблема 3

      Вычислить $$ \ displaystyle \ lim_ {x \ to 1} f (x) $$, если $$ f $$ определен следующим образом.+} \ frac 1 {x-1} = \ frac 1 0 \ qquad \ mbox {Деление на ноль!}
      \ end {выровнять *}
      $$

      Шаг 2

      Отвечать

      Ответ: $$ \ displaystyle \ lim_ {x \ to1} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

      Проблема 4

      Вычислить $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$, когда $$ f $$ определен, как показано ниже. +} \ left (2x + \ frac 8 3 \ right) = 2 (-5) + \ frac 8 3 = — \ frac {22} 3
      \ end {выровнять *}
      $$

      Шаг 2

      Отвечать

      Ответ: $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

      Проблема 5

      Определите значение $$ b $$, чтобы $$ \ displaystyle \ lim_ {x \ to-6} f (x) $$ существовал, когда $$ f $$ определен, как показано ниже.+} \ left (\ frac 1 2 x + 9 \ right) = \ frac {-6} 2 + 9 = -3 + 9 = 6
      \ end {выровнять *}
      $$

      Шаг 2

      Установите два односторонних предела равными друг другу и решите.

      Отвечать

      $$
      \ begin {align *}
      36 + b & = 6 \\
      b & = -30
      \ end {выровнять *}
      $$

      Ответ: $$ b = -30 $$

      Задача 6

      Определите значение $$ m $$, чтобы $$ \ displaystyle \ lim_ {x \ to3} f (x) $$ существовал, когда $$ f $$ определяется следующим образом. +} (mx-4) = 3m-4
      \ end {выровнять *}
      $$

      Шаг 2

      Приравняйте два предела и решите.

      Отвечать

      $$
      \\
      \ begin {align *}
      3м-4 & = 13 \\ [6pt]
      3м & = 17 \\ [6pt]
      m & = \ frac {17} 3
      \ end {выровнять *}
      \\
      $$

      Ответ: $$ m = \ frac {17} 3 $$

      Проблема 7

      Определите значение (я) $$ m $$ и $$ b $$, поэтому $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 10 $$, когда $$ f $$ определен, как показано ниже. +} (5x + b) = 20 + b.
      \ end {выровнять *}
      $$

      Шаг 2

      Поскольку оба предела должны равняться 10, составьте систему уравнений и решите.

      Отвечать

      $$
      \\
      \ begin {align *}
      4m + 2b & = 10 \\
      20 + b & = 10 \\ [12pt]
      %
      4m + 2b & = 10 \\
      b & = -10 && \ mbox {Решите относительно \ (b \) во втором уравнении.} \\ [12pt]
      %
      4m + 2 (-10) & = 10 && \ mbox {Подставьте значение \ (b \) в другое уравнение.} \\
      4м — 20 & = 10 \\
      4 м & = 30 \\ [6 пт]
      m & = \ frac {30} 4 \\ [6pt]
      m & = \ frac {15} 2
      \ end {выровнять *}
      \\
      $$

      Ответ: $$ m = \ frac {15} 2 $$ и $$ b = -10 $$.

      Ошибка: Нажмите «Не робот», затем повторите попытку.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *