Содержание
Формулы прогрессий. Арифметическая прогрессия. Геометрическая прогрессия
Понятие числовой последовательности
Введем два определения числовой последовательности:
Определение 1
Числовая функция, у которой область определения совпадает с натуральным рядом чисел, будет называться числовой последовательностью.
Определение 2
Отображения натурального ряда чисел на множество действительных чисел будет называться числовой последовательностью: $f:N→R$
Числовая последовательность обозначается следующим образом:
${p_k }={p_1,p_2,…,p_k,…}$
где $p_1,p_2,…,p_k,…$ — действительные числа.
Есть три различных способа для задания числовых последовательностей. Опишем их.
Аналитический.
В этом способе последовательность задается в виде формулы, с помощью которой можно найти любой член этой последовательности, подставляя в нее вместо переменной натуральные числа.
Рекуррентный.

Данный способ задания последовательности заключается в следующем: Дается первый (или несколько первых) член данной последовательности, а затем формула, которая связывает любой член ее с предыдущим членом или предыдущими членами.
Словесный.
При этом способе числовая последовательность просто описывается без введения каких-либо формул.
Двумя частными случаями числовых последовательностей являются арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Определение 3
Арифметической прогрессией называется последовательность, которая словесно описывается следующим образом: Задано первое число. Каждое же последующее определяется как сумма предыдущего с наперед заданным конкретным числом $d$.
В этом определении данное наперед заданное число будем называть разностью арифметической прогрессии.
Очевидно, что рекуррентно эту последовательность записываем следующим образом:
$p_1,p_{k+1}=p_k+d. $
$
Замечание 1
Отметим, что частным случаем арифметической прогрессии является постоянная прогрессия, при которой разность прогрессии равняется нулю.
Для обозначения арифметической прогрессии в ее начале изображается следующий символ:
Из рекуррентного соотношения для данной последовательности легко выводится формула для нахождения любого члена через первый:
$p_k=p_1+(k-1)d$
Сумма $k$ первых членов можно найти по формуле
$S_k=\frac{(p_1+p_k)k}{2}$ или $S_k=\frac{(2p_1+(k-1)d)k}{2} $
У арифметической прогрессии есть так называемое характеристическое свойство, которое определяется формулой:
$p_k=\frac{p_{k-1}+p_{k+1}}{2}$
Геометрическая прогрессия
Определение 4
Геометрической прогрессией называется последовательность, которая словесно описывается следующим образом: Задано первое число, не равное нулю. Каждое же последующее определяется как произведение предыдущего с наперед заданным конкретным не равным нулю числом $q$.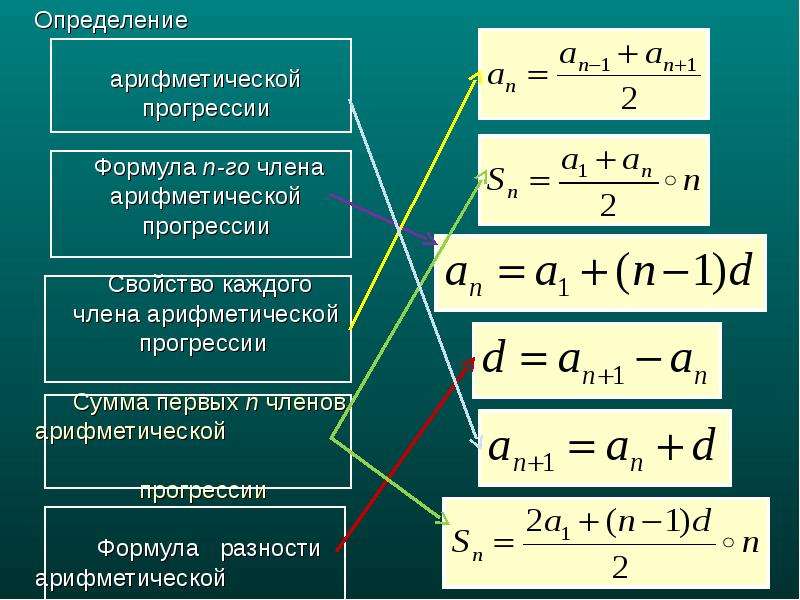 2=p_{k-1} p_{k+1}$
2=p_{k-1} p_{k+1}$
Примеры задач
Пример 1
Найти сумму $5$ членов прогрессии, описывающей четные положительные числа.
Решение.
Последовательность положительных четных чисел имеет вид
$2,4,6,8,10,…$
Она является арифметической.
Очевидно, что разность данной арифметической прогрессии равняется
$d=4-2=2$
Тогда по второй формуле суммы арифметической прогрессии, получим:
$S_5=\frac{2\cdot 2+(5-1)\cdot 2}{2\cdot 5}=30$
Ответ: $30$.
Пример 2
Найти сумму $5$ членов прогрессии, описывающей степени натуральных чисел тройки.
Решение.
Последовательность таких чисел имеет вид
$3,9,27,81,…$
Она является геометрической.
Очевидно, что знаменатель данной геометрической прогрессии равняется
$q=\frac{9}{3}=3$
Тогда по второй формуле суммы арифметической прогрессии, получим:
$S_5=\frac{3\cdot (3^5-1)}{3-1}=363$
Ответ: $363$.
Арифметическая прогрессия – Определение, Примеры, Формулы 9 класс
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
- Словесно — когда правило последовательности объясняется словами:
«Последовательность простых чисел: 4, 6, 10, 19, 21, 33…»
- Аналитически — когда указана формула ее n-го члена: yn = f(n).
Последовательность yn = C называют постоянной или стационарной.
- Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
- Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4…
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
- Последовательность {yn} называют возрастающей, если каждый ее член кроме первого больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < …
- Последовательность {yn} называют убывающей, если каждый ее член кроме первого меньше предыдущего:
y1 > y2 > y3 > … > yn > yn+1 > …
Возрастающие и убывающие последовательности называют монотонными последовательностями.
- Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: yn = yn+T.
 Число T — длина периода.
Число T — длина периода.
Разобраться во всех правилах и быстро щелкать задачки помогут внимательные учителя детской школы Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой, увлекательные математические комиксы и даже онлайн-доска, на которой можно чертить вместе с учителем.
Запишите вашего ребенка на бесплатный вводный урок математики: покажем, как все устроено и вдохновим на учебу.
Запишем числа, которые первые пришли в голову: 7, 19, 0, -1, 2, -11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2,…, a10…, an.
N-ый член последовательности можно задать формулой. Например:
- Формула an = 3n — 5 задает последовательность: −2, 1, 4, 7, 10…
- Формула an = 1 : (n + 2) задает последовательность: 13, 14, 15, 16…
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.
Арифметическая прогрессия — это числовая последовательность a1, a2,. .., an,… для которой для каждого натурального n выполняется равенство: .., an,… для которой для каждого натурального n выполняется равенство:an+1= an + d, где d — это разность арифметической прогрессии. |
Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.
Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:
Если известны первый член a1 и n-ый член прогрессии, разность можно найти так:
Арифметическая прогрессия бывает трех видов:
- Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.
Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.
- Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.

Пример: последовательность чисел 50, 48, 46, 44, 43… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.
- Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.
Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.
Свойство арифметической прогрессии
Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.
Рассмотрим пример арифметической прогрессии.
Дано: арифметическая прогрессия (an), где a1 = 0 и d = 2.
Найти: первые пять членов прогрессии и десятый член прогрессии.
Решение арифметической прогрессии:
- Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a2 = a1 + d = 0 + 2 = 2;
a3 = a2 + d = 2 + 2 = 4;
a4 = a3 + d = 4 + 2 = 6;
a5 = a4 + d = 6 + 2 = 8.

- Используем общую формулу an = a1 + d * (n — 1).
По условиям задачи n = 10, подставляем в формулу:
a10 = a1 + 2 * (10 — 1) = 0 + 2⋅9 = 18.
Формулы арифметической прогрессии
В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:
- Рекуррентной формулой:
- Формулой n-го члена: an = a1+ d · (n — 1).
- Формулой вида an = kn + b, где k и b — числа, n — число членов последовательности.
Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:
Формулы нахождения суммы n членов арифметической прогрессии:
Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:
Формула n-го члена арифметической прогрессии
Из определения арифметической прогрессии следует, что равенство истинно:
Поэтому:
и т. д.
д.
Значит,
Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.
Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.
Формулу an = a1 + d * (n — 1) называют формулой n-го члена арифметической прогрессии.
Доказательство формулы n-го члена арифметической прогрессии
Формулу n-го члена арифметической прогрессии можно доказать при помощи метода математической индукции.
Пусть дано:
Нужно доказать:
Как доказываем:
- Формула верна при n = 1.
Действительно,
- Предположим, что формула верна при n = k, то есть
- Докажем, что формула верна и при n = k + 1, то есть
- Из условия и предположения получаем:
Согласно принципу математической индукции формула верна для любого натурального числа.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.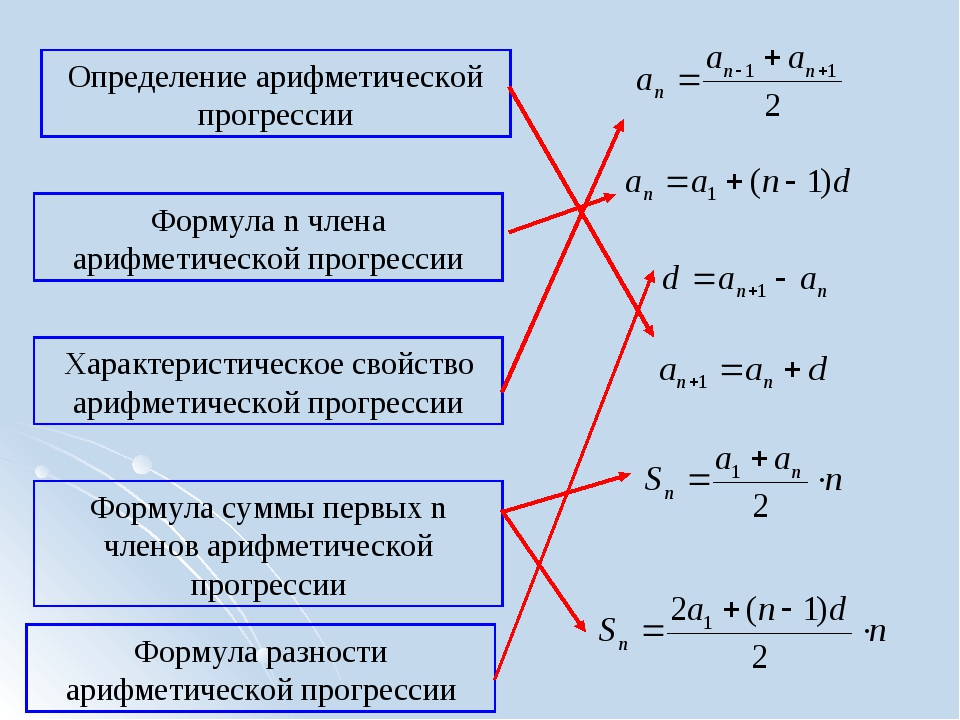
Если последовательность (bn) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:
| bn+1 = bn * q, где q — знаменатель геометрической прогрессии |
Если в геометрической прогрессии (bn) известен первый член b1 и знаменатель q, то можно найти любой член прогрессии:
- b2 = b1 * q;
- b3 = b2 * q = b1 * q * q = b1 * q²;
- b4 = b1 * q³;
- и т. д.
Общий член геометрической прогрессии bn можно вычислить при помощи формулы:
bn = b1 * qn−1, где n — порядковый номер члена прогрессии, b1 — первый член последовательности, q — знаменатель.
Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.
Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.
3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.
Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.
Приходите тренироваться: весело, современно и с результатом. В детской школе Skysmart знают, как подружить ребенка с самой коварной темой по математике и повысить оценки в школе.
1. Арифметическая и геометрическая прогрессии
Для \(14\) задания необходимо знать теорию арифметической и геометрической прогрессий.
Арифметическая прогрессия
Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
an+1=an+d, где an+1 — последующий член, an — предыдущий член и d — разность арифметической прогрессии.
Формула для нахождения разности: d=an+1−an.
Для арифметической прогрессии, где известен первый член a1 и разность d, её \(n\)-й член может быть найден по формуле:
an=a1+n
−1⋅d.
Свойство арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
an=an−1+an+12.
Сумма первых членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Sn=a1+an2⋅n.
И вторая формула для вычисления суммы: Sn=2a1+d⋅n−12⋅n.
Более подробно можно познакомиться с темой здесь.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
bn+1=bn⋅q, где bn+1 — последующий член, bn — предыдущий член и q — знаменатель геометрической прогрессии.
Формула для нахождения знаменателя: q=bn+1bn.
Для геометрической прогрессии, где дан первый член b1 и знаменатель q, её \(n\)-й член может быть найден по формуле:
bn=b1⋅qn−1.
Свойство геометрической прогрессии: каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому предшествующего и последующего членов.
bn2=bn−1⋅bn+1.
Сумму первых членов геометрической прогрессии со знаменателем, не равным нулю, можно найти по формуле:
Sn=b1⋅qn−1q−1, где q≠1.
Также можно найти сумму по формуле: Sn=bnq−b1q−1.
Более подробно можно познакомиться с темой здесь.
Алгебраическая и геометрическая прогрессии
Муниципальное общеобразовательное учреждение
«Ягельная средняя общеобразовательная школа»
Обобщение и систематизация по теме
«Алгебраическая и геометрическая прогрессии»
Учитель математики
Изекеева А.М.
2016/2017 учебный год
п. Ягельный
Ягельный
Обобщение и систематизация знаний по теме
«Арифметическая и геометрическая прогрессии»
Образовательные задачи:
обобщить и систематизировать знания об арифметической и геометрической прогрессиях с целью подготовки к итоговой аттестации;
контроль усвоения знаний и умений.
Развивающие задачи:
способствовать развитию умений анализировать, обобщать, сравнивать, самостоятельно применять знания, умения и навыки по теме, осуществлять их перенос в новые условия; развитию памяти, внимания, логического мышления, правильной математической речи, познавательного интереса.
Воспитательная задача:
способствовать воспитанию ответственности, активности, умения работать в группах, общей культуры.
План занятия:
Организационный момент.
Актуализация опорных знаний.
Фронтальная работа с классом.
Работа в группах.
Самостоятельная работа.
Подведение итогов урока.
Ход занятия
I. Организационный момент.
Цель:
Учитель: Тема нашего занятия «Обобщение и систематизация знаний по теме «Арифметическая и геометрическая прогрессии».
Для работы на занятии мы должны вспомнить: Демонстрируется слайд 1
определения АП и ГП, формулы п- го члена этих прогрессий и суммы n первых членов этих прогрессий.
II. Актуализация опорных знаний.
1. Устная фронтальная работа с классом с использованием мультимедийной
презентации.
Цель данного этапа урока: повторить известные учащимся сведения об
арифметической и геометрической прогрессиях.
Учитель: Даны две последовательности чисел (записаны на доске):
6; 8; 10;… (12; 14; 16;…)
3;6;12;…. (24; 48; 96;…)
Назовите следующие три члена первой последовательности.
Ученик:
12; 14; 16;…
Учитель:
Сформулируйте закономерность составления данной последовательности.
Ученик:
Каждый следующий член последовательности получен прибавлением числа 2 к
предшествующему числу.
Учитель:
Как называется такая последовательность чисел?
Ученик:
Такая последовательность чисел называется арифметической прогрессией.
Демонстрируется слайд 2.
Учитель: Устно решить задачу:
Назовите первые пять членов АП, если .
Ученик: .
Учитель: Какую закономерность можно заметить в первой последовательности?
Ученик: .
(Если затрудняются, задаем вопрос: Как получить 8, зная 6 и 10?)
Демонстрируется слайд 3 — характеристическое свойство АП
Учитель:
Рассмотрим вторую последовательность.
Назовите следующие три члена второй последовательности.
Ученик:
24; 48; 96;…
Учитель:
Сформулируйте закономерность составления данной последовательности.
Ученик:
Каждый следующий член последовательности получен умножением предшествующего числа на 2.
Учитель:
Как называется такая последовательность чисел?
Ученик:
Такая последовательность чисел называется геометрической прогрессией.
Демонстрируется слайд 4.
Учитель: Назовите первые пять членов ГП, если .
Ученик: .
Учитель: Сформулируйте закономерность для второй последовательности.
Ученик: .
Демонстрируется слайд 5 — характеристическое свойство ГП.
Учитель: Зная первый член арифметической прогрессии и ее разность можно найти любой член этой прогрессии. Вспомните формулу.
Ученик: .
Демонстрируется слайд 6 — формула n-го члена АП.
Учитель: Вспомните формулу п — го члена геометрической прогрессии.
Ученик: .
Демонстрируется слайд 7 – формула n – го члена ГП.
Учитель:
Решите задачу. (Два человека работают у доски – Чеботарев А — задача на АП, Ковтун Н — задача на ГП). (Для работающих у доски задача дается на листе). Класс делится на две группы.
Группа 1. Егоров А, Чеботарев А, Чанов С, Яценко М, Панкова Я. – решают задачу на АП.
Группа 2. Князькова Л, Гализянова Э, Ковтун Н, Чеботарева Е – решают задачу на ГП.
Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена арифметической прогрессии. Сформулируйте и решите аналогичную задачу для геометрической прогрессии.
Ученик: задача на АП.
Ученик: задача на ГП. (сформулировать).
Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.
Учитель: Решите задачу. (Демонстрируется слайд 8)
Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член
которой равен — 45,6, а пятнадцатый член равен 2.
Какую формулу нужно знать, чтобы решить эту задачу?
Ученик: Формулу суммы n первых членов АП.
Демонстрируется слайд 9
Задачу решают самостоятельно с последующей самопроверкой. Самопроверка осуществляется с помощью мультимедийного проектора. Решение появляется поочередно по действиям.
Демонстрируется слайд 10.
Учитель: Решите задачу: ( у доски работает Князькова Л)
В геометрической прогрессии найти число п членов, если . . Вспомните формулу суммы п первых членов геометрической прогрессии.
Ученик: .
Демонстрируется слайд 11.
Решение задачи.
Учитель: Повторили основные формулы по данной теме, а дальше будем применять их при решении задач.
Работа в группах.
Цель: — закрепить знания основных формул и умения применять их в новой измененной ситуации.
Группа 1. Егоров А, Яценко М, Чеботарев А, Чанов С, Панкова Я. (работают с учителем).
Решите задачу:
Компьютерная игра состоит в последовательном прохождении нескольких уровней. За прохождение каждого уровня игрок получает 50 баллов. Кроме того, начисляются и премиальные баллы по следующей схеме: 10 баллов за второй уровень и за каждый следующий уровень на 10 баллов больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать равно 1100 баллов?
Решение. (У доски работает Панкова Я)
Задача 2.
Найдите сумму семи первых членов геометрической прогрессии, у которой первый член равен 32, а знаменатель равен .
Решение.
(У доски работает Яценко М)
Ответ: 63,5.
Задачи для второй группы.
При свободном падении тело проходит в первую секунду 4,9 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.
Решение.
Ответ: 122,5 м.
В геометрической прогрессии Найти и сумму первых шести ее членов.
Решение.
Ответ: =0,125;=7,875.
Второй член арифметической прогрессии равен 18, а пятый член равен 9. Найти сумму первого и шестого членов этой прогрессии.
Решение.
1 способ:
2 способ.
Сумма первых шести членов геометрической прогрессии равна 910, знаменатель прогрессии равен 3. Найти сумму первого и пятого членов этой прогрессии.
Решение.
Проверочная работа (дифференцированная, в формате ЕГЭ 2010 г) – задания внесены в ноутбук, обучающиеся решают задачи в черновиках, ответы заносят в компьютер.

Задания для 1 группы.
1. Найдите номер члена арифметической прогрессии — 2; 3; 8;…, равного 28. Ответ: 7.
2. Известно, что в геометрической прогрессии первый член равен 4, а второй равен 2. Найдите шестой член прогрессии.
Ответ:0,125.
3. Найдите сумму первых двадцати членов арифметической прогрессии 5; 2; — 1; — 4; …
Ответ: — 470.
Задания для 2 группы.
1. Найдите первый член арифметической прогрессии, если известно, что сумма одиннадцати ее первых членов равна 165, а ее разность равна 7.
Ответ: — 20.
2. Найдите четвертый член геометрической прогрессии, если известно, что сумма пяти ее первых членов равна 713, а ее знаменатель равен 2.
Ответ: 184.
3. Пятый член арифметической прогрессии равен 14, а сумма первых десяти членов этой же арифметической прогрессии равна 155. Найдите произведение третьего и пятого членов этой прогрессии.
Найдите произведение третьего и пятого членов этой прогрессии.
Ответ: 112.
V. Подведение итогов.
Ребята, мы с вами на этом занятии повторили арифметическую и геометрическую прогрессии, решали задачи по данной теме. Некоторые из вас показали хорошие результаты. Но с некоторыми из вас нам следует вернуться к этой теме на консультациях.
Задачи в ноутбуке.
Группа 1.
1. Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена арифметической прогрессии.
2. Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член
которой равен — 45,6, а пятнадцатый член равен 2.
3. В геометрической прогрессии найти число п членов, если .
4. Компьютерная игра состоит в последовательном прохождении нескольких уровней. За прохождение каждого уровня игрок получает 50 баллов. Кроме того, начисляются и премиальные баллы по следующей схеме: 10 баллов за второй уровень и за каждый следующий уровень на 10 баллов больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать равно 1100 баллов?
Сколько уровней надо пройти, чтобы набрать равно 1100 баллов?
5. Найдите сумму семи первых членов геометрической прогрессии, у которой первый член равен 32, а знаменатель равен .
Группа 2.
1. Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.
2. Найдите сумму пятидесяти первых членов арифметической прогрессии, первый член
которой равен — 45,6, а пятнадцатый член равен 2.
3. В геометрической прогрессии найти число п членов, если .
4. При свободном падении тело проходит в первую секунду 4,9 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.
5. В геометрической прогрессии Найти и сумму первых шести ее членов.
6. Второй член арифметической прогрессии равен 18, а пятый член равен 9. Найти сумму первого и шестого членов этой прогрессии.
7. Сумма первых шести членов геометрической прогрессии равна 910, знаменатель прогрессии равен 3. Найти сумму первого и пятого членов этой прогрессии.
Найти сумму первого и пятого членов этой прогрессии.
Арифметические,геометрические прогрессии — Математика
Если каждому натуральному числу n (n = 1, 2,…) поставлено в соответствие число xn, то говорят, что задана числовая последовательность x1, x2,…, xn…, обозначаемая {xn}. Числаx1, x2,…, xn… называются членами последовательности, а член с номером n – ее n-м членом.
Арифметическая прогрессия
Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии: an+1 = an + d. Число Sn называется суммой n первых членов арифметической прогрессии.
Свойства арифметической прогрессии:
Геометрическая прогрессия
Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией.
Число q называется называется знаменателем прогрессии: bn+1 = bnq.
Число Sn называется суммой n первых членов геометрической прогрессии, Pn — произведением n первых членов геометрической прогрессии.
Свойства геометрической прогрессии:
Сумма первых трех членов возрастающей арифметической прогрессии равна 21. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 2, то полученные три члена составят геометрическую прогрессию. Найти сумму восьми первых членов геометрической прогрессии.
____________________________________________________________________________
Обозначим через ai — члены арифметической прогрессии c разностью d, через bi — геометрической, с знаменателем q.
Согласно формуле суммы арифметической прогрессии имеем S3 = (2a1 + 2d) · 3 / 2 = 21 или a1 + d = 7.
По условию a1 — 1, a1 + d — 1, a1 + 2d + 2 — три последовательных члена геометрической прогрессии. Используем свойство геометрической прогрессии:
(a1 + d — 1)2 = (a1 + 2d + 2)(a1 — 1).
После замены переменной a1 = 7 — d и открытия скобок получаем квадратное уравнение
d2 + 3d — 18 = 0, т.е. d1 = 3, d2 = -6.
Условию удовлетворяет лишь d1 = 3 (т.к. арифметическая прогрессия возрастающая). В этом случае a1 = 4. Находим b1 = a1 — 1 = 3. b2 = a1 + d — 1 = 6, откуда q = 2.
Наконец, согласно формуле суммы членов геометрической прогрессии получаем:
S8 = [b1(q8 — 1)] / (q — 1) = 765.
Ответ: S8 = 765.
Сумма трех чисел, которые составляют арифметическую прогрессию, равна 2, а сумма квадратов этих же чисел равна 14/9. Найти эти числа.
____________________________________________________________________________
Используя тот факт, что числа составляют арифметическую прогрессию, запишем их какa, a + d, a + 2d.
Согласно условию их сумма равна 2, т.е. 3a + 3d = 2, a = 2/3 — d.
Согласно второму условию a2 + (a + d)2 + (a + 2d)2 = 14/9.
После раскрытия скобок получаем 27a2 + 45d2 + 54ad = 14.
Делаем замену переменной a = 2/3 — d, раскрываем скобки и получаем:
d2 = 1/9.
d = ±1/3.
Теперь легко найти числа, составляющие арифметическую прогрессию. При любом из значений d = ±1/3 числа будут равны 1/3, 2/3, 1.
Ответ: 1/3, 2/3, 1.
Найти четыре числа, составляющие геометрическую прогрессию, в которой третий член больше первого на 9, а второй больше четвертого на 18.
____________________________________________________________________________
Используя тот факт, что числа составляют геометрическую прогрессию, запишем их какb, bq, bq2, bq3.
По условию:
1) bq2 = b + 9.
2) bq = bq3 + 18.
Домножаем первое уравнение на q и складываем со вторым:
9q + 18 = 0.
Откуда q = -2. Из первого уравнения находим b. b = 3.
Теперь легко найдем все числа: 3, -6, 12, -24.
Ответ: 3, -6, 12, -24.
Найти сумму всех трехзначных чисел, которые делятся на 7.
___________________________________________________
Сначала найдем минимальное и максимальное трехзначные числа, которые делятся на 7. Это числа 105 и 994 соотвественно. Запишем a1 = 105, am = 994.
Найдем m, т.е. количество трехзначных чисел, которые делятся на 7. Используем свойство прогрессии и получаем:
994 = 105 + 7(m — 1).
Откуда m = 128.
А теперь воспользуемся формулой суммы m членов арифметической прогрессии S128 = (105 + 994) · 128 / 2 = 70336.
Ответ: 70336.
Подготовка к ОГЭ. Последовательности. Арифметическая прогрессия.
Любой ученик девятого класса при желании легко сможет понять, что такое арифметическая или геометрическая прогрессия. Решение большинства задач на тему прогрессий из заданий ОГЭ по математике тоже не вызовет трудностей. Однако есть ряд задач, требующих понимания правильного использования формул прогрессий. Поэтому разберёмся, что такое арифметическая и геометрическая прогрессии и как применяются формулы этих прогрессий.
Запишем произвольный набор чисел, например: 2; 5; 8; 12; 19; 25;… Есть ли какая либо связь между этими числами? Как бы мы не пытались найти связь или закономерность, обнаружить этого нам не удастся. Единственное, что мы сможем сделать – это пронумеровать по порядку все числа. Тогда каждое число будет иметь свой порядковый номер, например, под номером 4 находится только число 12, и ни какое другое и т.д.
Набор чисел мы сможем рассматривать просто как числовую последовательность.
Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Теперь рассмотрим пару других наборов чисел, точнее, пару последовательностей:
-1; 2; 3; 4; 5; 6; …
— 5; 10; 15; 20; 25; … В этих последовательностях, кроме того, что каждое число или каждый элемент стоит на определённом месте, можно заметить и некоторую закономерность. В первой последовательности каждый следующий элемент на единицу больше предыдущего. Во второй последовательности каждый следующий элемент на 5 больше предыдущего. В обеих последовательностях каждый следующий элемент, начиная со второго, отличается от предыдущего на одно и то же число.
Такие последовательности называются арифметическими прогрессиями.
Сформулируем более точно определение арифметической прогрессии.
Арифметическая прогрессия – это числовая последовательность, каждый элемент которой равен предыдущему, сложенному с одним и тем же числом. Это число называют разностью арифметической прогрессии и обозначают буквой d.
Число d может быть положительным, в рассмотренных выше арифметических прогрессиях d=1 и d=5. Число d может быть отрицательным, например, прогрессия 100; 90; 80; 70;… Здесь число d = — 10. Легко можно заметить, что если разность прогрессии, число d , больше нуля, то прогрессия возрастающая. Если разность прогрессии меньше нуля, то прогрессия убывающая .
Если мы знаем, как образуется прогрессия и хотим записать некоторую прогрессию, которая начинается, например, с числа 8 и имеет разность прогрессии d = 4, то мы легко запишем первые её члены – 8; 12; 16; 20;… А если нам необходимо узнать член прогрессии под номером, например, 50. Прибавлять по 4 очень долго. В этом случае используют формулу аn = a1 +(n-1)d.
Для нашей задачи а50 = a1+(50 – 1)*4= 8 +49*4=204. На 50 месте будет находиться число 204.
Формулу аn = a1 +(n-1)d (1) называют уравнением арифметической прогрессии. Эту формулу используют при решении самых разных задач на арифметическую прогрессию.
Вспомним ещё одну формулу арифметической прогрессии. Начнём с интересной задачи. Допустим, есть последовательность — 1; 2; 3; 4; 5; 6; 7;…..98; 99; 100. и необходимо найти сумму всех её чисел. Заданная последовательность – это арифметическая прогрессия и нам необходимо найти сумму ста её чисел. Если будем складывать числа по порядку, то это займёт очень много времени. Давайте сделаем по-другому. Первое и последнее число в сумме дают 101, второе и предпоследнее в сумме также дают 101, третье и пред предпоследнее опять в сумме дают 101. Значит, объединяя определённым образом числа в пары, в сумме всегда, для данной прогрессии, будем получать 101. А сколько получится пар? Не сложно заметить, что пар будет ровно 50. Тогда сумма заданной прогрессии будет 101*50=5050.
Есть несколько предположений, легенд, по вопросу — кто первый начал считать, таким образом, сумму нескольких членов арифметической прогрессии. Возможно, это был великий математик Карл Гаус или строители египетских пирамид ( зная количество блоков в первом и последнем ряду, а также количество рядов можно рассчитать общее количество блоков) или математики древней Греции.
Формула суммы нескольких членов арифметической прогрессии является второй основной формулой арифметической прогрессии. Sn = (2a1+d(n-1))*n/2 (2)
Данная формула легко выводится, если рассуждать, как мы рассуждали выше, при расчёте суммы прогрессии от 1 до 100. Sn =( a1 +an)*n/2. Подставляя значение a n из формулы (1), получаем формулу (2).
В указанном видео https://youtu.be/fwWbim7yg1w мы решаем задачи на последовательности чисел и на арифметическую прогрессию. В задачах на прогрессию рассмотрели, как правильно использовать две основные формулы, указанные в статье.
Редакция не несет ответственности за наполнение блогов, они есть персональным мнением автора
Арифметическая прогрессия: определение, формулы, свойства
Арифметическая прогрессия – это числовая последовательность, в которой, начиная со второго числа, каждое последующее равняется предыдущему плюс постоянное слагаемое.
Общий вид арифметической прогрессии
a1, a1 + d, a1 + 2d, … a1 + (n – 1) d, …
d – шаг или разность прогрессии; это и есть постоянное слагаемое.
Члены прогрессии:
- a1
- a2 = a1 + d
- a3 = a2 + d = a1 + 2d
- и т.д.
Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.
Свойства и формулы арифметической прогрессии
1. Нахождение общего n-ого члена (an)
- an = an-1 + d
- an = a1 + (n – 1) d
- an = am – (m – n) d
2. Разность прогрессии
d = an – an-1
Также для нахождения шага используется такая формула:
3. Характеристическое свойство
Последовательность чисел a1, a2, a3 … является арифметической прогрессией, если для любого ее члена выполняется следующее условие:
4. Сумма первых членов прогрессии
Чтобы найти сумму первых членов арифметической прогрессии, необходимо воспользоваться формулой:
- n – количество суммируемых членов.
Если an заменить на a1 + (n – 1) d, то получится:
5. Сумма членов прогрессии с n-ого по m-ный
- (m – n + 1) – количество суммируемых членов.
Если am заменить на an + (m – n) d, то получим:
6. Сходимость прогрессии
Арифметическая прогрессия сходится при d = 0, во всех остальных случаях она расходится.
При этом, если:
- d > 0, прогрессия называется возрастающей;
- d < 0 – убывающей;
- d = 0 – стационарной.
Формулы геометрической прогрессии, геометрические ряды, бесконечные геометрические ряды
В математике геометрическая прогрессия (последовательность) (также неточно известная как геометрическая последовательность ) представляет собой последовательность
чисел, так что частное любых двух последовательных членов последовательности является константой, называемой
обычное отношение последовательности.
Геометрическую прогрессию можно записать как:
ar 0 = a, ar 1 = ar, ar 2 , ar 3 ,…
где r ≠ 0, r — обычное отношение, а a — коэффициент масштабирования (также первый член).
Примеры
Геометрическая прогрессия с общим соотношением 2 и масштабным коэффициентом 1 равна
1, 2, 4, 8, 16, 32 …
Геометрическая последовательность с общим соотношением 3 и масштабным коэффициентом 4 равна
4, 12, 36, 108, 324 …
Геометрическая прогрессия с общим соотношением -1 и масштабным коэффициентом 5 равна
5, -5, 5, -5, 5, -5, …
Формулы
Формулу для n-го члена можно определить как:
a n = a n-1 ⋅r
a n = a 1 r n-1
Формула обыкновенного отношения:
Если общее соотношение:
- Отрицательный, результаты будут чередоваться между положительными и отрицательными .
Пример:
1, -2, 4, -8, 16, -32 … — обычное отношение равно -2, а первый член равен 1. - Больше чем 1, будет экспоненциальный рост к бесконечности (положительный) .
Пример :
1, 5, 25, 125, 625 … — обычное отношение равно 5. - Менее -1, будет экспоненциальный рост к бесконечности (положительный и отрицательный) .
Пример :
1, -5, 25, -125, 625, -3125, 15625, -78125, 3, -1953125… — знаменатель -5.
- Между 1 и -1, будет экспоненциальный спад к нулю .
Пример :
4, 2, 1, 0,5, 0,25, 0,125, 0,0625 … — обычное отношение $ \ frac {1} {2} $
4, -2, 1, -0,5, 0,25, -0,125, 0,0625 … — обычное отношение $ — \ frac {1} {2} $. - Ноль, результаты останутся на нуле .
Пример :
4, 0, 0, 0, 0 … — обычное отношение равно 0, а первый член равен 4.
Свойства геометрической прогрессии
a 2 k = a k-1 ⋅a k + 1
a 1 ⋅a n = a 2 ⋅a n-1 =… = a k ⋅a n-k + 1
Формула суммы первых n чисел геометрического ряда
| S n = | a 1 — a n r 1 — г | = А 1 . | 1 — р н 1 — г |
Бесконечный геометрический ряд, где | r |
<1
Если | r | <1, затем n -> 0,
когда n -> ∞.
Сумма S такого бесконечного геометрического ряда определяется формулой:
что справедливо только при | r | <1.
1 — первый член.
Калькулятор геометрической прогрессии
Задачи геометрической прогрессии
Задача 1.
Последовательность 2, 4, 6, 8 … геометрическая прогрессия?
Решение: Нет, это не так. (2, 4, 8 — геометрическая прогрессия)
Задача 2
Если 2, 4, 8 … образуют геометрическую прогрессию. Какой 10-й срок?
Решение: Мы можем использовать формулу a n = a 1 ⋅ r n-1
a 10 = 2 ⋅ 2 10-1 = 2 ⋅ 512 = 1024
Задача 3
Найдите коэффициент масштабирования и командное отношение геометрической прогрессии, если
a 5 — a 1 = 15
a 4 — a 2 = 6
Решение: есть две геометрические прогрессии.У первого есть
масштабный коэффициент 1 и общее отношение = 2
второе решение -16, 1/2
Дополнительные задачи:
Геометрическая прогрессия — задачи
Задачи с прогрессиями
Геометрические прогрессии в математическом форуме
Присоединяйтесь к нашему математическому форуму (регистрация не требуется!)
Форумы с прогрессиями
арифметических и геометрических последовательностей | Purplemath
Purplemath
Две самые простые последовательности для работы — это арифметическая и геометрическая последовательности.
Арифметическая последовательность переходит от одного члена к другому, всегда добавляя (или вычитая) одно и то же значение. Например, 2, 5, 8, 11, 14, … является арифметическим, потому что каждый шаг добавляет три; а 7, 3, –1, –5, … является арифметическим, потому что каждый шаг вычитает 4.
Число, добавляемое (или вычитаемое) на каждом этапе арифметической последовательности, называется «общей разницей» d , потому что, если вы вычтите (то есть, если вы найдете разницу) последовательных членов, вы всегда получите это общая ценность.
MathHelp.com
Геометрическая последовательность переходит от одного члена к другому путем умножения (или деления) на одно и то же значение.Итак, 1, 2, 4, 8, 16, … геометрически, потому что каждый шаг умножается на два; и 81, 27, 9, 3, 1, 1/3, … геометрический, потому что каждый шаг делится на 3.
Число, умноженное (или разделенное) на каждом этапе геометрической последовательности, называется «общим соотношением» r , потому что, если вы разделите (то есть, если вы найдете соотношение) последовательных членов, вы всегда получите это общая ценность.
Найдите общую разницу и следующий член следующей последовательности:
Чтобы найти общую разницу, я должен вычесть пару следующих друг за другом членов.Неважно, какую пару я выберу, если они находятся рядом друг с другом. Чтобы быть внимательным, сделаю все вычитания:
11–3 = 8
19–11 = 8
27–19 = 8
35–27 = 8
Разница всегда равна 8, поэтому общая разница составляет d = 8.
Мне дали пять членов, так что шестой член последовательности будет следующим термином.Я нахожу следующий член, добавляя общее различие к пятому члену:
Тогда мой ответ:
общая разница: d = 8
шестой семестр: 43
Найдите общее отношение и седьмой член следующей последовательности:
Чтобы найти общее отношение, я должен разделить следующие пары членов.Неважно, какую пару я выберу, если они находятся рядом друг с другом. Чтобы быть внимательным, сделаю все деления:
Соотношение всегда 3, поэтому r = 3.
Мне дали пять сроков, так что шестой срок — это следующий семестр; седьмой будет срок после этого. Чтобы найти значение седьмого члена, я дважды умножу пятый член на обычное отношение:
a 6 = (18) (3) = 54
a 7 = (54) (3) = 162
Тогда мой ответ:
стандартное отношение: r = 3
седьмой семестр: 162
Поскольку арифметические и геометрические последовательности настолько хороши и правильны, у них есть формулы.
Для арифметических последовательностей общая разница составляет d , а первый член a 1 часто обозначается просто как « a ». Поскольку мы получаем следующий член, добавляя общую разницу, значение a 2 будет просто:
Продолжая, третий член:
a 3 = ( a + d ) + d = a + 2 d
Четвертый член:
a 4 = ( a + 2 d ) + d = a + 3 d
На каждом этапе общая разница умножалась на значение, которое было на единицу меньше индекса.Следуя этому шаблону, n -й член a n будет иметь форму:
Для геометрических последовательностей обычное отношение составляет r , а первый член a 1 часто обозначается просто как « a ». Поскольку следующий член мы получаем умножением на обыкновенное отношение, значение a 2 будет просто:
Продолжая, третий член:
Четвертый член:
На каждом этапе обычное отношение увеличивалось до степени, которая была на единицу меньше индекса.Следуя этому шаблону, n -й член a n будет иметь форму:
Запомните эти формулы n -го члена перед следующим тестом.
Найдите десятый член и
n -й член следующей последовательности:
Первое, что мне нужно сделать, это выяснить, какой это тип последовательности: арифметический или геометрический.Я быстро вижу, что различия не совпадают; например, разница между вторым и первым членами составляет 2 — 1 = 1, но разница между третьим и вторым членами составляет 4 — 2 = 2. Так что это не арифметическая последовательность.
С другой стороны, отношения последовательных членов одинаковы:
2 ÷ 1 = 2
4 ÷ 2 = 2
8 ÷ 4 = 2
(Я не делал деление с первым членом, потому что в нем участвовали дроби, и я ленив.Однако деление дало бы точно такой же результат.)
Итак, очевидно, что это геометрическая последовательность с общим отношением r = 2, а первый член равен a = 1/2. Чтобы найти n -й член, я могу просто подставить в формулу a n = ar ( n — 1) :
a n = (1/2) 2 n -1 = (2 -1 ) (2 n -1 )
= 2 (–1) + ( n — 1) = 2 n — 2
Чтобы найти значение десятого члена, я могу подставить n = 10 в формулу n -го члена и упростить:
Тогда мой ответ:
n -й член:
a n = 2 n –2
десятый семестр: 256
Найдите
n -й член и первые три члена арифметической последовательности, имеющей a 6 = 5 и d = 3/2
n -й член арифметической последовательности имеет вид a n = a + ( n — 1) d .В данном случае эта формула дает мне
a 6 = a + (6 — 1) (3/2) = 5. Решая эту формулу для значения первого члена последовательности, я получаю а = –5/2. Потом:
a 1 =
–5/2
a 2 =
–5/2 + 3/2 = –1
a 3 =
–1 + 3/2 = 1/2
Это дает мне первые три члена последовательности.Поскольку у меня есть значение первого члена и общая разница, я также могу создать выражение для n -го члена и упростить:
–5/2 + ( n — 1) (3/2)
= –5/2 + (3/2) n — 3/2
= –8/2 + (3/2) n = (3/2) n — 4
Тогда мой ответ:
n -й семестр:
(3/2) n — 4
первые три семестра:
–5/2, –1, 1/2
Найдите
n -й член и первые три члена арифметической последовательности, имеющей , 4 = 93 и , 8 = 65.
Поскольку a 4 и a 8 разделены на четыре позиции, то из определения арифметической последовательности я знаю, что я бы получил от четвертого члена до восьмого, добавив общую разность четыре раза к четвертому члену. ; Другими словами, определение говорит мне, что a 8 = a 4 + 4 d . Используя это, я могу найти общую разницу d :
65 = 93 + 4 д
–28 = 4 d
–7 = d
Кроме того, я знаю, что четвертый член относится к первому члену по формуле a 4 = a + (4-1) d , поэтому, используя значение, которое я только что нашел для d , я могу найти значение первого члена a :
93 = a + 3 (–7)
93 + 21 = а
114 = а
Теперь, когда у меня есть значение первого члена и значение общей разницы, я могу быстро найти значения первых трех членов и общую форму n -го члена:
a 1 = 114
a 2 = 114-7 = 107
a 3 = 107 — 7 = 100
a n = 114 + ( n — 1) (- 7)
= 114-7 n + 7 = 121-7 n
Тогда мой ответ:
n -й семестр: 121 — 7 n
первые три семестра: 114, 107, 100
Найдите
n, -й и 26-й члены геометрической последовательности: a 5 = 5/4 и a 12 = 160.
Два члена, для которых мне дали числовые значения, разнесены на 12-5 = 7 мест, поэтому, исходя из определения геометрической последовательности, я знаю, что перейду от пятого члена к двенадцатому, умножив пятый член по обыкновению семь раз; то есть a 12 = ( a 5) ( r 7 ). Я могу использовать это, чтобы найти значение общего отношения r :
160 = (5/4) ( r 7 )
128 = r 7
2 = r
Кроме того, я знаю, что пятый член относится к первому по формуле a 5 = ar 4 , поэтому я могу найти значение первого члена a :
5/4 = a (2 4 ) = 16 a
5/64 = а
Теперь, когда у меня есть значение первого члена и значение общего отношения, я могу вставить каждое из них в формулу для n -го члена, чтобы получить:
a n = (5/64) 2 ( n — 1)
= (5/2 6 ) (2 n –1 )
= (5) (2 –6 ) (2 n –1 )
= 5 (2 n –7 )
С помощью этой формулы я могу вычислить двадцать шестой член и упростить:
Тогда мой ответ:
n -й семестр:
(5/64) (2 n –1 )
26 семестр: 2,621,440
Когда мы узнаем, как работать с последовательностями арифметических и геометрических терминов, мы можем перейти к рассмотрению добавления этих последовательностей.
URL: https://www.purplemath.com/modules/series3.htm
геометрических последовательностей и серий | Безграничная алгебра
Геометрические последовательности
Геометрическая последовательность — это упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на константу, называемую [латекс] r [/ латекс], обычное отношение.{n-1} [/ латекс].
Ключевые термины
- геометрическая последовательность : упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением. Также известна как геометрическая прогрессия.
Определение геометрических последовательностей
Геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обычным соотношением [латекс] r [/ латекс ].{n-1} [/ latex]
Такая геометрическая последовательность также следует рекурсивному соотношению:
[латекс] a_n = ra_ {n-1} [/ латекс]
для каждого целого числа [латекс] n \ ge 1. [/ Latex]
Поведение геометрических последовательностей
Обычно, чтобы проверить, является ли данная последовательность геометрической, просто проверяют, все ли последовательные записи в последовательности имеют одинаковое соотношение. Обычное отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Поведение геометрической последовательности зависит от значения общего отношения. Если общее отношение:
- Положительно, все условия будут того же знака, что и начальный термин
- Отрицательный, члены будут чередоваться между положительным и отрицательным
- Больше, чем [latex] 1 [/ latex], будет экспоненциальный рост в сторону положительной бесконечности ([latex] + \ infty [/ latex]).
- [latex] 1 [/ latex], последовательность будет постоянной
- Между [латексом] -1 [/ латексом] и [латексом] 1 [/ латексом], но не [латексом] 0 [/ латексом], будет экспоненциальный спад в сторону [латекса] 0 [/ латекса]
- [латекс] -1 [/ латекс], прогрессия — чередующаяся последовательность (см. Чередующиеся серии)
- Меньше, чем [latex] -1 [/ latex], для абсолютных значений наблюдается экспоненциальный рост в сторону положительной и отрицательной бесконечности (из-за чередования знака)
Геометрические последовательности (с общим соотношением, не равным [латекс] -1 [/ латекс], [латекс] 1 [/ латекс] или [латекс] 0 [/ латекс]) показывают экспоненциальный рост или экспоненциальное затухание, в отличие от линейный рост (или снижение) арифметической прогрессии, такой как [латекс] 4, 15, 26, 37, 48, \ cdots [/ латекс] (с общим отличием [латекс] 11 [/ латекс]).Этот результат был получен T.R. Мальтуса в качестве математической основы его принципа народонаселения. {2} = ac [/ latex]
Суммирование первых n членов геометрической последовательности
Используя обычное отношение и первый член геометрической последовательности, мы можем суммировать его члены.{n}} {1-r}} [/ латекс].
Ключевые термины
- геометрическая серия : Бесконечная последовательность добавляемых чисел, члены которой находятся путем умножения предыдущего члена на фиксированное ненулевое число, называемое обычным отношением.
- геометрическая прогрессия : серия чисел, в которой каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением.
Геометрические ряды представляют собой примеры бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством.Исторически геометрические ряды играли важную роль в раннем развитии исчисления, и они по-прежнему занимают центральное место в изучении сходимости рядов. {n}}}} [/ латекс]
является геометрическим, потому что каждый последующий член может быть получен умножением предыдущего члена на [latex] \ displaystyle {\ frac {1} {2}} [/ latex].{n}}} [/ латекс]
Эту концепцию можно визуализировать с помощью диаграммы:
Бесконечная геометрическая серия: Каждый из фиолетовых квадратов получается путем умножения площади следующего большего квадрата на [latex] \ displaystyle {\ frac {1} {4}} [/ latex]. Площадь первого квадрата составляет [латекс] \ displaystyle {\ frac {1} {2} \ cdot \ frac {1} {2} = \ frac {1} {4}} [/ latex], а площадь второй квадрат — [латекс] \ displaystyle {\ frac {1} {4} \ cdot \ frac {1} {4} = \ frac {1} {16}} [/ latex].
Ниже приведены несколько геометрических рядов с разными общими отношениями.Поведение терминов зависит от общего соотношения [латекс] г [/ латекс]:
- [латекс] 4 + 40 + 400 + 4000 + \ точки [/ латекс] имеет общее соотношение [латекс] 10 [/ латекс]
- [латекс] \ displaystyle {9 + 3 + 1 + \ frac {1} {3} + \ frac {1} {9} + \ dots} [/ latex] имеет общее соотношение [латекс] {\ frac {1 } {3}} [/ латекс]
- [латекс] 3 + 3 + 3 + 3 + \ точки [/ латекс] имеет общее соотношение [латекс] 1 [/ латекс]
- [латекс] \ displaystyle {1- \ frac {1} {2} + \ frac {1} {4} — \ frac {1} {8} + \ dots} [/ latex] имеет общее соотношение [латекс] — \ frac {1} {2} [/ latex]
- [латекс] 3-3 + 3-3 + \ точки [/ латекс] имеет общее соотношение [латекс] -1 [/ латекс]
Значение [latex] r [/ latex] предоставляет информацию о характере серии:
- Если [латекс] r [/ латекс] находится между [латекс] -1 [/ латекс] и [латекс] +1 [/ латекс], члены ряда становятся все меньше и меньше, приближаясь к нулю в пределе, и ряд сходится к сумме.Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которых равна единице.
- Если [latex] r [/ latex] больше, чем [latex] 1 [/ latex] или меньше, чем [latex] -1 [/ latex], члены ряда становятся все больше и больше по величине. Сумма членов также становится все больше и больше, и в серии нет суммы. Сериал расходится.
- Если [latex] r [/ latex] равно [latex] 1 [/ latex], все члены серии совпадают.Сериал расходится.
- Если [latex] r [/ latex] равно [latex] -1 [/ latex], термины принимают поочередно два значения [latex] \ left (\ text {eg}, 2, -2,2, -2,2 , -2, \ cdots \ right) [/ латекс]. Сумма членов колеблется между двумя значениями [latex] \ left (\ text {eg.}, 2,0,2,0,2,0, \ cdots \ right) [/ latex]. Это другой тип дивергенции, и снова у ряда нет суммы.
Мы можем использовать формулу, чтобы найти сумму конечного числа членов в последовательности. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
Бесконечная геометрическая серия
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Вычислить сумму бесконечного геометрического ряда и определить момент схождения геометрического ряда
Основные выводы
Ключевые моменты
- Сумма геометрического ряда конечна, пока члены приближаются к нулю; поскольку числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
- Для бесконечного геометрического ряда, который сходится, его сумму можно вычислить по формуле [latex] \ displaystyle {s = \ frac {a} {1-r}} [/ latex].
Ключевые термины
- сходиться : приблизиться к конечной сумме.
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно изменяются с общим соотношением.
Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрической прогрессии или чьи последовательные члены имеют общее отношение. Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной. Когда числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
Говорят, что геометрический ряд с конечной суммой сходится. Ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы:
.
[латекс] \ левый | г \ право | <1 [/ латекс]
Что следует на примере бесконечного ряда с конечной суммой. Подсчитаем сумму [latex] s [/ latex] следующей серии:
[латекс] \ displaystyle {s = 1+ \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ cdots} [/ latex]
Эта серия имеет общее соотношение [латекс] \ displaystyle {\ frac {2} {3}} [/ latex].Если мы умножим на это обычное соотношение, то начальный член [латекс] 1 [/ latex] станет [latex] \ displaystyle {\ frac {2} {3}} [/ latex], [latex] \ displaystyle {\ frac {2} {3}} [/ latex] становится [latex] \ displaystyle {\ frac {4} {9}} [/ latex] и так далее:
[латекс] \ displaystyle {\ frac {2} {3} s = \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ frac {16} { 81} + \ cdots} [/ latex]
Эта новая серия такая же, как и исходная, за исключением того, что отсутствует первый член. Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
[латекс] \ displaystyle {\ begin {align} s- \ frac {2} {3} s & = 1 \\ \ поэтому s & = 3 \ end {align}} [/ latex]
Подобный метод можно использовать для вычисления любого самоподобного выражения.n \ rightarrow 0 \\ & = \ frac {a} {1-r} \ end {align}} [/ latex]
Следовательно, для [latex] | r | <1 [/ latex] мы можем записать бесконечную сумму как:
[латекс] \ displaystyle {s = \ frac {a} {1-r}} [/ latex]
Пример
Найдите сумму бесконечного геометрического ряда [латекс] 64+ 32 + 16 + 8 + \ cdots [/ latex]
Сначала найдите [latex] r [/ latex], или постоянное соотношение между каждым членом и тем, что ему предшествует:
[латекс] \ displaystyle {\ begin {align} r & = \ frac {32} {64} \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Подставьте [латекс] a = 64 [/ latex] и [latex] \ displaystyle r = \ frac {1} {2} [/ latex] в формулу суммы бесконечного геометрического ряда:
[латекс] \ displaystyle {\ begin {align} s & = \ frac {64} {1- \ frac {1} {2}} \\ & = \ frac {64} {\ frac {1} {2} } \\ & = 128 \ end {align}} [/ latex]
Применения геометрической серии
Геометрические ряды применяются в математике и естественных науках и являются одним из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Применение геометрических последовательностей и рядов к различным физическим и математическим темам
Основные выводы
Ключевые моменты
- Повторяющаяся десятичная дробь может рассматриваться как геометрическая последовательность, общее отношение которой равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].
- Архимед использовал сумму геометрического ряда, чтобы вычислить площадь, ограниченную параболой и прямой линией.
- Внутренняя часть снежинки Коха представляет собой союз бесконечного множества треугольников.При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры.
- Знание бесконечных рядов позволяет нам решать древние проблемы, такие как парадоксы Зенона.
Ключевые термины
- геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно изменяются с общим соотношением.
- фрактал : природное явление или математический набор, который демонстрирует повторяющийся узор, который можно увидеть в любом масштабе.
Геометрические ряды сыграли важную роль в раннем развитии исчисления и продолжают оставаться центральной частью изучения сходимости рядов. Геометрические ряды используются во всей математике. У них есть важные приложения в физике, инженерии, биологии, экономике, информатике, теории массового обслуживания и финансах.
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами, хотя не все они обладают этим свойством.
Повторяющаяся десятичная дробь
Повторяющееся десятичное число можно рассматривать как геометрический ряд, общее отношение которого равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].Например:
[латекс] \ displaystyle {0,7777 \ cdots = \ frac {7} {10} + \ frac {7} {100} + \ frac {7} {1000} + \ frac {7} {10000} + \ cdots} [/ латекс]
Формула суммы геометрического ряда может использоваться для преобразования десятичной дроби в дробь:
[латекс] \ displaystyle {\ begin {align} 0,7777 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {7} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {7} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {7} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {7} {9} \ end {align}} [/ latex]
Формула работает для любого повторяющегося термина.Еще несколько примеров:
[латекс] \ displaystyle {\ begin {align} 0.123412341234 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1234} {10000}} {1- \ frac {1 } {10000}} \\ & = \ frac {\ left (\ frac {1234} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left ( \ frac {1234} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1234} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,0
- 0909 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {100}} {1- \ frac {1 } {100}} \\ & = \ frac {\ left (\ frac {9} {100} \ right)} {\ left (\ frac {99} {100} \ right)} \\ & = \ left ( \ frac {9} {100} \ right) \ left (\ frac {100} {99} \ right) \\ & = \ frac {9} {99} \\ & = \ frac {1} {11} \ конец {align}} [/ latex]
- Найдите отношение второго члена к первому.
- Найдите отношение третьего члена ко второму.
- Продолжайте этот процесс, чтобы обеспечить постоянство отношения одного члена к предыдущему. Если да, то серия геометрическая.
- Если общее соотношение, [латекс] r [/ латекс], было найдено на шаге 3, проверьте, [латекс] -1
- Отношение второго члена к первому составляет [латекс] \ frac {\ text {2}} {\ text {3}} [/ latex],
, что не то же самое, что отношение третьего члена к второй, [латекс] \ frac {1} {2} [/ latex]. Серия не геометрическая. - Отношение второго члена к первому такое же, как отношение третьего члена ко второму. Ряд геометрический с общим соотношением [латекс] \ frac {2} {3} \ text {.} [/ Latex] Сумма бесконечного ряда определена.
- Данная формула является экспоненциальной с основанием [латекс] \ frac {1} {3} [/ latex]; серия является геометрической с общим соотношением [латекс] \ frac {1} {3} \ text {.} [/ latex] Сумма бесконечного ряда определена.
- Данная формула не является экспоненциальной; ряд не является геометрическим, потому что члены возрастают и поэтому не может дать конечной суммы.
S n = 244, r = –3, n = 5
S n = 15.75, r = 0,5, a n = 0,25
S n = 244, r = –3, n = 5
Используйте формулу 3:
S n = 15,75, r = 0,5, a n = 0,25
Используйте формулу 4:
25 + 20 + 16 + 12,8 +…
3 — 9 + 27 — 81 +…
25 + 20 + 16 + 12,8 +…
Сначала найдите r .
[латекс] \ displaystyle {\ begin {align} 0.143814381438 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1438} {10000}} {1- \ frac {1} {10000}} \\ & = \ frac { \ left (\ frac {1438} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left (\ frac {1438} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1438} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,9999 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {9} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {9} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {9} {9} \\ & = 1 \ end {align}} [/ латекс]
То есть повторяющаяся десятичная дробь с повторяющейся частью длины [латекс] n [/ latex] равна частному повторяющейся части (как целое число) и [латекс] 10 ^ n — 1 [/ latex].
Квадратура Параболы Архимеда
Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.
Теорема Архимеда: Разбиение Архимеда параболического сегмента на бесконечное количество треугольников.
Теорема Архимеда утверждает, что общая площадь под параболой равна [latex] \ displaystyle {\ frac {4} {3}} [/ latex] площади синего треугольника.{3} + \ cdots} [/ latex]
Первый член представляет площадь синего треугольника, второй член — площади двух зеленых треугольников, третий член — площади четырех желтых треугольников и так далее. Упрощение дробей дает:
[латекс] \ displaystyle {1+ \ frac {1} {4} + \ frac {1} {16} + \ frac {1} {64} + \ cdots} [/ latex]
Это геометрическая серия с общим соотношением [латекс] \ displaystyle {\ frac {1} {4}} [/ latex], а дробная часть равна [latex] \ displaystyle {\ frac {1} {3} }[/латекс].
Фрактальная геометрия
Снежинка Коха: Внутренняя часть снежинки Коха состоит из бесконечного количества треугольников.
Снежинка Коха — это фрактальная форма, внутренность которой состоит из бесконечного количества треугольников. При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры. В случае снежинки Коха ее площадь можно описать геометрическим рядом.
Построение снежинки Коха: первые четыре итерации: каждая итерация добавляет набор треугольников снаружи формы.
Область внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников. На диаграмме выше треугольники, добавленные во второй итерации, имеют размер [latex] \ displaystyle {\ frac {1} {3}} [/ latex], равный размеру стороны наибольшего треугольника, поэтому они имеют ровно [latex ] \ displaystyle {\ frac {1} {9}} [/ latex] область. Точно так же каждый треугольник, добавленный во второй итерации, имеет [latex] \ displaystyle {\ frac {1} {9}} [/ latex] площадь треугольников, добавленных в предыдущей итерации, и так далее.{3} + \ cdots} [/ latex]
Первый член этого ряда представляет площадь первого треугольника, второй член — общую площадь трех треугольников, добавленных во второй итерации, третий член — общую площадь двенадцати треугольников, добавленных в третьей итерации, и т. Д. . Исключая начальный термин [латекс] 1 [/ латекс], этот ряд является геометрическим с постоянным соотношением [латекс] \ displaystyle {r = \ frac {4} {9}} [/ latex]. Первый член геометрического ряда — [латекс] \ displaystyle {a = 3 \ frac {1} {9} = \ frac {1} {3}} [/ latex], поэтому сумма составляет:
[латекс] \ displaystyle {\ begin {align} 1+ \ frac {a} {1-r} & = 1 + \ frac {\ frac {1} {3}} {1- \ frac {4} {9 }} \\ & = \ frac {8} {5} \ end {align}} [/ latex]
Таким образом, снежинка Коха имеет [latex] \ displaystyle {\ frac {8} {5}} [/ latex] площади основного треугольника.
Парадоксы Зенона
Парадоксы Зенона — это набор философских проблем, изобретенных древнегреческим философом для поддержки учения о том, что истина противоречит нашим чувствам. Проще говоря, один из парадоксов Зенона гласит: есть точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний.
Использование формулы для геометрического ряда
Так же, как сумма членов арифметической последовательности называется арифметическим рядом, сумма членов геометрической последовательности называется геометрическим рядом .{k} [/ латекс]
Решение
Пример 5: Решение прикладной задачи с помощью геометрической серии
На новой работе стартовая зарплата сотрудника составляет 26 750 долларов. Он получает повышение на 1,6% годовых. Найдите его общий заработок по истечении 5 лет.
Решение
Задачу можно представить в виде геометрического ряда с [латексом] {a} _ {1} = 26,750 [/ latex]; [латекс] n = 5 [/ латекс]; и [латекс] r = 1,016 [/ латекс]. Подставьте значения для [latex] {a} _ {1} [/ latex], [latex] r [/ latex] и [latex] n [/ latex] в формулу и упростите, чтобы найти общую сумму заработка в конце. от 5 лет.{5} \ right)} {1 — 1.016} \ приблизительно 138 \ text {,} 099.03 \ hfill \ end {array} [/ latex]
К концу 5 лет он заработает в общей сложности 138 099,03 долларов.
Попробуй 8
На новой работе стартовая зарплата сотрудника составляет 32 100 долларов. Ежегодно она получает 2% -ное повышение. Сколько она заработает к концу 8 лет?
Решение
Использование формулы суммы бесконечного геометрического ряда
До сих пор мы рассматривали только конечные серии. Иногда, однако, нас интересует сумма членов бесконечной последовательности, а не сумма только первых [latex] n [/ latex] членов.{\ infty} 2k [/ latex], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно увеличивается по мере того, как мы добавляем новые члены. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд расходится на .
Определение, определена ли сумма бесконечного геометрического ряда
Если члены бесконечного геометрического ряда приближаются к нулю, можно определить сумму бесконечного геометрического ряда.{n} [/ latex] становятся очень маленькими и приближаются к нулю. Каждый последующий член влияет на сумму меньше, чем предыдущий член. По мере того, как каждый последующий член приближается к 0, сумма членов приближается к конечному значению. Члены любого бесконечного геометрического ряда с [latex] -1 Сумма бесконечного ряда определяется, если ряд геометрический и [латекс] -1 Определите, определена ли сумма бесконечного ряда. [латекс] \ frac {1} {3} + \ frac {1} {2} + \ frac {3} {4} + \ frac {9} {8} +.{k} [/ латекс] Решение Теперь, когда мы нашли сумму конечного числа членов, давайте рассмотрим случай бесконечного числа членов. Мы, конечно, не можем вручную суммировать бесконечные числа, поэтому нам придется найти общий подход. Начнем с обсуждения проблемы, с которой вы столкнулись в верхней части этой страницы: 12 + 24 + 38 + 416 + 532 + ⋯ =? \ Large \ dfrac {\ color {# 3D99F6} {1}} {\ color {# D61F06} {2}} + \ dfrac {\ color {# 3D99F6} { 2}} {\ color {# D61F06} {4}} + \ dfrac {\ color {# 3D99F6} {3}} {\ color {# D61F06} {8}} + \ dfrac {\ color {# 3D99F6} { 4}} {\ color {# D61F06} {16}} + \ dfrac {\ color {# 3D99F6} {5}} {\ color {# D61F06} {32}} + \ cdots = \,? 21 +42 +83 +164 +325 + ⋯ =? Допустим, данная серия является SSS, тогда S = 12 + 24 + 38 + 416 + 532 + ⋯.S = \ dfrac 12 + \ dfrac 24 + \ dfrac 38+ \ dfrac {4} {16} + \ dfrac {5} {32} + \ cdots.S = 21 +42 +83 +164 +325 + ⋯. Умножая SSS на 12 \ frac 1221, получаем S2 = 14 + 28 + 316 + 432 + 564 + ⋯. \ dfrac S2 = \ dfrac 14 + \ dfrac 28 + \ dfrac {3} {16} + \ dfrac {4} {32} + \ dfrac {5} {64} + \ cdots.2S = 41 +82 +163 +324 +645 + ⋯. Теперь вычитая S2 \ frac S22S из SSS, получаем S = 12 + 24 + 38 + 416 + 532 + ⋯ S2 = 0 + 14 + 28 + 316 + 432 + 564 + ⋯ S (1−12) = 12 + 14 + 18 + 116 + 132 + ⋯ ⇒S2 = 12 + 14 + 18 + 116 + 132 + ⋯, \ begin {array} {rlllllllll} , который является GP.2} = 2 1−21 21 + (1−21) 21 × 21 = 2. Решение 2: Данную серию можно записать как 14 + 38 + 516 + 732 + ⋯. \ Dfrac 14+ \ dfrac 38 + \ dfrac {5} {16} + \ dfrac {7} {32} + \ cdots .41 +83 +165 +327 + ⋯. Умножив и разделив ряд на 444, получим 14 (1 + 32 + 54 + 78 + ⋯).2} \ right) = \ dfrac 14 \ left (2 + 4 \ right) = 1,5. \ _ \ квадрат S = 41 ⎝⎜⎜⎜⎛ 1−21 1 + (1−21) 22⋅21 ⎠⎟⎟⎟⎞ = 41 (2 + 4) = 1,5. □ Решение проблем ниже позволит проверить, хорошо ли вы разбираетесь в концепциях и способах решения проблем: Найдите значение ppp для данного 3 + 14 (3 + p) +142 (3 + 2p) +143 (3 + 3p) + ⋯ = 8. n} n = 1∑∞ 3n2n может быть выражено в форме ab \ frac { a} {b} ba, где aaa и bbb взаимно простые положительные целые числа.Найдите a − b a — b a − b. Последовательности. Рассмотрим ряд натуральных чисел: 1, 2, 3,, n 1, n ,. u 1 , u 2 , u 3 ,, u n — 1 , u n « называется числовой последовательностью . Число u n называется общим термином числовой последовательности. 2, 4, 6, 8, 10,, 2 n ,; 1, 4, 9, 16, 25« n ²,; 1, 1/2, 1/3, 1/4, 1/5« 1/ n ,. Арифметическая прогрессия. Числовая последовательность, в которой каждый следующий член, начинающийся со второго, равен предыдущему члену, добавленному с константой для этого порядкового номера d , называется арифметической прогрессией .Число d называется общей разницей . Любой член арифметической прогрессии рассчитывается по формуле: a n = a 1 + d (n 1 ) . Сумма n первых членов арифметической прогрессии рассчитывается как: E x a m p l e. Найдите сумму первых 100 нечетных чисел. 1 = 1, d = 2 . Итак, имеем: Геометрическая прогрессия. Числовая последовательность, в которой каждый следующий член, начинающийся со второго, равен предыдущему члену, умноженному на константу для этого порядкового номера q , называется геометрической прогрессией . Число q называется обыкновенным отношением . Любой член геометрической прогрессии рассчитывается по формуле: b n = b 1 q n — 1 . Сумма n первых членов геометрической прогрессии вычисляется как: Бесконечно убывающая геометрическая прогрессия. Это геометрическая прогрессия с E x a m p l e. Найдите сумму в бесконечно убывающей геометрической прогрессии: S o l u t i o n. Воспользуйтесь последней формулой. Здесь b 1 = 1, q = 1/2. Итак, имеем: Преобразование повторяющейся десятичной дроби в простую дробь. Предположим, что мы хотим преобразовать повторяющийся десятичный 0.(3) до вульгарной фракции. Рассмотрим эту десятичную дробь в более естественной форме: Это бесконечно убывающая геометрическая прогрессия с первым членом 3/10 и общим отношением q = 1/10. Согласно приведенной выше формуле последняя сумма равна: Назад Геометрическая серия представляет собой сумму членов геометрической последовательности. Если в последовательности есть определенное количество членов, простая формула для суммы равна . Формула 3: Эта форма формулы используется, когда известно количество членов ( n ), первый член ( a 1 ) и обычное отношение ( r ). Другая формула суммы геометрической последовательности — Формула 4: Эта форма требует первого члена ( a 1 ), последнего члена ( a n ) и общего отношения ( r ), но не требует количества членов ( n ) . Найдите сумму первых пяти членов геометрической последовательности, в которой a 1 = 3 и r = –2. a 1 = 3, r = –2, n = 5 Используйте формулу 4: Найдите сумму геометрической последовательности, для которой. Используйте формулу 4: Найдите a 1 в каждом описанном геометрическом ряду. Формула 5: Если геометрический ряд бесконечен (то есть бесконечен) и –1 < r <1, то формула для его суммы принимает вид Если r > 1 или r <–1, то бесконечный ряд не имеет суммы. Найдите сумму каждого из следующих геометрических рядов. Общее примечание: определение того, определена ли сумма бесконечного геометрического ряда
Как сделать: учитывая первые несколько членов бесконечного ряда, определите, существует ли сумма ряда.
Решение
Попробуй 9
Арифметико-геометрическая прогрессия | Блестящая вики по математике и науке
S & = \ dfrac 12 & + \ dfrac 24 & + \ dfrac 38 & + \ dfrac {4} {16} & + \ dfrac {5} {32} + \ cdots \\
\ dfrac S2 & = 0 & + \ dfrac 14 & + \ dfrac 28 & + \ dfrac {3} {16} & + \ dfrac {4} {32} + \ dfrac {5} {64} + \ cdots \\
\ hline
S \ left (1- \ dfrac 12 \ right) & = \ dfrac 12 & + \ dfrac 14 & + \ dfrac 18 & + \ dfrac {1} {16} & + \ dfrac {1} {32} + \ cdots \ \
\ Rightarrow \ dfrac S2 & = \ dfrac 12 & + \ dfrac 14 & + \ dfrac 18 & + \ dfrac {1} {16} & + \ dfrac {1} {32} + \ cdots,
\ end {array} S2S S (1-21) ⇒2S = 21 = 0 = 21 = 21 +42 +41 +41 +41 +83 +82 + 81 +81 +164 +163 +161 +161 +325 + ⋯ + 324 +645 + ⋯ + 321 + ⋯ + 321 + ⋯,
Второе суммирование — это геометрическая прогрессия с суммой до бесконечности 141−12 = 12 \ frac {\ frac {1} {4}} {1 — \ frac {1} {2}} = \ frac {1} { 2} 1−21 41 = 21.
Следовательно, общая сумма равна 2−12 = 1,5 □ 2 — \ frac {1} {2} = 1,5 \ _ \ square 2−21 = 1,5 □. Вся элементарная математика — Учебное пособие — Алгебра
Последовательности. Числовые последовательности. Общий член числовой последовательности.
Арифметическая прогрессия. Геометрическая прогрессия. Бесконечно убывающая
геометрическая прогрессия. Преобразование повторяющейся десятичной дроби в обычную дробь.
Если заменить каждое натуральное число n в этой серии некоторым числом u n , подчиненным какому-либо закону, то получится новая серия чисел:
Примеры числовых последовательностей:
С о л ю т и н. Воспользуйтесь последней формулой. Здесь a
| q | <1. Для него понятие суммы бесконечно убывающей геометрической прогрессии определяется как число, к которому неограниченно приближается сумма первых n членов рассматриваемой прогрессии при неограниченном увеличении числа n .Бесконечно убывающая сумма геометрической прогрессии рассчитывается по формуле: Геометрическая серия
Пример 1
Пример 2
Пример 3
Пример 4
Так как этот бесконечный геометрический ряд имеет сумму.
