Содержание
Урок 16. окружность. задачи на построение — Геометрия — 7 класс
Геометрия
7 класс
Урок № 16
Окружность. Задачи на построение
Перечень рассматриваемых вопросов:
- Геометрическое место точек, примеры ГМТ.
- Изображение на рисунке окружности и ее элементов.
- Решение задач на построение.
- Выполнение построений прямого угла, отрезка, угла равного данному, биссектрисы угла, перпендикулярных прямых, середины отрезка с помощью циркуля и линейки.
Тезаурус:
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Хорда – отрезок, соединяющий две точки окружности.
Диаметр – хорда, проходящая через центр окружности.
Основная литература:
- Атанасян Л.
 С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М.А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали некоторые геометрические фигуры, например, угол, отрезок, треугольник, научились их строить и измерять. Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.
Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.
Для начала дадим определение геометрической фигуры, называемой окружностью.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Но можно использовать и другое определение окружности.
Окружность ‑ это геометрическое место точек, удалённых на одно и то же расстояние от точки, называемой центром окружности. Это расстояние называют радиусом окружности. В нашем случае точки О.
При этом стоит пояснить, что геометрическое место точек – это фигура речи, употребляемая в математике для определения геометрической фигуры, как множества всех точек, обладающих некоторым свойством.
Вспомним элементы окружности.
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
По определению окружности все её радиусы имеют одну и ту же длину.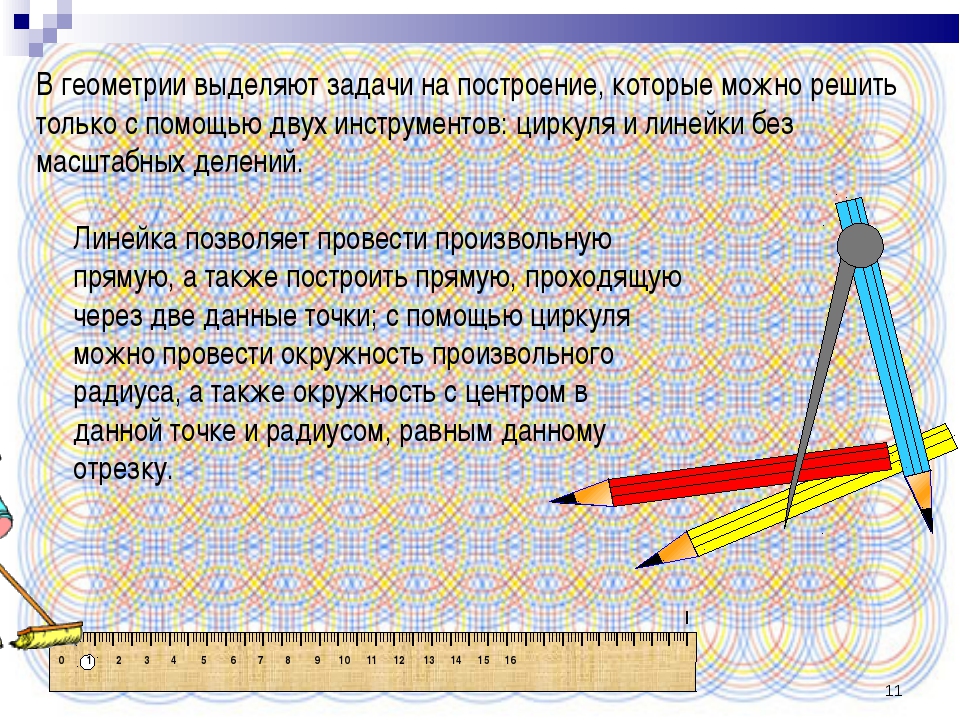 OM = OA
OM = OA
Отрезок, соединяющий две точки окружности, называется хордой.
AC, BD – хорды
Хорда, проходящая через центр окружности, называется диаметром.
AB – диаметр,
OB – радиус,
AB = 2OB,
O – середина диаметра.
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности.
AMB, ALB – дуги окружности.
Построим окружность радиусом 3 см. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки расстояние между ножками циркуля, равное 3 см. Поставим иголочку циркуля в точку О и построим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую кривую линию, которую называют окружностью.
Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, т. е. окружность ‑ граница круга.
Итак, мы можем с помощью циркуля строить окружность, но с его помощью можно построить и угол равный данному. Для построения воспользуемся ещё и линейкой.
Для построения воспользуемся ещё и линейкой.
Дано: A, OM – луч.
Построить: EOМ = A.
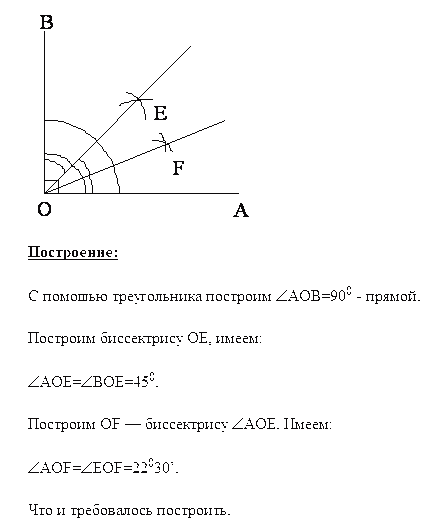
Построение.
1. Окр. (A; r), r – произвольный радиус.
2. Окр. (A; r) ∩ AB = B.
3. Окр. (A; r) ∩ AС = С.
4. Окр. (O; r) ∩ OM = D.
5. Окр. (D; BС) ∩ Окр. (O; r) = E
6. OЕ, ЕОD = BAC (из равенства ∆ОЕD и ∆ABC). EOM – искомый.
Теперь выполним построение биссектрисы угла.
Дано: CAB.
Построить: AE – биссектриса CAB.
Построение.
- Окр. (A; r), r – произвольный радиус.
- Окр. (A; r) ∩ AB = B.
- Окр. (A; r) ∩ AC = C.
- Окр. (C; CB) ∩ Окр. (B; CB) = E.
- AE – искомая биссектриса BAC, т. к. ABE =CBE (из равенства ∆ACE и ∆ABE).
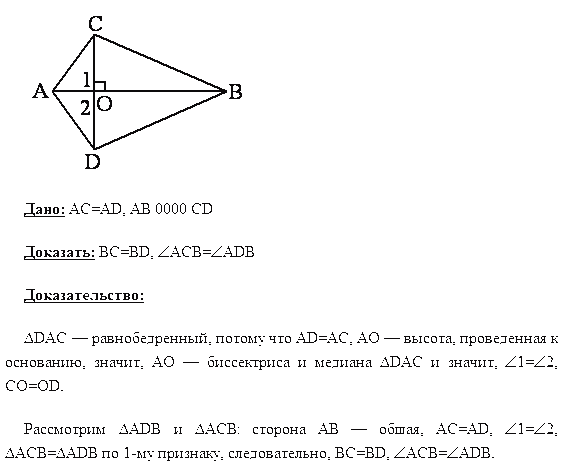
Рассмотрим ещё одно построение с помощью циркуля и линейки. Построим середину отрезка АВ.
Для этого построим две окружности с центрами на концах отрезка , т. е. в точках А и В.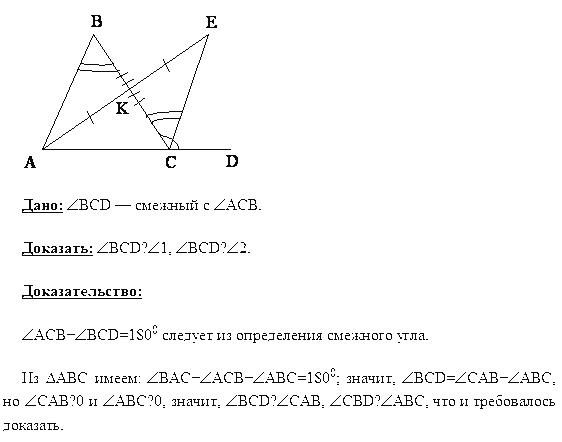 Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.
Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.
Разбор заданий тренировочного модуля.
№ 1. АВ и СК – диаметры окружности, с центром в точке О. По какому признаку равенства треугольников равны треугольники АОС и ОКВ?
Решение:
Так как О – центр окружности, то точка О делит диаметры пополам, следовательно отрезки АО, ОВ, ОС, ОК равны. ∠СОА = ∠КОВ (как вертикальные). Поэтому треугольники АОС и ОКВ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними).
Ответ: 1 признак равенства треугольников.
№ 2. На рисунке O – центр окружности, АВ – диаметр окружности.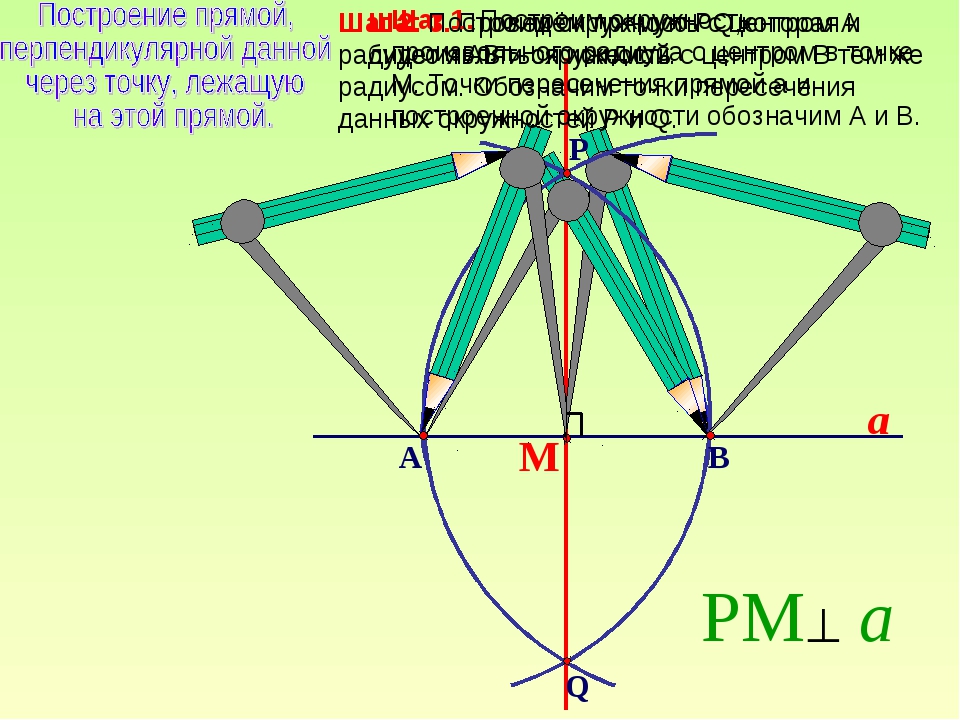 Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?
Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?
Решение:
Периметр треугольника AOD равен сумме сторон АО, AD, DO. Найдём эти стороны.
По условию O – центр окружности, то она делит диаметр пополам, следовательно отрезок АО равен отрезку ОВ, т. е. АО = АВ:2 = 8 см :2 = 4 см.
По условию отрезки АD и ВС, перпендикулярны к отрезку АВ, следовательно ∠СВО = ∠ОАD = 90°, ∠АОD = ∠СОВ (как вертикальные). Поэтому ∆АОD = ∆СОВ (по 2 признаку равенства треугольников). Следовательно, AD = СВ = 3 см, DO = ОС = 5 см.
Р∆AOD = АО + AD + DO = 4 см + 3 см + 5 см = 12 см.
Ответ: Р∆AOD = 12 см.
|
1. |
Отрезки и окружность
|
4 |
|
2. 
|
Радиус, диаметр и хорда окружности
|
1 |
|
3. |
Хорда, радиус и диаметр окружности
|
1 |
|
4. 
|
Диаметр окружности
|
1 |
|
5. |
Радиус окружности
|
1 |
|
6. 
|
Окружность или круг
|
1 |
|
7. |
Расположение окружностей
|
1 |
|
8. 
|
Общая часть окружностей или кругов
|
1 |
|
9. |
Радиусы и точки пересечения окружностей
|
1 |
|
10. 
|
Построение по основным конструкциям
|
1 |
|
11. |
Равные треугольники в окружности
|
3 |
|
12. 
|
Построение треугольника, равного данному
|
2 |
|
13. |
Общие точки окружностей
|
2 |
|
14. 
|
Диаметры окружности или круга
|
2 |
|
15. |
Построение треугольника по данным сторонам и медиане
|
8 |
Задачи на построение в геометрии.
 (7 класс)
(7 класс)
1. Уроки геометрии в 7-м классе
Уроки геометрии в 7м классе
Тема уроков:
«Задачи на построение»
Учитель математики
ГБОУ СОШ № 1194 г. Москва
Гаврилова Ирина Николаевна
2. План изучения темы: 1. Вступительная лекция: — Исторические сведения; — Инструменты для построения; 2. План решения задач на построение; 3. Выпо
План изучения темы:
1. Вступительная лекция:
Исторические сведения;
Инструменты для построения;
2. План решения задач на построение;
3. Выполнение простейших задачи на построение;
4. Решение задач на построение;
5. Задачи для самостоятельного решения.
2
Исторические сведения:
3
И в Вавилоне, и в Древнем Египте в IV–II
тысячелетиях до н.э. уже существовала
практическая математика (в виде правил
записи чисел, т.е. системы счисления, и
правил
различных
вычислений),
и
практическая геометрия – геометрия в
изначальном смысле слова: измерение
земли. Но и при измерениях, и при
Но и при измерениях, и при
строительных
построения.
работах
нужны
были
Инструменты для построения:
С помощью линейки выделить прямую из
множества всех прямых:
1.произвольную прямую;
2.произвольную прямую, проходящую через
заданную точку;
3.прямую, проходящую через две заданных точки;
С помощью циркуля выделить окружность
из множества всех окружностей:
1.произвольную окружность;
2.произвольную окружность с центром в
заданной точке;
3.произвольную окружность с радиусом, равным
расстоянию между двумя заданными точками;
4.окружность с центром в заданной точке и с
радиусом, равным расстоянию между двумя
заданными точками.
4
2. План решения задач на построение
Анализ:
Предположить, что задача решена, сделать примерный чертеж искомой
фигуры, отметить те отрезки и углы, которые известны из условия
задачи, и стараться определить, к нахождению какой точки (прямой, угла)
сводится решение задачи.
Построение:
Описать способ построения.
Доказательство:
Доказать, что множество точек , построенное описанным способом,
действительно
находится
в
заданном
соотношении
с
исходным
множеством точек.
Исследование:
Выяснить, всегда ли (при любых ли данных) описанное построение
возможно, нет ли частных случаев, в которых построение упрощается или
делается невозможным.
5
3. Выполнение простейших задачи на построение
Построение 1: построить треугольник по трем сторонам, т.е. построить
треугольник, стороны которого равны трем данным отрезкам а, b и с.
С помощью линейки проведем произвольную прямую и отметим на ней
произвольную точку B.
Раствором циркуля, равным a, описываем окружность с центром в точке B и
радиусом a. Пусть C – точка ее пересечения с прямой.
Описываем окружность с центром в точке B радиуса c и с центром в точке C
радиуса b. Пусть A – точка пересечения построенных окружностей. Треугольник ABC
Пусть A – точка пересечения построенных окружностей. Треугольник ABC
построен.
6
Построение 2: построить угол, равный данному, от данной полупрямой в
данную полуплоскость.
Анализ. (рис 2а) Пусть a – данный луч с вершиной A, а угол (ab) искомый. Выберем
точки B и C на лучах a и b соответственно. Соединив точки B и C, получим
треугольник ABC. В равных треугольниках соответственные углы равны, и отсюда
вытекает способ построения. Если на сторонах данного угла какимто удобным
образом выбрать точки C и B, от данного луча в данную полуплоскость построить
треугольник AB1C1, равный ABC (а это можно сделать, если знать все стороны
треугольника, см. предыдущую задачу), то задача будет решена.
7
Построение:
Проведем окружность с центром в вершине данного угла. Пусть B и C – точки
пересечения окружности со сторонами угла (рис. 2b).
Радиусом AB проведем окружность с центром в точке A1 – начальной точке
данного луча.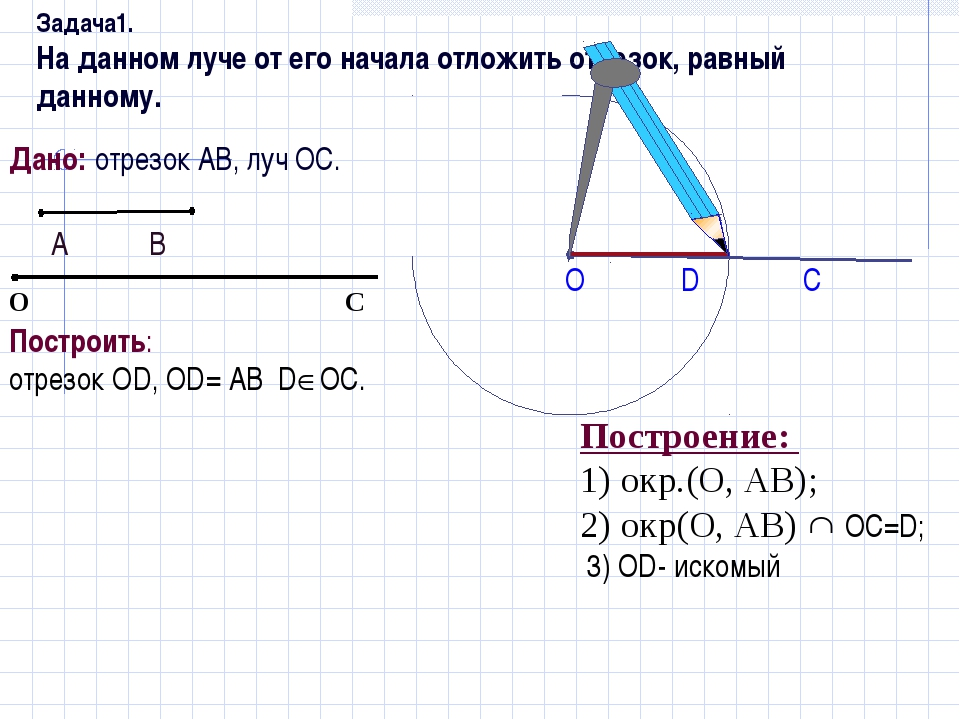 Точку пересечения этой окружности с данным лучом обозначим
Точку пересечения этой окружности с данным лучом обозначим
B1.
Опишем окружность с центром в B1 и радиусом BC. Точка пересечения C1
построенных окружностей в указанной полуплоскости лежит на стороне
искомого угла.
Доказательство:
Треугольники ABC и A1B1C1 (рис.2а) равны по трем сторонам. Углы A и A1 –
соответствующие углы этих треугольников. Следовательно, САВ = С1А1В1.
8
Построение 3: построить биссектрису данного угла.
Анализ (рис. 3b). Пусть луч AD – биссектриса данного угла A. Для построения
биссектрисы нам необходимо построить точку D на ней, отличную от A. Выберем
на разных сторонах угла точки C и B. Соединим их с точкой D. Если отрезки
AB и AC равны, т.е. AB = AC, то Δ ABD = Δ ACD и, следовательно, BAD = CAD
и луч AD – биссектриса.
9
Построение:
Из вершины A данного угла, как из центра,
опишем окружность произвольного радиуса.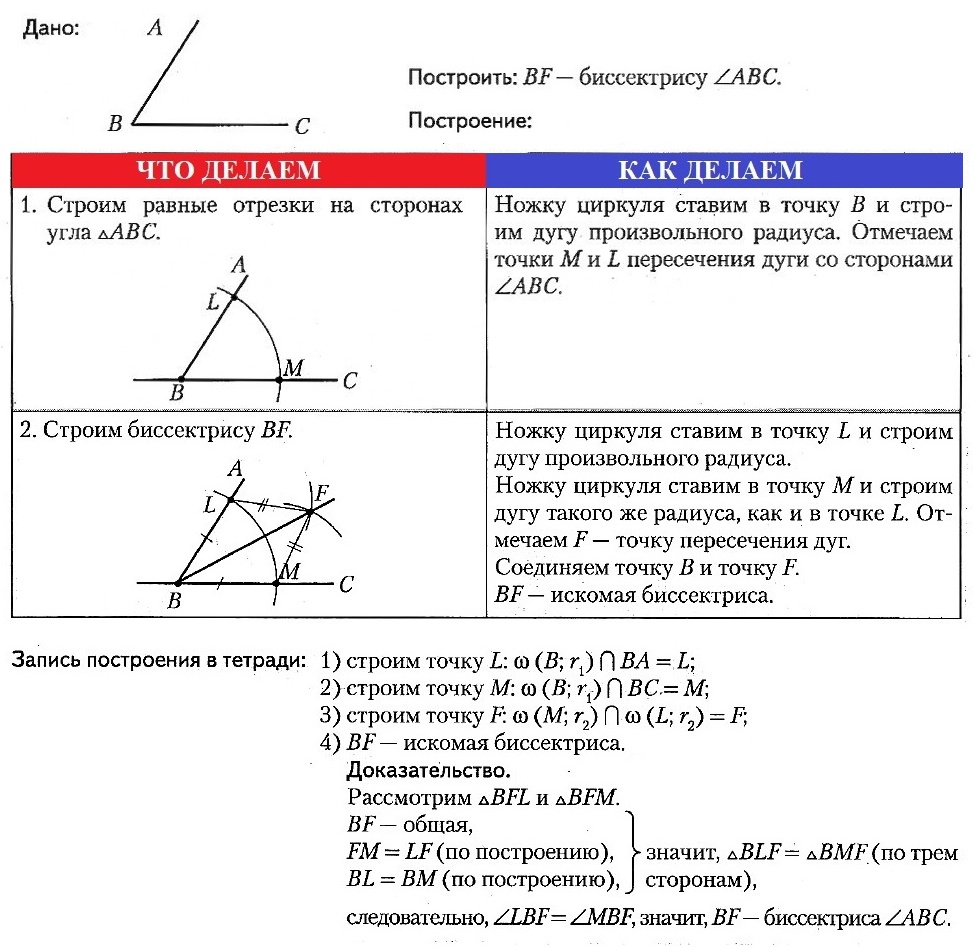
Пусть B и C – точки пересечения ее со
сторонами угла ( рис. 3).
Построим еще две окружности с тем же
радиусом с центрами в B и C. Пусть D – точка
их пересечения. Тогда луч AD – искомая
биссектриса угла A.
Доказательство: (рис.3а)
Соединим точку D с точками B и C.
Полученный четырехугольник ABDC –
ромб. AD – его диагональ. По свойству
диагоналей ромба луч AD – биссектриса
данного угла A.
10
Построение 4: деление отрезка пополам (одновременное построение
серединного перпендикуляра данного отрезка).
Анализ. Пусть AB – данный отрезок, точка O – его середина, прямая a – серединный
перпендикуляр к отрезку AB. Выберем произвольную точку C на прямой a, отличную
от точки O. В Δ ACB CO – одновременно медиана и высота. Следовательно, Δ ACB
равнобедренный, и AC = BC. Отсюда возникает следующий способ построения точки
O – середины отрезка AB.
Построение:
Из точек A и B циркулем описываем окружность радиусом AB.
Пусть C и C1 – точки пересечения этих окружностей. Они лежат
в разных полу плоскостях относительно прямой AB. (рис. 4а)
Доказательство:
Соединим точки C и C1 с концами отрезка AB. По построению
AC1 = AC = C1B = CB. Поэтому равнобедренные треугольники
CAC1 и CBC1 равны по трем сторонам. Отсюда следует
равенство углов ACO и BCO. В равнобедренном треугольнике
ABC CO – биссектриса, проведенная к основанию,
следовательно, она медиана и высота. Отсюда AO = OB, и точка
O – середина отрезка AB.
11
Построение 5: через точку O провести прямую, перпендикулярную данной
прямой a.
Возможны два случая:
точка O лежит на прямой a;
точка O не лежит на прямой a.
Случай 1.
Анализ. Пусть a – данная прямая, O – данная точка на ней, b – искомая прямая,
перпендикулярная прямой a и проведенная через точку O. Из предыдущей задачи нам
Из предыдущей задачи нам
известен способ построения серединного перпендикуляра к отрезку AB. Тогда, если
точка O – середина некоторого отрезка, то b – серединный перпендикуляр к этому
отрезку и проходит через точку O.
Построение: (рис. 5)
Отложим от точки O по разные стороны от
нее на прямой a одинаковые отрезки OA, OB.
Проведем
две
окружности
одинакового
радиуса AB с центром в точках A и B
соответственно. Они пересекаются в точке C.
Проведем прямую OC. Она перпендикулярна
прямой a.
12
Доказательство: (рис.5а)
Треугольник
ABC
–
равнобедренный
по
построению: AC = BC = AB. CO – медиана по
построению: AO = OB. Следовательно, СО ┴АВ.
Случай 2.
Анализ. (рис. 5b) Пусть O – данная точка,
лежащая вне данной прямой a, b – прямая,
проходящая
через
точку
O
и
перпендикулярная прямой a.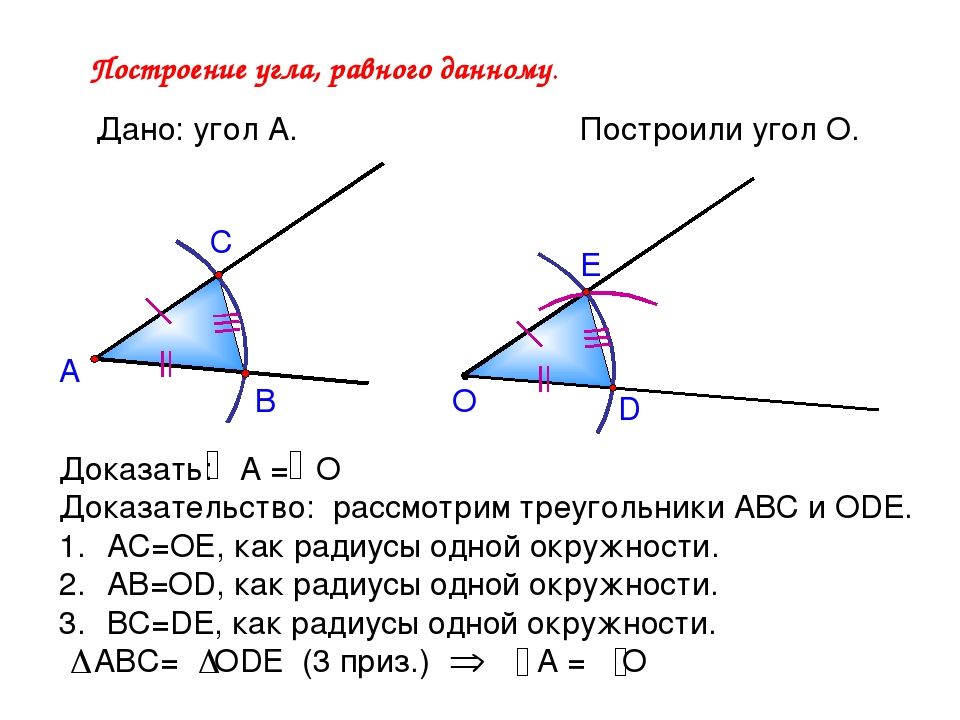 Чтобы
Чтобы
построить прямую, нам необходимо указать
(построить) еще какуюлибо ее точку. Для
этого проанализируем: какими свойствами
обладают
точки
прямой
b ┴ a?
В
частности, любые две равные наклонные к
прямой a, проведенные из точки O, имеют
одинаковые
проекции.
Поэтому,
если
OA = OB – такие наклонные, то должно
быть AC = CB, где C – точка пересечения
прямых a и b.
13
14
Построение: (рис. 5с)
Проведем окружность с центром в точке O,
пересекающую прямую a в двух точках A и B.
Проведем две окружности с центрами в точках A и B
и радиусом, равным OA. Пусть O1 – точка
пересечения, отличная от точки O, (O и O1 лежат в
разных
полуплоскостях).
Тогда
прямая
(OO1)
перпендикулярна данной прямой a.
•Через точку O проведем прямую, перпендикулярную
данной.
Доказательство:
По построению AO = OB = BO1 = AO1.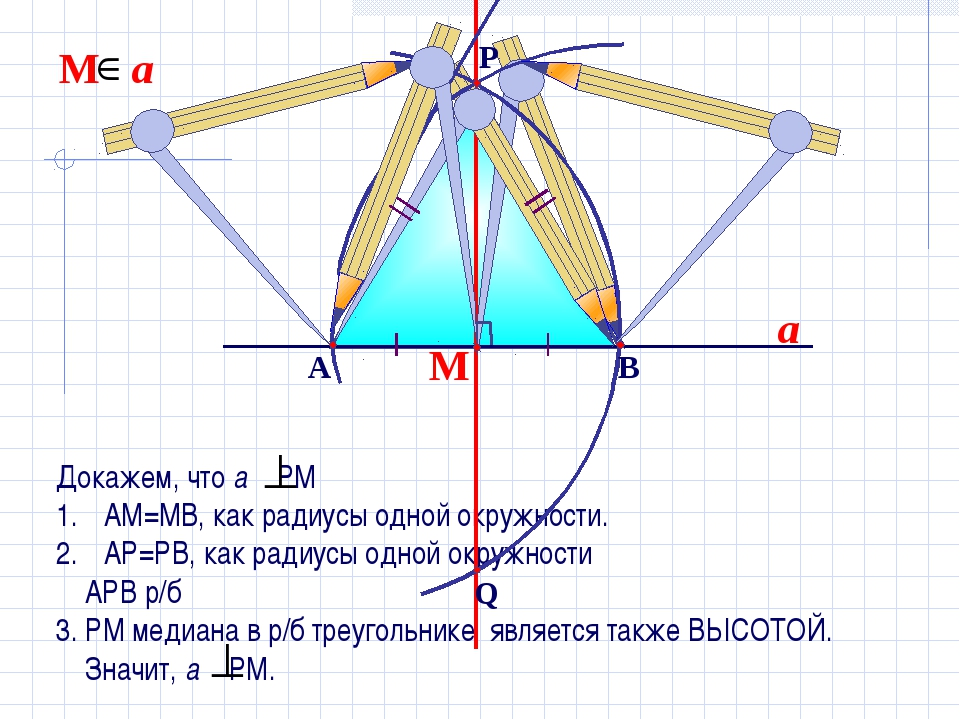 Четырехугольник AOBO1 – ромб. OO1и AB –
Четырехугольник AOBO1 – ромб. OO1и AB –
его диагонали. По свойству диагоналей ромба ОО1 ┴ АВ.
Построение 6: построение прямой , проходящей через данную точку А
параллельно данной прямой а.
Анализ. Если точка А лежит на прямой a, то задача
не имеет решения, поэтому, пусть A лежит вне прямой
a, и b || a – искомая прямая. Через точку A проведем
секущую AB, B a. По свойству параллельных прямых
внутренние накрест лежащие углы при параллельных
прямых и секущей равны. Верно и обратное: если
внутренние накрест лежащие углы при прямых a и b и
секущей AB равны, то a || b. Отсюда способ
построения.
Построение. (рис. 6)
Через заданную точку A и произвольную точку B прямой a проведем прямую AB.
Пусть C – произвольная, отличная от B точка прямой a. Построим от луча AB в
полуплоскость, не содержащую точку C, угол, равный углу ABC. Пусть AD – сторона
построенного угла. Тогда прямая AD || a.
Тогда прямая AD || a.
Через точку A проведем прямую, параллельную данной.
Доказательство: (рис. 6) Доказательство следует из признака параллельности
прямых (теорема: Если внутренние накрест лежащие углы равны, то прямые
параллельны.), ввиду равенства углов ABC и BAD как внутренних накрест лежащих при
прямых a, AD и секущей AB.
15
4. Решение задач на построение
Задача 1. Построить равнобедренный треугольник по углу при основании и
высоте, опущенной на основание.
16
Задача 2. Построить треугольник по данному периметру и двум углам.
По данному отрезку Р и двум углам требуется построить треугольник,
периметр которого равен Р, и два его угла равны двум данным углам.
17
Задача 3. Дан отрезок m и острый угол . Построить прямоугольный
треугольник с углом , в котором разность катетов равна m.
18
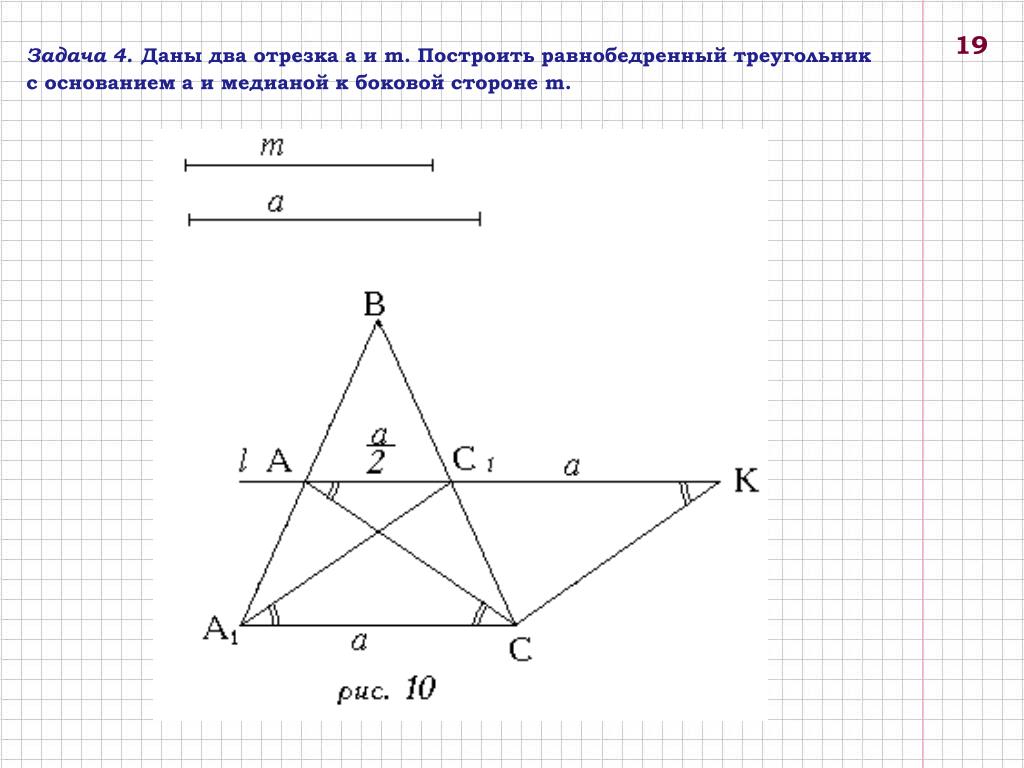
Задача 4. Даны два отрезка а и m. Построить равнобедренный треугольник
с основанием а и медианой к боковой стороне m.
19
5. Задачи для самостоятельного решения
Задача 1. Через данную точку провести
прямую под данным углом к данной
прямой.
Указание к решению задачи (рис. 13):
Построить угол, равный данному в
произвольной точке данной прямой, одна
из сторон которого лежит на этой
прямой; затем через данную точку
провести параллельную прямую.
20
21
Задача 2. описать окружность, которая
проходила бы через данную точку А и
касалась бы данной прямой в данной
на ней точке В.
Указание к решению задачи (рис. 14):
К
данной
перпендикуляр
прямой
из
восстановить
данной
точки
В,
построить серединный перпендикуляр к
отрезку АВ (А – другая данная точка). Их
пересечение – точка О – центр искомой
окружности, ОВ – радиус.
22
Задача
3.
Провести
в
треугольнике
прямую, параллельную основанию так,
чтобы
отрезок,
заключенный
между
боковыми сторонами был равен сумме
отрезков
боковых
сторон,
считая
от
основания.
Указание к решению задачи (рис. 15): Через
точку
прямую
пересечения
MN,
биссектрис
параллельную
провести
основанию.
Получим равнобедренные треугольники ONC и
ОМА (теорема о накрест лежащих углах при
параллельных прямых, свойства сторон и
углов в равнобедренном треугольнике).
23
Задача 4. На прямой АВ найти такую
точку С, чтобы лучи СМ и СN,
проведенные из С через данные точки
М и N, расположенные по одну сторону
от АВ, составляли с лучами СА и СВ
равные углы.
Указание к решению задачи (рис. 16):
Точка С – пересечение прямых M’N и АВ,
где
M’
–
точка,
относительно АВ.
симметричная
М
24
Список литературы:
1.Л.С. Атанасян, В.Ф. Бутузов и др., Геометрия 79, учебник для
общеобразовательных учреждений, «Просвещение», М., 2009;
2.Р.С. Сазоненко, Теоремы и задачи по планиметрии с перекрестными
ссылками 79 классы, Издательство института математики СО РАН,
Новосибирск, 1998;
3. Т.С. Пиголкина, Математика, задание № 2 для 8х классов ЗФТШ МФТИ,
Т.С. Пиголкина, Математика, задание № 2 для 8х классов ЗФТШ МФТИ,
Долгопрудный, 2005;
4.http://www.college.ru/mathematics/courses/planimetry/content/chapter8/
section/paragraph5/theory.html;
5.http://www.math.ru/lib/i/20/index.djvu?djvuopts&page=5.
Задачи на построение
Определение:
Окружность
— это геометрическая фигура, состоящая из всех точек плоскости, расположенных
на заданном расстоянии от данной точки.
Точка О — центром
окружности, а отрезок ОМ, соединяющий центр с точкой М, лежащей на
окружности, называется радиусом окружности. Радиус окружности обычно
обозначают буквой r.
Из определения окружности следует, что все радиусы имеют равную длину.
Возьмём
некоторую окружность с центром в точке О. Отметим на этой окружности две
произвольные точки А и В и соединим их.
Полученный
отрезок АВ называется хордой окружности.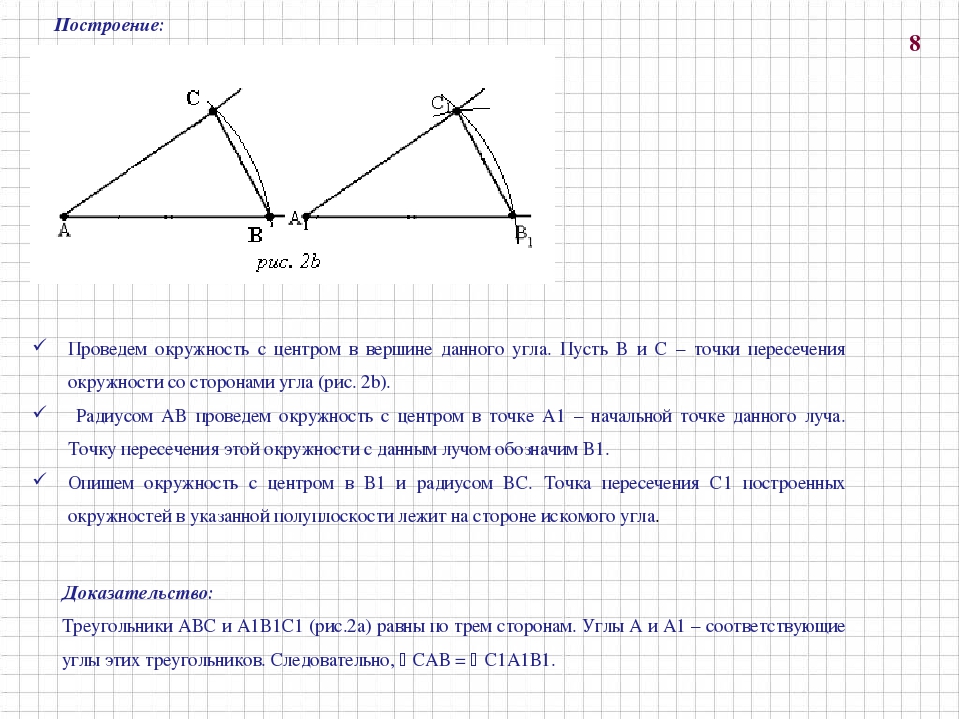 А вот хорда СD,
А вот хорда СD,
проходящая через центр окружности, называется диаметром. Диаметр
окружности в два раза больше её радиуса, то есть СD=ОD. Также отметим, что центр
окружности является серединой любого диаметра. Любые две точки окружности делят
её на две части, каждая из которых называется дугой окружности. CDB
и CAB
-
дуги окружности, ограниченные точками С и В.
Для
изображения окружности на чертеже используют циркуль. А вот на местности
окружность можно провести с помощью верёвки.
Часть
плоскости, ограниченная окружностью, называется кругом.
Ранее
вы уже проводили прямые и откладывали отрезки, чертили углы, треугольники и
другие геометрические фигуры.
При
этом вы использовали такие инструменты как масштабная линейка, транспортир,
циркуль, чертёжный угольник.
В
геометрии выделяют задачи на построение, которые можно решить, используя только
циркуль и линейку без масштабных делений.
С
помощью линейки можно:
·
провести
произвольную прямую;
·
построить
прямую, проходящую через две данные точки.
С
помощью циркуля можно:
·
провести
окружность произвольного радиуса;
·
провести
окружность с центром в данной точке и радиусом, равным данному отрезку.
Пример.
На
данном луче от его начала отложить отрезок, равный данному.
Изобразим
луч ОС и отрезок АВ.
Построим
окружность радиуса АВ с центром в точке О.
Полученная
окружность пересекает луч ОС в некоторой точке D. Отрезок OD и
является искомым.
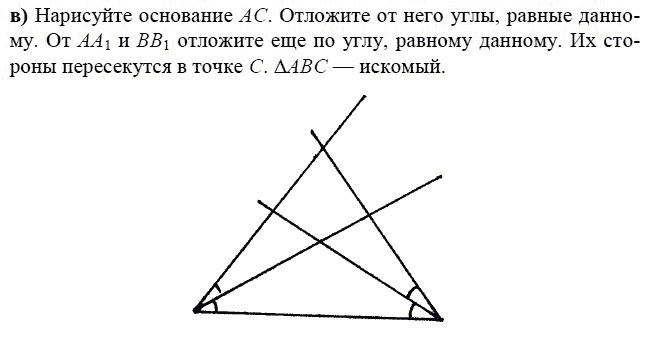
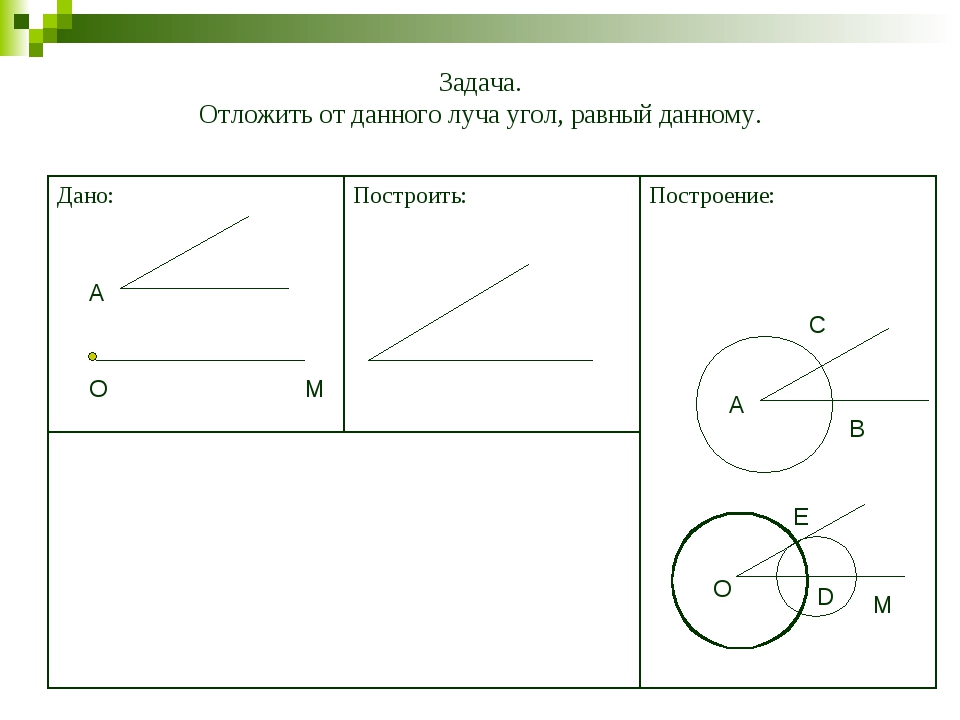
Пример.
Отложить
от данного луча угол, равный данному.
Возьмём
некоторый угол с вершиной в точке А и некоторый луч
ОМ.
Нам
нужно построить угол, равный углу А, так, чтобы одна
из его сторон совпала с лучом ОМ. Проведём окружность произвольного радиуса с
центром в точке А.
Окружность
пересекает стороны угла в точках В и С.
Проведём окружность такого же радиуса с
центром в точке О. Она пересекает луч в точке D.
Затем
построим окружность с центром в точке D,
радиус которой равен ВС.
Окружности
с центрами О и D пересекаются в двух точках.
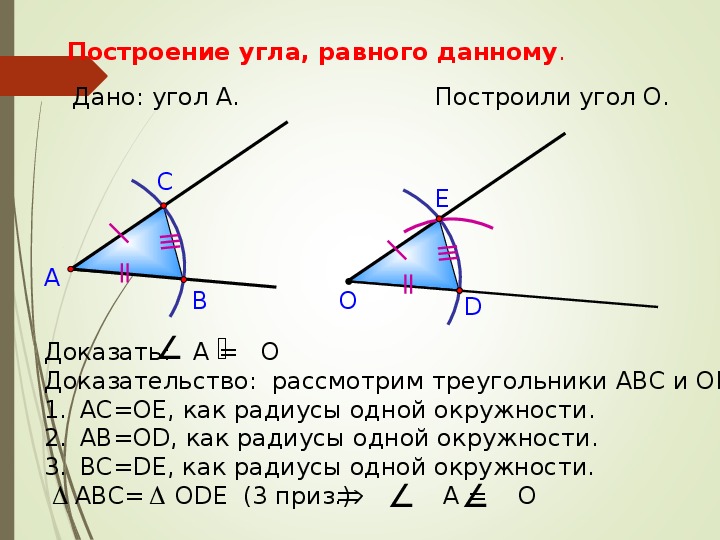
Докажем,
что ∠МОЕ
— искомый угол. Рассмотрим ∆ АВС и ∆ ODE.
Отрезки
АВ и АС — радиусы окружности с центром в точке А. OD и OE -
радиусы окружности с центром в точке О. По построению данные окружности имеют
равные радиусы, поэтому АВ=OD
и АС=ОЕ. А также по построению ВС=DE.
Следовательно,
треугольники АВС и ODE
равны по третьему признаку равенства треугольников. Поэтому ∠ВАС=∠DОЕ,
то есть построенный ∠MOE равен углу с вершиной в точке А.
Пример.
Даны
прямая а и точка М, лежащая на данной прямой. Построить
прямую, проходящую через данную точку и перпендикулярную этой прямой.
На
лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. Построим
окружность с центром в точке А радиуса АВ и окружность
с центром в точке В радиуса АВ.
Полученные
окружности пересекаются в точках P
и Q.
Проведя прямую МР, докажем, что эта прямая искомая.
Для этого рассмотрим треугольник АРВ, который является равнобедренным, так как
РА и РВ — равные радиусы окружностей с центром в точках А
и В соответственно.
РМ
является медианой треугольника, проведённой к основанию. А значит, является и
высотой, то есть прямая РМ перпендикулярна прямой а.
Следует
отметить, что не существует единого алгоритма решения задач на построение.
Каждая задача требует индивидуального подхода для решения.
| Класс | Название урока | Ссылка на учебные материалы |
| 7 | Прямая и отрезок | https://resh.edu.ru/subject/lesson/7284/main/250334/ |
| 7 | Луч и угол | https://resh.edu.ru/subject/lesson/7283/main/250509/ |
| 7 | Сравнение отрезков и углов | https://resh.edu.ru/subject/lesson/7282/main/250086/ |
| 7 | Измерение отрезков | https://resh.edu.ru/subject/lesson/7281/main/250474/ |
| 7 | Измерение углов | https://resh.edu.ru/subject/lesson/7286/main/249984/ |
| 7 | Смежные и вертикальные углы. Аксиомы и теоремы | https://resh.edu.ru/subject/lesson/7287/main/249702/ |
| 7 | Перпендикулярные прямые | https://resh.edu.ru/subject/lesson/7288/main/250076/ |
| 7 | Обобщение и систематизация знаний по теме «Простейшие геометрические фигуры и их свойства» | https://resh.edu.ru/subject/lesson/7285/main/249914/ |
| 7 | Треугольник | https://resh.edu.ru/subject/lesson/7292/main/272170/ |
| 7 | Медианы треугольника. Биссектрисы треугольника. Высоты треугольника | https://resh.edu.ru/subject/lesson/7290/start/250190/ |
| 7 | Перпендикуляр к прямой | https://resh.edu.ru/subject/lesson/7291/main/249774/ |
| 7 | Равнобедренный треугольник | https://resh.edu.ru/subject/lesson/7295/main/250019/ |
| 7 | Первый признак равенства треугольников | https://resh.edu.ru/subject/lesson/7294/main/249879/ |
| 7 | Второй и третий признаки равенства треугольников | https://resh.edu.ru/subject/lesson/7296/main/250229/ |
| 7 | Решение задач на признаки равенства треугольников | https://resh.edu.ru/subject/lesson/7297/main/249528/ |
| 7 | Обобщение и систематизация знаний по теме «Равные треугольники» | https://resh.edu.ru/subject/lesson/7293/main/249844/ |
| 7 | Параллельные прямые | https://resh.edu.ru/subject/lesson/7299/main/269607/ |
| 7 | Аксиома параллельных прямых | https://resh.edu.ru/subject/lesson/7300/main/249563/ |
| 7 | Признаки параллельности прямых | https://resh.edu.ru/subject/lesson/7298/main/249809/ |
| 7 | Свойства параллельных прямых | https://resh.edu.ru/subject/lesson/7301/main/249515/ |
| 7 | Обобщение и систематизация знаний по теме «Параллельные прямые» | https://resh.edu.ru/subject/lesson/7302/main/250439/ |
| 7 | Сумма углов треугольника | https://resh.edu.ru/subject/lesson/7308/main/249598/ |
| 7 | Соотношение между сторонами и углами треугольника. Неравенство треугольника | https://resh.edu.ru/subject/lesson/7307/main/271523/ |
| 7 | Прямоугольные треугольники | https://resh.edu.ru/subject/lesson/7309/main/249739/ |
| 7 | Расстояние от точки до прямой. Расстояние между параллельными прямыми | https://resh.edu.ru/subject/lesson/7306/main/250264/ |
| 7 | Построение треугольника по трём элементам | https://resh.edu.ru/subject/lesson/7305/main/250159/ |
| 7 | Окружность. Задачи на построение | https://resh.edu.ru/subject/lesson/7289/main/250391/ |
| 7 | Расстояние между фигурами | https://resh.edu.ru/subject/lesson/1289/ |
| 7 | Построение треугольника по трём элементам. Решение задач на построение | https://resh.edu.ru/subject/lesson/1356/ |
| 7 | Обобщение и систематизация знаний по теме «Соотношение между сторонами и углами треугольника» | https://resh.edu.ru/subject/lesson/7304/main/250562/ |
| 7 | Об истории геометрии. Решение задач | https://resh.edu.ru/subject/lesson/7303/main/250295/ |
| 7 | Повторение. Начальные геометрические сведения | https://resh.edu.ru/subject/lesson/7313/main/249388/ |
| 7 | Повторение. Треугольник. Равенство треугольников | https://resh.edu.ru/subject/lesson/7314/main/249422/ |
| 7 | Повторение. Равнобедренный треугольник и его свойства | https://resh.edu.ru/subject/lesson/7312/main/249458/ |
| 7 | Повторение. Параллельные и перпендикулярные прямые | https://resh.edu.ru/subject/lesson/7311/main/250404/ |
| 7 | Занимательные задачи. Итоговое обобщение и систематизация знаний | https://resh.edu.ru/subject/lesson/7310/main/249668/ |
| 7 | Углы с соответственно параллельными или перпендикулярными сторонами | https://znaika.ru/catalog/7-klass/geometry/Ugly-s-sootvetstvenno-parallelnymi-ili-perpendikulyarnymi-storonami.html |
| 7 | Геометрия как наука | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4485746 |
| 8 | Многоугольники. Четырёхугольник | https://resh.edu.ru/subject/lesson/1497/main/ |
| 8 | Параллелограмм. Свойства параллелограмма | https://resh.edu.ru/subject/lesson/1499/main/ |
| 8 | Признаки параллелограмма | https://resh.edu.ru/subject/lesson/1496/main/ |
| 8 | Трапеция | https://resh.edu.ru/subject/lesson/2009/main/ |
| 8 | Теорема Фалеса | https://resh.edu.ru/subject/lesson/2502/main/ |
| 8 | Прямоугольник. Ромб. Квадрат | https://resh.edu.ru/subject/lesson/1495/main/ |
| 8 | Осевая и центральная симметрия | https://resh.edu.ru/subject/lesson/2010/main/ |
| 8 | Симметрия. Виды симметрии | https://mosobr.tv/release/7879 |
| 8 | Площадь. Площадь прямоугольника | https://resh.edu.ru/subject/lesson/1484/main/ |
| 8 | Площадь параллелограмма | https://resh.edu.ru/subject/lesson/1493/main/ |
| 8 | Площадь треугольника | https://resh.edu.ru/subject/lesson/1492/main/ |
| 8 | Площадь трапеции | https://resh.edu.ru/subject/lesson/1491/main/ |
| 8 | Теорема Пифагора | https://resh.edu.ru/subject/lesson/1490/main/ |
| 8 | Формула Герона | https://resh.edu.ru/subject/lesson/2012/main/ |
| 8 | Определение подобных треугольников. Отношение площадей подобных треугольников | https://resh.edu.ru/subject/lesson/2014/main/ |
| 8 | Признаки подобия треугольников | https://resh.edu.ru/subject/lesson/2503/main/ |
| 8 | Средняя линия треугольника | https://resh.edu.ru/subject/lesson/2015/main/ |
| 8 | Свойство медиан треугольника | https://onliskill.ru/video/1537-geometrija-8-klass-svoistvo-median-treugolnika.html |
| 8 | Практическое приложение подобия треугольников | https://resh.edu.ru/subject/lesson/3140/main/ |
| 8 | Пропорциональные отрезки в прямоугольном треугольнике | https://resh.edu.ru/subject/lesson/3035/main/ |
| 8 | Синус, косинус и тангенс острого угла прямоугольного треугольника | https://resh.edu.ru/subject/lesson/2019/main/ |
| 8 | Значение синуса, косинуса и тангенса некоторых углов | https://resh.edu.ru/subject/lesson/2016/main/ |
| 8 | Решение задач по теме «Соотношение между сторонами и углами прямоугольного треугольника» | https://resh.edu.ru/subject/lesson/2017/main/ |
| 8 | Ломаная | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/5794942 |
| 8 | Взаимное расположение прямой и окружности | https://resh.edu.ru/subject/lesson/3036/main/ |
| 8 | Теорема о вписанном угле | https://resh.edu.ru/subject/lesson/2505/main/ |
| 8 | Градусная мера дуги окружности. Центральные углы | https://resh.edu.ru/subject/lesson/2027/main/ |
| 8 | Вписанная окружность | https://resh.edu.ru/subject/lesson/2023/main/ |
| 8 | Описанная окружность | https://resh.edu.ru/subject/lesson/2021/main/ |
| 8 | Свойства хорд окружностей | https://resh.edu.ru/subject/lesson/2504/main/ |
| 8 | Свойство биссектрисы угла | https://resh.edu.ru/subject/lesson/2026/main/ |
| 8 | Свойство серединного перпендикуляра | https://resh.edu.ru/subject/lesson/2025/main/ |
| 8 | Теорема о пересечении высот треугольника | https://resh.edu.ru/subject/lesson/2024/main/ |
| 8 | Фракталы вокруг нас | https://mosobr.tv/release/7963 |
| 9 | Понятие вектора. Равенство векторов. Откладывание вектора от данной точки | https://resh.edu.ru/subject/lesson/2506/main/ |
| 9 | Сумма двух векторов. Правило треугольника. Законы сложения векторов. Правило параллелограмма. Сумма нескольких векторов | https://resh.edu.ru/subject/lesson/2030/main/ |
| 9 | Вычитание векторов | https://resh.edu.ru/subject/lesson/2733/main/ |
| 9 | Умножение вектора на число | https://resh.edu.ru/subject/lesson/3037/main/ |
| 9 | Средняя линия трапеции | https://resh.edu.ru/subject/lesson/2029/main/ |
| 9 | Разложение вектора по двум неколлинеарным векторам | https://resh.edu.ru/subject/lesson/3038/main/ |
| 9 | Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах | https://resh.edu.ru/subject/lesson/2508/main/ |
| 9 | Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой | https://resh.edu.ru/subject/lesson/2028/main/ |
| 9 | Взаимное расположение двух окружностей. Использование уравнений окружности и прямой при решении задач | https://resh.edu.ru/subject/lesson/2033/main/ |
| 9 | Синус, косинус, тангенс, котангенс угла | https://resh.edu.ru/subject/lesson/2509/main/ |
| 9 | Основное тригонометрическое тождество. Формулы приведения. Формулы для вычисления координат точки | https://resh.edu.ru/subject/lesson/2510/main/ |
| 9 | Теорема о площади треугольника | https://resh.edu.ru/subject/lesson/2032/main/ |
| 9 | Теорема синусов | https://resh.edu.ru/subject/lesson/2034/main/ |
| 9 | Теорема косинусов | https://resh.edu.ru/subject/lesson/2041/main/ |
| 9 | Решение треугольников. Измерительные работы | https://resh.edu.ru/subject/lesson/2040/main/ |
| 9 | Угол между векторами. Скалярное произведение векторов | https://resh.edu.ru/subject/lesson/2039/main/ |
| 9 | Скалярное произведение в координатах. Свойства скалярного произведения векторов | https://resh.edu.ru/subject/lesson/2038/main/ |
| 9 | Правильный многоугольник. Окружность, описанная около правильного многоугольника. Окружность, вписанная в правильный многоугольник | https://resh.edu.ru/subject/lesson/2037/main/ |
| 9 | Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности | https://resh.edu.ru/subject/lesson/2512/main/ |
| 9 | Длина окружности | https://resh.edu.ru/subject/lesson/2513/main/ |
| 9 | Площадь круга. Площадь кругового сектора | https://resh.edu.ru/subject/lesson/2514/main/ |
| 9 | Решение практических задач с использованием формулы длины окружности, площади круга и кругового сектора | https://resh.edu.ru/subject/lesson/2515/main/ |
| 9 | Построение правильных многоугольников | https://resh.edu.ru/subject/lesson/2516/main/ |
| 9 | Отображение плоскости на себя. Понятие движения. Наложения и движения | https://resh.edu.ru/subject/lesson/2035/main/ |
| 9 | Параллельный перенос | https://resh.edu.ru/subject/lesson/3040/main/ |
| 9 | Поворот | https://resh.edu.ru/subject/lesson/3041/main/ |
| 9 | Решение задач на движение по теме «Движение» | https://resh.edu.ru/subject/lesson/2517/main/ |
| 9 | Предмет стереометрии. Многогранники | https://resh.edu.ru/subject/lesson/2780/main/ |
| 9 | Тела и поверхности вращения | https://resh.edu.ru/subject/lesson/2031/main/ |
| 9 | Применение векторов для решения задач | https://infourok.ru/videouroki/3293 |
| 9 | Осевая и центральная симметрия | https://znaika.ru/catalog/8-klass/geometry/Osevaya-i-tsentralnaya-simmetriya.html |
Уроков по геометрии 7 класс. Тема: «Задачи на построение»
Муниципальное общеобразовательное учреждение
Сорокинская средняя общеобразовательная школа №3
Разработки уроков по геометрии 7 класс.
Тема: «Задачи на построение».
Составитель: Щуракова Л.А.
учитель математики
2008г.
Пояснительная записка.
Услышишь — забудешь,
Увидишь — запомнишь,
Построишь — поймёшь.
Конфуций.
Задачи на построение являются традиционными задачами в курсе геометрии. Разработкой методов решения этих задач математики занимаются ещё со времён Древней Греции. Математики школы Пифагора (VI в. до н. э.) решили довольно сложную задачу построения правильного пятиугольника. В течение многих веков учёные проявляли живейший интерес к задачам на построение. Интерес к этим задачам обусловлен не только их красотой и оригинальностью методов решения, но и большой практической ценностью. Проектирование строительства, архитектура, конструирование различной техники основаны на геометрических построениях. Задачи на построение могут способствовать пониманию учащимися происхождения различных геометрических фигур, возможности их преобразования – всё это является важной предпосылкой развития пространственного мышления школьников. Они сильно развивают логическое мышление, геометрическую интуицию, а также такие качества личности, как внимание, настойчивость и целеустремленность, инициативу, изобретательность, дисциплинированность, трудолюбие. Задачи на построения не просты. Не существует единого алгоритма для решения таких задач. Каждая из них по-своему уникальна, и каждая требует индивидуального подхода для решения. Столкнувшись с этими вопросами, я стала искать решение. И, как мне кажется, кое-что нашла, что у меня неплохо получается и даёт неплохие результаты. При разработке данных уроков использованы различные педагогические технологии: информационно-коммуникационная, личностно-ориентированная, метод проектов. Использование новых информационных технологий непосредственно в рамках школьного курса геометрии может быть описано двумя моделями, различающимися по способу организации деятельности учащихся на уроке:
- Урок с компьютерным сопровождением;
- Урок в компьютерном классе
По вполне понятным причинам осуществить решение задачи по первой модели гораздо проще. Мультимедийную систему на своих уроках применяю в течении двух лет.
Мультимедийная система обеспечивает:
- Наглядность материала, в том числе, за счет звука, цвета, движения;
- Ускорение темпа урока;
- Свободу постоянного экспериментирования с целью улучшения методики преподавания;
- Последовательный характер обучения за счет планомерного накапливания наглядных электронных пособий, позволяющих с легкостью в любой момент вернуться к уже знакомым, эмоционально окрашенным образам пройденного материала, которые могут быть гораздо экспрессивнее всем известных опорных сигналов.
Компьютер на уроке — это педагогическая реальность, которая твердо вошла в нашу жизнь. При этом рассматриваю компьютер как ещё одно дополнение к процессу обучения, а не заменяющее учителя и учебник средство обучения.
На конкурс представлены уроки геометрии 7 класса по учебнику Л.С.Атанасяна и др. Данные уроки могут проводиться, как с сопровождением мультимедийной системы, так и в компьютерном кабинете.
Урок №1 «Задачи на построение»(1час)
Урок изучения нового материала с использованием электронного учебника.
Урок №2 «Построение треугольника по трём элементам»(2 часа)
Урок-практикум, «Конструкторское бюро» (решение задач на построение треугольника по трём элементам).
Урок №3 «Построение треугольника по трём элементам»(1 час)
Зачётная работа. Урок по технологии метода проектов. Краткосрочный проект по изготовлению плаката «Виды треугольников».
Ход урока:
I. Организационный этап.
II. Подготовка обучающихся к восприятию нового материала с использованием электронного учебника ( см. приложение1 урок 17):
2.1.
У круга есть подруга, Знакома всем её наружность. Она идёт по краю круга И называется окружность.
| |
|
2.2 Вводное слово учителя:
Проводя прямую, откладывая отрезок, измеряя угол и отрезок, изображая треугольник вы имели дело с геометрическими построениями. Вам знакомы такие инструменты, как масштабная линейка, циркуль, транспортир и другие. На этом уроке вы узнаете, как можно выполнить построения треугольника по трём элементам при помощи только циркуля и линейки без масштабных делений. Такая линейка позволяет провести произвольную прямую и построить, прямую, проходящую через две данные точки, но не позволяет откладывать отрезки, заданной длинны. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку.
Электронный учебник напоминает нам, как построить угол равный данному и биссектрису угла при помощи циркуля и линейки
( см.приложение1 урок ):
Построение с помощью циркуля и линейки угла равного данному.
(Используется анимация электронного учебника.)
1. 2. 3.
4. 5. 6.
Отработать на тренажёре алгоритм построения угла равного данному:
Построение биссектрисы данного угла:
1. 2. 3.
4. 5. 6.
III. Изучение нового материала. Работа с электронным учебником.
При изучении нового материала используется анимация (см. приложение1 урок 18).
3.1 Построение треугольника по трём сторонам:
1. 2. 3. 4. 5. 6.
7. 8.
3.2 Первичное закрепление. Используется тренажер (см. приложение1 урок18).
3.3 Практическая работа.
Обучающиеся работают самостоятельно используя таблицу, задача №1 (см. приложение2):
3.4 Построение треугольника по двум сторонам и углу между ними:
Обучающиеся выполняют задачу №2, используя анимацию электронного учебника (см. приложение2):
1. 2. 3.
4. 5. 6.
7. 8.
3.5 Построение треугольника по заданным стороне и двум углам:
Обучающиеся выполняют задачу №3, используя анимацию электронного учебника (см. приложение2):
1. 2. 3.
4. 5. 6.
7. 8.
9. 10. 11. 12.
IV. Предлагается обучающимся сделать выводы, какие построения можно выполнять
используя циркуль и линейку.
1) С помощью циркуля и линейки можно построить угол, равный данному.
2) С помощью циркуля и линейки можно построить биссектрису данного угла.
3) С помощью циркуля и линейки можно построить треугольник по трём заданным сторонам.
4) С помощью циркуля и линейки можно построить треугольник по двум заданным
сторонам и углу.
5) С помощью циркуля и линейки можно построить треугольник по заданным стороне
и двум углам.
V. Изучив материал урока, проверьте свои знания, ответив на вопросы итогового
тестирования.
Обучающимся предлагается выполнить итоговый тест с последующей проверкой с помощью электронного учебника и самостоятельным оцениванием (см. приложение 3).
VI. Рефлексия.
VII. Домашнее задание: п.38(задачи 1-3), №286.
Тема урока: «Конструкторское бюро»
( урок решения задач на построение треугольника по трем элементам)
Цели урока:
- расширить представления учащихся о построении треугольника по трём элементам;
- продолжить формирование навыков в решении задач на построение;
- развивать творческое мышление, память умение свободно пользоваться циркулем;
- способствовать воспитанию у обучающихся творческой активности и самостоятельности;
Педагогическая технология:
- личностно-ориентированная технология обучения;
- элементы информационной технологии;
Тип урока: урок-практикум
Оборудование:
- компьютер, проектор;
- циркуль;
- линейка;
- таблицы для практической работы;
- электронный учебник «Виртуальная школа Кирилла и Мефодия»
Уроки геометрии 7 класс.2005г.
Ход урока:
I. Организационный этап.
Информационный ввод учителя.
II. «Спешите видеть» (Устное решение задач по готовым чертежам).
Кто ничего не замечает,
Тот ничего не изучает,
Кто ничего не изучает,
Тот вечно хнычет и скучает.
В геометрии очень важно уметь смотреть и видеть, замечать и отличать различные особенности геометрических фигур.
- Внимательно посмотрите на рисунки и вычислите неизвестные углы треугольника (Рисунки предъявляются классу по одному)
- Сформулируйте теорему, которую применяли, решая предложенные задачи.
III. Историческая справка.
Великий немецкий математик Вильгельм Лейбниц сказал:
«Кто хочет ограничиться настоящим, без знания прошлого,
тот никогда ничего не поймёт».
Заглянем в прошлое.( Заслушиваем доклады учащихся).
Из истории геометрических построений циркулем и линейкой
Традиционное ограничение орудий геометрических построений восходит к глубокой древности. В своей книге «Начала» Евклид (III век до н. э.) строго придерживается геометрических построений, выполняемых циркулем и линейкой, хотя названий инструментов он нигде не упоминает. Ограничения, по-видимому, были связаны с тем, что эти инструменты заменили собой веревку, первоначально служившую как для проведения прямых, так и для описания окружностей. Но многие историки математики объясняют произведенный Евклидом отбор материала тем, что он, следуя Платону и пифагорейцам, считал только прямую и круг «совершенными» линиями.
Искусство построения геометрических фигур было в высокой степени развито в Древней Греции. Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем (это линейка) и двух заостренных палок, связанных на одном конце (это циркуль). Однако этих простейших инструментов оказалось достаточно для выполнения огромного множества различных построений. Древним грекам даже казалось, что любое разумное построение можно совершить этими инструментами, пока они не столкнулись с тремя знаменитыми впоследствии задачами.
Они издавна преобразовывали любую прямолинейную фигуру с помощью циркуля и линейки в произвольную прямолинейную фигуру, равновеликую ей. В частности, всякая прямолинейная фигура преобразовывалась в равновеликий ей квадрат. Поэтому понятно, что появилась мысль обобщить эту задачу: построить с помощью циркуля и линейки такой квадрат, площадь которого была бы равна площади данного круга. Это задача получила название квадратуры круга. Следы этой задачи можно усмотреть еще в древнегреческих и вавилонских памятниках второго тысячелетия до н.э. Однако ее непосредственная постановка встречается в греческих сочинениях V века до н.э.
Еще две задачи древности привлекали внимание выдающихся ученых на протяжении многих веков. Это задача об удвоении куба. Она состоит в построении циркулем и линейкой куба, имеющего объем вдвое больший, чем объем данного куба. Ее появление связывают с легендой, что на острове Делос в Эгейском море оракул, чтобы избавить жителей от эпидемии чумы, повелел удвоить алтарь, имевший форму куба. И третья задача трисекции угла о делении угла на три равные части с помощью циркуля и линейки.
Эти три задачи, так называемые 3 знаменитые классические задачи древности привлекали внимание выдающихся математиков на протяжении двух тысячелетий. И лишь в середине XIX века была доказана их неразрешимость, то есть невозможность указанных построений лишь с использованием только циркуля и линейки. В математике это были первые результаты о неразрешимости задач, когда средства решения указаны. Они были получены средствами не геометрии, а алгебры (с помощью перевода этих задач на язык уравнений), что еще раз подчеркнуло единство математики. Не поддаваясь решению, эти проблемы обогатили математику значительными результатами, привели к созданию новых направлений математической мысли.
Еще одной интереснейшей задачей на построение с помощью циркуля и линейки является задача построения правильного многоугольника с заданным числом сторон. Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон, и только их. Лишь в 1801 году великий немецкий математик К.Ф.Гаусс открыл способ построения правильного 17-угольника при помощи циркуля и линейки и указал все значения N, при которых возможно построение правильного N-угольника указанными средствами. Таким образом, была доказана невозможность построения с помощью циркуля и линейки правильных 7, 9, 11, 13, 18, 21, 22, 23 и т.д. угольников. Теория построения при помощи циркуля и линейки получила свое дальнейшее развитие. Был получен ответ на вопрос: можно ли решить задачу с помощью только одного из двух рассматриваемых инструментов, и достаточно неожиданный. Независимо друг от друга, датчанин Г.Мор в 1672 году и итальянец Л.Маскерони в 1797 году доказали, что любая задача на построение, разрешаемая циркулем и линейкой, может быть точно решена с помощью только одного циркуля. Это кажется невероятным, но это так. А в XIX веке было доказано, что любое построение, выполняемое с помощью циркуля и линейки можно провести лишь с помощью одной линейки, при условии, что в плоскости построения задана некоторая окружность и указан ее центр.
VI. «Знаю – не знаю» (Актуализация знаний по теме).
Опрос учащихся.
- Какие задачи можно назвать «задачами на построение?
(Задачи на построение — это такие задачи, при решении которых нужно построить геометрическую фигуру, удовлетворяющую условиям задачи, с помощью циркуля и линейки.)
- Какие задачи на построение вы знаете?
- Объясните, как построить треугольник:
- по двум сторонам и углу между ними;
- по стороне и двум прилежащим к ней углам;
- по трём сторонам. Всегда ли эта задача имеет решение?
V. «Проверка мастерства»
(Практическая работа, учебник геометрии стр.82-83,
№288а, 290(а, б), 291(а, б, д)).
Обучающимся предлагается познакомиться со схемой решения задач на построение и таблицами № 1,2, которые помогут в решении задач практической работы. Учащиеся испытывающие затруднения в ходе практической работы, могут обратиться к тренажёру (см. электронный учебник).
приложение 3
Рассмотрите схему, по которой обычно решают задачи на построение циркулем и линейкой. Она состоит из четырёх частей.
Схема решения задач на построение.
- Анализ. (Изображение искомой фигуры (рисунок), устанавливающее связи между данными задачи и искомыми элементами, и план построения)
- Построение по намеченному плану.
3) Доказательство, что данная фигура удовлетворяет условиям задачи.
4) Исследование (при любых ли данных задача имеет решение и,
если имеет, то сколько).
приложение 1
Таблица 1
| 288 а | ∆ ABC AB=PQ ∟ABC=∟hk ∟BAC=∟ | ||
| 290 а | ∆ ABC-прямоугольный AС=а СВ=b | ||
| 290 б | ∆ ABC-прямоугольный AС=а ∟BAC=∟M |
приложение 2
Таблица 2
| № | Дано | Требуется построить | Результат |
| 291 а | ∆ ABC-равнобедренный AС=AB=а ∟A=∟N | ||
| 291 б | ∆ ABC-равнобедренный AС=а ∟A=∟K ∟C=∟K | ||
| 291 д | ∆ ABC-равнобедренный СH=а — медиана AB=b |
VI. Итоги урока.
Учащиеся работают с листом контроля и определяют уровень своего мастерства.
VII.Рефлексия.
Оцени свою работу
VIII. Домашнее задание:
- п.38,№293;
- Построить три равносторонних треугольника таких, что стороны второго в три раза больше сторон первого, а стороны третьего в два раза меньше сторон второго.
- Верно ли высказывание: «Слово «цирк» и «циркуль» имеют одинаковое этимологическое происхождение». Для проверки рекомендуется воспользоваться этимологическим словарём.
Тема урока: Построение треугольника по трём элементам.
Цели урока:
- осмысление изученного материала, воспроизведение и применение знаний с целью их углубления;
- научить учащихся самостоятельно достигать поставленной цели;
- сформировать навыки проведения исследований, передачи и презентации полученных знаний, делового общения в группе;
- выявить уровень усвоения теоретического материала у учащихся;
- способствовать развитию познавательного интереса к геометрии;
- развитие коммуникативных связей;
Педагогическая технология:
- метод проектов.
Тип урока: зачётная работа.
Оборудование:
- компьютер, проектор;
- циркуль;
- линейка;
- ватман, миллиметровая и цветная бумага, маркеры.
Ход урока:
I. Организационный этап:
Обучающиеся делятся на группы. Знакомятся с раздаточным материалом, лежащим на столах.
II. Актуализация знаний, необходимых на уроке.
На доске прикрепляется карточка «Треугольник».
- С какой фигурой работаем сегодня на уроке?
(С треугольником.)
- Что такое треугольник?
( Треугольник – фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.)
- Какие треугольники различают?
(По сторонам: равносторонние, равнобедренные или разносторонние.)
На доске выставляются карточки-треугольники, соединяемые в схему:
Треугольник
по сторонам
Треугольники также различают (т.е. классифицируют) и по углам.
На доске дополняется схема.
Треугольник
по сторонам по углам
III. Постановка задачи.
Разработать плакат «Виды треугольников» с необходимыми доказательствами.
Каждой группе выдаётся задание.
1 группа:
Построить:
- равнобедренный треугольник по боковой стороне и углу при основании.
- прямоугольный треугольник по катету и прилежащему к нему острому углу.
- треугольник XYZ, по стороне и двум прилежащим к ней углам меньше 90˚.
- треугольник KLM, по двум сторонам и углу больше 90˚.
2 группа:
Построить:
- равносторонний треугольник.
- прямоугольный треугольник по катету и прилежащему к нему острому углу.
- равнобедренный треугольник KLM , по стороне и углу меньше 90˚.
- треугольник ABC, по двум сторонам и углу больше 90˚.
3 группа:
Построить:
- равнобедренный прямоугольный треугольник.
- прямоугольный треугольник по катету и прилежащему к нему острому углу.
- треугольник XYZ, по трём сторонам.
- треугольник KLM, по двум равным сторонам и углу между ними, больше 90˚.
Алгоритм работы над проектом:
1. Планирование.
2. Аналитический этап.
3. Этап обобщения информации.
4. Презентация (представление полученных результатов).
IV. Защита проекта.
Каждая группа представляет свой проект.
Ожидаемый результат плакат «Виды треугольника» (см. приложение 1).
V. Подведение итогов работы.
VI. Рефлексия.
VII. Домашнее задание.
« Геометрия в практической деятельности» ( подобрать материал, где в практической деятельности человека используются знания полученные по данной теме).
Например:
З а д а ч а : Для определения по карте места нахождения S судна с помощью радиопеленгатора определяют углы SAB и SBA, где А и В береговые радиомаяки, изображённые на карте. Ту же задачу решают с помощью радиолокатора, определяя расстояние от S до А и до В. как найти на карте месторасположение судна по данным: а) радиопеленгатора, б) радиолокатора?
Р е ш е н и е сводится к построению треугольника:
а) по стороне и двум углам,
б) по трём сторонам.
« Конструкторское бюро »
Лист контроля.
Ф.И._________________________________________
| № | Вид работы | Баллы |
| 1. | « Спешите видеть » (устное решение задач по готовым чертежам | |
| 2. | « Знаю – не знаю » | |
3. | « Проверка мастерства » № 288 – 3б | |
| № 290а – 1б | ||
| №290б – 2б | ||
| №291а – 2б | ||
| №291б – 3б | ||
| №291д – 4б |
Итог:____________
Примечание: ученик, набравший нужное количество баллов получает звание
Конструктор — 15 баллов
Ведущий технолог — 11-14 баллов
Технолог — 8-10 баллов
Поиск
Поиск
-
Школьный помощник- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая
предыдущая
вернуться на предыдущую страницу
Такой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Русский язык 7 класс
- Математика 6 класс
- Алгебра 7 класс
- Русский язык 5 класс
- Алгебра 8 класс
- Русский язык 6 класс
- Математика 5 класс
- Наименьшее общее кратное
- Наибольший общий делитель. Взаимно простые числа
- Доли. Обыкновенные дроби
- Деление и дроби
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Квадратный корень из неотрицательного числа
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Common Core Math 7 класс — Геометрия: Геометрическое построение — Видео и уроки
Воспользуйтесь видео-уроками и практическими тестами из этого сборника геометрических построений, чтобы помочь своим седьмым классам соответствовать Общим основным государственным стандартам по математике. Есть также советы и предложения о том, как использовать уроки и узнать, когда ваши ученики усвоили эти концепции.
Стандарт: Решение задач, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей из масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе.(CCSS.MATH.CONTENT.7.G.A.1)
Стандарт: Нарисуйте (от руки, линейкой и транспортиром, а также технологией) геометрические фигуры в заданных условиях. Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. (CCSS.MATH.CONTENT.7.G.A.2)
Стандарт: Опишите двумерные фигуры, полученные в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.(CCSS.MATH.CONTENT.7.G.A.3)
Об этой главе
Учащиеся, усвоившие эти стандарты Common Core, смогут рисовать, описывать и конструировать геометрические фигуры, а также описывать отношения между ними. Используйте уроки из этого сборника, чтобы научить своих учеников следующим навыкам:
- Применение масштабных коэффициентов к площади, объему и периметру подобных фигур
- Чтение и интерпретация масштабных чертежей
- Изготовление геометрических конструкций
- Построение типов треугольников
- Обозначение трехмерных фигур сверху, сбоку и спереди
Когда ваши ученики овладеют этими стандартами, вы узнаете, когда они смогут решать задачи, которые включают в себя масштабные чертежи геометрических фигур, рисование или построение геометрических фигур с использованием заданных условий и описывают двумерные формы, получаемые в результате нарезки трех Фигуры D.
Как использовать эти уроки в классе
Вот несколько советов по включению материалов коллекции в ваши планы уроков:
Построение геометрических фигур
Для занятий в классе попробуйте построить некоторые конструкции, описанные в видео «Практика создания геометрических конструкций с помощью инструментов». Предложите учащимся работать в небольших группах, чтобы они могли обмениваться инструментами и давать советы друг другу. После этого попросите каждого ученика записать названия своих конструкций и размеры, которые они использовали.
Сделайте масштабную модель Великой пирамиды в Гизе
Посмотрите уроки по масштабным коэффициентам и построению геометрических фигур. Затем создайте точную копию пирамиды Гизы, используя картон или плотную бумагу, ножницы и скотч. Измерения пирамиды легко получить в Интернете. Предложите учащимся использовать полученные знания для уменьшения масштаба. Используйте линейку, чтобы измерить и нарисовать стороны пирамиды, а затем вырежьте и соберите формы.
Назначьте уроки и тесты домашним заданием
Дополните регулярные задания видео и викторинами из этого сборника.Студенты могут просмотреть видео в качестве напоминания перед тем, как ответить на практические вопросы, соответствующие каждому уроку. В качестве бонусного задания предложите студентам придумывать собственные вопросы и отвечать на них на основе вопросов в практических тестах.
по математике, 7 класс, конструкции и углы
Кластер: рисуйте, конструируйте и описывайте геометрические фигуры и описывайте отношения между ними.
Стандарт: Нарисуйте (от руки, с помощью линейки и транспортира, а также с помощью техники) геометрические фигуры в заданных условиях.Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Кластер: решение реальных и математических задач, связанных с измерением угла, площади, площади поверхности и объема
Стандарт
: Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.
Кластер: математические практики
Стандарт
: разбираться в проблемах и настойчиво их решать. Учащиеся с математическими знаниями начинают с того, что объясняют себе смысл проблемы и ищут точки входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения.Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции.Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему. Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
Кластер: математические практики
Стандарт: Размышляйте абстрактно и количественно.Учащиеся с математическими знаниями понимают величины и их отношения в проблемных ситуациях. Учащиеся обладают двумя взаимодополняющими способностями для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагироваться от данной ситуации и представлять ее символически и манипулировать представляющими символами, как будто они живут своей собственной жизнью, не обязательно обращая внимание на своих референтов — и способность контекстуализировать, останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к их вычислению; знание и гибкое использование различных свойств операций и объектов.
Кластер: математические практики
Стандарт
: Придумывайте жизнеспособные аргументы и критикуйте рассуждения других. Математически опытные учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних классов. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Кластер: математические практики
Стандарт: Модель с математикой.Учащиеся со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах ученик может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
Кластер: математические практики
Стандарт: стратегически используйте соответствующие инструменты. Математически развитые студенты рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной степени знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезным, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
Кластер: математические практики
Стандарт: внимание к точности. Математически развитые ученики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом.Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме. Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
Кластер: математические практики
Стандарт: Ищите и используйте структуру.2 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
Кластер: математические практики
Стандарт: Ищите и выражайте закономерность в повторяющихся рассуждениях. Математически опытные ученики замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и придут к выводу, что у них есть повторяющаяся десятичная дробь.2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Область обучения: Геометрия
Стандарт
: рисовать, конструировать и описывать геометрические фигуры и описывать отношения между ними.
Показатель: Нарисуйте (от руки, линейкой и транспортиром, а также техникой) геометрические фигуры в заданных условиях. Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Область обучения: Геометрия
Стандарт: решение реальных и математических задач, связанных с измерением угла, площади, площади поверхности и объема
Индикатор
: используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.
Область обучения: математические практики
Стандарт: Математические практики
Показатель: разбирайтесь в проблемах и настойчиво пытайтесь их решать. Учащиеся с математическими знаниями начинают с того, что объясняют себе смысл проблемы и ищут точки входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения.Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции.Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему. Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Ť Они могут понимать подходы других к решению сложных проблем и определять соответствия между различными подходами.
Область обучения: математические практики
Стандарт: Математические практики
Показатель: Размышляйте абстрактно и количественно.Учащиеся с математическими знаниями понимают величины и их отношения в проблемных ситуациях. Учащиеся обладают двумя взаимодополняющими способностями для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать «абстрагировать данную ситуацию и представлять ее символически и манипулировать представляющими символами, как будто они живут своей собственной жизнью, не обязательно обращая внимание на своих референтов» Ó и возможность контекстуализировать, делать паузу, если необходимо, во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к их вычислению; знание и гибкое использование различных свойств операций и объектов.
Область обучения: математические практики
Стандарт: Математические практики
Показатель: Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.Математически опытные учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли.Математически опытные студенты также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян», объяснять, что это такое. Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних классов. Позже студенты учатся определять области, к которым применим аргумент.Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Область обучения: математические практики
Стандарт: Математические практики
Показатель: Модель с математикой. Учащиеся со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте.В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах ученик может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой. Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже.Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
Область обучения: математические практики
Стандарт: Математические практики
Индикатор
: стратегически используйте соответствующие инструменты.Математически развитые студенты рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной степени знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезным, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
Область обучения: математические практики
Стандарт: Математические практики
Индикатор
: Будьте внимательны. Математически развитые ученики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом.Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме. Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
Область обучения: математические практики
Стандарт: Математические практики
Индикатор
: Ищите и используйте структуру.2 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
Область обучения: математические практики
Стандарт: Математические практики
Показатель: Ищите и выражайте закономерность в повторяющихся рассуждениях. Математически опытные ученики замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и придут к выводу, что у них есть повторяющаяся десятичная дробь.2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Математика для 7-го класса — Блок 6: Геометрия
Краткое описание агрегата
В Блоке 6 ученики седьмого класса изучают широкий круг тем, от угловых отношений до кругов и многоугольников до твердых фигур.Стандарты геометрии седьмого класса относятся к категории дополнительных стандартов, однако в подразделении есть несколько возможностей, когда учащиеся заняты основной работой класса. В начале раздела учащиеся используют и решают уравнения, чтобы представить отношения между углами и найти недостающие меры углов. Исследуя круги, учащиеся обнаруживают пропорциональную связь между длиной окружности и ее диаметром и понимают π как отношение этих двух величин.Студенты также будут использовать свои навыки выражения для написания числовых выражений, которые можно использовать для определения площади поверхности и объема трехмерных фигур.
На протяжении всего раздела учащиеся сталкиваются с несколькими словарными словами, такими как дополнительные углы, вертикальные углы, радиус и окружность. Многие из этих слов позволяют студентам более точно общаться друг с другом (МР.6). Студенты также столкнутся со сложными диаграммами углов и трехмерными фигурами, где им нужно будет понять, какую информацию они могут почерпнуть из диаграммы, и спланировать путь решения, прежде чем приступить к работе (MP.1). Учащиеся должны иметь доступ к нескольким инструментам, которые они могут использовать на уроке, включая линейки, транспортиры, компасы и справочные листы (МР.5).
Основные навыки, необходимые для выполнения стандартов в этом блоке, относятся к четвертому – шестому классам. В четвертом классе ученики изучали принципы измерения углов и считали, что измерение угла является аддитивным. В пятом классе ученики развили понимание трехмерного объема, которое они в дальнейшем развили в шестом классе.Шестиклассники также начали различать трехмерное пространство, которое занимает объект, и площадь поверхности, которая его покрывает.
В восьмом классе ученики будут увеличивать масштаб прямоугольных треугольников и применять теорему Пифагора для определения длин сторон прямоугольных треугольников. Они также продолжат решать реальные приложения площади и объема с добавлением конусов, сфер и цилиндров.
Темп: 23 учебных дня (21 урок, 1 гибкий день, 1 контрольный день)
Инструкции по корректировке темпа на 2020-2021 учебный год из-за закрытия школ см. В нашем разделе «Рекомендуемые корректировки для 7-го класса и последовательности».
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (безымянные версии)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
PDST Математика после начального образования | Новые ресурсы: преподавание математики в среде DEIS
Этот веб-сайт использует Google Analytics для сбора анонимной информации, такой как количество посетителей сайта и наиболее популярные страницы.
Сохранение включенного файла cookie помогает нам улучшать наш веб-сайт.
Пожалуйста, сначала включите строго необходимые файлы cookie, чтобы мы могли сохранить ваши предпочтения!
Показать детали
| Имя | Провайдер | Назначение | Срок действия |
|---|---|---|---|
| _ga | Файл cookie Google Analytics, который используется для расчета данных о посетителях, сеансах и кампании, а также для отслеживания использования сайта для аналитического отчета сайта.Файлы cookie хранят информацию анонимно и присваивают случайно сгенерированный номер для идентификации уникальных посетителей. Отказаться на странице https://tools.google.com/dlpage/gaoptout | 730 дней | |
| _gat | Файл cookie Google Analytics, используемый для регулирования скорости запросов.Отказаться на странице https://tools.google.com/dlpage/gaoptout | 1 день | |
| _gid | Файл cookie Google Analytics используется для хранения информации о том, как посетители используют веб-сайт, и помогает в создании аналитического отчета о том, как работает веб-сайт.Собранные данные, включая количество посетителей, источник, откуда они пришли, и страницы, посещенные в анонимной форме. Отказаться на странице https://tools.google.com/dlpage/gaoptout | 1 день | |
| NID | Содержит уникальный идентификатор, который Google использует для запоминания ваших предпочтений и другой информации, например, предпочитаемого вами языка (например.грамм. Английский), сколько результатов поиска вы хотите отображать на странице (например, 10 или 20) и хотите ли вы, чтобы фильтр безопасного поиска Google был включен. |
Проект геометрии и задачи
Контрольные вопросы
Обратите внимание, что любые диаграммы или фотографии, включенные в вопрос, не масштабированы.
неделя № 1
Задача № 1
Задача № 1
неделя № 2
Задача № 2
Задача № 2
неделя № 3
Задача № 3
Задача № 3
неделя # 4
Задача # 4
Задача # 4
неделя # 5
Задача # 5
Задача # 5
неделя # 6
Задача # 6
Задача # 6
неделя № 7
Задача № 7
Задача № 7
неделя № 8
Задача № 8
Задача № 8
Проект геометрии
Повышение предела — постройка башни
Треугольники повсюду! Посмотрите вокруг, и вы увидите их в зданиях, мостах, велосипедах и многом другом.Вы даже найдете треугольники в своем проекте (мы надеемся).
Ваша цель — использовать изюм и зубочистки для создания разных башен, которые смогут удерживать один мяч для софтбола (на каждую башню) в течение одной минуты.
Мероприятие 1: Исследование
Создайте портфолио фотографий, цифровую презентацию, видео-презентацию или другое визуальное / мультимедийное шоу для отображения геометрических фигур в структурах. У вас должно быть не менее четырех различных геометрических (многоугольных) форм на четырех или более разных примерах.
Действие 2: Анализ
Используйте зубочистки и изюм, чтобы построить четыре различных геометрических (многоугольных) формы, которые вы наблюдали в упражнении 1. Какая форма, по вашему мнению, является наиболее устойчивой? Проверьте свой ответ, аккуратно покачивая фигуры. Добавьте дополнительные зубочистки к более слабым фигурам, чтобы попытаться сделать их такими же прочными, как и самая стабильная форма, которую вы сделали. Опишите в эссе, слайд-шоу или видео-презентации, что вы узнали о формах, и постарайтесь их укрепить.
Мероприятие 3: План
Нарисуйте эскиз башни, которую вы хотите построить. Рисунок должен быть выполнен на стандартном листе бумаги для принтера и не в масштабе. Возможно, вы захотите нарисовать более одного рисунка, но, пожалуйста, ограничьтесь не более чем тремя.
Мероприятие 4: Строительство
Используйте зубочистки и изюм для ОДНОГО из своих рисунков. Фактическая башня должна напоминать ваш дизайн и иметь высоту двенадцать или более дюймов.Запрещается использовать клей или другой крепежный материал. В строительстве башни можно будет использовать только зубочистки и изюм. Следите за тем, сколько изюма и сколько зубочисток вы используете в вышке. Постарайтесь сделать свою башню не только сильной, но и привлекательной.
Мероприятие 5: Тестирование
Проверьте прочность своей башни, осторожно поместив на нее мяч для софтбола. Если он начинает прогибаться, укрепите башню до того, как башня выйдет из строя.Если возможно, задокументируйте тестирование фотографиями или видео.
Представление класса:
Студенты представят свою башню для реального тестирования или свои фото- или видеопрезентации для наблюдения студентами.
Подсчет очков
Рубрика проекта
Рубрика проекта
Практическая геометрия 7 класс Дополнительные вопросы Математика 10
Практическая геометрия 7 класс Дополнительные вопросы Математика 10
Дополнительные вопросы для класса 7 по математике Глава 10 Практическая геометрия
Практическая геометрия Класс 7 Дополнительные вопросы Очень короткий ответ Тип
Вопрос 1.
Укажите, возможно ли построить треугольник, если
(a) В ΔABC, m∠A = 80 °, m∠B = 60 °, AB = 5,5 см
(b) В ΔPQR, PQ = 5 см, QR = 3 см, PR = 8,8 см
Раствор:
(а) m∠A = 80 °, m∠B = 60 °
m∠A + m∠B = 80 ° + 60 ° = 140 ° <180 °
Итак, ΔABC можно построить.
(b) PQ = 5 см, QR = 3 см, PR = 8,8 см
PQ + QR = 5 см + 3 см = 8 см <8,8 см
или PQ + QR
Вопрос 2.
Нарисуйте равносторонний треугольник, каждая сторона которого равна 4.5 см.
Решение:
Шаги построения:
(i) Нарисуйте AB = 4,5 см.
(ii) Нарисуйте две дуги с центрами A и B и одинаковым радиусом 4,5 см, чтобы они встретились в точке C.
(iii) Соедините CA и CB.
(iv) ΔCAB — искомый треугольник.
Вопрос 3.
Нарисуйте ΔPQR, в котором QR = 3,5 см, m∠Q = 40 °, m∠R = 60 °.
Решение:
Этапы построения:
(i) Нарисуйте QR = 3,5 см.
(ii) Нарисуйте ∠Q = 40 °, ∠R = 60 °, которые пересекаются друг с другом в точке P.
(iii) ΔPQR — это требуемый треугольник.
Вопрос 4.
Есть четыре варианта, из которых один правильный. Выберите правильный:
(i) Треугольник может быть построен с заданным размером.
(а) 1,5 см, 3,5 см, 4,5 см
(б) 6,5 см, 7,5 см, 15 см
(в) 3,2 см, 2,3 см, 5,5 см
(г) 2 см, 3 см, 6 см
( ii) (а) m∠P = 40 °, m∠Q = 60 °, AQ = 4 см
(б) m∠B = 90 °, m∠C = 120 °, AC = 6,5 см
(в) м ∠L = 150 °, m∠N = 70 °, MN = 3,5 см
(d) m∠P = 105 °, m∠Q = 80 °, PQ = 3 см
Решение:
(i) Вариант (a) возможно построить.
1,5 см + 3,5 см> 4,5 см
(ii) Вариант (а) правильный.
m∠P + m∠Q = 40 ° + 60 ° = 100 ° <180 °
Вопрос 5.
Какими будут другие углы прямоугольного равнобедренного треугольника?
Решение:
В прямоугольном равнобедренном треугольнике ABC B = 90 °
∠A + ∠C = 180 ° — 90 ° = 90 °
Но ∠A = ∠B
∠A = ∠C = \ (\ frac {90} {2} \) = 45 °
Следовательно, требуемые углы равны ∠A = ∠C = 45 °
Вопрос 6.
Каков размер внешнего угла равностороннего треугольника?
Решение:
Мы знаем, что размер каждого внутреннего угла = 60 °
Внешний угол = 180 ° — 60 ° = 120 °
Вопрос 7.
В ΔABC, A = ∠B = 50 °. Назовите пару равных сторон.
Решение:
∠A = ∠B = 50 °
AC = BC [∵ Стороны, противоположные равным углам, равны]
Следовательно, требуемые стороны — это AC и BC.
Вопрос 8.
Если один из других углов прямоугольного треугольника тупой, можно ли построить треугольник.
Решение:
Мы знаем, что углы прямоугольного треугольника, отличные от прямого, являются острыми углами.
Итак, построить такой треугольник невозможно.
Вопрос 9.
Укажите, конгруэнтны ли заданные треугольники.
Решение:
Здесь AB = PQ = 3,5 см
AC = PR = 5,2 см
∠BAC = ∠QPR = 70 °
ΔABC = ΔPQR [по правилу SAS]
Практическая геометрия Класс 7 Дополнительные вопросы Короткий ответ Тип
Вопрос 10.
Нарисуйте ΔABC, в котором BC = 5 см, AB = 4 см и m∠B = 50 °.
Решение:
Этапы построения:
(i) Нарисуйте BC = 5 см.
(ii) Нарисуйте ∠B = 50 ° и вырежьте AB = 4 см.
(iii) Присоединиться к AC.
(iv) ΔABC — искомый треугольник.
Вопрос 11.
Нарисуйте ΔPQR, в котором QR = 5,4 см, ∠Q = 40 ° и PR = 6,2 см.
Решение:
Этапы построения:
(i) Нарисуйте QR = 5,4 см.
(ii) Нарисуйте ∠Q = 40 °.
(iii) Возьмите R в качестве центра и с радиусом 6,2 см нарисуйте дугу, чтобы пересечь первую угловую линию на P.
(iv) Присоединиться к PR.
(v) ΔPQR — требуемый треугольник.
Вопрос 12.
Постройте ΔPQR, в котором m∠P = 60 ° и m∠Q = 30 °, QR = 4.8 см.
Решение:
m∠Q = 30 °, m∠P = 60 °
m∠Q + m∠P + m∠R = 180 ° (свойство суммы углов треугольника)
30 ° + 60 ° + m∠R = 180 °
90 ° + m∠R = 180 °
m∠R = 180 ° — 90 °
m∠R = 90 °
Этапы построения:
(i) Нарисуйте QR = 4,8 см.
(ii) Нарисуйте ∠Q = 30 °.
(iii) Нарисуйте ∠R = 90 °, которое пересекает первую угловую линию в точке P.
(iv) ∠P = 180 ° — (30 ° + 90 °) = 60 °
(v) ΔPQR — это требуемый треугольник.
Практическая геометрия Класс 7 Дополнительные вопросы Навыки мышления высшего порядка [HOTS] Тип
Вопрос 13.
Нарисуйте равнобедренный прямоугольный треугольник, гипотенуза которого равна 5,8 см.
Решение:
Прямоугольный треугольник — это равнобедренный треугольник.
Каждый из его острых углов = \ (\ frac {90} {2} \) = 45 °
Шаги построения:
(i) Нарисуйте AB = 5,8 см.
(ii) Постройте A = 45 ° и ∠B = 45 °, чтобы встретиться друг с другом при C.
(iii) ∠C = 180 ° — (45 ° + 45 °) = 90 °
(iv) ΔACB — это Требуется равнобедренный прямоугольный треугольник.
Вопрос 14.
Постройте ΔABC так, чтобы AB = 6.5 см, AC = 5 см, а высота от AP до BC составляет 4 см.
Решение:
Этапы построения:
(i) Нарисуйте линию l и возьмите любую точку P на ней.
(ii) Постройте перпендикуляр к l в точке P.
(iii) Отрежьте AP = 4 см.
(iv) Нарисуйте две дуги с центром A и радиусами 6,5 см и 5 см, чтобы разрезать линию l в точках B и C соответственно.
(v) Присоединитесь к AB и AC.
(vi) ΔABC — искомый треугольник.
Вопрос 15.
Постройте равносторонний треугольник высотой 4,5 см.
Решение:
Этапы построения:
(i) Нарисуйте любую линию l и возьмите на ней точку D.
(ii) Постройте перпендикуляр к l в точке D и вырежьте AD = 4,5 см.
(iii) Нарисуйте угол 30 ° по обе стороны от AD, чтобы пересечь линию l в точках B и C.
