2.
Решение.
- Функция степенная без каких-либо ограничений, поэтому область определения будет вся числовая прямая. Значения функции — вся числовая прямая.
- Четная или нечетная функция.
Подставим вместо переменной х значение —х и по результату сделаем вывод:
В результате получили, что функция не является ни четной, ни нечетной.
- Функция должна пересекаться с координатными осями. Вычислим точки пересечения функции с ними.
Для вычисления точек пересечения с осью Ох, подставим в функцию вместо переменной х число 0:
Функция пересекается с осью Ох в точке с координатами (0; 0).
Вычислим точку пересечения с осью Оу. Для этого подставим вместо переменной у значение 0 и решим полученное уравнение:
или
или
Функция пересекается с осью Оу в двух точках, первая— это пересечение с осью Ох, так как это начало координат — (0; 0). У второй точки координаты (1; 0).
У второй точки координаты (1; 0).
- Поскольку функция степенная, то должна иметь экстремумы. Вычислим их, рассчитав производную:
Запишем производную, как равную нулю, и вычислим корни уравнения:
или
или
Проверим полученные точки на экстремум. Для этого возьмем какую-нибудь точку из каждого полученного промежутка между найденными точками и найдем знак производной на всех полученных промежутках.
Первый промежуток от минус бесконечности до 0. Возьмем точку —1 и рассчитаем для нее производную:
— функция возрастает.
Второй промежуток от 0 до 2/3. Выберем точку 0,5 и вычислим от нее производную:
— функция убывает.
Третий промежуток от 2/3 до + бесконечности. Возьмем точку 1 и вычислим от нее производную:
— функция возрастает на этом промежутке.
Когда функция переходит через точку с абсциссой 0, она изменяет знак производной с + на —. Значит, это точка максимума, а при переходе через точку 2/3 знак производной меняется с — на +, значит, это точка минимума. 2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле
ax2 + bx + c = a(x — x1)(x — x2), где х1 и х2 — корни квадратных уравнений.
Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.
Итак, после разложения на множители функция примет такой вид:
Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.
После сокращения раскрываем оставшиеся скобки.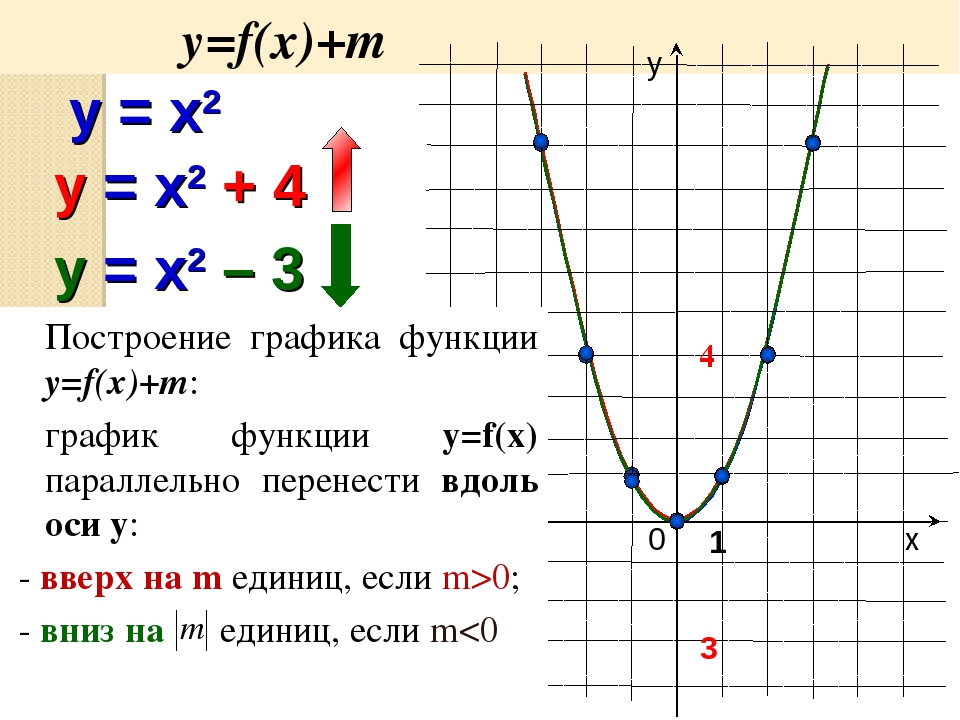
О, чудо! Это квадратичная функция! График — парабола!
Ищем ее вершину О (m; n).
Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.
А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.
В общем, вершина параболы имеет координаты (-0,5; -2,25).
Чертим координатную плоскость и отмечаем вершину.
Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.
Поскольку я мастер — обойдусь без таблицы 🙂
Не забываем про выколотые точки!
В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.
Ответ: 10; -2; -2,25.
P.S. Бывает так, что график нарисован очень криво. Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
Как не ошибиться в координатах выколотых точек? Очень просто. В нашей задаче x ≠ -1 и x ≠ 3. Подставь эти числа в функцию (упрощенную, разумеется), посчитай и найдешь, чему должны быть не равны координаты по игреку (у ≠ -2 и у ≠ 10).
Содержание
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3. Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.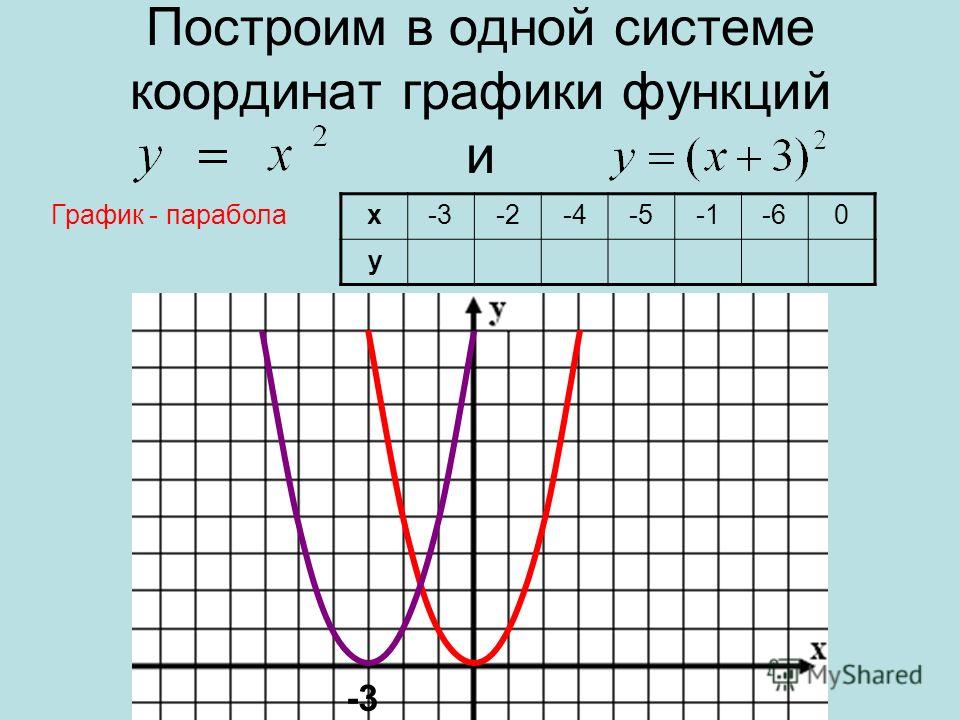
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно. Этот вариант нам подходит.
Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Пользователь публично извинился за критику Xiaomi Mi 10 Ultra
Суд усмотрел в действиях пользователя ложные обвинения в адрес Xiaomi Mi 10 Ultra за что тот и поплатился
В августе прошлого года один из китайцев приобрел два смартфона Xiaomi Mi 10 Ultra. Почти через неделю он выложил в сеть два отзыва о смартфоне и оба в негативном ключе. В частности, он сообщил о том, что за неделю он столкнулся с 8 случаями самопроизвольной перезагрузки и во время длительных игровых сессий смартфон нагревается до 50ºС. В числе недостатков Xiaomi Mi 10 Ultra он назвал плохую автономность и заявил, что «через 2 часа он разряжается».
Читать также: POCO F3 GT или OnePlus Nord 2: какой смартфон будет дешевле
Помимо перегрева среди проблем он перечислил не четкие снимки, медленную зарядку, «тормоза» и поставил под сомнение наличие водозащиты. Эти отзывы не прошли мимо Xiaomi, и она усмотрела в них ложные обвинения. Было решено через суд установить справедливость и опровергнуть обвинения.
Эти отзывы не прошли мимо Xiaomi, и она усмотрела в них ложные обвинения. Было решено через суд установить справедливость и опровергнуть обвинения.
В ходе судебного разбирательства было установлено, что пользователь приобрел смартфоны позже названого им срока. Самое интересно, что один из них он перепродал сразу после покупки. Первый негативный отзыв потребитель оставил спустя один день после покупки, а не через неделю. Любопытно, что его негативные комментарии о Xiaomi Mi 10 Ultra пользователи активно тиражировали и репостили. В итоге клиенты компании были введены в заблуждение и имиджу Xiaomi был нанесен ущерб.
Читать также: График выхода патчей безопасности для смартфонов Xiaomi, Redmi и POCO
Суд встал на сторону Xiaomi и вынес вердикт, которым признал ложными обвинения пользователя и обязал его выплатить в адрес компании $4640. А еще ему пришлось принести публичные извинения, что он на днях и сделал, почему эта история получила широкую огласку. Он признал, что его отзывы не имели под собой объективных оснований.
Он признал, что его отзывы не имели под собой объективных оснований.
Подписывайтесь на Andro News в Telegram, «ВКонтакте» и YouTube-канал.
Источник: gizchina
Автор:
Ирина Кошелева
Дата публикации:
14.07.2021
Поделиться статьей
Последние ролики на YouTube
Парабол
Квадратичная функция — это функция, которую можно записать в форме f (x) = ax2 + bx + c, где a, b и c — действительные числа и a 0. Эта форма называется стандартной формой квадратичной функции.
График квадратичной функции представляет собой U-образную кривую, которая называется параболой .
График уравнения y = x2, показанный ниже, представляет собой параболу. (Обратите внимание, что это квадратичная функция в стандартной форме с a = 1 и b = c = 0. )
)
На графике высшая или низшая точка параболы — это вершина.Вершиной графика y = x2 является (0,0).
Если a> 0 в f (x) = ax2 + bx + c,
парабола открывается вверх . В этом случае вершина является минимальной или самой низкой точкой параболы. Большое положительное значение a дает узкую параболу; положительное значение a, близкое к 0, делает параболу широкой.
Если a <0 в f (x) = ax2 + bx + c, парабола открывается вниз . В этом случае вершина — это максимальная или самая высокая точка параболы.Опять же, большое отрицательное значение a сужает параболу; значение, близкое к нулю, делает его широким.
Для уравнения в стандартной форме значение c дает пересечение графика y .
Линия, проходящая через вершину и разделяющая параболу на две симметричные части, называется осью симметрии.
Уравнение оси симметрии для графика y = ax2 + bx + c, где a ≠ 0, равно x = −b2a
На всех приведенных выше графиках ось симметрии — это ось y, x = 0. На графиках ниже ось симметрии другая (отмечена красным). Обратите внимание, что c по-прежнему дает точку пересечения с y.
На графиках ниже ось симметрии другая (отмечена красным). Обратите внимание, что c по-прежнему дает точку пересечения с y.
Если вы напишете квадратичную функцию типа x = f (y) = ay2 + by + c, где x является функцией y (вместо ay как функции x), вы получите параболу, в которой ось симметрии горизонтальна. .
Обратите внимание, что в этом случае c является точкой пересечения с координатой x. Если а положительно, график открывается вправо; если a отрицательно, график открывается слева.
Пример:
Напишите уравнение оси симметрии и найдите координаты вершины параболы y = −3×2−6x + 4.
Уравнение оси симметрии для графика y = ax2 + bx + c.
х = −b2a
Заменим −3 вместо a и −5 вместо b в уравнении оси симметрии.
х = −− 62 (−3) = −1
Итак, уравнение оси симметрии x = −1.
Поскольку уравнение оси симметрии имеет вид x = −1, а вершина лежит на оси, координата x вершины равна −1.
Чтобы найти y-координату вершины, сначала подставьте −1 вместо x в данном уравнении.
y = −3 (−1) 2−6 (−1) +4
Упростить.
у = −3 + 6 + 4 = 7
Следовательно, координаты вершины параболы равны (−1,7).
См. Также
Ось симметрии параболы
Вершина параболы
Построение квадратных уравнений с использованием оси симметрии
Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet
Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию.График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки, чтобы включить все точки.
Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
Пример
Постройте функцию y = x + 2
Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.
| X | Y = х + 2 | Заказанная пара |
| -2 | -2 + 2 = 0 | (-2, 0) |
| -1 | -1 + 2 = 1 | (-1, 1) |
| 0 | 0 + 2 = 2 | (0, 2) |
| 1 | 1 + 2 = 3 | (1, 3) |
| 2 | 2 + 2 = 4 | (2, 4) |
Теперь вы можете просто построить пять упорядоченных пар в координатной плоскости
На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.
Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.
Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).
Стандартная форма линейного уравнения —
$$ Ax + By = C, \: \: A, B \ neq 0 $$
Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.
$$ 2y-4x = 8 $$
$$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$
$$ 2y = 4x + 8 $$
$$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}}
$
$$ y = 2x + 4 $$
Отсюда вы можете построить уравнение, как в примере выше.
График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)
В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)
Видеоурок
Постройте график линейного уравнения y = 3x — 2
Wolfram | Примеры альфа: построение и графика
Функции
Изобразите функцию одной переменной в виде кривой на плоскости.
Постройте функцию одной переменной:
Укажите явный диапазон для переменной:
Постройте функцию с действительным знаком:
Постройте функцию в логарифмическом масштабе:
График в логарифмическом масштабе:
Другие примеры
3D графики
Изобразите функцию двух переменных как поверхность в трехмерном пространстве.
Постройте функцию от двух переменных:
Укажите явные диапазоны для переменных:
Другие примеры
Уравнения
Постройте набор решений уравнения с двумя или тремя переменными.
Постройте решение уравнения с двумя переменными:
Другие примеры
Неравенства
Постройте набор решений неравенства или системы неравенств.
Постройте область, удовлетворяющую неравенству двух переменных:
Постройте область, удовлетворяющую множеству неравенств:
Другие примеры
Полярные графики
Нарисуйте график точек или кривых в полярной системе координат.
Укажите диапазон для переменной theta:
Другие примеры
Параметрические графики
Графические параметрические уравнения в двух или трех измерениях.
Укажите диапазон для параметра:
Нарисуйте параметрическую кривую в трех измерениях:
Нарисуйте параметрическую поверхность в трех измерениях:
Другие примеры
Другие примеры
Числовые строки
Нанесите набор чисел или значений на числовую линию.
Визуализируйте набор действительных чисел на числовой строке:
Показать несколько наборов в числовой строке:
Другие примеры
Линейные уравнения и функции — Функции и их графики
Функции и их графики
Функция, функция, какова ваша функция? Вы личный тренер, известный шпион, ограничитель дверей или что-то совсем другое? Думаем, последний.
Функция принимает некоторые входные данные, обычно называемые x , в уравнение, f ( x ). Затем x проходит через уравнение, и в конце мы получаем некоторый результат, обычно известный как y . Обратите внимание, что y и f ( x ) на самом деле одно и то же. Может быть, y — знаменитый шпион?
Мы называем x независимой переменной , а y зависимой переменной .Итак, x — это хорошая работа, а x все еще живет дома. Все возможные значения x- — это область , а все возможные значения y- — это диапазон .
Пример задачи
Найдите область и диапазон y = 3 x — 4, где 0 ≤ x <4.
Если бы нам просто дали уравнение, y = 3 x — 4, не говоря больше ни о чем, мы бы сказали, что домен — это все действительные числа. При этом не учитываются воображаемые, фальшивые, бредовые и позерские числа.
При этом не учитываются воображаемые, фальшивые, бредовые и позерские числа.
Однако в данном случае мы не можем выбрать любой размер x , который нам нравится под солнцем. Проблема говорит, что 0 ≤ x <4. Это означает, что наш домен ограничен всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Пакмана).
А теперь ассортимент. Диапазон всех возможных значений: и . В нашем уравнении y = 3 x -4, значения y- — это то, что мы получаем, когда вставляем известные нам значения x-.Давайте составим таблицу, чтобы уточнить диапазон.
Диапазон этой функции: -4 ≤ y <8. Обратите внимание, что y меньше 8, потому что x не может равняться 4, поэтому y также никогда не может быть точно равным 8.
В этом случае диапазон легкий; мы могли бы посмотреть на наименьшее и наибольшее значения x , и они дают нам наименьшее и наибольшее значения y . Что, если бы у нас было что-то вроде y = — x 2 , с -2 < x <2?
Что, если бы у нас было что-то вроде y = — x 2 , с -2 < x <2?
Здесь, если мы просто подключим x = -2 и 2, мы получим y = -4 для них обоих.Однако мы знаем, что y не просто остаются на -4 все время. Мы должны проверить x = 0, чтобы найти, что y = 0, что дает нам диапазон -4 < y <0. Каждый раз, когда график может качаться или опускаться, проверьте различные числа, чтобы найти правильный диапазон.
Теперь поговорим на секунду о функциях построения графиков. Собственно, давайте поговорим и построим график одновременно. Только не просите нас тоже жевать жвачку.
Пример задачи
График y = 3 x — 4, где 0 ≤ x <4.
Ой, это снова ты. Вы собираетесь повторять вещь , не так ли?
Ничего страшного, потому что это означает, что мы уже проделали большую работу. Мы знаем домен и диапазон, и мы отметили несколько моментов.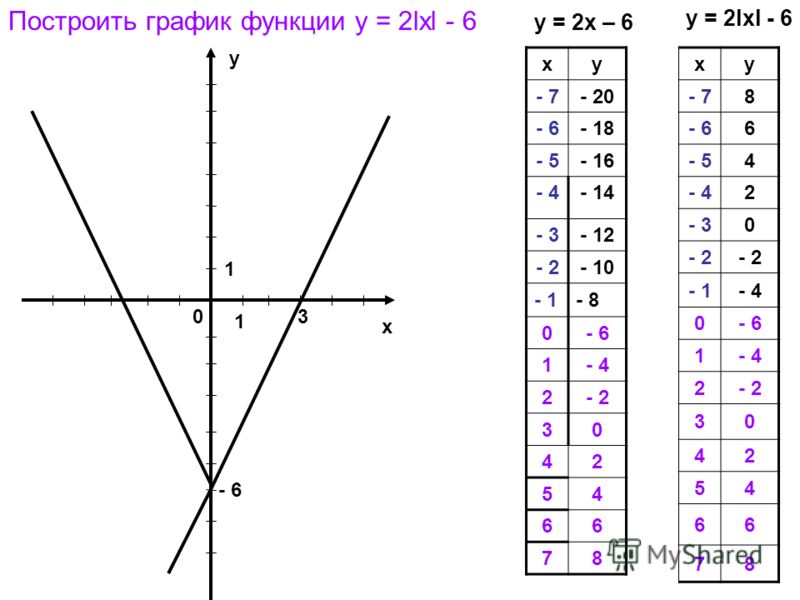
Начните с рисования координатной плоскости . Ось x замерзает на спине, лежа, в то время как ось y стоит по стойке смирно. Они встречаются посередине в исходной точке .Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Мы используем числа на осях для построения точек и линии. Мы делаем заказанных пар , которые выглядят так: ( x , y ). А x всегда вызывает дробовик, поэтому y никогда не попадает первым.
Начиная с начала координат (0, 0), положительные значения x перемещаются вправо, а положительные значения y перемещаются вверх. Переместите оба числа вместе, чтобы построить каждую точку из нашей таблицы.
Видите, как красиво они выстраиваются? Почему они не могли так красиво выглядеть на школьных фотографиях? Что ж, проведем через них черту, пока они сидят неподвижно.
У нас здесь ограниченная область, поэтому мы рисуем только линию, где функция действительно существует. Несуществующие линии на удивление легко рисовать, так что будьте начеку.
Вертикальность
В функциях есть кое-что очень важное. Фактически, это настолько важно, что мы собираемся поместить его в отдельную строку:
На каждые x есть только один y .Другими словами, каждый вход имеет только один выход. Один x входит, один y уходит.
Если уравнение нарушает этот принцип, это не функция. К счастью, нам не нужно подключаться и проверять каждое значение x- , чтобы увидеть, не совпадают ли какие-либо из них со значением y- . Это было бы утомительно и ужасно. Вместо этого мы можем использовать тест вертикальной линии . Какое имя, а?
Возьмем, к примеру, эти графики. Это именно то, на что похоже: рисование вертикальных линий поверх графика.Если какая-либо вертикальная линия может проходить через график более одного раза, тогда уравнение — это , а не как функция.
Смотрите? Мы можем сразу сказать, что является функцией, а что нет. И обратите внимание, что второй график посередине имеет одинаковое значение y- для двух разных значений x- (например, при y = 0). Это полностью разрешено. Мы просто не можем иметь одно и то же значение x- для нескольких значений y- , как на первом и третьем графиках.
С этого момента мы будем иметь дело с линейными уравнениями, которые легко классифицировать как линейные функции (ох, заголовок отсутствует). Это вертикальная линия? Если нет, то да, Вирджиния, это функция.
Функции — Алгебра — Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы алгебры.
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему то же самое значение y , известное на его изображении.
x → Функция → y
Буква f, g или h часто используется для обозначения функции. Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 . Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 . Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или, альтернативно, f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например, y = 3x).
- Если f (x) = 3x, а y является функцией x (т.е. y = f (x)), то значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4. «с.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x). Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Индивидуальные переговоры
Мы говорим, что функция взаимно однозначная , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x).f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Функции составления
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
.
Пример
Если f (x) = x 2 и g (x) = x — 1, то
gf (x) = g (x 2 ) = x 2 — 1
fg (x) = f (x — 1) = (х — 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией является функция, которая обращает действие исходной функции.Например, y = 2x, обратный y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» и сделайте y объектом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяет местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f -1 (x) = ½ (x — 1)
f -1 (x) — стандартное обозначение, обратное f (x).Говорят, что обратное существует тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
.
Обратите внимание, что график f -1 будет отражением f в линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить. Функция непрерывная , если на ее графике нет разрывов. Пример прерывного графа y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция периодическая , если ее график повторяется через равные промежутки времени, этот интервал известен как период.
Функция равна , даже если она не изменяется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция нечетная , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что «растяжение» фактически приводит к сжатию графика, если a — число больше 1]
Пример
График y = | x — 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так что точка V попадет на ось x в 1, а не в 0).
Линейные уравнения
Линейное уравнение — это уравнение для прямой линии
Это все линейные уравнения:
| у = 2х + 1 | ||
| 5x = 6 + 3 года | ||
| у / 2 = 3 — х |
Давайте внимательнее рассмотрим один пример:
Пример:
y = 2x + 1 — это линейное уравнение:
График y = 2x + 1 представляет собой прямую линию
- Когда x увеличивается, y увеличивается в два раза быстрее , поэтому нам нужно 2x
- Когда x равен 0, y уже равен 1.Так что +1 тоже нужен
- Итак: y = 2x + 1
Вот несколько примеров значений:
| x | г = 2х + 1 |
|---|---|
| -1 | y = 2 × (-1) + 1 = -1 |
| 0 | у = 2 × 0 + 1 = 1 |
| 1 | у = 2 × 1 + 1 = 3 |
| 2 | у = 2 × 2 + 1 = 5 |
Убедитесь сами, что эти точки являются частью линии выше!
Различные формы
Существует много способов написания линейных уравнений, но они обычно содержат констант (например, «2» или «c») и должны иметь простые переменных (например, «x» или «y»).
Примеры: Это линейные уравнения:
Но переменные (например, «x» или «y») в линейных уравнениях не имеют НЕ :
Примеры: это
НЕ линейных уравнений:
| y 2 — 2 = 0 | ||
| 3√x — y = 6 | ||
| х 3 /2 = 16 |
Форма пересечения откоса
Самая распространенная форма — уравнение угла наклона прямой:
Пример: y = 2x + 1
- Уклон: м = 2
- Перехват: b = 1
Форма точечного откоса
Еще одна распространенная форма — это форма угла наклона уравнения прямой линии:
y — y 1 = m (x — x 1 ) |
Пример: y — 3 = (¼) (x — 2)
Он имеет вид y — y 1 = m (x — x 1 ) где:
Общая форма
А есть еще Общая форма уравнения прямой:
Ax + By + C = 0 |
| (A и B не могут быть одновременно 0) |
Пример: 3x + 2y — 4 = 0
Он имеет вид Ax + By + C = 0 где:
Есть и другие, менее распространенные формы.
Как функция
Иногда линейное уравнение записывается как функция с f (x) вместо y:
| y = 2x — 3 |
| f (x) = 2x — 3 |
| Это такие же! |
И функции не всегда записываются с использованием f (x):
| y = 2x — 3 |
| w (u) = 2u — 3 |
| ч (z) = 2z — 3 |
| Это тоже такие же! |
Функция идентичности
Существует специальная линейная функция, называемая «Функция идентичности»:
f (x) = x
А вот его график:
Делает 45 ° (уклон 1)
Это называется «Идентификацией», потому что получается , идентичное тому, что входит:
| В | Из |
|---|---|
| 0 | 0 |
| 5 | 5 |
| -2 | −2 |
| …etc | … и т. Д. |
Постоянные функции
Другой особый тип линейной функции — это постоянная функция … это горизонтальная линия:
f (x) = C
Независимо от того, какое значение «x», f (x) всегда равно некоторому постоянному значению.
Использование линейных уравнений
Вы можете прочитать о том, что можно делать с помощью строк:
Как определить, является ли отношение функцией
Обновлено 24 ноября 2020 г.
Крис Дезиел
В математике функция — это правило, которое связывает каждый элемент в одном наборе, называемом доменом, ровно с одним элементом другого. набор, называемый диапазоном.На оси x — y домен представлен на оси x (горизонтальная ось), а домен — на оси y (вертикальная ось). Правило, которое связывает один элемент в домене с более чем одним элементом в диапазоне, не является функцией. Это требование означает, что при построении графика функции нельзя найти вертикальную линию, пересекающую график более чем в одном месте.
TL; DR (слишком долго; не читал)
Отношение является функцией, только если оно связывает каждый элемент в своем домене только с одним элементом в диапазоне.При построении графика функции вертикальная линия будет пересекать ее только в одной точке.
Математическое представление
Математики обычно обозначают функции буквами « f ( x )», хотя любые другие буквы работают точно так же. Вы читаете буквы как « f из x ». Если вы решите представить функцию как g ( y ), вы прочитаете ее как « g из y .2 + 2y + 1 \\ \, \\ p (m) = \ frac {1} {\ sqrt {m — 3}}
Определение домена
Набор чисел, для которых функция «работает» это домен. Это могут быть все числа или определенный набор чисел. Доменом также могут быть все числа, кроме одного или двух, для которых функция не работает. Например, домен для функции
f (x) = \ frac {1} {2-x}
— это все числа, кроме 2, потому что, когда вы вводите два, знаменатель равен 0, а результат не определен.2}
, с другой стороны, — это все числа, кроме +2 и −2, потому что квадрат обоих этих чисел равен 4.
Вы также можете определить область определения функции, посмотрев на ее график. Начиная с крайнего левого угла и двигаясь вправо, проведите вертикальные линии через ось x . Домен — это все значения x , для которых линия пересекает график.
Когда связь не является функцией?
По определению функция связывает каждый элемент в домене только с одним элементом в диапазоне.Это означает, что каждая вертикальная линия, проведенная через ось x , может пересекать функцию только в одной точке. Это работает для всех линейных уравнений и уравнений более высокой степени, в которых только член x возведен в степень. Это не всегда работает для уравнений, в которых члены x и y возведены в степень. Например, x 2 + y 2 = a 2 определяет круг. Вертикальная линия может пересекать круг более чем в одной точке, поэтому это уравнение не является функцией.
Как правило, отношение f ( x ) = y является функцией, только если для каждого значения x , которое вы подключаете к нему, вы получаете только одно значение для y . Иногда единственный способ узнать, является ли данное отношение функцией или нет, — это попробовать различные значения для x, чтобы увидеть, дают ли они уникальные значения для y .
Примеры: Определяют ли функции следующие уравнения?
y = 2x +1
Это уравнение прямой линии с наклоном 2 и пересечением 1 y , поэтому IS является функцией.
