Содержание
Функция y = x 2 и её график — презентация на Slide-Share.ru 🎓
1
Первый слайд презентации: Функция y = x 2 и её график
Урок алгебры в 7 классе.
Изображение слайда
2
Слайд 2: Величие человека в его способности мыслить»
Блез Паскаль
Изображение слайда
3
Слайд 3: Фалес:
— Что есть больше всего на свете?
— Пространство.
Что быстрее всего?
Ум.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого результата.
Изображение слайда
4
Слайд 4
(2;-2)
(- 2;2)
(1;2)
(-2; 2)
(-1;1)
(1;-1)
(2;2)
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Ф
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
У
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Н
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.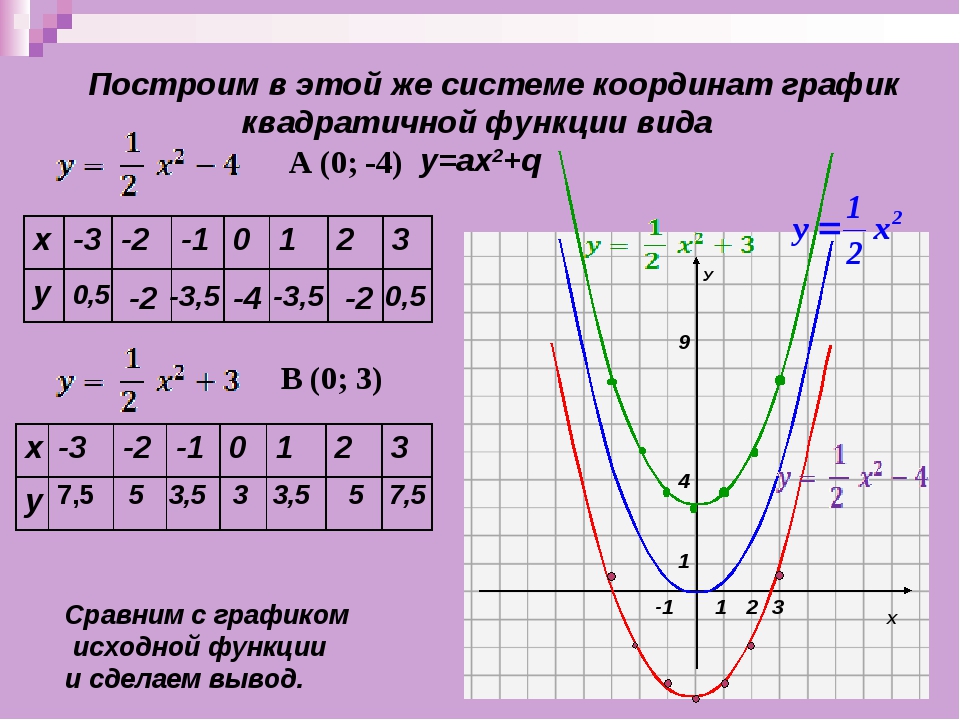
К
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Ц
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
И
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Я
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Изображение слайда
5
Слайд 5
Объясните термины
Функция
Область определения
Аргумент
График функции
Линейная функция
Изображение слайда
6
Слайд 6
Укажите
область определения функции:
y = 16 – 5 x
х ≠ 0
х ≠ 7
х – любое число
Изображение слайда
7
Слайд 7: Зависимость площади квадрата от длины его стороны
квадратичная функция
Зависимая
переменная
Независимая
переменная
y = x 2
y
x
Изображение слайда
8
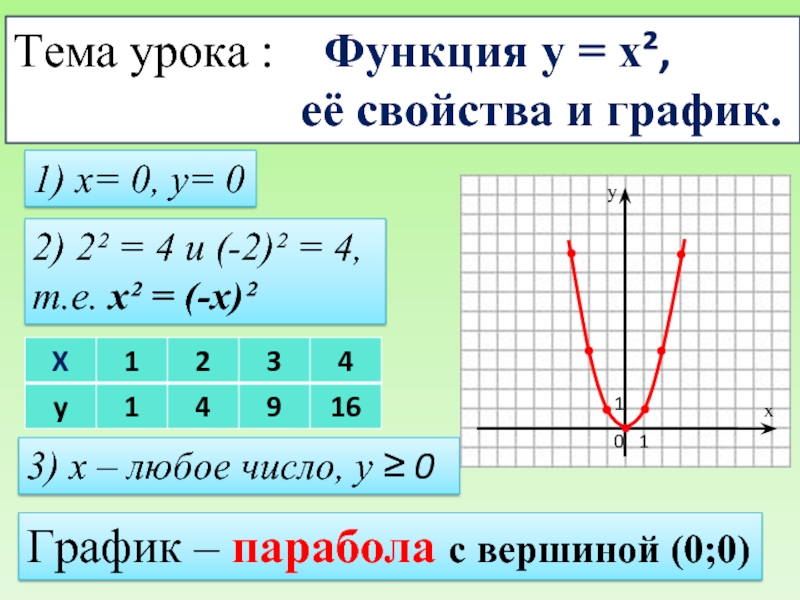
Слайд 8: Функция y = x 2 и её график
Изображение слайда
9
Слайд 9: Цели урока:
рассмотреть график и свойства функции у = х 2 ;
научиться строить и «читать» график данной функции.
Изображение слайда
10
Слайд 10
Ключом ко всякой науке является вопросительный знак?
Оноре де Бальзак
Изображение слайда
11
Слайд 11
Функция y = x 2
Математическое исследование
Изображение слайда
12
Слайд 12
х
— 3
— 2, 5
— 2
— 1,5
— 1
— 0,5
0
y
Заполните таблицу значений функции y = x 2 :
х
0
0, 5
1
1,5
2
2,5
3
y
9
6,25
4
2,25
1
0,25
0
0
0,25
1
2,25
4
6,25
9
Изображение слайда
13
Слайд 13
Постройте
график
функции y = x 2
парабола
Изображение слайда
14
Слайд 14
Древнегреческий математик
Аполлоний Пергский
( Перге, 262 до н. э. — 190 до н.э.)
э. — 190 до н.э.)
разрезав конус, линию среза назвал параболой, что в переводе с греческого означает «приложение» или «притча», о чём математик и написал в восьмитомнике «Конические сечения».
И долгое время параболой называли лишь линию среза конуса, пока не появилась квадратичная функция.
Историческая справка
Изображение слайда
15
Слайд 15
Траектория камня, брошенного под углом к горизонту
Знаете ли вы?
Изображение слайда
16
Слайд 16
Перевал Парабола
Невероятно,
но факт!
Изображение слайда
17
Слайд 17: Свойства функции y = x 2
Изображение слайда
18
Слайд 18
Область определения функции :
х – любое число.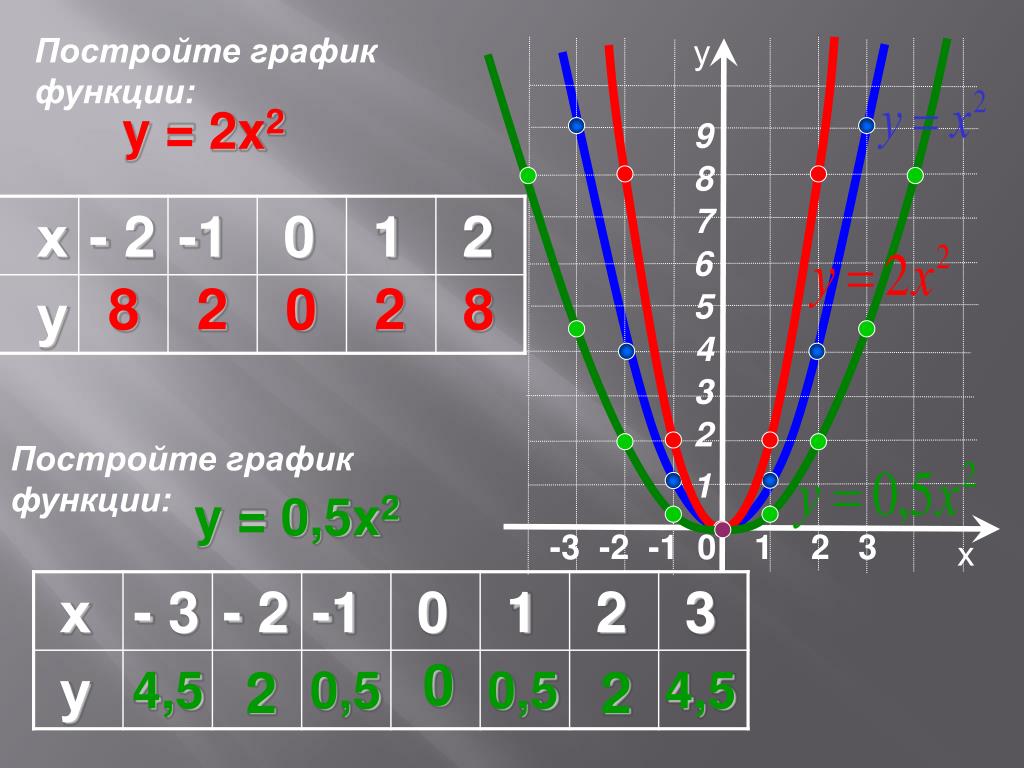
Область значений функции :
все значения у ≥ 0.
Изображение слайда
19
Слайд 19
Если х = 0, то у = 0.
График функции проходит через начало координат.
Изображение слайда
20
Слайд 20
Если х ≠ 0,
то у > 0.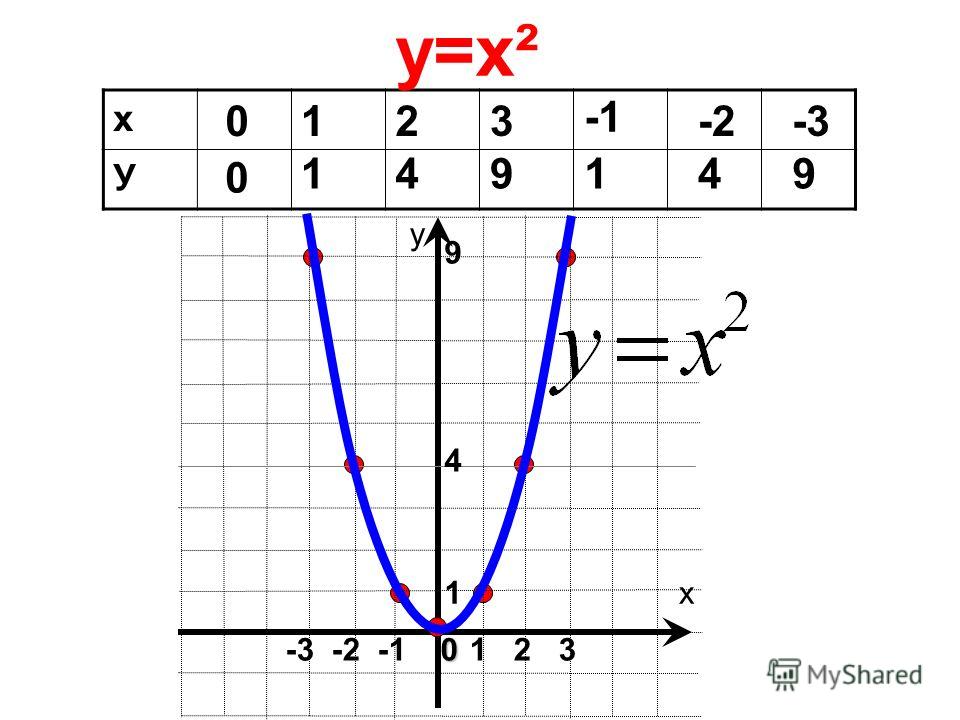
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
I
II
Изображение слайда
21
Слайд 21
Противоположным значениям х соответствует одно и то же значение у.
График функции симметричен относительно оси ординат.
(- х) 2 = х 2 при любом х
Изображение слайда
22
Слайд 22
Геометрические свойства параболы
Обладает симметрией
Ось разрезает параболу на две части: ветви параболы
Точка (0; 0) – вершина параболы
Парабола касается оси абсцисс
Ось симметрии
Изображение слайда
23
Слайд 23
«Знание – орудие,
а не цель»
Л.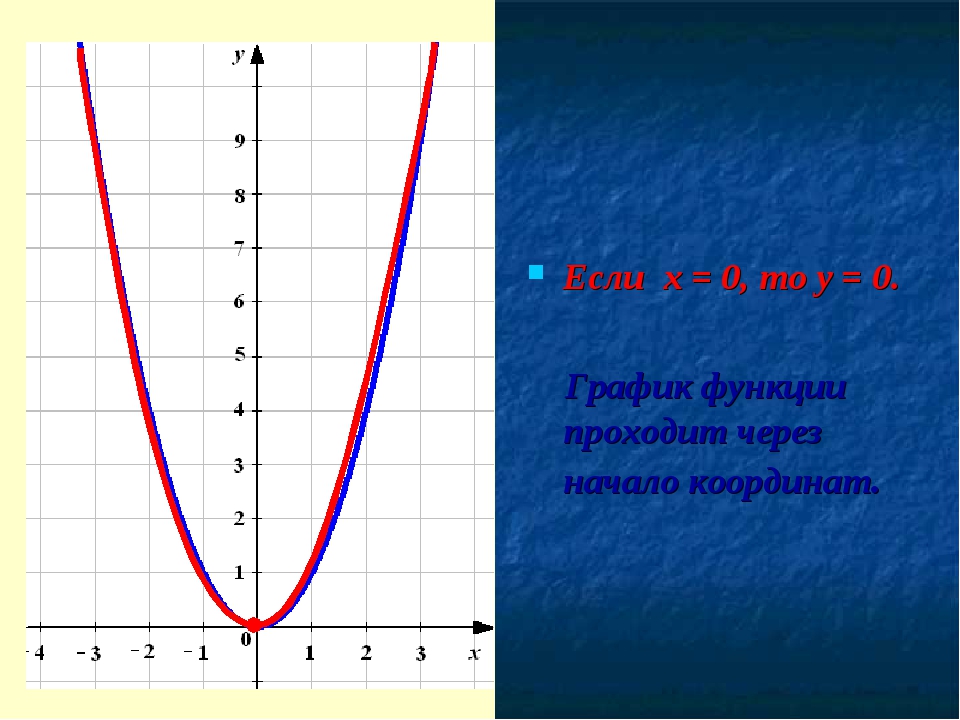 Н. Толстой
Н. Толстой
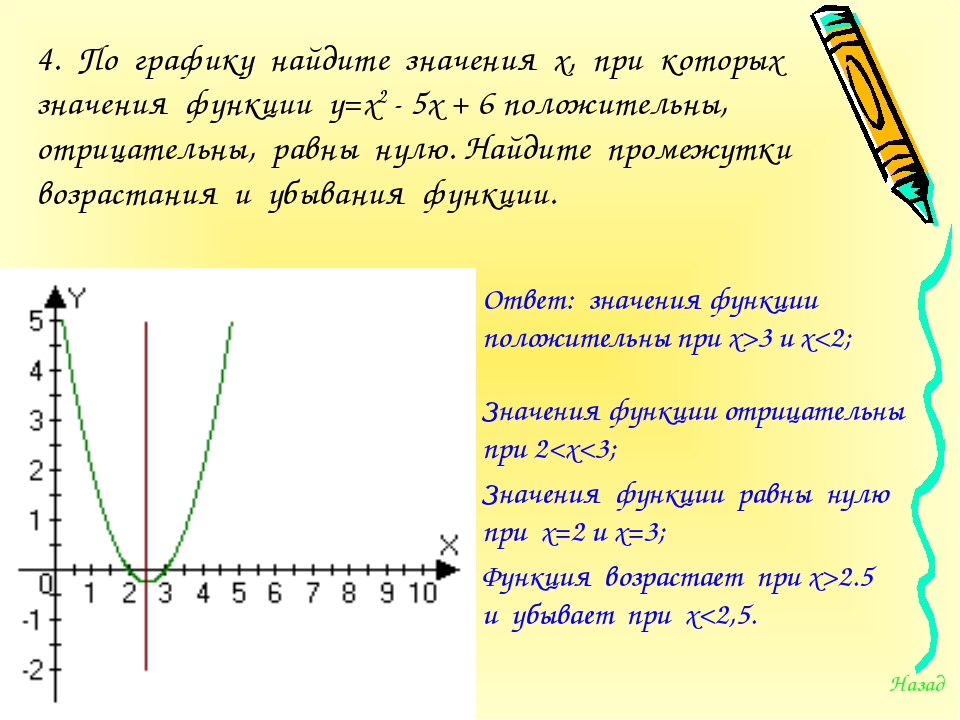
Найдите у, если:
х ≈ -2,5
х = — 2
у ≈ 1,9
у ≈ 6,7
у ≈ 9,6
х = 1,4
х = — 2,6
х = 3,1
у = 6
у = 4
Найдите х, если:
— 1,4
— 3, 1
х ≈ 2,5
х = 2
Изображение слайда
24
Слайд 24
Найдите
несколько значений х, при которых значения функции :
меньше 4
больше 4
Изображение слайда
25
Слайд 25
При каких значениях а точка Р(а; 64) принадлежит графику функции у = х 2.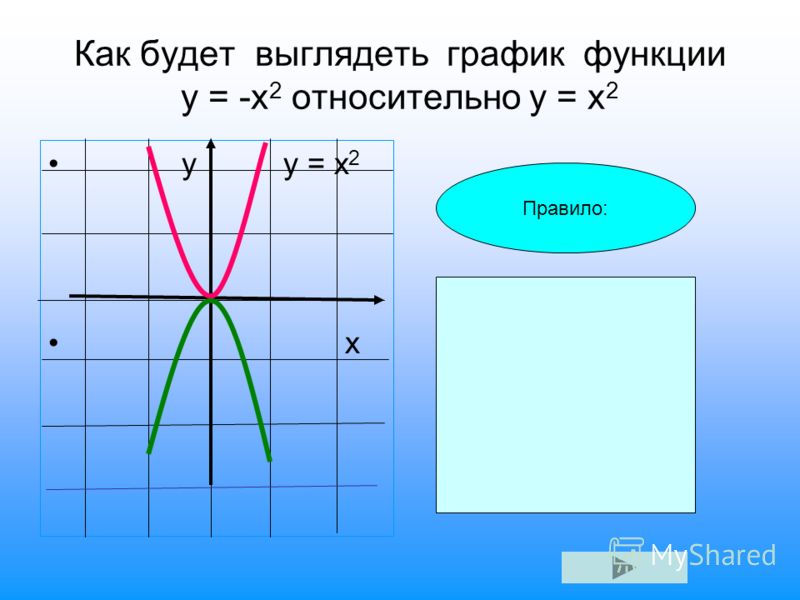
Принадлежит ли графику функции у = х 2 точка :
Не выполняя вычислений, определите, какие из точек не принадлеж ат графику функции у = х 2 :
P(-18; 324)
R(-99; -9081)
S(17; 279)
(-1; 1)
(0; 8)
(-2; 4)
(3; -9)
(1,8; 3,24)
(16; 0)
а = 8; а = — 8
принадлежит
не принадлежит
не принадлежит
Изображение слайда
26
Слайд 26
Решите графически уравнение:
х 2 = 5
х 2 = — 1
x 2 = х +1
y = — 1
y = x + 1
y = х 2
y = 5
нет решений
х ≈ — 2,2; х ≈ 2,2
х ≈ — 0,6; х ≈ 1,6
Изображение слайда
27
Слайд 27: Цели урока:
рассмотреть график и свойства функции у = х 2 ;
научиться строить и «читать» график данной функции.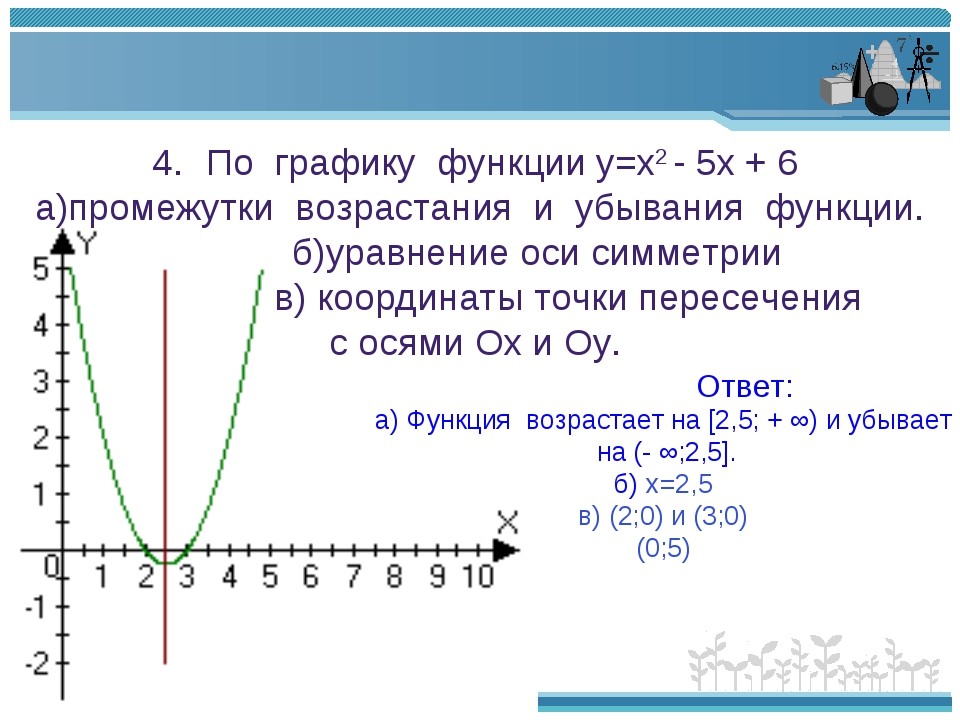
Изображение слайда
28
Последний слайд презентации: Функция y = x 2 и её график
Я узнал …
Я почувствовал ….
Я увидел….
Я сначала испугался, а потом ….
Я заметил, что ….
Я сейчас слушаю и думаю …..
Мне интересно следить за ….
Изображение слайда
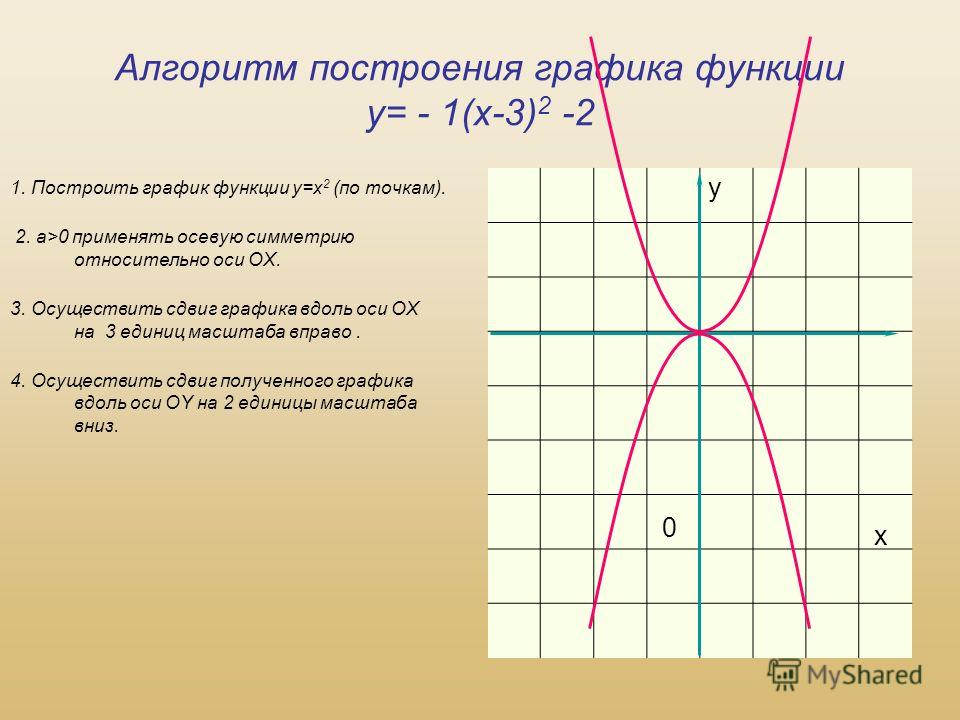
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
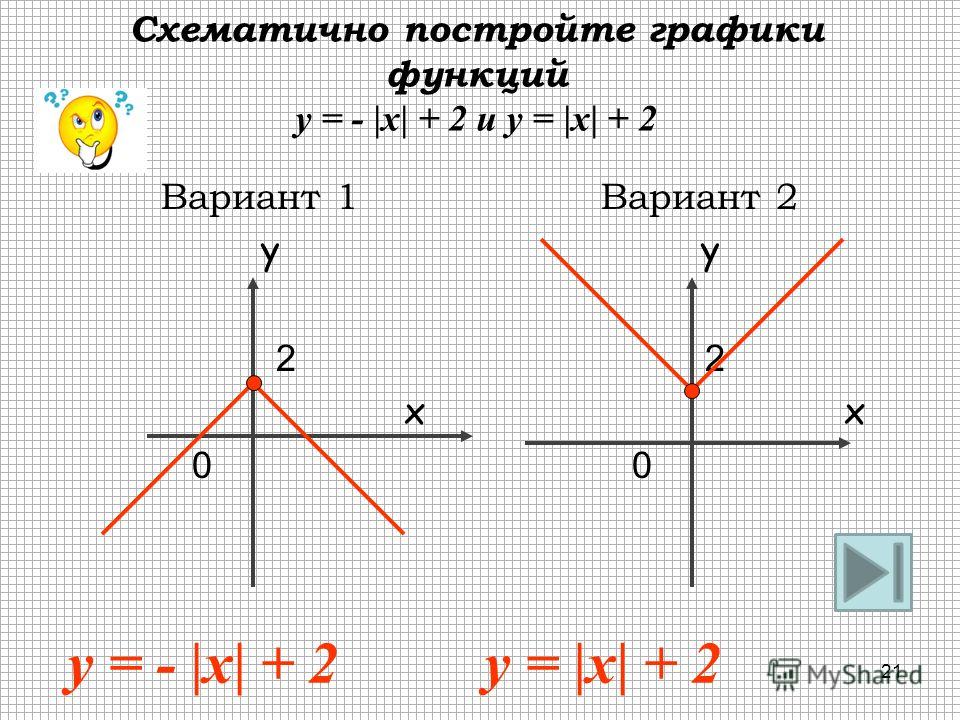
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
Сдвиги графиков функций
☰
Изменение значения k влияет на вид графика (степень крутизны в случае параболы), расположение ветвей в координатных четвертях и др. Однако точкой, через которую можно провести ось симметрии графиков, является точка O с координатами (0; 0).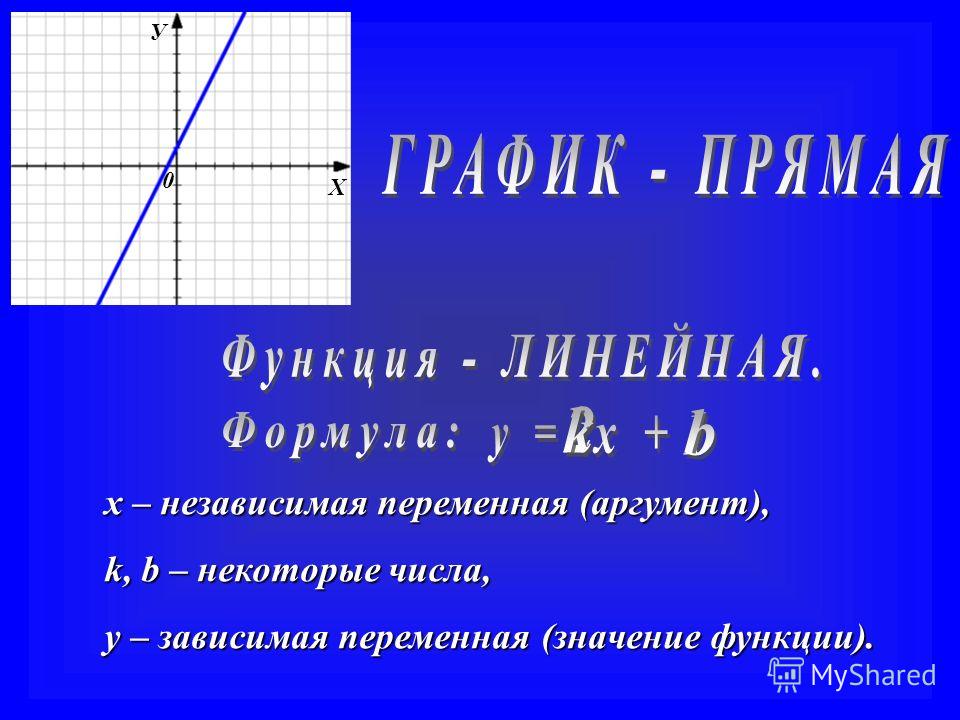
Если же рассматривать функций, подобные перечисленным выше, у которых к переменной x или ко всей исходной функции прибавляется (или вычитается) какое-либо число, то графики этих функций остаются такими же как у исходных, однако смещаются относительно точки (0; 0).
Если обозначить исходные функции как y = f(x), то прибавление к x числа дает функции вида y = f(x+l), а прибавление ко всей исходной функции значения дает вид y = f(x) + m.
Например, если исходная функция y = 2x2, то примером первого типа будет функция y = 2(x+5)2, а второго — y = 2x2 + 5.
Для функций вида y = f(x+l) график смещается влево на l единиц, если l прибавляется. Если же l вычитается, то график смещается вправо. Действительно, представим параболу функции y = x2 и сравним ее с функцией y = (x+1)2. Когда x = 1, то для первой функции y = 1, а для второй — y = 4. Когда x = 0, для первой y = 0, для второй y = 1. Когда x = –1, для первой y = 1, для второй y = 0.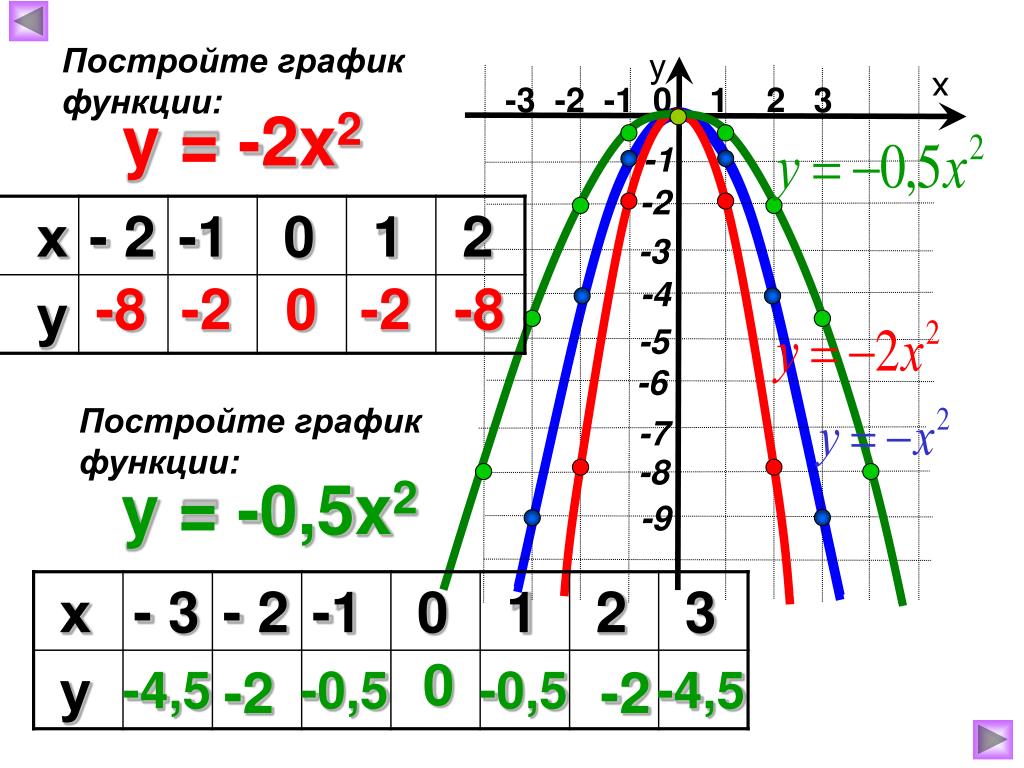
То есть график второй функции касается оси x в точке (–1; 0). Это значит, что график смещен влево по сравнению с исходным на 1.
Для функций вида y = f(x) + m график соответствующей функции y = f(x) смещается на m единиц, но уже по вертикальной оси (ось y). Здесь если m прибавляется, то график сдвигается вверх. Если m вычитается, то график сдвигается вниз.
Рассмотрим ту же параболу y = x2 и функцию y = x2 + 1. Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно. Это значит, что парабола имеет точку симметрии с координатами (0; 1), т. е. сдвинута от исходной вверх на 1.
«Смешанные» функции вида y = f(x + l) + m сдвигаются вдоль оси x и y. Вдоль оси x они сдвигаются на l, а вдоль y — на значение m.
График функции y = x 2
Как называется график функции y = x 2?
Сформулируйте свойства функции y = x
Как называется точка пересечения
параболы y = x 2
с её осью симметрии ?
2
y ax
2
4.
 Наша задача:
Наша задача:
Рассмотреть графики функций y = ax2.
Изучить свойства функции y = ax2
Научиться строить графики
функции y = ax2
y 2x
x
2
-3
-2
-1
0
1
2
3
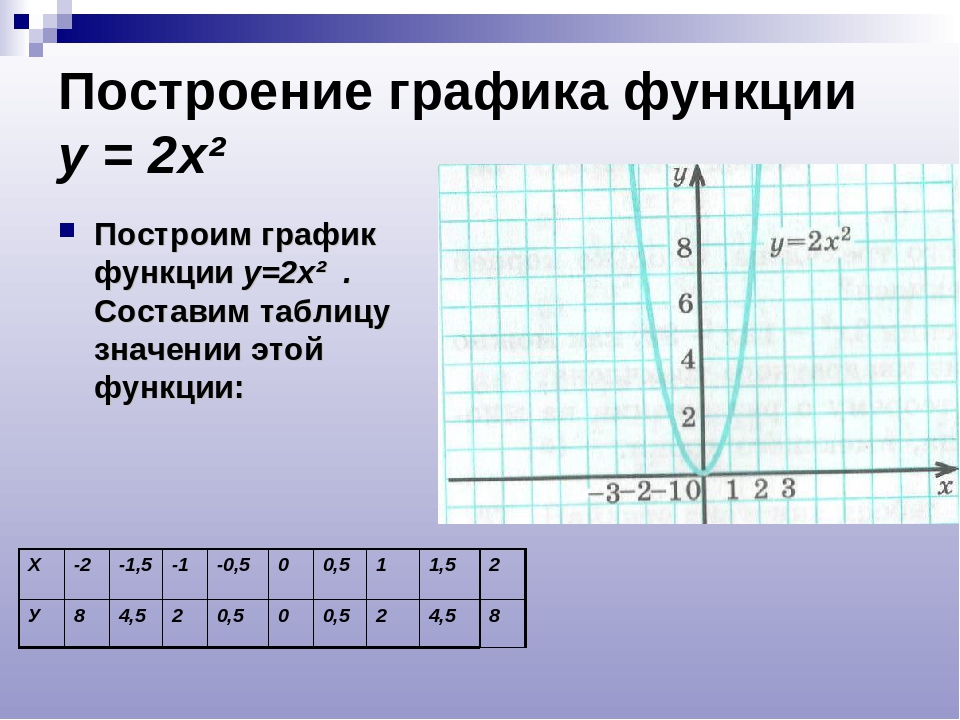
y 2x 2 18
8
2
0
2
8
18
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
1 2
3 4
5
6 7
X
8 9 10
10
Y
y=2×2
9
8
7
6
5
y=x2
4
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
X
1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
График функции y = 2×2 получается
растяжением
-9
графика функции y = x2 от-10оси Ox вдоль оси Oy
в 2 раза.
9
10
y 1/ 2x
2
x
-3
-2
-1
0
1
2
3
y 1/ 2×2
4,5
2
0,5
0
0,5
2
4,5
10
Y
y=x2
9
8
7
6
5
4
y = ½ x2
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
X
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
-6
-7
-8
-9
-10
График функции y = 1/2×2 получается сжатием
графика функции y = x2 к оси Ox вдоль оси Oy в 2
раза.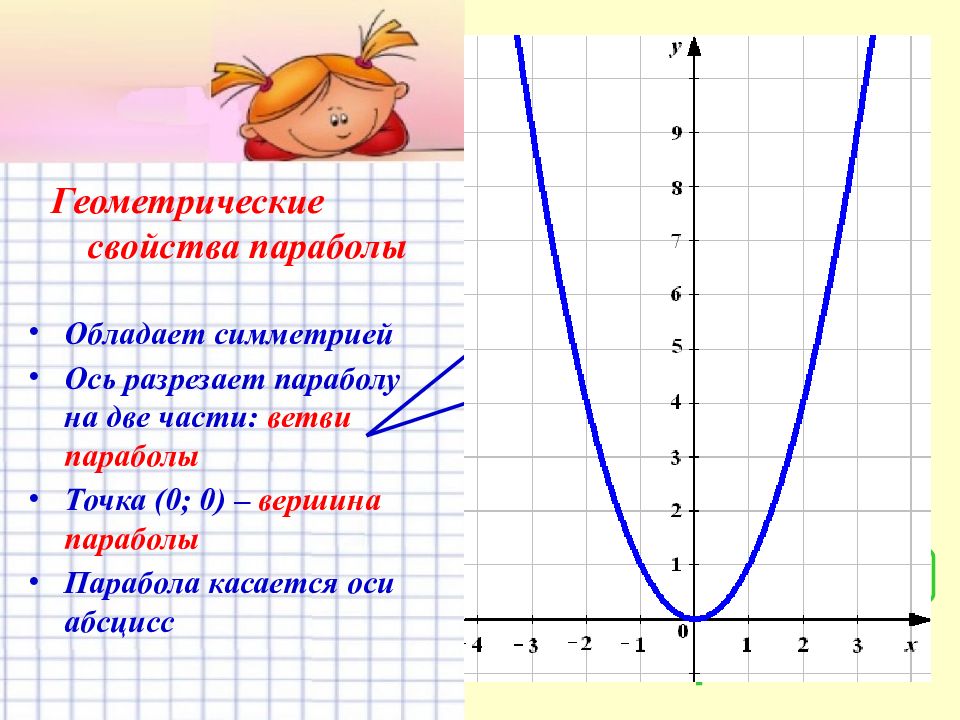
y x
x
2
-3
-2
-1
0
1
2
3
y x 2 -9
-4
-1
0
-1
-4
-9
10
Y
9
8
7
y=x2
6
5
4
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1 0
-1
X
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
-6
y=-x2
-7
-8
-9
-10
График функции y =
получается симметричным
отображением графика функции y = x2 относительно
оси Ox.
-x2
Вывод:
График функции y = a x 2 при любом
a ≠ 0 также называется параболой.
При a > 0 ветви параболы направлены
вверх,
а при a
направлены вниз.
С помощью графика функции y = -2×2 решить
неравенство: — 2 x2 ≤ — 8
10
Y
Ответ: x € (- ∞; — 2] U [2; +∞)
9
8
7
6
5
4
3
2
1
-10 -9
-8
-7
-6
-5
-4
-3
-2
-1 0
-1
X
1
2
3
4
5
6
7
8
9
-2
-3
-4
y = -2×2
-5
-6
-7
-8
-9
-10
y=-8
10
№ 599 (3)
§37 № 595
Хочется надеяться, что
сегодняшний урок
разбудит у вас жажду
новых познаний, ведь
«великий океан
истины по-прежнему
расстилается перед
вами не
исследованным до
конца».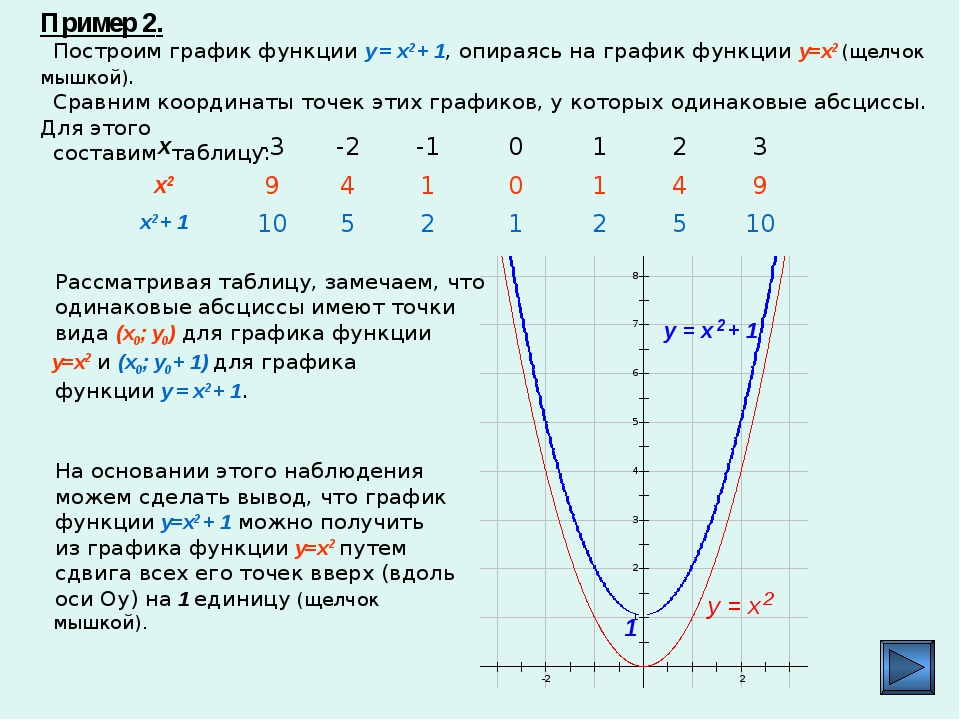
Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных
параметрически, то есть в виде
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе
Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. Выражение abs(x) эквивалентно |x|. Если функция содержит модуль подмодулем, то пользуйтесь abs(). Например, если вы хотите построить график функции |1-x+|x+5||,то нужно вводить abs(1-x+abs(x+5)). 3 дают 3 дают x в третьейстепени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа b по основанию a |
exp() | Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .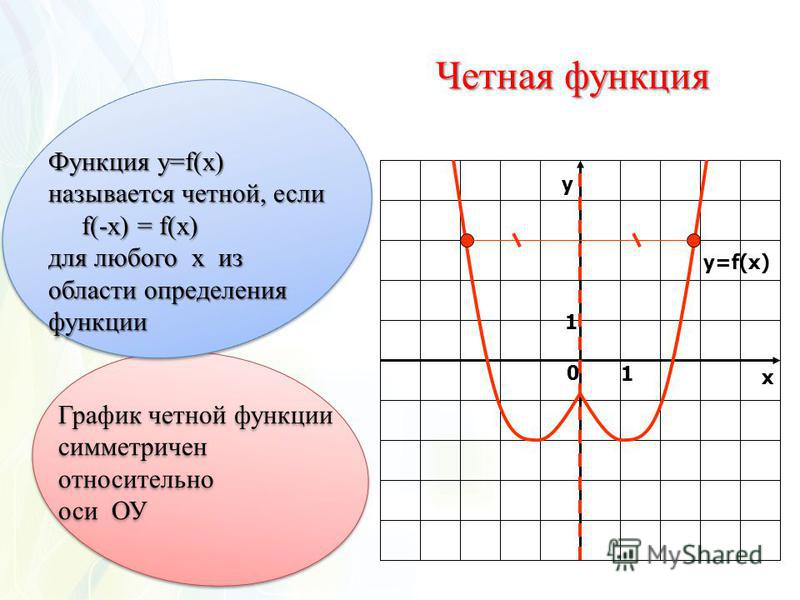
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах
(например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию
с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет
носить
ваше имя ;).
Графики линейных неравенств
Это график линейного неравенства:
Неравенство y ≤ x + 2
Вы можете увидеть линию y = x + 2, а заштрихованная область — это место, где y меньше или равно x + 2
Линейное неравенство
Линейное неравенство похоже на линейное уравнение (например, y = 2x + 1 ) …
… но у него будет неравенство типа <,>, ≤ или ≥ вместо = .
Как построить график линейного неравенства
Сначала нарисуйте линию «равно», затем заштрихуйте нужную область.
Есть три шага:
- Измените уравнение так, чтобы «y» находилось слева, а все остальное — справа.
- Постройте линию « y = » (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y < или y> )
- Затенение над линией для «больше чем» ( y> или y≥ )
или ниже линии для «меньше чем» ( y < или y≤ ).
Попробуем несколько примеров:
Пример: y≤2x-1
1. Неравенство уже имеет «y» слева и все остальное справа, поэтому нет необходимости переставлять
2. График y = 2x-1 (сплошная линия, потому что y≤ включает , равное )
3. Заштрихуйте область ниже (поскольку y на меньше или равно)
Пример: 2y — x ≤ 6
1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: 2y — x ≤ 6
Добавьте x к обеим сторонам: 2y ≤ x + 6
Разделить все на 2: y ≤ x / 2 + 3
2. Теперь постройте y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное )
Теперь постройте y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное )
3. Заштрихуйте область ниже (поскольку y на меньше или равно)
Пример: y / 2 + 2> x
1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: y / 2 + 2> x
Вычтем 2 с обеих сторон: y / 2> x — 2
Умножить все на 2: y> 2x — 4
2. Теперь постройте график y = 2x — 4 (пунктирная линия, потому что y> не включает равно)
3. Закрасьте область выше (поскольку y на больше )
Пунктирная линия показывает, что неравенство не включает линию y = 2x-4 .
Два особых случая
У вас также может быть горизонтальная или вертикальная линия:
| Здесь показано, где y меньше 4 (от линии y = 4 вниз, но не включая ее) Обратите внимание, что у нас есть пунктирная линия, чтобы показать, что она не включает где y = 4 | В этом даже нет y! Он имеет линию x = 1 и закрашен для всех значений x, превышающих (или равных) 1 |
Использование преобразований в графические функции
Вертикальный и горизонтальный перевод
Когда график функции изменяется по внешнему виду и / или местоположению, мы называем это преобразованием. Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.
Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.
Вертикальный сдвиг — жесткое преобразование, которое сдвигает график вверх или вниз.- жесткое преобразование, которое сдвигает граф вверх или вниз относительно исходного графа. Это происходит, когда к какой-либо функции добавляется константа. Если мы добавим положительную константу к каждой координате y , график сдвинется вверх. Если мы добавим отрицательную константу, график сместится вниз. Например, рассмотрим функции g (x) = x2−3 и h (x) = x2 + 3. Начните с вычисления некоторых значений независимой переменной x .
Теперь постройте точки и сравните графики функций g и h с основным графиком f (x) = x2, который показан ниже с помощью пунктирной серой кривой.
Функция g сдвигает основной график на 3 единицы вниз, а функция h сдвигает основной график на 3 единицы вверх. В общем, это описывает вертикальные переводы; если k — любое положительное действительное число:
Вертикальный сдвиг вверх k единиц: | F (x) = f (x) + k |
Вертикальный сдвиг вниз k единиц: | F (x) = f (x) −k |
Пример 1
Нарисуйте график функции g (x) = x + 4.
Решение:
Начните с базовой функции, определенной как f (x) = x, и сдвиньте график на 4 единицы вверх.
Ответ:
Горизонтальный сдвиг — жесткое преобразование, которое сдвигает график влево или вправо. — жесткое преобразование, которое сдвигает граф влево или вправо относительно исходного графа. Это происходит, когда мы добавляем или вычитаем константы из координаты x перед применением функции.Например, рассмотрим функции, определенные как g (x) = (x + 3) 2 и h (x) = (x − 3) 2, и создадим следующие таблицы:
Здесь мы складываем и вычитаем координаты x , а затем возводим результат в квадрат. Это дает горизонтальный перевод.
Обратите внимание, что это противоположное тому, что вы могли ожидать. В общем, это описывает горизонтальные переводы; если h — любое положительное действительное число:
Горизонтальный сдвиг влево ч единиц: | F (x) = f (x + h) |
Горизонтальный сдвиг вправо ч единиц: | F (x) = f (x − h) |
Пример 2
Нарисуйте график функции g (x) = (x − 4) 3.
Решение:
Начните с базовой функции кубирования, определяемой как f (x) = x3, и сдвиньте график на 4 единицы вправо.
Ответ:
Часто встречаются комбинации переводов.
Пример 3
Нарисуйте график функции g (x) = | x + 3 | −5.
Решение:
Начните с функции абсолютного значения и примените следующие преобразования.
y = | x | Базовая функция y = | x + 3 | Горизонтальный сдвиг влево на 3 единицы y = | x + 3 | −5 Вертикальный сдвиг вниз на 5 единиц
Ответ:
Порядок, в котором мы применяем горизонтальный и вертикальный переводы, не влияет на окончательный график.
Пример 4
Нарисуйте график функции g (x) = 1x − 5 + 3.
Решение:
Начните с обратной функции и определите переводы.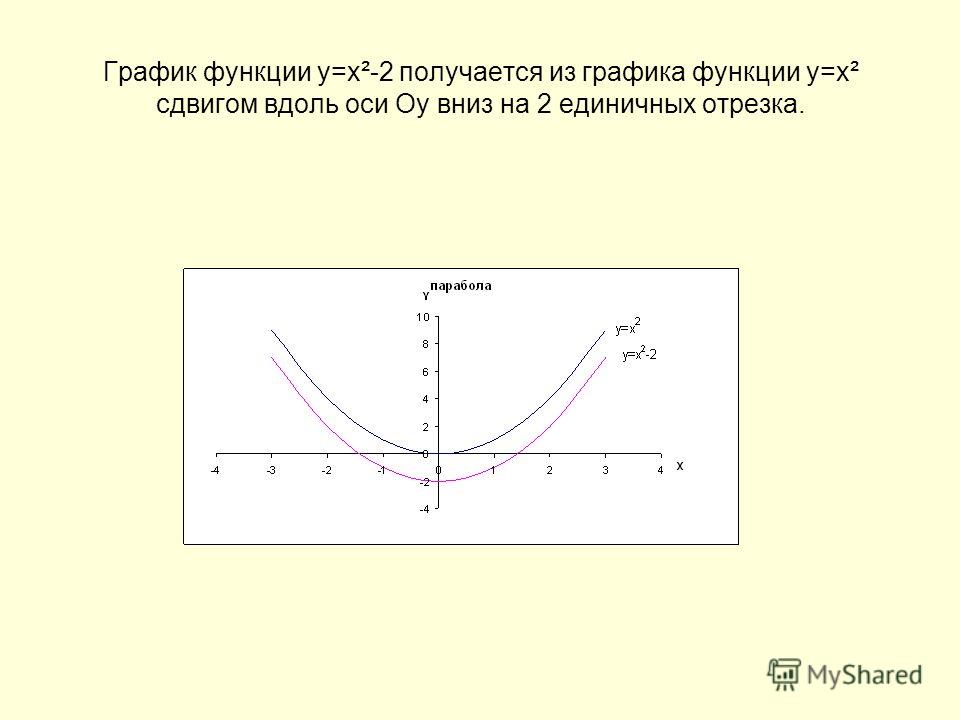
y = 1x Основная функция y = 1x − 5 Горизонтальный сдвиг вправо 5 единиц y = 1x − 5 + 3 Вертикальный сдвиг вверх на 3 единицы
Позаботьтесь о смещении вертикальной асимптоты с оси y на 5 единиц вправо и смещении горизонтальной асимптоты от оси x вверх на 3 единицы.
Ответ:
Попробуй! Нарисуйте график функции g (x) = (x − 2) 2 + 1.
Ответ:
Отражения
Отражение Преобразование, которое создает зеркальное отображение графика вокруг оси. представляет собой преобразование, при котором зеркальное отображение графика создается вокруг оси. В этом разделе мы рассмотрим отражения относительно осей x и y . График функции отражается относительно оси x- , если каждая координата y умножается на -1.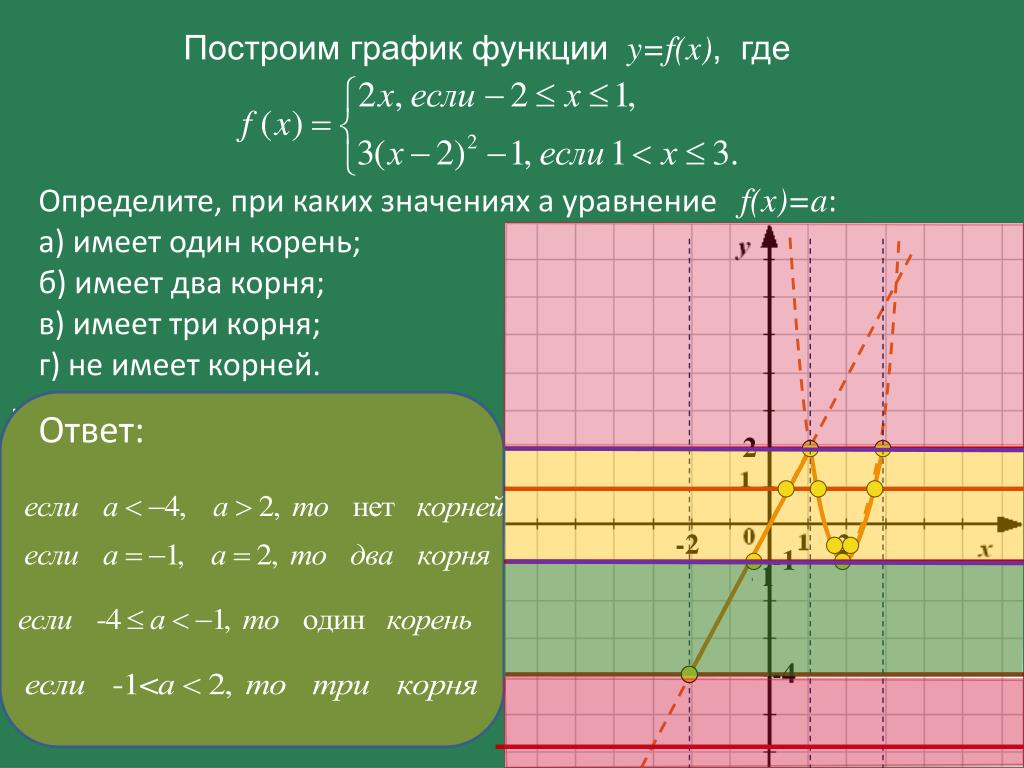 График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.
График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.
Сравните график g и h с базовой функцией квадратного корня, определяемой f (x) = x, показанной ниже серым пунктиром:
Первая функция g имеет отрицательный множитель, который появляется «внутри» функции; это дает отражение относительно оси y .Вторая функция h имеет отрицательный фактор, который появляется «вне» функции; это дает отражение около оси x . В целом верно, что:
Отражение относительно оси y : | F (x) = f (−x) |
Отражение относительно оси x : | F (x) = — f (x) |
При рисовании графиков с отражением сначала рассмотрите отражение, а затем примените вертикальный и / или горизонтальный перенос.
Пример 5
Нарисуйте график функции g (x) = — (x + 5) 2 + 3.
Решение:
Начните с функции возведения в квадрат, а затем определите преобразования, начиная с любых отражений.
y = x2 Основная функция. Y = −x2 Отражение относительно оси x. Y = — (x + 5) 2 Сдвиг по горизонтали влево на 5 единиц. Y = — (x + 5) 2 + 3 Сдвиг по вертикали на 3 единицы.
Используйте эти переводы, чтобы нарисовать график.
Ответ:
Попробуй! Нарисуйте график функции g (x) = — | x | +3.
Ответ:
Расстояния
Горизонтальные и вертикальные смещения, а также отражения называются жесткими преобразованиями, потому что форма основного графа остается неизменной или жесткой.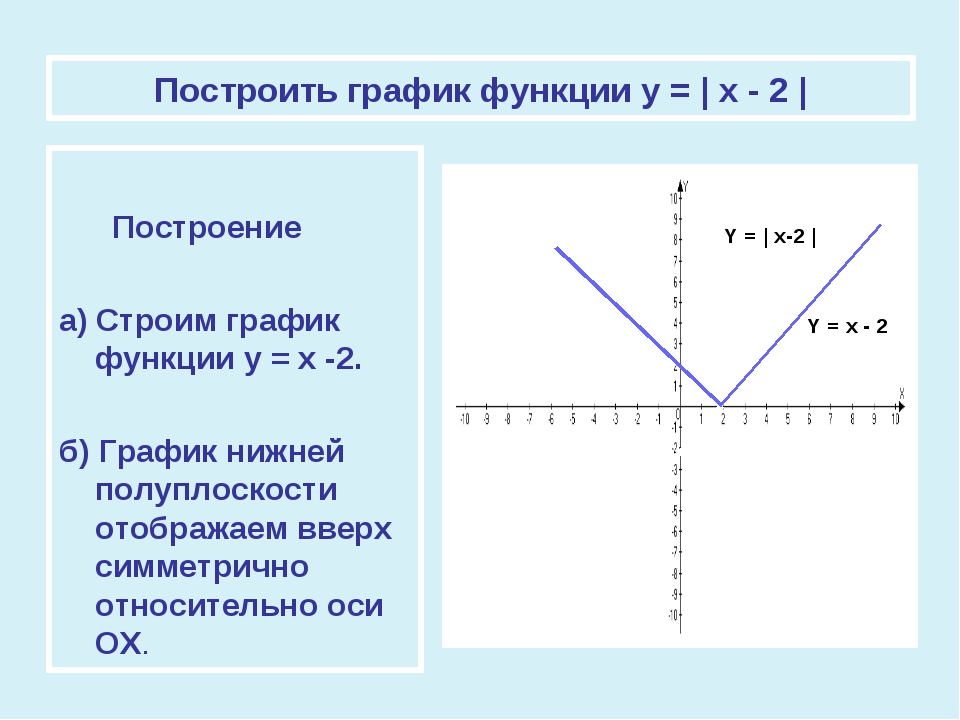 Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, по-видимому, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.
Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, по-видимому, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.
Сравните график g и h с базовой функцией возведения в квадрат, определяемой f (x) = x2, показанной ниже серым пунктиром:
Функция g круче, чем базовая функция возведения в квадрат, и ее график выглядит растянутым по вертикали. Функция h не такая крутая, как базовая функция возведения в квадрат, и, похоже, растянута по горизонтали.
В общем имеем:
Если множитель a представляет собой ненулевую дробь между -1 и 1, он растянет график по горизонтали. В противном случае график будет растянут по вертикали. Если коэффициент a отрицательный, то это также приведет к отражению.
В противном случае график будет растянут по вертикали. Если коэффициент a отрицательный, то это также приведет к отражению.
Пример 6
Нарисуйте график функции g (x) = — 2 | x − 5 | −3.
Решение:
Здесь мы начинаем с произведения −2 и основной функции абсолютного значения: y = −2 | x |.Это приводит к отражению и расширению.
xyy = −2 | x | ← Расширение и отражение − 1−2y = −2 | −1 | = −2⋅1 = −200y = −2 | 0 | = −2⋅0 = 01−2y = −2 | 1 | = −2⋅1 = −2
Используйте точки {(−1, −2), (0, 0), (1, −2)}, чтобы построить график функции отражения и расширения y = −2 | x |. Затем переместите этот график на 5 единиц вправо и на 3 единицы вниз.
y = −2 | x | Базовый график с растяжением и отражением относительно оси x. Y = −2 | x − 5 | Сдвиг вправо на 5 единиц. Y = −2 | x − 5 | −3 Сдвиг на 3 единицы вниз.
Ответ:
Таким образом, с учетом положительных вещественных чисел h и k :
Вертикальный сдвиг вверх k единиц: | F (x) = f (x) + k |
Вертикальный сдвиг вниз k единиц: | F (x) = f (x) −k |
Горизонтальный сдвиг влево ч единиц: | F (x) = f (x + h) |
Горизонтальный сдвиг вправо ч единиц: | F (x) = f (x − h) |
Отражение относительно оси y : | F (x) = f (−x) |
Отражение относительно оси x : | F (x) = — f (x) |
Основные выводы
- Идентификация преобразований позволяет нам быстро рисовать график функций.
 Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению. - Если к функции добавить положительную константу, f (x) + k, график сдвинется вверх. Если из функции f (x) −k вычесть положительную константу, график сдвинется вниз. Основная форма графика останется прежней.
- Если положительная константа добавляется к значению в области до применения функции, f (x + h), график сдвинется влево.Если положительная константа вычтена из значения в области до применения функции f (x − h), график сдвинется вправо. Основная форма останется прежней.
- Умножение функции на отрицательную константу -f (x) отражает ее график на оси x . Умножение значений в области на -1 перед применением функции f (-x) отражает график относительно оси y .
- При применении нескольких преобразований сначала примените отражения.

- Умножение функции на константу, отличную от 1, a⋅f (x), дает расширение. Если константа является положительным числом больше 1, график будет казаться растянутым по вертикали. Если положительная константа представляет собой дробную часть меньше 1, график будет казаться растянутым по горизонтали.
ответов
у = х; Сдвинуть вверх на 3 единицы; домен: ℝ; диапазон: ℝ
у = х2; Сдвинуть вверх на 1 единицу; домен: ℝ; диапазон: [1, ∞)
у = х2; Сдвиг вправо на 5 единиц; домен: ℝ; диапазон: [0, ∞)
у = х2; Сдвиг вправо на 5 единиц и на 2 единицы вверх; домен: ℝ; диапазон: [2, ∞)
у = | х |; Сдвиг влево на 4 единицы; домен: ℝ; диапазон: [0, ∞)
у = | х |; Сдвинуть вправо на 1 единицу и вниз на 3 единицы; домен: ℝ; диапазон: [−3, ∞)
у = х; Сдвинуть вниз на 5 единиц; домен: [0, ∞); диапазон: [−5, ∞)
у = х; Сдвиг вправо на 2 единицы и на 1 единицу вверх; домен: [2, ∞); диапазон: [1, ∞)
у = х3; Сдвиг вправо на 2 единицы; домен: ℝ; диапазон: ℝ
у = х3; Сдвинуть вправо на 1 единицу и вниз на 4 единицы; домен: ℝ; диапазон: ℝ
y = 1x; Сдвиг вправо на 2 единицы; область: (−∞, 2) ∪ (2, ∞); диапазон: (−∞, 0) ∪ (0, ∞)
y = 1x; Сдвинуть вверх на 5 единиц; область: (−∞, 0) ∪ (0, ∞); диапазон: (−∞, 1) ∪ (1, ∞)
y = 1x; Сдвинуть влево на 1 единицу и вниз на 2 единицы; область: (−∞, −1) ∪ (−1, ∞); диапазон: (−∞, −2) ∪ (−2, ∞)
Базовый график y = −4; домен: ℝ; диапазон: {−4}
у = х3; Сдвинуть вверх на 6 единиц и вправо на 2 единицы; домен: ℝ; диапазон: ℝ
Задача 5
Задача 5
5. Рисовать
Рисовать
график y = f ( x ) = x 2 + 2 x — 8.
- a) Что такое перехват y ?
- б) Какие корни?
- в) Какие координаты вершины?
- г) Запишите уравнение в стандарте или вершине
форма. - e) Решите относительно x
x 2 + 2 x -8 > 0
Прежде чем рисовать график, нужно ответить на вопросы а), б),
и в).
а) Что такое перехват и ?
Пересечение y — это точка на графике, координата которой x равна 0.
Итак, пусть x = 0 в уравнении, и мы получим
y = (0) 2 + 2 (0) — 8
= 0 + 0-8
= -8.
Это показывает, что интервал y всегда является постоянным членом
в полиноме.
верх
б) Какие корни?
Корни — это еще одно название перехватов x .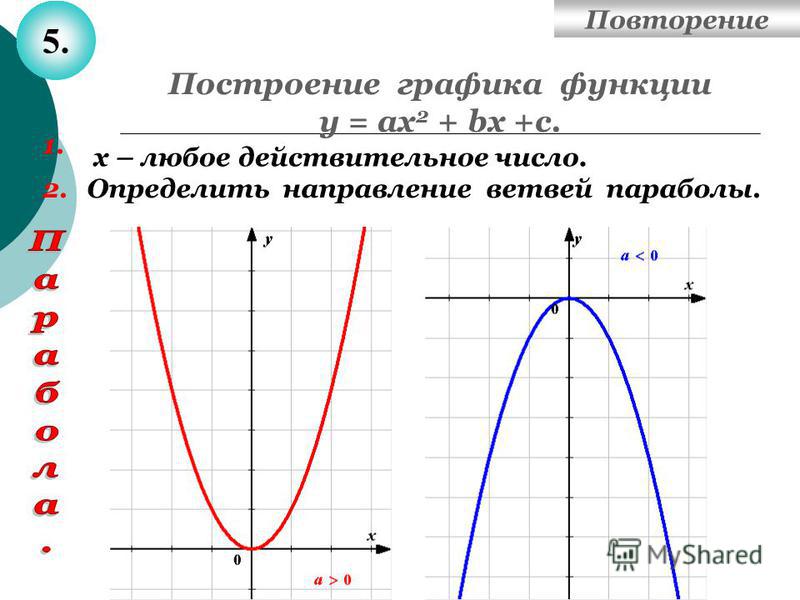 Они
Они
точек на графике, координаты которых y равны 0. Итак, пусть y = 0 в
уравнение и получаем
0 = x 2 + 2 x — 8
Это дает нам квадратное уравнение в x . & mbsp; Нам повезло
чтобы на одной стороне уже был 0, поэтому мы готовы к факторизации.
0 = ( x -2) ( x + 4)
Установите коэффициенты = 0.
x — 2 = 0 или x + 4 = 0
Решить относительно x
x = 2 или x = -4
верх
в) Какие координаты вершины?
Если мы воспользуемся формулой для координаты x вершины, то
получаем
или
х = -1
Теперь, когда у нас есть координата вершины x- , мы запускаем это
число через функцию, чтобы найти координату y-
y = f (-1) = (-1) 2 + 2 (-1) — 8
= 1-2-8
= -9
Итак, вершина находится в (-1, -9)
верх
Перед построением графика рекомендуется получить всю эту информацию.
точки, чтобы нарисовать график.Когда мы наносим точки, поскольку теперь мы знаем, что
координата x вершины равна -1, мы хотим, чтобы -1 находился в
середина x , которые мы рисуем. Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
Когда мы строим эти точки, получаем
верх
г) Запишите уравнение в виде вершины.
Уравнение равно
y = x 2 + 2 x — 8
Половина линейного коэффициента равна 1, а квадрат 1 равен 1, поэтому
складываем и вычитаем 1
y = x 2 + 2 x + 1-1-8
Это упрощается до
y = ( x + 1) 2 — 9
, и мы видим координаты вершины в уравнении.
верх
e) Решите относительно x
x 2 + 2 x — 8 ≥ 0
В процессе построения графика мы обнаружили
что корни были в -4 и 2.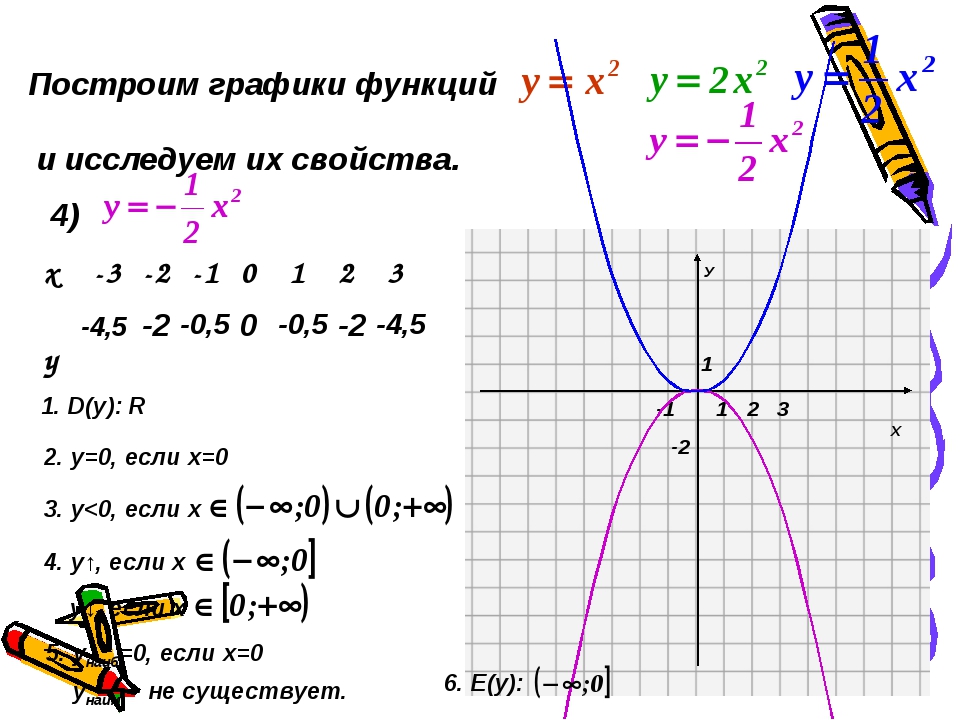 Когда мы делим вещественное число на прямую
Когда мы делим вещественное число на прямую
в промежутки между корнями, и проверьте x в каждом
интервал.
Поскольку равенство разрешено, конечные точки интервалов,
корни, являющиеся x , которые дадут ответы, равные 0
при подстановке в формулу будут решения.Итак, рисуем
квадратные скобки вокруг конечных точек.
Набор решений — это набор x , которые удовлетворяют
x ≤ -4 или x ≥ 2
В интервальной записи получается
.
(-∞, -4] ∪ [2, ∞)
верх
Вернуться к тесту
х | у = х 2 | (х, у) |
0 | 0 | (0,0) |
1 | 1 | (1,1) |
2 | 4 | (2,4) |
3 | 9 | (3,9) |
–1 | 1 | (-1,1) |
-2 | 4 | (-2,4) |
-3 | 9 | (-3,9) |
Х | у = 1 / х | (х, у) |
1/3 | 3 | (1 / 3,3) |
1/2 | 2 | (1 / 2,2) |
1 | 1 | (1, 1) |
2 | 1/2 | (2,1 / 2) |
3 | 1/3 | (3,1 / 3) |
-1/3 | -3 | (-1/3, -3) |
-1/2 | -2 | (-1/2, -2) |
–1 | –1 | (-1, -1) |
-2 | -1/2 | (-2, -1/2) |
-3 | -1/3 | (-3, -1 / 3) |
| | x | знак равно | x, если x ≥ 0, т. -x, если x |
График совпадает с линией y = x для x > 0 и с линией y = -x
для x <0.
график f (x) = -x
Объединяя эти два графика, получаем
график f (x) = | x |
Пример: 4 Нарисуйте график
t (x) = (x 2 — 4) / (x — 2) =
= ((х — 2) (х + 2) / (х — 2)) =
= (х + 2) х ≠ 2
Следовательно, эту функцию можно записать как
y = x + 2 x ≠ 2
График h (x) = x 2 — 4 Или x — 2
график y = x + 2 x ≠ 2
Пример: 4 Нарисуйте график
| г (х) = | 1, если x ≤ 2 x + 2, если x> 2 |
Графические функции переводчиками
— Предположим, что график f (x) известен
— Тогда мы можем найти графики
у = е (х) + с
у = f (х) — с
y = f (x + c)
y = f (x — c)
y = f (x) + c график f (x) переводит
UP по c единиц
y = f (x) — c график f (x) переводит
ВНИЗ по c единиц
y = f (x + c) график f (x) переводит
СЛЕВА по c единиц
y = f (x — c) график f (x) переводит
СПРАВА по c единиц
Пример: 5 Нарисуйте
график y = f (x) = | x — 3 | + 2
Перевести график y = | x | 3 единицы ВПРАВО, чтобы получить график
y = | x-3 |
Перевести график y = | x — 3 | 2 единицы к UP, чтобы получить график y = | x — 3 | + 2
Пример: 8
Нарисуйте график
y = x 2 — 4x + 5
— завершить квадрат
y + 4 = (x 2 — 4x + 5) + 4 y = (x 2 — 4x + 4) + 5 — 4
у = (х — 2) 2 + 1
В этой форме мы видим, что график может быть получен путем перевода графика y = x 2 вправо на 2 единицы из-за x — 2 и вверх на 1 из-за +1.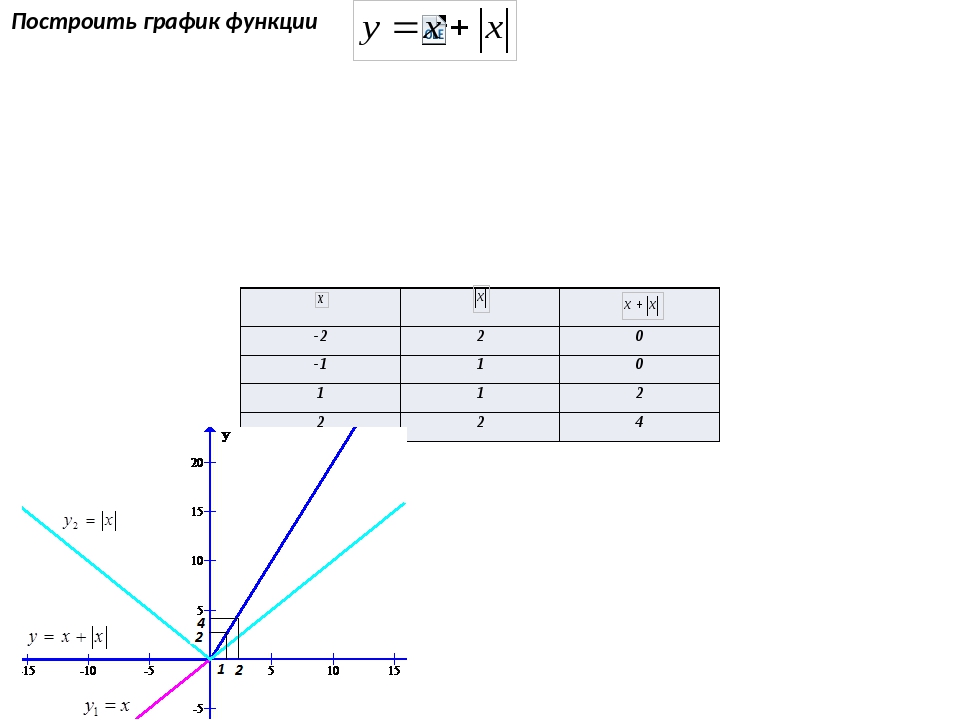
y = x 2 — 4x + 5
Отражения
(-x, y) — отражение (x, y) относительно оси y
(x, -y) — отражение (x, y) относительно оси x
Графики y = f (x) и y = f (-x) являются отражениями друг друга относительно оси y
Графики y = f (x) и y = -f (x) являются отражениями друг друга относительно оси x
График можно получить путем отражения и перевода:
— Нарисуйте график
— Отразите его вокруг оси Y, чтобы получить график
.
— Переведите этот график вправо на 2 единицы, чтобы получить график
Вот график
Если f (x) умножить на положительную константу c
График f (x) сжимается по вертикали, если 0 График f (x) растягивается по вертикали, если c> 1
Кривая не является графиком y = f (x) для любой функции f
Как построить график X через Y на калькуляторе TI-84
Обновлено 15 декабря 2020 г.
Джек Джерард
Калькулятор TI-84 предлагает ряд встроенных функций для решения и построения графиков уравнений. К сожалению, его основные параметры построения графиков ограничены функциями и уравнениями, которые включают Y в терминах X . Реже вам нужно построить график X с точки зрения Y , но если вы это сделаете, существующие параметры не совсем помогут. К счастью, TI-84 позволяет импортировать внешние приложения и использовать их во многом так же, как и приложения, поставляемые с калькулятором. Репозиторий TI Calc, поддерживаемый сообществом, содержит ряд этих внешних приложений, в том числе приложение под названием XGraph от Джоэла Смита, которое позволяет построить график X с точки зрения Y .
К сожалению, его основные параметры построения графиков ограничены функциями и уравнениями, которые включают Y в терминах X . Реже вам нужно построить график X с точки зрения Y , но если вы это сделаете, существующие параметры не совсем помогут. К счастью, TI-84 позволяет импортировать внешние приложения и использовать их во многом так же, как и приложения, поставляемые с калькулятором. Репозиторий TI Calc, поддерживаемый сообществом, содержит ряд этих внешних приложений, в том числе приложение под названием XGraph от Джоэла Смита, которое позволяет построить график X с точки зрения Y .
Что означает X в терминах Y?
Для большинства уравнений вы строите график Y через X . Это означает, что ваше уравнение основано на значении Y и интерпретируется через значение X ; Примером этого может быть y = x + 1. Значение Y зависит от того, каково значение X , поэтому для каждого X соответствующее значение Y равно значению X плюс 1.Построение графика X через Y меняет ситуацию. Вместо y = x + 1 вы должны создать график из x = y + 1. В этом случае ваше значение X зависит от для значения Y и для вычисления каждого X вы берете соответствующее значение Y и добавляете 1. К сожалению, это непросто построить график на калькуляторе TI-84, если вы не рассчитаете и нанесите отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в функциях построения графиков.
Значение Y зависит от того, каково значение X , поэтому для каждого X соответствующее значение Y равно значению X плюс 1.Построение графика X через Y меняет ситуацию. Вместо y = x + 1 вы должны создать график из x = y + 1. В этом случае ваше значение X зависит от для значения Y и для вычисления каждого X вы берете соответствующее значение Y и добавляете 1. К сожалению, это непросто построить график на калькуляторе TI-84, если вы не рассчитаете и нанесите отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в функциях построения графиков.
Установка XGraph
Одна вещь, которая есть у TI-84, — это средство расширения его функций с помощью закодированных приложений и программ. Приложение XGraph позаботится об этом, позволяя вводить уравнения в форме X через Y и строить их график.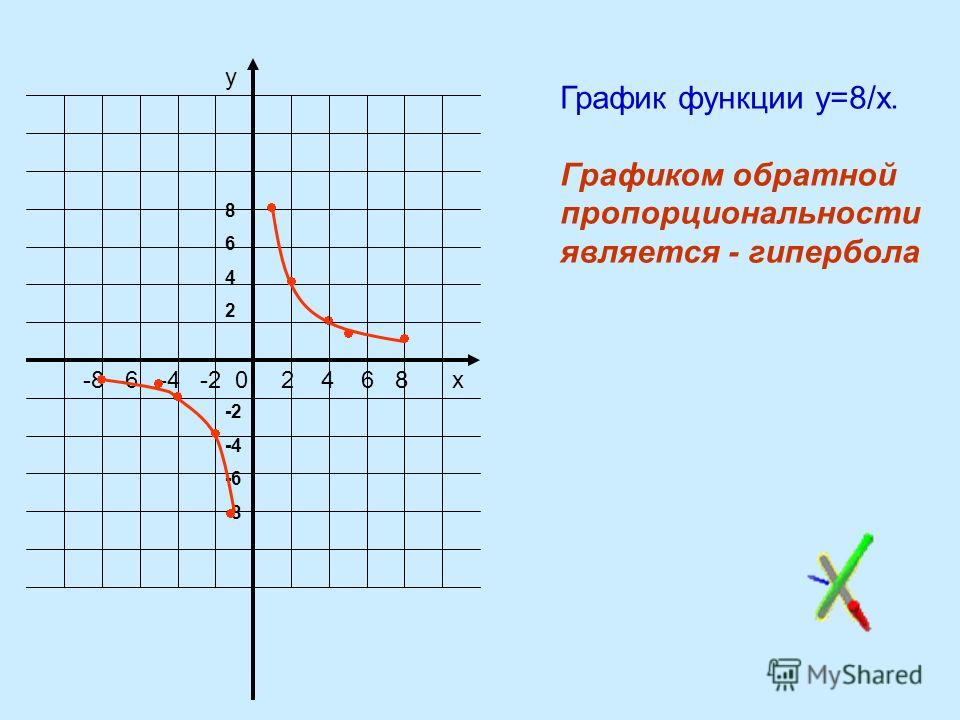 Файл загружается в виде файла .zip, который содержит XGRAPH.8XP и файл readme; извлеките файл XGRAPH.8XP в легкодоступное место. Подключите калькулятор TI-84 к компьютеру с помощью соединительного кабеля USB, поставляемого с калькулятором, а затем запустите программное обеспечение TI Connect от Texas Instruments (которое можно бесплатно загрузить с веб-сайта Texas Instruments, если оно еще не установлено. ).Выберите XGRAPH.8XP и подтвердите, что вы хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
Файл загружается в виде файла .zip, который содержит XGRAPH.8XP и файл readme; извлеките файл XGRAPH.8XP в легкодоступное место. Подключите калькулятор TI-84 к компьютеру с помощью соединительного кабеля USB, поставляемого с калькулятором, а затем запустите программное обеспечение TI Connect от Texas Instruments (которое можно бесплатно загрузить с веб-сайта Texas Instruments, если оно еще не установлено. ).Выберите XGRAPH.8XP и подтвердите, что вы хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
Использование приложения
Нажмите кнопку PRGM на калькуляторе TI-84 и найдите запись «XGRAPH» в списке программ. Нажмите клавишу ENTER, на вашем экране появится «prgmXGRAPH»; снова нажмите ENTER, чтобы запустить приложение. При появлении запроса введите уравнение, но используйте букву X вместо Y .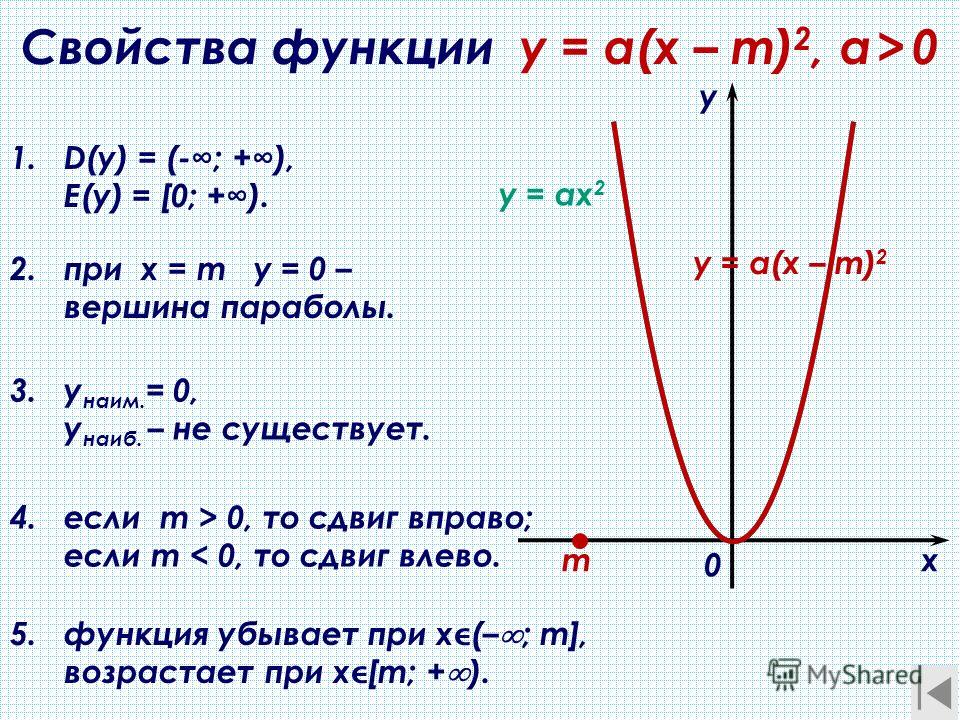


 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.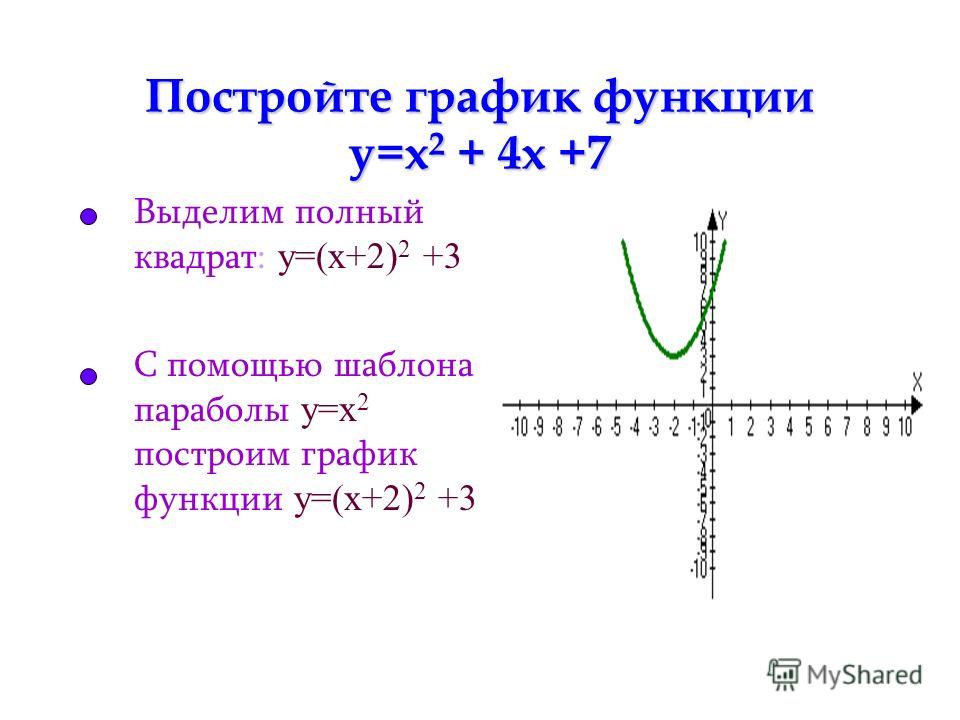 Если буквы x и y используются для обозначения
Если буквы x и y используются для обозначения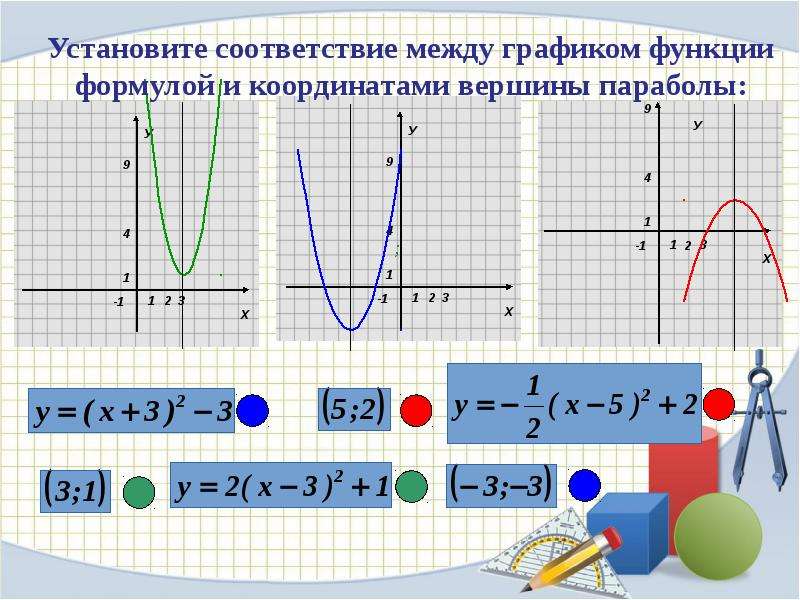
 В общем, только с техникой
В общем, только с техникой
 е.е. x неотрицателен
е.е. x неотрицателен