{2}} = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 34$$
$$x_{2} = 92$$
$$x_{3} = -100$$
$$x_{4} = 12$$
$$x_{5} = 80$$
$$x_{6} = 4$$
$$x_{7} = 70$$
$$x_{8} = -82$$
$$x_{9} = 90$$
$$x_{10} = -14$$
$$x_{11} = -78$$
$$x_{12} = -90$$
$$x_{13} = -46$$
$$x_{14} = -48$$
$$x_{15} = 46$$
$$x_{16} = 66$$
$$x_{17} = 22$$
$$x_{18} = 72$$
$$x_{19} = -66$$
$$x_{20} = -4$$
$$x_{21} = 82$$
$$x_{22} = 98$$
$$x_{23} = 74$$
$$x_{24} = 36$$
$$x_{25} = -70$$
$$x_{26} = -54$$
$$x_{27} = -74$$
$$x_{28} = -30$$
$$x_{29} = -32$$
$$x_{30} = -12$$
$$x_{31} = 52$$
$$x_{32} = 32$$
$$x_{33} = -60$$
$$x_{34} = -20$$
$$x_{35} = 40$$
$$x_{36} = 68$$
$$x_{37} = -86$$
$$x_{38} = -34$$
$$x_{39} = 24$$
$$x_{40} = -10$$
$$x_{41} = 18$$
$$x_{42} = -44$$
$$x_{43} = 62$$
$$x_{44} = -76$$
$$x_{45} = 50$$
$$x_{46} = -2$$
$$x_{47} = 88$$
$$x_{48} = 10$$
$$x_{49} = -94$$
$$x_{50} = -56$$
$$x_{51} = -52$$
$$x_{52} = 0$$
$$x_{53} = -80$$
$$x_{54} = -36$$
$$x_{55} = 78$$
$$x_{56} = 54$$
$$x_{57} = 60$$
$$x_{58} = -64$$
$$x_{59} = -40$$
$$x_{60} = -68$$
$$x_{61} = 26$$
$$x_{62} = 28$$
$$x_{63} = -38$$
$$x_{64} = -42$$
$$x_{65} = -22$$
$$x_{66} = -84$$
$$x_{67} = -50$$
$$x_{68} = 38$$
$$x_{69} = 64$$
$$x_{70} = 30$$
$$x_{71} = 14$$
$$x_{72} = 86$$
$$x_{73} = -6$$
$$x_{74} = -98$$
$$x_{75} = -28$$
$$x_{76} = 6$$
$$x_{77} = -18$$
$$x_{78} = 94$$
$$x_{79} = 48$$
$$x_{80} = 16$$
$$x_{81} = 20$$
$$x_{82} = 2$$
$$x_{83} = 96$$
$$x_{84} = -26$$
$$x_{85} = -92$$
$$x_{86} = -96$$
$$x_{87} = -8$$
$$x_{88} = 58$$
$$x_{89} = 76$$
$$x_{90} = -88$$
$$x_{91} = 8$$
$$x_{92} = -16$$
$$x_{93} = 100$$
$$x_{94} = -24$$
$$x_{95} = 42$$
$$x_{96} = 84$$
$$x_{97} = -62$$
$$x_{98} = 56$$
$$x_{99} = -58$$
$$x_{100} = -72$$
$$x_{101} = 44$$
Зн. экстремумы в точках:
экстремумы в точках:
(34, 1)
(92, 1)
(-100, -1)
(12, 1)
(80, 1)
(4, 1)
(70, 1)
(-82, -1)
(90, 1)
(-14, -1)
(-78, -1)
(-90, -1)
(-46, -1)
(-48, -1)
(46, 1)
(66, 1)
(22, 1)
(72, 1)
(-66, -1)
(-4, -1)
(82, 1)
(98, 1)
(74, 1)
(36, 1)
(-70, -1)
(-54, -1)
(-74, -1)
(-30, -1)
(-32, -1)
(-12, -1)
(52, 1)
(32, 1)
(-60, -1)
(-20, -1)
(40, 1)
(68, 1)
(-86, -1)
(-34, -1)
(24, 1)
(-10, -1)
(18, 1)
(-44, -1)
(62, 1)
(-76, -1)
(50, 1)
(-2, -1)
(88, 1)
(10, 1)
(-94, -1)
(-56, -1)
(-52, -1)
(0, -1)
(-80, -1)
(-36, -1)
(78, 1)
(54, 1)
(60, 1)
(-64, -1)
(-40, -1)
(-68, -1)
(26, 1)
(28, 1)
(-38, -1)
(-42, -1)
(-22, -1)
(-84, -1)
(-50, -1)
(38, 1)
(64, 1)
(30, 1)
(14, 1)
(86, 1)
(-6, -1)
(-98, -1)
(-28, -1)
(6, 1)
(-18, -1)
(94, 1)
(48, 1)
(16, 1)
(20, 1)
(2, 1)
(96, 1)
(-26, -1)
(-92, -1)
(-96, -1)
(-8, -1)
(58, 1)
(76, 1)
(-88, -1)
(8, 1)
(-16, -1)
(100, 1)
(-24, -1)
(42, 1)
(84, 1)
(-62, -1)
(56, 1)
(-58, -1)
(-72, -1)
(44, 1)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{101} = -30$$
$$x_{101} = -86$$
$$x_{101} = 50$$
$$x_{101} = -62$$
Максимумы функции в точках:
$$x_{101} = -48$$
$$x_{101} = 88$$
$$x_{101} = 64$$
Убывает на промежутках
[50, oo)
Возрастает на промежутках
(-oo, -86]
Содержание
Построение графика функции онлайн | umath.
 ru
ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.
- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных
параметрически, то есть в виде
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе
Режим позволяет построить график кривой, заданной в полярной системе
координат, то
есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. Выражение abs(x) эквивалентно |x|. Если функция содержит модуль подмодулем, то пользуйтесь abs(). Например, если вы хотите построить график функции |1-x+|x+5||,то нужно вводить abs(1-x+abs(x+5)). 3 дают 3 дают x в третьейстепени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа b по основанию a |
exp() | Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах
(например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию
с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет
носить
ваше имя ;).
Функции y=|x|, y=[x],y={x}, y=sign(x) и их графики. Функция f(x)=|x|
Функция $f(x)=|x|$
$|x|$ — модуль. Он определяется следующим образом: Если действительное число будет неотрицательным, то значение модуля совпадает с самим числом. Если же отрицательно, то значение модуля совпадает с абсолютным значением данного числа.
Математически это можно записать следующим образом:
Пример 1
Исследуем и построим её график.
- $D\left(f\right)=R$.
- По определению модуля действительного числа, получим, что$E\left(f\right)=[0,\infty )$
- $f\left(-x\right)=|-x|=|x|=f(x)$. Значит, функция четна.
- При $x=0,\ y=0$. Точка $\left(0,0\right)$ — единственное пересечение с координатными осями.
- \[f’\left(x\right)=\left\{ \begin{array}{c} {1,x >0,} \\ {-1,xФункция будет возрастать на промежутке $x\in (0,+\infty )$
Функция будет убывать на промежутке $x\in (-\infty ,0)$
Значения на концах области определения.
\[{\mathop{\lim }_{x\to -\infty } y\ }=+\infty \] \[{\mathop{\lim }_{x\to +\infty } y\ }=+\infty \]
Рисунок 1.
Функция $f(x)=[x]$
Функция $f\left(x\right)=[x]$ — функция целой части числа. Она находится округлением числа (если оно само не целое) «в меньшую сторону».
Пример: $[2,6]=2.$
Пример 2
Исследуем и построим её график.
- $D\left(f\right)=R$.
- Очевидно, что эта функция принимает только целые значения, то есть $\ E\left(f\right)=Z$
- $f\left(-x\right)=[-x]$.
 Следовательно, эта функция будет общего вида.
Следовательно, эта функция будет общего вида. - $(0,0)$ — единственная точка пересечения с осями координат.
- $f’\left(x\right)=0$
- Функция имеет точки разрыва (скачка функции) при всех $x\in Z$.
Рисунок 2.
Функция $f\left(x\right)=\{x\}$
Функция $f\left(x\right)=\{x\}$ — функция дробной части числа. Она находится «отбрасыванием» целой части этого числа.
$\{2,6\}=0,6$
Пример 3
Исследуем и построим график функции
$D\left(f\right)=R$.
Очевидно, что эта функция никогда не будет отрицательной и никогда не будет больше единицы, то есть $\ E\left(f\right)=[0,1)$
$f\left(-x\right)=\{-x\}$. Следовательно, данная функция будет общего вида.
Пересечение с осью $Ox$: $\left(z,0\right),\ z\in Z$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точки разрыва (скачка функции) при всех $x\in Z$
Рисунок 3.
Функция $f(x)=sign(x)$
Функция $f\left(x\right)=sign(x)$ — сигнум-функция. Эта функция показывает, какой знак имеет действительное число. Если число отрицательно, то функция имеет значение $-1$. Если число положительно, то функция равняется единице. При нулевом значении числа, значение функции также будет принимать нулевое значение.
Математически это можно записать следующим образом:
Пример 4
Исследуем и построим график функции
- $D\left(f\right)=R$.
- Непосредственно из определения, получим
- \[\ E\left(f\right)=\left\{-1\right\}\cup \left\{0\right\}\cup \{1\}\]
$f\left(-x\right)=sign\left(-x\right)=-sign(x)$. Следовательно, данная функция будет нечетной.
Пересечение с осью $Ox$: $\left(0,0\right)$
Пересечение с осью $Oy$: $\left(0,0\right)$
$f’\left(x\right)=0$
Функция имеет точку разрыва (скачка функции) в начале координат.
Рисунок 4.

линейная функция, квадратичная, кубическая и y=1/x
Степенной называется функция вида y=xn (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x2, y=x3, y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x
1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
Квадратичная функция y=x
2
Графиком квадратичной функции является парабола.
Общий вид параболы представлен на рисунке ниже.
Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2.
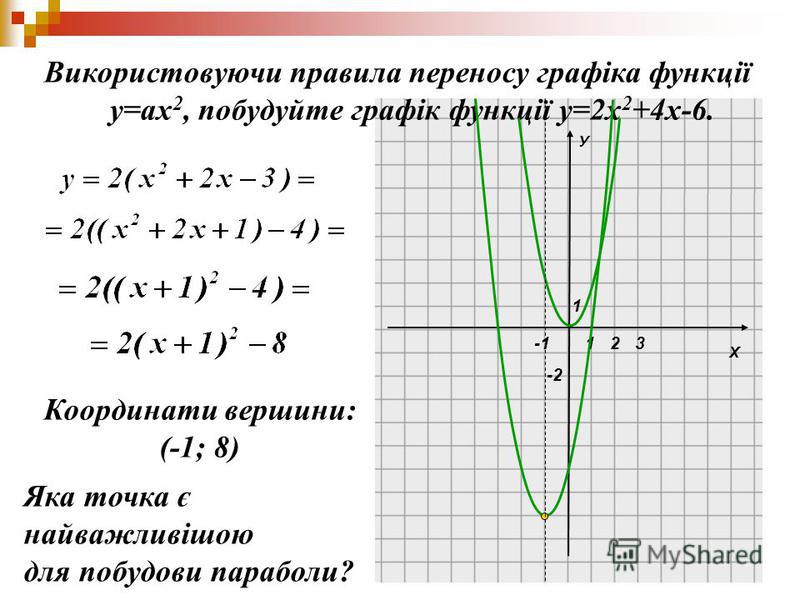 Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует. - 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;+∞).
- 4. Противоположным значениям х соответствует одинаковые значения y.
Кубическая функция y=x
3
Графиком кубической функции называется кубическая парабола.
Общий вид параболы представлен на рисунке ниже.
Основные свойства кубической функции:
- 1. При х =0, у=0. у>0 при х>0 и y
- 2. У кубической функции не существует не максимального ни минимального значения.
- 3. Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- 4. Противоположным значениям х, соответствуют противоположные значения y.
Функция вида y=x
-1 (y=1/x)
Графиком функции y=1/x называется гипербола.
Общий вид гиперболы представлен на рисунке ниже.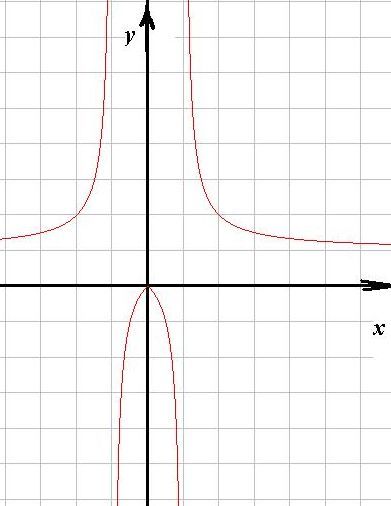
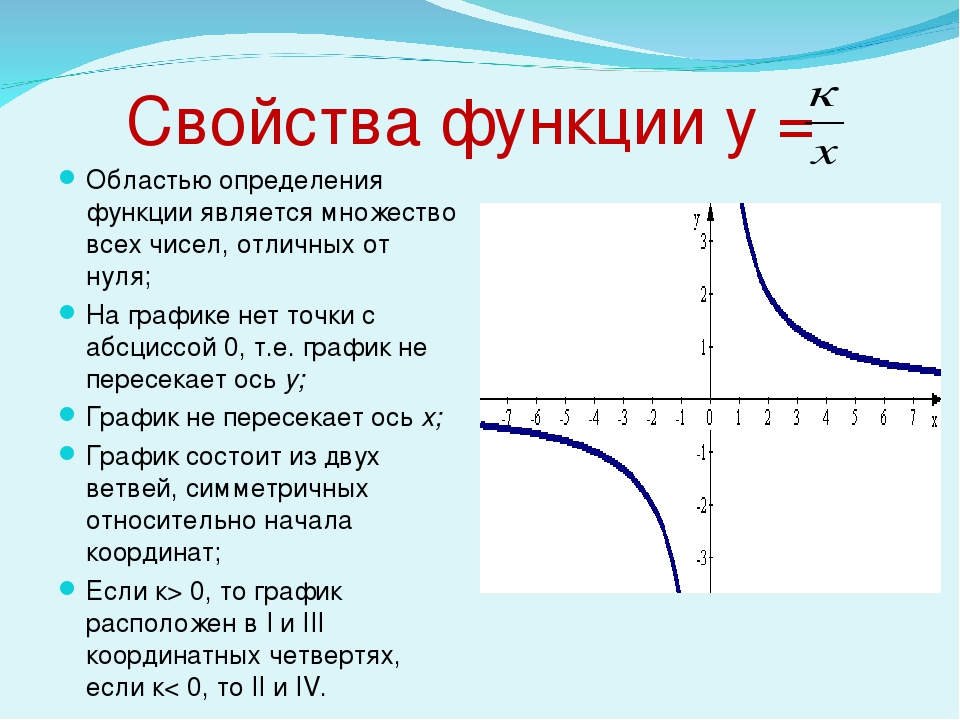
Основные свойства функции y = 1/x:
- 1. Точка (0;0) центр симметрии гиперболы.
- 2. Оси координат – асимптоты гиперболы.
- 3. Прямая y=x ось симметрии гиперболы.
- 4. Область определения функции все х, кроме х=0.
- 5. y>0 при x>0; y
- 6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
- 7. Функция не ограничена ни снизу, ни сверху.
- 8. У функции нет ни наибольшего, ни наименьшего значений.
- 9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
- 10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Нужна помощь в учебе?
Предыдущая тема: Четные и нечетные функции: графики и свойства
Следующая тема:   Определение корня n-ой степени: извлечение корня
ГИА — построение графиков функций со знаком модуля / Sandbox / Habr
Всем привет! Хотел бы сегодня объяснить такую тему, как построение графиков.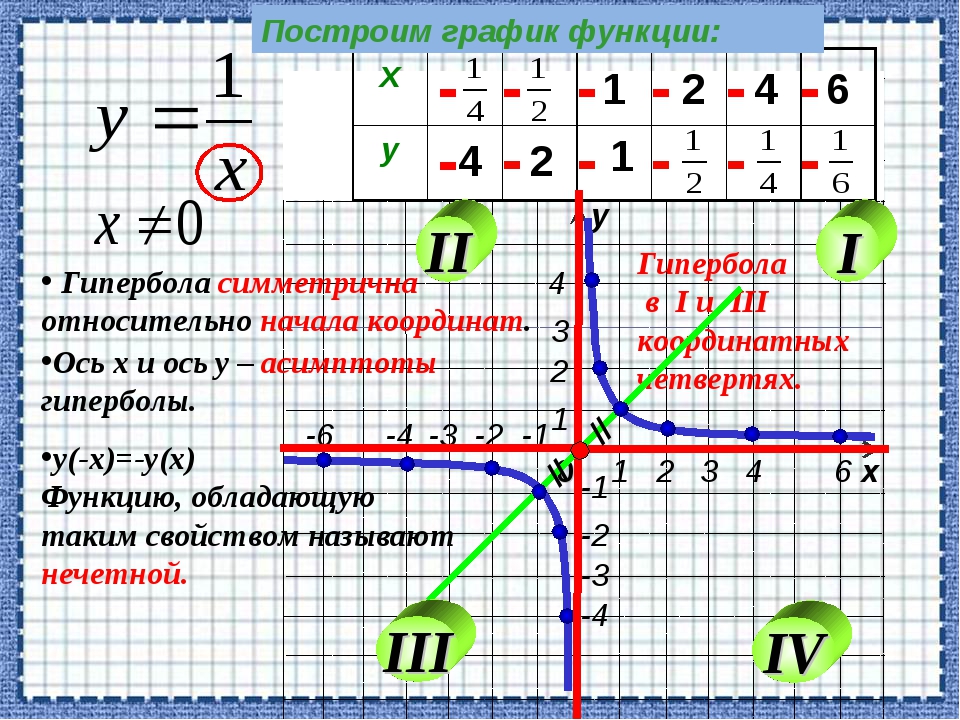 2 или y=1/x. А как строить графики со знаком модуля?
2 или y=1/x. А как строить графики со знаком модуля?
Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|. Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
(Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
Пусть -1< = x < = 4. Тогда х+1>0, |x+1|=x+1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(х+1)= -3х+13.
Пусть х>4. Тогда х+1>0, |x+1|=x+1, x-4>0; |x-4|=x-4; Следовательно у= 3(х-4)-х+х+1= 3х-11. 2 — |x| — 3|
2 — |x| — 3|
Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных
математических функций с помощью табличного
процессора Excel; - показать возможности использования программы
Excel для решения задач по математике; - закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с
основными приемами построения графиков функций
в программе Excel; - развивающие – формирование у учащихся
логического и алгоритмического мышления;
развитие познавательного интереса к предмету;
развитие умения оперировать ранее полученными
знаниями; развитие умения планировать свою
деятельность; - воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.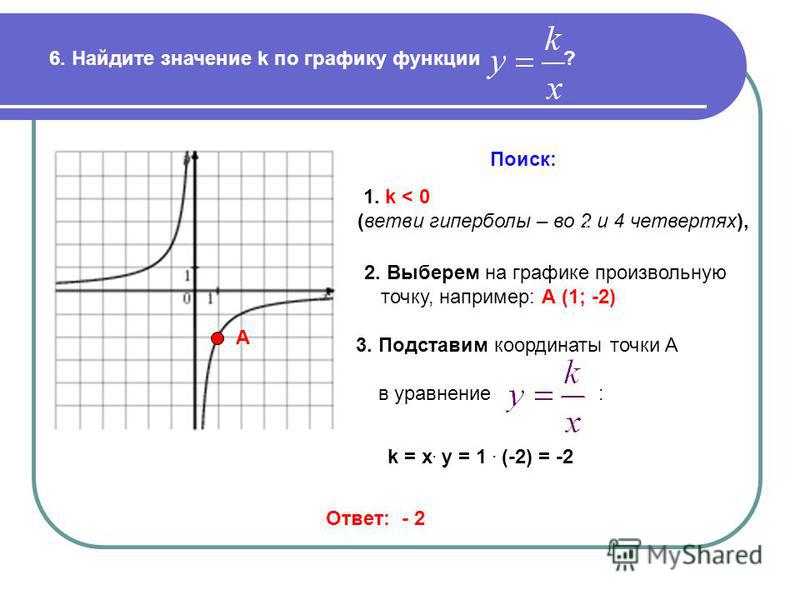
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред.
С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на
построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7
мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка
отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
(фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область
программы Excel? - Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она
задается? - Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как
изменить ориентацию бумаги? - Что такое функциональная зависимость у = f(х)?
Какая переменная является зависимой, а какая
независимой? - Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть
использован файл Excel с шаблонами задач (Приложение 1), который
выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного
процессора Excel для графиков функций. На
предыдущих практических вы уже строили
диаграммы к различным задачам, используя Мастер
диаграмм. Графики функций, так же как и диаграммы
строятся с помощью Мастера диаграмм программы
Excel.
Рассмотрим построение графиков функций на
примере функции у = sin x.
Вид данного графика хорошо известен вам по
урокам математики, попробуем построить его
средствами Excel.
Программа будет строить график по точкам: точки
с известными значениями будут плавно
соединяться линией. Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график.
- шаг переменной х, т.е. через какой промежуток
будут вычисляться значения функции.
Задача 1.Построить график функции у = sin
x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4
введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево
ячейки строки 4, до тех пор, пока получим значение
другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в
категории математические выберем функцию SIN, в
качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу
в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов
(х) и значений (у) функции у = sin x на отрезке [-2;2] с
шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на
кнопку “Удалить” (график изменений х нам не
нужен. График функции – это график изменения
значений у)
В поле Подписи оси Х нажать на кнопку.
Выделить в таблице ячейки со значениями х и
нажмите на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график
функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт
Формат оси….
Во вкладке Шкала установим: пересечение с осью
ОУ установите номер категории 5 (чтобы ось ОУ
пересекала ось ОХ в категории с подписью 0, а это
пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт.
Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на
построение графика функций. Эту задачу
попробуйте решить самостоятельно, сверяясь с
экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и
сформулировать следующую задачу.
Задача 2. Построить график функции у = х3
на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица
значений функции у = f(х).3
6. Маркером заполнения скопировать формулу в
ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица
аргументов (х) и значений (у) функции у = х3 на
отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7.
Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку
“Удалить” (график изменений х нам не нужен.
График функции – это график изменения значений
у) - В поле Подписи оси Х нажать на кнопку .
Выделить в таблице ячейки со значениями х и
нажать на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры
диаграмм таким образом, что бы все поместилось на
одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
14.Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем
График.
Самостоятельная работа.
Работа по карточкам с индивидуальными
заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде,
выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с
шагом h=c
2. Установить параметры страницы и размеры
графика таким образом, что бы все поместилось на
одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный
график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора. 3+ 1$.
3+ 1$.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
Функции и линейные уравнения (Алгебра 2, Как построить график функций и линейных уравнений) — Mathplanet
Если мы в следующем уравнении y = x + 7 присвоим значение x, уравнение даст нам значение для y.
Пример
$$ y = x + 7 $$
$$ если \; х = 2 \; затем
$
$$ y = 2 + 7 = 9 $$
Если бы мы присвоили другое значение x, уравнение дало бы нам другое значение y. Вместо этого мы могли бы присвоить значение y и решить уравнение, чтобы найти совпадающее значение x.
В нашем уравнении y = x + 7 у нас есть две переменные, x и y. Переменная, которой мы присваиваем значение, мы называем независимой переменной, а другая переменная является зависимой переменной, поскольку ее значение зависит от независимой переменной.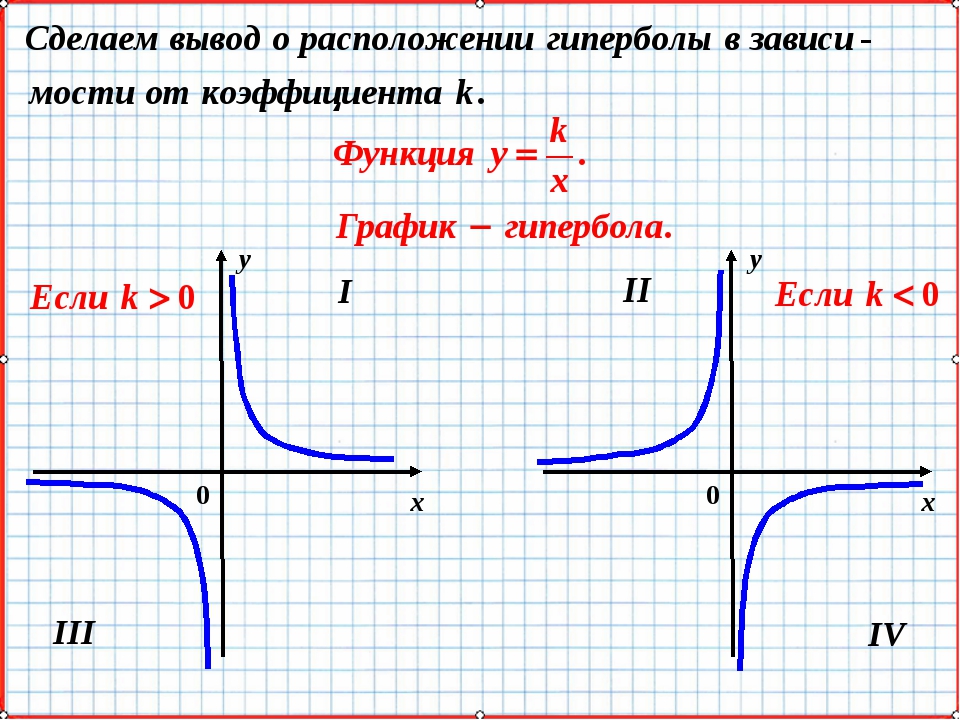 В нашем примере выше x — независимая переменная, а y — зависимая переменная.
В нашем примере выше x — независимая переменная, а y — зависимая переменная.
Функция — это уравнение, которое имеет только один ответ для y для каждого x. Функция назначает ровно один выход каждому входу указанного типа.
Обычно функцию называют f (x) или g (x) вместо y.f (2) означает, что мы должны найти значение нашей функции, когда x равно 2.
Пример
$$ f (x) = x + 7 $$
$$ если \; х = 2 \; затем
$
$$ f (2) = 2 + 7 = 9 $$
Функция линейна, если ее можно определить с помощью
.
$$ f (x) = mx + b $$
f (x) — значение функции.
м — уклон линии.
b — значение функции, когда x равно нулю, или координата y точки, в которой линия пересекает ось y в координатной плоскости.
x — значение координаты x.
Эта форма называется формой пересечения наклона. Если наклон m отрицательный, значение функции уменьшается с увеличением x и наоборот, если наклон положительный.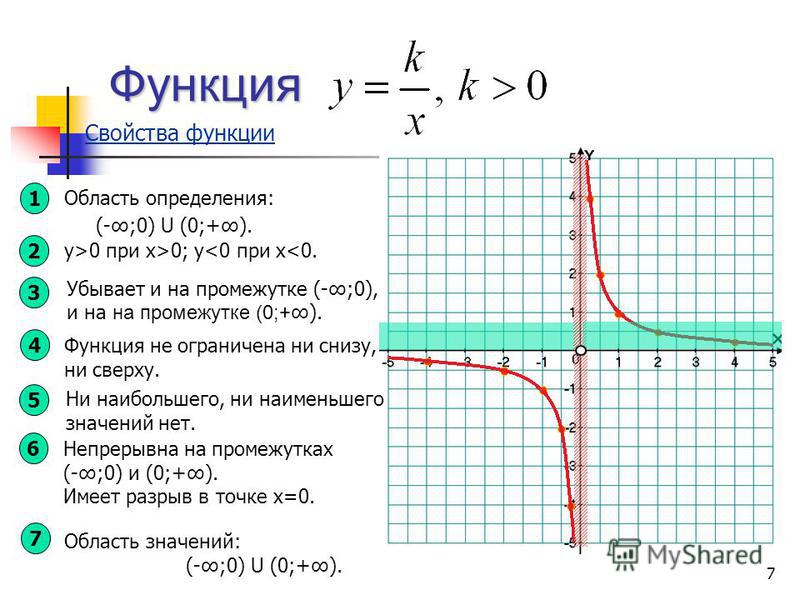
Уравнение, такое как y = x + 7 , является линейным, и существует бесконечное количество упорядоченных пар x и y, которые удовлетворяют этому уравнению.
Наклон m здесь равен 1, а наш b (точка пересечения с y) равен 7.
Наклон прямой, проходящей через точки (x1, y1) и (x2, y2), равен
$$ m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $$
$$ x_ {2} \ neq x_ {1} $$
Если двум линейным уравнениям задан один и тот же наклон, это означает, что они параллельны, а если произведение двух наклонов m1 * m2 = -1, два линейных уравнения называются перпендикулярными.
Видеоурок
Если x равен -1, какое значение имеет f (x), когда f (x) = 3x + 5?
Графические функции абсолютных значений | Purplemath
Purplemath
Принятие абсолютного значения отрицательного числа делает его положительным. По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили.Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу Т-диаграмму при построении графиков функций абсолютных значений. Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график.
По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили.Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу Т-диаграмму при построении графиков функций абсолютных значений. Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график.
Например, предположим, что ваш класс проходит следующую викторину:
MathHelp.com
Один из других учеников делает то, что обычно делает: он выбирает только положительные значения x для своей Т-диаграммы:
Затем он набирает свои очки:
Эти очки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график. В частности, они не содержат никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений что-то означают . В результате ученик забывает учесть эти столбцы и рисует ошибочный график:
В частности, они не содержат никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений что-то означают . В результате ученик забывает учесть эти столбцы и рисует ошибочный график:
НЕПРАВИЛЬНЫЙ ОТВЕТ!
Аааааи … он просто завалил викторину.
Но вы более осторожны.Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Итак, вы выбираете значения x , которые ставят «минус» внутри абсолютного значения, и выбираете еще несколько точек. Ваш T-график выглядит примерно так:
Затем вы наносите свои очки:
.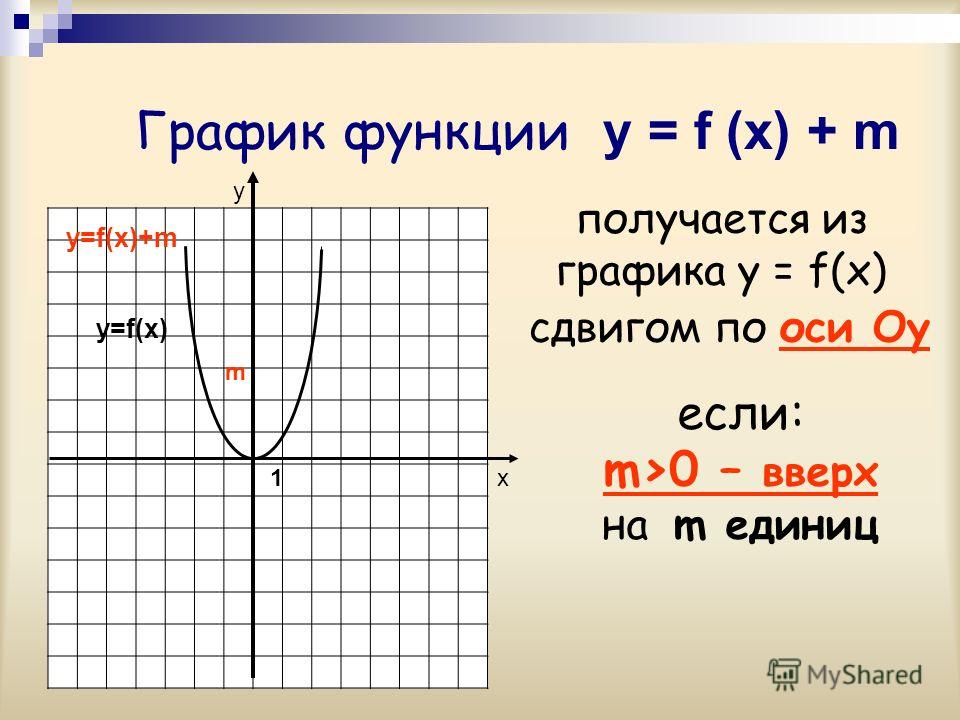 .. и, наконец, вы соединяете точки:
.. и, наконец, вы соединяете точки:
У вас есть правильный график:
Правильный ответ!
Ааааанд… вы только что успешно прошли викторину. Хорошая работа!
Хотя графики абсолютных значений имеют тенденцию выглядеть так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает в себя абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон значений x , потому что три соседних значения x почти наверняка не дадут вам достаточно информации, чтобы нарисовать достоверное изображение.
Примечание. Полоски абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (то есть положительные или нулевые). В результате буква «V» на приведенном выше графике появилась там, где знак внутри был равен нулю. Когда x было меньше –2, выражение x + 2 было меньше нуля, и столбцы абсолютных значений перевернули эти «минусовые» значения из-под оси x вверх. Когда x равняется –2, тогда аргумент (то есть выражение внутри столбцов) равен нулю.Для всех значений x справа от –2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не меняли.
Другими словами, графически столбцы абсолютных значений занимают этот график:
… и перевернул «минус» (зеленый на графике) снизу оси x наверх. Замечание, где аргумент столбцов абсолютного значения будет равен нулю, может быть полезным для проверки правильности построения графика.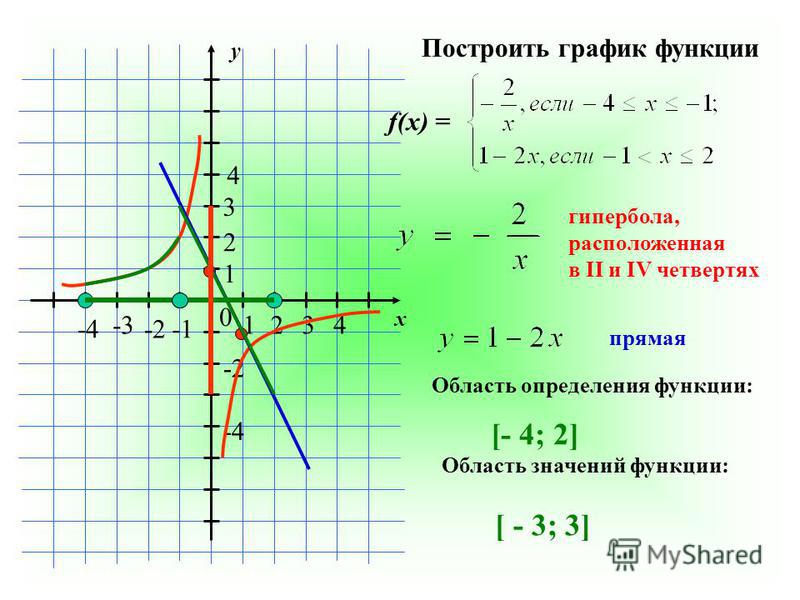
Эта функция почти такая же, как и предыдущая.
Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, когда x = 0, поэтому я должен ожидать увидеть локоть в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютных значений, я ожидаю, что мой график будет выглядеть как обычный график абсолютных значений (представляющий собой букву «V» с изгибом в начале координат), но смещенный вверх на две единицы. .
Сначала я заполню свою Т-диаграмму, выбирая по ходу несколько отрицательных значений x :
Затем нарисую точки и заполню график:
Партнер
Поскольку столбцы абсолютных значений всегда показывают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x .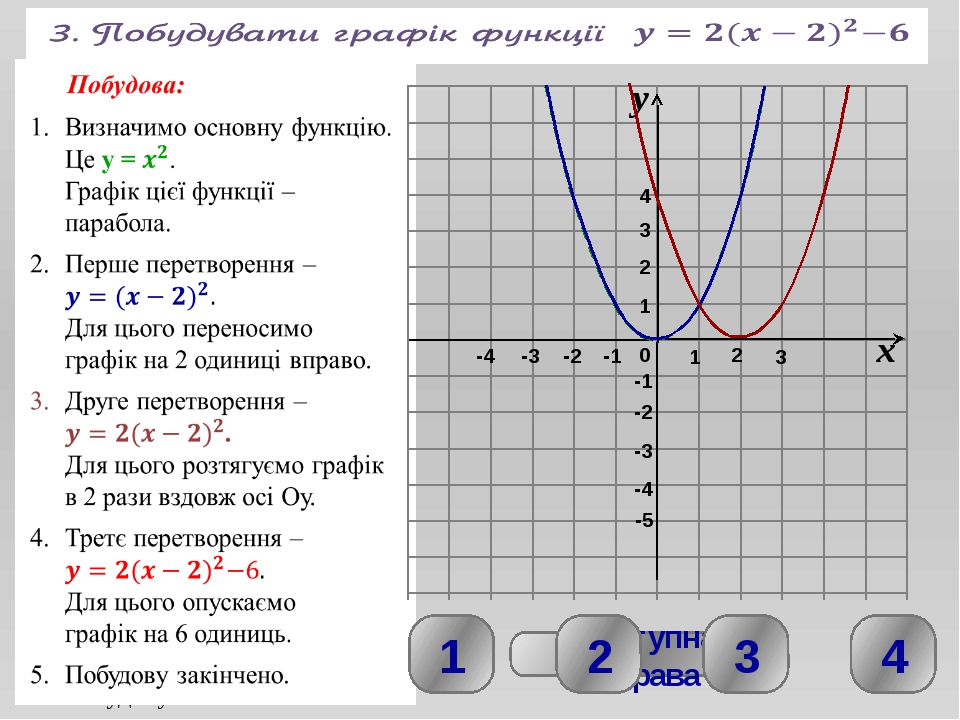 Но могут:
Но могут:
График
y = — | x + 2 |
Эта функция является своего рода противоположностью первой функции (см. Выше), потому что в выражении абсолютного значения в правой части уравнения стоит «минус». Из-за этого «минуса» все положительные значения, представленные столбцами абсолютных значений, будут переключены на отрицательные значения.Другими словами, я должен ожидать, что этот график будет иметь изгиб в точке (–2, 0), как и первый график выше, но остальная часть графика будет перевернута вверх дном, чтобы оказаться ниже оси x .
Сначала я заполню свою Т-диаграмму:
Затем делаю свой график:
Также не предполагайте, что какой-либо график абсолютных значений всегда будет находиться только на одной стороне оси x .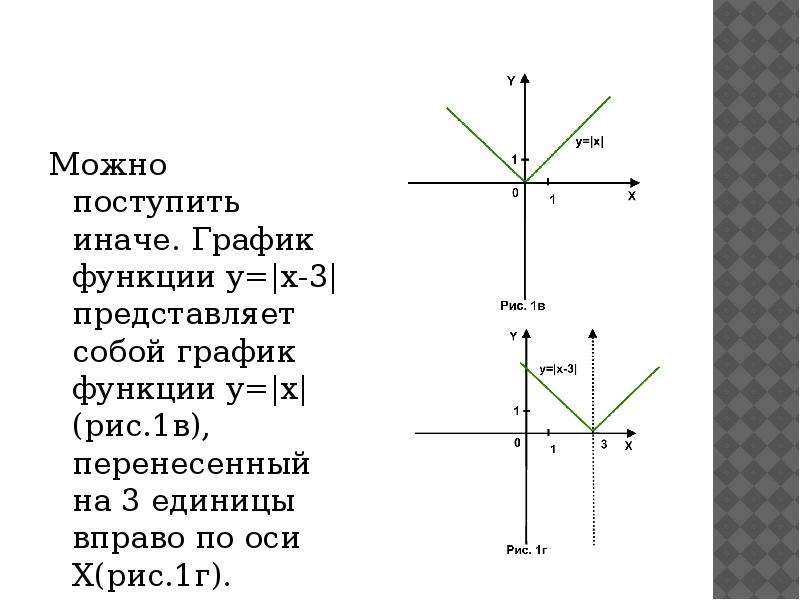 Графики могут пересекаться:
Графики могут пересекаться:
График
y = — | x | + 2
Моя Т-диаграмма:
… и мой график:
URL: https: // www.purplemath.com/modules/graphabs.htm
Графики функций квадратного корня
Родительская функция функций формы
ж
Икс
знак равно
Икс
—
а
+
б
является
ж
Икс
знак равно
Икс
.
Обратите внимание, что
домен
из
ж
Икс
знак равно
Икс
является
Икс
≥
0
и
диапазон
является
y
≥
0
.
График
ж
Икс
знак равно
Икс
—
а
+
б
можно получить, переведя график
ж
Икс
знак равно
Икс
к
а
единиц вправо, а затем
б
единиц вверх.
Пример:
Нарисуйте график
y
знак равно
Икс
—
1
+
2
из родительского графа
y
знак равно
Икс
.
Решение:
Шаг 1. Нарисуйте график
y
знак равно
Икс
.
Шаг 2. Переместите график
y
знак равно
Икс
от
1
единицы справа, чтобы получить график
y
знак равно
Икс
—
1
.
Шаг 3. Переместите график
y
знак равно
Икс
—
1
от
2
единиц до получения графика
y
знак равно
Икс
—
1
+
2
.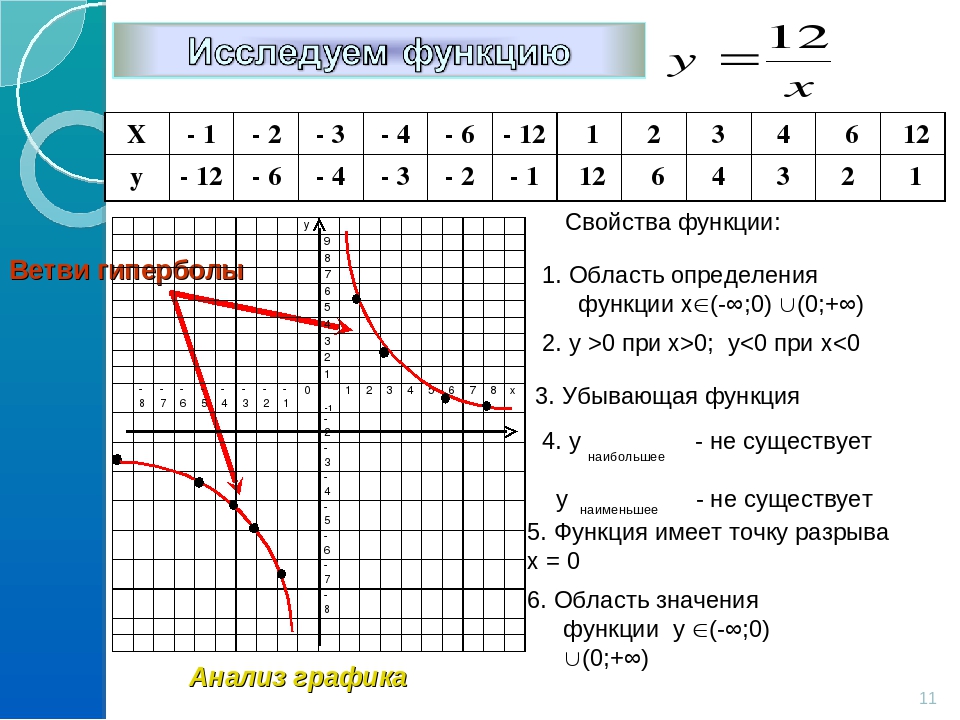
Область определения функции
y
знак равно
Икс
—
1
+
2
является
Икс
≥
1
.
Диапазон функции
y
знак равно
Икс
—
1
+
2
является
y
≥
2
.
Наибольшая целочисленная функция и график
Краткий обзор
- Функция наибольшего целого числа также известна как функция пола.
- Он записывается как $$ f (x) = \ lfloor x \ rfloor $$.
- Значение $$ \ lfloor x \ rfloor $$ — это наибольшее целое число, которое на меньше или равно $$ x $$.
Определение
Наибольшая целочисленная функция определяется как
$$ \ lfloor x \ rfloor = \ mbox {наибольшее целое число, которое} $$ меньше или равно $$ x $$.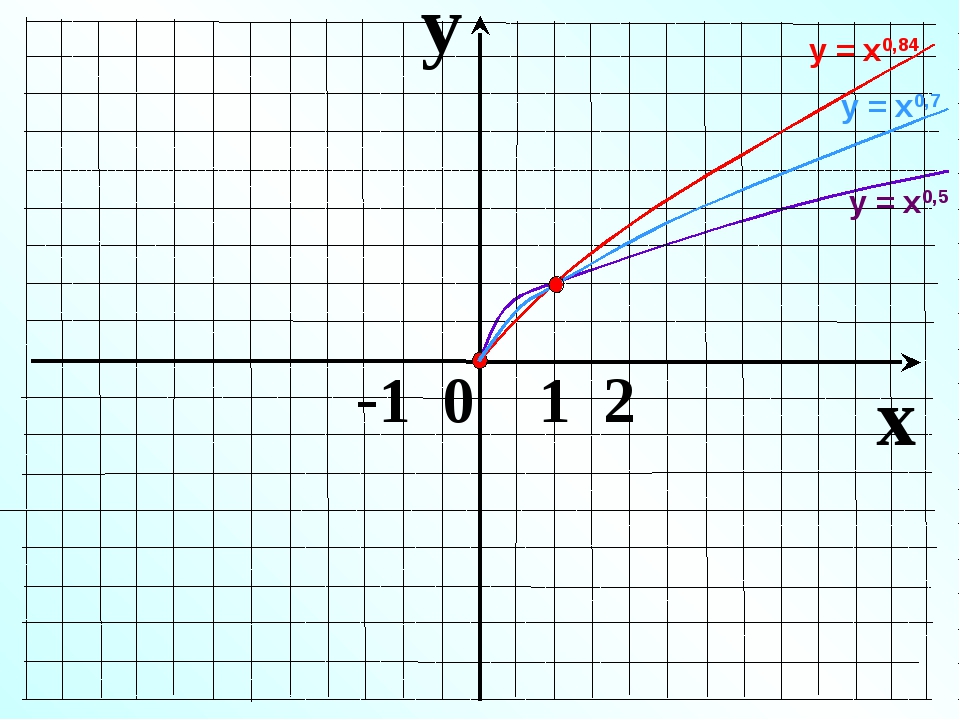
В математических обозначениях мы бы записали это как
$$
\ lfloor x \ rfloor = \ max \ {m \ in \ mathbb {Z} | m \ leq x \}
$$
Запись «$$ m \ in \ mathbb {Z} $$» означает «$$ m $$ — целое число».
Примеры
Пример 1 — Основные вычисления
Оцените следующее.
- $$ \ lfloor 2.7 \ rfloor $$
- $$ \ lfloor -1,4 \ rfloor $$
- $$ \ lfloor 8 \ rfloor $$
Решение
Если мы рассмотрим числовую строку с целыми числами и 2,7, нанесенными на нее, мы увидим
Наибольшее целое число, которое на меньше 2.7 равно 2.
 Итак, $$ \ lfloor 2.7 \ rfloor = 2 $$.
Итак, $$ \ lfloor 2.7 \ rfloor = 2 $$.Если мы рассмотрим числовую строку с целыми числами и нанесенными на нее -1,3, мы увидим
Поскольку наибольшее целое число, которое на меньше -1,3, равно -2, $$ \ lfloor -1,3 \ rfloor = -2 $$.
Поскольку $$ \ lfloor x \ rfloor = $$ наибольшее целое число, которое меньше или равно $$ x $$, мы знаем, что $$ \ lfloor 8 \ rfloor = 8 $$.
Построение графика наибольшей целочисленной функции
Чтобы понять поведение этой функции в терминах графика, давайте построим таблицу значений.
ТАБЛИЦА
$$
\ begin {array} {| c | c |}
\ hline
x & \ lfloor x \ rfloor \\
\ hline
-1.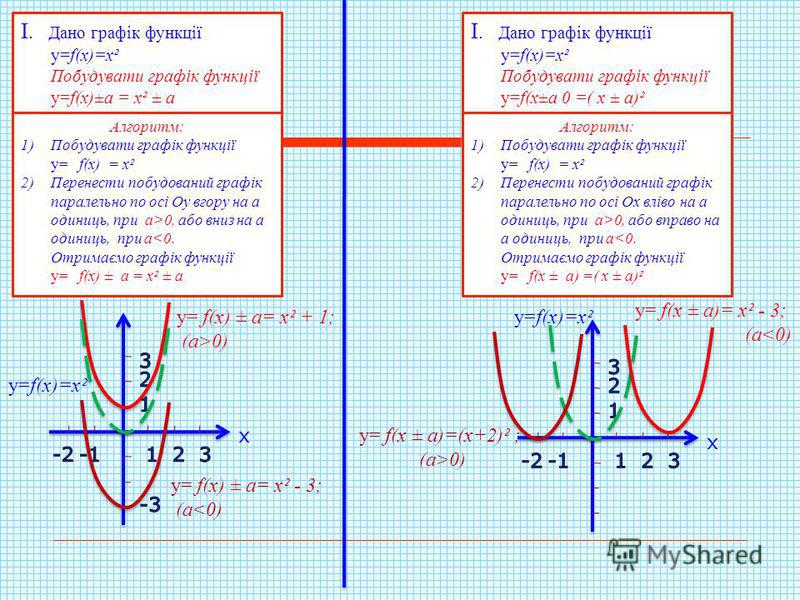 5 & -2 \\
5 & -2 \\
-1,25 & -2 \\
-1 & -1 \\
-0,75 & -1 \\
-0,5 & -1 \\
-0,25 и -1 \\
0 & 0 \\
0,25 & 0 \\
0,5 & 0 \\
0,75 & 0 \\
1 и 1 \\
1,25 и 1 \\
1.5 и 1 \\
\ hline
\ end {массив}
$$
Таблица показывает нам, что функция увеличивается до следующего наибольшего целого числа каждый раз, когда значение x становится целым числом. Это приводит к следующему графику.
Отвечать
Пример 2
Нарисуйте график $$ y = \ left \ lfloor \ frac 1 2x \ right \ rfloor $$.
Решение
Мы знаем, как должен выглядеть базовый график, поэтому нам просто нужно понять, как фактор $$ \ frac 1 2 $$ повлияет на вещи.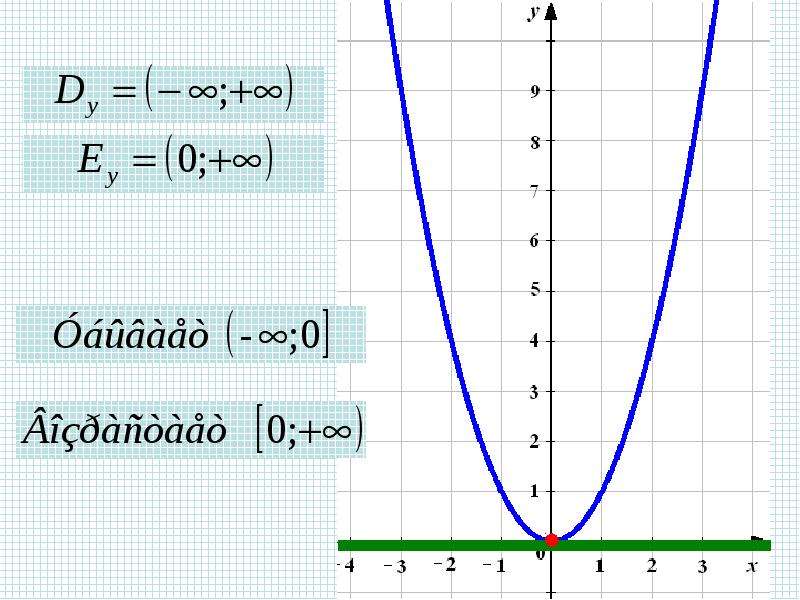 Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
ТАБЛИЦА
$$
\ begin {align *}
\ begin {array} {| c | c | c |}
\ hline
x & \ frac 1 2 x & \ left \ lfloor \ frac 1 2 x \ right \ rfloor \\ [6pt]
\ hline
-2 и -1.5 & -2 \\ [6pt]
-1,5 и -0,75 и -1 \\ [6pt]
-1 & -0,5 & -1 \\ [6pt]
-0,5 и -0,25 и -1 \\ [6pt]
0 & 0 & 0 \\ [6pt]
0,5 и 0,25 и 0 \\ [6pt]
1 & 0,5 & 0 \\ [6pt]
1,5 и 0,75 и 0 \\ [6pt]
2 и 1 и 1 \\ [6pt]
\ hline
\ end {массив}
\ end {выровнять *}
$$
Мы замечаем из таблицы, что значения функции переходят к следующему значению, когда $$ x $$ четно.
ПРЕОБРАЗОВАНИЕ
Мы можем интерпретировать $$ y = \ left \ lfloor \ frac 1 2 x \ right \ rfloor $$ как горизонтальный участок, который удваивает длину каждой части.
Отвечать:
Решение уравнений
Существует формула, которая может помочь нам при работе с уравнениями, включающими функцию пола.
$$ \ lfloor x \ rfloor = m \ qquad \ mbox {тогда и только тогда, когда} \ quad m \ leq x
(помните, $$ m $$ — целое число!)
Так, например, $$ \ lfloor x \ rfloor = 8 $$ тогда и только тогда, когда $$ 8 \ leq x
Пример 3
Решите уравнение $$ \ lfloor 2x + 5 \ rfloor = 9 $$.
Шаг 1
Перепишем уравнение, используя неравенство.
$$ 9 \ leq 2x + 5
Шаг 2
Решите неравенство.
$$
\ begin {align *}
9 & \ leq 2x + 5
Отвечать:
В интервальной записи уравнение верно для $$ x \ в [2, 2.5) $$.
Пример 4
Решите уравнение $$ \ lfloor 1.25 + \ lfloor x \ rfloor \ rfloor = 12 $$.
Шаг 1
Замените $$ \ lfloor x \ rfloor $$ на $$ u $$. Это называется «заменой переменной», и это облегчает работу с уравнением.
$$
\ begin {align *}
\ lfloor 1. 25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$
Шаг 2
Заменить уравнение одним из неравенств, где $$ m = 12 $$
$$
12 \ leq 1.25 + u
Шаг 3
Решите неравенство.
$$
\ begin {align *}
12 & \ leq 1.25 + u
Поскольку $$ \ lfloor x \ rfloor $$ является целым числом, единственный способ удовлетворить приведенные выше неравенства — $$ \ lfloor x \ rfloor = 11 $$.
Шаг 4
Определите значение $$ x $$.
Опять же, используя неравенства, мы знаем
$$
11 \ leq x
Отвечать:
$$
11 \ leq x
Продолжайте практиковать задачи
Ошибка: Нажмите «Не робот», затем повторите попытку.
Как построить график X через Y на калькуляторе TI-84
Обновлено 15 декабря 2020 г.
Джек Джерард
Калькулятор TI-84 предлагает ряд встроенных функций для решения и построения графиков уравнений. К сожалению, его основные параметры построения графиков ограничены функциями и уравнениями, которые характеризуют Y в терминах X . Реже вам нужно графически отображать X в терминах Y , но если вы это сделаете, существующие параметры не совсем помогут.К счастью, TI-84 позволяет импортировать внешние приложения и использовать их почти так же, как и приложения, поставляемые с калькулятором. Репозиторий TI Calc, поддерживаемый сообществом, содержит ряд этих внешних приложений, в том числе приложение под названием XGraph от Джоэла Смита, которое позволяет отображать X в терминах Y .
Что означает X в терминах Y?
Для большинства уравнений вы строите график Y в единицах X . Это означает, что ваше уравнение основано на значении Y и интерпретируется через значение X ; пример: y = x + 1. Значение Y зависит от значения X , поэтому для каждого X соответствующее значение Y равно этому значению X плюс 1. Построение графика X через Y меняет ситуацию. Вместо y = x + 1 вы должны создать график из x = y + 1.В этом случае ваше значение X зависит от значения Y , и для вычисления каждого X вы берете соответствующее ему значение Y и добавляете 1. К сожалению, это не так. На калькуляторе TI-84 легко построить график, если вы не рассчитываете и не наносите на график отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в его функциях построения графиков.
Это означает, что ваше уравнение основано на значении Y и интерпретируется через значение X ; пример: y = x + 1. Значение Y зависит от значения X , поэтому для каждого X соответствующее значение Y равно этому значению X плюс 1. Построение графика X через Y меняет ситуацию. Вместо y = x + 1 вы должны создать график из x = y + 1.В этом случае ваше значение X зависит от значения Y , и для вычисления каждого X вы берете соответствующее ему значение Y и добавляете 1. К сожалению, это не так. На калькуляторе TI-84 легко построить график, если вы не рассчитываете и не наносите на график отдельные точки вручную, поскольку TI-84 не имеет опции «X =» в его функциях построения графиков.
Установка XGraph
Одна вещь, которая есть у TI-84, — это средство расширения его функций с помощью закодированных приложений и программ. Приложение XGraph позаботится об этом, позволяя вводить уравнения в форме X через Y и отображать их в виде графика. Файл загружается в виде файла .zip, который содержит XGRAPH.8XP и файл readme; извлеките файл XGRAPH.8XP в легкодоступное место. Подключите калькулятор TI-84 к компьютеру с помощью соединительного кабеля USB, поставляемого с калькулятором, а затем запустите программное обеспечение TI Connect от Texas Instruments (которое можно бесплатно загрузить с веб-сайта Texas Instruments, если оно еще не установлено. ).Выберите XGRAPH.8XP и подтвердите, что хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
Приложение XGraph позаботится об этом, позволяя вводить уравнения в форме X через Y и отображать их в виде графика. Файл загружается в виде файла .zip, который содержит XGRAPH.8XP и файл readme; извлеките файл XGRAPH.8XP в легкодоступное место. Подключите калькулятор TI-84 к компьютеру с помощью соединительного кабеля USB, поставляемого с калькулятором, а затем запустите программное обеспечение TI Connect от Texas Instruments (которое можно бесплатно загрузить с веб-сайта Texas Instruments, если оно еще не установлено. ).Выберите XGRAPH.8XP и подтвердите, что хотите отправить его на свой калькулятор, и подождите, пока TI Connect отправит и установит приложение. По завершении вы можете закрыть TI Connect и отключить калькулятор.
Использование приложения
Нажмите кнопку PRGM на калькуляторе TI-84 и найдите запись «XGRAPH» в списке программ. Нажмите клавишу ENTER, на вашем экране появится «prgmXGRAPH»; снова нажмите ENTER, чтобы запустить приложение. При появлении запроса введите уравнение, но используйте букву X вместо Y .Если бы вы надеялись изобразить уравнение, такое как x = 2 y + 1, вместо этого ваш вход XGraph будет «X =? 2X + 1». Нажмите клавишу ENTER и подождите, пока программа построит график; несмотря на то, что вы вводите X , график будет нарисован как X с точки зрения Y (что для приведенного выше примера будет графиком x = 2 y + 1.) По завершении нажмите кнопку «ON», чтобы прервать программу, и выберите «1: Quit» для выхода.
При появлении запроса введите уравнение, но используйте букву X вместо Y .Если бы вы надеялись изобразить уравнение, такое как x = 2 y + 1, вместо этого ваш вход XGraph будет «X =? 2X + 1». Нажмите клавишу ENTER и подождите, пока программа построит график; несмотря на то, что вы вводите X , график будет нарисован как X с точки зрения Y (что для приведенного выше примера будет графиком x = 2 y + 1.) По завершении нажмите кнопку «ON», чтобы прервать программу, и выберите «1: Quit» для выхода.
Функции — Алгебра — Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы алгебры.
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему то же самое значение y , известное на его изображении.
x → Функция → y
Буква f, g или h часто используется для обозначения функции.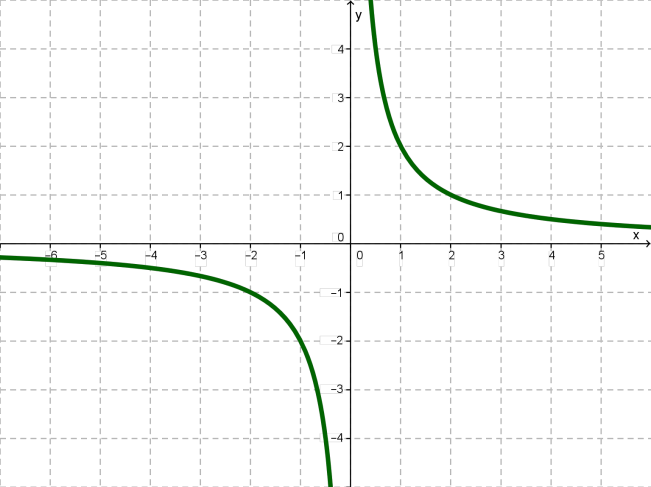 Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 .Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 .Это же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или, альтернативно, f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например, y = 3x).
- Если f (x) = 3x и y является функцией x (т.е. y = f (x)), тогда значение y, когда x равно 4, равно f (4), которое находится заменой x «s на 4» s.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x). Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Индивидуальные встречи
Мы говорим, что функция взаимно однозначная , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x).f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Функции компоновки
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
.
Пример
Если f (x) = x 2 и g (x) = x — 1, то
gf (x) = g (x 2 ) = x 2 — 1
fg (x) = f (x — 1) = (х — 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией является функция, которая обращает эффект исходной функции.Например, y = 2x, обратный y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» s и сделайте y предметом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяйте местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f -1 (x) = ½ (x — 1)
f -1 (x) — стандартное обозначение, обратное к f (x).Обратное считается существующим тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
.
Обратите внимание, что график f -1 будет отражением f на линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить в виде графиков. Функция непрерывная , если на ее графике нет разрывов. Пример прерывистого графа — y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция периодическая , если ее график повторяется через равные промежутки времени, этот интервал известен как период.
Функция равна , даже если она не изменяется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция нечетная , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что «растяжение» фактически приводит к сжатию графика, если a — число больше 1]
Пример
График y = | x — 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так, чтобы точка V ударилась о ось x на 1, а не на 0).
Mathscene — Функции 1 — Урок 3
Mathscene — Функции 1 — Урок 3
| 2007 Rasmus ehf и Jhann sak | Функции | Печать |
Урок 3
.
Функции второй степени
Давайте снова посмотрим на многочлены второй степени.Самая простая форма функции — f (x)
= х 2 . График представляет собой
параболу часто называют основной параболой.
Обратите внимание, что график симметричен относительно оси y-
ось. Ось ординат называется осью симметрии этой функции.
Теперь посмотрим, как коэффициенты влияют на внешний вид графика.
Коэффициент x 2 равен
обычно называется a. Если мы посмотрим на
параболы с разными значениями a мы видим, что некоторые из них шире, а некоторые —
уже основной параболы, где a = 1.
Вот графики парабол, где a = 4, 2,
ог.
а = 4
а = 2
а =
а =
Вот параболы с
отрицательные значения
а = −4
а = −2
а = —
а = —
Если значение a равно
положительный график изгибается вверх (как улыбка!) Чем больше значение
уже график.
По мере того, как становится мало
график становится более плоским и плоским до тех пор, пока, когда a не станет отрицательным, он не станет меньше (
как хмурый взгляд! ).
Пример 1
Теперь нарисуем график
из f (x) = x 2 + 1 и
сравните его с g (x) = x 2 .
| x | f (x) = х 2 + 1 | |
| -2 | (-2) 2 + 1 = 5 | |
| -1 | (-1) 2 + 1 = 2 | |
| 0 | 0 + 1 = 1 | |
| 1 | 1 2 + 1 = 2 | |
| 2 | 2 2 + 1 = 5 |
Значения функции (
y) в таблице значений для f (x) = x 2 +1 все
на единицу выше соответствующих значений в таблице значений для g (x) = x 2
и график был переведен по вертикали на 1 единицу.
Обратите внимание, что график f (x) =
x 2 + 1 не пересекает
ось абсцисс. Это говорит нам о том, что уравнение x 2
+ 1 = 0 не имеет решения. Мы уже знаем это, поскольку число в квадрате никогда не бывает
отрицательное, поэтому x 2 никогда не может быть равно -1.
Пример
2
Нарисуйте график f (x) = x 2
— 1 и сравните с g (x)
= х 2 .
| x | f (x) = х 2 — 1 | |
| -2 | (-2) 2 — 1 = 3 | |
| -1 | (-1) 2 — 1 = 0 | |
| 0 | 0 — 1 = -1 | |
| 1 | 1 2 — 1 = 0 | |
| 2 | 2 2 — 1 = 3 |
Теперь значения функции в
все таблицы f (x) на единицу ниже соответствующих значений в таблице для
g (x) = x 2 и график
сдвинулась на одну единицу.
Обратите внимание, что в этом примере
график f (x) = x 2
— 1 пересекает ось x в двух местах.
Это означает, что уравнение
x 2 — 1 = 0 имеет два
решения,
х 2 — 1 = 0
х 2 = 1
х = 1
, которые равны x = −1 и x
= 1.
Пример
3
Нарисуйте график f (x)
= (x + 1) 2 (или f (x)
= x 2 + 2x + 1) и сравните
это к основной параболе g (x) = x 2 .
| x | f (x) = (х + 1) 2 | |
| -3 | (-3 + 1) 2 = 4 | |
| -2 | (-2 + 1) 2 = 1 | |
| -1 | (-1 + 1) 2 = 0 | |
| 0 | (0 + 1) 2 = 1 | |
| 1 | (1 + 1) 2 = 4 |
Здесь мы прибавили 1 к x
и мы видим, что функция
значения в таблице значений сдвинуты на одну строку вверх по сравнению с базовыми
функция.
График f (x) — это
так же, как если бы мы переместили график g (x) = x 2 на одну единицу
Слева.
Мы говорим, что основной граф
переведено на -1 единиц по горизонтали. Ось симметрии теперь x
= -1.
Пример
4
Нарисуйте
график f (x) = (x — 2) 2
— 1 (или f (x) = x 2
— 4x + 3) и сравните его с базовым графиком g (x) = x 2 .
Если использовать тот же метод, что и в предыдущем
Например, мы можем предположить, что график переместился на две единицы вправо и одну
блок вниз. Теперь проверим это, составив таблицу
значения, начиная с x = 0 и
рисование графика.
| x | f (x) = (х — 2) 2 — 1 | |
| 0 | (0–2) 2 — 1 = 3 | |
| 1 | (1-2) 2 — 1 = 0 | |
| 2 | (2–2) 2 — 1 = -1 | |
| 3 | (3–2) 2 — 1 = 0 | |
| 4 | (4–2) 2 — 1 = 3 |
Обратите внимание, что ось симметрии теперь x = 2.
Мы можем найти, где график пересекает ось Y
без рисования графика. Мы делаем это, вычисляя f (0)
= 3 или путем умножения скобок и
видя, что постоянный член (член без x) равен 3.
f (x) = (x — 2) 2 — 1 = x 2
— 4x + 4 — 1 = x 2
— 4x + 3
или
f (0) = (x — 2) 2 — 1 = 4 — 1 = 3
Пример
5
Найдите график зависимости f (x) = (x — 2) 2
— 1 пересекает ось абсцисс.Положим y = f (x) = 0, а затем решим уравнение
для x.
| (x — 2) 2 — 1 = 0 | Первый переместите -1 над знаком равенства. |
| (x — 2) 2 = 1 | Далее, извлеките квадратный корень из обеих частей уравнения. Помните + и -. |
| x — 2 = 1 = 1 | Наконец переместите 2 на другую сторону и упростите результат. |
| x = 2 1 |
Точки пересечения:
х = 2 -1
= 1 и x = 2 + 1 = 3.
Легко видеть, что запись функции в виде f (x)
= (x — 2) 2 — 1 дает нам много информации.
Он сообщает нам, как переводится основной график
вертикально и горизонтально.
Он также сообщает нам, где находится ось симметрии.
Наконец, мы можем легко найти точки
пересечение с осями x и y.
Общий вид уравнения, записанного в этом
путь:
f (x) = a (x + r) 2 + s
a — коэффициент x 2
как мы уже видели.
ось симметрии имеет уравнение x = −r (или, можно сказать, то же
значение как r, но с обратным знаком).
Поэтому важно знать, как
перепишите функцию
f (x) =
ax 2 + bx + c в виде
f (x) = a (x + r) 2 + s
Пример
6
Теперь давайте посмотрим, как мы можем изменить секунду
функция степени от одной формы к другой.
Записываем f (x) = x 2 — 4x + 3 в виде f (x) = (x — 2) 2 .
— 1.
По сравнению с общей формой:
f (x) = ах 2
+ bx + c
f (х) = х 2
— 4x + 3
Здесь a
= 1
og b = −4
и c = 3 (поэтому график пересекает ось y в 3).
Посмотрите на правило возведения скобки в квадрат:
(x q) 2 = p 2
2xq
+ q 2 .
Мы видим, что коэффициент при x
составляет 2кв.
В нашем примере коэффициент при x равен
−4, что означает 2q = — 4 и, следовательно,
q = −2.
Если посчитать
(х — 2) 2
получаем x 2
— 4x + 4.
(х
— 2) 2 = х 2
— 4x + 4.
Если мы вычтем 1 с обеих сторон
мы получили :
(х — 2) 2
−1 = х 2 — 4x +
4−1 = x 2 — 4x
+ 3
Обобщая метод:
| f (x) = x 2 — 4x + 3 | Половина коэффициент при x равен −4 / 2 = −2, который мы возводим в квадрат (4) и добавить к уравнению. |
| = (x 2 — 4x + 2 2 ) — 2 2 + 3 | |
| = (x — 2) 2 — 4 + 3 | Если мы прибавив 4 к уравнению, мы также должны вычесть 4, чтобы уравнение без изменений Теперь упростим −4 + 3 = −1 |
| = (x — 2) 2 — 1 |
Из приведенного выше примера можно сделать вывод, что
график полинома второй степени, где a = 1 (f (x) = x 2 + bx + c) имеет ось симметрии в:
x = −b / 2 и обрезает y
ось, где y = c.
Пример
7
Найдите ось симметрии графика f (x) =
2x 2 — 12x + 10.
В этом случае a = 2, поэтому правило из предыдущего примера не применяется. Ни один
так же легко переписать функцию, как раньше.
Вместо этого мы переводим функцию вниз на 10
единиц путем вычитания 10 из уравнения. Перемещение графика по вертикали не
изменить положение оси симметрии.
Назовем эту новую функцию g (x) и найдем, где
g (x) отсекает ось x.
2x 2
— 12x = 0
2х (х — 6) = 0
Это уравнение имеет решения x = 0 и 6, поэтому
график g (x) пересекает ось x
в 0 и 6. Ось симметрии должна быть посередине этих двух точек, что
находится в x = 3 .
Пример
8
Перепишем функцию f (x) = 2x 2
— 12x + 10 в виде
е (х) = а (х + г) 2 + s.
| f (x) = 2x 2 — 12x + 10 | Дубль 2 вне скобки. Половина коэффициента при x равно −6 / 2 = −3, поэтому добавьте 3 2 внутри скобок. Мы действительно добавили 18, поэтому теперь нам нужно вычесть 23 2 = 18 за пределами скобки. |
| = 2 (x 2 — 6x + 3 2 ) — 2 3 2 + 10 | |
| = 2 (x 2 — 6x + 9) — 18 + 10 | |
| = 2 (х — 3) 2 — 8 |
Теперь мы, как и раньше, видим, что ось симметрии
находится в x = 3.
Коэффициенты x В приведенном выше примере (f (x)
= 2x 2 — 12x + 10)
равны a = 2, b = −12 и c = 10. Чтобы найти ось симметрии, мы
множитель 2 вынес за скобки. Это соответствует делению на 2. Тогда мы
завершил квадрат делением коэффициента при x
(−6) на 2.
Общая формула оси симметрии
функция
f (x) = ax 2
+ bx + c — это
следовательно:
Пример
9
Найдите вершину параболы f (x) = 2x 2
— 12x + 10.
Вершина (в которой вращается парабола) лежит
на оси симметрии, поэтому мы знаем значение x вершины (3).
Мы нашли
значение y путем вычисления f (3).
f (3) = 23 2
— 123 + 10 = 18 — 36 + 10 = −8.
Вершина параболы равна (3,
−8).
Примечание: Если a> 0, вершина является точкой минимума. Если
a <0 вершина является точкой максимума.
Попробуйте пройти тест 3 по функциям I.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
