Содержание
Пифагоровы штаны – на все стороны равны
Пифагоровы штаны – на все стороны равны.
Чтобы это доказать, нужно снять и показать.
Этот стишок известен всем со средней школы, с тех самых пор, когда на уроке геометрии мы изучали знаменитую теорему Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Для доказательства своей теоремы Пифагор нарисовал на песке фигуру из квадратов на сторонах треугольника. Cумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы А квадрат плюс В квадрат равно С квадрат. Был это 500 год до нашей эры. Сегодня теорему Пифагора проходят в средней школе. В книге рекордов Гиннесса теорема Пифагора — теорема с максимальным числом доказательств. Действительно, в 1940 году была опубликована книга, содержащая триста семьдесят доказательств теоремы Пифагора. Одно из них было предложено президентом США Джеймсом Абрамом Гарфилдом. Лишь одно доказательство теоремы до сих пор никому из нас не известно: доказательство самого Пифагора. Долгое время считалось, что доказательство Евклида — это и есть доказательство Пифагора, но теперь математики думают, что это доказательство принадлежит самому Евклиду.
Лишь одно доказательство теоремы до сих пор никому из нас не известно: доказательство самого Пифагора. Долгое время считалось, что доказательство Евклида — это и есть доказательство Пифагора, но теперь математики думают, что это доказательство принадлежит самому Евклиду.
Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.
Конструкция, используемая для доказательства, следующая: для прямоугольного треугольника ABC с прямым углом С, квадратов над катетами ACED и BCFG и квадрата над гипотенузой ABIK строится высота CH и продолжающий её луч s, разбивающий квадрат над гипотенузой на два прямоугольника АHJK и BHJI. Доказательство нацелено на установление равенства площадей прямоугольника АHJK с квадратом над катетом АC; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.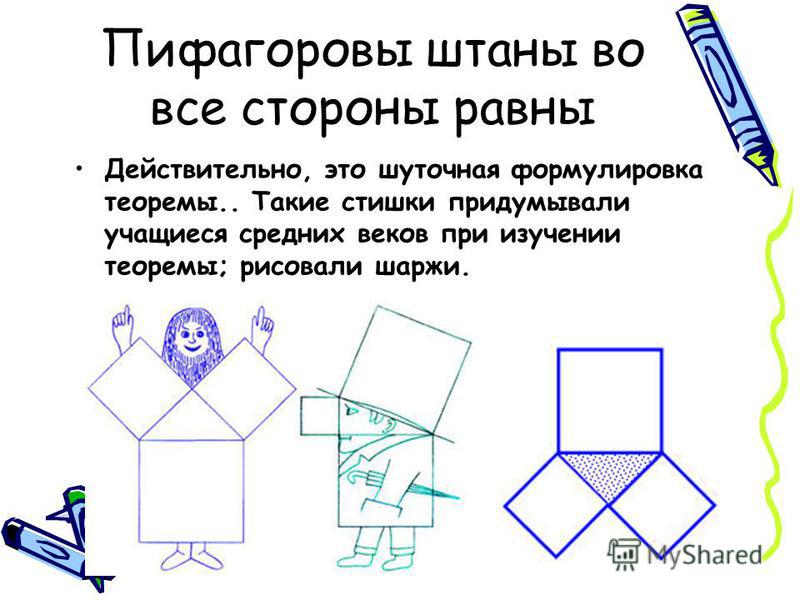
Равенство площадей прямоугольника АHJK и АCED устанавливается через конгруэнтность треугольников ACK и ABD, площадь каждого из которых равна половине площади прямоугольников AHJK и АCED соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямого угла и угла при A.
Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников АHJK и BHJI, равна сумме площадей квадратов над катетами.
Немецкий математик Карл Гаусс предложил в сибирской тайге вырубить из деревьев гигантские пифагоровы штаны. Глядя на эти штаны из космоса, инопланетяне должны убедиться, что на нашей планете обитают разумные существа.
Забавно, что сам Пифагор никогда не носил штаны – в те времена греки о таком предмете гардероба просто не знали.
Источники:
- sandbox.fizmat.vspu.ru
- ru.wikipedia.org
- kuchmastar.fandom.com
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
10 фактов о теореме Пифагора
Кто ж не помнит: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. А вот вам 10 фактов о знаменитой теореме.
Пифагоровы
штаны – на все стороны равны.
Чтобы это доказать, нужно снять и показать.
Этот стишок известен всем со средней школы, с тех самых
пор, когда на уроке геометрии мы изучали знаменитую теорему
Пифагора: квадрат длины гипотенузы прямоугольного треугольника
равен сумме квадратов катетов. А вот вам 10 фактов о знаменитой
теореме.
1. Происхождение штанов понятно: построенные на сторонах
Происхождение штанов понятно: построенные на сторонах
треугольника и расходящиеся в разные стороны квадраты напоминали
школьникам покрой мужских штанов. Правда, это как посмотреть:
средневековые школяры называли эту теорему «pons asinorum», что
означает «ослиный мост».
2. Книга рекордов Гиннесса называет теорему Пифагора теоремой с
максимальным числом доказательств. И поясняет в 1940 году была
опубликована книга, которая содержала триста семьдесят
доказательств теоремы Пифагора, включая одно предложенное
президентом США Джеймсом Абрамом Гарфилдом.
3. Теорему Пифагора доказывали через подобные треугольники,
методом площадей и даже через дифференциальные уравнения – это
сделал английский математик начала двадцатого века Годфри Харди.
Известны доказательства теоремы Пифагора, предложенные Евклидом и
Леонардо Да Винчи. А Электроник – мальчик из чемоданчика в книге
А Электроник – мальчик из чемоданчика в книге
Евгения Велтистова знал целых двенадцать способов, а среди них
«метод укладки паркета» и «стул невесты».
4. Только одно доказательство теоремы Пифагора нам не известно:
доказательство самого Пифагора. Долгое время считалось, что
доказательство Евклида и есть доказательство Пифагора, но теперь
считают, что это доказательство принадлежит Евклиду.
5. К настоящему моменту историки математики обнаружили, что
теорема Пифагора не была открыта Пифагором – ее знали в разных
странах задолго до древнегреческого философа и математика родом с
острова Самос, жившего в VI веке до н.э.
6. Крупнейший историк математики Мориц Кантор разглядел папирус
из Берлинского музея и обнаружил, что равенство три в квадрате
плюс четыре в квадрате равно пяти в квадрате было известно уже
египтянам около 2300 года до нашей эры во времена царя Аменемхета
I.
7. Приближенное вычисление гипотенузы прямоугольного треугольника
обнаруживается в вавилонских текстах времен правления царя
Хаммурапи, то есть за два тысячелетия до нашей эры. Весьма
вероятно, что теорема о квадрате гипотенузы была известна в Индии
уже около VIII века до нашей эры.
8. Голландский математик Бартель Ван дер Варден сделал важный
вывод: «Заслугой первых греческих математиков, таких как Пифагор,
является не открытие математики, но ее систематизация и
обоснование. В их руках вычислительные рецепты, основанные на
смутных представлениях, превратились в точную науку».
9. «В день, когда Пифагор открыл свой чертёж знаменитый,
Славную он за него жертву быками
воздвиг».
Со слов неизвестного древнего стихотворца легенда о гекатомбе –
жертвоприношении ста быков пошла гулять по умам и страницам
изданий. Остряки шутят, что с тех самых пор все скоты боятся
Остряки шутят, что с тех самых пор все скоты боятся
нового.
10. Сам Пифагор никогда не носил штанов – в те времена греки их
не знали.
Оригинальное доказательство теоремы Пифагора | by Сергей Базанов | Paradox Review
Знаменитую теорему Пифагора — «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» — знают все со школьной скамьи.
Ну, вы помните «Пифагоровы штаны», которые «во все стороны равны» — схематический рисунок, поясняющий теорему греческого ученого.
Здесь a и b — катеты, а с — гипотенуза:
Сейчас я вам расскажу об одном оригинальном доказательстве этой теоремы, о котором вы, возможно, не знали…
Но, сначала рассмотрим одну лемму — доказанное утверждение, которое полезно не само по себе, а для доказательства других утверждений (теорем).
Возьмем прямоугольный треугольник с вершинами X, Y и Z, где Z — прямой угол и опустим перпендикуляр с прямого угла Z на гипотенузу. Здесь W — точка, в которой высота пересекается с гипотенузой.
Эта линия (перпендикуляр) ZW разбивает треугольник на подобные копии самого себя.
Напомню, что подобными называются треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
В нашем примере образовавшиеся треугольники XWZ и YWZ подобны друг другу и также подобны исходному треугольнику XYZ.
Доказать это несложно.
Начнем с треугольника XWZ, обратите внимание, что ∠XWZ = 90, и поэтому ∠XZW = 180–90-∠X. Но 180–90-∠X — это именно то, что ∠Y, поэтому треугольник XWZ должен быть подобным (все углы равны) треугольнику XYZ. Такое же упражнение можно выполнить для треугольника YWZ.
Такое же упражнение можно выполнить для треугольника YWZ.
Лемма доказана! В прямоугольном треугольнике высота (перпендикуляр), опущенная на гипотенузу, разбивает треугольник на два подобных, которые в свою очередь подобны исходному треугольнику.
Но, вернемся к нашим «Пифагоровым штанам»…
Опустим перпендикуляр на гипотенузу c. В результате у нас образовались два прямогульных треугольника внутри нашего прямоугольного треугольника. Обозначим эти треугольники (на картинке вверху зеленым цветом) буквами A и B, а исходный треугольник — буквой С.
Разумеется, площадь треугольника С равна сумме площадей треугольников A и B.
Т.е. А + B = С
Теперь разобьем фигуру вверху («Пифагоровы штаны») на три фигурки-домика:
Как мы уже знаем из леммы, треугольники A, B и C подобны друг другу, поэтому и образовавшиеся фигурки-домики также подобны и являются масштабированными версиями друг друга.
Это означает, что соотношение площадей A и a², — это то же самое, что отношение площадей B и b², а также C и c².
Таким образом, мы имеем A / a² = B / b² = C / c² .
Обозначим это соотношение площадей треугольника и квадрата в фигуре-домике буквой k.
Т.е. k — это некий коэффициент, связывающий площадь треугольника (крыши домика) с площадью квадрата под ним:
k = A / a² = B / b² = C / c²
Из этого следует, что площади треугольников можно выразить через площади квадратов под ними таким образом:
A = ka², B = kb², и C = kc²
Но, мы помним, что A+B = C, а значит, ka² + kb² = kc²
Или a² + b² = c²
А это и есть доказательство теоремы Пифагора!
По материалам заметки Колина Фразера (Colin Fraser)
Сокровище геометрии | Наука и жизнь
Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI—XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.
Было это ещё в I веке до н. э. На рубеже XVI—XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.
Теорема Пифагора для случая равнобедренного прямоугольного треугольника.
Наука и жизнь // Иллюстрации
Иллюстрация к теореме Пифагора из «Трактата об измерительном шесте» (Китай, III век до н. э.) и реконструированное на его основе доказательство.
Наука и жизнь // Иллюстрации
С. Перкинс. Пифагор.
Чертёж к возможному доказательству Пифагора.
«Мозаика Пифагора» и разбиение ан-Найризи трёх квадратов в доказательстве теоремы Пифагора.
П. де Хох. Хозяйка и служанка во внутреннем дворике. Около 1660 года.
Я. Охтервелт. Бродячие музыканты в дверях богатого дома. 1665 год.
1665 год.
‹
›
Пифагоровы штаны
Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a < b < c, усмотреть соотношение a2 + b2 = c2 невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис.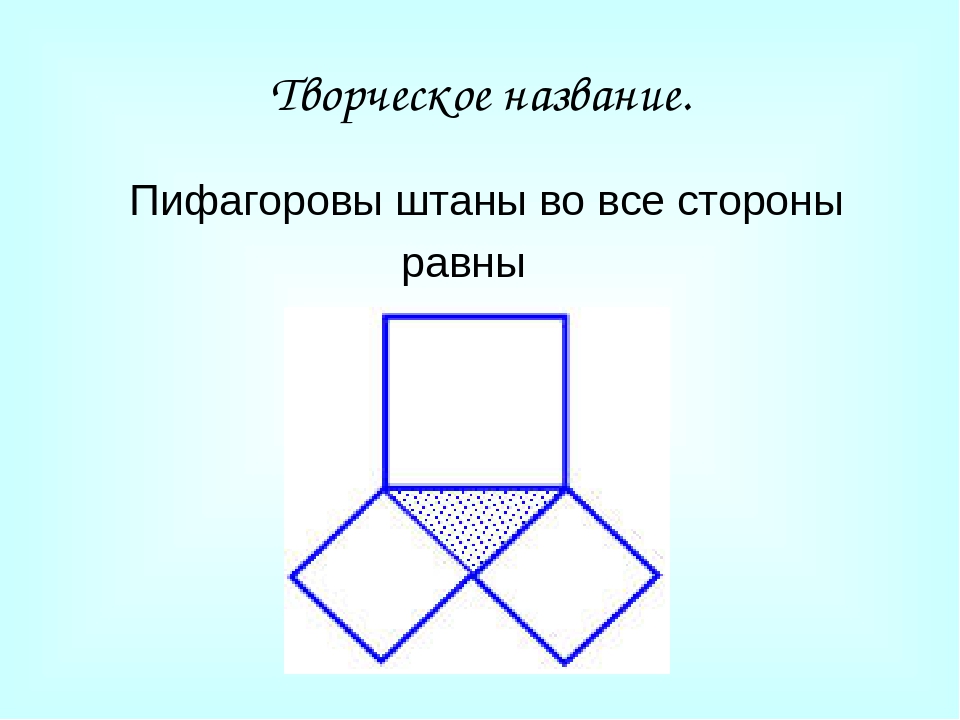 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.
1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.
Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением*. При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.
4000 лет спустя
История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a2 + b2 = c2 для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a2 + a2 = c2. Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.
Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!
И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!
Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV—III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.
3), и сразу проясняется его связь с задачей об удвоении площади квадрата.
Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его… самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!
Первый математик
Пифагора Самосского (570—495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII—VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.
Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII—VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.
Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.
Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.
Такое простое доказательство
Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a2 = c · m и b2 = c · n. Тогда a2 + b2 = = c · (m + n) = c2 (рис. 4).
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять. .. Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.
.. Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.
Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.
Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.
Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.
Мозаика Пифагора
Если покрыть плоскость квадратами двух разных размеров, окружив каждый малый квадрат четырьмя большими, получится паркет «мозаика Пифагора». Такой рисунок издавна украшает каменные полы, напоминая о древних доказательствах теоремы Пифагора (отсюда его название). По-разному накладывая на паркет квадратную сетку, можно получить разбиения квадратов, построенных на сторонах прямоугольного треугольника, которые предлагались разными математиками. Например, если расположить сетку так, чтобы все её узлы совпали с правыми верхними вершинами малых квадратов, проявятся фрагменты чертежа к доказательству средневекового персидского математика ан-Найризи, которое он поместил в комментариях к «Началам» Евклида. Легко видеть, что сумма площадей большого и малого квадратов, исходных элементов паркета, равна площади одного квадрата наложенной на него сетки. А это означает, что указанное разбиение действительно пригодно для укладки паркета: соединяя в квадраты полученные многоугольники, как показано на рисунке, можно заполнить ими без пробелов и перекрытий всю плоскость.
Легко видеть, что сумма площадей большого и малого квадратов, исходных элементов паркета, равна площади одного квадрата наложенной на него сетки. А это означает, что указанное разбиение действительно пригодно для укладки паркета: соединяя в квадраты полученные многоугольники, как показано на рисунке, можно заполнить ими без пробелов и перекрытий всю плоскость.
Комментарии к статье
* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.
узнаем новое об известной теореме. Обеспечительные меры как со стороны налоговых органов, так и со стороны налогоплательщиков
Теорема Пифагора всем известна со школьной поры. Выдающийся математик доказал великую гипотезу, которой в настоящее время пользуются многие люди. Звучит правило так: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. За многие десятилетия ни один математик не сумел переспорить данное правило.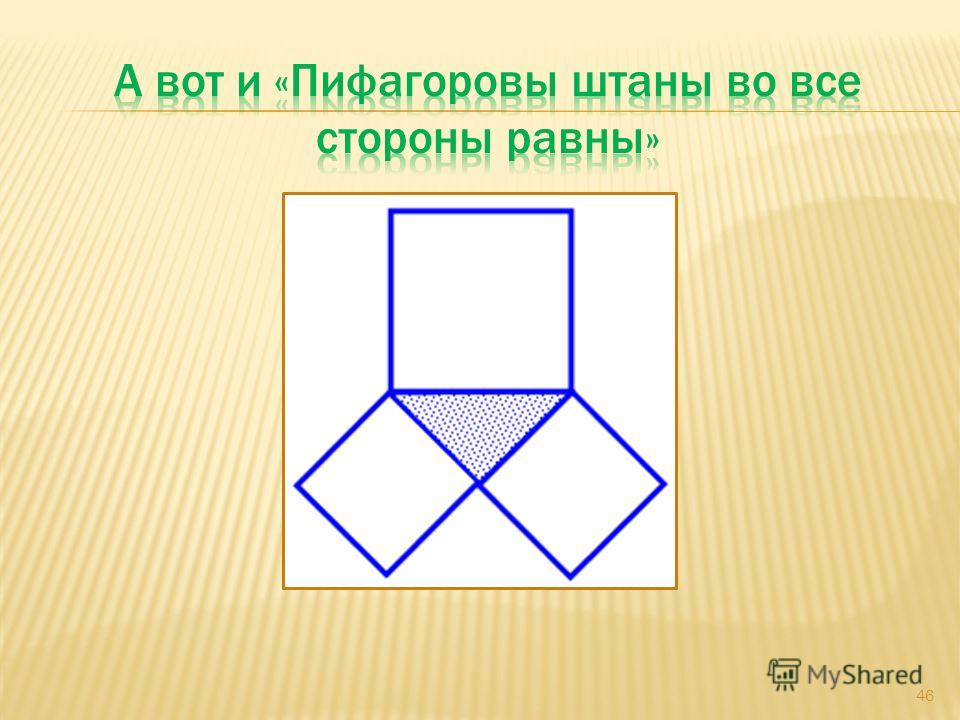 Ведь Пифагор долго шел к своей цели, чтобы в результате чертежи имели место в повседневной жизни.
Ведь Пифагор долго шел к своей цели, чтобы в результате чертежи имели место в повседневной жизни.
- Небольшой стих к данной теореме, который придумали вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагоровы штаны во все стороны равны»
. Это двустрочье отложилось в памяти у многих людей – по сей день стихотворение вспоминают при вычислениях. - Данная теорема получила название «Пифагоровы штаны» вследствие того, что при черчении по середине получался прямоугольный треугольник, по бокам которого располагались квадраты
. С виду данное черчение напоминало штаны – отсюда и название гипотезы. - Пифагор гордился разработанной теоремой, ведь данная гипотеза отличается от ею подобных максимальным количеством доказательств
. Важно: уравнение было занесено в книгу рекордов Гиннесса вследствие 370 правдивых доказательств. - Гипотезу доказывало огромное количество математиков и профессоров из разных стран многими способами
. Английский математик Джонс вскоре оглашения гипотезы доказал ее при помощи дифференциального уравнения.
- В настоящее время никому неизвестно доказательство теоремы самим Пифагором
. Факты о доказательствах математика сегодня не известны никому. Считается, что доказательство чертежей Евклидом — это и есть доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы. - Нынешние ученые обнаружили, что великий математик был не первым, кто открыл данную гипотезу
. Уравнение было известно еще задолго до открытия Пифагором. Данный математик сумел лишь воссоединить гипотезу. - Пифагор не давал уравнению название «Теорема Пифагора»
. Это название закрепилось после «громкого двустрочья». Математик лишь хотел, чтобы его старания и открытия узнал весь мир и пользовался ими. - Мориц Кантор — великий крупнейший математик нашел и разглядел на древнем папирусе записи с чертежами
. Вскоре после этого Кантор понял, что данная теорема была известна египтянам еще 2300 лет до нашей эры.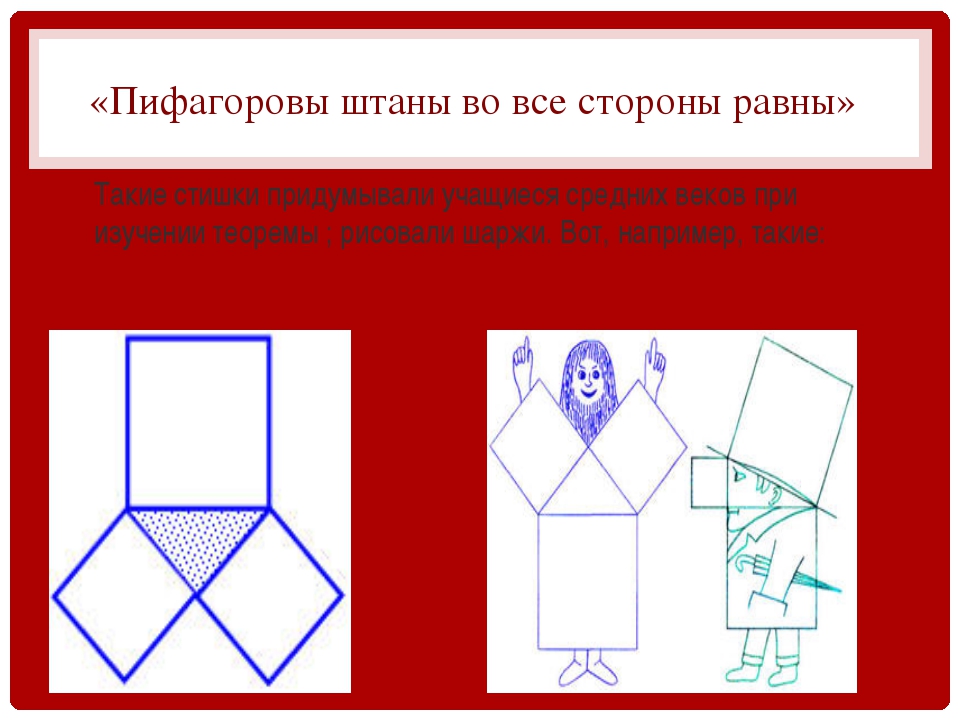 Только тогда ею никто не воспользовался и не стал пытаться доказать.
Только тогда ею никто не воспользовался и не стал пытаться доказать. - Нынешние ученые считают, что гипотеза была известна еще в 8 веке до нашей эры
. Индийские ученые того времени обнаружили приблизительное вычисление гипотенузы треугольника, наделенного прямыми углами. Правда в то время никто не смог доказать наверняка уравнение по приблизительным вычислениям. - Великий математик Бартель Ван дер Варден после доказательства гипотезы заключил важный вывод
: «Заслуга греческого математика считается не открытием направления и геометрии, а лишь ее обоснованием. В руках Пифагора были вычислительные формулы, которые основывались на предположениях, неточных вычислениях и смутных представлениях. Однако выдающемуся ученому удалось превратить из в точную науку». - Известный стихотворец сказал, что в день открытия своего чертежа он воздвиг быкам славную жертву
. Именно после открытия гипотезы пошли слухи, что жертвоприношение ста быков «пошло странствовать по страницам книг и изданий».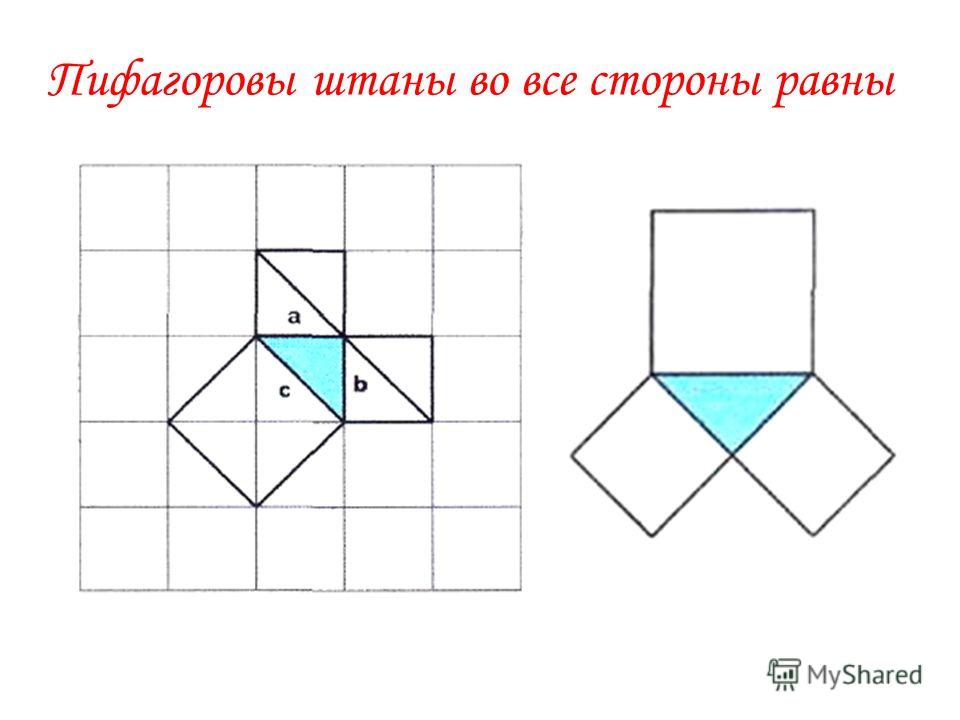 Остряки по сей день шутят, что с тех пор все быки боятся нового открытия.
Остряки по сей день шутят, что с тех пор все быки боятся нового открытия. - Доказательство того, что не Пифагор придумал стихотворение про штаны, дабы доказать выдвинутые им чертежи: во времена жизни великого математика штанов еще не было
. Они были придуманы через несколько десятилетий. - Размышления Пифагора о собственном правиле: секрет сущего на земле кроется в цифрах
. Ведь математик, опираясь на собственную гипотезу, изучил свойства чисел, выявил четность и нечетность, создал пропорции.
1
из 8
№ слайда 1
Описание слайда:
№ слайда 2
Описание слайда:
Это язвительное замечание (которое в полном виде имеет продолжение: чтобы это доказать, нужно снять и показать), придуманное кем-то, по-видимому, потрясенным внутренним содержанием одной важной теоремы евклидовой геометрии, как нельзя точно раскрывает отправную точку, из которой цепь совсем несложных размышлений быстро приводит к доказательству теоремы, а также к еще более значимым результатам. Теорема эта, приписываемая древнегреческому математику Пифагору Самосскому (6 век до нашей эры), известна чуть ли не каждому школьнику и звучит так: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Теорема эта, приписываемая древнегреческому математику Пифагору Самосскому (6 век до нашей эры), известна чуть ли не каждому школьнику и звучит так: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
№ слайда 3
Описание слайда:
Пожалуй, многие согласятся, что геометрическая фигура, обозванная шифровкой «пифагоровы штаны на все стороны равны», называется квадратом. Ну и с улыбкой на лице добавим безобидной шутки ради, что имелось в виду в продолжении шифрованного сарказма. Итак, «чтобы это доказать, нужно снять и показать». Ясно, что «это» — под местоимением подразумевалась непосредственно теорема, «снять» — это получить в руки, взять названную фигуру, «показать» — имелось в виду слово «покасать», привести в соприкосновение какие-то части фигуры. Вообще «пифагоровыми штанами» окрестили напоминавшую по виду штаны графическую конструкцию, получавшуюся на чертеже Евклида при весьма сложном доказательстве им теоремы Пифагора. Когда нашлось доказательство проще, быть может, какой-то рифмоплет сочинил эту скороговорку- подсказку, чтобы не запамятовать начало подхода к доказательству, а народная молва уж разнесла ее по свету как пустую поговорку.
Когда нашлось доказательство проще, быть может, какой-то рифмоплет сочинил эту скороговорку- подсказку, чтобы не запамятовать начало подхода к доказательству, а народная молва уж разнесла ее по свету как пустую поговорку.
№ слайда 4
Описание слайда:
Так вот если взять квадрат, и внутрь него поместить меньший квадрат так, чтобы центры их совпадали, и повернуть притом меньший квадрат до соприкосновения его углов со сторонами большего квадрата, то на большей фигуре окажутся выделены сторонами меньшего квадрата 4 одинаковых прямоугольных треугольник Отсюда уже лежит прямой путь к доказательству известной теоремы. Пусть сторону меньшего квадрата обозначим через c. Сторона большего квадрата равна a+b, и тогда его площадь равна (a+b) 2 =a 2 +2ab+b 2. Ту же площадь можно определить как сумму площади меньшего квадрата и площадей 4 одинаковых прямоугольных треугольников, то есть как 4·ab/2+c 2 =2ab+c 2. Поставим знак равенства между двумя вычислениями одной и той же площади: a 2 +2ab+b 2 =2ab+c 2.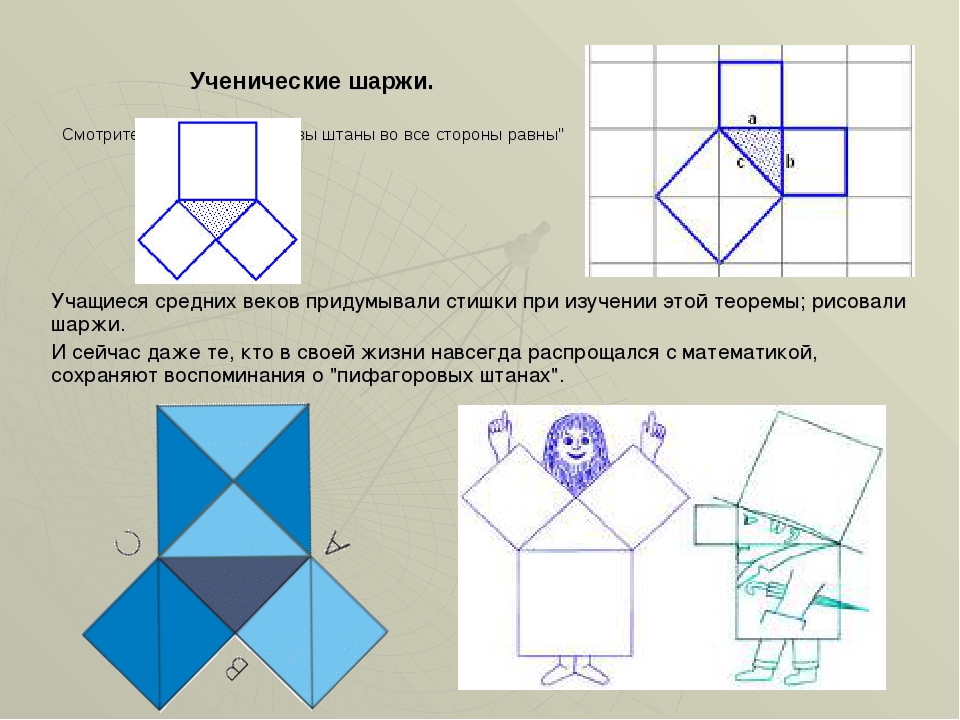 После сокращения членов 2ab получаем вывод: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов, то есть a 2 +b 2 =c 2.
После сокращения членов 2ab получаем вывод: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов, то есть a 2 +b 2 =c 2.
№ слайда 5
Описание слайда:
Сразу не каждый поймет, какой прок от этой теоремы. С практической точки зрения ее ценность состоит в служении базисом для многих геометрических вычислений, как например определения расстояния между точками координатной плоскости. Из теоремы выводятся некоторые ценные формулы, ее обобщения ведут к новым теоремам, перекидывающим мостик от вычислений на плоскости до вычислений в пространстве. Следствия теоремы проникают в теорию чисел, открывая отдельные подробности структуры ряда чисел. И многое другое, всего не перечислишь.
№ слайда 6
Описание слайда:
Взгляд с точки зрения праздного любопытства демонстрирует преподношение теоремой занимательных задачек, формулируемых до крайности понятно, но являющихся подчас крепкими орешками. В пример достаточно привести наиболее простую из них, так называемый вопрос о пифагоровых числах, задаваемую в бытовом изложении следующим образом: можно ли построить комнату, длина, ширина и диагональ на полу которой одновременно измерялись бы только целыми величинами, скажем шагами? Всего лишь малейшее изменение этого вопроса способно сделать задачу чрезвычайно сложной. И соответственно, найдутся желающие чисто из научного задора испытать себя в раскалывании очередного математического ребуса. Другое изменение вопроса — и еще одна головоломка. Часто в ходе поиска ответов на подобные проблемы математика эволюционирует, приобретает свежие взгляды на старые понятия, обзаводится новыми системными подходами и так далее, а значит теорема Пифагора, впрочем как и любое другое стоящее учение, с этой точки зрения имеет не меньшую пользу.
И соответственно, найдутся желающие чисто из научного задора испытать себя в раскалывании очередного математического ребуса. Другое изменение вопроса — и еще одна головоломка. Часто в ходе поиска ответов на подобные проблемы математика эволюционирует, приобретает свежие взгляды на старые понятия, обзаводится новыми системными подходами и так далее, а значит теорема Пифагора, впрочем как и любое другое стоящее учение, с этой точки зрения имеет не меньшую пользу.
№ слайда 7
Описание слайда:
Математика времен Пифагора не признавала иных чисел, кроме рациональных (натуральных чисел или дробей с натуральным числителем и знаменателем). Все измерялось целыми величинами или частями целых. Потому так понятно стремление делать геометрические вычисления, решать уравнения все больше в натуральных числах. Пристрастие к ним открывает путь в невероятный мир таинства чисел, ряд которых в геометрической интерпретации первоначально вырисовывается как прямая линия с бесконечным множеством отметин.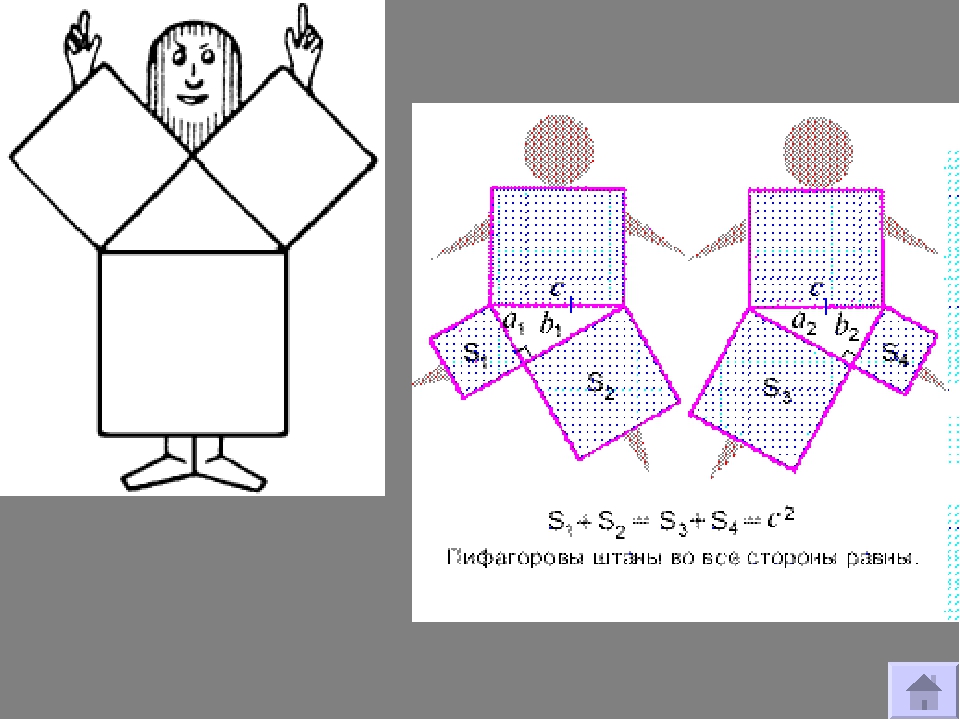 Иногда зависимость между какими-то числами ряда, «линейным расстоянием» между ними, пропорцией тотчас бросается в глаза, а иной раз самые сложные мыслительные конструкции не позволяют установить, каким закономерностям подчинено распределение тех или иных чисел. Выясняется, что и в новом мире, в этой «одномерной геометрии», старые задачи сохраняют силу, меняется лишь их постановка. Как например, вариант задания о пифагоровых числах: «От дома отец делает x шагов по x сантиметров каждый, а затем идет еще у шагов по y сантиметров. За ним шагает сын z шагов по z сантиметров каждый. Какими должны быть размеры их шагов, чтобы на z-том шаге ребенок вступил в след отца?»
Иногда зависимость между какими-то числами ряда, «линейным расстоянием» между ними, пропорцией тотчас бросается в глаза, а иной раз самые сложные мыслительные конструкции не позволяют установить, каким закономерностям подчинено распределение тех или иных чисел. Выясняется, что и в новом мире, в этой «одномерной геометрии», старые задачи сохраняют силу, меняется лишь их постановка. Как например, вариант задания о пифагоровых числах: «От дома отец делает x шагов по x сантиметров каждый, а затем идет еще у шагов по y сантиметров. За ним шагает сын z шагов по z сантиметров каждый. Какими должны быть размеры их шагов, чтобы на z-том шаге ребенок вступил в след отца?»
№ слайда 8
Описание слайда:
Справедливости ради полагается отметить некоторую сложность для начинающего математика пифагорейской методики развития мысли. Это особого рода стиль математического мышления, к нему нужно привыкать. Интересен один момент. Математики вавилонского государства (оно возникло задолго до рождения Пифагора, почти полторы тысячи лет до него) тоже, видимо, знали какие-то методы поиска чисел, которые впоследствии стали называться пифагоровыми.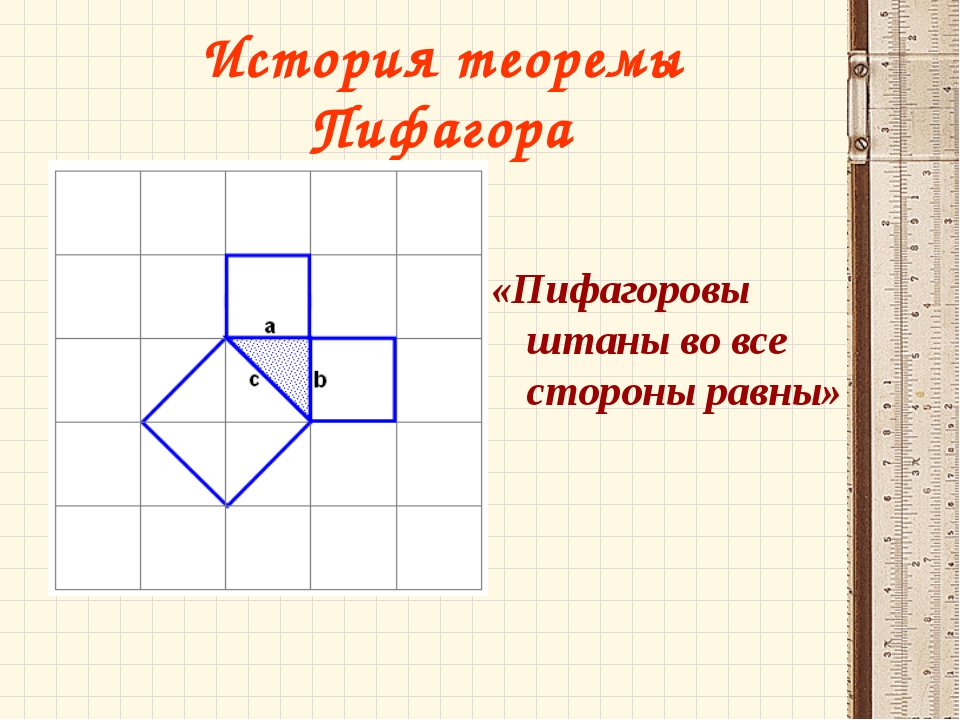 Были найдены клинописные таблички, где вавилонские мудрецы записали выявленные ими тройки таких чисел. Некоторые тройки состояли из чересчур больших чисел, в связи с чем наши современники стали предполагать наличие у вавилонян недурственных, и вероятно даже немудреных, способов их вычисления. К сожалению, ни о самих способах, ни об их существовании ничего не известно.
Были найдены клинописные таблички, где вавилонские мудрецы записали выявленные ими тройки таких чисел. Некоторые тройки состояли из чересчур больших чисел, в связи с чем наши современники стали предполагать наличие у вавилонян недурственных, и вероятно даже немудреных, способов их вычисления. К сожалению, ни о самих способах, ни об их существовании ничего не известно.
Некоторые дискуссии меня развлекают безмерно…
Привет, что делаешь?
-Да вот, задачки решаю из журнала.
-Ну ты даёшь! Не ожидал от тебя.
-Чего не ожидал?
-Что ты опустишься до задачек. Вроде умный ведь, а веришь во всякую ерунду.
-Извини, не понимаю. Что ты называешь ерундой?
-Да всю эту вашу математику. Ведь очевидно же, что фигня полная.
-Как ты можешь так говорить? Математика — царица наук…
-Вот только давай без этого пафоса, да? Математика — вообще не наука, а одно сплошное нагромождение дурацких законов и правил.
-Что?!
-Ой, ну не делай такие большие глаза, ты же сам знаешь, что я прав. Нет, я не спорю, таблица умножения — великая вещь, она сыграла немалую роль в становлении культуры и истории человечества. Но теперь-то это всё уже неактуально! И потом, зачем было всё усложнять? В природе не существует никаких интегралов или логарифмов, это всё выдумки математиков.
Нет, я не спорю, таблица умножения — великая вещь, она сыграла немалую роль в становлении культуры и истории человечества. Но теперь-то это всё уже неактуально! И потом, зачем было всё усложнять? В природе не существует никаких интегралов или логарифмов, это всё выдумки математиков.
-Погоди. Математики ничего не выдумывали, они открывали новые законы взаимодействия чисел, пользуясь проверенным инструментарием…
-Ну да, конечно! И ты этому веришь? Ты что, сам не видишь, какую чушь они постоянно несут? Тебе привести пример?
-Да уж, будь добр.
-Да пожалуйста! Теорема Пифагора.
-Ну и что в ней не так?
-Да всё не так! «Пифагоровы штаны на все стороны равны», понимаете ли. А ты в курсе, что греки во времена Пифагора не носили штанов? Как Пифагор мог вообще рассуждать о том, о чём не имел никакого понятия?
-Погоди. При чём тут штаны?
-Ну они же вроде бы Пифагоровы? Или нет? Ты признаёшь, что у Пифагора не было штанов?
-Ну, вообще-то, конечно, не было…
-Ага, значит, уже в самом названии теоремы явное несоответствие! Как после этого можно относиться серьёзно к тому, что там говорится?
-Минутку. Пифагор ничего не говорил о штанах…
Пифагор ничего не говорил о штанах…
-Ты это признаёшь, да?
-Да… Так вот, можно я продолжу? Пифагор ничего не говорил о штанах, и не надо ему приписывать чужие глупости…
-Ага, ты сам согласен, что это всё глупости!
-Да не говорил я такого!
-Только что сказал. Ты сам себе противоречишь.
-Так. Стоп. Что говорится в теореме Пифагора?
-Что все штаны равны.
-Блин, да ты вообще читал эту теорему?!
-Я знаю.
-Откуда?
-Я читал.
-Что ты читал?!
-Лобачевского.
*пауза*
-Прости, а какое отношение имеет Лобачевский к Пифагору?
-Ну, Лобачевский же тоже математик, и он вроде бы даже более крутой авторитет, чем Пифагор, скажешь нет?
*вздох*
-Ну и что же сказал Лобачевский о теореме Пифагора?
-Что штаны равны. Но это же чушь! Как такие штаны вообще можно носить? И к тому же, Пифагор вообще не носил штанов!
-Лобачевский так сказал?!
*секундная пауза, с уверенностью*
-Да!
-Покажи мне, где это написано.
-Нет, ну там это не написано так прямо. ..
..
-Как называется книга?
-Да это не книга, это статья в газете. Про то, что Лобачевский на самом деле был агент германской разведки… ну, это к делу не относится. Всё-равно он наверняка так говорил. Он же тоже математик, значит они с Пифагором заодно.
-Пифагор ничего не говорил про штаны.
-Ну да! О том и речь. Фигня это всё.
-Давай по порядку. Откуда ты лично знаешь, о чём говорится в теореме Пифагора?
-Ой, ну брось! Это же все знают. Любого спроси, тебе сразу ответят.
-Пифагоровы штаны — это не штаны…
-А, ну конечно! Это аллегория! Знаешь, сколько раз я уже такое слышал?
-Теорема Пифагора гласит, что сумма квадратов катетов равна квадрату гипотенузы. И ВСЁ!
-А где штаны?
-Да не было у Пифагора никаких штанов!!!
-Ну вот видишь, я тебе о том и толкую. Фигня вся ваша математика.
-А вот и не фигня! Смотри сам. Вот треугольник. Вот гипотенуза. Вот катеты…
-А почему вдруг именно это катеты, а это гипотенуза? Может, наоборот?
-Нет. Катетами называются две стороны, образующие прямой угол.
Катетами называются две стороны, образующие прямой угол.
-Ну вот тебе ещё один прямой угол.
-Он не прямой.
-А какой же он, кривой?
-Нет, он острый.
-Так и этот тоже острый.
-Он не острый, он прямой.
-Знаешь, не морочь мне голову! Ты просто называешь вещи как тебе удобно, лишь бы подогнать результат под желаемый.
-Две короткие стороны прямоугольного треугольника — это катеты. Длинная сторона — гипотенуза.
-А, кто короче — тот катет? И гипотенуза, значит, уже не катит? Ты сам-то послушай себя со стороны, какой ты бред несёшь. На дворе 21 век, расцвет демократии, а у тебя средневековье какое-то. Стороны у него, видишь ли, неравны…
-Прямоугольного треугольника с равными сторонами не существует…
-А ты уверен? Давай я тебе нарисую. Вот, смотри. Прямоугольный? Прямоугольный. И все стороны равны!
-Ты нарисовал квадрат.
-Ну и что?
-Квадрат — не треугольник.
-А, ну конечно! Как только он нас не устраивает, сразу «не треугольник»! Не морочь мне голову. Считай сам: один угол, два угла, три угла.
Считай сам: один угол, два угла, три угла.
-Четыре.
-Ну и что?
-Это квадрат.
-А квадрат что, не треугольник? Он хуже, да? Только потому, что я его нарисовал? Три угла есть? Есть, и даже вот один запасной. Ну и нефиг тут, понимаешь…
-Ладно, оставим эту тему.
-Ага, уже сдаёшься? Нечего возразить? Ты признаёшь, что математика — фигня?
-Нет, не признаю.
-Ну вот, опять снова-здорово! Я же тебе только что всё подробно доказал! Если в основе всей вашей геометрии лежит учение Пифагора, а оно, извиняюсь, полная чушь… то о чём вообще можно дальше рассуждать?
-Учение Пифагора — не чушь…
-Ну как же! А то я не слышал про школу пифагорейцев! Они, если хочешь знать, предавались оргиям!
-При чём тут…
-А Пифагор вообще был педик! Он сам сказал, что Платон ему друг.
-Пифагор?!
-А ты не знал? Да они вообще все педики были. И на голову трёхнутые. Один в бочке спал, другой голышом по городу бегал…
-В бочке спал Диоген, но он был философ, а не математик. ..
..
-А, ну конечно! Если кто-то в бочку полез, то уже и не математик! Зачем нам лишний позор? Знаем, знаем, проходили. А вот ты объясни мне, почему всякие педики, которые жили три тыщи лет назад и бегали без штанов, должны быть для меня авторитетом? С какой стати я должен принимать их точку зрения?
-Ладно, оставь…
-Да нет, ты послушай! Я тебя, в конце концов, тоже слушал. Вот эти ваши вычисления, подсчёты… Считать вы все умеете! А спроси у вас что-нибудь по существу, тут же сразу: «это частное, это переменная, а это два неизвестных». А ты мне в о-о-о-общем скажи, без частностей! И без всяких там неизвестных, непознанных, экзистенциальных… Меня от этого тошнит, понимаешь?
-Понимаю.
-Ну вот объясни мне, почему дважды два всегда четыре? Кто это придумал? И почему я обязан принимать это как данность и не имею права сомневаться?
-Да сомневайся сколько хочешь…
-Нет, ты мне объясни! Только без этих ваших штучек, а нормально, по-человечески, чтобы понятно было.
-Дважды два равно четырём, потому что два раза по два будет четыре.
-Масло масляное. Что ты мне нового сказал?
-Дважды два — это два, умноженное на два. Возьми два и два и сложи их…
-Так сложить или умножить?
-Это одно и то же…
-Оба-на! Выходит, если я сложу и умножу семь и восемь, тоже получится одно и то же?
-Нет.
-А почему?
-Потому что семь плюс восемь не равняется…
-А если я девять умножу на два, получится четыре?
-Нет.
-А почему? Два умножал — получилось, а с девяткой вдруг облом?
-Да. Дважды девять — восемнадцать.
-А дважды семь?
-Четырнадцать.
-А дважды пять?
-Десять.
-То есть, четыре получается только в одном частном случае?
-Именно так.
-А теперь подумай сам. Ты говоришь, что существуют некие жёсткие законы и правила умножения. О каких законах тут вообще может идти речь, если в каждом конкретном случае получается другой результат?!
-Это не совсем так. Иногда результат может совпадать. Например, дважды шесть равняется двенадцати. И четырежды три — тоже…
И четырежды три — тоже…
-Ещё хуже! Два, шесть, три четыре — вообще ничего общего! Ты сам видишь, что результат никак не зависит от исходных данных. Принимается одно и то же решение в двух кардинально различных ситуациях! И это при том, что одна и та же двойка, которую мы берём постоянно и ни на что не меняем, со всеми числами всегда даёт разный ответ. Где, спрашивается, логика?
-Но это же, как-раз, логично!
-Для тебя — может быть. Вы, математики, всегда верите во всякую запредельную хрень. А меня эти ваши выкладки не убеждают. И знаешь почему?
-Почему?
-Потому что я знаю
, зачем нужна на самом деле ваша математика. Она ведь вся к чему сводится? «У Кати в кармане одно яблоко, а у Миши пять. Сколько яблок должен отдать Миша Кате, чтобы яблок у них стало поровну?» И знаешь, что я тебе скажу? Миша никому ничего не должен
отдавать! У Кати одно яблоко есть — и хватит. Мало ей? Пусть идёт вкалывать, и сама себе честно заработает хоть на яблоки, хоть на груши, хоть на ананасы в шампанском.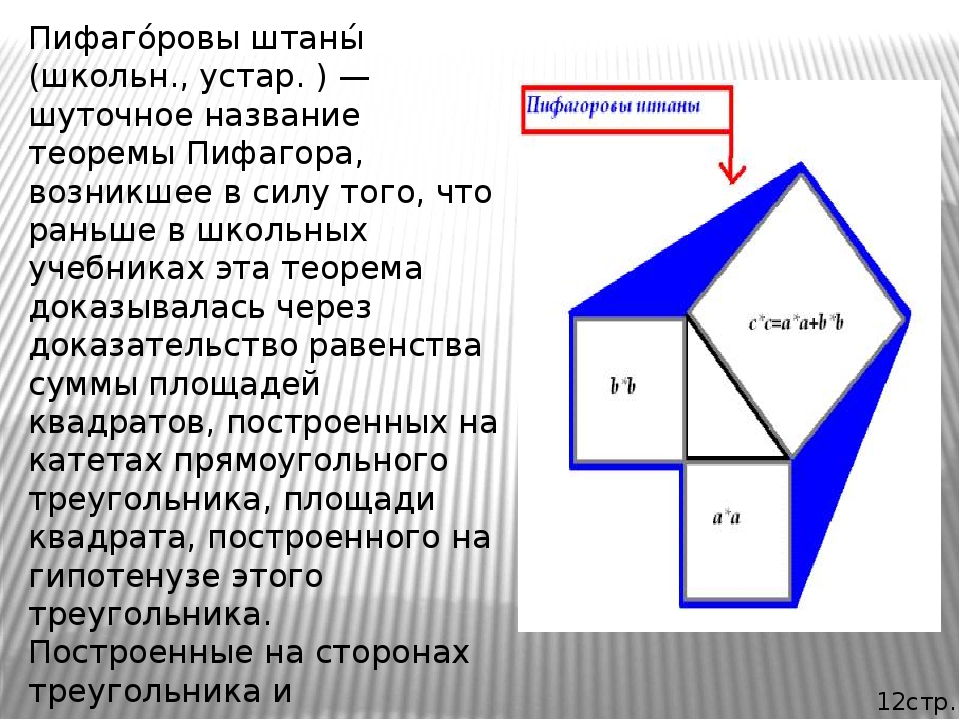 А если кто-то хочет не работать, а только задачки решать — пусть сидит со своим одним яблоком и не выпендривается!
А если кто-то хочет не работать, а только задачки решать — пусть сидит со своим одним яблоком и не выпендривается!
Жарг. шк. Шутл. Теорема Пифагора, устанавливающая соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
Пифагоровы штаны
— Шуточное название теоремы Пифагора, возникшее в силу того, что построенные на сторонах прямоугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов. Геометрию я любил… и на вступительном экзамене в университет получил даже от… … Фразеологический словарь русского литературного языка
пифагоровы штаны
— Шутливое название теоремы Пифагора, устанавливающей соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, что внешне на рисунках выглядит как покрой штанов … Словарь многих выражений
Иноск.: о человеке даровитом Ср. Это несомненности мудрец. В древности он наверное выдумал бы Пифагоровы штаны.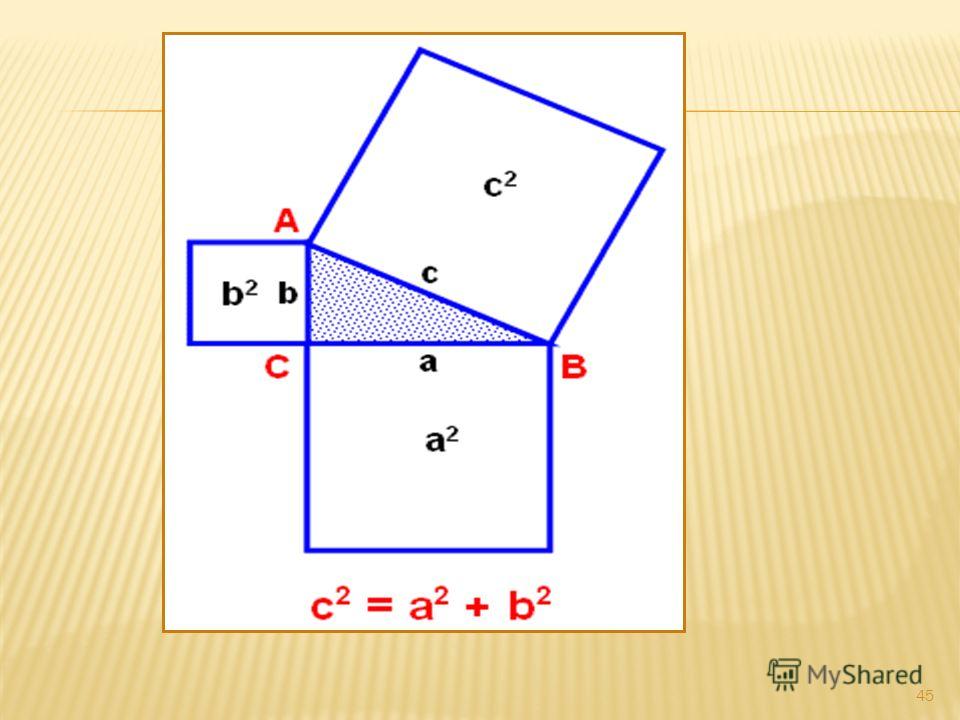 .. Салтыков. Пестрые письма. Пифагоровы штаны (геом.): в прямоугольнике квадрат гипотенузы равняется квадратам катетов (учение… … Большой толково-фразеологический словарь Михельсона
.. Салтыков. Пестрые письма. Пифагоровы штаны (геом.): в прямоугольнике квадрат гипотенузы равняется квадратам катетов (учение… … Большой толково-фразеологический словарь Михельсона
Пифагоровы штаны на все стороны равны
— Число пуговиц известно. Почему же хую тесно? (грубо) о штанах и мужском половом органе. Пифагоровы штаны на все стороны равны. Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах … Живая речь. Словарь разговорных выражений
Пиѳагоровы штаны (выдумать) иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны… Салтыковъ. Пестрыя письма. Пиѳагоровы штаны (геом.): въ прямоугольникѣ квадратъ гипотенузы… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
Пифагоровы штаны во все стороны равны
— Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля … Словарь народной фразеологии
Присл.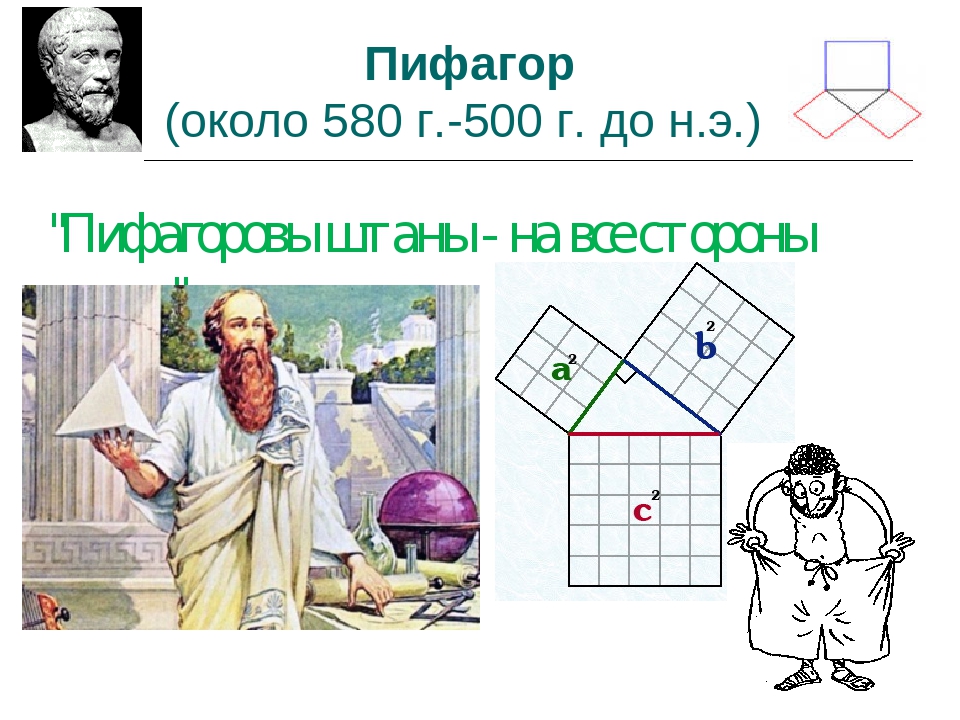 , груб …
, груб …
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ (ЧИСЛО ПУГОВИЦ ИЗВЕСТНО. ПОЧЕМУ ЖЕ ХУЮ ТЕСНО? / ЧТОБЫ ЭТО ДОКАЗАТЬ, НАДО СНЯТЬ И ПОКАЗАТЬ)
— присл., груб … Толковый словарь современных разговорных фразеологизмов и присловий
Сущ., мн., употр. сравн. часто Морфология: мн. что? штаны, (нет) чего? штанов, чему? штанам, (вижу) что? штаны, чем? штанами, о чём? о штанах 1. Штаны это предмет одежды, который имеет две короткие или длинные штанины и закрывает нижнюю часть… … Толковый словарь Дмитриева
Книги
- Как открывали Землю , Сахарнов Святослав Владимирович. Как путешествовали финикийцы? На каких кораблях плавали викинги? Кто открыл Америку, а кто впервые совершил кругосветное плавание? Кто составил первый в мире атласАнтарктиды, а кто изобрёл…
- Чудеса на колёсах , Маркуша Анатолий. Миллионы колёс крутятся по всей земле — катят автомобили, отмеряют время в часах, постукивают под поездами, выполняют бесчисленное множество работ в станках и разнообразных механизмах.
 Они…
Они…
Пифагоровы штаны
Шуточное название теоремы Пифагора, возникшее в силу того, что построенные на сторонах прямоугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов. Геометрию я любил… и на вступительном экзамене в университет получил даже от Чумакова, профессора математики, похвалу за то, что без доски, чертя руками по воздуху, объяснял свойства параллельных линий и пифагоровых штанов
(Н. Пирогов. Дневник старого врача).
Фразеологический словарь русского литературного языка. — М.: Астрель, АСТ
.
А. И. Фёдоров
.
2008
.
Смотреть что такое «Пифагоровы штаны» в других словарях:
Пифагоровы штаны
— … Википедия
Пифагоровы штаны
— Жарг. шк. Шутл. Теорема Пифагора, устанавливающая соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
пифагоровы штаны
— Шутливое название теоремы Пифагора, устанавливающей соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, что внешне на рисунках выглядит как покрой штанов … Словарь многих выражений
пифагоровы штаны(выдумать)
— иноск. : о человеке даровитом Ср. Это несомненности мудрец. В древности он наверное выдумал бы Пифагоровы штаны… Салтыков. Пестрые письма. Пифагоровы штаны (геом.): в прямоугольнике квадрат гипотенузы равняется квадратам катетов (учение… … Большой толково-фразеологический словарь Михельсона
: о человеке даровитом Ср. Это несомненности мудрец. В древности он наверное выдумал бы Пифагоровы штаны… Салтыков. Пестрые письма. Пифагоровы штаны (геом.): в прямоугольнике квадрат гипотенузы равняется квадратам катетов (учение… … Большой толково-фразеологический словарь Михельсона
Пифагоровы штаны на все стороны равны
— Число пуговиц известно. Почему же хую тесно? (грубо) о штанах и мужском половом органе. Пифагоровы штаны на все стороны равны. Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах … Живая речь. Словарь разговорных выражений
Пифагоровы штаны выдумать
— Пиѳагоровы штаны (выдумать) иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны… Салтыковъ. Пестрыя письма. Пиѳагоровы штаны (геом.): въ прямоугольникѣ квадратъ гипотенузы… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
Пифагоровы штаны во все стороны равны
— Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля … Словарь народной фразеологии
Присл. , груб …
, груб …
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ (ЧИСЛО ПУГОВИЦ ИЗВЕСТНО. ПОЧЕМУ ЖЕ ХУЮ ТЕСНО? / ЧТОБЫ ЭТО ДОКАЗАТЬ, НАДО СНЯТЬ И ПОКАЗАТЬ)
— присл., груб … Толковый словарь современных разговорных фразеологизмов и присловий
штаны
— сущ., мн., употр. сравн. часто Морфология: мн. что? штаны, (нет) чего? штанов, чему? штанам, (вижу) что? штаны, чем? штанами, о чём? о штанах 1. Штаны это предмет одежды, который имеет две короткие или длинные штанины и закрывает нижнюю часть… … Толковый словарь Дмитриева
Книги
- Как открывали Землю , Сахарнов Святослав Владимирович. Как путешествовали финикийцы? На каких кораблях плавали викинги? Кто открыл Америку, а кто впервые совершил кругосветное плавание? Кто составил первый в мире атласАнтарктиды, а кто изобрёл…
Пифагоровы штаны. От добермана до хулигана. Из имен собственных в нарицательные
Пифагоровы штаны
О том, что «пифагоровы штаны во все стороны равны», знали еще дореволюционные гимназисты, они-то и сочинили эту стихотворную шпаргалку. Да что там гимназисты! Наверное, уже великому Ломоносову, изучавшему геометрию в своей Славяно-греко-латинской академии, приходилось рисовать квадраты на катетах и на гипотенузе. Теорема Пифагора, вероятно, – самое знаменитое математическое положение. Благодаря ей любой школьник знает, что Пифагор Самосский (570 до н. э. – 490 до н. э.) был великим математиком и эту теорему доказал.
Да что там гимназисты! Наверное, уже великому Ломоносову, изучавшему геометрию в своей Славяно-греко-латинской академии, приходилось рисовать квадраты на катетах и на гипотенузе. Теорема Пифагора, вероятно, – самое знаменитое математическое положение. Благодаря ей любой школьник знает, что Пифагор Самосский (570 до н. э. – 490 до н. э.) был великим математиком и эту теорему доказал.
На самом деле Пифагор эту теорему не доказывал, а экспортировал в родную Грецию среди прочих тайн Востока. В 18-летнем возрасте он уехал в Египет, где прожил среди египетских жрецов 22 года. Потом ученый оказался на другом конце тогдашнего обитаемого мира, в Вавилоне, но не по своей воле: его увели среди прочих пленников воины персидского царя Камбиза, завоевавшие Египет в 525 году до н. э. В Вавилоне Пифагор тоже общался в основном со жрецами. Вавилонские жрецы были самыми лучшими в тогдашнем мире астрономами и, следовательно, математиками. В Вавилоне Пифагор прожил 12 лет.
Совсем не светочем цивилизации была тогда Греция, а периферией культурного мира. Трудно сказать, много ли было в Вавилоне знатоков греческого языка. Но Пифагор, вероятно, неплохо понимал вавилонян, ибо сам родился в финикийском городе Сидоне и тамошнее семитское наречие, родственное аккадскому языку Вавилона, знал с детства.
Трудно сказать, много ли было в Вавилоне знатоков греческого языка. Но Пифагор, вероятно, неплохо понимал вавилонян, ибо сам родился в финикийском городе Сидоне и тамошнее семитское наречие, родственное аккадскому языку Вавилона, знал с детства.
В почтенном уже по тем временам возрасте, в 56 лет, отягощенный многими знаниями, Пифагор вернулся на остров Самос, откуда когда-то уехал в Египет. Самосцы почитали возвратившегося Пифагора великим мудрецом и философом. Но Пифагор рассчитывал на большее. Он видел себя Великим жрецом, наставником народа и советником правителей. А на Самосе правил тиран Поликрат, который ревностно оберегал свою власть. Править он намеревался без всяких советников и следил, чтобы среди его подданных не появлялось слишком выдающихся личностей, претендентов на власть. Короче говоря, на Самосе стало Пифагору неуютно, поэтому он уплыл с восточной части заселенных греками территорий (остров Самос расположен у берегов нынешней Турции) в одну из самых западных греческих колоний, город Кротон в Южной Италии.
На новом месте Пифагор достиг того, чего давно хотел. Он стал главой философской школы (пожалуй, даже религиозной секты). Полученные им на востоке знания, в том числе и математические, Пифагор излагал ученикам нарочито туманно, обожествляя числа и геометрические фигуры. Кроме того, он проповедовал здоровый образ жизни, аскетизм и строгую мораль. А еще высказывался в том духе, что власть должна принадлежать касте мудрых и знающих людей, которым народ обязан подчиняться безоговорочно, как дети подчиняются отцу. Ясно, что на роль мудрого отца Пифагор определил себя.
До успеха, казалось, недалеко. Учеников у Пифагора набралось много. Были они молоды, не прочь подраться, и, не сильно разбираясь в деталях учения, попросту обожествляли своего учителя и идейного руководителя. Пифагорейцы едва не пришли к власти в Кротоне. Но что-то все же не срослось. Пифагор бежал из Кротона в другую греческую колонию – Метапонт, где и умер.
Пифагор и пифагорейцы, пожалуй, не зря обожествляли числа и прочие математические объекты. В самом деле, математика – наука удивительная. Числа и фигуры в реальном мире не существуют, живут они только в наших головах. Живут по своим строгим логическим законам. Но при этом математические абстракции обладают способностью точно и однозначно описывать окружающий нас мир.
В самом деле, математика – наука удивительная. Числа и фигуры в реальном мире не существуют, живут они только в наших головах. Живут по своим строгим логическим законам. Но при этом математические абстракции обладают способностью точно и однозначно описывать окружающий нас мир.
К чему далеко за примером ходить? Одним из основателей современной европейской математики считается Леонардо Пизанский (Leonardo Pisano; около 1170 – около 1250) по прозвищу Фибоначчи (Fibonacci). Он был купцом и сыном купца, жил в итальянском городе Пиза. Вместе с отцом Леонардо побывал в Египте, Сирии, Византии. Через Византию и через Египет в Европу поступали восточные товары. Ткани, пряности и драгоценности Востока очень ценились. Пизанские корабли постоянно пересекали Средиземное море, богатство города и его жителей прирастало.
Леонардо Пизанский вывозил с Востока не только дорогие товары. Он знал арабский язык. В арабском переводе Фибоначчи читал трактаты античных и индийских математиков. Эти трактаты в те времена размножали в библиотеках Багдада. Леонардо обобщил все, что узнал, в первом в средневековой Европе математическом труде, который назвал «Книгой абака». Абак – это древнеримские счеты, остававшиеся и во времена Фибоначчи главным «компьютером».
Леонардо обобщил все, что узнал, в первом в средневековой Европе математическом труде, который назвал «Книгой абака». Абак – это древнеримские счеты, остававшиеся и во времена Фибоначчи главным «компьютером».
В своей книге Фибоначчи сообщил европейцам о десятичной системе счисления, которую арабы переняли у индийцев. Привычная и понятная нам позиционная система счисления, позволяющая для написания любого (сколь угодно большого) числа обойтись всего десятью цифрами, была для европейцев того времени откровением. Раньше они пользовались римскими цифрами. При такой записи чисел процедуры сложения и вычитания превращались в хитроумные трюки, умножение же и деление были попросту высшим математическим пилотажем, не каждому доступным.
«Книга абака» включала в себя все известные на тот момент знания по арифметике и алгебре. Другая книга Фибоначчи, «Практика геометрии», была сводом знаний по геометрии. Обе книги выдержали испытание временем.
Едва ли не четыре сотни лет они были главными учебниками математики в Европе.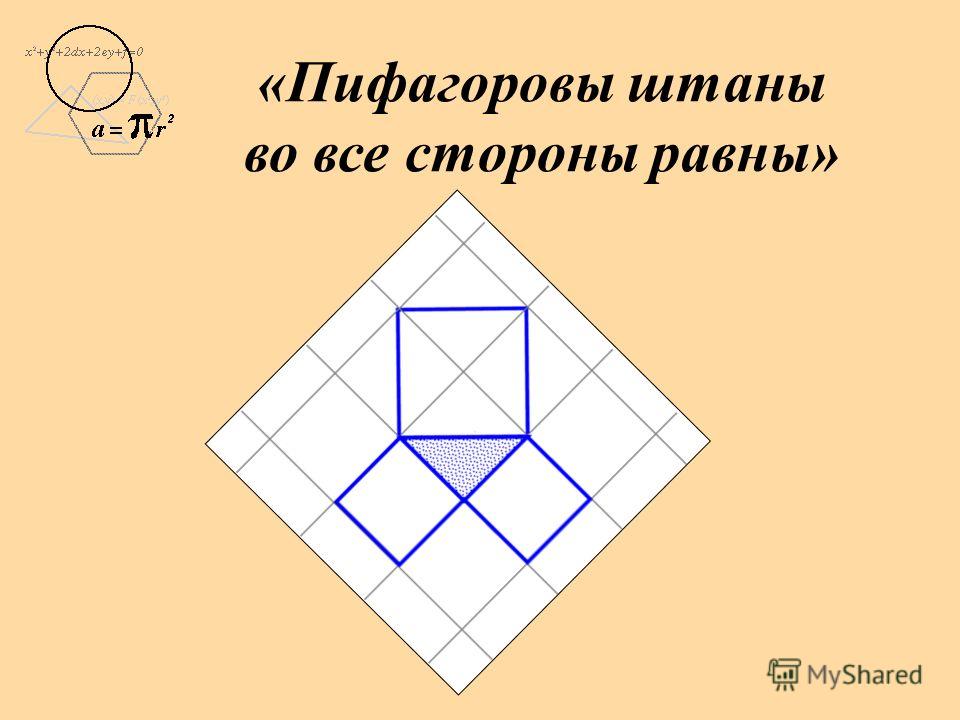
В «Книге абака» Фибоначчи описывает и свое собственное математическое изобретение – числовой ряд, в котором каждый последующий член равен сумме двух ему предшествующих.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Этот ряд – решение задачи о потомстве двух кроликов, сформулированной самим Фибоначчи. Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
С точки зрения математиков эта последовательность очень интересная. Одна из главных ее особенностей – отношение каждого последующего члена этого ряда к предыдущему неуклонно приближается к числу 1,618. «Волшебное» это число известно с античных времен и называется еще «золотым сечением». Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. Еще древнеегипетские и древнегреческие архитекторы установили, что если пропорции здания соответствуют золотому сечению, здание кажется нам красивым. К тому же оно оказывается наиболее устойчивым. Да и пропорции человеческого тела соответствуют «странной» цифре. Этот факт демонстрирует всем известный рисунок Леонардо да Винчи: фигура человека, помещенная в круг. Расстояние от ног человека до пупа (центра тела) и от пупа до головы находятся между собой в «золотой пропорции». Более того, многие существующие в природе спирали (рога животных, морские раковины, даже космические галактики) образуются как последовательность окружностей, радиусы которых относятся между собой, как числа Фибоначчи. Обычная для математики история. Математический объект возникает в результате решения какой-нибудь математической задачи, исследуется математиками по законам логики и возникает перед их мысленным взором во всей красе. И затем обнаруживается в самых разнообразных областях природы и жизни. Благодаря этому странному свойству математики возникла теоретическая физика, которая строит математические модели природы и с помощью этих моделей предсказывает новые физические эффекты.
Еще древнеегипетские и древнегреческие архитекторы установили, что если пропорции здания соответствуют золотому сечению, здание кажется нам красивым. К тому же оно оказывается наиболее устойчивым. Да и пропорции человеческого тела соответствуют «странной» цифре. Этот факт демонстрирует всем известный рисунок Леонардо да Винчи: фигура человека, помещенная в круг. Расстояние от ног человека до пупа (центра тела) и от пупа до головы находятся между собой в «золотой пропорции». Более того, многие существующие в природе спирали (рога животных, морские раковины, даже космические галактики) образуются как последовательность окружностей, радиусы которых относятся между собой, как числа Фибоначчи. Обычная для математики история. Математический объект возникает в результате решения какой-нибудь математической задачи, исследуется математиками по законам логики и возникает перед их мысленным взором во всей красе. И затем обнаруживается в самых разнообразных областях природы и жизни. Благодаря этому странному свойству математики возникла теоретическая физика, которая строит математические модели природы и с помощью этих моделей предсказывает новые физические эффекты.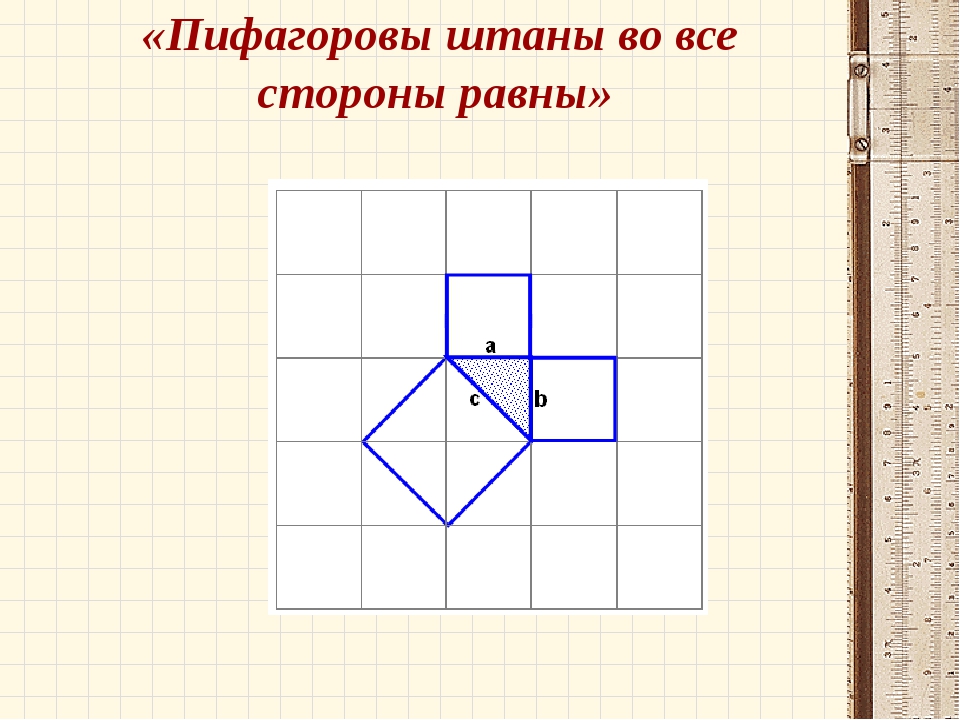
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
— Привет, что делаешь?
— Да… (Цитата из книги «Запасная книжка» Петра Бормора)
— Привет, что делаешь?
— Да вот, задачки решаю из журнала.
— Ну ты даешь! Не ожидал от тебя.
— Чего не ожидал?
— Что ты опустишься до задачек. Вроде умный, а веришь во всякую ерунду.
— Извини, не понимаю. Что ты называешь ерундой?
— Да всю эту вашу математику. Ведь очевидно же, что фигня полная.
— Как ты можешь так говорить? Математика — царица наук…
— Вот только давай без этого пафоса, да? Математика — вообще не наука, а одно сплошное нагромождение дурацких законов и правил.
— Что?!
— Ой, ну не делай такие большие глаза, ты же сам знаешь, что я прав. Нет, я не спорю, таблица умножения — великая вещь, она сыграла немалую роль в становлении культуры и истории человечества. Но теперь-то это все уже неактуально! И потом, зачем было все усложнять? В природе не существует никаких интегралов или логарифмов, это все выдумки математиков.
— Погоди. Математики ничего не выдумывали, они открывали новые законы взаимодействия чисел, пользуясь проверенным инструментарием…
— Ну да, конечно! И ты этому веришь? Ты что, сам не видишь, какую чушь они постоянно несут? Тебе привести пример?
— Да уж, будь добр.
— Да пожалуйста! Теорема Пифагора.
— Ну и что в ней не так?
— Да все не так! «Пифагоровы штаны на все стороны равны», понимаете ли. А ты в курсе, что греки во времена Пифагора не носили штанов? Как Пифагор мог вообще рассуждать о том, о чем не имел никакого понятия?
— Погоди. При чем тут штаны?
— Ну они же вроде бы Пифагоровы? Или нет? Ты признаешь, что у Пифагора не было штанов?
— Ну, вообще-то, конечно, не было…
— Ага, значит, уже в самом названии теоремы явное несоответствие! Как после этого можно относиться серьезно к тому, что там говорится?
— Минутку. Пифагор ничего не говорил о штанах…
Пифагор ничего не говорил о штанах…
— Ты это признаешь, да?
— Да… Так вот, можно я продолжу? Пифагор ничего не говорил о штанах, и не надо ему приписывать чужие глупости…
— Ага, ты сам согласен, что это все глупости!
— Да не говорил я такого!
— Только что сказал. Ты сам себе противоречишь.
— Так. Стоп. Что говорится в теореме Пифагора?
— Что все штаны равны.
— Блин, да ты вообще читал эту теорему?!
— Я знаю.
— Откуда?
— Я читал.
— Что ты читал?!
— Лобачевского.
Пауза.
— Прости, а какое отношение имеет Лобачевский к Пифагору?
— Ну, Лобачевский же тоже математик, и он вроде бы даже более крутой авторитет, чем Пифагор, скажешь, нет?
Вздох.
— Ну и что же сказал Лобачевский о теореме Пифагора?
— Что штаны равны. Но это же чушь! Как такие штаны вообще можно носить? И к тому же, Пифагор вообще не носил штанов!
— Лобачевский так сказал?!
Секундная пауза, с уверенностью:
— Да!
— Покажи мне, где это написано.
— Нет, ну там это не написано так прямо…
— Как называется книга?
— Да это не книга, это статья в газете. Про то, что Лобачевский на самом деле был агент германской разведки… ну это к делу не относится. Все равно он наверняка так говорил. Он же тоже математик, значит они с Пифагором заодно.
— Пифагор ничего не говорил про штаны.
— Ну да! О том и речь. Фигня это все.
— Давай по порядку. Откуда ты лично знаешь, о чем говорится в теореме Пифагора?
— Ой, ну брось! Это же все знают. Любого спроси, тебе сразу ответят.
— Пифагоровы штаны — это не штаны…
— А, ну конечно! Это аллегория! Знаешь, сколько раз я уже такое слышал?
— Теорема Пифагора гласит, что сумма квадратов катетов равна квадрату гипотенузы. И ВСЕ!
— А где штаны?
— Да не было у Пифагора никаких штанов!!!
— Ну вот видишь, я тебе о том и толкую. Фигня вся ваша математика.
— А вот и не фигня! Смотри сам. Вот треугольник. Вот гипотенуза. Вот катеты…
— А почему вдруг именно это катеты, а это гипотенуза? Может, наоборот?
— Нет. Катетами называются две стороны, образующие прямой угол.
Катетами называются две стороны, образующие прямой угол.
— Ну вот тебе еще один прямой угол.
— Он не прямой.
— А какой же он, кривой?
— Нет, он острый.
— Так и этот тоже острый.
— Он не острый, он прямой.
— Знаешь, не морочь мне голову! Ты просто называешь вещи как тебе удобно, лишь бы подогнать результат под желаемое.
— Две короткие стороны прямоугольного треугольника — это катеты. Длинная сторона — гипотенуза.
— А, кто короче — тот катет? И гипотенуза, значит, уже не катит? Ты сам-то послушай себя со стороны, какой ты бред несешь. На дворе 21 век, расцвет демократии, а у тебя средневековье какое-то. Стороны у него, видишь ли, не равны…
— Прямоугольного треугольника с равными сторонами не существует…
— А ты уверен? Давай я тебе нарисую. Вот, смотри. Прямоугольный? Прямоугольный. И все стороны равны!
— Ты нарисовал квадрат.
— Ну и что?
— Квадрат не треугольник.
— А, ну конечно! Как только он нас не устраивает, сразу «не треугольник»! Не морочь мне голову. Считай сам: один угол, два угла, три угла.
Считай сам: один угол, два угла, три угла.
— Четыре.
— Ну и что?
— Это квадрат.
— А квадрат что, не треугольник? Он хуже, да? Только потому, что я его нарисовал? Три угла есть? Есть, и даже вот один запасной. Ну и нефиг тут, понимаешь…
— Ладно, оставим эту тему.
— Ага, уже сдаешься? Нечего возразить? Ты признаешь, что математика — фигня?
— Нет, не признаю.
— Ну вот, опять снова-здорово! Я же тебе только что все подробно доказал! Если в основе всей вашей геометрии лежит учение Пифагора, а оно, извиняюсь, полная чушь… то о чем вообще можно дальше рассуждать?
— Учение Пифагора не чушь…
— Ну как же! А то я не слышал про школу пифагорейцев! Они, если хочешь знать, предавались оргиям!
— При чем тут…
— А Пифагор вообще был педик! Он сам сказал, что Платон ему друг.
— Пифагор?!
— А ты не знал? Да они вообще все педики были. И на голову трехнутые. Один в бочке спал, другой голышом по городу бегал…
— В бочке спал Диоген, но он был философ, а не математик…
— А, ну конечно! Если кто-то в бочку полез, то уже и не математик! Зачем нам лишний позор? Знаем, знаем, проходили. А вот ты объясни мне, почему всякие педики, которые жили три тыщи лет назад и бегали без штанов, должны быть для меня авторитетом? С какой стати я должен принимать их точку зрения?
А вот ты объясни мне, почему всякие педики, которые жили три тыщи лет назад и бегали без штанов, должны быть для меня авторитетом? С какой стати я должен принимать их точку зрения?
— Ладно, оставь…
— Да нет, ты послушай! Я тебя, в конце концов, тоже слушал. Вот эти ваши вычисления, подсчеты… Считать вы все умеете! А спроси у вас что-нибудь по существу, тут же сразу: «Это частное, это переменная, а это два неизвестных». А ты мне в о-о-о-общем скажи, без частностей! И без всяких там неизвестных, непознанных, экзистенциальных… Меня от этого тошнит, понимаешь?
— Понимаю.
— Ну вот объясни мне, почему дважды два всегда четыре? Кто это придумал? И почему я обязан принимать это как данность и не имею права сомневаться?
— Да сомневайся сколько хочешь…
— Нет, ты мне объясни! Только без этих ваших штучек, а нормально, по-человечески, чтобы понятно было.
— Дважды два равно четырем, потому что два раза по два будет четыре.
— Масло масляное. Что ты мне нового сказал?
— Дважды два — это два, умноженное на два. Возьми два и два и сложи их…
Возьми два и два и сложи их…
— Так сложить или умножить?
— Это одно и то же…
— Оба-на! Выходит, если я сложу и умножу семь и восемь, тоже получится одно и то же?
— Нет.
— А почему?
— Потому что семь плюс восемь не равняется…
— А если я девять умножу на два, получится четыре?
— Нет.
— А почему? Два умножал — получилось, а с девяткой вдруг облом?
— Да. Дважды девять — восемнадцать.
— А дважды семь?
— Четырнадцать.
— А дважды пять?
— Десять.
— То есть четыре получается только в одном частном случае?
— Именно так.
— А теперь подумай сам. Ты говоришь, что существуют некие жесткие законы и правила умножения. О каких законах тут вообще может идти речь, если в каждом конкретном случае получается другой результат?!
— Это не совсем так. Иногда результат может совпадать. Например, дважды шесть равняется двенадцати. И четырежды три — тоже…
— Еще хуже! Два, шесть, три, четыре — вообще ничего общего! Ты сам видишь, что результат никак не зависит от исходных данных.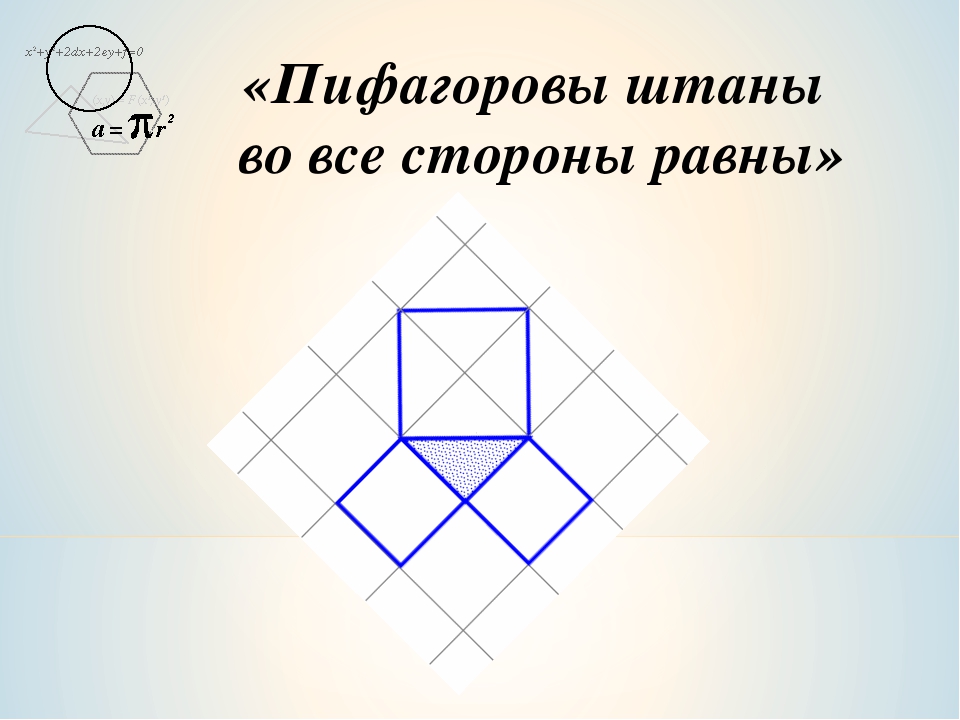 Принимается одно и то же решение в двух кардинально различных ситуациях! И это при том, что одна и та же двойка, которую мы берем постоянно и ни на что не меняем, со всеми числами всегда дает разный ответ. Где, спрашивается, логика?
Принимается одно и то же решение в двух кардинально различных ситуациях! И это при том, что одна и та же двойка, которую мы берем постоянно и ни на что не меняем, со всеми числами всегда дает разный ответ. Где, спрашивается, логика?
— Но это же, как раз, логично!
— Для тебя — может быть. Вы, математики, всегда верите во всякую запредельную хрень. А меня эти ваши выкладки не убеждают. И знаешь почему?
— Почему?
— Потому что я знаю, зачем нужна на самом деле ваша математика. Она ведь вся к чему сводится? «У Кати в кармане одно яблоко, а у Миши пять. Сколько яблок должен отдать Миша Кате, чтобы яблок у них стало поровну?» И знаешь, что я тебе скажу? Миша никому ничего не должен отдавать! У Кати одно яблоко есть — и хватит. Мало ей? Пусть идет вкалывать и сама себе честно заработает хоть на яблоки, хоть на груши, хоть на ананасы в шампанском. А если кто-то хочет не работать, а только задачки решать — пусть сидит со своим одним яблоком и не выпендривается!
штанов Пифагора во все стороны равны почему.
 Штаны Пифагора во всех направлениях равны. Из истории вопроса
Штаны Пифагора во всех направлениях равны. Из истории вопроса
В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенуз, любой взрослый смело бы смело: «Сумма квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но ее достаточно, чтобы кого-то доказать, и могут возникнуть трудности.Поэтому давайте вспомним и рассмотрим различные способы доказательства теоремы Пифагора.
Краткий обзор биографии
Теорема Пифагора знакома практически каждому, но почему-то биография человека, сделавшего ее на свет, не так популярна. Это поправимо. Поэтому, прежде чем изучать разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.
Пифагор — философ, математик, мыслитель, родом с сегодняшнего дня очень сложно отличить его биографию от легенд, сложившихся в память об этом великом человеке.Но как следует из трудов его последователей, Пифагор Самос родился на острове Самос.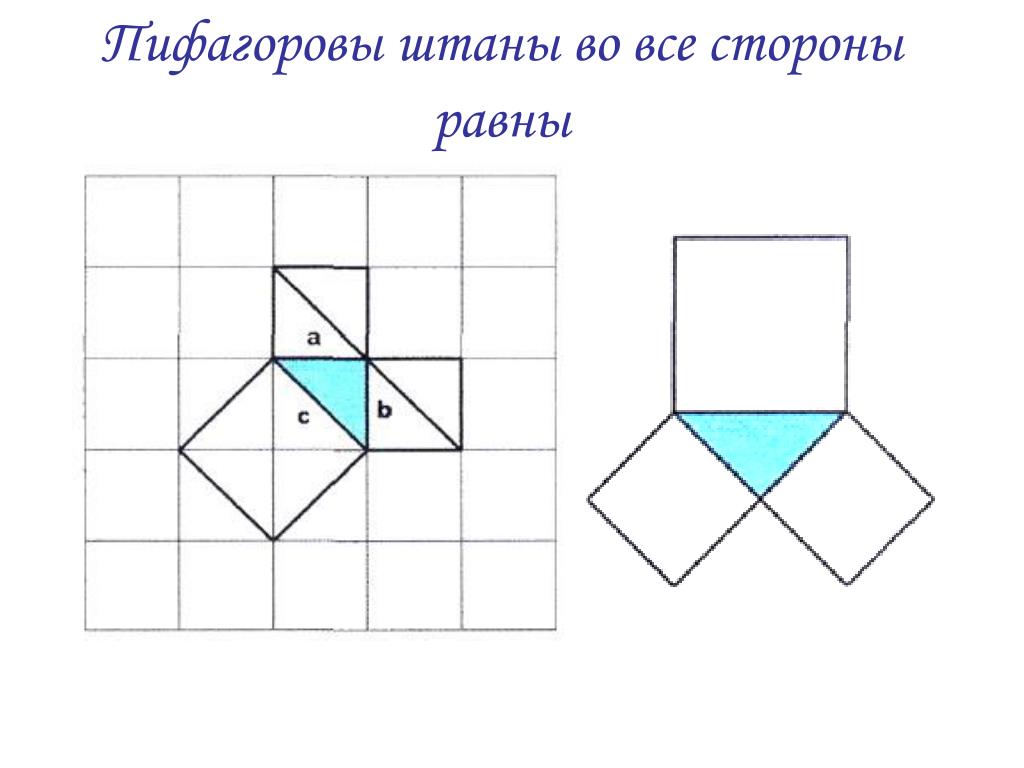 Его отцом был обычный Камнерис, но мать происходила из знатной семьи.
Его отцом был обычный Камнерис, но мать происходила из знатной семьи.
Судя по легенде, появление света Пифагора предсказала женщина по имени Пифия, в честь которой и назван мальчик. По ее предсказанию, рожденный мальчик должен был принести человечеству много пользы и добра. Что на самом деле он сделал.
Рождение теоремы
В юности Пифагор переехал в Египет, чтобы встретиться там со знаменитыми египетскими мудрецами.После встречи с ними он был принят в учебу, где знал все великие достижения египетской философии, математики и медицины.
Вероятно, именно в Египте Пифагор, вдохновленный величием и красотой пирамид, создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказал свою теорию. Но только передал свои знания последователям, которые потом выполнили все необходимые математические вычисления.
Как бы то ни было, сегодня существует не один метод доказательства этой теоремы, а сразу несколько.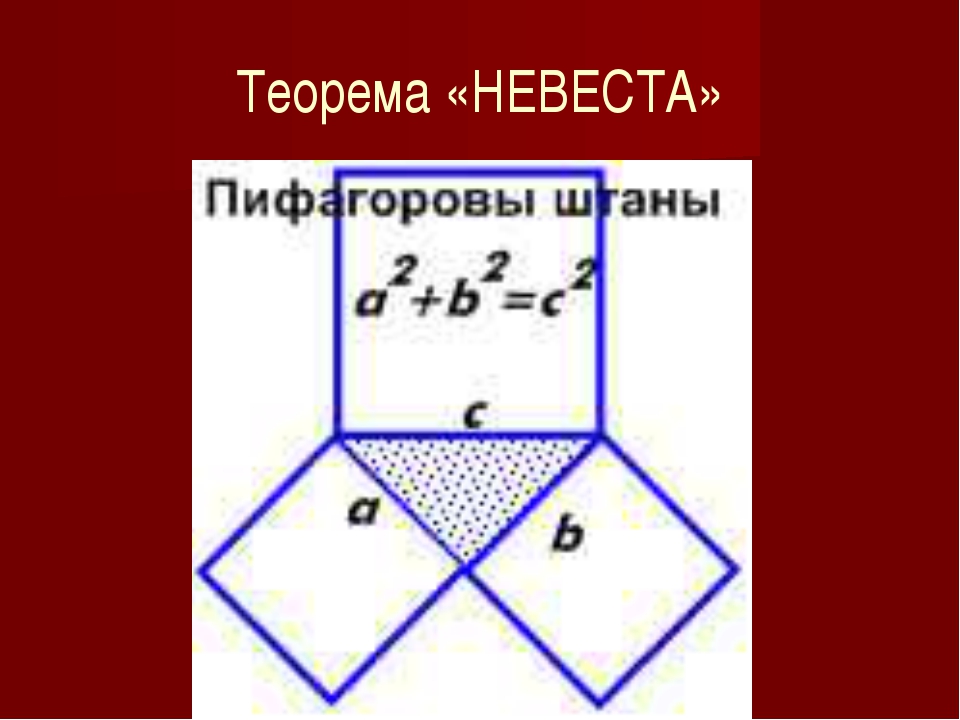 Сегодня остается только предположить, что именно древние греки производили свои вычисления, поэтому здесь мы рассмотрим различные способы доказательства теоремы Пифагора.
Сегодня остается только предположить, что именно древние греки производили свои вычисления, поэтому здесь мы рассмотрим различные способы доказательства теоремы Пифагора.
Теорема Пифагора
Перед тем, как начать какие-либо вычисления, вам нужно выяснить, какую теорию нужно доказать. Теорема Пифагора звучит так: «В треугольнике, в котором один из углов равен 90 o, сумма квадратов катетов равна квадрату гипотенузы».
Всего существует 15 различных способов доказательства теоремы Пифагора.Это довольно большая цифра, поэтому обратим внимание на самые популярные из них.
Fashion first
Сначала мы обозначаем то, что нам дается. Эти данные будут распространены на другие способы доказательства теоремы Пифагора, поэтому необходимо сразу запомнить все значения.
Предположим, что дан прямоугольный треугольник с катетиками A, B и гипотенузой, равными. Первый способ доказательства основан на том, что из прямоугольного треугольника нужно примерить квадрат.
Для этого нужно продеть катет в длину и провести отрезок равного катета внутрь, и наоборот. Значит, у квадрата должно быть две равных стороны. Осталось только провести две параллельные прямые, и квадрат готов.
Внутри получившейся фигуры нужно нарисовать еще один квадрат со стороной равной гипотезе исходного треугольника. Для этого есть два параллельных отрезка равной от. Таким образом, получается три стороны квадрата, одна из которых гипотенуза исходных прямоугольных треугольников.Осталось только решиться на четвертый отрезок.
На основании полученного рисунка можно сделать вывод, что площадь внешнего квадрата равна (A + B) 2. Если заглянуть внутрь фигуры, то можно увидеть, что помимо внутреннего квадрата есть четыре прямоугольных треугольника. Каждая область — 0.5AV.
Следовательно, площадь равна: 4 * 0,5Av + C 2 = 2AV + C 2
Отсюда (a + c) 2 = 2AV + C 2
И, следовательно, из 2 = a 2 + in 2
Теорема доказана.
Метод второй: подобные треугольники
Эта формула доказательства теоремы Пифагора была получена на основе одобрения геометрического раздела подобных треугольников. В нем говорится, что вращение прямоугольного треугольника является средним значением, пропорциональным его гипотенузе и отрезку гипотенузы, исходящему из вершины угла 90 o.
В нем говорится, что вращение прямоугольного треугольника является средним значением, пропорциональным его гипотенузе и отрезку гипотенузы, исходящему из вершины угла 90 o.
Исходные данные остались прежними, поэтому приступим сразу к доказательству. Проведем перпендикулярную сторону отрезка CD.На основании вышеописанного утверждения Картеты Треугольников равны:
AC = √AV * AD, SV = √AV * DV.
Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство должно быть построено на квадрате обоих неравенств.
AC 2 = AV * AD и SV 2 = AV * DV
Теперь нужно сложить полученные неравенства.
AC 2 + SV 2 = AV * (ад * дв), где ад + dv = av
Получается, что:
AC 2 + SV 2 = AV * AV
И, следовательно:
AC 2 + SV 2 = AB 2
Доказательство теоремы Пифагора и различные способы ее решения требуют разностороннего подхода к этой задаче.Однако этот вариант — один из самых простых.
Другой метод вычислений
Описание различных способов доказательства теоремы Пифагора может ничего не сказать, пока вы не пойдете на практику. Многие методики предусматривают не только математические вычисления, но и построение новых фигур из исходного треугольника.
В этом случае необходимо завершить еще один прямоугольный треугольник для другого прямоугольного треугольника из Cate. Таким образом, теперь есть два треугольника с общим катетом.
Зная, что площади таких фигур имеют отношение квадратов к их аналогичным линейным размерам, тогда:
S AVC * C 2 — S AVD * B 2 = S AVD * A 2 — S IT * A 2
S AVS * (C 2 -B 2) = a 2 * (s AVD -S IT)
c 2 -B 2 = a 2
c 2 = a 2 + in 2
Поскольку из разных способов доказательства теоремы Пифагора для 8 класса этот вариант вряд ли подходит, можно воспользоваться следующим методом.
Самый простой способ доказать теорему Пифагора.Отзывы
Как полагают историки, этот метод впервые применили для доказательства теоремы еще в Древней Греции. Это самый простой способ, не требующий абсолютно никаких расчетов. Если правильно нарисовать рисунок, то доказательством утверждения является то, что и 2 + в 2 = C 2 будут видны.
Условия для этого метода будут немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник ABC пустой.
Гипотенуза говорящих принимается стороной квадрата и самоубийством трех сторон.Кроме того, нужно провести две диагонали прямо в получившемся квадрате. Так что внутри него четыре неэффективных треугольника.
Так же надо дочки на квадрат и св, так же нужно провести по одной диагонали прямой в каждой из них. Первый направляет черные из вершины A, второй — из C.
Теперь нужно внимательно посмотреть на получившийся рисунок. Поскольку гипотенуза AU лежит на четырех треугольниках, равных исходному, и на двух категориях, это указывает на истинность этой теоремы.
Кстати, благодаря этому методу появилось доказательство теоремы Пифагора и знаменитая фраза: «Штаны Пифагора во всех направлениях равны».
Доказательство Дж. Гарфилд
Джеймс Гарфилд — двадцатый президент Соединенных Штатов Америки.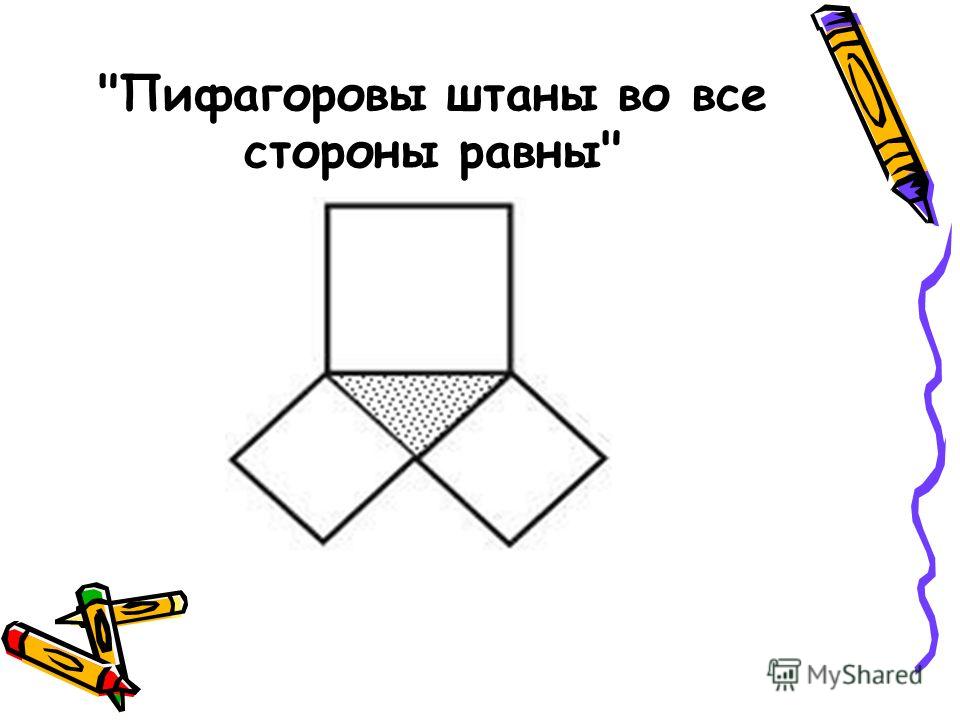 Кроме того, он оставил свой след в истории как правитель США, к тому же он был одаренным самоучкой.
Кроме того, он оставил свой след в истории как правитель США, к тому же он был одаренным самоучкой.
В начале карьеры он был рядовым учителем в народной школе, но вскоре стал директором одного из высших учебных заведений.Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядят так.
Для начала нужно нарисовать на листе бумаги два прямоугольных треугольника таким образом, чтобы катет на одном из них был продолжением второго. Вершины этих треугольников нужно совместить так, чтобы трапеция в конечном итоге получилась.
Как известно, площадь трапеции равна работе половины площадки по высоте.
S = a + in / 2 * (a + c)
Если рассматривать получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:
S = AV / 2 * 2 + C 2/2
Теперь необходимо выровнять два исходных выражения.
2AV / 2 + C / 2 = (A + B) 2/2
c 2 = a 2 + in 2
О теореме Пифагора и способах ее доказательства можно написать не одну из учебное пособие.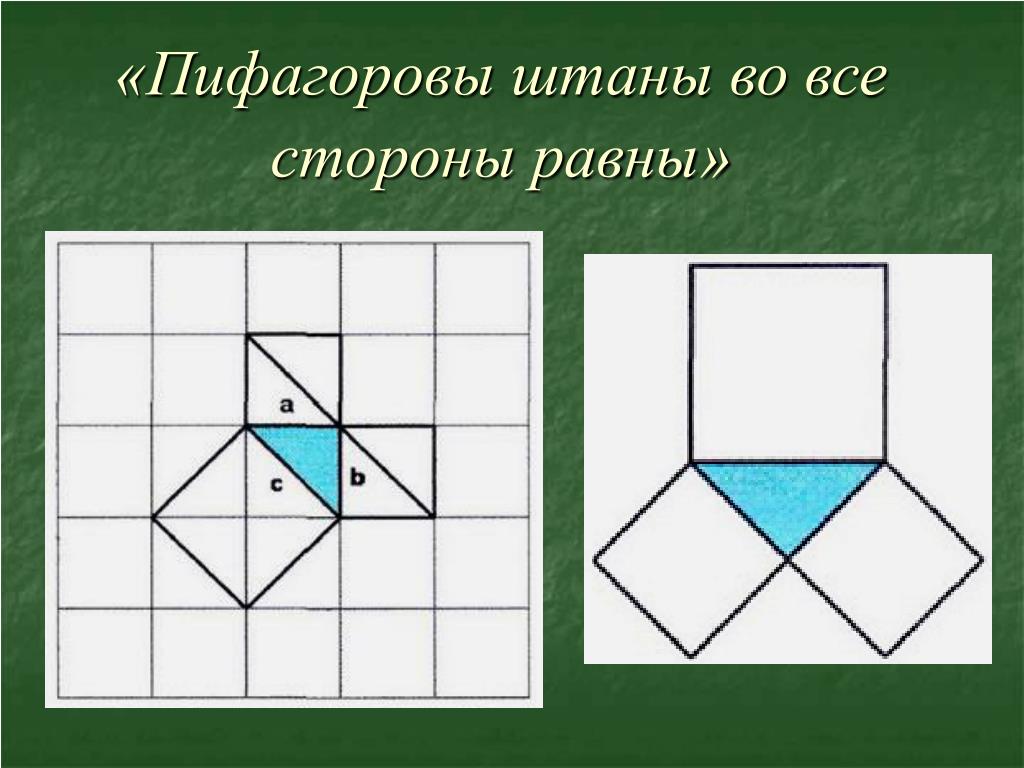 Но есть ли в этом смысл, когда эти знания нельзя применить на практике?
Но есть ли в этом смысл, когда эти знания нельзя применить на практике?
Практическое применение теоремы Пифагора
К сожалению, современные школьные программы предусматривают использование этой теоремы только в геометрических задачах.Выпускники скоро покинут школьные стены, и без обучения, и как они могут применить свои знания и умения на практике.
На самом деле применять теорему Пифагора в повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут быть крайне необходимы.
Коммуникационная теорема и астрономия
Казалось бы, звезды и треугольники на бумаге могут быть связаны.Фактически, астрономия — это научная сфера, в которой широко используется теорема Пифагора.
Например, рассмотрим движение светового луча в пространстве. Известно, что свет движется в обоих направлениях с одинаковой скоростью. Траекторию АВ, по которой движется луч света, назовем л. .
Траекторию АВ, по которой движется луч света, назовем л. .
И в половине случаев, когда свет необходим, чтобы добраться из точки A в точку B, давайте позвоним по номеру
т. . А скорость луча —
г. .
Получается, что: c * T = L
Если посмотреть на этот самый луч другого самолета, например, от космического лайнера, который движется со скоростью V, то при этом наблюдении тел , их скорость изменится. При этом даже неподвижные элементы будут двигаться со скоростью V в обратном направлении.
Предположим, комикс плывет вправо. Тогда точки A и B, между которыми устремляется луч, переместятся влево. Более того, когда луч движется из точки A в точку in, точка A успевает переместиться и, соответственно, свет попадет в новую точку S.Чтобы найти половину расстояния, на которое сместилась точка A, вам нужно умножить скорость луча на половину времени (T «).
И чтобы узнать, как за это время он смог пройти луч света, вам нужно обозначим половину пути нового бакена S и получим следующее выражение:
Если вы представите, что точки света C и B, а также космический лайнер являются вершинами равноправного треугольника, то отрезок от точки A к лайнеру разделит его на два прямоугольных треугольника. Следовательно, благодаря теореме Пифагора вы можете найти расстояние, на которое может пройти луч света.
Следовательно, благодаря теореме Пифагора вы можете найти расстояние, на которое может пройти луч света.
Этот пример, конечно, не самый удачный, так как только единицы могут стремиться опробовать его на практике. Поэтому мы рассматриваем более приземленные варианты использования этой теоремы.
Радиус передачи мобильного сигнала
Современную жизнь уже невозможно представить без смартфонов. Но сколько бы с них прибавилось, если бы они не могли подключать абонентов через мобильную связь ?!
Качество мобильной связи напрямую зависит от того, на какой высоте находится антенна мобильного оператора.Чтобы рассчитать, на каком расстоянии от мобильной вышки телефон может принимать сигнал, вы можете применить теорему Пифагора.
Предположим, вам нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.
АВ (высота башни) = х;
Солнце (радиус передачи сигнала) = 200 км;
ОС (радиус земного шара) = 6380 км;
Ov = OA + AVOV = R + x
Применяя теорему Пифагора, узнайте, что минимальная высота башни должна быть 2. 3 километра.
3 километра.
Теорема Пифагора в повседневной жизни
Как ни странно, теорема Пифагора может быть полезна даже в домашних делах, таких как, например, определение высоты шкафа. На первый взгляд нет необходимости использовать такие сложные вычисления, потому что вы можете просто удалить измерения с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.
Дело в том, что шкаф собирается в горизонтальном положении и только потом поднимается и устанавливается на стену.Поэтому боковины шкафа в процессе подъема конструкции должны свободно проходить как по высоте, так и по диагонали помещения.
Допустим, глубина шкафа составляет 800 мм. Расстояние от пола до потолка 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше высоты комнаты. Но почему именно 126 мм? Рассмотрим на примере.
При идеальном размере шкафа проверяем действие теоремы Пифагора:
AC = √AV 2 + √ WP 2
AC = √2474 2 +800 2 = 2600 мм — все сходится.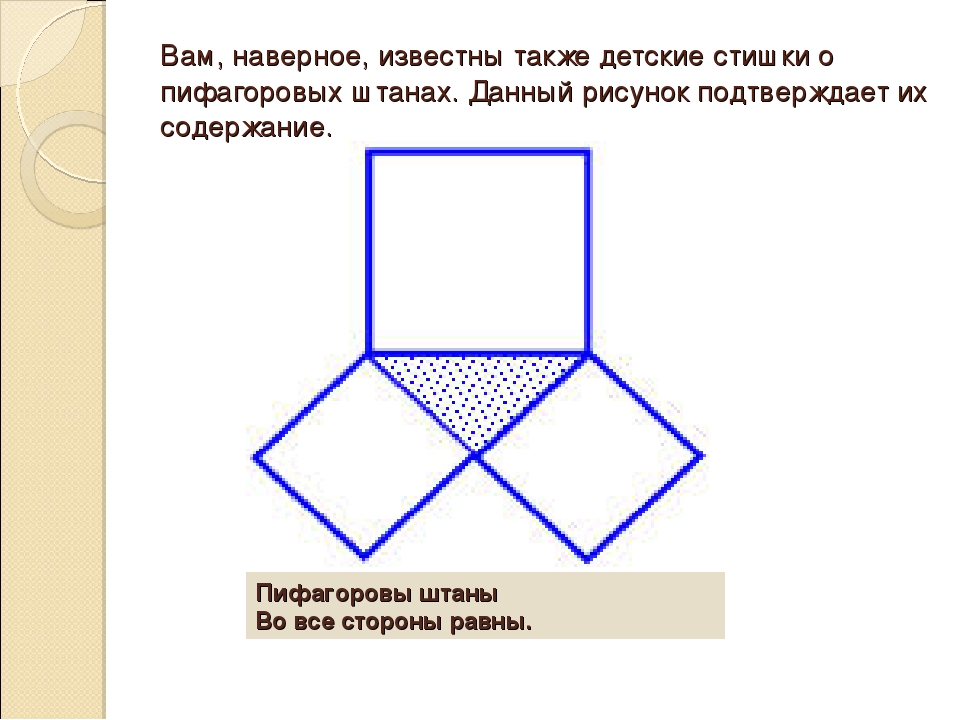
Допустим, высота шкафа не 2474 мм, а 2505 мм. Тогда:
АС = √2505 2 + √800 2 = 2629 мм.
Следовательно, этот шкаф не подходит для установки в этом помещении. Так как при подъеме в вертикальном положении повреждается корпус.
Возможно, рассматривая различные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что это больше, чем истина. Теперь вы можете использовать полученную информацию в своей повседневной жизни и быть полностью уверенными в том, что все расчеты будут не только полезными, но и верными.
»Заслуженный профессор математики Университета Варика, известный популяризатор науки Иэн Стюарт, посвященный роли чисел в истории человечества и актуальности их изучения в наше время.
Пытагорова Гипотенуза
Треугольники Пифагора имеют прямой угол и целые стороны. В простейшем из них самая длинная сторона имеет длину 5, остальные — 3 и 4. Правильных многогранников всего 5. Уравнение пятой степени невозможно решить с помощью корней пятой степени — или любых других корней. Решетки на плоскости и в трехмерном пространстве не обладают пятиточечной симметрией вращения, поэтому в кристаллах такие симметрии не отсутствуют. Однако они могут находиться в решетках в четырехмерном пространстве и в сложных структурах, известных как квазикристаллы.
Решетки на плоскости и в трехмерном пространстве не обладают пятиточечной симметрией вращения, поэтому в кристаллах такие симметрии не отсутствуют. Однако они могут находиться в решетках в четырехмерном пространстве и в сложных структурах, известных как квазикристаллы.
Гипотенуза наименьшей тройки Пифагорова
Теорема Пифагора утверждает, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) коррелирует с двумя другими сторонами этого треугольника очень просто и красиво: квадрат гипотенузы равен сумме квадратов двух других сторон.
Традиционно мы называем эту теорему Пифагора, но на самом деле история о ней довольно туманна. Глиняные пластины предполагают, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; Известность первооткрывателю принесла ему математический культ пифагорейцев, сторонники которых считали, что Вселенная основана на числовых законах. Древних авторов приписывали пифагорейцам — а значит, и Пифагор представляет собой разновидность математических теорем, но на самом деле мы понятия не имеем о том, какой математикой занимался сам Пифагор. Мы даже не знаем, смогли ли пифагорейцы доказать теорему Пифагора или просто поверили, что она верна. Или, скорее всего, у них были убедительные данные о его истинности, которых, тем не менее, было бы недостаточно для того, что мы сегодня считаем доказательством.
Мы даже не знаем, смогли ли пифагорейцы доказать теорему Пифагора или просто поверили, что она верна. Или, скорее всего, у них были убедительные данные о его истинности, которых, тем не менее, было бы недостаточно для того, что мы сегодня считаем доказательством.
Доказательство Пифагора
Первое доказательное доказательство теоремы Пифагора мы находим в «начале» Евклиды. Это довольно сложное доказательство с использованием рисунка, на котором викторианские школьники сразу узнают «Штаны Пифагора»; Рисунок и истина напоминают сушку доверенных лиц, сушащихся на веревке.Известны буквально сотни других свидетельств, большинство из которых делают доказанное одобрение более очевидным.
// Рис. 33. Штаны Пифагора
Одно из самых простых доказательств — это своего рода математическая головоломка. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата. На одной кладке мы видим квадрат на гипотенузе; С другой стороны, квадраты на двух других сторонах треугольника. Понятно, что квадрат в этом же случае равен.
Понятно, что квадрат в этом же случае равен.
// Рис.34. Слева: квадрат на гипотенузе (плюс четыре треугольника). Справа: сумма квадратов на двух других сторонах (плюс те же четыре треугольника). А теперь исключаем треугольники
Изготовление перигала — очередная пазл-пруф.
// Рис. 35. Перигальное рассечение
Существует также доказательство теоремы с использованием квадрата, лежащего на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему. Если вы посмотрите, как наклонный квадрат перекрывает два других квадрата, вы увидите, как разрезать большой квадрат на части, а затем сложить из них два меньших квадрата.Вы также можете увидеть прямоугольные треугольники, стороны которых соответствуют размеру трех задействованных квадратов.
// Рис. 36. Доказательство мощения
Есть интересные свидетельства использования подобных треугольников в тригонометрии. Известно не менее пятидесяти различных свидетельств.
Известно не менее пятидесяти различных свидетельств.
Пифагора Тройка
В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений. Тройка Пытагорова — это набор целых чисел a, b и c, таких что
Геометрически такой тройник определяет прямоугольный треугольник с целыми сторонами.
Наименьший гипотенус тройки Пифагора равен 5.
Две другие стороны этого треугольника равны 3 и 4. Здесь
32 + 42 = 9 + 16 = 25 = 52.
Следующая по величине гипотенуза — равно 10, потому что
62 + 82 = 36 + 64 = 100 = 102.
Однако, по сути, это тот же треугольник с двойными сторонами. Следующая самая большая и действительно другая гипотенуза — 13, для нее
52 + 122 = 25 + 144 = 169 = 132.
Евклидов знал, что существует бесконечное количество различных вариантов Пифагора Трока, и дал то, что можно было бы назвать формула их всех.Позже Диофант Александрийский предложил простой рецепт, в основном совпадающий с евклидовым.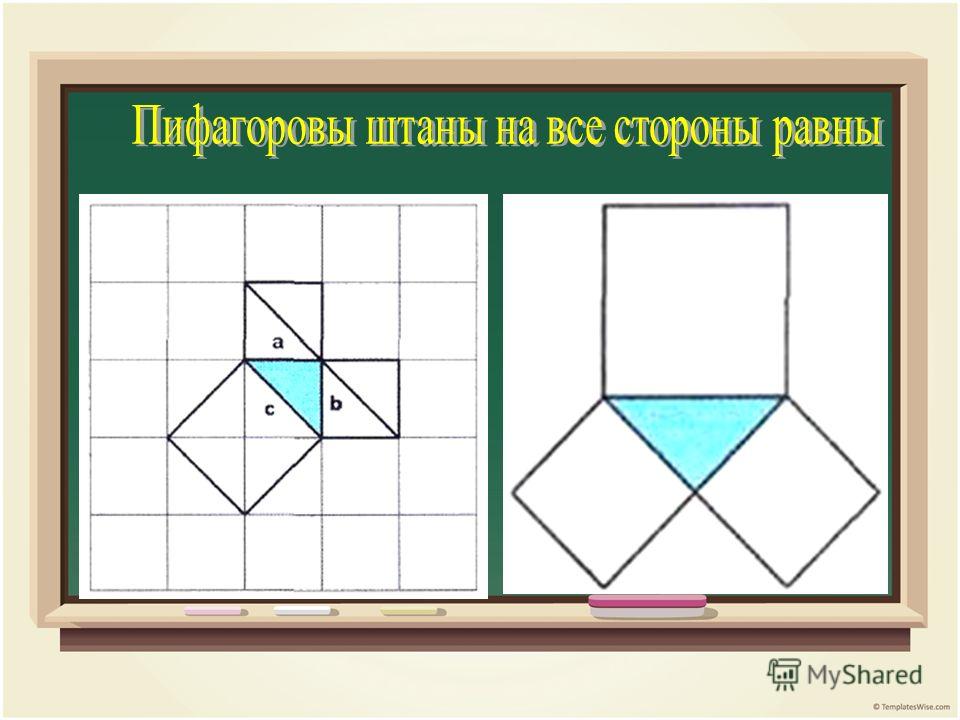
Возьмем любые два натуральных числа и вычислим:
их двойная работа;
разница между их квадратами;
сумма их квадратов.
Три полученных числа будут сторонами треугольника Пифажова.
Возьмем, например, числа 2 и 1. Вычислим:
двухстворчатая работа: 2 × 2 × 1 = 4;
разности квадратов: 22 — 12 = 3;
сумма квадратов: 22 + 12 = 5,
и мы получили знаменитый треугольник 3-4-5.Если взять вместо цифр 3 и 2, то получим:
двойная работа: 2 × 3 × 2 = 12;
разностей квадратов: 32 — 22 = 5;
суммирование квадрата: 32 + 22 = 13,
и мы получаем следующий треугольник 5-12-13, попробуем взять числа 42 и 23 и получим:
удфилды: 2 × 42 × 23 = 1932;
разностей квадратов: 422 — 232 = 1235;
сумма квадратов: 422 + 232 = 2293,
о треугольнике 1235-1932-2293 никто никогда не слышал.
Но работают и эти числа:
12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.
В Правиле диофантства есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять другое произвольное число и умножьте их на это. Таким образом, треугольник 3-4-5 можно превратить в треугольник 6-8-10, умножив все стороны на 2, или в треугольник 15-20-25, умножив все на 5.
Если перейти на язык алгебры, правило принимает следующую форму: пусть U, V и K — натуральные числа.Тогда прямоугольный треугольник со сторонами
2кув и k (u2 — v2) имеет гипотенузу
Есть и другие способы представления основной идеи, но все они сокращают описанное выше. Этот метод позволяет получить всю тройку Пифагора.
Правые многогранники
Имеется гладкий счет из пяти правильных многогранников. Правильный многогранник (или многогранник) — это объемная фигура с конечным числом плоских граней. Края сходятся друг с другом на линиях, называемых ребрами; Ребра находятся в точках, называемых вершинами.
Кульминация евклидова «начала» — доказательство того, что может быть только пять правильных многогранников, то есть многогранников, в которых каждая грань представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным количеством одинаковых лиц. Вот пять правильных многогранников:
тетраэдр с четырьмя треугольными ребрами, четырьмя вершинами и шестью ребрами;
куб или шестигранник с 6 квадратными гранями, 8 вершинами и 12 ребрами;
октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;
додекаэдр с 12 пираниоральными железами, 20 вершинами и 30 ребрами;
икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.
// Рис. 37. Пять правых многогранников
Правые многогранники встречаются в природе. В 1904 году Эрнст Гекель опубликовал рисунки крошечных организмов, известных как радолярии; Многие из них напоминают те самые пять правильных многогранников. Может быть, он немного поправил природу, и рисунки не полностью отражают облик конкретных живых существ. Первые три структуры также наблюдаются в кристаллах. Додекаэдр и икосаэдр в кристаллах вы не найдете, хотя иногда встречаются неправильные додекаэдры и икосаэдры.Настоящие додекаэдры могут существовать в виде квазикристаллов, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.
// Рис. 38. Рисунки Геккеля: Радиолярии в виде правильных многогранников
// Рис. 39. Сканеры правильных многогранников
Интересно делать модели правильных многогранников. многогранники из бумаги, вырезая заданный набор взаимосвязанных граней — это называется разверткой многогранника; Скан складываем по ребрам и склеиваем между собой соответствующие ребра.Полезно добавить дополнительную плату за клей к одному из краев каждой такой пары, как показано на рис. 39. Если такой площадки нет, можно использовать липкую ленту.
Уравнение пятой степени
Не существует алгебраической формулы для решения уравнений 5-й степени.
В целом уравнение пятой степени выглядит так:
aX5 + BX4 + CX3 + DX2 + EX + F = 0.
Задача состоит в том, чтобы найти формулу решения такого уравнения (может иметь до до пяти решений).Опыт обращения квадратных и кубических уравнений, а также уравнений четвертой степени подсказывает, что такая формула должна существовать для уравнений пятой степени, и в ней, по идее, должны фигурировать корни пятой, третьей и четвертой степени. Вторая степень. Опять же, можно смело предположить, что такая формула, если она существует, будет очень и очень сложной.
Это предположение в итоге оказалось ошибочным. На самом деле такой формулы не существует; По крайней мере, не существует формулы, состоящей из коэффициентов A, B, C, D, E и F, составленных с использованием сложения, вычитания, умножения и деления, а также извлечения корня.Таким образом, среди 5 5 есть что-то совершенно особенное. Причины такого необычного поведения пятерки очень глубоки, и на то, чтобы с ними разобраться, потребовалось много времени.
Первым признаком проблемы было то, что он, словно математик, пытался найти такую формулу, какими бы умными они ни были, они неизменно терпели неудачу. Некоторое время все считали, что причины кроются в невероятной сложности формулы. Считалось, что просто никто не сможет разгадать эту алгебру.Однако со временем некоторые математики начали сомневаться в том, что такая формула вообще существует, и в 1823 году Нильсу Хендрику Абелю удалось доказать обратное. Такой формулы не существует. Вскоре после этого Evarister Галуа нашел способ определить, является ли уравнение того или иного пути — 5-го, 6-го, 7-го, вообще каким-либо — с помощью такой формулы.
Вывод из всего этого простой: цифра 5 особенная. Вы можете решать алгебраические уравнения (используя корни N-й степени для различных значений N) для степеней 1, 2, 3 и 4, но не для 5-й степени.На этом очевидная закономерность заканчивается.
Никого не удивляет, что уравнения степеней больше 5 ведут себя еще хуже; В частности, с ними связана та же трудность: нет общих формул для их решения. Это не означает, что уравнения не имеют решений; Это не означает, что невозможно найти очень точные численные значения этих решений. Все это ограничивается традиционными инструментами алгебры. Напоминает о невозможности пересечения угла с помощью линейки и циркуляции.Ответ есть, но перечисленных методов недостаточно и они не позволяют определить, что это такое.
Кристаллографический предел
Кристаллы в двух и трех измерениях не обладают 5-лучевой симметрией вращения.
Атомы в кристалле образуют сетку, то есть структуру, периодически повторяющуюся в нескольких независимых направлениях. Например, рисунок на обоях повторяется по длине рулона; Кроме того, его обычно повторяют в горизонтальном направлении, иногда с переходом от одного куска обоев к другому.По сути, обои — это двухмерный кристалл.
На самолете 17 разновидностей рисунков обоев (см. Раздел 17). Они различаются по типу симметрии, то есть по методикам жестко перемещают рисунок таким образом, что он обязательно оставит сам себя в исходном положении. К типам симметрии относятся, в частности, различные варианты симметрии вращения, при которых рисунок должен быть повернут на определенный угол вокруг определенной точки — центра симметрии.
Порядок симметрии вращения — это то, сколько раз вы можете повернуть тело до полного круга, чтобы все детали чертежа вернулись в исходное положение.Например, поворот на 90 ° — это симметрия вращения 4-го порядка *. Список возможных типов симметрии вращения в кристаллической решетке снова указывает на необычность числа 5: ее там нет. Существуют варианты с симметрией вращения 2, 3, 4 и 6 порядков, но ни один рисунок обоев не имеет симметрии вращения 5-го порядка. Симметрия вращения на порядок больше 6 в кристаллах тоже не случай, но первое нарушение последовательности все же среди числа 5.
То же самое происходит с кристаллографическими системами в трехмерном пространстве. Здесь решетка повторяется в трех независимых областях. Существует 219 различных типов симметрии, или 230, если рассматривать зеркальное отражение узора отдельным вариантом, несмотря на то, что в данном случае нет зеркальной симметрии. Опять-таки соблюдается симметрия вращения 2-го, 3-го, 4-го и 6-го порядков, но не 5. Этот факт получил название кристаллографического предела.
В четырехмерном решетчатом пространстве с 5-м порядком симметрии существуют; В общем, для решеток достаточно большой возможной размерности возможен любой продвинутый порядок симметрии вращения.
// Рис. 40. Кристаллическая решетка поваренной соли. Темные шары изображают атомы натрия, светлые — атомы хлора
Квазикристаллы
Хотя симметрия вращения 5-го порядка в двумерных и трехмерных решетках невозможна, она может существовать в немного менее регулярных структурах, известных как квазикристаллы. Воспользовавшись зарисовками Кеплера, Роджер Пенроуз открыл плоские системы с более распространенным типом пятикратной симметрии. Они получили название квазикристаллов.
Квазикристаллы существуют в природе. В 1984 году Даниэль Шехтман обнаружил, что сплав алюминия и марганца может образовывать квазикристаллы; Первоначально кристаллографы встретили его сообщение с некоторым скептицизмом, но позже открытие подтвердилось, и в 2011 году Шехтман был удостоен Нобелевской премии по химии. В 2009 году группа ученых под руководством Люка Бинди обнаружила квазикристаллы в минерале из Корякского нагорья в России — сочетание алюминия, меди и железа. Сегодня этот минерал называется ИкосаДрит.Измеряя с помощью масс-спектрометра содержание в минерале различных изотопов кислорода, ученые показали, что этот минерал возник на Земле. Он сформировался около 4,5 миллиарда лет назад, когда Солнечная система только зародилась, и большую часть времени проводила в поясе астероидов, вращаясь вокруг Солнца, пока какое-то возмущение не изменило его орбиту и не привело в конце концов к Земле.
// Рис. 41. Слева: одна из двух квазикристаллических решеток с точной пятивременной симметрией.Справа: атомная модель икосаэдрического квазикристалла алюминия-палладия-марганца
.
Теорема Пифагора известна со школьной скамьи. Выдающийся математик доказал прекрасную гипотезу, которой сейчас пользуются многие. Звучит правило: квадрат длины гипотенуса прямоугольного треугольника равен сумме квадратов катетов. В течение многих десятилетий ни одному математику не удавалось повторить это правило. Ведь Пифагор долго шел к своей цели, чтобы рисунки имели место в повседневной жизни.
- Небольшой стих к этой теореме, придуманный вскоре после доказательства, напрямую доказывает свойства гипотезы: «Штаны Пифагора во всех направлениях равны». Этот двойник отложился в памяти многих людей — и по сей день стихотворение вспоминает при подсчете.
- Эта теорема получила название «Штаны Пифагора» из-за того, что при рисовании посередине получился прямоугольный треугольник, на сторонах которого располагались квадраты. По внешнему виду этот рисунок напоминал брюки — отсюда и название гипотезы.
- Пифагор гордится разработанной теоремой, потому что эта гипотеза отличается от нее как бы максимальным количеством доказательств. Важно: уравнение было занесено в Книгу рекордов Гиннеса благодаря 370 правдивым свидетельствам.
- Гипотезу доказало огромное количество математиков и профессоров из разных стран по-разному. . Английский математик Джонс вскоре объявил, что гипотеза доказана с помощью дифференциального уравнения.
- В настоящее время никому неизвестно доказательство теоремы Пифагора .Факты о доказательствах математики сегодня никому не известны. Считается, что доказательство рисунков Евклида также является доказательством Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид самостоятельно доказал теорему, без помощи создателя гипотезы.
- Современные ученые обнаружили, что Великий математик был не первым, кто открыл эту гипотезу . Уравнение было известно задолго до открытия Пифагором.Этому математику удалось только воссоединить гипотезу.
- Пифагор не давал уравнению названия «Теорема Пифагора» . Это название было исправлено после «громких двойных ударов». Математик только хотел, чтобы его усилия и открытия познали весь мир, и использовал их.
- Мориц Кантор — величайший математик, обнаруженный и увиденный на древних папирусных записях с рисунками . Вскоре после этого Кантор понял, что эта теорема была известна египтянам еще за 2300 лет до нашей эры.Только тогда этим никто не воспользовался и не пытался доказать.
- Современные ученые считают, что гипотеза была известна еще в 8 веке до нашей эры . Индийские ученые того времени открыли примерный расчет гипотенуса треугольника, наделенного прямыми углами. Правда в то время никто не мог точно доказать уравнение для приближенных расчетов.
- Великая математика Бартель Ван дер Варден После доказательства гипотезы сделал важный вывод : «Достоинством греческой математики считается не открытие направления и геометрии, а лишь ее обоснование.В руках Пифагора были вычислительные формулы, основанные на предположениях, неточных вычислениях и неопределенных представлениях. Однако выдающийся ученый сумел оказаться в точной науке. «
- В знаменитых стихах говорится, что в день открытия своего рисунка он воздвиг быков милой жертвы . Именно после открытия гипотезы пошли слухи, что жертва ста быков« ушла в блуждание. на страницах книг и публикаций.«Палки и по сей день шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что не Пифагор придумал стихотворение о штанах, чтобы доказать выдвинутые им рисунки: во время При жизни Великой математики штанов еще не было . Их изобрели спустя несколько десятилетий.
- Пекка, Лейбниц и несколько других ученых пытались доказать ранее известную теорему, но это никому не удалось. Название рисунков «Теорема Пифагора» означает «убедительность речи» .Так переводится слово Пифагор, которое математик взял за псевдоним.
- Размышления Пифагора о собственном правиле: секрет горения на Земле заключается в числах . Ведь математик, опираясь на собственную гипотезу, изучал свойства чисел, выявлял четность и нечетность, создавал пропорции.
Надеемся, вам понравилась подборка с картинками — интересные факты о теореме Пифагора: узнаем новое о знаменитой теореме (15 фото) онлайн в хорошем качестве.Пожалуйста, оставьте свое мнение в комментариях! Для нас важно каждое мнение.
Штаны Пифагора Шуточное название теоремы Пифагора, возникшей из-за того, что квадраты, построенные по сторонам прямоугольника и расходящиеся в разные стороны, напоминают штаны. Я любил геометрию … и получил в ВУЗ на вступительном экзамене в ВУЗ даже от Чумакова, профессора математики, похвалу за то, что без доски, рука за рукой объяснил свойства параллельных линий и pythagora брюки (Н.Пирогова. Дневник старого врача).
Фразеологический словарь русского литературного языка. — М .: Астрель, Аст. А. И. Федоров. 2008.
Посмотреть что такое «Штаны Пифагора» в других словарях:
Штаны — получите рабочий купон Academician на скидку SuperStep или выгодные штаны для покупки с бесплатной доставкой для продажи в Superstep
Штаны Pythagora — … Википедия
Штаны Пифагора — Жарг.шк. Желе Теорема Пифагора, которая устанавливает соотношение между квадратами квадратов, построенных на гипотенузе, и катетом прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
штаны пифагора — шутливое название теоремы Пифагора, устанавливающей связь между квадратами, построенными на гипотенусах, и формой прямоугольного треугольника, который внешне на рисунках выглядит как аисты … Словарь многих выражений
трусики из пифагора (изобрет.) — Иност.: about man Г. Даровит Это убожество. В древности он наверняка изобрел бы штаны Пифагорову … Салтыков. Письма о пестах. Штаны Пифагора (геометрия): В прямоугольнике квадрат гипотенузы равен квадрату катетов (учим … … Большой толсто-фразологический словарь Михельсона
Штаны Пифагора со всех сторон равны — Количество пуговиц известно. Зачем мне пристально? (Грубо) о штанах и мужских половых органах. Штаны Пифагора со всех сторон равны.Чтобы доказать это, нужно снять и показать: 1) о теореме Пифагора; 2) про широкие штаны … живая речь. Словарь устных выражений
Пифагор штаны дурак — ПиньяГоровы Штаны (изобретать) несправедливость. О человеческом петухе. Ср. Несомненно, это мудрец. В старину он бы изобрел штаны Пинягорова … Салтыков. Ходячие буквы. ПиньяГоровы штаны (геом.): В прямоугольнике квадрат гипотенузы … … Большой интеллектуально-фразеологический словарь Михельсона (орфография)
Штаны Пифагора во всех направлениях равны — шутливое доказательство теоремы Пифагора; Также в анекдоте про мешковатые штаны друга… Словарь народной фразеологии
Сел, грубо …
Штаны Пифагора по всем направлениям равны (количество пуговиц известно. Почему тесно? / Чтобы доказать, нужно снять и показать) — доволен, грубоват … Толковый словарь современных разговорных фраз и прогресса
брюки — СУМ., МН., УПОТР. по сравнению. Часто морфология: MN. какие? Штаны, (нет) что? Штаны, что? Штаны, (см.) Что? Штаны чем? Штаны, что? О штанах 1.Штаны Это предмет одежды, который имеет две короткие или длинные штаны и закрывает низ … … Толковый словарь Дмитриева
Книги
- Штаны Pythagora,. В этой книге вы найдете фантастику и приключения, чудеса и фантастику. Забавно и грустно, обыденно и загадочно … А что еще нужно для занимательного чтения? Главное, чтобы …
Римский архитектор Витрувий выделил теорему Пифагоры «из многочисленных открытий, которые послужили развитию человеческой жизни», и призвал относиться к ней с величайшим почтением.Это было еще в первом веке до н. е. На рубеже XVI-XVII веков известный немецкий астроном Иоганн Кеплер назвал его одним из сокровищ геометрии, сопоставимым с мерой золота. Вряд ли во всей математике будет более значимое и значимое одобрение, ведь по количеству научных и практических приложений теорема Пифагора не имеет себе равных.
Теорема Пифагора для случая равностороннего прямоугольного треугольника.
Наука и жизнь // иллюстрация
Иллюстрация к теореме Пифагора из «Трактовки с измерением шести» (Китай, III век до н.э.) и восстановленное на ее основе доказательство.
Наука и жизнь // иллюстрация
С. Перкинс. Пифагор.
Рисунок к возможному доказательству Пифагора.
Мозаика Пифагора и разделение AN-подданных на три квадрата в доказательстве теоремы Пифагора.
P. de Heh. Хозяйка и горничная во дворе. Около 1660 г.
I. OXTERVELT. Заблудшие музыканты в дверях богатого дома. 1665 год.
Штаны Пифагора
Теорема Пифагора — едва ли не самая узнаваемая и, несомненно, самая известная в истории математики.В геометрии он применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a
Рисунки на рис. 1 и 2, напоминают простейший орнамент из квадратов и равных их частей — геометрический узор, известный с незапамятных времен. Их можно полностью накрыть рубанком. Математика назвала бы такое покрытие плоскости полигональным паркетом или смешиванием. Что такое Пифагор? Оказывается, он первым решил задачу правильного паркета, с чего и началось изучение осмотров различных поверхностей.Итак, Пифагор показал, что плоскость вокруг точки может быть покрыта без пробелов равными правильным многоугольникам только трех видов: шести треугольников, четырех квадратов и трех шестиугольников.
4000 лет спустя
История теоремы Пифагора уходит в глубокую древность. Упоминание о нем до сих пор содержится в вавилонских клинических текстах царя Хаммурапи (XVIII век до н.э.), то есть за 1200 лет до рождения Пифагора. Теорема использовалась как готовое правило во многих задачах, самая простая из которых — найти диагональ квадрата на его стороне.Не исключено, что соотношение A 2 + B 2 = C 2 для произвольного прямоугольного треугольника вавилоняне получили, просто «суммируя» равенство A 2 + A 2 = C 2. Но им повезло — для практической геометрии древний, сводившийся к измерениям и расчетам, не требовал строгих обоснований.
Теперь, почти 4000 лет спустя, мы имеем дело с рекордсменом по количеству всех видов свидетельств. Кстати, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришелся на вторую половину XIX — начало XX века.И если первые коллекции содержат не более двух десятков свидетельств, то к концу XIX века их количество приблизилось к 100, а через полвека превысило 360, и это только те, которым удалось собрать разные источники. Кого только не взяли за решение этой нестабильной задачи — от известных ученых и популяризаторов науки до конгрессменов и школьников. И что примечательно, по оригинальности и простоте решения другие любители не уступали профессионалам!
До нас дошли самые древние из доказательств теоремы Пифагора, насчитывающие около 2300 лет.Одно из них строго аксиоматично — принадлежит к древнегреческому математику Евклиду, жившему в IV-III веках до нашей эры. е. В I, книге «Выгоды» теорема Пифагора выглядит как «предложение 47». Самые наглядные и красивые доказательства построены на картине «Пифагорейские штаны». Они похожи на хитрую головоломку для нарезки квадратов. Но заставьте фигуры двигаться правильно — и они откроют вам секрет знаменитой теоремы.
Вот какое изящное доказательство получено на основе рисунка из одного древнекитайского трактата (рис.3), и сразу же проясняет его связь с задачей удвоения квадрата квадрата.
Именно такое доказательство пытался объяснить своему младшему другу семилетнему Гвидо, не по годам, умному герою романа английского писателя Олдхоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность свидетельств, поэтому приписал ее … самому Пифагору. Но главный герой фантастического рассказа Евгении Веллистовой «Электроника — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данные Евклидом; Правда, ошибочно назвал его самым простым, хотя на самом деле в современном издании «началось» оно занимает полторы страницы!
Первый математик
Пифагор Самосский (570-495 до н.э.), имя которого давно и неразрывно связано с чудесной теоремой, в определенном смысле можно назвать первым математиком.Именно от него математика начинается как точная наука, где каждое новое знание является результатом не визуальных идей и правил, выведенных из опыта, а результатом логических рассуждений и выводов. Только так вы сможете навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод использовал только древнегреческий философ и ученый Фалез Милецкий, живший на рубеже VII-VI веков до н. Э. Он предложил идею доказательства, но применил ее не систематически, как правило, выборочно, к очевидным геометрическим утверждениям типа «Диаметр делит круг пополам».«Пифагор продвинулся намного дальше. Считается, что он ввел первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием« Традиция Пифагора ». теория чисел и стереометрия
Еще одна важная заслуга Пифагора — основание славной школы математиков, более века определявшей развитие этой науки в Древней Греции.Термин «математика» связан с его именем (от греческого μαθημA — учение, наука), объединившим четыре относительные дисциплины, созданные Пифагором и его последователями — пифагорейцами — системы знаний: геометрия, арифметика, астрономия и гармоника.
Невозможно отделить достижения Пифагора от достижений: по обычаю они приписывали собственные идеи и открывали своего учителя. Не осталось никаких очерков. Ранние пифагорейцы оставили всю информацию, которую они передавали друг другу устно.Итак, 2500 лет спустя у историков нет ничего другого, кроме восстановления утраченных знаний по переводам других, более поздних авторов. Отдадим должное грекам: они хоть и окружили имя Пифагора множеством легенд, но не приписывали ничего такого, что он не мог бы раскрыть или развить в теорию. И теорема, носящая его имя, не исключение.
Такое простое доказательство
Неизвестно, сам Пифагор открыл соотношение между длинами сторон прямоугольного треугольника или позаимствовал это знание.Античные авторы утверждали, что он сам и любил пересказывать легенду о том, как Пифагор принес в жертву быка в честь своего открытия. Современные историки склонны считать, что он узнал о теореме, познакомившись с вавилонской математикой. Мы также не знаем, что за формулировал теорему Пифагор: арифметика, как принято сегодня, — квадрат гипотенуз равен сумме квадратов катетов, или геометрически, в духе древних, квадрат, построенный на гипотеннеус прямоугольного треугольника равна сумме квадратов, построенных по Его обычаям.
Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Это точно не сохранилось. По одной из версий, Пифагор мог воспользоваться пропорциями, выработанными в его школе. Он был основан, в частности, на теории подобия, на которой основано рассуждение. Рисуем прямоугольный треугольник с высотой катетики A и B до гипотенузы C. Получаем три одинаковых треугольника, включая оригинал. Их соответствующие партии пропорциональны, a: c = m: a и b: c = n: b, откуда a 2 = c · m и b 2 = c · n.Тогда a 2 + b 2 = c · (m + n) = C 2 (рис. 4).
Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, очень простое: занимает всего несколько строк, не нужно ничего тащить, перекрашивать, вычислять … Неудивительно, что его неоднократно отбивали. Он содержится, например, в «Практике геометрии» Леонардо Писанского (1220 г.), и до сих пор лидирует в учебниках.
Такое свидетельство не противоречило взглядам пифагорейцев на Резюме: Первоначально они считали, что соотношение длин любых двух отрезков и, следовательно, площади прямолинейных фигур можно выразить натуральными числами.Никаких других чисел они не рассматривали, не допускали даже дробей, заменяя их отношениями 1: 2, 2: 3 и т. Д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости числа диагональ квадрата и его часть. Все попытки численно представить длину этой диагонали — в одном квадрате она равна √2 — ни к чему не привели. Было легче доказать, что задача не решена. В таком случае у математиков есть проверенный метод — доказательство от гадости.Кстати, и его приписывают Пифагору.
Существование отношений, не выражаемых натуральными числами, положило конец многим пифагорейским идеям. Стало понятно, что известных им чисел недостаточно для решения даже простых задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, ее центральной проблемы. Сначала это привело к развитию учения о несоизмеримых ценностях — иррациональностях, а затем к расширению понятия числа.Другими словами, началась многовековая история изучения многих действительных чисел.
Мозаика Пифагора
Если покрыть плоскость квадратами двух разных размеров, окружая каждый маленький квадрат до четырех больших, то получится мозаичный паркет Пифагора. Таким рисунком издавна украшали каменные полы, напоминая древнее свидетельство теоремы Пифагора (отсюда и его название). По-разному перекрывая квадратную сетку на паркете, можно получить разбиение квадратов, построенных по сторонам прямоугольного треугольника, которые предлагались разным математикам.Например, если вы расположите сетку так, чтобы все ее узлы совпадали с правыми верхними вершинами квадратиков, фрагменты чертежа будут показаны в доказательстве средневековой персидской математики Ан-Наирзи, которое он разместил в комментариях к «начало» Евклиды. Нетрудно заметить, что сумма площадей больших и малых квадратов, исходных элементов паркета, равна площади наложенной сетки одного квадрата. А это значит, что указанная перегородка действительно подходит для укладки паркета: соединяя получившиеся многоугольники в квадраты, как показано на рисунке, можно заливать ими без пробелов и перекрывать всю плоскость.
справочная информация, пруфы, примеры практического применения. Из истории выпуска
Все животные равны, но одни равнее других. Напоследок хотелось бы вспомнить людей, которые думают, что Косово может стать неким прецедентом. Мол, если населению Косово «мировое сообщество» (то есть США и ЕС) дает право решать свою судьбу
автор Литературная газета
Почти равный Клуб 12 стульев Почти равный ЖЕЛЕЗНАЯ ПРОЗА Смерть досталась одному бедолаге.И он был глухим. Так нормально, но глухо … А я плохо видел. Я почти ничего не видел. — Ой, у нас гости! Пожалуйста, передайте. Смерть говорит: — Подожди, чтобы радоваться,
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
МБОУ Бондарская общеобразовательная школа Студенческий проект на тему: «Пифагор и его теорема» Подготовил: Эктов Константин, ученик 7 класса А Научный руководитель: Долотова Надежда Ивановна, учитель математики 2015
2 слайда
Описание слайда:
3 слайда
Описание слайда:
Аннотация.Геометрия — очень интересная наука. Он содержит много разных теорем, но иногда так необходимых. Меня очень заинтересовала теорема Пифагора. К сожалению, в восьмом классе мы пропускаем только одно из самых важных утверждений. Я решил приоткрыть завесу тайны и исследовать теорему Пифагора.
4 слайда
Описание слайда:
5 слайдов
Описание слайда:
6 слайдов
Описание слайда:
Задания Изучить биографию Пифагора.Изучите историю происхождения и доказательства теоремы. Узнайте, как эта теорема используется в искусстве. Найдите исторические проблемы, в решении которых применяется теорема Пифагора. Познакомьтесь с отношением детей в разное время к этой теореме. Создайте проект.
7 слайдов
Описание слайда:
Прогресс исследований Биография Пифагора. Заповеди и афоризмы Пифагора. Теорема Пифагора. История теоремы.Почему «пифагорейские штаны равны во всех направлениях»? Различные доказательства теоремы Пифагора другими учеными. Применение теоремы Пифагора. Интервью. Выход.
8 слайд
Описание слайда:
Пифагор — кто он? Пифагор Самосский (580-500 до н.э.) — древнегреческий математик и философ-идеалист. Родился на острове Самос. Получила хорошее образование. Согласно легенде, Пифагор, чтобы познакомиться с мудростью восточных ученых, отправился в Египет и прожил там 22 года.Хорошо овладев всеми науками египтян, включая математику, он переехал в Вавилон, где прожил 12 лет и познакомился с научными знаниями вавилонских жрецов. Легенды связывают Пифагора с визитом в Индию. Это очень вероятно, поскольку Иония и Индия тогда имели торговые связи. Вернувшись на родину (ок. 530 г. до н. Э.), Пифагор попытался организовать собственную философскую школу. Однако по неизвестным причинам он вскоре покидает Самос и обосновывается в Кротоне (греческая колония на севере Италии).Здесь Пифагору удалось организовать свою школу, проработавшую почти тридцать лет. Школа Пифагора, или, как ее еще называют, Пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Статус пифагорейского союза был очень суровым. В своих философских взглядах Пифагор был идеалистом, защитником интересов рабовладельческой аристократии. Возможно, это было причиной его отъезда из Самоса, так как сторонники демократических взглядов имели очень большое влияние в Ионии.В социальных вопросах пифагорейцы понимали «порядок» как власть аристократов. Они осудили древнегреческую демократию. Пифагорейская философия была примитивной попыткой обосновать господство рабовладельческой аристократии. В конце 5 в. До н.э. по Греции и ее колониям захлестнула волна демократического движения. Демократия победила в Кротоне. Пифагор вместе со своими учениками покидает Кротон и направляется в Тарент, а затем в Метапон. Прибытие пифагорейцев в Метапонт совпало с началом там народного восстания.Почти девяностолетний Пифагор погиб в одной из ночных стычек. Его школа перестала существовать. Ученики Пифагора, спасаясь от преследований, расселились по всей Греции и ее колониям. Чтобы заработать на жизнь, они организовали школы, в которых преподавали в основном арифметику и геометрию. Информация об их достижениях содержится в трудах более поздних ученых — Платона, Аристотеля и др.
9 слайд
Описание слайда:
Заповеди и афоризмы Пифагора Мысль превыше всего среди людей на земле.Не садитесь на меру хлеба (то есть не живите праздно). Уходя, не оглядывайтесь (т.е. перед смертью не цепляйтесь за жизнь). Не ходите по проторенной дорожке (то есть следуйте не мнению толпы, а мнению немногих, кто понимает). Не держите в доме ласточек (то есть не принимайте разговорчивых и не сдержанных в языке гостей). Будьте с тем, кто сбрасывает груз, не будьте с тем, кто сбрасывает груз (то есть поощряйте людей не к праздности, а к добродетели, к работе).По полю жизни, как сеятель, шагай ровным и постоянным шагом. Истинное отечество там, где царит хорошая мораль. Не входите в образованное общество: самые мудрые, составляя общество, становятся простолюдинами. Чтите числа, вес и меру так же свято, как дети грациозного равенства. Измерьте свои желания, взвесьте свои мысли, посчитайте свои слова. Не удивляйтесь ничему: неожиданность произвела на себя богов.
10 слайдов
Описание слайда:
Формулировка теоремы.В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
11 слайдов
Описание слайда:
Доказательство теоремы. На данный момент в научной литературе зарегистрировано 367 доказательств этой теоремы. Теорема Пифагора, вероятно, единственная теорема с таким впечатляющим количеством доказательств. Конечно, все их можно разделить на небольшое количество классов.Самые известные из них: доказательства площади, аксиоматические и экзотические доказательства.
12 слайдов
Описание слайда:
Доказательство теоремы Пифагора Вам дан прямоугольный треугольник с катетами a, b и гипотенузой c. Докажем, что c² = a² + b² Допишем треугольник до квадрата со стороной a + b. Площадь S этого квадрата (a + b) ². С другой стороны, квадрат состоит из четырех равных прямоугольных треугольников, каждый из которых S равен ½ a b, и квадрата со стороной c.S = 4 ½ a b + c² = 2 a b + c² Таким образом, (a + b) ² = 2 a b + c², откуда c² = a² + b² c c c c c с a b
13 слайдов
Описание слайда:
История теоремы Пифагора История теоремы Пифагора интересна. Хотя эта теорема связана с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, в то время еще не знали его доказательства, а сама связь между гипотенузой и катетами была установлена эмпирически на основе измерений.Пифагор, кажется, нашел доказательства этой связи. Сохранилась древняя легенда, что в честь своего открытия Пифагор принес в жертву богам быка, а по другим свидетельствам — даже сотню быков. В течение следующих столетий были найдены различные другие доказательства теоремы Пифагора. В настоящее время их более сотни, но наиболее популярной является теорема о построении квадрата по заданному прямоугольному треугольнику.
14 слайдов
Описание слайда:
Теорема Древнего Китая «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет равна 5, когда основание равно 3, а высота равна 4».
15 слайдов
Описание слайда:
Теорема в Древнем Египте Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5 ² было известно египтянам уже около 2300 г. до н.э. До н.э., во времена короля Аменемхета (согласно папирусу 6619 Берлинского музея). Согласно Кантору, гарпедонапты, или «тяги веревки», строились под прямыми углами, используя прямоугольные треугольники со сторонами 3, 4 и 5.
16 слайдов
Описание слайда:
О теореме в Вавилонии «Заслуга первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, заключается не в открытии математики, а в ее систематизации и обосновании.В их руках вычислительные рецепты, основанные на расплывчатых представлениях, превратились в точную науку. «
17 слайд
Описание слайда:
Почему «пифагорейские штаны равны во всех направлениях»? На протяжении двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было доказательство Евклида. Он включен в его знаменитую книгу «Начало». Евклид опустил высоту КД от вершины прямого угла до гипотенузы и утверждал, что ее продолжение делит квадрат, завершенный на гипотенузе, на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.Рисунок, используемый для доказательства этой теоремы, в шутку называют «пифагорейскими штанами». Долгое время он считался одним из символов математической науки.
18 слайд
Описание слайда:
Отношение детей древности к доказательству теоремы Пифагора ученики Средневековья считали очень трудным. Слабые ученики, выучившие теоремы наизусть, не понимая, и потому получившие прозвище «ослы», не смогли преодолеть теорему Пифагора, которая служила для них непреодолимым мостом.Из-за рисунков, сопровождающих теорему Пифагора, студенты также называли ее «ветряной мельницей», сочиняли стихи, такие как «Пифагорейские штаны равны со всех сторон», и рисовали карикатуры.
19 слайд
Описание слайда:
Доказательства теоремы Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. В самом деле, достаточно просто взглянуть на мозаику из равнобедренных прямоугольных треугольников, чтобы убедиться в теореме.Например, для треугольника ABC: квадрат, построенный на гипотенузе AC, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два.
20 слайдов
Описание слайда:
«Стул невесты» На рисунке построенные на ножках квадраты расположены ступенями один за другим. Эта фигура встречается в свидетельствах, датируемых еще 9 веком нашей эры. э., индейцы называли «кресло невесты».
21 слайд
Описание слайда:
Применение теоремы Пифагора В настоящее время общепризнано, что успех развития многих областей науки и техники зависит от развития различных областей математики.Важным условием повышения эффективности производства является повсеместное внедрение математических методов в технику и народное хозяйство, что предполагает создание новых эффективных методов качественных и количественных исследований, позволяющих решать задачи, которые ставит практика.
22 слайда
Описание слайда:
Применение теоремы в строительстве В зданиях готического и романского стиля верхние части окон рассечены каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
23 слайда
Описание слайда:
24 слайда
Описание слайда:
Исторические задачи Для закрепления мачты необходимо проложить 4 троса. Один конец каждого кабеля должен быть закреплен на высоте 12 м, другой конец на земле на расстоянии 5 м от мачты. Достаточно ли 50 м кабеля для крепления мачты?
В одном можно быть на сто процентов уверенным, что на вопрос, каков квадрат гипотенузы, любой взрослый смело ответит: «Сумма квадратов катетов.«Эта теорема прочно вошла в сознание каждого образованного человека, но достаточно попросить кого-нибудь ее доказать, и тогда могут возникнуть трудности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.
Краткий биографический обзор
Теорема Пифагора знакома практически каждому, но почему-то биография человека, родившего ее, не так популярна. Это поправимо. Поэтому, прежде чем изучать различные способы доказательства теоремы Пифагора, необходимо: вкратце познакомимся с его личностью.
Пифагор — философ, математик, мыслитель. С сегодняшнего дня очень трудно отличить его биографию от легенд, сложившихся в память об этом великом человеке. Но, как следует из писаний его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычным каменотесом, а мать происходила из дворянской семьи.
Согласно легенде, рождение Пифагора предсказала женщина по имени Пифия, в честь которой и был назван мальчик.По ее предсказанию, рожденный мальчик должен был принести человечеству много пользы и добра. Что он на самом деле и сделал.
Рождение теоремы
В юности Пифагор переехал в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними его приняли на учебу, где он узнал все великие достижения египетской философии, математики и медицины.
Вероятно, именно в Египте Пифагор был вдохновлен величием и красотой пирамид и создал свою великую теорию.Это может шокировать читателей, но современные историки считают, что Пифагор не доказал свою теорию. Он только передал свои знания своим последователям, которые позже выполнили все необходимые математические вычисления.
Как бы то ни было, сегодня известен не один метод доказательства этой теоремы, а сразу несколько. Сегодня остается только догадываться, как именно древние греки проводили свои вычисления, поэтому здесь мы рассмотрим различные способы доказательства теоремы Пифагора.
Теорема Пифагора
Перед тем, как начать какие-либо вычисления, вам нужно выяснить, какая теория должна быть доказана.Теорема Пифагора звучит так: «В треугольнике, в котором один из углов равен 90 °, сумма квадратов катетов равна квадрату гипотенузы».
Всего существует 15 различных способов доказательства теоремы Пифагора. Это довольно большая цифра, поэтому обратим внимание на самые популярные.
Метод первый
Сначала обозначим то, что нам дано. Эти данные будут также применимы к другим методам доказательства теоремы Пифагора, поэтому вам следует немедленно запомнить все доступные обозначения.
Предположим, что дан прямоугольный треугольник с катетами a, b и гипотенузой, равной c. Первый метод доказательства основан на том, что вам нужно из прямоугольного треугольника начертить квадрат.
Для этого нужно провести отрезок, равный отрезку b, к отрезку длины a, и наоборот. Это должно создать две равные стороны квадрата. Осталось только провести две параллельные линии, и квадрат готов.
Внутри получившейся фигуры нужно нарисовать еще один квадрат со стороной, равной гипотенузе исходного треугольника.Для этого из вершин ac и sv нужно провести два параллельных отрезка, равных c. Таким образом, мы получаем три стороны квадрата, одна из которых — гипотенуза исходного прямоугольного треугольника. Осталось только закончить четвертый отрезок.
На основании полученного рисунка можно сделать вывод, что площадь внешнего квадрата составляет (a + b) 2. Если заглянуть внутрь фигуры, то можно увидеть, что помимо внутреннего квадрата она содержит четыре прямоугольные треугольники. Площадь каждого — 0.5 пр.
Следовательно, площадь равна: 4 * 0,5av + s 2 = 2av + s 2
Отсюда (a + b) 2 = 2ab + c 2
А, значит, c 2 = a 2 + b 2
Теорема доказана.
Метод второй: подобные треугольники
Эта формула для доказательства теоремы Пифагора была получена на основе утверждения из раздела геометрии о подобных треугольниках. Он говорит, что катет прямоугольного треугольника является пропорциональным средним для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 °.
Исходные данные остались прежними, поэтому приступим сразу к доказательству. Нарисуем отрезок SD перпендикулярно стороне AB. Исходя из приведенного выше утверждения, катеты треугольников равны:
AC = √AB * HELL, SV = √AB * DV.
Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство должно быть завершено возведением обоих неравенств в квадрат.
AC 2 = AB * HELL и SV 2 = AB * DV
Теперь нужно сложить полученные неравенства.
AC 2 + SV 2 = AB * (BP * DV), где BP + DV = AB
Получается, что:
AC 2 + SV 2 = AB * AB
А следовательно:
AC 2 + CB 2 = AB 2
Доказательство теоремы Пифагора и различные способы ее решения требуют разностороннего подхода к этой проблеме. Однако этот вариант — один из самых простых.
Другая вычислительная техника
Описание различных методов доказательства теоремы Пифагора может ничего не сказать, пока вы не начнете практиковать самостоятельно.Многие техники включают не только математические вычисления, но и построение новых фигур из исходного треугольника.
В этом случае необходимо завершить еще один прямоугольный треугольник ДПС от ножки ВС. Таким образом, теперь есть два треугольника с общей ногой BC.
Зная, что площади таких фигур имеют отношение квадратов к их аналогичным линейным размерам, тогда:
S avd * s 2 — S avd * a 2 = S avd * a 2 — S awd * a 2
S abc * (s 2 -v 2) = a 2 * (S abd -S vd)
s 2 -w 2 = a 2
c 2 = a 2 + b 2
Так как этот вариант Вряд ли из подходящих разных методов доказательства теоремы Пифагора для 8 класса можно воспользоваться следующей методикой.
Самый простой способ доказать теорему Пифагора. Отзывы
Историки считают, что этот метод впервые применили для доказательства теорем еще в Древней Греции. Он самый простой, не требует абсолютно никаких вычислений. Если нарисовать фигуру правильно, то будет хорошо видно доказательство утверждения, что 2 + в 2 = c 2.
Условия для этого метода будут немного отличаться от предыдущего. Для доказательства теоремы предположим, что прямоугольный треугольник ABC равнобедренный.
Возьмем гипотенузу переменного тока за сторону квадрата и разделим его на три стороны. Кроме того, в получившемся квадрате нужно провести две диагональные линии. Так что внутри него четыре равнобедренных треугольника.
К ножкам AB и CB также нужно провести квадрат и провести по одной диагональной линии в каждой из них. Первая линия проводится из вершины A, вторая — из C.
Теперь нужно внимательно посмотреть на получившийся рисунок. Поскольку есть четыре треугольника, равных исходному на гипотенузе AC, и два на катетах, это указывает на истинность этой теоремы.
Кстати, благодаря такому методу доказательства теоремы Пифагора родилась знаменитая фраза: «Пифагорейские штаны равны во всех направлениях».
Доказательства Дж. Гарфилда
Джеймс Гарфилд — 20-й президент Соединенных Штатов Америки. Он не только оставил свой след в истории как правитель Соединенных Штатов, но и был одаренным самоучкой.
В начале своей карьеры он был рядовым учителем в народной школе, но вскоре стал директором одного из высших учебных заведений.Стремление к саморазвитию позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения следующие.
Сначала нужно нарисовать на листе бумаги два прямоугольных треугольника так, чтобы ножка одного из них была продолжением второго. Вершины этих треугольников должны быть соединены, чтобы в конечном итоге образовалась трапеция.
Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.
S = a + b / 2 * (a + b)
Если рассматривать получившуюся трапецию как фигуру, состоящую из трех треугольников, то ее площадь можно найти следующим образом:
S = av / 2 * 2 + s 2/2
Теперь нужно выровнять два исходных выражения
2av / 2 + s / 2 = (a + b) 2/2
c 2 = a 2 + b 2
Подробнее О теореме Пифагора и методах ее доказательства можно написать не один том учебника. Но есть ли в этом смысл, когда эти знания нельзя применить на практике?
Практическое применение теоремы Пифагора
К сожалению, современные школьные программы предусматривают использование этой теоремы только в геометрических задачах.Выпускники скоро покинут школьные стены, так и не зная, как применить свои знания и умения на практике.
Фактически, каждый может использовать теорему Пифагора в своей повседневной жизни. И не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и методы ее доказательства могут оказаться крайне необходимыми.
Связь теоремы и астрономии
Казалось бы, как можно соединить звезды и треугольники на бумаге.Фактически, астрономия — это научная область, в которой широко используется теорема Пифагора.
Например, рассмотрим движение светового луча в пространстве. Известно, что свет движется в обоих направлениях с одинаковой скоростью. Траектория AB, по которой движется световой луч, называется l .
И половину времени, которое требуется свету, чтобы добраться из точки A в точку B, давайте позвоним по номеру
т … А скорость балки —
с . Получается, что: c * t = l
Если посмотреть на этот самый луч с другой плоскости, например с космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. В этом случае даже неподвижные элементы будут двигаться со скоростью v в обратном направлении.
Допустим, комикс плывет вправо. Тогда точки A и B, между которыми перебрасывается луч, переместятся влево. Более того, когда луч движется из точки A в точку B, точка A успевает переместиться и, соответственно, свет уже попадет в новую точку C.Чтобы найти половину расстояния, на которое сместилась точка A, вам нужно умножить скорость лайнера на половину времени прохождения луча (t «).
И найти, какое расстояние может пройти луч света за это время. раз нужно обозначить половину пути новой буквой s и получить следующее выражение:
Если представить, что точки света C и B, а также космический лайнер являются вершинами равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника.Следовательно, благодаря теореме Пифагора вы можете найти расстояние, которое может пройти луч света.
Этот пример, конечно, не самый удачный, так как лишь немногим посчастливится опробовать его на практике. Поэтому мы рассмотрим более приземленные приложения этой теоремы.
Радиус передачи мобильного сигнала
Современную жизнь уже невозможно представить без наличия смартфонов. Но были бы они полезны, если бы не могли подключать абонентов через мобильную связь ?!
Качество мобильной связи напрямую зависит от высоты антенны мобильного оператора.Чтобы вычислить, на каком расстоянии телефон может принимать сигнал от вышки мобильной связи, вы можете применить теорему Пифагора.
Допустим, вам нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.
АВ (высота башни) = х;
Самолет (радиус передачи сигнала) = 200 км;
ОС (радиус земного шара) = 6380 км;
OB = OA + ABOV = r + x
Применяя теорему Пифагора, выясняем, что минимальная высота башни должна быть 2.3 километра.
Теорема Пифагора в повседневной жизни
Как ни странно, теорема Пифагора может быть полезна даже в повседневных делах, таких как, например, определение высоты гардероба. На первый взгляд, в таких сложных вычислениях нет необходимости, ведь можно просто снимать мерки рулеткой. Но многие задаются вопросом, почему в процессе сборки возникают определенные проблемы, если все замеры были сняты более чем точно.
Дело в том, что шкаф собирается в горизонтальном положении и только потом поднимается и устанавливается у стены.Поэтому сторона шкафа в процессе подъема конструкции должна беспрепятственно проходить как по высоте, так и по диагонали помещения.
Допустим, у вас есть шкаф глубиной 800 мм. Расстояние от пола до потолка — 2600 мм. Опытный мебельщик подскажет, что высота шкафа должна быть на 126 мм меньше высоты комнаты. Но почему именно 126 мм? Давайте посмотрим на пример.
При идеальных габаритах шкафа проверяем действие теоремы Пифагора:
AC = √AB 2 + √BC 2
AC = √2474 2 +800 2 = 2600 мм — все сходится.
Допустим, высота шкафа не 2474 мм, а 2505 мм. Тогда:
АС = √2505 2 + √800 2 = 2629 мм.
Следовательно, этот шкаф не подходит для установки в этом помещении. Поскольку подъем его в вертикальное положение может повредить его корпус.
Возможно, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что это более чем верно. Теперь вы можете использовать полученную информацию в своей повседневной жизни и быть полностью уверенными, что все расчеты будут не только полезными, но и правильными.
Обращение теоремы Пифагора
Мы предполагаем, что вы знакомы с теоремой Пифагора.
Обратное к теореме Пифагора:
Если квадрат длины самой длинной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
То есть в
ΔABC, если c2 = a2 + b2, то
∠C — прямоугольный треугольник,
ΔPQR — прямой угол.
Мы можем доказать это от противного.
Предположим, что c2 = a2 + b2 в ΔABC и треугольник , а не прямоугольный.
Теперь рассмотрим другой треугольник.
ΔPQR.
Мы строим
ΔPQR так, чтобы
PR = a, QR = b и ∠R — прямой угол.
По теореме Пифагора (PQ) 2 = a2 + b2.
Но мы знаем, что a2 + b2 = c2, a2 + b2 = c2 и c = AB.
Итак, (PQ) 2 = a2 + b2 = (AB) 2.
То есть (PQ) 2 = (AB) 2.
Так как PQ и AB — длины сторон, мы можем взять положительные квадратные корни.
PQ = AB
То есть, все три стороны ΔPQR конгруэнтны трем сторонам ΔABC.
Итак, два треугольника конгруэнтны по свойству конгруэнтности сторона-сторона-сторона.
Поскольку ΔABC конгруэнтно ΔPQR, а ΔPQR — прямоугольный треугольник, ΔABC также должен быть прямоугольным треугольником.
Получили противоречие. Следовательно, наше предположение должно быть неверным.
Пример 1:
Проверьте, является ли треугольник со сторонами 6 см, 10 см и 8 см прямоугольным.
Проверьте, является ли квадрат длины самой длинной стороны суммой квадратов двух других сторон.
(10) 2 =? (8) 2+ (6) 2100 =? 64 + 36 100 = 100
Примените обратную теорему Пифагора.
Поскольку квадрат длины самой длинной стороны является суммой квадратов двух других сторон, согласно обратной теореме Пифагора, треугольник является прямоугольным.
Следствие теоремы подразделяет треугольники на острые, правые и тупые.
В треугольнике с длинами сторон a, b и c, где c — длина самой длинной стороны,
, если c2 если c2> a2 + b2, то треугольник тупой. Пример 2: Проверьте, является ли треугольник с длинами сторон 5, 7 и 9 единиц острым, прямым или тупым треугольником. Самая длинная сторона треугольника имеет длину 9 единиц. Сравните квадрат длины самой длинной стороны и сумму квадратов двух других сторон. Квадрат длины самой длинной стороны 92 = 81 кв. Ед. Сумма квадратов двух других сторон равна 52 + 72 = 25 + 49 = 74 кв. Единицы То есть 92> 52 + 72. Следовательно, согласно следствию, обратному теореме Пифагора, треугольник является тупым треугольником. Теорема Пифагора , также называемая «теоремой Пифагора, », возможно, является самой известной формулой в математике , которая определяет отношения между сторонами прямоугольного треугольника. Приписывают теорему греческому математику и философу по имени Пифагор (569-500 до н. Э.). Он внес большой вклад в математику, но теорема Пифагора — самая важная из них. Пифагору приписывают несколько вкладов в математику, астрономию, музыку, религию, философию и т. Д. Одним из его заметных вкладов в математику является открытие теоремы Пифагора. Пифагор изучил стороны прямоугольного треугольника и обнаружил, что сумма квадрата двух более коротких сторон треугольников равна квадрату самой длинной стороны. В этой статье e обсуждается, что такое теорема Пифагора , ее обратная формула и формула теоремы Пифагора . Прежде чем углубляться в тему, вспомним прямоугольный треугольник. Прямоугольный треугольник — это треугольник, внутренний угол которого равен 90 градусам. В прямоугольном треугольнике две короткие ножки встречаются под углом 90 градусов. Гипотенуза треугольника противоположна углу в 90 градусов. Теорема Пифагора — это математический закон, который гласит, что сумма квадратов длин двух коротких сторон прямоугольного треугольника равна квадрату длины гипотенузы . Теорема Пифагора алгебраически записывается как: a 2 + b 2 = c 2 Теорема Пифагора — объяснение и примеры
Что такое теорема Пифагора?
Как выполнить теорему Пифагора?
Рассмотрим прямоугольный треугольник выше.
Учитывая, что:
∠ ABC = 90 °.
Пусть BD — прямая, перпендикулярная стороне AC.
Подобные ∆s:
∆ADB и ∆ABC — подобные треугольники.
Из правила подобия
⇒ AD / AB = AB / AC
⇒ AD × AC = (AB) 2 —————– (i)
Аналогично;
∆BDC и ∆ABC — подобные треугольники.Следовательно;
⇒ DC / BC = BC / AC
⇒ DC × AC = (BC) 2 —————– (ii)
Комбинируя уравнения (i) и (ii), мы получаем
AD × AC + DC × AC = (AB) 2 + (BC) 2
⇒ (AD + DC) × AC = (AB) 2 + (BC) 2
⇒ (AC) 2 = (AB) 2 + (BC) 2
Следовательно, если мы положим AC = c; AB = b и BC = b, тогда;
⇒ c 2 = a 2 + b 2
Существует множество демонстраций теоремы Пифагора , приведенных разными математиками.
Другая распространенная демонстрация — это нарисовать 3 квадрата таким образом, чтобы они образовывали прямоугольный треугольник между ними, а площадь большего квадрата (тот, который находится в гипотенузе) равна сумме площади меньшего два квадрата (те, что с двух сторон).
Рассмотрим 3 квадрата ниже:
Они нарисованы таким образом, что образуют прямоугольный треугольник. Мы можем записать их площади в виде уравнения:
Площадь квадрата III = Площадь квадрата I + Площадь квадрата II
Предположим, что длина квадрата I , квадрата II, и квадрат III — это a, b и c соответственно.
Тогда
Площадь квадрата I = a 2
Площадь квадрата II = b 2
Площадь квадрата III = c 2
Следовательно, мы можем написать это как:
a 2 + b 2 = c 2
, что является теоремой Пифагора.
Обращение теоремы Пифагора
Обращение теоремы Пифагора — это правило, которое используется для классификации треугольников как прямоугольный, острый или тупой.
Учитывая теорему Пифагора, a 2 + b 2 = c 2 , затем:
- Для острого треугольника c 2 2 + b 2 , где c равно сторона, противоположная острому углу.
- Для прямоугольного треугольника c 2 = a 2 + b 2 , где c — сторона угла в 90 градусов.
- Для тупого треугольника c 2 > a 2 + b 2 , где c — сторона, противоположная тупому углу.
Пример 1
Классифицируйте треугольник с размерами; a = 5 м, b = 7 м и c = 9 м.
Решение
Согласно теореме Пифагора, a 2 + b 2 = c 2 тогда;
a 2 + b 2 = 5 2 + 7 2 = 25 + 49 = 74
Но, c 2 = 9 2 = 81
Сравните: 81> 74
Следовательно, c 2 > a 2 + b 2 (тупой треугольник).
Пример 2
Классифицируйте треугольник, длина сторон которого a, b, c равна 8 мм, 15 мм и 17 мм соответственно.
Решение
a 2 + b 2 = 8 2 + 15 2 = 64 + 225 = 289
Но, c 2 = 17 2 = 289
Сравните: 289 = 289
Следовательно, c 2 = a 2 + b 2 (прямоугольный треугольник).
Пример 3
Классифицируйте треугольник с длинами сторон: 11 дюймов, 13 дюймов и 17 дюймов.
Решение
a 2 + b 2 = 11 2 + 13 2 = 121 + 169 = 290
c 2 = 17 2 = 289
Сравните: 289 <290
Следовательно, c 2 2 + b 2 (острый треугольник)
Формула теоремы Пифагора
Формула теоремы Пифагора имеет следующий вид:
⇒ c 2
2 = a = a + b 2
где;
c = длина гипотенузы;
a = длина одной стороны;
b = длина второй стороны.
Эту формулу можно использовать для решения различных задач, связанных с прямоугольными треугольниками. Например, мы можем использовать формулу для определения третьей длины треугольника, когда известны длины двух сторон треугольника.
Применение формулы теоремы Пифагора в реальной жизни
- Мы можем использовать теорему Пифагора, чтобы проверить, является ли треугольник прямоугольным или нет.
- В океанографии формула используется для расчета скорости звуковых волн в воде.
- Теорема Пифагора используется в метеорологии и авиакосмической сфере для определения источника звука и его дальности.
- Мы можем использовать теорему Пифагора для расчета электронных компонентов, таких как экраны телевизоров, компьютерные экраны, солнечные панели и т. Д.
- Мы можем использовать теорему Пифагора для вычисления градиента определенного ландшафта.
- В навигации теорема используется для вычисления кратчайшего расстояния между заданными точками.
- В архитектуре и строительстве мы можем использовать теорему Пифагора для расчета уклона крыши, дренажной системы, плотины и т. Д.
Рабочие примеры теоремы Пифагора:
Пример 4
Две короткие стороны прямоугольного треугольника составляют 5 см и 12 см. Найти длину третьей стороны
Решение
Дано a = 5 см
b = 12 см
c =?
Из формулы теоремы Пифагора; c 2 = a 2 + b 2 , имеем;
c 2 = a 2 + b 2
c 2 = 12 2 + 5 2
c 2 = 144 + 25
√c 2 2 2 √169
c = 13.
Следовательно, третий равен 13 см.
Пример 5
Длина диагонали и одной стороны треугольной стороны составляет 25 см и 24 см соответственно. Каков размер третьей стороны?
Решение
Используя теорему Пифагора,
c 2 = a 2 + b 2 .
Пусть b = третья сторона
25 2 = 24 2 + b 2
625 = 576 + b 2
625-576 = 576-576 + b 2
49 = b 2
b 2 = 49
b = √49 = 7 см
Пример 6
Найдите размер экрана компьютера, размеры которого составляют 8 дюймов и 14 дюймов.
Подсказка: диагональ экрана равна его размеру .
Решение
Размер экрана компьютера совпадает с его диагональю.
Используя теорему Пифагора,
c 2 = 8 2 + 15 2
Решите относительно c.
c 2 = 64 + 225
c 2 = 289
c = √289
c = 17
Следовательно, размер экрана компьютера составляет 17 дюймов.
Пример 7
Найдите площадь прямоугольного треугольника, учитывая, что диагональ и основания составляют 8,5 см и 7,7 см соответственно.
Решение
Используя теорему Пифагора,
8,5 2 = a 2 + 7,5 2
Решите для a.
72,25 = a 2 + 56,25
72,25 — 56,25 = k 2 + 56,25 — 56,25
16 = a 2
a = √16 = 4 см
Площадь прямоугольного треугольника = ( ½) x основание x высота
= (½ x 7.7 x 4) см 2
= 15,4 см 2
Практические вопросы
- Канат длиной 20 м протягивается от вершины 12-метрового дерева до земли. Какое расстояние между деревом и концом веревки на земле?
- К стене прислонена лестница длиной 13 м. Если расстояние от основания лестницы до стены составляет 5 м, какова высота стены?
Предыдущий урок | Главная страница | Следующий урок
Теорема Пифагора делает возможным построение и GPS
Хорошо, время для популярной викторины.У вас есть прямоугольный треугольник, то есть тот, в котором две стороны сходятся, образуя угол в 90 градусов. Вы знаете длину этих двух сторон. Как определить длину оставшейся стороны?
Это легко, если вы изучали геометрию в средней школе и знали теорему Пифагора, математическое утверждение, которому тысячи лет.
Теорема Пифагора утверждает, что в прямоугольном треугольнике сумма квадратов двух сторон, образующих прямой угол, равна квадрату третьей, более длинной стороны, которая называется гипотенузой.В результате вы можете определить длину гипотенузы по уравнению a 2 + b 2 = c 2 , в котором a и b представляют две стороны прямого угла, а c — длинную сторону.
Кто был Пифагор?
Довольно ловкий трюк, а? Но человек, в честь которого назван этот математический трюк, почти не менее очарователен. Пифагор, древнегреческий мыслитель, родившийся на острове Самос и жил с 570 по 490 г. до н.э.К.Э. был своего рода странным персонажем — в равной степени философ, математик и лидер мистического культа. При жизни Пифагор не был известен как решающий вопрос длины гипотенузы, так как он был известен своей верой в реинкарнацию и приверженностью аскетическому образу жизни, который подчеркивал строгую вегетарианскую диету, соблюдение религиозных ритуалов и большую самодисциплину. этому он учил своих последователей.
Биограф Пифагора Кристоф Ридвег описывает его как высокую, красивую и харизматичную фигуру, чью ауру усиливала его эксцентричная одежда — белый халат, брюки и золотой венок на голове.Вокруг него ходили странные слухи — что он мог творить чудеса, что у него была золотая искусственная нога, скрытая под одеждой, и что он обладал способностью находиться в двух местах одновременно.
Пифагор основал школу недалеко от нынешнего портового города Кротоне на юге Италии, получившего название Полукруг Пифагора. Последователи, поклявшиеся соблюдать кодекс секретности, научились рассматривать числа подобно еврейскому мистицизму Кабаллы. В философии Пифагора каждое число имело божественное значение, и их комбинация открывала большую истину.
С такой гиперболической репутацией неудивительно, что Пифагору приписывают разработку одной из самых известных теорем всех времен, хотя на самом деле он не был первым, кто придумал эту концепцию. Китайские и вавилонские математики опередили его на тысячелетие.
«У нас есть доказательства того, что они знали пифагорейские отношения на конкретных примерах», — пишет Г. Дональд Аллен, профессор математики и директор Центра технологического обучения математике Техасского университета A&M.«Была найдена целая вавилонская табличка, на которой показаны различные тройки чисел, отвечающие условию: a 2 + b 2 = c 2 ».
Чем полезна теорема Пифагора сегодня?
Теорема Пифагора — это не просто увлекательное математическое упражнение. Он используется в широком спектре областей, от строительства и производства до навигации.
Как объясняет Аллен, одно из классических применений теоремы Пифагора заключается в закладке фундамента зданий.«Понимаете, чтобы сделать прямоугольный фундамент, скажем, для храма, вам нужно сделать прямые углы. Но как вы можете это сделать? Глядя на это на глаз? Это не сработает для большой конструкции. Но когда у вас есть длины и ширины, вы можете использовать теорему Пифагора, чтобы получить точный прямой угол с любой точностью ».
Кроме того, «Эта теорема и те, которые связаны с ней, дали нам всю нашу систему измерения», — говорит Аллен. «Это позволяет пилотам ориентироваться в ветреном небе, а кораблям — задавать курс.Благодаря этой теореме возможны все измерения GPS ».
В навигации теорема Пифагора предоставляет корабельному навигатору способ вычисления расстояния до точки в океане, которая, скажем, находится в 300 милях к северу и 400 милях к западу (480 км). к северу и 640 км к западу). Она также полезна картографам, которые используют ее для расчета крутизны холмов и гор.
«Эта теорема важна для всей геометрии, включая твердую геометрию», — продолжает Аллен. в других областях математики, большей части физики, геологии, всей механической и авиационной инженерии.Плотники используют это, и машинисты тоже. Когда у вас есть углы и вам нужны измерения, вам понадобится эта теорема ».
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov.ab.ca | |
Почему пифагорейские штаны. Пифагорейские штаны равны со всех сторон. Самый простой способ доказать теорему Пифагора. Отзывы
Теорема Пифагора всем известна со школьных времен. Выдающийся математик доказал прекрасную гипотезу, которую сегодня используют многие люди. Правило звучит так: квадрат длины прямоугольного треугольника гипотенузы равен сумме квадратов катетов.В течение многих десятилетий ни один математик не мог оспорить это правило. Ведь Пифагор долго шел к своей цели, чтобы в результате рисунки имели место в повседневной жизни.
- Краткий стих к этой теореме, придуманный вскоре после доказательства, напрямую доказывает свойства гипотезы: «Пифагорейские штаны во всех направлениях равны. «Эта двустрочка застряла в памяти многих людей — по сей день стихотворение помнят в расчетах.
- Эта теорема получила название« Пифагорейские штаны »из-за того, что при рисовании посередине прямоугольный треугольник Получилось, по сторонам которого были квадраты.По внешнему виду этот рисунок напоминал брюки — отсюда и название гипотезы.
- Пифагор гордился разработанной теоремой, поскольку эта гипотеза отличается от аналогичных максимальным количеством доказательств. Важно: уравнение было занесено в Книгу рекордов Гиннеса благодаря 370 правдивым свидетельствам.
- Гипотеза была доказана огромным количеством математиков и профессоров из разных стран разными способами. … Английский математик Джонс вскоре объявил гипотезу, доказав ее с помощью дифференциального уравнения.
- В настоящее время никто не знает доказательства теоремы самого Пифагора … Факты о доказательствах математиков сегодня никому не известны. Считается, что доказательство рисунков Евклида — это доказательство Пифагора. Однако некоторые ученые спорят с этим утверждением: многие считают, что Евклид доказал теорему самостоятельно, без помощи создателя гипотезы.
- Современные ученые обнаружили, что великий математик не был первым, кто открыл эту гипотезу. … Уравнение было известно задолго до открытия Пифагора. Этот математик смог только восстановить гипотезу.
- Пифагор не называл уравнение «теоремой Пифагора» … Это название прижилось после «громкого двустрочного». Математик лишь хотел, чтобы его усилия и открытия были признаны и использованы всем миром.
- Мориц Кантор — великий выдающийся математик, обнаруженный и обнаруженный на древних папирусных записях с рисунками …. Вскоре после этого Кантор понял, что эта теорема была известна египтянам еще в 2300 году до нашей эры. Только тогда этим никто не воспользовался и не пытался это доказать.
- Современные ученые считают, что эта гипотеза была известна еще в 8 веке до нашей эры. … Индийские ученые того времени открыли приблизительный расчет гипотенузы треугольника с прямыми углами. Правда, тогда еще никому не удавалось точно доказать уравнение приблизительными расчетами.
- Великий математик Бартель ван дер Варден после доказательства гипотезы пришел к важному выводу : «Заслуга греческого математика не в открытии направления и геометрии, а только в его оправдании.В руках Пифагора были вычислительные формулы, основанные на предположениях, неточных расчетах и расплывчатых идеях. Однако выдающемуся ученому удалось превратить это в точную науку. «
- Знаменитый поэт сказал, что в день открытия своего рисунка он воздвиг славное жертвоприношение быкам … Именно после открытия гипотезы распространились слухи о принесении в жертву сотни быков» ходил бродить по страницам книг и публикаций.»Остроумы до сих пор шутят, что с тех пор все быки боятся нового открытия.
- Доказательство того, что Пифагор придумал стихотворение о штанах не для того, чтобы доказать выдвинутые им рисунки: при жизни великого математика , штанов не было … Их изобрели несколько десятилетий спустя.
- Пекка, Лейбниц и еще несколько ученых пытались доказать известную ранее теорему, но ни у кого не получилось.
- Название рисунков «Теорема Пифагора» означает «убеждение речью» … Так переводится слово Пифагор, которое математик взял за псевдоним.
- Размышления Пифагора о собственном правиле: секрет существования на Земле кроется в числах … Ведь математик, опираясь на собственную гипотезу, изучал свойства чисел, обнаруживал четность и нечетность и создавал пропорции .
Надеемся, вам понравилась подборка с картинками — Интересные факты о теореме Пифагора: узнайте новое об известной теореме (15 фото) в хорошем качестве онлайн.Пожалуйста, оставьте свое мнение в комментариях! Для нас важно каждое мнение.
Брюки — получите рабочий купон на скидку в Paper Shop в Akademik или купите дешевые брюки с бесплатной доставкой в Paper Shop sale
Жарг. шк. Шаттл. Теорема Пифагора, устанавливающая связь между площадями квадратов, построенных на гипотенузе, и катетами прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
Штаны Пифагора — Шуточное название теоремы Пифагора, возникшей из-за того, что квадраты, построенные по сторонам прямоугольника и расходящиеся в разные стороны, напоминают разрез штанов.Любила геометрию … да еще почерпнула из … … фразеологического словаря русского литературного языка.
пифагорейские штаны — Юмористическое название теоремы Пифагора, которая устанавливает связь между площадями квадратов, построенных на гипотенузе, и сторонами прямоугольного треугольника, который выглядит как разрез штанов на картинках … Словарь много выражений
Иноск .: об одаренном человеке Ср. Это несомненный мудрец. В древности он наверняка изобрел пифагорейские штаны… Салтыков. Красочные буквы. Штаны Пифагора (геом.): В прямоугольнике квадрат гипотенузы равен квадрату катетов (учение … … Большой толковый фразеологический словарь Майкельсона
Пифагорейские штаны равны со всех сторон — Количество пуговиц известно. Почему член тесноват? (примерно) о штанах и мужских гениталиях. Пифагорейские штаны равны со всех сторон. Чтобы доказать это, необходимо убрать и показать: 1) о теореме Пифагора; 2) про широкие штаны… Живая речь. Словарь разговорных выражений
Пинягоровские штаны (изобрести) носок. о человеке одаренном. Ср. Это несомненный мудрец. В древности он, наверное, изобрел штаны Пинагора … Салтыков. Пестрые буквы. Брюки Пилягорова (геом.): В прямоугольном квадрате гипотенузы … … Большой толковый фразеологический словарь Михельсона (орфография)
Пифагорейские штаны равны во всех направлениях — Юмористическое доказательство теоремы Пифагора; также шутит о мешковатых штанах приятеля… Словарь народной фразеологии
Ex., Грубый …
БРЮКИ ПИФАГОРА НА ВСЕХ СТОРОНАХ РАВНЫ (КОЛИЧЕСТВО КНОПОК ИЗВЕСТНО. ПОЧЕМУ ТРАХАЕТСЯ? / ЧТОБЫ ДОКАЗАТЬ, НЕОБХОДИМО СНИМАТЬ И ПОКАЗАТЬ) — прил., Грубый … Толковый словарь современного разговорного фразеологизма единицы и поговорки
Существительное, множественное число, uptr. ср. часто Морфология: пл. какие? штаны, (нет) что? штаны, почему? штаны, (видите) что? штаны какие? штаны о чем? О штанах 1. Штаны — это предмет одежды, имеющий две короткие или длинные штанины и закрывающий нижнюю часть… … Толковый словарь Дмитриева
Книги
- Пифагорейские брюки ,. В этой книге вы найдете фантастику и приключения, чудеса и фантастику. Забавно и грустно, обыденно и загадочно … Что еще нужно для занимательного чтения? Главное, чтобы …
- Чудеса на колесах, Маркуша Анатолий. По всей земле вращаются миллионы колес — машины катятся, следят за временем, стучат под поездами, совершают бесчисленные работы на станках и различных механизмах.Они…
Некоторые дискуссии меня безмерно забавляют …
Привет, что ты делаешь?
-Да решаю задачи из журнала.
-Вау! Не ожидал от тебя.
-Чего ты не ожидал?
— То, что вы опускаетесь до проблем. Это все-таки кажется умным, но вы верите во всякую чепуху.
-Извините, я не понимаю. Что вы называете чушью?
-Да, вся ваша математика. Ведь очевидно, что фигня полная.
-Как ты можешь так сказать? Математика — королева наук…
— Да ладно, без пафоса? Математика — это вообще не наука, а сплошная куча дурацких законов и правил.
-Что ?!
-Эх, ну не делайте таких больших глаз, вы сами знаете, что я прав. Нет, не спорю, таблица умножения — великое дело, она сыграла значительную роль в формировании культуры и истории человечества. Но теперь все это уже неактуально! А зачем тогда все усложнять? В природе нет интегралов или логарифмов, это все изобретение математиков.
-Подождите минутку. Математики ничего не изобретали, они открыли новые законы взаимодействия чисел, используя проверенные инструменты …
-Да, конечно! И вы в это верите? Разве вы сами не видите, о чем они постоянно говорят? Могу я привести пример?
-Да, будьте добры.
-Да пожалуйста! Теорема Пифагора.
-Что с ней не так?
-Да, это не так! «Пифагорейские штаны равны со всех сторон», — видите ли. Знаете ли вы, что греки не носили штанов во времена Пифагора? Как мог Пифагор рассуждать о том, о чем он понятия не имел?
-Подождите минутку.При чем тут штаны?
-Ну, кажется, они Пифагор? Или нет? Вы признаете, что у Пифагора не было штанов?
— Ну на самом деле, конечно, не было …
-Ага, значит, в самом названии теоремы есть явное несоответствие! После этого, как вы можете серьезно относиться к тому, что там написано?
— Погодите. Пифагор ничего не сказал о штанах …
-Вы признаете это, верно?
-Да … Итак, я могу продолжить? О штанах Пифагор ничего не говорил, да и не надо приписывать ему чужую чушь…
-Ага, вы сами согласны, что это все ерунда!
— Я этого не говорил!
— Я только что сказал. Вы противоречите себе.
-Так. Стоп. Что говорит теорема Пифагора?
-Что все штаны равны.
— Блин, а вы хоть читали эту теорему ?!
-Я знаю.
-Откуда?
— Я читал.
-Что ты читал ?!
-Лобачевский.
* пауза *
-Извините, а какое отношение имеет Лобачевский к Пифагору?
-Ну, Лобачевский тоже математик, и он кажется даже более крутым авторитетом, чем Пифагор, скажите нет?
* вздох *
-Ну, а что Лобачевский сказал о теореме Пифагора?
-Что штаны ровные.Но это ерунда! Как можно носить такие штаны? К тому же Пифагор вообще не носил штанов!
-Лобачевский так сказал ?!
* вторая пауза, уверенно *
-Да!
-Покажи мне, где написано.
-Нет, ну так прямо там не написано …
-Какое название у этой книги?
-Да, это не книга, это газетная статья. Насчет того, что Лобачевский на самом деле был агентом немецкой разведки … ну, это не к делу. Во всяком случае, он, наверное, так сказал.Он тоже математик, поэтому он и Пифагор одновременно.
-Пифагор ничего не сказал о штанах.
-Ну да! Об этом и речь. Все это чушь собачья.
-Приходите в порядок. Откуда вы лично знаете, что говорит теорема Пифагора?
-Ах, давай! Все это знают. Спросите любого, сразу вам ответят.
-Пифагорейские штаны не штаны …
-И, конечно же! Это аллегория! Вы знаете, сколько раз я слышал это раньше?
— Теорема Пифагора гласит, что сумма квадратов катетов равна квадрату гипотенузы.И ВСЕ!
-Где брюки?
-Да, у Пифагора не было штанов !!!
-Понимаете, я об этом говорю. Вся ваша математика — чушь собачья.
-И это не фигня! Смотри сам. Вот треугольник. Вот гипотенуза. Вот ноги …
— А почему вдруг это ноги, а это гипотенуза? Может наоборот?
-Нет. Ноги — это две стороны, образующие прямой угол.
-Ну, вот вам еще один прямой угол.
— Он не натурал.
-Что он, криво?
— Нет, острый.
-Так что этот тоже острый.
— Он не острый, а прямой.
— Знаешь, не обманывай меня! Вы просто называете вещи как хотите, просто чтобы результат подогнать под желаемый.
— Две короткие стороны прямоугольного треугольника — ноги. Длинная сторона — гипотенуза.
-А кто короче — та нога? А гипотенуза уже не катится? Ты сам, послушай себя со стороны, что за чушь несешь.Сейчас 21 век, расцвет демократии, а у вас какое-то средневековье. Видите ли, его стороны не равны …
-Прямоугольного треугольника с равными сторонами не существует …
-Ты уверены? Позвольте мне нарисовать для вас. Вот посмотри. Прямоугольный? Прямоугольный. И все стороны равны!
— Вы нарисовали квадрат.
-И что?
-Квадрат не является треугольником.
-И, конечно же! Как только он нас не устраивает, сразу «не треугольник»! Не морочь мне голову. Сами посчитайте: один угол, два угла, три угла.
-Четыре.
-И что?
-Это квадрат.
-А квадрат не треугольник? Это хуже, не правда ли? Просто потому, что я это нарисовал? Есть три угла? Есть, и даже есть один запасной. Ну, тут ничего нет …
— Ладно, оставим эту тему.
-Ага, уже сдаешься? Не с чем спорить? Вы признаете, что математика — чушь собачья?
— Нет, не знаю.
-Ну, опять здорово! Я только что вам все подробно доказал! Если вся ваша геометрия основана на учении Пифагора, а это, прошу прощения, полная чушь… тогда о чем можно говорить дальше?
-Учение Пифагора — это не ерунда …
-Ну, конечно! И тогда я не слышал о школе пифагорейцев! Они, если хотите знать, баловались оргиями!
-При чем тут это …
-А Пифагор вообще был педиком! Сам он сказал, что Платон был его другом.
-Пифагор ?!
-Ты не знал? Да, все они были педиками. И три по голове. Один спал в бочке, другой бегал по городу голый…
-Диоген спал в бочке, но он был философом, а не математиком …
-И, конечно! Если кто-то залез в бочку, значит, он уже не математик! Зачем нам лишний стыд? Знаем, знаем, прошли. Но вы мне объясните, почему всякие педики, жившие три тысячи лет назад и бегавшие без штанов, должны быть для меня авторитетом? Почему я должен принимать их точку зрения?
-Ладно, уходи …
-Нет, послушай! В конце концов, я тоже вас послушал.Это ваши расчеты, расчеты … Вы все умеете считать! И тут же спросить кое-что по существу: «это частное, это переменная, а это две неизвестные». А вы мне говорите о-о-о-общем, без подробностей! И без какого-либо неизвестного, неизвестного, экзистенциального … От этого меня тошнит, понимаете?
-Понять.
— Ну, объясните мне, почему дважды два всегда четыре? Кто это придумал? И почему я вынужден принимать это как должное и не имею права сомневаться?
-Да, сколько угодно сомневайтесь…
-Нет, ты мне объясни! Только без этих ваших вещей, но нормально, по-человечески, чтобы было понятно.
-Дважды два равно четырем, потому что дважды два будет четыре.
-Масло масло. Что нового ты мне рассказал?
— Дважды два — это два раза два. Возьмите два и два и сложите их …
-Так что сложить или умножить?
-Это то же самое …
-Оба! Значит, если я сложу и умножу семь и восемь, получится то же самое?
-Нет.
-А почему?
-Потому что семь плюс восемь не равно…
— А если девять умножить на два, получится четыре?
-Нет.
-А почему? Два умножили — заработало, а с девяткой вдруг облом?
-Да. Дважды девять — восемнадцать.
-И дважды семь?
-Четырнадцать.
-И дважды пять?
-Десять.
— То есть четыре получается только в одном частном случае?
-Точно.
— А теперь подумайте сами. Вы говорите, что существуют строгие законы и правила умножения. О каких законах здесь можно говорить, если в каждом конкретном случае получается разный результат ?!
-Это не совсем правда.Иногда результат может быть таким же. Например, дважды шесть равняется двенадцати. И четыре раза по три — тоже …
— Хуже! Два, шесть, три, четыре — вообще ничего! Вы сами видите, что результат никак не зависит от исходных данных. Одно и то же решение принимается в двух принципиально разных ситуациях! И это при том, что одни и те же двое, которые мы берем постоянно и ни на что не меняем, всегда дают разный ответ со всеми числами. Где логика?
-Но это, опять же, логично!
— Для тебя — может быть.Вы, математики, всегда верите во всякую возмутительную чушь. И эти ваши расчеты меня не убеждают. А знаете почему?
-Почему?
-Потому что я, , знаю, , почему ваша математика действительно нужна. К чему все это сводится? «У Кати в кармане одно яблоко, а у Миши пять. Сколько яблок Миша должен дать Кате, чтобы у них было одинаковое количество яблок?» И знаете, что я вам скажу? Миша никому ничего не должен отдать! У Кати одно яблоко — и этого достаточно.Ей этого мало? Пусть усердно трудится и честно зарабатывает себе хоть на яблоки, хоть на груши, хоть на ананасы в шампанском. А если кто-то хочет не работать, а решать проблемы — пусть сидит с одним яблоком и не выпендривается!
»Заслуженный профессор математики Уорикского университета, известный популяризатор науки Ян Стюарт, посвятил себя роли чисел в истории человечества и актуальности их изучения в наше время.
Пифагорова гипотенуза
Пифагоровы треугольники имеют прямой угол и целые стороны. Самый простой из них имеет самую длинную сторону длиной 5, остальные — 3 и 4. Всего правильных многогранников 5. Уравнение пятой степени не может быть решено с использованием корней пятой степени или любых других корней. Решетки на плоскости и в трехмерном пространстве не обладают пятилепестковой симметрией вращения, поэтому такие симметрии отсутствуют и в кристаллах. Однако их можно найти в решетках в четырехмерном пространстве и в интересных структурах, известных как квазикристаллы.
Гипотенуза наименьшей пифагорейской тройки
Теорема Пифагора гласит, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) очень просто и красиво соотносится с двумя другими сторонами этого треугольника: квадрат гипотенузы равен сумме квадратов двух других сторон. .
Традиционно мы называем эту теорему именем Пифагора, но на самом деле ее история довольно туманна. Глиняные таблички предполагают, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; Известность первооткрывателю принес ему математический культ пифагорейцев, сторонники которых считали, что Вселенная основана на числовых законах.Древние авторы приписывали пифагорейцам — и, следовательно, Пифагору — множество математических теорем, но на самом деле мы понятия не имеем, какой математикой занимался сам Пифагор. Мы даже не знаем, смогли ли пифагорейцы доказать теорему Пифагора или они просто поверили, что это правда. Или, скорее всего, у них были убедительные доказательства его истинности, которых, тем не менее, было бы недостаточно для того, что мы сегодня считаем доказательством.
Доказательства Пифагора
Мы находим первое известное доказательство теоремы Пифагора в «Элементах» Евклида.Это довольно сложное доказательство, использующее рисунок, на котором викторианские школьники сразу узнают «пифагорейские штаны»; рисунок действительно напоминает сушку трусов на веревке. Известны буквально сотни других доказательств, большинство из которых делают аргументированное утверждение более очевидным.
// Рис. 33. Штаны Пифагора
Одно из простейших доказательств — это своего рода математическая головоломка. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата. При одной укладке мы видим квадрат на гипотенузе; с другой стороны, квадраты на двух других сторонах треугольника.Более того, видно, что площади в обоих случаях равны.
// Рис. 34. Слева: квадрат на гипотенузе (плюс четыре треугольника). Справа: сумма квадратов на двух других сторонах (плюс те же четыре треугольника). Теперь исключим треугольники.
Рассечение Перигаля — еще одна загадка с доказательством.
// Рис. 35. Рассечение Перигали
Существует также доказательство теоремы с использованием упаковки квадратов на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему.Если вы посмотрите, как наклонный квадрат перекрывает два других квадрата, вы увидите, как разрезать большой квадрат на части, а затем сложить их на два меньших квадрата. Вы также можете увидеть прямоугольные треугольники, стороны которых задают размеры трех задействованных квадратов.
// Рис. 36. Доказательство мощения
Есть интересные свидетельства использования подобных треугольников в тригонометрии. Известно не менее пятидесяти различных свидетельств.
Пифагорова тройка
В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений.Тройка Пифагора — это набор целых чисел a, b и c, таких что
Геометрически такая тройка определяет прямоугольный треугольник с целыми сторонами.
Наименьшая гипотенуза тройки Пифагора равна 5.
Две другие стороны этого треугольника равны 3 и 4. Здесь
32 + 42 = 9 + 16 = 25 = 52.
Следующая наибольшая гипотенуза равна 10, потому что
62 + 82 = 36 + 64 = 100 = 102.
Однако, по сути, это тот же треугольник с удвоенными сторонами.Следующая по величине и действительно отличная гипотенуза — 13, для нее
52 + 122 = 25 + 144 = 169 = 132.
Евклид знал, что существует бесконечное количество различных вариантов пифагоровых троек, и дал то, что можно назвать формула их всех. Позже Диофант Александрийский предложил простой рецепт, который в основном совпадает с евклидовым.
Возьмите любые два натуральных числа и вычислите:
их удвоенное произведение;
разница между их квадратами;
сумма их квадратов.
Три результирующих числа будут сторонами треугольника Пифагора.
Возьмем, например, числа 2 и 1. Вычислите:
двойное произведение: 2 × 2 × 1 = 4;
разность квадратов: 22 — 12 = 3;
сумма квадратов: 22 + 12 = 5,
и мы получили знаменитый треугольник 3-4-5. Если вместо этого взять числа 3 и 2, мы получим:
двойное произведение: 2 × 3 × 2 = 12;
разность квадратов: 32 — 22 = 5;
сумма квадратов: 32 + 22 = 13,
и мы получаем следующий по известности треугольник 5-12-13.Попробуем взять числа 42 и 23 и получить:
двойное произведение: 2 × 42 × 23 = 1932;
разность квадратов: 422 — 232 = 1235;
сумма квадратов: 422 + 232 = 2293,
о треугольнике 1235-1932-2293 никто никогда не слышал.
Но работают и эти числа:
12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.
В диофантовом правиле есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять другое произвольное число и умножьте их все на него.Таким образом, треугольник 3–4–5 можно превратить в треугольник 6–8–10, умножив все стороны на 2, или в треугольник 15–20–25, умножив все на 5.
Если мы перейдем к На языке алгебры правило принимает следующий вид: пусть u, v и k — целые числа … Тогда прямоугольный треугольник со сторонами
2kuv и k (u2 — v2) имеет гипотенузу
. представляя основную идею, но все они сводятся к описанной выше. Этот метод позволяет получить все триплеты Пифагора.
Правильные многогранники
Правильных многогранников ровно пять. Правильный многогранник (или многогранник) — это трехмерная фигура с конечным числом плоских граней. Грани сходятся друг с другом на линиях, называемых ребрами; ребра пересекаются в точках, называемых вершинами.
Кульминация евклидова «Начала» — доказательство того, что может быть только пять правильных многогранников, то есть многогранников, в которых каждая грань представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным количеством равномерно расположенных граней.Вот пять правильных многогранников:
тетраэдр с четырьмя треугольными гранями, четырьмя вершинами и шестью ребрами;
куб или шестигранник с 6 квадратными гранями, 8 вершинами и 12 ребрами;
октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;
додекаэдр с 12 пятиугольными гранями, 20 вершинами и 30 ребрами;
икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.
// Рис. 37. Пять правильных многогранников
Правильные многогранники также встречаются в природе.В 1904 году Эрнст Геккель опубликовал рисунки крошечных организмов, известных как радиолярии; многие из них по форме напоминают те самые пять правильных многогранников. Возможно, однако, он немного поправил природу, и рисунки не полностью отражают формы конкретных живых существ. Первые три структуры также наблюдаются в кристаллах. В кристаллах вы не найдете додекаэдра и икосаэдра, хотя иногда встречаются неправильные додекаэдры и икосаэдры. Истинные додекаэдры могут выглядеть как квазикристаллы, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.
// Рис. 38. Рисунки Геккеля: радиолярии в виде правильных многогранников
// Рис. 39. Развитие правильных многогранников
. бумага, предварительно вырезав набор соединенных между собой граней — это называется развёртыванием многогранника; скан складывается по краям, а соответствующие края склеиваются. Полезно добавить дополнительную клейкую подушку к одному из краев каждой такой пары, как показано на рис.39. Если такой зоны нет, можно использовать скотч.
Уравнение пятой степени
Не существует алгебраической формулы для решения уравнений 5-й степени.
В общих чертах уравнение пятой степени выглядит так:
ax5 + bx4 + cx3 + dx2 + ex + f = 0.
Задача состоит в том, чтобы найти формулу решения такого уравнения (оно может иметь до пяти решений). Опыт работы с квадратными и кубическими уравнениями, а также с уравнениями четвертой степени подсказывает, что такая формула должна существовать и для уравнений пятой степени, а теоретически — корней пятой, третьей и второй степеней. должно появиться в нем.Опять же, мы можем с уверенностью предположить, что такая формула, если она существует, будет очень и очень сложной.
Это предположение в итоге оказалось неверным. Действительно, такой формулы не существует; по крайней мере, не существует формулы для коэффициентов a, b, c, d, e и f, построенной с использованием сложения, вычитания, умножения и деления, а также извлечения корней. Итак, в числе 5 есть что-то особенное. Причины такого необычного поведения пятерки очень глубоки, и потребовалось много времени, чтобы их понять.
Первый признак проблемы в том, что независимо от того, насколько жесткие математики пытались найти такую формулу, независимо от того, насколько они умные были, они всегда не удалось. Некоторое время все считали, что причина кроется в невероятной сложности формулы. Считалось, что никто просто не может правильно понять эту алгебру. Однако со временем некоторые математики начали сомневаться в существовании такой формулы, и в 1823 году Нильс Хендрик Абель смог доказать обратное. Такой формулы нет.Вскоре после этого Эварист Галуа нашел способ определить, можно ли решить уравнение той или иной степени — 5-й, 6-й, 7-й, в общем, любой — с помощью такой формулы.
Вывод из всего этого простой: цифра 5 особенная. Вы можете решать алгебраические уравнения (используя корни n-й степени для разных значений n) для степеней 1, 2, 3 и 4, но не для 5-й степени. На этом очевидная закономерность заканчивается.
Ни для кого не удивительно, что уравнения степеней больше 5 ведут себя еще хуже; в частности, с ними связана та же трудность: нет общих формул для их решения.Это не означает, что уравнения не имеют решений; это также не означает, что невозможно найти очень точные численные значения этих решений. Все дело в ограничениях традиционных инструментов алгебры. Это напоминает невозможность разделить угол пополам линейкой и циркулем. Ответ есть, но перечисленных методов недостаточно и они не позволяют определить, что это такое.
Кристаллографическое ограничение
Кристаллы в двух и трех измерениях не обладают 5-лучевой вращательной симметрией.
Атомы в кристалле образуют решетку, то есть структуру, которая периодически повторяется в нескольких независимых направлениях. Например, рисунок на обоях повторяется по длине рулона; кроме того, это обычно повторяется по горизонтали, иногда со смещением от одного куска обоев к другому. По сути, обои — это двухмерный кристалл.
Есть 17 разновидностей плоских обоев (см. Главу 17). Они различаются видами симметрии, то есть способами жестко смещать рисунок так, чтобы он ровно лежал сам на себе в исходном положении.К видам симметрии относятся, в частности, различные варианты симметрии вращения, при которых изображение должно быть повернуто на определенный угол вокруг определенной точки — центра симметрии.
Порядок симметрии вращения — это то, сколько раз тело можно повернуть до полного круга, чтобы все детали чертежа вернулись в исходное положение. Например, поворот на 90 ° — это симметрия вращения 4-го порядка *. Список возможных типов вращательной симметрии в кристаллической решетке снова указывает на необычную цифру 5: ее там нет.Существуют варианты с симметрией вращения 2, 3, 4 и 6-го порядка, но ни один из обоев не имеет симметрии вращения 5-го порядка. В кристаллах симметрии вращения порядка более 6 также не существует, но первое нарушение последовательности все же происходит на цифре 5.
То же самое происходит с кристаллографическими системами в трехмерном пространстве. Здесь сетка повторяется в трех независимых направлениях. Существует 219 различных типов симметрии, или 230, если рассматривать зеркальное отображение рисунка как отдельную его версию — несмотря на то, что в данном случае нет зеркальной симметрии.Опять же, симметрии вращения наблюдаются на порядках 2, 3, 4 и 6, но не на 5. Этот факт называется кристаллографической связью.
В четырехмерном пространстве существуют решетки с симметрией 5-го порядка; в общем, для решеток достаточно больших размеров возможен любой заданный порядок симметрии вращения.
// Рис. 40. Кристаллическая решетка поваренной соли. Темные шары представляют собой атомы натрия, светлые — атомы хлора
Квазикристаллы
Хотя вращательная симметрия 5-го порядка невозможна в 2D- и 3D-решетках, она может существовать в немного менее регулярных структурах, известных как квазикристаллы.Используя наброски Кеплера, Роджер Пенроуз открыл плоские системы с пятичленной симметрией более общего типа. Их называют квазикристаллами.
Квазикристаллы существуют в природе. В 1984 году Даниэль Шехтман обнаружил, что сплав алюминия и марганца может образовывать квазикристаллы; Первоначально кристаллографы восприняли его сообщение с некоторым скептицизмом, но позже открытие подтвердилось, и в 2011 году Шехтман был удостоен Нобелевской премии по химии. В 2009 году группа ученых под руководством Луки Бинди обнаружила квазикристаллы в минерале из Корякского нагорья в России — сочетание алюминия, меди и железа.Сегодня этот минерал называется икосаэдритом. Измерив содержание различных изотопов кислорода в минерале с помощью масс-спектрометра, ученые показали, что этот минерал возник не на Земле. Он сформировался около 4,5 миллиардов лет назад, в то время, когда Солнечная система только зарождалась, и большую часть времени проводил в поясе астероидов, вращаясь вокруг Солнца, пока какое-то возмущение не изменило его орбиту и в конечном итоге не привело к Земле.
// Рис. 41. Слева: одна из двух квазикристаллических решеток с пятикратной точной симметрией.Справа: атомная модель икосаэдрического квазикристалла алюминия-палладия-марганца
.
Пифагорейские штаны Шуточное название теоремы Пифагора, возникшей из-за того, что квадраты, построенные по сторонам прямоугольника и расходящиеся в разные стороны, напоминают разрез штанов. Я любил геометрию … и на вступительном экзамене получил похвалу от профессора математики Чумакова за объяснение свойств параллельных линий и пифагорейских штанов без доски, рисование в воздухе руками (Н.Пирогова. Дневник старого врача).
Фразеологический словарь русского литературного языка. — М .: Астрель, АСТ … А.И. Федоров. 2008.
Посмотреть, что такое «Штаны Пифагора» в других словарях:
Брюки — получите рабочий купон на скидку в Paper Shop в Akademik или купите дешевые брюки с бесплатной доставкой в Paper Shop sale
Штаны Пифагора — … Википедия
Штаны Пифагора — Жарг.шк. Шаттл. Теорема Пифагора, устанавливающая связь между площадями квадратов, построенных на гипотенузе, и катетами прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
пифагорейские штаны — Юмористическое название теоремы Пифагора, которая устанавливает связь между площадями квадратов, построенных на гипотенузе, и сторонами прямоугольного треугольника, который выглядит как разрез штанов на картинках … Словарь много выражений
пифагорейские штаны (макияж) — сноска: об одаренном человеке Ср.Это несомненный мудрец. В древности он наверняка изобрел бы пифагорейские штаны … Салтыков. Красочные буквы. Штаны Пифагора (геом.): В прямоугольнике квадрат гипотенузы равен квадрату катетов (учение … … Большой толковый фразеологический словарь Майкельсона
Пифагорейские штаны равны со всех сторон — Количество пуговиц известно. Почему член тесноват? (примерно) о штанах и мужских гениталиях. Пифагорейские штаны равны со всех сторон.Чтобы доказать это, необходимо убрать и показать: 1) о теореме Пифагора; 2) про широкие штаны … живая речь. Словарь разговорных выражений
Пифагорейские штаны составляют — Пинагоровские штаны (изобретают) носок. о человеке одаренном. Ср. Это несомненный мудрец. В древности он, наверное, изобрел штаны Пинагора … Салтыков. Пестрые буквы. Брюки Пилягорова (геом.): В прямоугольном квадрате гипотенузы … … Большой толковый фразеологический словарь Михельсона (орфография)
Пифагорейские штаны равны во всех направлениях — Юмористическое доказательство теоремы Пифагора; также шутит о мешковатых штанах приятеля… Словарь народной фразеологии
Ex., Грубый …
БРЮКИ PYTHAGOR НА ВСЕХ СТОРОНАХ РАВНЫ (КОЛИЧЕСТВО КНОПОК ИЗВЕСТНО. ПОЧЕМУ ТАКОЕ ТУТ? / ЧТОБЫ ДОКАЗАТЬ, НЕОБХОДИМО СНИМАТЬ И ПОКАЗАТЬ) — прил., Грубый … Толковый словарь современного разговорного языка фразеологизмы и поговорки
брюки — существительное, множественное число, аптр.
