Содержание
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Определение 1
Угол наклона прямой y=kx+b называется угол α, который отсчитывается от положительного направления оси ох к прямой y=kx+b в положительном направлении.
На рисунке направление ох обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Определение 2
Угловой коэффициент прямой y=kx+b называют числовым коэффициентом k.
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
- Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0.
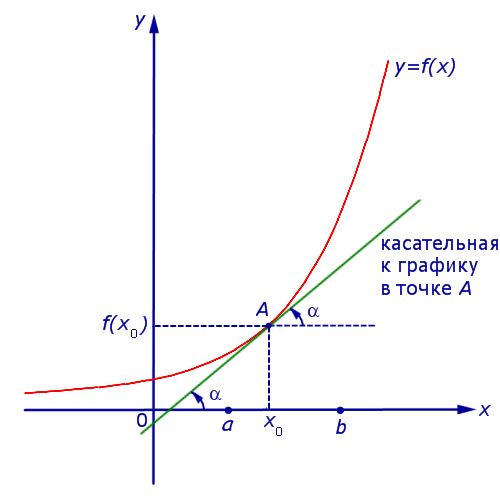 Значит, вид уравнения будет y=b.
Значит, вид уравнения будет y=b. - Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<π2 или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
- Если α=π2, тогда расположение прямой перпендикулярно ох. Равенство задается при помощи равенства x=c со значением с, являющимся действительным числом.
- Если угол наклона прямой y=kx+b тупой, то соответствует условиям π2<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f(x). Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
По рисунку видно, что АВ является секущей, а f(x) – черная кривая, α — красная дуга, означающая угол наклона секущей.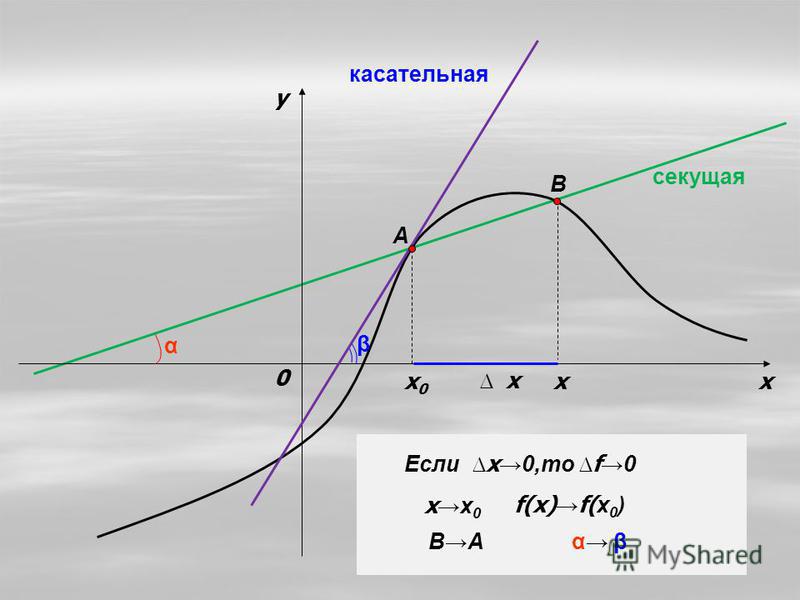
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника АВС можно найти по отношению противолежащего катета к прилежащему.
Определение 4
Получаем формулу для нахождения секущей вида:
k=tg α=BCAC=f(xB)-fxAxB-xA, где абсциссами точек А и В являются значения xA, xB, а f(xA), f(xB) — это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k=f(xB)-f(xA)xB-xA или k=f(xA)-f(xB)xA-xB, причем уравнение необходимо записать как y=f(xB)-f(xA)xB-xA·x-xA+f(xA) или
y=f(xA)-f(xB)xA-xB·x-xB+f(xB).
Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции.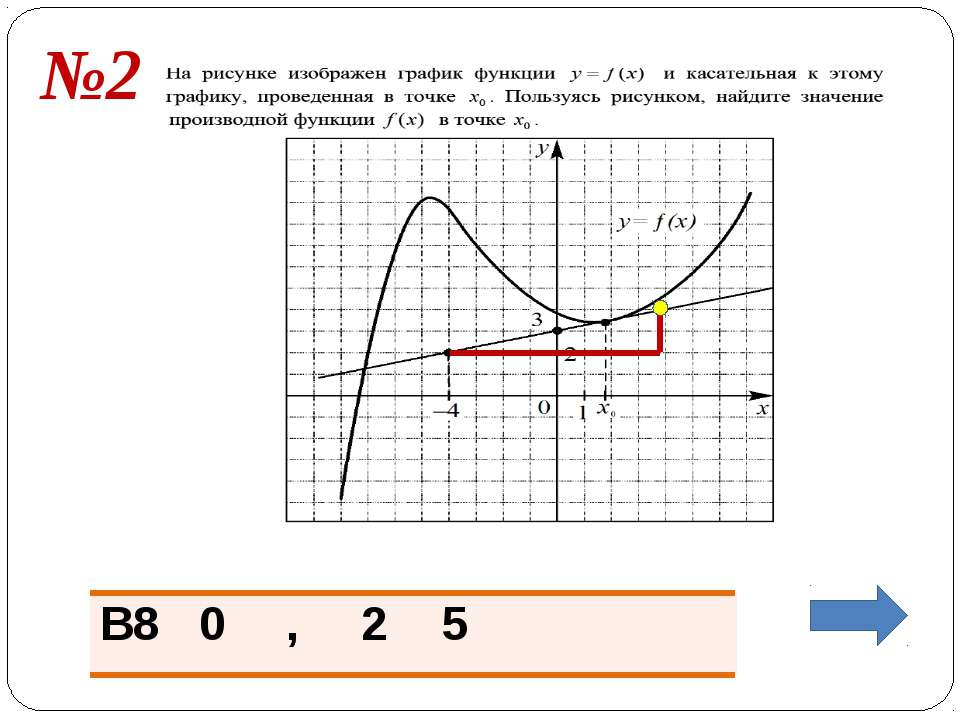 Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Если имеется уравнение вида у=0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Определение 5
Касательная к графику функции f(x) в точке x0; f(x0) называется прямая, проходящая через заданную точку x0; f(x0), с наличием отрезка, который имеет множество значений х, близких к x0.
Пример 1
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y=x+1, считается касательной к y=2x в точке с координатами (1; 2). Для наглядности, необходимо рассмотреть графики с приближенными к (1; 2) значениями. Функция y=2x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
Очевидно, что y=2x сливается с прямой у=х+1.
Для определения касательной следует рассмотреть поведение касательной АВ при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.
Секущая АВ, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной αx.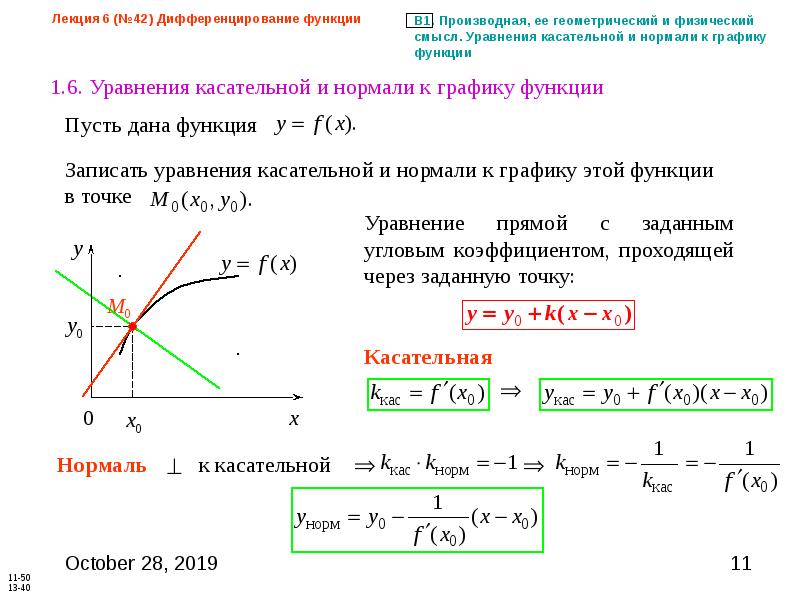
Определение 6
Касательной к графику функции y=f(x) в точке А считается предельное положение секущей АВ при В стремящейся к А, то есть B→A.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей АВ для функции f(x), где А и В с координатами x0, f(x0) и x0+∆x, f(x0+∆x), а ∆x обозначаем как приращение аргумента. Теперь функция примет вид ∆y=∆f(x)=f(x0+∆x)-f(∆x). Для наглядности приведем в пример рисунок.
Рассмотрим полученный прямоугольный треугольник АВС. Используем определение тангенса для решения, то есть получим отношение ∆y∆x=tg α. Из определения касательной следует, что lim∆x→0∆y∆x=tg αx. По правилу производной в точке имеем, что производную f(x) в точке x0 называют пределом отношений приращения функции к приращению аргумента, где ∆x→0, тогда обозначим как f(x0)=lim∆x→0∆y∆x.
Отсюда следует, что f'(x0)=lim∆x→0∆y∆x=tg αx=kx, где kx обозначают в качестве углового коэффициента касательной.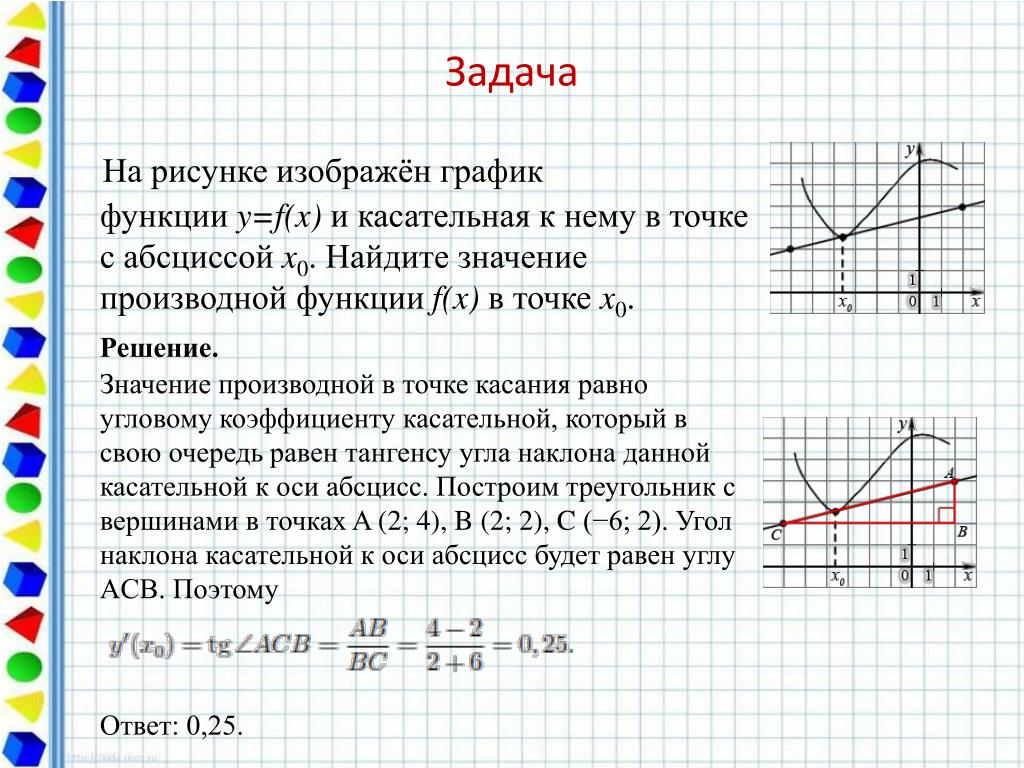
То есть получаем, что f’(x) может существовать в точке x0 причем как и касательная к заданному графику функции в точке касания равной x0, f0(x0), где значение углового коэффициента касательной в точке равняется производной в точке x0. Тогда получаем, что kx=f'(x0).
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x0 при пересечении.
Уравнение касательной к графику функции y=f(x) в точке x0, f0(x0) принимает вид y=f'(x0)·x-x0+f(x0).
Имеется в виду, что конечным значением производной f'(x0) можно определить положение касательной, то есть вертикально при условии limx→x0+0f'(x)=∞ и limx→x0-0f'(x)=∞ или отсутствие вовсе при условии limx→x0+0f'(x)≠limx→x0-0f'(x).
Расположение касательной зависит от значения ее углового коэффициента kx=f'(x0). При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
При параллельности к оси ох получаем, что kk=0, при параллельности к оу — kx=∞, причем вид уравнения касательной x=x0 возрастает при kx>0, убывает при kx<0.
Пример 2
Произвести составление уравнения касательной к графику функции y=ex+1+x33-6-33x-17-33 в точке с координатами (1; 3) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1; 3) является точкой касания, тогда x0=-1, f(x0)=-3.
Необходимо найти производную в точке со значением -1. Получаем, что
y’=ex+1+x33-6-33x-17-33’==ex+1’+x33′-6-33x’-17-33’=ex+1+x2-6-33y'(x0)=y'(-1)=e-1+1+-12-6-33=33
Значение f’(x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда kx=tg αx=y'(x0)=33
Отсюда следует, что αx=arctg33=π6
Ответ: уравнение касательной приобретает вид
y=f'(x0)·x-x0+f(x0)y=33(x+1)-3y=33x-9-33
Для наглядности приведем пример в графической иллюстрации.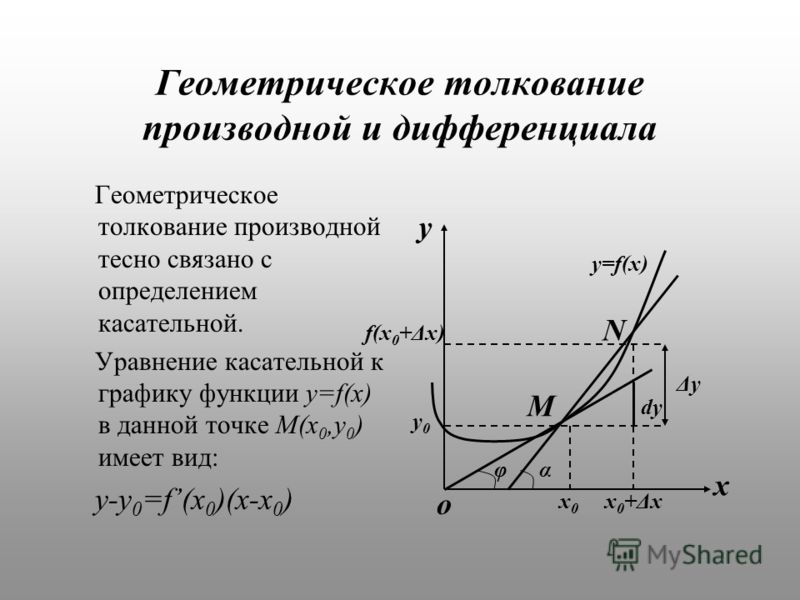
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Пример 3
Выяснить наличие существования касательной к графику заданной функции
y=3·x-15+1 в точке с координатами (1;1). Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y’=3·x-15+1’=3·15·(x-1)15-1=35·1(x-1)45
Если x0=1, тогда f’(x) не определена, но пределы записываются как limx→1+035·1(x-1)45=35·1(+0)45=35·1+0=+∞ и limx→1-035·1(x-1)45=35·1(-0)45=35·1+0=+∞, что означает существование вертикальной касательной в точке (1;1).
Ответ: уравнение примет вид х=1, где угол наклона будет равен π2.
Для наглядности изобразим графически.
Пример 4
Найти точки графика функции y=115x+23-45×2-165x-265+3x+2, где
- Касательная не существует;
- Касательная располагается параллельно ох;
- Касательная параллельна прямой y=85x+4.

Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x∈-∞; 2 и [-2; +∞). Получаем, что
y=-115×3+18×2+105x+176, x∈-∞; -2115×3-6×2+9x+12, x∈[-2; +∞)
Необходимо продифференцировать функцию. Имеем, что
y’=-115×3+18×2+105x+176′, x∈-∞; -2115×3-6×2+9x+12′, x∈[-2; +∞)⇔y’=-15(x2+12x+35), x∈-∞; -215×2-4x+3, x∈[-2; +∞)
Когда х=-2, тогда производная не существует, потому что односторонние пределы не равны в этой точке:
limx→-2-0y'(x)=limx→-2-0-15(x2+12x+35=-15(-2)2+12(-2)+35=-3limx→-2+0y'(x)=limx→-2+015(x2-4x+3)=15-22-4-2+3=3
Вычисляем значение функции в точке х=-2, где получаем, что
- y(-2)=115-2+23-45(-2)2-165(-2)-265+3-2+2=-2, то есть касательная в точке (-2;-2) не будет существовать.
- Касательная параллельна ох, когда угловой коэффициент равняется нулю.
 Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Тогда kx=tg αx=f'(x0). То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f’(x) и будут являться точками касания, где касательная является параллельной ох.
Когда x∈-∞; -2, тогда -15(x2+12x+35)=0, а при x∈(-2; +∞) получаем 15(x2-4x+3)=0.
Решим:
-15(x2+12x+35)=0D=122-4·35=144-140=4×1=-12+42=-5∈-∞; -2×2=-12-42=-7∈-∞; -2 15(x2-4x+3)=0D=42-4·3=4×3=4-42=1∈-2; +∞x4=4+42=3∈-2; +∞
Вычисляем соответствующие значения функции
y1=y-5=115-5+23-45-52-165-5-265+3-5+2=85y2=y(-7)=115-7+23-45(-7)2-165-7-265+3-7+2=43y3=y(1)=1151+23-45·12-165·1-265+31+2=85y4=y(3)=1153+23-45·32-165·3-265+33+2=43
Отсюда -5; 85, -4; 43, 1; 85, 3; 43 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 85 .
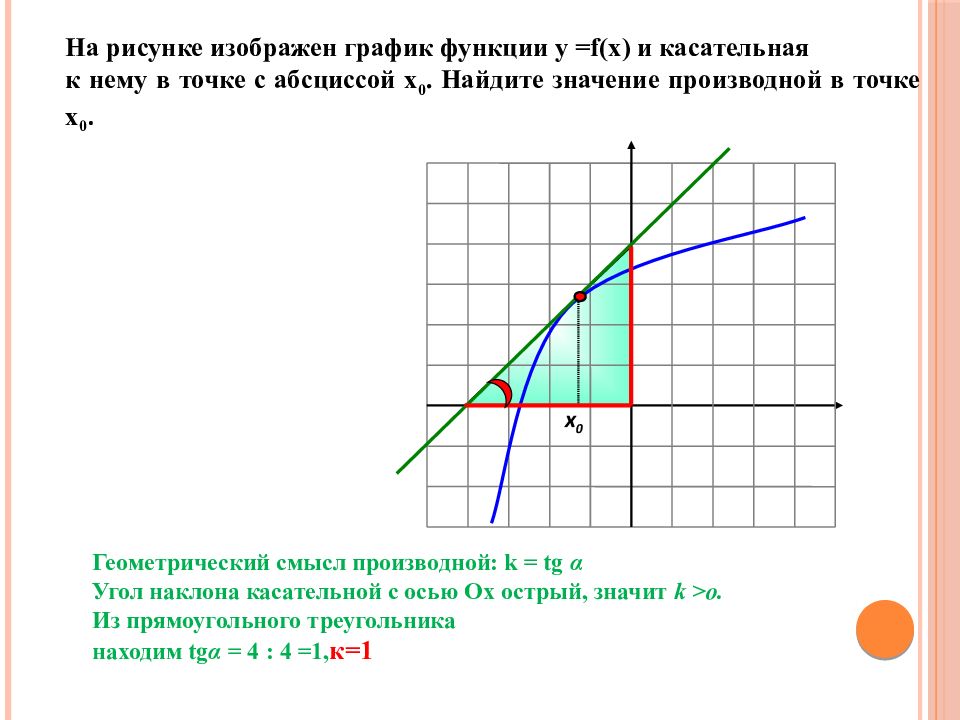 Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Для этого нужно решить уравнение вида y'(x)=85. Тогда, если x∈-∞; -2, получаем, что -15(x2+12x+35)=85, а если x∈(-2; +∞), тогда 15(x2-4x+3)=85.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
-15×2+12x+35=85×2+12x+43=0D=122-4·43=-28<0
Другое уравнение имеет два действительных корня, тогда
15(x2-4x+3)=85×2-4x-5=0D=42-4·(-5)=36×1=4-362=-1∈-2; +∞x2=4+362=5∈-2; +∞
Перейдем к нахождению значений функции. Получаем, что
y1=y(-1)=115-1+23-45(-1)2-165(-1)-265+3-1+2=415y2=y(5)=1155+23-45·52-165·5-265+35+2=83
Точки со значениями -1; 415, 5; 83 являются точками, в которых касательные параллельны прямой y=85x+4.
Ответ: черная линия – график функции, красная линия – график y=85x+4, синяя линия – касательные в точках -1; 415, 5; 83.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Возможно существование бесконечного количества касательных для заданных функций.
Пример 5
Написать уравнения всех имеющихся касательных функции y=3cos32x-π4-13, которые располагаются перпендикулярно прямой y=-2x+12.
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется -1, то есть записывается как kx·k⊥=-1. Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k⊥=-2, тогда kx=-1k⊥=-1-2=12.
Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x0 получаем, что kx=y'(x0). Из данного равенства найдем значения х для точек касания.
Получаем, что
y'(x0)=3cos32x0-π4-13’=3·-sin32x0-π4·32×0-π4’==-3·sin32x0-π4·32=-92·sin32x0-π4⇒kx=y'(x0)⇔-92·sin32x0-π4=12⇒sin32x0-π4=-19
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.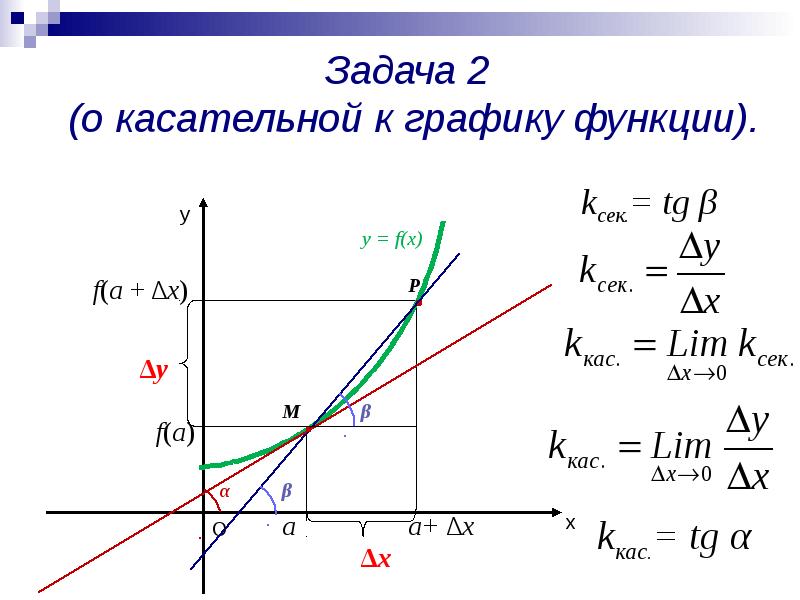
32×0-π4=arcsin-19+2πk или 32×0-π4=π-arcsin-19+2πk
32×0-π4=-arcsin19+2πk или 32×0-π4=π+arcsin19+2πk
x0=23π4-arcsin19+2πk или x0=235π4+arcsin19+2πk, k∈Z
Z- множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у:
y0=3cos32x0-π4-13
y0=3·1-sin232x0-π4-13 или y0=3·-1-sin232x0-π4-13
y0=3·1—192-13 или y0=3·-1—192-13
y0=45-13 или y0=-45+13
Отсюда получаем, что 23π4-arcsin19+2πk; 45-13, 235π4+arcsin19+2πk; -45+13 являются точками касания.
Ответ: необходимы уравнения запишутся как
y=12x-23π4-arcsin19+2πk+45-13,y=12x-235π4+arcsin19+2πk-45+13, k∈Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [-10;10], где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y=-2x+12. Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Для задания окружности с центром в точке xcenter; ycenter и радиусом R применяется формула x-xcenter2+y-ycenter2=R2.
Данное равенство может быть записано как объединение двух функций:
y=R2-x-xcenter2+ycentery=-R2-x-xcenter2+ycenter
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Для составления уравнения окружности в точке x0; y0, которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y=R2-x-xcenter2+ycenter или y=-R2-x-xcenter2+ycenter в указанной точке.
Когда в точках xcenter; ycenter+R и xcenter; ycenter-R касательные могут быть заданы уравнениями y=ycenter+R и y=ycenter-R, а в точках xcenter+R; ycenter и
xcenter-R; ycenter будут являться параллельными оу, тогда получим уравнения вида x=xcenter+R и x=xcenter-R.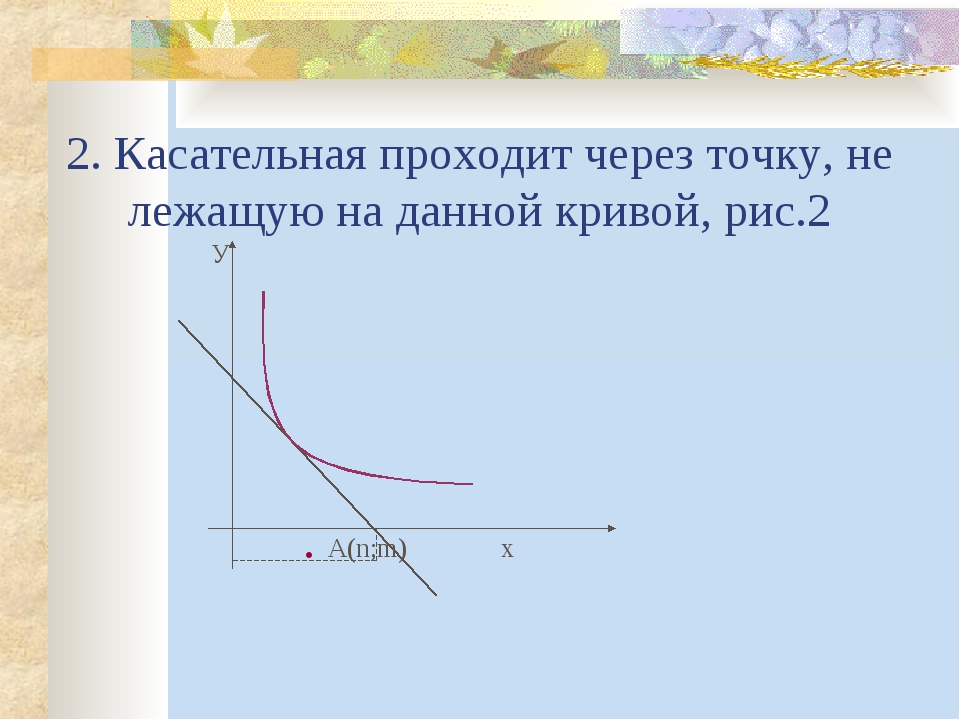
Касательная к эллипсу
Когда эллипс имеет центр в точке xcenter; ycenter с полуосями a и b, тогда он может быть задан при помощи уравнения x-xcenter2a2+y-ycenter2b2=1.
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y=ba·a2-(x-xcenter)2+ycentery=-ba·a2-(x-xcenter)2+ycenter
Если касательные располагаются на вершинах эллипса, тогда они параллельны ох или оу. Ниже для наглядности рассмотрим рисунок.
Пример 6
Написать уравнение касательной к эллипсу x-324+y-5225=1 в точках со значениями x равного х=2.
Решение
Необходимо найти точки касания, которые соответствуют значению х=2. Производим подстановку в имеющееся уравнение эллипса и получаем, что
x-324x=2+y-5225=114+y-5225=1⇒y-52=34·25⇒y=±532+5
Тогда 2; 532+5 и 2; -532+5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.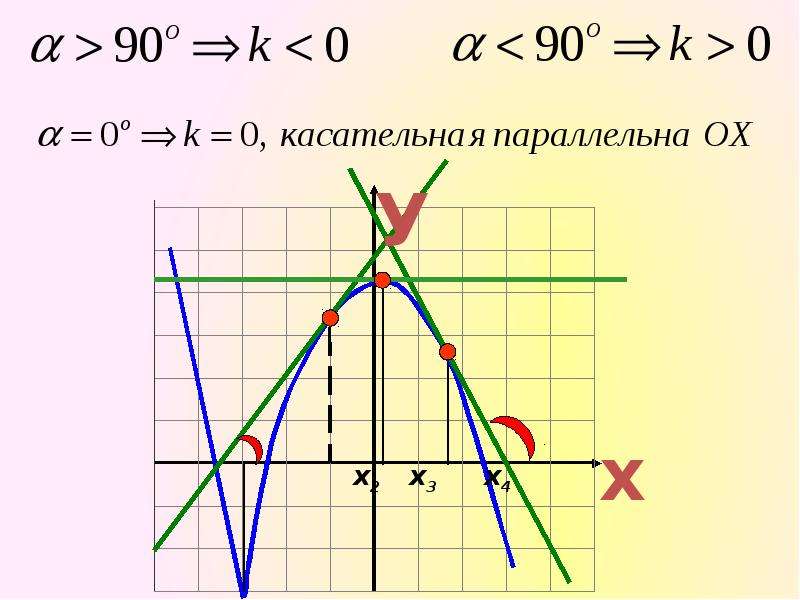
Перейдем к нахождению и разрешению уравнения эллипса относительно y. Получим, что
x-324+y-5225=1y-5225=1-x-324(y-5)2=25·1-x-324y-5=±5·1-x-324y=5±524-x-32
Очевидно, что верхний полуэллипс задается с помощью функции вида y=5+524-x-32, а нижний y=5-524-x-32.
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2; 532+5 будет иметь вид
y’=5+524-x-32’=52·124-(x-3)2·4-(x-3)2’==-52·x-34-(x-3)2⇒y'(x0)=y'(2)=-52·2-34-(2-3)2=523⇒y=y'(x0)·x-x0+y0⇔y=523(x-2)+532+5
Получаем, что уравнение второй касательной со значением в точке
2; -532+5 принимает вид
y’=5-524-(x-3)2’=-52·124-(x-3)2·4-(x-3)2’==52·x-34-(x-3)2⇒y'(x0)=y'(2)=52·2-34-(2-3)2=-523⇒y=y'(x0)·x-x0+y0⇔y=-523(x-2)-532+5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке xcenter; ycenter и вершины xcenter+α; ycenter и xcenter-α; ycenter, имеет место задание неравенства x-xcenter2α2-y-ycenter2b2=1, если с вершинами xcenter; ycenter+b и xcenter; ycenter-b, тогда задается при помощи неравенства x-xcenter2α2-y-ycenter2b2=-1.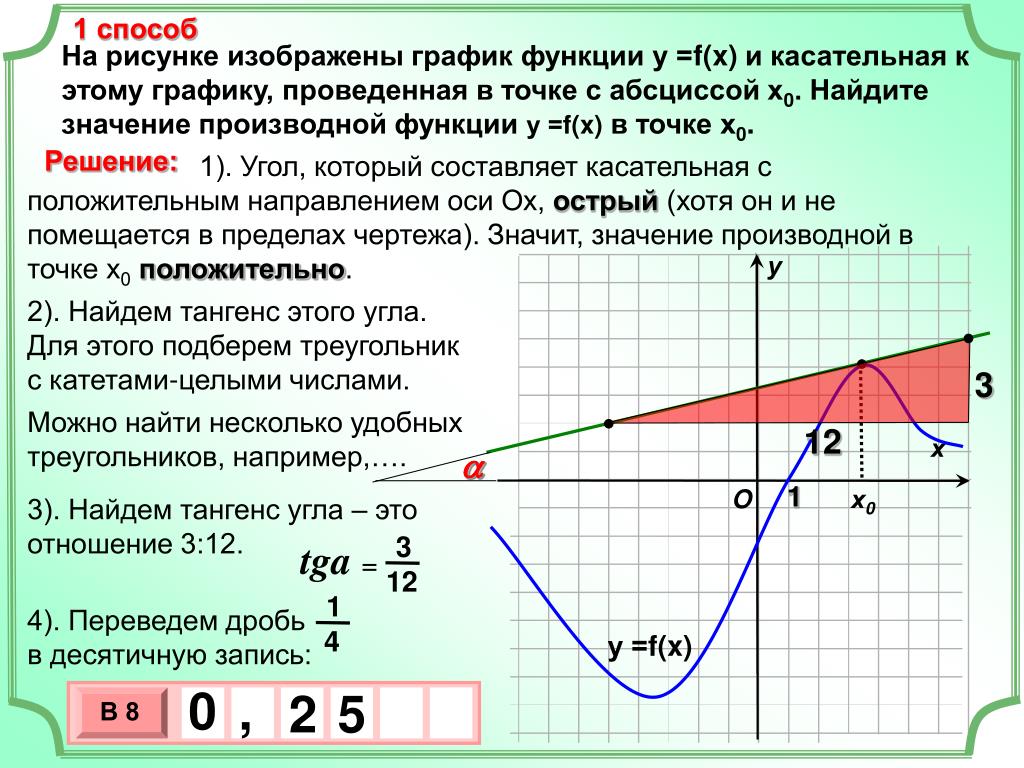
Гипербола может быть представлена в виде двух объединенных функций вида
y=ba·(x-xcenter)2-a2+ycentery=-ba·(x-xcenter)2-a2+ycenter или y=ba·(x-xcenter)2+a2+ycentery=-ba·(x-xcenter)2+a2+ycenter
В первом случае имеем, что касательные параллельны оу, а во втором параллельны ох.
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Пример 7
Составить уравнение касательной к гиперболе x-324-y+329=1 в точке 7; -33-3.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x-324-y+329=1⇒y+329=x-324-1⇒y+32=9·x-324-1⇒y+3=32·x-32-4 или y+3=-32·x-32-4⇒y=32·x-32-4-3y=-32·x-32-4-3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7; -33-3.
Очевидно, что для проверки первой функции необходимо y(7)=32·(7-3)2-4-3=33-3≠-33-3, тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y(7)=-32·(7-3)2-4-3=-33-3≠-33-3, значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
Получаем, что
y’=-32·(x-3)2-4-3’=-32·x-3(x-3)2-4⇒kx=y'(x0)=-32·x0-3×0-32-4×0=7=-32·7-37-32-4=-3
Ответ: уравнение касательной можно представить как
y=-3·x-7-33-3=-3·x+43-3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y=ax2+bx+c в точке x0, y(x0), необходимо использовать стандартный алгоритм, тогда уравнение примет вид y=y'(x0)·x-x0+y(x0). Такая касательная в вершине параллельна ох.
Следует задать параболу x=ay2+by+c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у. Получаем, что
x=ay2+by+c⇔ay2+by+c-x=0D=b2-4a(c-x)y=-b+b2-4a(c-x)2ay=-b-b2-4a(c-x)2a
Графически изобразим как:
Для выяснения принадлежности точки x0, y(x0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна оу относительно параболы.
Такая касательная будет параллельна оу относительно параболы.
Пример 8
Написать уравнение касательной к графику x-2y2-5y+3, когда имеем угол наклона касательной 150°.
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
-2y2-5y+3-x=0D=(-5)2-4·(-2)·(3-x)=49-8xy=5+49-8x-4y=5-49-8x-4
Значение углового коэффициента равняется значению производной в точке x0 этой функции и равняется тангенсу угла наклона.
Получаем:
kx=y'(x0)=tg αx=tg 150°=-13
Отсюда определим значение х для точек касания.
Первая функция запишется как
y’=5+49-8x-4’=149-8x⇒y'(x0)=149-8×0=-13⇔49-8×0=-3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150° для такой функции не существует.
Вторая функция запишется как
y’=5-49-8x-4’=-149-8x⇒y'(x0)=-149-8×0=-13⇔49-8×0=-3×0=234⇒y(x0)=5-49-8·234-4=-5+34
Имеем, что точки касания — 234; -5+34.
Ответ: уравнение касательной принимает вид
y=-13·x-234+-5+34
Графически изобразим это таким образом:
Внеклассный урок — Касательная к графику функции
Касательная к графику функции
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис.1).
Другое определение: это предельное положение секущей при Δx→0.
Пояснение: Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).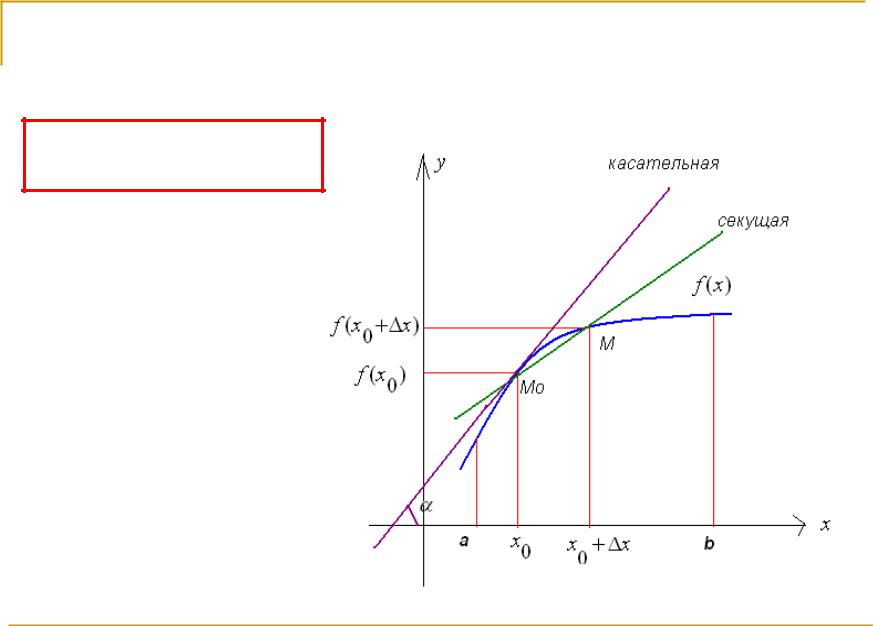
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.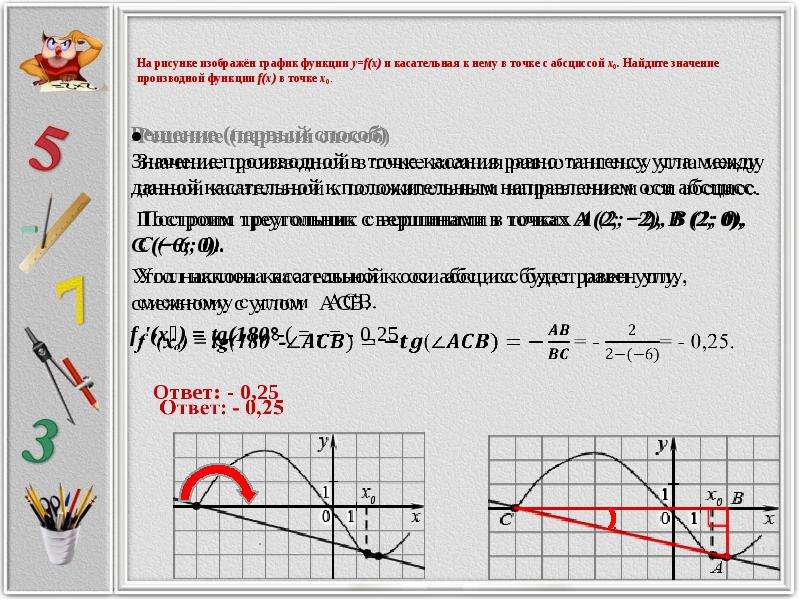 3).
3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
|
Алгоритм решения уравнения касательной к графику функции y = f(x):
1. 2. Вычислить производные f ′(x) и f ′(xо). 3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и решить его. |
Пример: Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2.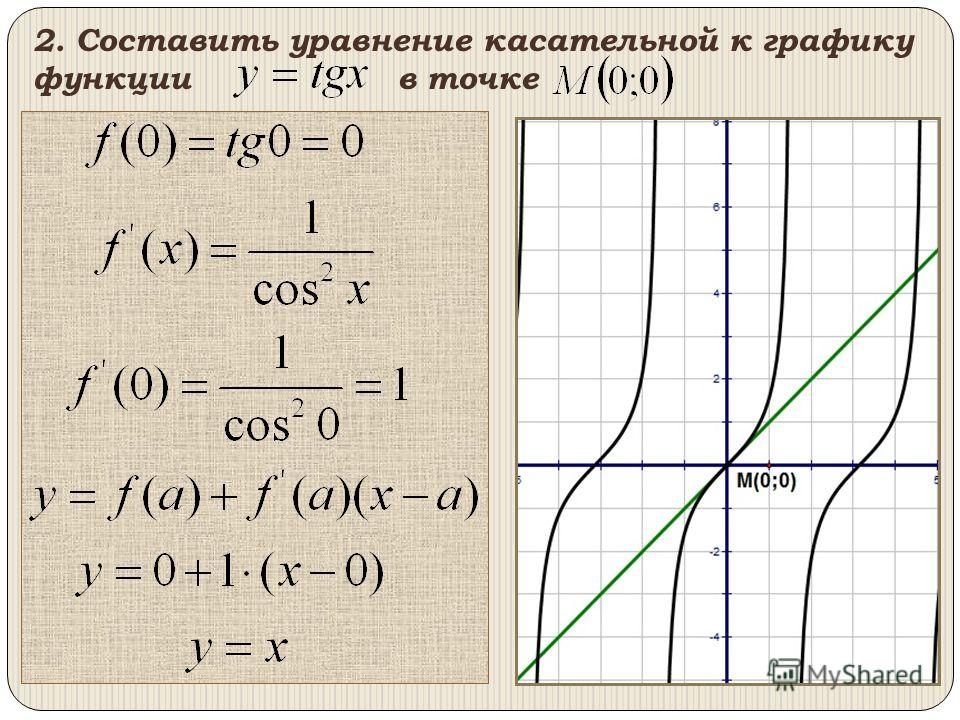 Значит:
Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ: у = 4х – 7.
Урок 14. геометрический смысл производной — Алгебра и начала математического анализа — 11 класс
Алгебра и начала анализа, 11 класса.
Урок №14. Геометрический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Геометрический смысл производной;
2) Алгоритм нахождения касательной к графику функции в точке;
3) Сравнение производных заданной функции по ее графику в различных точках.
Глоссарий по теме
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
– М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Напомним, что графиком линейной функции у=кх + b является прямая.
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Если k>0, то 0<α< π/2, в этом случае функция возрастает
Если k<0, то — π/2<α<0, в этом случае функция убывает
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Рассмотрим график функции y = f ( x ):
Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где — угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.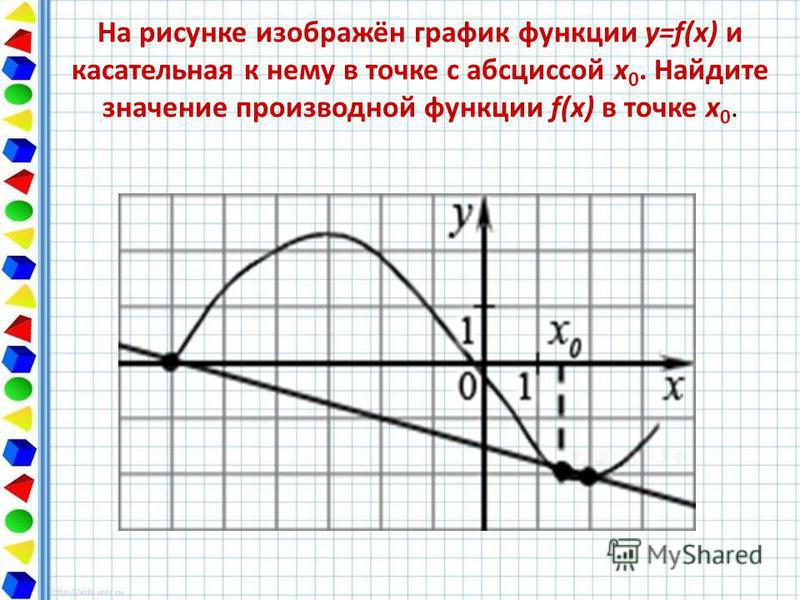
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует:
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной.
Уравнение касательной к графику функции y=f(x) в точке x0:
Примеры и разбор решения заданий тренировочного модуля
№1. Составить уравнение касательной к графику функции y=x+e-2x, параллельной прямой y=-x
Решение:
Угловой коэффициент касательной равен значению производной в точке касания x0. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x0) = -1.
Уравнение касательной:
Уравнение касательной: y=1-1(x-0) = 1-x
Ответ: y=1-x.
№2. На параболе у=х2-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.
Решение:
Определим угловой коэффициент касательной к параболе у=х2-2х-8:
k =у’=(х2-2х-8)’=2х-2.
Найдем угловой коэффициент прямой 4х+у+4=0:
у=-4х-4, k =-4.
Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.
2х-2=-4;
х=-1 – абсцисса точки касания.
Ординату точки касания М вычислим из уравнения данной параболы у=х2-2х-8, т.е.
у(-1)=(-1)2-2(-1)-8=-5, М(-1;-5).
Ответ: М(-1;-5).
Уравнение касательной к графику функции в заданной точке
Пусть у нас имеется график некоторой непрерывной и дифференцируемой на некотором отрезке функции y = f(x) и задана некоторая точка x0 из этого отрезка.
Мы хотим написать уравнение касательной к графику функции в этой точке.
Касательная – это прямая, а уравнение прямой, как известно, выражается формулой y = kx+c, коэффициент k равен тангенсу угла между этой прямой и положительным направлением оси ОХ.
Как, известно, геометрический смысл производной f'(x) – тангенс угла наклона касательной к графику функции f(x) в точке x. Значит в нашем случае k = f'(x0).
Уравнение прямой примет вид y = f'(x0)×x+c (*).
Неизвестным остается только один коэффициент – с. Найдем его следующим образом, раз это касательная в точке x0, то она проходит через принадлежащую графику точку (x0; f(x0)). А раз прямая проходит через эту точку, значит, ее координаты удовлетворяют уравнению прямой.
Получаем уравнение:
f(x0) = f'(x0)×x0+c;
c = f(x0)-f'(x0)×x0.
Подставляя выражение для с в уравнение (*), получаем уравнение касательной к графику функции в точке x0:
y = f'(x0)×x+f(x0)-f'(x0)×x0 = f'(x0)(x-x0)+f(x0).
Пример.
Найти уравнение касательной к графику функции y = x2+2x в точке x0 = 1.
Уравнение касательной имеет вид:
y = f'(x0)(x-x0)+f(x0).
В нашем случае:
f'(x) = (x2+2x)’ = 2x+2;
f'(x0) = 2×1+2 = 4;
f(x0) = 12+2×1 = 3.
Уравнение касательной запишется в виде:
y = 4×(x-1)+3 = 4x-4+3 = 4x-1;
y = 4x-1.
Уравнение касательной к графику функции
Вопросы
занятия:
·
рассмотреть
касательную к графику функции в точке;
·
вывести
уравнение касательной к графику функции в общем виде.
Материал
урока.
Прежде
чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.
Итак, мы с вами научились находить
производные различных функций. На предыдущих уроках мы говорили, что умение
находить производные – помогает в решении разных задач. На сегодняшнем уроке мы
разберём, как с помощью производных можно составить уравнение касательной к
графику функции и примеры применения производной к приближенным вычислениям.
Давайте сформулируем задачу.
Напомним, что если в некоторой точке к
графику функции можно провести касательную, то функция дифференцируема в этой
точке и f'(a)
существует.
Касательная – это прямая, значит, общее
уравнение касательной можно записать в виде y
= kx + m.
Наша задача сводится к нахождению коэффициентов k
и m.
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё
один пример.
Пример.
Решая примеры, мы выполняли практически
одни и те же действия. Давайте теперь попробуем сформулировать алгоритм
составления уравнения касательной к графику функции y = f(x).
Уравнение касательной имеет ещё одно
применение: с его помощью можно выполнять приближенные вычисления.
Рассмотрим общий приём.
Рассмотрим это на примере.
Пример.
Рассмотрим ещё один пример.
Пример.
Итак, давайте ещё раз выделим суть теории
приближенных вычислений. Сложная кривая в окрестности точки x0
заменяется прямой (касательной к графику функции) и если приращения аргумента
не велики, то для каждой функции можно вывести соответствующую формулу, по
которой осуществляются приближенные вычисления.
Уравнение касательной к графику функции
Лекция
Тема: Уравнение касательной к графику функции
Цель: Рассмотреть уравнений касательной к графику функции
1. Уравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую (см. рис.1).
Рис. 1. График функции .
Зафиксируем точку . Если , то значение функции равно . Значит, имеем точку с координатами (.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой , в которой — существует.
Уравнение касательной – это прямая, которая задается формулой
Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент .
Параметр найдем из условия, что касательная проходит через точку (, то есть .
.
Стало быть .
Запишем уравнение касательной
.
Или, .
Получили уравнение касательной к кривой в точке с абсциссой .
2. Смысл элементов уравнения касательной
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
2) — угловой коэффициент касательной к графику функции.
3) – произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что – это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
3. Алгоритм составления уравнения касательной к графику функции
Задача.
К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
Рис. 2. Касательная к графику функции .
Зафиксируем точку . Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти и точку касания.
— дано.Точка касания: (;.
2) Найти производную в любой точке .
.
3) Найти значение производной в точке с абсциссой .
.
4) Выписать и проанализировать уравнение касательной.
.
Упрощаем и получаем: .
Ответ: .
4. Сопутствующие задачи
Задача 1.
Пусть дано уравнение касательной .
Найдите точки пересечения касательной с осями координат.
Если , то . – это первая точка.
Если , то . — вторая точка.
Итак, первая точка – это точка с координатами . Вторая точка – точка пересечения с осью , точка с координатами (см. рис.3).
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .
Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .
5. Касательная к графику тригонометрической функции
Рассмотрим пример.
Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).
Рис. 4. Касательная к графику функции .
Нахождение точки касания.
1. Точка касания имеет координаты .
2. Найти .
3. Найти
И, последнее действие, – написать уравнение касательной.
4. .
Упростим и получим .
Заметим в точке синусоида и касательная соприкасаются. В районе точки синусоида и прямая почти не различаются.
Задачи для самостоятельного выполнения.
Написать уравнение касательной к графику функции в точке .
Написать уравнение касательной к графику функции в точке .
Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Дано уравнение касательной у=3х-1. Найдите точки пересечения касательной с осями координат. Если , то . – это первая точка. Если , то . — вторая точка.
10 класс. Алгебра. Производная. Уравнение касательной к графику функции. — Уравнение касательной к графику функции.
Комментарии преподавателя
Уравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую (см. рис.1).
Рис. 1. График функции .
Зафиксируем точку . Если , то значение функции равно . Значит, имеем точку с координатами (.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой , в которой — существует.
Уравнение касательной – это прямая, которая задается формулой
Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент .
Параметр найдем из условия, что касательная проходит через точку (, то есть .
.
Стало быть .
Запишем уравнение касательной
.
Или, .
Получили уравнение касательной к кривой в точке с абсциссой .
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
2) — угловой коэффициент касательной к графику функции.
3) – произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что – это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Задача.
К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
Рис. 2. Касательная к графику функции .
Зафиксируем точку . Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти и точку касания.
— дано.Точка касания: (;.
2) Найти производную в любой точке .
.
3) Найти значение производной в точке с абсциссой .
.
4) Выписать и проанализировать уравнение касательной.
.
Упрощаем и получаем: .
Ответ: .
Задача 1.
Пусть дано уравнение касательной .
Найдите точки пересечения касательной с осями координат.
Если , то . – это первая точка.
Если , то . — вторая точка.
Итак, первая точка – это точка с координатами . Вторая точка – точка пересечения с осью , точка с координатами (см. рис.3).
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .
Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .
Рассмотрим пример.
Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).
Рис. 4. Касательная к графику функции .
Нахождение точки касания.
1. Точка касания имеет координаты .
2. Найти .
3. Найти
И, последнее действие, – написать уравнение касательной.
4. .
Упростим и получим .
Заметим в точке синусоида и касательная соприкасаются. В районе точки синусоида и прямая почти не различаются.
Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/uravnenie-kasatelnoy-k-grafiku-funktsii
http://v.5klass.net/zip/457286d0df8865f8084b5db13cbd6e95.zip
http://school.xvatit.com/index.php?title=%D3%F0%E0%E2%ED%E5%ED%E8%E5_%EA%E0%F1%E0%F2%E5%EB%FC%ED%EE%E9_%EA_%E3%F0%E0%F4%E8%EA%F3_%F4%F3%ED%EA%F6%E8%E8
http://itest.kz/lekciya_uglovoj_koehfficzient_kasatelnoj_i_ee_uravnenie_ru
http://www.postupivuz.ru/vopros/12822.htm
График функции касательной
В
тригонометрические соотношения
также может рассматриваться как функция переменной, которая является мерой угла. Эту угловую меру можно указать в
градусы
или же
радианы
. Здесь мы будем использовать радианы.
С,
загар
(
Икс
)
знак равно
грех
(
Икс
)
потому что
(
Икс
)
касательная функция не определена, когда
потому что
(
Икс
)
знак равно
0
.Следовательно, касательная функция имеет
вертикальная асимптота
в любое время
потому что
(
Икс
)
знак равно
0
.
Точно так же каждая функция тангенса и синуса имеет нули в целых кратных
π
так как
загар
(
Икс
)
знак равно
0
когда
грех
(
Икс
)
знак равно
0
.
График
касательная
функция
y
знак равно
загар
(
Икс
)
выглядит так:
Свойства касательной функции,
y
знак равно
загар
(
Икс
)
.
Домен
:
Икс
∈
ℝ
,
Икс
≠
π
2
+
п
π
, где
п
целое число.
Диапазон
:
(
—
∞
,
∞
)
y
-перехват
:
(
0
,
0
)
Икс
-перехват
:
п
π
, где
п
целое число.
Период:
π
Симметрия: происхождение (нечетная функция)
Амплитуда и период касательной функции.
У тангенциальной функции нет амплитуды, потому что у нее нет максимального или минимального значения.
Период касательной функции,
y
знак равно
а
загар
(
б
Икс
)
, — расстояние между любыми двумя последовательными вертикальными асимптотами.
Период =
π
|
б
|
Также см
Тригонометрические функции
.
Тригонометрический Разделы: Следующая триггерная функция — касательная, Тангенс будет равен нулю везде, где его числитель Касательная будет undefined где бы то ни было Теперь мы можем использовать то, что знаем о синусе, Авторские права © Элизабет Между π / 2 и π, Поскольку синус и косинус периодичны, то
От Теперь мы можем завершить наш график: В Как видите, тангенс имеет период Для построения графиков нарисуйте нули в формате x = 0, π, 2π, Если вы предпочитаете запоминать графики, запомните << Предыдущий Наверх | 1 | 2 | 3 | Возвращаться
|
Графики других тригонометрических функций
Анализ графика y = tan x и его вариаций
Мы начнем с графика функции касательной , нанося точки, как мы делали для функций синуса и косинуса.Напомним, что
[латекс] \ tan x = \ frac {\ sin x} {\ cos x} \\ [/ latex]
Период касательной функции равен π , потому что график повторяется на интервалах kπ , где k — постоянная. Если построить график касательной функции на [latex] — \ frac {\ pi} {2} \\ [/ latex] к [latex] \ frac {\ pi} {2} \\ [/ latex], мы можем увидеть поведение графа на одном полном цикле. Если мы посмотрим на любой больший интервал, мы увидим, что характеристики графика повторяются.
Мы можем определить, является ли тангенс четной или нечетной функцией, используя определение тангенса.
[латекс] \ begin {array} \ tan (−x) = \ frac {\ sin (−x)} {\ cos (−x)} \ hfill & \ text {Определение касательной.} \\ = \ frac { — \ sin x} {\ cos x} \ hfill & \ text {Синус — нечетная функция, косинус — четный.} \\ = — \ frac {\ sin x} {\ cos x} & \ hfill \ text {Частное нечетной и четной функции является нечетной.} \ hfill \\ = — \ tan x \ hfill & \ text {Определение касательной.} \ end {array} \\ [/ latex]
Следовательно, тангенс — нечетная функция.Мы можем дополнительно проанализировать графическое поведение касательной функции, посмотрев значения для некоторых специальных углов, как указано в таблице ниже.
| x | [латекс] — \ frac {\ pi} {2} \\ [/ latex] | [латекс] — \ frac {\ pi} {3} \\ [/ latex] | [латекс] — \ frac {\ pi} {4} \\ [/ latex] | [латекс] — \ frac {\ pi} {6} \\ [/ latex] | 0 | [латекс] \ frac {\ pi} {6} \\ [/ latex] | [латекс] \ frac {\ pi} {4} \\ [/ latex] | [латекс] \ frac {\ pi} {3} \\ [/ latex] | [латекс] \ frac {\ pi} {2} \\ [/ latex] |
| желто-коричневый ( x ) | неопределенный | [латекс] — \ sqrt {3} \\ [/ латекс] | –1 | [латекс] — \ frac {\ sqrt {3}} {3} \\ [/ латекс] | 0 | [латекс] \ frac {\ sqrt {3}} {3} \\ [/ latex] | 1 | [латекс] \ sqrt {3} \\ [/ латекс] | неопределенный |
Эти точки помогут нам нарисовать наш график, но нам нужно определить, как график ведет себя там, где он не определен.Если мы более внимательно рассмотрим значения, когда [latex] \ frac {\ pi} {3}
| x | 1,3 | 1,5 | 1,55 | 1,56 |
| желто-коричневый x | 3.6 | 14,1 | 48,1 | 92,6 |
По мере приближения x к [latex] \ frac {\ pi} {2} \\ [/ latex] выходные данные функции становятся все больше и больше. Поскольку [latex] y = \ tan x \\ [/ latex] является нечетной функцией, мы видим соответствующую таблицу отрицательных значений в таблице ниже.
| x | -1,3 | -1,5 | -1,55 | -1,56 |
| желто-коричневый x | −3.6 | −14,1 | −48,1 | −92,6 |
Мы видим, что по мере приближения x к [latex] — \ frac {\ pi} {2} \\ [/ latex] выходы становятся все меньше и меньше. Помните, что есть некоторые значения x , для которых cos x = 0. Например, [latex] \ cos \ left (\ frac {\ pi} {2} \ right) = 0 \\ [/ latex] и [латекс] \ cos \ left (\ frac {3 \ pi} {2} \ right) = 0 \\ [/ latex]. При этих значениях касательная функция не определена, поэтому график [latex] y = \ tan x [/ latex] имеет разрывы в [latex] x = \ frac {\ pi} {2} \\ [/ latex ] и [латекс] \ frac {3 \ pi} {2} \\ [/ latex].При этих значениях график касательной имеет вертикальные асимптоты. На рисунке 1 представлен график [латекс] y = \ tan x \\ [/ latex]. Касательная положительна от 0 до [latex] \ frac {\ pi} {2} \\ [/ latex] и от π до [latex] \ frac {3 \ pi} {2} \\ [/ latex] , соответствующие квадрантам I и III единичной окружности.
Рисунок 1. График касательной функции
Графические вариации
y = tan x
Как и функции синуса и косинуса, функция тангенса может быть описана общим уравнением.
[латекс] y = A \ tan (Bx) \\ [/ латекс]
Мы можем идентифицировать горизонтальные и вертикальные растяжения и сжатия, используя значения A и B. Горизонтальное растяжение обычно можно определить по периоду графика. В случае касательных графиков часто бывает необходимо определить вертикальное растяжение, используя точку на графике.
Поскольку нет максимальных или минимальных значений тангенциальной функции, термин амплитуда не может быть интерпретирован так же, как для функций синуса и косинуса.Вместо этого мы будем использовать фразу , коэффициент растяжения / сжатия , когда будем ссылаться на константу A .
A Общее примечание: особенности графика
y = A tan ( Bx )
- Коэффициент растяжения | A | .
- Период [латекс] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Домен — это все действительные числа x , где [latex] x \ ne \ frac {\ pi} {2 | B |} + \ frac {\ pi} {| B |} k \\ [/ latex] такой что k — целое число.
- Диапазон составляет (−∞, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {2 | B |} + \ frac {\ pi} {| B |} k \\ [/ latex], где k — целое число.
- [latex] y = A \ tan (Bx) \\ [/ latex] — нечетная функция.
Построение графика одного периода растянутой или сжатой касательной функции
Мы можем использовать то, что мы знаем о свойствах функции касательной , чтобы быстро нарисовать график любой растянутой и / или сжатой касательной функции вида [latex] f (x) = A \ tan (Bx) \\ [ /латекс].Мы сосредотачиваемся на одном периоде функции, включая начало координат, потому что периодическое свойство позволяет нам расширить график до остальной области области функции, если мы хотим. Тогда наша ограниченная область — это интервал [latex] (- \ frac {P} {2}, \ frac {P} {2}) \\ [/ latex], а график имеет вертикальные асимптоты в [latex] \ pm \ frac {P} {2} \\ [/ latex], где [latex] P = \ frac {\ pi} {B} \\ [/ latex]. На [latex] (- \ frac {\ pi} {2}, \ frac {\ pi} {2}) \\ [/ latex] график выйдет из левой асимптоты в [latex] x = — \ frac {\ pi} {2} \\ [/ latex], пересекает начало координат и продолжает увеличиваться по мере приближения к правой асимптоте в [latex] x = \ frac {\ pi} {2} \\ [/ latex ].Чтобы функция приближалась к асимптотам с правильной скоростью, нам также необходимо установить вертикальный масштаб, фактически оценив функцию по крайней мере для одной точки, через которую будет проходить график. Например, мы можем использовать
[латекс] f \ left (\ frac {P} {4} \ right) = A \ tan \ left (B \ frac {P} {4} \ right) = A \ tan \ left (B \ frac {\ pi} {4B} \ right) = A \\ [/ latex]
, потому что [латекс] \ tan \ left (\ frac {\ pi} {4} \ right) = 1 \\ [/ latex].
Как: для функции [latex] f (x) = A \ tan (Bx) \\ [/ latex], построить график с одним периодом.
- Определите коэффициент растяжения | A |.
- Идентифицируйте B и определите период, [latex] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Нарисуйте вертикальные асимптоты в точках [latex] x = — \ frac {P} {2} \\ [/ latex] и [latex] x = \ frac {P} {2} \\ [/ latex].
- Для A > 0 график приближается к левой асимптоте при отрицательных выходных значениях и к правой асимптоте при положительных выходных значениях (обратная для A <0).
- Постройте контрольные точки в [latex] \ left (\ frac {P} {4} \ text {,} A \ right) \\ [/ latex] (0, 0) и ([latex] — \ frac {P } {4} \\ [/ latex], — A) и проведите график через эти точки.
Пример 1: Построение сжатой касательной
Нарисуйте график одного периода функции [latex] y = 0,5 \ tan (\ frac {\ pi} {2} x) \\ [/ latex].
Решение
Сначала мы идентифицируем A и B .
Рисунок 2
Поскольку [латекс] A = 0,5 [/ латекс] и [латекс] B = \ frac {\ pi} {2} \\ [/ latex], мы можем найти коэффициент растяжения / сжатия и период. Период равен [latex] \ frac {\ pi} {\ frac {\ pi} {2}} = 2 \\ [/ latex], поэтому асимптоты находятся в [latex] x = \ pm 1 [/ latex].За четверть периода от начала координат имеем
[латекс] \ begin {array} f (0,5) = 0,5 \ tan (\ frac {0,5 \ pi} {2}) \ hfill & \\ = 0,5 \ tan (\ frac {\ pi} {4}) \ hfill & \\ = 0,5 \ end {array} \\ [/ latex]
Это означает, что кривая должна проходить через точки (0,5,0,5), (0,0) и (-0,5, -0,5). Единственная точка перегиба находится в начале координат. На рисунке показан график одного периода функции.
Рисунок 3
Попробуй 1
Нарисуйте граф [латекс] f (x) = 3 \ tan \ left (\ frac {\ pi} {6} x \ right) \\ [/ latex].
Решение
Построение одного периода функции смещенного касания
Теперь, когда мы можем построить график касательной функции , которая растянута или сжата, мы добавим вертикальный и / или горизонтальный (или фазовый) сдвиг. В этом случае мы добавляем C и D к общей форме касательной функции.
[латекс] f (x) = A \ tan (Bx − C) + D \\ [/ латекс]
График преобразованной касательной функции отличается от базовой тангенциальной функции tan x несколькими способами:
A Общее примечание: особенности графика
y = A tan ( Bx — C ) + D
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {\ pi} {| B |} \\ [/ latex].
- Домен [latex] x \ ne \ frac {C} {B} + \ frac {\ pi} {| B |} k \\ [/ latex], где k — целое число.
- Диапазон составляет (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k \\ [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ tan (Bx) [/ latex] — нечетная функция, потому что это частное нечетных и четных функций (синус и косинус в перспективе).
Как сделать: для функции [latex] y = A \ tan (Bx − C) + D \\ [/ latex] нарисуйте график одного периода.
- Выразите заданную функцию в виде [латекс] y = A \ tan (Bx-C) + D \\ [/ latex].
- Определите коэффициент растяжения / сжатия , | A |.
- Идентифицируйте B и определите период, [latex] P = \ frac {\ pi} {| B |} \\ [/ latex].
- Идентифицируйте C и определите фазовый сдвиг, [latex] \ frac {C} {B} \\ [/ latex].
- Нарисуйте график [latex] y = A \ tan (Bx) \\ [/ latex], сдвинутый вправо на [latex] \ frac {C} {B} \\ [/ latex] и вверх на D .
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k \\ [/ latex], где k — нечетное целое число.
- Постройте любые три контрольные точки и проведите через эти точки график.
Пример 2: Построение графика одного периода функции смещенного касания
Изобразите один период функции [latex] y = −2 \ tan (\ pi x + \ pi) −1 \\ [/ latex].
Решение
Шаг 1. Функция уже записана в виде [латекс] y = A \ tan (Bx − C) + D \\ [/ latex].
Шаг 2. [латекс] A = -2 [/ латекс], поэтому коэффициент растяжения равен [латекс] | A | = 2 [/ латекс].
Шаг 3. [latex] B = \ pi [/ latex], поэтому период равен [latex] P = \ frac {\ pi} {| B |} = \ frac {\ pi} {\ pi} = 1 \\ [/ латекс].
Шаг 4. [latex] C = — \ pi [/ latex], поэтому сдвиг фазы равен [latex] \ frac {C} {B} = \ frac {- \ pi} {\ pi} = — 1 \\[/латекс].
Шаг 5–7. Асимптоты находятся в [latex] x = — \ frac {3} {2} \\ [/ latex] и [latex] x = — \ frac {1} {2} \\ [/ latex] и трех рекомендуемых реперные точки равны (−1.25, 1), (−1, −1) и (−0,75, −3). График показан на рисунке 4.
Рисунок 4
Анализ решения
Обратите внимание, что это убывающая функция, потому что A <0.
Попробуй 2
Как изменился бы график в примере 2, если бы мы сделали A = 2 вместо −2?
Решение
Как: по графику касательной функции определить горизонтальные и вертикальные отрезки.
- Найдите период P на основе расстояния между последовательными вертикальными асимптотами или x -пересечений.
- Запишите [латекс] f (x) = A \ tan (\ frac {\ pi} {P} x) [/ latex].
- Определите удобную точку ( x , f ( x )) на данном графике и используйте ее для определения A .
Пример 3: Определение графика растянутой касательной
Найдите формулу функции, показанной на рисунке 5.
Рисунок 5
Решение
График имеет форму касательной функции.
Шаг 1. Один цикл простирается от –4 до 4, поэтому период составляет [латекс] P = 8 [/ латекс]. Поскольку [latex] P = \ frac {\ pi} {| B |} \\ [/ latex], мы имеем [latex] B = \ frac {\ pi} {P} = \ frac {\ pi} {8} \\[/латекс].
Шаг 2. Уравнение должно иметь вид [latex] \ text {form} f (x) = A \ tan (\ frac {\ pi} {8} x) \\ [/ latex].
Шаг 3. Чтобы найти вертикальный участок A , воспользуемся точкой (2,2).
[латекс] 2 = A \ tan (\ frac {\ pi} {8} \ times2) = A \ tan (\ frac {\ pi} {4}) \\ [/ latex]
Поскольку [латекс] \ tan (\ frac {\ pi} {4}) = 1 \\ [/ latex], A = 2.
Эта функция будет иметь формулу [latex] f (x) = 2 \ tan (\ frac {\ pi} {8} x) \\ [/ latex].
Попробовать 3
Найдите формулу функции на рисунке 6.
Рисунок 6
Решение
Использование графиков тригонометрических функций для решения реальных задач
Многие реальные сценарии представляют периодические функции и могут быть смоделированы тригонометрическими функциями. В качестве примера вернемся к сценарию из начала раздела.Вы когда-нибудь наблюдали луч, образованный вращающимся светом на полицейской машине, и задавались вопросом о движении самого светового луча по стене? Периодическое поведение расстояния, на которое светит свет, как функция времени, очевидно, но как определить расстояние? Мы можем использовать касательную функцию.
Пример 4: Использование тригонометрических функций для решения реальных сценариев
Предположим, что функция [latex] y = 5 \ tan \ left (\ frac {\ pi} {4} t \ right) \\ [/ latex] отмечает расстояние в движении светового луча от верха полицейского автомобиль через стену, где t — время в секундах, а y — расстояние в футах от точки на стене прямо напротив полицейской машины.
- Найдите и интерпретируйте фактор растяжения и период.
- График на интервале [0, 5].
- Вычислите f (1) и обсудите значение функции на этом входе.
Решение
- Мы знаем из общего вида [latex] y = A \ tan (Bt) \\ [/ latex], что | A | — коэффициент растяжения, а π B — период.
Рисунок 7
Мы видим, что коэффициент растяжения равен 5. Это означает, что луч света переместится на 5 футов через половину периода.
Период [латекс] \ frac {\ pi} {\ frac {\ pi} {4}} = \ frac {\ pi} {1} \ times \ frac {4} {\ pi} = 4 \\ [ /латекс]. Это означает, что каждые 4 секунды луч света скользит по стене. Расстояние от места напротив полицейской машины увеличивается по мере приближения полицейской машины.
- Чтобы построить график функции, мы рисуем асимптоту при [latex] t = 2 [/ latex] и используем коэффициент растяжения и период. См. Рисунок 8.
Рисунок 8
- : [латекс] f (1) = 5 \ tan \ left (\ frac {\ pi} {4} \ left (1 \ right) \ right) = 5 \ left (1 \ right) = 5 \\ [ /латекс]; через 1 секунду луч переместился на 5 футов с места напротив полицейской машины.
Период
Анализ графиков y = sec x и y = cscx и их вариаций
Секущая была определена обратной идентичностью [латекс] \ sec x = \ frac {1} {\ cos x} [/ latex]. Обратите внимание, что функция не определена, когда косинус равен 0, что приводит к вертикальным асимптотам в [latex] \ frac {\ pi} {2} \ text {,} \ frac {3 \ pi} {2} \ text {и т. Д.} [/латекс]. Поскольку косинус никогда не превышает 1 по абсолютной величине, секанс, будучи обратной величиной, никогда не будет меньше 1 по абсолютной величине.
Мы можем построить график [latex] y = \ sec x [/ latex], наблюдая за графиком функции косинуса, потому что эти две функции являются обратными друг другу. См. Рисунок 9. График косинуса показан оранжевой пунктирной волной, поэтому мы можем видеть взаимосвязь. Когда график функции косинуса уменьшается, график функции секущей увеличивается. Когда график функции косинуса увеличивается, график функции секущей уменьшается. Когда функция косинуса равна нулю, секанс не определен.
Секущий график имеет вертикальные асимптоты при каждом значении x , где косинусный график пересекает ось x ; мы показываем их на приведенном ниже графике пунктирными вертикальными линиями, но не будем показывать явно все асимптоты на всех последующих графиках, включающих секанс и косеканс.
Обратите внимание: поскольку косинус является четной функцией, секанс также является четной функцией. То есть [латекс] \ сек (-x) = \ сек x [/ латекс].
Рис. 9. График функции секущей, [латекс] f (x) = \ sec x = \ frac {1} {\ cos x} [/ latex]
Как и для касательной функции, мы снова обратимся к константе | A | как фактор растяжения, а не амплитуда.
A Общее примечание: особенности графика
y = A сек ( Bx )
- Коэффициент растяжения | A |.
- Период [латекс] \ frac {2 \ pi} {| B |} [/ латекс].
- Домен [латекс] x \ ne \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Диапазон составляет (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются при [latex] x = \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ sec (Bx) [/ latex] — четная функция, потому что косинус — четная функция.
Подобно секансу, косеканс определяется обратной идентичностью [латекс] \ csc x = 1 \ sin x [/ latex]. Обратите внимание, что функция не определена, когда синус равен 0, что приводит к вертикальной асимптоте на графике в точках 0, π и т. Д. Поскольку синус никогда не превышает 1 по абсолютной величине, косеканс, будучи обратной величиной, никогда не будет меньше чем 1 по абсолютной величине.
Мы можем построить график [latex] y = \ csc x [/ latex], наблюдая за графиком синусоидальной функции, потому что эти две функции являются обратными друг другу. См. Рисунок 10. График синуса показан оранжевой пунктирной волной, поэтому мы можем видеть взаимосвязь. Когда график синусоидальной функции уменьшается, график функции косеканса увеличивается. Когда график функции синуса увеличивается, график функции косеканса уменьшается.
График косеканса имеет вертикальные асимптоты при каждом значении x , где синусоидальный график пересекает ось x ; мы показываем их на графике ниже вертикальными пунктирными линиями.
Обратите внимание, что, поскольку синус является нечетной функцией, функция косеканса также является нечетной функцией. То есть [латекс] \ csc (−x) = — \ csc x [/ latex].
График косеканса, показанный на рисунке 10, аналогичен графику секанса.
Рис. 10. График функции косеканса, [латекс] f (x) = \ csc x = 1 \ sin x [/ latex]
Общее примечание: особенности графика [латекса] y = A \ csc (Bx)
- Коэффициент растяжения | A |.
- Период [латекс] \ frac {2 \ pi} {| B |} [/ латекс].
- Домен [латекс] x \ ne \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон равен (−∞, — | A |] ∪ [| A |, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- [latex] y = A \ csc (Bx) [/ latex] — это нечетная функция, потому что синус — нечетная функция.
Графические вариации
y = sec x и y = csc x
Для смещенных, сжатых и / или растянутых версий секущих и косекансных функций мы можем использовать методы, аналогичные тем, которые мы использовали для тангенса и котангенса.То есть мы располагаем вертикальные асимптоты, а также оцениваем функции для нескольких точек (в частности, локальных экстремумов). Если мы хотим построить график только для одного периода, мы можем выбрать интервал для периода более чем одним способом. Процедура для секанса очень похожа, потому что идентичность кофункции означает, что граф секанса такой же, как граф косеканса, сдвинутый на полпериода влево. Вертикальный и фазовый сдвиги могут применяться к функции секущей таким же образом, как для секущей и других функций.Уравнения становятся следующими.
[латекс] y = A \ sec (Bx-C) + D [/ латекс]
[латекс] y = A \ csc (Bx-C) + D [/ латекс]
Общее примечание: особенности графика [латекса] y = A \ sec (Bx-C) + D [/ latex]
- Коэффициент растяжения | A |.
- Период [латекс] \ frac {2 \ pi} {| B |} [/ латекс].
- Домен [латекс] x \ ne \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Диапазон составляет (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
- Нет амплитуды.
- [latex] y = A \ sec (Bx) [/ latex] — четная функция, потому что косинус — четная функция.
Общее примечание: особенности графика [латекса] y = A \ csc (Bx-C) + D [/ latex]
- Коэффициент растяжения | A |.
- Период [латекс] \ frac {2 \ pi} {| B |} [/ латекс].
- Домен [латекс] x \ ne \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — целое число.
- Диапазон составляет (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Нет амплитуды.
- [latex] y = A \ csc (Bx) [/ latex] — это нечетная функция, потому что синус — нечетная функция.
Как: для функции вида [latex] y = A \ sec (Bx) [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ sec (Bx) [/ latex].
- Определите коэффициент растяжения / сжатия | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {2 \ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ cos (Bx) [/ latex].
- Используйте обратную связь между [latex] y = \ cos x [/ latex] и [latex] y = \ sec x [/ latex], чтобы нарисовать график [latex] y = A \ sec (Bx) [/ latex ].
- Изобразите асимптоты.
- Постройте любые две контрольные точки и проведите через эти точки график.
Пример 6: График изменения секущей функции
Изобразите один период [латекса] f (x) = 2,5 \ сек (0,4x) [/ latex].
Решение
Шаг 1. Данная функция уже записана в общем виде [latex] y = A \ sec (Bx) [/ latex].
Шаг 2. [латекс] A = 2,5 [/ латекс], поэтому коэффициент растяжения равен 2,5.
Шаг 3. [латекс] B = 0,4 [/ латекс], поэтому [латекс] P = \ frac {2 \ pi} {0,4} = 5 \ pi [/ латекс]. Период равен 5π единиц.
Шаг 4. Нарисуйте график функции [латекс] g (x) = 2,5 \ cos (0,4x) [/ latex].
Шаг 5. Используйте обратную связь функций косинуса и секанса, чтобы нарисовать функцию косеканса.
Шаги 6–7. Нарисуйте две асимптоты в [latex] x = 1,25 \ pi [/ latex] и [latex] x = 3,75 \ pi [/ latex]. Мы можем использовать две реперные точки: локальный минимум в (0, 2,5) и локальный максимум в (2,5π, −2,5). На рисунке 11 показан график.
Рисунок 11
Попробовать 4
Изобразите один период [латекса] f (x) = — 2.5 \ сек (0.4x) [/ латекс].
Решение
Вопросы и ответы
Влияют ли вертикальное смещение и растяжение / сжатие на диапазон секущей?
Да. Диапазон f (x) = A сек ( Bx — C ) + D равен (−∞, — | A | + D] ∪ [| A | + D, ∞) .
Как сделать: для функции вида [латекс] f (x) = A \ sec (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ sec (Bx-C) + D [/ latex].
- Определите коэффициент растяжения / сжатия, | A |.
- Идентифицируйте B и определите период, [latex] \ frac {2 \ pi} {| B |} [/ latex].
- Определите C и определите фазовый сдвиг, [latex] \ frac {C} {B} [/ latex].
- Нарисуйте график [латекс] y = A \ sec (Bx) [/ latex]. но сместите его вправо на [latex] \ frac {C} {B} [/ latex] и вверх на D .
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {2 | B |} k [/ latex], где k — нечетное целое число.
Пример 7: График изменения секущей функции
Изобразите один период [latex] y = 4 \ sec \ left (\ frac {\ pi} {3} x− \ frac {\ pi} {2} \ right) +1 [/ latex].
Решение
Шаг 1. Выразите заданную функцию в виде [latex] y = 4 \ sec \ left (\ frac {\ pi} {3} x− \ frac {\ pi} {2} \ right) +1 [ /латекс].
Шаг 2. Коэффициент растяжения / сжатия | A | = 4,
Шаг 3. Период
[латекс] \ begin {array} \ frac {2 \ pi} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {3}} \ hfill & \\ = \ frac {2 \ pi} {1} \ times \ frac {3} {\ pi} \ hfill & \\ = 6 \ end {array} [/ latex]
Шаг 4. Фазовый сдвиг
[латекс] \ begin {array} \ frac {C} {B} = \ frac {\ frac {\ pi} {2}} {\ frac {\ pi} {3}} \ hfill & \\ = \ frac { \ pi} {2} \ times \ frac {3} {\ pi} \ hfill & \\ = 1.5 \ end {array} [/ latex]
Шаг 5. Нарисуйте график [latex] y = A \ sec (Bx) [/ latex], но сдвиньте его вправо на [latex] \ frac {C} {B} = 1,5 [/ latex] и выше на D = 6.
Шаг 6. Нарисуйте вертикальные асимптоты, которые возникают при x = 0, x = 3 и x = 6.Существует локальный минимум в (1.5, 5) и локальный максимум в (4.5, −3). На рисунке 12 показан график.
Рисунок 12
Попробовать 5
Изобразите один период [латекса] f (x) = — 6 \ сек (4x + 2) −8 [/ latex].
Решение
Вопросы и ответы
Домен csc
x был задан как все x , так что [latex] x \ ne k \ pi [/ latex] для любого целого числа k . Будет ли домен [latex] y = A \ csc (Bx − C) + D [/ latex] быть [latex] x \ ne \ frac {C + k \ pi} {B} [/ latex]?
Да.Исключенные точки области следуют вертикальным асимптотам. Их расположение показывает горизонтальный сдвиг и сжатие или расширение, подразумеваемые преобразованием входных данных исходной функции.
Как: для функции вида [latex] y = A \ csc (Bx) [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [latex] y = A \ csc (Bx) [/ latex].
- | A |.
- Идентифицируйте B и определите период, [латекс] P = \ frac {2 \ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ sin (Bx) [/ latex].
- Используйте обратную связь между [latex] y = \ sin x [/ latex] и [latex] y = \ csc x [/ latex], чтобы нарисовать график [latex] y = A \ csc (Bx) [/ latex ].
- Изобразите асимптоты.
- Постройте любые две контрольные точки и проведите через эти точки график.
Пример 8: График изменения функции косеканса
Изобразите один период [латекса] f (x) = — 3 \ csc (4x) [/ latex].
Решение
Шаг 1. Данная функция уже записана в общем виде [latex] y = A \ csc (Bx) [/ latex].
Шаг 2. [латекс] | A | = | −3 | = 3 [/ латекс], поэтому коэффициент растяжения равен 3.
Шаг 3. [латекс] B = 4 \ text {, поэтому} P = \ frac {2 \ pi} {4} = \ frac {\ pi} {2} [/ latex]. Точка [латекс ] \ frac {\ pi} {2} [/ latex] единиц.
Шаг 4. Нарисуйте график функции [latex] g (x) = — 3 \ sin (4x) [/ latex].
Шаг 5. Используйте взаимное соотношение функций синуса и косеканса, чтобы построить функцию косеканса.
Шаги 6–7. Нарисуйте три асимптоты в [latex] x = 0 \ text {,} x = \ frac {\ pi} {4} \ text {и} x = \ frac {\ pi} {2} [/ latex]. Мы можно использовать две опорные точки: локальный максимум в [latex] \ left (\ frac {\ pi} {8} \ text {,} −3 \ right) [/ latex] и локальный минимум в [latex] \ left ( \ frac {3 \ pi} {8} \ text {,} 3 \ right) [/ latex]. На рисунке 13 показан график.
Рисунок 13
Попробуй 6
Изобразите один период [латекса] f (x) = 0,5 \ csc (2x) [/ latex].
Решение
Как сделать: для функции вида [латекс] f (x) = A \ csc (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите заданную функцию в виде [латекс] y = A \ csc (Bx-C) + D [/ latex].
- Определите коэффициент растяжения / сжатия, | A |.
- Идентифицируйте B и определите период, [latex] \ frac {2 \ pi} {| B |} [/ latex].
- Определите C и определите фазовый сдвиг, [latex] \ frac {C} {B} [/ latex].
- Нарисуйте график [latex] y = A \ csc (Bx) [/ latex], но сдвиньте его вправо на D вверх и вниз.
- Нарисуйте вертикальные асимптоты, которые встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
Пример 9: Графическое изображение косеканса, растянутого по вертикали, сжатого по горизонтали и смещенного по вертикали
Нарисуйте график [латекс] y = 2 \ csc \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex]. Каковы область и диапазон этой функции?
Решение
Шаг 1. Выразите заданную функцию в виде [латекс] y = 2 \ csc \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex].
Шаг 2. Определите коэффициент растяжения / сжатия, [латекс] | A | = 2 [/ латекс].
Шаг 3. Период [latex] \ frac {2 \ pi} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {2}} = \ frac {2 \ pi } {1} \ times \ frac {2} {\ pi} = 4 [/ латекс].
Шаг 4. Фазовый сдвиг [latex] \ frac {0} {\ frac {\ pi} {2}} = 0 [/ latex].
Шаг 5. Нарисуйте график [латекс] y = A \ csc (Bx) [/ latex], но сдвиньте его вверх [latex] D = 1 [/ latex].
Шаг 6. Нарисуйте вертикальные асимптоты, которые возникают при x = 0, x = 2, x = 4.
График этой функции показан на рисунке 14.
Рисунок 14
Анализ решения
Вертикальные асимптоты, показанные на графике, отмечают один период функции, а локальные экстремумы в этом интервале показаны точками. Обратите внимание, как график преобразованного косеканса соотносится с графиком [latex] f (x) = 2 \ sin \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex], показанным как оранжевая пунктирная волна.
Попробуйте 7
Учитывая график [латекса] f (x) = 2 \ cos \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex], показанный на рисунке 15, нарисуйте график [латекса] g (x) = 2 \ sec \ left (\ frac {\ pi} {2} x \ right) +1 [/ latex] на тех же осях.
Рисунок 15
Решение
Анализ графика y = cot x и его вариаций
Последняя тригонометрическая функция, которую нам нужно изучить, — это котангенс . Котангенс определяется обратной идентичностью [латекс] \ cot x = \ frac {1} {\ tan x} [/ latex]. Обратите внимание, что функция не определена, когда функция тангенса равна 0, что приводит к вертикальной асимптоте на графике в точках 0, π и т. Д. Поскольку выходные данные функции касательной являются действительными числами, выходные данные функции котангенса также являются все реальные числа.
Мы можем построить график [latex] y = \ cot x [/ latex], наблюдая за графиком касательной функции, потому что эти две функции являются обратными друг другу. См. Рисунок 16. Если график функции тангенса уменьшается, график функции котангенса увеличивается. Когда график функции тангенса увеличивается, график функции котангенса уменьшается.
Граф котангенса имеет вертикальные асимптоты при каждом значении x , где [latex] \ tan x = 0 [/ latex]; мы показываем их на графике ниже пунктирными линиями.Поскольку котангенс является обратной величиной касательной, [latex] \ cot x [/ latex] имеет вертикальные асимптоты при всех значениях x , где [latex] \ tan x = 0 [/ latex] и [latex] \ cot x = 0 [/ latex] при всех значениях x, где tan x имеет свои вертикальные асимптоты.
Рисунок 16. Функция котангенса
A Общее примечание: особенности графика
y = A кроватка ( Bx )
- Коэффициент растяжения | A |.
- Период [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Домен [латекс] x \ ne \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон составляет (−∞, ∞).
- Асимптоты встречаются в [latex] x = \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- [latex] y = A \ cot (Bx) [/ latex] — это нечетная функция.
Графические вариации
y = детская кроватка x
Мы можем преобразовать график котангенса почти так же, как мы это сделали для тангенса. Уравнение становится следующим.
[латекс] y = A \ cot (Bx − C) + D [/ латекс]
A Общее примечание: Свойства графика
y = A кроватка ( Bx −C) + D
- Коэффициент растяжения | A |.
- Точка [латекс] \ frac {\ pi} {| B |} [/ latex].
- Домен [latex] x \ ne \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Диапазон составляет (−∞, — | A |] ∪ [| A |, ∞).
- Вертикальные асимптоты встречаются в [latex] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Нет амплитуды.
- [latex] y = A \ cot (Bx) [/ latex] — нечетная функция, потому что это частное четных и нечетных функций (косинус и синус соответственно)
Как сделать: для данной модифицированной функции котангенса вида [латекс] f (x) = A \ cot (Bx) [/ latex], построить график с одним периодом.
- Выразите функцию в виде [латекс] f (x) = A \ cot (Bx) [/ latex].
- Определите коэффициент растяжения, | A |.
- Определите период, [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Нарисуйте график [латекс] y = A \ tan (Bx) [/ latex].
- Постройте любые две опорные точки.
- Используйте взаимное отношение между тангенсом и котангенсом, чтобы нарисовать график [латекс] y = A \ cot (Bx) [/ latex].
- Изобразите асимптоты.
Пример 10: Графики вариаций функции котангенса
Определите коэффициент растяжения, период и фазовый сдвиг [latex] y = 3 \ cot (4x) [/ latex], а затем нарисуйте график.
Решение
Шаг 1. Выражение функции в виде [латекс] f (x) = A \ cot (Bx) [/ latex] дает [latex] f (x) = 3 \ cot (4x) [/ latex].
Шаг 2. Коэффициент растяжения [латекс] | A | = 3 [/ латекс].
Шаг 3. Период [латекс] P = \ frac {\ pi} {4} [/ latex].
Шаг 4. Нарисуйте график [латекса] y = 3 \ tan (4x) [/ latex].
Шаг 5. Постройте две контрольные точки. Две такие точки: [latex] \ left (\ frac {\ pi} {16} \ text {,} 3 \ right) [/ latex] и [latex] \ left (\ frac {3 \ pi} {16} \ текст {,} −3 \ right) [/ latex].
Шаг 6. Используйте взаимное отношение, чтобы нарисовать [латекс] y = 3 \ cot (4x) [/ latex].
Шаг 7. Нарисуйте асимптоты, [latex] x = 0 [/ latex], [latex] x = \ frac {\ pi} {4} [/ latex].
Оранжевый график на Рисунке 17 показывает [латекс] y = 3 \ tan (4x) [/ latex], а синий график показывает [латекс] y = 3 \ cot (4x) [/ latex].
Рисунок 17
Как сделать: для данной модифицированной функции котангенса вида [латекс] f (x) = A \ cot (Bx − C) + D [/ latex], построить график с одним периодом.
- Выразите функцию в виде [латекс] f (x) = A \ cot (Bx-C) + D [/ latex].
- Определите коэффициент растяжения, | A |.
- Определите период, [латекс] P = \ frac {\ pi} {| B |} [/ latex].
- Определите фазовый сдвиг, [latex] \ frac {C} {B} [/ latex].
- Нарисуйте график [latex] y = A \ tan (Bx) [/ latex], сдвинутый вправо на [latex] \ frac {C} {B} [/ latex] и вверх на D .
- Нарисуйте асимптоты [латекс] x = \ frac {C} {B} + \ frac {\ pi} {| B |} k [/ latex], где k — целое число.
- Постройте любые три контрольные точки и проведите через эти точки график.
Пример 11: Построение модифицированного котангенса
Нарисуйте график одного периода функции [latex] f (x) = 4 \ cot (\ frac {\ pi} {8} x− \ frac {\ pi} {2}) — 2 [/ latex].
Решение
Шаг 1. Функция уже записана в общем виде [latex] f (x) = A \ cot (Bx − C) + D [/ latex].
Шаг 2. [латекс] A = 4 [/ латекс], поэтому коэффициент растяжения равен 4.
Шаг 3. [latex] B = \ frac {\ pi} {8} [/ latex], поэтому период равен [latex] P = \ frac {\ pi} {| B |} = \ frac {\ pi} {\ frac {\ pi} {8}} = 8 [/ latex].
Шаг 4. [latex] C = \ frac {\ pi} {2} [/ latex], поэтому сдвиг фазы равен [latex] \ frac {C} {B} = \ frac {\ frac {\ pi } {2}} {\ frac {\ pi} {8}} = 4 [/ латекс].
Шаг 5. Рисуем [латекс] f (x) = 4 \ tan \ left (\ frac {\ pi} {8} x− \ frac {\ pi} {2} \ right) −2 [/ latex ].
Шаг 6-7. Три точки, которые мы можем использовать для построения графика, — это (6,2), (8, −2) и (10, −6).Мы используем взаимное отношение тангенса и котангенса, чтобы нарисовать [латекс] f (x) = 4 \ cot (\ frac {\ pi} {8} x− \ frac {\ pi} {2}) — 2 [/ latex] .
Шаг 8. Вертикальные асимптоты [латекс] x = 4 [/ латекс] и [латекс] x = 12 [/ латекс].
График показан на рисунке 18.
Рисунок 18. Один период модифицированной функции котангенса.
Ключевые уравнения
| Функция сдвига, сжатия и / или растяжения по касательной | [латекс] y = A \ tan (Bx-C) + D [/ латекс] |
| Сдвинутая, сжатая и / или растянутая секущая функция | [латекс] y = A \ sec (Bx-C) + D [/ латекс] |
| Сдвинутый, сжатый и / или растянутый косеканс | [латекс] y = A \ csc (Bx-C) + D [/ латекс] |
| Функция котангенса со смещением, сжатием и / или растяжением | [латекс] y = A \ cot (Bx-C) + D [/ латекс] |
Ключевые понятия
- Касательная функция имеет период π.
- [латекс] f (x) = A \ tan (Bx-C) + D [/ latex] представляет собой касательную с вертикальным и / или горизонтальным растяжением / сжатием и сдвигом.
- Секанс и косеканс — периодические функции с периодом 2π. [latex] f (x) = A \ sec (Bx-C) + D [/ latex] дает сдвинутый, сжатый и / или растянутый график функции секущей.
- [latex] f (x) = A \ csc (Bx-C) + D [/ latex] дает смещенный, сжатый и / или растянутый график функции косеканса.
- Функция котангенса имеет период π и вертикальные асимптоты в точках 0, ± π, ± 2π,….
- Диапазон котангенса равен (−∞, ∞), и функция убывает в каждой точке своего диапазона.
- Котангенс равен нулю в [latex] \ ne \ frac {\ pi} {2} \ text {,} \ ne \ frac {3 \ pi} {2} [/ latex],….
- [латекс] f (x) = A \ cot (Bx-C) + D [/ latex] — котангенс с вертикальным и / или горизонтальным растяжением / сжатием и сдвигом.
- Реальные сценарии могут быть решены с использованием графиков тригонометрических функций.
Упражнения по разделам
1. Объясните, как можно использовать график синусоидальной функции для построения графика [латекс] y = \ csc x [/ latex].
2. Как можно использовать график [latex] y = \ cos x [/ latex] для построения графика [latex] y = \ sec x [/ latex]?
3. Объясните, почему период [latex] \ tan x [/ latex] равен π.
4. Почему на графике [latex] y = \ csc x [/ latex] нет перехватов?
5. Как период [latex] y = \ csc x [/ latex] сравнивается с периодом [latex] y = \ sin x [/ latex]?
Для следующих упражнений сопоставьте каждую тригонометрическую функцию с одним из следующих графиков.
6. [латекс] f (x) = \ tan x [/ латекс]
7. [латекс] f (x) = \ sec x [/ латекс]
8. [латекс] f (x) = \ csc x [/ латекс]
9. [латекс] f (x) = \ cot x [/ латекс]
Для следующих упражнений найдите период и горизонтальный сдвиг каждой функции.
10. [латекс] f (x) = 2 \ tan (4x − 32) [/ латекс]
11. [латекс] h (x) = 2 \ sec \ left (\ frac {\ pi} {4} (x + 1) \ right) [/ latex]
12. [латекс] m (x) = 6 \ csc \ left (\ frac {\ pi} {3} x + \ pi \ right) [/ latex]
13.Если tan x = −1,5, найдите tan (−x).
14. Если sec x = 2, найдите sec (- x ).
15. Если csc x = −5, найдите csc (- x ).
16. Если [латекс] x \ sin x = 2 [/ latex], найдите [латекс] (- x) \ sin (−x) [/ latex].
Для следующих упражнений перепишите каждое выражение так, чтобы аргумент x был положительным.
17. [латекс] \ cot (−x) \ cos (−x) + \ sin (−x) [/ latex]
18. [латекс] \ cos (−x) + \ tan (−x) \ sin (−x) [/ latex]
Для следующих упражнений нарисуйте два периода графика для каждой из следующих функций.Определите коэффициент растяжения, период и асимптоты.
19. [латекс] f (x) = 2 \ tan (4x − 32) [/ латекс]
20. [латекс] h (x) = 2 \ sec \ left (\ frac {\ pi} {4} \ left (x + 1 \ right) \ right) [/ latex]
21. [латекс] m (x) = 6 \ csc \ left (\ frac {\ pi} {3} x + \ pi \ right) [/ latex]
22. [латекс] j (x) = \ tan \ left (\ frac {\ pi} {2} x \ right) [/ latex]
23. [латекс] p (x) = \ tan \ left (x− \ frac {\ pi} {2} \ right) [/ latex]
24. [латекс] f (x) = 4 \ tan (x) [/ латекс]
25. [латекс] f (x) = \ tan \ left (x + \ frac {\ pi} {4} \ right) [/ latex]
26.[латекс] f (x) = \ pi \ tan \ left (\ pi x− \ pi \ right) — \ pi [/ latex]
27. [латекс] f (x) = 2 \ csc (x) [/ латекс]
28. [латекс] f (x) = — \ frac {1} {4} \ csc (x) [/ latex]
29. [латекс] f (x) = 4 \ сек (3x) [/ латекс]
30. [латекс] f (x) = — 3 \ cot (2x) [/ латекс]
31. [латекс] f (x) = 7 \ сек (5x) [/ латекс]
32. [латекс] f (x) = \ frac {9} {10} \ csc (\ pi x) [/ latex]
33. [латекс] f (x) = 2 \ csc \ left (x + \ frac {\ pi} {4} \ right) −1 [/ latex]
34. [латекс] f (x) = — \ sec \ left (x− \ frac {\ pi} {3} \ right) −2 [/ latex]
35.[латекс] f (x) = \ frac {7} {5} \ csc \ left (x− \ frac {\ pi} {4} \ right) [/ latex]
36. [латекс] f (x) = 5 \ left (\ cot \ left (x + \ frac {\ pi} {2} \ right) −3 \ right) [/ latex]
Для следующих упражнений найдите и изобразите два периода периодической функции с заданным коэффициентом растяжения | A |, период и фазовый сдвиг.
37. Касательная кривая, [латекс] A = 1 [/ latex], период [латекс] \ frac {\ pi} {3} [/ latex]; и фазовый сдвиг [латекс] (h \ text {,} k) = \ left (\ frac {\ pi} {4} \ text {,} 2 \ right) [/ latex]
38.Касательная кривая, [латекс] A = −2 [/ latex], период [латекс] \ frac {\ pi} {4} [/ latex] и фазовый сдвиг [латекс] (h \ text {,} k) = \ left (- \ frac {\ pi} {4} \ text {,} — 2 \ right) [/ latex]
Для следующих упражнений найдите уравнение для графика каждой функции.
39.
40.
41.
42.
43.
44.
45.
47. {2} (x) [/ latex].{2} х [/ латекс]
54. Функция [latex] f (x) = 20 \ tan \ left (\ frac {\ pi} {10} x \ right) [/ latex] отмечает расстояние в движении светового луча от полицейской машины. поперек стены на время x в секундах и расстояние [латекс] f (x) [/ латекс] в футах.
а. График на интервале [0,5].
г. Найдите и интерпретируйте фактор растяжения, период и асимптоту.
г. Оцените f (1) и f (2.5) и обсудите значения функции на этих входах.
55. Стоя на берегу озера, рыбак видит вдалеке лодку слева от себя.Пусть x , измеренный в радианах, будет углом, образованным линией обзора корабля и линией на север от его местоположения. Предположим, что север равен 0, а x измеряется отрицательно слева и положительно справа. (См. Рис. 19.) Лодка движется с запада на восток, и, игнорируя кривизну Земли, расстояние [латекс] d (x) [/ латекс] в километрах от рыбака до лодки определяется выражением функция [латекс] d (x) = 1,5 \ сек (x) [/ latex].
а. Каков разумный домен для [latex] d (x) [/ latex]?
г.График d (x) в этой области.
г. Найдите и обсудите значение любых вертикальных асимптот на графике [latex] d (x) [/ latex].
г. Вычислить и интерпретировать [латекс] d (- \ frac {\ pi} {3}) [/ latex]. Округлить до второго десятичного знака.
e. Вычислить и интерпретировать [латекс] d (\ frac {\ pi} {6}) [/ latex]. Округлить до второго десятичного знака.
ф. Какое минимальное расстояние между рыбаком и лодкой? Когда это происходит?
Рисунок 19
56. Лазерный дальномер зафиксирован на приближающейся к Земле комете.Расстояние [latex] g (x) [/ latex] в километрах от кометы после x дней для x в интервале от 0 до 30 дней определяется как [latex] g (x) = 250,000. \ csc (\ frac {\ pi} {30} x) [/ latex].
а. График [latex] g (x) [/ latex] на интервале [0,35].
г. Оцените [latex] g (5) [/ latex] и интерпретируйте информацию.
г. Какое минимальное расстояние между кометой и Землей? Когда это происходит? Какой константе в уравнении это соответствует?
г. Найдите и обсудите значение любых вертикальных асимптот.
57. Видеокамера сфокусирована на ракете на стартовой площадке в 2 милях от камеры. Угол подъема от земли до ракеты через x секунд составляет [latex] \ frac {\ pi} {120} x [/ latex].
а. Напишите функцию, выражающую высоту [латекс] h (x) [/ latex] в милях над землей после x секунд. Игнорируйте кривизну Земли.
г. График [latex] h (x) [/ latex] на интервале (0,60).
г. Оцените и интерпретируйте значения [латекс] h (0) [/ латекс] и [латекс] h (30) [/ латекс].
г. Что происходит со значениями [latex] h (x) [/ latex], когда x приближается к 60 секундам? Интерпретируйте значение этого с точки зрения проблемы.
График функции касания — Тригонометрия
График функции касания — Тригонометрия — Открытый справочник по математике
Тангенс угла откладывается от этой меры угла.
Попробуй это
Перетащите
вершине треугольника и посмотрите, как функция касательной изменяется с углом.
Чтобы построить график функции касательной, мы отмечаем угол по горизонтальной оси x, и для каждого угла мы помещаем тангенс этого угла на вертикальную ось y. Результат, как видно выше, представляет собой довольно изрезанную кривую, которая уходит в положительную бесконечность в одном направлении и в отрицательную бесконечность в другом.
На схеме выше перетащите точку A по круговой траектории, чтобы изменить угол CAB. При этом точка на графике перемещается в соответствии с углом и касательной к нему.(Если вы отметите поле «прогрессивный режим», кривая будет нарисована по мере перемещения точки A, а не по существующей кривой.)
Область касательной функции имеет дыры
Когда вы перетаскиваете точку A вокруг, обратите внимание, что после полного поворота вокруг точки B форма графика повторяется. Форма касательной кривой одинакова для каждого полного поворота угла, поэтому функция называется «периодической». Период функции равен 360 ° или 2π радиан.
Вы можете вращать точку сколько угодно раз.
Это означает, что вы можете найти тангенс любого угла, независимо от его размера, за одним исключением.
Если вы посмотрите на график выше, вы увидите, что tan90 ° не определен, потому что он требует деления на ноль.
Следовательно, такие углы не входят в область функций tan и дают неопределенный результат. Пытаться
tan90 ° на вашем калькуляторе, и вы получите ошибку, тогда как, скажем, 89,99 будет работать.
Таким образом, домен функции tan — это набор всех действительных чисел , кроме 90 °, -90 °, 270 °, -270 ° и т. Д.(или эквивалент в радианах: плюс / минус пи более 2, 3 пи более 2 и т. д.).
Диапазон
Диапазон функции — это набор значений результата, которые она может произвести. Функция касательной имеет диапазон от положительной бесконечности до отрицательной бесконечности.
Чтобы понять, почему это происходит, нажмите «Сброс», затем перетащите точку A против часовой стрелки. По мере приближения к точке 90 ° с почти вертикальным AB, вы можете видеть, что BC становится очень маленьким. Поскольку тангенс угла равен «противоположному по соседнему» (TOA), в результате деления числа на очень маленькое число получается очень большое.В конце концов, сторона BC приближается к нулю, а результат стремится к бесконечности.
То же самое происходит во втором квадранте, за исключением того, что BC тогда отрицательна, и поэтому функция приближается к отрицательной бесконечности.
Бесконечность не является действительным числом, поэтому tan90 ° фактически не определен. Однако, когда угол приближается к 90 °, функция возвращает очень большие числа. Например, загар (89,999 °) превышает 57000.
Функция арктангенса
Что, если бы нас попросили найти арктангенс числа, скажем 4.0? Другими словами, мы ищем угол, загар которого равен 4,0.
Если мы посмотрим на кривую выше, мы увидим четыре угла, тангенс которых равен 4,0 (красные точки). Фактически, поскольку график продолжается бесконечно в обоих направлениях, существует бесконечное количество углов, тангенс которых имеет заданное значение.
Так что же говорит калькулятор?
Если вы попросите калькулятор указать арктангенс (tan -1 или atan) числа, он не сможет вернуть бесконечно длинный список углов, поэтому по соглашению он находит только первый.Но помните, что их гораздо больше.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
графиков тангенса и котангенса | Блестящая вики по математике и науке
Из определения функций тангенса и котангенса имеем
tan (θ) = sin (θ) cos (θ), cot (θ) = cos (θ) sin (θ).\ tan (\ theta) = \ frac {\ sin (\ theta)} {\ cos (\ theta)}, \ quad \ cot (\ theta) = \ frac {\ cos (\ theta)} {\ sin (\ theta)}. tan (θ) = cos (θ) sin (θ), cot (θ) = sin (θ) cos (θ).
Таким образом, tan (θ) \ tan (\ theta) tan (θ) не определен для значений θ \ thetaθ таких, что cos (θ) = 0 \ cos (\ theta) = 0cos (θ) = 0. Теперь рассмотрим график cos (θ) \ cos (\ theta) cos (θ):
Из этого графика мы видим, что cos (θ) = 0 \ cos (\ theta) = 0cos (θ) = 0, когда θ = π2 + kπ \ theta = \ frac {\ pi} {2} + k \ piθ = 2π + kπ для любого целого kkk.Это означает, что касательная функция имеет вертикальные асимптоты при этих значениях θ \ thetaθ.
Стремится ли касательная функция к положительной или отрицательной бесконечности в этих асимптотах? Когда θ \ thetaθ приближается к π2 \ frac {\ pi} {2} 2π снизу (θ \ big (\ theta (θ принимает значения меньше π2 \ frac {\ pi} {2} 2π, приближаясь к π2), \ frac {\ pi} {2} \ big), 2π), sin (θ) \ sin (\ theta) sin (θ) принимает положительные значения, которые все ближе и ближе к 111, а cos ( θ) \ cos (\ theta) cos (θ) принимает положительные значения, которые все ближе и ближе к 000.Это показывает, что tan (θ) = sin (θ) cos (θ) \ tan (\ theta) = \ frac {\ sin (\ theta)} {\ cos (\ theta)} tan (θ) = cos ( θ) sin (θ) положительно и стремится к бесконечности, поэтому tan (θ) \ tan (\ theta) tan (θ) имеет положительную вертикальную асимптоту при θ → π2 \ theta \ rightarrow \ frac {\ pi} {2 } θ → 2π снизу. По аналогичному анализу, когда θ \ thetaθ приближается к π2 \ frac {\ pi} {2} 2π сверху (θ \ big (\ theta (θ принимает значения больше, чем π2 \ frac {\ pi} {2} 2π, в то время как все ближе и ближе к π2), \ frac {\ pi} {2} \ big), 2π), sin (θ) \ sin (\ theta) sin (θ) принимает положительные значения, которые все ближе и ближе к 111 , а cos (θ) \ cos (\ theta) cos (θ) принимает отрицательные значения, которые все ближе и ближе к 000.Это показывает, что tan (θ) \ tan (\ theta) tan (θ) имеет отрицательную вертикальную асимптоту при θ → π2 \ theta \ rightarrow \ frac {\ pi} {2} θ → 2π сверху. Ниже показан график касательной для области 0≤θ≤2π0 \ leq \ theta \ leq 2 \ pi0≤θ≤2π:
График касательной по всей области имеет следующий вид:
Аналогично, cot (θ) \ cot (\ theta) cot (θ) не определен для значений θ \ thetaθ, таких что sin (θ) = 0 \ sin (\ theta) = 0sin (θ) = 0.Из графика sin (θ), \ sin (\ theta), sin (θ) мы видим, что sin (θ) = 0 \ sin (\ theta) = 0sin (θ) = 0, когда θ = 0 + kπ \ theta = 0 + k \ piθ = 0 + kπ для любого целого kkk, что означает, что функция котангенса имеет вертикальные асимптоты при этих значениях θ: \ theta: θ:
Функция касания | График | Домен | Недвижимость
21 декабря 2020
Время чтения: 5 минут
Введение
Математика — это динамичный предмет, позволяющий лучше понять события, происходящие в мире природы.
Хорошие математические способности улучшают критическое мышление и развивают способность решать проблемы.
Одна особая область математических и геометрических рассуждений — тригонометрия, изучающая свойства треугольников.
Треугольники — это правда, одна из простейших геометрических фигур, но у них есть множество применений.
Тригонометрия происходит от греческого тригоно «треугольник» + метрон «мера».
Тригонометрия определяет отношения между длинами сторон и углами треугольников.
Тригонометрия также помогает нам находить углы и расстояния. Все дело в треугольниках.
Касательная функция — PDF
Если вы когда-нибудь захотите прочитать его столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.
| 📥 | Касательная функция: область, диапазон, свойства и приложения — PDF | Загрузить |
Также читайте,
Что такое касательная функция?
Мы определим функцию касательной или отношение касательной угла как отношение длины противоположной стороны к длине соседней стороны.
Загар полная форма: Полная форма загара — касательная.
Касательная функция обозначается tan (x). Это одна из шести распространенных тригонометрических функций. Касательная всегда почти связана с синусом и косинусом.
Коэффициент тангенса следующий:
Желто-коричневый = Напротив / Соседний = CB / BA
Кроме того, в терминах синуса и косинуса тангенциальное отношение может быть представлено как:
tan x = sin x / cos x
или, tan theta = sin theta / cos theta, где theta представляет собой угол
Мы знаем, что синус угла равен длине противоположной стороны, деленной на длину стороны гипотенузы, тогда как косинус угла — это отношение длины соседней стороны к отношению стороны гипотенузы.
То есть sin x = противоположная сторона / сторона гипотенузы
cos x = прилегающая сторона / сторона гипотенузы
Следовательно, tan x = противоположная сторона / смежная сторона
Что такое тангенс 30 °?
Решение: В гипотенузе треугольника 30 ° длиной 2, противоположной стороной длины 1 и смежной стороной √3:
Касательная = тангенс угла (30 °) = 1/1.732 = 0,577 |
Какова тангенс угла 35 °?
Решение: В треугольнике с углом 35 ° противоположная сторона имеет длину 2,8 и прилегающую сторону 4:
Касательная = тангенс (35 °) = 2,8 / 4,0 = 0,70 |
Какова тангенс угла 45 °?
Решение: В треугольнике 45 ° есть противоположная сторона длины 1 и смежная сторона 1:
Касательная = тангенс угла (45 °) = 1/1 = 1 |
Основные свойства функции загара
Четные и нечетные функции
Функция косинуса и функции Sec являются четными функциями; остальные функции — нечетные.Следовательно, функция tan нечетная.
f (-x) = f (x) …………………. Функция четности
f (-x) = -f (x) ………………… Нечетная функция
грех (-x) = -sin x
cos (-x) = cos x
tan (-x) = — tan x
детская кроватка (-x) = -cot x
csc (-x) = -csc x
сек (-x) = сек x
При некоторых углах функция касательной не определена, и проблема является фундаментальной для построения графика функции касательной.
Нахождение всех значений x на интервале [0,2π], таких что tan (x) не определено,
Начнем с использования определения касательной, чтобы переписать его как
тангенс (х) = грех (х) / соз (х)
Дробь не определена, где знаменатель равен 0, поэтому мы хотим решить уравнение
cos (x) = 0
В данной области решения равны x = π / 2 и x = 3π / 2 согласно функции арккосинуса.
График функции загара
Тангенс угла рассчитывается относительно этой меры угла, чтобы построить график тангенса.
Приведем пример:
загар (52 °) = 8,2 / 6,5 = 1,8. Размещение таких тригонометрических значений против угла дает желтовато-коричневый график.
График tan — это графическое представление функции tan x.
Это периодический график, тригонометрические значения которого могут быть вычислены по тригонометрической формуле: sin / cos = tan
Используя эту тригонометрическую формулу, мы понимаем все точки, в которых cos x равен 0, а значение tan x не определено.
Следовательно, мы получаем плавную кривую со значением загара, стремящимся к бесконечности, каждые 90 градусов или 3pi / 2.
Диапазон касательной, Период касательной и другие свойства
Касательная функция: tan (x)
Область касательной
Все действительные числа (R), кроме pi / 2 + k pi, k — целое число. R- {pi / 2 + kpi} k находится в Z
Диапазон касательной
Все числа
Период касательной
пи
x-перехватчики
x = k pi, место k — целое число.
Y-перехватчики
у = 0
Симметрия
, поскольку tan (-x) = — tan (x), то tan (x) — нечетная функция, а график tanx симметричен относительно начала координат.
Интервалы увеличения / уменьшения
За один период и от -pi / 2 до pi / 2 tan (x) увеличивается.
Вертикальные асимптоты
x = pi / 2 + k pi, где k — целое число, — вертикальные асимптоты для касательного графа.
Диапазон касательной
Диапазон функции — это набор значений результата, которые она может выдать.Функция касательной имеет диапазон, который автоматически изменяется от положительной бесконечности до отрицательной бесконечности.
Применение тригонометрических соотношений в реальной жизни
Можно ли использовать тригонометрию в повседневной жизни?
Тригонометрия не имеет прямого применения в решении практических задач, но используется в различных вещах, которые нам так нравятся.
Звук распространяется в форме волн, и тот же образец, хотя и не такой регулярный, как функция синуса или косинуса, по-прежнему полезен при разработке компьютерной музыки.
Компьютер не может слушать и понимать музыку, как мы, поэтому компьютеры математически представляют ее в виде составляющих ее звуковых волн.
Упоминаются некоторые области техники, в которых широко используются тригонометрические концепции.
- Астрономия,
- Навигация,
- Оптика,
- Акустика (наука об изучении механических волн в твердых телах, жидкостях и газах, которая также включает такие темы, как звук, инфразвук, ультразвук и вибрация),
- Электроника,
- Статистика,
- Теория чисел,
- Электротехника,
- Машиностроение,
- Компьютерная графика,
- Разработка игр,
- Гражданское строительство,
- Медицинская визуализация,
- Аптека,
- Картография (создание карт),
- Сейсмология (наука об изучении землетрясений),
- Кристаллография (Изучение расположения атомов в кристаллическом твердом теле).
Сводка
Тригонометрия имеет множество приложений, начиная от специализированных областей, таких как океанография, где она используется для расчета высоты приливов в океанах, и исчисления, где она используется в сочетании с алгеброй, до заднего двора нашего дома, где ее можно использовать для крыши дома. , чтобы сделать крышу наклонной в случае отдельных бунгало и рассчитать высоту крыши в зданиях и т. д.
Функция тангенса также известна как тангенс x, тангенс тета или тангенциальная функция, которая в основном является одной из шести тригонометрических функций.Tanx — это отношение длины противоположного к длине соседнего.
Также читайте,
О компании Cuemath
Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-классы для преподавателей и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для детей, развивающее несколько навыков.
Ознакомьтесь со структурой оплаты для всех классов и забронируйте пробное занятие сегодня!
Часто задаваемые вопросы (FAQ)
Что такое загар-тета или загар-функция?
тангенс тета или тангенс угла — это отношение длины противоположного угла к длине соседнего.
Значение tan 0?
Значение тангенса угла 0 градусов равно 0
Значение загара 30?
Значение тангенса угла 30 градусов равно 1 / √3
Значение загара 45?
Значение тангенса угла 45 градусов равно 1
Значение загара 60?
Значение тангенса угла 60 градусов равно √3
Значение загара 90?
Значение загара 90 градусов не определено
Что такое область касательной?
Все действительные числа (R), кроме pi / 2 + k pi, k — целое число.R- {pi / 2 + kpi} k находится в Z
График касательной функции — Концепция
Для графика функции касательной создайте таблицу значений и нанесите их на координатную плоскость. Поскольку tan (theta) = y / x, всякий раз, когда x = 0, касательная функция не определена (деление на ноль не определено). Эти точки при theta = pi / 2, 3pi / 2 и их кратные целые числа представлены на графике вертикальными асимптотами или значениями, с которыми функция не может равняться. Из-за симметрии единичного круга относительно оси y период равен пи / 2.
Я хочу построить график касательной функции. У меня есть таблица значений, написанная здесь, и определение функции касательной на единичной окружности. А вот и единичный круг. Я хочу напомнить вам, что еще один способ увидеть функцию касательной как наклон конечной стороны op. Это почему? Это потому, что вы нарисовали здесь этот маленький треугольник, вертикальная сторона треугольника — это y, а горизонтальная — это x, где x и y — эти координаты.И наклон этой линии будет y через x подъем за пробег. Итак, y над x — это наклон op, и это помогает нам увидеть, как ведет себя касательная. Но касательная дает мне наклон этой линии.
Хорошо. Давайте начнем с нанесения некоторых точек, я вернусь к проблеме наклона через секунду. Первая точка — 0 0, она идет прямо здесь. И я просто воспользуюсь этими двумя точками. Пи больше 4, 1. Пи больше 4 находится на полпути между 0 и пи больше 2, так что прямо здесь. И я собираюсь сделать это 1. Итак, здесь число пи больше 4, 1.И затем число пи больше 3, корень 3. Корень 3 равен примерно 1,7, поэтому я собираюсь отобразить это как 1,7, а число пи больше 3 составляет две трети пути от 0 до пи больше 2. Итак, это пи больше 3. . Хорошо. Если это 1,5, а это 2, то примерно 1,7. Вот моя точка зрения, и я рисую свою кривую. Он очень быстро растет и имеет вертикальную асимптоту. Он просто увеличивается круче и круче по мере приближения x или когда тэта приближается к пи, превышающему 2. И причина этого снова в том, что он снова возвращается к наклону.По мере того, как этот угол становится все ближе и ближе к пи, превышающему 2, наклон этой линии становится все круче и круче.

 Вычислить f(xо).
Вычислить f(xо).