Содержание
График линейного уравнения с двумя переменными: алгоритм построения
Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с. Здесь x и y есть две переменные, a,b,c – некоторые числа.
Решением линейного уравнения a*x + b*y = с , называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.
Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у – ординатой.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Алгоритм построения
Алгоритм построения графика линейного уравнения с двумя переменным.
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике
4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
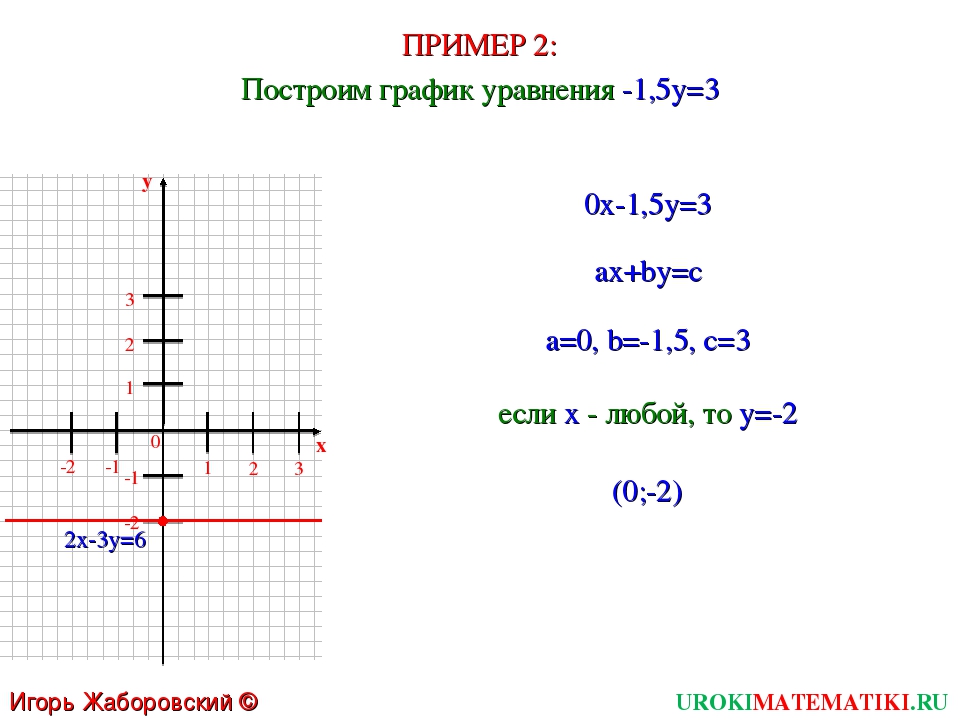
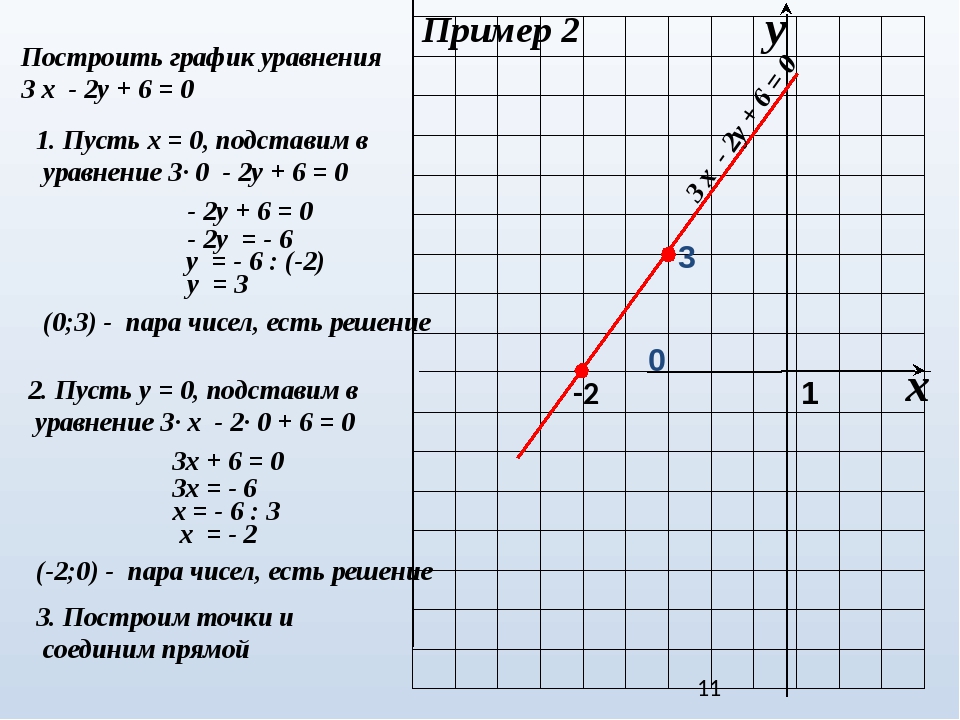
Пример: Построить график уравнения 3*x – 2*y =6;
Положим х=0, тогда – 2*y =6; y= -3;
Положим y=0, тогда 3*x = 6; x=2;
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её. Посмотрите на рисунок ниже, график должен получиться именно таким.
Посмотрите на рисунок ниже, график должен получиться именно таким.
Нужна помощь в учебе?
Предыдущая тема: Линейное уравнение с двумя переменными: решение и свойства
Следующая тема:   Системы линейных уравнений с двумя переменными
График линейного уравнения с двумя переменными
Вопросы
занятия:
·
ввести понятие «график линейного уравнения с двумя переменными»;
·
рассмотреть поведение графика в зависимости от значений коэффициентов перед
переменными.
Материал
урока
На
прошлом уроке мы с вами познакомились с линейным уравнением с двумя переменным.
Давайте, вспомним определение.
И
сегодня на уроке мы будем вести речь о графике такого уравнения.
Сформулируем
определение:
Графиком
уравнения с двумя переменными называется множество всех точек
координатной плоскости, координаты которых являются решениями этого уравнения.
Рассмотрим
уравнение:
Обратите
внимание, что полученная формула имеет вид линейной функции, графиком которой
является прямая.
Так
как прямая определяется двумя точками, то для построения графика нам достаточно
указать две точки. Так:
Таким
образом, получили две точки с координатами:
Теперь
на координатной плоскости отметим эти точки и проведём через них линию.
Эта
прямая является графиком исходного уравнения.
Все
точки, принадлежащие графику, – это пары чисел, которые являются решениями
нашего уравнения.
Теперь
рассмотрим уравнение, в котором коэффициент при одной из переменных равен нулю.
Например,
А
это постоянная функция. С предыдущих уроков нам известно, что график такой
функции – это прямая, которая проходит через точку с координатами (0; 2)
и параллельна оси Ox.
Все
точки, принадлежащие этой прямой, – это пары чисел, которые являются решениями
данного уравнения.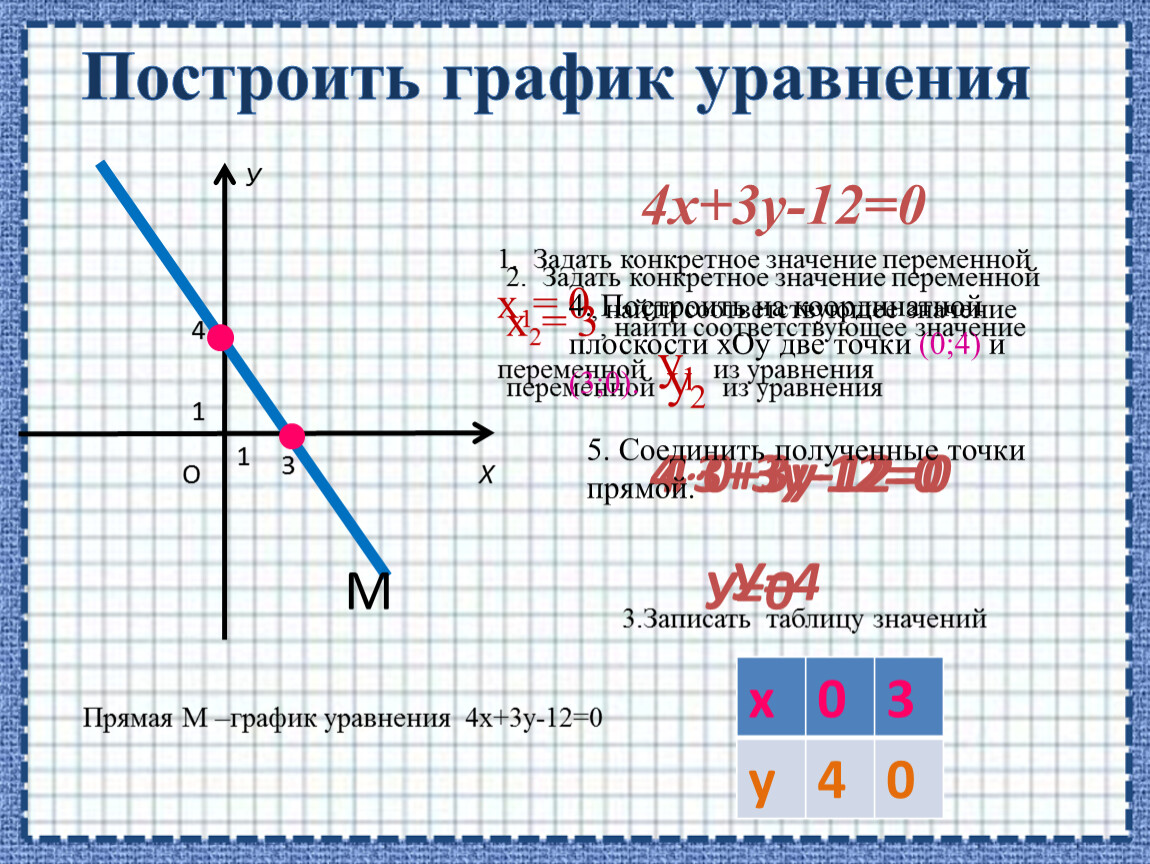 И таких решений бесконечно много.
И таких решений бесконечно много.
Сформулируем
определение.
Определение.
Графиком
линейного уравнения с двумя переменными, в котором хотя бы один
из коэффициентов при переменных не равен нулю, является прямая.
А
теперь давайте рассмотрим случай, когда в линейном уравнении оба коэффициента
при переменных равны нулю.
Давайте,
рассмотрим примеры построения графиков линейных уравнений.
Пример.
Пример.
Пример.
Итоги
урока.
Итак,
сегодня на уроке мы выяснили, что же представляет собой график линейного
уравнения с двумя переменными и научились строить такие графики.
Линейное уравнение с двумя переменными и его график, примеры
График линейного уравнения с двумя переменными
В линейном уравнении с двумя переменными ax+by=c , a и b называют коэффициентами при переменных, c — свободным членом.
Если хотя бы один из коэффициентов при переменных не равен нулю, графиком линейного уравнения с двумя переменными является прямая.
Действительно:
$$ ax+by = c \iff y = — \frac{a}{b} x+ \frac{c}{b} $$
Если сравним полученное уравнение $с y = kx+ \tilde b$ (см. §38 данного справочника), получаем:
$$ k = -\frac{a}{b} , \tilde b = \frac{c}{b}$$
Графиком $y = kx+ \tilde b$ является прямая, угловой коэффициент k определяет угол наклона, слагаемое $\tilde b$ – точку пересечения прямой с осью Y (см. §39 данного справочника).
Точки пересечения с осями координат:
${\left\{ \begin{array}{c} x = 0 \\ y = \frac{c}{b}\end{array} \right.}, {\left\{ \begin{array}{c} x = \frac{c}{a} \\ y = 0\end{array} \right.}$
Внимание!
График линейной функции ax+by=c с ненулевыми коэффициентами очень удобно чертить по двум точкам пересечения с осями координат: точка на оси X ( $\frac{c}{a}$;0) и точка на оси Y (0; $\frac{c}{b}$)
Равенство нулю коэффициентов при переменных:
$a = 0,b \neq 0$
$a \neq 0, b = 0$
$0x+2y = 4 \Rightarrow y = 2$
График – прямая, параллельная оси Х.
$3x+0y = 3 \Rightarrow x = 1$
График – прямая, параллельная оси У.
0x+0y = 0
x, $y \in \Bbb R$ — любое действительное число.
График – вся координатная плоскость
0x+0y = 5
Решений нет.
График – пустое множество.
Взаимное расположение графиков двух уравнений
$$ a_1 x+b_1 y = c_1 и a_2 x+b_2 y = c_2 $$
$ \frac{a_1}{a_2} \neq \frac{b_1}{b_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $
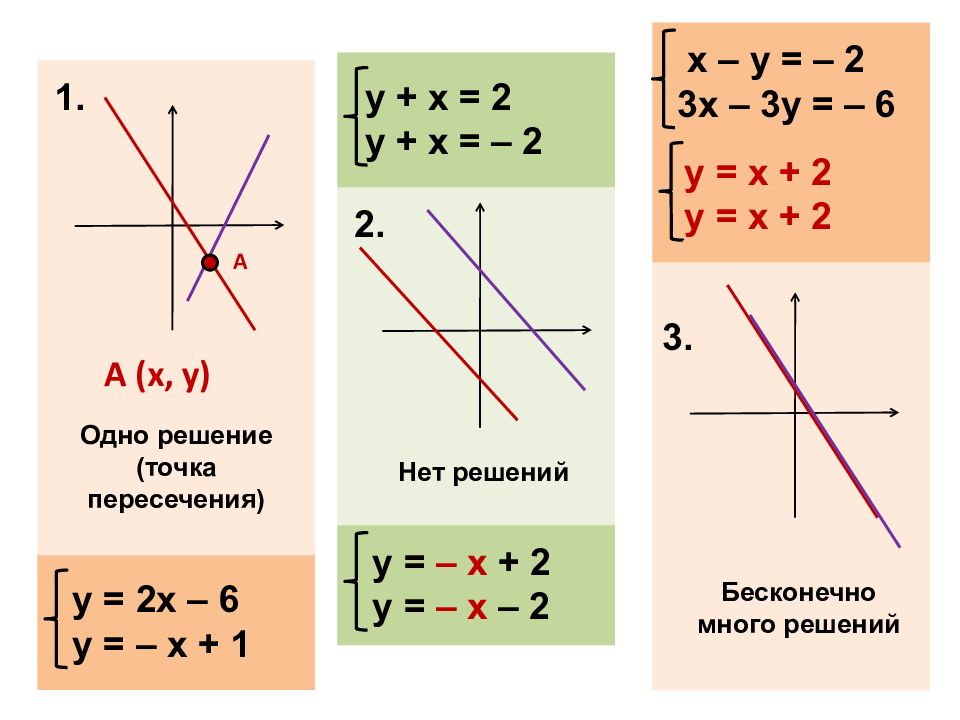
Прямые пересекаются
Прямые параллельны
Прямые совпадают
Примеры
Пример 1. Постройте график линейного уравнения по двум точкам пересечения с осями.
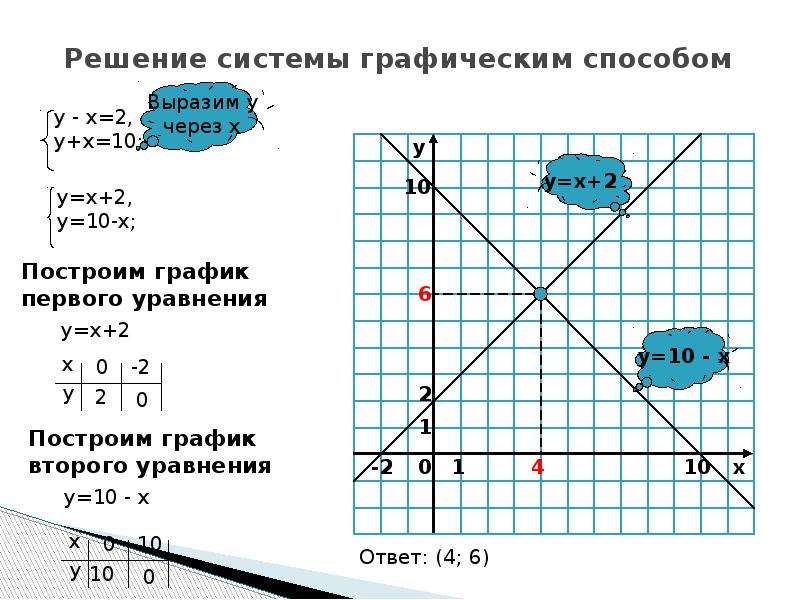
Пример 2. Постройте в одной координатной плоскости графики, найдите точку пересечения:
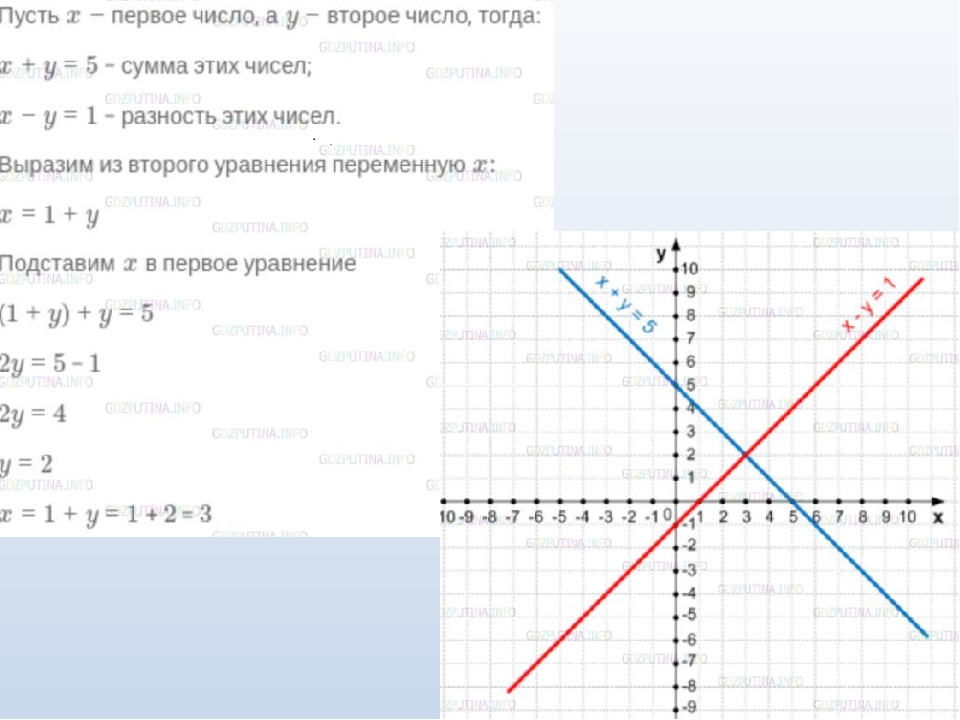
а) x+2y = 4 и x-2y = 4
Точка пересечения (4;0)
б) x+y = 4 и x-y = -1
Точка пересечения (1,5;2,5)
График линейного уравнения с двумя переменными
Текст этой презентации
Слайд 1
График линейного уравнения с двумя переменными
Слайд 2
Цель урока:
ввести понятие графика уравнения с двумя переменными;
повторить построение графика линейной функции по двум точкам; закрепить навыки нахождения одной переменной через другую.
Слайд 3
Устные упражнения
а) 3х – у = 14
б) 5у + х² = 16
в) 7ху – 5у = 12
г) 5х + 2у = 16 Ответ: 3х – у = 14 5х + 2у = 16
Слайд 4
Выбрать точку, которая принадлежит графику уравнения
2х + 5у = 12 А(-1; -2), В(2; 1), С(4; -4), D(11; -2). D(11; -2).
Слайд 5
x
8 6 4 2
-2
е ж з и к л м
а б в г д
у ф х ц ч ш щ
й э ю я п р с
н о т й
(6;4) (-2;-2) (4;4) (-2;-2) (4;6) (-6;4) (0;2)
М О Л О Д Е Ц
y
-8 -6 -4 -2 0 2 4 6 8
Слайд 6
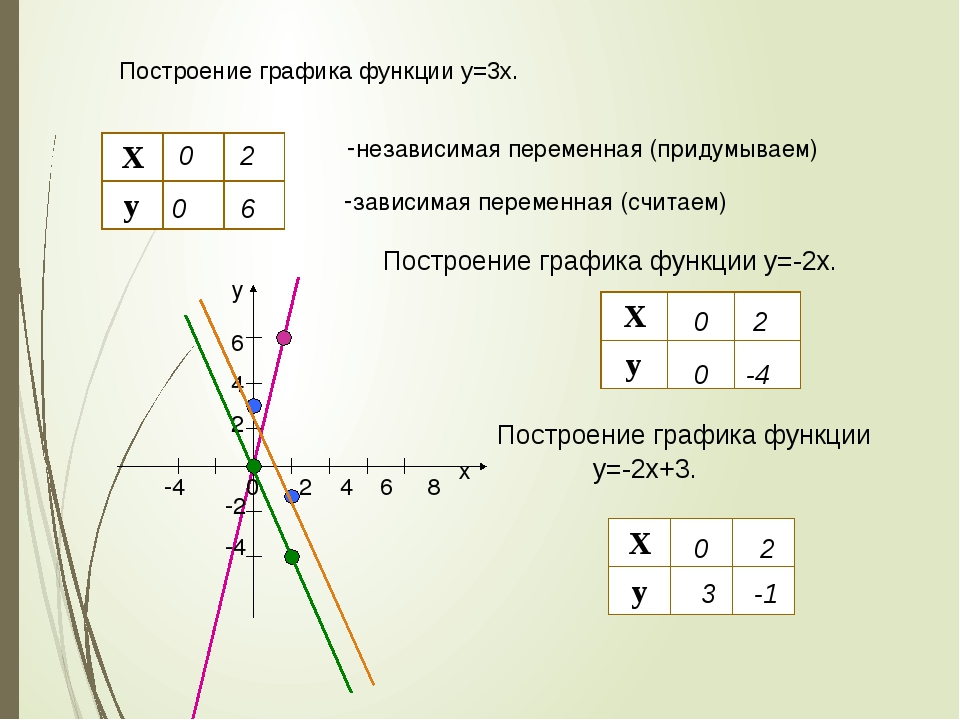
Построение графика функции y=3x.
Х
у
Х
у
Х
у
-независимая переменная (придумываем)
-зависимая переменная (считаем)
0
2
0
6
х
у
-4 0 2 4 6 8
6 4 2 -2
-4
Построение графика функции y=-2x.
Построение графика функции y=-2x+3.
0 2
0
-4
0 2
3
-1
Слайд 7
Каждая пара чисел, являющаяся решением уравнения с переменными х и у, изображается в координатной плоскости точкой, координатами которой служит пара чисел. Все эти точки образуют график уравнения.
Все эти точки образуют график уравнения.
Слайд 8
Выясним, что представляет собой график уравнения 3х+2у=6
Выразим переменную у через х у=-1,5х+3 Формулой у=-1,5х+3 задается линейная функция, графиком которой служит прямая. Уравнения 3х+2у=6 и у=-1,5х+3 равносильны, то эта прямая является и графиком уравнения 3х+2у=6
Слайд 9
Построим график функции y=-1,5x+3.
Х 0 2
у 3 0
х
у
3 2 1 -1
-2
Пары точек (0;3) и (2;0)
Являются решением данного уравнения 3х+2у=6
Слайд 10
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения
Слайд 11
Если в линейном уравнении коэффициент при х равен нулю, то графиком такого уравнения является прямая
y=kx +b – линейная функция.
y=0x +b, тогда y=b
Прямые параллельны оси х
х
у
6 4 2 -2
-4
у=6
у=4
у=-4
Слайд 12
Если в линейном уравнении коэффициент при у равен нулю, то графиком такого уравнения является прямая
y=kx +b – линейная функция. 0y+kx=b, тогда х=b/ k
Прямые параллельны оси у
0y+kx=b, тогда х=b/ k
Прямые параллельны оси у
у
6 4 2 -2
-4
х=-4
х=4
х=2
Слайд 13
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
Слайд 14
Уравнение ax+by=c, в котором оба коэффициента при переменных равны нулю, имеет вид 0x+0y=c. При с=0 любая пара чисел является решением этого уравнения, а его графиком -вся координатная плоскость. При с≠0 уравнение не имеет решений и его график не содержит ни одной точки
Слайд 15
ФизкультминуткаУпражнение 1 «Глядя в небо»
Цель этого упражнения — устранение вредных эффектов от неподвижного сидения в течение длительного периода времени и профилактика грыжи межпозвоночных дисков поясничного отдела. Поза: стоя
В положении стоя положите руки на бедра.
Медленно отклоняйтесь назад, глядя на небо или в потолок. Вернитесь в исходное положение. Повторите 10 раз.
Слайд 16
№1048(Б)
Слайд 17
Слайд 18
е
Слайд 19
№1051
Слайд 20
Самостоятельная работа
1 вариант
1. Какие из пар чисел (1;1), (6;5), (9;11) являются решением уравнения 5х – 4у — 1 =0?
2. Постройте график функции 2х + у = 4.
Какие из пар чисел (1;1), (6;5), (9;11) являются решением уравнения 5х – 4у — 1 =0?
2. Постройте график функции 2х + у = 4.
2 вариант
1. Какие из пар чисел (1;1), (1;2), (3;7) являются решением уравнения 7х – 3у — 1 =0?
2. Постройте график функции 5х + у – 4 = 0.
Слайд 21
Самостоятельная работа
1 вариант №1
(1;1), (9;11)
2 вариант №1 1. (1;2)
Слайд 22
Х
У
2
0
1 в
№2
4
Слайд 23
Х
У
1
0
2 в
№2
4
Слайд 24
Оцените свои знания, полученные на уроке
У меня все отлично
У меня все хорошо
Возникли трудности
Слайд 25
Домашняя работа.
П.41, №1045, 1048 (а, в,д)
§ 1. Линейные уравнения с двумя переменными — ЗФТШ, МФТИ
В первом задании мы рассмотрели линейные уравнения с одной переменной. Например, уравнения `2x+5=0`, `3x+(8x-1)+9=0` являются линейными уравнениями с переменной `x`. Уравнение, содержащее переменные `x` и `y`, называется уравнением с двумя переменными. 2=7` являются уравнениями с двумя переменными.
2=7` являются уравнениями с двумя переменными.
Уравнение вида `ax+by=c` называется линейным уравнением с двумя переменными, где `x` и `y` переменные, `a`, `b`, `c` — некоторые числа.
Например, уравнения `2x+y=3`, `x-y=0` являются линейными уравнениями с двумя переменными.
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Например, `x=3`, `y=4` является решением уравнения `2x+3y=18`, будем эту пару чисел записывать так `(3;4)`. Очевидно, что пара чисел `(4;3)` не является решением уравнения, т. к. `2*4+3*3=17!=18`. При нахождении решений с двумя переменными на первом месте в паре чисел пишем значение для переменной `x`, а на втором месте – значение переменной `y`.
Если каждое решение одного уравнения является решением второго уравнения и обратно, то данные уравнения называются равносильными. Например, решения уравнений `2x+y=3` и `4x+2y=6` совпадают, следовательно, эти уравнения равносильные.
1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Укажите три различных решения для уравнения `3x+y-2=0`.
Если `x=0`, то `y=2`; если `y=0`, то `x=2/3`; если `x=1`, то `y=-1`.
Таким образом, пары чисел `(0;2)`, `(2/3;0)`, `(1;-1)` являются решениями данного уравнения. Заметим, что данное уравнение имеет бесконечно много решений. Для заданного значения `x` значение `y=2-3x`, т. е. любая пара чисел `(x;2-3x)`, где `x` — любое число, является решением уравнения.
Рассмотрим координатную плоскость `Oxy` и отметим на ней все точки `(x,y)`, для которых пара чисел `x` и `y` является решениями уравнения. Например, рассмотрим уравнение `y=2`. Этому уравнению удовлетворяют все пары чисел `(x;2)`.Точки, для которых `x` — любое число, а `y=2`, лежат на прямой `y=2`. Эта прямая параллельна оси `x` и проходит через точку `(0;2)` (см. рис. 1).
Эта прямая параллельна оси `x` и проходит через точку `(0;2)` (см. рис. 1).
Рассмотрим уравнение `x=3`. Каждая пара чисел, являющаяся решением данного уравнения, изображается точкой с координатами `x` и `y` на координатной плоскости `Oxy`. Решениями данного уравнения являются пары чисел `(3;y)`. Точки с координатами `x=3` и `y` лежат на прямой `x=3`, эта прямая параллельна оси `Oy` и проходит через точку `(3;0)` (см. рис. 2).
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями данного уравнения.
На рис. 1 графиком уравнения является прямая `y=2`, на рис. 2 графиком уравнения является прямая `x=3`.
Рассмотрим теперь уравнение `2x+3y-1=0`. Выразим переменную `y` через `x`, получаем `y=1/3-2/3x`, это уравнение задаёт линейную функцию, и нам известно, что её графиком является прямая. Чтобы построить эту прямую, достаточно рассмотреть две точки, координаты которых удовлетворяют уравнению, а затем через эти две точки провести прямую. При `x=0` `y=1/3` и при `x=1/2` `y=0`. График данного уравнения приведён на рис. 3.
При `x=0` `y=1/3` и при `x=1/2` `y=0`. График данного уравнения приведён на рис. 3.
Рассмотрим уравнение `(x-4)(x+y-4)=0`. Произведение двух скобок равно нулю, каждая скобка может равняться нулю. Наше уравнение распадётся на два уравнения: `x=4` и `x+y-4=0`. Графиком первого уравнения является прямая, параллельная оси `Oy` и проходящая через точку `(4;0)`. Графиком второго уравнения является график линейной функции `y=4-x`, эта прямая проходит через точки `(4;0)` и `(0;4)`. График данного уравнения приведён на рис. 4.
Постройте график уравнения `|x|+|y|=1`.
Этот пример можно решать двумя способами. Пусть `x>=0` и `y>=0`, точки с такими координатами лежат в первой четверти. Получаем уравнение `x+y=1`, так как `|x|=x` и `|y|=y`. Графиком данного уравнения является прямая, проходящая через точки `A(1;0)` и `B(0;1)`. Графику исходного уравнения принадлежат точки полученной прямой, лежащие в первой четверти, т. е. графику принадлежат точки отрезка `AB`, где `A(1;0)` и `B(0;1)`.
Пусть теперь `x<=0` и `y>=0` тогда получаем уравнение `-x+y=1`, рассматриваем точки полученной прямой, лежащие во второй четверти. Это будет отрезок `BC`, где `C(-1;0)`. При `x<=0`, `y<=0` получим отрезок `CD` где `D(0;-1)`, и при `>=0`, `y<=0` получим отрезок `DA`. Таким образом, график данного уравнения состоит из точек квадрата `ABCD` (рис. 5).
Этот пример можно решать другим способом. Пусть `y>=0`, тогда наше уравнение эквивалентно уравнению `y=1-|x|`. В первом задании мы строили график функции `y=|x|` (см. рис. 6). График функции `y=-|x|` получается зеркальным отражением относительно оси `Ox` графика функции `y=|x|` (см. рис. 7). График функции `y=1-|x|` получается из графика функции `y=-|x|` сдвигом вдоль оси `Oy` на единицу вверх (см. рис. 8). У полученного графика рассматриваем только точки, для которых `y>=0`. Получим ломаную `ABC` с рис. 5.
Далее рассматриваем `y<=0`, получим, что графиком уравнения при `y<=0` является ломаная `CDA` с рис. 2=11`,
2=11`,
`(x+2-y-1)*(x+2+y+1)=11`.
Если `x` и `y` целые числа, то выражения, стоящие в скобках, являются целыми числами. А это могут быть числа `+-1` и `+-11`. Решаем `4` системы уравнений:
$$ \left\{\begin{array}{l}x+2-y-1=1,\\ x+2+y+1=11;\end{array}\right.$$
$$ \left\{\begin{array}{l}x+2-y-1=11,\\ x+2+y+1=1;\end{array}\right.$$
$$ \left\{\begin{array}{l}x+2-y-1=-1,\\ x+2+y+1=-11;\end{array}\right.$$
$$ \left\{\begin{array}{l}x+2-y-1=-11,\\ x+2+y+1=-1.\end{array}\right.$$
Решая эти системы, получаем `4` решения: `(4;4)`, `(4;-6)`, `(-8;-6)`, `(-8;4)`.
График линейного уравнения с двумя переменными
1. График линейного уравнения с двумя переменными
2. Графиком уравнения с двумя неизвестными называется множество всех точек координатной плоскости, координаты которых являются
решениями этого уравнения.
3. №1. Выразите у через х в уравнении:
а)
б)
в)
г)
3х – у = 2;
5х + 2у = 7;
х + 2у = 4;
2х – у = 11.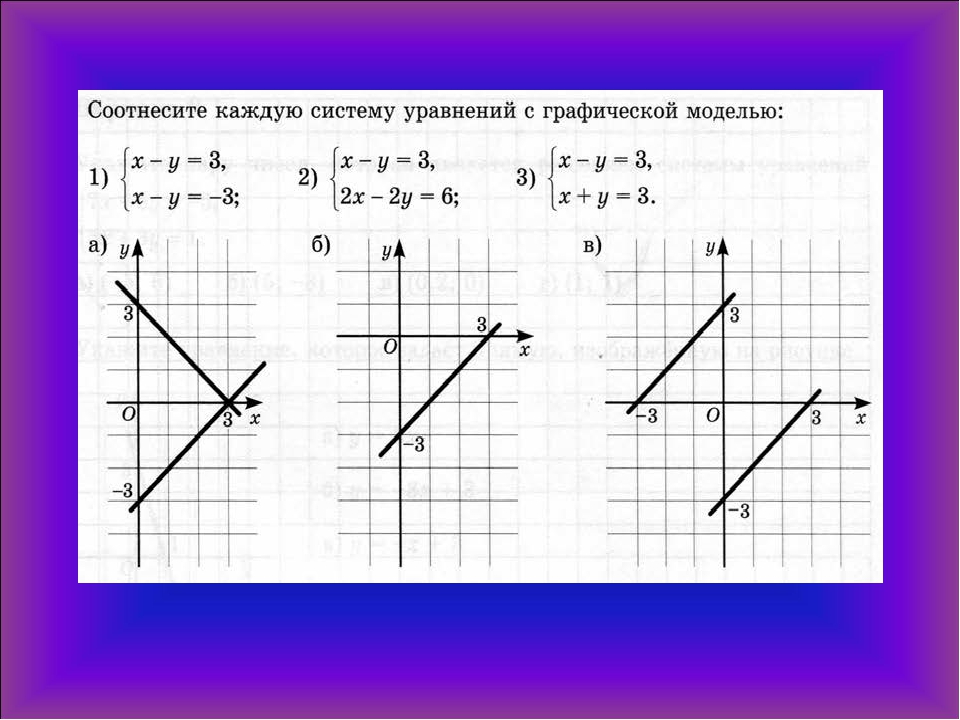
Проверь себя:
а) у = 3х – 2;
б) у = — 2,5х + 3,5;
в) у = — 0,5х + 2;
г) у = 2х – 11.
У = кх + b
4. №2. Из графиков, изображённых на рисунке, выберите: графики линейной функции; графики прямой пропорциональности.
5. № 3. Построить график уравнения 4х + 2у = 8.
Выразим переменную у
через х:
2у = 8 – 4х,
у = 4 – 2х.
у = -2х + 4 – линейная
функция, графиком
является прямая.
уу
у
4
4х+2у=8
1
х
у
0
4
2
0
0
12
х
aх + by = c
у
a = 0 => by = c,
y = c/b =>
=> график – прямая,
проходящая через
точку (0; c/b)
параллельно оси ОХ
c/b
0
х
aх + by = c
у
b = 0 => ax = c,
x = c/a =>
=> график – прямая,
проходящая через
точку (c/a; 0)
параллельно оси OY
0 c/a
х
8. Вывод: графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных отличен от
нуля, является прямая.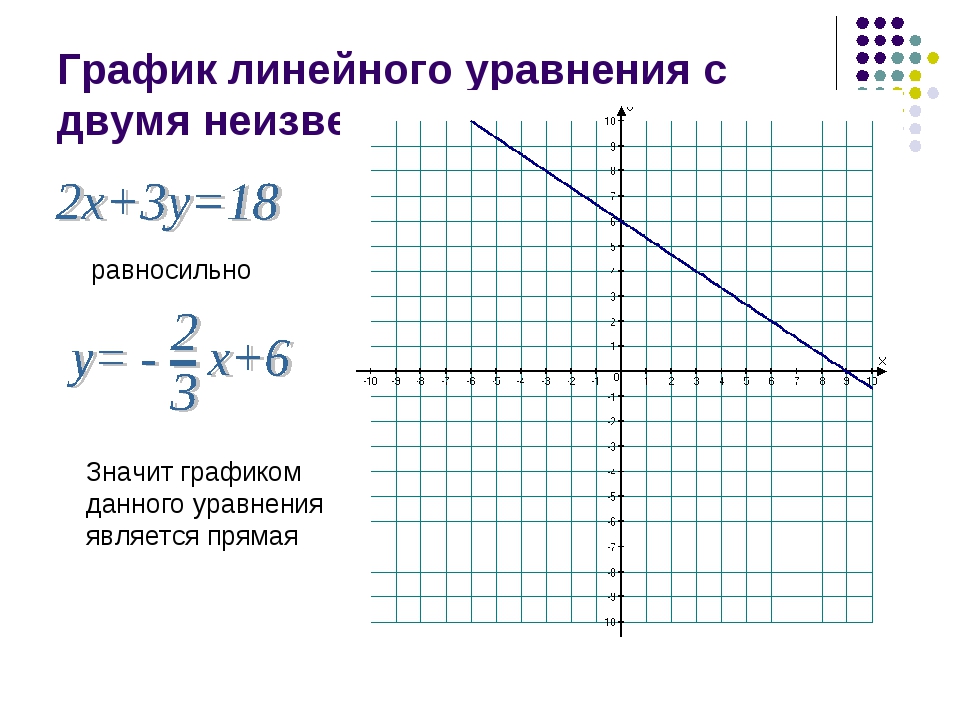
aх + by = c
а = 0 и b = 0 => 0 = c, =>
=> при с = 0 график – любая точка
координатной плоскости;
при с≠ 0 уравнение решений не имеет,
следовательно график построить
невозможно.
10. № 4. Покажите построением, что графики уравнений у= — х + 5; 2х – у = 16; х + 2у – 3 = 0 пересекаются в одной точке. Найдите
координаты этой точки.
11. Решение.
у
1) у = — х + 5.
х
0
у
5
2) 2х – у = 16,
у = 2х – 16
х
5
у
-6
5
0
8
0
3) х + 2у – 3 = 0,
2у = 3 – х,
у = — 0,5х + 1,5
х
у
0
1,5
3
0
5
4
3
2
У = -х +5
1
-3
0
1 2 3 4 5
-1
Х + 2у – 3 = 0
-2
-3
-4
-5
-6
6 7 8
А(7; — 2)
2х – у = 16
х
Домашнее задание: п.41,
№№ 1046, 1048 (а,в,д,е)
Построение графика квадратного уравнения с двумя переменными. Как построить график уравнения.
 Преимущества построения графиков онлайн
Преимущества построения графиков онлайн
На этом уроке мы подробно рассмотрим построение графиков уравнений. Вначале вспомним, что такое рациональное уравнение и множество его решений, образующее график уравнения. Подробно рассмотрим график линейного уравнения и свойства линейной функции, научимся читать графики. Далее рассмотрим график квадратного уравнения и свойства квадратичной функции. Рассмотрим гиперболическую функцию и ее график и график уравнения окружности. Далее перейдем к построению и изучению совокупности графиков.
Тема: Системы уравнений
Урок: Графики уравнений
Мы рассматриваем рациональное уравнение вида и системы рациональных уравнений вида
Мы говорили, что каждое уравнение в этой системе имеет свой график, если конечно имеются решения уравнений. Мы рассмотрели несколько графиков различных уравнений.
Сейчас мы систематически рассмотрим каждое из известных нам уравнений, т.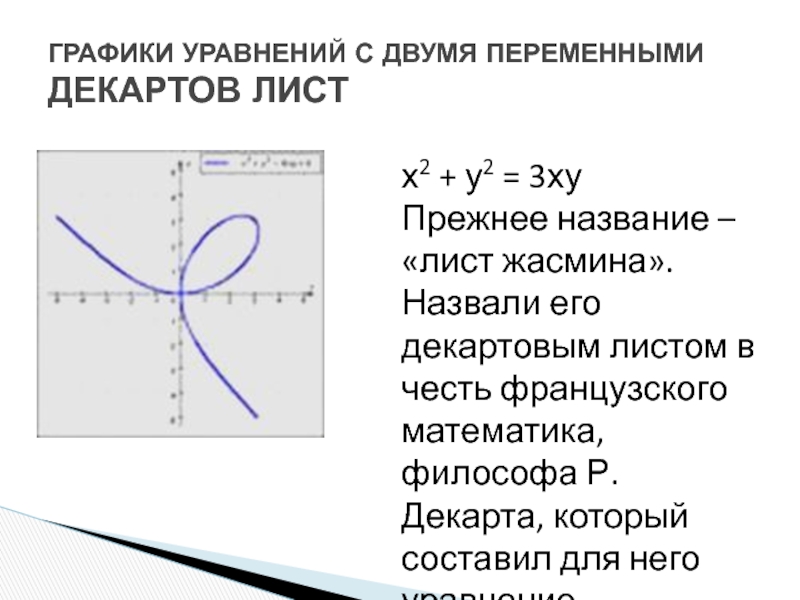 е. выполним обзор по графикам уравнений
е. выполним обзор по графикам уравнений
.
1. Линейное уравнение с двумя переменными
x, y — в первой степени; a,b,c — конкретные числа.
Пример:
Графиком этого уравнения является прямая линия.
Мы действовали равносильными преобразованиями — y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.
В данном случае
Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если сли
Эта функция возрастает, т.е. с увеличением x увеличивается y. Мы получили два частных решения, а как записать множество всех решений?
Если точка имеет абсциссу x, то ордината этой точки
Значит, чисел
У нас было уравнение, мы построили график, нашли решения.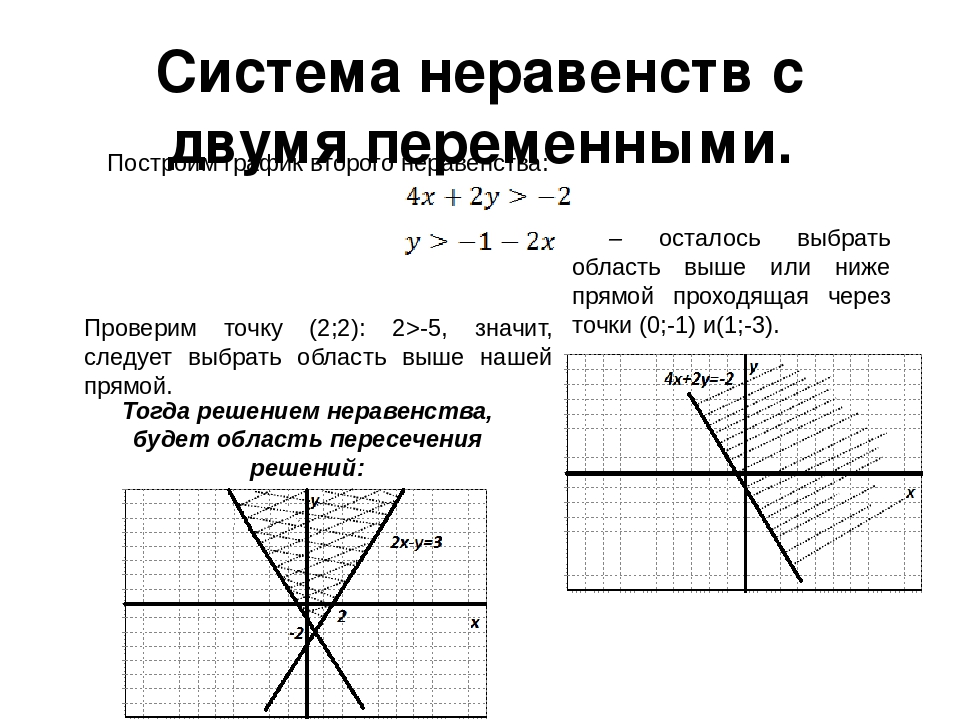 Множество всех пар — сколько их? Бесчисленное множество.
Множество всех пар — сколько их? Бесчисленное множество.
Это рациональное уравнение,
Найдем y, равносильными преобразованиями получаем
Положим и получаем квадратичную функцию, ее график нам известен.
Пример: Построить график рационального уравнения.
Графиком является парабола, ветви направлены вверх.
Найдем корни уравнения:
Схематически изобразим график (Рис. 2).
С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.
У уравнения бесчисленное множество решений, т.е. бесчисленное множество пар , удовлетворяющих уравнению, но все А каким может быть x? Любым!
Если мы зададим любое x, то получим точку
Решением исходного уравнения является множество пар
3. Построить график уравнения
Необходимо выразить y. Рассмотрим два варианта.
Графиком функции является гипербола, функция не определена при
Функция убывающая.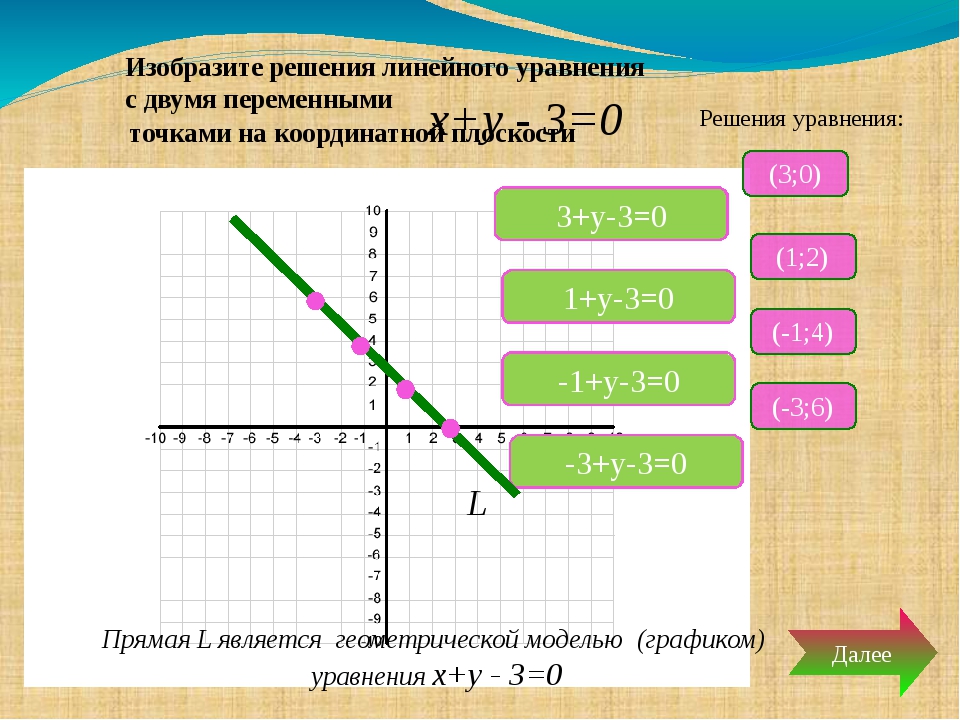
Если мы возьмем точку с абсциссой , то ее ордината будет равна
Решением исходного уравнения является множество пар
Построенную гиперболу можно сдвигать относительно осей координат.
Например, график функции — тоже гипербола — будет сдвинут на единицу вверх по оси ординат.
4. Уравнение окружности
Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке радиус равен R (Рис. 4).
Рассмотрим конкретные примеры.
a.
Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:
— получили уравнение окружности с центром в .
Построим график уравнения (Рис. 5).
b. Построить график уравнения
Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.
График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т. е. двух прямых.
е. двух прямых.
Построим его (Рис. 6).
Построим график функции Прямая будет проходить через точку (0; -1). Но как она пройдет — будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).
Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.
Координаты всех точек двух построенных прямых и являются решением уравнения.
Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Раздел College.ru по математике ().
2. Интернет-проект «Задачи» ().
3. Образовательный портал «РЕШУ ЕГЭ» ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А.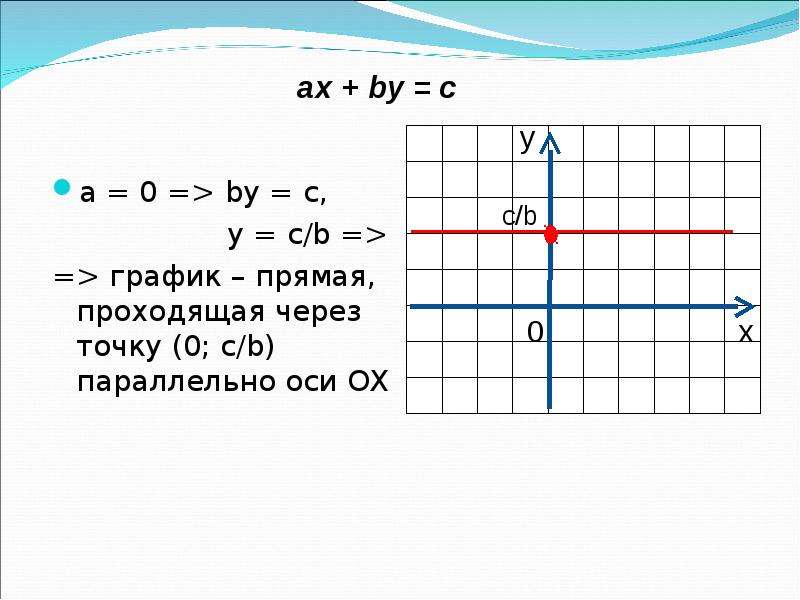 Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.
Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.
Пусть задано уравнение с двумя переменными F(x; y)
. Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.
Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.
Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a) 2 + (y – b) 2 = R 2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).
Пример 1.
Построить график уравнения x 2 – 9y 2 = 0.
Решение.
Разложим на множители левую часть уравнения.
(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.
Ответ: рисунок 1.
Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Первое уравнение равносильно системе
{f(x) ≥ 0,
{y = f(x) или y = -f(x).
То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.
Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).
Пример 2.
Построить график уравнения |y| = 2 + x.
Решение.
Заданное уравнение равносильно системе
{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.
Строим множество точек.
Ответ: рисунок 2.
Пример 3.
Построить график уравнения |y – x| = 1.
Решение.
Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.
Ответ: рисунок 3.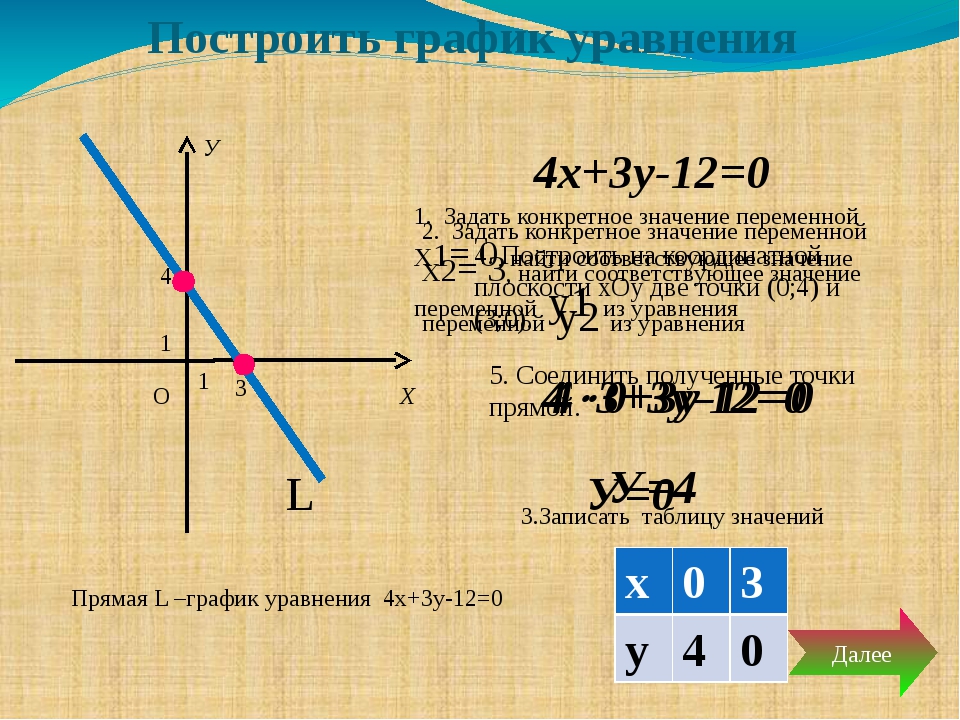
При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей
, основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.
Пример 4.
Построить график уравнения x + |x| + y + |y| = 2.
Решение.
В данном примере знак каждого подмодульного выражения зависит от координатной четверти.
1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:
2x + 2y = 2, а после упрощения x + y = 1.
2) Во второй четверти, где x
3) В третьей четверти x
4) В четвертой четверти, при x ≥ 0, а y
График данного уравнения будем строить по четвертям.
Ответ: рисунок 4.
Пример 5.
Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.
Решение.
Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.
| Область | Знак подмодульного выражения | Полученное уравнение после раскрытия модуля |
| I | x ≥ 1 и y ≥ 1 | x + y = 3 |
| II | x | -x + y = 1 |
| III | x | x + y = 1 |
| IV | x ≥ 1 и y | x – y = 1 |
Ответ: рисунок 5.
На координатной плоскости фигуры могут задаваться и неравенствами
.
Графиком неравенства
с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.
Рассмотрим алгоритм построения модели решений неравенства с двумя переменными
:
- Записать уравнение, соответствующее неравенству.
- Построить график уравнения из пункта 1.
- Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
- Изобразить графически множество всех решений неравенства.
Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.
1)
ax + bx + c ≥ 0. Рисунок 6
.
2)
|x| ≤ a, a > 0. Рисунок 7
.
3)
x 2 + y 2 ≤ a, a > 0. Рисунок 8
.
4)
y ≥ x 2 . Рисунок 9.
Рисунок 9.
5)
xy ≤ 1. Рисунок 10.
Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором
после того, как зарегистрируетесь . Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.
Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с
. Здесь x и y есть две переменные, a,b,c — некоторые числа.
Решением линейного уравнения a*x + b*y = с, называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.
Линейное уравнение имеет бесконечное множество решений.
Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у — ординатой.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Алгоритм построения
Алгоритм построения графика линейного уравнения с двумя переменным.
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
Отметить полученную точку на графике.
3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике
4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
Пример:
Построить график уравнения 3*x — 2*y =6;
Положим х=0, тогда — 2*y =6; y= -3;
Положим y=0, тогда 3*x = 6; x=2;
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её. Посмотрите на рисунок ниже, график должен получиться именно таким.
Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.
Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут
быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость
. В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости
В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости
и ts-плоскости
.
Упорядоченная пара
Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.
Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости
Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.
В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке
Определение графика
Графиком
уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения
Пример: нарисовать график y = x 2
Из-за того, что 1/x не определено, когда x=0, мы можем построить только точки, для которых x ≠0
Пример: Найдите все пересечения с осями
(a) 3x + 2y = 6
(b) x = y 2 -2y
(c) y = 1/x
Пусть y = 0, тогда 3x = 6 or x = 2
является искомой точкой пересечения оси x.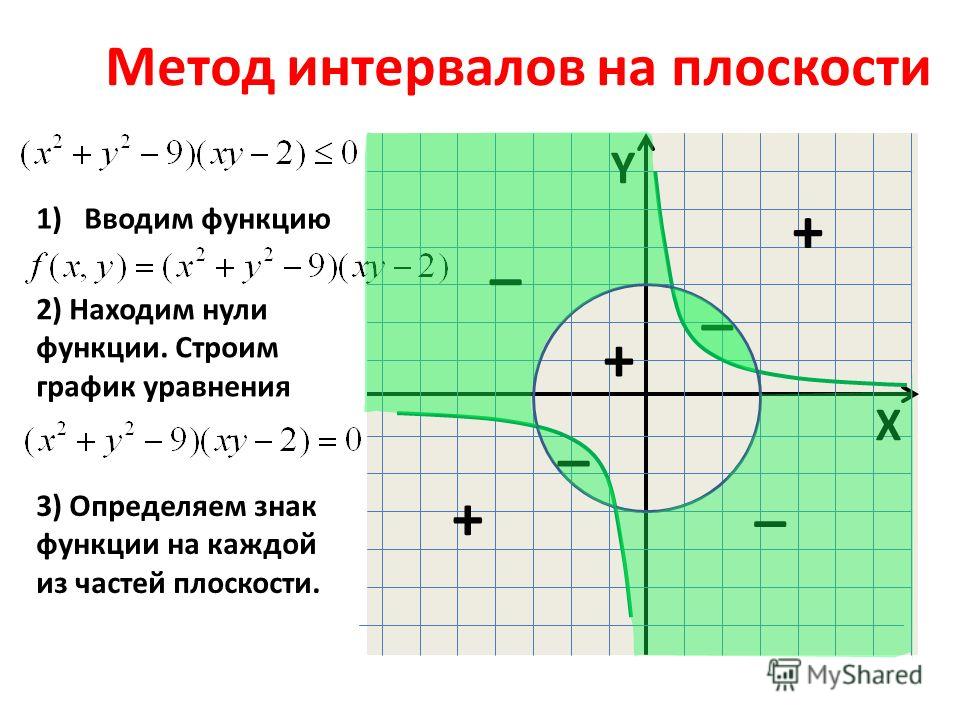
Установив, что х=0, найдем что точкой пересечения оси у является точка у=3.
Таким эе образом вы можете решить уравнение (b), а решения для (c) приведено ниже
x-пересечение
Пусть y = 0
1/x = 0 => x не может быть определено, то есть нет пересечения с осью у
Пусть x = 0
y = 1/0 => y также не определено, => нет пересечения с осью y
На рисунке внизу точки (x,y), (-x,y),(x,-y) и (-x,-y) обозначают углы прямоугольника.
График симметричен относительно оси х, если для каждой точки (x,y) графика, точка (x,-y) есть также точкой на графике.
График симметричен относительно оси y, если для каждой точки графика (x,y) точка (-x,y) также принадлежит графику.
График симметричен относительно центра координат, если для каждой точки (x,y) графика, точка (-x,-y) также принадлежит этому графику.
Определение:
График функции
на координатной плоскости определяется как график уравнения y = f(x)
Постройте график f(x) = x + 2
Пример 2. Постройте график f(x) = |x|
Постройте график f(x) = |x|
График совпадает с линией y = x для x>
0 и с линией y = -x
для x
graph of f(x) = -x
Соединяя эти два графика, мы получаем
график f(x) = |x|
Пример 3. Постройте график
t(x) = (x 2 — 4)/(x — 2) =
= ((x — 2)(x + 2)/(x — 2)) =
= (x + 2) x ≠ 2
Следовательно, эта функция может быть записана в виде
y = x + 2 x ≠ 2
График h(x)= x 2 — 4 Or x — 2
график y = x + 2 x ≠ 2
Пример 4. Постройте график
Графики функций с перемещением
Предположим, что график функции f(x) известен
Тогда мы можем найти графики
y = f(x) + c — график функции f(x), перемещённый
ВВЕРХ на c значений
y = f(x) — c — график функции f(x), перемещённый
ВНИЗ на c значений
y = f(x + c) — график функции f(x), перемещённый
ВЛЕВО на c значений
y = f(x — c) — график функции f(x), перемещённый
Вправо на c значений
Пример 5. Постройте
Постройте
график y = f(x) = |x — 3| + 2
Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график
Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2
Постройте график
y = x 2 — 4x + 5
Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:
y + 4 = (x 2 — 4x + 5) + 4 y = (x 2 — 4x + 4) + 5 — 4
y = (x — 2) 2 + 1
Здесь мы видим, что этот график может быть получен перемещением графика y = x 2 вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.
y = x 2 — 4x + 5
Отражения
(-x, y) есть отражением (x, y) относительно оси y
(x, -y) есть отражением (x, y) относительно оси x
Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y
Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x
График может быть получен отражением и перемещением:
Нарисуйте график
Найдём его отражение относительно оси y, и получим график
Переместим этот график вправо
на 2 значения и получим график
Вот искомый график
Если f(x) умножена на положительною постояную c, то
график f(x) сжимается по вертикали, если 0
график f(x) растягивается по вертикали, если c > 1
Кривая не является графиком y = f(x) для любой функции f
Графики и уравнения двух переменных
Декартова система
Декартова система координат используется для визуализации точек на графике путем отображения расстояний между точками по двум осям.
Цели обучения
Объясните, как нанести точки на декартовую плоскость и что это значит.
Основные выводы
Ключевые моменты
- Декартова система координат — это 2-мерная плоскость с горизонтальной осью, известной как [latex] x [/ latex] -ось, и вертикальной осью, известной как [latex] y [/ latex]-осью.
- В декартовой системе координат каждая точка однозначно определяется на плоскости с парой числовых координат, каждая из которых является расстоянием со знаком от точки до одной из двух осей.
- Числовые координаты точки представлены упорядоченной парой [latex] (x, y) [/ latex], где координата [latex] x [/ latex] — это расстояние точки от [latex] y [/ латекс] -оси, а координата [latex] y [/ latex] — это расстояние от [latex] x [/ latex] -оси.
- Декартова система координат разбита на четыре квадранта, обозначенных I, II, III и IV, начиная с верхнего правого угла и двигаясь против часовой стрелки.
- Независимая переменная находится на оси [latex] x [/ latex] и состоит из входных значений.
 Зависимая переменная находится на оси [latex] y [/ latex] и состоит из выходных значений.
Зависимая переменная находится на оси [latex] y [/ latex] и состоит из выходных значений.
Ключевые термины
- независимая переменная : произвольный ввод; в декартовой плоскости значение [латекс] х [/ латекс].
- Ось Y : ось на графике, которая обычно проводится снизу вверх, при этом значения растут дальше вверх.
- Квадрант : Одна из четырех четвертей декартовой плоскости, ограниченная осью [латекс] x [/ латекс] и осью [латекс] y [/ латекс].
- зависимая переменная : произвольный вывод; в декартовой плоскости значение [латекс] y [/ латекс].
- Ось x : ось на графике, которая обычно рисуется слева направо со значениями, увеличивающимися вправо.
- упорядоченная пара : набор, содержащий ровно два элемента в фиксированном порядке, используемый для представления точки в декартовой системе координат.Обозначение: [latex] (x, y) [/ latex].

Декартова система координат, названная в честь «отца аналитической геометрии», французского математика 17-го века Рене Декарта, представляет собой двумерную плоскость с горизонтальной осью и вертикальной осью. Обе оси простираются до бесконечности, а стрелки используются для обозначения бесконечной длины. Горизонтальная ось называется осью [latex] x [/ latex], а вертикальная ось — осью [latex] y [/ latex]. Точка пересечения осей называется началом координат.
Для построения точек используется декартова система координат. Точки задаются однозначно в декартовой плоскости парой числовых координат, которые представляют собой расстояния со знаком от точки до двух осей. Каждая точка может быть представлена упорядоченной парой [latex] (x, y) [/ latex], где координата [latex] x [/ latex] — это расстояние точки от оси [latex] y [/ latex]. а координата [latex] y [/ latex] — это расстояние от оси [latex] x [/ latex]. Таким образом, точка пересечения двух осей — [латекс] (0,0) [/ латекс]. На оси [latex] x [/ latex] числа увеличиваются вправо и уменьшаются влево; на оси [latex] y [/ latex] числа увеличиваются при движении вверх и уменьшаются при движении вниз.
На оси [latex] x [/ latex] числа увеличиваются вправо и уменьшаются влево; на оси [latex] y [/ latex] числа увеличиваются при движении вверх и уменьшаются при движении вниз.
Декартова система координат: Декартова система координат с 4 точками, нанесенными, включая начало координат, в [latex] (0,0) [/ latex].
Точки графика
Чтобы построить точку [latex] (2,3) [/ latex], например, вы начинаете с начала координат (где две оси пересекаются). Затем переместите три юнита вправо и два вверх.
Точка [латекс] (- 3,1) [/ latex] находится путем перемещения трех единиц влево от начала координат и одной единицы вверх.
Нецелочисленные координаты [latex] (- 1.5, -2.5) [/ latex] лежат между -1 и -2 на оси [latex] x [/ latex] и между -2 и -3 на [latex ] y [/ latex] -ось. Следовательно, вы перемещаете полторы единицы влево и две с половиной единицы вниз.
Независимые и зависимые переменные
Декартова плоскость особенно полезна для построения серии точек, которые показывают взаимосвязь между двумя переменными.
Например, существует взаимосвязь между количеством машин, которые моет автомойка, и деньгами, которые приносит бизнес (его доходом). Выручка или объем производства зависят от количества машин или материалов, которые они моют. Следовательно, доход — это зависимая переменная ([latex] y [/ latex]), а количество автомобилей — независимая переменная ([latex] x [/ latex]). Выручка отображается по оси [латекс] y [/ латекс], а количество вымытых автомобилей — по оси [латекс] x [/ латекс].
Квадранты
Декартова система координат разбита на четыре квадранта по двум осям.Эти квадранты обозначены I, II, III и IV, начиная с верхнего правого угла и продолжая против часовой стрелки, как показано на рисунке ниже.
Декартовы координаты: Четыре квадранта декартовой системы координат. Стрелки на осях указывают, что они бесконечно продолжаются в своих соответствующих направлениях.
Некоторые основные правила, касающиеся этих квадрантов, могут быть полезны для быстрого построения точек:
- Квадрант I: точки имеют положительные координаты [latex] x [/ latex] и [latex] y [/ latex], [latex] (x, y) [/ latex].

- Квадрант II: точки имеют отрицательные координаты [латекс] x [/ латекс] и положительные [латекс] y [/ латекс], [латекс] (- x, y) [/ latex].
- Квадрант III: точки имеют отрицательные координаты [latex] x [/ latex] и [latex] y [/ latex], [latex] (- x, -y) [/ latex].
- Квадрант IV: Точки имеют положительные [латекс] x [/ латекс] и отрицательные [латекс] y [/ латекс] координаты, [латекс] (x, -y) [/ latex].
- Точки, которые имеют значение 0 для любой координаты, лежат на самих осях и не считаются находящимися ни в одном из квадрантов (например,г., [латекс] (4,0) [/ латекс], [латекс] (0, -2) [/ латекс]).
Уравнения с двумя переменными
Уравнения с двумя неизвестными представляют собой взаимосвязь между двумя переменными и имеют ряд решений.
Цели обучения
Объясните, что представляет собой уравнение с двумя переменными
Основные выводы
Ключевые моменты
- Уравнение с двумя переменными имеет ряд решений, которые удовлетворяют уравнению для обеих переменных.
- Каждое решение уравнения с двумя переменными представляет собой упорядоченную пару и может быть записано в форме [латекс] (x, y) [/ latex].
Ключевые термины
- Декартовы координаты : координаты точки, измеренные от начала координат по горизонтальной оси слева направо (ось [латекс] x [/ латекс]) и по вертикальной оси снизу вверх ([латекс ] y [/ latex] -ось).
- упорядоченная пара : набор, содержащий ровно два элемента в фиксированном порядке, используемый для представления точки в декартовой системе координат.Обозначение: [latex] (x, y) [/ latex].
Уравнения с двумя неизвестными представляют собой взаимосвязь между двумя переменными. Уравнения с двумя переменными часто выражают взаимосвязь между переменными [latex] x [/ latex] и [latex] y [/ latex], которые соответствуют декартовым координатам.
Уравнения с двумя переменными имеют не одно решение, а серию решений, которые удовлетворяют уравнению для обеих переменных. Каждое решение представляет собой упорядоченную пару и может быть записано в виде [латекс] (x, y) [/ latex].
Каждое решение представляет собой упорядоченную пару и может быть записано в виде [латекс] (x, y) [/ latex].
Решение уравнений с двумя переменными
Для данного уравнения с двумя переменными выбор значения одной переменной определяет, каким будет значение другой переменной. Другими словами, если указано значение для одной переменной, то можно найти решение, удовлетворяющее уравнению. Это достигается заменой данного значения на эту переменную и вычислением значения другой.
Пример 1
Рассмотрим следующее уравнение:
[латекс] y = 2x [/ латекс]
Это уравнение с двумя переменными, которое имеет бесконечное количество решений.Для любого значения [latex] x [/ latex] соответствующее значение [latex] y [/ latex] будет в два раза больше его значения.
Например, [латекс] (1, 2) [/ латекс] является решением уравнения. Это можно проверить, указав значения [latex] x [/ latex] и [latex] y [/ latex]:
[латекс] (2) = 2 (1) [/ латекс]
Другое решение — [латекс] (30, 60) [/ латекс], потому что [латекс] (60) = 2 (30) [/ латекс]. Таким образом, существует бесконечное количество упорядоченных пар, удовлетворяющих уравнению. [Latex] [/ latex]
Таким образом, существует бесконечное количество упорядоченных пар, удовлетворяющих уравнению. [Latex] [/ latex]
Пример 2
Теперь рассмотрим следующее уравнение:
[латекс] y = 2x + 4 [/ латекс]
Является ли точка [латекс] (3, 10) [/ латекс] решением этого уравнения?
Обратите внимание, что упорядоченная пара [latex] (3, 10) [/ latex] сообщает нам, что [latex] x = 3 [/ latex] и [latex] y = 10 [/ latex].Чтобы оценить, является ли это решением уравнения, подставьте эти значения вместо переменных следующим образом:
[латекс] (10) = 2 (3) + 4 [/ латекс]
[латекс] 10 = 6 + 4 [/ латекс]
Это верное утверждение, поэтому [latex] (3, 10) [/ latex] действительно является решением этого уравнения.
Пример 3
Решите уравнение [латекс] y = 4x — 7 [/ latex] для значения [latex] x = 3 [/ latex].
Решение данного уравнения могло бы иметь вид [latex] (x, y) [/ latex], и нам дается значение [latex] x [/ latex]. Значение [latex] x [/ latex] можно подставить в уравнение, чтобы найти значение [latex] y [/ latex] в этой точке:
Значение [latex] x [/ latex] можно подставить в уравнение, чтобы найти значение [latex] y [/ latex] в этой точке:
[латекс] y = 4 (3) — 7 [/ латекс]
[латекс] y = 12–7 [/ латекс]
[латекс] y = 5 [/ латекс]
Для данного уравнения [латекс] y = 5 [/ латекс], когда [латекс] x = 3 [/ латекс]. Следовательно, решение — [латекс] (3, 5) [/ латекс].
Пример 4
Решите [латекс] x + 2y = 8 [/ latex] для [latex] x = 4 [/ latex].
Как и в приведенном выше примере, предоставляется значение [latex] x [/ latex], и нам нужно найти соответствующее значение [latex] y [/ latex].Сначала мы можем переписать уравнение в виде [латекс] y [/ латекс]:
[латекс] x + 2y -x = 8 -x [/ латекс]
[латекс] 2y = 8 — x [/ латекс]
[латекс] \ dfrac {2y} {2} = \ dfrac {8-x} {2} [/ латекс]
[латекс] y = \ dfrac {8} {2} — \ dfrac {x} {2} [/ латекс]
[латекс] y = 4 — \ dfrac {1} {2} x [/ латекс]
Теперь подставьте [latex] x = 4 [/ latex] в уравнение и решите относительно [latex] y [/ latex]:
[латекс] y = 4 — \ dfrac {1} {2} (4) [/ латекс]
[латекс] y = 4 — 2 [/ латекс]
[латекс] y = 2 [/ латекс]
Раствор [латекс] (4, 2) [/ латекс].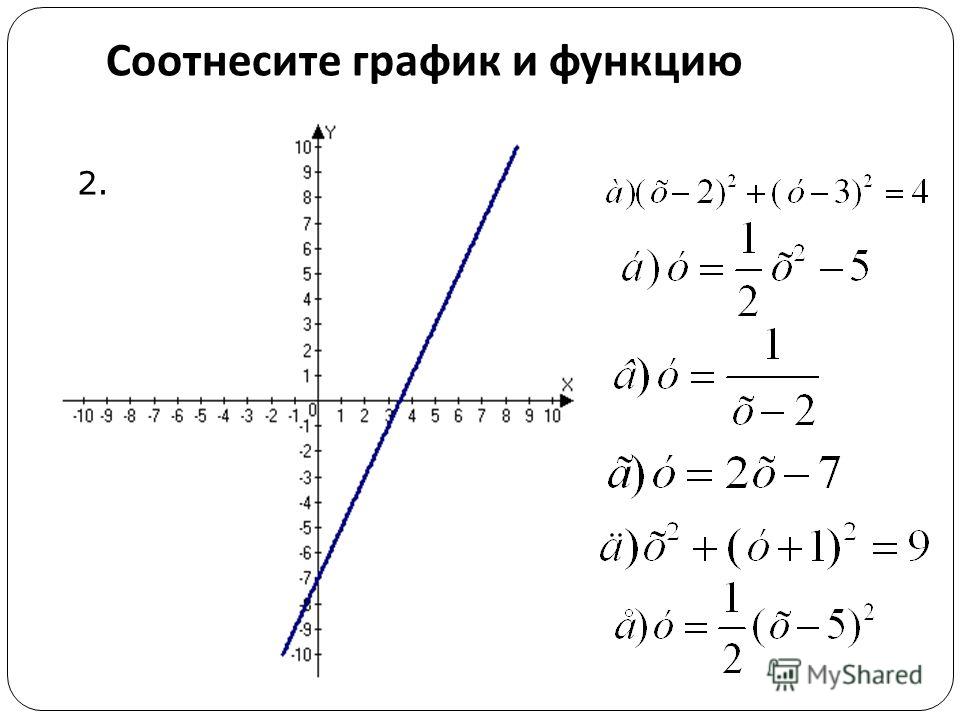
Графические уравнения
Уравнения и их взаимосвязи могут быть визуализированы в виде графиков различных типов.
Цели обучения
Практика построения графиков уравнений в декартовой плоскости
Основные выводы
Ключевые моменты
- Графики — важные инструменты для визуализации уравнений.
- Чтобы построить уравнение, выберите значение для [latex] x [/ latex] или [latex] y [/ latex], найдите переменную, которую вы не выбрали, изобразите упорядоченную пару как точку на декартовой плоскости и повторяйте, пока у вас не будет нанесено достаточно точек, чтобы вы могли соединить их для визуализации графика.
Ключевые термины
- график : диаграмма, отображающая данные; в частности, тот, который показывает взаимосвязь между двумя или более величинами, измерениями или числами.
- точка : объект, который находится в пространстве или на плоскости, но не имеет экстента.

Теперь, когда мы знаем, что такое уравнения, как нам их визуализировать? Для уравнения с двумя переменными, [latex] x [/ latex] и [latex] y [/ latex], нам нужен график с двумя осями: ось [latex] x [/ latex] и [latex] y. [/ latex] -ось.Мы будем использовать декартову плоскость, в которой ось [latex] x [/ latex] является горизонтальной линией, а ось [latex] y [/ latex] — вертикальной линией. Место пересечения двух осей называется началом координат.
Построение уравнения с двумя переменными
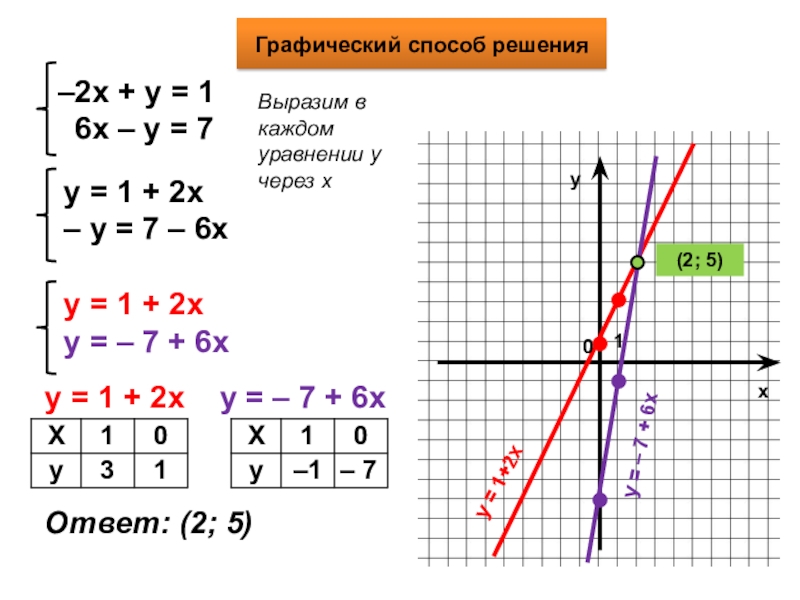
Начнем со следующего уравнения:
[латекс] y = 2x-3 [/ латекс]
Мы начнем с выбора нескольких значений [latex] x [/ latex], вставки их в это уравнение и решения для неизвестной переменной [latex] y [/ latex]. После создания нескольких упорядоченных пар [latex] x [/ latex] и [latex] y [/ latex] мы построим их на декартовой плоскости и соединим точки.
Для трех значений [latex] x [/ latex], давайте выберем отрицательное число, ноль и положительное число, чтобы мы включили точки с обеих сторон оси [latex] y [/ latex]:
- Если [латекс] x = -2 [/ латекс], то [латекс] y = -7 [/ латекс].
 {2} = 100 [/ латекс]
{2} = 100 [/ латекс]Давайте разберемся, выбрав несколько точек для построения графика.{2}} & = \ sqrt {100} \\ y & = \ pm10 \ end {align} [/ latex]
Итак, мы строим [латекс] (0,10) [/ латекс] и [латекс] (0, -10) [/ латекс].
Обратите внимание, что нам не всегда нужно выбирать значения для [latex] x [/ latex]. Например, давайте теперь попробуем установить [latex] y = 0 [/ latex].
Используя ту же арифметику, что и выше, мы получаем упорядоченные пары [латекс] (10,0) [/ латекс] и [латекс] (- 10,0) [/ латекс]. Постройте их также.
У нас все еще недостаточно очков, чтобы действительно понять, что происходит, поэтому давайте выберем еще несколько.2 + 9 [/ latex]: Этот график представляет собой параболу (открытая U-образная кривая, симметричная относительно линии). Параболы могут открываться вверх или вниз, вправо или влево; у них также есть максимальное или минимальное значение.
Графики уравнений как графики решений
Решение уравнения может быть нанесено на графики, чтобы лучше визуализировать поведение уравнения или функции.

Цели обучения
Осознайте, что графическое представление уравнения включает графическое представление его решений
Основные выводы
Ключевые моменты
- Чтобы решить уравнение, нужно определить, какие значения (числа, функции, множества и т. Д.)) удовлетворяют условию, сформулированному в форме уравнения.
- После того, как уравнение построено в виде графика, решения для любого конкретного значения [latex] x [/ latex] или [latex] y [/ latex] можно легко найти, просто взглянув на график.
- Чтобы найти переменную в уравнении, вы должны использовать алгебраические манипуляции, чтобы получить переменную сама по себе на одной стороне уравнения (обычно слева).
Ключевые термины
- уравнение : Утверждение, что два выражения эквивалентны (например,г., [латекс] х = 5 [/ латекс]).
- график : диаграмма, отображающая данные, обычно представляющие взаимосвязь между двумя или более величинами.

- выражение : расположение символов, обозначающих значения, выполняемые над ними операции и группирующие символы (например, [latex] (2x + 4) [/ latex]).
В математике решить уравнение — значит найти, какие значения (числа, функции, множества и т. Д.) Удовлетворяют условию, сформулированному в форме уравнения (два выражения, связанных равенством).Каждое из выражений содержит одно или несколько неизвестных.
В чем графическая разница между уравнениями с одной переменной и уравнениями с двумя переменными?
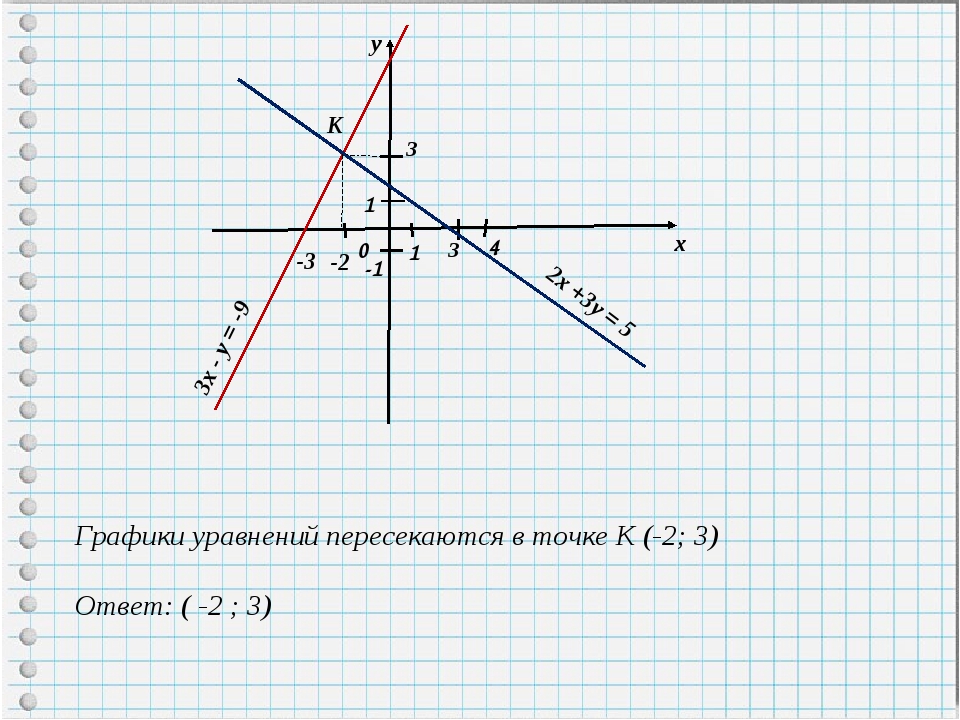
Графики линейных уравнений с одной переменной
Линейное уравнение с одной переменной может быть записано в форме [latex] ax + b = 0, [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] — действительные числа, а [latex] ] а \ neq 0 [/ латекс]. В уравнении, где [latex] x [/ latex] — действительное число, график представляет собой набор всех упорядоченных пар с любым значением [latex] y [/ latex] в паре с этим действительным числом для [latex] x [/ латекс].

Например, для построения графика уравнения [латекс] x-1 = 0, [/ latex] несколько упорядоченных пар будут включать:
- [латекс] (1, -3) [/ латекс]
- [латекс] (1,2) [/ латекс]
- [латекс] (1, -1) [/ латекс]
- [латекс] (1,0) [/ латекс]
- [латекс] (1,1) [/ латекс]
- [латекс] (1,2) [/ латекс]
- [латекс] (1,3) [/ латекс]
Их также можно найти, решив уравнение графика для [латекс] x [/ латекс], которое дает [латекс] x = 1 [/ латекс].Это означает, что значения [latex] y [/ latex] точек не имеют значения, пока их значения [latex] x [/ latex] равны 1. Таким образом, график представляет собой вертикальную линию, проходящую через эти точки, поскольку все точки имеют одинаковое значение [latex] x [/ latex].
То же самое верно и для уравнения, записанного, например, как [латекс] ay + b = 0 [/ latex] или [latex] y = -4 [/ latex]. График будет представлять собой горизонтальную линию, проходящую через точки, у которых все значения [latex] y [/ latex] равны -4.
 3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является многочленом 3-й степени, называемым кубическим многочленом. .
3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является многочленом 3-й степени, называемым кубическим многочленом. .Графики неравенств
Решения неравенств можно изобразить, нарисовав граничную линию, разделяющую координатную плоскость пополам, и заштриховав одну из этих частей.
Цели обучения
Практика построения графиков неравенств путем закрашивания в правильном сечении плоскости
Основные выводы
Ключевые моменты
- Все решения данного неравенства расположены в одной полуплоскости и могут быть изобразены.
- Чтобы изобразить неравенство, сначала рассмотрите его как линейное уравнение и нанесите на график соответствующую линию.Затем закрасьте правильную полуплоскость, чтобы представить все возможные решения неравенства.
- Если в неравенстве используется символ [латекс] \ leq [/ latex] или [латекс] \ geq [/ latex], граничная линия должна быть сплошной, что означает, что решения включают точки на самой линии.

- Если в неравенстве используется символ [latex] <[/ latex] или [latex]> [/ latex], граничная линия должна быть нарисована пунктиром, что означает, что решения не включают никаких точек на линии.
Ключевые термины
- полуплоскость : Одна из двух частей координатной плоскости, созданная при рисовании линии.
- граничная линия : прямая линия на графике неравенства, определяющая полуплоскость, содержащую решения неравенства.
В нашем исследовании линейных уравнений с двумя переменными мы заметили, что все решения уравнения — и только этих решений — были расположены на графике этого уравнения. Теперь мы хотим определить расположение решений линейных неравенств с двумя переменными.
Линейные неравенства двух переменных имеют одну из следующих форм:
- [латекс] ac + от
- [латекс] ac + by \ leq c [/ латекс]
- [латекс] ac + by> c [/ латекс]
- [латекс] ac + by \ geq c [/ латекс]
Напомним, что для линейного уравнения с двумя переменными упорядоченные пары, которые производят истинные утверждения при подстановке в уравнение, называются «решениями» этого уравнения.
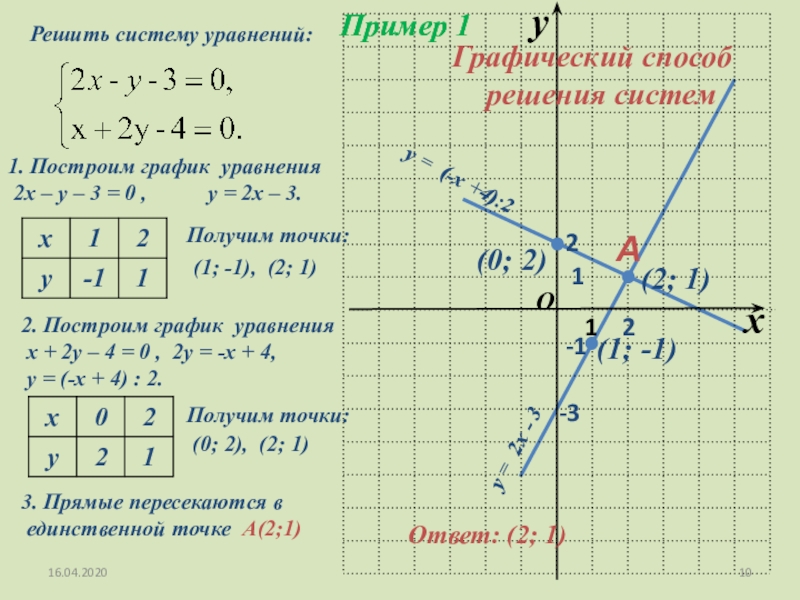
Мы можем сделать аналогичное утверждение относительно неравенств по двум переменным. Мы говорим, что неравенство с двумя переменными имеет решение, когда была найдена пара значений, такая что подстановка этих значений в неравенство приводит к истинному утверждению.
Как и в случае с уравнениями, решения линейных неравенств имеют определенные местоположения в координатной плоскости. При линейном равенстве двух переменных все решения расположены в одной цельной полуплоскости. Прямая линия, проведенная через плоскость, делит плоскость на две полуплоскости, как показано на схеме ниже.Показанная прямая линия называется граничной линией.
полуплоскости: показанная выше граничная линия делит координатную плоскость на две полуплоскости.
Например, рассмотрим следующее неравенство:
[латекс] 2x + 3y \ leq 6 [/ латекс]
На приведенном ниже графике показаны все решения этого неравенства, которые попадают на граничную линию и в заштрихованную полуплоскость.

График [латекс] 2x + 3y \ leq 6 [/ latex]: Все точки, лежащие на граничной линии и в заштрихованной полуплоскости, являются решениями этого неравенства.
Теперь рассмотрим следующее неравенство:
[латекс] y> 2 [/ латекс]
На графике ниже показаны решения этого неравенства: заштрихованная область над линией границы. Обратите внимание: поскольку в неравенстве используется символ [latex]> [/ latex], а не символ [latex] \ geq [/ latex], неравенство является строгим: точки на граничной линии не являются решениями, поэтому линия рисуется пунктирный.
График [latex] y> 2 [/ latex] : Все точки в заштрихованной полуплоскости над линией являются решениями этого неравенства.
Метод построения графиков линейных неравенств от двух переменных заключается в следующем.
Сначала рассмотрите неравенство как уравнение (т.е. замените знак неравенства знаком равенства) и нанесите это уравнение на график. Это называется пограничной линией.
 Примечание:
Примечание:- Если выполняется неравенство [латекс] \ leq [/ latex] или [латекс] \ geq [/ latex], нарисуйте сплошную линию границы. Это означает, что точки на линии являются решениями и являются частью графика.
- Если выполняется неравенство [латекс] <[/ латекс] или [латекс]> [/ латекс], нарисуйте линию границы пунктиром.Это означает, что точки на линии не являются решениями и не являются частью графика.
Определите, какую полуплоскость затенить, выбрав контрольную точку.
- Если при замене контрольная точка дает истинное утверждение, закрасьте содержащую ее полуплоскость.
- Если при замене контрольная точка дает ложное утверждение, заштрихуйте полуплоскость на противоположной стороне граничной линии.
Пример 1
Изобразите следующее неравенство:
[латекс] 3x — 2y \ geq -4 [/ латекс]
Во-первых, нам нужно построить граничную линию.Для этого рассмотрим неравенство как уравнение:
[латекс] 3x − 2y = −4 [/ латекс]
Напомним, что для построения графика уравнения мы можем подставить значение одной переменной и решить другую.
 Полученная упорядоченная пара будет одним из решений уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение:
Полученная упорядоченная пара будет одним из решений уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение:[латекс] \ begin {align} 3 (0) — 2y & = -4 \\ — 2y & = -4 \\ \ dfrac {-2y} {- 2} & = \ dfrac {-4} {- 2 } \\ y & = 2 \ end {align} [/ latex]
Теперь давайте подставим [латекс] y = 0 [/ latex], чтобы найти другое решение:
[латекс] \ begin {align} 3x — 2 (0) & = — 4 \\ 3x & = -4 \\ \ dfrac {3x} {3} & = \ dfrac {-4} {3} \\ x & = — \ dfrac {4} {3} \ end {align} [/ latex]
Теперь мы можем построить график двух известных решений: [latex] (0, 2) [/ latex] и [latex] (- \ frac {4} {3}, 0) [/ latex].Неравенство [латекс] \ geq [/ латекс], поэтому мы знаем, что нам нужно нарисовать линию сплошной. Это дает граничную линию ниже:
График граничной линии для [латекс] 3x — 2y \ geq -4 [/ latex]: График граничной линии, построенный с использованием двух решений для упорядоченных пар.
Затем выберите контрольную точку, чтобы выяснить, какую полуплоскость нам нужно закрасить.
 Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим [latex] (0, 0) [/ latex] в исходное неравенство:
Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим [latex] (0, 0) [/ latex] в исходное неравенство:[латекс] \ begin {align} 3 (0) — 2 (0) & \ geq -4 \\ 0 & \ geq -4 \ end {align} [/ latex]
Это верное утверждение, поэтому оттенок в полуплоскости, содержащей [латекс] (0, 0).[/ латекс]
График [latex] 3x — 2y \ geq -4 [/ latex]: График, показывающий все возможные решения данного неравенства. Решения лежат в заштрихованной области, включая граничную линию.
Как построить линейные уравнения с двумя переменными
Обновлено 3 ноября 2020 г.
Кевин Бек
Графики являются одними из самых полезных математических инструментов для передачи информации осмысленным образом. Даже те, кто не склонен к математике или испытывает явное отвращение к числам и вычислениям, могут найти утешение в базовой элегантности двумерного графа, представляющего отношения между парой переменных.
Линейные уравнения с двумя переменными могут иметь вид
Ax + By = C
, и результирующий график всегда представляет собой прямую линию.
 Чаще уравнение принимает вид
Чаще уравнение принимает видy = mx + b
, где m, — наклон линии соответствующего графика, а b — это интервал y , точка, в которой линия пересекает ось y .
Например, 4 x + 2 y = 8 является линейным уравнением, поскольку оно соответствует требуемой структуре.Но для построения графиков и большинства других целей математики пишут это как:
2y = -4x + 8
y = -2x + 4
Переменные в этом уравнении x и y. , а наклон и пересечение y — это константы .
Шаг 1. Определите точку пересечения оси y
Сделайте это, решив интересующее уравнение для y , если необходимо, и определив b .В приведенном выше примере интервал y равен 4.
Шаг 2: Обозначьте оси
Используйте масштаб, удобный для вашего уравнения.
 Вы можете столкнуться с уравнениями с необычно высокими или низкими значениями интервала y , такими как -37 или 89. В этих случаях каждый квадрат вашей миллиметровой бумаги может представлять десять единиц, а не одну, поэтому оба Ось x и y должны обозначать это.
Вы можете столкнуться с уравнениями с необычно высокими или низкими значениями интервала y , такими как -37 или 89. В этих случаях каждый квадрат вашей миллиметровой бумаги может представлять десять единиц, а не одну, поэтому оба Ось x и y должны обозначать это.Шаг 3. Постройте пересечение оси y
Нарисуйте точку на оси y в соответствующей точке.Между прочим, пересечение по оси Y — это просто точка, в которой x = 0.
Шаг 4: Определите наклон
Посмотрите на уравнение. Коэффициент перед x — это наклон, который может быть положительным, отрицательным или нулевым (последнее в случаях, когда уравнение просто y = b , горизонтальная линия). Наклон часто называют «нарастанием за пробегом» и представляет собой количество изменений единицы в y для каждого отдельного изменения единицы в x.
 В приведенном выше примере наклон равен -2.
В приведенном выше примере наклон равен -2.Шаг 5: Проведите линию через точку пересечения оси y с правильным наклоном
В приведенном выше примере, начиная с точки (0, 4), переместите две единицы в отрицательном направлении y -Направлении и один в положительном направлении x , так как наклон равен -2. Это приводит к точке (1, 2). Проведите линию через эти точки и продолжайте в обоих направлениях, насколько хотите.
Шаг 6: Проверьте график
Выберите точку на графике, удаленную от начала координат, и проверьте, удовлетворяет ли она уравнению.В этом примере точка (6, −8) лежит на графике. Подставляя эти значения в уравнение
y = -2x + 4
\ begin {align} -8 & = (-2) × 6 + 4 \\ -8 & = -12 + 4 \\ -8 & = — 8 \ end {align}
Таким образом, график правильный.
Графики линейных уравнений с двумя переменными — промежуточная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Построить точки в прямоугольной системе координат
- Постройте линейное уравнение, нанеся точки
- График вертикальных и горизонтальных линий
- Найдите точки пересечения по оси X и Y
- Постройте линию, используя точки пересечения
Перед тем, как начать, пройдите тест на готовность.
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Оценить, когда
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить относительно и :
Если вы пропустили эту проблему, просмотрите (рисунок).
Точки графика в прямоугольной системе координат
Подобно тому, как карты используют систему сеток для определения местоположений, система сеток используется в алгебре, чтобы показать взаимосвязь между двумя переменными в прямоугольной системе координат.
 Прямоугольная система координат также называется плоскостью xy или «координатной плоскостью».
Прямоугольная система координат также называется плоскостью xy или «координатной плоскостью».Прямоугольная система координат образована двумя пересекающимися числовыми линиями, горизонтальной и вертикальной. Горизонтальная числовая линия называется осью x . Вертикальная числовая линия называется осью y . Эти оси делят плоскость на четыре области, называемые квадрантами. Квадранты обозначаются римскими цифрами, начиная с верхнего правого угла и продолжаясь против часовой стрелки.См. (Рисунок).
В прямоугольной системе координат каждая точка представлена упорядоченной парой. Первое число в упорядоченной паре — это координата точки x , а второе число — координата точки y . Фраза «упорядоченная пара» означает, что порядок важен.
Заказанная пара
Упорядоченная пара дает координаты точки в прямоугольной системе координат.
 Первое число — это координата x .Второе число — координата y .
Первое число — это координата x .Второе число — координата y .Какая упорядоченная пара точек пересечения осей? В этой точке обе координаты равны нулю, поэтому ее упорядоченная пара — Точка имеет особое имя. Это называется происхождение.
Происхождение
Точка называется исходной точкой . Это точка пересечения осей x и y .
Мы используем координаты для определения точки на плоскости xy .Приведем точку в качестве примера. Сначала найдите 1 на оси x и слегка нарисуйте вертикальную линию через нее. Затем найдите 3 на оси y и нарисуйте горизонтальную линию через. Теперь найдите точку, в которой эти две линии пересекаются — это точка. с координатами См. (рисунок).
Обратите внимание, что сквозная вертикальная линия и сквозная горизонтальная линия не являются частью графика.
 Мы просто использовали их, чтобы найти точку
Мы просто использовали их, чтобы найти точку.
Когда одна из координат равна нулю, точка лежит на одной из осей.На (Рисунок) точка находится на оси y , а точка — на оси x .
Очки по топорам
Точки с координатой y , равной 0, находятся на оси x и имеют координаты
Точки с координатой x , равной 0, находятся на оси y и имеют координаты
Знаки координаты x и координаты y влияют на расположение точек.Вы могли заметить некоторые закономерности, когда рисовали точки в предыдущем примере. Мы можем суммировать знаковые паттерны секторов следующим образом:
Квадранты
До сих пор все решаемые вами уравнения были уравнениями только с одной переменной. Почти в каждом случае, когда вы решали уравнение, вы получали ровно одно решение.
 Но уравнения могут иметь более одной переменной. Уравнения с двумя переменными могут иметь вид. Уравнение такой формы называется линейным уравнением с двумя переменными.
Но уравнения могут иметь более одной переменной. Уравнения с двумя переменными могут иметь вид. Уравнение такой формы называется линейным уравнением с двумя переменными.Линейное уравнение
Уравнение формы, в которой A и B не равны нулю, называется линейным уравнением с двумя переменными.
Вот пример линейного уравнения с двумя переменными, x и y .
Уравнение также является линейным уравнением. Но это не похоже на форму. Мы можем использовать свойство сложения равенства и переписать его по форме.
Переписав, так как мы можем легко увидеть, что это линейное уравнение с двумя переменными, потому что оно имеет форму Когда уравнение находится в форме, мы говорим, что оно находится в стандартной форме линейного уравнения.
Стандартная форма линейного уравнения
Линейное уравнение в стандартной форме , когда оно записано
Большинство людей предпочитают, чтобы значения A , B и C были целыми числами и при написании линейного уравнения в стандартной форме, хотя это не является строго необходимым.

Линейные уравнения имеют бесконечно много решений. Каждому числу, которое заменяется на x , соответствует значение y .Эта пара значений является решением линейного уравнения и представлена упорядоченной парой. Когда мы подставляем эти значения x и y в уравнение, результатом будет истинное утверждение, потому что значение слева равно равно значению справа.
Решение линейного уравнения с двумя переменными
Упорядоченная пара — это решение линейного уравнения, если уравнение является истинным утверждением, когда в уравнение подставляются значения x и y упорядоченной пары.
Линейные уравнения имеют бесконечно много решений. Мы можем построить эти решения в прямоугольной системе координат. Точки будут идеально выровнены по прямой линии.
 Соединяем точки прямой линией, чтобы получился график уравнения. Мы помещаем стрелки на концах каждой стороны линии, чтобы указать, что линия продолжается в обоих направлениях.
Соединяем точки прямой линией, чтобы получился график уравнения. Мы помещаем стрелки на концах каждой стороны линии, чтобы указать, что линия продолжается в обоих направлениях.График — это визуальное представление всех решений уравнения. Это пример поговорки: «Картинка стоит тысячи слов.Линия показывает вам всех решений этого уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения. Пункты , а не на линии, не являются решениями!
График линейного уравнения
График линейного уравнения представляет собой прямую линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения представляет собой точку на этой прямой.
Показан график.
Для каждой заказанной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
А: В: С: D:
Подставьте значения x и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.

ⓐ
ⓑ Нанесите точки и
Точки и находятся на линии, а точка не находится на линии.
Точки, которые являются решениями, находятся на линии, но точка, которая не является решением, не находится на линии.
Использовать график Для каждой упорядоченной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
A B
ⓐ да, да ⓑ да, да
Использовать график Для каждой упорядоченной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
ⓑ Находится ли точка на линии?
A B
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения.Первый метод, который мы будем использовать, называется построением точек или методом точечного построения. Мы находим три точки, координаты которых являются решениями уравнения, и затем строим их в прямоугольной системе координат.
 Соединив эти точки в линию, мы получим график линейного уравнения.
Соединив эти точки в линию, мы получим график линейного уравнения.Как построить график линейного уравнения по точкам
Постройте уравнение, нанеся точки.
Изобразите уравнение, нанеся точки:
Изобразите уравнение, нанеся точки:
Шаги, которые необходимо предпринять для построения графика линейного уравнения с помощью точек, приведены здесь.
Постройте линейное уравнение путем нанесения точек.
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использовать три точки — хорошая привычка.
 Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между этими иллюстрациями.
Если уравнение включает дробь в качестве коэффициента, мы все равно можем заменить x любыми числами.Но арифметика будет проще, если мы сделаем «хороший» выбор для значений x . Таким образом мы избежим дробных ответов, которые сложно изобразить точно.
Изобразите уравнение:
Найдите три точки, которые являются решениями уравнения. Поскольку это уравнение имеет дробный коэффициент x , мы будем тщательно выбирать значения x . Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов.
 Почему значение, кратное двум, является хорошим выбором для значений x ? При выборе числа, кратного 2, умножение на упрощается до целого числа
Почему значение, кратное двум, является хорошим выбором для значений x ? При выборе числа, кратного 2, умножение на упрощается до целого числа.
Точки показаны на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Изобразите уравнение:
Изобразите уравнение:
Вертикальные и горизонтальные линии графика
Некоторые линейные уравнения имеют только одну переменную. У них может быть только x и не y , или только y без x . Это меняет то, как мы составляем таблицу значений, чтобы получить точки для построения.
Давайте рассмотрим уравнение. Это уравнение имеет только одну переменную, x . Уравнение говорит, что x — это , всегда равное , поэтому его значение не зависит от y .
 Независимо от того, каково значение y , значение x всегда равно
Независимо от того, каково значение y , значение x всегда равноИтак, чтобы составить таблицу значений, запишите все значения x . Затем выберите любые значения для y . Поскольку x не зависит от y , вы можете выбрать любые числа, которые вам нравятся.Но чтобы соответствовать точкам на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Постройте точки из таблицы и соедините их прямой линией. Обратите внимание, что мы нарисовали вертикальную линию.
Что делать, если в уравнении y , но нет x ? Давайте изобразим уравнение. На этот раз значение y- является константой, поэтому в этом уравнении y не зависит от x .
 Заполните 4 для всех y (рисунок), а затем выберите любые значения для x .Мы будем использовать 0, 2 и 4 для координат x .
Заполните 4 для всех y (рисунок), а затем выберите любые значения для x .Мы будем использовать 0, 2 и 4 для координат x .На этом рисунке мы изобразили горизонтальную линию, проходящую через ось и в точке 4.
График: ⓐ ⓑ
ⓐ Уравнение имеет только одну переменную, x , а x всегда равно 2. Мы создаем таблицу, где x всегда равно 2, а затем вводим любые значения для y . График представляет собой вертикальную линию, проходящую через ось x в точке 2.
ⓑ Точно так же уравнение имеет только одну переменную, y . Значение y постоянно. Все упорядоченные пары в следующей таблице имеют одинаковую координату y .
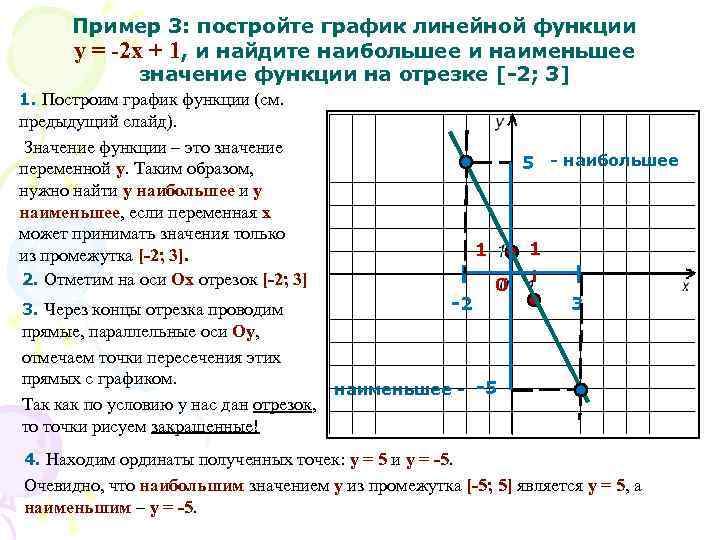 График представляет собой горизонтальную линию, проходящую через ось и в точке
График представляет собой горизонтальную линию, проходящую через ось и в точке.
Изобразите уравнения: ⓐ ⓑ
ⓐ
ⓑ
Изобразите уравнения: ⓐ ⓑ
ⓐ
ⓑ
В чем разница между уравнениями и
Уравнение имеет x и y .Значение y зависит от значения x , поэтому координата y изменяется в соответствии со значением x . Уравнение имеет только одну переменную. Значение y постоянно, оно не зависит от значения x , поэтому координата y всегда равна 4.
Обратите внимание: на графике уравнение дает наклонную линию, а дает горизонтальную линию.

График и в той же прямоугольной системе координат.
Мы замечаем, что первое уравнение имеет переменную x , а второе — нет. Мы составляем таблицу точек для каждого уравнения, а затем наносим на график линии. Показаны два графика.
Постройте уравнения в той же прямоугольной системе координат: и
Постройте уравнения в той же прямоугольной системе координат: и
Найти
x — и y — перехватить
Каждое линейное уравнение может быть представлено уникальной линией, которая показывает все решения уравнения.Мы видели, что при построении линии с помощью точек вы можете использовать любые три решения для построения графика. Это означает, что два человека, рисующие линию, могут использовать разные наборы из трех точек.
На первый взгляд, их две линии могут показаться не одинаковыми, поскольку на них будут обозначены разные точки.
 Но если вся работа была проделана правильно, линии должны быть точно такими же. Один из способов узнать, что это действительно одна и та же линия, — это посмотреть, где линия пересекает ось x и ось y .Эти точки называются пересечениями линии.
Но если вся работа была проделана правильно, линии должны быть точно такими же. Один из способов узнать, что это действительно одна и та же линия, — это посмотреть, где линия пересекает ось x и ось y .Эти точки называются пересечениями линии.Перехват линии
Точки, где линия пересекает ось x и ось y , называются пересечениями линии .
Давайте посмотрим на графики линий.
Во-первых, обратите внимание, где каждая из этих линий пересекает ось x . См. (Рисунок).
Теперь давайте посмотрим на точки, где эти линии пересекают ось y .
ось x в точке: Заказанная пара
для этой точки Линия
пересекает ось y- в точке: Заказанная пара
для этой точки Рисунок (a) 36 Рисунок (b) 4 Рисунок (c ) 5 Рисунок (d) 00 Общий рисунок a bВы видите закономерность?
Для каждой линии координата y точки, в которой линия пересекает ось x , равна нулю.
 Точка, где линия пересекает ось x , имеет форму и называется пересечением x линии.Перехват x происходит, когда y равно нулю.
Точка, где линия пересекает ось x , имеет форму и называется пересечением x линии.Перехват x происходит, когда y равно нулю.В каждой строке координата x — точки, в которой линия пересекает ось y , равна нулю. Точка, в которой линия пересекает ось y , имеет форму и называется пересечением оси y линии. Перехват y происходит, когда x равно нулю.
x — перехват и y — перехват строки
Пересечение x — это точка, в которой линия пересекает ось x .
Пересечение y — это точка, в которой линия пересекает ось y .
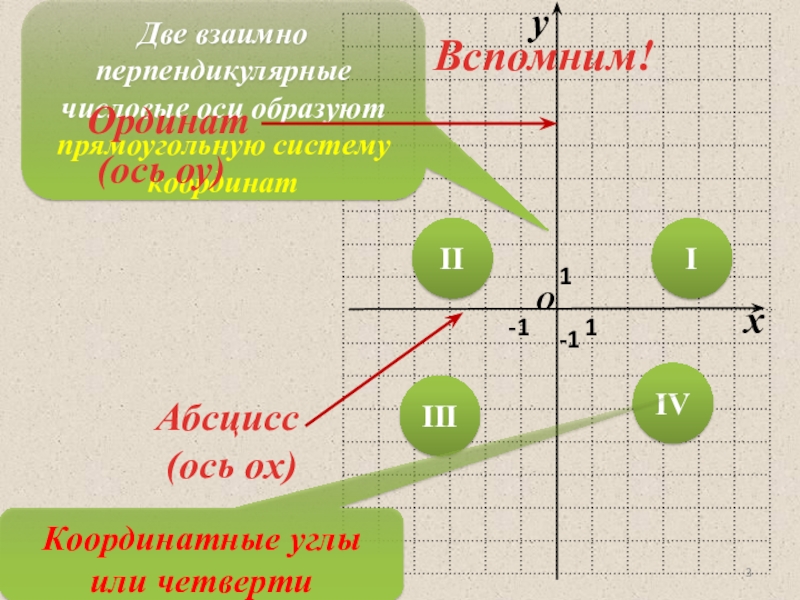
Найдите точки пересечения x и y на каждом показанном графике.
ⓐ График пересекает ось x в точке Пересечение x- составляет
График пересекает ось и в точке. Пересечение и составляет
.
ⓑ График пересекает ось x в точке Пересечение x составляет
График пересекает ось и в точке. Пересечение и составляет
.
ⓒ График пересекает ось x в точке Пересечение x составляет
График пересекает ось и в точке. Пересечение и составляет
.
Найдите точки пересечения x и y на графике.
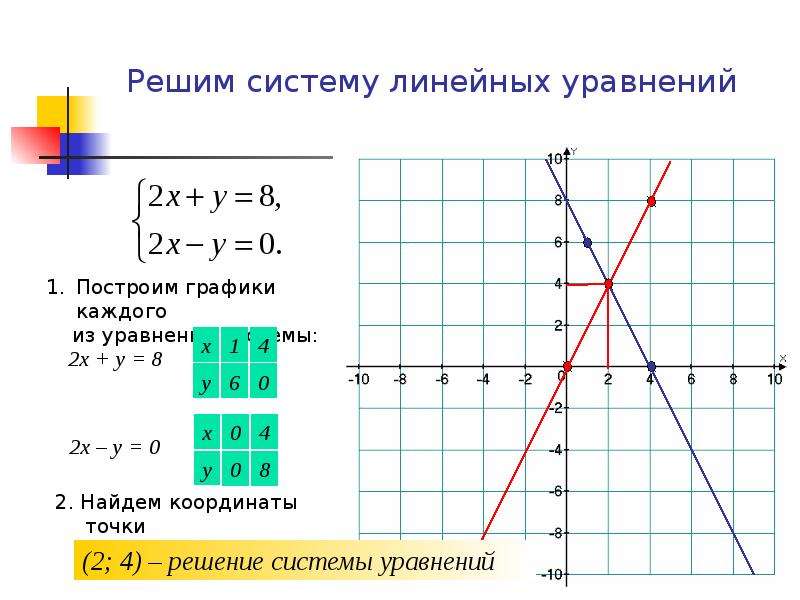
x -перехват:
y -перехват:
Найдите точки пересечения x и y на графике.
x -перехват:
y -перехват:
Признание того, что пересечение x происходит, когда y равно нулю, и что пересечение y происходит, когда x равно нулю, дает нам метод найти точки пересечения линии из ее уравнения.Чтобы найти перехват x , позвольте и решите для x . Чтобы найти перехват y , позвольте и решите относительно y .
Найдите точки пересечения x и y из уравнения прямой
Используйте уравнение линии.
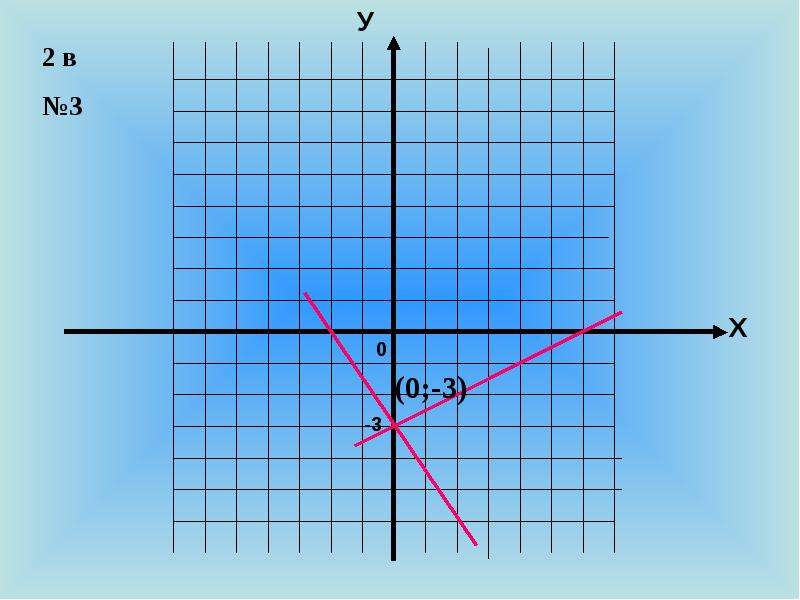 Чтобы найти:
Чтобы найти:- пересечение линии x , позвольте и решить для x .
- y -пересечение линии, позвольте и решить для y .
Найдите перехватчик
Давайте найдем перехват x , а найдем перехват y .Мы заполним таблицу, которая напоминает нам о том, что нам нужно найти.
Перехваты — это точки, как показано в таблице.
x y 4 0 0 8 Найдите точки перехвата:
x -перехват:
y -перехват:
Найдите точки перехвата:
x -перехват:
y -перехват:
Постройте линию с помощью точек пересечения
Чтобы построить линейное уравнение с помощью точек, необходимо найти три точки, координаты которых являются решениями уравнения.
 Вы можете использовать точки пересечения x- и y- как две из трех точек. Найдите точки пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают — затем проведите линию. Этот метод часто является самым быстрым способом построить линию.
Вы можете использовать точки пересечения x- и y- как две из трех точек. Найдите точки пересечения, а затем найдите третью точку, чтобы обеспечить точность. Убедитесь, что точки совпадают — затем проведите линию. Этот метод часто является самым быстрым способом построить линию.Как построить линию с помощью точек пересечения
График с использованием пересечений.
График с пересечениями:
График с пересечениями:
Шаги построения графика линейного уравнения с использованием точек пересечения приведены здесь.
Постройте линейное уравнение, используя точки пересечения.
- Найдите точки пересечения линии x и y .
- Позвольте и решить для x .
- Позвольте и решить для y .
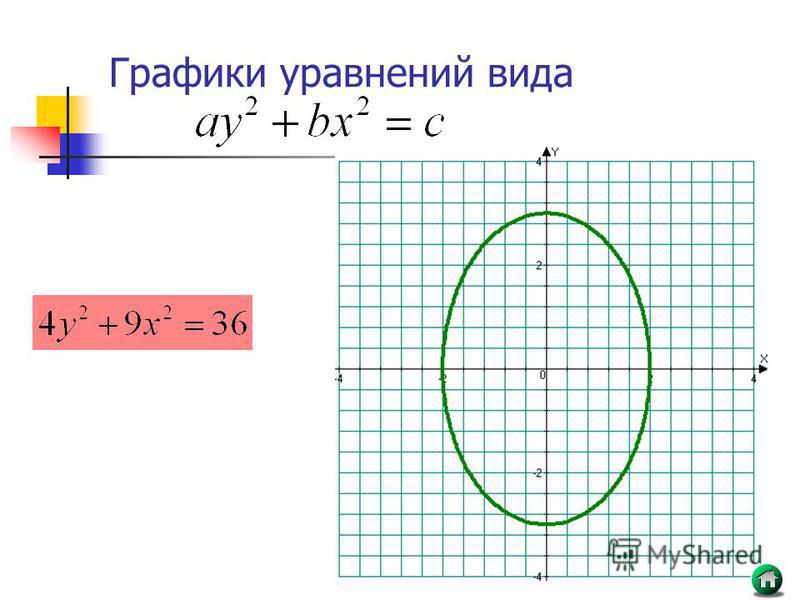
- Найдите третье решение уравнения.
- Постройте три точки и убедитесь, что они совпадают.
- Проведите линию.
График с использованием пересечений.
Найдите точки пересечения и третью точку.
Перечислим точки в таблице и покажем график.
График с пересечениями:
График с пересечениями:
Когда линия проходит через начало координат, точка пересечения x и точка пересечения y являются одной и той же точкой.
График с использованием пересечений.
Эта линия имеет только одну точку пересечения. Это точка
Для обеспечения точности нам нужно нанести три точки.Поскольку точки пересечения x и y — это одна и та же точка, нам нужно еще на две точек, чтобы построить линию.
Полученные три балла сведены в таблицу.
Постройте три точки, убедитесь, что они совпадают, и проведите линию.
График с пересечениями:
График пересечений:
Практика ведет к совершенству
Точки графика в прямоугольной системе координат
В следующих упражнениях нанесите каждую точку в прямоугольную систему координат и определите квадрант, в котором расположена точка.
В следующих упражнениях для каждой упорядоченной пары определите
ⓐ является ли упорядоченная пара решением уравнения? Ⓑ это точка на линии?
ⓐ A: да, B: нет, C: да, D: да ⓑ A: да, B: нет, C: да, D: да
ⓐ A: да, B: да, C: да, D: нет ⓑ A: да, B: да, C: да, D: нет
Построение линейного уравнения по точкам
В следующих упражнениях построите график путем нанесения точек.
График Вертикальные и горизонтальные линии
В следующих упражнениях нанесите на график каждое уравнение.
ⓐⓑ
ⓐⓑ
В следующих упражнениях нарисуйте каждую пару уравнений в одной прямоугольной системе координат.
и
и
Найти x- и y- Перехваты
В следующих упражнениях найдите точки пересечения x и y на каждом графике.
В следующих упражнениях найдите точки пересечения для каждого уравнения.
Построение линии с использованием точек пересечения
В следующих упражнениях построите график с использованием точек пересечения.
Смешанная практика
В следующих упражнениях нанесите на график каждое уравнение.
Письменные упражнения
Объясните, как выбрать три значения x , чтобы составить таблицу для построения графика линии
В чем разница между уравнениями вертикальной и горизонтальной линии?
Вы предпочитаете использовать метод построения точек или метод пересечения точек для построения графика уравнения. Почему?
Вы предпочитаете использовать метод построения точек или метод пересечения точек для построения графика уравнения. Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Если бы большинство ваших чеков было:
Уверенно. Поздравляю! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.
С некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не освоили, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент.К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?
Нет, не понимаю. Это предупреждающий знак, и вы должны его устранить. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
4.2: Графики линейных уравнений с двумя переменными
Распознать взаимосвязь между решениями уравнения и его графиком
В предыдущем разделе мы нашли несколько решений уравнения \ (3x + 2y = 6 \).Они перечислены в таблице \ (\ PageIndex {1} \). Итак, упорядоченные пары (0,3), (2,0) и \ ((1, \ frac {3} {2}) \) являются некоторыми решениями уравнения \ (3x + 2y = 6 \). Мы можем построить эти решения в прямоугольной системе координат, как показано на рисунке \ (\ PageIndex {1} \).
Таблица \ (\ PageIndex {1} \) 3x + 2y = 6 x y (х, у) 0 3 (0,3) 2 0 (2,0) 1 \ (\ frac {3} {2} \) \ ((1, \ frac {3} {2}) \) Рисунок \ (\ PageIndex {1} \)
Обратите внимание, как точки идеально совпадают? Соединяем точки линией, чтобы получить график уравнения 3x + 2y = 6.См. Рисунок \ (\ PageIndex {2} \). Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Рисунок \ (\ PageIndex {2} \)
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой. Пункты , а не на линии, не являются решениями.
Обратите внимание, что точка с координатами (−2,6) находится на линии, показанной на рисунке \ (\ PageIndex {3} \). Если вы подставите x = −2 и y = 6 в уравнение, вы обнаружите, что это решение уравнения.
Рисунок \ (\ PageIndex {3} \)
Итак, точка (−2,6) является решением уравнения \ (3x + 2y = 6 \). (Фраза «точка с координатами (−2,6)» часто сокращается до «точка (−2,6)».)
Рисунок \ (\ PageIndex {3} \). Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам всех решений уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения \ (3x + 2y = 6 \).
ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ
График линейного уравнения Ax + By = C представляет собой линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения представляет собой точку на этой прямой.
Упражнение \ (\ PageIndex {1} \)
Показан график y = 2x − 3.
Для каждой заказанной пары определите:
- Является ли упорядоченная пара решением уравнения?
- Точка на линии?
A (0, −3) B (3,3) C (2, −3) D (−1, −5)
- Ответ
Подставьте значения x и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
- 1.
- 2. Постройте точки A (0,3), B (3,3), C (2, −3) и D (−1, −5).
Точки, которые являются решениями для y = 2x − 3, находятся на линии, но точка, которая не является решением, не находится на линии.
Точки (0,3), (3,3) и (−1, −5) находятся на прямой y = 2x − 3, а точка (2, −3) не на прямой.
Упражнение \ (\ PageIndex {2} \)
Используйте график y = 3x − 1, чтобы решить, составляет ли каждая упорядоченная пара:
- решение уравнения.
- на линии.
- (0, -1)
- (2,5)
- Ответ
- да, да
- да, да
Упражнение \ (\ PageIndex {3} \)
Используйте график y = 3x − 1, чтобы определить, составляет ли каждая упорядоченная пара:
- решение уравнения
- по линии
- (3, -1)
- (-1, -4)
- Ответ
- нет, нет
- да, да
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения.Метод, который мы использовали для построения графика 3x + 2y = 6, называется построением точек или методом построения точек.
Упражнение \ (\ PageIndex {4} \): как построить график уравнения по точкам
Постройте уравнение y = 2x + 1, нанеся точки.
- Ответ
Упражнение \ (\ PageIndex {5} \)
Изобразите уравнение, нанеся точки: y = 2x − 3.
- Ответ
Упражнение \ (\ PageIndex {6} \)
Изобразите уравнение, нанеся точки: y = −2x + 4.
- Ответ
Действия, которые необходимо предпринять при построении линейного уравнения путем нанесения точек, приведены ниже.
ИЗОБРАЖЕНИЕ ЛИНЕЙНОГО УРАВНЕНИЯ ПО ТОЧКАМ
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использовать три точки — хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются.Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (a) и частью (b) на рисунке \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \)
Давайте рассмотрим другой пример. На этот раз мы покажем последние два шага в одной сетке.
Упражнение \ (\ PageIndex {7} \)
Изобразите уравнение y = −3x.
- Ответ
Найдите три точки, которые являются решениями уравнения. Здесь, опять же, проще выбрать значения для x.Вы понимаете почему?
Мы перечисляем точки в Таблице \ (\ PageIndex {2} \).
Таблица \ (\ PageIndex {2} \) y = −3x x y (х, у) 0 0 (0,0) 1 −3 (1, −3) -2 6 (-2,6) Постройте точки, убедитесь, что они совпадают, и проведите линию.
Упражнение \ (\ PageIndex {8} \)
Изобразите уравнение, нанеся точки: y = −4x.
- Ответ
Упражнение \ (\ PageIndex {9} \)
Изобразите уравнение, нанеся точки: y = x.
- Ответ
Когда уравнение включает дробь в качестве коэффициента при x, мы все равно можем заменять x любыми числами.Но математика будет проще, если мы сделаем «правильный» выбор значений x. Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Упражнение \ (\ PageIndex {10} \)
Изобразите уравнение \ (y = \ frac {1} {2} x + 3 \).
- Ответ
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь \ (\ frac {1} {2} \) является коэффициентом при x, мы будем тщательно выбирать значения x. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов.Почему кратное 2 — хороший выбор для значений x?
Точки показаны в таблице \ (\ PageIndex {3} \).
Таблица \ (\ PageIndex {3} \) y = 12x + 3 x y (х, у) 0 3 (0,3) 2 4 (2,4) 4 5 (4,5) Постройте точки, убедитесь, что они совпадают, и проведите линию.
Упражнение \ (\ PageIndex {11} \)
Изобразите уравнение \ (y = \ frac {1} {3} x — 1 \).
- Ответ
Упражнение \ (\ PageIndex {12} \)
Изобразите уравнение \ (y = \ frac {1} {4} x + 2 \).
- Ответ
До сих пор во всех уравнениях, которые мы построили, y было выражено через x.Теперь изобразим уравнение с x и y на одной стороне. Давайте посмотрим, что происходит в уравнении 2x + y = 3. Если y = 0, каково значение x?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем построить график этой точки, трудно быть точным, указав дроби. Помните, что в примере y = 12x + 3 мы тщательно выбирали значения x, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 3 относительно y, будет легче найти три решения уравнения.
\ [\ начало {выровнено} 2 x + y & = 3 \\ y & = — 2 x + 3 \ end {выровнено} \]
Решения для x = 0, x = 1 и x = −1 показаны в таблице \ (\ PageIndex {4} \).График показан на рисунке \ (\ PageIndex {5} \).
Таблица \ (\ PageIndex {4} \) 2x + y = 3 x y (х, у) 0 3 (0,3) 1 1 (1,1) -1-1 5 (-1,5) Рисунок \ (\ PageIndex {5} \)
Можете ли вы найти точку \ ((\ frac {3} {2}, 0) \), которую мы нашли, положив y = 0 на линии?
Упражнение \ (\ PageIndex {13} \)
Изобразите уравнение 3x + y = −1.
- Ответ
\ (\ begin {array} {lrll} {\ text {Найдите три точки, которые являются решениями уравнения.}} & {3 x + y} & {=} & {- 1} \\ {\ text {Первая решите уравнение для} y.} & {y} & {=} & {- 3 x-1} \ end {array} \)
Пусть x будет 0, 1 и −1, чтобы найти 3 точки. Упорядоченные пары показаны в таблице \ (\ PageIndex {5} \). Нанесите точки, убедитесь, что они совпадают, и проведите линию. См. Рисунок \ (\ PageIndex {6} \).
Таблица \ (\ PageIndex {5} \) 3x + y = -1 x y (х, у) 0 -1 (0, -1) 1 −4 (1, −4) -1 2 (-1,2) - Рисунок \ (\ PageIndex {6} \)
Упражнение \ (\ PageIndex {14} \)
Изобразите уравнение 2x + y = 2.
- Ответ
Упражнение \ (\ PageIndex {15} \)
Изобразите уравнение 4x + y = −3.
- Ответ
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают!
Уравнение в упражнении \ (\ PageIndex {13} \) было записано в стандартной форме, с x и y на одной стороне.Мы решили это уравнение относительно y всего за один шаг. Но для других уравнений в стандартной форме решить относительно y не так-то просто, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения графика, положив x = 0 и решив относительно y. Мы можем построить вторую точку, положив y = 0, а затем решив относительно x. Затем мы построим третью точку, используя другое значение для x или y.
Упражнение \ (\ PageIndex {16} \)
Изобразите уравнение \ (2x − 3y = 6 \).
- Ответ
\ (\ begin {array} {lrll} \ text {Найдите три точки, которые являются решениями уравнения} & 2 x-3 y & = & 6 \\ \ text {.} & 2 x-3 y & = & 6 \\ \ text {Сначала пусть} x = 0. & 2 (0) -3 y & = & 6 \\ \ text {Решить относительно} y. & -3 y & = & 6 \\ & y & = & — 2 \\\\ \ text {Теперь пусть} y = 0. & 2 x-3 (0) & = & 6 \\ \ text {Решить относительно} x. & 2 x & = & 6 \\ & x & = & 3 \\ \\ \ text {Нам нужна третья точка. Помните, мы можем} & 2 (6) -3 y & = & 6 \\ \ text {выбрать любое значение для x или y. Пусть x = 6.} & 12-3 y & = & 6 \\ \ text {Решить дляy.} & — 3 y & = & — 6 \\ & y & = & 2 \ end {array} \)
Мы перечисляем упорядоченные пары в Таблице \ (\ PageIndex {6} \).Нанесите точки, убедитесь, что они совпадают, и проведите линию. См. Рисунок \ (\ PageIndex {7} \).
Таблица \ (\ PageIndex {6} \) 2x − 3y = 6 x yT (х, у) 0 −2 (0, −2) 3 0 (3,0) 6 2 (6,2) Рисунок \ (\ PageIndex {7} \)
Упражнение \ (\ PageIndex {17} \)
Изобразите уравнение \ (4x + 2y = 8 \).
- Ответ
Упражнение \ (\ PageIndex {18} \)
Изобразите уравнение \ (2x − 4y = 8 \).
- Ответ
График вертикальные и горизонтальные линии
Можно ли построить уравнение только с одной переменной? Просто x и без y, или просто y без x? Как мы составим таблицу значений, чтобы получить точки для построения?
Рассмотрим уравнение x = −3.Это уравнение имеет только одну переменную x. Уравнение говорит, что x равен , всегда равно −3, поэтому его значение не зависит от y. Независимо от того, что такое y, значение x всегда равно −3.
Итак, чтобы составить таблицу значений, запишите −3 для всех значений x. Затем выберите любые значения для y. Поскольку x не зависит от y, вы можете выбирать любые числа, которые вам нравятся. Но чтобы соответствовать точкам на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. Таблицу \ (\ PageIndex {7} \)
Таблица \ (\ PageIndex {7} \) x = −3 x y (х, у) −3 1 (−3,1) −3 2 (−3,2) −3 3 (−3,3) Постройте точки из таблицы \ (\ PageIndex {7} \) и соедините их прямой линией.Обратите внимание на рис. \ (\ PageIndex {8} \), что мы построили вертикальную линию .
Рисунок \ (\ PageIndex {8} \)
ВЕРТИКАЛЬНАЯ ЛИНИЯ
Вертикальная линия — это график уравнения вида x = a.
Линия проходит по оси x в точке (a, 0).
Упражнение \ (\ PageIndex {19} \)
Изобразите уравнение x = 2.
- Ответ
Уравнение имеет только одну переменную, x, и x всегда равно 2.Мы создаем Table \ (\ PageIndex {8} \), где x всегда равно 2, а затем вводим любые значения для y. График представляет собой вертикальную линию, проходящую через ось x в точке 2. См. Рисунок \ (\ PageIndex {9} \).
Таблица \ (\ PageIndex {8} \) x = 2 x y (х, у) 2 1 (2,1) 2 2 (2,2) 2 3 (2,3) - Рисунок \ (\ PageIndex {9} \)
Упражнение \ (\ PageIndex {20} \)
Изобразите уравнение x = 5.
- Ответ
Упражнение \ (\ PageIndex {21} \)
Изобразите уравнение x = −2.
- Ответ
Что, если в уравнении есть y, но нет x? Построим график уравнения y = 4. На этот раз значение y — константа, поэтому в этом уравнении y не зависит от xx. Заполните 4 для всех y в таблице \ (\ PageIndex {9} \), а затем выберите любые значения для x.Мы будем использовать 0, 2 и 4 для координат x .
Таблица \ (\ PageIndex {9} \) y = 4 x y (х, у) 0 4 (0,4) 2 4 (2,4) 4 4 (4,4) График представляет собой горизонтальную линию, проходящую через ось y в точке 4.См. Рисунок \ (\ PageIndex {10} \).
Рисунок \ (\ PageIndex {10} \)
ГОРИЗОНТАЛЬНАЯ ЛИНИЯ
Горизонтальная линия представляет собой график уравнения вида y = b.
Линия проходит через ось y в точке (0, b).
Упражнение \ (\ PageIndex {22} \)
Изобразите уравнение y = −1.
- Ответ
Уравнение y = −1y = −1 имеет только одну переменную y. Значение y постоянно. Все упорядоченные пары в таблице \ (\ PageIndex {10} \) имеют одинаковую координату y .График представляет собой горизонтальную линию, проходящую через ось y в точке -1-1, как показано на рисунке \ (\ PageIndex {11} \).
Таблица \ (\ PageIndex {10} \) y = -1 x y (х, у) Ta − 1 (0, -1) -1 (3, -1) −3 -1 (-3, -1) - Рисунок \ (\ PageIndex {11} \)
Упражнение \ (\ PageIndex {23} \)
Изобразите уравнение y = −4.
- Ответ
Упражнение \ (\ PageIndex {24} \)
Изобразите уравнение y = 3.
- Ответ
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа y = 4x. В чем разница между уравнениями y = 4x и y = 4?
Уравнение y = 4x имеет как x, так и y. Значение y зависит от значения x.Координата y изменяется в соответствии со значением x. Уравнение y = 4 имеет только одну переменную. Значение y постоянно. Координата y всегда равна 4. Она не зависит от значения x. См. Таблицу \ (\ PageIndex {11} \).
Таблица \ (\ PageIndex {11} \) y = 4x г = 4 x y (х, у) x y (х, у) 0 0 (0,0) 0 4 (0,4) 1 4 (1,4) 1 4 (1,4) 2 8 (2,8) 2 4 (2,4) Рисунок \ (\ PageIndex {12} \)
Обратите внимание, на рисунке \ (\ PageIndex {12} \) уравнение y = 4x дает наклонную линию, а y = 4 дает горизонтальную линию.
Упражнение \ (\ PageIndex {25} \)
График y = −3x и y = −3 в той же прямоугольной системе координат.
- Ответ
Обратите внимание, что в первом уравнении есть переменная x, а во втором — нет. См. Таблицу \ (\ PageIndex {12} \). Эти два графика показаны на рисунке \ (\ PageIndex {13} \).
Таблица \ (\ PageIndex {12} \) y = −3x y = −3 x y (х, у) x y (х, у) (0,0) −3 (0, −3) −3 (1, −3) −3 (1, −3) −6 (2, −6) −3 (2, −3) - Рисунок \ (\ PageIndex {13} \)
Упражнение \ (\ PageIndex {26} \)
График y = −4x и y = −4 в той же прямоугольной системе координат.
- Ответ
Упражнение \ (\ PageIndex {27} \)
График y = 3 и y = 3x в одной прямоугольной системе координат.
- Ответ
Решение систем уравнений с двумя переменными (Алгебра 2, Как решить систему линейных уравнений) — Mathplanet
Система линейного уравнения состоит из двух или более уравнений, и одно ищет общее решение этих уравнений.В системе линейных уравнений каждое уравнение соответствует прямой линии, и каждый ищет точку, где две линии пересекаются.
Пример
Решите следующую систему линейных уравнений:
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right. $$
Поскольку мы ищем точку пересечения, мы можем изобразить уравнения:
Здесь мы видим, что прямые пересекаются друг с другом в точке x = 2, y = 8.Это наше решение, и мы можем называть его графическим решением задачи.
Но как найти решение, если линии никогда не пересекаются? Нельзя, система уравнений не имеет решения.
Можно также прийти к правильному ответу с помощью метода исключения (также называемого методом сложения или методом линейной комбинации) или методом подстановки.
При использовании метода подстановки мы используем тот факт, что если два выражения y и x имеют равное значение x = y, то x может заменить y или наоборот в другом выражении без изменения значения выражения.
Пример
Решите системы уравнений методом подстановки
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right. $$
Заменим y в верхнем уравнении на выражение для второго уравнения:
$$ \ begin {array} {lcl} 2x + 4 & = & 3x + 2 \\ 4-2 & = & 3x-2x \\ 2 & = & x \\ \ end {array} $$
Чтобы определить значение y , мы можем продолжить, вставив наше значение x в любое из уравнений.Выбираем первое уравнение:
$$ y = 2x + 4 $$
Подключаем x = 2 и получаем
$$ y = 2 \ cdot 2 + 4 = 8 $$
Таким образом, мы пришли к тому же ответу, что и в графическом решении.
Метод исключения требует, чтобы мы добавляли или вычитали уравнения, чтобы исключить либо x , либо y , часто нельзя приступить к сложению напрямую, не умножив сначала первое или второе уравнение на некоторое значение.
Пример
$$ 2x-2y = 8 $$
$$ x + y = 1 $$
Теперь мы хотим сложить два уравнения, но это не приведет к удалению ни x , ни y .Следовательно, мы должны умножить второе уравнение на 2 с обеих сторон и получить:
$$ 2x-2y = 8 $$
$$ 2x + 2y = 2 $$
Теперь мы пытаемся добавить нашу систему уравнений. Мы начинаем с терминов x слева, а затем с терминов и и, наконец, с чисел справа:
$$ (2x + 2x) + (- 2y + 2y) = 8 + 2 $$
Термины и были исключены, и теперь у нас есть уравнение только с одной переменной:
$$ 4x = 10 $$
$$ x = \ frac {10} {4} = 2.5 $$
После этого, чтобы определить значение y , мы вставляем x = 2,5 в одно из уравнений. Выбираем первое:
$$ \ begin {array} {lcl} 2 \ cdot 2.5-2y & = & 8 \\ 5-8 & = & 2y \\ -3 & = & 2y \\ \ frac {-3} {2} & = & y \\ y & = & -1,5 \\ \ end {array} $$
Видеоурок
Решите систему уравнений:
$$ \ left \ {\ begin {matrix} 2x-4y = 0 \\ -4x + 4y = -4 \ end {matrix} \ right.
$
Графические линейные уравнения
График линейного уравнения с двумя переменными представляет собой линию (поэтому его называют
линейный
).Если вы знаете, что уравнение линейно, вы можете построить его график, найдя любые два решения.
(
Икс
1
,
y
1
)
а также
(
Икс
2
,
y
2
)
,
нанесение этих двух точек на карту и построение линии, соединяющей их.
Пример 1:
Изобразите уравнение
Икс
+
2
y
знак равно
7
.
Вы можете найти два решения, соответствующие
Икс
-перехватывает
а также
y
-перехватывает
графика, установив сначала
Икс
знак равно
0
а потом
y
знак равно
0
.
Когда
Икс
знак равно
0
, мы получили:
0
+
2
y
знак равно
7
y
знак равно
3.5
Когда
y
знак равно
0
, мы получили:
Икс
+
2
(
0
)
знак равно
7
Икс
знак равно
7
Итак, две точки
(
0
,
3.5
)
а также
(
7
,
0
)
.
Постройте эти две точки и проведите линию, соединяющую их.
Если уравнение находится в
форма пересечения склонов
или же
точечно-наклонная форма
, вы также можете использовать
склон
чтобы помочь вам построить график.
Пример 2:
Постройте линию
y
знак равно
3
Икс
+
1
.
Из уравнения мы знаем, что
y
-перехват
1
, точка
(
0
,
1
)
и наклон
3
.Постройте точку
(
0
,
1
)
и оттуда идти вверх
3
единиц и вправо
1
единицы и нанесите на график вторую точку. Проведите линию, содержащую обе точки.
Горизонтальные и вертикальные линии
иметь очень простые уравнения.
Пример 3:
Горизонтальная линия:
y
знак равно
3
Вертикальная линия:
Икс
знак равно
—
2
графиков функций двух переменных
графиков функций двух переменных
Многие типы экономических проблем требуют, чтобы мы рассматривали две переменные в
в то же время.Типичный пример — соотношение между ценой товара и
спрос или предложение на этот товар. Отношение можно описать алгебраически
функцией или уравнением с двумя переменными. Но часто бывает полезно представить
отношение в двумерном графе. Такой график называется разбросом.
диаграмма. Это полезное устройство, потому что если существует простая взаимосвязь между
две переменные, это легко наблюдать, как только данные нанесены на график. Как
пословица гласит: «Картинка стоит тысячи слов.”Для графического представления функции мы используем две перпендикулярные линии, называемые осями.
Их точка пересечения называется началом координат. Этот способ представления
называется декартовой системой координат или плоскостью. Числовое значение одного
переменная измеряется по нижней или горизонтальной оси. Горизонтальная ось
называется осью x. Числовое значение другой переменной измеряется.
по боковой или вертикальной оси. Вертикальная ось называется осью y. В
четыре участка, на которые разбивается граф, называются квадрантами.Единицы
длины указаны по двум осям.Обратите внимание, что есть четыре квадранта. Если x положительный, мы перемещаемся вправо.
Если x отрицателен, мы перемещаемся влево. Если y положительно, мы движемся вверх. Если y отрицательно
мы спускаемся.Координаты
Координаты
позволяют нам увидеть взаимосвязь между парами чисел и
точки в плоскости. Координаты определяют положение точки P относительно
к происхождению.У нас есть координата x и координата y.
Пусть (x, y) представляет точку, координатами которой являются числа x и y.
Обратите внимание, что координата x идет первой. Две координаты говорят нам, как далеко
мы должны пройти сначала по оси x, а затем по оси y до точки
достигается.Построение координат: некоторые примеры
Пример 1
Найдите следующие точки
балла а
(2, 4)
точка b (4, -6)
точка c (-2, -6)
точка d (-6,
2)Пример 2
p = цена ящика с овощами за доллар
f (p) = предложение в тысячах ящиковУ менеджера магазина есть следующие данные, которые относятся к цене ящика
овощей в поставку:цена 4 6 8 10 14 снабжение 2 14 23 27 29 О чем говорят нам данные? График показывает, что, как и следовало ожидать, увеличение
в цене связано с увеличением предложения.
