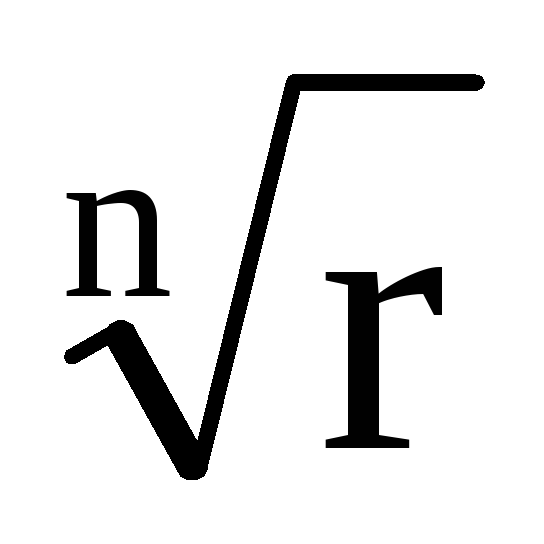Свойства числа 85849

Свойства числа 85849

Множители 293 * 293 Делители 1, 293, 85849 Количество делителей 3 Сумма делителей 86143 Предыдущее целое 85848 Следующее целое 85850 Простое число? NO Предыдущее простое 85847 Следующее простое 85853 85849th простое число 1101871 Является числом Фибоначчи? NO Число Белла? NO Число Каталана? NO Факториал? NO Регулярное число? NO Совершенное число? NO Полигональное число (s < 11)? квадрат(293) Двоичное 10100111101011001 Восьмеричная 247531 Двенадцатеричный 41821 Шестнадцатиричная 14f59 Квадрат 7370050801 Квадратный корень 293 Натуральный логарифм 11. 360345218034 Десятичный логарифм 4.9337352407082 Синус 0.96420924605962 Косинус -0.26514247078343 Тангенс -3.6365703435237

Математические настройки для вашего сайта

Выберите язык: Deutsch English Español Français Italiano Nederlands Polski Português Русский 中文 日本語 한국어

Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером

Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности. © 2021 numberempire.com Все права защищены

Число 85849

Сумма цифр	34
Произведение цифр	11520
Произведение цифр (без учета ноля)	11520
Количество цифр в числе	5 (пятизначное число)
Все делители числа	1, 293, 85849
Наибольший делитель из ряда степеней двойки	1
Количество делителей	3
Сумма делителей	86143
Простое число?	Нет
Полупростое число?	Да
Обратное число	0. 000011648359328588568
Индо-арабское написание	٨٥٨٤٩
Азбука морзе	—.. ….. —.. ….- —-.
Факторизация	293 * 293
Двоичный вид	10100111101011001
Троичный вид	11100202121
Восьмеричный вид	247531
Шестнадцатеричный вид (HEX)	14F59
Перевод из байтов	83 килобайта 857 байтов
Цвет	RGB(1, 79, 89) или #014F59
Наибольшая цифра в числе (возможное основание)	9 (10, десятичный вид)
Число Фибоначчи?	Нет
Нумерологическое значение	7 нематериальное, духовность, загадочное, познание, учеба, расставание, грусть, одиночество, тишина, спокойствие
Синус числа	0. 9642092460596192
Косинус числа	-0.26514247078342756
Тангенс числа	-3.6365703435237284
Натуральный логарифм	11.360345218034135
Десятичный логарифм	4.933735240708219
Квадратный корень	293
Кубический корень	44. 11420058479868
Квадрат числа	7370050801
Перевод из секунд	23 часа 50 минут 49 секунд
Дата по UNIX-времени	Thu, 01 Jan 1970 23:50:49 GMT
MD5	3f5edbc05f8e0879d31769c91cdfc77b
SHA1	c6e6ff55069fc3490b401e8039701622bf5eab18
Base64	ODU4NDk=
QR-код числа 85849

Таблица квадратов натуральных (целых) чисел от 1 до 999.

Таблица квадратных корней.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица квадратов натуральных (целых) чисел от 1 до 999. Таблица квадратных корней. Поделиться:    Таблица квадратов натуральных (целых) чисел от 1 до 999. Таблица квадратных корней. Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 0 0 1 4 9 16 25 36 49 64 81 1 100 121 144 169 196 225 256 289 324 361 2 400 441 484 529 576 625 676 729 784 841 3 900 961 1024 1089 1156 1225 1296 1369 1444 1521 4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401 5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 6 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761 7 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241 8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921 9 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801 10 10000 10201 10404 10609 10816 11025 11236 11449 11664 11881 11 12100 12321 12544 12769 12996 13225 13456 13689 13924 14161 12 14400 14641 14884 15129 15376 15625 15876 16129 16384 16641 13 16900 17161 17424 17689 17956 18225 18496 18769 19044 19321 14 19600 19881 20164 20449 20736 21025 21316 21609 21904 22201 15 22500 22801 23104 23409 23716 24025 24336 24649 24964 25281 16 25600 25921 26244 26569 26896 27225 27556 27889 28224 28561 17 28900 29241 29584 29929 30276 30625 30976 31329 31684 32041 18 32400 32761 33124 33489 33856 34225 34596 34969 35344 35721 19 36100 36481 36864 37249 37636 38025 38416 38809 39204 39601 20 40000 40401 40804 41209 41616 42025 42436 42849 43264 43681 Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 21 44100 44521 44944 45369 45796 46225 46656 47089 47524 47961 22 48400 48841 49284 49729 50176 50625 51076 51529 51984 52441 23 52900 53361 53824 54289 54756 55225 55696 56169 56644 57121 24 57600 58081 58564 59049 59536 60025 60516 61009 61504 62001 25 62500 63001 63504 64009 64516 65025 65536 66049 66564 67081 26 67600 68121 68644 69169 69696 70225 70756 71289 71824 72361 27 72900 73441 73984 74529 75076 75625 76176 76729 77284 77841 28 78400 78961 79524 80089 80656 81225 81796 82369 82944 83521 29 84100 84681 85264 85849 86436 87025 87616 88209 88804 89401 30 90000 90601 91204 91809 92416 93025 93636 94249 94864 95481 31 96100 96721 97344 97969 98596 99225 99856 100489 101124 101761 32 102400 103041 103684 104329 104976 105625 106276 106929 107584 108241 33 108900 109561 110224 110889 111556 112225 112896 113569 114244 114921 34 115600 116281 116964 117649 118336 119025 119716 120409 121104 121801 35 122500 123201 123904 124609 125316 126025 126736 127449 128164 128881 36 129600 130321 131044 131769 132496 133225 133956 134689 135424 136161 37 136900 137641 138384 139129 139876 140625 141376 142129 142884 143641 38 144400 145161 145924 146689 147456 148225 148996 149769 150544 151321 39 152100 152881 153664 154449 155236 156025 156816 157609 158404 159201 40 160000 160801 161604 162409 163216 164025 164836 165649 166464 167281 Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 41 168100 168921 169744 170569 171396 172225 173056 173889 174724 175561 42 176400 177241 178084 178929 179776 180625 181476 182329 183184 184041 43 184900 185761 186624 187489 188356 189225 190096 190969 191844 192721 44 193600 194481 195364 196249 197136 198025 198916 199809 200704 201601 45 202500 203401 204304 205209 206116 207025 207936 208849 209764 210681 46 211600 212521 213444 214369 215296 216225 217156 218089 219024 219961 47 220900 221841 222784 223729 224676 225625 226576 227529 228484 229441 48 230400 231361 232324 233289 234256 235225 236196 237169 238144 239121 49 240100 241081 242064 243049 244036 245025 246016 247009 248004 249001 50 250000 251001 252004 253009 254016 255025 256036 257049 258064 259081 51 260100 261121 262144 263169 264196 265225 266256 267289 268324 269361 52 270400 271441 272484 273529 274576 275625 276676 277729 278784 279841 53 280900 281961 283024 284089 285156 286225 287296 288369 289444 290521 54 291600 292681 293764 294849 295936 297025 298116 299209 300304 301401 55 302500 303601 304704 305809 306916 308025 309136 310249 311364 312481 56 313600 314721 315844 316969 318096 319225 320356 321489 322624 323761 57 324900 326041 327184 328329 329476 330625 331776 332929 334084 335241 58 336400 337561 338724 339889 341056 342225 343396 344569 345744 346921 59 348100 349281 350464 351649 352836 354025 355216 356409 357604 358801 60 360000 361201 362404 363609 364816 366025 367236 368449 369664 370881 Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 61 372100 373321 374544 375769 376996 378225 379456 380689 381924 383161 62 384400 385641 386884 388129 389376 390625 391876 393129 394384 395641 63 396900 398161 399424 400689 401956 403225 404496 405769 407044 408321 64 409600 410881 412164 413449 414736 416025 417316 418609 419904 421201 65 422500 423801 425104 426409 427716 429025 430336 431649 432964 434281 66 435600 436921 438244 439569 440896 442225 443556 444889 446224 447561 67 448900 450241 451584 452929 454276 455625 456976 458329 459684 461041 68 462400 463761 465124 466489 467856 469225 470596 471969 473344 474721 69 476100 477481 478864 480249 481636 483025 484416 485809 487204 488601 70 490000 491401 492804 494209 495616 497025 498436 499849 501264 502681 71 504100 505521 506944 508369 509796 511225 512656 514089 515524 516961 72 518400 519841 521284 522729 524176 525625 527076 528529 529984 531441 73 532900 534361 535824 537289 538756 540225 541696 543169 544644 546121 74 547600 549081 550564 552049 553536 555025 556516 558009 559504 561001 75 562500 564001 565504 567009 568516 570025 571536 573049 574564 576081 76 577600 579121 580644 582169 583696 585225 586756 588289 589824 591361 77 592900 594441 595984 597529 599076 600625 602176 603729 605284 606841 78 608400 609961 611524 613089 614656 616225 617796 619369 620944 622521 79 624100 625681 627264 628849 630436 632025 633616 635209 636804 638401 80 640000 641601 643204 644809 646416 648025 649636 651249 652864 654481 Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 81 656100 657721 659344 660969 662596 664225 665856 667489 669124 670761 82 672400 674041 675684 677329 678976 680625 682276 683929 685584 687241 83 688900 690561 692224 693889 695556 697225 698896 700569 702244 703921 84 705600 707281 708964 710649 712336 714025 715716 717409 719104 720801 85 722500 724201 725904 727609 729316 731025 732736 734449 736164 737881 86 739600 741321 743044 744769 746496 748225 749956 751689 753424 755161 87 756900 758641 760384 762129 763876 765625 767376 769129 770884 772641 88 774400 776161 777924 779689 781456 783225 784996 786769 788544 790321 89 792100 793881 795664 797449 799236 801025 802816 804609 806404 808201 90 810000 811801 813604 815409 817216 819025 820836 822649 824464 826281 91 828100 829921 831744 833569 835396 837225 839056 840889 842724 844561 92 846400 848241 850084 851929 853776 855625 857476 859329 861184 863041 93 864900 866761 868624 870489 872356 874225 876096 877969 879844 881721 94 883600 885481 887364 889249 891136 893025 894916 896809 898704 900601 95 902500 904401 906304 908209 910116 912025 913936 915849 917764 919681 96 921600 923521 925444 927369 929296 931225 933156 935089 937024 938961 97 940900 942841 944784 946729 948676 950625 952576 954529 956484 958441 98 960400 962361 964324 966289 968256 970225 972196 974169 976144 978121 99 980100 982081 984064 986049 988036 990025 992016 994009 996004 998001 Инструкция: в левом столбце — количество десятков, в первой строке — количество единиц. То есть, для того, чтобы узнать квадрат числа 123, требуется найти пересечение строки номер 12 со столбцом номер 3. Получим, что1232=15129. — 0 1 2 3 4 5 6 7 8 9 Справка проекта: Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

делители, простота, двоичный вид, куб, квадрат

Укажите число, чтобы получить всю информацию о нем:

Описание числа 293

Рациональное положительное число 293


является трехзначным. Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 293, равна 14, а их произведение равно 54.

Число 293 является нечетным и простым.
Всего число 293 имеет 2 делителей:
1,
293,
. Сумма делителей равна 294. Куб числа 293 равен 85849, а квадрат составляет 25153757.
Квадратный корень рассматриваемого числа равен 17,1172427686237. Кубический корень равен 6,64185219534421.
Число, которое является обратным к числу 293, выглядит как 0,00341296928327645.

© 2020 — ZeroInf

Большев Л.Н., Смирнов Н.В, Таблицы математической статистики (1983), страница 95

Квадраты целых чнсел 3 ! 4 и О 1 !21 441 96! !681 64 Зг4 784 И44 2304 а о4 ! ‘ 152! 24о! 4 484 !о!4 1764 ‘ 49 289 729 1369 2209 25 225 625 1225 гог» 9 169 529 1о89 1849 28о9 3969 6889 8649 гобо9 22769 25!29 27689 го449 о !оо 4оо 9оо 16оо 2»оо 36оо ~900 8!оо гбо1 5241 6561 8281 Зог», 4225’ 5625 7225 9ог»! 3249 4489 5929 7569 94о9 1!Ц9 16!29 18769 21629 24649 г7889 ЗЦ9 ЗВ 9 3498о69 2~04 44 6724 8464 ЗЭ64 462624 7744 96о4 и664 13924 16384 19044 219о4 348! 4761 6241 98о! в!ог». 13225′ 15625 18225 21025 и88! 1664! 1932 ! 22201 го4о4 12544 14884 174г4 го!64 !ого! !Ц21 146461 171 1 19881 !оооо 1 иоо 1464оо 196оо 1О 11 12 !3 14 25828! г 56! 3204! 357гг 396ог 23!о4 26144 29584 ЗЗ 4 36864 г4ог» 27225: 32625 34225 Зво25 г4964 28224 31684 Э5344 392о4 ггВо! 25921 29241 32761 3648 ! 234о9 26569 29929 33489 37249 225оо 256го 28902 324оо 36!оо 56 17 !8 ‘9 4озо4 .

492 4 449~4 5 564 5~824 63»о4 686484 739 4 $9524 5264 42о8~9 47 9 5!5г9 56169 61оо9 ббо489 7и 9 786729 2З69 882о9 4368! 47961 52441 57121 62оо! 42ог» 46и» »обг» 55225 боог» б»ог» 7оа25 ~5625 87ог» 4о4м Ж~ 53361 58081 4оооо 4424оо 529оо 57боо 2О г1 гг 23 24 67оВ! 723861 7 41 3521 894о1 615оо 676оо 729оо 84оо 41ао 63оо! 25 гб 27 28 29 9обог 967г1 1озо41 го9 561 и628! 93’2» 99225 го»625 112225 119025 95481 !о!761 гоВИ! 114921 !и Во! 92ооо 961оо !ог4оо !о89оо 1!56оо 91204 97344 го3684 ио224 и696» 94Ч9 1оо489 !о6923 113 569 120409 Эо 31 32 зз Э4 122»оо !296оо 1369оо И44оо 1521оо ибог» цЗ2 5 14обг5 ИВгг5 156ог» и888! цб!6! !4364! 151321 1592о1 1239о4 131044 138384 !45924 153664 16!6о4 169744 !866г4 195364 12320! гзо32! 137641 145161 152881 16ово1 168921 177241 !8576! 19448! 35 36 37 38 39 1274~9 1346 9 142129 И9769 1576о9 165649 73889 182329 !9о969 !99829 го8849 г!Во89 227529 237169 г47оо9 16оаоо !63!оо !764оо 184900 !936оо !64ог» 172225 18а625 !89гг» цВог5 4о и 42 43 44 !67281 !7556! 184041 192721 го!6о! гог5оо гибоо 2209оо 2 3о4оо 240100 4″ 46 47 48 49 ио68! 2!9961 22944! 239121 249оо ! го7ог5 2!62г5 гг5625 235225 24»о25 204324 213444 222784 232З24 242064 205209 2!4369 гг3729 233289 243о49 203401 2!г52! гг!841 гзцб! 24!281 — 390 4!229 45369 49729 54г89 59о49 64оо9 85849 91829 97969 !о4329 ио889 и 7649 1246о9 ц!769 !39129 !46689 154449 16г4о9 гто»69 1789г9 187489 !96249 !б 196 576 1!56 29Э6 2916 4о96 5476 8836 го816 12996,’ 15376 17956 го736 гэцб З 76 33856 37636 41616 45796 »о!76 54756 59536 64516 ‘ 69696 75о76 Во656 86436 9г416 98596 1о4976 1!1556 118336 125316 1324896 1Э9 76 И7456 Ц»236 163г!б 17!396 17~776 ,18 356 197 ц6 гобиб 215296 224676 234256 244о36 36 256 676 !г96 , гиб 32Ф 4356 5776 7396 9г!6 игзб 13456 15876 18496 гц!6 24336 27556 Зо976 3 4!6 3$596 424636 46 56 5!276 55696 бо»16 65536 7о75о 786176 !796 876!6 93636 99856 !обг76 112896 119716 и6736 133956 И!376 И8996 1568!6 164836 ‘1ро»6 1 И76 19оо96 !989!6 го7936 и7!56 226576 236196 г46о!6 43264 47524 51984 56644 61564 94864 1оИ24 !о7584 и4244 ггио4 128164 1354И !4И84 !5о544 1584о4 166464 174724 1’3184 !9!844 гоото4 го9764 гИог4 228484 238 И4 ИВоо4 . Таблица 7Я.

Факторналы, десятичные логарифмы факторналов, квадратные корни н обратные величины !оа„ц! л1′ 1, ООООСЮО а,7а71об8 57735о3 5оаааоа 4472!Эб о,4ааг483 3779645 3535534 3333333 3162270 о,За!5113 288675 ! 27735о! гб?26!г 250!909 о,25озооо 2425356 г35?аг3 2294157 223бо68 о,г!82179 2132007 го85!44 го4п41 2оаоаоз 1, ооаоаоо 1,4И2!Зб 1 732а5а0 2,ааоооао г,гзбоб8о 2,4494897 2,6457513 2, 0284271 3, ооооооо 3,1бгг777 3,3!ббг48 3,46Но!б 3 ба555’3 3,74′!6574 3,8729033 4,оозоаоо 4, п31о56 4,24гбза7 4 3588989 4.472’Збо 4, 50г5757 4, 6924!58 4, 7950315 4,8909795 5, аааоааа о, ооооооо а,за!аЗаа о, 778!5!3 1, 38огп г 2, 0791812 2 8573325 3,7о243о5 4, ба55га5 5, 559763о 6,559763о 7, боп557 8, 60о337о 9 79420оз 10,9404084 1г, И64996 13, Зго6196 И, 551оба5 15, 8о634!а !7, о85а946 18с 3861246 19,7о83439 21, озо?666 22, 41249Н 25, !За6457 26, бо5619о 28, о369828 29, 4841408 Зо, 94бя88 32, 4гЗббо! 33,915аг!8 35, 4!о!? г? 36,9386857 38,4?о!646 4о, о142326 41,57о535! 43; 1387369 Н, 7!85го5 46,3о9585! 4?,9п6451 49,5244289 51,!47678г 52,?Й!!467 54,4245993 56, о7701!9 57,74о5697 59,4!26676 61,о939о88 бг,?ЫНа49 64,403о749 1, ооооаоо а, 5ооааоа 3333333 25ааооо гаааоаа 1 6 24 по 1, Оааааа о, 5оооао 166667 416667 ЫЗЗЗЗЗ о, 138803 !984 И 248огб г75573 275573 0,25а52! го8768 ‘62592 !!47о? 7647!б о,477948 га 146 156!92 Ыггобз 41!аз! о,!95729 889679 386817 !6!!74 644695 1 3 4 5 6 7 0 9 га о, !666667 1420571 125озоа 1аааааа 720 5о4о 40320 36208а 3, 6288о 3,99168 4 79аог 6,22702 8, 71783 1, Зо?67 2,09228 3 55687 6, 4ог37 1, г1645 2,43г9о 5 10909 1,124оо г,585го б,го448 2! 55’!г о, 09о9091 оЫЗЗЗЭЗ 0769231 о?И!86 обббб67 о,об25ооо о588235 о555556 о5263!б о5сооао о,о476!92 о454545 о434783 о4!6667 а4оозза 11 гг 13 !4 ‘5 16 17 18 19 2о 21 22 гз 24 25 о,196116! 19245о! !889822 1856953 !025742 о,179ба53 1767767 174а777 17И986 169озо9 а, 1666667.

164399а гбпг14 гбоп8г 1581139 о, 156!738 1543а34 1524986 !5о7557 !4907!2 о,оз846!5 о37о37о а357’43 о3448г8 оЗЗЗЭЗЗ о,о32250! аз!25зо озозоЭз о!94118 со 057 И а, ог77778 о27ог7а о!63158 ог564 го огзоооо о, оИ3902 аг38095 о232550 агг7273 О222222 26 27 20 29 Зс’ 31 32 33 34 35 36 37 38 39 4о о,г479бо 918369 327989 .1цгоо 376999 а, п!6И 30аа39 1!5163 330716 967759 о,268822 726546 19!’96 49ог47 !ггзбг о,298931 7!!74! !65521 376184 835965 о, 18!732 386663 Ыа5540 16Н97 320?95 4,оЗг91 г,о8809 З,о!880 8, 84176 г,65253 8,2гг84 2,6313! 8, 68332 2 95233 » аззз! 3 7!993 1, 37630 5,гзо23 .г,о3979 0 159’5 3 34525 1,4о501 6, о4153 г,65827 1, !Збгг 5,5огбг 2,50623 1 И!39 6, оЫ282 Э а414! 5, а99о!95 5,196!5г4 5,г9!5згб 5,3851648 5,47?г256 5,5677644 5,656854г 5,?Н5626 5, Ыза9519 5,9!бо798 б,оооаооо б,а827625 б, 164414о 6,244998о б 3245553 6,4оЗ!г4г 6,48з?4о7 6,5574385 6,6332496 6,7002оз9 6,78гзэоа 6,0556546 6,9202азг 7,аааааоа ?,о?!о678 41 42 43 Н Н 46 47 40 49 5о о,зг!7391 огп?66 ого8333 ого4а8г о!ааааа о, И744га 145065о !нзз?б 142″57! 14142 ! 4 — 992 При л) 10 вместо я1 в таблице даны значения 10 ‘ лд где с — характеристика десятичного логарифма 1о0!е л1, Указанного в следУющем сталбее.

** Вместо 1/в! в таблице даны аначенил 10с?л1, гас с — хаРактеРистика аесл!износа лагаРифма 1оа,е л!! у ‘азаннага в цредыдущеи столбце. 7.6 !продолжение! ‘!аблнци и и!» ! р’ я !аа и! ! и !Од!еи! 66, !9064!о 67, 9о66484 69, 6309г43 71, 3633!00 73, го368о7 74, 85!8687 76,6о77436 78, 37!17!6 80,1420236 81, 920!748 83.7о55о47 85, 4978964 87, 2972369 89, 1а34169 9о, 91633оЗ 92, 7358742 94, 56!949о 96, 3944579 98, 2333070 100, 0784050 !о1, 9г96634 !а3, ?869959 го5,6503!07 107,5195505 109,3946п7 о, 644696 12398о 233925 433’94 787625 о, 140647 24675о 42543о 7г!а68 !го!78 0 197013 3!7763 Зо4386 788!оЗ 121247 о, 1837о7 г7419а 403220 504377 8348г4 о, !!758! 163307 ггз7о8 За!Зоб 4оЗо77 7, !4И284 7, п1!огб 7,28о!о99 7,3484692 7, 416!905 7 4833!48 7,5498344 ,7, 6157731 .7 681 И57 7, 7459667 7, 8!ог497 7,874оо79 7,9372539 В, оооооао 8, обп577 8,1240384 8,1053528 8, 2462п3 8,3оббгз9 8, 3666ооз 8,426!490 .

8′,48528!4 8,5440037 8, бог3253 8, 66о254о 51 5г 53 54 55 56 50 59 бо 61 бг 63 64 65 66 67 68 69 70 о, ИоогВо ц8675о ц736аб цбо828 1348400 о, ц36306 1324532 13ца64 ца1 803 гг9о994 о, пВо369 гг7аоо! !259882 п5оаао !240347 о, о!96о78 о!9гЗоВ ог88679 0185!85 о!8!818 а,о!78571 а!75439 о!72414 о!6949г о!66667 о, о!63934 о!6 п9о о!5873о о!5625о о!53846 о, 123о915 ггп 694 пп 678 гго3859 1195г29 о, п8678г 11785!! 1!704!! пбЦ76 п 5470! о, о! 51515 ОИ9254 о!47о59 о1449г8 о!42857 о,оИа845 0130889 оц6986 о!3513 5 О!33333 о, 53о365 688785 ВВЗо58 и г780 139724 о, !72499 г!о!65 25345г 30!728 354974 о, 41 2761 474438 539’34 бо 5769 673о76 о, 739644 Ва 3361 064474 9!9653 960256 О, 10С039 10 3958 10 6100 107151 го7’5! 8 7177979 8,7749644 8,83!76о9 8, 888 1944 11! 2754253 113,1619160 1!5, о54о!об пб 95!6377 п8,8547г77 !го,763ггг7 122, 677о266 124,5сга1047 иб, 520!В!о !28 4498029 130 38430!3 13г, 3 238206 134,г603033 !36, г176933 138, 1719358 Цо, 1 302772 Цг, о9!765о Ц4, о63248о Ц6, о363758′ ц8, оцо994 Ц9, 99637о7 151,983И24 153 9743685 15 5, 9 71»0 3 7 157, 9 7аоо37 а, П47о79 гцзбаб п32277 и 25088 П18о34 а, Цып! 1!043!5 1о976 !3 1о9!089 го 4652 о, 1о78328 .

Является ли 85 849 идеальным квадратом?

Почему 85 849 — это идеальный квадрат?

Полный квадрат — это число, которое может быть выражено как произведение двух равных целых чисел.

Единственный способ точно вычислить, является ли число точным квадратом, — это найти множители. Прежде чем мы займемся поиском факторов, есть небольшой трюк:
можно использовать, чтобы определить, нужна ли вам дополнительная работа.

Сначала попробуйте эти шаги:

1. Число, которое представляет собой идеальный квадрат, никогда не заканчивается на 2, 3, 7 или 8. Если ваше число заканчивается любым из этих чисел, вы можете остановиться на этом, потому что ваше число не является полным квадратом.
2. Получить цифровой корень числа. Цифровой корень по сути представляет собой сумму всех цифр. Если вы заблудились, не волнуйтесь, мы рассмотрим каждый шаг более подробно ниже.
3. Все возможные числа, представляющие собой полный квадрат, имеют цифровой корень из 1, 4, 7, 9.

Давай попробуем …

Шаг 1:

Какое последнее число из 85 849? Это номер:
85849.
Ответ: 9. Есть ли 9 в списке чисел, которые никогда не бывают полными квадратами (2, 3, 7 или 8)?

Ответ:
НЕТ, 9 нет в списке чисел, которые никогда не бывают полными квадратами. Перейдем к следующему шагу.

Шаг 2:

Теперь нам нужно получить цифровой корень числа.Вот как это сделать:

1. Разделите число и сложите каждую цифру вместе:

8 + 5 + 8 + 4 + 9 = 34

Если ответ состоит более чем из одной цифры, вы должны снова сложить каждую цифру ответа вместе:

3 + 4 = 7

Какой цифровой корень у числа 85 849?

Ответ: 7

Шаг 3:

Итак, теперь мы знаем, что цифровой корень 85 849
7 . Есть ли 7 в списке цифровых корней, которые всегда являются квадратным корнем (1, 4, 7 или 9)?

Ответ:
ДА, 7 находится в списке цифровых корней, которые всегда являются точными квадратами. Мы можем сделать вывод, что 85 849 могут быть идеальным квадратом!

Факторинг

Хорошо, теперь мы знаем, что 85,849 может быть идеальным квадратом. Мы должны найти множители числа, чтобы быть уверенными.

Вот все множители 85,849:

1 x 85,849293 x 293

Выше оранжевым цветом выделена комбинация факторов, которая делает 85,849 идеальным квадратом. Вы понимаете почему? Число может быть полным квадратом только в том случае, если произведение двух точно таких же чисел равно исходному числу.

Вот доказательство:
293 х 293 = 85 849

Другие примеры

Квадратный корень из 86100

кв. (86100).Найдите квадратный корень из 86100 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 86100 или что такое квадратный корень из 86100? Используйте калькулятор квадратного корня ниже, чтобы найти квадратный корень любого действительного числа, положительного или отрицательного. См. Также на этой странице диаграмму квадратного корня от 1 до 100.

Что такое квадратный корень? Определение квадратного корня

Квадратный корень из числа «x» — это такое число y, что y ² = x, другими словами, число y, квадрат которого равен y.Например, 293 — это квадратный корень из 85849, потому что 293 ² = 293 • 293 = 85849, -293 — квадратный корень из 85849, потому что (-293) ² = (-293) • (-293) = 85849. При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram

квадратный символ?

Вот символ квадратного корня. Он обозначается символом √, известным как знак корня или основание системы счисления.

Таблица квадратного корня 1-100

Квадратные корни от 1 до 100 с округлением до тысячных.

9010

число	квадрат	квадрат корень
1	1	1.000
2	4	1,414
3	9	1,732
0												2,236
6	36	2,449
7	49	2.646
8	64	2,828
9	81	3,000
10	100	3,162						9010				9011	144	3,464
13	169	3,606
14	196	3,742
15	225. 873
16	256	4.000
17	289	4,123
18	324	4,243				4,343						400	4,472
21	441	4,583
22	484	4,690
23	529 901.796
24	576	4.899
25	625	5.000

9010

9010

9010

9010

число	квадрат	квадрат корень
26	676	5,099
27	729	5,196
28	784	5,292
	2
30	900	5,477
31	961	5,568
32	1,024	5,657									1,156	5,831
35	1,225	5,916
36	1,296	6. 000
37	1,3083
38	1,444	6,164
39	1,521	6,245
40	1,600	6,325	1,600	6,325		1,764	6,481
43	1,849	6,557
44	1,936	6,633
45	2,0708
46	2,116	6,782
47	2,209	6,856
48	2,304 9010 9010 9010 9010 9010 9010 9010 9010 9011 9010 9010 9 9010	2,500	7,071

,410

85109 9010 9,165

9,409109.849

10

Квадратный корень из значений около 86100

404

Примеры квадратного корня

Что такое 85849/38 как смешанное число? (Преобразование неправильной дроби 85849/38 в смешанную дробь)

Пытаетесь узнать, как преобразовать 85849/38 в смешанное число или дробь? У меня есть для тебя ответ! В этом руководстве мы проведем вас через пошаговый процесс преобразования неправильной дроби, в данном случае 85849/38, в смешанное число.Читать дальше!

Хотите быстро узнать или показать студентам, как преобразовать 85849/38 в смешанное число? Воспроизведите это очень быстрое и веселое видео прямо сейчас!

Прежде чем мы начнем, давайте еще раз вернемся к некоторым основным терминам дроби, чтобы вы точно поняли, с чем мы здесь имеем дело:

• Числитель. Это число над дробной чертой. Для 85849/38 числитель 85849.
• Знаменатель. Это число под дробной чертой. Знаменатель 85849/38 равен 38.
• Неправильная дробь. Это дробь, в которой числитель больше знаменателя .
• Смешанный номер. Это способ выразить неправильную дробь, упростив ее до целых единиц и меньшей общей дроби. Это целое число (целое число) и правильная дробь.

Теперь давайте рассмотрим шаги, необходимые для преобразования 85849/38 в смешанное число.

Шаг 1. Найдите целое число

.

Сначала мы хотим найти целое число, и для этого делим числитель на знаменатель. Поскольку нас интересуют только целые числа , мы игнорируем любые числа справа от десятичной точки.

85849/38 = 2259,1842105263 = 2259

Теперь, когда у нас есть целое число для смешанной дроби, нам нужно найти наш новый числитель для дробной части смешанного числа.

Шаг 2. Получите новый числитель

Чтобы решить эту проблему, мы воспользуемся целым числом, вычисленным на первом этапе (2259), и умножим его на исходный знаменатель (38). Результат этого умножения затем вычитается из исходного числителя:

85849 — (38 x 2259) = 7

Шаг 3: Наша смешанная фракция

Мы упростили 85849/38 до смешанного числа.Чтобы увидеть это, нам просто нужно сложить целое число вместе с нашим новым числителем и исходным знаменателем:

2259

7
/
38

Шаг 4: Упрощение дроби

В этом случае нашу дробь (7/38) можно еще больше упростить.Для этого нам нужно вычислить GCF (наибольший общий множитель) этих двух чисел. Вы можете использовать наш удобный калькулятор GCF, чтобы вычислить это самостоятельно, если хотите. Мы уже сделали это, и GCF 7 и 38 составляет 1 .

Теперь мы можем разделить и новый числитель, и знаменатель на 1, чтобы упростить эту дробь до ее наименьших членов.

7/1 = 7

38/1 = 38

Когда мы сложим это вместе, мы увидим, что наш полный ответ:

2259

7
/
38

Надеюсь, это руководство помогло вам понять, как преобразовать любую неправильную дробь в смешанную дробь с целым числом и правильной дробью.Вы можете использовать наш калькулятор ниже, чтобы узнать больше, но постарайтесь научиться делать это самостоятельно. Обещаю, это намного веселее, чем кажется!

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

• Что такое 85849/38 как смешанное номер?

• «Что такое 85849/38 как смешанное число?». VisualFractions.com . По состоянию на 20 мая 2021 г. https://visualfractions.com/calculator/improper-to-mixed/what-is-85849-38-as-a-mixed-number/.

• «Что такое 85849/38 как смешанное число?». VisualFractions.com , https://visualfractions.com/calculator/improper-to-mixed/what-is-85849-38-as-a-mixed-number/. По состоянию на 20 мая 2021 г.

• Что такое 85849/38 как смешанное число ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/improper-to-mixed/what-is-85849-38-as-a-mixed-number/.

Калькулятор неправильной фракции в смешанную фракцию

Неверная дробь к смешанному числу

Введите неправильные числитель и знаменатель дроби

Что такое квадратный корень из 85423? Упрощение и пошаговые вычисления

Квадратные корни и свойства квадратного корня

Квадратный корень :

Квадратный корень из числа «а» — это то число, которое при умножении на само дает «а» в качестве произведения.
Таким образом, если b является квадратным корнем из числа ‘a’, то
bxb = a или = a
Квадратный корень из числа ‘a’ обозначается как
Отсюда следует, что
b = <=> = а.
, т.е. b является квадратным корнем из «a» тогда и только тогда, когда «a» является квадратом b.

Иллюстрация:
(i) = 2, потому что = 4
(ii) = 3, потому что = 9.
(iii) = 18, потому что = 324.
Замечание: Поскольку 4 = =, следовательно, 2 и -2 могут быть квадратными корнями из 4. Однако мы согласны с тем, что квадратный корень из числа будет равен быть только положительным квадратным корнем. Таким образом, имеем = 2.

Свойства квадратного корня:

Свойство 1: — Если число единиц измерения равно 2, 3, 7 или 8, то оно не имеет квадратного корня из N (набора натуральных чисел).

Пояснение: По свойству 1 квадратных чисел число, имеющее 2, 3, 7 или 8 на месте единицы, не может быть полным квадратом. Следовательно, число, состоящее из 2, 3, 7 или 8 в единицах, не имеет квадратного корня из N.

Свойство 2: — Если число заканчивается нечетным числом нулей, то оно не имеет квадратного корня. Если за квадратным числом следует четное количество нулей, оно имеет квадратный корень, в котором количество нулей в конце равно половине количества нулей в числе.

Пояснение: По свойству 2 квадратных чисел количество нулей в конце полного квадрата всегда четно и вдвое превышает количество нулей в конце числа.

Свойство 3: — Квадратный корень из четного квадратного числа является четным, а квадратный корень из нечетного квадратного числа является нечетным.

Пояснение: По свойству 3 квадратных чисел квадраты четных чисел являются четными числами, а квадраты нечетных чисел — нечетными числами.

Свойство 4: — Если число имеет квадратный корень из N, то его единица измерения должна быть 0, 1, 4, 5 или 9.

Пояснение: По свойству 6 цифры единиц квадратного и квадратного корня связаны следующим образом:

Свойство 5: — Отрицательные числа не имеют квадратного корня в системе рациональных чисел.

Пояснение: У нас есть, = 4, = 9, = 16 и так далее. Кроме того, = (–2) x (–2) = 4, = (–3) x (–3) = 9, = (–4) x (–4) = 16 и так далее.
Это означает, что квадрат числа, положительного или отрицательного, всегда положителен. Следовательно, отрицательные числа не являются полными квадратами.
Следовательно, отрицательные числа не имеют квадратных корней.

Свойство 6: — Сумма первых n нечетных натуральных чисел равна , т.е.
1 + 3 + 5 + 7 +… + (2n — 1) =.

Некоторые короткие пути для поиска квадратов:

Чтобы найти квадрат числа, мы умножаем данное число само на себя. Умножение удобно только для маленьких чисел. Для больших чисел умножение может быть трудоемким и трудоемким. В этом разделе показаны некоторые короткие методы нахождения квадратов натуральных чисел без использования умножения.

Колоночный метод:
Этот метод основан на старом индийском методе умножения двух чисел.Удобно находить квадраты только двухзначных чисел. По мере увеличения количества цифр этот метод становится трудным и требует много времени.

Этот метод использует identity = 2ab + для нахождения квадрата двузначного числа ab (где a — это цифра десятков, а b — цифра единиц). Мы выполняем следующие шаги, чтобы найти квадрат двузначного числа ab (где a — это цифра десятков, а b — цифра единиц).

Шаг I — Создайте три столбца и запишите значение, 2 x a x b и, соответственно, в эти столбцы следующим образом:

В качестве иллюстрации возьмем ab = 57.

а = 5 и б = 7.

Шаг II — Подчеркните цифру единиц b2 (в столбце III) и добавьте ее цифру десятков, 2xaxb (в столбце II).
, если есть, на 2xaxb (в столбце II).

Шаг III- Подчеркните цифру единиц в столбце II и добавьте число, образованное десятками и другими цифрами, если они есть, в столбец I.

Шаг IV- Под номером в графе I.

Шаг V- Напишите подчеркнутые цифры внизу каждого столбца, чтобы получить квадрат данного числа.
В данном случае = 3249.

Иллюстративные примеры:

Пример: Найдите квадраты следующих чисел, используя метод столбца:
(i) 25 (ii) 96
Решение: (i) Здесь a = 2 и b = 5.
Мы имеем,

= 625,

(ii) Здесь a = 9 и b = 6.

У нас,

= 9216,

Пример 2: Найдите квадраты следующих чисел, используя метод столбцов:
(i) 99 (ii) 89
Решение : (i) Здесь a = 9 и b = 9.
У нас,

= 9801.

(ii) Здесь a = 8 и b = 9

У нас,

= 7921,

Визуальный метод:
В методе столбца алгебраическое тождество = + 2ab + используется для вычисления квадрата двузначного числа. Квадрат положительного целого числа также можно вычислить, внимательно следя за визуальным представлением. Чтобы представить, мы рисуем квадрат со стороной a + b и делим его на два прямоугольника размером a x (a + b) и b x (a + b), рисуя вертикальную линию, как показано на рис.1 Мы также проводим горизонтальную линию, чтобы разделить квадрат на два прямоугольника размером (a + b) x b и (a + b) x a, как показано на рис. 3.1. Эти две линии делят квадрат на четыре части, а именно, два квадрата размером ax a и b x b и два прямоугольника размером ax b и b x a. Сумма площадей этих четырех частей составляет

.

a x a + a x b + b x a + b x b = + 2ab +

Мы используем это визуальное представление, чтобы найти квадрат числа.
Предположим, мы хотим найти квадрат 105.
У нас есть, 105 = 100 + 5
Итак, мы рисуем квадрат со стороной 105 единиц и делим его на четыре части, как показано на рисунке. Сумма площадей этих четырех частей равна квадрату 105.
= 10000+ 500 + 500 + 25 = 11025

Следующие примеры иллюстрируют вышеуказанный метод.

Иллюстративные примеры:

Пример 1: Визуальным методом находим квадрат следующих чисел:
(i) 54 (ii) 97
Решение: (i) У нас есть, 54 = 50 + 4
Итак, мы рисуем квадрат стороны 54 и разделите на части, как показано на рис.

Сумма площадей этих четырех частей равна квадрату 54.
= 2500 + 200 + 200 + 16 = 2916

(ii) Мы имеем, 97 = 90 + 7
Итак, мы рисуем квадрат со стороной 97 единиц и делим его на части, как показано на рис.
Сумма площадей этих четырех частей равна квадрату 97.
= 8100 + 630 + 630 + 49 = 9409

Пример 2: Визуальным методом найдите квадрат следующих чисел:
(i) 205 (ii) 315
Решение: (i) У нас есть, 205 = 200 + 5
Итак, нарисуем квадрат стороны 205 единиц и разделить на 4 части, как показано на рис.

= 40000 + 1000 + 1000 + 25 = 41025

(ii) У нас есть 315 = 300 + 15
Итак, давайте нарисуем квадрат со стороной 315 единиц и разделим его на части, как показано на рис.

.

Сумма площадей этих четырех частей равна квадрату 315.

=

+ 4500 + 4500 + 225 = 99225.

Диагональный метод:
Этот метод применим для нахождения квадрата любого числа независимо от количества цифр в номере. Чтобы найти квадрат числа этим методом, необходимо выполнить следующие шаги.

Шаг I — Получите число и посчитайте количество цифр в нем. Пусть число, которое нужно возвести в квадрат, состоит из n цифр.
Шаг II — Нарисуйте квадрат и разделите его на подквадраты одинакового размера, нарисовав (n —1) горизонтальные и (n —1) вертикальные линии.
Шаг III — Нарисуйте диагонали каждого квадрата. В качестве иллюстрации пусть число, которое нужно возвести в квадрат, будет 479.
Шаг IV — Напишите цифры числа, которое нужно возвести в квадрат вдоль левой вертикальной стороны и верхней горизонтальной стороны квадратов, как показано ниже.

Шаг V — Умножьте каждую цифру слева от квадрата на каждую цифру в верхней части столбца по одному. Напишите цифру единиц произведения под диагональю и цифру десятков над диагональю соответствующего подквадрата a, показанного ниже.

Шаг VI- Начиная с самой нижней диагонали, суммируйте цифры по диагоналям, полученным таким образом. Запишите цифру единиц суммы и перенесите цифру десятков (если есть) на диагональ выше, как показано ниже.

Шаг VII- Получите требуемый квадрат, записав цифры с левой стороны.

= 229441

Иллюстративные примеры:

Пример 1: Используя диагональный метод, найдите квадраты следующих элементов:
(i) 89 (ii) 68
Решение (i) Используя диагональный метод, мы имеем (ii) Используя диагональный метод, мы имеем

Пример 2: Найдите квадрат следующих чисел диагональным методом:
(i) 349 (ii) 293

Решение: (i) Используя диагональный метод, мы имеем

= 121801

(ii) Используя диагональный метод, получаем

= 85849

Список идеальных квадратов.Первые 1000 полных квадратов перечислены под

.

Список идеальных квадратов. Первые 1000 идеальных квадратов перечислены ниже.

1. Дом
2. Список идеальных квадратов

5.
Логарифм Напьера числа log _{1 / e} 85849 = -11,360345.

Тригонометрические функции

Косинус 85849 равен -0,265142.
Синус 85849 равен 0,