Содержание
Урок 3. Основні тригонометричні тотожності
Тригонометричною
тотожністю називається рівність, до якої входять тригонометричні функції і яка
задовольняється довільним допустимим значенням кута – аргументу
тригонометричних функцій, але не задовольняється, якщо кожну тригонометричну
функцію зокрема замінити довільною величиною.
Основні тригонометричні
тотожності.
З п’яти основних
тотожностей випливають три допоміжні.
Співвідношення між
тригонометричними функціями одного аргументу.
ПРИКЛАД:
Визначити
тригонометричні функції кута α, якщо
і 180⁰ < α < 270⁰.
За формулою
Знаходимо
За формулою
Знаходимо
Враховуючи,
що sec α
< 0 при
одержуємо
звідки
За формулою
Знаходимо
Значення sin α знайдемо
з формули
Враховуючи,
що sin α < 0 при
знаходимо
ПРИКЛАД:
Довести
тотожність
3(sin4 α + cos4 α) – 2(sin6 α + cos6 α) = 1.
Перетворимо спочатку ліву частину рівності, а
далі, скориставшись формулою
знайдемо
3(sin4 α + cos4 α) – 2(sin6 α + cos6 α) =
3(sin4 α + cos4 α) – 2(sin2 α + cos2 α) (sin4 α – sin2 α
cos2 α + cos4 α)
=
3sin4 α + 3cos4 α – 2sin4 α + 2sin2 α
cos2 α – 2cos4 α =
sin4
α + 2sin2
α cos2 α + cos4 α = (sin2 α + cos2 α)2 =
1.
Довести
тотожність
sin3
α (1 + ctg
α) + cos3
α (1 + tg
α) = sin
α + cos
α.
sin3 α (1 + ctg α) + cos3 α (1 + tg α) =
=
sin2 α (sin α + cos
α)
+ cos2
α
(cos α + sin α)
= (sin α + cos α) (sin2 α + cos2 α) = (sin α + cos α).
Спростити
вираз:
(1 – cos2 x)tg2 x = sin2 x tg2 x =
ВІДПОВІДЬ:
ПРИКЛАД:
Спростити
вираз:
cos2 x + tg2 x cos2 x
cos
x
=
0,6 або cos
x
=
–0,6.
Оскільки
аргумент належить другій чверті
cos
x
<
0, cos x = –0,6.
ВІДПОВІДЬ: cos
x
=
–0,6.
Знайдіть значення виразу:
якщо ctg x = 1/3.
Поділимо чисельник і знаменник дробу на sin x. Оскільки
ctg x = 1/3, то sin x не
приймає значення нуль.
ВІДПОВІДЬ: 11/13.
Тригонометричні тотожності і перетворення
Для вирішення деяких завдань буде корисною таблиця тригонометричних тотожностей, яка дозволить набагато простіше здійснювати перетворення функцій:
Найпростіші тригонометричні тотожності
Частка від ділення синуса кута альфа на косинус того ж кута одно тангенсу цього кута (Формула 1). Див. Також доказ правильності перетворення найпростіших тригонометричних тотожностей.
Див. Також доказ правильності перетворення найпростіших тригонометричних тотожностей.
Частка від ділення косинуса кута альфа на синус того ж кута одно котангенс цього ж кута (Формула 2)
Секанс кута дорівнює одиниці, поділеній на косинус цього ж самого кута (Формула 3)
Сума квадратів синуса і косинуса одного і того ж кута дорівнює одиниці (Формула 4). см. також доказ суми квадратів косинуса і синуса.
Сума одиниці і тангенса кута дорівнює відношенню одиниці до квадрату косинуса цього кута (Формула 5)
Одиниця плюс котангенс кута дорівнює частці від ділення одиниці на синус квадрат цього кута (Формула 6)
Твір тангенса на котангенс одного і того ж кута дорівнює одиниці (Формула 7).
Перетворення негативних кутів тригонометричних функцій (парність і непарність)
Для того, щоб позбутися від від’ємного значення градусної міри кута при обчисленні синуса, косинуса або тангенса, можна скористатися наступними тригонометричними перетвореннями (тотожністю), заснованими на принципах парності або непарності тригонометричних функцій.
Як видно, косинус і секанс є парною функцією, синус, тангенс і котангенс — непарні функції.
Синус негативного кута дорівнює від’ємному значенню синусу цього ж самого позитивного кута (мінус синус альфа).
Косинус «мінус альфа» дасть теж саме значення, що і косинус кута альфа.
Тангенс мінус альфа дорівнює мінус тангенс альфа.
Формули приведення подвійного кута (синус, косинус, тангенс і котангенс подвійного кута)
Якщо необхідно розділити кут навпіл, або навпаки, перейти від подвійного кута до одинарного, можна скористатися наступними тригонометричними тотожністями:
Перетворення подвійного кута (синуса подвійного кута, косинуса подвійного кута і тангенса подвійного кута) в одинарний відбувається за такими правилами:
Синус подвійного кута дорівнює подвоєному добутку синуса на косинус одинарного кута
Косинус подвійного кута дорівнює різниці квадрата косинуса одинарного кута і квадрата синуса цього кута
Косинус подвійного кута дорівнює подвоєному квадрату косинуса одинарного кута мінус одиниця
Косинус подвійного кута дорівнює одиниці мінус подвійний синус квадрат одинарного кута
Тангенс подвійного кута дорівнює дробу, чисельник якого — подвоєний тангенс одинарного кута, а знаменник дорівнює одиниці мінус тангенс квадрат одинарного кута
Котангенс подвійного кута дорівнює дробу, чисельник якого — квадрат котангенс одинарного кута мінус одиниця, а знаменник дорівнює подвоєному котангенсу одинарного кута
Формули універсальної тригонометричної підстановки
Зазначені нижче формули перетворення можуть стати в нагоді, коли потрібно аргумент тригонометричної функції (sin α, cos α, tg α) розділити на два і привести вираз до значення половини кута. Зi значення α отримуємо α / 2.
Зi значення α отримуємо α / 2.
Дані формули називаються формулами універсальної тригонометричної підстановки. Їх цінність полягає в тому, що тригонометричний вираз з їх допомогою зводиться до вираження тангенса половини кута, незалежно від того, які тригонометричні функції (sin cos tg ctg) були в вираженні спочатку. Після цього рівняння з тангенсом половини кута вирішити набагато простіше.
Тригонометричні тотожності перетворення половини кута
Зазначені нижче формули тригонометричного перетворення половинної величини кута до його цілого значення.
Значення аргументу тригонометричної функції α / 2 приводиться до значення аргументу тригонометричної функції α.
Тригонометричні формули додавання кутів
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс і котангенс суми кутів альфа і бета можуть бути перетворені за такими правилами перетворення тригонометричних функцій:
Тангенс суми кутів дорівнює дробу, чисельник якого — сума тангенса першого і тангенса другого кута, а знаменник — одиниця мінус твір тангенса першого кута на тангенс другого кута.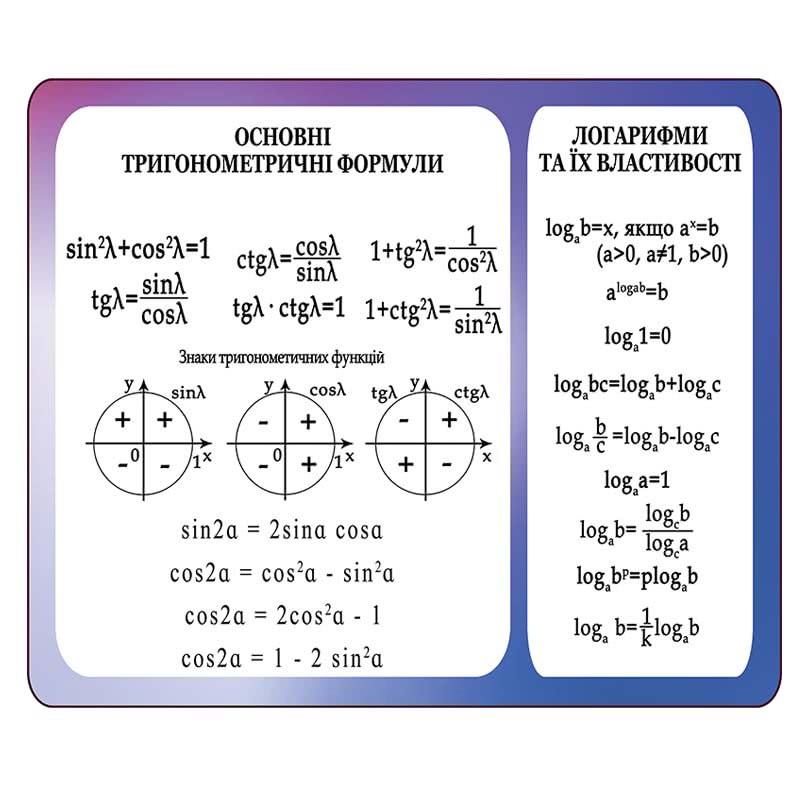
Тангенс різниці кутів дорівнює дробу, чисельник якого дорівнює різниці тангенса зменшуваного кута і тангенса від’ємника кута, а знаменник — одиниці плюс твір тангенсов цих кутів.
Котангенс суми кутів дорівнює дробу, числівник якого дорівнює добутку котангенс цих кутів плюс одиниця, а знаменник дорівнює різниці котангенс другого кута і котангенс першого кута.
Котангенс різниці кутів дорівнює дробу, чисельник якого — твір котангенсів цих кутів мінус одиниця, а знаменник дорівнює сумі котангенсів цих кутів.
Дані тригонометричні тотожності зручно застосовувати, коли потрібно обчислити, наприклад, тангенс 105 градусів (tg 105). Якщо його представити як tg (45 + 60), то можна скористатися наведеними тотожними перетвореннями тангенса суми кутів, після чого просто підставити табличні значення тангенса 45 і тангенса 60 градусів.
Формули перетворення суми або різниці тригонометричних функцій
Вирази, що представляють собою суму виду sin α + sin β можна перетворити за допомогою наступних формул:
Формули потрійного кута — перетворення sin3α cos3α tg3α в sinα cosα tgα
Іноді необхідно перетворити потрійну величину кута так, щоб аргументом тригонометричної функції замість 3α став кут α.
В цьому випадку можна скористатися формулами (тотожністю) перетворення потрійного кута:
Формули перетворення добутку тригонометричних функцій
Якщо виникає необхідність перетворити твір синусів різних кутів косинусів різних кутів або навіть твори синуса на косинус, то можна скористатися наступними тригонометричними тотожностями:
В цьому випадку твір функцій синуса, косинуса або тангенса різних кутів буде перетворено в суму або різницю.
Формули приведення тригонометричних функцій
Користуватися таблицею приведення потрібно в такий спосіб. У рядку вибираємо функцію, яка нас цікавить. У стовпці — кут. Наприклад, синус кута (α + 90) на перетині першого рядка та першого стовпчика з’ясовуємо, що sin (α + 90) = cos α.
См. також Повний список формул приведення тригонометричних функцій.
|
Кут |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
|
sin |
cos α |
-sin α |
-cos α |
cos α |
sin α |
-cos α |
-sin α |
|
cos |
-sin α |
-cos α |
sin α |
sin α |
-cos α |
-sin α |
cos α |
|
tg |
-ctg α |
tg α |
-ctg α |
ctg α |
-tg α |
ctg α |
-tg α |
|
ctg |
-tg α |
ctg α |
-tg α |
tg α |
-ctg α |
tg α |
-ctg α |
Основні тригонометричні тотожності.
 Формули зведення
Формули зведення
1. Основні тригонометричні тотожності. Формули зведення.
2. Мета
• Системазувати знання, уміння та навички з
теми: «Основні тригонометричні тотожності.
Формули зведення»; формувати вміння учнів
застосовувати тригонометричні формули для
перетворення тригонометричних виразів
різного рівня складності.
• Розвивати логічне мислення, уміння
аналізувати, навички самостійної та групової
роботи.
• Сприяти стійкому інтересу до вивчення
математики.
3. Епіграф
Предмет математики такий серйозний,
що корисно не нехтувати нагодою
робити його трохи цікавішим.
Блез Паскаль
Чому знання
тригонометрії необхідні
для сучасної людини?
5. Тригонометрія у фізиці
Коливання — найпоширеніша форма руху
в навколишньому світі та техніці.
Коливаються дерева під дією вітру,
поршні у двигуні автомобіля тощо.
Прикладами простих
коливальних систем
можуть
слугувати
вантаж на пружині
або
математичний
маятник
6.
 Математичний маятник
Математичний маятник
На малюнку зображені коливання
маятника, він рухається про кривій, яку
називають косинусоїдою.
На рисунку приведені графіки
координати x(t), швидкості v(t)
і прискорення а(t) тіла, що
здійснює гармонічні коливання.
8. Траекторія кулі (м’яча) і проекціі векторів на осі X та Y
9. Оптичні ілюзії
природні
штучні
мішані
10. Теорія райдуги
Вперше теорія райдуги
була запропонована
Рене Декартом в 1637р.
Він пояснив райдугу, як
явище пов’язане з
відображенням та
заломленням світла в
дощових краплях.
Райдуга виникає тому, що
сонячне світло зазнає
заломлення у краплях
води, зважених у повітрі за
законом заломлення:
sin α / sin β = n1 / n2
де n1=1, n2≈1,33 – відповідно
показники заломлення повітря і
води, α – кут падіння, а β – кут
заломлення світла.
11. Полярне сяйво
F q B q B sin
12. Тригонометрія в живій природі
Рух риб у воді відбувається за
законом синуса або косинуса,
якщо зафіксувати точку на хвості
а потім розглянути траекторію
руху.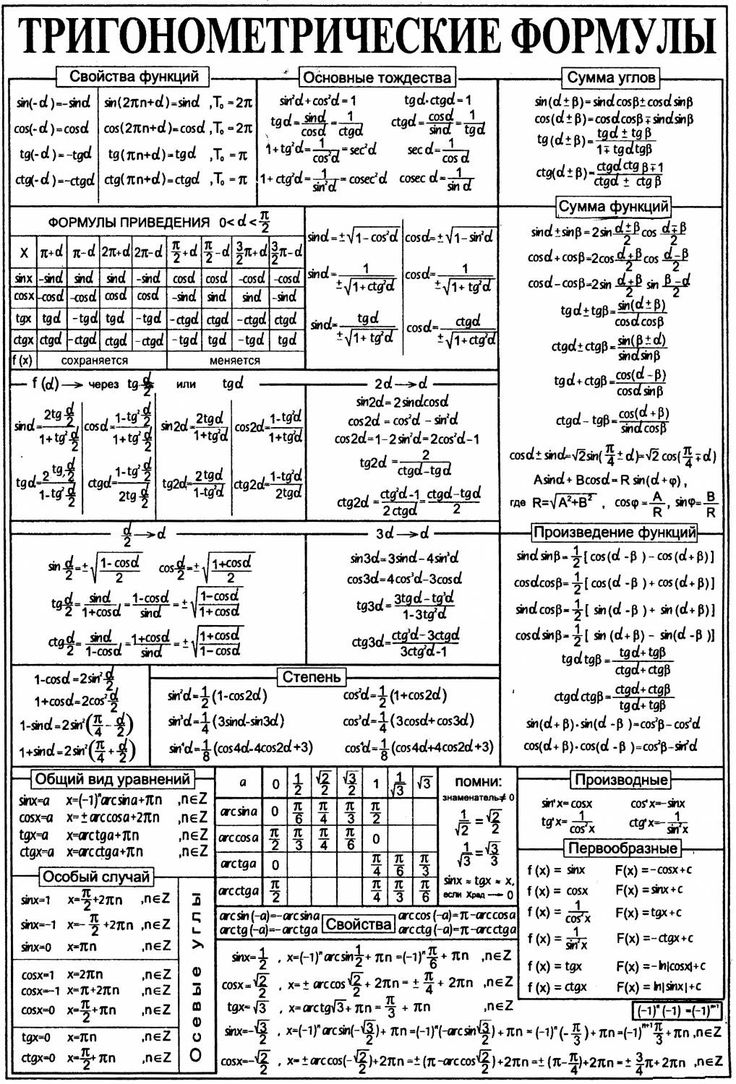
При плаванні тіло риби приймає
форму кривої, яка нагадує
графік функції y=tgx
Під час польоту птаха траєкторія помаху
крил утворює синусоїду
14. Тригонометрія в біології
Американські
вчені стверджують,
що мозок оцінює відстань до
об’єктів вимірюючи кут між
площиною землі та площиною зору.
Також
в біології використовують
поняття: синус сонний, синус
каротидний та венозний або
пещеристий синус.
Синус каротидний
(сонний)
Пещеристий синус
Тригонометрія
відіграє важливу роль
у медицині, за її допомогою іранські
вчені відкрили формулу серця –
комплексна алгебраїчнотригонометрична рівність, яка
складається з 8 виразів, 32
коефіцієнтів і 33 основних параметрів,
включаючи декілька додаткових для
розрахунків у випадках аритмії.
Біологічні
ритми, біоритми
пов’язані з тригонометрією.
17. Модель біоритмів
18. Тригонометрія у мистецтві
cos2 С + sin2 С = 1
АС – відстань від вершини статуї до очей
людини,
АН – висота статуї,
sin С — синус кута падіння погляду.
А
А
С
Н
Н
С
19. Фелікс Кандела Ресторан в Лос-Манантіалесі
20. Сантьяго Калатрава виноробня «Бодегас Ісіос»
21. Страхова корпорація Swiss Re у Лондоні
x=λ
y = f(λ)cos θ
z = f(λ)sin θ
22. Готична архітектура
Собор Паризької
Богоматері
1163р. – середина
XIV ст.
що таке? Як знайти синус, косинус і тангенс
Співвідношення між основними тригонометричними функціями — синусом, косинусом, тангенсом і котангенсом — задаються тригонометричними формулами. А так як зв’язків між тригонометричними функціями досить багато, то цим пояснюється і велика кількість тригонометричних формул. Одні формули пов’язують тригонометричні функції однакового кута, інші — функції кратного кута, треті — дозволяють знизити ступінь, четверті — висловити всі функції через тангенс половинного кута, і т.д.
У цій статті ми по порядку перерахуємо всі основні тригонометричні формули, яких достатньо для вирішення переважної більшості завдань тригонометрії.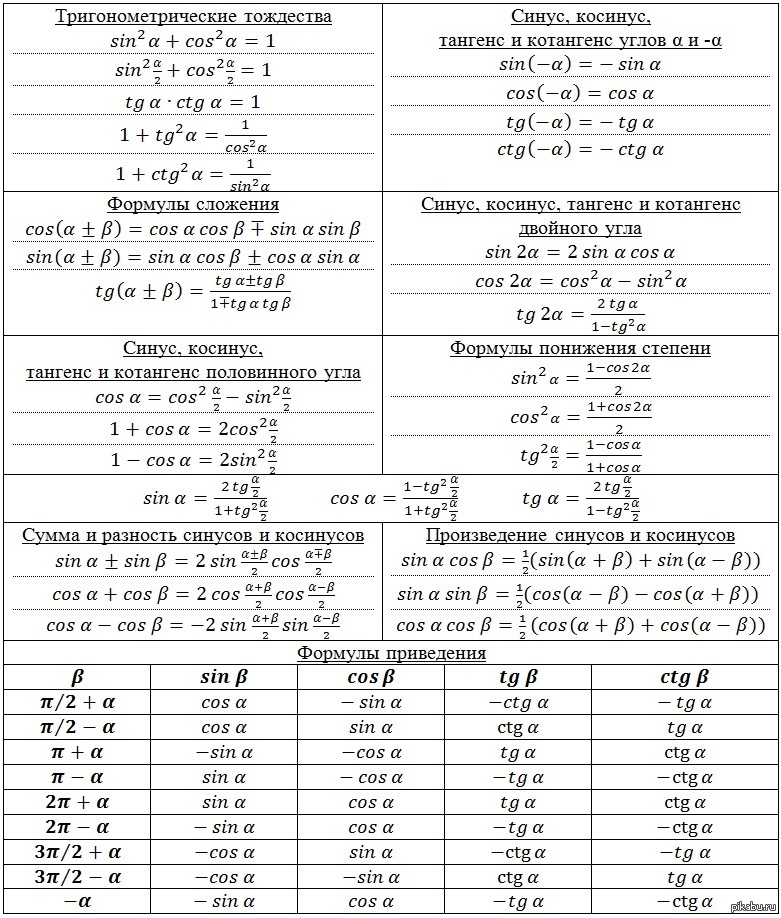 Для зручності запам’ятовування і використання будемо групувати їх за призначенням, і заносити в таблиці.
Для зручності запам’ятовування і використання будемо групувати їх за призначенням, і заносити в таблиці.
Навігація по сторінці.
Основні тригонометричні тотожності
Основні тригонометричні тотожності задають зв’язок між синусом, косинусом, тангенсом і котангенсом одного кута. Вони випливають з визначення синуса, косинуса, тангенса і котангенс, а також поняття одиничному колі. Вони дозволяють виразити одну тригонометричну функцію через будь-яку іншу.
Детальний опис цих формул тригонометрії, їх висновок і приклади застосування дивіться в статті.
формули приведення
формули приведення випливають з властивостей синуса, косинуса, тангенса і котангенс, тобто, вони відображають властивість періодичності тригонометричних функцій, Властивість симетричності, а також властивість зсуву на даний кут. Ці тригонометричні формули дозволяють від роботи з довільними кутами переходити до роботи з кутами в межах від нуля до 90 градусів.
Обгрунтування цих формул, мнемонічне правило для їх запам’ятовування і приклади їх застосування можна вивчити в статті.
формули додавання
Тригонометричні формули додавання показують, як тригонометричні функції суми або різниці двох кутів виражаються через тригонометричні функції цих кутів. Ці формули служать базою для виведення наступних нижче тригонометричних формул.
Формули подвійного, потрійного і т.д. кута
Формули подвійного, потрійного і т.д. кута (їх ще називають формулами кратного кута) показують, як тригонометричні функції подвійних, потрійних і т.д. кутів () виражаються через тригонометричні функції одинарного кута. Їх висновок базується на формулах складання.
Більш детальна інформація зібрана в статті формули подвійного, потрійного і т.д. кута.
Формули половинного кута
Формули половинного кута показують, як тригонометричні функції половинного кута виражаються через косинус цілого кута. Ці тригонометричні формули випливають з формул подвійного кута.
Ці тригонометричні формули випливають з формул подвійного кута.
Їх висновок і приклади застосування можна подивитися в статті.
Формули пониження степеня
Тригонометричні формули пониження степеня покликані сприяти переходу від натуральних ступенів тригонометричних функцій до синусів і косинусам в першого ступеня, але кратних кутів. Іншими словами, вони дозволяють знижувати ступеня тригонометричних функцій до першої.
Формули суми і різниці тригонометричних функцій
Основне призначення формул суми і різниці тригонометричних функцій полягає в переході до твору функцій, що дуже корисно при спрощення тригонометричних виразів. Зазначені формули також широко використовуються при вирішенні тригонометричних рівнянь, так як дозволяють розкладати на множники суму і різницю синусів і косинусів.
Формули твори синусів, косинусів і синуса на косинус
Перехід від добутку тригонометричних функцій до суми або різниці здійснюється за допомогою формул твори синусів, косинусів і синуса на косинус.
Copyright by cleverstudents
Всі права захищені.
Охороняється законом про авторське право. Жодну частину сайту www.сайт, включаючи внутрішні матеріали і зовнішнє оформлення, не може бути відтворена в будь-якій формі або використовувати без попередньої письмової згоди власника авторських прав.
— вже напевно зустрінуться завдання з тригонометрії. Тригонометрію часто не люблять за необхідність зубрити величезна кількість важких формул, що кишать синусами, косинусами, тангенс і котангенс. На сайті вже колись давалися поради, як згадати забуту формулу, на прикладі формул Ейлера і Піля.
А в цій статті ми постараємося показати, що досить твердо знати всього п’ять найпростіших тригонометричних формул, а про решту мати загальне уявлення і виводити їх по ходу справи. Це як з ДНК: в молекулі не зберігається повні креслення готового живої істоти. Там містяться, скоріше, інструкції по його збірці з наявних амінокислот. Так і в тригонометрії, знаючи деякі загальні принципи, ми отримаємо всі необхідні формули з невеликого набору тих, які потрібно обов’язково пам’ятати.
Будемо спиратися на наступні формули:
З формул синуса і косинуса сум, знаючи про парності функції косинуса і про непарності функції синуса, підставивши -b замість b, отримуємо формули для різниць:
- синус різниці: sin(A-b) = sinacos(-B)+cosasin(-B) = sinacosb—cosasinb
- косинус різниці: cos(A-b) = cosacos(-B)—sinasin(-B) = cosacosb+sinasinb
Поставляючи в ці ж формули a \u003d b, отримуємо формули синуса і косинуса подвійних кутів:
- Синус подвійного кута: sin2a = sin(A + a) = sinacosa+cosasina = 2sinacosa
- Косинус подвійного кута: cos2a = cos(A + a) = cosacosa—sinasina = cos 2 a—sin 2 a
Аналогічно виходять і формули інших кратних кутів:
- Синус потрійного кута: sin3a = sin(2a + a) \u003d sin2acosa+cos2asina = (2sinacosa)cosa+(cos 2 a—sin 2 a)sina = 2sinacos 2 a+sinacos 2 a—sin 3 a \u003d 3 sinacos 2 a—sin 3 a \u003d 3 sina(1-sin 2 a)-sin 3 a \u003d 3 sina-4sin 3 a
- Косинус потрійного кута: cos3a = cos(2a + a) \u003d cos2acosa—sin2asina = (cos 2 a—sin 2 a)cosa-(2sinacosa)sina = cos 3 a- sin 2 acosa-2sin 2 acosa = cos 3 a-3 sin 2 acosa = cos 3 a-3 (1 cos 2 a)cosa = 4cos 3 a-3 cosa
Перш ніж рухатися далі, розглянемо одну задачу.
Дано: кут — гострий.
Знайти його косинус, якщо
Рішення, дане одним учнем:
Оскільки , то sina \u003d 3, а cosa = 4.
(З математичного гумору)
Отже, визначення тангенса пов’язує цю функцію і з синусом, і з косинусом. Але можна отримати формулу, що дає зв’язок тангенса тільки з косинусом. Для її виведення візьмемо основне тригонометричну тотожність: sin 2
a+cos 2
a \u003d 1 і розділимо його на cos 2
a. отримаємо:
Так що вирішенням цього завдання буде:
(Оскільки кут гострий, при добуванні кореня береться знак +)
Формула тангенса суми — ще одна, важко піддається запам’ятовуванню. Виведемо її так:
Відразу виводиться і
З формули косинуса подвійного кута можна отримати формули синуса і косинуса для половинного. Для цього до лівої частини формули косинуса подвійного кута:
cos2
a = cos 2
a—sin 2
a
додаємо одиницю, а до правої — тригонометричну одиницю, тобто суму квадратів синуса і косинуса.
cos2a+1 = cos 2 a—sin 2 a+cos 2 a+sin 2 a
2cos 2
a = cos2
a+1
висловлюючи cosa через cos2
a і виконуючи заміну змінних, отримуємо:
Знак береться в залежності від квадранта.
Аналогічно, віднявши від лівої частини рівності одиницю, а від правої — суму квадратів синуса і косинуса, отримаємо:
cos2a-1 = cos 2 a—sin 2 a—cos 2 a—sin 2 a
2sin 2
a = 1-cos2
a
І, нарешті, щоб перетворити суму тригонометричних функцій у добуток, використовуємо наступний прийом. Припустимо, нам потрібно представити у вигляді добутку суму синусів sina+sinb. Введемо змінні x і y такі, що a \u003d x + y, b + x-y. тоді
sina+sinb = sin(X + y) + sin(X-y) \u003d sinx cosy + cosx siny + sinx cosy- cosx siny \u003d 2 sinx cosy.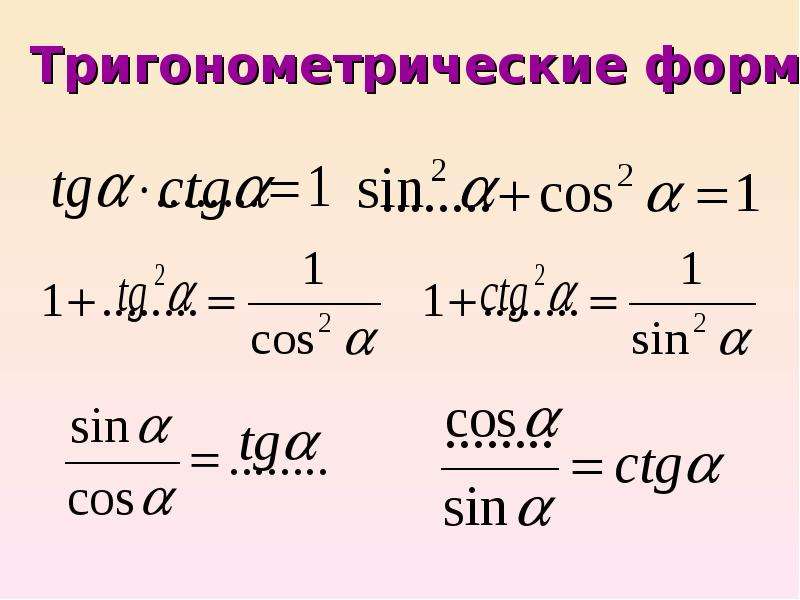 Висловимо тепер x і y через a і b.
Висловимо тепер x і y через a і b.
Оскільки a \u003d x + y, b \u003d x-y, то. Тому
Відразу ж можна вивести
- Формулу для розбиття твори синуса і косинуса в суму: sinacosb = 0.5(sin(A + b)+sin(A-b))
Рекомендуємо потренуватися і вивести самостійно формули для перетворення в твір різниці синусів і суми і різниці косинусів, а також для розбиття в суму творів синусів і косинусів. Проробивши ці вправи, ви досконально освоїте майстерність виведення тригонометричних формул і не заблукаєте навіть на найскладнішій контрольної, олімпіаді або тестуванні.
Вивчення тригонометрії ми почнемо з прямокутного трикутника. Визначимо, що таке синус і косинус, а також тангенс і котангенс гострого кута. Це основи тригонометрії.
Нагадаємо, що прямий кут — це кут, рівний 90 градусів. Іншими словами, половина розгорнутого кута.
Гострий кут — менший 90 градусів.
Тупий кут — більший 90 градусів. Стосовно до такого кутку «тупий» — не образа, а математичний термін 🙂
Стосовно до такого кутку «тупий» — не образа, а математичний термін 🙂
Намалюємо прямокутний трикутник. Прямий кут зазвичай позначається. Звернемо увагу, що сторона, яка лежить навпроти кута, позначається тією ж буквою, тільки маленькою. Так, сторона, що лежить навпроти кута A, позначається.
Кут позначається відповідною грецькою буквою.
гіпотенуза прямокутного трикутника — це сторона, що лежить навпроти прямого кута.
катети— сторони, що лежать навпроти гострих кутів.
Катет, що лежить навпроти кута, називається протилежними (По відношенню до кута). Інший катет, який лежить на одній зі сторін кута, називається прилеглим.
синус гострого кута в прямокутному трикутнику — це відношення протилежного катета до гіпотенузи:
косинус гострого кута в прямокутному трикутнику — відношення прилеглого катета до гіпотенузи:
тангенс гострого кута в прямокутному трикутнику — відношення протилежного катета до прилеглого:
Інше (рівносильне) визначення: тангенсом гострого кута називається відношення синуса кута до його косинусу:
котангенс гострого кута в прямокутному трикутнику — відношення прилеглого катета до протилежного (або, що те ж саме, відношення косинуса до синуса):
Зверніть увагу на основні співвідношення для синуса, косинуса, тангенса і котангенс, які наведені нижче. Вони стануть в нагоді нам при вирішенні завдань.
Вони стануть в нагоді нам при вирішенні завдань.
Давайте доведемо деякі з них.
Добре, ми дали визначення і записали формули. А для чого все-таки потрібні синус, косинус, тангенс і котангенс?
Ми знаємо, що сума кутів будь-якого трикутника дорівнює.
Знаємо співвідношення між сторонами прямокутного трикутника. Це теорема Піфагора:.
Виходить, що знаючи два кута в трикутнику, можна знайти третій. Знаючи дві сторони в прямокутному трикутнику, можна знайти третю. Значить, для кутів — своє співвідношення, для сторін — своє. А що робити, якщо в прямокутному трикутнику відомий один кут (крім прямого) і одна сторона, а знайти всі інші сторони?
З цим і зіткнулися люди в минулому, складаючи карти місцевості і зоряного неба. Адже не завжди можна безпосередньо виміряти всі сторони трикутника.
Синус, косинус і тангенс — їх ще називають тригонометричними функціями кута — дають співвідношення між сторонами і кутами трикутника. Знаючи кут, можна знайти все його тригонометричні функції за спеціальними таблицями. А знаючи синуси, косинуси і тангенси кутів трикутника і одну з його сторін, можна знайти інші.
Знаючи кут, можна знайти все його тригонометричні функції за спеціальними таблицями. А знаючи синуси, косинуси і тангенси кутів трикутника і одну з його сторін, можна знайти інші.
Ми теж намалюємо таблицю значень синуса, косинуса, тангенса і котангенс для «хороших» кутів від до.
Зверніть увагу на два червоних прочерку в таблиці. При відповідних значеннях кутів тангенс і котангенс не існують.
Розберемо кілька завдань з тригонометрії з Банку завдань ФІПІ.
1. У трикутнику кут дорівнює,. Знайдіть.
Завдання вирішується за чотири секунди.
Оскільки,.
2. У трикутнику кут дорівнює,,. Знайдіть.
Знайдемо по теоремі Піфагора.
Завдання вирішена.
Часто в задачах зустрічаються трикутники з кутами і чи з кутами і. Основні співвідношення для них запам’ятовуйте напам’ять!
Для трикутника з кутами і катет, що лежить навпроти кута в, дорівнює половині гіпотенузи.
Трикутник з кутами і — рівнобедрений. У ньому гіпотенуза в раз більше катета.
У ньому гіпотенуза в раз більше катета.
Ми розглянули завдання на рішення прямокутних трикутників — тобто на знаходження невідомих сторін або кутів. Але це не все! В варіантах ЄДІ з математики безліч завдань, де фігурує синус, косинус, тангенс або котангенс зовнішнього кута трикутника. Про це — в наступній статті.
Формули суми і різниці синусів і косинусів для двох кутів α і β дозволяють перейти від суми зазначених кутів до твору кутів α + β 2 і α — β 2. Відразу відзначимо, що не варто плутати формули суми і різниці синусів і косинусів з формулами синусів і косинусів суми і різниці. Нижче ми перерахуємо ці формули, наведемо їх висновок і покажемо приклади застосування для конкретних завдань.
Yandex.RTB R-A-339285-1
Формули суми і різниці синусів і косинусів
Запишемо, як виглядають формули суми і різниці для синусів і для косинусів
Формули суми і різниці для синусів
sin α + sin β \u003d 2 sin α + β 2 cos α — β 2 sin α — sin β \u003d 2 sin α — β 2 cos α + β 2
Формули суми і різниці для косинусів
cos α + cos β \u003d 2 cos α + β 2 cos α — β 2 cos α — cos β \u003d — 2 sin α + β 2 cos α — β 2, cos α — cos β \u003d 2 sin α + β 2 · β — α 2
Дані формули справедливі для будь-яких кутів α і β. Кути α + β 2 і α — β 2 називаються відповідно напівсумою і Полуразность кутів альфа і бета. Дамо формулювання для кожної формули.
Кути α + β 2 і α — β 2 називаються відповідно напівсумою і Полуразность кутів альфа і бета. Дамо формулювання для кожної формули.
Визначення формул сум і різниці синусів і косинусів
Сума синусів двох кутів дорівнює подвоєному добутку синуса напівсуми цих кутів на косинус полуразность.
Різниця синусів двох кутів дорівнює подвоєному добутку синуса полуразность цих кутів на косинус напівсуми.
Сума косинусів двох кутів дорівнює подвоєному добутку косинуса напівсуми і косинуса полуразность цих кутів.
Різниця косинусів двох кутів дорівнює подвоєному добутку синуса напівсуми на косинус полуразность цих кутів, взятому з негативним знаком.
Висновок формул суми і різниці синусів і косинусів
Для виведення формул суми і різниці синуса і косинуса двох кутів використовуються формули додавання. Наведемо їх нижче
sin (α + β) \u003d sin α · cos β + cos α · sin β sin (α — β) \u003d sin α · cos β — cos α · sin β cos (α + β) \u003d cos α · cos β — sin α · sin β cos (α — β) \u003d cos α · cos β + sin α · sin β
Також представимо самі кути у вигляді суми напівсумі і Полуразность.
α \u003d α + β 2 + α — β 2 \u003d α 2 + β 2 + α 2 — β 2 β \u003d α + β 2 — α — β 2 \u003d α 2 + β 2 — α 2 + β 2
Переходимо безпосередньо до висновку формул суми і різниці для sin і cos.
Висновок формули суми синусів
В сумі sin α + sin β замінимо α і β на вираження для цих кутів, наведені вище. отримаємо
sin α + sin β \u003d sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Тепер до першого висловом застосовуємо формулу складання, а до другого — формулу синуса різниць кутів (див. Формули вище)
sin α + β 2 + α — β 2 \u003d sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 \u003d sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 \u003d sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Розкриємо дужки, наведемо подібні доданки і отримаємо шукану формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 \u003d \u003d 2 sin α + β 2 cos α — β 2
Дії по висновку інших формул аналогічні.
Висновок формули різниці синусів
sin α — sin β \u003d sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 \u003d sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 \u003d \u003d 2 sin α — β 2 cos α + β 2
Висновок формули суми косинусів
cos α + cos β \u003d cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 \u003d cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 \u003d \u003d 2 cos α + β 2 cos α — β 2
Висновок формули різниці косинусів
cos α — cos β \u003d cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 \u003d cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 \u003d \u003d — 2 sin α + β 2 sin α — β 2
Приклади розв’язання практичних завдань
Для початку, зробимо перевірку однієї з формул, підставивши в неї конкретні значення кутів.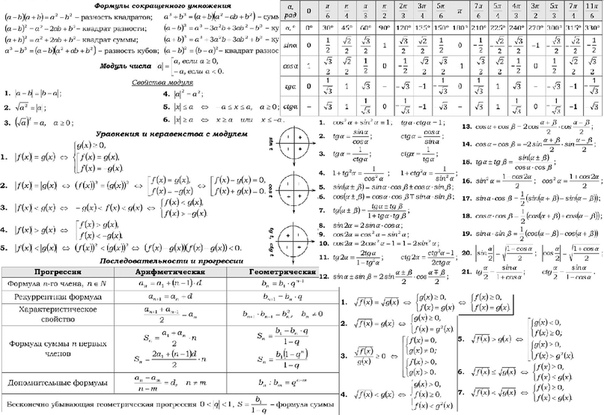 Нехай α \u003d π 2, β \u003d π 6. Обчислимо значення суми синусів цих кутів. Спочатку скористаємося таблицею основних значень тригонометричних функцій, а потім застосуємо формулу для суми синусів.
Нехай α \u003d π 2, β \u003d π 6. Обчислимо значення суми синусів цих кутів. Спочатку скористаємося таблицею основних значень тригонометричних функцій, а потім застосуємо формулу для суми синусів.
Приклад 1. Перевірка формули суми синусів двох кутів
α \u003d π 2, β \u003d π 6 sin π 2 + sin π 6 \u003d 1 + 1 2 \u003d 3 2 sin π 2 + sin π 6 \u003d 2 sin π 2 + π 6 2 cos π 2 — π 6 2 \u003d 2 sin π 3 cos π 6 \u003d 2 · 3 2 · 3 2 \u003d 3 2
Розглянемо тепер випадок, коли значення кутів відрізняються від основних значень, представлених в таблиці. Нехай α \u003d 165 °, β \u003d 75 °. Обчислимо значення різниці синусів цих кутів.
Приклад 2. Застосування формули різниці синусів
α \u003d 165 °, β \u003d 75 ° sin α — sin β \u003d sin 165 ° — sin 75 ° sin 165 — sin 75 \u003d 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 \u003d \u003d 2 · sin 45 ° · cos 120 ° \u003d 2 · 2 2 · — 1 | 2 \u003d 2 2
За допомогою формул суми і різниці синусів і косинусів можна перейти від суми або різниці до твору тригонометричних функцій. Часто ці формули називають формулами переходу від суми до твору. Формули суми і різниці синусів і косинусів широко використовуються при вирішенні тригонометричних рівнянь і при перетворенні тригонометричних виразів.
Часто ці формули називають формулами переходу від суми до твору. Формули суми і різниці синусів і косинусів широко використовуються при вирішенні тригонометричних рівнянь і при перетворенні тригонометричних виразів.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl + Enter
Тригонометричні перетворення | Математика, логіка, інтелект
Тригонометричні формули (або тригонометричні тотожності) — математичні вирази для тригонометричних функцій,
які виконуються при всіх значеннях аргумента.
Тригонометричні формули широко використовуються як в математиці, так і в фізиці. В математиці — при розв’язуванні трикутників, інтегруванні,
в теорії функцій комплексних змінних і т.д. В фізиці — при розв’язуванні задач, в яких векторні величини не лежать на одній прямій.
Співвідношення між тригонометричними функціями одного й того самого аргументу
Тут і далі запис \(k\in \mathbb{Z}\) означає, що \(k\) — будь-яке ціле число. {2} \alpha}, ~\alpha \ne \pi k\]
{2} \alpha}, ~\alpha \ne \pi k\]
Формули додавання
\[\sin(\alpha + \beta) = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta\]
\[\sin(\alpha — \beta) = \sin \alpha \cdot \cos \beta — \cos \alpha \cdot \sin \beta\]
\[\cos(\alpha + \beta) = \cos \alpha \cdot \cos \beta — sin \alpha \cdot \sin \beta\]
\[\cos(\alpha — \beta) = \cos \alpha \cdot \cos \beta + sin \alpha \cdot \sin \beta\]
\[\operatorname{tg}(\alpha + \beta) = \frac{\operatorname{tg} \alpha + \operatorname{tg} \beta} {1 — \operatorname{tg} \alpha \cdot \operatorname{tg} \beta}\]
\[\operatorname{tg}(\alpha — \beta) = \frac{\operatorname{tg} \alpha — \operatorname{tg} \beta}{1 + \operatorname{tg} \alpha \cdot \operatorname{tg} \beta}, ~\alpha, ~\beta, ~\alpha — \beta \ne \frac{\pi}{2} + \pi k, k\in \mathbb{Z}\]
Формули подвійного аргументу
\[\sin 2\alpha = 2\sin\alpha \cdot \cos \alpha\]
\[\cos 2\alpha = \cos^{2} \alpha — sin^{2} \alpha = 2\cos^{2} \alpha — 1 = 1 — 2\sin^{2} \alpha\]
\[\operatorname{tg} 2\alpha = \frac{2\operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha }\]
Формули половинного аргументу
\[\sin^{2} \frac{\alpha}{2} = \frac{1-\cos \alpha}{2}\]
\[\cos^{2} \frac{\alpha}{2} = \frac{1+\cos \alpha}{2}\]
\[\operatorname{tg} \frac{\alpha}{2} = \frac{\sin \alpha}{1+\cos \alpha} = \frac{1-\cos \alpha}{\sin \alpha}, ~\alpha \ne \pi + 2 \pi k, k\in \mathbb{Z}\]
Формули перетворення суми в добуток
\[\sin \alpha + \sin \beta = 2\sin\Big(\frac{\alpha + \beta}{2}\Big) \cdot \cos\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\sin \alpha — \sin \beta = 2\cos\Big(\frac{\alpha + \beta}{2}\Big) \cdot \sin\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\cos \alpha + \cos \beta = 2\cos\Big(\frac{\alpha + \beta}{2}\Big) \cdot \cos\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\cos \alpha — \cos \beta = — 2\sin\Big(\frac{\alpha + \beta}{2}\Big) \cdot \sin\Big(\frac{\alpha — \beta}{2}\Big)\]
\[\operatorname{tg} \alpha + \operatorname{tg} \beta = \frac{\sin( \alpha + \beta )}{\cos \alpha \cdot \cos \beta}\]
\[\operatorname{tg} \alpha — \operatorname{tg} \beta = \frac{\sin(\alpha — \beta)}{\cos \alpha \cdot \cos \beta}, ~\alpha, \beta \ne \frac{\pi}{2} + \pi k, k\in \mathbb{Z}\]
Формули перетворення добутку в суму
\[\sin \alpha \cdot \sin \beta = \frac{\cos(\alpha — \beta) — \cos(\alpha + \beta )}{2}\]
\[\cos \alpha \cdot \cos \beta = \frac{\cos(\alpha — \beta) + \cos(\alpha + \beta )}{2}\]
\[\sin \alpha \cdot \cos \beta = \frac{\sin(\alpha — \beta) + \sin(\alpha + \beta )}{2}\]
Співвідношення між \(\sin\alpha\), \(\cos\alpha\) і \(\operatorname{tg}\frac{\alpha}{2}\)
\[\sin \alpha = \frac{ 2\operatorname{tg}\large\frac{\alpha}{2} }{ 1+\operatorname{tg}^{2}\large\frac{\alpha}{2} }, ~\alpha \ne (2k+1) \pi\]
\[\cos \alpha = \frac{ 1-\operatorname{tg}^{2}\large\frac{\alpha}{2} }{ 1+\operatorname{tg}^{2}\large\frac{\alpha}{2} }, ~\alpha \ne (2k+1) \pi\]
Додаткові формули
\[\sin 3\alpha = 3\sin \alpha — 4\sin^{3}\alpha\]
\[\cos 3\alpha = 4\cos^{3}\alpha — 3\cos \alpha\]
Формули зведення
| \(x\) | \(\frac{\pi}{2} + \alpha\) | \(\pi + \alpha\) | \(\frac{3\pi}{2} + \alpha\) | \(-\alpha\) | \(\frac{\pi}{2} — \alpha\) | \(\pi — \alpha\) | \(\frac{3\pi}{2} — \alpha\) |
| \(\sin x\) | \(\cos \alpha\) | \(-\sin \alpha\) | \(-\cos \alpha\) | \(-\sin \alpha\) | \(\cos \alpha\) | \(\sin \alpha\) | \(-\cos \alpha\) |
| \(\cos x\) | \(-\sin \alpha\) | \(-\cos \alpha\) | \(\sin \alpha\) | \(\cos \alpha\) | \(\sin \alpha\) | \(-\cos \alpha\) | \(-\sin \alpha\) |
| \(\operatorname{tg}x\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) |
| \(\operatorname{ctg}x\) | \(-\operatorname{tg} \alpha\) | \(\operatorname{ctg} \alpha\) | \(-\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) | \(-\operatorname{ctg} \alpha\) | \(\operatorname{tg} \alpha\) |
Значення тригонометричних функцій деяких кутів
| \(\alpha\) | \(0 (0^{\circ})\) | \(\frac{\pi}{6} (30^{\circ})\) | \(\frac{\pi}{4} (45^{\circ})\) | \(\frac{\pi}{3} (60^{\circ})\) | \(\frac{\pi}{2} (90^{\circ})\) |
| \(\sin \alpha\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
| \(\cos \alpha\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) |
| \(\operatorname{tg} \alpha\) | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | Не існує |
| \(\operatorname{ctg} \alpha\) | Не існує | \(\sqrt{3}\) | \(1\) | \(\frac{\sqrt{3}}{3}\) | \(0\) |
| \(\alpha\) | \(\pi (180^{\circ})\) | \(\frac{3\pi}{2} (270^{\circ})\) | \(2 \pi (360^{\circ})\) |
| \(\sin \alpha\) | \(0\) | \(-1\) | \(0\) |
| \(\cos \alpha\) | \(-1\) | \(0\) | \(1\) |
| \(\operatorname{tg} \alpha\) | \(0\) | Не існує | \(0\) |
| \(\operatorname{ctg} \alpha\) | Не існує | \(0\) | Не існує |
Значення тригонометричної функції
Значення тригонометричної функції будь-якого гострого кута
Обчислення кута за тригонометричною функцією
Основні тригонометричні тотожності презентація — irinaseregina.
 ru
ru
Скачать основні тригонометричні тотожності презентація txt
Тригонометрические тождества Основное тригонометрическое тождество (1) Тригонометрическое тождество (2) Тригонометрическое тождество (3). Основное тригонометрическое тождество (1) x 1 -1 -1 1 M 0 α sin 2α + cos 2α = 1 x2 + y 2 = 1 y cosα sinα. Тригонометрическое тождество (2) sin2α + cos2α = 1. Тригонометрическое тождество (3) sin2α + cos2α = 1.
Пользовательское соглашение. [email protected] X. Чтобы скачать данную презентацию, порекомендуйте её своим друзьям в любой соц. сети. После этого кнопка ЗАГРУЗКИ станет активной! Кнопки рекомендации: загрузить презентацию. ВКонтакте – универсальное средство для общения и поиска друзей и одноклассников, которым ежедневно пользуются десятки миллионов человек. Мы хотим, чтобы друзья, однокурсники, одноклассники, соседи и коллеги всегда оставались в контакте. Слайд 8 из презентации «Основные тригонометрические формулы».
Размеры: х пикселей, irinaseregina.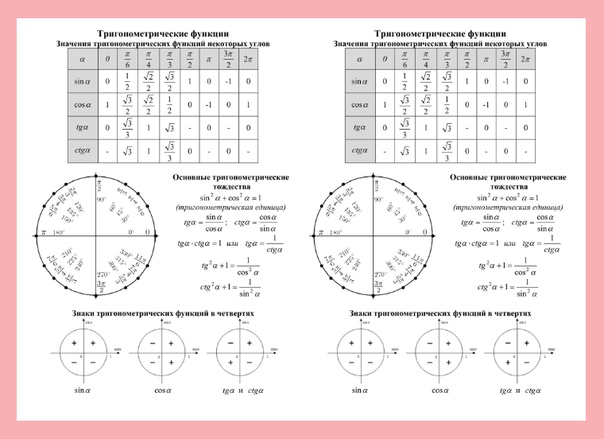 ru Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как». Скачать всю презентацию «Основные тригонометрические irinaseregina.ru» можно в zip-архиве размером КБ. Скачать презентацию. Основное тригонометрическое тождество, доказательство и определение. Связь тангенса, синуса и косинуса. Основное тригонометрическое тождество.
ru Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как». Скачать всю презентацию «Основные тригонометрические irinaseregina.ru» можно в zip-архиве размером КБ. Скачать презентацию. Основное тригонометрическое тождество, доказательство и определение. Связь тангенса, синуса и косинуса. Основное тригонометрическое тождество.
Там, где заканчиваются границы привычной и давно знакомой алгебры, начинаются владения тригонометрии. Давайте вооружимся всеми необходимыми формулами, чтобы в полном обмундировании преодолеть любые тригонометрические испытания. Повторение формул тригонометрии с помощью компьютерной презентации.
Применение тригонометрических формул к преобразованию выражений. Выполнение теста. Работа на компьютерах с презентацией: “Основные формулы тригонометрии”. Предварительно напомнить технику безопасности. Основные тригонометрические тождества. V. Применение тригонометрических формул к преобразованию выражений.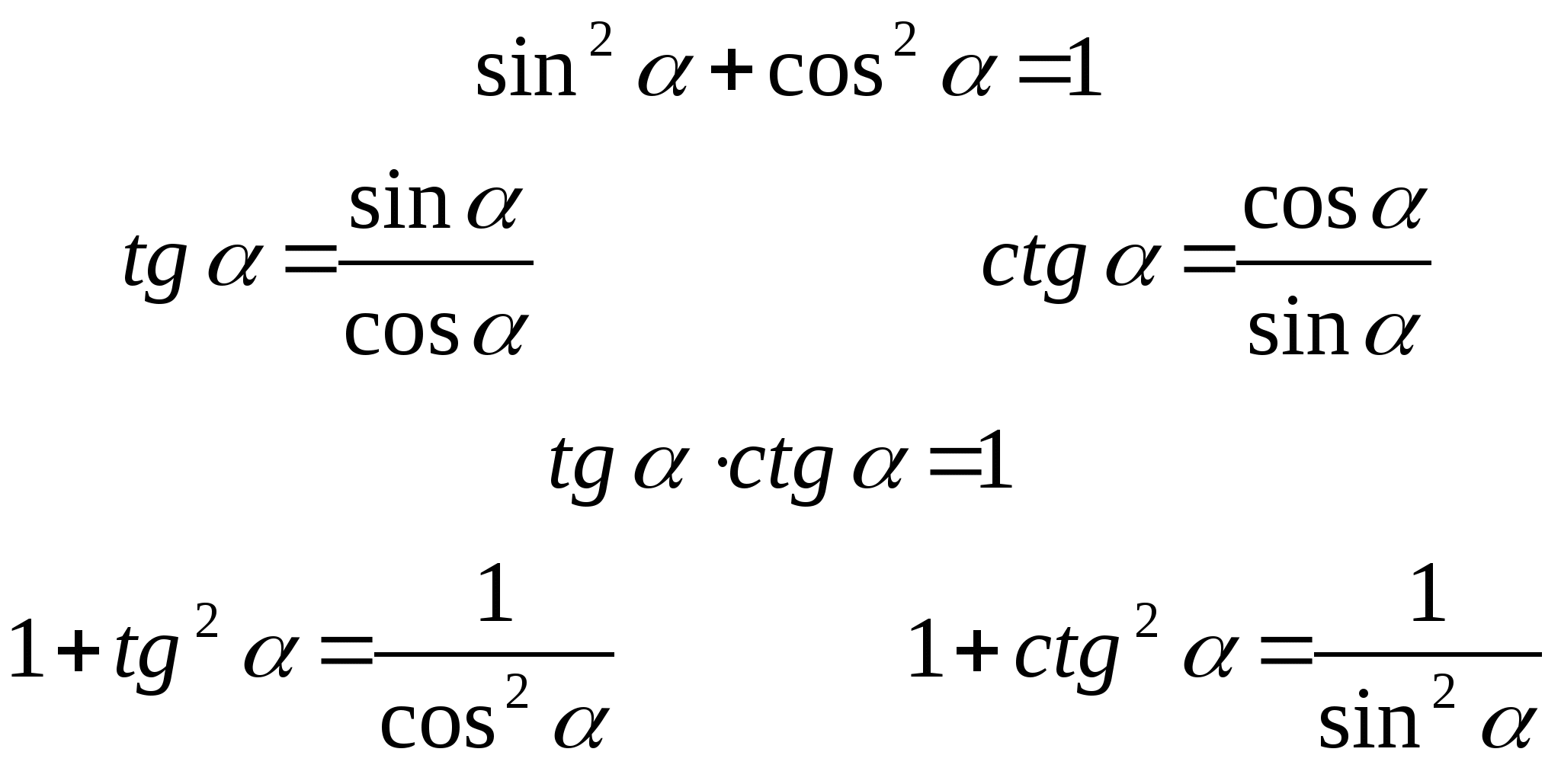 Упростить выражение 7 cos — 5. Ученики умеют работать с интерактивной доской и компьютерной презентацией.
Упростить выражение 7 cos — 5. Ученики умеют работать с интерактивной доской и компьютерной презентацией.
Но следует отметить,не все ученики смогли принять участие при устных ответах на уроке. Опубликовано в в группе «Преподаватели математики».
Повторение формул тригонометрии с помощью компьютерной презентации. Применение тригонометрических формул к преобразованию выражений. Выполнение теста. Работа на компьютерах с презентацией: “Основные формулы тригонометрии”.
Предварительно напомнить технику безопасности. Основные тригонометрические тождества. V. Применение тригонометрических формул к преобразованию выражений. Упростить выражение 7 cos — 5. Ученики умеют работать с интерактивной доской и компьютерной презентацией. Но следует отметить,не все ученики смогли принять участие при устных ответах на уроке. Опубликовано в в группе «Преподаватели математики». Презентация предназначена для изучения данной темы в группах колледжа.формирование понятия тождестваумения доказывать тождества.
• Системазувати знання, уміння та навички з теми: «Основні тригонометричні тотожності. Формули зведення»; формувати вміння учнів застосовувати тригонометричні формули для перетворення тригонометричних виразів різного рівня складності.
• Розвивати логічне мислення, уміння аналізувати, навички самостійної та групової роботи. • Сприяти стійкому інтересу до вивчення математики.
rtf, doc, djvu, txt
Похожее:
Українська мова 11 клас контрольна робота 1
Фізика 7 клас зошит лабораторних робіт відповіді божинова
Історія україни 10 клас відповіді до підручника
Позбавлення батьківських прав курсова робота
Examination card 9 клас відповіді
Основні тригонометричні формули. Співвідношення між тригонометричними функціями одного и того самого аргументу (реферат)
Реферат з математики
Основні тригонометричні формули. Співвідношення між тригонометричними
Співвідношення між тригонометричними
функціями одного и того самого аргументу
Розглянемо, як пов’язані між собою синус і косинус одного й того самого
кута.
Нехай при повороті радіуса ОА навколо точки О на кут ? дістали радіус ОВ
(мал. 77). Тоді за означенням
,
де х — абсциса точки В, а у — її ордината, а R — довжина радіуса ОА.
Звідси
x = R cos ?, y = R sin ?.
Оскільки точка В належить колу з
центром у початку координат, радіус якого дорівнює R, то її координати
задовольняють рівняння
x2+y2 = R2
Підставивши в це рівняння замість х і у вирази R cos ? і R sin ?,
дістанемо:
(R cos ?)2 + (R sin ?)2=R2.
Поділивши обидві частини останньої рівності на R2, знайдемо, що
sin2? + cos2? = l. (1)
Рівність (1) справджується при будь-яких значеннях ?.
З’ясуємо тепер, як пов’язані між собою тангенс, синус і косинус одного і
того самого кута.
. Оскільки y = R sin ?, х= R cos ?, то
.
Отже,
(2)
Аналогічно
,
тобто
, (3)
0.
За допомогою формул (1) – (3) можна вивести інші формули, які виражають
співвідношення між тригонометричними функціями одного й того самого
аргументу.
З різностей (2) і (3) дістанемо:
= 1,
тобто
tg ?-ctg ? = l. (4)
Рівність (4) показує, як пов’язані між собою тангенс і котангенс кута ?.
Вона справджується при всіх значеннях ?, при яких tg ? і ctg ? мають
зміст.
Зазначимо, що формулу (4) можна вивести і безпосередньо з означення
тангенса і котангенса.
Виведемо тепер формули, які виражають співвідношення між тангенсом і
косинусом, а також між котангенсом і синусом одного й того самого кута.
Поділивши обидві частини рівності (1) на cos2? дістанемо:
,
тобто
. (5)
Якщо обидві частини рівності (1) поділити на sin2a, то матимемо:
.
тобто
(6)
0.
Рівності (1) – (6) є тотожностями, їх називають основними
тригонометричними тотожностями. Розглянемо приклади використання цих
Розглянемо приклади використання цих
тотожностей для знаходження значень тригонометричних функцій за відомим
значенням однієї з них.
Нашли опечатку? Выделите и нажмите CTRL+Enter
30 Янв 2007
Сводка тригонометрических формул
Сводка тригонометрических формул
Эти формулы относятся к длине и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Идентичности не относятся к конкретным геометрическим фигурам, но верны для всех углов.
Формулы дуг и секторов окружностей
Вы можете легко найти как длину дуги, так и площадь сектора для угла θ в окружности радиуса r .
| Длина дуги. Длина дуги равна радиусу r, в умноженному на угол θ , где угол измеряется в радианах. Чтобы преобразовать градусы в радианы, умножьте количество градусов на π /180. | |
Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах. |
Формулы для прямоугольных треугольников
Наиболее важные формулы для тригонометрии — формулы для прямоугольного треугольника.Если θ — один из острых углов в треугольнике, то синус тэты — это отношение противоположной стороны к гипотенузе, косинус — это отношение соседней стороны к гипотенузе, а тангенс — это отношение сторона, противоположная соседней стороне.
Эти три формулы известны мнемоническим языком SohCahToa. Помимо этого, существует очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.
Зная, что два острых угла дополняют друг друга, то есть они складываются в 90 °, вы можете решить любой прямоугольный треугольник:
- Если вы знаете две из трех сторон, вы можете найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Формулы наклонных треугольников
Эти формулы работают для любого треугольника, будь то острый, тупой или прямой.Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначаются прописными буквами A , B и C , а три противоположные им стороны соответственно обозначаются строчными буквами a , . b и c .
Есть две важные формулы для наклонных треугольников. Их называют законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники.В нем говорится, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумме квадратов двух других сторон минус 2. ab cos & nbsp C , удвоить их произведение, умноженное на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне является одинаковым отношением для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Если вы знаете два угла и сторону, вы можете найти третий угол и две другие стороны.
- Если вы знаете две стороны и включенный угол, вы можете найти третью сторону и оба других угла.
- Если вы знаете две стороны и угол, противоположный одной из них, есть две возможности для угла, противоположного другой (острый и тупой), и для обеих возможностей вы можете определить оставшийся угол и оставшуюся сторону.
Формулы площади для треугольников
Есть три разные полезные формулы для определения площади треугольника, и какая из них вы используете, зависит от того, какая информация у вас есть.
Половина основания, умноженная на высоту. Это обычный вариант, поскольку он самый простой и обычно у вас есть такая информация. Выбирайте любую сторону, чтобы позвонить по базе b . Тогда, если h — это расстояние от противоположной вершины до b , то площадь равна половине bh . | |
| Формула Герона. Это полезно, когда вы знаете три стороны треугольника: a , b и c , и все, что вам нужно знать, — это площадь. Пусть с будет половиной их суммы, называемой полупериметром . Тогда площадь является квадратным корнем из произведения s , s — a , s — b и s — c . | |
| Формула стороны-угла-стороны. Используйте это, если вам известны две стороны, a и b , и включенный угол C . Площадь равна половине произведения двух сторон, умноженного на синус включенного угла. |
Формула тригонометрии — [Sin, Cos, Tan, Cot, Sec и Cosec]
Формула тригонометрии : Тригонометрия — это хорошо известное имя в геометрической области математики, которое актуально в этой области с давних времен, а также применяется практически во многих случаях.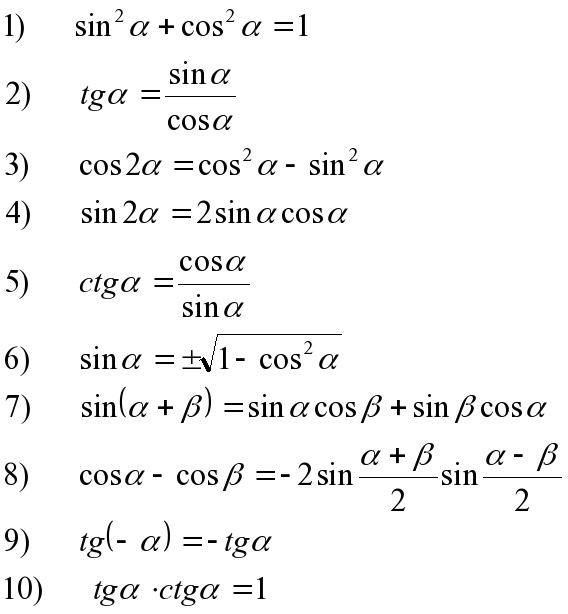
На простом языке тригонометрию можно определить как ту ветвь алгебры, которая связана с треугольником. В этом разделе мы в основном изучаем взаимосвязь между углами и длиной стороны данного треугольника. При таком подробном изучении треугольника формируется несколько типов уравнений, которые, следовательно, решаются для упрощения взаимосвязи между длинами сторон и углов такого треугольника.
Тригонометрия считается одним из старейших компонентов алгебры, существующей примерно с 3 века.Существует практическое использование тригонометрии в нескольких контекстах, таких как астрономия, геодезия, оптика или периодические функции.
Формулы тригонометрии
Что ж, будь то алгебра или геометрия, обе эти области математики основаны на научных вычислениях уравнений, и мы должны выучить различные формулы, чтобы их было легко вычислить.
Как мы знаем, в тригонометрии мы в основном измеряем разные стороны треугольника, из которых формируются несколько уравнений.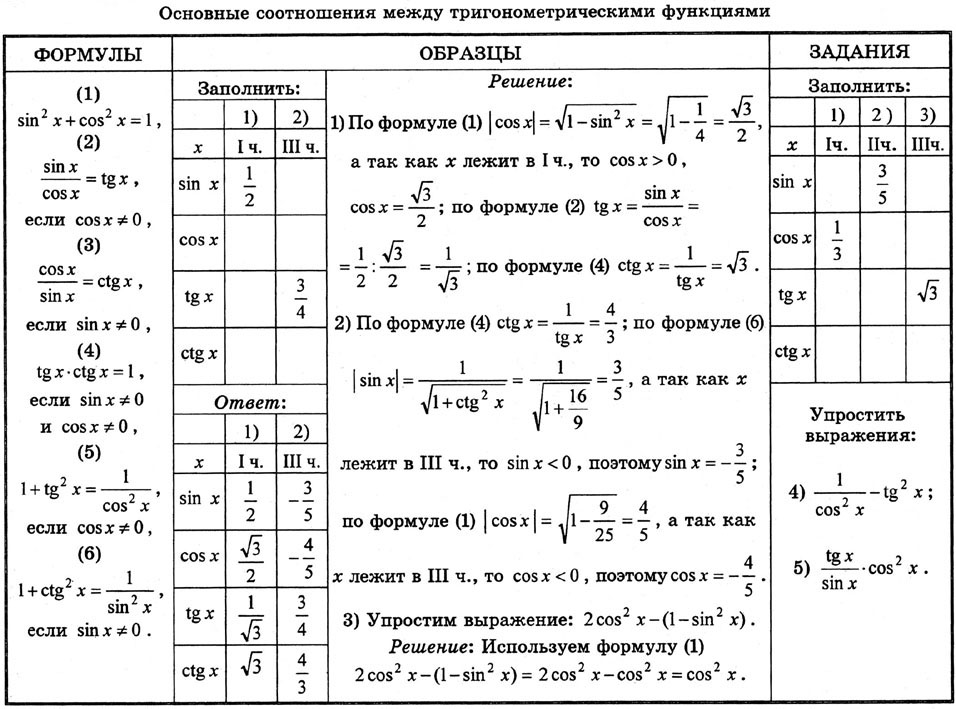 Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .
Далее формулы тригонометрии составлены в соответствии с различными отношениями, используемыми в области, такими как синус, тангенс, косинус и т. Д. Таким образом, в основном есть номера формул, которые обычно используются в тригонометрии для измерения сторон треугольника. .
Здесь мы приводим список различных типов формул тригонометрии.
Основная формула тригонометрии
2. Sin Cos Tan на 0, 30, 45, 60 градусов
3.Пифагорейские тождества
4. Знак греха, Cos, Tan в разных квадрантах
A dd– S ugar – T o –C оферта
5. Радианы
1 градус = 60 минут
Пример: 1 ° = 60 ′
1 минута = 60 секунд
Пример: 1 ′ = 60 дюймов
6. Отрицательные углы [четно-нечетные отождествления]
Sin (-x) = — Sin x
Cos (-x) = Cos x
Tan (-x) = — Tan x
Cot (-x) = — Cot x
Sec (-x) = Sec x
Cosec (-x) = — Cosec x
7.
 Значение Sin, Cos, Tan повторяется после 2𝛑
Значение Sin, Cos, Tan повторяется после 2𝛑
Sin (2𝛑 + x) = Sin x
Cos (2𝛑 + x) = Cos x
Tan (2𝛑 + x) = Tan x
8. Идентификация периодичности — углы смещения на 𝛑 / 2, 𝛑, 3𝛑 / 2
9. Идентификаторы суммы углов и разностей
10. Формула двойного угла
11. Формула тройного угла
12. Полугловые идентичности
13. Сумма идентичностей
14.Идентификационные данные продукта
15. Закон греха
Здесь,
- ABC — вершины треугольника ABC.
- Место, противоположное углу A, — это a. то есть до н.э.
- Место, противоположное углу B, — это b. т.е. AC
- Место, противоположное углу C, равно c. т.е. AB
16. Закон косинуса
17. Обратная тригонометрическая функция
Если Sin θ = x
, затем поместите Sin на правую сторону
Таким образом, вы можете видеть, что Sin — это угол. То же, что и обратная функция для всех функций Trignomentry, — это угол.
То же, что и обратная функция для всех функций Trignomentry, — это угол.
18. Область и диапазон функций обратной тригонометрии
19. Формула обратной тригонометрии
20. Замена обратной тригонометрии
Как и любой другой раздел математики, формулы тригонометрии не менее важны, поскольку без этих формул вы не можете использовать значения треугольников для целей измерения. Эти формулы упрощают стороны треугольника, так что вы можете легко измерить все его стороны.
Мы призываем всех ученых понять эти формулы, а затем легко применять их для решения различных типов задач тригонометрии.
3.1: Основные тригонометрические идентичности — математика LibreTexts
Пока мы знаем несколько соотношений между тригонометрическими функциями. Например, нам известны отношения взаимности:
- \ (\ csc \; \ theta ~ = ~ \ dfrac {1} {\ sin \; \ theta} \ qquad \), когда \ (\ sin \; \ theta \ ne 0 \)
- \ (\ sec \; \ theta ~ = ~ \ dfrac {1} {\ cos \; \ theta} \ qquad \), когда \ (\ cos \; \ theta \ ne 0 \)
- \ (\ cot \; \ theta ~ = ~ \ dfrac {1} {\ tan \; \ theta} \ qquad \), когда определено \ (\ tan \; \ theta \), а не \ (0 \)
- \ (\ sin \; \ theta ~ = ~ \ dfrac {1} {\ csc \; \ theta} \ qquad \), когда определено \ (\ csc \; \ theta \), а не \ (0 \)
- \ (\ cos \; \ theta ~ = ~ \ dfrac {1} {\ sec \; \ theta} \ qquad \), когда определено \ (\ sec \; \ theta \), а не \ (0 \)
- \ (\ tan \; \ theta ~ = ~ \ dfrac {1} {\ cot \; \ theta} \ qquad \), когда определено \ (\ cot \; \ theta \), а не \ (0 \)
Обратите внимание, что каждое из этих уравнений верно для всех углов \ (\ theta \), для которых определены обе части уравнения.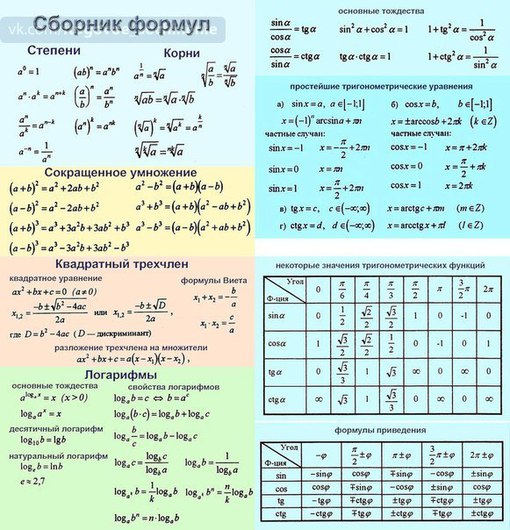 Такие уравнения называются тождествами , и в этом разделе мы обсудим несколько тригонометрических тождеств , то есть тождеств, включающих тригонометрические функции. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
Такие уравнения называются тождествами , и в этом разделе мы обсудим несколько тригонометрических тождеств , то есть тождеств, включающих тригонометрические функции. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
\ [\ tan \; \ theta ~ = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} \ qquad \ text {when} \ cos \; \ theta \ ne 0 \ label {3.1 } \]
Чтобы доказать это тождество, выберите точку \ ((x, y) \) на конечной стороне \ (\ theta \) на расстоянии \ (r> 0 \) от начала координат, и предположите, что \ (\ cos \ ; \ theta \ ne 0 \).Тогда \ (x \ ne 0 \) (поскольку \ (\ cos \; \ theta = \ frac {x} {r} \)), поэтому по определению
\ [\ nonumber
\ frac {\ sin \; \ theta} {\ cos \; \ theta} ~ = ~ \ dfrac {~ \ dfrac {y} {r} ~} {~ \ dfrac {x} {r } ~} ~ = ~ \ frac {y} {x} ~ = ~
\ tan \; \ theta ~.
\]
Обратите внимание, как мы доказали тождество, расширив одну из его сторон (\ (\ frac {\ sin \; \ theta} {\ cos \; \ theta} \)) до тех пор, пока не получили выражение, равное другой стороне ( \ (\ tan \; \ theta \)). 2 \; \ theta \ label {3.2 \; \ theta ~ + ~ 4
2 \; \ theta \ label {3.2 \; \ theta ~ + ~ 4
\ end {align *} \]
Пример 3.3
Докажите, что \ (\; \ tan \; \ theta ~ + ~ \ cot \; \ theta ~ = ~ \ sec \; \ theta ~ \ csc \; \ theta \; \).
Решение
Раскроем левую часть и покажем, что она равна правой стороне:
\ [\ nonumber \ begin {alignat *} {3}
\ tan \; \ theta + \ cot \; \ theta ~ & = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} ~ + ~
\ frac {\ cos \; \ theta} {\ sin \; \ theta} & {} \ qquad & \ text {(автор \ ref {3.2 \; \ theta} {\ cos \; \ theta ~ \ sin \; \ theta} & {} \ qquad
& \ text {(после получения общего знаменателя)} \\ \ nonumber
& = ~ \ frac { 1} {\ cos \; \ theta ~ \ sin \; \ theta} & {} \ qquad & \ text {(by \ ref {3.3})} \\ \ nonumber
& = ~ \ frac {1} {\ cos \; \ theta} ~ \ cdot ~ \ frac {1} {\ sin \; \ theta} \\ \ nonumber
& = ~ \ sec \; \ theta ~ \ csc \; \ theta
\ end {alignat * } \]
В приведенном выше примере, как мы узнали, что нужно развернуть левую сторону вместо правой? В целом, хотя этот метод не всегда работает, более сложную сторону идентичности, вероятно, будет легче раскрыть. 2 \; \ theta} {\ sec \; \ theta} ~ = ~ \ csc \; \ theta ~ \ cot \; \ theta \; \ ).2 \; \ theta} {\ sec \; \ theta}
2 \; \ theta} {\ sec \; \ theta} ~ = ~ \ csc \; \ theta ~ \ cot \; \ theta \; \ ).2 \; \ theta} {\ sec \; \ theta}
& {} \ qquad & \ text {(by \ ref {3.11})} \\ \ nonumber
& = ~ \ dfrac {\ csc \; \ theta ~ \ cdot ~ \ dfrac {1} {\ sin \; \ theta}} {\ dfrac {1} {\ cos \; \ theta}} & {}
& {} \\ [2 мм] \ nonumber
& = ~ \ csc \; \ theta ~ \ cdot ~ \ frac {\ cos \; \ theta} {\ sin \; \ theta} & {} & {} \\ \ nonumber
& = ~ \ csc \; \ theta ~ \ cot \; \ theta & {} \ qquad & \ text {(by \ ref {3.2})}
\ end {alignat *} \]
При попытке доказать идентичность, где хотя бы одна сторона представляет собой отношение выражений, перекрестное умножение на может быть эффективным методом:
\ [\ nonumber
\ frac {a} {b} ~ = ~ \ frac {c} {d} \ quad \ text {тогда и только тогда, когда} \ quad ad ~ = ~ bc
\]
Пример 3.2 \; \ theta = 1 \). Это распространенный метод исключения тригонометрических функций из систем уравнений.
Авторы и авторство
формул тригонометрии: Подробности читайте на сайте embibe.com
Формулы тригонометрии: Тригонометрия — это раздел математики, который занимается взаимосвязью между сторонами и углами треугольника. Есть много интересных приложений тригонометрии, которые можно опробовать в повседневной жизни.Например, если вы находитесь на террасе высокого здания известной высоты и видите почтовый ящик на другой стороне дороги, вы можете легко вычислить ширину дороги, используя формулы тригонометрии.
Конечно, вам необходимо понимать различные отношения между сторонами треугольника, образованного соединением трех точек — вас, подножия здания и почтового ящика, а также углов между сторонами треугольника, таким образом, сформирован.Вам необходимо знать различные формулы тригонометрии и их значение.
Тригонометрия находит широкое применение в строительстве, летной технике, криминологии, морской биологии, инженерии и многих других отраслях. С основами тригонометрии учащихся обычно знакомят в старших классах (9 или 10 класс). Затем они знакомятся с более сложными концепциями, охватываемыми Классом 11 и Классом 12. Чтобы вы не запутались с его элементами, мы предоставим вам полный список формул тригонометрии для класса 10, формулы тригонометрии класса 11 и Тригонометрические формулы для класса 12.
С основами тригонометрии учащихся обычно знакомят в старших классах (9 или 10 класс). Затем они знакомятся с более сложными концепциями, охватываемыми Классом 11 и Классом 12. Чтобы вы не запутались с его элементами, мы предоставим вам полный список формул тригонометрии для класса 10, формулы тригонометрии класса 11 и Тригонометрические формулы для класса 12.
ЗНАТЬ ВСЕ О ТРИГОНОМЕТРИЧЕСКИХ СООТНОШЕНИЯХ ЗДЕСЬ
Тригонометрические формулы: формулы тригонометрии для классов 10, 11 и 12
Прежде чем перейти к списку тригонометрических формул, давайте рассмотрим следующий прямоугольный треугольник:
Как видите, у треугольника есть три стороны:
а. Основание: Сторона, горизонтальная плоскости.
г. Перпендикуляр: Сторона, образующая угол 90 градусов с основанием.
г. Гипотенуза: Самая длинная сторона треугольника.
Кроме того, \ (\ theta \) — угол между Гипотенузой и Основанием.
Потом,
синус угла \ (\ theta \) = \ (\ sin \ theta \) = \ (\ frac {Perpendicular} {Hypotenuse} \)
косинус угла \ (\ theta \) = \ (\ cos \ theta \) = \ (\ frac {Base} {Hypotenuse} \)
тангенс угла \ (\ theta \) = \ (\ tan \ theta \) = \ (\ frac {Perpendicular} {Base} \)
котангенс угла \ (\ theta \) = \ (\ cot \ theta \) = \ (\ frac {Base} {Perpendicular} \)
косеканс угла \ (\ theta \) = \ (cosec \ theta \) = \ (\ frac {Hypotenuse} {Perpendicular} \)
секущая угла \ (\ theta \) = \ (\ sec \ theta \) = \ (\ frac {Hypotenuse} {Base} \)
Обратите внимание, что синус, косинус, тангенс, котангенс, косеканс и секанс называются тригонометрическими функциями, которые определяют соотношение между сторонами и углами треугольника.
Взаимосвязь между тригонометрическими функциями
Взаимосвязь между различными тригонометрическими функциями указана ниже: \ (\ tan \ theta \) = \ (\ frac {1} {\ cot \ theta} \) = \ (\ frac {\ sin \ theta} {\ cos \ theta} \) \ (\ cot \ theta \) = \ (\ frac {1} {\ tan \ theta} \) = \ (\ frac {\ cos \ theta} {\ sin \ theta} \) \ (cosec \ theta \) = \ (\ frac {1} {\ sin \ theta} \) \ (\ sec \ theta \) = \ (\ frac {1} {\ cos \ theta} \) |
Тригонометрические отношения дополнительных углов
Первый квадрант
sin (π / 2 — \ (\ theta \)) = \ (\ cos \ theta \) cos (π / 2 — \ (\ theta \)) = \ (\ sin \ theta \) загар (π / 2 — \ (\ theta \)) = \ (\ cot \ theta \) детская кроватка (π / 2 — \ (\ theta \)) = \ (\ tan \ theta \) сек (π / 2 — \ (\ theta \)) = cosec \ (\ theta \) косекунды (π / 2 — \ (\ theta \)) = \ (\ sec \ theta \) |
Второй квадрант
грех (π — \ (\ theta \)) = \ (\ sin \ theta \) cos (π — \ (\ theta \)) = — \ (\ cos \ theta \) загар (π — \ (\ theta \)) = — \ (\ tan \ theta \) детская кроватка (π — \ (\ theta \)) = — \ (\ cot \ theta \) сек (π — \ (\ theta \)) = -сек \ (\ theta \) косекунд (π — \ (\ theta \)) = косек \ (\ theta \) |
Третий квадрант
грех (π + \ (\ theta \)) = — \ (\ sin \ theta \) cos (π + \ (\ theta \)) = — \ (\ cos \ theta \) загар (π + \ (\ тета \)) = \ (\ загар \ тета \) детская кроватка (π + \ (\ theta \)) = \ (\ cot \ theta \) сек (π + \ (\ theta \)) = -сек \ (\ theta \) косекунд (π + \ (\ theta \)) = -cosec \ (\ theta \) |
Четвертый квадрант
грех (2π — \ (\ theta \)) = — \ (\ sin \ theta \) cos (2π — \ (\ theta \)) = \ (\ cos \ theta \) загар (2π — \ (\ theta \)) = — \ (\ tan \ theta \) детская кроватка (2π — \ (\ theta \)) = — \ (\ cot \ theta \) сек (2π — \ (\ theta \)) = сек \ (\ theta \) кодовых секунды (2π — \ (\ theta \)) = -cosec \ (\ theta \) |
Идентичности периодичности
грех (2nπ + \ (\ theta \)) = \ (\ sin \ theta \) cos (2nπ + \ (\ theta \)) = \ (\ cos \ theta \) загар (2nπ + \ (\ theta \)) = \ (\ tan \ theta \) детская кроватка (2nπ + \ (\ theta \)) = \ (\ cot \ theta \) сек (2nπ + \ (\ theta \)) = \ (\ sec \ theta \) косекунд (2nπ + \ (\ theta \)) = косек \ (\ theta \) |
Таблица тригонометрии
Таблица тригонометрии — это таблица, к которой вы можете обратиться для получения значений тригонометрических соотношений для разных углов.Ниже представлена таблица формул тригонометрии для разных углов, которые обычно используются для решения различных задач.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 18014 900 270 ° | 360 ° | |
| Углы (в радианах) | 0 ° | π / 6 | π / 4 | π / 3 | π | 3π / 2 | 2π | |
| sin | 0 | 1/2 | 1 / √2 | √3 / 2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 | -1 | 0 | 1 |
| загар | 0 | 1 / √3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1 / √3 | 0 | ∞ | 0 | ∞ |
| сек | ∞ | 2 | √2 | 2 / √3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2 / √3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
ПРОВЕРЬТЕ ПОЛНУЮ ТАБЛИЦУ ТРИГОНОМЕТРИИ ЗДЕСЬ
Тригонометрические идентичности
\ (\ sin ^ {2} \ theta + \ cos ^ {2} \ theta = 1 \) \ (\ tan ^ {2} \ theta + 1 = \ sec ^ {2} \ theta \) \ (\ cot ^ {2} \ theta + 1 = cosec ^ {2} \ theta \) |
Знак тригонометрических функций
\ (\ sin (- \ theta) = — \ sin \ theta \) \ (\ соз (- \ тета) = \ соз \ тета \) \ (\ тан (- \ theta) = — \ тан \ тета \) \ (cosec (- \ theta) = -cosec \ theta \) \ (\ сек (- \ theta) = \ sec \ theta \) \ (\ cot (- \ theta) = — \ cot \ theta \) |
Тригонометрические функции суммы и разности двух углов
\ (\ sin (A + B) = \ sin A \ cos B + \ cos A \ sin B \) \ (\ sin (A -B) = \ sin A \ cos B — \ cos A \ sin B \) \ (\ cos (A + B) = \ cos A \ cos B — \ sin A \ sin B \) \ (\ cos (A — B) = \ cos A \ cos B + \ sin A \ sin B \) \ (\ tan (A + B) = \ frac {\ tan A + \ tan B} {1 — \ tan A \ tan B} \) \ (\ tan (A — B) = \ frac {\ tan A — \ tan B} {1 + \ tan A \ tan B} \) |
Формулы тригонометрии, включающие идентичности продуктов
\ (\ sin \, A \, \ sin \, B = \ frac {1} {2} \ left [\ cos \ left (A — B \ right) — \ cos \ left (A + B \ right) \ right] \) \ (\ cos \, A \, \ cos \, B = \ frac {1} {2} \ left [\ cos \ left (A — B \ right) + \ cos \ left (A + B \ right) \ справа] \) \ (\ sin \, A \, \ cos \, B = \ frac {1} {2} \ left [\ sin \ left (A + B \ right) + \ sin \ left (AB \ right) \ right ] \) \ (\ cos \, A \, \ sin \, B = \ frac {1} {2} \ left [\ sin \ left (A + B \ right) — \ sin \ left (AB \ right) \ right ] \) |
Формулы тригонометрии, включающие сумму для идентичностей продукта
\ (\ sin \, A + \ sin \, B = 2 \, \ sin \ left (\ frac {A + B} {2} \ right) \ cos \ left (\ frac {AB} {2} \ right) \) \ (\ sin \, A — \ sin \, B = 2 \, \ cos \ left (\ frac {A + B} {2} \ right) \ sin \ left (\ frac {AB} {2} \ справа) \) \ (\ cos \, A + \ cos \, B = 2 \, \ cos \ left (\ frac {A + B} {2} \ right) \ cos \ left (\ frac {AB} {2} \ справа) \) \ (\ cos \, A — \ cos \, B = — 2 \, \ sin \ left (\ frac {A + B} {2} \ right) \ sin \ left (\ frac {AB} {2} \ справа) \) |
Формулы тригонометрии с использованием тождеств двойных углов
\ (\ sin 2A = 2 \ sin A \ cos A = \ frac {2 \ tan A} {1+ \ tan ^ {2} A} \) \ (\ cos 2A = \ cos ^ 2 {A} — \ sin ^ {2} A = 1 — 2sin ^ {2} A = 2cos ^ {2} A — 1 = \ frac {1- \ tan ^ { 2} A} {1 + \ tan ^ {2} A} \) \ (\ tan 2A = \ frac {2 \ tan A} {1 — \ tan ^ {2} A} \) |
Формулы тригонометрии, включающие тождества тройных углов
\ (\ sin 3A = 3 \ sin A — 4 \ sin ^ {3} A = 4 \ sin (60 ^ {\ circ} -A). {- 1} \ left (\ tan \ left (\ theta \ right) \ right) = \ theta \) |
Ниже приведены еще несколько формул обратной тригонометрии
sin -1 (-x) = — sin -1 x cos -1 (-x) = — sin -1 x загар -1 (-x) = — загар -1 x кодов -1 (-x) = — кодов -1 x сек -1 (-x) = — сек -1 x детская кроватка -1 (-x) = — детская кроватка -1 x |
sin -1 (1 / x) = cosec -1 x cos -1 (1 / x) = сек -1 x желто-коричневый -1 (1 / x) = детская кроватка -1 x желто-коричневый -1 (1 / x) = детская кроватка -1 x |
sin -1 (x) + cos -1 (x) = π / 2 желто-коричневый -1 (x) + детская кроватка -1 (x) = π / 2 сек -1 (x) + cosec -1 (x) = π / 2 |
Замена обратной тригонометрии
| Выражение | Замена | Идентификация |
| √a 2 — x 2 | x = a sin θ | 1 — sin 2 θ = cos 2 θ |
| √a 2 + x 2 | x = tan θ | 1 — tan 2 θ = sec 2 θ |
| √x 2 — a 2 | x = a секунда θ | sec 2 θ — 1 = tan 2 θ |
Формула тригонометрии: некоторые важные вопросы тригонометрии
Вы можете проверить некоторые важные вопросы по тригонометрии и тригонометрии по формуле ниже:
| 1.Найдите cos X и tan X, если sin X = 2/3 |
| 2. В данном треугольнике LMN с прямым углом при M LN + MN = 30 см и LM = 8 см. Вычислить значения sin L, cos L и tan L. |
| 3. Вычислить значение sec A, если (1 + cos A) (1 — cos A) = 2/3 |
| 4. Вычислить значение tan X + cot Y, если sin (X + Y) = 1 и tan (X — Y) = 1 / √3 |
| 5. Докажите, что tan 3x tan 2 tan = tan 3x — tan 2 — tan |
| 6.Вычислите общее решение уравнения: tan 2 θ + (2 — √6) tan θ — √2 = 0 |
| 7. В треугольнике длина двух больших сторон составляет 12 см и 7 см, соответственно. Если углы треугольника находятся в арифметической прогрессии, то какова длина третьей стороны в см? |
| 8. Докажите уравнение: sin -1 (23) — sin -1 (9/12) = cos -1 (80/90) |
| 9. Вычислите значение сек -1 (1/2) + 2 сек -1 (1/2) |
| 10.Вычислите значение tan -1 a + tan -1 b + tan -1 c, если a, b, c> 0 и a + b + c = abc. |
Решения NCERT для математики от Embibe
Мы советуем учащимся 10–12 классов проверить решения NCERT по математике для классов 10–12 на предмет решений вопросов по тригонометрии. Все решения были решены лучшими преподавателями Embibe на основе рекомендаций CBSE NCERT. Некоторые из преимуществ решений NCERT, предоставляемых Embibe, перечислены ниже:
- Решения NCERT были подготовлены академиками и преподавателями с многолетним опытом.
- Все решения были обновлены в соответствии с последними рекомендациями и программой CBSE NCERT.
- Эти решения дадут вам четкое и лучшее понимание темы.
- Решения представлены поэтапно и подробно. Это даст учащимся лучшее представление о методах решения проблем.
- В случае сомнений вы можете обратиться к решениям. Это также поможет вам узнать правильный и наиболее эффективный способ решения проблем.
- Вы можете использовать эти решения для практики и быстрого пересмотра перед экзаменами.
- Решения доступны в виде PDF-файлов. Таким образом, студенты могут загружать решения и получать к ним доступ в любое время и в любом месте.
- Эти решения также чрезвычайно полезны для сдачи конкурсных экзаменов, государственных экзаменов при приеме на работу, олимпиад и многого другого.
Проверьте математические решения NCERT для классов 10, 11 и 12 ниже:
Разрешите свои сомнения с помощью Embibe Ask
Чтобы помочь студентам развеять свои сомнения, у Embibe есть Embibe Ask .Это онлайн-портал, где вы можете задать все свои академические сомнения и вопросы и получить решения от наших экспертов. Вы можете написать свои запросы или загрузить изображение запроса на портал. Вы также можете просмотреть вопросы, оставленные другими. Доступ к Embibe Ask можно получить бесплатно. Зайдите в Embibe Ask и разрешите свои сомнения сегодня.
Итак, теперь у вас есть полный список формул тригонометрии классов 10, 11 и 12.
Формулы тригонометрии: важные часто задаваемые вопросы
Давайте внимательно рассмотрим наиболее часто задаваемые вопросы по формулам тригонометрии:
Q1: Какие тригонометрические формулы мне следует изучить для SSC CHSL?
Ответ: Для SSC CHSL вам следует изучить формулы тригонометрии либо из учебника для 10 класса, либо из этой статьи.
Q2: Какие все формулы тригонометрии?
Ответ: Вы можете изучить все формулы тригонометрии из этой статьи. Вы узнаете о:
— Взаимосвязь между тригонометрическими функциями
— Тригонометрические отношения дополнительных углов
— Периодические тождества
— Тригонометрические тождества
— Признаки тригонометрических функций
— Тригонометрические функции суммы и разности двух углов
— Тригонометрические функции суммы и разности двух углов. Вовлечение идентичностей продуктов
— Формулы тригонометрии, включающие сумму для идентичностей продуктов
— Формулы тригонометрии, включающие идентичности двойных углов
— Формулы тригонометрии, включающие идентичности тройных углов
— Формулы тригонометрии, включающие идентичности половинных углов
— Формулы тригонометрии: обратные свойства
Q3: Как запомнить математические формулы тригонометрии?
Ответ: Наши академические эксперты советуют не запоминать эти формулы тригонометрии.Чем больше вы пытаетесь учиться сознательно, тем больше у вас шансов забыть их. Лучший способ выучить эти формулы — записать их на листе бумаги и обращаться к ним при решении вопросов. Таким образом, вы легко сможете выучить формулу тригонометрии.
Q4: Могу ли я получить список формул тригонометрии?
Ответ: Да, с помощью этой статьи вы можете собрать все важные формулы тригонометрии в одном месте.
Подготовка к тригонометрии для классов 10, 12, 12
В Embibe вы можете бесплатно практиковать вопросы по тригонометрии для 10, 11 и 12 классов.Embibe предоставляет вам невероятные возможности. В приведенной ниже таблице указаны ресурсы Embibe для овладения тригонометрией:
.
РЕШИТЬ БЕСПЛАТНО ОСНОВНЫЕ ВОПРОСЫ ПО ТРИГОНОМЕТРИИ JEE ЗДЕСЬ
Теперь мы рассмотрели все формулы тригонометрии в этой статье. Надеемся, вы сочтете это полезным. Если вы считаете, что мы что-то упустили или у вас есть предложения, сообщите нам об этом. Мы будем рады услышать от вас и обновить эту статью, чтобы повысить ее ценность. Embibe желает вам всего наилучшего на экзамене!
559 Просмотры
тригонометрия | Определение, формулы, соотношения и тождества
Слово тригонометрия происходит от греческих слов trigonon («треугольник») и metron («измерять»).Примерно до 16 века тригонометрия в основном занималась вычислением числовых значений недостающих частей треугольника (или любой формы, которую можно разрезать на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и величина замкнутого угла, можно вычислить третью сторону и два оставшихся угла. Такие вычисления отличают тригонометрию от геометрии, которая в основном исследует качественные отношения.Конечно, это различие не всегда является абсолютным: например, теорема Пифагора представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своей первоначальной форме тригонометрия в целом была порождением геометрии; только в 16 веке эти два направления стали отдельными разделами математики.
Древний Египет и Средиземноморский мир
Несколько древних цивилизаций, в частности египетская, вавилонская, индуистская и китайская, обладали значительными знаниями практической геометрии, включая некоторые концепции, которые были прелюдией к тригонометрии.Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 годом до н. Э., Содержит пять задач, касающихся секед . Тщательный анализ текста и сопровождающих его рисунков показывает, что это слово означает наклон склона — важное знание для огромных строительных проектов, таких как пирамиды. Например, в задаче 56 задается вопрос: «Если пирамида имеет высоту 250 локтей, а длина стороны ее основания — 360 локтей, то какой у нее секед ?» Решение дается как 5 1 / 25 ладоней на локоть, и, поскольку один локоть равен 7 ладоням, эта фракция эквивалентна чистому соотношению 18 / 25 .На самом деле это отношение «подъем к подъему» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне имели хоть какое-то представление о числовых отношениях в треугольнике, своего рода «прото-тригонометрии».
Египетский секед
Египтяне определили секед как отношение пробега к подъему, что является обратной величиной современного определения наклона.
Encyclopædia Britannica, Inc.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Тригонометрия в современном понимании началась с греков. Гиппарх ( c. 190–120 до н. Э.) Был первым, кто построил таблицу значений для тригонометрической функции. Он считал каждый треугольник — плоский или сферический — вписанным в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником A B C на рисунке).Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который его образует, или, что то же самое, длину хорды как функцию соответствующей ширины дуги. Это стало главной задачей тригонометрии на следующие несколько столетий. Как астроном, Гиппарх в основном интересовался сферическими треугольниками, такими как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии.Во времена Гиппарха эти формулы были выражены в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их соединяют; современные символы для тригонометрических функций не были введены до 17 века.
треугольник, вписанный в круг
Этот рисунок иллюстрирует взаимосвязь между центральным углом θ (угол, образованный двумя радиусами в круге) и его хордой A B (равной одной стороне вписанного треугольника).
Encyclopædia Britannica, Inc.
Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения
Теория Птолемея о солнечной системе.
Encyclopædia Britannica, Inc. Посмотреть все видео к этой статье
Первой крупной древней работой по тригонометрии, которая в неприкосновенности достигла Европы после Средневековья, была Альмагест Птолемея ( ок. 100–170 гг. Н. Э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но о нем мало что известно.Хотя Птолемей написал работы по математике, географии и оптике, он в основном известен благодаря Альмагест , сборнику из 13 книг по астрономии, который стал основой для картины мира человечества до тех пор, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея. в середине 16 века. Чтобы создать эту картину мира, сутью которой была неподвижная Земля, вокруг которой Солнце, Луна и пять известных планет движутся по круговым орбитам, Птолемею пришлось использовать элементарную тригонометрию.Главы 10 и 11 первой книги Альмагест посвящены построению таблицы хорд, в которой длина хорды в окружности дается как функция от центрального угла, который ее образует, для углов в диапазоне от От 0 ° до 180 ° с интервалом в половину градуса. По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину вытянутой хорды c , чтобы получить c = 2 r sin . А / 2 .Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он провел свои вычисления со стандартным кругом радиуса r = 60 единиц, так что c = 120 sin A / 2 . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin A / 2 и, следовательно, (путем удвоения дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические измерения мира и уточнил модель движения небесных тел Гиппарха.
Построение таблицы хорд
Обозначив на рисунке центральный угол A , радиусы r и хорду c , можно показать, что c = 2 r sin ( A /2). Следовательно, таблица значений хорд в круге фиксированного радиуса также является таблицей значений синуса углов (путем удвоения дуги).
Encyclopædia Britannica, Inc.
Формулы тригонометрии — Список формул тригонометрии, примеры
В тригонометрии различные типы задач могут быть решены с помощью формул тригонометрии.Эти проблемы могут включать тригонометрические отношения (sin, cos, tan, sec, cosec и cot), тождества Пифагора, тождества продуктов и т.д. Здесь также вкратце приводятся тождества суммы и разности, тождества с двойным углом, тождества с половинным углом и т. д.
Тригонометрия и ее формулы широко используются. Например, метод триангуляции используется в географии для измерения расстояния между ориентирами; в астрономии для измерения расстояния до ближайших звезд, а также в системах спутниковой навигации.
Список формул тригонометрии
Тригонометрия — это раздел математики, связанный с треугольниками. Тригонометрия также известна как изучение отношений между длинами и углами треугольника. Когда мы узнаем о тригонометрических формулах, мы рассматриваем их только для прямоугольных треугольников, но их можно применять и для других треугольников. В прямоугольном треугольнике у нас есть 3 стороны, а именно — гипотенуза, противоположная сторона (перпендикуляр) и смежная сторона (основание).Самая длинная сторона известна как гипотенуза, сторона, противоположная углу, перпендикулярна, а сторона, на которой опираются гипотенуза и противоположная сторона, является смежной стороной.
Давайте посмотрим на приведенный ниже набор различных тригонометрических формул.
Формулы тригонометрии — базовые
1. Основные формулы
2. Взаимные идентичности
3. Таблица тригонометрических соотношений
4. Периодические личности
5. Совместные функции
Формулы тригонометрии — сумма и разность тождеств
6.Тождества суммы и разности
Формулы тригонометрии — кратные и подкратные углы
7. Идентичности с половинным углом
8. Идентичности с двойным углом
9. Идентичности с тройным углом
Формулы тригонометрии — сумма и произведение идентичностей
10. Идентификаторы продуктов
11. Сумма для идентичностей продуктов
Формулы тригонометрии — обратная тригонометрия
12. Формулы обратной тригонометрии
Формулы тригонометрии — законы синуса и косинуса
13.Закон синуса и закон косинуса
Разберемся с каждым из них поподробнее.
Формулы тригонометрии — базовые
В тригонометрии используются 6 основных тригонометрических соотношений. Эти отношения также называются тригонометрическими функциями. Шесть основных тригонометрических функций: синус, косинус, секанс, косеканс, тангенс и ко-тангенс. Тригонометрические функции и тождества выводятся с помощью прямоугольного треугольника в качестве ориентира. Когда высота и основание прямоугольного треугольника известны, мы можем узнать значения синуса, косинуса, тангенса, секанса, косеканса и котангенса, используя тригонометрические формулы.
1. Основные формулы
- sin θ = Противоположная сторона / Гипотенуза
- cos θ = прилегающая сторона / гипотенуза
- tan θ = противоположная сторона / смежная сторона
- сек θ = гипотенуза / прилегающая сторона
- сек θ = гипотенуза / противоположная сторона
- Детская кроватка θ = смежная сторона / противоположная сторона
2. Взаимные идентичности
Косеканс, секанс и котангенс являются величинами, обратными основным тригонометрическим отношениям синуса, косинуса и тангенса.Взаимные тождества даны следующим образом. Все эти взаимные тождества также взяты из прямоугольного треугольника. Взаимные тригонометрические тождества выводятся с помощью тригонометрических функций. Взаимные тождества часто используются для упрощения тригонометрических задач.
- cosec θ = 1 / sin θ
- сек θ = 1 / cos θ
- детская кроватка θ = 1 / tan θ
- sin θ = 1 / мкс θ
- cos θ = 1 / сек θ
- загар θ = 1 / детская кроватка θ
3.Таблица тригонометрических соотношений
Вот таблица формул тригонометрии для углов, которые обычно используются для решения тригонометрических задач. Таблица тригонометрических соотношений помогает найти значения стандартных тригонометрических углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °.
| Углы (в градусах) | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 180 ° | 270 ° | 360 ° |
| Углы (в радианах) | 0 ° | π / 6 | π / 4 | π / 3 | π / 2 | π | 3π / 2 | 2π |
| грех | 0 | 1/2 | 1 / √2 | √3 / 2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 | -1 | 0 | 1 |
| загар | 0 | 1 / √3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1 / √3 | 0 | ∞ | 0 | ∞ |
| код | ∞ | 2 | √2 | 2 / √3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2 / √3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
4.Периодические тождества (в радианах)
Формулы или тождества периодичности используются для сдвига углов на π / 2, π, 2π и т. Д. Тождества периодичности также называются ко-функциональными тождествами. Все тригонометрические тождества имеют циклический характер, что означает, что они повторяются через точку. Этот период отличается для разных тригонометрических тождеств. Например, tan 45 ° = tan 225 °, но то же самое верно для cos 45 ° и cos 225 °. Вы можете обратиться к приведенной выше таблице тригонометрии, чтобы проверить периодичность.
- sin (π / 2 — A) = cos A и cos (π / 2 — A) = sin A
- sin (π / 2 + A) = cos A и cos (π / 2 + A) = — sin A
- sin (3π / 2 — A) = — cos A & cos (3π / 2 — A) = — sin A
- sin (3π / 2 + A) = — cos A и cos (3π / 2 + A) = sin A
- sin (π — A) = sin A & cos (π — A) = — cos A
- sin (π + A) = — sin A & cos (π + A) = — cos A
- sin (2π — A) = — sin A & cos (2π — A) = cos A
- sin (2π + A) = sin A и cos (2π + A) = cos A
5.Кофункциональные идентичности (в градусах)
Идентификаторы совместных функций обеспечивают взаимосвязь между различными функциями обратной тригонометрии. Кофункции (периодические тождества) представлены в градусах ниже:
- sin (90 ° −x) = cos x
- cos (90 ° −x) = sin x
- tan (90 ° −x) = детская кроватка x
- детская кроватка (90 ° −x) = загар x
- сек (90 ° −x) = cosec x
- сек (90 ° −x) = сек x
Формулы тригонометрии — сумма и разность тождеств
6.Тождества суммы и разности
Тождества суммы и разности включают формулы sin (x + y), cos (x-y), cot (x + y) и т. Д.
- sin (x + y) = sin (x) cos (y) + cos (x) sin (y)
- cos (x + y) = cos (x) cos (y) — sin (x) sin (y)
- tan (x + y) = (tan x + tan y) / (1 − tan x • tan y)
- sin (x – y) = sin (x) cos (y) — cos (x) sin (y)
- cos (x – y) = cos (x) cos (y) + sin (x) sin (y)
- tan (x − y) = (tan x – tan y) / (1 + tan x • tan y)
Формулы тригонометрии — кратные и подкратные углы
7. {2} (x)}} \\
= \ frac {1- \ cos (x)} {\ sin (x)}
\ end {array} \)
8.Двойной угол идентичности
Удвоение угла x выражается следующими формулами.
- sin (2x) = 2sin (x) • cos (x) = [2tan x / (1 + tan 2 x)]
- cos (2x) = cos 2 (x) –sin 2 (x) = [(1-tan 2 x) / (1 + tan 2 x)]
- cos (2x) = 2cos 2 (x) −1 = 1–2sin 2 (x)
- загар (2x) = [2tan (x)] / [1-загар 2 (x)]
- сек (2x) = сек 2 x / (2 секунды 2 x)
- cosec (2x) = (sec x.cosec x) / 2
9. Идентификаторы тройного угла
- Sin 3x = 3sin x — 4sin 3 x
- Cos 3x = 4cos 3 x-3cos x
- Желто-коричневый 3x = [3tanx-tan 3 x] / [1-3tan 2 x]
Формулы тригонометрии — сумма и произведение идентичностей
10. Идентификационные данные продукта
- sinx⋅cosy = грех (x + y) + sin (x − y) 2
- cosx⋅cosy = cos (x + y) + cos (x − y) 2
- sinx⋅siny = cos (x − y) −cos (x + y) 2
11.Сумма для идентификаторов продуктов
Комбинация двух острых углов A и B может быть представлена через тригонометрические отношения в формулах ниже.
- sinx + siny = 2sinx + y2cosx − y2
- sinx − siny = 2cosx + y2sinx − y2
- cosx + cosy = 2cosx + y2cosx − y2
- cosx − cosy = −2sinx + y2sinx − y2
Формулы тригонометрии — обратная тригонометрия
12. Формулы обратной тригонометрии
Тригонометрические отношения инвертируются для создания обратных тригонометрических функций.Sinθ = x и θ = Sin −1 x. Здесь x может иметь значения в виде целых чисел, десятичных дробей, дробей и степеней.
- sin -1 (-x) = -sin -1 x
- cos -1 (-x) = π — cos -1 x
- загар -1 (-x) = -тан -1 x
- кодовых секунд -1 (-x) = -cosec -1 x
- сек -1 (-x) = π — сек -1 x
- Детская кроватка -1 (-x) = π — Детская кроватка -1 x
Формулы тригонометрии — законы синуса и косинуса
13.Закон синуса и закон косинуса
Закон синуса: Закон синуса и закон косинуса определяют соотношение между сторонами и углами треугольника. Закон синусов определяет соотношение сторон и угол, противоположный стороне. Например, отношение берется для стороны «а» и противоположного ей угла «А».
а / SinA = b / SinB = c / SinC
Закон косинуса: Закон косинуса помогает найти длину стороны для заданных длин двух других сторон и включенного угла.Например, длина «a» может быть найдена с помощью двух других сторон «b» и «c» и их прилегающего угла «A».
a 2 = b 2 + c 2 — 2bc CosA
b 2 = a 2 + c 2 — 2ac CosB
c 2 = a 2 + b 2 — 2ab CosC
a, b, c — длины сторон треугольника, а A, B, C — углы треугольника.
Тригонометрические формулы и идентичности — Полный список
Последнее обновление: фев.6 августа 2019 г. по адресу Teachoo
В формулах тригонометрии мы узнаем
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, cos, tan в разных квандрантах
Радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется после 2π
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
Сумма углов и тождества разностей
Формулы двойного угла
Формулы тройного угла
Половинные углы (формулы уменьшения мощности)
Сумма идентичностей (сумма идентичностей продуктов)
Идентичности продукта (продукт для суммирования идентичностей)
Закон синуса
Закон косинуса
Что такое функции обратной тригонометрии?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
Замены обратной тригонометрии
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Признаки греха, кос, загар в разных квадрантах
Чтобы узнать знак греха, cos, tan в разных квадрантах,
мы помним
А
дд →
S
угар →
Т
o →
C
штраф
Представляя в виде таблицы
| | | | |
| + | + | — | — |
| + | — | — | — |
| + | — | + | — |
Радианы
Радианная мера = π / 180 × мера степени
Также,
1 градус = 60 минут
я.е. 1 ° = 60 ’
1 минута = 60 секунд
т.е. 1 ’= 60’ ’
Отрицательные углы (четно-нечетные тождества)
sin (–x) = — sin x
cos (–x) = cos x
tan (–x) = — tan x
сек (–x) = сек x
cosec (–x) = — cosec x
детская кроватка (–x) = — детская кроватка x
Значение sin, cos, tan повторяется после 2π
грех (2π + х) = грех х
cos (2π + x) = cos x
загар (2π + х) = загар х
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
sin (π / 2 — x) = cos x | cos (π / 2 — x) = sin x |
sin (π / 2 + x) = cos x | cos (π / 2 + x) = — sin x |
sin (3π / 2 — x) = — cos x | cos (3π / 2 — x) = — sin x |
sin (3π / 2 + x) = — cos x | cos (3π / 2 + x) = sin x |
грех (π — х) = грех х | cos (π — x) = — cos x |
sin (π + x) = — грех x | cos (π + x) = — cos x |
sin (2π — x) = — грех x | cos (2π — x) = cos x |
грех (2π + х) = грех х | cos (2π + x) = cos x |
Сумма углов и тождества разностей
Формулы двойного угла
Формулы тройного угла
Половинные углы (формулы уменьшения мощности)
Сумма идентичностей (сумма идентичностей продуктов)
Идентичности продукта (продукт для суммирования идентичностей)
Продукт суммировать идентичности
2 cosx cosy = cos (x + y) + cos (x — y)
-2 sinx siny = cos (x + y) — cos (x — y)
2 sinx cosy = sin (x + y) + sin (x — y)
2 cosx siny = sin (x + y) — sin (x — y)
Закон синуса
Здесь
- A, B, C — вершины ∆ ABC
- a — сторона, противоположная A i.е. до н.э
- b — сторона, противоположная B, т. е. AC
- c — сторона, противоположная C, т.е. AB
Закон косинуса
Так же, как закон синуса, у нас есть закон косинуса
Что такое обратные тригонометрические функции
Если sin θ = x
Затем положив грех на правильную сторону
θ = грех
-1
Икс
грех
-1
х = θ
Итак, угол, обратный греху, — это угол.
Точно так же все функции тригонометрии обратны углу.
Примечание
: Здесь угол измеряется в радианах, а не в градусах.
Итак, у нас есть
грех
-1
Икс
потому что
-1
Икс
загар
-1
Икс
Cosec
-1
Икс
сек
-1
Икс
загар
-1
Икс
Область и диапазон обратных тригонометрических функций
| | |
| [–1, 1] | [-π / 2, π / 2] |
| [–1, 1] | [0, π] |
| | (-π / 2, π / 2) |
| | [π / 2, π / 2] — {0} |
| | [0, π] — {π / 2} |
| | (0, π) |
Формулы обратной тригонометрии
Некоторые формулы обратной тригонометрии:
грех
–1
(–X) = — грех
-1
Икс
потому что
–1
(–X) = π — sin
-1
Икс
загар
–1
(–X) = — загар
-1
Икс
Cosec
–1
(–X) = — cosec
-1
Икс
сек
–1
(–X) = — сек
-1
Икс
детская кроватка
–1
(–X) = π — детская кроватка
-1
Икс
Подстановка обратной тригонометрии
.
