| 1 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень 1 | |
| 69 | Упростить | квадратный корень 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Постройте график функции y 2×2
Здравствуйте!
Постройте график функции y = 2x – 2, пожалуйста.
Спасибо!
Задание.
Постройте график функции y = 2x — 2
Решение.
Функция представлена в виде , следовательно, она линейная.
Начнем с вычисления области определения функции. Поскольку функция является линейной, то она имеет область определения всю числовую прямую.
Такой же вывод можно сделать и об области значений функции.
В таком случае для графика никаких ограничений не будет.
Проверим функцию, является ли она четной или нечетной. С этой целью подставим вместо переменной х переменную —х:
В результате получили, что данная функция является ни четной, ни нечетной.
Как упоминалось выше, функция — линейная. Тогда будет достаточно двух точек, чтобы построить ее график. С этой целью вычислим точки пересечения с координатными осями:
При пересечении оси Ох переменная х = 0. Подставим это значение в функцию:
При пересечении оси Оу переменная у = 0.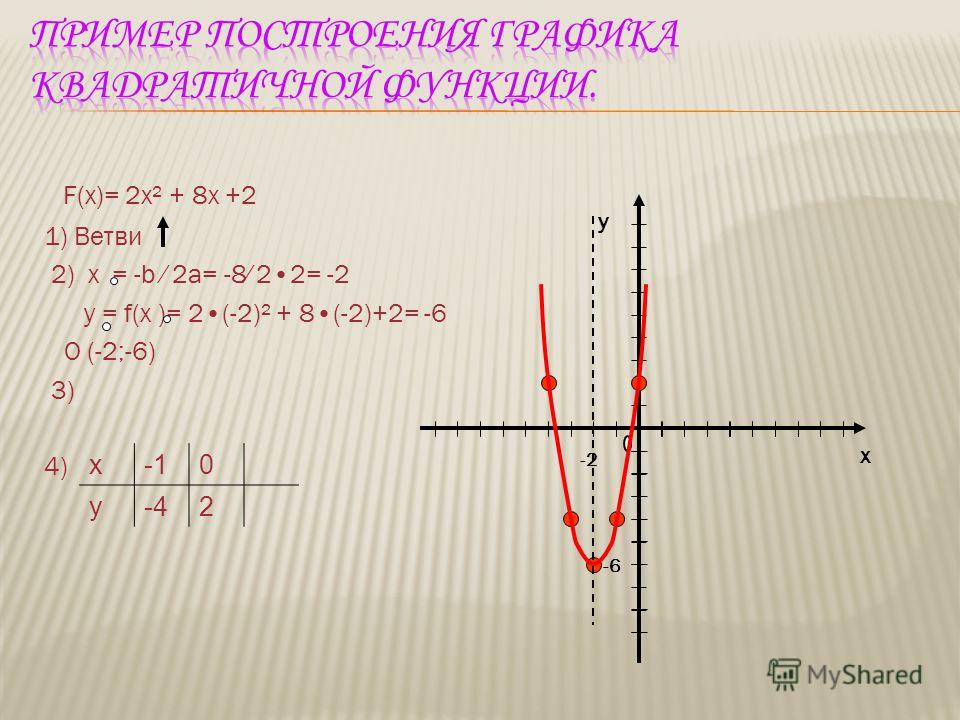 Решим уравнение:
Решим уравнение:
Итак, получили две точки пересечения с координатами:
(0; —2) и (1; 0).
Поскольку для линейной функции не существует точек минимума или максимума, то производную находить не будет.
Как уже упоминалось, достаточно двух точек, чтобы построить линейную функцию.
Здравствуйте!
Постройте график функции y = –2x + 2, пожалуйста.
Спасибо!
Задание.
Построить график функции y = —2x + 2
Решение.
Функции подобного вида строятся очень просто, так как они являются линейными. А как известно линию можно провести всего через две точки. Поэтому все решение сводится к тому, что нужно определить две точки, которые принадлежат этой функции, нанести их на координатную плоскость и провести через них линию. Это и будет графиком заданной функции.
Проведем небольшой анализ данной функции.
Поскольку функция представлена в виде , то, как уже упоминалось выше, она называется линейной. Как известно, линия бесконечна, поэтому и область определения функции, и область ее значений будет вся числовая прямая.
Как известно, линия бесконечна, поэтому и область определения функции, и область ее значений будет вся числовая прямая.
Функция может быть четной, нечетной или ни той, ни другой. Определим это с помощью несложных вычислений:
Получили, что функция является ни той, ни другой.
Для получения точек линейной прямой, через которые можно будет построить график заданной функции, найдем точки пересечения этой прямой с координатными осями.
Сначала найдем точку пересечения с координатной осью Оу. Для этого подставим значение х = 0 в функцию:
Точка пересечения с осью Оу будет иметь координаты (0; 2).
Теперь найдем точку пересечения с координатной осью Ох. Для этого подставим значение у = 0 в функцию и решим полученное простое уравнение:
Точка пересечения с осью Оx будет иметь координаты (1; 0).
Отметим на координатной плоскости полученные точки и проведем через них прямую.
Заданная функция построена.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться.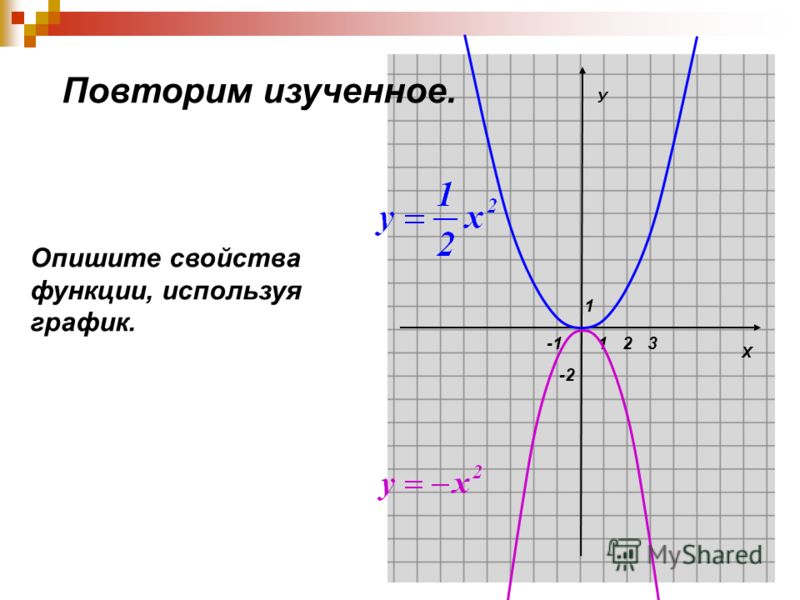 Cледите за масштабом – если графика на рисунке нету, значит стоит поварьировать значения a и b
Cледите за масштабом – если графика на рисунке нету, значит стоит поварьировать значения a и b
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
© Контрольная работа РУ – калькуляторы онлайн
Квадратичная функция: ее график и свойства 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 4.
Всем привет! Сегодня мы поговорим об одной из самых важных функций, о квадратичной функции.
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.
Построим в одной системе координат
y = x2; y = 2x2; y = 3x2.
y = x2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 2x2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При любом x ≠ 0 значение функции y = x2 в 2 раза больше соответствующих значений функции y = x2. То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
Аналогично, график функции y = 3x2 можно получить из графика функции y = x2 растяжением от оси x в 3 раза.
Построим теперь в одной системе координат графики функции y = x2, y=12×2, y=13×2.
y=12×2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что при любом x ≠ 0 значения функции y=12×2меньше соответствующих значений функции y = x2 в 2 раза.
Таким образом, график функции y=12×2 можно получить из параболы y = x2 сжатием к оси x в 2 раза.
y=13×2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично график функции y=13×2 можно получить из графика функции = x2 сжатием к оси x в 3 раза.
Давай сделаем вывод:
График функции y = ax2 можно получить из параболы y = x2 растяжением от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0 a
Рассмотрим теперь случай, когда a y=-13×2. Составим таблицу значений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравним графики функций y=13×2 и y=-13×2. При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
То есть графики функций y = ax2 и y = —ax2 при a ≠ 0 симметричны относительно оси x. Графиком функции y = ax2, как и графиком функции y = x2 является парабола
Сформулируем свойства функции y = ax2 при a > 0.
-
Область определения -∞;+∞; -
Область значений функций 0;+∞ -
Если x = 0, то y = 0, т.е. график функции проходит через начало координат. -
Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости. -
График функции симметричен относительно оси y.
-
Функция убывает в промежутке -∞;0 и возрастает в промежутке 0;+∞. -
При x = 0 функция принимает наименьшее значение, равное 0. Наибольшего значения функции нет.
Сформулируем свойства функции y = ax2 при a
-
Область определения -∞;+∞; -
Область значений функций -∞;0 -
Если x = 0, то y = 0, т.е. график функции проходит через начало координат. -
Если x ≠ 0, то y -
График функции симметричен относительно оси y. -
Функция убывает в промежутке 0;+∞ и возрастает в промежутке -∞;0. -
При x = 0 функция принимает наибольшее значение, равное 0. Наименьшего значения функции нет.
От коэффициента a зависит направление ветвей параболы. Если a > 0, то ветви параболы направлены вверх, если a
Если a > 0, то ветви параболы направлены вверх, если a
Построение графика, симметричного данному относительно оси x, или сжатие к оси x – различные виды преобразований графиков функций. Преобразования графиков функции, рассмотренные нами сегодня для функций y = ax2, применимы к любой функции.
График функции y=-fx можно получить из графика функции y=fx с помощью симметрии относительно оси абсцисс.
График функции y=afx можно получить из графика функции y=fx с помощью растяжения от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0
постройте график функции y 2 x 2
Вы искали постройте график функции y 2 x 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и постройте график функции y 2x 2, не
исключение.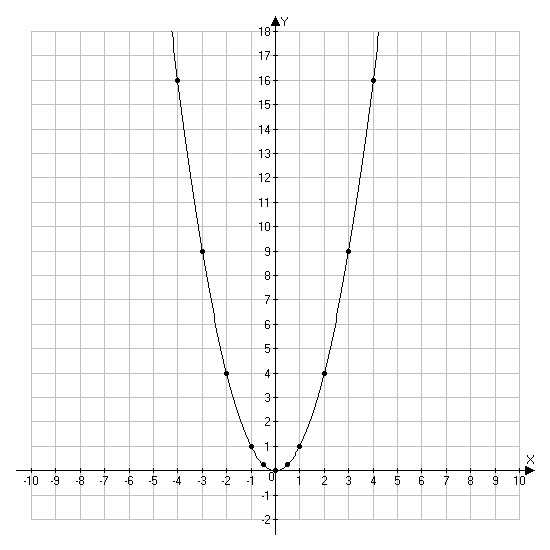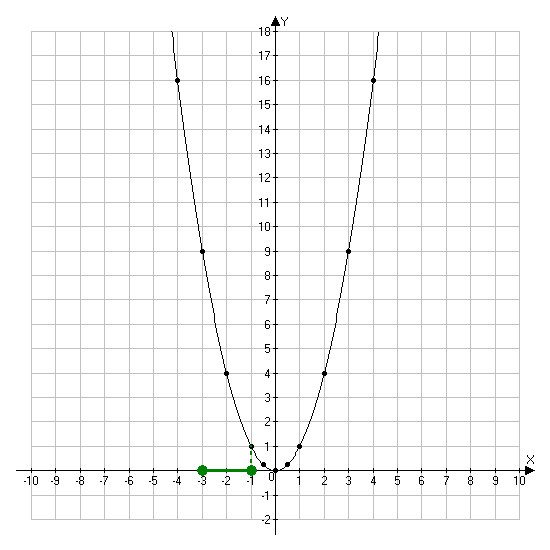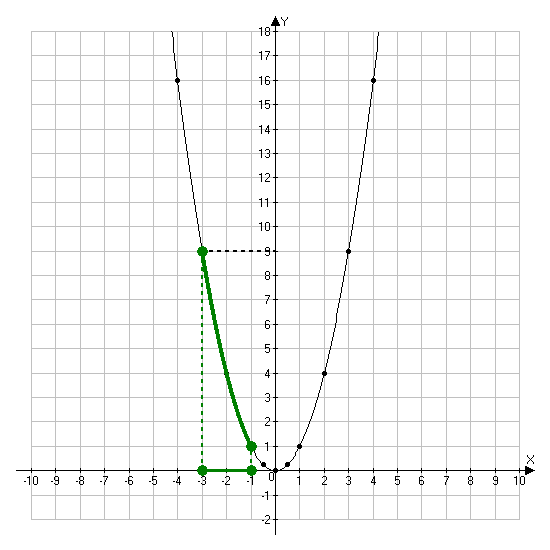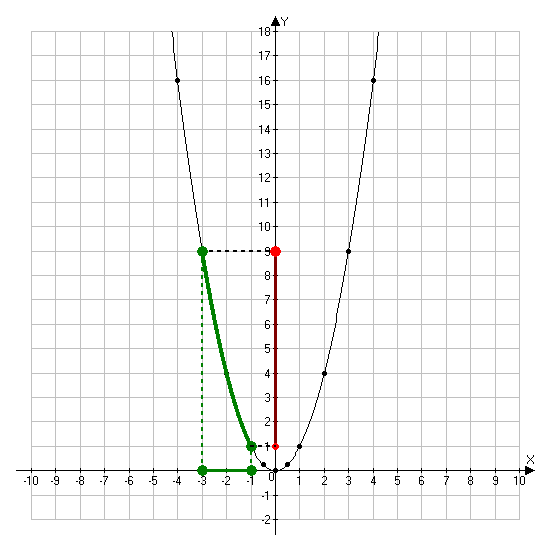 Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «постройте график функции y 2 x 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как постройте график функции y 2 x 2,постройте график функции y 2x 2,постройте график функции y 2×2,постройте график функции y x2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и постройте график функции y 2 x 2. Просто введите задачу в окошко и нажмите
Просто введите задачу в окошко и нажмите
«решить» здесь (например, постройте график функции y 2×2).
Где можно решить любую задачу по математике, а так же постройте график функции y 2 x 2 Онлайн?
Решить задачу постройте график функции y 2 x 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
|
КВАДРАТИЧНАЯ ФУНКЦИЯ
Используются технологии uCoz |
График трехчлена y = ax² + bx + c
y = x2 (1)
и
y = 2x2. (2)
Мы видим, что при одном и том же значении аргумента x значение y функции (2) будут в 2 раза больше значений функции (1). Например:
Например:
Это значит, что ордината каждой точки графика функции (2) равна удвоенной ординате точки с той же абсциссой графика функции (1).
Отсюда следует, что график функции (2) можно получить так: построить график функции (1) (черт. 74) и удвоить ординату каждой его точки.
Наглядно это преобразование можно представить при помощи следующей модели.
Представим себе ось OX в виде неподвижной планки, а верхнюю полуплоскость — в виде растяжимой (например, резиновой) пленки, на которой начерчена парабола y = x2. Если теперь растянуть пленку по направлению вверх в 2 раза, то парабола y = x2 перейдет в параболу y = 2x2 (черт. 75).
Полученная линия (черт. 75) и будет графиком функции (2). Эта линия тоже называется параболой. По сравнению с параболой y = x2 она «более круто» поднимается вверх.
Рассмотрим теперь функцию
. (3)
Чтобы перейти от графика (1) к графику (3), достаточно все ординаты точек графика (1) уменьшить в 2 раза.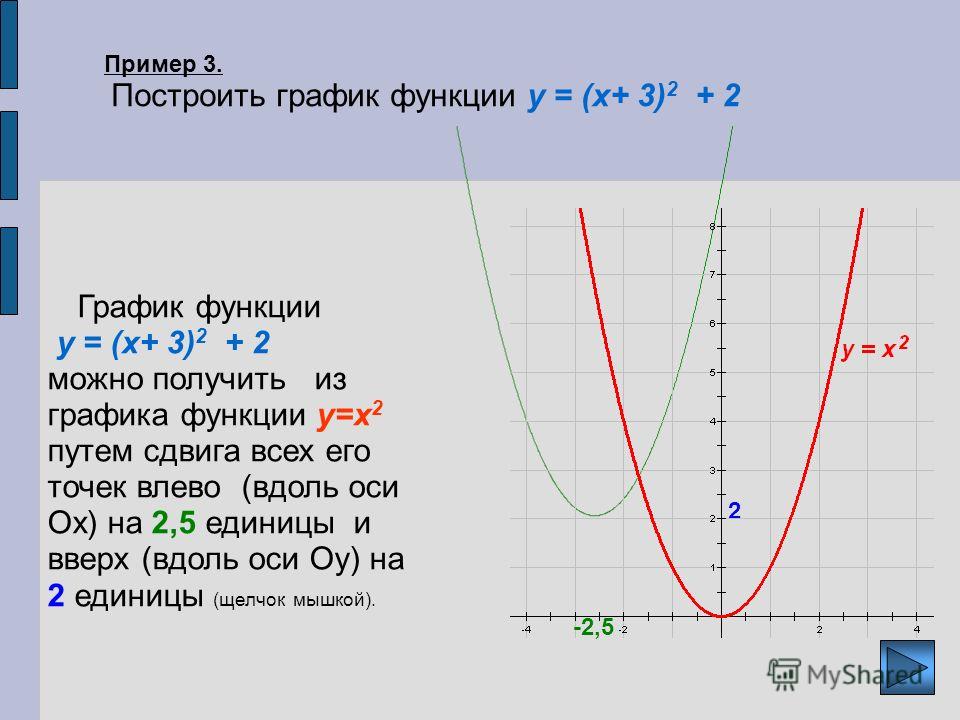
На нашей модели это будет соответствовать не растяжению, а сжатию пленки в 2 раза. Вообще, чтобы построить график функции y = ax2, где a — положительное число, достаточно все ординаты точек параболы y = x2 умножить на a.
При помощи нашей модели этот переход можно пояснить как растяжение при a > 1 (в a раз) либо сжатие при a < 1 (в раза) основной параболы y = x2.
Рассмотрим график функции
y = –2x2. (4)
Очевидно, при любом значении x значения y в (2) и (4) будут равны по абсолютной величине и противоположны по знаку. Это значит, что точки графиков функций (2) и (4) с одной и той же абсциссой имеют противоположные ординаты, то есть расположены симметрично относительно оси абсцисс.
Отсюда следует, что и весь график функции (4) будет симметричен с графиком (2) относительно оси абсцисс.
Таким образом, график функции y = –2x2 можно получить, повернув (в пространстве) график функции y = 2x2 на 1800 вокруг оси абсцисс.
Иначе говоря, парабола y = –2x2 получается зеркальным отражением параболы y = 2x2 в оси абсцисс.
Вообще, при a < 0 график функции y = ax2 можно получить из основной параболы y = x2 так: умножить ординаты точек параболы y = x2 на |a| (растяжение либо сжатие), а затем зеркально отразить полученную параболу в оси абсцисс.
На чертеже 76 изображен ряд парабол y = ax2 при различных значениях a. Мы видим, что при a > 0 параболы обращены вогнутостью вверх, а при a < 0 — вниз.
Построим график полного квадратного трехчлена, например:
y = 2x2 + 4x + 6.
Проделаем такие преобразования. Вынесем за скобку коэффициент при x2, а затем выделим полный квадрат:
y = 2(x2 + 2x + 3) = 2(x2 + 2x + 1 + 2)
и, наконец,
y = 2(x + 1)2 + 4.
Этот график можно получить из параболы y = x2 постепенными преобразованиями так:
1) перенесем параболу y = x2 на 1 единицу влево (черт. 77a), получим:
77a), получим:
y = (x + 1)2;
2) умножим все ординаты на 2 (растяжение в 2 раза), получим:
y = 2(x + 1)2;
3) перенесем последний график вверх на 4 единицы, получим искомый график (черт. 77б):
y = 2(x + 1)2 + 4.
Примечание. Практически можно ограничиться построением лишь одной параболы. Для этого достаточно через точку O1 (–1; 4) провести оси O1X1 и O1Y1, параллельные осям XOY, и во вспомогательной системе координат X1O1Y1 построить (например, по точкам) параболу y1 = 2x12.
Рассмотрим еще пример: построим график
Представим данную функцию в следующем виде:
.
Строим график постепенно так:
1) переносим параболу y = x2 на 3 единицы вправо:
y = (x – 3)2;
2) умножаем ординаты на (сжатие): ;
3) отражаем зеркально в оси абсцисс:
;
4) переносим вверх на 2 единицы:
.
Все сказанное применимо к квадратному трехчлену с любыми коэффициентами.
Рассмотрим квадратный трехчлен в общем виде:
y = ax2 + bx + c.
Выполним такие преобразования:
,
и, наконец,
.
Мы видим, что искомый график можно получить, перенеся параболу y = x2 на в направлении оси абсцисс, умножив ординаты точек полученной параболы на a и перенеся последний график на в направлении оси ординат.
В результате этих преобразований вершина параболы окажется в точке ; при этом парабола обращена вогнутостью вверх при a > 0 и вниз при a < 0.
Оператор | Описание | ||||
| + — * : / () [] {} | Сложение, вычитание, умножение, деление и группирующие символы. 3 значит x в кубе, также можно написать xxx или x*x*x. 3 значит x в кубе, также можно написать xxx или x*x*x. | ||||
| root(x,n) | Корень n-ой степени из x.
Например: root(x,3) есть корень 3й степени из x. | ||||
| sqrt() | Квадратный корень. Эквивалентно root(аргумент,2) | ||||
| cbrt() | Кубический корень. Эквивалентно root(аргумент,3) | ||||
| logn(x,a) | Логарифм x пооснованию a | ||||
| ln() | Натуральный логарифм
(с основанием е) | ||||
| lg() | Логарифм по основанию 10 (Десятичный логарифм), то же, что и logn(аргумент,10). аргумент аргумент | ||||
| sin() | Синус | ||||
| cos() | Косинус | ||||
| tan() | Тангенс | ||||
| cot() | Котангенс | ||||
| sec() | Секанс, определяется как 1/cos() | ||||
| csc() | Косеканс, определяется как 1/sin() | ||||
| asin() | Арксинус | ||||
| acos() | Арккосинус | ||||
| atan() | Арктангенс | ||||
| acot() | Арккотангенс | ||||
| asec() | Арксеканс, обратный секанс | ||||
| acsc() | Арккосеканс, обратный косеканс | ||||
| sinh() | Гиперболический синус, шинус | ||||
| cosh() | Гиперболический косинус, чосинус | ||||
| tanh() | Гиперболический тангенс | ||||
| coth() | Гиперболический котангенс | ||||
| sech() | Гиперболический секанс | ||||
| csch() | Гиперболический косеканс | ||||
| asinh() | Гиперболический арксинус, функция обратная sinh() | ||||
| acosh() | Гиперболический арккосинус, функция обратная cosh() | ||||
| atanh() | Гиперболический арктангенс, функция обратная tanh() | ||||
| acoth() | Гиперболический арккотангенс, функция обратная cotanh() | ||||
| asech() | Гиперболический арксеканс, функция обратная sech() | ||||
| acsch() | Гиперболический арккосеканс, функция обратная csch() | ||||
| gaussd(x,среднее,сигма) | Нормальное распределение (Распределение Гаусса). Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1. Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1. | ||||
| min(число1,число2) | Вычисляет наименьшее из 2х значений | ||||
| max(число1,число2) | Вычисляет наибольшее из 2х значений | ||||
| round() | Округляет аргумент до целого значения | ||||
| floor() | Округление вниз | ||||
| ceil() | Округление вверх | ||||
| abs() или | | | Модуль (абсолютное значение) | ||||
| sgn() | Функция сигнум, определяет знак аргумента
| ||||
| rand | Случайное число от 0 до 1 |
ПРИМЕР 1 Изобразите функцию вида y = ax 2 График y = 2x 2.
 Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для.
Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для.
Презентация на тему: «ПРИМЕР 1 График функции вида y = ax 2 График y = 2x 2. Сравните график с графиком y = x 2. ШАГ РЕШЕНИЯ 1 Составьте таблицу значений для.» — стенограмма презентации :
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
ПРИМЕР 1 График функции вида y = ax 2 График y = 2x 2.Сравните график с графиком y = x 2. РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для y = 2x 2. ШАГ 2 Постройте точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
ШАГ 2 Постройте точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
2
ПРИМЕР 1 Изобразите функцию вида y = ax 2 ШАГ 4 Сравните графики y = 2x 2 и y = x 2. Оба они открываются и имеют одинаковую вершину и ось симметрии. График y = 2x 2 уже, чем график y = x 2.
3
ПРИМЕР 2 Изобразите функцию вида y = ax 2 + c График y = — сравните график с графиком x 2 + 3 1212 y = x 2 ШАГ РЕШЕНИЯ 1 Составьте таблицу значений для y = — x 2 + 3 1212 ШАГ 2 Нанесите точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.
4
ПРИМЕР 2 Постройте график функции вида y = ax 2 ШАГ 4 Сравните графики y = — и y = x 2.Оба графика имеют одну и ту же ось симметрии. Однако график y = — открывается вниз и шире, чем график y = x 2. Кроме того, его вершина на 3 единицы выше. х 2 + 3 1212 1212
х 2 + 3 1212 1212
5
РЕКОМЕНДАЦИИ для примеров 1 и 2 Изобразите функцию. Сравните график с графиком y = x 2. 1. y = — 4x 2 РЕШЕНИЕ ШАГ 1 Составьте таблицу значений y = — 4x 2. X — 2 — 102 Y — 16-40 — 16 — 4
6
ПРАКТИЧЕСКИЕ ПРАКТИКИ для примеров 1 и 2 ШАГ 2 Обозначьте точки из таблицы.ШАГ 3 Проведите плавную кривую через точки. ШАГ 4 Сравните графики y = — 4x 2 и y = x 2. Та же ось симметрии и вершина, раскрывается вниз и уже. ОТВЕТ
7
РЕКОМЕНДАЦИИ для примеров 1 и 2 2. y = — x 2 — 5 РЕШЕНИЕ ШАГ 1 Составьте таблицу значений для y = — x 2 — 5. X — 2 — 102 Y — 9 — 6 — 5 — 9 — 6 ШАГ 2 Нанесите точки из таблицы. ШАГ 3 Проведите плавную кривую через точки.ШАГ 4 Сравните графики y = — x 2-5 и y = x 2.
8
ПРАКТИЧЕСКИЕ ПРАКТИКИ для примеров 1 и 2 ОТВЕТ Ось симметрии та же, вершина смещена на 5 единиц вниз и открывается вниз.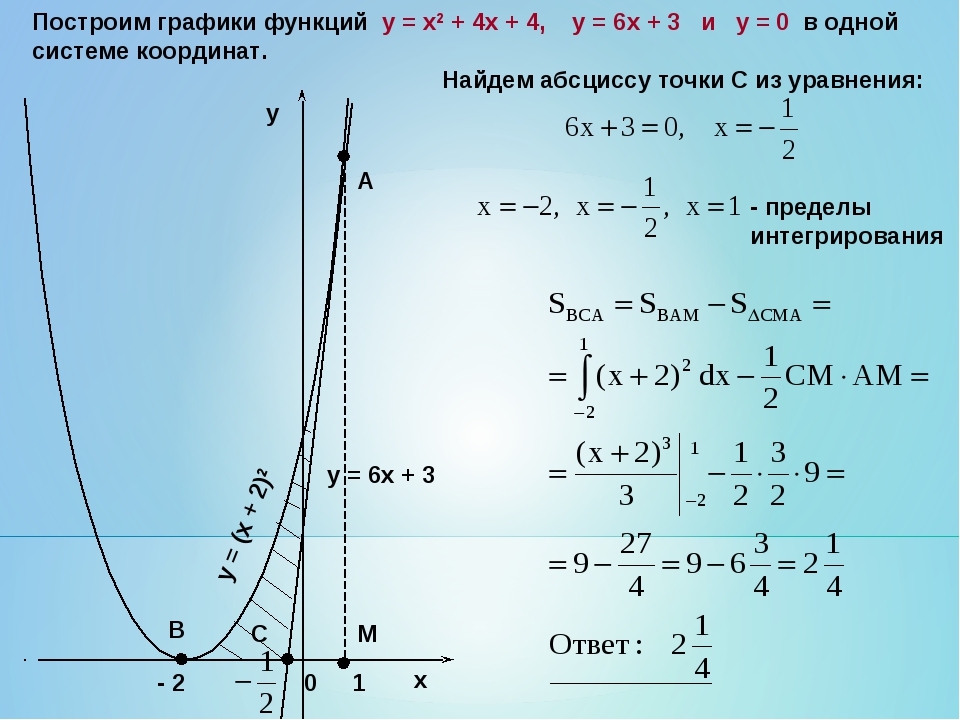
9
РЕКОМЕНДАЦИИ для примеров 1 и 2 3. f (x) = РЕШЕНИЕ ШАГ 1 X — 4 — 20 — 4 2 Y — 2 4264 ШАГ 2 Нанесите точки из таблицы.2-4x + 3
Продолжение ……….
График параболы в форме пересечения:
Интервальная форма квадратного уравнения (уравнение параболы): y = a (x — p) (x — q) , где p и q — точки пересечения с x, а
- Если a> 0 , то парабола открывается вверх.
- Если a <0 , то парабола открывается вниз.
Функция f (x) = y = — 2x 2 — 4x + 3.
Запишите уравнение параболы в виде перехвата.
Разложите выражение на множители — 2x 2 — 4x + 3.
— 2x 2 — 4x + 3, является квадратичным, поэтому используйте формулу корней квадратного уравнения, чтобы найти корни соответствующего квадратного уравнения.
x = [- b ± √ (b 2 — 4ac)] / 2a.
Подставляем a = — 2, b = — 4 и c = 3.
x = [4 ± √ (16 + 24)] / 2 * -2
x = — [4 ± √40] / 4
х = — [2 ± √10] / 2.
Из фольги: y = — 1 (x — [- (2 — √10) / 2]) (x — [(√10 +2) / 2])
Сравните уравнение с интегральной формой квадратного уравнения (уравнение параболы): y = a (x — p) (x — q) .
- a = — 1> 0 (отрицательный), поэтому график функции открывается вниз и имеет максимальное значение.
- x — точки пересечения p и q равны — (2 — √10) / 2 и (√10 +2) / 2 .
- y — точка пересечения — это a (- p) (- q) = — 1 ([(2 — √10) / 2]) (- (√10 +2) / 2) = 3.
- Пересечение оси y равно (0, 3), поэтому точка, соединенная с ним на другой стороне оси симметрии, равна (- 2, 3) и имеет то же значение y -.
- Так как ось симметрии делит параболу на две равные части, то если есть точка (0, 3) с одной стороны, есть соответствующая точка с другой стороны, которая находится на таком же расстоянии от оси симметрии и имеет тот же у — стоимость.
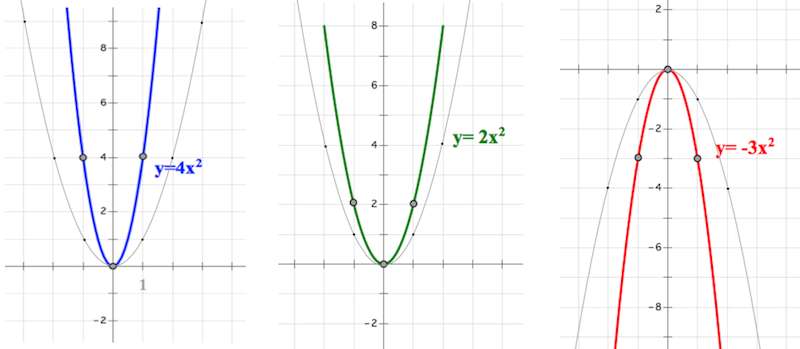
- Расстояние между точками (0, 3) и (- 1, 3) = 1 = Расстояние между (-1, 3) и точкой, спаренной с ним на другой стороне оси симметрии, имеет то же значение y — значение.
- Расстояние между (- 1, 3) и спаренной с ним точкой по другую сторону оси симметрии. = — 1 — 1 = — 2.
- Следовательно, точка, соединенная с ней на другой стороне оси симметрии, равна (- 2, 3).
- Так как ось симметрии делит параболу на две равные части, то если есть точка (0, 3) с одной стороны, есть соответствующая точка с другой стороны, которая находится на таком же расстоянии от оси симметрии и имеет тот же у — стоимость.
- Ось симметрии — это линия x = (p + q) / 2.
Ось симметрии x = (- (2 — √10) / 2 + ((√10 +2) / 2) ) / 2 = — 4/4 = — 1 .{2}
$
Самая низкая или самая высокая точка параболы называется вершиной. Вершина имеет координату x
$$ x = — \ frac {b} {2a} $$
Координата Y вершины — это максимальное или минимальное значение функции.
a> 0 парабола открывает минимальное значение
<0 парабола раскрывается до максимального значения
Практическое правило напоминает нам, что когда у нас есть положительный символ перед x 2 , мы получаем счастливое выражение на графике, а отрицательный символ передает печальное выражение. {2} + 2x + 1 $$
{2} + 2x + 1 $$
Составьте таблицу значений для некоторых значений x.Используйте как положительные, так и отрицательные значения!
| x | y = x 2 + 2x + 1 |
| -3 | 4 |
| -2 | 1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
| 2 | 9 |
| 3 | 16 |
Постройте точки, проведите плавную линию через точки и продолжите ее в обоих направлениях
Обратите внимание, что у нас есть точка минимума, обозначенная положительным значением a (a = 1).Вершина имеет координаты (-1, 0), которые вы получите, если воспользуетесь формулой для координаты x вершины
.
$$ x = — \ frac {b} {2a} = — \ frac {2} {2 \ cdot 1} = — 1 $$
и что линия имеет точку пересечения по оси y (0, 1), которая могла быть определена из значения c, равного 1.
Если у вас абсолютное значение a больше 1, парабола будет уже, чем родительская квадратичная функция. И наоборот, если у вас есть абсолютное значение a, которое меньше 1, тогда парабола будет шире, чем родительская квадратичная функция.{2}} $
2
Данные варианты включают параболу и гиперболу. Давайте посмотрим, что такое парабола, гипербола и эллипс.
Парабола — это плоская кривая, которая является зеркально-симметричной с единственной открытой кривой, которая продолжается до бесконечности и имеет U-образную форму.Гипербола — это открытая кривая с двумя несвязанными ветвями и двумя осями симметрии. Эллипс — это плоская кривая, имеющая две фокусные точки и напоминающая круг.
Из графика мы можем сделать вывод, что форма является U-образной и простирается до бесконечности. Он не имеет двух осей симметрии и не похож на круг. Следовательно, данная функция является параболой.
Следовательно, данная функция является параболой.
Теперь посмотрим, проходит ли он через начало координат. Мы знаем, что в начале координат x и y равны 0. То есть точка $ \ left (0,0 \ right) $.{2}} $ проходит через исходную точку.
Другими словами, мы можем сказать, что когда возводится в квадрат либо x, либо y, но не оба сразу, данное уравнение будет уравнением параболы.
Когда x и y возведены в квадрат, а коэффициенты положительны, но различны, то данное уравнение является уравнением эллипса.
Когда x и y возведены в квадрат, и ровно один из коэффициентов отрицателен, а ровно один из коэффициентов положителен, тогда это напоминает гиперболу.
% PDF-1.6
%
513 0 объект
>
эндобдж
xref
513 711
0000000016 00000 н.
0000016494 00000 п.
0000016640 00000 п.
0000017729 00000 п.
0000017780 00000 п.
0000017831 00000 п.
0000017882 00000 п.
0000017933 00000 п.
0000020467 00000 п.
0000020518 00000 п.
0000020627 00000 н.
0000020678 00000 п.
0000021217 00000 п.
0000024735 00000 п.
0000025275 00000 п.
0000025520 00000 п.
0000025628 00000 п.
0000025729 00000 п.
0000025778 00000 п.
0000026154 00000 п.
0000026205 00000 п.
0000026737 00000 п.
0000026844 00000 п.
0000027030 00000 п.
0000027355 00000 п.
0000028210 00000 п.
0000029405 00000 п.
0000033102 00000 п.
0000033357 00000 п.
0000033943 00000 п.
0000034180 00000 п.
0000040292 00000 п.
0000040766 00000 п.
0000040824 00000 п.
0000041067 00000 п.
0000041242 00000 п.
0000041485 00000 п.
0000042184 00000 п.
0000042833 00000 п.
0000043487 00000 п.
0000044018 00000 п.
0000044127 00000 п.
0000044506 00000 п.
0000046049 00000 п.
0000046112 00000 п.
0000046361 00000 п.
0000046588 00000 п.
0000046936 00000 п.
0000047279 00000 н.
0000047473 00000 п.
0000047578 00000 п.
0000048118 00000 п.
0000048782 00000 п.
0000050035 00000 п.
0000050279 00000 н.
0000050485 00000 п.
0000050629 00000 п.
0000050922 00000 п.
0000051462 00000 п.
0000054524 00000 п.
0000055039 00000 п.
0000056290 00000 п.
0000058903 00000 п.
0000059230 00000 п.
0000059383 00000 п.
0000061307 00000 п.
0000061586 00000 п.
0000061735 00000 п.
0000063433 00000 п.
0000063583 00000 п.
0000064655 00000 п.
0000064908 00000 н.
0000064986 00000 п.
0000065517 00000 п.
0000066030 00000 п.
0000066315 00000 п.
0000066680 00000 п.
0000067087 00000 п.
0000067497 00000 п.
0000067552 00000 п.
0000068441 00000 п.
0000068697 00000 п.
0000068790 00000 п.
0000068921 00000 п.
0000070024 00000 н.
0000070767 00000 п.
0000071307 00000 п.
0000074184 00000 п.
0000074511 00000 п.
0000074695 00000 п.
0000078835 00000 п.
0000079284 00000 п.
0000079613 00000 п.
0000080801 00000 п.
0000080855 00000 п.
0000081514 00000 п.
0000085085 00000 п.
0000085481 00000 п.
0000085735 00000 п.
0000086093 00000 п.
0000086296 00000 п.
0000087223 00000 п.
0000088441 00000 п.
00000 00000 п.
0000091375 00000 п.
0000091615 00000 п.
0000091811 00000 п.
0000092393 00000 п.
0000092637 00000 п.
0000092879 00000 п.
0000092930 00000 н.
0000092985 00000 п.
0000093225 00000 п.
0000093454 00000 п.
0000093506 00000 п.
0000093898 00000 п.
0000094329 00000 п.
0000094569 00000 п.
0000099124 00000 п.
0000104314 00000 н.
0000105835 00000 п.
0000106426 00000 н.
0000106477 00000 н.
0000106924 00000 н.
0000106978 00000 п.
0000107027 00000 н.
0000107196 00000 п.
0000138897 00000 н.
0000139136 00000 н.
0000139187 00000 н.
0000143019 00000 н.
0000143256 00000 н.
0000143306 00000 н.
0000145328 00000 н.
0000145571 00000 н.
0000145622 00000 н.
0000151799 00000 н.
0000152038 00000 н.
0000152089 00000 н.
0000153780 00000 н.
0000154024 00000 н.
0000154075 00000 н.
0000157236 00000 н.
0000201394 00000 н.
0000203005 00000 н.
0000204337 00000 н.
0000204678 00000 н.
0000204729 00000 н.
0000209702 00000 н.
0000218799 00000 н.
0000219039 00000 н.
0000219281 00000 п.
0000219623 00000 п.
0000219919 00000 п.
0000219980 00000 н.
0000221124 00000 н.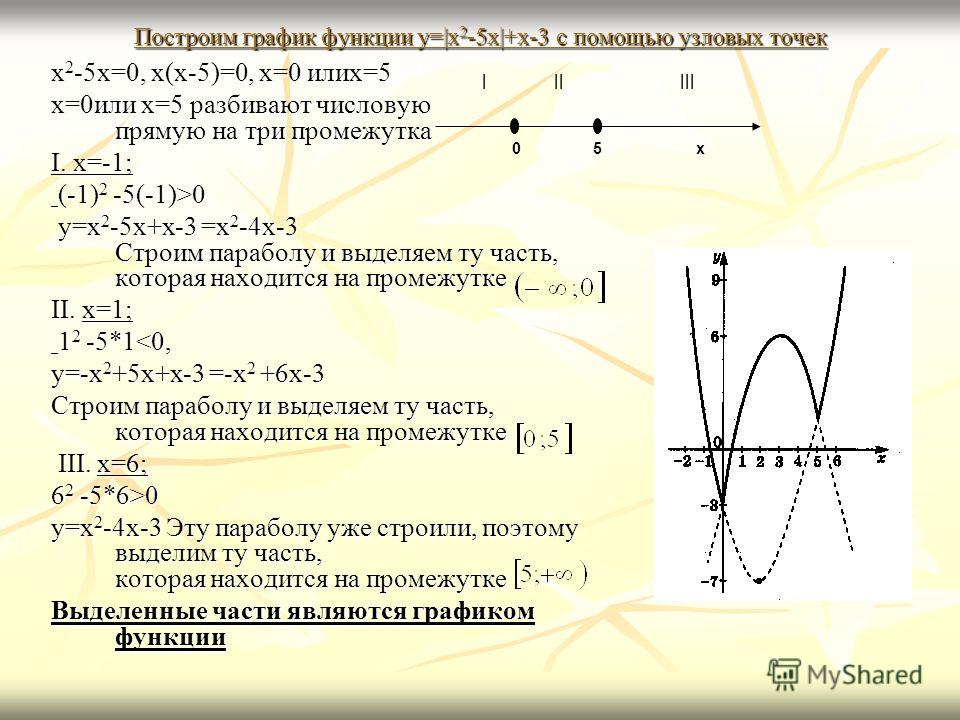
0000221397 00000 н.
0000221685 00000 н.
0000221782 00000 н.
0000222157 00000 н.
0000222524 00000 н.
0000222872 00000 н.
0000223197 00000 н.
0000223591 00000 н.
0000223906 00000 н.
0000224280 00000 н.
0000224664 00000 н.
0000225047 00000 н.
0000225476 00000 н.
0000225782 00000 н.
0000226179 00000 н.
0000226465 00000 н.
0000226770 00000 н.
0000227126 00000 н.
0000227534 00000 н.
0000227895 00000 н.
0000228255 00000 н.
0000228328 00000 н.
0000228427 00000 н.
0000228536 00000 н.
0000228653 00000 н.
0000228770 00000 н.
0000228855 00000 н.
0000228913 00000 н.
0000229012 00000 н.
0000229070 00000 н.
0000229158 00000 н.
0000229216 00000 н.
0000229310 00000 п.
0000229367 00000 н.
0000229453 00000 н.
0000229510 00000 н.
0000229601 00000 п.
0000229658 00000 н.
0000229757 00000 н.
0000229814 00000 н.
0000229903 00000 н.
0000229960 00000 н.
0000230088 00000 н.
0000230168 00000 н.
0000230225 00000 н.
0000230360 00000 н.
0000230488 00000 н.
0000230568 00000 н.
0000230625 00000 н.
0000230760 00000 н.
0000230888 00000 н.
0000230968 00000 н.
0000231025 00000 н.
0000231160 00000 н.
0000231289 00000 н.
0000231369 00000 н.
0000231426 00000 н.
0000231561 00000 н.
0000231689 00000 н.
0000231769 00000 н.
0000231826 00000 н.
0000231946 00000 н.
0000232072 00000 н.
0000232150 00000 н.
0000232207 00000 н.
0000232327 00000 н.
0000232424 00000 н.
0000232481 00000 н.
0000232579 00000 н.
0000232636 00000 н.
0000232739 00000 н.
0000232796 00000 н.
0000232891 00000 н.
0000232948 00000 н.
0000233053 00000 н.
0000233174 00000 п.
0000233275 00000 н.
0000233382 00000 п.
0000233474 00000 н.
0000233531 00000 н.
0000233615 00000 н.
0000233706 00000 н.
0000233763 00000 н.
0000233856 00000 н.
0000233913 00000 н.
0000234006 00000 н.
0000234063 00000 н.
0000234156 00000 н.
0000234213 00000 н.
0000234306 00000 п.
0000234363 00000 п.
0000234456 00000 п.
0000234513 00000 п.
0000234606 00000 н.
0000234663 00000 п.
0000234756 00000 п.
0000234813 00000 п.
0000234930 00000 н.
0000235047 00000 н.
0000235164 00000 п.
0000235281 00000 п.
0000235398 00000 н.
0000235515 00000 н.
0000235632 00000 н.
0000235747 00000 н.
0000235804 00000 н.
0000235896 00000 н.
0000235953 00000 п.
0000236076 00000 н.
0000236199 00000 н.
0000236316 00000 н.
0000236373 00000 н.
0000236490 00000 н.
0000236605 00000 н.
0000236662 00000 н.
0000236779 00000 п.
0000236871 00000 н.
0000236928 00000 н.
0000237012 00000 н.
0000237103 00000 н.
0000237160 00000 н.
0000237251 00000 н.
0000237308 00000 н.
0000237401 00000 н.
0000237458 00000 н.
0000237551 00000 н.
0000237608 00000 н.
0000237701 00000 н.
0000237758 00000 н.
0000237851 00000 п.
0000237908 00000 н.
0000238001 00000 н.
0000238058 00000 н.
0000238151 00000 н.
0000238208 00000 н.
0000238301 00000 н.
0000238358 00000 н.
0000238475 00000 н.
0000238592 00000 н.
0000238709 00000 н.
0000238826 00000 н.
0000238943 00000 н.
0000239060 00000 н.
0000239177 00000 н.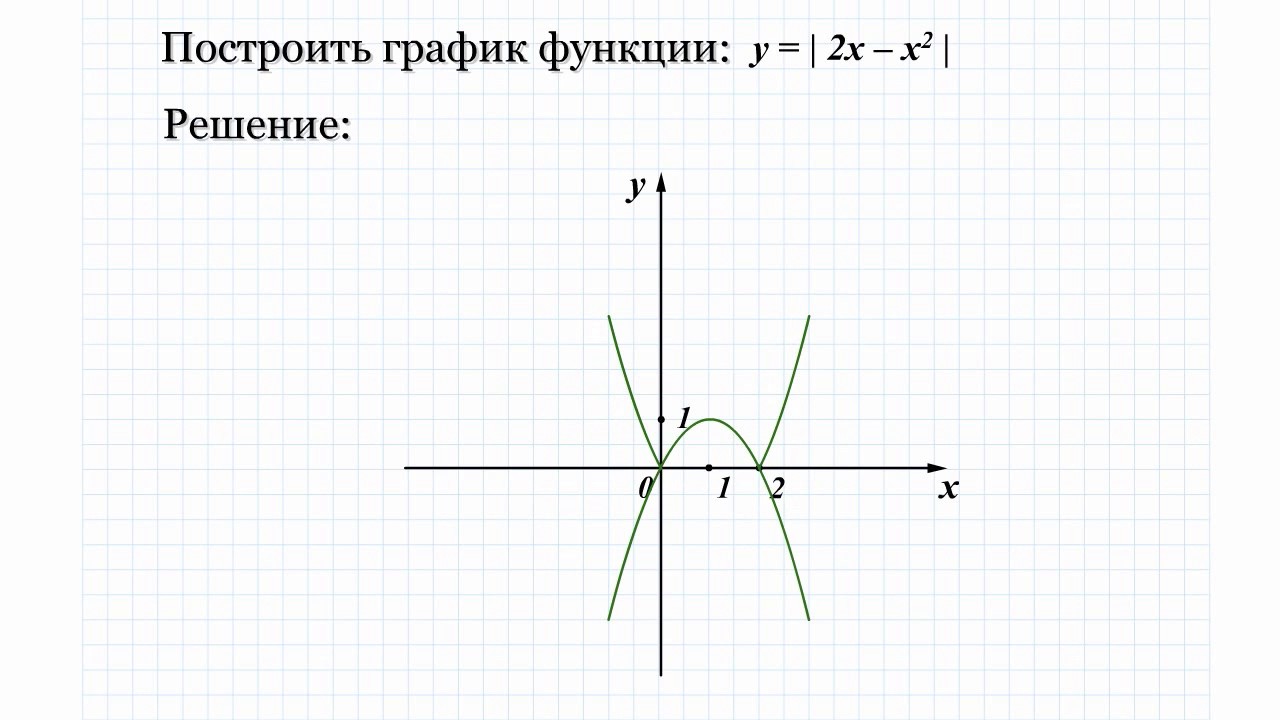
0000239294 00000 н.
0000239409 00000 н.
0000239466 00000 н.
0000239558 00000 н.
0000239615 00000 н.
0000239738 00000 н.
0000239861 00000 н.
0000239978 00000 н.
0000240035 00000 н.
0000240152 00000 н.
0000240267 00000 н.
0000240324 00000 н.
0000240441 00000 п.
0000240555 00000 н.
0000240612 00000 н.
0000240710 00000 н.
0000240809 00000 н.
0000240866 00000 н.
0000240959 00000 н.
0000241016 00000 н.
0000241109 00000 н.
0000241166 00000 н.
0000241259 00000 н.
0000241316 00000 н.
0000241409 00000 н.
0000241466 00000 н.
0000241559 00000 н.
0000241616 00000 н.
0000241709 00000 н.
0000241766 00000 н.
0000241859 00000 н.
0000241916 00000 н.
0000242009 00000 н.
0000242066 00000 н.
0000242183 00000 н.
0000242300 00000 н.
0000242417 00000 н.
0000242534 00000 н.
0000242651 00000 н.
0000242768 00000 н.
0000242885 00000 н.
0000243002 00000 н.
0000243117 00000 н.
0000243174 00000 н.
0000243275 00000 н.
0000243332 00000 н.
0000243455 00000 н.
0000243578 00000 н.
0000243695 00000 н.
0000243752 00000 н.
0000243869 00000 н.
0000243984 00000 н.
0000244041 00000 н.
0000244158 00000 н.
0000244272 00000 н.
0000244329 00000 н.
0000244427 00000 н.
0000244526 00000 н.
0000244583 00000 н.
0000244675 00000 н.
0000244732 00000 н.
0000244825 00000 н.
0000244882 00000 н.
0000244975 00000 н.
0000245032 00000 н.
0000245125 00000 н.
0000245182 00000 н.
0000245275 00000 н.
0000245332 00000 н.
0000245425 00000 н.
0000245482 00000 н.
0000245575 00000 н.
0000245632 00000 н.
0000245725 00000 н.
0000245782 00000 н.
0000245875 00000 н.
0000245932 00000 н.
0000246049 00000 н.
0000246166 00000 н.
0000246283 00000 н.
0000246400 00000 н.
0000246517 00000 н.
0000246634 00000 н.
0000246751 00000 н.
0000246868 00000 н.
0000246987 00000 н.
0000247102 00000 н.
0000247159 00000 н.
0000247260 00000 н.
0000247317 00000 н.
0000247440 00000 н.
0000247563 00000 н.
0000247680 00000 н.
0000247737 00000 н.
0000247854 00000 н.
0000247969 00000 н.
0000248026 00000 н.
0000248143 00000 н.
0000248257 00000 н.
0000248314 00000 н.
0000248412 00000 н.
0000248511 00000 н.
0000248568 00000 н.
0000248661 00000 н.
0000248718 00000 н.
0000248811 00000 н.
0000248868 00000 н.
0000248961 00000 н.
0000249018 00000 н.
0000249111 00000 п.
0000249168 00000 н.
0000249261 00000 н.
0000249318 00000 н.
0000249411 00000 н.
0000249468 00000 н.
0000249561 00000 н.
0000249618 00000 н.
0000249711 00000 н.
0000249768 00000 н.
0000249885 00000 н.
0000250002 00000 н.
0000250119 00000 п.
0000250236 00000 п.
0000250353 00000 п.
0000250470 00000 н.
0000250587 00000 н.
0000250704 00000 н.
0000250819 00000 н.
0000250876 00000 н.
0000250977 00000 н.
0000251034 00000 н.
0000251157 00000 н.
0000251280 00000 н.
0000251397 00000 н.
0000251454 00000 н.
0000251571 00000 н.
0000251686 00000 н.
0000251743 00000 н.
0000251860 00000 н.
0000251974 00000 н.
0000252031 00000 н.
0000252129 00000 н.
0000252228 00000 н.
0000252285 00000 н.
0000252377 00000 н.
0000252434 00000 н.
0000252527 00000 н.
0000252584 00000 н.
0000252677 00000 н.
0000252734 00000 н.
0000252827 00000 н.
0000252884 00000 н.
0000252977 00000 н.
0000253034 00000 н.
0000253127 00000 н.
0000253184 00000 н.
0000253277 00000 н.
0000253334 00000 н.
0000253427 00000 н.
0000253484 00000 н.
0000253577 00000 н.
0000253634 00000 н.
0000253751 00000 н.
0000253868 00000 н.
0000253985 00000 н.
0000254102 00000 н.
0000254219 00000 н.
0000254336 00000 н.
0000254453 00000 н.
0000254570 00000 н.
0000254687 00000 н.
0000254804 00000 н.
0000254861 00000 н.
0000254962 00000 н.
0000255019 00000 н.
0000255142 00000 н.
0000255265 00000 н.
0000255382 00000 н.
0000255439 00000 н.
0000255556 00000 н.
0000255671 00000 н.
0000255728 00000 н.
0000255845 00000 н.
0000255972 00000 н.
0000256107 00000 н.
0000256234 00000 н.
0000256365 00000 н.
0000256494 00000 н.
0000256610 00000 н.
0000256754 00000 н.
0000256840 00000 н.
0000256921 00000 н.
0000256980 00000 н.
0000257066 00000 н.
0000257197 00000 н.
0000257279 00000 н.
0000257338 00000 н.
0000257425 00000 н.
0000257557 00000 н.
0000257639 00000 н.
0000257698 00000 н.
0000257785 00000 н.
0000257917 00000 п.
0000257999 00000 н.
0000258058 00000 н.
0000258145 00000 н.
0000258276 00000 н.
0000258358 00000 н.
0000258417 00000 н.
0000258504 00000 н.
0000258563 00000 н.
0000258657 00000 н.
0000258716 00000 н.
0000258812 00000 н.
0000258871 00000 н.
0000258967 00000 н.
0000259026 00000 н.
0000259122 00000 н.
0000259181 00000 н.
0000259277 00000 н.
0000259336 00000 н.
0000259432 00000 н.
0000259491 00000 п.
0000259587 00000 н.
0000259646 00000 н.
0000259742 00000 н.
0000259801 00000 п.
0000259897 00000 н.
0000259956 00000 н.
0000260114 00000 п.
0000260272 00000 н.
0000260430 00000 н.
0000260588 00000 н.
0000260746 00000 н.
0000260904 00000 н.
0000261062 00000 н.
0000261220 00000 н.
0000261376 00000 н.
0000261534 00000 н.
0000261692 00000 н.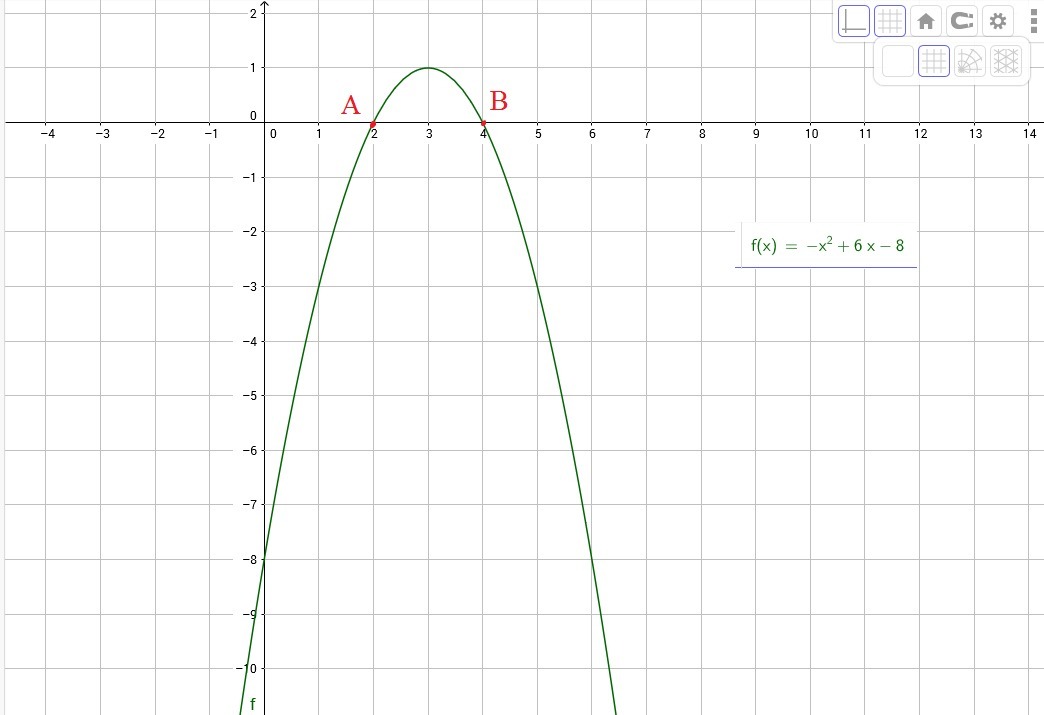
0000261751 00000 н.
0000261909 00000 н.
0000261968 00000 н.
0000262062 00000 н.
0000262121 00000 н.
0000262217 00000 н.
0000262276 00000 н.
0000262372 00000 н.
0000262431 00000 н.
0000262527 00000 н.
0000262586 00000 н.
0000262682 00000 н.
0000262741 00000 н.
0000262837 00000 н.
0000262896 00000 н.
0000262992 00000 н.
0000263051 00000 н.
0000263147 00000 н.
0000263206 00000 н.
0000263302 00000 н.
0000263361 00000 н.
0000263517 00000 н.
0000263673 00000 н.
0000263829 00000 н.
0000263985 00000 н.
0000264141 00000 п.
0000264297 00000 н.
0000264453 00000 н.
0000264609 00000 н.
0000264763 00000 н.
0000264919 00000 н.
0000265075 00000 н.
0000265134 00000 н.
0000265290 00000 н.
0000265349 00000 п.
0000265443 00000 п.
0000265502 00000 н.
0000265599 00000 н.
0000265658 00000 н.
0000265754 00000 п.
0000265813 00000 н.
0000265909 00000 н.
0000265968 00000 н.
0000266064 00000 н.
0000266123 00000 н.
0000266219 00000 п.
0000266278 00000 н.
0000266374 00000 н.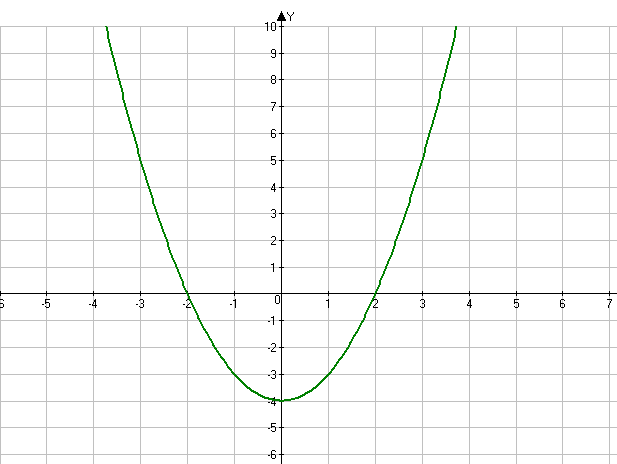
0000266433 00000 н.
0000266529 00000 н.
0000266588 00000 н.
0000266684 00000 н.
0000266743 00000 н.
0000266839 00000 н.
0000266898 00000 н.
0000267054 00000 н.
0000267210 00000 н.
0000267366 00000 н.
0000267522 00000 н.
0000267678 00000 н.
0000267834 00000 н.
0000267990 00000 н.
0000268146 00000 н.
0000268302 00000 н.
0000268456 00000 п.
0000268612 00000 н.
0000268768 00000 н.
0000268827 00000 н.
0000268983 00000 п.
0000269042 00000 н.
0000269136 00000 н.
0000269195 00000 н.
0000269291 00000 н.
0000269350 00000 н.
0000269446 00000 н.
0000269505 00000 н.
0000269601 00000 н.
0000269660 00000 н.
0000269756 00000 н.
0000269815 00000 н.
0000269911 00000 н.
0000269970 00000 н.
0000270066 00000 н.
0000270125 00000 н.
0000270221 00000 н.
0000270280 00000 н.
0000270376 00000 п.
0000270435 00000 н.
0000270591 00000 н.
0000270747 00000 н.
0000270903 00000 н.
0000271059 00000 н.
0000271215 00000 н.
0000271371 00000 н.
0000271527 00000 н.
0000271683 00000 н.
0000271837 00000 н.
0000271993 00000 н.
0000272149 00000 н.
0000272208 00000 н.
0000272364 00000 н.
0000272423 00000 н.
0000272516 00000 н.
0000272575 00000 н.
0000272671 00000 н.
0000272730 00000 н.
0000272825 00000 н.
0000272884 00000 н.
0000272979 00000 н.
0000273038 00000 н.
0000273133 00000 н.
0000273192 00000 н.
0000273287 00000 н.
0000273346 00000 н.
0000273441 00000 н.
0000273500 00000 н.
0000273595 00000 н.
0000273654 00000 н.
0000273749 00000 н.
0000273808 00000 н.
0000273903 00000 н.
0000273962 00000 н.
0000274118 00000 н.
0000274274 00000 н.
0000274430 00000 н.
0000274586 00000 н.
0000274742 00000 н.
0000274898 00000 н.
0000275054 00000 н.
0000275210 00000 н.
0000275366 00000 н.
0000275520 00000 н.
0000275676 00000 н.
0000275832 00000 н.
0000275891 00000 н.
0000276047 00000 н.
0000276128 00000 н.
0000276187 00000 н.
0000276273 00000 н.
0000276332 00000 н.
0000276425 00000 н.
0000276484 00000 н.
0000276579 00000 н.
0000276638 00000 н.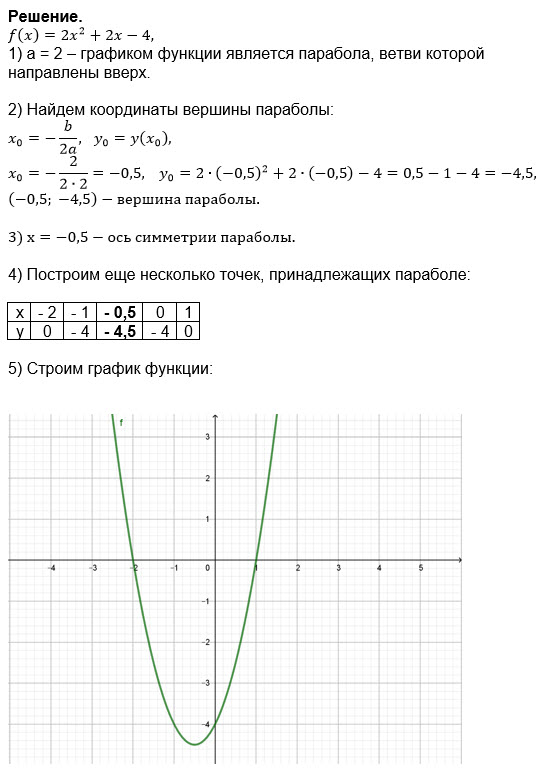 ks˽ «EDA #! Ii1DnC &: ࠉ2bZ> b! 41uѺ (wfz
ks˽ «EDA #! Ii1DnC &: ࠉ2bZ> b! 41uѺ (wfz
Конструктор квадратичных графиков
Запишите квадратное уравнение в стандартной форме.Добавьте 5 к обеим сторонам уравнения. x 2 + 2x = -5: Шаг 2: Определите значения a, b и c. a = 1, b = 2, c = 5: Шаг 3: подставьте значения a, b и c в формулу корней квадратного уравнения. Замените 1 на a, 2 на b и 5 на c. Шаг 4. Упростите. Упростим подкоренное выражение и знаменатель.
2 ноября 2020 г. · Существуют различные способы решения квадратичной функции и уравнений, которые были рассмотрены в Уроках 8-1, 8-2, 8-3 и 8-6. Если вы только что научились решать эти уравнения, то приведенная ниже викторина идеально подходит для вас.Попробуйте и отточите свои навыки.
квадратичных неравенств Подготовьте гизмо: установите a на 1,0, b на 0,0 и c на 0,0. Выбирать . 1. График, показанный в Gizmo, должен иметь y> x2. Нарисуйте график y> x2 на сетке справа. A. Нанесите на график точки (1, 5) и (4, 7). B. Подставим 1 вместо x и 5 вместо y, чтобы проверить, делает ли (1, 5) истинным y> x2. Покажи свою работу ниже.
Покажи свою работу ниже.
Откройте для себя удивительный мир графиков. Создайте свой собственный и посмотрите, что дают разные функции.
09 января 2016 · Знание, как построить параболу или решить квадратное уравнение, или даже понять, какое влияние все параметры квадратного уравнения в форме вершины оказывают на график уравнения, не сразу делает это очевидным. как написать уравнение с учетом трех точек, даже если эти точки специально выбраны для устранения необходимости …
Oct 03, 2019 · 3.1 Квадратичные функции в вершинной форме SLO: Я могу нарисовать график квадратичной функции с помощью преобразований.1. Постройте график следующих функций с помощью преобразований. Обязательно укажите трансформации и покажите все этапы. Обязательно используйте миллиметровую бумагу и линейку !! a) y = 2×2 — (x-1) 2-3 10-12-10-8-6-4-2 0 2 4 6 8 10 …
8B: квадратичные графики и приложения. Студенты развивают методы построения графиков квадратных уравнений, уделяя особое внимание корням и вершинам. Они используют эти графики для поиска максимумов и минимумов в текстовых задачах. 8C: Работа с квадратиками
Они используют эти графики для поиска максимумов и минимумов в текстовых задачах. 8C: Работа с квадратиками
Какая пара уравнений формирует графики с одной и той же вершиной
Студент ожидает применения понятий наклона и 𝑦-пересечения к графикам, уравнениям и пропорциональным отношениям.2/2.
Пара (g, d) в dp [i] означает путь от v к вершине i, у которого НОД вершин пути равен g, а его длина равна d, где v — один из правнуков вершины i. Очевидно, мне не нужно хранить пары (g, d), где g = 1, а также я могу игнорировать вершину i, где a [i] = 1.
a, b и c — коэффициенты квадратного уравнения n = количество значений или элементов Σ x = сумма первых баллов Σ y = сумма вторых баллов Σ x 2 = сумма квадратов первых баллов Σ x 3 = Сумма куба первых баллов Σ x 4 = сумма степеней четверки первых баллов Σ xy = сумма произведения первого и второго баллов Σ x 2 y = сумма квадратов…
Если d = 2, получается более прямоугольный график, такой как: уравнение которого, следовательно, если вершина находится где-то в другом месте, кроме начала координат, то все измерения производятся относительно нее (например, расстояния до фокуса и направляющей) и уравнение принимает следующий вид: Мы называем это стандартной формой параболы.


 Растяжение графика функции y = x 2 вдоль оси y в 2 раза
Растяжение графика функции y = x 2 вдоль оси y в 2 раза