Содержание
Универсальная лестница Эйфель Премьер 2 х 3 + 2 х 4 — цена, отзывы, характеристики, фото
Универсальная лестница Эйфель Премьер 2 х 3 + 2 х 4 подходит для выполнения разного рода работ. Удобна для маляров, монтажников и прочих строительных работников. Лестница быстро трансформируется из простой приставной лестницы в стремянку с двусторонним заходом, в лестницу с консолью для доступа под нависающие конструкции. А сборка в виде помоста заменит раскладной стол. Модель изготовлена из анодированного алюминия, который не меняет свой цвет на протяжении всего периода и не подвержен коррозии, а также руки останутся чистыми при работе на ней.
- Тип трансформер
- Max рабочая нагрузка, кг 150
- Настил в комплекте нет
- org/PropertyValue»> Рабочая высота, м 5,02
- Высота площадки, м 1,22
- Материал алюминий
- Общая длина, м 3,97
- Размер в сложенном состоянии, см 125х35х30
- min длина в сложенном состоянии, м 1.25
- Ширина ступеней, мм 28
- Ширина лестницы, мм 350
- org/PropertyValue»> Толщина профиля, мм 1.4
- Вес, кг 14,6
- Габариты, мм 3970х350
- Помост да
- Количество ступеней, шт 2х4+2х3
- Показать еще
Этот товар из подборок
Комплектация *
- Лестница поставляется в защитной плёнке с информационным плакатом.
Параметры упакованного товара
Единица товара: Штука
Вес, кг: 14,60
Длина, мм: 1250
Ширина, мм: 350
Высота, мм: 300
Преимущества
|
Произведено
- Россия — родина бренда
- Россия — страна производства*
- Информация о производителе
* Производитель оставляет за собой право без уведомления дилера менять характеристики, внешний вид, комплектацию товара и место его производства.
Указанная информация не является публичной офертой
На данный момент для этого товара нет расходных материалов
Сервис от ВсеИнструменты.ру
Мы предлагаем уникальный сервис по обмену, возврату и ремонту товара!
Вернем вам деньги, если:
- С момента приобретения прошло не более 120 дней.
 3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x3 -2x +1.
Оператор partial fractions разложит отношение многочленов в сумму простейших дробей.
minimize минимизирует функцию, а maximize максимизирует
Число «Пи» записывается, как pi
Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan
Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0
Производные и интегралы
Чтобы найти предел, необходимо в начале функции подставить lim, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity).
 8
8Оператор factor раскладывает число на множители
! выводит факториал, например 123!
Оператор gcd выводит наибольший общий делитель, например gcd 164, 88 выводит наибольший общий делитель чисел 164 и 88
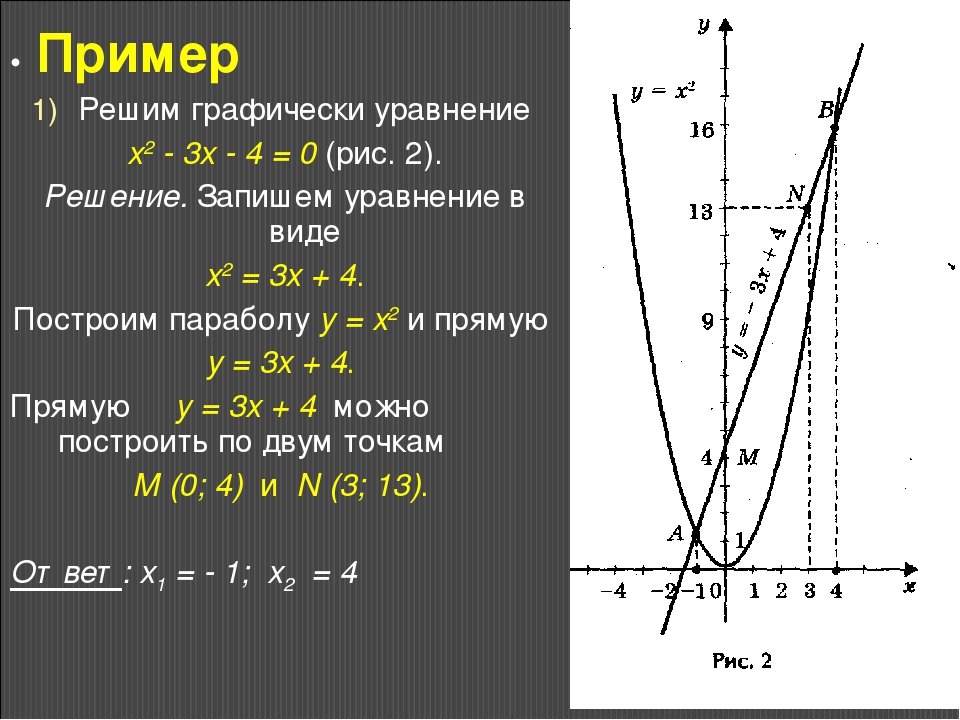
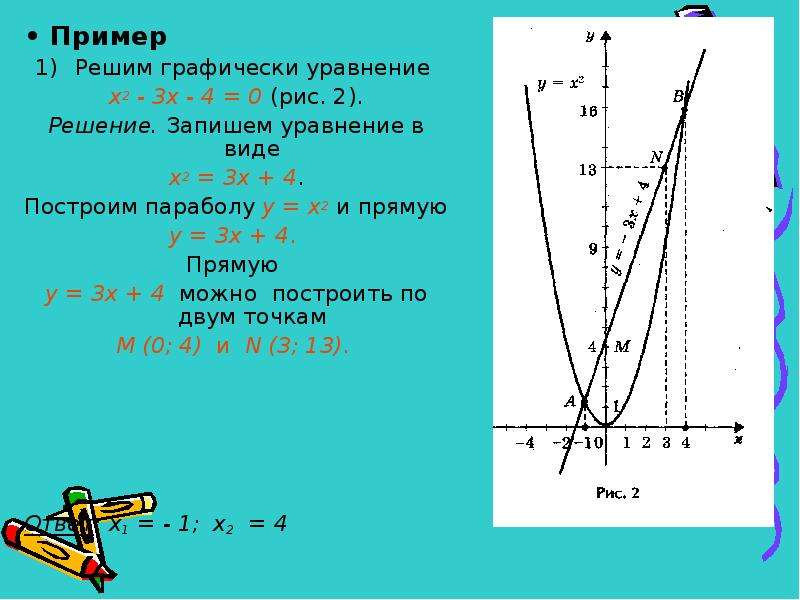
Целые уравнения. Алгебра, 9 класс
Название материала: Самостоятельная работа по теме: «Целые уравнения». Алгебра, 9 класс
Образовательная организация:
МОУ «Средняя школа №35» городского округа Саранск Республики Мордовия
ФИО автора: Глушкова Светлана Юрьевна
Должность: учитель математики
Вариант №1
Решите уравнения.
1) х4-16х2+63=0; 2) 9х3-7х2-2х=0; 3) х3+х2-4х-4=0; 4) (х2+4х)(х2+4х-17)= -60
Вариант №2
Решите уравнения.
1) 9х4-42х2+49=0; 2) х3+18х2-63х=0; 3)3х3+5х2+5х+3=0; 4) (х2-2х)2-2(х2-2х)=3
Вариант №3
Решите уравнения.

1) 3х4-13х2+10=0; 2) х3-10х2+9х=0; 3) х3+х2-9х-9=0;4) (х2-5х)(х2-5х+10)+24= 0
Вариант №4
Решите уравнения.
1) х4-2х2-35=0; 2) 4х3-36х2+81х=0; 3) 4х3+7х2+7х+4=0; 4) (х2-4х)2+9(х2-4х)=-20
Вариант №5
Решите уравнения.
1) 16х4-40х2+25=0; 2) х3-13х2+36х=0; 3) х3+х2-16х-16=0; 4) (х2+3)2+28= 11(х2+3)
Вариант №6
Решите уравнения.
1) 7х4-9х2+2=0; 2) х3-5х2+4х=0; 3) х3+х2-25х-25=0; 4) (х2+х+2) (х2+х-1) -40=0
Вариант №7
Решите уравнения.
1) х4-20х2+91=0; 2) 9х3+5х2— 4х=0; 3) х3+3х2-16х-48=0; 4) (2х2+х-1) (2х2+х-4) =-2
Вариант №8
Решите уравнения.

1) 4х4-28х2+49=0; 2) х3-50х2+49х=0; 3) х3+х2-36х-36=0; 4) (х2+х) (х2+х-5) -84=0
Вариант №9
Решите уравнения.
1) 9х4-7х2-2=0; 2) х3-3х2-4х=0; 3) х3+3х2-9х-27=0;4) (х2-4х+4) (х2-4х+3) =12
Вариант №10
Решите уравнения.
1) х4+18х2-63=0; 2) 4х3-5х2+х=0; 3) х3+х2-49х-49=0; 4) (х2-6х+9) (х2-6х+8) =20
Вариант №11
Решите уравнения.
1) 4х4-36х2+81=0; 2) х3+х2-20х=0; 3) х3+3х2-25х-75=0; 4) (х2-3х) (х2-3х+3) =24
Вариант №12
Решите уравнения.
9х4+5х2— 4=0; 2) х3+3х2-4х=0; 3) х3+х2-64х-64=0; 4) (х2-5х) (х2-5х-24) +108=0
Вариант №13
Решите уравнения.
1) х4-10х2+9=0;2) 9х3-13х2+4х=0; 3) х3-3х2-16х+48=0; 4) (х2+8х+16) (х2+8х-20) +243=0
Вариант №14
Решите уравнения.
х4-13х2+36=0; 2) 4х3+5х2-9х=0; 3) х3+х2-81х-81=0; 4) (х2+9х) (х2+9х+20) +96=0
Вариант №15
Решите уравнения.
1) х4-5х2+4=0; 2)9х3+23х2-12х=0; 3)х3-3х2-9х+27=0; 4) (х2+8х) (х2+8х+15) +56=0
Вариант №16
Решите уравнения.
1) х4-50х2+49=0; 2)9х3-42х2+49х=0; 3)х3-х2-9х+9=0; 4) (х2-5х+4) (х2-5х+6) =24
Вариант №17
Решите уравнения.
х4-3х2-4=0; 2)3х3-13х2+10х=0; 3) х3-3х2-25х+75=0; 4) (х2-9х+18) (х2-9х+20) =1680
Вариант №18
Решите уравнения.

1) х4+х2-20=0; 2)16х3-40х2+25х=0;3) х3-х2-16х+16=0; 4) (х-2)2 (х2-4х+3) =12
Вариант №19
Решите уравнения.
1) х4+3х2-4=0; 2) 7х3-9х2+2х=0;3) х4+2х3-х-2=0; 4) (х2+6х)2-2 (х+3)2 -17=0
Вариант №20
Решите уравнения.
1) х4-4х2-5=0; 2)4х3-28х2+49х=0; 3)х3-х2-49х+49=0; 4) (х2-7х+13)2 -(х-4)(х-3) =1
Вариант №21
Решите уравнения.
1) 4х4-5х2+1=0;2) х3-8х2-9х=0; 3)х4+2х3-8х-16=0; 4) (х2-5х+7)2 -(х-2)(х-3) =1
Вариант №22
Решите уравнения.
1) 9х4-13х2+4=0; 2)х3+3х2-10х=0; 3)х3-х2-25х+25=0; 4) (2х2+х-1) (2х2+х-4) +2=0
Вариант №23
Решите уравнения.

1) 4х4+5х2-9=0; 2)х3-20х2+100х=0; 3)х4+2х3-27х-54=0; 4) (х2-4х+4) (х2-4х+3) -12=0
Вариант №24
Решите уравнения.
1) 9х4+23х2-12=0; 2)х3-4х2-5х=0; 3 )х3-х2-64х+64=0; 4) (х2-3х) (х2-3х+3) -24=0
Вариант №25
Решите уравнения.
1) х4-8х2-9=0; 2)9х3-7х2-2х=0; 3)х4-2х3-х+2=0; 4)(х2+4х)(х2+4х-17)+60=0
Вариант №26
Решите уравнения.
1) х4+3х2-10=0; 2)4х3-36х2+81х=0; 3)х3-х2-81х+81=0; 4)(х2-2х)2-2(х2-2х)-3=0
Вариант №27
Решите уравнения.
х4-20х2+100=0; 2)9х3-7х2-2х=0; 3) х4-2х3-8х+16=0; 4)(х2-5х)(х2-5х+10)=-24
Вариант №28
Решите уравнения.

1) х4-47х2-98=0; 2)4х3-36х2+81х=0; 3)х3-х2-4х+4=0; 4) (х2-4х+4) (х2-4х+3) -12=0
Вариант №29
Решите уравнения.
1) х4+18х2-63=0; 2) 16х3-40х2+25х=0; 3) х4-2х3-27х+54=0; 4) (х2+8х) (х2+8х+15) = -56
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/298338-samostojatelnaja-rabota-po-teme-celye-uravnen
10.5. Нахождение рациональных корней многочлена с целыми коэффициентами.
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.

Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0.
(1)
Умножим обе части равенства (1) на (q ≠ 0). Получаем
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0.
(2)
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.

Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d),
(3)
где а, b, с и d — неопределенные (пока что) коэффициенты.
 Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:х4+ х3+ 3х2 + х + 6 = x4+ cx3+ dx2+
+ ax3+ acx2+ adx +
+ bx2+ bcx + bd.
Получаем систему
(4)
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6.
 Все возможные варианты запишем в таблицу.
Все возможные варианты запишем в таблицу.Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3).

(5)
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.

- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
 6> 0 \ подразумевает
6> 0 \ подразумевает— 1
0
а также
— 1
1> — x 1> — x 2> 0 ⟹ 1> — x 1> — x 2> 0 ⟹ 1> -x_1> -x_2> 0 \ подразумевает
2> 1 — x 1> 1 — x 2> 1 ⟹ 2> 1 — x 1> 1 — x 2> 1 ⟹ 2> 1-x_1> 1-x_2> 1 \ подразумевает
1 2
Умножая (4) (4) \\ (4) \ \ и (5) (5) \ \ (5) \ \ получаем
0
(1 — x 1) (x 5 1 + x 4 1 + x 3 1 + x 2 1 + x 1 + 1) 1 — x 1
x 5 1 + x 4 1 + x 3 1 + x 2 1 + x 1 + 1
f (x 1)
поэтому f (x) f (x) \ \ f (x) \ \ монотонно возрастает, когда x ∈ (- 1, 0) x ∈ (- 1, 0) \ \ x \ in (-1,0)
что в конечном итоге доказывает, что ff \ \ f \ \ монотонно возрастает во всех интервалах (- ∞, — 1), (- 1, 0) (- ∞, — 1), (- 1, 0) (- \ infty, — 1), \ \ (-1,0) \ \ и (0, + ∞) (0, + ∞) \ (0, + \ infty) \ \, и поскольку ff \ \ f \ \ является полиномиальной функцией, она всюду непрерывно, и мы можем заключить, что ff \ \ f \ \ монотонно возрастает всюду в RR \ R, что в итоге дает нам
∀ x ∈ R, f ′ (x)> 0 ⟹ ∀ x ∈ R, f ′ (x)> 0 ⟹ \ forall x \ in \ R \, \ \ f ‘(x)> 0 \ влечет
f ′ (x) ≠ 0 ⟹ f ′ (x) ≠ 0 ⟹ f ‘(x) \ neq 0 \ подразумевает
5 x 4 + 4 x 3 + 3 x 2 + 2 x + 1 ≠ 0 5 x 4 + 4 x 3 + 3 x 2 + 2 x + 1 ≠ 0 \ в штучной упаковке {5x ^ 4 + 4x ^ 3 + 3x ^ 2 + 2x + 1 \ neq 0}
К сожалению, на этот раз нет реальных решений для вас 🙂
Самостоятельная работа по математике на тему: «Линейные уравнения»
Карточка 1
1.
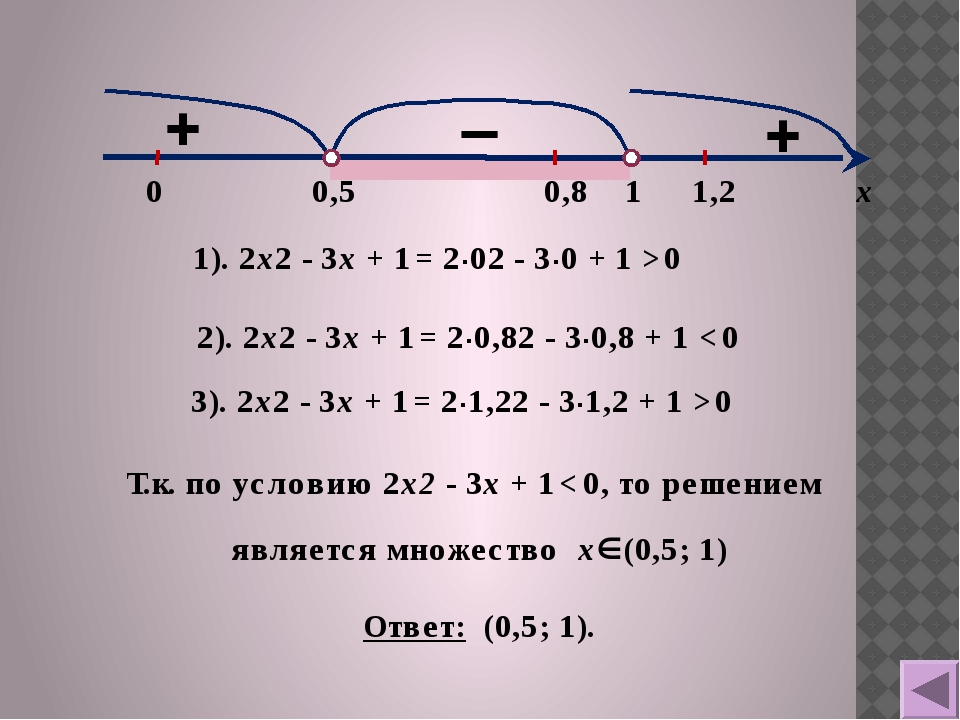 – 0,7х = -0, 21
– 0,7х = -0, 212. 2х + 4 = 0
3. 5х – 8 = 9 + 3х4. 9х + (6 – 2х) = 15
5. 3(-2у+5) — 4(6 – у) =13Карточка 2
1. 20х = -2
2. 7х – 0,2 = 0,4
3. 12 – 2х = 3х-104. 2х – (5х + 4) = — 8
5. -3(4-2х)+4(х-1)= -12Карточка 3
1. – 3х = — 21
2. 0,8х + 0,5 = 0
3. 8х – 2 = 7 + 2х4. 5 – 3(2х – 7) = -6х
5. 6(х-3) — 2(7-2х) = 5
Карточка 4
1. 0,2х = -0,5
2. 3х – 7 = 2
3. 11 – 4х = 2х -1
4. 6х – (2х + 5) = — 4
5. -5(3-2х) +4(х-3) =6
Карточка 5
1. – 0,5х = — 0,15
2. 8х – 5 = 3х3. 4х – 3 = 2 + 7х
4. 5 (2х +2) – 5х = 135. 3(1-2х) — 2(х+3)= -9
Карточка 6
1. 40х = -5
2. 16 – 0,8х = 0,2х
3. 5-2х=4х-74. 2х + (4 – 3х) = 11
5. -5(2-х) + (5х – 4) =28
Карточка 7
1. – 0,8х = — 0,16
2. 3х – 2 = 83. 4х – 3= 4 + 2х
4. 7х – (8х + 4) = — 3
5. 2(6-2х) – 4(х+2) = 10Карточка 8
1.
 0,5 х =-2,5
0,5 х =-2,52. 4х+3=11
3. 0,7 + 2х = 3х+ 1,7
4. -2(х-4) +4(х-2) =0
5. 2(4-х) – (8+х) =2
Карточка 9
1. – 0,6х = — 0,18
2. 5х – 3 = 4
3. 2х – 5 = 9 + 6х
4. 7х + (2– 3х) = 195. 5(6-х) – 6(2х + 3) =24
Карточка 10
1. 0,7х=-4,9
2. 15-3х=3
3. –х-6=8+6х
4. 2(4х +6) – 5х = 10
5. –(6х-4) +2(5-х) =20
Карточка 11
1. 0,5 х = -20
2. 12х-16=8
3. 3х – 10 = х + 6
4. 5х – (7х -43) = 9
5. 3(4-2х) – 2(х+3) = 10
Карточка 12
1. 0,7х = -0, 28
2. 2х — 4 = 0
3. 5х – 8 = 9 + 3х4. 9х + (6 – 2х) = 15
5. 3(-2у+5) — 4(6 – у) =13Карточка 13
1. 40х = -5
2. 16 – 0,8х = 0,2х
3. 5-2х=4х-74. 2х + (4 – 3х) = 11
5. -5(2-х) + (5х – 4) =28
Карточка 14
1. 0,3х = — 0,18
2. 5х – 3 = 4
3. 2х – 5 = 9 + 6х
4. 7х + (2– 3х) = 195. 5(6-х) – 6(2х + 3) =24
Карточка 15
1.
 – 0,3х = — 0,45
– 0,3х = — 0,45
2. 8х – 5 = 3х3. 4х – 3 = 2 + 7х
4. 5 (2х +2) – 5х = 135. 3(1-2х) — 2(х+3)= -9
Карточка 16
1. – 3х = 4,8
2. 0,8х + 0,5 = 0
3. 8х – 2 = 7 + 2х4. 5 – 3(2х – 7) = -6х
5. 6(х-3) — 2(7-2х) = 5
Карточка 17
1. 0,6х = — 36
2. 3х – 2 = 83. 4х – 3= 4 + 2х
4. 7х – (8х + 4) = — 3
5. 2(6-2х) – 4(х+2) = 10Карточка 18
1. 0,5 х = -20
2. 12х-16=8
3. 3х – 10 = х + 6
4. 5х – (7х -43) = 9
5. 3(4-2х) – 2(х+3) = 10
Карточка 19
1. 0,1х = -0,5
2. 3х – 6 = 2
3. 11 – 4х = 2х -1
4. 6х – (2х + 5) = — 4
5. -5(3-2х) +4(х-3) =6
Карточка 20
1. -0,4х = -0,2
2. 7 — 2х= 3
3. 10 – 3х = 2х -2
4. х – (3х + 2) = — 3
5. -2(3- х) +3(2х-3) =7
Карточка 21
1. 0,4х = -0,2
2. 7х + 3 = -4
3. 14 – 3х = 6х -4
4. 2(4х +6) – 5х = 10
5. -3(х+4) + 2(5-х) = 3
Карточка 22
1.
 -0,3х=-0,6
-0,3х=-0,62. 15-3х=3
3. –х-6=8+6х
4. 2(4х +6) – 5х = 10
5. –(6х-4) +2(5-х) =20
Карточка 23
1. 0,2х=1,6
2. 11-3х=2
3. 27-4х=х+31
4. 3х-(7х-2) =18
5. -(х+6) +3(х+2) =0
Карточка 24
1. – 0,5х = — 2,5
2. 16 – 8х = 2х
3. 7-2х = 3+4х
4. 6(2х +5) – 7х = 17
5. 4(х+2) –(6-3х) = 3
Карточка 25
1. 0,3х = — 0,18
2. -0,8х + 0,5 = 0
3. 8х – 2 = 7 + 2х4. 5х – (7х -26) = 8
5. 2(4-х) – (8+х) =12
Карточка 26
1. 0,2х=-2,8
2. 12-2х=-2
3. 26-3х=х+30
4. 2х-(5х-2) =18
5. 3(х+6) — (х+2) =0
Карточка 27
1. -0,4х=-3,2
2. -15+3х=3
3. –х-6=8+6х
4. 2(4х +6) – 5х = 10
5. –(6х-4) +2(5-х) =-20
Карточка 28
1. 0,4х = -0,2
2. -7х – 0,2 = 0,4
3. 12 – 3х = 2х-104. 2х – (5х + 4) = — 8
5. 3(4-2х) — 4(х-1)= -12Карточка 29
1. 0,8х = — 0,64
2. -2х + 0,4 = 0
-2х + 0,4 = 0
3. 8х – 2 = 7 + 2х4. 5 – 3(2х – 7) = -6х
5. 2(х-3) — (7-2х) = 5
Карточка 30
1. -0,5 х =-2,5
2. 4х — 3=-11
3. 0,7 + 2х = 3х+ 1,7
4. -2(х-4) +4(х-2) =0
5. -(4-х) +2 (8+х) =2
Решите уравнение:а) (х + 4)2 = 3х + 40; б) (2х
Решите уравнение:
а) (х + 4)2 = 3х + 40; б) (2х — 3)2 = 11х — 19;
в) 3(х + 4)2 = 10x + 82; г) 15х2 + 17 = 15(х + 1)2;
д) (х + 1)2 = 7918 — 2х; е) (х + 2)2 = 3131 — 2х;
ж) (x + 1)2 = (2х — 1)2; з) (х — 2)2 + 48 = (2 — 3х)2.Решение:
а) (х + 4)2 = 3х + 40; х2 + 8х + 16 — 3х-40 = 0; х2 + 5х — 24 = 0;
D = 25 + 4 • 24 = 25 + 96 = 121; х = (-5±11)/2; x1 = -8; х2 = 3;
б) (2х — 3)2 = 11х — 19; 4х2 — 12х + 9 — 11х + 19 = 0; 4х2 — 23х + 28 = 0;
D = 232 — 4 • 4 • 28 = 529 — 448 = 81; х = (23±9)/8; x1 = 1,75; х2 = 4;
в) 3(х + 4)2 = 10x + 82; 3х2 + 24х + 48 = 10х + 32; 3х2 + 14х + 16 = 0;
D = 72 — 3 • 16 = 49 — 48 = 1; х = (-7±1)/3; x1 = — 2 2/3; х2 = — 2;
г) 15х2 + 17 = 15(х + 1)2; 15х2+ 17 = 15х2 + 30х + 15; 30x = 2; x = 1/15;
д) (х + 1)2 = 7918 — 2х; х2 + 2х + 1 — 7918 + 2х = 0; х2 + 4х — 7917 = 0;
D1 = 22 + 7917 = 7921; х = -2 ± 89; x1 = -91; х2 = 87;
е) (х + 2)2 = 3131 — 2х; х2 + 4х + 4 — 3131 + 2х = 0; х2 + 6х — 3127 = 0;
D1 = 32 + 3127 = 3136; х = -3 ± 56; x1 = -59; х2 = 53;
ж) (x + 1)2 = (2х — 1)2; (2х — 1)2 — (х + 1)2 = 0; (2х — 1 — х — 1) (2х — 1 + x + 1) = 0; (х — 2) • х = 0; х2 — 2х = 0; х(х — 2) = 0; x1 = 0; х2 = 2;
з) (х — 2)2 + 48 = (2 — 3х)2; х2 — 4х + 4 + 48 = 4 — 12х + 9х2; 8х2 — 8х — 48 = 0; х2 — х — б = 0;
D = 1 + 24 = 25; х = (1±5)/2; x1 = -2; х2 = 3.
Похожие задачи:
2 = 0 Tiger Algebra Solver
Пошаговое решение:
Шаг 1:
Уравнение в конце шага 1:
((x 4 ) - (2 • (x 3 ))) - 2x 2 = 0
Шаг 2:
Уравнение в конце шага 2:
((x 4 ) - 2x 3 ) - 2x 2 = 0
Шаг 3:
Шаг 4:
Условия вытягивания:
4.1 Факторы вытягивания:
x 4 — 2x 3 — 2x 2 = x 2 • (x 2 — 2x — 2)
Попытка разложить на множители путем разделения среднего члена
4.2 Факторинг x 2 — 2x — 2
Первый член, x 2 , его коэффициент равен 1.
Средний член равен -2x, его коэффициент равен -2.
Последний член, «константа», равен -2Шаг-1: Умножьте коэффициент первого члена на константу 1 • -2 = -2
Шаг-2: Найдите два множителя -2, сумма которых равен коэффициенту среднего члена, равному -2.

-2 + 1 = -1 -1 + 2 = 1 Наблюдение: Два таких фактора не могут быть найдены !!
Вывод: трехчлен не может быть разложен на множителиУравнение в конце шага 4:
x 2 • (x 2 - 2x - 2) = 0
Шаг 5:
Теория — Истоки продукта:
5.1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы один из членов должен быть равен нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте
Любое решение term = 0 также решает product = 0.
Решение уравнения с одной переменной:
5.2 Решение: x 2 = 0
Решение: x 2 = 0
Парабола, поиск вершины:
5.
 3 Найдите вершину y = x 2 -2x-2
3 Найдите вершину y = x 2 -2x-2Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A).В нашем случае координата x равна 1.0000
Подставив в формулу параболы 1.0000 для x, мы можем вычислить координату y:
y = 1.0 * 1.00 * 1.00 — 2.0 * 1.00 — 2.0
или y = -3.000Parabola, Графическое изображение вершины и пересечения X:
Корневой график для: y = x 2 -2x-2
Ось симметрии (пунктирная линия) {x} = {1,00}
Вершина в точке {x, y} = {1,00, — 3.00}
x -Перехват (корни):
Корень 1 при {x, y} = {-0.73, 0.00}
Корень 2 при {x, y} = {2.73, 0.00}Решите квадратное уравнение, заполнив квадрат
5.4 Решение x 2 -2x-2 = 0, заполнив квадрат.
Добавьте 2 к обеим сторонам уравнения:
x 2 -2x = 2Теперь умный бит: возьмите коэффициент при x, равный 2, разделите его на два, получив 1, и возведите его в квадрат, получив 1
Добавьте 1 к обеим частям уравнения:
В правой части мы имеем:
2 + 1 или, (2/1) + (1/1)
Общий знаменатель двух дробей равен 1 Сложение (2 / 1) + (1/1) дает 3/1
Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем:
x 2 -2x + 1 = 3Добавление 1 завершило левую часть в идеальный квадрат:
x 2 -2x + 1 =
(x-1) • (x-1) =
(x-1) 2
Вещи, которые равны одному и тому же, также равны друг другу. Поскольку
Поскольку
x 2 -2x + 1 = 3 и
x 2 -2x + 1 = (x-1) 2
, то согласно закону транзитивности
(x-1) 2 = 3Мы будем называть это уравнение уравнением. # 5.4.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-1) 2 равен
(x-1) 2/2 =
(x-1) 1 =
x-1Теперь, применяя Принцип квадратного корня для уравнения.# 5.4.1 получаем:
x-1 = √ 3Добавьте 1 к обеим сторонам, чтобы получить:
x = 1 + √ 3Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — 2x — 2 = 0
имеет два решения:
x = 1 + √ 3
или
x = 1 — √ 3Решите квадратное уравнение с помощью квадратичной формулы
5.5 Решение x 2 -2x-2 = 0 по квадратичной формуле.

Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2AВ нашем случае A = 1
B = -2
C = -2Соответственно B 2 — 4AC =
4 — (-8) =
12Применение квадратичной формулы:
2 ± √ 12
x = —————
2Можно ли упростить √ 12?
Да! Разложение 12 на простые множители равно
2 • 2 • 3
Чтобы можно было удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).√ 12 = √ 2 • 2 • 3 =
± 2 • √ 3√ 3, округленное до 4 десятичных цифр, составляет 1,7321
Итак, теперь мы смотрим на:
x = (2 ± 2 • 1,732) / 2Два реальных решения:
x = (2 + √12) / 2 = 1 + √ 3 = 2,732
или:
x = (2-√12) / 2 = 1-√ 3 = -0,732
Было найдено три решения:
- x = (2-√12) / 2 = 1-√ 3 = -0,732
- x = (2 + √12) / 2 = 1 + √ 3 = 2,732
- x 2 = 0
Как вы множите x ^ 4 + 2x ^ 3 — 8x -16?
Дано: # x ^ 4 + 2x ^ 3-8x-16 #
Первое наблюдение: # 2xx8 = 16 #, поэтому у нас есть возможное соединение.
 2) #
2) #Где #color (white) («d») — (- b) a = + ab #
Решите уравнение (2x + 3 / x — 4) — (2x — 8 / 2x + 1) = 1
Решите уравнение (2x + 3 / x — 4) — (2x — 8 / 2x + 1) = 1
Ответ
Для начала мы должны найти общий знаменатель между двумя дробями.
При решении сложных задач, которые включают буквы и цифры, проще всего умножить знаменатель каждой дроби вместе следующим образом:
(х — 4) (2x + 1)
Это будет общий знаменатель левой части знака равенства.
Чтобы учесть этот новый знаменатель, мы должны также изменить числитель.
Например, мы должны умножить (2x + 3) на (2x +1), а затем (2x — 8) на (x — 4), чтобы оставить все уравнение без общего знаменателя (x — 4) (2x + 1)
Итак, новое уравнение выглядит следующим образом:
(2x + 3) (2x + 1) — (2x — 8) (x — 4) / (x — 4) (2x + 1) = 1
Теперь нам нужно раскрыть скобки:
(2x + 3) (2x + 1) превратится в (4x 2 + 2x + 6x + 3), когда вы начнете с умножения первого числа в первой скобке на первое число во второй скобке, затем вы умножите первое число в первой скобке на второе число во второй скобке, затем вы умножаете второе число в первой скобке на первое число во второй скобке, затем, наконец, вы умножаете второе число в первой скобке на второе число в вторая скобка.

(4x 2 + 2x + 6x + 3) затем можно упростить до (4x 2 + 8x + 3)
(2x — 8) (x — 4) превратится в (2x 2 — 8x — 8x + 32), поскольку вы выполните тот же процесс, что и выше. Затем это можно упростить до (2x 2 — 16x + 32)
Общий знаменатель (x — 4) (2x + 1) станет (2x 2 + x — 8x — 4), который можно упростить до (2x 2 — 7x — 4)
Итак, теперь уравнение в целом выглядит так:
(4x 2 + 8x + 3) — (2x 2 — 16x + 32) / (2x 2 — 7x — 4) = 1
Теперь вы снимаете скобки и упрощаете числитель. NB — при снятии скобок во втором уравнении чрезвычайно важно учитывать знак «-»
Таким образом, числитель выглядит как 4x 2 + 8x + 3 — 2x 2 + 16x (поскольку двойной минус дает плюс) — 32
Это тогда равно 2x 2 + 24x — 29
Уравнение теперь выглядит так:
2x 2 + 24x — 29 / 2x 2 — 7x — 4 = 1
Теперь вы должны посмотреть, чтобы убрать знаменатель.
 Для этого вы должны переместить его на другую сторону от знака равенства, туда, где стоит единица. Это делается путем умножения 1 на (2x 2 — 7x — 4)
Для этого вы должны переместить его на другую сторону от знака равенства, туда, где стоит единица. Это делается путем умножения 1 на (2x 2 — 7x — 4)Итак,
2x 2 + 24x — 29 = 2x 2 — 7x — 4
Чтобы переставить это, 2x 2 будут отменены, — 7x станет + 7x при перемещении в левую часть уравнения и станет + 25, когда — 29 станет + 29 после него. присоединяется к правой части уравнения.
31x = 25
Теперь, наконец, чтобы изолировать x, вы должны разделить x на 31
х = 25/31
Следовательно, x = 0,8064516129 или 0,81 (2 десятичных знака)
Алгебраическое решение уравнений
Алгебраическое решение уравнений
Содержание: Эта страница соответствует § 2.4
(с. 200) текста.Предлагаемые задачи из текста:
с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87,
88, 95, 97Квадратные уравнения
Уравнения с радикалами
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения
Квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0.
Факторинг
Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то
хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое.
Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2 или x = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt (k).
Пример 2.
x 2 — 9 = 0.
x 2 = 9.
x = 3 или x = -3.
Пример 3.
Пример 4.
x 2 + 7 = 0.

х 2 = -7.
х = ±.
Обратите внимание, что = =,
так что решенияx = ±, два комплексных числа.
Завершение квадрата
Идея завершения квадрата заключается в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат
корневой принцип.Пример 5.
x 2 + 6x — 1 = 0.
x 2 + 6x = 1.
x 2 + 6x + 9 = 1 + 9.
9, добавленные к обеим сторонам, были возведены в квадрат половинного коэффициента при x, (6/2) 2 = 9. Причина
выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами).
Поэтому эта процедура называется — завершение квадрата .[Заинтересованный читатель может видеть, что это
верно, учитывая (x + a) 2 = x 2 + 2ax + a 2 . Чтобы получить «а» нужно всего лишь
Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .](x + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
x = -3 ± sqrt (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент
(коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив
обе части уравнения на 2.x 2 + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат,
(3/2) 2 = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.x 2 + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от
проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня
могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.Пример 7.
x 2 = 16.
x 2 — 16 = 0.
(x + 4) (x — 4) = 0.
x = -4 или x = 4.
В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.

Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае
мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие:
всегда одинаковы, поэтому их можно применить к общему квадратному уравнениютопор 2 + bx + c = 0.
Результатом завершения квадрата в этом общем уравнении является формула для решений уравнения
называется квадратной формулой.Квадратичная формула
Решение уравнения ax 2 + bx + c = 0:
Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае,
где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его
в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения.

Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика
функции f (x) = 2x 2 + 6x — 5.Пример 9.
4x 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует обратить внимание на две вещи.

- Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
- Решение упрощено, так что квадратный корень не используется. Это означает, что уравнение могло быть
решается факторингом. (Все квадратные уравнения могут быть решены факторизацией! Я имею в виду, что это могло быть
решено легко факторингом.)
4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0.
х = -1/2.
Пример 10.
х 2 + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов.
функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2
+ x + 1 не имеет пересечений по x.
Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом
уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.
Примечания к проверке растворов
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример
3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения,
потому что при решении уравнений очень легко сделать невнимательные ошибки.Алгебраический метод, который заключается в подстановке числа обратно в уравнение и проверке того, что
полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда
решение предполагает радикальное.
Например, в предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) 2 +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2.
Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический
проверить или использовать калькулятор для алгебраической проверки быстрее.Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x 2 + 6x — 5 и проследите график, чтобы приблизительно определить, где
х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение.Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и перешли непосредственно к графику
утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя
(алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень
близко к найденным вами числам, значит, вы, наверное, правы!Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3x 2 -5x — 2 = 0. Ответ
(b) (x + 1) 2 = 3. Ответ
(c) x 2 = 3x + 2. Ответ
Вернуться к содержанию
Уравнения с участием радикалов
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы
радикальный член сам по себе на одной стороне уравнения.Пример 11.
Теперь, когда мы изолировали радикальный член в правой части, возводим обе стороны в квадрат и решаем полученное уравнение
для x.Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно
раствор .Решение : x = 3.
Примечание: Решением является координата x точки пересечения графиков y = x и
у = sqrt (х + 1) +1.
Посмотрите, что произошло бы, если бы мы возводили обе части уравнения в квадрат до , выделив радикал
срок.Это хуже того, с чего мы начали!
Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью
возведение в степень один раз. Однако мы можем на уменьшить количество радикальных членов на , возведя в степень.Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и
возвести в степень. Затем мы повторяем этот процесс.Пример 12.
Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат
снова обе стороны.Чек:
Подстановка x = 5/4 в исходное уравнение дает
sqrt (9/4) + sqrt (1/4) = 2.

3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание к проверочным решениям:
В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что
нет решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение
— координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).Упражнение 2:
Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее. Когда мы встречаемся
Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой.Нулевая постоянная
Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий
x, чтобы начать задачу.Пример 13.
2x 3 + 3x 2 -5x = 0.
x (2x 2 + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x 2 + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом.
Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, мы могли бы прибегнуть к
к использованию квадратичной формулы.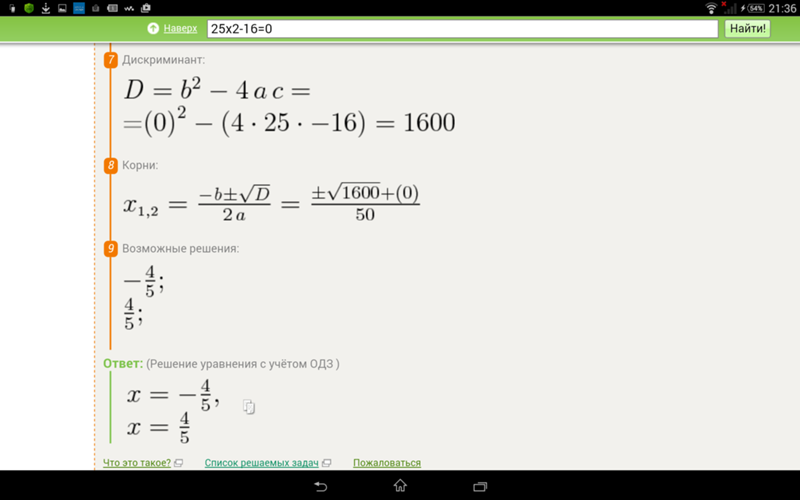 [Убедитесь, что вы получили те же результаты, что и ниже.]
[Убедитесь, что вы получили те же результаты, что и ниже.]x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x 3
+ 3x 2 -5x.Фактор по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0.
Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между
коэффициенты при третьем и четвертом членах. Группа термины один и два, а также термины третий и четвертый.x 2 (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x 2 — 9) = 0.
Когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.

x — 2 = 0 или x 2 — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x 3
-2x 2 -9x +18.Квадратичная форма
Пример 15.
x 4 — x 2 — 12 = 0.
Этот многочлен неквадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x 2 .
(x 2 ) 2 — (x 2 ) — 12 = 0.
Это может помочь вам фактически заменить z на x 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на
x 2 и решите полученные уравнения.x 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i или x = — i.
Итак, есть четыре решения, два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x 4
— х 2 — 12.График f (x) = x 4 — x 2 -12 и масштабирование, показывающее его локальную
экстремумы.Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения, содержащие дробные выражения или абсолютные значения
Пример 16.
Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы
убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков.
из y = 1 и y = 2 / x-1 / (x + 2).Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения
столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности,
и все решения должны быть проверены.Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (х — 1) = х + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение становится
-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты
точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).Упражнение 4:
(а) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ
Вернуться к содержанию
Распределительная собственность — ChiliMath
Распределительное свойство умножения над сложением позволяет нам исключить символ группировки, обычно в форме круглых скобок.Следующая диаграмма иллюстрирует основной шаблон или формулу, как ее применять.
Основная «формула» распределительной собственности
Несколько заметок:
- Это делается путем умножения внешнего члена на каждый член в скобках.
- Таким образом, возьмите член a, стоящий вне скобок, и распределите его по каждому члену внутри скобок.
- Обратите внимание, что ab означает a, умноженное на b.
- Точно так же ac означает a, умноженное на c.
Объединение одинаковых терминов с использованием свойства распределения
Пример 1: Распределить, а затем упростить приведенное ниже выражение.
Можно ли сразу скомбинировать x-термины? Не так быстро! Член 2x находится внутри скобок, а 3x — снаружи. Мы не можем объединить их, потому что они находятся в разных местах.
Что нам нужно сделать, так это сначала удалить символ круглой скобки, прежде чем мы сможем объединить похожие термины, которые могут возникнуть при сложении или вычитании.Вот где полезность этого свойства вступает в игру.
На этом этапе скобки опущены, и все x-члены можно комбинировать. Я бы переставил их, поместив похожие термины рядом, прежде чем выполнять требуемую операцию.
Пример 2: Распределить, а затем упростите приведенное ниже выражение.
Поскольку здесь две круглые скобки, мы должны применить свойство дважды. Это должно избавить нас от символов группировки и позволить нам комбинировать похожие термины.
После удаления двух круглых скобок теперь можно комбинировать похожие термины. Перед выполнением требуемой операции сложения или вычитания убедитесь, что вы переставили термины таким образом, чтобы одинаковые термины располагались рядом.
Пример 3: Распределить, а затем упростить приведенное ниже выражение.
Я надеюсь, что теперь вы можете увидеть закономерность. Имея три круглые скобки, мы также должны применить его трижды.
Поскольку все термины теперь находятся за пределами круглых скобок, продолжайте комбинировать похожие термины.
Пример 4: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Пример 5: Распределить, а затем упростите приведенное ниже выражение.
Решение:
Пример 6: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Сначала примените свойство распределения к внутренним скобкам и объедините похожие термины.Наконец, избавьтесь от символа квадратной скобки, распределив еще раз.
Вы также можете использовать свойство распределения при решении уравнений .
Решение линейных уравнений с использованием распределительного свойства
Пример 7: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Как видите, внешнее число 3, находящееся непосредственно слева от круглой скобки, предполагает, что мы можем применить свойство для удаления символа группировки.
- Возьмите это число 3 и умножьте на каждый член в скобках.
- После этого символ скобки должен исчезнуть. Затем мы можем перейти к обычным шагам решения уравнения. В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
Пример 8: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Наличие двух круглых скобок в левой части уравнения означает, что мы должны распределить дважды.
Избавившись от символов группировки, теперь мы можем комбинировать похожие термины и изолировать переменную в левой части уравнения.
Пример 9: Используйте свойство распределения, чтобы решить уравнение.
Решение:
Начните с распределения 4 в первые скобки, а затем — 1 во вторую скобку.Затем объедините похожие термины, которые возникают после исключения скобок. Наконец, решите x, выделив его слева.
Пример 10: Используйте свойство распределения для решения уравнения.
Решение:
Здесь мы видим две круглые скобки, которые означают, что мы будем распределять дважды, по одной с каждой стороны уравнения, чтобы исключить символы группировки. Затем решите линейное уравнение как обычно. 😀
Инверсия функции — объяснение и примеры
Что такое обратная функция?
В математике обратная функция — это функция, отменяющая действие другой функции.
Например, , сложение и умножение являются противоположностью вычитания и деления соответственно.
Обратную функцию можно рассматривать как отражение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
Мы используем символ f — 1 для обозначения обратной функции. Например, если f (x) и g (x) противоположны друг другу, то мы можем символически представить это утверждение как:
g (x) = f — 1 (x) или f (x) = g −1 (x)
Об обратной функции следует отметить то, что обратная функция не совпадает с обратной, т.е.е., f — 1 (x) ≠ 1 / f (x). В этой статье мы обсудим, как найти обратную функцию.
Поскольку не все функции имеют инверсию, важно проверить, есть ли у функции инверсия, прежде чем приступать к определению инверсии.
Мы проверяем, есть ли у функции инверсия, чтобы не тратить время на поиск чего-то несуществующего.
Индивидуальные функции
Итак, как мы можем доказать, что данная функция имеет обратную? Функции, у которых есть обратные, называются взаимно однозначными функциями.
Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.
Другими словами, домен и диапазон однозначной функции имеют следующие отношения:
- Область f −1 = Диапазон f.
- Диапазон f −1 = Область f.
Например, чтобы проверить, является ли f (x) = 3x + 5 взаимно однозначной заданной функцией, f (a) = 3a + 5 и f (b) = 3b + 5.
⟹ 3a + 5 = 3b + 5
⟹ 3a = 3b
⟹ a = b.
Следовательно, f (x) является взаимно однозначной функцией, потому что a = b.
Рассмотрим другой случай, когда функция f задается формулой f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция взаимно однозначна, потому что ни одно из ее значений y не встречается более одного раза.
А как насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, потому что значение y, равное –9, встречается более одного раза.
Вы также можете графически проверить взаимно однозначную функцию, проведя вертикальную и горизонтальную линии через график функции. Функция взаимно однозначна, если и горизонтальная, и вертикальная линии проходят через график один раз.
Как найти обратную функцию?
Найти инверсию функции — несложный процесс, хотя нам действительно нужно быть осторожными с парой шагов. В этой статье мы будем предполагать, что все функции, с которыми мы будем иметь дело, относятся друг к другу.
Вот процедура нахождения обратной функции f (x):
- Заменить обозначение функции f (x) на y.
- Поменять местами x на y и наоборот.
- Начиная с шага 2, решите уравнение относительно y. Будьте осторожны с этим шагом.
- Наконец, измените y на f −1 (x). Это обратная функция.
- Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:
⟹ (f ∘ f −1 ) (x) = x
⟹ (f −1 ∘ f) (x) = x
Давайте поработаем пару примеров.
Пример 1
Дана функция f (x) = 3x — 2, найти обратную ей.
Решение
f (x) = 3x — 2
Заменить f (x) на y.
⟹ y = 3x — 2
Поменять местами x на y
⟹ x = 3y — 2
Решить для y
x + 2 = 3 года
Разделим на 3, чтобы получить;
1/3 (x + 2) = y
х / 3 + 2/3 = у
Наконец, заменим y на f −1 (x).
f −1 (x) = x / 3 + 2/3
Проверить (f ∘ f −1 ) (x) = x
(f ∘ f −1 ) (x) = f [f −1 (x)]
= f (x / 3 + 2/3)
⟹ 3 (х / 3 + 2/3) — 2
⟹ х + 2 — 2
= х
Следовательно, f −1 (x) = x / 3 + 2/3 — правильный ответ.
Пример 2
Дано f (x) = 2x + 3, найдите f −1 (x).
Решение
f (x) = y = 2x + 3
2x + 3 = y
Поменять местами x и y
⟹2y + 3 = x
Теперь решите для
y
⟹2y = х — 3
⟹ y = x / 2 — 3/2
Наконец, заменим y на f −1 (x)
⟹ f −1 (x) = (x– 3) / 2
Пример 3
Задайте функцию f (x) = log 10 (x), найдите f −1 (x).
Решение
f (x) = log₁₀ (x)
Заменен f (x) на y
⟹ y = журнал 10 (x) ⟹ 10 y = x
Теперь поменяйте местами x на y, чтобы получить;
⟹ y = 10 x
Наконец, заменим y на f −1 (x).
f -1 (x) = 10 x
Следовательно, обратное значение f (x) = log 10 (x) равно f -1 (x) = 10 x
Пример 4
Найдите обратную функцию следующей функции g (x) = (x + 4) / (2x -5)
Решение
г (x) = (x + 4) / (2x -5) ⟹ y = (x + 4) / (2x -5)
Поменять местами y с x и наоборот
y = (x + 4) / (2x -5) ⟹ x = (y + 4) / (2y -5)
⟹ х (2у − 5) = у + 4
⟹ 2xy — 5x = y + 4
⟹ 2xy — y = 4 + 5x
⟹ (2x — 1) y = 4 + 5x
Разделите обе части уравнения на (2x — 1).
⟹ у = (4 + 5x) / (2x — 1)
Заменить y на g — 1 (x)
= г — 1 (x) = (4 + 5x) / (2x — 1)
Проба:
(г г -1 ) (x) = г [г -1 (x)]
= г [(4 + 5x) / (2x — 1)]
= [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5]
Умножьте числитель и знаменатель на (2x — 1).
⟹ (2x — 1) [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5] (2x — 1).
⟹ [4 + 5x + 4 (2x — 1)] / [2 (4 + 5x) — 5 (2x — 1)]
⟹ [4 + 5x + 8x − 4] / [8 + 10x — 10x + 5]
⟹13x / 13 = x
Следовательно, g — 1 (x) = (4 + 5x) / (2x — 1)Пример 5
Определите значение, обратное следующей функции f (x) = 2x — 5
Решение
Заменить f (x) на y.
f (x) = 2x — 5⟹ y = 2x — 5
Переключите x и y, чтобы получить;
⟹ x = 2y — 5
Изолировать переменную y.
2у = х + 5
⟹ у = х / 2 + 5/2
Измените y обратно на f –1 (x).
⟹ f –1 (x) = (x + 5) / 2
Пример 6
Найти обратную функцию к функции h (x) = (x — 2) 3 .
Решение
Измените h (x) на y, чтобы получить;
h (x) = (x — 2) 3 ⟹ y = (x — 2) 3
Поменять местами x и y
⟹ х = (у — 2) 3
Изолятор ул.
y 3 = x + 2 3
Найдите кубический корень из обеих частей уравнения.
3 √y 3 = 3 √x 3 + 3 √2 3
y = 3 √ (2 3 ) + 2
Заменить y на h — 1 (x)
ч — 1 (x) = 3 √ (2 3 ) + 2
Пример 7
Найти обратную величину h (x) = (4x + 3) / (2x + 5)
Решение
Заменить h (x) на y.
h (x) = (4x + 3) / (2x + 5) ⟹ y = (4x + 3) / (2x + 5)
Поменять местами x и y.
⟹ х = (4у + 3) / (2у + 5).
Решите относительно y в приведенном выше уравнении следующим образом:
⟹ х = (4у + 3) / (2у + 5)
Умножаем обе стороны на (2y + 5)
⟹ х (2у + 5) = 4у + 3
Распределить х
⟹ 2xy + 5x = 4y + 3
Изолятор ул.
⟹ 2xy — 4y = 3 — 5x
⟹ y (2x — 4) = 3-5x
Разделим на 2x — 4, чтобы получить;
⟹ y = (3-5x) / (2x — 4)
Наконец, замените y на h — 1 (x).
⟹ ч — 1 (x) = (3 — 5x) / (2x — 4)
Практические вопросы
Найдите обратное из следующих функций:
- г (x) = (2x — 5) / 3.
- h (x) = –3x + 11.
- г (x) = — (x + 2) 2 — 1.
- г (х) = (5/6) х — 3/4
- f (x) = 3 x — 2.
- h (x) = x 2 + 1.
- г (x) = 2 (x — 3) 2 -5
- f (x) = x 2 / (x 2 + 1)
- h (x) = √x — 3.
- f (x) = (x — 2) 5 + 3
- f (x) = 2 x 3 — 1
- f (x) = x 2 — 4 x + 5
- г (x) = 5 √ (2x + 11)
- h (x) = 4x / (5 — x)
Предыдущий урок | Главная страница | Следующий урок
Три правила экспонент — Полный курс алгебры
Урок 13, Раздел 2
Вернуться в раздел 1
Правило 1.Та же база
Правило 2. Мощность продукта
Правило 3. Степень мощности
Правило 1. То же основание
«Чтобы умножить степени одного основания, сложите экспоненты».
Например, a 2 a 3 = a 5 .
Почему мы добавляем экспоненты? Из-за того, что означают символы. Секция 1.
Пример 1. Умножение 3 x 2 · 4 x 5 · 2 x
Решение . Задача означает (Урок 5): умножьте числа, затем сложите степени x :
3 x 2 · 4 x 5 · 2 x = 24 x 8
Два фактора x — x 2 — умножить на пять факторов x — x 5 — умножить на один фактор x , произвести всего 2 + 5 + 1 = 8 множителей x : x 8 .
Задача 1. Умножить. Примените правило Same Base.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!а) 5 x 2 · 6 x 4 = 30 x 6 б) 7 x 3 · 8 x 6 = 56 x 9 в) x · 5 x 4 = 5 x 5 г) 2 x · 3 x · 4 x = 24 x 3 e) x 3 · 3 x 2 · 5 x = 15 x 6 е) x 5 · 6 x 8 y 2 = 6 x 13 y 2 г) 4 x · y · 5 x 2 · y 3 = 20 x 3 y 4 ч) 2 x y · 9 x 3 y 5 = 18 x 4 y 6 i) a 2 b 3 a 3 b 4 = a 5 b 7 к) a 2 bc 3 b 2 ac = a 3 b 3 c 4 к) x м y n x p y q = x n + q л) a p b q ab = a p + 1 b q + 1 Проблема 2.Различают следующие:
x · x и x + x .
x · x = x ². x + x = 2 x .
Пример 2. Сравните следующее:
а) x · x 5 б) 2 · 2 5
Решение .
a) x · x 5 = x 6
b) 2 · 2 5 = 2 6
Часть b) имеет ту же форму , что и часть a). Это часть а) с x = 2.
Один множитель 2 умножает пять множителей 2, давая шесть множителей 2.
2 · 2 = 4 здесь неверно.
Проблема 3. Примените правило Same Base.
а) x x 7 = x 8 б) 3 · 3 7 = 3 8 в) 2 · 2 4 · 2 5 = 2 10 г) 10 · 10 5 = 10 6 д) 3 x · 3 6 x 6 = 3 7 x 7 Проблема 4.Примените правило Same Base.
а) x n x 2 = x n + 2 б) x n x = x n + 1 в) x n x n = x 2 n г) x n x 1- n = x e) x · 2 x n — 1 = 2 x n е) x n x м = x n + m г) x 2 n x 2- n = x n + 2 Правило 2: Сила произведения факторов
«Увеличьте каждый коэффициент до той же степени.«
Например, ( ab ) 3 = a 3 b 3 .
Почему мы можем это сделать? Опять же, в соответствии с тем, что означают символы:
( ab ) 3 = ab · ab · ab = aaabbb = a 3 b 3 .
Порядок факторов не имеет значения:
ab · ab · ab = aaabbb .
Задача 5. Применить правила экспонент.
а) ( x y ) 4 = x 4 y 4 б) ( pqr ) 5 = p 5 q 5 r 5 в) (2 abc ) 3 = 2 3 a 3 b 3 c 3 d) x 3 y 2 z 4 ( xyz ) 5 = x 3 y 2 z 4 · x 5 y 5 z 5 Правило 2. = x 8 y 7 z 9 То же основание. Правило 3: Сила силы
«Чтобы взять степень степени, умножьте экспонент».
Например, ( a 2 ) 3 = a 2 · 3 = a 6 .
Почему мы это делаем? Опять же, из-за того, что означают символы:
( a 2 ) 3 = a 2 a 2 a 2 = a 3 · 2 = a
1
9
Задача 6. Примените правила экспонент.
а) ( x 2 ) 5 = x 10 б) ( a 4 ) 8 = a 32 в) (10 7 ) 9 = 10 63 Пример 3.Примените правила экспонент: (2 x 3 y 4 ) 5
Решение . В скобках указаны три фактора: 2, x 3 и y 4 . Согласно Правилу 2 мы должны брать пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,
(2 x 3 y 4 ) 5 = 2 5 x 15 y 20
Проблема 7.Применяйте правила экспонент.
а) (10 a 3 ) 4 = 10 000 a 12 б) (3 x 6 ) 2 = 9 x 12 в) (2 a 2 b 3 ) 5 = 32 a 10 b 15 г) ( xy 3 z 5 ) 2 = x 2 y 6 z 10 e) (5 x 2 y 4 ) 3 = 125 x 6 y 12 е) (2 a 4 bc 8 ) 6 = 64 a 24 b 6 c 48 Проблема 8.Применяйте правила экспонент.
a) 2 x 5 y 4 (2 x 3 y 6 ) 5 = 2 x 5 y
9 · 4
908 2 5 x 15 y 30 = 2 6 x 20 y 34
b) abc 9 ( a 2 b 3 c 4 ) 8
= abc 9 · a 16 b 24 c 32 = a 17 b 25 c 11Проблема 9.Используйте правила экспонент, чтобы вычислить следующее.
a) (2 · 10) 4 = 2 4 · 10 4 = 16 · 10 000 = 160 000
б) (4 · 10 2 ) 3
= 4 3 · 10 6 = 64 000 000в) (9 · 10 4 ) 2
= 81 · 10 8 = 8 100 000 000В степени 10 столько же нулей, сколько в экспоненте 10.
Пример 4. Квадрат x 4 .
Решение . ( x 4 ) 2 = x 8 .
Чтобы возвести в квадрат степень, удвойте экспоненту.
Проблема 10. Возведите следующее.
а) x 5 = x 10 б) 8 a 3 b 6 = 64 a 6 b 12 в) −6 x 7 = 36 x 14 г) x n = x 2 n Часть c) иллюстрации: Квадрат числа никогда не бывает отрицательным.
(−6) (- 6) = +36. Правило знаков.
Задача 11. Примените правило экспонент — если возможно.
а) x 2 x 5 = x 7 , Правило 1. б) ( x 2 ) 5 = x 10 , Правило 3. в) x 2 + x 5 Невозможно. Правила экспонент применяют только к умножению. В итоге: Добавьте показателей степени, когда одно и то же основание появляется дважды: x 2 x 4 = x 6 . Умножьте экспоненты, когда основание появится один раз — и в скобках:
( x 2 ) 5 = x 10 .Задача 12. Примените правила экспонент.
а) ( x n ) n = x n · n = x n 0 9109 2 900
б) ( x n ) 2 = x 2 n Проблема 13.Примените правило экспонент или добавьте похожие термины — если возможно.
а) 2 x 2 + 3 x 4
Невозможно. Это не похоже на термины .б) 2 x 2 · 3 x 4 = 6 x 6 . Правило 1.
c) 2 x 3 + 3 x 3
= 5 x 3 .Как термины. Показатель степени не меняется.г) x 2 + y 2
Невозможно. Это не похоже на термины.e) x 2 + x 2
= 2 x 2 . Как термины.f) x 2 · x 2
= x 4 . Правило 1г) x 2 · y 3
Невозможно.Разные базы.ч) 2 · 2 6
= 2 7 . Правило 1i) 3 5 + 3 5 + 3 5 =
3 · 3 5 (При добавлении подобных терминов) = 3 6 .

 22 м до 3.97 м;
22 м до 3.97 м;