Содержание
Несобственный интеграл онлайн
Определённый интеграл называется несобственным, если выполняется хотя бы одно из двух условий:
Один (или оба) из пределов интегрирования равен
или
. В этом случае, интеграл называется
несобственным интегралом первого рода, например:
.
В любой точке на отрезке интегрирования, подинтегральная функция терпит бесконечный разрыв. В этом случае, интеграл называется
несобственным интегралом второго рода, например:
в точке
.
Рассмотрим в качестве примера
несобственный интеграл
первого рода
. График подинтегральной функции
на отрезке интегрирования
имеет вид:
Геометрически, данный несобственный интеграл равен площади под графиком функции
на отрезке
. Рассматриваемый интеграл является сходящимся, потому что указанная площадь равна
Рассматриваемый интеграл является сходящимся, потому что указанная площадь равна
12
— конечному числу. Однако, несобственные интегралы бывают и расходящимися, например:
Алгоритм вычисления несобственного интеграла первого рода выглядит следующим образом:
Сначала мы заменяем бесконечный предел на некоторый параметр, например
и получаем определенный интеграл. Этот интеграл мы вычисляем обычным образом: берем
неопределенный интеграл
и далее используем формулу Ньютона-Лейбница. На завершающем этапе, мы вычисляем
предел
при
и, если, данный предел существует и конечен, тогда исходный несобственный интеграл является сходящимся, а в противном случае — расходящимся.
Алгоритм вычисления несобственного интеграла второго рода заключается в разбивке интервала интегрирования на отрезки в каждом из которых подинтегральная функция является непрерывной (разрывы допускаются только на концах отрезка). Далее, вычисляются полученные
определенные интегралы, а при подстановке значений в формулу Ньютона-Лейбница вычисляются соответствующие пределы. И если все эти пределы существуют и конечны, тогда, как и раньше, интеграл является сходящимся, а в противном случае — расходящимся. Приведем пример:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен вычислить очень многие типы несобственных интегралов. При этом, если интеграл расходится, калькулятор выдает сообщение:
integral does not converge.
Вычислить несобственные интегралы или установить их расходимость. Определенный интеграл онлайн
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно.
И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B.
Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов.
Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница.
которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение».
Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн.
Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО
(точно так же, как в определенном интеграле), или доказать, что он расходится
(то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода
. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна
на промежутке , и этот важный факт следует проверять в первую очередь!
Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция
Для определённости предположим, что и тогда типичная криволинейная трапеция
будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл
численно равен её площади
. При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что несобственный интеграл расходится
.
2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится
.
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным
.
Важно!
Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно
. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений
У кого с ними плохо, изучите урок Пределы функций. Примеры решений
, ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике
строить чертежи в данном задании не нужно
.
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций
.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией
– непрерывна она на промежутке интегрирования или нет
. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва
на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего)
, либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности
, следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать
, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела
.
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей
.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов
. Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода
. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
. В этой связи проверим и верхний предел: . Здесь всё хорошо.
В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
*
по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа.
Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа
.
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле
.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом
. В данном случае у нас правосторонний предел
.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
Определенный
интеграл как предел интегральной суммы
может
существовать (т.е. иметь определенное
конечное значение) лишь при выполнении
условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a
;
)
его нельзя разбить на п
частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес
[a
;
b
]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с
,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными
.
Определение.
Пусть
функция
определена на промежутке [a
;
)
и интегрируема на любом конечном отрезке
[a
;
b
],
т.е. существует
для любого b
> a
.
Предел вида
называютнесобственным
интегралом
первого
рода
(или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся
.
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится
.
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–;
b
]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где
а
– произвольная точка. Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На
случай интеграла с бесконечным пределом
можно обобщить и формулу
Ньютона-Лейбница
:
=
=F(+
)
– F(a
),
где
F(+
)
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы
рассмотрели обобщение понятия
определенного интеграла на случай
бесконечного промежутка.
Рассмотрим теперь
обобщение для случая неограниченной
функции.
Определение
Пусть
функция
определена на промежутке [a
;
b
),
неограниченна в некоторой окрестности
точки b
,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел вида
называетсянесобственным
интегралом второго рода
(или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким
образом, несобственный интеграл от
неограниченной в точке b
функции есть по определению
=
.
Если
предел справа существует и конечен, то
интеграл называется сходящимся
.
Если конечного предела не существует,
то несобственный интеграл называется
расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа
:
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно слагаемое.
С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.
Во
многих задачах, приводящих к несобственным
интегралам, не обязательно знать, чему
равен этот интеграл, достаточно лишь
убедиться в его сходимости или
расходимости. Для этого используют
признаки
сходимости
.
Признаки
сходимости несобственных интегралов:
1)
Признак
сравнения
.
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся
).
Признаки
сходимости и расходимости несобственных
интегралов от неограниченных функций
аналогичны сформулированным выше.
Примеры
решения задач.
Пример
1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а)
По определению
имеем:
.
б)
Аналогично
Следовательно,
данный интеграл сходится и равен
.
в)
По определению
=
+
,
причем,а
– произвольное число. Положим в нашем
случае
,
тогда получим:
Данный
интеграл сходится.
Значит, данный
интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно,
данный интеграл расходится.
Пример
2.
Исследовать
сходимость интеграла
в зависимости от п
.
Решение.
При
имеем:
Если
,
то
и.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно,
интеграл сходится.
Если
,
то
следовательно,
интеграл расходится.
Таким
образом,
Пример
3.
Вычислить
несобственный интеграл или установить
его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
Интеграл сходится и равен
.
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
Следовательно,
интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.
Несобственный интеграл с бесконечным пределом интегрирования
Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .
Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif»>?
Нет, не всегда. Подынтегральная функция
https://pandia.ru/text/80/057/images/image007_0.gif»>
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:
Несобственный интеграл
https://pandia.ru/text/80/057/images/image009_0.gif»>», иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что, что несобственный интеграл расходится
.
2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится
Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится
.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.
: .
Пример 1
Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif»>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif»>
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>
Гуд..gif»>
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Сначала попытаемся найти первообразную функцию (неопределенный интеграл).
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif»>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала..
Несобственные интегралы от неограниченных функций
Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif»>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif»>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
.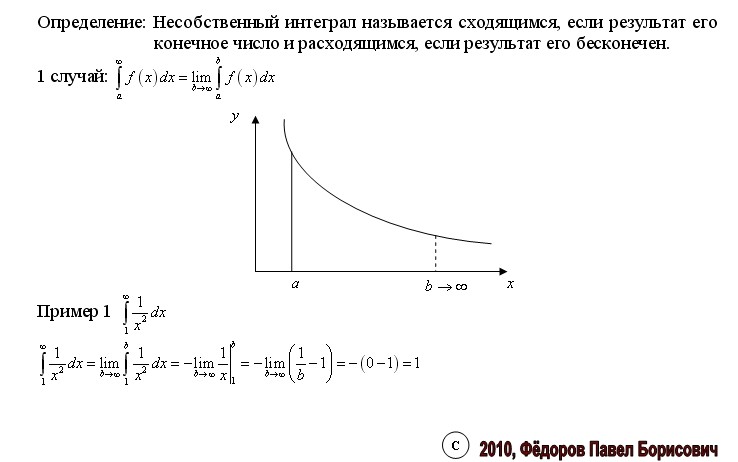 .jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>
.jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению
https://pandia.ru/text/80/057/images/image052.gif»> справа
.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif»>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению
https://pandia. 3+1}.
3+1}.
\]
Несобственный интеграл 2 рода онлайн калькулятор. Несобственные интегралы. Примеры решений
Определенный
интеграл как предел интегральной суммы
может
существовать (т.е. иметь определенное
конечное значение) лишь при выполнении
условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a
;
)
его нельзя разбить на п
частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес
[a
;
b
]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с
,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными
.
Определение.
Пусть
функция
определена на промежутке [a
;
)
и интегрируема на любом конечном отрезке
[a
;
b
],
т.е. существует
для любого b
> a
.
Предел вида
называютнесобственным
интегралом
первого
рода
(или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся
.
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится
.
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–;
b
]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где
а
– произвольная точка. Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На
случай интеграла с бесконечным пределом
можно обобщить и формулу
Ньютона-Лейбница
:
=
=F(+
)
– F(a
),
где
F(+
)
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы
рассмотрели обобщение понятия
определенного интеграла на случай
бесконечного промежутка.
Рассмотрим теперь
обобщение для случая неограниченной
функции.
Определение
Пусть
функция
определена на промежутке [a
;
b
),
неограниченна в некоторой окрестности
точки b
,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т. е.
е.
существует). Предел вида
называетсянесобственным
интегралом второго рода
(или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким
образом, несобственный интеграл от
неограниченной в точке b
функции есть по определению
=
.
Если
предел справа существует и конечен, то
интеграл называется сходящимся
.
Если конечного предела не существует,
то несобственный интеграл называется
расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа
:
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно слагаемое.
С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.
Во
многих задачах, приводящих к несобственным
интегралам, не обязательно знать, чему
равен этот интеграл, достаточно лишь
убедиться в его сходимости или
расходимости. Для этого используют
признаки
сходимости
.
Признаки
сходимости несобственных интегралов:
1)
Признак
сравнения
.
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся
).
Признаки
сходимости и расходимости несобственных
интегралов от неограниченных функций
аналогичны сформулированным выше.
Примеры
решения задач.
Пример
1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а)
По определению
имеем:
.
б)
Аналогично
Следовательно,
данный интеграл сходится и равен
.
в)
По определению
=
+
,
причем,а
– произвольное число. Положим в нашем
Положим в нашем
случае
,
тогда получим:
Данный
интеграл сходится.
Значит, данный
интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно,
данный интеграл расходится.
Пример
2.
Исследовать
сходимость интеграла
в зависимости от п
.
Решение.
При
имеем:
Если
,
то
и.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно,
интеграл сходится.
Если
,
то
следовательно,
интеграл расходится.
Таким
образом,
Пример
3.
Вычислить
несобственный интеграл или установить
его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
Интеграл сходится и равен
.
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
Следовательно,
интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.
Несобственный интеграл с бесконечным пределом интегрирования
Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .
Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif»>?
Нет, не всегда.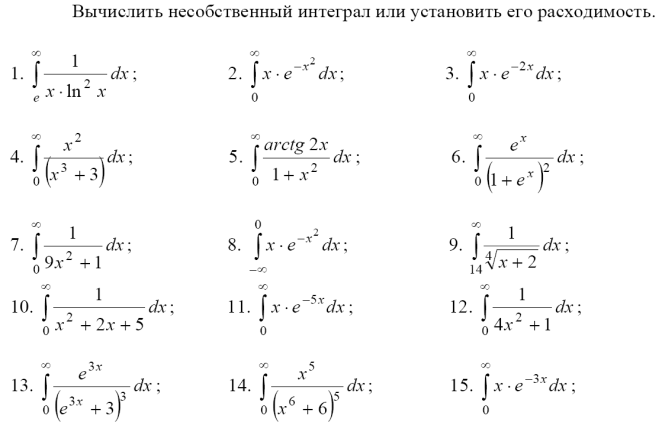 Подынтегральная функция
Подынтегральная функция
https://pandia.ru/text/80/057/images/image007_0.gif»>
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:
Несобственный интеграл
https://pandia.ru/text/80/057/images/image009_0.gif»>», иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что, что несобственный интеграл расходится
.
2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится
.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.
: .
Пример 1
Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif»>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы https://pandia. ru/text/80/057/images/image018_0.gif»>
ru/text/80/057/images/image018_0.gif»>
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Сначала попытаемся найти первообразную функцию (неопределенный интеграл).
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif»>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. .
.
Несобственные интегралы от неограниченных функций
Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif»>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif»>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
..jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению
https://pandia.ru/text/80/057/images/image052.gif»> справа
.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif»>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению
https://pandia. ru/text/80/057/images/image052.gif»> мы должны бесконечно близко приблизиться к точке разрыва слева
ru/text/80/057/images/image052.gif»> мы должны бесконечно близко приблизиться к точке разрыва слева
.
Тема
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла
для случая конечного промежутка
и ограниченной функции
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности
,
,
то придем к интегралу от неограниченной
функции:
,
где
.
2.
Пусть тело массой
движется
по инерции в среде с силой сопротивления
,
где
— скорость тела. Используя второй закон
Ньютона (
,
где
ускорение),
получим уравнение:
,
где
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функция
Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т. е. до момента,
е. до момента,
когда
,
то придем к интегралу по бесконечному
промежутку:
I Определение
Пусть
функция
определена и непрерывна на промежутке
.
Тогда для любого
она интегрируема на промежутке
,
то есть существует интеграл
.
Определение
1
.
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции
по промежутку
и обозначают символом
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (
или не существует) – расходящимся.
Итак,
по определению
Примеры
2.
.
3.
– не существует.
Несобственный
интеграл из примера 1 сходится, в примерах
2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть
— некоторая первообразная для функции
(сущест-вует на
,
т.к.
— непрерывна). Тогда
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела
.
Если этот предел обозначить
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
где
.
Примеры
.
5.
.
6.
Более сложный пример:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл
,
учитывая,
что
:
III
Свойства
Приведем
ряд свойств несобственного интеграла
(1), которые вытекают из общих свойств
пределов и определенного интеграла:
IV
Другие определения
Определение
2
.
Если
непрерывна
на
,
то
.
Определение
3
.
Если
непрерывна
на
,
то принимают по определению
(–
произвольное),
причем
несобственный интеграл в левой части
сходится, если только оба ин-теграла в
правой части сходятся.
Для
этих интегралов, как и для интеграла
(1) можно написать соответствующие
формулы Ньютона – Лейбница.
Пример
7
.
§2.
Признаки сходимости несобственного
интеграла 1-го рода
Чаще
всего несобственный интеграл вычислить
по определению не-возможно, поэтому
используют приближенное равенство
(для
больших
).
Однако,
это соотношение имеет смысл лишь для
сходящихся интегралов. Необходимо иметь
методы выяснения поведения интеграла
минуя определение.
I
Интегралы от положительных функций
Пусть
на
.
Тогда определенный интеграл
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1
.
Несобственный интеграл 1 го
рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция
остается
ограниченной при увеличении.
Эта
теорема – следствие общих свойств
монотонных функций. Практического
смысла теорема почти не имеет, но
позволяет получить т.н. признаки
сходимости.
Теорема
2
(1-й признак сравнения). Пусть функции
и
непре-рывны на
и удовлетворяют неравенству
.
Тогда:
1)
если интеграл
сходится, то и
сходится;
2)
если интеграл
расходится, то и
расходится.
Доказательство
.
Обозначим:
и
.
Так как
,
то
.
Пусть интеграл
сходится, тогда (в силу теоремы 1) функция
‒ ограничена. Но тогда и
ограничена,
а значит, интеграл
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от
или сходимости интеграла от
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3
(2-й признак сравнения). Пусть функции
и
непрерывны и неотрицательны на
.
Тогда, если
при
,
то несобственные интегралы
и
сходятся или расходятся одновременно.
Доказательство
.
Из условия теоремы получим такую цепочку
равно-сильных утверждений:
,
,
.
Пусть,
например,
.
Тогда:
Применим
теорему 2 и свойство 1) из §1 и получим
утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция
,
.
Предлагаем студентам самим доказать,
что интеграл
сходится
при
и расходится при
.
Примеры
.
1.
.
Рассмотрим
подынтегральную функцию на промежутке
:
,
.
Интеграл
сходится, ибо
.
По 2-му признаку сравнения сходится и
интеграл
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2.
.
Так
как
,
тоcуществует
такое, что при
.
Для таких значений переменной:
Известно,
что логарифмическая функция растет
медленнее степенной, т.е.
,
а
значит, начиная с некоторого значения
переменной, эта дробь меньше 1. Поэтому
.
Интеграл
сходится как эталонный. В силу 1-го
признака сравнения сходится и
.
Применяя 2-й признак, получим, что и
интеграл
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Как вычислить несобственный интеграл и выяснить сходимость
Несобственные интегралы первого рода. По сути это тот же определённый интеграл,
но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела
интегрирования бесконечны.
Несобственные интегралы второго рода. По сути это тот же
определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций,
подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет,
обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f(x) непрерывна на отрезке [a, b], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений.
Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто.
В случае, когда график функции y = f(x)
находится выше оси Ox, определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y = f(x),
осью абсцисс и ординатами x = a, x = b.
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями
y = f(x) (на рисунке ниже — красного цвета), x = a
и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных
интервалов:
,
.
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный
интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный
интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного
интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как
отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом
интегрирования от непрерывной функции f(x) на промежутке
от a до ∞ называется
предел интеграла этой функции с верхним пределом интегрирования b
и нижним пределом интегрирования a при условии, что верхний предел
интегрирования неограниченно растёт, т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень
икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость.
То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится,
а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл
(нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда
, то есть
, и не существует, когда
, то есть
.
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл
сходится при и
расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница ,
можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Решение. С помощью метода замены переменной можно получить очень полезную формулу:
Доказывать эту формулу нет необходимости, но запомнить стоит — пригодится. Итак, применяя эту формулу для нахождения первообразной получим
Итак, несобственный интеграл сходится и равен 1.
Пример 4. Вычислить несобственный интеграл (если он сходится).
Решение. Находим
.
Но предел не существует, т. е. данный несобственный интеграл расходится.
Пример 5. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке, поэтому определённый
интеграл от неё на отрезке [0, b] существует
при всяком b. Находим этот интеграл:
.
Находим предел этого интеграла:
.
По определению, значение данного несобственного интеграла:
.
Несобственные интегралы с бесконечным нижним пределом
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, обозначаемый символом , а именно
.
Если этот предел существует (и, значит, конечен, то есть, равен некоторому числу, а не бесконечности), то данный несобственный интеграл называется сходящимся.
Пример 6. Вычислить несобственный интеграл
с бесконечным
нижним пределом(если он сходится).
Решение. Находим предел данного интеграла:
Вывод: данный несобственный интеграл сходится, а его значение равно -1/2.
Несобственные интегралы с двумя бесконечными пределами
Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом , нужно
предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним
пределом интегрирования, другой — с конечным нижним пределом интегрирования, т.е.
.
По определению,
,
причём этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.
Пример 7. Вычислить несобственный интеграл
с двумя бесконечными пределами (если он сходится).
Решение. На основании определения несобственного интеграла с двумя бесконечными
пределами представляем данный интеграл как сумму двух несобственных интегралов:
.
Преобразуем подынтегральное выражение к форме ,
с помощью выделения полного квадрата:
По формуле
находим:
(Эта формула, которой мы воспользовались, а также другие формулы, пригодные для интегрирования
дробей, приведены в уроке Интегрирование некоторых рациональных дробей и иррациональностей).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного
интеграла с двумя бесконечными пределами:
.
Пусть функция f(x) задана на
отрезке от a до b
и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b,
в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f(x)
на отрезке от a до b
называется предел интеграла этой функции с верхним пределом интегрирования c,
если при стремлении c к b
функция неограниченно возрастает, а в точке x = b
функция не определена, т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется
сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим:
.
Это также обобщённая формула Ньютона-Лейбница. Именно она применяется в решении задач на вычисление несобственных интегралов от неограниченных функций.
Пример 8. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция при неограниченно возрастает, а в точке x = 0 функция не определена, то есть, не существует. Применяем обобщённую формулу Ньютона-Лейбница:
(так как при x = 0 первообразная непрерывна). Вывод: данный несобственный интеграл сходится и равен -3/2.
Пример 9. Вычислить несобственный интеграл (если он сходится).
Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка
[0, 1]. В точке x = 1
функция обращается в бесконечность. Если взять ,
то на [0, c] подынтегральная функция непрерывна и,
следовательно, существует интеграл.
.
Найдём предел этого интеграла:
Результат предыдущих действий: несобственный интеграл сходится и его значение мы нашли.
Пример 10. Исследовать на сходимость несобственный интеграл
(верхний предел интегрирования больше нижнего).
Решение. Подынтегральная функция обращается в бесконечность при
x = b, в остальных точках она непрерывна.
Предположим сначала, что ,
тогда для :
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда
, то есть
, и не существует,
когда , то есть
.
В первом случае, то есть при
.
Если , то
.
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл
сходится при и
расходится при .
Начало темы «Интеграл»
Продолжение темы «Интеграл»
Поделиться с друзьями
вычисление интегралов определенных онлайн
Вы искали вычисление интегралов определенных онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определенного интеграла, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычисление интегралов определенных онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление интегралов определенных онлайн,вычисление определенного интеграла,вычисление определенного интеграла онлайн,вычисление определенного интеграла онлайн с подробным решением,вычисление определенных интегралов,вычисление определенных интегралов онлайн,вычисление определенных интегралов онлайн с подробным решением,вычислите определенный интеграл,вычислить значение определенного интеграла,вычислить интеграл онлайн с подробным решением определенный,вычислить несобственный интеграл онлайн,вычислить определенные интегралы,вычислить определенные интегралы онлайн с решением,вычислить определенный интеграл,вычислить определенный интеграл онлайн,вычислить определенный интеграл онлайн калькулятор,вычислить определенный интеграл онлайн с подробным решением,вычислить определенный интеграл онлайн с решением,интеграл онлайн определенный,интеграл определенный онлайн,интеграл решение определенный,интегралы онлайн несобственные,интегралы онлайн определенные,интегралы определенные онлайн,интегралы определенные онлайн с подробным решением,как вычислить определенный интеграл,калькулятор интегралов онлайн определенных,калькулятор интегралов онлайн определенных интегралов,калькулятор интегралов определенных,калькулятор онлайн вычислить определенный интеграл,калькулятор онлайн определенные интегралы,калькулятор онлайн определенный интеграл,калькулятор онлайн определенный интеграл с подробным решением,калькулятор онлайн определенных интегралов,калькулятор определенного интеграла,калькулятор определенного интеграла онлайн,калькулятор определенный интеграл,калькулятор определенных интегралов,калькулятор определенных интегралов онлайн,калькулятор определенных интегралов онлайн с решением,калькулятор определенных интегралов онлайн с решением подробным,калькулятор определенных интегралов с подробным решением онлайн,калькулятор определенных интегралов с решением онлайн,найти определенный интеграл,найти определенный интеграл онлайн,найти определенный интеграл онлайн с подробным решением,нахождение определенного интеграла,нахождение определенного интеграла онлайн,несобственные интегралы онлайн,несобственный интеграл онлайн,онлайн вычисление определенных интегралов,онлайн калькулятор вычислить определенные интегралы,онлайн калькулятор интегралов определенных,онлайн калькулятор интегралов с подробным решением определенных,онлайн калькулятор интегралы определенные,онлайн калькулятор определенного интеграла,онлайн калькулятор определенные интегралы,онлайн калькулятор определенный интеграл,онлайн калькулятор определенных интегралов,онлайн калькулятор определенных интегралов с подробным решением,онлайн нахождение определенного интеграла,онлайн решение определенного интеграла,онлайн решение определенного интеграла с подробным решением,онлайн решение определенных интегралов,онлайн решение определенных интегралов с подробным решением,определенные интегралы калькулятор онлайн,определенные интегралы онлайн,определенные интегралы онлайн калькулятор,определенные интегралы онлайн с подробным решением,определенный интеграл калькулятор,определенный интеграл калькулятор онлайн,определенный интеграл калькулятор онлайн с подробным решением,определенный интеграл онлайн,определенный интеграл онлайн калькулятор,определенный интеграл онлайн калькулятор с подробным решением,определенный интеграл онлайн с подробным решением,определенный интеграл онлайн тройной,определенный интеграл решение,определенный интеграл решить,определенный интеграл решить онлайн,определенный интеграл решить онлайн с подробным решением,посчитать интеграл онлайн определенный,посчитать онлайн определенный интеграл,посчитать определенный интеграл онлайн,решение интегралов онлайн определенных,решение несобственных интегралов онлайн,решение определенного интеграла,решение определенного интеграла онлайн,решение определенного интеграла онлайн с подробным решением,решение определенный интеграл,решение определенных интегралов,решение определенных интегралов онлайн,решение определенных интегралов онлайн с подробным решением,решение определенных интегралов онлайн с подробным решением бесплатно,решить интеграл определенный,решить онлайн определенный интеграл,решить определенный интеграл,решить определенный интеграл онлайн,решить определенный интеграл онлайн с подробным решением,сходимость интеграла онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление интегралов определенных онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление определенного интеграла онлайн).
Где можно решить любую задачу по математике, а так же вычисление интегралов определенных онлайн Онлайн?
Решить задачу вычисление интегралов определенных онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Несобственные интегралы
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
Если предел (1.1) есть конечное число, то несобственный интеграл называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл
Решение. Вычислим определенный интеграл
Имеем
Следовательно, заданный интеграл сходится и он равен
Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:
Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл определяется равенством:
где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:
Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:
Решение.
а) функция
ограничена и непрерывна, а потому и интегрируемая. Предельное значение
существует; таким образом,
ограничена и непрерывна, но
расходится.
Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение
Решение.
если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;
если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:
так и при 0 < α < 1:
Пример 1.4. Найти несобственный интеграл
Решение. Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:
Решение.
то есть, несобственный интеграл расходится
то есть, несобственный интеграл I2 сходится и равен .
Пример 1.5. Исследовать на сходимость интегралы:
Решение.
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Несобственный интеграл
Пользователи также искали:
исследовать на сходимость несобственный интеграл не вычисляя его,
несобственный интеграл 1 рода,
несобственный интеграл 2 рода,
несобственный интеграл это,
несобственный интеграл от экспоненты,
несобственный интеграл по бесконечному промежутку,
несобственный интеграл с бесконечными пределами,
несобственный интеграл с логарифмом,
Несобственный,
несобственный,
интеграл,
Несобственный интеграл,
рода,
сходимость,
несобственный интеграл от экспоненты,
несобственный интеграл это,
несобственный интеграл с логарифмом,
вычисляя,
промежутку,
логарифмом,
несобственный интеграл рода,
экспоненты,
бесконечными,
пределами,
исследовать,
бесконечному,
несобственный интеграл с бесконечными пределами,
исследовать на сходимость несобственный интеграл не вычисляя его,
несобственный интеграл по бесконечному промежутку,
несобственный интеграл 2 рода,
несобственный интеграл 1 рода,
несобственный интеграл,
интегральное исчисление. несобственный интеграл,
…
3 (х).
В следующей таблице перечислены поддерживаемые операции и функции:
| Тип | Получить |
| Константы | |
| e | e |
| pi | `pi` |
| i | i (мнимая единица) |
| Операции | |
| a + b | a + b |
| ab | ab |
| a * b | `a * b` |
| a ^ b, a ** b | ` a ^ b` |
| sqrt (x), x ^ (1/2) | `sqrt (x)` |
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` |
| root (x, n), x ^ (1 / n) | ` root (n) (x) ` |
| x ^ (a / b) | ` x ^ (a / b) ` |
| x ^ a ^ b | ` x ^ (a ^ b) ` |
| abs (x) | ` | x | ` |
| Функции | |
| e ^ x | `e ^ x` |
| ln (x), журнал (x) | ln (x) |
| ln (x) / ln (a) | `log_a (x)` |
| Тригонометрические функции | |
| sin (x) | sin (x) |
| cos (x) | cos (x) |
| tan (x) | tan (x), tg (x) |
| кроватка (x) | кроватка (x), ctg ( x) |
| sec (x) | sec (x) |
| csc (x) | csc (x), cosec (x) |
| Обратные тригонометрические функции | |
| asin (x) , arcsin (x), sin ^ -1 (x) | asin (x) |
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) |
| атан (x), arctan (x), tan ^ -1 (x) | atan (x) |
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) |
| asec (x), arcsec (x), sec ^ -1 (x) | asec (x) |
| acsc (x), arccsc (x), csc ^ -1 (x) | |
| Гиперболические функции | |
| sinh (x) | sinh (x) |
| cosh (x) | cosh (x) |
| tanh (x) | tanh (x) |
| coth (x) | coth (x) |
| 1 / cosh (x) | sech (x) |
| 1 / sinh (x) | csch (x) |
| Обратные гиперболические функции | |
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) |
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) |
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) |
| acoth (x), arccoth (x) , кроватка ^ -1 (x) | acoth (x) |
| acosh (1 / x) | asech (x) |
| asinh (1 / x) | acsch (x) |
Неправильные интегралы
Цель этого урока — распространить понятие определенного интеграла \ (\ int \ limits_a ^ b {f \ left (x \ right) dx} \) на несобственные интегралы. n {f \ left (x \ right ) dx}.x}}} \ normalsize} \) также сходится по сравнительному тесту \ (1. \)
Исчисление II — неправильные интегралы
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана (, то есть , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-8: Неправильные интегралы
В этом разделе нам нужно взглянуть на несколько различных видов интегралов.Оба они являются примерами интегралов, которые называются несобственными интегралами.
Начнем с первого типа несобственных интегралов, которые мы собираемся рассмотреть.
Бесконечный интервал
В этом виде интеграла один или оба предела интегрирования бесконечны. В этих случаях говорят, что интервал интегрирования составляет бесконечный интервал.
Давайте взглянем на пример, который также покажет нам, как мы собираемся работать с этими интегралами.t = 1 — \ frac {1} {t} \]
Теперь мы можем получить площадь под \ (f \ left (x \ right) \) на \ (\ left [{1, \, \ infty} \ right) \), просто взяв предел \ ({A_t } \) при стремлении \ (t \) к бесконечности.
\ [A = \ mathop {\ lim} \ limits_ {t \ to \ infty} {A _ {\, t}} = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ left ({1 — \ гидроразрыв {1} {t}} \ right) = 1 \]
Вот как мы будем делать сам интеграл.
\ [\ begin {align *} \ int _ {{\, \, 1}} ^ {{\, \ infty}} {{\ frac {1} {{{x ^ 2}}} \, dx}} & = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ int _ {{\, \, 1}} ^ {{\, t}} {{\ frac {1} {{{x ^ 2}} } \, dx}} \\ & = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ left.t \\ & = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ left ({1 — \ frac {1} {t}} \ right) = 1 \ end {align *} \]
Итак, вот как мы будем иметь дело с такими интегралами в целом. Мы заменим бесконечность переменной (обычно \ (t \)), сделаем интеграл, а затем возьмем предел результата, поскольку \ (t \) стремится к бесконечности.
Кстати, обратите внимание, что площадь под кривой на бесконечном интервале не была бесконечностью, как мы могли предположить.На самом деле это было на удивление мало. Конечно, так будет не всегда, но достаточно важно отметить, что не все области на бесконечном интервале дадут бесконечные области.
Давайте теперь разберемся с некоторыми определениями. Мы будем называть эти интегралы сходящимися , если связанный предел существует и является конечным числом (, т.е. это не плюс или минус бесконечность), и расходящийся , если связанный предел либо не существует, либо равен (плюс или минус) бесконечности. .{{\, \ infty}} {{f \ left (x \ right) \, dx}} \]
Где \ (c \) — любое число. Также обратите внимание, что для этого требуется, чтобы ОБА интегралов сходились, чтобы этот интеграл также был сходящимся. Если один из двух интегралов расходится, то и этот интеграл тоже.
Давайте взглянем еще на пару примеров.
Пример 2 Определите, сходится ли следующий интеграл или расходится, и если он сходится, найдите его значение.t \\ & = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ left ({\ ln \ left (t \ right) — \ ln 1} \ right) \\ & = \ infty \ end { выровнять*}\]
Итак, предел бесконечен, а значит, интеграл расходится.
Если мы вернемся к мышлению в терминах площади, обратите внимание, что область под \ (g \ left (x \ right) = \ frac {1} {x} \) на интервале \ (\ left [{1, \, \ infty} \ right) \) бесконечно. Это контрастирует с областью под \ (f \ left (x \ right) = \ frac {1} {{{x ^ 2}}} \), которая была довольно маленькой.p}}} \, dx}} \]
сходится, если \ (p> 1 \), и расходится, если \ (p \ le 1 \).
В связи с этим фактом следует отметить одну вещь: по сути, он говорит о том, что если подынтегральное выражение обращается к нулю достаточно быстро, то интеграл сходится. Насколько быстро достаточно быстро? Если мы воспользуемся этим фактом в качестве ориентира, похоже, что интегранты, которые стремятся к нулю быстрее, чем \ (\ frac {1} {x} \) стремятся к нулю, вероятно, сойдутся.
Давайте взглянем еще на пару примеров.
Пример 3 Определите, сходится или расходится следующий интеграл.2}}} \, dx}} \]
Показать решение
В этом случае у нас есть бесконечности в обоих пределах. Процесс, который мы используем для работы с бесконечными пределами, требует только одного бесконечного предела в интеграле, поэтому нам нужно будет разбить интеграл на два отдельных интеграла. Мы можем разделить интеграл в любой точке, поэтому давайте выберем \ (x = 0 \), так как это будет удобная точка для процесса оценки. 2}}} \, dx}} \]
Теперь мы должны рассмотреть каждый из индивидуальных ограничений.t \\ & = \ mathop {\ lim} \ limits_ {t \ to \ infty} \ left ({\ cos 2 — \ cos t} \ right) \ end {align *} \]
Этого предела не существует, поэтому интеграл расходится.
В большинстве примеров класса Calculus II, которые обрабатываются на бесконечных интервалах, предел либо существует, либо бесконечен. Однако есть ограничения, которых не существует, как показал предыдущий пример, поэтому не забывайте о них.
Интегральная функция с разрывом
Теперь нам нужно рассмотреть второй тип несобственных интегралов, которые мы рассмотрим в этом разделе.{{\, b}} {{f \ left (x \ right) \, dx}} \]
Где \ (c \) — любое число. Опять же, это требует, чтобы ОБА интегралов сходились, чтобы этот интеграл также был сходящимся.
Обратите внимание, что пределы в этих случаях действительно должны быть правыми или левыми. Поскольку мы будем работать внутри интервала интеграции, нам нужно будет убедиться, что мы остаемся внутри этого интервала. Это означает, что мы будем использовать односторонние ограничения, чтобы оставаться в пределах интервала.2}}} + \ frac {1} {8}} \ right) \\ & = — \ infty \ end {align *} \]
На этом мы закончили. Один из интегралов расходится, что означает, что интеграл, на который нас попросили посмотреть, расходится. Нам даже не нужно возиться со вторым интегралом.
Прежде чем покинуть этот раздел, отметим, что у нас также могут быть интегралы, которые включают оба этих случая. Рассмотрим следующий интеграл.
Пример 8 Определите, сходится или расходится следующий интеграл.2}}} \, dx}} \]
Показать решение
Это интеграл по бесконечному интервалу, который также содержит разрывную подынтегральную функцию. Чтобы получить этот интеграл, нам нужно разделить его на два интеграла, чтобы каждый интеграл содержал только одну точку разрыва. Важно помнить, что все процессы, с которыми мы работаем в этом разделе, так что каждый интеграл содержит только одну проблемную точку.
Мы можем разделить его где угодно, но выберем значение, удобное для целей оценки.+}} \ left ({- 1 + \ frac {1} {t}} \ right) \\ & = \ infty \ end {align *} \]
Итак, первый интеграл расходится, а значит, и весь интеграл расходится.
Несобственные интегралы — исчисление 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
7.8: Неправильные интегралы — математика LibreTexts
Площадь между графиком \ (f (x) = \ dfrac {1} {x} \) и осью \ (x \) на интервале \ ([1 , + ∞) \) конечное или бесконечное? Если эта же область вращается вокруг оси \ (x \), будет ли объем конечным или бесконечным? Удивительно, но площадь описываемой области бесконечна, но объем твердого тела, полученный вращением этой области вокруг оси \ (x \), конечен.t_af (x) \, dx \) можно интерпретировать как площадь для различных значений \ (t \). Другими словами, мы можем определить несобственный интеграл как предел, взятый как неограниченное увеличение или уменьшение одного из пределов интегрирования.
Рисунок \ (\ PageIndex {1} \): Чтобы интегрировать функцию на бесконечном интервале, мы рассматриваем предел интеграла, когда верхний предел неограниченно возрастает.
Определение: неправильный интеграл
- Пусть \ (f (x) \) непрерывно на интервале вида \ ([a, + ∞) \).{+ ∞} _af (x) \, dx \) для любого значения a.).
В нашем первом примере мы возвращаемся к вопросу, который мы поставили в начале этого раздела: является ли область между графиком \ (f (x) = \ frac {1} {x} \) и \ (x \ ) -ось на отрезке \ ([1, + ∞) \) конечна или бесконечна?
Пример \ (\ PageIndex {1} \): поиск области
Определите, является ли область между графиком \ (f (x) = \ dfrac {1} {x} \) и осью \ (x \) — на интервале \ ([1, + ∞) \) конечной. или бесконечно.
Решение
Сначала мы делаем быстрый набросок рассматриваемой области, как показано на рисунке \ (\ PageIndex {2} \).t_1 \ tag {Найдите первообразную} \\ [4pt] = \ lim_ {t → + ∞} (\ ln | t | — \ ln 1) \ tag {Вычислите первообразную} \\ [4pt] = + ∞. \ tag {Оцените предел.} \ end {align *} \]
Поскольку несобственный интеграл расходится на \ (+ ∞, \), площадь области бесконечна.
Пример \ (\ PageIndex {2} \): поиск тома
Найдите объем твердого тела, полученный вращением области, ограниченной графиком \ (f (x) = \ dfrac {1} {x} \) и осью \ (x \) на интервале \ ([1 , + ∞) \) вокруг оси \ (x \) -.t_1 \ quad \ text {Найдите первообразную.} \\ [4pt]
& = π \ lim_ {t → + ∞} \ left (- \ frac {1} {t} +1 \ right) \ quad \ text { Вычислите первообразную.} \\ [4pt]
& = π \ end {align *} \]
Несобственный интеграл сходится к \ (π \). Следовательно, объем тела вращения равен \ (π \).
В заключение, хотя площадь области между осью \ (x \) и графиком \ (f (x) = 1 / x \) на интервале \ ([1, + ∞) \) бесконечна. объем твердого тела, образующийся при вращении этой области вокруг оси \ (x \), конечен.Образовавшееся твердое тело известно как Рог Габриэля.
Примечание. Рог Габриэля (также называемый трубой Торричелли) представляет собой геометрическую фигуру, имеющую бесконечную площадь поверхности и конечный объем единиц. Название относится к традиции, отождествляющей архангела Гавриила с ангелом, который трубит в рог, чтобы объявить Судный день, связывая божественное или бесконечное с конечным. Свойства этой фигуры впервые были изучены итальянским физиком и математиком Евангелистой Торричелли в 17 веке.
Пример \ (\ PageIndex {3} \): Дорожно-транспортные происшествия в городе
Предположим, что на оживленном перекрестке дорожно-транспортные происшествия происходят в среднем один раз в три месяца. После жалоб жителей изменили светофор на перекрестке. Прошло восемь месяцев с момента внесения изменений, и несчастных случаев не было. Были ли изменения эффективны или 8-месячный интервал без происшествий — это случайность?
Рисунок \ (\ PageIndex {4} \): Модификация работы Дэвида МакКелви, Flickr.2_0 \ frac {1} {x} \, dx \) в предельной форме с использованием уравнения \ ref {implperundefa}.
- Ответ
\ (+ ∞ \), расходится.
Теорема сравнения
Непосредственное вычисление несобственного интеграла не всегда просто или даже возможно; однако, сравнивая его с другим тщательно подобранным интегралом, можно определить его сходимость или расхождение. Чтобы убедиться в этом, рассмотрим две непрерывные функции \ (f (x) \) и \ (g (x) \), удовлетворяющие \ (0≤f (x) ≤g (x) \) для \ (x≥a \) ( Рисунок \ (\ PageIndex {6} \)).t_af (x) \, dx≤L \) для всех \ (t≥a. \)
Если площадь области между графиком \ (g (x) \) и осью \ (x \) над \ ([a, + ∞) \) конечна, то площадь области между график \ (f (x) \) и \ (x \) — ось над \ ([a, + ∞) \) также конечен.
Эти выводы резюмируются в следующей теореме.
Теорема сравнения
Пусть \ (f (x) \) и \ (g (x) \) непрерывны над \ ([a, + ∞). t_ag (x) \, dx = + ∞.{+ ∞} _e \ frac {\ ln x} {x} \, dx \) расходится.
Преобразование Лапласа
В последних нескольких главах мы рассмотрели несколько способов использования интеграции для решения реальных проблем. В этом следующем проекте мы собираемся изучить более сложное приложение интеграции: интегральные преобразования. В частности, мы описываем преобразование Лапласа и некоторые его свойства. Преобразование Лапласа используется в инженерии и физике для упрощения вычислений, необходимых для решения некоторых проблем.{−st} dt \). Обратите внимание, кстати, что мы определили \ (g (t), du = f (t) dt. \))
Как и следовало ожидать, вы должны увидеть, что
\ [L {g (t)} = \ frac {1} {s} ⋅L {f (t)}. \]
Интеграция во временной области упрощается до деления на \ (s \) в частотной области.
3.7 Неправильные интегралы — том 2 исчисления
Цели обучения
- 3.7.1 Вычислить интеграл на бесконечном интервале.
- 3.7.2 Вычислить интеграл по замкнутому интервалу с бесконечным разрывом внутри интервала.
- 3.7.3 Используйте теорему сравнения, чтобы определить, сходится ли определенный интеграл.
Является ли область между графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) конечной или бесконечной? Если эта же область вращается вокруг оси x , будет ли объем конечным или бесконечным? Удивительно, но площадь описываемой области бесконечна, но объем твердого тела, полученный путем поворота этой области вокруг оси x , конечен.
В этом разделе мы определяем интегралы по бесконечному интервалу, а также интегралы от функций, содержащих разрыв на интервале. Интегралы этих типов называются несобственными интегралами. Мы исследуем несколько методов вычисления несобственных интегралов, все из которых связаны с определением пределов.
Интегрирование в бесконечном интервале
Как нам подойти к определению интеграла типа ∫a + ∞f (x) dx? ∫a + ∞f (x) dx? Мы можем интегрировать ∫atf (x) dx∫atf (x) dx для любого значения t, t, поэтому разумно посмотреть на поведение этого интеграла, когда мы подставляем большие значения t.т. Рисунок 3.17 показывает, что ∫atf (x) dx∫atf (x) dx можно интерпретировать как площадь для различных значений t.t. Другими словами, мы можем определить несобственный интеграл как предел, взятый как неограниченное увеличение или уменьшение одного из пределов интегрирования.
Рис. 3.17. Чтобы интегрировать функцию на бесконечном интервале, мы рассматриваем предел интеграла, когда верхний предел неограниченно возрастает.
Определение
- Пусть f (x) f (x) непрерывна на интервале вида [a, + ∞).[а, + ∞). Тогда
A + ∞f (x) dx = limt → + ∞∫atf (x) dx, ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx,3,16
при условии, что этот предел существует.
- Пусть f (x) f (x) непрерывна на интервале вида (−∞, b]. (- ∞, b]. Тогда
∫ − ∞bf (x) dx = limt → −∞∫tbf (x) dx, ∫ − ∞bf (x) dx = limt → −∞∫tbf (x) dx,3,17
при условии, что этот предел существует.
В любом случае, если предел существует, то говорят, что несобственный интеграл сходится. Если предел не существует, то говорят, что несобственный интеграл расходится. - Пусть f (x) f (x) непрерывна на (−∞, + ∞). (- ∞, + ∞). Тогда
− ∞ + ∞f (x) dx = ∫ − ∞0f (x) dx + ∫0 + ∞f (x) dx, ∫ − ∞ + ∞f (x) dx = ∫ − ∞0f (x) dx + ∫0 + ∞f (x) dx,3,18
при условии, что ∫ − ∞0f (x) dx∫ − ∞0f (x) dx и ∫0 + ∞f (x) dx∫0 + ∞f (x) dx сходятся. Если любой из этих двух интегралов расходится, то ∫ − ∞ + ∞f (x) dx∫ − ∞ + ∞f (x) dx расходится. (Можно показать, что на самом деле ∫ − ∞ + ∞f (x) dx = ∫ − ∞af (x) dx + ∫a + ∞f (x) dx∫ − ∞ + ∞f (x) dx = ∫− ∞af (x) dx + ∫a + ∞f (x) dx для любого значения a.) A.)
В нашем первом примере мы возвращаемся к вопросу, который мы поставили в начале этого раздела: является ли область между графиком f (x) = 1xf (x) = 1x и осью xx на интервале [1, + ∞) [1, + ∞) конечное или бесконечное?
Пример 3.47
В поисках места
Определите, является ли область между графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) конечной или бесконечной.
Решение
Сначала мы делаем быстрый набросок рассматриваемой области, как показано на следующем графике.
Рис. 3.18. Мы можем найти площадь между кривой f (x) = 1 / xf (x) = 1 / x и осью x на бесконечном интервале.
Мы видим, что площадь этой области определяется как A = ∫1∞1xdx.А = ∫1∞1xdx. Тогда у нас
A = ∫1∞1xdx = limt → + ∞∫1t1xdx Перепишите несобственный интеграл как предел. = Limt → + ∞ln | x || 1t Найдите первообразную. = Limt → + ∞ (ln | t | −ln1) Вычислите первообразную . = + ∞. Вычислить предел. A = ∫1∞1xdx = limt → + ∞∫1t1xdx Перепишите несобственный интеграл как предел. = Limt → + ∞ln | x || 1t. Найдите первообразную. = Limt → + ∞ (ln | t | −ln1) Вычислить первообразную. = + ∞. Вычислить предел.
Поскольку несобственный интеграл расходится до + ∞, + ∞, площадь области бесконечна.
Пример 3.48
В поисках тома
Найдите объем твердого тела, полученный вращением области, ограниченной графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) относительно оси xx.
Решение
Твердое тело показано на Рисунке 3.19. Дисковым методом видим, что объем V равен
V = π∫1 + ∞1x2dx. V = π∫1 + ∞1x2dx.
Рис. 3.19. Тело вращения можно создать, вращая бесконечную область вокруг оси x .
Тогда у нас
V = π∫1 + ∞1x2dx = πlimt → + ∞∫1t1x2dx Перепишите как предел. = Πlimt → + ∞ − 1x | 1t Найдите первообразную. = Πlimt → + ∞ (−1t + 1) Вычислите первообразную. = Π.V = π∫1 + ∞1x2dx = πlimt → + ∞∫1t1x2dx Перепишем как предел.= πlimt → + ∞ − 1x | 1t Найти первообразную. = πlimt → + ∞ (−1t + 1) Вычислить первообразную. = π.
Несобственный интеграл сходится к π.π. Следовательно, объем тела вращения равен π.π.
В заключение, хотя площадь области между осью x и графиком f (x) = 1 / xf (x) = 1 / x на интервале [1, + ∞) [1, + ∞ ) бесконечен, объем твердого тела, образованного вращением этой области вокруг оси x , конечен. Сгенерированное твердое тело известно как Gabriel’s Horn .
Пример 3.49
Начало главы: Дорожные происшествия в городе
Рисунок 3.20 (кредит: модификация работы Дэвида МакКелви, Flickr)
В начале главы мы сформулировали следующую проблему: предположим, что на оживленном перекрестке дорожно-транспортные происшествия происходят в среднем один раз в три месяца. После жалоб жителей изменили светофор на перекрестке. Прошло восемь месяцев с момента внесения изменений, и несчастных случаев не было.Были ли изменения эффективны или 8-месячный интервал без происшествий — это случайность?
Теория вероятностей говорит нам, что если среднее время между событиями равно k, k, вероятность того, что X, X, время между событиями, находится между aa и bb, равна
.
P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <0ke − kxifx≥0.P (a≤x≤b) = ∫abf (x) dxwheref (x) = {0ifx < 0ke − kxifx≥0.
Таким образом, если несчастные случаи происходят с частотой один раз в 3 месяца, то вероятность того, что X, X, время между несчастными случаями, находится между aa и bb, равна
.
P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <03e − 3xifx≥0.P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <03e − 3xifx≥0.
Чтобы ответить на вопрос, мы должны вычислить P (X≥8) = ∫8 + ∞3e − 3xdxP (X≥8) = ∫8 + ∞3e − 3xdx и решить, вероятно ли, что 8 месяцев могли бы пройти без ДТП, если не было улучшения дорожной обстановки.
Решение
Нам нужно вычислить вероятность как неправильный интеграл:
P (X≥8) = ∫8 + ∞3e − 3xdx = limt → + ∞∫8t3e − 3xdx = limt → + ∞ − e − 3x | 8t = limt → + ∞ (−e − 3t + e − 24) ≈ 3.8 × 10−11.P (X≥8) = ∫8 + ∞3e − 3xdx = limt → + ∞∫8t3e − 3xdx = limt → + ∞ − e − 3x | 8t = limt → + ∞ (−e − 3t + e − 24) ≈3.8 × 10-11.
Значение 3,8 × 10–113,8 × 10–11 представляет вероятность отсутствия аварий в течение 8 месяцев при начальных условиях. Поскольку это значение очень и очень мало, можно сделать вывод, что изменения вступили в силу.
Пример 3.50
Вычисление неправильного интеграла за бесконечный интервал
Вычислить ∫ − ∞01×2 + 4dx.∫ − ∞01×2 + 4dx. Укажите, сходится или расходится несобственный интеграл.
Решение
Начнем с переписывания ∫ − ∞01×2 + 4dx∫ − ∞01×2 + 4dx в качестве предела, используя уравнение 3.17 из определения. Таким образом,
∫ − ∞01×2 + 4dx = limx → −∞∫t01x2 + 4dx Перепишите как предел. = Limt → −∞12tan − 1×2 | t0 Найдите первообразную. = 12limt → −∞ (tan − 10 − tan − 1t2) Вычислите первообразную. = π4. Вычислить предел и упростить. − ∞01×2 + 4dx = limx → −∞∫t01x2 + 4dx Перепишите как предел. = limt → −∞12tan − 1×2 | t0 Найдите первообразную. = 12limt → −∞ (tan − 10 −tan − 1t2) Вычислить первообразную. = Π4. Вычислить предел и упростить.
Несобственный интеграл сходится к π4.π4.
Пример 3.51
Вычисление несобственного интеграла на (−∞, + ∞) (- ∞, + ∞)
Вычислить ∫ − ∞ + ∞xexdx.∫ − ∞ + ∞xexdx. Укажите, сходится или расходится несобственный интеграл.
Решение
Начнем с разделения интеграла:
− ∞ + ∞xexdx = ∫ − ∞0xexdx + ∫0 + ∞xexdx.∫ − ∞ + ∞xexdx = ∫ − ∞0xexdx + ∫0 + ∞xexdx.
Если либо ∫ − ∞0xexdx∫ − ∞0xexdx, либо ∫0 + ∞xexdx∫0 + ∞xexdx расходится, то − ∞ + ∞xexdx∫ − ∞ + ∞xexdx расходится. Вычислите каждый интеграл отдельно. Для первого интеграла
∫ − ∞0xexdx = limt → −∞∫t0xexdx Перепишите как предел. = Limt → −∞ (xex − ex) | t0Используйте интегрирование по частям, чтобы найти антипроизводную.(Здесь u = xanddv = exdx.) = Limt → −∞ (−1 − tet + et) Вычислить первообразную. = — 1. Вычислить предел. Примечание: limt → −∞tetisin, определенное в виде 0 · ∞. Таким образом, limt → −∞tet = limt → −∞te − t = limt → −∞ − 1e − t = limt → −∞ − et = 0 по правилу Л.Гопиталя. ∫ − ∞0xexdx = limt → −∞∫t0xexdx Перепишите как предел. = Limt → −∞ (xex − ex) | t0Используйте интегрирование по частям, чтобы найти антипроизводную. (Здесь u = xanddv = exdx.) = Limt → −∞ (−1 − tet + et) Вычислить первообразную. = — 1. Вычислить предел. Примечание: limt → −∞tetisin определяет форму 0 · ∞. Таким образом, limt → −∞tet = limt → −∞te − t = limt → −∞ − 1e − t = limt → −∞ − et = 0 по правилу Л.Гопиталя.
Первый несобственный интеграл сходится. Для второго интеграла
∫0 + ∞xexdx = limt → + ∞∫0txexdx Перепишите как предел. = Limt → + ∞ (xex − ex) | 0t Найдите первообразную. = Limt → + ∞ (tet − et + 1) Вычислите первообразную. = Limt → + ∞ ((t − 1) et + 1) Перепишите. (Tet − etis неопределенно.) = + ∞. Вычислите предел. ∫0 + ∞xexdx = limt → + ∞∫0txexdx Перепишите как предел. = Limt → + ∞ (xex − ex) | 0t Найти первообразную. = limt → + ∞ (tet − et + 1) Вычислить первообразную. = limt → + ∞ ((t − 1) et + 1) Перепишите. (tet − etis неопределенный.) = + ∞. Вычислить предел.
Таким образом, ∫0 + ∞xexdx∫0 + ∞xexdx расходится.Поскольку этот интеграл расходится, ∫ − ∞ + ∞xexdx∫ − ∞ + ∞xexdx также расходится.
КПП 3.27
Вычислить ∫ − 3 + ∞e − xdx. − 3 + ∞e − xdx. Укажите, сходится или расходится несобственный интеграл.
Интегрирование разрывного подынтегрального выражения
Теперь рассмотрим интегралы от функций, содержащих бесконечный разрыв в интервале, на котором происходит интегрирование. Рассмотрим интеграл вида abf (x) dx, ∫abf (x) dx, где f (x) f (x) непрерывна над [a, b) [a, b) и разрывна в b.б. Поскольку функция f (x) f (x) непрерывна по [a, t] [a, t] для всех значений tt, удовлетворяющих a Рис. 3.21. Когда t приближается к b слева, значение площади от a до t приближается к области от a до b . Мы используем аналогичный подход для определения ∫abf (x) dx, ∫abf (x) dx, где f (x) f (x) непрерывно над (a, b] (a, b] и разрывно в aa. приступить к формальному определению. Определение
Abf (x) dx = limt → b − ∫atf (x) dx.Abf (x) dx = limt → b − ∫atf (x) dx.
3,19
Abf (x) dx = limt → a + ∫tbf (x) dx.abf (x) dx = limt → a + ∫tbf (x) dx.
3,20
В любом случае, если предел существует, то говорят, что несобственный интеграл сходится. Если предел не существует, то говорят, что несобственный интеграл расходится.
Abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx, ∫abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx,
3.21
при условии, что ∫acf (x) dx∫acf (x) dx и ∫cbf (x) dx∫cbf (x) dx сходятся. Если любой из этих интегралов расходится, то расходится ∫abf (x) dx∫abf (x) dx.
Следующие примеры демонстрируют применение этого определения.
Пример 3.52
Интегрирование разрывного подынтегрального выражения
Оцените ∫0414 − xdx, ∫0414 − xdx, если возможно. Укажите, сходится ли интеграл или расходится.
Решение
Функция f (x) = 14 − xf (x) = 14 − x непрерывна на [0,4) [0,4) и разрывна на 4.Используя уравнение 3.19 из определения, перепишите ∫0414 − xdx∫0414 − xdx как предел:
∫0414 − xdx = limt → 4 − ∫0t14 − xdxПерепишите как предел. = Limt → 4 — (- 24 − x) | 0tНайдите первообразную. = Limt → 4 — (- 24 − t + 4) Вычислите первообразную. = 4. Вычислить предел. 0414 − xdx = limt → 4 − ∫0t14 − xdx Перепишите как предел. = Limt → 4 — (- 24 − x) | 0t Найдите первообразную. = Limt → 4 — (- 24 − t +4) Вычислить первообразную. = 4. Вычислить предел.
Несобственный интеграл сходится.
Пример 3.53
Интегрирование разрывного подынтегрального выражения
Оценить ∫02xlnxdx.∫02xlnxdx. Укажите, сходится ли интеграл или расходится.
Решение
Поскольку f (x) = xlnxf (x) = xlnx непрерывно на (0,2] (0,2] и разрывно в нуле, мы можем переписать интеграл в предельной форме, используя уравнение 3.20:
∫02xlnxdx = limt → 0 + ∫t2xlnxdxПерепишите как предел. = Limt → 0 + (12x2lnx − 14×2) | t2Evaluate∫ xlnxdx используя интегрирование по частям с u = lnxanddv = xdx. = Limt → 0 + .Оценка первообразной. = 2ln2−1.Оценка предела .limt → 0 + t2lnt является неопределенным.Чтобы оценить это, перепишите как частное и примените правило L’Hôpital. 02xlnxdx = limt → 0 + ∫t2xlnxdx Перепишите как предел. = Limt → 0 + (12x2lnx − 14×2) | t2Evaluate∫ xlnxdx, используя интегрирование по частям. = limt → 0 + (2ln2−1−12t2lnt + 14t2). Вычислить первообразную. = 2ln2−1. Вычислить limit.limt → 0 + t2lnt не определено. Чтобы оценить его, перепишите как частное и примените правило Л’Опиталя.
Несобственный интеграл сходится.
Пример 3.54
Интегрирование разрывного подынтегрального выражения
Вычислить ∫ − 111x3dx.∫ − 111x3dx. Укажите, сходится или расходится несобственный интеграл.
Решение
Поскольку f (x) = 1 / x3f (x) = 1 / x3 имеет разрыв в нуле, используя уравнение 3.21, мы можем записать
− 111x3dx = ∫ − 101x3dx + ∫011x3dx.∫ − 111x3dx = ∫ − 101x3dx + ∫011x3dx.
Если один из двух интегралов расходится, то исходный интеграл расходится. Начнем с ∫ − 101x3dx: ∫ − 101x3dx:
∫ − 101x3dx = limt → 0 − ∫ − 1t1x3dx Перепишите как предел. = Limt → 0 — (- 12×2) | −1t Найдите первообразную. = Limt → 0 — (- 12t2 + 12) Вычислите первообразную.= + — ∞. Вычислить предел. − 101x3dx = limt → 0 − ∫ − 1t1x3dx Перепишите как предел. = Limt → 0 — (- 12×2) | −1t Найдите первообразную. = Limt → 0 — (- 12t2 + 12) Вычислить первообразную. = + — ∞. Вычислить предел.
Следовательно, ∫ − 101x3dx∫ − 101x3dx расходится. Поскольку ∫ − 101x3dx∫ − 101x3dx расходится, − 111x3dx∫ − 111x3dx расходится.
КПП 3.28
Оценить ∫021xdx.∫021xdx. Укажите, сходится ли интеграл или расходится.
Теорема сравнения
Непосредственное вычисление несобственного интеграла не всегда просто или даже возможно; однако, сравнивая его с другим тщательно подобранным интегралом, можно определить его сходимость или расхождение.Чтобы убедиться в этом, рассмотрим две непрерывные функции f (x) f (x) и g (x) g (x), удовлетворяющие 0≤f (x) ≤g (x) 0≤f (x) ≤g (x) для x ≥ax≥a (рисунок 3.22). В этом случае мы можем рассматривать интегралы этих функций по интервалам вида [a, t] [a, t] как области, поэтому мы имеем соотношение
0≤∫atf (x) dx≤∫atg (x) dxfort≥a.0≤∫atf (x) dx≤∫atg (x) dxfort≥a.
Рисунок 3.22. Если 0≤f (x) ≤g (x) 0≤f (x) ≤g (x) для x≥a, x≥a, то для t≥a, t≥a, ∫atf (x) dx ≤∫atg (x) dx.∫atf (x) dx≤∫atg (x) dx.
Таким образом, если
∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = + ∞, ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = + ∞,
, затем
∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞.То есть, если площадь области между графиком f (x) f (x) и осью x над [a, + ∞) [a, + ∞) бесконечна, то площадь области между графиком g (x) g (x) и осью x над [a, + ∞) [a, + ∞) также бесконечно.
С другой стороны, если
∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L для некоторого действительного числа L, L , затем
∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx должен сходиться к некоторому значению, меньшему или равному L , L, поскольку atf (x) dx∫atf (x) dx увеличивается с увеличением tt и ∫atf (x) dx≤L∫atf (x) dx≤L для всех t≥a.t≥a.
Если площадь области между графиком g (x) g (x) и осью x над [a, + ∞) [a, + ∞) конечна, то площадь области между график f (x) f (x) и оси x над [a, + ∞) [a, + ∞) также конечен.
Эти выводы резюмируются в следующей теореме.
Теорема 3.7
Теорема сравнения
Пусть f (x) f (x) и g (x) g (x) непрерывны над [a, + ∞). [A, + ∞). Предположим, что 0≤f (x) ≤g (x) 0≤f (x) ≤g (x) для x≥a.x≥a.
- Если ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = + ∞, ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = + ∞, то A + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞.∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞.
- Если ∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L, ∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L, где LL — вещественное число, то ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = M∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx = M для некоторого действительного числа M≤LM≤L.
Пример 3.55
Применение теоремы сравнения
Используйте сравнение, чтобы показать, что ∫1 + ∞1xexdx∫1 + ∞1xexdx сходится.
Решение
Мы видим, что
0≤1xex≤1ex = e − x, 0≤1xex≤1ex = e − x,
, поэтому если ∫1 + ∞e − xdx∫1 + ∞e − xdx сходится, то сходится и ∫1 + ∞1xexdx.∫1 + ∞1xexdx. Чтобы вычислить ∫1 + ∞e − xdx, ∫1 + ∞e − xdx, сначала перепишите его как предел:
∫1 + ∞e − xdx = limt → + ∞∫1te − xdx = limt → + ∞ (−e − x) | t1 = limt → + ∞ (−e − t + e – 1) = e – 1.∫ 1 + ∞e − xdx = limt → + ∞∫1te − xdx = limt → + ∞ (−e − x) | t1 = limt → + ∞ (−e − t + e – 1) = e – 1.
Поскольку ∫1 + ∞e − xdx∫1 + ∞e − xdx сходится, то же самое происходит и с ∫1 + ∞1xexdx.∫1 + ∞1xexdx.
Пример 3.56
Применение теоремы сравнения
Используйте теорему сравнения, чтобы показать, что ∫1 + ∞1xpdx∫1 + ∞1xpdx расходится для всех p <1.р <1.
Решение
Для p <1, p <1, 1 / x≤1 / (xp) 1 / x≤1 / (xp) по [1, + ∞). [1, + ∞). В примере 3.47 мы показали, что ∫1 + ∞1xdx = + ∞.∫1 + ∞1xdx = + ∞. Следовательно, ∫1 + ∞1xpdx∫1 + ∞1xpdx расходится при всех p <1.p <1.
КПП 3.29
Используйте сравнение, чтобы показать, что ∫e + ∞lnxxdx∫e + ∞lnxxdx расходится.
Студенческий проект
Преобразования Лапласа
В последних нескольких главах мы рассмотрели несколько способов использования интеграции для решения реальных проблем.В этом следующем проекте мы собираемся изучить более сложное приложение интеграции: интегральные преобразования. В частности, мы описываем преобразование Лапласа и некоторые его свойства. Преобразование Лапласа используется в технике и физике для упрощения вычислений, необходимых для решения некоторых задач. Он принимает функции, выраженные в терминах времени, и преобразует их в функции, выраженные в терминах частоты. Оказывается, что во многих случаях вычисления, необходимые для решения задач в частотной области, намного проще, чем вычисления, необходимые для временной области.
Преобразование Лапласа определяется в терминах интеграла как
L {f (t)} = F (s) = ∫0∞e − stf (t) dt.L {f (t)} = F (s) = ∫0∞e − stf (t) dt.
Обратите внимание, что входные данные для преобразования Лапласа являются функцией времени, f (t), f (t), а выходные данные — функцией частоты, F (s) .F (s). Хотя многие примеры из реального мира требуют использования комплексных чисел (включая мнимое число i = −1), i = −1), в этом проекте мы ограничиваемся функциями действительных чисел.
Начнем с простого примера.Здесь мы вычисляем преобразование Лапласа f (t) = tf (t) = t. Имеем
L {t} = ∫0∞te − stdt.L {t} = ∫0∞te − stdt.
Это неправильный интеграл, поэтому мы выражаем его через предел, который дает
L {t} = ∫0∞te − stdt = limz → ∞∫0zte − stdt.L {t} = ∫0∞te − stdt = limz → ∞∫0zte − stdt.
Теперь мы используем интегрирование по частям для вычисления интеграла. Обратите внимание, что мы интегрируем относительно t , поэтому мы рассматриваем переменную s как константу. У нас
u = tdv = e − stdtdu = dtv = −1se − st.u = tdv = e − stdtdu = dtv = −1se − st.
Тогда получаем
limz → ∞∫0zte − stdt = limz → ∞ [[- tse − st] | 0z + 1s∫0ze − stdt] = limz → ∞ [[- zse − sz + 0se − 0s] + 1s∫0ze − stdt] = limz → ∞ [[- zse − sz + 0] −1s [e − sts] | 0z] = limz → ∞ [[- zse − sz] −1s2 [e − sz − 1]] = limz → ∞ [−zsesz ] −limz → ∞ [1s2esz] + limz → ∞1s2 = 0−0 + 1s2 = 1s2.limz → ∞∫0zte − stdt = limz → ∞ [[- tse − st] | 0z + 1s∫0ze − stdt] = limz → ∞ [[- zse − sz + 0se − 0s] + 1s∫0ze − stdt] = limz → ∞ [[- zse − sz + 0] −1s [e − sts] | 0z] = limz → ∞ [[ −zse − sz] −1s2 [e − sz − 1]] = limz → ∞ [−zsesz] −limz → ∞ [1s2esz] + limz → ∞1s2 = 0−0 + 1s2 = 1s2.
- Вычислите преобразование Лапласа f (t) = 1. f (t) = 1.
- Вычислите преобразование Лапласа f (t) = e − 3t.f (t) = e − 3t.
- Вычислите преобразование Лапласа для f (t) = t2.f (t) = t2. (Обратите внимание, вам придется интегрировать по частям дважды.)
Преобразования Лапласа часто используются для решения дифференциальных уравнений. Дифференциальные уравнения подробно не рассматриваются до конца этой книги; а пока давайте посмотрим на взаимосвязь между преобразованием Лапласа функции и преобразованием Лапласа ее производной.
Начнем с определения преобразования Лапласа. У нас
L {f (t)} = ∫0∞e − stf (t) dt = limz → ∞∫0ze − stf (t) dt.L {f (t)} = ∫0∞e − stf (t) dt = limz → ∞∫0ze − stf (t) dt. - Используйте интегрирование по частям, чтобы оценить limz → ∞∫0ze − stf (t) dt.limz → ∞∫0ze − stf (t) dt. (Пусть u = f (t) u = f (t) и dv = e − stdt.) Dv = e − stdt.)
После интеграции по частям и оценки предела вы должны увидеть, что
L {f (t)} = f (0) s + 1s [L {f ′ (t)}]. L {f (t)} = f (0) s + 1s [L {f ′ (t)}. ].
Затем
L {f ′ (t)} = sL {f (t)} — f (0). L {f ′ (t)} = sL {f (t)} — f (0).
Таким образом, дифференцирование во временной области упрощается до умножения на с в частотной области.
Последнее, что мы рассмотрим в этом проекте, — это то, как связаны преобразования Лапласа функции f (t) f (t) и ее первообразной. Пусть g (t) = ∫0tf (u) du.g (t) = ∫0tf (u) du. Затем
L {g (t)} = ∫0∞e − stg (t) dt = limz → ∞∫0ze − stg (t) dt.L {g (t)} = ∫0∞e − stg (t) dt = limz → ∞∫0ze − stg (t) dt. - Используйте интегрирование по частям, чтобы оценить limz → ∞∫0ze − stg (t) dt.limz → ∞∫0ze − stg (t) dt. (Пусть u = g (t) u = g (t) и dv = e − stdt.dv = e − stdt. Кстати, обратите внимание, что мы определили g (t), g (t), du = f (t) dt.) du = f (t) dt.)
Как и следовало ожидать, вы должны увидеть, что
L {g (t)} = 1s · L {f (t)}.L {g (t)} = 1s · L {f (t)}.
Интеграция во временной области упрощается до деления на с в частотной области.
Раздел 3.7 Упражнения
Вычислите следующие интегралы. Если интеграл не сходится, ответьте «расходится».
347.
∫24dx (x − 3) 2∫24dx (x − 3) 2
348.
∫0∞14 + x2dx∫0∞14 + x2dx
349.
∫0214 − x2dx∫0214 − x2dx
350.
∫1∞1xlnxdx∫1∞1xlnxdx
351.
∫1∞xe − xdx∫1∞xe − xdx
352.
∫ − ∞∞xx2 + 1dx∫ − ∞∞xx2 + 1dx
353.
Без интегрирования определите, сходится или расходится интеграл ∫1∞1×3 + 1dx∫1∞1×3 + 1dx, сравнивая функцию f (x) = 1×3 + 1f (x) = 1×3 + 1 с g (x) = 1×3. г (х) = 1×3.
354.
Без интегрирования определить, сходится или расходится интеграл ∫1∞1x + 1dx∫1∞1x + 1dx.
Определите, сходятся или расходятся несобственные интегралы. Если возможно, определите значение сходящихся интегралов.
355.
∫0∞e − xcosxdx∫0∞e − xcosxdx
356.
∫1∞lnxxdx∫1∞lnxxdx
359.
∫ − ∞∞1×2 + 1dx∫ − ∞∞1×2 + 1dx
361.
− 22dx (1 + x) 2∫ − 22dx (1 + x) 2
362.
∫0∞e − xdx∫0∞e − xdx
363.
∫0∞sinxdx∫0∞sinxdx
364.
∫ − ∞∞ex1 + e2xdx∫ − ∞∞ex1 + e2xdx
368.
∫01dx1 − x2∫01dx1 − x2
369.
∫031x − 1dx∫031x − 1dx
371.
∫355 (x − 4) 2dx∫355 (x − 4) 2dx
Определите сходимость каждого из следующих интегралов путем сравнения с заданным интегралом. Если интеграл сходится, найдите число, к которому он сходится.
372.
∫1∞dxx2 + 4x; ∫1∞dxx2 + 4x; сравните с ∫1∞dxx2.∫1∞dxx2.
373.
∫1∞dxx + 1; ∫1∞dxx + 1; сравните с ∫1∞dx2x.∫1∞dx2x.
Вычислите интегралы. Если интеграл расходится, ответьте «расходится».
378.
∫ − ∞0dxx2 + 1∫ − ∞0dxx2 + 1
379.
∫ − 11dx1 − x2∫ − 11dx1 − x2
382.
∫0∞xe − xdx∫0∞xe − xdx
383.
∫ − ∞∞x (x2 + 1) 2dx∫ − ∞∞x (x2 + 1) 2dx
384.
∫0∞e − xdx∫0∞e − xdx
Вычислите несобственные интегралы.Каждый из этих интегралов имеет бесконечный разрыв либо в конце, либо во внутренней точке интервала.
386.
∫ − 271dxx2 / 3∫ − 271dxx2 / 3
387.
∫03dx9 − x2∫03dx9 − x2
388.
∫624dttt2−36∫624dttt2−36
389.
∫04xln (4x) dx∫04xln (4x) dx
390.
∫03×9 − x2dx∫03×9 − x2dx
391.
Вычислить ∫.51dx1 − x2.∫.51dx1 − x2. (Будьте осторожны!) (Выразите свой ответ, используя три десятичных знака.)
392.
Оценить ∫14dxx2−1.∫14dxx2−1. (Выразите ответ в точной форме.)
393.
Вычислить ∫2∞dx (x2−1) 3 / 2.2∞dx (x2−1) 3/2.
394.
Найдите площадь области в первом квадранте между кривой y = e − 6xy = e − 6x и осью x .
395.
Найдите площадь области, ограниченной кривой y = 7×2, y = 7×2, осью x и слева x = 1.x = 1.
396.
Найдите площадь под кривой y = 1 (x + 1) 3/2, y = 1 (x + 1) 3/2, ограниченной слева x = 3.x = 3.
397.
Найдите площадь под y = 51 + x2y = 51 + x2 в первом квадранте.
398.
Найдите объем твердого тела, образованного вращением вокруг оси x в области под кривой y = 3xy = 3x от x = 1x = 1 до x = ∞.x = ∞.
399.
Найдите объем твердого тела, образованного вращением вокруг оси y в области под кривой y = 6e − 2xy = 6e − 2x в первом квадранте.
400.
Найдите объем твердого тела, образованного вращением вокруг оси x области под кривой y = 3e − xy = 3e − x в первом квадранте.
Преобразование Лапласа непрерывной функции на интервале [0, ∞) [0, ∞) определяется как F (s) = ∫0∞e − sxf (x) dxF (s) = ∫0∞e − sxf ( x) dx (см. Студенческий проект). Это определение используется для решения некоторых важных начальных задач в дифференциальных уравнениях, о которых будет сказано ниже. Область F — это набор всех действительных чисел s , так что неправильный интеграл сходится. Найдите преобразование Лапласа F для каждой из следующих функций и задайте домен F .
405.
Используйте формулу для длины дуги, чтобы показать, что длина окружности x2 + y2 = 1×2 + y2 = 1 равна 2π.2π.
Неотрицательная функция является функцией плотности вероятности, если она удовлетворяет следующему определению: ∫ − ∞∞f (t) dt = 1. − ∞∞f (t) dt = 1. Вероятность того, что случайная величина x находится между a и b , определяется как P (a≤x≤b) = ∫abf (t) dt. b 0.{-0,6} \\
\ amp \ приблизительно 0.1422 \ text {.}
\ end {выровнять *}
Таким образом, около 14,22% всех лампочек выходят из строя между \ (t = 2 \) и \ (t = 3 \ text {.} \). Очевидно, мы могли бы отрегулировать пределы интегрирования, чтобы измерить долю лампочек, которые выходят из строя в любое время. интересующий период.
Предварительный просмотр деятельности 6.5.1.
У компании с большой клиентской базой есть колл-центр, который принимает тысячи звонков в день. Изучив данные, показывающие, как долго вызывающие абоненты ждут помощи, они обнаруживают, что функция \ (p (t) = 0.б п (т) \, дт \ текст {.}
\ end {уравнение *}
Используйте эту информацию, чтобы ответить на следующие вопросы.
Определите долю вызывающих абонентов, которые ждут от 5 до 10 минут.
Определите долю вызывающих абонентов, которые ждут от 10 до 20 минут.
Далее давайте изучим долю, которая ждет определенное количество минут:
Какая доля абонентов ожидает от 0 до 5 минут?
Какая доля абонентов ожидает от 0 до 10 минут?
От 0 до 15 минут? От 0 до 20?
Пусть \ (F (b) \) представляет долю вызывающих абонентов, которые ждут от \ (0 \) до \ (b \) минут.
