Содержание
«Трапеция». 8-й класс
Цель:
- Ввести понятие трапеции, её элементов, виды трапеций.
- Рассмотреть некоторые свойства трапеции.
- Применение знаний при решении задач.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Кроссворд.
Ключевое слово кроссворда – является темой нашего урока.
- Любой многоугольник разделяет плоскость на две части, одна из которых
называется … - Четырехугольник, у которого противоположные стороны попарно параллельны.
- Отрезок, соединяющий любые две не соседние вершины многоугольника.
- Сумма длин всех сторон многоугольника.
- Две вершины многоугольника, принадлежащие одной стороне, называются…
- В конце урока каждый ученик ждет хорошую …
- Две несмежные стороны четырехугольника называются …
- Любой многоугольник разделяет плоскость на две части, одна из которых
внутренняя, а другая
Ответы:
III.
 Новый материал.
Новый материал.
Трапеция – (от греч. trapezion, букв. – столик).
Трапеция – четырёхугольник, у которого две стороны параллельны,
а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон,
называется средней линией трапеции.
Виды трапеции.
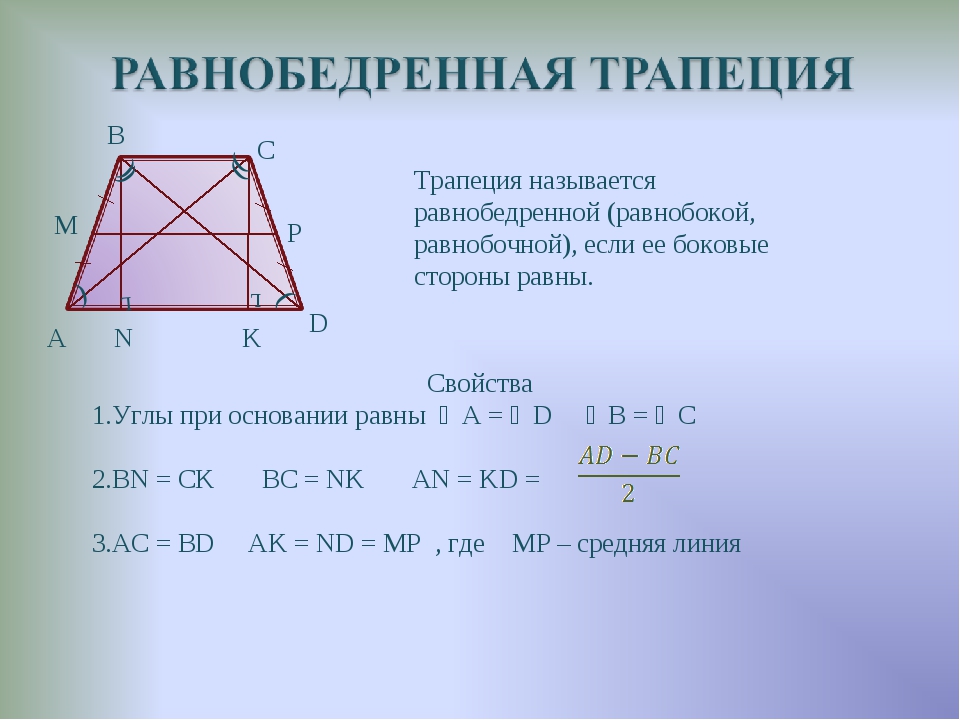
Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Работа в группах.
Группы с четными номерами – исследуют диагонали
равнобедренной трапеции. Группы с нечетными номерами – исследуют углы
равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать
решения.
Свойства равнобедренной трапеции.
Теорема. В равнобедренной трапеции углы при каждом основании равны.
Доказательство.
Проведем СЕ
АВ.
ABCD – параллелограмм (АВ
СЕ, ВС
AD).
CD = AB = CE,
СDE – равнобедренный,
СDЕ =
СЕD.
АВ
СЕ, тогда
СЕD =
ВАЕ,
СDЕ =
СЕD =
ВАЕ.
ABC = 180°
– СDЕ =
180° – ВАЕ =
BCD.
Теорема. В равнобедренной трапеции диагонали равны.
Доказательство.
ABC =
DСВ (АВ = С, ВС
– общая сторона,
АВС =
ВСD) тогда АС = ВD.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать
решения.
1. Если углы при основании трапеции равны, то она равнобедренная.
Доказательство.
Проведем ЕС
АВ.
ABCЕ – параллелограмм, тогда АВ
СЕ,
А =
СЕD,
СЕD –
равнобедренный (D =
СЕD), тогда СЕ = СD.
АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.
2. Если диагонали трапеции равны, то она равнобедренная.
Доказательство.
Проведем СК
ВD.
ВСКD – параллелограмм (т.к. СК
ВD, ВС
АК).
АСК – равнобедренный, т.к. АС = ВD = СК,
САD =
СDА.
СК ВD,
ВDА =
СКD, тогда
САD =
СКD.
АВD =
DСА, т.к. АС=ВD, АD
– общая сторона,
САD =
СКD, тогда АВ = СD, т.е. АВСD –
равнобедренная трапеция.
IV. Закрепление.
Решение задач по готовым чертежам.
V. Итог урока:
VI. Домашнее задание.
Параграф 44, вопросы: 10-11, №386, №388.
Диагонали трапеции
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).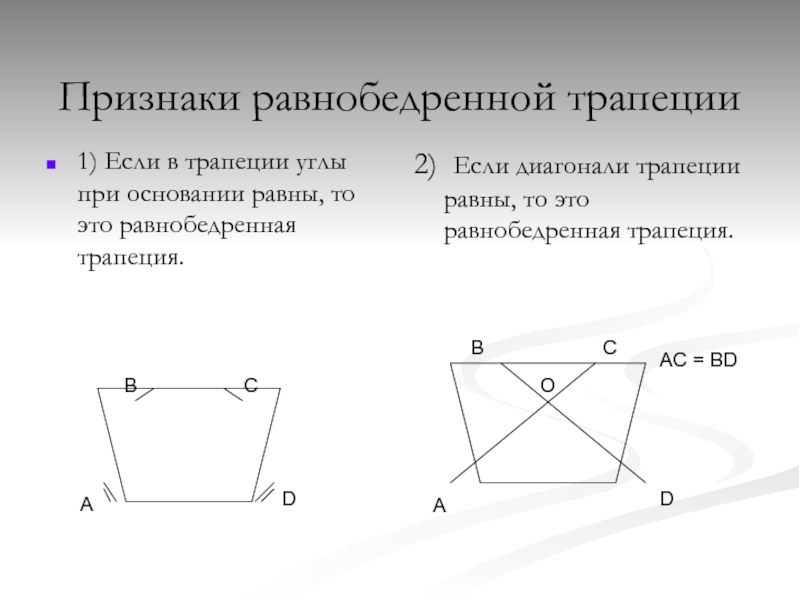
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.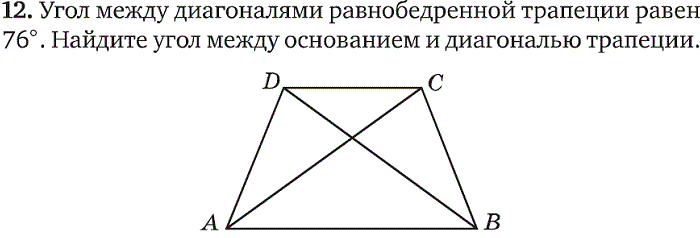
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).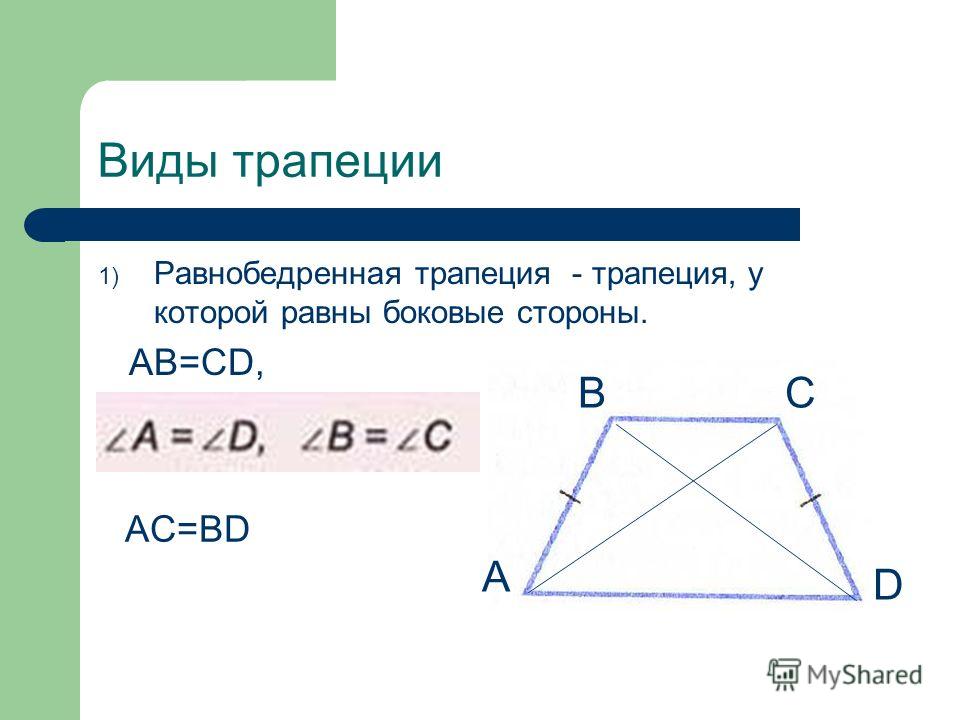
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание.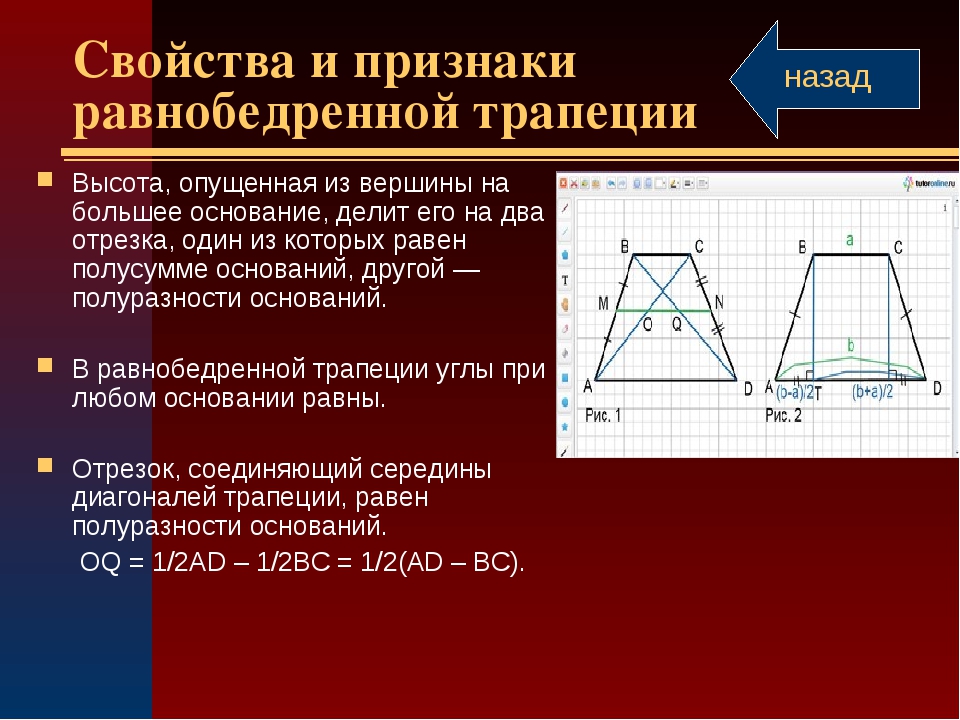 В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ: 16 см
Задача.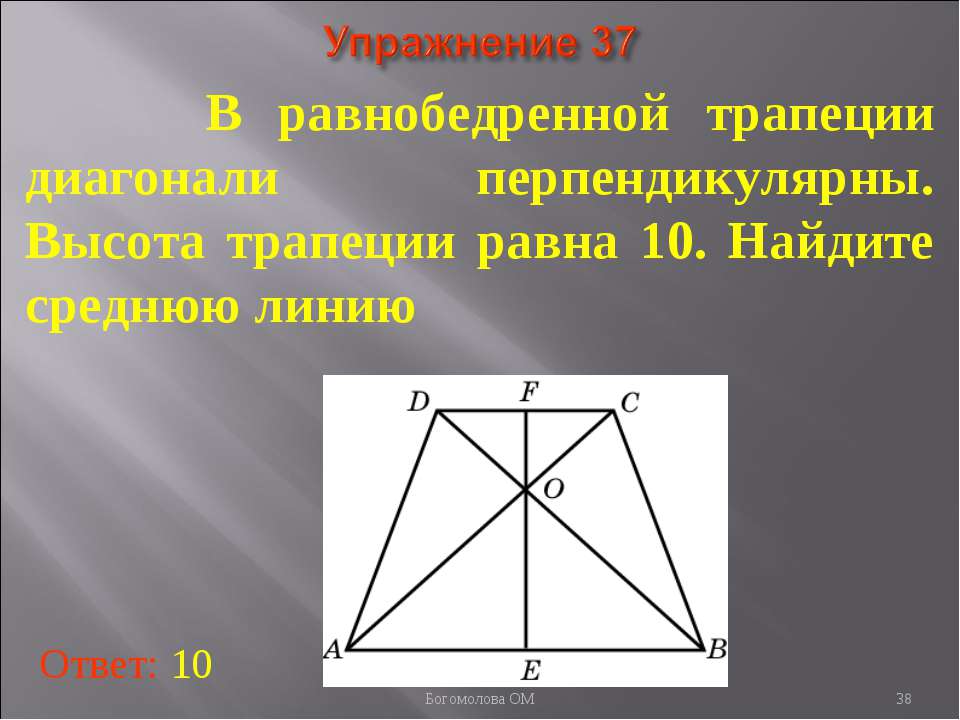
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
h2 + (24 — a)2 = (5√17)2
и
h2 + (24 — b)2 = 132
Учтем, что a = 16 — b , тогда в первом уравнении
h2 + (24 — 16 + b)2 = 425
h2 = 425 — (8 + b)2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора.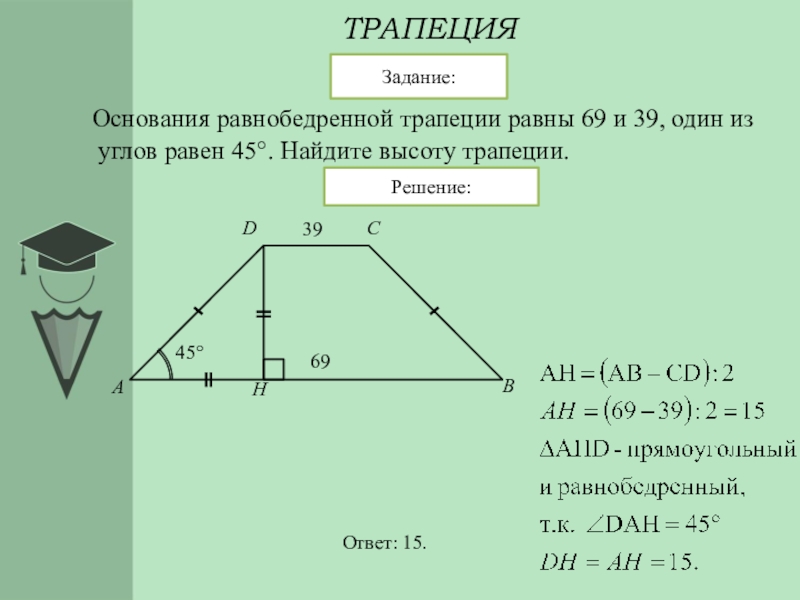 Получим:
Получим:
425 — (8 + b)2 + (24 — b)2 = 169
-(64 + 16b + b)2 + (24 — b)2 = -256
-64 — 16b — b2 + 576 — 48b + b2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h2 = 425 — (8 + b)2 = 425 — (8 + 12)2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см2
Ответ: площадь трапеции равна 80 см2.
Трапеция (задачи про основания) |
Описание курса
| Прямоугольная трапеция
Как доказывать признаки равнобедренной трапеции. Диагонали трапеции. Теоремы: свойства равнобедренной трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.
Данный отрезок параллелен основаниям трапеции
.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.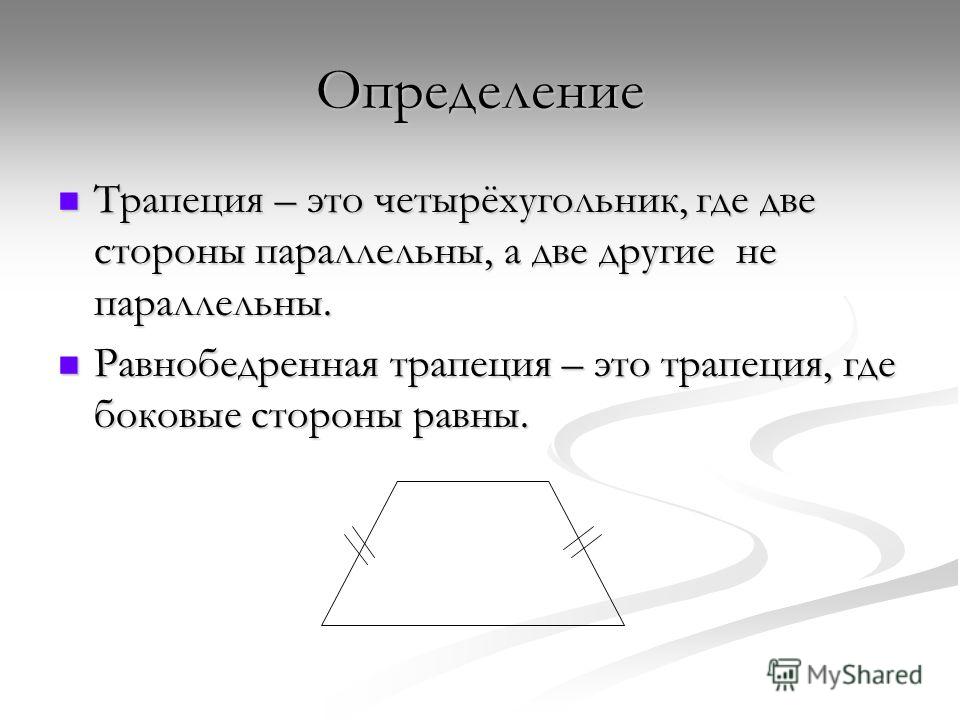
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b
— основания трапеции
c, d
— боковые стороны трапеции
d1 d2
— диагонали трапеции
α β
— углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.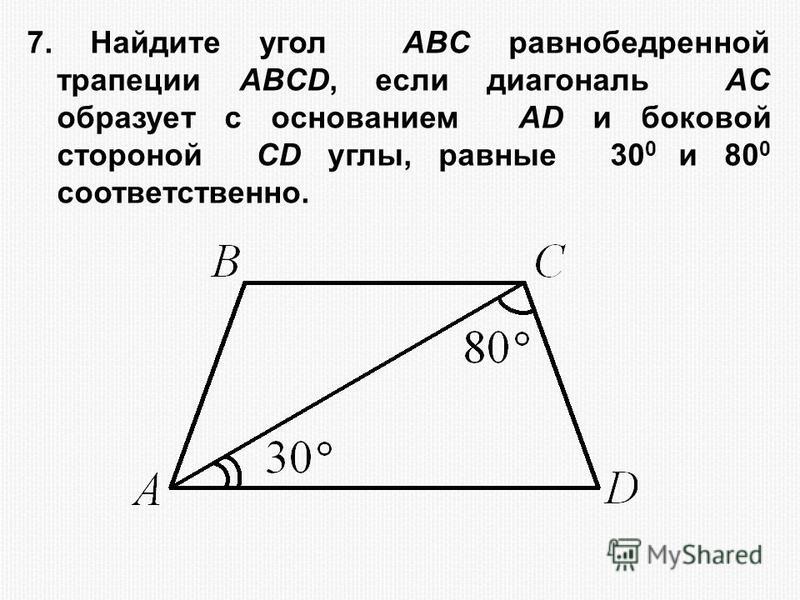
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.
Задача
.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение
.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ
: 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты.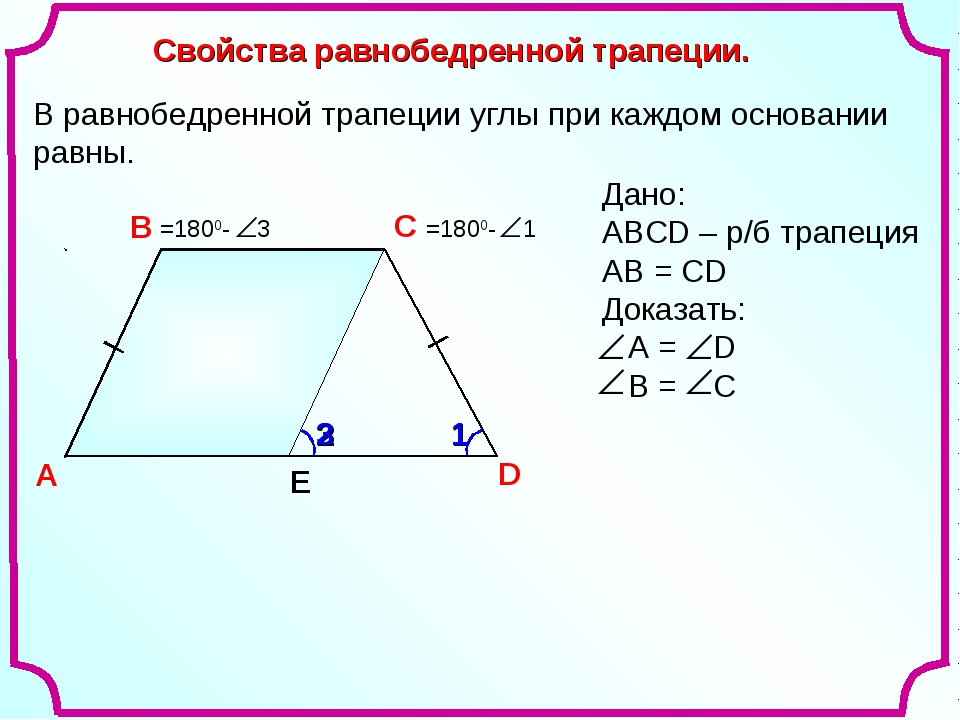 Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ
: площадь трапеции равна 80 см 2 . \circ\)
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
.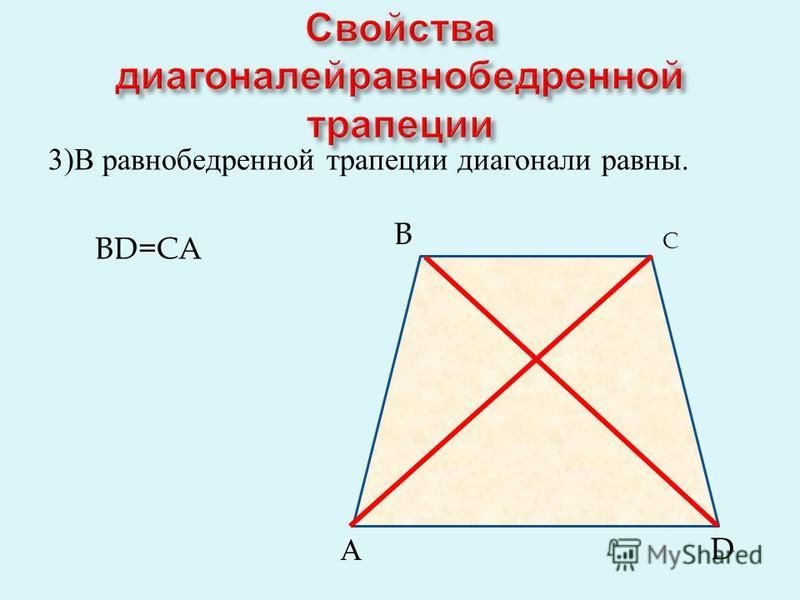 Пусть \(BB»\cap MN=M», CC»\cap
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.
Таким образом:
\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.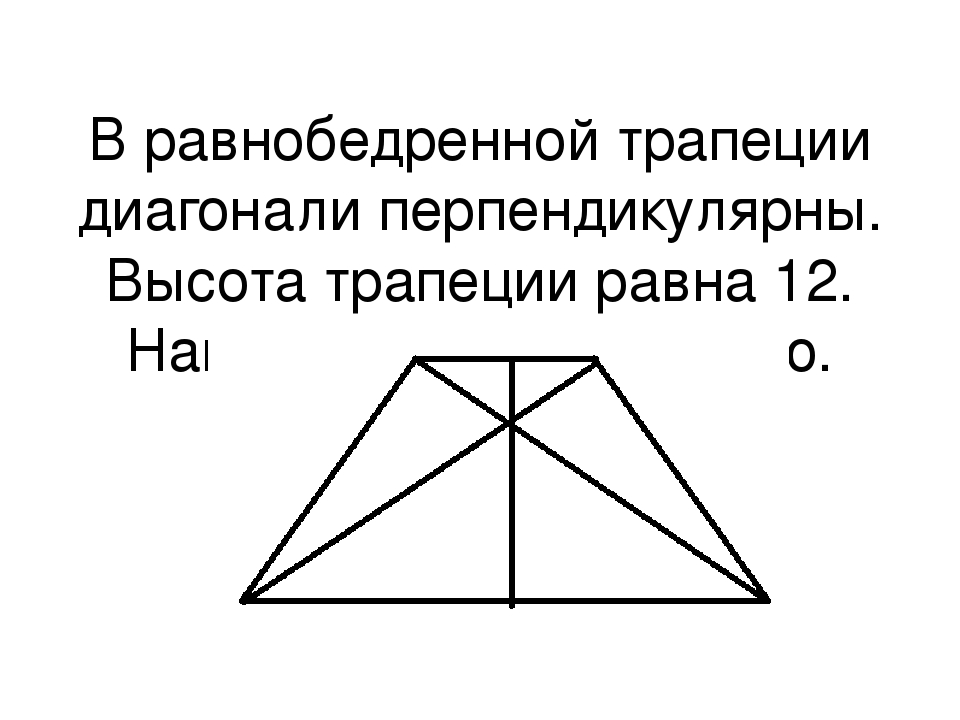
Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.
2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.
Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.
3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.
Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.
В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.
2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Поэтому одну из них мы назовем большим
, вторую — малым основанием
трапеции. Высотой
Высотой
трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник)
Теорема 20
. Радиус вписанной в трапецию окружности равен половине высоты основания.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
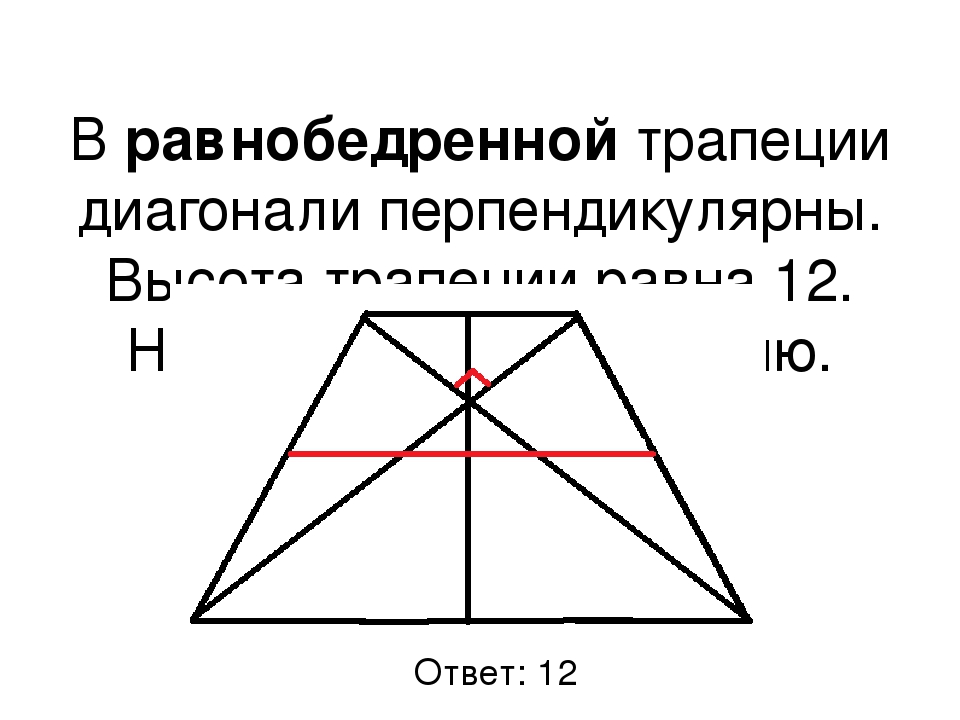
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
то
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
откуда
[PDF] Document — Free Download PDF
Download Document…
Трапеция свойства и признаки
Свойства и признаки равнобедренной трапеции Трапеция – это четырехугольник, у которого две стороны параллельны а две другие не параллельны Равнобедренная Трапеция – это трапеция, у которой боковые стороны равны Свойства
Признаки
У равнобедренной трапеции углы при основании равны
Если углы, прилежащие к одному из оснований трапеции, равны, то трапеция равнобедренная.
У равнобедренной трапеции диагонали равны
Если диагонали трапеции равны, то трапеция равнобедренная
Решение задач Доказать что диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки
B
A
C
D
B
C 3 4 1
2
O A
Решение задач Дано: ABCD – трапеция AB=CD Доказать: BO=OC, AO=OD D Доказательство
1. ABD ACD по двум сторонам и углу между ними (AB=CD, AD – общая, A D ) 2. 1 2 как соответственные элементы 3. C B, 1 2 следовательно 3 4 4. Треугольник BOC – равнобедренный, значит BO=OC
5. BD=AC и BO=OC, значит AO=OD
Свойство трапеции Мы доказали ещё одно свойство равнобедренной трапеции, давайте его запишем Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки
Решение задач Доказать, что если диагонали трапеции точкой пересечения делятся на соответственно равные отрезки, то эта трапеция будет равнобедренной
B
A
C
D
Решение задач B
C 1
Дано: ABCD – трапеция BO=OC, AO=OD
2
O A
Доказать: ABCD – равнобедренная трапеция D
Доказательство
1. ABO CDO по двум сторонам и углу между ними (BO=OC, AO=OD, 1 2 ) 2. AB=CD как соответственные элементы
Признак трапеции Мы доказали ещё один признак равнобедренной трапеции, давайте его запишем Если диагонали трапеции точкой пересечения делятся на соответственно равные отрезки, то эта трапеция будет равнобедренной
Домашнее задание
1. Трапеция, ее виды и свойства Свойства трапеции, которые часто используются при решении задач
Раздел 2. Четырехугольники
I.
Справочные материалы.
1.
Трапеция, ее виды и свойства
Свойства
трапеции, которые часто используются
при решении задач:
1)
Диагонали трапеции разбивают её на
четыре треугольника с общей вершиной.
Площади треугольников, прилежащие к
боковым сторонам, равны.
2) В
любой трапеции середины оснований,
точка пересечения диагоналей и точка
пересечения прямых, на которой лежат
боковые стороны, лежат на одной прямой
(точки М, N, О и К).
3) В
равнобокой трапеции углы при основании
равны.
4) В
равнобокой трапеции прямая, проходящая
через середины оснований, перпендикулярна
основаниям и является осью симметрии
этой трапеции,
5) В
равнобокой трапеции диагонали равны.
6) В
равнобокой трапеции высота, опущенная
на большее основание из конца меньшего
основания, делит его на два отрезка,
один из которых равен полуразности
оснований, а другой их полусумме.
7) Во
всякой трапеции серединам боковых
сторон и середины диагоналей лежат на
одной прямой.
8) Во
всякой трапеции отрезок, соединяющий
середины диагоналей, параллелен
основаниям и равен полуразности
оснований.
9) во
всякой трапеции сумма квадратов
диагоналей равна сумме квадратов боковых
сторон и удвоенного произведения
оснований.
10)
Трапецию можно вписать в окружность
тогда и только тогда, когда она равнобокая.
11)
Трапецию можно описать около окружности
тогда и только тогда, когда сумма
оснований равна сумме боковых сторон.
2.Вписанные
и oписанные
четырёхугольники.
1)Если
четырёхугольник вписан в окружность,
то сумма противолежащих углов равна
180°.
Верно
и обратное: если сумма противолежащих
углов четырёхугольника равна 180°, то
около этого четырёхугольника можно
описать окружность.
2)Около
параллелограмма можно описать окружность
тогда и только тогда, когда этот
параллелограмм есть прямоугольник.
3)Около
трапеции можно описать окружность, если
она равнобокая.
четырёхугольник
называется описанным около окружности,
если окружность касается всех его
сторон.
4)Если
четырёхугольник описан около окружности,
то суммы противолежащих сторон равны.
5)Если
в выпуклом четырёхугольнике суммы
противоположных сторон равны, то в этот
четырёхугольник можно вписать окружность.
3. Площади
четырёхугольников.
Площадь
выпуклого четырёхугольника равна
половине произведения диагоналей на
синус угла между ними.
Ромб
1.
Диагонали ромба взаимно перпендикулярны
и делят углы пополам.
2.
Площадь определяется формулами:
Параллелограмм
1.
Сумма квадратов диагоналей равна сумме
квадратов всех его сторон.
2. Площадь
определяется формулой
S=ah
S=аb·sinА
.
II.
Дополнительные материалы
1)Свойства
вписанного выпуклого четырехугольника.
а)В
выпуклом вписанном четырехугольнике
сумма противоположных углов равна двум
прямым
б)Обратно:
если в выпуклом четырехугольнике сумма
противоположных углов равна двум прямым,
то около него можно описать окружность
Доказательство.
а)
Пусть АВСD есть вписанный выпуклый
четырехугольник; требуется доказать„
что
Так как
сумма всех четырех углов сякого выпуклого
четырехугольника равна 4d,
то достаточно доказать только одно из
требуемых равенств.
докажем,
например, что
Углы В
и D как вписанные, измеряются:
первый—половиной дуги ADC,
второй- половиной дуги АВС;
Следовательно,
сумма ½ ﬞ ADC+ ½ ﬞ
ABC , а эта сумма равна
1/2 (ﬞ ADС+ ﬞ ABC),
т. е. равна половине окружности; значит,
б) Пусть
АВСD есть такой выпуклый
четырехугольник, у которого
Через
какие-нибудь три его вершины, например,
через A,В и С, проведем
окружность (что всегда можно сделать).
Четвертая
вершина D должна находиться
на этой окружности, пoтoму
что в противном случае вершина угла В
лежала бы или внутри круга, или вне его,
и тогда этот угол не измерялся бы
половиной дуги АВС; поэтому cyммa
измерялась
бы полусуммой дуг ADC и АВС
и, значит, сумма
Следствия
1) из
всех параллелограммов только вокруг
прямоугольника можно описать окружность.
2) около
трапеции можно описать окружность
только тогда, когда она равнобокая.
2)
Свойство описанного четырехугольника.
В описанном четырехугольнике суммы
противоположных сторон равны.
Пусть
АВСD будет описанный
четырехугольник, Т.е, стороны его касаются
окружности; требуется доказать, что
АВ+СВ=ВС+АD
Обозначим
точки касания буквами M,
N, Р и Q. Так
как две касательные, проведенные из
одной точки окружности, равны, то АМ.=АQ,
ВМ=ВN, CN=СР, DP=DQ.
Следовательно,
АМ+МВ+СР+РD=AQ+QD+BN+NC.
Т.е. АВ+СD=АD+ВС.
III. Вводные задачи.
Задача 1.
Средняя линия трапеции ABCD равна 15.
AD – большее основание трапеции,
A
= 90°,
D
= 60°,
BAC
= 30°. Найдите длину стороны CD.
Решение.
В
∆ABC (он прямоугольный) BC =
– по свойству катета, лежащего против
угла в 30°.
BAC
= 30°, значит,
CAD
= 90° – 30° =
= 60°, следовательно, ∆ACD
равносторонний,
т. е. AC = CD = AD
= 2BC.
Средняя линия MN =
3BC = 30,
BC = 10, значит,
CD = 2 · 10 = 20.
Ответ:20.
Задача
2.
Сторона AB параллелограмма ABCD
равна а его диагонали равны 20 и
24. Найдите сторону BC.
Решение.
Для
любого выпуклого четырехугольника
справедливо
где
a, b, c и d – стороны
четырехугольника, а d1, d2
– его диагонали.
В
параллелограмме
202 + 242 = 2(( )2
+ b2), b > 0; b2 + 88 =
488,b2 = 400, b = 20.
Ответ: 20.
Задача
3.
Основания трапеции равны 4 и 10, а ее
боковые стороны – и 15. Найдите
косинус наименьшего угла этой трапеции.
Решение.
1)
Проведем BM ∥
CD, значит,
BMA
=D,
ВСDМ – параллелограмм, так как ВМ
|| MD, ВМ || СD. Следовательно,
ВС = MD = 4,
BM = CD = 15, AM
= AD – MD = 10 – 4 = 6.
2) В ∆AMB против большей стороны
(выбирая из AB и BM) лежит больший
угол: AB BM, значит,
BMA
A.
cos α = .
.
Ответ: 0,8.
Задача 4.
Определите периметр равнобокой трапеции,
у которой длина меньшего основания
равна 7, диагонали перпендикулярны
боковым сторонам и равны
.
Решение.
1)
Проведем в трапеции ABCD высоту
CF,
тогда
∆ACD ∼ ∆AFC,
2) Пусть FD = x, тогда AF = 7 + x
( )2 = (x + 7) (7 + 2x),
36 · 2 = 49 + 21x + 2x2,
2x2 + 21x – 23 = 0,
D = 212 + 4 · 2 · 23 = 625,
х1,2 =
3) Итак, AD = 7 +2 = 9;
CD =
P = 9 + 7 + 2 · 3 = 22.
Ответ: 22.
Задача 5.
В ромбе высота, проведенная из вершины
тупого угла, делит сторону ромба пополам.
Найдите периметр и высоту ромба, если
меньшая диагональ его равна 7
Решение.
1)
В треугольнике ABD BK – высота и
медиана, значит, ∆ABD -равнобедренный
с основанием AD, т. е. AB = BD = 7
см. Тогда ∆ABD -равносторонний, значит,
A
=
ABD
=
BDA
= 60°.
2) P = 4AB = 4 · 7 = 28 (см).
3)
BKD
– прямоугольный, BK = AD sin
BDK.
BK = 7 · sin 60° = (см). Ответ:
28 см; 3,5 см.
Задача 6.
Основание AB трапеции ABCD вдвое
длиннее основания CD и вдвое длиннее
боковой стороны AD. Длина диагонали
AC равна 12, длина боковой стороны BC
равна 5. Найдите площадь трапеции.
Решение.
1)
По условию AB = 2AD = 2DC.
Пусть
M – середина AB, тогда AM = MB
= CM,
т. е. CM – медиана треугольника
ABC и CM = AB, значит, ∆ABC
прямоугольный с гипотенузой AB.
По
теореме Пифагора AB2 = AC2
+ BC2; AB = =
= = 13.
CM
= MB = = 6,5.
2) CK – высота трапеции и высота ∆MCB.
По
формуле Герона S∆ =
где ;
S(∆MBC)
=
= 3 · 2 · 2,5 = 15.
CK =
S(ABCD) =
Ответ: 4,5.
IV.
Дополнительные задачи
№ 1.
Вершина C параллелограмма
ABCD соединена с точкой N
на стороне AB. Отрезок CN
пересекает диагональ BD
в точке P. Площадь
треугольника BNP равна 8,
а площадь треугольника BCP
равна 12. Найдите площадь параллелограмма
ABCD.
Решение:
1)
Треугольники BNP и BPC
имеют общую высоту BH=>
SBNP/SBPC=PN/PC=>PN/NC=2/3;
2)
Треугольники BPN и DPC
подобны по
двум
углам => SBPN/SDPC=(PN/PC)2
SDPC=9/4;
SBPN
= (9/4)·8=18;
3)
SBCD=SBPC+SDPC=12+18=30;
4)
SABCD=2·SBCD=60;
Ответ: 60
№ 2.
На стороне AB параллелограмма
ABCD, как на диаметре,
построена окружность, проходящая через
точку пересечения диагоналей и середину
стороны AD. Найдите углы
параллелограмма.
Решение:
1) По
условию, AB – диагональ=>
o=>ABCD – ромб
P – середина АВ: по условию
Q – середина AD=>PQ
– средняя линия ∆ABD=BD=2PQ;PQ=R=>BD=2R;PO=R – средняя
линия ∆АBD=>AD=2·PO=R∆ABD – правильный =>
o=>
o.
Ответ:
60o и 120o.
№ 3.
Угол между сторонами АВ и СD четырехугольника
ABCD=φ. Докажите, что AD2=AB2+BC2+CD2-2(AB·BCcosB
+ BC·CDcosC+CD·ABcosφ)
Решение.
По
теореме косинусов AD2=AC2+CD2-2AC·CD·cosACD
и AC2=AB2+BC2-2AB·BCcosB. A
так как длина проекции отрезка АС на
прямую l , перпендикулярную CD, равна
сумме длин проекций отрезков АВ и ВС на
прямую l, то ACcosACD=ABcosφ+BCcosC
V.Задачи для
самостоятельного решения
№1. Докажите, что если ABCD прямоугольник,
а Р- произвольная точка, то
АР2 +СР2 =DP2 +BP2
№2. Перпендикуляр, опущенный из вершины
параллелограмма на диагональ, делит
ее на отрезки длиной 6 и 15. Найдите
большую сторону параллелограмма, если
известно, что разность сторон равна 7.
Ответ: 7
№3. Одно из оснований трапеции равно
24, а расстояние между серединами
диагоналей 4. найдите другое основание.
Ответ: 16
№4. Длины оснований равнобедренной
трапеции относятся как 5:12, а длина ее
высоты равна 17. Найдите радиус окружности,
описанной около трапеции, если средняя
линия равна высоте.
Ответ: 13
№5. В трапеции ABCD диагональ АС
перпендикулярна боковой стороне СD.
Окружность, описанная возле треугольника
АВС, касается прямой CD, пересекает
основание AD в точке М. Найдите площадь
трапеции АBCD, если АМ=8, СМ=4.
Ответ: 36
№6. Окружность, центр которой лежит
внутри квадрата PQRS, касается стороны
PQ в точке К, пересекает сторону PS в точках
А и В,, а диагональ PR в точках С и D. Найдите
радиус окружности, если АВ=16, СD=2√92
Ответ: 10
№7. В параллелограмме ABCD угол АВС=3п/4.
окружность, описанная возле треугольника
АВD, касается прямой CD. Найдите площадь
параллелограмма, если диагональ BD=2
Ответ: 4
№8. Вершина С параллелограмма ABCD соединена
с точкой N на стороне АВ. Отрезок CN
пересекает диагональ BD в точке Р. Площадь
треугольника BNP равна 8, а SВСР=12.
Найдите площадь параллелограмма АВСD.
Ответ:
60
№9.
Найдите площадь трапеции, основания
которой 6 и 26, а боковые стороны – 12 и
16.
Ответ:
153,6
№10. На
стороне АВ параллелограмма АВСD как на
диаметре построена окружность, проходящая
через точку пересечения диагоналей и
середину стороны АD. Найдите углы
параллелограмма.
Ответ:
60,120,60,120.
VI.
Контрольные задачи.
Вариант № 1.
1) В равнобедренную трапецию, площадь
которой равна 80, вписана окружность
радиуса 4. Найдите периметр трапеции.
2) Найдите диаметр окружности, вписанной
в равнобедренную трапецию, если сумма
оснований трапеции 26, а разность оснований
равна 10.
3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К. Найдите периметр
параллелограмма, если АК = 12, СМ = 24, МК =
18.
Вариант
№ 2.
1) В круг с площадью 169π вписана
равнобедренная трапеция, меньшее
основание которой равно 10. найдите
площадь трапеции, если центр описанного
круга лежит на её большем основании.
2) Найдите диаметр окружности, вписанной
в равнобедренную трапецию, если сумма
оснований трапеции 15, а разность оснований
равна 9.
3)В параллелограмме АВСД биссектриса
угла Д пересекает сторону АВ в точке К
и прямую ВС в точке Р. Найдите периметр
∆ СДР, если ДК = 18, РК = 24, АД=15.
Вариант
№ 3.
1) В равнобедренную трапецию, площадь
которой 20, а синус одного из углов равен
0,8, вписана окружность. Найдите радиус
этой окружности.
2) Основание СМ и ОР трапеции СМОР равны
3 и 6 соответственно, диагонали трапеции
пересекаются в точке Н, а площадь
треугольника СРН равна 4. Найдите площадь
трапеции.
3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К. Найдите периметр
∆ АМК, если СД = 12, СМ = 14, СВ = 30.
Вариант
№ 4.
1) Найдите площадь равнобедренной
трапеции, если её высота равна 4, а тангенс
угла между диагональю и основанием
равен
.
2) В равнобедренную трапецию, площадь
которой равна 80, вписана окружность
радиуса 4. Найдите периметр трапеции.
3) В параллелограмме АВСД биссектриса
угла В пересекает сторону СД в точке Т
и прямую АД в точке М. Найдите
периметр ∆ АВМ, если ВТ = 18, ТМ = 12, ВС =
15.
Четырехугольники
Параллелограмм
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
- Диагональ разбивает параллелограмм на два равных треугольника.
- Противоположные стороны параллелограмма попарно равны.
- Противоположные углы параллелограмма попарно равны.
- Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
- Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
- Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм.
- Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник – параллелограмм.
Свойство середин сторон четырёхугольника
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника.
Прямоугольник
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
- Диагонали прямоугольника равны.
- Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.
Квадрат
Квадратом называется прямоугольник, все стороны которого равны.
Ромб
Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба
- Диагонали ромба перпендикулярны.
- Диагонали ромба делят его углы пополам.
- Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
- Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны.
Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция
Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции
- Углы при основании равнобедренной трапеции равны.
- Диагонали равнобедренной трапеции равны.
- Если углы при основании трапеции равны, то она равнобедренная.
- Если диагонали трапеции равны, то она равнобедренная.
- Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Докажите, что диагонали равнобедренной трапеции совпадают
Чтобы доказать, что диагонали равнобедренной трапеции совпадают, рассмотрим равнобедренную трапецию, показанную ниже. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя одну и ту же трапецию.
Первый способ — показать, что треугольник ABC конгруэнтен треугольнику DCB
.
Дано : Равнобедренная трапеция ABCD с отрезком AB ≅
сегмент DC
Prove : сегмент AC ≅ сегмент BD
Поскольку трапеция равнобедренная, углы основания совпадают.
Следовательно, ∠CBA ≅ ∠BCD
Кроме того, отрезок BC должен отрезать BC по рефлексивному свойству конгруэнтности.
Согласно постулату SAS, треугольник ABC ≅ треугольник DCB.
Следовательно, сегмент AC ≅ сегмент BD
О чем нужно помнить, когда вы доказываете, что диагонали равнобедренной трапеции совпадают.
Вот некоторые вещи, которые вы должны знать о приведенном выше доказательстве.
- Утверждение , если трапеция равнобедренная, то базовые углы равны , также требует доказательства.Однако мы не будем здесь доказывать.
- У равнобедренной трапеции равные стороны всегда непараллельны. На трапеции выше мы показываем эти стороны красными отметками.
- Рефлексивное свойство относится к числу, которое всегда равно самому себе. Например, 9 = 9 или y = y являются примерами рефлексивного свойства.
- SAS означает «сторона, угол, сторона». Возможно, вам стоит повторить урок о равных треугольниках.
- Чтобы доказать, что диагонали равнобедренной трапеции совпадают, вы могли бы также использовать треугольник ABD и треугольник DCA.
Другой способ доказать, что диагонали равнобедренной трапеции совпадают. На этот раз мы покажем, что треугольник BAD конгруэнтен треугольнику CDA
.
Дано : Равнобедренная трапеция ABCD с отрезком AB ≅
сегмент DC
Prove : сегмент AC ≅ сегмент BD
Поскольку трапеция равнобедренная, базовые углы совпадают
Следовательно, ∠BAD ≅ CDA
Обратите внимание, что на этот раз мы не используем те же базовые углы, что и перед.Базовые углы, которые мы сейчас используем, связаны с основанием на вершине или сегментом AD.
Кроме того, отрезок AD ≅ должен отрезать AD по рефлексивному свойству конгруэнтности.
Согласно постулату SAS, треугольник BAD ≅ треугольник CDA
Следовательно, сегмент AC ≅ сегмент BD
доказывают, что диагонали равнобедренной трапеции равны
Докажите, что в равнобедренном треугольнике углы, противоположные равным сторонам, также равны
Докажите, что в равнобедренном треугольнике углы, противоположные равным сторонам, также равны.
Если две высоты треугольника равны, докажите, что треугольник равнобедренный.
Если две высоты треугольника равны, докажите, что он равнобедренный.
Равнобедренная трапеция с периметром 40 см описана в круге с радиусом r = # sqrt (21) #. Определите длину его сторон?
Равнобедренная трапеция с периметром 40 см описана в круге с радиусом r = # sqrt (21) #.Определите длину его сторон?
диагонали равнобедренной трапеции — 17, высота — 8, верхнее основание — 9.
диагонали равнобедренной трапеции равны 17, высота 8 и верхнее основание 9. Найдите периметр трапеции.
Завершите доказательство того, что диагонали равнобедренной трапеции совпадают 19 Дано: …
Завершите доказательство того, что диагонали равнобедренной трапеции совпадают 19 Дано: Трапеция EFGH с FE = GH Fb, c) G (b, c) Докажите: EG = HF E (-a, 0) 01 H (a, 0) Доказательство: по формуле расстояния EG = a.? а ВЧ = b._? По транзитивному свойству сравнения EG = HF. Следовательно, EG = HF по определению сравнения. Заполните пробел для поля a. Доказательство: по формуле расстояния EG = a ….
Докажите следующее
— AD конгруэнтно BC (диагонали совпадают)
— AB параллельна …
Докажите следующее
— AD конгруэнтно BC (диагонали совпадают)
— AB параллельно CD
— угол SUT меньше пи / 2
— RS меньше или равно TU
2 Рассмотрим следующие четырехугольники в Neutal acome ky 乃
евклидова геометрия
пошаговый процесс
1.(7 баллов) Докажите, что диагонали прямоугольника …
евклидова геометрия
пошаговый процесс
1. (7 баллов) Докажите, что диагонали прямоугольника совпадают. 2. (18 баллов) На диаграмме ниже докажите, что M является серединой AC и BD тогда и только тогда, когда ABCD — параллелограмм. 3. (9 баллов) Используйте пункты 1 и 2 выше, чтобы доказать, что диагонали квадрата разрезают друг друга на 4 равных сегмента. Используйте # 3, чтобы доказать, что диагонали квадрата — это биссектрисы угла …
Вопрос 1.Докажите обратное к теореме о равнобедренном треугольнике: если треугольник имеет два угла …
Вопрос 1. Докажите обратное к теореме о равнобедренном треугольнике: если в треугольнике два угла равны, то стороны, противоположные равным углам, равны.
доказать, что треугольник равнобедренный тогда и только тогда, когда две высоты
конгруэнтны.
докажи и то, и другое …
доказать, что треугольник равнобедренный тогда и только тогда, когда две высоты
конгруэнтны.
доказать оба пути
доказать, что диагонали ромба делят ромб на четыре равных треугольника
докажите, что диагонали ромба делят ромб на четыре равных треугольника.Спасибо.
Диагонали равнобедренной трапеции
Это был день перед тестированием на полигонах, и я подумал, что написание доказательства и последующий отзыв о доказательстве другой команды могут быть полезны.
Студенты работали в одиночестве в течение нескольких минут, думая о том, что им было дано и что могло подразумеваться. Затем они вместе со своей командой обсудили свои идеи и начали планировать доказательство.
Некоторым было положено хорошее начало.
Некоторые, очевидно, практиковали , ищут и используют структуру .
Некоторые застряли.
Я поговорил с несколькими группами, выслушал их план и задал несколько вопросов, чтобы они разобрались.
А потом я достал цветную бумагу, чтобы написать групповое доказательство.
Время шло, но я подумал, что они наверняка смогут обменяться доказательствами с другой командой для получения обратной связи в течение нескольких минут.
Я разговаривал с другой группой. Они отражали ∆ABC относительно линии AC.
Каким будет изображение ∆ABC около линии AC?
Ответ? ∆ACD.
Конечно, это неправильно. Кажется настолько очевидным, что ∆ABC не конгруэнтно ∆ACD. И мне также интересно, как это помогает нам доказать, что AC = BD, поскольку BD не входит ни в один из этих треугольников. Но вот где находится эта команда студентов. Теперь у меня есть возможность поддержать их продуктивную борьбу , или я могу остановить продуктивную борьбу на ее пути, дав им свое объяснение.
Мой выбор? Ножницы.И бумага. И еще раз.
Что произойдет, если вы отразите ∆ABD относительно линии AC?
Ой! Треугольники не совпадают.
Так есть ли совпадающие треугольники, которые могут привести нас к диагоналям?
∆ABC конгруэнтно ∆BAD.
Откуда ты знаешь?
Отражение.
О чем?
Вот этот карандаш!
Так что же важного в линии, проводимой карандашом?
Это линия симметрии трапеции.
Проходит через средние точки.
(Один из членов команды использовал программу динамической геометрии, чтобы отразить ∆ABC посреди нашего разговора, но у меня нет фотографий ее работы.)
Итак, план состоял в том, чтобы команда написала свои доказательства на цветной бумаге, а затем обменялась с другими командами для получения отзывов. Отличная идея, правда? Так что же делать с оставшимися 15 минутами? Действовать, как запланировано, и позволить им высказывать свое мнение без обсуждения всего класса? Или провести обсуждение со всем классом, чтобы связать студенческие работы? Потому что, как выяснилось, никакие две команды не доказали совпадение диагоналей одинаково.Я выбрал второе.
Я попросил первую команду поделиться своей работой.
Их доказательство требует доработки. Но у них есть хорошая идея.
Они доказали ∆AMDAM∆BMC, что делает соответствующие стороны конгруэнтными, поэтому с помощью подстановки и Постулата сложения сегментов мы можем показать, что диагонали конгруэнтны.
Затем я попросил команду рассказать, кто доказал ∆ABC≅∆BAD, используя отражение линии, которая содержит средние точки оснований.Их письменное доказательство тоже нуждается в доработке. Но у них была хорошая идея.
Другая команда доказала ∆ACD≅∆BDC.
Другая команда построила серединные перпендикулярные основаниям. Поскольку основания параллельны, линия, перпендикулярная одному, будет перпендикулярна другому. Я не уверен, что они добрались до причины, по которой срединные перпендикуляры должны совпадать. Они могли бы использовать ∆AZD≅∆BZC, чтобы показать это. Вместо этого они использовали точку Z на обоих серединных перпендикулярах (они знают, что любая точка на серединном перпендикуляре сегмента равноудалена от конечных точек сегмента), чтобы обосновать, что ∆AZB и ∆DZC равнобедренные, и затем использовали добавление сегмента. Постулат и подстановка, чтобы показать, что диагонали совпадают.Не идеально. Но хорошее начало.
Обсуждение
NCTM Принципов действий по поддерживает продуктивную борьбу в изучении математики гласит: «Учителя иногда воспринимают разочарование учеников или отсутствие немедленных успехов как индикаторы того, что они каким-то образом не справились со своими учениками. В результате они бросаются «спасать» студентов, разбивая задачу на части и помогая студентам шаг за шагом преодолевать трудности. Несмотря на благие намерения, такое «спасение» подрывает усилия учащихся, снижает когнитивные требования к задаче и лишает учащихся возможности полностью погрузиться в понимание математики.”
Итак, хотя я не спас своих учеников, мы так и не смогли создать образцового доказательства того, что диагонали равнобедренной трапеции совпадают. Разве они узнают что-то о имеют смысл проблем и настойчивость в решении их ? Конечно. Этого достаточно?
Было бы полезно начать урок следующего года с этой студенческой работы? Или это убирает продуктивную борьбу ?
Неужели мы просто должны найти баланс между продуктивной борьбой и тем, как выглядит образцовая работа, которая на одних уроках легче, чем на других? Если так, то на этом уроке мне не удалось добиться этого баланса.Тем не менее, путешествие продолжается…
Нравится:
Нравится Загрузка …
Связанные
Трапеция
и ее теоремы
Covid-19 привел мир к феноменальному переходу.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе мы обсудим некоторую трапецию и ее теоремы.
Трапеция — это четырехугольник, по крайней мере, с одной парой параллельных сторон. AB || CD. (если есть две пары параллельных прямых, то это параллелограмм)
Если непараллельные стороны трапеции равны, то это равнобедренная трапеция.
Теорема 1: Трапеция является равнобедренной тогда и только тогда, когда базовые углы совпадают.
Дано: ABCD — равнобедренная трапеция. AD = BC и AB || CD. Докажите, что: ∠C = ∠D
| Утверждения | Причины |
| 1) ABCD представляет собой трапецию. | 1) Дано |
| 2) AB || CD | 2) Дано |
| 3) AD = BC | 3) Дано |
| 4) DA || CE | 4) По конструкции |
| 5) ADCE — параллелограмм. | 5) По свойствам параллелограмма. |
| 6) DA = CE и DC = AE | 6) По свойствам параллелограмма. |
| 7) BC = CE | 7) BC = AD и AD = CE (переходное свойство) |
| 8) ∠CEB ≅ & CBE | 8) Если BC ≅ CE, то противоположный им угол конгруэнтен. |
| 9) ∠DAB ≅ ∠ABC | 9) свойство параллелограмма и углов линейной пары |
| 10) ∠A + ∠D = 180 и ∠B + ∠C = 180 | 10) внутренние углы на с той же стороны трансверсали являются дополнительными. |
| 11) ∠A + ∠D = ∠C + ∠B | 11) Транзитивность (правые части совпадают, поэтому левые части равны) |
| 12) ∠D = ∠C | 12) Сверху (∠A = ∠B) |
Пример: В форме трапеции PQRS, PQ || RS и PS = QR.Если ∠S = 60 0 , найдите оставшиеся углы.
Решение:
PQ || RS и PS = QR, поэтому трапеция PQRS является равнобедренной трапецией.
У равнобедренной трапеции углы основания равны (трапеция и ее теоремы)
∠S = ∠R и ∠P = ∠Q
Но ∠S = 60 0
∴ ∠R = 60 0
Пусть ∠P = ∠Q = x
Сумма всех углов в четырехугольнике равна 360.
∴ ∠P + ∠Q + ∠S + ∠R = 360
x + x + 60 + 60 = 360
2x +120 = 360
2x = 360-120
2x = 240
∴ x = 240/2
x = 120
∠P = ∠Q = 120 0
__________________________________________________________________
Некоторые важные теоремы трапеций приведены ниже:
| 1.Трапеция является равнобедренной тогда и только тогда, когда базовые углы совпадают. |
| 2. Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. |
| 3. Если трапеция равнобедренная, противоположные углы являются дополнительными. |
| Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. |
| Никогда не предполагайте, что трапеция равнобедренная, если вам не предоставят (или не можете доказать) эту информацию. |
Практика
1) В трапеции ABCD, AB || CD и BC = AD. Если m∠C = 65 0 , найдите m∠D.
2) PQRS — это трапеция, в которой PQ || RS. Если ∠P = ∠Q = 40, найдите размеры двух других углов.
3) В трапеции ABCD ∠B = 120 0 Найдите m∠C.
4) В четырехугольнике HELP, если EP = LH, то что это за четырехугольник?
5) В четырехугольнике углы имеют соотношение 4: 5: 3: 6.Найдите размеры каждого угла.
6) Если три угла трапеции равны 130 0 , 120 0 , 50 0 и 2x 0 . Найдите x и 4-й угол.
7) Нарисуйте равнобедренную трапецию с именем PQRS, PS || QR и PQ = SR.
Четырехугольник
• Введение в четырехугольник
• Типы четырехугольника
• Свойства четырехугольника
• Параллелограмм и его теоремы
• Прямоугольник и его теоремы
• Квадрат и его теоремы
• Ромб и его теоремы
• Трапеции и его теоремы
• Воздушный змей и его теоремы
• Теорема средней точки
Геометрия
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
509 Превышен предел пропускной способности
509 Превышен предел пропускной способности
Сервер временно не может обслуживать ваш
запрос из-за того, что владелец сайта достиг своего
ограничение пропускной способности.Пожалуйста, повторите попытку позже.
Завершите аналитическое доказательство каждой теоремы в упражнениях с 1 по 17. Диагонали равнобедренной трапеции равны по длине.
Вычислите алгебраические выражения в задачах 35-57 для заданных значений переменных. Цели 2 2 (a + b) …
Промежуточная алгебра
36. Сложные проценты Если 1000 долларов инвестируются в течение x лет под 10%, непрерывно начисляются, будущая стоимость r …
Математические приложения для управления , Жизнь и общественные науки
Вы разработали серию вопросов для измерения удовлетворенности работой водителей автобусов в Нью-Йорке.Случайный …
Основы статистики
Определите, является ли дифференциальное уравнение линейным. 3. uet = t + tdudt
Calculus: Early Transcendentals
Исследователь проводит исследование, сравнивая два различных метода лечения с выборкой из n = 16 участников в каждом t …
Статистика для поведенческих наук (список курсов MindTap)
Участие детей в спортивных, культурных и молодежных группах, по-видимому, связано с улучшением самооценки…
Основы статистики для поведенческих наук (список курсов MindTap)
Заполните каждый пробел: 4 mi = ft
Элементарная техническая математика
Локальные экстремумы и асимптоты Нарисуйте график функции и используйте его для определения асимптот и местные …
Precalculus: Mathematics for Calculus (Standalone Book)
Поиск единичных векторов В упражнениях 79-82 найдите единичный вектор (a) в направлении v и (b) в направлении …
Исчисление: ранние трансцендентные функции
Вычислите выражение sin Упражнения 116. (2) 3
Конечная математика
Найдите fx и fy и граф f, fx и fy с областями и точками обзора, которые позволяют вам видеть отношения между ставками …
Многопараметрическое исчисление
В упражнении 1728 используйте логарифм, чтобы получить недостающую величину.
Прикладное исчисление
Статистическая грамотность Какие из следующих переменных являются непрерывными, а какие дискретными? (а) Количество тра…
Основные сведения о статистике
В упражнениях 27–30 определите, является ли первый набор правильным подмножеством второго набора. Набор countin …
Mathematical Excursions (MindTap Course List)
В каждом случае определите значение константы c, которая делает утверждение вероятности правильным. а. (c) = .983 …
Вероятность и статистика для инженерии и науки
В упражнении 4756 решите данное уравнение для указанной переменной.5x + 1 = 1125
Конечная математика и прикладное исчисление (список курсов MindTap)
В упражнениях 2730 определите все значения x, для которых каждая функция является прерывистой. 30. f (x) = | 2x | x
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
Используйте форму определения интеграла, приведенную в теореме 4, для вычисления интеграла. 25 (42x) dx
Исчисление одной переменной: ранние трансцендентальные методы, том I
Дан график f.Нарисуйте графики следующих функций. (a) y = f (x 8) (b) y = f (x) (c) y = 2 f (…
Исчисление одной переменной
Вычислить интеграл. 1 + sinx1 + cosxdx
Исчисление ( Список курсов MindTap)
Поиск области и диапазона функции В упражнениях 17-24 найдите область и диапазон функции. Используйте …
Исчисление: прикладной подход (список курсов MindTap)
Для каждого следующих уравнений, решите для (a) решений всех степеней и (b), если 0360.Не используйте вычисления …
Тригонометрия (список курсов MindTap)
Для следующих утверждений подчеркните ключевые слова и переведите в уравнения. Число составляет 5 раз B a …
Современная математика для бизнеса и потребителей
ЗАДАЧА НА ЭКЗАМЕНАХ НА ПУТНАМЕ Найдите минимальное значение | sinx = cosx + tanx + cotx + secx + cscx | для действительных чисел x. Эта проблема …
Исчисление одной переменной
Как вы оцениваете sinmxcosnxdx, если m нечетно? Что, если n нечетное? Что, если m и n четные?
Исчисление одной переменной: ранние трансцендентальные методы
Верно или неверно
Отметьте каждое из следующих утверждений как истинное или ложное.Набор всех целых чисел не …
Элементы современной алгебры
Анализ уравнений хищник-жертва В упражнениях 79 и 80, (а) используйте данные значения, чтобы написать набор хищников-p …
Исчисление: ранние трансцендентные функции (список курсов MindTap)
Определите графически набор решений для следующих систем неравенств. a.2x + y10x + 3y15x4x0, y0 b.2x + y8 …
Конечная математика для управленческих, жизненных и социальных наук
Для непрерывной функции справа и данного значения N сколько точек c удовлетворяет заключение…
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные методы, 8-е
Рассмотрим следующие два набора рейтингов для шести пунктов. Обратите внимание, что в первом случае рейтинги идентичны …
Статистика для бизнеса и экономики, пересмотренная (список курсов MindTap)
Нахождение векторов скорости и ускорения в пространстве В упражнениях 37-40 вектор положения r описывает путь. ..
Исчисление
Использование функции Рассмотрим функцию f (x, y) = (x3 + y3) 1/3.(a) Найдите fx (0,0) и fy (0,0). (b) Определите точку …
Многопараметрическое исчисление
Бумага Неправильное использование кредитных карт, отношение к деньгам и принудительное покупательское поведение: сравнение внутреннего и внешнего …
Введение в статистику и анализ данных
Раунд следующего десятичные дроби с указанным количеством десятичных знаков. 11.0.03894 (2 места)
Математика для машинной техники
В этой главе мы описали исследование, в котором Skjoeveland (2001) изучал влияние уличных парков на социальную среду…
Методы исследования поведенческих наук (список курсов MindTap)
Преобразование полярной формы в прямоугольную В упражнениях 35-44 преобразуйте полярное уравнение в прямоугольную форму и сделайте набросок i …
Исчисление (список курсов MindTap)
В упражнениях 29-36 переведите два утверждения в символическую форму и используйте таблицу истинности, чтобы определить, …
Математика: практическая одиссея
Истина или ложь:
Учебное пособие по многомерному исчислению Стюарта, 8-й
Упростите каждое выражение.-10i24
College Algebra (Список курсов MindTap)
Следующие данные показывают структуру результатов, которые были получены в исследовании Liguori and Robinson (2001), экзамен …
Методы исследования поведенческих наук (Список курсов MindTap) )
Следующие данные показывают годовой доход (в миллионах) и оценочную стоимость команды (в миллионах) для 30 Majo …
СТАТИСТИКА F / BUSINESS + ECONOMICS-TEXT
Дайте рекурсивное определение для набора всех строк Значения «а» и «б» означают ровно один а.
Дискретная математика с приложениями
Экзамен с несколькими вариантами ответов. Рассмотрим экзамен с несколькими вариантами ответов из 50 вопросов. Каждый вопрос имеет четыре возможных …
Основы статистики для бизнеса и экономики
6. Ежедневное отслеживающее исследование Gallup показало, что средние ежедневные дискреционные расходы американцев, зарабатывающих более 9 долларов …
Современная бизнес-статистика с Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)
Напоминание Округлите все ответы до двух десятичных знаков, если не указано иное.Равновесное решение Найдите равновесие …
Функции и изменения: подход к моделированию алгебры колледжа (Список курсов MindTap)
Написание n-го члена геометрической последовательности В упражнениях 33-38 найдите формулу для n-го члена последовательности. …
College Algebra
В задачах 29 и 30 действуйте, как в примере 5, и найдите явное решение данной задачи начального значения ….
Первый курс дифференциальных уравнений с приложениями моделирования (список курсов MindTap )
Для следующих упражнений нарисуйте уравнения и закрасьте область между кривыми.Определить …
Calculus Volume 2
Используйте следующую информацию, чтобы ответить на следующие два упражнения: Маркетинговые компании заинтересованы в том, чтобы знать …
Вводная статистика
В следующих упражнениях используйте свойства логарифмов, чтобы записать выражения в виде суммы, разности и или …
Calculus Volume 1
Покажите, что диагонали трапеции делят ее на четыре треугольника, два из которых имеют одинаковую площадь? «Equi-extension»
Обычно трапеция определяется как четырехугольник с двумя параллельными сторонами.Равнобедренная трапеция — это особый случай трапеции, которая имеет боковую симметрию, что означает, что одна сторона будет зеркалом другой.
На изображении выше изображена равнобедренная трапеция, # «ABCD» #. Должно быть очевидно, что треугольники # «ABE» # и # «DCE» # имеют равные площади, поскольку они являются зеркальным отображением друг друга. Поэтому давайте сосредоточимся на попытке доказать, что эти два треугольника должны иметь одинаковую площадь для всех трапеций.
Площадь треугольника можно определить по тождеству:
#A = 1/2 (B xx H) #
Где # B # — основание треугольника, а # H # — высота.Треугольники # «ABE» # и # «DCE» # не имеют общих сторон, которые мы могли бы рассматривать как общую основу, однако треугольники # «ACD» # и # «DBA» # имеют общую сторону, основание трапеции. .
Если мы рассматриваем сторону # «AD» # как основание для обоих треугольников, то высота для обоих — это расстояние между линией # «AD» # и # «BC» #. Поскольку основание и высота у обоих треугольников равны, площадь обоих треугольников также должна быть одинаковой.
#A_ «ABD» = A_ «DCA» #
Теперь мы также можем видеть, что треугольник # «ABD» # состоит из треугольников # «ABE» # и # «AED» #.Кроме того, треугольник # «DCA» # состоит из треугольников # «DCE» # и # «AED» #.
#A_ «ABD» = A_ «ABE» + A_ «AED» #
#A_ «DCA» = A_ «DCE» + A_ «AED» #
Если мы вычтем площадь AED из ABD и DCA, мы увидим, что площади ABE и DCE действительно равны.
#A_ «ABD» = A_ «DCA» #
#A_ «ABE» + цвет (красный) отмена (цвет (черный) (A_ «AED»)) = A_ «DCE» + цвет (красный) отмена (цвет ( черный) (A_ «AED»)) #
#A_ «ABE» = A_ «DCE» #
Хотя я проиллюстрировал это доказательство с помощью равнобедренной трапеции, ни одна из работ не относилась конкретно к правильной трапеции.

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.