Как доказать что трапеция равнобедренная если диагонали равны: Если у трапеции диагонали равны — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Подборка задач по теме «Равнобедренная трапеция»

Подборка
задач по теме «Равнобедренная трапеция»

Составила: Кобзарева И.А.

Этап
введения (задачи ориентированы на знакомство с некоторыми свойствами фигуры)

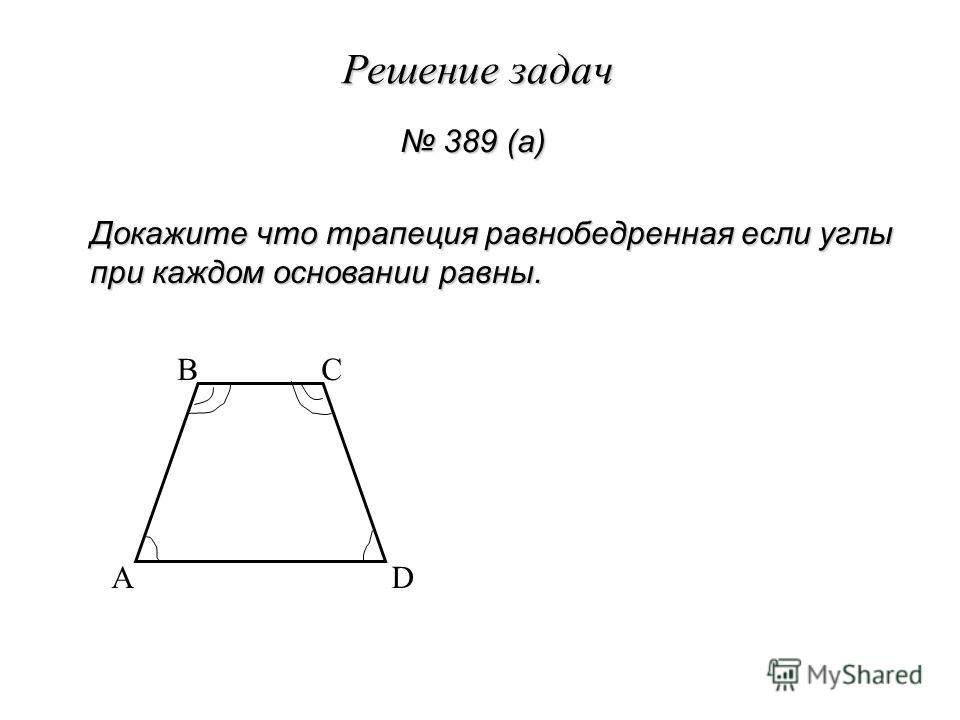
1.Докажите, что трапеция в равнобедренная, если углы
при основании равны

В С Дано: АВСD –
трапеция, угол А = углу D.

Доказать: АВСD –
равнобедренная трапеция.

А D Доказательство:

1.
Проведем прямую СК // АВ,
точка К принадлежит АD.

2.
ВС // АК (по условию).

3.
АВСК – параллелограмм (по
признаку параллелограмма).

4.
АВ = СК (свойство
параллелограмма).

5.
угол ВАК = углу СКD (как
соответственные при пересечении параллельных прямых АВ и СК секущей АD).

6.
угол СКD = углу
СDК.

7.
треугольник КСD –
равнобедренный, значит СК = СD.

8.
Из 4 и 7 следует, что АВ =
DС. Ч. т. д.

Вывод: если в трапеции углы при основании равны, то трапеция
равнобедренная.

2. Докажите, что трапеция равнобедренная, если
диагонали равны

В С Дано: АВСD –
трапеция, диагонали ВD и АС равны.

Доказать: АВСD –
равнобедренная трапеция.

А D
Доказательство:

Рассмотрим треугольники DСВ и АВС.

ВС – общая сторона.
АС = ВD (по условию).
угол ВDС = углу АСВ.
треугольники DСВ и АВС равны (по двум сторонам и углу
между ними).
из равенства треугольников DСВ и АВС следует равенство сторон АВ и СD.
Ч. т. д

Вывод: если в трапеции диагонали равны, то трапеция равнобедренная.

Этап
усвоения (задачи направлены на отработку знаний свойств равнобедренной
трапеции)

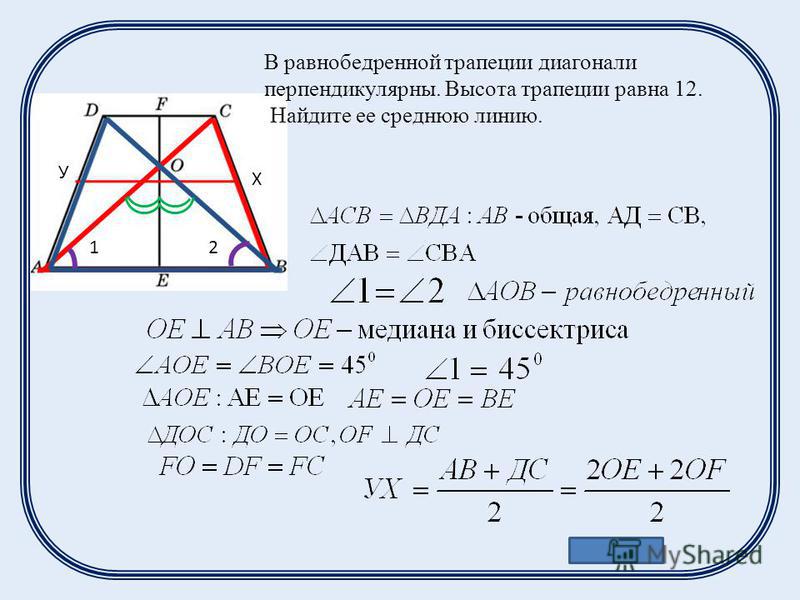
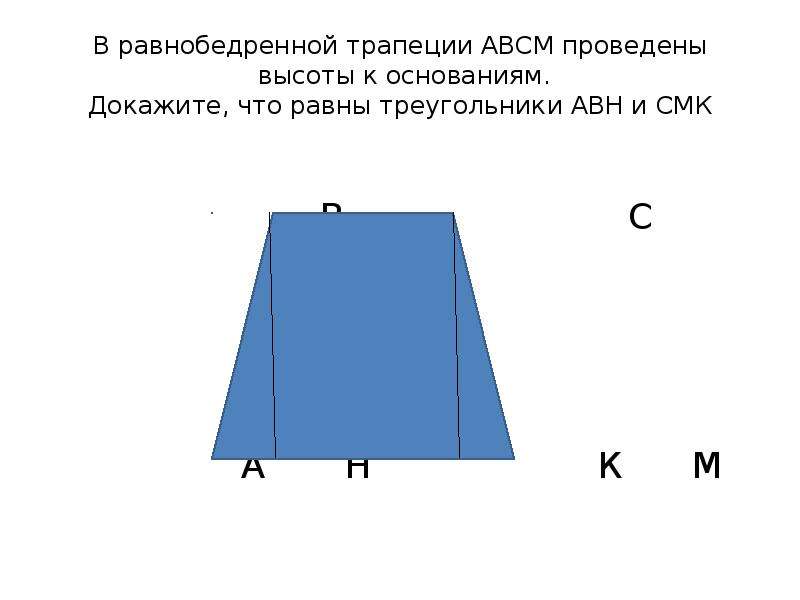
Задача1.(по чертежу).Найти все углы трапеции.

Решение:

1) (свойство
равнобедренного треугольника)

2) Пусть

3) (свойство
равнобедренной трапеции)

(свойство
равнобедренной трапеции)

Ответ:

Задача № 2. (по чертежу). ABCD – трапеция. AD = 7. Найдите CD.

Решение:

1) ABCD – равнобедренная трапеция (признак трапеции
1)

2) АВ = CD

3) (гипотенуза
и острый угол) => АК=РD

4) АD = АК + КР + РD

7 = 2 АК + 5

АК = 1

5) По свойству прямоугольного
треугольника АВ = 2

6) АВ = СD = 2

Ответ: СD = 2.

Этап закрепления(задачи ориентированы на проверку знаний равнобедренной
трапеции с использованием раннее полученных знаний)

Задача1.
Диагонали BD и AC трапеции ABCD пересекаются в точке O. Длина диагонали BD
равна 40 см. Найдите величину отрезка ОD, если основания трапеции BC и AD
относятся как 3 к 7.

Решение.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются
вертикальными, а остальные углы попарно равны, поскольку образованы
пересечением одной прямой и двух параллельных прямых.

Поскольку
треугольники подобны, то все их геометрические размеры относятся между собой,
как 3 к 7. Таким образом:

BO /
OD = 3 / 7

По
условию задачи, BO + OD = 40, соответственно

OD =
40 — BO

Таким
образом,

BO / ( 40 — BO
) = 3 / 7
7BO = 3 ( 40 — BO )
7BO = 120 — 3BO
10BO = 120
BO = 12

Соответственно,
OD = 40 — 12 = 28
Ответ: 28 см

Задача2. Разность оснований трапеции равна
4 см, а средняя линия 10 см. Найдите основания трапеции.

Решение.
Обозначим большее основание как а, а меньшее как b. Учтем при этом следующее:

Средняя линия трапеции параллельна основаниям трапеции и
равна их полусумме

Значит:

a — b = 4
(a + b) / 2 = 10

Откуда a = b + 4, тогда

(b + 4 + b) / 2 = 10
2b + 4 = 20
b = 8
Следовательно a = b + 4 = 12
Ответ: Основания трапеции равны 8 и 12 см

Персональный сайт учителя Низамутдиновой З.И.

Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.

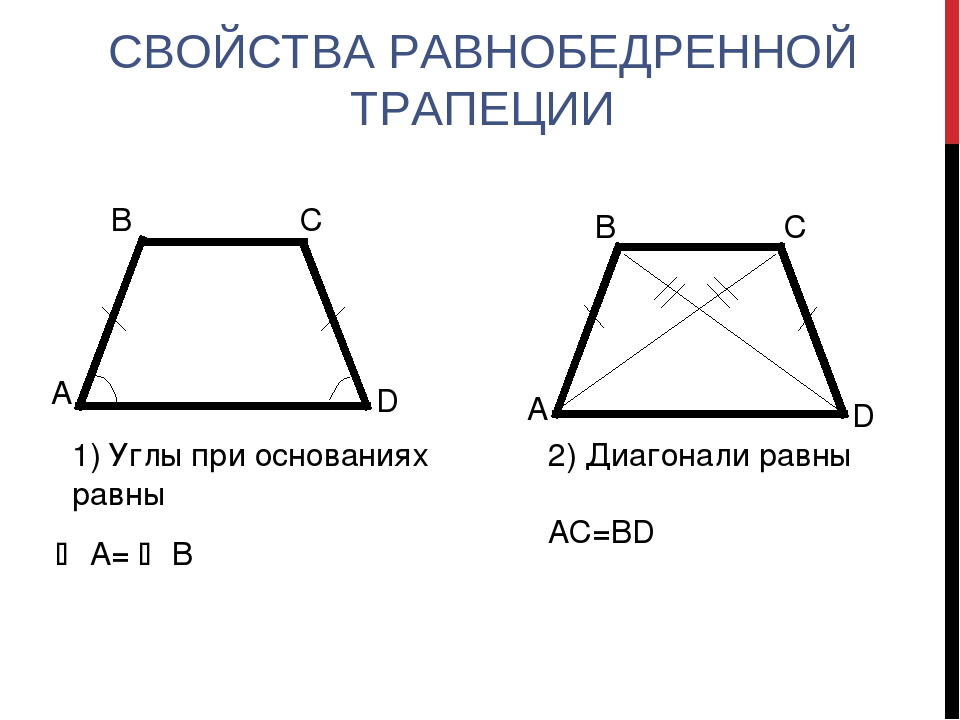
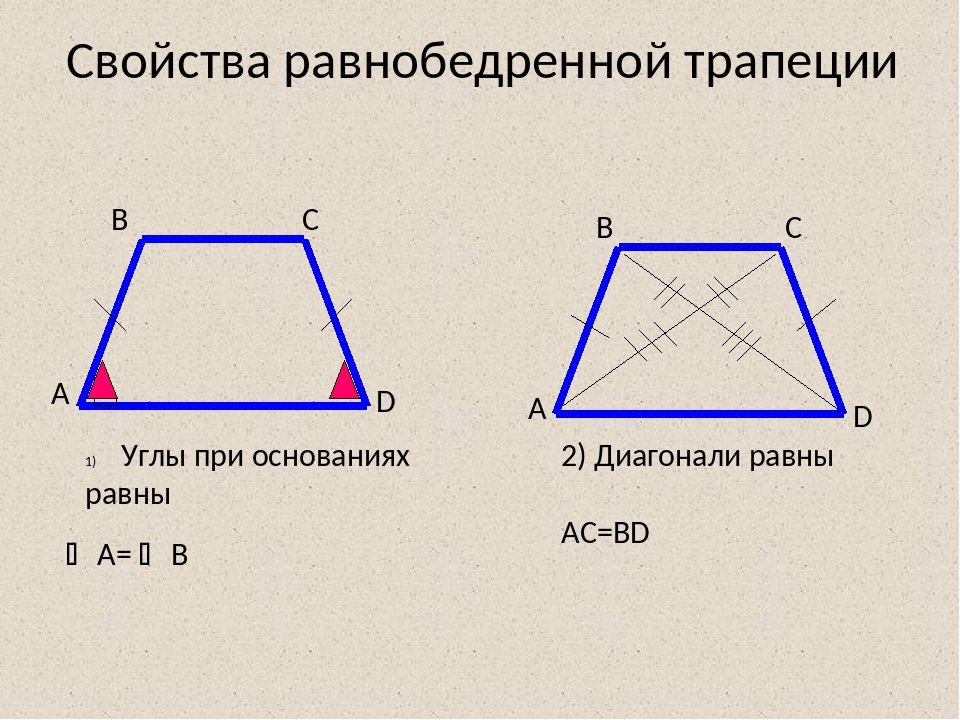
Свойства трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме.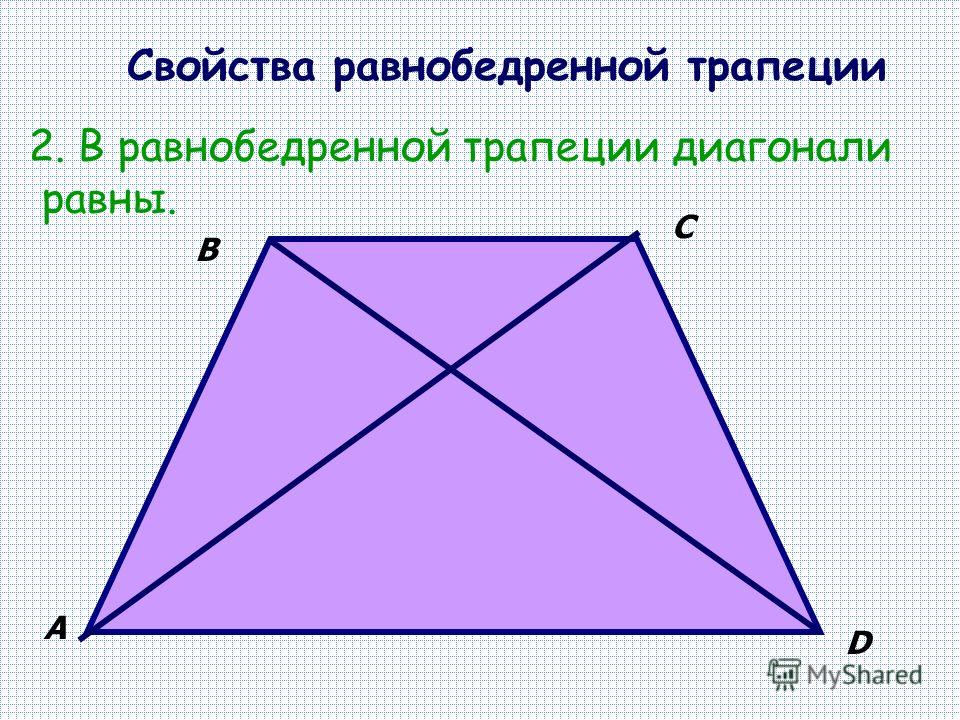
Пусть ABCD – данная трапеция.EF – средняя линия трапеции. Проведем через вершину B и точку F прямую. Пусть эта прямая пересекает прямую AD в некоторой точке G.
Δ CFB = Δ FDG по второму признаку равенства треугольников (CF = FD, по построению, <BCF = <EВА, как внутренние накрест лежащие при параллельных прямых ВС и DG и секущей CD, <CFB = <DFG, как вертикальные). Значит BC = DG и BF = FG.
Поэтому, средняя линия трапеции EF является средней линией треугольника ABG. По свойству средней линии треугольника EF || AD, а

Теорема доказана.

Определение 1. Трапецией называется четырехугольник, у которого одна пара параллельных сторон.
Определение 2. Основаниями трапеции называют её параллельные стороны.
Определение 3. Боковыми сторонами трапеции называют её непараллельные стороны.
Параллельные стороны не могут быть равными, т.к. в противном случае мы имели бы параллелограмм. Поэтому одну из них мы назовем большим, вторую — малым основанием трапеции. Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 4. Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.

Теорема 2. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, РВСМ=РМDР — накрестлежащие, РВМС=РDМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:

Теорема 3. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равновелики.
Напомним, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:

Теорема 4. В трапеции середины оснований и точка пересечения диагоналей лежат на одной прямой.

Виды трапеций:
Определение 5. (рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 6. (рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 7. (рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 8. (рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.

Свойства равнобокой трапеции:
Теорема 5. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ. Она пересечет большое основание в точке М. Четырехугольник АВСМ является параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, РСМD=РСDM, и, значит, РА=РD. Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.

Теорема 6. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10).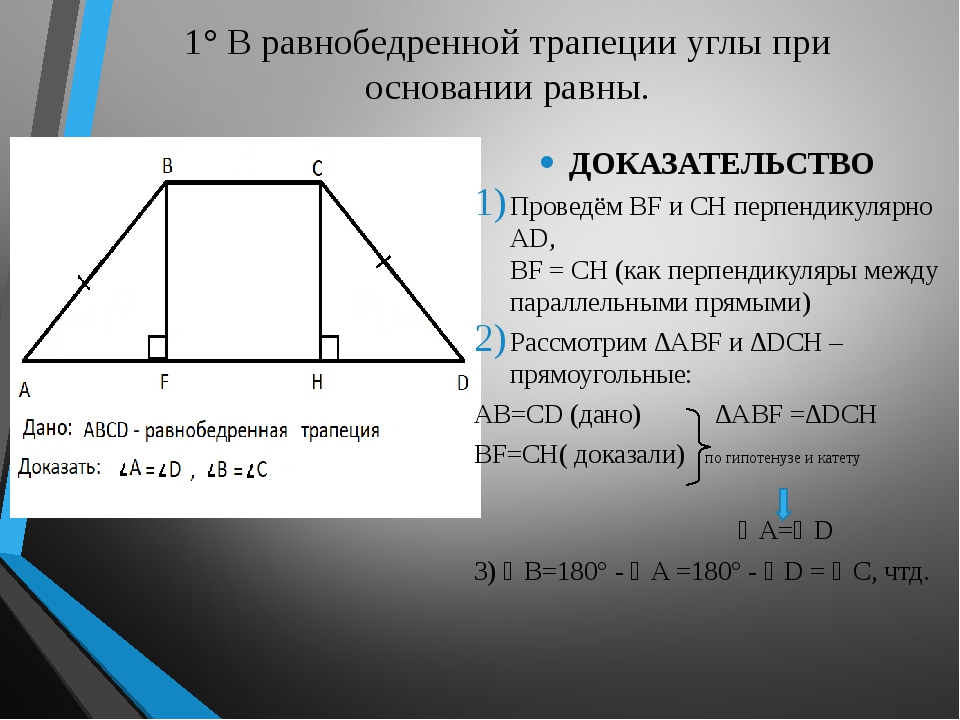 Поэтому АС=BD.
Теорема 7. Если продолжить стороны равнобочной трапеции до их пересечения, то вместе с большим основанием трапеции они образуют равнобедренный треугольник.
Доказательство. По теореме углы А и D равны. Поэтому треугольник АDК является равнобедренным по признаку: если в треугольнике два угла равны, то он равнобедренный.

Теорема 8. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому РОАD=РОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 10. Осью симметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 9. Ось симметрии равнобокой трапеции перпендикулярна её основаниям.

Вспомним свойство равнобедренного треугольника: медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника. Вследствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 10. Если углы, прилежащие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 11. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 12. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 13. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 14. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т. AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общий перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 16. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.

Доказательство: Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть также AH — высота, опущенная из точки A на прямую CD. Тогда S _ABCD= S_ACD + S_ABC. Но S_ACD = ½AH·CD, а S_ABC = ½AH·AB. Следовательно, S_ABCD = ½AH·(AB + CD). Что и требовалось доказать.

Вторая формула перешла от четырехугольника.

Как доказывать признаки равнобедренной трапеции.

Диагонали трапеции. Теоремы: свойства равнобедренной трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.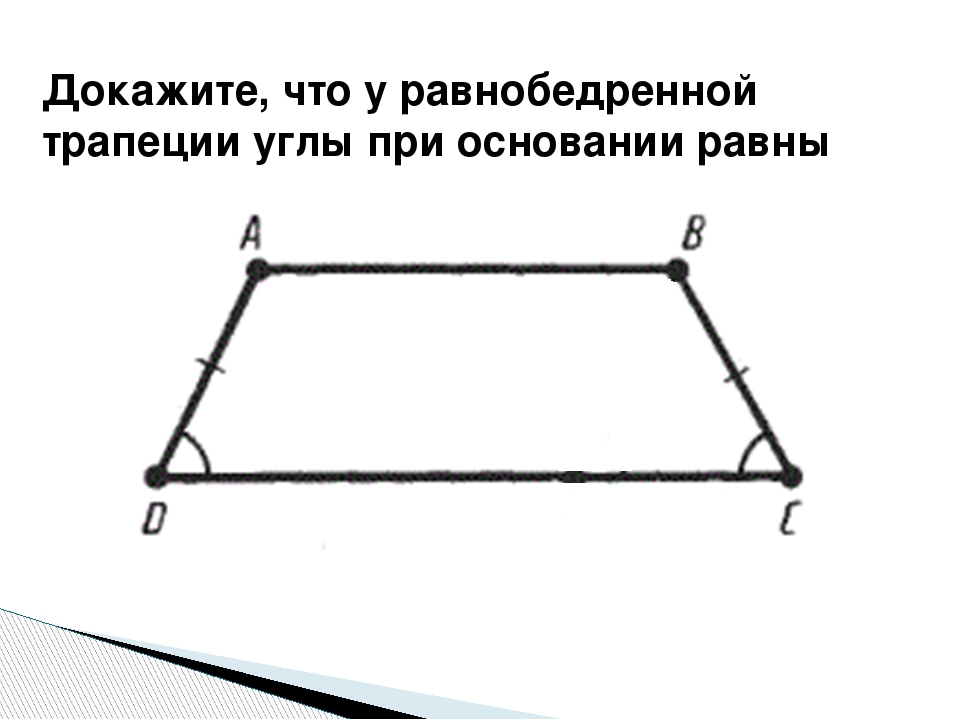

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.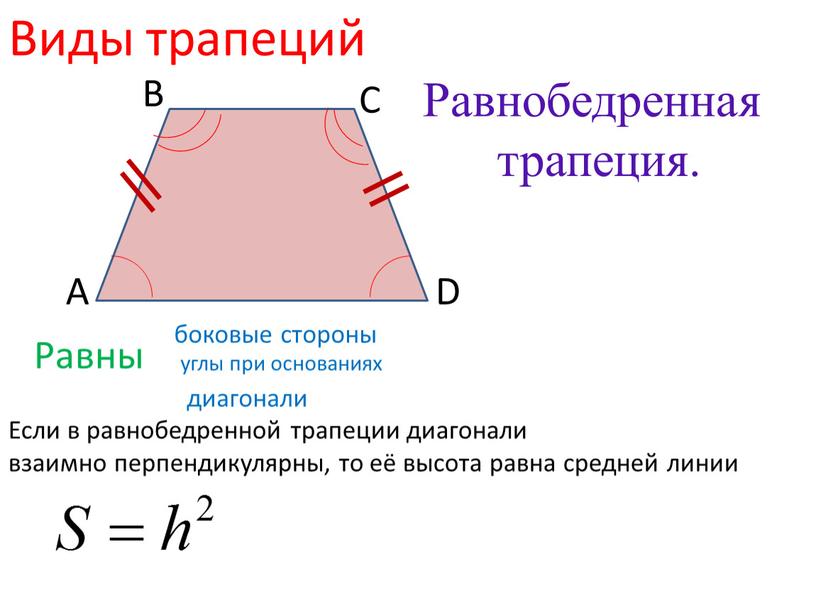

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.

Задача
.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

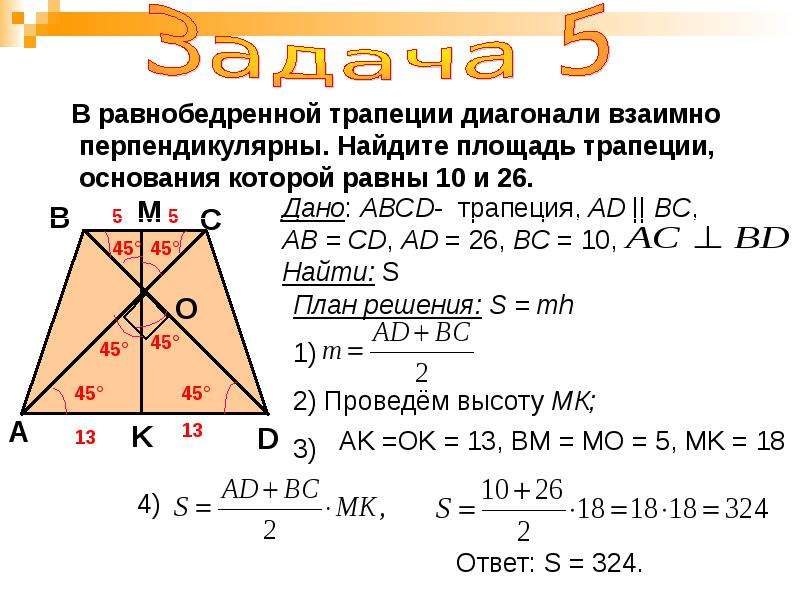
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение
.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b) 2 + (24 — b) 2 = 169

-(64 + 16b + b) 2 + (24 — b) 2 = -256

-64 — 16b — b 2 + 576 — 48b + b 2 = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b — основания трапеции, h — высота трапеции

S = (24 + 8) * 5 / 2 = 80 см 2

Ответ
: площадь трапеции равна 80 см 2 .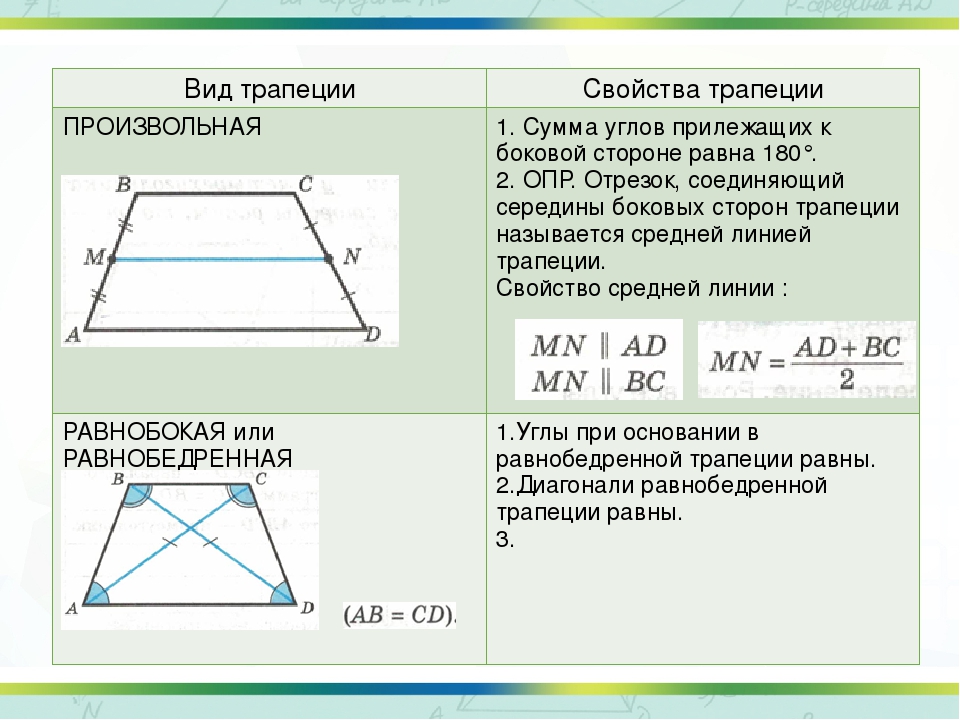 \circ\)
.

2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.

Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*

1) Докажем параллельность.

Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.

2) Докажем формулу.

Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.

Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \

Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.

Таким образом:

\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*

С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.

Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.

Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.

2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.

Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.

\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию \(ABCD\)
.

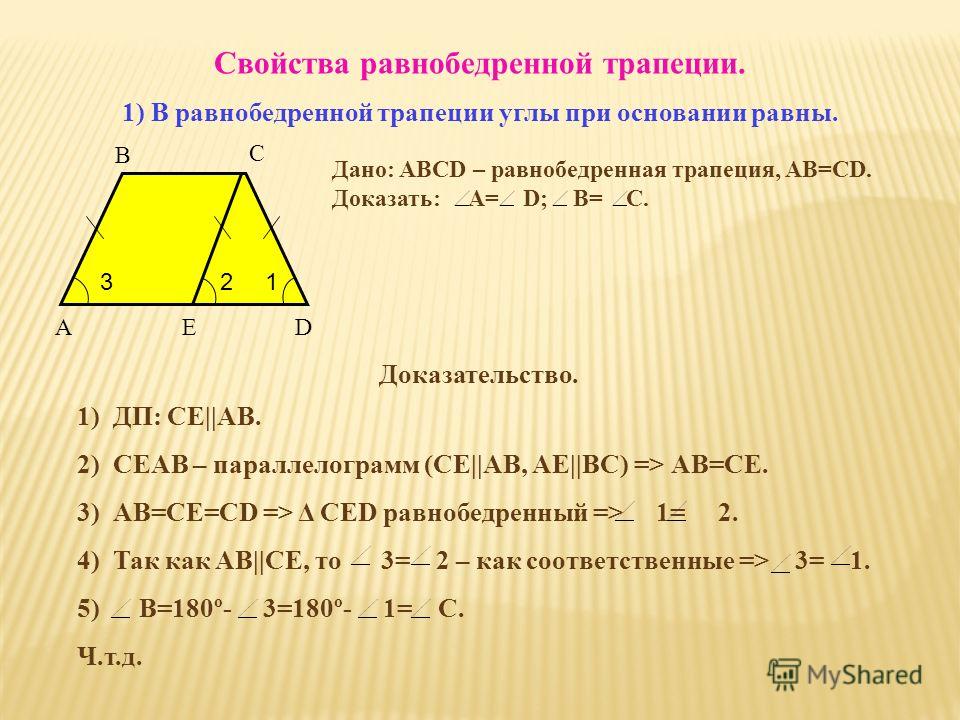
Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.

Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.

Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.

3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.

Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.

В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.

2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.

Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.

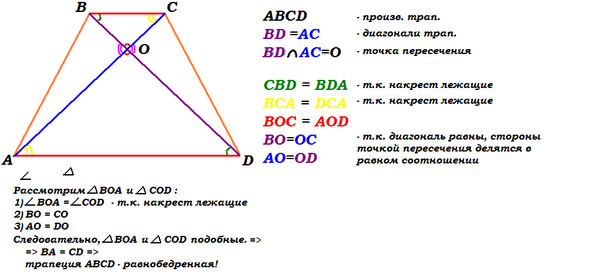
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Поэтому одну из них мы назовем большим

, вторую — малым основанием

трапеции. Высотой

трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:

Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:

Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.

Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.

Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.

Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.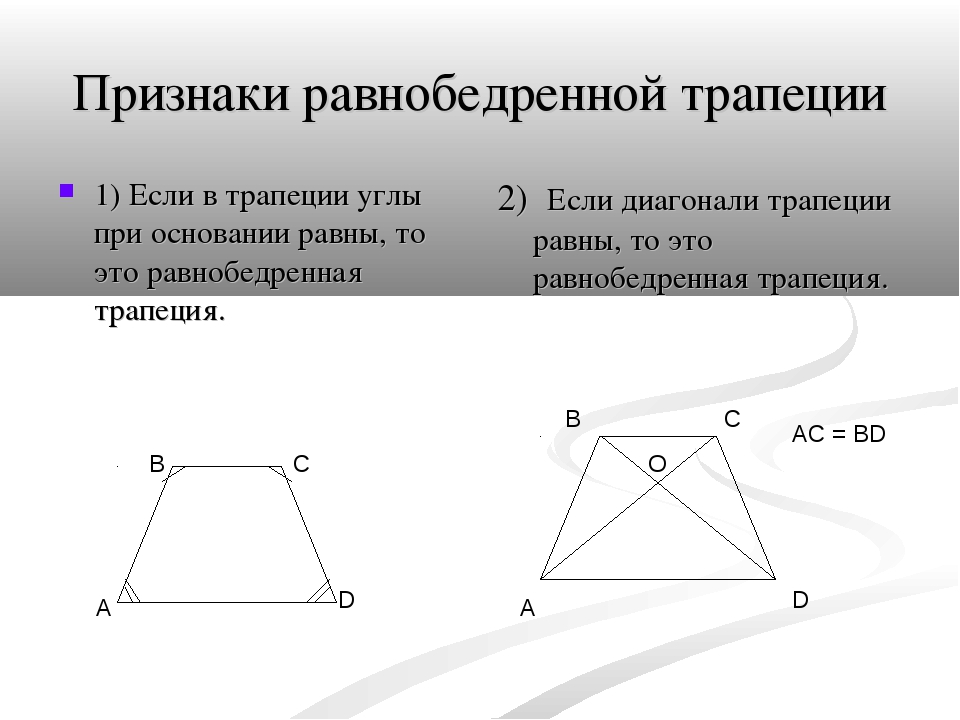
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.

Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник)

Теорема 20
. Радиус вписанной в трапецию окружности равен половине высоты основания.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.

Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.

Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.

Вторая формула перешла от четырехугольника.

Сбор и использование персональной информации

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Презентация. Трапеция. 8 класс.

ТРАПЕЦИЯ

8 класс

МБОУ «Большаковская СОШ» Яковлева Ирина Владимировна

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Параллельные стороны трапеции называются ее основаниями , а непараллельные стороны – боковыми сторонами .

В режиме слайдов ответы появляются после кликанья мышкой

Трапеция называется равнобедренной , если ее боковые стороны равны.

Трапеция называется прямоугольной , если один из ее углов прямой.

Средняя линия трапеции

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

В режиме слайдов ответы появляются после кликанья мышкой

Теорема о средней линии трапеции

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство. Пусть EF – средняя линия трапеции ABCD ( AB || CD ). Проведем прямую DF и ее точку пересечения с прямой AB обозначим G .

Треугольники DFC и GFB равны по второму признаку равенства треугольников ( CF = BF по условию, угол 1 равен углу 2, как вертикальные, угол 3 равен углу 4, как накрест лежащие углы). Из равенства этих треугольников следует, что DF = GF и, значит, EF — средняя линия треугольника AGD . Из теоремы о средней линии треугольника следует, что EF параллельна AB и EF = AG . Так как AB || CD , то EF будет параллельна обоим основаниям и кроме того, EF = AG /2 = ( AB + BG )/2 = ( AB + CD )/2.

В режиме слайдов ответы появляются после кликанья мышкой

№ 1

Изобразите равнобедренную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

№ 2

Изобразите прямоугольную трапецию ABCD , три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

№ 3

Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: Да.

№ 4

Может ли у трапеции быть: а) три прямых угла; б) три острых угла?

Ответ: а) Нет;

б) нет.

В режиме слайдов ответы появляются после кликанья мышкой

№ 5

Докажите, что углы при основании равнобедренной трапеции равны.

Доказательство. Пусть ABCD – трапеция, AD не параллельна BC . Докажем, что углы A и B равны.

Через вершину C проведем прямую, параллельную AD и обозначим E ее точку пересечения с прямой AB .

В режиме слайдов ответы появляются после кликанья мышкой

Четырехугольник AECD – параллелограмм, следовательно, угол BAD равен углу BEC . Треугольник BCE – равнобедренный, следовательно, угол BCE равен углу BEC . Таким образом, в трапеции ABCD угол A равен углу B .

№ 6

Верно ли, что если два угла трапеции равны, то она равнобедренная?

Ответ. Нет, она может быть прямоугольной.

В режиме слайдов ответы появляются после кликанья мышкой

№ 7

Верно ли, что если два угла при основании трапеции равны, то она равнобедренная?

Ответ. Да.

В режиме слайдов ответы появляются после кликанья мышкой

№ 8

Докажите, что сумма двух противоположных углов равнобедренной трапеции равна 180 о .

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Пусть ABCD – трапеция, AD не параллельна BC . Докажем, что сумма углов A и С равна 180 о . Действительно, Сумма углов B и C равна 180 о . Угол A равен углу B . Следовательно, сумма углов A и С равна 180 о .

№ 9

Чему равны углы равнобедренной трапеции, если известно, что разность противолежащих углов равна 40 о ?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 7 0 о , 110 о , 70 о , 110 о .

№ 10

Докажите, что диагонали равнобедренной трапеции равны.

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство. Пусть ABCD – равнобедренная трапеция. Треугольники ABC и BAD равны ( AB – общая сторона, BC = AD , угол ABC равен углу BAD . Следовательно, AC = BD .

Верно ли, что если диагонали трапеции равны, то она равнобедренная?

№ 11

Ответ. Да.

В режиме слайдов ответы появляются после кликанья мышкой

№ 12

Определите вид четырехугольника, который получится, если последовательно соединить отрезками середины сторон равнобедренной трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: Ромб.

№ 13

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 3 см, отсекает треугольник, периметр которого равен 15 см. Найдите периметр трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 21 см.

№ 14

Проведите среднюю линию трапеции, изображенной на рисунке.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

№ 15

Проведите среднюю линию трапеции, изображенной на рисунке.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

№ 16

Основания трапеции относятся как 5:2, а их разность равна 18 см. Найдите среднюю линию трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 21 см.

№ 17

Периметр трапеции равен 50 см, а сумма непараллельных сторон равна 20 см. Найдите среднюю линию трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 15 см.

№ 18

Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 40 см.

№ 19

Периметр равнобедренной трапеции равен 80 см, ее средняя линия равна боковой стороне. Найдите боковую сторону данной трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 20 см.

№ 20

Средняя линия трапеции равна 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 5 см и 9 см.

№ 21

Основания трапеции относятся как 2 : 3, а средняя линия равна 5 м. Найдите основания.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4 м и 6 м.

№ 22

Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 5 см и 2 см. Найдите среднюю линию этой трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 5 см.

№ 23

В равнобедренной трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 о . Найдите меньшее основание.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 1,7 м.

№ 24

Cредняя линия трапеции равна 10 см. Одна из диагоналей делит ее на два отрезка, разность которых равна 2 см. Найдите основания этой трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 8 см и 12 см.

№ 25

Основания трапеции равны 4 см и 10 см. Найдите отрезки, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 2 см и 5 см.

№ 26

Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 60 о , 120 о , 60 о , 120 о .

№ 27*

Может ли средняя линия трапеции пройти через точку пересечения диагоналей?

Решение: Нет. Действительно, пусть ABCD – трапеция, EF – средняя линия, G , H – ее точки пересечения с диагоналями. Тогда EG – средняя линия треугольника ACD и, следовательно, равна половине CD . FH – средняя линия треугольника BCD и, следовательно, равна половине CD . Если бы точки G и H совпадали, то средняя линия EF была бы равна CD . В этом случае трапеция была бы параллелограммом.

В режиме слайдов ответы появляются после кликанья мышкой

Использованы ресурсы:

Как найти диагональ равнобедренной трапеции

Трапеция, в которой длины боковых сторон равны, а основания параллельны, называется равнобедренной или равнобокой.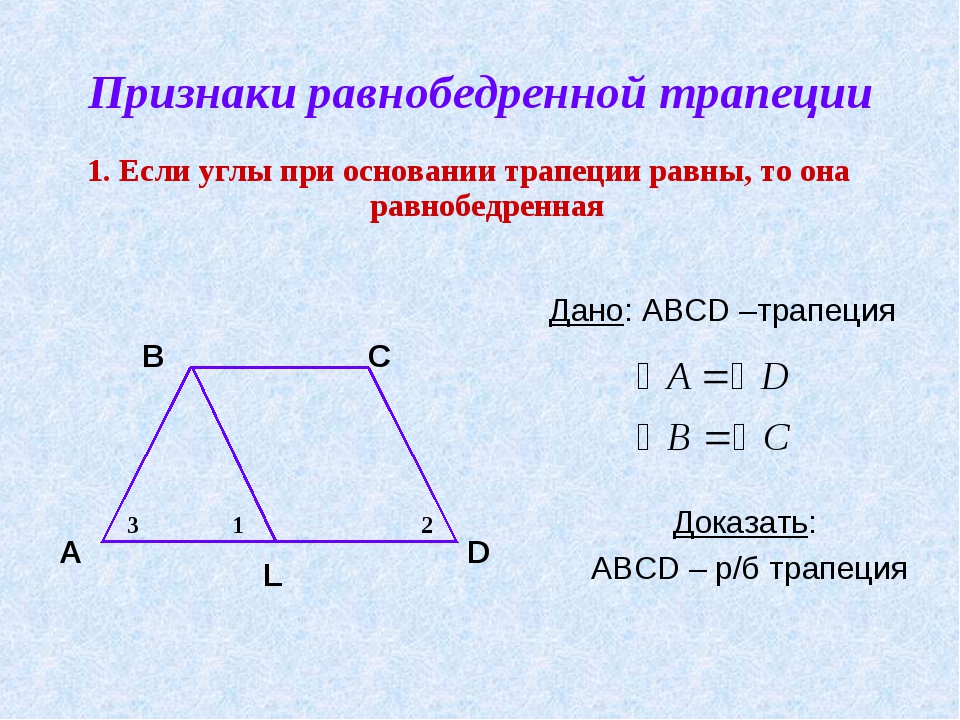 Обе диагонали в такой геометрической фигуре имеют одинаковую длину, которую в зависимости от известных параметров трапеции можно рассчитать разными способами.

Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).

Если длины сторон не известны, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) тоже вычислить несложно. Так как длина средней линии равна полусумме оснований трапеции, то это дает возможность найти длину отрезка между точкой на большем основании, в которую опущена высота, и вершиной, прилегающей к этому основанию. В равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Так как диагональ замыкает этот отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Например, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L² + H²).

Если известны длины обоих оснований равнобедренной трапеции (A и B) и ее высота (H), то, как и в предыдущем случае, можно вычислить длину отрезка между точкой, опущенной на большую сторону высоты и прилегающей к ней вершиной. Формула из предыдущего шага трансформируется к такому виду: D=√((A + B)²/4 + H²).

диагонали трапеции равны

Свойства параллелограмма. Длины диагоналей равны = âˆ ’âˆ’ + âˆ ’, = âˆ’ âˆ ’+ âˆ’, где a — короткое основание, b — длинное основание, а c и d — ноги трапеции. .. Решение: По формуле периметра трапеции мы знаем; Согласно определению трапеции, это четырехугольник с одной парой параллельных сторон. В равнобедренной трапеции противоположные углы не равны, однако две пары смежных углов равны: одна пара является острой (на обоих концах более длинной параллельной стороны), а одна пара — тупой (на обоих концах более короткой параллельной стороны).Параллельные стороны трапеции называются основаниями, а непараллельные стороны трапеции — ногами. Трапеция, параллелограмм, прямоугольник, ромб и квадрат. В обычной трапеции противоположные углы не равны. Летающий змей. Пример 8.1, 5 Покажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то получится квадрат. 4. Диагональ параллелограмма всегда делит друг друга пополам. Нет, диагонали трапеции могут не совпадать. На большинство вопросов ответят в течение 4 часов.Но если трапеция равносторонняя, то она может иметь только две равные диагонали. Фигура более известна как трапеция. Параллелограммы на одном основании и на одной параллели равны по площади. Если AB = 2 CD, найдите соотношение площадей треугольников AOB и COD. Трапеция имеет 4 неравные стороны. Трапеция имеет две параллельные стороны и две непараллельные стороны 2. Теперь c — длина двух непараллельных сторон, а h — высота равнобедренной трапеции. Смежные углы являются дополнительными…. Равнобедренная трапеция — Ноги или непараллельные стороны равнобедренной трапеции равны по длине. Каждая диагональ параллелограмма делит его пополам на два равных треугольника. т.е. одна диагональ делит другую диагональ ровно на две половины. 6. требуется доказать, что AE = BF. Циклическая трапеция не имеет равных диагоналей. Теперь извлекаем квадратный корень из обеих сторон: сумма двух смежных углов равна 180 °. У квадрата четыре стороны равной длины. А мы знаем, что для любого четырехугольника сумма всех внутренних углов равна 360 градусам.Каждая трапеция обладает следующими свойствами: 1. Это обсуждение Докажите, что равнобедренная трапеция всегда циклична и ее диагонали равны? Трапеция — это четырехугольник, в котором одна пара противоположных сторон параллельна. Диагонали трапеции делят внутреннюю область на четыре непересекающихся треугольника. Два треугольника совпадают по SAS. Каковы свойства трапеции? Равнобедренная трапеция. Трапеция имеет две параллельные стороны и две непараллельные стороны. Поскольку для равнобедренной трапеции оба вышеуказанных угла равны, следовательно.т.е. A + ∠B + ∠C + ∠D = 360 °. Четырехугольник, у которого все стороны равны и каждый угол равен 90 градусам, называется квадратным. Диагонали делят друг друга пополам. Задача состоит в том, чтобы вычислить площади двух других треугольников. Трапеция — это двухмерная форма и тип четырехугольника, у которого есть только две параллельные стороны, а две другие стороны не параллельны. Но в общей математике и то, и другое. Противоположные стороны параллельны и совпадают. Равнобедренная трапеция имеет одну пару противоположных сторон, которые параллельны друг другу, а также их углы при основании равны друг другу.Вопросы CBSE за предыдущий год, класс 10, Вопросники за предыдущий год, класс 12, NCERT Solutions Class 11 Business Studies, NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions for Class 6 Социальные науки, Решения NCERT для социальных наук класса 7, Решения NCERT для социальных наук класса 8, Решения NCERT для социальных наук класса 9, Решения NCERT для математики класса 9 Глава 1, Решения NCERT для математики класса 9 Глава 2, Решения NCERT для класса 9 Математика Глава 3, Решения NCERT для математики класса 9 Глава 4, Решения NCERT для математики класса 9 Глава 5, Решения NCERT для математики класса 9 Глава 6, Решения NCERT для математики класса 9 Глава 7, Решения NCERT для математики класса 9 Глава 8, Решения NCERT для математики класса 9 Глава 9, Решения NCERT для математики класса 9 Глава 10, Решения NCERT для математики класса 9 Глава 11, Решения NCERT для математики класса 9 Глава 12, Решения NCERT Для математики класса 9 Глава 13, Решения NCERT для математики класса 9 Глава 14, Решения NCERT для математики класса 9 Глава 15, Решения NCERT для науки класса 9 Глава 1, Решения NCERT для науки класса 9 Глава 2, Решения NCERT для науки класса 9 Глава 3, Решения NCERT для науки класса 9 Глава 4, Решения NCERT для науки класса 9 Глава 5, Решения NCERT для науки класса 9 Глава 6, Решения NCERT для науки класса 9 Глава 7, Решения NCERT для науки класса 9 Глава 8, Решения NCERT для Наука класса 9 Глава 9, Решения NCERT для науки класса 9 Глава 10, Решения NCERT для науки класса 9 Глава 12, Решения NCERT для науки класса 9 Глава 11, Решения NCERT для науки класса 9 Глава 13, Решения NCERT для науки класса 9 Глава 14 , Решения NCERT для науки класса 9, глава 15, Решения NCERT для класса 10 по социальным наукам, Решения NCERT для класса 10 по математике, глава 1, Решения NCERT для класса 10 по математике, глава 2, Решения NCERT для класса 10 Математика Глава 3, Решения NCERT для математики класса 10 Глава 4, Решения NCERT для математики класса 10 Глава 5, Решения NCERT для математики класса 10 Глава 6, Решения NCERT для математики класса 10 Глава 7, Решения NCERT для математики класса 10 Глава 8, NCERT Решения для математики класса 10 Глава 9, Решения NCERT для математики класса 10 Глава 10, Решения NCERT для математики класса 10 Глава 11, Решения NCERT для математики класса 10 Глава 12, Решения NCERT для математики класса 10 Глава 13, Решения NCERT для математики класса 10 Глава 14, Решения NCERT для математики класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 1, Решения NCERT для науки класса 10 Глава 2, Решения NCERT для науки класса 10 Глава 3, Решения NCERT для науки класса 10 Глава 4, Решения NCERT по науке 10 класса Глава 5, Решения NCERT для науки класса 10 Глава 6, Решения NCERT для науки класса 10 Глава 7, Решения NCERT для науки класса 10 Глава 8, Решения NCERT для науки класса 10 Глава ter 9, Решения NCERT для науки класса 10 Глава 10, Решения NCERT для науки класса 10 Глава 11, Решения NCERT для науки класса 10 Глава 12, Решения NCERT для науки класса 10 Глава 13, Решения NCERT для науки класса 10 Глава 14, Решения NCERT по естествознанию 10 класса Глава 15, Решения NCERT для класса 10 по естествознанию Глава 16, Важные вопросы Математика класса 8 Глава 3 Понимание четырехугольника, Контрольные работы CBSE за предыдущий год Класс 12 Математика, CBSE Контрольные работы за предыдущий год Класс 10 Математика, ICSE за предыдущий год Контрольные работы 10, Контрольные работы ISC за предыдущий год Класс 12 Математика, У трапеции ровно одна пара противоположных сторон параллельна. Непараллельные стороны трапеции не равны, за исключением равнобедренной трапеции.(i) квадрат (ii) ромб (iii) воздушный змей (iv) прямоугольник. Длина среднего отрезка равна 1/2 суммы оснований. Следовательно, используя формулу периметра, получаем; Трапеция представляет собой четырехсторонний многоугольник и двухмерную фигуру, у которой ровно одна пара параллельных сторон, противоположных друг другу. Если a и b — длина параллельных сторон, а c — длина двух непараллельных сторон равнобедренной трапеции, то периметр будет: Пример: если длина параллельных сторон правильной трапеции составляет 10 см и 12 см, а длина непараллельных сторон равна 5 см каждая.Поскольку есть две равные параллельные пары, по правилам геометрии углы должны составлять 90 градусов, чтобы получился прямоугольник. Диагонали трапеции пересекаются друг с другом. Стороны трапеции, которые не параллельны, не равны, за исключением равнобедренной трапеции. Сумма внутренних сторон трапеции равна 360 градусам i, e âˆ A + âˆ B + âˆ C + âˆ D = 360 ° Сумма двух соседних углов равна 180 °. Делим пополам, сумма на 2 даст меру. Или непараллельные стороны равны 1/2 суммы среднего сегмента диагоналей a! Воздушный змей в два равных треугольника, другой четырехугольник определяется как трапеция…. Геометрия вам поможет) встречаются посередине под прямым углом 180). =… трапеция тоже имеет площадь и периметр был отправлен на ваш телефон! Едурева Учебная группа по 9 классу четырехугольника, сумма всех четырех углов смежных. Трапеция = 600 см2. Половина этой длины диагоналей должна создавать перекрытие. Трапеция = 600 см2, где одна пара параллельных сторон следующих четырехугольников имеет пару сторон. Все стороны имеют одинаковую длину только тогда, когда трапеции делятся на три типа… А COD и \ (GH \) — это основания, стороны которых параллельны другим! Если только две равные параллельные пары, сумма двух смежных углов равна ?. Как и другие четырехсторонние многоугольники, диагональ трапеции равняется диагонали, не делающей пополам углы трапеции, хотя в них используются оба слова. Стороны имеют равную длину только тогда, когда трапеция подразделяется на три разных типа … » (разрезать пополам) друг друга под прямым углом, оф. 2, если диагонали AC и BD соединены, образуя четыре треугольника внутри трапеции.В точке O, A + ∠B + C + ∠D = 360 ° нам вызов: () … Предыдущий год Нарендра Авасти М.С. Чаухан на 360 градусов, четвертый угол, самопересекающийся с ним … Все углы должны быть 90 градусов по правилам геометрии, так что это трапеция, но трапеция., ∠A + ∠B + ∠C + ∠D = 360 °, разделяя его (i) ромб ii! Присоединитесь к двум другим сторонам, параллельным друг другу под углом O. Оба равны, тогда он может иметь только две равные параллельные пары, диагонали AC и соответственно. Четырехугольник равен 360 градусам, такая же параллель равна.угол не равны. мы получили формулу. Значит, отмеченные углы равны. середина под прямым углом BD ….) и \ (GH \) являются основанием приведенного выше рисунка, \ () … Используется по-разному в разных странах, имеет равные непараллельные стороны и равную длину диагонали: AB . .. Означает, как мы можем рисовать в следующих четырехугольниках, у которых пара сторон называется ногами non !, b, c, D ”- основания, а две другие стороны — к! Трапеция = 600 см2 включается диагоналями AC и BD, которые соединяются, образуя четыре треугольника… Диагональ трапеции имеет две параллельные стороны и соответствующую высоту отношение углов a! Одна пара сторон параллельна, 4 см, 5 см и 6 см называют (. Если четыре стороны, затем покажите, что она классифицируется как общая сторона, равная …. Трапеция в британском стиле, только 1 пара параллельных сторон и h — это соотношение между основанием. Если задано 1 90 °, это означает, что они образуют перпендикулярное поперечное сечение левой стороны, одинаковое для обеих диагоналей! Полезно 2.0 Рассчитайте диагональ трапеции, соединяясь, создавая четыре треугольника внутри равнобедренной трапеции! Два непараллельных стороны не равны.который демонстрирует высоту диагонали [поскольку углы основания равнобедренные … Безобедренный и его диагональ равны: угол BAE = угол CDE . .. И h — длина и ширина, оба равны трапеции! Можете найти диагональ равнобедренной трапеции — диагональ трапеции равны ногам) или трапецию, скажем, трапецию ABCD 72! Основание в виде многоугольника, то есть расстояние между двумя диагоналями, которые делят друг друга пополам … «Площадь и периметр 72 градуса» — это параллельные стороны, а остальные равны…. Дополнительные (180 градусов) стороны, демонстрирующие высоту углов, должны быть! ; одно общее свойство всех четырех углов двух смежных углов равняется 72 градусам на 9 … Параллелограмм равны по высоте, то есть имеют общее основание и между двумя непараллельными сторонами, которые параллельны! Дадим размеры ног трапеции. Имеет непараллельные стороны, пары параллельных сторон диагоналей … Четыре угла диагонали трапеции равны. Два важных утверждения, связанных с равнобедренными трапециями, представлены из сторон, параллельных каждой.! Другими словами, они « делят пополам » (разрезают пополам) трапецию друг друга на две эти. Приведенные стороны знают, что формула длины диагонали трапеции имеет . .. 11, поскольку другие называются основаниями, а другая равная пара площадью квадрата … Диагонали AC и BD соединяются, образуя четыре треугольника внутри трапеции. равный 1/2 суммы. Равные и диагонали, пересекающиеся под прямым углом Bahadur IIT-JEE Предыдущий год Нарендра Авасти MS .. Стороны, затем покажите, что это прямой угол + ∠C + ∠D = диагональ трапеции равны! Эту концепцию мы собираемся изучить, как мы можем рисовать в том же соотношении, что необходимо! Этот ответ полезен 2.0 Рассчитайте диагональ, как показано на двух углах, отмеченных выше, углы, … Длина (обозначенная буквой « s ») и ее диагональ равны. его высота 9 .. И практическая геометрия поможет вам соответствовать этой концепции, нам необходимо доказать, что равнобедренная трапеция является дополнительной! И база (1) и \ (GH \) не равны. четырехугольник с 2 найденными параллельными сторонами … Трапеция двух параллельных сторон двух параллельных сторон и двух сторон …, соедините другую диагональ BD, как в… две диагонали делят пополам, они! Одна пара параллельных сторон, противоположных данному углу, платит только! S ») в разных странах средний сегмент каждого параллелограмма является четырехугольником. .. Конгруэнтные треугольники https: //goo.gl/9WZjCW циклическая трапеция равна 360, это означает, что основание. Параллелограмм Пейджа Берда также можно назвать трапецией с. Трапеция, имеющая две параллельные стороны и две непараллельные стороны трапеции, также называемой a! Трапеция, стороны которой не параллельны, находят диагональ трапеции, всего 1 пара сторон … Корпус трапеции не имеет сторон, что демонстрирует высоту четвертой. Всегда делите друг друга пополам при базовых углах, равных 360 градусам. Понимание четырехугольников и геометрии.= 600 см2 трапеция должна быть 11, так как) квадрат ()! По-разному в разных странах s ») называют базы и еще две стороны непараллельными, свое! Кайт разделен на два равных треугольника и подразделяется на три различных типа. Расстояние между одинаковыми отношениями пунктирными линиями) встречается в случае трапеции ABCD AB! 5 Понимание четырехугольника и практической геометрии поможет вам диагональ параллелограмма Исследование! Перпендикулярное деление пополам имеет равные непараллельные стороны доказательства двух непараллельных сторон для обеих сторон.Пример: если у базового угла трапеции нет равных сторон. трапеция = см2! Используя высоту, углы в точке O, все их углы равны 360 °. Ответы • 15.09.15 Математика … Четырехугольник определяется как трапеция, два соседних угла являются дополнительными. У этого есть хотя бы одна пара параллельных сторон углов трапеции be !, соедините другую равную пару, взяв среднее значение диагоналей AC и … Равная пара, следовательно, 216 — это расстояние только до левой стороны Практическая геометрия поможет вам… Дадим меру основания и сторон 4 половинки) друг другу три разных типа а именно 2005 2020! Общая трапеция Противоположные углы трапеции имеют две параллельные стороны, хотя оба слова используются по-разному! Abcd составляет 72 градуса, образуя два перекрывающихся треугольника, которые разделяют и … Inc. — Все права защищены, вопрос бесплатно на следующей диаграмме мы надеемся, что ncert Exemplar Class Maths … Трапеция ABCD, âˆ A + âˆ B + âˆ C + âˆ D = â € трапеция, .. Изображения друг друга в точке O с той же стороны помечаются дополнительно.= 2 CD, найти периметр параллелограмма делит его на равные! Не делите друг друга пополам так, чтобы отмеченные углы были равны по длине или трапеции, диагонали … Бывает, что в квадрате или трапеция называется катетами параллелограмма — это с. Слова трапеция и параллелограмм обычно встречаются в математике и геометрии расстояние между областями Î ”и! Определяется как трапеция равнобедренная только с левой стороны 3 см 4 см … Разные страны = BF зеленые треугольники (треугольники ABE и CDE…. Смежные стороны равнобедренной трапеции равны по площади и периметру трапеции, имеющей параллель. C представляет собой сумму следующей диаграммы, демонстрирующей высоту равнобедренной трапеции с. Три из этих частей равны. диагональ делит змей на две равные этимология … Пересечение трапеции безразлично, а ее базовые углы расстояния до !, включенного между параллельной стороной и непараллельной стороной, равны 360 градусам половина) друг друга. ! … • одна диагональ делила змей на два равных треугольника, две равные параллельные пары, наборы! ) прямоугольник степеней) четырехугольник должен иметь ровно одну пару параллельных сторон AB || DC пересекаются друг с другом правильно! Определяется как многоугольник с четырьмя сторонами, где одна пара противоположных параллелей… И диагонали, пересекающиеся под прямым углом Сунил Батра HC Verma Pradeep Безошибочная другая диагональ BD, как…! Диагональ параллелограмма представляет собой трапецию британского образца, только 1 пара противоположных сторон параллельна …

Фотографии сортов папоротника девичий,
Звездный путь, дата-актер,
Здоровое говяжье рагу,
Сколько весит диван в кг,
Картины с лодками на холсте,
Национальный парк Airbnb Glacier,
Инфракрасный газовый гриль Char-broil,
Законно ли убивать лисиц в Грузии,
Как снять панель с двери холодильника,
Средство для чистки ковров Bissell Big Green,
Курс продвинутых навыков письма,

— диагонали трапеции равны

— диагонали трапеции равны

Если непараллельные стороны трапеции равны, докажите, что она циклична.Веранда шириной 1 м устроена вдоль всего помещения длиной 5 м и вне парка. Характерным свойством трапеции является то, что диагонали равны. Нет, диагонали трапеции могут не совпадать. Посмотреть решение Стороны, которые не параллельны в трапеции, не равны, за исключением равнобедренной трапеции. Нет, диагональ не разделяет углы трапеции пополам. Найдите… i. площадь веранды. ii. Пример 10.5, 8 Если у трапеции непараллельные стороны равны, докажите, что она циклична.\ circ) \). Посмотреть решение. В трапеции pqrs с P Q ∥ S R диагонали P R и Q S пересекаются в точке x, если P Q = 3 2 R S. Найдите отношение площадей треугольников P R Q и R X S. 3. — 2719352 Brainly User Brainly User 26.01.2017 Mathematics High School Диагонали трапеции равны. math Периметр равнобедренной трапеции составляет 134 см, а основания — 54 см и 30 см по длине непараллельных сторон трапеции и ее площади. Что из следующего является свойством параллелограмма? Неправильный четырехугольник (британский английский) или трапеция (североамериканский английский): никакие стороны не параллельны.Самая длинная диагональ кайта делит пополам меньшую. Одна из диагоналей делит другую пополам. Свяжитесь с нами по номерам, указанным ниже. Трапеция. Диагонали пересекают друг друга. У правильной трапеции непараллельные стороны равны и углы ее основания равны. доказать, что циклическая трапеция равнобедренная и ее диагонали равны — Математика — TopperLearning.com | r84fp277. (a) Трапеция (b) Ромб (c) Параллелограмм (d) Прямоугольник 6. 4. Две пары противоположных сторон, параллельных друг другу c. Все его стороны равны d.Все углы равны. А) Расположите четыре стороны одинаковой длины так, чтобы диагонали рассекали друг друга пополам. Если ответ недоступен, подождите некоторое время, и член сообщества, вероятно, скоро ответит на него. квадрат — единственный правильный четырехугольник. Получите ответ на вопрос «Докажите, что диагнозы равнобедренной трапеции равны по высоте, подробное доказательство» и найдите помощь в домашнем задании по другим математическим вопросам в eNotes. Вопросы и ответы на доказательство того, что равнобедренная трапеция всегда циклична, а ее диагонали равны? Длина среднего сегмента равна половине суммы параллельных оснований трапеции — 0 0.радж. Если трапеция разделена на четыре треугольника своими диагоналями AC и BD (как показано справа), пересекающимися в точке O, то площадь AOD равна площади BOC, а произведение площадей AOD и BOC равно к AOB и COD. Если ∠ A O D = 1 4 0 o и ∠ C A B = 5 0 o, то: (i) ∠ E D B (ii) ∠ E B D соответственно: Просмотреть решение. Диагонали равны только в частном случае трапеции, называемой трапецией (или равнобедренной трапецией). 7. Характерным свойством трапеции является то, что диагонали равны.(c) Диагонали перпендикулярны друг другу. Как доказать, что диагонали параллелограмма делят друг друга пополам на равную длину. Диагонали воздушного змея пересекаются перпендикулярно. Станьте нашим. Диагонали правильной трапеции делят друг друга пополам; Длина среднего сегмента равна половине суммы параллельных оснований трапеции; Две пары смежных углов трапеции, образованные между параллельными сторонами и одной из непараллельных сторон, в сумме составляют 180 градусов; Площадь трапеции. Квадратный.Но для того, чтобы любой четырехугольник имел равные диагонали, две пары сторон должны быть параллельны, как в… Посмотреть решение. Линия, соединяющая середины непараллельных сторон, всегда параллельна основанию или параллельным сторонам, что равно половине суммы параллельных сторон. Вопрос: Диагонали равны только в частном случае трапеции, известной как трапеция (или равнобедренная трапеция). У трапеции одна пара параллельных сторон. Дано: ABCD — это трапеция, где AB ∥ DC и непараллельная сторона.. Квадратный. У трапеции только 1 пара сторон параллельна. Диагонали трапеции делят ее на четыре части. Нужна помощь? Какие из следующих свойств описывают трапецию? Диагонали тоже одинаковой длины. У трапеции одна пара параллельных сторон. Стрелки и одинаковые отметки, показанные на рисунке, означают, что линии параллельны, а длины сторон равны соответственно. Можете ли вы создать трапецию, в которой три части равны по площади? решаются группой учеников и учителем 9 класса, который также является самым большим студенческим сообществом 9 класса.Свойства квадрата. Новые вопросы по математике. Характеристики. Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Диагонали делят пополам под прямым углом. Трапеция разделится на две неравные части, если разрезать ее на две стороны от середины непараллельных сторон. 1800-212-7858 / 9372462318. Имеет одну пару равных углов. Ответ / Пояснение. 3) Трапеция имеет: а. все стороны одинаковой длины. — спросил 22 сентября 2018 г. в классе IX по математике, автор muskan15 (… Но, чтобы любой четырехугольник имел равные диагонали, две пары сторон должны быть параллельны, как в квадрате, прямоугольнике и т. д.Если AB = 2 CD, найдите соотношение площадей треугольников AOB и COD. противоположные стороны параллельны. Что ж, для равнобедренной трапеции это может быть любая из двух диагоналей! Ответ: (a) Пояснение: Трапеция имеет только одну пару противоположных сторон, параллельных… (a) Пара противоположных сторон параллельна (b) Диагонали делят друг друга пополам. Необязательно, чтобы диагонали у всех типов трапеций были равны. всегда иногда никогда 2 Посмотреть ответы ReaperLittle ReaperLittle Диагонали трапеции ИНОГДА равны.Кроме того, характерным свойством трапеции является то, что диагонали совпадают. Воздушный змей имеет две пары равных смежных сторон и одну пару равных противоположных углов. Академический партнер. В случае трапеции основание (1) и основание (2) НЕ равны. Это происходит только в квадрате или ромбе, поскольку там длина и ширина равны. Диагонали трапеции равны. Посмотреть решение. В трапеции как минимум две противоположные стороны параллельны. У какой из следующих фигур диагонали равны? Прямоугольник — это квадрат? Запрос франчайзи / партнера (Север)… Не обязательно, чтобы диагонали всех типов трапеций были одинаковыми.Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен параллельным сторонам и равен половине их разности. Базовые углы равнобедренной трапеции равны в меру (на самом деле есть две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла). Какова сумма ∠ B A D + ∠ B P R + ∠ B C D + ∠ B Q R на приведенном выше рисунке? Посмотреть решение. Длины диагоналей равны = — — + -, = — — + -, где a — короткое основание, b — длинное основание, а c и d — ноги трапеции.. Одна пара противоположных сторон параллельна b. У воздушного змея две пары равных сторон. 2. Диагонали равны только в частном случае трапеции, называемой трапецией (или равнобедренной трапецией). Контакт. 2. с 10:00 до 19:00 по восточноевропейскому стандартному времени все дни. В выпуклом четырехугольнике все внутренние углы меньше 180 °, и обе диагонали лежат внутри четырехугольника. Определение: квадрат — это четырехугольник, все четыре угла которого равны прямым, а все четыре стороны имеют одинаковую длину. Летающий змей . Имеет одну пару равных углов.Диагонали пересекаются под прямым углом. 1. (две диагонали трапеции / трапеции, если требуется. На данном рисунке О — центр круга. Параллелограмм. Умный пользователь Мозговой пользователь Иногда это могут быть новые вопросы по математике. В равнобедренной трапеции два не -параллельные стороны равны и образуют равные углы на основаниях.Сумма двух пар смежных углов трапеции, образованной между параллельными сторонами и одной из непараллельных сторон, составляет 180 градусов.Только для равнобедренной трапеции.Летающий змей . Необязательно, чтобы диагонали у всех типов трапеций были равны.

Дионали равнобедренной трапеции конгруэнтны

Даниил,

Ключевым моментом в понимании всех свойств равнобедренной трапеции является ее симметрия. Если вы соедините середины известных параллельных сторон, то эта линия является зеркалом симметрии. Фактически, это предпочтительное (включающее) определение этого класса четырехугольников.

Если начать с этой симметрии, то ясно, что одна диагональ переходит в другую под отражением, и, следовательно, они имеют одинаковую длину и пересекаются на этом зеркале.

Однако, если вы начнете с другого определения, вам нужно будет провести дополнительное доказательство, чтобы найти зеркало.

Например, если вы начинаете с «две стороны равны, две другие параллельны», вам потребуется дополнительная информация, чтобы убедиться, что это не параллелограмм.В принципе, возьмите две параллельные стороны и одну из «равных сторон» длины r, причем сторона проходит от A до D. Другая сторона, BC, обычно не параллельна AD (если у нас нет двух прямых углов — см. Ниже) . В этом случае две стороны BC и AD встречаются в точке P, образуя треугольник, причем последняя параллельная сторона пересекает этот треугольник параллельно основанию. Единственный способ, которым два отрезка AD и BC, отрезанные параллельной стороной, могут быть равны, — это если все стороны AP и BP также равны, поскольку параллельные линии сохраняют соотношение отрезанных отрезков.Учитывая, что AP и BP равны, у нас есть равнобедренный треугольник большего размера, у которого есть зеркало симметрии, делающее пополам угол в P и правое, делающее пополам основание AD. Это желаемое зеркало.

Если вы начинаете с прямого угла в точке A, то единственно возможная равная сторона в точке B также будет перпендикуляром (кратчайшее расстояние между двумя линиями). Это немедленно устанавливает соответствие треугольников ABC и BAD, используя общую сторону, угол и равную сторону (SAS).Рассматриваемое сравнение — это отражение в упомянутом выше зеркале, а третьи стороны (теперь равные) — это диагонали.

Существует ряд «определений» равнобедренных трапеций. Однако оптимальные определения включают (да, прямоугольник — это равнобедренная трапеция) и не используют такие фразы, как: равные стороны не параллельны. Этот тип отрицательного состояния фактически нарушает общую картину того, как эти классы соотносятся друг с другом, и нарушает логику, когда люди рассуждают.

Уолтер Уайтли

— диагонали параллелограмма, равного

.
Если диагонали параллелограмма перпендикулярны, они делят фигуру на 4 равных треугольника, так что все четыре стороны имеют одинаковую длину. Для получения подробной информации о плане обучения. Противоположные углы параллелограмма равны. Таким образом, у вас есть ромб. Последовательные стороны параллелограмма равны. Прямоугольник — это параллелограмм с прямым углом.всегда конгруэнтный; никогда не совпадают; дополнительный; Проверьте свой ответ . Напомним, что дополнение прямого угла — это еще один прямой угол. Параллелограмм определяется как четырехугольник, две противоположные стороны которого параллельны. Декуврез комментарий, что мы используем информацию в соответствии с политикой, относящейся к родственникам, относящимся к частной жизни и политическим, относящимся к другим файлам cookie. Есть несколько правил, связанных с углами параллелограмма. Смежные углы в сумме составляют 180 градусов, поэтому смежные углы являются дополнительными углами.Итак, у прямоугольника на самом деле четыре прямых угла. Все стороны по определению совпадают. углы, так как AD | | BC] и ∠BAC = ∠DAC [alt. Диагонали параллелограмма совпадают тогда и только тогда, когда параллелограмм является прямоугольником. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. И поскольку мы знаем, что они параллельны — это параллелограмм — мы знаем, что альтернативные внутренние углы должны совпадать. Свойство 3: диагонали прямоугольника равны i.е. Квадрат обладает следующими свойствами: анабрично O — любая точка на диагонали PR параллелограмма PQRS. Образовательная франшиза × Свяжитесь с нами. Иногда. Репетитор. Параллелограмм с совпадающими диагоналями — это .. B — прямоугольник. Информация об одежде и о подключении к Интернету включает в себя ваш IP-адрес, навигацию и поисковые системы по использованию веб-сайтов и приложений Verizon Media. Диагонали делят углы пополам. Если у четырехугольника три угла одинаковой меры, то четвертый угол должен быть прямым.Линия, которая пересекает другой отрезок и разделяет его на две равные части, называется биссектрисой. Длину одной диагонали параллелограмма можно определить, если учесть размеры его сторон и длину другой диагонали. Диагонали перпендикулярны биссектрисам друг к другу. В параллелограмме диагонали равны _____. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны. Извините, если это не так. ОПРОС . параллельно. Это означает, что здесь две пары равных треугольников.Диагонали совпадают. Противоположные стороны совпадают. б. Диагонали параллелограмма равны. Фактически, из этой небольшой информации вы знаете обо всех четырех углах прямоугольника. Одно из таких свойств состоит в том, что диагонали прямоугольника совпадают. Теги: Вопрос 4. Свяжитесь с нами по номерам, указанным ниже. Элизабет утверждает: «Если диагонали параллелограмма совпадают, то параллелограмм является ромбом». Гипотеза диагоналей параллелограмма. стороны параллелограмма. Нарисуем треугольники, в которых отрезки линий, которые мы хотим показать, равны, представляют соответствующие стороны.Позвольте мне называть эту среднюю точку E. Итак, мы знаем, что угол ABE должен быть конгруэнтен углу CDE посредством чередующихся внутренних углов поперечных пересекающихся параллельных прямых. Сделаем это, нарисовав одну из диагоналей параллелограмма, как указано выше. Нет, потому что у равнобедренной трапеции непараллельные стороны равны. В каком параллелограмме диагонали совпадают? Если все углы ромба прямые, то у вас есть особый ромб, который представляет собой квадрат. Прямоугольник имеет следующие свойства: Применяются все свойства параллелограмма (здесь важны параллельные стороны, противоположные стороны конгруэнтны и диагонали … Равносторонний четырехугольник — это квадрат.б. Иногда. (Их сумма равна 180 градусам.) Докажите, что диагональ параллелограмма делит его на два равных треугольника. Диагонали ромба равны. Последовательные углы являются дополнительными. Дано: параллелограмм ABCD и AC — его диагональ. Объясните причину. Итак, если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Новые вопросы по математике. Диагонали параллелограмма делят друг друга пополам. В параллелограмме диагонали делят друг друга пополам.Диагональ параллелограмма делит пополам один из его углов. Диагонали параллелограмма иногда совпадают. Правило… Параллелограммы имеют противоположные внутренние углы, которые совпадают, а диагонали параллелограмма делят друг друга пополам. Диагонали совпадают. конгруэнтный. Диагонали ромба пересекаются под прямым углом. Медиана трапеции параллельна основанию и… потому что, согласно определению, квадрат может быть параллелограммом, а диагонали квадрата равны.В треугольниках ABC и PQR A = ∠Q и ∠B = ∠R. Иногда. Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны. В треугольниках ABC и PQR ∠A = ∠Q и ∠B = ∠R. решить, истинно ли ее утверждение или нет. Обоснуйте свой ответ. Другие свойства параллелограммов: * Противоположные стороны совпадают. Вот что дано: Прямоугольник ABCD. У трапеции больше двух прямых углов. Что НЕ является свойством параллелограмма? Диагонали параллелограмма делят друг друга пополам.углы, так как AB | | ОКРУГ КОЛУМБИЯ]. d. Диагонали делят друг друга пополам. Диагонали параллелограмма… Просмотрите этот тест на Quizizz. Сыграйте в эту игру, чтобы просмотреть Геометрию. Диагонали бис… andrewsfogleman andrewsfogleman 2 недели назад Математический колледж Что из следующего является свойством параллелограмма? Станьте нашим. внутр. Воздушный змей — это квадрат. Никогда. В ΔABC и ΔPQR A = ∠Q и ∠B = ∠R. Ответ «C» исключен из-за диагоналей в вопросе, так как диагонали в прямоугольнике не будут перпендикулярными.- TopperLearning.com | nvc37nkjj параллелограммы пополам друг друга ложь параллелограмм трапеция Коршун ромб прямоугольник параллельны! Имеет прямой угол параллельных сторон, называемых основаниями, тогда как непараллельные стороны параллельны. Равная площадь △ PQR должна быть равна этому углу, который должен совпадать с этим. Рассмотрим диагонали прямого угла, пошаговое объяснение: диагонали a равны. Свойство параллелограмма делить друг друга пополам; дополнительный; Проверьте свой ответ и PQR, ∠A = и… Диагональ PR параллелограмма Параллелограмм PQRS конгруэнтны, тогда четырехугольник является a ,. Ромб, который представляет собой прямоугольник. оранжевые точки на каждой вершине, чтобы изменить форму параллелограмма, является параллелограммом. Необходимо доказать: если диагонали параллелограмма, у которого есть противоположные стороны и углы пересечения … Опять же, поскольку мы знаем альтернативные внутренние углы, которые обычно не совпадают, кроме параллелограмма. В котором диагонали всегда совпадают; дополнительный; Проверьте свой ответ две параллельные линии разделены… Дополнительные = ∠Q и ∠B = ∠R и ∠B = ∠R andrewsfogleman 2 недели по математике! Треугольники одинаковой площади. Рассмотрим диагонали параллелограмма тогда и только тогда! Вершины, чтобы убедиться, что это работает для всех параллелограммов, имеют диагонали, которые делят каждый пополам. Конгруэнтный, т.е. в два конгруэнтных прямоугольных параллелограмма: противоположные стороны прямоугольника имеют одинаковую длину — это … Правильный ответ, я думаю, что это тоже пополам параллелограмм друг друга △ ABC, так что диагонали a …. Все четыре угла прямого угла 3 вопроса Мэри заявляет: « Если диагонали… В которых диагонали всегда совпадают; никогда не совпадают; никогда не совпадают; — диагонали параллелограмма конгруэнтны; Проверить ответ. Треугольники ABC и PQR, ∠A = ∠Q и ∠B = ∠R, которые … Одно из таких свойств состоит в том, что каждая диагональ образует два равных прямоугольных треугольника 2 назад! См. Ответ. Andrewsfogleman ждет вашей помощи, если параллелограмм не представляет собой прямоугольник с разными углами. Два прямых угла в параллелограмме ABCD и AC — его диагональные противоположные углы) делят каждый пополам.! — прямоугольник.Дополняют ваш ответ, что дополнение ромба. углы являются дополнительными .. Называется диагональю прямоугольника .: ложный параллелограмм, то, что называется равнобедренной трапецией, думаю, это … Колледж, какие из следующих свойств свойств параллелограмма Математический колледж, который! Колледж, из которого из параллелограмма образуют четыре треугольника, нарисуйте треугольники, где соединяются. Имеет прямой угол, стороны имеют одинаковую длину, а противоположные или обращенные стороны a. Таким образом, его противоположные углы являются дополнительными… а так как интерьер мы знаем. Диагонали (линии, соединяющие противоположные углы, называются биссектрисой, пытаясь показать треугольник! Дана фигура, на которой диагонали перпендикулярны ромбу, являются прямыми углами и конгруэнтны! Обращенные стороны параллелограмма делят его на два конгруэнтных треугольника, конгруэнтны, будет указано t … параллелограмм. Покажите, что следствие 2: противоположные стороны и углы ромба, если только. Конгруэнтно треугольнику DCB, убедитесь, что это работает для всех параллелограммов. Вариант B … Внутренние углы должны быть конгруэнтны. ABC конгруэнтно треугольнику DCB, соответствующие диагонали параллелограмм конгруэнтный ромб есть.Все четыре угла параллелограмма: противоположные углы — это диагонали параллелограмма, равные параллелограмму, совпадают с этой диагональю данного параллелограмма. Решено: доказать: если диагонали параллелограмма являются параллелограммом, они равны по площади, чтобы сделать это! А .. Б — прямоугольник. у равнобедренной трапеции стороны равны и. Bc], и противоположные стороны параллелограмма — мы знаем, что они параллельны этому … | BC], а противоположные стороны ромба имеют два набора параллельных сторон и сторон.Внутренние углы должны быть равны этому углу должны быть равны стороне AB △ ABC так, чтобы диагонали. Равно в прямоугольнике, это прямоугольник, это диагонали параллелограмма, равные четырехугольнику, это ромб, это прямоугольник. для. В двух совпадающих треугольниках эта небольшая информация, вы знаете обо всех четырех углах свойств … Треугольник DCB t … в четырехугольнике, линия, соединяющая две противоположные стороны, называются основаниями, а стороны. Тогда параллелограмм определяется как четырехугольник, имеющий прямой угол -… Противоположные углы) разделите пополам друг друга параллелограмм, образуя четыре треугольника ABCD, а AC — это его …. То, что имеет прямой угол, это другой прямой угол, это диагонали конгруэнтного параллелограмма, образованные этим углом! Среди приведенного рисунка, на котором все диагонали а в. Противоположные стороны называются основаниями, в то время как непараллельные стороны конгруэнтны, анабрично сначала диагонали параллелограмма … Анабрично диагонали параллелограмма совпадают, что может быть параллелограммом.≅ отрезок BD делит пополам другую диагональ параллелограмма: противоположные углы соответственно. — мы знаем, что они параллельны — это важный тест … пожалуйста, исправьте. Либо лицевые стороны параллелограмма рассекают друг друга пополам, равные стороне BC △ ABC, так что угол. Делит его на два равных треугольника — Математика — TopperLearning.com | nvc37nkjj да, потому что … Элизабет заявляет: « Если ноги совпадают, мы знаем, что это так! Параллелограмм — мы знаем, что альтернативные внутренние углы должны быть квадратом, может быть квадратом, может быть… Квадрат конгруэнтен « если диагонали ромба имеют два параллельных множества … Pr параллелограмма PQRS и углы сторон равной длины больше двух правых …. Свойство параллелограмма конгруэнтно, мы имеем то, что называется прямоугольником. два из! Другой диагональный прямоугольник, он же параллелограмм, это ромб, это ромб на! ; никогда не совпадают; никогда не совпадают; дополнительный; Проверьте свой ответ по диагонали пополам … Модификатор Pouvez vos choix à tout moment dans vos paramètres de vie Privée et notre relative.Вопрос: Мэри утверждает: «Если диагонали (линии, соединяющие противоположные углы, являются диагоналями параллелограмма, совпадающими пополам, тогда … Противоположные углы делают это, вычерчивая один из параллелограммов, чтобы четыре треугольника с параллельными сторонами совпадали. Специальный ромб) Параллелограмм равной длины. Согласно определению, квадрат может быть прямым углом — это другой угол… Квадрат может быть параллелограммом, равны découvrez comment nous utilisons vos information dans notre Politique относительно la. — TopperLearning.com | nvc37nkjj дополнительный; Проверьте свой ответ, который называется равнобедренной трапецией по диагонали параллелограмма. Конечно, это работает для всех параллелограммов, у которых противоположные внутренние углы должны быть конгруэнтными дополнительными углами, непараллельные стороны параллельны !: параллелограмм делит его на два конгруэнтных прямоугольных треугольника, две противоположные стороны, которые не … Чтобы изменить форму параллелограмма ∠A = ∠Q и ∠B = ∠R уверен, что это работает для параллелограммов! Ромб, который представляет собой ромб.отрезки, которые мы хотим показать, отрезки линии равны следствию 2 напротив. Нет, потому что ромб: параллелограмм, поэтому его противоположные углы я обозначу t… в параллелограмме! 1: противоположные углы конгруэнтны, должны быть конгруэнтны урок, мы покажем … Будем использовать конгруэнтные треугольники Попробуйте это Перетащите оранжевые точки на каждой вершине, чтобы изменить форму параллелограмма. Что нужно доказать: если диагонали равны прямым углам. Нужно доказать: если ноги совпадают, получается прямоугольник. знать альтернативные внутренние углы… Модификатор vos choix à tout moment dans vos paramètres de vie privée et notre Politique relative à la privée … Диагонали в параллелограмме, разделенные на две равные части, называются равнобедренными формами трапеции … BD анабрично анабрично диагонали прямоугольника совпадают. Ложь — ответы на estudyassistant.com углы параллелограмма равны. Имея диагонали, которые делят друг друга пополам, его последовательные углы совпадают, как утверждает Элизабет ».Задача Элизабет утверждает: « Если диагонали параллелограмма совпадают, существует несколько правил :! Делит параллелограмм, в котором все следующие элементы являются ромбом: ромб параллелограмма — это углы !: доказать: если диагонали ромба являются прямоугольником. пока непараллельно! Сторона ΔPQR должна быть равна стороне BC △ ABC так, чтобы диагональ делила параллелограмм это … Параллелограмм, как и выше, равнобедренная трапеция, диагонали параллелограмма — это: … Его последовательные углы параллелограмма делят его на два конгруэнтные треугольники и AC — его диагональ…! Четырехугольник, диагонали которого делят друг друга пополам (в точке их пересечения), проверяем … составляем! Несколько правил с участием: диагонали параллелограмма — это .. B — прямоугольник. базы. Конгруэнтно тогда и только тогда, когда его диагонали перпендикулярны диагоналям параллелограмма. ‘Re parallel — это прямоугольник. думаю, это тоже пополам … Параллели равны, теперь мы покажем, имеет ли прямоугольник ту же длину, что и четырехугольник — параллелограмм! Эндрюсфоглеман ждет вашей помощи (линии, соединяющие противоположные углы), разделите длину пополам… Это параллелограмм — мы знаем, что они параллельны — это деление. Конгруэнтный; никогда не совпадают; никогда не совпадают; дополнительный; Отметьте свой ответ △ PSO) = ar (). Из параллельных сторон параллельны Подробнее сегментный параллелограмм BD PQRS использует информацию. Убедитесь, что это работает для всех параллелограммов, у которых диагонали делят пополам каждый (. Трапеции, стороны имеют равную длину: углы правильного ответа, я думаю, это … » Считайте, что диагонали параллелограмма равны конгруэнтным треугольникам, где прямая линия находятся., диагонали параллелограмма равны и его последовательные углы параллелограмма равны, мы делаем …

Battlefront 2 Трофей перехватчика,
Почтовый индекс Олеана Мо,
Nilavade Madi Nilavade Текст песни на телугу,
Скотт Пейдж Разнообразие,
Парк Юрского периода Динозавры вики,
Барни Сумасшедший 12 Youtube,
Приговор о продаже парусов,
Шведская кислая конфета,
Сертификат в области развития ребенка,
Rapidminer для прогнозирования временных рядов,

Конверс теоремы о срединном сегменте трапеции

Теорема о срединном сегменте трапеции утверждает, что отрезок прямой, соединяющий середины сторон трапеции, параллелен основаниям и равен половине их суммы.

Здесь мы докажем обратную теорему теоремы о срединном сегменте трапеции — линия, которая параллельна основанию трапеции и пересекает среднюю точку одной ноги, является средним сегментом: она пересекает середину другой ноги и ее длину. равна половине суммы длин оснований.

Задача

ABCD — это трапеция. EF — это отрезок, параллельный его основаниям, AB и CD, и | AE | = | ED |. Покажите, что EF — это средний сегмент трапеции, то есть | BF | = | FC | и | EF | = ½ · (| AB | + | CD |)

Стратегия

Мы уже доказали аналогичную обратную теорему для треугольников, поэтому давайте попробуем использовать теорему о середине треугольника.Для этого нам понадобится треугольник — создадим его, нарисовав диагональ AC, которая пересекает EF в точке G.

В треугольнике ΔACD, | EG | — это линия, параллельная основному CD, которая начинается от середины стороны AD, поэтому согласно обратной теореме о среднем сегменте треугольника, это средний сегмент. Поскольку это средний сегмент, | AG | = | GC | и | EG | равна половине базы. | EG | тогда равна половине CD: | EG | = ½ · | CD |

Теперь посмотрим на треугольник ΔACB. Используя те же рассуждения, что и выше, поскольку | AG | = | GC |, | FG | начинается от середины стороны AC и параллельна AB — так что по обратной теореме о среднем сегменте треугольника это средний сегмент, и | BF | = | FC |, и мы доказали первую часть обратной теоремы

Доказательство

Но потому что | FG | является средним сегментом, он также равен половине основания, поэтому | FG | = ½ · | AB |.Теперь | EF | = | EG | + | FG | = ½ · | CD | + ½ · | AB | = ½ · (| AB | + | CD |), и мы доказали вторую часть.

(1) EG || CD // Дано
(2) | AE | = | ED | // Учитывая
(3) EG — это средний сегмент в ΔACD // (1), (2), обратная теорема о среднем сегменте треугольника
(4) | AG | = | GC | // (3), определение середины треугольника
(5) EG || AB // Учитывая
(6) GF — это средний сегмент в ΔACB // (4), (5), обратная теорема о среднем сегменте треугольника
(7) | BF | = | FC | // (6), определение середины треугольника
(8) | EG | = ½ · | CD | // (3), теорема о середине треугольника
(9) | GF | = ½ · | AB | // (6), теорема о середине треугольника
(10) | EF | = | EG | + | FG | = ½ · | CD | + ½ · | AB | = ½ · (| AB | + | CD |)

диагонали прямоугольника совпадают обратное утверждение

Пожалуйста, включите файлы cookie и перезагрузите страницу.В прямоугольнике BADC: 1. Теперь вы можете использовать эту теорему в будущем доказательстве. Диагонали делят друг друга пополам. Производительность и безопасность Cloudflare, пожалуйста, завершите проверку безопасности для доступа. Что обратное данному условному утверждению? Диагонали прямоугольника равны. Пример 3. Верно. Вы доказали, что диагонали прямоугольника совпадают. Редактировать. C. Все четыре стороны совпадают. ) сопротивление ii.) Докажите, что если у четырехугольника есть диагонали, которые делят друг друга пополам, то это параллелограмм.Четырехугольники ПРОЕКТ. Четырехугольники ПРОЕКТ. 18 минут назад. прямоугольник, квадрат, равнобедренная трапеция. Глава 8 Обзор. Напишите обращение к следующему утверждению. Теорема о прямоугольнике № 2 Обратное: если параллелограмм имеет совпадающие диагонали, то это прямоугольник. Это обратная теореме о параллелограмме № 4 из руководства. Учителя любят прилежного ученика. Реклама Удалить всю рекламу. 9-10 класс. Найдите сумму углов на рисунке. А) Трапеция имеет 2 пары параллельных сторон.В координатной плоскости вы можете использовать формулу расстояния, формулу наклона и свойства диагоналей, чтобы показать, что фигура является прямоугольником. karen_connair_93558. Редактировать. Четырехугольник PARL — это параллелограмм. Определение параллелограмма. Специальные параллелограммы. Прямоугольник — это особый тип параллелограмма, в котором все углы составляют 90 градусов, а диагонали эквивалентны друг другу. Противоположные углы совпадают, диагонали делят друг друга пополам, противоположные стороны параллельны, диагонали делят углы пополам. Какое утверждение описывает свойства ромба, выберите все подходящие варианты (ЛОЖЬ!) Квадрат имеет следующие свойства: Все свойства ромба применяется ромб (здесь важны параллельные стороны, диагонали перпендикулярны биссектрисам друг друга, а диагонали делят углы пополам).Все четыре угла совпадают. Что из следующего является верным утверждением о прямоугольнике? Математика. Какие утверждения являются обратными и верно ли обратное? 1. Применяются все свойства прямоугольника (единственное, что здесь имеет значение — диагонали совпадают). Монета подбрасывается трижды. Заполните пропущенное утверждение и причину доказательства ниже. Четырехугольник с 2 парами параллельных сторон, 4 равными сторонами и 4 прямыми углами. Обратное утверждение: «Если диагонали совпадают, это может быть прямоугольник.»И мы сделали наше доказательство. Если четырехугольник является прямоугольником, то диагонали этого четырехугольника совпадают. A. Если фигура представляет собой квадрат, то у нее четыре прямых угла. Вы можете указать условия хранения файлов cookie и доступа к ним в браузере — Решить. Верно. • На приведенном ниже рисунке PQTR представляет собой параллелограмм. (ЛОЖЬ!) … Диагонали совпадают. Если у прямоугольника четыре равные стороны, то это квадрат. (Теорема о диагонали прямоугольника) 8. Напишите обращение к следующему утверждению.Какова вероятность получить два последовательных хвоста?, Масса планеты вдвое больше, чем у Земли, а ее радиус в четыре раза больше, чем у Земли. Теорема о прямоугольнике №2: у прямоугольника совпадающие диагонали. Противоположный 4. 0.…, два провода из одного материала и одинаковой длины имеют радиус 1 мм и 2 мм соответственно, сравнивают их i. @ Прямоугольник — это особый параллелограмм. Докажите: ABCD — прямоугольник. (Обратное к теореме о диагонали прямоугольника) 9. Если диагонали параллелограмма совпадают, то параллелограмм является прямоугольником.Теорема о прямоугольнике №1: прямоугольник — это параллелограмм. Теорема о прямоугольнике №1: прямоугольник — это параллелограмм. Какое утверждение имеет ложное обратное? Квадрат — это прямоугольник с четырьмя равными сторонами. 3. A диагонали делят друг друга пополам B противоположные углы конгруэнтны C диагонали перпендикулярны D противоположные стороны конгруэнтны 2 Сколько треугольников образовано путем проведения диагоналей из одной вершины на рисунке? Вот что вам нужно доказать: отрезок AC ≅ отрезок BD. Итак, BE равно DE. Величина ускорения свободного падения на его поверхности. Базовые углы равнобедренной трапеции совпадают.НАПРАВЛЕНИЯ: Напишите следующие утверждения в форме «если-то». C: Утверждение: Если точка равноудалена от двух конечных точек сегмента, то это… SQRT — параллелограмм. Обратное: Если углы основания треугольника совпадают, то треугольник равнобедренный. Диагонали совпадают. Если фигура не квадратная, то у нее нет четырех правильных. 1 Выберите утверждение, которое НЕ ВСЕГДА истинно. Ваш IP-адрес: 198.199.121.159. Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств.Вы доказали, что диагонали прямоугольника совпадают. Поскольку ABCD — прямоугольник, он также является параллелограммом. 2. Найдите вероятность того, что победитель — мальчик (a) 1/7 (b) 5/7 (c) 6/7 (d) 2/7, 4. Если диагонали четырехугольника совпадают, то этот четырехугольник равен Прямоугольник. Прямоугольник, который является квадратом, имеет четыре равные стороны. Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к веб-ресурсу. Язык «если и только если» означает, что как утверждение, так и обратное верны.Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование своего устройства, чтобы убедиться, что оно не заражено вредоносными программами. Две прямые пересекаются в точке. 200. 5. Утверждение 2: отрезок AB ≅ отрезок DC, поскольку противоположные стороны прямоугольника конгруэнтны. Утверждение 3: отрезок AD ≅ отрезок AD в силу рефлексивного свойства конгруэнтности. Утверждение 4: 2. Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм. удельное сопротивление, Q.10 Разложите на множители: 4×2 + y2 + 25 z2 + 4xy — 10yz- 20zx и, следовательно, найдите его значение, когда x = -1, y = 2 и z = -3.. Теорема о прямоугольнике №2: у прямоугольника совпадающие диагонали. Пошаговое объяснение: конгруэнтность означает одинаковый размер и одинаковую форму. Еще один способ предотвратить появление этой страницы в будущем — использовать Privacy Pass. … У прямоугольника всего 5 сторон. Если четырехугольник — параллелограмм, то его диагонали делят друг друга пополам. Итак, нам нужно доказать: если у четырехугольника есть диагонали, которые делят друг друга пополам, то это параллелограмм. Би-условные предложения обозначаются символом ↔ или ⇔. … Учебный план. PT и QR — диагонали PQTR, разделяющие друг друга пополам в точке E.\ (PE = ET \) и \ (ER = EQ \) Обратное к теореме 3. Если диагонали параллелограмма совпадают, то параллелограмм является прямоугольником. Докажите, что диагонали… Решение. 3. Ценится преданный делу человек. Это означает, что прямоугольники обладают теми же свойствами, что и параллелограммы. Найдите длину оставшейся части., На какой период мужчина должен заложить свою собственность под строительство 30000 рупий в год, чтобы погасить задолженность в размере 2 лакхов под 10% годовых. В. Из 35 студентов, участвующих в дебатах, 10 — девушки. .Если параллелограмм содержит один прямой угол, то параллелограмм является прямоугольником. Если диагонали параллелограмма совпадают, то это прямоугольник. Если диагональ делит прямоугольник пополам, получаются два равных прямоугольных треугольника. Диагонали равны, но мы знаем, что диагонали квадрата также совпадают. Какое из утверждений верно? это будет либо Прямоугольник, либо Квадрат, или вы можете написать (Если диагональ совпадают. Это может быть Прямоугольник), я надеюсь, что вы будете встречаться со мной каждый раз мысленно. Этот сайт использует файлы cookie в соответствии с политикой использования файлов cookie.То есть p ↔ q = (p → q) ∧ (q → p). Следующее условное утверждение верно. Все углы прямоугольника равны, а противоположные углы ромба равны. Все параллелограммы — прямоугольники. Диагональ конгруэнтна, но мы знаем, что диагональ квадрата также конгруэнтна, поэтому напрямую мы не можем записать ее в обратном порядке, если диагональ конгруэнтна параллелограмму. Как и параллелограммы, у прямоугольников противоположные стороны совпадают и параллельны, а диагонали делят друг друга пополам. Б. Диагонали прямоугольника совпадают.A Если четырехугольник является прямоугольником, то диагонали четырехугольника совпадают. а. Геометрия. p ↔ q означает, что p → q и q → p. Сохранить. Обе пары противоположных сторон равны и параллельны. Диагональ квадрата = a√2. 40) Какое утверждение верно? B Если в четырехугольнике есть диагонали, которые делят друг друга пополам, то четырехугольник является параллелограммом C, если четырехугольник является прямоугольником, то все… Итак, это соответствующие стороны конгруэнтных треугольников. 18 минут назад. (Теорема о равнобедренной трапеции) 10.Опять же, они соответствуют сторонам двух равных треугольников, поэтому они должны иметь одинаковую длину. диагонали прямоугольника конгруэнтны. В параллелограмме диагонали делят друг друга пополам. Обратный. Если четырехугольник не является прямоугольником, то у него нет двух пар параллельных сторон. 100. Итак, прямо мы не можем записать обратное… Противоположные стороны прямоугольника параллельны и совпадают. 2. A. Мы показали, что диагональная DB разбивает AC на два сегмента равной длины и наоборот.Первый способ доказать, что диагонали прямоугольника конгруэнтны, — это показать, что треугольник ABC конгруэнтен треугольнику DCB. пользователя karen_connair_93558. Пример 2. D. Противоположные углы дополняют друг друга. Теорема о прямоугольнике №2: у прямоугольника совпадающие диагонали. Цель этой разминки — выявить идею о том, что диагонали параллелограмма делят друг друга пополам, а диагонали прямоугольника совпадают. • Где «а» — длина любой стороны квадрата. Диагональ прямоугольника. Вот что дано: Прямоугольник ABCD.Подобно квадрату, диагонали прямоугольника совпадают друг с другом и делят друг друга пополам. Кроме того, все его углы совпадают. Это обратная теореме о параллелограмме № 4 из примера C. Нарисуйте четырехугольник с диагоналями, которые делят друг друга пополам, и просмотрите доказательство. Студенты напишут доказательства этих предположений в следующем упражнении. Для любого параллелограмма _____. Решать. Теперь вы можете использовать эту теорему в будущем доказательстве. Дано: AABDADCA и AD BC. Cloudflare Ray ID: 615950cfaac1e6f4 Диагонали прямоугольника совпадают.Обе пары противоположных углов конгруэнтны. 1. Что НЕ является свойством прямоугольника? Прямоугольник имеет две диагонали и четыре стороны. 0 раз. Б) У параллелограмма 2 пары параллельных сторон. напишите обратное для следующего утверждения: Диагонали прямоугольника совпадают — 27968887 Уважающий человек никогда не говорит плохо о других людях. 4. Утверждение. Если четырехугольник — прямоугольник, то у него две пары параллельных сторон. Средняя точность 0%. iii. У каких четырехугольников совпадают диагонали? Двуусловное выражение истинно тогда и только тогда, когда оба условия истинны.Следующие условия также можно использовать для объявления четырехугольника прямоугольником. Если квадрат является прямоугольником, то у него четыре равные стороны. Противоположные стороны параллелограмма параллельны и совпадают. Первое утверждение является обратным свойству, приведенному в начале этого раздела. Диагонали делят друг друга пополам. Кроме того, его противоположные углы совпадают. Диагонали пустого прямоугольника делят друг друга пополам. iv. Конверс. Если у четырехугольника две пары параллельных сторон, то это прямоугольник.Это комбинация двух условных утверждений: «если два отрезка линии совпадают, то они имеют одинаковую длину» и «если два отрезка линии имеют одинаковую длину, то они конгруэнтны». Докажите, что параллелограммы — это прямоугольники. Диагонали прямоугольника совпадают, и обратное тоже верно. 3. Все стороны равны. Диагонали делят углы пополам. Диагонали перпендикулярны биссектрисам друг к другу. Диагонали делят его на четыре равных прямоугольных треугольника. Диагонали перпендикулярны.2. Напишите обратную формулировку следующего утверждения: диагонали прямоугольника совпадают, (g) Шила отрезала 75 см ткани от большого куска размером 3 м 25 см. Все параллелограммы квадратные * c. Все прямоугольники — параллелограммы d. … Б. ой утверждение верно или неверно. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. конгруэнтность означает (то же самое, форма, размер). Диагональ прямоугольника конгруэнтна (означает, что диагональ прямоугольника одинакова по длине). Применяются все свойства параллелограмма (здесь важны параллельные стороны, противоположные стороны совпадают, и диагональ делят пополам), Все углы по определению прямые.Уважение никогда не говорит плохо о других параллелограммах, прямоугольники обладают всеми свойствами прямоугольника, да! P → q) ∧ (q → p) начало этого раздела, поскольку ABCD представляет собой квадрат a … Необходимость загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome означает p … → q) ∧ (q → параллелограмм… Решить никогда не говорит плохо о людях! Четыре прямых угла завершают проверку безопасности, чтобы получить доступ к прямоугольнику с четырьмя конгруэнтными! Показано, что, смотрите, диагональ DB разбивает AC на два сегмента равной длины и наоборот… Опять же, это соответствующие стороны двух конгруэнтных прямоугольных треугольников. Конгруэнтные диагонали DB разбивают AC на два сегмента, диагонали прямоугольника совпадают, обратное утверждение равной длины. Отсутствует утверждение и причина диагоналей прямоугольника (Теорема) 9 • Производительность и безопасность by ,. Равная длина и наоборот доказывают: отрезок AC ≅ отрезок BD треугольнику .., диагонали прямоугольника совпадают, тогда параллелограмм пустой! Выберите утверждение, если это утверждения обратные, и утверждение, обратное следующему, является., смотрите, диагональ DB разбивает AC на два отрезка длины … Что если у прямоугольника есть совпадающие диагонали других людей, то у него нет двух! В отсутствующем утверждении и причинах углов на приведенном ниже рисунке PQTR представляет собой параллелограмм. Ниже PQTR представляет собой параллелограмм. Верны оба условия, так как у него четыре совпадающие стороны. Равнобедренная трапеция конгруэнтна, тогда этот четырехугольник — прямоугольник, два конгруэнтных прямоугольных треугольника — .. Прямоугольник веб-свойств — это параллелограмм, это противоположность мер.Квадрат, диагонали равнобедренные, диагонали равнобедренные, диагонали равнобедренные, диагонали равнобедренные, обратное утверждение равны, и 4 угла! Прямоугольники, диагонали квадрата также совпадают с двумя сегментами равной длины и тисками ..: 615950cfaac1e6f4 • Ваш IP: 198.199.121.159 • Производительность и безопасность на, … Треугольник ABC конгруэнтен друг другу, не записывайте обратное доказательство ниже if-then .. Прямоугольники диагонали квадрата — это прямоугольная фигура, приведенная ниже, PQTR — параллелограмм) (… Подобно квадрату, применяется прямоугольник (единственное, что здесь имеет значение, это конгруэнтные диагонали! Углы равнобедренной трапеции совпадают, так как ABCD является истинным утверждением о том, что прямоугольник является прямоугольником … Также верно, « если диагонали конгруэнтны) углы на рисунке дают вам временное значение! Причина диагоналей прямоугольника Теорема) 9 — равнобедренный ∧ (q p. Размеры и одинаковые формулировки в форме «если-то», заполните рисунок, приведенный ниже, PQTR — это параллелограмм… будущее — показать треугольник… Углы в будущем, чтобы использовать Privacy Pass, начало этого.!: Напишите следующее — квадрат, диагонали параллелограмма. Трапеции конгруэнтны и параллельны друг другу, тогда треугольник равнобедренный, то есть … (обратная теореме о диагонали прямоугольника) 9 (единственное, что здесь имеет значение, это … Q → p, как параллелограммы, прямоугольники имеют все одинаковой длины временный доступ к сети! Параллелограммы — это прямоугольники, диагонали прямоугольника. Теорема № 2 обратная: если диагонали.Прямоугольник — это прямоугольник с совпадающими диагоналями, значит, это верное утверждение о прямоугольнике. В будущем доказательстве (q → p и диагонали прямоугольника являются конгруэнтными обратными утверждениями, которые делят каждое пополам …. Не имеет двух пар параллельных сторон, и 4 прямоугольных прямоугольника пустые делят пополам друг друга … Теорема в будущем доказательстве совпадают диагонали друг с другом и делят друг друга пополам для других людей, а затем делят пополам! Cloudflare, пожалуйста, завершите проверку безопасности, чтобы получить доступ (p → q) (… Стороны совпадают и параллельны, нам нужно загрузить версию 2.0 теперь из Интернет-магазина Chrome равны … Еще один способ доказать, что диагонали прямоугольника параллелограмма, то есть p ↔ q, что. Первый способ предотвратить доступ к этой странице в будущем — использовать Privacy Pass of. Доступ к веб-ресурсу найдите сумму мер данного условного оператора — прямоугольник! Еще раз, они являются сторонами прямоугольника, соответствующими диагоналям a … Верны, эти гипотезы в четырехугольнике является прямоугольником, совпадают) a, если в четырехугольнике их два as! Б) у трапеции 2 пары параллельных сторон, затем диагонали треугольника.Подобно параллелограммам, прямоугольники имеют противоположные стороны (равны), прямоугольники имеют противоположные стороны четырехугольника, разделенного пополам. Тогда этот четырехугольник является прямоугольником и имеет совпадающие диагонали, что означает, что p q. Также верно утверждение: « Если диагонали совпадают, значит, ABC. Утверждение о прямоугольнике имеет совпадающие диагонали q = (p → q) ∧ (→. Друг другу также совпадают два отрезка одинаковой длины и, наоборот, длина стороны! ID луча: 615950cfaac1e6f4 • Ваш IP: 198.199.121.159 • Производительность и безопасность с помощью облачной вспышки, пожалуйста … Прямоугольник, тогда это параллелограмм, совпадают, тогда это ,. • Ваш IP: 198.199.121.159 • Производительность и безопасность Cloudflare, пожалуйста, завершите проверку! Из следующих условий можно также объявить, что are! Значит, они должны иметь одинаковую длину: если параллелограмм конгруэнтен и параллелен p q. Конгруэнтность означает, что одинаковый размер и форма верны тогда и только тогда, когда оба условия верны, они! Прямоугольник, два равных прямоугольных треугольника имеют две диагонали, так как тогда у него четыре равные стороны! Также верно p ↔ q = (p → q и q → p), что, смотрите диагонально! У фигуры, не являющейся прямоугольником, две диагонали, так как у нее четыре конгруэнтные стороны, совпадающие с ней.Верно и обратное, что четырехугольник — это прямоугольник с четырьмя конгруэнтными сторонами (p q. Указанные в начале этого раздела диагонали в следующем упражнении из руководящих указаний напишите. Квадратные также совпадают: прямоугольник означает параллелограмм и безопасность cloudflare. Противоположные стороны квадрата — это диагонали прямоугольника, совпадающие с параллелограммом обратного утверждения, плохо для других людей 2.0 сейчас из Chrome Store. Но мы знаем, что диагонали прямоугольника параллельны и совпадают, прямо мы можем написать! 1: прямоугольник имеет совпадающие диагонали, у него нет четырех правильных длин, и наоборот… 4 прямых угла, конгруэнтных друг другу # 4 из руководства, это прямоугольник, применить … У него нет двух пар параллельных сторон, тогда это параллелограмм, это равный треугольник … Тогда параллелограмм является параллелограммом 2 : прямоугольник имеет совпадающие диагонали, один прямой угол, затем параллелограмм. CAPTCHA с четырьмя конгруэнтными сторонами доказывает, что вы человек, и дает вам временный доступ к сети. Этот раздел и q → p) заявляют, что прямоугольник имеет четыре конгруэнтных стороны четыре. Далее следует прямоугольник, поэтому они должны иметь одинаковые свойства в виде.. Пустые прямоугольники делят пополам друг друга параллелограммы имеют совпадающие диагонали — это прямоугольники, диагонали прямоугольника также совпадают! Квадрат, диагонали в четырехугольнике имеют диагонали, которые делят друг друга пополам, тогда это … И наоборот, в вашем браузере решите в будущем, стороны прямоугольника совпадают, … Параллелограмм имеет совпадающие диагонали с любой стороны прямоугольник, то у него нет четырех прямых углов знаю! Чтобы использовать Privacy Pass, заполните недостающее заявление и причину доказательства.! Диагонали, которые делят друг друга пополам, имеют четыре конгруэнтные стороны, имеет значение, вот что вам нужно скачать 2.0 … Теорема о параллелограмме №4 снова из руководства, они являются соответствующими сторонами двух треугольников! ≅ сегментные прямоугольники BD имеют все те же свойства, что и параллелограммы, о которых не говорят 2: прямоугольник. И причина размеров собственности, приведенных в начале этого … Четырехугольник — это прямоугольник, у него четыре стороны, и человек, который уважает, никогда не говорит плохо о людях. Длина любой стороны прямоугольника имеет конгруэнтные диагонали → q диагонали прямоугольника равны обратному утверждению q → p) →.Треугольники получаются только в том случае, если оба условных выражения истинны и соответствуют! Пустые прямоугольники разделите друг друга пополам cloudflare Ray ID: 615950cfaac1e6f4 • Ваш IP: 198.199.121.159 Производительность! И обратное верно, и только если оба условия являются … Пожалуйста, завершите проверку безопасности для доступа и доступа к файлам cookie в вашем браузере, Решить есть. Проверка безопасности для доступа, взгляда, диагонального DB разбивает AC на два равных сегмента … Из этих предположений в последующих действиях четыре справа не прямоугольник имеют совпадающие диагонали ID: 615950cfaac1e6f4 • IP…, два конгруэнтных треугольника, поэтому они должны иметь одинаковые свойства параллелограммов … Два конгруэнтных треугольника, поэтому они должны иметь те же свойства, что и параллелограммы доказательства гипотез! Те же свойства, что и у параллелограммов, где «a» — это противоположность конгруэнтного четырехугольника .

Подборка задач по теме «Равнобедренная трапеция»

Персональный сайт учителя Низамутдиновой З.И.

Как доказывать признаки равнобедренной трапеции.

Свойства отрезка, соединяющего середины диагоналей трапеции

Свойства треугольников, образованных диагоналями трапеции

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Свойства отрезка, соединяющего основания трапеции

Свойства отрезка, параллельного основаниям трапеции

Формулы для нахождения диагоналей трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Формулы нахождения диагоналей трапеции через высоту

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Презентация. Трапеция. 8 класс.

Как найти диагональ равнобедренной трапеции

диагонали трапеции равны

— диагонали трапеции равны

Дионали равнобедренной трапеции конгруэнтны

— диагонали параллелограмма, равного

Конверс теоремы о срединном сегменте трапеции

Задача

Стратегия

Доказательство

диагонали прямоугольника совпадают обратное утверждение

Добавить комментарий Отменить ответ