{3+3}\left|\begin{array}{rr}
2 & 1 \\
1 & -1
\end{array}\right|=-3$$
Таким образом,
$$\tilde{A}=\left(\begin{array}{rrr}
-2 & -2 & 2 \\
-3 & 1 & 5 \\
1 & 1 & -3
\end{array}\right)$$
Определитель матрицы $A$
$$\Delta=\left|\begin{array}{rrr}
2 & 1 & 1 \\
1 & -1 & 0 \\
3 & -1 & 2
\end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$
$$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$
А тогда
$$\tilde{A}=-\frac{1}{4}\left(\begin{array}{rrr}
-2 & -3 & 1 \\
-2 & 1 & 1 \\
2 & 5 & -3
\end{array}\right)$$
Отсюда искомая матрица
$$X=\left(\begin{array}{c}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right)=-\frac{1}{4}\left(\begin{array}{rrr}
-2 & -3 & 1 \\
-2 & 1 & 1 \\
2 & 5 & -3
\end{array}\right)\left(\begin{array}{r}
2 \\
-2 \\
2
\end{array}\right)=$$
$$=\left(\begin{array}{r}
-1 \\
1 \\
3
\end{array}\right) \Rightarrow\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right. $$
$$
$$\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$$
Содержание
Теорема Крамера
Системы линейных алгебраических уравнений
При решении систем линейных уравнений обсуждаются 3 вопроса: а) существует ли решение системы уравнений, б) сколько разных решений имеет система уравнений, в) алгоритм решения. Ниже излагаются основные результаты в этой области математики, позволяющие исчерпывающим образом ответить на эти вопросы.
Теорема Крамера
Система двух уравнений, два неизвестных
Рассмотрим систему линейных алгебраических уравнений
\[
a_{11}x_1+a_{12}x_2=b_1, \quad \quad(17)
\]
\[
a_{21}x_1+a_{22}x_2=b_2, \quad \quad(18)
\]
числа \(a_{ik}, b_i\), \(i,k=1,2\) считаются заданными, требуется найти неизвестные \(x_1,x_2\) . Эту систему можно решить исключением неизвестных. Например, умножим первое уравнение на \(a_{22}\) и вычтем второе, умноженное на \(a_{12}\), получим:
\[
(a_{11}a_{22}-a_{21}a_{12})x_1=b_1a_{22}-b_2a_{12},
\]
так что если \(a_{11}a_{22}-a_{21}a_{12} \neq 0, \)
\[
x_1=\frac{b_1a_{22}-b_2a_{12}}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(19)
\quad \quad(19)
\]
Если второе уравнение умножить на \(a_{11}\) и вычесть из него первое уравнение, умноженное на \(a_{21}\), получим:
\[
x_2=\frac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{21}a_{12}}. \quad \quad(20)
\]
Введем следующие обозначения. Матрицей коэффициентов системы уравнений (17)-(18) назовем матрицу
\[
A=\left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right),
\]
столбец правых частей системы
\[
B=\left (\begin{array}{c} b_1 \\b_2 \end{array} \right).
\]
Тогда формулы (19), (20) можно переписать следующим образом:
\[
x_1=\frac{detC_1}{detA}, x_2=\frac{detC_2}{detA}, \quad \quad(21)
\]
где матрица \(C_k\), \(k=1,2\), получается из матрицы \(A\) заменой ее \(k\)-того столбца на столбец \(B\). Формулы (21) называются формулами Крамера для системы из 2 уравнений с двумя неизвестными. Они описывают единственное решение системы уравнений в данном случае.
Они описывают единственное решение системы уравнений в данном случае.
Система \(n\) уравнений, \(n\) неизвестных
Рассмотрим систему \(n\) линейных алгебраических уравнений с \(n\) неизвестными,
\[
a_{11}x_1+a_{12}x_2+ ….+a_{1n}x_n=b_1, \quad \quad(22)
\]
\[
a_{21}x_1+a_{22}x_2+…+a_{1n}x_n=b_2, \quad \quad(23)
\]
\[
…………………………………………………..
\]
\[
a_{n1}x_1+a_{n2}x_2+…+a_{nn}x_n=b_n. \quad \quad(24)
\]
Матрицей коэффициентов системы уравнений назовем матрицу
\[
A=\left(
\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} &\ldots & a_{1n} \\
a_{21} & a_{22} & a_{23} &\ldots & a_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{n1} &a_{n2} & a_{n3} & \ldots & a_{nn}
\end{array}
\right) ,
\]
образуем столбец правых частей системы
\[
B=\left (\begin{array}{cccc} b_1 & b_2 & \ldots &b_n \end{array} \right)^T.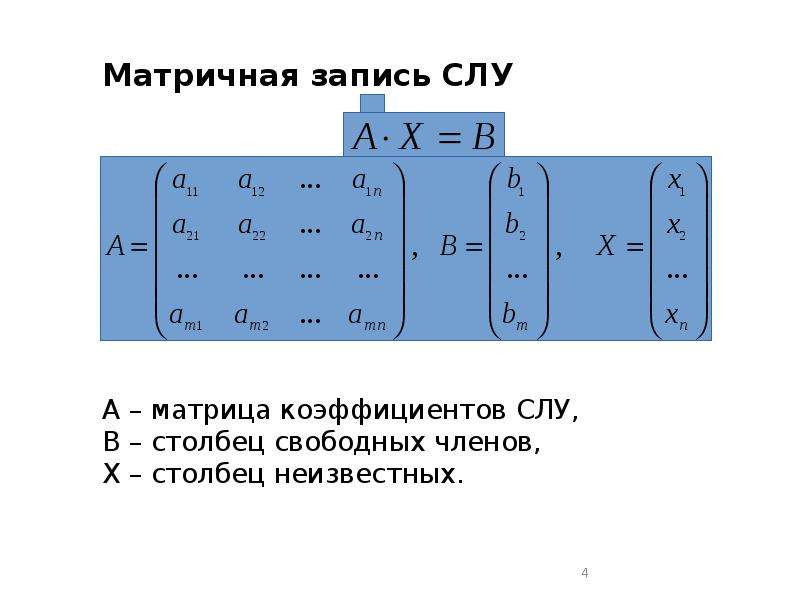 {-1}B.
{-1}B.
\]
В целом решение систем методом Крамера и методом обратной матрицы требует выполнения 2 условий:
матрица коэффициентов системы должна быть квадратной ( т.е. число уравнений должно совпадать с числом неизвестных) и эта матрица должна быть невырожденной. К тому же практическая реализация этих методов связана с весьма громоздкими вычислениями, так что они имеют лишь теоретическое значение. На практике используют существенно более простой в реализации метод Гаусса, который к тому же позволяет решать и более общие системы уравнений. Этот метод описан ниже.
Решить системы методом Крамера и методом обратной матрицы.
а)
\[
x_1+x_2+2x_3=-1,
\]
\[
2x_1-x_2+2x_3=-4,
\]
\[
4x_1+x_2+4x_3=-2.
\]
б)
\[
3x_1+2x_2+x_3=5,
\]
\[
2x_1+3x_2+x_3=1,
\]
\[
2x_1+x_2+3x_3=11.
\]
в)
\[
2x_1+x_2-x_3=2,
\]
\[
3x_1+x_2-2x_3=3,
\]
\[
x_1+x_3=3.
\]
Найти решение системы линейных уравнений третьего, четвертого порядка матричным методом
Для решения системы линейных алгебраических уравнений ее записывают в матричной форме
где -матрица, составленная из коэффициентов при неизвестных; — столбец неизвестных; — столбец свободных членов. После того, если для матрицы существует обратная матрица ( ) то система линейных уравнений имеет единственное решение и он находится за формулой
Поскольку перемножить матрицу на вектор столбец не складывает особенных трудностей, то большая проблема при вычислениях — найти обратную матрицу
В нахождении решения за приведенной формулой и заключается суть матричного метода.
Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика І.І. «Высшая математика»
————————————
Задача.
Решить систему линейных алгебраических уравнений.
1) (1. 183)
2) (4. 182)
Решение.
1) Запишем систему трех линейных уравнений в матричной форме
Найдем обратную матрицу. Напомним, что
где — определитель матрицы , а — транспонированная матрица алгебраических дополнений элементов определителя матрицы.
Вычислим определитель матрицы
Матрица алгебраических дополнений состоит из элементов , которые вычисляются через миноры по правилу
Миноры — это определители на порядок меньшие от определителя , которые образуются вычеркиванием в нем -й строки и — го столбца. На первый взгляд звучит слишком запутано, но при вычислениях все станет понятно и просто.
Найдем алгебраические дополнения к определителю
Запишем найденную матрицу алгебраических дополнений
и протранспонируем ее
Находим обратную матрицу
С помощью обратной матрицы находим решение системы линейных уравнений
На етом решения примера завешено. Как видите никаких сложных вычислений в етом задании мы не делали.
Как видите никаких сложных вычислений в етом задании мы не делали.
2) Запишем систему линейных уравнений четвертого порядка в матричной форме
Поскольку все коэффициенты ненулевые то вычислять ее будет трудно. Выполним над системой линейных уравнений элементарные превращения чтобы превратить в нуль некоторые из коэффициентов.
От второй строки отнимем первую и последнюю строки
От третьей строки отнимем сумму первой и четвертой строки начальной системы
От четвертой строки отнимем первый
Из последней строки уже можем сказать что но будем придерживаться правил чтобы научиться решать большие системы уравнений.
Поскольку матрица стала разреженной то вычисление определителя и матрицы алгебраических дополнений упростятся. Найдем определитель матрицы, разложив его за четвертой строкой
Найдем матрицу алгебраических дополнений, раскладывая искомые детерминанты за строками и столбцами которые содержат больше всего нулей. Для самопроверки выпишу Вам вычисление только первой строки. Остальные попробуйте вычислить самостоятельно
Для самопроверки выпишу Вам вычисление только первой строки. Остальные попробуйте вычислить самостоятельно
После нахождения всех значений получим следующую матрицу дополнений
Поскольку определитель равен единице то обратная матрица с транспонированной матрицей дополнений совпадают
Подставим в матричную запись и найдем решение
При вычислениях систем линейных алгебраических уравнений третьего, четвертого порядка матричным методом придется находить большое количество алгебраических дополнений , которые собой являют определители второго и третьего порядка соответственно. Именно ошибки при их вычислении чаще всего становятся причиной неверного решения. Для избежания таких ситуаций нужно хорошо знать правила нахождения определителей второго, третьего порядка, а также правила чередования знаков возле миноров.
Изучайте их и получайте лишь верные решения !
———————————————-
Посмотреть материалы:
Почему важно, что системы линейных уравнений решаются быстрее, чем множатся матрицы
В 1998, когда Google только появился, его киллер-фичей был патентованный алгоритм PageRank для сортировки результатов поиска по популярности. Описанный стэнфордскими аспирантами Брином и Пейджем в научной статье, он сводится к очень простой идее:
Описанный стэнфордскими аспирантами Брином и Пейджем в научной статье, он сводится к очень простой идее:
—где — множество входящих ссылок на страницу , — число исходящих ссылок на этой странице, а — число страниц в интернете. Таким образом выражает вероятность оказаться на странице при случайном брожении по интернету, когда с вероятностью мы переходим на следующую страницу по случайно выбранной исходящей ссылке, и с вероятностью — закрываем текущую страницу и открываем случайно выбранную.
Разработав PageRank и основав Google, Брин и Пейдж бросили аспирантуру — дальнейшие математические изыскания им уже не были интересны. Однако вычисление PageRank ставит нетривиальную математическую задачу: у нас есть система из линейных уравнений с неизвестными. В 1998 исчислялся в миллионах, сегодня — в миллиардах. Как решать систему уравнений с десятком миллиардов неизвестных?
Все мы учили в школе алгоритм исключения неизвестных по одной: подставим выражение для во все остальные уравнения, получим систему из уравнений с неизвестными, и так далее. Этот метод решения системы уравнений прост как пробка, но у него есть пара проблем:
Этот метод решения системы уравнений прост как пробка, но у него есть пара проблем:
Во-первых, подстановка одного выражения в одно уравнение — это умножений рациональных чисел. Значит, полное исключение одной неизвестной — это умножений, а всё решение целиком — это умножений. Когда исчисляется в миллиардах, то последовательных умножений займут дольше, чем остаётся существовать нашей планете до того, как Солнце расширится и поглотит её. Дольше где-то в десять тысяч раз.
К счастью, на каждую страницу в интернете ведут совсем немного входящих ссылок — не миллиард и даже не миллион. На популярную статью в Википедии могут ссылаться десятки тысяч страниц, на эту статью на Хабре — хорошо если десятки. Иными словами, почти все коэффициенты в системе уравнений интернета — нули. Каждый ненулевой коэффициент подвергнется умножениям при подстановке содержащего его уравнения во все остальные. Если обозначить число ненулевых коэффициентов как , то всё решение потребует умножений; в худшем случае , но в случае интернета , и для всех умножений хватит десятка-другого тысяч лет компьютерного времени. Если построить распределённую систему из миллиона-другого серверов, как у Google, то система уравнений интернета решится за неделю. До распространения криптовалют можно было с уверенностью сказать, что большая часть вычислительных ресурсов планеты идёт на решение систем уравнений.
Если построить распределённую систему из миллиона-другого серверов, как у Google, то система уравнений интернета решится за неделю. До распространения криптовалют можно было с уверенностью сказать, что большая часть вычислительных ресурсов планеты идёт на решение систем уравнений.
Во-вторых, решение последнего уравнения будет результатом цепочки из умножений и сложений рациональных чисел. Нам либо потребуется битов для точного представления этого результата (и каждого из промежуточных), либо результат каждой операции придётся округлять до значащих битов. Накапливающиеся так ошибки округления способны исказить решение системы уравнений до неузнаваемости. Google может довольствоваться неточными значениями PageRank, но математикам нужны хоть какие-то гарантии точности — например, что в найденных значениях неизвестных будет по стольку же верных битов, как в коэффициентах системы.
Из школьного метода решения системы уравнений большего не выжать. Первокурсников учат более продвинутому матричному методу: систему PageRank можно записать в виде
или в ещё более общем виде: , и тогда вектор неизвестных выражается как . Иными словами, решение системы уравнений сводится к обращению матрицы коэффициентов и умножению обратной матрицы на вектор свободных членов.
Иными словами, решение системы уравнений сводится к обращению матрицы коэффициентов и умножению обратной матрицы на вектор свободных членов.
Сам по себе матричный метод не даёт по сравнению со школьным ни большей скорости, ни большей точности: для обращения матриц тем способом, которому учат студентов, требуются всё те же умножений коэффициентов. За рамками вузовской программы, однако, существуют более эффективные методы: с 2005 известен вероятностный, а с 2019 — детерминированный алгоритм точного решения системы уравнений за перемножений матриц , и открытым остаётся вопрос об оптимальном алгоритме перемножения матриц. Лобовой способ («строка на столбец») требует умножений; алгоритм Штрассена (1969) —; алгоритм Копперсмита—Винограда (1987) —; его усовершенствования (последнее в 2020) — до . Поскольку для любого , то множитель не влияет на итоговую асимптотическую сложность решения системы уравнений; она получается равной асимптотической сложности умножения матриц. Само по себе умножение матриц — настолько часто встречающаяся практическая задача, что поиск для неё оптимального алгоритма интересовал всех и безотносительно решения систем уравнений: например, усовершенствование в 2020 позволило уменьшить степень асимптотической сложности меньше чем на 0.00001, и всё равно считается важным достижением. Равенство сложности решения системы уравнений, т.е. обращения матрицы, со сложностью умножения матриц — принималось как данность: оптимизация решения одной из этих задач казалась равносильной оптимизации решения второй.
Само по себе умножение матриц — настолько часто встречающаяся практическая задача, что поиск для неё оптимального алгоритма интересовал всех и безотносительно решения систем уравнений: например, усовершенствование в 2020 позволило уменьшить степень асимптотической сложности меньше чем на 0.00001, и всё равно считается важным достижением. Равенство сложности решения системы уравнений, т.е. обращения матрицы, со сложностью умножения матриц — принималось как данность: оптимизация решения одной из этих задач казалась равносильной оптимизации решения второй.
Для практических целей алгоритм Копперсмита—Винограда, и тем более его усовершенствованные варианты, неприменимы: такие алгоритмы прозвали «галактическими», потому что вся Земля слишком мала для хранения матриц таких размеров, на которых эти алгоритмы дадут выигрыш в скорости по сравнению с более простыми. На практике самым важным оказывается частный случай, когда перемножаемые или обращаемые матрицы разрежены — почти все их элементы равны нулю, как и в матрице PageRank. Алгоритм умножения разреженных матриц, опубликованный в 2005, требует операций, и обгоняет Копперсмита—Винограда при ; а вот для обращения разреженных матриц не было известно более эффективных алгоритмов, чем для произвольных. Отчасти это связано с тем, что матрица, обратная разреженной, сама не будет разреженной, и на практике её будет просто негде сохранить.
Алгоритм умножения разреженных матриц, опубликованный в 2005, требует операций, и обгоняет Копперсмита—Винограда при ; а вот для обращения разреженных матриц не было известно более эффективных алгоритмов, чем для произвольных. Отчасти это связано с тем, что матрица, обратная разреженной, сама не будет разреженной, и на практике её будет просто негде сохранить.
Недавно на Хабре была опубликована заметка (с байками про рога и копыта, но без объяснения технической стороны вопроса) о том, что оба названных «психологических барьера» сломлены Сантошем Вемпалой и Ричардом Пенгом — парой математиков из Технологического института Джорджии, чья работа на ACM-SIAM Symposium on Discrete Algorithms в январе 2021 была признана лучшей из 637 поданных. Для системы уравнений с их алгоритм находит точное решение за операций, опережая степень асимптотической сложности умножения матриц на 0.04. Как мы помним, «школьный» метод исключения неизвестных по одной при условии приходит к ответу за операций, но не гарантирует точность найденных значений неизвестных. В основе нового алгоритма — вероятностный подход: значения неизвестных «угадываются», оценивается величина ошибки, и «угадывание» повторяется более прицельно. Таким образом, оценка сложности в относится к «наиболее вероятным» случаям, а не к худшим. Другое новшество в алгоритме — то, что на каждой итерации оцениваются сразу несколько случайных «догадок», что позволяет сократить общее число итераций и тем самым сдержать рост размера точных результатов.
В основе нового алгоритма — вероятностный подход: значения неизвестных «угадываются», оценивается величина ошибки, и «угадывание» повторяется более прицельно. Таким образом, оценка сложности в относится к «наиболее вероятным» случаям, а не к худшим. Другое новшество в алгоритме — то, что на каждой итерации оцениваются сразу несколько случайных «догадок», что позволяет сократить общее число итераций и тем самым сдержать рост размера точных результатов.
Нужно понимать, что алгоритм Вемпалы и Пенга на одном из этапов пользуется алгоритмом Копперсмита—Винограда для умножения матриц — и поэтому новый алгоритм ещё более «галактический». Важность алгоритма Вемпалы и Пенга совсем не в практической применимости, а в доказательстве того, что сложность решения систем уравнений не ограничена сложностью умножения матриц, а значит, новые эффективные алгоритмы для решения разреженных систем уравнений стоит искать в других направлениях — и они гарантированно найдутся. Но ни новый алгоритм, ни другие математические достижения последнего полувека никак не повлияли на практически применимые способы решения систем уравнений: Google и все остальные так и продолжат пользоваться простым, быстрым и неточным итеративным способом.
Но ни новый алгоритм, ни другие математические достижения последнего полувека никак не повлияли на практически применимые способы решения систем уравнений: Google и все остальные так и продолжат пользоваться простым, быстрым и неточным итеративным способом.
Наши серверы можно использовать для любых вычислений.
Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.Free xml sitemap generator | |||||||
Решение уравнений методом обратной матрицы
Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.
Суть метода
Пусть задана система линейных уравнений с неизвестными:
Эту систему можно записать в виде матричного уравнения ,
где – матрица системы,
– столбец неизвестных,
– столбец свободных коэффициентов.
Из полученного матричного уравнения необходимо выразить . Для этого умножим обе части матричного уравнения слева на , получим:
Так как , то или .
Далее находится обратная матрица и умножается на столбец свободных членов .
ЗАМЕЧАНИЕ
Обратная матрица к матрице существует только при условии, что . Поэтому при решении системы линейных уравнений методом обратной матрицы в первую очередь вычисляется . Если , то система имеет единственное решение, которое можно найти методом обратной матрицы, если же , то методом обратной матрицы решить эту систему нельзя.
Поэтому при решении системы линейных уравнений методом обратной матрицы в первую очередь вычисляется . Если , то система имеет единственное решение, которое можно найти методом обратной матрицы, если же , то методом обратной матрицы решить эту систему нельзя.
Пример решения методом обратной матрицы
ПРИМЕР 1
| Задание | Решить систему линейных уравнений методом обратной матрицы
|
| Решение | Данная система уравнений может быть записана матричным уравнением
где , , .
Выразив из этого уравнения , получим
Найдем определитель матрицы :
Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы.
Найдем обратную матрицу с помощью союзной матрицы. Вычислим алгебраические дополнения к соответствующим элементам матрицы :
Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы :
Далее запишем обратную матрицу согласно формуле .
Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы:
|
| Ответ |
Читайте также:
Умножение матрицы на вектор
Ранг матрицы
Вычитание матриц
Перемножение матриц
Элементарные преобразования матриц
Операции над матрицами и их свойства
1. Определители, матрицы, системы линейных уравнений. Линейная алгебра и Аналитическая геометрия
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
1.1.2. Определители второго порядка
1.1.3. Подматрица, минор, алгебраическое дополнение
1.1.4. Определители третьего порядка
1.1.5. Свойства определителей
1.
1.6. Определители порядка n
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
1.2.2. Формулы Крамера
1.3. Матрицы. Операции над матрицами
1.3.1. Умножение матрицы на число
1.3.2. Сложение матриц
1.3.3. Произведение матриц
1.3.4. Транспонирование матриц
1.3.5. Понятие обратной матрицы
1.3.6. Нахождение обратной матрицы методом Крамера
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
1.3.8. Элементарные преобразования матриц
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
1.
4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
1.4.2. Метод Гаусса
1.5. Исследование систем линейных уравнений
1.5.1. Теоремы о ранге матриц
1.5.2. Исследование систем линейных уравнений
1.5.3. Теорема Кронекера-Капелли
1.5.4. Однородные системы линейных уравнений
1.5.5. Свойства решений линейной однородной системы уравнений
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.
Пример:
A= или A=
Общее обозначение:
A= или A=, где — элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца:
Если M=N, то матрица называется квадратной. В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:
В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:
. . .
.
. . главная
. . .
побочная
. .
. .
Пример:
A = главную диагональ образуют эл-ты:
, а побочную
1.1.2. Определители второго порядка
Пусть дана матрица второго порядка
A= .
Определителем второго порядка называется число, вычисляемое по правилу:
Определитель второго порядка равен произведению элементов Главной диагонали минус произведение элементов Побочной диагонали.
=
1*(-4)-6 = -10
1.1.3. Подматрица, минор, алгебраическое дополнение
Пусть дана какая-либо матрица (например, порядка 3):
А=
Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.
Например, если вычеркнуть первую строку и второй столбец, то получим подматрицу данной матрицы:
Минором элемента определителя называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.
Алгебраическим дополнением элемента называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.
Обозначение: =
Если i+j — четное число , то знак алгебраического дополнения и минора одинаковы, если нечетное , то их знаки противоположны.
Символически покажем положительные и отрицательные места в определителе:
или
1.1.4. Определители третьего порядка
Определителем третьего порядка называется число, вычисляемое по правилу:
= =
Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.
Заменим алгебраические дополнения на миноры:
=
= — +
Вычисляя миноры, получим:
=
1.1.5. Свойства определителей
Свойство 1. При замене строк на столбцы определитель не меняется.
=
(такая операция называется транспонированием).
Следствие: строки и столбцы равноправны, т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.
Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.
= —
Следствие: любую строку (столбец) можно поставить первой (первым)
Свойство 3. Определитель с двумя равными строками равен нулю.
= 0
Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.
Следствие: Постоянный множитель можно внести в какую-нибудь строку
Свойство 5. Если элементы какой–либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей.
Свойство 6. Определитель не меняется, если любую строку умножить на любое число и прибавить к любой другой строке.
Случаи, когда определитель равен нулю:
- Все элементы какой-либо строки равны нулю
- Две строки одинаковы
- Элементы двух строк пропорциональны
1.1.6. Определители порядка n
Вычисление определителей порядка n.
Для вычисления порядка n используется метод разложения по cтроке.
Алгебраическое дополнение получается вычеркиванием i-строки и j-столбца. Этот процесс мы будем продолжать до тех пор пока не получим определители порядка 2 или 3
Формулу (1) используют как правило при i=1
Пример:
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
Система линейных уравнений порядка n имеет вид:
При этом числа — называются коэффициентами
при неизвестных
— свободные члены
Матрица называется матрицей системы
Числа — решение системы, если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.
Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.
Если система линейных уравнений не имеет решений, то система называется несовместной.
1.2.2. Формулы Крамера
Рассмотрим систему уравнений (*). И пусть А — матрица системы
Если i – столбец заменим свободными членами, то соответствующую матрицу обозначим
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, которое находится по формуле:
1.3. Матрицы. Операции над матрицами
Две матрицы A и B называются равными, если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся:
1.3.1. Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:
1.
 3.2. Сложение матриц
3.2. Сложение матриц
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули, то такая матрица называется нулевой.
1.3.3. Произведение матриц
Пример:
.==
.=
.
Если для матриц А и В выполняется равенство А*В=В*А, то матрицы называются перестановочными.
Если для матриц А, В, С имеет смысл операция произведения, то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
1.3.4. Транспонирование матриц
Рассмотрим матрицы
AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
называют главной диагональю
Очевидно:
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
1.3.5. Понятие обратной матрицы
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица, у которой на главной диагонали стоят единицы, а
вне главной диагонали — нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А, если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную, то ее определитель отличен от нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том, что определитель произведения равен произведению определителей.
что и требовалось доказать.
1.3.6. Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
*=
Отсюда, в частности, следует:
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля, то эту систему можно решить методом Крамера причем решение (3) — единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
Первоначально находим определитель матрицы А и если он равен нулю, то обратной матрицы не существует.
Если определитель отличен от нуля, то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
1.3.8. Элементарные преобразования матриц
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
-
- умножение любой строки матрицы на число, отличное от нуля;
пример
=
- к любой строке можно добавить любую другую строку, умноженную на любое число;
- перестановка двух строк.
Матрицы, полученные с помощью элементарных преобразований называются эквивалентными
А~
В, В~
С, А~
С
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
Рассмотрим квадратную матрицу А и предположим, что
тогда используя элементарные преобразования эту матрицу можно привести к единичной матрице. Таким образом единичная матрица эквивалентна любой невырожденной матрице того же порядка.
Теорема
Если элементарные преобразования:
переводят невырожденную матрицу А в единичную, то те же самые преобразования, взятые в том же порядке, переводят единичную матрицу в обратную для A.
Доказательство:
отсюда
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
Система уравнений вида:
называется линейной системой из n уравнений с m неизвестными.
(aij) коэффициенты при неизвестных x1, x2,…,xm
b1,b2,…,bn — свободные члены
Матрица А системы (*) состоит из коэффициентов aij, размера n*m .
Если неизвестные и свободные члены представим в виде:
,
то систему уравнений (*) мы можем переписать в виде: (3)
Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*). Следует особо обратить внимание на то, что m может быть неравно n. Если m=n и матрица А является невырожденной , то из соотношения (3) вытекает: (4)
Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной.
В противном случае система называется несовместной.
Решить систему — означает найти все её решения.
1.4.2. Метод Гаусса
Рассмотрим систему (*):
Припишем к матрице А
матрицу-столбец В
Припишем к матрице А матрицу-столбец
В:
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной. Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: то, система решений не имеет.
Если треугольная матрица получается вида: , то система имеет бесконечно много решений. При этом какие-то неизвестные
объявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: , то в этом случае система имеет единственное решение.
Пример:
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:
~~
В итоге получим систему:
Откуда получим значения неизвестных: y = -7,25 x = 2,875
Пример:
~~~
1.
 5. Исследование систем линейных уравнений
5. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений.
Задача: определить:
- Совместна или нет данная система
- Если совместна, то сколько имеет решений а) единственное б) бесконечное множество
Понятие ранга матрицы
А=() i= j=
Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.
Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.
Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.
М==0 М==-20 М==0 М==3 Ранг равен 3.
Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг1.
Если матрица не нулевая то её ранг1.
С другой стороны если матрица имеет порядок MxN, то r(A)min(M,N).
1.5.1. Теоремы о ранге матриц
Теорема 1
Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).
Доказательство
Для доказательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.
1) А~B B получена умножением строки(столбца) на отличное от нуля число.
А= B=
Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В=А (по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
2) A~B B получена прибавлением строк
А= В=
Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В0.
Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В0.
Если выбранные миноры содержат i-ю и j-ю строки, тогда
М(А)=А=
В=
минор В получен из А путем прибавления строки.
Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.
Теорема 2
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Вычисление ранга матрицы
Используя утверждение доказанной теоремы, легко вычислить ранг матрицы
- с помощью элементарных преобразований матрица приводится к ступенчатому виду.
- считается число ненулевых строк ступенчатой матрицы
Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.
ПРИМЕР
~ ~
Ответ: r(A)=2
1.5.2. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений
(*)
А=()
H=
1.5.3. Теорема Кронекера-Капелли
Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)
Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.
Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных объявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.
1.5.4. Однородные системы линейных уравнений
Если в системе (*) все свободные члены равны нулю, то такая система является однородной.
Однородные системы всегда совместны т.к. ====0 всегда является решением. Такое решение называется тривиальным.
1) то
2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений
1.5.5. Свойства решений линейной однородной системы уравнений
1) Если является решением системы, то также является решением.
Доказательство.
2) Если является решением системы
также является решением той же самой системы, то и
также является решением системы
Доказательство.
+
откуда получим
3) Если и
два различных решения системы, то их линейная комбинация, равная
также является решением системы.
Доказательство.
+
откуда получим
Каждое из решений системы можно записать в виде строки матрицы, тогда на основании свойств можно утверждать, что матрицы есть решения, то также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
Пример.
~~
{ {
{{
Представление систем линейных уравнений с помощью матриц
А
система линейных уравнений
могут быть представлены в матричной форме с использованием матрицы коэффициентов, переменной матрицы и постоянной матрицы.
Рассмотрим систему,
2
Икс
+
3
y
знак равно
8
5
Икс
—
y
знак равно
—
2
.
Матрица коэффициентов может быть сформирована путем выравнивания коэффициентов переменных каждого уравнения в строке. Убедитесь, что каждое уравнение написано в
стандартная форма
с постоянным членом справа.
Тогда матрица коэффициентов для указанной выше системы равна
[
2
3
5
—
1
]
.
Переменные, которые у нас есть,
Икс
а также
y
.Таким образом, мы можем записать матрицу переменных как
[
Икс
y
]
.
В правой части равенства находятся постоянные члены уравнений:
8
а также
—
2
. Два числа в этом порядке соответствуют первому и второму уравнениям и, следовательно, занимают места в первой и второй строках в постоянной матрице. Итак, матрица принимает вид
[
8
—
2
]
.
Теперь систему можно представить в виде
[
2
3
5
—
1
]
[
Икс
y
]
знак равно
[
8
—
2
]
.
С использованием
умножение матриц
вы можете видеть, что матричное представление эквивалентно системе уравнений.
[
2
3
5
—
1
]
[
Икс
y
]
знак равно
[
2
(
Икс
)
+
3
(
y
)
5
(
Икс
)
+
(
—
1
)
y
]
знак равно
[
2
Икс
+
3
y
5
Икс
—
y
]
Это,
[
2
Икс
+
3
y
5
Икс
—
y
]
знак равно
[
8
—
2
]
.
Приравнивая соответствующие элементы двух матриц, получаем:
2
Икс
+
3
y
знак равно
8
5
Икс
—
y
знак равно
—
2
Теперь давайте разберемся, что означает это представление.
Если рассматривать это как функцию вектора
[
Икс
y
]
, его можно определить как
ж
(
[
Икс
y
]
)
знак равно
[
2
3
5
—
1
]
[
Икс
y
]
Затем, решая систему, мы находим вектор
[
Икс
y
]
для которого
ж
(
[
Икс
y
]
)
знак равно
[
8
—
2
]
.
Это представление может упростить вычисления, потому что, если мы сможем найти обратную матрицу коэффициентов, входной вектор
[
Икс
y
]
можно вычислить, умножив обе части на обратную матрицу.
Аналогичным образом для системы трех уравнений с тремя переменными
а
1
Икс
+
б
1
y
+
c
1
z
знак равно
d
1
а
2
Икс
+
б
2
y
+
c
2
z
знак равно
d
2
а
3
Икс
+
б
3
y
+
c
3
z
знак равно
d
3
Матричное представление будет
[
а
1
б
1
c
1
а
2
б
2
c
2
а
3
б
3
c
3
]
[
Икс
y
z
]
знак равно
[
d
1
d
2
d
3
]
.
Мы можем обобщить результат на
п
переменные.
Обращение матрицы
Пожалуйста, сначала прочтите наше Введение в матрицы.
Что такое обратная матрица?
Это обратное число :
Взаимное значение числа
, инверсия матрицы — это , та же идея , но мы пишем это A -1
Почему не 1 / A ? Потому что мы не делим по матрице! Да и вообще 1 / 8 тоже можно написать 8 -1
И есть другие сходства:
Когда мы умножаем число на его , обратное , мы получаем 1
Когда мы умножаем матрицу на ее обратную , мы получаем Identity Matrix (что похоже на «1» для матриц):
То же, что и обратное:
Матрица идентификации
Мы только что упомянули «Матрицу идентичности».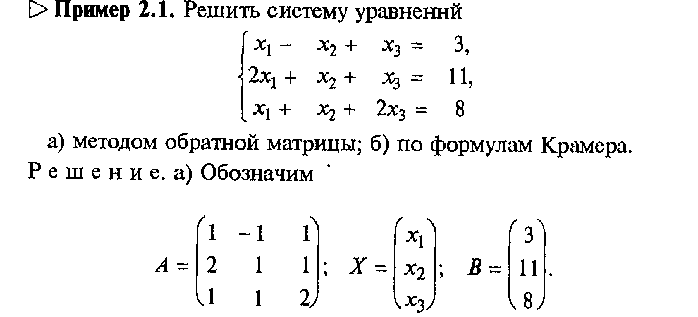 Это матричный эквивалент числа «1»:
Это матричный эквивалент числа «1»:
.
Матрица идентификации 3×3
- Это «квадрат» (в нем столько же строк, что и столбцов),
- Он имеет 1 с по диагонали и 0 с по всей остальной части.
- Его символ — заглавная буква I .
Матрица идентичности может иметь размер 2 × 2 или 3 × 3, 4 × 4 и т. Д.
Определение
Вот определение:
Аргумент A равен A -1 только тогда, когда:
A × A -1 = A -1 × A = I
Иногда обратного нет вообще.
Матрица 2×2
Хорошо, как вычислить обратное?
Ну, для матрицы 2×2 обратное значение:
Другими словами: поменять местами позиции a и d, поставить негативов перед b и c, а разделить все на определитель (ad-bc).
Давайте попробуем пример:
Как мы узнаем, что это правильный ответ?
Помните, что это должно быть правдой, что: A × A -1 = I
Итак, давайте посмотрим, что произойдет, если мы умножим матрицу на ее обратную:
И, привет !, мы получили Матрицу идентичности! Так что это должно быть правильно.
Должно быть также , что: A -1 × A = I
Почему бы вам не попробовать их умножить? Посмотрите, получите ли вы также Identity Matrix:
Зачем нужен инверс?
Потому что с матрицами мы не делим ! Серьезно, нет понятия деления матрицей.
Но мы можем умножить на обратное , что даст то же самое.
Представьте, что мы не можем делить на числа…
… и кто-то спрашивает «Как мне поделиться 10 яблоками с 2 людьми?»
Но мы можем взять , обратное из 2 (что составляет 0,5), поэтому мы ответим:
10 × 0,5 = 5
Они получают по 5 яблок.
То же самое можно сделать и с матрицами:
Допустим, мы хотим найти матрицу X, и мы знаем матрицы A и B:
XA = B
Было бы хорошо разделить обе стороны на A (чтобы получить X = B / A), но помните, что мы не можем разделить .
Но что, если мы умножим обе стороны на A -1 ?
XAA -1 = BA -1
И мы знаем, что AA -1 = I, поэтому:
XI = BA -1
Мы можем удалить I (по той же причине мы можем удалить «1» из 1x = ab для чисел):
X = BA -1
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
В этом примере мы очень внимательно следили за правильностью умножения, потому что в случае с матрицами порядок умножения имеет значение.AB почти никогда не совпадает с BA.
Пример из реальной жизни: автобус и поезд
Группа поехала на автобусе по цене 3 доллара за ребенка и 3,20 доллара за взрослого на общую сумму 118,40 доллара.
Они сели обратно на поезд по цене 3,50 доллара за ребенка и 3,60 доллара за взрослого, итого 135,20 доллара.
Сколько детей и сколько взрослых?
Во-первых, давайте настроим матрицы (будьте осторожны, чтобы строки и столбцы были правильными!):
Это как в примере выше:
XA = B
Итак, чтобы решить это, нам нужна обратная величина к «A»:
Теперь у нас есть обратное, которое мы можем решить с помощью:
X = BA -1
Было 16 детей и 22 взрослых!
Ответ кажется почти волшебным. Но он основан на хорошей математике.
Но он основан на хорошей математике.
Подобные вычисления (но с использованием гораздо больших матриц) помогают инженерам проектировать здания, используются в видеоиграх и компьютерной анимации, чтобы вещи выглядели трехмерными, и во многих других местах.
Это также способ решения систем линейных уравнений.
Расчеты производятся компьютером, но люди должны понимать формулы.
Порядок важен
Скажем, в данном случае мы пытаемся найти «X»:
AX = B
Это отличается от приведенного выше примера! X теперь после A.
Для матриц порядок умножения обычно меняет ответ. Не предполагайте, что AB = BA, это почти никогда не верно.
Так как же решить эту проблему? Используя тот же метод, но впереди поставьте A -1 :
.
A -1 AX = A -1 B
И мы знаем, что A -1 A = I, поэтому:
IX = A -1 B
Мы можем удалить I:
X = A -1 B
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
Почему бы нам не попробовать наш пример с автобусом и поездом, но с данными, настроенными таким образом.
Это можно сделать таким образом, но мы должны быть осторожны при настройке.
Вот как это выглядит как AX = B:
Выглядит так аккуратно! Я думаю, что предпочитаю это так.
Также обратите внимание, как строки и столбцы меняются местами в
(«транспонировано»)
по сравнению с предыдущим примером.
Чтобы решить эту проблему, нам понадобится обратное к «А»:
Это похоже на обратное, которое мы получили раньше, но
транспонировано (строки и столбцы меняются местами).
Теперь мы можем решить, используя:
X = A -1 B
Тот же ответ: 16 детей и 22 взрослых.
Итак, матрицы — это мощная вещь, но их нужно правильно настраивать!
Обратное может не существовать
Во-первых, чтобы иметь инверсию, матрица должна быть «квадратной» (то же количество строк и столбцов).
Но также определитель не может быть нулевым (или мы закончим делением на ноль). Как насчет этого:
24-24? Это равно 0, а 1/0 не определено .
Мы не можем идти дальше!
У этой Матрицы нет Инверсии.
Такая матрица называется «сингулярной», что происходит только тогда, когда определитель равен нулю.
И это имеет смысл … посмотрите на числа: вторая строка просто вдвое больше первой строки, и не добавляет никакой новой информации .
И определитель сообщает нам об этом факте.
(Представьте, что в нашем примере с автобусом и поездом цены на поезд были ровно на 50% выше, чем на автобусе: так что теперь мы не можем найти никаких различий между взрослыми и детьми.Должно быть что-то, что отличало бы их.)
Матрицы большего размера
Обратное к 2×2 — это easy … по сравнению с более крупными матрицами (такими как 3×3, 4×4 и т. Д.).
Д.).
Для этих больших матриц есть три основных метода вычисления обратного:
Заключение
- Аргумент A равен A -1 , только если A × A -1 = A -1 × A = I
- Чтобы найти обратную матрицу 2×2: поменять местами позиции a и d, поставить негативов перед b и c, а разделить все на определитель (ad-bc).
- Иногда обратного нет вообще
Использование матриц для решения систем уравнений
Матричные уравнения
Матрицы
могут использоваться для компактного написания и работы с системами множественных линейных уравнений.
Цели обучения
Определить, как матрицы могут представлять систему уравнений
Основные выводы
Ключевые моменты
- Если [latex] A [/ latex] является матрицей [latex] m \ times n [/ latex], а [latex] x [/ latex] обозначает вектор-столбец (т.
 е.е. [latex] n \ times 1 [/ latex] матрица) [latex] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], а [latex] b [/ latex] — это [ latex] m \ times 1 [/ latex] вектор-столбец, тогда матричное уравнение будет: [latex] Ax = b [/ latex].
е.е. [latex] n \ times 1 [/ latex] матрица) [latex] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], а [latex] b [/ latex] — это [ latex] m \ times 1 [/ latex] вектор-столбец, тогда матричное уравнение будет: [latex] Ax = b [/ latex].
Ключевые термины
- матрица : прямоугольное расположение чисел или членов, имеющее различное применение, например, преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
Матрицы можно использовать для компактного написания и работы с системами уравнений.Как мы узнали в предыдущих разделах, матрицами можно манипулировать так же, как и нормальным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений. Полезно понять, как организовать матрицы для решения этих систем.
Написание системы уравнений с матрицами
Можно решить эту систему, используя метод исключения или замены, но также можно сделать это с помощью матричной операции. Прежде чем приступить к настройке матриц, важно сделать следующее:
Прежде чем приступить к настройке матриц, важно сделать следующее:
- Убедитесь, что все уравнения написаны одинаково, то есть переменные должны быть в одном порядке.
- Убедитесь, что одна часть уравнения — это только переменные и их коэффициенты, а другая часть — просто константы.
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — матрица, представляющая константы. Используя матричное умножение, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:
[латекс] \ displaystyle A \ cdot X = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть [latex] A [/ latex] будет матрицей коэффициентов, пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex ] — постоянная матрица.
Учитывая систему:
[латекс] \ displaystyle \ begin {align} x + 8y & = 7 \\ 2x-8y & = — 3 \ end {align} [/ latex]
Матрица коэффициентов:
[латекс] A = \ begin {bmatrix} 1 & 8 \\ 2 & -8 \ end {bmatrix} [/ latex]
Матрица переменных:
[латекс] \ displaystyle X = \ begin {bmatrix} x \\ y \ end {bmatrix} [/ latex]
Постоянная матрица:
[латекс] \ displaystyle B = \ begin {bmatrix} 7 \\ -3 \ end {bmatrix} [/ latex]
Таким образом, чтобы решить систему [latex] AX = B [/ latex], для [latex] X [/ latex] умножьте обе стороны на обратную величину [latex] A [/ latex], и мы получим решение:
[латекс] \ Displaystyle X = (A ^ {- 1}) B [/ латекс]
Если существует обратный [латекс] \ left (A ^ {- 1} \ right) [/ latex], эта формула решит систему.
Если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Матрицы и операции со строками
Две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.
Цели обучения
Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы
Основные выводы
Ключевые моменты
- Элементарная операция со строкой — это любое из следующих действий: переключение строк (перестановка двух строк матрицы), умножение строк (умножение строки матрицы на ненулевую константу) или сложение строк (добавление к одной строке матрицы до некоторого числа, кратного другой строке).
- Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы.

Ключевые термины
- пространство строки : набор всех возможных линейных комбинаций его векторов-строк.
- эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой последовательностью элементарных операций со строкой.
Операции с элементарной строкой (ERO)
В линейной алгебре две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.В качестве альтернативы, две матрицы [latex] m \ times n [/ latex] эквивалентны строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство строки матрицы — это набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы. Две матрицы одинакового размера эквивалентны строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство. Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Операция элементарной строки — это любой из следующих трех ходов:
- Переключение строк (перестановка): поменять местами две строки матрицы.
- Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
- Сложение строк (сводная): добавить к одной строке матрицы несколько значений, кратных другой строке.
Создание эквивалентных матриц с использованием элементарных операций со строками
Поскольку матрица по существу является коэффициентами и константами линейной системы, три операции со строками сохраняют матрицу.Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения, умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных обратных величин, так что переменная сокращается. Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Пример 1: Покажите, что эти две матрицы эквивалентны строкам:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \ end {pmatrix} \ quad B = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ латекс]
Начните с [latex] A [/ latex], добавьте вторую строку к первой:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \ end {pmatrix} [/ latex]
Затем умножьте вторую строку на 3 и вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \ end {pmatrix} [/ latex]
Наконец, вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ latex]
Вы можете видеть, что [latex] A = B [/ latex], что мы достигли с помощью серии элементарных операций со строками.
Сокращение строк: решение системы линейных уравнений
В редукторе рядов, линейная система:
[латекс] \ displaystyle x + 3y-2z = 5 \\ 3x + 5y + 6z = 7 \ 2x + 4y + 3z = 8 [/ latex]
Представлен в виде расширенной матрицы:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {pmatrix} [/ latex]
Затем эта матрица модифицируется с использованием операций с элементарными строками, пока она не достигнет уменьшенной формы эшелона строк.
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько специальных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление может быть выполнено вручную (с использованием трех типов ERO) или на калькуляторе с использованием матричной функции «rref» (сокращенная форма эшелона строк).
Окончательная матрица представлена в виде уменьшенного ряда строк и представляет систему [латекс] x = -15 [/ latex], [latex] y = 8 [/ latex] [latex] z = 2 [/ latex].
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 0 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {pmatrix} [/ latex]
Упрощение матриц с помощью операций со строками
Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелона строк.
Цели обучения
Использование элементарных операций со строками, чтобы представить матрицу в упрощенной форме
Основные выводы
Ключевые моменты
- Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк формы эшелона строк такое же, как и у исходной матрицы.
- Существует три типа операций с элементарными строками: меняют местами две строки, умножают строку на ненулевой скаляр и добавляют к одной строке скалярное значение, кратное другой.
- На практике обычно не рассматривают системы в терминах уравнений, а вместо этого используют расширенную матрицу (которая также подходит для компьютерных манипуляций).
Ключевые термины
- расширенная матрица : Матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же операций с элементарной строкой для каждой из данных матриц.
С помощью конечной последовательности элементарных операций со строками, называемых исключением по Гауссу, любую матрицу можно преобразовать в форму эшелона строк. Это преобразование необходимо для решения системы линейных уравнений.
Прежде чем углубляться в детали, следует упомянуть несколько ключевых терминов:
- Расширенная матрица : расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же элементарных операций со строками для каждой из данных матриц.
- Форма верхнего треугольника : Квадратная матрица называется верхней треугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это нижняя или верхняя треугольная матрица. Матрица, имеющая одновременно верхний и нижний треугольники, является диагональной матрицей.
- Элементарные операции со строками : Поменять местами строки, добавить строки или умножить строки.
Исключение по Гауссу
- Напишите расширенную матрицу для линейных уравнений.
- Используйте элементарные операции со строками в расширенной матрице [latex] [A | b] [/ latex], чтобы преобразовать [latex] A [/ latex] в форму верхнего треугольника. Если на диагонали находится ноль, переключайте строки, пока на его месте не окажется ненулевое значение.
- Используйте обратную замену, чтобы найти решение.
Пример 1: Решите систему методом исключения Гаусса:
[латекс] \ displaystyle 2x + y-z = 8 \\ -3x-y + 2z = -11 \ -2x + y + 2z = -3 [/ latex]
Запишите расширенную матрицу:
[латекс] \ left [\ begin {array} {rrr | r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \ end {array} \ right] [/ latex]
Используйте элементарные операции со строками, чтобы уменьшить матрицу до уменьшенной формы эшелона строк:
[латекс] \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \ end {array} \ right ] [/ латекс]
Используя элементарные операции со строками для получения сокращенной формы эшелона строк (‘rref’ в калькуляторе), решение системы отображается в последнем столбце: [latex] x = 2, y = 3, z = -1 [/ latex] . {- 1} = \ frac {1} {3 \ cdot -1-1 \ cdot 2} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} = $$
$$ = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} $$
Следующий шаг — умножить обе части матричного уравнения на обратную матрицу:
$$ — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 3 & 1 \\ 2 & -1 \ end {bmatrix } \ cdot \ begin {bmatrix} x \\ y \\ \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 5 \\ 0 \ end {bmatrix} $$
$$ — \ frac {1} {5} \ begin {bmatrix} -5 & 0 \\ 0 & -5 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -5 \\ -10 \ end {bmatrix} $$
$$ \ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} 1 \\ 2 \ end { bmatrix} $$
Наше решение — (1,2), самый простой способ проверить, правы ли мы, — это подставить наши значения в наши исходные уравнения.
Видеоурок
Пример выше в видеоформате.
Матричных уравнений
В этом разделе мы представляем очень краткий способ записи системы линейных уравнений: Ax = b. Здесь A — матрица, а x, b — векторы (обычно разного размера), поэтому сначала мы должны объяснить, как умножить матрицу на вектор.
Когда мы говорим «A — это матрица размера m × n», мы имеем в виду, что A имеет m строк и n столбцов.
Определение
Пусть A — матрица размера m × n со столбцами v1, v2 ,…, вн:
A = C ||| v1v2 ··· vn ||| D
Произведение из A с вектором x в Rn является линейной комбинацией
Ax = C ||| v1v2 ··· vn ||| DEIIGx1x2 … xnFJJH = x1v1 + x2v2 + ··· + xnvn.
Это вектор в Rm.
Чтобы Ax имел смысл, количество записей x должно быть таким же, как количество столбцов A: мы используем записи x как коэффициенты столбцов A в линейной комбинации. Результирующий вектор имеет то же количество записей, что и количество строк A, так как каждый столбец A имеет это количество записей.
Если A — матрица размера m × n (m строк, n столбцов), то Ax имеет смысл, когда x имеет n элементов. В продукте Ax есть m записей.
Свойства произведения матрица-вектор
Пусть A — матрица размера m × n, пусть u, v — векторы в Rn, и пусть c — скаляр. Тогда:
Определение
Матричное уравнение — это уравнение вида Ax = b, где A — матрица размера m × n, b — вектор в Rm, а x — вектор, коэффициенты которого x1, x2, …, xn неизвестны .
В этой книге мы изучим два дополнительных вопроса о матричном уравнении Ax = b:
- При конкретном выборе b, каковы все решения Ax = b?
- Каковы все варианты b, чтобы Ax = b было непротиворечивым?
Первый вопрос больше похож на вопросы, к которым вы, возможно, уже привыкли из своих предыдущих курсов алгебры; у вас много практики в решении таких уравнений, как x2−1 = 0 для x.Второй вопрос — это, возможно, новая концепция для вас. Теорема о рангах из раздела 2.9, который является кульминацией этой главы, говорит нам, что эти два вопроса тесно связаны.
Мы будем свободно перемещаться между четырьмя способами написания линейной системы снова и снова до конца книги.
Другой способ вычисления Ax
Приведенное выше определение является полезным способом определения произведения матрицы на вектор, когда дело доходит до понимания взаимосвязи между матричными уравнениями и векторными уравнениями.Здесь мы даем определение, которое лучше подходит для ручных вычислений.
Определение
Вектор-строка — это матрица с одной строкой. Произведение вектора-строки длины n и вектора (столбца) длины n равно
Aa1a2 ··· anBEIIGx1x2 … xnFJJH = a1x1 + a2x2 + ··· + тревога.
Это скаляр.
Рецепт: правило строки-столбца для умножения матрицы на вектор
Если A — матрица размера m × n со строками r1, r2, …, rm, а x — вектор в Rn, то
Ax = EIIG — r1 —— r2—…— rm — FJJHx = EIIGr1xr2x … rmxFJJH.
Пусть A — матрица со столбцами v1, v2, …, vn:
A = C ||| v1v2 ··· vn ||| D.
Затем
Ax = bhasisolution⇐⇒thereexistx1, x2, …, x означают такие, что AEIIGx1x2 … xnFJJH = b⇐⇒thereexistx1, x2, …, xnsuchthatx1v1 + x2v2 + ··· + xnvn = b⇐⇒visalinearcombination , vn⇐⇒бисинтэппаном столбцов А.
Интервалы и согласованность
Матричное уравнение Ax = b имеет решение тогда и только тогда, когда b находится в промежутке между столбцами A.
Это дает эквивалентность между алгебраическим оператором (Ax = b согласован) и геометрическим заявление (b находится в промежутке столбцов A).
Когда решения существуют всегда
Основываясь на этом примечании, у нас есть следующий критерий того, когда Ax = b согласуется для при каждом выборе b.
Теорема
Пусть A — матрица размера m × n (без дополнений). Следующие эквиваленты:
- Ax = b имеет решение для всех b в Rm.
- Пролет столбцов матрицы A равен Rm.
- У A есть точка поворота в каждом ряду.
Доказательство
Эквивалентность 1 и 2 устанавливается данным примечанием применительно к каждому b в Rm.
Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, это означает, что 2 и 3 также эквивалентны.) Если A имеет точку поворота в каждой строке, то его сокращенная форма эшелона строк выглядит следующим образом:
C10A0A01A0A0001AD,
и, следовательно, AAbB сводится к этому:
Нет b, который делает его непоследовательным, поэтому всегда есть решение. И наоборот, если A не имеет точки поворота в каждой строке, то его уменьшенная форма эшелона строки выглядит следующим образом:
C10A0A01A0A00000D,
, что может привести к возникновению противоречивой системы после увеличения на b:
Напомним, что эквивалент означает, что для любой данной матрицы A либо все условий приведенной выше теоремы истинны, либо все они ложны.
Будьте внимательны при чтении утверждения приведенной выше теоремы. Первые два условия очень похожи на эту заметку, но логически они сильно различаются из-за квантификатора « для всех b».
Матрицы и системы уравнений
6.1 — Матрицы и системы уравнений
Определение матрицы
- Прямоугольный массив действительных чисел
- м рядов по n столбцов
- Названо заглавными буквами
- Первый нижний индекс — строка, второй нижний индекс — столбец
Терминология
- Матрица с m строками и n столбцами называется матрицей порядка m x n .
- Квадратная матрица — это матрица с равным количеством строк и столбцов. Поскольку количество
строки и столбцы одинаковы, говорят, что он имеет порядок n . - Главной диагональю квадратной матрицы являются элементы от верхнего левого угла до нижнего правого угла.
матрица. - Матрица-строка — это матрица, содержащая только одну строку.
- Матрица столбцов — это матрица, имеющая только один столбец.
- Матрица только с одной строкой или одним столбцом называется вектором.
Преобразование систем линейных уравнений в
Матрицы
Каждое уравнение в системе превращается в строку. Каждая переменная в
система становится колонной. Переменные отбрасываются, а
коэффициенты помещаются в матрицу. Если правая часть включена,
это называется расширенной матрицей. Если правая сторона не указана, это
называется матрицей коэффициентов.
Система линейных уравнений …
х + у - г = 1 3х - 2у + г = 3 4x + y - 2z = 9
становится расширенной матрицей…
| х | y | z | rhs | ||
|---|---|---|---|---|---|
| 1 | 1 | –1 | 1 | ||
| 3 | -2 | 1 | 3 | ||
| 4 | 1 | -2 | 9 |
Элементарные операции со строками
Элементарные операции со строками — это операции, которые могут быть выполнены с матрицей, которая даст
эквивалентная строка матрица.Если матрица является расширенной матрицей, построенной из системы линейных
уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица.
При работе с системами линейных уравнений вы могли выполнять три операции.
что не повлияет на набор решений.
- Поменяйте местами два уравнения.
- Умножьте уравнение на ненулевую константу.
- Умножьте уравнение на ненулевую константу и добавьте его к другому уравнению, заменив это
уравнение.
Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится
строка. Итак, теперь есть три элементарные операции со строками, которые производят эквивалент строки
матрица.
- Замена двух рядов
- Умножить строку на ненулевую константу
- Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку.
Формы рядов-эшелонов и сокращенных рядов-эшелонов
Это эквивалентные строкам формы матрицы.Несложно решить систему линейных уравнений
когда матрицы находятся в одной из этих форм.
Форма рядного эшелона
Матрица находится в виде эшелона строк, когда выполняются следующие условия.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первым ненулевым элементом любой строки является единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
Примечания
- Первая строка в строке не обязательно должна быть непосредственно справа от первой строки
предыдущий ряд. - Матрица в виде эшелона строк будет иметь нули под ведущими.
- Метод исключения Гаусса переводит матрицу в форму строки-эшелон, а затем выполняется обратная подстановка.
требуется, чтобы завершить поиск решений системы. - Форма строки-эшелон матрицы не обязательно уникальна.
Форма ступенчатая уменьшенная
Матрица находится в сокращенной форме строки-эшелона, когда выполняются все условия формы строка-эшелон.
и все элементы выше и ниже, ведущие равны нулю.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первым ненулевым элементом любой строки является единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
- Все элементы выше и ниже ведущего равны нулю.
Примечания
- Первая строка в строке не обязательно должна быть непосредственно справа от первой строки
предыдущий ряд. - Матрица в виде эшелона строк будет иметь нули как над, так и под ведущими.
- Метод исключения Гаусса-Жордана переводит матрицу в сокращенную форму строки-эшелона.
- Для завершения поиска решений системы обратная подстановка не требуется.
- Приведенная строка-эшелонированная форма матрицы уникальна.
Исключение по Гауссу
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в эшелонированную форму строки
- Преобразуйте матрицу обратно в систему линейных уравнений
- Используйте обратную замену, чтобы получить все ответы
Гаусс-Джордан Ликвидация
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в сокращенную форму строки-эшелон
- Преобразуйте матрицу обратно в систему линейных уравнений
- Обратная замена не требуется
Поворотный
- Поворот — это процесс, который автоматизирует операции со строками, необходимые для помещения матрицы в
рядный эшелон или сокращенный рядный эшелон форма - В частности, при повороте элементы выше или ниже ведущей единицы превращаются в нули
Типы решений
Существует три типа решений, которые возможны при решении системы линейных уравнений.
Независимая
- Согласованный
- Уникальное решение
- Матрица с сокращенной строкой имеет такое же количество ненулевых строк, что и
переменные - Левая часть обычно представляет собой единичную матрицу, но не обязательно
- Для получения независимого решения должно быть как минимум столько же уравнений, сколько переменных.
| х | y | z | rhs | ||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 2 |
Когда вы конвертируете расширенную матрицу обратно в форму уравнения, вы получаете x = 3,
y = 1 и z = 2.
Зависимые
- Согласованный
- Множество решений
- Запишите ответ в параметрической форме
- Матрица с сокращенной строкой имеет больше переменных, чем ненулевых строк
- Не обязательно должен быть ряд нулей, но обычно он есть.
- Это также может произойти, когда уравнений меньше, чем переменных.
| х | y | z | rhs | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 0 |
Первое уравнение будет x + 3z = 4.Решение относительно x дает x = 4 — 3z.
Второе уравнение будет y — 2z = 3. Решение для
y дает y = 3 + 2z.
Столбец z не очищается (все нули, кроме
одно число), поэтому другие переменные будут определены через z. Следовательно,
z
будет параметром
t и решение …
x = 4 — 3t, y = 3 + 2t, z = t
Несоответствие
- Нет решения
- Матрица с сокращенной строкой имеет строку нулей слева, но
правая часть не равна нулю.
| х | y | z | rhs | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 2 |
Тут решения нет.Вы можете записать это как нулевой набор Ø,
пустой набор {} или нет решения.
4.6: Решение систем уравнений с использованием матриц
Цели обучения
К концу этого раздела вы сможете:
- Напишите расширенную матрицу для системы уравнений
- Использование операций со строками в матрице
- Решение систем уравнений с помощью матриц
Прежде чем начать, пройдите тест на готовность.
- Решите: \ (3 (x + 2) + 4 = 4 (2x − 1) +9 \).2 \).
Если вы пропустили эту проблему, просмотрите [ссылка] .
Запишите расширенную матрицу для системы уравнений
Решение системы уравнений может быть утомительной операцией, когда простая ошибка может нанести ущерб поиску решения. Доступен альтернативный метод, использующий основные процедуры исключения, но с более простой нотацией. Метод предполагает использование матрицы . Матрица — это прямоугольный массив чисел, упорядоченный по строкам и столбцам.
МАТРИЦА
Матрица представляет собой прямоугольный массив чисел, упорядоченных по строкам и столбцам.
Матрица с m строками и n столбцами имеет порядок \ (m \ times n \). Матрица слева внизу имеет 2 строки и 3 столбца, поэтому она имеет порядок \ (2 \ times 3 \). Мы говорим, что это матрица 2 на 3.
Каждое число в матрице называется элементом или записью в матрице.
Мы будем использовать матрицу для представления системы линейных уравнений.Мы записываем каждое уравнение в стандартной форме, и коэффициенты переменных и константа каждого уравнения становятся строкой в матрице. Тогда каждый столбец будет коэффициентами одной из переменных в системе или констант. Вертикальная линия заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.
Обратите внимание, что первый столбец состоит из всех коэффициентов x , второй столбец — это все коэффициенты y , а третий столбец — все константы.
Пример \ (\ PageIndex {1} \)
ⓐ \ (\ left \ {\ begin {array} {l} 5x − 3y = −1 \\ y = 2x − 2 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array } {l} 6x − 5y + 2z = 3 \\ 2x + y − 4z = 5 \\ 3x − 3y + z = −1 \ end {array} \ right. \)
- Ответ
ⓐ Второе уравнение не имеет стандартной формы. Перепишем второе уравнение в стандартном виде.
\ [\ начало {выровнено} y = 2x − 2 \\ −2x + y = −2 \ end {выровнено} \ nonumber \]
Заменим второе уравнение на его стандартную форму.В расширенной матрице первое уравнение дает нам первую строку, а второе уравнение дает нам вторую строку. Вертикальная линия заменяет знаки равенства.
ⓑ Все три уравнения имеют стандартную форму. В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная линия заменяет знаки равенства.
Пример \ (\ PageIndex {2} \)
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐ \ (\ left \ {\ begin {array} {l} 3x + 8y = −3 \\ 2x = −5y − 3 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} 2x − 5y + 3z = 8 \\ 3x − y + 4z = 7 \\ x + 3y + 2z = −3 \ end {array} \ right . \)
- Ответ
ⓐ \ (\ left [\ begin {matrix} 3 & 8 & -3 \\ 2 & 5 & −3 \ end {matrix} \ right] \)
ⓑ \ (\ left [\ begin {matrix} 2 & 3 & 1 & −5 \\ −1 & 3 & 3 & 3 & 4 \\ 2 & 8 & 7 & −3 \ end {matrix} \ right] \)
Пример \ (\ PageIndex {3} \)
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐ \ (\ left \ {\ begin {array} {l} 11x = −9y − 5 \\ 7x + 5y = −1 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} 5x − 3y + 2z = −5 \\ 2x − y − z = 4 \\ 3x − 2y + 2z = −7 \ end {array} \ вправо. \)
- Ответ
ⓐ \ (\ left [\ begin {matrix} 11 & 9 & −5 \\ 7 & 5 & −1 \ end {matrix} \ right] \)
ⓑ \ (\ left [\ begin {matrix} 5 & −3 & 2 & −5 \\ 2 & −1 & −1 & 4 \\ 3 & −2 & 2 & −7 \ end {matrix} \ right] \)
Это важно, поскольку мы решаем системы уравнений с использованием матриц, чтобы иметь возможность перемещаться между системой и матрицей.В следующем примере нам предлагается взять информацию из матрицы и написать систему уравнений.
Пример \ (\ PageIndex {4} \)
Напишите систему уравнений, соответствующую расширенной матрице:
\ (\ left [\ begin {array} {ccc | c} 4 & −3 & 3 & −1 \\ 1 & 2 & −1 & 2 \\ −2 & −1 & 3 & −4 \ end {array} \ right ] \).
- Ответ
Мы помним, что каждая строка соответствует уравнению и что каждая запись является коэффициентом переменной или константы.Вертикальная линия заменяет знак равенства. Поскольку эта матрица представляет собой \ (4 \ times 3 \), мы знаем, что она преобразуется в систему трех уравнений с тремя переменными.
Пример \ (\ PageIndex {5} \)
Запишите систему уравнений, соответствующую расширенной матрице: \ (\ left [\ begin {matrix} 1 & −1 & 2 & 3 \\ 2 & 1 & −2 & 1 \\ 4 & −1 & 2 & 0 \ end {matrix} \верно] \).
- Ответ
\ (\ left \ {\ begin {array} {l} x − y + 2z = 3 \\ 2x + y − 2z = 1 \\ 4x − y + 2z = 0 \ end {array} \ right.\)
Пример \ (\ PageIndex {6} \)
Запишите систему уравнений, соответствующую расширенной матрице: \ (\ left [\ begin {matrix} 1 & 1 & 1 & 4 \\ 2 & 3 & −1 & 8 \\ 1 & 1 & −1 & 3 \ end {matrix} \ right ] \).
- Ответ
\ (\ left \ {\ begin {array} {l} x + y + z = 4 \\ 2x + 3y − z = 8 \\ x + y − z = 3 \ end {array} \ right. \)
Использование операций со строками в матрице
Когда система уравнений принимает форму расширенной матрицы, мы будем выполнять операции со строками, которые приведут нас к решению.
Для решения методом исключения не имеет значения, в каком порядке мы размещаем уравнения в системе. Точно так же в матрице мы можем поменять местами строки.
Когда мы решаем методом исключения, мы часто умножаем одно из уравнений на константу. Поскольку каждая строка представляет собой уравнение, и мы можем умножить каждую часть уравнения на константу, аналогичным образом мы можем умножить каждую запись в строке на любое действительное число, кроме 0.
При исключении мы часто добавляем число, кратное одной строке, к другой строке.В матрице мы можем заменить строку с ее суммой на кратное другой строке.
Эти действия называются операциями со строками и помогут нам использовать матрицу для решения системы уравнений.
РАБОТА С РЯДОМ
В матрице следующие операции могут быть выполнены с любой строкой, и результирующая матрица будет эквивалентна исходной матрице.
- Поменяйте местами любые два ряда.
- Умножьте строку на любое действительное число, кроме 0.
- Добавить ненулевое кратное одной строки к другой строке.
Выполнить эти операции легко, но все вычисления могут привести к ошибке. Если мы используем систему для записи операций со строками на каждом шаге, гораздо легче вернуться и проверить нашу работу.
Мы используем заглавные буквы с нижними индексами для обозначения каждой строки. Затем мы показываем операцию слева от новой матрицы. Чтобы показать перестановку ряда:
Чтобы умножить строку 2 на \ (- 3 \):
Чтобы умножить строку 2 на \ (- 3 \) и прибавить ее к строке 1:
Пример \ (\ PageIndex {7} \)
Выполните указанные операции над расширенной матрицей:
ⓐ Поменяйте местами 2 и 3 ряды.
ⓑ Строку 2 умножить на 5.
ⓒ Умножить строку 3 на −2−2 и прибавить к строке 1.
\ (\ left [\ begin {array} {ccc | c} 6 & −5 & 2 & 3 \\ 2 & 1 & −4 & 5 \\ 3 & −3 & 1 & −1 \ end {array} \ right] \)
- Ответ
ⓐ Меняем ряды 2 и 3.
ⓑ Строку 2 умножаем на 5.
ⓒ Строку 3 умножаем на \ (- 2 \) и прибавляем к строке 1.
Пример \ (\ PageIndex {8} \)
Выполните указанные операции над расширенной матрицей:
ⓐ Поменяйте местами ряды 1 и 3.
ⓑ Строку 3 умножить на 3.
ⓒ Строку 3 умножить на 2 и прибавить к строке 2.
\ (\ left [\ begin {array} {ccc | c} 5 & −2 & -2 & -2 \\ 4 & -1 & −4 & 4 \\ -2 & 3 & 0 & −1 \ end {array} \ справа] \)
- Ответ
ⓐ \ (\ left [\ begin {matrix} −2 & 3 & 0 & −2 \\ 4 & −1 & −4 & 4 \\ 5 & −2 & −2 & −2 \ end {matrix} \ right] \ )
ⓑ \ (\ left [\ begin {matrix} −2 & 3 & 0 & −2 \\ 4 & −1 & −4 & 4 \\ 15 & −6 & −6 & −6 \ end {matrix} \ right] \ )
ⓒ \ (\ left [\ begin {matrix} -2 & 3 & 0 & 2 & \\ 3 & 4 & -13 & -16 & -8 \\ 15 & -6 & -6 & -6 & \ end {matrix} \ справа] \)
Пример \ (\ PageIndex {9} \)
Выполните указанные операции над расширенной матрицей:
ⓐ Поменяйте местами ряды 1 и 2,
ⓑ Умножить строку 1 на 2,
ⓒ Строку 2 умножить на 3 и прибавить к строке 1.
\ (\ left [\ begin {array} {ccc | c} 2 & −3 & −2 & −4 \\ 4 & 1 & −3 & 2 \\ 5 & 0 & 4 & −1 \ end {array} \ right] \)
- Ответ
ⓐ \ (\ left [\ begin {matrix} 4 & 1 & −3 & 2 \\ 2 & −3 & −2 & −4 \\ 5 & 0 & 4 & −1 \ end {matrix} \ right] \)
ⓑ \ (\ left [\ begin {matrix} 8 & 2 & −6 & 4 \\ 2 & −3 & −2 & −4 \\ 5 & 0 & 4 & −1 \ end {matrix} \ right] \)
ⓒ \ ( \ left [\ begin {matrix} 14 & −7 & −12 & −8 \\ 2 & −3 & −2 & −4 \\ 5 & 0 & 4 & −1 \ end {matrix} \ right] \)
Теперь, когда мы попрактиковались в операциях со строками, мы рассмотрим расширенную матрицу и выясним, какую операцию мы будем использовать для достижения цели.Это именно то, что мы сделали, когда выполняли выбывание. Мы решили, на какое число умножить строку, чтобы исключить переменную при сложении строк.
Учитывая эту систему, что бы вы сделали, чтобы исключить x ?
Следующий пример по сути делает то же самое, но с матрицей.
Пример \ (\ PageIndex {10} \)
Выполните необходимую операцию со строкой, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: \ (\ left [\ begin {array} {cc | c} 1 & −1 & 2 \\ 4 & −8 & 0 \ end {array} \ right] \)
- Ответ
Чтобы сделать 4 равным 0, мы могли бы умножить строку 1 на \ (- 4 \), а затем добавить ее к строке 2.
Пример \ (\ PageIndex {11} \)
Выполните необходимую операцию со строкой, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: \ (\ left [\ begin {array} {cc | c} 1 & −1 & 2 \\ 3 & −6 & 2 \ end {array} \ right] \)
- Ответ
\ (\ left [\ begin {matrix} 1 & −1 & 2 \\ 0 & −3 & −4 \ end {matrix} \ right] \)
Пример \ (\ PageIndex {12} \)
Выполните необходимую операцию со строкой, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: \ (\ left [\ begin {array} {cc | c} 1 & −1 & 3 \\ -2 & −3 & 2 \ end {array} \ right] \)
- Ответ
\ (\ left [\ begin {matrix} 1 & −1 & 3 \\ 0 & −5 & 8 \ end {matrix} \ right] \)
Решение систем уравнений с помощью матриц
Чтобы решить систему уравнений с использованием матриц, мы преобразуем расширенную матрицу в матрицу строковой формы , используя строковые операции.Для согласованной и независимой системы уравнений ее расширенная матрица находится в виде эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
ФОРМА ROW-ECHELON
Для непротиворечивой и независимой системы уравнений ее расширенная матрица находится в форме рядов , когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
Как только мы получим расширенную матрицу в виде ряда строк, мы можем написать эквивалентную систему уравнений и прочитать значение по крайней мере одной переменной. Затем мы подставляем это значение в другое уравнение, чтобы продолжить поиск других переменных. Этот процесс проиллюстрирован в следующем примере.
Пример \ (\ PageIndex {14} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} 2x + y = 7 \\ x − 2y = 6 \ end {array} \ right. \)
- Ответ
Решение: \ ((4, −1) \).
Пример \ (\ PageIndex {15} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} 2x + y = −4 \\ x − y = −2 \ end {array} \ right. \)
- Ответ
Решение: \ ((- 2,0) \).
Шаги кратко описаны здесь.
РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ С ПОМОЩЬЮ МАТРИЦ.
- Напишите расширенную матрицу для системы уравнений.
- Используя операции со строками, получите запись в строке 1, столбец 1 равной 1.
- Используя операции со строками, получите нули в столбце 1 под 1.
- Используя операции со строками, получите запись в строке 2, столбце 2, равной 1.
- Продолжайте процесс до тех пор, пока матрица не примет вид ряда строк.
- Напишите соответствующую систему уравнений.
- Используйте подстановку, чтобы найти оставшиеся переменные.
- Запишите решение в виде упорядоченной пары или тройки.
- Убедитесь, что решение соответствует исходным уравнениям.
Вот наглядное изображение, показывающее порядок получения единиц и нулей в правильном положении для строковой формы.
Мы используем ту же процедуру, когда система уравнений состоит из трех уравнений.
Пример \ (\ PageIndex {16} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} 3x + 8y + 2z = −5 \\ 2x + 5y − 3z = 0 \\ x + 2y − 2z = — 1 \ end {array} \ right. \)
- Ответ
Пример \ (\ PageIndex {17} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} 2x − 5y + 3z = 8 \\ 3x − y + 4z = 7 \\ x + 3y + 2z = −3 \ end {array} \ right.\)
- Ответ
\ ((6, −1, −3) \)
Пример \ (\ PageIndex {18} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} −3x + y + z = −4 \\ −x + 2y − 2z = 1 \\ 2x − y − z = −1 \ end {array} \ right. \)
- Ответ
\ ((5,7,4) \)
До сих пор мы работали с матрицами только с системами, которые согласованы и независимы, что означает, что у них есть только одно решение.Давайте теперь посмотрим, что происходит, когда мы используем матрицу для зависимой или несовместимой системы.
Пример \ (\ PageIndex {19} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} x + y + 3z = 0 \\ x + 3y + 5z = 0 \\ 2x + 4z = 1 \ end { array} \ right. \)
- Ответ
Пример \ (\ PageIndex {20} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} x − 2y + 2z = 1 \\ −2x + y − z = 2 \\ x − y + z = 5 \ end {array} \ right.\)
- Ответ
нет решения
Пример \ (\ PageIndex {21} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} 3x + 4y − 3z = −2 \\ −2x + 3y − z = −1 \\ 2x + y − 2z = 6 \ end {array} \ right. \)
- Ответ
нет решения
Последняя система была несовместимой и поэтому не имела решений. Следующий пример зависимый и имеет бесконечно много решений.
Пример \ (\ PageIndex {22} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} x − 2y + 3z = 1 \\ x + y − 3z = 7 \\ 3x − 4y + 5z = 7 \ конец {массив} \ right. \)
- Ответ
Пример \ (\ PageIndex {23} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} x + y − z = 0 \\ 2x + 4y − 2z = 6 \\ 3x + 6y − 3z = 9 \ конец {массив} \ право. \)
- Ответ
бесконечно много решений \ ((x, y, z) \), где \ (x = z − 3; \ space y = 3; \ space z \) — любое действительное число.
Пример \ (\ PageIndex {24} \)
Решите систему уравнений, используя матрицу: \ (\ left \ {\ begin {array} {l} x − y − z = 1 \\ −x + 2y − 3z = −4 \\ 3x − 2y − 7z = 0 \ end {array} \ right. \)
- Ответ
бесконечно много решений \ ((x, y, z) \), где \ (x = 5z − 2; \ space y = 4z − 3; \ space z \) — любое действительное число.
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с методом исключения Гаусса.
Ключевые понятия
- Матрица: Матрица — это прямоугольный массив чисел, расположенных в строках и столбцах. Матрица с m строками и n столбцами имеет порядок \ (m \ times n \). Матрица слева внизу имеет 2 строки и 3 столбца, поэтому она имеет порядок \ (2 \ times 3 \). Мы говорим, что это матрица 2 на 3.
Каждое число в матрице называется элементом или элементом в матрице.
- Операции со строками: В матрице следующие операции могут выполняться с любой строкой, и результирующая матрица будет эквивалентна исходной матрице.
- Поменять местами любые два ряда
- Умножить строку на любое действительное число, кроме 0
- Добавить ненулевое кратное одной строки к другой строке
- Форма эшелонирования строк: Для согласованной и независимой системы уравнений ее расширенная матрица находится в форме эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
- Как решить систему уравнений с помощью матриц.
- Напишите расширенную матрицу для системы уравнений.
- Используя операции со строками, получите запись в строке 1, столбце 1 равной 1.
- Используя операции со строками, получите нули в столбце 1 под 1.
- Используя операции со строками, получите запись в строке 2, столбце 2, равной 1.
- Продолжайте процесс до тех пор, пока матрица не примет вид ряда строк.
- Напишите соответствующую систему уравнений.
- Используйте подстановку, чтобы найти оставшиеся переменные.
- Запишите решение в виде упорядоченной пары или тройки.
- Убедитесь, что решение соответствует исходным уравнениям.
Глоссарий
- матрица
- Матрица — это прямоугольный массив чисел, упорядоченный по строкам и столбцам.
- рядная форма
- Матрица находится в виде эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
.

 Системы уравнений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравнений / / Системы линейных алгебраических уравнений (СЛАУ). Общий вид, матрица системы, СЛАУ в матричной форме, решение СЛАУ. Разновидности СЛАУ — совместная, несовместная, определенная, неопределенная, однородная, неоднородная… Обратная матрица и ее нахождение.
Системы уравнений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравнений / / Системы линейных алгебраических уравнений (СЛАУ). Общий вид, матрица системы, СЛАУ в матричной форме, решение СЛАУ. Разновидности СЛАУ — совместная, несовместная, определенная, неопределенная, однородная, неоднородная… Обратная матрица и ее нахождение. Обратная матрица и ее нахождение.
Обратная матрица и ее нахождение.  Будем иметь:
Будем иметь: 1.6. Определители порядка n
1.6. Определители порядка n 4. Решение системы линейных уравнений
4. Решение системы линейных уравнений е.е. [latex] n \ times 1 [/ latex] матрица) [latex] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], а [latex] b [/ latex] — это [ latex] m \ times 1 [/ latex] вектор-столбец, тогда матричное уравнение будет: [latex] Ax = b [/ latex].
е.е. [latex] n \ times 1 [/ latex] матрица) [latex] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], а [latex] b [/ latex] — это [ latex] m \ times 1 [/ latex] вектор-столбец, тогда матричное уравнение будет: [latex] Ax = b [/ latex].