x нулевое

Вы искали x нулевое? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и игрек нулевое формула, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «x нулевое».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как x нулевое,игрек нулевое формула,икс нулевое формула,как найти x нулевое,как найти y нулевое,как найти игрек нулевое,как найти икс нулевое,как найти у нулевое,как найти х нулевое,как найти х0 в физике,формула x нулевое,формула игрек нулевое,формула нулевого х,формула х нулевого,х нулевое,х нулевое как найти,х нулевое формула. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и x нулевое. Просто введите задачу в окошко и нажмите
«решить» здесь (например, икс нулевое формула).

Где можно решить любую задачу по математике, а так же x нулевое Онлайн?

Решить задачу x нулевое вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Формула вершины параболы

☰

Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.

Квадратичная функция имеет вид: y = ax² + bx + c.

Ее график — это парабола с вершиной, координаты которой определяются по формулам:

Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.

Например, если дана функция y = 2x² – 4x + 5, то координата x ее вершины будет равна:

x = –(–4 / (2 × 2)) = 1

Координату же y вычислим, подставив найденный x в саму функцию:

y = 2 × 12 – 4 × 1 + 5 = 3

Таким образом, вершина графика функции y = 2x² – 4x + 5 находится в точке с координатами (1; 3).

В остальном парабола квадратичной функции вида y = ax² + bx + c такая же как функции вида y = ax². Отличие лишь в сдвиге вершины по сравнению с функцией y = ax². Так в приведенном выше примере (y = 2x² – 4x + 5) парабола будет по форме и направлению ветвей такой же, как для функции y = 2x². Разница лишь в координатах вершин парабол.

Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b²) / 4a. То есть l и m — это координаты x₀ и y₀ соответственно.

Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax² + bx + c. При этом выполняются следующие преобразования:

1. Объединим первые два члена многочлена: y = (ax² + bx) + c

2. Вынесем коэффициент a за скобку, при этом b разделится на a:

3. Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:

4. Выделим квадрат суммы:

5. Умножим на a:

6. Приведем к общему знаменателю свободные члены:

7. Поменяем знак:

Таким образом, мы привели функцию y = ax² + bx + c к виду y = a(x + l)² + m, что соответствует функции y = f(x + l) + m, где f(x) = ax². А как строить графики последней известно.

Нулевая скорость, нулевое ускорение?

Я хочу пойти другим путем, чем другие ответы. Это будет одна большая ручная волна, а не строгий математический аргумент, но я надеюсь, что она поможет понять идею интуитивно.

Прежде всего, как я отметил в комментарии, и, как отмечает hft, вы используете «v» для обозначения «скорости как функции времени» и «скорости как функции положения». Это сбивает с толку, но там нет никаких фундаментальных проблем. Кроме…

За исключением того, что ваша математика зависит от способности различать скорость относительно позиции. Это требует, чтобы скорость действительно была функцией положения.

При каких обстоятельствах одномерная скорость может фактически быть функцией положения? Должна быть ровно одна скорость для каждой позиции. Что это означает о нашей скорости? Это никогда не должно менять знак! Потому что, если она меняет знак, то наша частица иногда движется вперед, а иногда назад, и поэтому должна существовать позиция, которая перемещается как назад, так и вперед, и, следовательно, скорость не будет функцией положения.

Итак, без ограничения общности, давайте предположим, что скорость никогда не бывает отрицательной. Давайте также предположим, что функции положения, скорости и ускорения непрерывны и дифференцируемы и все такое хорошее.

Теперь давайте подумаем о физичности этой ситуации в отношении ускорения.

Предположим, что скорость положительна, а ускорение равно нулю или положительно.

Частица движется вправо, ее положение становится все более и более положительным, все время быстрее, если ускорение положительное, и не медленнее, если оно равно нулю. Очевидно, что скорость никогда не будет равна нулю, если это будет продолжаться.

Итак, давайте предположим, что скорость положительна, а ускорение отрицательно. Наша частица становится все медленнее и медленнее. Имейте в виду, что всегда двигайтесь вправо, потому что по предположению скорость является функцией положения. Но все медленнее и медленнее.

Теперь предположим, что он становится все медленнее и медленнее, но никогда не достигает нулевой скорости в любое время. Нет проблем там. Ускорение должно становиться все ближе и ближе к нулю, но ни ускорение, ни скорость не доходят до нуля.

Итак, мы исключили кучу случаев из рассмотрения — случай, когда ускорение равно нулю, а скорость никогда не меняется, случай, когда ускорение положительно, а скорость никогда не уменьшается, и случай, когда ускорение отрицательно, а скорость приближается и ближе к нулю, но никогда не добирается туда. Мы заботимся только о ситуациях, когда скорость достигает нуля.

Теперь давайте рассмотрим случай, когда скорость начинается как положительная, ускорение отрицательное, и в результате скорость через некоторое время достигает нуля. Что должно произойти с ускорением в точке, где скорость становится равной нулю ? Ускорение не может быть отрицательным в этой точке, потому что если бы это было так, тогда частица начала бы двигаться назад, и мы знаем, что этого не происходит. Ускорение должно быть либо нулевым в этой точке, либо положительным.

Предположим, что ускорение положительно в тот момент, когда скорость равна нулю. Очевидно, что это было отрицательным, прежде чем скорость стала нулевой; мы не могли бы замедлиться до нуля с положительной скорости, если бы ускорение было положительным или равным нулю. Но это противоречит нашему предположению, что функция ускорения была хорошей гладкой дифференцируемой функцией! Ускорение мгновенно перешло от отрицательного значения к положительному значению без прохождения через ноль и, следовательно, не было хорошей непрерывной функцией.

Единственная оставшаяся возможность состоит в том, что ускорение равно нулю в точке, где скорость равна нулю. Это именно то, что вы хотели показать.

Я могу вспомнить несколько ситуаций, когда частица имеет ненулевое ускорение, несмотря на мгновенный покой. Что тут происходит?

То, что происходит, заключается в том, что во всех этих ситуациях либо ускорение в этой точке прерывисто, либо скорость на самом деле не является функцией положения, как того требует ваша математика.

Нулевая точка станка и направления перемещений

Система координат станка с ЧПУ является главной расчетной системой, определяющей перемещения исполнительных органов. Оси координат располагают параллельно направляющим станка, что позволяет при создании УП легко задавать направления и расстояния перемещений.

Рис. 4.1. Оси координатной системы расположены параллельно направляющим

Правая система координат является стандартной для всех станков с ЧПУ. В этой системе положительные направления координатных осей определяются по правилу «правой руки». Если большой палец указывает положительное направление оси X, указательный – оси Y, то средний укажет на положительное направление оси Z. В качестве положительного направления оси Z принимают вертикальное направление вывода инструмента (например, сверла) из заготовки. То есть ось Z всегда связана со шпинделем станка. Как правило, за X принимают ось, вдоль которой возможно наибольшее перемещение исполнительного органа станка. При этом ось X перпендикулярна оси Z и параллельна плоскости рабочего стола. Если вы определили на станке направления осей X и Z, то по правилу «правой руки» вы однозначно сможете сказать, куда «смотрит» ось Y. Оси X, Y, Z указывают положительные направления перемещений инструмента относительно неподвижных частей станка.

При создании УП программист всегда исходит из правила, что именно инструмент перемещается относительно неподвижной заготовки.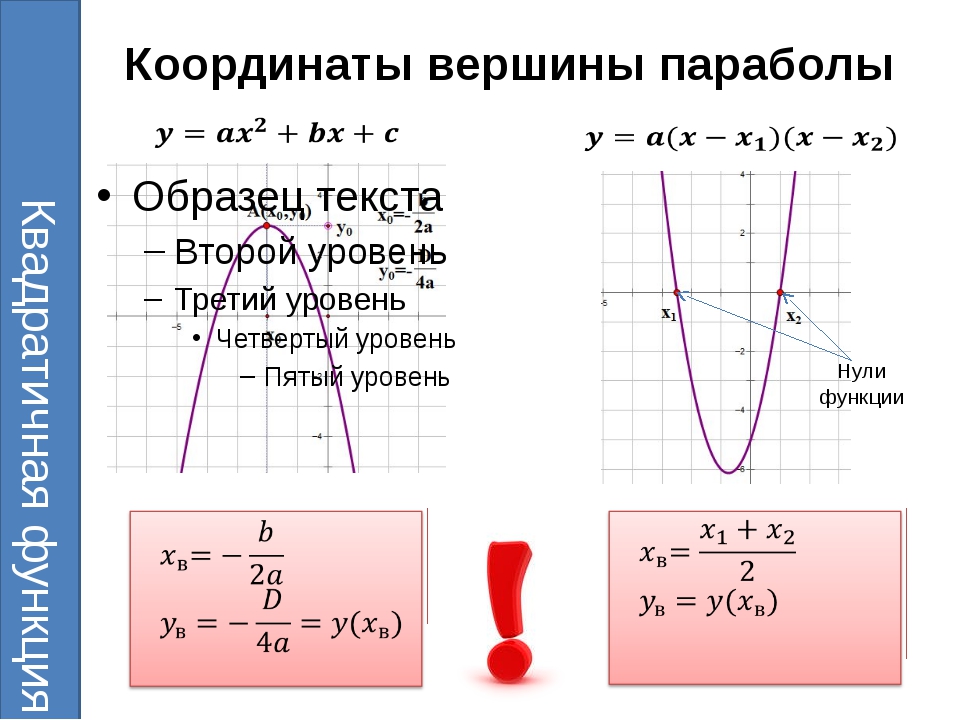

Дело в том, что одни станки с ЧПУ действительно перемещают колонну, шпиндель и, соответственно, вращающийся инструмент относительно неподвижной заготовки, а другие станки, наоборот, перемещают рабочий стол с заготовкой относительно вращающегося инструмента. Получаем противоположные направления перемещений. Если бы не было этого правила, то программист вынужден был бы думать: а что, собственно, перемещается и в какую сторону. А так все просто – система ЧПУ сама определит, в каком направлении нужно переместить тот или иной узел станка.

Кроме линейных перемещений, конструкция некоторых станков позволяет совершать круговые перемещения. Под круговым перемещением подразумевается, например, поворот оси шпинделя фрезерного станка. Однако само рабочее вращение шпинделя не входит в это понятие. Круговые перемещения инструмента обозначают латинскими буквами А (вокруг оси X), В (вокруг оси Y) и С (вокруг оси Z). Положительные направления вращений вокруг этих осей определяются очень просто. Если расположить большой палец по направлению оси, то другие согнутые пальцы покажут положительное направление вращения.

Рис. 4.4. Головка этого станка способна поворачиваться вокруг своей оси

Положения исполнительных органов характеризуют их базовые точки, которые выбираются с учетом конструкции станка. Например, базовой точкой для шпинделя фрезерного станка с ЧПУ является точка пересечения его торца с собственной осью вращения. Для рабочего стола – точка пересечения его диагоналей или один из углов. Положение базовой точки относительно начала координат станка с ЧПУ (нулевой точки станка) называется позицией исполнительного органа в системе координат станка или машинной позицией (от англ. machine станок). При работе станка в любой момент времени вы можете увидеть на экране стойки ЧПУ текущую машинную позицию (например, рабочего стола) по любой из осей относительно «нуля станка». В документации станка пределы возможных перемещений рабочих органов, как правило, указывают пределами смещений базовых точек. Эти данные являются очень важной характеристикой станка, так как они определяют максимально возможные габариты обрабатываемой заготовки.

Рис. 4.5. Расстояния Xm, Ym и Zm от нулевой точки станка до базовых точек исполнительных органов определяют машинные позиции

Нулевая точка станка – это физическая позиция, установленная производителем станка при помощи концевых выключателей или датчиков. После включения станка необходимо переместить исполнительные органы в его нулевую точку, для того чтобы СЧПУ смогла определить или «обнулить» их машинную позицию, или, другими словами, нужно синхронизировать СЧПУ и станок. Дело в том, что в момент включения станка СЧПУ еще не знает реального положения исполнительных органов, и если не выполнить возврата в нуль, то станок просто «откажется» работать. Когда исполнительный орган приходит в нулевую точку станка, то происходит замыкание контактов специального датчика или конечного выключателя, СЧПУ получает электрический сигнал и машинная позиция обнуляется. Процедура возврата в нуль станка является стандартной, и для ее осуществления любой станок имеет специальный режим и соответствующие клавиши на панели УЧПУ.

Расчёт сопротивления нулевой последовательности линии

Величина сопротивления нулевой последовательности используется в расчетах однофазного короткого замыкания методом симметричных составляющих. Но, зачастую проблематично найти значение этой величины в справочниках для различного исполнения электрических сетей, и, следовательно, невозможно выполнить расчет. При этом значения сопротивлений фазного и нулевого проводников в справочниках присутствуют. Как же быть?

Можно использовать следующие формулы расчета сопротивления нулевой последовательности:

где R0л (X0л) – активное (индуктивное) сопротивление нулевой последовательности линии;

Rф (Xф) – активное (индуктивное) сопротивление фазного проводника;

Rн (Xн) – активное (индуктивное) сопротивление нулевого проводника.

Вывод формул смотри ниже.

Сразу следует подчеркнуть, что этими формулами следует пользоваться, если сопротивление нулевой последовательности неизвестно. Если есть выбор, использовать справочные данные, или выполнить расчет сопротивления нулевой последовательности, то, наверное, следует отдать предпочтение справочным данным.

Итак, основным документом, регламентирующим расчеты токов короткого замыкания до 1000 В, является ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ». В справочном приложении 2 этого ГОСТ, в таблицах №№ 6-14 содержатся данные о сопротивлениях прямой и нулевой последовательностей для различного исполнения кабельных линий. К сожалению, есть варианты исполнения линий, довольно распространенные, для которых нет подходящей таблицы в этом стандарте. Например, нельзя найти параметры 4-жильного кабеля с алюминиевыми жилами в непроводящей оболочке, если сечение жил одинаковое (в табл.11 сечение нулевого провода меньше, чем сечение фазного). Также, отсутствуют аналогичные данные для кабеля с медными жилами (в табл.14 приведены данные для кабеля в стальной оболочке; да и номенклатура сечений неполная).

В то же время, в справочниках есть данные сопротивлений для любого исполнения линий. Вот только приведены эти данные в виде сопротивлений фазного и нулевого проводников (для применения в расчетах тока однофазного короткого замыкания методом петли «фаза-ноль»), а не сопротивлений прямой, обратной и нулевой последовательностей.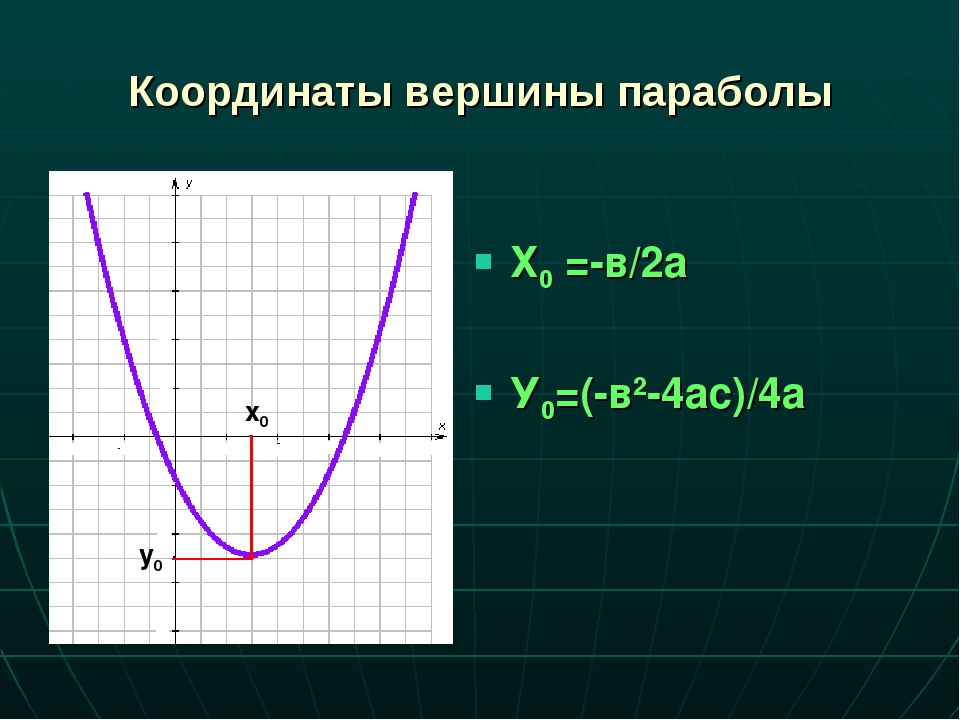

Логично предположить, что если результаты расчета по двум разным методам:

— методу петли «фаза-ноль»;

— методу симметричных составляющих,

приравнять, то можно сделать вывод о соотношениях сопротивлений, используемых в этих методах.

Формула расчета тока однофазного КЗ методом петли «фаза-ноль» выглядит следующим образом (см. [2] и [3]):

где U – линейное напряжение сети;

Uф – фазное напряжение сети;

Zпт – полное сопротивление петли фаза-ноль от трансформатора до точки КЗ;

Zс.т. – сопротивление системы и трансформатора току однофазного КЗ.

где Х1т, Х2т, Х0т, R1т, R2т, R0т – индуктивные (Х) и активные (R) сопротивления трансформатора токам прямой (1), обратной (2) и нулевой (0) последовательностей;

Хс – индуктивное сопротивление питающей сети;

Rд – сопротивление электрической дуги.

Перепишем формулу (3) в более удобной форме, при этом:

— учтем, что сопротивления прямой и обратной последовательностей равны;

— умножим числитель и знаменатель на 3;

— в знаменателе будем складывать не модули полных сопротивлений, а отдельно их активные и индуктивные составляющие (это сделает расчет более точным).

где Rф (Rн) – активное сопротивление фазного (нулевого) проводника линии;

Xф (Xн) – индуктивное сопротивление фазного (нулевого) проводника линии.

Вот формула расчета тока однофазного КЗ методом симметричных составляющих (см. [1], п.8.2.1, формула 24):

где R1сум. (R0сум.) – суммарное активное сопротивление прямой (нулевой) последовательности;

X1сум. (X0сум.) – суммарное индуктивное сопротивление прямой (нулевой) последовательности.

Перепишем формулу (6), подставив в нее значение фазного напряжения, а также расписав более подробно суммарные величины сопротивлений прямой и обратной последовательностей:

где R1л (R0л) – суммарное активное сопротивление прямой (нулевой) последовательности линии;

X1л (X0л) – суммарное индуктивное сопротивление прямой (нулевой) последовательности линии.

После сравнения формул (5) и (7) получим следующие выражения:

Считая, что Rф=R1л, Xф=X1л, выразим из соотношений (8) и (9) величины сопротивлений нулевой последовательности:

Итак, при отсутствии справочных значений о величине сопротивления нулевой последовательности линии, эти значения можно рассчитать, используя справочные данные сопротивлений фазного и нулевого проводников линии.

Используемая литература

ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ».

Кужеков С. Л. Практическое пособие по электрическим сетям и электрооборудованию / С.Л. Кужеков, С. В. Гончаров. – Ростов н/Д.: Феникс, 2007.

Тульчин И. К., Нудлер Г. И. Электрические сети и электрооборудование жилых и общественных зданий. – 2-е изд., перераб. и доп. – М.: Энерготамиздат, 1990.

Правило Крамера (Лекция №15)

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях
равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠
0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах
интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы
система линейных однородных уравнений имела ненулевое
решение, необходимо и достаточно, чтобы Δ
≠ 0.

Итак, если определитель Δ ≠ 0, то
система имеет единственное решение. Если же Δ
≠ 0, то система линейных однородных уравнений
имеет бесконечное множество решений.

Примеры.

1. , а значит x=y=z=0.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец,
высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

,

где λ – некоторое число.
Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ,
при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то
матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде
системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения
координат x₁, x₂,
x₃ вектора X. Чтобы система имела
ненулевые решения необходимо и достаточно, чтобы определитель системы был равен
нулю, т.е.

Это
уравнение 3-ей степени относительно λ. Оно называется характеристическим
уравнением матрицы A и служит для определения
собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X,
координаты которого определяются из системы при соответствующем значении λ.

Примеры.

1. Найти собственные векторы и соответствующие им собственные значения матрицы .

   Составим характеристическое уравнение и найдём собственные значения

   1. При λ₁ = –1 получаем систему уравнений

      Если x₁ = t, то, где tÎR.

   2. Если λ₂ = 5

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые
полностью определяются заданием их численных значений, например, длина,
площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых,
кроме численного значения, необходимо знать также их направление в
пространстве, например, сила, действующая на тело, скорость и ускорение тела
при его движении в пространстве, напряжённость магнитного поля в данной точке
пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём
отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный
отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у
которого одна из ограничивающих его точек принимается за начало, а вторая – за
конец. Если A – начало
вектора, B – его конец, то вектор
обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его
направление стрелкой.

Модулем или длиной вектора называют длину
определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого
начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и
модуль его равен нулю ||=0.

Векторы и называются коллинеарными, если они расположены на
одной прямой или на параллельных прямых. При этом если
векторы и одинаково
направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных
одной и той же плоскости, называются компланарными.

Два вектора и называются равными, если они коллинеарны,
одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить
параллельно самому себе, помещая его начало в любую точку пространства.

Например.

1. Если дан вектор , то, выбрав любую точку , можем построить вектор , равный данному, и притом только один, или, как говорят,
   перенести вектор в точку .
2. Если рассмотреть квадрат ABCD, то на основанииопределения
   равенства векторов, мы можем написать и , но , , хотя все они имеют одинаковую длину.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

1. Умножение вектора на число.

   Произведением вектора на число λ называется новый вектор
   такой, что:

   1. ;
   2. вектор коллинеарен
      вектору ;
   3. векторы и направлены
      одинаково, если λ>0
      и противоположно, если λ<
      0. (Если λ=0, то
      из условия 1 следует, что ).

   Произведение вектора на число λ обозначается
   .

   Например, есть вектор,
   направленный в ту же сторону, что и вектор , и имеющий длину, вдвое меньшую, чем вектор .

   Введённая операция обладает следующими свойствами:

   1. Для любых чисел a и b и вектора выполняется
      равенство .

      Действительно, векторы, стоящие в обеих частях равенства имеют одинаковую
      длину . Кроме того, ясно, что они одинаково направлены, т.к.
      их направление совпадает с направлением вектором , если a и b одного знака, и противоположно направлению , если a и b разных знаков.

   2. Пусть дан вектор . Для любого коллинеарного ему вектора найдётся и притом
      только одно число l,
      удовлетворяющее равенству .

      Доказательство свойства 2:

      1. Пусть . Рассмотрим вектор . Очевидно, . Кроме того , поэтому . Из этих двух свойств следует, что , а значит .
      2. Аналогично, если . Тогда .

         Единственность
         числа λ следует из того, что при умножении
         вектора на два разных
         числа, получаем два разных вектора.

2. Сложение векторов.

   Пусть и – два
   произвольных вектора. Возьмём произвольную точку O и
   построим вектор . После этого из точки A отложим вектор . Вектор , соединяющий начало первого вектора c концом
   второго , называется суммой
   этих векторов и обозначается .

   Сформулированное определение сложения векторов называют правилом параллелограмма, так как ту же
   самую сумму векторов можно получить следующим образом. Отложим от точки O векторы и . Построим на этих векторах параллелограмм ОАВС. Так как векторы , то вектор , являющийся диагональю параллелограмма, проведённой из вершины O, будет
   очевидно суммой векторов .

   
   

   Легко проверить следующие свойства сложения векторов.

   1. Ясно, что прибавление
      нулевого вектора к некоторому вектору ā
      не меняет вектора , т.е. .
   2. Сложение векторов
      коммутативно, т.е. .

      Это свойство сразу следует из правила параллелограмма.

   3. Сложение векторов ассоциативно, т.е. для любых трёх векторов . Поэтому сумму трёх векторов часто записывают просто .

      Сумму трёх векторов можно получить следующим образом. Из произвольной
      точки O откладывается вектор, равный первому вектору. К его концу
      присоединяется начало второго, к концу второго – начало третьего. Вектор, соединяющий
      начало первого вектора с концом последнего, будет суммой данных векторов.
      Аналогично строится сумма любого конечного числа векторов.

   4. Для любого числа λ и
      любых векторов и .

      Заметим, что при умножении векторов на число λ меняются только размеры векторов, т.е. масштаб чертежа,
      фигуры остаются подобными. Поэтому, так как векторы образуют
      стороны и диагональ параллелограмма, то, умножив все члены на λ,
      т.е. изменив лишь размеры векторов одинаковым образом, мы получим снова параллелограмм,
      а значит, сохранится равенство .

   5. Для любых чисел a и b и любого вектора выполняется
      равенство .

3. Разность векторов.

   Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный,
   называется противоположным вектором
   для вектора и обозначается . Противоположный вектор можно рассматривать
   как результат умножения вектора на число λ = –1: .

   Разностью двух векторов и называется вектор , равный сумме векторов и , т.е. .

   Очевидно, что , для любого вектора .

   Легко показать, что .

   Действительно,

   Таким образом, если .

   Из определения суммы двух векторов вытекает правило построения вектора
   разности. Откладываем векторы и из общей точки O. Чтобы найти вектор-разность, нужно к добавить вектор или . Тогда . Вектор , соединяющий концы векторов и и направленный от
   «вычитаемого» к «уменьшаемому» (т.е. от второго вектора к первому), и будет
   разностью . Действительно, по правилу сложения векторов или .

   Таким образом, если на векторах и , отложенных из общей точки O,
   построить параллелограмм OACB, то вектор , совпадающий с одной диагональю параллелограмма, равен
   сумме , а вектор , совпадающий с другой диагональю, равен разности .

Урок 10. определение производной. физический смысл производной — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №10. Определение производной. Физический смысл производной.

Перечень вопросов, рассматриваемых в теме

1) Определение производной;

2) Физический смысл производной;

2) Приращение функции;

3) Скорость материальной точки в заданный момент времени по данному закону движения.

Глоссарий по теме

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.

Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Итак, x₁-x₀=Δx, значит, x₁=x₀+Δx.

f(x₁)-f(x₀)=Δy, значит, 

Δy=f(x₀+Δx)-f(x₀). (1)

Нельзя истолковывать термин «приращение» как «прирост».

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найдем приращение Δx и Δf в точке x_0, если f(x)= x², x₀=2 и х=1,9

Решение:

Δx= x₁−x₀=1,9-2=-0,1

Δf= f(1,9) –f(2)=1,9²-2²=-0,39

Ответ: Δx=-0,1; Δf =-0,39

Пример 2.

Найдем приращение Δx и Δf в точке x_0, если f(x)= x², x₀=2 и х=2,1

Решение:

Δx= x₁−x₀=2,1-2=0,1

Δf= f(1,9) –f(2)=2,1²-2²=0,41

Ответ: Δx=0,1; Δf =0,41

Пример 3.

Найдем приращение Δf функции в точке x₀,если приращение аргумента равно x₀.

Решение:

по формуле (1) находим:

.

Ответ: .

С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀; t₀+∆t]. Если точка движется по прямой и известна ее координата x(t), то

Эта формула верна и для ∆t<0 (для промежутка [t₀+∆t; t₀]).

Аналогично выражение называют средней скорость изменения функции на промежутке с концами х₀ и х₀+∆х.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Обозначение: y’ или f’(x)

Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

Схема вычисления производной функции

1. Найти приращение функции на отрезке [x; x+Δx]:

∆y=y(x+∆x)-y(x)

1. Разделить приращение функции на приращение аргумента:

1. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Пример 4.

Вычислить производную функции y=x²

Решение: Используем схему вычисления производной по действиям:

1. ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²

Ответ: y’=2x.

Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).

Таким образом, скорость – есть производная от пути по времени.

Пример 5.

Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.

Решение:

найдем ∆t= 1-0,8=0,2

S(0,8)= 1-2·0,8= -0,6=S(t)

S(1)= 1-2·1= -1=S(t+∆t)

.

Ответ: _.

Необходимое и достаточное условие дифференцируемости

Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.

Трехчлен совершенного квадрата — объяснение и примеры

Квадратное уравнение — это многочлен второй степени, обычно имеющий форму f (x) = ax ² + bx + c, где a, b, c, ∈ R и a ≠ 0. Термин «a» относится к как старший коэффициент, а ‘c’ — абсолютный член f (x).

Каждое квадратное уравнение имеет два значения неизвестной переменной, обычно известных как корни уравнения (α, β). Мы можем получить корни квадратного уравнения, разложив уравнение на множители.

Что такое идеальный квадратный трехчлен?

Способность распознавать особые случаи многочленов , которые мы можем легко учесть, является фундаментальным навыком для решения любых алгебраических выражений, содержащих многочлены.

Один из этих многочленов « легко разложить на множители » является трехчленом полного квадрата. Мы можем вспомнить, что трехчлен — это алгебраическое выражение, состоящее из трех членов, связанных сложением или вычитанием.

Точно так же бином — это выражение , состоящее из двух членов .Следовательно, трехчлен полного квадрата можно определить как выражение, которое получается возведением в квадрат бинома

Изучение того, как распознать трехчлен полного квадрата , является первым шагом к его факторизации.

Ниже приведены советы, как распознать трехчлен полного квадрата:

• Проверьте, являются ли первое и последнее члены трехчлена полными квадратами.
• Умножьте корни первого и третьего членов вместе.
• Сравните средние члены с результатом на втором шаге
• Если первый и последний члены являются точными квадратами, а коэффициент среднего члена в два раза больше произведения квадратных корней из первого и последнего членов, тогда выражение будет полный квадрат трехчлена.

Как разложить на множители идеальный квадратный трехчлен?

После того, как вы определили трехчлен полного квадрата, факторизация — довольно простой процесс.

Давайте посмотрим, как разложить на множители полный квадратный трехчлен.

• Определите квадрат чисел в первом и третьем членах трехчлена.
• Проверьте средний член, если он положительный или отрицательный. Если средний член трехчлена положительный или отрицательный, то множители будут иметь знак плюс и минус соответственно.
• Запишите условия, используя следующие идентификаторы:

(i) a ² + 2ab + b ² = (a + b) ² = (a + b) (a + b)
(ii) a ² — 2ab + b ² = (a — b) ² = (a — b) (a — b)

Формула трехчлена идеального квадрата

Выражение, полученное из квадрата a биномиальное уравнение является трехчленом в виде полного квадрата.Выражение называется трехчленом полного квадрата, если оно принимает вид ax ² + bx + c и удовлетворяет условию b ² = 4ac.

Формула полного квадрата принимает следующие формы:

• (ax) ² + 2abx + b ² = (ax + b) ²
• (ax) ² −2abx + b ² = (ax − b) ²

Пример 1

Фактор x ² + 6x + 9

Решение

Мы можем переписать выражение x ² + 6x + 9 в форме a ² + 2ab + b ² as;
x ² + 6x + 9 ⟹ (x) ² + 2 (x) (3) + (3) ²
Применяя формулу a ² + 2ab + b ² = (a + б) ² к выражению дает;
= (x + 3) ²
= (x + 3) (x + 3)

Пример 2

Фактор x ² + 8x + 16

Решение

Запишите выражение x ² + 8x + 16 как a ² + 2ab + b ²

x ² + 8x + 16 ⟹ (x) ² + 2 (x) (4) + (4) ²
Теперь применим формулу полного квадрата трехчлена;

= (x + 4) ²
= (x + 4) (x + 4)

Пример 3

Фактор 4a ² — 4ab + b ²

Решение

4a ² — 4ab + b ² ⟹ (2a) ² — (2) (2) ab + b ²

= (2a — b) ²

= (2a — b) (2a — b)

Пример 4

Фактор 1- 2xy- (x ² + y ² )

Решение

1- 2xy- (x ² + y ² )
= 1 — 2xy — x ² — y ²
= 1 — (x ² + 2xy + y ² )
= 1 — (x + y) ²
= (1) ² — (x + y) ²

= [1 + (x + y)] [1 — (x + y)]

= [1 + x + y] [1 — x — y]

Пример 5

Фактор 25y ² — 10y + 1

9 0115 Решение

25 лет ² — 10 лет + 1⟹ (5 лет) ² — (2) (5) (y) (1) + 1 ²

= (5y — 1) ²

= (5y– 1) (5y — 1)

Пример 6

Фактор 25t ² + 5t / 2 + 1/16.

Раствор

25t ² + 5t / 2 + 1/16 ⟹ (5t) ² + (2) (5) (t) (1/4) + (1/4) ²

= (5т + 1/4) ²

= (5т + 1/4) (5т + 1/4)

Пример 7

Фактор x ⁴ — 10x ² y ² + 25y ⁴

Решение

x ⁴ — 10x ² y ² + 25y ⁴ ⟹ (x ² ) ^{2 — 2 (x ) (5y 2 ) + (5y 2 ) 2}

Примените формулу a ² + 2ab + b ² = (a + b) ² , чтобы получить,
= (x ² — 5y ² ) ²
= (x ² — 5y ² ) (x ² — 5y ² )

Практические вопросы

Факторизуйте следующие триномины полного квадрата :

1. x ² + 12x + 36
2. 9a ² — 6a + 1
3. (m + n) ² + 12 (m + n) + 36
4. x ² + 4x + 4
5. x ² + 2x + 1
6. x ² + 10x + 25
7. 16x ² — 48x + 36
8. x ² + x + ¼
9. Z ² + 1 / z ² — 2 .
10. 4x ² — 20x + 25

Ответы

1. (x + 6) (x + 6)
2. (3a — 1) (3a — 1)
3. (m + n + 6) (m + n + 6)
4. (x + 2) (x + 2)
5. (x + 1) (x + 1)
6. (x + 5) (x + 5)
7. (4x– 6) (4x — 6)
8. (x + 1/2) (x + 1/2)
9. (z — 1 / z ² ) (z — 1 / z ² )
10. (2x — 5) (2x — 5)

Предыдущий урок | Главная страница | Следующий урок

Как найти нули функции

При работе с функциями иногда необходимо вычислить точки, в которых график функции пересекает ось x.Эти точки возникают, когда значение x равно нулю и являются нулями функции. В зависимости от типа функции, с которой вы работаете, и ее структуры, она может не иметь нулей или иметь несколько нулей. Независимо от того, сколько нулей имеет функция, вы можете вычислить все нули одинаково.

TL; DR (слишком долго; не читал)

Вычислить нули функции, установив функцию равной нулю, а затем решив ее. Многочлены могут иметь несколько решений для учета положительных и отрицательных результатов даже экспоненциальных функций.

Нули функции

Нули функции — это значения x, при которых полное уравнение равно нулю, поэтому вычислить их так же просто, как установить функцию равной нулю и решить относительно x. Чтобы увидеть базовый пример этого, рассмотрим функцию f (x) = x + 1. Если вы установите функцию равной нулю, тогда она будет выглядеть как 0 = x + 1, что дает вам x = -1 после вычитания 1 с обеих сторон. Это означает, что нуль функции равен -1, поскольку f (x) = (-1) + 1 дает результат f (x) = 0.

Хотя не для всех функций так легко вычислить нули, тот же метод используется даже для более сложных функций.

Нули полиномиальной функции

Полиномиальные функции потенциально усложняют задачу. Проблема с полиномами заключается в том, что функции, содержащие переменные, возведенные в четную степень, потенциально могут иметь несколько нулей, поскольку как положительные, так и отрицательные числа дают положительные результаты при умножении на себя четное число раз.Это означает, что вам нужно вычислять нули как для положительных, так и для отрицательных возможностей, хотя вы все равно решаете, устанавливая функцию равной нулю.

Пример поможет понять это. Рассмотрим следующую функцию: f (x) = x ² — 4. Чтобы найти нули этой функции, вы начинаете таким же образом и устанавливаете функцию равной нулю. Это дает вам 0 = x ² –4. Добавьте 4 с обеих сторон, чтобы изолировать переменную, что дает вам 4 = x ² (или x ² = 4, если вы предпочитаете писать в стандартной форме).Отсюда извлекаем квадратный корень из обеих частей, в результате получаем x = √4.

Проблема в том, что и 2, и -2 дают вам 4 в квадрате. Если вы укажете только один из них как ноль функции, вы проигнорируете законный ответ. Это означает, что вы должны указать оба нуля функции. В данном случае это x = 2 и x = -2. Однако не все полиномиальные функции имеют нули, которые так точно совпадают; более сложные полиномиальные функции могут дать существенно разные ответы.

Действительный ноль функции

А

настоящий ноль

из

функция

это

настоящий номер

что делает значение функции равным нулю.

Настоящее число,

р

, является нулем функции

ж

, если

ж

(

р

)

знак равно

0

.

Пример:

ж

(

Икс

)

знак равно

Икс

2

—

3

Икс

+

2

Находить

Икс

такой, что

ж

(

Икс

)

знак равно

0

.

0

знак равно

Икс

2

—

3

Икс

+

2

0

знак равно

(

Икс

—

2

)

(

Икс

—

1

)

Икс

знак равно

2

или же

Икс

знак равно

1

ж

(

2

)

знак равно

2

2

—

3

(

2

)

+

2

знак равно

0

ж

(

1

)

знак равно

1

2

—

3

(

1

)

+

2

знак равно

0

С

ж

(

2

)

знак равно

0

а также

ж

(

1

)

знак равно

0

, оба

2

а также

1

находятся

настоящие нули

функции.

Нахождение нулей функций — Видео и стенограмма урока

Что такое ноль функции?

Нуль функции — это значение x , которое при подключении к функции дает нулевое значение y . Он имеет другие имена, такие как x -перехват и корень функции. Если задана как упорядоченная пара, она всегда будет иметь номер в качестве координаты x , за которым следует 0 для координаты y .Например, (4,0), (-2,0) и (0,0) могут быть нулями некоторой функции. Графически ноль функции — это пересечение оси x и графика функции. У разных типов функций разное количество нулей. График некоторых функций не пересекает ось x и поэтому не имеет нулей (интервалы x ). Другие функции имеют одну или несколько. Найти эти нули — очень распространенная задача в алгебре.

Линейные и квадратичные функции

Линейные функции — это функции, которые можно представить в форме y = mx + b .Их графики всегда представляют собой линии. У линейных функций будет не более одного нуля. Нуль линейной функции можно найти, заменив y нулем и затем решив для x .

Квадратичные функции — это функции, которые можно представить в форме f ( x ) = ax 2 + bx + c , которая называется стандартной формой. Графически эти графики представляют собой параболы. Нули функции там, где f ( x ) = 0.Эти функции могут иметь 0, 1 или 2 действительных нуля. Существует несколько методов нахождения нулей квадратичной функции, включая свойство извлечения квадратного корня, разложение на множители, завершение квадрата и квадратную формулу. Из всех этих методов квадратичная формула является наиболее полезной, потому что она работает для всех квадратичных функций. Для этого необходимо определить значения a , b и c , а затем подставить эти значения в формулу корней квадратного уравнения.

Другие функции

Давайте посмотрим на пару других функций, которые существуют.

1. Многочлены высшего порядка

Для многочленов со степенью больше 2 поиск нулей становится намного сложнее. Существует небольшая вероятность того, что многочлен будет множителем. Вы также можете использовать теорему о рациональном корне , которая гласит, что если многочлен имеет рациональный корень (ноль), он будет существовать при значении x , так что x является одним из множителей постоянного члена, деленного на один из факторов коэффициента к ведущему члену.Обратите внимание, что это была большая IF — многочлен часто не имел рационального корня. Для полиномов более высокого порядка самый простой способ найти ноль — это использование графического калькулятора.

2. Экспоненциальные и логарифмические функции

Экспоненциальные функции будут иметь форму ab x . Если экспоненциальная функция соответствует этой форме и значение b не равно нулю; тогда у функции не будет нуля. График никогда не пересечет ось x .Расположение точки перехвата y будет (0, a ). Логарифмические функции — это функции, обратные экспоненциальным функциям. Если экспоненциальная функция имеет точку пересечения y в точке (0, a ), то ее обратная логарифмическая функция будет иметь точку пересечения x (ноль) в точке ( a , 0).

3. Рациональные функции

Наконец, рациональные функции — это функции в форме f ( x ) = p ( x ) / q ( x ), где p ( x ) и q ( x ) являются полиномами, а q ( x ) не может равняться нулю.Чтобы найти нуль рациональной функции, найдите нули p ( x ).

Использование графического калькулятора

Графический калькулятор можно использовать для нахождения действительных корней функций. Чтобы найти нули функции с помощью графического калькулятора, выполните следующие действия. Приведенные здесь указания относятся к графическим калькуляторам марки TI-83 и 84. Другие бренды будут выполнять те же операции с аналогичными кнопками.

1. Введите функцию в банк функций y = (верхняя левая кнопка).
2. Постройте график функции, используя кнопку «График» (верхняя правая кнопка).
3. Используйте стандартное окно 10 на 10, выбрав кнопку «Масштаб», а затем z-стандарт.
4. Если вы не видите пересечения графика и оси x , увеличивайте значения x -min и x -max, пока не увидите.
5. Как только вы окажетесь в поле зрения, выберите 2-й расчетный.
6. Выберите ноль.
7. На экране появится надпись «Граница слева»; переместите курсор влево от нуля и нажмите «Ввод».’
8. На экране появится надпись «Правая граница»; переместите курсор вправо от нуля и нажмите «Ввод».
9. На экране появится надпись «Угадай»; нажмите «Ввод».
10. Ваше значение x — это ваш ноль или корень.

Графический калькулятор не найдет ненастоящие корни.

Резюме урока

Хорошо, давайте на минутку рассмотрим, что мы узнали о нахождении нулей функции, при этом функция представляет собой процесс, который принимает один фрагмент данных (ввод), а затем выполняет определенные операции над входом и выдает выход.Как мы узнали, нахождение нуля функции означает нахождение точки ( a , 0), где пересекаются график функции и пересечение точки y . Чтобы найти значение a из точки ( a , 0), вам нужно установить функцию равной нулю, а затем решить для x . Это предполагает использование различных методов в зависимости от типа выполняемой вами функции. Мы рассмотрели следующие функции:

• Линейные функции , которые могут быть представлены в форме y = mx + b .
• Квадратичные функции , которые представляют собой функции, которые могут быть представлены в форме f ( x ) = ax 2 + bx + c , которая называется стандартной формой.
• Полиномы более высокого порядка, но с использованием теоремы о рациональном корне , которая гласит, что если многочлен имеет рациональный корень (ноль), то он будет существовать при значении x , так что x является одним из факторов постоянный член, деленный на один из множителей коэффициента к главному члену.
• Экспоненциальные функции , который имеет форму ab x .
• Логарифмические функции , функции, обратные экспоненциальным функциям.
• Рациональные функции , которые представляют собой функции в форме f ( x ) = p ( x ) / q ( x ), где p ( x ) и q ( x ) являются полиномами. и q ( x ) не может равняться нулю.

Мы также узнали, как можно найти нуль функции, построив график функции на графическом калькуляторе и затем выполнив поиск точки пересечения.

колледж алгебры обзоры

Определение: Рациональные функции — это функции, которые могут быть записаны как отношение двух многочленов. Вы можете вспомнить, что многочлен — это алгебраическое выражение, в котором показатели всех переменных являются целыми числами и никакие переменные не появляются в знаменателе.

Технически полином также является рациональной функцией, так же как целое число также является рациональным числом со знаменателем 1. Обычно мы говорим о неполиномиальных рациональных функциях ПОСЛЕ того, как мы обсудили полиномиальные функции, чтобы мы могли использовать некоторые из общих характеристики.

Что нужно знать о рациональных функциях?

По сути, вас попросят узнать шесть вещей о рациональных функциях.

(1) Знать определение и уметь распознавать его

(2) Найдите нули и точки пересечения по оси Y

(3) Сформулируйте вертикальные асимптоты

(4) Сформулируйте асимптоты конечного поведения (горизонтальные или наклонные)

(5) Уметь подготовить числовую строку для изменения знака и построить график функции

(6) Приведите несколько примеров того, где они могут быть использованы

Давайте рассмотрим каждый из этих шести пунктов.

(1) Знать определение рациональной функции и уметь распознавать его

Как было сказано ранее, рациональная функция — это функция, которую можно записать как отношение двух полиномов. Вот несколько примеров:

Разделите все общие множители между числителем и знаменателем, прежде чем находить нули или асимптоты или строить график функции. Если вы разделите общий множитель, вы также должны указать, что домен не включает число, которое сделало бы знаменатель равным нулю.Например,

(2) Найдите нули и точки пересечения по оси Y

ZEROS: При обсуждении полиномиальных функций нас часто интересовали нули функции. То есть мы хотели знать значения в Домене (вход) функции, которые сделали бы Диапазон (выход) равным нулю. На этом этапе графики функций обычно показывают область на горизонтальной оси — это означает, что нули будут отображаться как значения на горизонтальной оси, где график касается или пересекает.

Когда рациональная функция равна нулю (то есть ее выход равен нулю), то ее НОМЕР равен нулю. Итак, чтобы найти нули рациональной функции, мы просто находим нули ЧИСЛА.

ПРИМЕР: Нули функции h (x), описанной выше, можно найти, установив НОМЕР, равный нулю.

То есть 3x — 6 = 0

Ноль равен x = 2.

Можете ли вы определить нули для функций f (x) и g (x), описанных выше?
(ответ: 0 — это ноль функции f (x), а — 2 — ноль функции g (x))

ПЕРЕСЕЧЕНИЯ ПО Y: Точка, в которой график пересекает ось Y, называется пересечением по оси Y.В этой точке координата x всегда будет равна 0. Итак, чтобы найти точку пересечения оси y, вы просто замените x на 0.

ПРИМЕР: Пересечение оси y функции h (x), описанной выше, равно h (0) = -6/5.

Можете ли вы определить точки пересечения y = для f (x) и g (x), описанные выше?
(ответ: f (0) = 0 и g (0) = -8)

(3) Сформулируйте вертикальные асимптоты

Линия является асимптотой, если расстояние между кривой и линией приближается к нулю по мере того, как мы продвигаемся все дальше и дальше по линии.Можно сказать, что асимптота «моделирует» поведение кривой.

Когда вертикальная линия является асимптотой, график становится все ближе и ближе к вертикальной линии. График становится вертикальным, поэтому вертикальная линия представляет собой модель того, как выглядит график по мере приближения графика к линии.

Мы находим вертикальные асимптоты, устанавливая ЗНАЧИТЕЛЬ функции равным нулю. Но подождите, кричите вы (!), Знаменатель на самом деле не может быть равен нулю. Совершенно правильно и очень проницательно с вашей стороны замечать.Когда знаменатель функции приближается к нулю, величина диапазона (выхода) функции приближается к бесконечности, что и указывает вертикальная линия. График никогда не касается вертикальной линии, поэтому знаменатель никогда не бывает нулевым. В случае вертикальной асимптоты мы просто описываем линию, к которой график приближается, но никогда не касается.

Помните, что вы уже разделили все общие множители между числителем и знаменателем, прежде чем находить нули или асимптоты или строить график функции.Если вы разделите общий множитель, вы также должны указать, что домен не включает число, которое сделало бы знаменатель равным нулю.

ПРИМЕР: Вертикальную асимптоту функции h (x) = (3x-6) / (5 + 4x), описанной выше, можно найти, установив ДЕНОМИНАТОР равным нулю.

То есть 5 + 4x = 0

Вертикальная асимптота x = — 5/4

Можете ли вы определить вертикальные асимптоты для f (x) и g (x)?

Ответ: f (x) не имеет вертикальных асимптот, поскольку x ² + 6 не может равняться нулю
g (x) имеет вертикальные асимптоты x = 1 и x = — 1

(4) Сформулируйте асимптоты конечного поведения (горизонтальные или наклонные)

Как следует из названия, асимптоты конечного поведения моделируют поведение функции на левом и правом концах графика.Расстояние между кривой и линией приближается к нулю по мере того, как мы продвигаемся все дальше и дальше по линии.

Чем может быть полезна асимптота? Функция описывает отношения между двумя наборами, так что для каждого входа существует ровно один выход. График функции — это визуальное представление отношения, описанного правилом функции. В некоторых случаях правило, описывающее взаимосвязь функций, может быть довольно сложным и требовать много времени для оценки, но если существует линейная асимптота, то ее можно использовать для аппроксимации выходных данных функции без прохождения сложного определения функции.Это будет показано на примерах ниже.

Есть три ситуации, в которых у нас будут асимптоты линейного поведения конца.

(i.) Если степень числителя меньше степени знаменателя.

(ii.) Если степень числителя равна степени знаменателя.

(iii.) Если степень числителя на единицу больше степени знаменателя.

Несмотря на то, что в двух из этих трех случаев существуют короткие пути нахождения асимптоты конечного поведения, все они происходят из одной и той же процедуры.Сначала я кратко изложу процедуру, затем объясню, почему она работает, а затем приведу несколько примеров, основанных на функции, определенной в начале.

Найти асимптоту конечного поведения

Используйте длинное деление, чтобы разделить знаменатель на числитель, отбросьте остаток. Асимптота конечного поведения будет y = частное.

Почему это работает?

Рассмотрим функцию g (x) = (x ³ + 8) / (x ² — 1), определенную выше.

Используйте длинное деление, чтобы разделить (x ² — 1) на
(x ³ + 8).

Мы получаем частное от x и остаток от x + 8, и затем можем переписать
(x ³ + 8) / (x ² — 1) следующим образом.

Асимптота конечного поведения позволит нам аппроксимировать поведение функции на концах графика. То есть, когда x -> бесконечность или x -> — бесконечность.

Чтобы исследовать поведение функции (x ³ + 8) / (x ² — 1) , когда x стремится к бесконечности, мы можем вместо этого исследовать поведение правой части тождества выше, х + (х + 8) / (х ² — 1)

Значит, когда x -> бесконечность, мы имеем

Асимптота конечного поведения (уравнение, которое аппроксимирует поведение исходной функции на концах графика) будет просто y = частное.

В этом случае асимптота будет y = x (наклонная или наклонная линия).

Если бы мы хотели приблизиться к g (8000000000), мы могли бы сделать это с помощью асимптоты.

y = x приближает значение y = g (x). Когда x = 8000000000, y = x, поэтому y = 8000000000.

г (8000000000) = 8000000000 (приблизительно).

ПРИМЕР: В этом примере давайте воспользуемся функцией h (x) = (3x — 6) / (5 + 4x), описанной выше.Разделить ЗНАЧИТЕЛЬ (4x + 5) делится на ЗНАЧИТЕЛЬ (3x — 6).

Частное 3/4, остаток -39/4. Отбросьте остаток.

Асимптота конечного поведения y = 3/4. (горизонтальная линия).

Вот набросок графика

горизонтальная асимптота — черная горизонтальная линия
вертикальная асимптота — розовая вертикальная линия

Обратите внимание, что горизонтальная линия y = 3/4 приближается к форме графика на левом и правом концах кривой, в то время как кривая становится довольно вертикальной, когда x приближается к -5/4 (мы говорим, что вертикальная линия x = — 5/4 моделирует форму графика, когда x приближается к 2).

Если бы мы хотели аппроксимировать h (-555555555), мы могли бы сделать это с помощью вертикальной асимптоты.

y = 3/4 аппроксимирует значение y = h (x), когда значения x приближаются к бесконечности. Когда x = -555555555, y = 3/4, поэтому h (-555555555) = 3/4

ПРИМЕР: В этом примере давайте воспользуемся функцией f (x) = 3x / (6 + x ² ), как описано выше.

Еще раз, чтобы найти асимптоту конечного поведения, мы разделим знаменатель (6 + x ² ) на числитель 3x.

Поскольку знаменатель имеет степень БОЛЬШУ, чем степень числителя, знаменатель разделится на числитель 0 раз. То есть частное будет равно нулю.

Конечная асимптота поведения будет y = 0. Это всегда будет иметь место, когда степень знаменателя больше степени числителя.

5) Уметь подготовить числовую линию смены знака и построить график функции

Используйте методы, описанные в методе «точка / крест» для решения неравенства, чтобы нарисовать числовую линию смены знака для рациональной функции. На интервалах, где числовая линия смены знака равна +, график рациональной функции будет находиться над осью абсцисс. На интервалах, где идет числовая линия смены знака — график будет ниже оси абсцисс.

ПРИМЕР: Для функции h (x) числовая строка изменения знака будет выглядеть так:

Из числовой строки смены знака можно сделать вывод, что

• h (x)> 0, когда x <- 5/4 или x> 2 ——>, поэтому график будет выше горизонтальной оси
• h (x) <0, когда x находится в интервале (- 5/4, 2) ----->, поэтому график будет ниже горизонтальной оси

Посмотрите на график на графическом калькуляторе (или посмотрите на график функции, показанной выше), чтобы убедиться, что это так.

(6.) Приведите несколько примеров использования рациональных функций.

Сходите в библиотеку и посмотрите видеосюжет «Алгебра колледжа: простыми словами № 17». Вы можете проверить это или посмотреть в библиотеке — это всего около 27 минут. В этом видео не только рассматриваются некоторые из перечисленных здесь шагов, но и приводятся некоторые примеры рациональных функций, используемых для моделирования событий.

© 1999 Джо Стейг

Нахождение нулей многочлена из графа

Нули многочлена — это решения уравнения p (x) = 0, где p (x) представляет собой многочлен.Если мы изобразим этот многочлен как y = p (x), то вы увидите, что это значения x, где y = 0. Другими словами, это точки пересечения с x на графике.

Нули полинома можно найти, определив, где график полинома пересекает или касается оси x.

объявление

Давайте попробуем это на примере!

Пример

Рассмотрим многочлен f (x), который изображен ниже. Какие нули у этого многочлена?

Чтобы ответить на этот вопрос, вы хотите найти точки пересечения по оси x.Чтобы найти их, посмотрите, где график проходит через ось x (горизонтальная ось).

Это показывает, что нули полинома: x = –4, 0, 3 и 7.

Хотя здесь все нули были представлены графиком, фактически пересекающим ось x, это не всегда так. Рассмотрим следующий пример, чтобы увидеть, как это может работать.

Пример

Найдите нули полинома, изображенного ниже.

Как и раньше, ищем x-перехватчики.Но это любые значения, где y = 0, и поэтому возможно, что график просто касается оси x в точке пересечения с x. Вот в чем дело!

Отсюда видно, что функция имеет ровно один ноль: x = –1.

Связь с факторами

Возможно, вы помните, что решение уравнения типа f (x) = (x — 5) (x + 1) = 0 приведет к ответам x = 5 и x = –1. Это алгебраический способ найти нули функции f (x). Каждый из нулей соответствует коэффициенту: x = 5 соответствует коэффициенту (x — 5), а x = –1 соответствует коэффициенту (x + 1).

Итак, если мы вернемся к самому первому примеру многочлена, нули были: x = –4, 0, 3, 7. Это говорит нам, что у нас есть следующие множители:

(x + 4), x, (x — 3), (x –7)

Однако без дополнительного анализа мы не можем сказать ничего большего. Например, обе следующие функции будут иметь следующие коэффициенты:

f (x) = 2x (x + 4) (x – 3) (x – 7)

и

г (x) = x (x + 4) (x – 3) (x – 7)

Во втором примере единственный ноль был x = –1.Итак, только по нулям мы знаем, что (x + 1) является множителем. Если вы много изучили алгебру, вы поймете, что график является параболой и имеет форму, где a> 0. Но только знание нуля не даст вам этой информации *.

* вы действительно можете сказать по графику И нулю. Поскольку график не пересекает ось x (только касается ее), вы можете определить, что степень на множителе четная. Но это немного выходит за рамки того, что мы пытаемся узнать в этом руководстве!

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Свойство нулевого продукта

«Свойство нулевого продукта» говорит, что:

Если a × b = 0, то a = 0 или b = 0
(или оба a = 0 и b = 0)

Это может помочь нам решить уравнения:

Пример: Решить (x − 5) (x − 3) = 0

«Свойство нулевого продукта» говорит:

Если (x − 5) (x − 3) = 0, то (x − 5) = 0 или (x − 3) = 0

Теперь мы просто решаем каждую из них:

Для (x − 5) = 0 получаем x = 5

Для (x − 3) = 0 получаем x = 3

И решения:

x = 5 или x = 3

Вот оно на графике:

y = 0, когда x = 3 или x = 5

Стандартная форма уравнения

Иногда мы можем решить уравнение, поместив его в стандартную форму, а затем используя свойство нулевого продукта:

«Стандартная форма» уравнения:

(некоторое выражение) = 0

Другими словами, «= 0» находится справа, а все остальное — слева.

Пример: поместите x

² = 7 в стандартную форму

Ответ:

x ² — 7 = 0

Стандартная форма и свойство нулевого продукта

Итак, давайте попробуем:

Пример: Решить 5 (x + 3) = 5x (x + 3)

Заманчиво разделить на (x + 3), но это деление на ноль, когда x = −3

Таким образом, вместо этого мы можем использовать «Стандартную форму»:

5 (x + 3) — 5x (x + 3) = 0

Что можно упростить до:

(5−5x) (x + 3) = 0

5 (1-х) (х + 3) = 0

Тогда «Свойство нулевого продукта» говорит:

(1 − x) = 0 или (x + 3) = 0

И решения:

x = 1 , или x = −3

И еще пример:

Пример: решить

x ³ = 25x

Заманчиво разделить на x, но это деление на ноль, когда x = 0

Итак, давайте использовать стандартную форму и свойство нулевого продукта.

Перенести все в левую сторону:

x ³ — 25x = 0

Выносим за скобки:

х (х ² -25) = 0

x ² -25 — это разница квадратов и может быть разложена на (x — 5) (x + 5):

х (х — 5) (х + 5) = 0

Теперь мы видим три возможных варианта, по которым он может оказаться нулевым:

x = 0 , или x = 5 , или x = −5

.