Квадратное уравнение где дискриминант равен 0. Нахождение дискриминанта, формула, сравнение с нулём

Квадратное уравнение это уравнение которое выглядит как ax 2 + dx + c = 0
. В нем значение а,в
и с
любые числа, при этом а
не равно нулю.

Все квадратные уравнения разделяются на несколько видов, а именно:

Уравнения в которых только один корень.
-Уравнения с двумя разными корнями.
-Уравнения в которых корней нет совсем.

Это и различает линейные уравнения в которых корень всегда единый, от квадратных. Для того что бы понять какое количество корней в выражении и нужен Дискриминант квадратного уравнения
.

Допустим наше уравнение ax 2 + dx + c =0. Значит дискриминант квадратного уравнения
—

D = b 2 — 4 ac

И это нужно запомнить навсегда. С помощью этого уравнения мы и определяем количество корней в квадратном уравнении. И делаем мы это следующим образом:

Когда D меньше нуля, в уравнении нет корней.
— Когда D равно нулю, имеется только один корень.
— Когда D больше нуля, соответственно, в уравнении два корня.
Запомните что дискриминант показывает сколько корней в уравнении, не меняя знаков.

Рассмотрим для наглядности:

Нужно выяснить какое количество корней в данном квадратном уравнении.

1) х 2 — 8х + 12 = 0
2)5х 2 + 3х + 7 = 0
3) х 2 -6х + 9 = 0

Вписываем значения в первое уравнение, находим дискриминант.
а = 1, b = -8, c = 12
D = (-8) 2 — 4 * 1 * 12 = 64 — 48 = 16
Дискриминант со знаком плюс, значит в данном равенстве два корня.

Делаем тоже самое со вторым уравнением
a = 1, b = 3, c = 7
D = 3 2 — 4 * 5 * 7 = 9 — 140 = — 131
Значение минусовое, значит корней в данном равенстве нет.

Следующее уравнение разложим по аналогии.
а = 1, b = -6, с = 9
D = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0
как следствие имеем один корень в уравнении.

Важно что в каждом уравнении мы выписывали коэффициенты. Конечно это не много длительный процесс, но это помогло нам не запутаться и предотвратило появление ошибок. Если очень часто решать подобные уравнения, то вычисления сможете производить мысленно и заранее знать сколько у уравнения корней.

Рассмотрим еще один пример:

1) х 2 — 2х — 3 = 0
2) 15 — 2х — х 2 = 0
3) х 2 + 12х + 36 = 0

Раскладываем первое
а = 1, b = -2, с = -3
D =(-2) 2 — 4 * 1 * (-3) = 16, что больше нуля, значит два корня, выведем их
х 1 = 2+?16/2 * 1 = 3, х 2 = 2-?16/2 * 1 = -1.

Раскладываем второе
а = -1, b = -2, с = 15
D = (-2) 2 — 4 * 4 * (-1) * 15 = 64, что больше нуля и так же имеет два корня. Выведем их:
х 1 = 2+?64/2 * (-1) = -5, х 2 = 2-?64/2 *(-1) = 3.

Раскладываем третье
а = 1, b = 12, с = 36
D = 12 2 — 4 * 1 * 36 =0, что равно нулю и имеет один корень
х = -12 + ?0/2 * 1 = -6.
Решать данные уравнения не сложно.

Если нам дано неполное квадратное уравнение. Такое как

1х 2 + 9х = 0
2х 2 — 16 = 0

Данные уравнения отличаются от тех что были выше, так как оно не полное, в нем нет третьего значения. Но не смотря на это оно проще чем полное квадратное уравнение и в нем дискриминант искать не нужно.

Что делать когда срочно нужна дипломная работа или реферат, а времени на его написание нет? Всё это и многое другое можно заказать на сайте Deeplom.by (http://deeplom.by/) и получить высший балл.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.

Дискриминант

Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D
   = 0, есть ровно один корень;
3. Если D
   > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x
   2 − 8x
   + 12 = 0;
2. 5x
   2 + 3x
   + 7 = 0;
3. x
   2 − 6x
   + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x
   2 − 2x
   − 3 = 0;
2. 15 − 2x
   − x
   2 = 0;
3. x
   2 + 12x
   + 36 = 0.

Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.

D
> 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.

D
> 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x
   2 + 9x
   = 0;
2. x
   2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0.

Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax
   2 + c
   = 0 выполнено неравенство (−c
   /a
   ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c
   /a
   )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x
   2 − 7x
   = 0;
2. 5x
   2 + 30 = 0;
3. 4x
   2 − 9 = 0.

x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.

5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.

Квадратное уравнение – решается просто! *Далее в тексте «КУ».
Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше.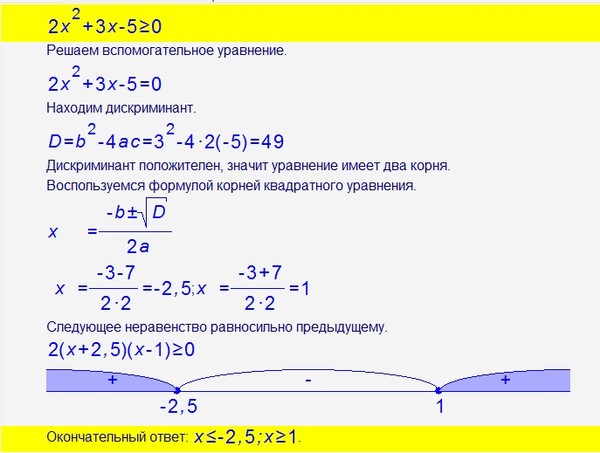 Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим!
Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a,
b
и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

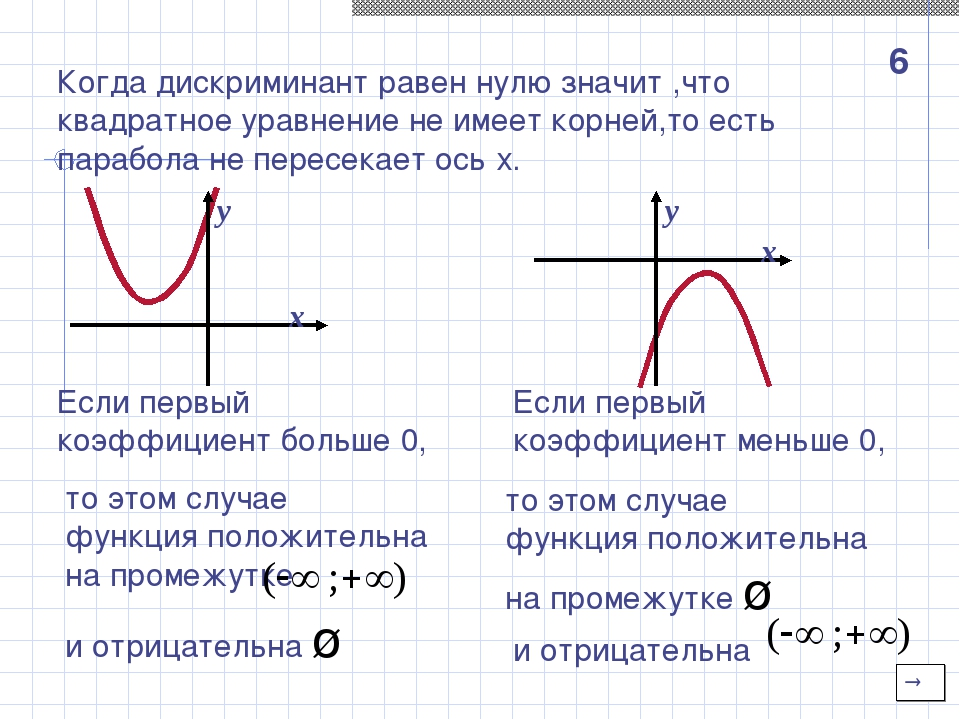
Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1:
Решить 2x
2
+8
x
–192=0

а=2 b=8 c= –192

D = b
2
–4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2:
Решить

x 2
–22
x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3:
Решить

x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi

– это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а
x
2
+
bx
+
c
=0
выполняется равенство

a
+
b
+ с = 0,
то

— если для коэффициентов уравнения а
x
2
+
bx
+
c
=0
выполняется равенство

a
+ с =
b
,
то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001
x
2
–4995
x
– 6=0

Сумма коэффициентов равна 5001+(–
4995)+(–
6) = 0, значит

Пример 2: 2501
x
2
+2507
x
+6=0

Выполняется равенство a
+ с =
b
,
значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.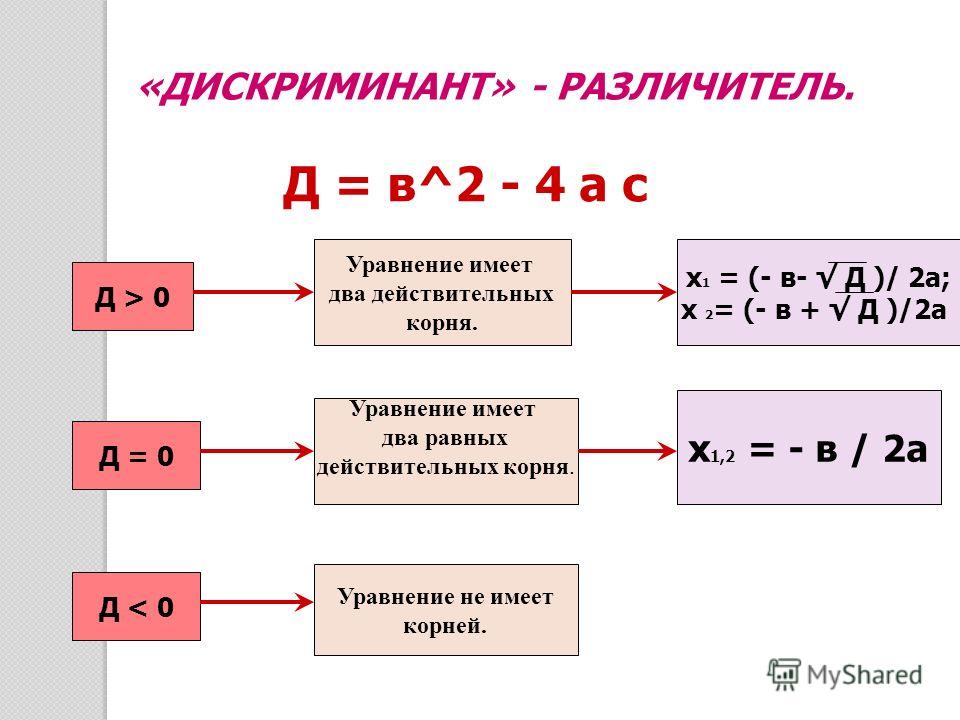

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении
ax 2
+ bx
–
c = 0
коэффициент «b»

равен (a 2

– 1), а коэффициент «c»

численно равен коэффициенту «a»
,
то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а
± b+c
≠ 0, то используется прием переброски, например:

2х
2 – 11х+
5 = 0 (1) => х
2 – 11х+
10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1
= 5 х 2
=
0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.

Предлагаю вам подробный алгоритм решения неравенств методом интервалов
, следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств
.

Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i
2 = — 1.

Вместе с тем

(- i

) 2 = (- 1 i

) 2 = (- 1) 2 i

2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i

и — i

. Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi

равен — 1. Тогда

(а + bi

) 2 = — 1,

а
2 + 2аbi

— b

2 = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а

и b

должно равняться нулю. Если b

= 0, то из первого уравнения получается а

2 = — 1. Число а

действительное, и поэтому а

2 >
0. Неотрицательное число а

2 не может равняться отрицательному числу — 1. Поэтому равенство b

= 0 в данном случае невозможно. Остается признать, что а

= 0, но тогда из первого уравнения системы получаем: —b

2 = — 1, b

= ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i

и —i

, Условно это записывается в виде:

√-1 = ± i

.

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а

. Такими числами являются √ai

и -√ai

. Условно это записывается так:

√— а

= ± √ai

.

Под √a

здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i

, √-9= ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x

2 + 2х

+ 5 = 0; тогда

х
1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i

.

Итак, данное уравнение имеет два корня: х

1 = — 1 +2i

, х

2 = — 1 — 2i

. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Понятие комплексного числа

Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
   a = b и c = d .
2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число
   a + c + i (b + d).
3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число
   ac – bd + i (ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,

№ 4 .1.
В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множествавещественных чисел или множества комплексных чисел .

График функции

Фрагмент графика функции

Способы задания функции

[править]Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

[править]Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

[править]Графический способ

Осциллограмма задаёт значение некоторой функции графически.

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

[править]Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

• факториал;
• числа Фибоначчи;
• функция Аккермана.

[править]Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

• функция, возвращающая цифру в записи числа пи по её номеру;
• функция, возвращающая число атомов во вселенной в определённый момент времени;
• функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида , где . 

— коэффициент при  , или старший коэффициент.

— коэффициент при х, или второй коэффициент.

— свободный член.

Например, в уравнении   , , .

B уравнении   , ,

Если в квадратном уравнении  или  , то такое квадратное уравнение называется НЕПОЛНЫМ.

Неполное квадратное уравнение решается с помощью разложения на множители.

1. Если , то нужно вынести за скобки общий множитель.

Например,

Приравняем каждый множитель к нулю:

или

Ответ: {0,  }

2. Если , то нужно разложить на множители по формуле разности квадратов:

Например:

Приравниваем каждый множитель  к нулю, получаем:

или 

Коротко это уравнение решается так:

В этом месте важно не забыть знак  перед корнем!

Ответ: {}

Если  в квадратном уравнении  и  , то такое квадратное уравнение называется ПОЛНЫМ.

Полное квадратное уравнение решается с помощью нахождения ДИСКРИМИНТА.

Дискриминант квадратного уравнения  вычисляется по формуле:

.

Формулы для вычисления корней квадратного уравнения выглядят так:

В этих формулах дискриминант присутствует под знаком квадратного корня, поэтому

Eсли , то квадратное уравнение не имеет действительных корней.

Если , то квадратное уравнение имеет два различных действительных корня, которые можно найти по приведенным выше формулам.

Если ,  то квадратное уравнение имеет два совпадающих корня:

.

Иногда  говорят, что в этом случае квадратное уравнение имеет один корень.

Итак, при решении квадратного уравнения удобно пользоваться таким алгоритмом:

1. Определяем, является ли квадратное уравнение полным, или неполным.

2. Если уравнение неполное, раскладываем левую часть на множители и приравниваем каждый множитель к нулю.

3. Если уравнение полное, то

• находим дискриминант квадратного уравнения по формуле
• если дискриминант меньше нуля, то записываем, что квадратное уравнение не имеет действительных корней
• если дискриминант равен нулю, то находим корни квадратного уравнения по формуле 
• если дискриминант больше нуля, то находим корни квадратого уравнения по формулам:, 

Если коэффициент   квадратного уравнения — четное число, то есть его можно записать как , или  то для нахождения корней квадратного уравнения удобно пользоваться формулами для четного второго коэффициента:

Два полезных замечания:

1. Если для коэффициентов квадратного уравнения  выполняется равенство , то , 

2. Если для коэффициентов квадратного уравнения  выполняется равенство , то , 

Эти свойства помогают устно решать некоторые громоздкие квадратные уравнения. Например, в квадратном уравнении  сумма коэффициентов равна 0, поэтому ,  .

В уравнении выполняется равенство , поэтому ,  

Рассмотрим несколько примеров.

Решим квадратные уравнения:

1.

а) найдем дискриминант этого уравнения:

Дискриминант больше нуля, значит уравнение имеет два различных корня.

б) Тогда: , 

Ответ:   {1; 1/2}

2.  

а) Найдем дискриминант этого уравнения:

. Очевидно, что  , и даже нет необходимости вычислять его точное значение.

Ответ: уравнение не имеет действительных корней.

3. 

а) Найдем дискриминант этого уравнения:

б) Так как , уравнение имеет два совпадающих корня,

Если внимательно посмотреть на квадратный трехчлен, стоящий в левой части уравнения, то становится очевидно, то что его можно преобразовать по формуле квадрата разности к выражению

, отсюда 

Ответ: 1/4.{2}+px+q=0,\quad p={\frac {b}{a}},\quad q={\frac {c}{a}}.}

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на пример — и сами все поймете:

Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;                                                                      Выпишем коэффициенты для первого уравнения и найдем дискриминант:

   a = 1, b = −8, c = 12;
   D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

   Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. 

2.                 Корни квадратных уравнений

3. Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

   Основная формула корней квадратного уравнения

   Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

4.                   Неполные квадратные уравнение

   Бывает, что квадратное уравнение несколько отличается от того, что дано в определении.2-bx=0     x(ax-b)=0   x1=0   ax-b=0    ax=b     x2=b:a

5. Вынесение общего множителя за скобку. Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни.
6. Задания для отработки квадратных уравнений:тренировочные задания по квадратным уравнениям

Как решается через дискриминант. Решение квадратных уравнений

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D=0: у уравнения всего один корень, и он является действительным числом.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

», то есть
уравнения первой степени. В этом уроке мы разберем, что называют квадратным
уравнением
и как его решать.

Что называют квадратным уравнением

Важно!

Степень уравнения определяют по наибольшей
степени, в которой
стоит неизвестное.

Если максимальная степень, в которой стоит неизвестное — «2
»,
значит, перед вами квадратное
уравнение.

Примеры квадратных уравнений

• 5x 2 − 14x + 17 = 0
• −x 2 + x + = 0
• x 2 + 0,25x = 0
• x 2 − 8 = 0

Важно!

Общий вид квадратного уравнения выглядит так:

A
x 2 + b
x + c
= 0

«a
», «b
» и «c
» — заданные числа.

• «a
  » — первый или старший коэффициент;
• «b
  » — второй коэффициент;
• «c
  » — свободный член.

Чтобы найти «a
», «b
» и «c
»
нужно сравнить свое уравнение с общим видом квадратного уравнения
«ax 2 + bx + c = 0
».

Давайте потренируемся определять
коэффициенты «a
», «b
»
и «c
» в квадратных уравнениях.

5x 2 − 14x + 17 = 0

−7x 2 − 13x + 8 = 0

−x 2 + x + = 0

x 2 + 0,25x = 0

Уравнение	Коэффициенты
a = −7 b = −13 с = 8
x 2 − 8 = 0

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная
формула для нахождения корней
.

Запомните!

Чтобы решить квадратное уравнение нужно:

• привести квадратное уравнение к общему виду «ax 2 + bx + c = 0
  ».
  То есть в правой части должен остаться только «0
  »;
• использовать формулу для корней:

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

X 2 − 3x − 4 = 0

Уравнение «
x 2 − 3x − 4 = 0
» уже приведено к общему виду «ax 2 + bx + c = 0
» и не требует дополнительных упрощений.
Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения
.

Определим коэффициенты «a
», «b
» и
«c
» для этого уравнения.

x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =

С её помощью решается любое
квадратное уравнение.

В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».

Рассмотрим другой пример квадратного уравнения.

x 2 + 9 + x = 7x

В данном виде определить коэффициенты «a
», «b
» и
«c
» довольно сложно.
Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0
».

X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0

Теперь можно использовать формулу для корней.

X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =

x = 3

Ответ: x = 3

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0
, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2
– 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2

+ х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет
.

Решить уравнение 2х 2

+ 5х – 7 = 0
.

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1
.

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2


+ bx + c,
иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2



, затем с меньшим –
bx
, а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2



равен единице и уравнение примет вид х 2 + px + q = 0
. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а
, стоящий при х 2



.

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2



+ 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3
. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

Квадратное уравнение где дискриминант равен 0. Решение квадратных уравнений с помощью дискриминанта

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

x=0 или 8х — 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X 2 — 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D

О корнях и их формуле

В нашем случае дискриминант равен: 256 — 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0

Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x 2 + 21x — 54 = 0

Для простоты преобразуем выражение:

x 2 + 7x — 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.

Библиографическое описание:
Гасанов А. Р., Курамшин А. А., Ельков А. А., Шильненков Н. В., Уланов Д. Д., Шмелева О. В. Способы решения квадратных уравнений // Юный ученый. — 2016. — №6.1. — С. 17-20..03.2019).



Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.

Что же такое «квадратные уравнения»?

Квадратное уравнение
— уравнение вида ax
2
+ bx + c = 0
, где a
, b
, c
— некоторые числа (a ≠ 0
), x
— неизвестное.

Числа a, b,c называются коэффициентами квадратного уравнения.

• a называется первым коэффициентом;
• b называется вторым коэффициентом;
• c — свободным членом.

А кто же первый «изобрёл» квадратные уравнения?

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Вавилонские математики примерно с IV века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта
(Индия, VII столетие нашей эры).

Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax2 + bх = с, а>0

В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

В алгебраическом трактате Аль-Хорезми
дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах2 = bх.

2) «Квадраты равны числу», т. е. ах2 = с.

3) «Корни равны числу», т. е. ах2 = с.

4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах2.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи
. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли
среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона
и других ученых способ решения квадратных уравнений принимает современный вид.

Рассмотрим несколько способов решения квадратных уравнений.

Стандартные способы решения квадратных уравнений из школьной программы:

1. Разложение левой части уравнения на множители.
   
   
2. Метод выделения полного квадрата.
   
   
3. Решение квадратных уравнений по формуле.
   
   
4. Графическое решение квадратного уравнения.
   
   
5. Решение уравнений с использованием теоремы Виета.
   
   

Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.

Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.

Пример.
x
2
-5x+6=0

Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.

Ответ: x
1
=2, x
2
=3.

Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.

Пример.
3x
2
+2x-5=0

Берём первый коэффициент и умножаем его на свободный член: x 2 +2x-15=0

Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.

Ответ: x
1
=-5/3, x
2
=1

6. Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение ах 2 + bх + с = 0, где а≠0.

Умножая обе его части на а, получаем уравнение а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у 2 + by + ас = 0, равносильному данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.

Окончательно получаем х 1 = у 1 /а и х 2 = у 2 /а.

При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример.
2х
2
— 11х + 15 = 0.

«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у 2 — 11у + 30 = 0.

Согласно обратной теореме Виета

у 1 = 5, х 1 = 5/2, х 1 =2,5 ;у 2 = 6, x 2 = 6/2, x 2 = 3.

Ответ: х
1
=2,5; х
2
= 3.

7. Свойства коэффициентов квадратного уравнения.

Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.

1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1.

2. Если а — b + с = 0, или b = а + с, то х 1 = — 1.

Пример.
345х
2
— 137х — 208 = 0.

Так как а + b + с = 0 (345 — 137 — 208 = 0), то х 1 = 1, х 2 = -208/345.

Ответ: х
1
=1; х
2
= -208/345
.

Пример.
132х
2
+ 247х + 115 = 0

Т.к. a-b+с = 0 (132 — 247 +115=0), то х 1 = — 1, х 2 = — 115/132

Ответ: х
1
= — 1; х
2
=- 115/132

Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.

8. Решение квадратных уравнений с помощью номограммы.

Рис 1. Номограмма

Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0
. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис. 1):

Полагая ОС = р, ED = q, ОЕ = а
(все в см), из рис.1 подобия треугольников САН
и CDF
получим пропорцию

откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0,
причем буква z
означает метку любой точки криволинейной шкалы.

Рис. 2 Решение квадратных уравнения с помощью номограммы

Примеры.

1) Для уравнения z
2
— 9z + 8 = 0
номограмма дает корни z 1 = 8,0 и z 2 = 1,0

Ответ:8,0; 1,0.

2) Решим с помощью номограммы уравнение

2z
2
— 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение z 2 — 4,5z + 1 = 0.

Номограмма дает корни z 1 = 4 и z 2 = 0,5.

Ответ: 4; 0,5.

9. Геометрический способ решения квадратных уравнений.

Пример.
х
2
+ 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».

Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25

Рис. 3 Графический способ решения уравнения х 2 + 10х = 39

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

10. Решение уравнений с использованием теоремы Безу.

Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т.е. значению P(x) при x = α).

Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.

Пример.
х²-4х+3=0

Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3

х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0

х-1=0; х=1, или х-3=0, х=3; Ответ: х
1
=2, х
2
=3.

Вывод:
Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.

Литература:

1. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
2. Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
3. https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
4. Глейзер Г.И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодшего. — М.: Просвещение, 1964.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант
.

Дискриминант

Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D
   = 0, есть ровно один корень;
3. Если D
   > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x
   2 − 8x
   + 12 = 0;
2. 5x
   2 + 3x
   + 7 = 0;
3. x
   2 − 6x
   + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x
   2 − 2x
   − 3 = 0;
2. 15 − 2x
   − x
   2 = 0;
3. x
   2 + 12x
   + 36 = 0.

Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.

D
> 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.

D
> 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x
   2 + 9x
   = 0;
2. x
   2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0.

Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax
   2 + c
   = 0 выполнено неравенство (−c
   /a
   ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c
   /a
   )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x
   2 − 7x
   = 0;
2. 5x
   2 + 30 = 0;
3. 4x
   2 − 9 = 0.

x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.

5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5.

КОМПЛЕКСНЫЕ ЧИСЛА XI § 253. Извлечение корней квадратных из отрицательных чисел. Решение квадратных уравнений с отрицательными дискриминантами Как мы знаем, i 2 = — 1. Вместе с тем (- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1. Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1? Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда (а + bi ) 2 = — 1, а 2 + 2аbi — b 2 = — 1 Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому { а 2 — b 2 = — 1 ab = 0 (1) Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: — b 2 = — 1, b = ± 1. Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i и —i , Условно это записывается в виде: √-1 = ± i . Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а . Такими числами являются √a i и -√a i . Условно это записывается так: √— а = ± √a i . Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому √-4 = + 2i , √-9 = ± 3i Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда х 1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i . Итак, данное уравнение имеет два корня: х 1 = — 1 +2i , х 2 = — 1 — 2i . Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета. Упражнения 2022. (У с т н о.) Решить уравнения: а) x 2 = — 16; б) x 2 = — 2; в) 3x 2 = — 5. 2023. Найти все комплексные числа, квадраты которых равны: а) i ; б) 1 / 2 — √ 3 / 2 i ; 2024. Решить квадратные уравнения: а) x 2 — 2x + 2 = 0; б) 4x 2 + 4x + 5 = 0; в) x 2 — 14x + 74 = 0. Решить системы уравнений (№ 2025, 2026): 2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными. 2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом. 2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются: a) х 1 = 5 — i , х 2 = 5 + i ; б) х 1 = 3i , х 2 = — 3i . 2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i ) (2i — 4). 2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 — i 1- 3i .

Дискриминант квадратного уравнения и его геометрический смысл

Одна из немногих формул, которую удается выучить к концу девятого класса практически всем ученикам, это формула нахождения дискриминанта и формулы корней квадратного уравнения.2-4ac, которое и называют дискриминантом. Пример из учебника алгебры Бевз Г.П. (2016 год):

Обосновывается это название следующим образом:

Если D < 0, то данное уравнение не имеет корней — ведь невозможно, чтобы квадрат некоторого вещественного выражения был отрицательным числом.

Если D = 0, то данное уравнение имеет один корень — ведь только квадрат нуля равен нулю.

Если D > 0, то данное уравнение имеет два корня.

В результате ученик вынужден заучивать не только формулы нахождения корней квадратного уравнения, но и эти три утверждения — взаимосвязь дискриминанта с количеством корней.

На мой взгляд, методически правильнее сначала довести разбор понятия «дискриминант» до логического конца, указав, что дискриминант равен квадрату расстояния между корнями уравнения. 

Рассмотрим для простоты приведенное квадратного уравнение (напомню, что любое квадратное уравнение легко привести к приведенному виду, разделив все коэффициенты на старший коэффициент). Итак, с учетом теоремы Виета:

Таким образом, если корни приведенного квадратного уравнения существуют, то расстояние между ними равно корню из дискриминанта. 

Грубо говоря, чем больше дискриминант, тем больше расстояние между корнями. Вот что показывает дискриминант — насколько далеки корни друг от друга, если они существуют. А связь с количеством корней — это всего лишь следствие этого простого факта.

Теперь взаимосвязь между дискриминантом и количеством корней ясна как на ладони: если дискриминант равен нулю, то расстояние между корнями равно нулю, они совпадают — два корня, образно говоря, наложились друг на друга и превратились в один корень. Далее, расстояние не может быть меньше нуля, а значит, при отрицательном дискриминанте корней нет. Если же дискриминант строго положителен, то корней два и расстояние между ними как раз и равно корню из дискриминанта.

Эти выводы интуитивно понятны и не требуют отдельного заучивания. Более того, понимание геометрического смысла дискриминанта помогает упростить и ускорить нахождение самих корней.

Начинающий ученик действует обычно по следующей схеме:

1) определяет коэффициенты уравнения;

2) записывает формулу дискриминанта, подставляет в нее значения коэффициентов, вычисляет значение;

3) извлекает квадратный корень из дискриминанта;

4) записывает формулу корней и поочередно вычисляет каждый из них.

Шаг 4 можно упростить, найдя меньший корень и затем для нахождения большего корня останется только прибавить корень из дискриминанта — а он у нас уже посчитан на шаге 3. 

(В случае неприведенного квадратного уравнения нужно не забыть корень из дискриминанта разделить на старший коэффициент).

Вывод. Знание геометрического смысла дискриминанта квадратного уравнения позволяет ученикам получить наглядное представление о взаимосвязи корней и коэффициентов уравнения, упростить расчеты, уменьшить объем заучиваемой информации.

Редакція не несе відповідальності за наповнення блогів, вони є персональною думкою автора

Страница не найдена — Fandroid.info

2 294

[:ru] Перевод документации официального сайта developer.android.com LinearLayout представляет собой view group, которая выравнивает все

5 738

В этом уроке вы увидите, как сделать простейший браузер, который отобразит страницу в интернете

4 138

Библиотека поддержки  Android Design Support Library облегчает разработку, обеспечивая обратную совместимость множества компонентов в материальном стиле, вплоть

3 509

Продолжаем изучать Android Data Binding. На прошлом уроке мы просто отобразили статичные данные пользователю, но возможности

550

Виктория Сулейманова из Rambler поделится опытом тестирования RxJava. За последний год реактивное программирование прочно

1 018

В этом уроке узнаем, какие ресурсы (файлы музыки, изображений или xml файлы) может использовать

Дискриминанты и определение числа действительных корней квадратного уравнения

Что такое дискриминант?

Дискриминант — это величина, вычисляемая по квадратному уравнению. Он использует его, чтобы «различать» корни (или решения) квадратного уравнения.

Квадратное уравнение имеет вид: ax ² + bx + c

Дискриминант, D = b ² — 4ac

Примечание. Это выражение внутри квадратного корня квадратной формулы

.

Дискриминант бывает в трех случаях;

Корпус 1:

b ² — 4ac> 0

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных (разных) корня .

Пример

х ² — 5х + 2 = 0

а = 1, б = -5, в = 2

Дискриминант, D = b ² — 4ac

= (-5) ² — 4 * (1) * (2)

= 17

Следовательно, квадратное уравнение

имеет два действительных различных корня.

х ² — 5х + 2.

Корпус 2:

b ² — 4ac <0

Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет действительных корней .

Пример

3x ² + 2x + 1 = 0

а = 3, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ^{2 —} 4 * (3) * (1)

= — 8

Следовательно, у квадратного уравнения 3x ² + 2x + 1 нет действительных корней.

Корпус 3:

b ² — 4ac = 0

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет два действительных идентичных корня .

Пример

х ² + 2х + 1 = 0

а = 1, б = 2, с = 1

Дискриминант, D = b ² — 4ac

= (2) ² — 4 * (1) * (1)

= 0

Следовательно, есть два действительных идентичных корня квадратного уравнения x ² + 2x + 1.

Сводка

Квадратное уравнение: ax ² + bx + c

Определитель D = b ² — 4ac

D> 0 означает два реальных, различных корня.

D = 0 означает два настоящих одинаковых корня /

D <0 означает отсутствие реальных корней.

Теперь попробуйте эти (будьте осторожны со знаками минус)

вопросов

Q1.х ² — 7x + 2 = 0

Q2. — 3x ² + 2x — 1 = 0

Q3. 9x ² — 12x + 4 = 0

Q4. — х ² + х + 1 = 0

ответов

Q1. D = 41 означает два реальных, различных корня.

Q2. D = -16, означает отсутствие настоящих корней.

Q3. D = 0 означает два настоящих одинаковых корня.

Q4. D = 5 означает два реальных, различных корня.

BioMath: квадратичные функции

В этом разделе мы узнаем, как найти корень (корни) квадратного уравнения.Корни также называются перехватами x или нулями. Квадратичная функция графически представлена ​​параболой с вершиной, расположенной в начале координат, ниже оси x или выше оси x . Следовательно, квадратичная функция может иметь один, два или нулевой корень.

Когда нас просят решить квадратное уравнение, нас действительно просят найти корни. Мы уже видели, что завершение квадрата — полезный метод решения квадратных уравнений.Этот метод можно использовать для вывода квадратной формулы, которая используется для решения квадратных уравнений. Фактически, корни функции

f ( x ) = ax ² + bx + c

даются по формуле корней квадратного уравнения. Корни функции — это перехваты x . По определению, координата y точек, лежащих на оси x , равна нулю. Следовательно, чтобы найти корни квадратичной функции, мы устанавливаем f ( x ) = 0 и решаем уравнение:

ось ² + bx + c = 0.

Мы можем сделать это, заполнив квадрат как,

Решая для x и упрощая, получаем

Таким образом, корни квадратичной функции равны,

Эта формула называется квадратной формулой , и ее вывод включен, чтобы вы могли видеть, откуда она взялась. Мы называем термин b ² −4 ac дискриминантом .Дискриминант важен, потому что он говорит вам, сколько корней имеет квадратичная функция. В частности, если

1. b 2 −4 ac <0 Настоящих корней нет. 2. b 2 −4 ac = 0 Существует один действительный корень. 3. b 2 −4 ac > 0 Есть два действительных корня.

Рассмотрим каждый случай индивидуально.

Случай 1: Нет настоящих корней

Если дискриминант квадратичной функции меньше нуля, эта функция не имеет действительных корней, а парабола, которую она представляет, не пересекает ось x . Поскольку квадратная формула требует извлечения квадратного корня из дискриминанта, отрицательный дискриминант создает проблему, потому что квадратный корень из отрицательного числа не определяется по действительной прямой. Пример квадратичной функции без действительных корней дается формулой

.

f ( x ) = x ² — 3 x + 4.

Обратите внимание, что дискриминант f ( x ) отрицательный,

b ² −4 ac = (−3) ² — 4 · 1 · 4 = 9 — 16 = −7.

Эта функция графически представлена ​​открывающейся вверх параболой, вершина которой лежит выше оси x. Таким образом, график никогда не может пересекать ось x и не имеет корней, как показано ниже,

Случай 2: Один настоящий корень

Если дискриминант квадратичной функции равен нулю, эта функция имеет ровно один действительный корень и пересекает ось x в одной точке.Чтобы увидеть это, мы устанавливаем b ² −4 ac = 0 в формуле корней квадратного уравнения, чтобы получить,

Обратите внимание, что это координата x вершины параболы. Таким образом, парабола имеет ровно один действительный корень, когда вершина параболы лежит прямо на оси x . Простейший пример квадратичной функции, имеющей только один действительный корень, —

y = x ² ,

, где действительный корень равен x = 0.

Другой пример квадратичной функции с одним действительным корнем:

f ( x ) = −4 x ² + 12 x — 9.

Обратите внимание, что дискриминант f ( x ) равен нулю,

b ² −4 ac = (12) ² — 4 · −4 · −9 = 144 — 144 = 0.

Эта функция графически представлена ​​параболой, которая открывается вниз и имеет вершину (3/2, 0), лежащую на оси x .Таким образом, график пересекает ось x ровно в одной точке (т.е. имеет один корень), как показано ниже,

.

Случай 3: Два настоящих корня

Если дискриминант квадратичной функции больше нуля, эта функция имеет два действительных корня ( x -перехватывания). Извлечение квадратного корня из положительного действительного числа хорошо определено, и два корня равны,

Пример квадратичной функции с двумя действительными корнями:,

f ( x ) = 2 x ² -11 x + 5.

Обратите внимание, что дискриминант f ( x ) больше нуля,

b ² — 4 ac = (−11) ² — 4 · 2 · 5 = 121 — 40 = 81.

Эта функция графически представлена ​​открывающейся вверх параболой, вершина которой лежит ниже оси x . Таким образом, график должен пересекать ось x в двух местах (т.е. иметь два корня), как показано ниже,

.

*****

В следующем разделе мы будем использовать квадратную формулу для решения квадратных уравнений.

Решение квадратных уравнений

Как найти дискриминант квадратного уравнения и прокомментировать природу корней?

Если, у нас есть квадратное уравнение вида

, где a, b, c — действительные числа, а

, тогда как мы можем определить природу корней такого квадратного уравнения?

Ответ: С помощью дискриминанта можно определить природу корней любого квадратного уравнения.Теперь возникает вопрос, что такое дискриминант.

Мы часто используем квадратичную формулу,

, чтобы найти корни любого квадратного уравнения. Подчасти (

) квадратичной формулы называется дискриминантом квадратного уравнения.

Следовательно, дискриминант любого квадратного уравнения =

Давайте возьмем пример, у нас есть квадратное уравнение,

, если сравнить его с общей формой квадратного уравнения

, получаем

и

.

Дискриминант =

=

Аналогичным образом можно найти дискриминант других квадратных уравнений.

Теперь вопрос в том, как определить природу корней по значению дискриминанта квадратного уравнения.

Если, Дискриминант> 0, то два корня квадратного уравнения различны и действительны.

Если Дискриминант = 0, то два корня квадратного уравнения действительны и равны.

Если Дискриминант <0, то для данного квадратного уравнения нет действительных корней.

Возьмем три разных примера, по одному для каждого случая. Допустим, у нас есть три квадратных уравнения:

(1)

(2)

(3)

Теперь мы определим природу корней этих трех квадратных уравнений с помощью дискриминанта.

(1)

Сравнение этого уравнения с общей формой

, получаем

и

.

Дискриминант =

Следовательно, дискриминант уравнения больше 0. Следовательно, уравнение имеет действительные и различные корни. Вы также можете проверить это, фактически найдя корни уравнения. Корни уравнения будут

и

, которые являются различными и действительными числами.

(2)

Сравнение этого уравнения с общей формой

, получаем

и

.

Дискриминант =

Следовательно, дискриминант уравнения равен нулю. Следовательно, уравнение имеет равные и действительные корни. Вы также можете проверить это, фактически найдя корни уравнения. Корней получится

и

, которые являются равными и действительными числами.

(3)

Сравнение этого уравнения с общей формой

, получаем

и

.

Дискриминант =

Следовательно, дискриминант уравнения меньше нуля. Следовательно, уравнение не имеет реальных корней. Вы также можете проверить это, фактически пытаясь найти корни уравнения. Когда вы примените квадратичную формулу,

, чтобы найти корни уравнения, вы получите

в корне квадратном.Все мы знаем, что квадрата отрицательного числа не существует. Следовательно, у этого квадратного уравнения не будет решения. Или вы можете сказать, что у этого квадратного уравнения нет реального решения.

Примечание *: Решение таких квадратных уравнений может быть сложным, но это выходит за рамки книг, которые мы изучаем в десятом классе. Так что вам не нужно об этом беспокоиться. Вам просто нужно не писать решения или нет реального решения для таких квадратных уравнений.

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения
Часть 1

Напомним, что квадратное уравнение ax ² + bx + c = 0 может быть решено с помощью квадратной формулы:

Для получения дополнительной информации о квадратичной формуле см. Следующие сообщения:

Квадратичная формула — Часть 1 Квадратичная формула — Часть 2

Прежде чем мы продолжим, вы можете также просмотреть информацию о квадратных корнях, которую можно найти здесь:

Основы квадратного корня

Дискриминант квадратного уравнения ax ² + bx + c = 0 — это величина Δ , определяемая

Δ = b ² — 4 ac

Другими словами, дискриминант — это просто выражение, которое появляется под квадратным корнем в формуле корней квадратного уравнения.

Хотя вычисление дискриминанта квадратного уравнения не дает корней (решений) уравнения, оно дает нам много информации о природе корней и графике уравнения.

Например, если дискриминант квадратного уравнения ax ² + bx + c = 0 равен 0, то квадратная формула упрощается до

x = — b / 2a ,

, и мы видим, что есть только одно решение.

Если коэффициенты a и b являются целыми числами, то единственным решением будет рациональное число.

Графически это означает, что график функции y = ax ² + bx + c представляет собой параболу, которая пересекает ось x в одной точке.

Пример дается красной параболой на изображении выше.

Примечание: Дискриминант не сообщает , открывается ли парабола вверх или вниз.Однако это легко определить, просто посмотрев на значение a .

Если a > 0 (т.е. a — положительное число), то парабола открывается вверх.

Если a <0 (т.е. a — отрицательное число), то парабола открывается вниз.

Итак, красная парабола на изображении выше имеет уравнение вида y = ax ² + bx + c , где a <0 и Δ = 0

Пример: Найдите дискриминант x ² + 6 x + 9 = 0 .Затем опишите характер корней уравнения и опишите график функции y = x ² + 6 x + 9 .

Я опубликую решение этой проблемы завтра, а затем обсудю другие возможности для определителя. Не стесняйтесь размещать свои собственные решения в комментариях.

Если вам понравилась эта статья, поделитесь ею со своими друзьями на Facebook:

Комментарии

комментария

Понимание дискриминанта в квадратной формуле

Квадратное уравнение в алгебре — это уравнение, в котором наибольшая степень неизвестной переменной равна 2.Вы пишете квадратные уравнения, используя следующую формулу: ax² + bx + c = 0

Вот несколько быстрых примеров квадратных уравнений:

• 2x² + 5x - 8 = 0
• 7x² + 9 = 0
• xx² - 26 = 3x

В этой статье я покажу вам, как дискриминант влияет на решения квадратных уравнений. Дискриминант квадратной формулы — это часть квадратной формулы, которая определяет тип корня в квадратном уравнении (мнимое, действительное, сингулярное).

Решения квадратного уравнения

Решения квадратного уравнения — это значения неизвестной переменной, которые делают уравнение истинным. Есть четыре стандартных способа найти корни квадратного уравнения.

Метод факторизации

Этот метод применим, если вы можете разложить коэффициенты квадратного уравнения на множители как av + bx + c = a (rx + n) (px + m) = 0 . Где n и m — корни квадратного уравнения.

Квадратный метод

Этот метод полезен, когда вы не можете факторизовать коэффициенты квадратного уравнения, как показано выше.При завершении метода квадратов квадратное уравнение выражается в виде

• ax² + bx + c = x2 + (b / a) x + (c / a) = 0
• x² + (b / a) x + (c / a) = (x + ½b) 2 + (c / a) - (b² / 4) = 0
• (x + ½b) 2 = (b² / 4) - (c / a)

Решение относительно x дает корни квадратного уравнения.

Квадратичная формула

Вы получите квадратную формулу, выполнив метод квадратов.Если квадратное уравнение задано как ax² + bx + c , то корни квадратного уравнения даются как x = (-b + - (b² – 4ac) 1/2) / 2a .

Графический метод

В этом методе вы строите квадратное уравнение, и точки, в которых график пересекает ось x, являются корнями уравнения.

Однако в рамках этой темы мы сосредоточимся на квадратной формуле.

Дискриминант квадратичной формулы

Вы можете решить все квадратные уравнения, используя метод квадратной формулы.Из-за его универсальности мы называем его всемогущей формулой. Вы можете найти корни квадратного уравнения, используя x = (-b + - (b² - 4ac) 1/2) / 2a .

Член b² - 4ac под квадратным корнем определяет корни квадратного уравнения и является дискриминантом квадратного уравнения. Для дискриминанта есть три возможных исхода.

b² - 4ac> 0

Это происходит, когда b ² больше 4ac. В этом случае вы получите два действительных корня квадратного уравнения.Это верно, потому что квадратный корень любого положительного числа является положительным числом. Если вы построите график квадратного уравнения, он срежет ось x в двух точках.

b² - 4ac = 0

Это происходит, когда b² равно 4ac. Если это ваш результат, у квадратного уравнения есть только один действительный корень. Квадратный корень из нуля равен нулю. Если вы построите график квадратного уравнения, он коснется оси x только в одной точке.

(b² - 4ac) = 0

Это происходит, когда b ² меньше 4ac.Это работа для мнимых корней. Корни мнимые, поскольку квадратный корень отрицательного числа является мнимым числом. График такого квадратного уравнения не будет касаться оси абсцисс.

Проиллюстрируем различные случаи, когда дискриминант определяет корни квадратных уравнений.

Пример 1

Найдите корни следующих квадратных уравнений:

1. x² + 7x + 3 = 0
2. 3x² - 13x - 12 = 0
3. 6y² + 10y = 0

Так как мы хотим продемонстрировать, как дискриминант влияет на корни квадратного уравнения, мы будем использовать метод формулы для решения вышеупомянутых задач.

Квадратичная формула: x = (-b + - (b² - 4ac) 1/2) / 2a

Уравнение 1

x² + 7x + 3 = 0

a = 1, b = 7 и c = 3

Подставьте значения коэффициентов a, b и c в формулу корней квадратного уравнения.

• (-7 + - (72-4 * 1 * 3) 1/2) / (2 * 1)

Дискриминант здесь равен (72 - 4 * 1 * 3) и равен 37. Поскольку 37 больше 0, это означает, что у нас есть два действительных корня.Решим и получим корни!

• (-7 + - (72-4 * 1 * 3) 1/2) / (2 * 1)
• (-7 + - 371/2) / (2 * 1)
• (-7 + - 6,08) / (2 * 1)

Корни

• (-7 + 6,08) / (2 * 1) и (-7 - 6,08) / (2 * 1)
• -0,46 и -6,54

Корни x² + 7x + 3 = 0 равны -0,46 и -6,54

Уравнение 2

3x² - 13x - 12 = 0

a = 3 , b = -13 и c = -12

После подстановки значений a, b и c в формулу получаем

• (- (- 13) + - (-132 - 4 * 3 * -12) 1/2) / (2 * 3)
• (13 + - (313) 1/2) / (2 * 3)
• (13 + - 17.69) / (2 * 3)

Корни

• (13 + 17,69) / (2 * 3) и (13-17,69) / (2 * 3)
• 5,11 и -0,78

Корни 3x2 - 13x - 12 = 0 равны 5,11 и -0,78

Уравнение 3

6y² + 10y = 0

a = 6 , b = 10 и c = 0

Коэффициент c равен нулю, поэтому он не фигурировал в вопросе.

После подстановки значений a, b и c в формулу корней квадратного уравнения получаем:

• (-10 + - (102-4 * 6 * 0) 1/2) / (2 * 6)
• (-10 + - (102) 1/2) / (2 * 6)

Корни следующие:

• (-10 + 10) / 12 и (-10-10) / 12
• 0 и -1.67

Для всех вопросов дискриминант был больше 0. Все корни действительные и попарно.

Пример 2

Ваше квадратное уравнение: 2x2 + 4x + 2 = 0 .

a = 2 , b = 4 и c = 2

Подставьте значения коэффициентов для a, b и c в квадратное уравнение.

• (-4 + - (42-4 * 2 * 2) 1/2) / 2 * 2
• (-4 + - 0) / 4

Корни

• (-4 + 0) / 4 или (-4-0) / 4
• -1 и -1

Корень квадратного уравнения равен -1.В этом примере дискриминант равен 0, и мы пришли только к одному корню.

Пример 3

Найдите корни 3x2 + 2x + 7 = 0 .

a = 3 , b = 2 и c = 7

Введите значения a, b и c в формулу корней квадратного уравнения.

• (-2 + - (22-4 * 3 * 7) 1/2) / 2 * 2
• (-2 + - (-80) 1/2) / 4
• (-2 + - 8,9j) / 4

Корни

• (-2 + 8.9j) / 4 и (-2 - 8,9j) / 4
• Вы не можете дальше упрощать корни.

Корни здесь мнимые. Они содержат мнимую переменную j, которую мы определяем как (-1) 1/2 или квадратный корень из -1. Мы пришли к мнимым корням, потому что дискриминант был меньше нуля.

Завершение

Понять, как дискриминант влияет на результат решения квадратного уравнения, так же просто, как запомнить формулу. Если вы когда-либо сталкивались с этой математической задачей, всегда выбирайте квадратную формулу.

Оставьте первый комментарий ниже.

Сколько корней?

Когда вы решаете корни квадратного уравнения, есть несколько возможных результатов.

• У вас может быть два вещественных числа. Если вы установите x равным любому решению, результат будет равен нулю оба раза.
• Может быть только одно вещественное число.
• Уравнение может иметь два решения комплексных чисел. Реальных числовых решений не существует.

Не волнуйтесь; есть простой способ узнать, сколько существует решений, еще до того, как вы начнете использовать формулу. Просто взгляните на b ² -4 ac часть формулы квадратичного уравнения. Этот небольшой кусок называется дискриминантом , и это ключевой вид нашей маленькой квадратичной экосистемы. Без него все развалится.

• Если значение b ² -4 ac положительно, тогда существует два решения с действительными числами.
• Если b ² -4 ac = 0, тогда существует только одно решение для вещественных чисел.
• Если значение b ² -4 ac отрицательно, тогда существует два решения комплексных чисел.

Все это происходит непосредственно из формулы корней квадратного уравнения. Если дискриминант положительный, то у вас есть, что приводит к двум ответам с действительными числами. Если он отрицательный, то да, что дает два сложных результата. И если b ² -4 ac равно 0, то у вас есть, поэтому у вас есть только одно решение.

Пример задачи

Сколько корней имеет x ² — 3 = 0?

Чтобы использовать дискриминант, сначала отметим, что a = 1, b = 0 и c = -3.

b ² — 4 ac = (0) ² — 4 (1) (- 3) = 12

Итак, у нас есть два настоящих корня. Ха! Слишком легко.

Хорошо, как насчет этого?

Сколько корней имеет 2 x ² + 8 x + 8 = 0?

Эй, прекрати с этой губой, подзаголовок.Почему бы просто не сказать «Пример задачи», как обычно? В любом случае дискриминант для этого уравнения равен

b ² — 4 ac = (8) ² — 4 (2) (8) = 64 — 64 = 0

Это означает, что у нас есть один действительный числовой корень для этого уравнения.

Тогда как вам этот?

Сколько корней у 0,7731 x ² — 2,3812 x + 4,1111 = 0?

Это просто подло — но мы все еще можем это сделать.Просто позвольте нам быстро найти наш калькулятор.

b ² -4 ac = (-2,3812) ² -4 (0,7731) (4,1111) ≈ 5,6701 — 12,7132 = -7,0431

Это отрицательное значение, поэтому у этого уравнения есть два комплексных корня . Кроме того, калькулятор находился в массажном кабинете Шмоопа, рядом с грудой учебников по алгебре. Если вам интересно.

Что он там делал?

В то время мы могли выполнять несколько задач одновременно. Знаешь, мы очень заняты.

Квадратичные уравнения | Решенные задачи и практические вопросы

В этой статье мы рассмотрим квадратные уравнения — определения, форматы, решенные задачи и примеры вопросов для практики.

Квадратное уравнение — это многочлен, наибольшая степень которого равна квадрату переменной (x ² , y ² и т. Д.)

Определения

Моном — это алгебраическое выражение, содержащее только один член.

Пример: x ³ , 2x, y ² , 3xyz и т. Д.

Многочлен — это алгебраическое выражение, содержащее более одного члена.

В качестве альтернативы можно указать —

Многочлен формируется путем сложения / вычитания нескольких одночленов.

Пример: x ³ + 2y ² + 6x + 10, 3x ² + 2x-1, 7y-2 и т. Д.

Многочлен, содержащий два члена, называется биномиальным выражением .

Многочлен, содержащий три члена, называется выражением трехчлена .

Стандартное квадратное уравнение выглядит так:

топор ² + bx + c = 0

Где a, b, c — числа и a≥1.

a, b называются коэффициентами x, ^{, 2,} и x соответственно, а c называется константой.

Ниже приведены примеры некоторых квадратных уравнений:

1) x ² + 5x + 6 = 0, где a = 1, b = 5 и c = 6.

2) x ² + 2x-3 = 0, где a = 1, b = 2 и c = -3

3) 3x ² + 2x = 1

→ 3x ² + 2x-1 = 0, где a = 3, b = 2 и c = -1

4) 9x ² = 4

→ 9x ² -4 = 0, где a = 9, b = 0 и c = -4

Для каждого квадратного уравнения может быть одно или несколько решений.Они называются корнями квадратного уравнения.

Для квадратного уравнения ax ² + bx + c = 0,

сумма его корней = –b / a и произведение его корней = c / a.

Квадратное уравнение может быть выражено как произведение двух биномов.

Например, рассмотрим следующее уравнение

x ² — (a + b) x + ab = 0

x ² -ax-bx + ab = 0

х (х-а) -b (х-а) = 0

(х-а) (х-б) = 0

x-a = 0 или x-b = 0
x = a или x = b

Здесь a и b называются корнями данного квадратного уравнения.

Теперь давайте вычислим корни уравнения x ² + 5x + 6 = 0.

Мы должны взять два числа, сложить которые мы получим 5 и умножить получим 6. Это 2 и 3.

Выразим средний член как сложение 2х и 3х.

→ х ² + 2х + 3х + 6 = 0

→ х (х + 2) +3 (х + 2) = 0

→ (х + 2) (х + 3) = 0

→ x + 2 = 0 или x + 3 = 0

→ x = -2 или x = -3

Этот метод называется факторингом .

Ранее мы видели, что сумма корней равна –b / a, а произведение корней равно c / a. Давайте проверим это.

Сумма корней уравнения x ² + 5x + 6 = 0 равна -5, а произведение корней равно 6.

Корни этого уравнения -2 и -3 при сложении дают -5, а при умножении дают 6.

Решенные примеры квадратных уравнений

Решим еще несколько примеров этим методом.

Задача 1: Решить для x: x ² -3x-10 = 0

Решение :

Выразим -3x как сумму -5x и + 2x.

→ х ² -5x + 2x-10 = 0

→ х (х-5) +2 (х-5) = 0

→ (х-5) (х + 2) = 0

→ x-5 = 0 или x + 2 = 0

→ x = 5 или x = -2

Задача 2: Решить относительно x: x ² -18x + 45 = 0

Решение :

Числа, которые в сумме дают -18 и дают +45 при умножении: -15 и -3.

Переписывая уравнение,

→ х ² -15x-3x + 45 = 0

→ х (х-15) -3 (х-15) = 0

→ (х-15) (х-3) = 0

→ x-15 = 0 или x-3 = 0

→ x = 15 или x = 3

До сих пор коэффициент x ² был равен 1.Давайте посмотрим, как решить уравнения, в которых коэффициент при x ² больше 1.

Задача 3: Решить относительно x: 3x ² + 2x = 1

Решение :

Переписывая наше уравнение, получаем 3x ² + 2x-1 = 0

Здесь коэффициент при x ² равен 3. В этих случаях мы умножаем константу c на коэффициент x ² . Следовательно, произведение выбранных нами чисел должно быть равно -3 (-1 * 3).

Выражение 2x как суммы + 3x и –x

→ 3x ² + 3x-x-1 = 0

→ 3х (х + 1) -1 (х + 1) = 0

→ (3x-1) (x + 1) = 0

→ 3x-1 = 0 или x + 1 = 0

→ x = 1/3 или x = -1

Задача 4: Решить для x: 11x ² + 18x + 7 = 0

Решение :

В этом случае сумма выбранных чисел должна быть равна 18, а произведение чисел должно быть равно 11 * 7 = 77.

Это можно сделать, представив 18x как сумму 11x и 7x.

→ 11x ² + 11x + 7x + 7 = 0

→ 11x (x + 1) +7 (x + 1) = 0

→ (х + 1) (11x + 7) = 0

→ x + 1 = 0 или 11x + 7 = 0

→ х = -1 или х = -7/11.

Факторинг — простой способ найти корни. Но этот метод применим только к уравнениям, которые можно разложить на множители.

Например, рассмотрим уравнение x ² + 2x-6 = 0.

Если мы возьмем +3 и -2, их умножение даст -6, но их сложение не даст +2. Следовательно, это квадратное уравнение нельзя разложить на множители.

Для этого вида уравнений мы применяем формулу корней квадратного уравнения, чтобы найти корни.

Квадратичная формула для нахождения корней,

x = [-b ± √ (b ² -4ac)] / 2a

Теперь давайте найдем корни приведенного выше уравнения.

x ² + 2x-6 = 0

Здесь a = 1, b = 2 и c = -6.

Подставляя эти значения в формулу,

x = [-2 ± √ (4 — (4 * 1 * -6))] / 2 * 1

→ x = [-2 ± √ (4 + 24)] / 2

→ x = [-2 ± √28] / 2

Когда мы получаем неполный квадрат в квадратном корне, мы обычно пытаемся выразить его как произведение двух чисел, одно из которых является точным квадратом. Это сделано для упрощения. Здесь 28 может быть выражено как произведение 4 и 7.

→ x = [-2 ± √ (4 * 7)] / 2

→ x = [-2 ± 2√7] / 2

→ x = 2 [-1 ± √7] / 2

→ х = -1 ± √7

Следовательно, √7-1 и -√7-1 являются корнями этого уравнения.

Рассмотрим другой пример.

Решить относительно x: x ² = 24 — 10x

Решение :

Переписывая уравнение в стандартную квадратичную форму,

x ² + 10x-24 = 0

Какие два числа при сложении дают +10, а при умножении — -24? 12 и -2.

Значит, это можно решить методом факторинга. Но давайте решим его новым методом, применив формулу корней квадратного уравнения.

Здесь a = 1, b = 10 и c = -24.

x = [-10 ± √ (100 — 4 * 1 * -24)] / 2 * 1

x = [-10 ± √ (100 — (- 96))] / 2

x = [-10 ± √196] / 2

x = [-10 ± 14] / 2

x = 2 или x = -12 — корни.

Дискриминант

Для уравнения ax ² + bx + c = 0, b ² -4ac называется дискриминантом и помогает в определении природы корней квадратного уравнения.

Если b ² -4ac> 0, корни действительны и различны.

Если b ² -4ac = 0, корни действительны и равны.

Если b ² -4ac <0, корни не являются действительными (они комплексные).

Рассмотрим следующий пример:

Задача: Найти природу корней уравнения x ² + x + 12 = 0.

Решение :

b ² -4ac = -47 для этого уравнения. Итак, у него сложные корни. Давайте проверим это.

→ [-1 ± √ (1-48)] / 2 (1)

→ [-1 ± √-47] / 2

√-47 обычно записывается как i √47, что означает, что это мнимое число.

Значит проверено.

Тест по квадратным уравнениям: решите следующие

Проблема 1

Решить относительно x: x ² -15x + 56 = 0

A. x = 14 или x = 4
B. x = 8 или x = 7
C. x = 28 или x = 2
D. Все вышеперечисленное

Ответ 1

Б.

Пояснение

Только 8 и 7 удовлетворяют условиям сложения до 15 и получения произведения 56.

Проблема 2

Найдите x, если 2x ² + 7x + 4 = 0

A. -7 ± √17 / 4
B. -7 ± √7 / 4
C. [-7 ± √17] / 4
D. [-7 ± √17] / 2

Ответ 2

C.

Пояснение :

Применяя формулу корней квадратного уравнения и подставляя a = 2, b = 7 и c = 4, мы получаем ответ как C.

Проблема 3

При каком значении k уравнение x ² -12x + k = 0 имеет действительные и равные корни?
А.6
Б. 35
В. 12
Д. 36

Ответ 3

Д.

Пояснение

b ² -4ac = 0, чтобы уравнение имело действительные и равные корни.
144-4к = 0 → к = 36

Пройдите этот доступный онлайн-курс по квадратным уравнениям. Из решения, построения графиков и записи квадратного уравнения вы узнаете все шаг за шагом.