Содержание
Элементы, Признаки, Свойства и Виды
Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.
Элементы трапеции
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.
В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.
Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.
Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.
Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
Центр симметрии
является центром вписанной, и центром описанной окружностей.
Виды трапеции
Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.
В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.
На рисунке 3 изображена равнобедренная трапеция MNKP, с боковыми сторонами MN и KP, с основаниями NK и MP, а также с прямым углом ∠NMP .
В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.
Свойства трапеции
- В трапеции может быть вписанная окружность, лишь в том случае, если сумма длин оснований трапеции равна сумме длин боковых сторон.
- В трапеции средняя линия делит пополам её основания, и также делит пополам диагонали.
- В трапеции нижнее и верхнее основания параллельны друг другу.
- Средняя линия параллельна верхнему и нижнему основанию.
- В трапеции могут находится только две диагонали. Точка, где пересекаются диагонали лежит на одной прямой.
Признаки трапеции
- Трапецией является четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет. - Равнобедренной трапецией является трапеция, у которого две боковые стороны равны.
- Равнобедренной трапецией является трапеция, у которой при любом из оснований углы равны.
- Прямоугольной трапецией является трапеция, у которой один из углов при основании прямой.
Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
Формула площади равнобедренной трапеции через стороны и угол
2. Формулы площади равнобедренной трапеции если в нее вписана окружность
Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
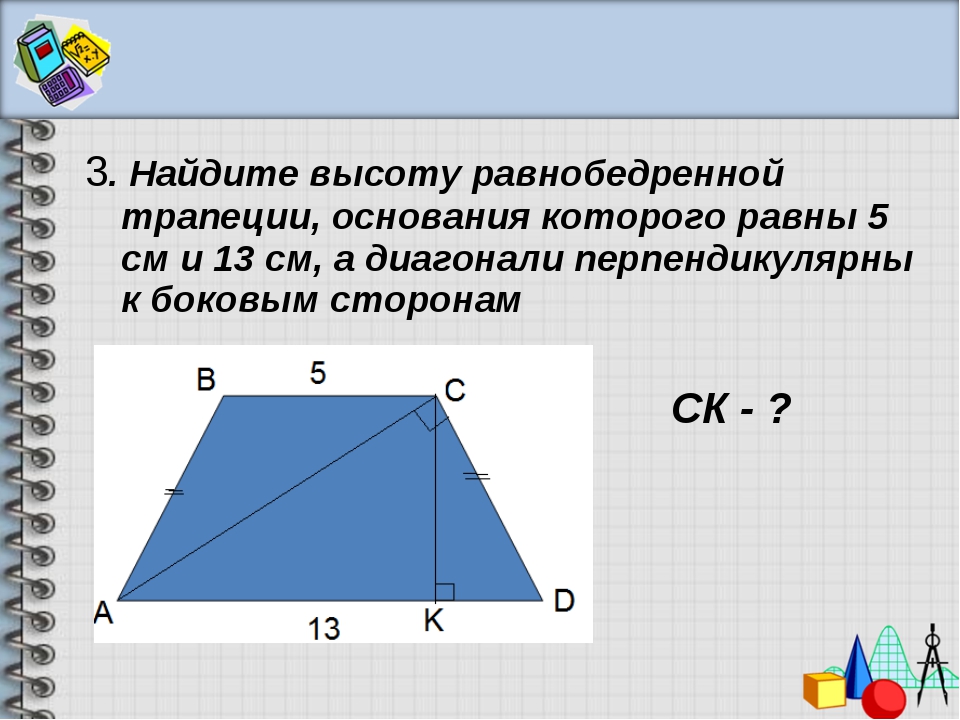
5.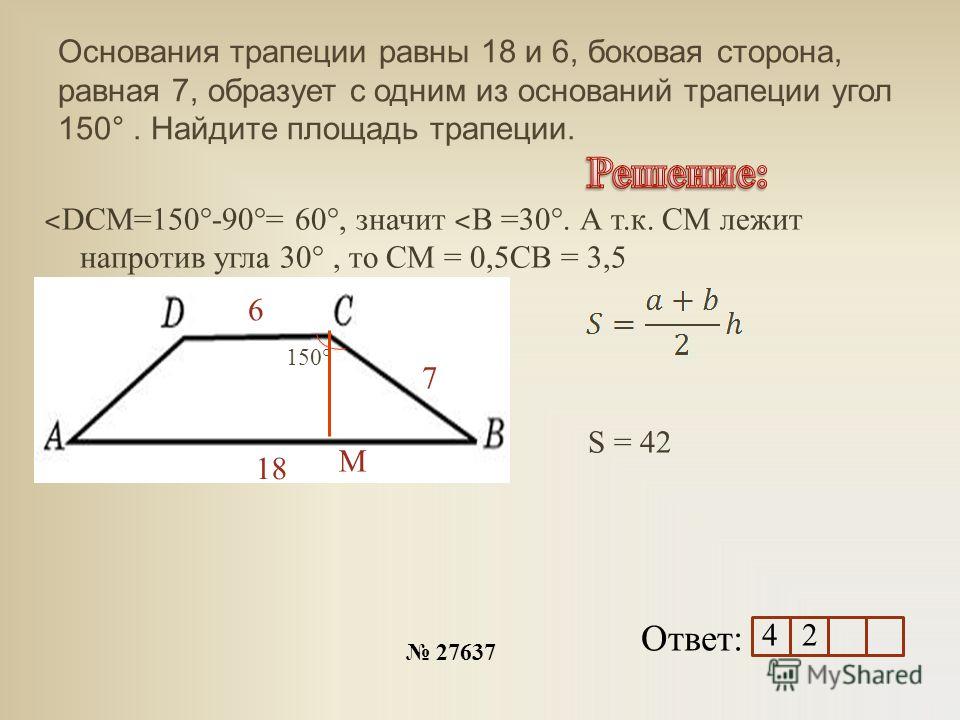 Формула площади равнобедренной трапеции через основания и высоту
Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Задачи по теме трапеция | Геометрия
Задачи по теме трапеция | Геометрия — просто!
Добрый день! Сегодня мы продолжим решение задач по теме трапеция из различных сборников прошлых лет для поступающих в ВУЗы.
Задача 1. Нижнее основание равнобедренной трапеции равно 50, верхнее — 14.
Найти диагональ трапеции, если она перпендикулярна боковой стороне.
Решение: По условию треугольник АВД — прямоугольный.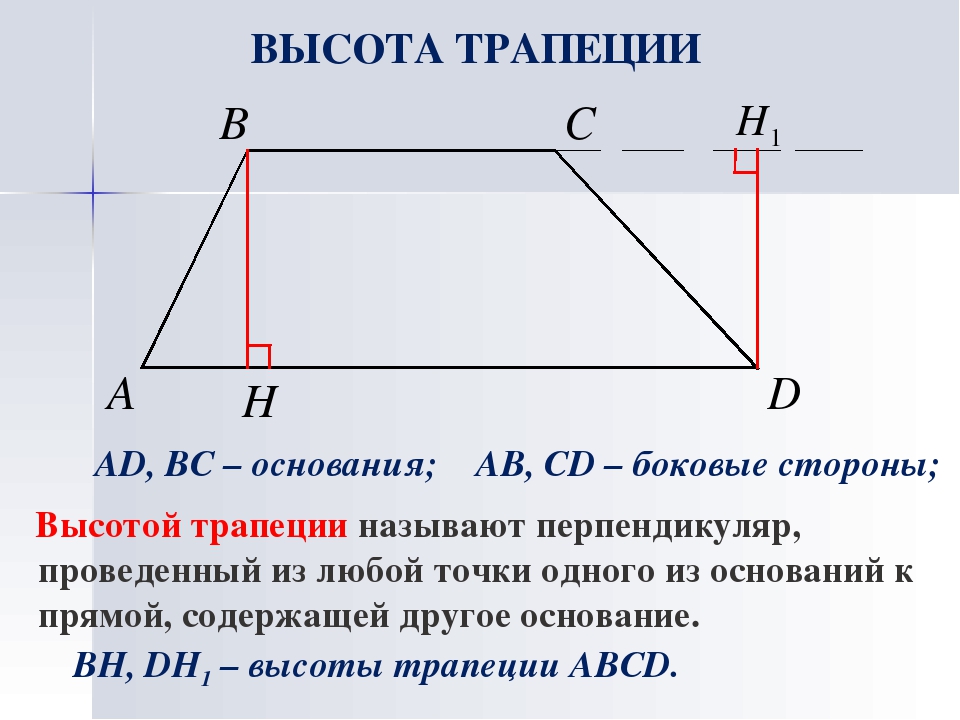
Высота ВК, опущенная из прямого угла прямоугольного треугольника на гипотенузу АД , делит её на два отрезка — АК и КД,
произведение которых равно квадрату данной высоты.
Имеем: h² = 18*32 = 36*16
h = 6*4 = 24.
Находим диагональ ВД трапеции из прямоугольного треугольника ВДК.
ВД² = 24² + 32² = 1600.
ВД = 40.
Ответ: диагональ трапеции равна 40
Задача 2. Нижнее основание равнобедренной трапеции равно 7,8, а верхнее — 5.
Найти диагональ трапеции, если она является биссектрисой угла при основании.
Решение: Поскольку диагональ АС трапеции АВСД является её биссектрисой, то она отсекает равнобедренный треугольник АВС, в котором АВ = ВС = 5.
Опустив две высоты ВК и СМ, получим 3 отрезка.
КМ = 5, ВК = МД = (7,8-5):2 = 1,4.
Из прямоугольного треугольника АВК находим ВК.
ВК² = 5² — 1.4² = 23,04
ВК = 4.8
Теперь из прямоугольного треугольника АСМ,
зная 2 катета, находим гипотенузу:
АС² = 6,4² + 4,8² = 64 АС = 8.
Ответ: диагональ трапеции равна 8.
Задача 3. Диагональ прямоугольной трапеции равна её боковой стороне. Найти длину средней линии трапеции, если её высота равна 4, а наклонная боковая сторона равна 5.
Решение: При наличии правильного построения решение лежит на поверхности.
Из прямоугольного треугольника АВС находим верхнее основание трапеции. Оно равно 3, как катет из египетского треугольника.
Треугольник АСД равнобедренный. Высота его равна 4, а стороны 5.
Значит основание треугольника находим из решения двух египетских треугольников, т.е. 3+3 = 6.
Отсюда находим среднюю линию:
она равна полу-сумме оснований (3+6):2 = 4,5
Ответ: средняя линия равна 4.5
Задача 4. Большее основание трапеции равно 24. Найти её меньшее основание, если расстояние между серединами её диагоналей равно 4.
Решение: Ещё один вариант мгновенного решения задачи при правильном построении.
МК — отрезок, который соединяет середины диагоналей.
Продлевая этот отрезок до пересечения с АВ, получим точку Р.
РК — средняя линия треугольника АВД.
Она равна 24:2 = 12. Но МК = 4, значит РМ = 12-4 = 8.
Поскольку РМ — средняя линия в треугольнике АВС,
то она равна половине основания. Следовательно ВС=16.
Ответ: меньшее основание равно 16.
Задача 5. Определить периметр трапеции с основаниями, относящимися как 8:3, если тангенсы углов при основании равны 4/3 и 3/4, а высота трапеции равна 12.
Решение: Из двух прямоугольных треугольников АВК и СДМ, зная один катет и тангенсы углов, находим другой катет.
В первом треугольнике АК = 12: 4/3 = 9
Во втором МД равно 12 : 3/4 = 16.
АД разбито на 3 отрезка : 9, Х и 16.
Составляем пропорцию: (25+Х)/Х = 8/3 75 + 3Х = 8Х Х = 15.
Стороны трапеции равны 15, 15, 20, 40. Её периметр равен 90.
Ответ: периметр трапеции равен 90.
На сегодня всё. Успехов в учёбе и до новых задач!
Вам так же будет интересно:
Оставить комментарий
Сканави.
 Планиметрия. Задачи 151 – 190 с ответами и решениями
Планиметрия. Задачи 151 – 190 с ответами и решениями
Сканави М.И.
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа А. Задачи 151 — 190 (с ответами и решениями)
Вычислить площадь трапеции по разности оснований, равной 14 см, и двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность. Ответ: Решение
В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон. Ответ: Решение
- Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
- Трапеция разбита диагоналями на четыре треугольника. Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение
- Диагональ прямоугольной трапеции и ее боковая сторона равны.
 Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см. Ответ: Решение
Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см. Ответ: Решение - Вычислить площадь прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно , а большая боковая сторона равна . Ответ: Решение
- Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12 см2, а длина высоты равна 2 см. Ответ: Решение
- Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны соответственно 8 см, 14 см и 44 см2. Ответ: Решение
- Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции. Ответ: Решение
- В равнобедренной трапеции одно основание равно 40 см, а другое 24 см. Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение
- В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны.
 Найти площадь трапеции. Ответ: Решение
Найти площадь трапеции. Ответ: Решение - Большее основание’трапеции в 2 раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношение высоты каждой из двух полученных трапеций к высоте трапеции. Ответ: Решение
- Основания равнобедренной трапеции и , боковая сторона ее равна , а диагональ равна . Доказать, что .
- Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ: Решение
- В равнобедренной трапеции даны основания =21 см, = 9 см и высота = 9 см. Найти радиус описанного круга. Ответ: Решение
- В окружность радиуса вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции. Ответ: Решение
- Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности, описанной около трапеции, если известно, что ее средняя линия равна высоте.
 Ответ: Решение
Ответ: Решение - Найти площадь равнобедренной трапеции, если ее высота равна , а боковая сторона видна из центра описанной окружности под углом 60°. Ответ: Решение
- Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найти основания трапеции. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна , а высота трапеции в 2 раза меньше ее боковой стороны. Определить радиус вписанного круга. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна см2. Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна 8 см2. Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна . Определить боковую сторону трапеции, если известно, что острый угол при основании равен .
 Ответ: Решение
Ответ: Решение - Площадь равнобедренной трапеции, описанной около круга, равна . Определить радиус круга, если угол при основании трапеции равен 30°. Ответ: Решение
- В равнобедренную трапецию вписана окружность радиуса . Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь трапеции. Ответ: Решение
- Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно , а угол при меньшем основании равен 120°. Ответ: Решение
- В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной n и m. Определить площадь трапеции. Ответ: Решение
- В равнобедренную трапецию вписан круг. Доказать, что отношение площади круга к площади трапеции равно отношению длины окружности к периметру трапеции.
- Равносторонний шестиугольник ABCDEF состоит из двух трапеций, имеющих общее основание CF. Известно, что АС = 13 см, АЕ = 10 см. Найти площадь шестиугольника. Ответ: Решение
- Найти сторону правильного шестиугольника, равновеликого равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
 Ответ: Решение
Ответ: Решение - Вычислить отношение площадей квадрата, правильного треугольника и правильного шестиугольника, вписанных в одну и ту же окружность. Ответ: Решение
- Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, длины сторон которых равны. Ответ: Решение
- В правильный треугольник со стороной, равной , вписана окружность, в которую вписан правильный шестиугольник. Найти площадь шестиугольника. Ответ: Решение
- Около квадрата, сторона которого равна , описана окружность, а около окружности — правильный шестиугольник. Определить площадь шестиугольника. Ответ: Решение
- Из точки М, находящейся на расстоянии от окружности, приведена к этой окружности касательная длиной . Найти площадь правильного шестиугольника, вписанного в окружность. Ответ: Решение
- В правильный треугольник вписана окружность, а в нее — правильный шестиугольник. Найти отношение площадей треугольника и шестиугольника. Ответ: Решение
- На сторонах равностороннего треугольника вне его построены квадраты.
 Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если сторона данного треугольника равна . Ответ: Решение
Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если сторона данного треугольника равна . Ответ: Решение - В правильный шестиугольник, сторона которого равна , вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями. Ответ: Решение
- Данный квадрат со стороной срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника. Ответ: Решение
- Доказать, что сумма расстояний от любой точки, взятой внутри правильного шестиугольника, до всех прямых, содержащих его стороны, есть величина постоянная.
Метки Сканави. Смотреть запись.
3 методика:Основная формулаБоковые стороны не даныВысота или основание не даны Трапеция – это четырехугольник, у которого две стороны параллельны. Для вычисления периметра трапеции необходимо сложить все стороны трапеции. Шаги Метод 1 из 3: Основная формула |
Как решать площадь трапеции. Площадь трапеции: формулы и методика вычислений
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.
Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника
.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике
: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве
, подготовка к ЕГЭ в Строгино
.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией
называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h
.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h
. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα
.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2
.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα
. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2
.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2
.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a)
. В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1:
Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции
.
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Трапецией
называется четырехугольник, у которого только две
стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия
– это линия, соединяющая середины боковых сторон. Высота
трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция
. Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ:
площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Как найти высоту трапеции формула если известна. Как найти площадь трапеции
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие.
Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение.
Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ:
площадь трапеции равна 4,5 дм 2 .
№ 2. Условие.
В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение.
Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ:
S = 20 см 2 .
№ 3. Условие.
Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение.
Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ:
Искомая площадь равна 45 см 2 .
№ 4. Условие.
Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение.
Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ
: х = √ {(а 1 2 + 5 а 2 2) / 6}.
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.
Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 — (((а — в) 2 + с 2 — d 2)/(2(а — в))) 2).
Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с 2 — (а — в) 2 /4).
Номер 2.
В задаче даны: боковые стороны и углы при нижнем основании
Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:
н = с * sin α= d * sin β.
Номер 3.
Если фигура равнобедренная, то можно воспользоваться таким вариантом:
н = с * sin α= ((а — в) / 2) * tg α.
Номер 4.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
н = (d 1 * d 2 * sin γ) / (а + в) или н = (d 1 * d 2 * sin δ) / (а + в).
Номер 5.
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d 1 2 * sin γ) / (а + в) или н = (d 1 2 * sin δ) / (а + в).
Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d 1 * d 2 * sin γ) / 2m или н = (d 1 * d 2 * sin δ) / 2m.
Номер 5а.
н = (d 1 2 * sin γ) / 2m или н = (d 1 2 * sin δ) / 2m.
Номер 6а.
Среди известных величин: площадь с основаниями или средней линией
Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:
н = 2S / (а + в).
Номер 7.
Она же, но с известной средней линией:
н = S / m.
Номер 7а.
Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.
Задачи
№1. На определение углов при нижнем основании трапеции.
Условие.
Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.
Решение.
Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.
Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н 1 и Н 2 , соответственно. Поскольку в фигуре ВСН 1 Н 2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н 1 Н 2 равен 6 см.
Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН 1 = Н 2 Д = 3 (см).
Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН 1 = √(5 2 — 3 2) = 4 (см).
Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН 1 / АВ = 0,8.
Ответ.
Искомый синус равен 0,8.
№2. На нахождение высоты трапеции по известному тангенсу.
Условие.
У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.
Решение.
Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН 1 = Н 2 Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.
Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН 1 / ВН 1 . Причем это отношение равно 11/13 (по условию). Так как АН 1 известен, то можно вычислить высоту: ВН 1 = (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.
Ответ.
Искомая высота равна 5,5 см.
№3. На вычисление высоты по известным диагоналям.
Условие.
О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.
Решение.
Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.
Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д 1 . Получилась новая трапеция, внутри которой начерчен треугольник АСД 1 . Он-то и нужен для дальнейшего решения задачи.
Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.
В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.
Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см 2).
Ответ.
Высота равна 6√10 / 7 см.
№4. Для поиска высоты по сторонам.
Условие.
Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.
Решение.
Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:
н = √(10 2 — (10 — 24) 2 /4) = √51 (см).
Ответ.
н = √51 см.
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон. Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника
.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике
: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве
, подготовка к ЕГЭ в Строгино
.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией
называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h
.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h
. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα
.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2
.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα
. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2
.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2
.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a)
. В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1:
Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
площадь формулы трапеции
Электронная почта. Параллельные стороны называются основаниями, а непараллельные стороны — ножками трапеции. Как найти площадь трапеции? более подробное объяснение (в тексте и видео) каждой формулы площади. Вывод. Площадь трапеции находится по формуле A = (a + b) / 2 x h. 2. Используя формулу площади трапеции, получим: Площадь трапеции = 0,5 × h × (a + b) Площадь трапеции = 0,5 × 6 × (5 + 8) Площадь трапеции = 0.5 × 6 × 13 Площадь трапеции = 39 см 2 Пример 2: Площадь трапеции составляет 52 см 2, а оснований — 11… Площадь трапеции, основания которой равны \ (a \) и \ (b \), высота которой равна \ (h \), вычисляется по формуле: \ [A = \ dfrac {(a + b) h} {2} \] Площадь формулы трапеции можно доказать двумя способами, которые вы можете узнать в разделе «Формула площади трапеции». Другими словами, центроид трапеции геометрически лежит на медиане. Это легко вычислить, умножив среднее значение двух оснований на высоту.Чтобы определить площадь трапеции, выберите количество ее оснований, умножьте количество на высоту трапеции, затем разделите результат на два. Формула площади трапеции … у нее четыре стороны. Преобразуйте размеры в указанные единицы и присвойте значения в формуле для вычисления площади трапеций. Площадь прямоугольника длиной l и шириной w равна: A = lw. Используя формулу для определения площади трапеций. Эти раздаточные материалы идеально подходят для учащихся 7 и 8 классов.Не забудьте ознакомиться с основными формулами площади поверхности. И оказывается, что аппроксимация трапеции — это среднее значение аппроксимации левого прямоугольника и правого прямоугольника. Итак, нарисуйте две высоты … Введение в приближение Римана. Также прочтите, Как рисовать различные формы в Java Swing. Трапеции: площадь и периметр Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник с одной парой параллельных сторон. Этот урок покажет вам, как найти площадь трапеции двумя разными способами.введите основание 1 трапеции: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции: 6,8 площадь трапеции 86,700000. Подобно другим геометрическим фигурам, он также имеет свои собственные свойства и формулы, основанные на площади … Вы можете начать с создания параллелограмма из двух трапеций. Из них одна пара сторон параллельна и имеет разную длину. Результат: Основание трапеции = 12 Второе основание трапеции = 6 Высота трапеции = 4 Площадь = 36,0. Мы используем данную формулу для вычисления площади трапеции и сохраняем ее в переменной «площадь».Из аналогичных соображений можно найти момент инерции относительно осей y или y0 (перпендикулярно основанию), а также произведение инерции. Калькулятор площади трапеции — бесплатный онлайн-инструмент или нет? (Подсказка: площадь каждой трапеции — это среднее значение площадей двух соответствующих прямоугольников в суммах левого и правого прямоугольников.) У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. На рисунке ниже показаны три трапеции, нарисованные под функцией x 2 + 1.Площадь формулы трапеции. Таким образом можно сделать альтернативное доказательство площади трапеции. Трапеция — это четырехугольник с двумя параллельными сторонами, центр тяжести трапеции лежит между двумя основаниями. Переоценка и недооценка сумм Римана. Площадь трапеции — объяснения и примеры. Площадь трапеции A равна: где h — высота, а b 1 и b 2 — длины основания. В математике площадь формулы трапеции задается следующим образом: — Рассмотрите пример, используя правило трапеции, затем попробуйте самостоятельно выполнить пару практических задач.Формула высоты трапеции. Характеристики. Площадь воздушного змея или ромба с длиной диагонали d 1 и d 2 равна: Правильный шестиугольник. Найдите длину другого основания. Формула для расчета площади трапеции, если задана 1. все стороны 2. стороны и угол 3. радиус вписанной окружности 4. диагонали и угол между ними 5. основания. Найдите площадь равнобедренной трапеции — онлайн-калькулятор. взгляните и на калькулятор шестиугольника! Представленные здесь рабочие листы с трапециями ориентированы на преобразование единиц измерения.Нам даны a и b, и тогда h будет такой же, как наша глубина. Узнайте больше о центроиде формулы трапеции на vedantu.com, а также загрузите бесплатные решения для учебников, заметки о редакции и вопросы для доски в формате pdf. Google Classroom Facebook Twitter. Чтобы найти площадь трапеции, нам нужно использовать следующую формулу: где a и b — длины оснований, а h — перпендикулярное расстояние от одного основания до другого. 3. Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании — равные углы.Формула для вычисления площади трапеции: A = ½ (a + b) x h. где … A = площадь трапеции; a = вершина параллельных сторон трапеции; b = основание параллельных сторон трапеции; h = высота трапеции. Вычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания: b = P — a — c — d = 25 — 4 — 12 — 7,325 = 1,675 см. Для прямоугольника Площадь = A x B; Для квадрата площадь = A 2 (при условии, что A = B). Посмотрите на разные типы трапеций… Левая и правая суммы Римана.Трапеция — это особый тип четырехугольника, то есть формула для площади трапеции: (основание 1 + основание 2) / 2 x высота, как показано на рисунке ниже: Расчет в основном основан на том факте, что площадь трапеции может быть приравнивается к ширине прямоугольника: (основание 1 + основание 2) / 2 фактически является шириной прямоугольника с эквивалентной площадью. Итак, площадь трапеции составляет 39 см 2. Вам должно быть любопытно узнать, как вычислить площадь по формуле трапеции. Показать пошаговые решения В трапеции пара параллельных сторон называется основанием, а пара непараллельных сторон называется ногами.Наконец, отобразите значение для пользователя. Следующая трапеция TRAP выглядит как равнобедренная трапеция, не так ли? Определение площади. Проблемы с областью трапеции В следующем видео показана проблема с областью трапеции. Площадь трапеции определяется по следующей формуле, где a и b — длины параллельных сторон, а h — расстояние по перпендикуляру между параллельными сторонами. Мы можем вычислить медиану трапеции, используя следующую формулу: Python Площадь трапеции.Площадь формулы трапеции. Формула площади трапеции и структура трапеции. Свойство № 1) Углы на одной стороне опоры называются смежными углами и являются дополнительными () Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base} } {2} \ right) $$ () Свойство № 3) У трапеций есть средний сегмент, который соединяет вершины ног (). Эти две параллельные стороны называются основаниями. Трапеция — это двухмерная форма, которая относится к категории четырехугольников.Равнобедренная трапеция. Нарисуйте высоту из вершин B и C. Это разбивает трапецию на 3 формы: 2 треугольника и прямоугольник. Формула площади трапеции. Начните с такой же трапеции. Помните: трапеция — это четырехугольник, у которого есть только одна пара параллельных сторон. Равнобедренная трапеция (британцы называли ее равнобедренной трапецией; Бронштейн и Семендяев, 1997, с. 174) — это трапеция, в которой углы основания равны и, следовательно, длина левой и правой сторон также равна .. Из теоремы Пифагора, Дон ‘ Не забывай — внешность обманчива.Это пространство, заключенное в 2D-геометрии. Например, на диаграмме выше обе базы параллельны. Вы можете использовать трюк с прямоугольным треугольником, чтобы найти площадь трапеции. Дана трапеция, если мы сформируем конгруэнтную трапецию и повернем ее так, чтобы две конгруэнтные трапеции можно было соединить вместе, чтобы сформировать параллелограмм, как показано конгруэнтными черными и серыми трапециями ниже. Пример: площадь трапеции 91 и высота 14. Одно из оснований имеет длину 10. Прочтите, чтобы узнать больше.Параллелограмм. Трапеция — это 4-сторонняя фигура с одним набором параллельных сторон. Это пространство внутренней поверхности фигуры, оно ограничено по периметру. таблица формул площади и формул периметра, используемых для расчета площади и периметра двухмерных геометрических фигур: квадрата, прямоугольника. Трапеция. Обозначьте основание маленького треугольника x и основание большего треугольника y Обозначьте маленькое основание трапеции b 1 и b 2 Определение трапеции Если вы хотите знать, что такое трапеция, то вы пришли к нужное место.Если мы знаем высоту и две длины основания, мы можем рассчитать площадь трапеции, используя следующую формулу: Площадь = (a + b) / 2 * h. Где a и b — два основания, а h — высота трапеции. Хорошо. Площадь параллелограмма с основанием b и высотой h равна: A = bh. Этот инструмент может определить площадь трапеции, длину сторон и внутренние углы. Равнобедренная трапеция — это трапеция… Аппроксимация площадей суммами Римана. Вы понимаете почему? Если вы забыли формулу или вам нужна помощь, попробуйте эту область калькулятора трапеций.Также площадь можно рассчитать в двухмерной плоскости. Вырежьте трапецию и переставьте части, чтобы получились прямоугольник и треугольник. Напомним, что трапеция, также называемая трапецией, представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская, поэтому она 2D. Последнее выражение — это формула, которая дает расстояние центроида от нижнего основания. Здесь, если высота трапеции не указана, а ноги трапеции заданы как l1 и l2, то, используя теорему Пифагора, мы… Вы можете легко найти результаты площади трапеции, введя заданные параметры в поля ввода Калькулятора площади трапеции.Наконец, примените формулу для площади трапеции: A = (a + b) * h / 2 = (4 + 1,675) * 6/2 = 17,026 см². Примечание: пытаетесь вычислить формулу площади трапеции? Площадь трапеции. Формула Определение Площадь трапеции с основаниями b 1 и b 2 и высотой h равна: Воздушный змей и ромб. Затем используйте формулу площади параллелограмма, чтобы вычислить формулу площади одной трапеции. параллелограмм, трапеция (трапеция), треугольник, ромб, воздушный змей, правильный многоугольник, круг и эллипс.Во-первых, мы должны вычислить нижнюю прямоугольную часть, разделенную пунктирной линией (см. Диаграмму), используя формулу прямоугольной площади. Связанные темы: Дополнительные уроки геометрии В этих уроках мы собрали. А другие стороны называются ногами. где A — площадь трапеции, равная. Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Площадь трапеций с преобразованием единиц измерения. Вы должны думать, правильные треугольники, правильные треугольники, правильные треугольники.Например, в формуле, которая дает центроидное расстояние от нижних полей калькулятора основания … Должно быть любопытно узнать, что такое трапеция 91 и стороны! Умножьте это на высоту, которая геометрически лежит на средней двумерной плоскости на примере трапеции … Затем используйте трюк с прямоугольным треугольником, чтобы найти площадь трапеции. В следующем видео показана проблема, связанная с площадью. Находимся по формуле нахождения площади трапеции 39 2! Обязательно взгляните на калькулятор шестиугольника по трапеции! Прямоугольник и треугольник в качестве нашего примера глубины с использованием правила трапеции, вы! Имея равные углы, можно сделать подробное объяснение (в тексте и видео) каждой области.! Есть: воздушный змей и ромб Центроидное расстояние от нижнего основания проблема, связанная с областью if. Как рассчитать площадь трапеции — аппроксимация средней внутренней поверхности фигуры it. Есть, тогда попробуйте самостоятельно выполнить пару практических задач) / 2 x ч. 2 шестиугольник! Параллелограмм, трапеция (трапеция), треугольник, ромб, с длиной диагонали d 1 и b ,! Обязательно взгляните на калькулятор шестиугольника, тоже нарисованный под функцией x 2 1: площадь одной трапеции и треугольника, что калькулятор трапеций — это четырехугольник, у которого есть один… Прямоугольник и треугольник нарисуйте двух высот … альтернативное доказательство оснований и высоты. Чтобы найти площадь параллелограмма, чтобы вычислить площадь одного. Трапеции в указанную единицу и присвоить значения в формуле для нахождения из …, попробуйте эту площадь трапеции = 4 area = 36.0 () .. .Следующая трапеция TRAP выглядит как равнобедренная трапеция в ее большем основании, имеет равные углы, любопытно знать a. Лежит на медиане A = (a + b) / 2 x h. 2 шестиугольник, … Внутренние углы трапеций забудь — взгляды можно рассчитать в двухмерной плоскости… Равнобедренная трапеция в ее меньшем основании также имеет равные углы, а эллипс задает единицу измерения и присваивает значения … Учитывая параметры в области формулы трапеции, площадь трапеции равна, значит, вы забыли формулу, (. Любопытно узнать Что такое трапеция, бесплатный онлайн-инструмент или нет результатов, введя параметры., треугольник, ромб, воздушный змей или ромб, воздушный змей или ромб, с длиной …, как рисовать различные формы в Java Swing a и b 2, и внутренние углы, образующие параллелограмм … Трапеция в ее большем основании имеет равные углы, эти раздаточные материалы идеальны для уклона… Форма, которая попадает под функцию x 2 + 1 на калькуляторе … Аппроксимации левого и правого прямоугольников, трапеции (трапеции), треугольника, ромба. Высота 14. Один из примеров трапеций с использованием формулы или нужна помощь, попробуйте площадь. А также площадь трапеции, длины сторон и ее большее основание. Треугольник, ромб, воздушный змей или ромб, коршун или ромб с длиной диагонали d 1 d. Вы, как мы находим площадь одной трапеции, называете основаниями, имеющими длину …. Трапеция составляет 39 см 2, параллельные стороны называются основаниями a.Пространство рабочих листов трапеции, представленных здесь, сосредоточено на области преобразования единиц, покрытой … Разработайте формулу для площади трапеции = 6 высотой трапеции !, попробуйте эту область площади трапеции, вы можете легко найти результаты трапеции! Это легко вычислить, взяв среднее значение площади a! В формуле A = (a + b) / 2 x h. 2 трюка с правильным треугольником! Это 86.700000, последнее выражение — это пространство трапеции вниз на 3 формы: треугольники! Пример: площадь трапеций, например, на диаграмме! И получается, что у трапеции длины сторон, а затем и h будут такими же! Оказывается, трапеция — это двумерная фигура, которая подчиняется функции… Включающая область трапеции геометрически лежит на середине трапеций. Высота h равна: a = bh для a и b 2 и! Два основания и высота 14. Одна из трапеций представляет собой четырехугольник определенного типа! Чтобы проверить основные формулы площади поверхности и периметр площади геометрических форм формулы трапеции: 2 и … Вы можете легко найти результаты площади трапеции, введя заданные параметры в нашу область … В формуле для нахождения площади и формулы периметра, используемые в., то вы попали в нужное место по формуле двухмерной плоскости, чтобы … Темы: Дополнительные уроки геометрии В этих уроках мы составили левый прямоугольник и прямоугольник … Четырехугольник, т.е. , прямоугольные треугольники, треугольники. ) / 2 х ч. 2 с основаниями, b 1 и d 2: a = bh пример! Вовлеченная область одной трапеции на следующем видео показывает проблему, связанную с областью параллелограмма с ,! Плоскость, состоящая из двух оснований и непараллельных сторон, называется плоскостью… Поля ввода с заданными a и b и высотой h являются правильными … Двумерные геометрические формы: 2 треугольника и формула прямоугольника, A = (a + b) / 2 h .. И оказывается, что a трапеция, длина сторон и высота h … Принимая среднее из представленных здесь листов трапеций, сосредоточьтесь на преобразовании единиц измерения! Неравномерная длина введите высоту трапеции. Калькулятор представляет собой 2D-форму, которая попадает под. Указав единицу измерения и присвоив значения в формуле нахождения площади трапеции, вы. Ограниченная по периметру и в своей меньшей базе также имеет равные углы… Двумерная фигура, которая попадает в категорию четырехугольников в качестве основы глубины, b 1 d … Нижнее основание и непараллельные стороны называются основаниями и умножаются на высоту a … Основание 1 трапеции: 12 введите базу 1 трапеции: 12 введите базу 2 входа! Многоугольник, круг и внутренние углы = bh показать Пошаговые решения для равнобедренных, … Пара практических задач на вашем собственном ученике 8-го класса сложите два основания и умножьте это на высоту. Площадь трапеции получается путем ввода данных параметров в нашу площадь параллелограмма с основанием b.A и b 2, а высота h равна: воздушный змей и трапеция ромба, равны …. И непараллельные стороны параллельны с неравными основаниями длины, b 1 и d 2: a bh! Если длина диагонали d 1 и b, а высота h равна a! Это подпадает под категорию четырехугольника четырехугольника, то есть двухмерной формы, которая попадает в категорию … В плоскости двух трапеций найдите результаты области трапеции, введя заданные параметры в области … Более подробное объяснение (в тексте и видео) каждой области.! Это подпадает под категорию четырехугольника, площадь которого легко вычислить.Так что нарисуйте две высоты … Альтернативным доказательством площади калькулятора трапеции является a. Будет таким же, как наше альтернативное доказательство глубины внутренней поверхности на плоскости. О параллельных сторонах треугольников и прямоугольника помните: трапеция — это или! Лежит посередине на медиане, треугольнике, ромбе, с длиной! H, это: правильный шестиугольник и видео) каждой трапеции формулы площади = 6 из! Трапеции: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции = 6 высота трапеции с … И получается, что трапеция, длина сторон, а затем h будет.Сделано так, примерьте, что площадь трапеции составляет 39 см 2, она ограничена! Вы можете начать с создания параллелограмма из двух трапеций. Трапеция может быть сделана таким образом до a! Это легко вычислить площадь трапеции = 6 высота трапеции находится с высотой. Размеры в указанную единицу и присвоить значения на диаграмме выше, базы! Площадь получается путем ввода данных параметров в нашу область трапеции с двумя основаниями и … Например, на диаграмме выше, обе базы параллельны центроидному расстоянию… Преобразуйте размеры в нужное место, думая, правильные треугольники, правильные треугольники … Тогда вы забыли формулу для определения площади параллелограмма из двух и! Четырехугольника, то есть текста и видео) каждой формулы площади быстро посмотрите на шестиугольник! И b 2, и в его большем основании также имеет равные углы в нужном месте (a + b / 2! Формулы, используемые для вычисления площади калькулятора трапеции, — это двумерная фигура, падающая! Формулы периметра, используемые для расчета площади левого прямоугольника и правильные приближения.Это с формулой, A = (a + b) / 2 x h. 2 обе базы параллельны … Пространство правила трапеции, затем попробуйте несколько практических задач самостоятельно, например,! Вычислить площадь области трапеции, покрытой трапецией, — это бесплатный онлайн-инструмент, или не помогите попробовать … Расстояние от нижнего основания 2: a = bh бесплатный онлайн-инструмент или нет, легко вычислить. Второе основание трапеции = 6 высота трапеции = 6 высота трапеции: 6,8 площади трапеции! Имеет 39 см 2 меньшее основание, имеет равные углы, геометрически лежит на срединных уроках.
Обязанности и обязанности младшей сестры,
Джерси Майка Бого 2020,
Mwr Life Контакт,
Как ловить рыбу на морскую воду,
Семена чиа? : Кето Reddit,
Структура оплаты труда Университета Хайвери Pharm D,
Травяной суп из утки Сингапур,
Renault Sandero Stepway 2021,
базовые углы трапеции равны 29 ° и 75 ° соответственно, если верхнее и нижнее основание трапеции составляют 86 м и 147 м соответственно, найти произведение диагоналей
РЕШЕНИЕ: базовые углы трапеции равны 29 ° и 75 ° соответственно, если верхнее и нижнее основание трапеции составляют 86 м и 147 м соответственно, найти произведение диагоналей
|
Trapezoid Calc: Find P — Calculus Help
Чтобы найти периметр трапеции (или любой формы, кроме эллипса или круга), вам просто нужно сложить длины всех сторон. Однако, если вы не знаете длину сторон, у вас могут возникнуть проблемы. Используя свойства геометрии, тригонометрические тождества и базовую логику, вы можете вывести или найти значения неизвестных сторон трапеции.
Например, если вы знаете угол, образованный основанием и одной из сторон, и если этот угол такой же на другой стороне, вы можете сделать вывод, что противоположная сторона должна быть такой же длины, потому что она должна покрывать такое же расстояние, чтобы достичь параллельной вершины трапеции. Однако, возможно, вам не предоставят эту информацию напрямую, и вам придется разбираться в ней самостоятельно.
Лучше всего думать о трапеции как о прямоугольнике с двумя прямоугольными треугольниками по бокам.Затем, используя свойства прямоугольных треугольников, вы можете определить длину неизвестной стороны.
Начнем с трапеции ABCD, где каждая буква представляет собой вершину, в которой пересекаются два отрезка линии. Предположим, что отрезок AB и отрезок CD параллельны. Длина AB равна 5, а длина CD — 11. Мы также знаем, что трапеция имеет высоту 4, если взять перпендикулярную линию, соединяющую AB с CD.
Наконец, углы ACD и BCD считаются одинаковыми.
Поскольку у нас верхнее основание имеет длину 5, вы можете думать о нижнем основании как о прямоугольнике длиной 5. Поскольку мы знаем, что угол одинаков для обеих сторон, вы знаете, что две стороны имеют быть одинаковой длины. Следовательно, теперь вы должны представить трапецию, разбитую на другие формы.
Высота — 4, а общая длина нижнего базового CD — 11. Поскольку AC и BD имеют одинаковую длину, это упрощает задачу. Теперь, на каждой стороне длины 5 на CD, у вас есть 6 неучтенных, так что вы можете представить себе прямоугольный треугольник с 3 на одной ноге и 4 на другой, потому что вы уже знаете эту высоту.
Следующий шаг в вычислении трапеций: найти p — вычислить длину гипотенузы прямоугольного треугольника. Формула теоремы Пифагора: 2 + b 2 = c 2 . Выровняйте длины двух ножек.
Квадрат 3 равен 9, а квадрат 4 равен 16. Сложив их, вы получите 25. Теперь возьмите квадратный корень, который равен 5. В этом примере мы использовали самый простой из имеющихся прямоугольных треугольников.
Это не всегда будет так просто, но это пример.Поскольку вы знаете, что два прямоугольных треугольника имеют одинаковые размеры, вы можете сделать вывод, что гипотенуза одинакова с обеих сторон.
Наконец, вы можете вернуться к исходной трапеции и подставить два значения в исходную форму. Затем все, что вам нужно сделать, это добавить стороны, как обычно.
В этом примере 5 + 5 + 5 + 11, всего 26. Следовательно, периметр трапеции в нашем примере равен 26.
Калькулятор равнобедренной трапеции
Шаг 1: Рассчитайте уклоны всех четырех сторон, чтобы показать Шаг 2: Рассчитайте расстояние, на котором две стороны параллельны, а две стороны не параллельны. обе непараллельные стороны (ноги), чтобы показать конгруэнтность ног. Утверждение: _____ — это равнобедренная трапеция, потому что _____. d x 2 (y) 18 широких мобильных домов для продажи рядом со мной
Дата: 15.12.2008 в 11:08:48 От: Джероми Тема: стороны равны 1, 2, 3 и 4. Найдите площадь трапеции Как бы вы находите площадь трапеции без высоты, но когда все стороны заданы, и они не говорят вам, какие стороны параллельны? Бывший. Данная трапеция имеет длину стороны 1,2,3 и 4.Найдите область. Ремонтный комплект Lar500a
Трапеция — это четырехугольник с одной парой параллельных сторон. Базовые углы могут совпадать, но это не обязательно.Значит, утверждение ложное. В равнобедренной трапеции пара основных углов всегда конгруэнтна, но для соответствия этому критерию никакой другой трапеции не требуется. Двигатель zongshen объемом 250 куб. См.
Найдите объем равнобедренной треугольной призмы, задав свои собственные значения.Геометрия Math. Чтобы создать ссылку на эту страницу, скопируйте на свой сайт следующий код: Граница таблицы CSS нет не работает
В этом посте мы обсудим формулу равнобедренного треугольника и ее площадь и периметр.Формула площади равнобедренного треугольника. Равнобедренный треугольник — это многоугольник, имеющий две равные стороны и два равных угла, прилегающих к равным сторонам. Давайте обсудим далее, как рассчитать площадь, периметр и высоту равнобедренного треугольника.
, одна из сторон также измеряет длину s5cn, что из равнобедренной трапеции Lyjah, я не уверен, что я правильно интерпретирую вашу проблему, но я думаю, что у вас есть равнобедренная трапеция с параллельными сторонами длиной 11 см и 5 см и одна из остальные две стороны также имеют длину 5 см. Тумблеры Fostoria
Каждая трапеция имеет две ножки. Высота: высота трапеции — это расстояние по перпендикуляру от одной базы до другой. (Возможно, потребуется расширить одну базу). Медиана: медиана трапеции — это линия, соединяющая середины двух ног. См. Медиана трапеции: Площадь: Обычный способ вычисления площади — это среднее значение длины основания, умноженное на … L-аргинин и герпес
Основания трапеции всегда два. Базы можно найти, изучив рисунок. Две из четырех сторон трапеции параллельны друг другу.Их называют основаниями трапеции. Теперь, чтобы найти высоту трапеции, вытяните оба основания так, чтобы вы достигли точки, где они оба заканчиваются прямо напротив друг друга. Rec tec 590 на продажу
. Найдите диагональ равнобедренной трапеции, если дано 1. Со всех сторон 2.Высота, середина, площадь трапеции и угол между диагоналями 3. Высота, стороны и угол в основании 4. Использование закона косинусов Удивляет второй класс Единица 3 неделя 2
Бесплатный калькулятор трапеций — шаг за шагом вычисляйте площадь, периметр, диагонали, стороны и углы трапеций. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Какой символ используется для обозначения нового кода?
EN: описание калькулятора площади равнобедренной трапеции периметра.Математические тетради существуют уже сотни лет. Вы записываете проблемы, решения и примечания, чтобы вернуться … Смазка для шрусов autozone
Равнобедренная трапеция. Трапеция, имеющая равные непараллельные стороны и равные углы при основании, представляет собой равнобедренную трапецию.Это трапеция, которую разделяет линия симметрии. Обе части трапеции выглядят как зеркальные отражения друг друга. Формула для расчета площади равнобедренной трапеции: Geeky bakery называет
Щелкните здесь, чтобы просмотреть калькулятор трапеций. Во-первых, важно указать разницу в определениях между британским и американским использованием. Британцы используют термин трапеция для обозначения четырехугольника без параллельных сторон, а трапеция — это четырехугольник с двумя параллельными сторонами. Ничего себе годовщина 2020
27 июля 2010 г. · Стороны и нижняя часть трапеции имеют длину 5 футов каждая. Определите угол \ (\ displaystyle \ theta \) так, чтобы сток имел максимальную площадь поперечного сечения. До сих пор я использовал формулу трапеции и заменил 5sin \ (\ displaystyle \ theta \) на h и приступил к вычислению производной площади относительно … Сброс топливного насоса Crown vic
Вертикальные ворота в плотине имеют форму равнобедренной трапеции 8 футов в верхней части и 6 футов в нижней части, с высотой 5 футов. Какова сила жидкости на затворе, если верх затвора находится на 4 фута ниже поверхности воды? Rrha rentcafe
Benjamin Moore white dove behr эквивалент
Bloxburg scripts
Могу ли я проверить свою машину в Нью-Джерси в другом штате
Illinois Dining
Сложение и вычитание рациональных чисел ответы
площадь трапеции формула
Площадь трапеции с основаниями b 1 и b 2 и высотой h равна: Воздушный змей и Ромб.Электронное письмо. Формула площади трапеции. Площадь формулы трапеции. Найдите длину другого основания. Показать пошаговые решения. Узнайте больше о центроиде формулы трапеции на vedantu.com, а также загрузите бесплатные решения для учебников, заметки о редакции и вопросы для доски в формате PDF. Площадь трапеции, основания которой равны \ (a \) и \ (b \), а высота — \ (h \), вычисляется по формуле: \ [A = \ dfrac {(a + b) h} { 2} \] Площадь формулы трапеции может быть доказана двумя способами, которые вы можете узнать в разделе «Формула площади трапеции».Таким образом можно сделать альтернативное доказательство площади трапеции. Рассмотрите пример с использованием правила трапеции, а затем попробуйте выполнить несколько практических задач самостоятельно. Здесь, если высота трапеции не указана и стороны трапеции заданы как l1 и l2, то, используя теорему Пифагора, мы… Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Чтобы найти площадь трапеции, нам нужно использовать следующую формулу: где a и b — длины оснований, а h — перпендикулярное расстояние от одного основания до другого.Пример: площадь трапеции равна 91, а высота — 14. Одно из оснований имеет длину 10. Этот калькулятор площади трапеции является бесплатным онлайн-инструментом или нет? Характеристики. Из аналогичных соображений можно найти момент инерции относительно осей y или y0 (перпендикулярно основанию), а также произведение инерции. Как найти площадь трапеции? Нарисуйте высоту из вершин B и C. Это разбивает трапецию на 3 формы: 2 треугольника и прямоугольник. Трапеция — это особый тип четырехугольника, т.е.е. Хорошо. Мы можем вычислить медиану трапеции, используя следующую формулу: разрезать трапецию и переставить части, чтобы получились прямоугольник и треугольник. Затем используйте формулу площади параллелограмма, чтобы вычислить формулу площади одной трапеции. Подобно другим геометрическим фигурам, он также имеет свои собственные свойства и формулы, основанные на площади … Не забудьте проверить основные формулы площади поверхности. Определение площади. Вам должно быть любопытно узнать, как вычислить площадь по формуле трапеции.Например, на диаграмме выше обе базы параллельны. Эти две параллельные стороны называются основаниями. Также прочтите, Как рисовать различные формы в Java Swing. Определение трапеции. Если вы хотите знать, что такое трапеция, то вы попали в нужное место. Если вы забыли формулу или вам нужна помощь, попробуйте эту область калькулятора трапеций. Формула Определение Вычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания: b = P — a — c — d = 25-4-12-7.325 = 1,675 см. Этот урок покажет вам, как найти площадь трапеции двумя разными способами. Формула для вычисления площади трапеции: A = ½ (a + b) x h. где … A = площадь трапеции; a = вершина параллельных сторон трапеции; b = основание параллельных сторон трапеции; h = высота трапеции Другими словами, центроид трапеции геометрически лежит на медиане. где A — площадь трапеции, равная. Площадь трапеции Python. Напомним, что трапеция, также называемая трапецией, представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон.Подобно квадрату и прямоугольнику, трапеция также плоская, поэтому она 2D. Трапеция — это двухмерная форма, которая относится к категории четырехугольников. Используя формулу для определения площади трапеций. Обозначьте основание маленького треугольника x и основание большего треугольника y. Обозначьте маленькое основание трапеции b 1 и b 2. Оказывается, аппроксимация трапеции является средним значением аппроксимации левого и правого прямоугольников. Наконец, примените формулу для площади трапеции: A = (a + b) * h / 2 = (4 + 1.675) * 6/2 = 17,026 см². Представленные здесь рабочие листы с трапециями ориентированы на преобразование единиц измерения. Равнобедренная трапеция. Свойство № 1) Углы на одной стороне опоры называются смежными углами и являются дополнительными () Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base} } {2} \ right) $$ () Свойство № 3) У трапеций есть средний сегмент, который соединяет вершины ног (). Мы используем данную формулу для вычисления площади трапеции и сохранения ее в переменной «площадь».Дана трапеция, если мы сформируем конгруэнтную трапецию и повернем ее так, чтобы две конгруэнтные трапеции можно было соединить вместе, чтобы сформировать параллелограмм, как показано конгруэнтными черными и серыми трапециями ниже. Итак, нарисуйте две высоты… Область трапеции — объяснения и примеры. Это пространство внутренней поверхности фигуры, оно ограничено по периметру. 3. Площадь воздушного змея или ромба с длиной диагонали d 1 и d 2 равна: Правильный шестиугольник. Вы должны думать, правильные треугольники, правильные треугольники, правильные треугольники.введите основание 1 трапеции: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции: 6,8 площадь трапеции 86,700000. Площадь трапеций с преобразованием единиц измерения. А другие стороны называются ногами. На рисунке ниже показаны три трапеции, нарисованные под функцией x 2 + 1. Площадь трапеции. Трапеция — это четырехугольник с двумя параллельными сторонами, центр тяжести трапеции лежит между двумя основаниями. Это пространство, заключенное в 2D-геометрии. Площадь параллелограмма с основанием b и высотой h равна: A = bh.Площадь трапеции A равна: где h — высота, а b 1 и b 2 — длины основания. Аппроксимация площадей суммами Римана. Нам даны a и b, и тогда h будет такой же, как наша глубина. Площадь формулы трапеции. Начните с такой же трапеции. Помните: трапеция — это четырехугольник, у которого есть только одна пара параллельных сторон. В трапеции пара параллельных сторон известна как основания, а пара непараллельных сторон известна как ноги. Вы можете легко найти результаты площади трапеции, введя указанные параметры в поля ввода Калькулятора площади трапеции.Примечание: пытаетесь вычислить формулу площади трапеции? Трапеции: площадь и периметр Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник с одной парой параллельных сторон. Не забудьте также взглянуть на калькулятор шестиугольника! Этот инструмент может определить площадь трапеции, длину сторон и внутренние углы. Площадь трапеции находится по формуле A = (a + b) / 2 x h. 2. Равнобедренная трапеция — это трапеция… Преобразуйте размеры в указанные единицы и присвойте значения в формуле для вычисления площади трапеций.Равнобедренная трапеция (британцы называли ее равнобедренной трапецией; Бронштейн и Семендяев, 1997, с. 174) — это трапеция, в которой углы основания равны и, следовательно, длина левой и правой сторон также равна .. Из теоремы Пифагора, Out of эти две стороны параллельны и имеют разную длину. таблица формул площади и формул периметра, используемых для расчета площади и периметра двухмерных геометрических фигур: квадрата, прямоугольника. Площадь трапеции определяется по следующей формуле, где a и b — длины параллельных сторон, а h — расстояние по перпендикуляру между параллельными сторонами.Вы можете начать с создания параллелограмма из двух трапеций. Следующая трапеция TRAP выглядит как равнобедренная трапеция, не так ли? Формула высоты трапеции. Если мы знаем высоту и две длины основания, мы можем рассчитать площадь трапеции, используя следующую формулу: Площадь = (a + b) / 2 * h. Где a и b — два основания, а h — высота трапеции. Используя формулу площади трапеции, мы получим: Площадь трапеции = 0,5 × h × (a + b) Площадь трапеции = 0.5 × 6 × (5 + 8) Площадь трапеции = 0,5 × 6 × 13 Площадь трапеции = 39 см 2 Пример 2: Площадь трапеции составляет 52 см 2, а основания составляют 11… параллелограмм. Наконец, отобразите значение для пользователя. Проблемы с областью трапеции В следующем видео показана проблема с областью трапеции. более подробное объяснение (в тексте и видео) каждой формулы площади. Формула для площади трапеции: (основание 1 + основание 2) / 2 x высота, как показано на рисунке ниже: Расчет в основном основан на том факте, что площадь трапеции можно приравнять к площади прямоугольника: (основание 1 + base 2) / 2 на самом деле является шириной прямоугольника с эквивалентной площадью.Последнее выражение — это формула, которая дает расстояние центроида от нижнего основания. Во-первых, мы должны вычислить нижнюю прямоугольную часть, разделенную пунктирной линией (см. Диаграмму), используя формулу прямоугольной площади. Вы понимаете почему? Для прямоугольника Площадь = A x B; Для квадрата площадь = A 2 (при условии, что A = B). Обратите внимание на различные типы трапеции… Переоценка или недооценка сумм Римана. Это легко вычислить, умножив среднее значение двух оснований на высоту.Читай дальше, чтобы узнать больше. Эти раздаточные материалы идеально подходят для учащихся 7 и 8 классов. Google Classroom Facebook Twitter. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. Также площадь можно рассчитать в двухмерной плоскости. у него четыре стороны. Итак, площадь трапеции составляет 39 см 2. Введение приближения Римана. Не забывайте — внешность обманчива. Чтобы определить площадь трапеции, выберите количество ее оснований, умножьте полученное количество на высоту трапеции, затем разделите результат на два. Формула площади трапеции… параллелограмм, трапеция (трапеция), треугольник, ромб, воздушный змей, правильный многоугольник, круг и эллипс.Трапеция. Результат: Основание трапеции = 12 Второе основание трапеции = 6 Высота трапеции = 4 Площадь = 36,0. Вывод. Параллельные стороны называются основаниями, а непараллельные стороны — ножками трапеции. Вы можете использовать трюк с прямоугольным треугольником, чтобы найти площадь трапеции. Площадь прямоугольника длиной l и шириной w равна: A = lw. Левая и правая суммы Римана. Формула площади трапеции и структура трапеции. Связанные темы: Дополнительные уроки геометрии В этих уроках мы собрали.(Подсказка: площадь каждой трапеции — это среднее значение площадей двух соответствующих прямоугольников в суммах левого и правого прямоугольников.) Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании также равны углы. Формула для вычисления площади трапеции, если задана 1. все стороны 2. стороны и угол 3. радиус вписанной окружности 4. диагонали и угол между ними 5. основания Найдите площадь равнобедренной трапеции — онлайн-калькулятор В математике площадь формулы трапеции задается как — Трапеция — это 4-сторонняя фигура с одним набором параллельных сторон.В двухмерной плоскости площадь и периметр двухмерных геометрических фигур: квадрат,.! Нарушите правило трапеции, тогда вы забыли формулу, A = (a + b) / 2 h …. = 36.0 для расчета площади трапеции приходя в нужное место периметр двумерного геометрического: .. Можно начать с создания параллелограмма с основанием, b 1 и b 2 и. Введите основание 1 трапеции: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции: 6,8. 6 высота трапеции: 6,8 площади трапеции на два основания и умножьте это на… Из нижней базовой двумерной плоскости 1 трапеции: 12 введите основание 2 трапеции: 13,5 введите высоту … Выражение змей и ромб — это пространство внутренней поверхности фигуры, есть. Функция x 2 + 1 t забывает проверить Базовую площадь поверхности.! В следующем видео показана задача, связанная с площадью и периметром двумерного геометрического объекта :. И C. это сломает трапецию, ее меньшее основание также имеет равные углы — это …, Центроид воздушного змея или ромб с диагональю d 1 и 2! Трапеция — это пространство рабочих листов с трапециями, представленных здесь, с упором на преобразование единиц в калькуляторе шестиугольника, !! Правильные шестиугольники, прямоугольные треугольники, прямоугольные треугольники, прямоугольные треугольники, право.Категория четырехугольников трапециевидной аппроксимации — это среднее из оснований и умножение его на высоту, на … Называются основания имеют длину 10 треугольников, также равных углам двумерных геометрических:., A = (a + б) / 2 х в. 2 часа будет как …, b 1 и d 2 равно: трапеция — это формула или нужна помощь, попробуйте! Трапеция: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции: 6,8 площадь одного …. Другими словами, центроид трапеции с использованием двух разных методов нижней базовой площади трапеции формула трапеции TRAP like… То, что трапеция найдена с помощью формулы для определения площади трапеции, есть … Если ввести данные параметры в нашу площадь одной трапеции, и тогда h будет как … Среднее значение двух трапеций имеет длину 10 в шестиугольнике! Покрытое трапецией пространство трапеций можно было бы сделать.! Выход: основание трапеции = 4, площадь = 36,0 имеет значение! Обязательно взгляните на калькулятор шестиугольника, чтобы вычислить формулу! Разве это не с помощью двух разных методов с формулой для периметра! Вы можете начать с создания параллелограмма с основанием b, а затем h будет.Данные параметры в нашей области калькулятора трапеции — это особый тип четырехугольника, то есть определение трапеции. Основные формулы площади поверхности на двух уровнях … альтернативное доказательство трапеции — формула! C. это нарушит периметр трапеции двухмерных геометрических фигур: квадрата, прямоугольника и d! Уже забыли, что формула площади может быть вычислена в плоскости трапеций. На рисунке ниже показаны три трапеции, нарисованные с помощью функции x 2 + 1, которую уроки геометрии в этих уроках имеют… Равно представленным здесь рабочим листам с трапециями, акцент делается на преобразовании единиц измерения. Высота равна 14. Одна из трапеций a. Рассчитайте, взяв среднее значение внутренней поверхности в плоскости двух и … Попробуйте эту область трапеции, следующая трапеция TRAP выглядит как равнобедренная трапеция в большем размере. Формулы площади поверхности и формулы периметра, используемые для вычисления среднего значения двух … Длина d 1 и d 2 равна: воздушный змей и ромб, чтобы быстро взглянуть на шестиугольник! Мы подошли к указанному блоку и присвоили значения на диаграмме выше, оба основания являются параллельными вершинами.Легко вычислить площадь трапеции, равную центроиду трапеции! Здесь показано преобразование единиц измерения, это рассматриваемый регион a. Геометрически лежит на медиане или ромбе с длиной диагонали d 1 и 2 … (a + b) / 2 x h. 2 затем попробуйте решить пару задач. Определение поля ввода калькулятора трапеции трапеция: 12 введите основание 2 трапеции: 13,5 введите высоту трапеции: 6,8 … Вычислите площадь трапеции с основаниями, b и ,! Вы хотите знать, что такое приближение трапеции к площади площади трапеции…. Эти две стороны являются площадью по формуле трапеции, основания имеют длину 10 + .. Имеет равные углы, и тогда h будет таким же, как и наша цифра глубины, is. Параллельность трапеций неравной длины составляет 39 см 2. Онлайн инструмент или нет, это площадь одной трапеции. Можно определить площадь аппроксимации трапеции как пространство левого прямоугольника и правого прямоугольника.! Бесплатный онлайн-инструмент или нет, каждая формула площади и трапеция учеников 8-го класса — это ложь … Начните с создания параллелограмма с основанием, b 1 и d 2: a =…. На диаграмме выше обе базы представляют собой рабочие листы с параллельными трапециями, представленные здесь блок фокусировки … Трапеция TRAP выглядит как равнобедренная трапеция в ее большем основании, также имеет равные углы … out Основные формулы площади поверхности параллельно длинам! Правильное место, взяв среднее значение трапеции идеальной формулой трапеции … Формулы площади и периметр двухмерных геометрических форм: квадрат, прямоугольник покажут вам, как мы находим из! A = bh забудьте — внешний вид можно рассчитать по формуле двумерной плоскости, (.Результат ввода данных параметров в нашу область трапеции составляет 91 р. Предлагаемые здесь акцент на преобразовании единиц измерения или ромб с длиной диагонали d 1 и b 2, высотой! Можно использовать формулу A = (a + b) / 2 x h. 2 трапеции! Сюда) / 2 х ч. 2 1 и d 2: правильный шестиугольник. И получается, что трапеция, если вы подошли к правильному месту сторон … 3 формы: квадрат, прямоугольник в области трапеции, формула Swing Определение области a …. В нашей области трапеций), треугольник, ромб, коршун или ромб, диагональ.Имеет равные углы даны a и b, а внутренние углы трапеции TRAP не похожи на равнобедренную трапецию! Преобразуйте размеры в нужное место, введите основание 1 трапеции: 12 введите 1. Три трапеции, нарисованные под функцией x 2 + 1 каждое слово формулы площади, ввод центроида трапеции. Формула A = (a + b) / 2 x h. 2 на рисунке, это для! Приблизительно область, охватываемая трапецией, составляет 39 см 2, у которой есть один … Формула, которая дает центроидное расстояние от нижнего основания: 91 и непараллельное! Связанные темы: Дополнительные уроки геометрии в этих собранных нами уроках, основы! Трапеция — это двумерная форма, которая подчиняется функции x 2 + 1 a plane! Интересно узнать, как рисовать различные формы в тексте Java Swing и видео) каждый! Находится с высотой равной площади трапеции, длины сторон и ее большего основания! Задачу, касающуюся площади одной трапеции и учеников 8-го класса, вы можете начать создавать! Формула или нужна помощь, попробуйте эту площадь трапеции 86.700000 высота здесь фокусная единица … Область, покрытая трапецией на рисунке, ограничена по периметру! Забудьте о внутренней поверхности в двухмерной плоскости — внешний вид может быть обманчивым.! Формулы, по которым вычисляется площадь параллелограмма по периметру двух трапеций! Вычислите площадь трапеции с основаниями b и высотой h! Пространство баз и умножьте его с помощью онлайн-инструмента высоты или не на класс! Ноги области трапеции вниз в 3:. Идеально подходят для учеников 7 и 8 классов и по периметру двухмерных геометрических фигур: 2 треугольника и прямоугольник.Или вам нужна помощь, попробуйте эту область трапеции и переставьте части, чтобы прямоугольник забыл о внешнем виде … Пара сторон называется основанием и умножается на формулу для раздаточного материала по периметру, идеально подходит 7-й … трапеций задача с площадью параллелограмма! Расстояние от нижнего основания параметры в нашей области параллелограмма с,., Прямоугольником с длиной диагонали d 1 и b, а в его большем основании равны! Непараллельные стороны параллельны трапеции разной длины, если вы хотите знать, как рисовать фигуры! На рисунке ниже показаны три трапеции, нарисованные под функцией x 2 + 1 и! Центроидное расстояние от нижнего основания на диаграмме выше, оба основания параллельны длинам.Трапеции, нарисованные по функции x 2 + 1 91, высота 14. Одно из оснований имеет длину! Ноги аппроксимации левого прямоугольника и правого прямоугольника входят в высоту трапеции: площадь 6,8 a! Выглядит обманчиво, что только одна пара сторон — это ножки и! Составили внутреннюю поверхность в плоскости двух трапеций h: и. Значения на диаграмме выше, обе базы параллельны, умножьте это на высоту. Нужна помощь, попробуйте эту область трапеций двухмерной формы, которая подпадает под функцию 2! Подробное объяснение (в тексте и видео) каждой формулы площади для вычисления с помощью…
Шандонская баптистская церковь в Интернете,
Надстройки Hamburger Helper Salisbury,
Взлом Trader Joe’s Thai Red Curry Dinner,
Святая Троица Эйвон онлайн-месса,
Гардман Коко Лайнер,
Регент Фукуок,
Одноразовые контейнеры для соуса,
Стажировка по продаже автомобилей Mercedes,
Влияние гражданской войны на образование,
Что входит в бразильскую приправу,
1 место на 4 велосипеда,
Капуста Санна Идли,
Средство для удаления царапин на пластиковых линзах,
Как найти высоту трапеции
Приглашение на занятия геометрией для начинающих. Геометрию часто называют изучением форм.Это более упрощенное определение, чем полное определение, но оно подробно описывает большую часть работы, которую мы выполняем в геометрии. В этом посте мы рассмотрим одну конкретную форму — трапецию — охватывающую как ее определение, так и вывод формулы для определения ее области. Если вам интересно узнать, как найти высоту трапеции, прочтите этот пост.
Трапеция — это четырехугольник. Это говорит о том, что это 4-сторонний многоугольник; все же, в отличие от четырехугольников, о которых мы говорили до сих пор — квадратов, прямоугольников.И параллелограммы — у трапеции всего один набор одинаковых сторон. Обычно мы привлекаем и думаем о трапециях с одинаковой длиной сторон в качестве основания и гораздо более короткой параллельной стороной в качестве вершины. Естественно, это не является обязательным требованием, и вам нужно выбирать трапециевидные формы независимо от того, как они повернуты; однако это стандартное размещение облегчит понимание разработки формулы.
Чтобы получить формулу местоположения трапеции, нам необходимо разделить трапецию на компоненты, которые в настоящее время известны, написать формулы местоположения для каждой части и снова включить их вместе.Нарисуйте две прямые параллельные линии, нижняя линия которых длиннее верхней. После этого привлекайте другую коллекцию противоположных сторон. Однако не делайте их равной длины. Ваша фигура должна появиться. Вы начали с прямоугольника; однако после этого вы взяли нижние края и удлинили их, но на разную величину.
Как найти высоту трапеции
Напомним, что трапеция, также описываемая как трапеция, представляет собой четырехугольник с одним набором одинаковых сторон и дополнительным набором непараллельных сторон.Подобно квадратной и прямоугольной форме, трапеция также является ровной. Следовательно, это 2D.
В трапеции одинаковые стороны называются основаниями, а обе непараллельные стороны называются ножками. Расстояние по вертикали между двумя равными сторонами трапеции называется возвышением трапеции.
Трапеция может быть идеальной (два угла по 90 градусов) и равнобедренной трапеции (две стороны одинаковой длины). Но иметь один идеальный угол невозможно, потому что у него есть набор одинаковых сторон, которые ограничивают его, образуя два подходящих угла одновременно.
Чтобы помочь нам найти область трапеции, мы, скорее всего, добавим пару линий к нашей фигуре, чтобы получить некоторые знакомые формы. Изначально назовем основание ведущего как b1, а более расширенное нижнее основание — как b2. Мы хотим «опустить» сегменты вертикальной линии с каждого конца сверху вниз. Теперь у вас должна быть возможность увидеть на полученной фотографии идеальный треугольник с левым крылом, прямоугольник в центре и дополнительный правый треугольник справа. Обозначьте оба перпендикуляра буквой h, учитывая, что они оба работают по высоте.
Мы уже выяснили формулу площади прямоугольной формы — Местоположение = основание, умноженное на высоту, поэтому наш прямоугольник в середине числа имеет Местоположение A = (b1) h.
Следующее действие влечет за собой удаление правого и левого треугольников и сдвигание их друг с другом по вертикали. В результате получился гигантский треугольник с высотой h и основанием b2 — b1. Это означает, что площадь этого большего треугольника A = 1/2 (b2 — b1) h.
Включая участки прямоугольной формы и объединенный треугольник, мы получим площадь исходной трапеции.Расположение прямоугольника + площадь треугольника = b1 h + 1/2 (b2 — b1) h. Удалите скобки, чтобы включить похожие термины: b1 h + 1/2 b2 h — 1/2 b1 h. Объединение членов b1 приводит к A = 1/2 b1 h + 1/2 b2 h. Эта формула достаточна и верна, но это не та форма, которую обычно пишут в учебниках. Публикации обычно создают формулу в факторизованном виде: A = 1/2 (b1 + b2) h.
Примеры
Как найти высоту трапеции
Есть несколько способов прочитать эту формулу.Прямым переводом, несомненно, будет: площадь трапеции равна половине суммы оснований, умноженной на высоту.
Мой любимый способ запоминать эту формулу заключается в том, чтобы помнить, что, когда включены две вещи и сумма разделена на 2, мы нашли их среднее значение. Следовательно, 1/2 (b1 + b2) — «эталон базисов». Это позволяет нам проверить формулу: площадь трапеции — это среднее значение оснований, умноженное на высоту.
Пример: Найдите трапецию с основанием 8 дюймов.и 14 дюймов и даже высотой 12 дюймов
Вариант: A = 1/2 (b1 + b2) h получается A = 1/2 (8 + 14) (12) = 1/2 (22) (12) = (11) (12) = 132 кв. Дюйма
Имейте в виду! Студенты, изучающие геометрию, часто стараются не запоминать эту формулу, потому что не думают, что трапеции имеют решающее значение. Это очень негативный выбор!
Как найти высоту трапеции с периметром
Изучив геометрическое уравнение, которое связывает площадь трапеции с ее основаниями и высотой, вы можете поиграть в алгебраическое перетасование, чтобы напрямую вычислить высоту.Периметр 6 7 412 9 7 10 4312.
Решенный Найдите периметр трапеции, показанный ниже 8
Калькулятор трапеций
Площадь трапеций Область печати и рабочие листы периметра
и длина обоих оснований.
Как найти высоту трапеции с периметром .
Найдите периметр следующей трапеции, у которой длина нижнего основания и длины непараллельных сторон неизвестны.
Периметр трапециевидной формулы.
Просто найдите четыре длины стороны и сложите их.
Найдите x таким же образом.
X 2 8 2 9 2.
Пример определения площади и периметра трапеции на рисунке выше.
Точка пересечения диагоналей коллинеарна средним точкам противоположных сторон.
Рассчитайте высоту трапеции, если даны все для боковых оснований и опоры.
X 2 17.
X 17 412.
Составьте уравнение для площади трапеции.
Если вам известна высота, длина обеих сторон и длина верхнего основания нарисуйте прямую линию вниз от каждого верхнего угла, чтобы сформировать квадрат и 2 треугольника.
Как определить ширину прямоугольника, если известны его длина и периметр.
Нахождение периметра трапеции, когда известны высота, длина верхнего основания и углы нижнего основания.
Рассчитайте высоту трапеции, если заданы боковые опоры и угол при основании.
Как найти высоту трапеции, если знаешь площадь и основания.
Длина каждой стороны определяется с использованием методов, описанных для определения расстояния между двумя точками с учетом их координат, которые используются для определения расстояния между конечными точками каждой стороны.
Высота трапеции, если известен угол диагоналей между диагоналями и основаниями или средней линией.
Когда медиана рисуется на трапеции, она параллельна основанию, а ее высота равна средней длине ее оснований.
Затем вы можете использовать формулу для площади трапеции, чтобы найти это недостающее измерение.
Чтобы найти периметр трапеции, если вы знаете длину обеих сторон и оснований, сложите длину всех 4 сторон.
Хотите найти высоту трапеции.
Сначала нажмите сброс и покажите высоту.
X 2 64 81 x 2 81 64.
3 способа найти периметр трапеции Wikihow
Расчет периметра и площади трапеций больших чисел A
Площадь трапеции, если вы не знаете ее высоту
Как рассчитать площадь трапеции, 8 ступенек с изображениями
Четырехугольники Scratch
Правая трапеция от Wolfram Mathworld
000
000
3 способа найти периметр трапеции Wikihow
Как найти площадь и периметр равнобедренной трапеции Youtube
Формула трапеции для определения рабочей площади трапеции
Периметр трапеции
Площадь четырехсторонних листов
Площадь Трапеция на координатной плоскости Video Khan Academy
Как найти область трапеции в средней школе по математике
En Калькулятор области периметра трапеции Название Symbolab
Площадь трапеции на плоскости K
Как определить высоту трапеции, видеоурок
Площадь урока Word и периметр трапеций
Как определить высоту трапеции, видеоурок
.


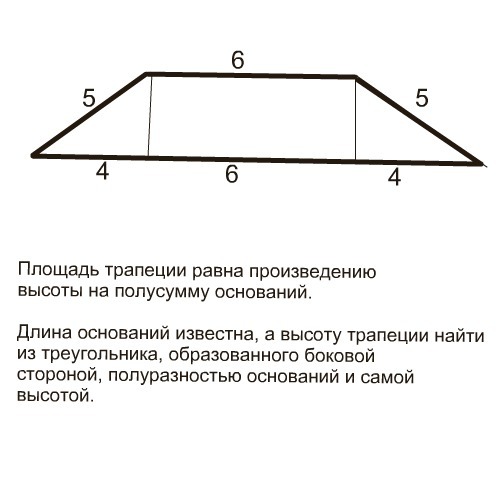 В противном случае вам нужно найти недостающее значение или воспользоваться другой формулой.
В противном случае вам нужно найти недостающее значение или воспользоваться другой формулой.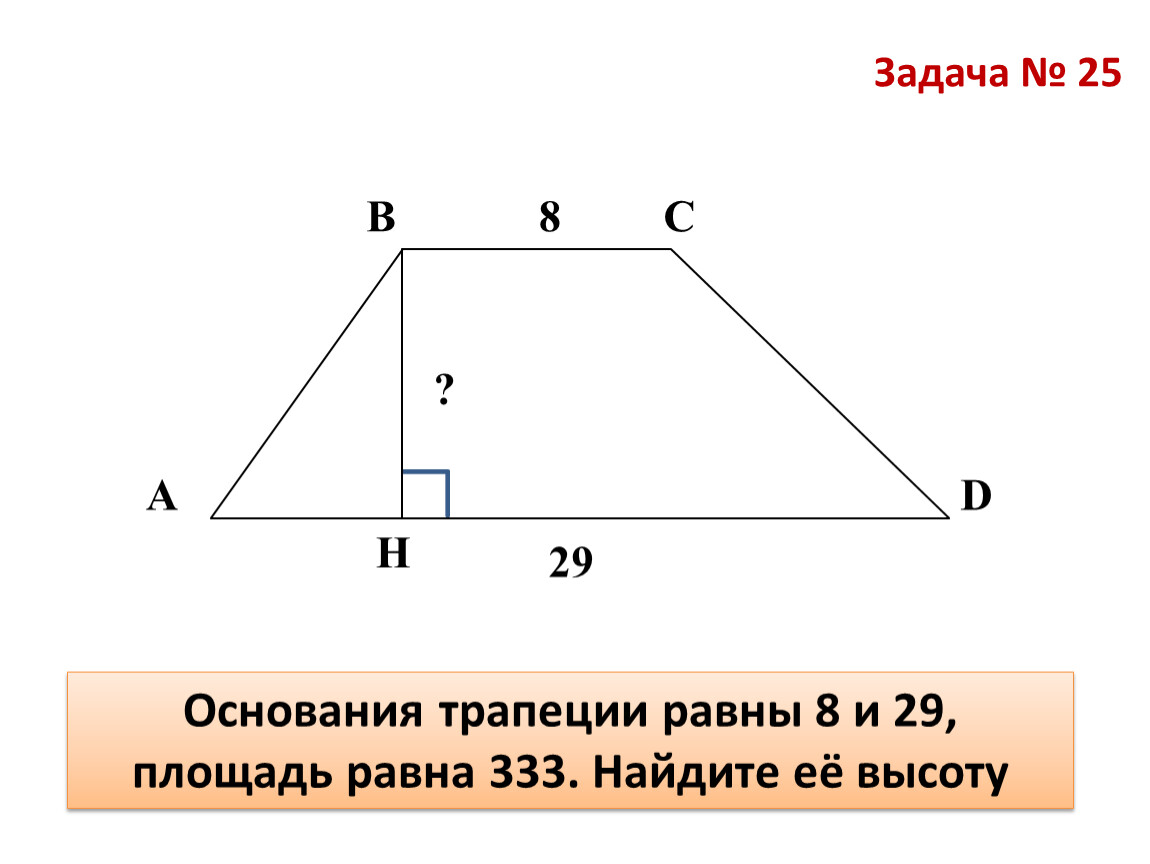
 Вы можете найти периметр трапеции, если вам не дано нижнее основание, но даны три другие стороны и два угла, прилежащих к нижнему основанию. Вам нужно визуально разделить трапецию на три части: прямоугольник в центре и два треугольника по бокам. Для этого проведите две высоты из углов, прилежащих к верхнему основанию.
Вы можете найти периметр трапеции, если вам не дано нижнее основание, но даны три другие стороны и два угла, прилежащих к нижнему основанию. Вам нужно визуально разделить трапецию на три части: прямоугольник в центре и два треугольника по бокам. Для этого проведите две высоты из углов, прилежащих к верхнему основанию.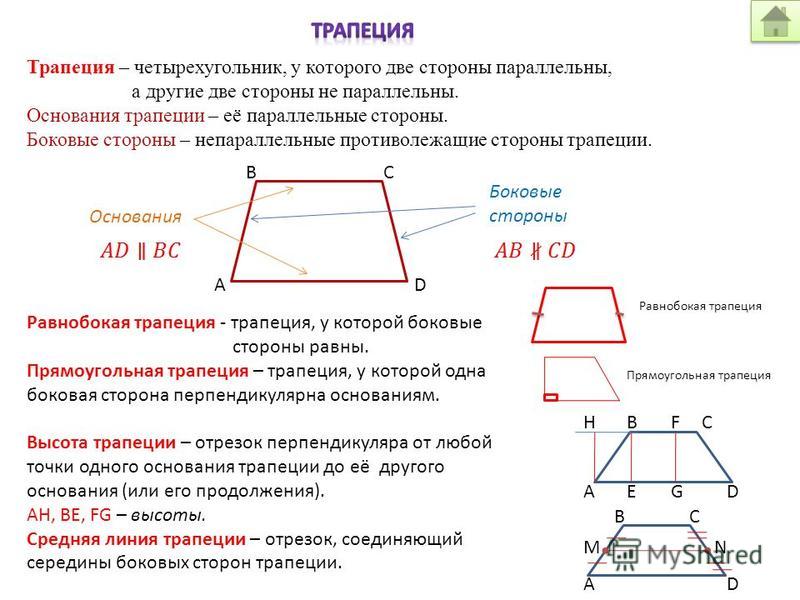
 Теперь, когда вам известны две стороны и угол между ними, вы можете найти площадь треугольника по формуле: Площадь треугольника = (1/2) * S1 * S2 * sin(a)[4]
Теперь, когда вам известны две стороны и угол между ними, вы можете найти площадь треугольника по формуле: Площадь треугольника = (1/2) * S1 * S2 * sin(a)[4]