Содержание
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Как найти верхнее основание равнобедренной трапеции
Читайте также: Беспроводные наушники капельки для телефона рейтинг лучших
Радиус окружности, описанной вокруг равнобокой трапеции, ищется как радиус описанной окружности треугольника, образованного ее диагональю со сторонами. (рис.104.4) R=abd/√((a+b+d)(a+b)(a+d)(b+d))
(рис.104.4) R=abd/√((a+b+d)(a+b)(a+d)(b+d))
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 – 2 ac cos α
d 1 = √ b 2 + c 2 – 2 bc cos β
4. Формула длины диагонали через высоту и основания:
Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 – ( a – b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p – a )( p – c )( p – d 1) |
где
a – большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
1. Формула длины основания равнобедренной трапеции через среднюю линию
a – нижнее основание
b – верхнее основание
m – средняя линия
Формулы длины основания :
2. Формулы длины сторон через высоту и угол при нижнем основании
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α – угол при основании трапеции
h – высота трапеции
Формулы всех четырех сторон трапеции :
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
d – диагонали
α , β – углы между диагоналями
h – высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a – нижнее основание
b – верхнее основание
c – равные боковые стороны
α , β – углы при основаниях
m – средняя линия
h – средняя линия
Формулы длины сторон равнобедренной трапеции через площадь :
“>
Найти большее основание трапеции
Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Рассмотрим задачи:
27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Площадь трапеции (формула):
Нам известны основания и площадь, можем записать:
Ответ: 8
27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Формула площади при данных обозначениях вершин:
Нам известны основание, площадь и высота, можем записать:
Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.
27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Найдите высоту трапеции.
Формула площади при данных обозначениях вершин:
Нам известны средняя линя и площадь, можем записать:
Ответ: 8
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:
Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:
Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):
По теореме Пифагора:
Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:
Выполним дополнительные построения:
Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:
Таким образом площадь будет равна:
Ответ: 160
27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:
Теперь выполним дополнительные построения (опустим высоты):
Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:
Ответ: 5
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:
Высоту нашли, вычисляем площадь:
Ответ: 42
27593. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Ответ выразите в градусах.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
Основание трапеции равно боковой стороне
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
1) Если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Рассмотрим трапецию ABCD, в которой боковая сторона AB равна меньшему основанию BC.
1) Так как AB=BC, треугольник ABC — равнобедренный с основанием AC. Значит, у него углы при основании равны:∠BAC=∠BCA.
2)∠BCA=∠∠CAD (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
3) Отсюда следует, что ∠BAC=∠CAD, а значит, AC — биссектриса угла BAD.
2) Если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
Рассмотрим трапецию ABCD, в которой большее основание AD равно ее боковой стороне AB.
1) Так как треугольник ABD — равнобедренный с основанием BD, то его углы при основании равны: ∠ABD=∠ADB.
2) ∠CBD=∠ADB (как внутренние накрест лежащие при AD ∥ BC и секущей BD).
3) Отсюда ∠CBD=∠ABD, следовательно, BD — биссектриса угла ABC.
Аналогично доказываются утверждения для прямоугольной и равнобедренной трапеции.
3) Если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
4) Если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
5) Если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
6) Если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
7) Если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
8) Если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
В частности, так как сумма противолежащих углов равнобедренной трапеции равна 180º, соответственно, ∠ACD+3∠BCA=180º и ∠BAC+3∠CAD=180º.
Как найти основание равнобедренной трапеции
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите все формулы, которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Найдите катет AH, следуя теореме Пифагора, которую вы уже записали. Пусть он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
Выразите через площадь трапеции неизвестную величину. У вас должно получиться: AD=2*S/h-BC или y=2*S/h-x.
После этого подставьте данные числовые значения в полученную систему уравнений и решите ее. Решение любой системы уравнений можно найти автоматически в программе MathCAD.
Формулы и свойства трапеции
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка к ОГЭ и ЕГЭ.
«Формулы и свойства трапеции»
Методическая разработка
учителя математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
Определения 4
Частные случаи трапеции 5
Свойства произвольной трапеции 6-7
Свойства равнобедренной трапеции 8-10
Свойства биссектрисы угла трапеции 10-12
Свойства треугольников, образованных диагоналями трапеции 12-13
Формулы нахождения диагоналей трапеции 13-14
Трапеция и окружность 14-17
Дополнительные построения в трапеции 17-23
Для тех, кому интересно. Теоремы.
 23-27
23-27Задачи с решениями.27-35
Список используемой литературы .
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует от учащихся знаний «непрограммных» свойств трапеции. (Программными считаются свойство средней линии трапеции, свойства диагоналей и углов
равнобедренной трапеции.) Свойства, необходимые для решения задач, отсутствуют в учебниках или перенесены в задачи и не воспринимаются как теоретические положения.
Какими же замечательными свойствами обладает трапеция? Как решать геометрические задачи, требующие глубоких знаний? Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач, к которым традиционные методы (метод цепочек равных треугольников, метод геометрических преобразований, векторный метод и др.) либо вовсе не применимы, либо дают сложные и громоздкие решения. Во многих случаях решать такого рода задачи помогает введение в чертеж дополнительных линий – так называемое дополнительное построение. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют от решающего достаточно большого опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно достраивать до фигуры другого типа, можно с многоугольной фигурой связывать окружность, а можно целью дополнительного построения ставить выделение на чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в большинстве случаев позволяет решать, казалось бы, сложные геометрические задачи просто, понятно и красиво.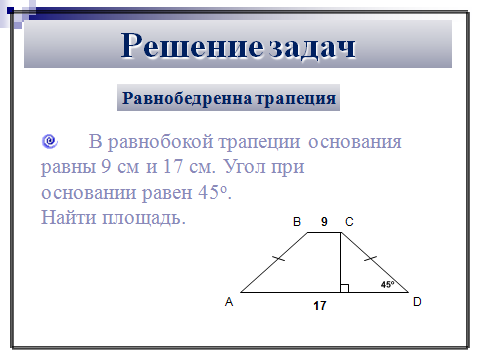
В этой разработке собраны формулы, свойства и подсказки для решения задач связанных с трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.
Kаждый из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота.
2.Частные случаи трапеции.
Прямоугольной трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна основаниям.
У нее два прямых угла при меньшей боковой стороне.
Эта сторона одновременно является и высотой трапеции.
произвольная
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны.
Трапеция, у которой боковые стороны равны, называется равнобедренной
(равнобокой, равнобочной).
3.Свойства произвольной трапеции.
1. Во всякой трапеции сумма углов , прилежащих к одной ее боковой стороне, равна 1800.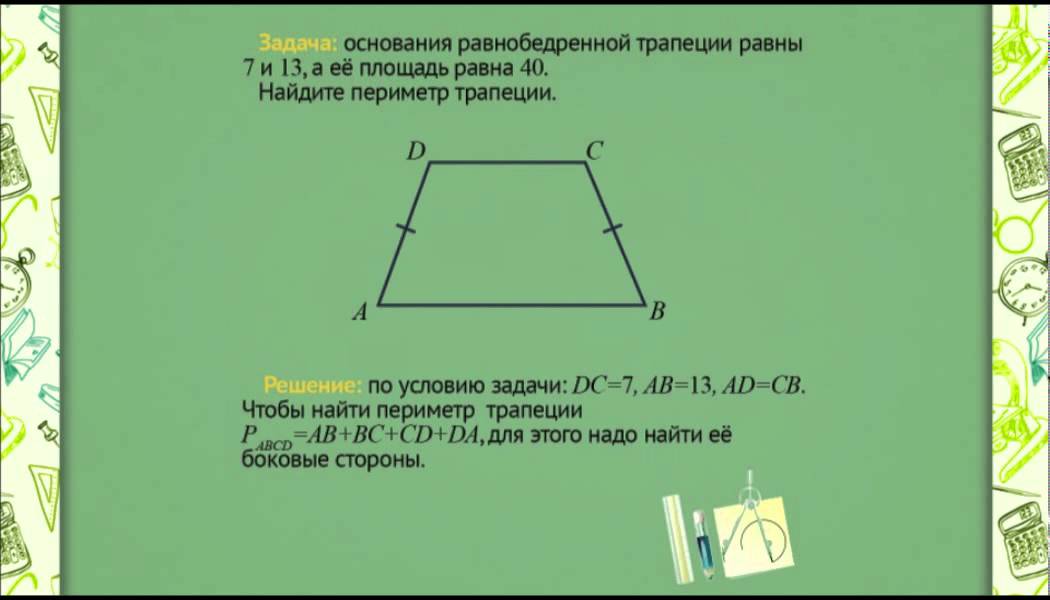
2. Во всякой трапеции средняя линия параллельна ее основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.
MК =
3.Четыре замечательные точки трапеции:
Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
4. Во всякой трапеции если сумма углов при большем основании равна 900, то боковые стороны лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины оснований, равна полуразности оснований.
5. Свойства отрезка, соединяющего основания трапеции
Отрезок, соединяющий основания всякой трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции.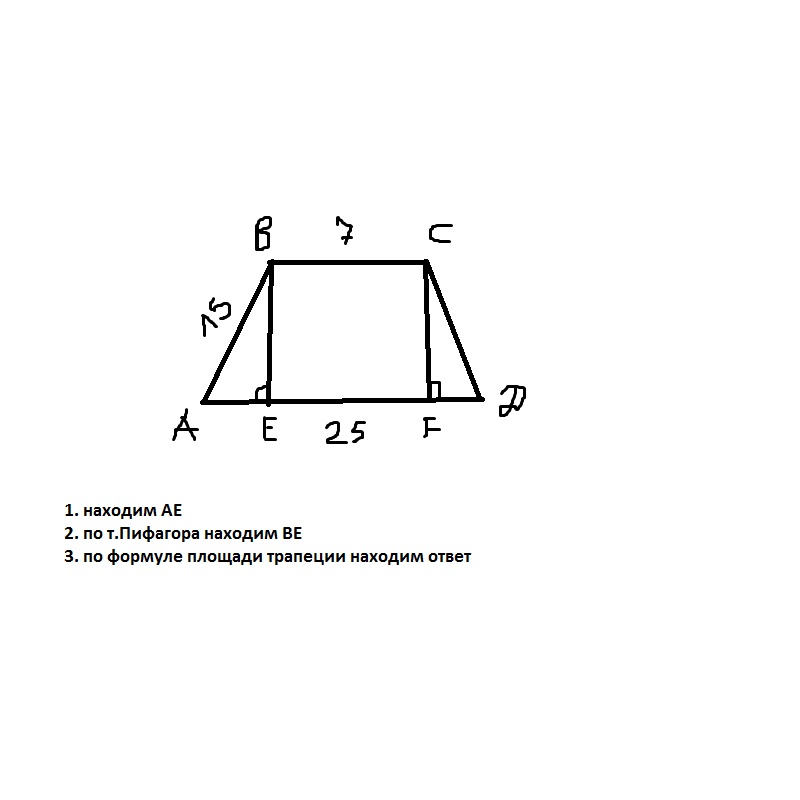
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам, то есть КО=ОМ
*Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна
KM = .
7.Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему геометрическому оснований, если он делит трапецию на две трапеции, подобные между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему квадратичному оснований, если он делит трапецию на две трапеции равной площади (равновеликие).
9.Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
d12 + d22 = c2 + d2+ 2ab, d- боковая сторона. d1 и d2 – диагонали.
Свойства равнобедренной трапеции.
Трапеция является равнобедренной тогда и только тогда, когда
*углы, прилежащие к одному основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;
AC = BD
*отрезки диагоналей, соединяющих точку пересечения с концами одного основания, равны; BO = OC, AO = OD.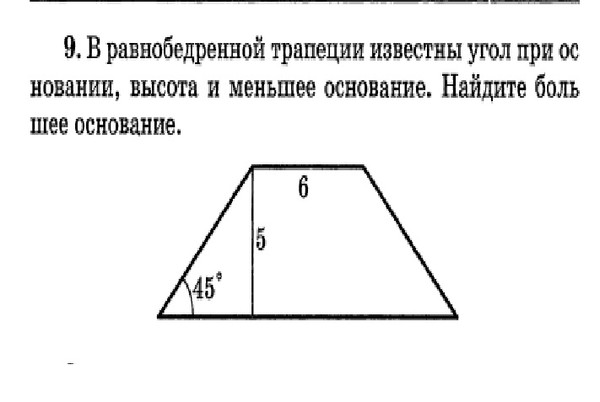
*вокруг этой трапеции можно описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.
* высота, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны, то
1)квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4) площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).
*если в равнобокой трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через точку пересечения диагоналей, в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна им и является осью симметрии трапеции.
*отрезки, последовательно соединяющие середины смежных сторон равнобедренной трапеции, образуют ромб.
MNKE – ромб, то есть
MN=NK=KE= ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его боковой стороны плюс произведение оснований: d2 = c2 + a b
*площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
S =
Свойства биссектрисы угла трапеции.
*биссектриса угла отсекает от трапеции равнобедренный треугольник.
*точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
*если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
* если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
* если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом.
*Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
*В подобных треугольниках длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис, медиан (проведенных из равных углов) подобных треугольников равны отношению соответствующих сторон (лежащих против равных углов) или равны коэффициенту подобия.
*Площади подобных треугольников относятся как квадраты соответствующих сторон или равно квадрату коэффициента подобия.
*Площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Эта группа формул отражает одно из основных свойств диагоналей трапеции:
*Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем теорему косинусов.
*Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
*Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d12 — d22 = a2 – b2
*Если диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований
h2 = a ∙ b
2) Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии. Площадь трапеции определяется произведением средней линии на высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
. CF =m, FD =n, OF = r.
∠COD=90º, т.к. ∠ADC+∠BCD=180º — так
как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD равна 1800.
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как r = .
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно описать окружность, то проекция диагонали на большее основание, равна боковой стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
AB+CD=AD+BC
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
1)Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции (четырехугольника) взаимно перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности или удвоенному квадрату боковой стороны:
a2 + b2 = 4R2 = 2c2.
6) Если в трапецию вписана окружность, то вершина трапеции, центр вписанной в нее окружности и основание перпендикуляра, опущенного из другой вершины на основание, лежат на одной прямой.
Дополнительные построения как прием при решении задач
Дополнительные построения являются эффективным методом решения геометрических задач. Наиболее часто используются при решении задач:
1. Опускание высот из концов одного основания на другое основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину
3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину .
5. Продолжение боковых сторон до пересечения.
Рассмотрим каждое их них.
При решении задач на отыскание площади дополнительным построением считается построение ее высоты или высот. Если построение высоты не помогает решить задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом найти площадь полученного треугольника, который будет равновеликим исходной трапеции.
1. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину.
При дополнительном построении, когда переносится диагональ, образуется треугольник, площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим CF // BD и получим SACF = SABCD. Почему?
ABC = CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит, для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF = АD + ВС — сумма оснований трапеции. По условию задачи средняя линия трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF. Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172 = 82 + 152
289 = 64 + 225.
289 = 289.
ACF – прямоугольный. SACF = AC*CF = 8*15 = 60. SABCD= 60.
Если ACF разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2. Продолжение боковых сторон до пересечения.
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника.
*Если ABCD равнобедренная трапеция, то KL является биссектрисой, медианой и высотой одновременно.
Это дополнительное построение позволяет перейти от трапеции к треугольнику. Если сумма углов при большем основании равна 900, топродолжив боковые стороны мы получим прямоугольный треугольник.
Задача.
В трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна 900. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ = 18.
Решение.
Центром О данной окружности будет точка пересечения серединного перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые стороны трапеции и получим прямоугольный треугольник АМD. KMNO – прямоугольник, где KM = MN = NO =КО = R.
BMC AMD.
= , то есть и x = 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого — одно из оснований и высота трапеции) и два прямоугольных треугольника (в которых один из катетов – высота трапеции, а гипотенузы – боковые стороны трапеции)
Построение 1 Построение 2
Задача. Найдите площадь трапеции с основаниями 8 и 13 и боковыми сторонами 3 и 4.
Решение.
Проведем ВН и СM — высоты и получим ABD (египетский треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту трапеции: h= 2S:5 = 2*6:5= 2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4 делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в треугольник.
5. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см и 12 см. Найдите высоту трапеции.
Решение. Пусть АВСД трапеция, заданная в условии.
Проведем через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД в точке М.
Тогда АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так как 92+122=152, то, применив обратную теорему Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим, что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают. Для определения искомой высоты применим метод площадей. Пусть искомая высота равна х. Тогда для определения х составим уравнение, дважды вычислив площадь треугольника МСД:
.
Решив это уравнение находим: х=7,2. Ответ: 7,2.
Задача. Боковые стороны AB и CD трапеции ABCD равны 15 и 12 соответственно. Найдите градусную величину угла D, если одно из оснований трапеции на 9 больше другого.
Решение.
Из вершины угла проведем прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на параллелограмм и треугольник. Противоположные стороны параллелограмма равны, значит, длина стороны треугольника равна разности длин оснований трапеции. Данный треугольник определен по трем сторонам. По теореме косинусов определим искомый угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию, искомый угол прямой.
Ответ:
Для тех, кому интересно.
Теорема.
Задачи с решениями.
Пример 1.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD — равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
AB = CD = 10 по условию.
AB + CD = AD + BC по свойству вписанной окружности.
AD + BC = 10 + 10 = 20.
FE = 2r = 2 · 4 = 8.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20 · 8 = 20/2 · 8 = 10 · 8 = 80.
Пример 2.Основания трапеции равны 10 м и 31 м, а боковые стороны — 20 м и 13 м. Найдите высоту трапеции.
Решение.
Пусть HK = BC = 10 м, BH = CK = x, AH = y, тогда KD = 21 – y
По теореме Пифагора:x2 + y2 = 132x2 + (21 – y)2 = 202x2 + y2 = 169 (1)
x2 + 441 – 42y + y2 = 400 (2)
Вычтем из (2) уравнения (1):441 – 42y = 23142y = 210y = 5AH = 5 м
По теореме Пифагора:BH2 = AB2 – AH2BH2 = 132 – 52BH2 = 169 – 25BH2 = 144
BH = 12
Пример 3.Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Решение.
Пример 4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие треугольников.
Квадраты соответствующих сторон относятся как площади треугольников.
Введем параметры треугольников: стороны оснований и высоты треугольников.
Площади трапеции и треугольников определим по известным формулам.
Решение.
Ответ:
Пример 5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников по катету и гипотенузе: ABD = ACD, поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для определения боковой стороны трапеции.
Высоту трапеции определим из равенства площадей.
Проекцию боковой стороны на большее основание легче определить из подобия треугольников, чем по теореме Пифагора.
Длину средней линии в равнобокой трапеции можно определять как разность большего основания и проекции боковой стороны на основание.
Площадь трапеции находим как площадь прямоугольника АМСК, который получим, если достроим трапецию.
Пример 6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции.
Анализ.
Задача решается построением.
Достроим прямоугольники и используем свойство прямоугольника: диагонали прямоугольника равны и в точке пересечения делятся пополам.
Длина средней линии равна полусумме длин оснований.
Длина отрезка, соединяющая середины оснований, равна полусумме длин диагоналей двух построенных треугольников.
Пример 7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного основаниям и заключенного между боковыми сторонами, который делит трапецию на две равновеликие части.
Анализ.
Провести из вершины тупого угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей трапеций.
Определить отношение при подобии треугольников.
Рациональные алгебраические преобразования приведут к результату.
Решение.Ответ:
Пример 11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине средней линии.
Применяем теорему Пифагора для нахождения высоты трапеции.
Площадь трапеции определяем по доступной формуле.
Пример 8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно вписать окружность, а средняя линия делит ее на части, площади которых относятся как 5: 11. Найдите длину большего основания трапеции.
Анализ.
Трапеция является описанной.
Сумма длин оснований равна сумме боковых сторон.
Средняя линия делит трапецию на две трапеции, высоты которых равны.
Задача сводится к системе уравнений.
Длина средней линии равна половине суммы длин боковых сторон.
Пример 9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.
Анализ.
Трапеция равнобедренная.
Длина средней линии равна боковой стороне.
Площадь трапеции определяется произведением средней линии на высоту трапеции.
Опустим высоту трапеции из тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту трапеции через боковую сторону.
Пример 10.В прямоугольной трапеции, описанной около окружности, большая боковая сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание трапеции.
Анализ.
Необходимо использовать свойство сторон четырехугольника, описанной около окружности: сумма длин противоположных сторон равна между собой.
Кроме того, длина средней линии равна полусумме длин сторон оснований.
Проведем из вершины тупого угла высоту трапеции.
Воспользуемся теоремой Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример 11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности.
Анализ.
Важное положение, что трапеция является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны равна длине средней линии.
Введем параметр боковой стороны, из прямоугольного треугольника по заданному углу определим высоту трапеции, которая является диаметром вписанной окружности. Площадь трапеции определяется как произведение средней линии на высоту трапеции.
.
Пример 12.Найдите площадь равнобедренной трапеции, у которой большее основание равно 13, средняя линия равна 8, а биссектриса тупого угла является диагональю трапеции.
Анализ.
При проведении биссектрисы тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем высоту трапеции.
Площадь трапеции находим по формул.
Список используемой литературы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция | Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции | |
| Определение | Диагонали трапеции | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции | |
| Определение | Высота трапеции | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение | |
| Свойство | Точка пересечения диагоналей | Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве | |
| Определение | Средняя линия трапеции | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции | |
| Свойство | Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | ||
| Свойство | Биссектрисы углов при боковой стороне трапеции | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Трапеция |
Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Диагонали трапеции |
Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Высота трапеции |
Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Точка пересечения диагоналей |
Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Средняя линия трапеции |
Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство |
| Биссектрисы углов при боковой стороне трапеции |
Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренная трапеция | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство | Равенство углов при основании | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
| Свойство | Равенство диагоналей | Если трапеция является равнобедренной, то её диагонали равны. | |
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность | Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
| Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство: равенство углов при основании | |
| Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак: равенство углов при основании | |
| Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | |
| Свойство: равенство диагоналей | |
| Если трапеция является равнобедренной, то её диагонали равны. | |
| Признак: равенство диагоналей | |
| Если у трапеции диагонали равны, то она является равнобедренной | |
| Свойство: углы, которые диагонали образуют с основаниями | |
| Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак: углы, которые диагонали образуют с основаниями | |
| Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | |
| Свойство: описанная окружность | |
| Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак: описанная окружность | |
| Если около трапеции можно описать окружность, то она является равнобедренной. | |
| Свойство: высоты трапеции | |
| Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований | |
| Равнобедренная трапеция |
Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Равенство углов при основании |
Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Равенство диагоналей |
Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной. |
| Углы, которые диагонали образуют с основаниями |
Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Описанная окружность |
Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной. |
| Высоты трапеции |
Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти длину стороны трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Геометрия
— Поиск углов в равнобедренной трапеции Геометрия
— Поиск углов в равнобедренной трапеции — Mathematics Stack Exchange
Сеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
392 раза
$ \ begingroup $
Мне задали следующий вопрос:
PQRS — равнобедренная трапеция.Если угол TRS = 100 градусов, угол T = 35 градусов и PS = TS , найдите размеры пронумерованных углов.
Прилагается рисунок представленной схемы.
.
У меня большие трудности с этим. Я знаю, что угол PRS будет 80 градусов, потому что он является дополнительным к углу TRS . Но остальное я не могу понять. Я вижу взаимосвязь между углами и т. Д., Но не могу определить ни одно из этих измерений. Я тоже не понимаю, почему вопрос предусматривает то, что PS = TS .Ничего полезного от этого, похоже, не прибавилось. Это не может сказать мне, что треугольники совпадают, потому что тогда угол PRS должен быть 100 градусов, а это не так.
Есть мысли?
Создан 23 июн.
BurtBurt
1,69511 золотых знаков55 серебряных знаков2626 бронзовых знаков
$ \ endgroup $
$ \ begingroup $
Как вы заметили, $ \ angle {PRS} = 80 ° $.Возьмем треугольник $ \ треугольник {TRS} $: мы знаем два угла из трех, так что $ \ angle {TSR} = 45 ° $. Теперь возьмем равнобедренный треугольник $ \ треугольник {PTS} $: два угла, примыкающие к основанию $ PT $, равны $ 35 ° $, поэтому третий угол $ \ angle {PST} = 110 ° $, а затем $ \ angle { PSR} = 65 ° $. Это один из двух углов, примыкающих к основанию равнобедренной трапеции: зная его, вы можете легко завершить решение.
Создан 23 июн.
Анатолий Анатолий
16.\ circ $. Вы можете закончить отсюда?
Я предположил, что точки $ P, R, T $ лежат на одной прямой в соответствии с рисунком.
Создан 23 июн.
пользователь
22.7k22 золотых знака1717 серебряных знаков5050 бронзовых знаков
$ \ endgroup $
2
Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками геометрия или задайте свой вопрос.
Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
Основания трапеции, ножки, углы и площадь, правила и формулы
Трапеция — это четырехугольник с одной парой параллельных линий
Основания — две параллельные линии называются основаниями.
Ноги — две непараллельные линии — это ноги.
Недвижимость
- Свойство № 1) Углы на одной стороне ножки называются смежными углами и являются дополнительными (еще )
- Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base}} {2} \ right) $$ (еще )
- Объект № 3) Трапеции имеют средний сегмент, который соединяет мипоинты ног (еще )
Смежные углы трапеции
Углы на одной стороне ножки называются смежными углами, например $$ \ angle A $$ и $$ \ angle D $$ являются дополнительными.По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.
Задача 1
$$ \ angle ZWX = 180 — 44 = 136 ° $$
Проблема 2
Используйте теорему о смежных углах для вычисления m $$ \ angle MLO $$.
Покажи ответ
$$ \ angle MLO = 180-124 = 56 ° $$
Задача 3
Найдите значение x на трапеции ниже, затем определите меру углов $$ \ angle WXY $$ и $$ \ angle XYZ $$.
Покажи ответ
Проблема 4
Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией, основываясь на предоставленной информации) .
Покажи ответ
Если LMNO — трапеция, и ее основания LO и MN параллельны, то $$ \ angle MNO $$ и $$ \ angle NOL $$, которые должны быть дополнительными, сумма этих углов не равна 180 111 + 68 ≠ 180. 2
$
Средняя часть трапеции:
Проблема 6
Используйте теорему о среднем сегменте, чтобы определить длину включения среднего сегмента.
Длина мидсегмента
Чтобы вычислить длину среднего сегмента, найдите среднее значение длины оснований среднего сегмента = (6 + 4) / 2 = 5.
Быстрый обзор Midpoint
Самая важная вещь, о которой следует помнить, — это то, что средняя точка делит линию пополам (разрезает линию на две равные половины).
Показать среднюю точку
Средняя точка красного сегмента, изображенного ниже, — это точка $$ (A, 2b) $$ (нажмите кнопку ниже, чтобы увидеть).
Средний сегмент трапеции — это сегмент, соединяющий середины непараллельных сторон трапеции.
На трапеции ниже середины непараллельных сторон — это точки S и V. Средний сегмент — это красный отрезок линии от S до V.
Пример среднего сегмента
Трапеция # 10
Шаг 1
Расчет длины оснований. Верхняя база:
$$ 35–16 = 9 $$
Шаг 2
Расчет низкой базы:
$$ 45 — 0 = 45
$$
Шаг 3
Расчет суммы оснований
$$ 9 + 45 = 54 $$
Шаг 4
Разделите сумму на 2
$$ \ frac {54} {2} = \ boxed {27} $$
Проблема 8
Какова длина среднего сегмента SV трапеции ниже?
Покажи ответ
Шаг 1
Расчет длины оснований.Верхняя база:
$$ 17–8 = 9 $$
Шаг 2
Расчет низкой базы:
$$ 20 — 0 = 20
$$
Шаг 3
Расчет суммы оснований
$$ 9 + 20 = 29 $$
Шаг 4
Разделите сумму на 2
$$ \ frac {29} {2} = \ boxed {14.5} $$
Проблема 9
Красный сегмент ниже среднего сегмента?
Покажи ответ
Это не настоящий средний сегмент, потому что его длина не равна половине суммы длин оснований.
Свойства трапеции — Задача 1
Равнобедренная трапеция имеет две конгруэнтные стороны и одну пару параллельных сторон. Базовые углы совпадают друг с другом, а при одинаковых боковых внутренних углах верхние углы дополняют соответствующие базовые углы, что означает, что они оба равны 180 ° (мера базового угла).
Итак, если дана мера одного из верхних углов, вы знаете, что его базовый угол является дополнительным к нему, поэтому вычтите его значение из 180 °, чтобы найти меру базового угла. Затем вспомните, что у равнобедренной трапеции углы основания совпадают. Другой верхний угол является дополнительным к его базовому углу, поэтому он соответствует верхнему углу. Таким образом, только по одному углу равнобедренной трапеции можно найти размеры других углов.
В этой задаче у нас есть равнобедренная трапеция, что означает, что у нас есть две конгруэнтные ноги, когда у нас есть пара параллельных сторон.Итак, давайте посмотрим, что мы знаем о равнобедренных трапециях.
Итак, мы видим, что базовые углы, поэтому, если я смотрю на два базовых угла, они будут конгруэнтны друг другу. Мы также знаем, что те же боковые внутренние углы здесь, поэтому я смотрю на эти треугольники прямо здесь, будут дополнительными, что является определением того же внутреннего бокового угла.
Итак, вернемся к нашей проблеме. Если я посмотрю на единственное, что мы знаем об этой трапеции, а именно на угол B, равный 110 градусам, я могу начать с определения угла C.Хорошо, я знаю, что эти два должны быть дополнительными, потому что они находятся на одной стороне этого поперечного BC. Итак, если B равно 110 C, что должно быть? 180 минус 110, что 70 градусов. Итак, я собираюсь написать здесь, что C должно быть 70 градусов.
Теперь вам просто нужно помнить, что ваши базовые углы конгруэнтны друг другу. Итак, я напишу, что D должно быть 70 градусов, а A должно быть 110 градусов. Итак, А, как мы сказали, было 110, а D, как мы сказали, было 70 градусов. Ключевым моментом здесь было помнить, что одни и те же боковые внутренние углы являются дополнительными и что базовые углы в равнобедренной трапеции всегда совпадают.
Трапеция
(Перейти к области трапеции или периметру трапеции)
Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечены стрелками ниже):
| Трапеция | Равнобедренная трапеция |
Трапеция:
| имеет пару параллельных сторон | |
— это равнобедренная трапеция , когда она имеет равных углов от параллельной стороны | |
| называется « трапеция » в Великобритании (см. Ниже) |
Игра с трапецией:
Параллельные стороны — это «основания»
Две другие стороны — «ножки»
Расстояние (под прямым углом) от одной базы до другой называется «высотой».
Площадь
трапеции
Площадь — это среднее значение двух базовых длин, в раз превышающее высоту : Площадь = a + b 2 × h |
Пример: два основания трапеции составляют 6 м и 4 м, а высота — 3 м.Какова его площадь?
Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2
Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.
Периметр трапеции
Периметр — это расстояние по краям.
Периметр равен сумме длин всех сторон : Периметр = a + b + c + d |
Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см. Каков ее периметр?
Периметр = 5 см + 12 см + 4 см + 15 см = 36 см
Медиана трапеции
Медиана (также называемая средней линией или срединным сегментом) — это линейный сегмент на полпути между двумя основаниями. Средняя длина — это среднее значение двух базовых длин: м = а + б 2 |
Вы можете рассчитать площадь, зная медианное значение, это просто медиана, умноженная на высоту:
Площадь = mh
Трапеция
A trapezium (UK: trapezoid) — четырехугольник без параллельных сторон.
Определения США и Великобритании поменялись местами, например:
| Трапеция | Трапеция | |
| США: | Пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | Пара параллельных сторон |
Равнобедренная трапеция — формула, свойства, определение, примеры
Трапеция — это четырехугольник, у которого параллельна только одна сторона.Равнобедренная трапеция — это трапеция с совпадающими углами при основании и совпадающими непараллельными сторонами. Равнобедренная трапеция обладает множеством интересных свойств, которые делают ее уникальной и помогают нам отличать ее от других четырехугольников. Обсудим их подробнее.
Равнобедренная трапеция, определение
Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны и углы основания имеют одинаковую меру. Другими словами, если две противоположные стороны (основания) трапеции параллельны, а две непараллельные стороны имеют одинаковую длину, то это равнобедренная трапеция.Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.
Свойства равнобедренной трапеции
Ниже приведены свойства равнобедренной трапеции в соответствии с приведенным ниже рисунком.
- Имеет ось симметрии. Он не имеет вращательной симметрии и одной линии симметрии, соединяющей середину параллельных сторон.
- Одна пара сторон параллельна, и они являются сторонами основания.(AB II DC на данном изображении)
- Остальные стороны, кроме основания, не параллельны и имеют одинаковую длину. (c = d на данном изображении)
- Диагонали одинаковой длины. (AC = BD)
- Базовые углы такие же. (∠D = ∠C, ∠A = ∠B)
- Сумма противоположных углов составляет 180 ° или дополнительные. (A + ∠C = 180 ° и ∠B + ∠D = 180 °)
- Отрезок, соединяющий середины параллельных сторон, перпендикулярен основаниям. (PQ ⊥ DC)
Формула равнобедренной трапеции
Ниже приведены формулы для расчета площади и периметра равнобедренной трапеции.
Площадь равнобедренной трапеции
Чтобы найти площадь равнобедренной трапеции, мы должны сложить стороны основания или параллельные стороны и разделить ее на 2, а затем умножить результат на высоту.
Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × h
Периметр равнобедренной трапеции
Чтобы найти периметр равнобедренной трапеции, мы должны сложить все стороны равнобедренной трапеции.
Периметр равнобедренной трапеции = сумма всех сторон
Статьи по теме о равнобедренной трапеции
Ознакомьтесь с интересными темами, чтобы узнать больше о равнобедренной трапеции.
Часто задаваемые вопросы о равнобедренной трапеции
Каковы характеристики равнобедренной трапеции?
У равнобедренной трапеции четыре стороны. Две противоположные стороны (основания) параллельны друг другу, а две другие стороны равны по длине, но не параллельны друг другу.
Если один базовый угол равнобедренной трапеции равен 30 °, найдите другой базовый угол.
Согласно свойству равнобедренной трапеции, базовые углы равны, поэтому, если один базовый угол равен 30 °, то другой базовый угол будет равен 30 °.
В чем разница между трапецией и равнобедренной трапецией?
У трапеции каждая сторона имеет разную длину и диагонали не совпадают, тогда как у равнобедренной трапеции непараллельные стороны равны, углы основания равны, диагонали совпадают, а противоположные углы являются дополнительными.
Какова формула площади равнобедренной трапеции?
Формула для вычисления площади равнобедренной трапеции: Площадь = (сумма параллельных сторон ÷ 2) × высота.
Какова формула периметра равнобедренной трапеции?
Формула для расчета периметра равнобедренной трапеции: Периметр = сумма всех сторон равнобедренной трапеции
Урок трапеции — Бесплатная справка по математике
Определение трапеции
Трапеция — четырехугольник с одной парой параллельных сторон. Как показано на рисунке ниже, параллельные стороны трапеции ABCD называются основаниями , а стороны, которые не параллельны, называются ножками .
Факты о трапециях
Сумма четырех углов в градусах дает 360 градусов . На самом деле это верно для любого четырехугольника. Пусть строчные буквы a, b, c и d представляют углы трапеции ABCD.
Тогда: a + b + c + d = 360 градусов.
Соответствующие пары базовых углов, такие как A и B или C и D, являются дополнительными (в сумме составляют 180 градусов).
угол a + угол b = 180 градусов
угол c + угол d = 180 градусов
Равнобедренная трапеция
Существует особый вид трапеции, называемый равнобедренной трапецией и .Равнобедренная трапеция — это трапеция, у которой ноги равны по длине. Помните, что ноги — это непараллельных сторон , в отличие от параллельных оснований. Вы заметите, что в первой трапеции этого урока (выше) ноги НЕ равны.
Это равнобедренная трапеция, называемая ABCD:
.
Имеет следующие характеристики:
Два нижних базовых угла имеют одинаковую меру, а два верхних базовых угла имеют одинаковую меру.
угол a = угол d
угол b = угол c
Диагонали одинаковой длины.
диагональ AC = диагональ BD
Пример задачи
В равнобедренной трапеции MATH сторона HT параллельна стороне MA, отрезок MH конгруэнтен отрезку AT. Градусная мера угла MHT = 60 градусов. Каковы размеры остальных трех углов?
Решение:
Мы знаем, что две ноги совпадают, так что это равнобедренная трапеция. Учитывая это, мы знаем, что два основных угла (T, H) имеют одинаковую меру. Поскольку нам задан угол H равным 60, мы также можем сказать, что
Поскольку верхний и нижний углы дополняют друг друга, мы знаем, что
Угол M = 180-60
Угол M = 120
По той же логике, угол A = 120 градусов.
Урок, проводимый г-ном Фелизом
.
